Training DNN with Reduced Precision Floating-Point Format

< 목차 >

• Motivation
• 3 Popular Floating-Point Formats for DNN
  • FP32 format
• Training DNN with Reduced Floating-Point Format
  • FP16
  • What's Wrong with FP16 ?
  • Mixed Precision Training
    • Range of FP16
    • 1. Gradient Accumulation in FP32
    • 2. Gradient Scaling
    • 3. FP16 arithmetic with accumulation in FP32
  • BF16
    • Pros and Cons of BF16
• Automatic Mixed Precision (AMP)
• Reference

Motivation

Computer가 어떤 실수 값을 이해하는 방식에는 여러가지가 있다. 어떤 방식으로 수를 표현을 할 것인지는 Deep Learning (DL)에서만 논의되는 것은 아니겠지만, Deep Neural Network (DNN)은 각 layer별로 input tensor와 weight matrix를 곱하는 연산을 무수히 많이 반복하기 때문에 각 layer inpuut, weight matrix (and bias) 그리고 activation을 얼마나 정밀하게 표현하는지가 중요하다. 하지만 DNN의 특성을 이용해 아니면 정밀도 (precision)을 조금 포기하더라도 빠르게 연산을 할 것인가?를 선택할 수도 있는데, 이 때 안정적인 training 및 inference를 하기 위해서는 고려할 것이 많다. 더 낮은 precision의 체계를 쓰는 것은 분명 위험할 수 있지만 안정적인 장치만 잘 해준다면 성능의 감소가 거의 없음에도 performance improvement를 수 배 가져올 수도 있다.

Fig.

그런데 DNN은 matrix multiplication이 수 십, 수 백번 일어나기 때문에 감소된 정밀도 (reduced precision)이 가져오는 error가 누적되기 쉬운 구조를 가지고 있다. 그래서 아무리 안전 장치를 잘 해주더라도 model forward시 최종 output이 NN weight을 표현하는 precision에 따라서 확달라질 수도 있다. 이를 해결하기 위해 Mixed Precision Training같은 것들이 제안된 지 벌써 5년이 넘었지만, 대부분의 large scale model들에는 이것이 필수이며 precision의 기본 개념과 mixed precision training같은 것을 잘 이해하는 것이 large scale model의 training 및 inference가 망가졌을 때 debugging을 하는 중요한 단서가 되기 때문에 반드시 잘 숙지를 해야 한다.

이제 이것들에 대해서 자세하게 알아보도록 하자.

3 Popular Floating-Point Formats for DNN

먼저 어떻게 computer가 실수를 표현하는지와 여러가지 floating-point format의 표현력에 대해 알아보자. DNN에서 input, weight matrix를 표현하는 데 주로 쓰이는 floating-point format은 크게 3가지가 있다.

• Single-precision (or full precision) floating-point format (FP32, float32)
• Half-precision floating-point format (FP16, float16)
• bfloat16 floating-point format (BF16, bfloat16)

먼저 fp32는 가장 기본적인 format으로 floating-point variable를 가장 넓은 range로 표현하며 하나의 variable당 4byte를 먹는다. 그 다음 fp16은 표현력은 줄어들지만 (smaller range), 하나의 variable이 2 byte 밖에 먹질 않는다. 마지막 bf16은 Google Brain이 효율적인 NN training 학습을 위해 개발한 것으로, 표현력은 fp32에 버금가지만 먹는 용량은 fp16과 같이 2 byte 밖에 되질 않는다. “오 그러면 무조건 bf16을 쓰는게 이득 아닌가?” 라는 생각이 들 수 있지만, version이 낮은 GPU에서는 쓸 수 없으며 fp16과는 다른 방향으로 잠재적으로 문제점을 가지고 있기 때문에 무조건 좋은 것은 아니다.

일단 세 가지 data type (앞으로 dtype 이라고 부르겠다)에 대해서 좀 더 알아보자.

Fig. Source from here

Computer가 어떤 수를 인식하는 방법에 대해 간단히 recap해 보자. Computer는 0과 1로 모든 수를 표현하는데 이를 1 bit라고 한다. 만약 bit가 16개라면 모든 bit가 1일 때 10진수 65535와 같고 모든 bit가 0일 때 0되므로, 표현할 수 있는 값의 범위는 정수값 [0, 65535]가 된다.

만약 우리가 부호가 있는 정수 (signed integer)를 원한다면 2의 보수 (two’s completion)를 사용해 [-32768, +32767]를 표현할 수 있다.

하지만 이런 16bits 체계는 0.15625, -118.625같은 소수가 포함된 수를 dynamic하게 표현할 수 없다. 물론 16개 bits중 왼쪽 8개는 정수 부분을 (integer part), 오른쪽 8개는 소수점 이하 부분을 (fractional part)를 표현할 수 있다. 가령 \(0.15625\)는 integer가 \(0\)이고 fraction이 \(00101\)이므로 \((00000000.00101000)_2\)로 표현할 수 있다.

이런 방식을 고정 소수점 (fixed point)라고 하는데, 이 방식은 정해진 format을 벗어난 값은 다 표현할 수 없는데, 이는 다른 format들도 마찬가지지만 fixed point는 표현할 수 있는 수의 범위와 정밀도가 특히 낮다. 정밀도가 낮다는 것은 fraction으로 표현이 되지 않는 소수점 아래의 수가 반 올림이나 반 내림되어거나 심한 경우 0 처리 된다는 걸 의미한다.

이를 해결하기 위해 등장한 것이 바로 부동 소수점 (floating point) 이다. 이는 움직이지 않는다는 의미의 ‘부동 (fixed)’이 아니라 소수점의 위치가 이리저리 바뀐다는 의미의 ‘부동 (floating)’을 쓰며, 약 40년 전 쯤 comouter scientist들이 도입한 IEEE 754가 대표적인 format이다. 이름에서도 알 수 있듯 Institute of Electrical and Electronics Engineers (IEEE)에서 개발한 것이며 컴퓨터에서 부동 소수점을 표현할 때 가장 널리 쓰이는 표준 방식이다. 이 방식은 아래와 같은 intuition으로 수를 표현한다.

IEEE 754 standard에 대해 조금 더 알아보자. 754의 single precision floating point (fp32)는 세 가지로 구성되어 있다.

• 최상위 bit 1개는 부호 (sign)를 표현
• 그 다음 8 bits는 지수 부분 (exponent)을 표현
• 마지막 23 bits는 가수 부분 (fraction or significand or mantissa)을 표현

최상위 bit가 sign을 표현한다는 rule은 그다지 어려울 것이 없고, 그 다음 8개 bits는 말 그대로 2의 지수부, \(2^e\)의 e를 의미하기 때문에 exponent라는 이름이 붙었다. 최종적으로 \(-5\)같은 값이 exponent를 사용해 정해졌으면 나머지 23개 bits가 그 이하 소수점을 정밀하게 표현하기 때문에 이를 fraction이라고 부르기도 하고 (아마 이 정밀함까지 더해져야 진짜 수 이므로) true significand라고 표현하기도 하는 것 같다.

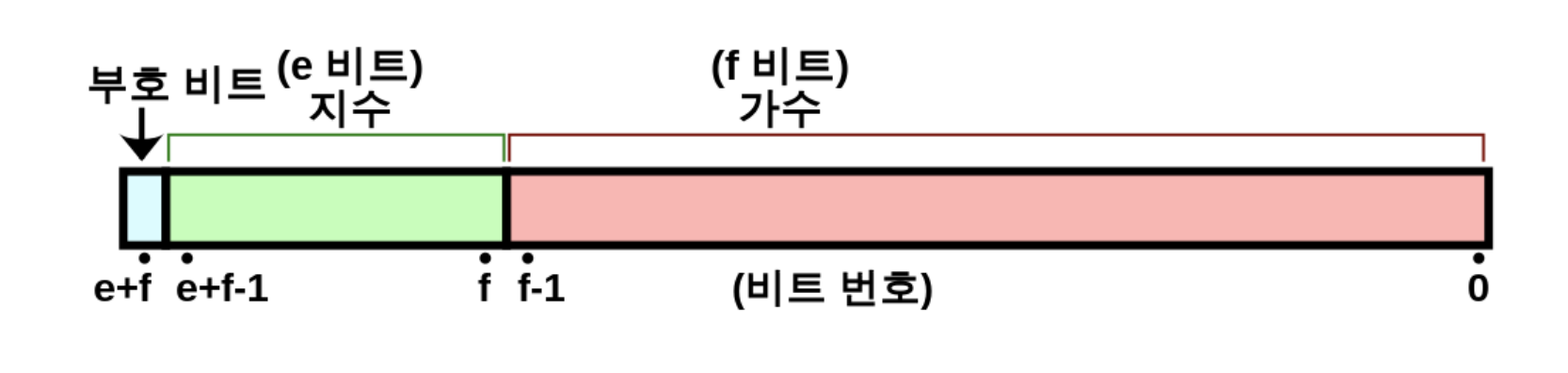Fig. Source from Wiki

이제 우리는 앞서 얘기했던 \(0.15625, -118.625\)를 표현할 수 있게 되었는데, 아래와 같이 bit 32개를 구성하면 된다.

Fig. Source from Wiki

Fig. Source from Wiki

FP32 format

Single precision (FP32)로 수를 표현하는 방법에 대해 조금 더 자세히 알아보자. 먼저 \(0.15625\)의 sign은 양수이므로 아래처럼 간단하게 처리할 수 있다.

Exponent를 계산하기 위해서는 먼저 10진수의 integer, fraction part를 2진수로 변환하고,

이 숫자를 \(1.xxxx \times 2^n\)으로 정규화 (normalize)를 해야한다.

그런데 IEEE 574는 exponent part에 bias를 -127만큼 가지고 있다. 그 이유는 아주 작은 숫자를 표현하기 위해서이며, 그렇기 때문에 \(2^{E-127} = 2^{-3}\)을 만족하는 exponent, \(124\)가 우리가 bits로 표현할 값이 된다.

마지막으로 fraction (mantisa)는 \(1.01\)이므로 이를 bits로 표현하면되는데, 여기서 앞의 \(1\)은 생략하고 \(0.01\)만 표현하면 된다.

최종적으로 우리는 \(0.15625\)를 32개의 bits로 표현할 수 있게 되었다.

마찬가지로 \(-118.625\)도 아래처럼 표현할 수 있다.

• 2진수 변환: \(−118.625=−(1110110.101)_2\)
• 정규화: \(−(1110110.101)_2 =−1.110110101 \times 2^6\)
• sign bit: 음수이므로 \(1\)
• exponent bits: \(E-127=6\)이므로 \(E=133=(10000101)_2\)
• fraction (mantisa) bits: \(1.110110101\)에서 \(1\)생략하고 표현
• 최종 표현: \([1][10000101][11011010100000000000000]\)

하지만 아무리 정교한 방식을 쓰더라도 computer는 모든 실수를 cover할 수가 없는데, 이는 당연하게도 0~1 사이에 존재하는 수만 해도 무한대이기 때문이며, 우리가 어떤 variable을 선언했을 때 설령 이것이 아주 간단한 \(0.01\)같은 수여도 실제로는 이 값이 아닐 수 있다는 점에 주의해야한다.

# 나누어 떨어지지 않는 수
>>> print(f'{0.01:.5f}'); print(f'{0.01:.60f}');
0.01000
0.010000000000000000208166817117216851329430937767028808593750

# 딱 나누어 떨어지는 수
>>> print(f'{0.15625:.5f}'); print(f'{0.15625:.60f}');
0.15625
0.156250000000000000000000000000000000000000000000000000000000

# 정수
>>> print(f'{10:.5f}'); print(f'{10:.60f}');
10.00000
10.000000000000000000000000000000000000000000000000000000000000

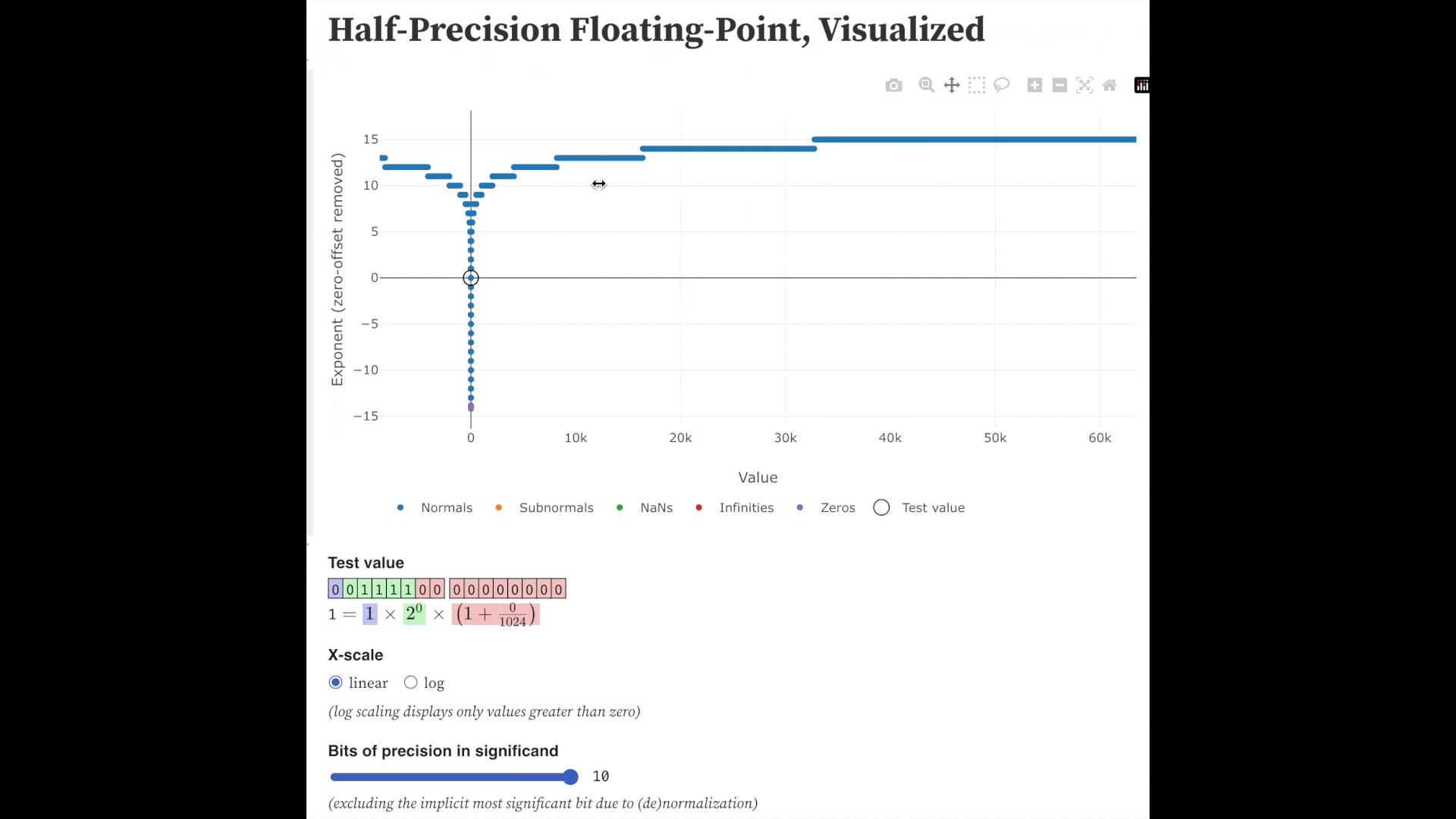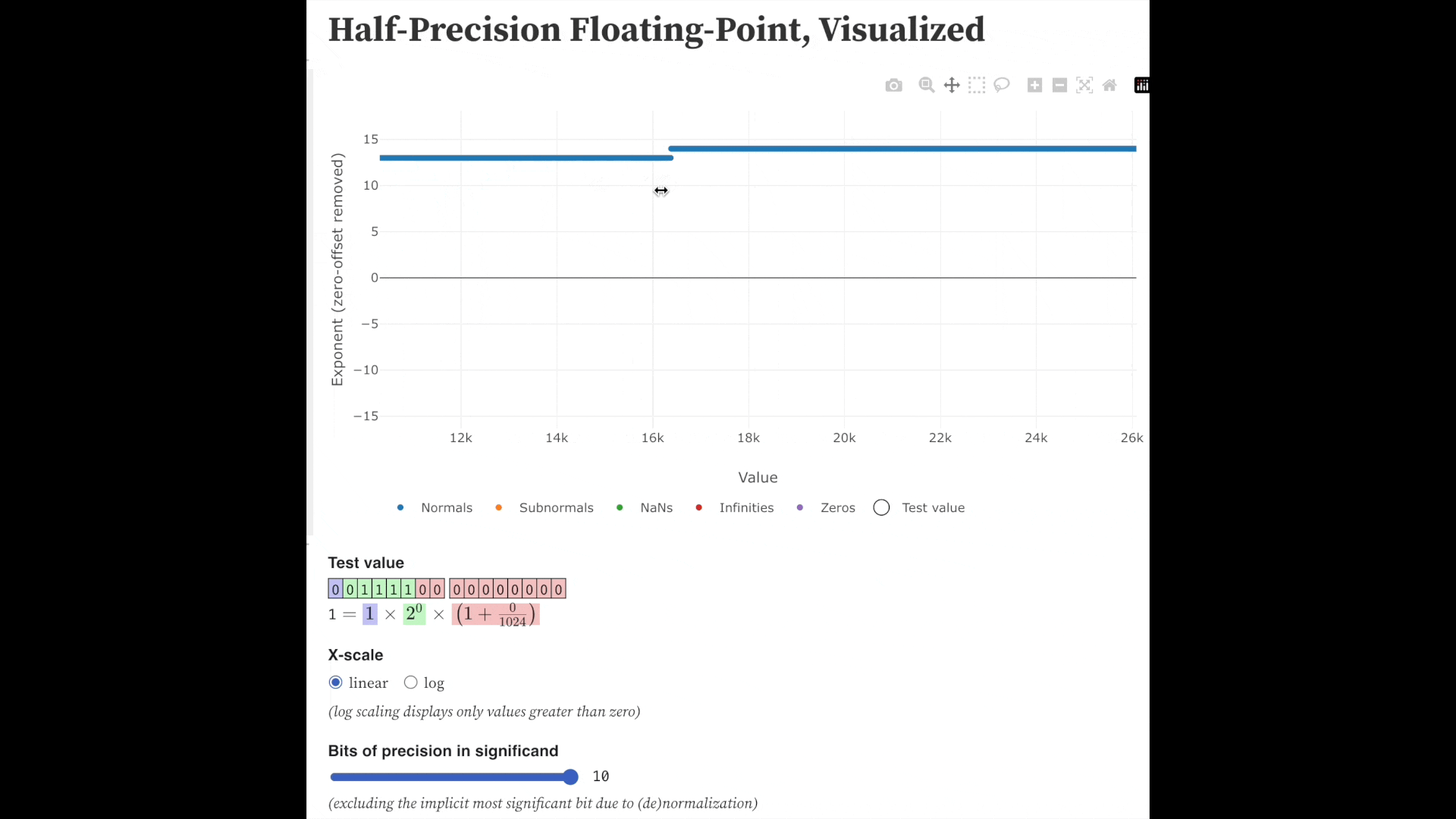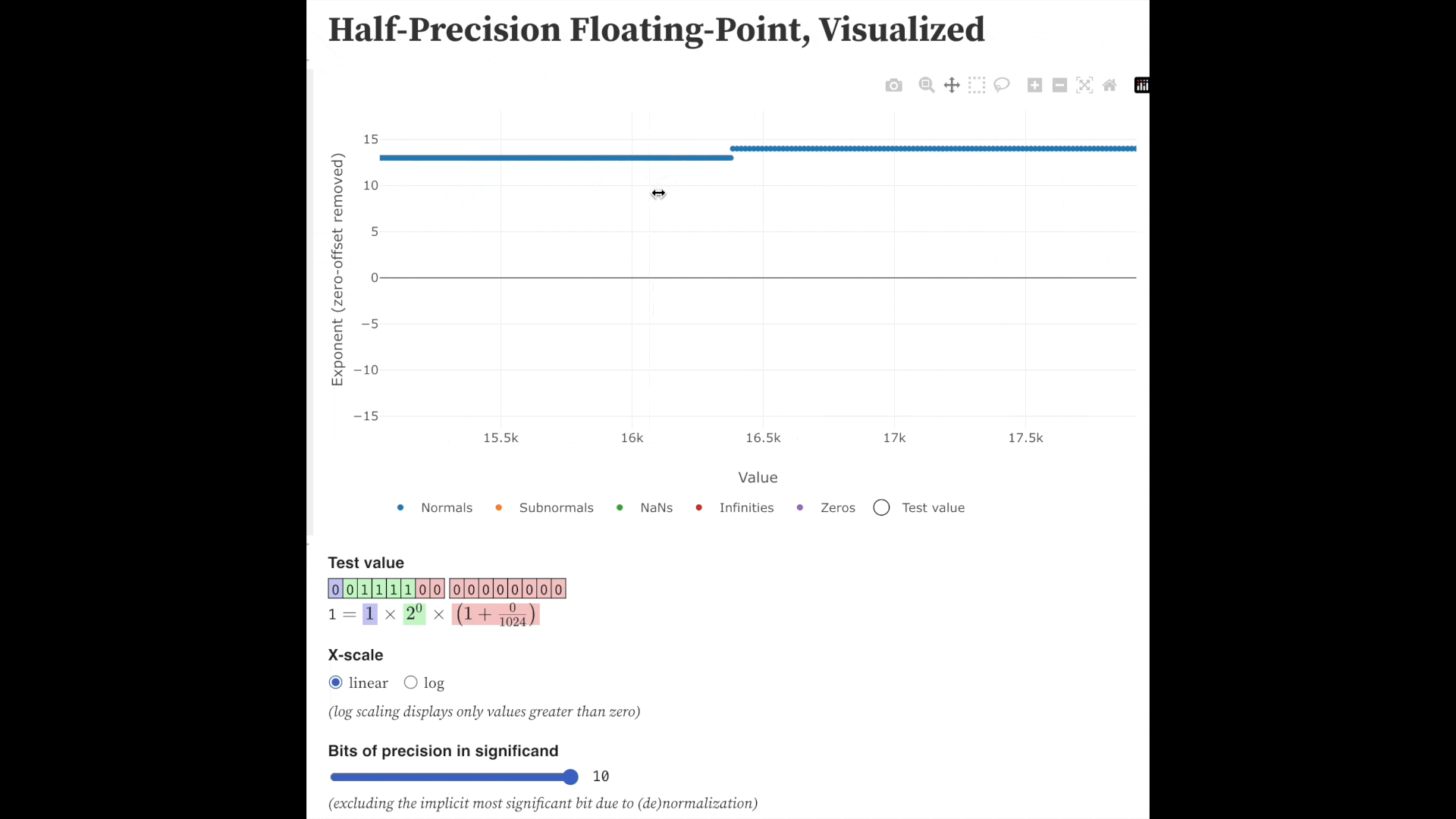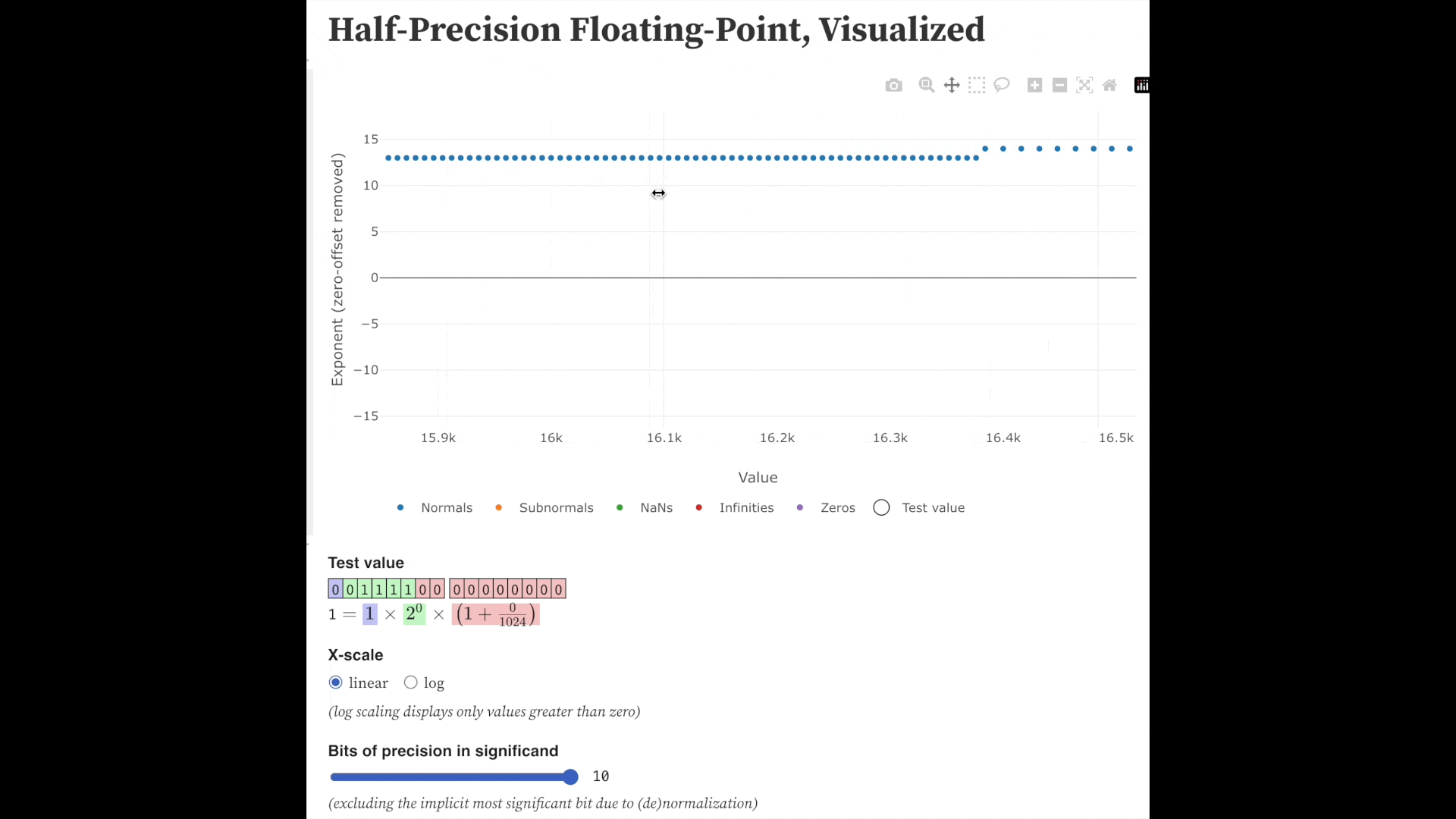Fig. fp16의 각 exponent별 표현할 수 있는 수. 당연하게도 무한대인 실수를 다 표현할 수는 없다. Source from here

그리고 이러한 수 체계는 exponent가 커질수록 더 커진 수, \(2^{E-127}\)에 fraction을 곱하는 형태가 되기 때문에, 직관적으로 정확도가 낮아질 것이다.

Training DNN with Reduced Floating-Point Format

FP16

한 편, fp16은 fp32에서 exponent에서 3bits, mantisa에서 13bits 줄어든 형태이다. 즉 표현력이 대폭 감소했다고 할 수 있는데, exponent가 줄어들었다는 것 (bias가 줄어들었다는 것)은 거시적으로 표현할 수 있는 수 자체가 줄어들었다는 것이고 (최대값이 \(3.4 \times 10^{38} \rightarrow 65504\)로 감소), mantisa가 줄어들었다는 것은 똑같은 \([9~10]\) 구간에 대해서도 나타낼 수 있는 수가 확 줄어들었다는 의미로, 원래는 예를 들어 설명하자면 \(0.00000015\)같은 수가 반 내림 되어 \(0.0000001\)이 된다는 걸 의미한다 (말 그대로 정밀함이 감소한 것; reduced precision).

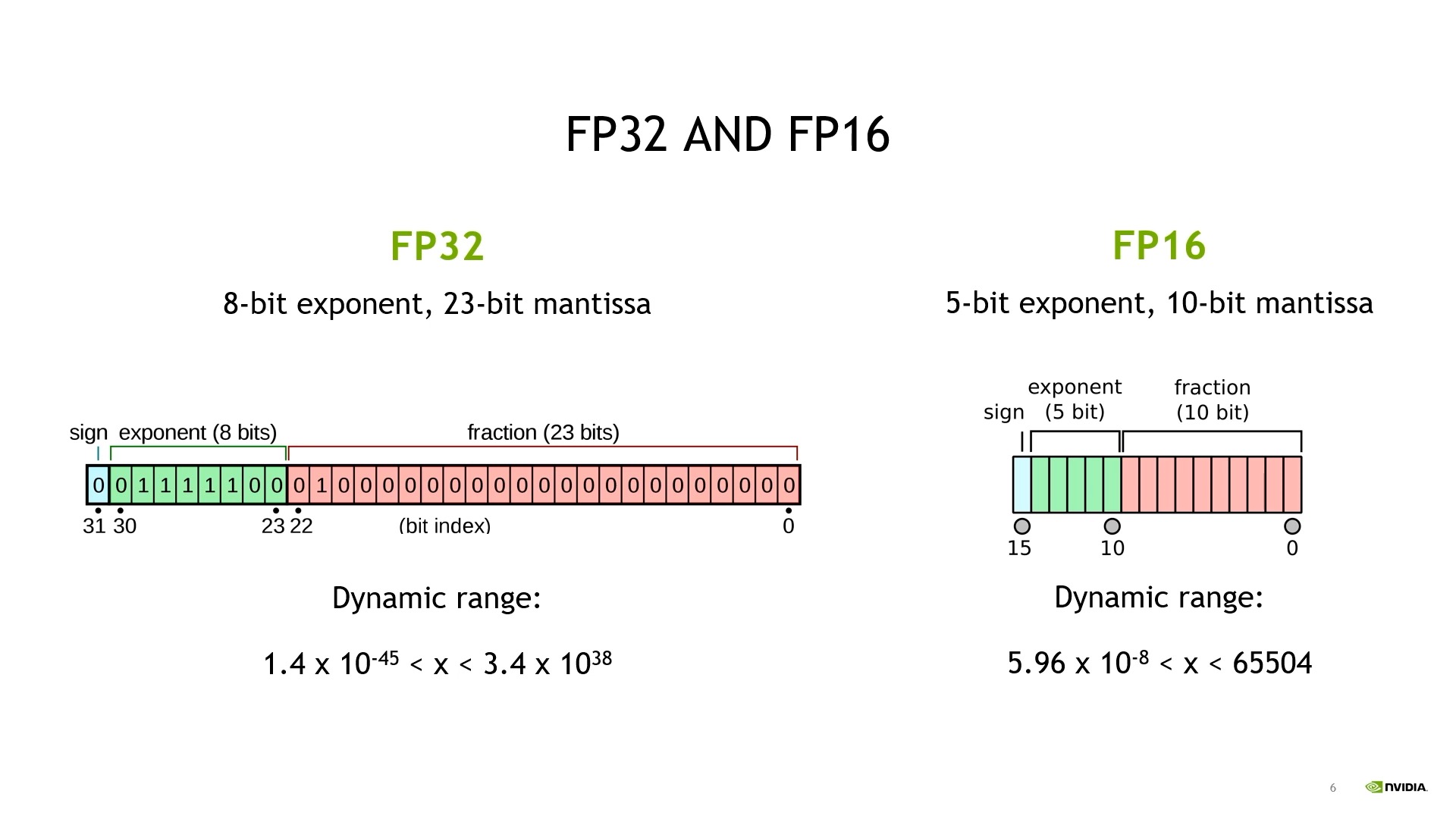Fig.

물론 fp16의 bias가 줄어들긴 했어도 실수를 표현하는것은 fp32와 크게 다르진 않다.

Fig. Source from here

하지만 dynamic range가 줄어들었기 때문에 어떤 4096차원의 vector 16이라는 수를 채워넣으면 fp16은 무한대 (infinity; inf)를 return하게 되는 문제가 있으며,

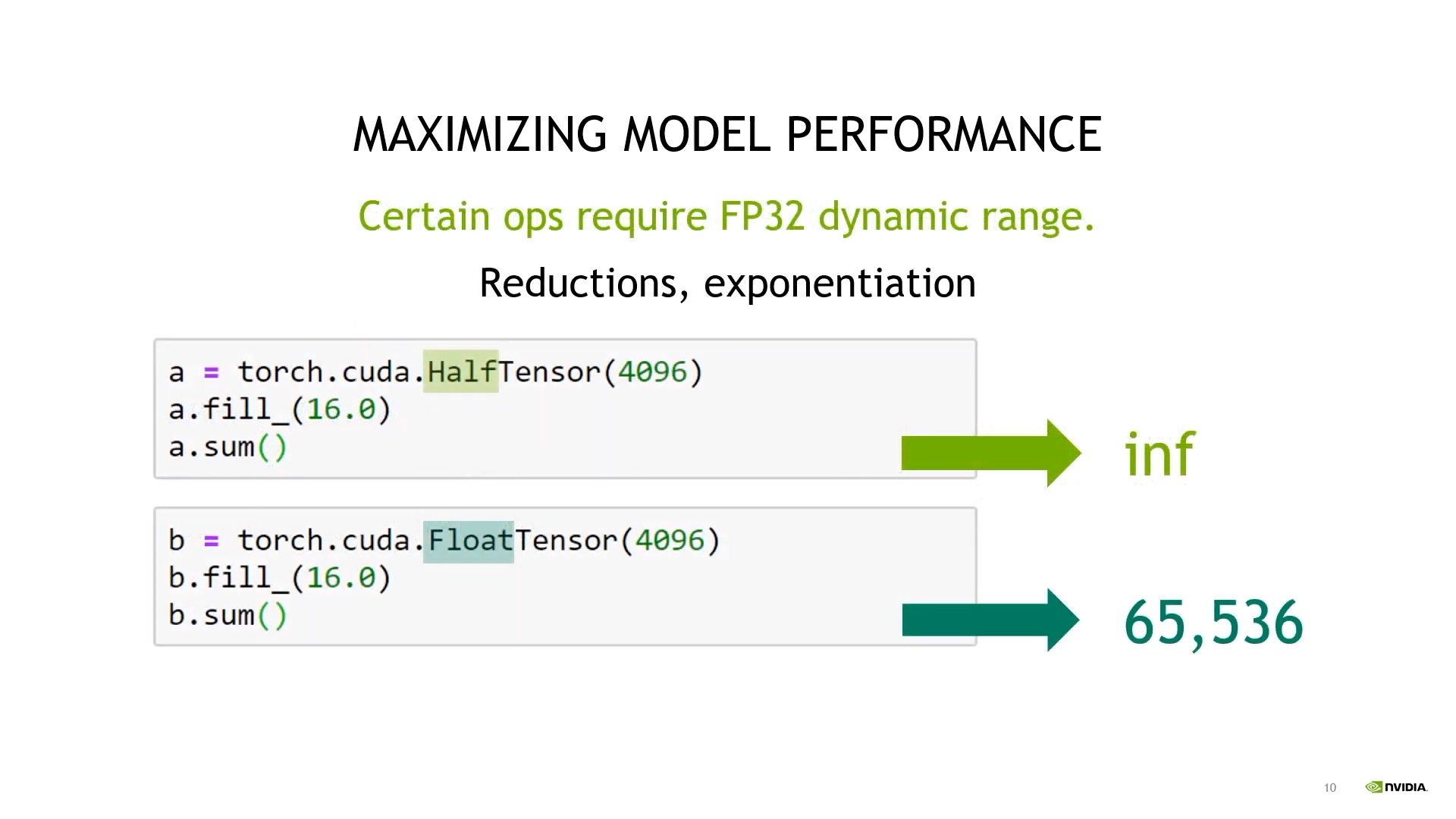Fig.

precision bits가 줄어들었기 때문에 정밀하지 못한 수를 쓸 수 밖에 없다.

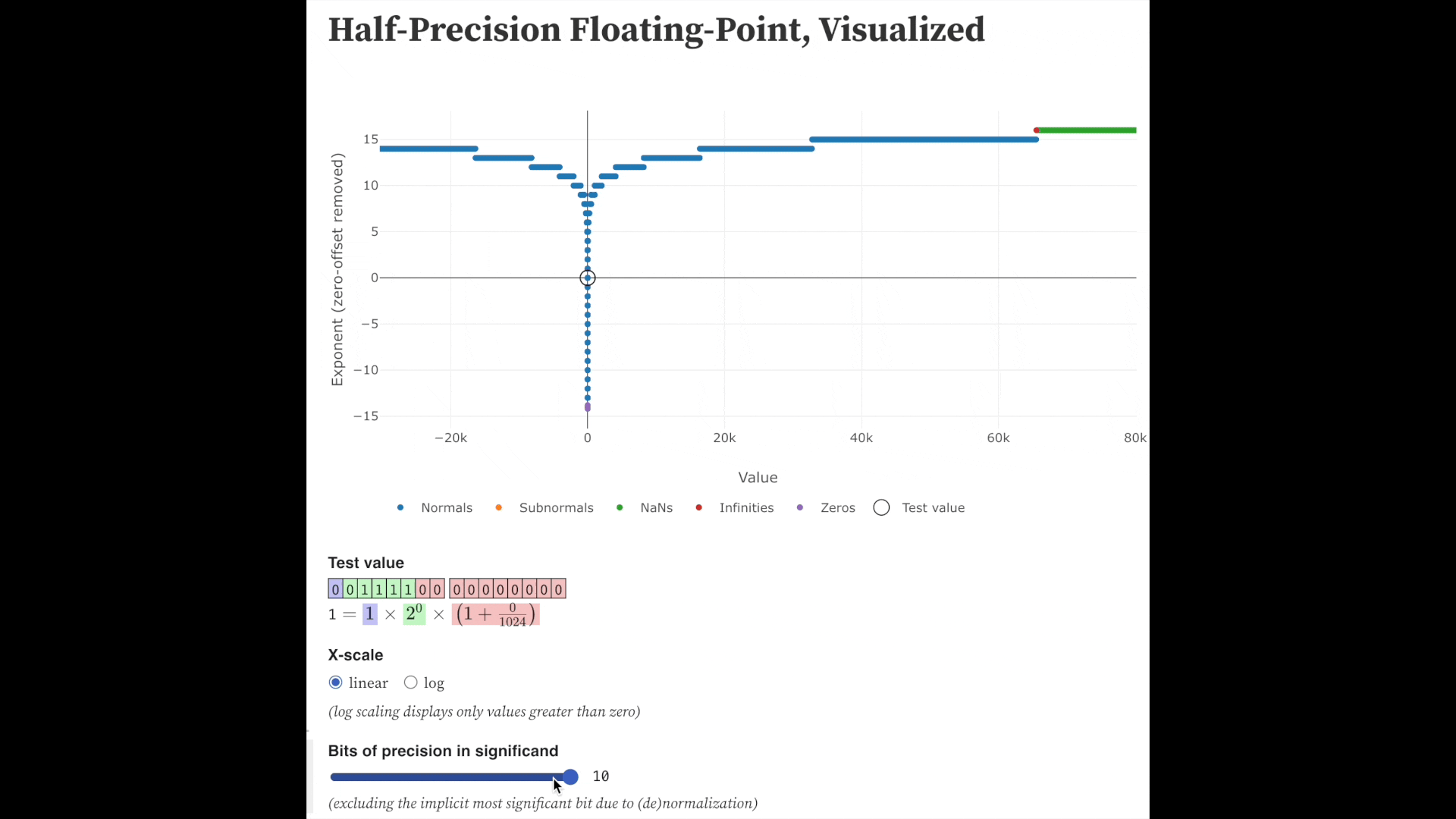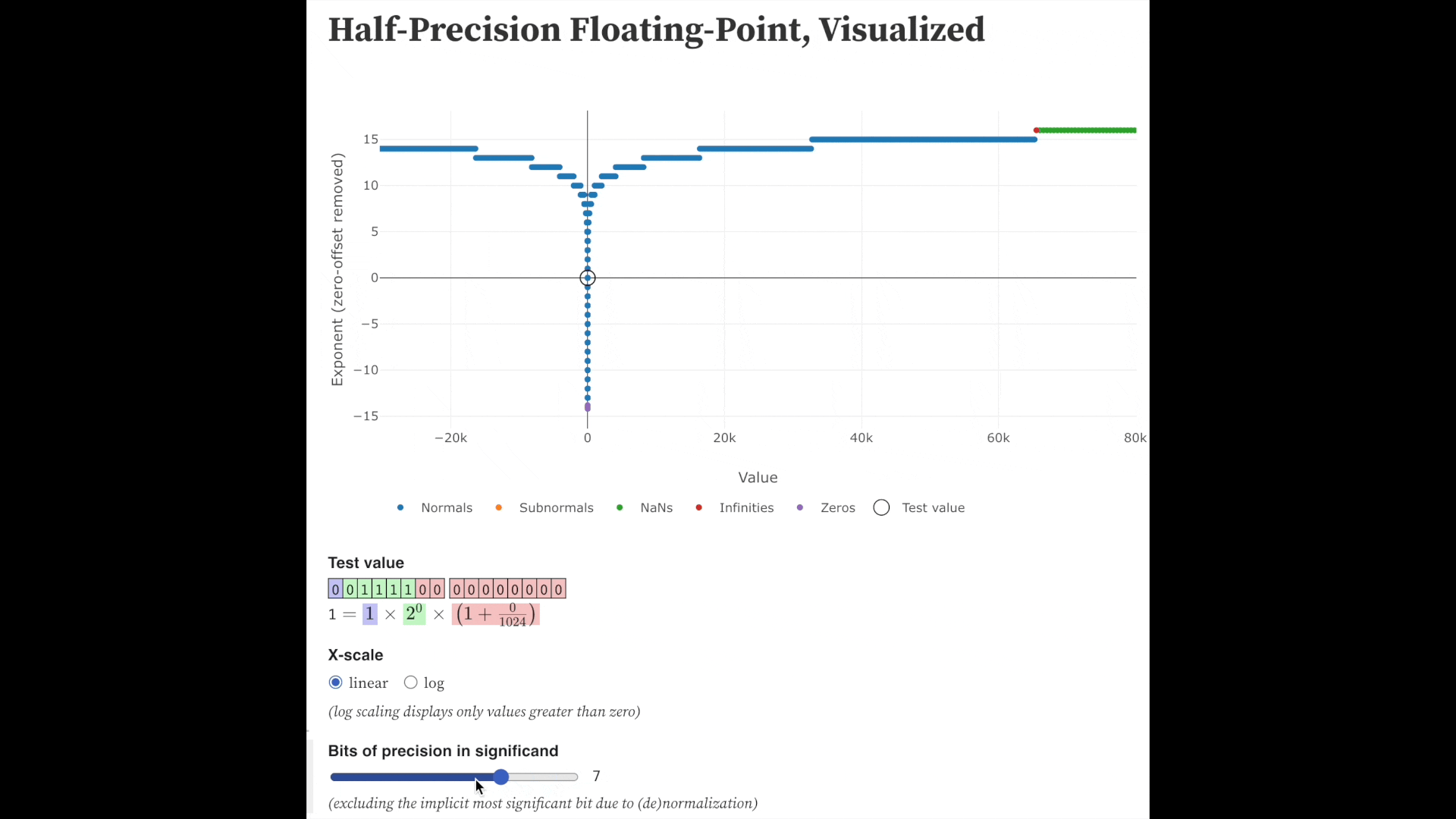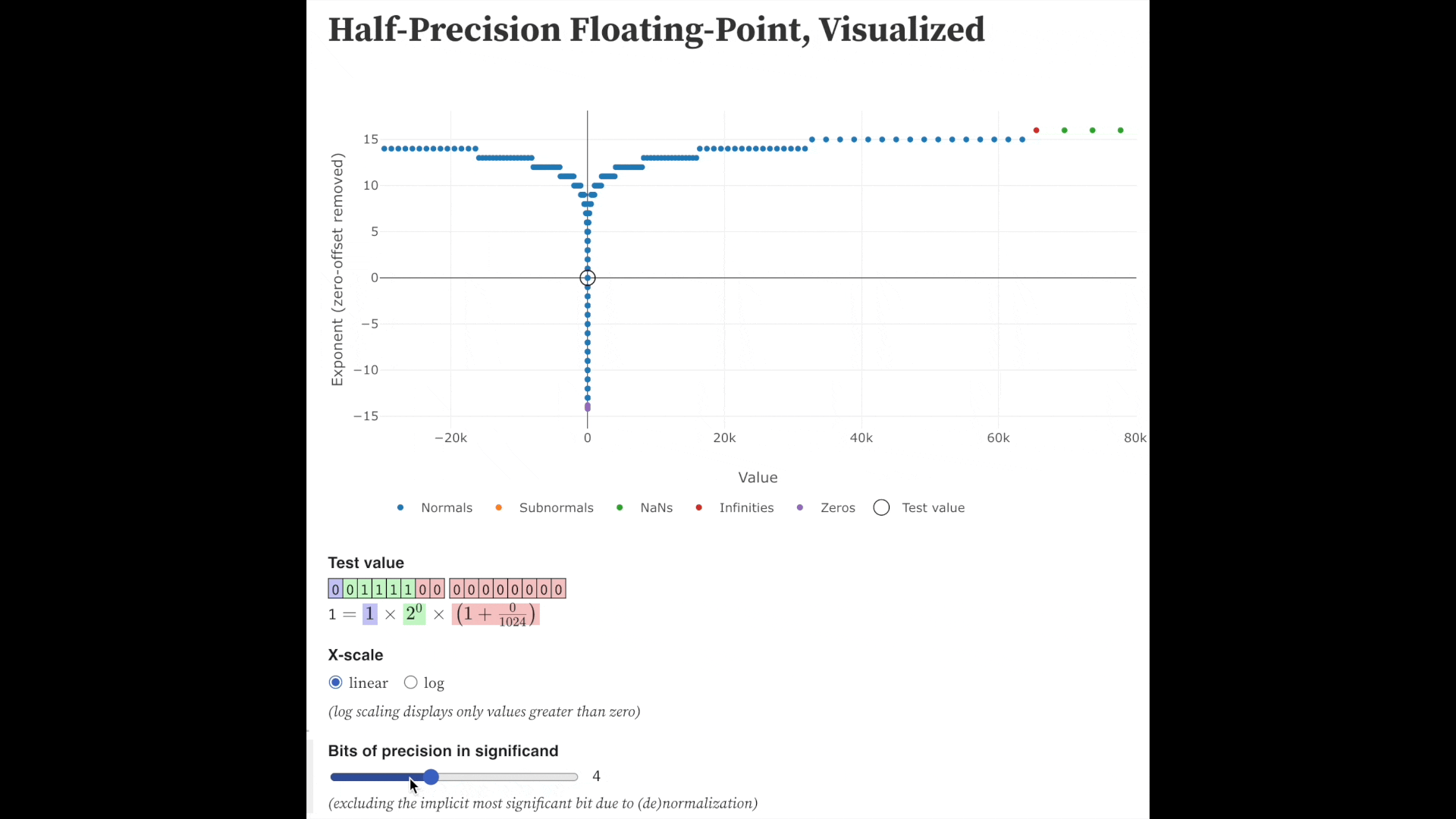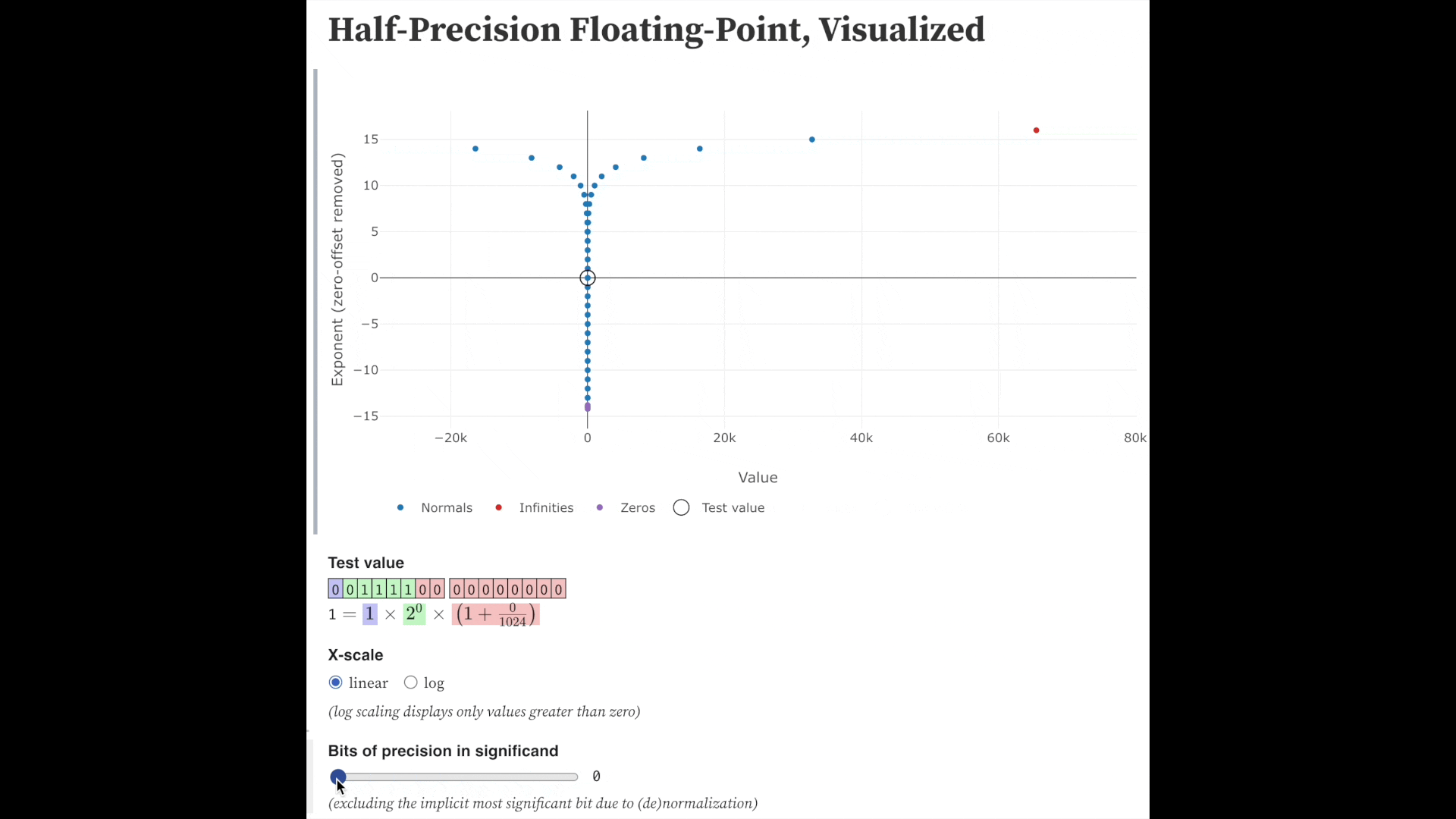Fig. precision bits를 줄일 수록 같은 exponent 내에서 표현가능한 실수는 줄어든다. Source from here

그런데 이것이 DNN을 학습할 때 왜 문제가 된다는 것일까? 지금부터 이에 대해 알아보자.

What's Wrong with FP16 ?

FP16은 fp32와 대비해 dynamic range가 감소했다는 건 자명하다. 여기서 문제는 매우 작은 값이 다 0으로 처리된다는 것이다. 또 다른 문제는 reduced precision이 작은 누적 (small accumulation)을 무시할 수 있다는 점이다.

Fig.

우리가 NN을 학습하기위해 gradient descent를 쓴다고 치자.

여기서 \(L(\theta)\)는 \(\theta\) parameterized NN을 통해 구한 loss값이며 1차 미분을 통해 gradient를 계산 해 learning rate만큼 update를 한다는 것을 의미한다. 그런데 만약 어떤 parameter가 값이 \(1\)인데 update가 \(0.0001\)인 경우 fp16을 사용하면 parameter가 update되지 않을 수 있다.

Fig.

그 이유는 상대적으로 매우 큰 weight에 작은 update량을 더하려고 해서 그런데, fp16에서는 이 비율이 \(\text{update} / \text{param} < 2^{-11}\)인 경우 update가 아무런 효과가 없다고 한다 (2048배 이상 차이날 경우라고 한다).

Fig.

게다가 만약 gradient가 작아지다 못해 fp16의 표현 범위를 벗어나게 되면 어떻게 될까? 이를 해결하기 위한 기술이 바로 mixed precision training method이다.

Mixed Precision Training

Mixed precision training은 3가지 technique을 적용해서 fp16으로도 DNN model을 가능하게 했다.

• (기본) 대부분의 forward/backward 연산은 fp16으로 한다.
• fp32의 weight을 copy한 master copy를 따로 관리하며 매 training step마다 fp16 weight으로 forwarding해서 구한 gradient는 fp32 weight에 더해 update하고 fp16은 이를 copy해서 쓴다. (매 번 copy가 일어남)
• gradient value가 0이될 경우의 수를 줄이기 위해 loss를 scaling해서 gradient를 계산한 뒤, 나중에 다시 unscaling한다.
• 특정 operation들은 fp16이 아닌 fp32로 한다.

여기서 만약 loss scaling을 해주지 않으면 아래와 같이 loss가 갑자기 폭발하는 것을 볼 수 있다.

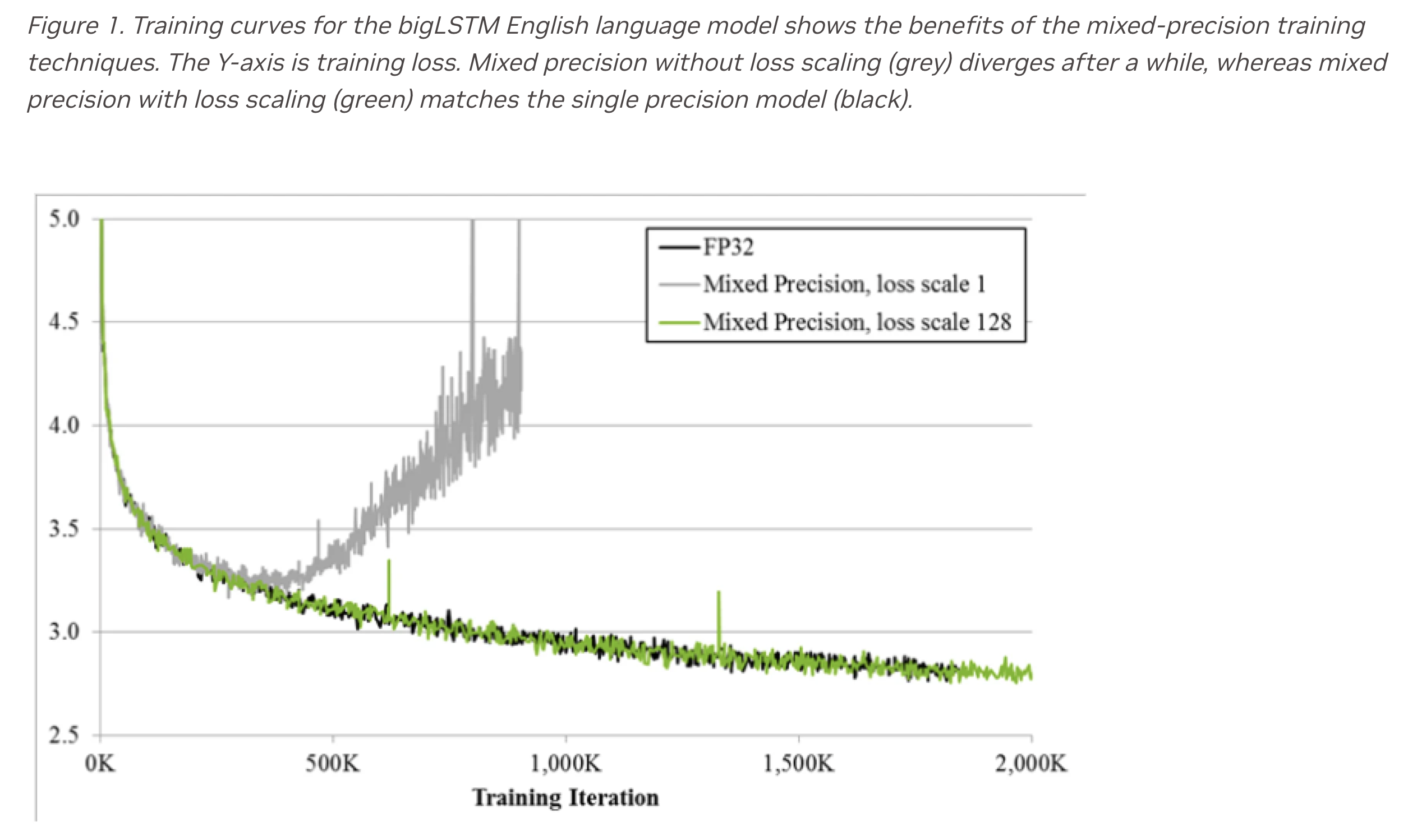Fig.

Range of FP16

본격적으로 mixed precision training의 3가지 technique에 대해 논하기 전에 fp16의 실제 표현 범위 (dynamic range)와 비정규 값 (denormal number, subnormal number)에 대해 정리하고 넘어가자. Denormal number는 이름 그대로 normalization 되지 않은 수를 의미하는데, 0과 1사이에 있는 매우작은 값들을 표현하기 위해 사용된다. fp32, fp16 모두 아래와 같은 rule을 따르는데,

• 0 : exponent == all zero, frcation == all zero
• Inf (Infinity) : exponent == all one, fraction == all zero
• Not a Number (NaN) : exponent == all one, fraction != all zero
• Denormal number : exponent == all zero, fraction != all zero

fp32에서 0과 1사이에 있는 값들 중에서도 \(0.0123\)과 같은 값은 \(1.23 \times 10^{-2}\)로 표현되긴 하지만 denormal number는 그보다 훨씬 작은 수인 \(1 \times 2^{-126} \times 2^-23\)같은 값은 것 (이 값이 제일 작은 값임) 들을 말한다. 즉 이를 통해서 원래 fp32의 exponent가 표현할 수 있는 범위가 \([-126, 127]\)였는데 \(2^{-126} \times 2^{-23} = 2^{-149}\)가 되기 때문에 실제로 fp32의 exponent가 표현할 수 있는 range는 \([-149, 127]\)라고 할 수 있는 것이다. 따라서 fp16도 exponent \([-14,15]\)에 denomal number를 포함하면 \([-24,-14]\)가 된다. 이들은 underflow를 어느정도 방지해주지만 정밀도 손실이 발생할 수 있으며, 때로는 계산 속도가 느려질 수 있다고 한다.

• maximum normalized of fp16 : \(65504\)
• minimum normalized : \(2^{-14} = \sim 6.10 e^{-5}\)
• minimum denormal : \(2^{-24} = \sim 5.96 e^{-8}\)

1. Gradient Accumulation in FP32

먼저 fp32 master copy를 따로 두고 gradient update하는 데 쓰는 것에 대해 얘기해보자. 이것을 도입한 이유는 paper에서 2가지로 설명되는데, 첫 번째는 앞서 gradient update가 weight과 2048배 차이나는 경우 update가 되지 않는다는 점이고, 두 번째는 gradient가 정상적으로 range안에 들어왔어도 1보다 훨씬 작은 learning rate이 곱해지면서 결국 0이되는 것이다 (값이 \(2^{-24}\)보다 작아져 버린 것). 전자의 경우 weight과 binary point을 맞추기 위해 오른쪽으로 shift하는 덧셈 연산 과정에서 0이 된다고 한다.

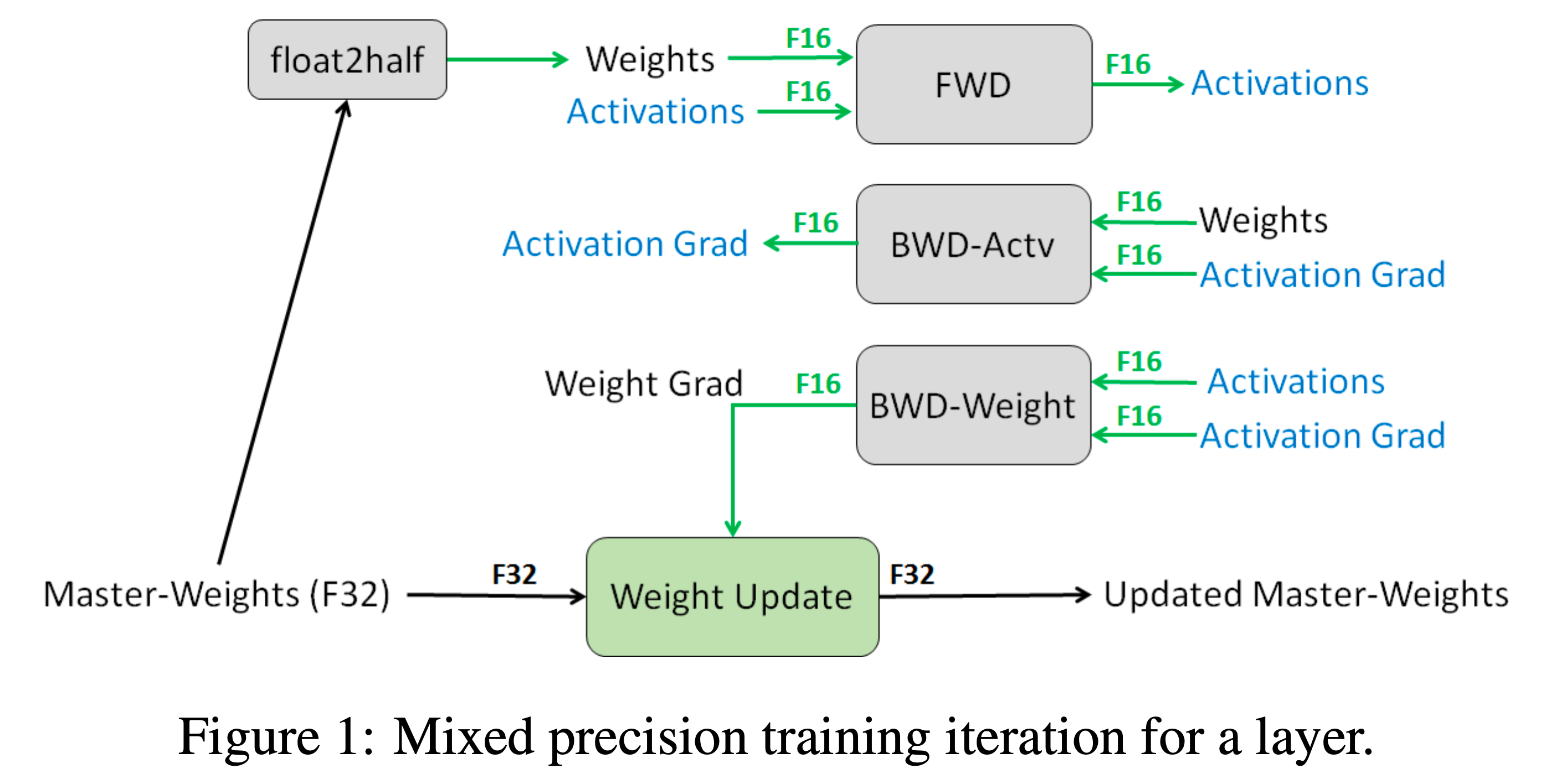Fig.

이를 해결하기 위해 fp32 master copy를 두는 technique은 위 figure에 나와있는 것 처럼 forward, backward로 gradient까지 잘 구한 뒤에 update는 fp32로 하는 걸 의미하는 것으로, mixed precision 이라는 이름 그 자체를 설명한다. 아래 figure의 (a)는 fp32 copy의 유무에 따른 중국어 (Mandarin) 음성 인식 (Automatic Speech Recognition; ASR) model의 loss curve를 의미하는데, 성능차이가 매우 큰 것으로 보인다. (아무래도 loss scaling까지는 적용되었고 fp32 copy만 없앤 것으로 보이는데 사실 loss scaling이 없으면 아예 학습이 안되었을 것이다.)

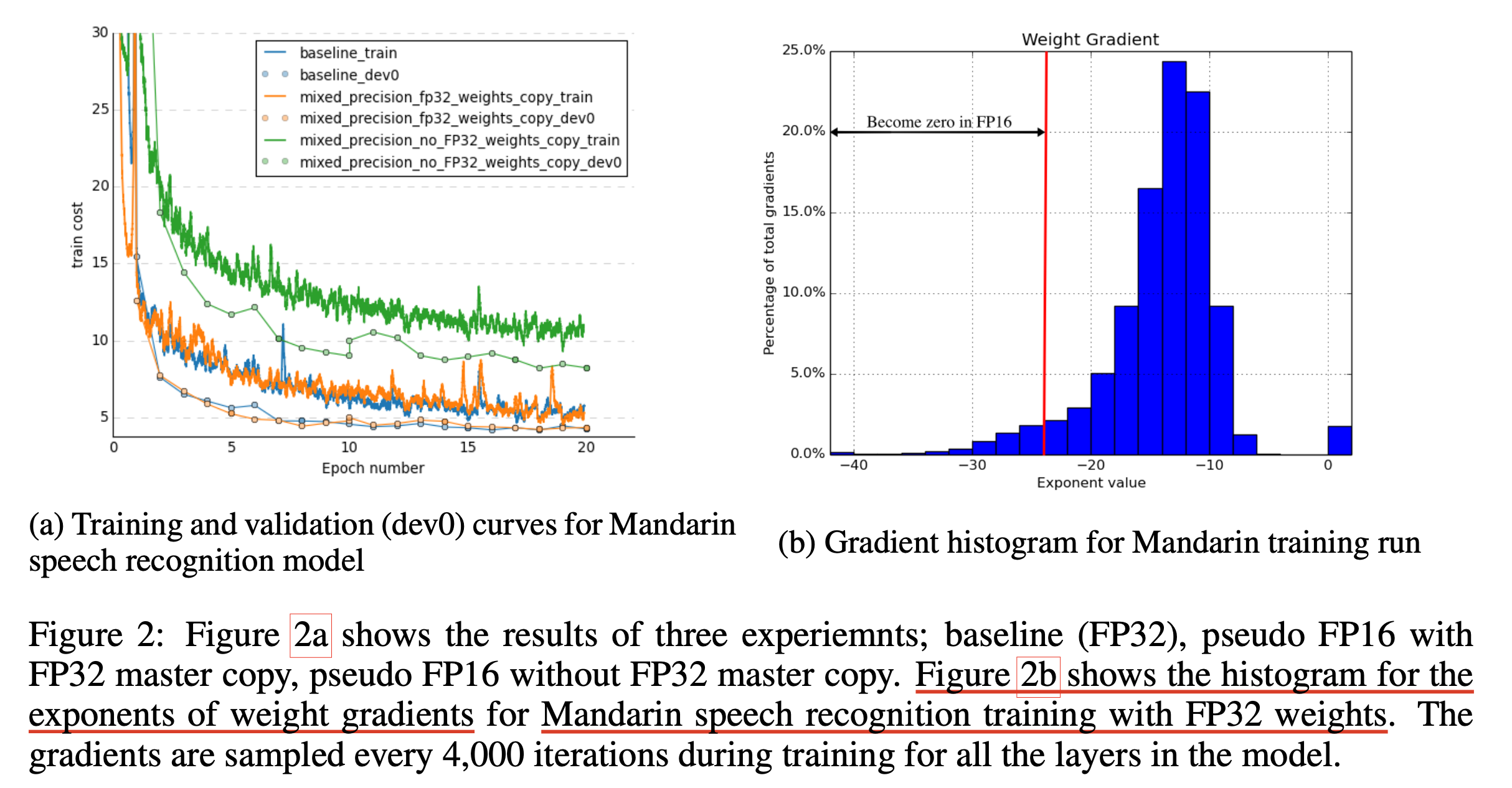Fig.

그리고 여기서 sub-figure (b)는 model을 fp32로 학습했을 때 각 weight들의 gradient의 exponent의 histogram을 나타낸 것인데, 매우 많지는 않지만 일정 fp16 range를 벗어나 gradient가 0이 되어 소실되는 것을 보여준다.

(하지만 이렇게 할 경우 update시 마다 model copy가 발생한다는 점과 원본 model의 fp32 copy만큼의 memory가 추가적으로 필요하다는 문제가 있다. 이는 model size가 작을 때는 별 문제가 되지 않지만 model size가 커질수록 엄청난 GPU memory 문제를 야기한다. 이를 해결하기 위한 technique이 바로 Zero Redundancy Optimizer (ZeRO)라는 것인데, 더 관심이 있는 사람들은 이 post를 읽어보길 바란다.)

2. Gradient Scaling

그 다음은 gradient scaling이다. 아래 figure는 Multibox SSD detector network라는 model을 fp32로 학습했을 경우 전 layer에 걸쳐 얻은 activation gradient의 value를 나타낸 것이다.

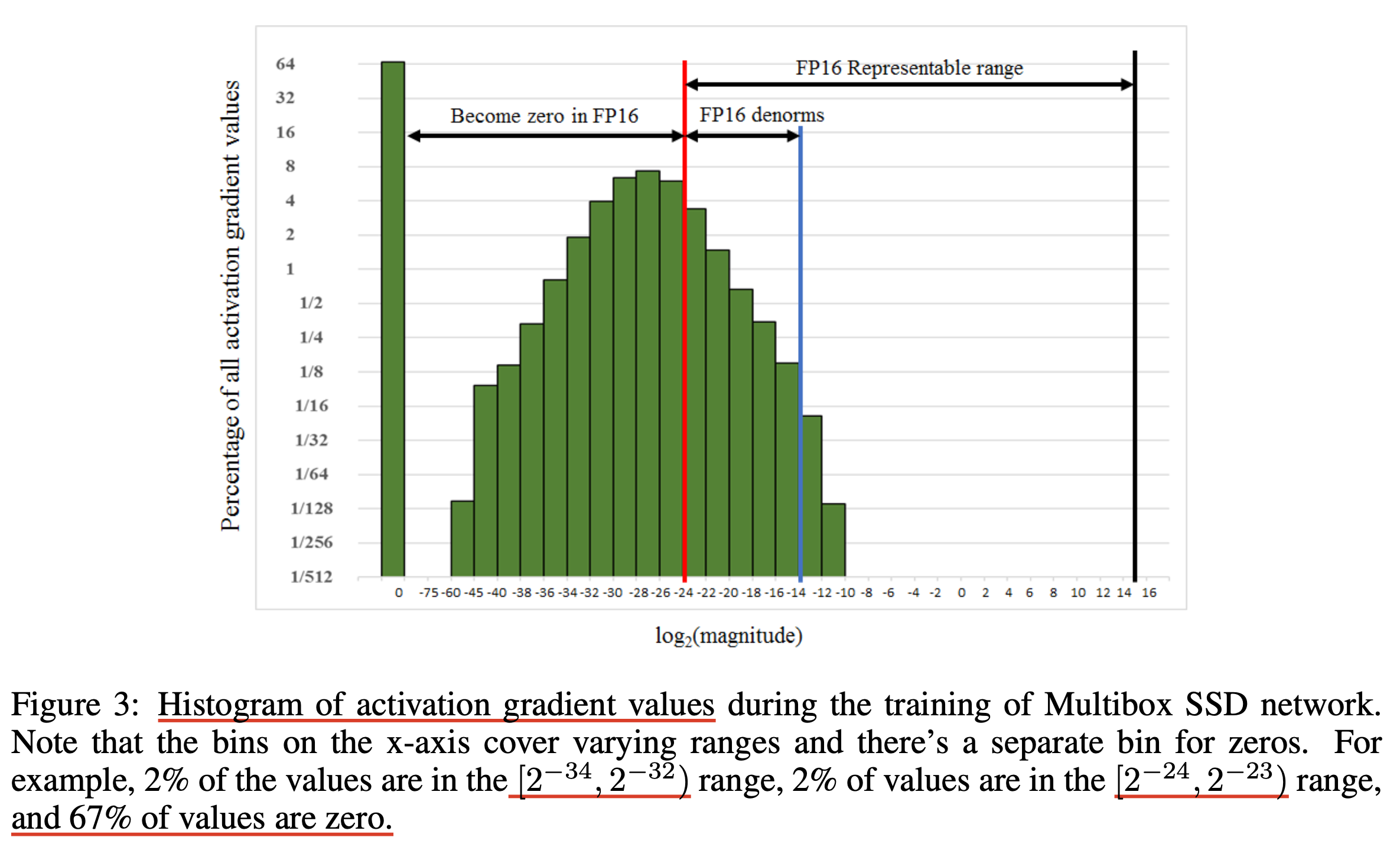Fig.

여기서 주목할만한 것은 대부분의 gradient가 fp16의 range를 넘어 0이 된다는 점과 fp16의 오른쪽 range는 전혀 사용되지 않았다 것이다. 즉 이 histogram을 오른쪽으로 shift 시킨 뒤 나중에 다시 recover를 하면 된다는 아주 간단한 idea가 gradient scaling 이다. 하지만 실제로는 gradient를 scaling하지는 않고 loss를 scaling하는데, 그 이유는 어차피 error backpropagation을 할 때 chain rule에 의해 gradient가 loss scale의 영향을 받기 때문이다. 아래 figure를 보면 원래는 0이 될 gradient들을 loss scaling 해줌으로써 underflow가 되지 않도록 먼저 보존해준다.

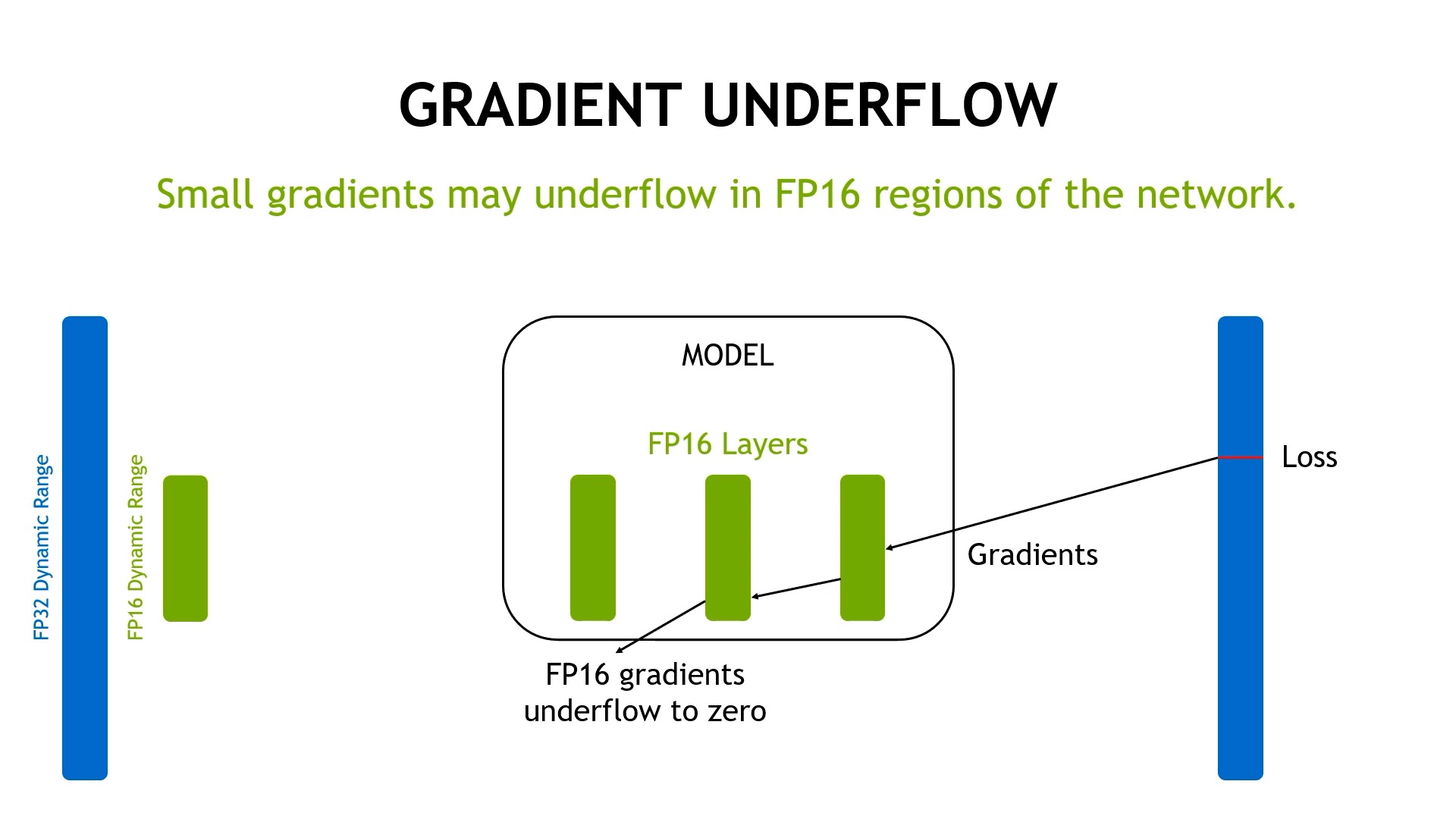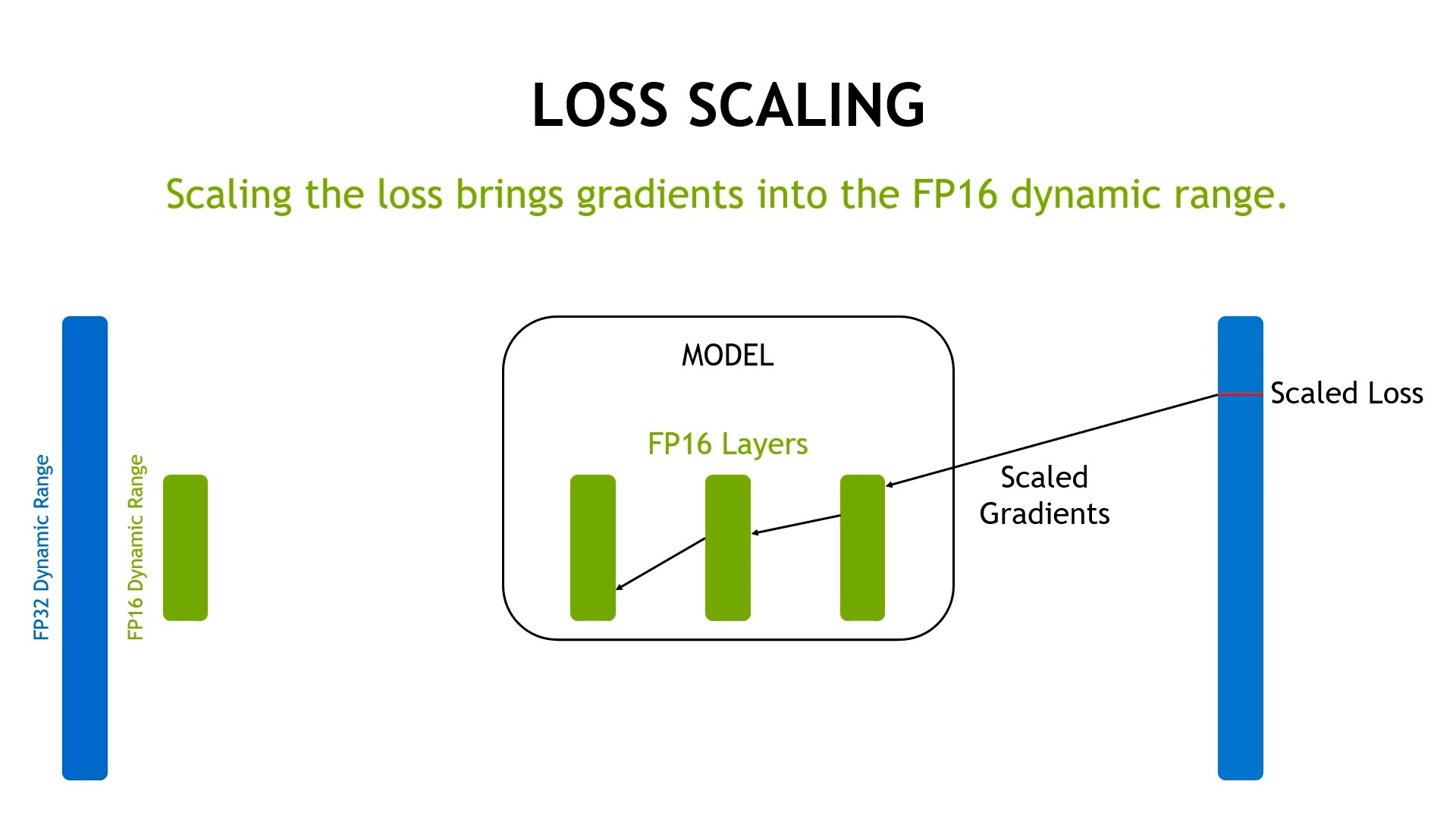Fig.

Fig.

그 뒤에 fp32로 gradient update를 할 때 다시 원래 gradient의 크기가 되도록 unscale을 해주면 된다.

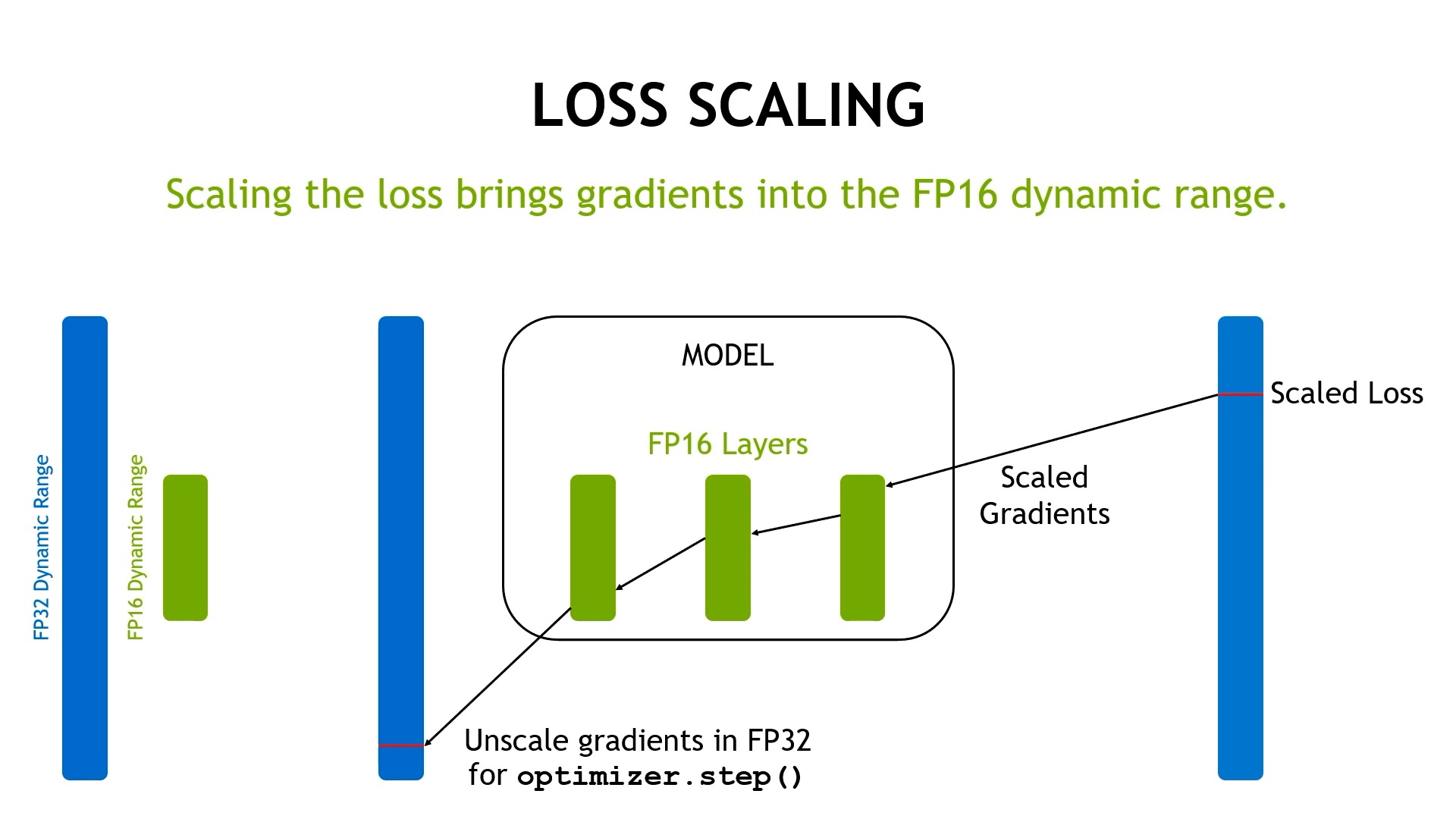Fig.

보통 \(8\)정도를 scaling factor로 써서 loss에 곱해주는데 (즉 exponent를 3배 키우는 것), 직관적으로 \(2^{-27}\)이하의 gradient는 학습에 무관한 (무시할만한) 수준이라고 판단했기 때문이라고 한다. 이것만으로 충분할 때도 있고 아닐 때도 있기 때문에 hyperparameter로서 user가 설정해줘야 한다. 혹은 training dynamics에 따라 이 값을 자동으로 늘리거나 줄이는 방향으로 adaptation 하도록 할 수도 있다. Adaptation을 할 경우 일반적으로 맨처음에는 large scaling factor, S를 고른 뒤, N번의 iteration step동안 아무 문제가 없었다면 S를 키우고 (보통 2배) overflow같은 문제 (\(65504\)보다커지면 생김)가 생겼으면 batch를 버리거나 다음 iteration으로 넘긴 뒤 S를 줄이는 것 (보통 1/2배)이다. (별 문제 없을 때 키우는 이유는 최대한 많은 gradient를 보존하기 위해서 인 것 같다)

1. Maintain a primary copy of weights in FP32.
2. Initialize S to a large value.
3. For each iteration:
    a. Make an FP16 copy of the weights.
    b. Forward propagation (FP16 weights and activations).
    c. Multiply the resulting loss with the scaling factor S.
    d. Backward propagation (FP16 weights, activations, and their gradients).
    e. If there is an Inf or NaN in weight gradients:
        i. Reduce S.
        ii. Skip the weight update and move to the next iteration.
    f. Multiply the weight gradient with 1/S.
    g. Complete the weight update (including gradient clipping, etc.).
    h. If there hasn’t been an Inf or NaN in the last N iterations, increase S.

그런데 overflow는 어떻게 알 수 있을까? paper에서는 gradient statistics를 구할 수 있으면 (즉 torch.isnan or torch.isinf같은걸 쓰면) 된다는 하는데, model size가 클 경우 이를 검사하는 것 자체가 training의 bottleneck이 될 수 있으므로 주의해야 한다.

import torch
>>> torch.isinf(torch.tensor([1, float('inf'), 2, float('-inf'), float('nan')]))
tensor([False,  True,  False,  True,  False])

아래는 pytorch level의 simple implementation인데, 어려운 작업이 아님을 알 수 있다.

Fig.

3. FP16 arithmetic with accumulation in FP32

마지막으로 특정 operation들을 fp32로 수행하는 것인데, batch normalization이나 softmax activation 혹은 (개인적으로) residual connection 같은 것들이 이에 해당된다. 이들은 여전히 fp16으로 읽고 쓰기 때문에 memory saving효과는 있지만 내부적으로는 fp32로 연산이 수행된다는 것 같다.

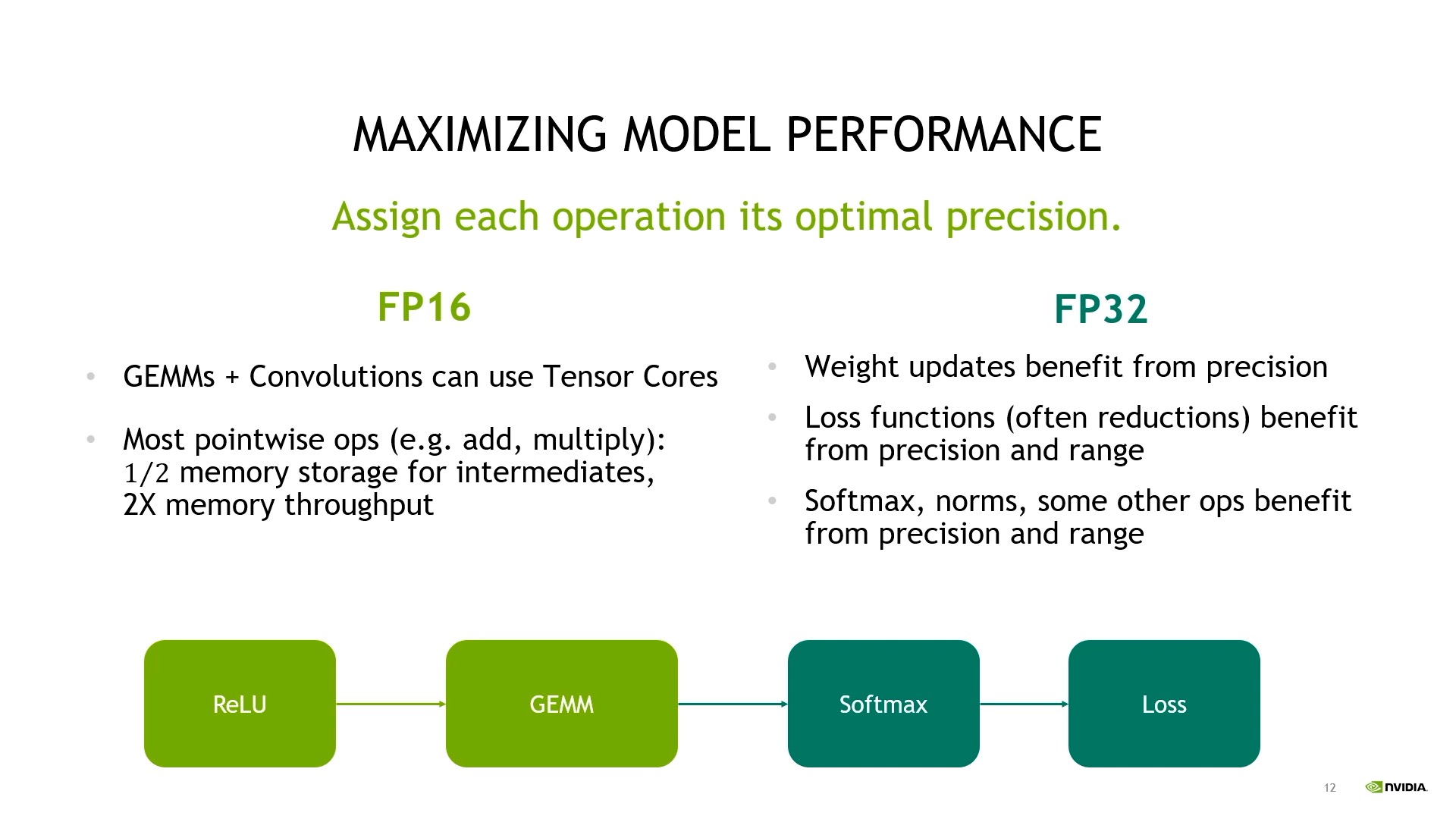Fig.

이런 precision에 민감한 operation들을 fp32로 upcasting하는 것은 아래처럼 간단하게 구현할 수 있는데, 이것이 paper에서 말하는 read, write이 fp16인 것을 의미하는 지는 모르겠다.

def get_attn_weights(Q, K, attn_mask):
    attn_weights = (Q @ K) / math.sqrt(Q.dim(-1)) + attn_mask
    return nn.functional.softmax(attn_weights, dtype=torch.float32).to(Q.dtype)

class Fp32LayerNorm(nn.LayerNorm):
    def __init__(self, *args, **kwargs):
        super().__init__(*args, **kwargs)

    def forward(self, input):
        output = F.layer_norm(
            input.float(),
            self.normalized_shape,
            self.weight.float() if self.weight is not None else None,
            self.bias.float() if self.bias is not None else None,
            self.eps,
        )
        return output.type_as(input)

BF16

Bf16은 Google Brain이 고효율 ML 학습을 위한 custom 16-bits floating point format 이다. 표현할 수 있는 값의 최대, 최소 range는 exponent가 8개이기 때문에 fp32와 아예 동일하지만 (The dynamic range of bfloat16 and float32 are equivalent), mantisa가 7개 이기 때문에 fp16보다 정밀도가 더 떨어진다. (variable당 2 byte의 memory가 필요하다는 점에서 fp16과 같은 이점이 있다)

Fig.

Brain team은 NN training가 mantisa의 크기보다 exponent 크기에 더 민감하다는 가설을 세웠다. 그렇기 때문에 fp16보다 exponent의 크기를 더 키운 것인데, 그 결과 Underflow, overflow, NaN의 동작이 fp32과 같아지게 되었다 (당연함). 다만 fp32와 동일한 것은 당연히 아니기에 denormal numbers를 처리하는 방식이 다른데, bf16은 denormal numbers를 0으로 flush해버린다고 한다 (?..).

Pros and Cons of BF16

bf16의 장단점을 알아보자. 먼저 장점으로는 bf16이 fp32와 같은 dynamic range를 갖기 때문에 mixed precision training의 loss scaling같은 건 필요하지 않을 수 있다는 것이 있다. 앞서 gradient statistics를 계산하는 것 자체가 bottleneck이 될 수 있다고 얘기했는데, 이 과정 자체가 fp16보다 없으므로 시간을 더 save할 수 있다.

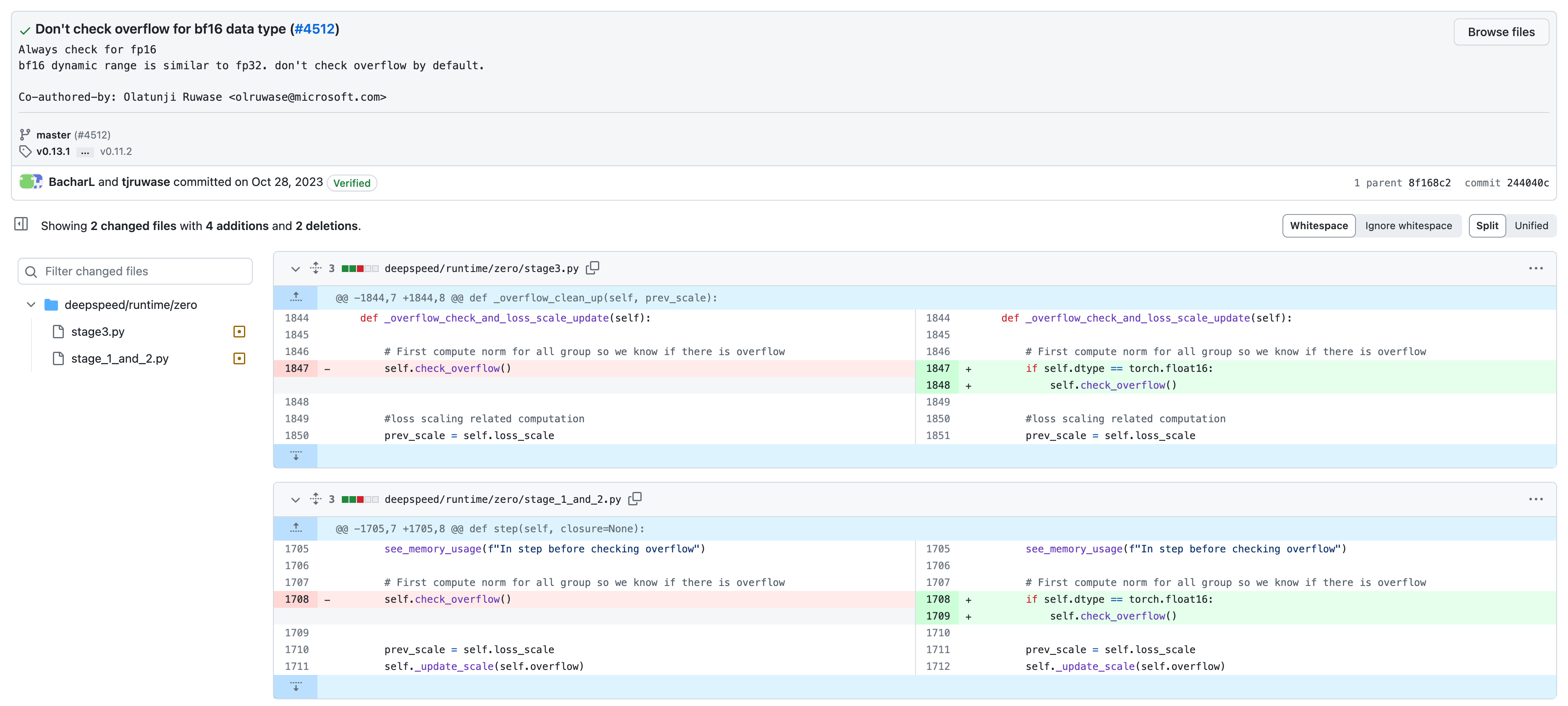Fig. deepspeed의 최근 commit에서 bf16이 fp16이 하는 overflow 를 검사하는 logic을 제거해서 속도 개선을 이뤄냈다. (이렇게 거대한 library도 실수할 수 있다)

그 다음 단점에 대해서는 먼저 당연히 매우 작은 gradient들은 무시된다는 점이지만 이는 매우 작은 gradient가 training에 큰 영향을 끼치지 못한다면 넘어가도 될 문제다. 하지만 precision bits가 fp16과 대비해서도 5개나 줄어들었기 줄어들었기 때문에 수를 정밀하게 표현하는데 있어서는 더 불리해 졌다.

Fig. precision bits를 줄일 수록 같은 exponent 내에서 표현가능한 실수는 줄어든다. Source from here

물론 bf16으로 학습했을 때 문제가 없다는 report가 많이 있다. 특히 large scale model을 pre-training할 때 loss explosion을 막기 위해서 bf16을 쓴다는 reference가 많이 있는것으로 알려져 있다. 하지만 어떤 학습을 할 때 정밀한 확률 값을 계산해야 한다거나할 때는 굉장히 큰 문제를 만들 수 있다. 예를 들어 어떤 layer의 activation output의 mean값이 5라고 하자. 그리고 다음 곱해질 weight matrix의 mean은 0이지만 variance가 꽤 크고, bias는 3~4 정도라고 치자. 충분히 가능한 weight distribution인데 물론 bf16 으로 학습됐으니 bf16으로 forwarding을 할 경우 큰 문제가 없을 수도 있지만, 여기에 flash attention이나 다른 technique과 sampling등이 추가되면 operation 순서가 많이 바뀌거나 한다면 결과가 천차만별로 바뀔 수 있다.

자세한 내용은 다룰 수 없어 이만 줄이겠으나 언제나 돌다리도 두들겨보고 건너야 한다는 점에 주의해야 할 것이다. bf16은 만능이 아니다.

Automatic Mixed Precision (AMP)

한 편, Pytorch에서는 nvidia와 합작하여 Automatic Mixed Precision (AMP)라는 것을 제공하고 있는데, 이 class를 사용하면 정밀한 연산은 fp32로 자동 upcasting해서 연산해주고 loss scaling, fp32 copy등도 자동으로 처리해주므로 귀찮게 이를 구현할 필요는 없다. (원래는 따로 있었다가 torch로 정식 편입되고 deprecated)

Fig.

혹은 microsoft의 deepspeed같은 library는 이런 technique들을 manually 구현하기도 한다.

Reference

• Papers
  • Mixed Precision Training
  • A Study of BFLOAT16 for Deep Learning Training
• Videos
  • NVAITC Webinar: Automatic Mixed Precision Training in PyTorch
• Blogs
  • Train With Mixed Precision
  • Accelerating AI Training with NVIDIA TF32 Tensor Cores
  • What’s the Difference Between Single-, Double-, Multi- and Mixed-Precision Computing?
  • The bfloat16 numerical format
  • Accelerating Large Language Models with Mixed-Precision Techniques
  • Half-Precision Floating-Point, Visualized from Ricky Reusser
  • Neural Network Quantization & Number Formats From First Principles from DYLAN PATEL
  • Mixed-Precision Training of Deep Neural Networks
  • BINARY REPRESENTATION OF THE FLOATING-POINT NUMBERS