Regression (1/7) - Linear Regression
21 Jan 2021< 목차 >
- Regression VS Classification
- Linear Regression
- Linear Regression in formula
- Connection to Mean Squared Error (MSE) Loss
- Bayesian Linear Regression
- Further Study
- References
Regression VS Classification
Machine Learning (ML) algorithm으로 다양한 문제를 풀 수 있다. 이런 대부분의 Application 들은 사실 회귀 (Regression), 분류 (Classification) 문제의 연장선이라고 할 수 있는데, regression 과 classification 두 가지 task는 아래의 표에서 볼 수 있듯 input과 output이 어떤 형태냐 (어떤 distribution를 따라느냐)에 따라서 단순하게 나눌 수 있다.
 Fig. 회귀 (Regression) vs 분류 (Classification)
Fig. 회귀 (Regression) vs 분류 (Classification)
Linear Regression
1차원 x값에 대해서 이에 대응하는 y값이 존재하는 data를 생각해보자. 우리의 목적은 예를들어 이 data를 가장 잘 설명하는 직선 하나를 찾는것이 될 수 있다.
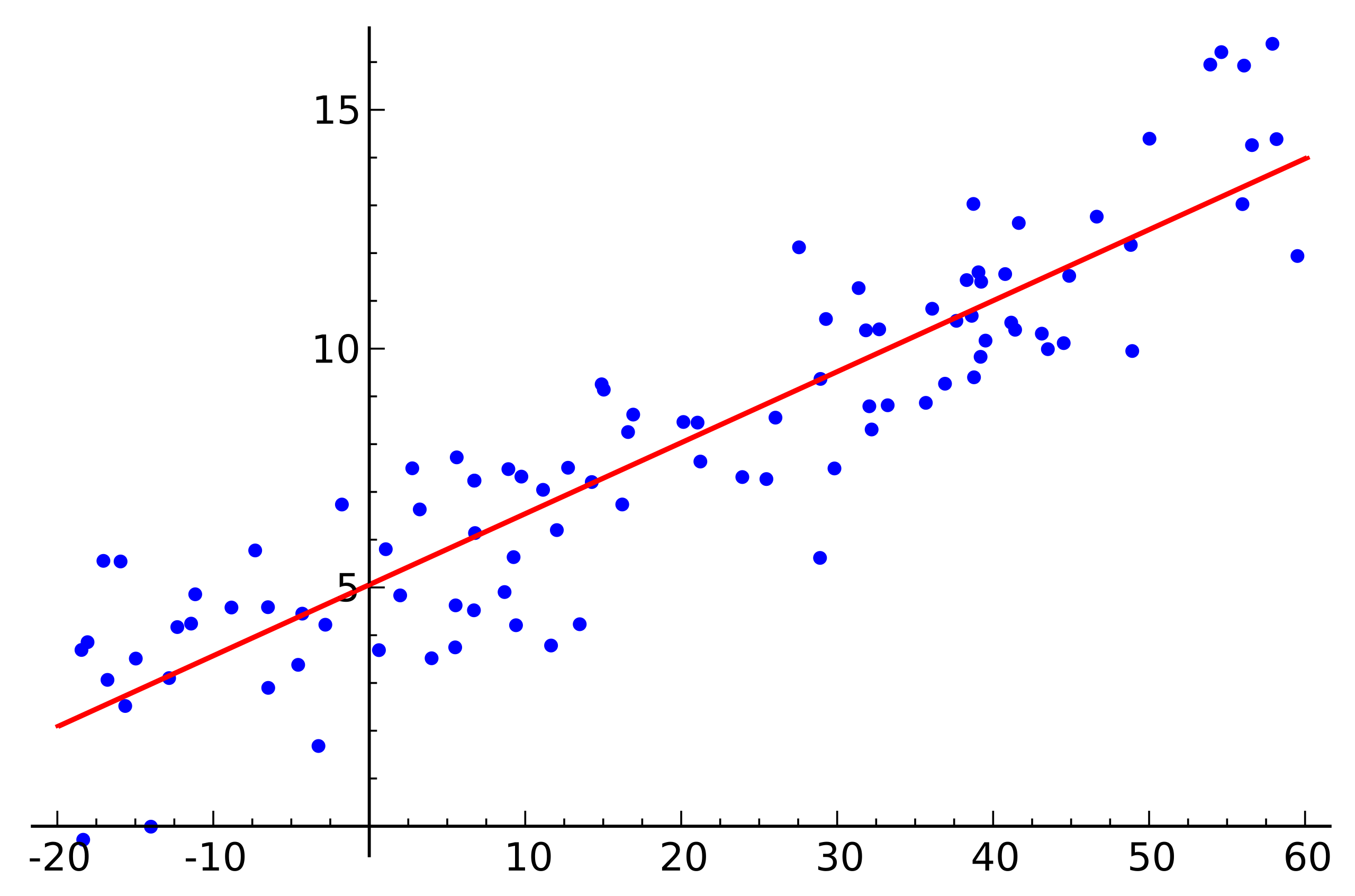 Fig. data를 가장 잘 설명하는 직선은 무엇일까?. Source from link
Fig. data를 가장 잘 설명하는 직선은 무엇일까?. Source from link
당연히 data를 잘 설명하는 curve가 직선이 아닐 수도 있다. 가령 \(y=ax+bx^2+cx^3\) 같은 curve를 찾아내야 할 수도 있다. 이를 비선형 회귀 (non linear regression)이라고 하는데, 이는 독립 변수와 종속 변수 간의 관계가 비선형이라는 것을 의미한다. 이 수식에서는 x에 대해서는 비선형 (non linear) 이지만 우리가 구하고자 하는 계수는 a,b,c이기 때문에 이에 대해서는 선형이라고 할 수 있지만, 어쨌든 이런 curve를 찾으면 다양한 data 분포에 맞는 curve를 구할 수 있다. (non linear regression은 다음 post에서 다룰 예정임. Ref 2
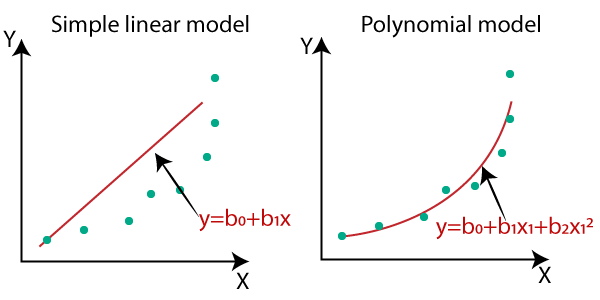 Fig. Linear vs Polynomial Regression. 다항식 피팅 곡선도 선형 regression라 할 수 있는데 왜냐하면, 우리가 추정하고자 하는 parameter에 대해서 수식이 선형이기 때문이다. Source from here
Fig. Linear vs Polynomial Regression. 다항식 피팅 곡선도 선형 regression라 할 수 있는데 왜냐하면, 우리가 추정하고자 하는 parameter에 대해서 수식이 선형이기 때문이다. Source from here
만약 data가 총 3차원 (입력 x 2차원, 결과 y 1차원) 이라면 우리는 data를 잘나타내는 평면의 방정식의 법선 vector를 구하는 것이 목적이 된다.
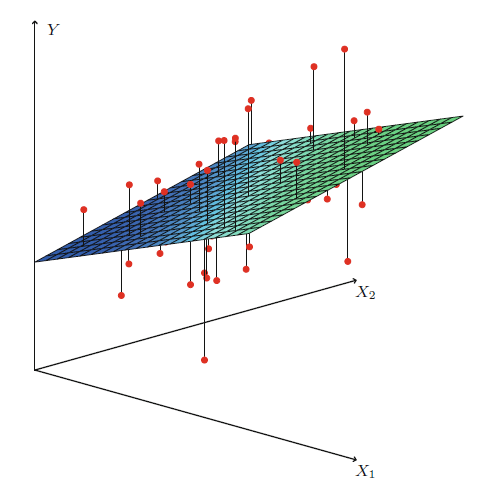 Fig. 2차원 data에서의 regression. Source from link
Fig. 2차원 data에서의 regression. Source from link
Intuitive Animation for Linear Regression
다음은 입력 x 1차원, 출력 y 1차원 data에 대한 linear regression이 학습 되는 과정에 대한 animation이다. 아래는 직선 \(y=\theta_0 + \theta_1 x\) 을 피팅하는 과정이고
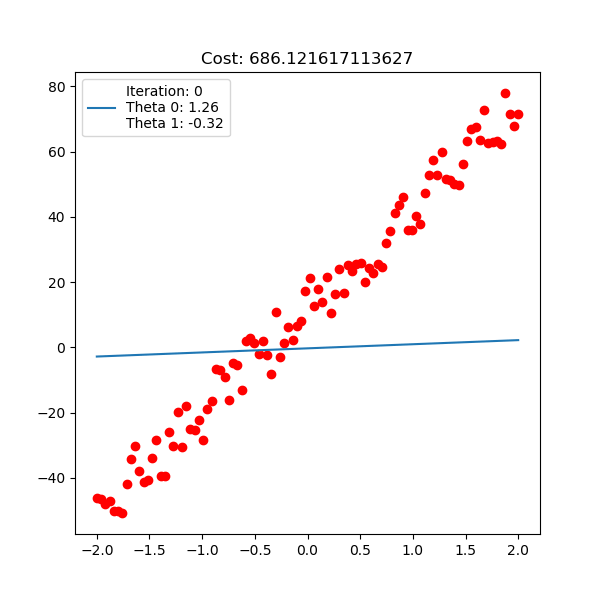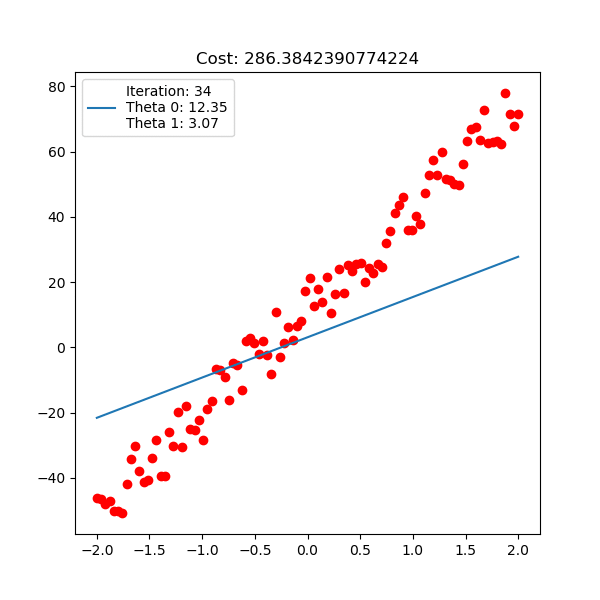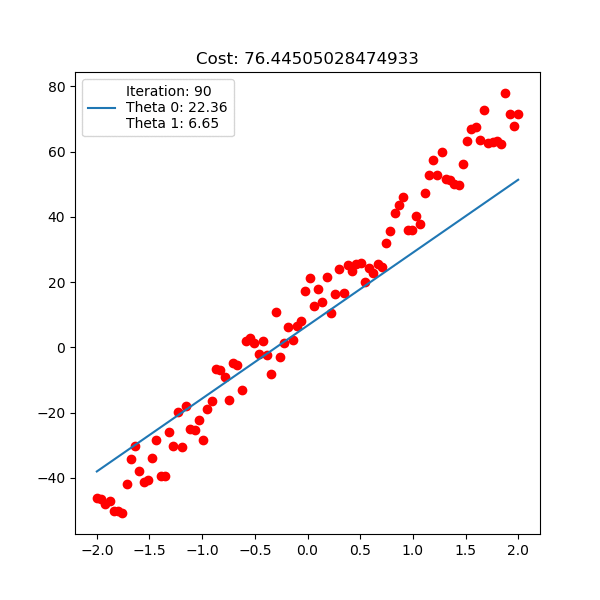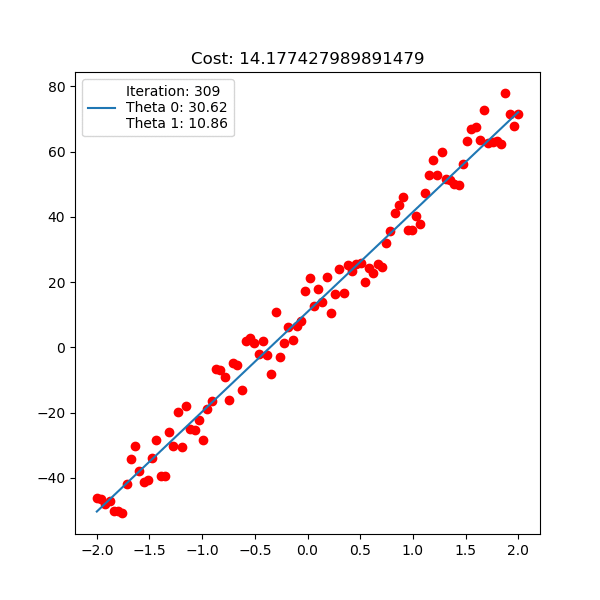 Fig. Linear Regression Animation
Fig. Linear Regression Animation
아래는 마찬가지로 linear regression 이지만, 직선 \(y=\theta_0 + \theta_1 x + \theta_2 x^2\) 인 polynomial linear regression을 피팅하는 과정에 대한 것이다.
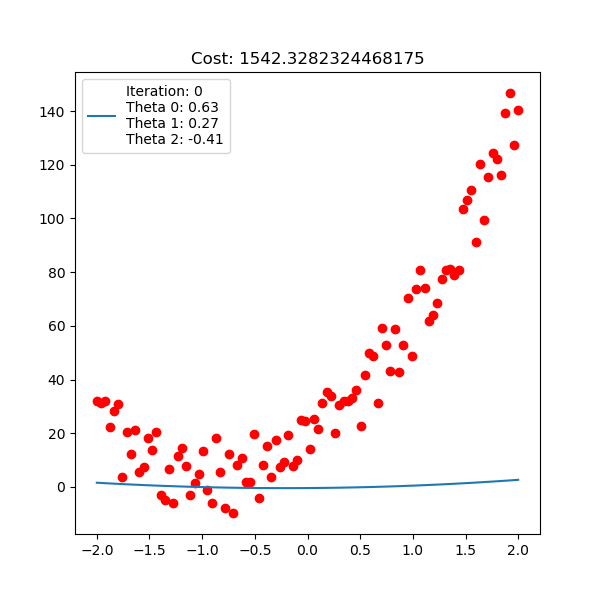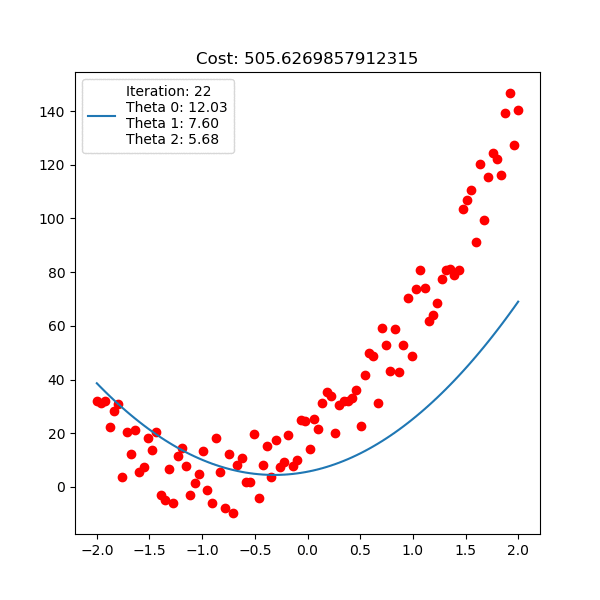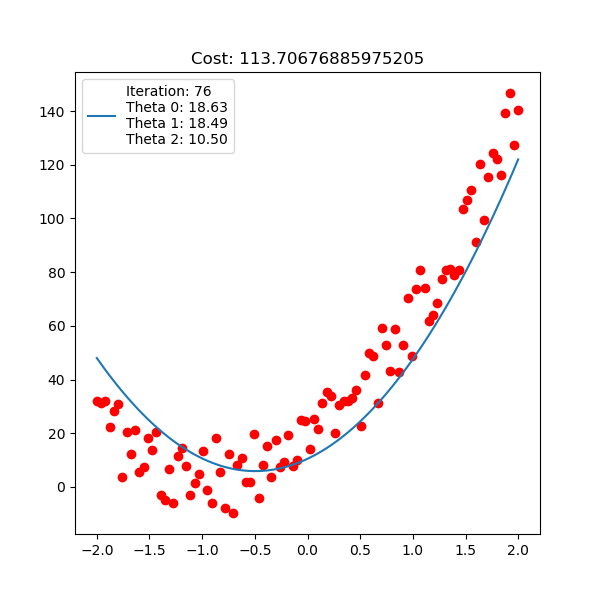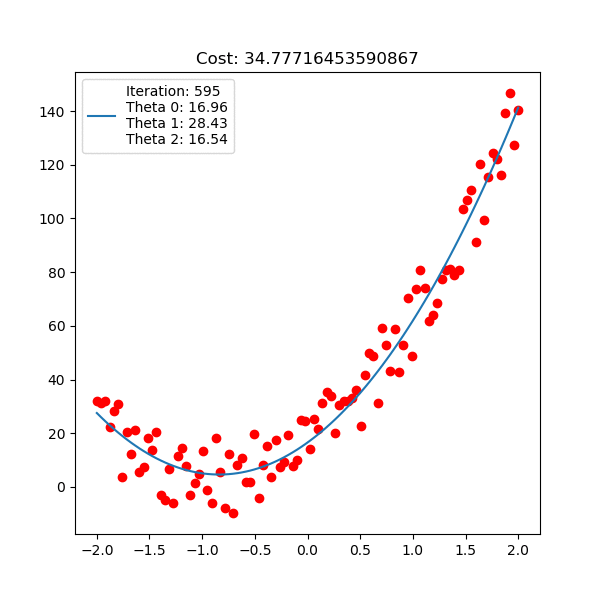 Fig. Linear Regression Animation2. Source from link
Fig. Linear Regression Animation2. Source from link
다시 본론으로 돌아가서, data는 x 1차원, y 1차원이니 총 2차원 평면에 뿌려져있고, 우리는 중고등학교때 y절편과 직선의 기울기, 이렇게 두 가지를 알면 직선의 방정식을 구할 수 있다고 배웠다/.
\[y=ax+b\]그러니까 우리가 data로부터 학습을 통해 찾아야 될 직선은 a랑 b인 것이다.
하지만 확률론적인 관점에서 (probabilistic perspective) 우리가 linear regression을 하는 것은 \(x_i\)가 주어졌을 때 이에 대응하는 \(y_i\) distribution를 찾는 것이라고 할 수 있다. 무슨말이냐면 단순히 직선의 방정식을 찾는것은 \(x_i=4\)일 때 \(y_i = x_i \cdot 4 + 5 = 4 \cdot 4 + 5\)이런식으로 scalar값을 리턴한다는 것인데, 확률론적인 관점에서 원하는 것은 이것을 mean (mean)으로 하는 distribution를 찾는 것이다. 어떤 input이 있을 때 output값이 정해지는 결정론적인 것 보다는 “음 \(x_i=4\)면 \(y_i=21\)일 가능성이 크겠지만 다른 값일 확률도 존재하겟지?” 라고 생각하는게 더 자연스럽기 때문이다.
우리가 각 input에 대한 distribution을 구한다 (modeling한다고 하는데) 할 때, 하필 이 distribution이 gaussian distribution를 따른다고 생각해보자. 그렇다면 우리가 추정하고자 하는 regression 모양은 위의 그림 (b) 같이 된다.
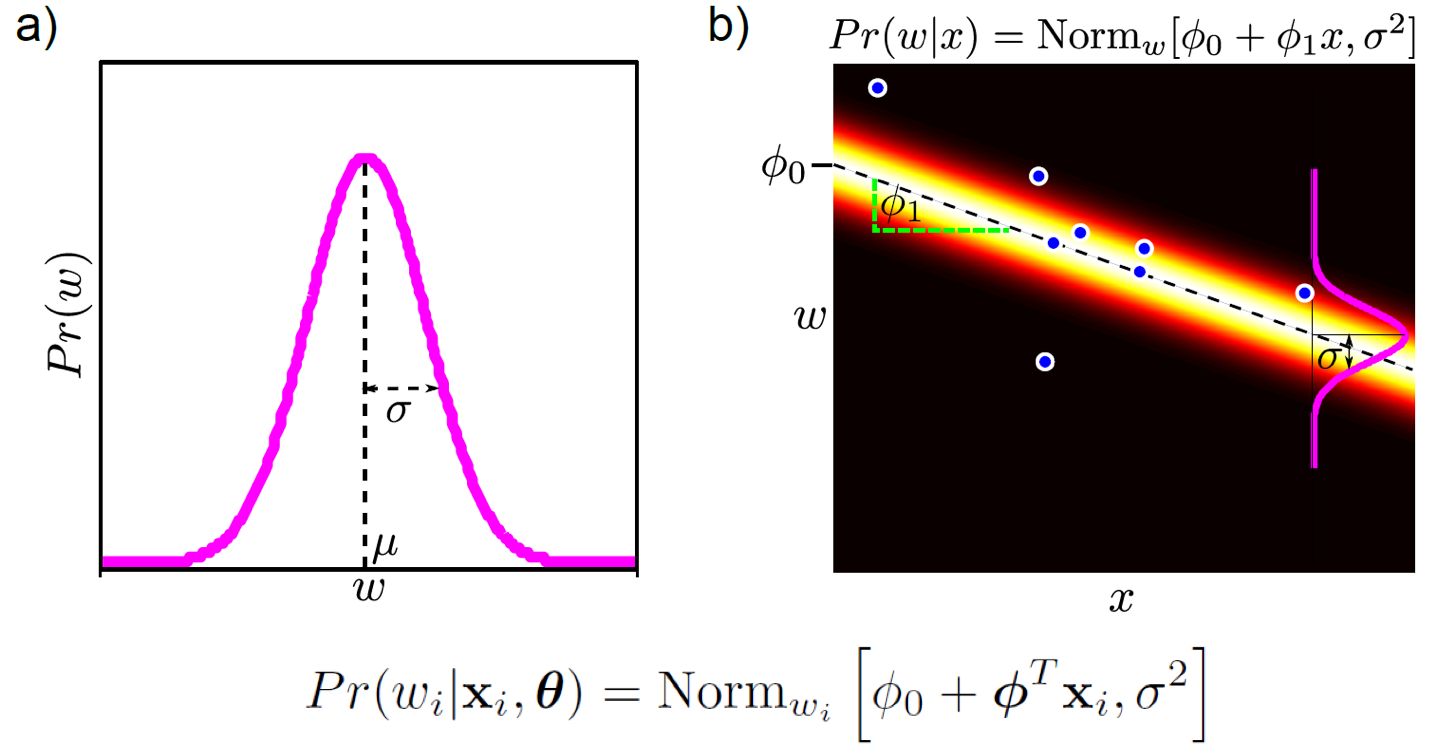 Fig. 선형 regression 문제는 data x가 주어졌을때 출력 y값이 어떤 distribution의 형태로 나타날까?를 모델링한다. 그림은 gaussian distribution를 가정한다.
Fig. 선형 regression 문제는 data x가 주어졌을때 출력 y값이 어떤 distribution의 형태로 나타날까?를 모델링한다. 그림은 gaussian distribution를 가정한다.
이 때 \(y_i\)의 mean과 variance이 있을텐데 mean은 \(y_i=ax_i+b\) 를 따르는 것입니다. 마치 빔을 쏘는 것 처럼 됐는데, 여기서 빔의 두께가 gaussian의 variance (variance)를 의미할 것이다. 지금은 모든 x에 대해서 variance가 같은데, 직관적으로 data point가 적은 부근에는 우리가 예측하는 걸 좀 더 조심스럽게 하는게 좋을 것이다. 그럴 때에는 variance를 크게 잡아 표현하는게 좋은데, 이는 현재 post의 scope을 벗어나기에 그 다음 post에서 다루도록 하겠다.
Linear Regression in formula
이제 수식적으로 linear regression을 보자.
Notation
input state, data 입력값 : \(x\)
world state, x에 대응하는 값 : \(w\)
parameter, 우리가 알고싶은, 추정하려는 값 : \(\theta\)
우리가 위에서 w (혹은 y인데 책에서는 같은 의미로 world state, w를 사용)에 대해서 gaussian distribution를 가정했기 때문에 우리가 모델링 하고자 하는 distribution는 다음과 같다.
\[Pr(w_i \mid x_i,\theta) = Norm_{w_i}[\phi_0 + \phi^T x_i, \sigma^2]\]즉, 각 \(x_i\)에 대응하는 \(y_i\)의 distribution인 것. x가 1차원이지만 notation을 쉽게 만들기 위해서 모든 \(x_i\)에 1을 붙힌다.
\[x_i \leftarrow [1 \space x_{i}^{T}]^T\]그리고 \(\phi\)도 합쳐서 표현한다.
\[\phi \leftarrow [\phi_0 \space \phi^{T}]^T\]그러면 위의 모델링 하고자 하는 distribution를 아래처럼 다시 쓸 수 있다.
\[Pr(w_i \mid x_i,\theta) = Norm_{w_i}[\phi^T x_i, \sigma^2]\]이제 우리는 모든 x,y data pair에 대한 식을 위처럼 얻게 되었다.
likelihood
앞서 Maximum Likelihood Estimation MLE post에서 다룬 것 처럼,
우리가 원하는 것은 입출력 관계를 gasussian으로 modeling했을 때 전체 data point를 가장 잘 표현하는 (fitting하는) gaussian distribution의 mean, vairnace를 찾는 것이다.
우리는 이를 Likelihood라고 한다고 했다.
Likelihood는 각각의 distribution를 전부 곱한것과 같기 때문에 (모든 sample은 i.i.d 이므로) 아래와 같이 쓸 수 있다.
\[Pr(w \mid X) = Norm_{w}[X^T \phi, \sigma^2I]\] \[where X = [x_1,x_2, ... x_I] \space and \space w=[w_1,w_2,...,w_I]^T\]이제 likelihood를 maximize하는 parameter point하나를 고르면 됐다.
\[\hat{\theta} = \arg \max_{\theta}[Pr(w|X,\theta)] = \arg \max_{\theta}[logPr(w|X,\theta)]\]우리가 구하고자 하는 parameter, \(\theta\)는 지금은 \(\phi_0\), \(\phi_1\), \(\sigma^2\) 세 개 이므로 위의 식을 다시 쓰면 다음과 같다. (계산의 편의성을 위해 log를 취한다)
\[\hat{\phi}, \hat{\sigma^2} = \arg \max_{\phi,\sigma^2}[ -\frac{Ilog[2\pi]}{2} - \frac{Ilog[\sigma^2]}{2} - \frac{(w-X^T\phi)^T(w-X^T \phi)}{2\sigma^2} ]\]이제 미분을 해서 0인 지점을 찾으면 우리는 likelihood를 가장 크게하는, 그러니까 현재 data를 가장 likely하게 표현하는 세 가지 parameter를 구할 수 있게 된다.
solution
위의 방법대로 풀면 우리가 Maximum likelihood 방법을 통해 구한 솔루션은 아래와 같게 된다.
\[\hat{\phi} = (XX^T)^{-1}Xw\]먼저 구한 mean을 결정하는 parameter들을 통해 variance 마저 구한다.
\[\hat{\phi} = \frac{(w-X^T\phi)^T(w-X^T \phi)}{I}\]Connection to Mean Squared Error (MSE) Loss
어떤 사람들은은 위의 솔루션이 맘에 들지 않을 수도 있다.
왜냐하면 대부분의 ML book, lecture에서 \(X(x_1,x_2...)\)와 \(X(y_1,y_2...)\) data에 대한 curve fitting을 할 때, Mean Squared Error (MSE) Loss를 통해 solution을 구한다고 얘기하기 때문이다.
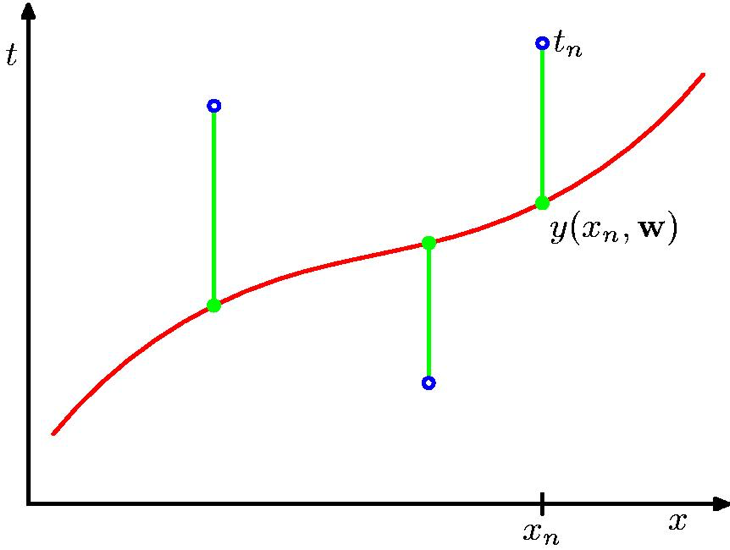 Fig. curve fitting의 예시 from PRML
Fig. curve fitting의 예시 from PRML
MSE Loss는 다음과 같이 나타낼 수 있다.
\[Loss(\theta) = \frac{1}{2} \sum_{i=1}^{I}{ \{ f(x_i,\theta)-y_i \} }^2\] \[\hat{\theta} = \arg \min_{\theta}\frac{1}{2} \sum_{i=1}^{I}{ \{ f(x_i,\theta)-y_i \} }^2\]직관적으로 위의 수식이 의마하는 바는 Loss는 모든 data point에 대해서 실제 정답 label과의 error (거리 차이; euclidean distance)를 의미하며, Loss를 minimize하는 parameter를 solution으로 얻겠다는 걸 의미한다. 그런데 이는 사실 우리가 각 target distribution을 gaussian distribution으로 가정하고 MLE를 한 것과 같다.
\[\hat{\phi}, \hat{\sigma^2} = \arg \max_{\phi,\sigma^2}[ -\frac{Ilog[2\pi]}{2} - \frac{Ilog[\sigma^2]}{2} - \frac{(w-X^T\phi)^T(w-X^T \phi)}{2\sigma^2} ]\]왜냐하면 위의 수식에서 parameter, \(\theta\)와 관련없는 term들은 미분 시 cancel되기 때문이다. 이를 다시쓰면 다음과 같다.
\[\hat{\phi}, \hat{\sigma^2} = \arg \max_{\phi,\sigma^2} - \frac{1}{2}\frac{1}{\sigma^2}{\sum_{i=1}^{N}{\{f(x_i,\phi)-w_i\}}^2}\]여기서 variance에 대한건 잊어버리고 argmax는 식에 -를 붙혀 argmin하는것과 같으니 우리는 MSE loss와 정확히 같은 수식을 얻을 수 있다.
Bayesian Linear Regression
앞서 우리는 MLE과 Maximum A Posteriori (MAP)의 차이에 대해서 공부했었다. MAP에서 사후 확률 (posterior)는 likelihood에 prior 정보를 추가해 data가 별로 없을 때 likelihood를 보완해주는 것이라고 했었다.
\[\text{posterior} \propto \text{likelihood} \times \text{prior}\] \[Pr(\theta \mid x,w) \propto Pr(w \mid x,\theta) \times Pr(\theta)\]prior는 \(\theta\)에 대한 선입견을 주입하는 것이므로 (likelihood가 gaussian distribution이기 때문에 “mean, variance가 0부근의 값을 가질 확률이 높더라” 같은 정보를 주입한다), 다음과 같이 0 mean gaussian distribution로 prior를 선정할 수 있고
\[Pr(\theta \mid \alpha^2) = Norm_{\theta}[0,\alpha^2]\] \[Pr(\theta \mid \alpha^2) = \frac{1}{\sqrt{2\pi\alpha^2}}exp[-0.5\frac{(\theta-0)^2}{\alpha^2}]\]posterior를 최대화 하는 solution을 구하면 다음을 최소화 하는 것과 같은 solution을 구할 수 있게 된다.
\[\frac{1}{2\sigma^2} \sum_{i=1}^{I}{ \{ f(x_i,\phi)-y_i \} }^2 + \frac{1}{2\alpha^2}{\phi^T \phi}\]이는 MSE Loss를 최소화 하는 것은 맞는데, 동시에 parameter가 0에 가깝지 않고 너무 값이 커지면 Loss가 증가할 것이기 때문에 두 조건을 모두 만족하라고 하는 것과 같다. 이를 정규화 (regularization) 혹은 weight decay라고 부르며, 이는 Deep Learning (DL)에서도 흔히 쓰이는 technique이다.
여기서 \(\lambda = \frac{\sigma^2}{\alpha^2}\) 라고 할 때, \(\lambda\) 에 따른 정규화 term이 곡선 피팅에 끼치는 영향은 다음과 같다. Data point가 별로 없기 때문에 regularization의 영향력이 작을수록 overfitting하는 경향이 심하다.
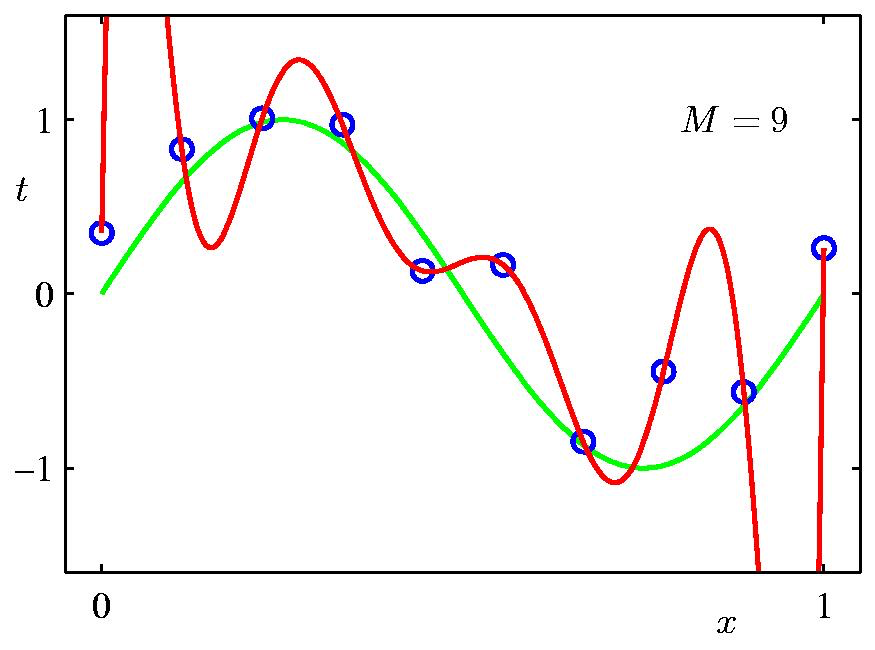
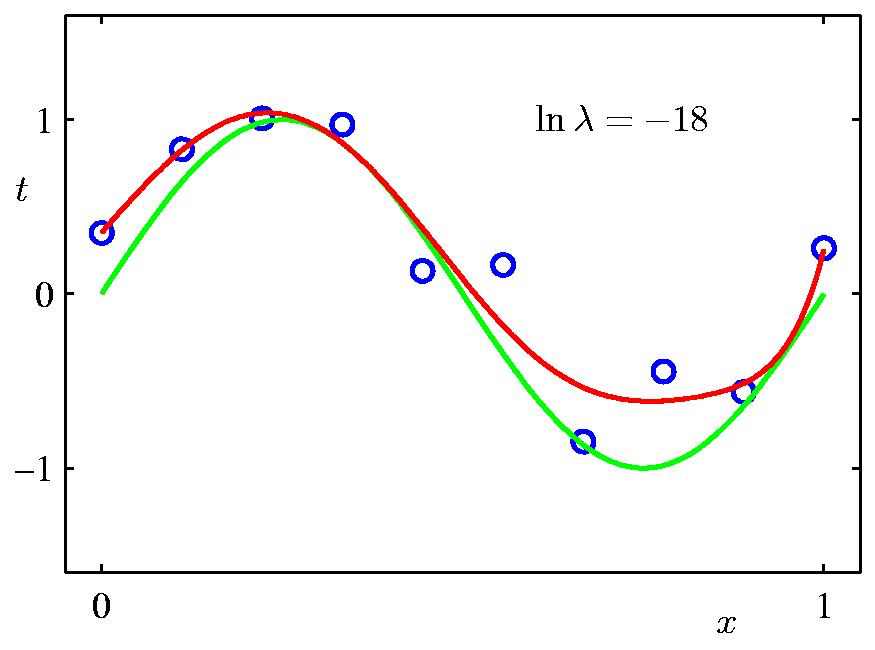
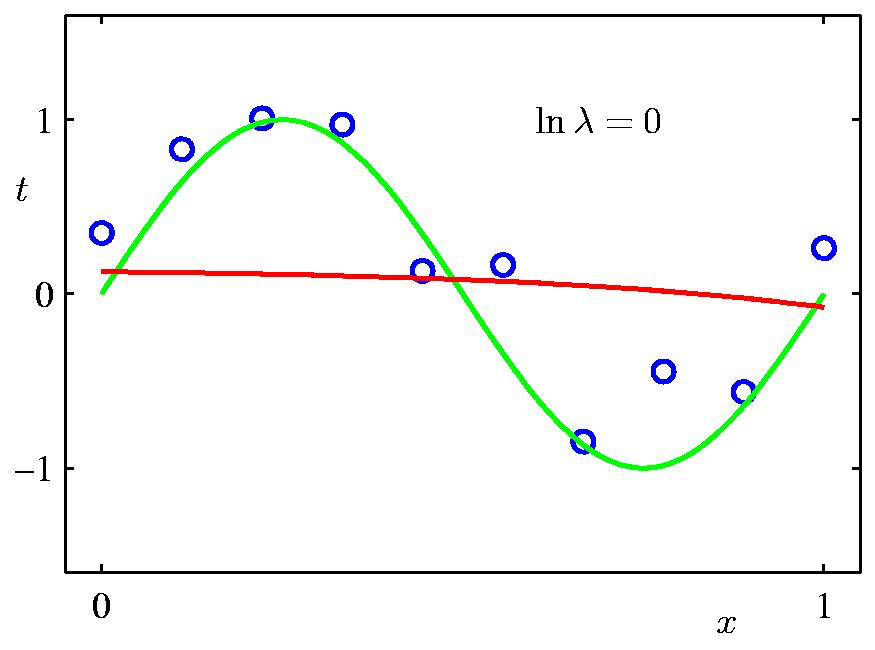 Fig. Regularization의 영향력에 따른 regression 곡선 표현력의 차이
Fig. Regularization의 영향력에 따른 regression 곡선 표현력의 차이
Further Study
지금까지 이야기 한 것 외에도, Bayesian Regression 방법과 Non-linear Regression 등등의 다양한 upgrade 버전이 있는데, 이는 다음 post에서 다루도록 하겠다.
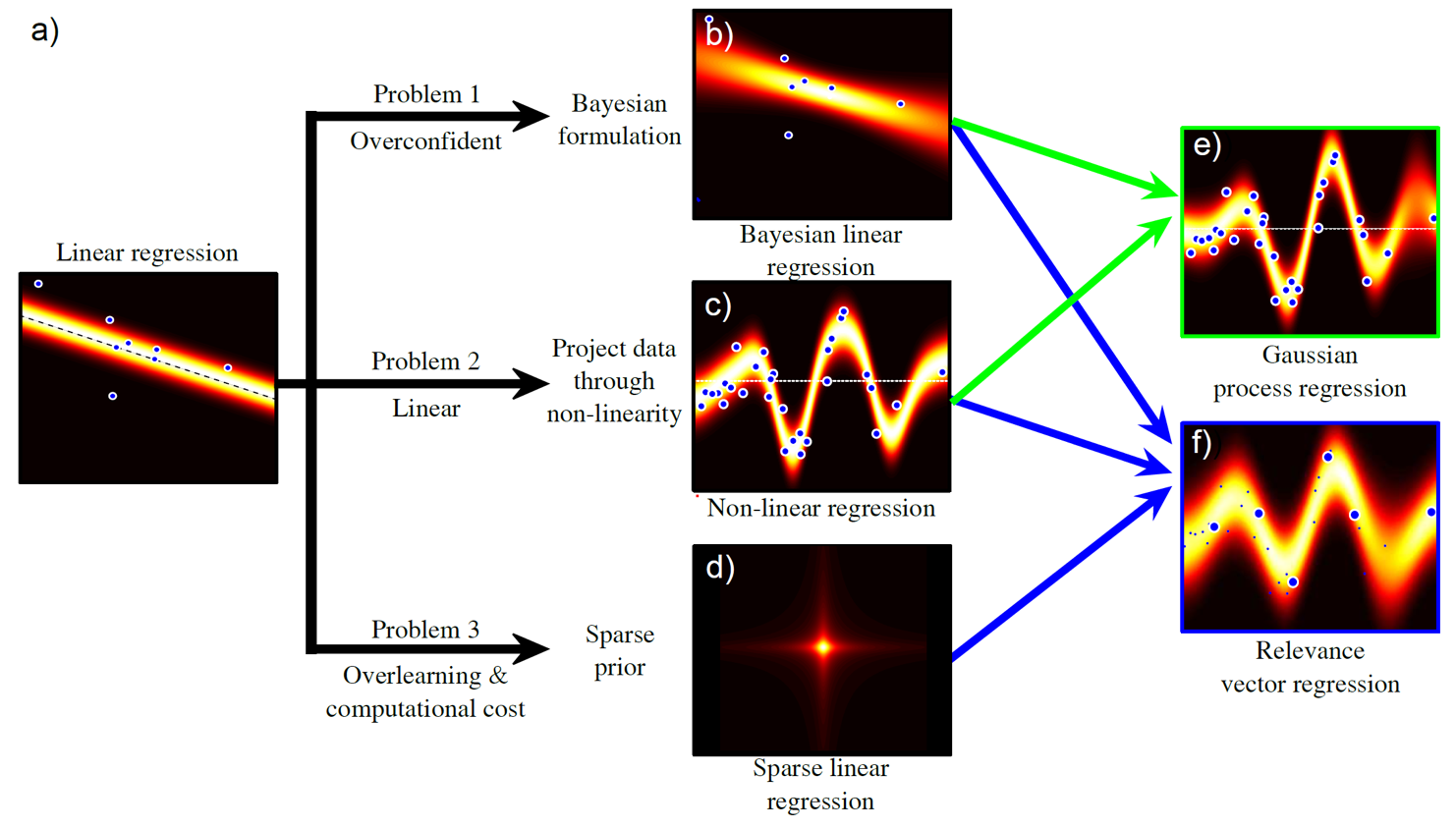 Fig. 다양한 regression 문제를 풀기 위한 Variation들
Fig. 다양한 regression 문제를 풀기 위한 Variation들