Notes

(CS285) Lecture 8 - Deep RL with Q-Functions

03 Dec 2023

이 글은 UC Berkeley 의 교수, Sergey Levine 의 심층 강화 학습 (Deep Reinforcement Learning) 강의인 CS285를 듣고 작성한 글 입니다.

Lecture 8의 강의 영상과 자료는 아래에서 확인하실 수 있습니다.

< 목차 >

이번 lecture 에서 다룰 내용은 lecture 7 에 이어 value-based method의 대표적인 algorithm인 Q-Learning을 발전시킨 Deep Q-Learning 입니다.

slide1 Slide. 1.

Recap: Q-learning

Q-iteration에 대한 Recap으로 강의를 시작합니다.

Value-based 강화학습 algorithm들은 policy를 따로 명시적으로 (explicitly) 나타내지 않아도 됐죠. 하지만 Transition Probability를 알아야 하는 대부분의 Model-based Value-based algorithm들은 문제가 됐습니다. 이를 개선하기 위해서 \(V(s)\) 를 \(Q(s,a)\)로 대체한 Model-free Value-based algorithm인 Q-Learning을 유도해냈습니다. Q-Learning 은 optimal policy를 얻는 것이 보장되지 않은 algorithm이었으나 잘 design하면 충분히 real-world에서 잘 작동할 수 있음을 알 수 있었습니다.

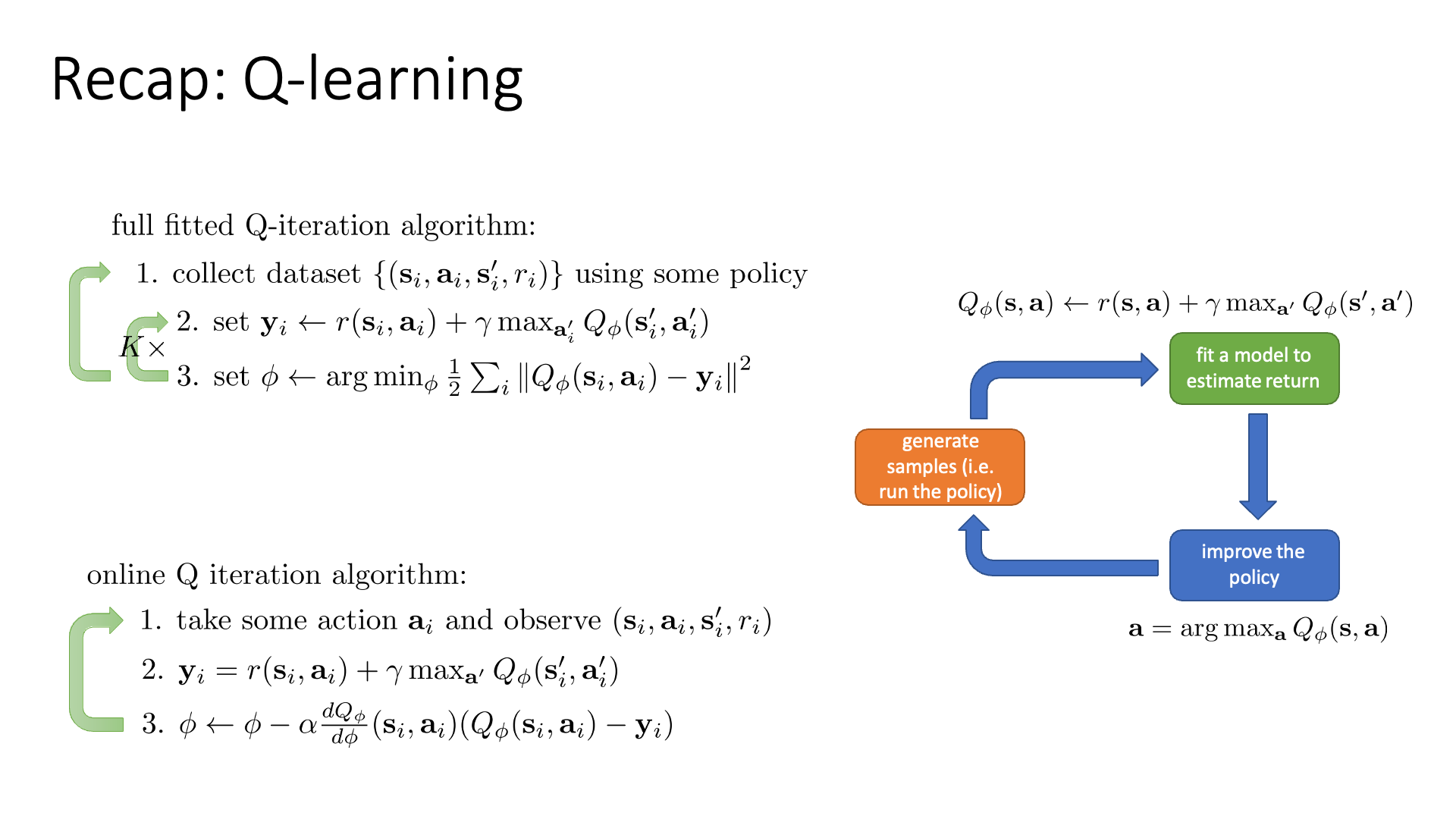slide2 Slide. 2.

슬라이드의 왼쪽에는 Batch-mode Q-Iteration과 Online-mode Q-Iteration이 나와있는데, update step을 몇 번 가져갈지?에 따라서 Fitted Q-Iteration은 Online Q-Iteration이 되는데 이를 Q-Learning이라고 했습니다.

Problems of Q-Learning

그런데 Q-Learning을 하는데 있어 몇 가지 문제점이 있습니다.

아래는 몇 가지 DL과 RL의 차이와 그에 따른 stability issue에 대한 slides 입니다. 이 문제점을 해결하는 다 해결한 것이 바로 그 유명한 Deep Q Network (DQN)로 가는 길입니다.

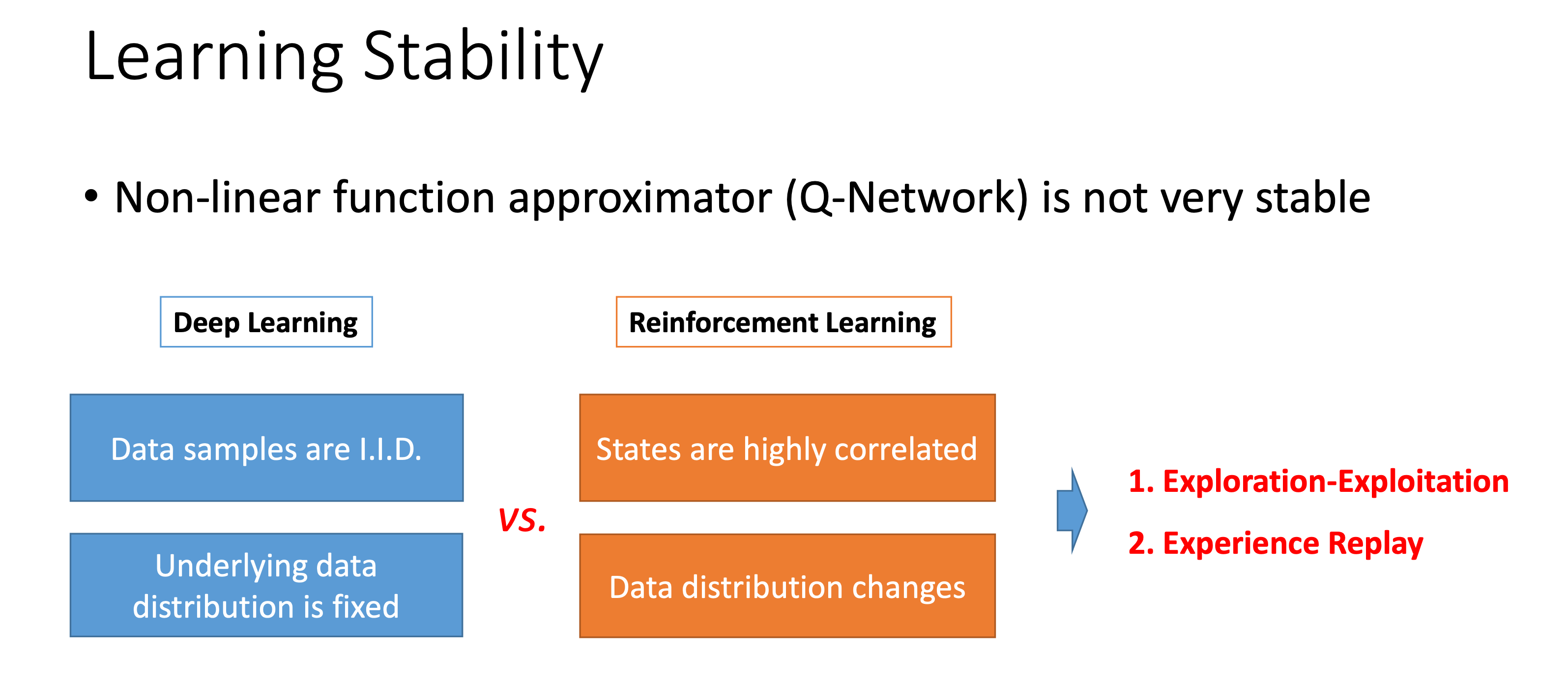dl_vs_rl_stability_fig1 Fig. DQN이전에는 Non linear function approximator를 쓴다는 것 자체가 Challenge였으며, RL은 DL과 다르게 sample들이 highly correlate 되어있다. Source from Jiang Guo’s slide

dl_vs_rl_stability_fig2 Fig. Source from Bowen Xu’s slide

Sergey의 lecture에서도 똑같은 문제점을 언급합니다. 가장 첫 번째 문제는 아래 slide 3에서 볼 수 있듯 step 3가 gradient descent처럼 보이지만 사실은 그렇지 않다는 겁니다. 수식을 보면 target, y를 구하는 과정에 max operator가 있기 때문에 gradient가 흐르지 않습니다.

slide3 Slide. 3.

이를 해결하기 위한 방법으로 residual gradient algorithm이라는 algorithm을 쓸 수 있으나 잘 작동하지 않는다고 합니다. (아마 moving target 문제를 얘기하는 것 같습니다.)

또 다른 문제점은 한 번에 하나의 transition만 sample하면 sequential transition들이 highly correlated되어 있는 것이라고 합니다. 다시 말해서 1 step씩 update를 하는 경우에 step을 거듭할수록 보는 sampling되는 state들인 \(s_t\)와 \(s_{t+1}\)는 굉장히 유사할거라는 겁니다.

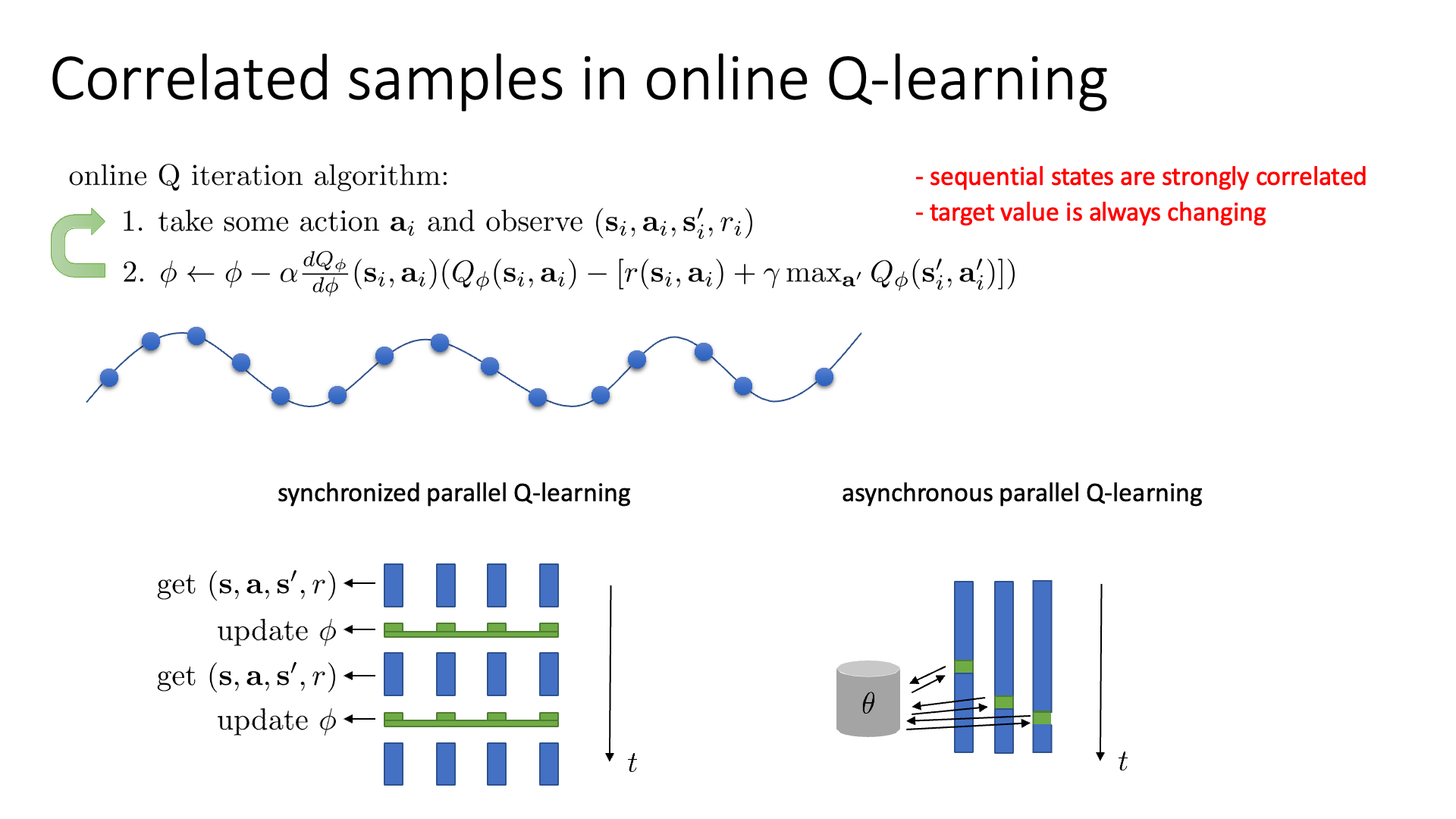slide4 Slide. 4.

이게 왜 문제냐면 비슷한 입력과 결과를 내는 데이터를 매우 많이 학습하는것은 비효율적이고 Network가 오버피팅되는 등의 악영향을 줄 수 있기 때문입니다. ML algorithm들이 일반적으로 하는 일을 생각해 봅시다. 어떤 \(\sin x\)로 부터 sample된 data point 몇 개를 가지고 원래 함수를 추정하는 문제를 푸는 상황에서, 만약 data point들이 한 지점에 몰려서 뽑혔다면, 그 data들을 가지고 원래 함수를 근사하기란 힘들겁니다.

correlation1 Fig. sampling된 data point가 몰려있다면?

correlation2 Fig. Trajectory 1-2

correlation3 Fig. Trajectory 1-3

그러니까 매우 비슷한 sample들로 model update를 하는 것은 overfitting을 야기할 수 있는겁니다.

(그리고 곧 또 다루겠지만 또 다른 문제로는 후에 다룰거지만 Optimization 하는 과정이 MSE Loss를 사용한 Supervised Regression 문제 같이 보이지만 Target Value가 계속 변화하는 문제가 있다고 합니다.)

Actor-Critic의 경우를 잠시 생각해 봅시다. 우리는 infinite horizon 같은 경우를 해결하기 위해서 sample을 뽑는 즉시 replay buffer에 넣고 거기서 sampling된 여러 transition points를 가지고 model을 update했습니다 (Online Actor-Critic). 혹은 여러 Worker들을 사용해서 sample을 각자 뽑아 공유하는 것으로 다양성을 높히기도 했습니다.

그런데 Online Actor-Critic을 하려면 뭔가 Critic의 Traget value도 고쳐주고… 하는 전략이 필요했었습니다. 왜일까요? 원래 Actor-Critic은 On-policy algorithm이기 때문이었습니다. 하지만 Q-Learning 자체는 지난 lecture 에서 얘기했듯 애초에 Off-Policy algorithm이므로 더 손쉽게 이런 technique들을 적용할 수 있습니다.

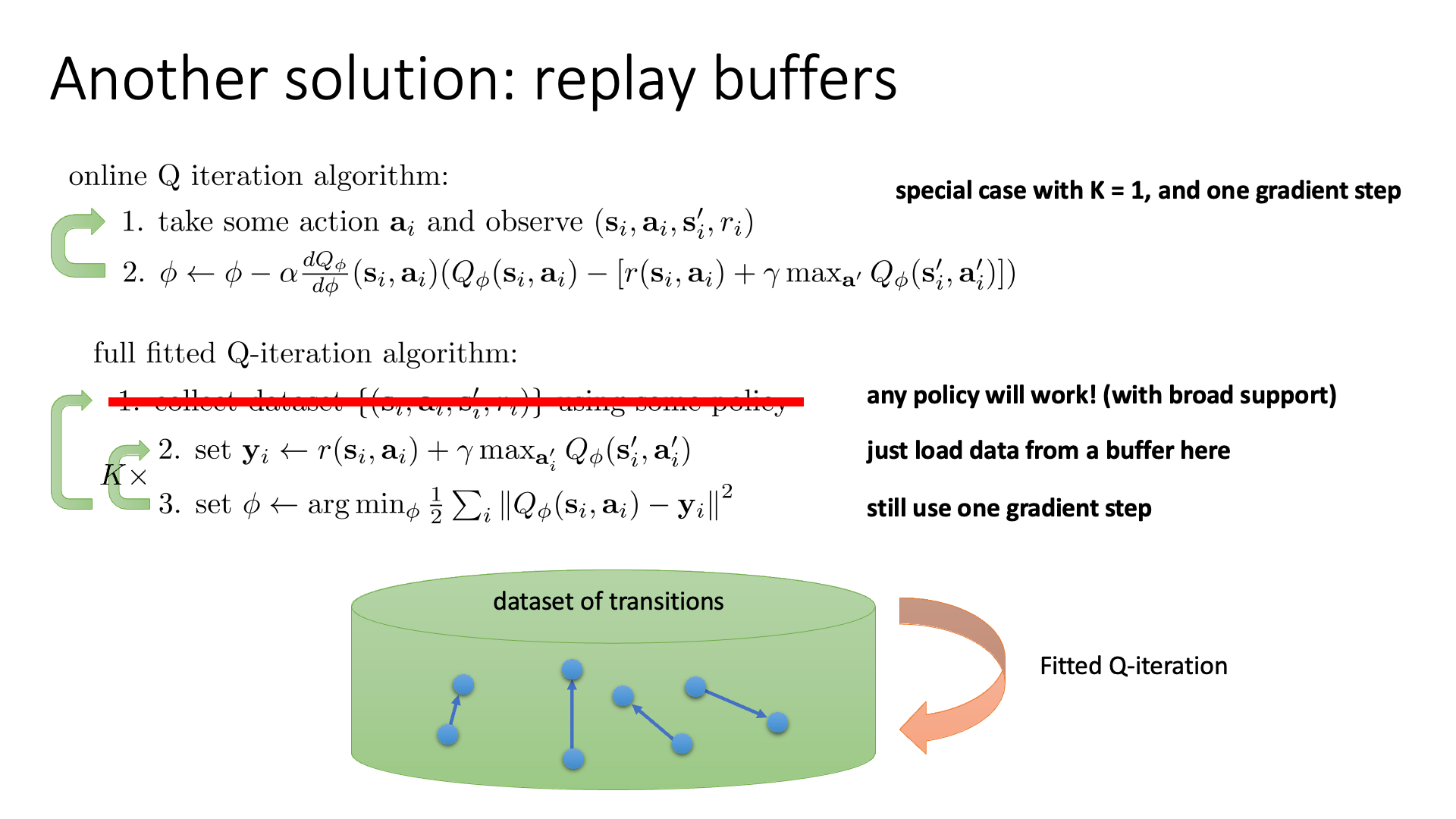slide5 Slide. 5.

이렇게 replay buffer에 넣어두고 transition을 batch size만큼 꺼내 학습하는 경우, 전형적인 Deep Learning의 Supervised Learning처럼 상황이 변하게 됩니다.

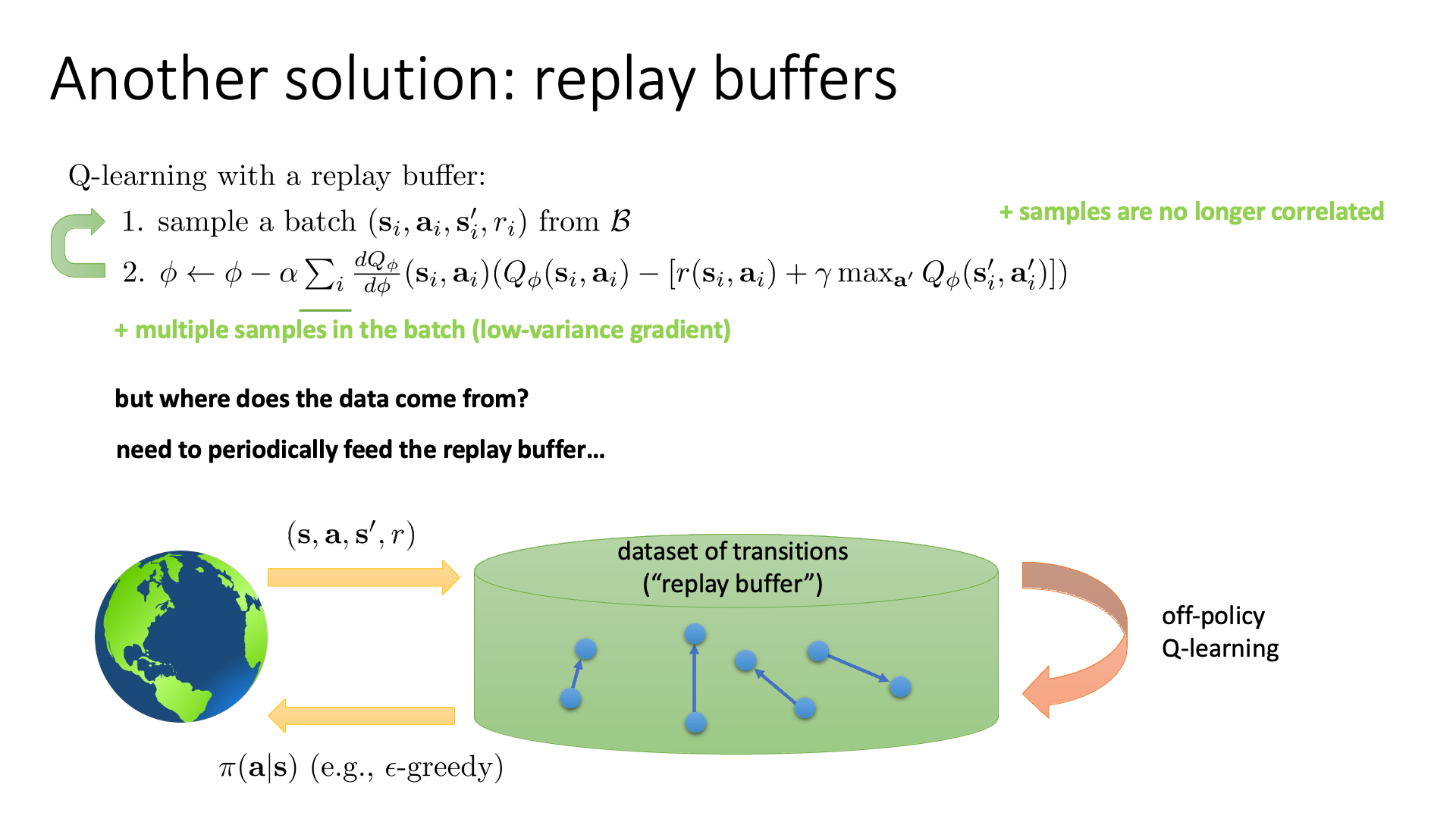slide6 Slide. 6.

위의 슬라이드에서 보시면 이제 데이터를 그냥 배치를 원하는 만큼 샘플합니다. (이 때 데이터들은 딥러닝 algorithm들이 사용하는 데이터가 iid라고 가정하는 것과 같아진다고 합니다.)

그리고 배치를 1이 아닌 4,8 이런식으로 여러번 하고 gradient를 합쳐서 업데이트 하면 low variance gradient를 얻을 수도 있습니다.

하지만 리플레이 버퍼를 사용할 때의 문제점이 아직 존재합니다. “리플레이 버퍼에 넣을 데이터를 어디서 sample하지?”, “시간이 지날수록 어떻게 더 유의미한 data를 학습에 쓸 수 있을까?” 인데요, 초기 policy는 랜덤하거나 매우 좋지않은 policy이기 때문에 (\(s,a,r,s'\))이 별로 좋지 않을 수 있기 때문에, 학습이 진행될 수록 업데이트된 그럴싸한 policy를 사용해서 추가적으로 뽑은데이터를 넣거나 해야 수렴이 더 잘된다는 겁니다.

지금까지 말한 전략을 figure로 나타내면 아래와 같습니다.

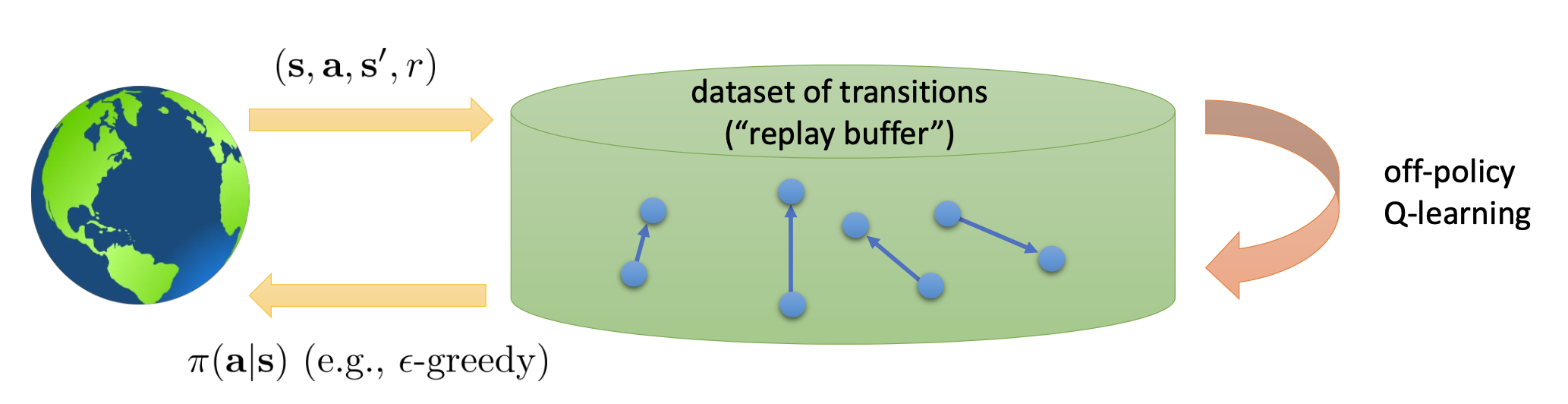replay_buffer_update Fig. How to update replay buffer

  • 우선 \((s,a,r,s')\) 같은 transition data를 매우 많이 sample 해서 buffer에 가지고 있는다.
  • 학습을 조금 진행한 뒤에 이 buffer 최근 policy로 구한 transition data를 더 추가한다.

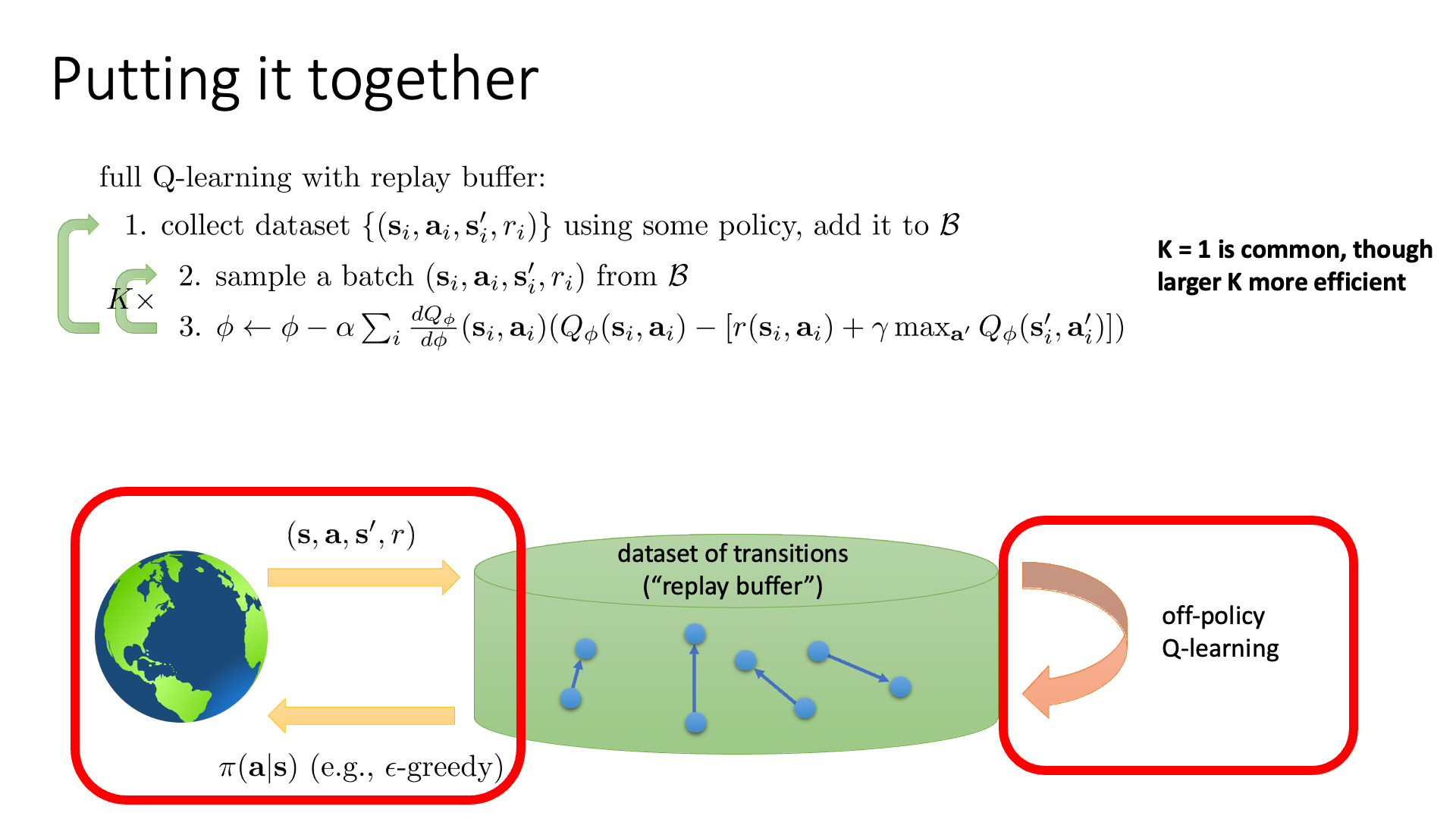slide7 Slide. 7. 방금까지 내용을 정리한 slide

Target Networks

지금까지 Q-Learning의 몇가지 문제점에 대해 생각해보고 이를 해결하면서 practical한 algorithm을 만들려고 노력했지만 아직 trolling을 하는 term이 있습니다. 이것 때문에 Replay Buffer를 사용했음에도 여전히 학습이 불안정한데요,

slide9 Slide. 9.

바로 Objective의 두 번째 term인 max term 입니다. Q-Learning은 gradient descent 같이 보이지만 그건 아니라고 했고 (Sergey피셜), 또한 moving target을 따라가야 하는 문제를 가지고 있습니다. 그러니까 예를 들어 MSE Loss를 쓰는 회귀문제에서 target이 움직이는거나 다름 없기 때문에 Network가 수렴하기 어렵습니다.

slide10 Slide. 10.

그렇기 때문에 우리는 Q-Learning에 어떤 Target Network라고 하는 것을 사용해서 Full Batch Fitted Q-Iteration과 Online Q-Learning을 결합한(?) 방법을 써보려고 합니다.

slide11 Slide. 11.

그러니까 문제는 Target이 움직이는건데, 왜 움직이는지를 생각해보면 원래 Q-Learning의 target은 \(Q_{ \color{red}{\phi}}(s',a')\), 즉 \(\phi\)로 파라메터화된 Network의 output을 사용하는건데, update step에서 파라메터 \(\phi\)가 업데이트되기 때문에 그게 문제인겁니다. 이를 피하기 위해서 제안된 아이디어는 “\(\phi'\)를 써보면 어떨까?” 입니다. 그러니까 Q-Network, \(Q_{\phi}\)의 파라메터가 자꾸 변하니까 Target Network, \(Q_{\color{blue}{\phi'}}\)를 따로 두자는 거죠.

target_network Fig.

그 결과 algorithm은 버퍼에서 데이터를 샘플해서 데이터에 대해서 Q-Network를 충분히 여러번 반복적으로 업데이트 하고 충분히 업데이트 했으면 Target Network를 다시 최근의 Q-Network로 업데이트해주고, 다시 또 Target은 고정을 하고… 를 반복하는 겁니다. (Slide. 11. 에서 1번과 4번의 \(\phi'\)가 핵심입니다.)

target_network2 Fig.

여기서 K는 1~4정도의 값으로 반복하고, N은 10000정도가 될 수 있다고 합니다. 이제 여태까지 배운 것을 바탕으로 Deep Q-Learning (Deep-Q-Network; DQN)을 정의할 수 있는데, “Classic” DQN의 경우 k=1일 때를 말합니다 (special case).

slide12 Slide. 12.

Averaging Traget

그런데 “Classic” DQN을 보면 5번의 update rule이 조금 위험하게 느껴질 수 있습니다., 바로 우리가 Moving Target 문제를 해결하고자 \(\phi'\)로 고정된 Network로 타겟을 생성하고 이를 바탕으로 \(\phi\)를 업데이트 하고 있었는데 이게 어느순간 \(\phi\)로 확 변해버려서 결국엔 Moving Target처럼 느껴질 수 있다는 점입니다.

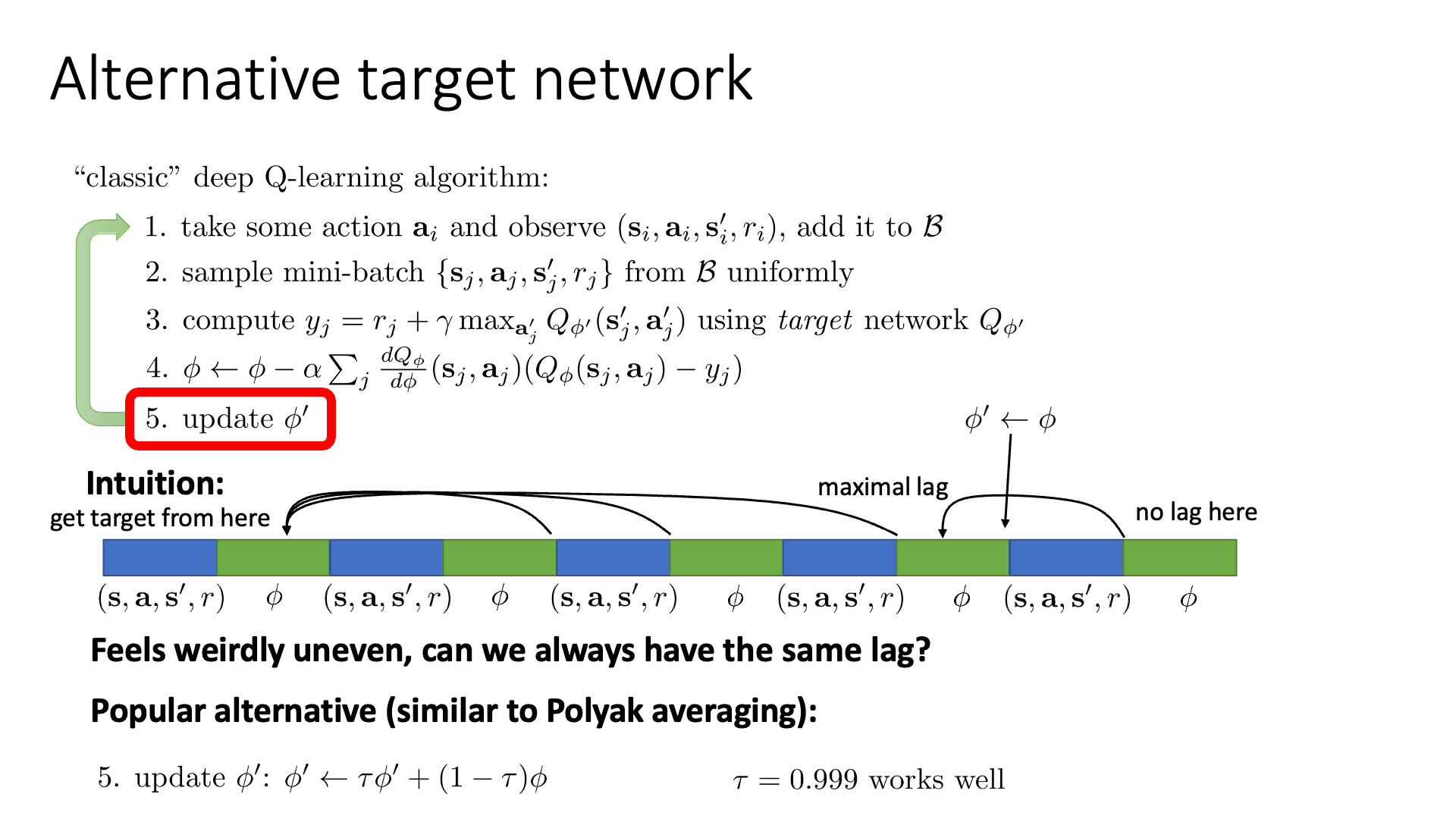slide13 Slide. 13.

그러니까 K=1 (gradient step 반복 횟수), N=4 (배치 데이터 샘플 횟수, 실제론 매우 큼) 라고 생각할 때, N=4에서 5로 넘어가는 순간 갑자기 \(\phi\)가 되버리는게 문제가 될 수 있다는 겁니다 (실제로는 별로 큰문제는 아니라고는 합니다).

그래서 \(\phi' \leftarrow \phi\) 가 아니라 조금 더 자연스럽게 \(\phi' \leftarrow (\tau)\phi' + (1-\tau)\phi\) 로 업데이트하는 방식을 쓰기도 한다고 하며, 이와 비슷한 방법론을 Polyak Averaging라고 한다고 합니다.

\[\phi' \leftarrow ( \color{red}{ \tau } )\phi' + ( 1 - \color{red}{ \tau } )\phi, \text{ where } \tau \text{ is large value, like } \color{red}{ 0.999 }\]

여기서 “NN은 선형적이지 않은데 linearly interpolation을 해도 되나?” 하는 의문점이 들 수 있는데요, old policy가 current policy의 set이라서 (유사해서) 별로 문제가 되지 않는다고(?) 합니다. (Sergey는 non-linear function들에 대한 linear interpolation이 궁금하시다면 Polyak Averaging을 살펴보라고 하네요.)

* (Paper) Deep Q-Learning

이렇게 Replay Buffer, Fixed Target 을 도입함으로써 우리는 stable한 Fixed Q-Learning algorithm을 얻게 되었는데, 이것이 바로 Deep Q-Network (DQN)입니다.

dl_vs_rl_stability_fig3 Fig. Source from Bowen Xu’s slide

Lecture에는 없지만 이번에는 실제 DQN paper에서는 실제로 어떤 얘기를 하는지 알아봅시다. 여러 번 말씀드렸지만 DQN은 2013년에 제안된 Deep Neural Network (DNN)와 RL을 결합한 method로, Atari라는 비디오 게임에서 human level의 performance 보여준 현대 DL, RL 분야의 역사적인 paper 중 하나입니다. 이전에도 DNN과 RL을 결합한 Approach는 있었으나 잘 안되었으며, 2013년에 DeepMind가 공개한 Playing Atari with Deep Reinforcement Learning라는 논문이 첫 성공 사례라고 합니다. (이 논문은 2년 후에 Nature지에 Human-level control through deep reinforcement learning 라는 이름으로 출판됩니다.)

dqn_paper_fig1 Fig. 2013년에 DeepMind가 제안한 DQN은 Q-Learning의 variant로 CNN과 결합해서 control policy 를 direct로 배워 atari라는 당시에는 꽤 복잡한 task에서 human level에 도달한 최초의 성공 사례이다.

사실 앞서 우리가 살펴본 문제점들은 모두 DQN paper에서 언급되었고, Q Function을 Neural Network (NN)로 근사해서 쓴다는 것과 replay buffer를 쓴다는 개념 자체가 DQN의 핵심입니다. 그러니까 우리는 이미 다 알고있는 것들인 것이죠.

dqn_paper_fig2 Fig. paper에 언급된 RL의 문제점들

  • Computer Vision, Speech Recognition 등지에서 Deep Learning 이 대단한 성공을 이뤘지만 이들은 모두 대량의 hand-labelled training data를 필요로 했으나 RL은 그런게 없다 (on-policy의 경우 그렇단 말임).
  • 게다가 Atari 나 Go (바둑) 같은 우리가 풀고자 하는 문제들은 모두 sparse reward problem으로, 매 행동이 어땠는지에 대한 guide를 즉각적으로 제대로 주기 힘들고 (미래에 어떤 결과를 초래할지를 예측해야 함)
  • 마지막으로 data sample 이 서로 너무나 correlate 되어있다.

2013년 이전에 RL에서의 가장 혁신적이었던 성공 중 하나인 1995년의 TD-gammon이라는 algorithm에 대해서 언급하는데 이는 단 하나의 game을 위한 algorithm이었으며 on-policy였던 점 (off-policy일 경우 발산하는 듯?)과 이는 Q Function을 안정적으로 학습하기 위해서 linear function을 사용했다는 것 등을 문제삼아 DQN이 풀고자 하는 문제는 모든 atari game을 푸는 generalize된 단 하나의 network를 학습한 것임을 강조했다는 겁니다.

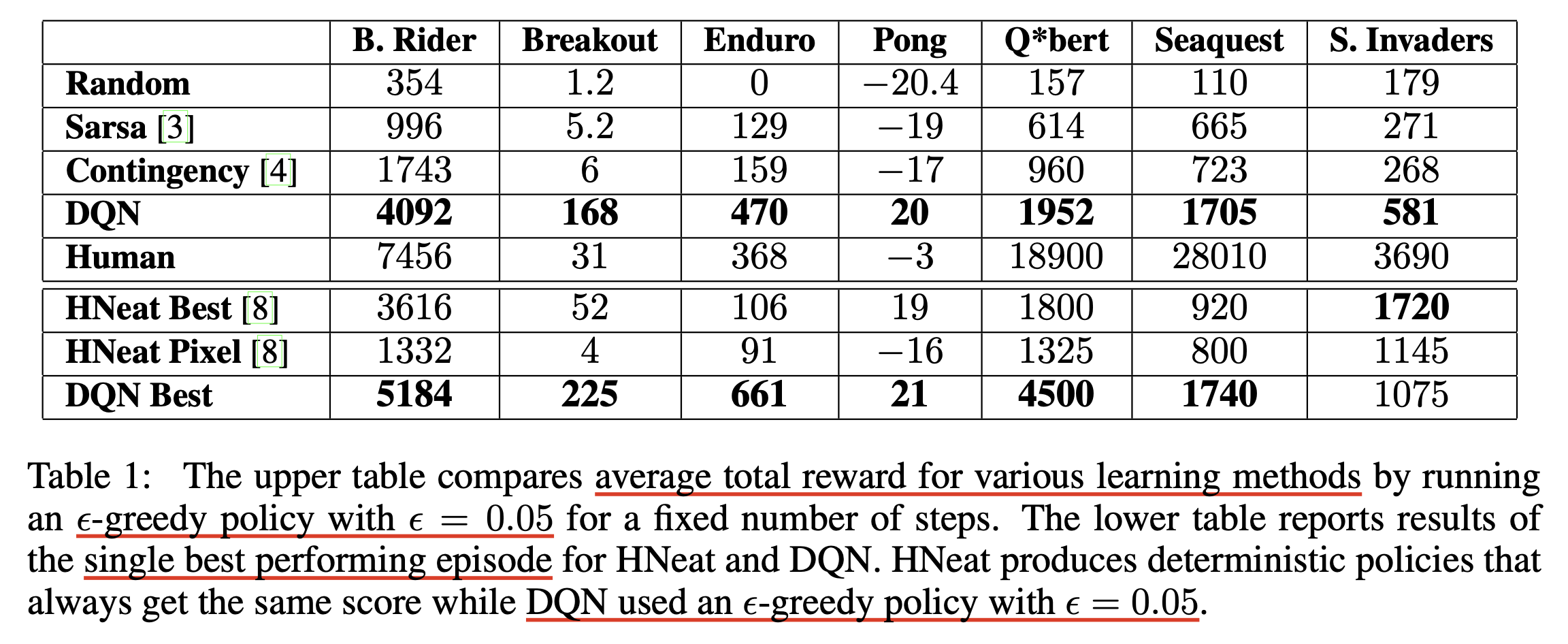
2013_dqn Fig. Screenshots from five Atari 2600 Games: (Left-to-right) Pong, Breakout, SpaceInvaders, Seaquest, Beam Rider. 이 모든 game을 play하는 network는 단 하나의 network로, game별로의 specific한 feature를 따로 줬다던가 하지 않았음.

논문의 중간쯤에보면 왜 atari를 풀기 위해서 Q-Learning을 선택했는지, 그리고 TD-Gammon 등에서 사용한 Online Q-Learning 대비 experience replay buffer를 활용한 것이 왜 주요했는지에 대한 언급이 있습니다. 언급한 3가지 문제점을 해결하기 위해서였는데, 특히 Deep Learning 성공의 key point는 large scale dataset이었고, 이를 학습하기 위해서는 on-policy가 아닌 off-policy였기 때문임이 가장 critical 했다고 할 수 있겠습니다.

dqn_paper_fig4

우리가 이전까지 언급하지 않은 내용은 DQN model 구조가 Q Network의 front-end에 Convolution Neural Network (CNN)이 붙혔다는 것 정도입니다. 왜냐하면 video game의 경우 초당 60개의 210x160 RGB frame이 들어오는 상황이기 때문입니다. 그런데 이는 당시 GPU 상황으로는 부담이 되는 setting이어서 인지 frame 하나 기준 gray-scale 에 110x84 size로 downsampling을 하고 84x84로 crop해서 CNN에 넣어서 feature를 뽑아서 CNN에 넣어주고, 그렇게 뽑은 feature를 Q-Network 에 넣어서 Q 값을 prediction 하도록 학습했다고 합니다. 추가로 실제로 game에서는 초당 60 frame이 들어온다고 했으니 직전 4개 frame까지를 stack해서 넣어줬다고 합니다.

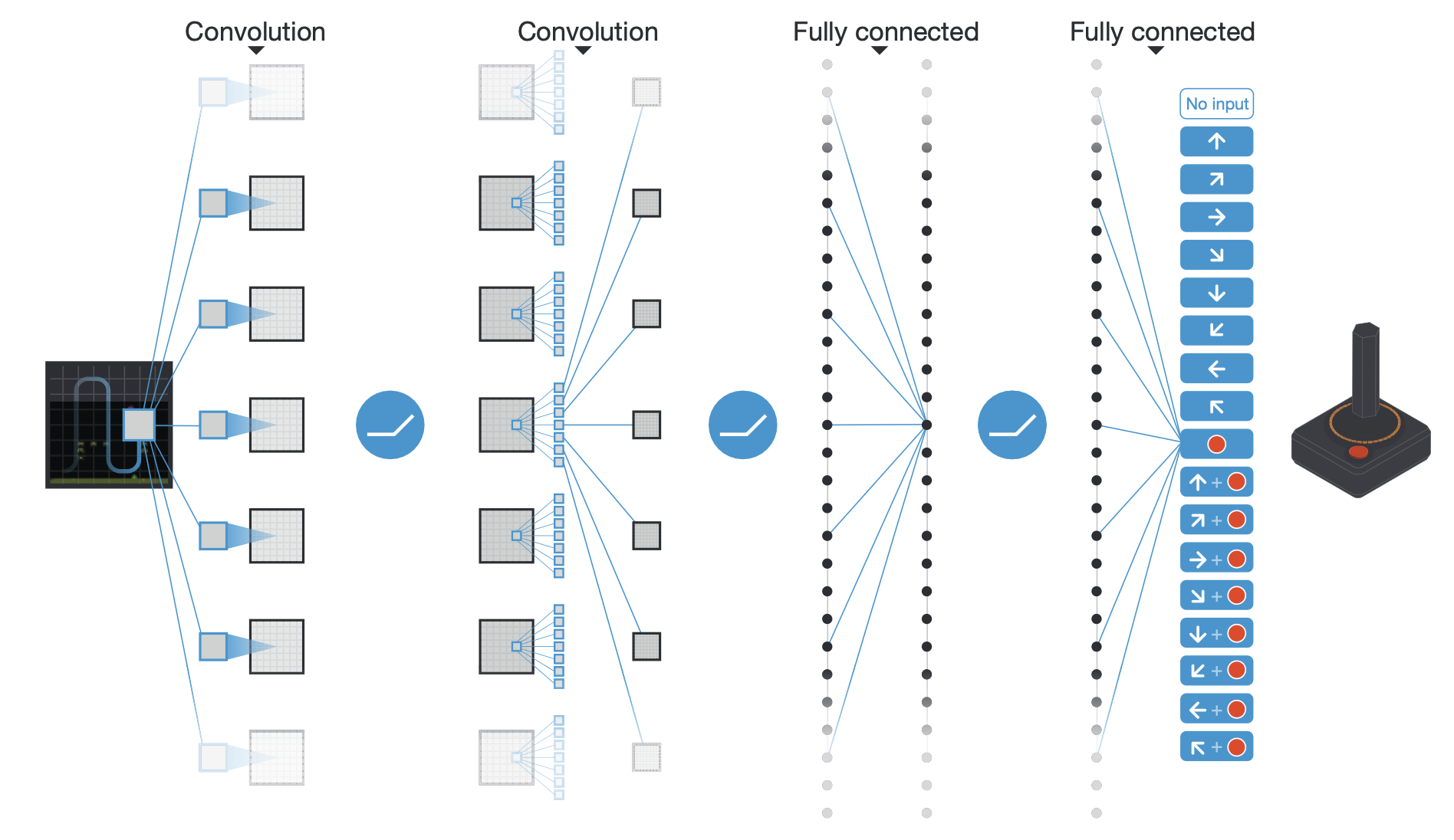2015_dqn Fig. Schematic illustration of the convolutional neural network in Deep-Q-Network (DQN). from 2015, Human-level control through deep reinforcement learning

DQN을 제안한 원본 논문에서는 아래와 같이 algorithm을 설명하고 있습니다. Sergey의 slide와 크게 다르지 않고

dqn_annotated Fig. Original DQN Algorithm from 2013, Playing Atari with Deep Reinforcement Learning

여기서 gradient descent에 사용된 target을 생성하는 target network는 바로 앞서 말씀드린 것 처럼 고정이 되어있습니다.

dqn_paper_fig5

결과적으로 7장에서 언급드린 SARSA (TD-gammon이 이러함) 같은 algorithm들 대비 훨씬 고득점을 낼 수 있게 되었습니다.

dqn_paper_fig6

Additional) Training and Inference Flow Chart

아래는 Inference 와 Training 을 나타낸 Flow charts 입니다. 여기서 Q-Network가 input s를 받으면 각 action 별 value를 다 출력합니다. 즉 Network가 근사하는 건 \(Q(s,a)\)지만 network input은 state, \(s\) 인 것입니다.

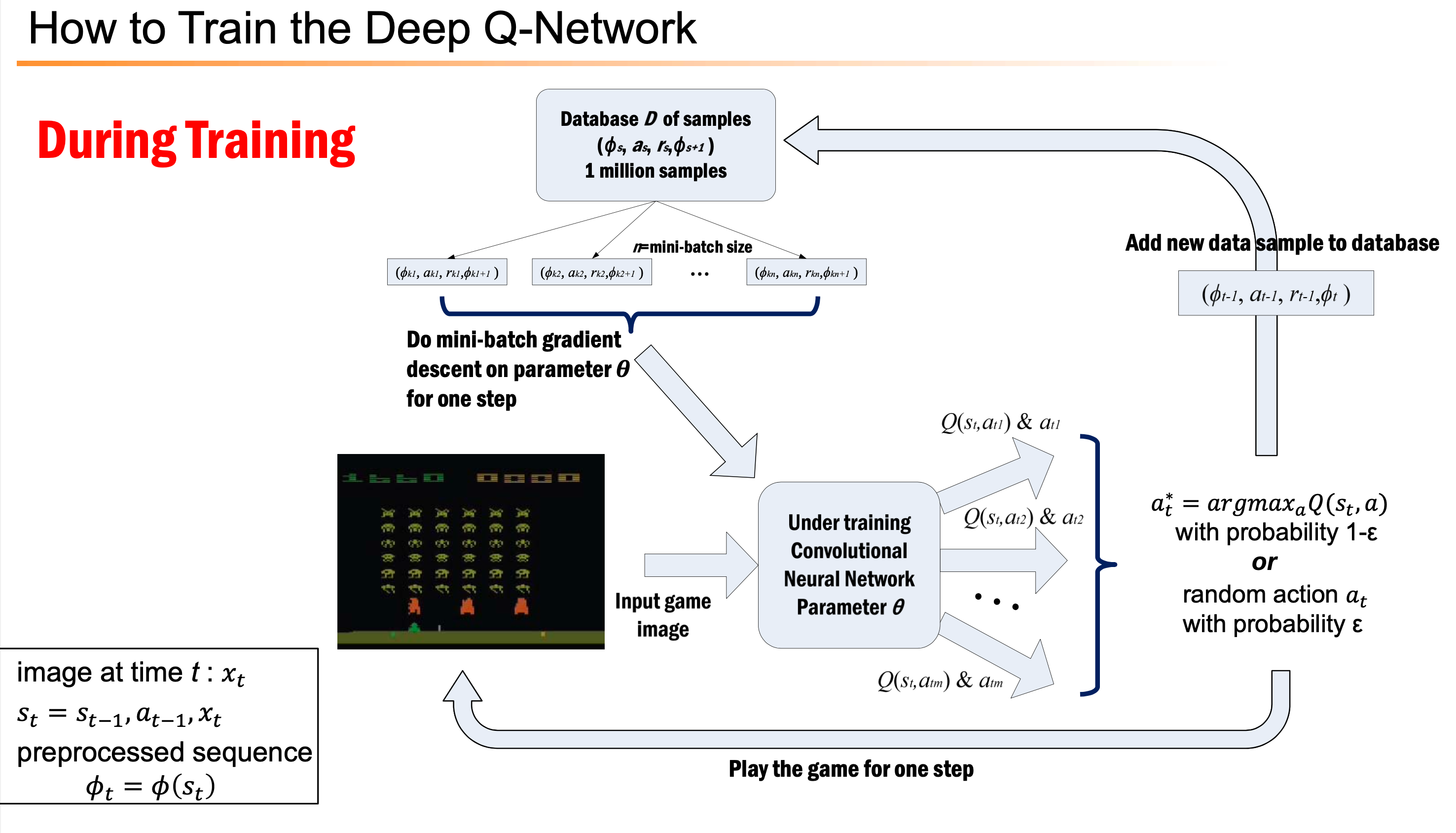how_to_train_dqn_fig1 Fig. Source from Bowen Xu’s slide

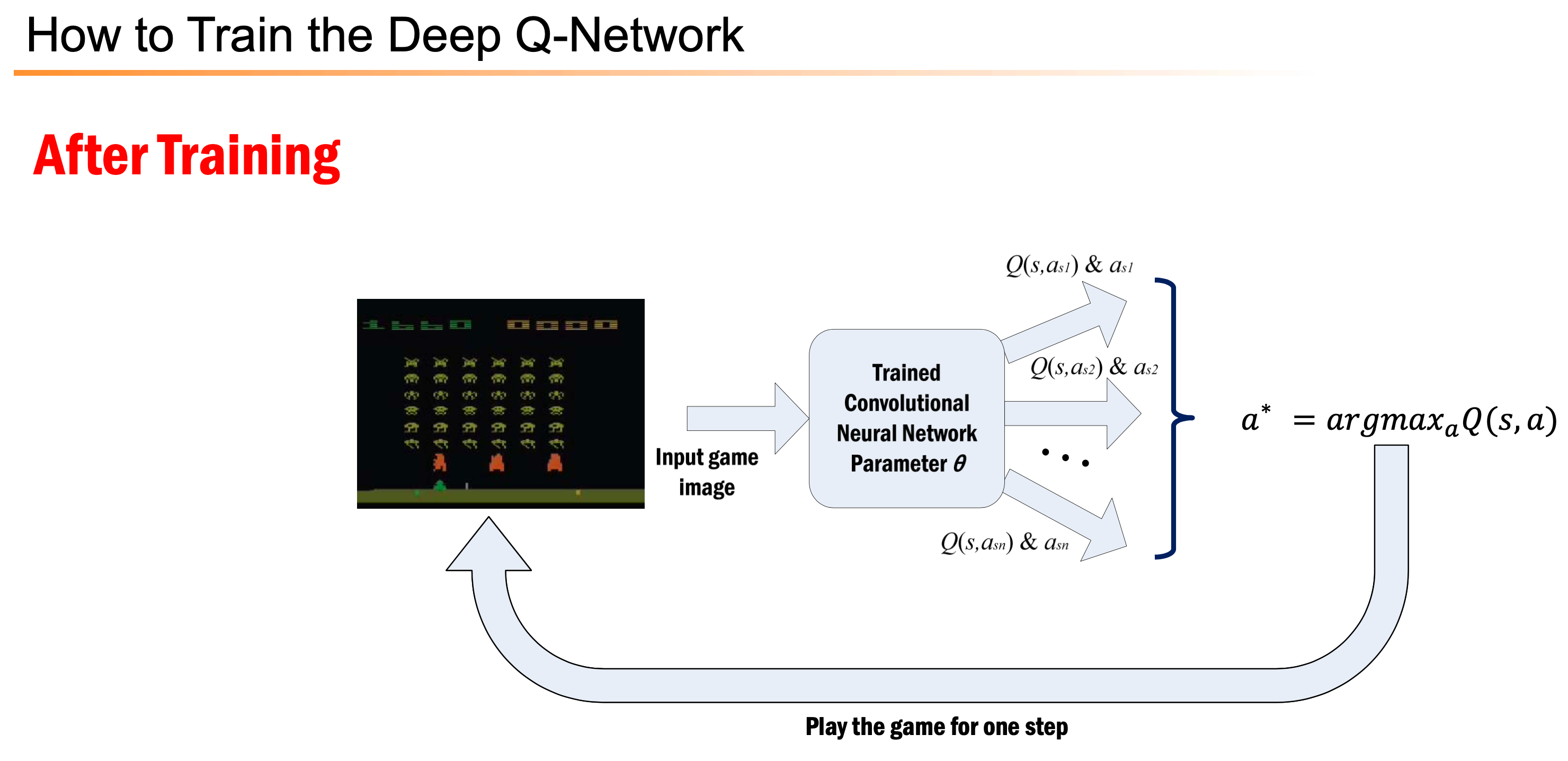how_to_train_dqn_fig2 Fig. Source from Bowen Xu’s slide

A General View of Q-Learning

다시 lecture로 돌아오겠습니다. 이번 subsection에서는 그동안 살펴 본 다양한 버전의 Q Value based algorithm들을 하나의 General한 Framework로 표현하려고 한다고 합니다. (사실 별로 내용은 없는 것 같으나 복습차원에서 넣은 것 같습니다)

slide15 Slide. 15.

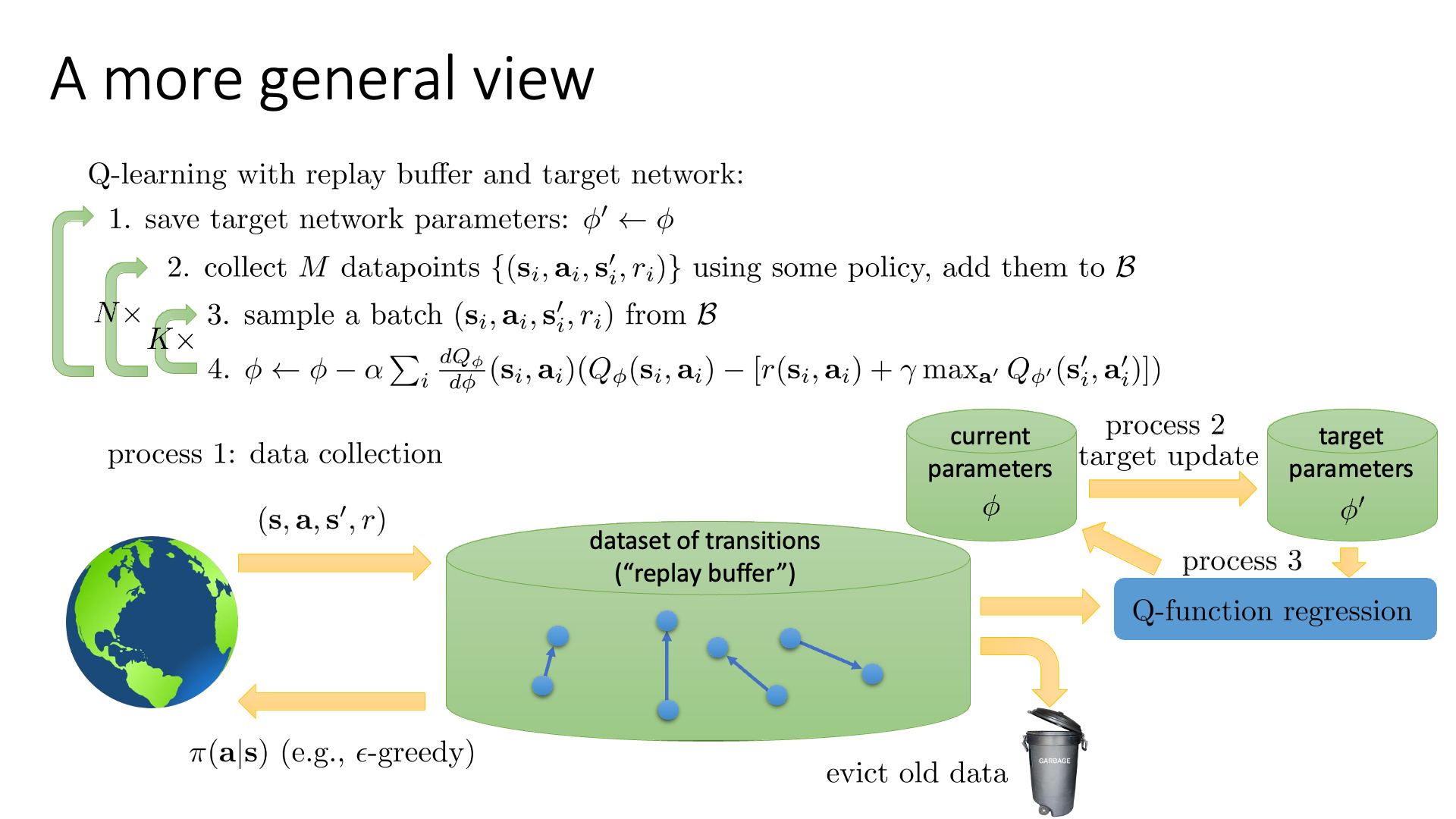slide16 Slide. 16.

여기서 replay buffer는 유한 차원의 사이즈를 가지고 있기 때문에, 오래된 데이터는 실제로는 주기적으로 버린다고 합니다. 예를 들어 100만개의 transition이 담겨져 있으면 하나 추가될 때 마다 가장 오래된 걸 하나 버리는거죠.

Slide. 16.의 flow 에서 N, K가 값이 몇이냐에 따라서 DQN이 될 수도 있고, process 1,2,3 을 어떻게 구성하느냐에 따라서 여태까지 배운 algorithm 들이 나뉜다고 할 수 있겠습니다. (필요한 algorithm을 상황에 맞게 쓰면 되겠으나 DQN말고는 거의 쓸 일 없겠죠?)

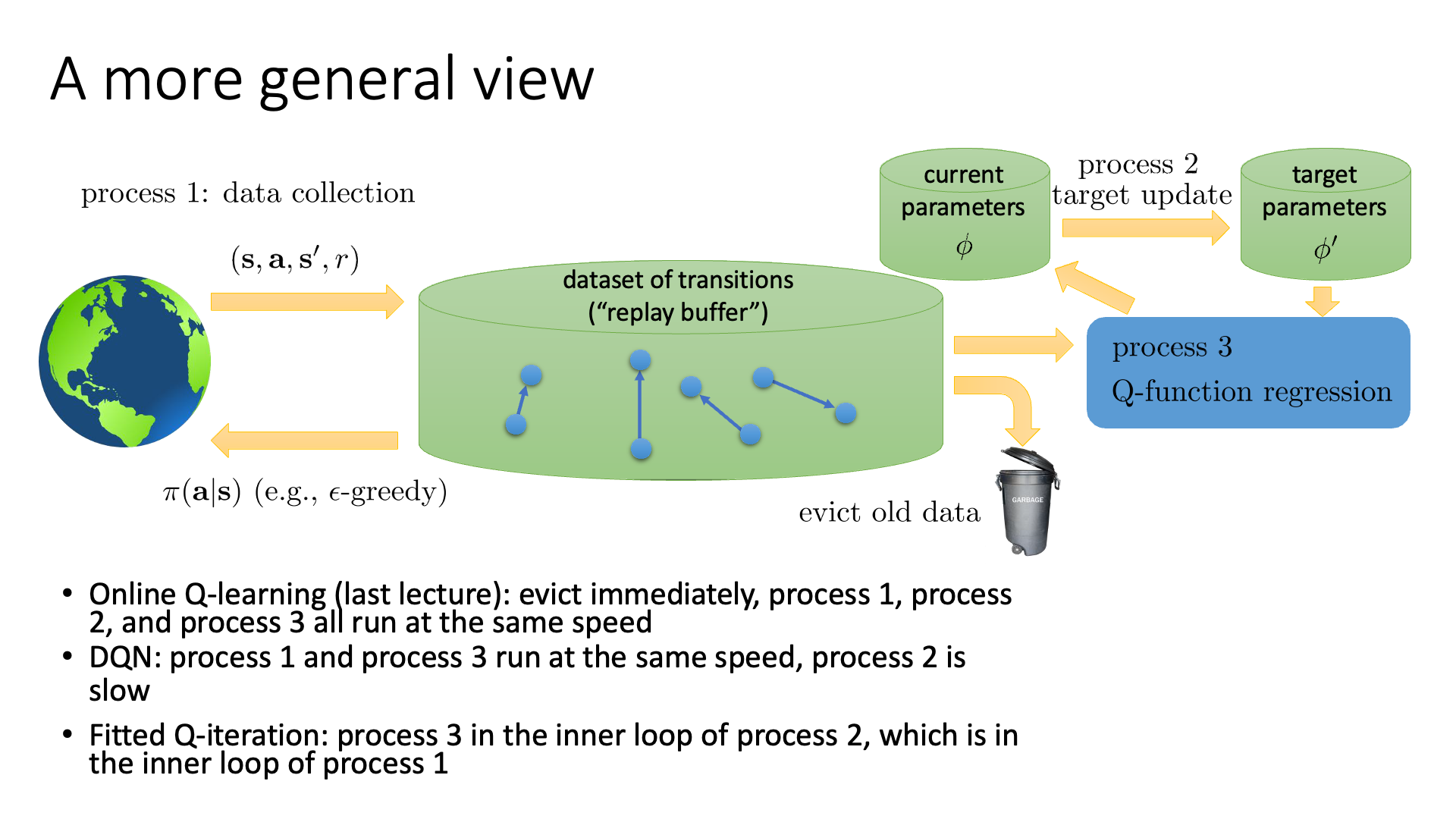slide17 Slide. 17.

Improving Q-Learning

이번 subsection에서 다룰 내용은 "Are the Q-values accurate?"라는 질문으로 시작됩니다.

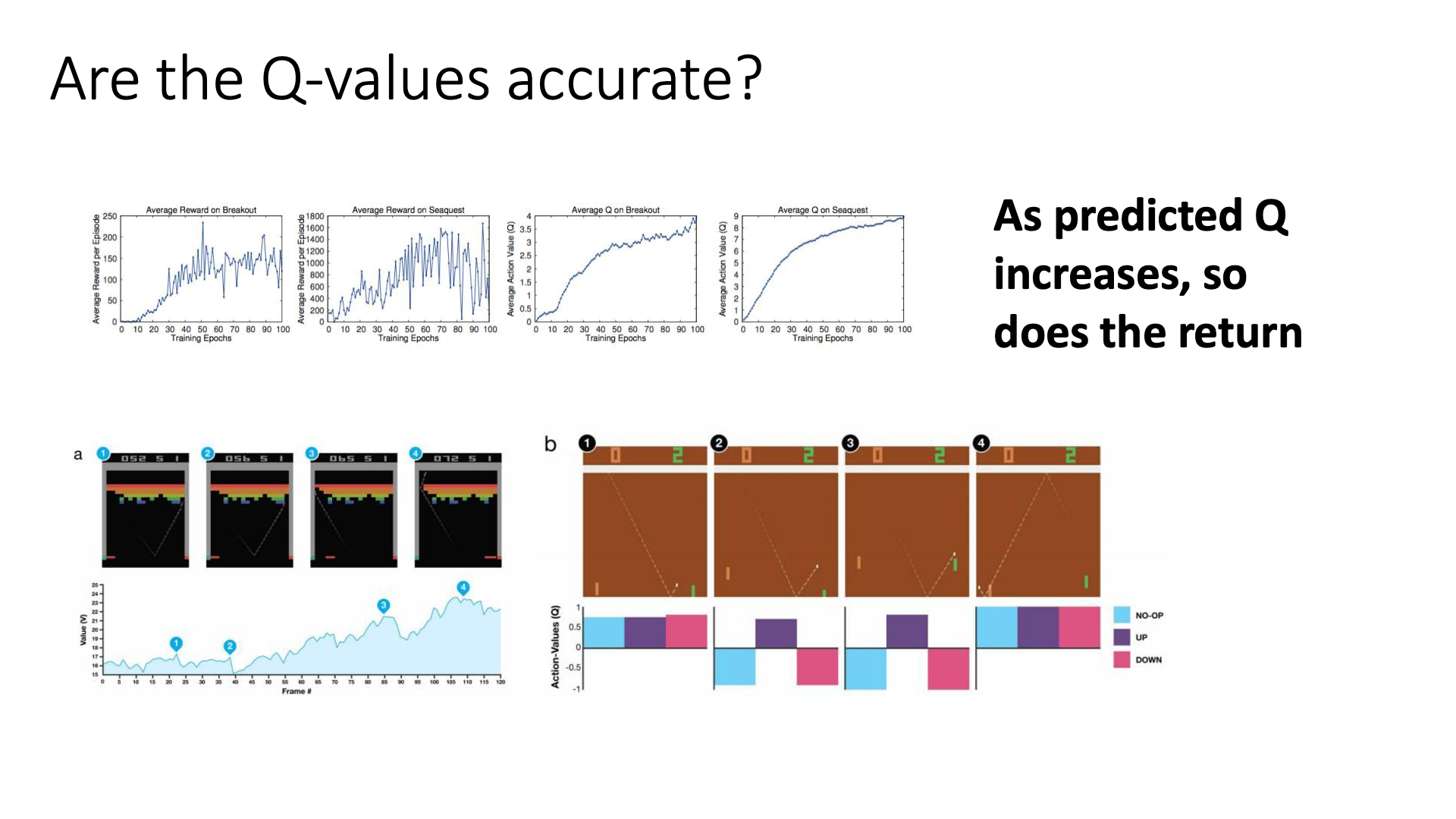slide19 Slide. 19.

Q-Function은 어떤 state에서 어떤 action을 했을때 미래에 내가 얻을 수 있는 reward들의 합을 의미하죠. Slide. 19.의 상단에 나와있는 그림을 확대해 봅시다.

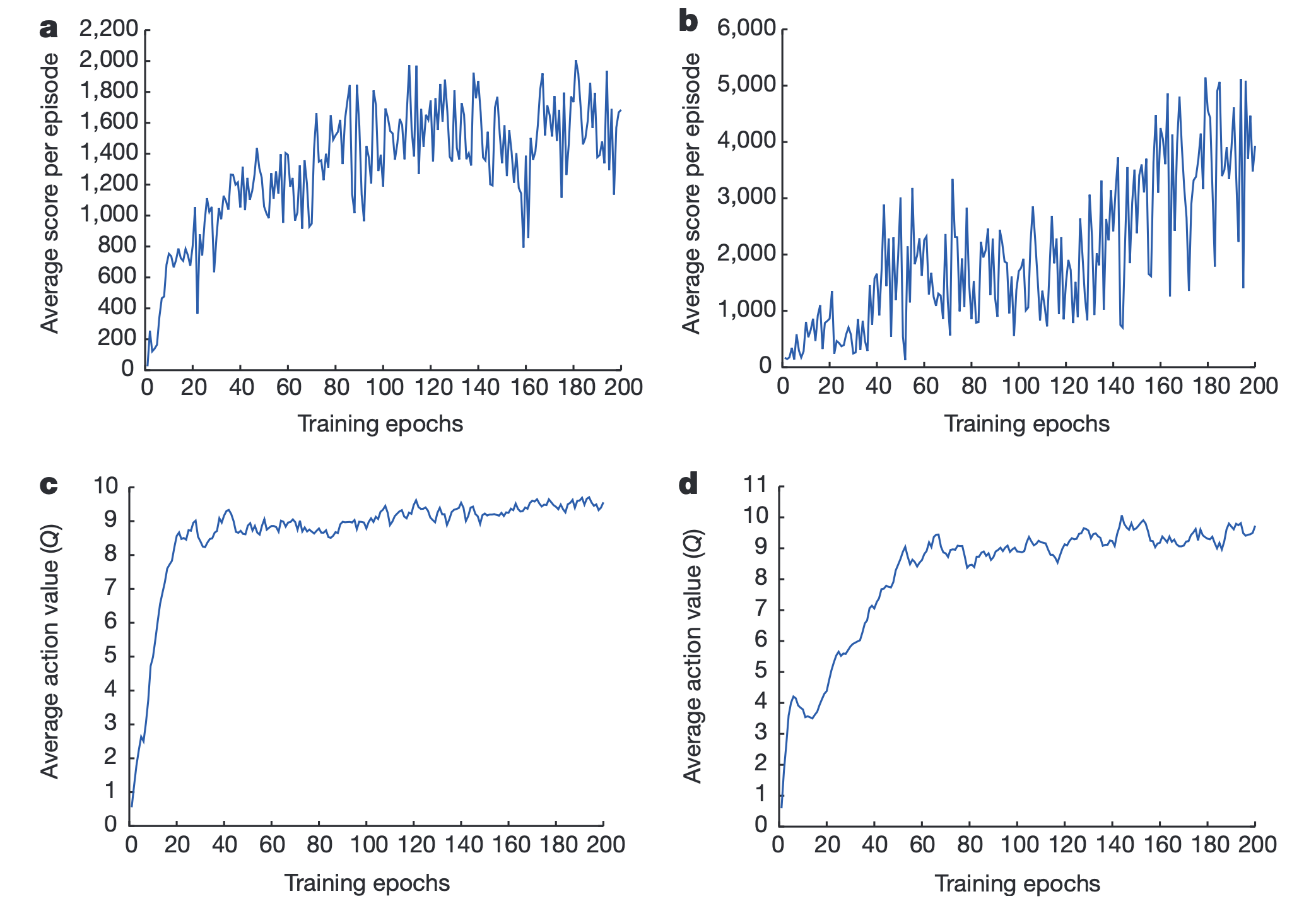dqn_paper_figure1 Fig. Source from Human-level control through deep reinforcement learning

그래프의 x축은 Training Epoch이고 y축은 위의 두개는 episode당 average reward 이며, 아래 두개는 Average Q-Value 입니다. 이는 Atari 게임을 play하는 Agent를 DQN으로 학습시켰을 때의 결과이며, 학습이 진행될수록 평균 Q-Value와 Reward 둘 다 증가하는 것을 볼 수 있습니다.

그 다음으로 우리는 실제 게임에서 매 state (게임 화면) 마다 우리가 가진 Network가 Value, \(V(s)\)를 어떻게 예측하는지를 살펴볼 수 있는데요, 아래의 그림은 Atari게임 중 “Breakout (벽돌 깨기)”를 플레이할 때 게임 진행 과정 동안 Value가 어떻게 변하는지를 나타냅니다.

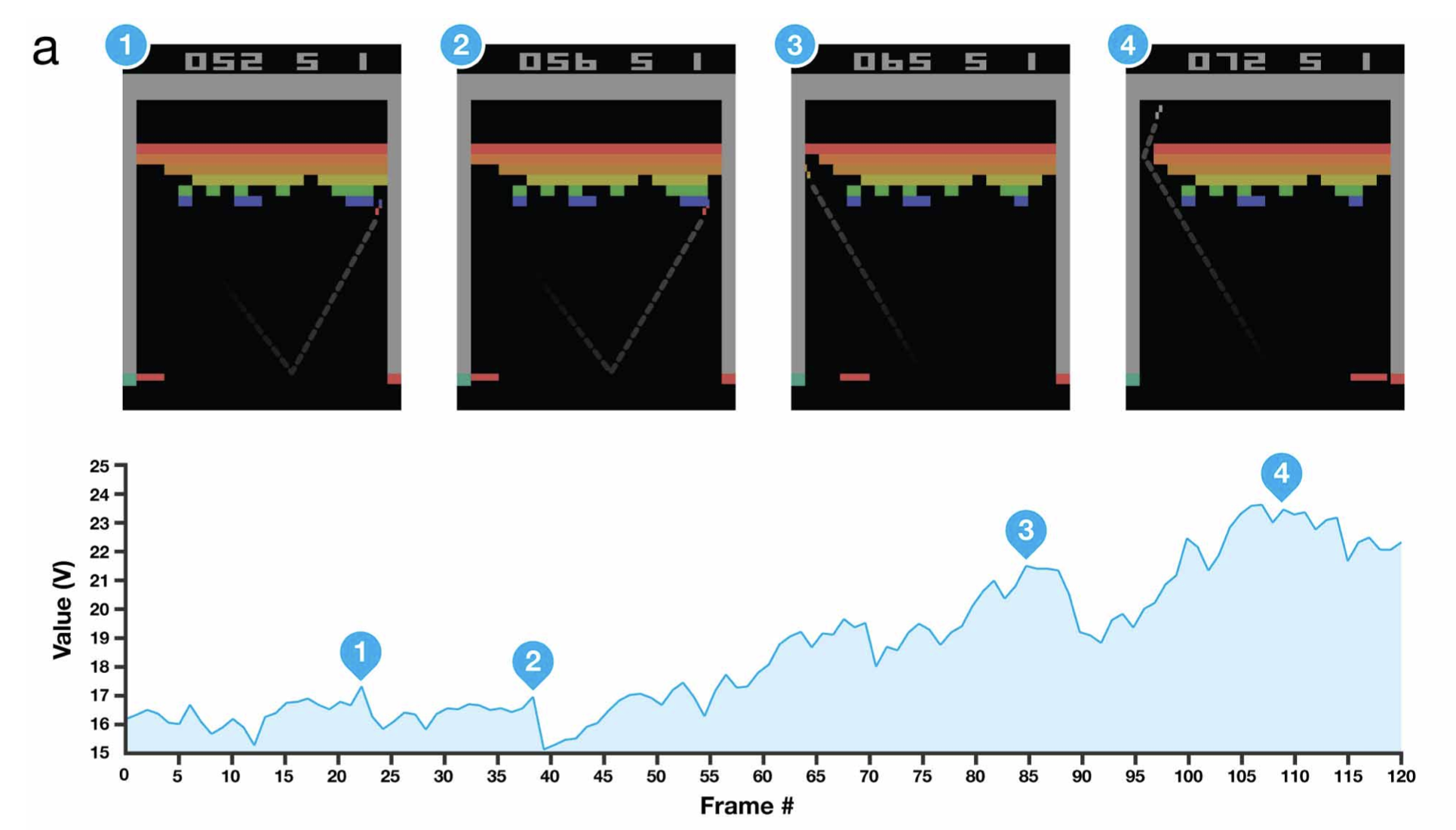dqn_paper_figure2 Fig. Source from Human-level control through deep reinforcement learning

벽돌 깨기를 실제로 해보신 분들은 아시겠지만, 그림 3번에서처럼 벽돌의 한쪽을 공략한 뒤 그 뒤로 공을 넘겨버리면 천장을 다 부숴버리면서 좋은 점수를 얻을 수 있는데, 잘 학습된 Network는 3번 state에서 공을 벽돌 천장 위로 보내는 action이 좋다는 걸 알고 행동을 취하게 됩니다. 4번에서는 천장 위로 공을 보내는 행위가 직접적으로 벽돌을 깨는 행위는 아닌데도 가장 높은 Value를 리턴합니다. 알려준 적은 없지만 DQN으로 사람같이 어떤 action이 좋은지를 추론할 수 있게 된거죠.

마지막으로 Pong이라는 탁구로 상대를 이기는것이 목표인 게임에서의 결과입니다. 2번의 순간에 위로 올라가야 한다는 걸 Q(s,a(위))가 가장 높은 값을 리턴함으로써 알려주네요.

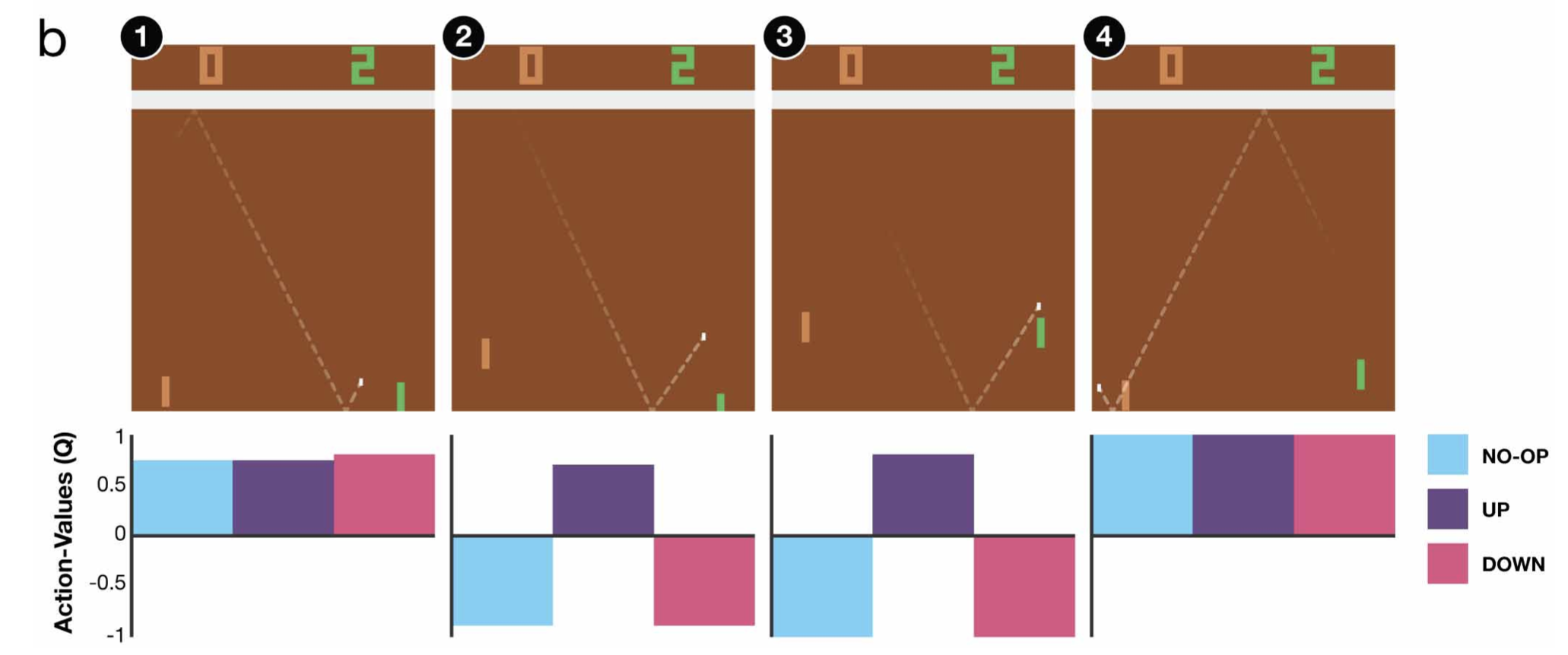dqn_paper_figure3 Fig. Source from Human-level control through deep reinforcement learning

그런데 Q가 높아지는것이 항상 좋은 policy를 학습한 것이냐? total reward가 높아지는 것과 관련이 있느냐? 라고 하면 그건 아닐 수 있다고 합니다. 아래의 그림은 250번 정도의 optimization step을 거쳐 DQN을 학습한 경우를 나타냅니다. DQN True value라 함은 250번 학습을 한 후의 parameter를 가지고 해당 task를 inference해봤을 때 실제로 emulator로부터 얻는 실제 discounted reward의 총 합으로 ground truth 이고 DQN estimate value라 함은 Q Network가 추정한 값을 누적한 겁니다.

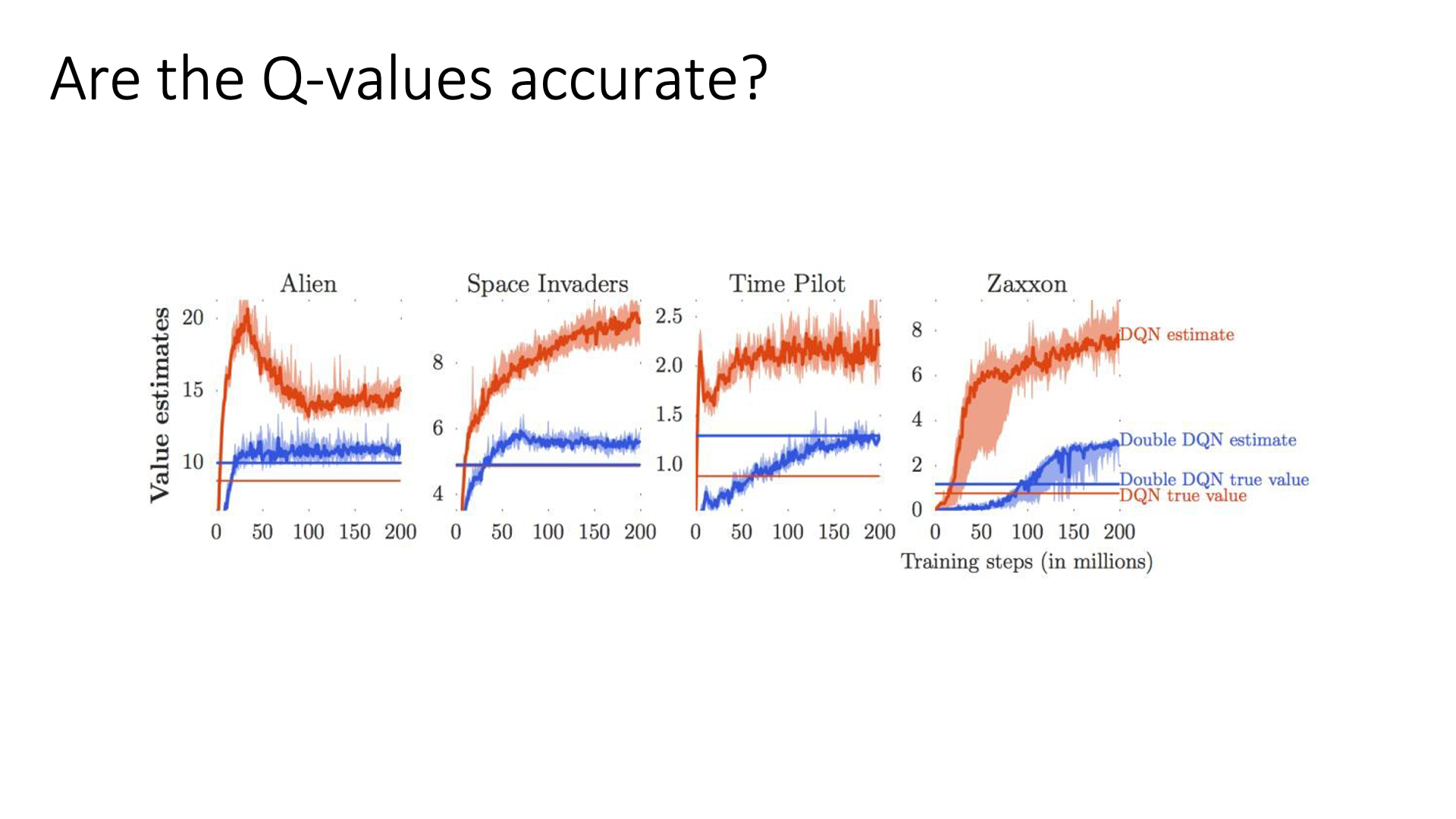slide20 Slide. 20.

보시면 DQN이 예측한 값이 굉장히 높아지는데 실제로 Q Network가 의마하는 바는 s에서 a를 택할 경우 끝까지 가본다면 몇 점을 얻을 수 있는가?를 나타내는 것으로 true value와 비슷한 값으로 수렴을 해야하는데 실제로는 그렇지가 않은 것이죠. 이를 Overestimation Problem이라고 합니다. (아마 true value는 step 1에서의 value값을 의미하는 것 같습니다만 step 1에서 v(s)를 취하는 것이 실제로 expected sum of total reward 이므로 그게 그거입니다.)

반면에 Slide. 20.에서 파란색 선은 Double DQN이라고 되어있는데 이는 꽤 근사한 값을 출력해주는 것을 볼 수 있으며, 우리가 이제 알아볼 algorithm이 바로 이것입니다만 그 전에 잠시 Double Q-Learning에 대해 얘기해 보려고 합니다.

Overestimation and Double Q-Learning

2015년까지의 value-based methods의 굵직한 timeline 은 다음과 같습니다.

지금 얘기하려는 것은 Double Q-Learning 이며 이는 Overestimation 문제를 tackle합니다. Overestimation 은 왜 발생하는 것이며 이것이 발생하다고 해서 어떤 문제가 생기게 되는 것일까요?

slide21 Slide. 21.

Q-Learning이 Overestimation 하는 이유는 max operation 때문 이라고 알려져 있습니다.

\[y_j = r_j + \gamma \color{red}{\max_{a'_j}} Q_{\phi'}(s'_j,a'_j)\]

Sergey는 어떤 두 random variable \(X_1, X_2\)를 가지고 이 문제를 설명하려고 했는데, 저는 이를 주사위를 굴리는 task로 설명드려보려고 합니다 (random variable 을 6개로 확장). 우리가 주사위를 던져서 나오는 수의 expected value는 3.5임이 자명합니다.

\[\frac{1}{6}(1+2+3+4+5+6) = 3.5\]

그런데 만약에 우리가 주사위를 5번 굴린다고 생각하면 게중에는 3.5보다 큰 값도 있고 작은 값도 있을겁니다. 그런데 이 5번의 sampled value에 max를 취하면 대부분의 경우 3.5보다 큰 값이 나올겁니다. 즉 내가 하려는 task의 분포에는 당연히 noise가 끼어있을 테고 (variance가 존재함), 거기서 sample한 경우 negative, positive error가 포함되어 있을 수 있는데 max를 하는 경우 항상 expected value에 조금의 positive error가 낄 가능성이 있는겁니다.

또 하나 sutton book의 예시를 들어보겠습니다. 아래와 같이 언제나 \(A\) state에서 출발하고 가능한 action이 left, right밖에 없는 MDP를 생각해 보겠습니다. A에서 right을 선택하면 reward, return 모두 0이고, left를 선택하면 B로 간 뒤에, B에서 선택할 수 있는 action은 무수히 많은데, 이 action들을 선택했을 때 얻을 수 있는 reward는 mean이 -0.1이고 variance가 1.0인 normal distribution에서 sampling 된다고 생각해 봅시다. 따라서 A에서 left action을 취하는 경우 어떤 trajectory라도 expected return은 -0.1인 겁니다. 그러므로 언제나 left는 mistake 가 되는게 맞습니다.

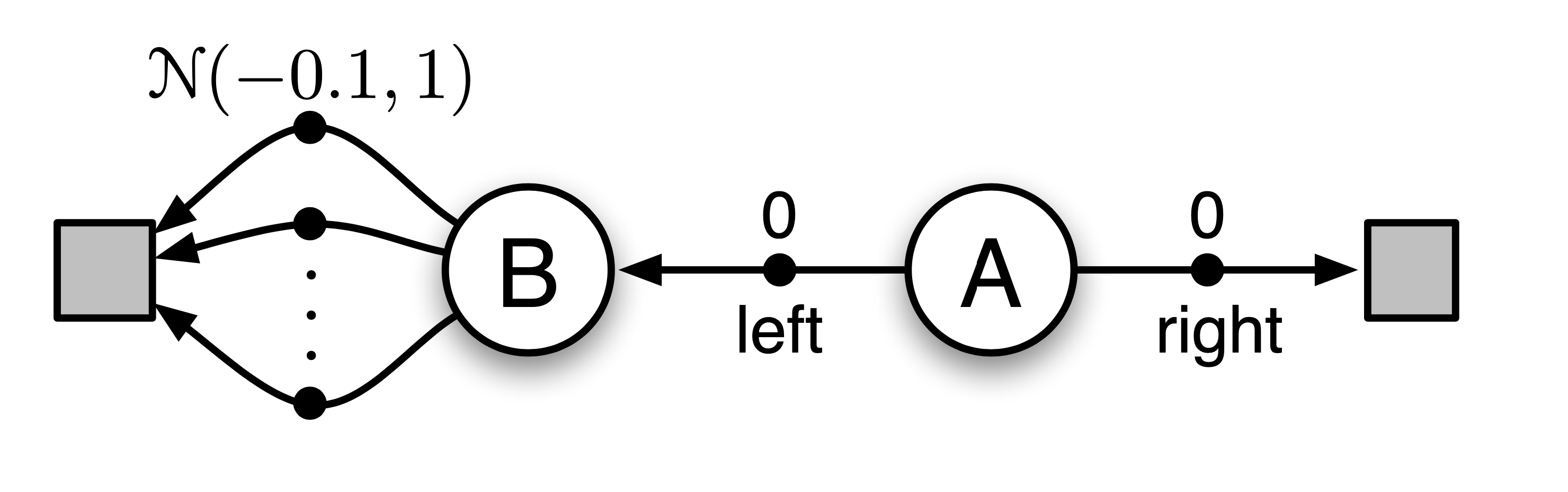sutton_book_overestimation_fig1 Fig.

하지만 이 agent는 left로 가는걸 선호하게 된다고 합니다. 왜 그럴까요?

바로 Overestimation 문제, 즉 maximization bias가 있기 때문입니다. 이것이 B가 positive value를 갖는 것 처럼 만들어 버린다고 합니다. 왜냐하면 우리가 B에서 가능한 action 들 중 대부분의 action은 -0.1부근의 reward를 받겠으나, 어떤 action은 이 reward 분포로 부터 많이 벗어나 (variance가 1이므로) positive reward를 받을 수 있을 거고, Q-Learning으로 학습한 agent는 \(Q(A, left)\) 의 target으로 \((0 + \max_a Q(B,a)) = +0.2\)같은 값을 사용할 수 있기 때문입니다.

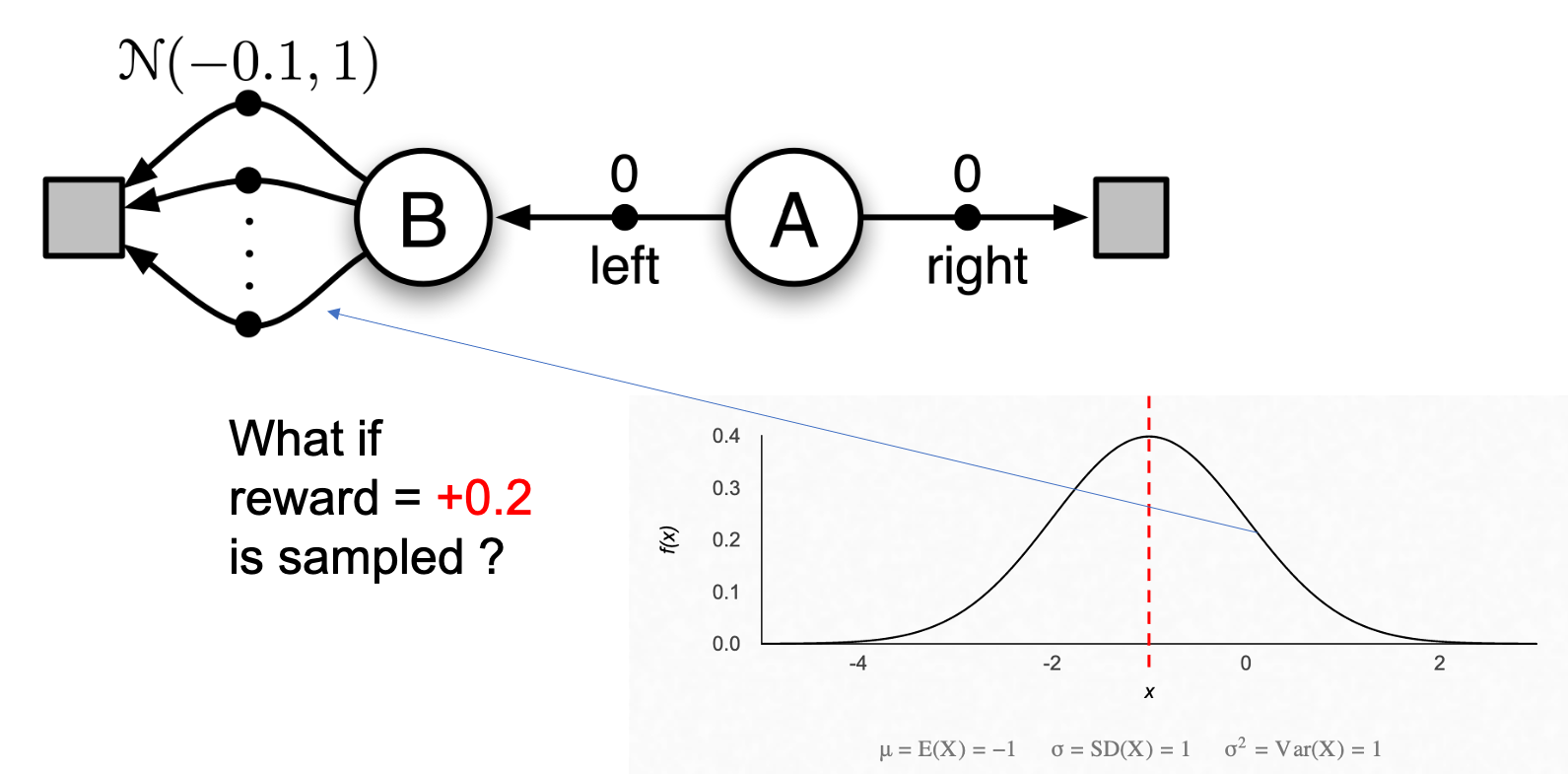sutton_book_overestimation_fig1_edited Fig.

그러면 Agent는 음 대부분의 경우 음의 reward를 받겠으나 아주 낮은 확률로 reward가 좋을 수도 있잖아?라는 이상한 긍정적인 생각을 하게 되고, left 라는 action의 Q값으로 양수가 propagate되는 이상한 상황이 발생합니다.

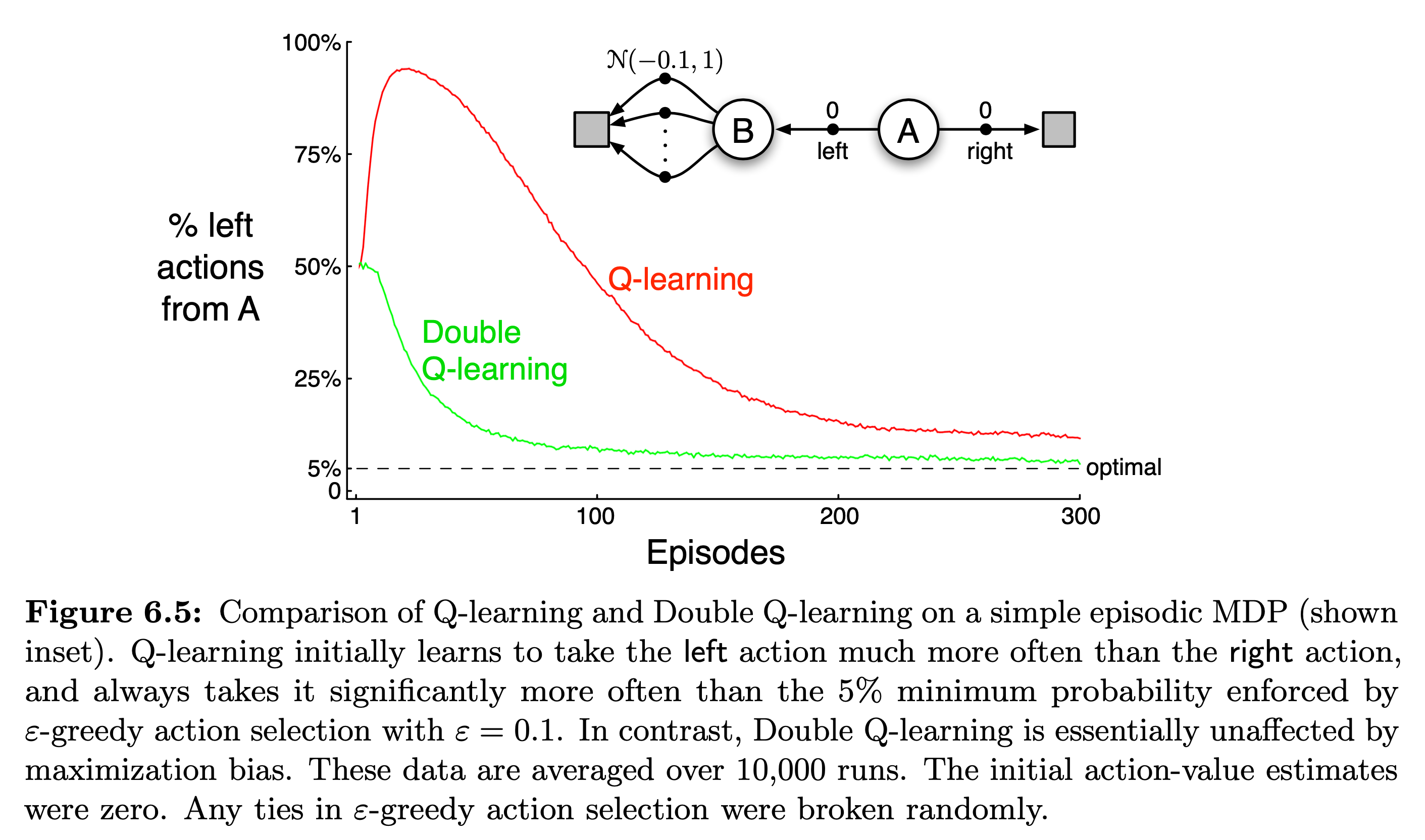sutton_book_overestimation_fig2 Fig.

Q-Learning은 그렇기 때문에 초반에 left 를 취할 확률이 폭증했다가 다시 내려오지만, 점근선에 다다랐음에도 불구하고 (학습이 된 후에도) A에서 left 를 선택할 확률의 optimal 값인 0.05 (0이 아닌 이유는 epsilon greedy 때문에)보다 0.05나 더 큰 값을 갖게 됩니다.

이제 Q-Learning에 대해서 생각해봅시다. Q-Learning이 추정한 특정 state에서 action에 대한 value값들의 분포도 noise가 껴있을 것입니다. 여기서 앞선 toy example들과 같은 논리로 max 를 취하게 되면, 이 error가 껴있는 값들 중에서도 max인 값을 고를 것이기 때문에, 하필 negative, positive error 중에서 positive error가 낀 값이 계속 채택되고 이것이 반복됨으로써 그 action에 대한 target이 커지고 학습된 추정치도 계속 커지는 겁니다. 즉 max operator를 쓰는 Q-Learning은 구조적으로 거듭된 반복으로 Q-Value를 overestimate (과대평가) 할 수 밖에 없다는 결론에 다다르게 된다고 합니다. (아마 지금은 간단한 toy problem에 대해서 얘기했지만 왼쪽으로 갈 확률이 optimal할 경우 0.05 여야 하는데 그렇지 않은걸 보면 분명히 overestimation이 더 복잡한 problem에 대해서는 더 큰 문제를 일으킬 가능성이 높을 것 같습니다.)

그렇다면 어떻게 이 문제를 해결할 수 있을까요?

가장 먼저 할 일은 우리가 할 일은 Q-Learning의 원래 수식을 조금 변형해서 생각하는 겁니다.

\[\begin{aligned} & Q(s,a) = r + \max_{a'} Q_{\phi'}(s',a') \\ & Q(s,a) = r + Q_{\phi'}(s', \arg \max_{a'} Q_{\phi'} (s',a') ) & \\ \end{aligned}\]

그러면 우리는 비로소 Q-Network가 사실은 두 가지 중요한 일을 한다는 걸 볼 수 있는데, 각 action들을 평가해서 best action을 고르는 일과 그 action에 대한 Q 값을 계산하는 일입니다. 사실상 한 번에 할 수 있는일이고 같은 network가 하는 일이지만 일단 나눠본 것입니다.

Sergey는 이 두 가지 일을 하는 network의 noise 를 decorrelate 할 수 있다면 해결할 수 있다고 얘기하는데요,

slide22 Slide. 22.

key idea는 action 을 고르는 Q-Network와 이를 평가하는 Q-Network에 각자 서로 다른 network를 쓰는 것입니다. 직관적으로 왜 이것이 working하는가?는 우리가 결국 학습하고자 하는 것은 Q value의 시간 차 (Temporal Difference; TD)이기 때문입니다. 만약 모든 action들이 다 과대평가 됐다면 어차피 그 차이는 변하지 않을 것인데, 지금 문제가 되는 것은 주어진 state에 대해서 지속적으로 한 action에 대해서 계속 과대평가를 하는 것이 문제이기 때문입니다. 만약 두 network를 쓰게 된다면 (번갈아서), 이들은 서로 다른 sample \((s,a,s',r)\)을 보고 학습될 가능성이 크며, 이 둘은 적어도 서로 다른 action에 대해 과대평가 할 것이므로 error가 누적되는 것을 막을 수 있기 때문입니다.

\[\begin{aligned} & \color{red}{ Q_{\phi_A} }(s,a) \leftarrow r + \gamma \color{blue}{ Q_{\phi_B} } (s', \arg \max_{a'} \color{red}{ Q_{\phi_A} } (s',a') ) & \\ & \color{blue}{ Q_{\phi_B} } (s,a) \leftarrow r + \gamma \color{red}{ Q_{\phi_A} } (s', \arg \max_{a'} \color{blue}{ Q_{\phi_B} } (s',a') ) & \\ \end{aligned}\]

이렇게 하면 우리가 문제삼았던 아래의 수식에서

\[\max_{a'} Q_{\phi'}(s',a') = Q_{\phi'}(s', \arg \max_{a'} Q_{\phi'} (s',a') )\]

noise가 두 번 추가되는 (?) 부분이 서로 관련이 없어진다고 생각할 수 있기 때문에 noise들이 설령 껴있다고 하더라도 둘은 서로 출처가 다른것이 되는데, 아래의 경우를 예로 들어보면 \(Q_{\phi_A}\)를 통해 positive noise가 낀 액션을 골랐어도 \(Q_{\phi_B}\)가 낮은 값을 리턴하기 때문에 보완이 된다는 겁니다.

\[\color{red}{ Q_{\phi_A} }(s,a) \leftarrow r + \gamma \color{blue}{ Q_{\phi_B} } (s', \arg \max_{a'} \color{red}{ Q_{\phi_A} } (s',a') )\]

이를 self-correcting이 된다고 표현한다고도 합니다.

실제 Sutton book의 Double Q-Learnign algorithm을 보면 아래와 같은데, 0.5의 확률로 어떤 network를 update할지를 정하는 것 같습니다.

sutton_book_overestimation_fig3 Fig.

Double DQN (DDQN)

하지만 실제로 Double Q-Learning을 구현할 때는 다른 \(Q_A,Q_B\)를 또 추가하는 것이 아니라 다른 방식을 쓴다고 합니다. 이것이 Double DQN (DDQN)에서 제안된 방법인데, 우리는 optimization step에 따라서 \(\phi, \phi'\)과 같이 current, target network를 두 개나 가지고 있고 이 둘의 noise 분포는 다르기 때문에 이 network들을 Dobule Q-Learning approach의 module들로 써도 문제가 없다고 합니다.

slide23 Slide. 23.

즉 moving target 문제를 피하기 위해서 Target Network로 여전히 Q값을 평가하긴 하지만, 액션을 고르기 위해서는 Current Network를 쓰게 되는 것이고, 이는 \(\phi\)와 \(\phi'\)이 비슷해지지 않는이상 decorrelated 되게 된다고 합니다.

물론 이렇게 함으로써 moving target 문제가 좀 생긴다고 하며, \(Q'\)는 가장 최근의 \(Q\)로 고정된 Network이기 때문에 둘은 완전 decorrelated 하지 않아서 완벽한 해법은 아니라고 하지만 practical하게는 이렇게 쓴다고 합니다.

DDQN의 실제 algorithm은 다음과 같습니다.

ddqn_algorithm Fig. Source from DDQN paper

Over-Estimation Analysis from DDQN paper

TBC (DDQN paper에 재밌는 분석 내용이 있음)

Dueling-DQN

추가적으로 강의에서 언급하지는 않았지만 Double DQN이 제안된 2016년 즈음에 Dueling-DQN이라는 방법론도 제안됐었습니다. Algorithm 이름이 비슷해서 잠깐 봤는데, 마찬가지로 Research Affiliation은 DQN, DDQN을 제안한 DeepMind 이지만 이 paper에서 tackle하고자 하는 문제는 overestimation은 아니었습니다. Paper에서는 \(Q(s,a) = V(s) + A(s,a)\) 라는 정의를 이용해 직접적으로 \(Q\)를 예측하는 network를 두는 것보다 \(V,A\)를 예측하는 network를 2개 둬서 간접적으로 Q를 예측함으로써 더 효율적이고 안정적이게 Q-Learning을 할 수 있는 것이었습니다.

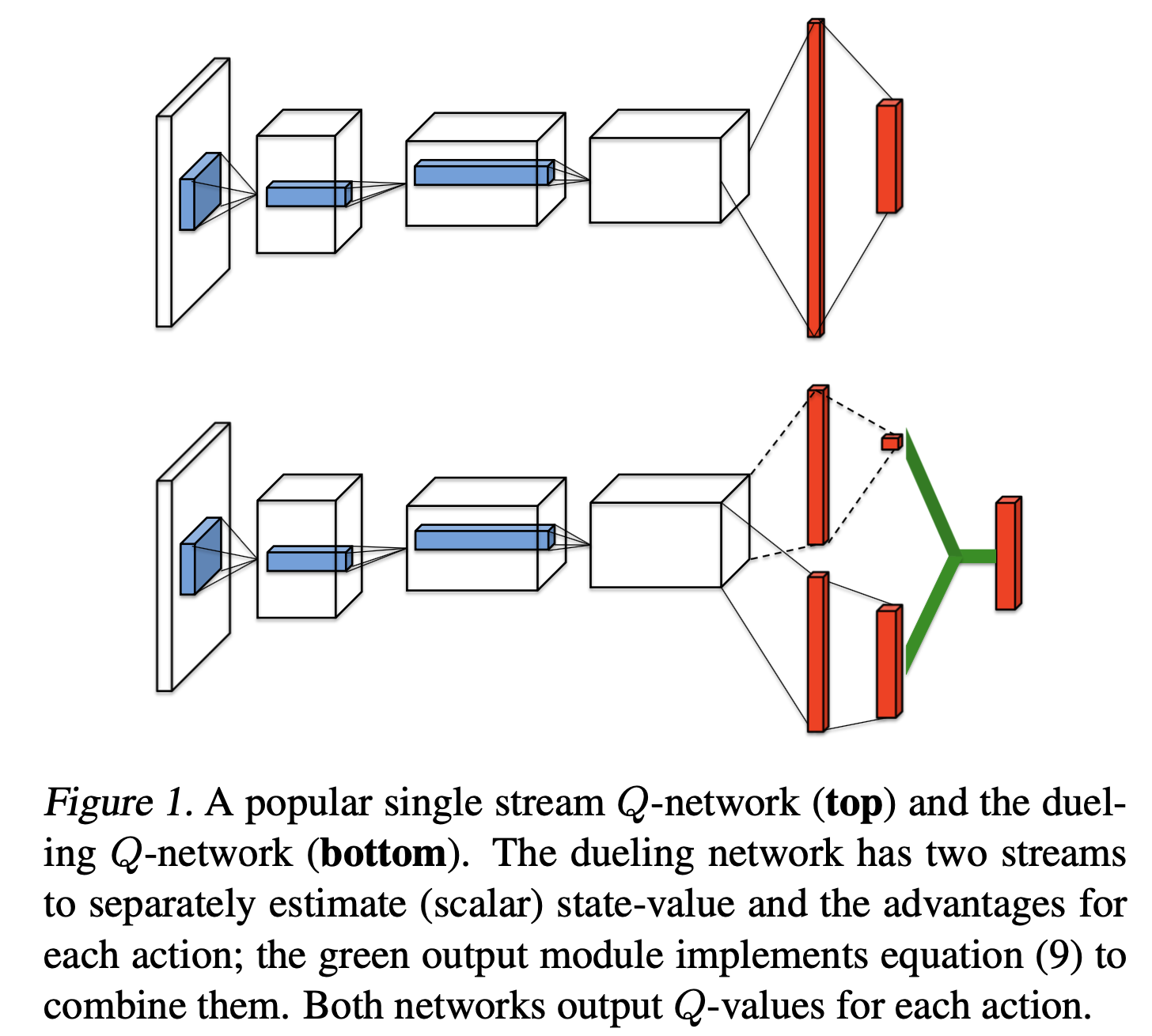dueling_dqn1 Fig. DQN (위) vs DDQN (아래)

더 관심이 있으신 분들은 원 논문인 Dueling Network Architectures for Deep Reinforcement Learning를 찾아보시길 바랍니다.

Q-Learning with Multi-Step Returns

그 다음으로 알아볼 것은 Multi-Step Return Q-Learning 입니다. 이는 Actor-Critic에서 살펴봤던 방법과 비슷합니다.

  • Actor-Critic의 다양한 Advantage Function Recap
\[\begin{aligned} & \hat{A}_{\color{red}{C}}^{\pi} (s_t,a_t) = r(s_t,a_t) + \gamma \hat{V}_{\phi}^{\pi} (s_{t+1}) - \hat{V}_{\phi}^{\pi} (s_{t}) & \\ & \hat{A}_{\color{red}{MC}}^{\pi} (s_t,a_t) = \sum_{t=t'}^{\infty} \gamma^{t'-t} r(s_{t'},a_{t'}) - \hat{V}_{\phi}^{\pi} (s_{t}) & \\ \end{aligned}\]

Policy-based에서 그 action이 얼마나 좋았는가?를 의미하는 advantage라는 quantity는 우리가 직접 rollout해보는 Monte Carlo (MC) 방법과 Critic이 추론한 값을 쓰는 방법 두 가지가 있었는데, MC는 bias가 없는대신 variance가 크고 Critic-based 는 variance가 작은대신 더이상 unbiased가 아니었습니다. 그렇기때문에 둘을 교묘하게 결합한 n step 방법론, 더 나아가서 Generalized Advatnage Estimator (GAE)를 쓰는것으로 algorithm을 update 했었습니다.

\[\hat{A}_{ \color{red}{n} }^{ \pi } (s_t,a_t) = \sum_{t=t'}^{t+n} \gamma^{t'-t} r(s_{t'},a_{t'}) - \hat{V}_{\phi}^{\pi} (s_{t}) + \color{blue}{ \gamma^n \hat{V}_{\phi}^{\pi} (s_{t+n}) }\]

slide24 Slide. 24.

Q-Learning 에도 n step estimator같은 방식을 적용해보도록 합시다.

\[y_{j,t} = r_{j,t} + \gamma \max_{a_{j,t+1}} Q_{\phi'}(s_{j,t+1},a_{j,t+1})\]

Q-Learning는 current reward + expected future reward라고 할 수 있습니다. 그런데 학습 초기에는 \(Q_{\phi'}\)이 구릴 것이므로 current reward, \(r\) 가 더 중요할 것이고 처음에는 noise같았던 \(Q_{\phi'}\)는 나중에 가서는 잘 될 것이므로 그제서야 future reward를 더한 target을 쓰면 된다는 idea입니다.

Q-Learning은 기본적으로 한 스텝만으로 target을 정하는 이른 바 one step back up 방법으로 maximum bias 이며 minimum variance 한 특성을 지니고 있다고 하는데요, 이를 Actor-Critic에서 처럼 바꿔줍니다.

\[\begin{aligned} & y_{j,t} = r_{j,t} + \gamma \max_{a_{j,t+1}} Q_{\phi'}(s_{j,t+1},a_{j,t+1}) & \scriptstyle{ \text{ og Q-Learning target } } \\ & y_{j,t} = \sum_{t'=t}^{t+N-1} \gamma^{t-t'} r_{j,t'} + \gamma^N \max_{a_{j,t+N}} Q_{\phi'}(s_{j,t+N},a_{j,t+N}) & \scriptstyle{ \text{ Multi-Step target like Actor-Critic } } \\ \end{aligned}\]

(당연히 여기서 N이 1이면 standard form이 됩니다.)

이는 여러번 reward값을 더하고 N step뒤의 state, action에 기반한 Q값을 사용하기 때문에 Actor-Critic에서와 비슷하게 N-step Estimator라고도 부르며, 마찬가지로 one-step에서 n-step이 됐기 때문에 variance는 조금 높아졌으며 bias는 낮아지는 효과가 생깁니다 (bias variance trade-off). 하지만 N-Step Return을 사용할 경우 몇 가지 문제점이 있을 수 있다고 합니다.

slide25 Slide. 25.

그 중 하나는 N번이나 transition을 진행하기 때문에 off-policy sample을 사용할 경우 더이상 return값이 정확하지 않다는 겁니다.

이를 해결하는 방법은 세 가지 정도가 있을 수 있는데요,

  • Ignore the problem
  • Cut the trace - dynamically choose N to get only on-policy data
  • Importance sampling

더 자세한 내용은 Safe and Efficient Off-Policy Reinforcement Learning 논문을 찾아보시면 좋을 것 같습니다. (또 DeepMind paper 입니다.)

Q-Learning with Continuous Actions

Lecture 7에서 Q-Iteration 을 Fitted Q-Iteration으로 바꾼 이유가 기억나실겁니다. State 수가 우주에 존재하는 원자 수 보다 많아지기 때문에 모든 state를 방문할 수 없으며, policy evaluation을 위한 계산이 오래걸리기 때문에 NN를 써서 \(Q(s,a)\)를 근사하는 것이었죠. 하지만 이 때 우리는 action이 무수히 많은 경우, 즉 continuous action space를 갖는 경우에 대해서는 아직 얘기해보지 않았습니다.

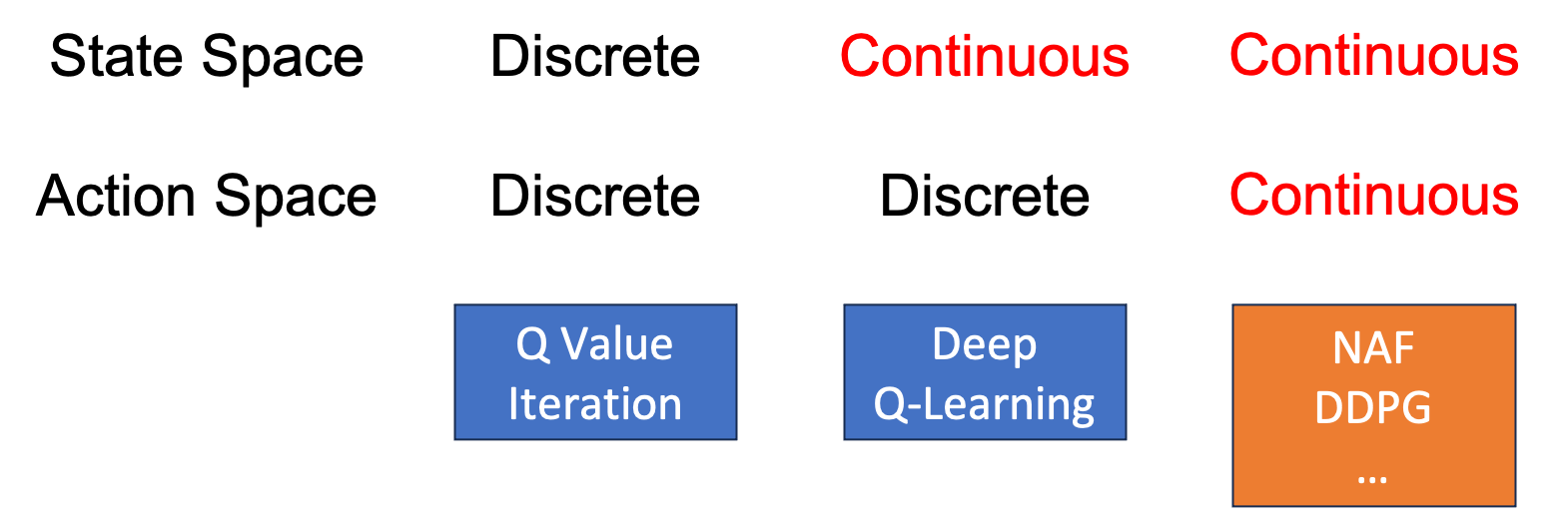continuous_value_based Fig. state가 continuous 하다기 보다는 “매우 많은 state가 존재하는 경우에 대해서” 라고 생각하시면 될 것 같습니다. 사실상 무한대에 가까운 state가 있어도 Q-Learning은 학습할 수 있으므로? continuous라고 표기했습니다.

Atari등의 게임은 모두 방향키와 버튼을 누르는 수준의 10차원 내외의 discrete space를 갖는 쉬운 문제 였습니다.

하지만 real world problem 중에서 가령 robotics 같은 경우 robot의 관절이 예를 들어 4~50개 씩 존재하는데, 각각의 관절을 매 순간 순간 몇도 만큼 어느 방향으로 틀어야하는가? 같은 task는 discrete 하지 않습니다. 자율주행을 하는 경우에도 left, right, stop 같이 action을 discrete하게 정의할 수는 있으나 실제로는 핸들을 어디로 몇도 돌려야 하는가? 같이 continuous 할 겁니다.

discrete_vs_continuous1 Fig. Discrete Action Space vs Continuous Action Space

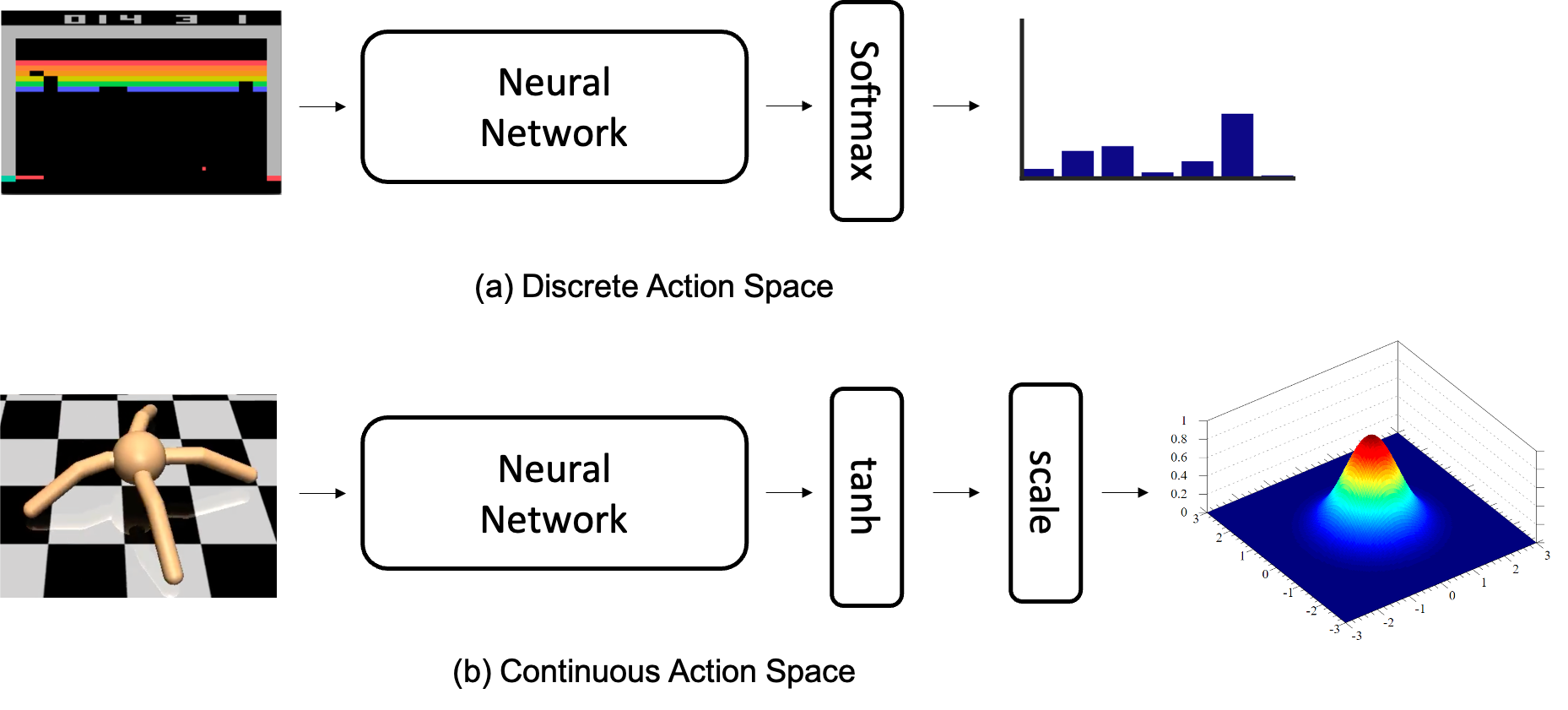discrete_vs_continuous2 Fig. Discete case는 마지막에 Softmax Layer를 통과시켜 Categorical Distribution을 출력하고, Continuous case는 Multivariate Gaussian Distribution을 추론하는 것으로 생각할 수 있겠습니다.

과연 어떻게 이런 setting 의 agent를 학습할 수 있을까요? 3가지의 idea를 살펴보려고 합니다.

Option 1 : Optimization

첫 번째는 Stochastic Optimization을 이용하는 것이라고 하는데, 그냥 random sampling 한다고 생각할 수 있겠습니다.

slide27 Slide. 27.

원래는 action이 up, down, left, right 4개라면 4개의 Q값 중 가장 큰 Q를 고르면 됐습니다만 continuous distribution인 경우 다 해볼 수는 없기 때문에 ramdon하게 sampling 해서 얻은 N개의 action들의 Q값을 측정하고 이 중 max를 취하는 것이죠. 일반적으로는 별로 정확하지는 않을 수 있으며 sampling을 하는만큼 computational cost가 들기 때문에 좋지 않은 방식이겠으나 action space가 작다거나 하면 꽤 나쁘지 않은 선택이라고 합니다.

slide28 Slide. 28.

Cross-Entropy Meothd (CEM)이나 CMA-ES 등의 improved method가 존재한다고 하는데, 궁금하신 분들은 관련 자료를 더 찾아보시면 좋을 것 같습니다.

(사실 reference 를 많이 못읽어봐서 그런지 어느 구석이 optimization based Q-Learning 이라는건지 모르겠습니다.)

Option 2 : Normalized Adantage Functions (NAF)

두 번째 옵션은 Continuous Deep Q-Learning with Model-based Acceleration 라는 논문의 방법론으로 Normalized Advantage Function (NAF) 입니다.

Key idea는 2차식 형태 (quadratic form)로 Q-Function을 나타내는 겁니다. 이렇게하면 2차식이 일반적으로 concave한 형태가 되기 때문에 현재 state에서 action에 대한 function, Q를 maximize하기 위해서 미분을 하면 \(\arg \max_a Q(s,a)\)인 a를 얻을 수 있겠죠?
(즉 closed-form 형태로 구할 수 있도록 NN을 미리 design한 것)

slide29 Slide. 29.

NAF에서는 어떤 NN이 state, \(s\)를 인풋으로 받아 \(\mu,P,V\)로 표현되는 세 가지 qunatity를 출력값으로 뱉습니다. 어떻게 vector와 matrix만으로 2차식을 만들어내는지는 어떤 함수를 테일러 전개했을 때 2차 항 까지만 표현하는 방법을 생각하시면 될 것 같습니다 (?). NAF에서는 이런 design 덕분에 \(\mu_{\phi}(s)\)로 표현할 수 있고, 그 때의 Q값은 \(V_{\phi}(s)\)를 inference하면 얻을 수 있습니다. 지금은 2차식 형태로 표현하기로 했기 때문에 representational power를 잃게되는 단점이 있지만 효율적으로 연속적인 행동 공간에 놓여진 문제를 Q-Learning으로 풀 수 있다고 합니다.

Pseudo Code

다음은 NAF algorithm을 구현한 pseudo code 입니다.

naf_algorithm Fig. NAF algorithm

그리고 아래는 실제 model의 입출력 관계를 나타낸 flow chart 인데, 실제 loss를 구하기 위해서 current Q network와 target Q network가 마찬가지로 존재하고, predicted \(Q(s,a)\)를 계산하기 위해서는 \(\mu, P, V\) heads를 전부 통과 시켜 얻은 값을 사용하고, TD target을 위해 \(Q(s',a')\)을 얻기 위해서는 \(V\)만 통과시키면 되는 것 같습니다.

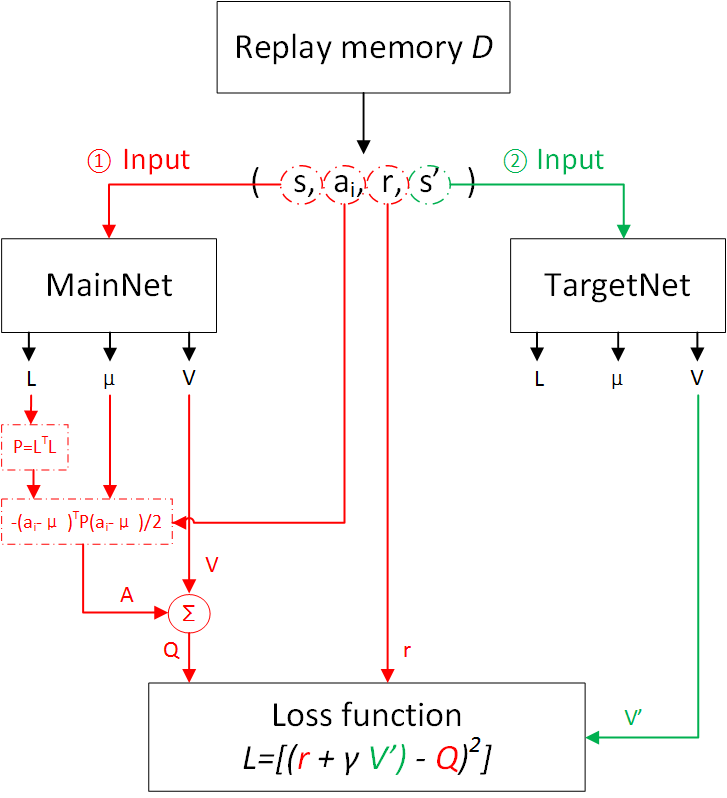naf_flowchart Fig. NAF Flowchart. Source from Deep reinforcement learning-continuous action control DDPG, NAF

Option 3 : Deep Deterministic Poliy Gradient (DDPG)

마지막 옵션은 approximate maximizer를 따로 학습하는 방법으로, Continuous control with deep reinforcement learning 라는 논문에서 소개된 방법론입니다. 이 paper에서 제시하는 algorithm은 Deep Deterministic Policy Gradient (DDPG)라고 불립니다.

DDPG는 사실 DQN + Deterministic Poliy Gradient (DPG)이기 때문에 실제로는 DPG를 알아야 합니다. OpenAI Spinning Up의 algorithm 종류를 보면 DDPG, SAC, TD3 같은 algorithm들은 Interpolating Between Policy Optimization and Q-Learning라고 소개되고 있습니다. “아니 Actor-Critic이 이미 value-based와 policy-based의 hybrid 아님?”이라고 생각할 수 있지만 이는 variance를 줄이기 위해 learnable critic을 도입한 것이지 일반적으로 policy optimization로 분류합니다. 즉 DPG는 일반적인 Actor-Critic과는 반대로 continuous action space에서의 DQN을 하기 위해서 actor를 도입한 것이라고도 생각할 수 있겠습니다. 문서에 따르면 “불행하게도 Q-Learning과 Policy Optimization은 양립할 수 없지만…“이라고 하는 문구가 보일 것인데, 아마 off-policyness 때문에 그런 것 같습니다 (Q-Learning은 대표적인 off-policy algorithm). 아무튼 주의할점은 DDPG는 policy based가 아니고 DQN에 더 초첨을 맞춘 hybrid method라는 겁니다.

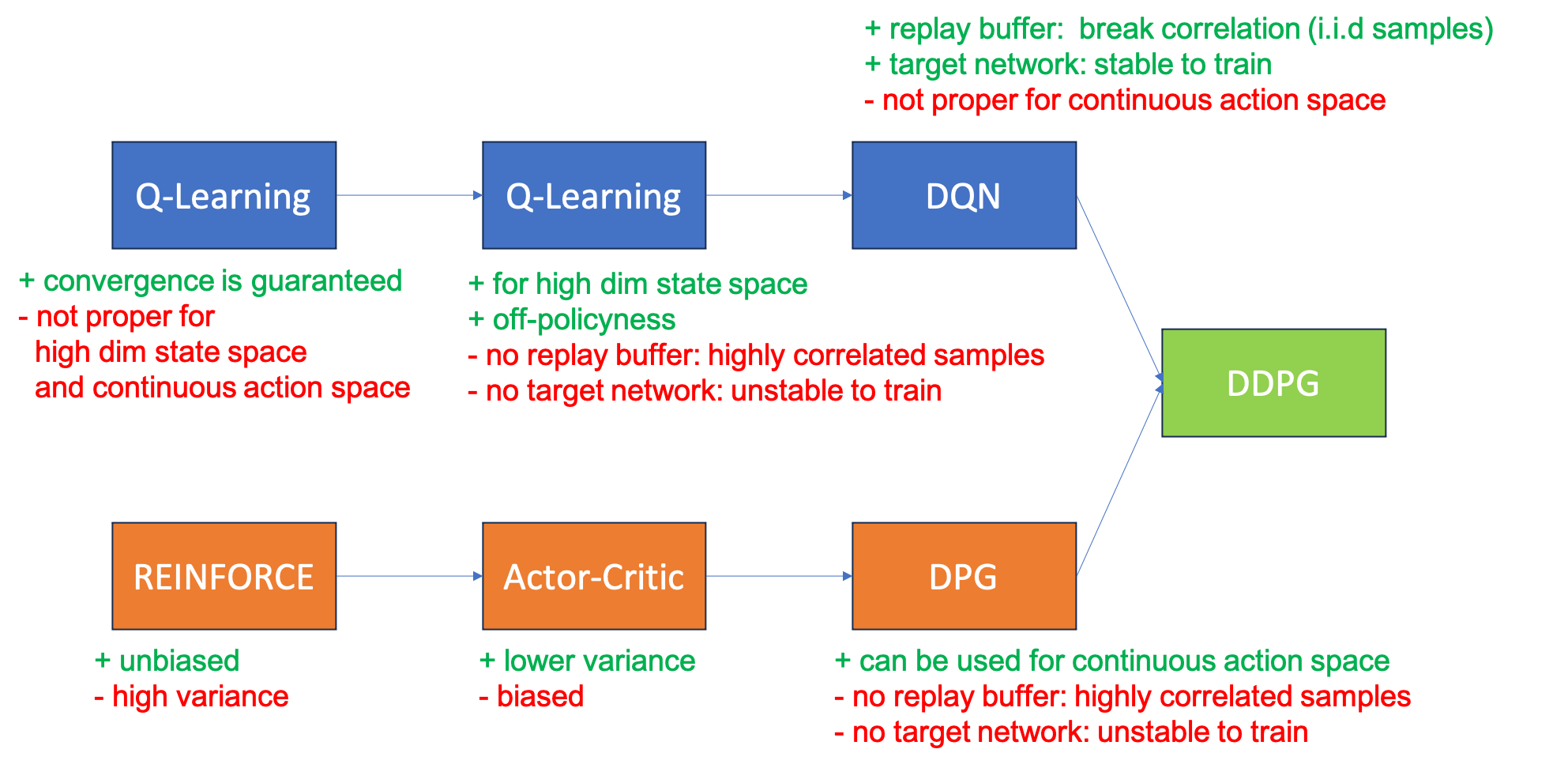from_dqn_dpg_to_ddpg Fig. 여태 배운 algorithm 의 장단점 비교. modified version of this slide

그럼 이제 DPG와 DDPG에 대해서 알아봅시다 (자세한 내용은 paper를 보시는 것을 추천드리지만 간단하게 느낌만). DPG의 핵심 아이디어는 다음의 역할을 하는 \(\theta\)로 파라메터화 된 NN를 학습하는 겁니다.

\[\mu_{\theta} (s) \approx \arg \max_a Q_{\phi}(s,a)\]

즉 이제 network가 두개인겁니다 (\(\phi, \theta\)).

slide30 Slide. 30.

여기서 \(\mu_{\theta}\)가 state를 input으로 받아 action을 return하는데, action 의 distribution을 뱉는 것이 아니라 무조건 (가장 likely한) action 하나만을 return하기 때문에 deterministic policy라고 불립니다. 반면에 우리가 lecture 5, 6에서 배운 policy들은 action의 distribution을 알려주기 때문에 (보통 categorical or gaussian), stochastic policy라고 부릅니다. (여기서 확률적으로 sampling을 할 수도 있죠)

그런데 이러면 “Actor, \(\theta\)는 어떻게 학습하지?”같은 생각이 바로 들겁니다. 왜냐하면 더이상 확률 분포가 아니기 때문에 likelihood에 log를 씌워서 gradient 를 계산하는 문제가 아니게 되었기 때문이죠. 이는 아래의 optimization problem을 풀면 된다고 하는데,

\[\theta \leftarrow \arg \max_{\theta} Q_{\phi} (s, \mu_{\theta}(s))\]

왜 이수식을 쓰게 됐는지 잠깐만 생각해봅시다. 우리가 지금 continuous action space 를 다루기 때문에 어떤 state에서 모든 action들을 했을 때의 \(Q^{\mu}(s,a)\)를 계산하고 그 중 max를 고르는 approach를 쓸 수 없죠. (여기서 \(\mu\)가 policy를 의미함)

\[\mu^{k+1} (s) = \arg \max_a Q^{\mu^k} (s,a)\]

즉 매 step마다 \(Q\)를 globally maximization을 하는 것은 불가능에 가깝다는 것인데, 그래서 DPG에서는 \(Q\)의 gradient 방향으로 policy를 살짝 update하는 단순한 대안책을 제안합니다.

\[\theta^{k+1} = \theta^{k} + \alpha \mathbb{E}_{s \sim \rho^{\mu^k}} [ \nabla_{\theta} Q^{\mu^k} (s, \mu_{\theta} (s) ) ]\]

여기서 \(\mu(s)\)가 determinisitc policy이기 때문에 더이상 action의 distribution을 출력하는 것이 아니라 action 값 하나만을 return하는 형태이고, 이 수식에 chain rule을 쓰면 policy improvement 는 action-value function, \(Q\)의 gradient와 policy의 gradient의 곱으로 decomposition 될 수 있습니다.

\[\begin{aligned} & \theta^{k+1} = \theta^{k} + \alpha \mathbb{E}_{s \sim \rho^{\mu^k}} [ \nabla_{\theta} Q^{\mu^k} (s, \color{red}{ \mu_{\theta} (s) } ) ] \\ & = \theta^{k} + \alpha \mathbb{E}_{s \sim \rho^{\mu^k}} [ \nabla_{\theta} \color{red}{ \mu_{\theta}(s) } \nabla_a Q^{\mu^k} (s,a) \vert_{\color{red}{ a = \mu_{\theta}(s) } } ] \\ \end{aligned}\]

여기서 \(\nabla_{\theta} \mu_{\theta} (s)\)는 jacobian matrix 라는데, 간단히 말해서 actor가 그 state에서 action을 sample해주면 Q network를 통과시켜 Q값을 얻은 뒤에 backpropagation을 하면 actor의 parameter, \(\theta\)까지 전파가 된다는 겁니다. (자세한 내용은 paper에)

실제 DDPG의 algorithm은 아래와 같은데,

slide31 Slide. 31.

앞서 말씀드렸지만 Actor-Critic 처럼 NN이 2개이므로 (\(\theta,\phi\)), 둘 다 update 해줘야 한다는 점을 잊으면 안됩니다.

이하 같은 내용이지만 paper의 algorithm을 보면 \(\mathcal{N}_t\)에서 sampling한 noise를 \(\mu(s_t)\)에 더해줌으로써 (reparameterization trick), discrete action space에서의 epsilon greedy 같은 exploration를 하는 걸 알 수 있습니다.

ddpg_algorithm Fig. DDPG algorithm

추가적으로 강의에서 언급하진 않았지만 NFQCA나 TD3, SAC등의 기법들도 있으니 관심있으신 분들은 더 찾아보시면 좋을 것 같습니다.

Pseudo Code and Implementation

아래는 DDPG algorithm을 구현한 pseudo code 입니다.

ddpg_pseudo_code Fig. Source from here

그리고 아래는 실제 model의 입출력 관계를 나타낸 flow chart 입니다.

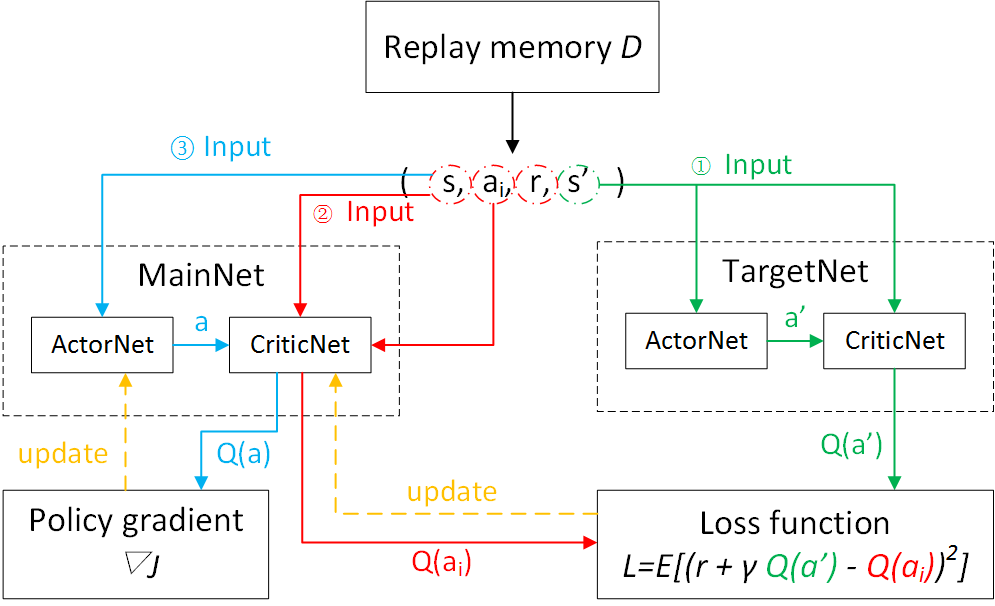ddpg_flowchart Fig. DDPG Flowchart. Source from Deep reinforcement learning-continuous action control DDPG, NAF

실제 CleanRL의 DDPG 구현체를 보면 좀 더 이해가 쉬울 것 같아 불필요한 부분을 제외하고 주석을 달아 첨부합니다.

  ## set env and replaybuffer (it's pseudocode!)
  device = 'cuda:0'
  envs = gym.vector.SyncVectorEnv()
  rb = ReplayBuffer()

  ## define Actor
  actor = Actor(envs).to(device)
  target_actor = Actor(envs).to(device)
  target_actor.load_state_dict(actor.state_dict())

  ## define Critic
  qf1 = QNetwork(envs).to(device)
  qf1_target = QNetwork(envs).to(device)
  qf1_target.load_state_dict(qf1.state_dict())

  ## define optimizer 
  actor_optimizer = optim.Adam(list(actor.parameters()), lr=args.learning_rate)
  q_optimizer = optim.Adam(list(qf1.parameters()), lr=args.learning_rate)

  ## generate samples
  obs, _ = envs.reset(seed=args.seed)

  ## training loop
  for global_step in range(args.total_timesteps):

    ## get (s,a,r,s') from current state, s
    with torch.no_grad():
      actions = actor(torch.Tensor(obs).to(device))
      actions += torch.normal(0, actor.action_scale * args.exploration_noise)
      actions = actions.cpu().numpy().clip(envs.single_action_space.low, envs.single_action_space.high)
    next_obs, rewards, terminations, truncations, infos = envs.step(actions)

    ## save transition to replay buffer
    real_next_obs = next_obs.copy()
    for idx, trunc in enumerate(truncations):
        if trunc:
            real_next_obs[idx] = infos["final_observation"][idx]
    rb.add(obs, real_next_obs, actions, rewards, terminations, infos)

    obs = next_obs

    ## sample from replay buffer
    data = rb.sample(args.batch_size)

    ## get TD target using Actor and Critic
    with torch.no_grad():
      next_state_actions = target_actor(data.next_observations)
      qf1_next_target = qf1_target(data.next_observations, next_state_actions)
      next_q_value = (
        data.rewards.flatten() 
        + (1 - data.dones.flatten()) * args.gamma * (qf1_next_target).view(-1)
      )
    qf1_a_values = qf1(data.observations, data.actions).view(-1)
    qf1_loss = F.mse_loss(qf1_a_values, next_q_value)

    ## optimize Critic 1 step
    q_optimizer.zero_grad()
    qf1_loss.backward()
    q_optimizer.step()

    ## get Actor Loss and optimize Actor 1 step
    actor_loss = -qf1(data.observations, actor(data.observations)).mean()
    actor_optimizer.zero_grad()
    actor_loss.backward()
    actor_optimizer.step()

    ## Update target networks
    for param, target_param in zip(actor.parameters(), target_actor.parameters()):
        target_param.data.copy_(args.tau * param.data + (1 - args.tau) * target_param.data)
    for param, target_param in zip(qf1.parameters(), qf1_target.parameters()):
        target_param.data.copy_(args.tau * param.data + (1 - args.tau) * target_param.data)

가장 궁금했던 것은 실제로 deterministic actor의 loss가 어떻게 전파되는가? 였는데, 어떻게 이게 구현이 되어있는지 봅시다.

slide31 Fig. 5번의 actor update 수식이 의미하는 바는 정확히 무엇일까?

먼저 actor가 scalar value를 return하면 거기에 noise (variance 와 exploration noise)를 더해서 최종적으로 \(s_t\)에서의 가장 likely한 action, \(a_t\)을 얻습니다. 그리고 \((s_t,a_t)\)를 통해 environment로부터 \((r,s_{t+1})\)를 얻습니다. 그리고 target actor를 통해서 \(a_{t+1}\) 를 또 얻고, 최종적으로 target critic을 통해 \(Q(s_{t+1}, a_{t+1})\)을 얻습니다. 이제 TD target을 조립하면 되는데, current reward, \(r\)과 discounted next Q를 더해서 계산하면 됩니다. 이제 그대로 critic은 update하면 되고, 문제는 actor인데 Q network에 \((s_t, a_t)\)를 feeding 해서 \(Q(s_t, a_t)\)를 얻습니다 (당연히 내부적으로 computattional graph를 들고있습니다). 그리고 그냥 그 값에 log 없이 negative (-1) 를 곱해줍니다. 그리고 backpropagation을 하면 됩니다. 즉 deterministic actor에 gradient를 흘리기 위해서 Q를 이용한 겁니다.

DPG, DDPG 그리고 SAC등에 대해서는 따로 post를 작성할 것이므로 더 궁금하신 분들은 참고하시면 좋을 것 같습니다.

Implementation Tips and Examples

마지막 subsection은 Q-Learning algorithm을 구현할 때 practical한 tip과 몇 가지 Q-Learning을 사용한 paper 예시들 입니다.

Implementation Tips

slide33 Slide. 33.

Q-Learning은 실제로 사용하기에 Policty Gradient보다 더 까다롭다고 (finicky) 합니다. 학습하는 데 있어서 stability가 항상 문제가 된다고 하는데 Sergey는 우선 DQN 같은 algorithm을 구현했으면 쉬운 task부터 학습하고 test 해 보면서 하면서 bug가 있지는 않은지? 잘 구현했는지?를 체크해보라고 합니다. 그 다음에 hyperparameter를 tuning하고 실제 문제에 적용해 보는 것을 추천한다고 합니다. (deep learning methods 도 다 그러지 않나…?)

dqn_implementation1 Figure from Prioritized Experience Replay

위의 그림이 나타내는 바는 똑같은 algorithm을 다른 random seed로 실험했을때의 차이를 나타내는데 어려운 문제일수록 seed에 따라서 학습에 실패할 경우도 있고 성공할 경우도 있다고 합니다. (그러니까 쉬운 task 부터 적용해보라고 하는거같네요)

강의에서 언급하는 몇가지 팁을 정리해보자면 아래와 같습니다.

  • 쉬운 task 부터 검증해봐라
  • Replay Buffer를 1 milion 정도로 크게 만들어서 써라
  • 인내심을 가져라 (…)
  • epsilon 을 크게가져가서 점점 줄여라 (초기에 exploration 많이 하라는 뜻)

(사실 다 deep learning에도 다 통용되는 말 같습니다;)

slide34 Slide. 34.

그 다음으로 언급하는 문제는 Q-Target과 Prediction 사이의 Error Gradient가 너무 클 경우 입니다. 해결책은 바로 일정치 이상의 경우에 graident를 clip해버린다던가 Huber Loss를 사용하는 방법을 써보라고 하네요. Huber Loss는 Absolute Loss와 Square Loss를 적절히 interpolation한 간단한 방법으로 Robust Linear Regression 에 사용되는 방법이라고 합니다.

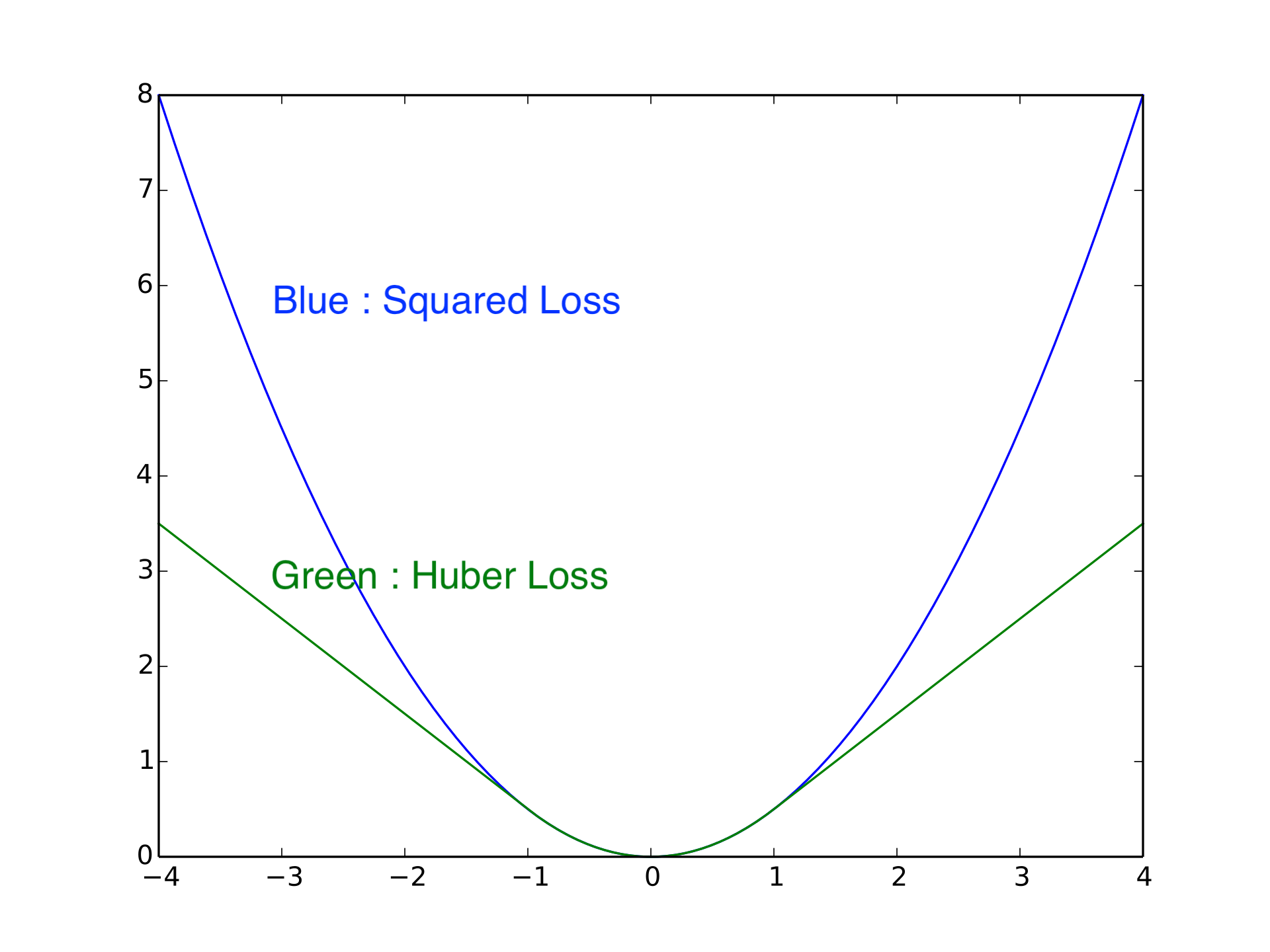huber_vs_squared Fig. Squared Loss vs Huber Loss

실제로 Q-Learning을 할 때 Double Q-Learning을 쓰는 것도 굉장히 잘 작동한다고 합니다. N-step return을 사용하는 방법 같은 경우는 좋긴 하지만 앞서 얘기한 것 처럼 bias를 증가시키기 때문에 성능 감소 (downside)를 가져올 수도 있으니 주의하라고 합니다. 그리고 앞서 말한 것 처럼 Exploration Scheduling을 하거나 (처음에 exploration을 많이 하고 학습이 될수록 감쇠시킴), 딥러닝에서 자주 쓰이는 Learning Rate (LR) scheduling 를 한다거나 Adam 을 쓴다거나 하는 것도 잘 먹힌다고 합니다.

마지막으로 디버깅을 할 때 다양한 random seed로 여러번 실험해서 algorithm을 검증해야 한다고 합니다. (RL은 random seed에 따라 결과가 천차만별인 경우가 많다고 하므로 좋은 paper에서 제안된 algorithm들 중에서도 작동하지 않는게 많다고 들은 것 같습니다)

Some Papers and Examples

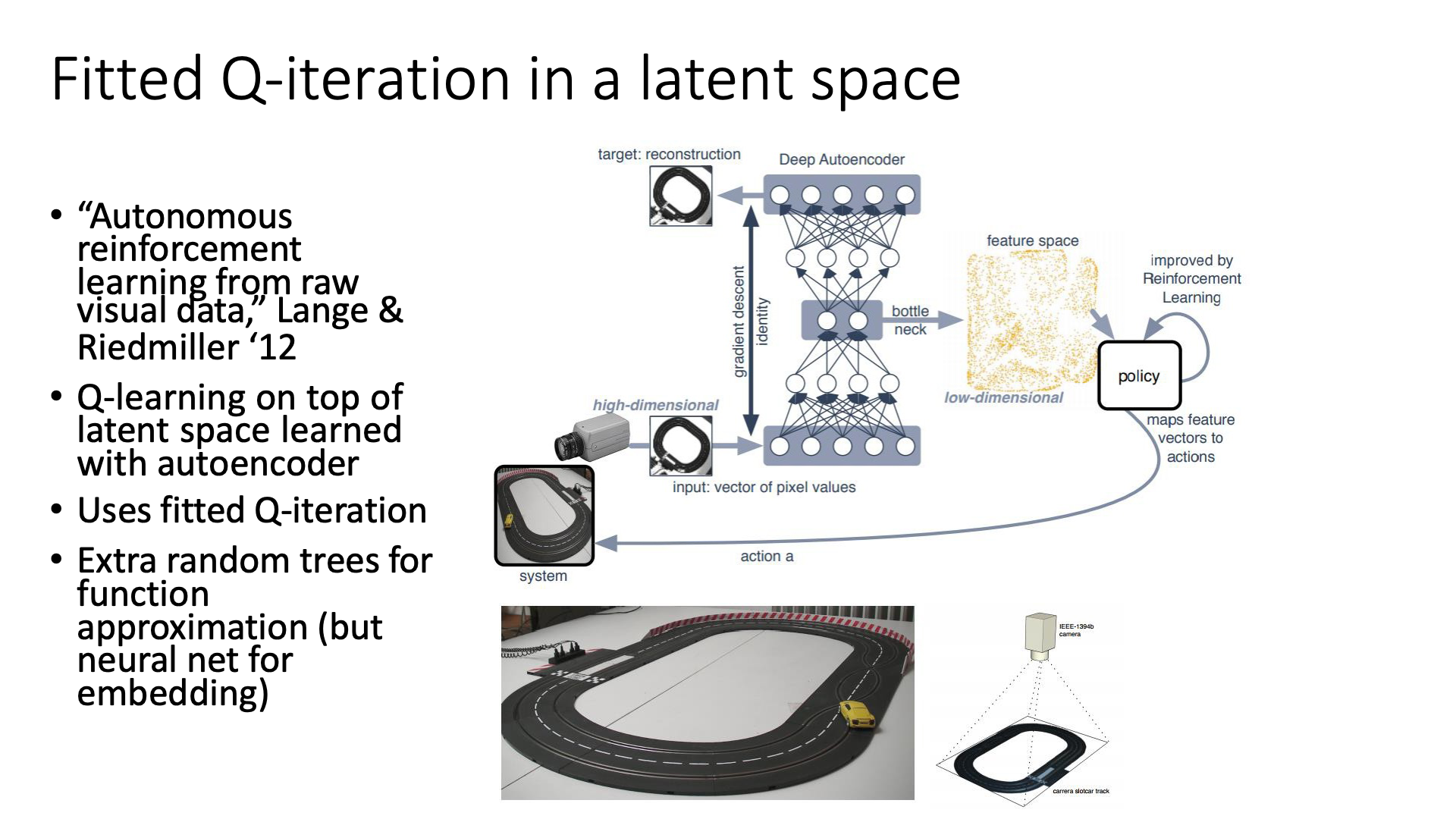
다음은 몇 가지 실전 예시들 입니다. 첫 번째는 Autonomous reinforcement learning on raw visual input data in a real world application로 Deep Learning과 Fitted Q-Iteration을 결합한 거의 최초의 논문이라고 합니다.

slide35 Slide. 35.

사실 이 paper는 여태 커버한 내용과는 다르게 우리가 후에 다루게될 Model-based Q-Iteration과 관련이 있다고 하는데요, 이는 입력 이미지를 오토인코더로 뽑은 latent vector로 바꾼 뒤에 Q-Iteration을 쓰는데요 중요한 점은 여기서 Neural Network로 모델링된 Q-Network를 쓰는건 아니고 tree구조를 썼다고 합니다.

그 다음으로 소개드릴 paper는 제가 여러번 말씀드린 Human-level control through deep reinforcement learning입니다. 그 유명한 Atari 게임을 사람 수준으로 플레이하는 모습을 보여줬죠.

slide36 Slide. 36.

이미 많이 설명했으니 여태까지 배운 keyword들로 짧게 요약하고 넘어가도록 하겟습니다.

  • Q-Learning with CNN
  • Large Replay Buffer
  • One-step backup
  • One gradient step
  • DDQN 으로 더 좋은 성능 도달 가능

그 다음은 Continuous control with deep reinforcement learning인데요, DDPG가 제안된 논문이죠.

slide37 Slide. 37.

이것도 넘어가도록 하겠습니다.

마지막 Slide. 38의 내용은 Deep Reinforcement Learning for Robotic Manipulation with Asynchronous Off-Policy Updates 라는 논문의 내용인 것 같은데 Real World에서 먹히는 Continuous Action Space를 가지는 Robotics 문제를 풀기 위해서 NAF를 사용한 논문입니다. Sergey가 교신저자입니다.

slide38 Slide. 38.

여러 로봇이 parallel하게 문을 여는걸 학습하는 off-policy 방법이라고 하는데, 여기서는 실제 로봇이 행동하는 걸로 sample을 모으기 때문에 굉장히 비효율적이라서 한스텝씩 업데이트하기가 쉽지 않으므로, 가능한 적은 데이터로 최고 효율을 내기 위해서 4번씩 gradient step을 했다고 합니다.

마지막 예시는 QT-Opt: Scalable Deep Reinforcement Learning for Vision-Based Robotic Manipulation입니다. 2018년에 제안된 논문으로 마찬가지로 Sergey가 교신저자입니다.

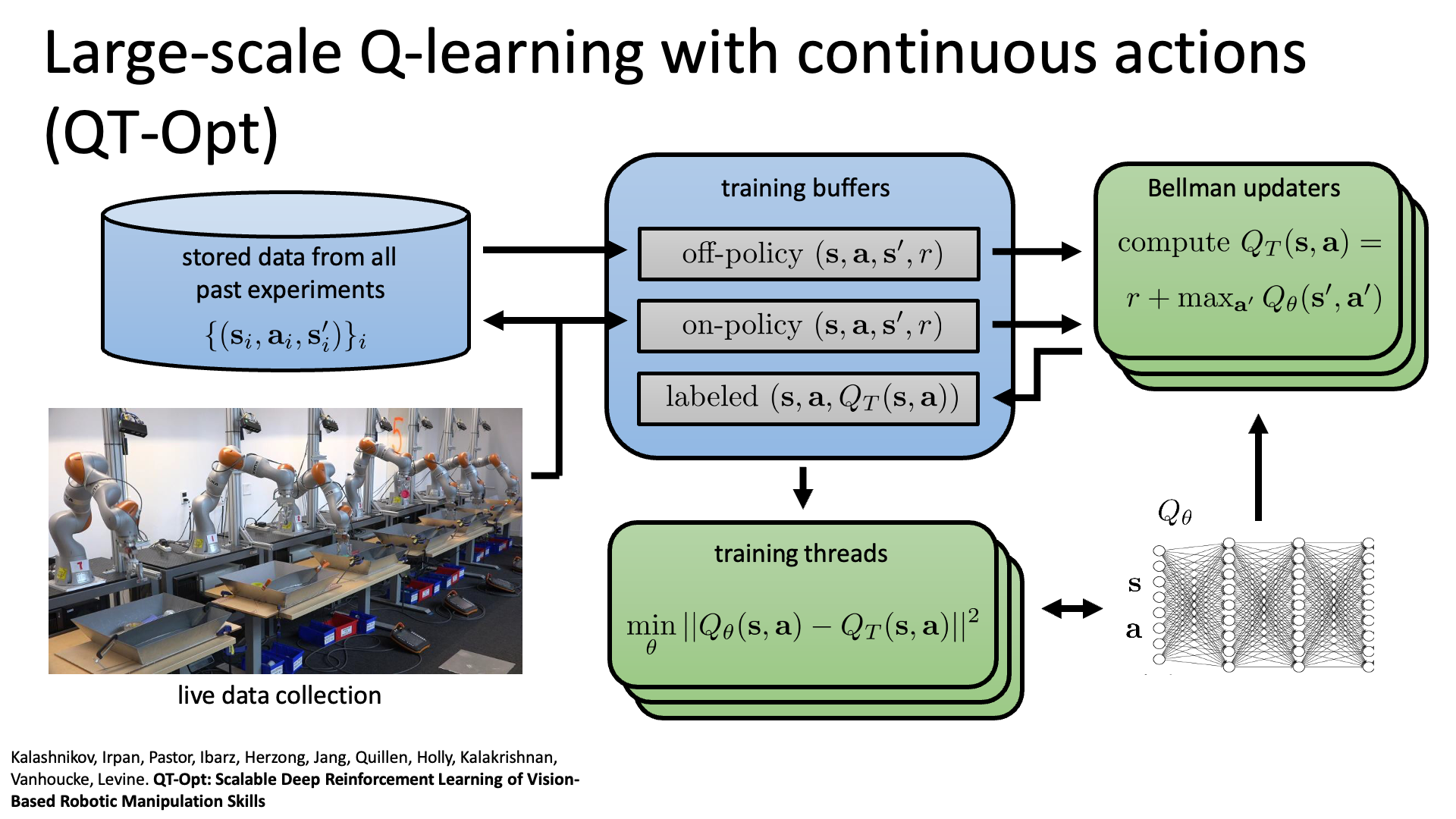slide39 Slide. 39.

끝으로 Sergey가 궁금해 할 독자들을 위해 읽을만한 paper를 listup 해주고 review를 하면서 강의는 끝이 납니다.

slide40 Slide. 40. Paper list

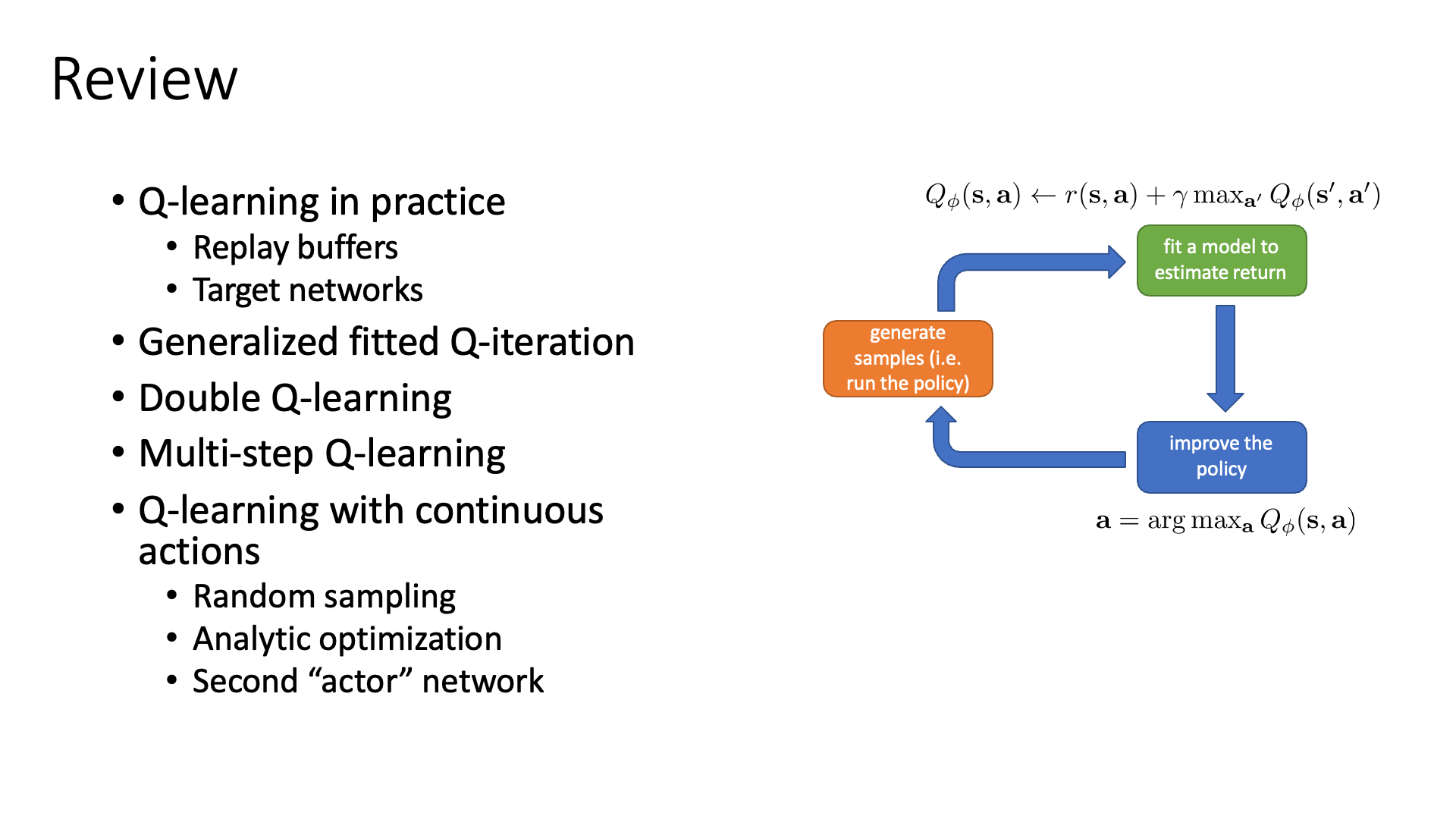slide41 Slide. 41. Review는 생략

Reference