Machine FLOPs Utilization (MFU)
04 Jul 2024< 목차 >
Why Machine FLOPs Utilization (MFU) ?
Large Scale Distributed Training을 위한 기술을 소개하는 blog post들을 보면 Machine FLOPs Utilization (MFU)라는 용어를 심심치않게 볼 수 있다.
이는 말 그대로 “Training time 동안 hardward가 낼 수 있는 peak Floating point operations per second (FLOPS, flops or flop/s) 대비 얼마나 많은 FLOPs를 점유했는가?”를 의미하는 metric이다.
여기서 FLOPs는 초당 GPU가 몇 개의 부동 소수점 (floating-point) 연산 (operation)을 할 수 있는 지를 의미한다. FLOPS가 높으면 같은 시간 동안 더 많은 operation을 처리했다는 뜻이다. 단위는 1000000 FLOPS = 1 GFLOPS, 1000 GFLOPS = 1 TFLOPS, 1000 TFLOPS = 1 PFLOPS 등을 사용한다.
아래 pytorch blog의 table을 보자. 이들은 pytorch의 internal distributed optimizer인 Fully Sharded Data Parallel (FSDP)와 Just In Time (JIT)에 한번에 묶어서 연산이 가능한 것들은 알아서 합쳐주는 (kernel fusion) 기능인 torch.compile를 홍보하기 위해, 각 technique을 llama model에 적용한 뒤 MFU를 측정했고 결과는 다음과 같다.
이들은 서로 다른 4개의 model size를 2개 GPU cluster에 대해서 측정했는데, 하나는 128 A100 GPUs로 이루어져있으며 400 Gbps inter-node connectivity를 가지고 있고, 다른 하나는 464 H100 GPUs에 3.2 Tbps connectivity를 가지고 있다고 한다.
 Fig. 128 A100, 400 Gbps
Fig. 128 A100, 400 Gbps
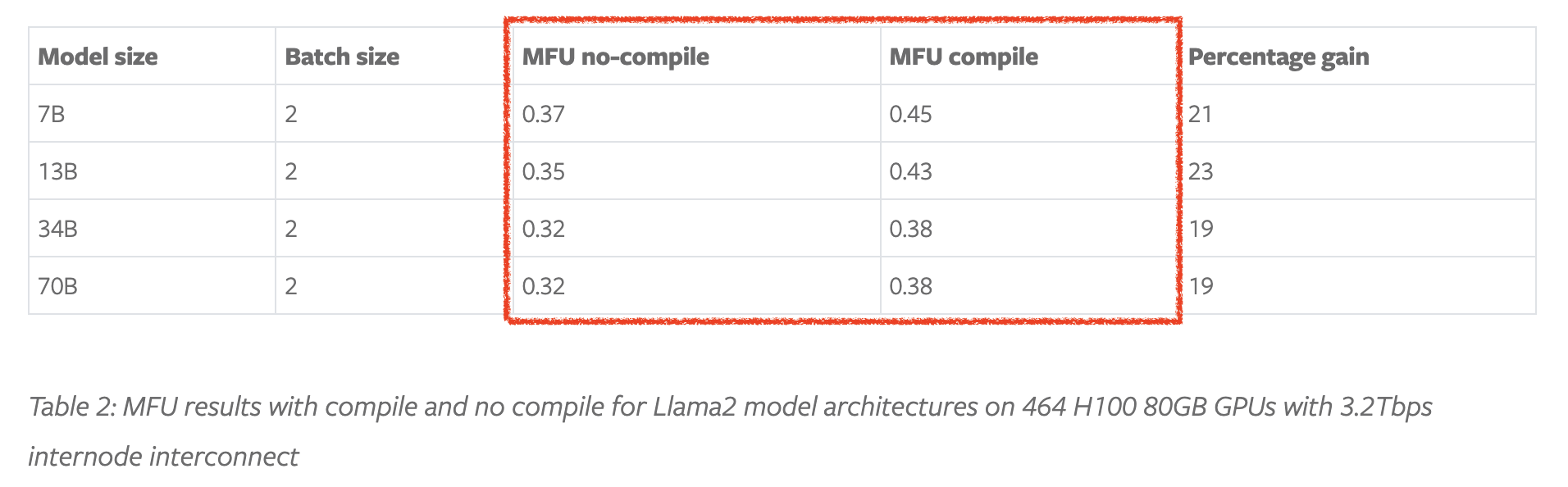 Fig. 464 A100, 3.2 Tbps
Fig. 464 A100, 3.2 Tbps
대충 "아 이정도 규모에서는 이정도 MFU가 나와야 평타는 치는구나"로 받아들이면 될 것 같은데,
H100이 더 느린 이유에 대해서 infiniband issue가 있다고 했던가? 그렇게 들은 것 같다.
이들은 결과적으로 448 GPUs (H100인지 A100인지 모르겠다)를 selective activation checkpointing과 torch.compile을 사용해 global batch size를 3.7e6 (M)으로 setting해서 4e12 (T) tokens를 사용해 llama2 model arch를 학습하는 데 고작 13 days 10 hours만 걸렸다고 한다.
하지만 model size가 커질 때 MFU가 linear하게 증가하지 않는 것을 볼 수 있는데, 저자들은 node가 매우 많을 때에는 Tensor Parallel (TP)같은 technique가 필요하다거나 하는 부분을 지적하고 있다. 어쨌든 MFU가 50이 넘는건 사실 굉장히 잘 나오는거라고 할 수 있다.
이번에는 NVIDIA의 Megatron LM repo를 보자. Megatron에서도 성능 지표로 model size별 MFU를 측정하고 있다.
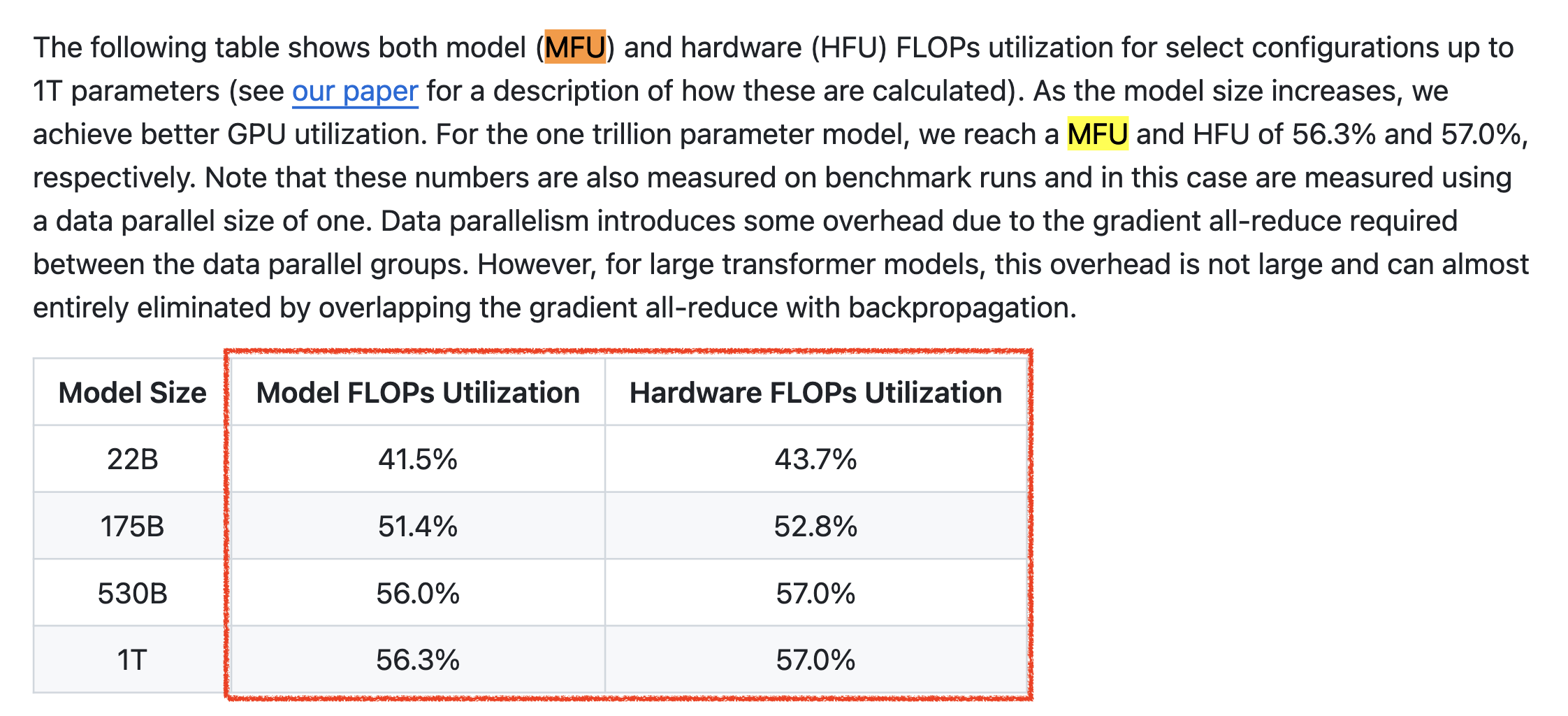 Fig.
Fig.
NVIDIA의 경우도 linear하게 증가하는지는 모르겠으나, 그래도 우상향 하는 trend를 확인할 수 있다.
이렇듯 어떤 “distributed system이 좋은지?”, “이 distributed setting이 해당 model size에 최적인지?”, “우리 연구 그룹이 최대한 GPU를 잘 활용하고 있는지? 어딘가에 병목이 있는건 아닌지?”, “어디를 집중적으로 최적화 (kernel fusing) 해야 하는지?” 등등을 판단하기 위해서는 MFU를 재는 것이 필수라고 할 수 있다.
How To Measure MFU
How To Compute The Number of Parameter and FLOPs per Tokens
MFU를 측정하기 위해서는 먼저 내가 학습하려는 model의 token당 Floating point operations per second (FLOPS, flops or flop/s)를 계산할 수 있어야 한다. 이는 Kaplan et al.의 Scaling Law paper에 자세히 나와있는데, paper를 참고해도 좋고 이를 code로 구현한 karpath의 notebook이나 blog post 등을 참고하면 좋을 것 같다.
- MFU, FLOPs per token에 대해 정의 및 언급한 paper list
먼저 계산에 사용될 notation들은 다음과 같다.
- model size: \(N\)
- number of layers: \(n_{\text{layer}}\)
- hidden size: \(d_{\text{model}}\)
- intermediate hidden size: \(d_{\text{ff}} = 4 d_{\text{model}}\)
- attention output dim size: \(d_{\text{attn}} = d_{\text{model}}\)
- number of attention heads per layer: \(n_{\text{heads}}\)
- context length: \(n_{\text{ctx}}\)
이제 이 term들을 따라서 model size, \(N\)과 model을 forward하는데 필요한 FLOPs는 다음 table과 같이 정리가 된다.

대부분은 Feed Forward Network (FFN)의 intermediate dim, \(d_{\text{ff}}\)는 \(d_{\text{model}}\)의 4배로 설정되고, attention output hidden size, \(d_{\text{attn}}\)는 \(d_{\text{model}}\)와 같은게 일반적이므로, model size는 다음과 같이 쓸 수 있다.
\[\begin{aligned} & N \approx 2 d_{\text{model}} n_{\text{layer}} (2 d_{\text{attn}} + d_{\text{ff}}) & \\ & = 12 n_{\text{layer}} d_{\text{model}}^2 & \\ \end{aligned}\]여기서 bias등은 model size에 contirubte 하지 않는데 (제외되는데), 이것 말고도 embedding matrix, \(n_{\text{vocab}} d_{\text{model}}\)과 positional embeddings, \(n_{\text{ctx}} d_{\text{model}}\)도 제외된다. 이는 Kaplan et al.이 Scaling Law prediction을 할 때 더 부드러운 plot을 얻기 위해서라고 paper에 쓰여있다.
Transformer의 forward pass, \(C_{\text{forward}}\)는 대략적으로 다음과 같이 계산되는데,
\[C_{\text{forward}} \approx 2 N + 2 n_{\text{layer}} n_{\text{ctx}} d_{\text{model}}\]여기서 model size에 계수가 2 붙는 이유는 matmul을 할 때 multiply-accumulate (아마 multiply-add 얘기하는듯) operation이 사용되기 때문이다.
FLOPs에 대해 헷갈릴 수 있어 recap하자면 \(K \times M\), \(M \times N\) matrix 두 개를 곱할 때 총 \(M * N * K\)의 Fused Multiply-Adds (FMAs)가 발생하고 (link 참고), 각각 FMA는 덧셈과 곱셈 2개의 operation으로 이루어져 있으므로 총 \(2*M*N*K\) FLOPs가 필요하게 된다. 그렇기 때문에 여기서 한 token에 대해서 QKV attention projection을 하려면 Transformer는 self attention이 residual block마다 있으니 layer 갯수만큼 곱해주고, 한 token vector \(1 \times d_{\text{model}}\)과 \(d_{\text{attn}} \times d_{\text{attn}}\)의 weight matrix 3번이 곱해지므로 \(2 n_{\text{layer}} d_{\text{model}} 3 d_{\text{attn}}\)이 되는 것이다.
이 table에서 아마 다른 건 다 이해가 갈텐데,
attention: mask라는 operation에 대해서는 따로 설명이 쓰여있지 않다.
이 연산은 \(2 n_{\text{layer}} n_{\text{ctx}} d_{\text{attn}}\)이고,
sequence length (context length)에 비례하는 것으로 보아 \(QK^T\)를 의미하는 것 같다.
아무튼 Kaplan et al.에서의 총 forward 연산은 \(C_{\text{forward}} \approx 2 N + 2 n_{\text{layer}} n_{\text{ctx}} d_{\text{model}}\)가 되는데, Kaplan은 \(d_{\text{model}} > n_{\text{ctx}}/12\)인 경우 \(C \approx 2N\)로 근사할 수 있다고 하는데, GPT-3를 학습하던 시절에는 이게 성립하기 때문에 무시할 수 있었던 것으로 보인다. 여기에 backward가 보통 forward의 2배라는 점을 고려하면 non-embedding compute는 \(C \approx 6N\)이 되는 것이다. 이것이 한 token당의 forward + backward FLOPs가 되므로 한 iteration step에 쓰인 token갯수를 곱하면 우리는 \(6ND\)라는 수식을 얻게 된다.
한 편, model parameter와 token당 FLOPs를 재는 공식에는 또 다른 이견이 있는데, Hoffmann et al.의 Chinchilla Optimal paper를 보면 이에 대한 수식이 나와있다. 이들과 Kaplan의 가장 큰 차이는 attention에 드는 FLOPs와 embedding matrix의 contribution을 정확히 계산했다는 것이다.
 Fig.
Fig.
그 결과 아래와 같은 Kaplan et al.과 Hoffmann et al.에는 아래와 같은 차이가 있었다고 하는데, model size가 커질수록 embedding matrix의 contribution이 작기 때문에 그렇게 큰 차이가 안나는 것 같고 작을수록 많이 나는 것 같다.
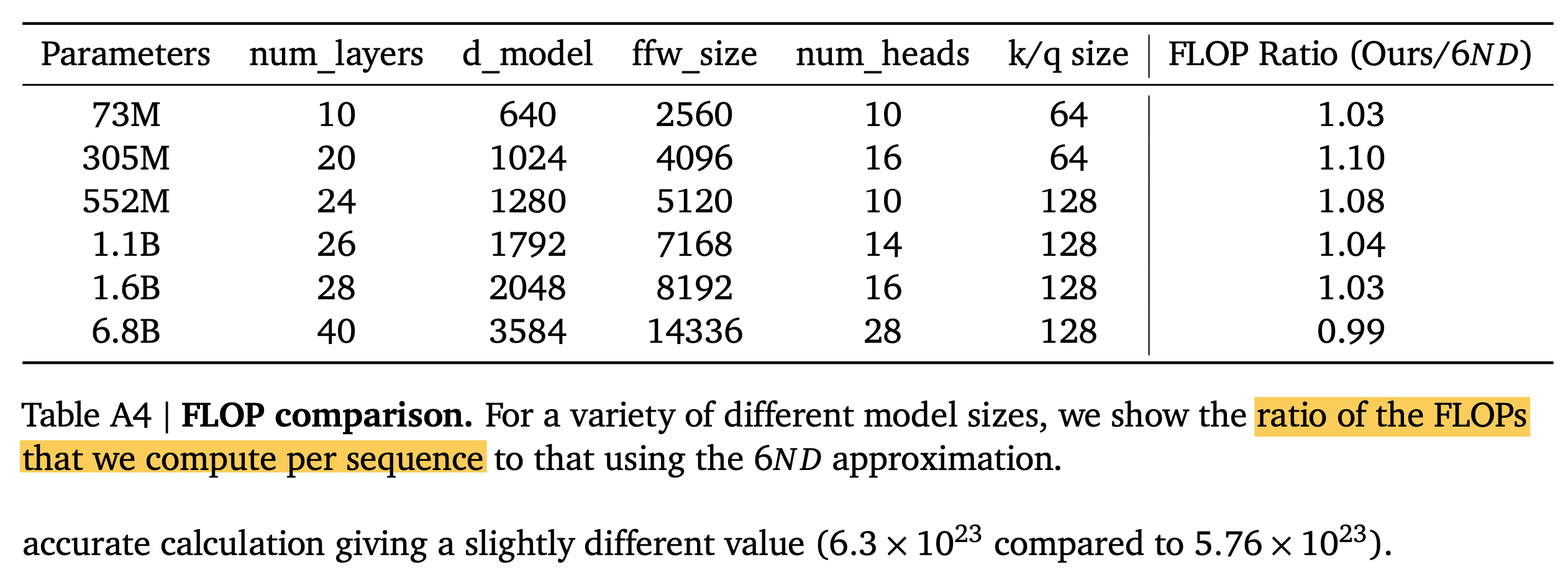 Fig.
Fig.
Code implementation은 다음과 같다 (reference).
def openai_flops_per_token(n_layers, n_heads, d_model, n_ctx, n_vocab, ff_ratio=4):
"""
Open AI method for forward pass FLOPs counting of decoder-only Transformer
"""
d_attn = d_model // n_heads
d_ff = d_model * ff_ratio
embeddings = 4 * d_model
attn_qkv = 2 * n_layers * d_model * 3 * (d_attn * n_heads)
attn_mask = 2 * n_layers * n_ctx * (d_attn * n_heads)
attn_project = 2 * n_layers * (d_attn * n_heads) * d_model
ff = 2 * n_layers * 2 * d_model * d_ff
logits = 2 * d_model * n_vocab
return embeddings + attn_qkv + attn_mask + attn_project + ff + logits
def deepmind_flops_per_sequence(n_layers, n_heads, d_model, n_ctx, n_vocab, ff_ratio=4):
"""
DeepMind method for forwad pass FLOPs counting of decoder-only Transformer
"""
d_attn = d_model // n_heads
d_ff = d_model * ff_ratio
embeddings = 2 * n_ctx * n_vocab * d_model
attn_qkv = 2 * n_ctx * 3 * d_model * (d_attn * n_heads)
attn_logits = 2 * n_ctx * n_ctx * (d_attn * n_heads)
attn_softmax = 3 * n_heads * n_ctx * n_ctx
attn_reduce = 2 * n_ctx * n_ctx * (d_attn * n_heads)
attn_project = 2 * n_ctx * (d_attn * n_heads) * d_model
total_attn = attn_qkv + attn_logits + attn_softmax + attn_reduce + attn_project
ff = 2 * n_ctx * (d_model * d_ff + d_model * d_ff)
logits = 2 * n_ctx * d_model * n_vocab
return embeddings + n_layers * (total_attn + ff) + logits
이 외에도 PaLM paper와 karpathy의 nanoGPT version들도 있는데, 각각 수치가 조금씩 다르지만 대략적으로는 비슷하다고 할 수 있겠다.
def karpathy_flops(n_layer, n_embd, n_head, block_size):
# we only count Weight FLOPs, all other layers (LayerNorm, Softmax, etc) are effectively irrelevant
# we count actual FLOPs, not MACs. Hence 2* all over the place
# basically for any matrix multiply A (BxC) @ B (CxD) -> (BxD) flops are 2*B*C*D
out = OrderedDict()
head_size = n_embd // n_head
# attention blocks
# 1) the projection to key, query, values
out['attention/kqv'] = 2 * block_size * (n_embd * 3*n_embd)
# 2) calculating the attention scores
out['attention/scores'] = 2 * block_size * block_size * n_embd
# 3) the reduction of the values (B, nh, T, T) x (B, nh, T, hs) -> (B, nh, T, hs)
out['attention/reduce'] = 2 * n_head * (block_size * block_size * head_size)
# 4) the final linear projection
out['attention/proj'] = 2 * block_size * (n_embd * n_embd)
out['attention'] = sum(out['attention/'+k] for k in ['kqv', 'scores', 'reduce', 'proj'])
# MLP blocks
ffw_size = 4*n_embd # feed forward size
out['mlp/ffw1'] = 2 * block_size * (n_embd * ffw_size)
out['mlp/ffw2'] = 2 * block_size * (ffw_size * n_embd)
out['mlp'] = out['mlp/ffw1'] + out['mlp/ffw2']
# the transformer and the rest of it
out['block'] = out['attention'] + out['mlp']
out['transformer'] = n_layer * out['block']
out['dense'] = 2 * block_size * (n_embd * vocab_size)
# forward,backward,total
out['forward_total'] = out['transformer'] + out['dense']
out['backward_total'] = 2 * out['forward_total'] # use common estimate of bwd = 2*fwd
out['total'] = out['forward_total'] + out['backward_total']
return out
# compare our param count to that reported by PyTorch
f = karpathy_flops()
flops_total = f['forward_total']
print(f"{'name':20s} {'flops':14s} {'ratio (%)':10s}")
for k,v in f.items():
print(f"{k:20s} {v:14d} {v/flops_total*100:10.4f}")
def palm_flops():
"""estimate of the model flops following PaLM paper formula"""
# non-embedding model parameters. note that we do not subtract the
# embedding/token params because those are tied and get used in the last layer.
N = params()['total'] - params()['emebedding/position']
L, H, Q, T = n_layer, n_head, n_embd//n_head, block_size
mf_per_token = 6*N + 12*L*H*Q*T
mf = mf_per_token * block_size
return mf
print(f"palm_flops: {palm_flops():d}, flops: {flops()['total']:d}, ratio: {palm_flops()/flops()['total']:.4f}")
Karpathy의 flops는 거의 bias를 제외하고 모든 matmul의 contribution을 정확히 계산한 것으로 보이고, PaLM approach는 embedding을 제외하지 않았다. (개인적으로는 Karpathy’s가 제일 맘에든다)
Scaling Of FLOPs Contribution
Sequence length, \(n_{\text{ctx}}\)가 4096일 때, model size가 커질수록 FLOPs contribution이 어떻게 변하는지 한 번 관찰해 보자.
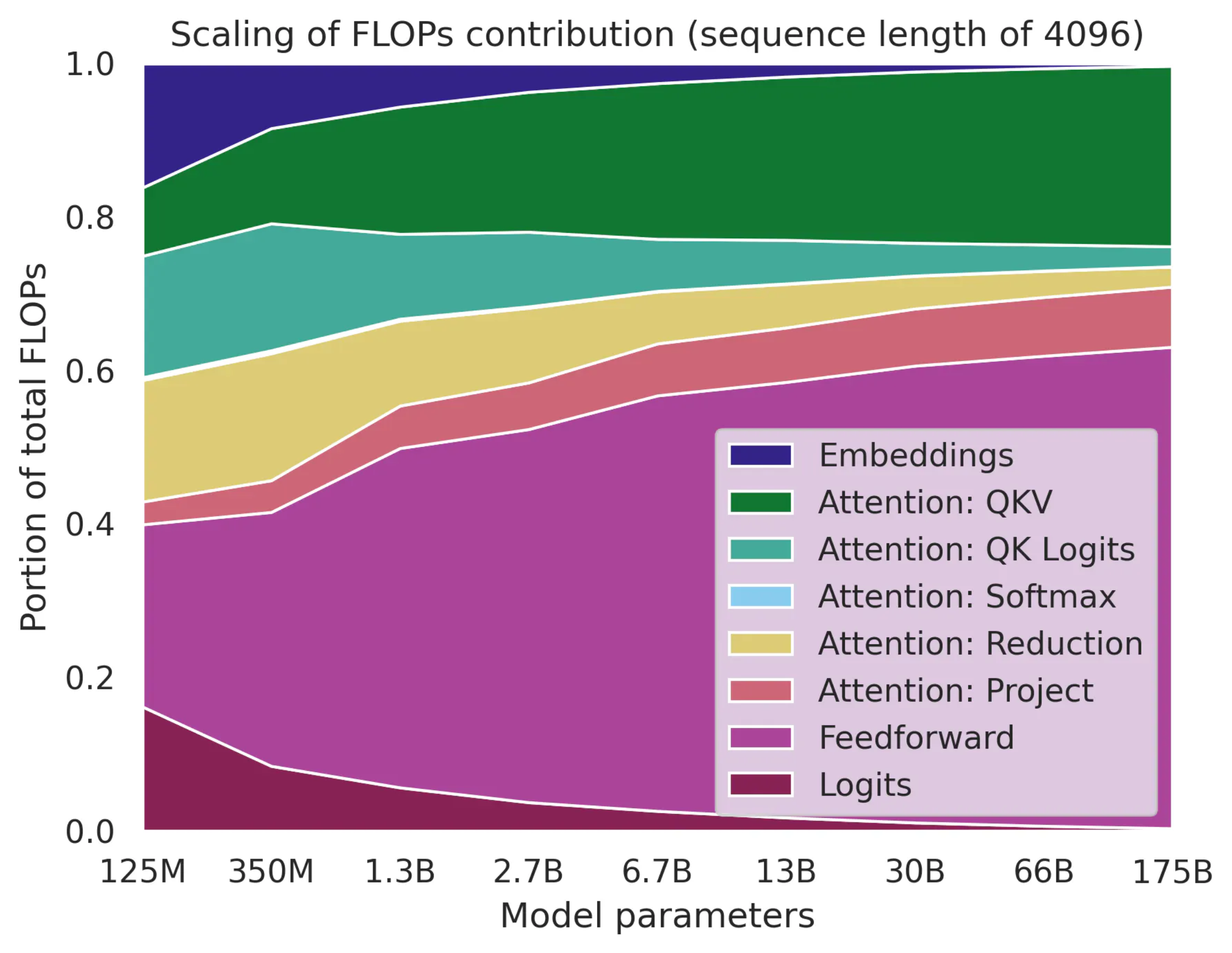 Fig. Source from here
Fig. Source from here
먼저 model size (보통 width, \(d_{\text{model}}\))가 커질수록 FFN이나 QKV projection의 기여도가 높아지는 걸 볼 수 있다. 그리고 embedding과 logit의 기여도는 줄어들게 된다. 그리고 Chinchilla 기준 sequence length에 linear인 term과 quadratic인 term이 있는데,
- Linear
- Embeddings
- Attention: QKV
- Attention: Project
- Feedforward
- Logits
- Quadratic
- Attention: QK logits
- Attention: Softmax
- Attention: Reduction
이들의 contribution은 다음과 같다.
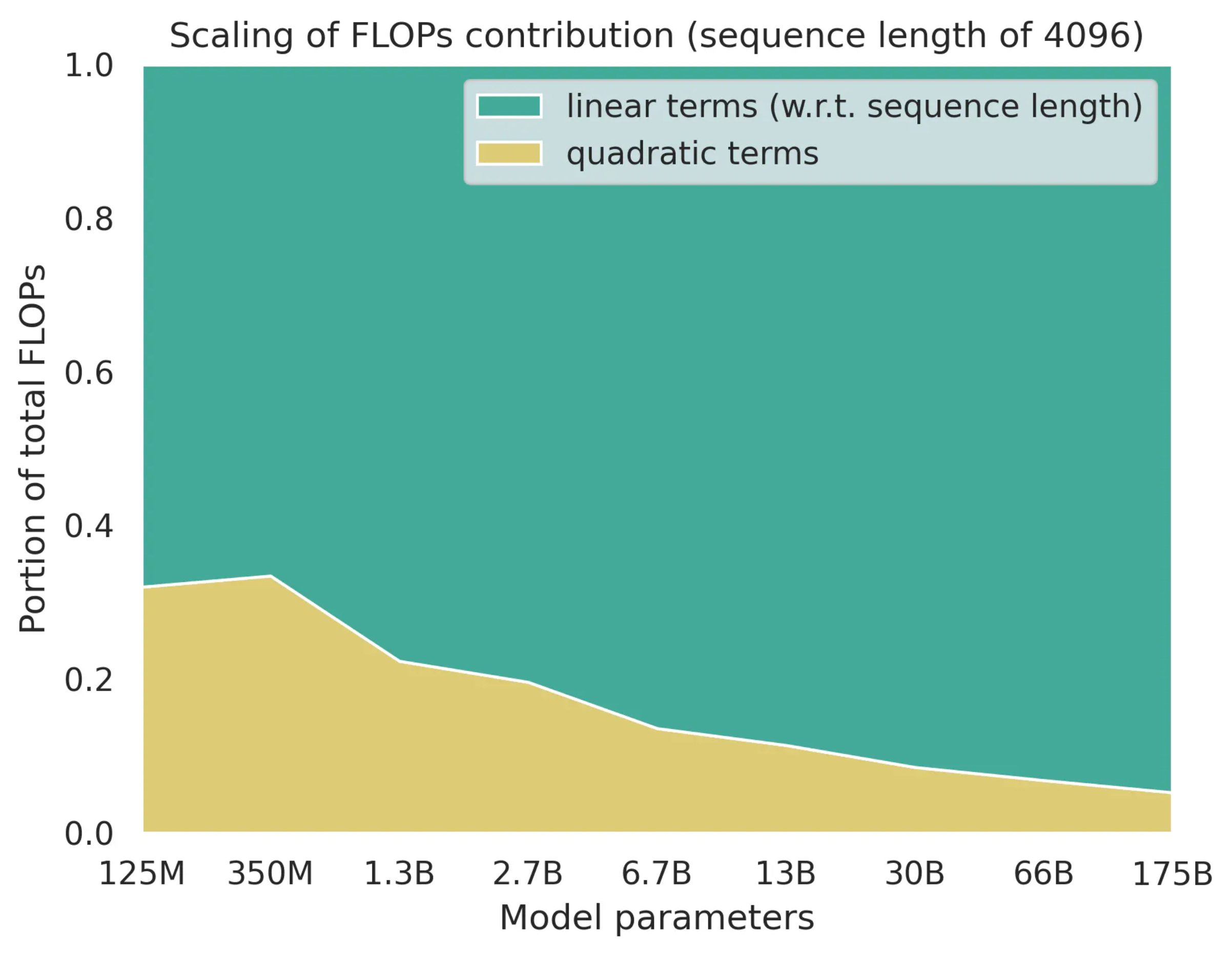 Fig. Source from here
Fig. Source from here
그리고 sequence length가 증가할 수록 contribution은 다음과 같이 변화한다.
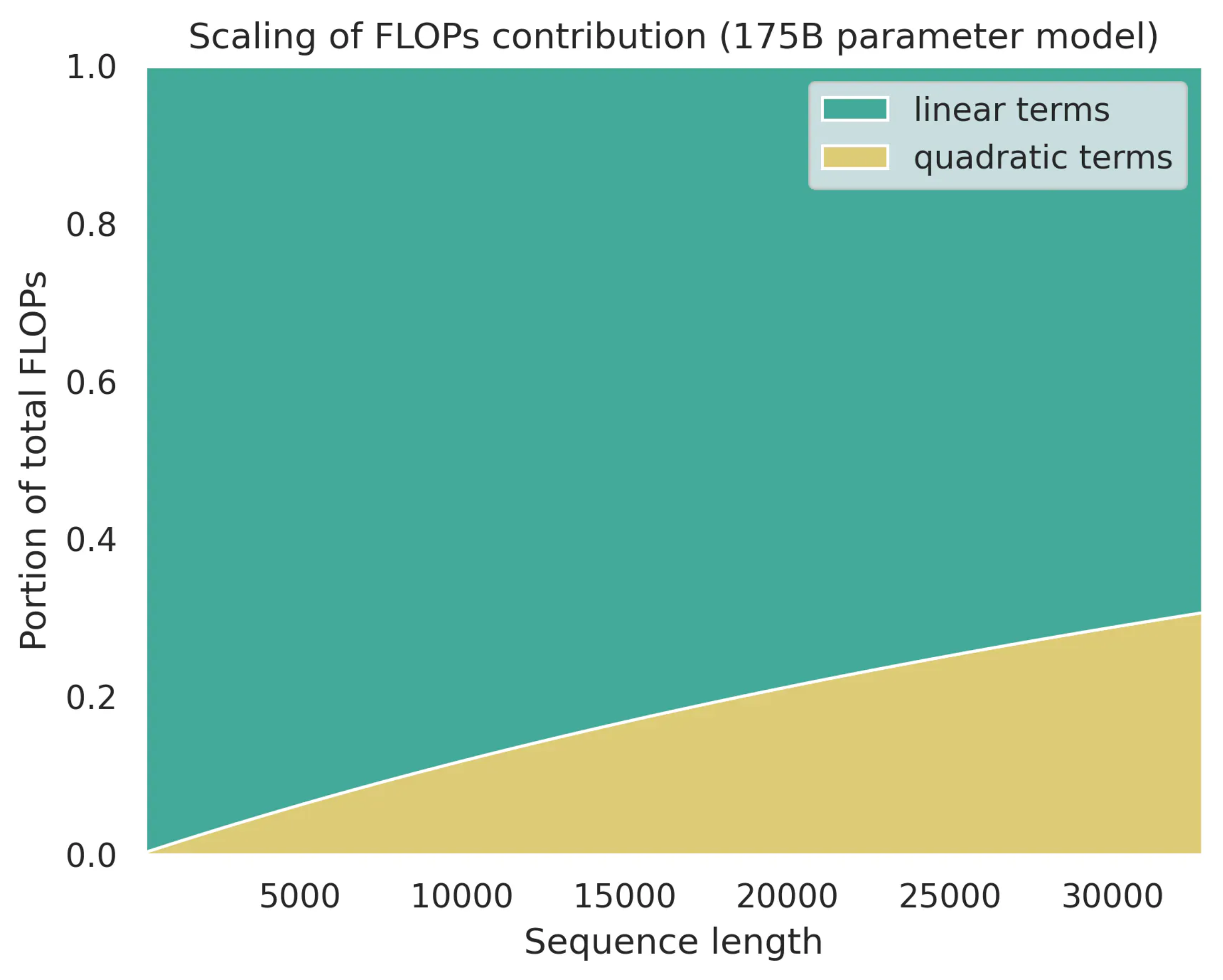 Fig. Source from here
Fig. Source from here
이 점들을 잘 파악해서 어떤부분을 optimize해야할지 결정하는것이 중요할 것이다.
MFU
이제 MFU를 계산해보도록 하자.
Model FLOPs Utilization (MFU)는 PaLM paper의 Appendix B를 보면 그 정의가 잘 나와있는데,
사실 MFU 말고도 LLM Training efficiency를 측정하는 metric에는 Hardware FLOPs Utilization (HFU)라는 것도 있고,
이게 더 오래된 metric이다.
하지만 Google 저자진들은 HFU가 가지고 있는 문제점을 지적하는데 요약하자면 아래와 같다.
- HFU는 주어진 device 에서의 observed FLOPs와 theoretical peak FLOPs의 비율을 의미함
- 그런데 HFU가 측정하는 FLOPs는
GPU Kernel구현이나 system에 의존해서 다른 system에서 training된 model끼리 비교가 어려움- ex) Nvidia megatron 530B는 Nvidia에서 개발한 A100 General Purpose Unit (GPU)에서 학습됨
- Google PaLM은 Google에서 개발한 Tensor Processing Unit (TPU)에서 학습됨
- Large NN을 학습할 때에는 VRAM memory가 부족한 경우가 많기 때문에 Activation Checkpointing (Gradient Checkpointing)같은 걸 쓰는데 HFU는 이것도 포함해서 계산함. (PaLM paper에서는
Re-materialization이라고 하기도 함)- 그런데 실제로는 이걸 측정할 필요가 없음.
연산이 더 쓰이더라도 초당 처리하는 token량, Throughput (tokens/sec)만 좋으면 장땡임
 Fig.
Fig.
그래서 저자들이 제안한 게 바로 MFU인데,
이는 theoretical maximum throughput 대비 observed throughput을 의미한다.
즉 decoder-only transformer에서 초당 처리할 수 있는 tokens량이 이론적으로 100인데,
30개밖에 못 처리했으면 30인 것이다.
MFU를 계산하는 수식은 아래와 같은데,
\[\begin{aligned} & R =\frac{P}{6N + 12LHQT} & \\ & N: \text{the number of model parameter} & \\ & L: \text{the number of layers} & \\ & H: \text{the number of heads} & \\ & Q: \text{the head dimension} & \\ & T: \text{the sequence length} & \\ & P: \text{peak matmul throughput of P FLOPs per sec} & \\ \end{aligned}\]여기서 \(12LHQT\)는 token당 self attention에 들어가는 FLOPs를 계산하는 수식인데, 충분히 큰 large NN에 대해서는 무시할만한 수준이기 때문에 사살싱 numerator에 들어가는 값은 \(6N\)이라고 할 수 있다. 이는 앞서 Kaplan et al.에서 계산한 \(6N\)와 같은 값이며, 자세한 내용은 아래와 같다.
 Fig.
Fig.
이제 예를 들어서 MFU를 계산해 보도록 하자. 아래 code는 MFU, HFU를 위한 naive implementation이라고 할 수 있다.
GPU_AVAILABLE_FLOPS = 3e12 # A100 bf16 peak FLOPs
flops_per_token = 2 * n_params
flops_per_seq = flops_per_token * seq_len
mfu* = 3 * flops_per_seq * seq_per_sec / (gpu_num * GPU_AVAILABLE_FLOPS)
attn_flops_per_seq = n_layers * 2 * 2 * (d_model * (seq_len**2))
mfu = (3 * flops_per_seq + 3 * attn_flops_per_seq) * seq_per_sec / (gpu_num * GPU_AVAILABLE_FLOPS)
GPU_AVAILABLE_FLOPS = 3e12 # A100 bf16 peak FLOPs
hfu* = 4 * flops_per_seq * seq_per_sec / (gpu_num * GPU_AVAILABLE_FLOPS)
hfu = (4 * flops_per_seq + 4 * attn_flops_per_seq) * seq_per_sec / (gpu_num * GPU_AVAILABLE_FLOPS)
Nvidia에서 megatron을 실험한 training setting이 530B LLM을 2240개 A100에 대해서 실험했고 결과적으로 throughput이 \(65.43K\) tokens/sec을 달성했다고 한다. 그러니까 이 경우에는 A100이 bf16, fp16에 대해서 \(312e12\) peak matmul FLOP/s를 갖는데, 총 2240개를 썼기 때문에 theoretical throughput은 \(312e12 * 2240\)이 된다. 그러므로 계산된 MFU값은 아래와 같다.
\[\frac{ (65.43) \times \text{tokens/sec} \times (6 \times 530) \times \text{FLOPs/token} }{ (3e12 \times 2240) \times \text{FLOPs/token} }\] Fig.
Fig.
한 편, PaLM은 TPU를 사용했고 Nvidia와 다른 codebase를 썼고, activation checkpointing의 여부 등이 모두 다르겠지만 그것들과 독립적인 training efficiency를 측정할 수 있고, 결과적으로 GPT-3, Gopher, Megatron-Turing NLG등과 비교했을 때 PaLM이 더 높은 MFU를 달성했음을 자랑한다.
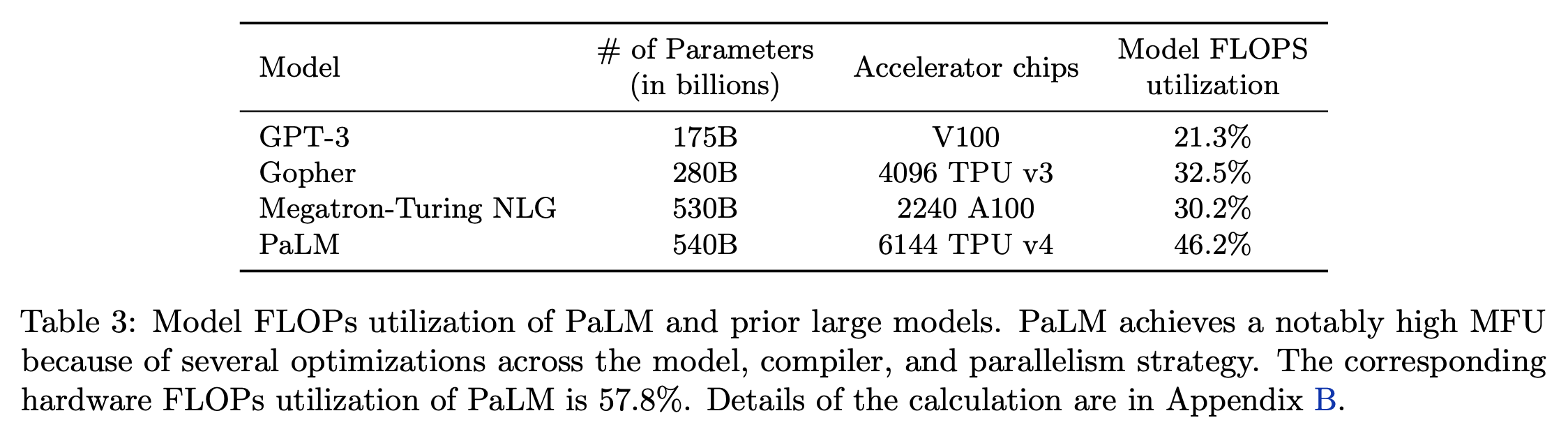 Fig.
Fig.
여기서 중요한 점은 activation checkpointing이 forward pass re-computation을 함으로써 FLOPs가 더 많이 들긴 하지만, 이 전략을 쓰면 memory save를 함으로써 batch를 늘릴 수 있기 때문에 결과적으로 throughput이 늘어난다는 점이다. 저자들은 PaLM 540B에 대해서 이 전략을 취했다고 한다. 즉 FLOPs만을 측정하는 HFU는 이런 점을 catch할 수가 없을 수 있는데 MFU는 catch를 한 것이다.
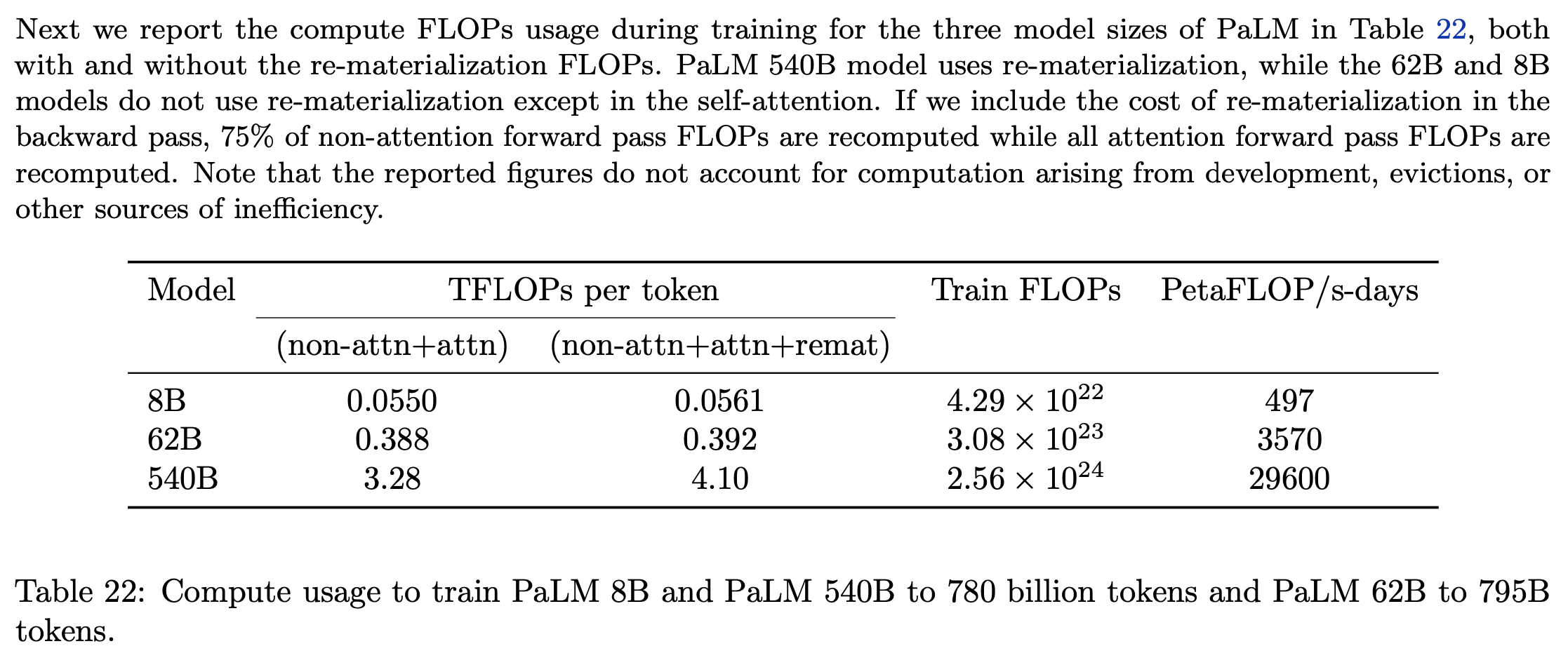 Fig.
Fig.
Example Code Snippets for MFU
마지막으로 내가 사용하는 MFU를 측정할 수 있는 code implemenation을 공유하고 post를 정리하려고 한다. (Karpathy의 notebook을 참고함)
def simplified_mfu(
num_params,
TP_degree,
MP_degree,
batch_size,
block_size,
fwdbwd_per_iter,
grad_accum,
):
# a100_promised = 300e12*MP_degree*TP_degree
a100_promised = 312e12*MP_degree*TP_degree # bfloat16
achieved = (6*num_params/fwdbwd_per_iter)*(batch_size*block_size)*grad_accum # 6ND is approximated FLOPs per token for forward + backward
mfu = achieved/a100_promised
print(f"num_params: {num_params * 1e-9}B")
print(f"fwdbwd_per_iter: {fwdbwd_per_iter}")
print(f"MFU: {mfu*100:.2f}%")
print()
return mfu
def estimate_mfu(
num_params,
n_layer,
n_head,
n_embd,
block_size,
fwdbwd_per_iter,
dt
):
""" estimate model flops utilization (MFU) in units of A100 bfloat16 peak FLOPS """
# first estimate the number of flops we do per iteration.
# see PaLM paper Appendix B as ref: https://arxiv.org/abs/2204.02311
N = num_params
L, H, Q, T = n_layer, n_head, n_embd//n_head, block_size
flops_per_token = 6*N + 12*L*H*Q*T
flops_per_fwdbwd = flops_per_token * T
flops_per_iter = flops_per_fwdbwd * fwdbwd_per_iter
# express our flops throughput as ratio of A100 bfloat16 peak flops
flops_achieved = flops_per_iter * (1.0/dt) # per second
flops_promised = 312e12 # A100 GPU bfloat16 peak flops is 312 TFLOPS
mfu = flops_achieved / flops_promised
print(f"MFU: {mfu}")
return mfu
+Updated) 실제로 MFU와 MFU을 이용해 training wall clock을 계산해보자. torchtitan의 reference table을 보면 llama3에 대해서 FSDP1만 적용했을 때 Word Per Second (WPS)가 2900쯤 된다는 것을 볼 수 있는데, 이 경우 MFU가 56.8이 나온다. 이제 이 수치를 재현해보자.
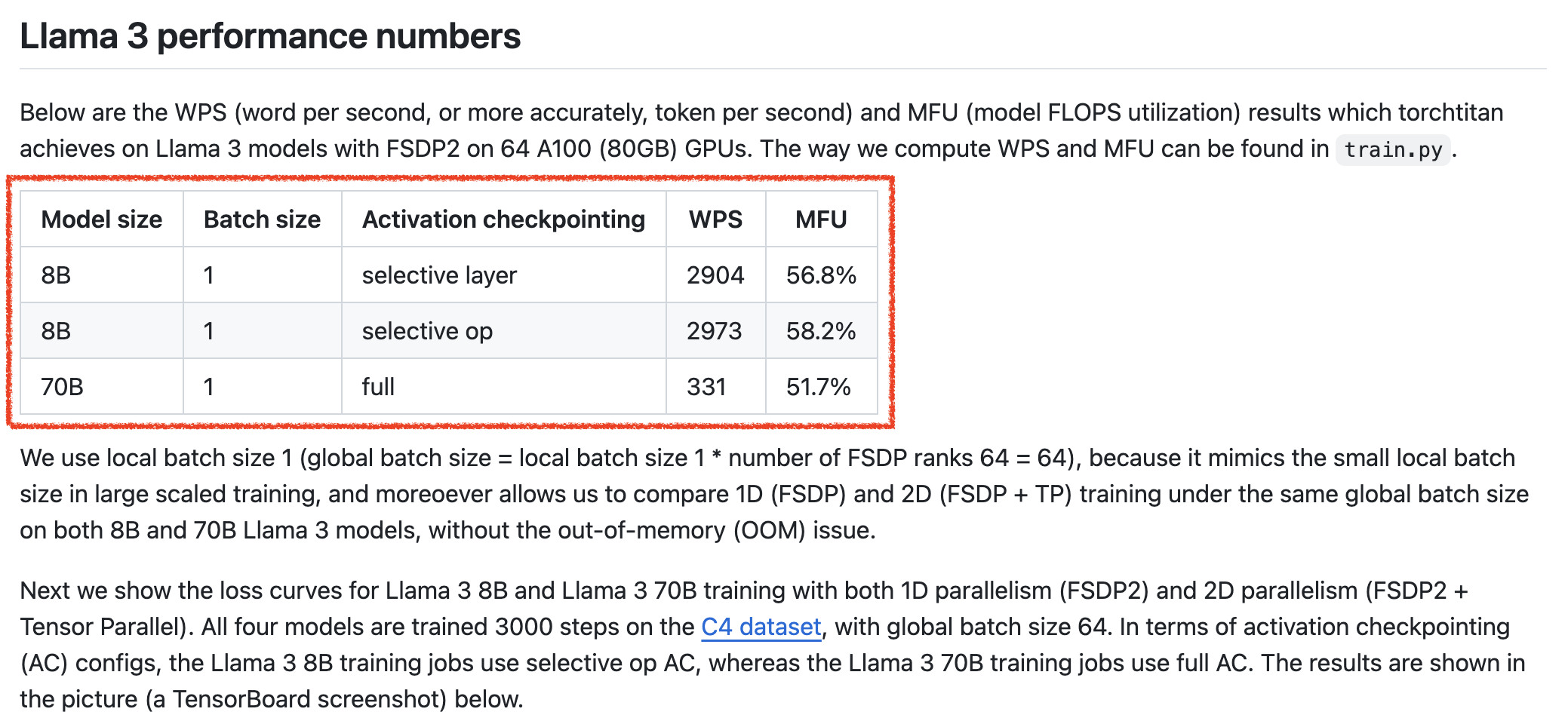 Fig.
Fig.
먼저 simplified_mfu를 사용해서 계산해볼건데,
llama3는 seq_len=8192이며 위 table의 training setting은 node를 8개 (즉 GPU를 64개) 썼으며,
따라서 local batch_size는 1이 된다.
그리고 초당 token 처리량 (throughput)과 같은 말인 WPS가 2904이므로,
한 token을 처리하는데 걸리는 fwd+bwd iteration time은 1/2904가 된다.
이를 simplified_mfu에 대입하면 우리는 44.68을 얻을 수 있다.
# https://github.com/pytorch/torchtitan/blob/main/docs/performance.md
non_embedding_params = 8e9
# non_embedding_params = 8e9 - 1*4096*128256 # torch titan exclude embedding 1 times
# non_embedding_params = 8e9 - 2*4096*128256 # if embedding is tied and exclude them all
TP_degree, MP_degree = 1, 1
micro_batch_size, seq_len, accum, num_nodes = 1, 8192, 1, 8
num_steps = 3000
num_tokens = num_steps * micro_batch_size * accum * num_nodes * 8 * seq_len
wps = 2904
fwdbwd_per_iter = 1/wps*micro_batch_size*seq_len # 2.82 sec
# fwdbwd_per_iter = 2.3*3600/num_steps
# wps = micro_batch_size*seq_len/fwdbwd_per_iter
args = {
'num_params': non_embedding_params,
'TP_degree': TP_degree,
'MP_degree': MP_degree,
'batch_size': micro_batch_size,
'block_size': seq_len,
'fwdbwd_per_iter': fwdbwd_per_iter, # sec
'grad_accum': accum,
}
print(f'non_embedding_params: {non_embedding_params/1e9:.2f}B')
print(f'num_tokens: {num_tokens/1e9:.2f}B')
print(f'wps: {wps:.2f}')
mfu = simplified_mfu(**args)
non_embedding_params: 8.00B
num_tokens: 1.57B
wps: 2904.00
num_params: 8.0B
fwdbwd_per_iter: 2.8209366391184574
MFU: 44.68%
여기서 주석처리해둔 것 중에 fwdbwd_per_iter=2.3*3600/num_steps로 계산한 부분이 있는데,
이는 tensorboard에 logging된 wall clock time을 기준으로 한 step당 걸린 시간을 계산한 것이며,
이를 WPS를 계산해도 거의 같은 fwd+bwd time을 얻을 수 있다.
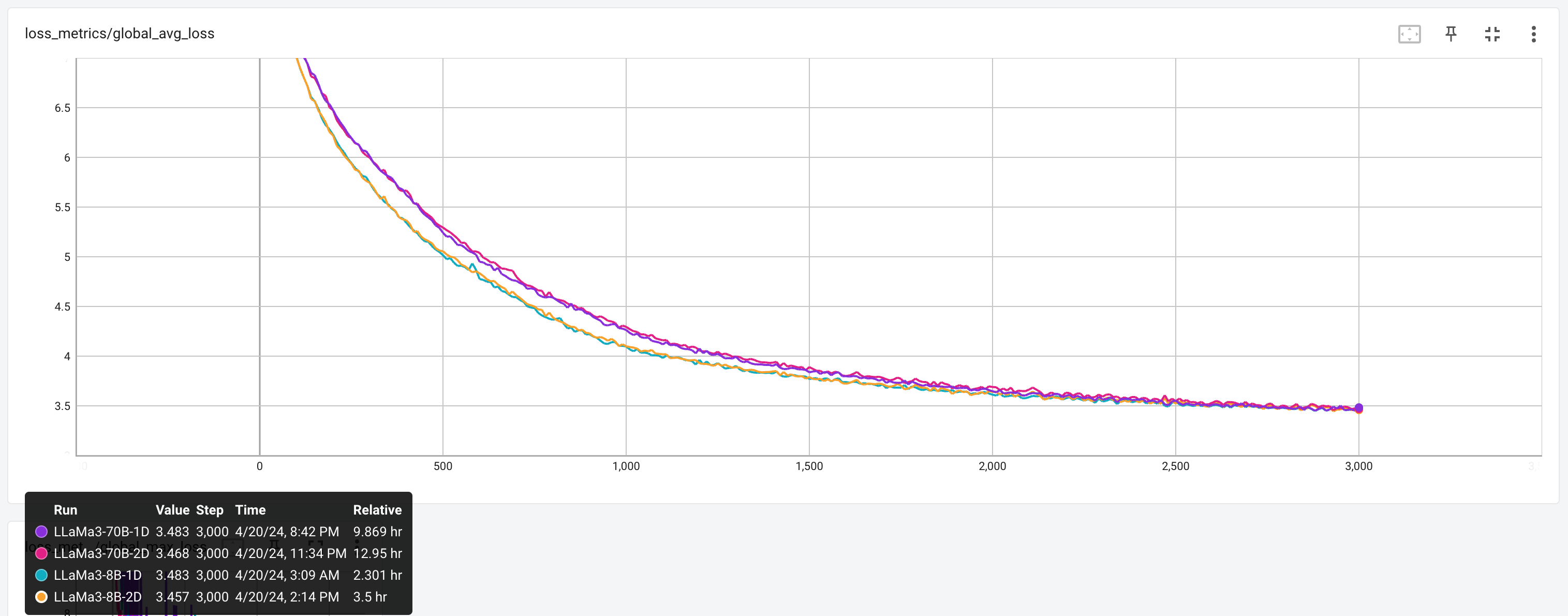 Fig.
Fig.
그런데 torchtitan에서 report하는 MFU는 44.68보다 훨씬 높은 56.8이다. 어디서 이런 차이가 생긴걸까? 앞서 Kaplan et al.은 \(d_{model} >> n_{ctx} / 12\)인 경우 attention과 관련된 fwd+bwd term을 무시할 수 있다고 했는데, 요즘은 8k 이상의 context length를 쓰기 때문에 해당 term의 contribution을 무시할 수가 없게 된 것이다.
그러므로 torchtitan의 결과를 재현하기 위해서 PaLM에서 제안한 방식 대로 12*LHQT만큼을 더해줘야 하는 것이다.
additional_mfu = (12*32*32*128*seq_len)*wps/312e12
print(f'for torchtitan, approx {100*additional_mfu:.2f} should be added')
print(f'so, PaLM MFU is {100*(mfu+additional_mfu):.2f}')
for torchtitan, approx 11.99 should be added
so, PaLM MFU is 56.67
Torchtitan의 code snippet들을 모아 대충 training loop에서 MFU를 측정하는 code를 작성해보면 아래와 같다.
# https://github.com/pytorch/torchtitan/blob/81c555f8bd6791ccd575a52bdcaaf816f4de7ee6/train.py#L345C1-L354C70
def simplified_train_loop_with_mfu(dataloader, model, model_config, optimizer, seq_len):
# https://github.com/pytorch/torchtitan/blob/81c555f8bd6791ccd575a52bdcaaf816f4de7ee6/torchtitan/utils.py#L118C1-L133C26
def get_num_flop_per_token(num_params: int, model_config, seq_len) -> int:
l, h, q, t = (
model_config.n_layers,
model_config.n_heads,
model_config.dim // model_config.n_heads,
seq_len,
)
# Reasoning behind the factor of 12 for the self-attention part of the formula:
# 1. each self-attention has 2 matmul in the forward and 4 in the backward (6)
# 2. the flash attention does 1 more matmul recomputation in the backward
# but recomputation should not be counted in calculating MFU (+0)
# 3. each matmul performs 1 multiplication and 1 addition (*2)
# 4. we follow the convention and do not account for sparsity in causal attention
flop_per_token = 6 * num_params + 12 * l * h * q * t
return flop_per_token
# get num_params, flops per token
num_params = get_num_params(model)
num_flop_per_token = get_num_flop_per_token(num_params, model_config, seq_len)
gpu_peak_flops = utils.get_peak_flops(gpu_memory_monitor.device_name) # 312e12
# training loop
time_last_log = time.perf_counter()
for inputs, labels in dataloader():
# num tokens
ntokens_since_last_log += labels.numel()
# impl fwd+bwd and count time
optimizer.zero_grad()
loss = model(inputs)
loss.backward()
optimizer.step()
lr_scheduler.step()
time_delta = time.perf_counter() - time_last_log
# tokens per second, abbr. as wps by convention (model parallel (tensor parallel) degree should be count)
# https://github.com/pytorch/torchtitan/blob/81c555f8bd6791ccd575a52bdcaaf816f4de7ee6/torchtitan/parallelisms/parallel_dims.py#L69-L70
wps = ntokens_since_last_log / (time_delta * parallel_dims.model_parallel_size)
# model FLOPS utilization
# For its definition and calculation, please refer to the PaLM paper:
# https://arxiv.org/abs/2204.02311
mfu = 100 * num_flop_per_token * wps / gpu_peak_flops # \approx 100 * 6 * N * D / fwd_bwd_iter_time / (312e12 * MP_degree * TP_degree)
time_last_log = time.perf_counter()
이제 training wall clock time을 계산해보자. 나는 보통 아래 두 가지 함수를 만들어서 사용하는데, 하나느 MFU를 기반으로 측정하는 것이고, 하나는 fwd+bwd iteration time으로 측저하는 것인데 이 둘은 결과적으로 같아야 한다.
def cal_with_mfu(N, D, nodes, mfu):
C=6*N*D
a100_promised=312e12
gpus=nodes*8
training_hours=C/(a100_promised*mfu*gpus)/3600
training_days=training_hours/24
print(f'training_hours: {training_hours:.2f} hours (computed by MFU)')
print(f'training_days: {training_days:.2f} days (computed by MFU)')
def cal_with_iter_time(D, bsz, fwd_bwd_time):
num_steps=D//bsz
training_hours=num_steps*fwd_bwd_time/3600
training_days=training_hours/24 # should be sec
print(f'training_hours: {training_hours:.2f} hours (computed by fwd bwd iter time)')
print(f'training_days: {training_days:.2f} days (computed by fwd bwd iter time)')
cal_with_mfu(non_embedding_params, num_tokens, num_nodes, mfu)
cal_with_iter_time(num_tokens, micro_batch_size*accum*num_nodes/TP_degree/MP_degree*8*seq_len, fwdbwd_per_iter)
결과를 보면 torchtitan에서 report하는 tensorboard log와 거의 같은 시간을 재현할 수 있었음을 알 수 있는데,
MFU를 56.8로 두고 계산할 경우 cal_with_mfu에서 C=6*N*D가 아니라 C=6*N*D + 12L*H*Q*T로 계산해야 하는 걸 잊지 말자.
(귀찮아서 생략)
training_hours: 2.35 hours (computed by MFU, MFU: 44.68)
training_days: 0.10 days (computed by MFU), MFU: 44.68
training_hours: 2.35 hours (computed by fwd bwd iter time)
training_days: 0.10 days (computed by fwd bwd iter time)
Updated) Megatron-LM's MFU macro
# https://github.com/NVIDIA/Megatron-LM/blob/54f1f78529cbc2b9cddad313e7f9d96ac0420a27/megatron/training/training.py#L90
def num_floating_point_operations_megatron_lm(
padded_vocab_size,
num_layers,
hidden_size,
num_attention_heads,
group_query_attention,
num_query_groups,
kv_channels,
ffn_hidden_size,
swiglu,
num_experts,
moe_router_topk,
world_size,
global_batch_size,
seq_length,
elapsed_time_per_iteration,
):
# Attention projection size.
query_projection_size = kv_channels * num_attention_heads
query_projection_to_hidden_size_ratio = query_projection_size / hidden_size
# Group Query Attention.
if not group_query_attention:
num_query_groups = num_attention_heads
# MoE.
num_experts_routed_to = 1 if num_experts is None else moe_router_topk
gated_linear_multiplier = 3 / 2 if swiglu else 1
# The 12x term below comes from the following factors; for more details, see
# "APPENDIX: FLOATING-POINT OPERATIONS" in https://arxiv.org/abs/2104.04473.
# - 3x: Each GEMM in the model needs to be performed 3 times (forward pass,
# backward wgrad [weight gradient], backward dgrad [data gradient]).
# - 2x: GEMMs of a particular size are stacked twice in the standard Transformer model
# architectures implemented in this codebase (e.g., h->ffn_h GEMM and ffn_h->h GEMM
# in MLP layer).
# - 2x: A GEMM of a m*n tensor with a n*k tensor requires 2mnk floating-point operations.
expansion_factor = 3 * 2 * 2
FLOPs = (
expansion_factor
* global_batch_size
* seq_length
* num_layers
* hidden_size
* hidden_size
* (
# Attention.
(
(
1
+ (num_query_groups / num_attention_heads)
+ (seq_length / hidden_size)
) * query_projection_to_hidden_size_ratio
)
# MLP.
+ (
(ffn_hidden_size / hidden_size)
* num_experts_routed_to
* gated_linear_multiplier
)
# Logit.
+ (padded_vocab_size / (2 * num_layers * hidden_size))
)
)
TFLOPs_per_gpu = FLOPs / (elapsed_time_per_iteration * 10**12 * world_size)
MFU = TFLOPs_per_gpu/312
print(f'throughput per GPU (TFLOP/s/GPU): {TFLOPs_per_gpu:.2f}')
print(f'MFU using megatron-LM: {100*(MFU):.2f}%')
return MFU
LLaMa-3 8B에 대한 argument를 넣어 test해보자.
args = {
'padded_vocab_size': 128256,
'num_layers': 32,
'hidden_size': 4096,
'num_attention_heads': 32,
'group_query_attention': True,
'num_query_groups': 8,
'kv_channels': 128,
'ffn_hidden_size': 14336,
'swiglu': True,
'num_experts': None,
'moe_router_topk': None,
'world_size': 64,
'global_batch_size': 64*1,
'seq_length': 8192,
'elapsed_time_per_iteration': fwdbwd_per_iter, # sec
}
megatron_lm_mfu = num_floating_point_operations_megatron_lm(**args)
params: 8.00B (not exclude embedding)
num_tokens: 1.57B
wps: 2904.00
num_params: 8.00B
fwdbwd_per_iter: 2.82
MFU: 44.68%
==================================================
training_hours: 2.35 hours (computed by MFU, num_tokens: 1.5729B, nodes: 8, MFU: 44.68)
training_days: 0.10 days (computed by MFU), num_tokens: 1.5729B, nodes: 8, MFU: 44.68
training_hours: 2.35 hours, num_tokens: 1.5729B, fwd_bwd_time: 2.82 (computed by fwd bwd iter time)
training_days: 0.10 days, num_tokens: 1.5729B, fwd_bwd_time: 2.82 (computed by fwd bwd iter time)
==================================================
for torchtitan, approx 11.99 should be added
so, MFU using PaLM is 56.67%
==================================================
throughput per GPU (TFLOP/s/GPU): 168.18
MFU using megatron-LM: 53.90%
FAQ?
It doesnt reflect number of nodes?
자주 나오는 질문인데 “node 수는 MFU 수식에 안들어가는 거니까 증가에 따른 communication cost는 반영이 안되는건가요?”에 답하자면, throughput이 이미 한 iteration의 mini-batch를 처리하는데 걸리는 시간이 몇초인가?가 반영됐기 때문에 distributed plan이 좋은지 나쁜지는 여기에 반영된다. 즉 throughput이 안좋다는건 한 iteration당 걸리는 시간이 오래걸린다는 거고 당신의 distributed training plan에 문제가 있다는 것을 의미한다.
\[MFU = \frac{ \text{Required FLOPS per a token (FLOPs/token)} \times \color{red}{\text{Throughput (tokens/sec)}} }{ \text{Peak FLOPs of bf16/A100} (FLOPs) }\]References
- Papers
- Blogs and Others
- Benchmarks