Notes

(WIP) GPU Programming (2/6) - GPU Programming (CPU vs GPU / Parallel Matmul)

06 Mar 2024

< 목차 >

Introduction and Motivation

이번 post의 목적은 CPU 와 GPU 는 구조적으로 어떤 차이가 있는지, Deep Learning을 하는 데 왜 GPU computing이 더 이득이며 사용하는 Computed Unified Device Architecture (CUDA)란 무엇인지? 그리고 Triton란 무엇인지? 등에 대해서 알아보는 것이다.

그런데 왜 GPU Programming을 할 줄 알아야 하는 걸까? 사실 그동안은 system engineer나 CUDA kernel engineer가 아니라면 distributed training, GPU programming에 대해 크게 알 필요가 없다는 인식이 컸던 것 같다. 하지만 이는 Large Language Model (LLM)이 등장하기 전 까지만 해당되는 말이었다. LLM 시대에 접어들면서 model size가 수십억 (billion; B)단위를 우습게 넘어가면서 General Matrix Multiplications (GEMMs)도 엄청나게 증가하게 되었다. 즉 그동안 small size model에서는 “크게 문제가 되지 않았 보였던” 최적화 문제들이 수면위로 드러나게 된 것이다.

과연 나는 "design하고자 하는 model architecture의 training, inference시 bottleneck이 어딘지 파악하고 이를 개선할 수 있는가?"에 대해 답할 수 있을까? 이를 해결하지 못하면 frontier lab들은 같은 FLOPs의 model을 학습하는데 30일 걸리지만 우리 lab은 60일이 걸릴 수도 있고, 같은 size model을 inference 하는 데 드는 token당 비율이 열배 이상씩 차이가 날 수도 있다. 그런데 일반적으로 "측정할 수 없다면 개선할 수 없다 (If you can not measure, you can not manage)"는 말이 있듯, 어디를 최적화 해야 하는지?를 정량화 해서 분석할 수 없으면 이를 개선할 수 없는 것이다.

물론 training, inference 모두에 대해 어느정도 최적화를 가능하게 해주는 멋진 opensource project들이 존재한다.

여기서 megatron, vllm, sglang등은 자신들만의 inference optimization과 더불어 tri dao가 만든 fused attention kernel등을 사용하면서 초당 토큰 처리량 (tokens/sec throughput)을 계속 개선해 나가고 있기 때문에, 어느정도 scale의 model은 학습하고 배포할 수 있다. 그런데 이렇게 opensource에만 의존하게 되면, flash attention에 버그가 있거나 원하는 기능이 있을 때마다 tri dao가 patch해주지 않으면 쓸 수 없는 상황에 놓일 수 있다.

tri_dao_flash_meme Fig. “Literally only @tri_dao can debug Flash Attention 2 when things go wrong.”. Source from Hieu Pham’s tweet

실제로 huggingface’s transformer에 flash attention kernel을 다 적용하는데 1년이 넘는 시간이 걸렸을 정도로, kernel을 짜는 일이 아니라 갖다 쓰는 것 마저도 opensource는 매우 오래걸린다는 것을 알 수 있다. 그리고 flash attention을 쓰는 이상 prefix-LM을 구현할 수도 없다. 이를 위해 pytorch team에서 Flex Attention를 구현해줬지만 VLM같은 task에서 prefix-LM이 더 좋을 수 있음에도 불구하고 남이 해주지 않으면 실험조차 할 수 없었던 것이다.

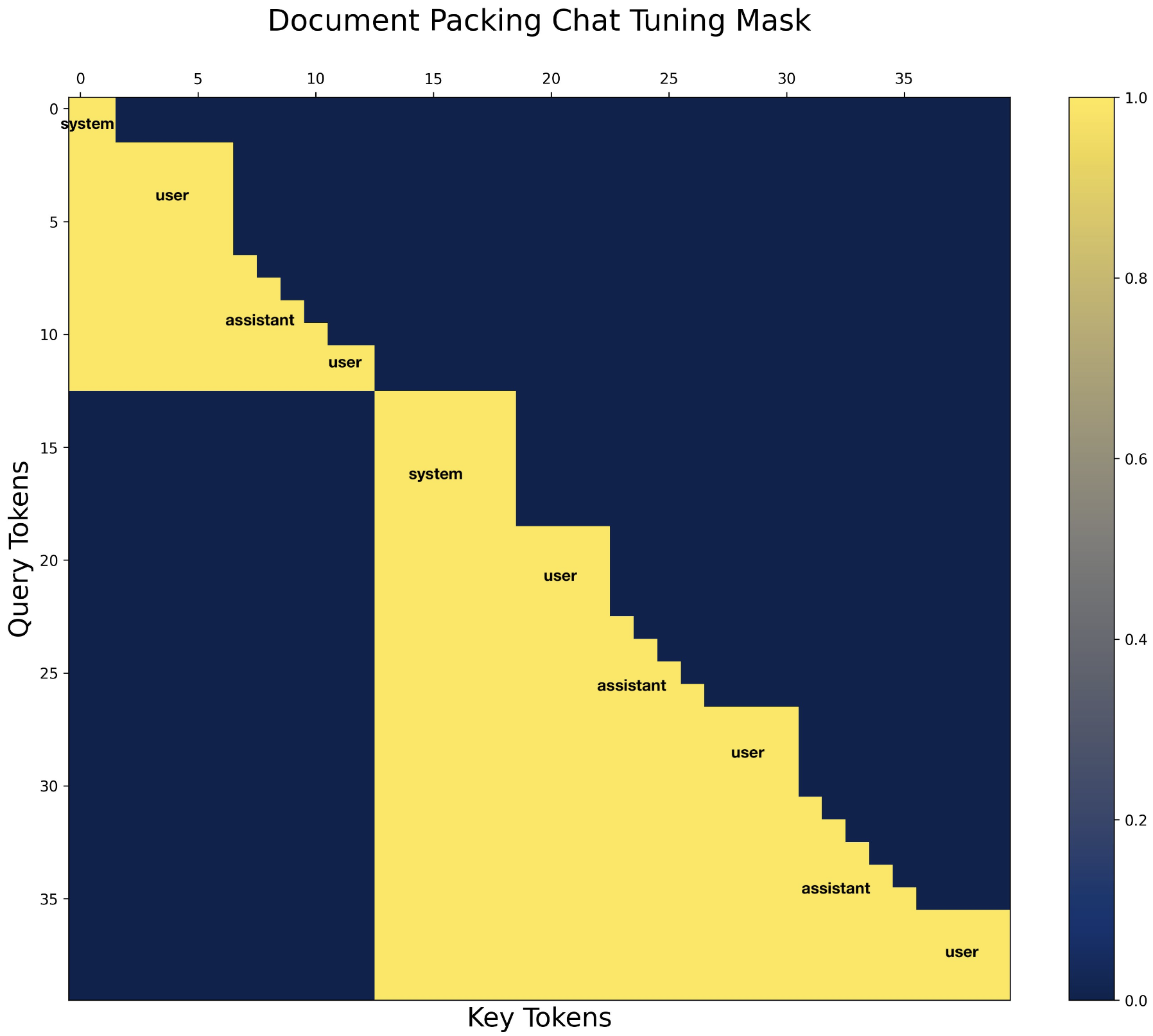prefix_lm_example Fig. tweet from Jonathan Chang

게다가 flash attention의 저자인 Tri Dao도 자선사업가는 아니기 때문에 together.ai라는 스타트업을 운영하고 advanced kernel들이나 inference engine은 돈을 받고 판매한다. 아래는 Together Kernel Collection (TKC)의 성능 지표인데, Noam architecture (a.k.a llama architecture)의 경우 SwiGLU가 연산량을 많이 점유하고 있기 때문에 이를 최적화 함으로써 inference throughput을 많이 올린 걸 확인할 수 있다.

TKC

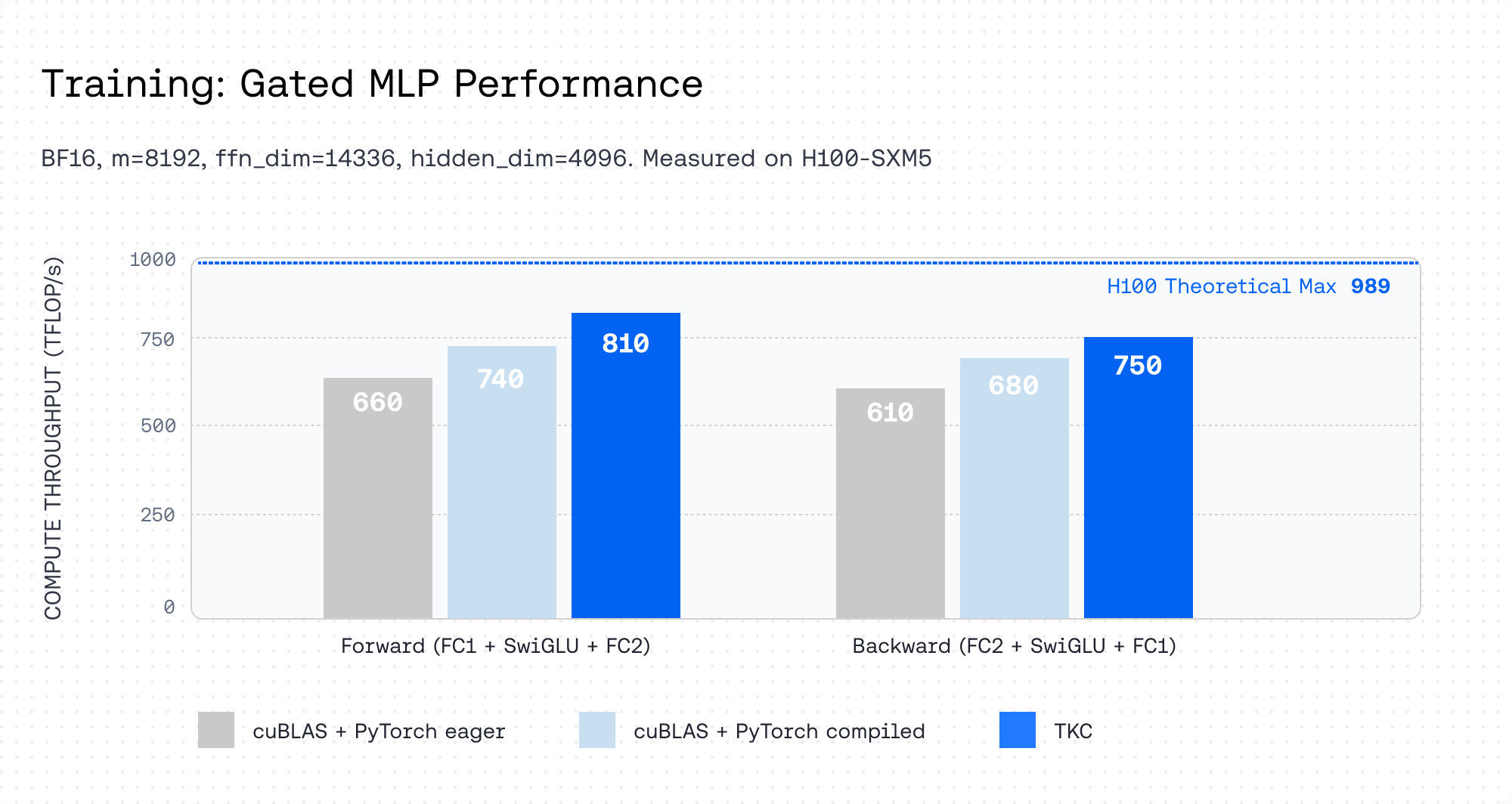
이렇듯 LLM을 하는 기관이라면 어느정도 optimization을 할 줄 모르면, GPU programming을 이해하거나 distributed training system을 분석할 수 없으면 살아남기가 힘들다. hard하게 kernel작성까진 아니더라도 어디가 bottleneck인지 분석하고 (communication이 문제인지? 즉 compute bound인지 memory bound인지) 어느정도 개선할 수는 있어야 하는 것이다.

CUDA_GIGACHAD Fig. GPU Programming를 할 줄 모르면 남이 해줄 때 까지 기다릴 수 밖에 없다.

이를 할 줄 알면 수 없이 반복하여 optimum을 찾는 deep learning 실험의 특성상 iteration speed를 20~30%정도만 개선해도 개선 이후의 실험들은 다 빨라지기 때문에 비용과 성능개선을 매우 개선할 수 있게 된다. 실제로 Anthropic이나 Xai같은 frontier lab들의 pretraining team의 job description을 보면 data processing, model architecture 개선, traning dynamics등을 고려한 learning algorithm, optimizer 개선 등은 당연하고 GPU programming이나 distributed system을 개선할 수 있는 strong engineering background를 요구한다.

anthropic_pretraining_jd

xai_pretraining_jd

사실 training dynamics를 포함해서 model을 어떻게 scale up해야 안전하게 학습할 수 있는지? 어떤 distributed plan을 써야 Model FLOPS Utilization (MFU) 손해 없이 GPU device를 더 투입할 수 있는지?를 알지 못한다면 "그 기관은 scale up하는 방법을 모른다"라고 할 수 있다. Scaling Law paper나 요즘 나오는 LLM들을 보고 “음 연산량만 더 투입하면 저런 모델이 나온다는 말이지?”라고 생각했다면 이는 매우 잘못된 생각이다. 상기한 내용을 모르면 제대로, 효율적으로 scale up이 안된다고 보면 된다.

이 post의 목적은 GPU가 왜 parallism에 특화되었는지?에 대해 이해하고 parallel matmul을 구현함으로써 아래 질문들에 대답할 수 있는 정도가 되는 것이다. (아마 글을 작성하는데 꽤 오래걸릴 것 같지만 일단 이렇게 시작해본다)

tweet_from_Hieu_Pham Fig. 당신은 이 질문에 대답할 수 있는가?. Source from Hieu Pham’s tweet

iceberg_meme_matmul Fig. Iceberg Meme about Matmul Implementations. Source from spike’s tweet

Central Processing Unit (CPU) vs Graphic Processing Unit (GPU)

우리가 GPU Programming을 이해하기 위해서는 먼저 중앙 처리 장치 (Central Processing Unit; CPU)와 그래픽 처리 장치 (Graphic Processing Unit; GPU)의 차이에 대해서 제대로 알고, GPU device의 계층 구조 (hierarchy)를 이해해야 할 것이다.

이 section의 목표는 아래와 같은 개념들을 익히는 것이다.

  • Core, Process, Thread
  • Arithmetic Logic Unit (ALU)
  • Cache
    • Level 1 Cache
    • Level 2 Cache
  • Random Access Memory (RAM)
    • Dynamic RAM (DRAM)
    • Static RAM (SRAM)
    • Video RAM (VRAM)
  • Local Memory
  • Shared Memory
  • Global, Constant, Texture Memory
  • Grid
  • Block
  • Register
  • Kernel
  • Warp
  • Warp Scheduler
  • Dispatch Unit
  • Register File

보통 CPU와 GPU를 각각 전문가 1명, 초등학생 10000명으로 비유하는데, CPU는 정교한 연산 (방정식 같은 것)을 적은 유닛이 순차적으로 (sequential) 수행하는 일을 하지만, GPU는 비교적 덜 정교한 연산 (산수 같은 것) 을 훨씬 많은 유닛이 병렬적으로 (parallel) 처리하기 때문이다.

cpu Fig. CPU 는 순차적으로 그림을 그린다.

cpu Fig. GPU 는 한번에 (병렬적으로) 그림을 그린다. 이게 가능한 이유는 여러개의 유닛이 있는 GPU 를 이용해 이런 연산을 묶어서 한번에 처리하는 CUDA kernel 이라는 것이 구현되어 있기 때문이다.

This difference in capabilities between the GPU and the CPU exists 
because they are designed with different goals in mind. 

While the CPU is designed to excel at executing a sequence of operations, 
called a thread, as fast as possible 
and can execute a few tens of these threads in parallel, 
the GPU is designed to excel at executing thousands of them in parallel 
(amortizing the slower single-thread performance to achieve greater throughput).

CPU는 이름 처럼 중앙에서 모든 걸 관장하는 computer의 뇌라고 불린다. Computer가 무언가를 처리하고 표현하는 과정이 모두 숫자 0, 1로 이루어져 있다는 건 잘 알려져 있는데, 이 역할을 하기 위해서 전기 신호에 따라서 0, 1을 표현하는 트랜지스터 (transistor)가 수십업 개 모인것이 바로 CPU이다. CPU는 컴퓨터 및 운영 체제에 필요한 명령과 프로세스를 실행하며 web surfing 등 우리가 computer로 하는 모든 job들 (program)의 실행 속도를 결정하는 데 중요한 영향을 끼친다.

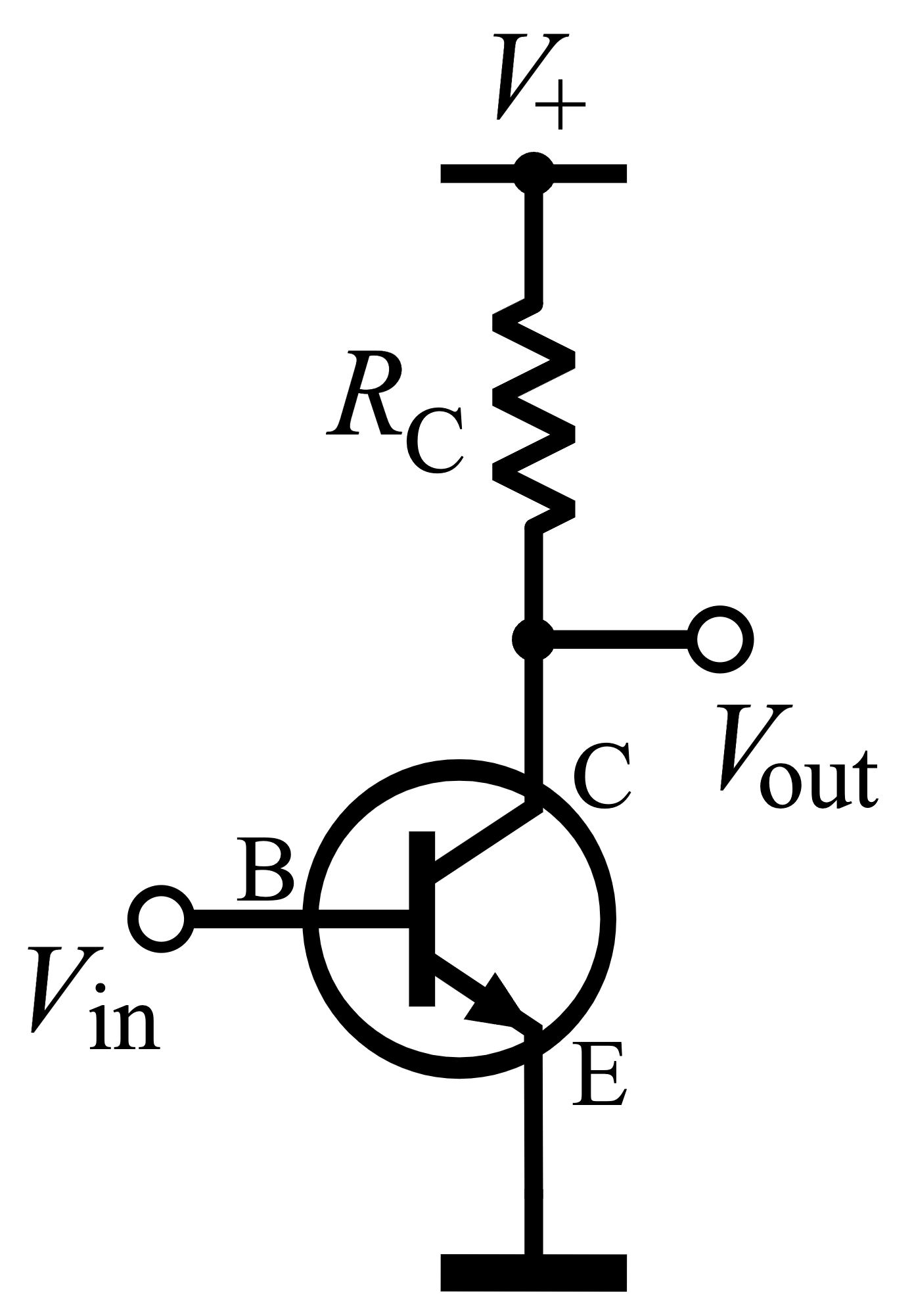transistor Fig. Source from wiki

GPU는 더 작고 보다 전문화된 코어로 구성된 처리기 (processor)로, 처리해야 하는 작업을 동시에 (또는 병렬로) 여러 코어 간에 분할할 수 있을 때 엄청난 효과를 발휘한다. GPU는 게임으로 치면 더 높은 품질의 visual과 끊김없는 원활한 play를 지원하므로 현대 gaming을 위한 필수 구성 요소이다. 그리고 gaming을 위한 processor가 GPU인 이유가 곧 Deep Learning에 GPU가 유리한 이유가 된다.

먼저 CPU와 GPU는 똑같이 반도체 (silicon)를 이용한 processor임은 같지만, 그 목적이 다르듯 아래 figure처럼 design에 차이가 있다.

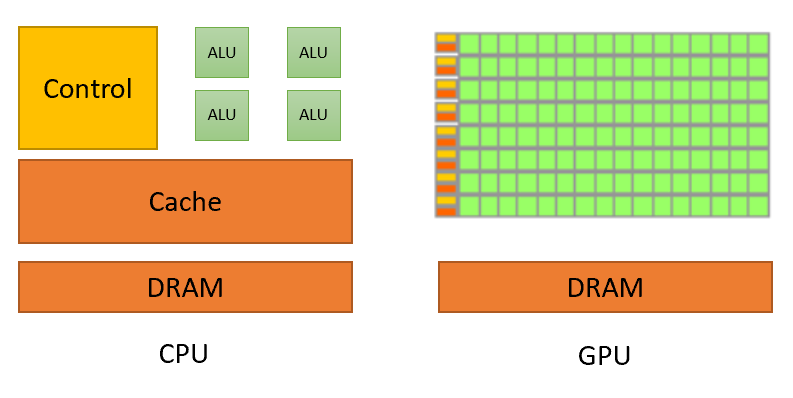cpu_gpu_transistor Fig. Source from here

Central Processing Unit (CPU), Process, Thread and Core

CPU는 먼저 제어 장치 (Control Unit; CU), 산술 논리 장치 (Arithmetic Logic Unit; ALU), 캐시 (Cache) 그리고 동적 램 (Dynamic Random Access Memory; DRAM)으로 이루어져 있다. ALU는 덧셈, 뺄셈 같은 두 숫자의 산술연산과 배타적 논리합, 논리곱, 논리합 같은 논리연산을 계산하는 디지털 회로로 산술 논리 장치는 컴퓨터 중앙처리장치의 기본 설계 블록이라고 한다.

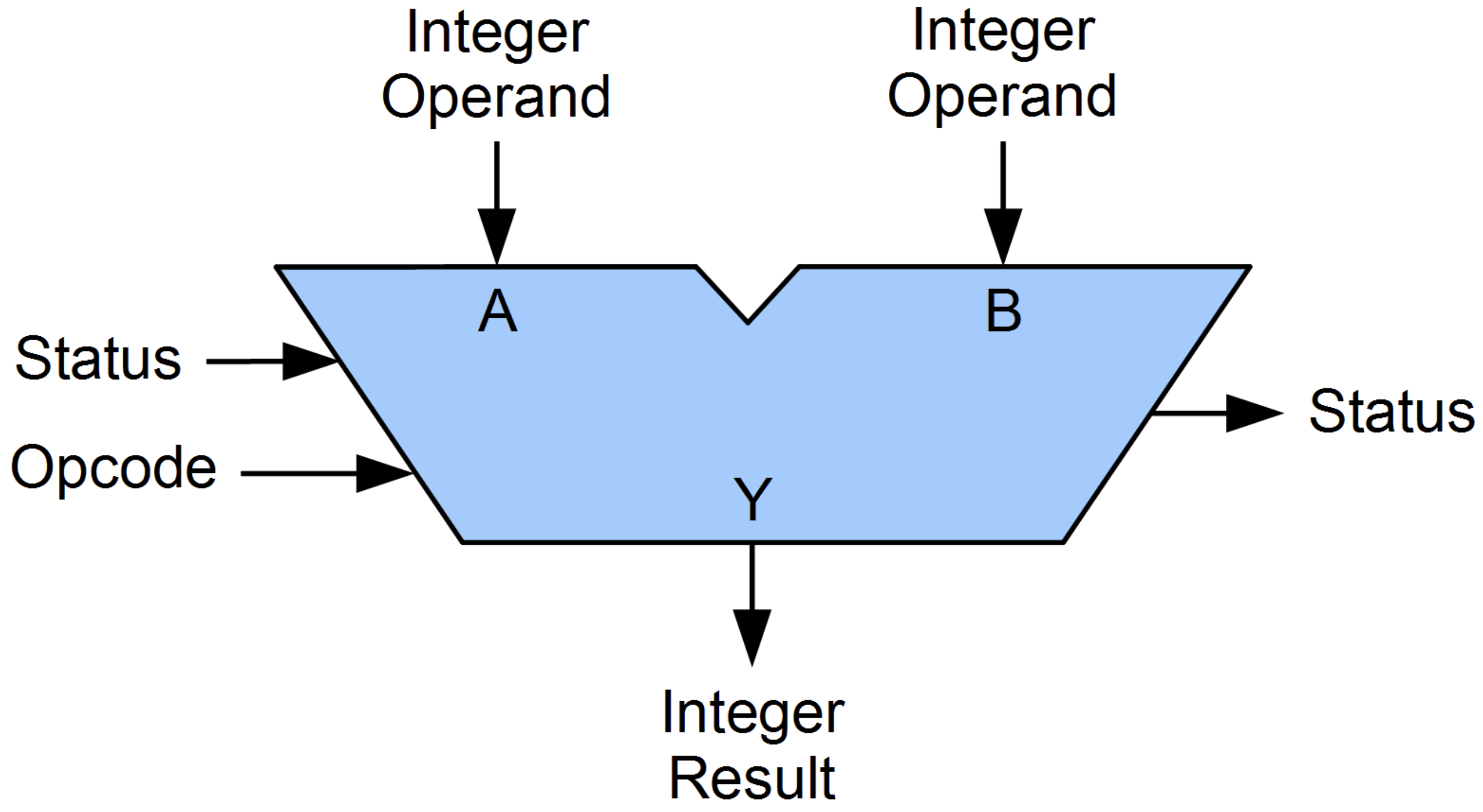ALU_wiki Fig. ALU. Source from wiki

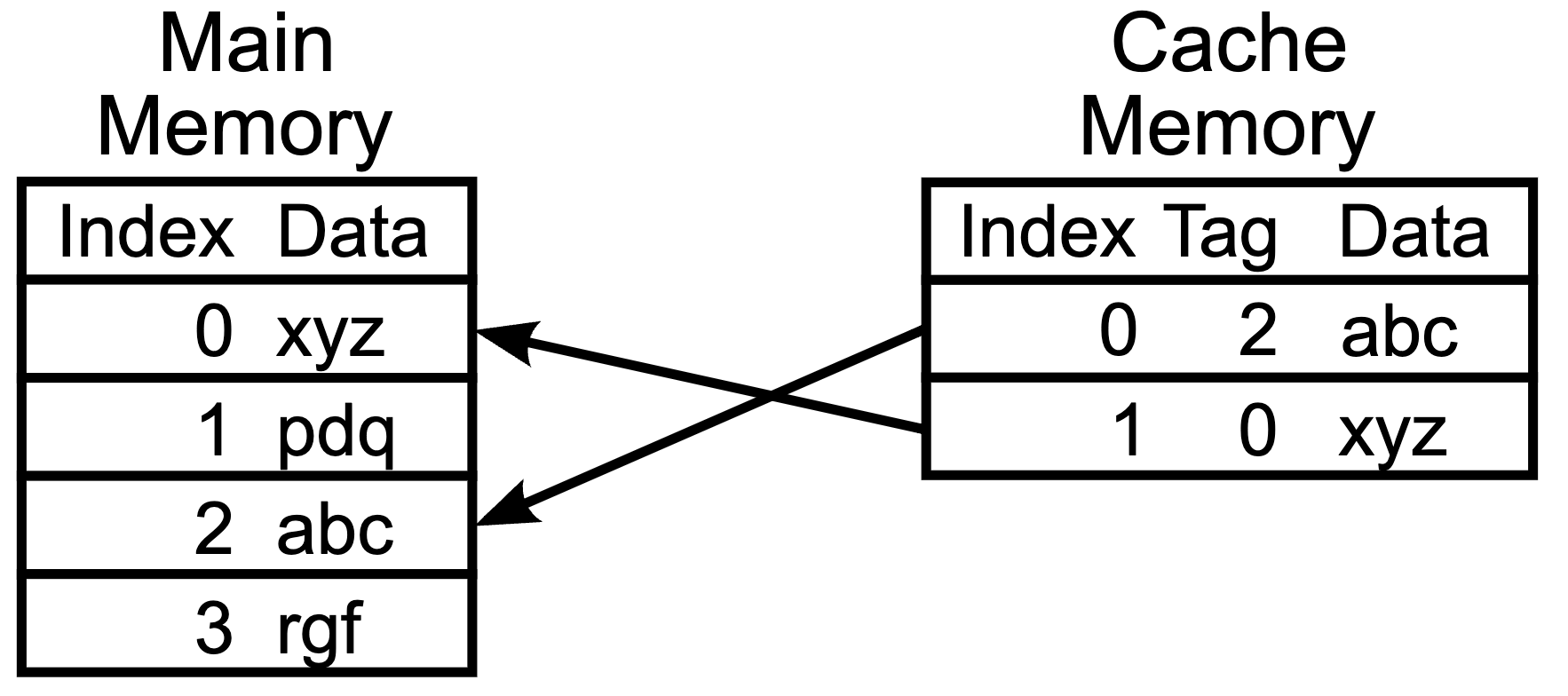cache Fig. Cache. Source from wiki

차근차근 살펴보겠으나 우리가 정말로 관심있는 것은 GPU이며, 위의 figure를 다시보면 GPU는 CPU보다 훨씬 많은 transistor가 달려있다는 걸 알 수 있다. GPU는 훨씬많은 ALU를 가지고 있는데 이는 CPU의 그것들보다 energy efficient하지만 연산 정확도는 떨어지며, cache 크기에 차이가 있는 등 여러 부분에서 차이점이 있다.

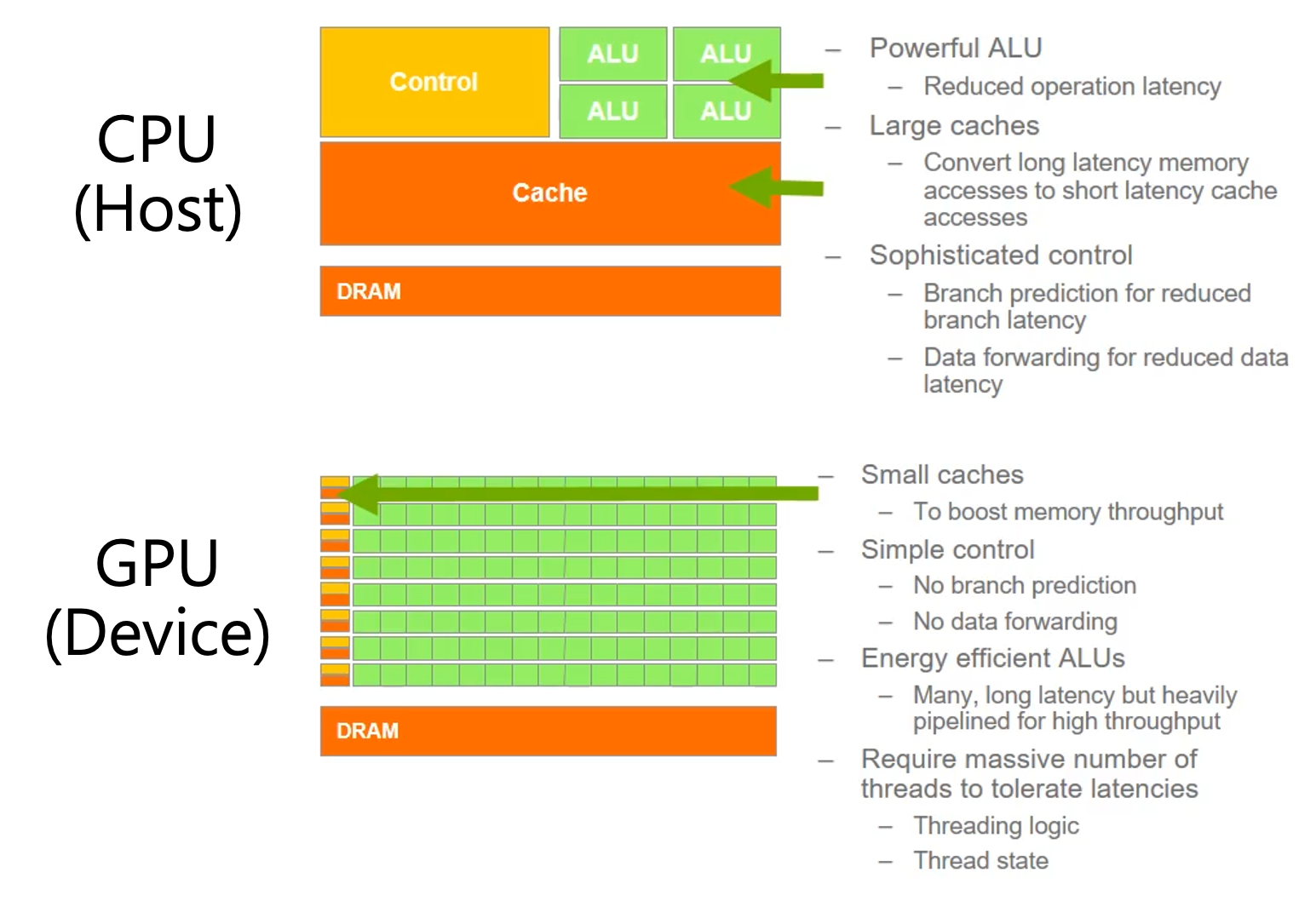cpu_gpu Fig.

우선 계속해서 CPU에 대해 알아보자면, Computer가 task를 수행할 수 있도록 주어지는 instruction set을 computer program이라고 부른다. Program이 실행되면 Window, MacOS, Linux같은 Operating System (OS)가 (Random Access) Memory에 program을 loading하고 registers, program counter, stack 그리고 heap 같은 필요한 자원을 제공한다. 이 때, data를 미리 복사해놓는 임시 장소 (temporary buffer)가 바로 앞서 말한 cache이다.

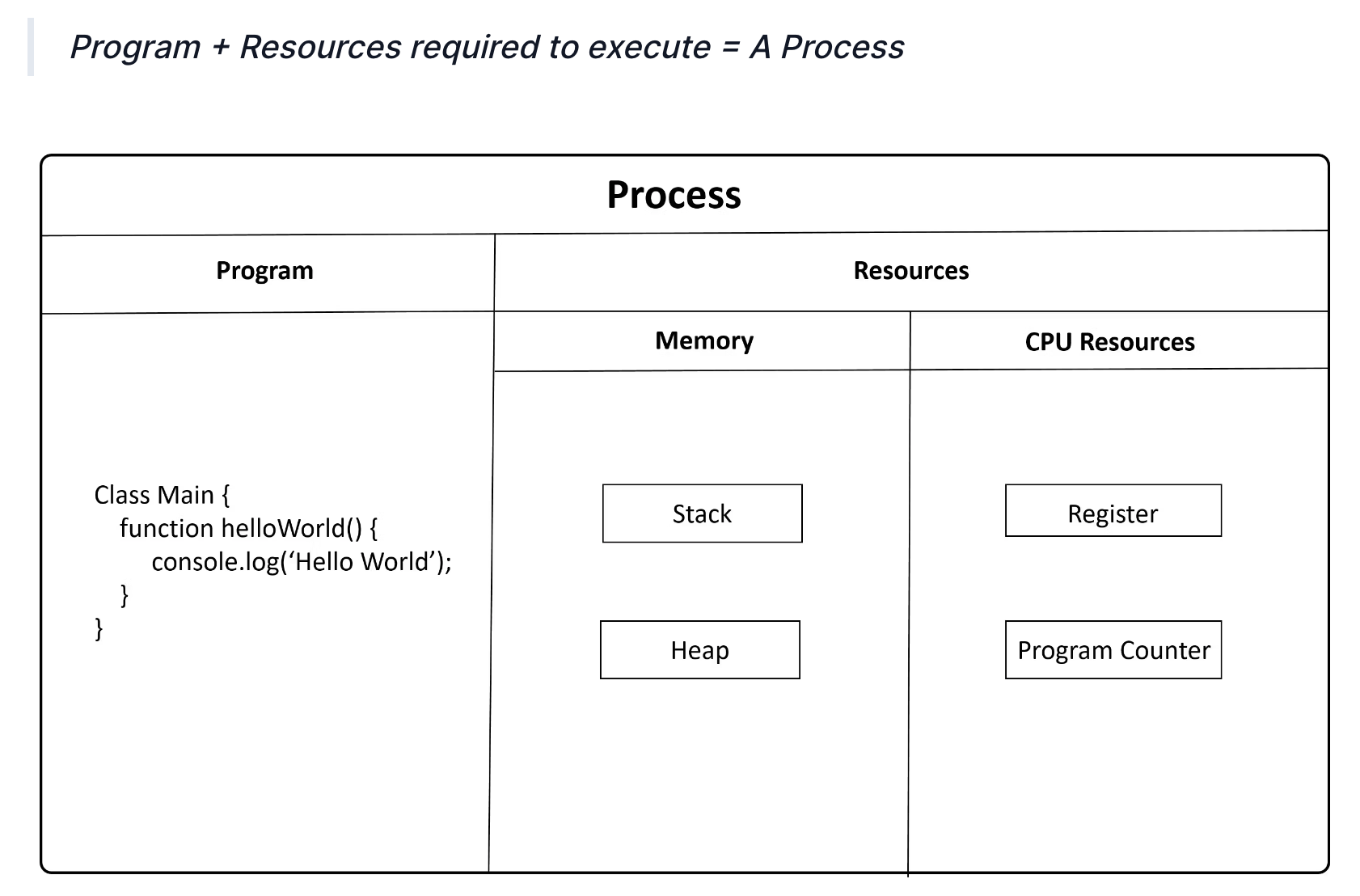cpu_multi_thread_fig1 Fig. Source from here

CPU가 처리하는 일련의 연산 과정을 thread라고 부르는데 (process의 실행 단위), CPU는 이런 thread를 동시에 여러개 띄워서 처리할 수도 있으며, 이를 multi-thread라고 한다. 당연하게도 thread가 1개짜리라면 (single thread) process가 곧 thread가 된다. Multi-thread 상황에서 process가 시작되면, memory와 연산을 위한 resource들이 할당 (allocate) 되는데, 각 thread는 모두 같은 memory와 resource를 공유 (share) 하지만, stack 만큼은 공유하지 않고 각 thread별로 갖게 된다.
Single thread의 경우 한 번에 하나의 task만 처리할 수 있지만, multi-threaded process의 경우 여러개의 task를 동시에 처리할 수 있다고 한다.

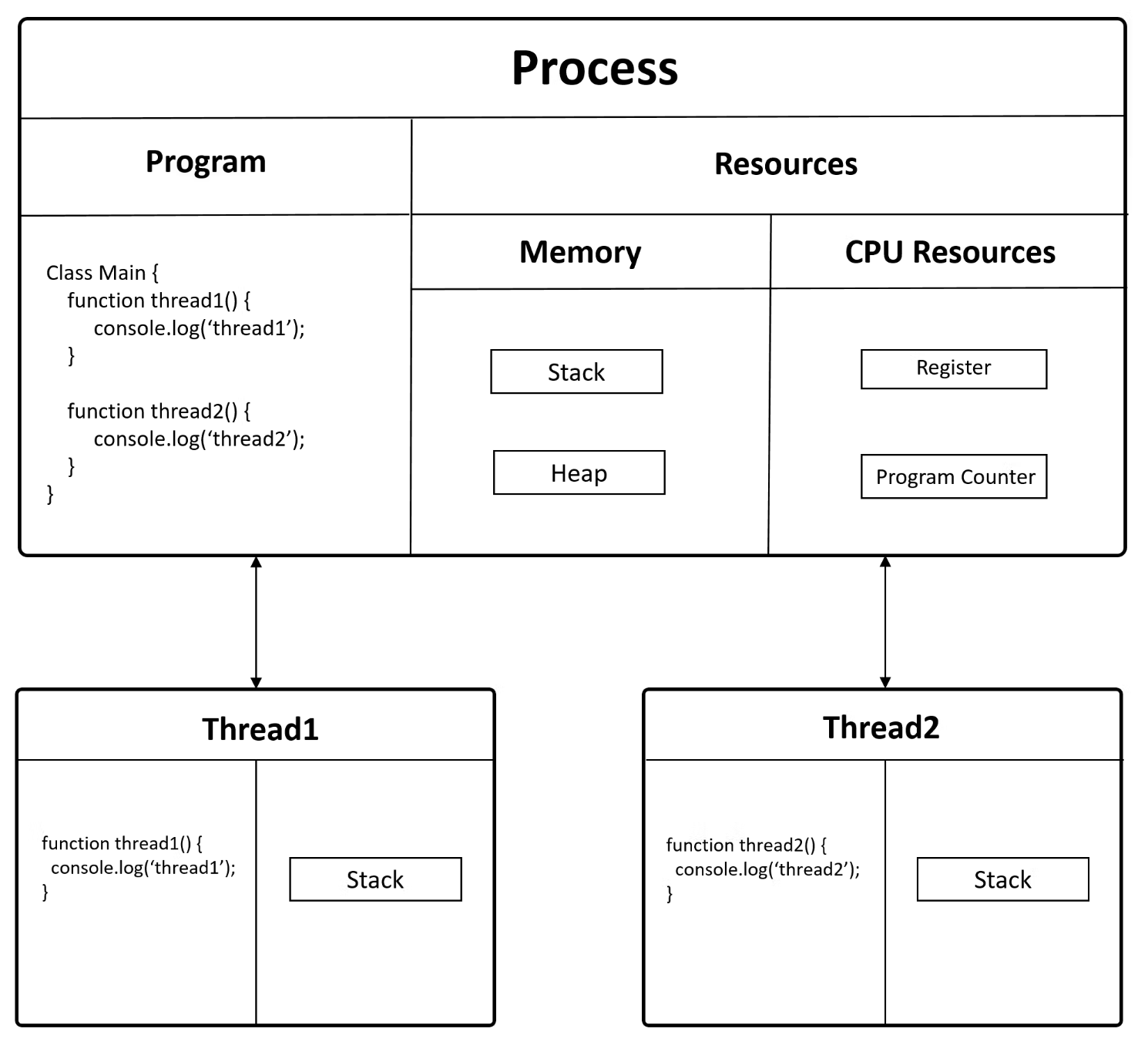cpu_multi_thread_fig2 Fig. Source from here

위 figure에서 어떤 program이 실제로 task를 수행하기 위해선 function 1을 처리하고 function 2까지 처리해야 하는데, 아마 thread가 1개라면 이를 순차적으로 처리해야 할 것이다 (이런 의미에서 CPU가 sequential job을 처리한다는 뜻인듯). Multi-thread면 task를 쪼개서 처리하는 아예 동시에 처리할 수 있는 이른 바 병렬화 (parallelism)가 가능해 보이지만, 실제로는 그렇지 않다고 한다. 그런데 이 process를 왔다갔다 하는 context switching를 negligible time동안 효율적으로 할 수 있었기 때문에 마치 multi processing을 하는 듯한 착각을 불러일으키며, 어떤 process나 thread가 무한루프에 빠지면 망하는 구조였다고 한다. 그럼 언제 thread를 건너뛰면서 처리할 수 있는가?에 대해서는 어떤 thread가 memory에서 data를 기다리는 등의 대기 상태에 빠졌을 때 다른 thread를 실행한다던가 하는 식으로 이루어진다고 한다. 대표적인 multi-threading 기술에는 동시 다발성 멀티스레딩(Simultaneous Multithreading, SMT)가 있으며, CPU의 대가 Intel에서는 이를 하이퍼스레딩(Hyper-Threading)이라고도 부른다고 한다.

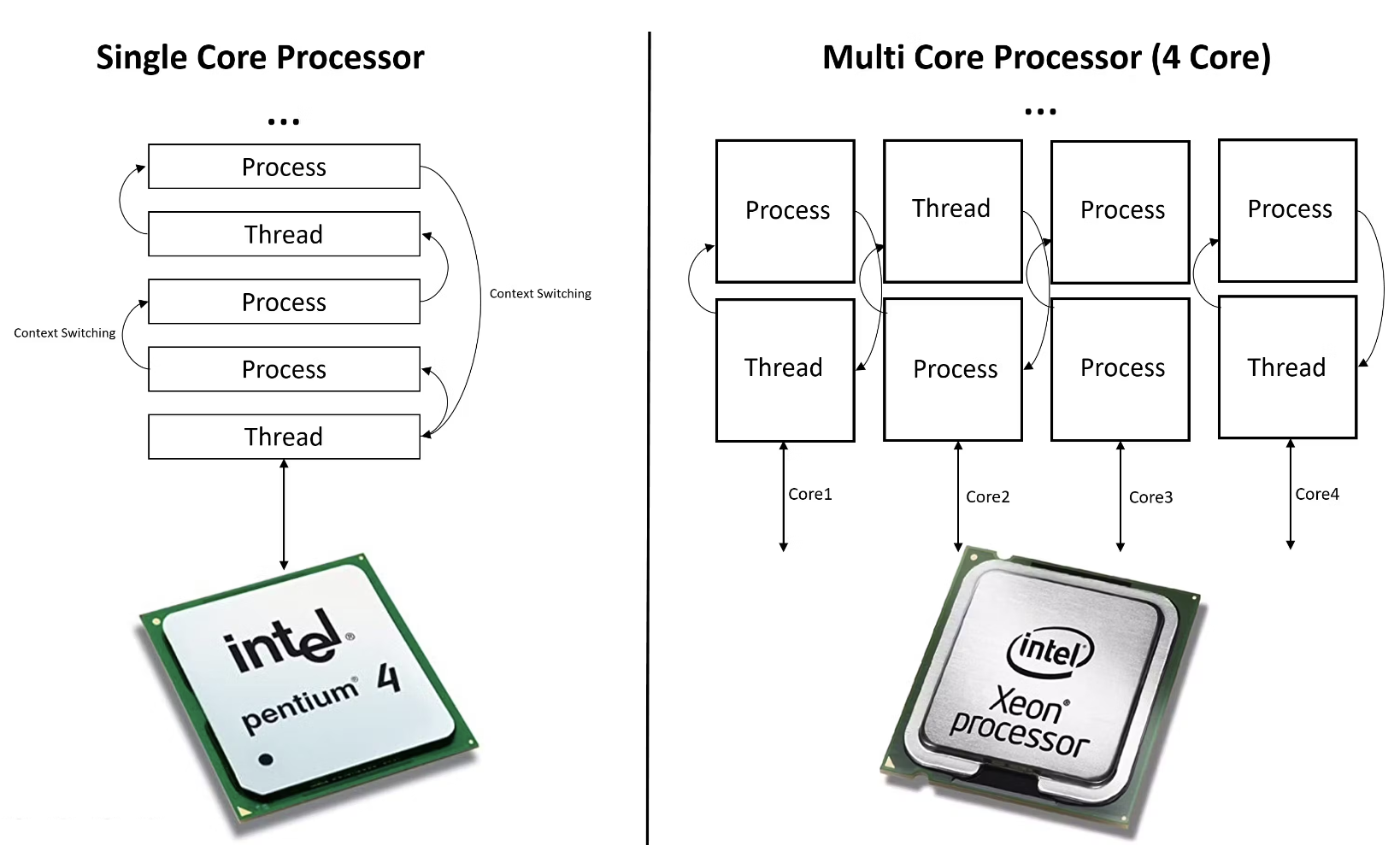cpu_multi_thread_fig3 Fig. Source from here

한 편, 옛날 옛적 pentium 4 시절에는 CPU가 single core processor였고, 한 번에 하나의 process나 thread만 처리가 가능했다고 한다. 물론 CPU의 성능을 발전시키기 위해서 응답 시간 (Latency), 클락 (clock) 등의 성능을 높혀왔는데, 이는 말 그대로 더빨리 switching 하라고 processor를 채찍질 하는것이나 다름이 없었지만 이것만으로는 부족했다.

당연하게도 이 문제를 해결하기 위해서 여러개의 CPU를 장착한다는 발상을 할 수 있는데, modern CPU들은 보통 2~16개 정도의 Core를 가지고 있고 thread는 16개 안팎이 된다고 하는 이른 바 multi-core processor이며, 이는 single physical processor가 그 안에 CPU를 하나 이상 가지고 있는 것을 의미하며 이를 바로 Core라고 부른다고 한다. 앞서 말한 것 처럼 Core는 한 번에 하나의 작업만을 수행할 수 있기 때문에, 완전한 동시성을 달성하기는 어려웠고, multi-threading이란 기술로 이러한 물리적 한계를 극복하기 위해, 대기 시간을 최소화하고 CPU의 사용률을 최대화하는 방법으로 설계 되었으나. multi-core의 경우 진짜 물리적으로 처리장치가 늘어났으며 각 Core는 자체적인 연산 resource를 가지므로 진정한 의미의 병렬화 (parallelism)이 가능해진다고 한다. 만약 core가 4개면 4개의 (quad)라는 접두사를 붙혀 quad core라고 부른다.

어쨌든 우리는 하나의 Core만 가지고도 photoshop, web surfing, game 등을 동시에 할 수는 있겠으나 (multi-threading으로 동시에 하는 것으로 보임), 만약 당신의 website가 loading이 너무 느리다면 (이것도 하나의 process) single core CPU를 multi core CPU로 교체해야 할 것이다. (하지만 multi-core를 쓴다고 모든 program는 아니라고 한다. 왜냐하면 program code자체가 single core에 대해서 최적화되어 있을 수 있기 때문이라고 한다.)

HDD, RAM and Cache Memory

GPU로 넘어가기전에 Memory에 대해서 얘기를 잠깐 해보자. Modern CPU는 아래처럼 Core가 4개 이상이라고 할 수 있는데, 잘 보면 Cache가 L1, L2, L3 이렇게 있는걸 알 수 있다. 이는 (L)evel을 의미하는데, processor에 가까울수록 Level이 낮고고 DRAM에 가까울수록 level이 높다.

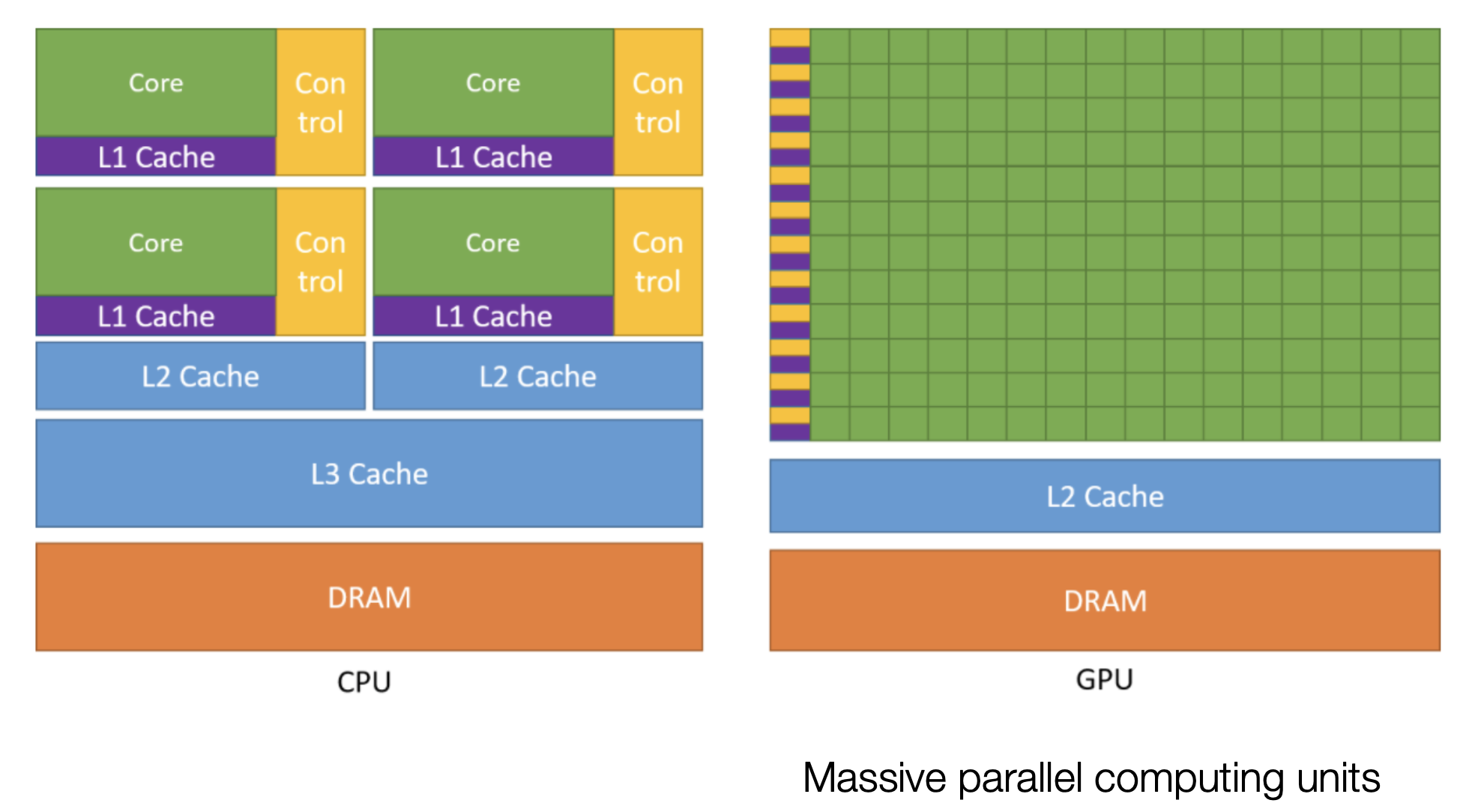modern_cpu_gpu Fig. Modern CPU and GPU. 앞선 figure와 비교해서 CPU가 4코어가 됐고 GPU는 L2 Cache가 생겼다

Computer를 구성하는 memory는 크게 세 가지가 있는데 이는 요약하자면 다음과 같다.

    1. 하드 디스크 (Hard Disk; HDD)
      • 정의: 하드디스크는 자기 저장 장치로, 컴퓨터의 주요 비휘발성 저장 매체로 전원이 꺼진 후에도 데이터를 보관.
      • 용도: 주로 운영 체제, 프로그램, 사용자 데이터 등의 장기 저장을 위해 사용됨.
      • 특징: 비교적 읽기/쓰기 속도가 느리지만, 대용량 데이터를 저장할 수 있고 비용 효율적.
    1. 램 (Random Access Memory; RAM)
      • 정의: 램은 컴퓨터의 휘발성 메모리로, 전원이 공급되는 동안에만 데이터를 유지.
      • 용도: CPU가 현재 실행 중인 프로그램과 프로그램이 사용하는 데이터를 빠르게 읽고 쓸 수 있도록 임시 저장공간으로 사용됨.
      • 특징: 데이터 접근 속도가 매우 빠르며, 프로그램의 실행 속도에 직접적인 영향을 미칩니다. 다만, 전원이 꺼지면 저장된 모든 정보가 사라짐.
    1. 캐시 (Cache)
      • 정의: 캐시는 CPU 내부에 위치한 매우 빠른 휘발성 메모리.
      • 용도: 자주 사용되는 데이터와 명령어를 저장하여, CPU가 램이나 하드디스크에서 데이터를 가져오는 시간을 줄여줌.
      • 특징: 캐시는 크기가 상대적으로 작지만, 데이터 접근 속도가 매우 빠릅니다. CPU와 가장 가까운 메모리 계층이며, 여러 단계(L1, L2, L3 등)로 구성될 수 있음.

Computer game을 실행하는 것으로 비유하자면 우리가 전원을 키는 순간 HDD에서 OS를 loading한다. 그리고 game file도 HDD에 있으므로 OS가 load된 이후 game을 실행하면 HDD의 file을 RAM으로 가져와서 load한다 (data를 이동시키는것과 같음). 실제 game이 시작되고나면 CPU는 RAM에서 data를 가져와 실행하는데, 이 때 많은 game data들 중 현재 play에 필요한 data를 processor가 빨리 처리할 수 있도록 가장 가까운 곳에 임시로 (temporary) 두고 쓰게 되는데, 이게 바로 cache로 load를 하는 것이 된다.

Cache 중에서도 L1 cache는 물리적으로도 processor와 가깝기 때문에 (그래서 on-chip memory라고 부른다) 훨씬 속도가 빠르지만 만드는데 드는 비용이 크고, chip 내부에 있어야 하기 때문에 용량에 한계가 있다. RAM은 지속적으로 game play에 필요한 data를 유지하지만 만약 user가 map을 이동하거나 하면 추가 data를 HDD에서 load한다. 만약 user가 원하는 data가 cache에 없으면 RAM, RAM에 없으면 HDD로 가서 data를 찾아야 하며, cache에는 내가 최근에 사용한 것들 위주로 data가 구성되는데 빠른처리를 위해서는 이를 잘 설계해야 할 것으로 보인다.

Graphic Processing Unit (GPU)

GPU는 이러한 parallelism을 매우 극한으로 끌어올린 것이라고 볼 수 있다. 아래 figure를 보면 GPU는 Core개수가 매우 많은데, 즉 대부분의 transistor가 데이터 처리를 위해 사용되고 나머지가 cache에 쓰인다데 CPU보다 cache의 크기는 작다.

modern_cpu_gpu Fig. Modern CPU and GPU. 앞선 figure와 비교해서 CPU가 4코어가 됐고 GPU는 L2 Cache가 생겼다

왜 이렇게 발전했는가?

Computing 분야에는 무어의 법칙 (Moore’s Law)이라는 용어가 있는데, 이는 micro chip 기술의 발전 속도에 관한 일종의 법칙으로, micro chip에 저장할 수 있는 데이터 분량이 18-24개월 마다 두 배씩 증가한다는 법칙을 말한다. 이는 컴퓨터 성능이 거의 5년마다 10배, 10년마다 100배씩 개선된다는 것을 의미하는데, moore’s law는 PC의 처리속도와 memory 양이 2배로 증가하고 비용은 상대적으로 떨어지는 효과를 가져 왔다.

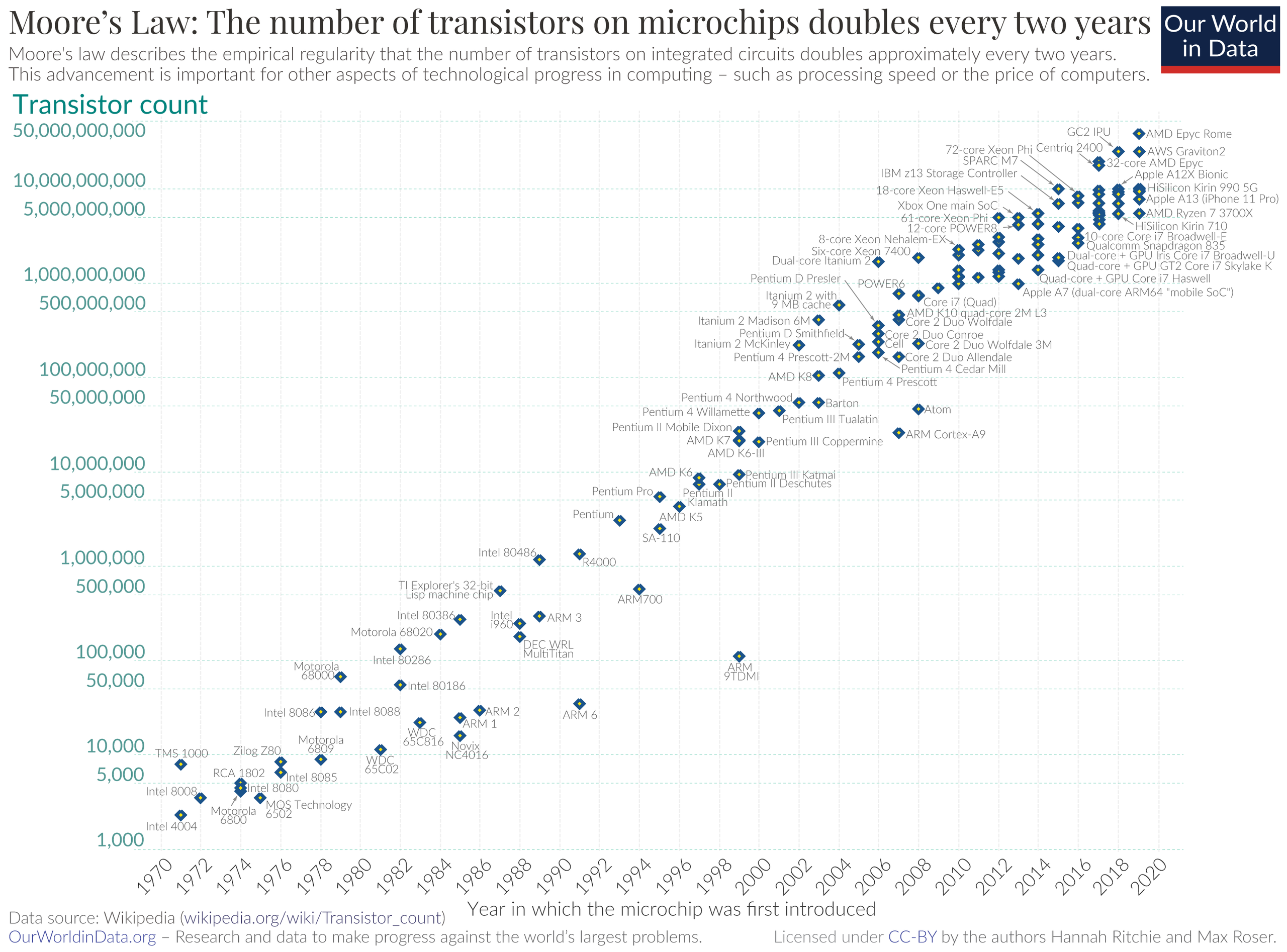moore_law Fig.

그러나 비슷한 크기의 chip에 더 많은 transistor의 개수를 욱여넣을 수 있게 되더라도, CPU는 2000년대 초반까지 single core를 쓰는 등 computing 성능은 transistor의 갯수에 비례해서 늘지 않았다고 한다.

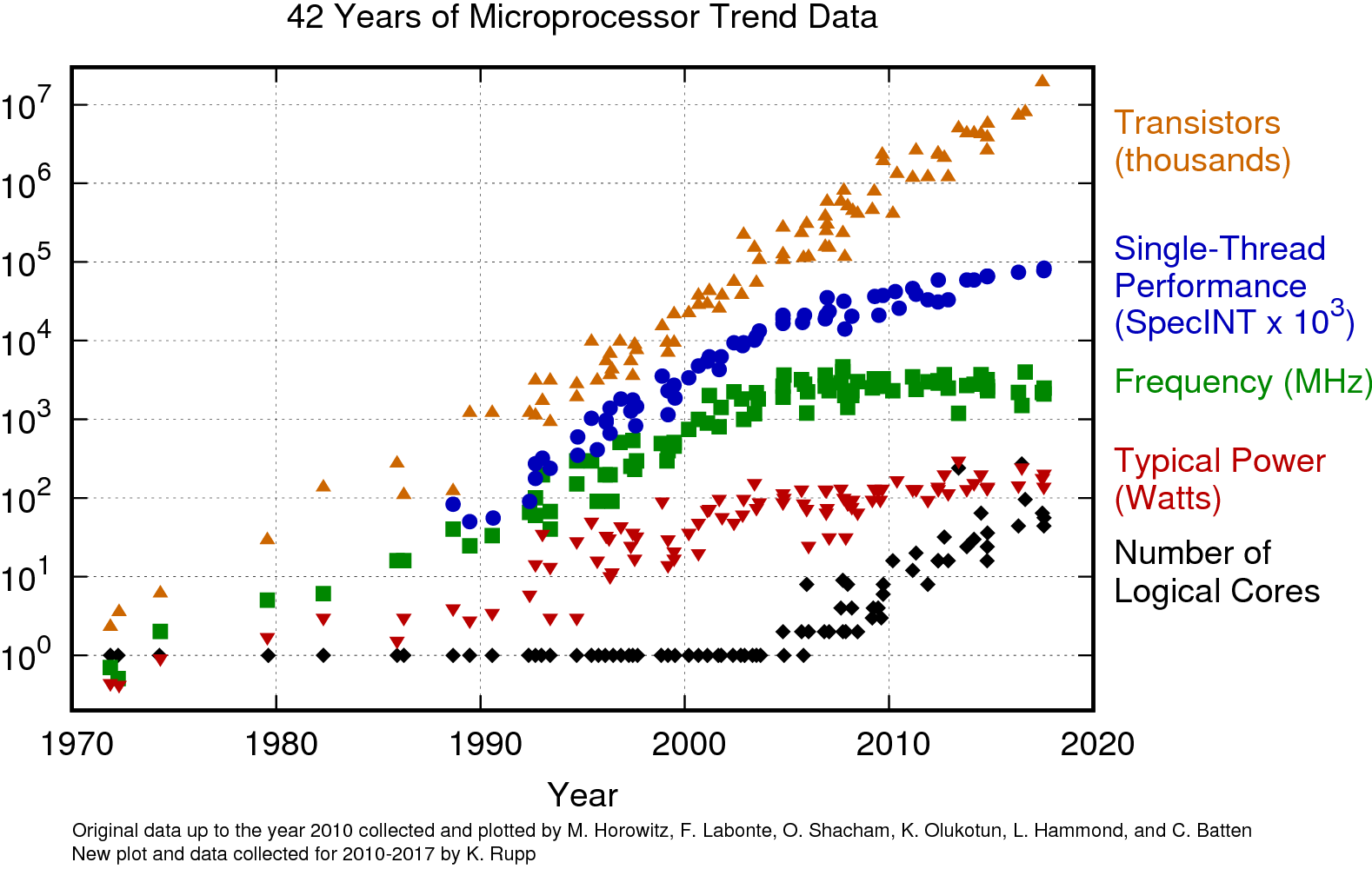42_years_processor_trend Fig.

하지만 GPU는 달랐다. 병렬 처리 (parallelism)에 특화된 이 processor는 잘만 logic을 짜주면 초당 부동 소수점 연산 수 (Floating point operations per second; FLOPs)를 기하급수적으로 끌어 올릴 수 있었다.

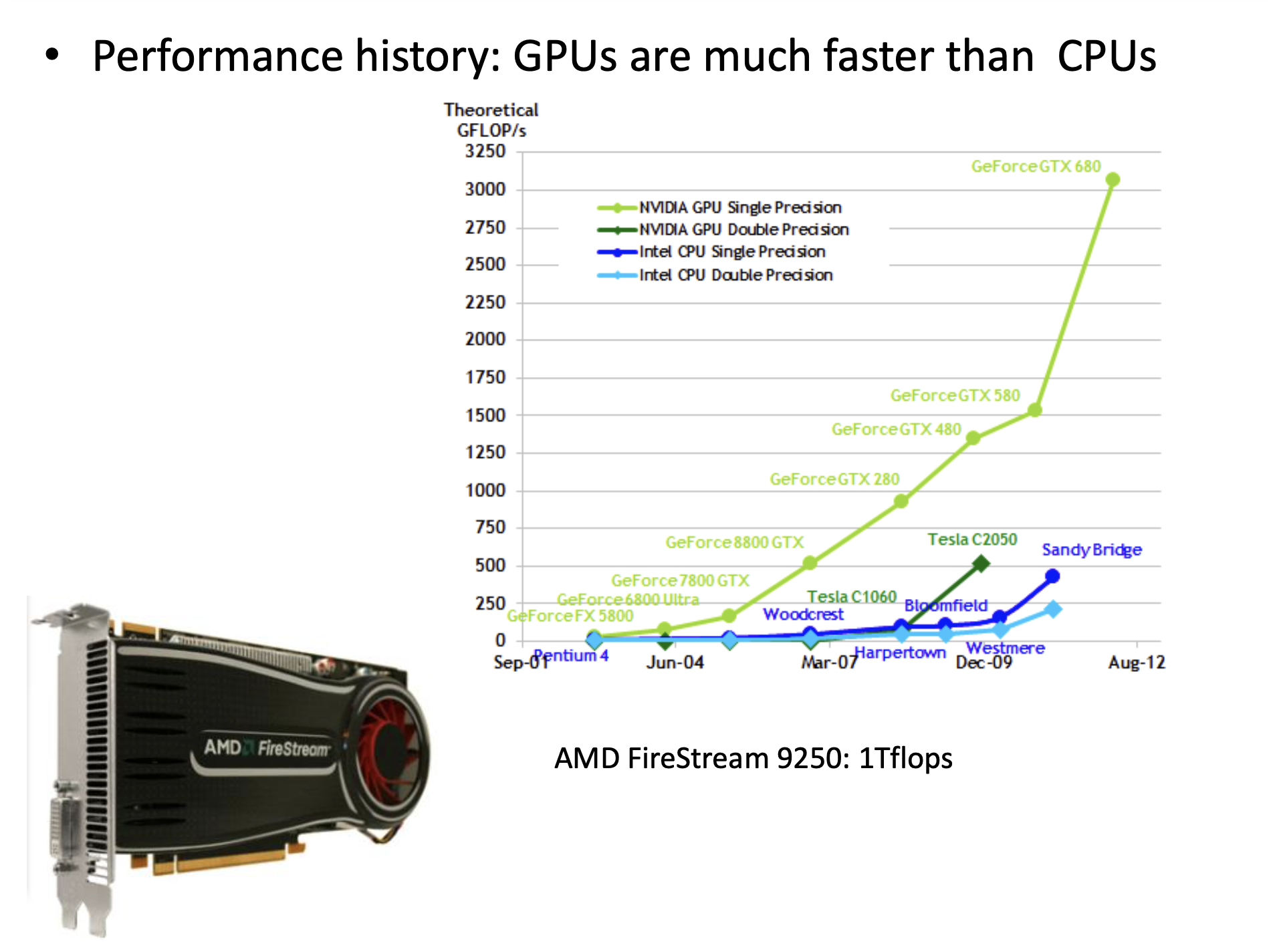flops_cpu_gpu_years Fig.

GPU는 고처리량 processor, 혹은 throughput processor라고 불리기도 하는데, CPU가 latency가 빠르지만 처리량은 적은 예를 들어 슈퍼카 같은 존재라면 GPU는 좀 느려도 처리하는 승객량이 많은 버스라고 보면 될 것 같다.

H100을 제외하고 GPGPU중에서 가장 성능이 좋은 A100은 아래처럼 생겼다. 총 108개의 Streaming Multiprocessors (SMs)를 가지고 있으며 각각은 L1 cache를 갖고 있고, 40MB의 L2 cache를 가지며 80GB의 HBM2 memory로부터 초당 data를 얼마나 전송할 수 있는지를 measure하는 metric인 bandwidth는 2039 GB/s이다.

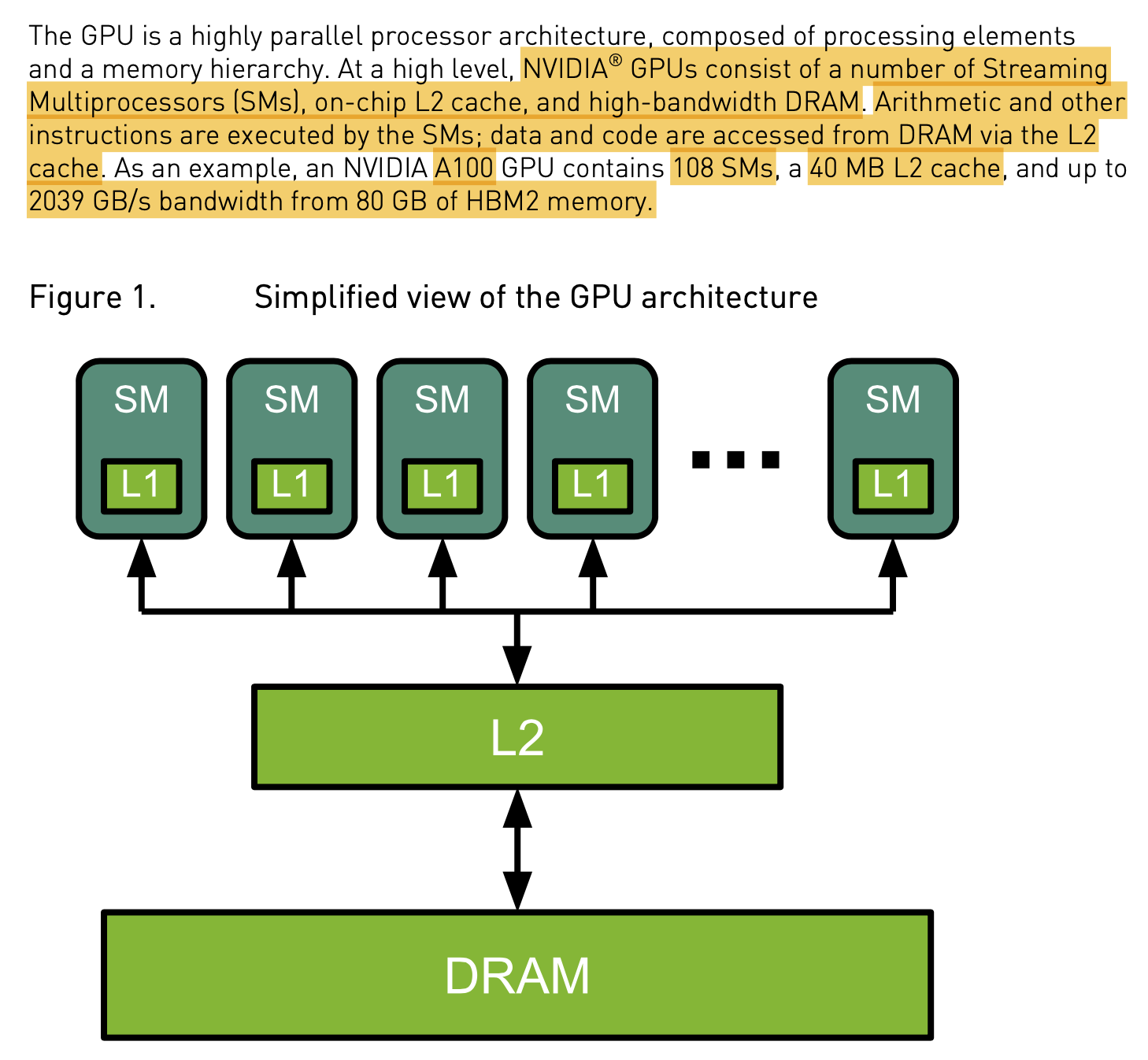a100_arch Fig.

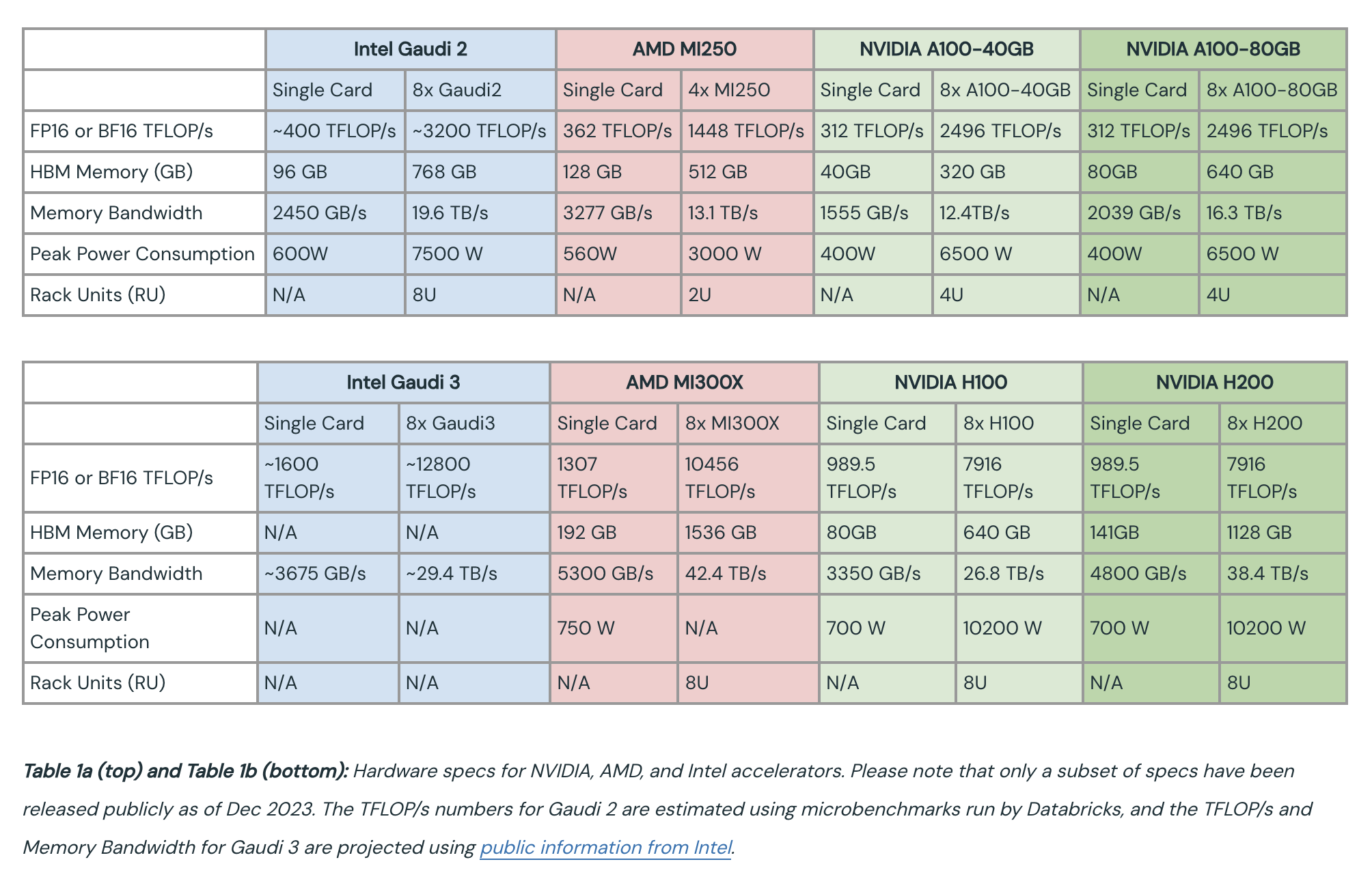acclerator_specs Fig. Source from link

Operations of Nerual Networks

Understanding Performance (Arithmetic Intensity)

우선 GPU의 어떤 연산에 대해 이것이 Math bound인지? 아니면 Memory bound인지? 논하기 위해서는 Arithmetic Intensity (Compute Intensity)을 알아야 한다. Arithmetic Intensity는 다음과 같이 표현하는데,

\[\begin{aligned} & \text{Arithmetic Intensity} = \frac{ \text{number of FLOPS} }{ \text{number of byte accesses} } & \\ \end{aligned}\]

직관적으로 행렬 곱 (matrix mutliplication), \(C=AB\)을 생각할 때 C를 만들기 위해서 A와 B의 row, column을 조회해야 하고, 가져온 vector를 내적해서 C의 element로 채워넣으면 된다. 이 때 data를 조회하는 것이 memory에 access한다고 하며, 실제 계산을 수행하는것이 math, arithmetic 이라고 하며 초당 부동 소수점 연산 수 (Floating point operations per second; FLOPs)라고도 한다. 여기서 만약 Arithmentic Intensity가 현재 GPU hardware의 어떤 기준 수치보다 작으면 이 연산은 memory access에 시간을 많이 쓰는 것이므로 memory bound라 부르고, 그 반대는 math bound라고 부른다. 만약 memory bound라면 memory access속도를 개선하거나 다른 방법을 찾아 이를 개선할수록 performance가 좋아질 것이다.

그렇다면 arithmetic intensity가 어떤 값보다 크냐 작냐를 판단하는 기준은 뭘까? 사실 주어진 GPU hardware에 대해서 어떤 function의 performance를 재는 것은 세 가지 요소라고 한다.

  • memory bandwidth
  • math bandwidth
  • latency

대역폭 (Bandwidth)란 단위 시간 동안 전송될 수 있는 data의 양을 의미하는데, memory bandwitdh는 보통 도로의 차선에 비유하곤 하며, 차선의 폭이 넓을수록 데이터가 시간당 전송되는 양이 늘어난다.

다시 \(T_{mem}\)이 memory access에 드는 시간이라 하고, math operation에 쓰는 시간은 \(T_{math}\)라고 정의하자. 마찬가지로 math에 걸리는 시간이 더 길면 math limited, 그 반대면 memory limited이다. 그런데 어떤 algorithm (function)이 memory와 math에 얼마나 시간을 쓰는지는 processor의 bandwidth와도 관련이 있다. Memory time, \(T_{meme}\)은 아까 arithmetic intensity를 계산할 때 정의한 byte accessed의 수, \(\# bytes\)인데 이를 GPU의 bandwidth로 나눈 \(\# bytes / BW_{mem}\)이 된다. 당연히 P40, V100, A100, H100으로 갈수록 bandwidth가 좋아지는데 memory access수만 가지고 이것이 memory bound인지를 논할순 없지 않은가?

마찬가지로 Math time, \(T_{math}\)도 \(\# ops / BW_{math}\)가 된다. 즉 우리는 math limited (math bound)냐, memory limited (memory bound)냐를 정하기 위해 아래의 수식을 써야 하는 것이다.

\[\begin{aligned} && T_{math} > T_{mem} && \\ && \# ops / BW_{math} > \# bytes / BW_{mem} && \\ \end{aligned}\]

이를 간단한 algebra에 의해 다시 표현하면 다음과 같은데, 왼쪽에 있는게 arithmetic intensity가 되면 오른쪽이 주어진 GPU의 performance를 재는 기준이 되는 것으로, 이를 ops:byte ratio라고 한다.

\[\# ops / \# bytes > BW_{math} / BW_{mem}\]

NVIDIA Volta V100 GPU의 경우 이 값이 40~139정도 라고 하는데, 이는 다음을 따르기 때문이다.

arithmetic_intensity_fig1 Fig.

그렇다면 Neural Network (NN)를 구성하는 function들은 무엇에 bound되어 있을까? 아래 table을 보면 대부분은 arithmetic intensity가 낮은 memory bound라고 할 수 있음을 알 수 있다.

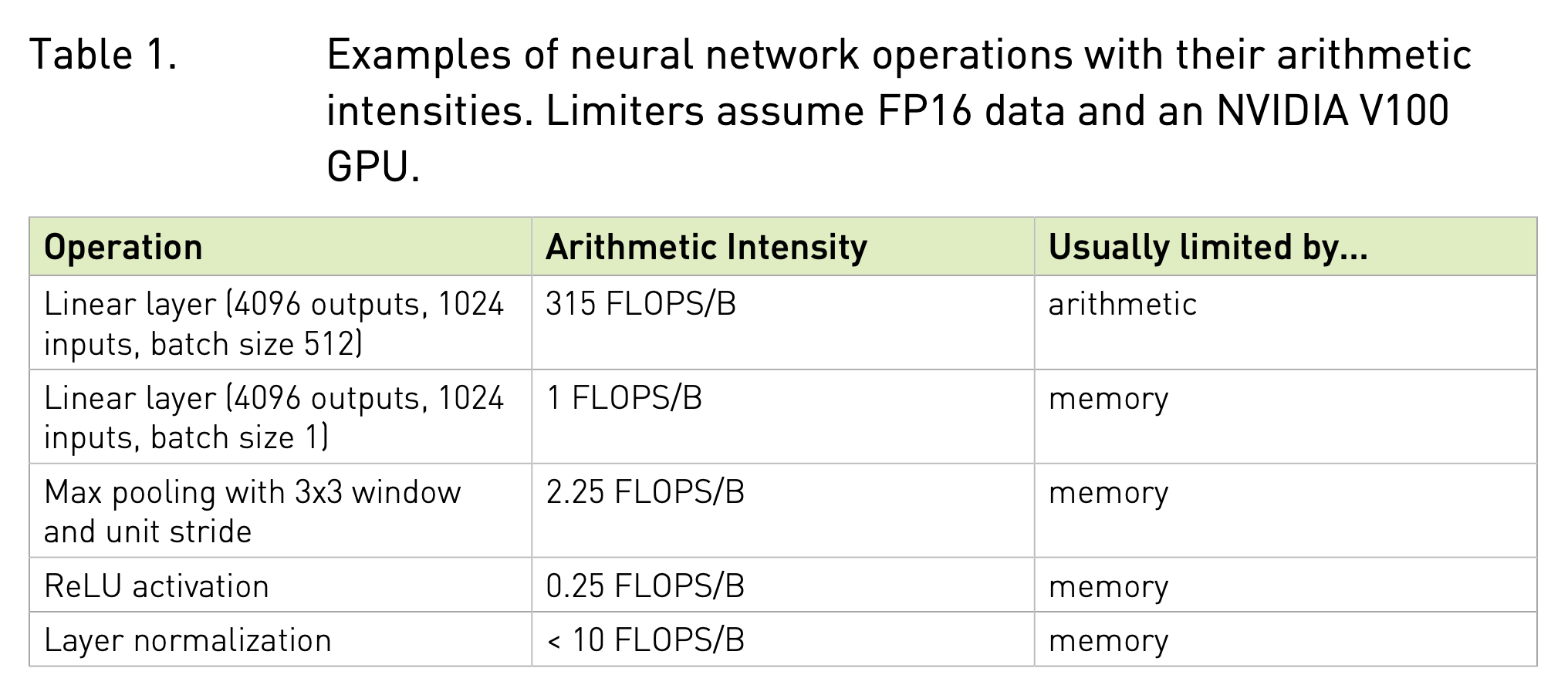example_of_nn_operations Fig.

하지만 이 분석방법은 multiple memory access를 고려하지 않는다던가, 실제 function (algorithm)이 실행할때 갖는 address calculation등을 포함하지 않는 등의 문제가 있기 때문에 실제 profiling 결과를 바탕으로 design을 고려해야 한다고 하니 주의하자.

arithmetic_intensity_fig2 Fig.

나머지는 내용은 NVIDIA의 blog post, GPU Performance Background User’s Guide를 참고하길 바란다.

example_of_nn_operations2 Fig.

example_of_nn_operations3 Fig.

GEneral Matrix-to-matrix Multiplication (GEMM)

한 편, 행렬 곱을 지칭하는 term으로 GEneral Matrix-to-matrix Multiplication (GEMM)이라는 것이 있다. GEMM은 Neural Network (NN)의 수많은 연산을 구성하는 가장 근본적인 building block으로, 말 그대로 matrix multiplication인데, 이를 수식으로 나타내면 다음과 같다.

\[\begin{aligned} && C = \alpha AB + \beta C && \\ \end{aligned}\]

NN의 한 layer를 생각해보면 A는 activation input이고 B는 weight matrix일 것이며 C는 output matrix이다. 여기서 \(\alpha=1, \beta=0\)이면 그냥 matrix mutliplication이고 \(\alpha=1, \beta=1\)이면 원래 output C가 다시 더해지는 형태로 residual connection을 의미한다.

우선 단순하게 \(\alpha, \beta\)를 무시하고 오로지 \(C=AB\)에 대해 생각해보자. Matrix, A가 M-bt-K의 크기를 갖고 B가 K-by-N을 가진다면 output matrix의 크기는 M-by-N 이 될 텐데 K가 충분히 크면 이 coefficient들은 무시할만한 수준이 된다. 이 때 Arithmetic Intensity는 다음과 같이 표현할 수 있다.

\[\begin{aligned} && \text{Arithmetic Intensity} = \frac{ \text{number of FLOPS} }{ \text{number of byte accesses} } && \\ && \frac{ 2 \cdot (M \cdot N \cdot K) }{ 2 \cdot (M \cdot K + N \cdot K + M \cdot N) } && \\ && \frac{ M \cdot N \cdot K }{ M \cdot K + N \cdot K + M \cdot N } && \\ \end{aligned}\]

C의 각 element들은 k-elements vector들인 A와 B의 row, column vector들의 내적 값 (inner product)이라고 할 수 있다. 즉 matmul은 vector간 내적의 총 집합인 셈이며, 두 vector를 내적한다는 것은 각 element끼리 곱하고 더하는 것으로 총 \(M * N * K\)의 Fused Multiply-Adds (FMAs)를 한다고 얘기한다. 당연히 각 FMA는 곱셈 (multiply)과 덧셈 (add) 2개 연산을 합쳐서 부르는 것이므로 총 \(2 * M * N * K\) FLOPs가 요구된다. 이것이 분자가 \(2 \cdot (M \cdot N \cdot K)\)인 이유이다. 분모의 number of byte access가 위처럼 계산되는 이유는 \(M \cdot K, N \cdot K\)는 A, B matrix를 읽는 데 (read) 드는 access비용, 나머지 \(M \cdot N\)은 output matrix C를 쓰는 데 (write)드는 비용이기 때문이다. 앞에 계수 2가 곱해지는 이유는 write, read 모두 float16, bfloat16인 경우 2 bytes가 들기 때문이다.

예를 들어 M x N x K = 8192 x 128 x 8192 GEMM에 대해서 생각해보자. 이는 arithmetic intensity가 124.1 FLOPS/B로 V100의 ops:bytes인 139보다 낮기 때문에 memory bound이다. 그런데 GEMM size가 8192 x 8192 x 8192가 된다면 (output matrix의 column개수인 N이 매우커짐), 2730이 되어 math bound가 된다. 또한 M=1이거나 N=1인 Matrix-vector products (general matrix-vector product or GEMV)에 대해서는 intensity가 1보다 작게 되기 때문에 언제나 memory limited가 된다고 한다.

Implementation of GEMM

이제 NN의 heart인 Matmul에 대해서 구현하는 경우에 대해 생각해보자. Matrix, A가 M-bt-K의 크기를 갖고 B가 K-by-N을 가질 때 가장 간단한 방식은 아래처럼 단순 무식하게 for loop을 돌면서 output matrix, C의 element를 채우는 것이다.

gemm_fig1 Fig.

M-by-N크기의 matrix, C의 (i,j)번째 element는 A의 i번째 row와 B의 j번째 column의 dot product일 것이다. 물론 이게 최적의 구현이라면 당연히 말도 꺼내지 않았을텐데 당연히 이는 몇 가지 문제점을 가지고 있다. 왜냐하면 \(C[i][j]\)를 계산하기 위해서는 \(A[i][k]\)의 한 행과 \(B[k][j]\)의 한 열을 반복적으로 access해야 하기 때문이다. A의 각 행과 B의 각 열은 N번 혹은 M번 access되어야 하는데, 이 경우 k가 제일 안쪽 loop에 위치해 있을 때 데이터 재사용 (data reuse)가 제한적이며, 행렬의 크기가 커지면 cache memory의 용량을 초과할 수 있다고 한다.

이상적으로, 이 Matmul의 performance는 processor의 arithmetic throughput에 의해 제한되어야 할 것이고, 매우 큰 M=N=K에 대해서 math operation의 수는 O(N^3)인 반면 필요한 data의 양은 O(N^2)이므로 이론적인 compute intensity를 사용하려면 모든 element를 O(N)번 재사용 해야 한다고 한다.

반면 아래와 같이 K를 최외곽에 두게 되면, 데이터 재사용(data reuse)과 메모리 액세스 패턴(memory access patterns)에서 장점을 가질 수 있다.

gemm_fig2 Fig.

이 경우 A의 각 열과 B의 각 행을 한 번씩만 읽어서 C의 모든 요소에 대한 누적 계산을 진행할 수 있다. 이 구조는 루프를 통한 계산이 연속적으로 이어지도록 하여 memory에서 processor로의 데이터 전송 지연을 최소화 할 수 있다고 한다.

마지막으로 이런 efficient matmul을 block (tile) 단위로 쪼개서 처리할 수가 있다.

gemm_fig3 Fig.

Tiled MatMul

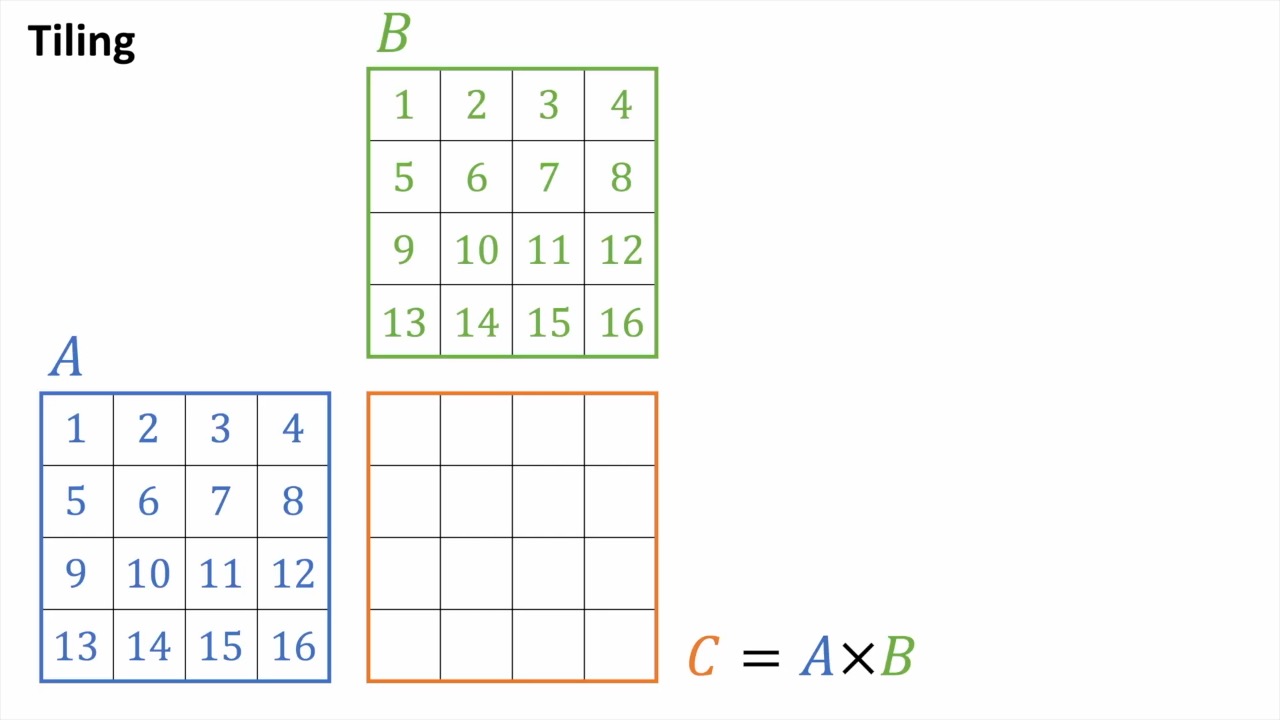tiled_matmul_example_fig1 Fig.

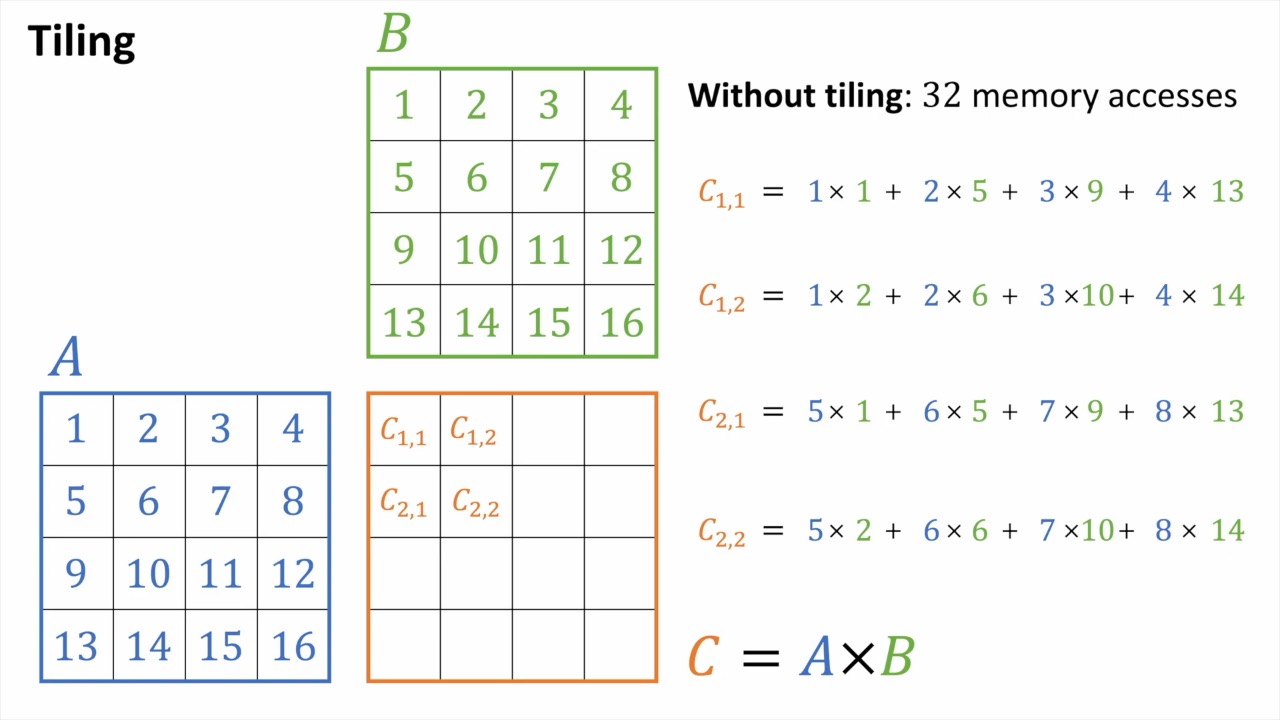tiled_matmul_example_fig2 Fig.

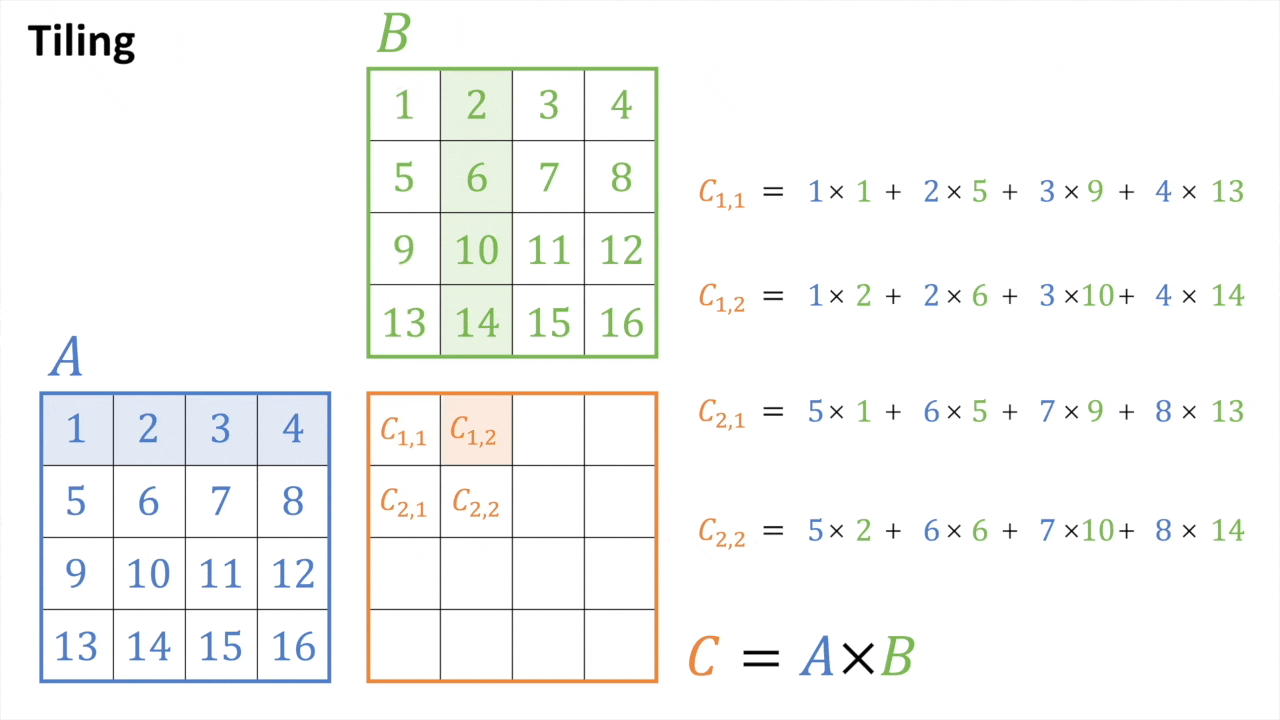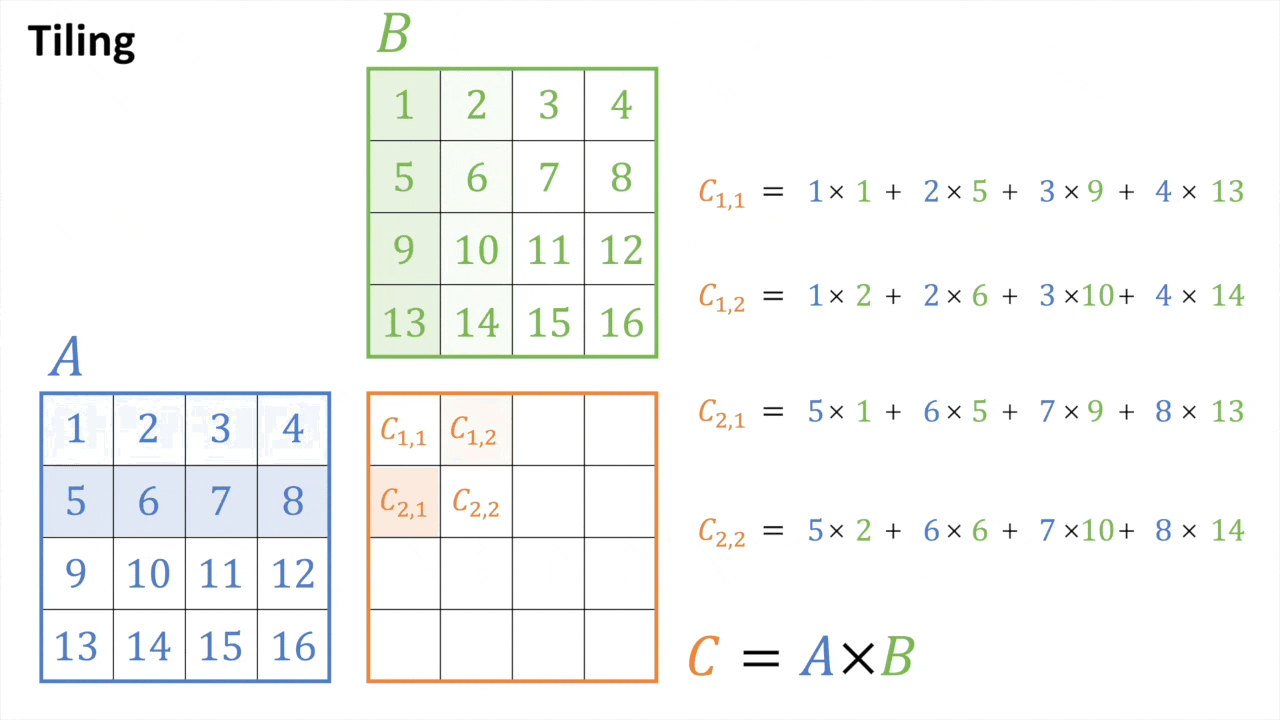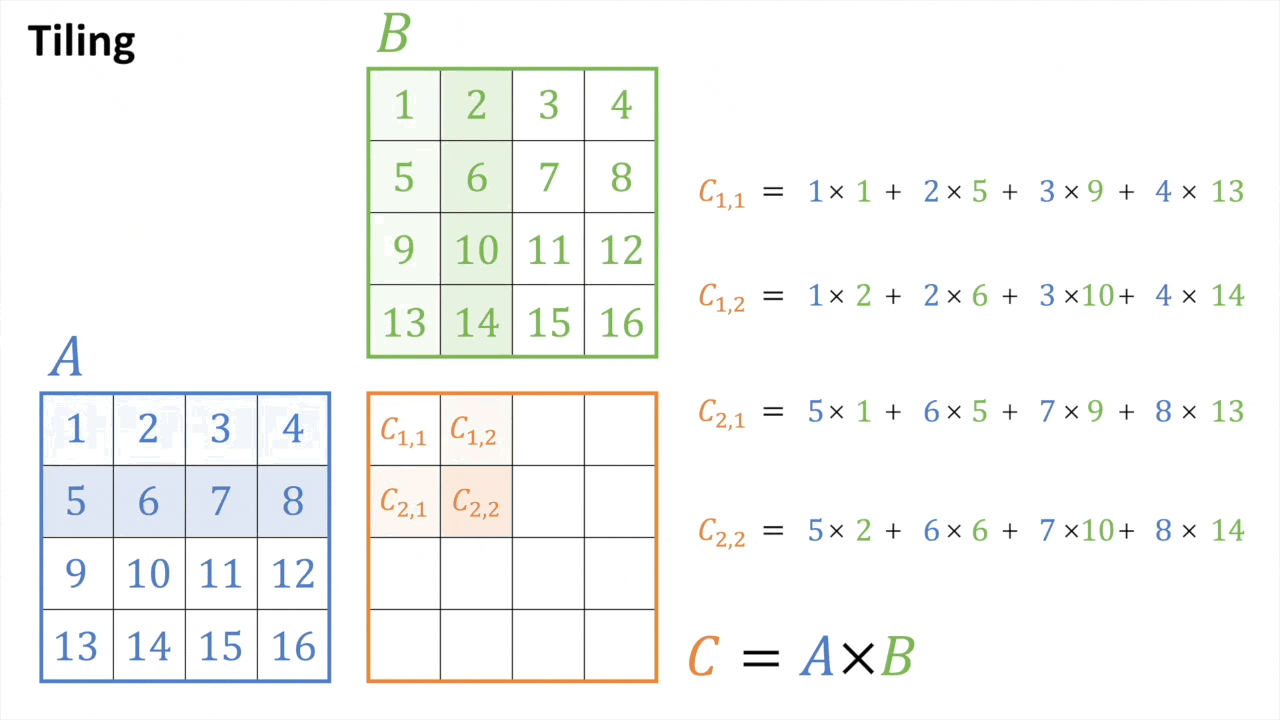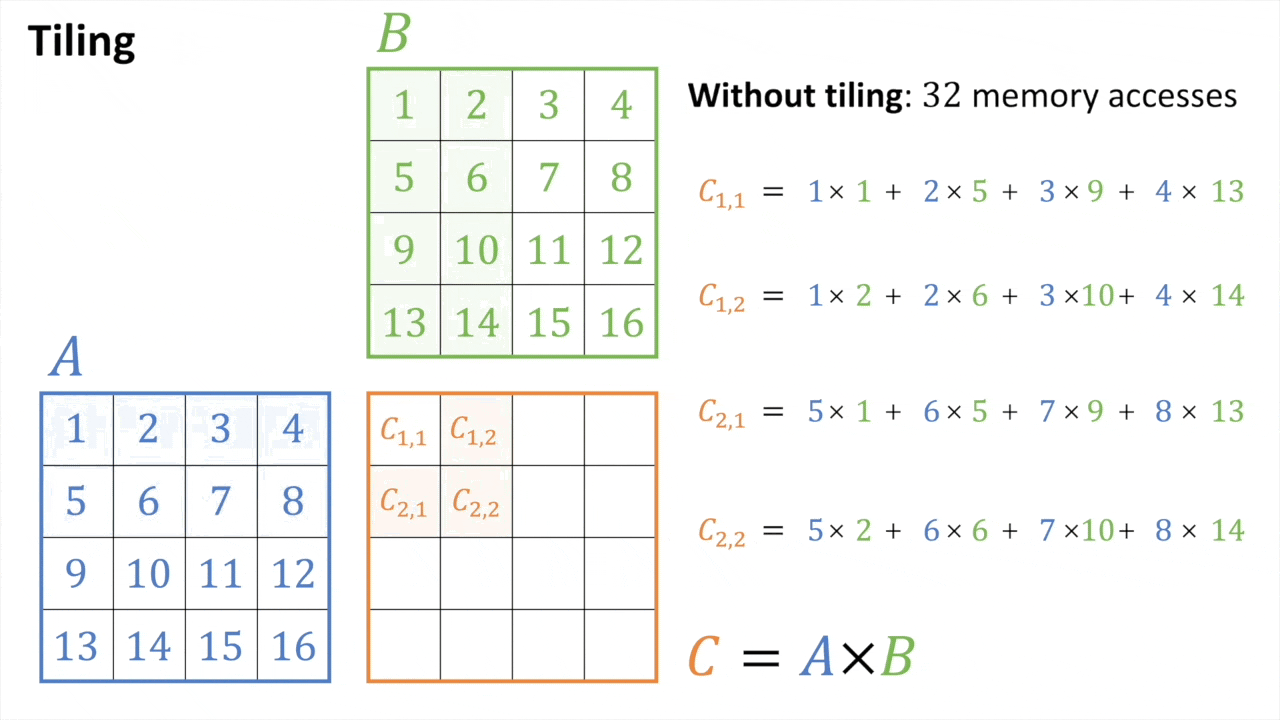tiled_matmul_example_animation1 Fig.

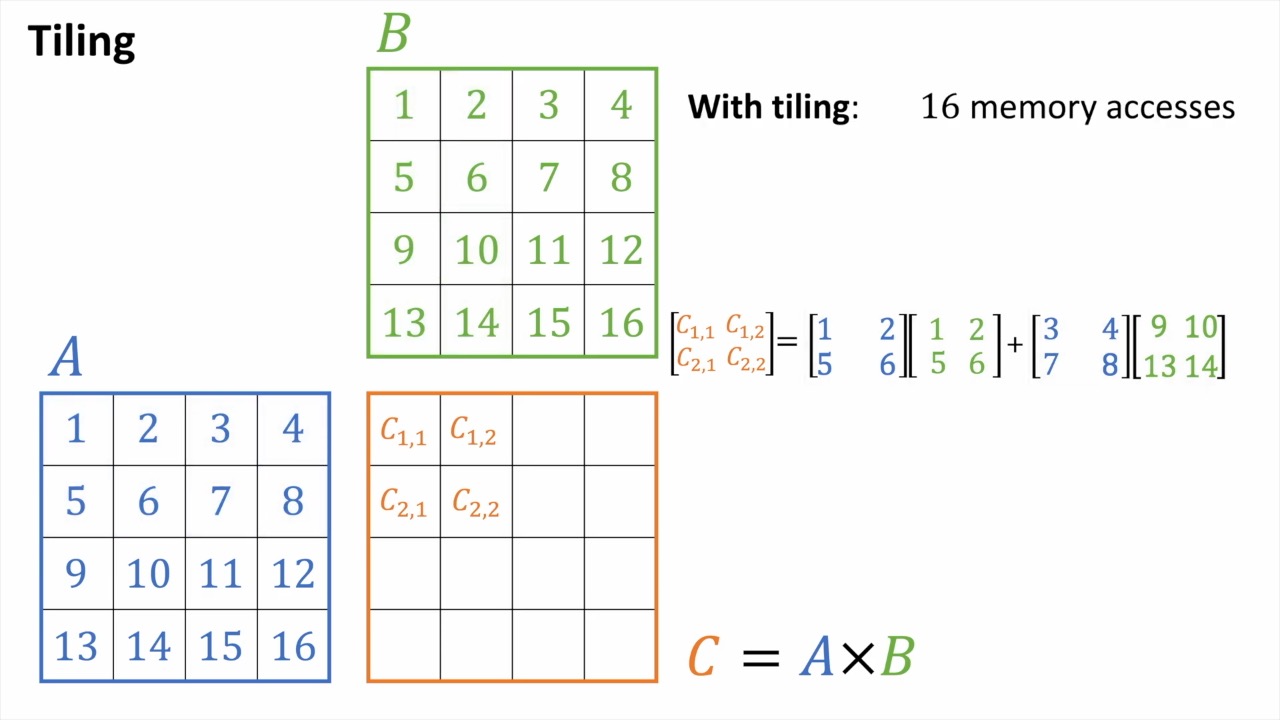tiled_matmul_example_fig3 Fig.

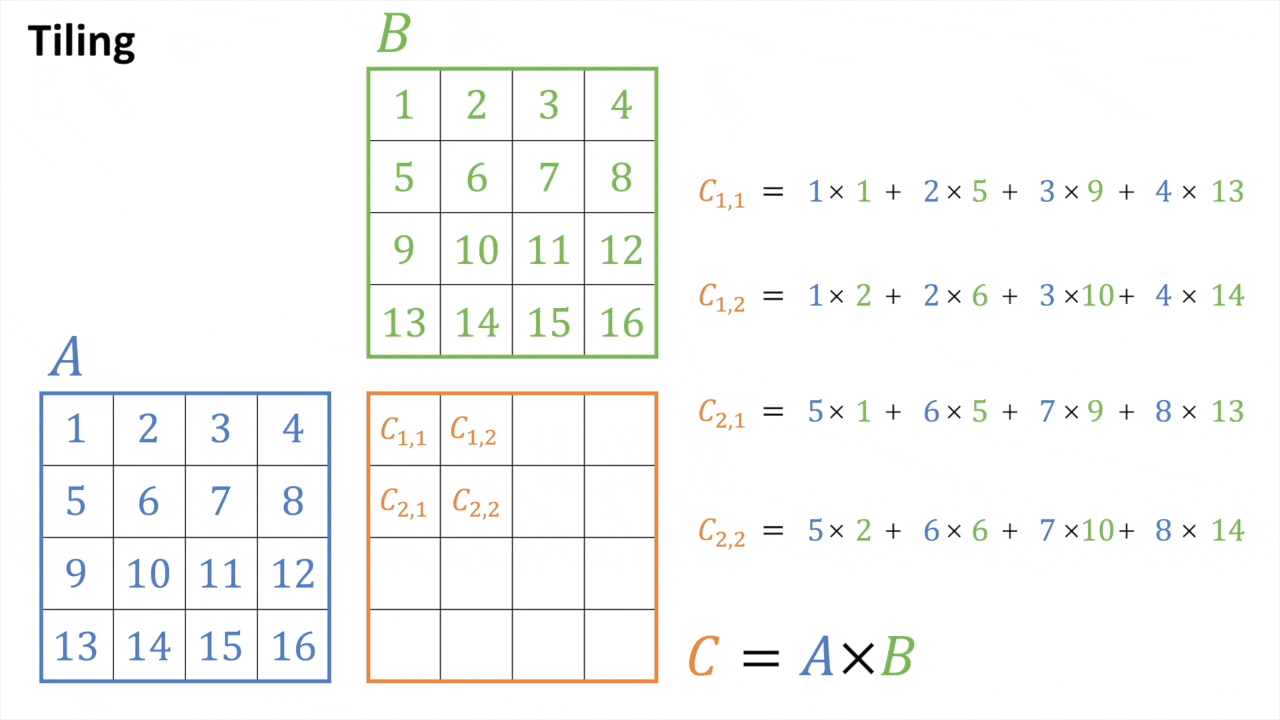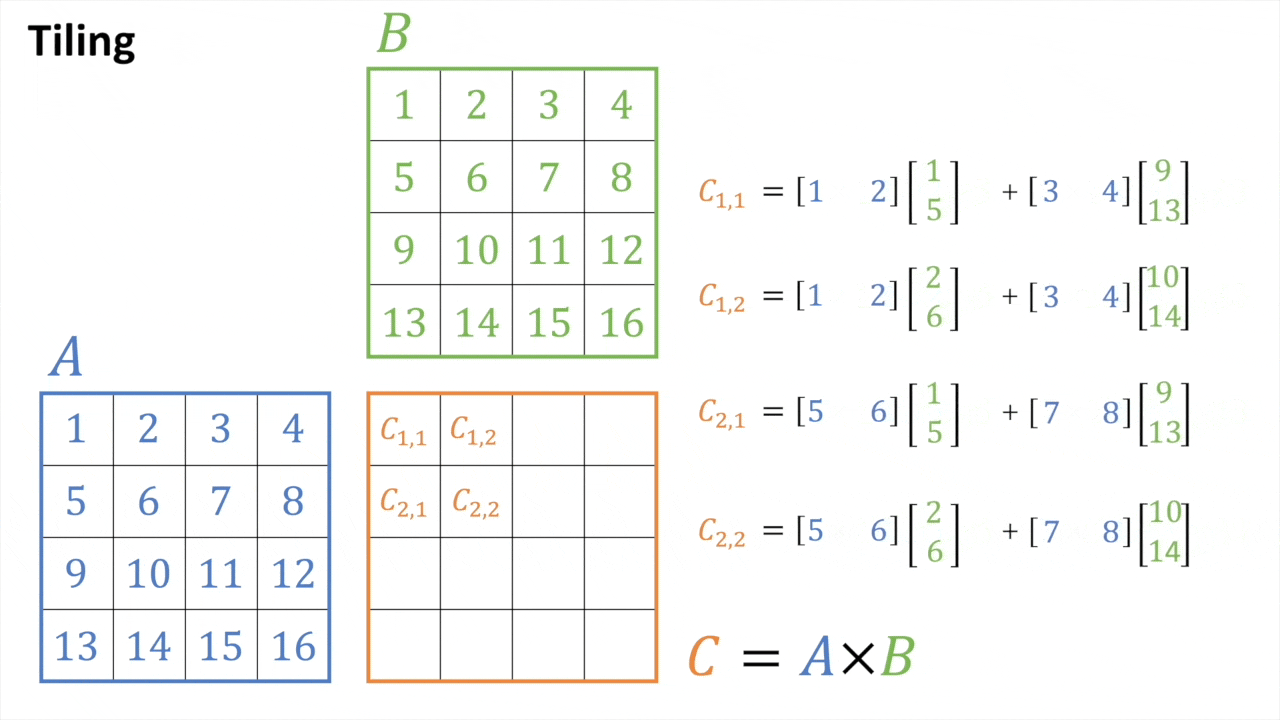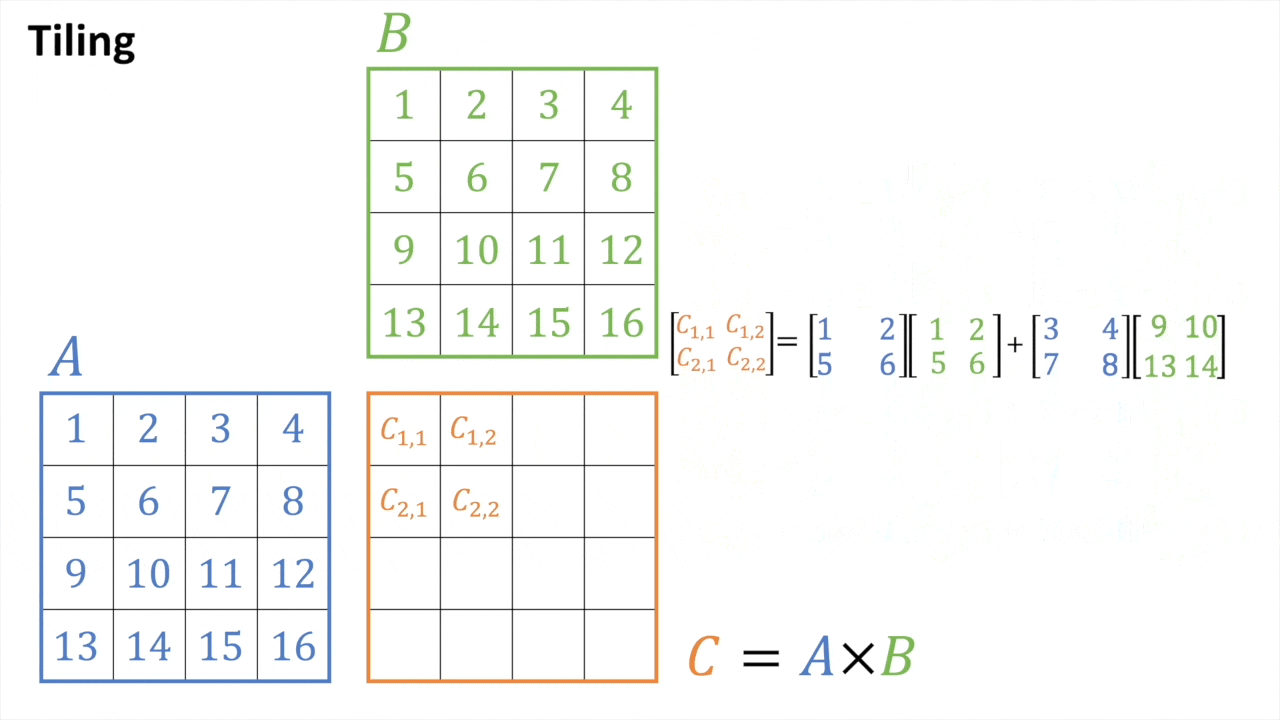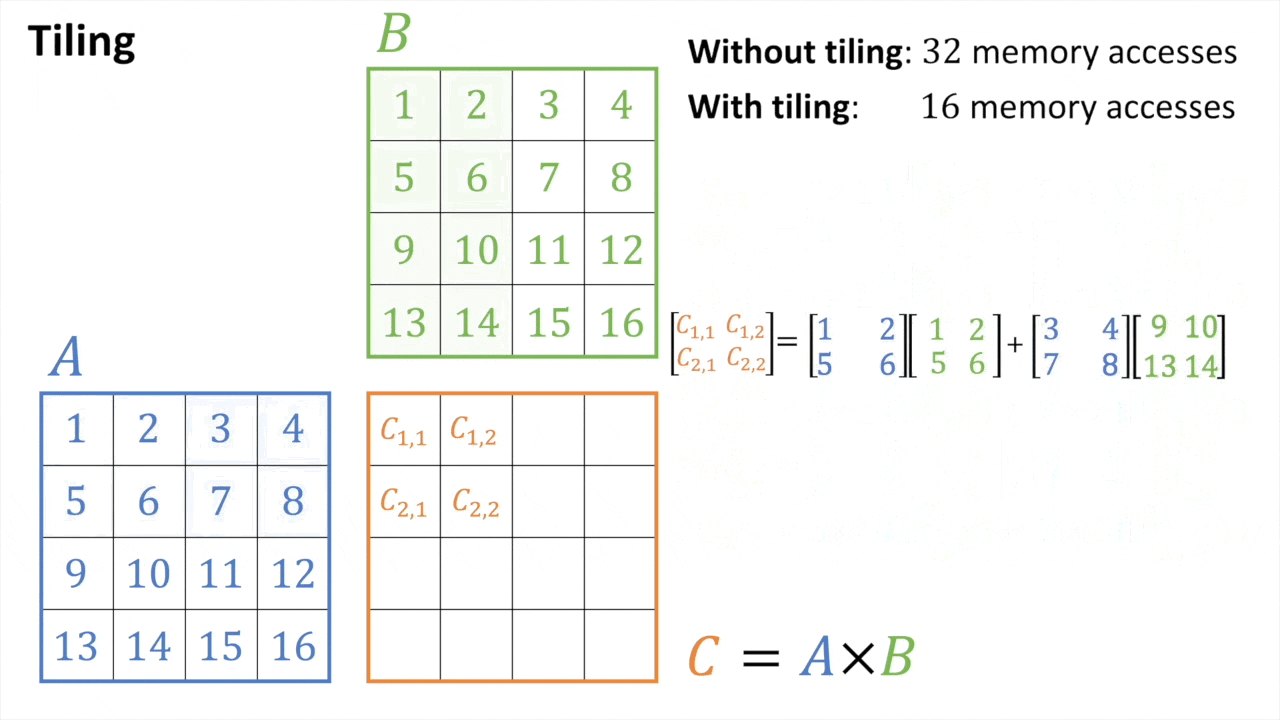tiled_matmul_example_animation2 Fig.

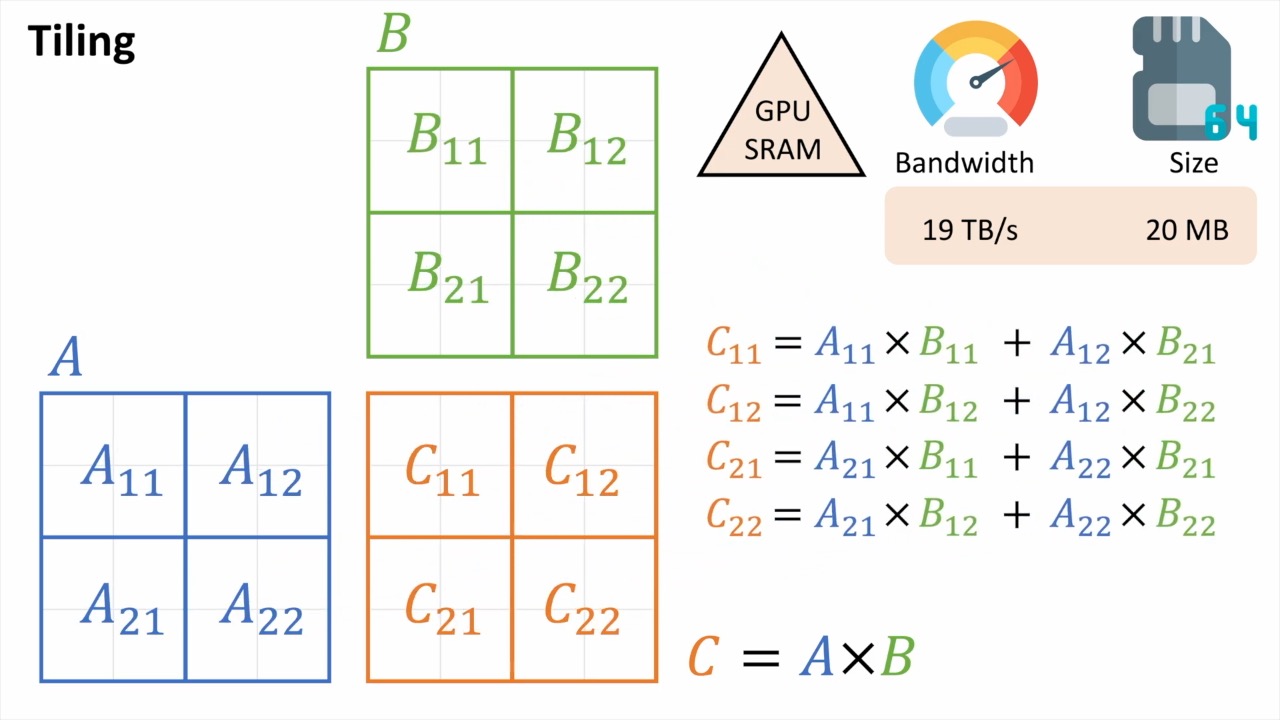tiled_matmul_example_fig4 Fig.

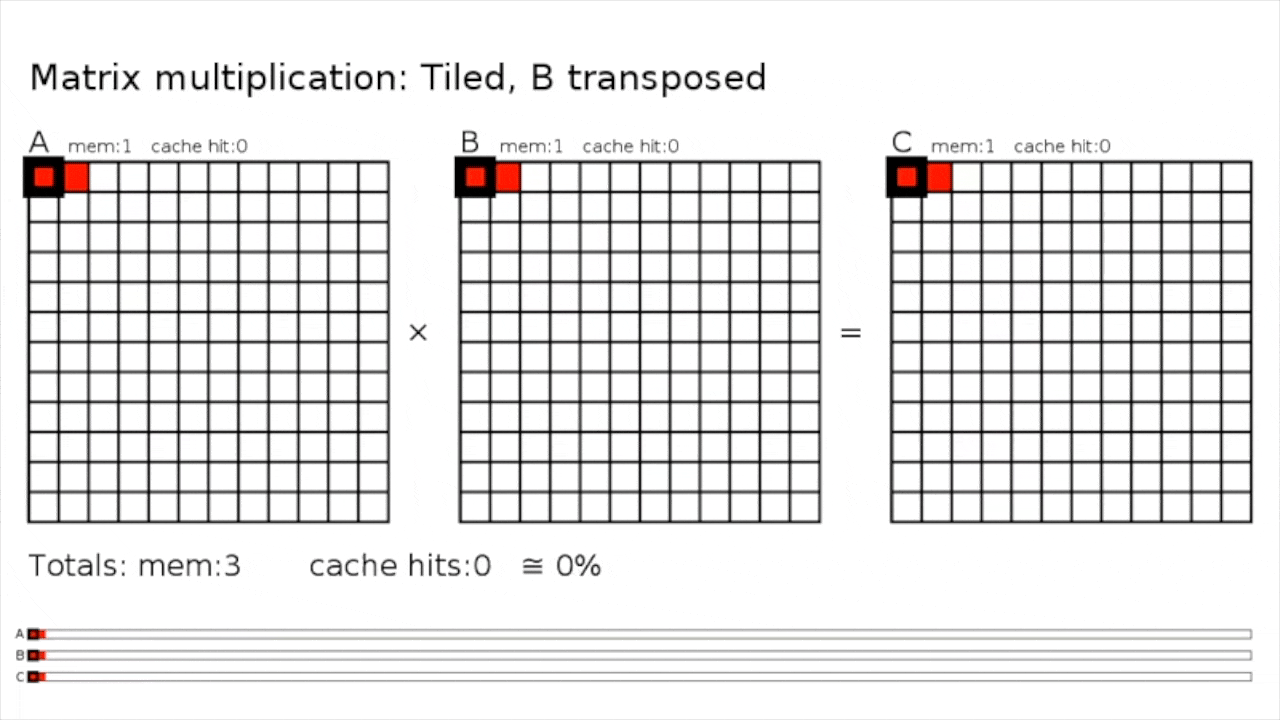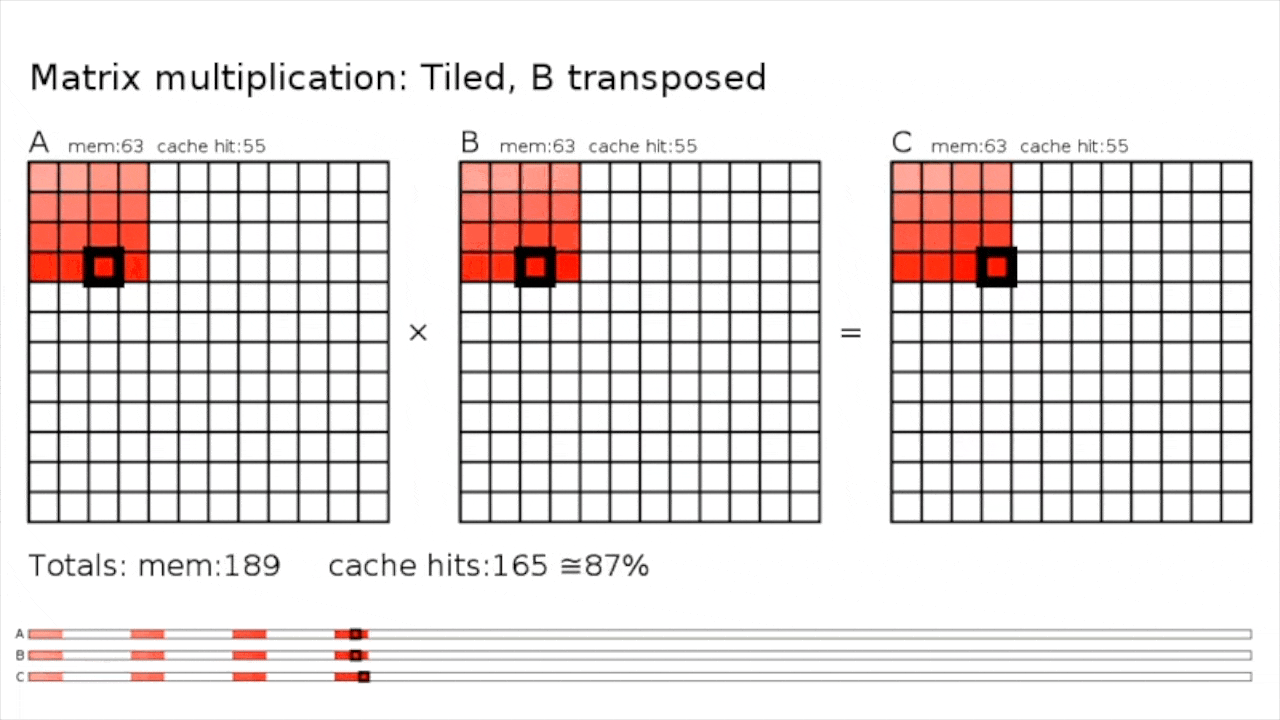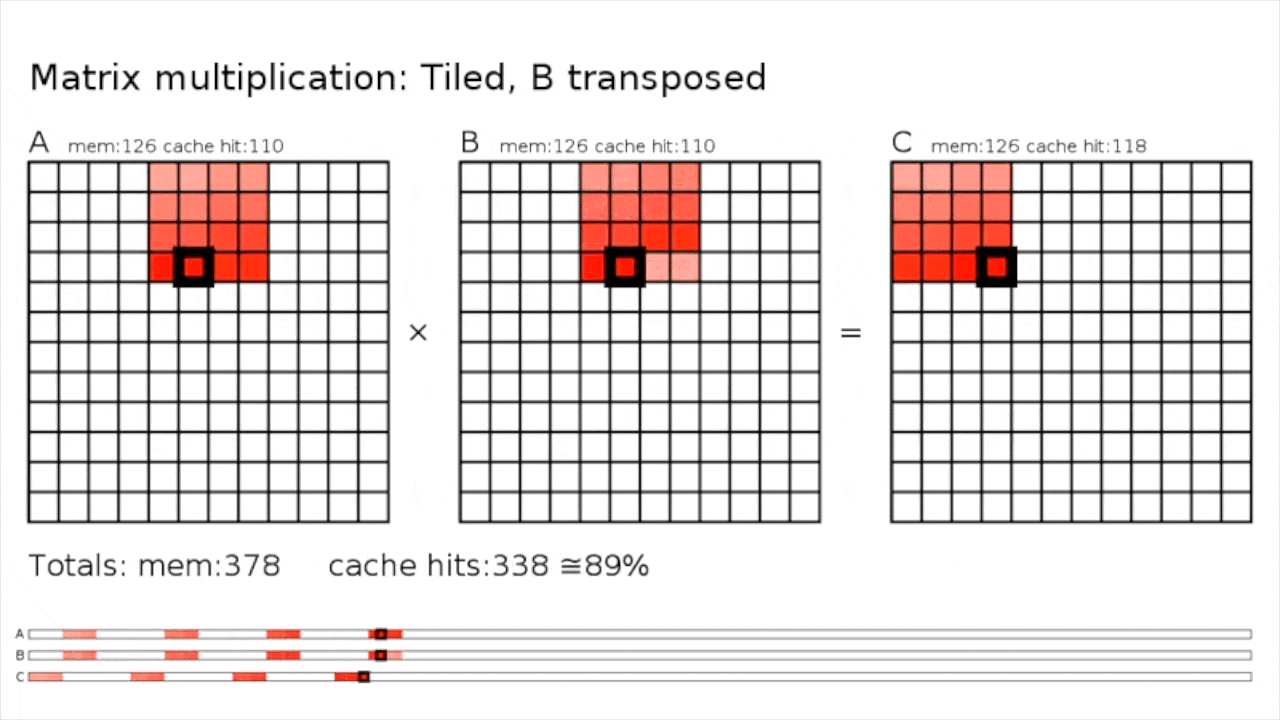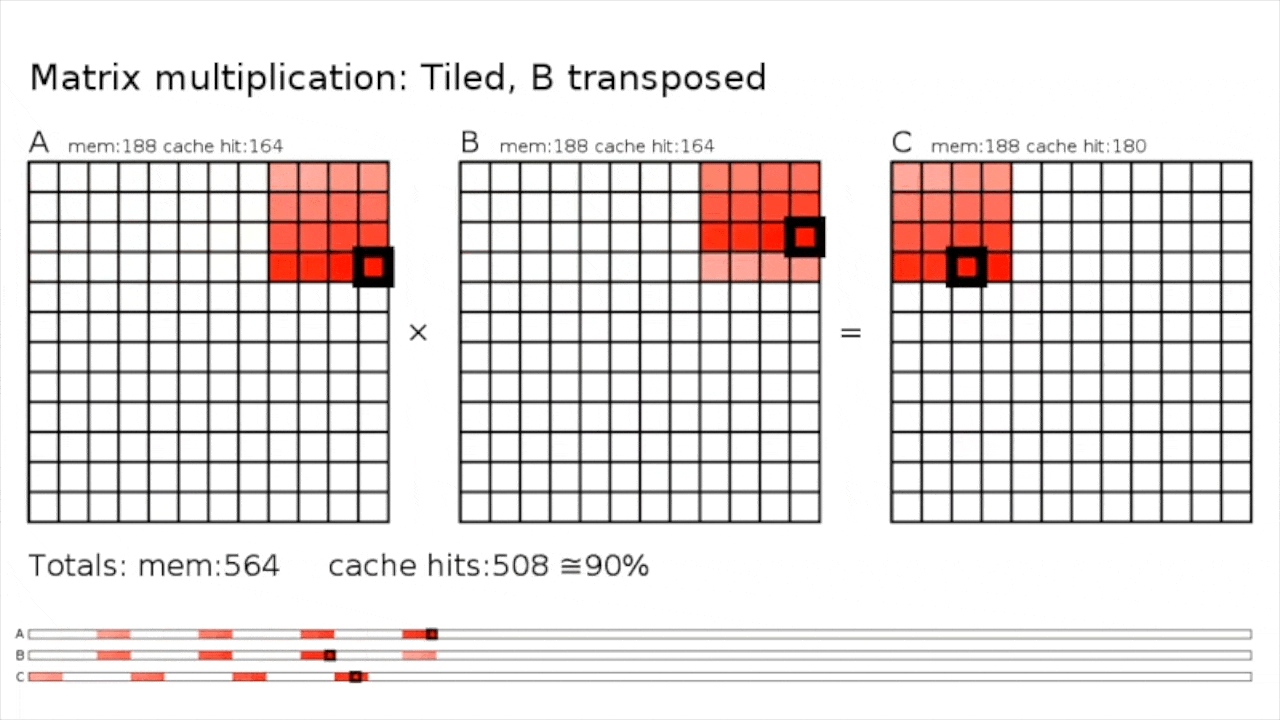tiled_matmul_example_animation3 Fig.

tmp

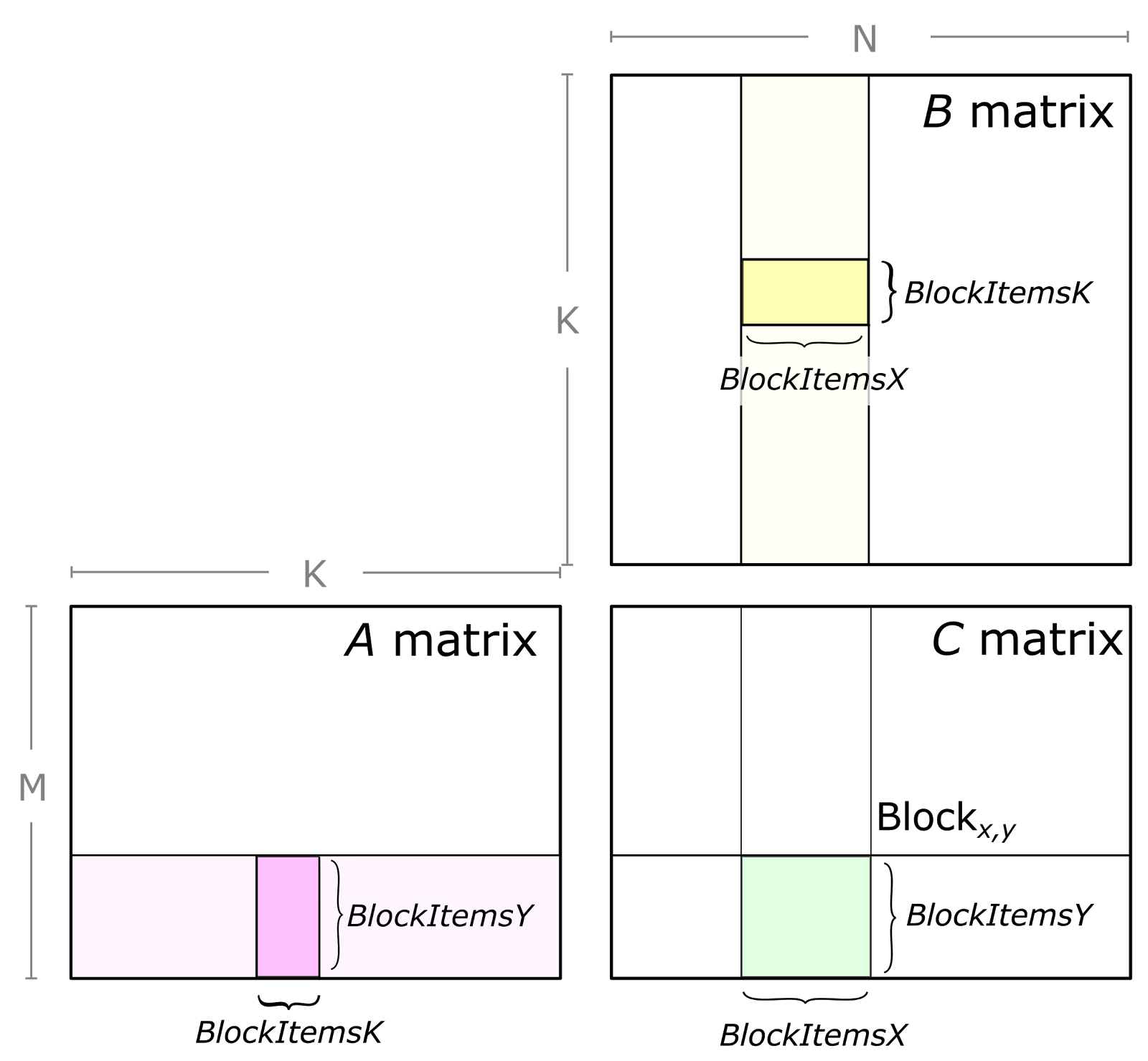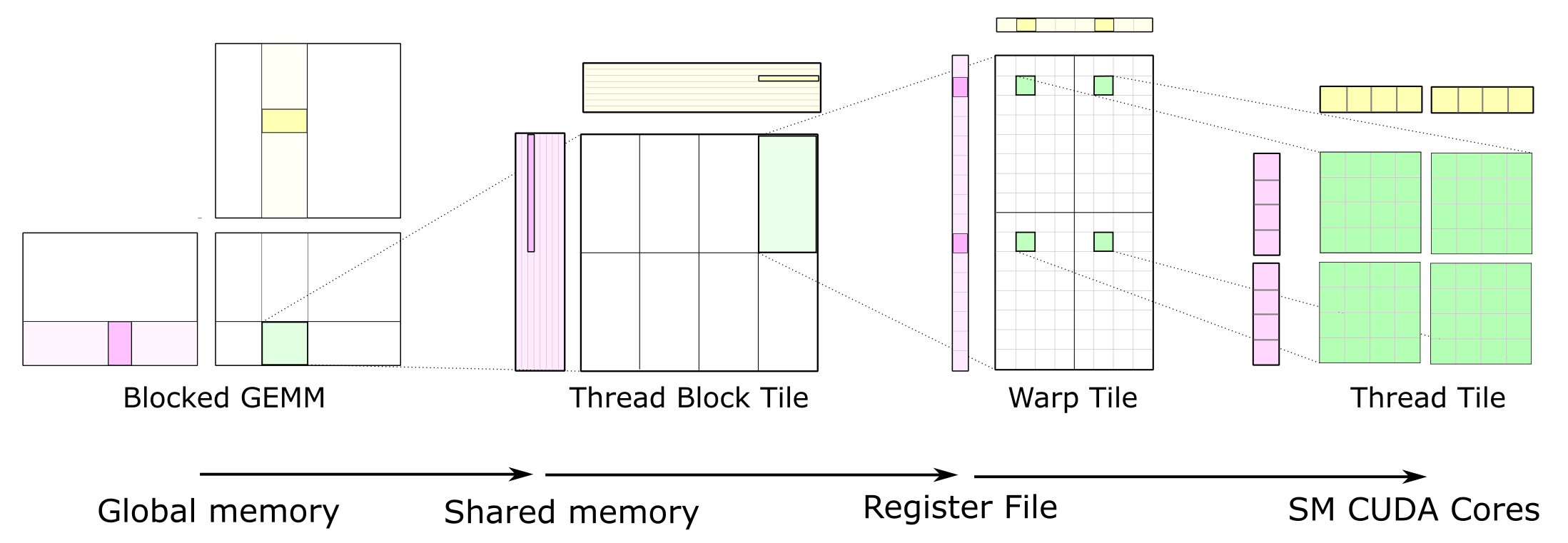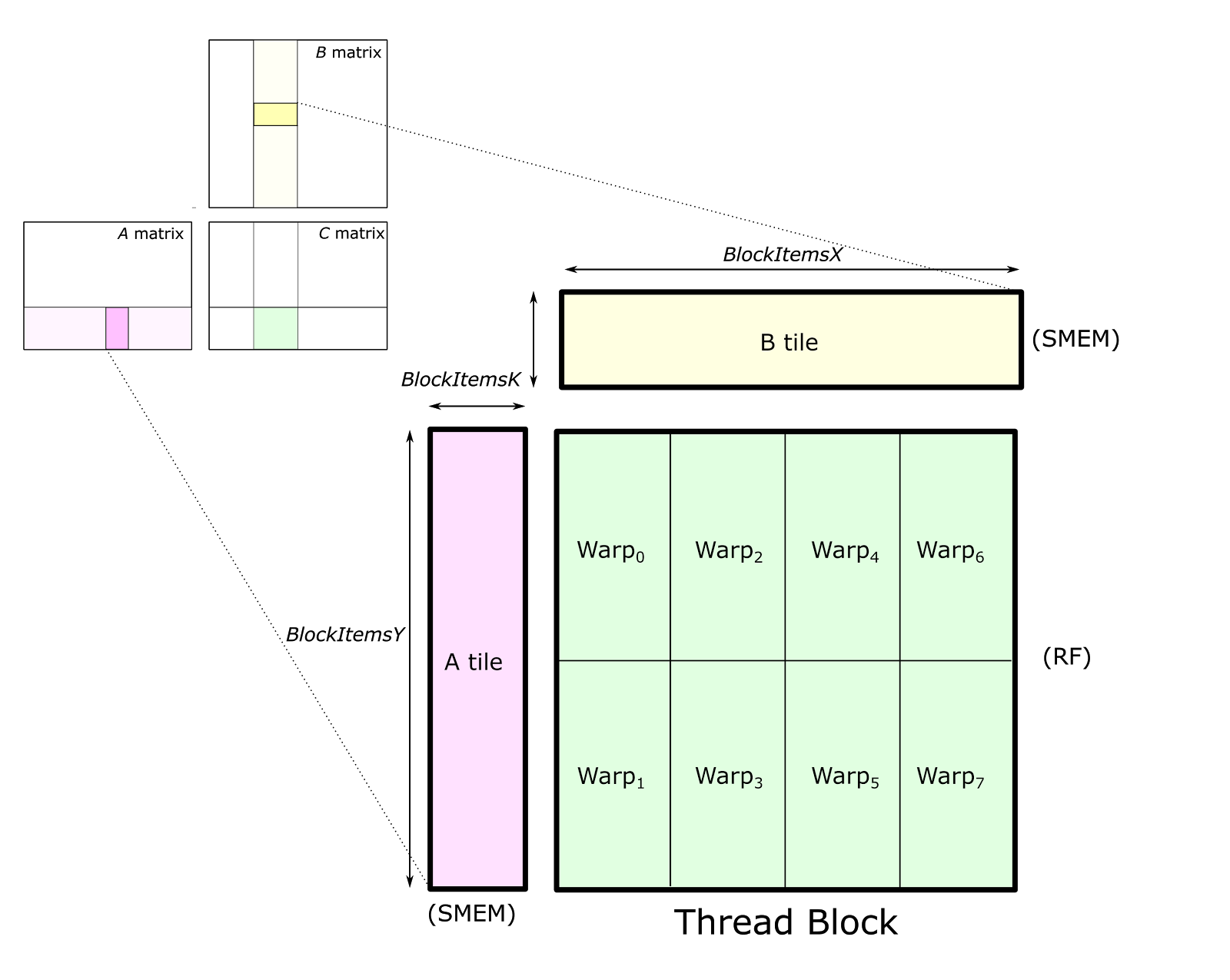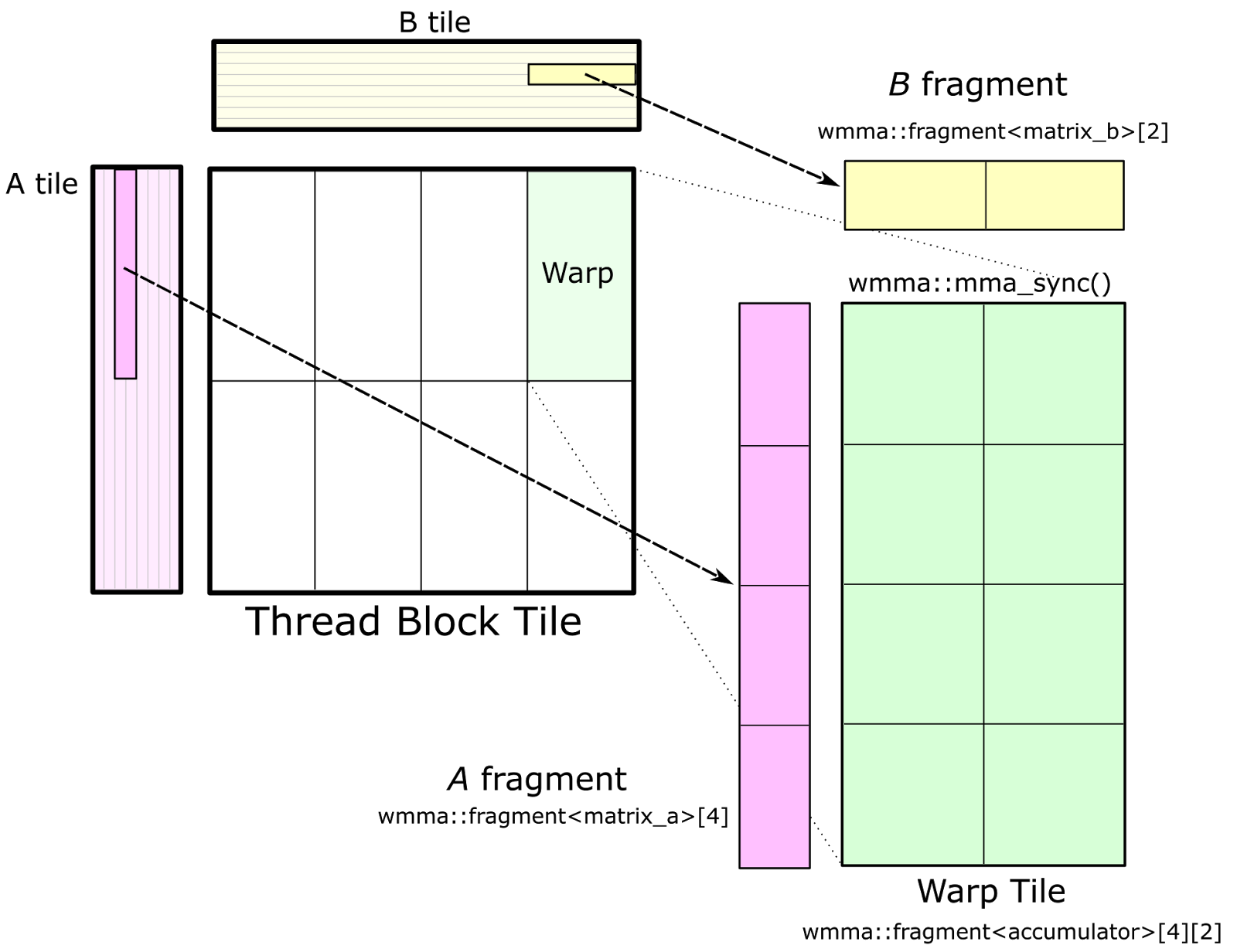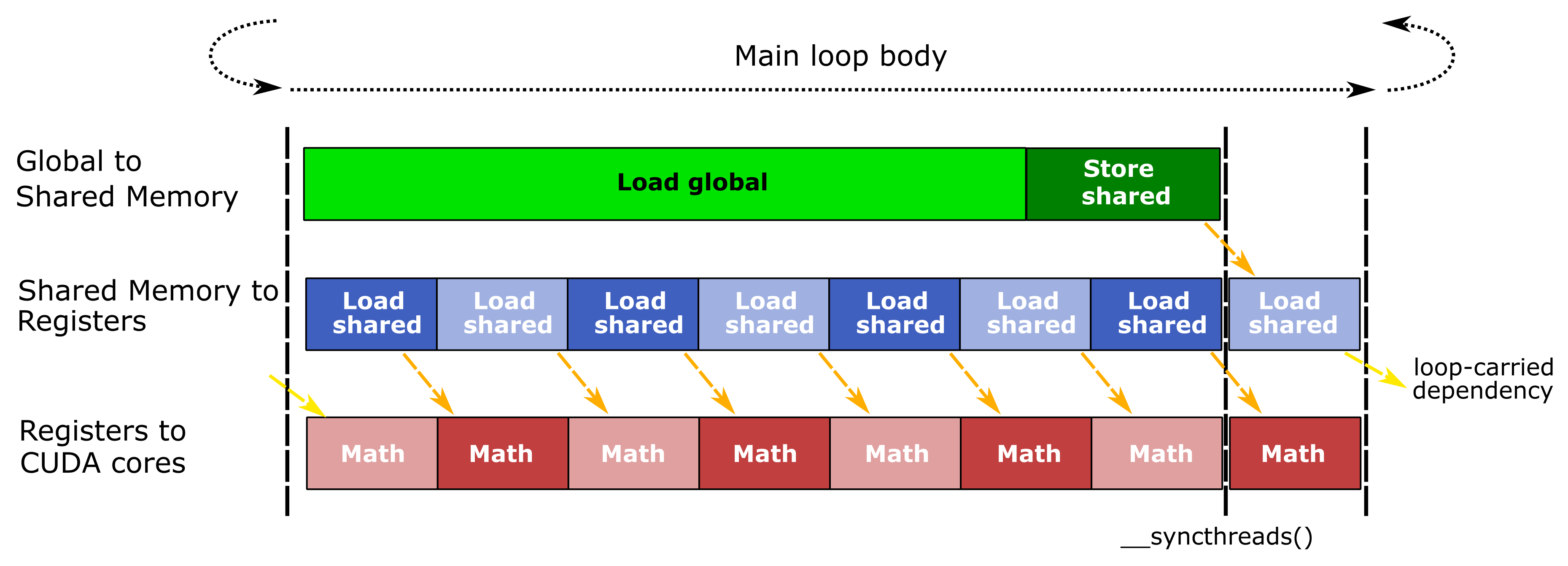tiled_matmul_fig2 Fig. tiled_matmul_fig1 Fig. tiled_matmul_fig3 Fig. tiled_matmul_fig4 Fig. tiled_matmul_fig5 Fig. tiled_matmul_fig6 Fig. tiled_matmul_fig7 Fig. tiled_matmul_fig8 Fig.

Open Computing Language (OpenCL) and Computed Unified Device Architecture (CUDA)

Open Computing Language (OpenCL)는

Computed Unified Device Architecture (CUDA)는

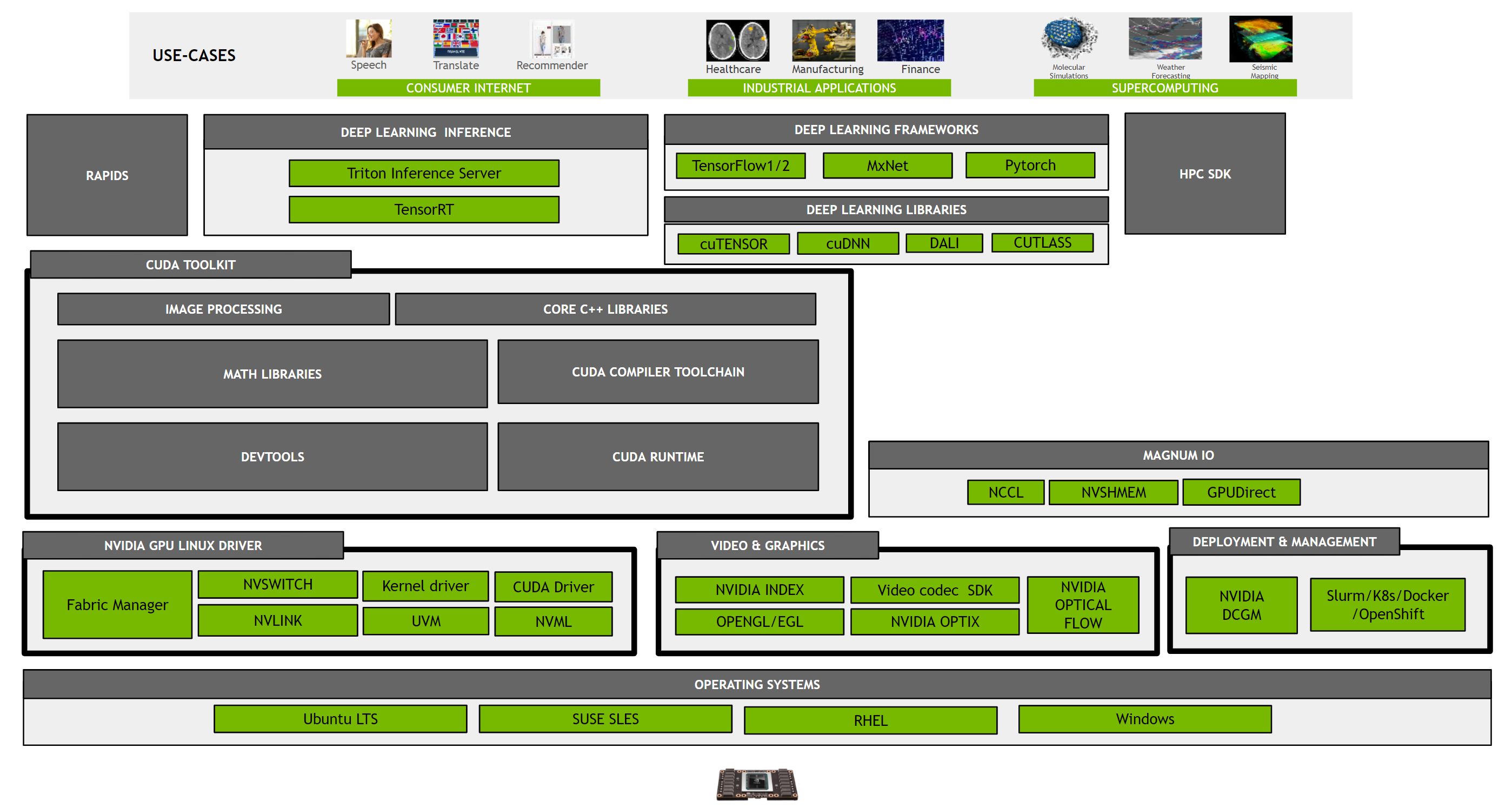cuda_taxonomy Fig. Overview of CUDA Toolkit and Associated Products

Install the NVIDIA drivers (do not install CUDA Toolkit as this brings in additional dependencies that may not be necessary or desired)
Install the CUDA Toolkit using meta-packages. This provides additional control over what is installed on the system.
Install other components such as cuDNN or TensorRT as desired depending on the application requirements and dependencies.

cuBLAS (CUDA Basic Linear Algebra Subroutine) and cuTLASS (CUDA Templates for Linear Algebra Subroutines)

Why use CUTLASS instead of CUBLAS for GEMM? What are the advantages of CUTLASS ?

CUDA Deep Neural Network (cuDNN)

CUDA Deep Neural Network (cuDNN)는

Nvidia CUDA Compiler (NVCC)

Nvidia CUDA Compiler (NVCC)는

NVIDIA Collective Communications Library (NCCL)

NVIDIA Collective Communications Library (NCCL)

The NVIDIA Collective Communication Library (NCCL) implements multi-GPU 
and multi-node communication primitives optimized for NVIDIA GPUs and Networking. 
NCCL provides routines such as all-gather, all-reduce, broadcast, reduce, reduce-scatter 
as well as point-to-point send and receive that are optimized to achieve high bandwidth 
and low latency over PCIe and NVLink high-speed interconnects 
within a node and over NVIDIA Mellanox Network across nodes.

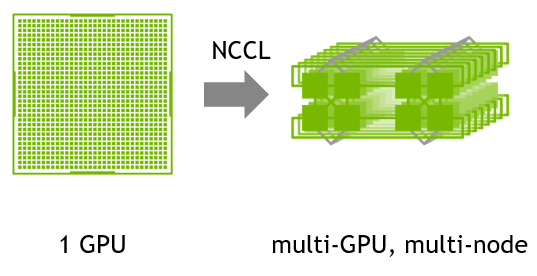nccl Fig. NCCL

References