Distributed Training for Large Scale Transformer (2/6) - Tensor Parallelism (TP)

< 목차 >

• Overview of Tensor Parallelism (TP)
  • Connection to (ZeRO) Data Parallelism (DP)
  • Connection to Pipeline Parallelism (PP)
• Implementation
• +Updated) communication cost for TP with ZeRO?
• References

Overview of Tensor Parallelism (TP)

Tensor Parallelism (TP)는 NVIDIA의 Megatron-LM에서 처음 제안되었다고 할 수 있다. 정확히는 Transformer model을 여러 GPU에 효율적으로 나눠 연산하기 위한 전반적인 methodology가 그렇다는 것이고, 내가 알기로는 Neural Network (NN)를 여러 GPU로 나눠 처리하는 것 자체는 Alexnet이 더 오래된 것으로 알고있고, 고성능 컴퓨팅 (High Performance Computing; HPC)분야에서는 이미 많이 쓰던 테크닉이라고 듣기도 했다.

Fig.

Fig.

(그 시절에는 마땅한 ML framework도 없어서 손수 module, backprop을 low-level에서 돌아가도록 GPU programming까지 다 했다고 알고있는데, 이미 이런 approach도 다 해봤다니 respect가 안생길수가 없는듯)

본래 각 GPU device별로 model을 띄우고 서로 다른 data를 처리한 뒤 gardient를 모아서 update하는 Data Parallelism (DP)는 model 크기가 수 Billion (B)에 달하면서 그 부족함을 드러냈다. DP를 할 때 optimizer state를 따로 들고 있어도 된다는 ZeRO같은 Distributed Optimizer가 등장하기 전에, “model이 너무 크면 GPU별로 model을 나눠 들면 되잖아?” 라는 idea가 이미 있었고, 이를 Model Parallelism (MP) 이라 부르게 됐다. 하지만 가장 먼저 제안된 MP의 경우 Transformer Layer가 12층이고 GPU가 4개라면 Model을 아래처럼 block단위로 나누곤 했는데, 이는 앞단의 layer의 activation이 뒤로 전파되어야만 그 다음 device가 연산을 할 수 있어 bottleneck (보통 bubble이라고 함)이 존재했다.

GPU 0: Layers 0, 1, 2
GPU 1: Layers 3, 4, 5
GPU 2: Layers 6, 7, 8
GPU 3: Layers 9, 10, 11

이에 대한 해결책으로 TP가 등장했는데, TP도 그냥 model을 device가 나눠갖는 MP와 같지만 model을 vertical로 나눴다고 점에 차이가 있다.

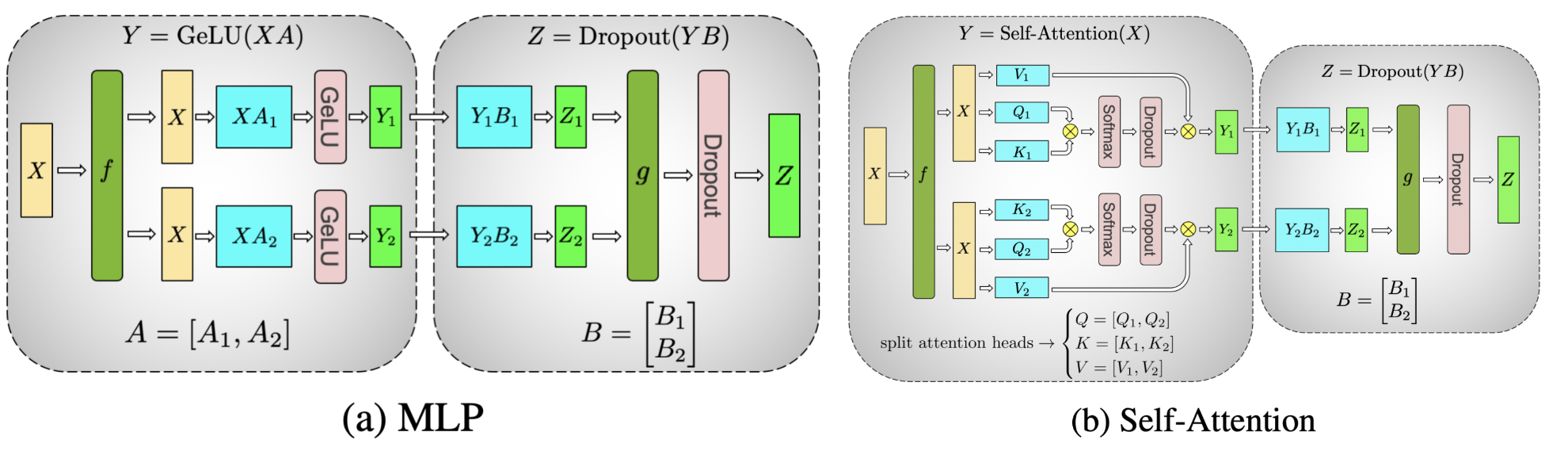Fig.

위 figure가 megatron white paper에 등장하는 TP의 예시이다. 어떻게 TP가 가능한지에 대해서 이해하기 위해서는 간단한 Feedforward Neural Network (FFN) 연산을 생각해보면 되는데,

위 연산이 weight matrix를 column기준으로 잘라 계산한 뒤 이어붙히는 것과 동일하다는 것은 당연하다.

이를 Column-Wise Parallel이라고 하며, 이런 방식이 아니라 input matrix (혹은 3차원 tensor)를 column-wise로 자르고 weight matrix를 row-wise로 자를 경우에도 같은 결과를 얻을 수 있다는 것도 이해하기 쉬울 것이다.

이를 Row-Wise Parallel이라고 부른다. 이 두가지를 아래 figure처럼 도식화 할 수 있는데, 사실 이것이 TP의 거의 전부라고 할 수 있다.

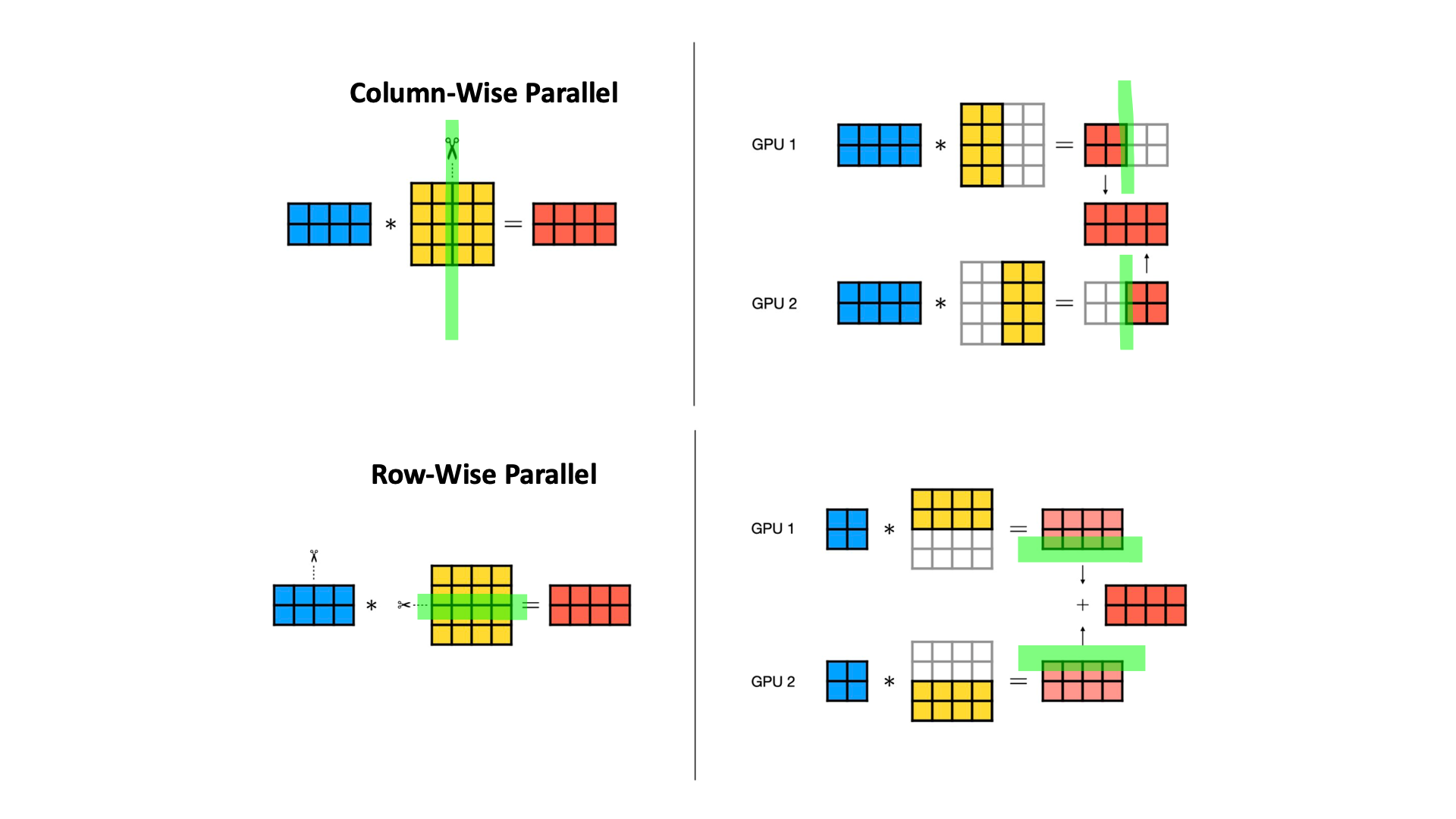Fig.

그런데 왜 이렇게 다른 2가지 방법이 필요한걸까?

그 이유는 통신 비용 (communication cost)이 줄기 때문이다. 예를 들어 Transformer Layer의 MLP module을 생각해보자.

여기에 TP를 적용해서 GPU별로 나눠서 연산한 결과물을 하나로 합치는 것이 당연하다고 생각할 수 있는데, 그 이유는 GeLU같은 non linear activation function연산은 linearity가 성립하지 않기 때문이다. 즉 나눠서 연산한 결과물에 따로 따로 GeLU를 취한 뒤 더하는 것이 성립되지 않는 것인데,

이는 Row-Parallel 을 적용할 경우 생기는 문제이다. 만약 우리가 Row-Parallel 을 적용하면 TP를 하고 난 결과물을 더한 뒤 GeLU를 사용하고 \(y_2\)를 사용할 때 또 나눠야 하는 문제가 있는데, 이 때 device간 all-gather operation이나 all-reduce을 써야 하므로 communication cost가 발생한다.

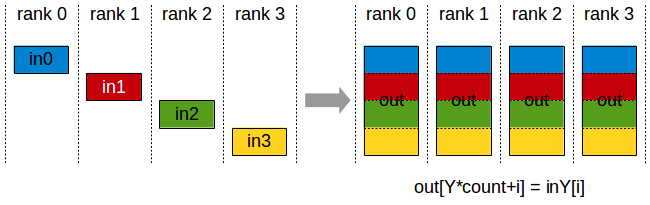Fig. All-Gather

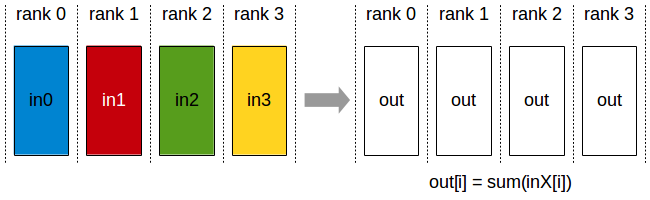Fig. All-Reduce

그런데 이 MLP module의 연산에 대해서 column-wise, row-wise를 적절히 배치하게 되면, 우리는 all-gather통신을 줄일 수 있다. 아래 처럼 column-wise, row-wise 순서로 배치할 경우 마지막에 한 번만 all-gather를 해서 각 device별로 tensor를 공유한 뒤 더해주면 되는데,

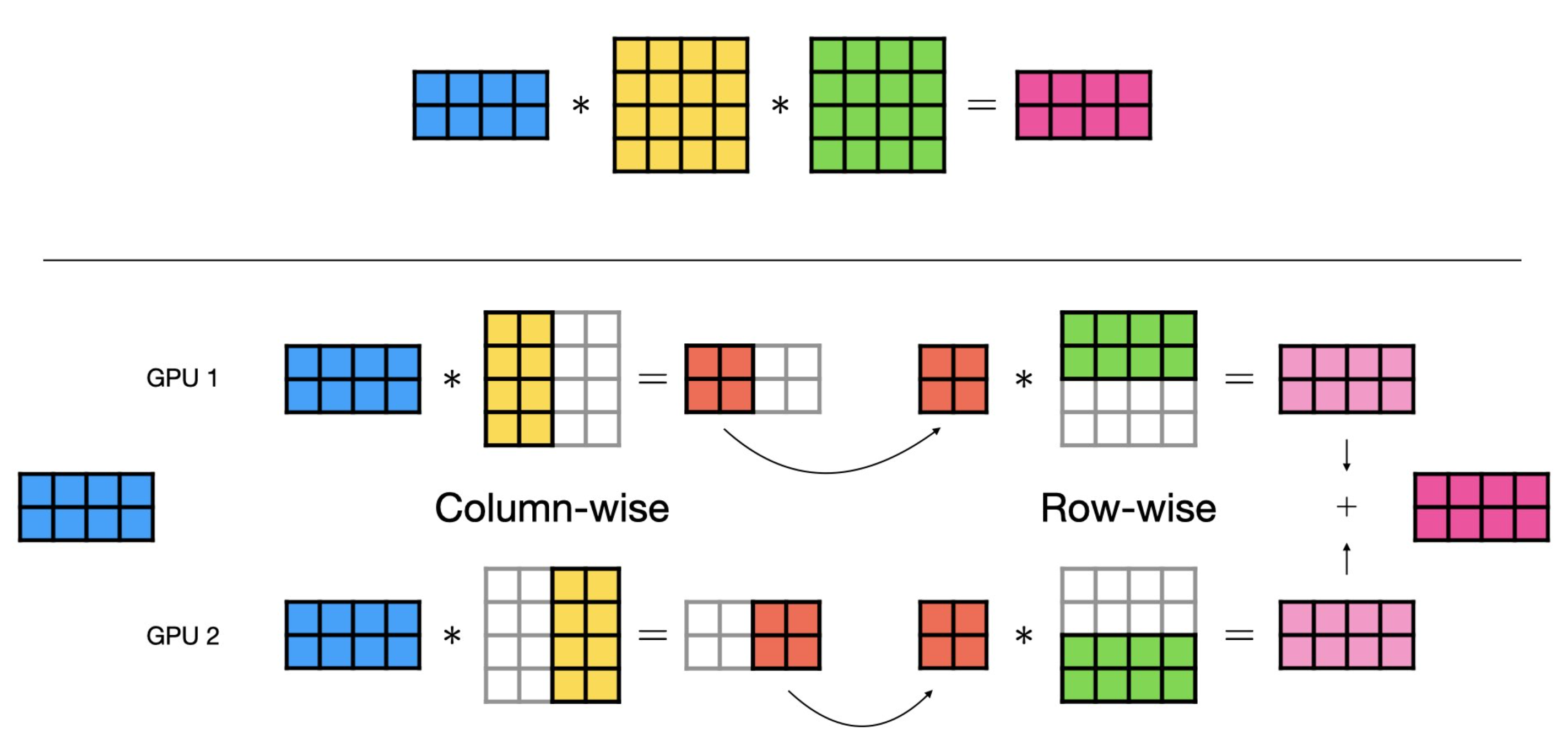Fig.

이 경우 column-wise parallel 을 한 결과물에 GeLU를 적용하는것에 아무런 문제가 없다. 당연하게도 element-wise로 연산을 하는 것이므로 다른 element들과는 독립이기 때문이다. 즉 우리는 MLP에 대해서 col-wise, row-wise parallel을 순차적으로 해주고 (device별로 나눠주고),

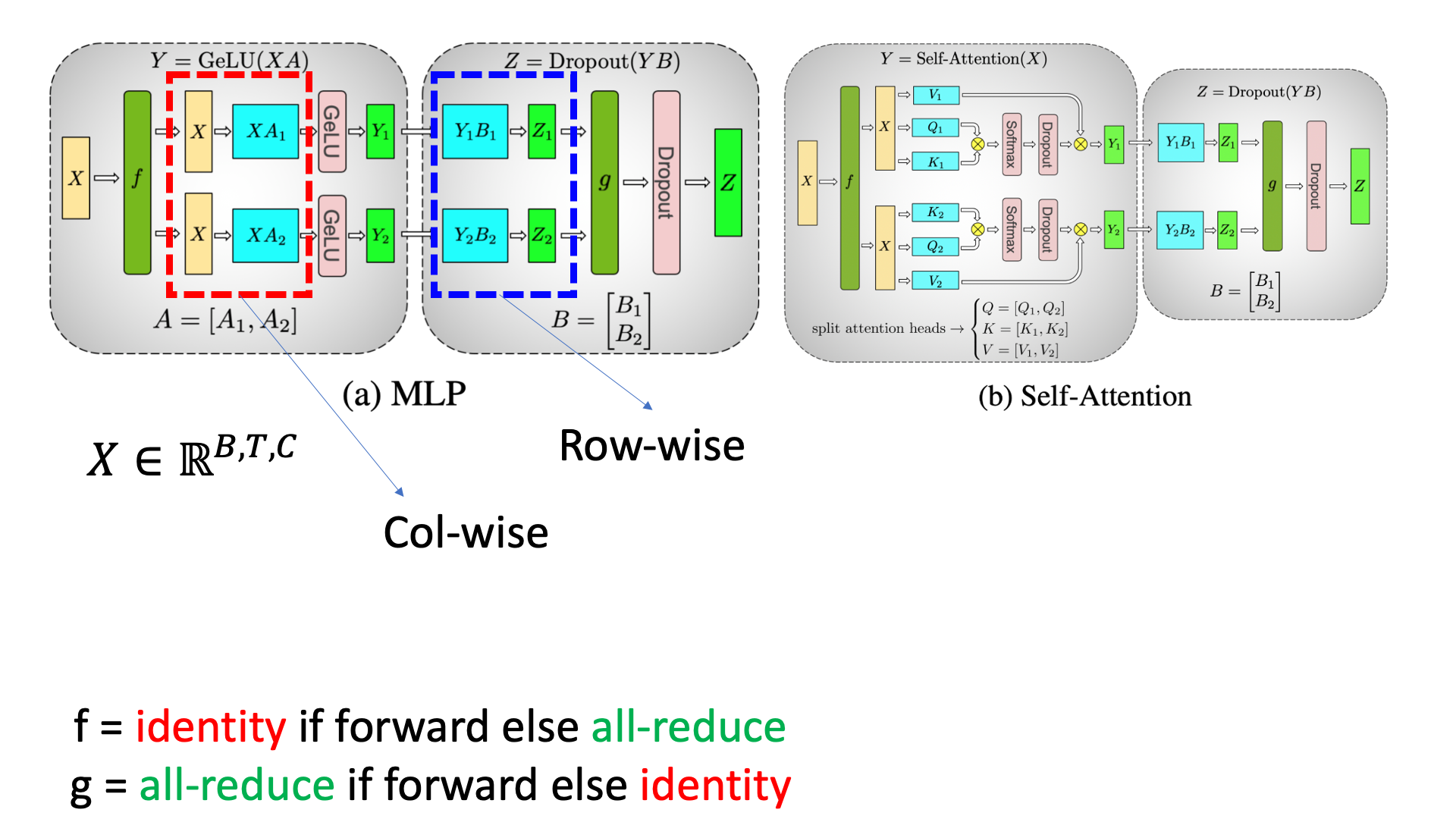Fig.

forward시에는 MLP의 output projection을 한 뒤에 element-wise로 더해줘야 하므로 all-reduce를 쓰면 된다.

Self attention layer에 대해서도 비슷하게 연산을 수행해주면 되는데, 원래 input tensor가 batch, seq_len, hidden_size, \(B \times T \times C\)라고 할 때, 사실 hidden_size C는 head dimension과 head의 갯수를 곱한 값이며 transformer자체가 head 갯수로 연산을 parallelize 하기 쉽게 만들었기 때문에 쉽게 column-wise parallel를 쓸 수 있다.

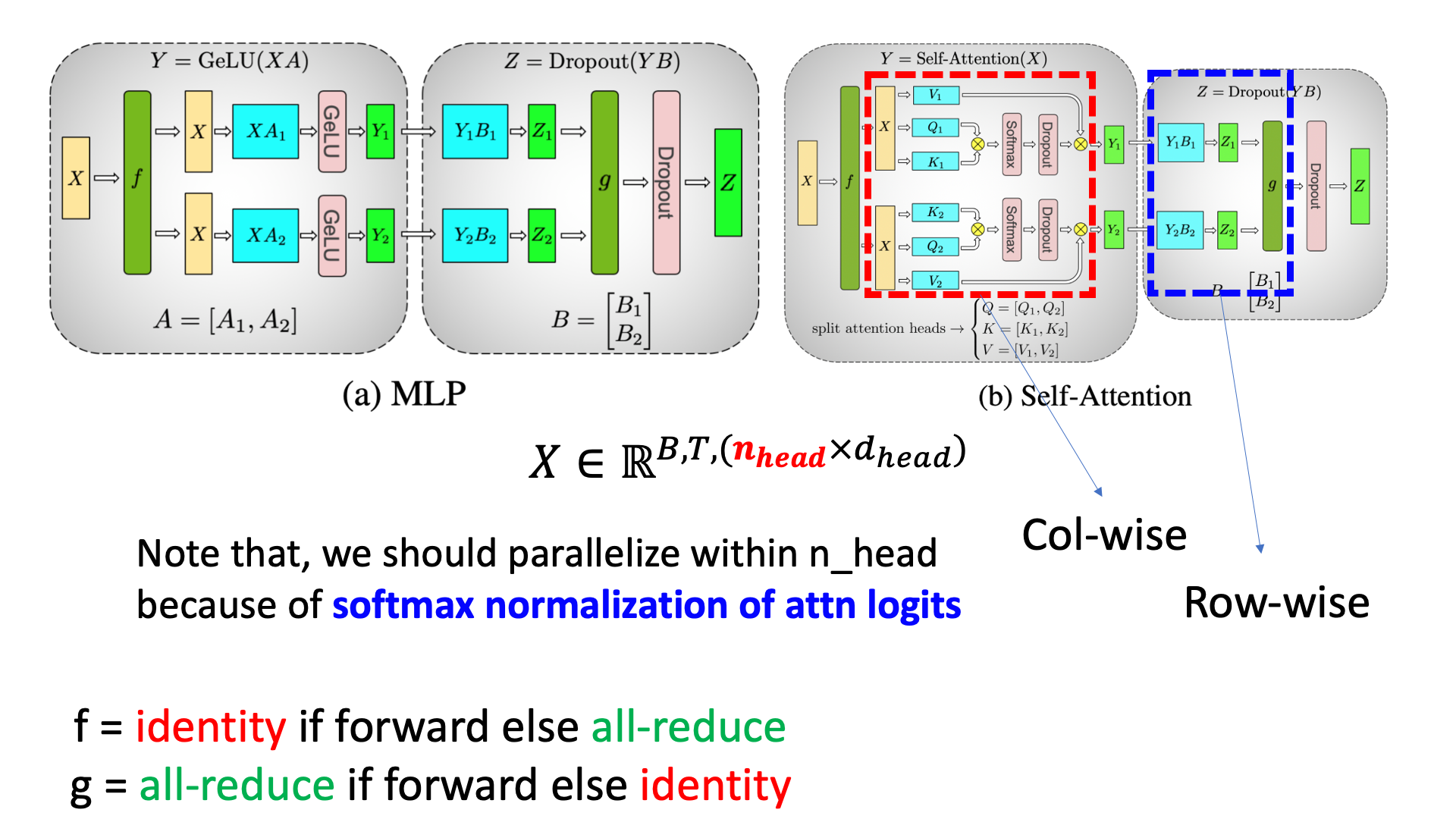Fig.

단 논문에 적혀있지 않는 것 같지만, 당연하게도 head 갯수를 넘어서 parallelize 하게 되면 \(QK^T\)에 대해서 row-wise softmax를 할 때 모든 element가 필요하므로 all-gather를 해야 할 수가 있으므로 주의해야 할 것 같다. 마찬가지로 forward시에 마지막 output projection이후 all gather를 해주면 된다.

여기서 f, g라는 module이 하는 일에 대해 forward와 backward시 수행하는 연산이 다르다고 적어놨는데, forward에 대해서는 다들 이해할 것 같고, backward에 대해서 f가 all reduce가 되는 이유는 각 device가 들고있는 weight matrix가 쪼개져 있기 때문에 Loss, \(L\)에 대한 upstream gradient \(\frac{\partial L}{\partial z}\)와 weight matrix의 outer product로 표현되는 local gradient가 나눠져있기 때문에 그렇다.

그래서 TP를 할 경우 각 transformer residual block마다 forward에 (activation에 대해) all-reduce 2번, backward에 (gradient에 대해 ) all-reduce 2번이 필요하게 된다.

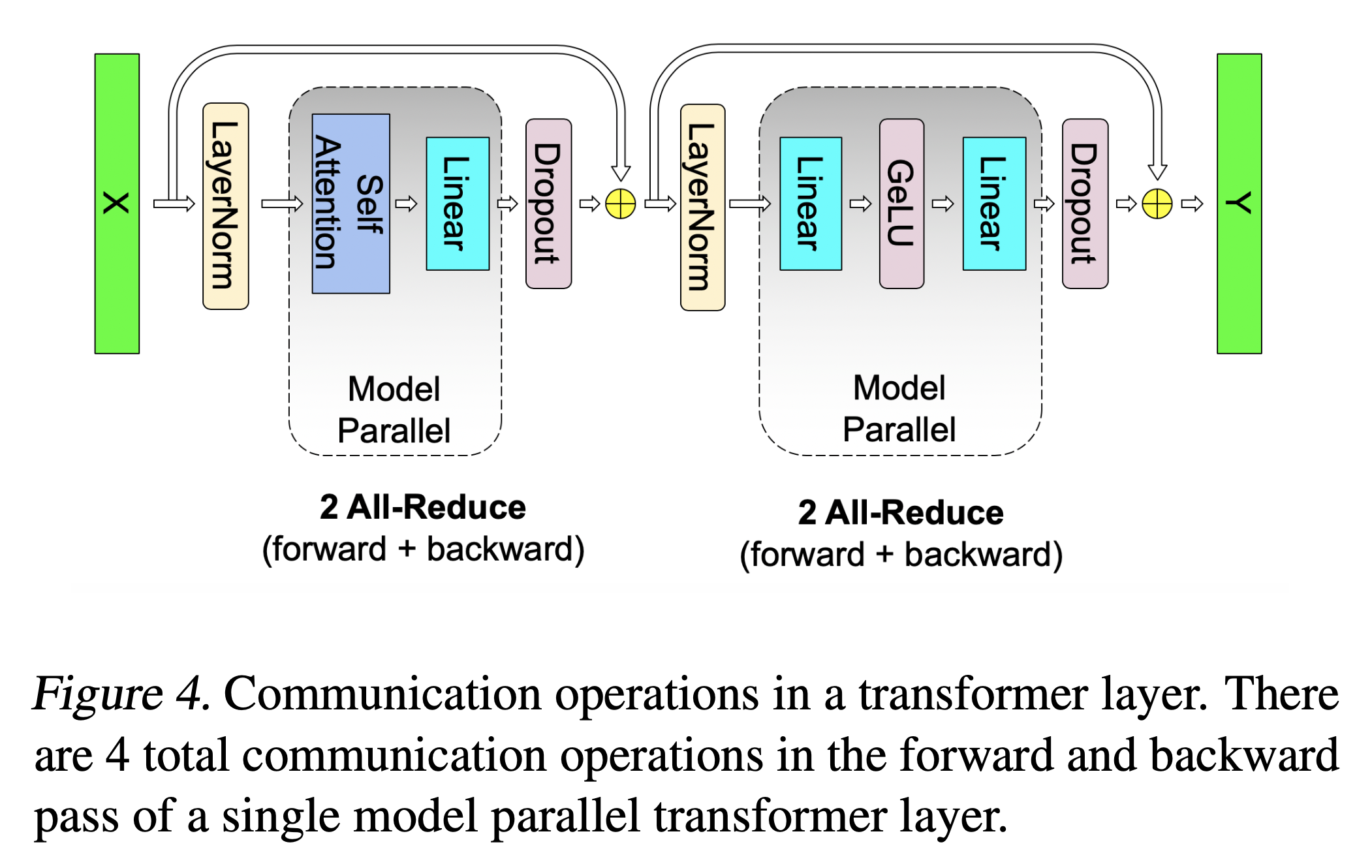Fig.

여기에 추가적으로 embedding weight에 대한 TP도 있는데, megatron에서는 vocab dimension을 따라 column-wise parallel을 적용한다.

이러면 embedding table의 일부만 들고 있게 되므로 input embedding 을 계산한 뒤 all-reduce가 필요하게 된다 (즉 forward에 all-reduce, backward에 identity인 g가 필요). 예를 들어 hidden_size가 8192, vocab_size가 102400인데 device가 8개면 각 device는 8192x12800 만큼만 들고있게 된다는 것 같은데, 그렇다면 GPU 0은 12800개의 one-hot vector에 대해서만 look-up 할 수 있게 되는 것 같다. (그럼 어떤 device는 device assertion error가 나지 않나…? 아마 처리를 했을 것을 보인다.)

그런데 transformer의 embedding과 unembedding weight은 묶을 수 있는데 (tying), 이럴 경우 각 device가 연산한 결과물을 합쳐줘야 한다. 즉 cross entropy 연산 하기 전에 all-gather를 해줘야 한다.

그런데 all-gather를 하기 위해서는 각 device가 8등분 된 logit을 합치기 위해 batch size, seq_len, vocab_size에 대해서 \(B\times T \times V\)만큼의 communication volumn이 발생하게 된다. 하지만 우리는 loss값, 즉 scalar만 알고 있으면 backpropagation을 할 수 있으므로 각 device에서 loss까지 구한 뒤에 scalar를 합쳐주는 방식을 취하면 된다.

이 경우 backpropagation에 대해서도 큰 문제가 없어 보이는데, logit을 분산해서 들고 있기 때문에 우리가 구해야 하는 \(\frac{\partial L}{\partial X}, \frac{\partial L}{\partial E}\) 중 \(\frac{\partial L}{\partial X} = \frac{\partial L}{\partial z} logits^T\)를 계산할 때 분산된 logit을 사용해 각자 계산한 뒤 gradient만 all-reduce하면 된다.

Connection to (ZeRO) Data Parallelism (DP)

한 편, TP는 DP와 orthogonal하게 사용이 가능하다. 하지만 TP를 사용할 때는 주의할 점이 있다. 바로 node 내에서 (intra-node) model partition을 하는 것은 communication cost가 그리 크지 않지만, node 간 partition을 하게 되면 (inter-node) communication cost가 매우 증가한다는 것이다. ZeRO paper의 내용을 잘 읽어보면 이에 대한 언급이 있다. 먼저 아래 ZeRO paper의 figure를 보자.

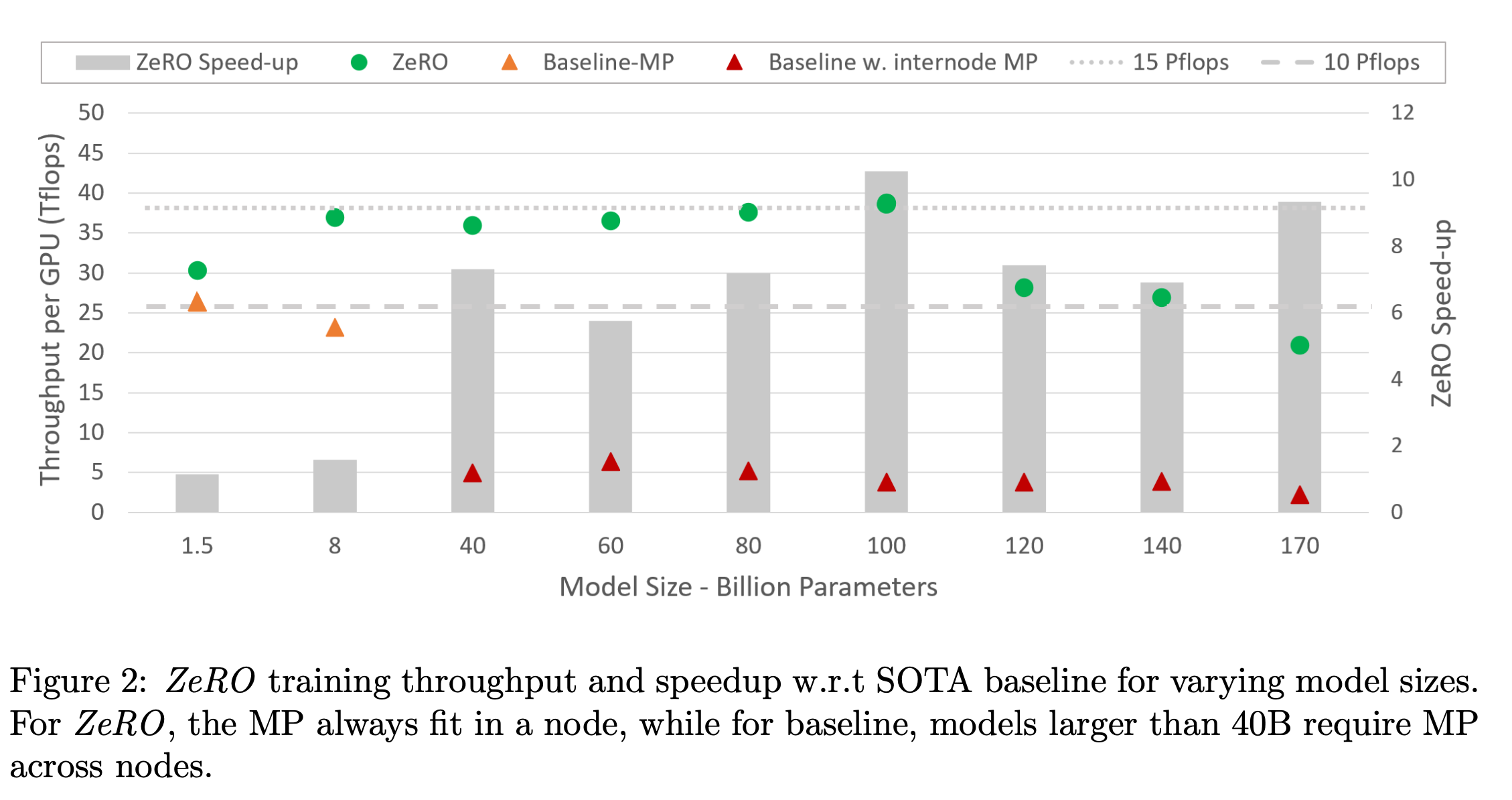Fig.

Baseline이 바로 Megatron-TP를 한 것인데, intra-node의 경우 V100-32GB GPU에서 처리 가능한 model 크기는 16~20B 수준이라고 되어있고, 그 이상의 scale을 처리하기 위해서는 inter-node partition을 해야 한다.

Fig.

하지만 이럴 경우 inter-node bandwidth 때문에 efficiency가 확 떨어진다고 한다.

Fig.

그렇기 때문에 ZeRO의 기능을 같이 쓰는 것을 추천하는데, 물론 TP를 한다는 것 자체가 model param을 GPU에 나눠 담겠다는 것이므로 이미 optimizer state등은 partition이 되어있는 것과 다름 없으므로 ZeRO-DP의 기능은 탐나지 않을 수 있다. 하지만 ZeRO에는 gradient, optimizer state 그리고 parameter를 partition하는 ZeRO-DP 외에 TP와 결합 될 경우 activation partioning해서 checkpointing하는 기능도 있으며, 이것이 VRAM memory를 확 줄여주기 때문에 batch size를 늘림으로써 inter-node TP의 throughput을 늘릴 수 있다는 것이 핵심이다.

Fig.

ZeRO paper에서는 GPU device 나 training setting에 따라서 TP가 유리할 수도 있는 상황에 대해 언급하는데, 보통 GPU가 128~256대 이상인 경우이다. 뭐가 더 나은지를 고려할 때는 두 가지, Model FLOPs Utilization (MFU)와 critical batch size를 잘 고려해야 하는데, 아래 figure에서 slow convergence가 언급한 critical batch size와 관련이 있다.

Fig.

이는 parallelism으로 batch size를 늘려봐야 gradient가 더 정교해지기 어려워 training time을 줄여주는 효과가 없는 지점을 말한다. 즉 이런 경우 ZeRO-3보다 TP가 낫다는 것인데, ZeRO-3의 경우 device에 비례해서 model param, optimizer state등에 필요한 VRAM memory를 줄여주기 때문에 activation을 제외한 VRAM memory를 거의 0에 가깝게 줄일 수 있지만 그 댓가로 보통 일반적인 DP나 ZeRO보다 1.5배 정도의 communication volume이 더 든다고 알려져 있다. 하지만 communication volume이 model size의 1.5배로 고정인 것과 별개로 ring all-reduce를 하는데서 오는 ring latency가 문제가 된다고 한다.

Fig. Source from link

즉 device가 늘어날수록 throughput이 떨어진다는 것인데, 앞서 말한 것 처럼 critical batch size를 넘길 필요는 없기 때문에 GPU가 1024개면 1024개에 partition을 모두 해버리는 ZeRO를 쓰는 것 보다 GPU memory를 좀 희생해서 batch size가 좀 줄더라도 critical batch size에 근접하기만 하면 더 빠른 TP를 쓰는 것이 나을 수 있다.

주의할 점은 TP를 쓴다고 해도 앞서 언급한 것 처럼 ZeRO를 같이 써야 한다는 점과, TP를 모든 inter-node에 대해서 하는건 아니라는 것이다. 가장 좋은 것은 node를 넘어 partitioning하지 않는 것이다. 하지만 model size가 충분히 크면 이는 불가능할 수 있고, 예를 들어 1024개 GPUs에 대해서 TP를 16-way하게 되면 (TP degree=16) 2 node, 16 GPUs에 대해서 TP를 하겠다는 것이고, 이 경우 1024/16=64 way가 DP degree가 된다.

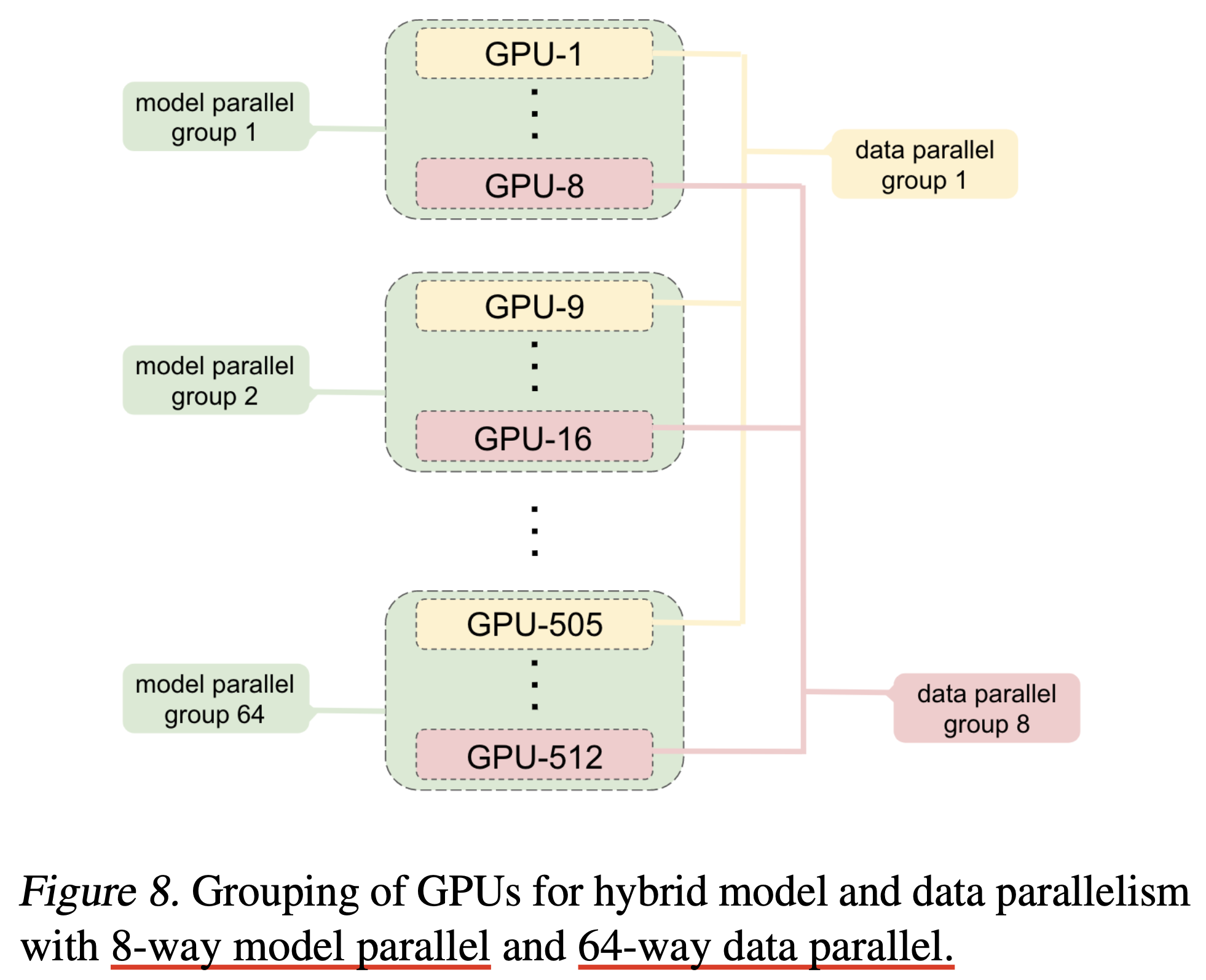Fig.

추가) 이 부분에 대해서 좀 더 생각해본 뒤 slide를 만들어왔다. 바로 아래 figure는 256 GPUs에 대해서 ZeRO-3를 할 때를 요약한 것이다.

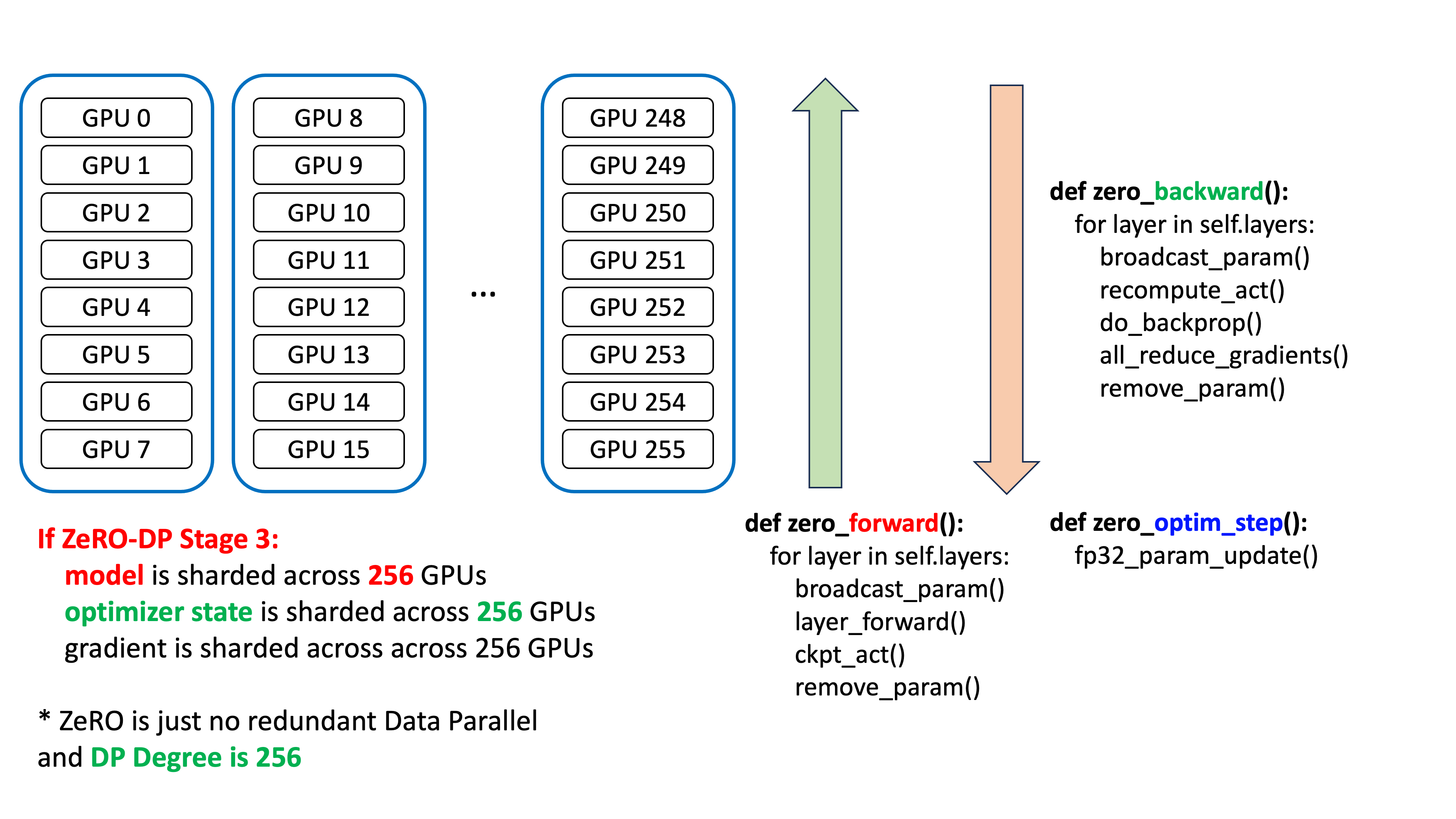Fig.

이 경우 model param이 node를 넘어 256개로 partition되며, optimizer state도 그렇게 된다. 다시 한 번 명심해야 할 것은 ZeRO는 Data Parallel (DP)라는 것이다. 그리고 forward, backward, optimizer step 을 보면 어떤 communication operation이 사용되는지 알 수 있다.

반면 TP+ZeRO-1을 할 경우는 아래와 같은데, 중요한 점은 optimizer state가 partition되는 ZeRO world size, 즉 DP degree가 32로 줄어들었다는 것이다. ZeRO가 DP degree로 256를 갖기 때문에 optimizer가 256개로 쪼개진 것과 다르게 TP+ZeRO-1는 32개로 찢어질 수 있고, memory가 충분하다면 node 내에서만 sharding하는 것, 즉 8개로도 쪼갤 수 있으며 memory가 반대로 부족하다면 256개로 찢을 수도 있다.

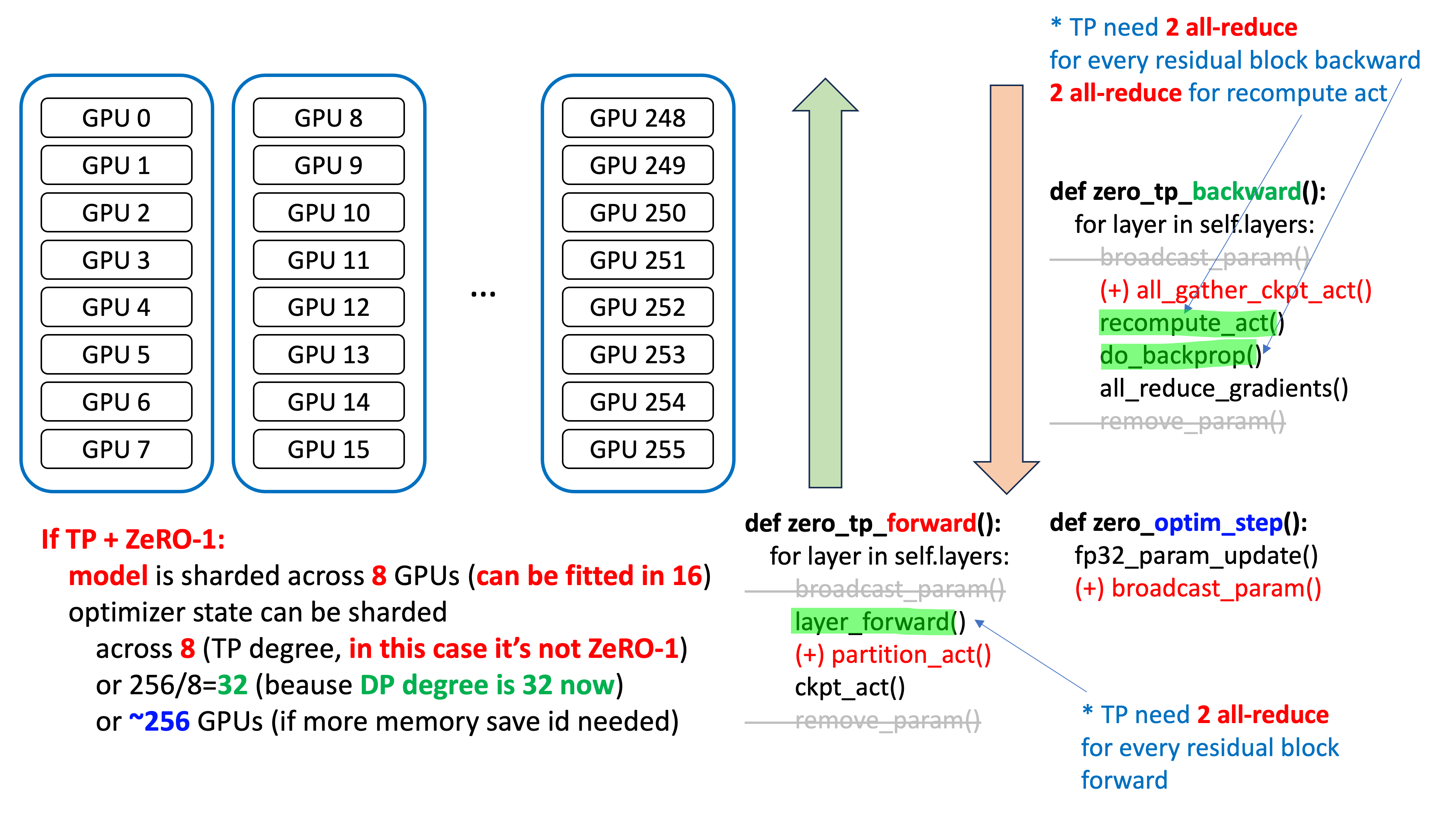Fig.

암튼 memory가 부족하지 않다면 gradient의 all-reduce가 32개 이하의 process에 대해서 이루어지는 것이기 때문에 256개에 대해서 이루어지는 ZeRO-3와는 많은 차이가 나게 된다.

추가로 ring all-reduce의 communication volume과 latency에 대한 slide를 만들었는데, latency를 이렇게 계산하는 것이 맞는지는 모르겠지만 맞다고 치면

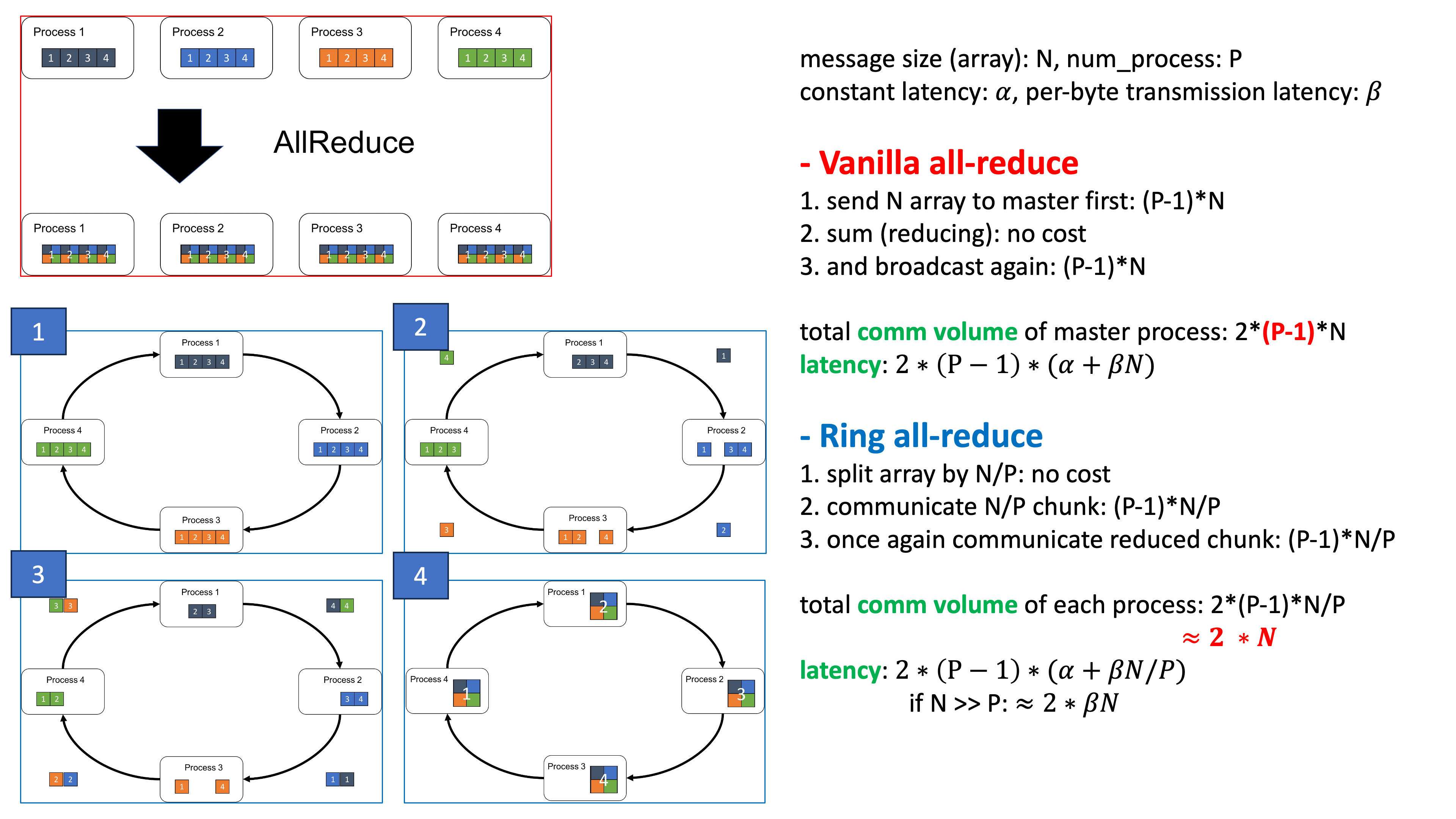Fig.

the number of processes 에 따른 ring latency는 아래처럼 plot할 수 있다.

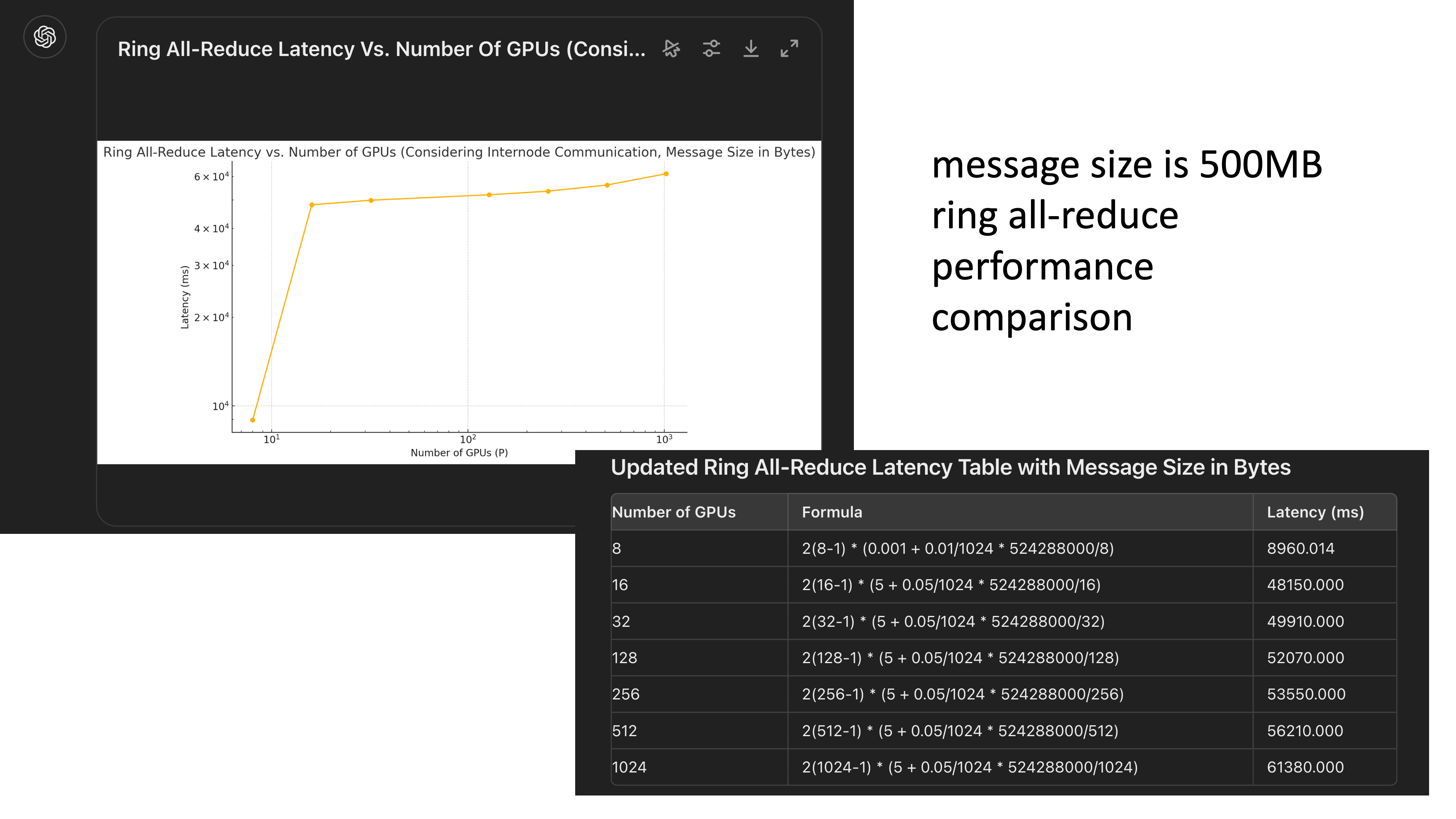Fig.

(distributed training plan을 구성할 때 반드시 ring latency 등을 고려해야 할 것 같다)

이렇듯 TP (MP variant)와 DP를 같이 쓰는 경우를 우리는 distributed plan 차원이 2차원이라고 하여 2D Parallelism이라고 부르며, 여기에 Pipeline Parallelism (PP) 까지 합쳐지면 3차원이 되기에 3D Parallelism이라 부른다.

Connection to Pipeline Parallelism (PP)

PP까지만 잠깐 언급하자면 아래처럼 Transformer layer가 예를 들 어 2개이고 GPU가 4개라고 생각해보자. TP만 적용하면 1, 2층의 parameter들을 알맞게 col-wise, row-wise parallel하여 GPU 4개가 나눠갖게 되는데, 이 경우 inter-node communcation을 하면 communication cost가 너무 커진다고 앞서 얘기했다. 그러므로 이를 최대한 줄이기 위해서 Transformer layer 1층의 param을 GPU 0, 1에 TP를 한다. 그리고 2층의 param은 GPU 2, 3에 TP를 하여 마치 horizontal (?) Model Parallelism (MP)과 vertical MP (즉 TP)를 같이 하는 것이다.

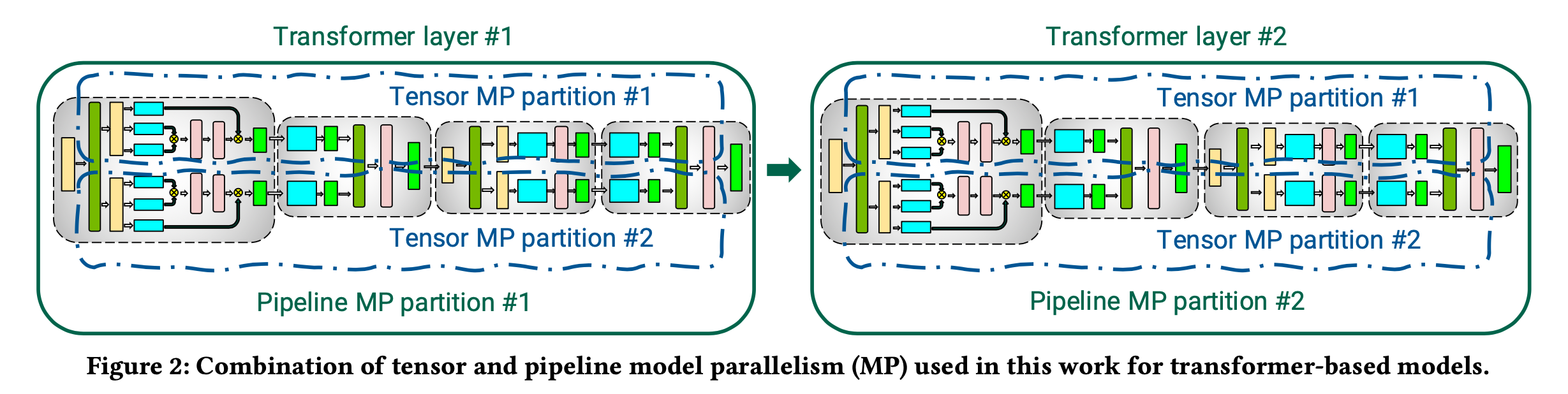Fig.

PP를 적용할 경우 문제는 아래처럼 앞선 1층의 output이 나와야 2층이 연산을 시작할 수 있다는 것인데, 아래 figure에서 Forward (F), Backward (B) operation를 수행하는 시점을 제외한 gray 영역은 GPU device가 놀고 있는 것으로, 이를 bubble이라고 부른다.

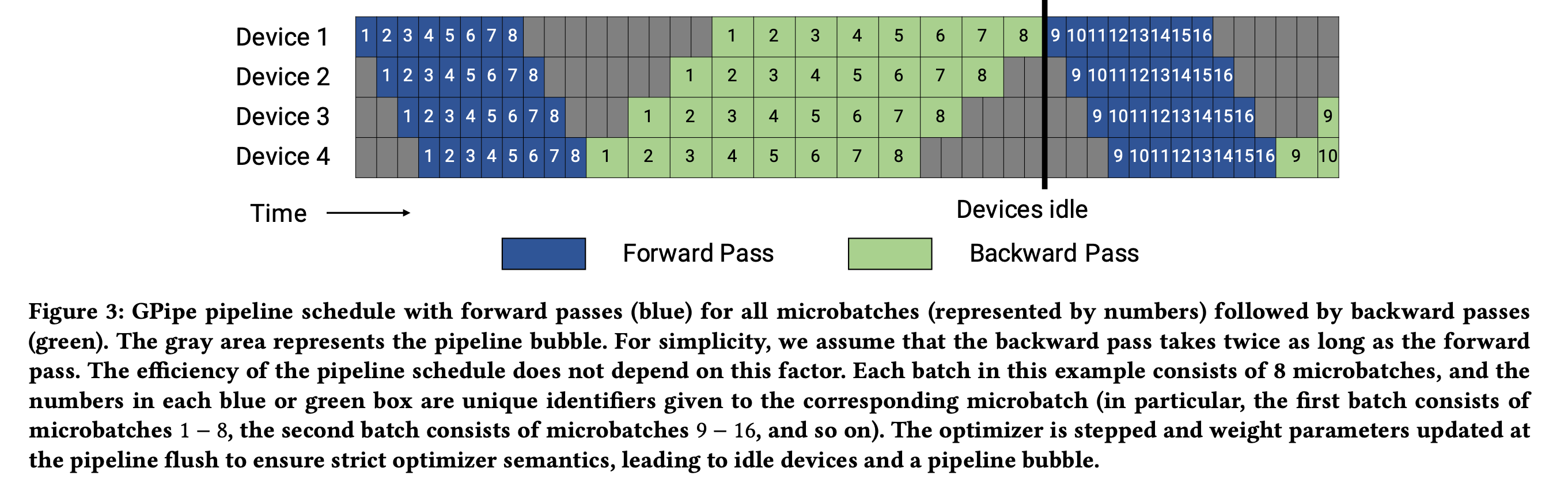Fig.

이를 해결하기 위해서 PP는 아래 figure처럼 최대한 large batch를 micro batch로 잘게 쪼개어 F, B에 드는 시간을 줄인 뒤에, 이를 dynamic 하게 배치해서 중간 중간 끼워넣는 (interleaving)한다.

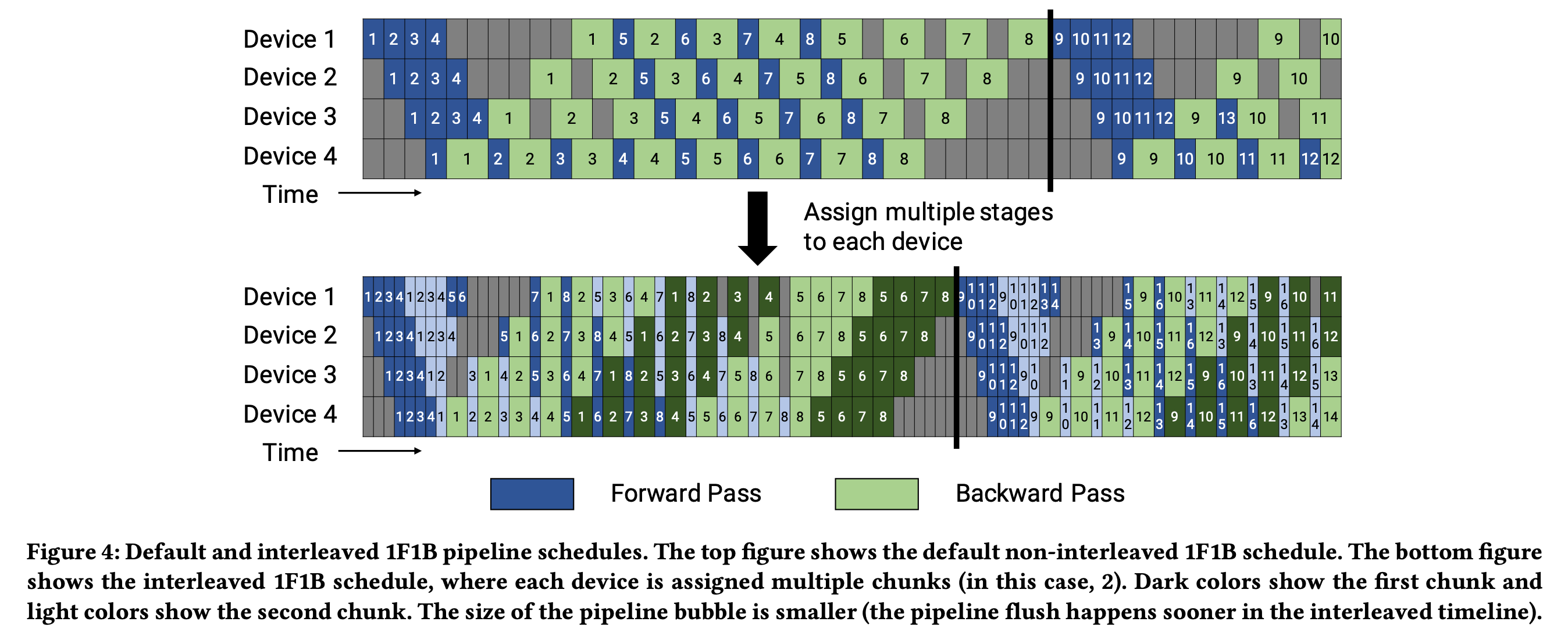Fig.

이를 잘 하면 예를 들어 GPU 32개에 대해서 아래와 같이 3차원 parallelism을 수행할 수 있게 된다.

• TP degree: 4
• PP degree: 4
• PD degree: 2

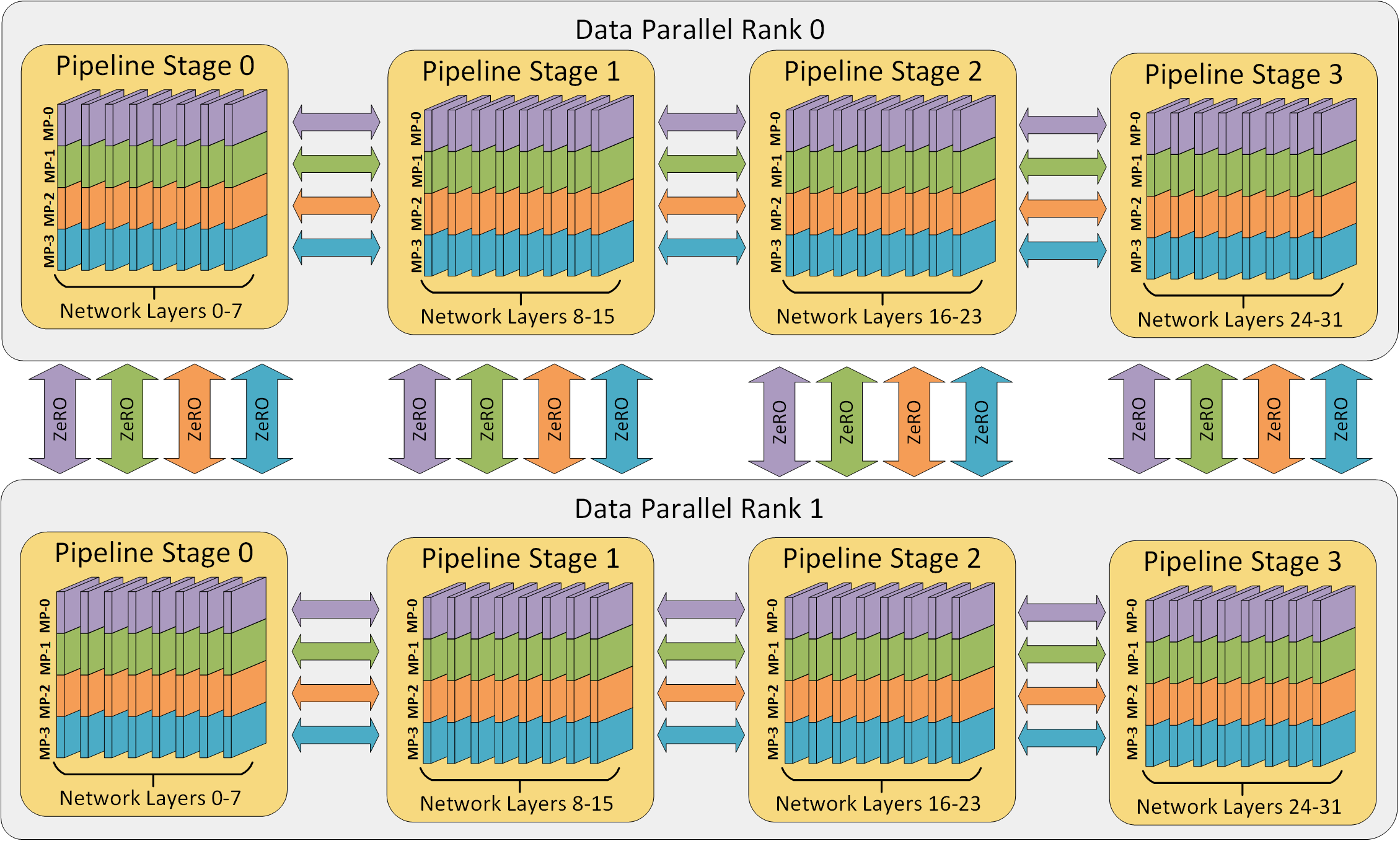Fig. Example 3D parallelism with 32 workers. Layers of the neural network are divided among four pipeline stages. Layers within each pipeline stage are further partitioned among four model parallel workers. Lastly, each pipeline is replicated across two data parallel instances, and ZeRO partitions the optimizer states across the data parallel replicas. Source from deepspeed blog

Implementation

Megatron처럼 엄청 효율적으로 구현한 것은 아니지만 TP가 어떻게 작동하는지 알고싶다면, 이 post를 확인하길 바란다.

+Updated) communication cost for TP with ZeRO?

최근 megatron-lm를 다시 보니까 model parameters, optimizer states, 그리고 아마 gradient 까지 계산해서 (activaiton은 일단 제외) theoritical memory consumption이 얼마나 드는지 계산하는 부분을 보니 TP + ZeRO-1을 하는 것이 내 생각과는 다른 것 같다. pytorch blog를 보면 앞서 설명했던 것 처럼 DP degree가 늘어나면 ring latency가 너무 늘어나기 때문에 TP를 같이 하는 것이 더 scalable하다고 했는데,

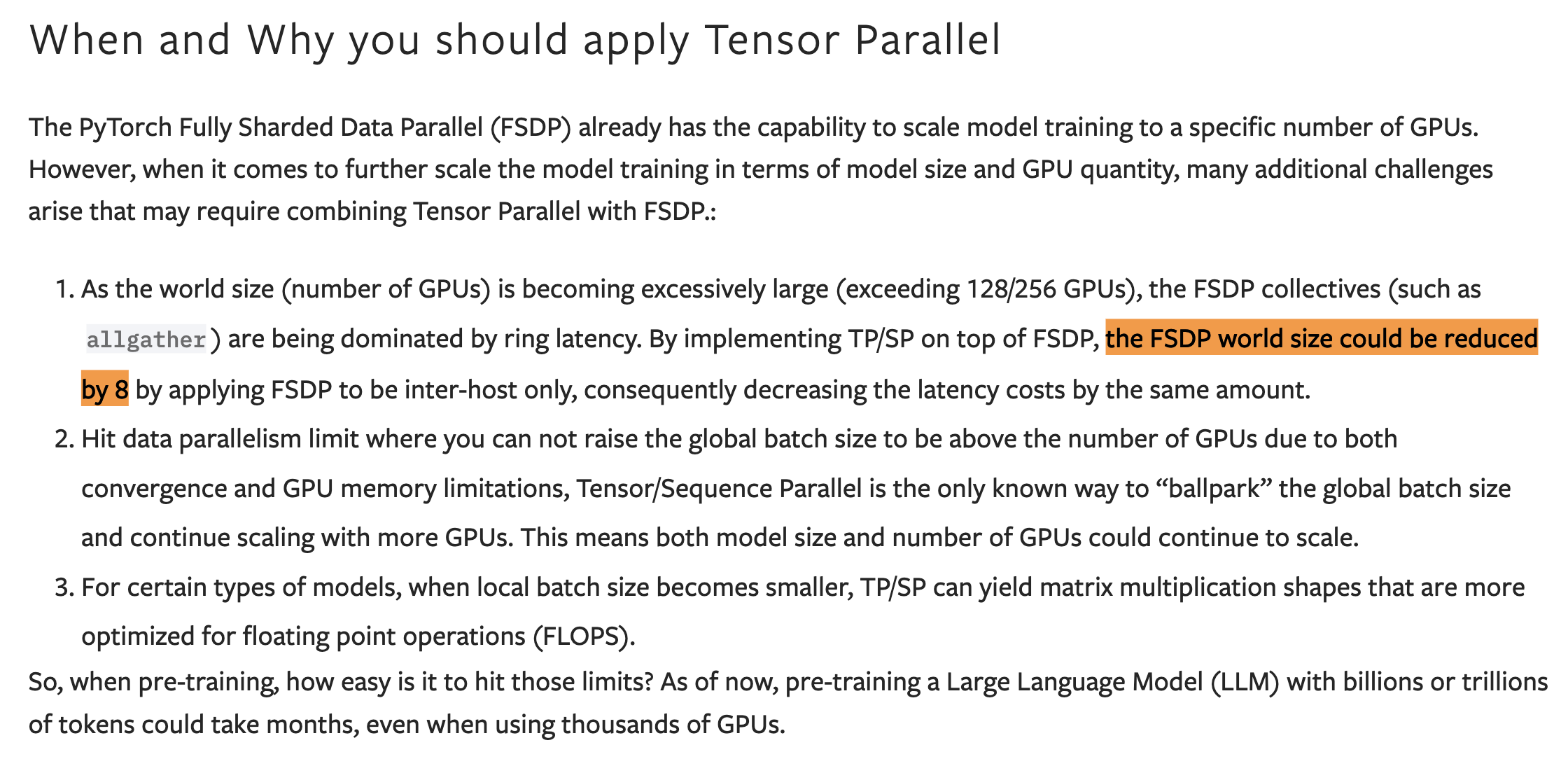Fig.

Fig.

megatron sharding strategy를 보면 optimizer state가 DP degree뿐 아니라 TP, PP degree로도 partition이 되어있었다. 이렇게 memory를 더 아껴서 activation recomputation 같은걸 안한다거나, comm overlap이나 다른 걸로 커버가 되는건지는 모르겠는데 생각을 좀 해봐야 할 것 같다.

Fig.

Torchtitan에도 torch native 개발 roadmap에서 3d parallelism을 중요하게 다루고 있는 이유에 대해 얘기한 부분이 있는데, 이는 다음과 같다.

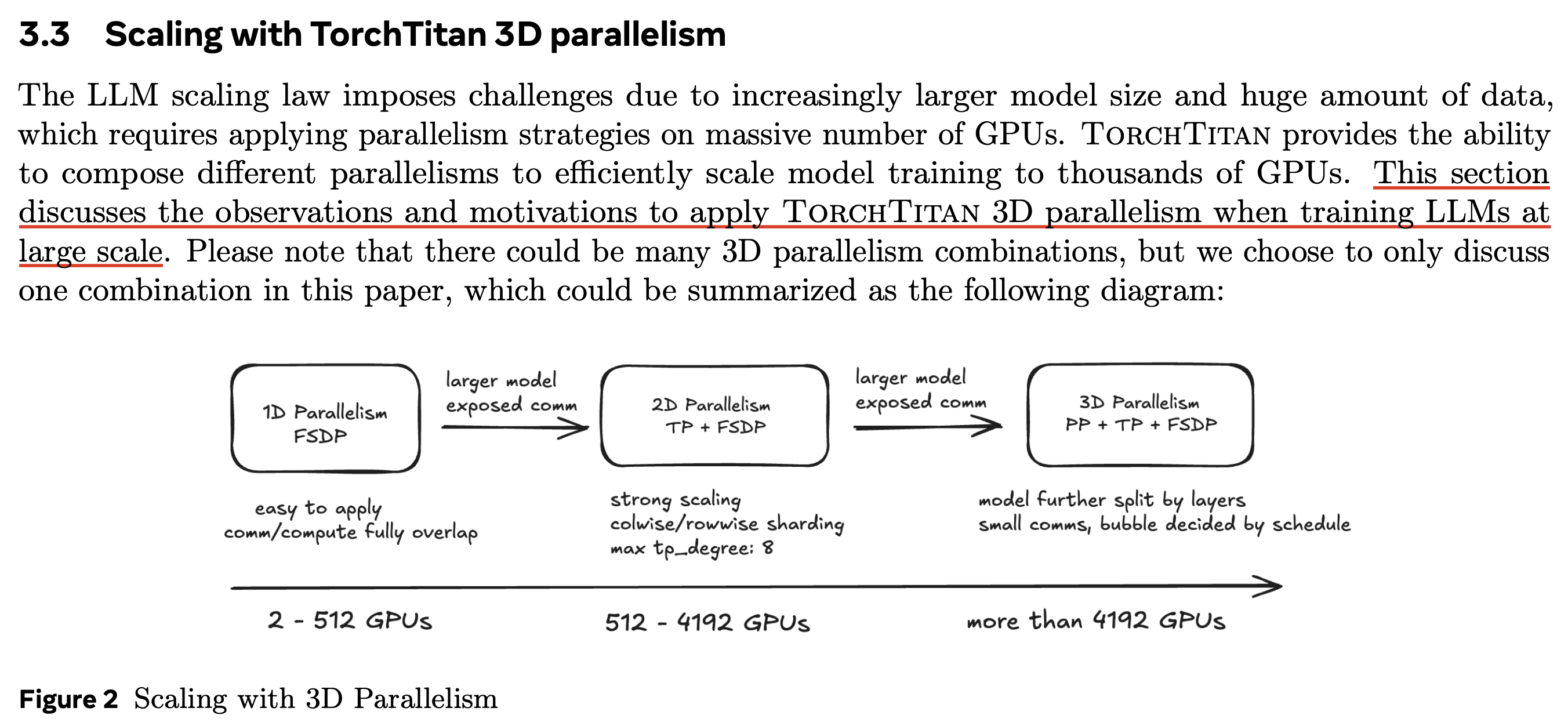Fig. Source from TorchTitan white paper

Fig. Source from TorchTitan white paper

References

• Papers
  • Mesh-TensorFlow: Deep Learning for Supercomputers
  • Megatron-LM
  • Efficient Large-Scale Language Model Training on GPU Clusters Using Megatron-LM
  • ZeRO
• Blogs and Others
  • Parallelisms Docs from NVIDIA
  • Large Scale Transformer model training with Tensor Parallel (TP)
  • Tensor Parallelism from Torch Lightening
  • Tensor Parallelism from UvA DL Notebooks
  • random tweet
• Codes
  • BreadcrumbsMegatron-LM/megatron/core/tensor_parallel/
  • BreadcrumbsMegatron-LM/megatron/core/tensor_parallel/layers.py
  • Megatron-LM/megatron/core/transformer/transformer_block.py

  • Megatron-LM/megatron/legacy/mpu/tests/test_layers.py

  • NeMo/nemo/lightning/megatron_parallel.py

  • fairseq/fairseq/model_parallel/models/transformer.py

  • https://github.com/huggingface/transformers/issues/10321

  • torchtitan/parallelisms/parallelize_llama.py