(ASR) A Long Way To CTC BeamSearch (1)

< 목차 >

• Big Picture of ASR
• Various Decoding Strategy
  • Greedy Decoding
  • Beam-Search Decoding
  • Beam-Search Decoding for CTC trained Model
• References

이번 post에서는 음성 인식 (Automatic Speech Recognition, ASR) 모델들 중 CTC로 학습한 모델의 Decoding 방법에 대해 다뤄보려고 합니다.

Big Picture of ASR

ASR의 goal은 간단합니다. 음성 feature를 입력받아 text를 출력으로 뱉으면 되죠. 최근 들어 ASR 모델은 심층 신경망 (Deep Neural Network)로 구성되어 여러 모듈을 따로 학습할 필요 없이 End-to-End (E2E)로 학습할 수 있게 되었습니다. 이런 E2E 모델은 크게 두 가지 step으로 구성되어 있다고 할 수 있는데요, 각각은 아래와 같습니다.

• Encoder : 음성 feature 를 입력으로 해서 Representation을 뽑는다.
• Decoder : Hidden Representation을 text로 바꿔준다.

이런 인코더와 디코더를 E2E로 학습하기 위한 Objective 는 Connectionist Temporal Classification (CTC) Loss, Cross Entropy (CE) Loss 그리고 Transducer Loss 가 대표적입니다. 이 중에서 CTC Loss는 2006년에 Alex Graves 라는 세계적인 석학이 제안했는데요, 간단히 말해서 CTC Loss 는 어떤 음성의 정답이라고 할 수 있는, 예를 들어 “cat” 이라는 text에 blank token을 추가하여 만들 수 있는 가능한 모든 path를 정의?하고 이에 대한 likelihood를 최대화 하는 방향으로 파라메터를 업데이트 하는 Objective 입니다.

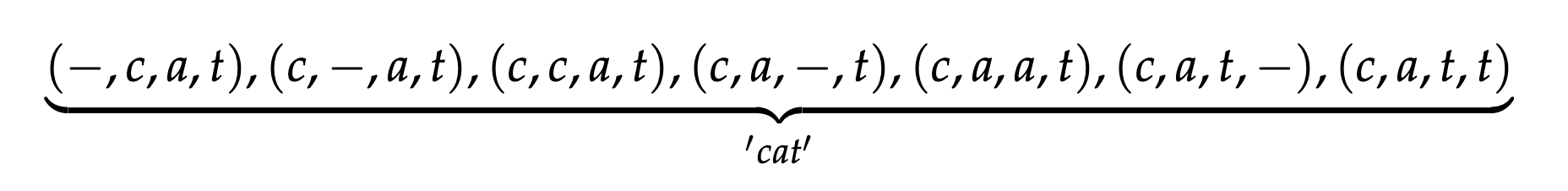Fig. 정답은 “cat” 세 글자 이지만 수백개에 달하는 음성 frame들 중 어디서부터 어디까지가 c 인지 알 수 없기 때문에 가능한 조합을 다 고려한다.

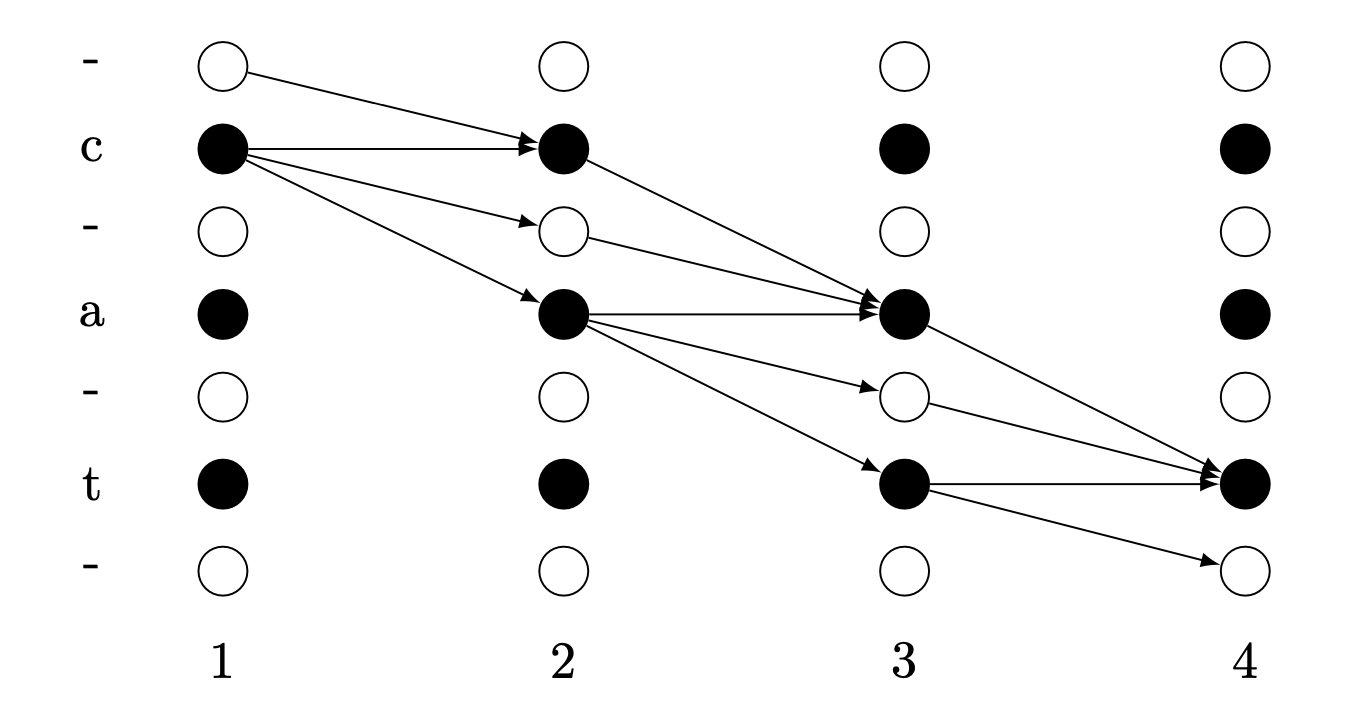Fig. 격자 (lattice) 구조로 나타내면 위와 같다.

CTC Loss를 수식으로 나타내면 아래와 같은데요

여기서 \(\hat{y}=\left(\hat{y}_{1}, \cdots, \hat{y}_{T}\right) \in A_{C T C}(x, y)\)는 정답에 대응하는 가능한 path들을 나타내고, 입력 음성이 각 path들을 뱉을 확률은 아래와 같으며, 이 중 어떤 특정 path \(\pi\)는 아래와 같이 표현할 수 있고,

여기서 \(Z^{\prime T}\) 는 정답 label (Vocabulary) \(Z^{\prime}\) 에 대한 확률 분포를 나타내는 토큰 T개 입니다.

(CTC에 대해 더 알고싶으시다면 link를 참고해 주세요.)

학습이 끝났다면 모델은 음성을 입력받고 해당 음성 벡터 frame들 마다 Vocabulary 에 정의된 Token 들의 확률 분포를 뽑아주고 (Token은 character ,sub-word 그리고 word 다 가능합니다) 이를 디코딩하게 됩니다.

가장 간단한 방법으로는 frame 마다 확률이 가장 높은 token들만 찍어보면 되는데요, 실제로 찍어보면 같은 결과를 얻을 수 있습니다.

디코딩 된 모든 토큰들의 예시 1 : "c - a a - t -"
디코딩 된 모든 토큰들의 예시 2 : "c - a - t t -"

위의 경우는 frame이 7개 인 경우이고 최종적으로 여기서 중복된 글자는 축약시키고, blank token이라 불리우는 ‘-‘는 없애는 등 몇 가지 규칙에 따르면 후처리된 최종 출력을 얻을 수 있습니다.

후처리 함수가 \(\mathcal{B}\) 라고 할 때

이므로

최종 출력 : "c a t"

이 되는 겁니다.

하지만 방금 말씀드린 Greedy Decoding (혹은 Best-path decoding) 이라고 하는 것은 실제 상황에서 꽤 좋지 않은 결과를 냅니다. 왜냐면 CTC Loss 라는 Objective 는 최종 출력을 만들어낼 때 다른 Seq2Seq Loss (CE Loss) 나 Transducer Loss 와는 다르게 각 각 frame 마다의 Conditional Independence 를 가정하기 때문입니다.

즉 앞뒤 맥락을 보지 않고 소리나는 대로만 디코딩 할 수 있다는 건데요, 이를 테면 어떤 음성이 I ate food 가 정답인데 이를 소리 나는 대로 I eight food 로 디코딩 할 수도 있다는 겁니다. 하지만 이는 앞에 I 가 나왔을 경우 보통 동사인 ate가 나온다는 걸 학습했다면, 즉 언어 모델 (Language Model, LM) 의 기능이 있다면 안그러겠죠? Seq2Seq 같은 모델은 바로 Decoder Module 이 Implicit LM 역할을 해서 이런 문제가 덜할 수 있지만 CTC 는 Objective 디자인 부터가 앞뒤 맥락과는 별개의 결과를 낼 수 있기 때문에 외부 LM 을 넣어줘야 더 좋은 결과를 낼 수 있는겁니다.

그리고 또한 이런 Greedy Decoding 방법은 CTC 로 학습된 모델에 좋지 않습니다. 그 이유는 앞서 말한 CTC의 특성 때문인데요,

아래의 그림을 봅시다.

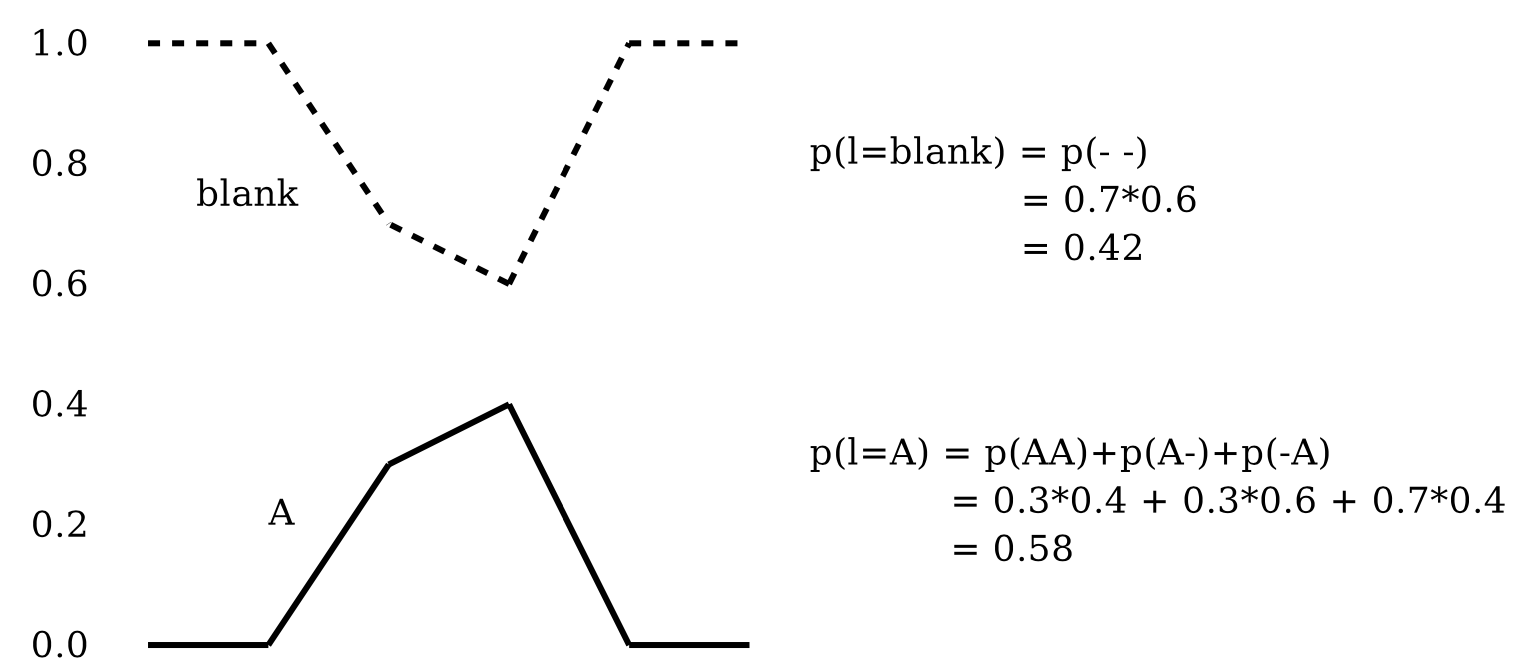Fig. Best Path Decoding 의 문제점.

frame 별로 A일 확률과 blank 일 확률이 있습니다. frame 은 두 개 밖에 없고 vocab도 2개니까 총 4개의 경우의 수를 낼 수 있는데요, 여기서

A-
AA
-A

이 세 가지는 전부 CTC의 후처리 규칙에 따라 A를 나타냅니다. 즉 Greedy Decoding은 각 문장을 여러개의 path로 나타낼 수 있다는 대전제를 제대로 반영하지 못한 겁니다.

근데 각 프레임마다 max인 값만 생각하는 greedy decoding 의 경우 -가 정답으로 나오게 되고 이 문장의 확률은 \(0.7*0.6=0.42\) 입니다. 하지만 A가 정답으로 나오게 될 확률은 그림에도 나와있듯 \(0.3*0.4+0.3*0.6+0.7*0.4=0.58\) 입니다.

즉 우리가 모든 timestep의 frame들을 쭉 보면서 나올 수 있는 문장들을 전부 구하고 CTC의 후처리 규칙에 따라 같은 문장을 나타내는 문장들의 확률은 전부 더하는 (merge) 식으로 하면 가장 그럴듯한 문장을 만드는게 가능해 집니다.

즉 우리는 CTC로 학습된 모델에 Beam Search 같은 방법을 써서 더 좋은 문장을 만들 수 있는거죠. 하지만 CTC의 경우 Beam Search 만으로는 충분하지 않고 앞서 말씀드린 것 처럼 LM을 더해서 디코딩 하는 것 까지 해줘야 결과가 많이 좋아집니다.

이러한 일련의 과정은 아래와 같은 그림으로 나타낼 수 있는데요,

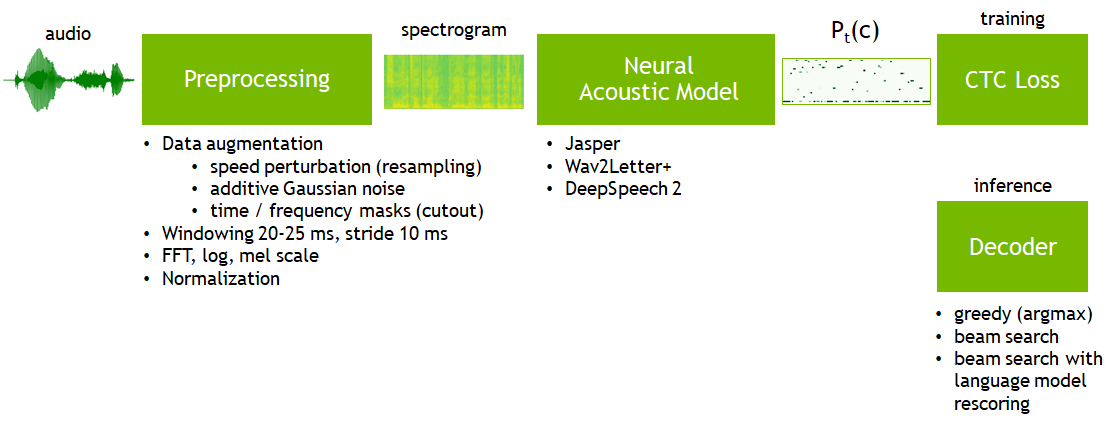Fig. Overview of E2E ASR Training with CTC Loss. Image Source

이번 post는 위의 그림에서 바로 추론 (Inference) 단계에 해당하는 Decoding 방법을 다루게 되겠습니다.

Various Decoding Strategy

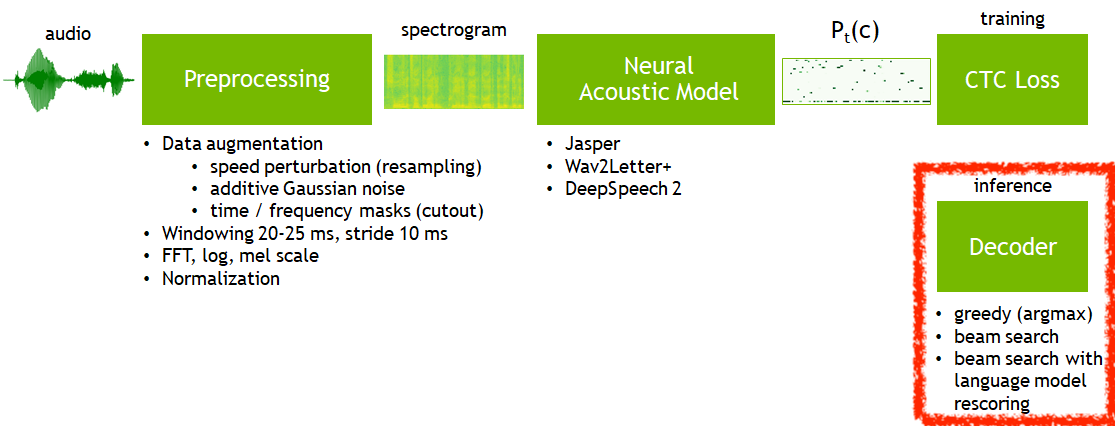Fig. E2E ASR Model은 CTC로 학습하든 어텐션과 CE Loss를 사용해서 학습하든, 실제 추론 시 다양한 Decoding 전략을 사용할 수 있다.

위의 그림에서 추론 과정이라 하는 것은 아래 테이블 처럼 학습한 ASR 모델 (Acoustic Model ; AM) 과 언어 모델 (Language Model ; LM)을 다양한 결합해서 최선의 결과를 내는 겁니다.

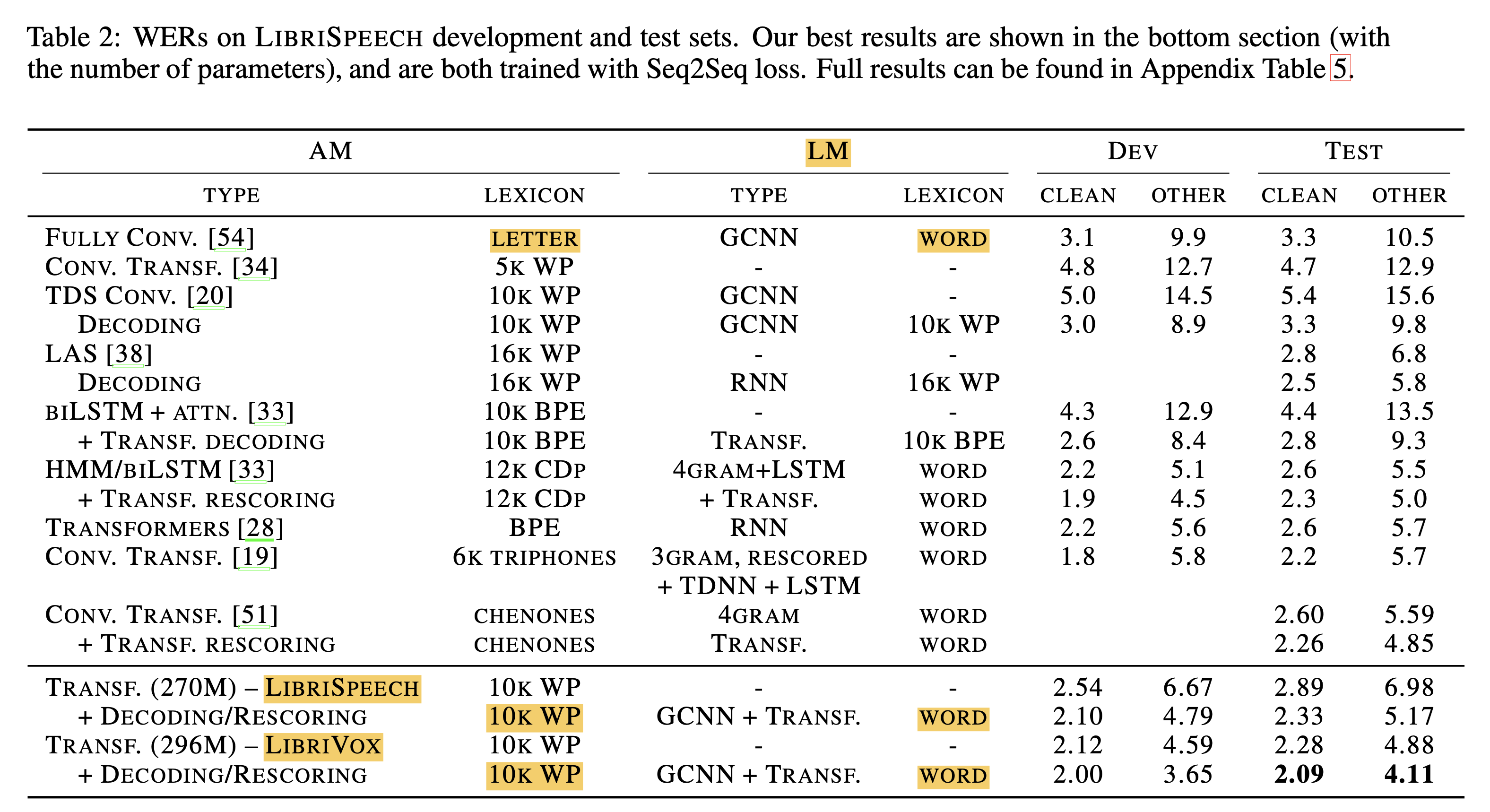Fig. AM에 LM을 붙혀 디코딩 하는 과정이 다양할 수 있으며 심지어 학습된 AM과 다른 vocab을 사용하는 LM도 존재한다.

여기서 디코더 라고하는게 ASR 모델이 어떤 거냐에 따라서 조금 헷갈리실 수도 있는데요, 
예를 들어 어떤 CTC 기반 모델은 ASR Encoder 와 그 끝에 붙은 Linear Projection Layer 까지 해서 AM 이라고 부릅니다. 

반면에 Sequence-to-Sequence (Seq2Seq) 모델에는 explicit 하게 Encoder, Decoder 라는 모듈이 존재합니다. 

즉 CTC는 사실 디코더라고 부를 만한 모듈이 없는 셈인데 실제 CTC 모델을 추론할 때는 ctc output을 먼저 뽑고 
맨 첫 프레임 부터 전진하면서 LM 확률을 더해주면서 빔 서치 등을 진행하며 이를 디코더 라고 부릅니다.

즉 CTC의 입장에서 디코더는 학습할 요소가 있는 parametric module은 아닌 셈인거죠.

헷갈리실 수 있으니 주의해 주세요.

CTC Decoding에는 앞서 말씀드린 것 처럼 AM의 출력물만 사용해서 Greedy Decoding을 하는 경우, Beam Search Decoding 를 하는 경우, 여기에 LM 까지 더하는 경우 그리고 마지막으로 Beam Search 결과에 Rescoring LM으로 Rescoring 하는 방법이 있습니다.

1.Greedy
2.Beam Search
3.Beam Search + LM
4.Beam Search + LM + Rescoring LM

어떤 음성 샘플에 대해 CTC 출력을 뽑고 각각 출력 결과를 비교해 봅시다.

### Example 1
GREEDY DECODING:
mister qualter as the apostle of the middle classes and we re glad twelcomed his gospe
BEAM SEARCH DECODING:
mister qualter as the apostle of the middle classes and we are glad twelcomed his gospel
BEAM SEARCH DECODING WITH LM:
mister quilter is the apostle of the middle classes and we are glad to welcome his gospel

### Example 2
GREEDY DECODING:
alloud laugh followed at chunkeys expencs
BEAM SEARCH DECODING:
alloud laugh followed at chunkeys expense
BEAM SEARCH DECODING WITH LM:
a loud laugh followed at chunkys expense

### Example 3
GREEDY DECODING:
but no ghoes tor anything else appeared upon the angient wall
BEAM SEARCH DECODING:
but no ghoest tor anything else appeared upon the angient walls
BEAM SEARCH DECODING WITH LM:
but no ghost or anything else appeared upon the ancient walls

LM을 넣어 빔서치를 했더니 glad twelcomed 같은게 glad to welcome으로 바뀌는 걸 확인할 수 있습니다. 그럼 이제 차근차근 Decoding 방법들에 대해서 알아보도록 하겠습니다.

Greedy Decoding

앞서 얘기했지만 실제 CTC output 을 가지고 얘기해보죠. Greedy Decoding이란 모든 time-step에 대해서 가장 높은 확률을 나타내는 토큰을 선택하는 가장 쉬운 방법입니다.

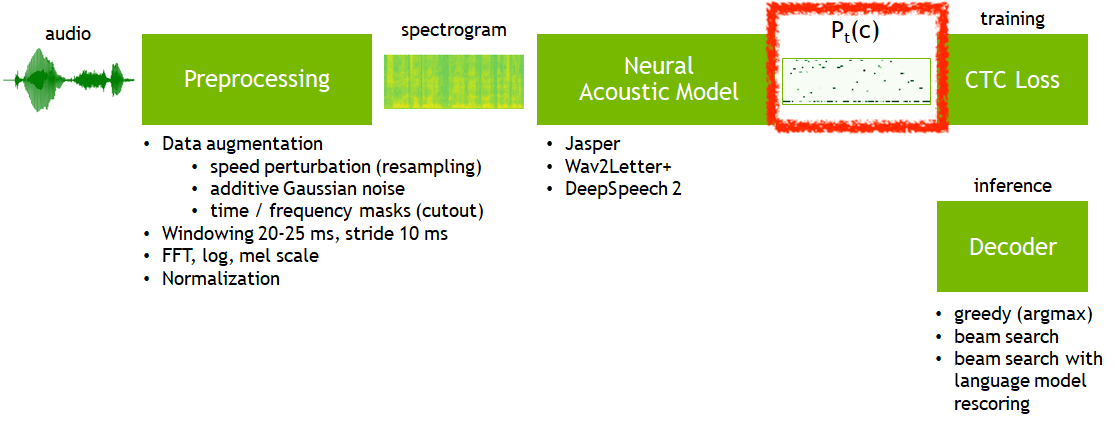Fig.

위의 그림에서 빨간 박스인 CTC Output는 실제로 아래와 같이 생겼는데요,

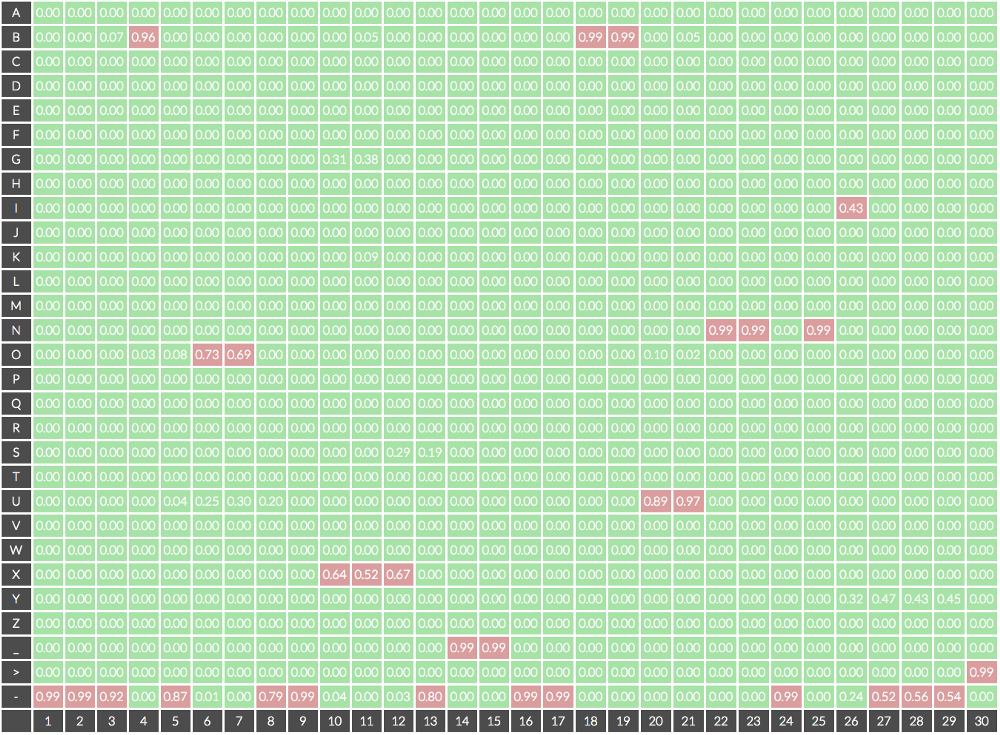Fig. 실제 CTC Output, 매 token 마다 vocab에 있는 label들에 대한 확률이 나온다. Image Source

Greedy Decoding (Greedy Search)는 모든 time step 에 대해서 가장 확률이 큰 정답만을 방법으로 실제로 수식은 아래와 같습니다.

위의 예시의 그림에서 골라보자면 정답은

---B-OO--XXX-__--BBUUNN-NI--->

가 되는데, 여기서 -는 blank token이며, _는 띄어쓰기, >는 문장의 끝을 나타내는 토큰이므로, CTC 논문에서 제안된 방법에 따라 후처리를 해주면 실제 추론 결과는

BOX BUNNI

가 됩니다.

Fig. Bugs Bunny 말하는거니…?

위의 예시에서는 프레임 개수가 30개밖에 안되지만
실제 상황의 음성 샘플은 보통 300~700개 정도의 프레임 개수가 있습니다. 
이 중에서 실제 의미가 있는 프레임 개수는 몇개 안되는데요 (spiky),
지금 다룰 것은 아니지만 CTC를 개선한 ASG라는 알고리즘으로 학습하면 이를 개선할 수 있다고 합니다.

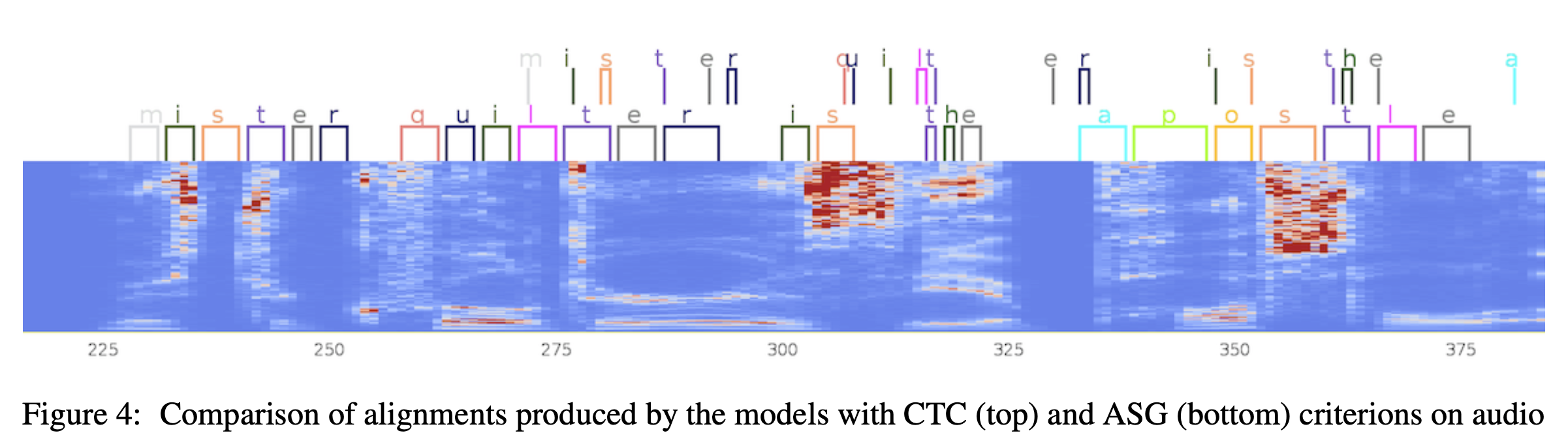Fig. CTC vs ASG. 어쨌든 둘 다 blank가 많기는 하다.

Beam-Search Decoding

그 다음은 Beam Search Decoding 입니다. Beam Search는 무엇이며 왜 해야 하는 걸까요?

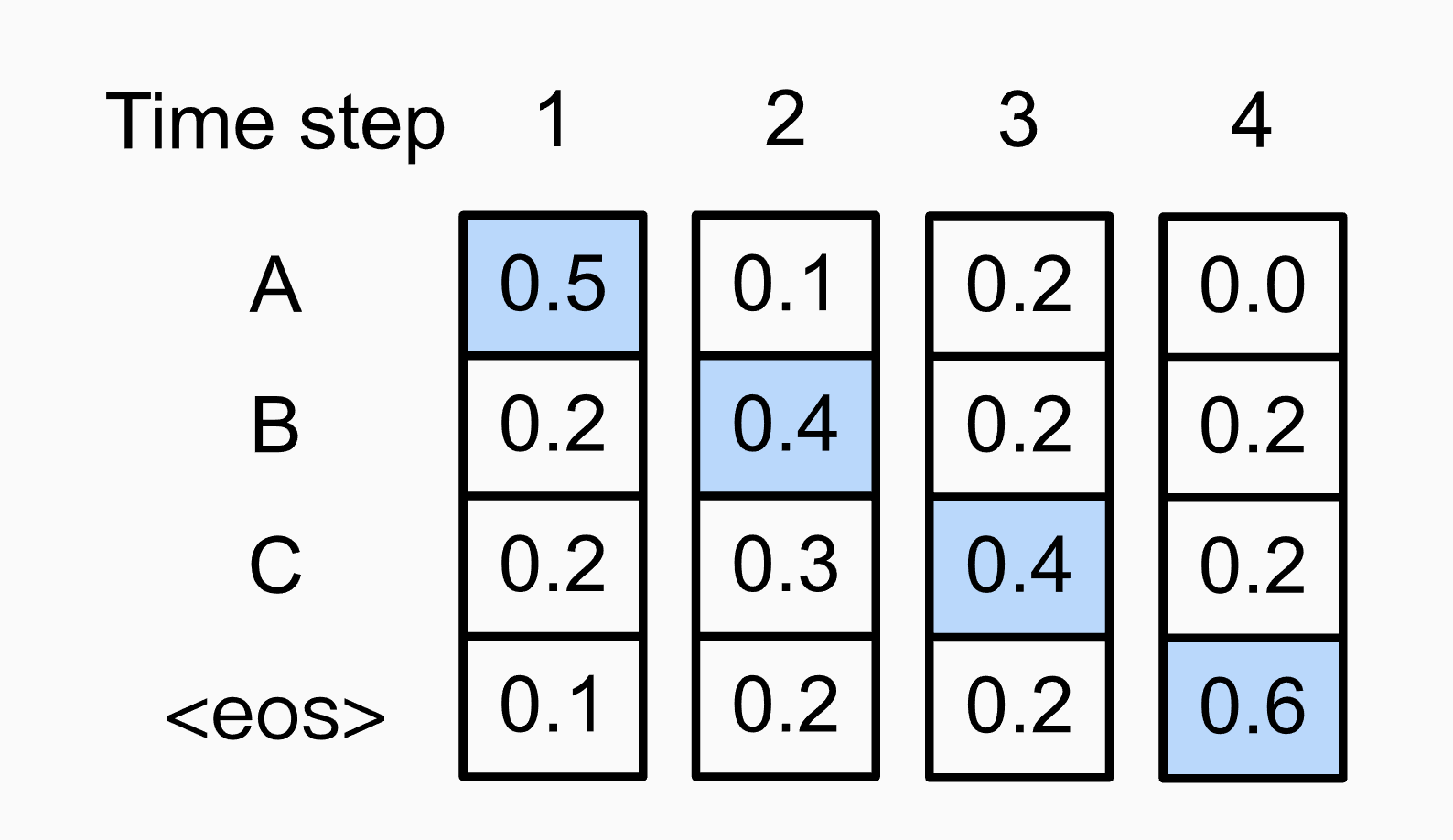Fig. Greedy Search Example. Image Source

위 그림은 Greedy Decoding을 한경우를 나타냅니다. time-step마다 max값만 골랐죠.

근데 이렇게 구한 문장의 확률을 구해보면 다음과 같습니다.

그런데 다음 경우를 생각해 볼까요?

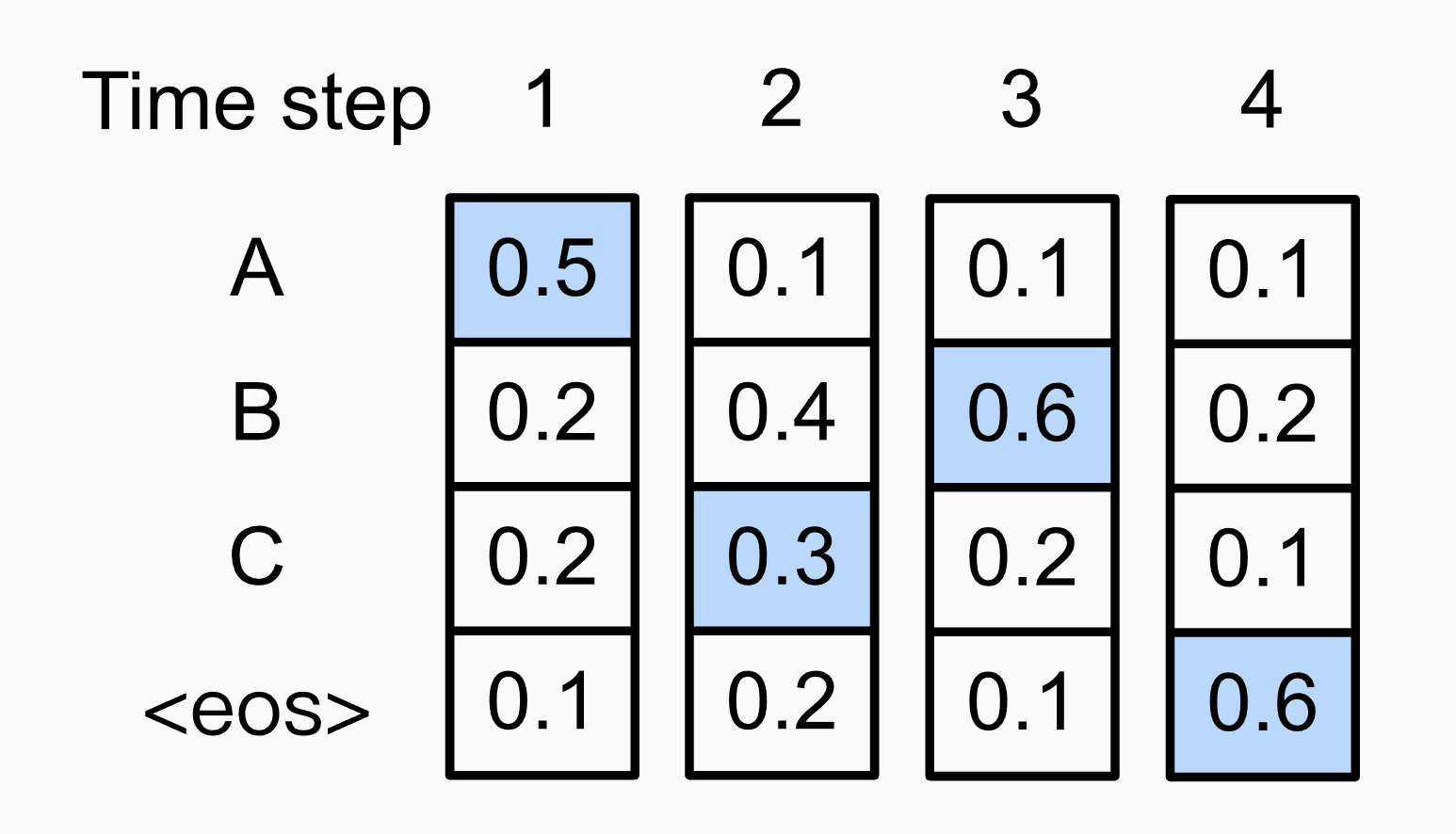Fig.

0.054가 Greedy Search를 한 경우의 0.048 보다 큽니다.

위의 경우는 2번째에서 B 보다 확률이 적은 C 토큰을 선택했지만 그럼으로써 3번째 토큰 확률 분포가 달라졌고 3,4번째 토큰은 또 max를 선택함으로써 결과가 달라진겁니다. 각 토큰별 확률값을 곱한 문장의 확률이 더 높다는건 데이터에 기반해서 학습한 모델이 아래의 문장을 더 그럴듯하다고 느낀다는 것이고 우리는 이런 문장을 답으로 내길 원하죠.

허나 Greedy Search를 하는 순간 두 번째 스텝에서 B를 골라야만 하기 때문에 위와 같은 문장을 찾아낼 수 없습니다. 이런 문제를 해결하기 위해서 각 time-step 마다 1개보다 더 많은 토큰을 골라서 여러 경우의수를 생각하면서 search를 해보자는 아이디어가 나온건데요, 만약 극단적으로 모든 경우의 수를 다 생각해본다면 만약 우리가 가지고 있는 label이 alphabet 개수 + _ + - + > 라면 총 29개이고, time-step이 100일 때, \(29^{100}\)만큼의 가능한 path들을 살펴보고 이중에서 최고를 고르면 됩니다.

근데 이렇게 모든 path를 다 고려하는건 너무 말이 안되기 때문에 약간의 타협을 하게 되는데요, 바로 매 time-step마다 얼만큼의 후보를 (candidate token) 보고 얼만큼의 가지를 뻗어나갈 것이냐를 고정하는 겁니다. 이것이 바로 Beam Search 입니다. 이 때 ‘각 timestep 마다 얼만큼의 가지를 뻗어나갈 것이냐?’ 는 Beam Width 라고 하는 하이퍼파라메터에 의해 정해집니다. 일반적으로 이게 클수록 서치하는 path가 많아지니 성능이 좋아지나 특정 값을 넘어가면 더이상 성능은 오르지 않고 시간만 잡아먹으니 잘 골라야 하는 값이죠. (이 외에도 빔 서치를 최적화 하기 위해 필요한 다양한 하이퍼파라메터가 있습니다.)

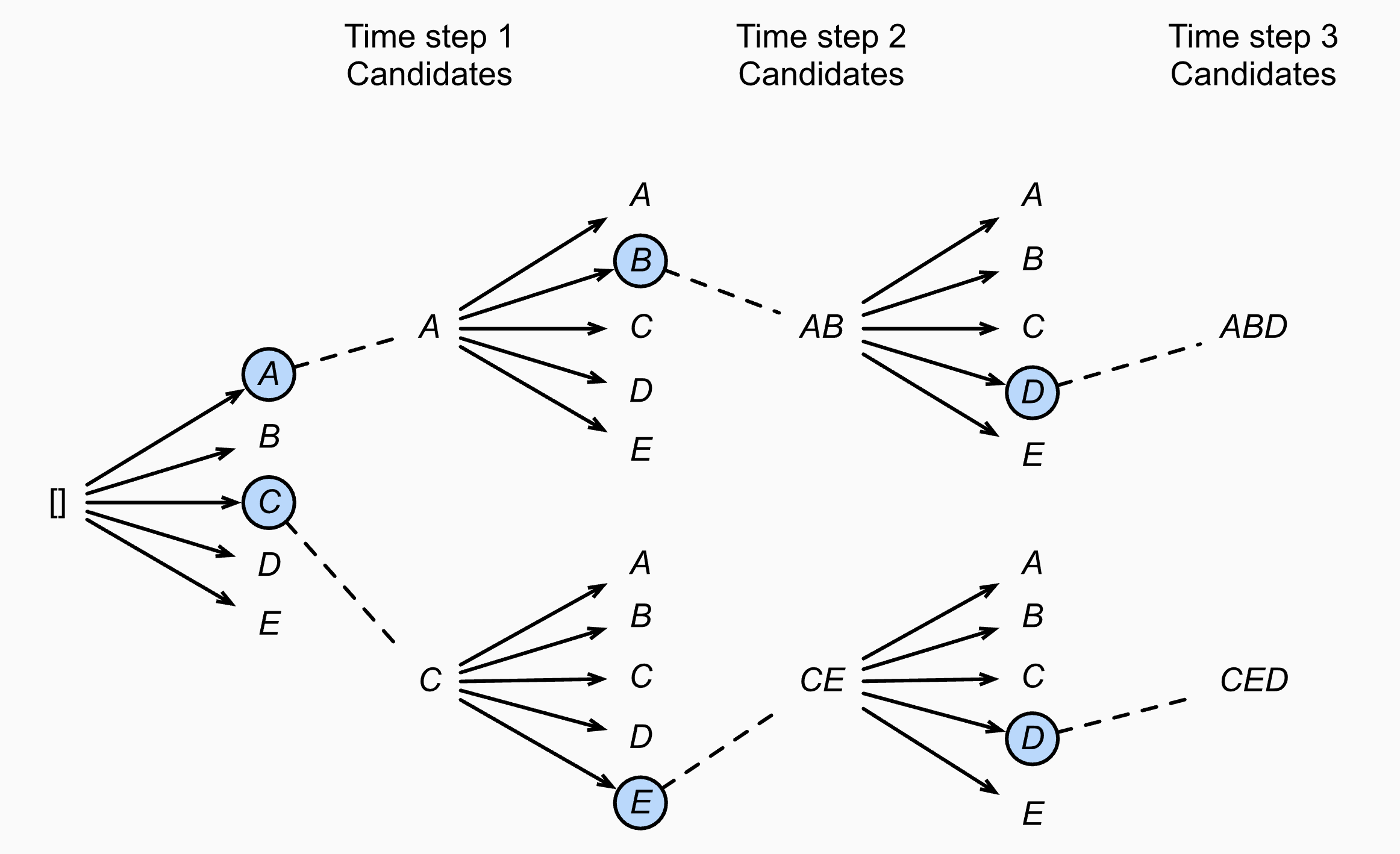Fig. Beam Width가 2인 경우 각각의 time-step에서 candidate은 A, C, AB, CE, ABD 그리고 CED가 된다.

Beam Search는 Beam Width가 n개 일 경우 n개의 가장 높은 확률의 n-best 문장을 찾아내주며 (나중에 다룰 pruning이란 개념이 들어가면 n개가 보장이 안될수도 있습니다), Greedy Search는 Beam Search의 special case 라고 할 수 있겠습니다.

Beam-Search Decoding for CTC trained Model

앞서 Beam Search 가 어떤 것이며, Greedy Search 대비 어떤 이득이 있는지 까지 직관적으로 알아봤습니다. 이번에는 CTC로 학습된 음성인식 모델에 대해서 Beam Search를 하는 경우에 대해 살펴보도록 하겠습니다.

먼저 빔 서치를 하기 위해서 CTC Loss로 학습한 ASR Model의 경우 일단 AM으로 아레와 같이 CTC output을 쭉 뽑습니다.

이제 t=1 부터 빔 서치를 하면서 빔들을 만들어가면 되는데요 이 때 LM 이 있으면 LM score도 더할 수 있습니다.

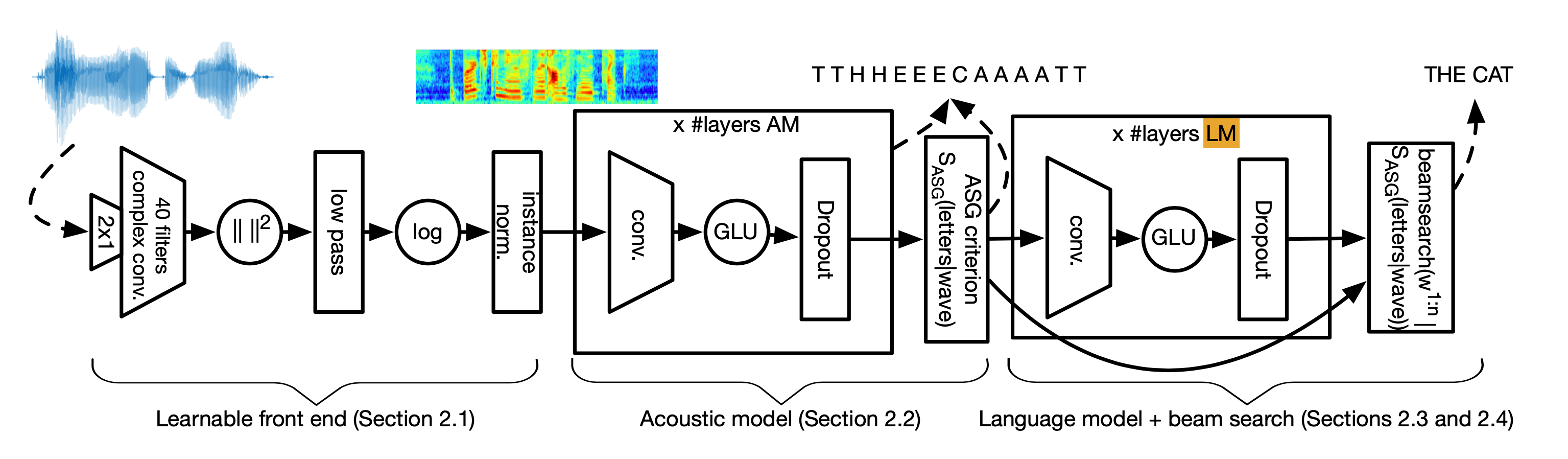Fig. LM을 활용한 빔서치의 모식도

독자분들 중 음성인식에 친숙하지 않으신 분들이 계실 것 같아서 다시 말씀드리자면 이는 Seq2Seq 모델처럼 Autoregressive 하게 token을 뽑아가면서 LM확률을 더해주는 Shallow Fusion과는 살짝 다릅니다. t=1 부터 전진하는 건 맞지만 말씀드린 것 처럼 CTC 확률을 t=1~T 까지 쭉 뽑아두고 처음부터 다시 빔서치를 한다는 걸 잊지 말아주시기 바랍니다.

다시 요약하자면 CTC로 학습된 모델의 빔 서치 과정은 다음과 같습니다.

• 1.ASR Model (어떤 논문에서는 AM이라고 하기도 함)이 frame별로 학습한 Vocabulary 사이즈의 Token Distribution을 쫙 뽑아냄.
• 2.뽑아낸 time-step별 확률을 알고 있고, 맨 처음부터 beam search를 하게 되는데, 이 때 Language Model의 보조를 받아서 Beam을 찾게 됨.
• 3.최종 출력물
  • 여기서 추가적으로 n-best list에 대해서 다시 LM을 사용해 ppl을 재서 re-order 할 수도 있는데 이를 re-scoring 이라고 함.

Rescoring 을 빼고 빔서치 하는 과정을 수식으로 나타내면 아래와 같습니다.

여기서 \(\alpha\)는 language model weight로 빔서치를 하면서 LM의 영향을 얼마나 받을 것인가를 정하는 요소이며 \(\beta\)는 word insertion penalty로 문장 길이에 따라 패널티를 주는 요소입니다. 이 값이 필요한 이유는 Beam Search라는 것은 결국 각 time-step 에서의 token의 확률을 곱해서 문장의 확률을 표현하는 것인데, 0~1사이 값인 확률을 계속 곱하면 길이가 긴 문장일수록 낮아질 수 밖에 없기 때문에 아무리 좋은 문장이어도 문장이 길어지면 확률이 작아져서 결국 덜 좋은문장보다 최종 스코어가 작아지게 돼서 선택받지 못하는 일이 발생하기 때문입니다.

이 \(\beta\)값은 양수 일 수도 있고 음수일 수도 있는데요, 이 값이 음수이면 문장별로 빔 서치 최종 확률값이 같아도 긴 문장에 더 많은 점수를 할당해서 결과가 길게 나오게끔 장려하는 것이 되고 양수면 반대가 됩니다.

그 밖에도 빔 서치를 할 때는 silence weight, \(\gamma\) 나 아래의 수식에는 없지만 <unk> weight, 특히 Seq2Seq의 경우에 EOS-penalty, 등의 인자가 추가될 수도 있습니다.

그런데 왜 CTC로 학습한 빔서치는 기존의 Vanilla 빔서치와 다르다는 걸까요? 그 이유는 바로 blank token 이 존재하고, CTC output을 후처리 하는 CTC의 특수성 때문입니다.

CTC는 alignment 를 알 수 없는 가변 길이의 (variable length) 입력 sequence 와 정답 sequence 간의 관계를 학습하기 위해 정답으로 매핑 가능한 모든 path를 학습한 결과 한 문장을 여러 path로 표현할 수 있게 됐습니다.

#some examples
“to” → “---ttttttooo”, or “-t-o-”, or “to”
“too” → “---ttttto-o”, or “-t-o-o-”, or “to-o”, but not “too”
“hello” → ‘h-elllll-ll-ooo’, ‘hel-lo’, …
“a” → ‘aa’, ‘a-’, ‘-a’, …

즉 CTC로 학습한 모델의 입장에선 Blank와 중복 토큰을 제외했을 때 (collapse) 같은 문장들은 사실상 같은 출력 결과나 다름없기 때문입니다. 이 경우는 어떻게 해야할까요? 빔을 통합해야하나요?

네 맞습니다, CTC로 학습한 모델의 빔서치를 할 경우에는 후처리 했을 때 같은 문장을 나타내는 path들은 확률을 합쳐서 (merge) 생각하는 trick 등을 써야 제대로 path를 찾을 수 있게 됩니다.

만약에 그렇게 하지 않고 Vanilla Beam Serach를 쓴다면 어떻게 될까요? 아까의 예시를 가져와 봅시다.

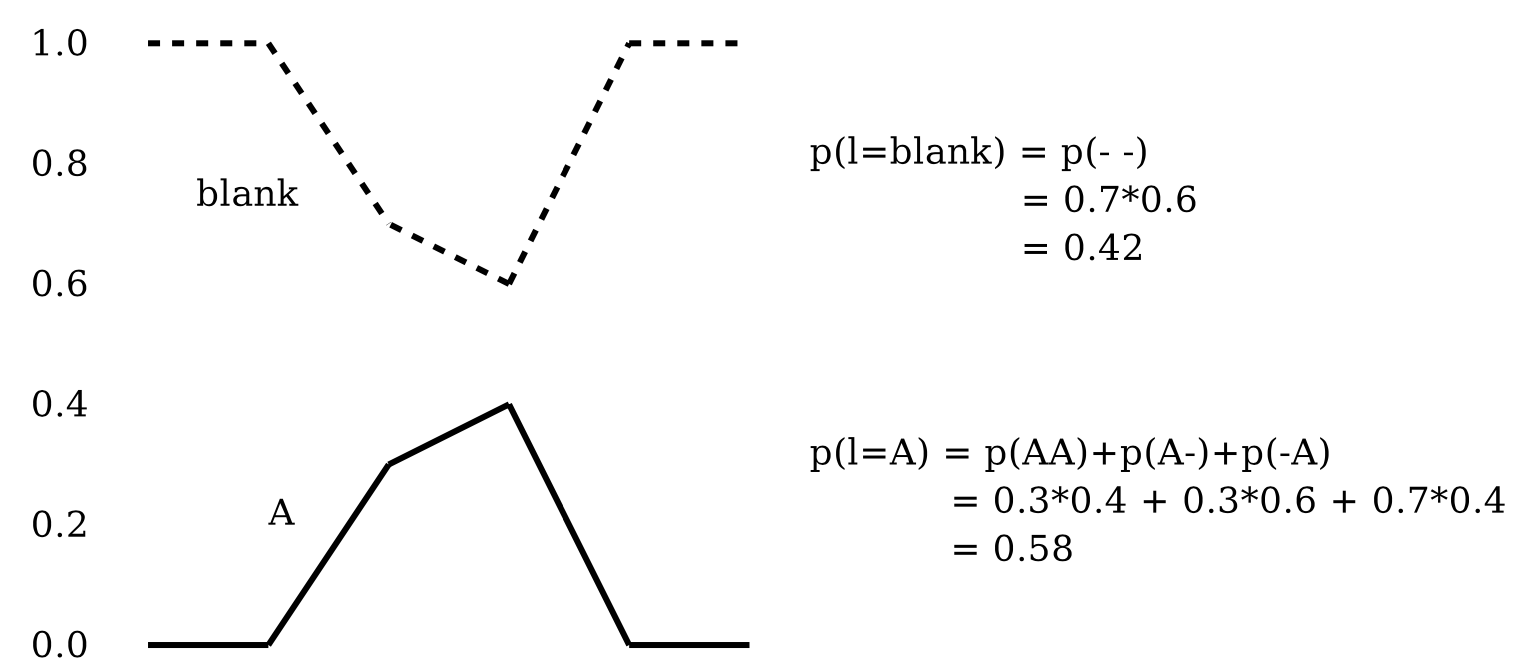Fig. Best Path Decoding 의 문제점.

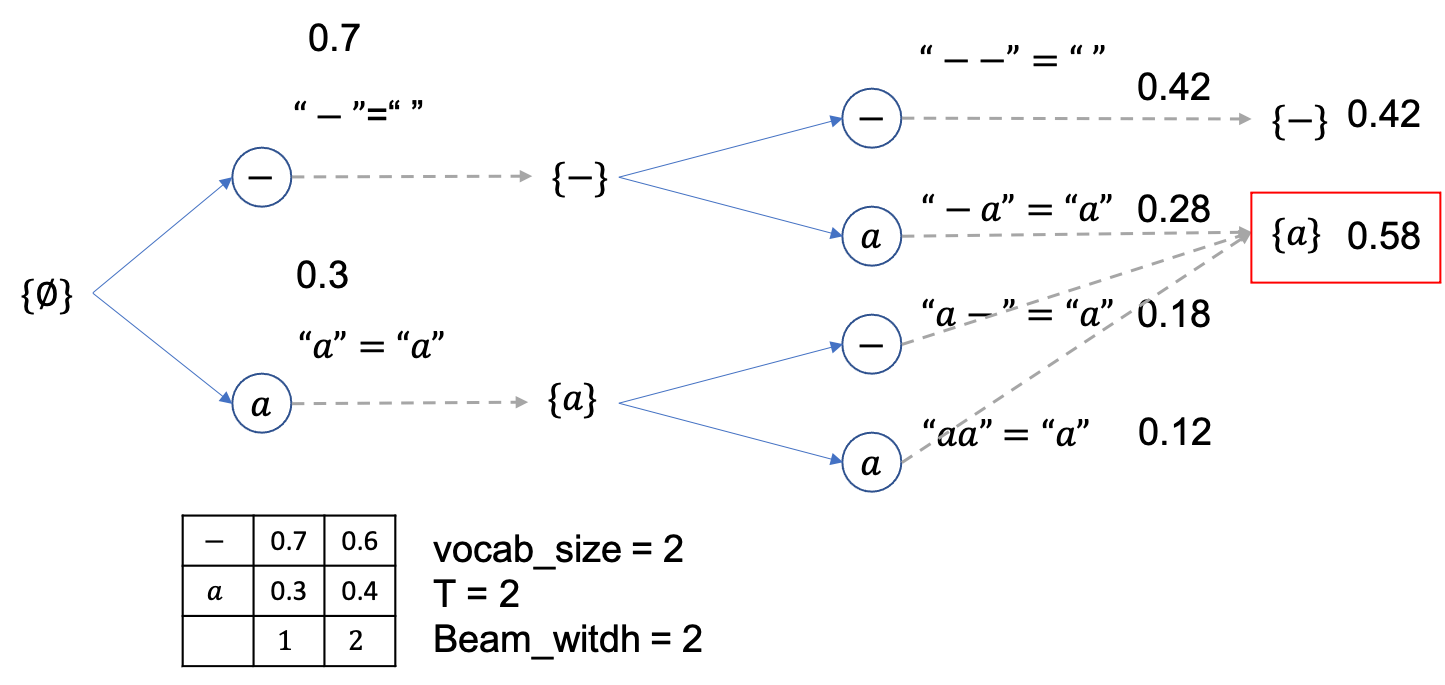
이런 경우 Greedy Decoding 을 하면 0.42 의 --를 찾기 떄문에 결과적으로 후처리를 했을 때 empty sequence 를 얻게 되죠.

빔서치를 하면 이를 막을 수 있다고 했는데 과연 그런지 살펴봅시다.

총 timestep=2 이고 vocab_size=2 로 [-,a] 밖에 경우의 수가 없으며 확률은 위의 figure와 같고 마지막으로 beam_size=2 생각합시다. 먼저 \(\emptyset\) 에서 부터 출발하고 각각 -,a 로 뻗어나갈 확률은 0.7, 0.3 입니다.

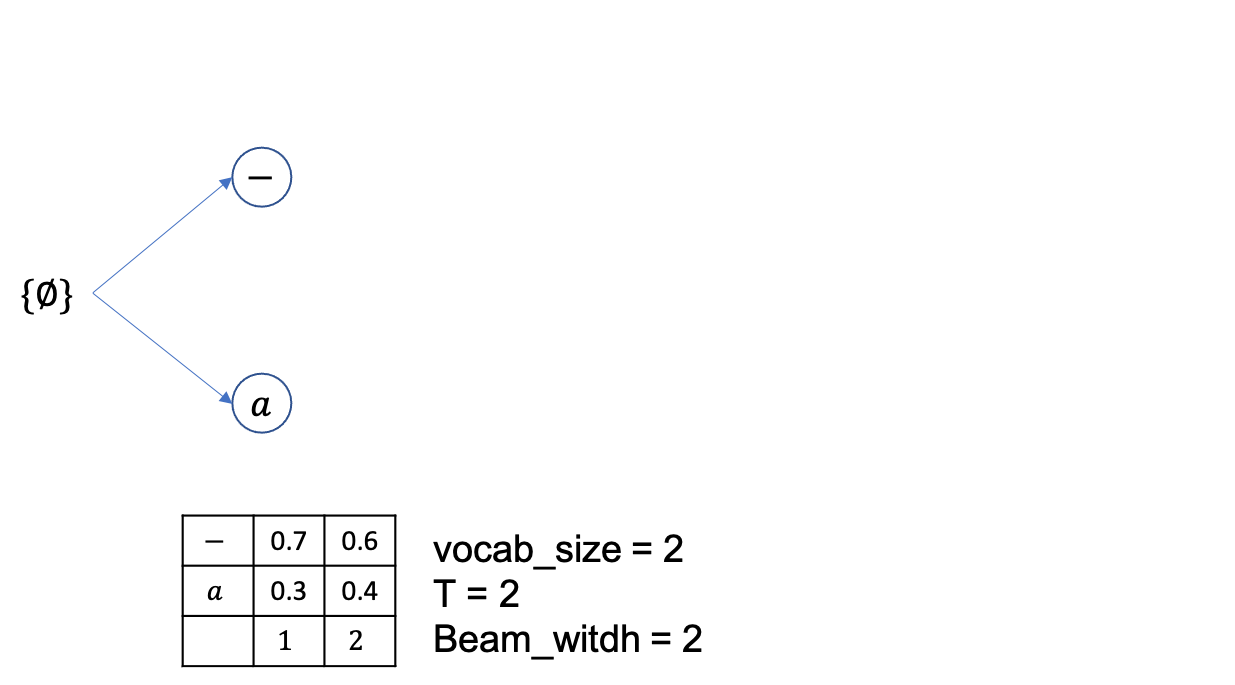
Vanilla beam search 이므로 현재 beam 은 2개 각 각 {-},{a} 입니다.

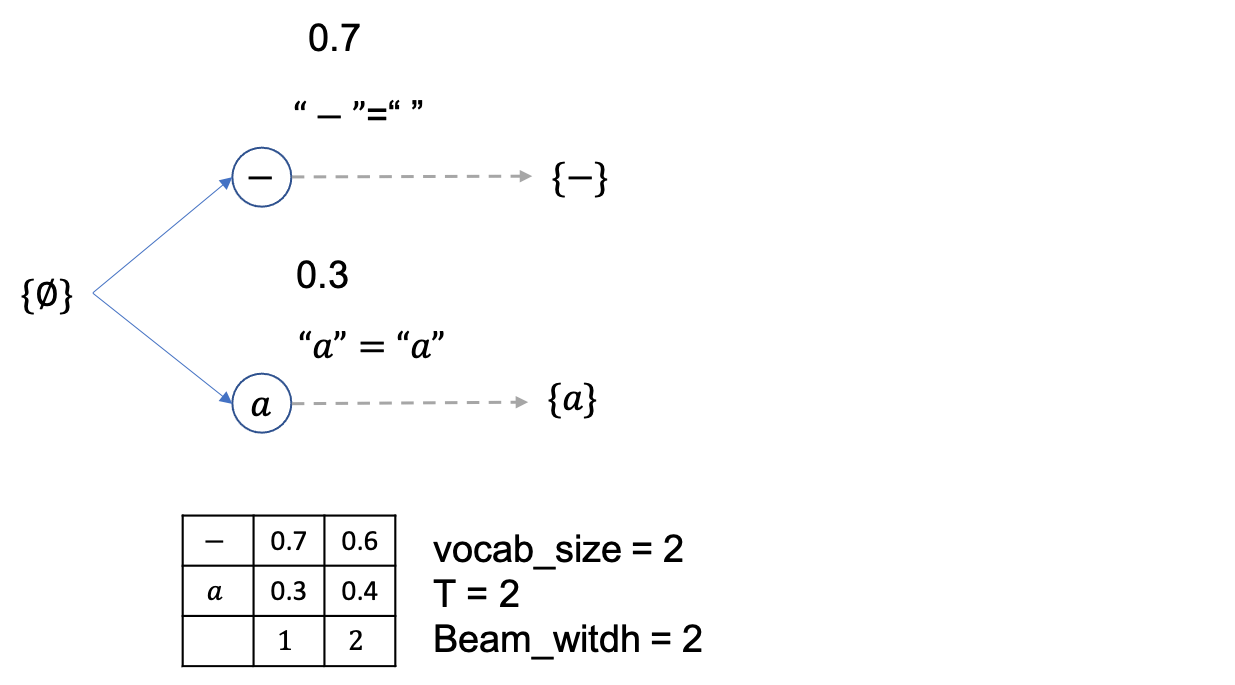
여기서 빔 1개당 2개씩 candidate 이 있으므로 총 4개의 beam candidate 이 만들어 질 수 있고

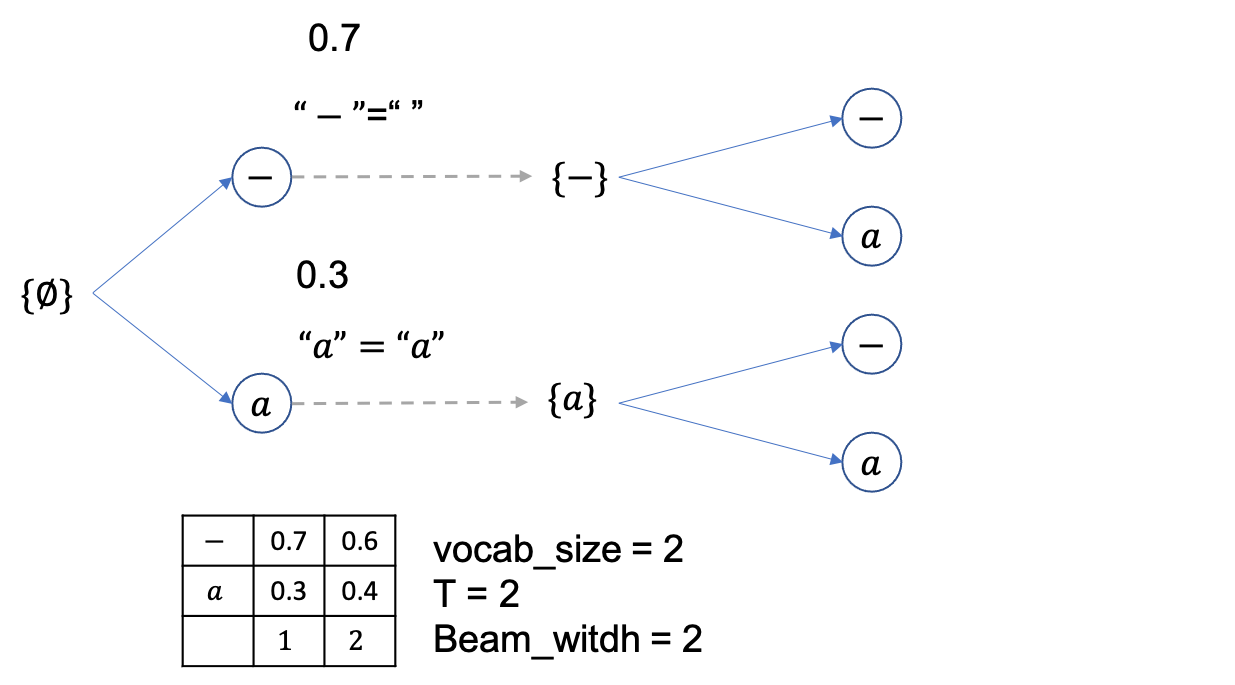
이 때의 beam 확률 (문장 확률) 들은 각각 아래처럼 됩니다.

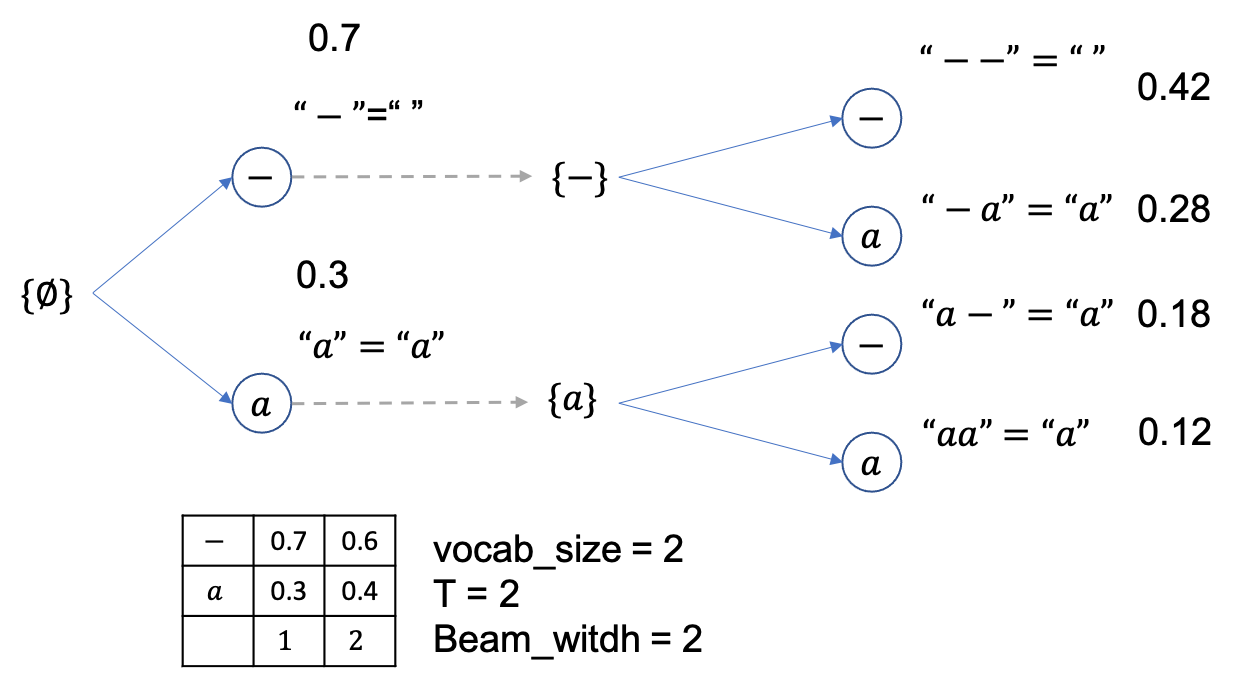
beam size는 2니까 총 4개의 후보중에 상위 2개만 빼고 다 버리면 아래처럼 {--},{-a} 두개만 남습니다.

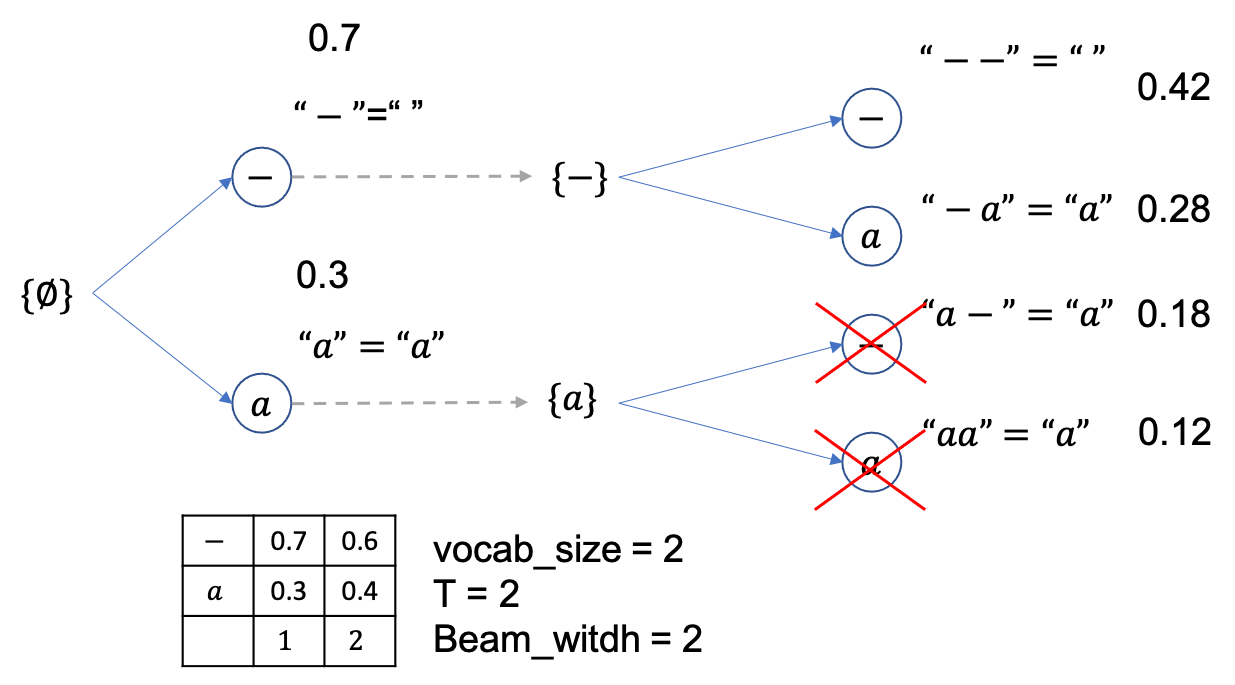
마지막 step이었으니 여기서 제일 높은 확률을 지니는 문장을 채택하면 되는데 정답이 Greedy Decoding 때처럼 0.42 확률을 갖는 {--} 입니다.

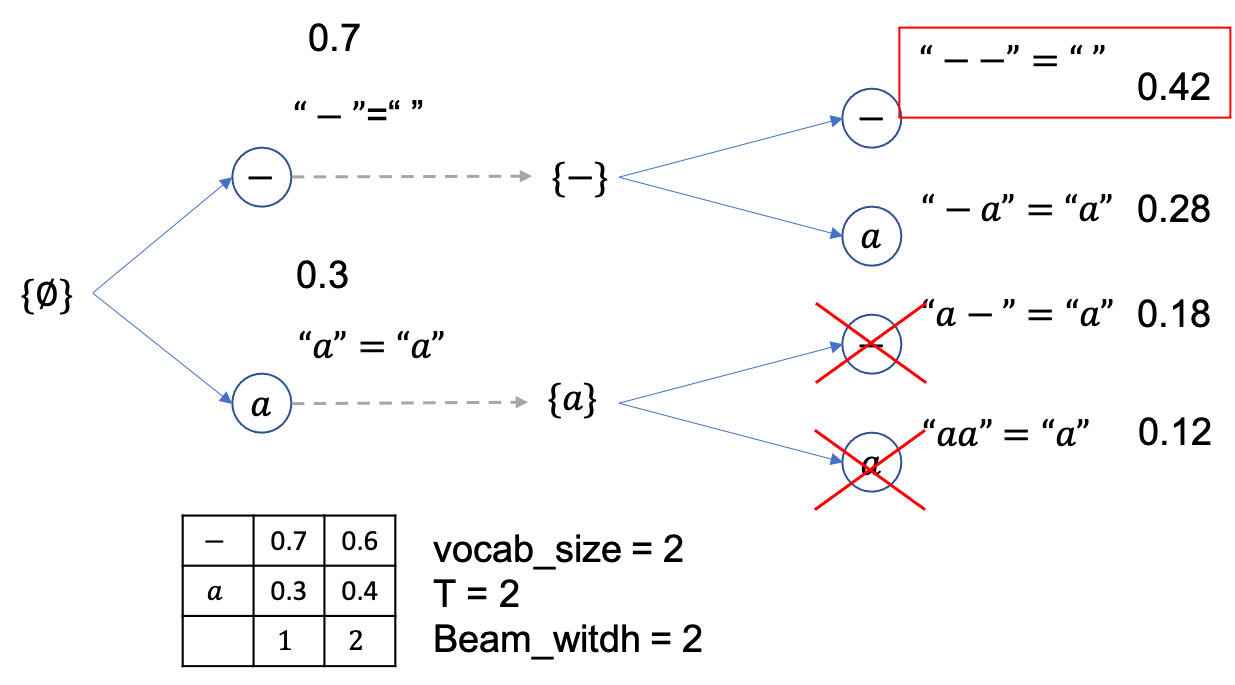
후처리하면 아예 empty sequence가 나오죠. 그렇습니다. 단순히 Vanilla Beam Search를 하면 우리의 바람처럼 모든 a 를 나타내는 path를 합쳐서 고려하지 않기 때문에 CTC로 학습된 모델의 특성을 반영할 수 없습니다. 그러므로 우리는 마지막에 빔 확률을 산정할 때 a를 나타내는 beam candidate들은 모두 merge를 생각해야 하는데요,

앞으로 Tricky한 Beam Serach에 대해서 알아보도록 할것입니다.

CTC를 위한 Beam Search Decoding은 CTC의 창시자인 Alex Graves가 2014년에 ICML에 출판한 논문인 Towards End-To-End Speech Recognition with Recurrent Neural Networks에 자세히 기술해 두었습니다.

Fig. Beam Search for CTC Algorithm

하지만 위의 Pseudo Code만 보고 단번에 알고리즘을 파악하기란 쉽지 않은데요 (적어도 저는 그랬습니다…), 그래서 중요한 부분을 따로 말로 적어봤습니다.

Fig. CTC Beam Serach 의 직관적인 해석

아마 이렇게 말로 표현해도 와닿지 않으실 것 같아 예시를 또 준비했습니다. 이번 예제 vocab_size=3 로 [-,a,b] 밖에 경우의 수가 없으며 beam_size=2 라고 생각하겠습니다. 마찬가지로 \(\emptyset\) 에서 부터 출발합니다.

vocab 이 [-,a,b] 세 개 이므로 맨 처음 candidate 도 세 개 입니다. 각각의 candidate 들은 CTC 의 후처리를 따르는데요, \(\emptyset\) 에는 blank token -를 더해도 여전히 empty 가 됩니다.

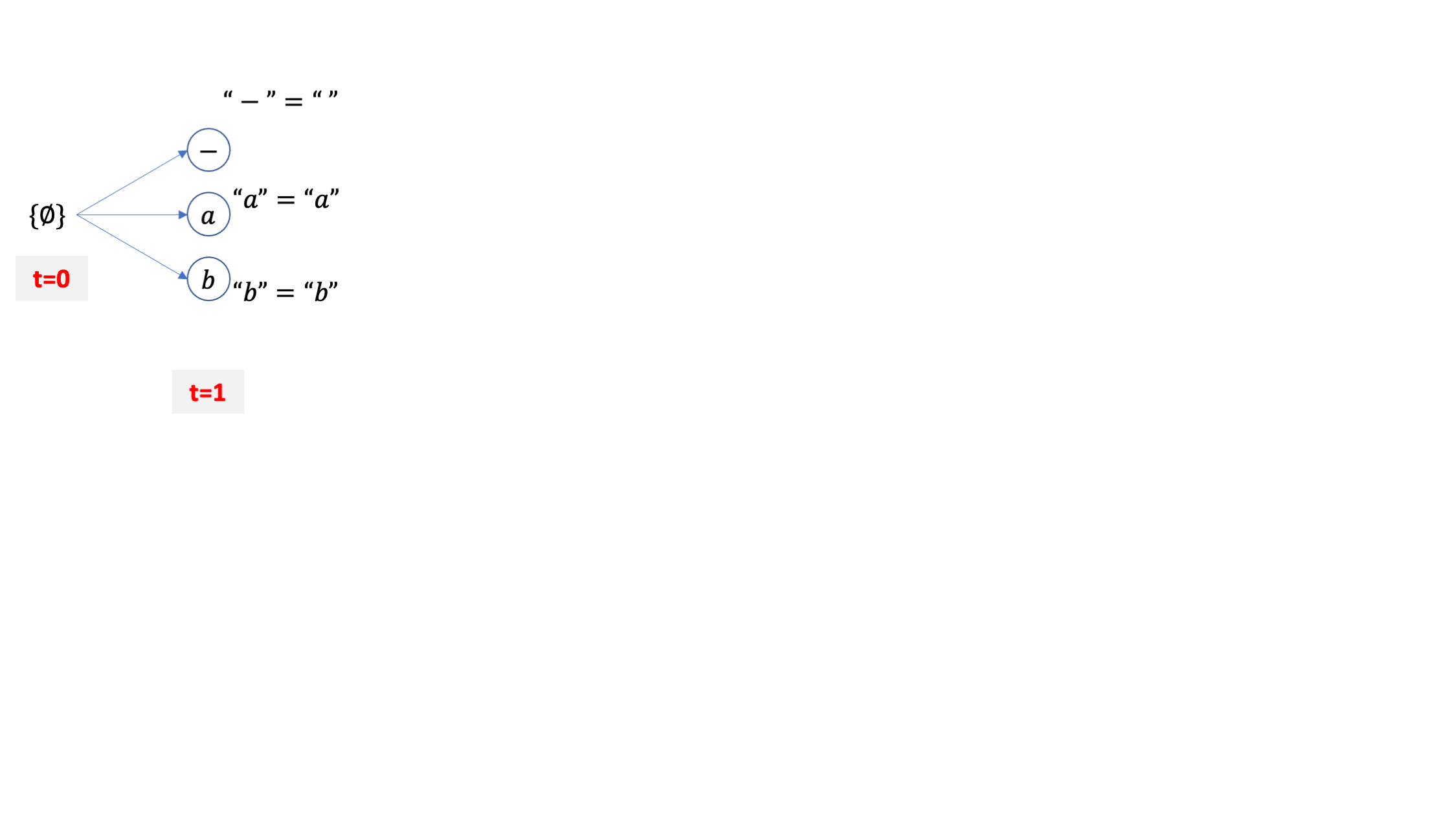
여기서 {b} 라는 beam candidate 이 가장 확률이 적었다고 칩시다. 그럼 beam size=2 이기 때문에 이 beam은 탈락합니다.

살아남은 beam들에 대해서 또 vocab size 만큼 각각 candidate을 만들어 줍시다. beam 2개가 각각 3개의 candidate을 갖기 때문에 총 6개의 후보가 생깁니다.

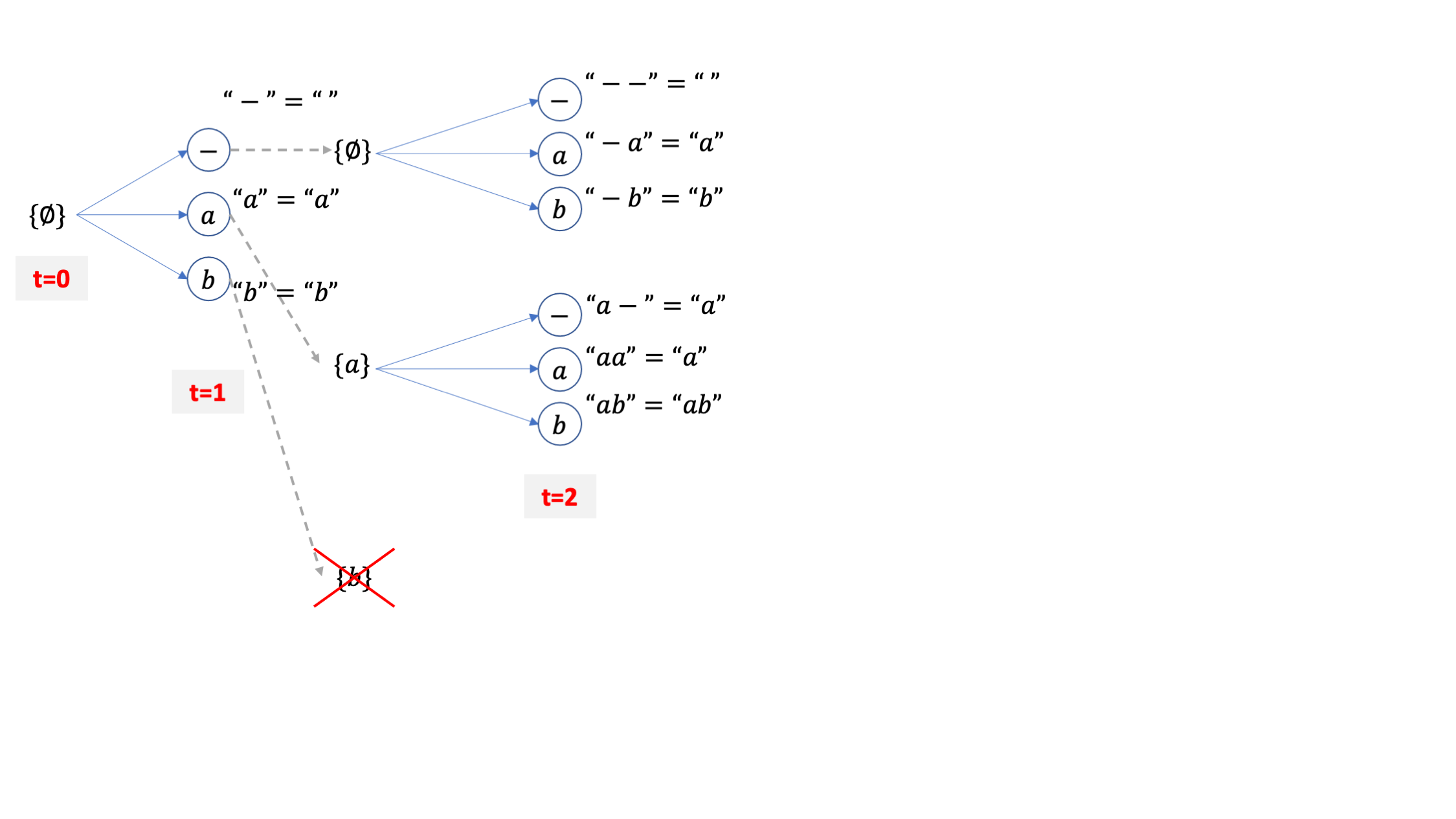
하지만 여기서 CTC 후처리를 따르면 총 beam candidate 은 6개가 아니라 4개로 줄어드는 것을 알 수 있습니다. 그 이유는 아래의 세 beam path가 모두 {a} 를 가리키기 때문입니다.

-a
aa
a-

이 때 {a} 가 세 개의 path 의 확률값을 더한 값을 beam 확률 값으로 갖는게 맞기는 한데요, 여기서 굉장히 중요한게 하나 있습니다.

그것은 {a}라는 path 가 -로 끝나는 경우와 a로 끝나는 경우의 path를 합친 것이기 때문에 여기서 다음 beam candidate 을 뽑을 때 [-,a,b] 세 가지 토큰 중 a가 붙는 경우는 특수한 경우가 생기기 때문입니다. 한번 생각해 봅시다. -a, aa 같은 path들 뒤에 a가 붙으면 candidate은 결국 {a}가 될 것이지만 a- 라는 path 뒤에 붙으면 candidate 은 {aa}가 되기 때문에 이 경우를 신경 써 줘야 하는 것입니다. 바로 이런 경우를 나누기 위해서 같은 {a} 내에 blank로 끝나는 확률을 blank prob 이라고 해서 따로 정의하고 a로 끝나는 확률을 non-blank prob 이라고 따로 정의하며 이 둘을 합친 {a} 자체의 확률을 total prob 이라고 정의하는 건데 이 내용이 바로 위의 pseudo code에 복잡하게 정의되어 있는 겁니다.

아무튼 이런 사실을 인지하고 또 4개의 후보중에 2개를 탈락시켜서 {a}, {ab} 두 개의 빔이 남았다고 칩시다.

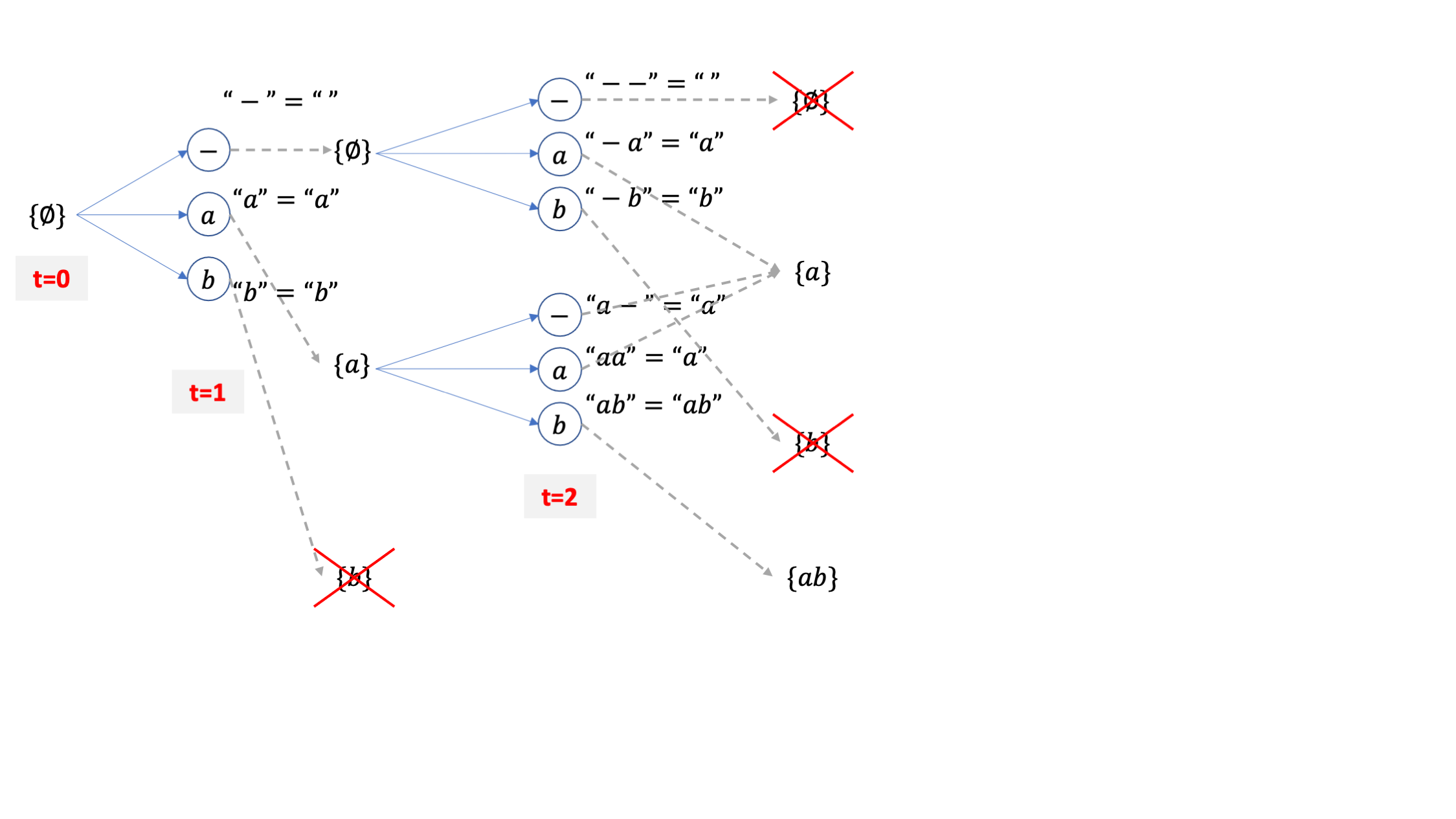
여기서 또 candidate token 3개씩이 있으니 또 6개의 후보가 되고,

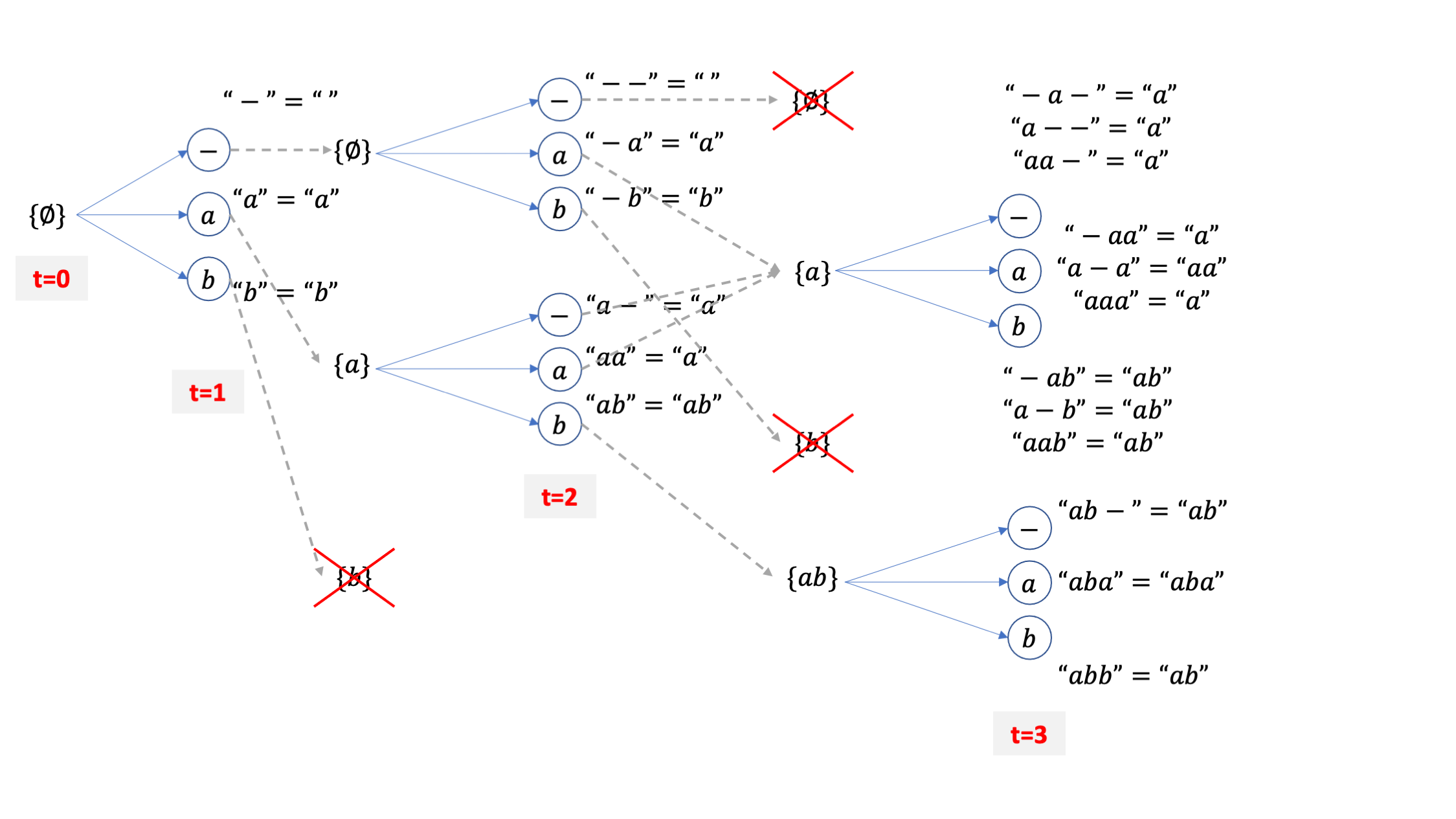
여기서 또 collapse 이후 같은 문장이 되는 빔들을 합치고 이를 끝날때까지 반복하는 것이 바로 CTC 빔서치가 되겠습니다.

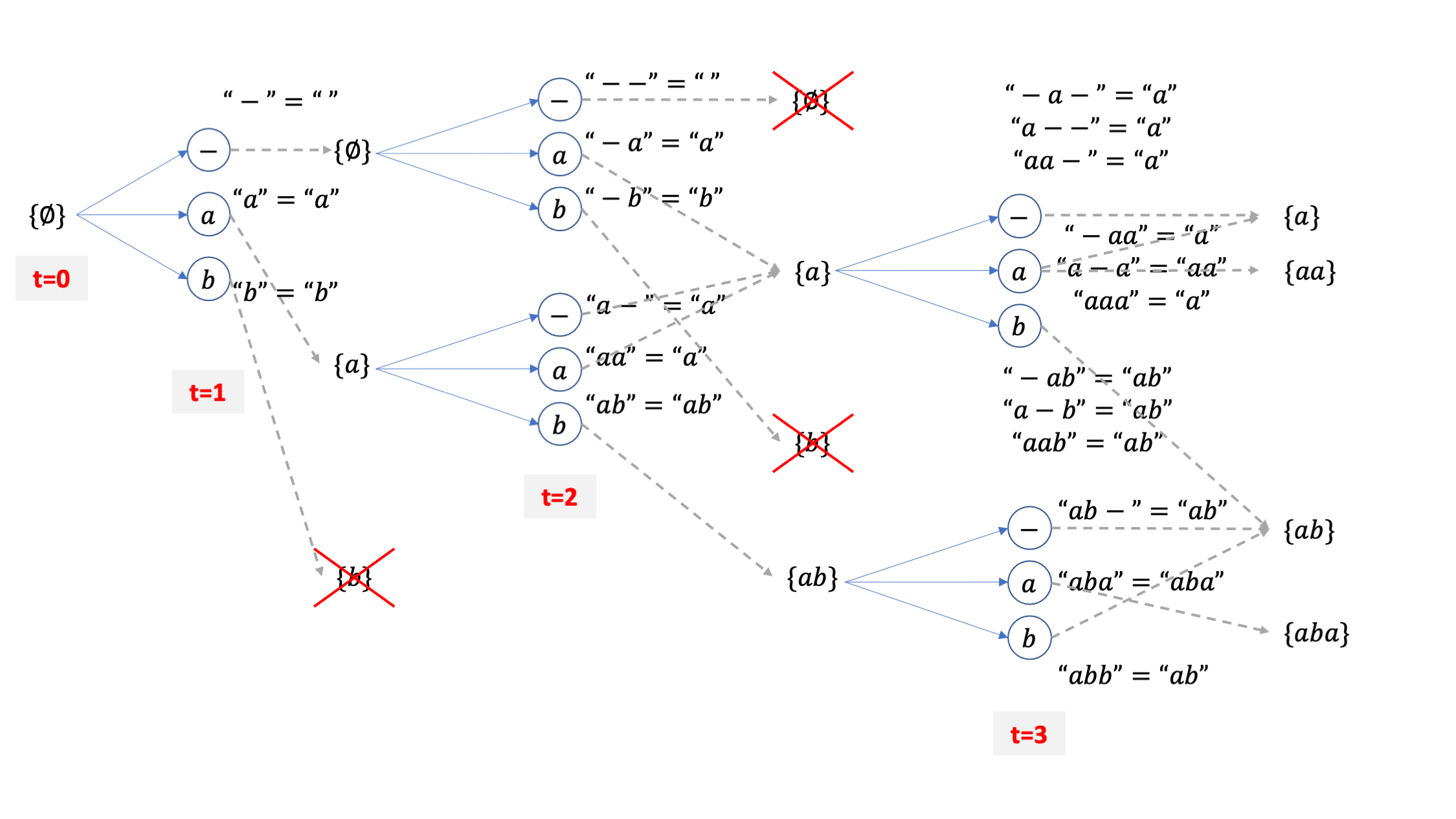
자 이제 어느정도 직관적으로 CTC Beam Search를 이해 하셨으리라 믿고 이제는 위의 예제에 실제 확률값들을 부여해 각 beam 들의 blank prob, non blank prob, total prob 을 계산하면서 논문과 pseudo code에 수식을 같이 이해해 보도록 하겠습니다.

Fig. Beam Search for CTC Algorithm

pseudo code를 이해하기 위해 Notation을 몇 가지 알아봅시다.

• \(Pr^{-}(y,t)\) : t 시점에서 빔 서치에 의해 출력 문장 y에 할당된 Blank Prob
• \(Pr^{+}(y,t)\) : t 시점에서 빔 서치에 의해 출력 문장 y에 할당된 Non-Blank Prob
• \(Pr(y,t) = Pr^{-}(y,t) + Pr^{+}(y,t)\) : Total Prob (두개 더한거, 즉 beam 의 최종 확률)

예제를 통해 알 수 있었던 것 처럼 위의 수식은 거창하게 적혀있지만 CTC의 특성상 어떤 beam candidate 문장은 끝나는 경우가 blank 일 수도 있고 아닐 수도 있기 때문에 이를 나눠서 갖고 있는거고 이를 더한게 total prob이 되는겁니다. 즉 모든 빔들은 저마다 확률을 2개씩 저장하고 있다고 보시면 됩니다.

여기에 t 시점에서 label k 에 의해 만들어질 문장 y에 대한 Extention Prob 이라고 하는 \(Pr(k,y,t)\) 은 다음과 같이 정의 하는데요,

(결합 분포 (joint probability) 입니다.)

여기서 우항의 각 항들의 의미는 아래와 같습니다.

• \(Pr(k,t \vert x)\) : t 시점에서 label k 에 대한 CTC Emission Prob (Softmax 취해짐)
• \(Pr(k \vert y)\) : \(y\)에서 \(y+k\)로 전이될 확률 (Transition Prob)
• \(y^{e}\) : 문장 y 의 마지막 label

일반적인 경우 \(Pr(k \vert y)\)는 사용하지 않을 경우 (standard CTC version) 1로 둘 수있다고 하므로 (언어모델 확률까지 끌어다 쓰려면 이게 필요합니다.)

The transition probabilities Pr(k|y) can be used to integrate prior linguistic information into the search.
If no such knowledge is present (as with standard CTC) then all Pr(k|y) are set to 1.

편의를 위해 제거하면

라고 볼 수 있습니다.

즉 현재 문장의 마지막 label 과 지금 디코딩 하려는 k가 같을 경우와 아닌 경우에 따라서 Extention Probability가 나눠져 있는건데 이건 beam candidate 을 만들 때 사용합니다. (아직 이해가 안가셔도 됩니다, 예제와 함께 알아보면 되니까요)

마지막으로

• \(\hat{y}\) : 마지막 label이 제거된 y
• \(\emptyset\) : empty sequence
• \(Pr^{+}(\emptyset,t)=0 \forall t\) : 전체 t에 대해서 \(Pr^{+}(y,t)\) 의 확률은 0이라는 뜻으로, 즉 y가 공백 문장이면 확률은 계산하지 않는다는 뜻

까지 정의하면 준비가 거의 끝났습니다.

자 이제 위의 예제를 pseudo code 의 흐름을 따라 빔 서치를 다시 해봅시다.

앞으로 빔 서치 결과는 { } 라는 Bucket \(B\) 에 담을거고 맨 처음 \(B\) 에는 아무것도 없습니다. 즉 empty sentence만 들어있는거죠.

그리고 논문에는 맨 처음 \(t\) 가 어느 값이던 (어느 시점이던), empty space 에 대한 non-blank prob은 0 이며

어느 시점이던 \(\{ \emptyset \}\) 에 대한 blank prob = 1 으로 정의하겠다고 했습니다.

이는 당연한게 empty sentence 는 곧 - 만 있는 경우와 같은데 (왜냐하면 후처리하면 아무것도 안남으니까), 이런 문장은 무조건 blank 로 끝날 수 밖에 없으므로 blank prob 만 존재하고 non-blank prob은 존재 자체를 안하는 겁니다.

앞으로 그림에서 빨간색은 해당 beam candidate 의 blank prob, 파란색은 non-blank prob, 그리고 초록색은 이 둘을 합친 total prob으로 나타낼 것입니다. 그리고 AM 이 뽑은 ctc emission probs 은 그림에 표기해 둔 것 처럼 timestep 별로 확률을 가질것이며 총 시간 T=3, voca_size=3 이며 마지막으로 빔 사이즈는 2 로 세팅했습니다.

시작해봅시다. 원래 맨 처음에 \(Pr(\emptyset,t=0)\) 을 기반으로 \(Pr(\emptyset,t=1)\) 확률을 구한 뒤에 beam candidate 을 만들어서 각 빔마다 확률을 부여한다는 흐름인데 편의를 위해 그림에는 모든 가지를 먼저 만들어 두겠습니다.

이제 pseudo code에 따르면 각 후보들마다

• blank prob
• non-blank prob
• total prob

을 부여하면 되죠?

우리가 가지고 있는 beam bucket 에는 \(\emptyset = "-"\) 밖에 없으므로 아래의 pseudo code 의 맨 마지막 라인만 쓰면 됩니다.

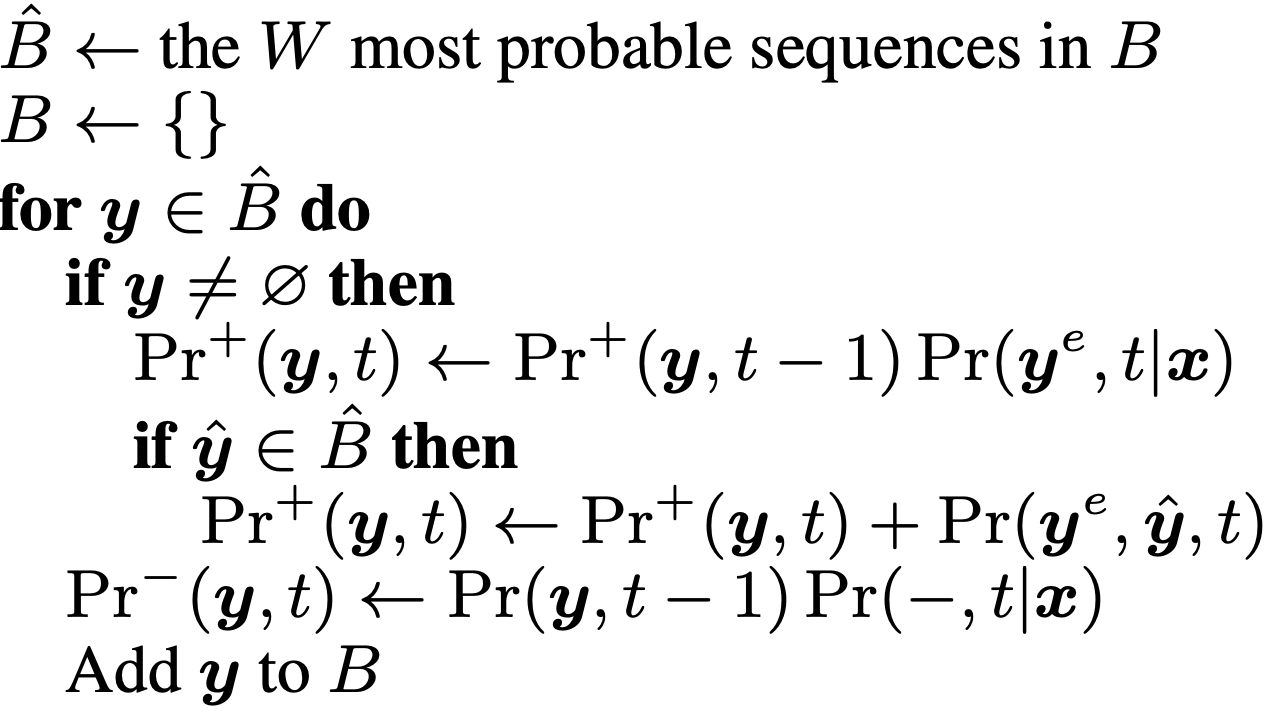
이를 현 상황에 맞게 쓰면

이 됩니다.

그러니까 t=1에서의 blank prob 은 ctc emission 의 t=1 시점의 blank 확률인 0.4 와 t=0 일 때의 total prob이 곱해져 0.4가 되고, 여전히 empty sentence이기 때문에 논문에서의 대 전제에 따라 non-blank prob은 계속해서 0이 됩니다.

즉 t=1 일 때 empty sentence 를 나타내는 빔의 확률은 totla prob은 0.4가 되는겁니다. (여기서 주의할점은 non-blank + blank prob 은 합쳐서 1인게 보장되지 않는다는 겁니다.)

그리고 이제 beam candiate 을 더 만들어주면 되는데요, 여기서 blank 가 붙어서 만들어질 candidate 은 방금 처리했으니 나머지 a,b 토큰으로 candidate이 만들어지는 경우는 아래의 psuedo code를 따르게 됩니다.

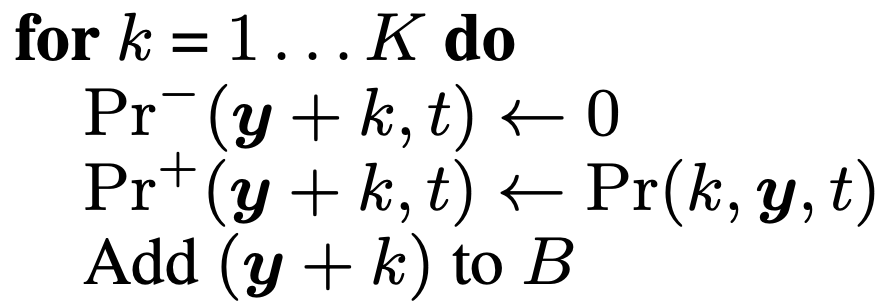
여기서 \(for \space k=1,\cdots,K\) 가 vocab size 만큼 candidate을 만들곘다는 것이고

각 candidate 문장은 이전 빔 가지에서 \(k\) 번째 vocab token 을 이어부힐거니 \(y+k\) 로 나타내구요, 각각의 blank prob = 0 이며 non-blank prob은 \(Pr(k,y,t)\) 를 따릅니다.

직접 계산해보자면

이 됩니다.

여기서 \(Pr(k,y,t)\) 라는 결합 확률이 Pr(a,1 \mid x)Pr(-,0)가 되는 이유는 논문에 정의된 것 처럼 현재 extend 에 쓰이는 token이 이전 beam의 마지막 토큰과 다르기 때문입니다.

이를 b에도 마찬가지로 적용하고 각각의 확률값들을 실제로 적용하면 아래와 같은 beam candidate의 각각의 blank prob, non-blank prob을 얻을 수 있습니다.

하지만 사실 복잡한 수식을 따라갈 필요가 없고 직관적으로 이해할 수도 있습니다. 진짜 단순하게 생각하면 되는데요 왜냐하면 맨 처음 empty sentence, 즉 blank 만 있은 문장에서 출발했을 때 그 다음 토큰으로 -,a,b가 각각 붙는다면 -가 붙는 경우에는 무조건 blank로 끝나니까 blank prob 만 존재하니까 이전의 total prob (=1) 에 - 가 나올 AM확률만 곱해서 blank prob으로 해주면 되고, a가 붙는 경우에는 마찬가지로 a가 붙어서 -a 가 되는 경우 밖에 없기 때문에 반대로 blank prob은 존재할 수가 없고 따라서 non blank prob만 이전 beam의 total prob 에 AM의 t=1일 때의 a일 확률만 곱해줘서 non-blank prob 으로 가지고 있으면 되는 것이기 때문입니다.

이렇게 직관적으로 각 빔마다의 non-blank, blank prob을 계산할 수 있어야 나중에 빔서치를 한참 진행하고 난 뒤에 헷갈리지 않게 beam 을 계산할 수 있기 때문에 구현을 위한 수식 말고 이런식으로 ‘이렇게 될 수밖에 없겠구나’ 를 생각하시는걸 추천드립니다.

어쨌든 현재 beam candidate 3개 중에 total prob이 가장 낮은 {b} 라는 문장의 빔은 제거됩니다.

그 다음으로 또 살아남은 빔 2개 마다 3개씩 candidate을 만들어 봅시다.

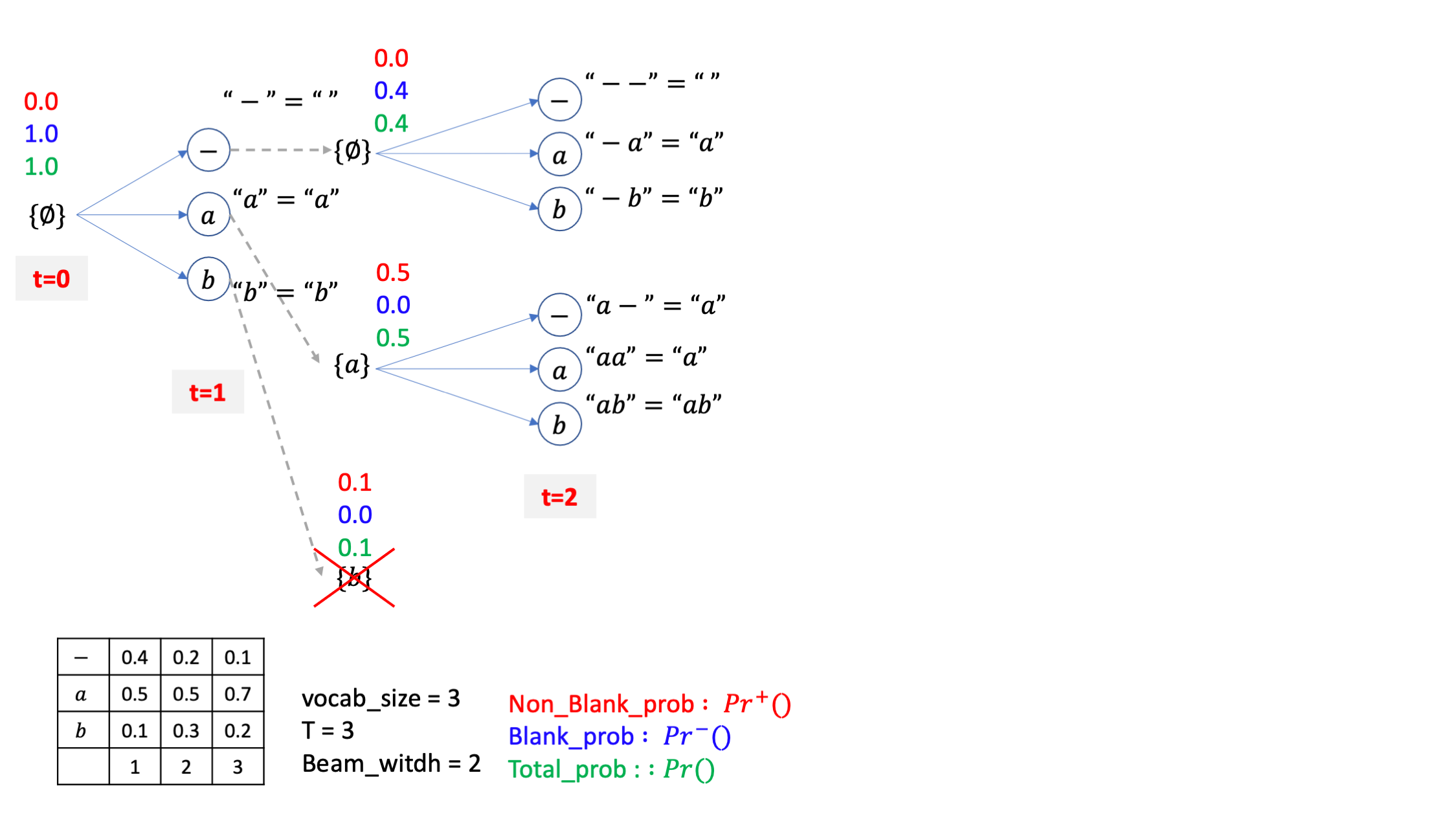
{-}, {a}라는 이전 빔들에 -,a,b 세 개를 붙힐 수 있는데요, CTC의 후처리 규칙에 따라서 이 candidate 들은

-- = -
-a = a
-b = b

a- = a
aa = a
ab = ab

가 됩니다. 그리고 같은 문장 {a}를 가리키는 candidate 들은 merge가 됩니다.

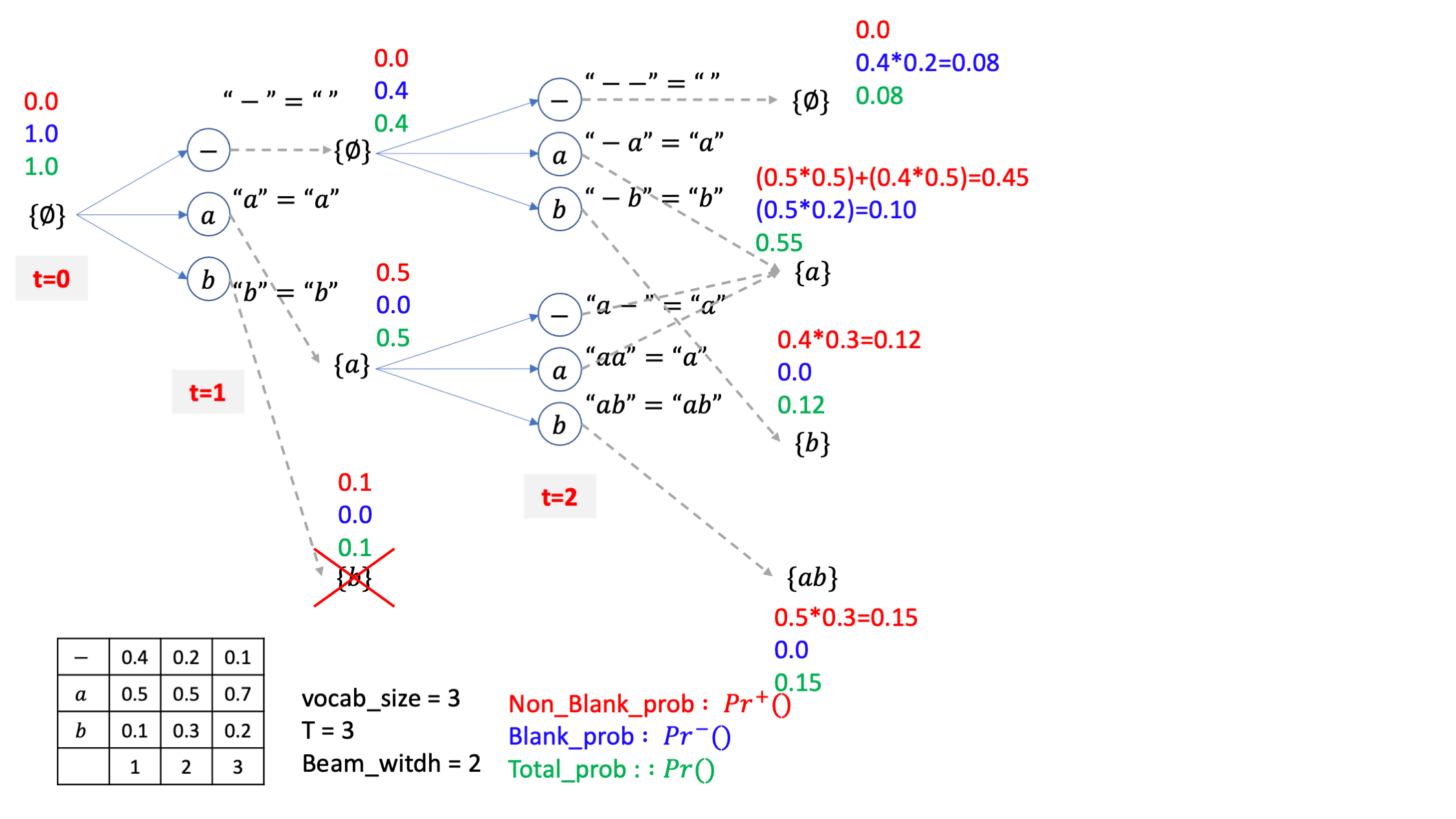
자 위의 그림을 보시면 굉장히 복잡하게 blank prob, non-blank prob이 계산된 것 처럼 보이죠. 바로 아래의 pseudo code를 적용해서 그런건데요,

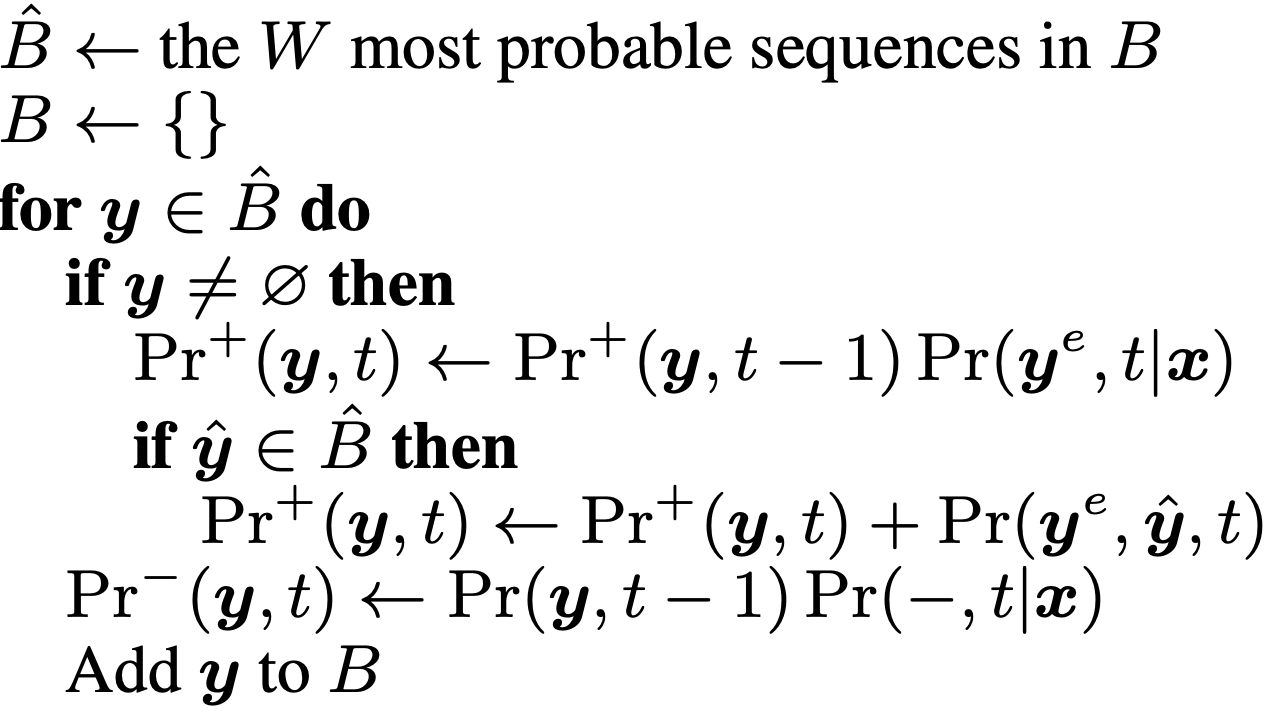
여기서 잘 보면 아시겠지만 {-}의 경우는 여전히 후처리하면 아무것도 아닌 empty sentence, \(\emptyset\) 이기 때문에 마지막에 라인만 적용됩니다.

여전히 이전의 {-} 빔에 -가 붙어서 {--}={-}=" " 인 빔의 확률은 total prob에 t=2 시점의 -에 대한 AM 확률을 곱하는게 blank prob이고 blank로 끝나니까 non-blank 은 없으며 이 둘을 더한게 total prob이 됩니다.

하지만 여기서 {-} 나 {a} 라는 beam 이 {a} 라는 beam candidate 으로 될 확률은 {-a},{a-},{aa} 라는 beam candidate 들의 확률들을 merge를 해야 하는데요,

이 부분이 조금 복잡하게 수식으로 표현되어 있습니다.

위의 pseudo code에서 if 문 내의 값을 보면

를 먼저 계산해서 t=2 일때의 a 라는 beam candidate 의 non-blank prob을 나이브하게 계산하구요, 만약 {a} 에서 마지막 토큰을 뗀 경우, 그러니까 \(\{-\}=\{\empty\}\) 라는 게 이전 beam에 존재하면, 즉 t=1에서 2로 넘어올 때 이런 빔이 살아남았다면

을 또 계산해서 더해줍니다.

그러니까 최종적으로

가 되는거죠.

그리고 blank prob 은 pseudo code 의 마지막 라인에 따라

가 됩니다.

이게 수식이 좀 많아보이고 이리 갔다가 저리 갔다가 하니 되게 복잡해 보이지만 사실은 생각해보면 당연한건데요, 아까 처럼 직관적으로 생각해보면 {a} 라는 beam candidate 은 CTC 특성상 -로 끝나던지 a로 끝나던지 결국 a인 거죠?

여기서 -로 끝나는 경우는 {a-} 밖에 없고 a로 끝나는 경우는 {-a},{aa} 두 가지 입니다. 그니까 여기서 -로 끝나는 blank prob을 계산하려면 {a} 라는 beam 에 -가 붙을 확률 만 계산해주면 되니 {a} total 확률에 t=2 인 시점의 AM의 blank 확률을 곱해주면 끝인겁니다. 그리고 a로 끝나는 non-blank prob의 확률을 계산하려면 {-a},{aa} 두 가지를 생각해야 하니까 그림에서 처럼 두 가지 term을 더해줘야 하는건데요, 그러니까{-} 라는 빔에 AM이 t=2에 a라고 할 확률을 곱해주고 {a} 라는 빔에 마찬가지로 a 일 AM 확률을 곱해주는게 되는겁니다.

좀 더 진행해 봅시다, 마찬가지로 {b},{ab}라는 candidate 의 각각의 확률들은 b 가 되려면 {-}에 b 토큰이 붙는 경우 단 한가지 밖에 없으니 {-} 라는 beam의 total 확률에 b AM 확률을 곱해주는 식으로 하고 {ab}도 마찬가지가 됩니다.

그리고 4개의 빔 중에 total prob이 높은 2개만또 남깁시다.

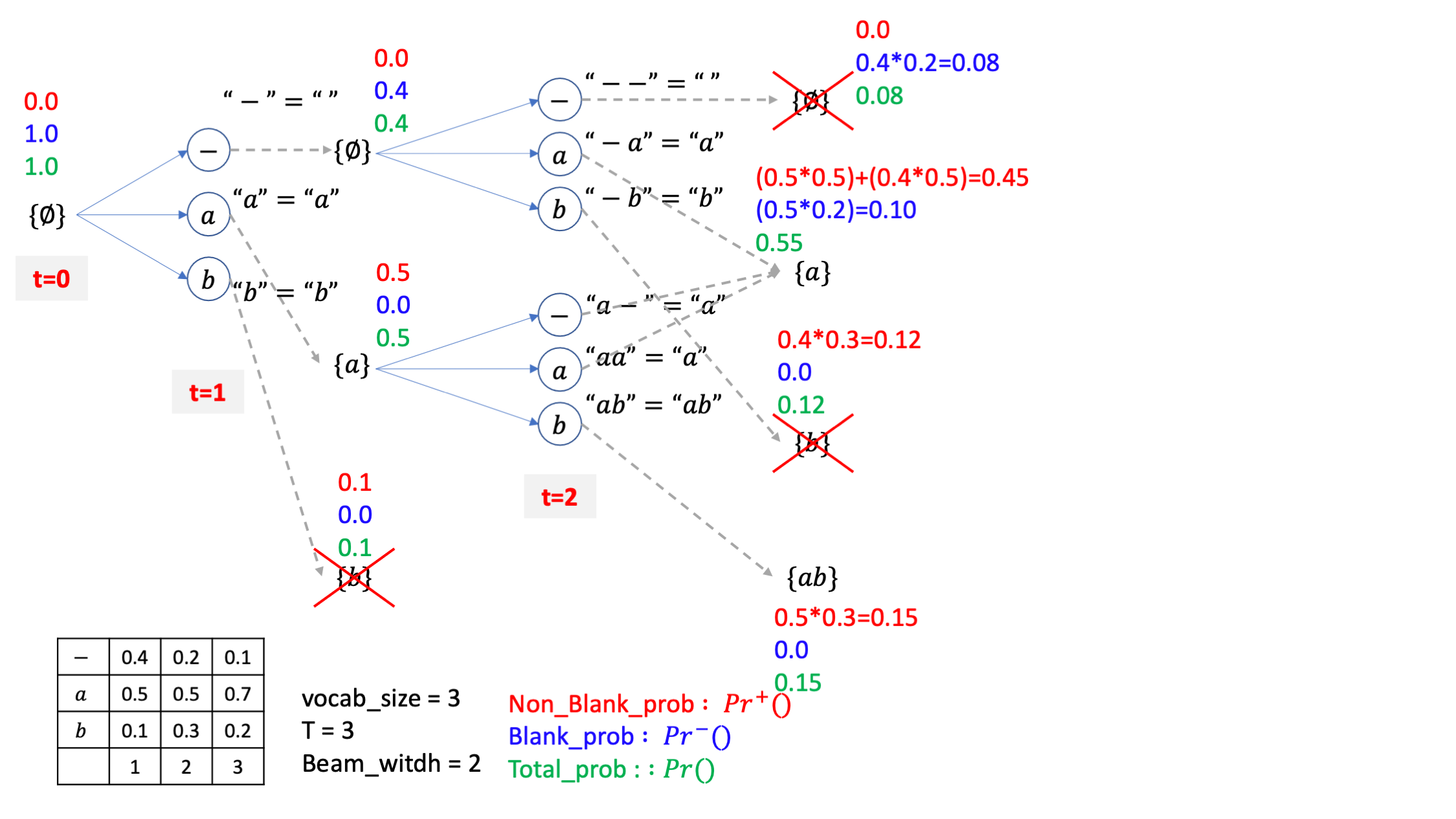
이제 또 2개 살아남은 빔에 3개씩 붙혀서 6개를 만들면 되는데요

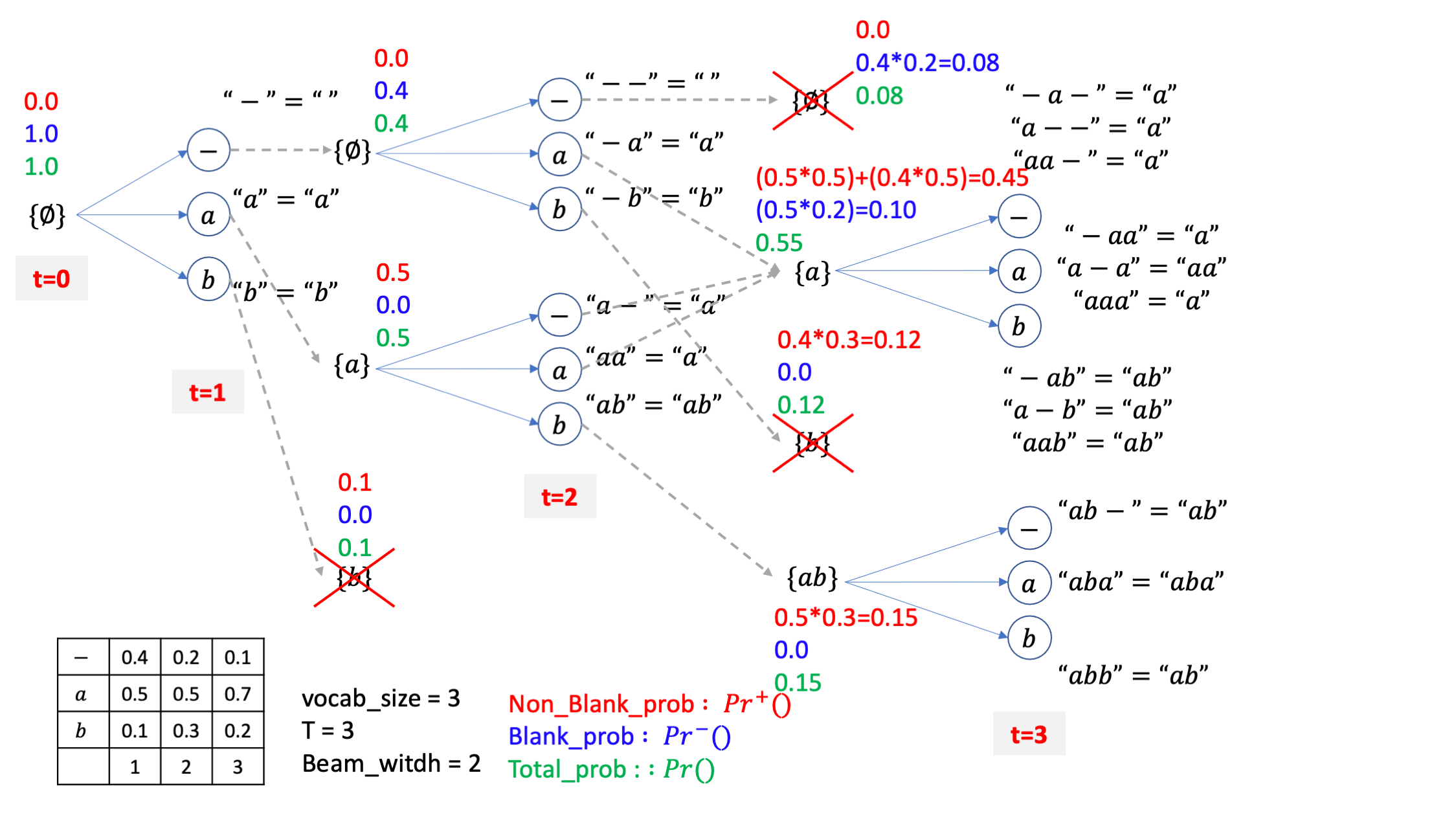
마찬가지로 직관적으로 값들을 계산하면 아래처럼 됩니다.

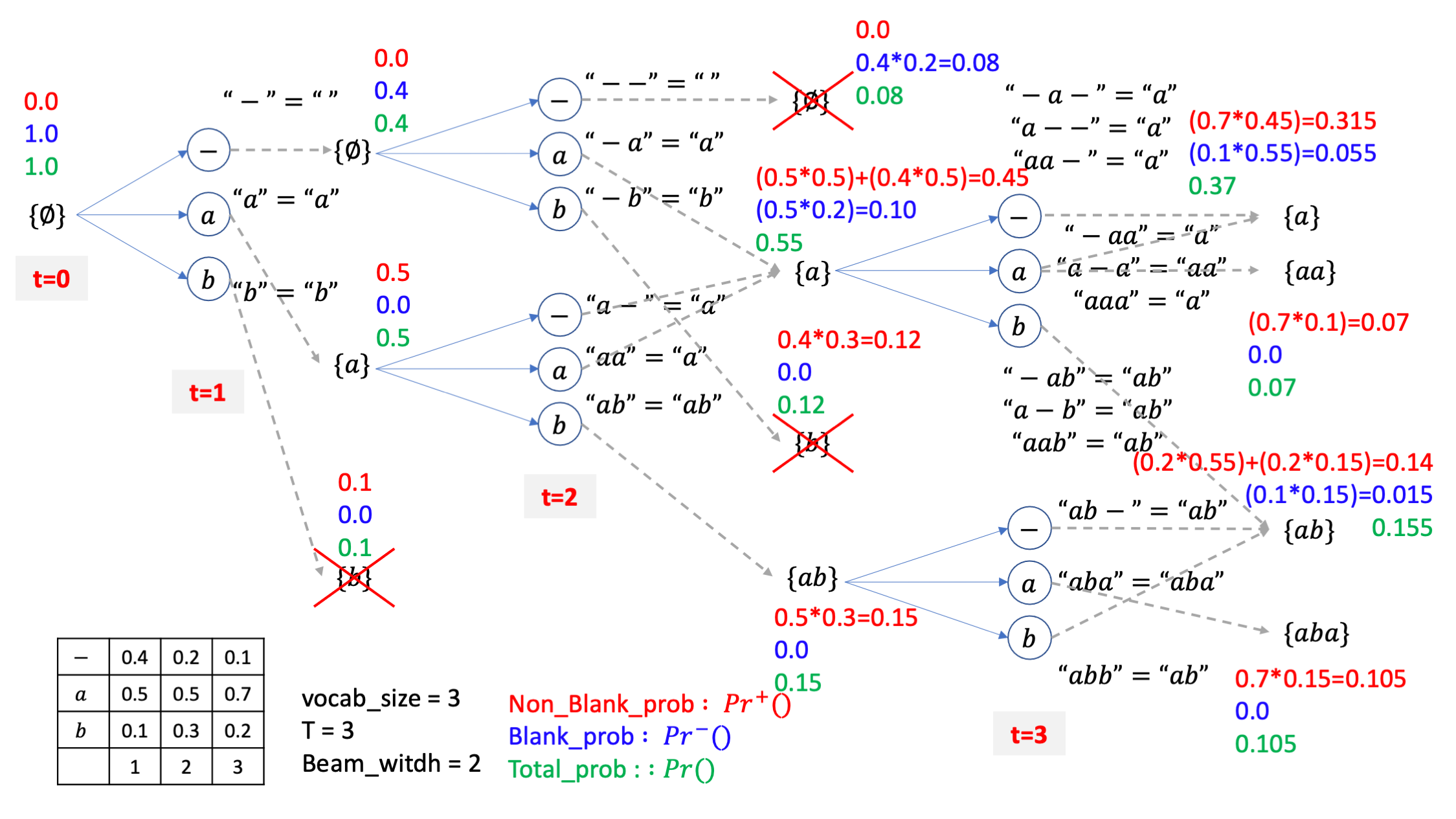
아마 이제 다 이해가 가시겠지만 여기서 처음보는 케이스가 잇습니다. 살아남은 {a},{ab}라는 두 개의 빔이 {aa} 같은 candidate 으로 mapping 되는 경우는 {a} 빔이 blank로 끝나는 케이스, 즉 같은 a 문장이지만 실제로는 a-인 경우에 a 토큰이 붙는 경우밖에 없다는 겁니다.

그러니까 자연스럽게 마지막 시점의 {aa} 라는 beam candidate 의 경우는 blank prob 만 존재하고 non-blank prob은 없게 되는겁니다.

이제 마찬가지로 4개의 빔 중에 상위 2개의 빔만 남기고

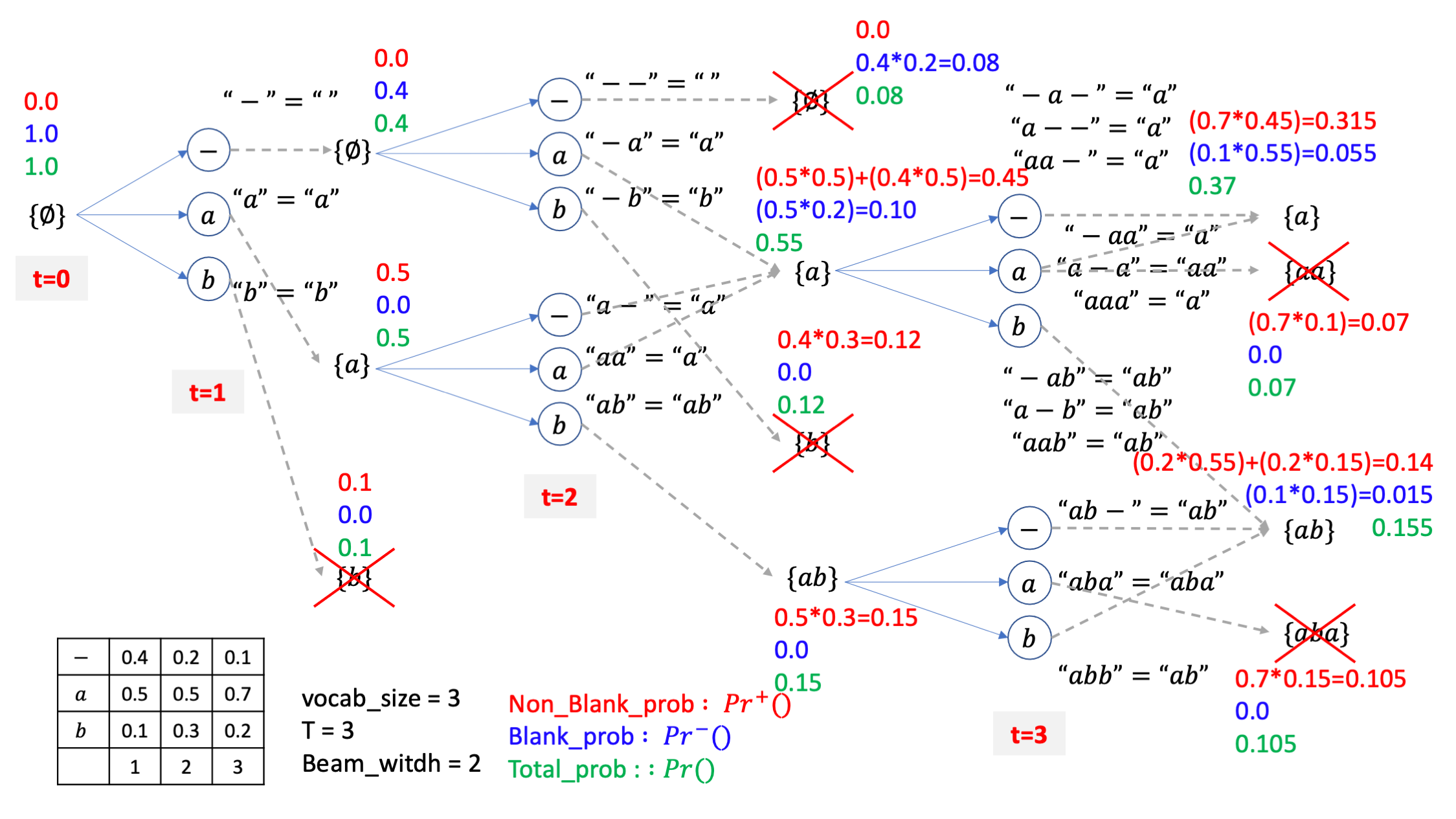
마지막 step 이었으니 여기서 가장 우수한 beam만 한번 더 골라내면 이게 빔 서치의 최종 출력이 됩니다.

이렇게 해서 상당히 복잡해보이는 CTC 의 특수성을 고려한 Beam Search 에 대해 알아봤는데요, 여기에 N-gram 이나 RNN, Transformer 등으로 모델링한 Neural Net 의 매 step 별로의 token 확률을 더해주면 더 정확도가 좋아집니다.

References

• Papers
  • 2014, Towards End-To-End Speech Recognition with Recurrent Neural Networks
  • Supervised Sequence Labelling with Recurrent Neural Networks (Alex Graves thesis)
  • 2014, First-Pass Large Vocabulary Continuous Speech Recognition using Bi-Directional Recurrent DNNs
  • wav2letter++: The Fastest Open-source Speech Recognition System
• Codes
  • githubharald/CTCDecoder
  • corticph/prefix-beam-search
  • awni/ctc_decoder.py
  • Wav2Letter : flashlight/wav2letter
    • Flashlight : flashlight/wav2letter/recipes/sota/2019
      • dependency 1 : pytorch/fairseq
      • dependency 2 : kpu/kenlm
• Blogs
  • Sequence Modeling With CTC
  • Beam Search Decoding in CTC-trained Neural Networks from Harald Scheidl
  • CTC Networks and Language Models, Prefix Beam Search Explained from Lasse Borgholt
  • A contemplation of logsumexp
  • The Log-Sum-Exp Trick