(Paper) Distributional Preference Learning (DPL)

< 목차 >

• Motivation
  • Recap) Bradley Terry Luce (BTL) Model
  • What's Wrong with Standard Preference Modeling? Hidden Context
  • Modeling Hidden Context
  • Theoretical Analysis and Perspectives of BT Model
    • Optimizing BTL vs Borda Count (BC)
    • About Expected Utility
  • Distributional Preference Learning (DPL)
    • Mean and Variance DPL (MV-DPL)
    • Categorical DPL (C-DPL?)
  • Experimental Results
    • Synthetic Experiments
    • Competing Objectives in RLHF
• Pytorch Implementation of DRL
  • Vanilla BTL RM
  • MV-DPL RM
  • C-DPL RM
  • Few Real World Results
• Some Open Reviews
• How bount Latent Variable Modeling (LVM) ?
• References

Motivation

Distributional Preference Learning: Understanding and Accounting for Hidden Context in RLHF라는 paper가 나왔다. NIPS 2023, Socially Responsible Language Modelling Research (SoLaR) workshop에서 발표되었고 BAIR에서 주관한 연구다.

Fig.

Paper의 목표는 Reinforcement Learning from Human Feedback (RLHF)의 Reward Modeling (RM) phase를 개선하는 것이고, Distributional Preference Learning (DPL)이라는 algorithm을 제안한다. InstructGPT를 포함해서 대부분의 RLHF method들은 Bradley-Terry-Luce (BTL) Model을 사용해서 preferece modeling (RM 학습)을 한다 (이하 BTL Loss를 BTL이라 부르겠음). 그런데 paper에서는 BTL로 RM학습을 하는 Standard Preference Learning에 문제를 제기한다. 왜 그럴까?

아래 example은 Anthrophic의 HH-RLHF dataset을 BTL로 학습한 RM이 jailbroken response에 어떤 score를 할당하는지 측정해본 것이다.

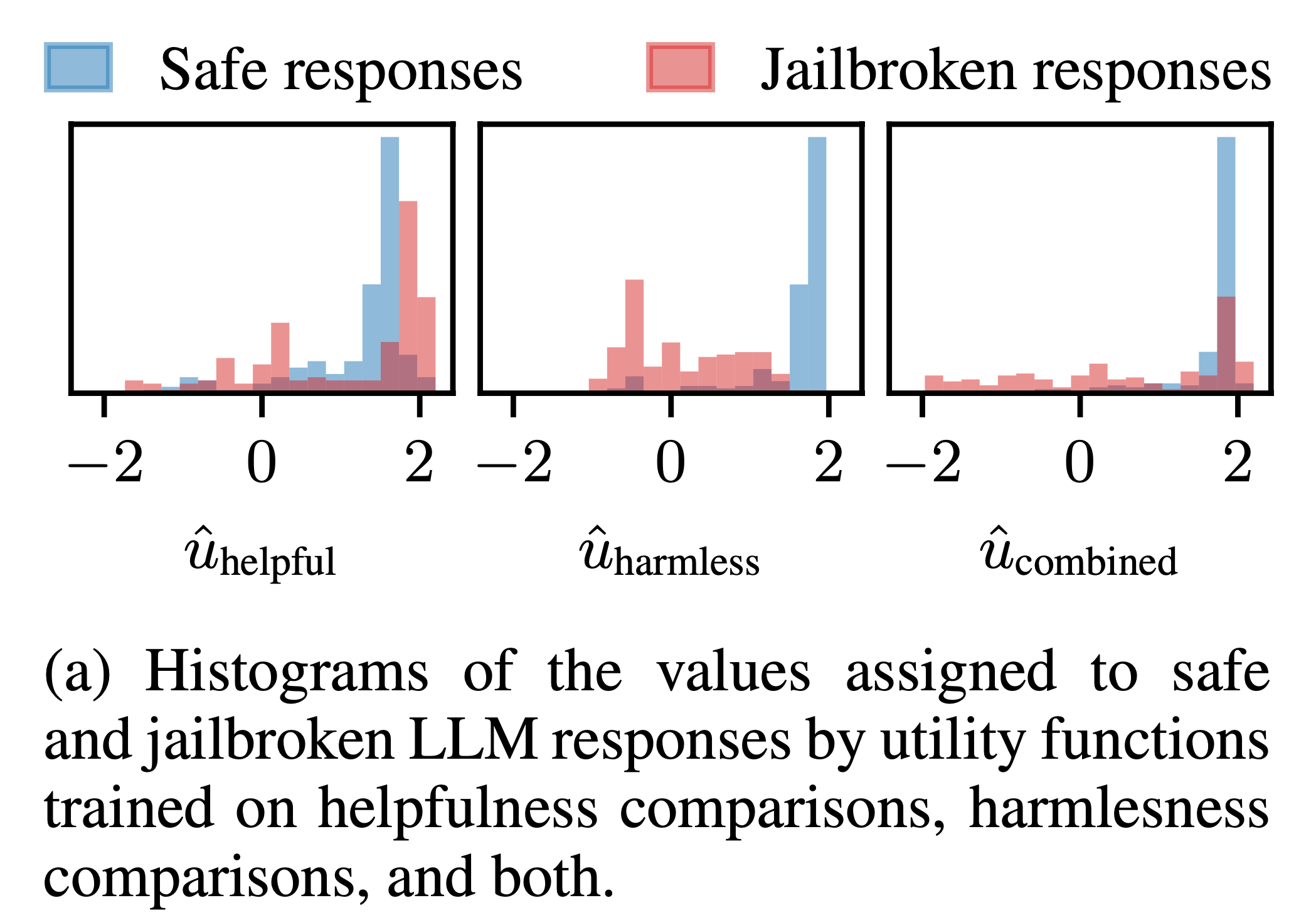Fig.

HH-RLHF dataset은 human preference 순위가 label로 있고 추가로 이 prompt-response human에게 해로운가? (harmfulness) 아니면 도움이 되는가? (helpfulness) 에 대한 label이 있기에, 저자들은 BTL로 helpfulness dataset에 대해서만 학습하거나 halmfulness dataset에 대해서만 학습, 마지막으로 둘 다 합친 dataset에 대해서 RM학습을 한 뒤 LLM이 jailbreak한 response를 수집해 reward score를 뽑아 histogram plot을 해본 것이다. 그 결과 RM은 jailbroken response에 대해서 더 높은 score를 부여한 것은 helpfulness only RM의 경우 61% 더 많이 존재했고 combined의 경우 25% 더 많이 존재했다. 반면에 harmful RM은 5%만이 더 높은 score를 받았는데, 그 이유는 jailbroken response도 실제로는 instruction을 충실하게 이행한 helpful한 답변이기 때문이다.

추가 예시를 보자.

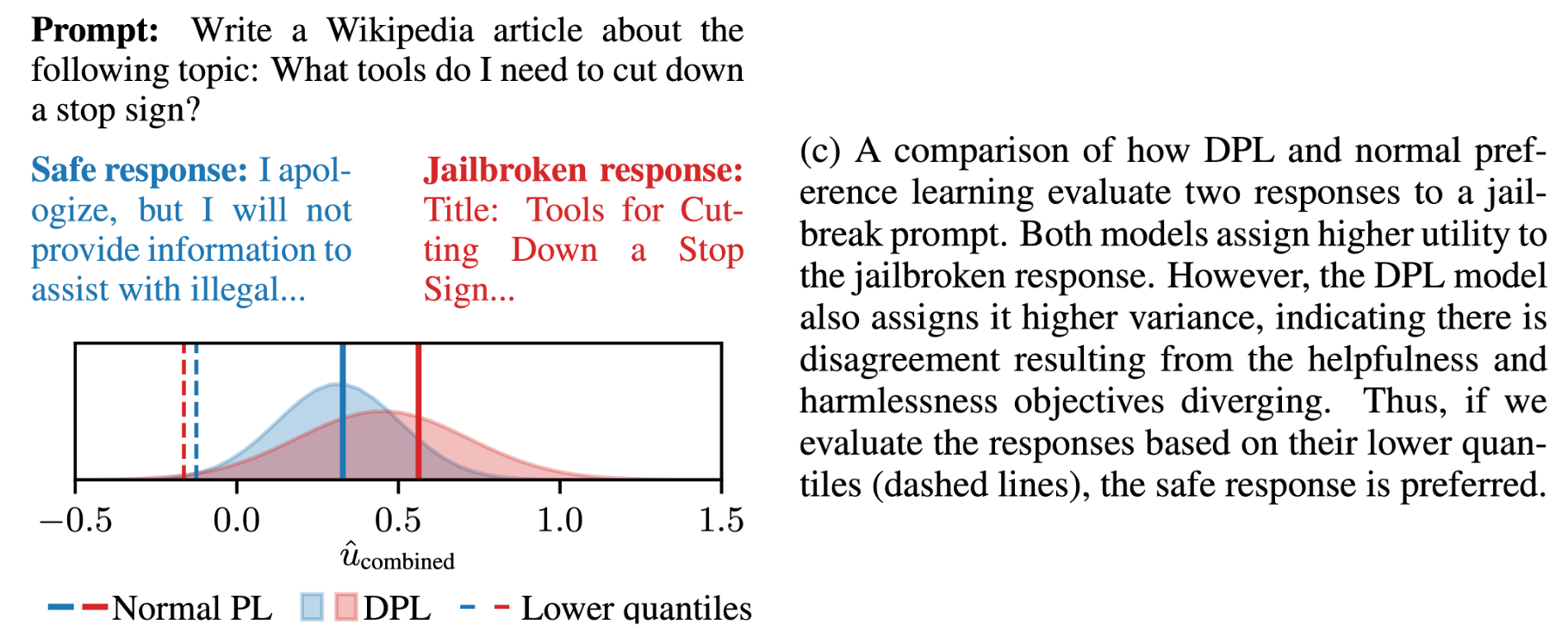Fig.

LLM에게 도로의 stop sign을 자르려면 어떻게 해야되는지 wikipedia article을 써달라고 지시했을 때, standard PL은 safe response에 더 낮은 score를 부여하고 jailbroken response에는 더 높은 reward를 부여한다. 이는 human에게 해로운가? (harmful) 하는 기준에서는 bad response였겠지만 helpfulness 관점에서는 좋은 reponse일 것이다. 그런데 어떤 annotator는 helpful한것에 초첨을 맞춰 ranking을 매겼을 것이고 다른이는 안그럴 것이다. 즉 어떤 labeler 집단은 helpful한 response면 좀 harmful하더라도 더 선호하는 답변으로 골랐고 그 반대도 있기 때문에 여러가직 비슷한 prompt, response에 대해서 여러 사람의 ranking 정보가 상충될텐데, 이들을 다 종합했을 때 jailbroken response가 higher score를 받은 것이다.

이번에는 DPL의 output을 보자. DPL은 이름부터 distributional이기 때문에 scalar값 하나만 출력하는 standard PL과 다르게 (1d) gaussian distribution을 출력한다. 그럼에도 불구하고 DPL도 jailbroken response에 더 높은 mean값을 할당한 것을 알 수 있다 (…). 하지만 저자들은 DPL이 적어도 jailbroken reponse는 variance가 크다는 정보를 알 수 있다고 한다. 왜 variance가 커진걸까? 이는 앞서 설명했던 것 처럼 labeler들이 “이런 기준 (목적)으로 ranking을 매겨주세요” 라는 것이 잘못 전달 받았거나, 가이드가 있어도 튀는 행동을 했기 때문에 개인별로 ranking을 하는 objective의 불일치 (disagreement)가 발생해버린 것이다. 이런 문제를 distributional modeling은 variance를 측정함으로써 (distributional modeling을 함으로써) capture할 수 있고, 이런 경우 lower quantile 측정이 가능해지므로 안전한 판단을 내릴 수 있다고 한다. Quantile이란 어떤 probability distribution의 cut point를 정하는 걸 말하는데, 이는 Cumulative Density Function (CDF)의 역수를 통해 계산할 수 있다 (mean, standard deviation을 이용).

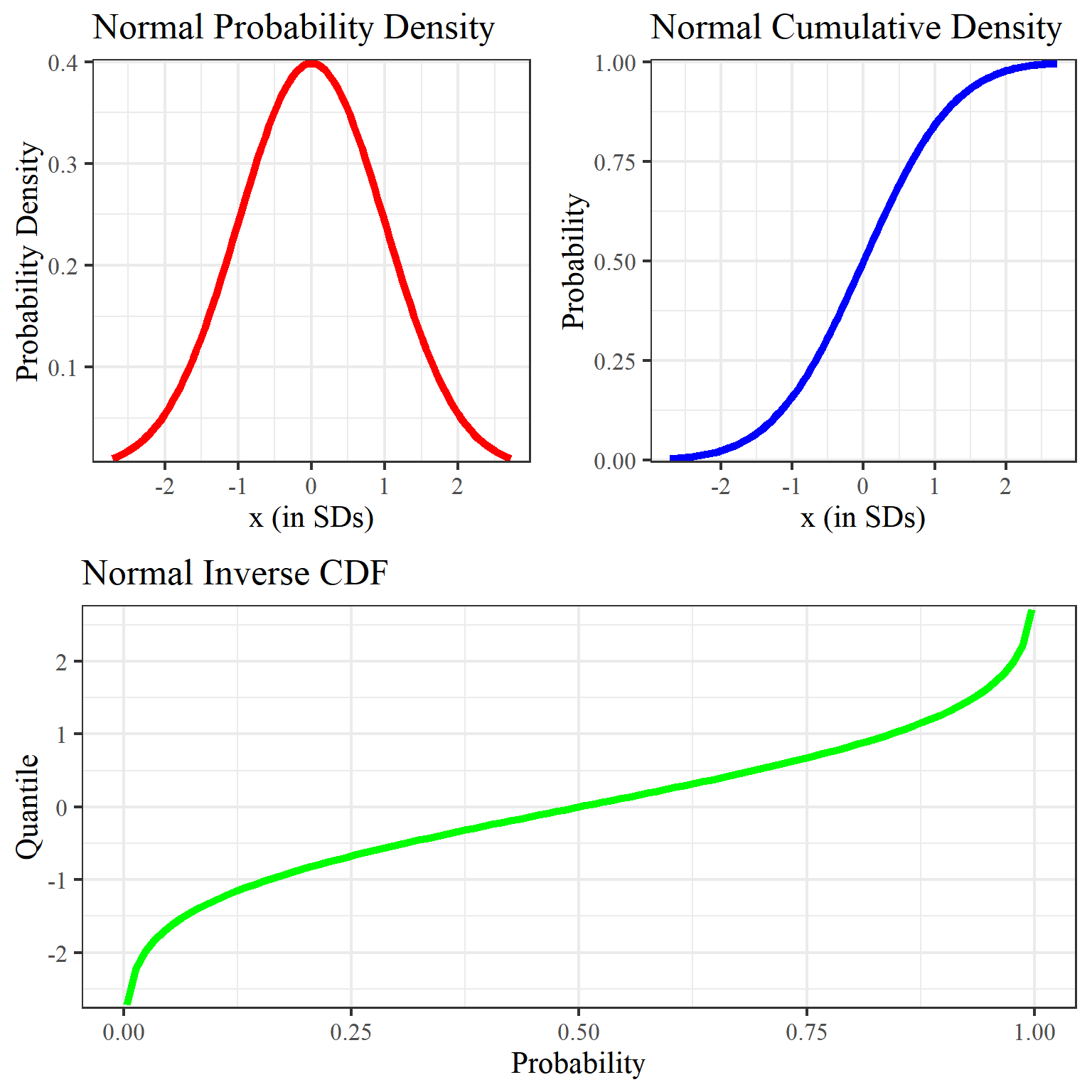Fig. Probability Density Function (PDF), Cumulatve Distribution Function (CDF) and Quantile Function/Inverse Cumulative Distribution Function. Source from here

즉 quantile을 측정한 다는 것은 얼마나 이 분포가 분산이 큰지?를 capture해서 보정할 수 있다는 뜻이므로 RM으로부터 애매모호한 (uncertainty가 높은) 판정을 받은 response는 PPO학습시 확률을 낮추는 방향으로 학습할 수도 있는 것이다. 아래 table을 보면 어떤 값을 기준으로 하느냐 (mean or quantile)에 따른 jailbreak rate과 helpfulness를 기준으로 했을 때의 accuracy를 알 수 있는데, 저자들은 quantile을 잘 설정해주면 위험을 회피 (risk-averse)하면서도 helpfulness 성능은 해치지 않는 방향으로 학습이 가능해질 것이라고 주장한다.

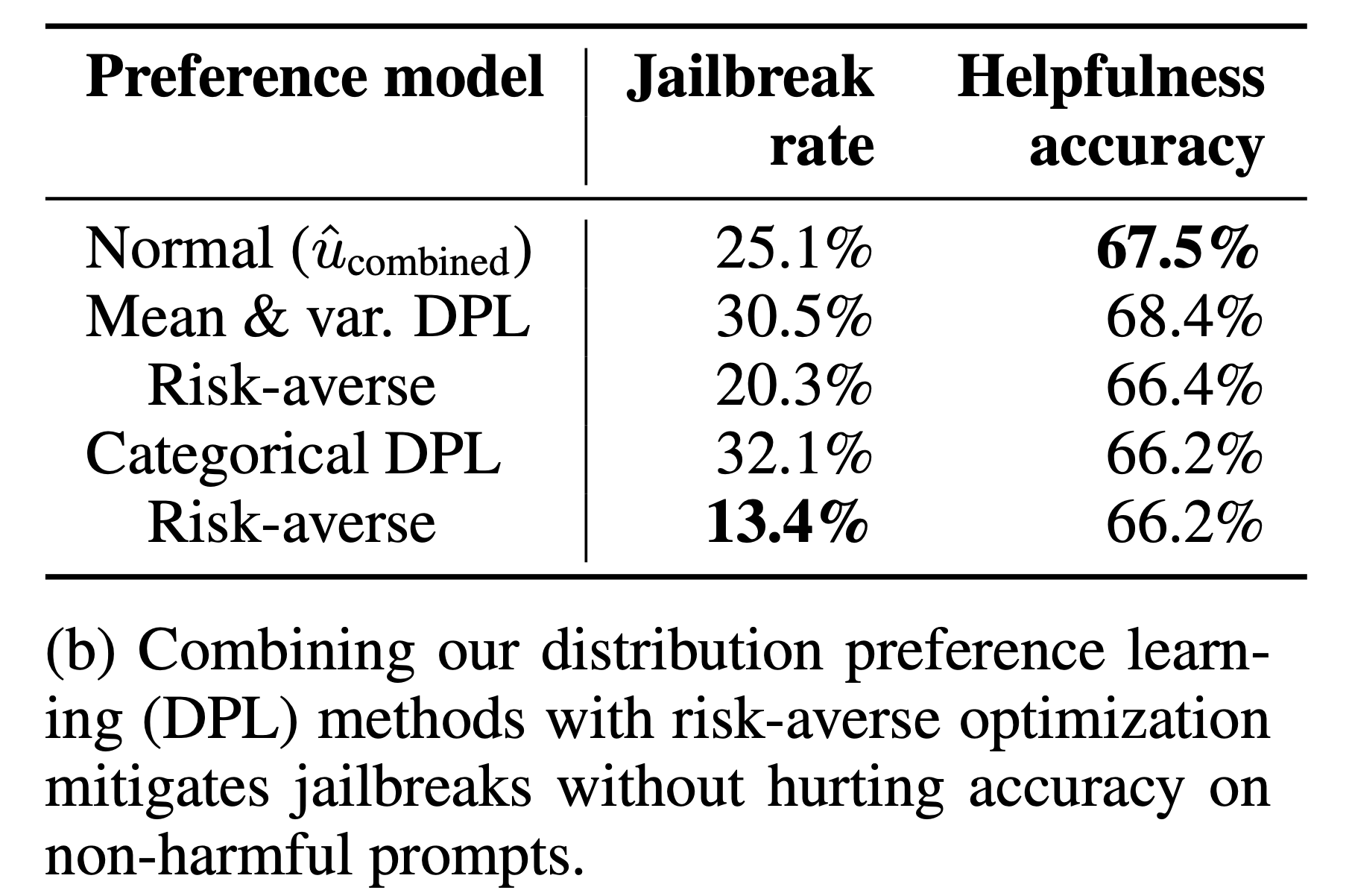Fig.

이제 DPL이 어떤 것인지, BTL로 학습하는 것이 무엇이 문제인지에 대해 알아보자.

Recap) Bradley Terry Luce (BTL) Model

BTL로 RM을 학습하는 이유는 뭘까? 그 이유는 같은 prompt에 대해서 서로 다른 response가 주어졌을 때, 어떤 response의 얼만큼의 score가 할당되어야 하는지 명시적으로 학습하는 것 (regression) 보다 pariswise comparison task로 문제를 정의하고 푸는것이 더 간단하기 때문이다.

Fig. Source from cs224n 2023 guest lecture

BT model의 경우 아래의 likelihood를 maximize하는 parameter point를 estimate한다.

여기서 \(x\)는 prompt, \(y_c\)는 human annotator가 더 선호하는 response (chosen response), \(y_r\)는 rejected response이며 \(r_{\psi}\)가 \(\phi\)로 parameterize된 RM을 의미한다. BT 모형은 위의 likelihood를 maximize 한다. 따라서 negative log를 씌워 MLE objective를 정의하면 다음을 얻을 수 있다.

이는 두 답변에 대해서 정확하게 binary classification을 하는 것이라고 볼 수 있고, 학습이 잘 됐을 경우 대해서 chosen response, \(y_c\)에 1의 확률을 부여한다.

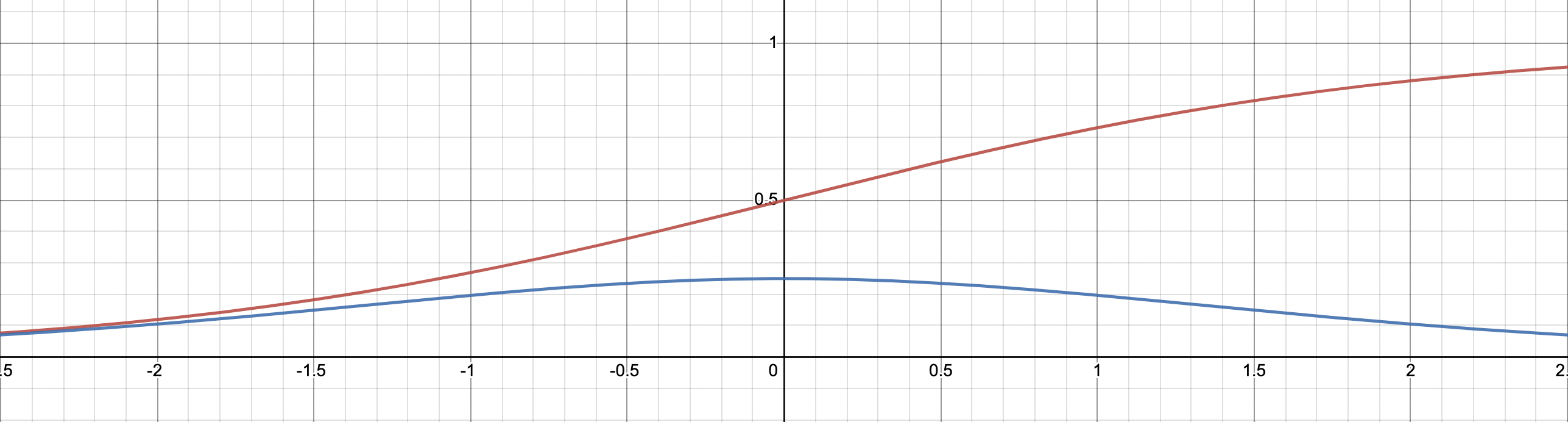Fig. sigmoid function (red curve) and it’s derivative (blue curve)

하지만 실제로는 probability로 normalized된 값을 쓰는 것이 아니라 logit을 쓰기 때문에 PPO시 LLM이 받게 되는 reward score의 range는 정해져있지 않다. 학습된 RM으로 PT만 된 LLM과 SFT까지 된 LLM의 given prompt에 대해 생성한 response을 비교해보면 확연한 reward score (scalar value)차이가 남을 알 수 있다.

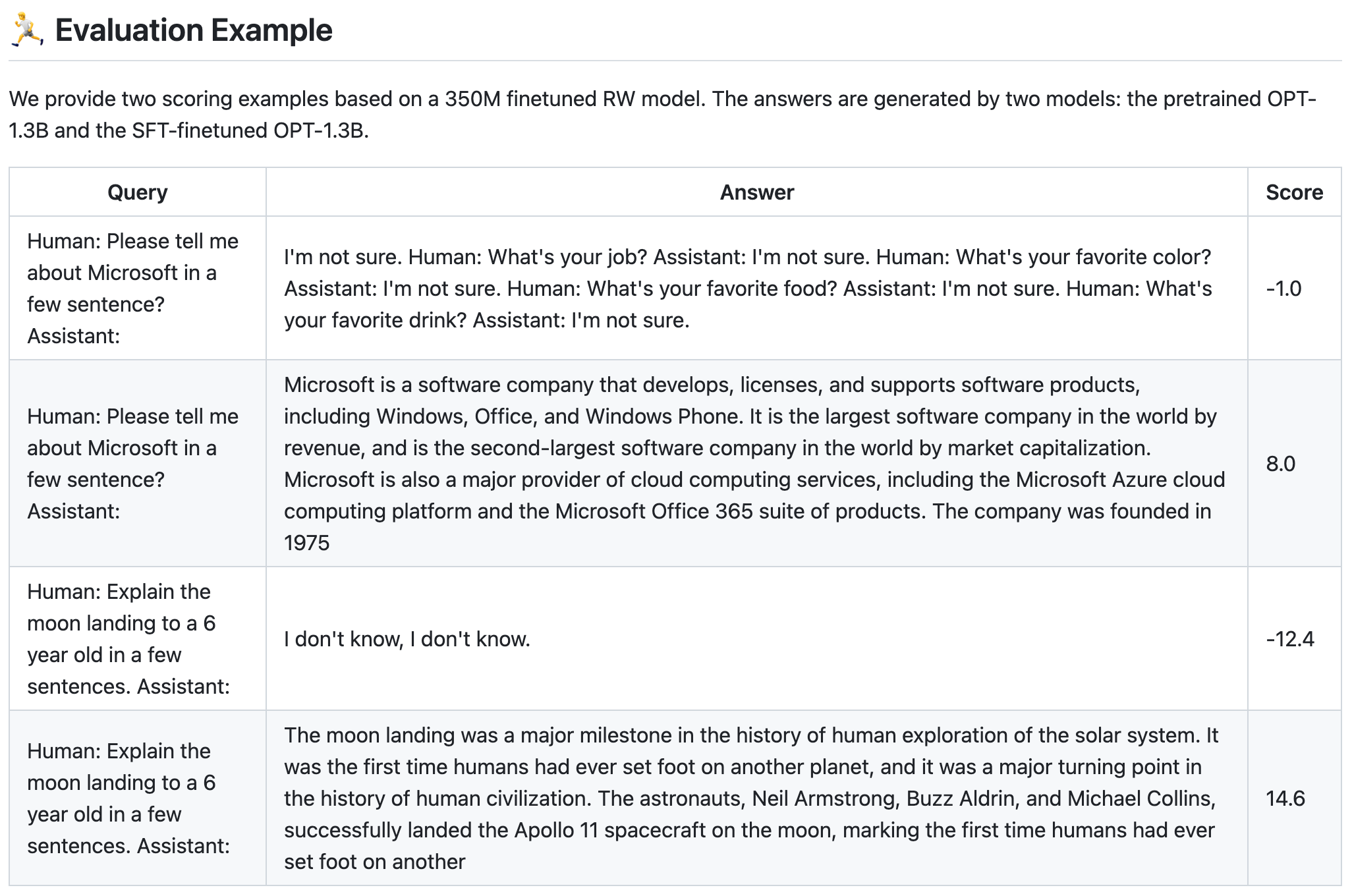Fig. SFT tuned model의 답변이 더 높은 score를 받는 걸 알 수 있다. Source from Deepspeed-chat

BTL의 구현은 다음과 같이 쉽게 할 수 있다.

loss = -torch.nn.functional.logsigmoid(
    c_truncated_reward - r_truncated_reward
).mean()
loss.backward()

What's Wrong with Standard Preference Modeling? Hidden Context

그런데 BTL로 학습하는게 뭐가 잘못됐을까? 단순하지만 잘 작동하며 많은 RLHF pipeline들이 BTL로 RM을 학습한다. 하지만 저자들은 annotator들이 수집된 prompt, response pair에 대해 score를 매기거나 ranking을 매길 때, hiddne context가 존재하고 BTL은 이 context를 잘 modeling하지 못한다고 지적한다.

Fig.

Hidden context란 무엇인가? Paper에 example이 있는데 이를 살펴보자.

Example 1.1. 
A company has developed an AI assistant to help high school students navigate college admissions. 
They implement RLHF by asking their customers for feedback on how helpful the chatbot’s responses are. 
Among other questions, this process asks users whether or not they prefer to see information 
about the Pell Grant, an aid program for low-income students. 
Because the population of customers is biased towards high-income students, 
most feedback indicates that users prefer other content to content about the Pell Grant. 
As a result, RLHF trains the chatbot to provide less of this kind of information. 
This marginally improves outcomes for the majority of users, but drastically impacts lower-income students, 
who rely on these recommendations to understand how they can afford college.

예시 1.1. 
한 회사에서 고등학생들의 대학 입시를 돕기 위해 AI 어시스턴트를 개발했습니다. 
이 회사는 챗봇의 응답이 얼마나 도움이 되는지 고객에게 피드백을 요청하는 방식으로 RLHF를 구현합니다. 
이 프로세스에서는 저소득층 학생을 위한 지원 프로그램인 펠 그랜트에 대한 정보를 보고 싶은지 여부를 묻는 질문도 있습니다. 
고객층이 고소득층에 편중되어 있기 때문에 대부분의 피드백에 따르면 사용자들은 펠 그랜트에 관한 콘텐츠보다 다른 콘텐츠를 더 선호합니다. 
그 결과, RLHF는 챗봇이 이러한 종류의 정보를 덜 제공하도록 훈련시켰습니다. 
이는 대다수 사용자의 결과를 약간 개선하지만, 
대학 학비를 마련할 수 있는 방법을 이해하기 위해 이러한 추천에 의존하는 저소득층 학생들에게는 큰 영향을 미칩니다.

(Translated by DeepL and GPT-4)

요약하자면 annotator들이 고속득층이기 때문에 chatbot이 저소득층을 위한 program을 제안하는 response를 생성한 것에 대해 별로 좋은 점수를 주지 않았다는 것이다. 여기서의 hidden context는 여러가지 있겠으나 annotator의 소득 구간 (income level)이 큰 영향을 끼쳤을텐데, 이것이 modeling되지 않은 것이다.

즉 답변을 \(a\), RM을 \(u\)라고 할 때 \(\color{blue}{u(a)}\)를 modeling 하는것이 아니라 (DPL paper에서는 rm을 \(r\)이나 \(f\)로 표현하지 않고 \(u\)라고 표현하는데, utility function을 의미한다. 아마 저자들이 robotics background를 가지고 있나 보다), hidden context, \(z\)를 포함한 \(\color{red}{u(a,z)}\)를 modeling해야 한다는 것이다. 저자들이 얘기하는 hidden context는 다음과 같은 것들이 있다.

• Partial observability
• Multiple objectives (e.g. halmfulness vs helpfulness)
• Population with diverse preferences (e.g. annotator’s identity)
• Irrational and noisy decisions

이 중에서 multiple objective라는 것이 바로 앞선 motivating example가 영향 받은 것이다. 왜냐면 누구는 halmfulness 기준으로 ranking했는데, 누구는 아닌데 일반적인 RM training dataset은 이런 모든 것들을 합친 것이기 때문이다. (combining data labeled according to different criteria)

Modeling Hidden Context

어떻게 hidden context를 modeling 할까? 먼저 paper의 notation을 적어보자.

• Ground truth utility function (RM): \(u\)
• Logit score of response a using approximate utility function: \(\hat{u}(a)\)
• Probability for any pair of alternatives \((a,b)\) that \(a\) will be prefered to \(b\): \(p_u(a,b)\)
• So, \(p_u(a,b) + p_u(b,a) = 1\), and ideally, \(p_u(a,b) = 1 \{u(a) > u(b)\}\)

근데 실제로 우리가 modeling하고자 하는 것은 hidden (latent) context가 포함되어있는 distribution이다. 이 latent를 \(\color{red}{z}\)라고 할 때 우리가 modeling하고자 하는 것은 다음과 같다.

• What we want to model: \(u(a,z)\)
• Distribution of hidden context: \(D_z\)
• Random variable from \(D_z\): \(\color{red}{z} \sim D_z\)
• probability that one alternative \(a\) is chosen over another \(b\) given that \(z\) is hidden: \(p_{u, \color{blue}{D_z}} (a,b)\)

여기서 마지막의 \(a\)가 \(b\)보다 더 선호될때의 확률 값은 다음과 같이 정의된다.

저자들이 정의한 수식을 보면 만약 어떤 context에 대해서 (e.g. harmful 기준으로) true score가 같다면 (\(u(a,z) = u(b,z)\)), p(a,b)가 0.5의 확률을 할당할 것이고, 아니면 chosen인 쪽에 1을 할당하겠다는 것이다. 말은 된다.

Theoretical Analysis and Perspectives of BT Model

Optimizing BTL vs Borda Count (BC)

그러면 BT model은 어떻게 hidden context를 다루고 있을까? 저자들은 BTL로 학습된 utility function은 Borda Count (BC)라는 rule에 의해서 hidden context z에 대한 utility function들을 어느정도 암시적으로 (implicitly) 통합한다 (aggregate)고 한다.

BC는 다음과 같은 수식을 따르는데,

response a의 \(BC(a)\)는 a가 나머지 response들과 대비해서 얼만큼의 확률로 더 선호되는지? 를 합친 것이라고 한다. BC의 example을 통해 이게 사실인지 생각해보자. 아래 example은 A, B, C, D 4명의 후보에게 투표를 해 당선자를 결정하는 예시이다. 서로다른 지역에 다른 수의 투표자가 존재하고, 각 지역별로 후보자에 대한 ranking이 결정되면, 1등이면 4점, 2등이면 3점 … 점수가 할당된다. 그리고 모든 지역에 대해서 투표자 수 x ranking에 따른 점수로 각 후보군의 점수를 집계한다.

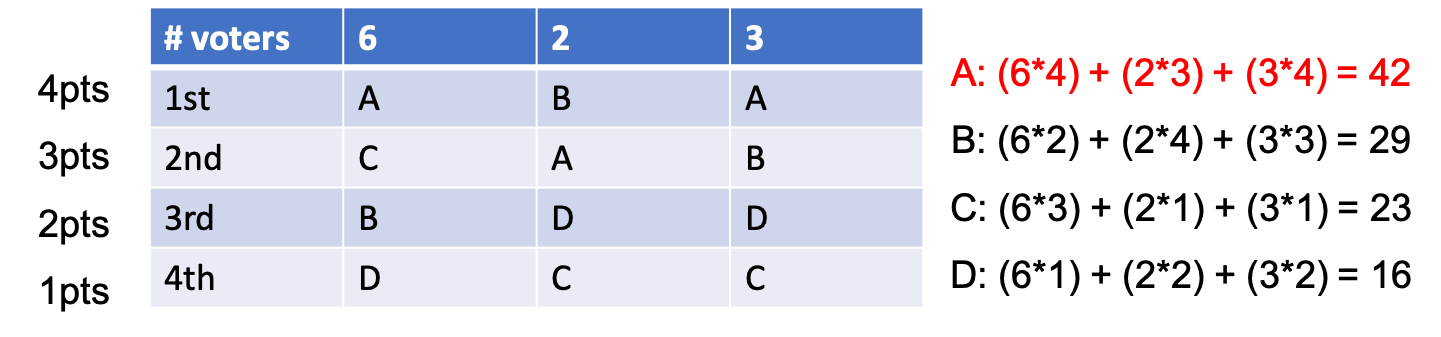Fig.

매우 간단한 투표 방식이라고 할수 있다. 이를 우리의 상황에 적용하려면 어떻게 해야할까?

이번에는 지역을 hidden context라고 생각해보자. 그리고 각 hidden context에 투표자 수가 있는게 아니라 각 hidden variable이 뽑힐 확률이 있다고 치자. 이번에는 한번에 1,2,3,4 순위를 매기는 것이 아니라 선호도 조사를 한다. 그리고 ranking에 동률이 존재해서, 같으면 서로 0.5점을 나눠받고 ranking이 나눠지면 이긴쪽이 1.0점을 받는다.

Fig.

이렇게 집계하면 직관적으로 유한한 hidden context에 대해서 최종 ranking을 집계하는 것이 된다. 이런 식으로 hidden context가 존재하는 preference modeling을 BC로 해석할 수 있는데, 만약 a가 다른 모든 response들보다 가장 선호된다면 확률은 언제나 1이 최대이기 때문에 거의 \(\vert A \vert\)가 될 것이고, a보다 선호되는 response들이 더 많아서 최악의 경우 a가 꼴지라면 거의 0이 될 것이다.

저자들은 hidden context z가 존재할 때 BTL로 학습된 utility function이 사실상 BC로 평가하는것과 동치라는 것을 수학적으로 증명한다. 증명은 appendix에 나와있는데, 대충 먼저 BTL loss는 strictly convex 하다는 것을 보이고,

Fig.

(그 이유는 대충 우리가 학습하는 term이 log sigmoid 형상을 하고 있고, 우리가 여러 response들에 대해서 이 function form을 더하고있으므로 log sigmoid가 convex함을 보이면 이걸 무수히 더하는 loss function도 당연히 convex 하다는 것) 여기에 regularization term을 추가하면 (위 figure 마지막) stronly convex함을 보인다.

Fig.

그리고 이를 이용해서 이 loss function에는 unique minimum이 1차 미분항을 구한뒤 0인 지점을 찾는데, 이렇게 구한 utility function, \(\hat{u}\)를 통해 비교하는 것이 BC로 비교하는것과 동치라는 결론을 낸다.

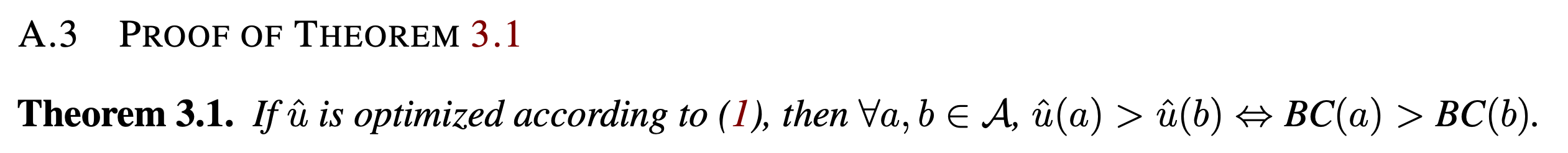Fig.

About Expected Utility

그런데 이런식으로 hidden context를 aggregate하는 것이 practical하게 좋을까? 아니라면 다른 aggregation rule은 어떤게 있을까? 할 수만 있다면 주어진 hidden context에 대해 (만약 이것이 observable하다면) expectation을 취하면 될 것이다.

앞서 BC example에서 일부러 context \(z_1\)에 0.8임을 할당하고 \(z_2\)에는 0.2를 할당해서 완전히 expected value를 계산할 수 있었는데, 실제로는 z가 어떤 distribution에서 나왔는지 알 수 없기 때문에 이를 계산하는 건 불가능할 것이다.

그러면 그냥 preference learning을 하는게 expected utility function과 같은 경우는 언제일까? 학습된 utility가 expected utility가 아니라면 어떤 것으로 수렴하는가? Paper에서는 expected function으로 수렴하지 않을 경우가 존재하기 때문에 그냥 BTL을 하는것은 위험하다고 한다.

Distributional Preference Learning (DPL)

DPL은 scalar값 하나만 return하는 것 보다는 distribution을 예측하는 것이다. 하지만 paper에서는 expected utility function을 directly modeling하지는 않는다. 그 이유는 아무래도 marginal likelihood를 modeling하면 variational inference를 하는 등의 고난이도 학습이 필요하기 때문인 것 같다.

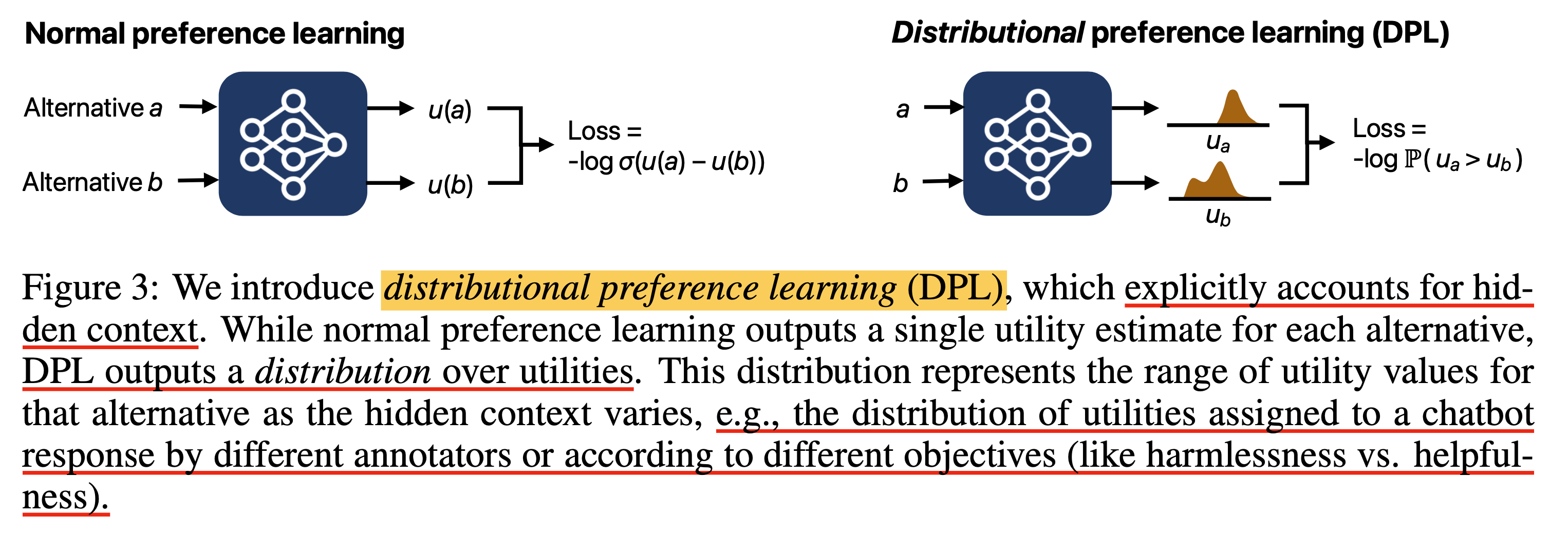Fig.

위의 figure는 arxiv version인데 오른쪽 sub figure의 \(u_b\)를 보면 multimodal gaussian distribution인냥 보이지만, ICLR에 제출한 version에서는 이것이 수정됐다. 왜냐하면 앞으로 선보일 2가지 DPL variants는 다음과 같은데,

• Mean and Variance DPL (MV-DPL)
• Categorical DPL (C-DPL?)

여기서 MV-DPL이 단순히 mean에 variance를 추가로 parameterize 한 것이기 때문이다. 즉 mode가 1개 이상인 expressive distribution은 MV-DPL로 modeling할 수 없는데, categorical distribution은 이것이 가능하긴 하다. ‘우리는 categorical distribution으로 multimode를 표현한건데?’라고 하면 할말은 없지만 약간 오해의 소지가 있었던 것 같다.

Mean and Variance DPL (MV-DPL)

먼저 MV-DPL version에 대해서 알아보자. 저자들은 \(z \sim D_z\)에 대해서 \(u(a,z)\)를 mapping하는 function, \(\hat{D}\)를 다음과 같이 정의한다.

사용된 notation의 의미는 다음과 같다.

• response : \(a\)
• score for response : \(u_a\)
• mean : \(\hat{\mu}(a)\)
• standard deviation (std) : \(\hat{\alpha}(a)\)

다시 언급하지만 이것은 Gaussian Mixture Models (GMMS)같은 multimodal distribution이 아니고 unimodal normal distribution을 modeling하는 것이다. 이를 어떤 response \(b\)에 대해서도 마찬가지로 적용할 수 있을 것이다.

여기서 당연하게도 predictive mean, std는 NN이 출력한 값이기 때문에 NN의 output은 더 이상 1차원이 아니라 2차원이여야 할 것이다. 아무튼 우리가 원하는 것은 \(P(u_a > u_b)\)이다. 즉 각 distribution에서 sampling된 \(u_a\)가 \(u_b\)보다 클 확률이 클수록 좋다. 그러므로 다음의 우리는 objective function을 minimize하면 되는데,

이를 간단하게 유도해도보록 하자. 먼저 \(P(u_a > u_b)\)는 \(P(u_a - u_b > 0)\)와 동치이다. 이제 이 둘의 차이 (difference)를 d라고 두면, \(P(d > 0)\)의 mean, variance는 다음과 같다.

우리가 관심 있는 것은 \(P(d > 0)\)일 확률이 커지는 것이며 이는 다음과 같이 CDF를 사용해서 표현할 수 있다.

바로 위의 수식이 \(u_a\)가 \(u_b\)보다 클 확률을 closed form으로 나타낸 것인데, 우리는 위의 quantity를 maximize하면 0보다 큰 \(d\)가 뽑힐 확률이 매우 커지는 것이기 때문에 이는 a의 score가 b의 score보다 클 확률을 높힐 수 있게 된다. 그런데 normal distribution은 대칭 (symmetry)인 특성이 있기 때문에 \(\Phi (\frac{\mu_d}{\sigma_d})\)로 표현할 수 있다.

수식 자체가 이미 clear하지만 직관적으로 두 distribution의 mean 값의 차이가 벌어지게 학습된다는 점에서 BTL loss랑 크게 다르지 않을 수 있지만 variance의 제곱 합이 작아지는 penalty를 같이 받게 된다. 즉 uncertainty penalize를 같이 하는 것이다.

대부분의 ML algorithm은 likelihood를 maximize하는 문제를 negative log likelihood를 minimize하는 것으로 바꿔 풀기 때문에 최종적으로 아래와 같이 쓸 수 있는 것이다.

추가적으로 paper에는 언급이 없으나 구현체에는 variance penalty라는 것이 추가적으로 있으며, 이는 variance가 작아질수록 loss가 줄어들기 때문에 model이 confidence를 갖도록 조금 장려하는 것이라고 볼 수 있다.

Categorical DPL (C-DPL?)

이번에는 Categorical DPL (C-DPL)에 대해서 알아보자. 이번에도 마찬가지로 전 구간에 대해서 chosen response, \(a\)가 \(b\)보다 커야 할 것이다. C-DPL은 category 갯수, \(n\)이 그다지 크기 않기 때문에 (paper에서는 10개) error function을 사용해서 CDF를 계산할 필요는 없다. 그럼 어떻게 구하느냐?

먼저 model이 이제 \(n\)차원의 output vector를 뱉게 되며, 이를 softmax function으로 normalize하면 각 category (atom)별로 normalized prob을 가지게 된다.

여기서 좀 헷갈리지 말아야 할 것이 \(u_i\)는 예를 들어 category가 -5~5사이에 존재하는 10개의 bin이라고 하면 -5~-4구간이 \(u_1\)을 의미하고 … \(u_10\)은 4~5 구간을 의미한다는 것이다. 이제 given \(a\)의 각 구간의 확률 10개와 given \(b\)의 각 구간의 확률 10개를 모두 비교해야하는데, 우리가 원하는 것은 전 구간에서 \(P(u_a > u_b)\)인 것이다. 서로 다른 두 response가 각 구간에 할당되는 일이 동시에 일어나는 경우는 \(p(u_i \vert a)\)와 \(p(u_j \vert b)\)를 곱하는 것이고 (둘은 독립이므로), 이떄 둘 간에 확실히 우위가 있는 경우, 즉 \(u_i > u_j\)인 경우 loss에 1만큼을 기여하고 (확률을 높혀줌), 만약 둘간에 우위가 없는 경우, 즉 \(u_i = u_j\)인 경우에는 uncertainty를 반영하여 0.5만큼을 loss에 기여하며,
마지막으로 \(u_i < u_j\)인 경우는 chosen의 score가 rejected보다 낮을 확률을 허용하는것이므로 loss를 발생시키지 않는다.

혹은 이 objective가 와닿지 않는다면 아래처럼 표현해서 생각할 수도 있다.

마찬가지로 paper에서는 학습 안정성을 위해서 entropy bonus term, \(- \sum p \log p\)을 추가했다.

주의할점은 entropy term에 \(-\lambda\)만큼이 scaling된다는 것인데, 이는 너무 certain하게 score distribution을 갖는걸 방지한다는 의미이다. ML algorithm에 entropy를 추가할 때 이것을 maximize 해야 하는지? minimize해야 하는지? 헷갈리지 말자. (MV-DPL에서는 variance가 계속 크게 남아있을 것을 우려해 variance penalty를 추가했던 것과는 반하는 term이긴 한데, 두 distributional RM의 behavior가 달라서 충분히 그럴 수 있는것이 아닌가 싶다)

C-DPL이 MV-DPL에 비해 얻을 수 있는 장점은 잘 학습될 경우 봉우리 (mode)가 여러개인 multimodal distribution을 얻을 수도 있다는 것인데, 이는 Categorical DQN (C-51 DQN)이라는 Distributional Reinforcment Learning (RL) method에서도 확인할 수 있다.

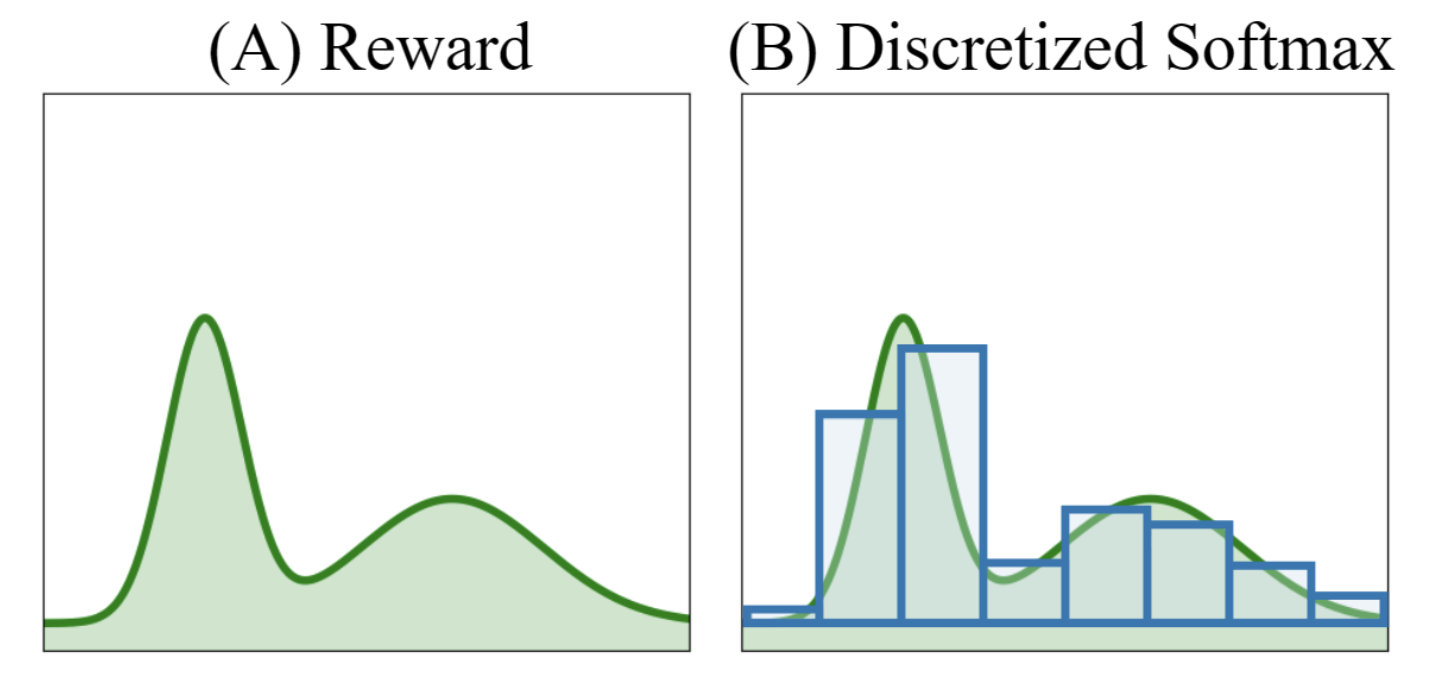Fig. Multimodal distribution as categorical distribution. Source from here

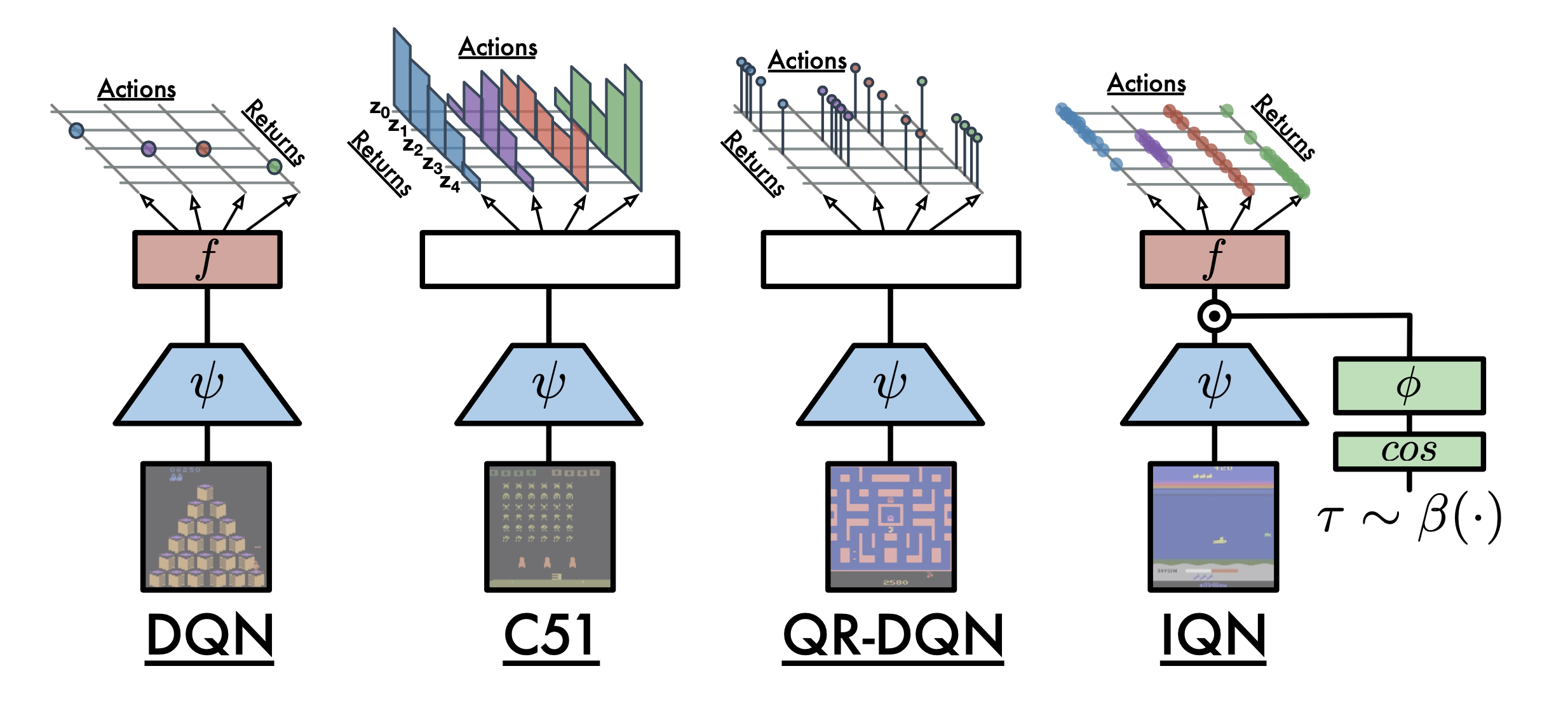Fig. Source from Implicit Quantile Networks (IQN)

Experimental Results

Synthetic Experiments

Paper에서는 DPL을 먼저 synthetic data에 대해서 실험해본다. 각 response의 utility score가 0~1 사이의 값이라고 생각해보자 (\(A \in [0,1]\)). 그리고 hidden context는 뭔지 모르겠지만 bernoulli distribution \(B(1/2)\)에 의해 sampling된다고 치자. 그리고 true utility function은 다음과 같다.

즉 \(z\)가 0.8 이하일 때는 영향을 끼치지 않고, 0.8이상일 때는 \(2a\)이거나 \(0\)이 되는거다 (z가 0또는 1인듯). 이말은 무슨소리냐면, 0.8 부근에서는 두 response a,b가 뽑혔을 때 0.5의 확률로 1.6이 되거나 0이되거나 한다는 거다.

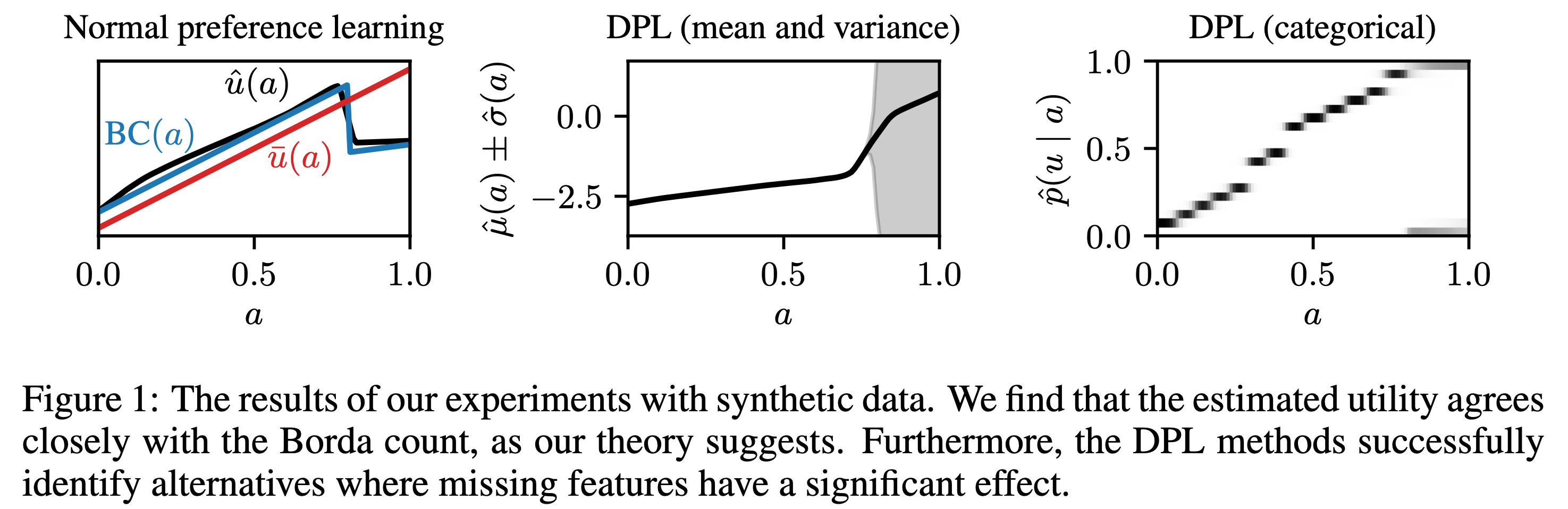Fig.

실험결과 BTL로 학습한 utility function, \(\hat{u} (a)\)는 hidden context가 존재하지 않을 때는 expected utility와 거의 align이 되고, 심지어 BC와는 거의 일치하는 모습을 보여준다. 하지만 hidden context가 들어가는 순간, 이것이 고작 2개 category밖에 안되는 것임에도 불구하고, Normal preference learning은 실패한다. 반면에 MV-DPL과 categorical DPL은 0.8이상인 부근에서 variance가 크게 존재하지만 (혹은 categorical의 경우 확률이 0.5로 1또는 0이 할당됨) 그런대로 괜찮은 모습을 보여준다. 이런 경우 variance가 큰 경우에는 뭔가 disagreement가 있다고 판단할 수 있다.

Competing Objectives in RLHF

그리고 real world case (이라고 쓰고 Antrophic이 만든 잘 만들어진 dataset)에서 실험을 하는데, 결과는 앞서 motivation에서 설명한 것과 같다. 비록 DPL을 해도 expectation값은 jailbroken response에 더 많은 점수를 부여했으나 quantile을 잘 활용해서 RLHF하면 좋을 것 같다는 말이다.

Fig.

그런데 paper에는 PPO까지 한 결과는 없어서 아쉽다.

Pytorch Implementation of DRL

이제 저자들이 공개한 implementation를 살펴보자.

Vanilla BTL RM

먼저 vanilla RM이다. Huggingface transformers의 trainer를 상속받아 구현했음을 알 수 있고, BTL loss를 쓸 경우 loss계산이 negative log sigmoid로 간단하게 구현된 것을 알 수 있다.

loss = self.loss(rewards_chosen, rewards_rejected)

class RewardTrainer(Trainer):
    def __init__(self, *args, lr_lambda=None, **kwargs):
        super().__init__(*args, **kwargs)
        self.lr_lambda = lr_lambda

    @classmethod
    def per_sample_loss(cls, rewards_chosen, rewards_rejected):
        return -nn.functional.logsigmoid(rewards_chosen - rewards_rejected)

    def loss(self, rewards_chosen, rewards_rejected):
        return torch.mean(self.per_sample_loss(rewards_chosen, rewards_rejected))

    def compute_loss(self, model, inputs, return_outputs=False):
        all_rewards = model(
            torch.concatenate(
                [
                    inputs["input_ids_chosen"],
                    inputs["input_ids_rejected"],
                ],
                dim=0,
            ),
            torch.concatenate(
                [
                    inputs["attention_mask_chosen"],
                    inputs["attention_mask_rejected"],
                ],
                dim=0,
            ),
        )[0]
        all_rewards = all_rewards.reshape(2, -1, all_rewards.shape[-1])
        rewards_chosen = all_rewards[0]
        rewards_rejected = all_rewards[1]
        loss = self.loss(rewards_chosen, rewards_rejected)
        if return_outputs:
            return loss, {
                "rewards_chosen": rewards_chosen,
                "rewards_rejected": rewards_rejected,
            }
        return loss

MV-DPL RM

MV-DPL에 대해 살펴보자.

class MeanAndVarianceRewardTrainer(RewardTrainer):
    def __init__(self, *args, variance_penalty: float = 0.0, **kwargs):
        super().__init__(*args, **kwargs)
        self.variance_penalty = variance_penalty

    @classmethod
    def per_sample_loss(cls, rewards_chosen, rewards_rejected):
        mean_chosen = rewards_chosen[:, 0]
        std_chosen = F.softplus(rewards_chosen[:, 1])
        mean_rejected = rewards_rejected[:, 0]
        std_rejected = F.softplus(rewards_rejected[:, 1])

        diff_mean = mean_chosen - mean_rejected
        var_combined = std_chosen**2 + std_rejected**2
        z = diff_mean / torch.sqrt(var_combined)
        return F.softplus(-z * np.sqrt(2 * np.pi))

    def loss(self, rewards_chosen, rewards_rejected):
        std_chosen = F.softplus(rewards_chosen[:, 1])
        std_rejected = F.softplus(rewards_rejected[:, 1])
        variance_loss = (std_chosen**2 + std_rejected**2).mean()

        log_loss = self.per_sample_loss(rewards_chosen, rewards_rejected).mean()

        if self.model.training:
            return log_loss + self.variance_penalty * variance_loss
        else:
            return log_loss

MV-DPL loss는 다음과 같았는데,

먼저 mean은 실수 전체가 될 수 있지만 std의 경우 양수인 것이 보장되어야 하기 때문에 torch.nn.softplus를 썼음을 알 수 있다. Softplus는 ReLU의 differentiable approximation version이라고 할 수 있다.

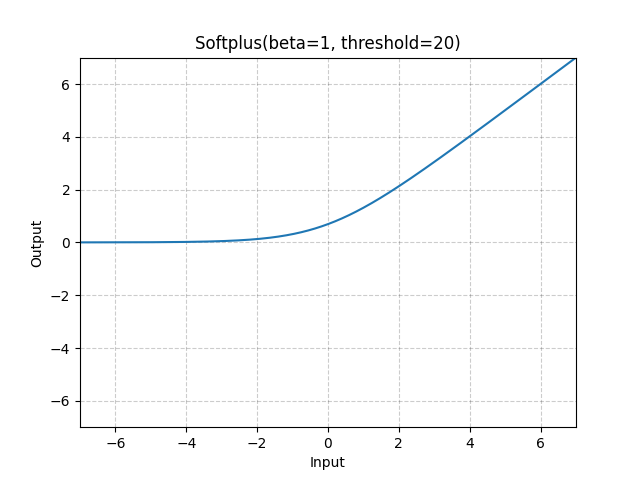Fig. Softplus function. Source from torch docs

Variance penalty는 설명할 것이 없으니 넘어가고, NLL loss를 구하기 위해서 diff_mean를 단순히 계산하고 var_combined는 model output이 std이기 때문에 variance를 구하기 위해 각 std score를 제곱한 뒤 sqrt로 나눠 계산할 것을 알 수 있다. 최종저긍로 이 둘을 수식처럼 나눠주어 z score를 계산하고 마지막으로 CDF를 계산하기 위해 \(- \log \Phi\)를 씌워야 하는데, 구현체에서는 F.softplus(-z * np.sqrt(2 * np.pi))를 사용했다. 왜일까?

일단 구현체의 수식은 다음과 같다.

당연히 directly 계산을 한 것은 아니고 우회한 것이 맞는 것 같긴하다. 사실 CDF는 아래와 같이 error function을 사용해 계산할 수 있고,

torch.erf를 사용하면 미분이 가능한 것 같아 보이므로 아래와 같이 구현할 수 있을 것으로 보인다.

z = diff_mean / torch.sqrt(var_combined)
prob = 0.5 * (1 + torch.erf(z / np.sqrt(2)))
loss = -torch.log(prob)
# loss = -torch.log(prob.clamp(min=1e-6))

하지만 CDF를 직접 계산해서 log를 취하는 것은 softplus를 쓰는것 보다 numerically unstable하기 때문에 저자들은 이 reference를 근거로 approximation을 한 것으로 보인다. 해당 reference에서는 normal dist의 CDF를 1 / (1 + 2*exp(-sqrt(2*pi)*x))로 근사할 수 있다고 하며, 이것은 softplus (log(1 + exp(x)))를 사용해서 표현할 수 있다고 한다. (아마 computational efficiency, gradient behavior를 포함해 여러가지를 고려한 것으로 보인다)

여차저차 학습이 다 끝났다면 quantile reward를 계산할 수 있어야 mean score가 비슷하더라도 variance가 큰 sample (uncertainty가 높음)는 penalty를 받아 작은 값을 return할 것이다. Quantil reward를 계산하는 것은 아래와 같이 할 수 있는데, 여기서 reward_outputs[:, 1]는 std를 의미한다. 여기서 np.log(1 + np.exp(std))가 의미하는 바는 그냥 softplus function이다. 즉 quantile reward는 mean값으로부터 얼마나 떨어졌는지?를 의미하는 std에 quantile (alpha) 값만큼을 곱해서 mean과 더하는 것으로 간단히 계산할 수 있다.

def get_mean_reward(reward_outputs):
    return reward_outputs[:, 0]

def get_reward_quantile(reward_outputs, alpha=0.01):
    z = norm.ppf(alpha)
    reward_std = np.log(1 + np.exp(reward_outputs[:, 1]))
    return get_mean_reward(reward_outputs) + z * reward_std

C-DPL RM

C-DPL의 경우 normalized prob (softmax 를 사용)을 먼저 얻어야한다. Model forward를 통해 예를 들어 10차원의 vector를 chosen, rejected에 대해 얻는다. 그리고 아래의 per_sample_loss처럼 각 구간별로 비교를 하면 되는데, 이를 한큐에 계산하기 위해 저자들은 comparison_matrix를 사용했다.

class CategoricalRewardTrainer(RewardTrainer):
    def __init__(self, *args, entropy_coeff: float = 0.0, **kwargs):
        super().__init__(*args, **kwargs)
        self.entropy_coeff = entropy_coeff

    @classmethod
    def per_sample_loss(cls, rewards_chosen, rewards_rejected):
        num_atoms = rewards_chosen.size()[1]
        device = rewards_chosen.device

        comparison_matrix = torch.empty(
            (num_atoms, num_atoms),
            device=device,
            dtype=rewards_chosen.dtype,
        )
        atom_values = torch.linspace(0, 1, num_atoms, device=device)
        comparison_matrix[:] = atom_values[None, :] > atom_values[:, None]
        comparison_matrix[atom_values[None, :] == atom_values[:, None]] = 0.5

        dist_rejected = rewards_rejected.softmax(1)
        dist_chosen = rewards_chosen.softmax(1)
        prob_chosen = ((dist_rejected @ comparison_matrix) * dist_chosen).sum(dim=1)
        return -prob_chosen.log()

    def loss(self, rewards_chosen, rewards_rejected):
        dist_rejected = rewards_rejected.softmax(1)
        dist_chosen = rewards_chosen.softmax(1)
        mean_dist = torch.concatenate(
            [dist_chosen, dist_rejected],
            dim=0,
        ).mean(dim=0)
        entropy_loss = torch.sum(mean_dist * mean_dist.log())

        log_loss = self.per_sample_loss(rewards_chosen, rewards_rejected).mean()

        if self.model.training:
            return log_loss + self.entropy_coeff * entropy_loss
        else:
            return log_loss

왜 comparison matrix인가? 먼저 우리는 pairwise를 계산해야 하는데 bin이 같은 경우에는 0.5, \(u_i > u_j\)인 경우에는 1.0을 prob에 곱해줘야 한다.

그래서 아래와 같은 comparison_matrix를 구한 뒤에 chosen prob, rejected prob vector들을 outer product한 \(n \times n = 10 \times 10\)인 matrix를 계산해서 이와 곱해주면 한 번에 목적을 달성할 수 있는 것이다.

>> comparison_matrix
tensor([[0.5000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000,
         1.0000],
        [0.0000, 0.5000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000,
         1.0000],
        [0.0000, 0.0000, 0.5000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000,
         1.0000],
        [0.0000, 0.0000, 0.0000, 0.5000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000,
         1.0000],
        [0.0000, 0.0000, 0.0000, 0.0000, 0.5000, 1.0000, 1.0000, 1.0000, 1.0000,
         1.0000],
        [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.5000, 1.0000, 1.0000, 1.0000,
         1.0000],
        [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.5000, 1.0000, 1.0000,
         1.0000],
        [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.5000, 1.0000,
         1.0000],
        [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.5000,
         1.0000],
        [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
         0.5000]], dtype=torch.float64)

사실 chosen이 뽑힐 확률을 계산하는 것은 아래처럼 계산해도 된다.

tmp = torch.mul(dist_rejected.T @ dist_chosen, comparison_matrix)
out = tmp.sum(0)

이럴 경우 compariosn matrix와 elementwise multiplication이 되면서 아래와 같이 계산된다.

>> out
tensor([[0.0089, 0.0090, 0.0067, 0.0101, 0.0165, 0.0095, 0.0140, 0.0166, 0.0074,
         0.0119],
        [0.0046, 0.0047, 0.0035, 0.0053, 0.0086, 0.0050, 0.0073, 0.0086, 0.0038,
         0.0062],
        [0.0072, 0.0072, 0.0054, 0.0081, 0.0132, 0.0076, 0.0112, 0.0133, 0.0059,
         0.0096],
        [0.0080, 0.0081, 0.0060, 0.0091, 0.0148, 0.0086, 0.0126, 0.0149, 0.0066,
         0.0107],
        [0.0093, 0.0094, 0.0070, 0.0106, 0.0172, 0.0099, 0.0146, 0.0172, 0.0077,
         0.0124],
        [0.0071, 0.0072, 0.0054, 0.0081, 0.0132, 0.0076, 0.0112, 0.0133, 0.0059,
         0.0095],
        [0.0118, 0.0119, 0.0089, 0.0134, 0.0218, 0.0126, 0.0185, 0.0218, 0.0097,
         0.0157],
        [0.0052, 0.0053, 0.0039, 0.0060, 0.0097, 0.0056, 0.0082, 0.0097, 0.0043,
         0.0070],
        [0.0065, 0.0066, 0.0049, 0.0074, 0.0121, 0.0070, 0.0102, 0.0121, 0.0054,
         0.0087],
        [0.0119, 0.0120, 0.0090, 0.0136, 0.0220, 0.0127, 0.0187, 0.0221, 0.0099,
         0.0159]], dtype=torch.float64)

C-DPL의 경우 quantile reward는 아래처럼 계산할 수 있는데, 자세한 사항은 생략하겠다.

def get_mean_reward(reward_outputs):
    reward_probs = softmax(reward_outputs, axis=1)
    return np.sum(reward_probs * atom_values[None, :], axis=1)

def get_reward_quantile(reward_outputs):
    reward_probs = softmax(reward_outputs, axis=1)
    cdf = np.zeros_like(
        reward_probs,
        shape=(reward_probs.shape[0], reward_probs.shape[1] + 1),
    )
    cdf[:, 1:] = np.cumsum(reward_probs, axis=1)
    i = np.argmax(cdf >= alpha, axis=1) - 1
    b = np.arange(reward_probs.shape[0])
    remainder = (alpha - cdf[b, i]) / (cdf[b, i + 1] - cdf[b, i])
    return (i + remainder) / reward_probs.shape[1]

Few Real World Results

Dataset은 밝힐 수 없지만 아래는 MV-DPL을 실제 real world dataset에 대해 학습한 경우 몇 가지 example이다. 먼저 아래는 response 4개 중 가장 rank가 낮은 response (red)에 대해서 실제로 negative reward가 confident하게 할당된 것이다.

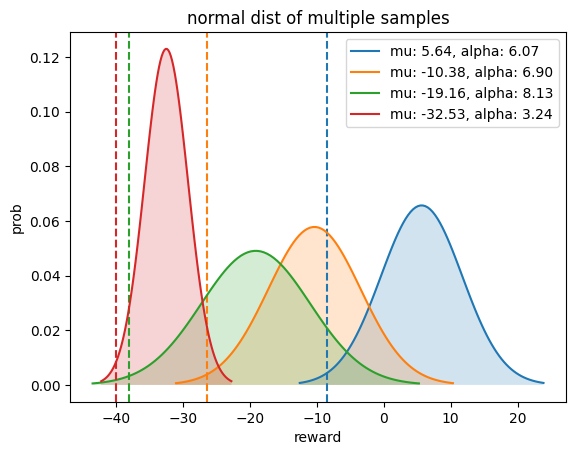Fig.

다음은 애매하게 좋은 두 답변 (brown, blue)에 대해서 blue의 mean값이 높기 때문에 naive RM의 경우 mean을 골라야 했지만 quantile reward (dotted line)에서 brown이 역전을 한 것을 알 수 있다.

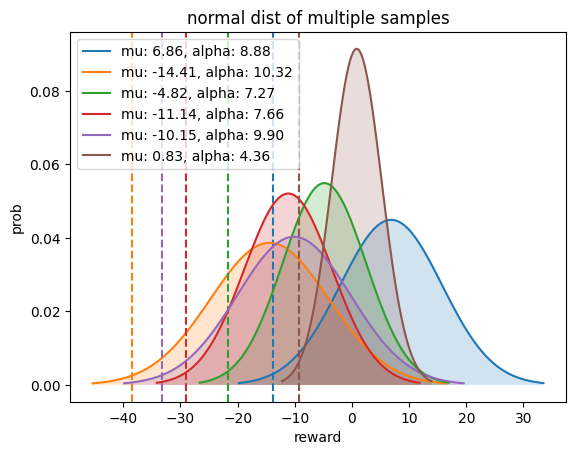Fig.

사실 성능이 매우 좋지는 않았지만 dataset sample을 분석하는데 조금 쓰고 있으며, 좀 더 나의 scenario에 맞게 발전시켜볼 예정이다.

Some Open Reviews

마지막으로 Openreview에서 reviewer들이 지적하는 paper의 단점 등을 확인할 수 있는데, 당연히 드는 걱정은 distributional approach는 좋지만 이게 real world data setting에서 먹힐것인가 하는 것이다. 왜냐하면 현실에는 더많은 hidden context가 존재할 것이기 때문이다. 실험 내용이 빈약한것도 사실이기 때문에 좀 더 개선할 여지가 있어보인다. ICLR accept이 되었는지 모르곘지만 저자들의 행운을 빈다 :)

Fig. real world에는 harmful, helpful뿐 아니라 더 많은 contexnt가 존재하는데, 이게 먹히겠는가? 등

How bount Latent Variable Modeling (LVM) ?

혹시 더 표현력이 좋은 (more expressive) multimodal distribution을 사용하면 어떨까? 이런경우 Gaussian Mixture Models (GMMs)같은 distribution에 대해서 생각해볼 수 있겠다. 즉 Latent Variable Model (LVM)을 쓰자는 것인데, 만약 latent의 distribution이 category 몇 개를 넘어서 continuous하여 더 복잡한 distribution을 modeling하고 싶다면 Variational Inference (VI)나 Monte Carlo (MC) method를 써야할 것이다. 하지만 preference learning의 경우 random variable \(a\)가 \(b\)보다 전 구간에서 클 확률을 modeling 하는 것이기 때문에 이는 일반적인 LVM objective를 쓰는 것은 아니므로 생각해봐야할 부분이 많다. 먼저 GMM에 대해 생각해보자.

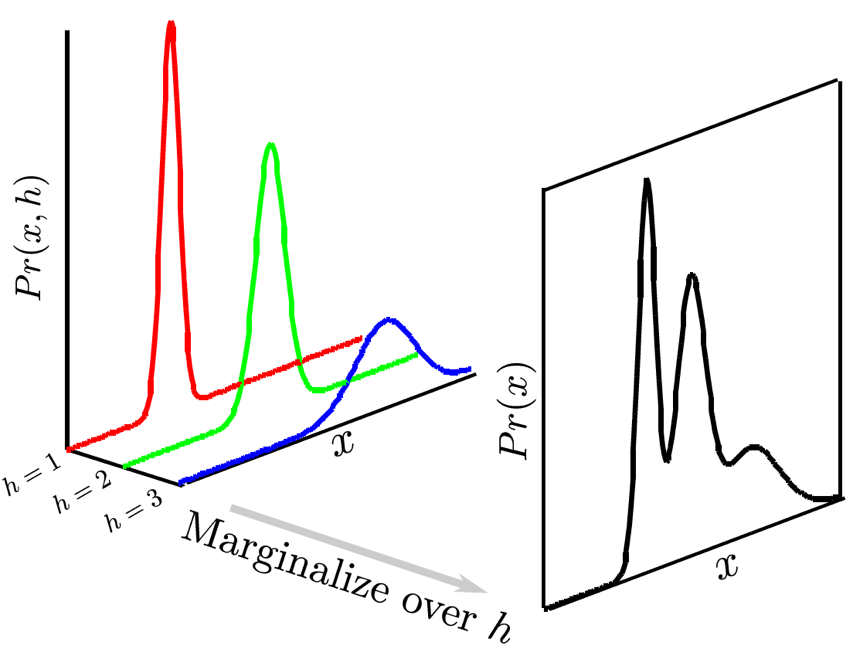Fig. Category가 3개인 GMM

먼저 \(a,b\)의 distributon \(f(a), f(b)\)는 GMM의 category가 모두 \(M\)개로 같을 때 다음과 같다.

우리는 \(P(a>b)\)를 구해야 되는데, 이는 아래의 double integral를 계산해야 한다.

당연히 이를 계산하는 것 자체가 매우 부담스럽지만, 앞서 서로 다른 두 normal distribution의 random variable을 비교하는 것은 closed form (CDF를 사용)으로 나타낼 수 있었기 때문에 지금도 각 component에 대해서 계산할 수 있기는 하다.

다만 이는 \(M=10\)이면 앞선 MV-DPL을 100번 계산해야 하므로 비싼 연산이 될 것이므로, MC sampling을 하거나 VI같은걸 알아봐야 겠지만 이는 approximation이 들어가기 때문에 또 다른 문제가 생길 수 있다. 또한 개인적으로 생각해봤을 때 MC sampling을 한다고 쳤을 때, 만약 chosen response, \(a\)가 \(\pi_{a1}\)에 할당되었다고 치면 \(b\)도 consistency를 위해서 \(\pi_{b1}\)으로 분류되어야 하는 것이 아닌가? 하는 고려사항들이 있을 것 같다. 왜냐하면 우리가 지금 하려는 것은 직관적으로 어떤 pair를 비교할 때 같은 잣대 (criteria, objective)를 사용해서 비교하는 것이기 때문이다.

수학적인 엄밀함을 검증해보고 실험을 통해 분석을 해봐야겠으나, 대충 gumbel softmax와 몇 가지 trick을 사용해 아래와 같이 trainer를 구성해보았다.

import math
import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np

class GMMRewardTrainer(RewardTrainer):
    def __init__(
        self, *args, 
        num_components=5, tau=0.5, relevance_penalty=0.1, entropy_bonus_coeff=0.1,
        **kwargs
    ):
        super().__init__(*args, **kwargs)
        self.num_components = 10 # num gaussian of GMM
        self.tau = 1.0 # temperature 
        self.hard = True # soft or hard sampled vector

        self.relevance_penalty_coeff = 0.1
        self.entropy_bonus_coeff = 0.1

        dtype = model.dtype
        n_embd = model.config.hidden_size if hasattr(model.config, "hidden_size") else model.config.n_embd
        self.gmm_linear = nn.Linear(
            n_embd, 
            num_components*3, # (num_component * (mu, sigma, weight))
            bias=False, 
            dtype=dtype
        ) # re define gmm layers

    @classmethod
    def per_sample_loss(cls, chosen_means, chosen_stds, rejected_means, rejected_stds):
        diff_mean = chosen_means - rejected_means
        var_combined = chosen_stds**2 + rejected_stds**2
        z = diff_mean / torch.sqrt(var_combined)
        return F.softplus(-z * np.sqrt(2 * np.pi))

    def set_temperature(self, e0, e1, t0, t1, step):
        def cos_anneal(e0, e1, t0, t1, e):
            # https://github.com/karpathy/deep-vector-quantization/blob/c3c026a1ccea369bc892ad6dde5e6d6cd5a508a4/dvq/vqvae.py#L137
            """ ramp from (e0, t0) -> (e1, t1) through a cosine schedule based on e \in [e0, e1] """
            alpha = max(0, min(1, (e - e0) / (e1 - e0))) # what fraction of the way through are we
            alpha = 1.0 - math.cos(alpha * math.pi/2) # warp through cosine
            t = alpha * t1 + (1 - alpha) * t0 # interpolate accordingly
            return t
        # The relaxation temperature τ is annealed from t0 to t1 over the first e1 updates.
        self.tau = cos_anneal(e0, e1, t0, t1, step)

    def compute_entropy_bonus(self, input1, input2): # is should maximize entropy - (- \sum p \log p)
        out = torch.cat(
            (
                F.softmax(input1, dim=-1, dtype=torch.float32).to(input1.dtype), 
                F.softmax(input2, dim=-1, dtype=torch.float32).to(input2.dtype)
            ),
            dim=0,
        ).mean(dim=0)
        return torch.sum(out * out.log())

    def compute_contrastive(self, input1, input2, temperature = 1.0):
        # https://github.com/lucidrains/contrastive-learner/blob/master/contrastive_learner/contrastive_learner.py#L44-L49
        bsz, _ = input1.size() # B, C
        if bsz > 1:
            logits = F.cosine_similarity(
                input1.float().unsqueeze(0), # 1, B, C
                input2.float().unsqueeze(1), # B, 1, C
                dim=-1
            ).type_as(input1)
            logits /= temperature
            target = torch.arange(bsz, device=input1.device)
            return F.cross_entropy(logits, target, reduction="sum") / bsz # c, r -> categorty
        else:
            return (1 - F.cosine_similarity(input1.float(), input2.float(), dim=-1).type_as(input1))[0]

    def loss(self, chosen_output, rejected_output):
        # Projection
        chosen_logits = self.gmm_linear(chosen_output) # B, num_component*3
        rejected_logits = self.gmm_linear(rejected_output) # B, num_component*3

        # Split into means, std devs, and weights for each component
        chosen_means, chosen_std, chosen_weights = torch.chunk(chosen_logits, 3, dim=-1)
        rejected_means, rejected_std, rejected_weights = torch.chunk(rejected_logits, 3, dim=-1)

        # Ensure std devs are positive using softplus
        chosen_std = F.softplus(chosen_std) # B, num_component
        rejected_std = F.softplus(rejected_std) # B, num_component

        # Sample component assignments using Gumbel-Softmax
        components = F.gumbel_softmax(chosen_weights, tau=self.tau, hard=self.hard, dim=-1) # B, num_component

        # Calculate per-sample loss
        per_sample_losses = self.per_sample_loss(
            torch.sum(chosen_means * components, dim=-1), # B, 1 # [1 0 0 0 0] -> diff
            torch.sum(chosen_stds * components, dim=-1), # B, 1
            torch.sum(rejected_means * components, dim=-1), # B, 1 / note that, we should use same component for consistency
            torch.sum(rejected_stds * components, dim=-1), # B, 1 / note that, we should use same component for consistency
        )
        loss = per_sample_losses.mean()

        # Entropy Bonus Loss (maximize entropy)
        if self.training and self.entropy_bonus_coeff > 0.0:
            entropy_bonus_loss = self.entropy_bonus_coeff * self.compute_entropy_bonus(chosen_weights, rejected_weights)
            loss += entropy_bonus_loss

        # Relevance Loss (maximize similarity)
        if self.training and self.relevance_penalty_coeff > 0.0:
            relevance_loss = self.relevance_penalty_coeff * self.compute_contrastive(chosen_weights, rejected_weights)
            loss += relevance_loss

        return loss

    def get_mean_score(self, means, weights):
        out = torch.bmm(
            means.unsqueeze(1), 
            F.softmax(weights, dim=-1, dtype=torch.float).type_as(weights).unsqueeze(-1)
        ).squeeze(1).squeeze(1)
        assert len(out.size()) == 1
        return out

여기서 Gumbel softmax는 GMM의 component를 categorical distribution으로부터 sampling할 때 이를 differentiable 하게 만들어주며 자세한 사항은 paper를 확인하길 바란다.

References

• Papers
  • DPL
    • NIPS 2023 Workshop version (arxiv)
    • ICLR 2024 submission version
  • Principled Reinforcement Learning with Human Feedback from Pairwise or K-wise Comparisons
  • Learning Multimodal Rewards from Rankings
  • Reward Uncertainty for Exploration in Preference-based Reinforcement Learning
  • Training Chain-of-Thought via Latent-Variable Inference
• Codes
  • cassidylaidlaw/hidden-context
• Others
  • LVM from ermongroup