(WIP) Expectation Maximization (EM) vs Variational Inference (VI)

< 목차 >

• Modeling Expressive Probabilistic Distribution
• How to train LVM?: Marginal Likelihood Training
  • The Expectation-Maximization (EM) algorithm
• EM vs Variational Inference (VI)
  • Properties of EM
• Learning Deep Generative Models
  • What's Wrong with EM?
  • Auto-Encoding Variational Bayes (AEVB)
  • The Variational Auto-Encoder
• References

This post is highly inspired by class notes from Stefano Ermon’s research group.

Modeling Expressive Probabilistic Distribution

Machine Learning (ML)에서는 dataset, model parameter 그리고 내가 풀고자 하는 likelihood나 posterior의 형태가 결정되면 objective function이 결정된다. 그리고 objective function을 maximize하는 parameter를 찾게 되는데, 보통 likelihood를 maximize하는 parameter를 찾기 때문에 Maximum Likelihood Estimation (MLE)라고 부른다.

여기서 target distribution (likelihood)가 continuous이길 바라면 보통 unimodal gaussian distribution을 사용하게 되고 이런 문제를 회귀 문제 (regression problem)이라고 부르고 이 때의 loss function은 Mean Squared Error (MSE) loss가 된다.

그런데 만약 내가 modeling하고자 하는 distribution이 unimodal이 아니라

훨씬 복잡한 distribution이면 어떻게 해야할까? 예를 들어 gaussian이긴 한데 봉우리 (mode)가 여러 개 있는 경우를 생각해보자.

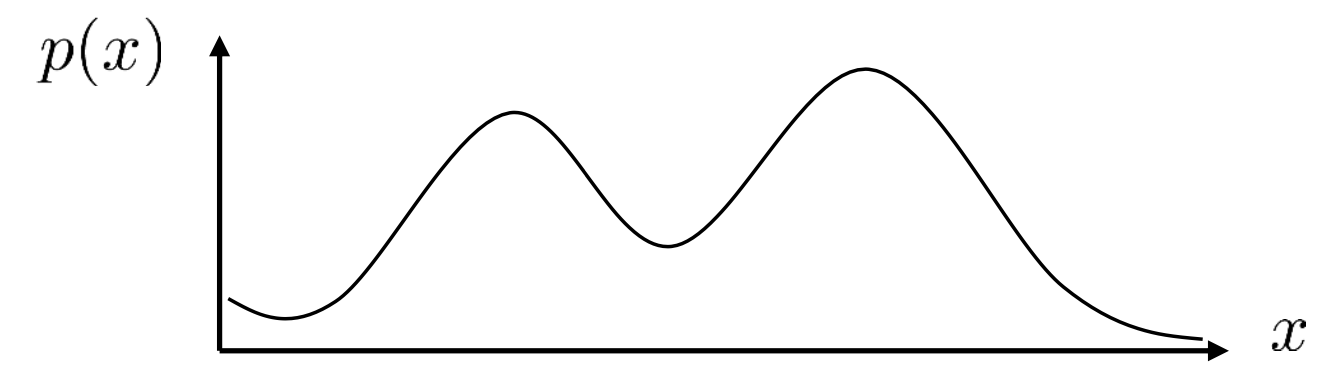Fig. mode가 2개인 bimodal distribution

왜 이런 경우가 생기는 걸까?

직관적으로 생각해보자. 내가 image 100장으로 이루어진 dataset을 가지고 있다. 그런데 50장은 cat image고 나머지 50장은 dog image 이다. 그럴 리 없겠지만 image가 1차원이라고 생각할 때, cat image는 \(x=5\)인 지점에서 많이 몰려있다고 하자 (즉 다른말로 \(x=5\)인 지점에서 sampling하면 cat이 나올 확률이 높은 것). 그리고 dog image는 \(x=20\)부근에 몰려있다고 생각해보자. 즉 위와 같은 distribution이 이상적인 것이다.

이런 경우 우리는 image sample dataset에 “이 image는 cat입니다”라는 label이 따로 달려있지는 않지만, 이런 label이 숨겨져 있지 (잠재) 않을까?라는 생각을 해볼 수 있다. 즉 data sample들에는 우리가 모르는 어떤 잠재 변수 (latent variable)이라는 것이 존재할 수가 있는 것이다. 어떻게 이런게 있다고 가정하고 modeling할 수 있을까? 만약 latent variable이 3개 category로 나눠질 수 있다면 (cat, dog, turtle class), 각 dataset은 각 category로 mapping된 후, 그 mapping된 category에서 maximum likelihood를 하는 식으로 학습을 하고, 나중에 이를 합치면 우리가 원하는 distribution을 흉내낼 수 있을것이다.

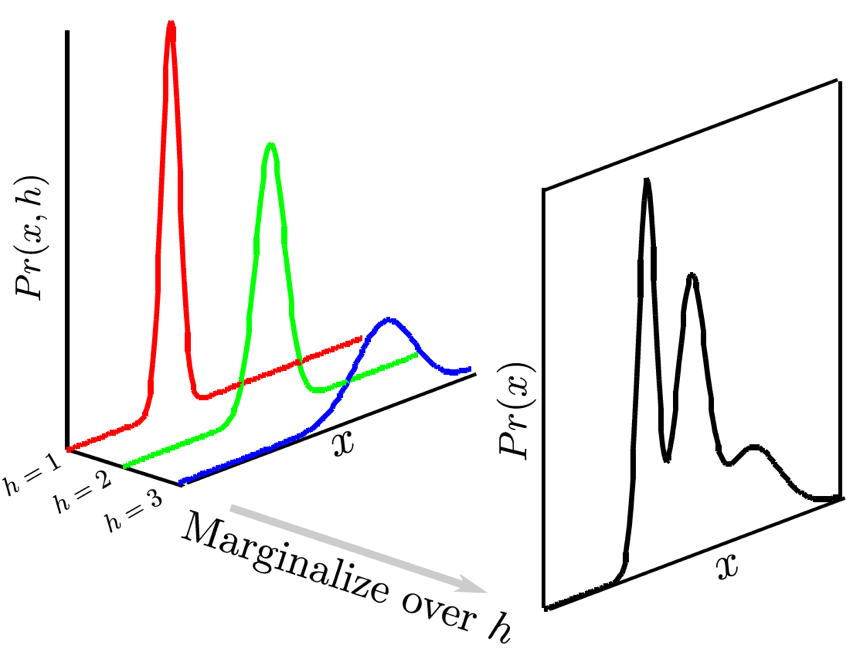Fig. latent가 3개 class라고 가정해보자.

이럴 경우 단순히 gaussian distribution을 합치면 되는데, 이것이 합쳐지는 과정을 살펴보자. 먼저 각 discrete한 \(z=k\) class에서의 likelihood를 정의하는 trainable parameter들이 당연히 존재하겠다.

그리고 \(p(x \vert z)\)는 \(\pi_k\)라는 trainable weight에 의해서 weighted sum 된다.

이런 distribution을 합치는 과정은 다음과 같이 나타낼 수 있다.

이는 당연히 expectation이 discrete z에 대해서는 summation이 되고, continuous z에 대해서는 integral이 되기 때문에 동치이다. 여기서 \(\color{red}{ p(x, z) }\) 를 modeling한다는 것이 중요한 부분인데, 앞서 말했듯 원래 우리같은 사람은 dataset file을 볼 때 이 \(z\)라는 column을 볼 수 없지만 이것이 있다고 가정하고 같이 modeling한다고 하는 것을 의미하기 때문이다.

아무튼 이렇게 latent variable이 dataset 자체에는 존재하지만 우리가 이것이 내재되어 있다고 생각하고 같이 modeling하는 것을 잠재 변수 모델 (Latent Variable Model; LVM)이라고 부르고, gaussian distribution에 대해서 discrete latent, \(z\) 를 modeling하는 것을 특별히 여러 guassian을 섞는다 해서 가우시안 혼합 모델 (Gaussian Mixture Model; GMM)이라고 부른다. (혹은 Mixture of Gaussian (MoG)라고 부르는 사람도 있다)

GMM으로 modeling을 할 경우 우리는 model이 알아서 비슷한 data에 mode를 생성함으로써 군집화 (clustering) 할 수 있게 해주는 것을 알 수 있다.

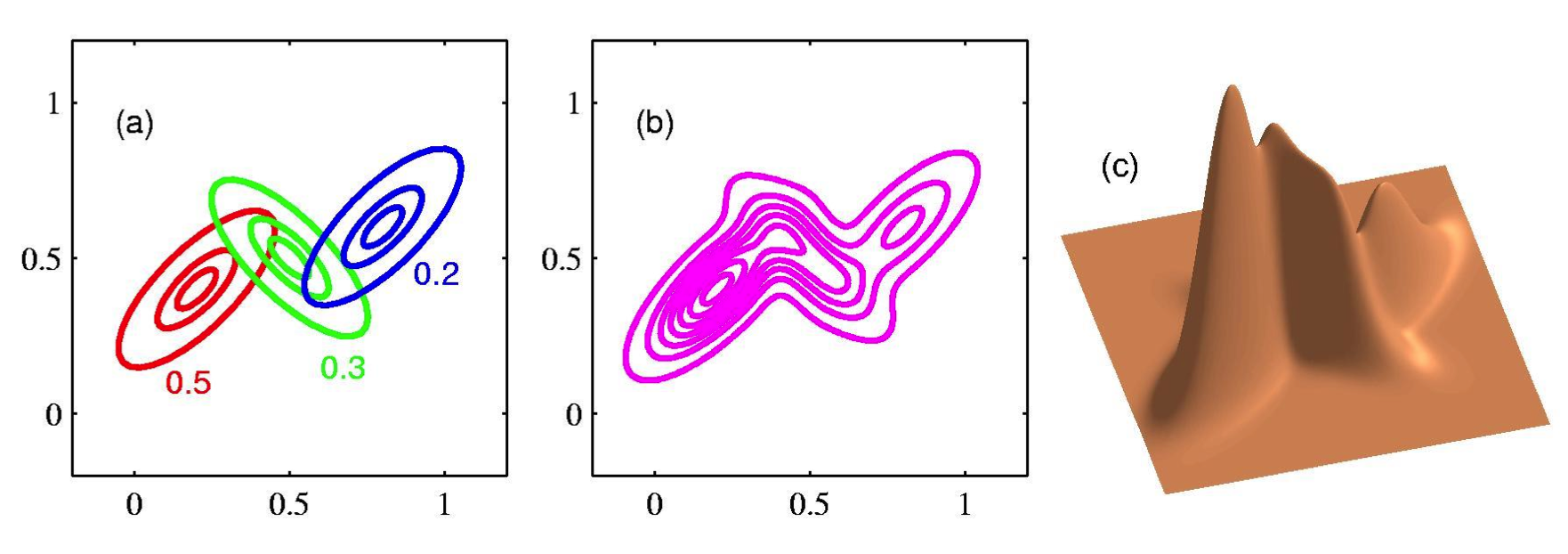Fig. 2변수 data에 대해서 bivariate guassian distribution을 3개 mixture하는 경우. 3d로 보면 z축이 likelihood를 의미한다. 어떤 class (latent)를 주느냐에 따라서 red, blue, green curve를 얻을 수 있다. 주의할 점은 원래 dataset에는 각 data point의 class가 red냐 blue냐 같은 정보는 주어지지 않았다는 것이다.

그리고 이런 LVM은 data에 숨겨진 variable을 발견하는 것으로 볼 수 있어 이렇게 modeling된 distribution을 표현력이 풍부한 (expressive) distribution 이라고도 한다.

How to train LVM?: Marginal Likelihood Training

그럼 어떻게 LVM을 학습할까?

Latent variable이 생겼지만 여전히 우리의 goal은 \(p(x)\)를 maximize하는 것이다. 이를 marginal likelihood라고 하는데, 그 이유는 \(p(x,z)\)의 z를 expectation으로 없애버렸기 때문이다 (marginal out했다고 한다). 학습을 위해서는 marginal log likelihood를 전체 dataset, \(D\)에 대해서 계산해야 한다.

이는 regular log likelihood와는 학습 난이도가 자체가 다른데, 왜냐하면 log안에 있는 summation term이 \(p(x)\)를 log-factor 들로 decompose하는걸 불가능하게 하기 떄문이다. 예를 들어 gaussian distribution에서는 log를 씌우면 모든 term들이 덧셈으로 나눠지고 parameter와 관련없는 term들은 무시해도 되었지만, latent variable이 추가되면서 이것이 불가능해진 것이다. 그러므로 우리는 closed-form solution을 얻을 수 없다.

게다가 summation 안의 term은 예를 들어 gaussian이 여러 개 겹친 것이라고 볼 수 있고 gaussian distribution은 오목 (concave)함에도 불구하고, 이를 무수히 많이 더한 \(p(x)\)는 더이상 concave하거나 convex하지 않기 때문에 이를 풀기 위해서는 special algorithm이 필요한데, 그것이 바로 Expectation Maximization (EM) algorithm 이다.

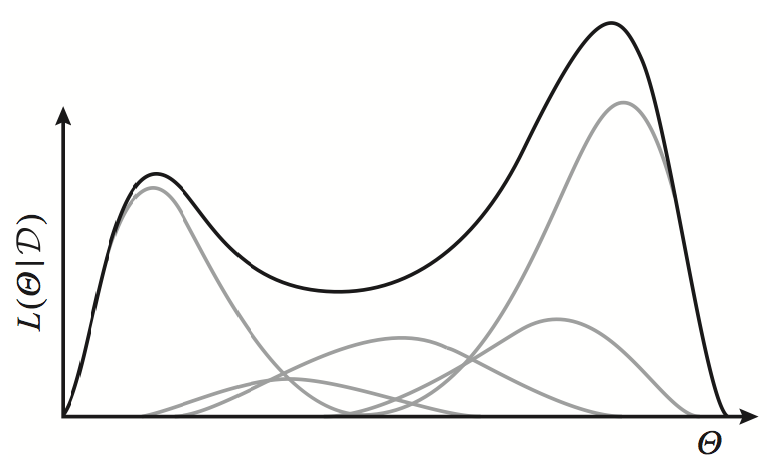Fig. Exponential family distributions (gray lines) have concave log-likelihoods. However, a weighted mixture of such distributions is no longer concave (black line).

The Expectation-Maximization (EM) algorithm

우리가 deep learning을 할 때 loss surface가 convex하지 않기 때문에 극값을 찾는 것으로 (first order condition) optimal solution을 찾지 못한다는 것은 알려진 사실이다. 이런 경우 gradient based optimization을 하는 것 처럼 점진적으로 parameter update를 해야한다. 먼저 아래의 illustration으로 EM의 대략적인 concept을 이해해보자.

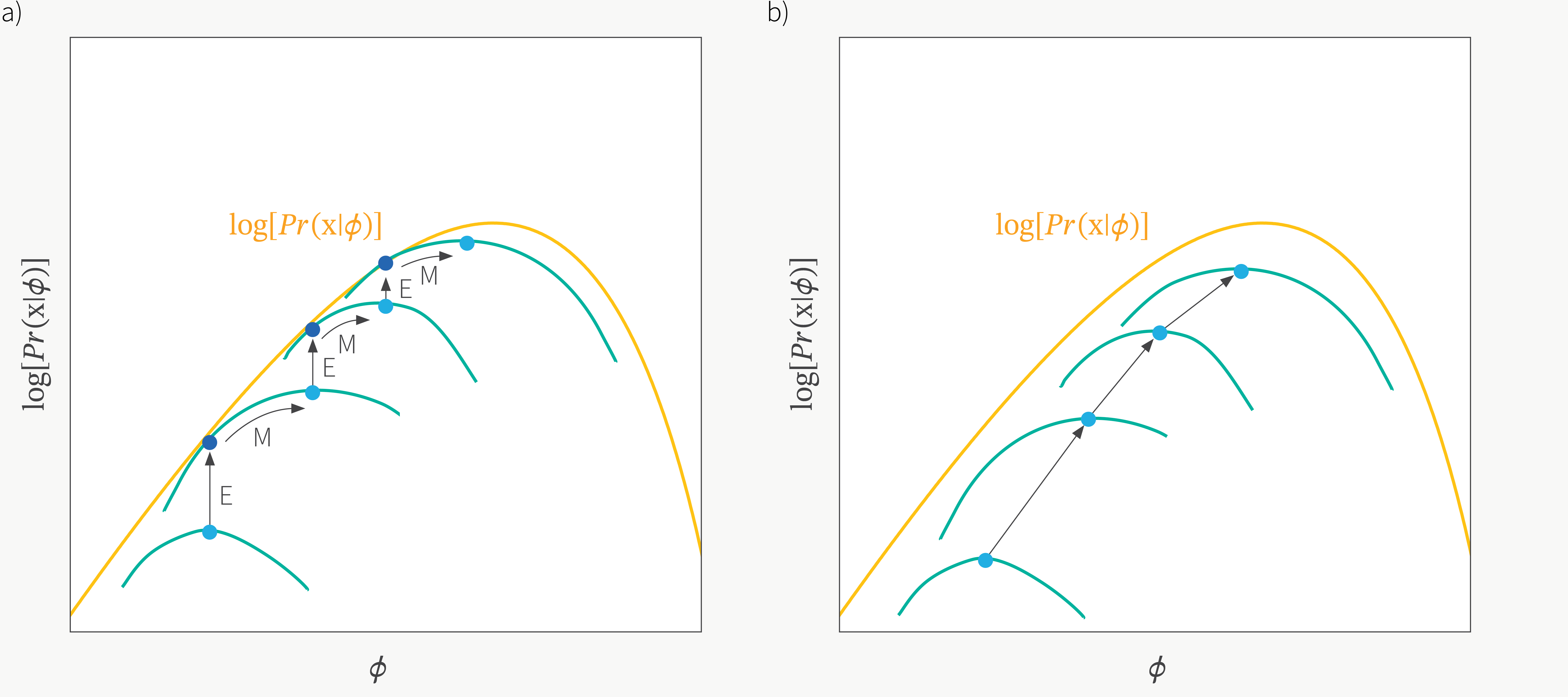Fig.

EM은 Expectation (E)와 Maximization (M) step을 반복하는 algorithm인데, 전체 dataset을 \(D\)라고 할 때 다음의 step을 따르면 된다.

• Starting at intital \(\theta_0\), repeat until convergence for 1,2, …:
  • E-Step: for each \(x \in D\), compute the posterior, \(p( z \vert x; \theta_t)\)
  • M-step: compute new parameters via: \(\theta_{t+1} = \arg \max_{\theta} \sum_{x \in D} \mathbb{E}_{z \sim p(z \vert x; \theta_t)} [ \log p(x, z; \theta) ]\)

여기서 posterior, \(p(z \vert x; \theta)\)라는 것이 처음 언급되었는데, 이것은 data sample, \(x\)와 현재 model parameter, \(\theta_{t}\)를 가지고 있다면 latent를 유추할 수 있다는 것이다. 그냥 category label이라고 생각할 경우 image input이 주어졌을 때 이것이 개인지 고양이인지에 대한 distribution이 있고 거기서부터 sampling을 하겠다는 것이다. 그리고 EM같은 algorithm을 쓸 때 우리가 받아들여야 할 것은 ‘이렇게 뽑힌 latent variable, z가 맞다고 생각하는 것 (use it to “hallucinate” values for z)’이다. 일단 현재 주어진 상황에서 각 sample, \(x_i\)마다 \(z_i\)가 모두 정해졌으면 (sample 됐으면), 이제 optimization을 해서 (maximize), 다음 parameter, \(\theta_{t+1}\)로 parameter update가 이루어지는 것이다. 만약에 이 \(z\) distribution이 너무 큰 차원을 갖지 않는다면 (예를 들어 GMMs은 3차원 categorical distribtuon임)

GMMs에 대해서 EM을 해보자. 먼저 각 data point, \(x_i\)마다 posterior를 계산해야 한다.

이것이 E-step인데, E-step의 결과물은 여기서는 k 차원의 vector가 된다. 예를 들어 3개 gaussian을 mix한다면 3차원 vector인 것이며 모든 component의 합은 1이 된다.

이제 우리가 가 sample별 \(z\)를 뽑았으니 M-step을 진행하면 되는데, 이는 maximume likelihood 문제를 푼다고 생각하면 된다.

위 수식을 분리해서 optimize할 수 있는데, 지금 model이 gaussian을 weighted sum할 것이므로 \(p(x \vert z_k ; \theta) = \mathcal{N}(x; \mu_k, \Sigma_k)\)로 두고 아래 수식을 maximize하는 mean, variance를 찾으면 된다.

그런데 이 수식은 아래처럼 표현할 수 있고,

여기서 \(c_k=\sum_{x \in D} p(z_k \vert x; \theta_t)\)는 \(\theta\)와 관련없는 상수 (constant)이며 (왜냐하면 \(\theta_t\)는 정해진 값이고 변수가 아니기 때문), 새롭게 정의된 distribution, \(Q_k(x)\)는 다음과 같다.

이는 \(Q_k\)라는 normalized probability distribution하의 epxectation인데, 우리는 이를 maximization 해야 한다. 그런데 우리는 대부분의 ML algorithm이 수행하는 MLE를 한다는 것은 사실 data가 sampling된 ture distribution과 model이 예측한 predictive distribution과의 KL divergence를 minimize 하는 것과 동일하다는 것을 알고있다.

그러므로 우리가 계산하고자하는 \(Q_k\) distribution 하의 liklihood expectation 값은 결과적으로 두 분포간의 KL divergence를 minimze하는 것과 같은데, KL divergence의 최소값인 0이 되는 순간은 \(Q_k = p(x \vert z_k; \theta)\)인 순간이다. 그리고 \(p(x \vert z_k; \theta)\)는 언제나 gaussian distribution, \(\mathcal{N}(x; \mu_k, \Sigma_k)\)이다. 그렇기 때문에 \(\mu_k, \Sigma_k\)는 정확하게 아래 처럼 계산이 된다.

즉 우리는 \(\theta\)를 그저 cluster affinities에 따라서 weight을 부여한 data의 mean, variance로 update하면 된다는 것을 알 수 있다. 유사하게 class prior도 아래처럼 계산할 수 있다.

이런 GMM의 E-M fitting과정은 아래 figure 처럼 시각화 될 수 있다.

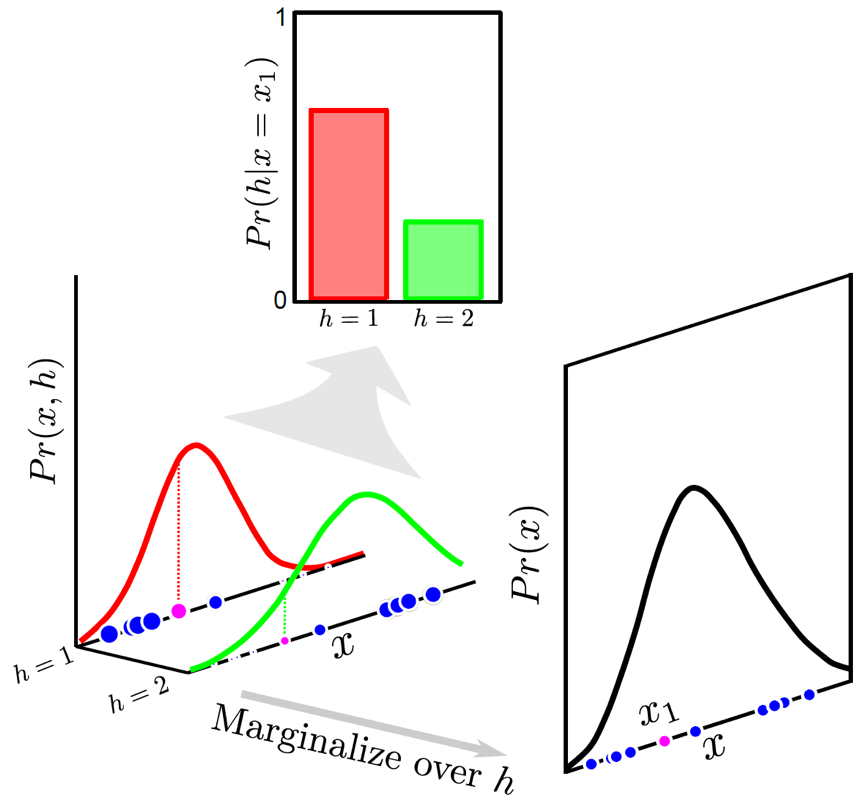Fig. Expectation. Pink sample이 각 cluster (component)로 할당될 확률이 몇인지를 계산할 수 있다.

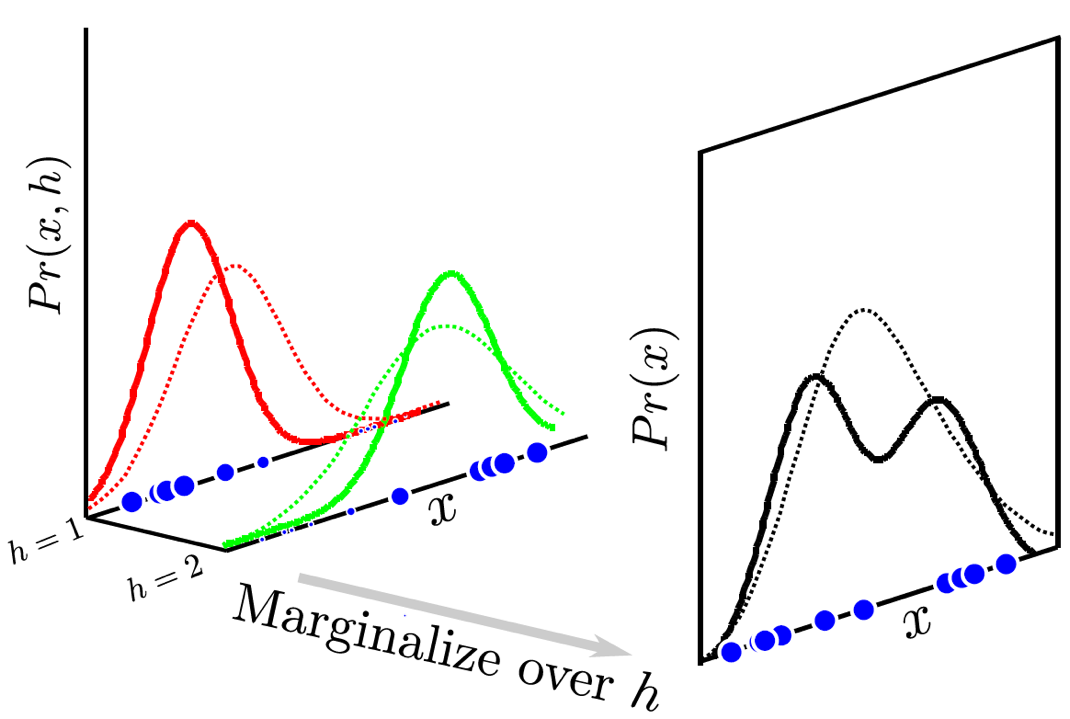Fig. Maximization을 통해 mean variance를 update한다.

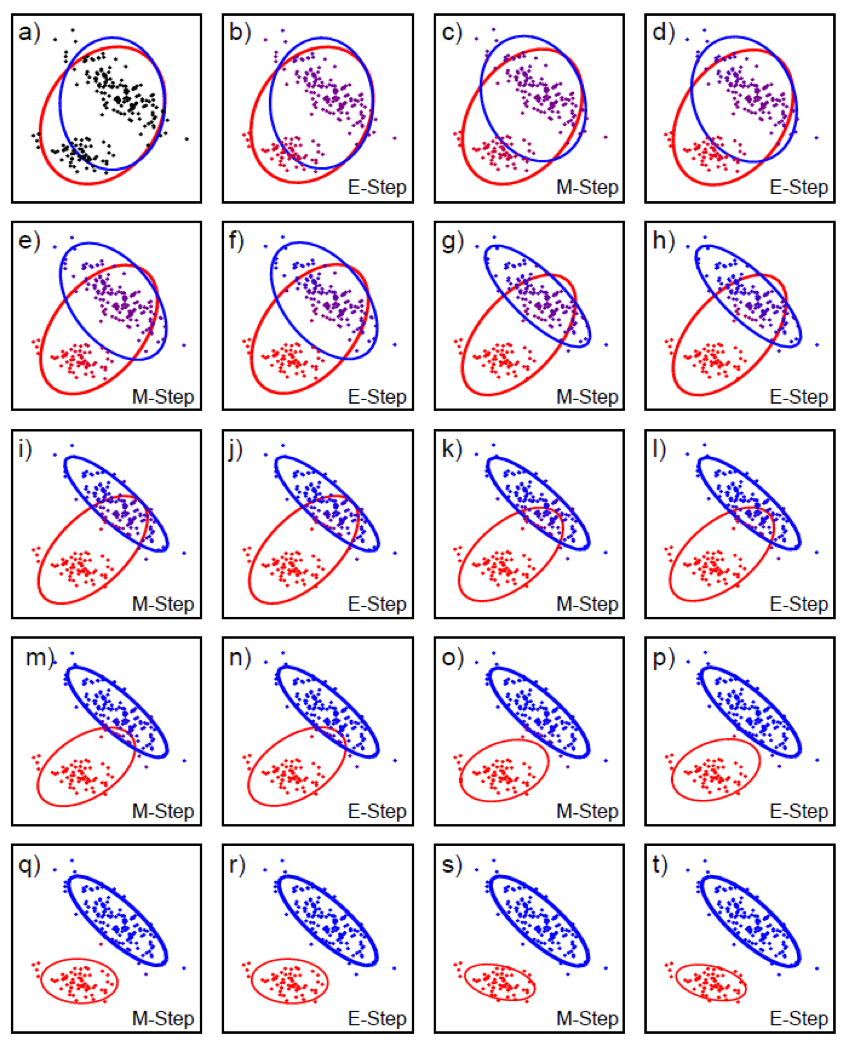Fig. 2차원 feature dim인 경우에 어떻게 clustering이 되는지 볼 수 있다.

추가적으로 원래의 objective function을 미분해서 0을 놓고 문제를 풀어도 GMM에서는 충분히 \(\mu_k, \Sigma_k\)를 찾을 수 있다.

이는 PRML등의 자료를 찾아보길 바란다. 어쨌든 한 번에 marginal liklihood를 maximize할 수 없어, \(\theta_t\)를 기준으로 \(Q_k\)를 구하고 (E-step), 구한 \(Q_k\)를 기준으로 \(\theta_t \rightarrow \theta_{t+1}\) update를 한다는 걸 (M-step) 반복함으로써 문제를 푼다는 것을 기억하면 된다.

EM vs Variational Inference (VI)

그런데 왜 EM이 수렴 (converge)하는 것일까? 그리고 \(z\)의 distribution이 더 복잡하다면 (continuous하다면) 어떻게 posterior를 계산해야 할까? 이번에는 EM을 Variational Inference (VI) framework로 casting해서 생각해보려고 한다.

VI는 말 그대로 inference 를 위한 method이다. 보통 bayesian approach같은데서 \(p(x \vert \theta)\)가 아니라 \(p(\theta \vert x)\)같은 posterior를 modeling하여 추론 시 test sample, \(x^{\ast}\)에 대해서 \(\int p(\theta \vert x, x^{\ast})\)를 계산 하는데, 이는 posterior distribution을 계산하고 적분을 해야 하므로 사실상 계산이 불가능하다.

이런 inference를 optimization 문제로 바꿔 푸는 대표적인 방법론들이 바로 Laplace Approximation, VI 같은 것들인데, 쉽게 말하자면 \(p(\theta \vert x)\)를 우리가 다루기 쉬운 distribution인 예를 들어 zero mean, unit variance의 gaussian distribution 으로 modeling하는 식으로 학습을 한 뒤에 inference시에 이것을 사용한다고 생각하면 된다.

먼저 variational lower bound를 계산해보자.

여기서 부등식이 들어가는 부분에서 expectation과 log의 위치가 바뀌는데, 이는 Jensen’s Inequality를 사용했기 때문이다.

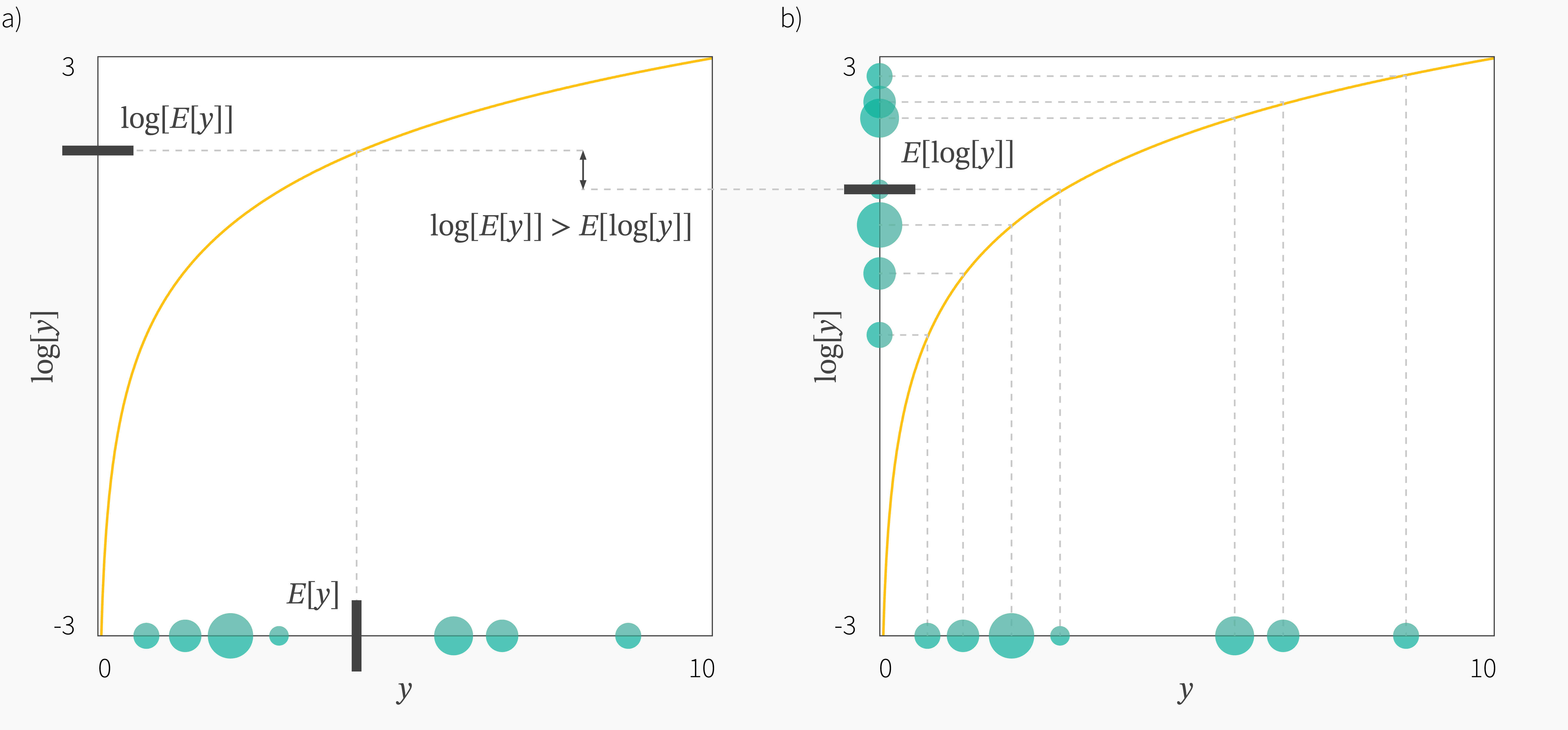Fig. Jensen’s Inequality

Jansen’s inequality 때문에 우리는 원래 maximize 하려는 수식과는 조금 다른 lower bound를 얻게 되었는데, 이를 Evidence Lower BOund (ELBO)라고 부른다.

이 때 약간의 error가 발생하게 됐는데, 이는 아래 수식처럼 현재 parameter, \(\theta\)를 가지고 계산한 posterior \(p(z \vert x; \theta)\)와 \(q(z)\)라는 임의로 도입한 distribution이 얼마나 다른가? 를 의미하는 KL divergence 만큼이다.

그러면 과연 언제 ELBO가 커질까? 바로 KL term이 0이 될 때로 \(q=p(z \vert x)\)인 순간이다. 이를 bound가 tight해진다고 하는데, 아래 그림을 보면 EM처럼 번갈아가면서 bound를 tight하게 만들고 (q에 대해 optimization, E-step), 그 bound내에서 maximization이 되는 parameter로 update를 하는 것 (\(\theta\)에 대해 optimization M-step)을 반복하게 되는데, 이는 EM을 하는것과 같다.

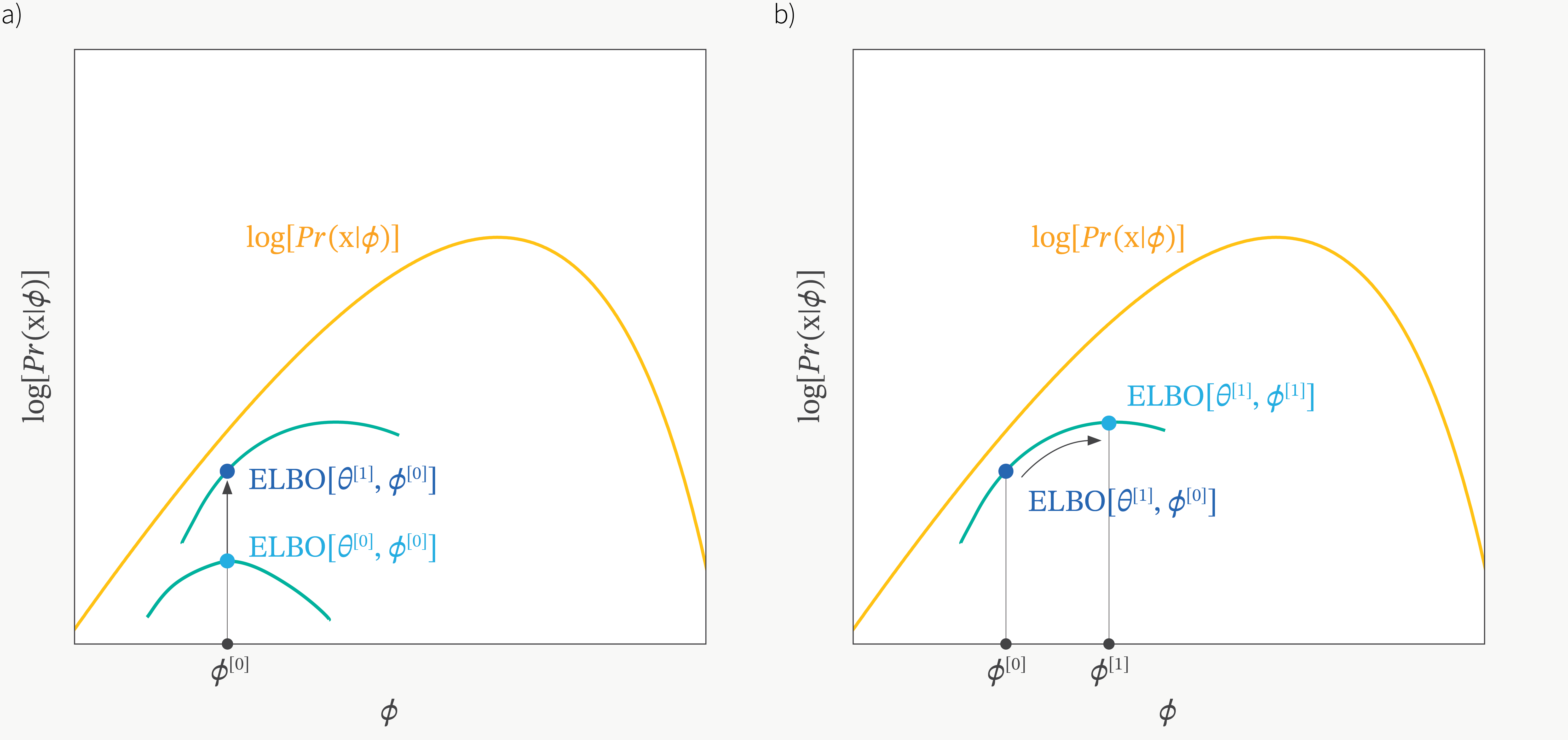Fig. figure에는 \(\phi, \theta\) 두 개의 parameter 가 등장하는데, 이는 posterior를 approximate하는 parameter를 추가했기 때문이며 곧 다루도록 하겠다.

Properties of EM

앞선 discussion들에 의해 우리는 EM이 다음의 두 가지 특성이 있음을 알 수 있다.

• 1.marginal likelihood는 매 EM cycle마다 증가한다.
• 2.marginal likelihood는 true global maximum에 의해 upper-bound되어 있으며 1번에 의해 매 cycle마다 marginal likelihood가 증가하므로 결국 EM은 수렴한다.

그러나 안타깝게도 우리는 non-convex optimization을 하기 때문에 매 iteration마다 global optimum을 찾을 수 있다는 보장이 없다. 사실 practical하게는 EM은 매번 local optimum으로 수렴할 수는 있고, 더욱이 이는 model parameter의 initialization에 크게 의존하기에 여러 intial point, \(\theta_0\)이 각기 다른 solution을 return 한다. 그러므로 EM을 쓸 때는 여러 번 algorithm을 restart해서 best one을 찾는 것이 흔하며 좋은 init point를 찾는 것이 중요한 연구 분야 중 하나라고 한다.

Learning Deep Generative Models

What's Wrong with EM?

앞서 LVM을 EM으로 충분히 학습할 수 있음을 배웠다. 하지만 deep generative model을 EM으로 학습하기 하기위해 E step에서 approximate posterior, \(p(z \vert x)\)를 계산하는 부분이 너무 어려워진다. 이를 사실상 계산 불가능하다 (intractable) 라고 얘기한다.

그리고 M step에서는 전체 dataset을 보고 optimize를 해야 하는 문제가 있는데, deep learning의 dataset size를 생각할 때 이는 불가능하다. Mini-batch로 계산하는 online EM이 존재하기 때문에 이를 쓰면 되긴 한다고 한다.

Auto-Encoding Variational Bayes (AEVB)

The Variational Auto-Encoder

References

• Stefano Ermon Group’s Lecture Notes
  • MAP inference
  • Variational inference
  • Learning in latent variable models
  • The variational auto-encoder
  • Bayesian Learning
• Others
• LATENT VARIABLE MODELS from DLVU
• Variational Inference from David M. Blei