Precision, Recall and F1 Score
30 Aug 2022< 목차 >
Introduction
Classification (분류) 문제를 풀 때는 Accuracy (정확도) 를 재는 것이 일반적입니다.
하지만 accuracy만 metric 으로 쓰는 것이 좋은 것은 아닙니다.
좀 더 디테일하게 결과를 분석하기 위해 Precision, Recall 그리고 F1-Score 라는 것을 더 중요한 지표로 볼 때가 있습니다.
Precision, Recall을 직관적으로 이해하기 위해 다음의 예시를 살펴봅시다. Image에서 사람을 자동으로 검출해주는 program 이 두 개가 있다고 칩시다.
- A program: 99%의 성능으로 사람을 검출함.
- B program: 50%의 성능으로 사람을 검출함.
문득 보기에는 A program 이 대단하다고 생각할 수 있겠으나, 이는 A와 B에 오검출이 없다는 가정이 깔렸을 때 그렇습니다. 만약에 A program은 사실 image 한장당 평균 10건의 오 검출을 범하고 있다고 칩시다. 즉 정확히 사람이 아니어도 사람같기만 하면 다 사람이라고 하는건데, 반면에 B program은 검출돼야 할 사람 100명 중 50명 밖에 검출이 안됐지만 오검출은 왠만하면 안나온다고 칩시다. 그러면 A와 B중 어떤게 더 좋은 program이 되는걸까요?
혹은 주어진 4~5 개의 문장으로 이루어진 하나의 문단에 대해서 .,!? 등 구두점을 검출해주는 program의 경우도 생각해 봅시다. 이는 음성 인식이 된 결과물에 보통 구두점이 없기 때문에 사용되는데 구두점이 안찍혀 있어도 문장을 끊어읽을 수 없어 보기 힘들겠지만, 아무데나 구두점이 매우 빈번하게 찍힌다면 그건 그거대로 문제가 될겁니다.
이 때 얼마나 원하는 target을 빠뜨리지 않고 잘 잡아냈는가 (구두점을 잘 찍었는가? 사람을 잘 찾아냈는가?)를 나타내는 지표를 Recall (재현율, 검출율) 이라고 하며, 검출된 결과물이 얼마나 정확한가?를 Precision (정밀도) 라고 합니다.
그럼 어떤 평가 지표 (metric)를 더 중요하게 봐야할까요? 이는 내가 만들고자하는 application이 무엇인지에 따라 다릅니다. 사람을 찾아주는 program에 대해 다시 생각해 봅시다. 만약 이것이 범죄자 (의 얼굴)을 탐지하는 application이라고 생각해 봅시다. 이 때는 실제 범죄자를 놓치지 않고 다 잡아야 할겁니다. 즉 Recall이 높아야 합니다.
그러면 Program은 아마도 target을 빠뜨리지 않고 잘 잡아내기 위해서는 조금만 비슷한 output이어도 다 그렇다고 대답해야 할겁니다. 그런데 이렇게 되면 마치 과녁에 화살을 많이 쏘게 됨으로써 오류가 날 가능성이 높아지게 (precision은 낮아지게) 될 수 있습니다. 사실 precision도 높고 recall도 높은 model을 만들기란 매우 어렵습니다. 왜냐하면 둘은 방금 설명드린 것 처럼 tension 관계에 있기 때문에 recall이 높아지면 precision은 낮아지기 마련이기 때문입니다. (그렇지만 무고한 시민을 camera가 detect 하더라도 다시 훈방조치 하면 되니까 이 경우에는 recall에 신경쓰면 될겁니다.)
구두점 검출기의 경우에는 recall이 높다는 것은 문장의 끝이나 중요한 구분점을 놓치지 않는 것이 중요하다고 판단되면 recall을 중요하게 보고, 잘못된 위치에 구두점이 찍히면 문장의 의미가 왜곡될 수 있으므로, 이러한 상황에서는 precision이 더 중요할겁니다.
이렇게 둘 다 중요하기 때문에 한쪽에 가중치를 두지 못하겠다 싶으면 다른 metric을 보는 경우도 있는데 보통 이 둘을 조합한 F1-Score라는 것을 봅니다.
F1-Score에 대해서는 Precision, Recall에 대해서 좀 더 자세히 알아본 뒤 설명드리도록 하겠습니다.
Precision and Model Bias
한가지 더 생각해 볼 점이 있다면, 정밀도라는 의미의 precision 은 model의 accuracy와 어떻게 다르냐? 입니다.
우리가 훈려소에서 사격을 한다고 칩시다. 비슷한 곳에 탄착군이 형성되는 건 precision가 높다는 의미입니다. 하지만 precision이 높아도 탄착군이 정 중앙에서 조금 벗어난 곳에 형성될 수도 있습니다. 이럴 경우 정확도는 낮다고 하며 중앙과 떨어진 만큼 model bias가 있다고 합니다. (bias는 2차원 평면에 직선을 그릴때 절편이라고 할 수 있으니 원점에서 얼마나 벗어났는지를 의미하기도 합니다)
그러니까 preicison은 매우 높지만 accuracy는 낮은 경우가 있을 수 있고, 그 반대일 수도 있고, 이상적인 경우로는 둘 다 높은 경우도 있을 수 있습니다.
우리가 마찬가지로 분류 문제를 푼다고 할 때, 만든 model이 preicison이 높다는 것은 같은 (비슷한) sample을 여러 번 평가했을 때 이것이 모두 다 비슷한 쪽으로 분류되는가? 즉 유사한 sample에 대해서 true, false… 라고 계속 헷갈리면서 말하면 반복 정밀도인 precision이 낮다고 얘기할 수도 있겠습니다.
Example: Binary Classification
이번에는 이진 분류 (Binary Classification) 문제를 통해 더 정확히 Precision, Recall에 대해 알아봅시다. 어떤 data sample이 실제 정답이 1인데 모델이 이를 1로 예측한 경우와 0으로 예측한 경우, 또는 반대로 data sample이 실제 정답은 0인데 모델이 이를 1 로 예측한 경우와 0 으로 예측한 경우 총 4가지를 나눌 수 있고 이를 각각 아래처럼 나타낼 수 있습니다.
| Predicted : 1 | Predicted : 2 | |
|---|---|---|
| Actual : 1 | True Positive (TP) | False Negative (FN) |
| Actual : 0 | False Positive (FP) | True Negative (TN) |
이를 Confusion Matrix 라고 합니다.
이해를 돕기 위해서 분류 문제가 암 세포가 양성인지 아닌지를 판단하는 문제라고 한번 생각해 보겠습니다.
그렇다면 각 TP, FN, FP, TN은 다음과 같은 의미를 가지게 됩니다.
TruePositive (TP) : Positive Instance 가 Positive 로 분류됐을 경우 (종양이 양성인데 모델이 양성이라고 예측한 경우 (정답))- False Negative (FN) : Positive Instance 가 Negative 로 분류됐을 경우 (종양이 양성인데 모델이 양성이 아니라고 예측한 경우)
- False Positive (FP) : Negative Instance 가 Positive 로 분류됐을 경우. (종양이 음성인데 모델이 양성이라고 예측한 경우)
TrueNegative (TN) : Negative Instance 가 Negative 로 분류됐을 경우 (종양이 음성인데 모델이 양성이 아니라고 예측한 경우 (정답))
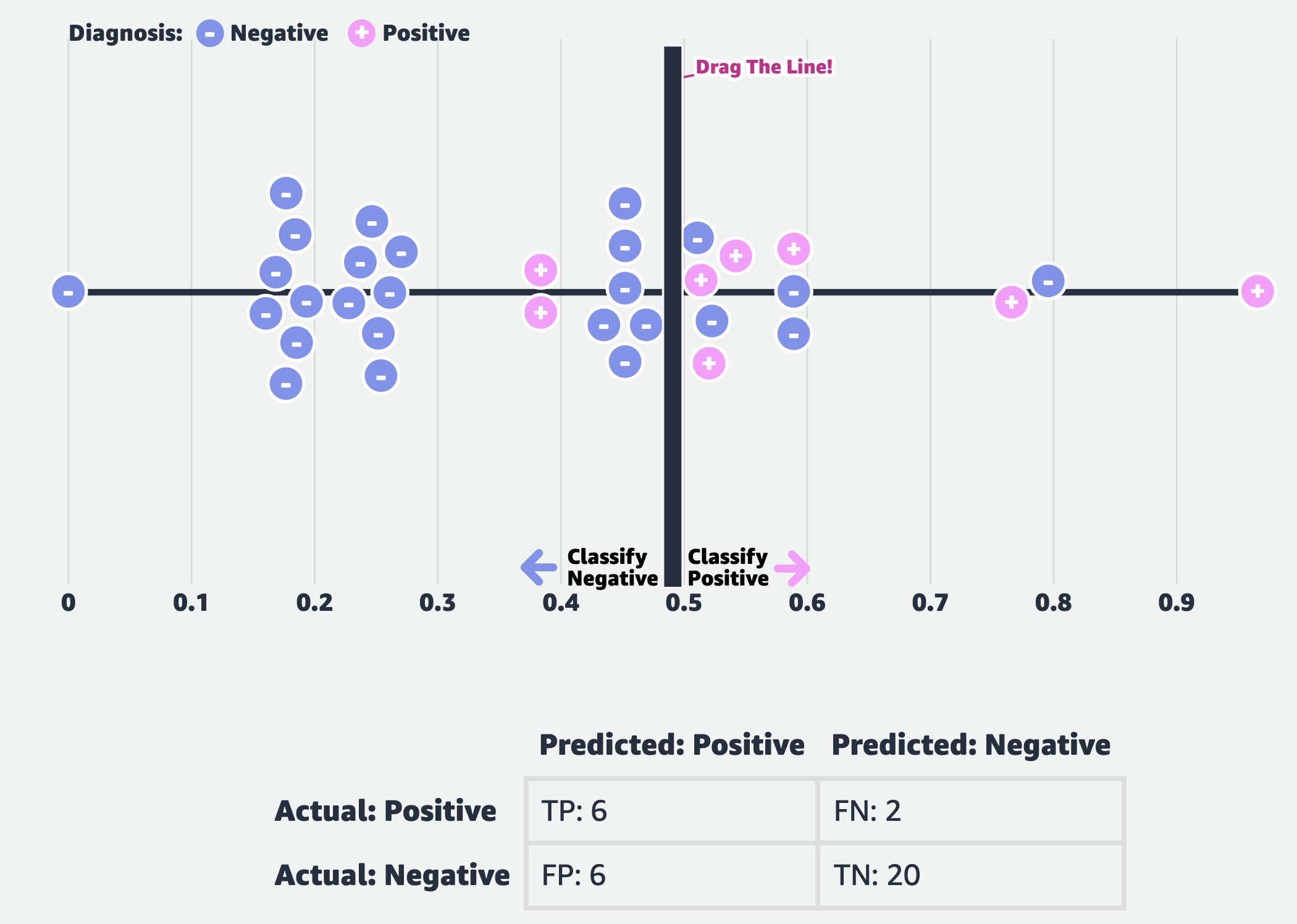 Fig. TP, FP, FN, TN when Decision boundary at 0.5
Fig. TP, FP, FN, TN when Decision boundary at 0.5
여기서 한번 정확도 (Accuracy) 를 재 보도록 하겠습니다.
\[\text{Accuracy} = \frac{\text{TP} + \text{TN}}{\text{TP} + \text{FP} + \text{FN} + \text{TN}} = \frac{27}{34} \approx 79 \%\]하지만 이렇게 단순히 Accuracy 를 재는 것은 문제가 있을 수 있는데, 그 이유는 바로 Data Imbalance (데이터 불균형) 이 심하다는 것입니다. 왜 이것이 문제일까요?
이런 경우 만약 모델이 전체 sample 을 다 음성이라고 예측해버려도 정확도만 본다면 \(76 \%\) 의 정확도는 나오게 됩니다.
즉 우리에게 중요한건 눈 먼 accuracy 보다는 실제로 양성인 경우를 실제로 양성으로 분류했느냐? 같은 detail한 metric 일 수도 있는 것인데요,
이것이 바로 앞서 설명드린 Preicison, Recall 같은 값이 됩니다.
Precision and Recall
먼저 Positive Instance 에 대한 TP, FP 만 살펴봅시다.
모델이 양성으로 예측한 sample들 중 실제로 양성이었던 케이스에 대해서 실제 양성이었던 경우를 생각해보면 아래와 결과를 내게 됩니다.
이를 바로 Precision 이라고 부릅니다.
Precision은 사전적 의미만 보면 Accuracy와 비슷한데,
말씀드린 것 처럼 모델이 얼마나 Positive Prediction 을 잘 했느냐 (정확하게 했느냐) 를 나타냅니다.

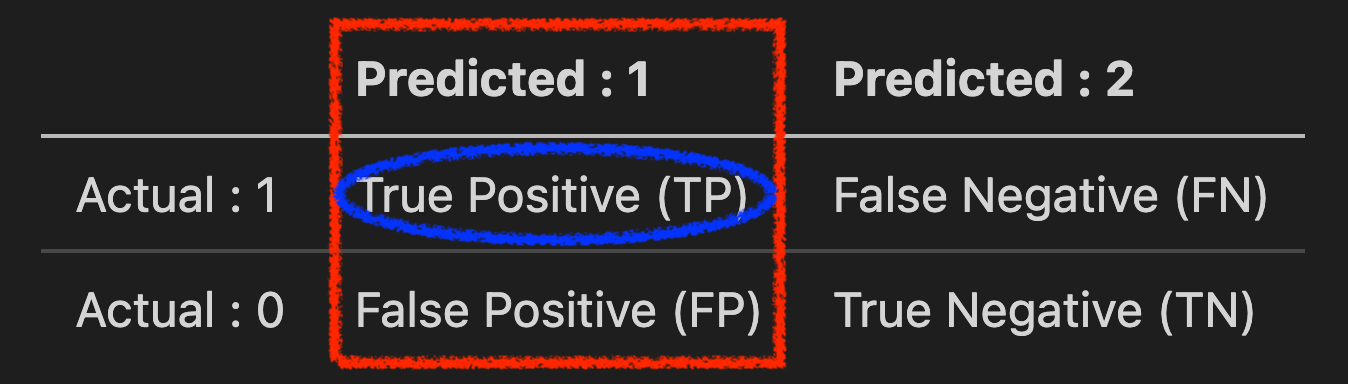
이는 FP 가 FN 보다 더 중요하다고 생각될 때 쓰기 좋은 Metric 이라고 하는데, 분모에 FP 가 들어가 있기 때문에 FP 가 늘어날수록 Precision 의 값이 작아질 것이라는 걸 알 수 있습니다.
예를 들어 아래의 두 가지 대푲거인 이진 분류 task 를 생각해봅시다.
- 종양을 양성인지 음성인지 분류하는 task
- E-mail 을 spam 인지 아닌지 분류하는 task
E-mail 분류 문제는 먼저 이렇게 생각할 수 있습니다.
- Program이 spam이라고 분류한 것들은 실제로 다 spam 이었길 기대함.
- 즉
실제로 spam이 아닌 메일을 spam으로 분류하는 경우 (FP)가 spam인 메일을 spam이 아니라고 예측하는 경우 (FN) 보다 중요함.
무슨 말이냐? spam인 mail이 잘못분류돼서 휴지통으로 들어가지 않아도 user입장에서는 문제가 없지만, 만약 중요한 mail을 휴지통으로 잘못 보내버리면 이것은 큰 문제가 될 수도 있다는 겁니다.
하지만 종양을 분류하는 task에서는 종양이 음성일 때 양성으로 분류 하는 경우 (FP) 가 종양이 양성일 때 음성으로 분류하는 경우 (FN) 보다 중요할까요? 아닙니다, 이 때는 FN이 중요합니다. 둘 다 오진 (False)이 맞지만 전자의 경우 (FP) 치료비 잠깐 더 내면 되는 데 반해 후자 (FN) 의 경우는 사람이 죽기 때문에 아주 치명적이게 되는거죠.
- Program이 실제로 양성 종양인 sample은 모두 양성이라고 잡아내길 기대함.
- 즉
종양이 양성일 때 음성으로 분류하는 경우 (FN)에 더 초첨을 맞춤.
이런 경우에 쓰는 것이 바로 Recall입니다.
Recall 은 Positive Instance 를 실제로 얼마나 정확하게 예측했느냐를 의미합니다.
즉 Positive Instance 가 잘 분류 됐느냐 마느냐는 TP, FN 이 나타내고 이를 이용해
로 나타낼 수 있습니다.

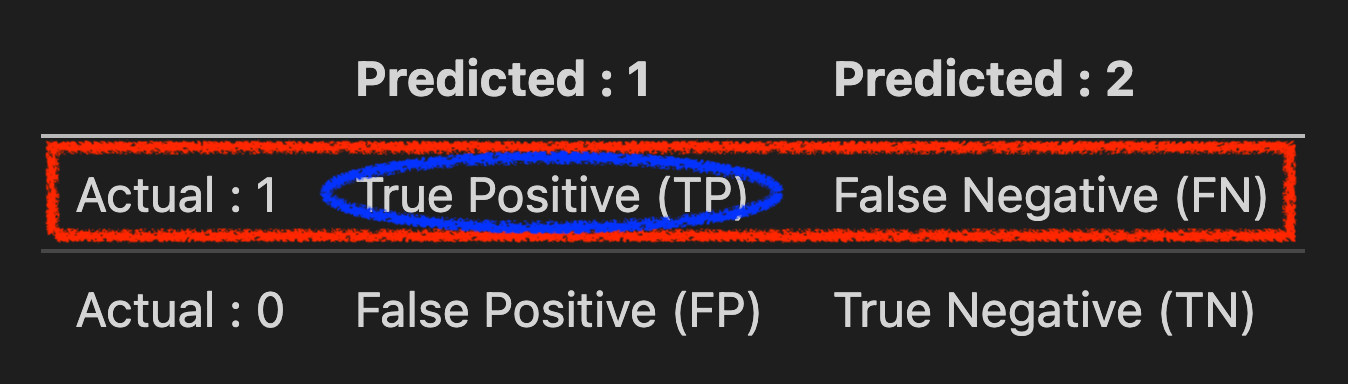
마찬가지로 아까의 예시에 대해 Recall을 계산해 봅시다.
\[\text{Recall} = \frac{\text{TP}}{\text{TP} + \text{FN}} = \frac{6}{8} \approx 75 \%\]Recall은 실제로 양성인 Sample들을 양성으로 잘 분류했느냐를 판단하는 Metric 이 되기 때문에 아까 종양 분류 task의 경우에 더 적합할 겁니다.
학습한 모델이 실제로 Recall 과 Precision 가 둘 다 높으면 이상적이겠지만 실제 상황에서는 두 값 사이에 tension이 존재한다고 앞서 말씀드렸죠. 이런 경우 둘 다 반영한 Metric이 있다고 말씀드렸는데, 바로 F1-Score 입니다.
F1-Score
F1-Score (F-Measure) 는 아래와 같이 계산됩니다.
Recall과 Precision 의 조화 평균 (Harmonic mean) 을 의마하는데, Precision 과 Recall 이 각각 TP, FP, FN 에 대한 수식이기 때문에 이를 풀어서 쓰면 아래와 같습니다.
\[F_1 = \frac{ \text{TP} }{ \text{TP} + \color{blue}{ \frac{1}{2} ( \text{FP} + \text{FN} ) } }\]Precision 과 Recall 이 아래와 같았다는 걸 생각해보면
\[\text{Precision} = \frac{\text{TP}}{\text{TP} + \text{FP}}\] \[\text{Recall} = \frac{\text{TP}}{\text{TP} + \text{FN}}\]F1 Score 는 두 Measure 에서 중요하게 생각하는 FN, FP 가 더해져 분모에 들어갔기 때문에 둘 다 고려한 값이라고 생각할 수 있습니다.
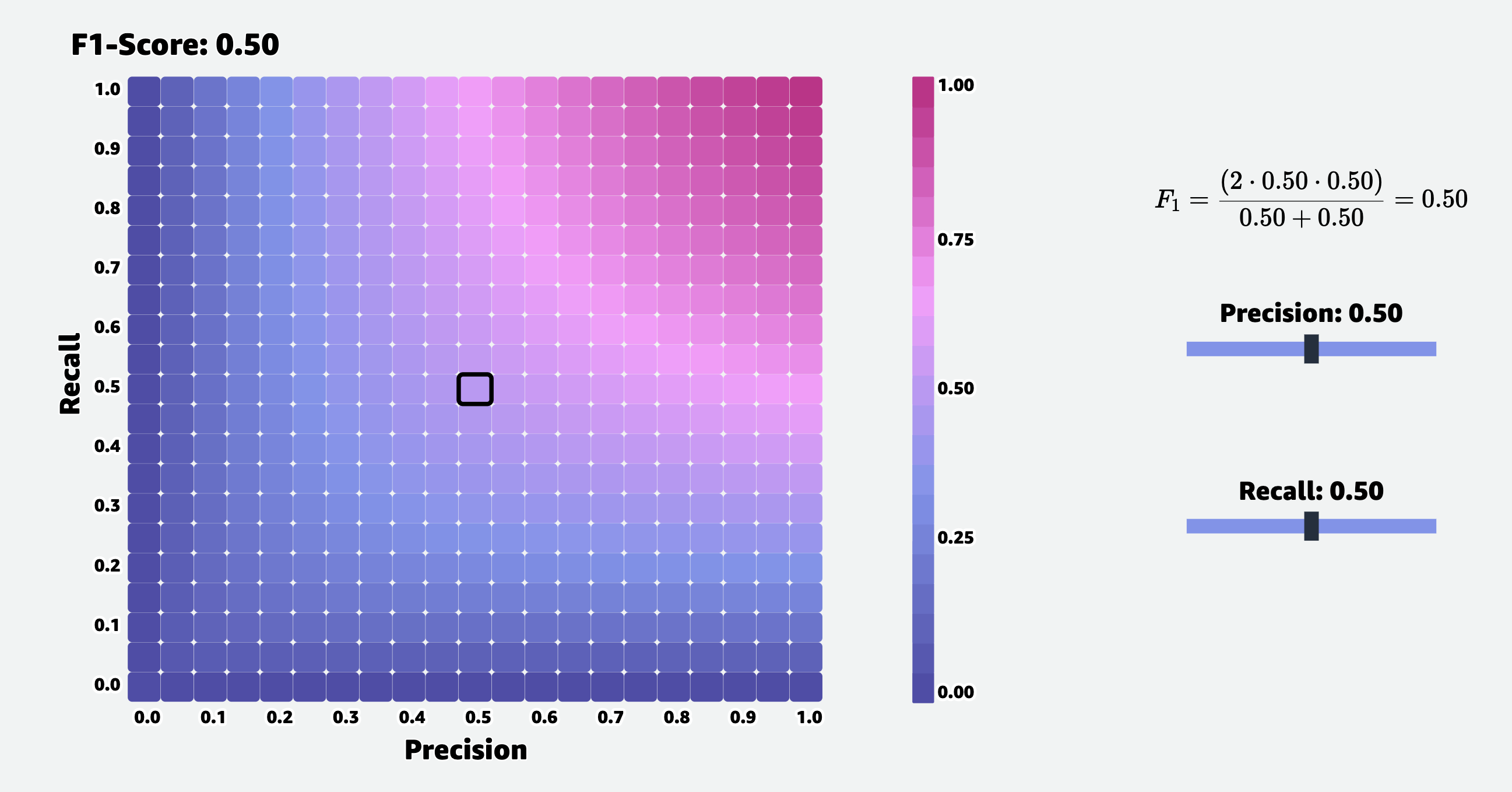
하지만 F1-Score 도 만능은 아닌데요, Negative 에 대한 값들을 고려하지 않았기 때문입니다. 그래서 True Negative 등이 중요하다고 생각되면 다른 Metric을 써야 한다고 합니다.
Trade-Off
앞서 종양을 분류하는 task를 다시 생각해 봅시다.
 Fig. TP, FP, FN, TN when Decision boundary at 0.5
Fig. TP, FP, FN, TN when Decision boundary at 0.5
분류 문제를 푼다는 것은 실제로는 결정 경계면 (Decision Boundary) 를 긋는다는 것과 같습니다. 그리고 이 decision boundary의 위치는 program (model)의 예측값이 0.5인 부근을 기준으로 나눌것이냐? 즉 threshold가 어떤 값이냐? 에 따라서 이동하게 되는데요, decision boundary의 위치에 따라 Accuracy, Precision, Recall 그리고 F1-Score 등이 바뀌는지를 살펴봅시다.
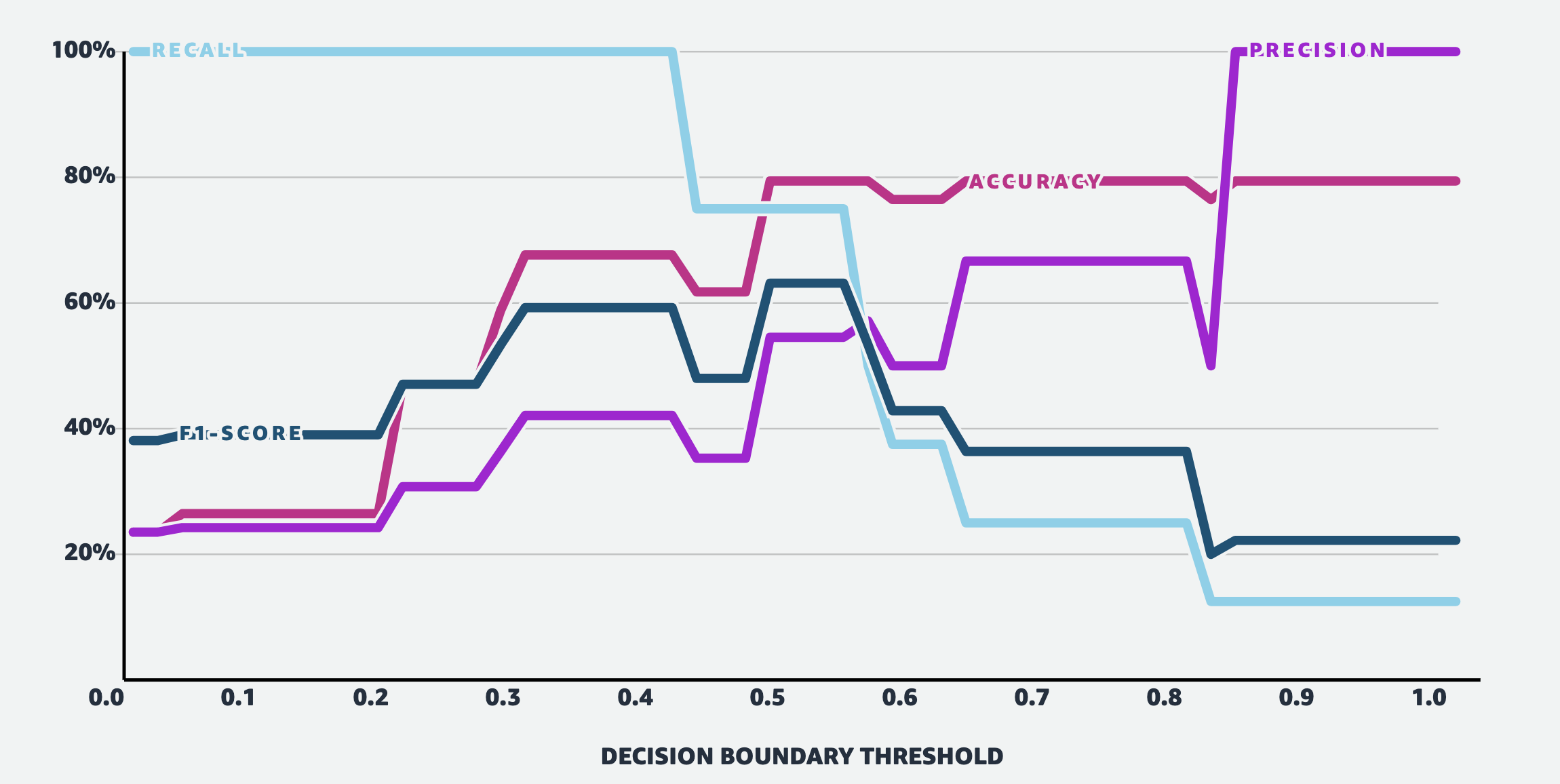 Fig. Trade-off between Accuracy, Precsion, Recall and F1-Score
Fig. Trade-off between Accuracy, Precsion, Recall and F1-Score
아까 말씀드린 것 처럼 Precision 과 Recall 사이에는 Trade-Off 가 있는 걸 알 수 있습니다. Recall의 경우 threshold가 낮을경우 100%가 나오는 걸 볼 수 있습니다. 이는 당연하게도 threshold==0.1인 경우를 생각해보면 model이 어떤 input에 대해서 positive, negative 중 positive의 확률을 0.1만 할당해도 그 sample은 positive가 되기 때문입니다. 이러면 모든 환자가 암 양성이라고 하는것이 되죠.
반면에 Preicison은 threshold값이 올라갈수록 (기준이 깐깐해 지는거죠), 그 값이 올라가게 됩니다.
F1-Score는 왼쪽부터 Threshold 가 증가할수록 값이 커지다가 다시 줄어드는걸 알 수 있네요. 그리고 Accuracy 는 Precision 과 유사하게 거의 우샹향이지만 threshold가 0.5 이던 0.8, 1.0 이던 Accuracy 는 비슷해서 어떤 model이 더 좋은지 알수 없는 반면, F1-Score를 기준으로 보면 0.55 부근에서 고점을 찍고 내려오기 때문에 model을 판단하는 기준으로 F1이 꽤 괜찮은 metric으로 쓰일 수 있다는 걸 알 수 있습니다.
F1-Score in Deep Learning Application
F1-Score 는 고전 ML 분류 문제에만 사용되는 것이 아니라 DL application들에도 많이 쓰입니다. 특히 객체 탐지 (Object Detection) 같은 분야에서는 accuracy보다는 precision이나 f1-score를 많이 쓴다는 것 같고, 자연어 처리 (Natural Langueg Processing; NLP) 의 질의 응답 (Question Answering; QA) task 나 음성 인식 (Automatic Speech Recogniton; ASR) task 의 Rare word detection, punctuation detection 같은 데서도 쓰입니다.
(Macro-averaged) F1-Score in Question Answering (QA)
Stanford University 는 Stanford Question Answering Dataset (SQuAD) 라는 데이터 셋을 공개하면서 이에 대한 평가 Metric 으로 Exact Match (EM) Score 와 F1-Score 를 예시로 들었는데요,
 Fig. SQuAD 는 deep learning model이 sentence embedding을 통해 feature를 뽑은 뒤 Question 에 맞는 답을 내는 task이다.
Fig. SQuAD 는 deep learning model이 sentence embedding을 통해 feature를 뽑은 뒤 Question 에 맞는 답을 내는 task이다.
EM 은 모델이 내놓은 정답이 실제 정답과 정확히 일치해야 하는것이며, F1 Score 는 우리가 알고있는 Precision Recall 을 내서 조화 평균을 낸 값입니다.
왜 이렇게 했는지?에 대해 생각해보자면, deep learning model이 주어진 문단에서 정답에 해당하는 단어 구를 추출 (Parsing) 해 와야 하는데 만약 정답이 5 단어로 이루어져 있다고 치면 여기서 하나라도 틀리면 틀렸다고 하는것이 너무 가혹하기 때문일 것 같습니다. 뭐 다른 의미가 없는 단어가 몇 개 포함되더라도, 질문에 대한 정답으로 꼭 포함돼야하는 의미있는 단어가 포함되기만 하면 되니 Recall같은걸 보면 되겠지만 우리는 F1이 더 안전하고 보수적인? 걸 알기 때문에 이 값을 쓴 것 같습니다.
SQuAD 논문에서는 아래와 같은 Table 로 두 Measure를 비교했습니다.
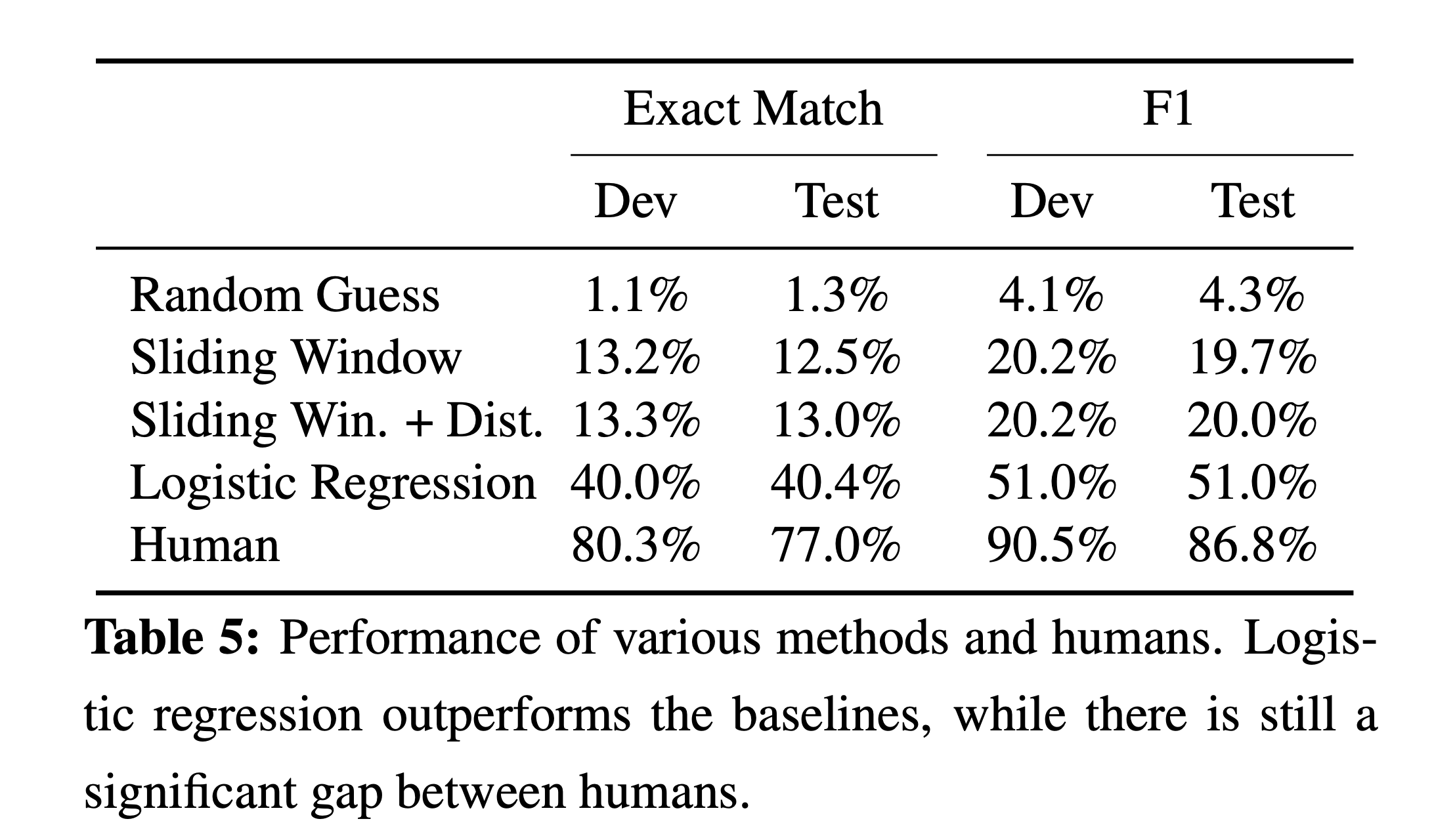 )
Fig. EM 과 F1 비교. 단어를 다 맞춰야 하는 EM과 달리 F1이 더 느슨한 (loosen) Measure 라고 할 수 있다.
)
Fig. EM 과 F1 비교. 단어를 다 맞춰야 하는 EM과 달리 F1이 더 느슨한 (loosen) Measure 라고 할 수 있다.
여기서 생각해 볼 점은 EM이 높으면 과연 무조건 좋은 model일 것이냐? 라는 건데, 제 의견이지만 EM이 100인것은 완전히 Overfitting했다는 의미일 수도 있어서 마냥 좋은건 아닐 수도 있을 것 같습니다.
Python Implementation
마지막으로 이해를 돕기위해 이를 구현체를 가져왔습니다.
아래처럼 정답과 예측한 문장을 Normalize 해주고 F1 Score 는 예측한 문장의 단어이 정답 문장에 있는 지를 Set 함수를 사용하고 이를 예측한 문장의 길이로 나눠 Precision 을 계산하고 실제 정답 문장의 길이로 나눠 Recall 을 구합니다. 그리고 이를 평균내서 F1-Score를 구합니다.
반면 EM은 정확히 문장이 일치 (==) 하지 않으면 0 을 return 하는 걸 볼 수 있고,
def normalize_text(s):
"""Removing articles and punctuation, and standardizing whitespace are all typical text processing steps."""
import string, re
def remove_articles(text):
regex = re.compile(r"\b(a|an|the)\b", re.UNICODE)
return re.sub(regex, " ", text)
def white_space_fix(text):
return " ".join(text.split())
def remove_punc(text):
exclude = set(string.punctuation)
return "".join(ch for ch in text if ch not in exclude)
def lower(text):
return text.lower()
return white_space_fix(remove_articles(remove_punc(lower(s))))
def compute_exact_match(prediction, truth):
return int(normalize_text(prediction) == normalize_text(truth))
def compute_f1(prediction, truth):
pred_tokens = normalize_text(prediction).split()
truth_tokens = normalize_text(truth).split()
# if either the prediction or the truth is no-answer then f1 = 1 if they agree, 0 otherwise
if len(pred_tokens) == 0 or len(truth_tokens) == 0:
return int(pred_tokens == truth_tokens)
common_tokens = set(pred_tokens) & set(truth_tokens)
# if there are no common tokens then f1 = 0
if len(common_tokens) == 0:
return 0
prec = len(common_tokens) / len(pred_tokens)
rec = len(common_tokens) / len(truth_tokens)
return 2 * (prec * rec) / (prec + rec)
실제 아래와 같은 Question 이 들어왔을 때 모델이 예측한 값이 "water bodies" 일 경우,
이 질문에 대한 사람이 Labeling 한 정답이 아래처럼 세 개는 되기 때문에 이들과 EM, F1-Score 를 각각 재면서 그 값들 중 가장 큰 값들을 각각 계산해 최종 EM, F1-Score 로 씁니다.
question = "Where on Earth is free oxygen found?"
prediction = "water bodies"
gold_answers = ['water', "in solution in the world's water bodies", "the world's water bodies"]
em_score = max((compute_exact_match(prediction, answer)) for answer in gold_answers)
f1_score = max((compute_f1(prediction, answer)) for answer in gold_answers)
print(f"Question: {question}")
print(f"Prediction: {prediction}")
print(f"True Answers: {gold_answers}")
print(f"EM: {em_score} \t F1: {f1_score}")
Question: Where on Earth is free oxygen found?
Prediction: water bodies
True Answers: ['water', "in solution in the world's water bodies", "the world's water bodies"]
EM: 0 F1: 0.8
이 외에도 추천 시스템 (Recommendation System) 등에서도 많이 쓰인다는 것 같으니 관심있으신 분들은 더 찾아보시면 좋을 것 같습니다.