Notes

Support Vector Machine (SVM) and Kernel Trick

06 Jul 2022

< 목차 >

Generalization Problem in Frequentist Solution

이진 분류 (Binary Classification) 문제를 푼다고 생각해보죠. Logistic Regression 을 해야 할 텐데요,

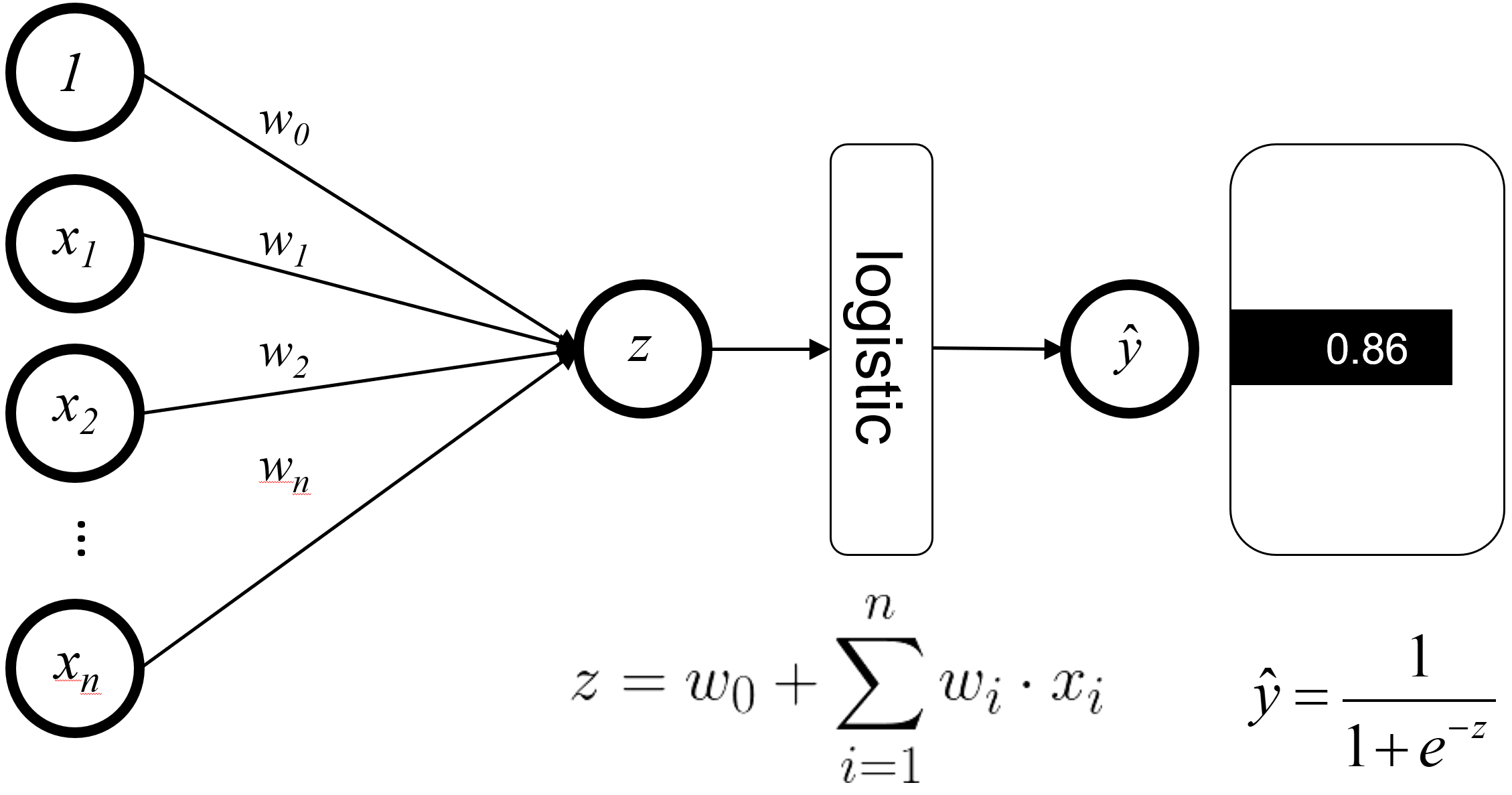logistic_vs_nn_fig1 Fig. Logistic Regression. Source From Link

Maximum Likelihood Estimation (MLE) 방법을 사용해서 파라메터 셋을 하나 찾을겁니다. 즉 결정 경계 (Decision Boundary)를 딱 하나 긋는, 점 추정 (Point Estimation) 을 하는 것이 일반적일 겁니다.

하지만 이럴 경우 얼마 있지도 않은 데이터에 오버피팅 할 수 있는 문제가 있습니다. 즉 일반화 (Generalization) 문제가 있는 건데요,

nyu_svm_slide_fig1 Fig.

이는 Prior를 도입해 Bayesian Approach (MAP나 Bayesian Inferece)를 사용함으로써 어느정도 해결할 여지가 보이긴 하나 계산량이 너무 많이드는 문제점이 있을 수 있습니다.

여기에 추가로 비선형적인 (Non-Linear) Decision Boundary 를 구하기 위해 층을 하나 더 쌓아 Neural Network (NN) 알고리즘을 사용한다고 생각해 봅시다.

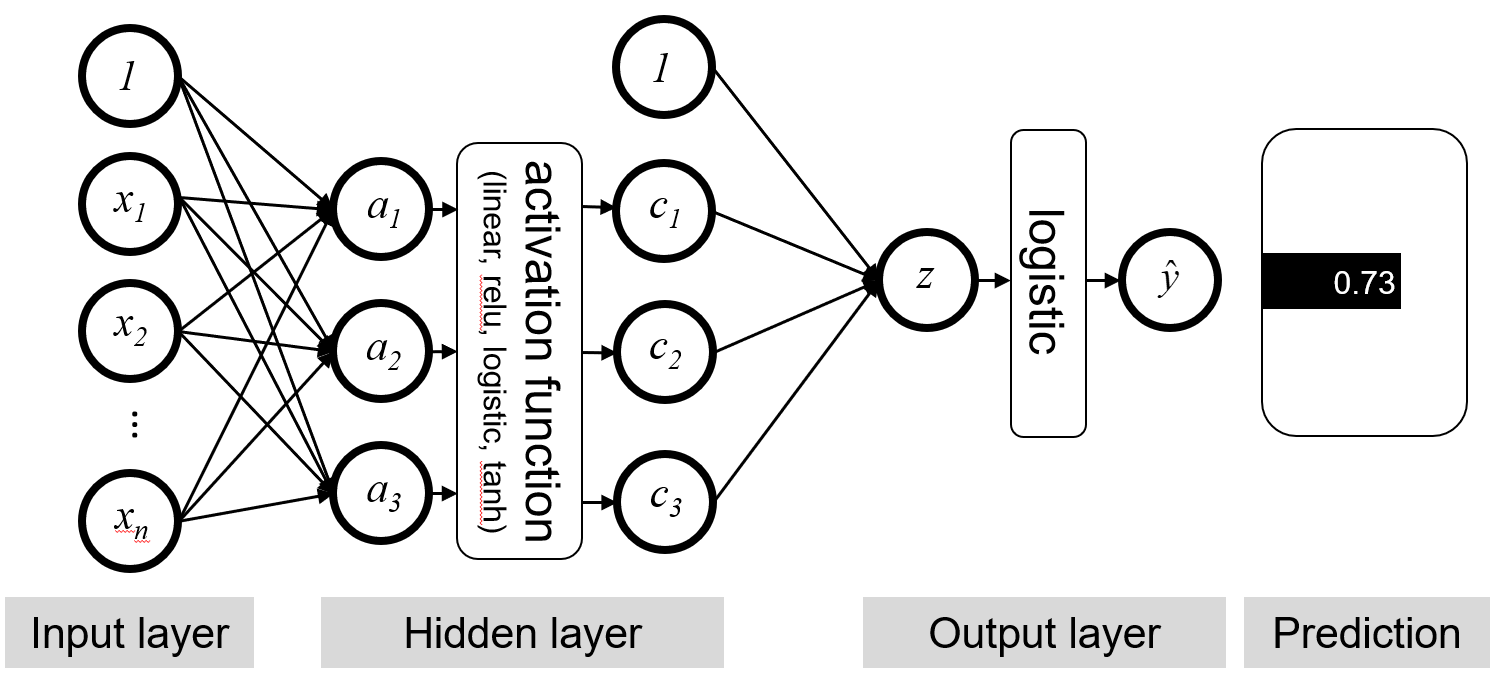logistic_vs_nn_fig2 Fig. Neural Network for Binary Classification

이 경우에는 또한 Local Minima 에 빠진다거나 이론적 근거가 부족하다는 것이 문제가 된다고 하는데요,

Non Linearity 를 적용한다는 점에서 Closed Form Solution 을 한번에 구할 수 없게 되고,
이런 Non Linearity 가 적용된 층이 여러곂으로 쌓일수록 최적화 시 문제가 생길 수 있습니다.

idiot_svm_slide_fig1 Fig.

Support Vector Machine (SVM) 은 이런 문제들을 상당 부분 해결해 준다고 알려져 있는데요, 실제로 정교하게? 디자인된 Neural Network 와 견주는 성능을 내면서도 연산이 효율적이며 실제 Test Time에도 잘 작동하기 (일반화가 잘 된거죠) 때문에 현대 딥러닝 시대가 도래하기 전까지는 굉장히 각광받는 알고리즘으로 사용됐다고 합니다.

nyu_svm_slide_fig2 Fig.

SVM

알고리즘의 아이디어는 굉장히 간단한데요, 초평면 (Hyperplane) (Decision Boundary) 을 그을 때 전체 data points 중 몇 개를 기준으로 최대한 Margin 이 큰 경우를 고르자 라는 것입니다.

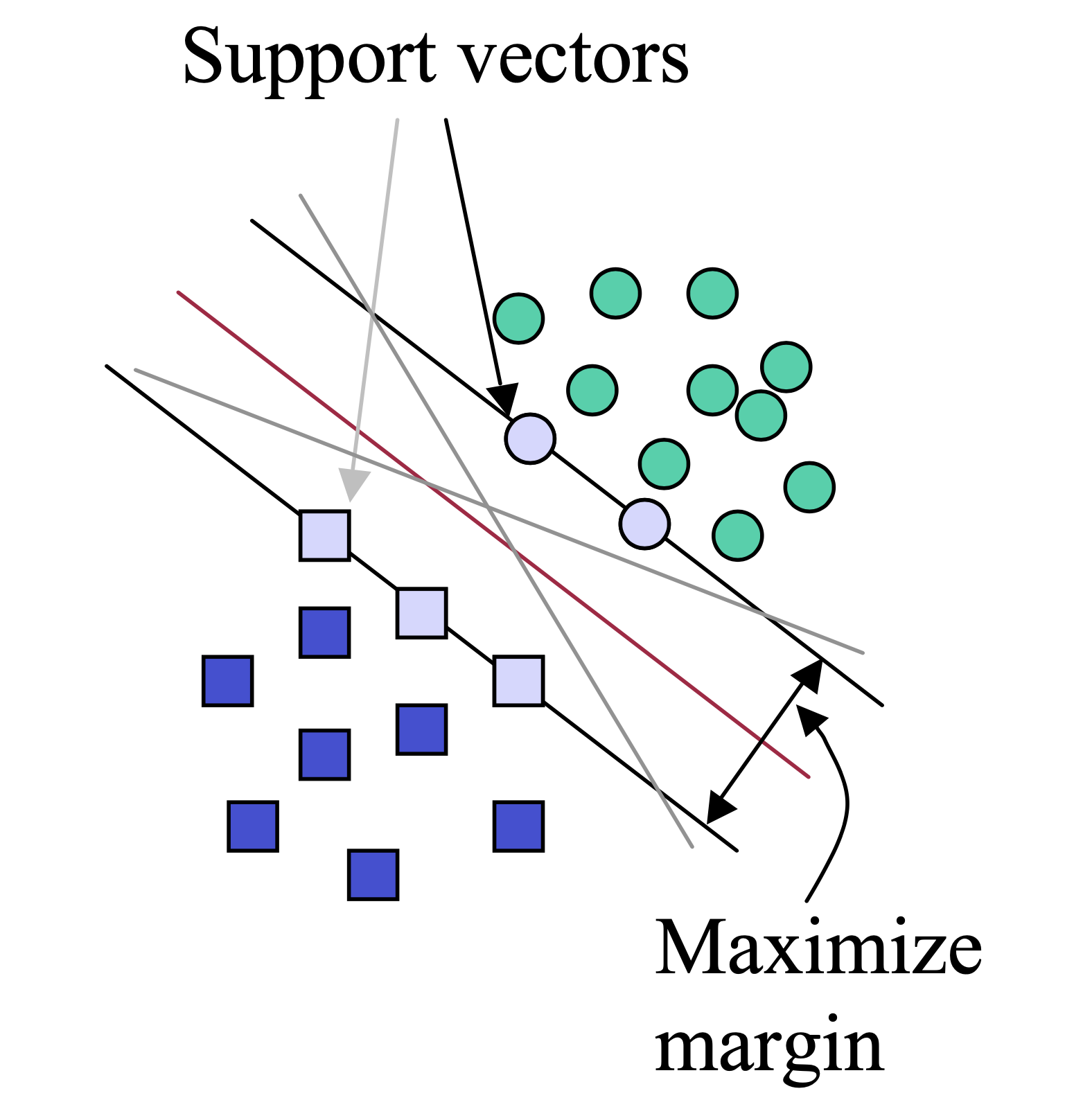idiot_svm_slide_fig2 Fig.

이 때 data point 몇 개가 바로 초평면을 만드는 근거가 되기 때문에 Support Vector가 되는 겁니다.

SVM 이 NN 보다 효율적으로 학습할 수 있는 이유는 바로 이 Supprot Vector 에 대해서만 계산을 해서 결정 경계면을 정하는 model weight 를 수정하기만 하면 되기 때문인데요, 가령 데이터 전체가 100개의 데이터 샘플을 포함하고 있다고 가정하면 NN은 결정경계면의 위치를 나타내는 파라메터 w를 업데이트할 때 100개를 가지고 업데이트를 해야 하지만 Support Vector를 5개로 제한한다면 5개에 대해서만 연산하면 됩니다. (물론 NN의 경우 SGD를 하려면 몇개로 나눠서 여러번 업데이트 해야겠죠.)

여기서 Vector 란 좌표평면상의 점을 의미하는 것과 같습니다. (고등학생때 기하와 벡터가 생각나네요…)

그렇다면 어떻게 Support Vector가 정해지느냐?가 궁금하실 수 있는데요, 이는 결정 경계면 주변의 가장 가까운 점들로 자동으로 정해지게 됩니다. 결정 경계면이 최적화되면서 위치가 조금씩 바뀌면 그에 따라 Support Vector 들도 조금씩 변하죠.

Quadratic Programming (QP) Problem

이제 어떻게, 즉 어떠한 Objective 를 가지고 최적화를 해야하는지 알아봅시다.

먼저 우리는 결정 경계면을 나타내기 위한 방정식을 알고 있어야 합니다.

2차원 x, y 좌표 상에서 직선을 나타내는 식은

\[\begin{aligned} & w_1 x + w_2 y + b=0 \\ \end{aligned}\]

으로 나타낼 수 있습니다.

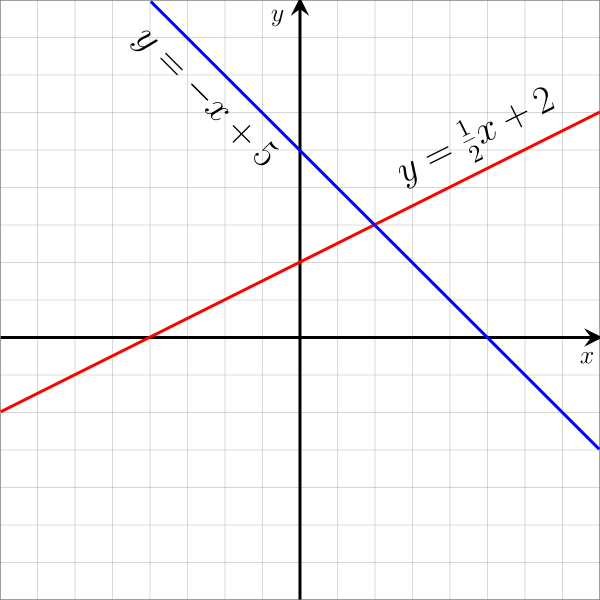linear_equation Fig. Example of Linear Equation

이를 3차원으로 확장시켜 어떤 공간을 구분 짓는 평면 (경계면)을 그리기 위한 수식은 다음과 같습니다.

\[\begin{aligned} & (w_1, w_2, w_3) \cdot (x-x_0,y-y_0,z-z_0) = 0 \\ & w_1 (x-x_0) + w_2 (y-y_0) + w_3 (z-z_0) = 0 \\ & w_1x + w_2y + w_3 z - (w_1 x_0 + w_2 y_0 + w_3 z_0) = 0 \\ & w_1x + w_2y + w_3 z + b = 0 \\ \end{aligned}\]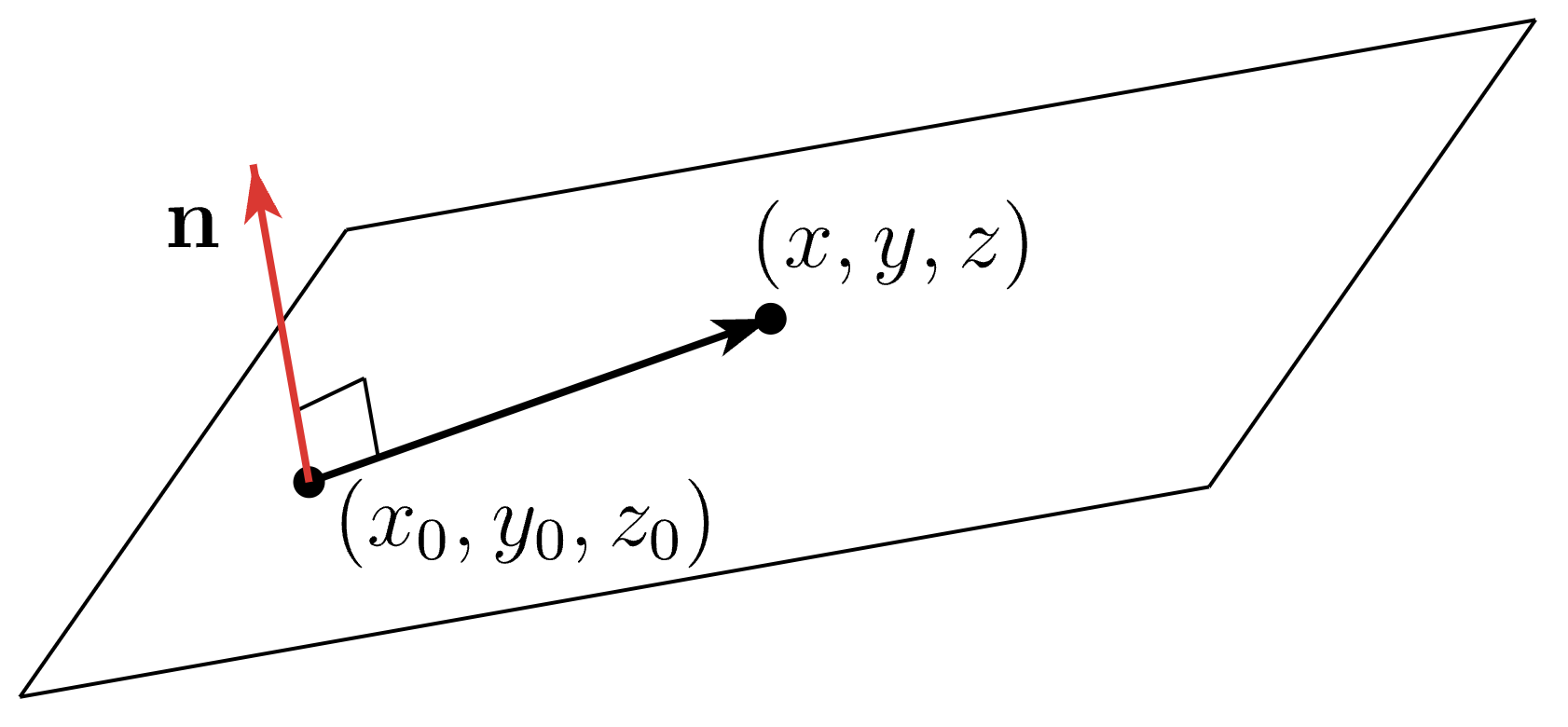

plane_equation Fig.

즉 법선 벡터 (normal vector) 와 점 하나만 알면 결졍 경계면, 평면 하나를 정의할 수 있게 되는데요, 이를 적당히 model weight vector 와 data point 의 feature vector 로 나타내면 우리가 잘 아는 form 으로 나타낼 수 있습니다.

\[w \cdot x + b = 0\]

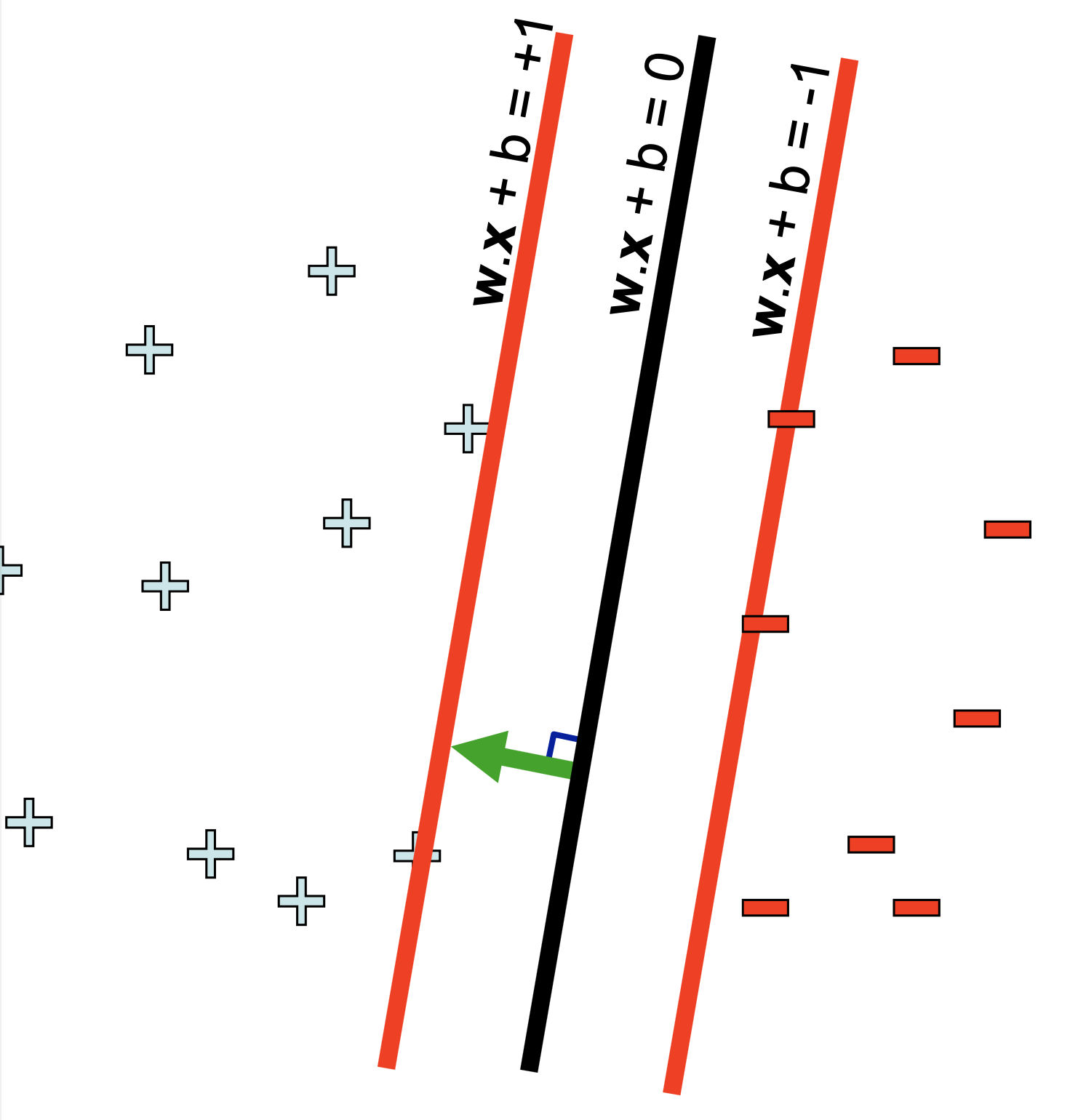vanilla_svm Fig.

이제 이 평면을 기준으로 0보다 큰 영역, 작은 영역을 나누면

\[\begin{aligned} & w \cdot x + b \geq 0 \\ & w \cdot x + b \leq 0 \\ \end{aligned}\]

아래처럼 결정면을 경계로 나눠진 영역을 나타낼 수 있게 되는데요,

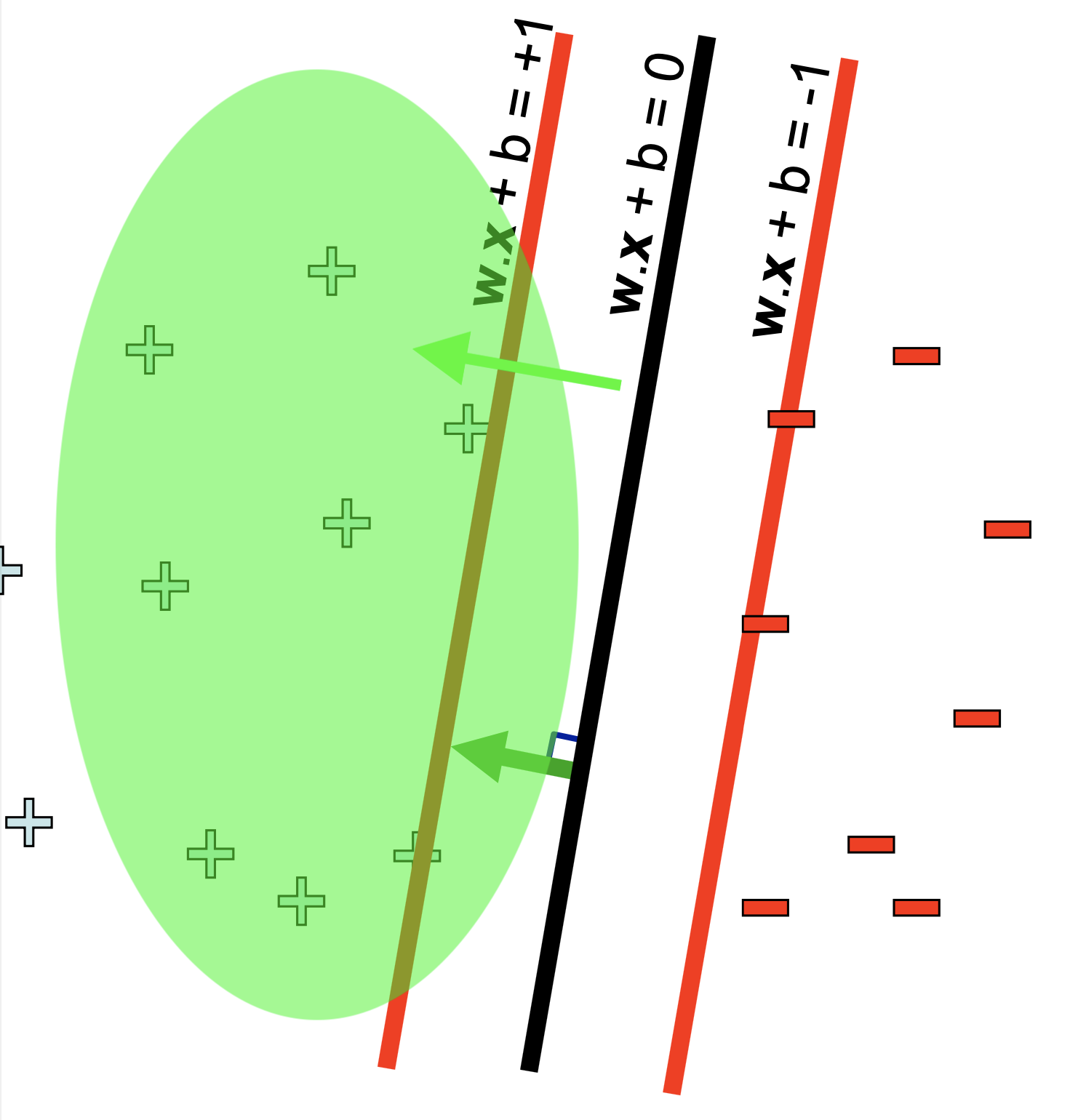vanilla_svm_geq Fig.

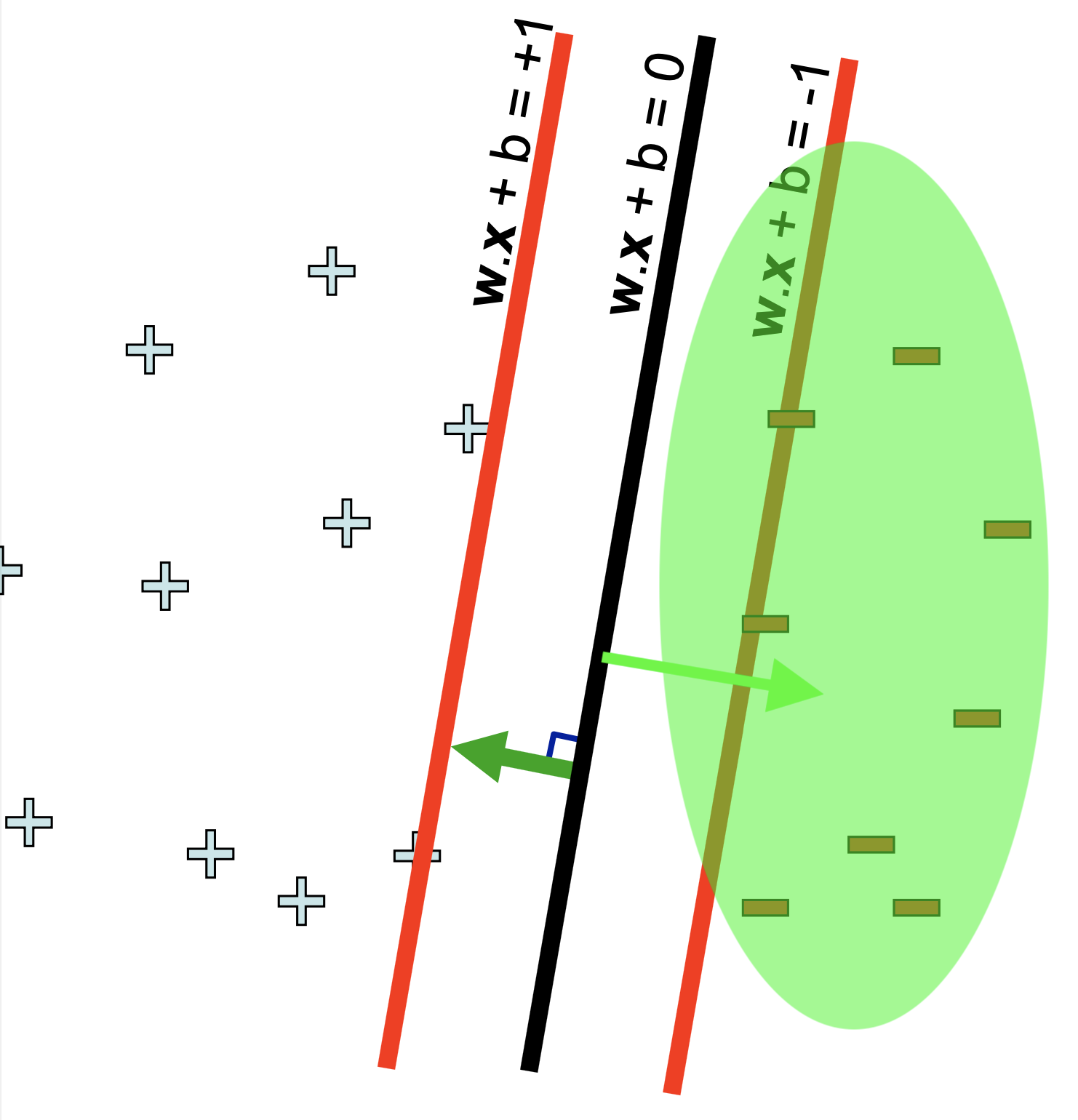vanilla_svm_leq Fig.

우리가 원하는 건 Margin을 \(\gamma\) (혹은 distance, d 라고 표현) 정도 앞 뒤로 유지하면서 Support Vector를 올바르게 나눠주는 결정 경계면이기 때문에 결정 경계면과 거리가 조금 떨어져 있지만 법선벡터는 같아 평행한 빨간색 평면 을 정의해서 사용할겁니다.

\[\begin{aligned} & w \cdot x + b = 1 \\ & w \cdot x + b = -1 \\ \end{aligned}\]

이것을 기준으로 한쪽은 +1 Class, 다른 쪽은 -1 Class 로 나눌 계획입니다.

\[\begin{aligned} & w \cdot x + b \geq 1 \text{ when } y_i = +1 \\ & w \cdot x + b \leq -1 \text{ when } y_i = -1 \\ \end{aligned}\]

여기서 주의할 점은 \(wx+b=0\) 과 \(wx+b=+-1\) 같은 평면 사이의 거리가 항상 1은 아니라는 점입니다. (햇갈리실까봐)

\[\begin{aligned} & w \cdot x + b = 1 \\ & w \cdot x + b = 0 \\ \end{aligned}\]

위의 수식을 따르는 두 평면 (혹은 직선) 가 존재할 때 이 둘 사이의 거리는 그것을 정의하는 법선벡터 (기울기) 에 따라서 천차만별로 달라질 수 있습니다.

svm_d_2 Fig.

다시 정리하면 우리는 2가지를 충족시키는 결정 경계면을 그리길 원하는데요, 바로

  • 1.결정경계면이 data point 들을 올바르게 분류해줬으면 좋겠다.
  • 2.결정경계면 앞뒤로 Margin d 를 갖고 싶은데 이 d가 최대한 컸으면 좋겠다.

입니다.

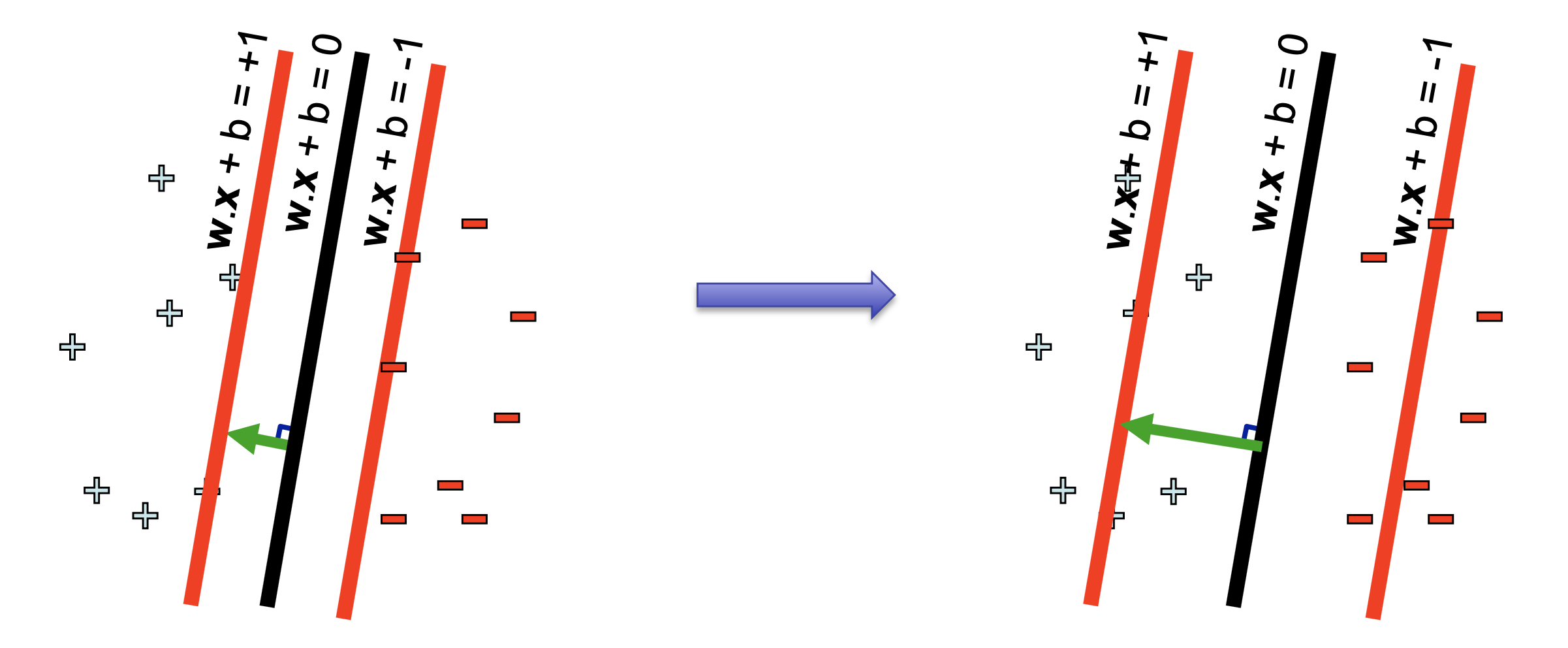svm_d Fig.

2번에 대해서 먼저 생각해보기 위해 2차원으로 생각해보도록 하겠습니다.

\[\begin{aligned} & w \cdot x + b = 1 \\ & w \cdot x + b = 0 \\ \end{aligned}\]

라는 평면이 존재할 때 각각의 평면은 \(x_1, x_2\) 라는 점을 지난다고 생각합시다. 그러면 이는

\[\begin{aligned} & (w x_1 + b) - (w_x2 + b) = 1 \\ & w (x_1 - x_2) = 1 \\ \end{aligned}\]

을 만족하게 되고, 여기에 \((x_1 - x_2)\) 벡터는 법선벡터와 방향이 같고 (평행), 그 벡터의 길이는 두 평면사이의 거리, 즉 \(\gamma\) 만큼의 상수배 라는 사실을 이용하면

\[x_1 - x_2 = \gamma \frac{ w }{ \parallel w \parallel }\]

다음과 같은 결론을 얻을 수 있습니다.

\[w ( \gamma \frac{ w }{ \parallel w \parallel } ) = \frac{\gamma}{\parallel w \parallel} w \cdot w = \gamma \parallel w \parallel\]

즉 두 평면 사이의 거리는 법선 벡터, model weight 인 \(w\) 로 쉽게 정의되는 것입니다.

\[\gamma = \frac{1}{\parallel w \parallel}\]

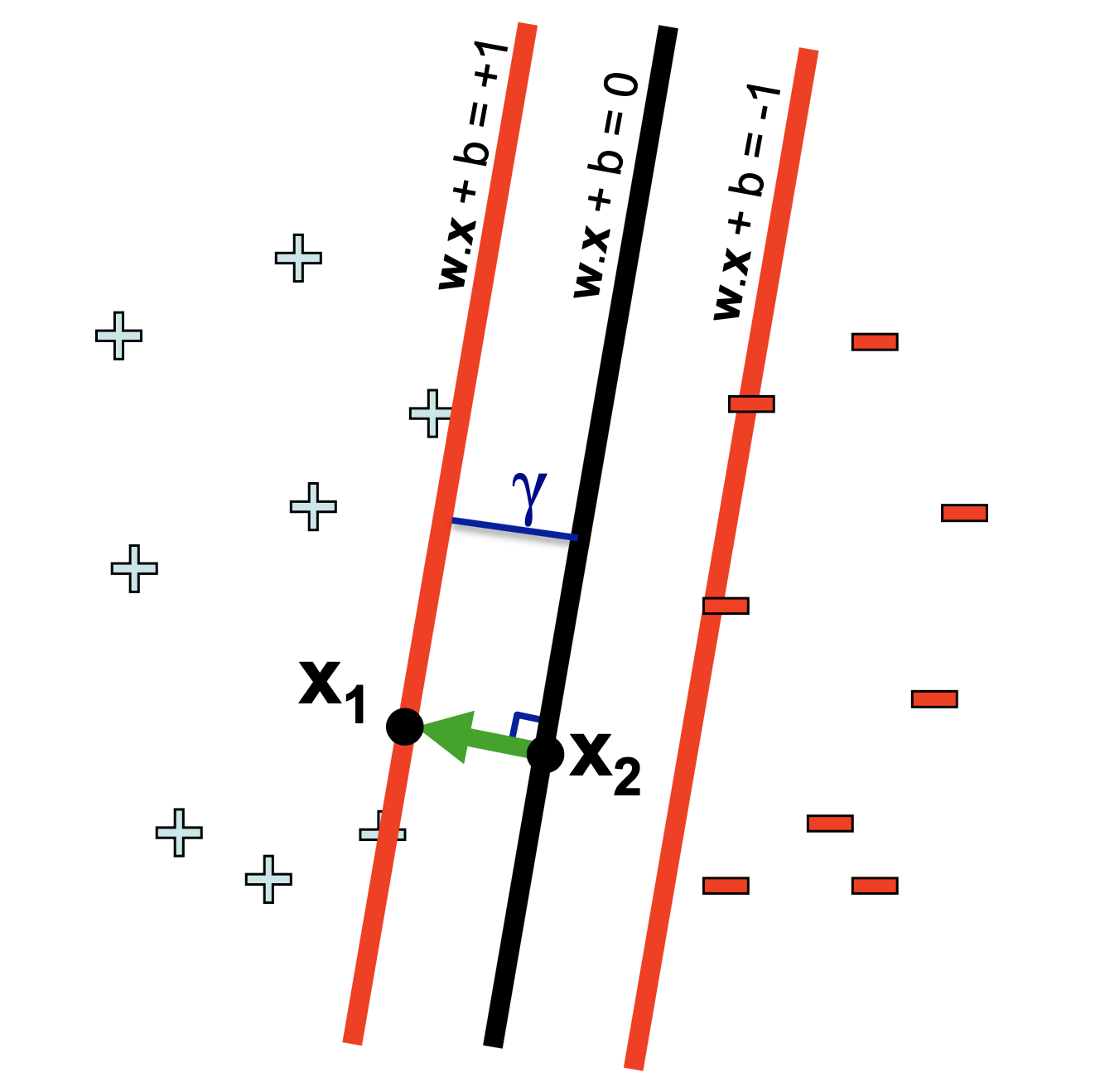svm_d_3 Fig.

여기서 margin은 앞뒤로 2개가 있으니 실제 최적화 하고 싶은 거리는 \(2d = 2\gamma\) 로

\[2\gamma = \frac{2}{\parallel w \parallel}\]

입니다.

그 다음으로 첫 번째 가장 조건인 주어진 x, y 데이터를 올바르게 분류하고 싶다 라는 것 까지 만족해야 하므로 이를 수식으로 나타내야 하는데요,

앞서 우리는 어떤 data point \(x_i, y_i\) 가 있을 때 (SVM 은 Supervised Learning 입니다),

\[\begin{aligned} & w \cdot x + b \geq 1 \text{ when } y_i = +1 \\ & w \cdot x + b \leq -1 \text{ when } y_i = -1 \\ \end{aligned}\]

를 만족하면 된다고 했는데요, 이를 하나의 수식으로 표현하면

\[y_i(w \cdot x_i + b) \geq 1\]

로 표현할 수 있습니다.

최종적으로 우리는 Margin 거리를 최대화 하면서 위의 수식을 만족하는 Objective 를 앞서 정의했으니 여기에 방금 정의한 조건식을 넣어 수식으로 표현하면

\[\underbrace{max_{w,b} \frac{2}{\parallel w \parallel} }_{\color{red}{\text{maximize margin}}} \underbrace{\text{ s. t. }y_i(w \cdot x_i + b) \geq 1 \space \forall i = 1, \cdots, N}_{\color{blue}{\text{separating hyperplane}}}\]

를 얻습니다.

하지만 여기서 Margin 을 최대화 하는 첫 번째 항은 최적화를 하기 위해 미분을 취할 경우 원점에서 문제가 발생합니다. 그렇기 때문에 이를 2차식 (Quadratic) 으로 바꿔 문제를 풀게 되는데요,

\[min_{w,b} \frac{1}{2}\parallel w \parallel^2 \text{ s. t. }y_i(w \cdot x_i + b) \geq 1 \space \forall i = 1, \cdots, N\]

그렇게 하면 미분을 할 경우 기울기가 1차식으로 떨어지기 때문에 편리해 집니다. (수식의 Norm 이 제곱으로 바뀌고 분자로 가면서 max 를 해야 하는 문제에서 min 을 해야 하는 문제로 바뀌었습니다.)

이게 가능한 이유는

\[max_{w,b} \frac{2}{\parallel w \parallel_2}\]

는

\[min_{w,b} \parallel w \parallel_2\]

를 최적화 하는 것과 같은 문제이며,

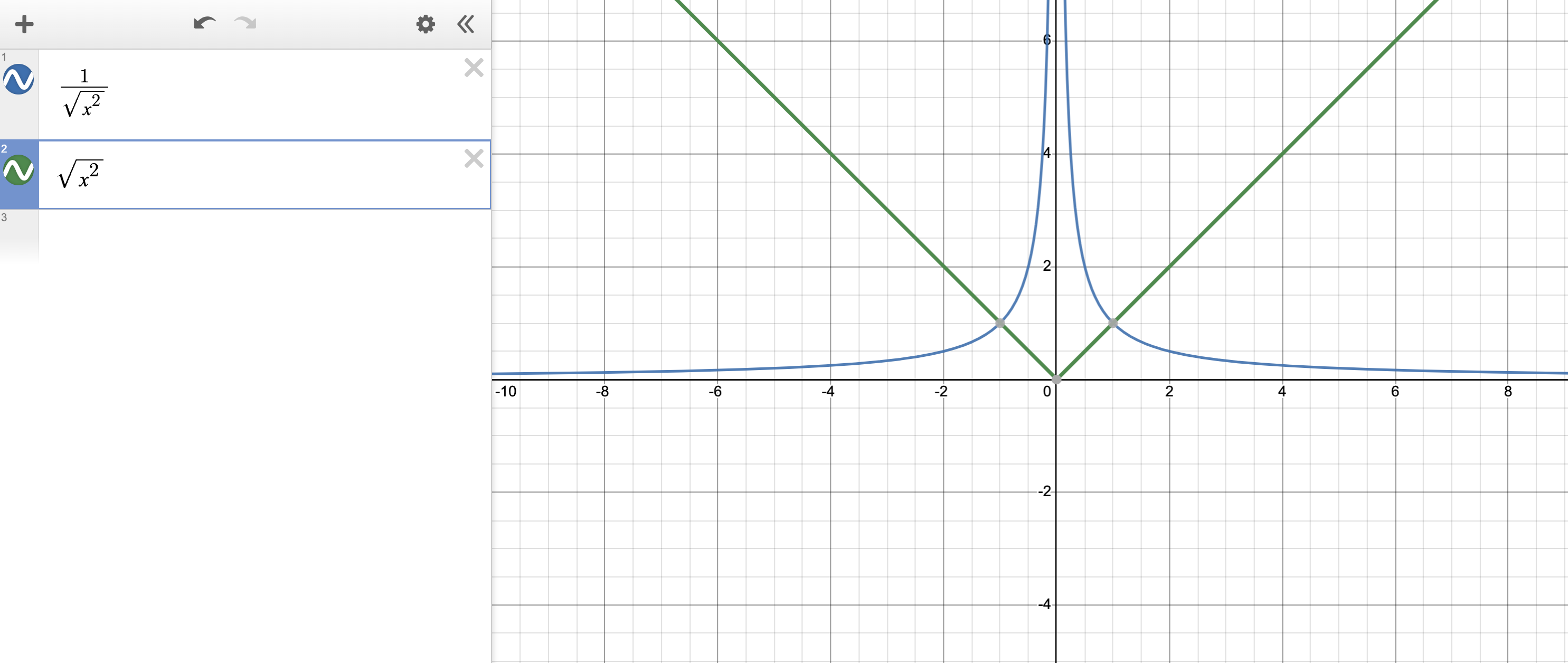qp_fig1 Fig.

\[min_{w,b} \parallel w \parallel_2\]

를 푸는 것은 사실상,

\[min_{w,b} \parallel w \parallel_2^2\]

를 푸는 것과 같은 문제이기 때문입니다.

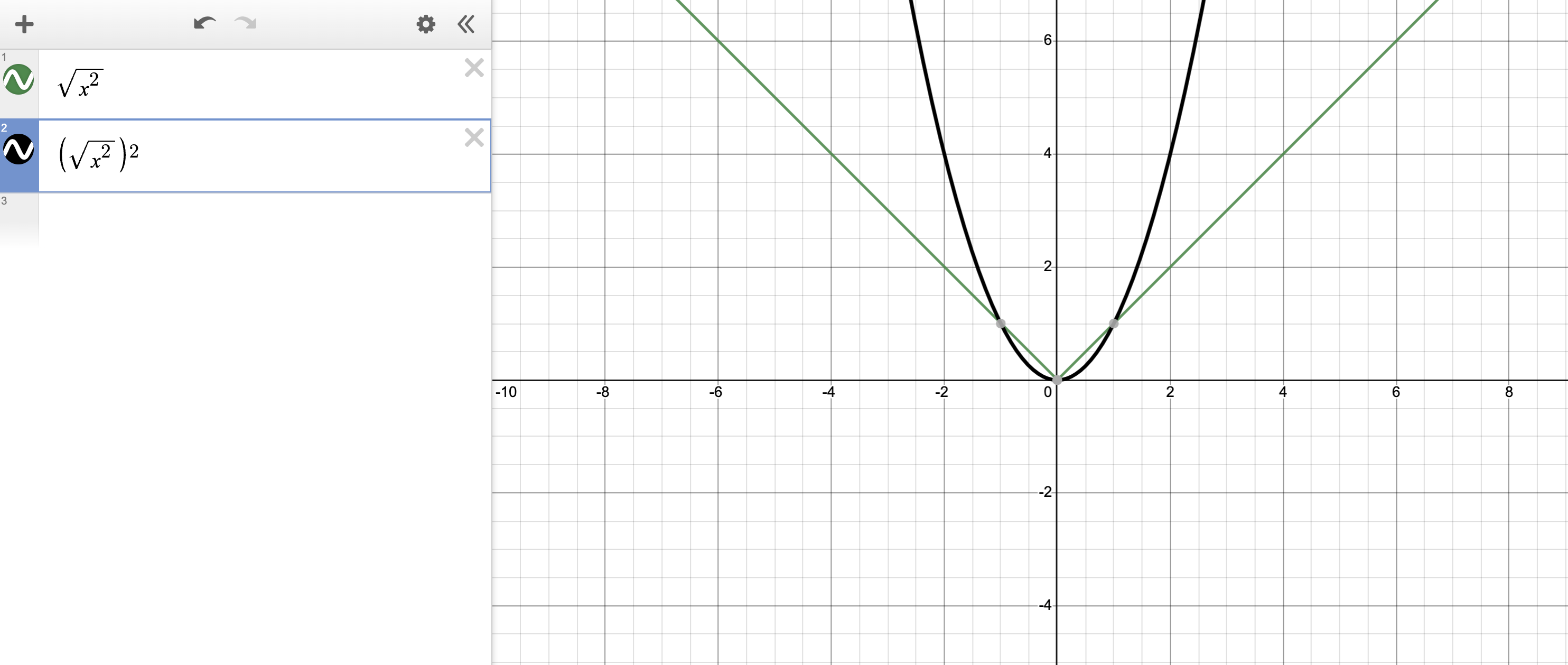qp_fig2 Fig.

이제 Objective 는 Quadratic 이고 같이 만족해야하는 제약식, Constraint 는 Linear 한 수식을 얻었습니다. 이는 QCQP (Quadratically Constrained Quadratic Program) 라고 부릅니다.

Constrained Optimization Problem (Solved by Lagrangian Multiplier)

\[\begin{aligned} & \min{ L_P } = \frac{1}{2} \parallel w \parallel^2 - \sum_{i=1}^{l} a_i y_i (x_i \cdot w + b ) + \sum_{i=1}^l a_i \\ & \text{s.t. } \forall i \space a_i \geq 0\text{where } l \text{ is the } \#\text{ of training points} \\ \end{aligned}\]

Lagrangian Duality (vs Primal)

\[\begin{aligned} & \min{ L_P } = \frac{1}{2} \parallel w \parallel^2 - \sum_{i=1}^{l} a_i y_i (x_i \cdot w + b ) + \sum_{i=1}^l a_i \\ & \text{s.t. } \forall i \space a_i \geq 0\text{where } l \text{ is the } \#\text{ of training points} \\ \end{aligned}\] \[\begin{aligned} & \max{ L_D } (a_i)= \sum_{i=1}^{l} a_i - \frac{1}{2} \sum_{i=1}^{l} a_i a_j y_i y_j (x_i \cdot x_j) \\ & \text{s.t. } \sum_{i=1}^{l} a_i y_i = 0 \space \& \space a_i \geq 0 \\ \end{aligned}\]

Kernel Trick

Polynomial Kernel

Radial Basis Function (RBF) Kernel

tmp

Soft Margin SVM

Multi Class SVM

(2019 NIPS) Learning Imbalanced Datasets with Label-Distribution-Aware Margin Loss (LDAM-DRW Loss)

References