Principle Component Analysis (PCA) and AutoEncoder (AE)

< 목차 >

• Motivation
• Principle Component Analysis (PCA)
  • Learning a Subspace
    • Minimizing the Reconstruction Error
    • Maximizing the Variance of the Projected Data
    • Equivalence of Maximizing Variance and Minimizing Reconstruction Error
  • Solution of PCA
  • PCA using Singular Value Decomposition (SVD)
  • Decorrelation
  • Application: Eigenface
• Connection to AutoEncoder (AE)
  • PCA vs AE
  • Sparse AE
  • Encoding to a Higher Dimensional Space
• PCA vs Linear Discriminant Analysis (LDA)
• Outro
• References

Motivation

Machien Learning (ML)에서 차원 축소 (dimensionality reduction)는 중요한 개념 중 하나이다.

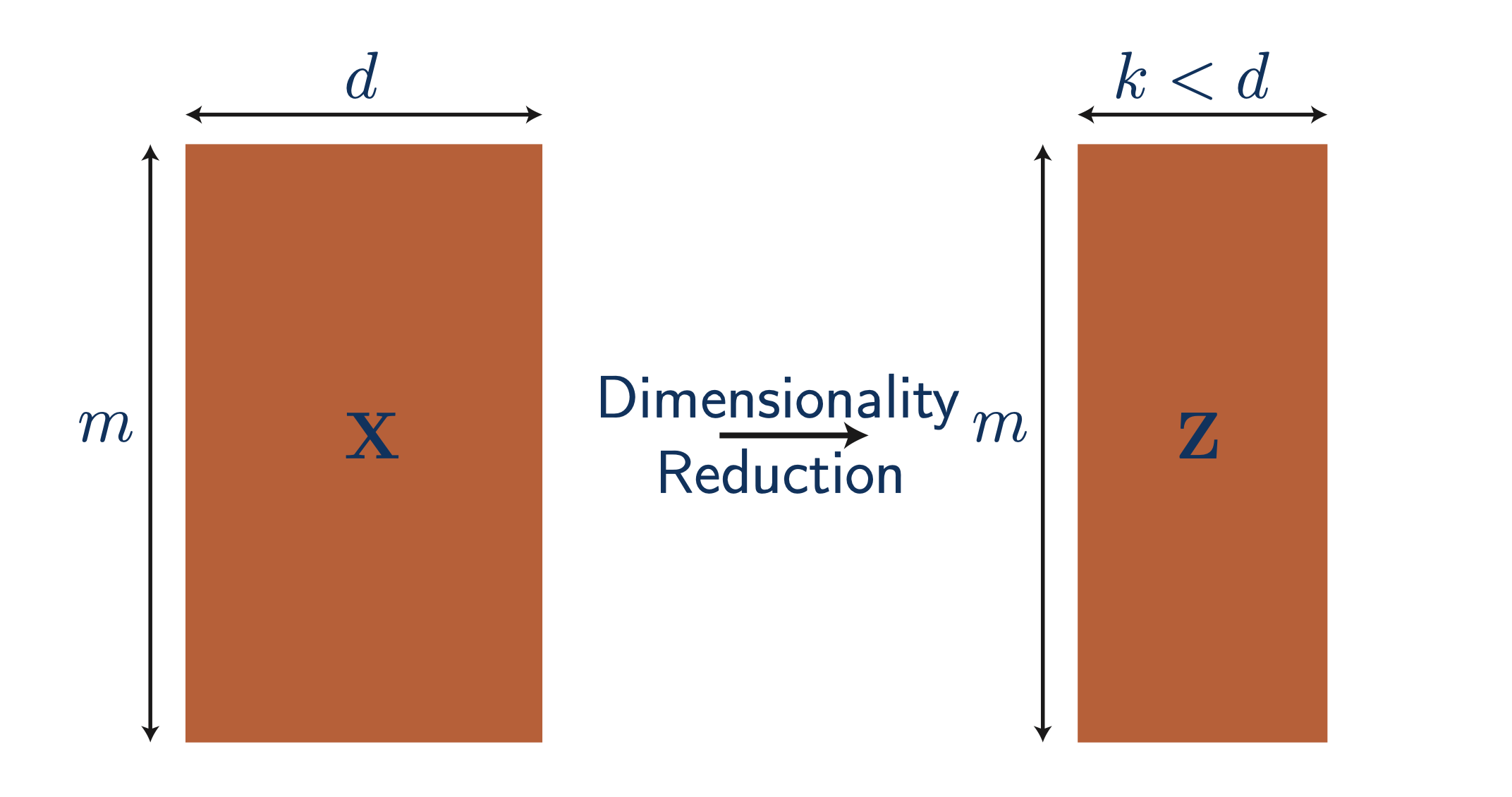Fig. 원래 d차원인 input feature를 k차원으로 줄여보자.

왜 차원을 축소하는게 의미가 있을까?

우리가 가지고 있는 dataset가 feature가 100개라고 해보자. 그러면 data sample 하나는 100개의 feature에 대한 값들을 가지고 있는 \(\mathbb{R}^{1 \times 100}\)차원의 vector가 된다.

전체 dataset은 이러한 data가 여러 개 (N개) 있는 것이므로 \(\mathbb{R}^{n \times 100}\)차원이 될 것이다. 만약 우리가 이 data를 가지고 linear regression을 한다고 치면 100차원 상에서 이 data sample들을 가장 잘 표현하는 직선을 찾아야 하는데 이것은 쉽지 않은 일이 될 수 있다. 그런데 100개의 feature가 모두 유의미한 feature일까? Regression의 예시로 집 가격을 예측하는 예시를 많이 드니까 대충 이 예시를 생각해보자. 부동산이 있는 위치, 집이 지어진 시기, 부대 내 편의시설이나 교통 편의성 등 집값을 결정하는데 유의미한 feature들이 있겠지만 그렇지 않은 feature도 있을 것이다. 이런 feature들은 집값을 구분하는데 아무런 도움도 안될 수도 있기 때문에 noise라고 할 수 있다. 만약 좋은 차원축소 algorithm을 사용해 100개의 feature중 불필요한 (redundant) feature를 제거할 수 있을까?

가능하다. 차원 축소 algorithm의 application 중 하나가 바로 data의 noise를 효과적으로 제거하는 것이다.

만약 효과적으로 data의 차원을 축소할 수 있다면 (e.g. 100차원 -> 3차원), 우리는 data를 disc에 저장할 때에도 엄청난 memory save를 할 수 있을 것이다. (zip 같은 lossless 압축 방법들이 있긴 하지만)

차원축소 algorithm들은 시각화 (visualization)에도 많이 쓰이는데, 우리가 볼 수 있는 차원의 한계는 2차원 혹은 3차원이기 때문에 100차원 data를 2, 3차원으로 사영 (projection)시키는 것이 시각화에 도움이 된다.

Fig. Applications of PCA. Source from here

그런데 당연하게도 원래 차원의 data를 1,2,3 차원등의 subspace (1차원은 line, 2,3차원은 plane)로 projection 할 때 아무 random한 subspace로 projection하는 것은 좋지 않다. 앞서 얘기했던 feature의 유의미함 (반대로는 noise) 과 관련이 있는데, projection이 되었을 때 data를 잘 구분지어 줄 수 있는 subspace를 골라야 한다. 이 subspace를 찾는 algorithm 중 가장 일반적으로 쓰이는 것이 바로 이번 post에서 알아볼 주 성분 분석 (Principle Component Analysis; PCA)라는 것인데, 이 주 성분 (Principle Component; PC)라는 것은 training (최적화; optimization)을 하거나 선형 대수 (linear algebra)적인 특성을 사용하면 알아낼 수 있다.

이제 PCA는 무엇인지? 그리고 오토 인코더 (AutoEncoder; AE)와는 무슨 관련이 있는지 알아보도록 하자.

Principle Component Analysis (PCA)

어떻게하면 수많은 feature중에서 유의미한 feature를 찾아 그 subspace로 data를 mapping할 수 있을까?

내가 가지고 있는 dataset이 2차원 data라고 치자. 그리고 이를 1차원 직선 (line)에 projection 하고 싶다. 아래 figure중 어떤 option이 더 좋은 projection일까?

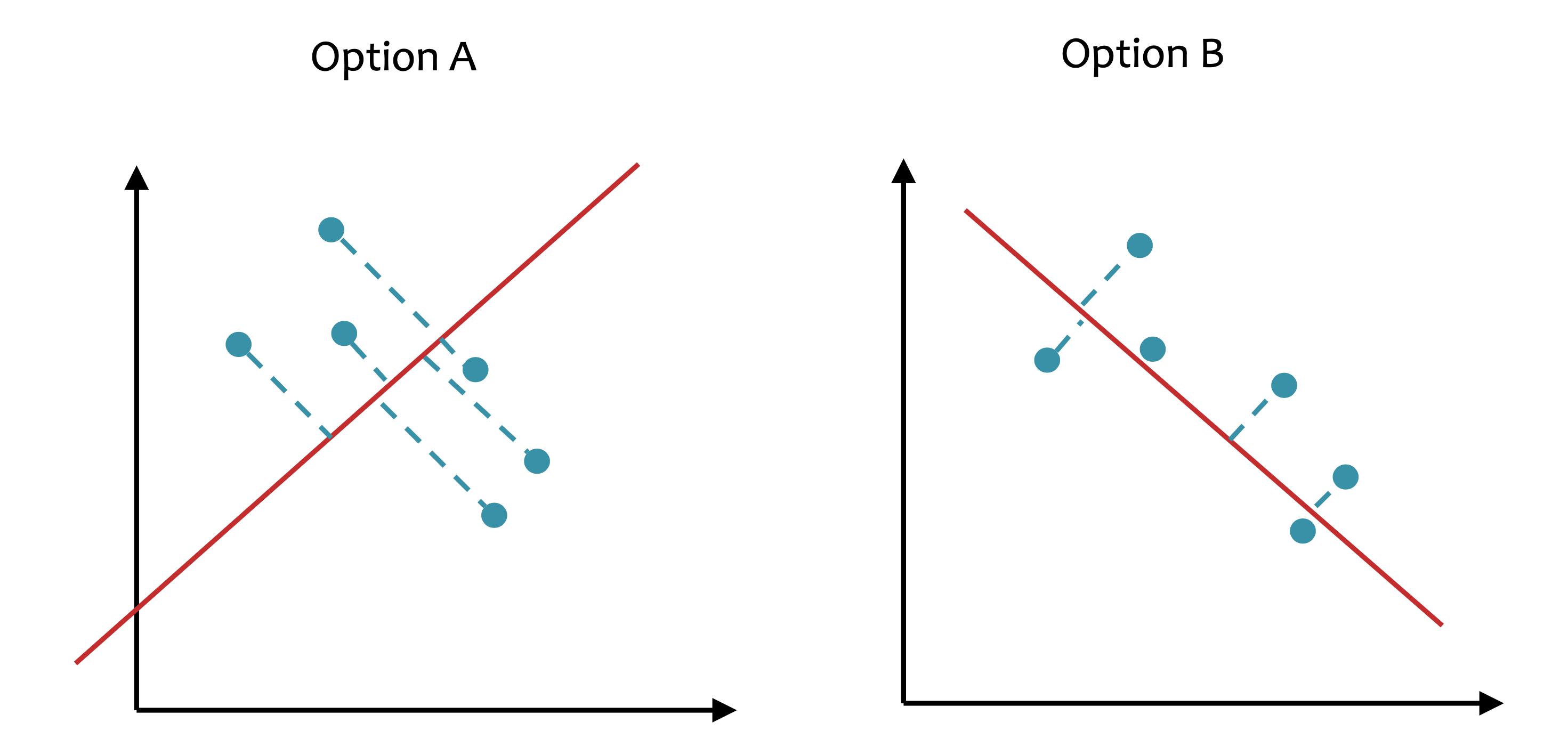Fig. Which Projection is good ?

가장 쉽게 1차원으로 data를 projection하는 방법은 x축이나 y축으로 projection 해버리는 것 일 것이다. 하지만 이렇게 하면 너무 infomation loss가 많다. 부동산 가격 예측을 하는데, 평수만 제외하고 모든걸 0으로 만들어버리는 것과 같은 것인데, 이것이 좋은 projection일 리 없다.

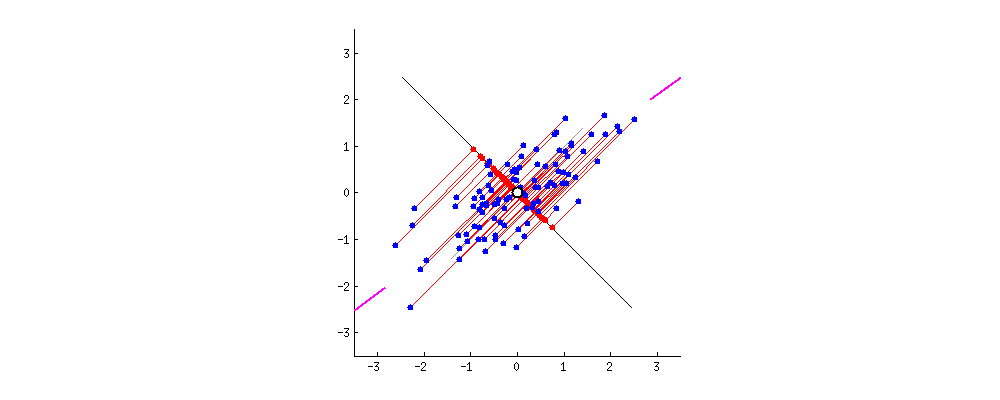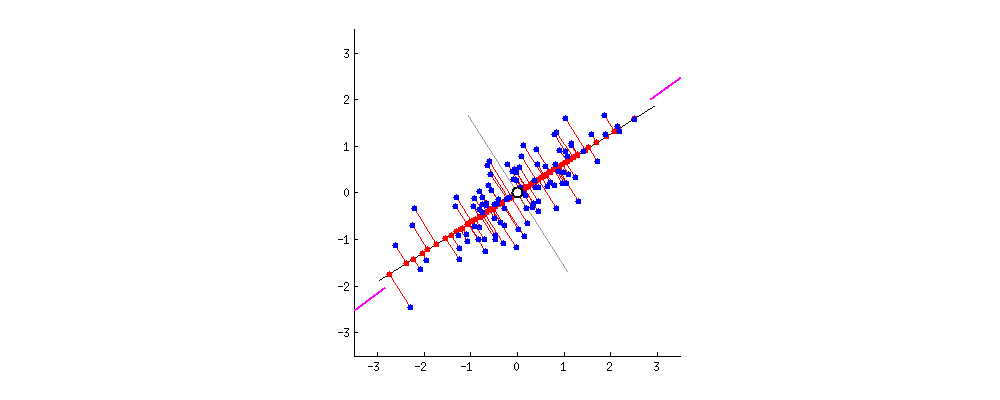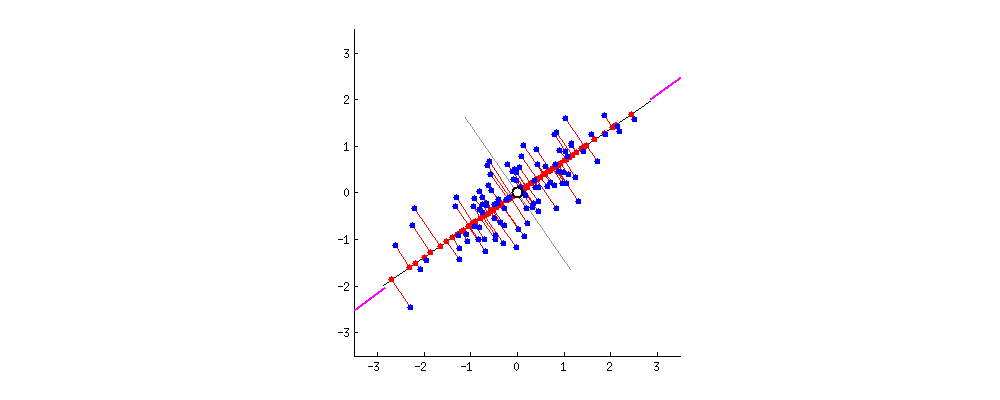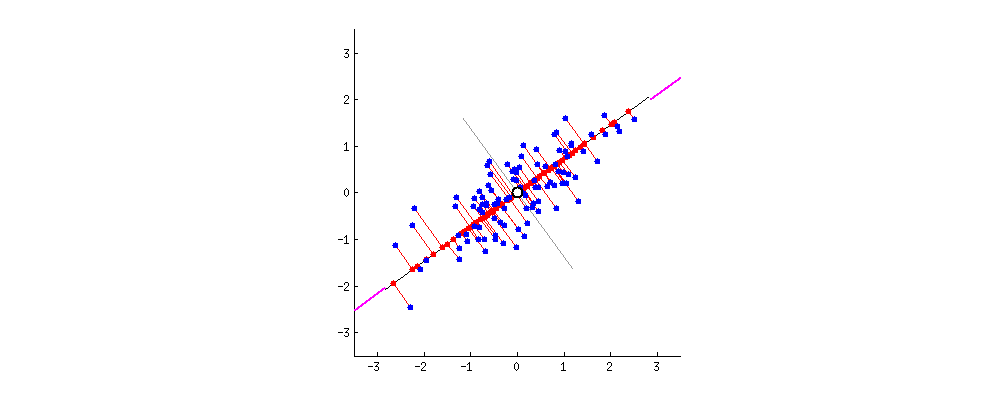Fig. 원래의 2차원 data (blue dots)가 1차원으로 projection 되는 모습 (red dots). 이 중에서 가장 loss가 적은 line은 뭘까?

Learning a Subspace

우리가 찾고싶은 어떤 subspace가 2차원이라면 이는 2개의 vector가 span하는 공간이므로 우리가 찾아야 하는 것은 미지의 basis vector 2개가 될 것이다. 이 vector 하나 Principle Component (PC)라고 한다. PC를 찾는 approahc는 크게 3가지가 유명한데,

Fig.

bishop의 probabilistic formulation은 나중에 따로 기회가 있으면 알아보도록 하고, 이번 post에서 알아볼 것은 projected variance를 maximize하는 것과 reconstruction error를 minimize하는 것 두 가지이다.

Minimizing the Reconstruction Error

먼저 reconstruction error를 minimize하는 것으로 PC를 찾아보자.

주어진 dataset은 i 개의 data sample로 이루어져 있다 (\(D= \{ x_1, \cdots, x_i\}\)). 이 data sample들의 mean은 \(\mu = \frac{1}{N} \sum_{i=1}^N x_i\)로 계산된다. 우리의 목표는 zero centered된 \(x_i - \mu\)를 어떤 subspace에 잘 projection 시키는 것이다. 이제 어떤 subspace의 basis vector가 k개 존재하고 (\((u_1, \cdots, u_k)\)) 이들은 서로 직교하며 크기가 1인 정규 직교 (orthonormal)하다고 생각하자. 그렇다면 이 subspace로 어떤 n차원의 data point, \(x \in \mathbb{R}^{1 \times n}\)가 projection되는 경우는 다음과 같다.

그런데 우리가 원하는 것은 다시 이를 원래의 space로 복원 (reconstruction)하는 것이다. 정규 직교 행렬 (orthornomal matrix)의 역 행렬 (inverse matrix)는 전치 행렬 (transpose matrix)와 같기 때문에, reconstructed vector는 아래와 같이 표현될 수 있다.

이렇게 data point들이 projection 됐다가 다시 원래 차원으로 돌아오는 과정은 아래 figure를 보면 이해하기 쉬운데, 아무리 잘 복구한다고 해도 원래의 data point를 찾아가는건 쉽지 않음을 알 수 있다.

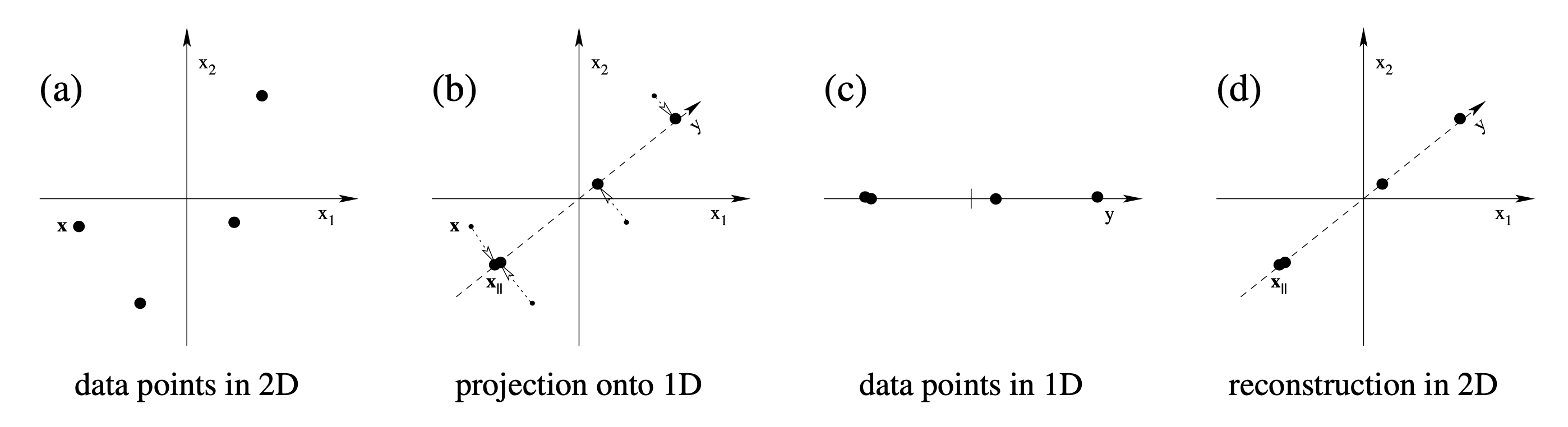Fig. 2D to 1D projection example

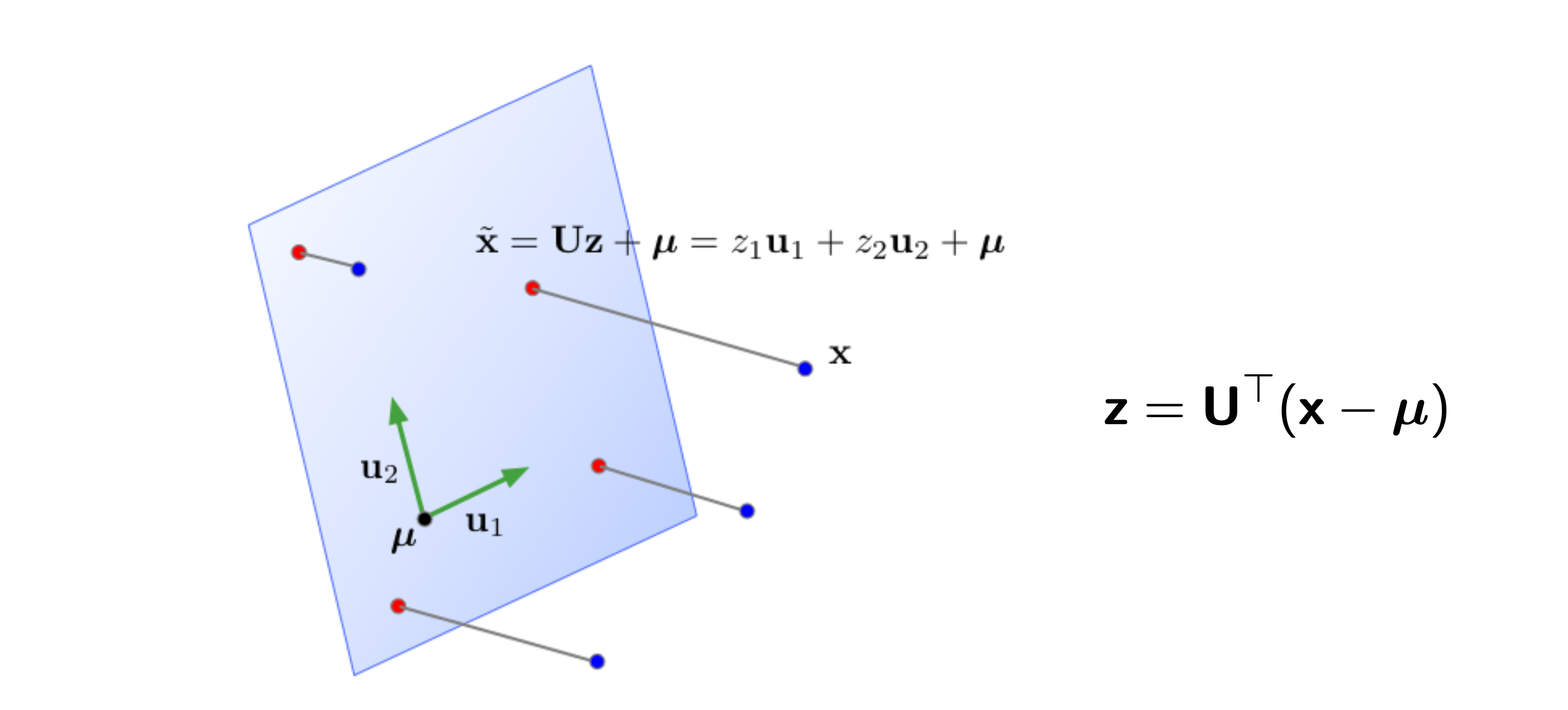Fig. 3D to 2D projection example

즉 reconstruction error는 존재할 수 밖에 없는데, 이를 그나마 최소화 하는것이 우리의 목적 (objective)이다. 만약에 좋은 subspace로 vector들이 projection이 됐다면 이를 다시 원래 차원으로 되돌려놨을 때 원래 vector와 크게 다르지 않아야 한다는 것이 이 approach의 직관이다.

Learning objective function은 original vector와 reconstruction error와의 euclidean distance를 minimize하는 space, \(U\)를 찾는것이므로 아래와 같이 정의할 수 있겠다.

이제 이를 gradient descent같은 iterative optimization method로 subspace를 구성하는 basis vector를 찾아도 될 것 같지만, 일단은 solution을 구하는 건 보류하고 다음 approach에 대해 먼저 알아보자.

Maximizing the Variance of the Projected Data

다음은 projected vector들의 variance를 maximize하는 approach이다. 마찬가지로 projected vector는 다음과 같이 표현할 수 있다.

Learning objective는 \(z\)의 variance를 maximize하는 것인데, 이 때 z가 3차원이라면 모든 차원에 대해서 variance를 maximize 할 것이다.

여기서 \(\bar{z}\)는 mean을 의미하며, 당연히 subspace를 구성하는 PC들은 서로 orthonormal 하다. 이제 이 objective를 가장 잘 만족하는 PC를 마찬가지로 구하면 되겠다.

Equivalence of Maximizing Variance and Minimizing Reconstruction Error

그런데 다른 approach처럼 써놨지만 사실 이 둘은 같은 goal을 좇는 objective를 가지고 있다. 왜 그럴까?

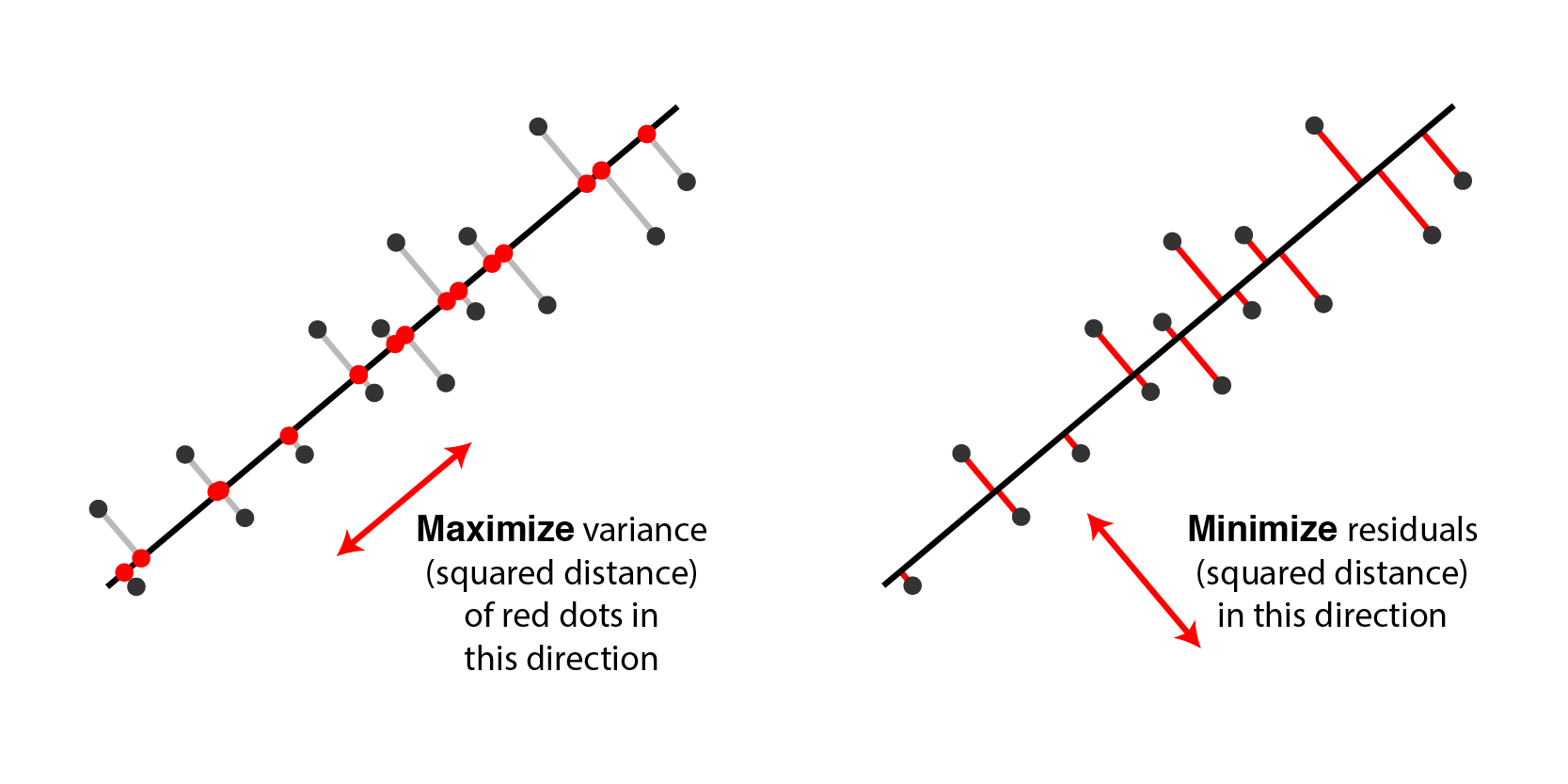Fig. Two equivalent views of principal component analysis. 사실 두 관점은 달라보이지만 solution을 구해보면 같다는 걸 알 수 있다.

아래 figure를 봐 보도록 하자.

어떤 point, \(\mu\)로 부터 projected vector의 variance와 그 vector, \(\tilde{x}\)와 원래 data간의 거리, 그리고 \(\mu\)에서 원래 data point, \(x\)는 서로 피타고라스의 정리 (Pythagorean theorem)를 따른다는 것을 이해할 수 있다. 우리가 보통 PCA를 할 때 original data point들을 zero centered (dataset 전체의 mean을 각각 빼줌) 시키기 때문에 원점 (origin)부터의 distance로 생각해도 된다.

이 수식에 따르면 원점 (origin)으로 부터 original data의 거리가 변하지 않는 상수 (constant)이기 떄문에 projection을 해도 남아있는 variance를 maximize하는 것과 reconstruction error를 최소화 (즉 손실된, lost variance를 최소화) 하는 것이 결국 같은 것이 된다. 아래 animation을 통해서 우리는 실제로 같은 PC에 대해서 두 objective가 나타내는 curve는 정확하게 일치하는 것을 볼 수 있다.

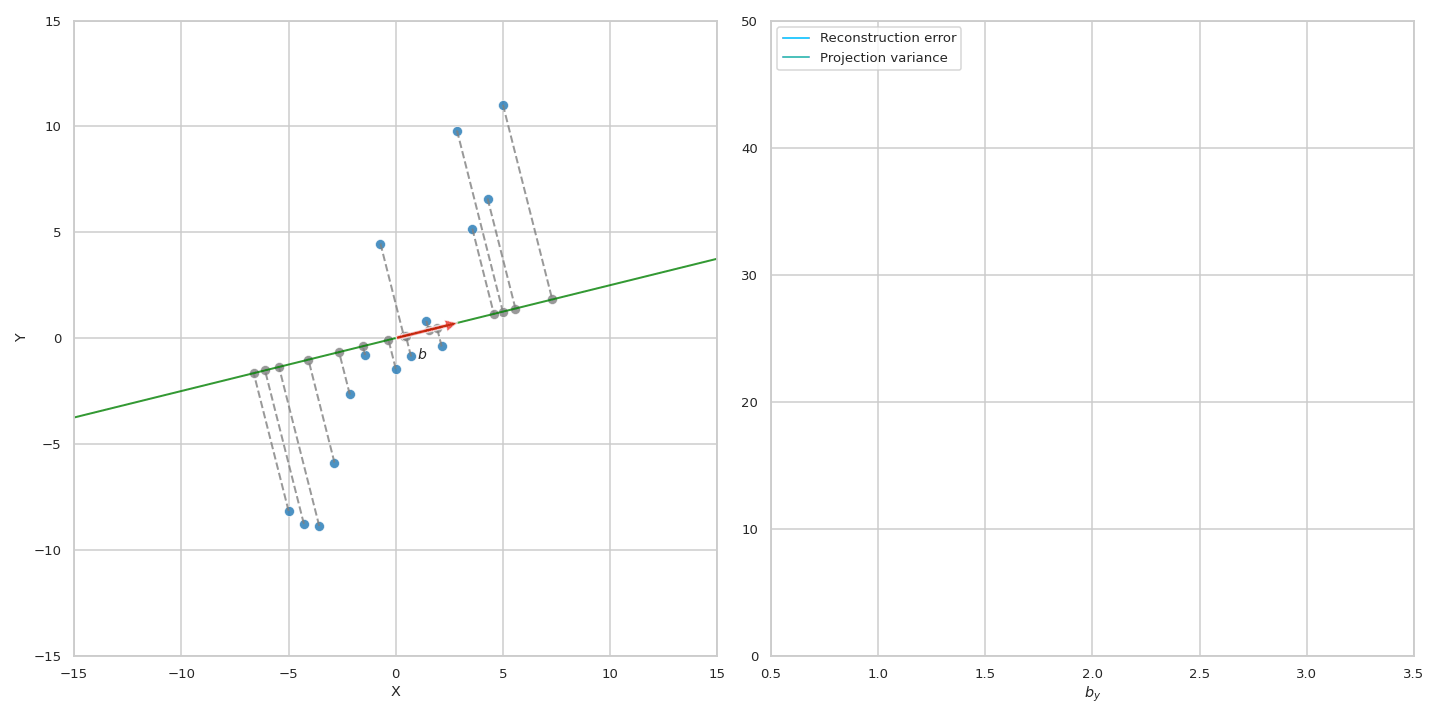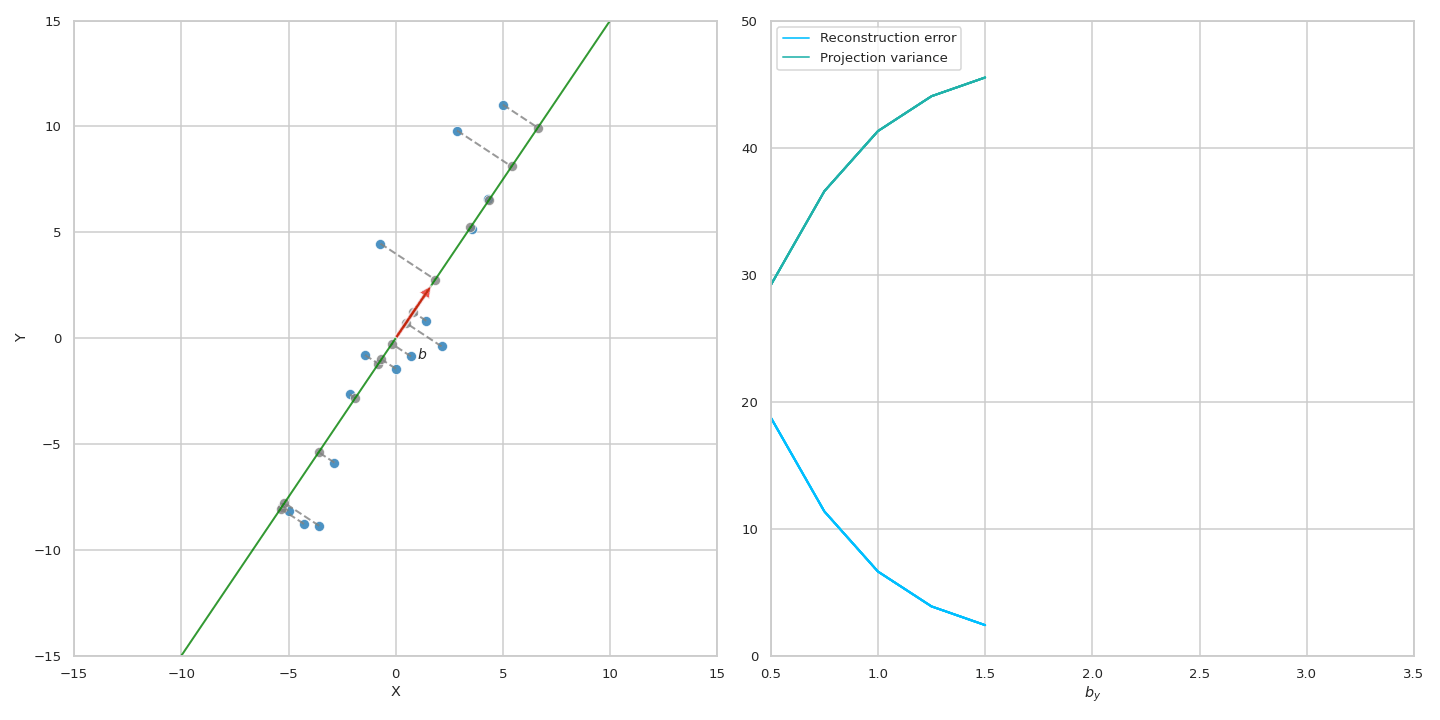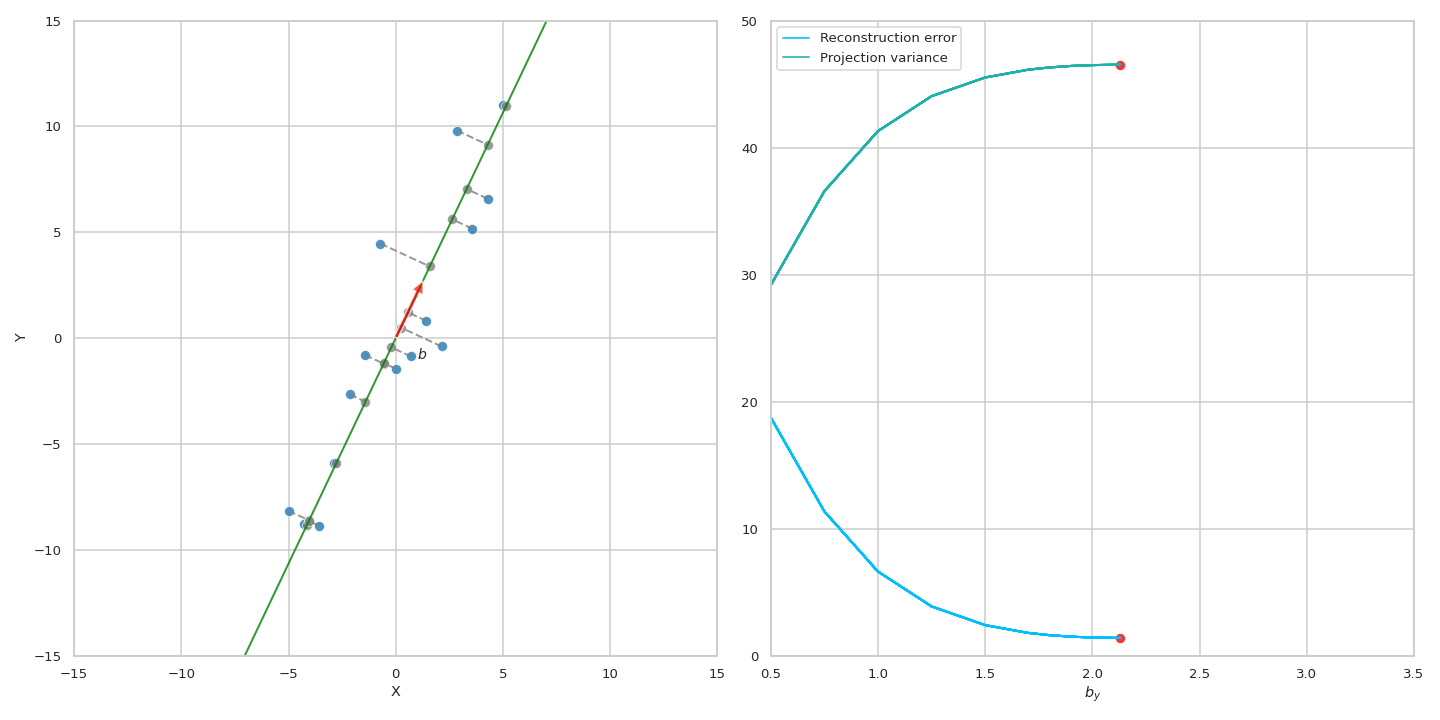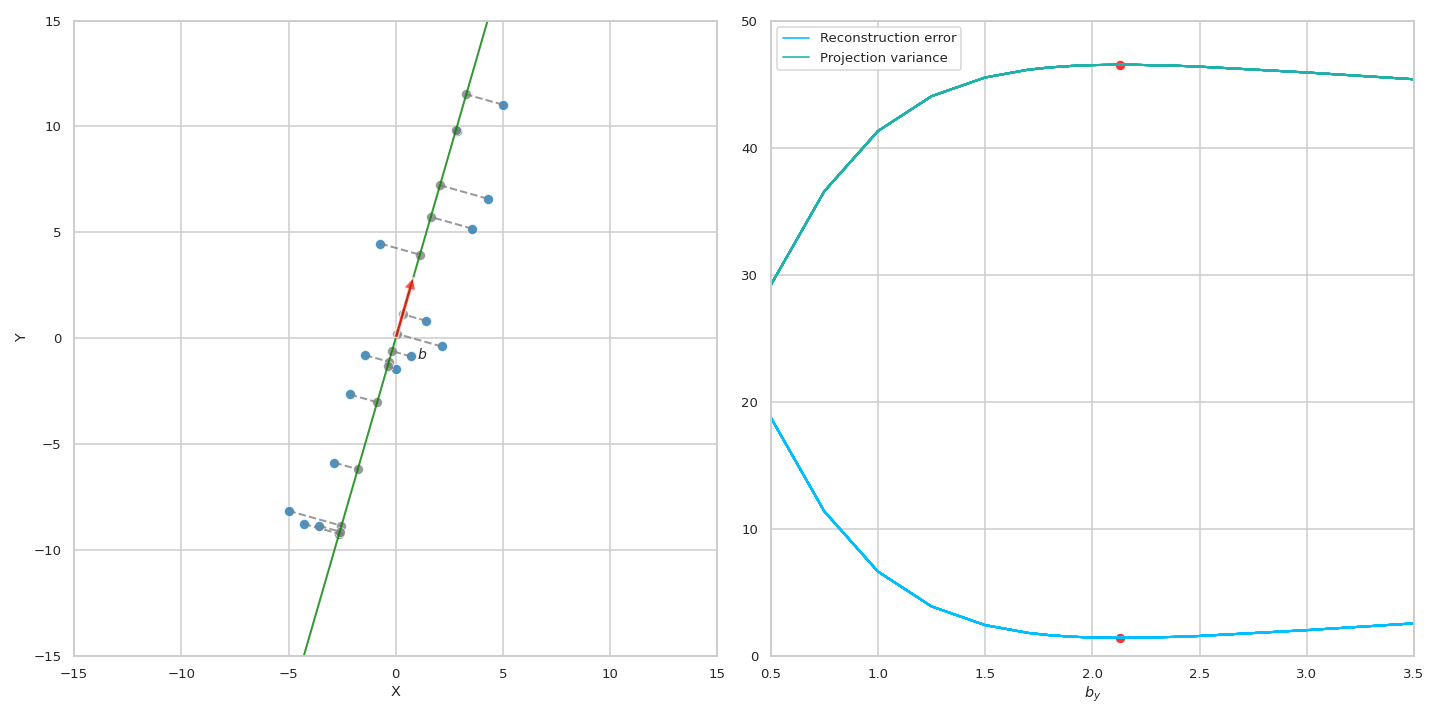Fig. Source from here

혹은 이런 gemoetry view가 아니더라도 수식적으로도 이를 증명할 수 있을 것이다.

Solution of PCA

이제 PCA의 solution을 구해보도록 하자. 아마 이 post를 보는 사람들 중에서도 PCA를 모르는 사람은 아마 없을 것이다. (다만 좀 더 insight를 얻기 위해 읽을 뿐)

그래서 결론부터 말하자면 PC를 찾는 solution은 보통 original dataset의 공분산 행렬 (Covariance Matrix)를 구한 뒤, 이 matrix를 고유값 분해 (Eigenvalue Decomposition)해서 eigen vector를 구하고, 마지막으로 eigen value 순서대로 정렬된 eigen vector 중 상위 r 개의 component를 구하는 것으로 설명할 수 있다. 만약 3차원으로 projection하고 싶다면 eigen value 순서대로 정렬한 eigen vector의 상위 3개를 사용해 \(U\) matrix를 구성하면 된다.

왜 이것이 성립하는지 수많은 derivation이 있지만, 그 중 가장 간단한 방법 하나만 소개하려고 한다.

먼저 어떤 dataset distribution의 분산 (variance), \(\sigma^2\)는 내가 가지고 있는 dataset의 sample mean이 \(\hat{\mu}\)일 때 다음을 이용해 계산할 수 있다.

그러나 우리가 관심이 있는 것은 covariance matrix이다. 이는 random variable (data sample)간의 상관 관계 (correlation)를 의미한다. Covariance matrix는 다음과 같이 구할 수 있다.

Fig. 다양한 covariance를 갖는 data cloud 예시들. correlation이 강할수록 각 feature가 redundant할 가능성이 높다.

이제 eigenvalue decomposition에 대해서 생각해보자. 어떤 정방 행렬 (square matrix)에 대해서 선형 변환 (linear transformation)을 하더라도 그 크기는 변할 지언정 (stretch) 방향 (direction)은 변하지 않는 vector가 존재하는데, 이를 고유 벡터 (eigenvector) 라고 하며 이에 대응되는 scaling factor를 고유 값 (eigenvalue) 라고 한다.

위 수식은 A라는 matrix에 의해 vector, \(u\)가 변하는 것은 \(\lambda\)배 scaling 되는 것 밖에 없다는 걸 의미한다. 당연히 matrix, A에 대해서 eigenvector, eigenvalue는 여러 개 있을 수 있기 때문에 이를 matrix form으로 표현하면 아래의 수식처럼 쓸 수 있다.

한 편, 우리가 풀고자 하는 것은 projected vector의 covariance를 maximize하는 것 이었다.

그리고 이는 다음과 같이 전개될 수 있다.

우리는 제약 조건 (constraint)이 걸린 문제 (constraint problem)의 solution을 찾아야 하므로, Lagrange Multiplier를 사용해서 문제를 풀 것인데, 수식을 단순화 하기 위해서 우리가 PC를 1개만 찾는다고 생각해 보자. 원래 feature차원이 \(d\)일 때, \(U \in \mathbb{R}^{d \times 1}\) 이므로 vector, \(u\)로 나타낼 수 있다. 이제 PC 1개에 대한 optimal solution (가장 variance를 크게 유지해주는 vector)는 다음과 같이 찾을 수 있다.

당연히 PC를 여러개로 확장해서 matrix form으로 해도 비슷한 수식이 유도될 것인데, 여기서 중요한 점은 유도된 수식이 사실상 covariance matrix의 eigenvector와 다름이 없다는 것이다. 즉 우리는 eigenvalue decomposition을 covariance matrix에 대해 수행하기만 하면 모든 PC vector를 한 번에 다 얻을 수 있는 것이다.

그렇다면 eigenvector들 중에서 어떤 vector가 가장 variance를 크게 만들까? 직관적으로 data간의 상관관계를 나타내는 \(\Sigma\)와 eigenvector를 곱한 것은 eigenvector의 특성상 eigenvalue를 곱해서 vector를 상수 배 늘린 것 (stretch)과 같다. 그러므로 eigenvalue가 가장 큰 값을 고르면 된다. 보통 eigenvalue decomposition을 scikit-learn등의 package 로 구하게 되면 eigenvalue순으로 정렬이 되니 top-1 vector를 뽑으면 그걸로 끝인 것이다.

좀 더 이를 이해해보자. 아래 서로 다른 covariance를 갖는 data cloud들을 다시 보자.

Fig. 다양한 covariance를 갖는 data cloud 예시들.

먼저 가장 왼쪽의 첫 번째 sub figure는 이미 covriance가 diagonal matrix이다. 즉 diagonalization을 할 필요가 없는 것이다. 이 때는 PC가 \(x_1,x_2\) 축 두 개 일텐데, 여기서 data가 더 넓게 분포해있는 축은 \(x_2\)이므로 1차원 projection을 하고싶다면 \(x_2\)로 projection 하면 된다. 반면에 가운데 sub figure는 그렇지 않다. 이 경우 Ccvariance matrix를 diagnoalize 해야 비로소 PC가 보이게 되는데, 바로 이 diagonalization 과정이 eigenvalue decomposition이 되는 것이다.

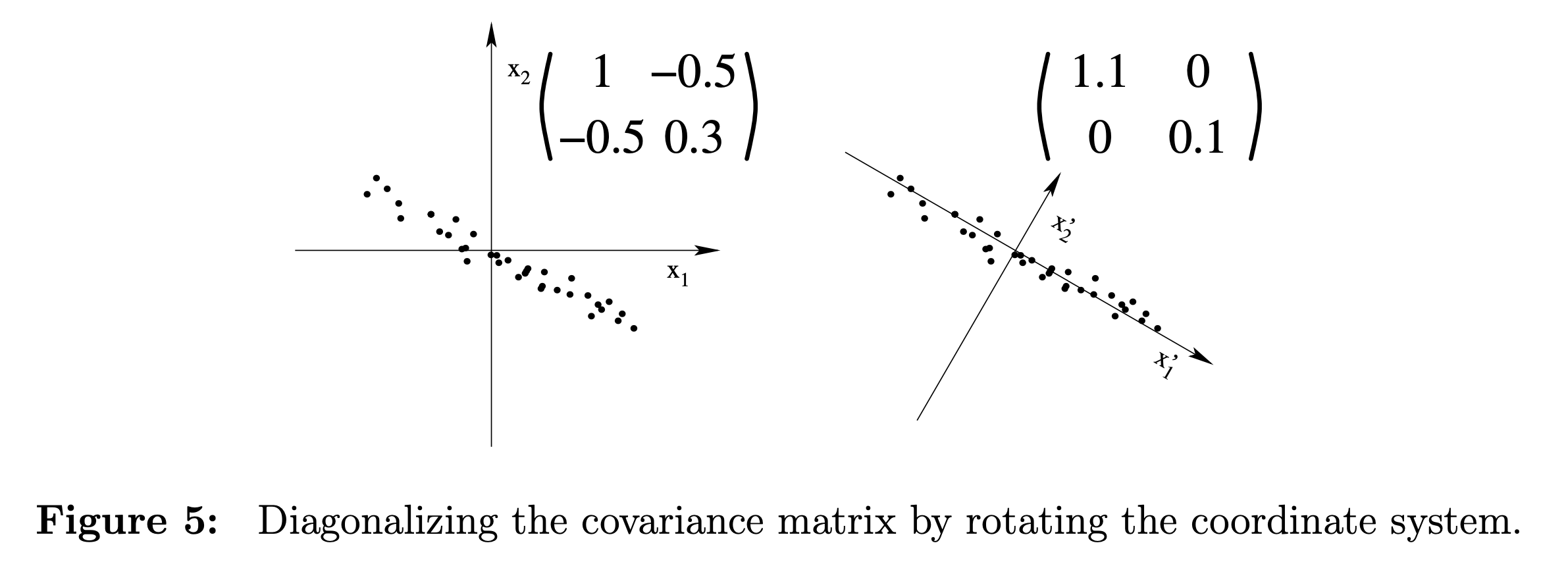Fig. some examples of different dataset with different covariance matrix

원래 data의 covaraince를 diagnoalize 하고 나면 비로소 PC가 보이게 되는데, 이 때도 eigenvalue가 큰 값을 고르면 data 분포가 가장 널리 퍼지게 된다. 이것이 바로 covariance의 eigenvector를 구해서 이 공간으로 projection 하는 이유이다.

(추가로 누군가는 위의 constraint problem을 gradient descent로 풀어도 되는 것 아니냐고 할 수 있다. 하지만 우선 이것이 수렴하는지 잘 모르겠고 (자료를 자세히 못 찾아봤지만 이런 얘기가 있는 듯 하다), eigenvalue decomposition이라는 efficient solution이 있는 상황에서 굳이 optimization을 해야 하는지 모르겠으므로 이는 넘어가도록 하겠다.)

PCA using Singular Value Decomposition (SVD)

앞서 PC를 찾는 가장 쉬운 방법은 covariance matrix의 eigenvector를 구하는 것이라고 했다. 하지만 이것보다 더 간단한 방법이 존재한다.

Fig. 다양한 방법으로 PC를 구할 수 있다.

그건 바로 \(X\)자체에 대해서 (not covariance, but dataset itself) 특이값 분해 (Singular Value Decomposition; SVD)를 쓰는 것이다. 두 approach 모두 decomposition을 한 뒤에는 구한 eigen (or signular) vector를, eigen (or singular) value순으로 정렬한 뒤 내가 원하는 subspace갯수 k개 만큼을 뽑으면 된다.

원래 matrix를 대각화 (diagonalization) 하는 방법은 eigenvalue decomposition가 대표적인데, 이는 row, column dimension이 같은 \(m \times m\) 정방 행렬 (Square matrix)이 아닌 경우 사용할 수 없다. 하지만 원본 dataset은 sample 수가 N개고 feature가 d개라면 \(\mathbb{R}^{N \times d}\)이기 때문에 eigenvalue decomposition은 쓸 수도 없으며, 쓴다고 하더라도 의미가 없다 (왜냐하면 covariance가 아니기 때문에).

SVD에 대해서 조금 recap 해 보자. SVD는 아래와 같이 matrix를 3가지 성분으로 분해해주는데,

가운데 있는 \(S\) matrix는 off-diagonal 성분이 0이고 diagonal 성분으로 singular value가 채워져 있는 diagonal matrix이며, 그 외의 matrix, \(U,V^T\)를 각각 diagonal matrix 왼쪽, 오른쪽에 있다 하여 left-singular vector matrix와 right-singular vector matrix 라고 한다.

그런데 사실 SVD와 eigenvalue decomposition은 서로 관계가 있다. 우리가 구해야 하는것은 \(X^TX\)의 eigenvector들 이었는데, 사실 이 covariance의 eigenvector를 구하는 것은 \(X\)의 singular vector를 구하는 것과 거의 같다.

여기서 matrix \(V\)는 단지 covariance matrix의 eigenvector들이며, matrix \(S\)는 실제 covraince matrix를 eigenvalue decomposition해서 얻은 eigenvalue의 square root 값이라는 차이가 있을 뿐이다.

이제 SVD를 사용해 matrix decomposition을 한 몇 가지 예시를 살펴보자. 먼저 square matrix에 대한 예시이다.

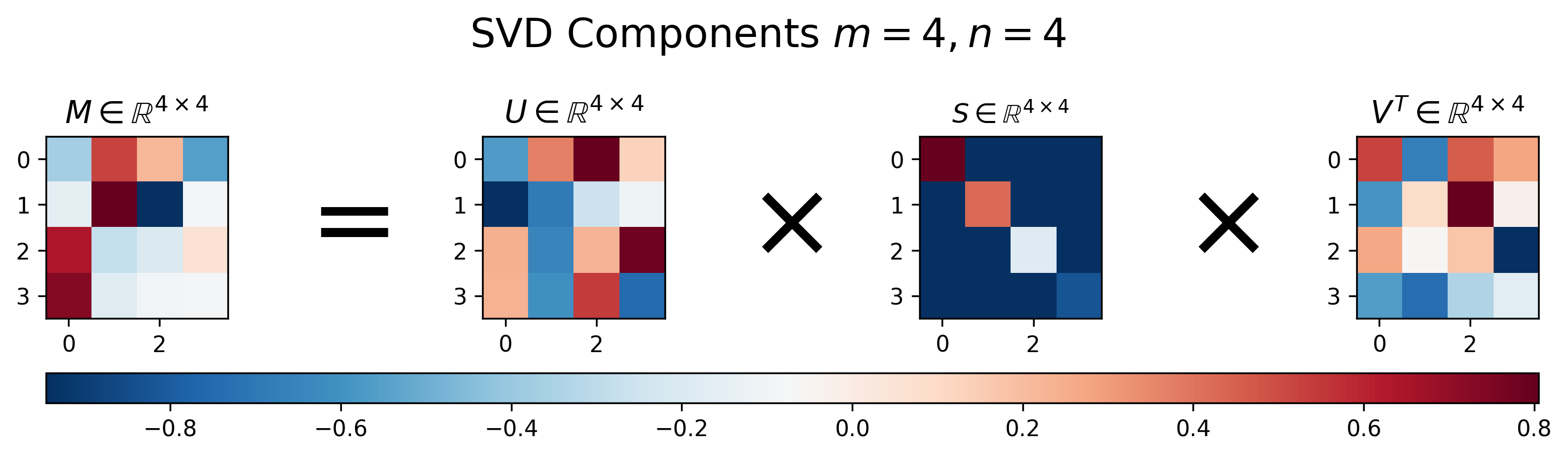Fig. SVD of Square Matrix. Source from here

Matrix \(U\)는 각 column vector 들이 모두 서로 직교하며 크기가 1인 orthonormal matrix이며, matrix \(V^T\)는 row vector들이 그러한 관계에 놓여져 있다. 앞서 말한 것 처럼 SVD는 square matrix가 아닌 경우에도 적용할 수 있다. 아래 \(4 \times 8\), \(8 \times 4\)인 matrix를 보자.

Fig. SVD of 4x8 Matrix. Source from here

Fig. SVD of 8x4 Matrix. Source from here

위에서 보다시피 원래 SVD를 하면 \(m \times n\)크기의 matrix에 대해서 \(U \in \mathbb{R}^{m \times n}, S \in \mathbb{R}^{n \times n}, V^T \in \mathbb{R}^{n \times m}\)의 matrix들을 얻을 수 있다.

그런데 어떤 matrix에 대해 SVD를 활용하면 매우 아름다운 일을 할 수 있다. 그 이유는 matrix를 표현하기 위해서 singular vector와 sigular value를 모두 가지고 있을 필요가 없기 때문이다. 어떤 matrix는 column vector가 형식적으로는 8개이지만 이 중 몇개의 vector는 나타내는 바가 같아서 실제로는 redundant할 수 있기 때문이다. 즉 어떤 vector는 어떤 vector의 n배를 한 것이나 다름 없을 수도 있다. 이런 경우 matrix의 rank가 8이하인 4가 될 수도 있고 이런 경우 full rank가 아니라고 한다.

이런 경우 SVD를 통해 얻은 \(U,S,V^T\)중 몇개의 성분은 날려버려도 전혀 문제가 없다. 아래의 figure를 보면 맨 왼쪽의 경우 column이 4개이지만 rank도 4여서 full rank이다. 즉 redundancy가 없지만, 가운데 matrix는 그렇지 않다. 가운데 matrix는 column vector는 8개이지만 rank가 4 이므로 SVD를 했을 때 left singular matrix 중 하위 4개 버리고, diagonal matrix와 right singular matrix에서도 그에 대응되는 matrix를 버려도 원본 matrix를 정확히 복원해낼 수 있다.

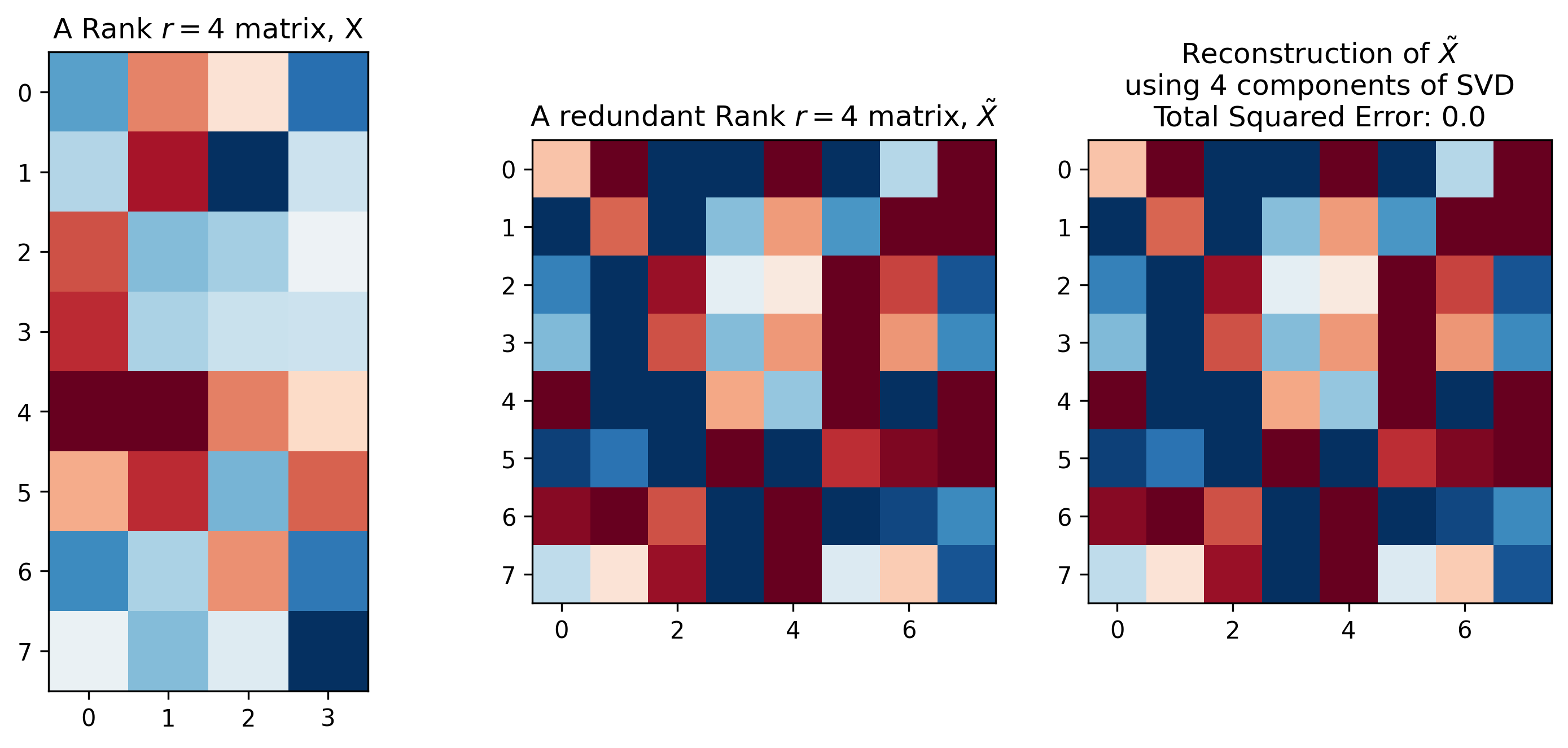Fig. 어떤 matrix는 full rank가 아니므로 SVD를 통해 많이 압축해도 loss가 0이다. Source from here

혹은 만약에 data가 full rank 여서 완전히 복구를 할 수 없더라도 필요에 따라서 우리는 우선 순위가 낮은 vector들을 날려버릴 수 있는데, 이렇게하면 강제로 rank가 낮아지는 것이고, 이를 Low Rank Approximation (LRA)라고 한다.

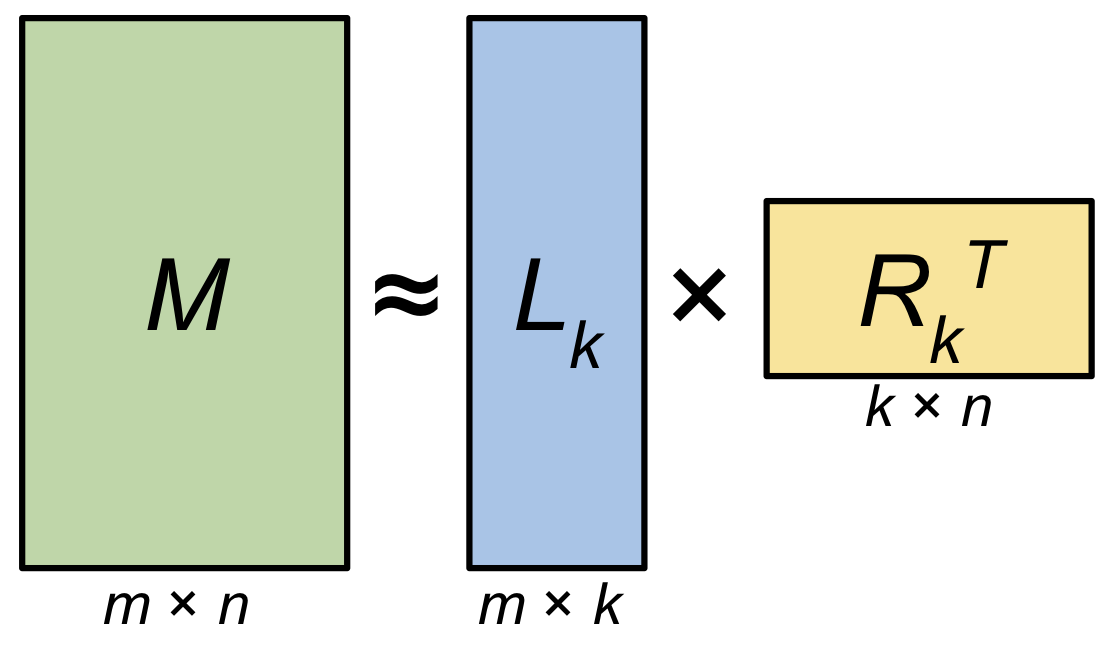Fig. Low Rank Approximation. Source from here

이를 이용해 image 같은 high dimensional matrix를 압축할 수 있는데,

이렇게 압축된 matrix는 무수히 많은 singular vector들을 계산한 것을 signular value 만큼 weighted sum한 것이나 다름 없게 된다.

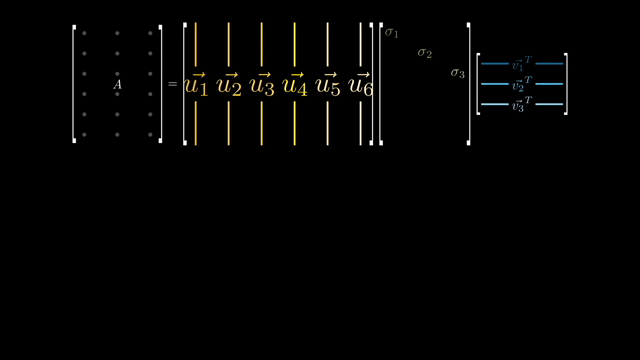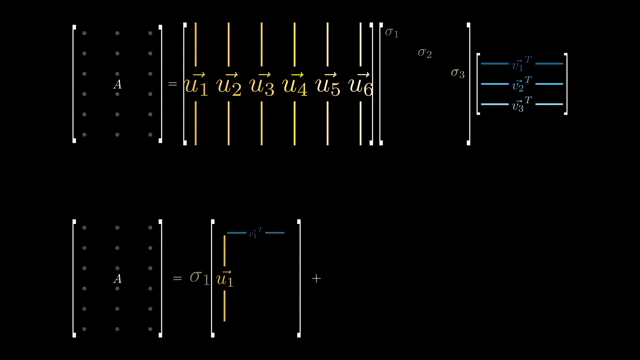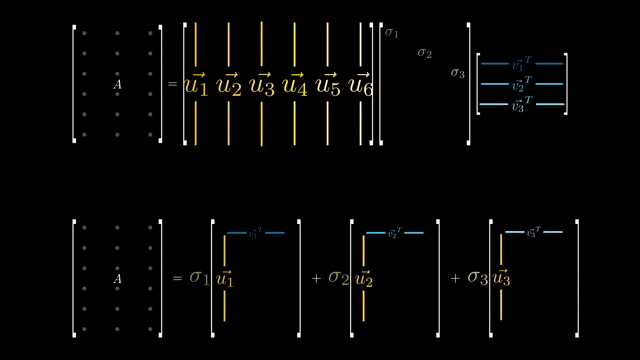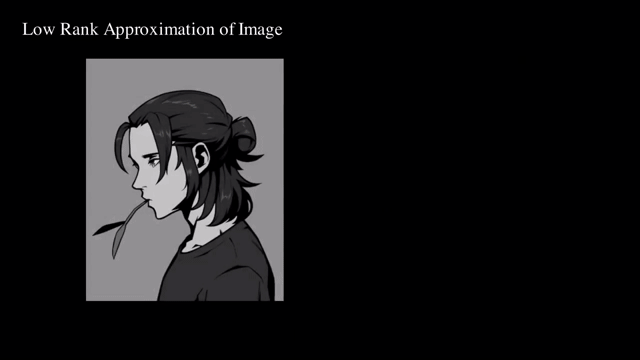
우리는 지금 원본 dataset (feature 차원이 d이며 갯수가 N; \(\mathbb{R}^{N \times d}\))를 SVD하고 그 중에서 상위 r개만 뽑아 \(\mathbb{R}^{N \times r}\)인 subspace 상의 vector들을 얻고싶다. 그리고 이것은 곧 LRA를 하는것과 같은 것이 된다.

아래와 같이 feature dim이 8인 data가 12 개 (\(X \in \mathbb{R}^{12 \times 8}\)) 있다고 생각해 보자. 이 data matrix에 대해서 SVD를 수행해서 top 1~N개 정도의 vector (component)들을 고를 수 있다. (앞서 covariance matrix, \(X^TX\)를 구하고 eigenvalue decomposition을 해도 된다고 했다.)

그러면 우리는 n개의 components \(U \in \mathbb{R}^{8 times n}\)을 사용해 \(Z = X U \in \mathbb{R}^{8 \times 3}\)의 matrix를 얻을 수 있다. 만약 vector (component)를 1개 골랐다면 1차원 line으로 8차원 data를 projection 하는 것이 된다. 만약 approximate 된 matrix \(W\)에 다시 \(C\) matrix를 외적한다면 우리는 원본 matrix를 얻을 수 있는데, matrix \(\tilde{X} = Z U^T = X U U^T\)는 rank가 1인 matrix가 된다.

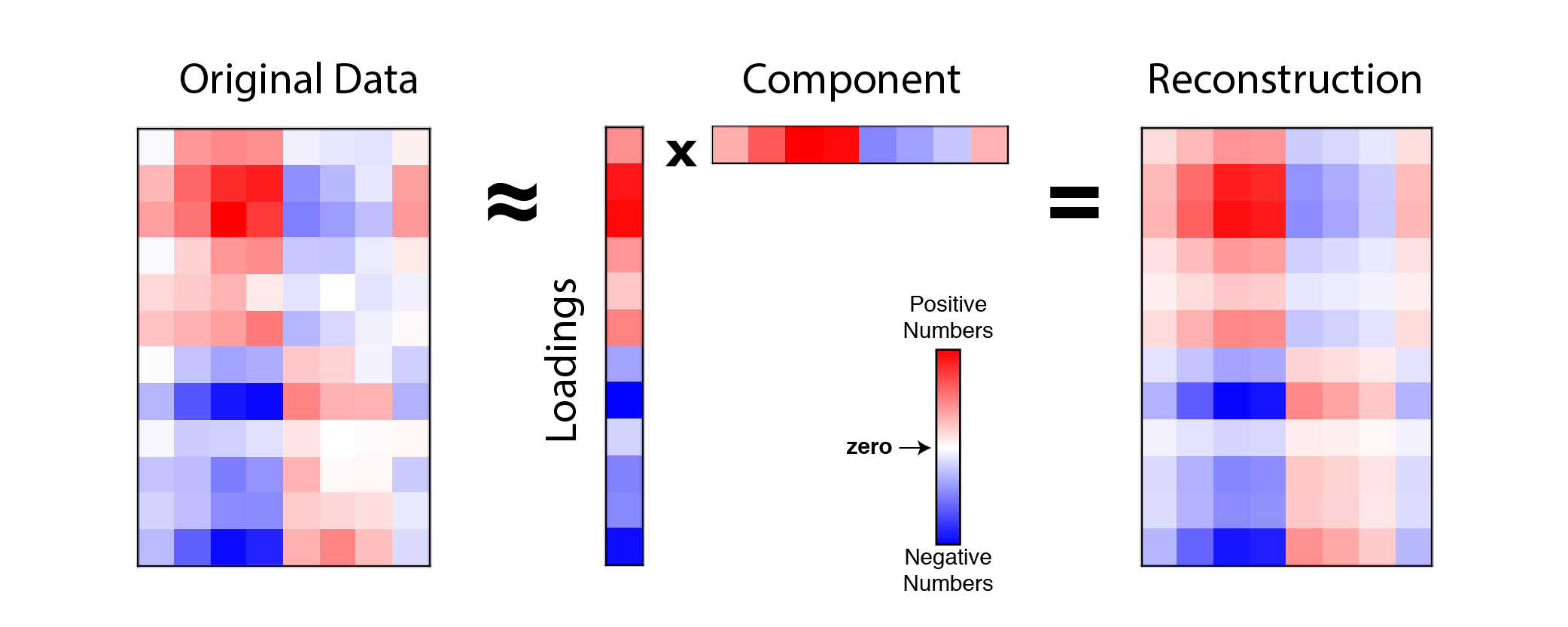Fig. rank=1. Source from here

3개의 component를 골라 차원으로 projection 한다면 차원은 증가하지만 information을 너무 많이 잃지 않는 선에서 적당히 차원 축소가 가능함을 알 수 있다.

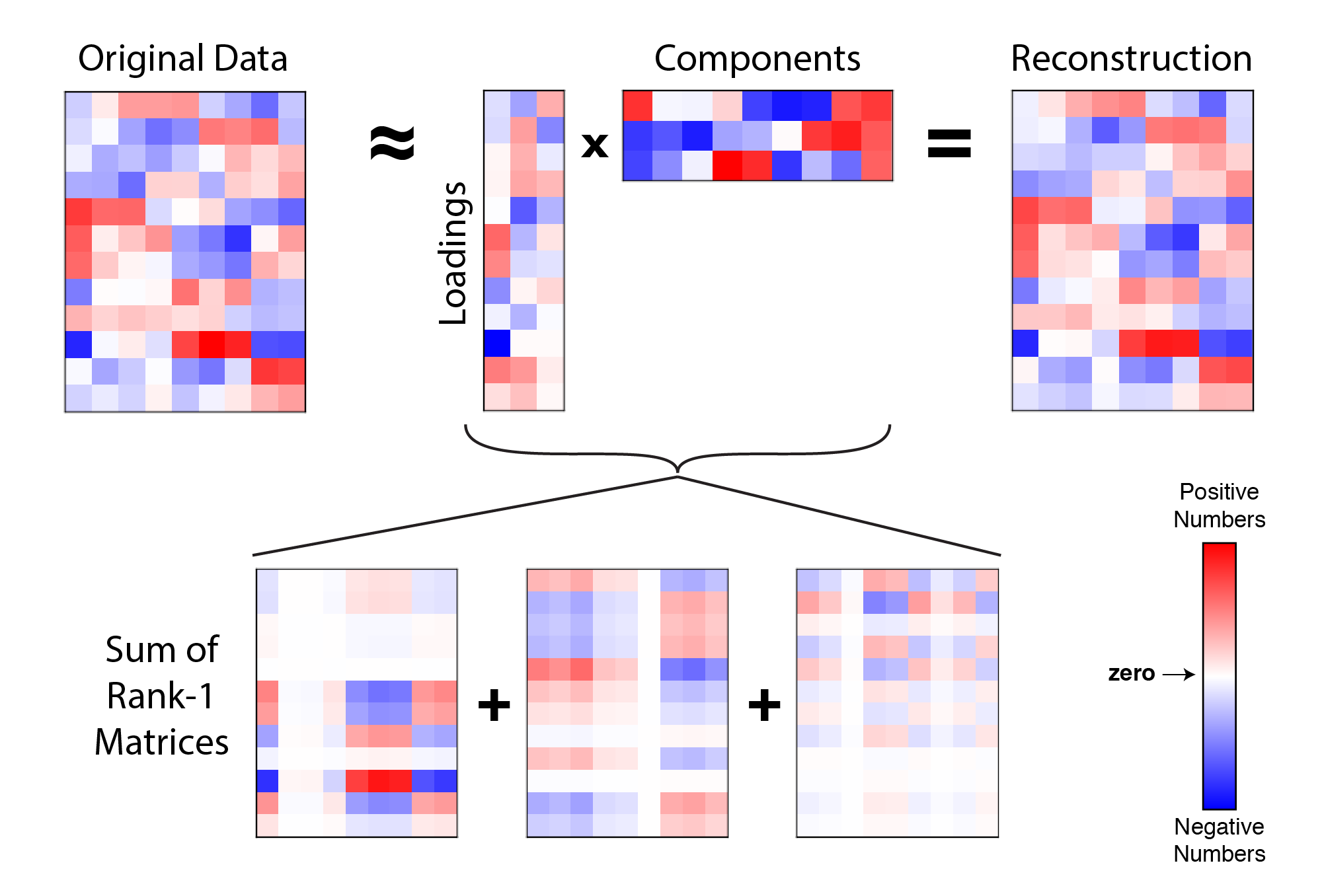Fig. rank=3. Source from here

내가 가지고있는 dataset을 information loss가 심하지 않으면서도 적당한 subspace로 projection하기 위해서는 몇 개의 component가 필요한가? 를 plot해 볼 수도 있는데, 이를 고려해서 PC의 개수를 정해야 할 것이다.

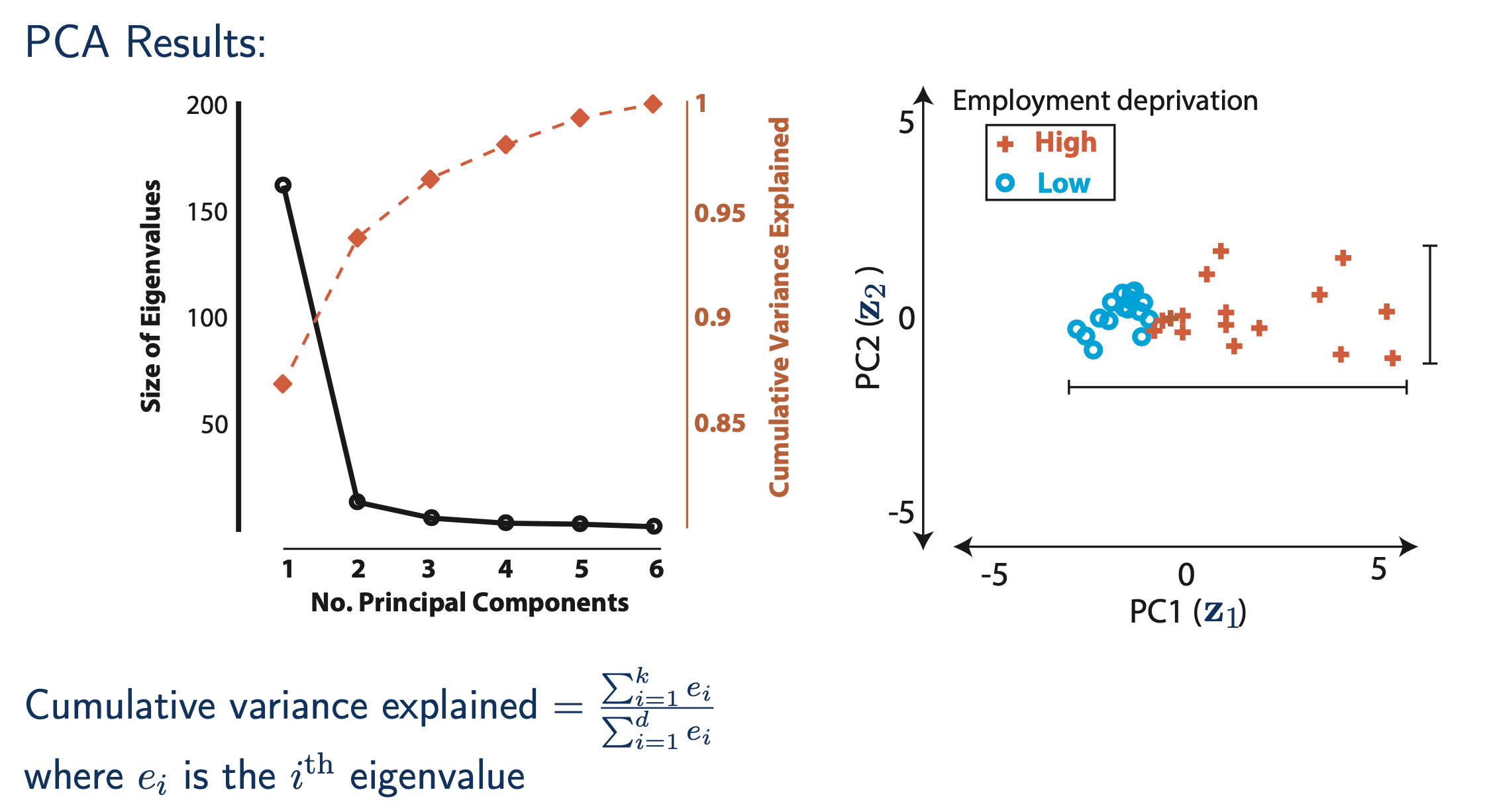Fig.

Decorrelation

PCA를 통해 얻은 subspace projected vector, \(z\)들은 서로 얼마나 correlation이 있을까? 사실 PCA를 하면 각 feature들이 decorrleration 되는 효과가 있다고 한다. 이를 증명하기 위해서는 아래처럼 \(z\) vector들의 covariance를 재보면 되는데,

covariance matrix가 diagonal 하면 (off-diagonal이 모두 0), 각 feature 는 uncorrleated 하다고 하는데 \(z\) vector들이 서로 그러한 것이다. 이는 다르게 말하면 redundancy가 없다고 할 수도 있다.

Application: Eigenface

끝으로 PCA의 유명한 application 중에는 Eigenface라는 것이 있다. PCA로 3개 PC를 뽑은 뒤 classifer를 학습한 것이 Gaussian Mixture Model (GMM) 같이 복잡한 모델보다 더 좋은 performance를 보였다는 것이다.

Fig.

Connection to AutoEncoder (AE)

한 편, ML algorithm 중 오토 인코더 (Auto Encoder; AE)라는 것이 있다. 보통 고전 ML algorithm들은 굳이 따지자면 layer가 1개이고 비선형성 (non linearity)라는 것이 없지만, Neural Network (NN)는 그렇지 않다. 층이 2개 이상이며 각 층을 통과할 때마다 non-linearity 를 주입해 더 복잡한 curve fitting을 할 수 있다. 그런데 층이 2개인 경우 특히 가운데 병의 목 (bottle neck) 구조를 가지고 있어 feature dimension이 확 줄어들었다가 다시 원래의 feature dimension으로 되돌아가는 형태가 있는데, 이를 AE라고 한다.

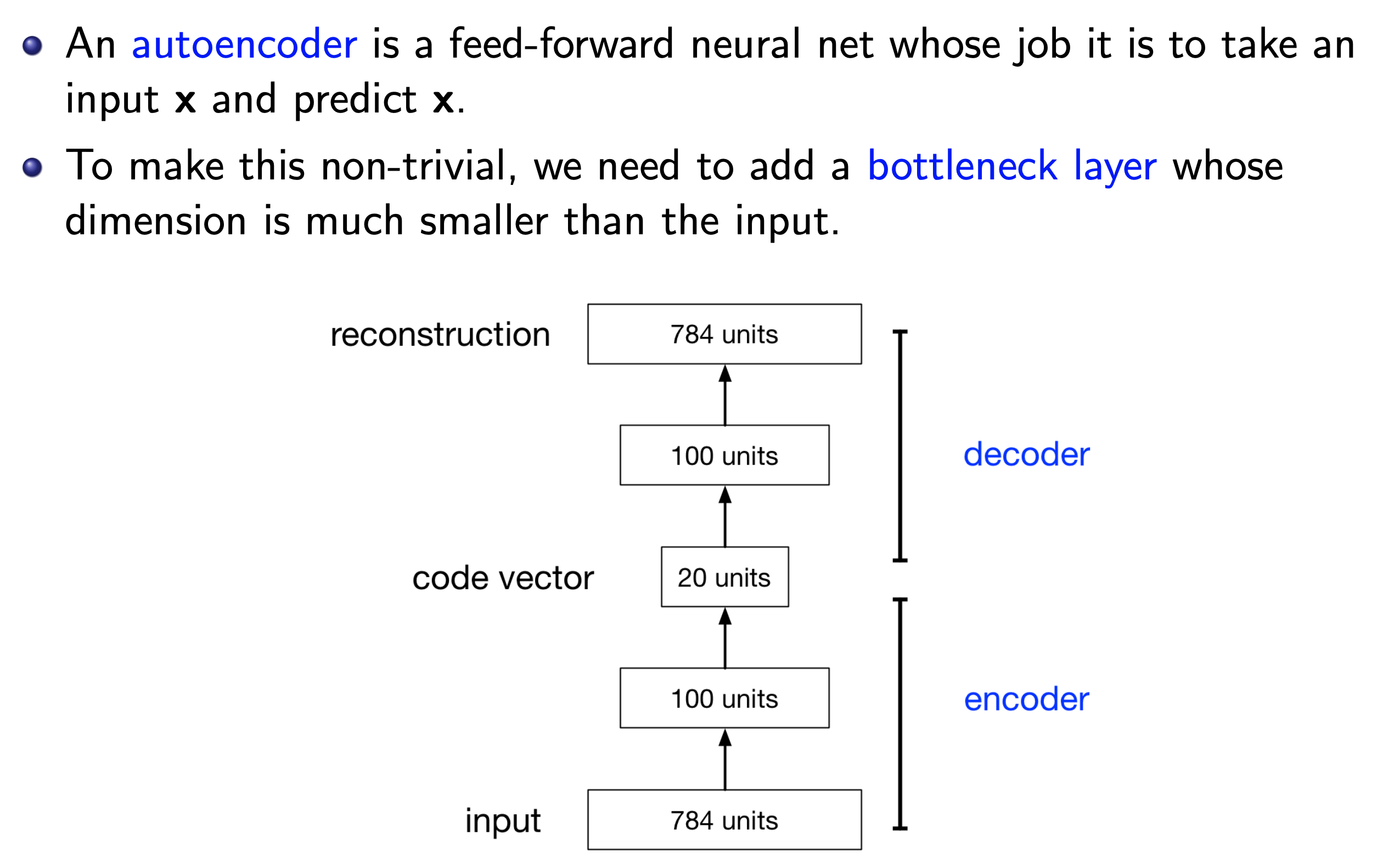Fig.

예를 들어 AE는 input \(x\)가 예를 들어 784차원인데 (보통 28x28 gray scale image가 딱 이 크기다), 이를 첫 layer에 통과시키면 4차원이 되도록 만든 다음 (\(z\)), 다시 layer를 통과시켜 784차원의 원래 feature를 복원 (\(x'\))하도록 한다. 그리고 이 architecture를 training하는 learning objective는 원본 input을 복원하는 것으로 architecture와 learning objective를 구성할 수 있다.

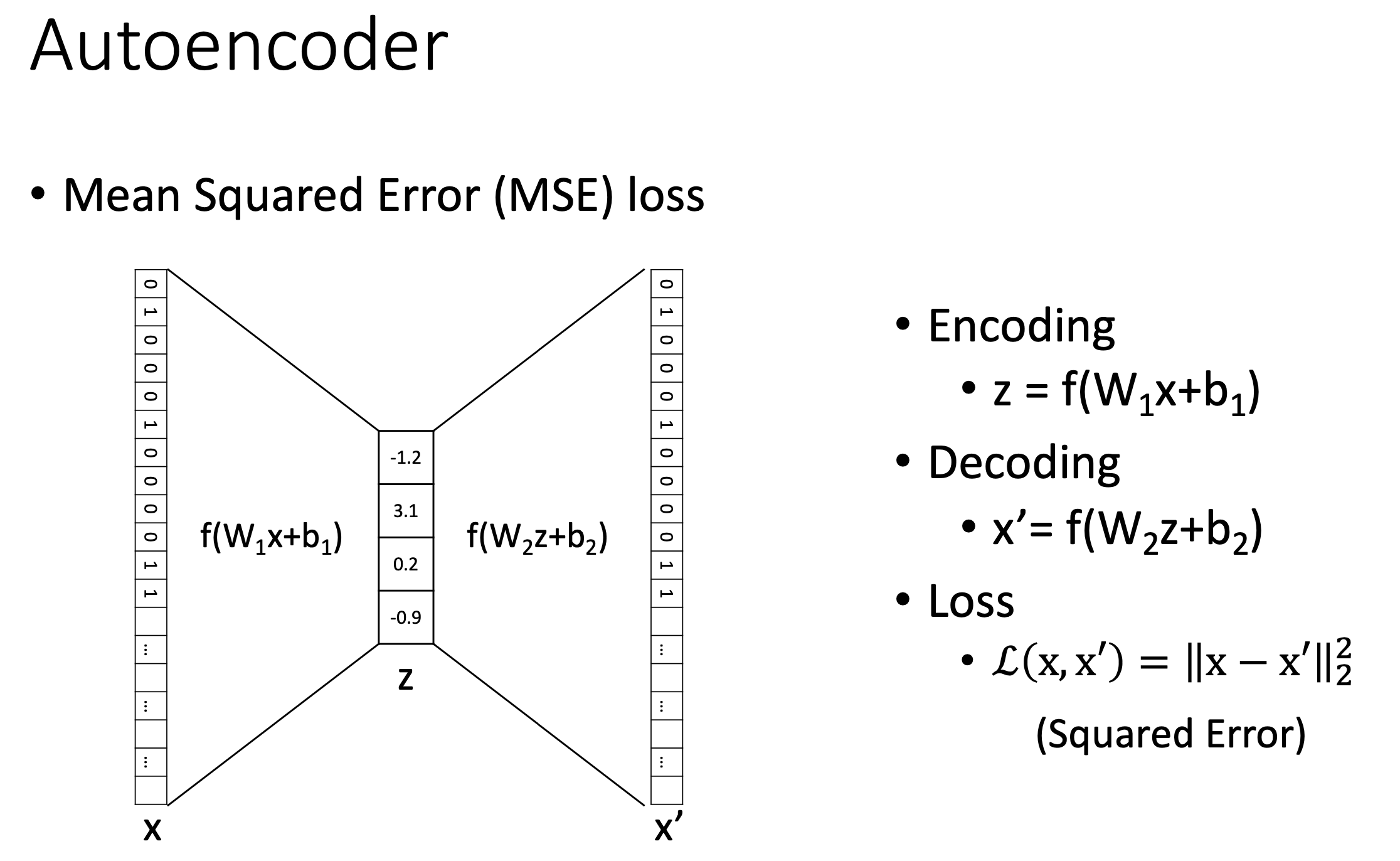Fig. Slide adopted from here

아마 여기까지만 봐도 AE와 PCA는 거의 같은 일을 한다는 느낌이 왔을 것이다. 첫 번째 layer가 input data의 차원을 축소해주긴 하는데, 그것도 유의미하게 축소를 해주도록 알아서 training이 되는 것이다. 즉 우리는 어떤 image input을 받았을 때, 예를 들어 image size가 \(28 \times 28 = 784\) 차원을 가지고 있다면, training된 AE로부터 4개의 유의미한 feature를 찾을 수 있고 여기에 classifier 를 붙혀서 이 image가 남자인지? 여자인지? 판단하는 binary classification 같은 task를 풀 수 있다. (즉 DL에서 널리 쓰이는 pre-training을 고전 ML에서도 하고 있었던 것)

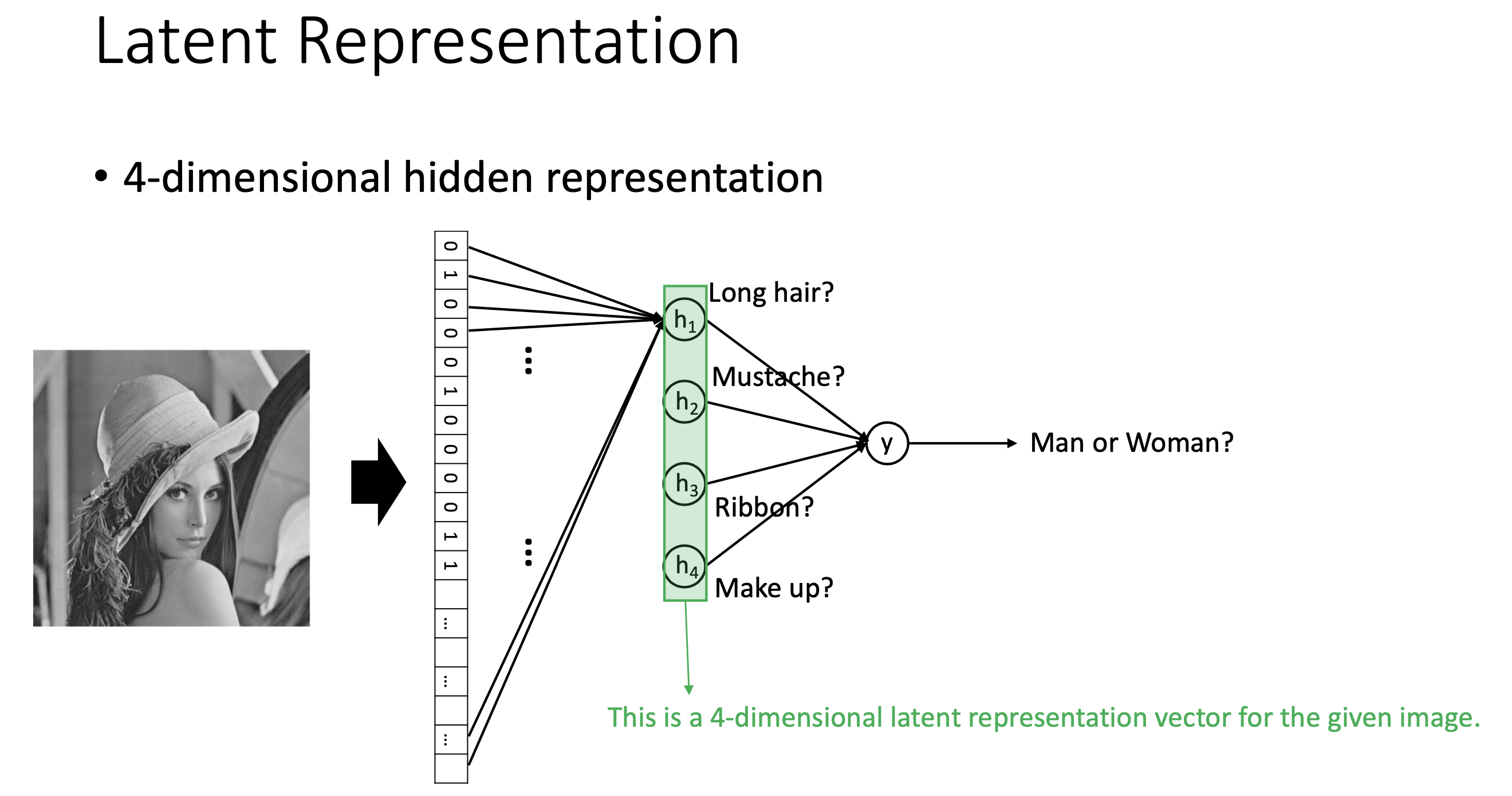Fig. Slide adopted from here

이렇게 저차원의 유의미한 feature를 input data들 속에 숨어있는 잠재 표현 vector (latent representation vector)라고 하며, 그리고 이 latent vector가 존재하는 공간을 latent space라고 한다.

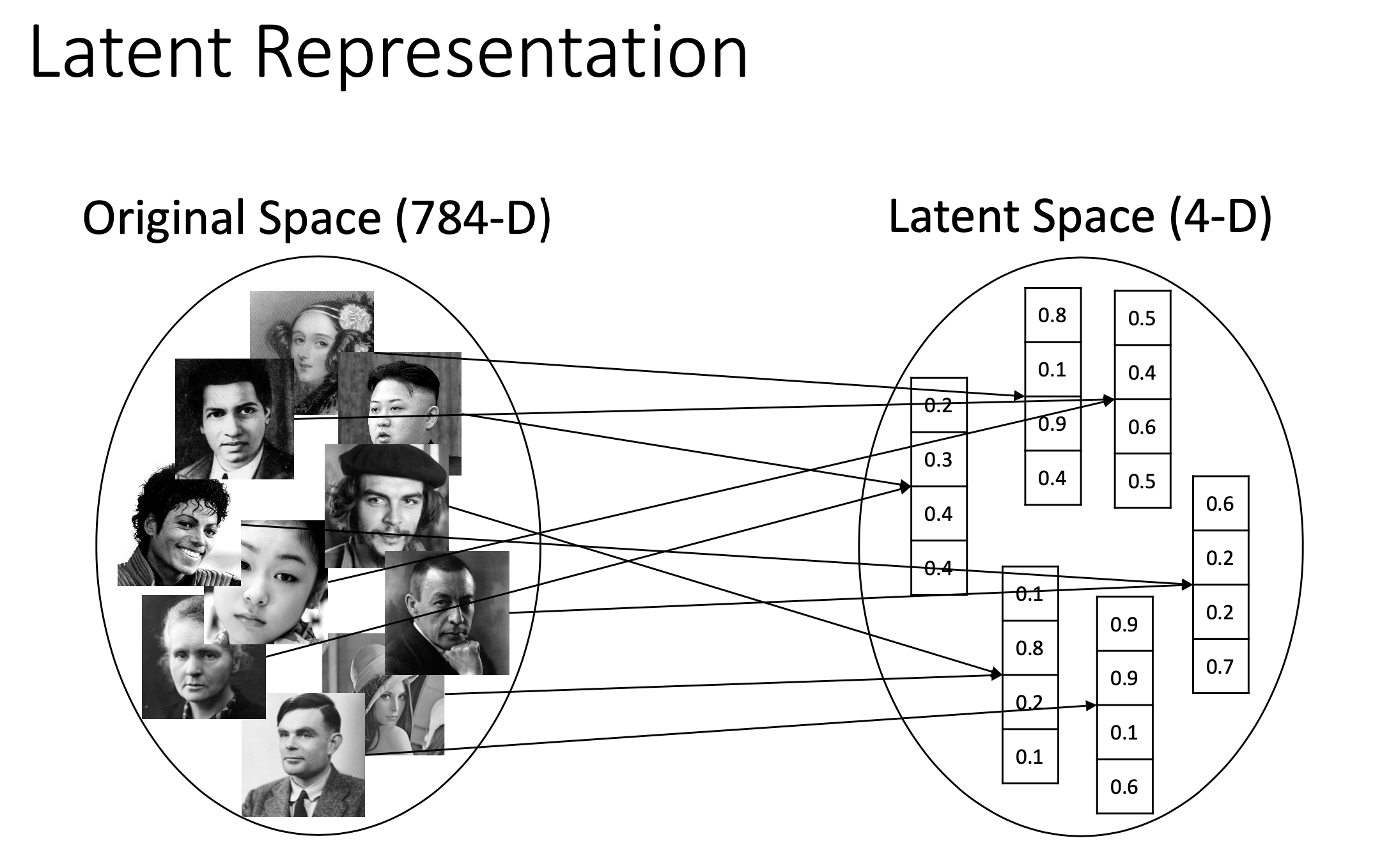Fig. Slide adopted from here

이 latent space는 우리가 training하고자 하는 objective function이 무엇인가에 따라 달라진다.

Fig. Slide adopted from here

한 편, 이 4차원짜리 latent vector (혹은 information bottleneck)은 우리가 원하는 것처럼 해석 가능한 (interpretable) feature들일까? 그럴 가능성은 낮다고 한다. 사실 PCA에서도 이건 마찬가지 라고 한다. 우리가 여자, 남자 image로 부터 머리길이, 턱수염의 유무 같은 유의미한 feature들만 뽑고 싶겠지만 그럴 순 없는 것이다.

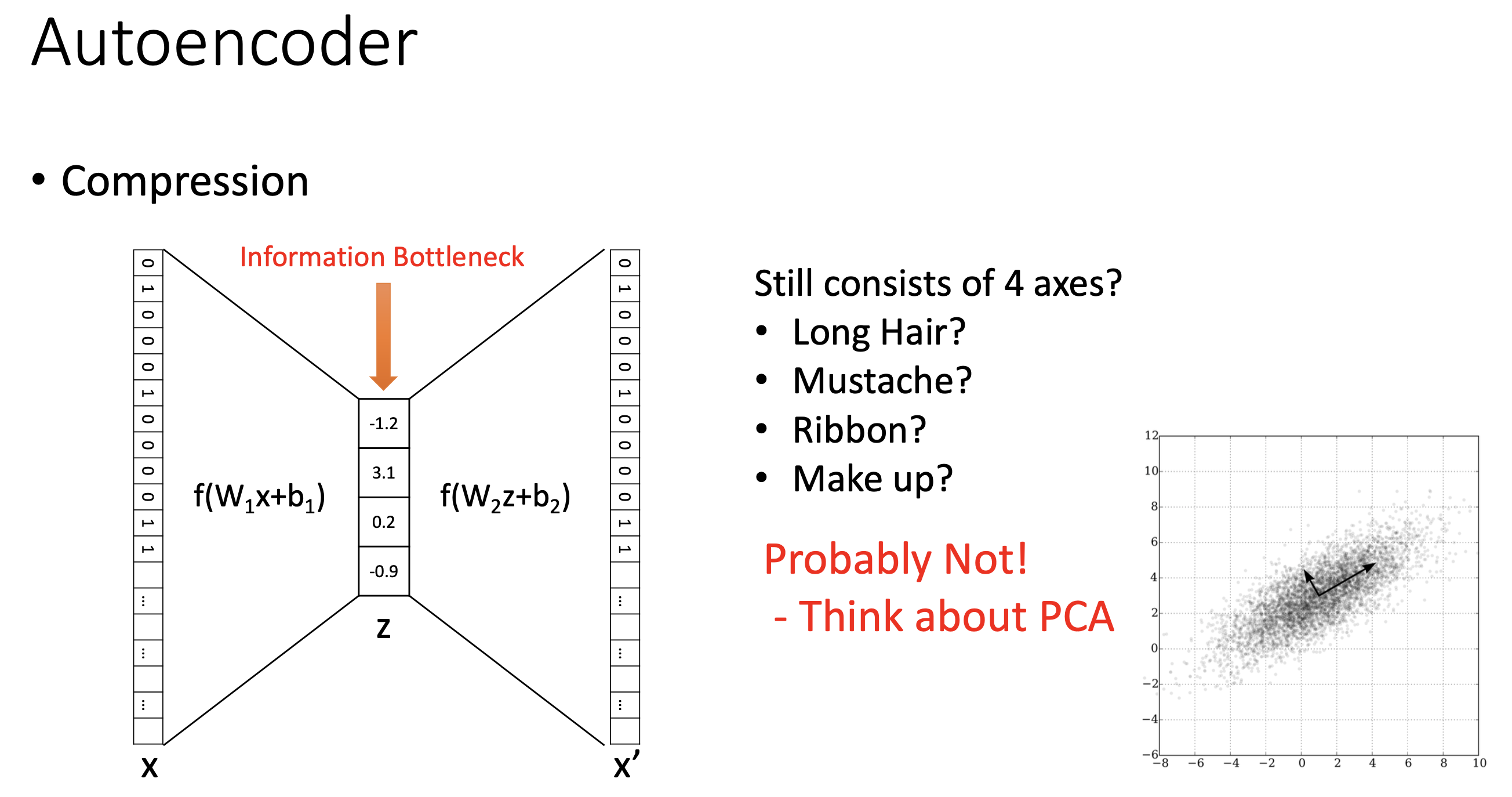Fig. Slide adopted from here

다만 해석하기는 어려워도 비슷한 input은 비슷한 vector로 mapping 되어야 잘 training이 된 것이라고 할 수 있다. (이를 강제하기 위해서 regularization term을 objective에 추가할 수도 있을 것이다)

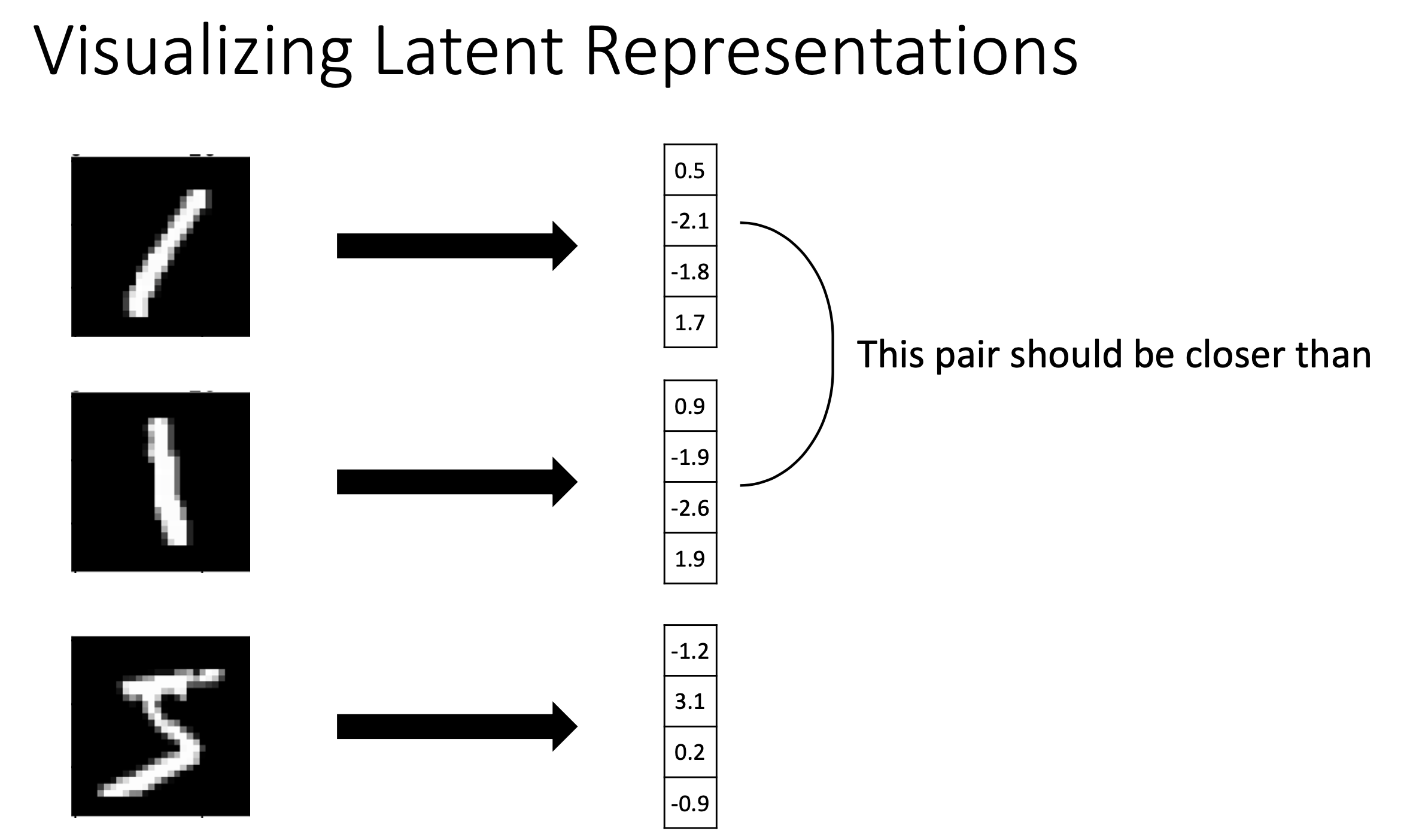Fig. Slide adopted from here

PCA vs AE

그래서 PCA와 AE는 뭐가 다른가? Objective가 reconstruct error를 minimize 한다고 해서 PCA와 AE가 같은 것은 아니다. 왜냐하면 AE는 layer를 통과할 때마다 비선형성 (non-linearity)이 추가되기 때문이다.

Fig. Slide adopted from here

물론 non-linearity가 존재하지 않는 linear AE는 PCA와 optimal solution이 같다고 할 수 있다. 왜냐하면 linear AE의 경우 AE의 output 1st layer의 weight matrix가 \(W_1\), 2nd layer의 weight matrix가 \(W_2\)라고 할 때 \(y = W_2 W_1 x\)이기 때문이다. 그러면 당연히 objective function은 다음과 같이 쓸 수 있을텐데,

이것은 정확히 PCA의 objective와 같다. 당연히 optimal solution은 eigenvector를 구하는 것과 같을 것이다.

그러나 Non-linearity AE는 PCA와 전혀 다른 차원의 dimensionality reduction을 할 수 있는데, 예를 들어 아래 왼쪽과 같이 data가 구성되어 있을 때 (roll cake같이 생겨서 swiss roll data라고 한다) nonlinear projection을 잘 학습하면 3차원에서 2차원으로 mapping하더라도 data를 잘 구분할 수 있을 정도로 좋은 space를 얻을 수 있다.

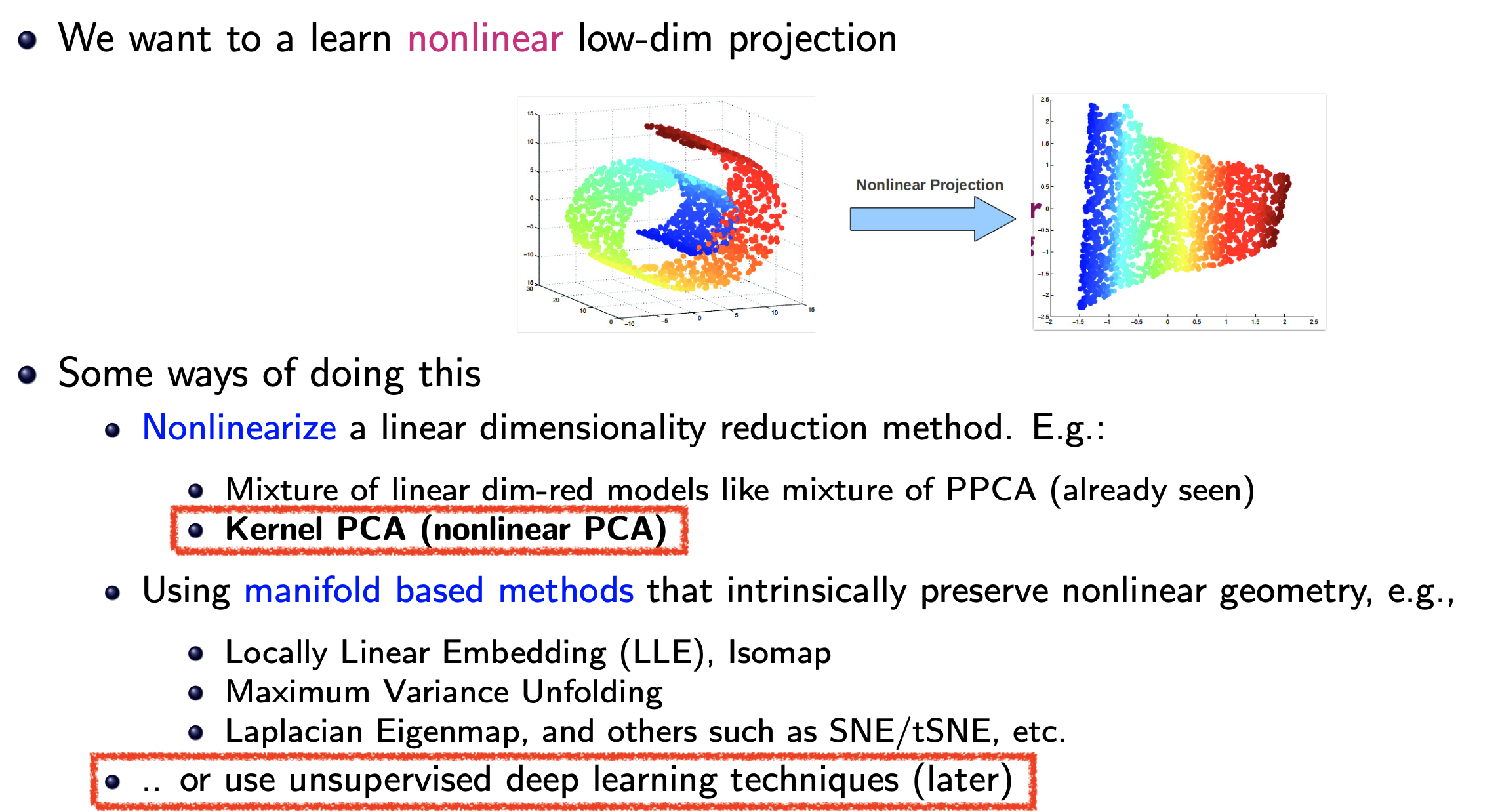Fig. Source from here

반면에 PCA는 어떻게 해도 결국에 linear projection을 하는 것에 지나지 않기 때문에 3차원 swiss roll data를 2차원으로 projection 하는 데 한계가 있을 수 밖에 없다.

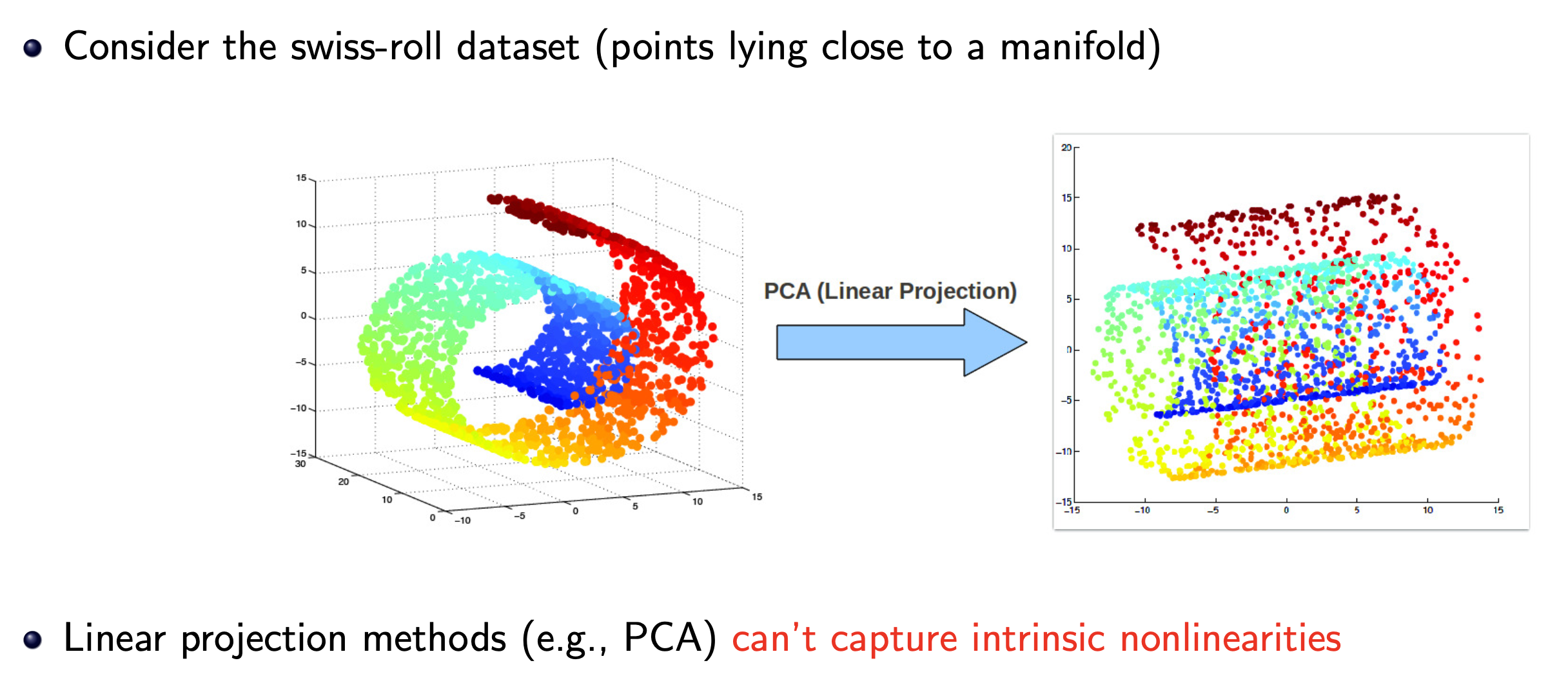Fig. Source from here

이렇게 data가 swiss roll처럼 기이하게 뿌려져 있을 때 이 data들이 사는 공간을 manifold라고 하는데, nonlinear projector들은 이를 펴는 (unrolling) 능력을 가질 수 있다.

아래 PCA와 AE를 통해 찾은 space를 보면 원래 vector를 복원하는 데 있어 상당한 성능 차이가 있다는 걸 알 수 있다. (역시 DL이다.)

Fig.

Sparse AE

더 좋은 subspace를 찾기 위해서는 어떻게 할까? 사실 AE의 variant들은 굉장히 많다. 그 중에서 Sparse AE에 대해서만 잠깐 알아보도록 하자.

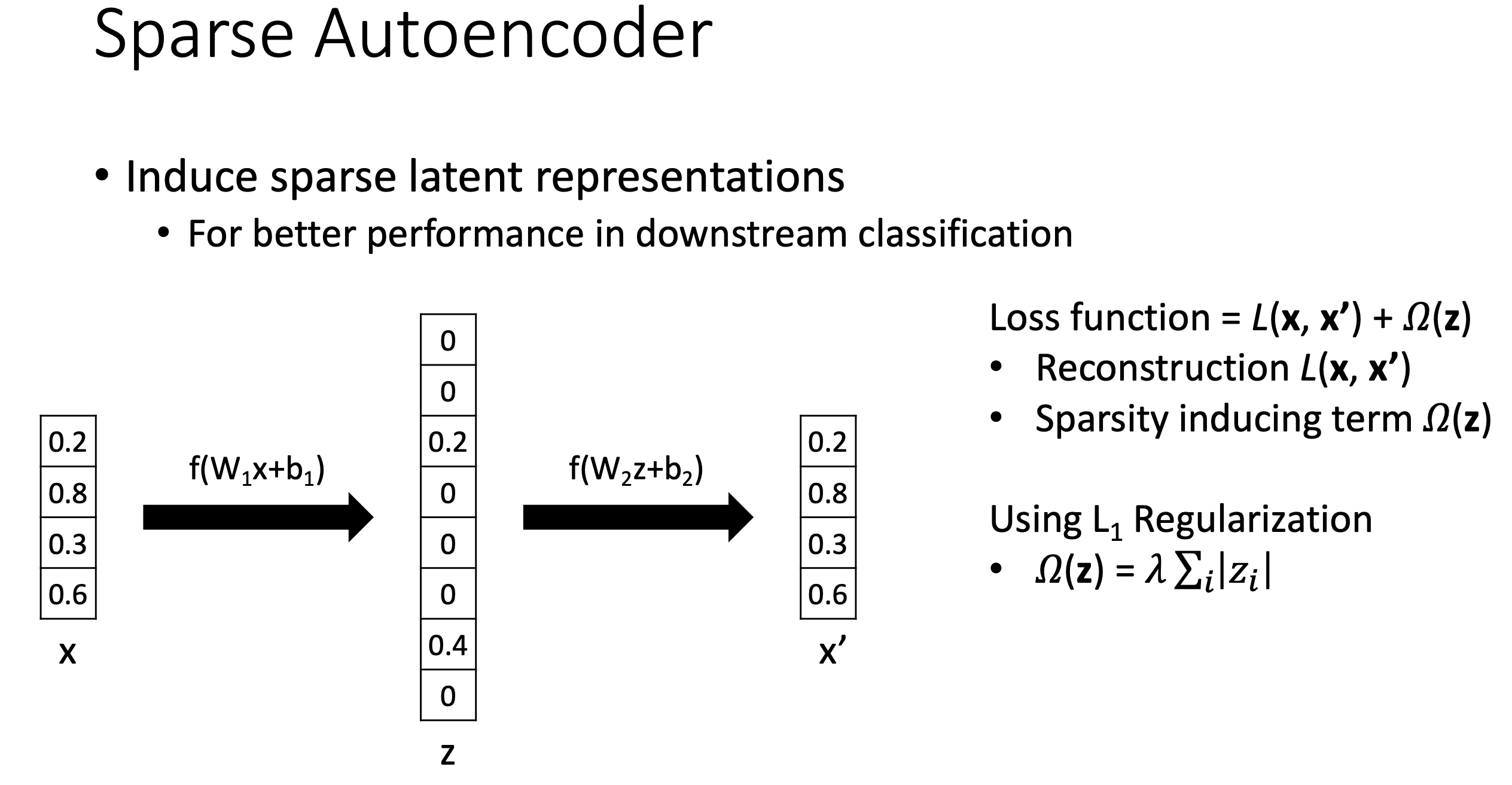Fig. Slide adopted from here

Sparse AE는 solution matrix가 희박 (sparse)하다는 걸 의미한다. ML에서 sparse solution이라 함은 learned matrix (weight)의 element의 대부분이 0인 걸 의미하는데, 따라서 subspace로 projection해주는 matrix가 sparse한 걸 말한다.

보통 이 문제를 풀기 위해서는 원래의 objective function에 regularization을 추가해주면 되는데, L1 regulaizer를 추가하면 sparse solution을 얻을 수 있다. 이걸 해석하는 방법은 다양할 수 있는데, weight distribution이 0에 몰려있을 것이라는 prior를 주고 bayesian solution을 얻는 것으로 해석할 수도 있고, 기하학적으로 objective와 L1 penalty를 둘 다 만족하기 위해서는 sparse solution이 되어야만 하기 때문이라고 해석할 수도 있을 것이다. (자세한 내용은 블로그 내 L1, L2 regulaization에 대한 post 참고)

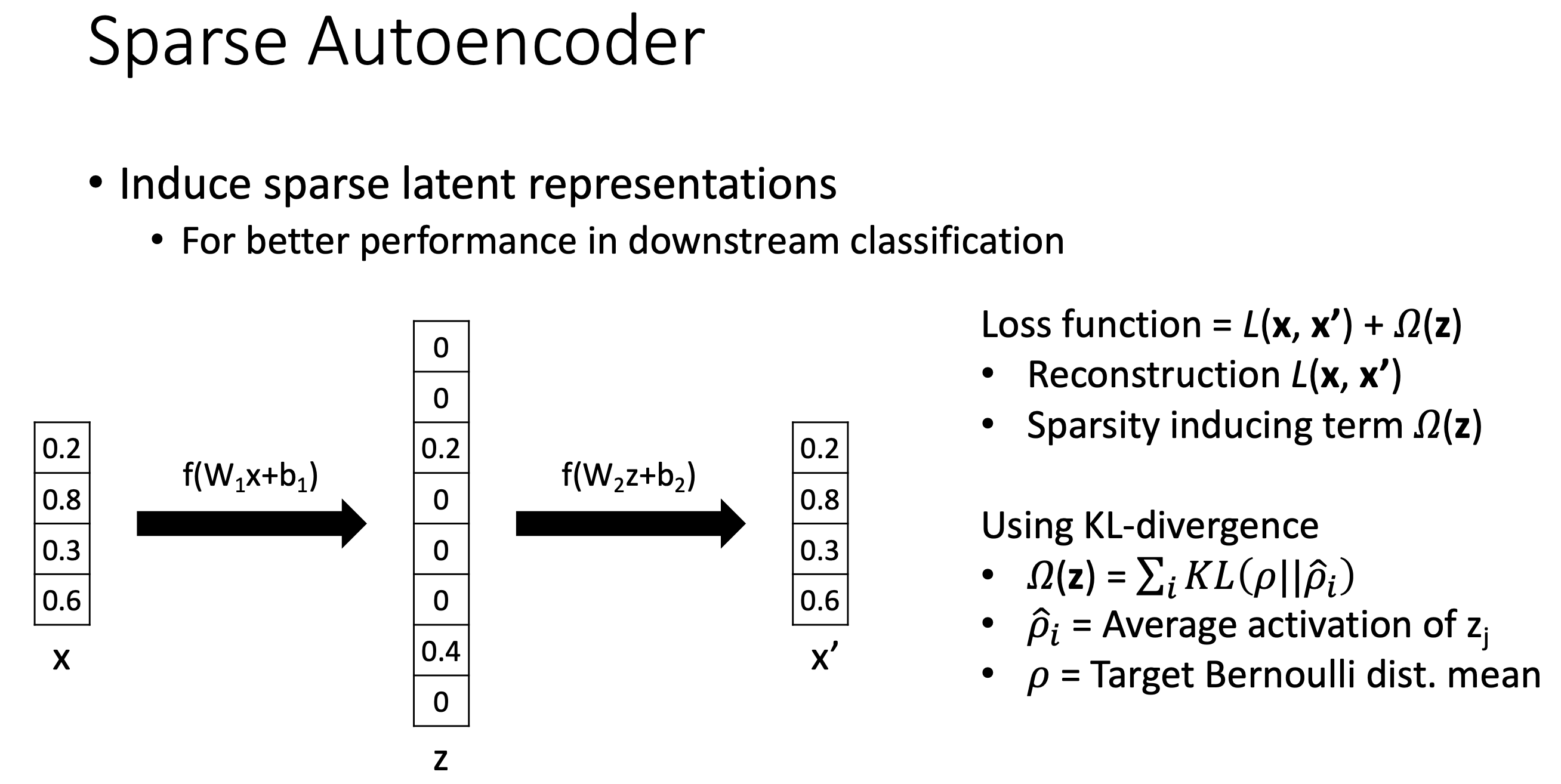Fig. Slide adopted from here

혹은 KL divergence를 쓰는 방법도 있는데, 깊게 생각해보진 않았지만 큰 틀에서 같은 역할을 할 것으로 생각된다.

(PCA도 Sparse PCA라는 것이 있다. 앞서 non-linearity만 빼면 정확히 같은 solution을 도출하기 때문에 비슷한 방식으로 sparse PCA도 구현할 수 있을 것이다. 다만 이때는 eigenvalue decomposition으로 쉽게 solution을 구하진 못할 것이다.)

Encoding to a Higher Dimensional Space

그런데 위의 Sparse AE를 보면 가운데 latent space의 차원을 input 차원보다 크게 설정된 것을 볼 수 있다 \((k > d)\). 이런식으로 하면 어떤 solution이 도출될까?

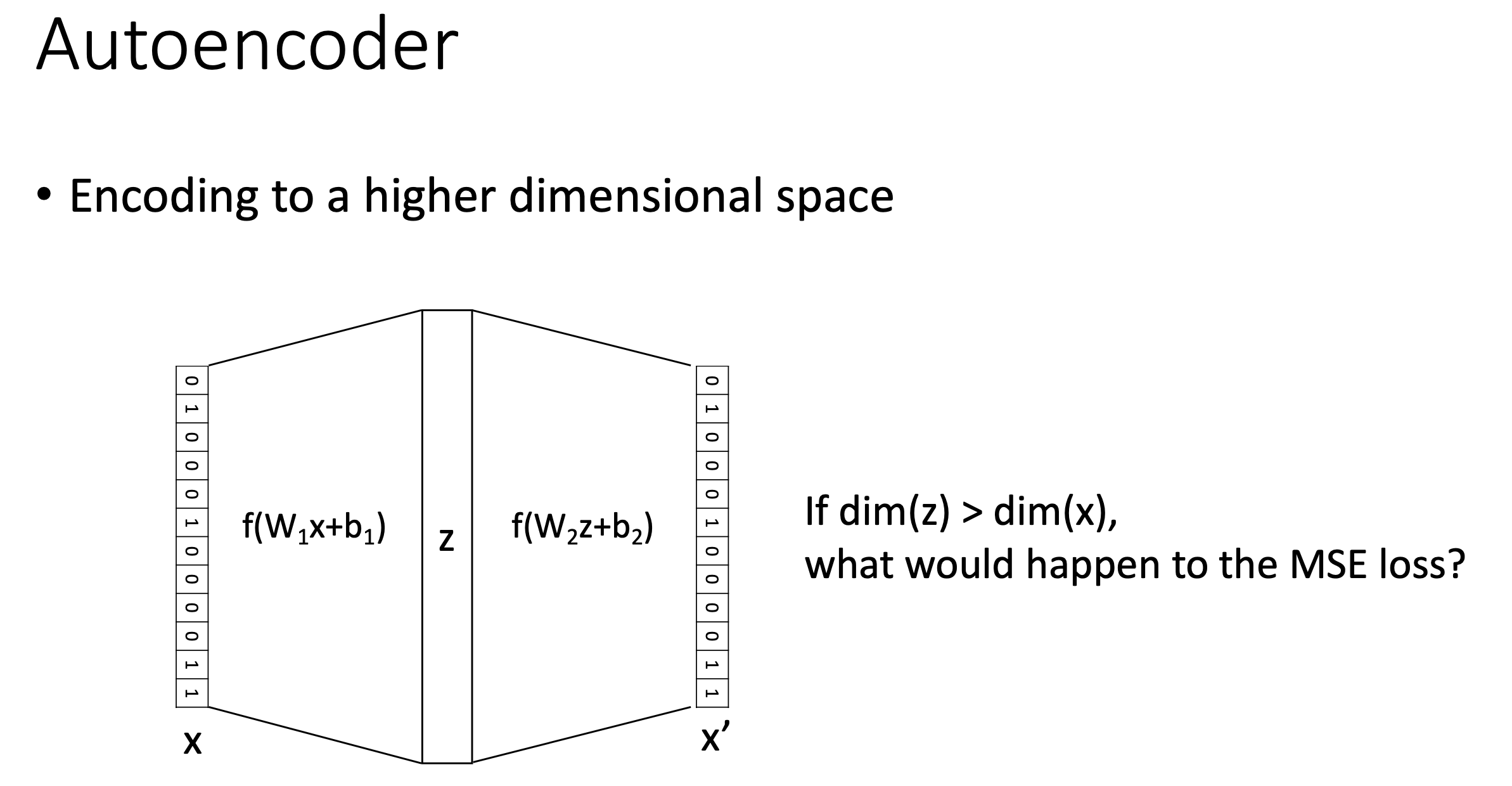Fig. Slide adopted from here

사실 non-linear AE에서도 그런지는 모르겠으나 linear AE라면 subspace projector는 identity matrix와 0항으로 이루어진 matrix가 될 수도 있다. 이는 어찌보면 당연한데, 원본으로 reconstruct을 가장 잘 하기 위해서는 제자리에서 안움직이면 되기 때문이다. 지금은 sparse solution을 강제하기 때문에 이런 일은 아마 안 일어날 것이다.

(DL 분야의 유명한 architecture인 Transformer의 block 하나 하나가 각각 layernorm, attention, feedforward network (FFN)의 조합으로 이뤄져있는데, 여기서 FFN의 구조체가 딱 이렇게 생겼지만 같은 현상이 일어나는지? 이를 의도한것인지? 에 대해서는 깊게 생각해보지 못했지만 독자들의 상상을 위해 우선 언급하고 넘어가려고 한다)

PCA vs Linear Discriminant Analysis (LDA)

차원 축소 algorithm 는 다양하다. t-distributed Stochastic Neighbor Embedding (t-SNE)나 Uniform Manifold Approximation and Projection (UMAP) 같은 것들도 존재한다.

Fig. Slide adopted from here

그리고 선형 판별 분석 (Linear Discriminant Analysis; LDA)라는 것도 있다. (Topic modeling에 쓰이는 Latent Dirichlet allocation (LDA)와 헷갈리지 말자) LDA는 PCA와 마찬가지로 data를 linear transformation 한다는 데서 공통점이 있지만, 판별 (classification, discrimination) task를 풀기 용이하게 차원을 축소한다는 점에서 차이가 있다.

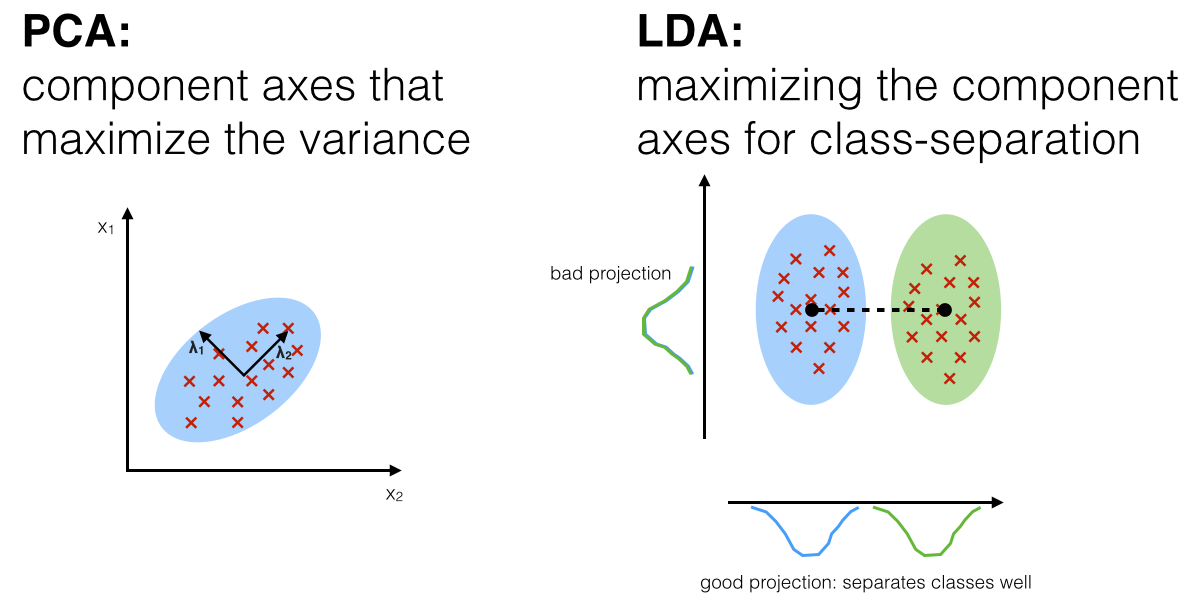Fig. Source from here

위 figure를 봤을 때 두 blue, green class label을 무시하고 단순히 variance를 maximize하는 basis들을 찾아 그 subspace로 projection 하는 것보다는 class aware한 subspace로 projection 하는 것이 더 좋다는 걸 한번에 느낄 수 있을 것이다. 하지만 LDA를 한 feature로 classifier를 training하는것이 언제나 PCA를 하고 training하는 것 보다 좋지는 않다고 한다. LDA에 대해서는 시간이 되면 다른 post에서 다뤄보도록 하겠다.

Outro

끝으로 PCA와 AE에 대해서 어떤 algorithm을 써야 할지에 대해 짧게 생각해보자. 만약 우리가 어떤 real world data를 분석해달라는 의뢰를 받았다. 그러면 data의 특성을 파악하고 normalization을 하고 visualization 해보고… 같은 일들을 해야할 것이다. 그리고 이 data를 분류하는 application을 만들어달라고 했다면 training도 한 번 해봐야 할 것이다.

당연히 이 data들로부터 좋은 representation을 뽑아준다면 PCA, AE중 어떤걸 써도 상관없을 것이지만 처음 접한 종류의 data이고 알려진 정보가 없다면 바로 해볼 수 있는 것은 PCA일 것이다. training도 PCA를 한 feature들로 NN을 training하는게 raw feature들로 training하는 것 보다 빨리 결과를 가져다 줄 수 있다. (만약 classification을 한다면 LDA가 더 좋겠다)

그러나 만약 우리가 받은 data가 자연어 (natural language) data라고 쳐보자. 이런 자연어 data를 대규모로 training해서 이미 자연어로부터 유의미한 feature를 뽑아주는 encoder들이 많이 인터넷에 공개되어 있다. 그 중 BERT는 너무 유명한 pre-trained encoder이다. 만약 우리가 이 text data를 한번 clustering도 해보고 싶고, visualization을 해보거나 간단하게 network를 training시켜서 PoC해보고 싶을 때는 raw feature를 쓰는 것 보다 BERT를 통과시켜 뽑은 BERT embedding을 쓰는 것이 나을 것이다. 물론 BERT가 완전히 AE 방법론으로 training된 것은 아니지만 거의 유사하게 training되었다.

물론 요즘 대부분의 model을 end-to-end로 training하는 경우 이런 PCA나 BERT같은 feature extractor를 사용해 feature를 뽑고 model을 training하는 경우는 거의 없긴 하지만, 여전히 고급 architecture를 사용하는 경우에도 중간에 이를 사용해서 dim reduction을 하고 clustering을 한다거나 하는 경우가 존재한다. 그러므로 가능성을 열어두고 좋은 성능을 내기만 한다면 PCA를 같이 쓰는것도 고려해봄직 할 것이다.

References

• Papers
  • A Tutorial on Principal Component Analysis from Jonathon Shlens
  • Lecture Notes on Principal Component Analysis from Laurenz Wiskott
• Lecture Slides
  • CSC 411 Lecture 12: Principal Component Analysis from Mengye Ren and Matthew MacKay
  • Lecture 18: Principal Component Analysis (PCA) from Kia Nazarpour
  • Principal Component Analysis (PCA) from Matt Gormley
  • AI504 2020 Class 4: Autoencoder from Edward Choi
    • Video
• Others
  • Everything you did and didn’t know about PCA from Alex Williams
  • Singular Value Decomposition: The Swiss Army Knife of Linear Algebra
  • SVD and Data Compression Using Low-rank Matrix Approximation
  • [선형대수학 #4] 특이값 분해(Singular Value Decomposition, SVD)의 활용 from 다크 프로그래머
  • [선형대수학 #6] 주성분분석(PCA)의 이해와 활용 from 다크 프로그래머
• Videos
  • 3Blue1Brown (3B1B) Official Website
  • Essence of linear algebra from 3Blue1Brown
  • SVD Visualized, Singular Value Decomposition explained, SEE Matrix , Chapter 3
  • What is the Singular Value Decomposition?