Notes

Neural Network (NN) and Representation

07 Feb 2021

< 목차 >

Neural Networks (NN)

신경 망 (Neural Network; NN) algorithm은 고전 머신 러닝 (Machine Learning; ML)을 넘어 딥 러닝 (Deep Learning; DL)으로 가는 길목에 있는 architecture 이다. Layer를 2개 사용한 NN의 concept은 DL 시대가 도래하기 전에도 이미 ML textbook에 실리던 concept이다 (꾸준히 연구되어 왔다고 한다). 아마 나를 포함해서 2020년 즈음에서야 ML을 접한 사람들은 고전 ML에 대해서는 잘 모를 것이다. DL이 대중화 되기 전까지는 classification problem을 풀기 위해서는 Support Vector Machine (SVM)을 쓰고 regression을 하기 위해서는 Linear Regression을 쓰거나 Kernel Regression을 썼다고 한다. 하지만 2012년 AlexNet이 image classification challenge에서 압도적인 성능을 보이며 SVM 같은 algorithm을 다 깨부수기 시작하며 NN을 여러번 stack한 심층 신경망 (Deep NN)이 본격적으로 연구되기 시작했다는 것은 이제 전혀 새로운 사실이 아니다.

NN algorithm은 hardware의 한계와 dataset의 크기 등 (internet의 발전이 더딤)의 한계에 부딪혀 이론상으로만 잘 되는 approach 느낌이었다고 한다. 고전 ML algorithm들은 대부분 굳이 따지자면 layer가 1개인 것들로 linear regression을 하거나 linear decision boundary를 찾는데 그쳤으나, NN은 layer가 2층 이상인 것을 말하고 이것이 깊게 쌓이면 Deep NN이라고 부르며 non-linear decsioun boundary를 찾거나 non-linear regression을 가능하게 했다. (물론 kernel regression 등을 하면 고전 ML도 non-linear regression이 가능하지만 이는 learnable 하지 않은 feature extractor를 가지고 있다)

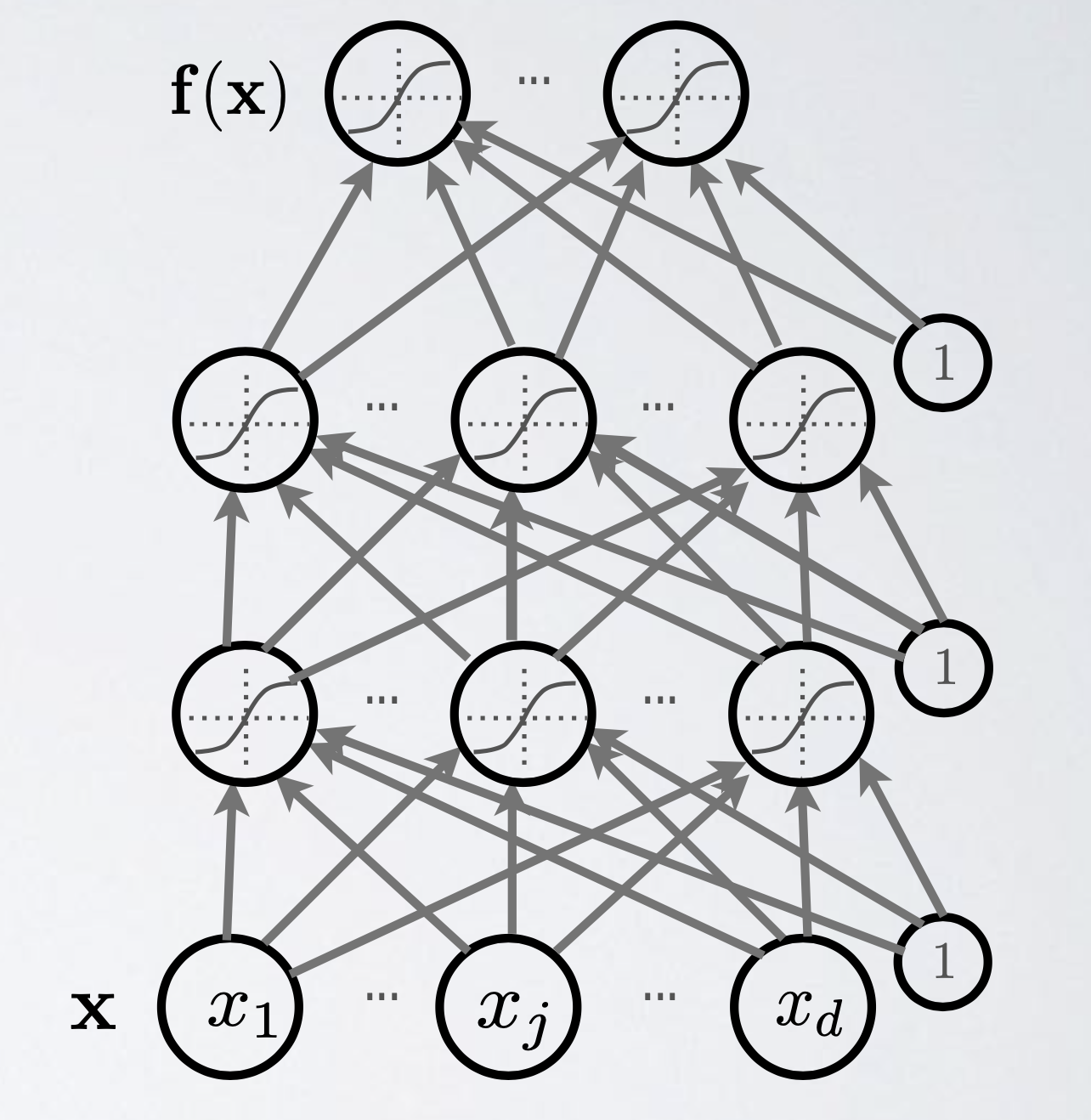fig1 Fig. Neural Network (NN) with 3 layers (2 hidden layers and 1 classifier). Source from from Hugo Larochelle’s lecture slide

위의 figure는 hidden layer 2개와 그것을 구성하는 weight vector들, 그리고 non-linearity를 주입하기 위한 activation function으로 이루어져 있다. 그런데 왜 NN은 층이 2개 이상인 걸까? 이렇게 함으로써 우리가 얻을 수 있는것은 무엇일까?

닳고 닳은 주제이지만 이에 대해서 알아보도록 하자.

Neural Networks and Logistic Regression for Classification

왜 NN이 필요한지에 대해서 얘기해보기 위해 toy problem에 대해 생각해보자. 아래 figure는 binary classification 을 하기 위한 Logistic Regression을 NN-like하게 표현한 것이다.

fig2

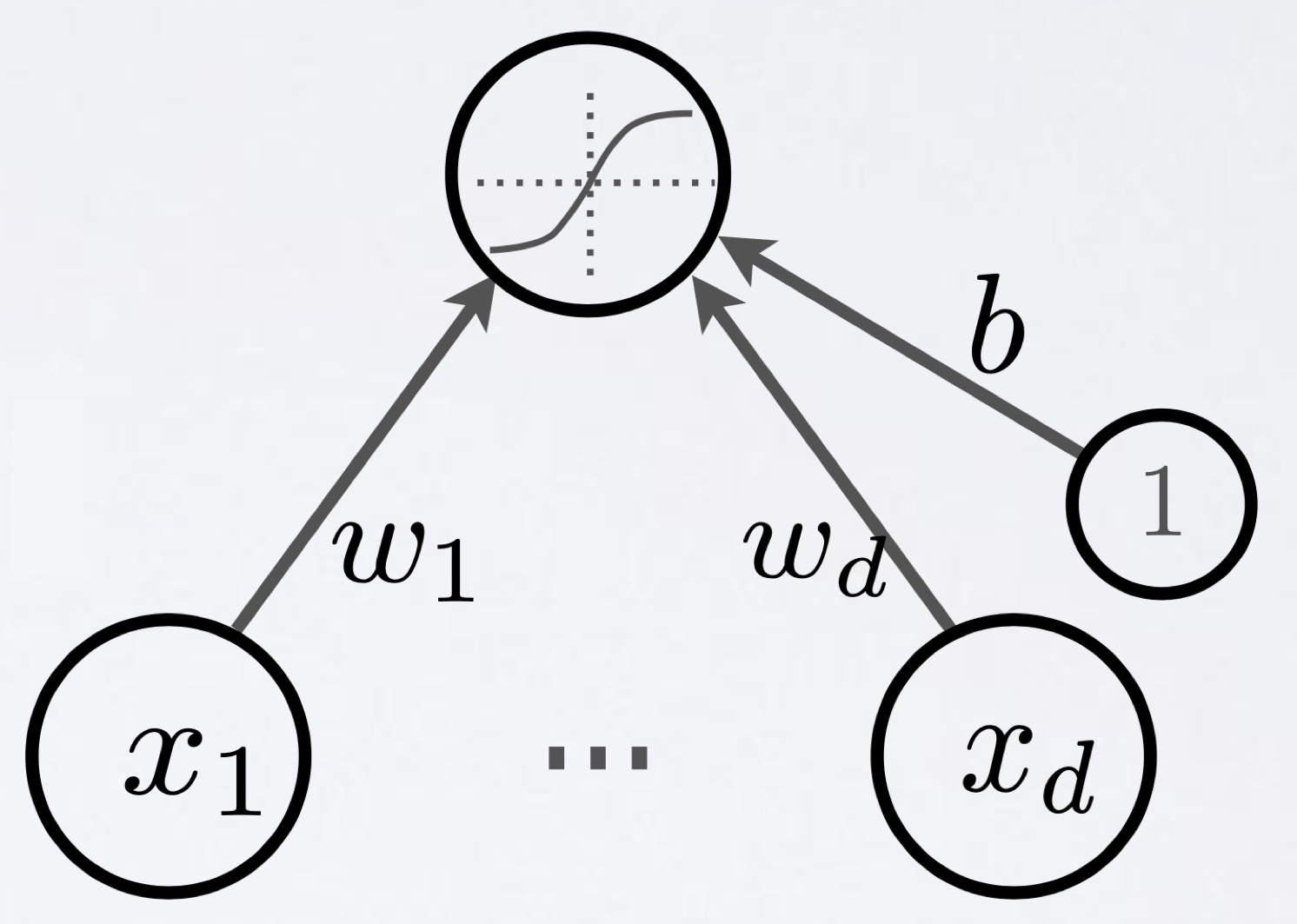
Fig. Logistic Regression

Input을 받아 weight matrix를 곱한다음에 sigmoid function으로 계산된 logit을 0~1사이값으로 mapping해 주는 것이 전부이다. 이런 모형은 NN이라고 부르지 않지만 (최소 2층 이상이며 층을 통과할때 non-linear activation 이 있어야 비로소 NN이라 함), 굳이 정의하자면 1층짜리 NN이라고 할 수 있겠다.

Binary classification을 풀기 위해서는 (decision boundary를 찾기 위해서는) target distribution 을 bernoulli distribution 으로 가정하고 Maximum Likelihood Estimation (MLE)를 수행하면 되는데, gradient based optimization을 parameter, likleihood가 최대가 될 때의 \(w_1, \cdots, w_d\)를 구하면 아래와 같은 decision boundary를 얻게 된다.

fig3 Fig. d=2차원 데이터의 Logistic Regression의 결과로 얻어지는 Decision Boundary

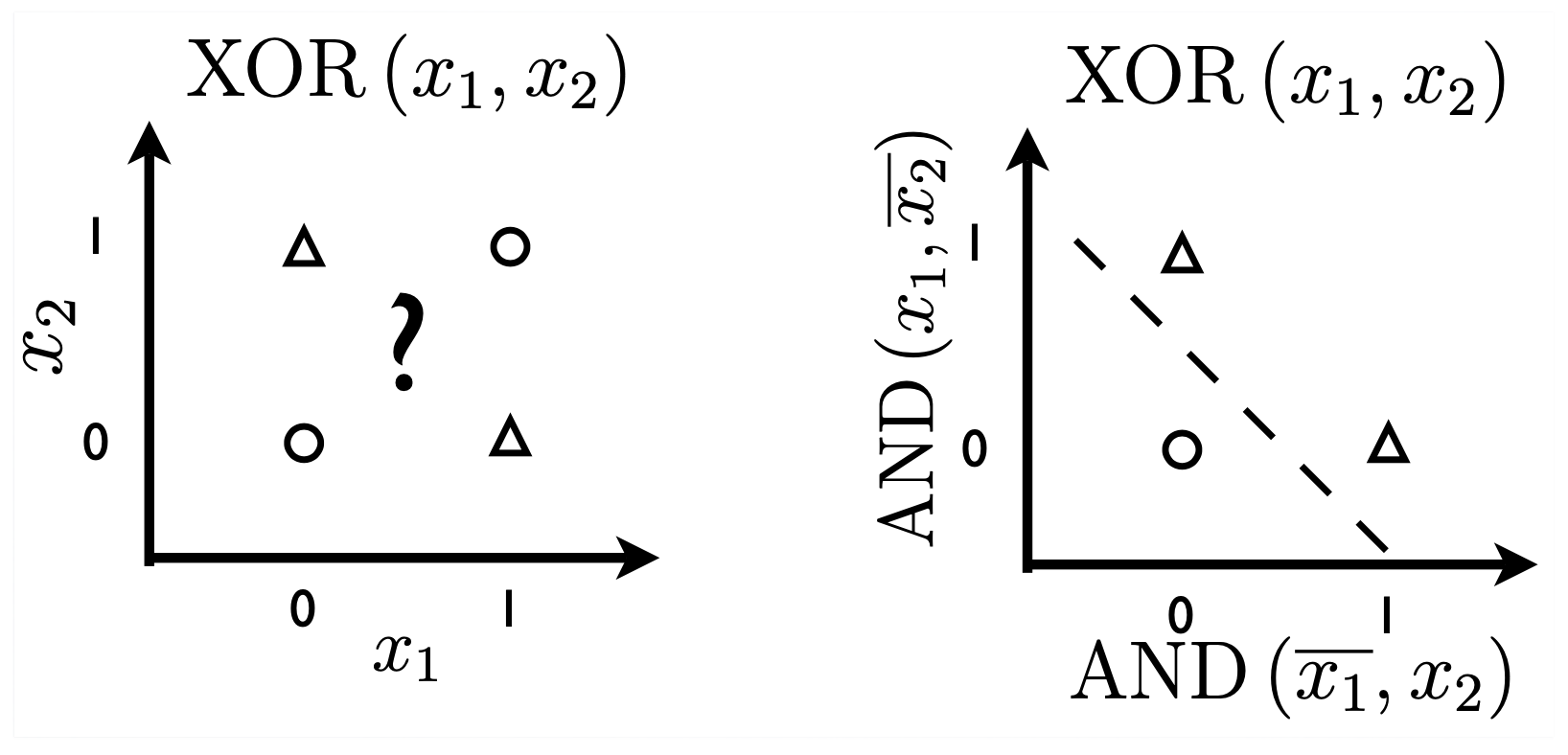
XOR Problem

이제 조금 더 어려운 문제를 풀어보자. NN을 얘기할 때 꼭 등장하는 example로 XOR classification problem을 풀어보는 것이다. 어떻게 decision boundary를 그려야 할까?

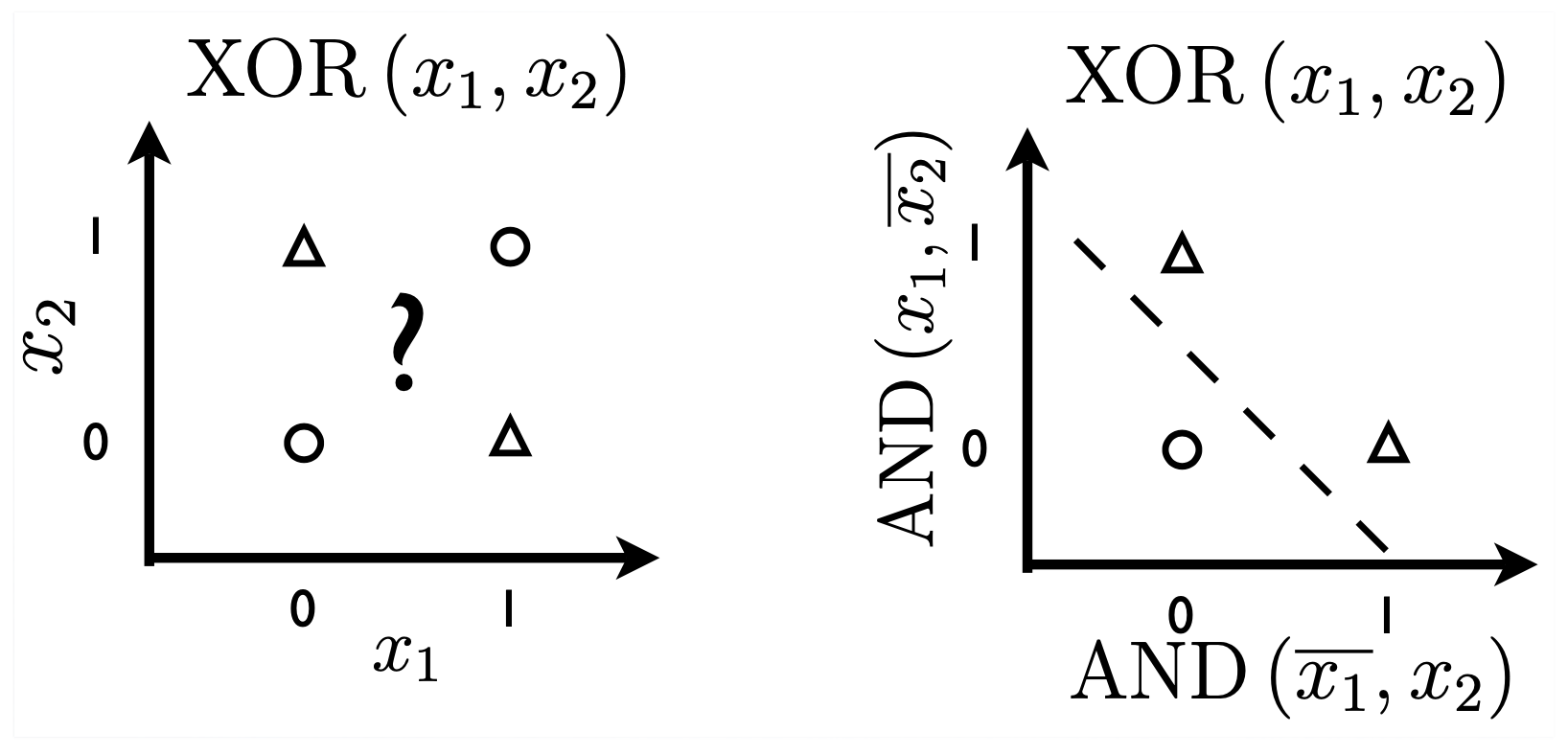fig4 Fig. XOR 문제, 이는 decision boundary 하나로 풀 수 없는 문제라고 알려져있다.

위 figure에 나와있듯, 이는 단순히 하나의 decision boundary로는 분류할 수 없는 문제로 알려져 있다. 즉 단순 logistic regression 로는 풀 수 없다.

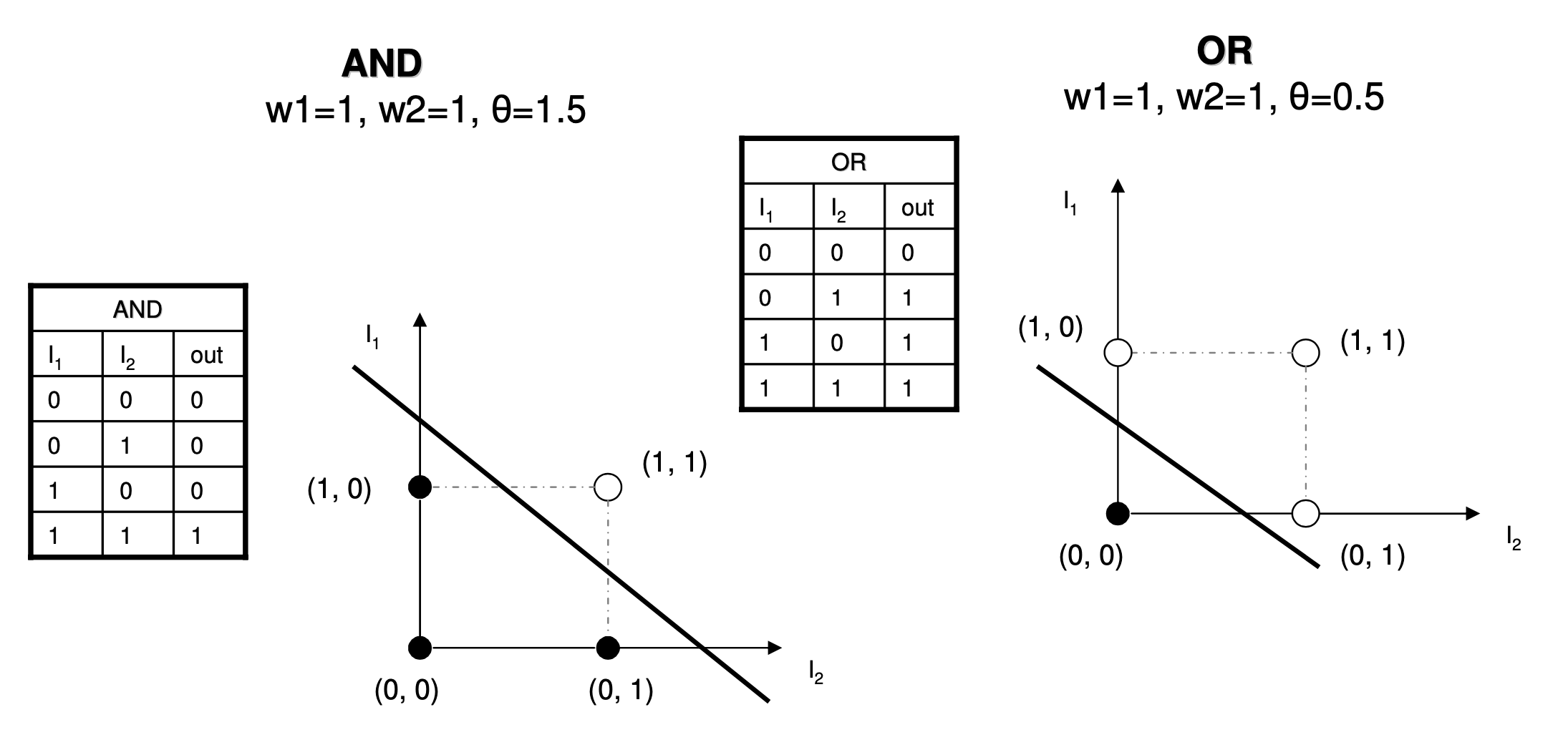fig5 Fig. AND gate, OR gate problem. Source from link

반면 AND, OR gate problem은 단일 decision boundary로 문제를 풀 수 있음이 위 figure에 잘 나타나 있다. 그럼 XOR은 어떻게 할까? 우선 XOR의 논리 table 을 그려보자.

fig6

x1 x2 y
0 0 0
0 1 1
1 0 1
1 1 0

이 논리 table을 잘 보면 문제를 풀기위해 x1, x2를 입력받아 뭔가 중간 결과를 얻고, 그 다음 중간 결과를 바탕으로 y 에 대한 decision boundary를 그리면 될 것 같다는 힌트를 얻을 수 있다. 즉 아래와 같이 x1, x2 에서 어떤 function을 통과시켜 h1, h2를 얻고 이를 또 다른 function에 통과시켜 최종 output으로 가는 것이다.

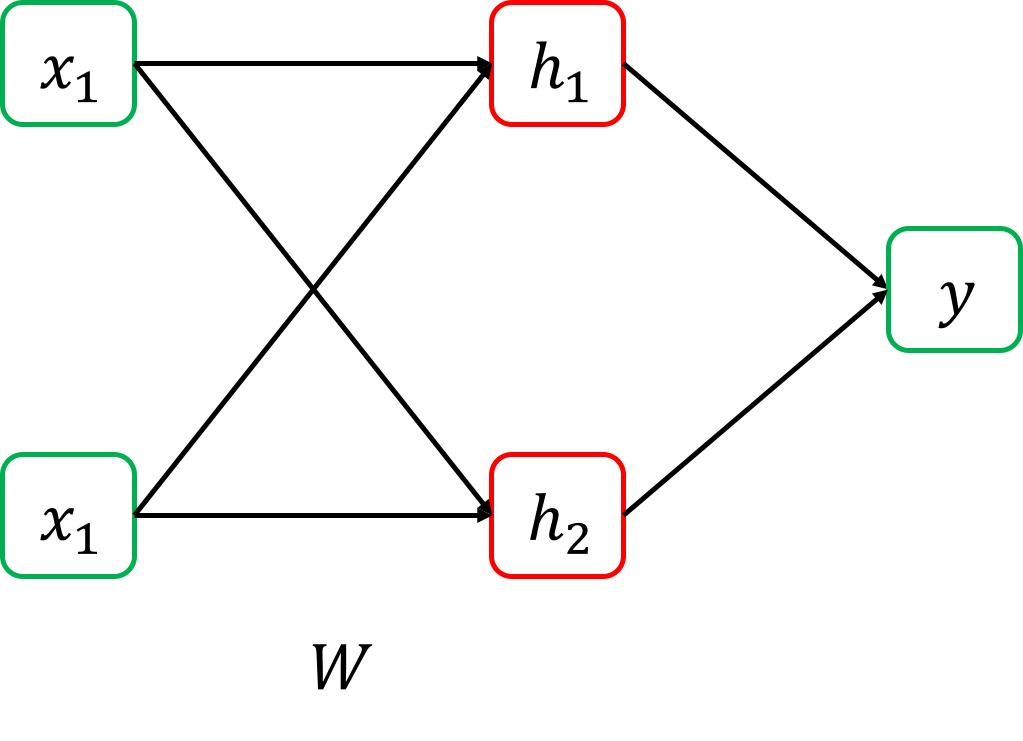
fig7_0

즉 W에 아래와 값을 주게 되면 x1=0, x2=1일 때, 중간 결과가 h1=1, h1=1 이런식으로 나오게 되고, 둘다 1이면 y=1 이 되는 식으로 문제를 푸는 것이다.

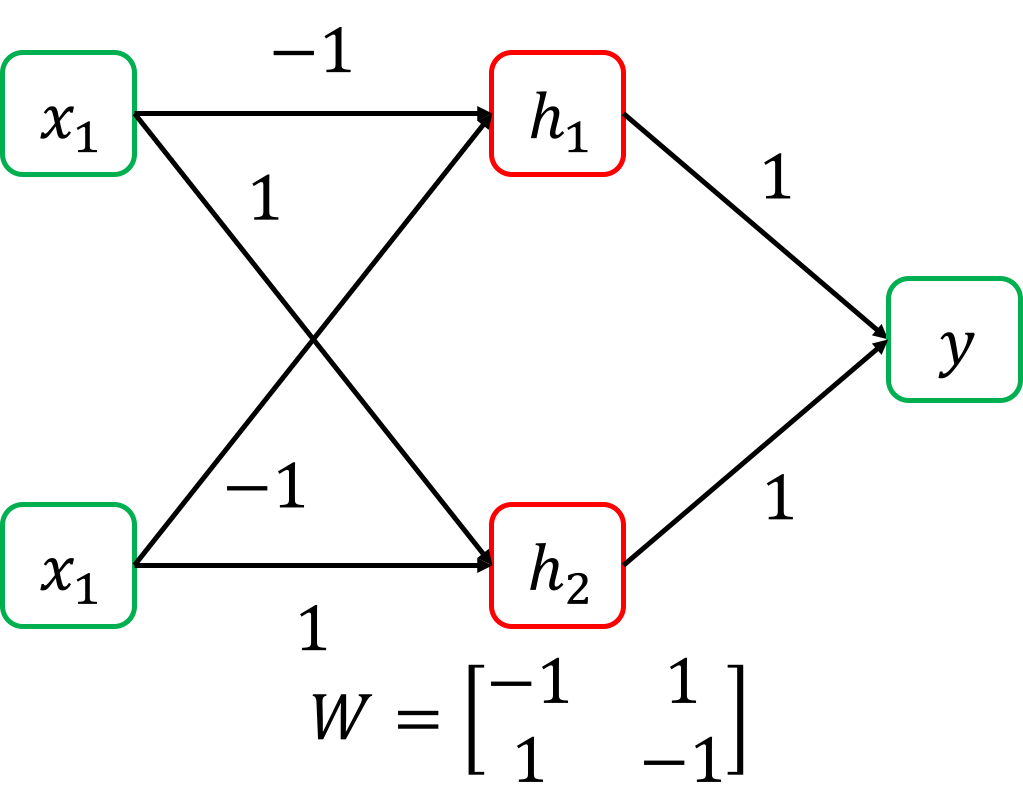fig7_1 Fig. XOR을 풀기 위한 Nerual Network

여기서 h1, h2 는 뭘까? 사실 이 둘은 NAND gate와 OR gate의 output을 의미한다. 그리고 h1, h2 를 y 로 분류하는 문제는 decision boundary 하나로 풀 수 있는 문제였다.

x1 x2 h1(NAND) h2(OR) y(XOR)
0 0 1 0 0
0 1 1 1 1
1 0 1 1 1
1 1 0 0 0

즉 XOR는 classification을 2번 하는 것으로 해결할 수 있다는 것이다. 여기서 NN이 뭘 하는지 직관적으로 이해를 할 수 있을 것인데, NN은 logistic regression을 여러 개 쌓은 것이라고 간단하게 생각해볼 수 있다.

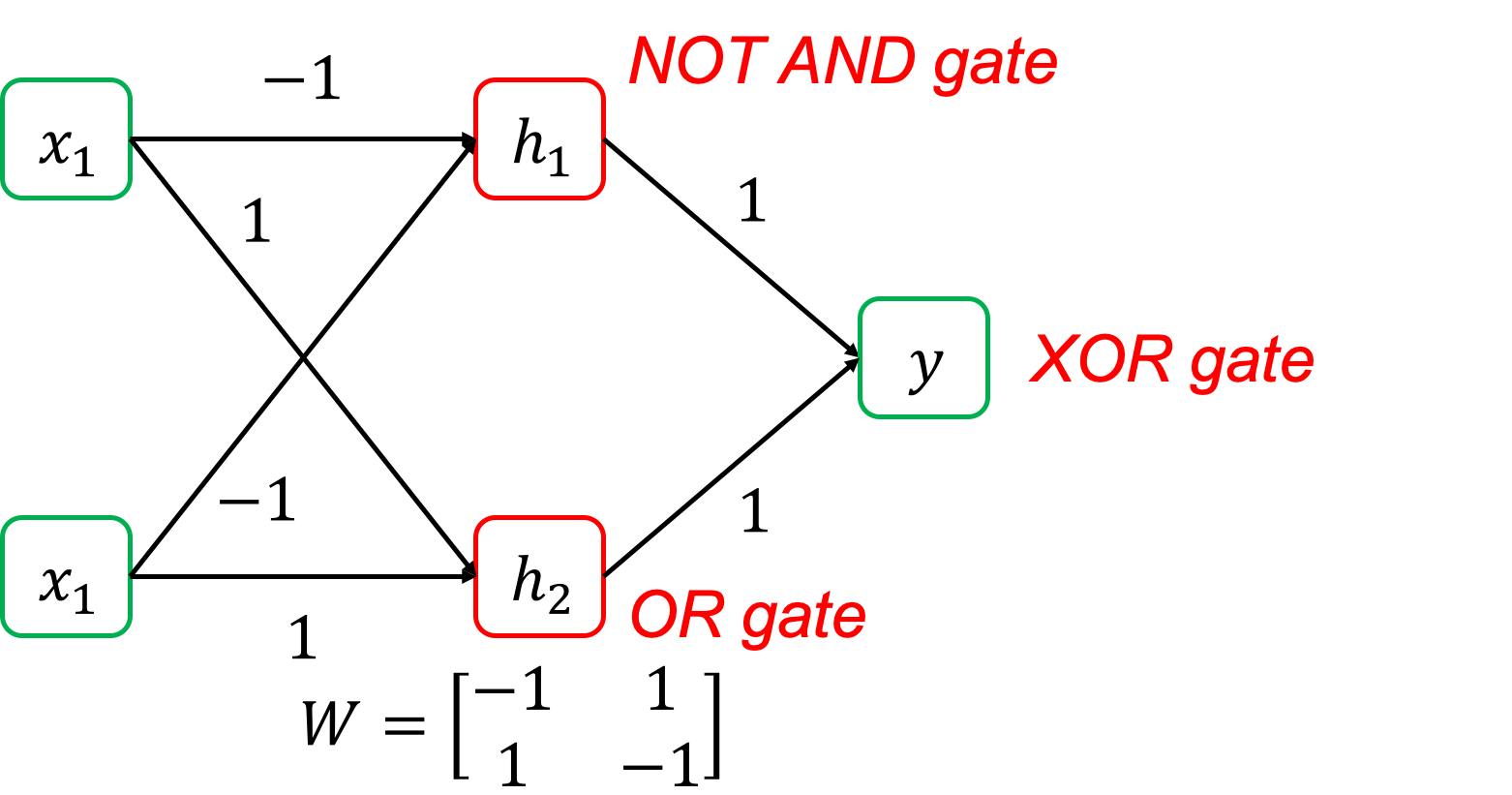fig7_2 Fig. 각각의 hidden layer neuron의 의미

Classification을 한다는 것은 앞서 decision boundary를 어디에 그릴지를 결정하는 것이었다. 그러므로 우리는 model이 decisoun boundary 2개를 합쳐서 최종적으로 non-linear decision boudnary 갖는걸로 생각할 수 있다.

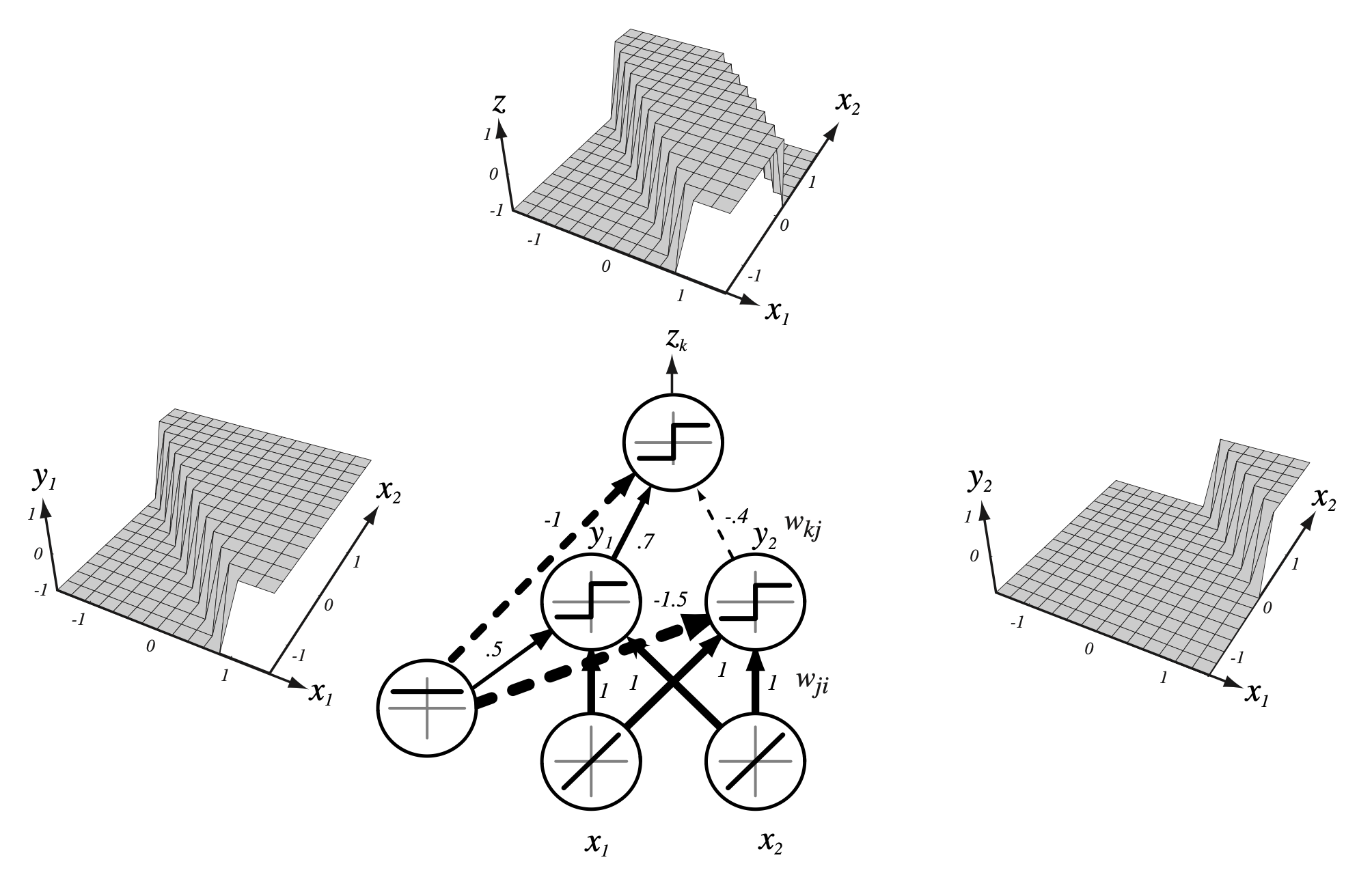fig8 Fig. 각각의 hidden layer neuron의 의미는 사실상 결정 경계면 두개이다. from Pascal Vincent’s slide

이런 XOR같은 문제를 linear (직선) decision boundary 하나로는 풀 수 없다 하여 Non-Lineary separable problem이라고 한다. 반대로 AND, OR 같은 문제들을 Linearly separable problem 이라고 하는데, 직관적으로 non-lineary separable 문제는 lineary-separable 여러 개로 나눠 풀 수 있다는 것을 알 수 있다.

Another Non-Linearly Seperable Problem

조금 더 복잡한 example을 보자. XOR문제에서는 hidden layer가 1개이며 (2 layer NN), hidden neuron은 2개였다. 이제 이를 4개로 늘려보자.

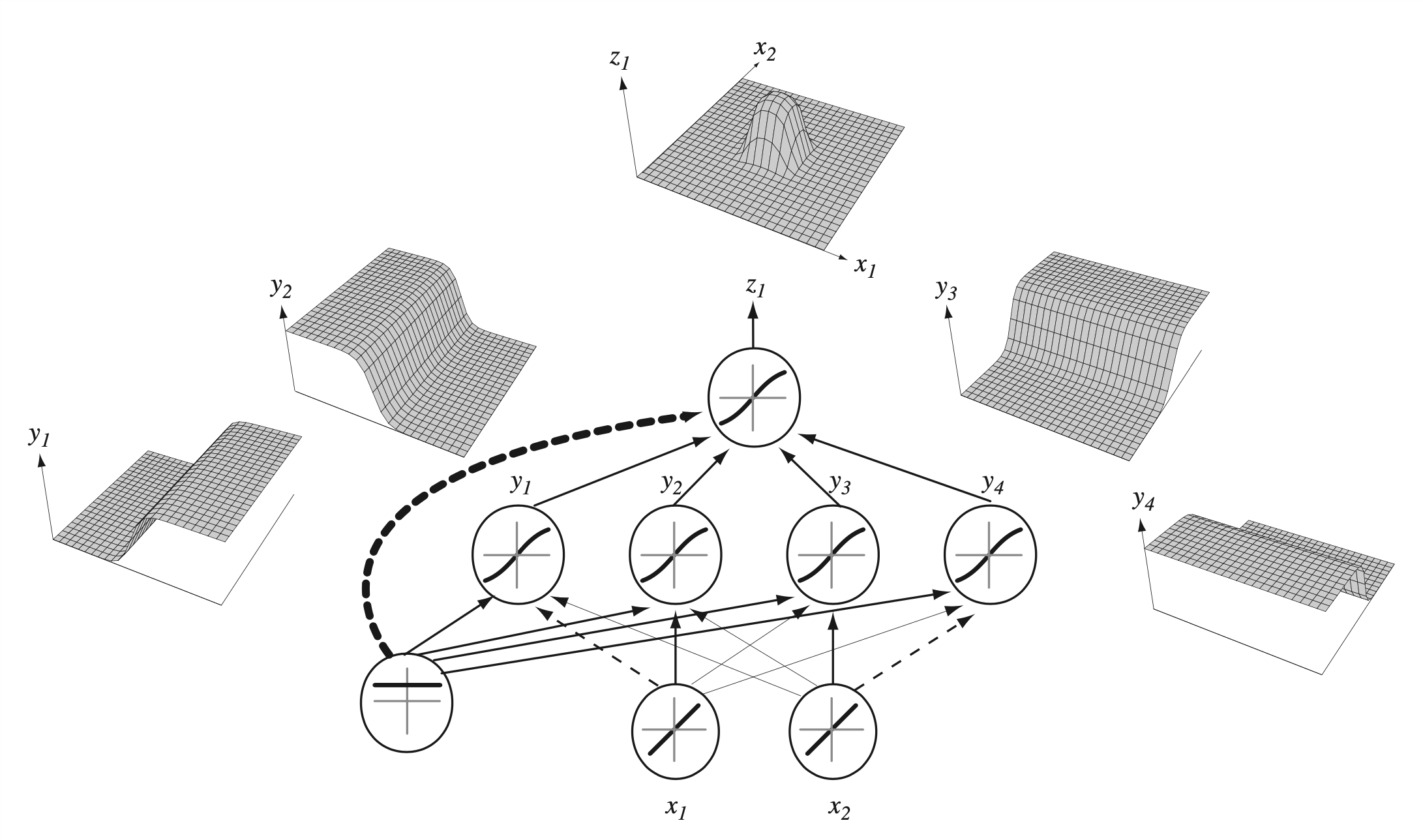fig9.png Fig. 5개의 hidden neuron이 합쳐져 만든 결정 경계

그러면 우리는 decision boundary를 결합해서 더 복잡한 최종 decision boundary를 정할 수 있게 된다. 아래와 도넛 모양의 non-linearly seperable dataset을 분류한다고 생각해보자. 가능할까?

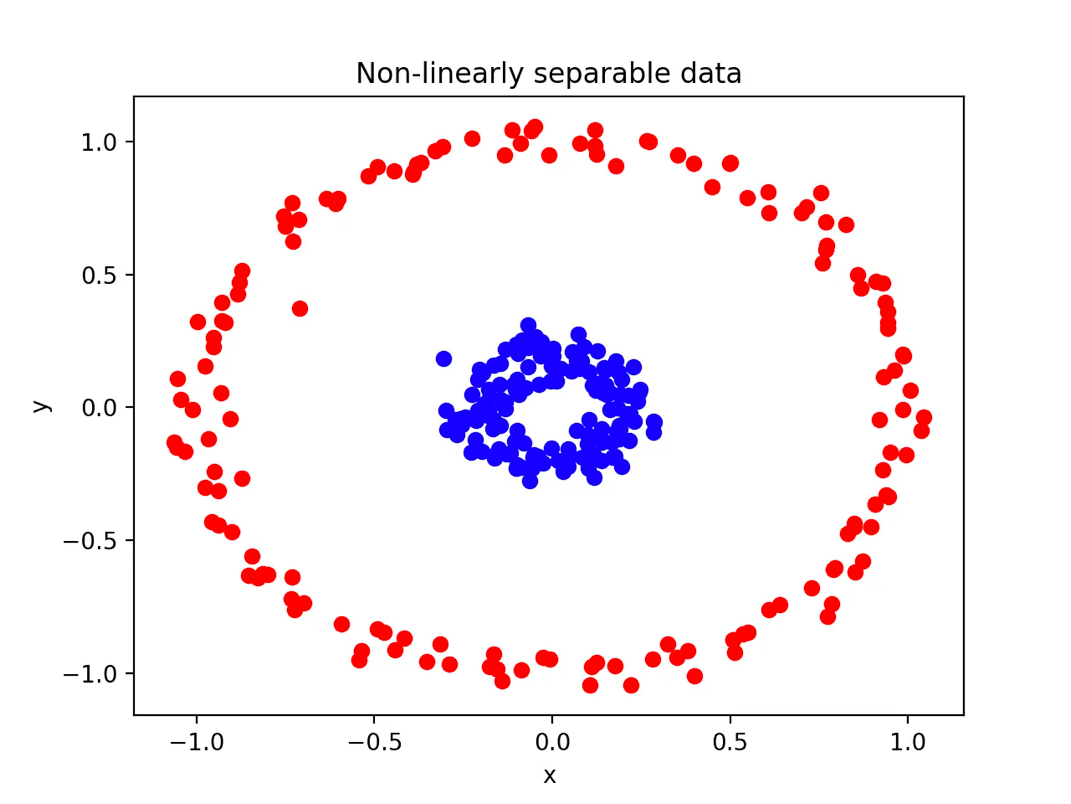fig10.png Fig. 도넛 모양의 Non-linearly seperable dataset

Neuron을 더 많이 쓰면 원에 가까운 decision boundary를 그릴 수 있을 것이므로 당연히 가능할 것이다. 이렇게 neuron을 늘려갈수록 점점 더 유연한 boundary를 그릴 수 있는데 (regression이라면 더 복잡한 curve를 그릴 수 있음), 이를 두고 표현력 (representation) 을 늘린다고 표현하곤 한다.

더 복잡한 dataset에 대해서도 분류를 할 수가 있는데,

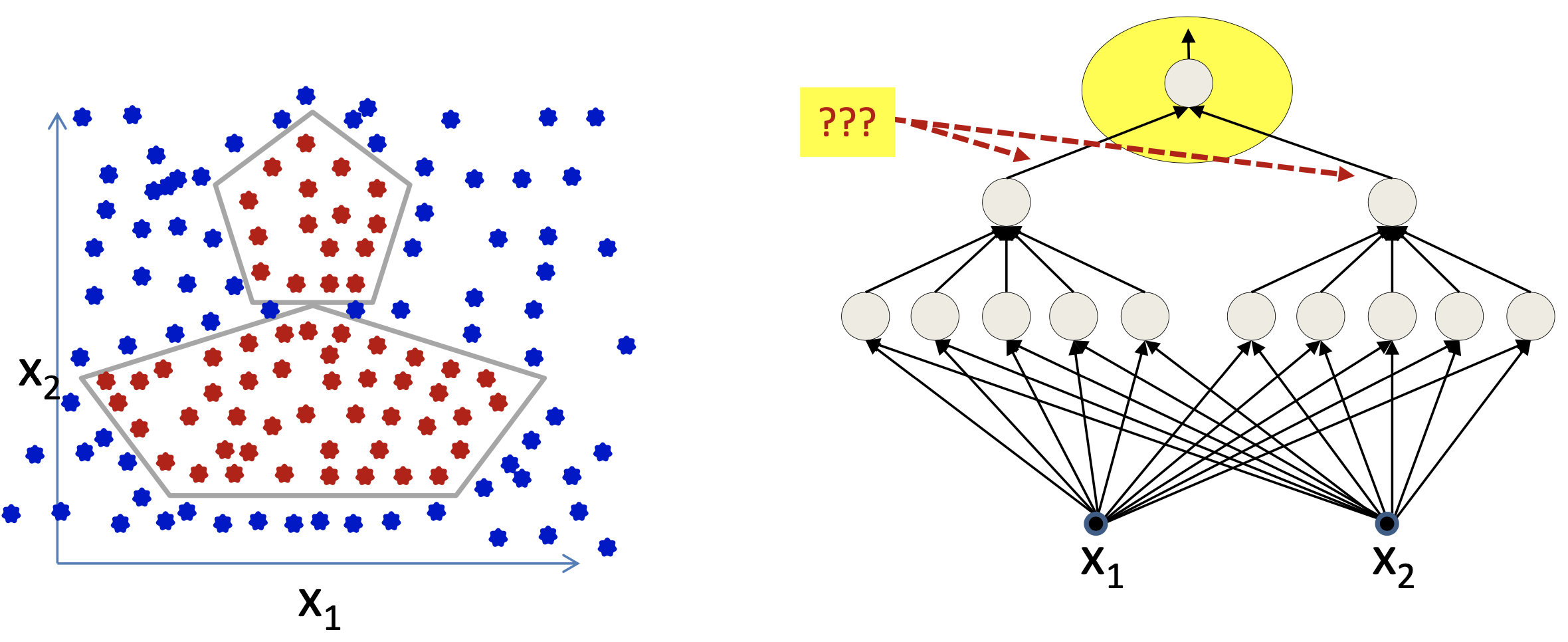fig11.png Fig. 조금 더 복잡한 오리모양?의 Non-linearly seperable dataset

좀 복잡하다 싶으면 hidden layer를 늘려서 총 3 layer를 갖는 NN을 설계하면 된다. 이러면 1st layer가 오각형 boundary를 그려내고, 이를 또 받은 2nd layer가 받고 최종적으로 마지막 layer가 classification을 한다.

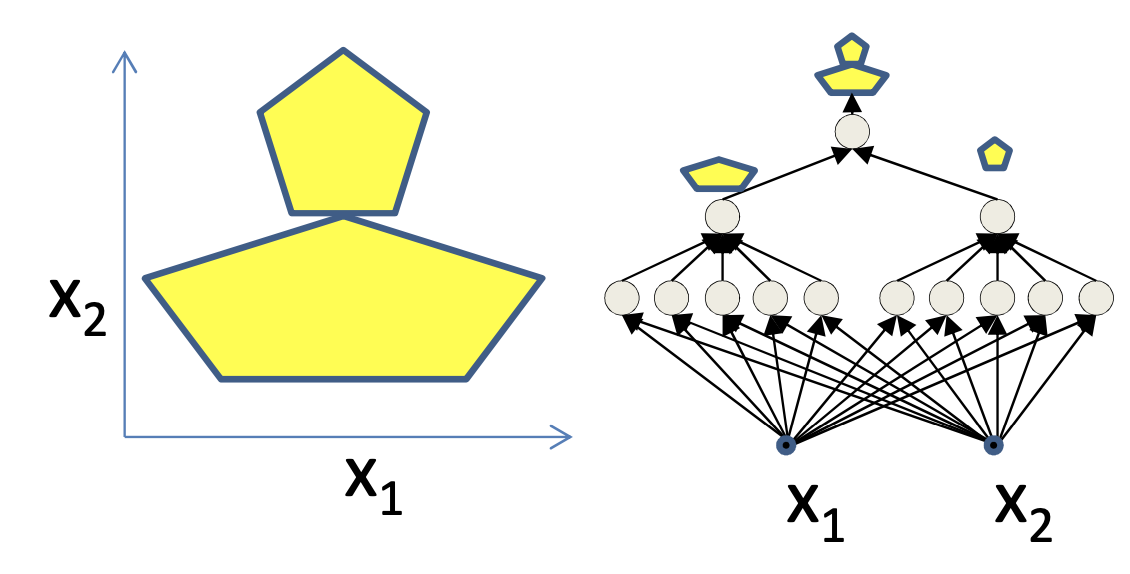fig12.png Fig. 2 layer NN

이렇듯 NN은 사실상 무한대에 가까운 경우의 수의 decision boundary를 그리거나 curve를 fitting할 수 있다.

Another Perspective : Linear Transformation

이번에는 NN이 하는 일을 조금 다른 관점에서 보도록 하자. Linear algebra에서 data (vector)와 matrix(NN 각 layer의 weight)를 곱하는 것은 선형 변환 (linear transformation) 한다는 것을 의미한다. 다시 말해서 weight을 곱하는 원래 data vector와 곱하는 것은 이 data sample을 회전 (rotation) 하고 늘리고 (scale)하는 것이다. 그런데 NN은 linear transformation을 한 다음 그 vector들을 non linear function (sigmoid 등)에 통과시킨다. 이게 무슨 의미로 해석될 수 있을까?

다시 XOR문제를 생각해보도록 해보자.

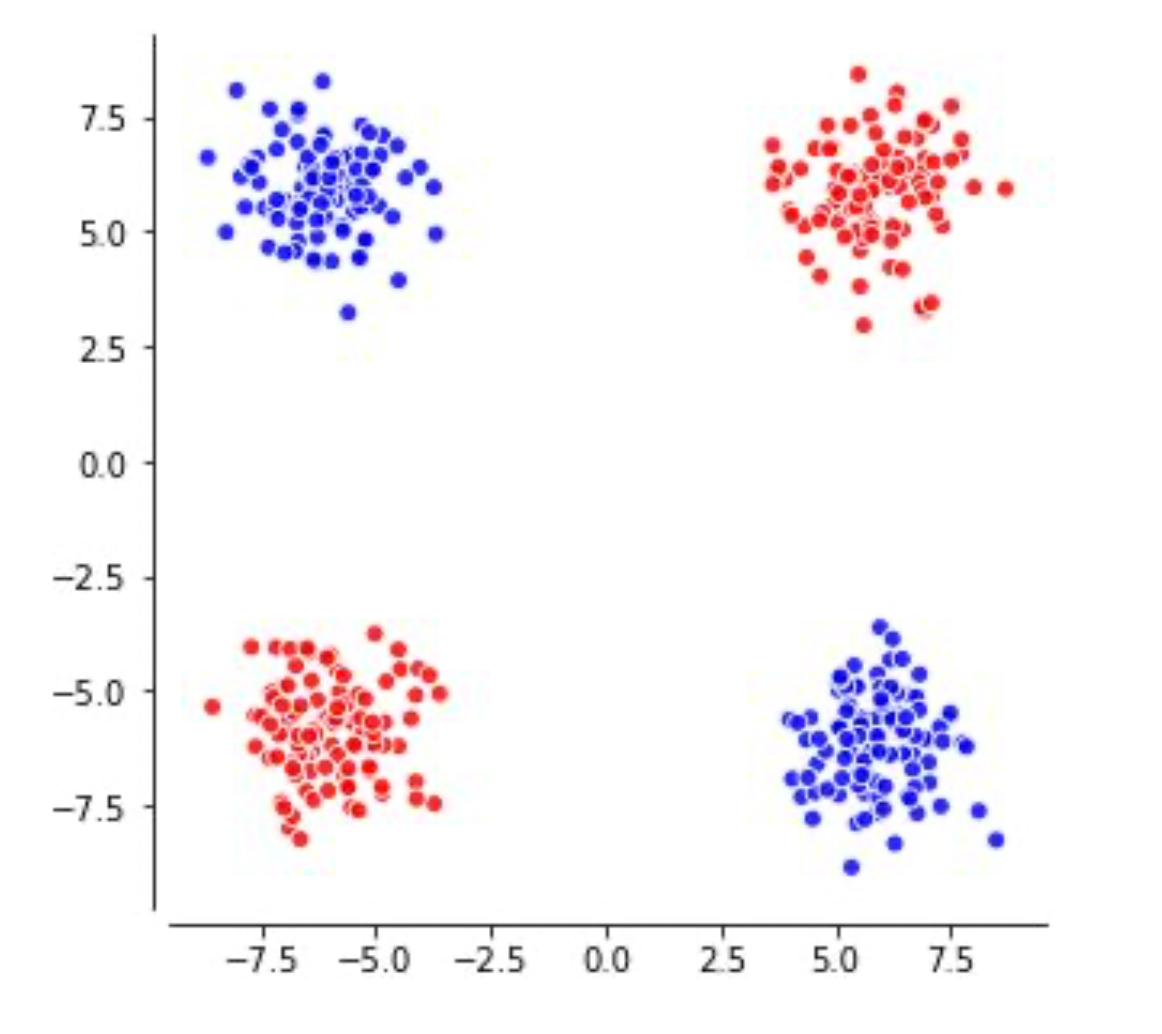fig15 Fig. Recap. XOR problem. Source from UCLxDeepmind lecutre

편의상 색을 바꿔서 표현해 보겠다.

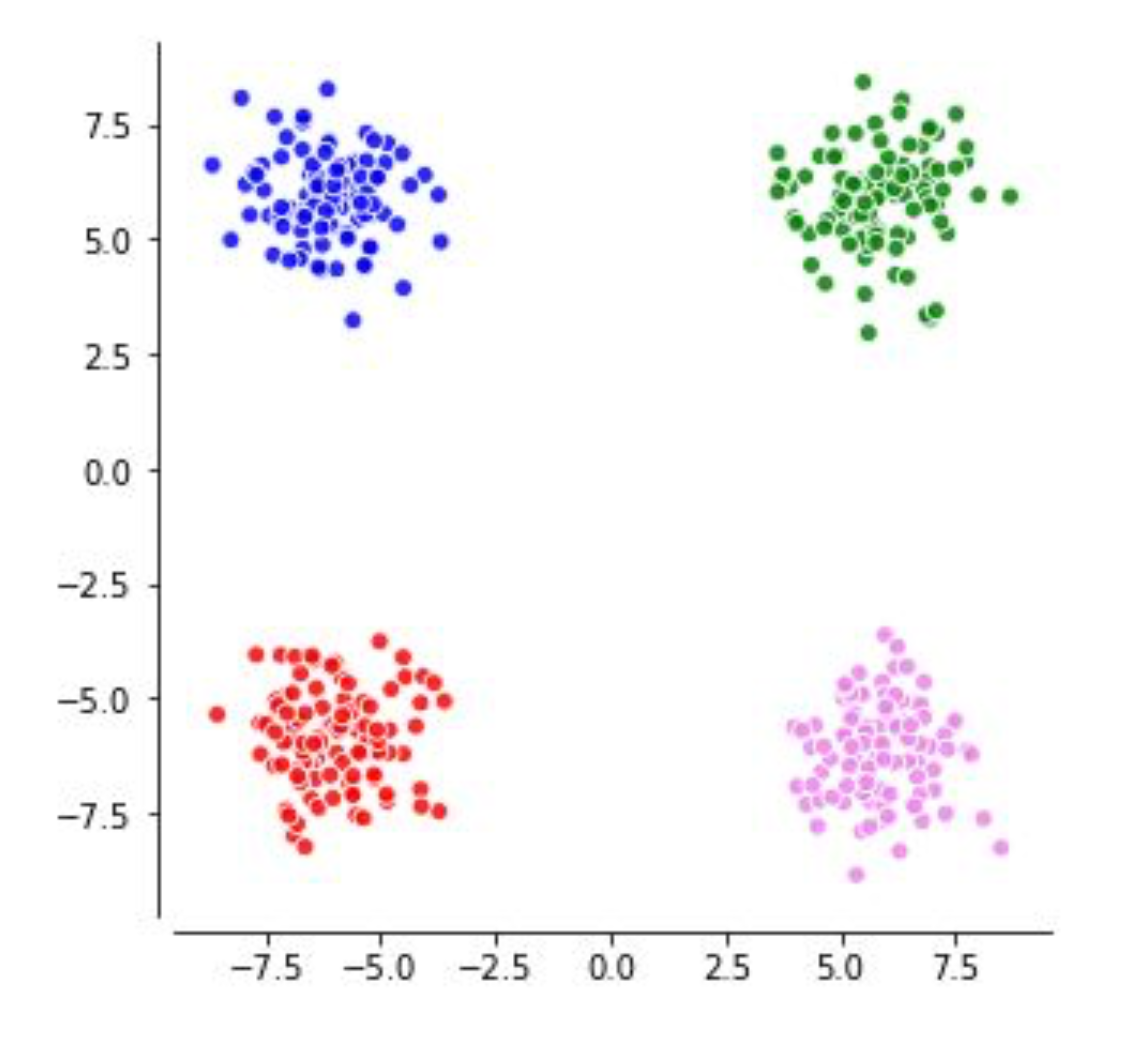fig16 Fig. Recap. XOR problem

그리고 아까의 2 layer NN을 다시 생각해보자.

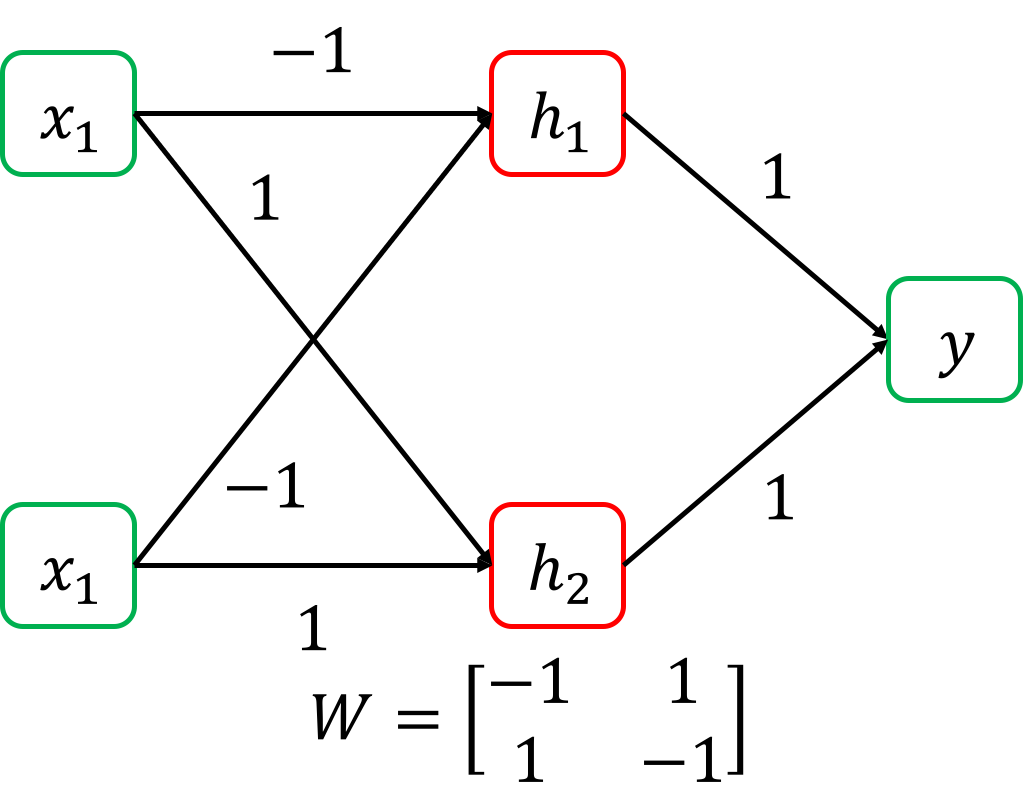fig17 Fig. recap 2 layer NN for XOR problem

아까는 각각의 neuron 하나가 decision boundary를 만든다는 접근을 썼는데, 이번에는 matrix multiplication이 data를 다른 차원으로 mapping 해준다고 생각해보자.

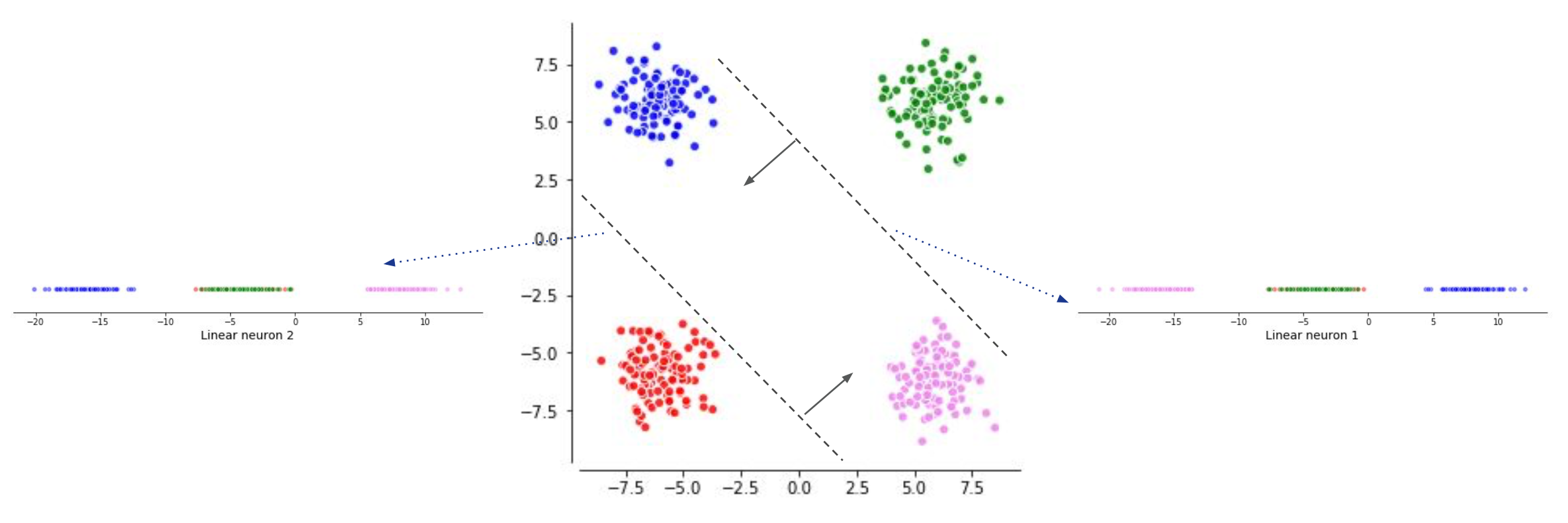
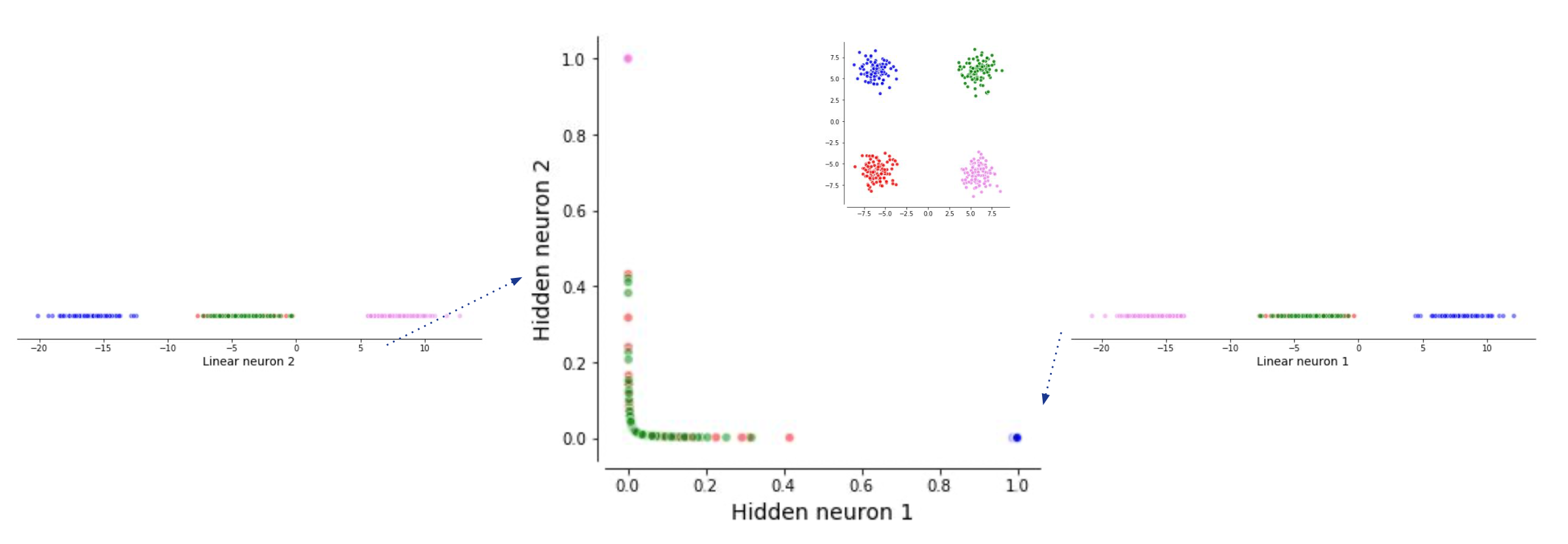fig18.png fig19.png Fig. 새롭게 2차원상에 (2차원 ->2차원) 뿌려진 data sample들

NN의 1st layer가 하는 일은 원래 2차원 space의 data를 neuron 한 개당 1차원으로 projection 하는 것과 다름이 없다. 지금은 neuron이 2개 이므로 1차원 두개로 각각 data가 projection 되는 것이다. 이제 새롭게 정의된 1차원 vector space 두 개는 하나의 2차원 space를 만드는데 (두 basis가 span하는 공간), 이 공간에서 decision boundary를 하나 그리는 것이 2nd layer (classifier)가 하는 일이 된다.

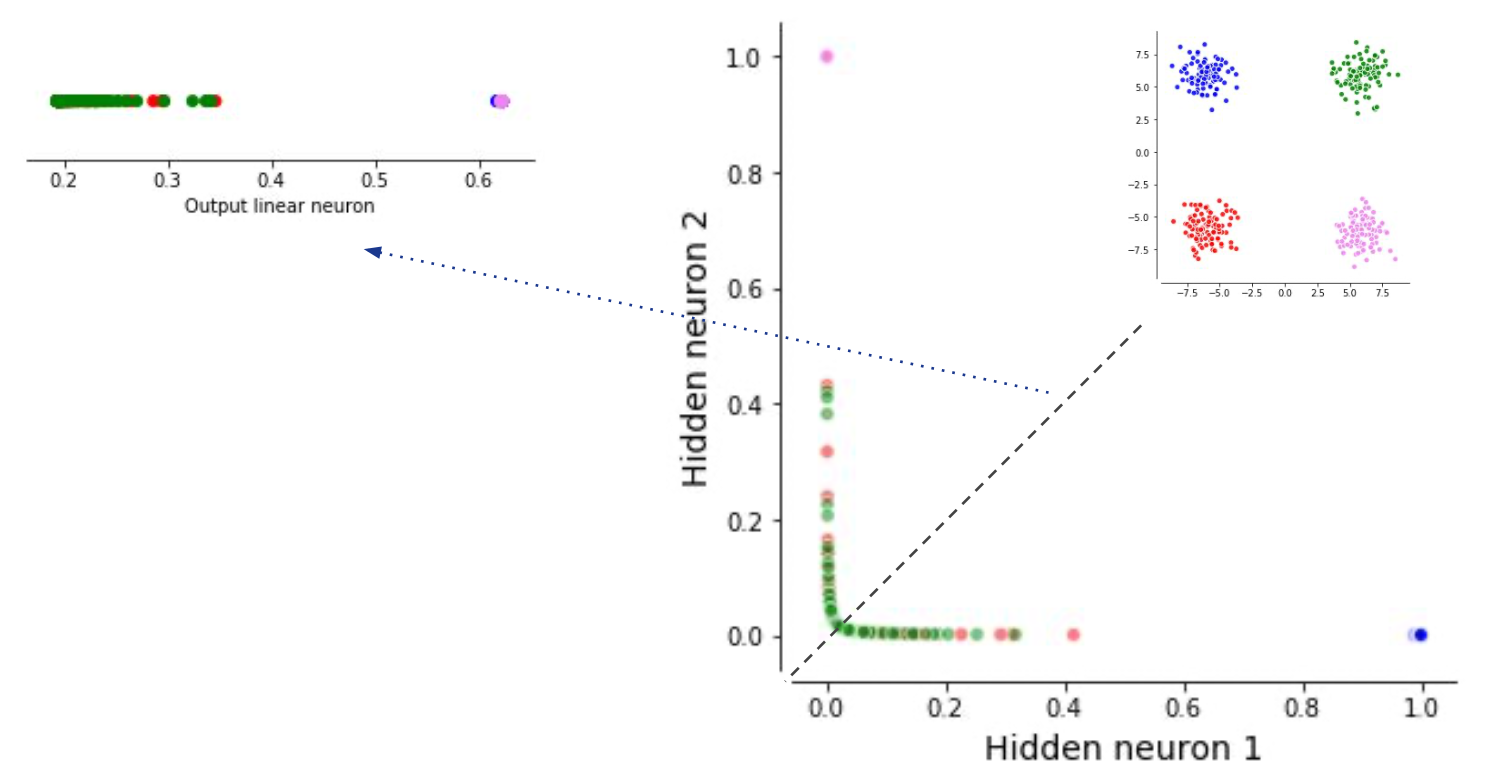
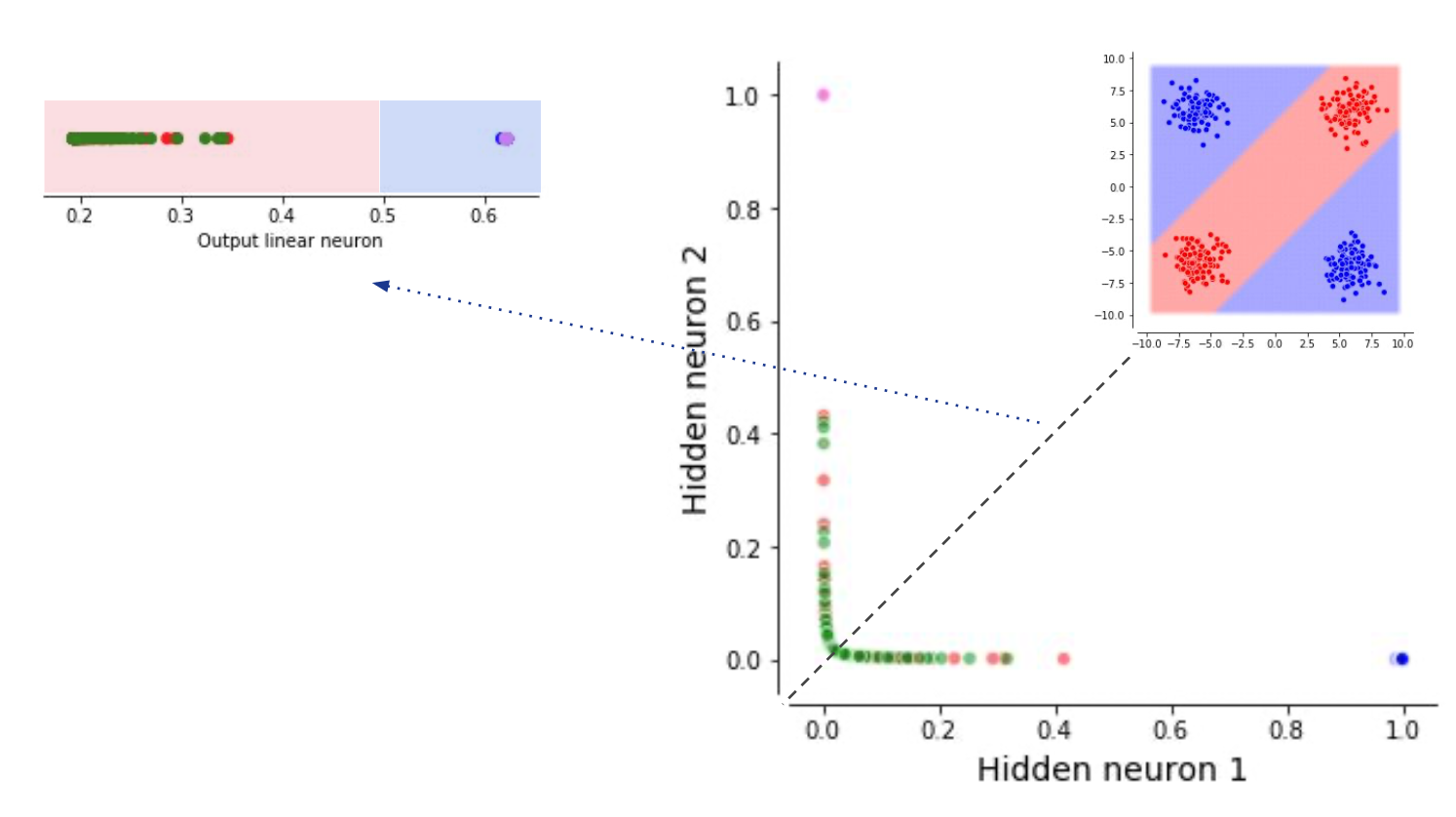fig20 fig21 Fig. Neural Network Classifier for XOR problem. lecturer가 그림이 조금 이상하다고 한다.

이처럼 decision boundary를 여러개 그린다는 해석 말고도 NN은 hidden layer가 data를 linearly separable하도록 만든다고도 해석할 수 있다. 당연히 더 복잡한 distribution을 갖는 dataset도 이런식으로 해석할 수 있다.

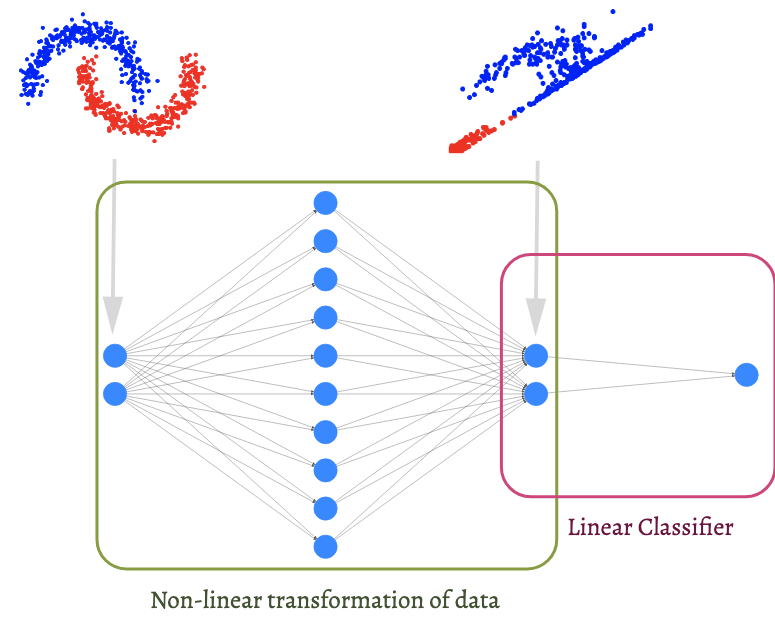fig24 Fig. NN classify complex data points by linearly transforming original vectors. Source from here

그런데 2차원을 2차원으로 mapping하는 것만 가능할까? 사실 2차원을 더 고차원을 보낼 수도 있다. 아까의 도넛 모양 data cloud를 생각해 보자. 이는 아래와 같은 3차원으로 mapping하면 쉬운 문제로 치환할 수 있다.

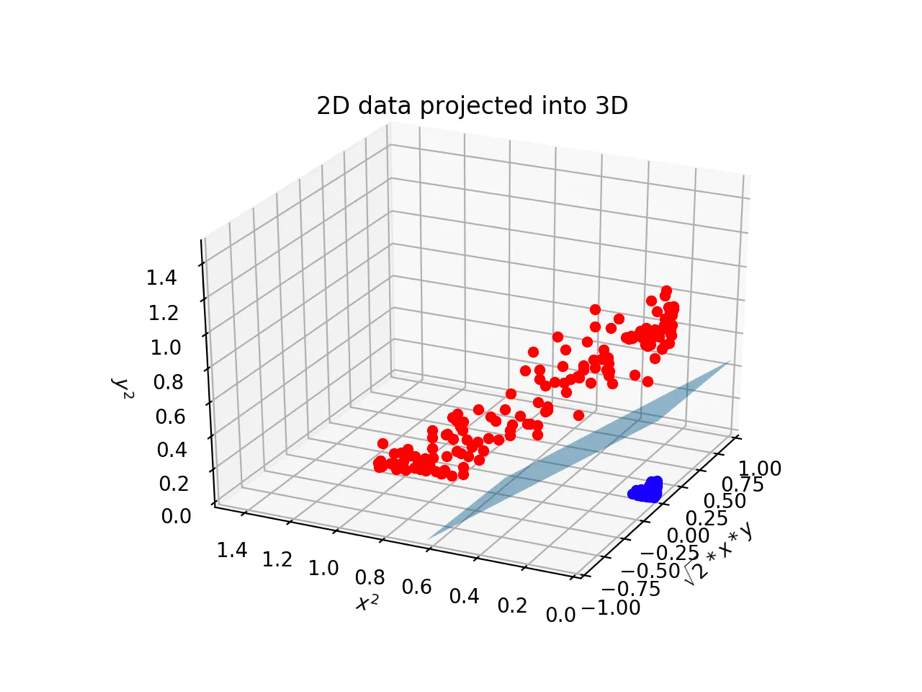fig26 Fig. 3차원에 projection 된 도넛 모양의 data cloud

이 때의 Decision boundary는 더 이상 1차원이 아니라 2차원 plane 이라는 점을 주의하자. 바로 이런 mechanism으로 훨씬 복잡한 high dimensional data인 image data들도 분류할 수가 있는 것이다.

fig27 Fig. MNIST dataset

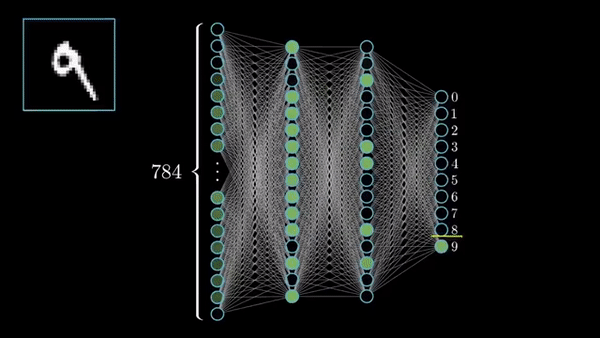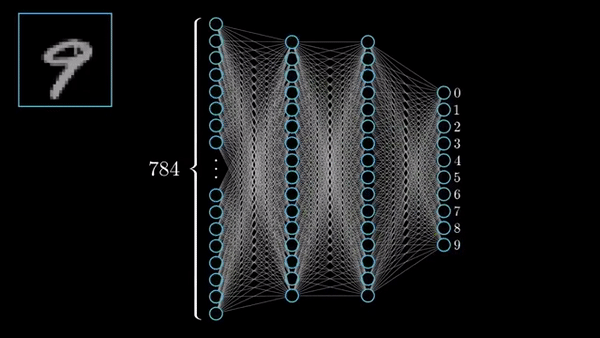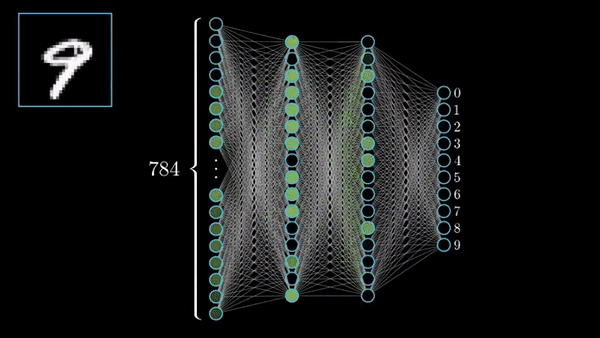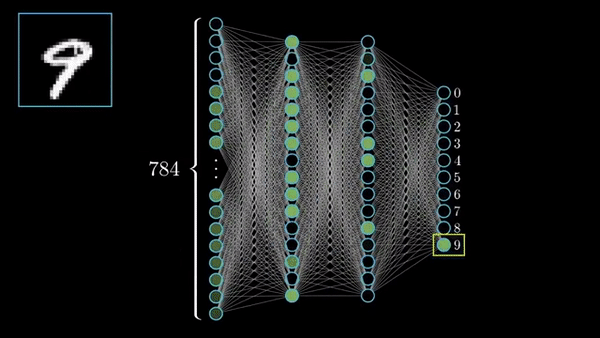fig28 Fig. NN trained on MNIST. Source from here

이 경우는 binary classification이 아니기 때문에 여러 class에 대해서 각각 decision boundary가 존재한다. (숫자 1을 판단하는 decision boundary, 2를 판단하는 …)

fig29 Fig. MNIST dataset의 embedding space. 사실 3차원이 아니라 더 고차원으로 mapping되지만 (NN의 hidden layer가 2차원일 리는 없으므로) 시각화를 위해 3차원으로 mapping한 것일 뿐이다. Source from here

이처럼 data가 원래의 space를 떠나 새로운 non linear space 로 mapping 하는 것을 model이 학습하는 것을 표현력을 배운다 (representation learning)라고 표현하기도 하며, vector들이 mapping된 공간 자체는 representation space 혹은 embedding space 등으로 부르기도 한다.

Measuring Correlation and Convolutional Neural Network (CNN)

마지막으로 input date를 각 layer에 통과시키는 것은 예를 들어 각 image의 특정 성분이 존재하는가?를 검사하는 filter가 있고, 이 filter와 input data간의 상관 관계 (correlation)를 재는 것이라고 볼 수도 있다.

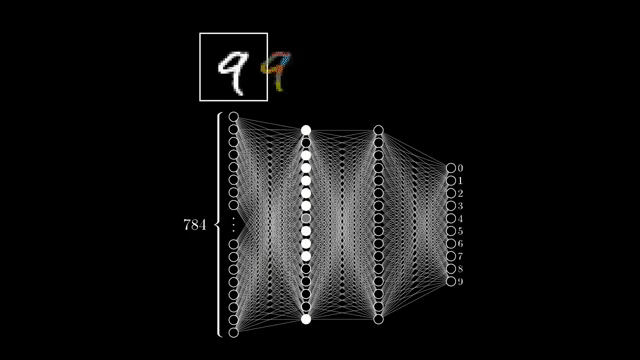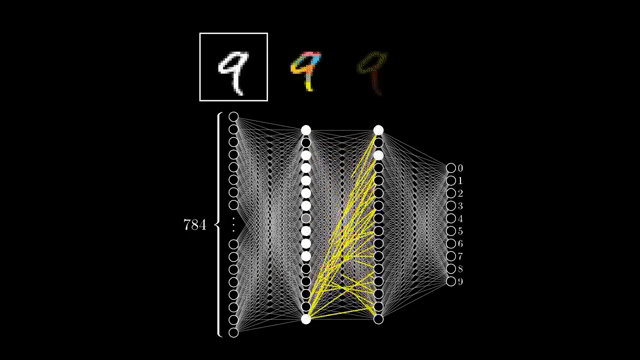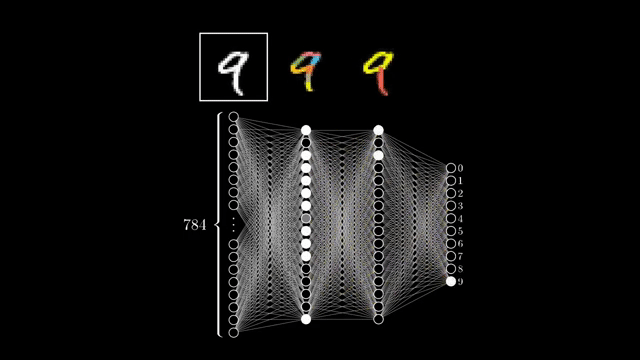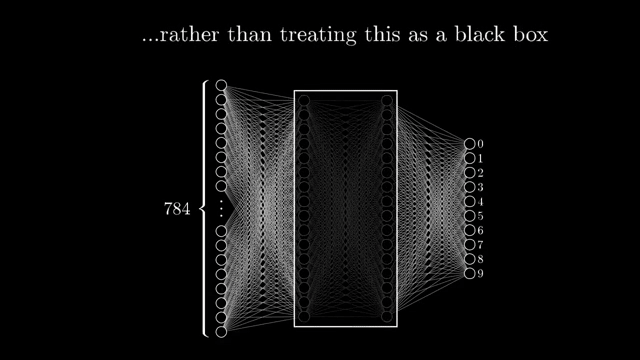fig31 Fig. Source from here

예를 들어 마지막 classifier layer는 hidden layer를 많이 통과하면서 얻은 representation vector와 숫자 2를 의미하는 vector와의 correlation을 보는 것과 같다. 만약 input data가 MNIST data라면 \(x \in \mathbb{R}^{1 \times 784}\)이고, hidden layer의 neuron 수가 128개라면 \(h = Wx^T \in \mathbb{R}^{1 \times 128}\) 이다 (weight matrix는 \(W \in \mathbb{R}^{128 \times 784}\)). 그리고 2를 의미하는 classifer의 vector, \(W_{\text{Digit 2}}\)는 \(1 \times 128\)크기의 vector일 것이므로, 이를 곱하면 \(W_{\text{Digit 2}} h^T = 0.8\) 이런 vector간 내적 값 (similarity를 잰 것)이 나올 것이다.

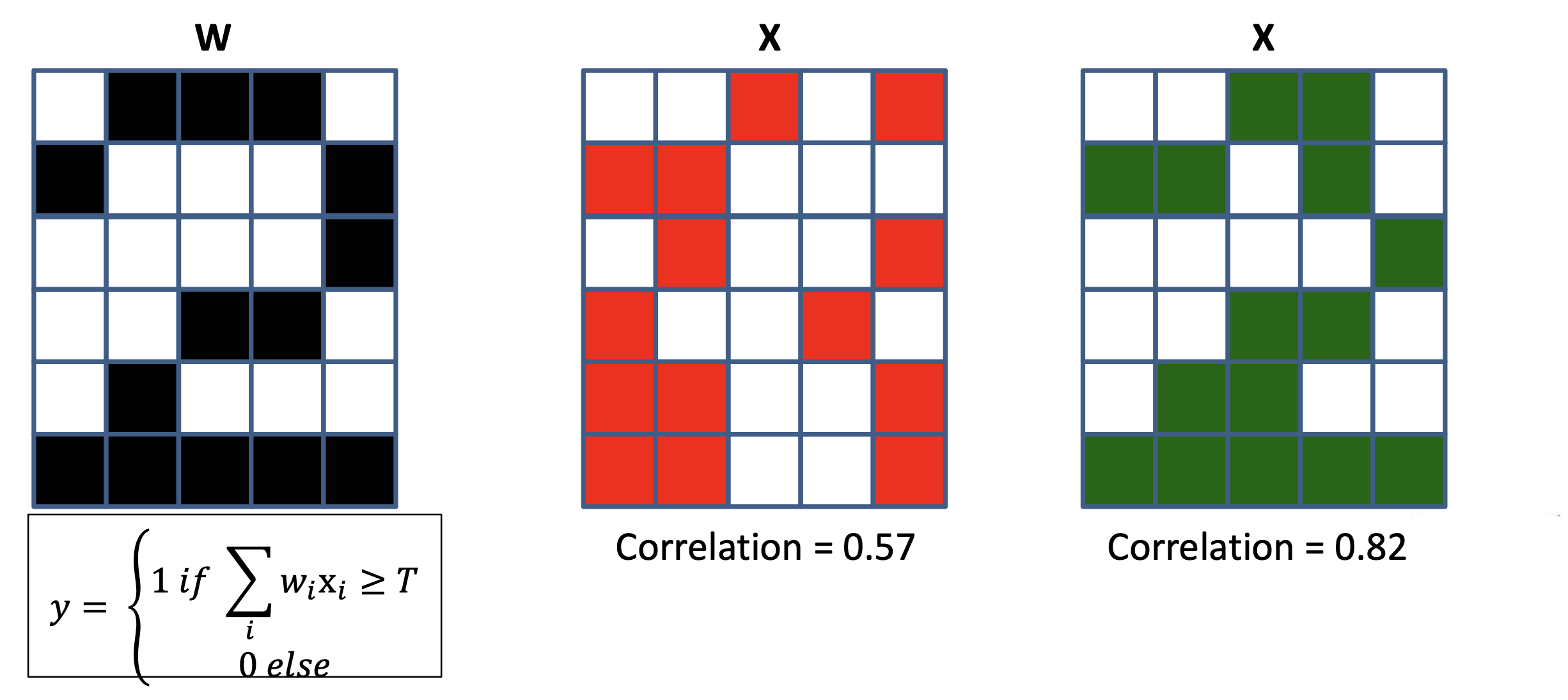fig30 Fig.

만약 다른 숫자의 classifier 대비 2와의 correlation이 가장 높으면 2로 분류되는 것이다. 그럼 hidden layer는 무슨일을 하고있을까? Hidden layer의 각 neuron들은 (마찬가지로 vector) 예를 들어 숫자의 곡선, 둥근 부분, 직선을 검사 하는 일 (각 숫자를 나타내는 성분과 correlation 계산)을 한다고 생각할 수 있다.

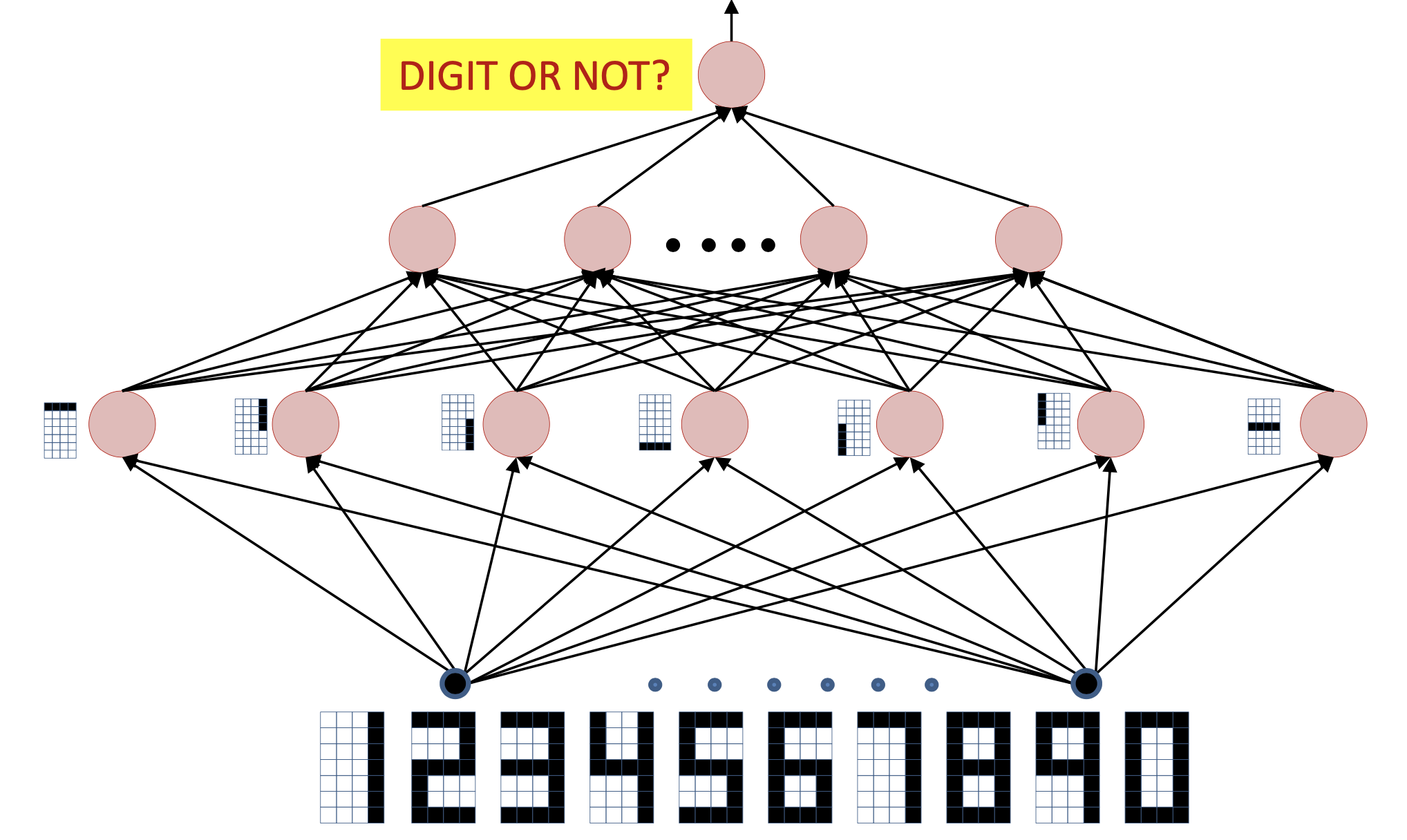fig32 Fig.

아마 이 post를 읽고있는 대부분이 DL을 아예 모르는 것은 아닐 것이다. 그리고 DL에 입문한 누구라도 Convolutional Neural Netowrks (CNNs)을 알 것이다.

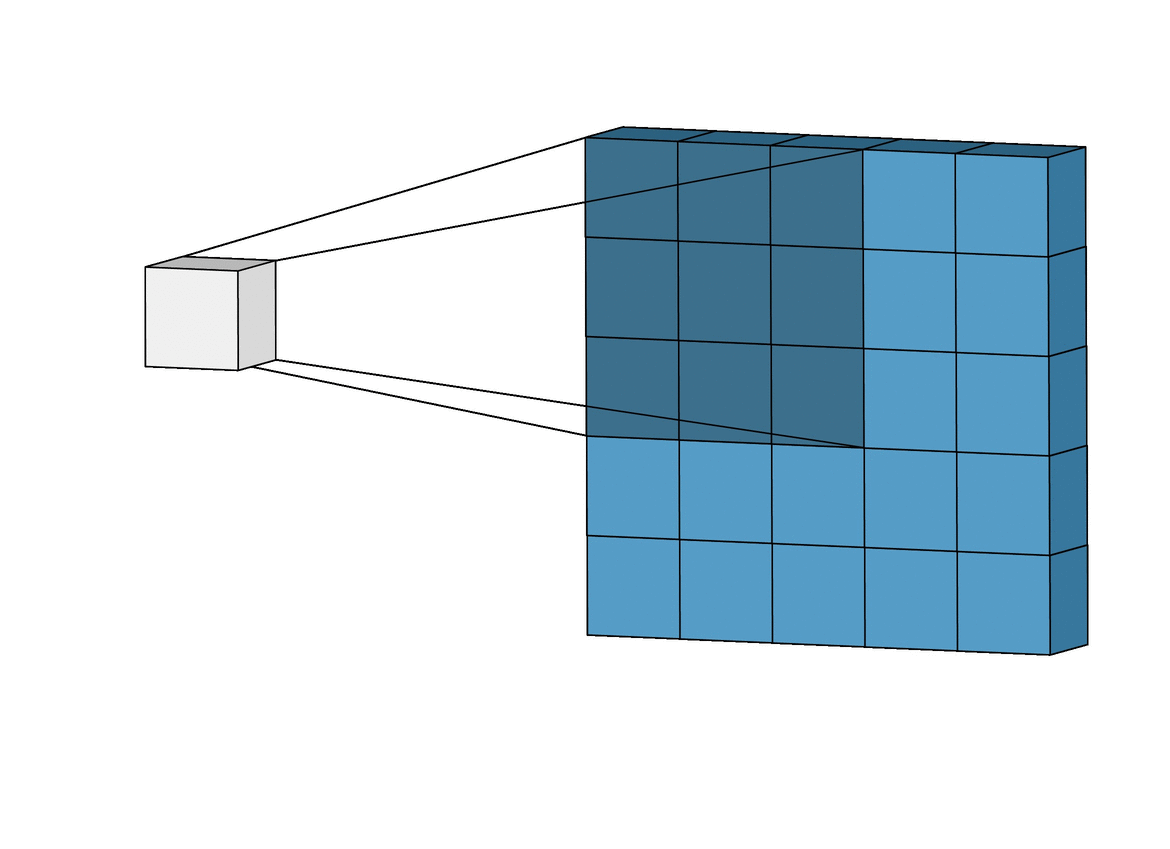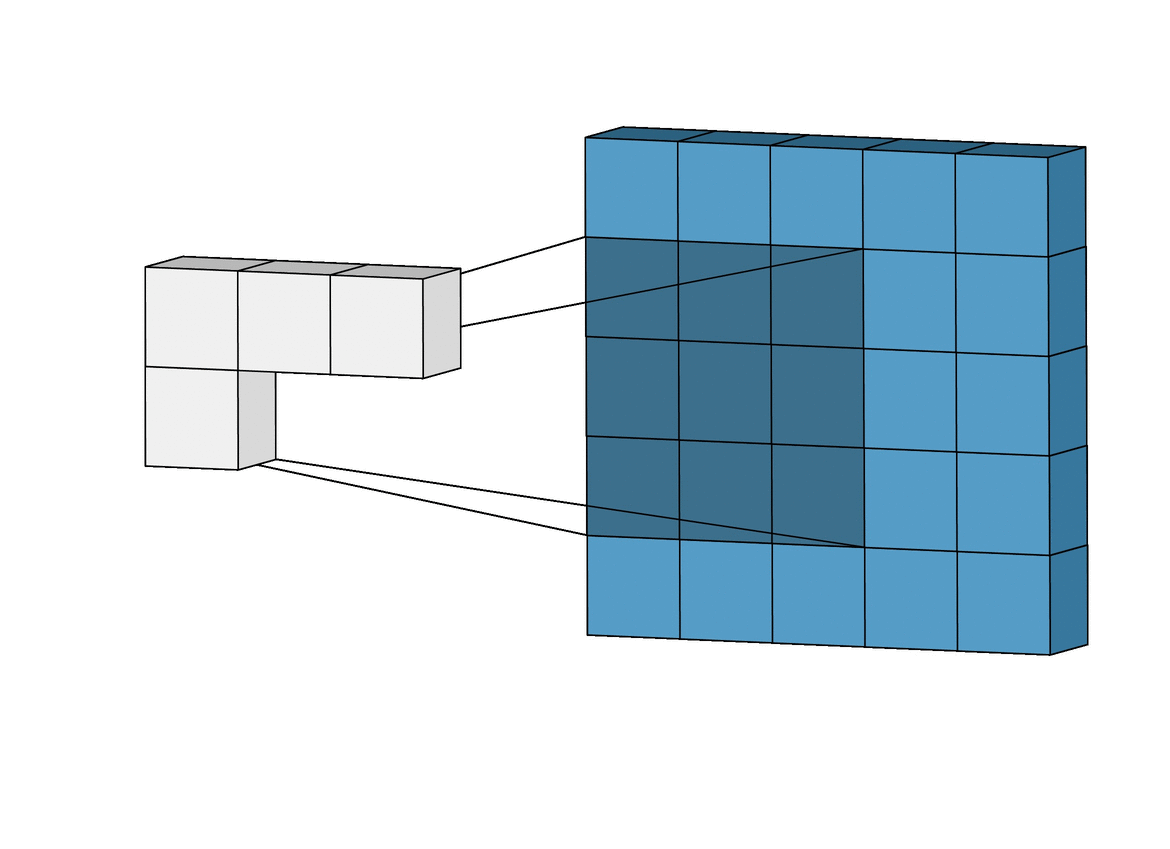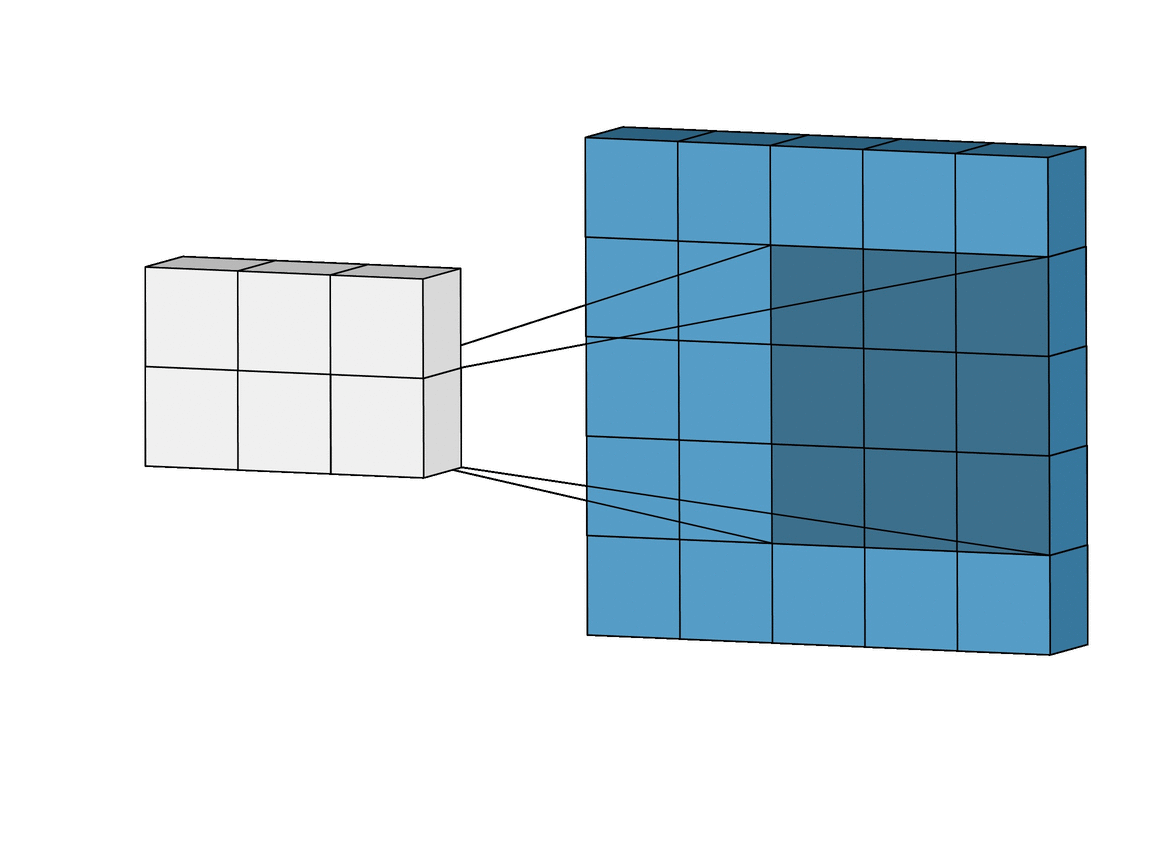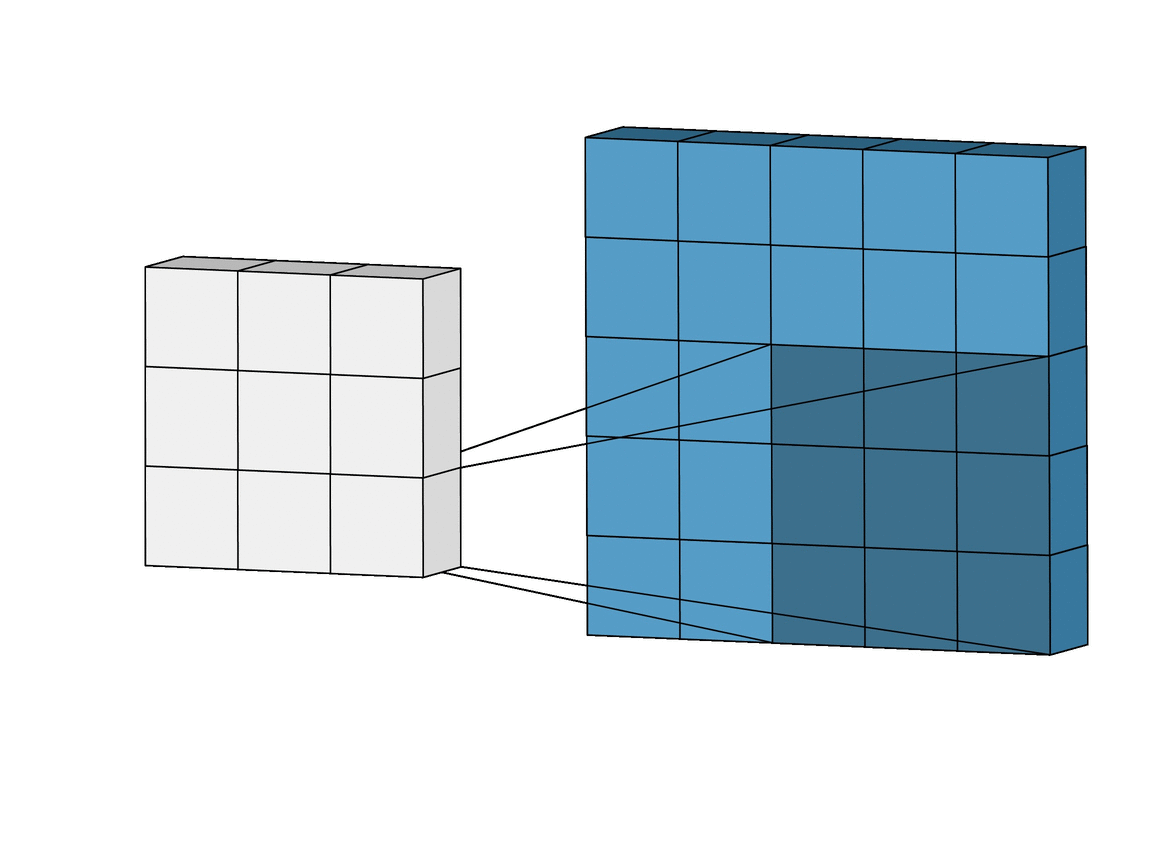fig33 Fig. 이 필터 연산도 사실상 correlation 계산을 하는것과 같다.

CNN의 각 filter들은 아래 처럼 image의 특징을 catch한다고 알려져 있는데, 이것 또한 앞선 MNIST에서 neuron들이 하는 일과 matching됨을 알 수 있다.

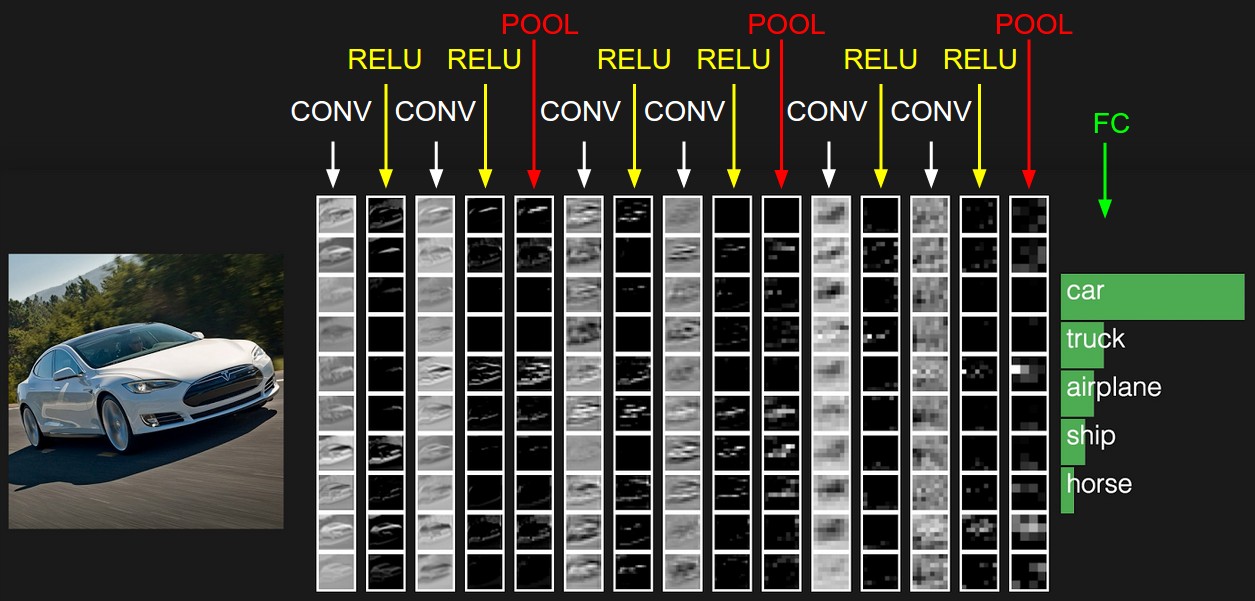fig34 Fig. What Filters Learn. Source from cs231n

물론 CNN은 우리가 지금까지 배운 NN과 다르게 생겼다. 이 post에서 다룬 NN은 layer의 input과 layer의 weight matrix가 완전히 곱해지는 Fully Connected (FC) 형태였다. 하지만 중요한 점은 결국 CNN도 NN의 각 neruon들이 input 과 weight matrix 간의 correlation 을 계산한다는 concept을 벗어나지는 않는다는 것이다.

+Updated) Inspiring Videos for NN Training and Manifold Hypothesis

요즘은 3B1B처럼 수학/물리/ML 등의 개념을 시각화하는 자료가 점점 더 많아지는 것 같다. 몇 가지 좋은 자료를 링크한다.

References