Notes

Generative vs Discriminative Models

25 Jan 2021

< 목차 >

Learning and Inference

어떤 input image \(x\)가 들어왔을 때, 이 이미지가 개인지 고양인지 구분하는 알고리즘을 만들고 싶다고 생각해봅시다. 이때 model을 만드는데 필요한 procedure는 다음과 같습니다.

  1. 입력 x와 출력 w의 관계를 설명할 model을 설정한다.
  2. 학습 데이터 \(x_i,y_i\)들을 통해서 model의 파라메터를 학습한다. (Learning)
  3. 학습이 끝난 후 모델을 이용해 주어진 테스트 입력 x에 대한 \(Pr(w \mid x)\) 를 구한다. (Inference)

어떤 방식(ML, MAP, Bayesian)으로 어떤 분포를 모델링하던지, 그리고 x에 대한 분포나 w에 대한 분포 중 어떤 것을 모델링 하던지, 우리가 실제로 Inference 할 때 필요한 것은 \(Pr(w \mid x)\)가 됩니다. 왜냐면 궁금한것은 \(x\) 가 들어갔을때 개인지 고양이 인지에 대한 확률이니까요.

Generative vs Discriminative Models

그런데 목적이 \(Pr(w \mid x)\) 를 하는것이라면 \(Pr(w \mid x, \theta)\) 를 학습하면 되지 왜 \(Pr(x \mid w, \theta)\) 를 모델링 하는 방법도 있는걸까요? 일반적으로 \(Pr(x \mid w)\) 를 모델링하는 것을 생성 모델 (Generative Model) 이라고 부르고 \(Pr(w \mid x)\) 를 모델링 하는 것을 판별 모델 (Discriminative Model) 이라고 합니다.

여기서 우리가 생성모델 \(Pr(x \mid w)\)를 모델링한다는 것은 예를들어 이진 분류 문제를 풀 때 두 개의 클래스 (개,고양이) 중에서 개라는 이미지의 데이터가 실제로 어떤 분포를 띄고 있을까? 를 알게되는 것과 같습니다. 예를 들어 개 모양의 이미지들의 분포가 가우시안 모양을 하고 있다고 가정해봅시다.

\[Pr(x \mid w_{\color{red}{dog}}) = Norm [ \mu_{\color{red}{dog}}, \sigma_{\color{red}{dog}}^2 ]\]

즉 “아 개에 대한 image 는 이런 분포를 형성하고 있구나” 를 알고있는 상황인데, 그러면 개가 뽑힐 확률이 높은 곳 이 존재하겠죠? 바로 mean 값 근처가 되는데 이 부근에서 x 를 sampling 하면 어떻게 될까요?
그러면 새로운 우리는 새로운 data point 를 얻을 수 있게 됩니다. 즉 새로운 데이터를 생성 (혹은 합성)해 낸것이죠.

만약에 이런 정보가없었다면 아무런 x 나 뽑는다고 해서 새로운 data를 생성 하는 것은 불가능에 가깝습니다. 만약 이미지 x 가 1,2차원 보다 조금 고차원인 10차원이라고 해봅시다. 10차원에서 아무거나 sampling == 랜덤한 수의 element 10개로 이뤄진 vector 를 만들어내는건데요 이것이 개 이미지 일 확률은 매우 낮을테니까요.

반면에 다이렉트로 \(Pr(w \mid x)\) 를 학습한 것은 (Logistic Regression 을 한다느 것은) 단순히 클래스 두 개를 분류하는 어떤 Decision Boundary 가 어디에 어떻게 그려질까? 를 학습하는 것일 뿐 개 image 의 분포, 고양이 image 의 분포 따위는 알 수 없는 일입니다.

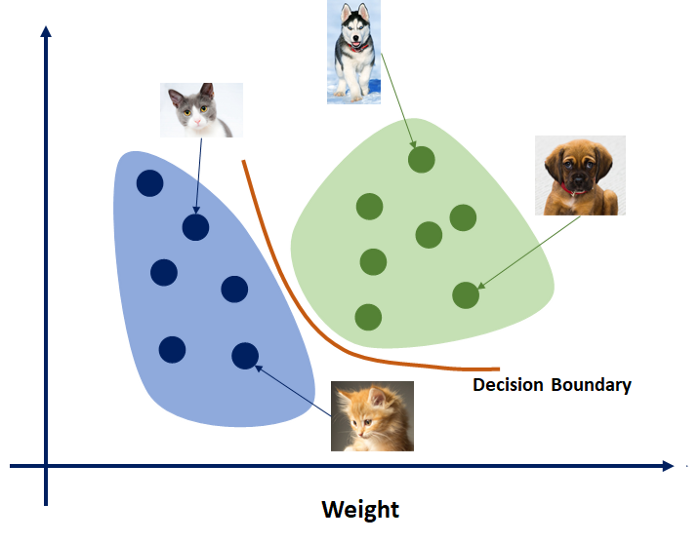fig17 Fig. Source From link

생성 모델\(Pr(w \mid x, \theta)\) 를 학습한 뒤에는 그러면 \(Pr(w \vert x)\) 를 알 수 없을까요? 아닙니다 x에 대한 분포를 모델링하고도 어떤 x를 넣었을때 개일확률과 고양이일 확률 (w의 확률) 을 알 수 있는데, 바로 Bayes’ Rule 을 사용하는 겁니다.

아주 간단하게 설명하면 어떤 test image 를 \(Pr(\text{test image} \vert w_{dog}) = 0.57\), \(Pr(\text{test image} \vert w_{cat}) = 0.4\) 로 각 class 에서의 확률값을 기준으로 더 확률이 높은 (more likely) 쪽의 class 를 선택하는 식인거죠.

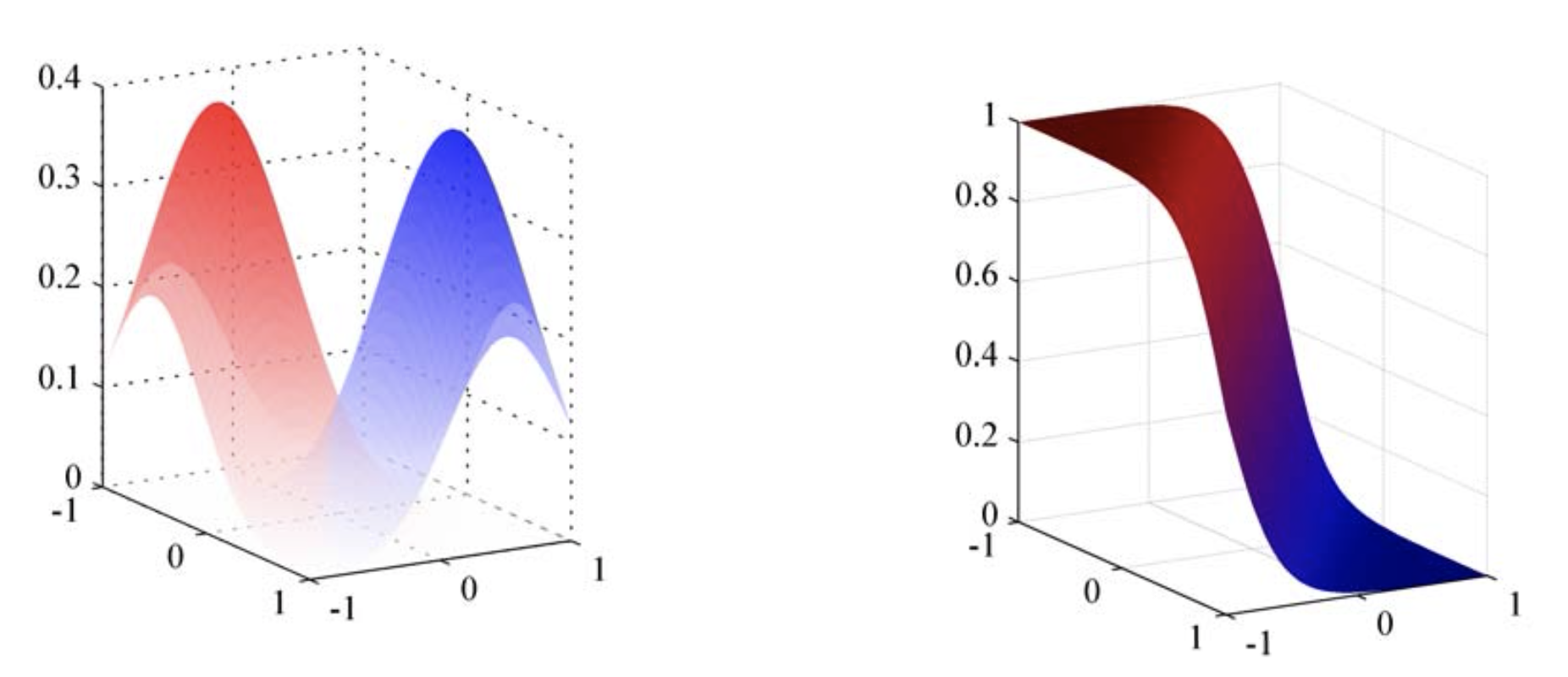prml_generative Fig. input x, 개(파랑), 고양이(빨강)의 분포를 학습한 경우 (좌)에도 decision boundary 를 결정할 수 있다 (우)

앞으로 Regression, Classification 문제를 풀 때 어떻게 Generative Model 을 적용하는지 알아봅시다.

Example 1 : Regression

Regression : Discriminative

먼저 Linear Regression Task 를 풀고싶은 경우입니다. Discriminative Regression Model 을 사용하는 경우 전체 procedure 는 다음과 같습니다.

  1. 모델링할 \(Pr(w \mid x,\theta)\) 분포가 무엇일지 정한다.
  2. 간단하게 \(Pr(w \mid x,\theta) = Norm_w[\theta^T x, \sigma^2]\)라고 정의한다.
  3. 가우시안 분포 이므로 학습할 파라메터는 \(\theta, \sigma^2\) 이다.

Parameter \(\theta\)를 Maximum Likelihood Estimation (MLE), Maximum A Posteriori (MAP), Bayesian Aprroach 등으로 학습하면 됩니다. 추론을 할 때는 어떻게할까요? 애초에 \(Pr(w \mid x,\theta)\)에 대해 가우시안 분포라고 정의하고, 그 파라메터를 학습한것이기 때문에 추론을 할 때에는 학습된 \(\theta\)와 \(x\) 를 곱해 넣고 \(w\)의 좌표를 읽으면 끝입니다.

fig2

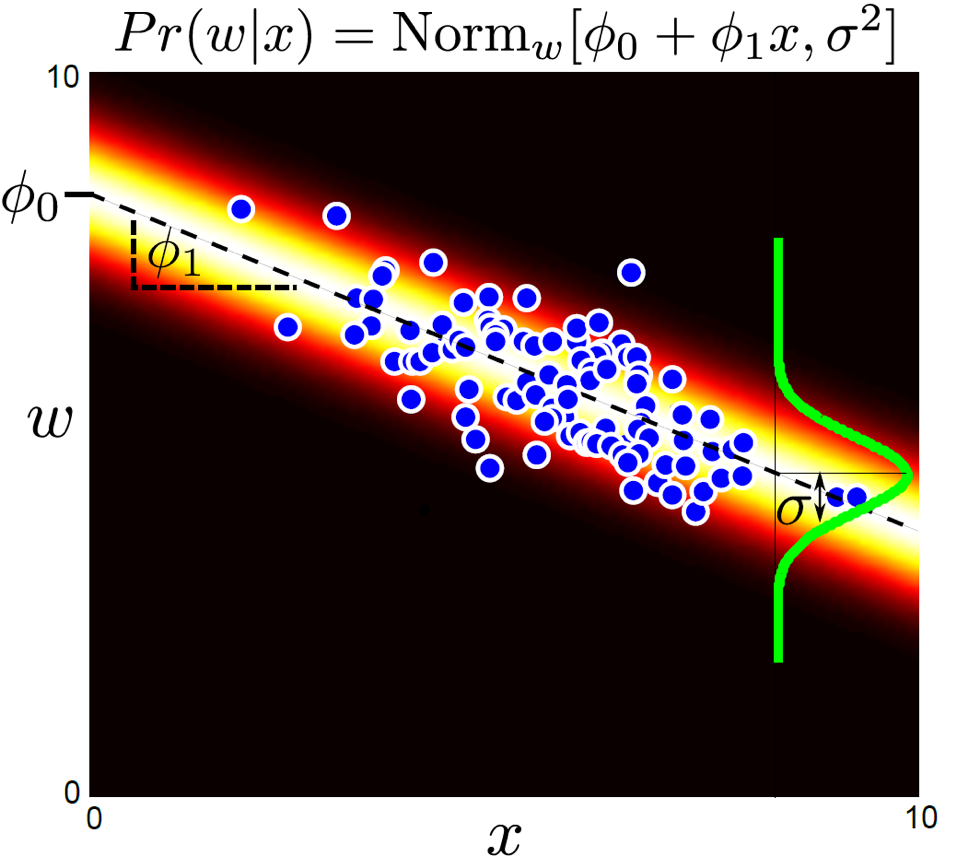
Regression : Generative

Generative Regression Model의 경우를 살펴봅시다.

  1. 모델링할 \(Pr(x \mid w,\theta)\) 분포가 무엇일지 정한다.
  2. 마찬가지로 간단하게 가우시안 분포 \(Pr(x \mid w,\theta) = Norm_x[\theta^T w, \sigma^2]\)라고 정의한다.
  3. 학습할 파라메터는 \(\theta, \sigma^2\) 이다.

판별 모델과 차이가 없어보이지만 우리가 학습하고자 정의한 분포가 \(Pr(x \mid w,\theta)\) 라는게 점이 바뀌었죠. w 값이 1.72일 때 x 는 어떤 분포를 가지고 있을까? 를 학습하는 것이죠. 판별모델은 x가 들어가면 정답 label w의 분포가 어떻게 되어있느냐? 였는데 반대인거죠.

fig4

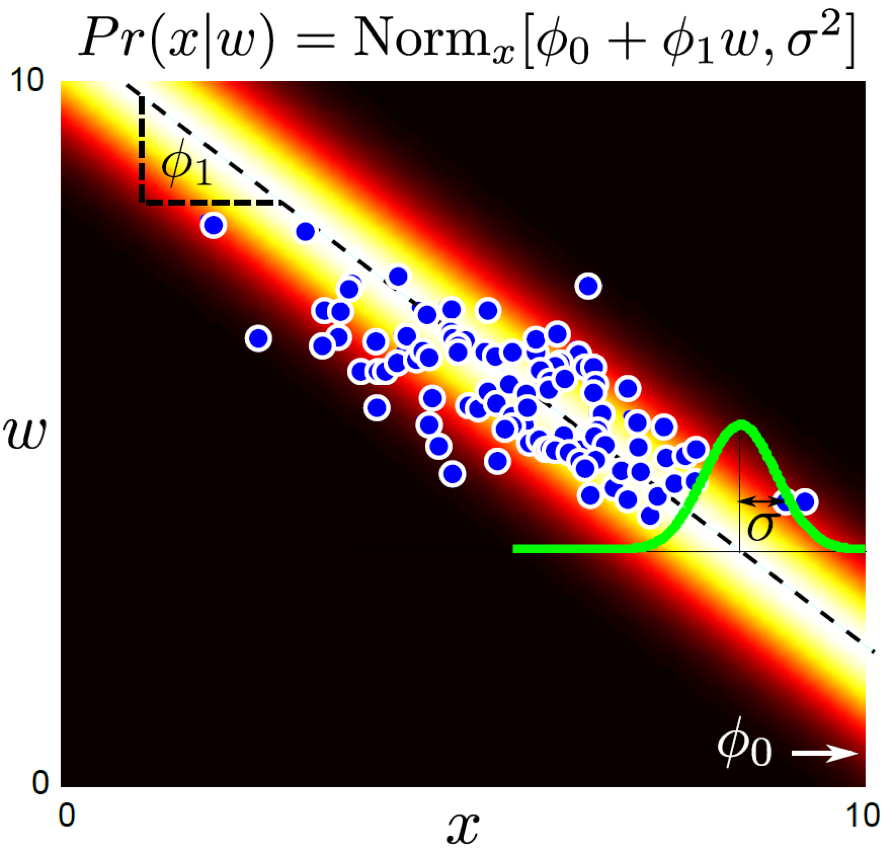
하지만 우리가 앞서 말한 것처럼 어떤 모델을 사용하던, 두 모델 모두 추론할 때 하고싶은것은 \(Pr(w \mid x)\) 입니다. 어떻게하면 원하는 바를 이룰 수 있을까요? Bayes’ Rule을 사용하면 됩니다.

\[Bayes' \space Rule : Pr(w \mid x) = \frac{Pr(x \mid w)Pr(w)}{\int{Pr(x \mid w)}{Pr(w)}dw}\]

학습을 통해 x,w의 관계는 \(Pr(x \mid w, \theta)\) 로 모델링해서 잘 학습했습니다. 여기서 \(Pr(w)\) 는 실제로 우리가 학습하려는 dataset의 w 분포입니다. 이것도 적당히 가우시안 분포로 생각할 수 있스니다. 다시 말해서 “음 가지고 있는 데이터의 w label 의 평균을 내봤더니 대충 1.5 에 몰려있고 variance 는 얼마군?” 하고 그냥 계산해서 얻을 수 있다는거죠.

가우시안 끼리의 곱은 여전히 가우시안 이기때문에 \(p(w \vert x)\) 를 쉽게 얻을 수 있습니다.

fig5

fig8

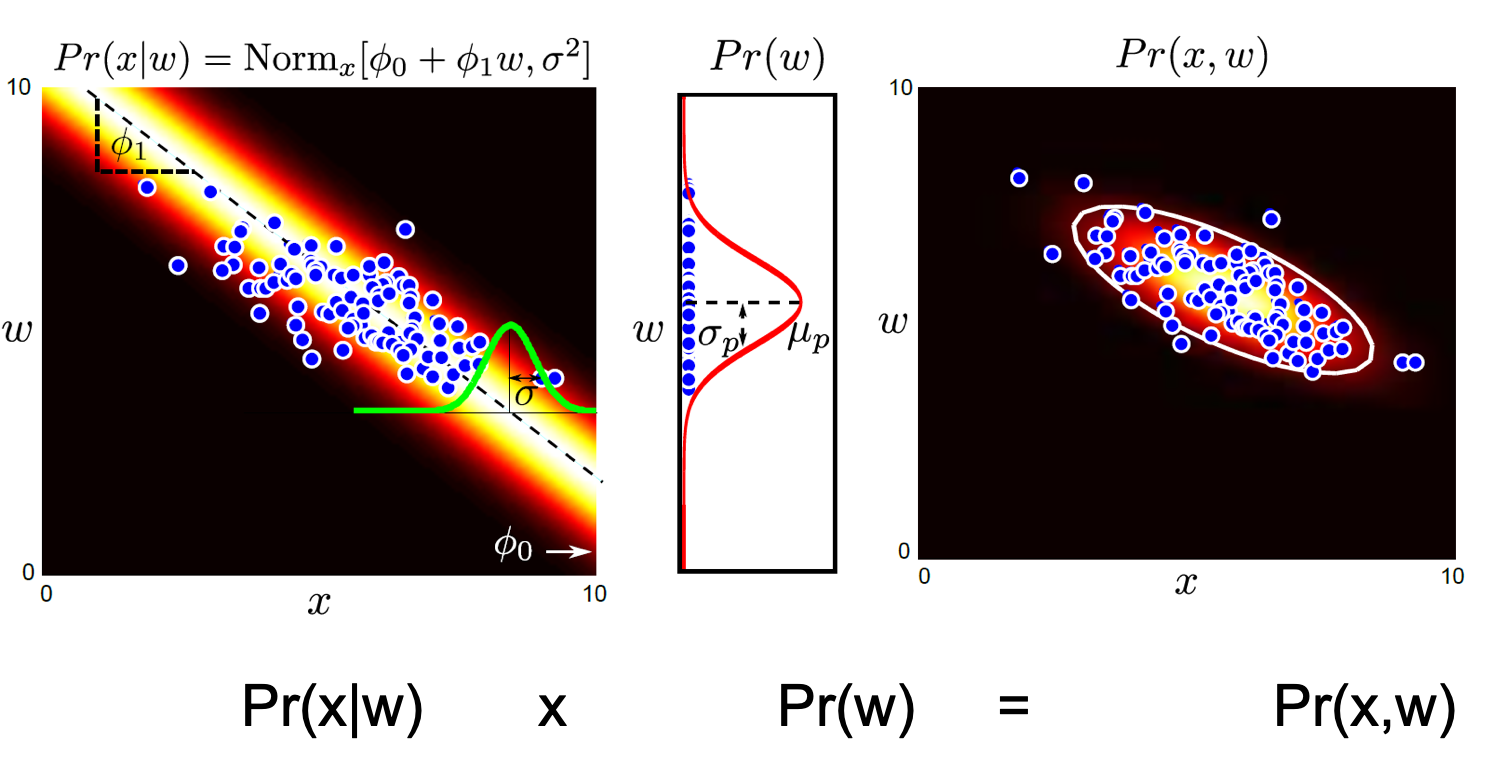
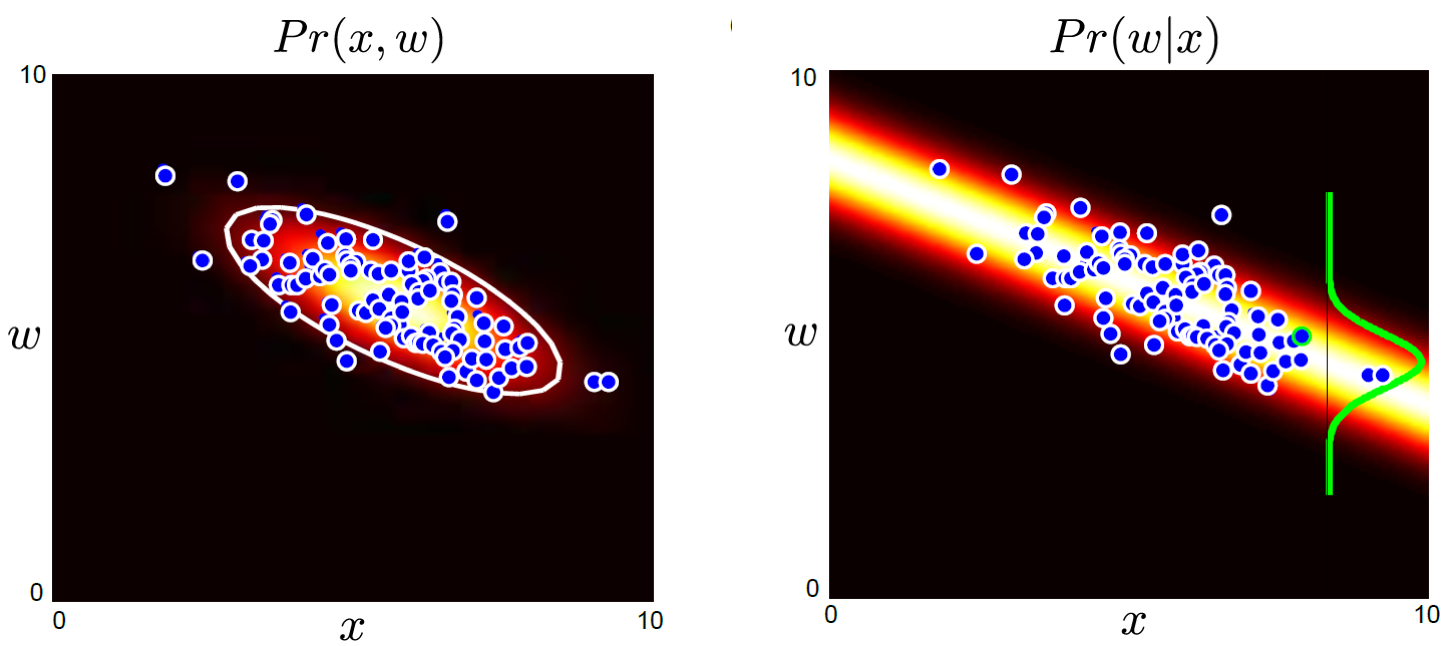
한편 위의 figure 에서 \(Pr(x,w)\) 가 튀어나오는 것을 알 수 있는데요, 이는 Bayes’ Rule 에서 \(Pr(x,y) = Pr(x \mid y)Pr(y) = Pr(y \mid x)Pr(x)\) 이 성립하기 때문입니다. (분모의 적분 결과가 \(Pr(x)\)임.)

그래서 생성모델을 설명할 때 결합 분포 (Joint Probability) \(Pr(x,w)\) 를 모델링하는 method 라고 설명하기도 합니다.

Example 2 : Classification

2개의 클래스를 판별하는 이진 분류 모델에 대해서 생각해보도록 하겠습니다.

Classification : Discriminative

Discriminative Classification Model의 경우

  1. Target distribution을 \(Pr(w \mid x) = Bern_w[\frac{1}{1+exp[-\theta_0 -\theta_1 x]}]\) 라고 정의한다.
  2. 학습할 파라메터는 \(\theta_0,\theta_1\) 이다.

Bernoulli distribution 을 target distribution 으로 설정하고 \(\theta\) 를 구하면 되겠습니다. Regression 때와 마찬가지로 \(Pr(w \mid x)\) 에 대한 분포를 정의하고 그 분포의 파라메터를 학습했으니, 바로 입력 데이터 x를 넣어 추론할 수 있습니다.

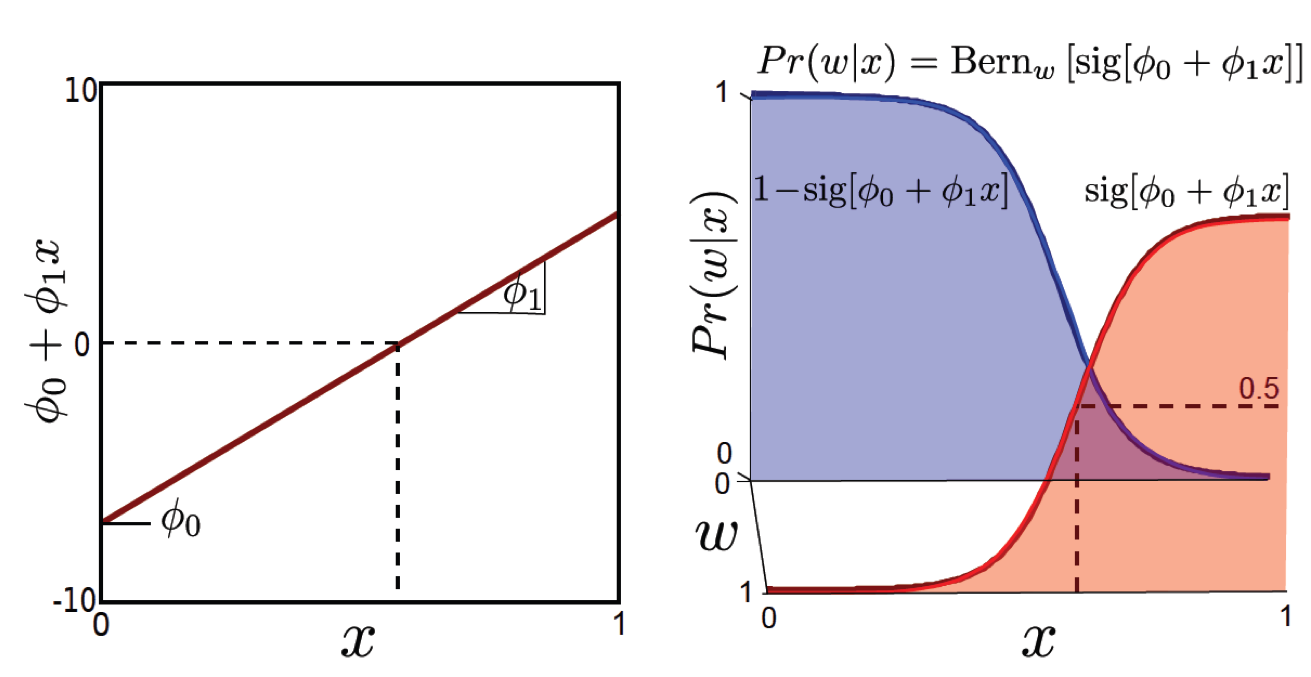
fig10

그림에서 \(Pr(w \vert x)=0.5\) 가 되는 부근이 decision boundary 가 그어지는 부분이니 x가 어느 지점에 떨어지는지만 알면 되겠네요.

Classification : Generative

Generative Classification Model의 경우를 살펴봅시다. 이번에도 마찬가지로 \(Pr(x \mid w)\)를 학습하겠죠?

  1. Target distribution을 \(Pr(x \mid w) = Norm_x[\mu_w, \sigma_w^2]\) 라고 정의한다.
  2. 학습할 파라메터는 \(\mu_0,\mu_1,\sigma_0^2,\sigma_1^2\) 입니다.

현재 이진 분류 문제를 예시로 들었으니, 우리가 찾아야 할 것은 continuous한 입력에 대해 가우시안 분포로 모델링 했기 때문에 각 클래스 당 mean,variance 1개 씩 총 \(\mu_0,\mu_1,\sigma_0^2,\sigma_1^2\) 4개가 됩니다.

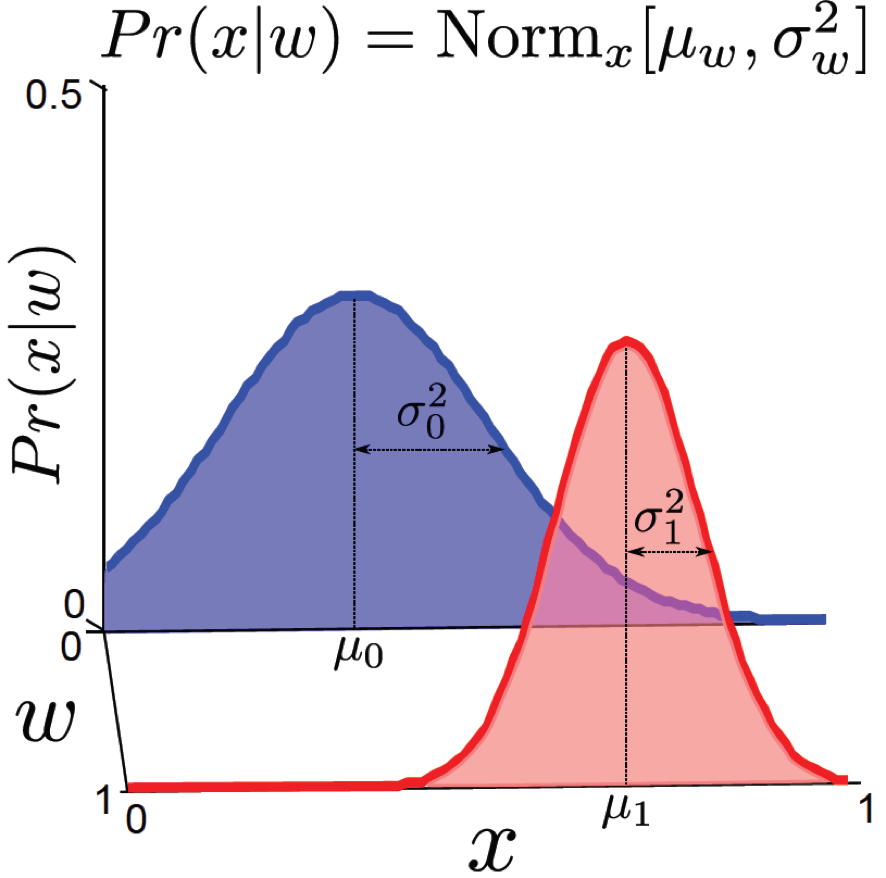
fig12

이제 학습 데이터에서 바로 정답 클래스의 분포 \(Pr(w)\)를 구할 수 있습니다. 이진 분류 문제이기 때문에 정답 분포는 \([0,1,0,1,1,1,0,...,0]\) 이런식으로 되어있으니 쉽게 통계를 낼 수 있습니다.

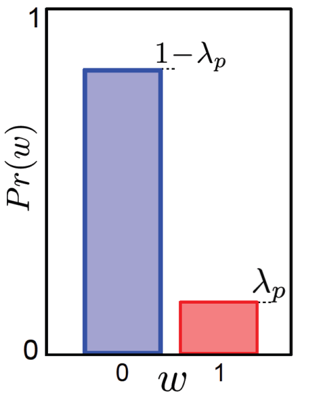
fig13

만약 이 생성모델로 classification 을 하고 싶다면 (판별을 하고싶다면) 원하는 것은 \(Pr(w \mid x)\) 이기 때문에 마찬가지로 Bayes’ Rule을 이용해 구해보면 다음과 같은 결과를 얻을 수 있습니다. 실제로 \(Pr(x \mid w)\)를 학습한 뒤 구한 \(Pr(w \mid x)\) 분포와 vs 다이렉트로 \(Pr(w \mid x)\)를 학습한 분포는 아래와 같은 차이 조금 차이가 납니다.

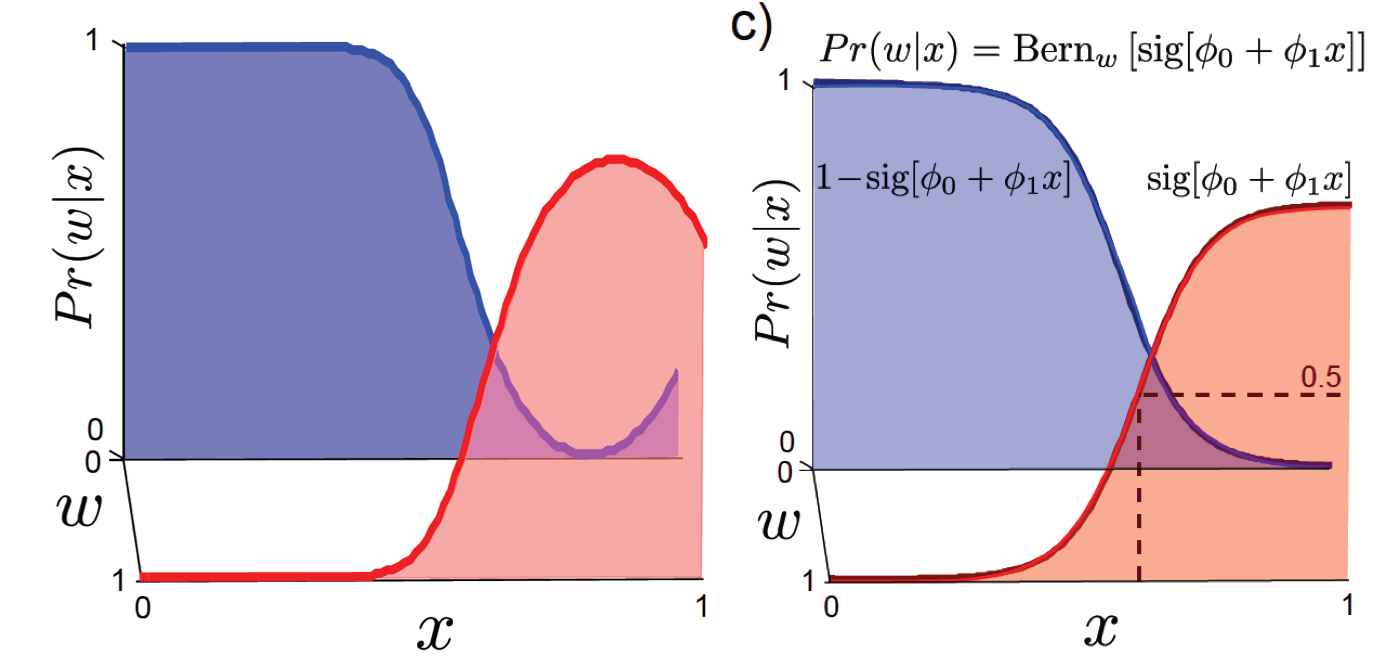fig14 Fig. 생성 모델로 부터 얻은 w given x (좌) vs 판별 모델(우)

별로 차이는 사실 안나죠. 이런 경우 데이터 생성도 할 수 있고 판별도 할수있는 생성모델이 최고 아닌가? 라고 생각할 수도 있습니다. 하지만 생성모델은 학습이 어렵다는 단점과 추론할때마다 Bayes’ Rule 을 계산해야하는 등의 단점이 있습니다. 만약 우리가 만들고싶은 모델이 가 그냥 개 고양이 판독기라면 생성 모델까지 필요한게 과연 맞을까요?

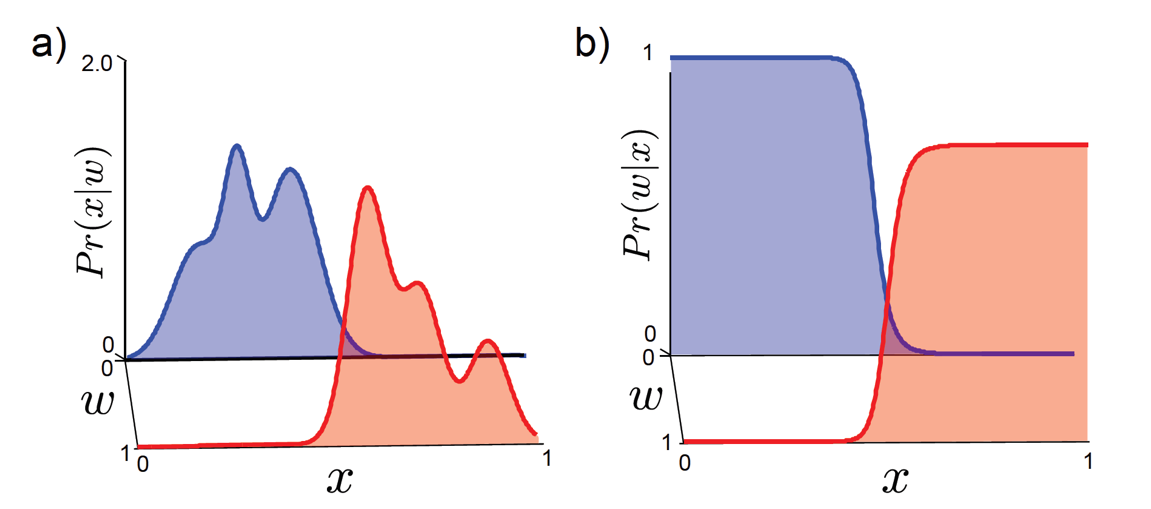fig16 Fig 생성 모델의 class conditional 분포를 더 복잡하게 만들수도 있다. 다른 post들 참고

Task에 따라서 잘 맞는 model type 을 고르는게 당연히 현명할 겁니다.

Generative Model vs Discriminative Model Pros and Cons

생성 모델과 판별 모델의 장단점을 나열해보면 다음과 같습니다.

  • Generative Model
    • Pros
      • 1.각 클래스가 어떤 분포로 부터 근거했는지 근본적인 부분에 대해서 생각할 수 있다.
      • 2.찾은 분포를 통해 새로운 데이터를 생성 할 수 있다.
      • 3.베이지안 정리를 통해 p(x)의 주변 밀도까지 구할 수 있다. (\(\rightarrow\) 이를 바탕으로 발생 확률이 낮은 새 데이터 포인트들을 미리 발견할 수 있다. 이런 데이터들은 낮은 정확도를 뱉을 것이기 때문에 이상점 검출 등에 사용 될 수 있다.)
      • 4.Unsupervised Learning에 적합하다.
    • Cons
      • 1.보통 입력 데이터의 차원이 크기 때문에 그것을 모델링하기란 쉽지 않다. (모델 파라메터가 엄청 많아지고 계산량이 많아짐)
      • 2.일정 수준 이상의 제대로 된 분포를 찾기 위해서는 학습 데이터가 많이 필요하다.
      • 3.사후 확률을 계산하는데 영향을 미치지 않는 추가적인 정보가 많이 포함되어 있을 수도 있다.
    • Examples
      • Naive Bayes
      • Gaussian mixture model
      • Hidden Markov Models (HMM)
  • Discriminative Model
    • Pros
      • 1.계산량이 적다.
      • 2.필요한 데이터도 적다. (물론 데이터가 많으면 좋겠지만 생성모델처럼 데이터 요구량이 엄청 많지는 않다.)
    • Cons
      • 1.해석하기 어렵다.
      • 2.단순히 분류를 할 뿐 (decision boundary를 만들어낼 뿐) 데이터를 만들어 낼 수는 없다.
      • 3.Unsupervised Learning에 부적합하다.
    • Examples
      • Logistic regression
      • SVM
      • Neural Networks

어떤 모델이 더 우수하다고는 할 수 없습니다.
대부분의 경우에 Discriminative Model이 계산량이 적고 모델링 하기 쉽기 때문에 인기가 많습니다. 하지만 과거 고전적인 음성인식 모델이 Generative Modeling 을 해야만 하는 상황이 있을 수 있고, 당연히 실제로 있을법한 나만의 합성 이미지를 만들어낸다거나 새로운 음악을 만든다거나, 생성형 챗봇을 만드는 등의 경우에는 Generative Modeling 이 필요합니다.

Large Scale 에서 학습이 어렵다는 단점은 GPU computing 이 발전함에따라, 그리고 Variational AutoEncoder (VAE) 같은 모델이 등장함에 따라 많이 해소가 되었습니다. 앞으로 Blog 에서 Deep Neural Network (DNN) 을 사용한 Deep Generative Model 도 많이 다뤄보도록 하겠습니다.

References

  1. Prince, Simon JD. Computer vision: models, learning, and inference. Cambridge University Press, 2012.

  2. Bishop, Christopher M. Pattern recognition and machine learning. springer, 2006.