Notes

Information Theory, Entropy and Kullback-Leibler Divergence (KLD)

25 Jan 2021

이번 글은 Bishop, Christopher M. Pattern recognition and machine learning. springer, 2006. 를 기반으로 작성되었습니다. 비숍의 PRML 책을 보면, 정보 이론 (Information Theory) 이 패턴 인식 (Pattern Recognition)과 머신 러닝 (Machine Learning; ML) technique들을 이해하는 데 있어 확률론, 결정 이론과 함께 중요한 역할을 하게 될 역할을 한다는 문구가 있습니다.

(in PRML 48 page)

In this chapter, we have discussed a variety of concepts from probability theory 
and decision theory that will form the foundations for much of the subsequent discussion in this book. 
We close this chapter by introducing some additional concepts from the field of information theory, 
which will also prove useful in our development of pattern recognition and machine learning techniques.

어떤의미에서 그렇다는건지, 그리고 ML 과의 connection 은 무엇인지 알아보도록 합시다.

< 목차 >

Information Theory

Information

어떤 이산 확률 변수 (discrete random variable) \(x\)에 대해 생각해 봅시다. 이 변수가 특정 값을 가지고 있는 것을 확인했을 때 전해지는 정보량 (Information)은 얼마만큼일까요? Information은 놀라움의 정도라고 표현되기도 합니다.

아래 example figure를 보시면 일기예보에서 내일 비가 올 확률이 제일 크다는 것을 알 수 있습니다. (사각형이 클수록 확률이 큼)

fig2

그렇다면 내일 진짜 비가와서 우산을 들고 나갈 때 쯤이면 우리는 놀랄까요? 아닙니다. 우리는 매우 일어날 가능성이 높은 사건이 일어났다는 소식을 전해 들었을 때 보다 일어나기 힘든 사건이 발생했다는 사실을 전해 들었을 때 더 많은 정보 를 전달받게 됩니다. 이렇게 Information이 많다는 것을 informative 하다고 합니다. 따라서 앞으로 우리가 쓸 Information은 데이터 x의 발생 확률을 의미하는 분포 \(p(x)\)에 종속적인 함수가 됩니다. 이는 아래처럼 수식으로 표현할 수 있는데

\[\begin{aligned} & h(x) = - \log_2 p(x) \\ & = \log_2 \frac{1}{p(x)} \\ \end{aligned}\]

저는 Information을 \(h(x)\)라고 표현했지만 누군가는 \(I(x)\)라고 쓰기도 합니다.

fig3

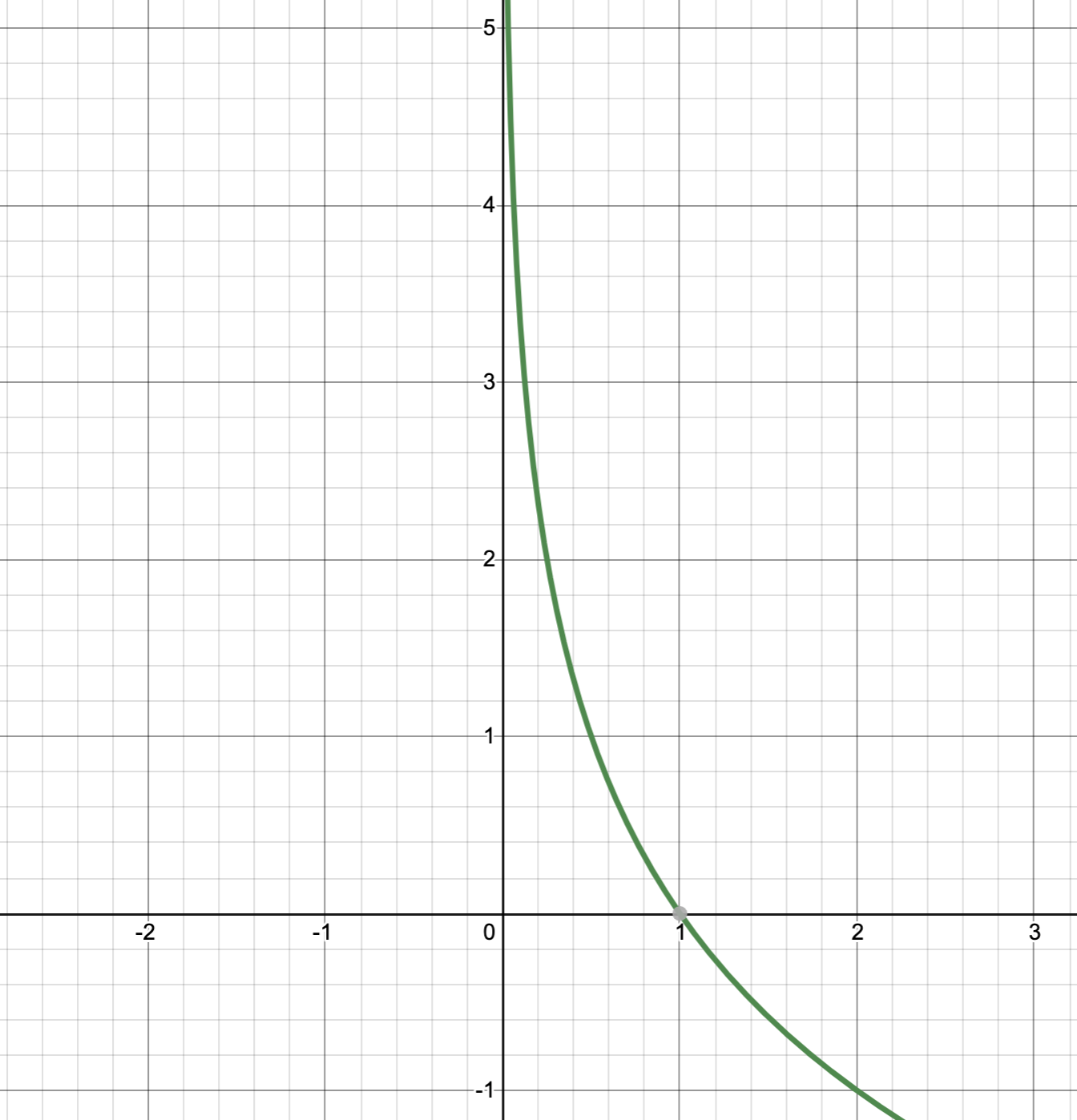
일반적으로 ML에서는 확률 분포를 다루는데 확률 값이 0~1 사이의 값이기 때문에 당연히 Information은 음수를 가질 수 없으며 확률이 0에 가까워질수록 무한대에 가까운 값을 가지게 됩니다. 즉 로또에 당첨될 확률의 이벤트는 Information이 많은것 입니다.

로그의 밑이 2인 것은 정보 이론 학계의 관습 이라고 하며 이렇게 할 경우 h(x)의 단위는 bit가 된다고 합니다. (이진 비트; binary bit)

Entropy

이번에는 누군가 어떤 확률 변수의 값을 다른 사람에게 전송하고자 하는 상황을 가정해 보겠습니다. 전송에 필요한 Information의 평균치는 p(x)에 대한 Information의 기대값으로 구할 수 있습니다.

\[H[x] = - \sum_{x \in X} p(x) \log_2 p(x) = \mathbb{E}[ - \log(X) ]\]

이 값을 바로 엔트로피 (Entropy) 라고 부릅니다. 확률 밀도 \(p(x)\)가 베르누이 분포를 따를 경우 Entropy는 아래와 같습니다.

fig4

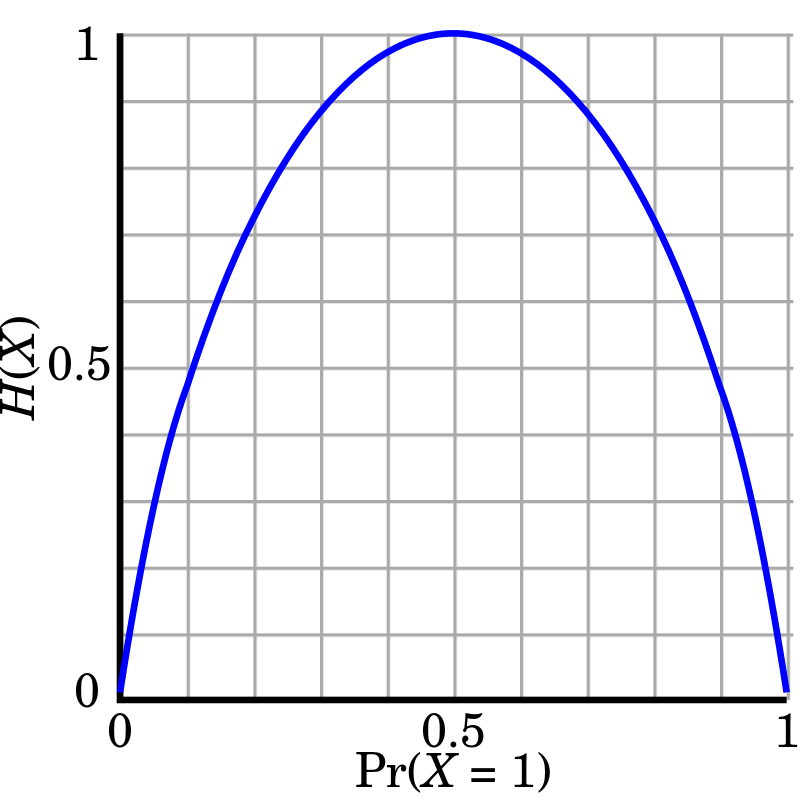
Entropy 경우 질서가 있는것이 무질서한 것 보다 훨씬 높은 값을 return합니다. 가령 아래의 분포를 보면 확률이 고르게 분포되어 특정 값들이 나올 확률이 굉장히 높은 경우보다 여러 값들이 나올 확률이 고만고만한게 더 값이 높은걸 알 수 있습니다.

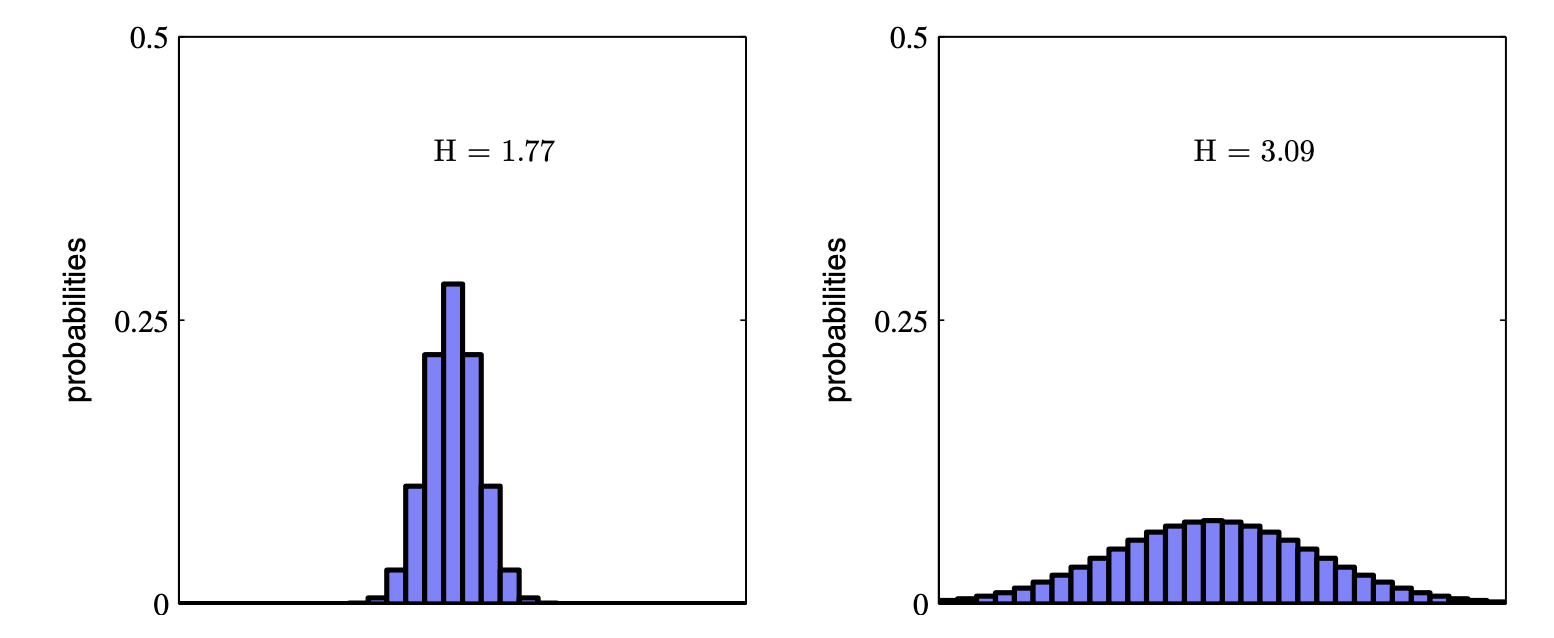
fig4_1

즉 Entropy 는 확률분포에서 어떤 분포가 더 균일한지를 measure 하는 척도입니다.

Entropy for Continuous Distribution

이번에는 이산 확률 변수가 아닌, 연속적인 확률 변수 ((continuous random variable)에 대해 생각해 보도록 합시다.

fig5

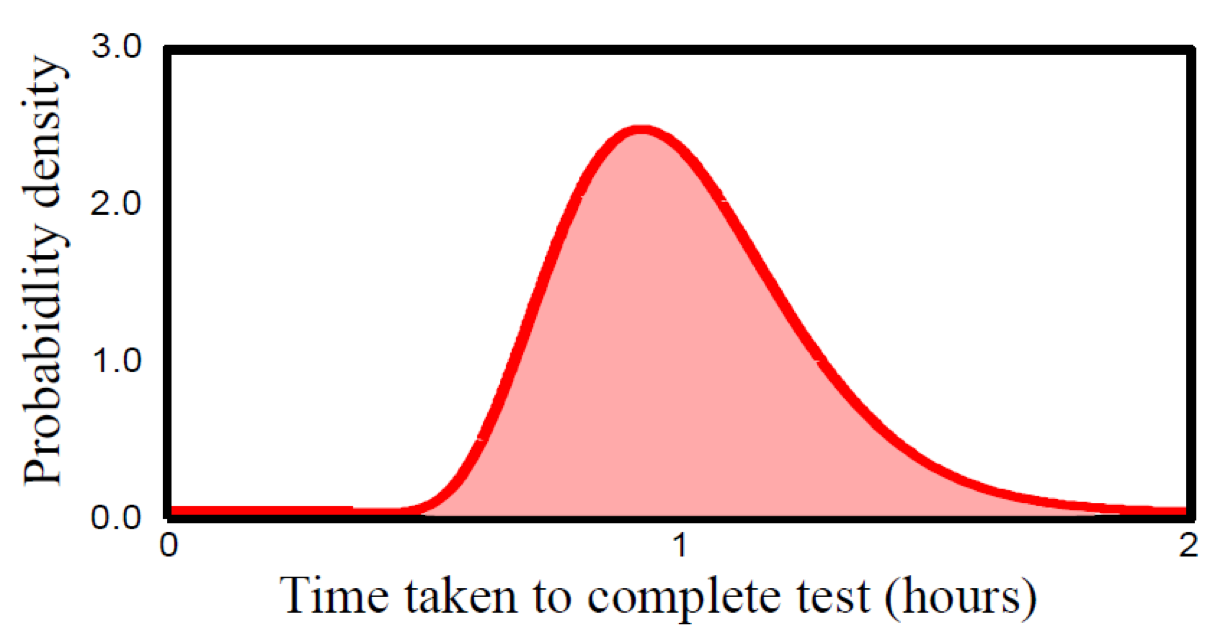
연속 변수 \(x\)에 대한 분포 \(p(x)\)를 Entropy 정의에 포함시켜 보려고 합니다. 먼저 구간 \(x\)를 너비 \(\Delta\)의 여러 구간으로 나눕니다. 그러면 \(p(x)\)가 연속적이라는 가정 하에, ‘평균값의 정리’에 따라서 다음을 만족시키는 \(x_i\)값이 존재합니다.

\[\int_{i\Delta}^{(i+1)\Delta} p(x) dx = p(x_i) \Delta\]

이제 모든 \(x\) 값에 대해서 해당 값이 \(i\) 번째 칸에 속할 경우에 \(x_i\)를 할당하도록 합니다. 이 경우 \(x_i\)를 관측하게 될 확률은 \(p(x_i)\Delta\)가 됩니다. 이산 확률 변수의 Entropy를 구하는 것과 유사하게 계산을 하게 되면 아래의 수식을 얻을 수 있습니다.

\[H_{\Delta}=-\sum_i p(x_i)\Delta \ln (p(x_i)\Delta) = - \sum_i p(x_i) \Delta \ln p(x_i) - \ln \Delta\]

이제 오른쪽 항의 \(-\ln \Delta\) 를 제외하고 \(\Delta \rightarrow 0\) 를 사용하게 되면

\[\lim_{\Delta} \{ -\sum_i p(x_i)\Delta \ln (p(x_i)\Delta) \} = - \int p(x) \ln p(x) dx\]

연속 확률 변수의 Entropy를 구할 수 있게 됩니다.

여기서 오른쪽 변을 미분 Entropy (differential entropy)라고 합니다. 우리가 아까 \(\ln \Delta\)를 제외하고 계산했기 때문에 이를 포함해서 생각한다면 \(\lim_{\Delta} \ln \Delta\) 만큼이 이산 Entropy와 미분 Entropy간의 차이라고 할 수 있음을 알 수 있습니다.

한 편, \(\lim_{\Delta} \ln \Delta\) 는 무한대로 발산하는 값이기 때문에, 연속 변수의 Entropy를 정확하게 지정하기 위해서는 아주 많은 수의 비트가 필요하다고 합니다. 어쨌든 여러 연속 변수들에 대해 정의된 밀도의 경우 (x를 벡터라고 생각) 최종적으로 미분 Entropy는 아래와 같습니다.

\[H[x] = - \int p(x) \ln p(x) dx\]

이산 확률 변수 때와 마찬가지로 증명하지는 않겠지만 \(p(x)\)를 가우시안 분포로 고정하고 분산을 변화시켜보면 분산이 클 때, 즉 분포가 더 넓게 퍼져서 균일분포에 가까워질수록 Entropy가 커짐을 알 수 있습니다. (균일할수록 Entropy가 커지며 뾰족해질수록 작아짐)

Entropy for Joint Distribution

이번에는 \(x\)값과 \(y\)값을 함께 뽑는 결합 분포 \(p(x,y)\)에 대해 고려해 본다고 생각해봅시다.

fig6

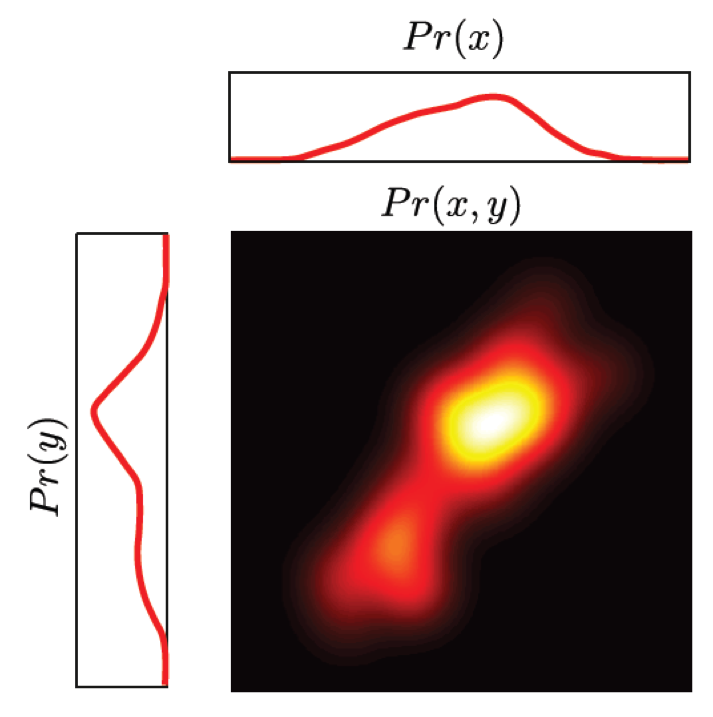
만약 x의 값이 이미 알려져 있다면, 그에 해당하는 y값을 알기 위해 필요한 정보는 \(-\ln p(y \mid x)\)로 주어집니다.

fig7

따라서 y를 특정하기 위해 추가로 필요한 정보의 평균값은 다음과 같습니다.

\[H[y|x] = - \int \int p(y,x) \ln p(y|x) dy dx\]

이를 x에 대한 y의 조건부 Entropy(conditional entropy) 라고 합니다.

그 다음 확률의 곱 법칙을 이용하면 우리는 원하는 결합 분포의 Entropy를 알 수 있습니다.

\[H[x,y] = H[y|x] + H[x]\]

Relative Entropy and Mutual Information

이번에는 정보 이론의 중요 개념들을 ML에 어떻게 적용시킬 수 있는지를 살펴봅시다. 어떤 알려지지 않은 분포 \(p(x)\)에 대해 먼저 생각해봅시다. 대부분의 ML algorithm의 목적은 실제 데이터 분포 \(p(x)\)를 찾는 것 입니다.

fig8

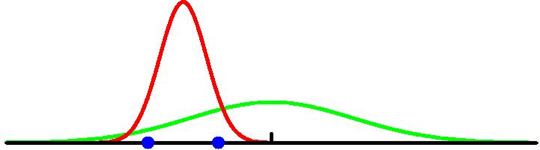
(위의 그림에서 녹색 분포, 즉 데이터가 실제로 샘플링된 리얼 분포)

여차저차 학습 데이터를 모델링해 분포 q(x)를 구할 수 있었다고 생각해봅시다. 만약 우리가 \(q(x)\)를 사용해 x의 값을 누군가에게 전달하기 위해 코드를 만든다고 하면, 우리는 \(p(x)\) 가 아닌 \(q(x)\)를 사용했기 때문에 추가적인 정보를 더 포함해서 수신자에게 전달해야 합니다. 이때 추가로 필요한 정보의 양은 다음과 같이 주어집니다.

\[KL(p \parallel q) = - \int p(x) \ln q(x) dx - (-\int p(x) \ln p(x) dx)\] \[KL(p \parallel q) = - \int p(x) (\ln q(x) - \ln p(x)) dx\] \[KL(p \parallel q) = - \int p(x) \ln \frac{q(x)}{p(x)} dx\]

위의 \(KL(p \parallel q)\)를 두 분포간의 상대 Entropy (relative entropy) 혹은 쿨백 라이블러 발산 (Kullback-Leibler divergence, KL divergence, KLD)이라고 합니다. (여기서 Divergence는 우리가 흔히 알고 있는 수학적 의미의 발산을 의미하는게 아니라 ‘차이, 상이’ 정도로 해석되는게 맞는 것 같습니다.)

아래의 그림은 서로 다른 가우시안 분포의 \(D_{KL}\)을 나타낸 그림입니다. 전체 면적이 그 값이 될 것입니다.

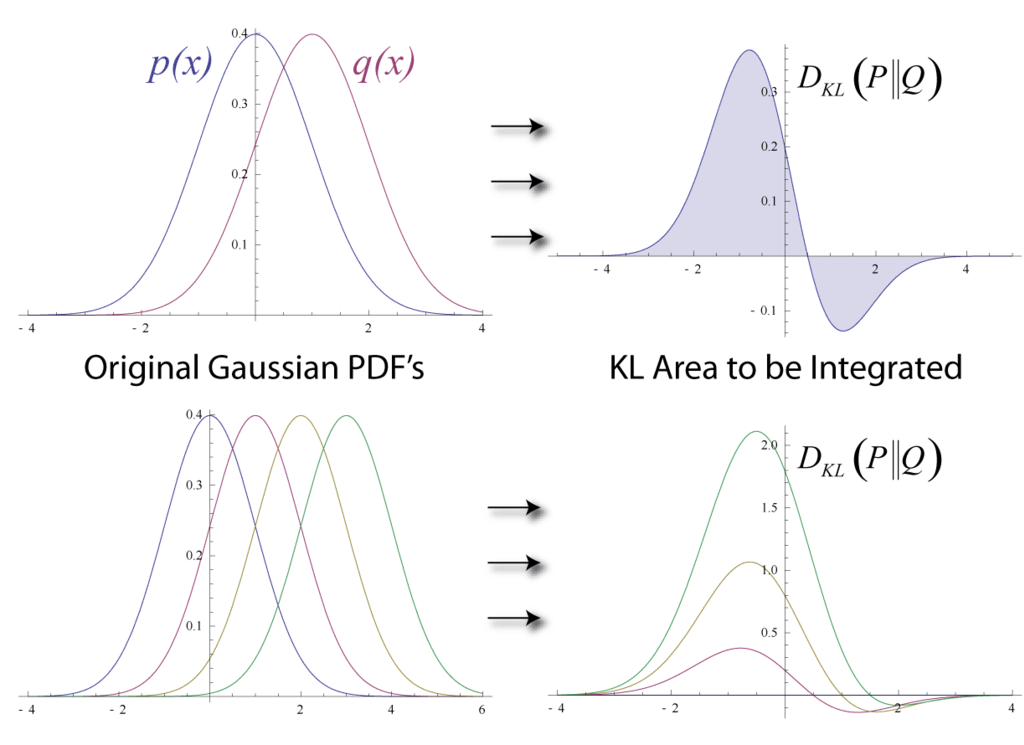fig9 Fig. KLD. Source From link

어떤 데이터 \(x\)(벡터) 에 대해 이 연속 변수들에 대해 정의된 밀도의 경우, 미분 Entropy가 아래와 같이 주어졌던걸 생각해보면 두 분포(실제 분포, 실제가 아닌 분포)를 이용해서 데이터를 전달하기 위해 필요한 Information의 차가 위 수식처럼 주어지는지 알 수 있을겁니다.

\[cf) H[x] = - \int p(x) \ln p(x) dx\]

이 quantity는 대칭적이지 않다는 특징이 있습니다.

\[KL(p \parallel q) \not\equiv KL(q \parallel p)\]

또한 \(KL(p \parallel q)=0\) 일 때는 \(KL(p \parallel q) \geqslant 0\) 에서 \(p(x) = q(x)\) 인 것과 동치입니다. (자세한 내용은 PRML 이나 wiki 참조)

Example

KLD 값을 한 번 계산해 봅시다. 어떤 두 이산 분포 \(p,q\)의 KLD는 다음과 같습니다.

\[D_{KL}(p \parallel q) = \sum_{x \in \chi}p(x) \ln ( \frac{q(x)}{p(x)} )\]

다음과 같은 두 분포가 있다고 생각해보도록 하겠습니다.

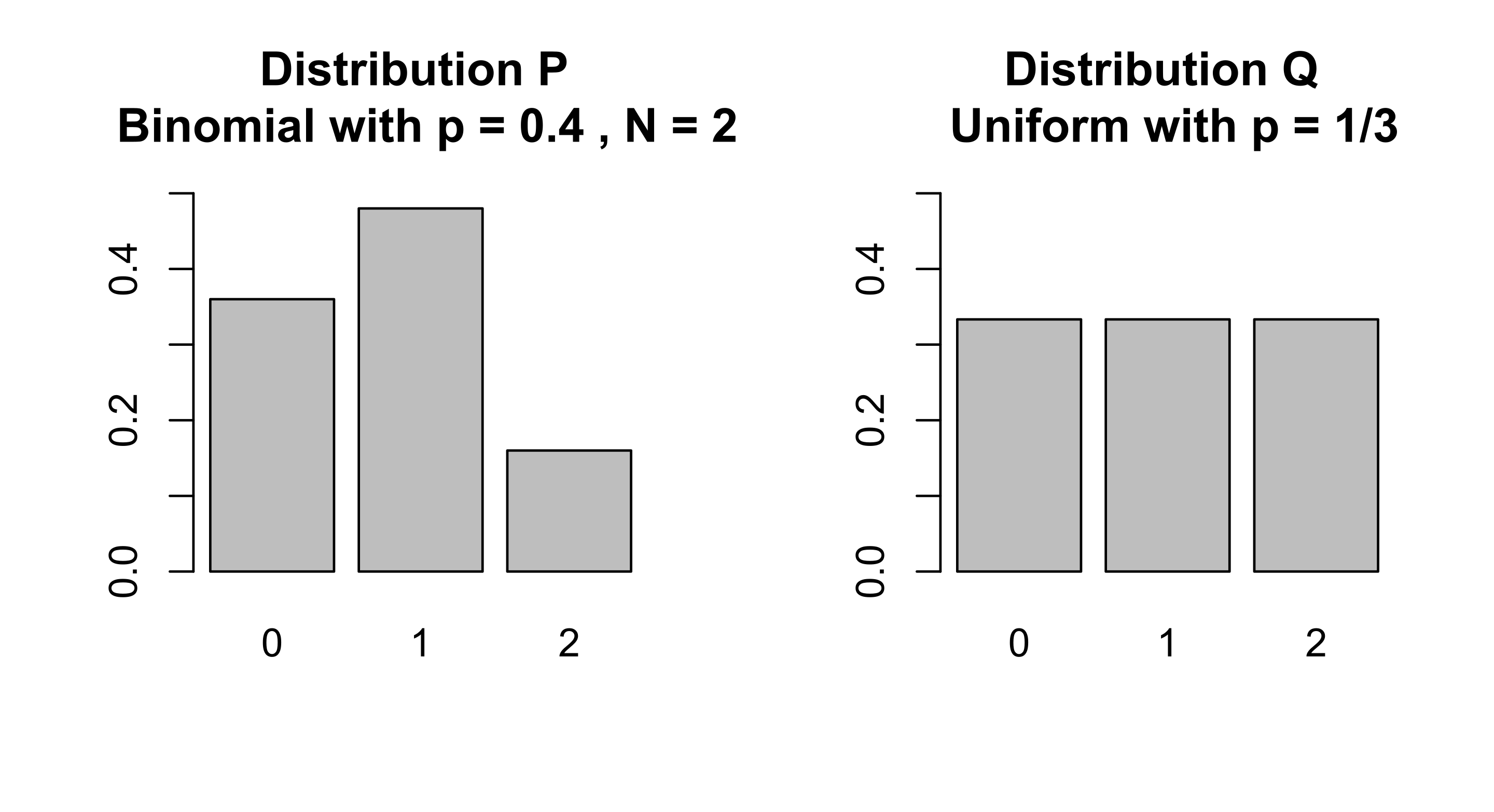
fig10

x 0 1 2
Distribution p(x) 9/25 12/25 4/25
Distribution q(x) 1/3 1/3 1/3

두 분포가 얼마나 다른지를 measure하는 KLD를 계산해 보면 다음과 같은 값을 얻을 수 있습니다.

\(D_{KL}(p \parallel q) = \sum_{x \in \chi}p(x) \ln ( \frac{q(x)}{p(x)} )\) \(= \frac{9}{25} \ln (\frac{\frac{9}{25}}{\frac{1}{3}}) + \frac{12}{25} \ln (\frac{\frac{12}{25}}{\frac{1}{3}}) + \frac{4}{25} \ln (\frac{\frac{4}{25}}{\frac{1}{3}})\) \(= \frac{1}{25} (32\ln (2) + 55\ln (3) - 50\ln (5)) \approx 0.0852996\)

\(D_{KL}(q \parallel p) = \sum_{x \in \chi}q(x) \ln ( \frac{p(x)}{q(x)} )\) \(= \frac{1}{3} \ln (\frac{\frac{1}{3}}{\frac{9}{25}}) + \frac{1}{3} \ln (\frac{\frac{1}{3}}{\frac{12}{25}}) + \frac{1}{3} \ln (\frac{\frac{1}{3}}{\frac{4}{25}})\) \(= \frac{1}{3} (-4\ln (2) - 6\ln (3) + 6\ln (5)) \approx 0.097455\)

Connection to Machine Learning

KLD vs Cross Entropy Loss in ML

이번에는 KLD가 ML과 직접적으로 어떤 관련이 있는지 알아봅시다. KLD를 사용해서 서로 다른 두 분포 p(x)와 q(x)가 얼마나 다른 분포인지를 measure 할 수 있었습니다. 이제 우리가 해볼 것은 KLD를 사용해 우리가 가지고 있는 data들이 sampling 됐을 original data distribution 과 ML model 이 학습한 distribution 간의 차이를 measure해 보는 겁니다.

이는 ML이 probability distribution을 추정하는 것 (실제로는 알 수 없으나 가지고잇는 data 로 부터 실제 distribution 을 모델링하는 문제)이 전송하는 data를 압축하는 데는 밀접한 연관이 있기 때문입니다. 왜냐하면 실제 분포에 대해서 알고 있을 때 가장 효율적인 압축이 가능해서인데, 실제 분포와 다른 분포를 바탕으로 modeling이 이루어졌을 경우에는 압축 자체가 덜 효율적이게 되고, 따라서 두 분포 사이의 mismatch 만큼, 즉 KLD 만큼의 정보가 추가적으로 전송되어야 하는 것입니다.

예를 들어 현재 우리가 가지고 있는 dataset은 \(p(x)\)로부터 한 100개정도 sampling 된 것들입니다. 우리는 보통 이 분포가 regression 이면 gaussian, classification 이면 categorical distribution 일거라고 생각하고 MLE 등으로 문제를 풀죠.

이번에는 KLD를 사용해서 가장 likely 한 parameter 를 찾아봅시다, 즉 두 분포 \(p(x)\)와 \(q(x \mid \theta)\) 사이의 KLD를 최소화 하도록 하는 \(\theta\)를 찾는 겁니다.

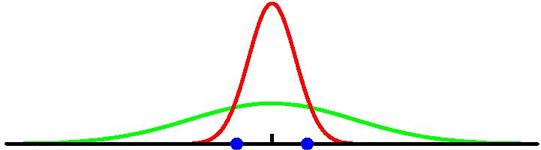fig11 Fig. 실제 데이터 분포 (녹), 모델이 찾은 분포 (적)

하지만 우리는 실제 데이터 분포 \(p(x)\)는 아예 모르는 상태이고 (그러니까 어디서 샘플링했는지는 모르는 겁니다), 학습 데이터들만 가지고 있습니다. (\(x_n, \space n=1,2,...,n\)) 그렇기 때문에 우리는 KL Term 을 근사시켜야 합니다.

\[\begin{aligned} &KL(p \parallel q) = - \int p(x) \ln q(x) dx - (-\int p(x) \ln p(x) dx) \\ & \simeq - \frac{1}{N} \sum_{n=1}^{N} \{ -\ln q(x_n \mid \theta) + \ln p(x_n) \} \\ & \simeq - H_p[X] + H_{p,q}[X]\\ \end{aligned}\]

실제로 적분을 할 수는 없겠고 sampling 된 data point들의 합으로 \(p(x)\)에 대한 기대값을 구한 것이죠. 여기서 우변의 두 번째 항은 추정하고자 하는 \(\theta\)와 독립이니 생각하지 않아도 되고, 첫 번째 항인 \(q(x \mid \theta)\) 하에서 \(\theta\) 에 대한 것만 남기게 되면 우리는 이것이 음의 로그 가능도 함수 (Negative Log Likelihood, NLL)을 최소화 하는 것에 같은 것임을 알 수 있습니다.

\[KL(p \parallel q) \simeq - \frac{1}{N} \sum_{n=1}^{N} \{ -\ln q(x_n \mid \theta) \}\]

즉 KLD를 최소화 하는 것이 Maximum Likelihood Estimation을 하는 것과 사실 같은거죠.

from Cross Entropy (CE) to KLD

이번엔 반대로 해보려고 합니다. 우리가 분류 문제를 풀기 위해 categorical distribution 을 정의함으로써 Cross Entropy (CE) Loss 를 최적화 한다고 생각해보겠습니다. 정보 이론에서 Cross Entropy 는 다음과 같이 쓸 수 있습니다.

\[Hp,q[X] = -\sum_{n=1}^{N} p(x_n) \ln q(x_n)\]

Entropy 는 Entropy 인데 random variable \(x_n\) 들이 sampling 된 진짜 분포 \(p(x_n)\) 이 아니라 현재 model parameter 가 만든 분포 \(q(x_n)\) 를 사용한거죠. 직관적으로 q랑 p가 많이다르다면 이 값은 클 수 밖에 없습니다. 왜냐면 실제 데이터셋에서 variable 이 많이 샘플링된 구간의 확률이 높아야되는데, q 분포가 이를 잘못 모델링했다면 여기에 작은 확률값들이 할당될 것이고 따라서 negative log 을 취하면 엄청 커지는 것이죠.

이진 분류 문제를 예시로 들어 이 Cross Entropy 를 풀어보면 이는 아래와 같이 전개할 수 있습니다.

\[\begin{aligned} & Hp,q[Y|X] = -\sum_{n=1}^{N} \sum_{y \in \{0,1\}} p(y_i | x_i) \ln q(y_i | x_i) \\ & = -\sum_{n=1}^{N} [ p(y_i=1 | x_i) \ln q(y_i =1 | x_i) + p(y_i=0 | x_i) \ln q(y_i =0 | x_i) ] \\ & = -\sum_{n=1}^{N} [ p(y_i=1 | x_i) \ln q(y_i =1 | x_i) + (1-p(y_i=1 | x_i)) \ln (1-q(y_i =1 | x_i)) ] \\ & = -\sum_{n=1}^{N} [ p(y_i) \ln q(y_i) + (1-p(y_i)) \ln (1-q(y_i)) ] \\ & = -\sum_{n=1}^{N} [ p(y_i) \ln q(y_i) + (1-p(y_i)) \ln (1-q(y_i)) ] \\ & = D_{KL}(p \parallel q)) + H_p[X] \\ \end{aligned}\]

마찬가지로 \(H_p[X]\) 는 parameter 와 독립인 term 이기 때문에 이를 제외하면 \(H_{p,q}[Y \vert X] = D_{KL}(p \parallel q)\) 가 됩니다.

Additional) Forward-KL vs Reverse-KL

Traget distribution p가 mode가 여러개인 multi-modal gaussian distribution이고 이를 근사하려는 q는 mode가 1개인 unimodal이라고 생각을 해 봅시다. 이 때 우리가 학습하는데 쓰는 Objective를 forward kl인 KL(p,q)를 쓸 경우와 reverse kl KL(q,p)를 쓰는 경우가 각각 학습하는 distribution의 모양이 다르다고 알려져 있습니다. 일반적으로 forward kl인 경우 p 분포의 중간 지점을 찾아가는 mean seeking을 하게되고, reverse kl인 KL(q,p)는 어떤 하나의 mode를 찾아가는 mode seeking을 하게 된다고 알려져 있습니다.

그래서 지금 post의 범위를 벗어나긴 하나 deep learning의 경량화 기법중 large model의 distribution 을 small model이 전이 학습하는 Knowledge Distillation (KD)에서 보통 KL divergence를 쓰는데 이 때 forward, reverse 중 어떤 걸 쓰느냐에 따라 성능이 달라지기도 한다고 합니다.

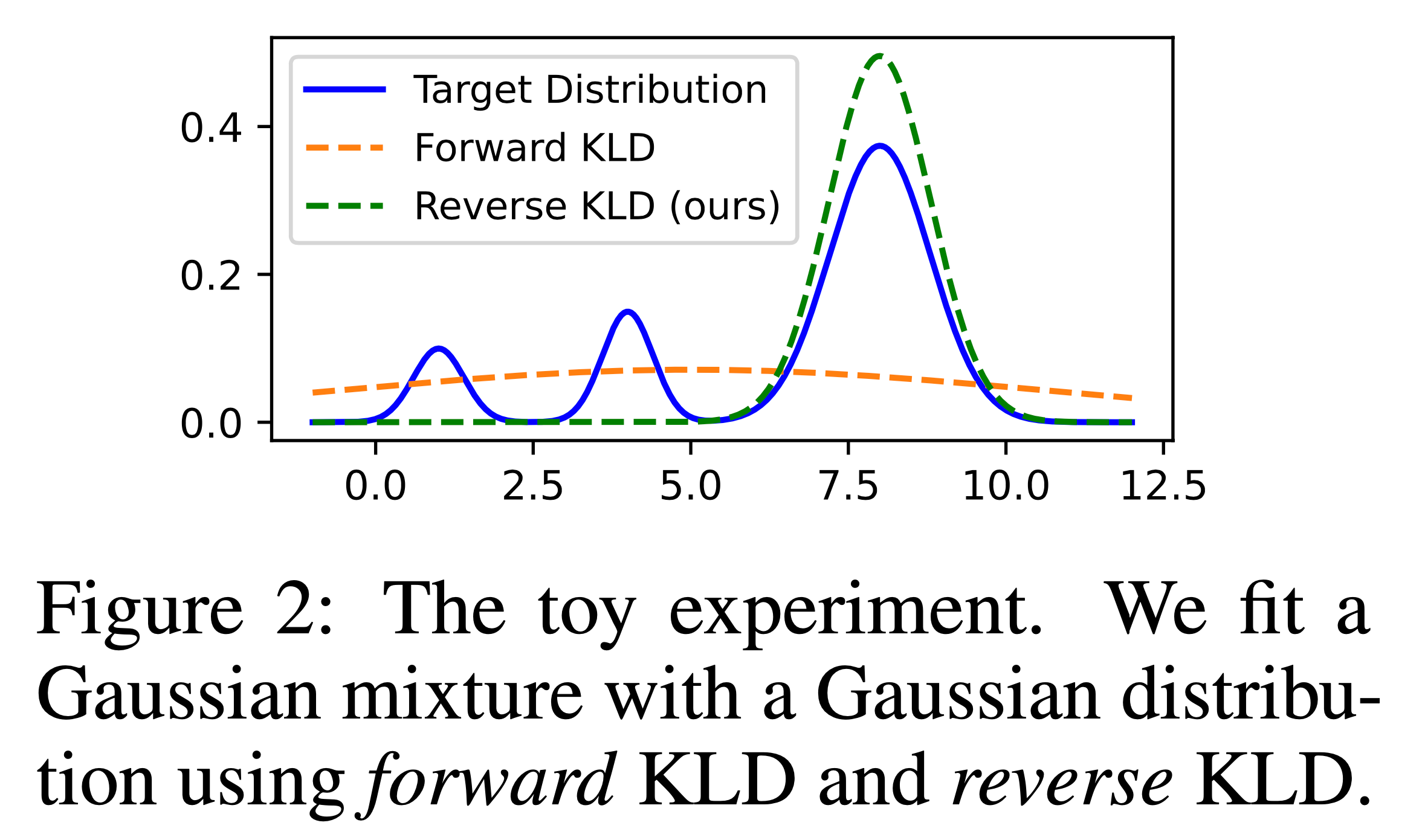kd_llm_reverse_kl_fig Fig. Source from here

Bayesian Inference using Variational Approximation

Linear Regression 을 다루면서 데이터를 잘 나타내는 Parameter 를 추정하는 방법에는 MLE, MAP 말고도 Bayesian Inference 라는 것이 있죠. Bayesian Linear Regression의 경우를 다시 살펴보면 아래와 같은 notation 을 따를 때

input state, 데이터 입력값 : \(x\)
world state, x에 대응하는 값 : \(w\)
parameter, 우리가 알고싶은, 추정하려는 값 : \(\phi,\sigma^2\)

test sample \(x^{\ast}\) 의 결과값 \(w^{\ast}\) 는 아래 처럼 전체 parameter space 에 대해서 inference 를 다 해본 것이라고 할 수 있습니다.

\[\begin{aligned} & Pr(w^{\ast}|x^{\ast},X,W) = \int Pr(w^{\ast}|x^{\ast},\phi) Pr(\phi|X,W) d\phi \\ \end{aligned}\]

이 때 \(Pr(\phi \vert X,W)\) 를 사후 분포 (posterior)라고 하며 이게 어떻게 생겼는지는 학습을 통해서 구하면 됩니다.

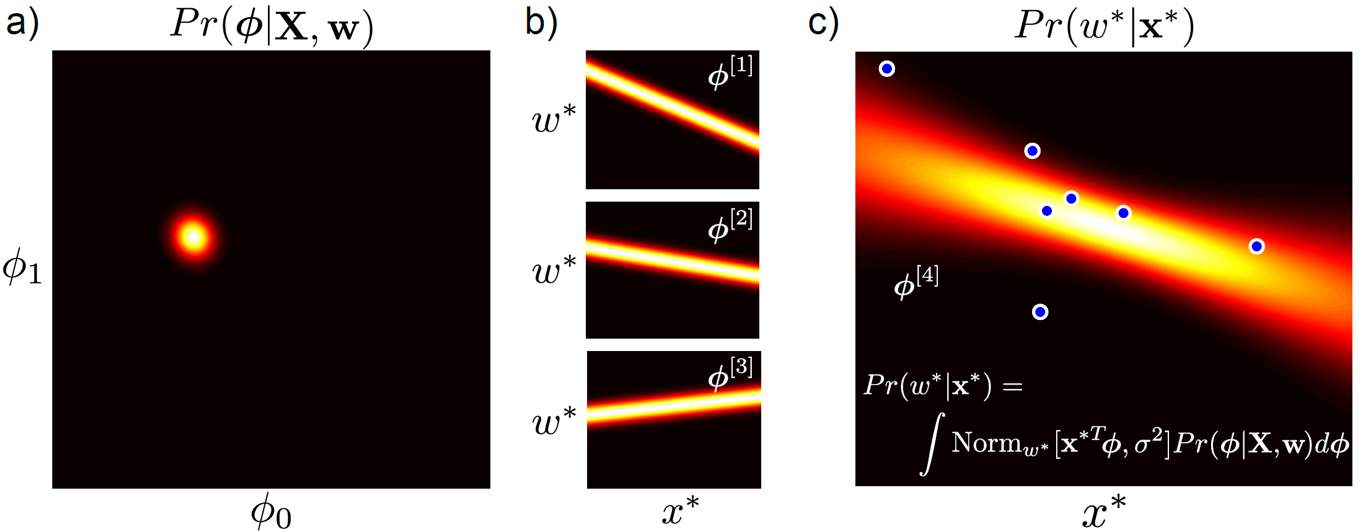fig12 Fig. Bayesian Linear Regression

우리가 위와같이 매 test data 의 결과값을 구하려고 할 때마다 Bayesian Inference를 하면 좋겠지만 Logistic Regression 이나 Neural Network (NN) 등을 쓰는 경우에는 계산을 하기가 쉽지 않습니다. 이는 다양한 이유가 있을 수 있는데 주로 posterior 가 더이상 가우시안 분포가 아니기 때문에 parameter \(\phi\) 에 대해 정확한 적분을 할 수 없기 때문입니다. (data나 model이 훨씬 고차원이 되기 때문에 사실상 불가능, + 분포들이 conjugate 도 아님)

바로 아래의 식에서 분모의 적분 term (evidence) 이 계산이 어렵기 때문인데

\[posterior : p(\phi \mid X,W) = \frac{p(W \mid X, \phi)p(\phi)}{p(W \mid X)}\] \[p(W \mid X) = \int p(W|X,\phi)p(\phi) d\phi\]

이런 경우 실제 \(posterior = p(\phi \mid X, W)\) 를 쓰는 것이 아니라 비슷한 모양이지만 훨씬 간단한 근사 분포 (approximate distribution) \(q(\phi \vert \theta)\) 를 사용하는 방법이 있습니다.

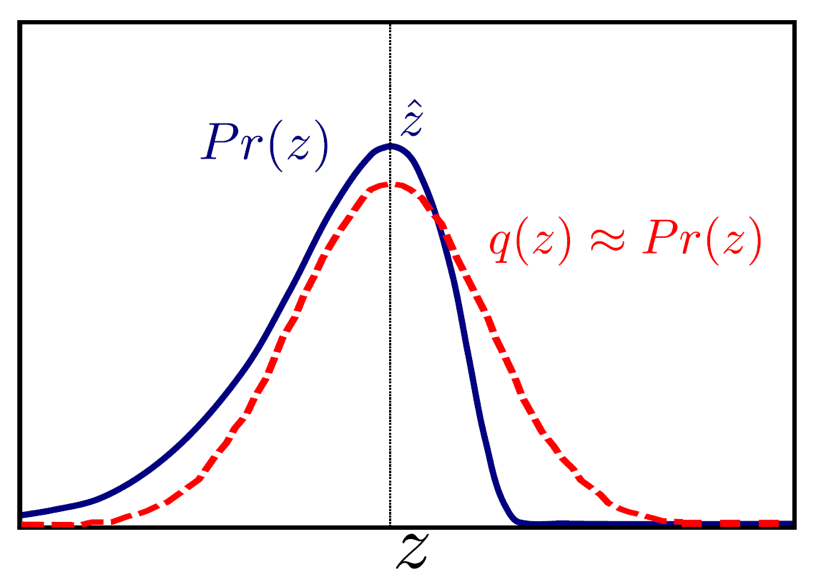fig13 Fig. 복잡한 P 보다 훨씬 간단한 Q를 사용하자.

진짜 posterior 대신 q를 써서 추론을 하는거죠.

\[p(w^{\ast}|x^{\ast},X,W) = \int p(w^{\ast}|x^{\ast},\phi) q^{\ast}(\phi \vert \theta) d\phi\]

하지만 우리가 아무 관련없는 \(q(\phi \vert \theta)(w)\)를 갖다 쓸 수는 없으니, 학습을 하는 과정에서 최대한 \(p\)와 유사한 \(q\)를 쓰고싶겠죠? 위와같은 경우에 p와 비슷하지만 더 쉬운 분포인 gaussian, q 를 쓴다고 할 때 p와 최대한 비슷할 mean 값만 적당히 잘 구해보는거죠. 이런 경우에 KLD를 쓰는겁니다. 즉 우리가 원하는 것은

\[q^{\ast}(\phi \vert \theta) = \arg \min_{\color{red}{\theta}} KL (q (\phi \vert \color{red}{\theta}) \parallel p(\phi \vert X,W))\]

입니다.

수식을 전개해보면 아래와 같이 정리되는데,

\[\begin{aligned} & KL(q(\phi \vert \theta) \parallel p(\phi \mid X,W) ) = \int q(\phi \vert \theta) \log ( \frac{ q(\phi \vert \theta) }{ p(\phi \mid X,W) } ) d\phi \\ & = \int _{\theta}(\phi) \log (q(\phi \vert \theta)) d\phi - \int _{\theta}(\phi) \log (p(\phi \mid X,W)) d\phi \\ & = \mathbb{E}_{q(\phi \vert \theta)} [ \log (q(\phi \vert \theta))] - \mathbb{E}_{q(\phi \vert \theta)} [ \log (p(\phi \mid X,W))] \\ \end{aligned}\]

여기서 실제 posterior, \(p(\phi \vert X, W)\) 는 Bayes’ Rule에 의해 다음과 같이 정리되므로

\[p(\phi \vert X, W) = \frac{ p( W \vert X, \phi) \cdot p(\phi)}{ p(W \vert X)}\]

다시 KL 식은

\[\begin{aligned} & KL(q(\phi \vert \theta) \parallel p(\phi \mid X,W) ) = \mathbb{E}_{q(\phi \vert \theta)} [ \log (q(\phi \vert \theta))] - \mathbb{E}_{q(\phi \vert \theta)} [ \log (p(\phi \mid X,W))] \\ & = \mathbb{E}_{q(\phi \vert \theta)} [ \log (q(\phi \vert \theta))] - \mathbb{E}_{q(\phi \vert \theta)} [ \color{red}{ \log (p(W \vert X, \phi) + \log ( p(\phi) ) - \log (P(W \vert X) )} ] \\ \end{aligned}\]

이 됩니다. 여기서 prior 는 고정이라고 치고, \(\log (P(W \vert X))\) 는 parameter 가 없으니 무시하면

\[\begin{aligned} & KL(q(\phi \vert \theta) \parallel p(\phi \mid X,W) ) = - \mathbb{E}_{q(\phi \vert \theta)} [ \log (p(W \vert X, \phi) ] + \mathbb{E}_{q(\phi \vert \theta)} [ \log (q(\phi \vert \theta))] \\ \end{aligned}\]

로 정리가 됩니다.

직관적으로 위의 수식에서 좌변의 첫번째 항이 q 분포로부터의 모든 parameter 에 대해서의 negative log likelihood 를 계산하는 것아고, 두번째 항은 q의 음의 entropy 를 계산하는 것이 됩니다.

\[\begin{aligned} & KL(q(\phi \vert \theta) \parallel p(\phi \mid X,W) ) = - \mathbb{E}_{q(\phi \vert \theta)} [ \log (p(W \vert X, \phi) ] - H_q[\phi] \\ \end{aligned}\]

우리는 두 분포간의 KL을 최소화 하고 싶으니 이 수식 자체를 작아지게하면 어떤일이 일어나나요? negative likelihood 가 작아지니까 maximum likelihood 가 되는것과 동시에 q 분포의 entropy 가 커지게 됩니다 (음의 entropy 가 작아지게 되므로).

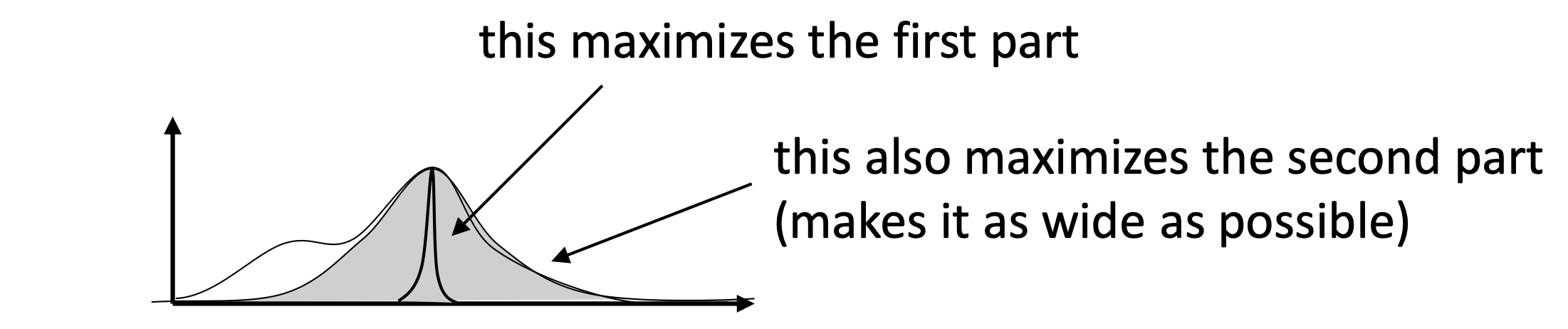
cs285_lec18_entropy

이런 방식을 변분 근사 (Variational Approximation), 혹은 변분 추론 (Variational Inference) 한다고 하는데 이렇게 불리는 이유는 변분법 (Calculus of variations) 에서 기인했기 때문이라고 합니다. (유사하게 posterior 를 근사하기 위한 방법으로 Laplace Approximation 도 있음)

Mutual Information

두 변수 \(x\), \(y\)의 결합 분포 \(p(x,y)\)에 대해 생각해봅시다. 만약 두 변수가 독립이라면 \(p(x,y)=p(x)p(y)\)가 될 겁니다. 이 둘의 KLD 값을 통해 우리는 변수들이 얼마나 독립적인지도 판단할 수 있는데

\[\begin{aligned} & I[x,y] \equiv KL(p(x,y) \parallel p(x)p(y) ) \\ & = -\int \int (p(x,y) \ln ( \frac{p(x)p(y)}{p(x,y)} ) dx dy \\ \end{aligned}\]

이 식을 바로 상호 Information (mutual information) 이라고 합니다. 이 상호 Information은 x,y가 서로 독립일때만 0이 됩니다.

더 나아가 확률의 합과 곱 법칙을 적용하면 상호 Information은 아래와 같아집니다.

\[I[x,y] = H[x] - H[x|y] = H[y] - H[y|x]\]

이는 y에 대해 알고 있을 때 x값에 대한 불확실성 (혹은 그 반대)를 표현한 것이 곧 상호Information이라는 뜻입니다. 베이지안 관점에서는 \(p(x)\)를 x에 대한 사전 분포로, \(p(x \mid y)\)를 새로운 데이터 y를 관찰한 후의 사후 분포로 볼 수 있기 때문에, 상호Information은 새 관찰값 y의 결과로 줄어드는 x에 대한 불확실성을 의미하기도 합니다.

References