MLE & Bayesian Series (2/3) - Maximum A Posteriori (MAP)
20 Jan 2021- MLE & Bayesian Series (1/3) - Maximum Likelihood Estimation (MLE)
- MLE & Bayesian Series (2/3) - Maximum A Posteriori (MAP)
- MLE & Bayesian Series (3/3) - Bayesian Approach
< 목차 >
What is Maximum A Posteriori (MAP) ?
지난 글에서 Maximum Likelihood Estimation (MLE)에 대해서 간단하게 살펴봤다.
이번 post에서는 Maximum A Posteriori (MAP)에 대해서 이야기해보도록 하겠다.
- likelihood : \(p(x\mid\theta)\)
- posterior : \(\text{posterior} \propto \text{likelihood} \times \text{prior} = p(\theta \mid x) \propto p(x \mid \theta)p(\theta)\)
MAP는 사후 확률 분포 (Posterior distribution)이라는 것을 정의하고,
MLE에서 했던 것 처럼 그 distribution 에서 가장 posterior값이 큰 parameter를 추정하는 방법이다.
Posterior 는 likelihood distribution과 사전 분포 (prior distribution) 의 곱으로 표현되며,
사전 분포 정보를 추가해준다는 것은 음 mean, variance는 각각 0~1 사이일 거야라는 선입견, prior를 model에게 알려주고 MLE를 하겠다 정도로 해석할 수 있다.
Maximum A Posteriori (MAP)
지난 글에서 MLE의 문제점에 대해 이야기하면서 MAP를 잠깐 언급했었다.
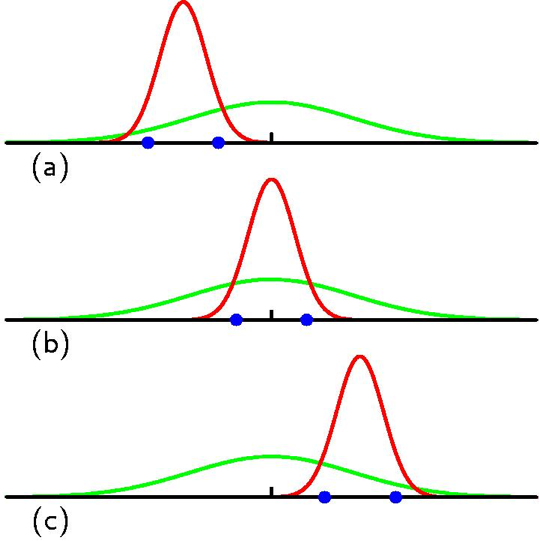Fig. MLE의 문제점은 ta 수가 적으면 심각하 over-fitting 한다는 것이다.
MAP는 likelihood에 prior를 곱해 posterior distribution을 구하고 이것을 maximize하는 parameter를 찾는 것이다.
MAP를 쓸 경우 data가 적을 때는 prior의 영향력이 커서 추정 값이너무 편향되지게 잡아주고, data가많을 경에는 likelihood의 영향력이 커져 결국 data로부터 얻은 정보를대한 활용하게 된다.
한 편, MAP는 바로 다음 post에서 언급할 베이지안 방법론 (Bayesian Approach)과 MAP는 같은 철학을 공유하고 있다. 하지만 Bayesian은 posterior disribution의 가능한 모든 parameter를 고려하여 input data에 대한 확률값을 return한다는 점이 MAP와 다르다. MAP는 가장 확률값이 클 딱 한 parameter만 얻은 뒤에 이 paramter를 통해서 input data의 확률을 return 한다. 그래서 MAP나 MLE같은 방법론들은 점 추정 (Point Estimation)을 한다고 표현하기도 한다.
MAP와 MLE를 통해 data을 가장 잘 표현하는 distribution의 parameter를 찾는데 그 distribution이 Gaussian distriubtion이라고 생각해 보자. 아래의 figure는 오른쪽 부터 왼쪽으로 posterior, prior 그리고 likelihood 를 나타낸다.
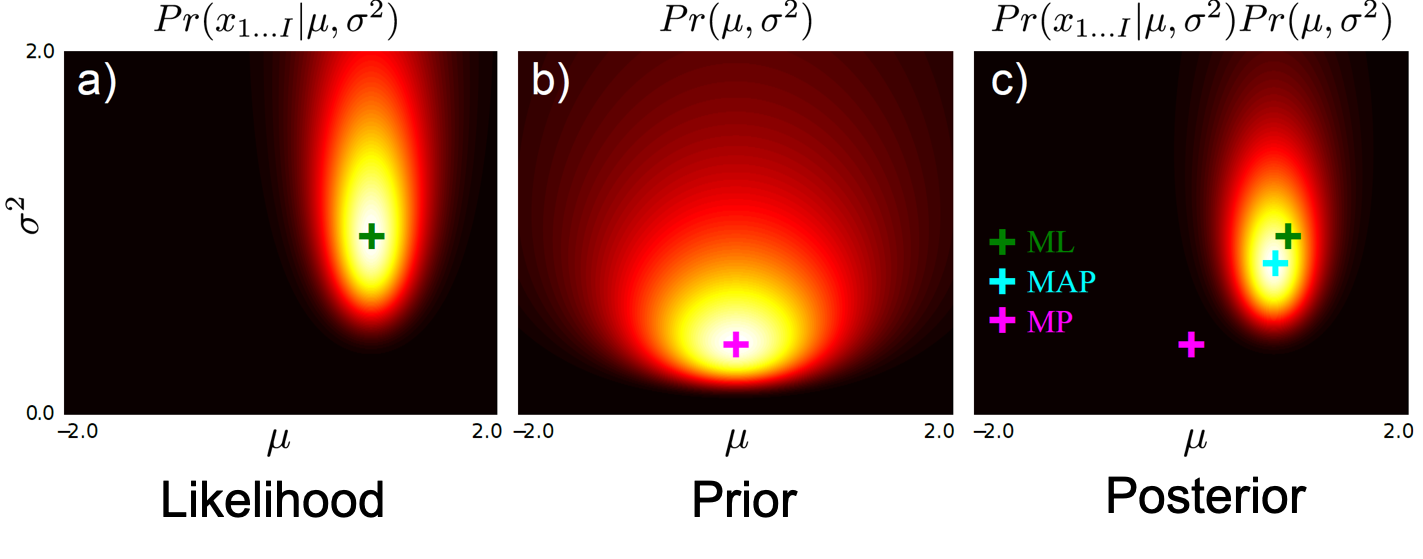
한눈에 봐도 likelihood 분포에서 peak를 찍는것과 posterior에서 peak를 찍는 것은 달라 보인다. 이는 앞서 설명드린 것 처럼 data수가 적을수록 확연히 달라진다.
Prior Distribution and Conjugate Family
앞서 간략하게 말했지만 prior는 말그대로 사전 지식 (선입견)으로, ‘실험은 안해봤지만 그냥 일반적으로 보니까 mean, variance가 값이 1일 확률이 가장 높던데?’ 같은 정보를 준다고 했었다. 그리고 prior는 likelihood와 곱해져 posterior를 표현하는데 쓰인다고 했다. 그런데 서로 다른 두 확률 분포를 막무가내로 곱하면 결과물이 엉망이 될 수 있고, 우리가 MLE때 처럼 log를 씌우고 미분하는 데 지장을 줄 수 있다.
\[\text{posterior} \propto \text{likelihood} \times \text{prior} : p(\theta \mid x) \propto p(x \mid \theta)p(\theta)\]그러므로 prior는 likelihood의 conjugate distribution으로 정하는 것이 좋다. 예를 들어 likelihood가 Gaussian distribution (Normal distribution) 따른다면 prior로는 conjugate distribution인 Normal Inverse Gamma Distribution을 따르는 것이 좋다. 왜냐면 아래의 수식처럼 둘을 곱할건데 Conjugate Family인 분포로 모델링을 하게 되면 수학적으로 굉장히 쉽게 계산이 되기 때문이다.
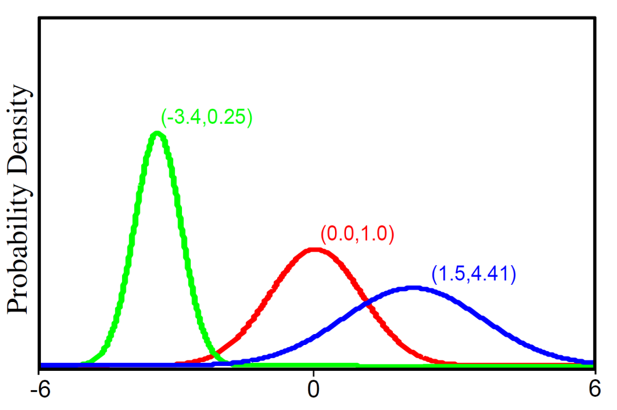
Fig. Univarite Gaussia (Normal distribution) distribution 수식과 그림.
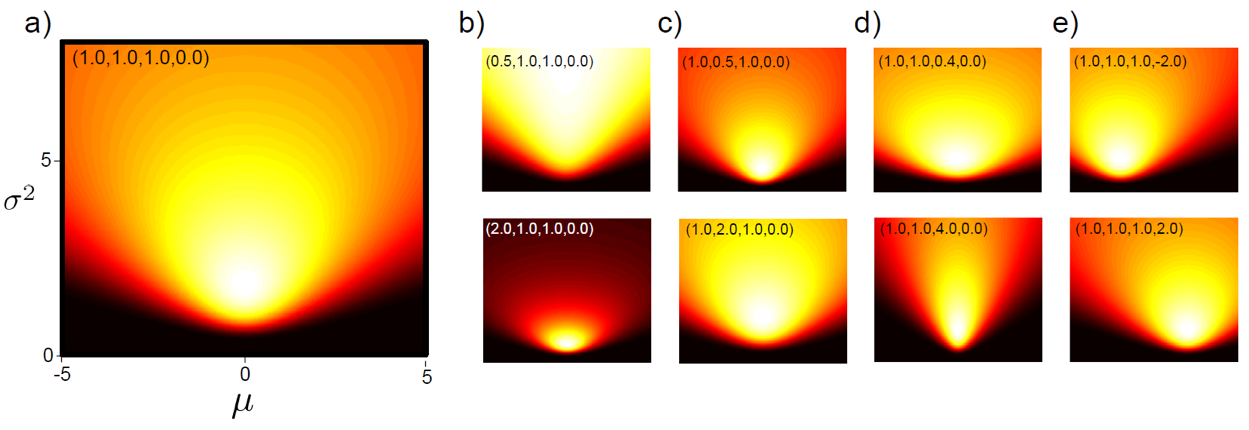
Fig. Normal Inverse Gamma Distribution의 수식과 그림.
위의 두 distribution는 Conjugate Distributions 이다.
MAP in formula
이제 MLE처럼 MAP를 수식으로 표현해 보도록 해보자. 우리가 하고 싶은것은 likelihood, prior를 어떤 distribution으로 할 지 정하고 이 둘을 곱해서 posterior distribution을 표현한 뒤에 해당 분포 하에서 posterior가 maximize 되는 parameter를 찾는 것이다.
\[\hat{\Theta}=\arg \max_\theta[Pr(\theta \mid x_{1...I})]\]Posterior는 likelihood와 prior의 곱과 비례한다고 했는데, 사실 이는 Bayes’ Rule에서 기인한 것이다.
\[Pr(\theta \mid x_{1...I})=\frac{Pr(x_{1...I} \mid \theta)Pr(\theta)}{Pr(x_{1...I})}\] \[\hat{\Theta}=\arg \max_\theta[\frac{Pr(x_{1...I} \mid \theta)Pr(\theta)}{Pr(x_{1...I})}]\] \[\hat{\Theta}=\arg \max_\theta[\frac{\prod_{i=1}^{I}Pr(x_i \mid \theta)Pr(\theta)}{Pr(x_{1...I})}]\]위 수식의 분모에 있는 것은 증거 값 (Evidence) 라고 하는데, Advanced ML을 하다보면 이 값을 계산하는것도 중요하지만 현재는 우리가 추정하고자 하는 parameter와 관련이 없으므로 떼어놓고 생각할 수 있다.
\[\hat{\Theta}=\arg \max_\theta[ {\prod_{i=1}^{I} Pr(x_i \mid \theta) Pr(\theta)} ]\]MAP solution
이제 MLE solution을 구한것과 마찬가지로 Gaussian distribution을 fitting하는 경우에 대한 MAP solution을 구해보도록 하겠다.
\[\hat{\Theta}=\arg \max_\theta[ {\prod_{i=1}^{I} Pr(x_i \mid \theta) \cdot Pr(\theta)} ]\]likelihood는 다음의 Gaussian distribution을 따르고
\[Pr(x\mid\mu,\sigma^2)=Norm_x[\mu,\sigma^2]=\frac{1}{\sqrt{2\pi\sigma^2}}exp[-0.5\frac{(x-\mu)^2}{\sigma^2}]\]prior는 다음의 Normal inverse gamma 분포를 따른다.
\[Pr(\mu,\sigma^2) = NormInvGam_{\mu,\sigma^2}[\alpha, \beta, \gamma, \delta]\] \[Pr(\mu,\sigma^2) = \frac{sqrt{\gamma}}{\alpha\sqrt{2\pi}} \frac{\beta^{\alpha}}{\Gamma[\alpha]}(\frac{1}{\sigma^2})^{\alpha+1}exp[-\frac{2\beta+\gamma(\delta-\mu)^2}{2\sigma^2}]\]그러므로 사후 확률은 다음과 같이 계산할 수 있다.
\[\hat{\mu},\hat{\sigma^2}=\arg \max_{\mu,\sigma^2}[posterior]\] \[\hat{\mu},\hat{\sigma^2}=\arg \max_{\mu,\sigma^2}[likelihood \times prior]\] \[\hat{\mu},\hat{\sigma^2}=\arg \max_{\mu,\sigma^2}[\color{red}{\prod_{i=1}^{I}Pr(x_{i}\mid\mu,\sigma^2)} \cdot \color{blue}{ Pr(\mu,\sigma^2) } ]\] \[\hat{\mu},\hat{\sigma^2}=\arg \max_{\mu,\sigma^2}[\prod_{i=1}^{I} \color{red}{Norm_{x_i}[\mu,\sigma^2]} \cdot \color{blue}{NormInvGam_{\mu,\sigma^2}[\alpha,\beta,\gamma,\delta] } ]\]ML때와 마찬가지로 log를 취해 maximize해도 원래의 식을 maximize하는것과 다름 없기 때문에 계산상의 편의를 위해 log를 취한다.
\[\hat{\mu},\hat{\sigma^2}=\arg \max_{\mu,\sigma^2}[\sum_{i=1}^{I} \log [Norm_{x_i}[\mu,\sigma^2]] + \log [NormInvGam_{\mu,\sigma^2}[\alpha,\beta,\gamma,\delta]]]\]위에서는 그대로 log 때문에 두 distribution가 분리되는 것처럼 보이는데, 이는 두 distribution이 conjugate distribution 이기 때문이다. Normal 과 Normal Inverse 의 곱은 Normal이라는 것이 널리 알려져 있다.
이제 미분을 취해 값을 0 으로 두고 그 때의 mean, variance 값을 구하면 됩니다.
\[\hat{\mu} = \frac{\sum_{i=1}x_i+\gamma\delta}{I+\gamma}\] \[\hat{\mu} = \frac{I\bar{x}+\gamma\delta}{I+\gamma}\]마찬가지로 variance, \(\sigma\)에 대해서도 구할 수 있다.
MLE vs MAP
MAP를 사용하는것에도 단점 (비판)이 있을 수 있다.
MLE를 사용하는 빈도적 확률 관점(frequent) 과 prior를 추가해 posterior를 사용하는 베이지안 확률 관점 (MAP가 bayes' rule에서 기인함) 중 어떤 것이 더 상대적으로 우수한지에 대해서는 끊임없이 논쟁이 있다고 한다.
여기서 베이지안 접근법 (Bayesian Approach)에 대해 널리 알려진 비판 중 하나는 “prior distribution이 실제 사전의 믿음을 반영하기 보다는 수학적인 편리성을 위해 선택하는 것이 아니냐” 라는 것이라고 한다.
위에서 말한 prior를 likelihood의 conjugate distribution으로 설정하는것이 주관이 포함된게 아니냐는 것인데,
그렇기 때문에 MAP, bayesian을 사용할 때 Jeffreys Prior 등의 주관이 들어가지 않은,
무 정보적 (non-informative) prior distribution를 사용하는 방버이 있다고 한다.
그리고 앞서 얘기했던 것 처럼 MAP 하는것은 data point가 몇개냐?에 다라서도 MLE와 결과많이 달라 수 있다고 했는데, 아래 figure를 보면 data 개수가 많아지면 MAP와 MLE가 굉장히 유사한 것을 볼 수 있고 (likelihood가 prir를 압도하면서 prior가 무시됨), data가 적을 때는 다른 것을 볼 수 있다 (prior가 압도적임).
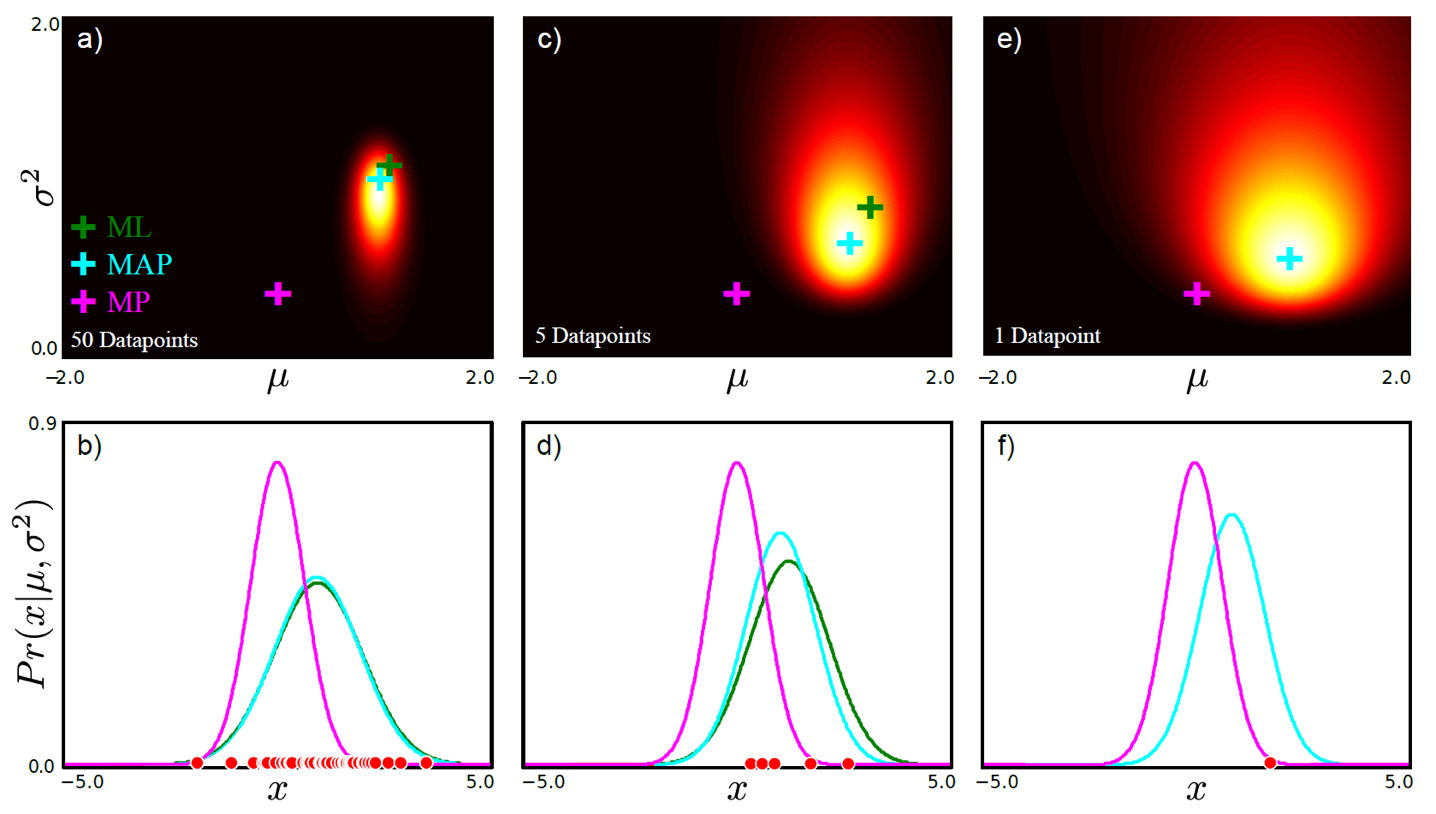Fig. data가 많아지 많이질수록 posterior 분포의 크기가 줄어드는 것을 알 수 있다.
Bayesian?
앞서 Bayesian Approach에 대해서 짧게 얘기했었는데, 이는 MAP와 거의 유사합니다만 한가지 매우 다른 점이 있다. 둘 다 likelihood와 prior로 부터 posterior distribution을 구해야 하는건 같다. (둘을 구분짓기가 좀 애매한데 사실 MAP도 Bayesian Perspective로 문제를 푸는 것이기 때문이다. 다시 말해서 MAP도 엄밀히는 Bayesian Approach의 하나인데 둘을 구분짓는게 어색할 수 있다.)
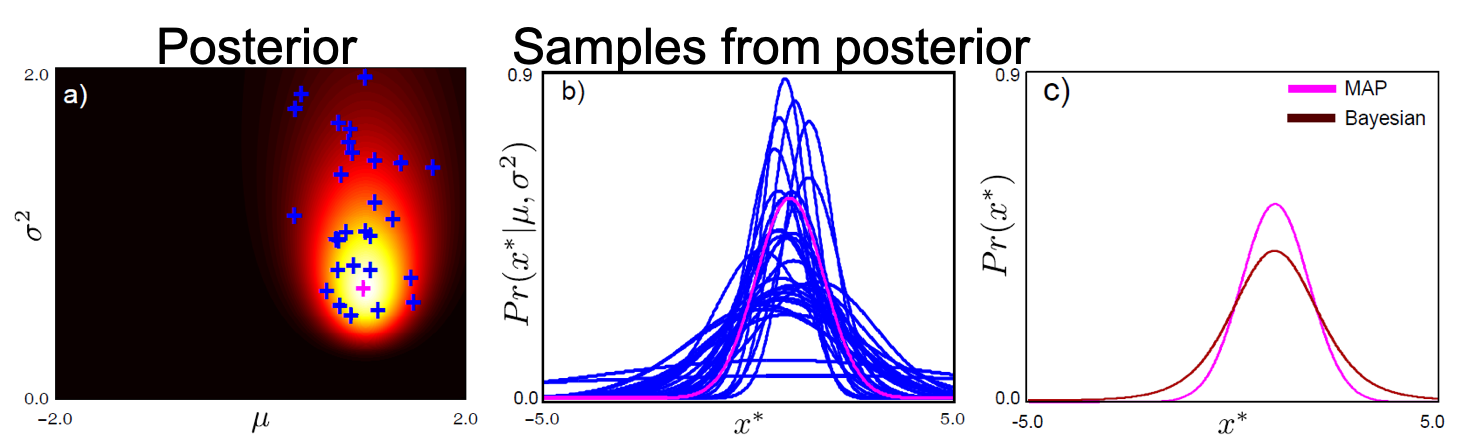Fig. MAP vs Bayesian
Posterior distrubiton 은 확률 분포이기 때문에 발생 가능한 parameter이 여럿 있을테고 각각의 parameter가 얼마나 확률이 높은지? 가장 그럴듯한 parameter인지?를 알려준다. MAP는 그 중 가장 그럴듯한 parameter하나만을 고른다 (점 추정)고 얘기했었는데 Bayesian Approach은 가능한 모든 parameter로 input data의 output을 계산하여 이를 합쳐 결과를 낸다고 할 수 있다. Parameter별로 posterior값이 다를테니 그만큼을 곱해줘 weighted sum 한다고 할 수 있는 것이다 (sum이 무한대이므로 적분).
위의 그림에서 posterior로 부터 샘플링한 분포를 보여주는 (b)의 파란색 선들은 일부를 보여준 것이다. Parameter가 달라지면 data 를 설명하는 distribution도 달라지는데 이를 모두 짬뽕하는 것이다.
Bayesian Approach는 적분이 들어간다는 것 부터가 계산 비용 (computational cost)가 많이 드는 방법론이겠으나, 모든 parameter를 고려해서 output distribution을 만든다는 것에서 꽤 좋은 approach일 것이다. 적분이 문제라면 몇개의 parameter만 확률적으로 sampling해서 weighted sum할 수도 있고 아니면 다른 방법을 강구할 수도 있겠다. (여전히 비싸지만요)
Bayesian Approach는 다음 post에서 detail하게 알아보도록 하겠다.