GPU/GRAD_ACCUM/BSZ (4/1/4) vs (2/2/4) Is Not Same
28 Jun 2024< 목차 >
tmp
(이 post는 당연하지만 헷갈릴 사람을 위해 작성되었다.)
사실 아래 setting들은 소위 말하는 total_batch_size가 같기 때문에 loss, gradient가 같아야 할 것 같다는 생각이 들 수 있다.
| num. GPUs | grad_accum | batch_size | total_batch_size |
|---|---|---|---|
| 4 | 1 | 4 | 16 |
| 4 | 2 | 2 | 16 |
| 4 | 1 | 4 | 16 |
| 2 | 1 | 8 | 16 |
| 2 | 2 | 4 | 16 |
| 2 | 4 | 2 | 16 |
| 2 | 8 | 1 | 16 |
하지만 실제로는 그렇지 않다.
아래는 XEntropy Loss로 Language Modeling (LM) 학습을 한 것이며, GPU, grad accum에 변화를 주었을 때 실제 loss curve들이다. software로는 Hf trainer, deepspeed를 사용했다.
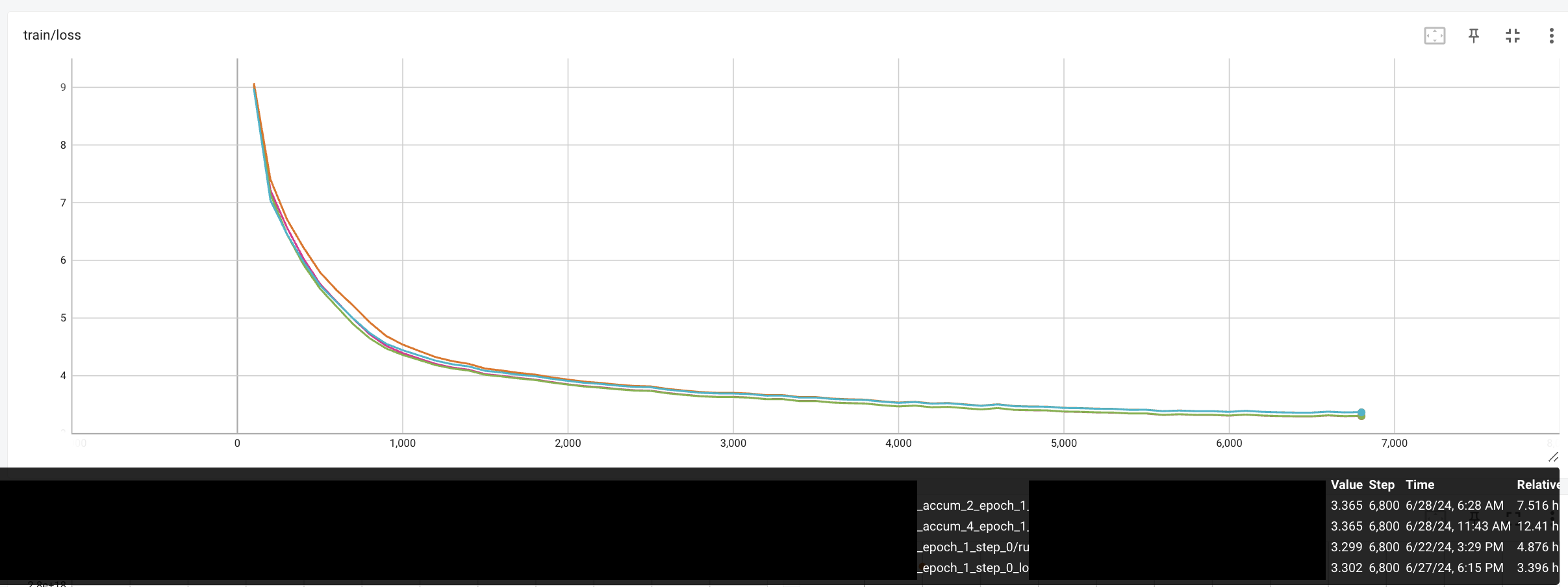 Fig.
Fig.
Training loss가 비슷해보이지만 다른걸 알 수 있고, 이는 gradient도 마찬가지이다.
왜 그럴까?
사실 좀만 생각해보면 당연하다. 왜냐하면 HF trainer같은 opensource의 경우 XEntropy를 계산할 때 아래와 같이 계산하는데, 보통 reduction=’mean`이기 때문이다.
loss = nn.CrossEntropyLoss(reduction=reduction)(x, y)
가령 batch_size가 32이며 grad_accum = 2라고 쳐보자. 그럼 우리가 얻을 loss는 다음과 같다.
\[\text{accumulated loss} = \frac{ \text{loss}(x[:16],y[:16]) + \text{loss}(x[16:],y[16:]) }{2}\]만약 이게 reduction=’mean’이라고 치자, 앞 16개는 num_valid_tokens가 m개, 뒤 16개는 n개라고 하면 accumulation한 것과 한번에 32개를 계산한 것은 다르다.
\[\frac{\text{loss}(x[:], y[:])}{m+n} \neq\frac{ \frac{\text{loss}(x[:16],y[:16])}{m} + \frac{\text{loss}(x[16:],y[16:])}{n} }{2}\]이것이 reduction=’sum’이더라도 마찬가지이다.
물론 아마 \(m=n\)이면 이 값은 같을 것이다.
하지만 \(n \neq m\)인 경우 gradient를 같아지진 않을 것이다.
Report 하는 값 자체는 accumulation loop를 도는 동안 전체 loss sum한 값과 num_valid_tokens를 같이 tracking하다가,
accumulation을 끝내는 boundary에서 loss.sum()/num_valid_tokens인 값을 report하면 똑같은 값을 얻을 수도 있을 것 같지만 사실 이것도 아니다.
왜냐하면 report되는 loss가 정교해질 수는 있겠으나 결국 gradient는 각자 backward한 값을 (서로의 평균 loss값에 대해서 backprop),
all reduce로 합친 뒤에 \(1/2\)배 해서 평균을 취하기 때문에 gradient가 같아질 수는 없기 때문이다.
total_loss = 0.0
total_valid_tokens = 0.0
for accum in range(num_accum):
x_ = x[accum * (bsz // num_accum):(accum + 1) * (bsz // num_accum), :, :]
y_ = y[accum * (bsz // num_accum):(accum + 1) * (bsz // num_accum), :]
logits_, targets_ = model_(x_, y_)
loss_, valid_tokens_ = compute_loss(logits_, targets_) # reduction = 'none'
total_loss += loss_
total_valid_tokens += valid_tokens_
(loss_ / valid_tokens_).backward() # Normalize by valid token count
avg_loss = total_loss / total_valid_tokens
여기에 float point를 쓰는 상황에서 2+1과 1+2도 엄밀히는 값이 다르기 때문에 numerical error까지 추가되면 둘은 같을 확률이 거의 없을 것이다. 아래 full code를 돌려보면서 grad diff가 얼마나 발생하는지 알아보면서 post를 마치도록 하자.
(하지만 padding이 없는 pre-training같은 경우에는 같아질 수는 있다)
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import copy
# Set random seed for reproducibility
import random
import numpy as np
def set_seed(seed_val: int = 42):
random.seed(seed_val)
np.random.seed(seed_val)
torch.manual_seed(seed_val)
torch.cuda.manual_seed_all(seed_val)
# set
seed = 42
vocab_size = 32768
d_embd = 1024
bsz = 32
seq_len = 512
n = d_embd
dtype = torch.bfloat16
# create input and target
set_seed(seed)
x = torch.randn((bsz, seq_len, d_embd)).cuda().to(dtype=dtype)
y = torch.randint(0, vocab_size, (bsz, seq_len)).cuda()
y[-1, -20:] = -100 # force padding
class Model(nn.Module):
def __init__(self, vocab_size, d_embd):
super(Model, self).__init__()
self.vocab_size = vocab_size
self.ffn = nn.Linear(d_embd, d_embd, bias=False)
self.unemb = nn.Linear(d_embd, vocab_size, bias=False)
def forward(self, x, y, reduction):
x = self.unemb(F.relu(self.ffn(x))).float()
x = x.contiguous().view(-1, self.vocab_size)
y = y.contiguous().view(-1).to(x.device)
assert x.size(0) == y.size(0), f"x.size()({x.size()}) != y.size(){y.size()}"
loss = nn.CrossEntropyLoss(reduction=reduction)(x, y)
num_valid_tokens = (y != -100).sum()
if reduction == 'sum':
loss = loss / num_valid_tokens
print(f'x.size(): {x.size()}, num_valid_tokens: {num_valid_tokens}')
return loss
set_seed(seed)
model = Model(vocab_size, d_embd).cuda().to(dtype=dtype)
optimizer = optim.Adam(model.parameters(), lr=0.001)
set_seed(seed)
model_ = Model(vocab_size, d_embd).cuda().to(dtype=dtype)
optimizer_ = optim.Adam(model_.parameters(), lr=0.001)
reduction='sum'
# reduction='mean'
num_accum = 2
for epoch in range(5):
loss = model(x, y, reduction)
loss.backward()
ffn_grad_cache = copy.deepcopy(model.ffn.weight.grad)
unemb_grad_cache = copy.deepcopy(model.unemb.weight.grad)
optimizer.step()
optimizer.zero_grad()
avg_loss = 0.0
for accum in range(num_accum):
x_ = x[accum * (bsz // num_accum):(accum + 1) * (bsz // num_accum), :, :]
y_ = y[accum * (bsz // num_accum):(accum + 1) * (bsz // num_accum), :]
loss_ = model_(x_, y_, reduction)
avg_loss += loss_
loss_.backward()
avg_loss /= num_accum
ffn_grad_cache_ = copy.deepcopy(model_.ffn.weight.grad)
unemb_grad_cache_ = copy.deepcopy(model_.unemb.weight.grad)
optimizer_.step()
optimizer_.zero_grad()
print(f'''
reduction: {reduction}
num_accum: {num_accum}
loss (not accum): {loss}
loss (accum): {avg_loss}
loss diff? : {loss-avg_loss}
ffn_grad allclose?: {torch.allclose(ffn_grad_cache, ffn_grad_cache_)}, abs diff max: {(ffn_grad_cache.abs()-ffn_grad_cache_.abs()).max()}
ffn_grad allclose?: {torch.allclose(unemb_grad_cache, unemb_grad_cache_)}, abs diff max: {(unemb_grad_cache.abs()-unemb_grad_cache_.abs()).max()}
''')
x.size(): torch.Size([16384, 32768]), num_valid_tokens: 16364
x.size(): torch.Size([8192, 32768]), num_valid_tokens: 8192
x.size(): torch.Size([8192, 32768]), num_valid_tokens: 8172
reduction: sum
num_accum: 2
loss (not accum): 10.424154281616211
loss (accum): 10.424150466918945
loss diff? : 3.814697265625e-06
ffn_grad allclose?: False, abs diff max: 1.1622905731201172e-06
ffn_grad allclose?: False, abs diff max: 5.2619725465774536e-08
x.size(): torch.Size([16384, 32768]), num_valid_tokens: 16364
x.size(): torch.Size([8192, 32768]), num_valid_tokens: 8192
x.size(): torch.Size([8192, 32768]), num_valid_tokens: 8172
reduction: sum
num_accum: 2
loss (not accum): 9.981513977050781
loss (accum): 9.981494903564453
loss diff? : 1.9073486328125e-05
ffn_grad allclose?: False, abs diff max: 2.372264862060547e-05
ffn_grad allclose?: False, abs diff max: 6.444752216339111e-07
x.size(): torch.Size([16384, 32768]), num_valid_tokens: 16364
x.size(): torch.Size([8192, 32768]), num_valid_tokens: 8192
x.size(): torch.Size([8192, 32768]), num_valid_tokens: 8172
reduction: sum
num_accum: 2
loss (not accum): 9.553024291992188
loss (accum): 9.553009033203125
loss diff? : 1.52587890625e-05
ffn_grad allclose?: False, abs diff max: 2.2530555725097656e-05
ffn_grad allclose?: False, abs diff max: 9.387731552124023e-07
x.size(): torch.Size([16384, 32768]), num_valid_tokens: 16364
x.size(): torch.Size([8192, 32768]), num_valid_tokens: 8192
x.size(): torch.Size([8192, 32768]), num_valid_tokens: 8172
reduction: sum
num_accum: 2
loss (not accum): 9.134072303771973
loss (accum): 9.134047508239746
loss diff? : 2.47955322265625e-05
ffn_grad allclose?: False, abs diff max: 2.6702880859375e-05
ffn_grad allclose?: False, abs diff max: 1.2218952178955078e-06
x.size(): torch.Size([16384, 32768]), num_valid_tokens: 16364
x.size(): torch.Size([8192, 32768]), num_valid_tokens: 8192
x.size(): torch.Size([8192, 32768]), num_valid_tokens: 8172
reduction: sum
num_accum: 2
loss (not accum): 8.720924377441406
loss (accum): 8.7208251953125
loss diff? : 9.918212890625e-05
ffn_grad allclose?: False, abs diff max: 2.956390380859375e-05
ffn_grad allclose?: False, abs diff max: 1.8328428268432617e-06