REINFORCE and Actor-Critic
15 Jan 2022이 글은 Pytorch의 공식 구현체를 통해서 실제 강화학습 알고리즘이 어떻게 구현되어있는지를 알아보는 것이 goal이다. Reference code-base는 다음과 같다.
- pytorch/examples/reinforcement_learning/reinforce.py
- pytorch/examples/reinforcement_learning/actor_critic.py
< 목차 >
REINFORCE
REINFORCE를 통해 Agent의 Policy를 학습하기 위해서는 우선 아래의 5개의 element (term)를 정의해야 한다.
- 1.Agent가 행동을 할 장소인 env 설정 (환경 설정)
- 2.
Policy: Neural Network 기반의 Policy 구현체 (클래스) - 3.
select_action: Policy와 현재 state를 기반으로 action을 sampling할 함수 - 4.
finish_episode: episode가 한 번 끝날 때 마다 Policy를 업데이트 해주는 함수 - 5.위의 구현체드를 통해 loop를 돌리는 부분 (main)
Actor-Critic의 내용을 까먹으셨다면 제 블로그 내 Actor-Critic post를 참고하면 좋을 것 같다.
Initialize Environment
우리가 REINFORCE로 학습하려는 task는 cartpole이다. 주어진 물체의 밸런스를 잘 잡아서 최대한 오랜 시간 유지하는 것이 objective이다. 이를 위해서 가장 먼저 해야하는 것은 환경을 세팅하는 것이다.
왠만하면 OpenAI에서 제공해주는 open-source package인 gym을 사용하므로 먼저 install을 잘 해주고 위의 코드처럼 environment를 만들어주면 된다.
gamma:Rewards-to-go를 산정할 때 사용하는 discount factor \(\gamma\) 값seed: 랜덤시드 설정 (어려운 태스크에서는 이에 따라 수렴을 할수도 안할수도 있음)render: 강화학습이 진행되면서 어떻게 agent가 행동하는지 실시간 모니터링할지log-interval: log를 언제마다 찍을지 결정하는 값
같은 변수들을 선언해주고 Openai Gym의 CartPole-v1 환경을 만들어 준다.
env = gym.make('CartPole-v1')
env.seed(args.seed)
torch.manual_seed(args.seed)
그러면 랜더링할 경우 아래와 같은 cartpole을 볼 수 있다.
Cartpole 말고도 다양한 환경이 존재하지만, 복잡한 환경에서 Agent를 학습하기 전에 우선 state space와 action space가 상대적으로 작은 Cartpole을 통해 알고리즘의 구현체를 이해하는 것이 본 post의 goal이다.
Policy
그 다음은 Policy network를 만드는 것이다. 우리는 Deep RL을 하고있으니 아래와 같은 Neural Network (NN)을 선언해주면 된다.
굉장히 간단한 NN인데 현재 CartPole 이라는 환경의 이미지,
즉 state는 4차원 이므로 첫 layer는 4차원 input을 128차원으로 mapping해주며 여기에 비선형성을 더해주는 ReLU와 Dropout 이 추가되었다.
그리고 마지막으로 Action Space로 mapping해주는 linear Layer가 있다.
Policy(
(affine1): Linear(in_features=4, out_features=128, bias=True)
(dropout): Dropout(p=0.6, inplace=False)
(affine2): Linear(in_features=128, out_features=2, bias=True) # 좌, 우 행동
)
다른 Supervised Learning (SL)과 달리 강화학습을 해야하기 때문에 log prob에 Advantage, A 값을 계산해서 곱해줘야 한다.
이를 계산하기 위해 log prob, reward를 caching할 list 을 선언한다.
self.saved_log_probs = []
self.rewards = []
Sampling Action
그 다음은 현재 state에서 어떤 행동을 할 지를 샘플링하는 부분이다.
먼저 4차원의 state를 받아 policy network에 태워서 현재 state에서의 2지선다 (좌,우) 행동에 대한 확률을 얻는다.
(Pdb) state
tensor([[ 0.0026, 0.0269, -0.0137, -0.0200]])
(Pdb) policy(state)
tensor([[0.4246, 0.5754]], grad_fn=<SoftmaxBackward>)
그리고 이를 Categorical 분포로 감싸주면 아래와 같이 되는데 (현재는 액션이 2개뿐이니 Bernoulli Distribution 이라고 할 수 있음), 이렇게 해주는 이유는 우리가 RL을 할 때 각 state에 대해 action을 sampling 해줘야만 항상 확률이 max인 action이 아니라 확률이 낮은 action에 대해서도 평가하고 학습하는 데 쓸 수 있기 때문이다 (exploration).
(Pdb) Categorical(probs)
Categorical(probs: torch.Size([1, 2]))
이제 이 분포로부터 샘플링을 하면 앞서 구한 [0.4246, 0.5754] 확률에 따라서 액션을 샘플링 한다.
(Pdb) m.sample()
tensor([0])
(Pdb) m.sample()
tensor([1])
(Pdb) m.sample()
tensor([0])
(Pdb) m.sample()
tensor([1])
(Pdb) m.sample()
tensor([0])
(Pdb) m.sample()
tensor([0])
위에는 여러번 샘플링했을 때 결과가 어떻게 되는지 한번 보려고 찍어본 예시이고, 실제 python debugger로 각 라인을 찍어본 결과는 아래와 같다.
(Pdb) action
tensor([1])
(Pdb) m.log_prob(action)
tensor([-0.6252], grad_fn=<SqueezeBackward1>)
(Pdb) probs
tensor([[0.4246, 0.5754]], grad_fn=<SoftmaxBackward>)
(Pdb) torch.log(probs)
tensor([[-0.7661, -0.6252]], grad_fn=<LogBackward>)
최종적으로 해당 액션이 있으면, 그 액션이 나올 확률에 log를 취해서 이를 Policy network에 저장한다. 나중에 log_prob * A 를 해준 뒤에 backprop을 하기 위해서 이다.
Update Policy Network
이제 Policy를 업데이트해야 되는데요, 이부분이 어떻게 구성되어있는가?
먼저 Loop를 끊임없이 돌면서 매 episode 마다 \((s_1,a_1,r_1,s_2,a_2,r_2,\cdots, s_T,a_T,r_T)\) 를 쭉 뽑아야 한다.
이런 Trajectory를 뽑는 부분은 딱 아래의 부분으로 설명할 수 있는데,
action = select_action(state)
state, reward, done, _ = env.step(action)
이는 \(s_t\)를 받아서 \(a_{t+1}\)을 sample하고 \(r_{t+1},s_{t+1}\)을 env로부터 얻는것이다. episode를 진행하면서 전체 episode에 대한 reward를 계속 누적시키면서 저장해준다.
그리고 이를 무한정 반복할 수 없기 때문에 현재 환경,
즉 Cartpole에 지정되어있는 reward_threshold 를 기준으로 이를 넘으면 loop를 탈출하는데 이 기준은
running_reward가 정하며 이는 코드에 나와있다.
근데 for loop 중간에 finish_episode()라는 함수가 있다.
이 부분이 바로 매 episode가 끝날 때 마다 Policy를 업데이트 하는 부분이다.
함수는 아래와 같이 구현되어 있는데,
보면 환경과 상호작용하면서 action을 sample하면서 매 time-step, \(t\) 마다의 reward가 저장되어 있으며 이는 아래와 같다.
(Pdb) len(policy.rewards[::-1])
78
(Pdb) policy.rewards[::-1]
[1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0,
1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0,
1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0,
1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0,
1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0,
1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0]
중간에 환경이 78step에서 멈췄기 때문에 78개의 reward만이 저장되어 있다.
이제 아래의 코드에 따라서,
for r in policy.rewards[::-1]:
R = r + args.gamma * R
returns.insert(0, R)
(아래의 수식과 동치인데, post를 보신분들은 알겠지만 이는 그 action이 얼마짜리인지를 평가하는 방법 중 가장 간단한 방법인 Monte Carlo Estimator 이다. REINFORCE이므로 Critic은 아직 없다)
\[R_t = \sum_{t=0}^T \gamma^t r_t\]해당 step마다 감가상각을 맞은 (discounted) reward를 재산정 한다.
(Pdb) len(returns)
78
(Pdb) returns
[54.33902522560851, 53.87780325819041, 53.41192248302062, 52.94133584143497,
52.465995799429265, 51.98585434285784, 51.500862972583676, 51.01097269957947,
50.51613403997926, 50.016297010080066, 49.511411121292994, 49.00142537504343,
48.48628825761963, 47.96594773496932, 47.44035124744376, 46.90944570448865,
46.37317747928146, 45.831492403314606, 45.284335760923845, 44.73165228376146,
44.1733861452136, 43.60948095476121, 43.03987975228405, 42.46452500230712,
41.88335858818901, 41.29632180625153, 40.70335535985003, 40.10439935338387,
39.49939328624633, 38.888276046713464, 38.27098590577118, 37.647460510879974,
37.01763687967674, 36.38145139361287, 35.73883979152815, 35.08973716315975,
34.4340779425856, 33.77179590160162, 33.10282414303194, 32.42709509397166,
31.744540498961268, 31.05509141309219, 30.358678195042614, 29.655230500043047,
28.944677272770754, 28.22694674017248, 27.501966404214627, 26.76966303456023,
26.02996266117195, 25.282790566840355, 24.528071279636723, 23.76572856528962,
22.995685419484467, 22.21786406008532, 21.4321859192781, 20.638571635634445,
19.8369410460954, 19.027213177874142, 18.209306240276913, 17.383137616441328,
16.54862385499124, 15.705680661607312, 14.854222890512437, 13.994164535871148,
13.12541872310217, 12.247897700103202, 11.361512828387072, 10.466174574128356,
9.561792499119552, 8.64827525163591, 7.72553055720799, 6.793465209301,
5.8519850599, 4.90099501, 3.9403989999999998, 2.9701, 1.99, 1.0]
마지막에는 그냥 리턴이 1이고 (현재 episode는 10000step 중에서 78번째만에 성공을 한 것이다) 이를 다시 normalize 해주면 아래와 같다.
(Pdb) returns # returns = (returns - returns.mean()) / (returns.std() + eps)
tensor([ 1.4914e+00, 1.4619e+00, 1.4321e+00, 1.4020e+00, 1.3716e+00,
1.3409e+00, 1.3098e+00, 1.2785e+00, 1.2468e+00, 1.2148e+00,
1.1825e+00, 1.1499e+00, 1.1169e+00, 1.0836e+00, 1.0500e+00,
1.0160e+00, 9.8171e-01, 9.4705e-01, 9.1204e-01, 8.7667e-01,
8.4095e-01, 8.0486e-01, 7.6842e-01, 7.3160e-01, 6.9441e-01,
6.5685e-01, 6.1890e-01, 5.8058e-01, 5.4187e-01, 5.0276e-01,
4.6326e-01, 4.2336e-01, 3.8306e-01, 3.4235e-01, 3.0123e-01,
2.5970e-01, 2.1774e-01, 1.7536e-01, 1.3256e-01, 8.9319e-02,
4.5643e-02, 1.5266e-03, -4.3036e-02, -8.8049e-02, -1.3352e-01,
-1.7944e-01, -2.2583e-01, -2.7269e-01, -3.2002e-01, -3.6783e-01,
-4.1613e-01, -4.6491e-01, -5.1418e-01, -5.6395e-01, -6.1423e-01,
-6.6501e-01, -7.1631e-01, -7.6812e-01, -8.2046e-01, -8.7332e-01,
-9.2672e-01, -9.8066e-01, -1.0351e+00, -1.0902e+00, -1.1458e+00,
-1.2019e+00, -1.2586e+00, -1.3159e+00, -1.3738e+00, -1.4323e+00,
-1.4913e+00, -1.5509e+00, -1.6112e+00, -1.6720e+00, -1.7335e+00,
-1.7956e+00, -1.8583e+00, -1.9217e+00])
이제 마지막으로 실제 REINFORCE의 수식처럼
\[\nabla_{\theta} J(\theta) \approx \sum_{i}\left(\sum_{t} \nabla_{\theta} \log \pi_{\theta}\left(\mathbf{a}_{t}^{i} \vert \mathbf{s}_{t}^{i}\right)\right)\left(\sum_{t} r\left(\mathbf{s}_{t}^{i}, \mathbf{a}_{t}^{i}\right)\right)\]아래의 코드를 통해 policy loss를 계산하면
for log_prob, R in zip(policy.saved_log_probs, returns):
policy_loss.append(-log_prob * R)
아래처럼 되고 이를 BackPropagation 하면 Policy가 업데이트 된다.
(Pdb) policy_loss #torch.cat(policy_loss)
tensor([ 9.3239e-01, 1.2561e+00, 1.0801e+00, 9.0076e-01, 9.1203e-01,
1.0779e+00, 1.1815e+00, 1.0848e+00, 9.9581e-01, 9.0983e-01,
8.1994e-01, 1.0329e+00, 5.9475e-01, 8.0361e-01, 7.4601e-01,
5.4984e-01, 4.3901e-01, 8.2733e-01, 5.4570e-01, 5.6544e-01,
6.9274e-01, 6.7476e-01, 5.3832e-01, 7.2206e-01, 5.2357e-01,
2.8371e-01, 3.2219e-01, 1.6687e-01, 3.3372e-01, 3.7222e-01,
2.6276e-01, 2.3098e-01, 2.5936e-01, 2.3791e-01, 2.3465e-01,
1.7208e-01, 1.5607e-01, 1.4481e-01, 1.2690e-01, 7.3750e-02,
2.7267e-02, 1.1812e-03, -2.7377e-02, -7.4695e-02, -1.2630e-01,
-1.2419e-01, -1.5823e-01, -2.0956e-01, -1.9456e-01, -2.6148e-01,
-2.5040e-01, -3.6716e-01, -3.0935e-01, -3.6311e-01, -5.2213e-01,
-3.1056e-01, -3.7007e-01, -4.5262e-01, -5.0509e-01, -5.5682e-01,
-6.6902e-01, -5.3275e-01, -6.6688e-01, -6.5198e-01, -6.2906e-01,
-1.3167e+00, -1.0709e+00, -1.0465e+00, -8.2307e-01, -1.0744e+00,
-8.1389e-01, -6.9362e-01, -1.0453e+00, -8.1829e-01, -2.0383e+00,
-1.4645e+00, -1.2171e+00, -1.3923e+00], grad_fn=<CatBackward>)
(Pdb) policy_loss #torch.cat(policy_loss).sum()
tensor(0.6655, grad_fn=<SumBackward0>)
- Recap) REINFORCE
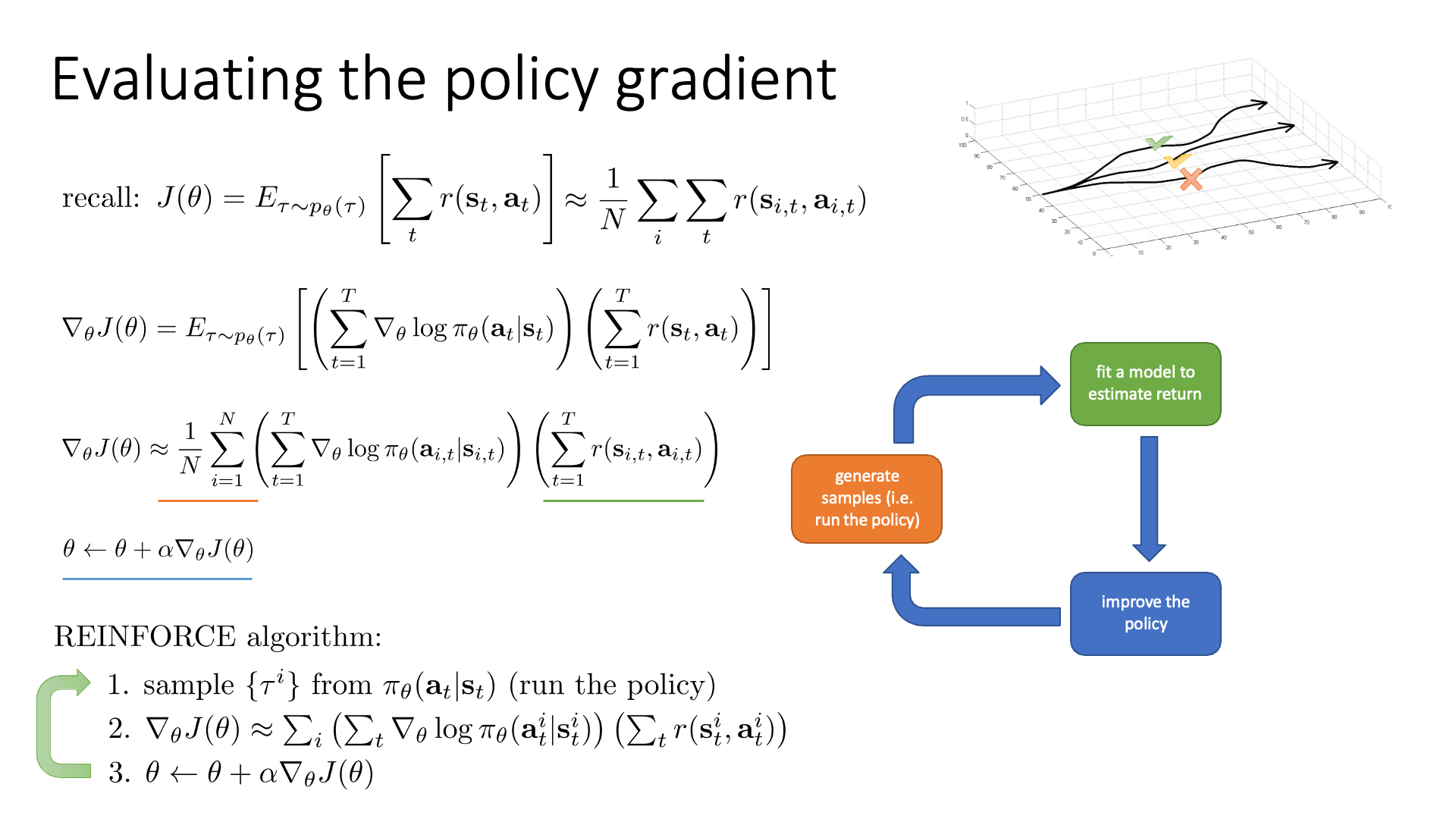Fig. CS285의 REINFORCE 수식
Iteration
마지막으로 Loop를 돌린 실제 결과를 처음부터 끝까지 보면 아래와 같다.
root@e5bcb446a9ee:/workspace/tutorial# python reinforce.py
Episode 10 Last reward: 26.00 Average reward: 16.00
Episode 20 Last reward: 16.00 Average reward: 14.85
Episode 30 Last reward: 49.00 Average reward: 20.77
Episode 40 Last reward: 45.00 Average reward: 27.37
Episode 50 Last reward: 44.00 Average reward: 30.80
Episode 60 Last reward: 111.00 Average reward: 42.69
Episode 70 Last reward: 131.00 Average reward: 70.39
Episode 80 Last reward: 87.00 Average reward: 76.68
Episode 90 Last reward: 100.00 Average reward: 96.49
Episode 100 Last reward: 115.00 Average reward: 115.31
Episode 110 Last reward: 333.00 Average reward: 150.83
Episode 120 Last reward: 500.00 Average reward: 248.35
Episode 130 Last reward: 500.00 Average reward: 338.73
Episode 140 Last reward: 291.00 Average reward: 345.93
Episode 150 Last reward: 112.00 Average reward: 256.34
Episode 160 Last reward: 117.00 Average reward: 198.14
Episode 170 Last reward: 278.00 Average reward: 227.55
Episode 180 Last reward: 336.00 Average reward: 250.06
Episode 190 Last reward: 195.00 Average reward: 237.52
Episode 200 Last reward: 227.00 Average reward: 228.20
Episode 210 Last reward: 500.00 Average reward: 279.83
Episode 220 Last reward: 395.00 Average reward: 340.28
Episode 230 Last reward: 500.00 Average reward: 395.89
Episode 240 Last reward: 500.00 Average reward: 437.66
Episode 250 Last reward: 500.00 Average reward: 458.68
Episode 260 Last reward: 500.00 Average reward: 463.04
Solved! Running reward is now 475.476968005226 and the last episode runs to 500 time steps!
+ Back Propagation with Sampling
앞서 구현체에서 pytorch의 Categorical Distribution method를 사용해 \(t\) 시점의 state, \(s_t\)에서 Action Space에 대한 확률 분포에 따라서 ㅁction을 샘플링 했던 게 기억이 날 것이다.
\[a_{t+1} \sim \pi (a_t \vert s_t)\]Policy가 뱉는 분포로 부터 argmax를 취한다면 가장 높은 확률을 가지는 행동을 deterministic하게 뽑아낼 수 있는데,
우리가 Categorical 객체를 이 만들어서 사용하는 이유는 매번 같은 행동이 나오지 않게 하기 위해서이다.
이는 강화학습에서 가장 중요하다고도 할 수 있는 두 가지 핵심 개념인 아래 두 가지를 적절히 하기 위해서 인 것이다.
- expolitation : 가지고있는 policy를 기반으로 최적의 수를 두는 것
- exploration : 확률은 낮지만 가보지 않은 길을 개척해보는 것
이 sampling 하는 부분은 RL뿐 아니라 generative modeling이나 representation learning을 할때도 자주 쓰이는 기법이다. 그런데 이 sampling하는 행위는 미분이 불가능 (non-differentiable) 해서 backpropagation이 불가능해지는 문제가 있다. (Torch official docs의 distributions package 참고)
이를 해결할 수 있는 방법이 몇 가지가 있는데 아래와 같은 것들이다.
- Score Function-based Gradient Estimator (Score Function estimator (such as REINFORCE) / likelihood ratio estimato)
- Path Derivative Gradient Estimator
그런데 여기서 보시면 1번이 REINFORCE인 것을 볼 수 있다.
probs = policy_network(state)
# Note that this is equivalent to what used to be called multinomial
m = Categorical(probs)
action = m.sample()
next_state, reward = env.step(action)
loss = -m.log_prob(action) * reward
loss.backward()
원래는 sampling 을 함으로써 미분이 불가능한데 (non-differentiable),
그 action의 시행확률이 몇인지를 sampling전에 log를 씌워 log_prob에 저장하고 reward를 곱함으로써 미분 불가능함을 우회한 것이다.
또 다른 방법은 resample()이라는 함수를 통해서 reparameterization trick 을 사용해서 sampling하는 효과를 내면서도 미분 가능성을 잃지 않게 하는 것이다.
이를 앞서 말한 것 처럼 Pathwise Derivative라고 한다.
params = policy_network(state)
m = Normal(*params)
# Any distribution with .has_rsample == True could work based on the application
action = m.rsample()
next_state, reward = env.step(action) # Assuming that reward is differentiable
loss = -reward
loss.backward()
위 두 방식은 아래 처럼 차이가 조금 있는데,
# REINFORCE
loss = -m.log_prob(action) * reward
loss.backward()
# reparameterization trick
loss = -reward
loss.backward()
Categorical Reparameterization with Gumbel-Softmax 논문을 보시면 이 방법론들에 대해서 자세히 잘 설명해주고 있다 (Categorical 분포에 대해서 어떻게 Reparameterization Trick을 사용하는지에 대해서).
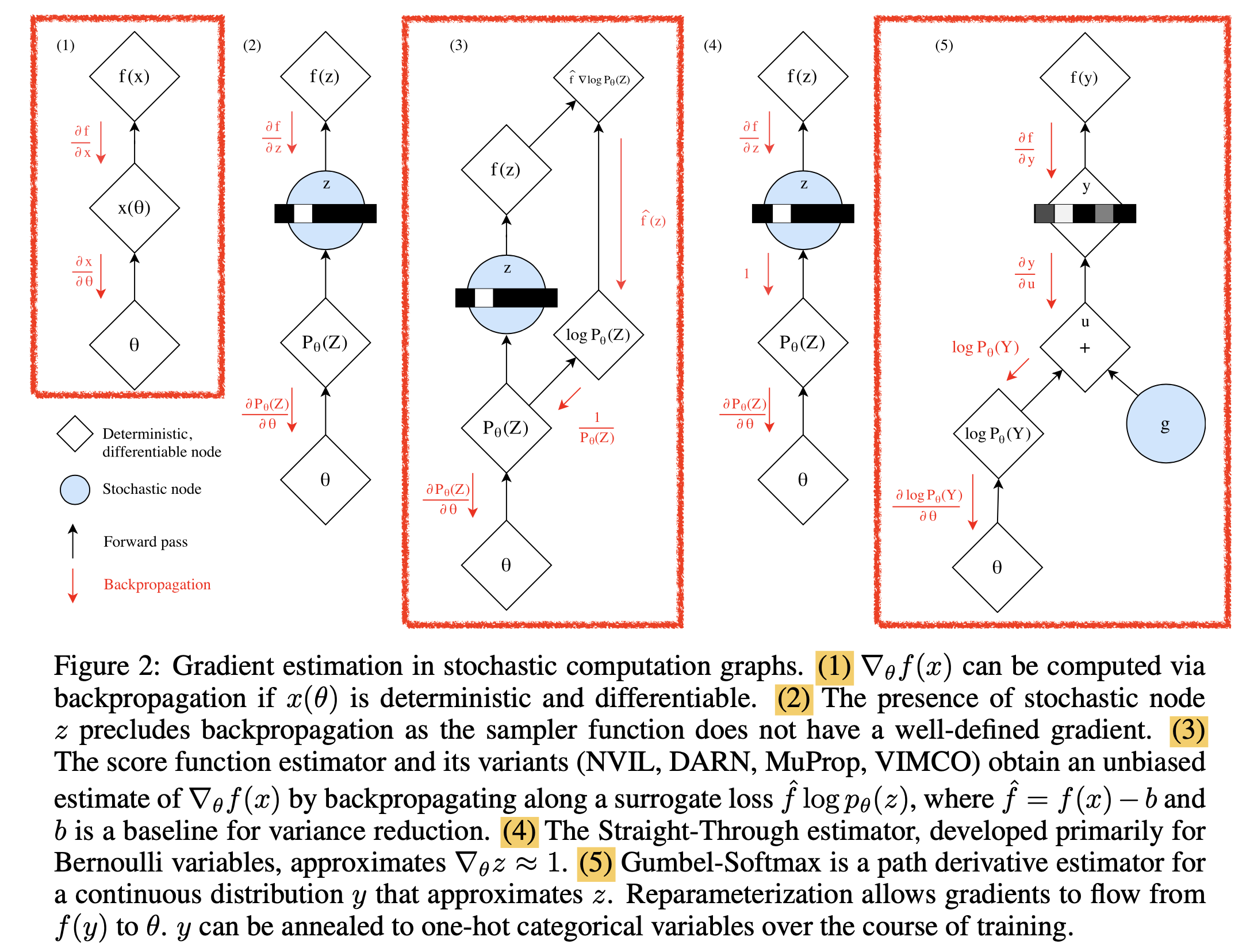Fig 미분 불가능한 샘플링 기법이 적용된 알고리즘에서 미분을 가능하게 하는 5가지 방식들.
- 1번은 그냥 함수의 출력값부터 network parameter \(\theta\) 까지 graident가 잘 흐르는 모습이고, 2번부터는 미분 불가능한 (Non-Differentiable) Node 가 포함되어 있다.
- 아무런 장치가 없는 2번은 그래디언트가 제대로 흐르지 못하고,
- 3번이 바로 REINFORCE 방법이라 생각할 수 있다.
- 4번 방법은 샘플링이 들어갔으나 이것의 미분체를 그냥 1로 처리하는것에 그쳤고,
- 5번 방법이 z를 근사한 연속 분포 y를 위한
Path Derivative Estimator, 즉Gumbel-Softmax앞서 말한Reparameterization 과 같은 것이며 본 논문에서 제안한 방법론 이다. g에는 그래디언트가 흐르지 않지만 출력값부터 \(\theta\)까지는 문제없이 그래디언트가 흐르는 걸 알 수 있죠.
이 중에서 Gumbel-Softmax가 또 유명한데, 이는 다른 post에서 다루도록 하고,
우리가 가져갈 수 있는 것은 미분 불가능한 연산에 대해서 REINFORCE가 쓰인다이며 다른 방식으로도 이런 문제를 해결할 수 있다는 것이다.
Actor-Critic
이번에는 REINFORCE 의 업그레이드 버전인 Actor-Critic에 대해서 알아보도록 하자. Actor는 Policy Network로 state가 주어졌을 때 action space에 대한 probabilistic distribution을 return하는것이며, Critic은 그 action이 얼마나 좋았는지를 평가해준다. 이를 위해서는 아래의 REINFORCE 수식에서
\[\nabla_{\theta} J(\theta) \approx \sum_{i}\left(\sum_{t} \nabla_{\theta} \log \pi_{\theta}\left(\mathbf{a}_{t}^{i} \vert \mathbf{s}_{t}^{i}\right)\right)\left(\sum_{t} r\left(\mathbf{s}_{t}^{i}, \mathbf{a}_{t}^{i}\right)\right)\]Log prob에 곱해지는 rewards-to-go를 monte carlo estimator가 아닌 Advantage Function 값으로 바꿔 주어야 한다.
그리고 이 \(A_{t}^i\)값을 bootstrapped estimator를 쓰면 \(r_{s_{t}^i,a_{t}^i} + V(s_{t+1}^i) - V(s_{t}^i)\) 가 된다.
Fig. CS285의 Actor-Critic 알고리즘 설명
수식을 간단히해서 한 trajectory 만 sample 했다면 아래와 같은 수식을 구현해주면 되며, 여기서 \(V\) network가 바로 Critic 이며 우리는 앞으로 Policy를 나타낼 파라메터 \(\pi\)와 state의 Value를 나타낼 파라메터 \(\phi\)를 둘 다 학습하면 된다. (REINFORCE는 Policy만 학습하면 됐음)
\[\hat{A}^{\pi}\left(\mathbf{s}_{i}, \mathbf{a}_{i}\right)=r\left(\mathbf{s}_{i}, \mathbf{a}_{i}\right)+\hat{V}_{\phi}^{\pi}\left(\mathbf{s}_{i}^{\prime}\right)-\hat{V}_{\phi}^{\pi}\left(\mathbf{s}_{i}\right)\] \[\nabla_{\theta} J(\theta) \approx \sum_{i} \nabla_{\theta} \log \pi_{\theta}\left(\mathbf{a}_{i} \mid \mathbf{s}_{i}\right) \hat{A}^{\pi}\left(\mathbf{s}_{i}, \mathbf{a}_{i}\right)\]Initialize Environment
맨 처음 환경 설정은 크게 다를것이 없으니 넘어가도록 하자.
Policy
Policy 의 Neural Network 구현체도 크게 다를 것이 없어 보이지만 보면 head가 두개 있다.
# actor's layer
self.action_head = nn.Linear(128, 2)
# critic's layer
self.value_head = nn.Linear(128, 1)
즉 Actor, Critic을 아예 독립된 network로 두지 않고 shared network 구조를 쓰겠다는 것이다.
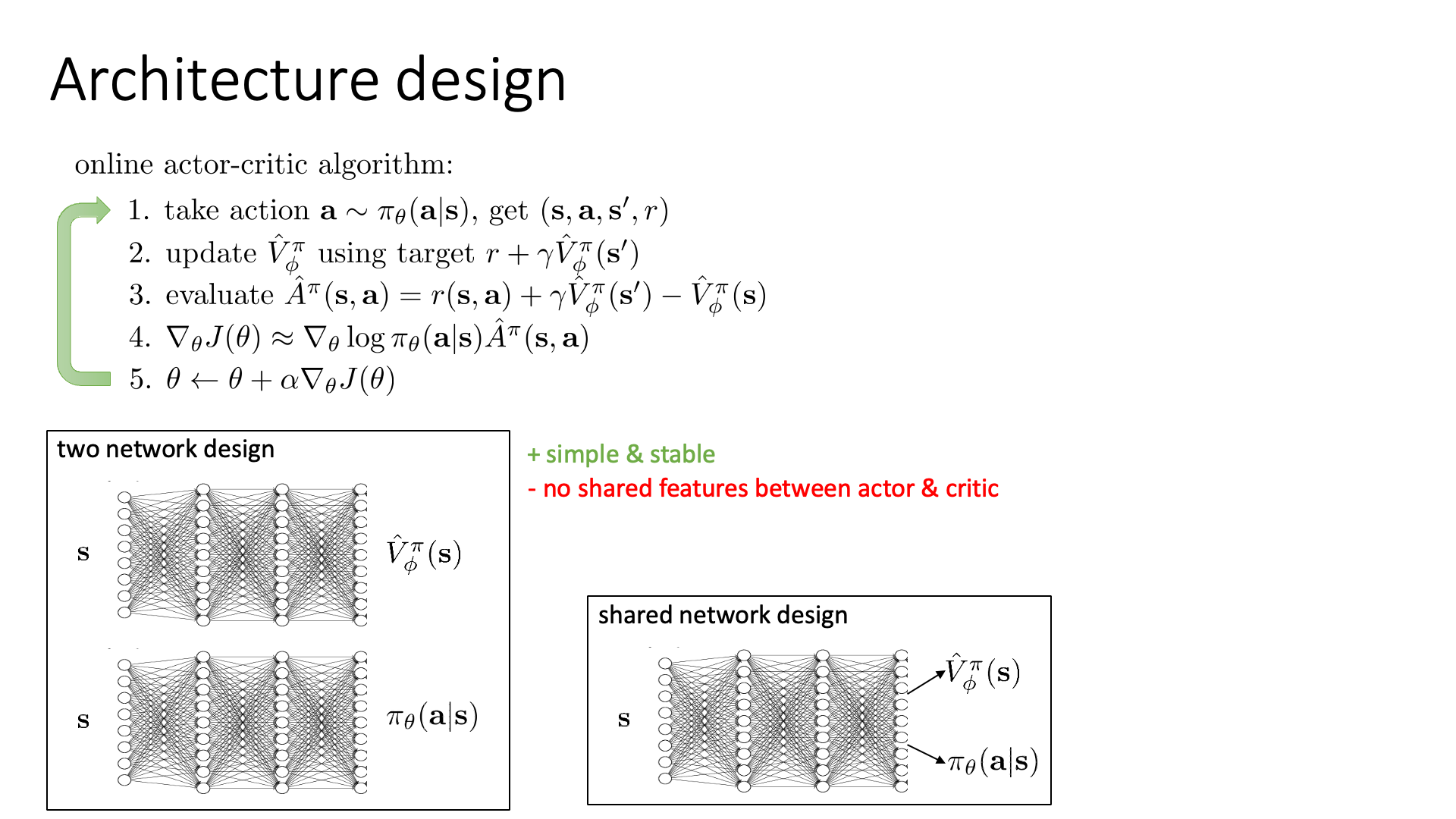Fig. Network Body를 공유하는 경우 (twin-head)
위의 그림에서 보시는 바와 같이, Actor와 Critic을 선언하는데 있어 완전히 독립적인 network를 두 개 선언하는 방식이 있고, body는 공유하되 head만 두개로 빼는 방법이 있는데 여기서는 후자인 셈인 거죠. (각각의 장단점에 대해서는 문헌을 더 찾아보시길 바란다)
Model class가 return하는 것을 보시면 action에 대한 prob 이외에도, value 값도 뱉는 것을 알 수 있다. 이 때 value는 당연히 1차원, 즉 Scalar 값이다.
Sampling Action
select_action함수도 REINFORCE와 다를게 없는데,
마찬가지로 Categorical Class로 Policy가 뱉은 \(\pi(a \vert s)\) Action Prob을 감싸주고, 이 분포로부터 샘플링을해준 action 과 현재 state가 얼마나 좋은지를 평가하는 value값을 각각 의 bucket에 저장한다.
Update Policy and Value Network
이제 이 각각의 network를 업데이트 하는 부분이다.
각 time-step, \(t\) 별로의 returns은 마찬가지로 discount를 해서 역순으로 계산한다.
R = 0
returns = []
for r in model.rewards[::-1]:
# calculate the discounted value
R = r + args.gamma * R
returns.insert(0, R)
returns = torch.tensor(returns)
returns = (returns - returns.mean()) / (returns.std() + eps)
이제 여기서 REINFORCE와 차이가 생기는데, 우리가 gradient를 계산하기 위해 구하는 quantity는 log_prob과 Advantage, A를 곱해야 얻을 수 있다.
saved_actions = model.saved_actions
policy_losses = [] # list to save actor (policy) loss
value_losses = [] # list to save critic (value) loss
for (log_prob, value), R in zip(saved_actions, returns):
advantage = R - value.item()
# calculate actor (policy) loss
policy_losses.append(-log_prob * advantage)
# calculate critic (value) loss using L1 smooth loss
value_losses.append(F.smooth_l1_loss(value, torch.tensor([R])))
# sum up all the values of policy_losses and value_losses
loss = torch.stack(policy_losses).sum() + torch.stack(value_losses).sum()
# perform backprop
loss.backward()
Total Loss는 Value Loss와 Policy Loss를 더한 값인데, Policy Loss를 계산하는 방법은 log_prob에 Advantage라는 값이 곱해지며 이는 다음과 같다.
\[r(s_t,a_t) + \gamma \sum_{t'=t+1}^T r(s_{t'},a_{t'}) - V (s_t)\]Value network의 output을 사용해서 계산이 되긴 하지만, 정확히 bootstrapped estimator가 아니다. 그리고 Value Loss를 계산할 때 Value Network의 target도 아래의 수식에 따라 계산된다.
\[r(s_t,a_t) + \gamma \sum_{t'=t+1}^T r(s_{t'},a_{t'})\]그리고 계산한 returns에 대해서 (각 timestep별 r + sum of discounted future rewards) 평균을 빼주는 걸 알 수 있다. 원래라면 Advantage Function이 아래와 같고
\[\hat{A}^{\pi}\left(\mathbf{s}_{i}, \mathbf{a}_{i}\right)=r\left(\mathbf{s}_{i}, \mathbf{a}_{i}\right)+\hat{V}_{\phi}^{\pi}\left(\mathbf{s}_{i}^{\prime}\right)-\hat{V}_{\phi}^{\pi}\left(\mathbf{s}_{i}\right)\]실제로는 현재 Value Network가 예측한 값인 \(\hat{V}_{\phi}^{\pi}\left(\mathbf{s}_{i}\right)\) 가 \(r\left(\mathbf{s}_{i}, \mathbf{a}_{i}\right)+\hat{V}_{\phi}^{\pi}\left(\mathbf{s}_{i}^{\prime}\right)\) 를 따라가도록 학습되어야 한다. 사실 뭐가 맞다 틀리다 할 순 없는것이 bootstrapped target을 사용하면 (ideal target을 씀) variance가 더 낮아지지만 bias가 생길 수 있고, 지금의 구현 예제대로 하면 variance는 조금 크지만 우리가 구한 gradient는 unbias 한다.
bootstrapped target을 구하고싶다면 아래처럼 loop을 구성해도 되겠다.
log_probs = [ log_prob for log_prob, value in saved_actions ]
values = [ value for log_prob, value in saved_actions ]
rewards = model.rewards
for timestep, (log_prob, r) in enumerate(zip(log_probs, rewards)):
value = values[timestep]
next_value = values[timestep+1] if timestep < len(log_probs) - 1 else torch.tensor([0.0])
value_target = torch.tensor([r]) + gamma * next_value.item() # r + V(s_{t-1})
advantage = value_target - value # r + V(s_{t-1}) + V(s_{t})
policy_losses.append(-log_prob * advantage.detach().item()) # - log_prob * ( r + V(s_{t-1}) + V(s_{t}) )
value_losses.append(F.smooth_l1_loss(value, value_target.detach())) # || V(s_{t}) - r + V(s_{t-1}) ||^2
optimizer.zero_grad()
actor_loss = torch.stack(policy_losses).sum()
critic_loss = torch.stack(value_losses).sum()
loss = (actor_loss + critic_loss)
loss.backward()
optimizer.step()
Iteration
마지막으로는 Loop를 돌려 trajectory를 계속 샘플링해가면서 Policy, Value networks를 업데이트 하면 된다.
아래는 monte carlo estimator를 활용한 Actor-Critic이고
root@e5bcb446a9ee:/workspace/tutorial# python actor_critic.py
Episode 10 Last reward: 9.00 Average reward: 10.67
Episode 20 Last reward: 10.00 Average reward: 14.35
Episode 30 Last reward: 11.00 Average reward: 12.54
Episode 40 Last reward: 10.00 Average reward: 11.31
Episode 50 Last reward: 12.00 Average reward: 10.79
Episode 60 Last reward: 9.00 Average reward: 10.43
Episode 70 Last reward: 9.00 Average reward: 10.51
Episode 80 Last reward: 12.00 Average reward: 11.04
Episode 90 Last reward: 10.00 Average reward: 10.78
Episode 100 Last reward: 32.00 Average reward: 12.34
Episode 110 Last reward: 12.00 Average reward: 13.97
Episode 120 Last reward: 26.00 Average reward: 19.78
Episode 130 Last reward: 38.00 Average reward: 28.38
Episode 140 Last reward: 65.00 Average reward: 48.45
Episode 150 Last reward: 75.00 Average reward: 70.96
Episode 160 Last reward: 108.00 Average reward: 71.93
Episode 170 Last reward: 100.00 Average reward: 83.27
Episode 180 Last reward: 12.00 Average reward: 78.75
Episode 190 Last reward: 19.00 Average reward: 74.03
Episode 200 Last reward: 35.00 Average reward: 53.71
Episode 210 Last reward: 53.00 Average reward: 54.67
Episode 220 Last reward: 51.00 Average reward: 57.19
Episode 230 Last reward: 64.00 Average reward: 60.95
Episode 240 Last reward: 109.00 Average reward: 88.45
Episode 250 Last reward: 200.00 Average reward: 106.18
Episode 260 Last reward: 117.00 Average reward: 109.89
Episode 270 Last reward: 77.00 Average reward: 108.43
Episode 280 Last reward: 137.00 Average reward: 112.53
Episode 290 Last reward: 197.00 Average reward: 129.27
Episode 300 Last reward: 171.00 Average reward: 152.55
Episode 310 Last reward: 179.00 Average reward: 156.38
Episode 320 Last reward: 200.00 Average reward: 173.89
Episode 330 Last reward: 98.00 Average reward: 179.26
Episode 340 Last reward: 60.00 Average reward: 149.99
Episode 350 Last reward: 152.00 Average reward: 131.80
Episode 360 Last reward: 200.00 Average reward: 142.50
Episode 370 Last reward: 200.00 Average reward: 165.57
Episode 380 Last reward: 200.00 Average reward: 179.39
Episode 390 Last reward: 200.00 Average reward: 187.66
Episode 400 Last reward: 200.00 Average reward: 166.43
Episode 410 Last reward: 200.00 Average reward: 171.87
Episode 420 Last reward: 200.00 Average reward: 183.16
Episode 430 Last reward: 200.00 Average reward: 189.92
Episode 440 Last reward: 200.00 Average reward: 193.96
Episode 450 Last reward: 200.00 Average reward: 189.47
Episode 460 Last reward: 200.00 Average reward: 193.70
Episode 470 Last reward: 200.00 Average reward: 187.99
Episode 480 Last reward: 200.00 Average reward: 192.81
Solved! Running reward is now 195.2293344612271 and the last episode runs to 200 time steps!
아래는 bootstrapped estimator를 쓴 경우이다.
Episode 10 Last reward: 9.00 Average reward: 10.89
Episode 20 Last reward: 15.00 Average reward: 11.33
Episode 30 Last reward: 23.00 Average reward: 15.46
Episode 40 Last reward: 13.00 Average reward: 19.20
Episode 50 Last reward: 76.00 Average reward: 29.51
Episode 60 Last reward: 133.00 Average reward: 51.61
Episode 70 Last reward: 29.00 Average reward: 67.07
Episode 80 Last reward: 200.00 Average reward: 93.90
Episode 90 Last reward: 200.00 Average reward: 136.47
Episode 100 Last reward: 200.00 Average reward: 161.97
Episode 110 Last reward: 79.00 Average reward: 164.56
Episode 120 Last reward: 95.00 Average reward: 168.45
Episode 130 Last reward: 141.00 Average reward: 146.15
Episode 140 Last reward: 200.00 Average reward: 158.77
Episode 150 Last reward: 181.00 Average reward: 165.11
Episode 160 Last reward: 80.00 Average reward: 139.79
Episode 170 Last reward: 200.00 Average reward: 129.22
Episode 180 Last reward: 200.00 Average reward: 146.80
Episode 190 Last reward: 200.00 Average reward: 168.15
Episode 200 Last reward: 200.00 Average reward: 180.93
Episode 210 Last reward: 200.00 Average reward: 188.58
Episode 220 Last reward: 200.00 Average reward: 190.74
Episode 230 Last reward: 200.00 Average reward: 194.46
Solved! Running reward is now 195.24610193969923 and the last episode runs to 200 time steps!