Notes

(WIP) (Sparse) Mixture Of Experts (MoE)

11 Oct 2024

< 목차 >

Why Mixture Of Experts (MoE)?

Mixture of Experts (MoE)는 아마 내가 조사한 자료들에 의하면 90년대에 최초로 제안된 method로, 유출됐다고 알려진 바에 의하면 GPT-4에서 사용됐을 가능성이 높다.

아마 Switch Transformers를 제안한 google researcher들이 지금은 대부분 OpenAI에서 일하고 있기도 하고, 같은 computing budget을 쓴 경우 더 좋은 scaling exponent를 보이는 방법 중 확실히 검증 된 것 중 하나가 MoE인 것이 이유가 아닐까 싶다.

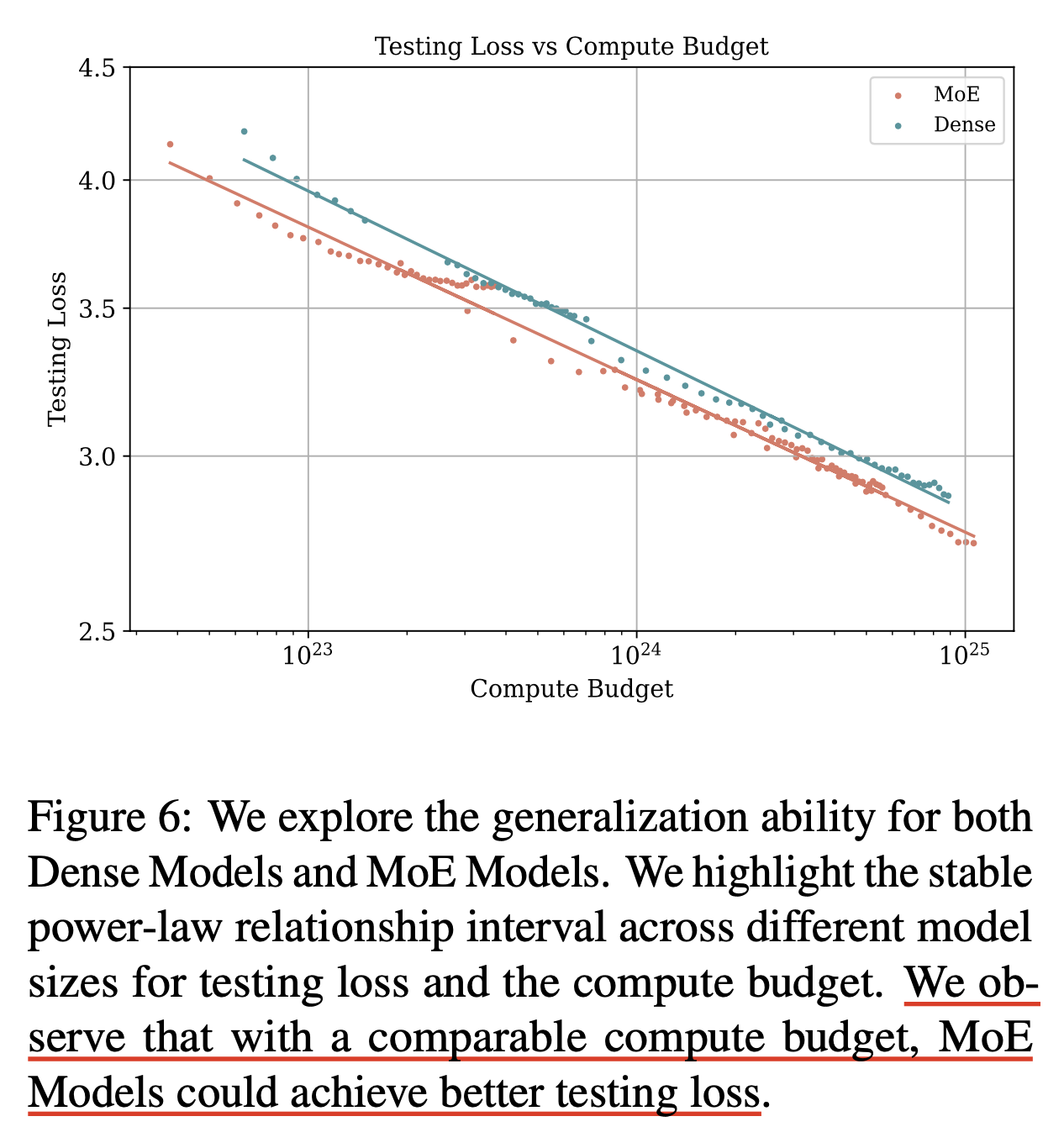moe_scaling_law_paper_fig6 Fig. Source from Scaling Laws Across Model Architectures: A Comparative Analysis of Dense and MoE Models in Large Language Models

아래 switch transformer의 figure를 보도록 하자. "for a fixed training duration and computational budget, should one train a dense or a sparse model?"

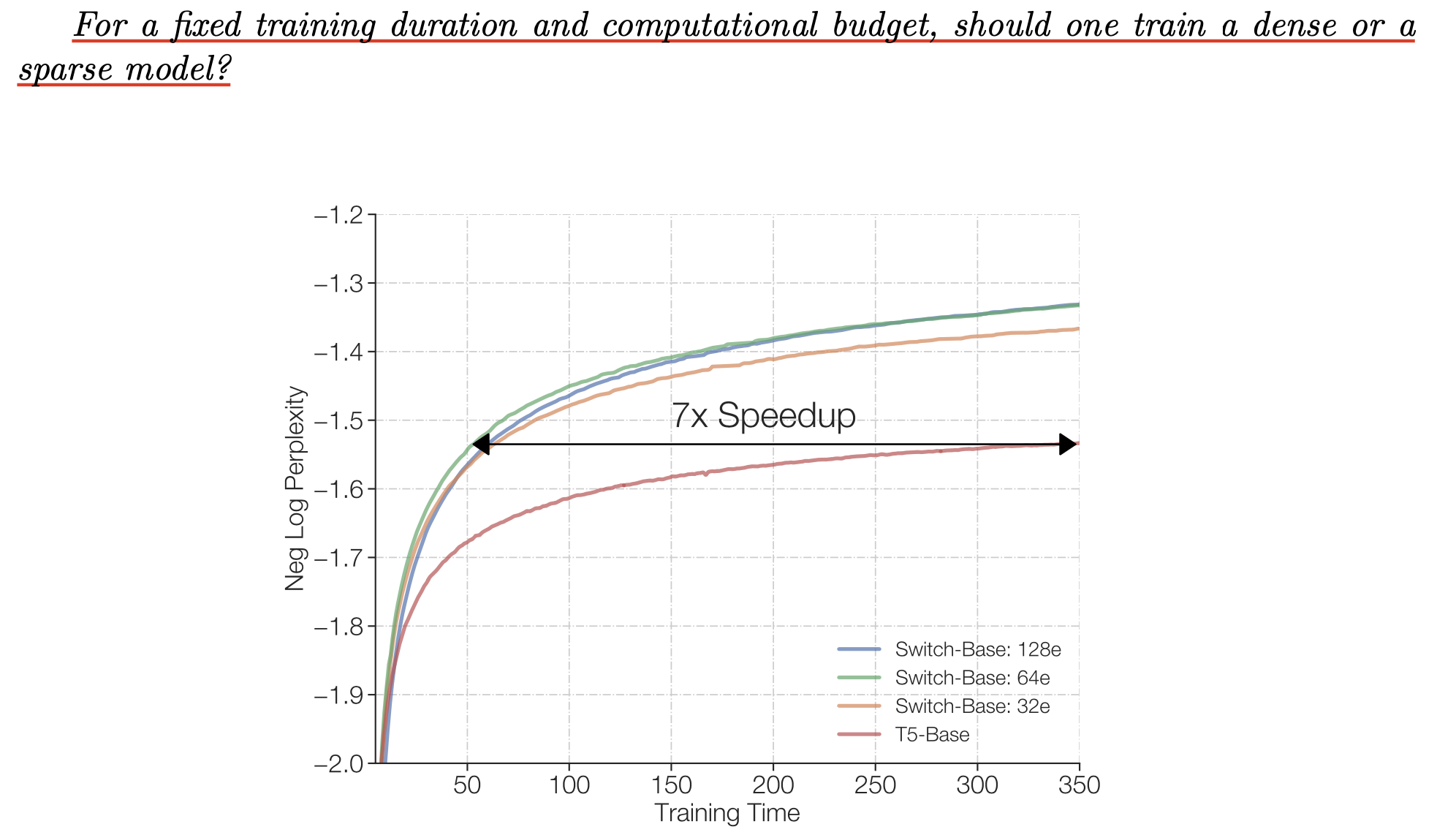
switch_transformer_paper_fig5

이에 대한 답은 moe다. moe를 사용하면 dense가 도달하고자 하는 perplexity에 도달하는 데 7배나 빠르게 도달할 수 있다. 실제로 from scratch로 학습된 Large Language Model (LLM) 중 정보가 공개된 것 중 하나인 DeepSeekMoE의 성능을 보면 (switch transformer는 T5 였으므로), 같은 activated parameter에 대해서 압도적인 성능을 보이는 걸 볼 수 있다. MoE에서 activated parameter 라는 것은 예를 들어 expert가 실제로는 16개인데 token마다 활성화 되는 expert는 그 token과 matching될 확률이 가장 높은 expert 1개 혹은 2개 라는 의미이며, 보통 model forward 시 같은 actiavted parameter를 쓰면 dense model과 MoE model 모두 공평하게 비교한다고 생각한다.

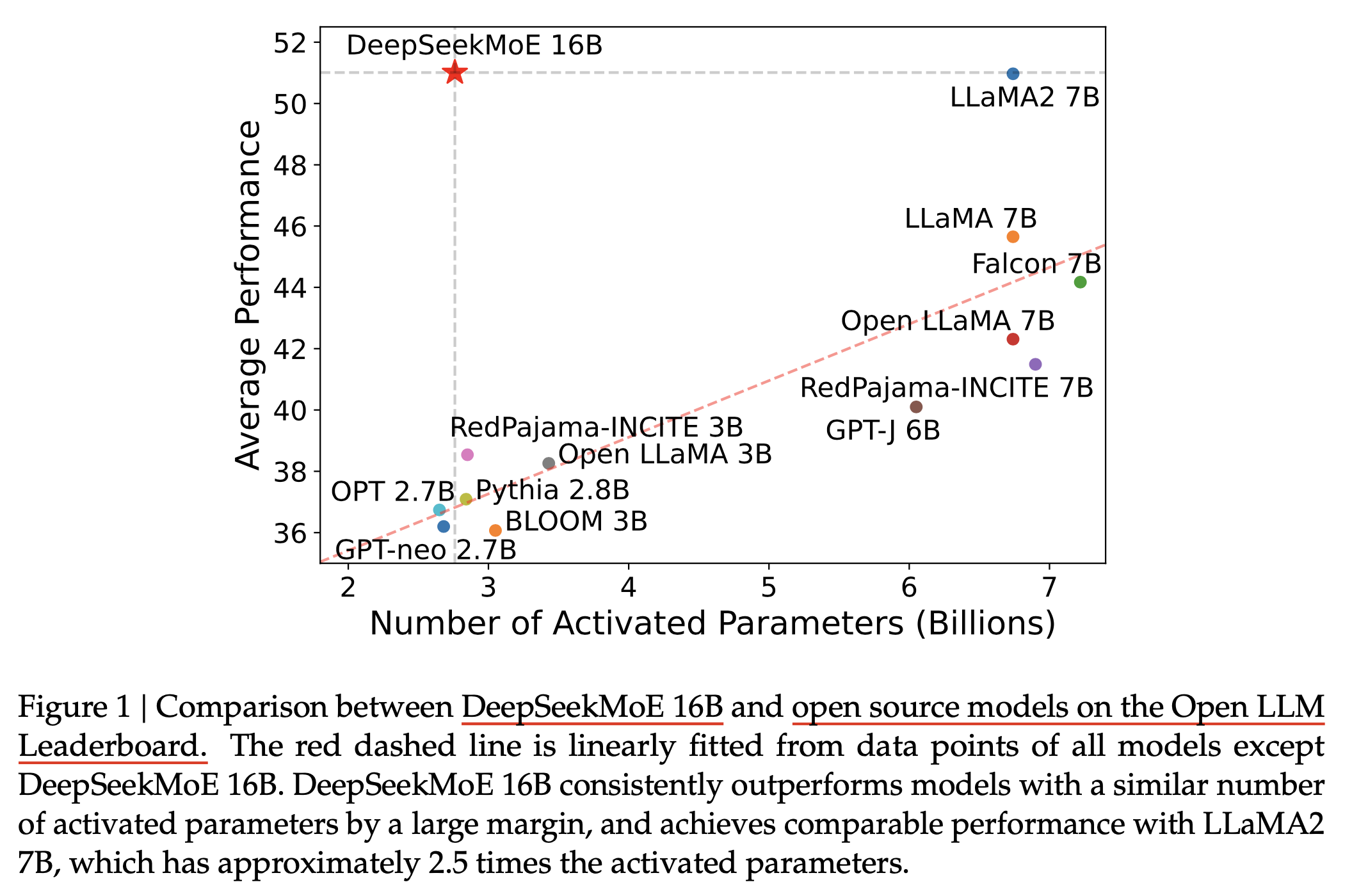deepseek_moe_paper_fig1 Fig.

물론 MoE와 dense를 비교할 때는 주의해야 할 점이 있는데, expert들이 모두 GPU device에 올라가서 대기하고 있어야 하므로 space complexity는 그만큼 더 점유하겠지만 초당 부동 소수점 연산량인 FLOPs가 그렇다는 것이라는 점이다.

아래 table을 보면 total parameter가 10배 가까이 차이나지만 activated parameter와 한 batch (2k tokens)를 처리하는데 드는 FLOPs 는 거의 유사하며, 이 때 똑같은 학습량 (training tokens)을 쓴다면 token당 FLOPs를 MoE가 좀 더 많이 쓰기 때문에 compute budget을 더 쓰는 셈이 되지만 MoE가 성능이 더 좋음을 확인할 수 있다.

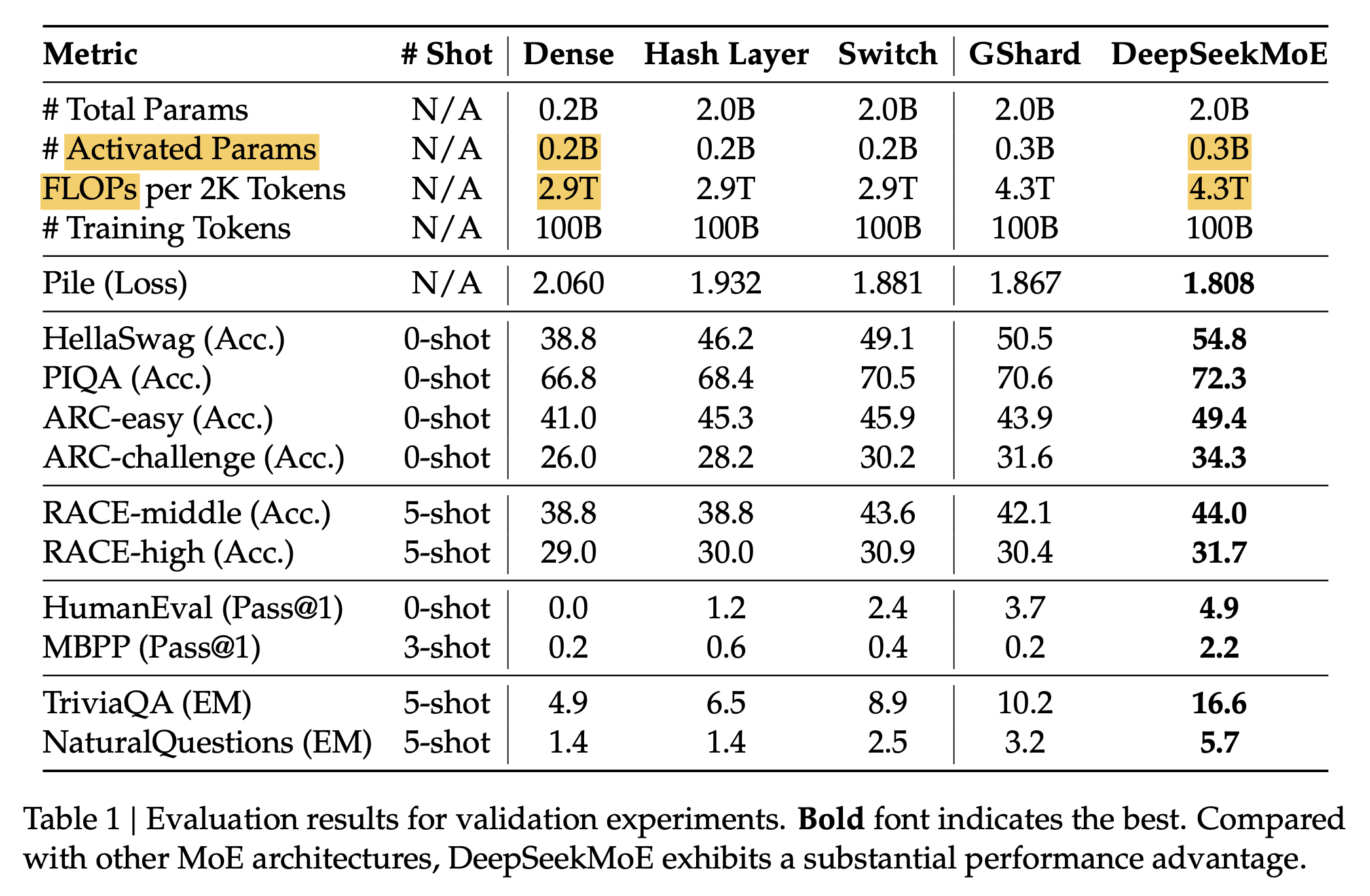deepseek_moe_paper_table1 Fig.

위의 small scale을 더 확장한 아래 두 table을 확인하면 같거나 훨씬 적은 token당 FLOPs를 쓰고도 MoE가 훨씬 압도적인 성능을 보여준다는 것을 확인 할 수 있다.

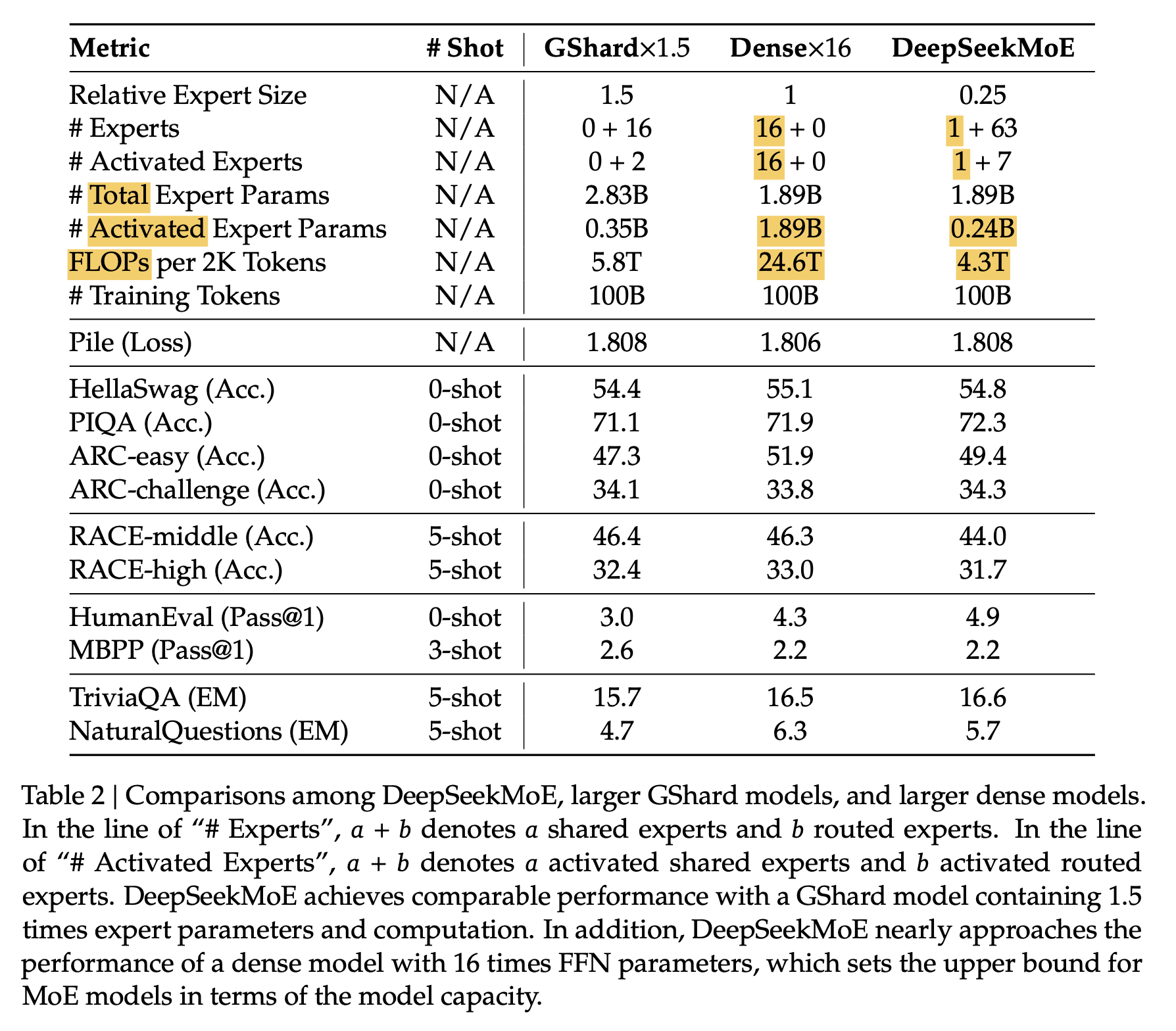deepseek_moe_paper_table2 Fig.

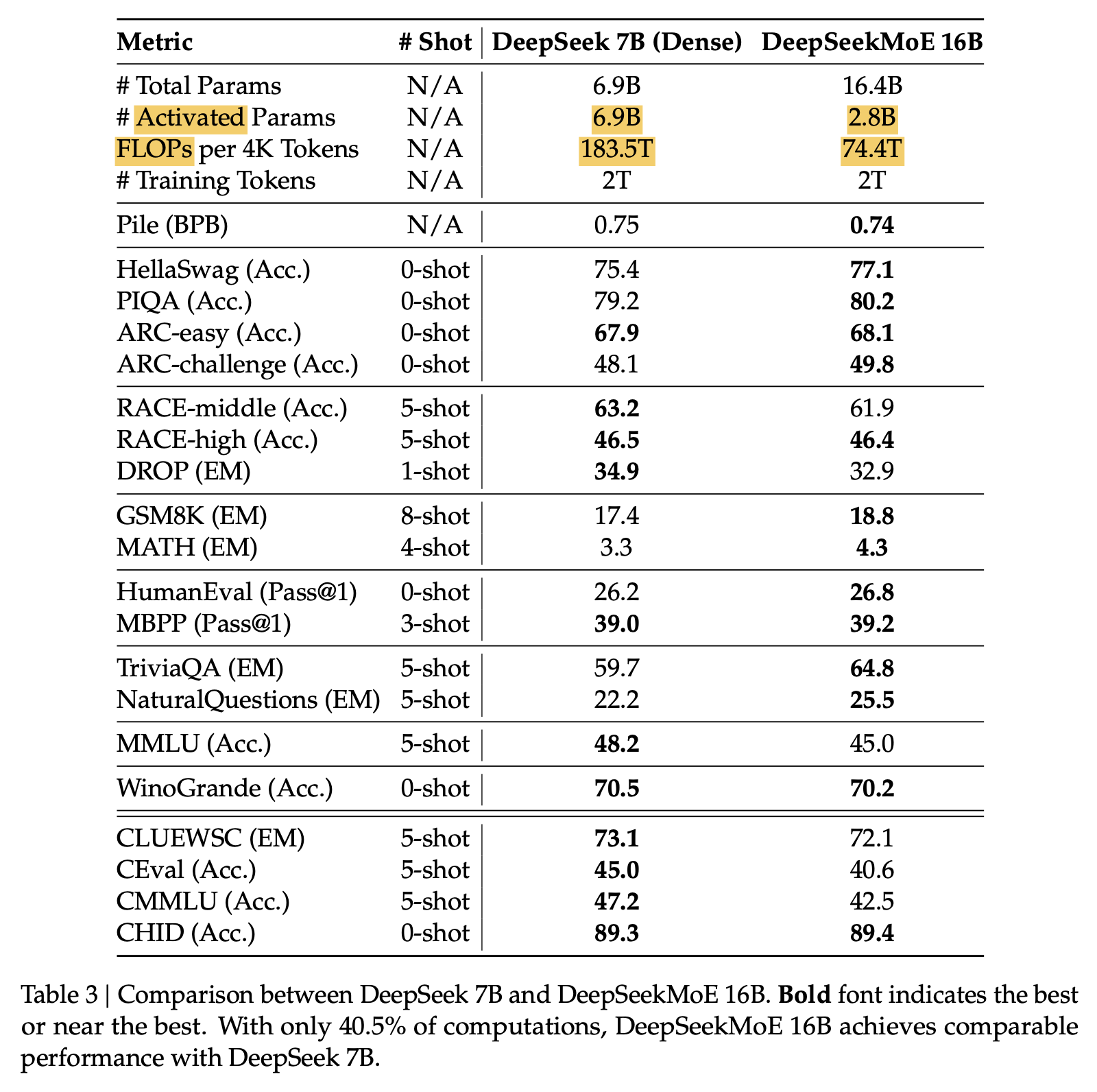deepseek_moe_paper_table3 Fig.

MoE가 좋은 또 다른 이유는 inference 효율이 좋기 때문이다. 사실 정확히 말하면 user가 instruction query와 함께 주는 document나 code를 prefilling 할 때 효율이 좋다는 것으로 보인다. 후에 잠깐 디스커션 하겠으나 실제로는 dense model에 비해 inference시 필요한 물리적인 gpu수가 더 많이 필요하며, token이 expert별로 나눠질 것이기 때문에 생성시에는 효율이 안 좋을 수 있다. 아무튼, 최근 화제가 되고있는 Cursor team의 interview를 보면, 언급 가능한 것들 중 breakthrough를 가져다 준 두 가지 ML detail 중 하나는 단연 MoE 였으며, 나머지 하나는 speculative decoding였다고 한다.

cursor_moe Fig. Source from Lex Fridman’s Podcast (transcription)

Code generation 같은 task에서 MoE가 좋은 이유는 예를 들어 code context가 10000 tokens 정도 된다고 칠 때 (debugging하려는 code context는 매우 길다), 예를 들어 어떤 1 layer Transformer의 FFN model의 사이즈가 16*8=200B일 경우 이를 모든 token에 쓰는 것 보다 16개로 쪼개서 각 token별로 8B씩 할당하는게 훨씬 효율이 좋기 때문이다. 이런 철학은 AlphaCode같은 데서도 드러나는데, AlphaCode는 Machine Translation (MT) task를 풀던 Encoder-Decoder Vanilla Transformer의 구조가 Encoder가 deep했던 것과 달리 Decoder가 매우 deep한데, 직접 저자에게 물어본 바로는 code context가 매우 길기 때문에 inference효율을 생각해서 이렇게 디자인했음에도 성능 열화가 없어서 decoder가 깊은 구조로 결정을 하게 됐다고 들었다.

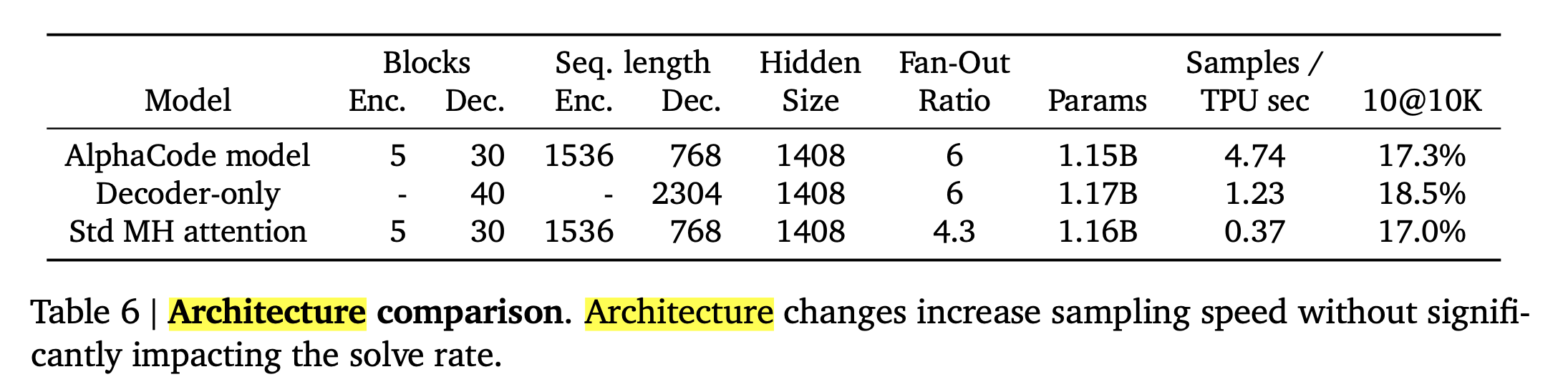alphacode_arch Fig.

MoE구조를 갖는 잘 학습된 Language Model (LM)의 경우에는 기대하건데 말 그대로 각 expert가 각자의 전문성을 가져야 할 것이다. 예를 들어 어떤 layer의 expert는 code에 특화되어있다던가 해야 할 것이다. 즉 선호하는 token이 있다는 것인데, Google의 ST-MoE paper에는 비록 encoder-decoder 구조에 MoE를 적용한 것이지만 아래와 같은 분석이 있다.

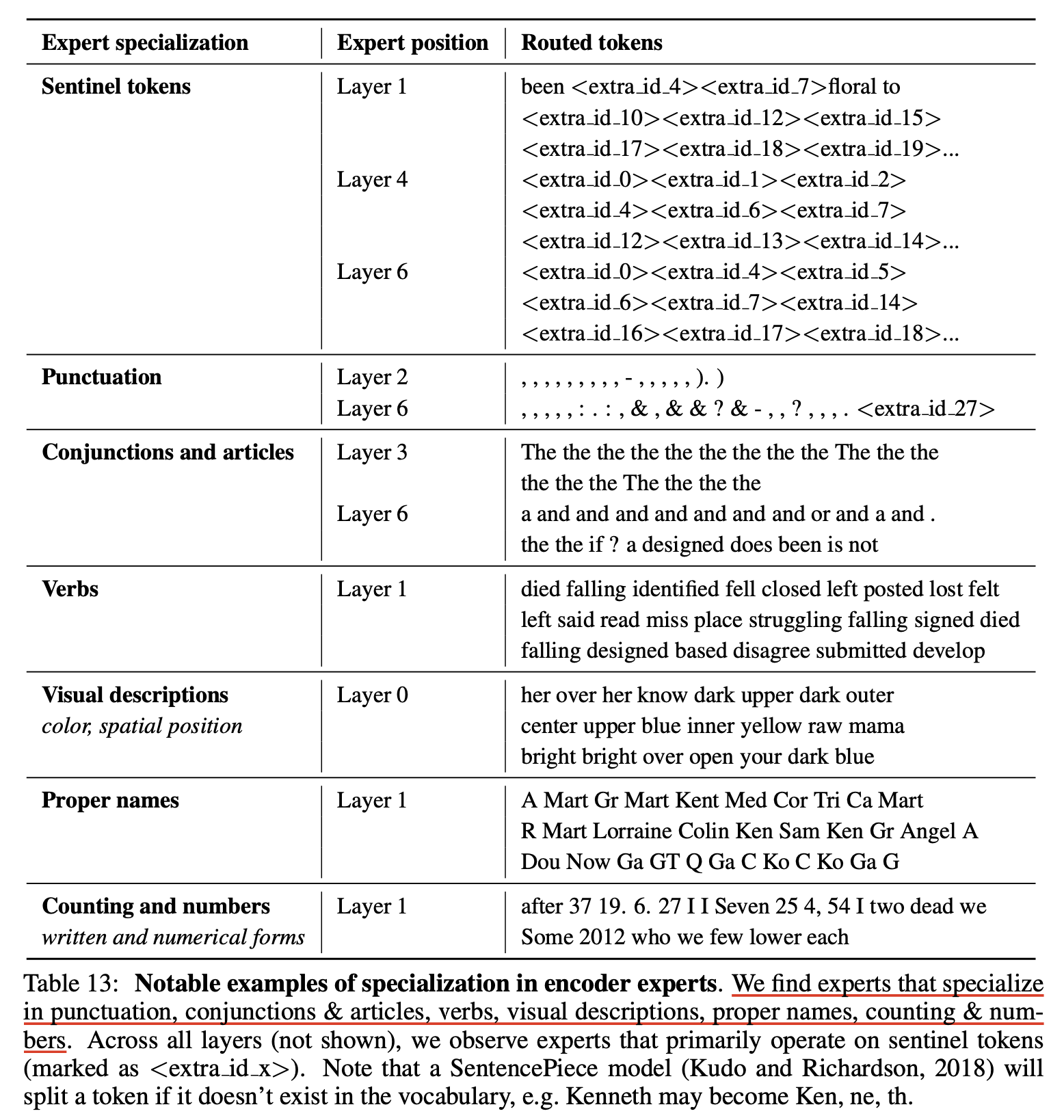st_moe_paper_fig13 Fig.

내가 바라는대로 high level 에서 domain에 따라 expert가 나뉘는 것은 아니고 punctuation 등에 따라 나눠지는 것을 알 수 있다. 또 비슷한 분석이 MoE model들에 종종 있는데, Mistral.ai의 Mixtral의 routing anaylsis를 보면 아래와 같이 pile testset의 subset domain에 따라서 각 layer별로 어떤 expert가 활성화 되는지와 code snippet에 대해서 어떻게 expert가 활성화되는지를 확인해볼 수 있다.

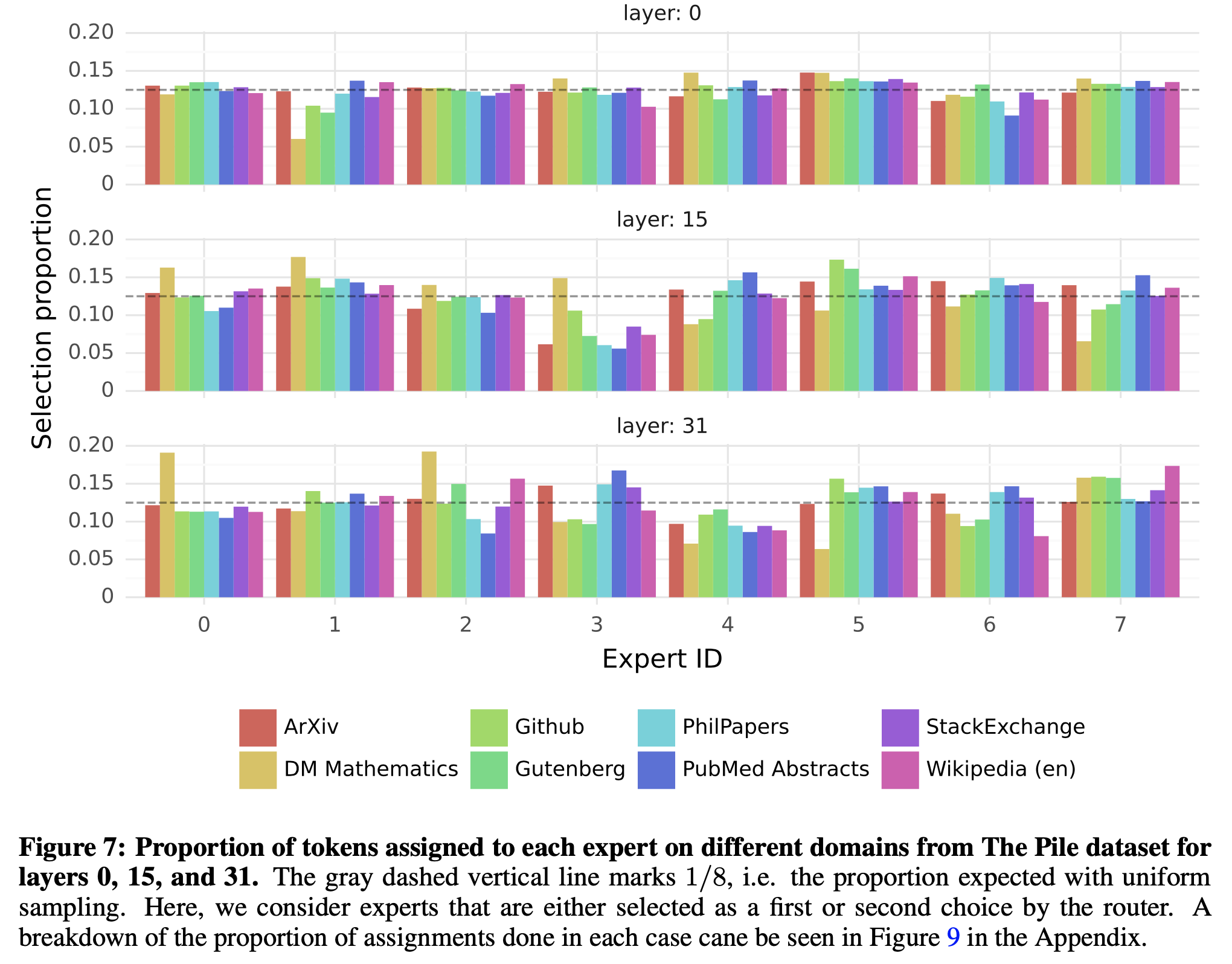mixtral_paper_fig7 Fig.

mixtral_paper_fig8 Fig.

사실 엄청난 일관성이 있는지는 모르겠으나 마지막 layer의 특정 expert가 거의 대부분의 indent token을 처리한다는 것 정도는 쉽게 눈에 들어온다. (paper들을 읽으면서 차차 insight를 더해보자)

(2022) Switch Transformer

이제 본격적으로 MoE paper들을 살펴보자.

이번 section에서는 Switch Transformers: Scaling to Trillion Parameter Models with Simple and Efficient Sparsity에 대해 살펴볼건데, 물론 Switch Transformer 이전에 Outrageously Large Neural Networks: The Sparsely-gated Mixture-of-Experts Layer나 GShard: Scaling Giant Models with Conditional Computation and Automatic Sharding같은 훨씬 오래된 paper들이 존재한다. 그리고 약 30년 전에 이미 Hinton et al.이 Adaptive Mixtures of Local Experts라는 paper에서 MoE의 개념을 제안했지만, Noam Shazeer 등의 Sparsely-gated Mixture-of-Experts 는 Recurrent Neural Network (RNN)에 대한 얘기이기 때문에 Switch Transformer 부터 다루려는 것이다.

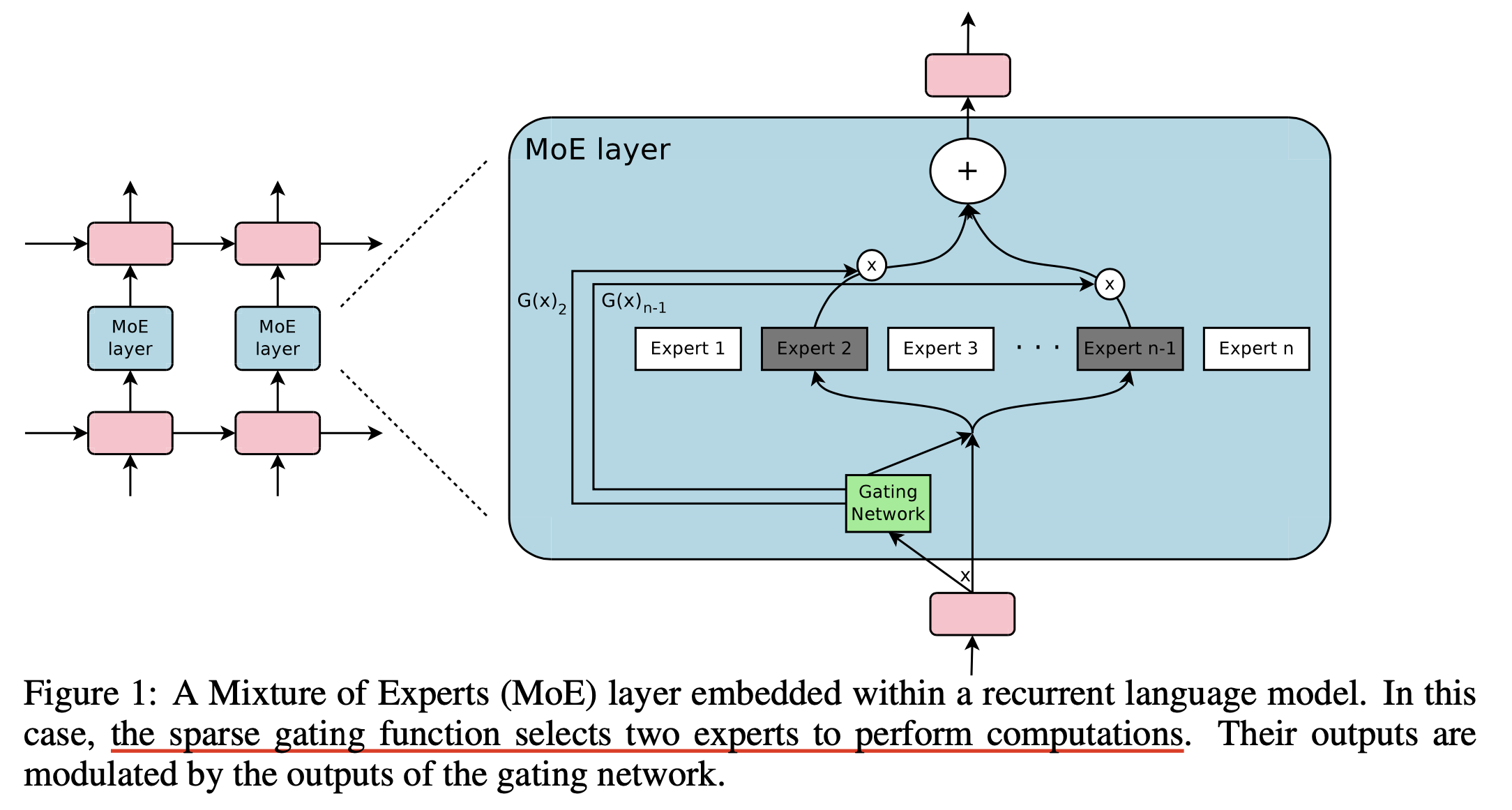sparsely_gated_rnn_moe_paper_fig1 Fig. MoE + RNN

Switch Transformer는 Google이 2021년 publish한 paper로, Transformer based MoE model 중 가장 단순한 (?) model 구성을 갖는다고 볼 수 있다. vision task와 LM task 모두에서 MoE가 훨씬 더 scalable하다는 것을 보였다.

먼저 expert가 \(N\)개라고 하면 input, \(X \in \mathbb{R}^{B \times L \times d}\)는 router module을 통과하면 각 expert에 대한 logit값을 뱉게 되고, \(\text{Router}(X) \in \mathbb{R}^{B \times L \times N}\), 이를 softmax activation function에 통과시켜 각 router로 갈 확률을 뽑아 가장 확률이 큰 router로 각 token을 할당해서 expert FFN에 개별적으로 통과시키게 된다. 그리고 나온 output값은 prob weight와 곱해져 다음 residual block으로 가게된다.

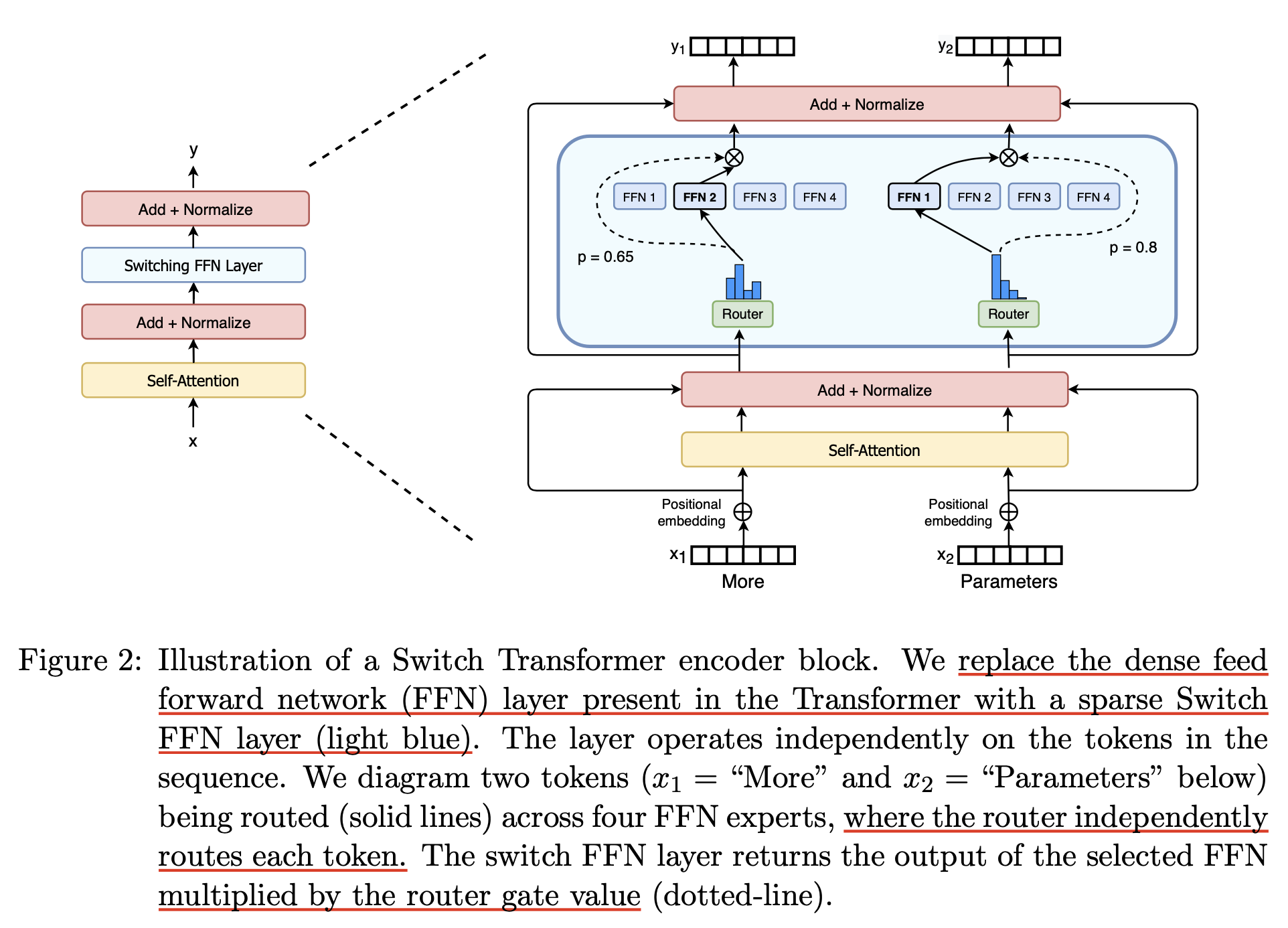switch_transformer_paper_fig2 Fig.

Switch transformer는 각 token이 하나의 expert만 선택할 수 있는데, 여기서 문제가 있는 것이 모든 token이 하나의 expert만 선택한다거나 하면 안된다는 것이다. 그러면 training efficiency 관점에서도 안좋고 (한쪽으로 쏠리니 OOM이 날 수도 있고 OOM이 안나더라도 나머지 expert들은 기다리는 상황이 발생하므로 비효율적), 성능상도 MoE를 하는 이유가 없어지게 된다. 그래서 capacity factor, \(c\)라는 개념을 도입하게 되는데, 이 factor에 따라서 각 expert가 할당받을 수 있는 최대 token 수가 결정된다.

\[\text{expert capacity} = \frac{ \text{tokens per batch} }{ \text{number of experts} } \times \text{capacity factor}\]

그런데 그럼에도 불구하고 expert가 처리하는 token량은 한계가 있는데, 가령 batch당 token이 128개인데, epxert가 16개이고 factor가 2.0이라면 8*2.0 = 16개 토큰을 각 expert가 처리하게 되지만 이를 넘어가는 token은 버려야 하는데, 이를 drop 한다라고 표현한다.

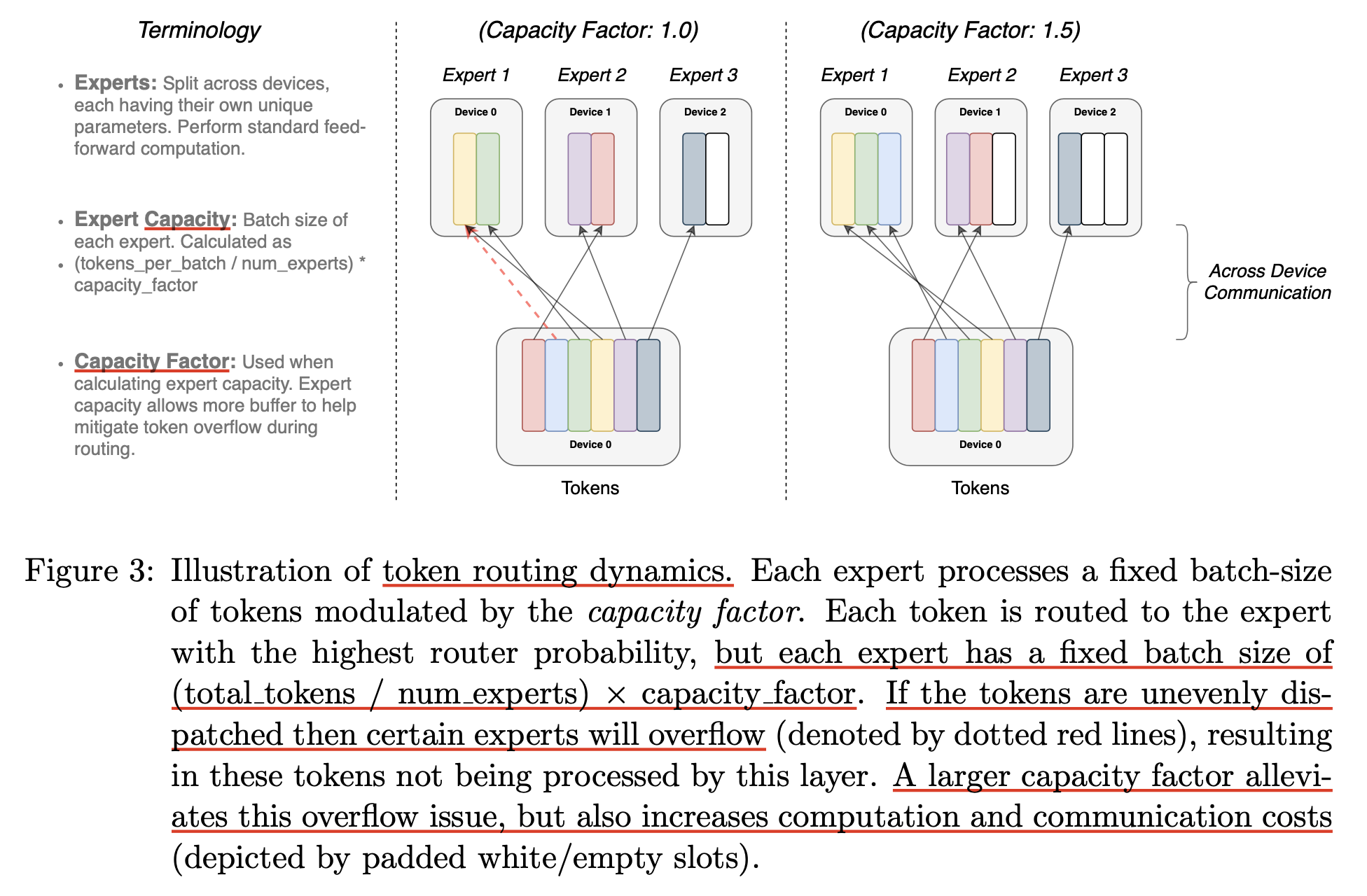switch_transformer_paper_fig3 Fig.

A Differentiable Load Balancing Loss

Experimental Results

(2022) Mixture-of-Experts with Expert Choice Routing

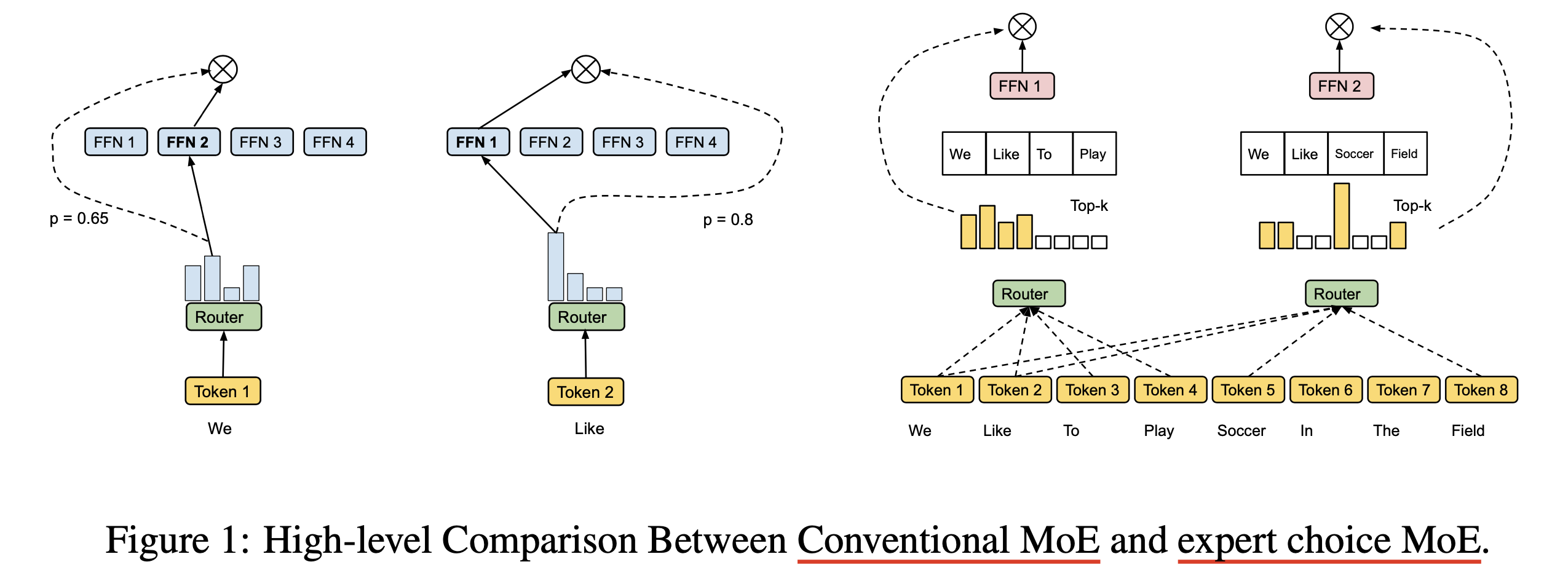expert_choice_moe_paper_fig1 Fig.

expert_choice_moe_paper_contribution Fig.

observations from OLMOE (2024)

olmoe_paper_TC_vs_EC_fig1 Fig.

olmoe_paper_TC_vs_EC_fig2 Fig.

(2022) ST-MoE: Designing Stable and Transferable Sparse Expert Models

st_moe_paper_contributions Fig.

GPT-4 Leaked Details

다음으로 넘어가기 전에 intro에서 얘기햇던 gpt-4 leaked details에 대해 조금만 얘기해보자.

gpt4_leaked_fig1 Fig.

  • 먼저 gpt-4는 111B의 MLP가 16개로 구성된 MoE구조에 attention parameters가 대략 55B로 1.8T에 달하며, expert는 token당 2개가 선택됐음
  • 13T 학습됨
  • 4k로 학습되고 8k로 further training됨

leak도니 시점이 7월쯤인 것으로 보이고 이게 맞는 정보인지는 모르겠지만, 우선 맞다는 가정하에 생각해보면 모델 규모는 릴리즈 당시 매우 느렸던것과 성능을 생각해보면 말이 되는 크기인 것 같아보인다. 그리고 13T로 학습됐다는 것은 지금 SOTA open weight model들이 10T가까이 학습되는걸 생각해보면 그 당시에도 compute optimal로 학습한 것은 아닌 것으로 보인다 (over-training regime에 대해 더 빨리 알고있었던 듯 하다).

gpt4_leaked_fig2 Fig.

그 다음은 distributed training plan인데, tensor parallel (TP): pipeline parallel (PP)=8:16을 쓰고 zero-1 같은 optimizer state를 sharding하는 distributed optimizer를 썼다고 한다. 흠 근데 expert parallel (EP)에 대한 정보가 없어서 이게 맞는지는 모르겠다. 왜냐면 최근 llama3 paper를 보면 405B dense model을 학습하는데 정확히 8:16이 쓰였고 이는 VRAM memory가 더 큰 H100일 때의 얘기이기 때문이다. 물론 gpt-4의 경우 4k로 학습된것이고, batch tokens가 모든 expert를 합쳐 60M인 것이면 activation memory가 더 작아서 가능한지도 모르겠지만 말이다.

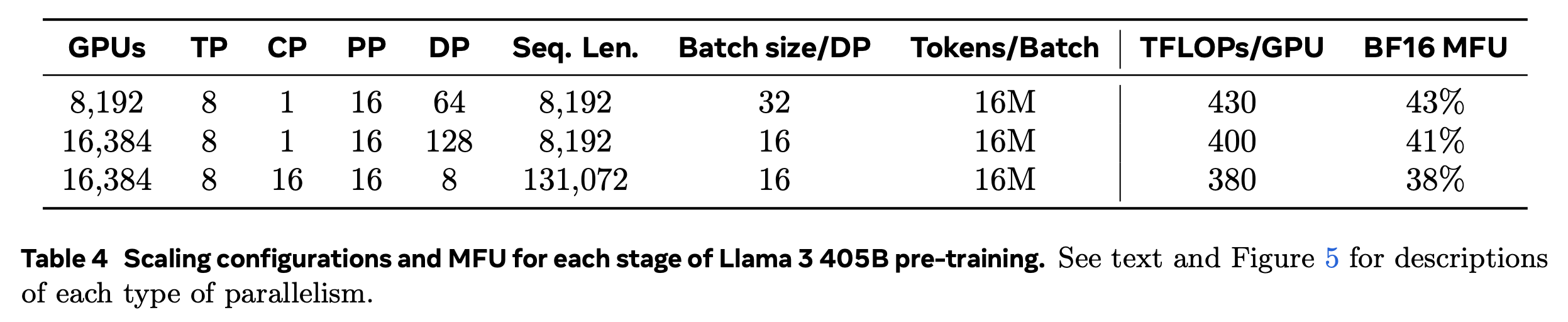llama3_paper_405b_distributed_training_plan Fig. Source from llama3

아무튼 A100 25000대로 MFU 32~36정도로 90~100일 정도 학습을 했다고 하는데, 보통 GPU수가 만대를 넘어가는 스케일이면 communication cost 때문에 MFU를 잘 뽑기 힘든 상황에서 (아마 Llama3 405B도 16k 정도 gpu를 썼고 mfu는 40안팎이었던 것 같다), 이정도면 대단한 것 같다. H100도 아니고 A100으로 이걸 해냈다는 것도 대단한데, 생각해보면 scaling 하는 데 있어서 선구자들인 oai는 GPT-3도 지금보면 너무 구려서 못쓰겠는 V100으로 해냈었다.

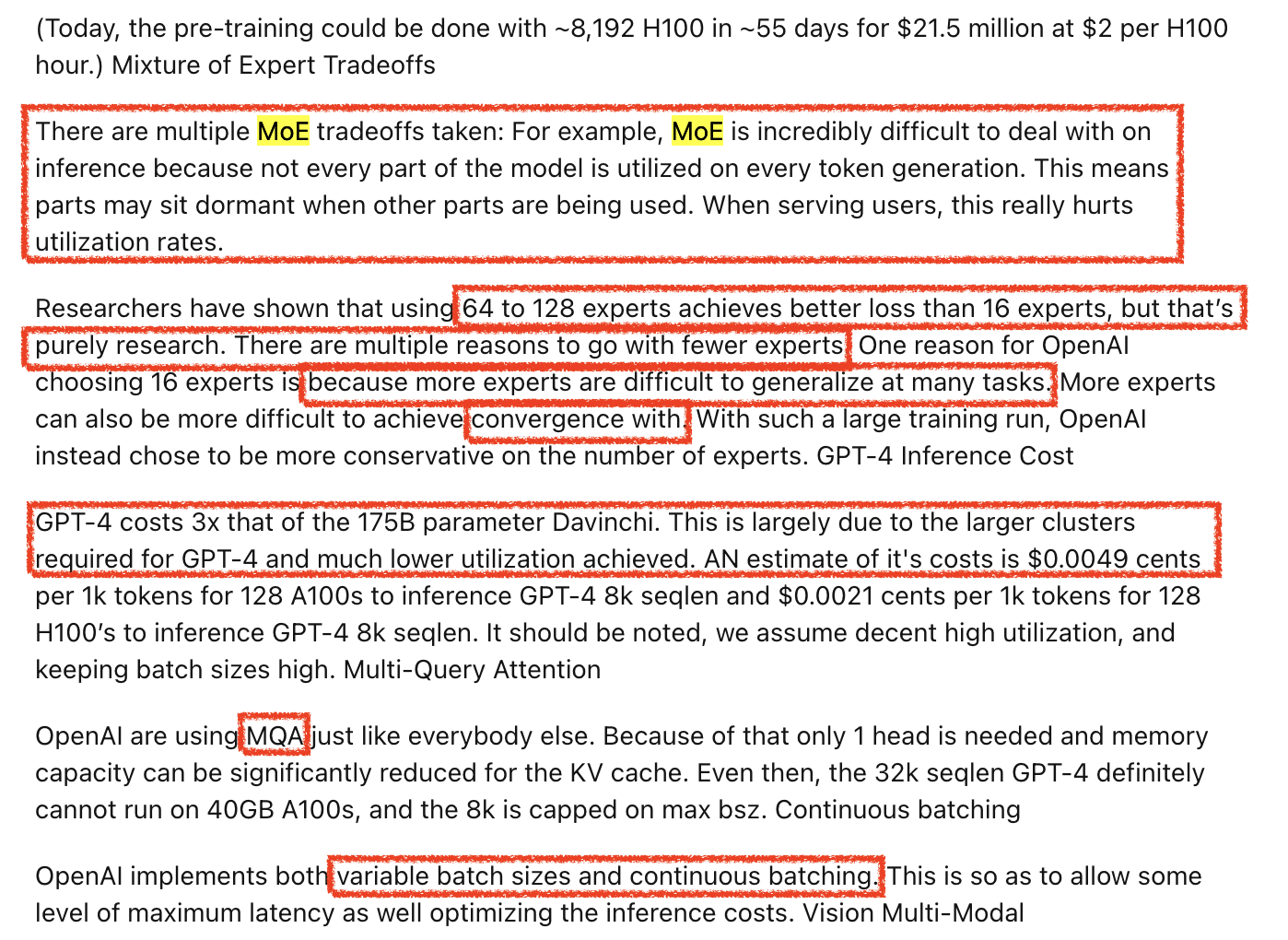gpt4_leaked_fig3 Fig.

그 다음은 Multi Query Attention (MQA)를 썼다는것과 MoE를 왜 16개밖에 쓰지 않았는가?에 대한 얘기인데, 후자에 대해서는 수렴성과 task generalization 때문이라고 하는데 좀 생각해봐야 할 부분인 것 같다. 다만 MQA같은 부분은 Grouped Query Attention (GQA), Multi-head Latent Attention (MLA), Cross Layer Attention (CLA) 등 key-value caching memory complexity와 연산량을 줄이기 위한 노력이 gpt-4이후의 model들에서 계속 공유되고 있기 때문에 합리적인 것으로 보인다.

gpt4_leaked_fig4 Fig.

gpt4_leaked_fig5 Fig.

이하 inference에 대한 얘기는 일단 넘어가도록 하는데, FSDP 얘기는 왜 나오는지 모르겠다. (누가 이만한 규모에서 ring latency가 gpu 갯수만큼 선형으로 늘어나는 FSDP를 쓴다고..?)

Upcycled MoE

MoE model을 만드는 방법으로는 from scratch부터 학습하는 것 이외에 Upcycling이라는 방법이 있다. 이번 post에서는 Google의 Sparse Upcycling: Training Mixture-of-Experts from Dense Checkpoints와 NVIDIA의 Upcycling Large Language Models into Mixture of Experts를 주로 살펴볼 것이다.

(2022) Sparse Upcycling: Training Mixture-of-Experts from Dense Checkpoints

Upcycling이라 함은 아래처럼 FFN layer를 expert 갯수만큼 copy해서 MoE로 만드는 것이다. 이 때 parameter는 당연히 copy되고 optimizer state도 각 gpu device로 copy되는데, optional하게 copy된 expert들을 random init하거나 optimizer state를 loading하지 않을 수도 있다. 이럴 경우 optimizer는 adam을 쓸 경우 당연하게도 momentum이 없는 상태로 시작 될 것이다. 그리고 각 token을 어디로 할당할지 정하는 router module은 당연히 어디서 copy할 수 없기 때문에 random init하게 된다.

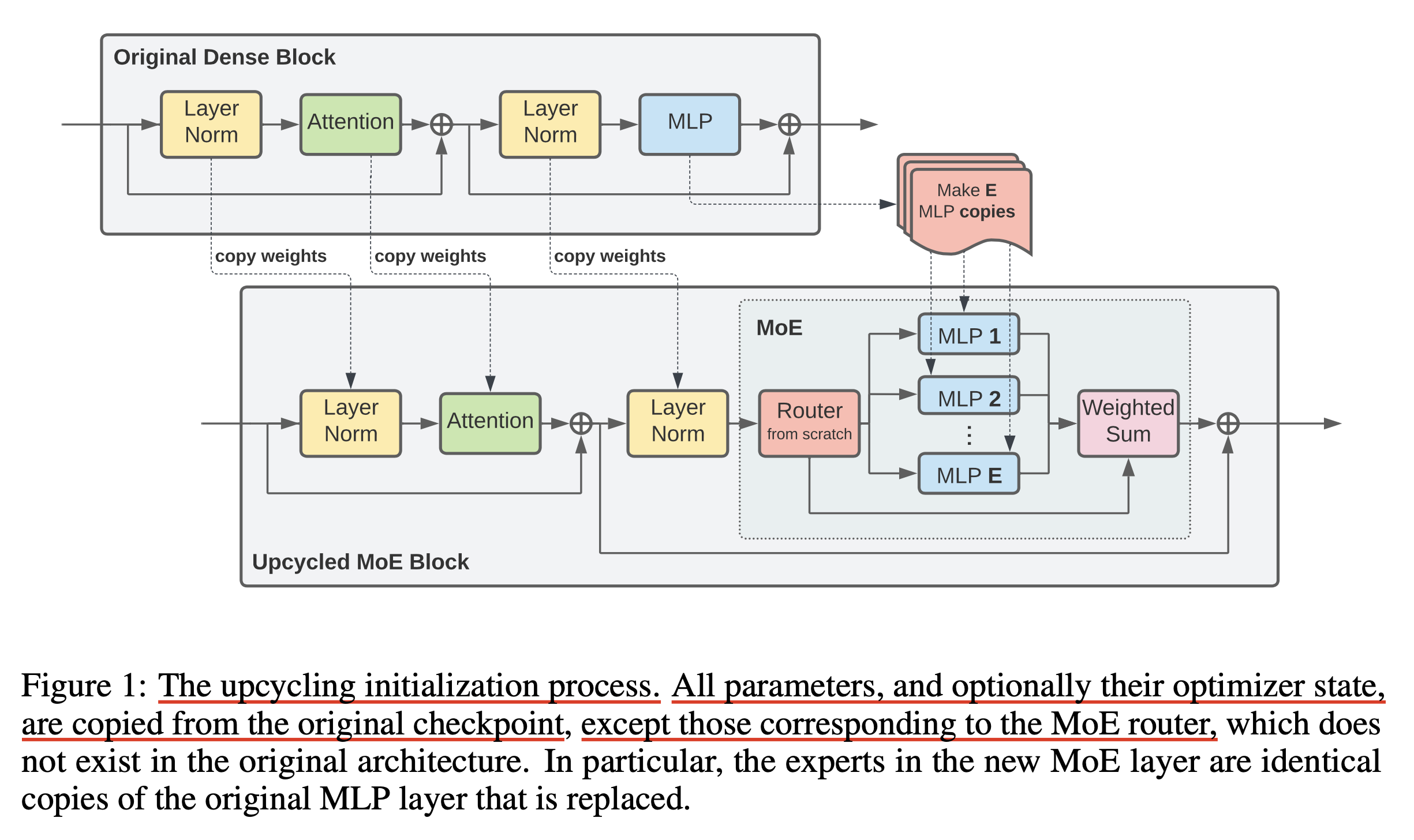sparse_upcycling_paper_fig1 Fig.

이 paper에서 중점적으로 확인한 것은 dense model을 예를 들어 1T tokens 학습한 경우 upcycling을 했을 때와 dense model을 그대로 further pre-training했을 경우 누가 더 좋고 얼마나 더 좋냐는 것이다. 그리고 나아가 upcycling이 아닌 from scratch로 학습한 경우는 dense model로 init한 upcycled MoE와 얼마나 차이가 나며, 얼만큼 시간이 경과하면 이 둘이 역전이 되는가를 봤다. 여기에 추가로 그동안 google이 리소스를 많이 투자해서 연구한 MoE인 만큼 다양한 design choice를 ablation했으며, 주요 목록은 다음과 같다.

sparse_upcycling_paper_ablation_module_fig1 Fig.

sparse_upcycling_paper_ablation_module_fig2 Fig.

observations from OLMOE (2024)

olmoe_paper_sparse_upcycling_fig1 Fig.

olmoe_paper_sparse_upcycling_fig2 Fig.

(2024) Upcycling Large Language Models into Mixture of Experts

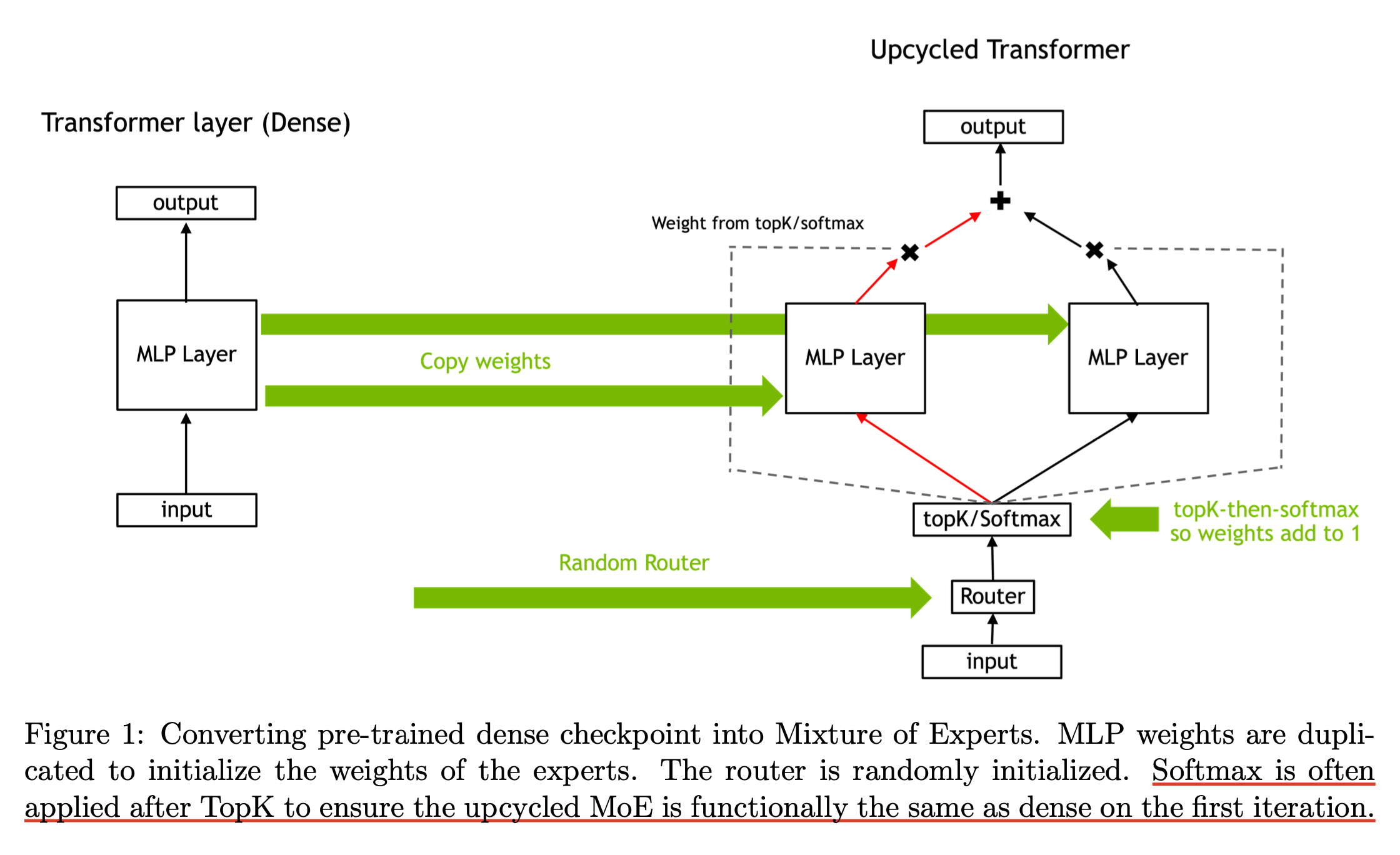nvidia_upcycling_paper_fig1 Fig.

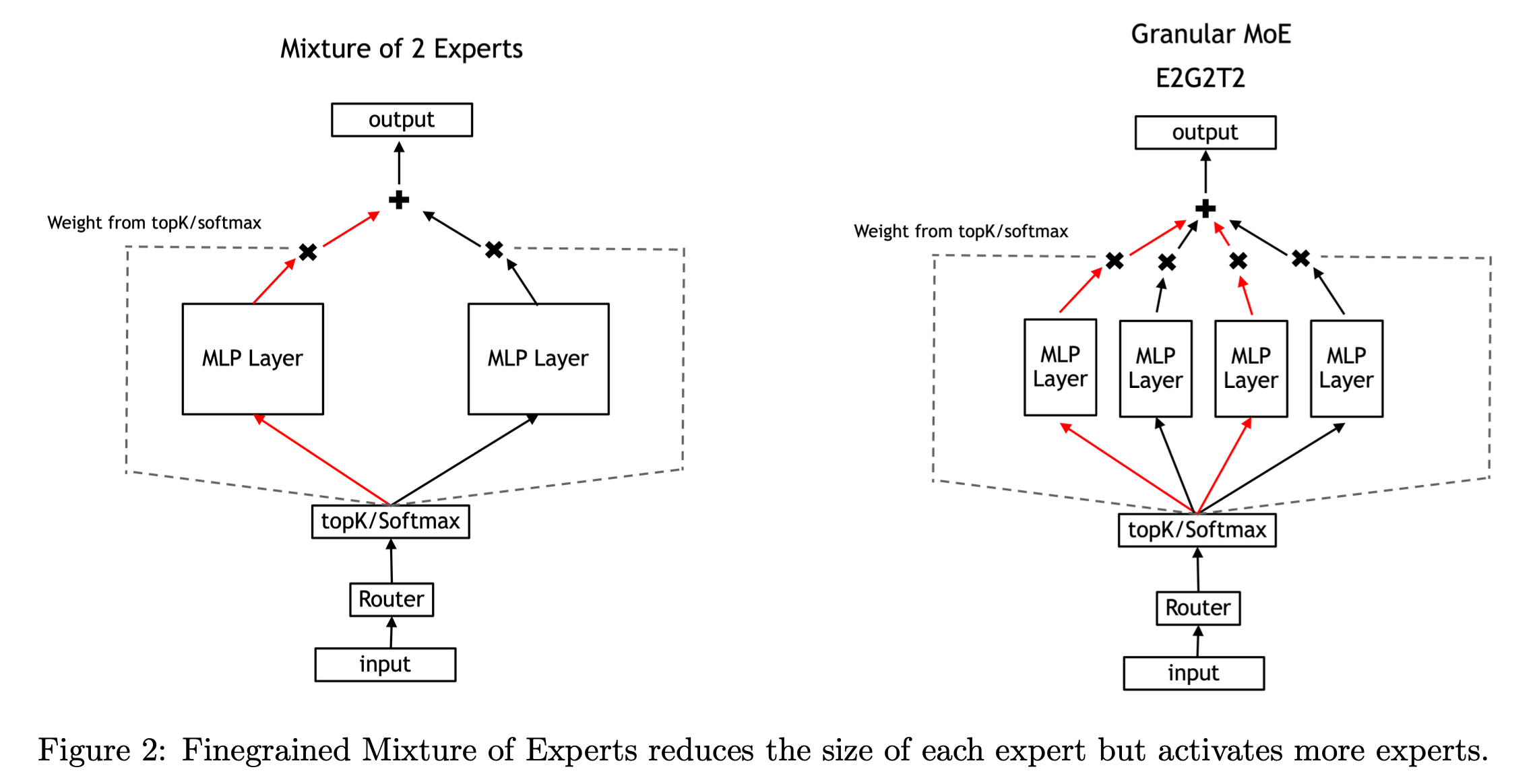nvidia_upcycling_paper_fig2 Fig.

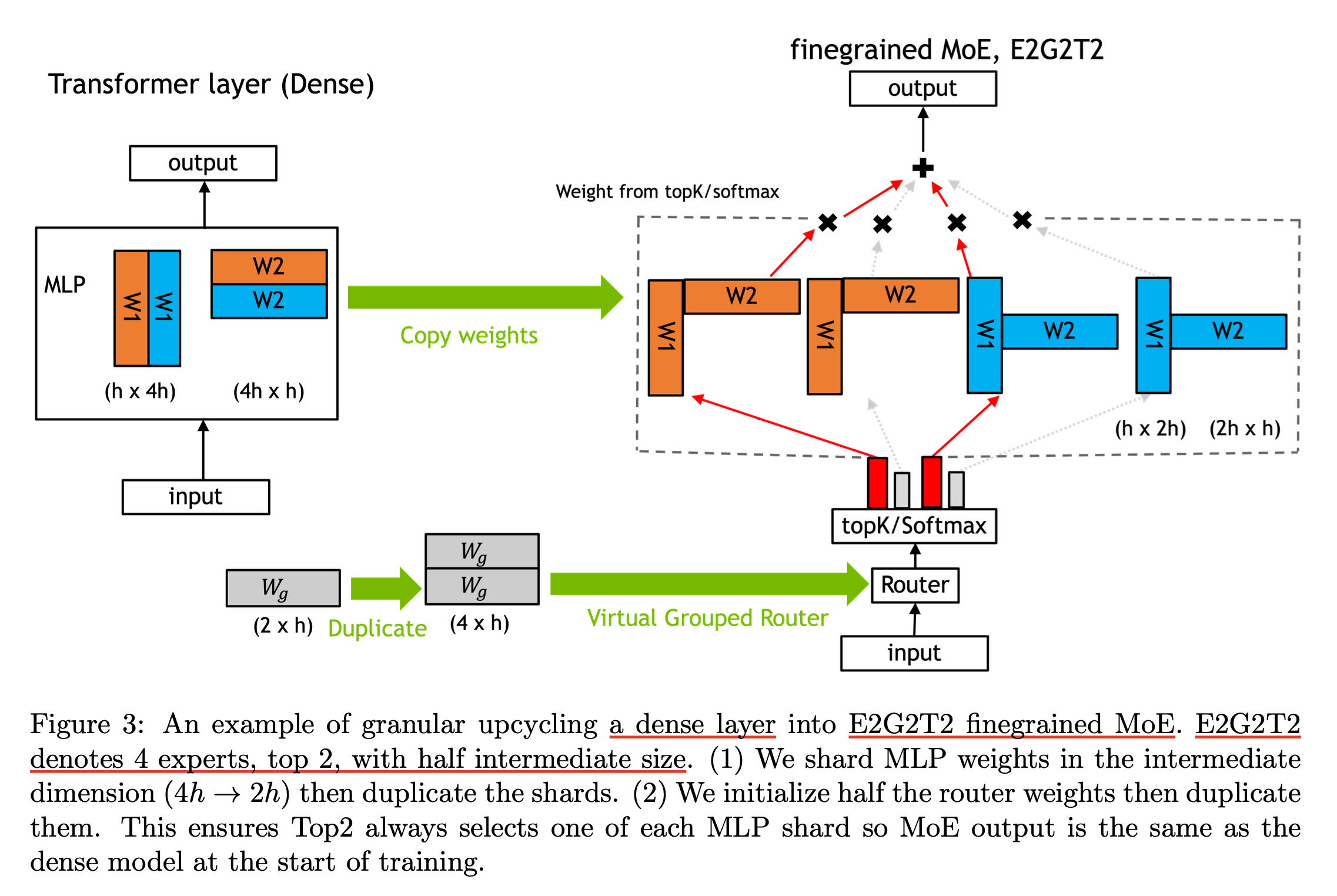nvidia_upcycling_paper_fig3 Fig.

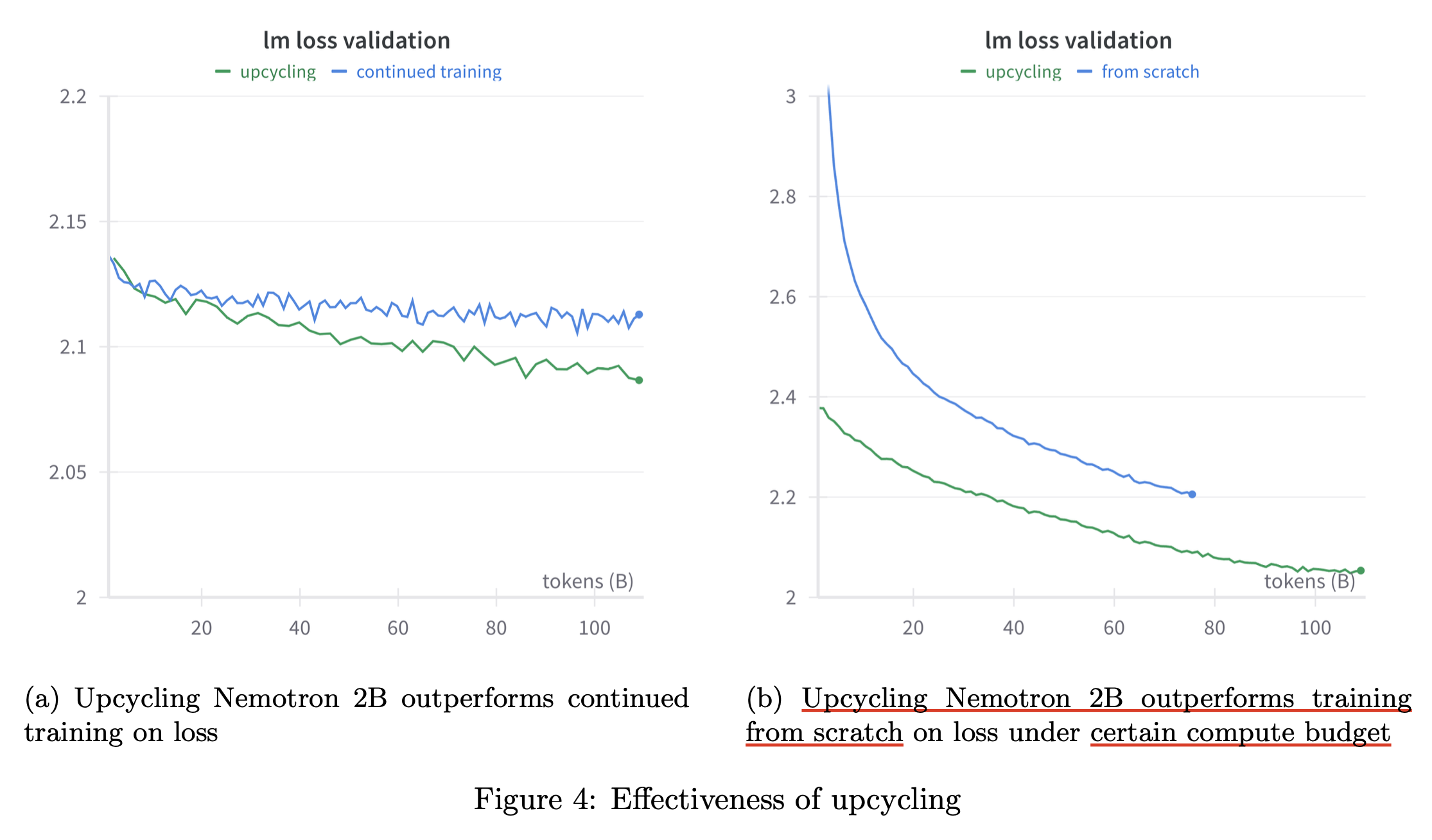nvidia_upcycling_paper_fig4 Fig.

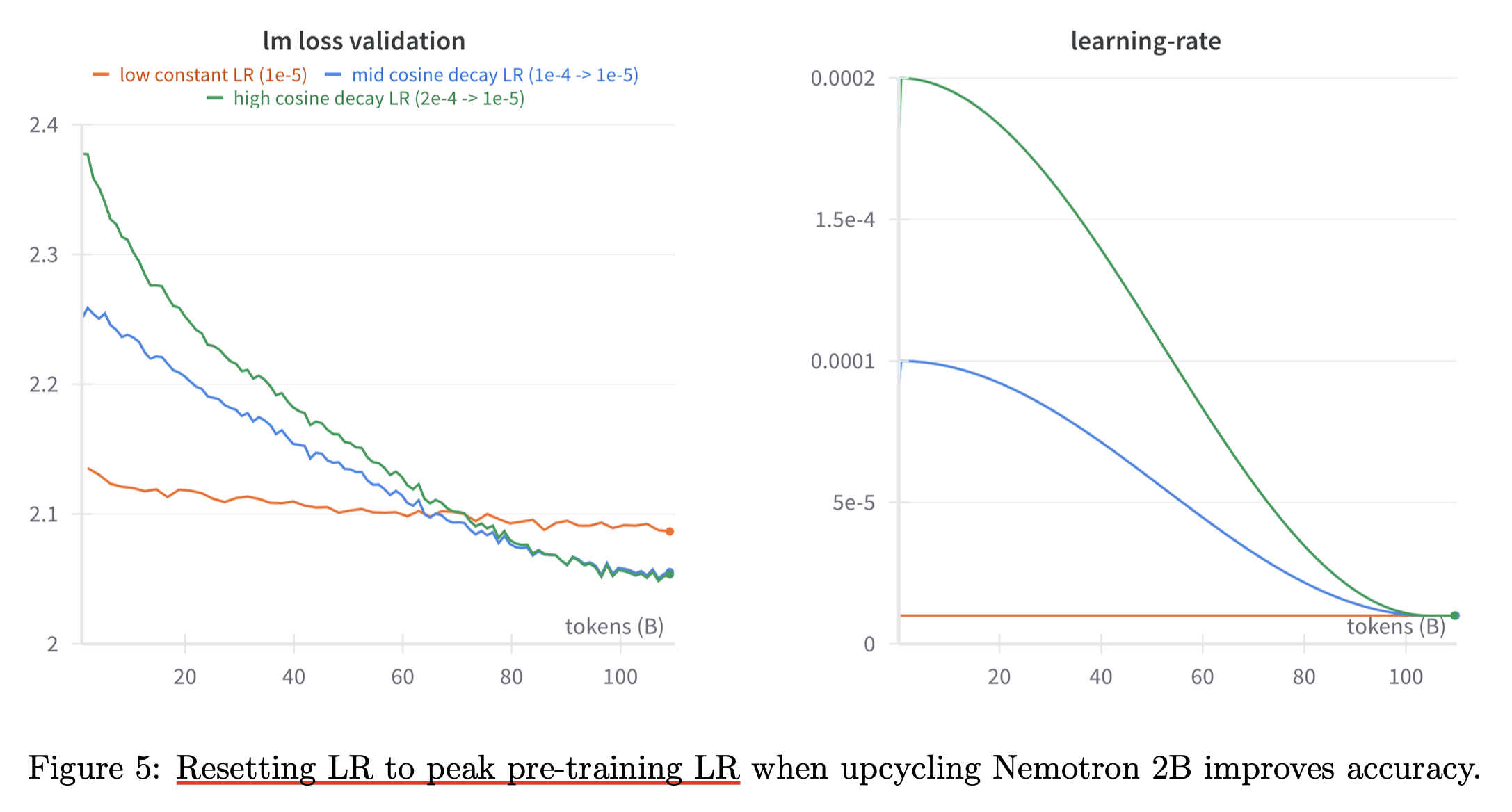nvidia_upcycling_paper_fig5 Fig.

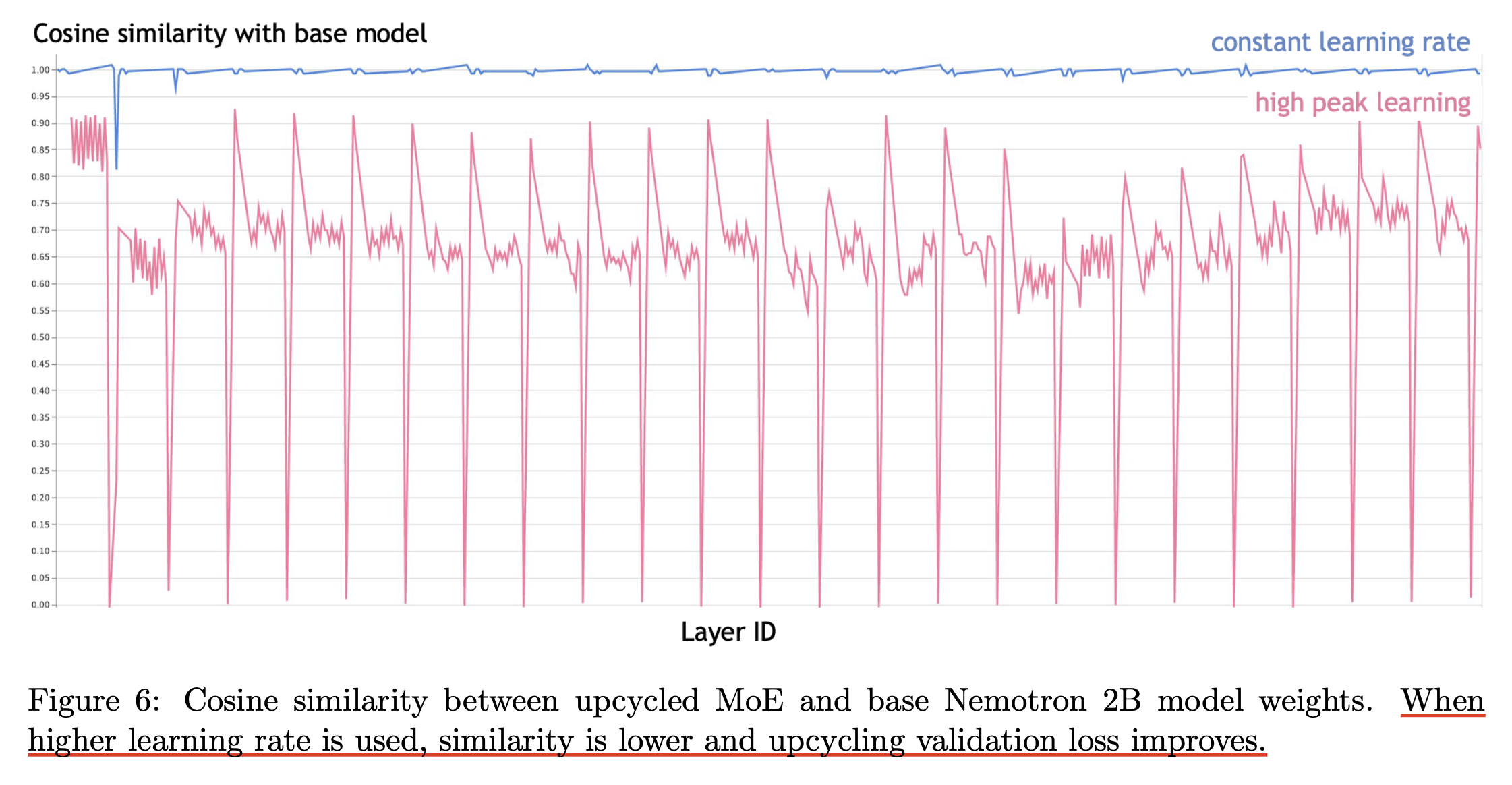nvidia_upcycling_paper_fig6 Fig.

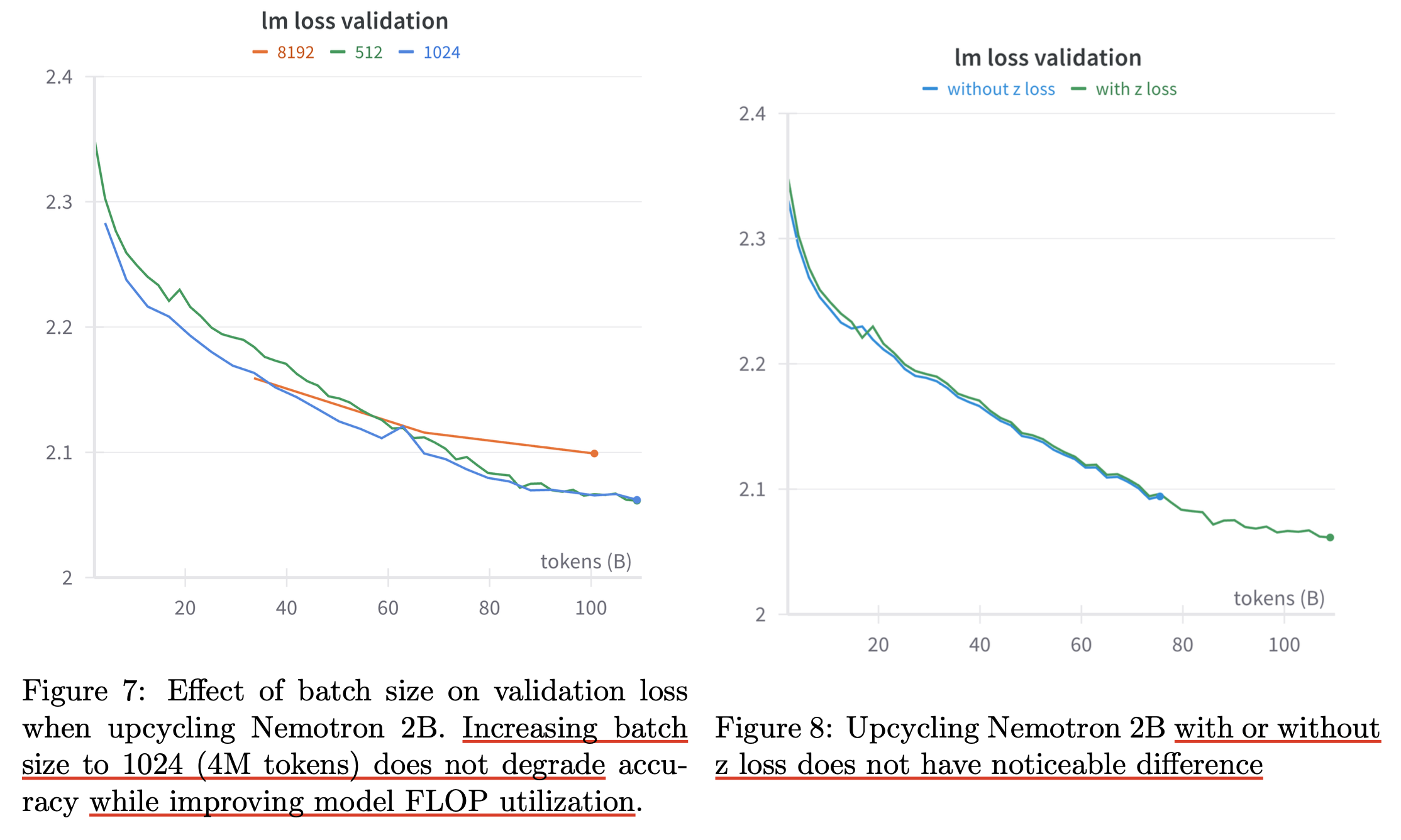nvidia_upcycling_paper_fig7 Fig.

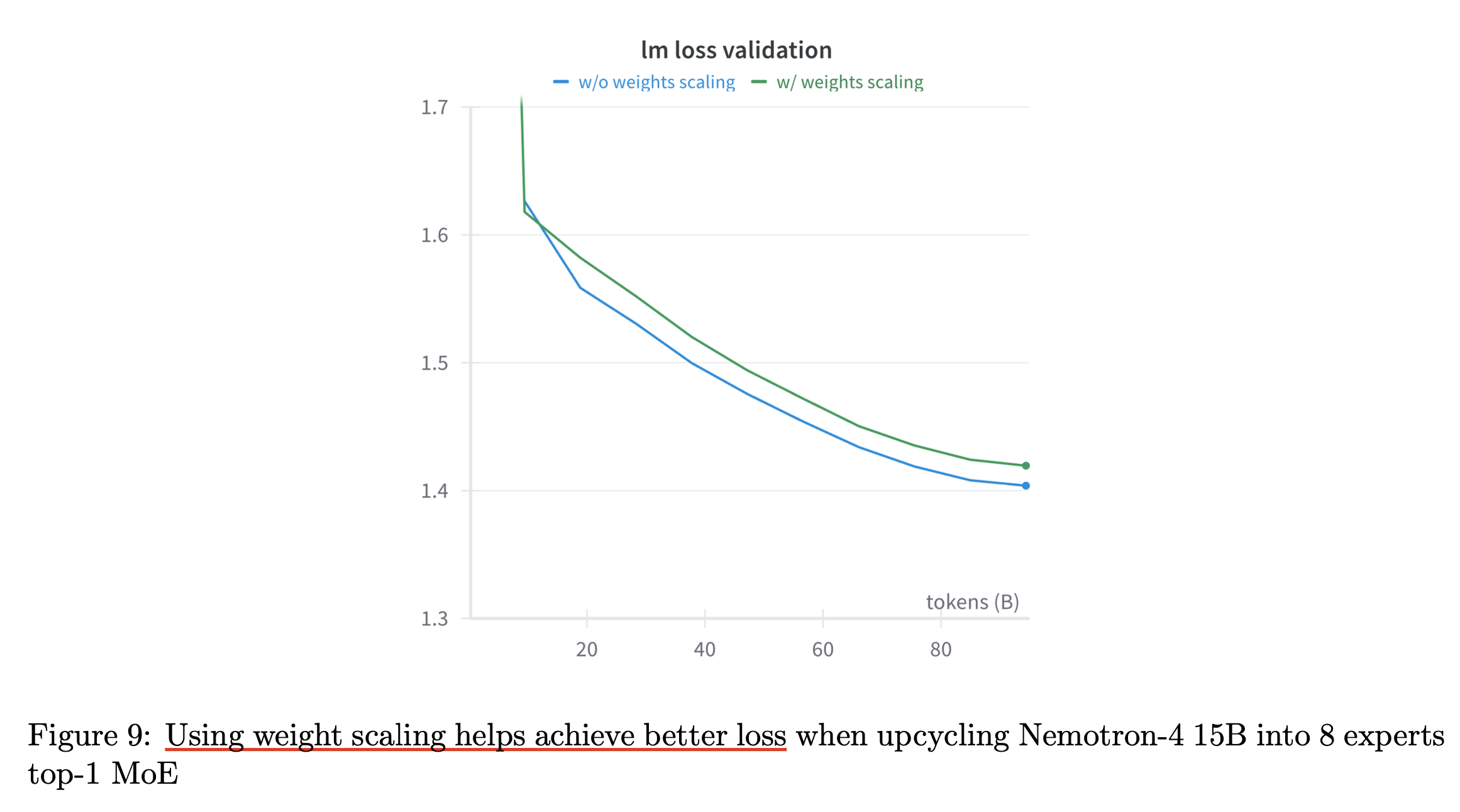nvidia_upcycling_paper_fig9 Fig.

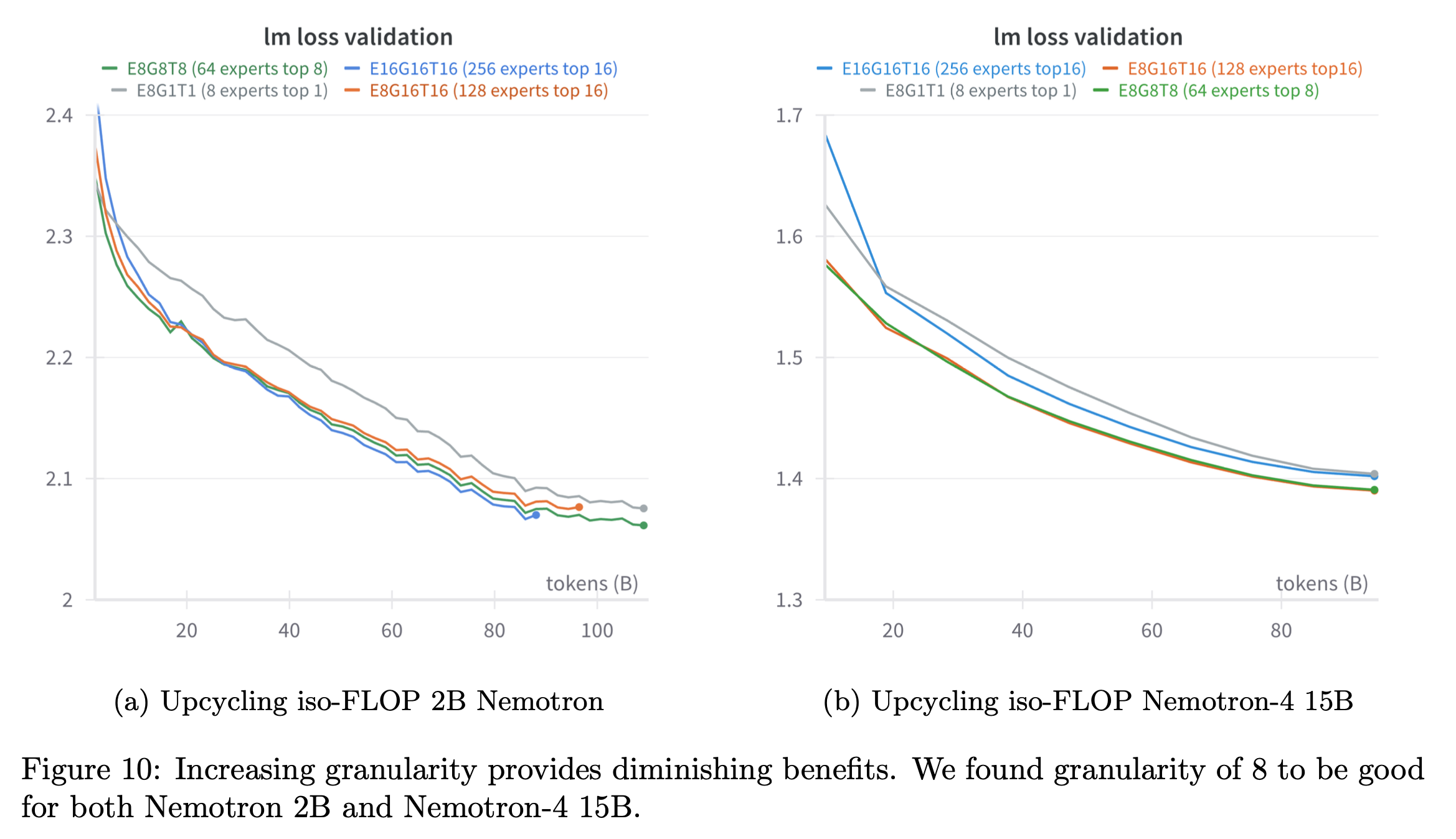nvidia_upcycling_paper_fig10 Fig.

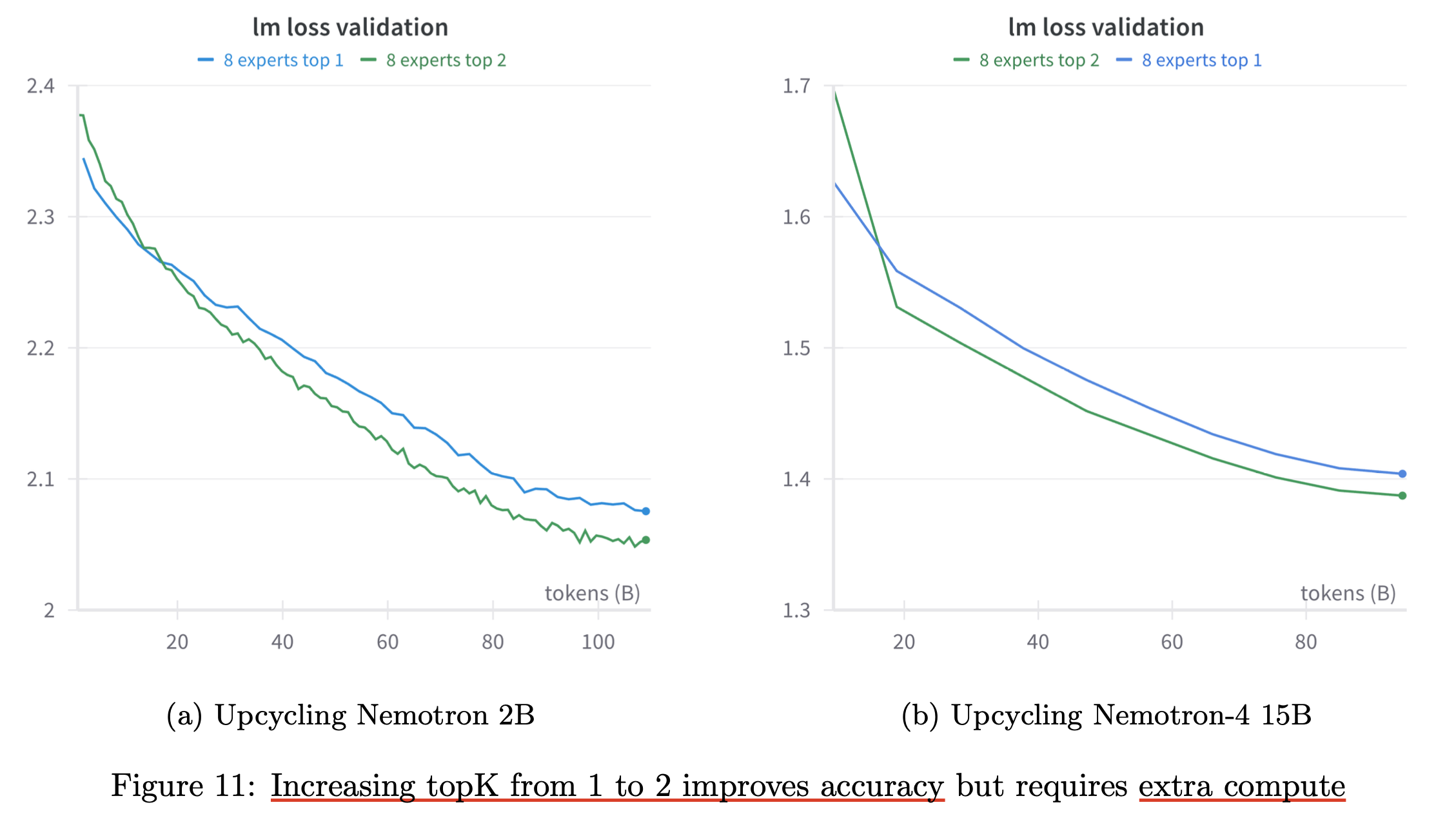nvidia_upcycling_paper_fig11 Fig.

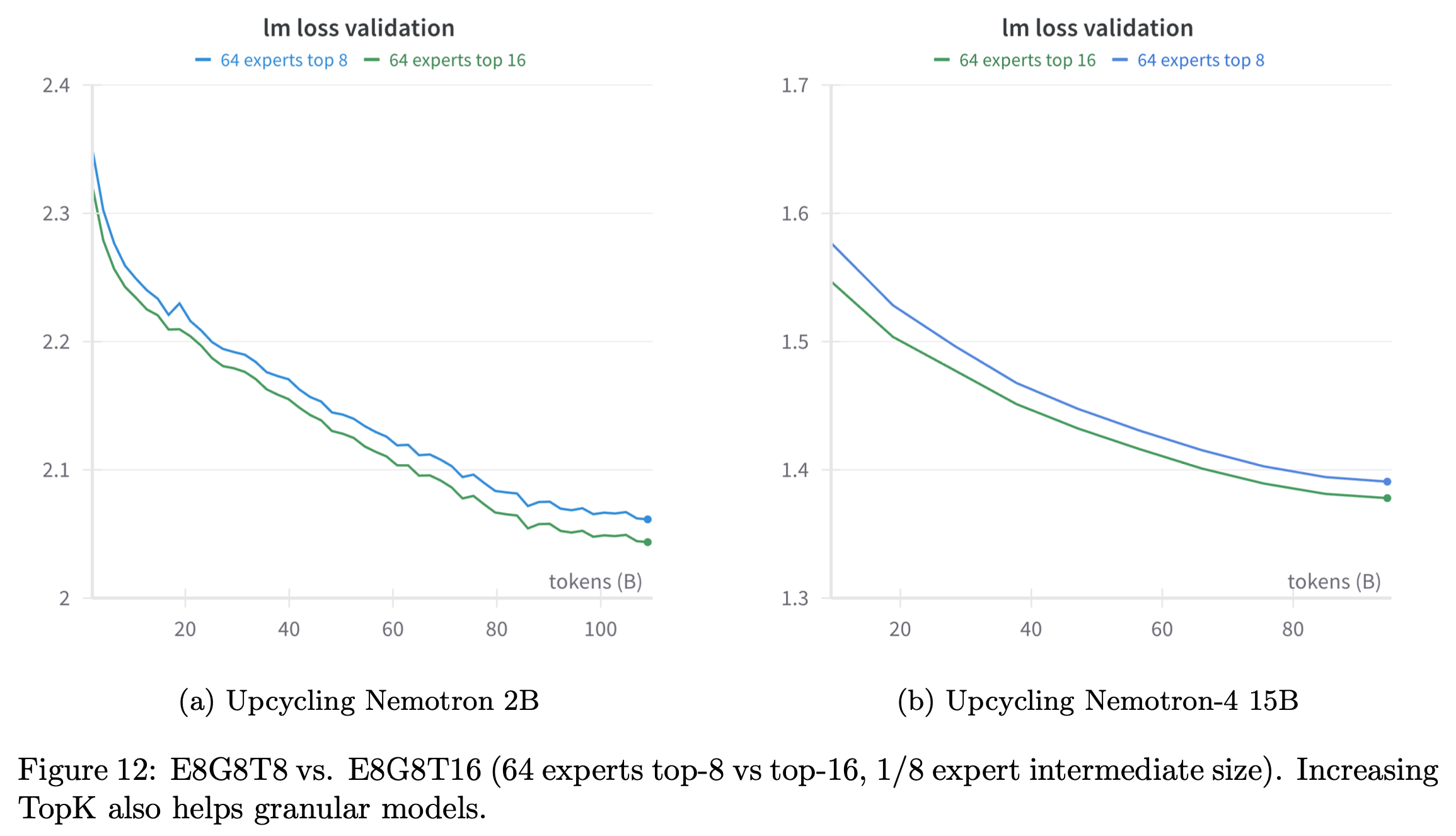nvidia_upcycling_paper_fig12 Fig.

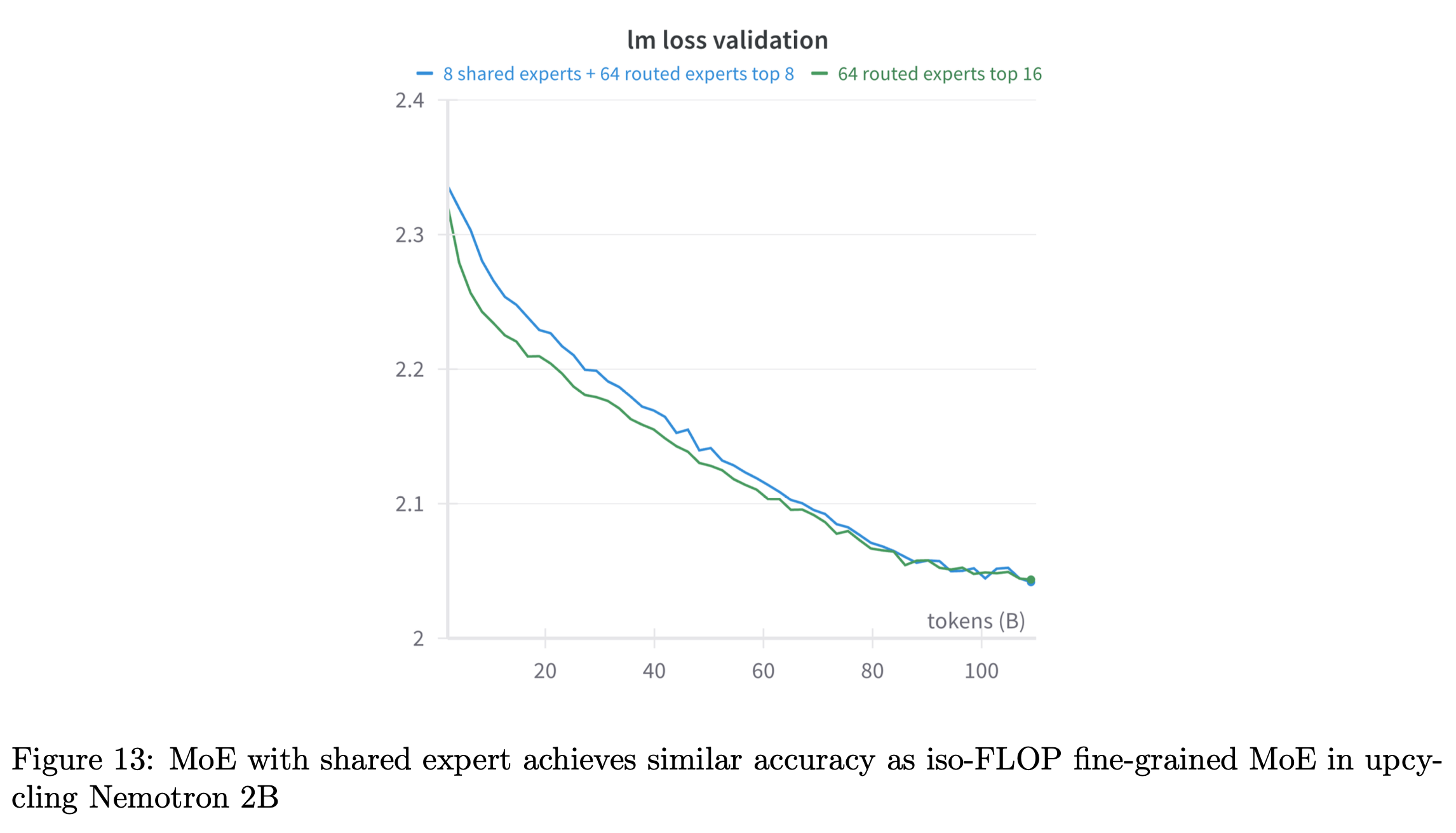nvidia_upcycling_paper_fig13 Fig.

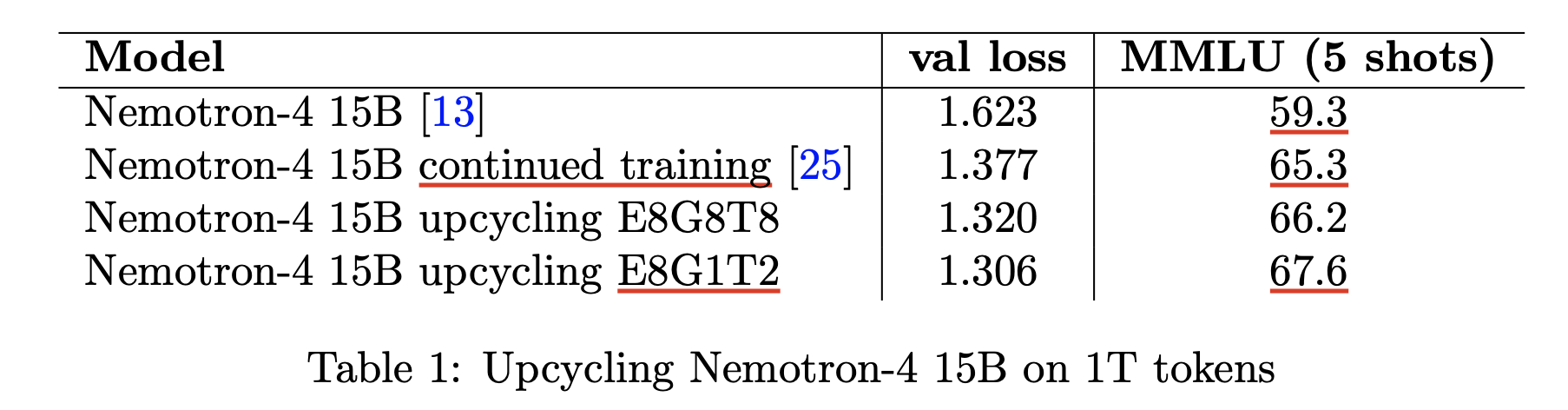nvidia_upcycling_paper_table1 Fig.

nvidia_upcycling_paper_future_work Fig.

Granular Upcycling

Softmax - TopK Order

Experimental Results

Pre-training 과 구분되는 training phase를 따로 갖을 때 LR scheduler를 어떻게 설정해야하는가?에 대한 언급은 Arctic-SnowCoder: Demystifying High-Quality Data in Code Pretraining에도 있는데,

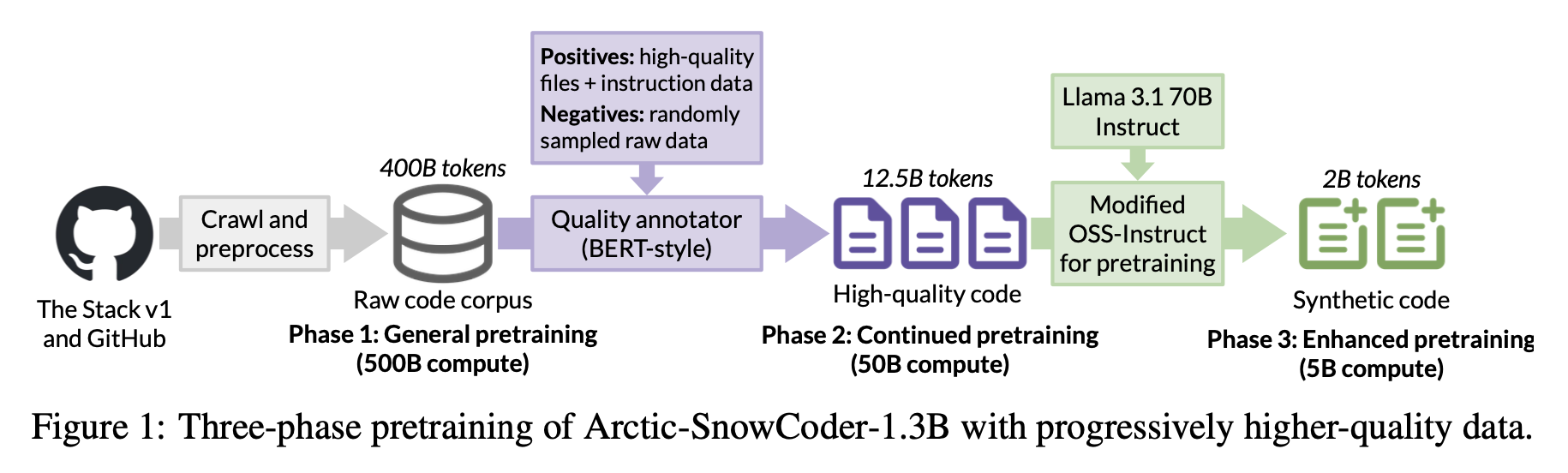arctic_coder_paper_fig1 Fig.

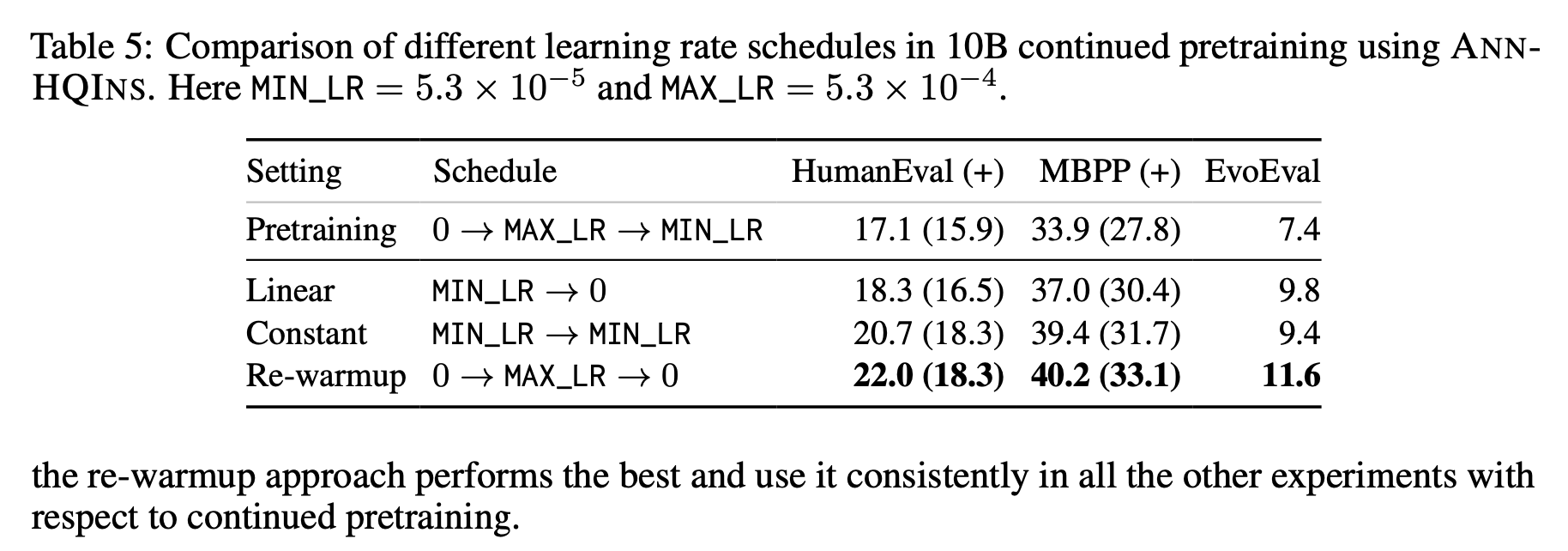arctic_coder_paper_fig2 Fig.

Reuse, Don’t Retrain: A Recipe for Continued Pretraining of Language Models

reuse_dont_retrain_fig1 Fig.

More Efficient Alogrithms for MoE Training

Megablocks (Block Sparse Kernel for More Scalable Training)

MoE는 위 처럼 self attention module을 통과해 FFN을 통과시키는 것을 expert 갯수만큼 늘린 것이다. 어떤 sequence가 N개의 token으로 이뤄져있다면, 각 token들이 어떤 expert에 들어가게 될 지는 expert space로 projection 한 뒤 softmax를 해서 그 확률값을 바탕으로 결정하고, 이를 routing이라고 했다.

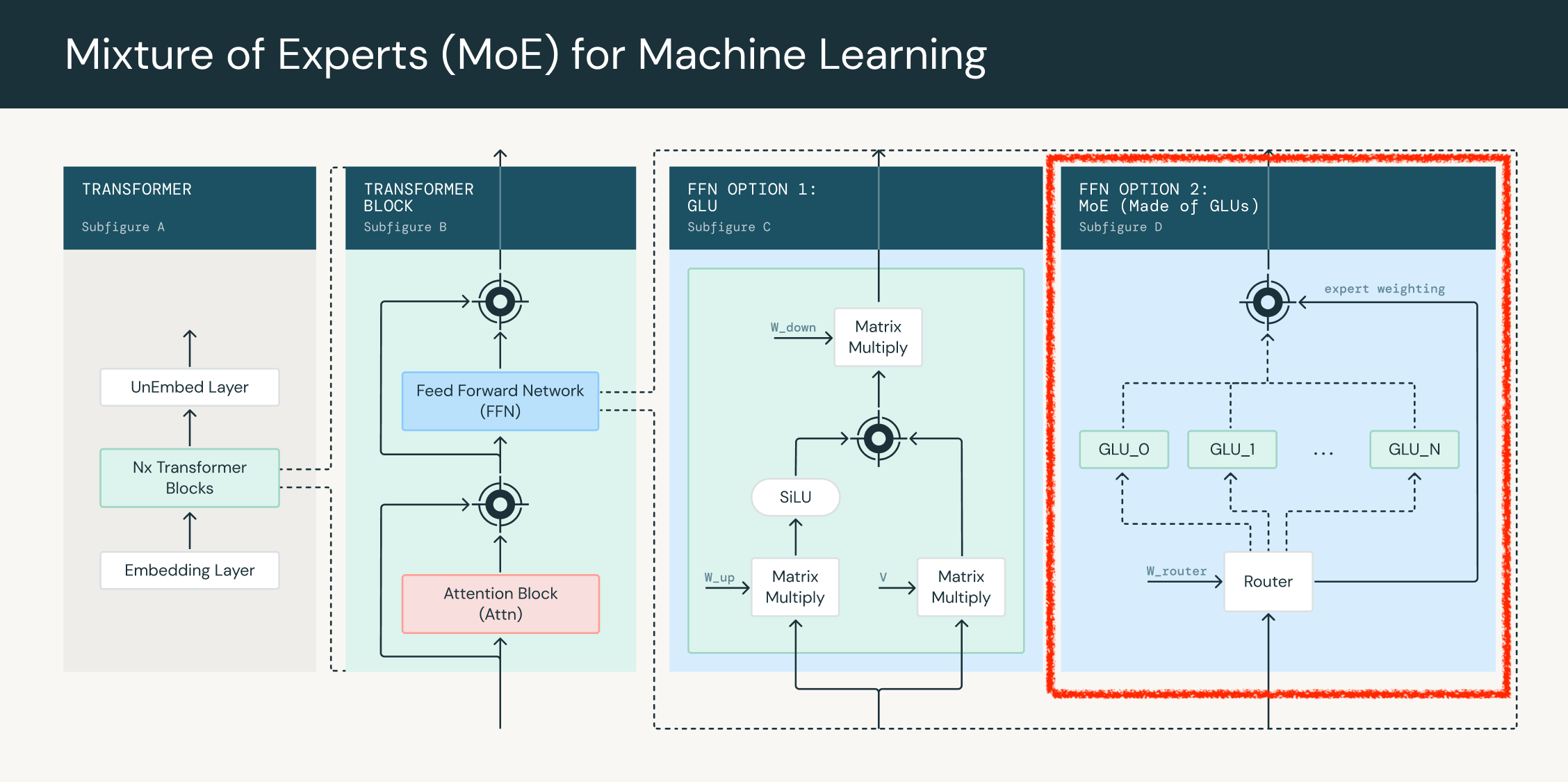dbrx_megablocks_fig1 Fig.

MoE를 학습하기 위해서는 FFN experts들을 통과할 때 routing을 포함해 아래 네 가지 연산을 하게 되는데,

  • Routing: 각 token들이 어떤 expert로 향하게 될지 정하는 단계. softmax prob을 구하고 top-k 개를 선택함
  • Permutation: 각 GPU별로 expert를 가지고 있으니 각 device로 token들을 정렬해서 배치화
  • Computation: matmul, activation 등 수행
  • Un-permutation: 연산이 끝난 vector들을 원래 sequence order로 재배치 한 뒤 만약 top-k가 top-2였다면 2개 expert output을 score에 따라 weighted sum 수행

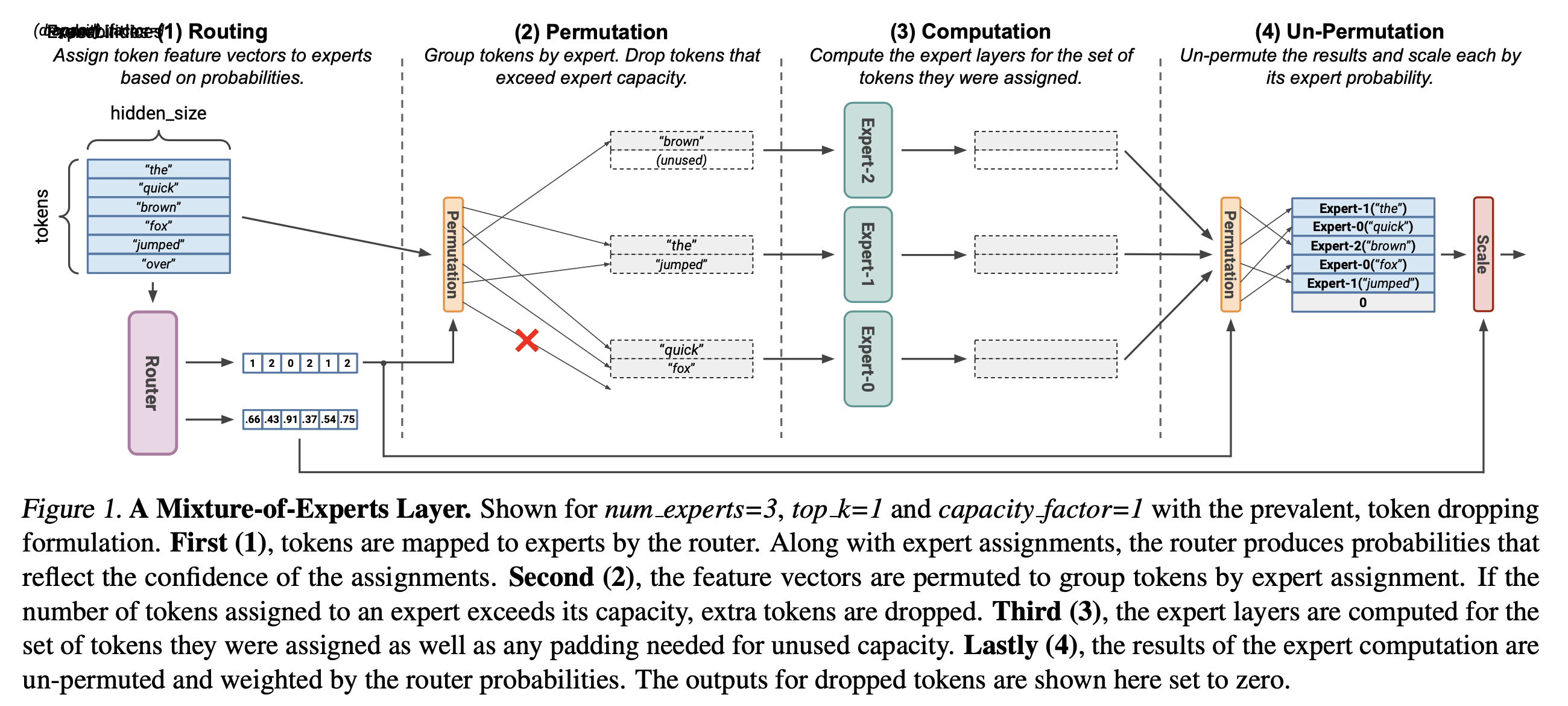megablocks_paper_fig1 Fig.

여기서 permutation 부분이 MoE 연산의 핵심이라고 할 수 있는데, 예를 들어서 input shaepd이 \(x = \mathbb{R}^{B \times T} = \mathbb{R}^{1 \times 256}\)이라고 생각했을 때, 각 expert로 향할 수 있는 token들의 갯수는 user가 정할 수 있으며 이를 expert capacity 라고 부른다고 앞서 얘기한 바 있다.

\[expert \space capacity = \frac{num \space tokens}{num \space epxerts} \times capacity \space factor\]

보통 expert factor는 1.5~2정도로 설정되는데, 그렇다는 것은 각 expert가 받을 수 있는 tokens 수는 expert가 8개, factor가 2일 경우 256개 중에서 64개가 된다.

\[\frac{256}{8} \times 2 = 64\]

switch_transformer_fig3_expert_capa_factor Fig.

MoE는 factor가 1.0이냐 1.5냐에 따라서 device (즉 expert)별로 받을 수 있는 tokens수의 상한이 정해지는데, 이렇게 하는 이유는 computation efficiency 때문이었다. 보통 capacity를 1.5 정도로 설정하면 각 expert가 받을 수 있는 token수를 넘게 할당받으면 이를 버리게 되는데, 이를 token drop이라고 하며, 반대로 64개까지 받을 수 있는데 10개밖에 받지 못하면 54개를 padding해야 한다고 했다 (안해도 될 것 같기도 하지만 기다리는 시간은 마찬가지다). 결국 이런 weight matrxi와 expert input의 shape을 fix하는 방식은 MoE parallelism에서 흔한 method이지만, 이렇게 학습이 되는 경우 sequence token들이 expert에 골고루 가도록 학습이 되리란 보장이 없다. 결과적으로 이는 model performance 저하로 이어지는데, 그렇기 때문에 보통 load balancing loss라는 걸 추가적으로 사용했다.

moe_permutation_problem Fig.

쉽게 말해서 routing prob의 entropy를 높히는 방향으로 penalizing을 하는 것인데, megablocks paper에서는 이런 노력들이 여전히 balancing에 도움이 되지 않았다고 한다.

dmoe_motivation Fig.

Megablocks는 바로 이 부분을 tackle 하는 것인데, megablocks에서 제안하는 것이 바로 dropless MoE (dMoE)이다. 말 그대로 drop하는 것 없도록 하겠다는 것인데, traditional MoE가 아래 그림과 같이 capacity를 넘어가면 drop하고 아니면 padding하는 모양새였는데,

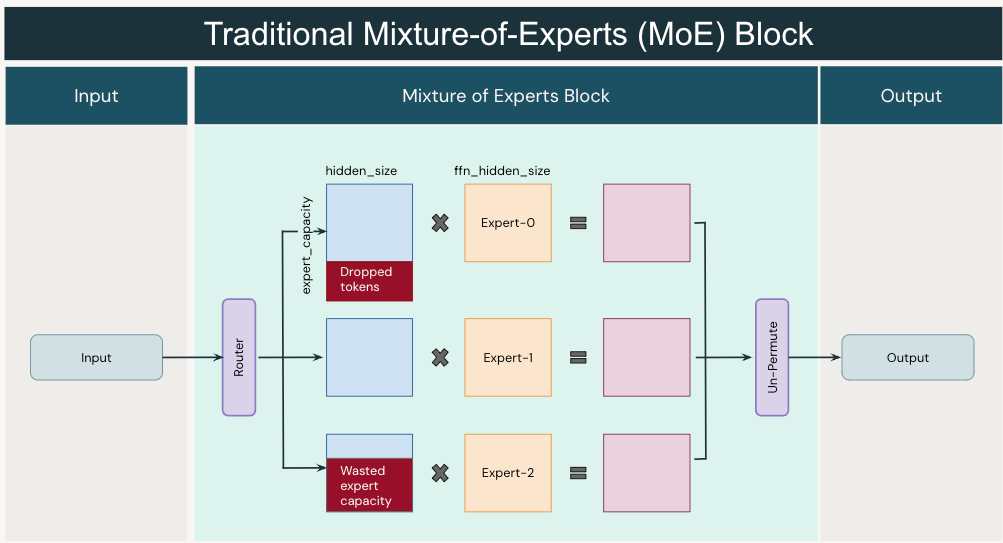dbrx_megablocks_fig2 Fig.

dMoE는 아래처럼 input, weight matrix를 재 구성해서 버리는 token 없이 효율적으로 연산할 수 있게 되었다고 한다.

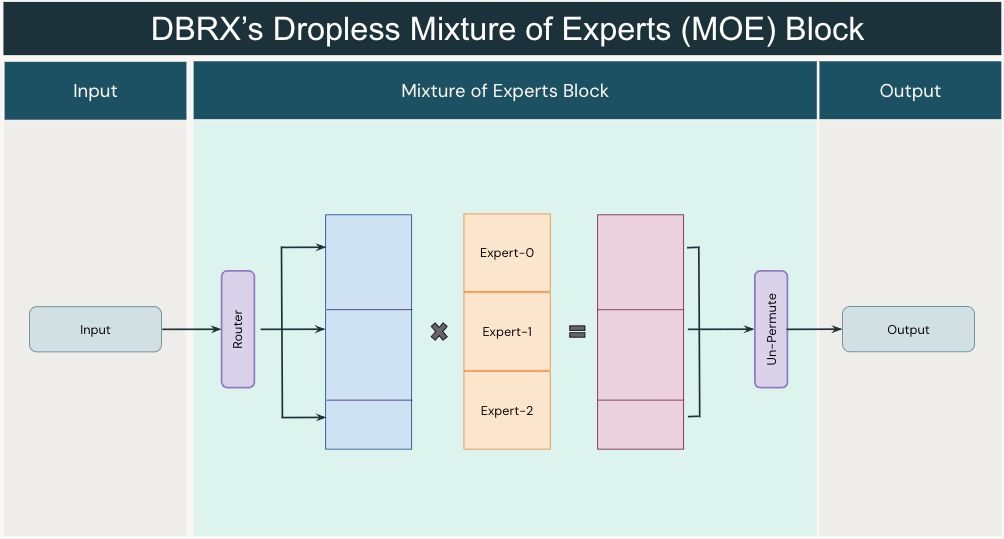dbrx_megablocks_fig3 Fig.

사실 이런 방식은 Microsoft의 Tutel에서도 제안이 되었다고 하는데, 여기서는 dynamic capacity factor mechanism라는 걸 제안했다고 하며 이것도 dMoE의 한 종류로 분류되는 것 같다. (dropless moe는 megablocks만 있는 것은 아니기 때문에 dMoE==Megablocks라고 하는 것은 비약이라고 할 수 있다.)

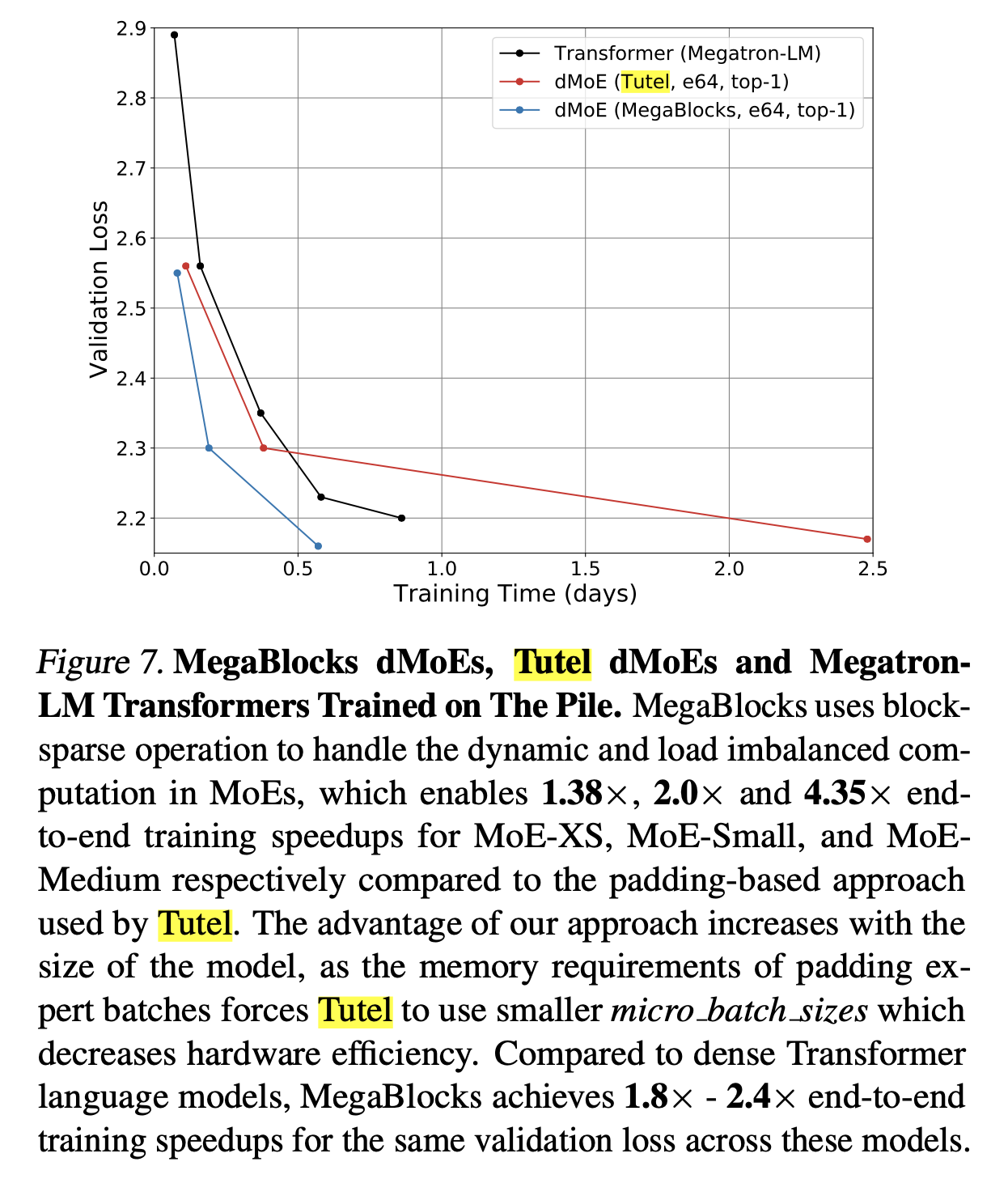megablocks_paper_fig7 Fig.

하지만 위 megablocks paper figure를 보면 같은 dmoe라 하더라도 tutel에 비해 megablocks dMoE가 훨씬 빠른속도로 학습이 되는 것을 볼 수 있다.

그래서 어떻게 token drop을 하지 않고 학습할 수 있는가? 핵심은 Block-Sparse Kernel을 사용하는 것이다.

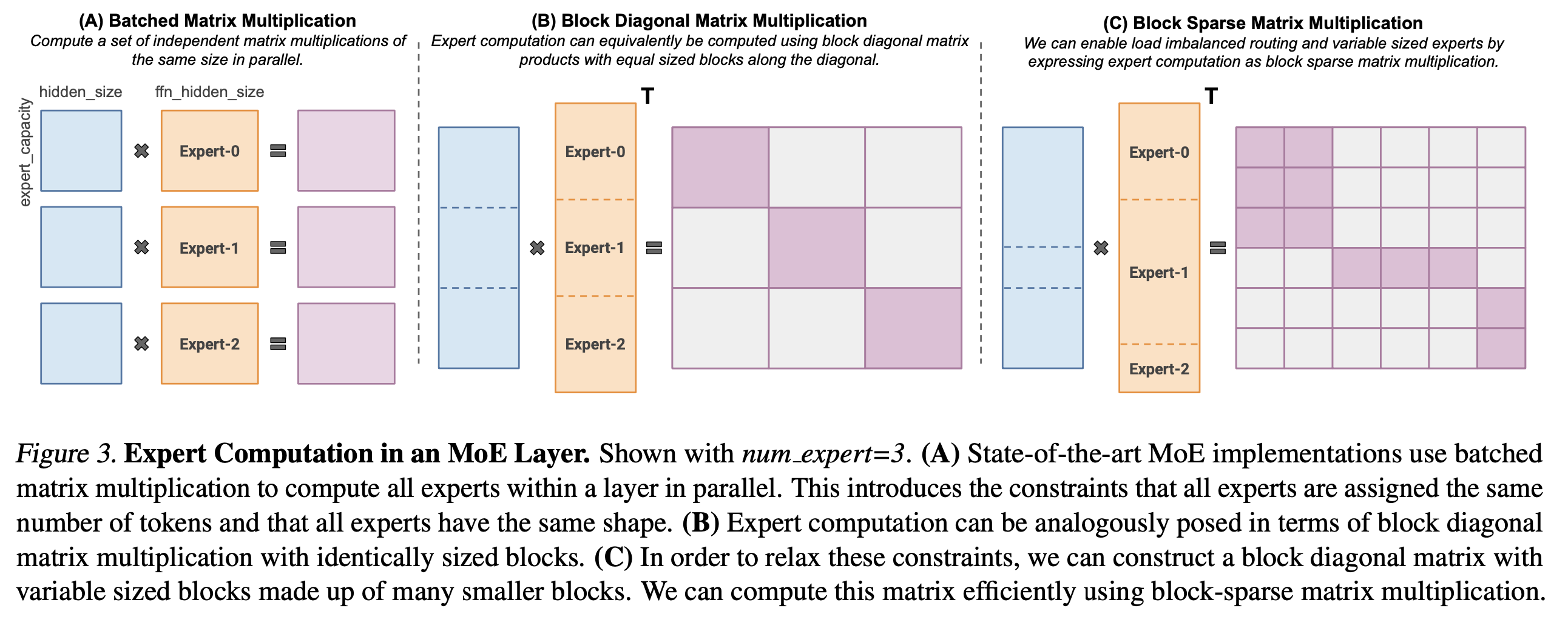megablocks_paper_fig3 Fig.

Mega-blocks라는 이름의 blocks는 blocksparse를 의미하는 것이지만 Mega-는 아마 Megatron-LM 구현체 위에서 dMoE를 구현한 하나의 system 이기 때문에 붙은 것 같다.

what_is_megablocks Fig.

그런데 초기에는 Megatron dependency가 있었으나 megablocks는 어차피 moe ffn들의 weight을 모아 block sparse matrix를 만들어 연산에 쓰는 것이기 때문에 어디서나 쓸 수 있어야 정상이고, llm-foundry라는 databricks의 opensource library를 보면 Megatron-LM같은 dependency가 없이도 사용이 가능하다는 걸 알 수 있다. (databricks CTO가 megablocks 의 교신저자)

llm_foundry Fig.

BlockSparse Matrix Multiplication

Block-Sparse는

megablocks_impl_fig1 Fig.

megablocks_impl_fig2 Fig.

megablocks_impl_fig3 Fig.

megablocks_paper_fig3 Fig.

megablocks_impl_fig4 Fig.

A Peek into Megablocks Kernel Design

megablocks_contributions Fig.

  • blocked compressed sparse row (BCSR)
  • hybrid blocked-CSR-COO sparse matrix format

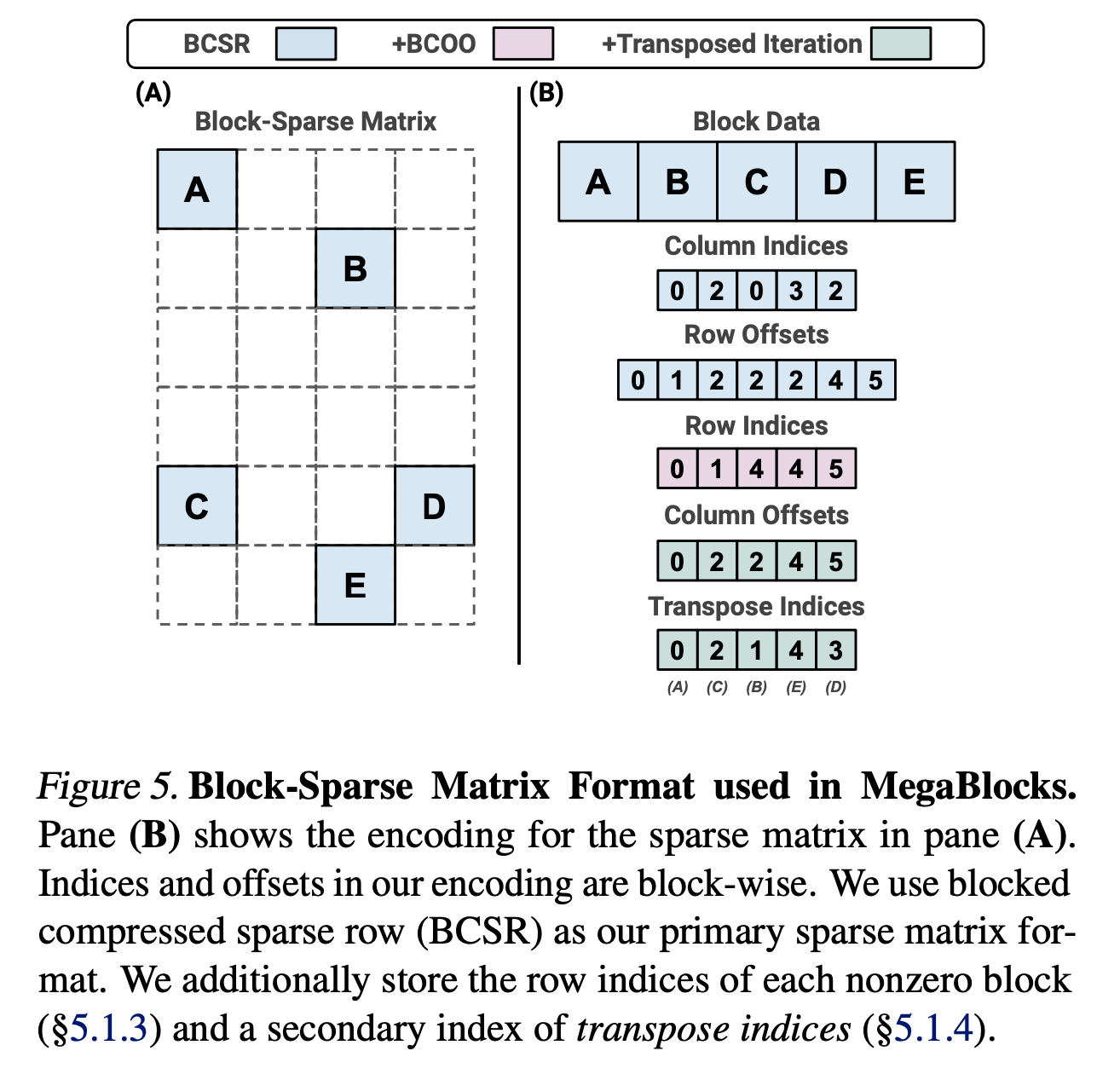megablocks_paper_fig5 Fig.

Experimental Results

megablocks_paper_table1 Fig.

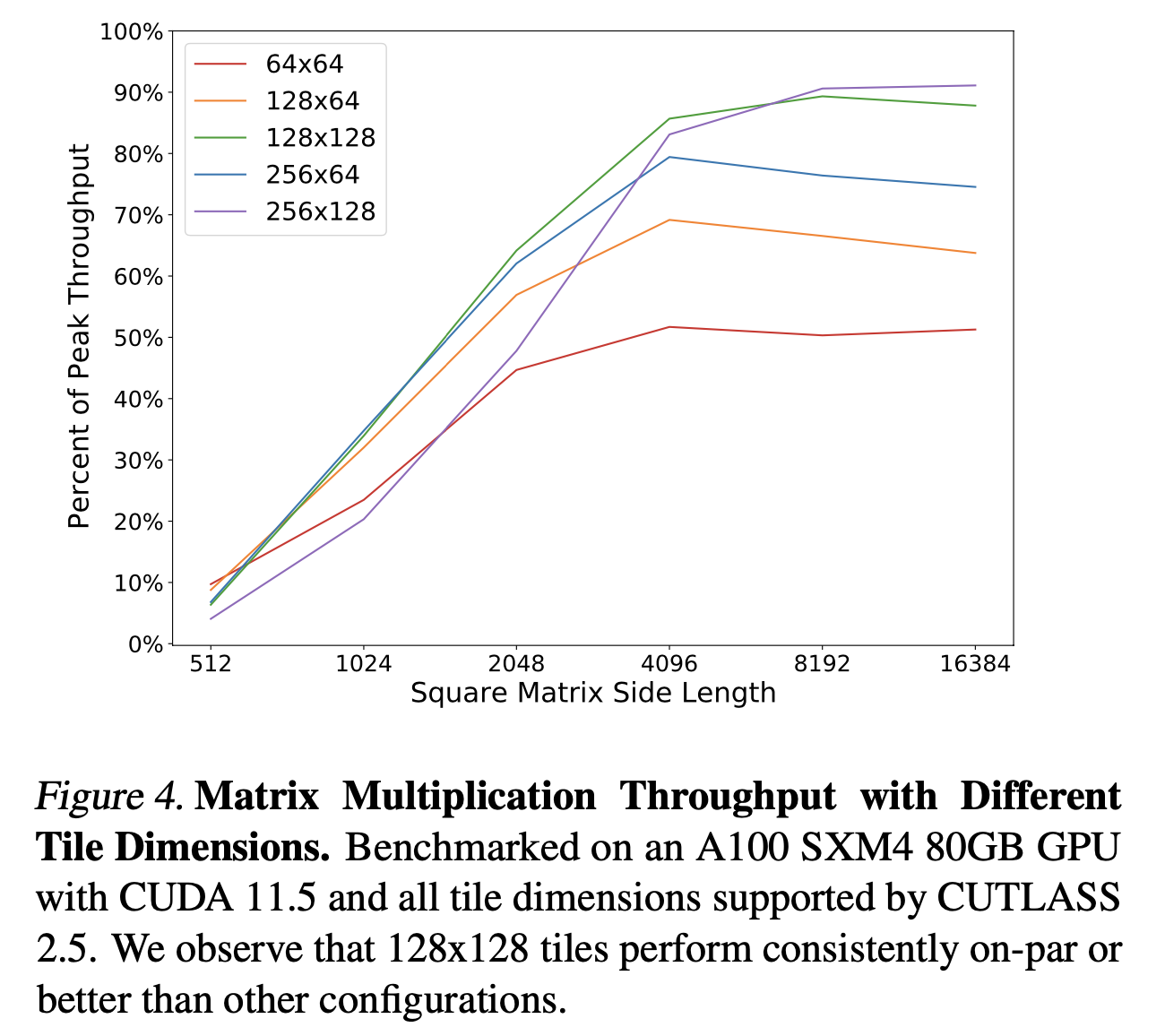megablocks_paper_fig4 Fig.

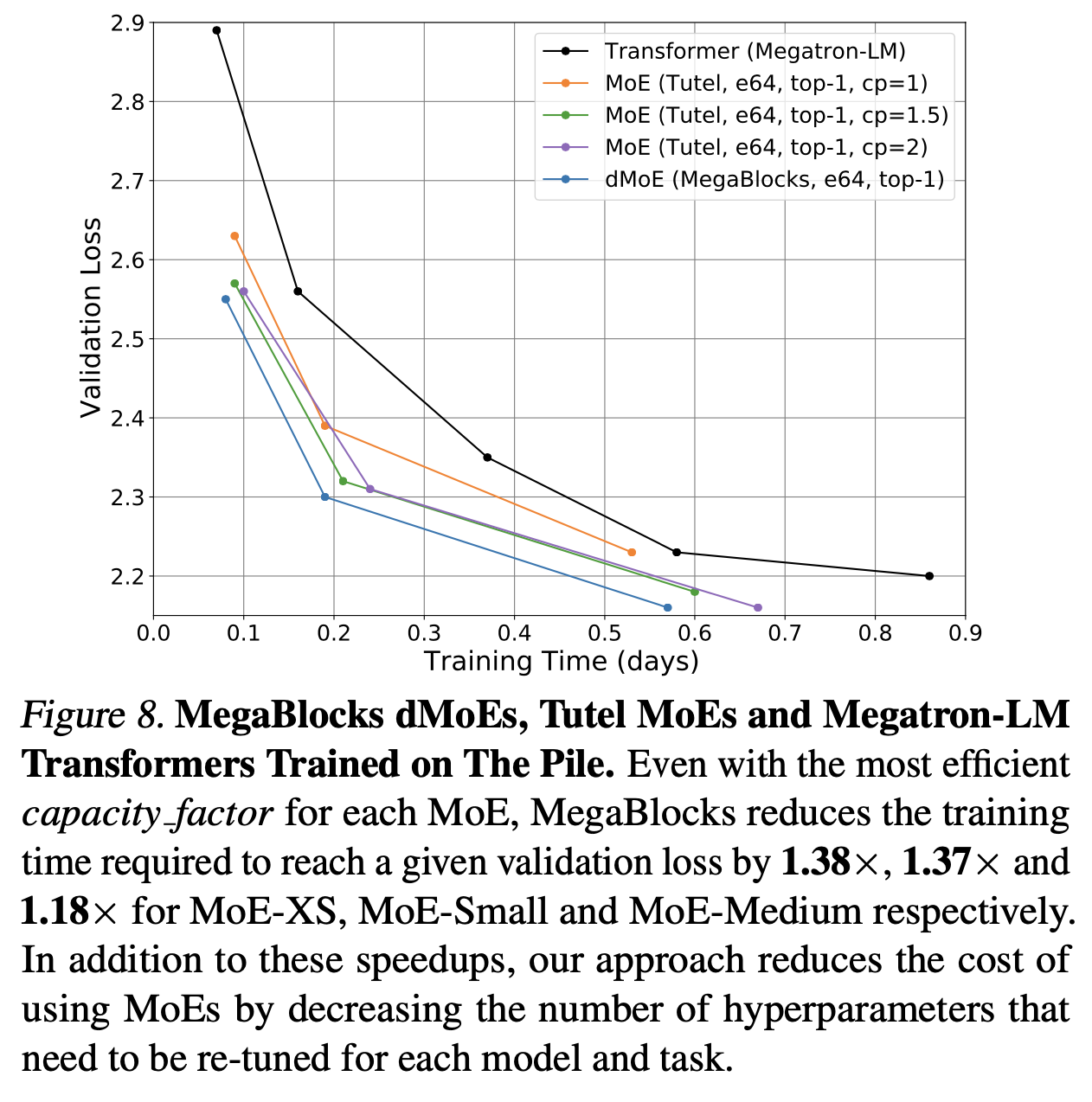megablocks_paper_fig8 Fig.

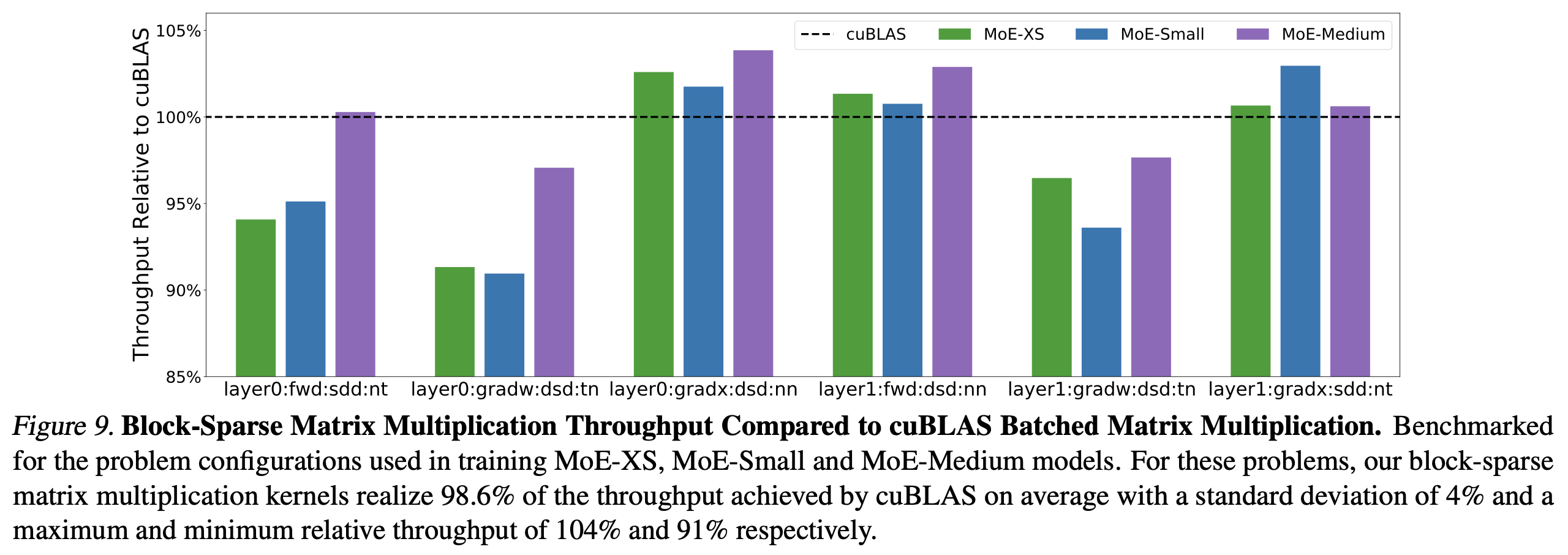megablocks_paper_fig9 Fig.

LLMs trained using Megablocks

Open weight model중에서 가장 빨리 공개된 model은 Mixtral이었다.

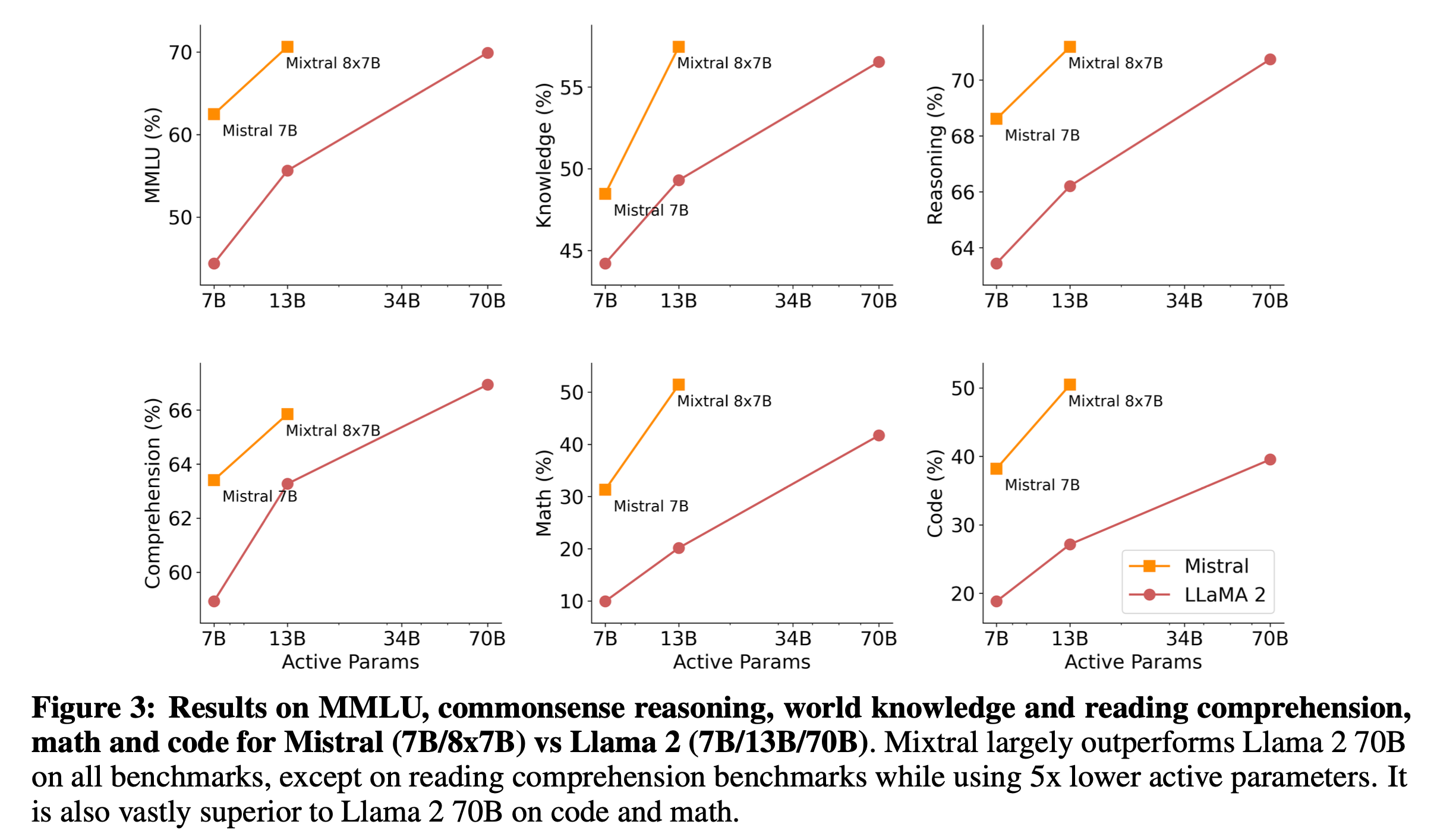mixtral_paper_fig3 Fig.

자세한 언급은 없지만 model이 공개된 시점과 관련 트윗들을 봤을 때 mixtral은 아마 upcycling model인 것으로 보이는데, white paper에 megablocks에 대한 언급이 있다.

mixtral_paper_megablocks_fig1 Fig.

그런데 이게 학습에 dropless moe를 썼다는 것인지는 사실 불분명 하다. dropless moe의 효율성에 대해 얘기하는 걸 보면 학습에 썼을 수도 있지만 말이다.

mixtral_paper_megablocks_fig2 Fig.

그 다음은 최근 공개된 OLMoE이다.

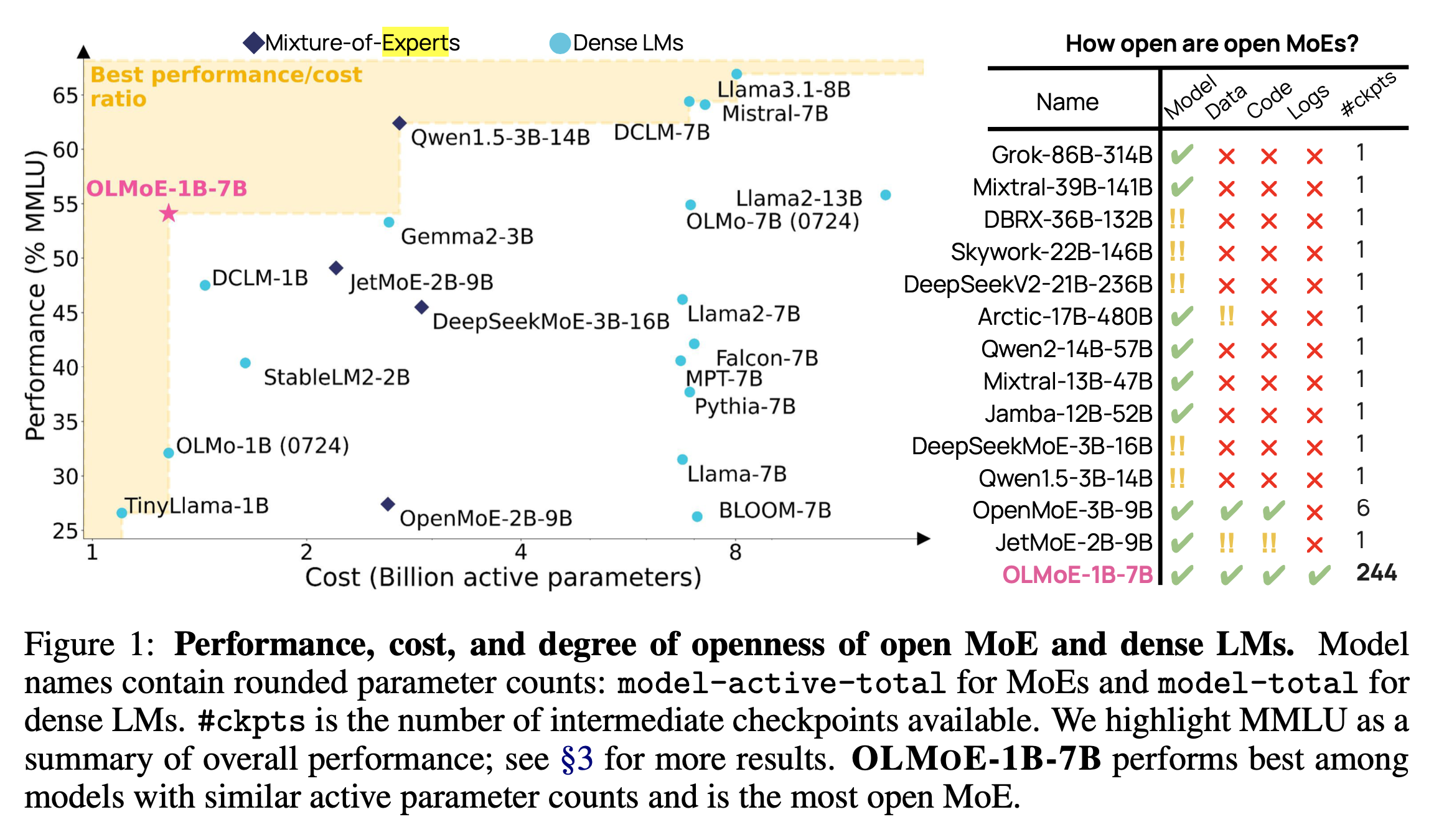olmoe_paper_fig1 Fig.

olmoe에서는 megablocks와 일반 moe에 대한 정량적인 비교 수치는 없지만 megablocks가 성능이 훨씬 좋았다고 언급하며 학습에 megablocks를 썼다고 명시했다.

olmoe_megablocks_fig1 Fig.

그 밖에 databricks의 DBRX는 당연히 megablocks의 교신저자가 CTO이므로 megablocks를 썼을것이나 full training code는 공개되어있지 않았고, JetMoE또한 MoE가 dense model보다 훨씬 경제적이라고 주장함과 동시에 megablocks를 썼다고 언급하지만 정확한 code는 공개하지 않았다.

olmoe_megablocks_fig2 Fig.

olmoe_megablocks_fig3 Fig.

+Updated) ScatterMoE

Aaron Courville lab 에서 24년 3월에 Scattered Mixture-of-Experts Implementation (ScatterMoE)라는 paper를 발표했다. ScatterMoE는 megablocks랑 거의 같은 철학을 공유하는 Sparse MoE (SMoE)지만 megablocks보다 더 높은 throughput과 더 낮은 memory footprint를 보인다고 주장한다. (이러면 megablocks를 쓸 이유가 없다)

(tmp) Implementations

Training and Inference Inefficiency of MoE

이제 MoE를 사용하는것의 단점에 대해서 얘기해보자.

이는 OLMoE에도 잘 나와있는 내용인데, 우리가 1.3B-1_activated-64_experts-7B_total MoE model을 학습한다고 치면 이것의 quality equivalent counter part는 어떤 것인지 모르겠으나, activation param만 놓고보면 1.3B dense model과 같을 것이다. Switch transformer에서도 언급했듯 token 학습량에 따라서 3배에서 크게는 7배까지 moe model과 dense model의 수렴 속도가 차이나는데, 이는 FLOPs로 계산했을 때 그렇다는 것이지 실제로 wall clock time이 3배 빠른 것은 아니다.

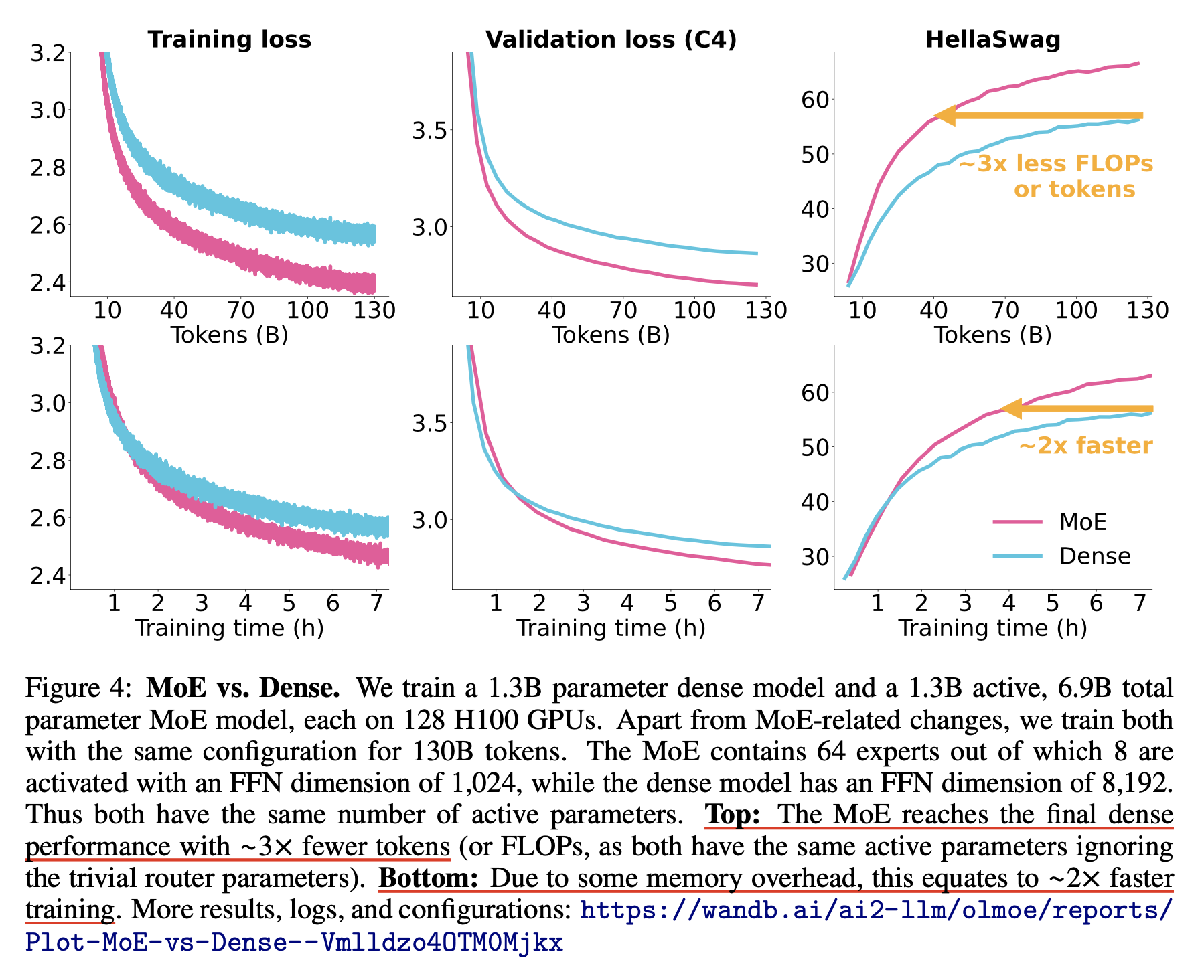olmoe_megablocks_inefficiency Fig.

왜냐하면 지금 예시로 든 상황에서 roughly parameter가 5~6배 차이나기 때문에 VRAM memory에 들고있어야 하는 model, optimizer state parameter가 5~6배 차이가 난다. 그렇기 때문에 실제로는 batch size를 작게 쓰거나 memory flush를 주기적으로 하거나 cpu offloading을 하는 데서 wall clock time을 소비해야 하기 때문에 실제 물리적인 시간은 2배 밖에 차이가 안나는 것이다.

If inference efficiency sucks, then why should we use MoE?: Distillation from Large Sparse Model

switch_transformer_paper_distillation_fig1 Fig.

Google의 Gemini 1.5 Flash

gemini_moe_distillation_fig1 Fig.

gemini_moe_distillation_fig2 Fig.

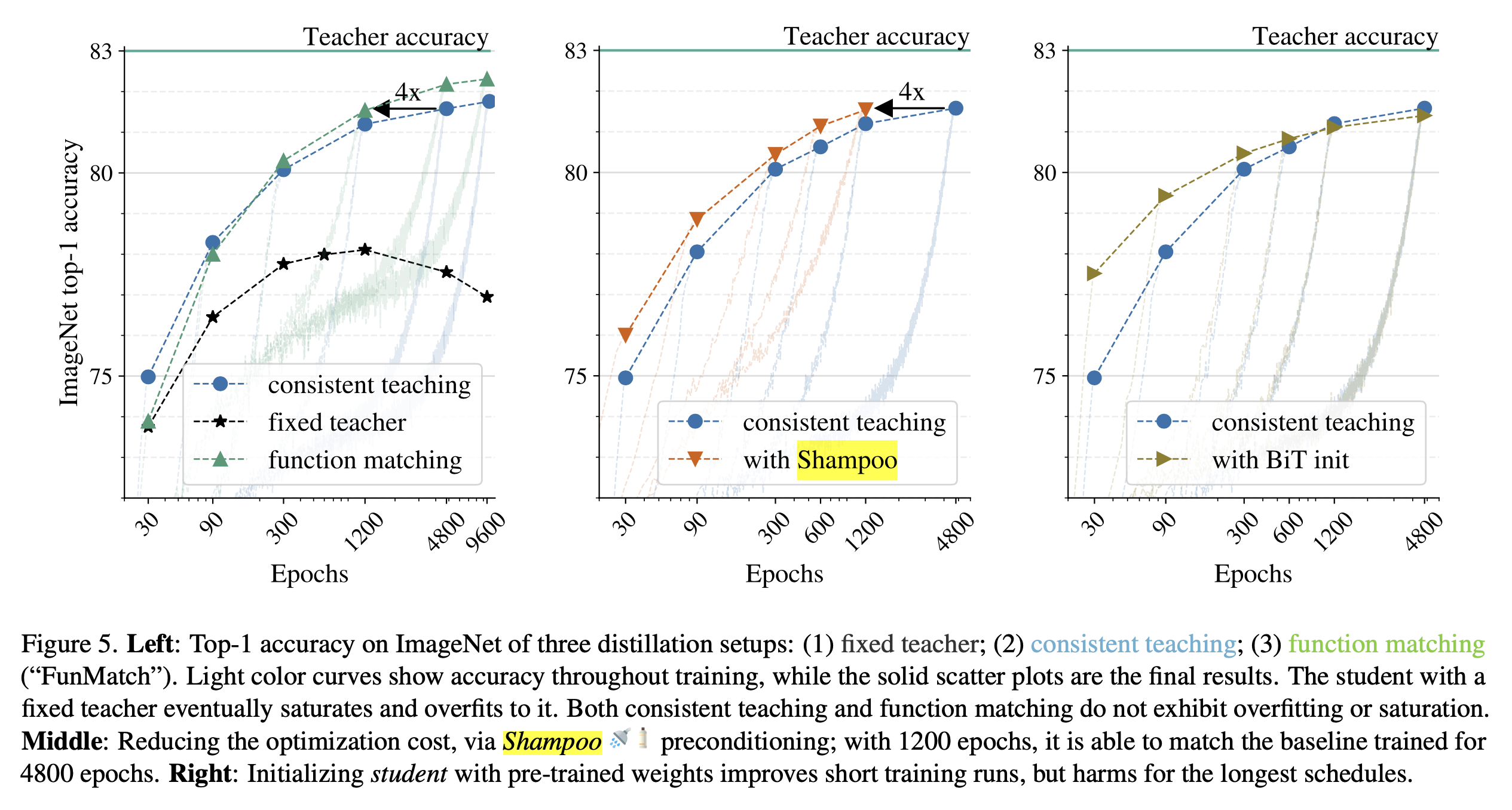gemini_moe_distillation_fig3 Fig.

switch_transformer_paper_distillation_fig2 Fig.

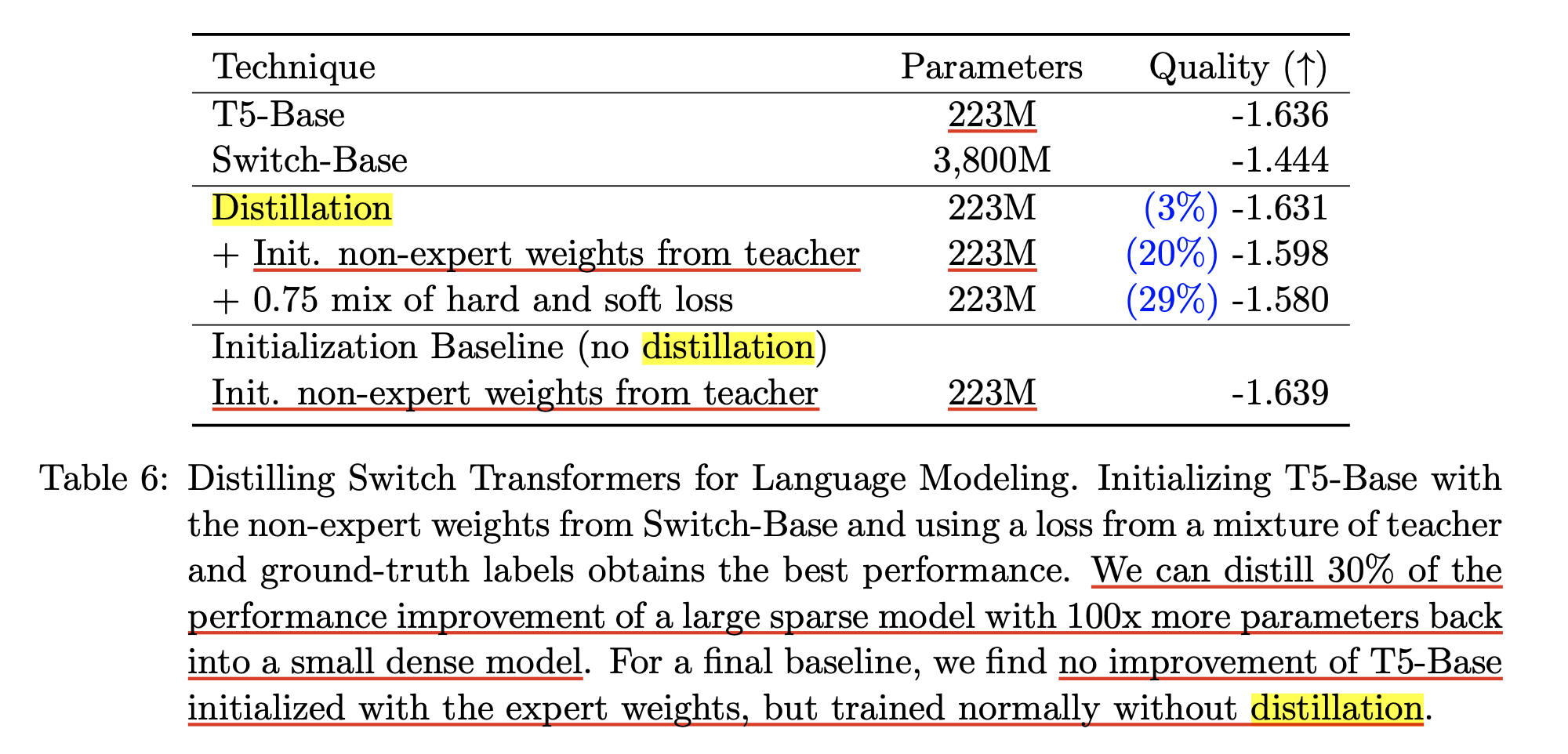switch_transformer_paper_distillation_fig3 Fig.

Others

Hunyuan-Large

Tencent AI에서 공개한 Hunyuan-Large의 technical report를 조금 살펴보겠다. 중국 모델들이 최근 좋은 model들을 많이 뽑고 있는데 deepseek의 경우 moe로 아예 가닥을 잡은 것 같고, alibaba의 qwen도 1.5 release 당시 moe upcycling을 했는데 어떤이유로 포기했는지 모르겠으나 (inference, 가성비 관점인지?) 좋은 중국 연구 기관들은 moe를 많이 시도하는 느낌이다. 그 중에서도 Hunyuan-Large는 최근에 공개돼서 그런지 매우 인상적인 성능을 보인다.

물론 이 model도 qwen 같은 chinese open weight model들이 많이 하는 전략인 instruction data를 합성해서 pre-training corpus에 넣는 방식을 썼기 때문에, benchmark는 많이 뻥튀기 됐을 가능성이 있기 때문에 이 점에 주의해야한다.

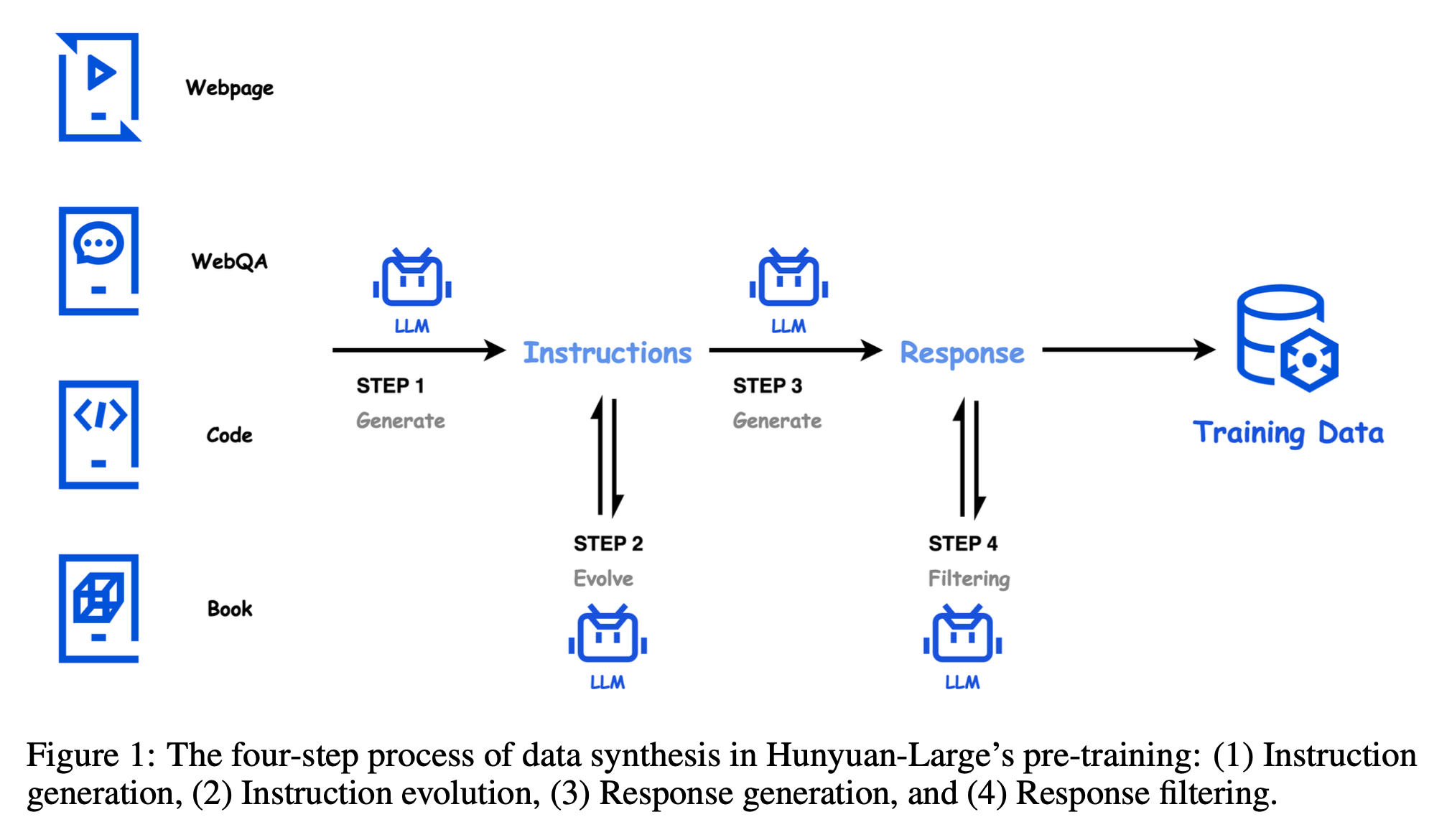hunyuan_paper_fig1 Fig.

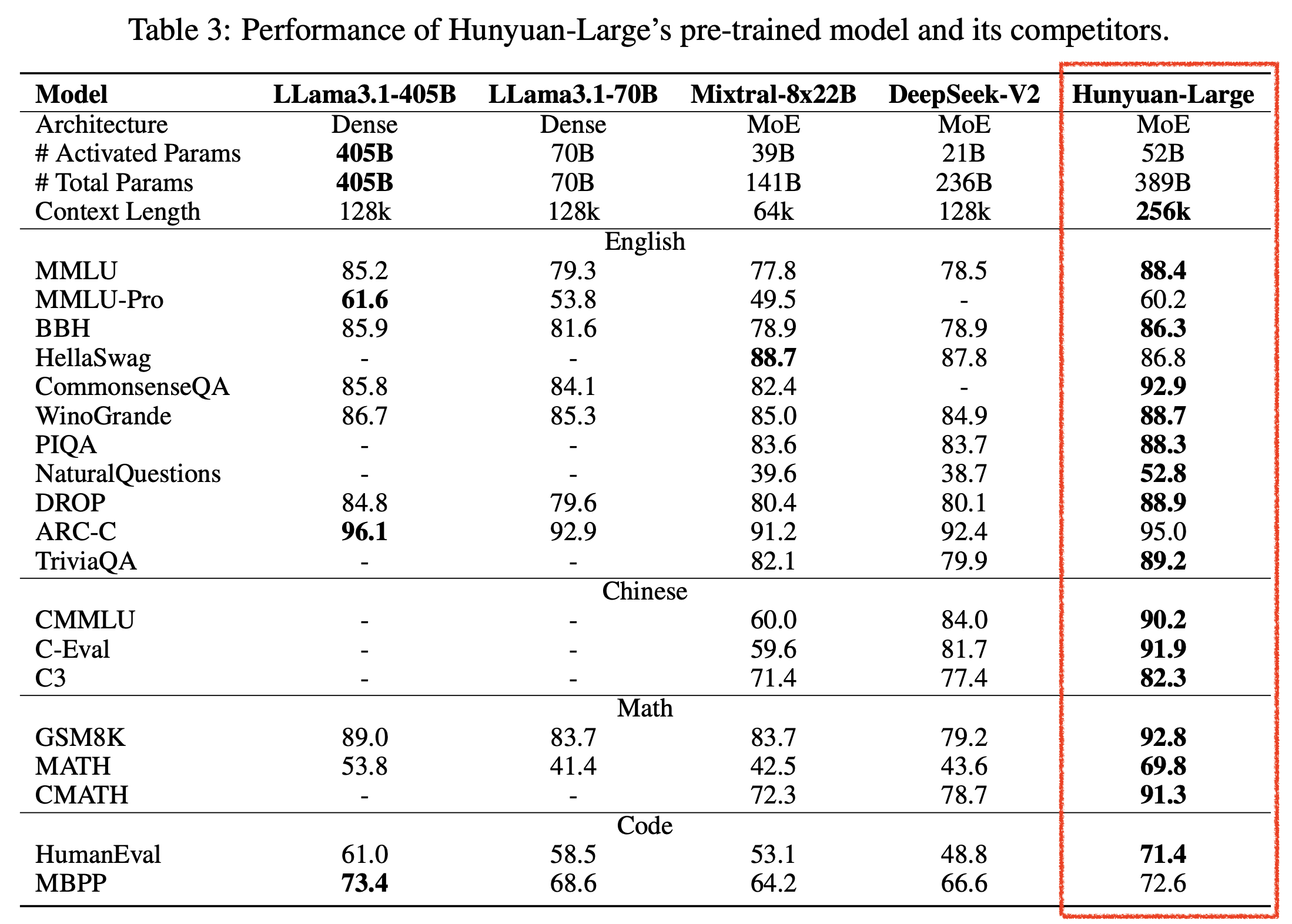hunyuan_paper_table3 Fig.

아마 evol instruct나 llm으로 filtering하는 것들 대부분 rlhf aligned llm이 필요한 것이고 많이 기관들이 gpt-4를 암묵적으로 사용하는 것으로 알고 있는데, gpt-4의 압도적인 MMLU 성능이 이런 방식에서 기인한 것은 아닐 확률이 높기 때문에 (그 당시에는 gpt-3.5말고는 이렇다할 aligne llm이 없었으므로) 이런 방식에 나는 좀 회의적이긴 하다.

아무튼 사실 성능 얘길 하고싶었던 건 아니고 hunyuan의 moe detail에 대해 좀 읽어볼까 해서 subsection을 만들었으며 내용은 다음과 같다.

  • moe random routing
  • moe lr scaling
  • moe scaling law

먼저 deepseek-moe처럼 Cross Layer Attention (CLA)와 shared expert를 쓴 것 외에 random routing이란 것을 적용했는데,

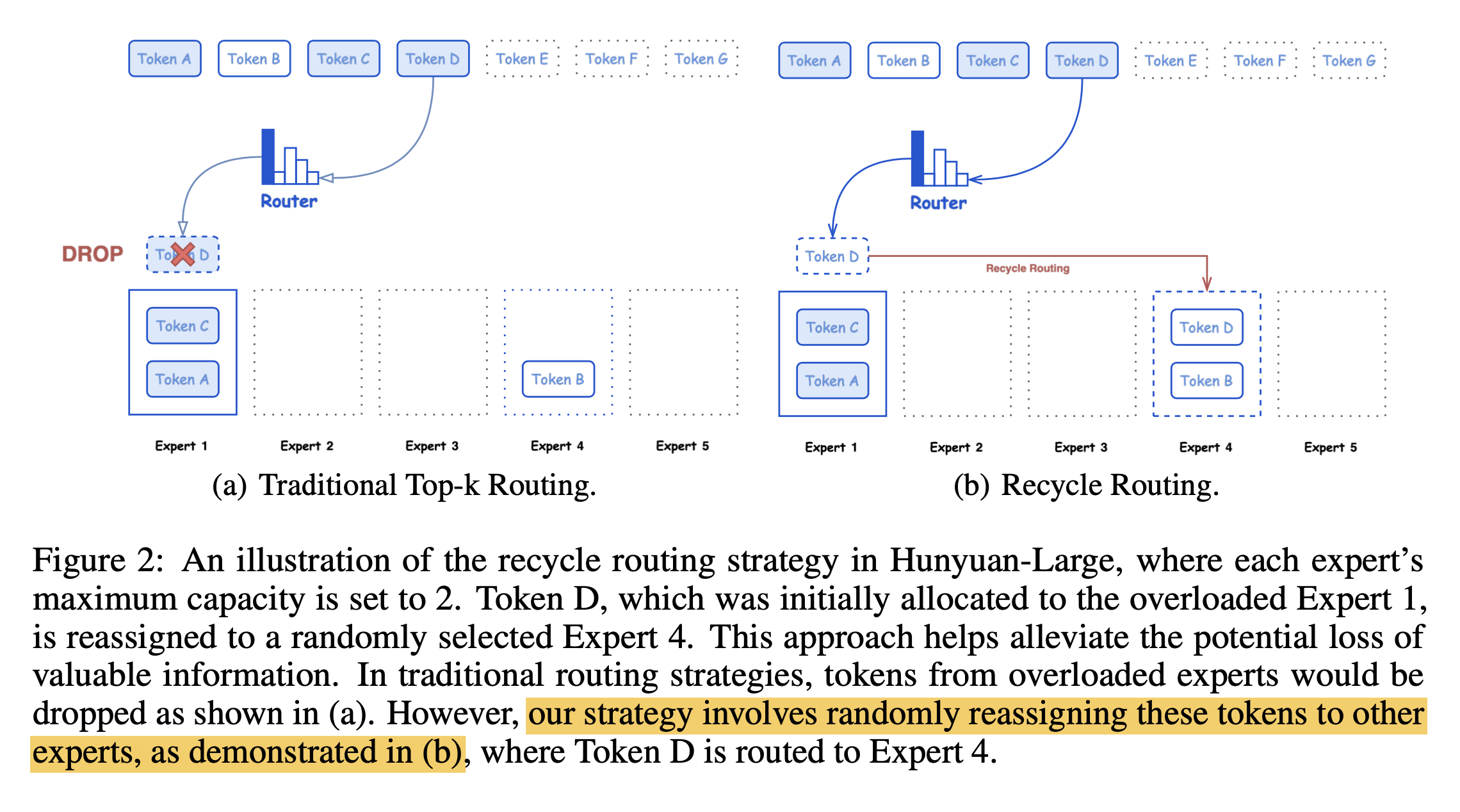hunyuan_random_routing_fig1 Fig.

token이 버려지는게 아까워서 discard되는 애들은 다른 router에 넣는다는 것이다.

hunyuan_random_routing_fig2 Fig.

말이 되는 것 같다.

그 다음은 moe ffn들의 lr을 조절하는 것인데, 예를 들어 training tokens가 16k라면 expert별로 1k씩 이상적으로 나눠진다면 shared expert는 16k를 다 받는 반면에 나머지들은 gradient average하는 량이 1/16이기 때문에 adamw lr을 조절해줘야 한다는 내용이었고 이것도 말이 되는 것 같다.

hunyuan_lr_scaling Fig.

마지막은 scaling law인데 같은 activated parameter인 dense model과의 scaling exponent를 비교한 게 없어서 아쉽긴 하지만, 요지는 dense model의 computing budget을 계산하는 것 처럼 C=6ND로 계산하지 않고 변형된 attention과 (GQA, CLA) moe를 고려해서 C를 계산해야 것이고, 수식은 아래 figure를 보면 된다.

hunyuan_moe_scaling_law Fig.

여기에 critical batch size관련된 내용이 있는데, 왜 이게 나왔는지 약간 헷가릴게 써놨다. 그래서 실제 학습할 때 쓰는 target batch size를 써서 scaling law 실험을 했다는걸까? 사실 그렇다면 말이 안되는 것으로 나는 생각하는데, 왜냐하면 batch size가 커지면 (병렬화를 많이 하면) gradient 평균이 정교해지지만 parameter update가 줄어들기 때문에 learning rate을 높혀주는게 맞지만, 어느 시점, 즉 critical batch size를 넘어가면 이것이 불가능한데, 작은 computing budget에서 training tokens가 작을 때 실제 389B moe model의 target batch를 쓴다고 하면 update가 너무 적어서 제대로 예측하기 어려울 것이기 때문이다.

Hunyuan paper에 나와있는 (3)번 수식은 원래 아래의 의미를 갖고 있는데,

scaling_law_paper_critical_batch_size Fig. Source from Kaplan et al.

예를 들어 batch token size, \(B 2^{19} = 500k\)인 경우 어떤 validation loss, \(L\)에 도달하기 위해 필요한 training steps가 \(S\)라고 치자. 그리고 critical batch size, \(B_{crit} (L)\)가 있다고 할 때, 이는 도달하고자 하는 loss에 대한 함수이기 때문에 이미 정해진 것이나 다름이 없고 (예를 들어 2M), 이 때 batch size가 \(B_{crit}\)보다 매우 큰 경우에 한해서 B가 커질수록 denominator가 1에 가까워지기 때문에 매우 큰 batch size로 학습할 경우 training steps가 \(2^{19}\)로 학습할 때 필요한것 만큼 필요하다는 것을 의미한다. 즉 병렬처리 아무리 많이해도 training wall clock time은 줄어들지 않는다는 얘기다.

이는 아래 llama3에서 했던 scaling law prediction을 보면 compute budget별로 적당한 batch size를 사용했다는 것에서도 확인할 수 있다.

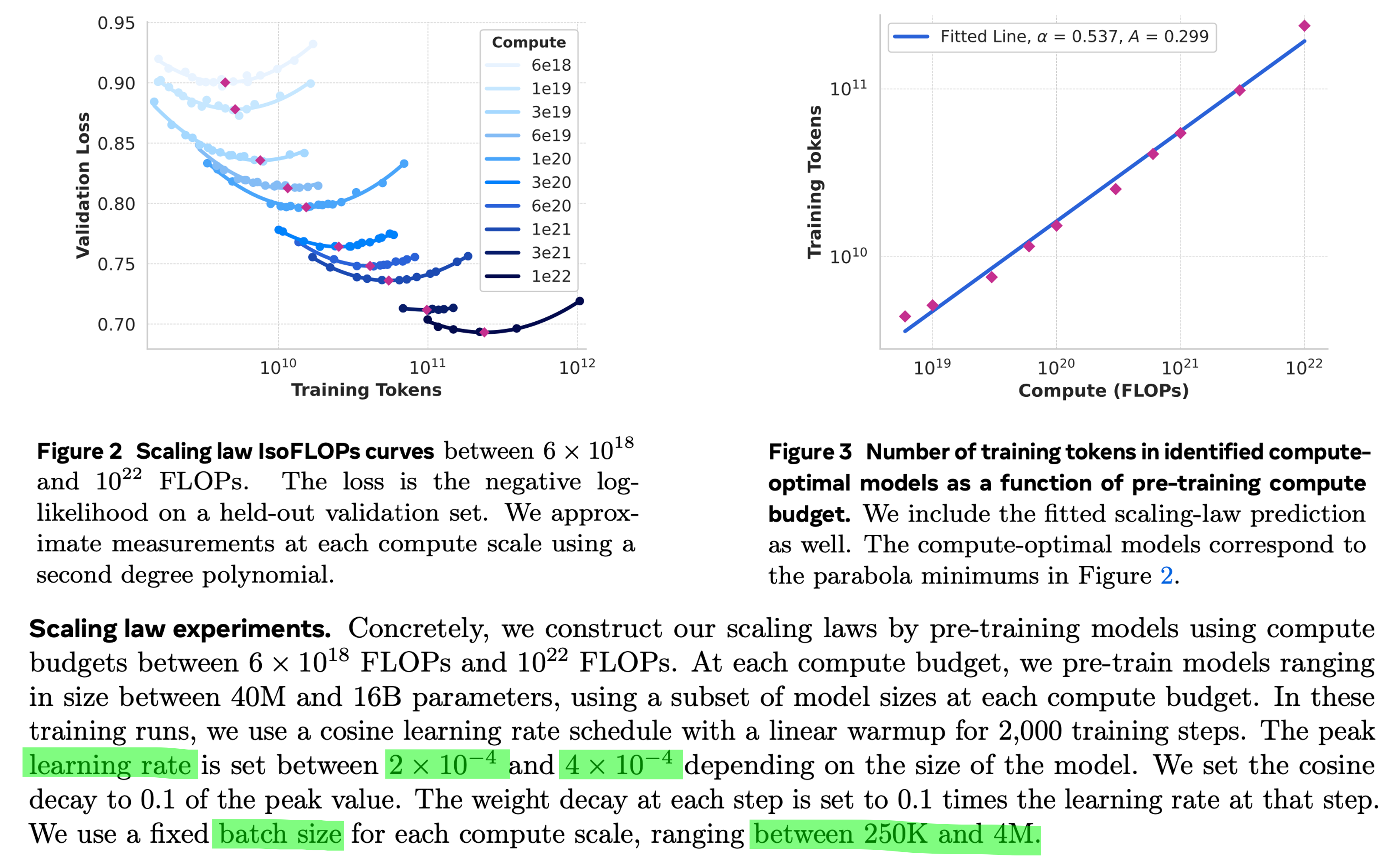llama3_paper_405b_scaling_law_prediction Fig.

그래서 나는 hunyuan이 갑자기 이 얘기를 moe scaling law에서 왜 했는지 이해가 잘 가지 않지만, 아무튼 scaling law측정한대로 나름 compute optimal인 것 보다 좀 더 token량을 써서 학습했음을 알 수 있다.

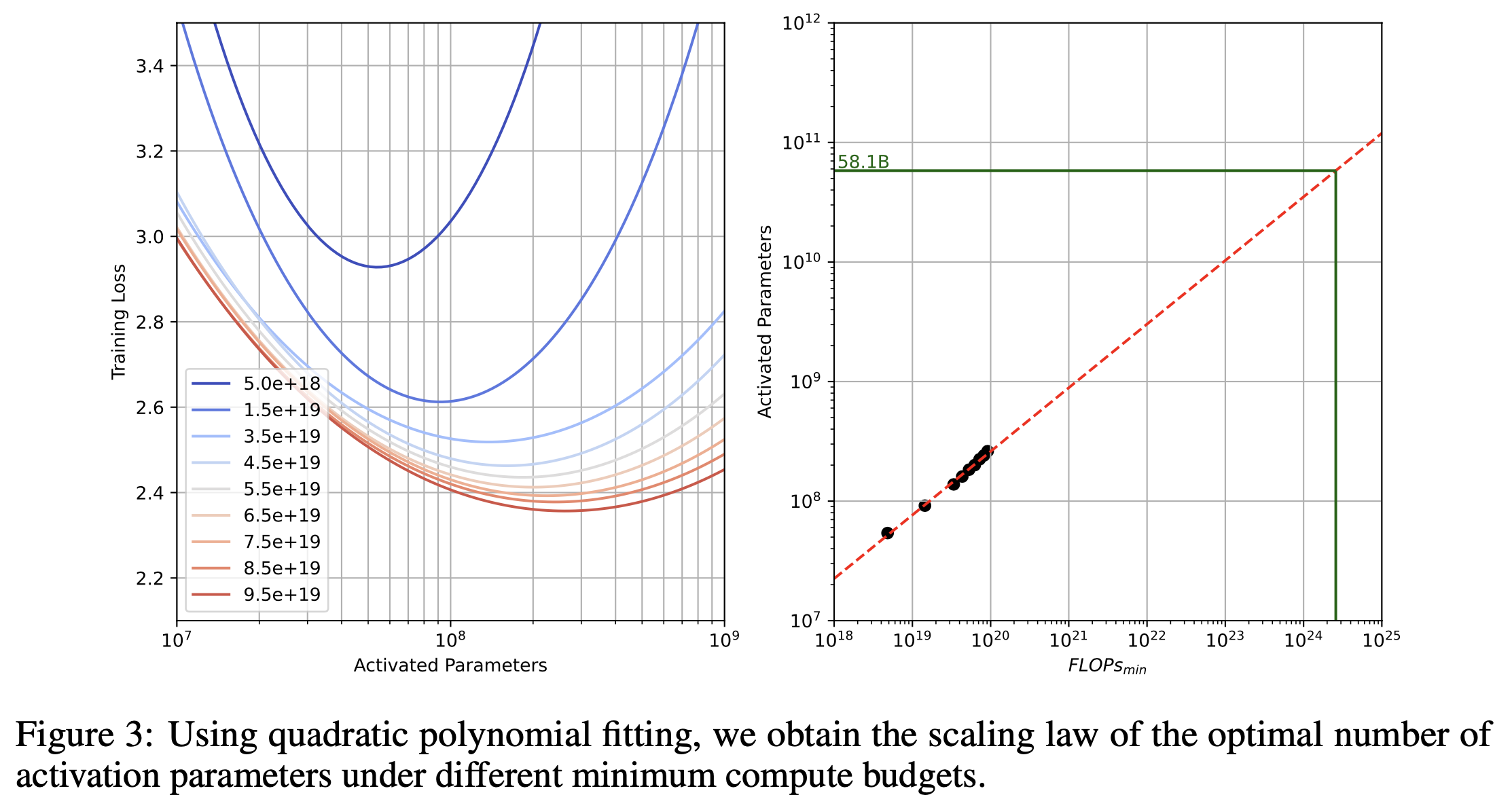hunyuan_paper_fig3 Fig.

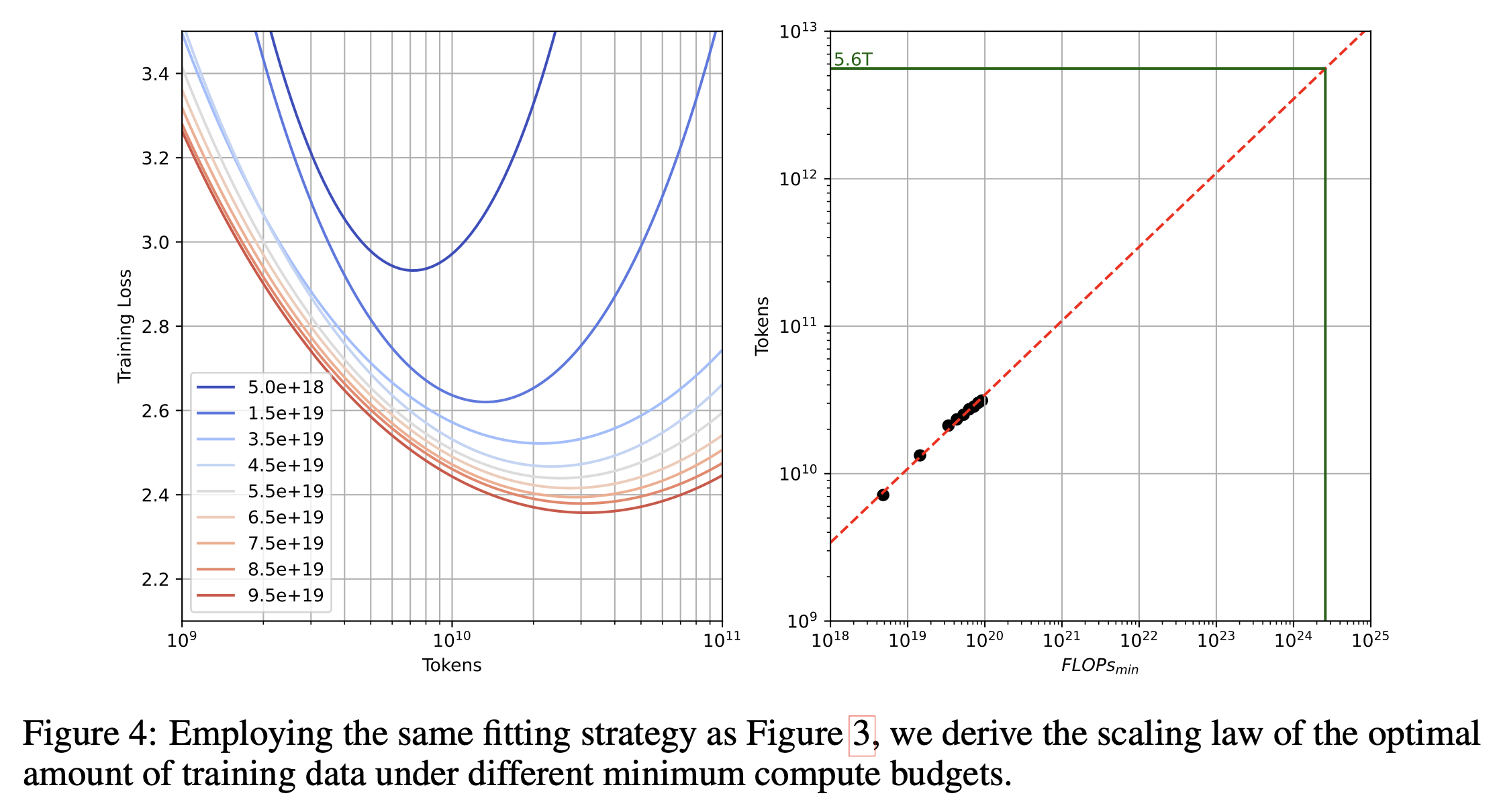hunyuan_paper_fig4 Fig.

(실제로는 7T학습함)

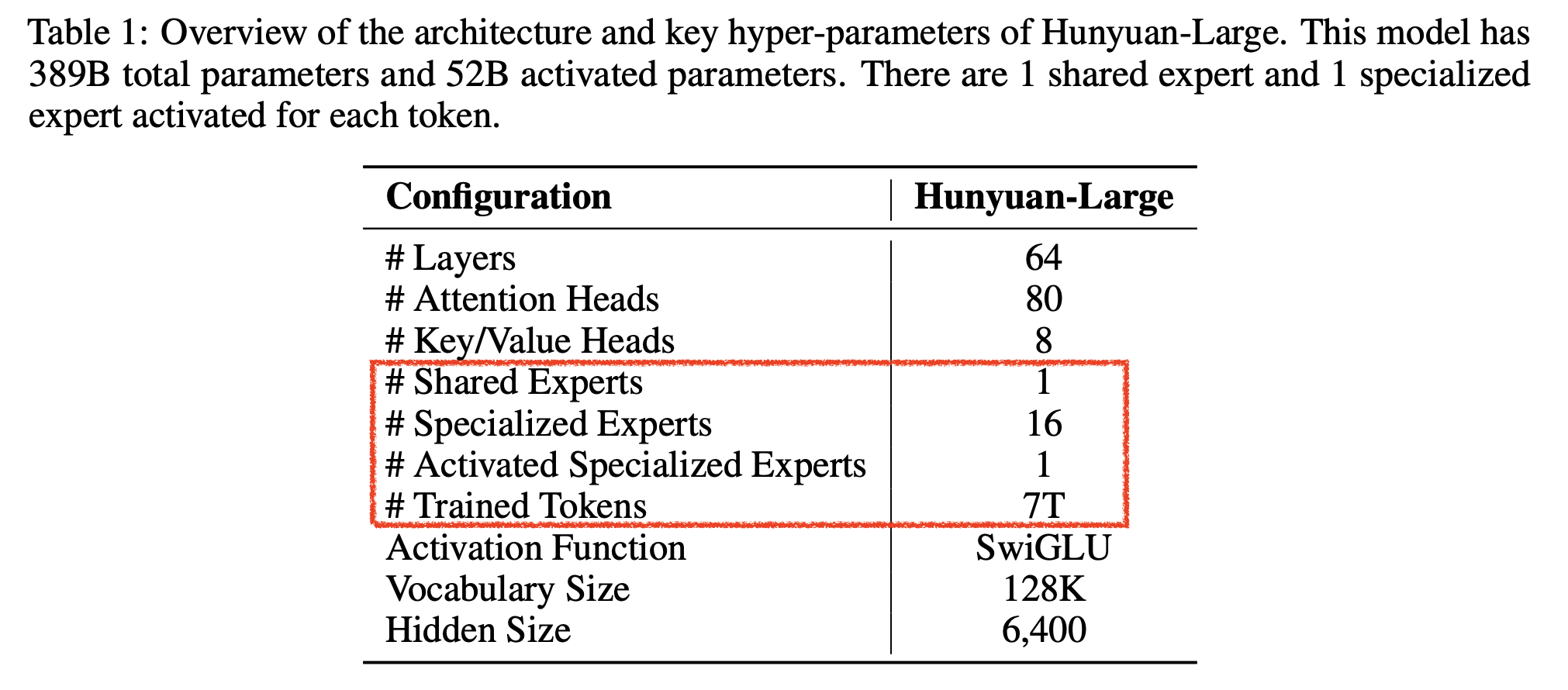hunyuan_paper_table1 Fig.

References