(WIP) Activation Functions and Gated Linear Unit (GLU)
29 Sep 2024< 목차 >
Overview of Activatin Functions
Activation function이 training dynamics에 끼치는 영향은 무엇인가? 왜 Noam architecture들은 swish, gelu 등의 activation을 사용할까? 기초적이지만 한 번 정리하면 좋을 것 같아 post를 작성하게 되었다.
고전 Machine Learning (ML)의 algorithm들과 Neural Network (NN)을 구분짓는 가장 큰 차이는 hidden layer의 존재 유무라고 할 수 있다. 쉽게 말하면 logistic regression 의 기능을 수행하는 module이 여러개가 모여 implicitly decision boundary를 형성한다고 생각할 수도 있겠다. 즉 NN에는 logistic regression의 sigmoid activation function 같은 것이 여러 번 들어간다고 할 수 있는데, Deep Neural Network (DNN)는 NN의 hidden layer가 매우 깊은 architecture를 의미한다. 그리고 같은 시간동안 좀 더 빠르게 model이 수렴할 수 있도록 (converge) optimizer, model architecture 등은 발전해왔다.
어떤 임의의 DNN에서 중간 layer 하나의 output은 input과 그 layer의 weight matrix를 사용해 아래와 같이 표현할 수 있는데,
\[\begin{aligned} & \text{let's say } x \in \mathbb{R}^{N \times D}, W \in \mathbb{R}^{D \times M}, b \in \mathbb{R}^{N \times D} & \\ & z = Wx + b & \\ & \text{then layer output is } y = f(z) \in \mathbb{R}^{N \times M} & \\ & \\ \end{aligned}\]sigmoid function이 쓰이면 아래와 같은 \(f\)를 사용하게 된다.
\[f(x) = \sigma(x) = \frac{1}{1 + \exp^{-x}}\]아마 이 글을 읽는 그 누구도 이에 대해서 모르지 않겠지만, 좀만 더 내 생각을 얘기해보자면 sigmoid function은 앞서 얘기한 것 처럼 logistic regression을 풀던 데 쓰이던 것이었고, 그런 binary classificaion problem을 풀 때는 output probability가 bernoulli distribution이 되므로 어느 한 쪽의 값이 0~1 사이로 mapping되는 것은 매우 자연스러웠다. 게다가 DNN으로 넘어와서도 어떤 hidden layer의 ouput matrix의 element 하나가 0 or 1로 표현되는것은 소위 “음 이 neuron이 활성화가 됐구나 (neural firing)”라고 해석하기 좋기에 별 문제가 없었다고 생각했다고 알고있다.
하지만 문제는 우리가 실제로 model training이라고 부르는 행위는 “고차원에서 optimal solution을 찾기 위해 gradient descent같은 iterative optimization algorithm를 사용해 weight update를 하는 것”에 지나지 않는 다는 것이며, 이를 위해서는 backpropagation을 해야 하며, 바로 이 때 sigmoid function은 매우 큰 단점을 지니고 있다는 것이었다. 우리가 원하는 것은 아래 수식처럼 loss function에 대한 현재 weight point의 미분체 (derivative)를 구하고 Learning Rate (LR), \(\eta\)만큼 update하는 것이다.
\[W_{\text{new}} = W_{\text{old}} - \eta \cdot \frac{\partial L}{\partial W}\]그리고 loss에 대한 임의의 hidden layer의 weight의 derivative는 아래와 같이 쓸 수 있는데,
\[\begin{aligned} & \frac{\partial L}{\partial W} = \underbrace{\frac{\partial L}{\partial f(z)}}_{\text{upstream grad}} \cdot \underbrace{\frac{\partial f(z)}{\partial z}}_{\text{grad for act func}} \cdot \underbrace{\frac{\partial z}{\partial W}}_{\text{local grad}} & \\ & = x^T \cdot \frac{\partial L}{\partial f(x)} \cdot \frac{\partial f(z)}{\partial z} & \\ \end{aligned}\]여기서 layer input과 weight matrix의 matrix multiplication 결과인 \(z\)가 activation function을 통과하기 때문에 activation function이 미분했을 때 어떤 특성을 갖는지는 굉장히 중요하며, 이에 따라 학습이 아예 안 될 수도 있거나 같은 training wallclock time 동안 수십배의 성능이 차이날 수도 있다 (즉 수렴이 늦게 된다는 말).
예를 들어 sigmoid function에 대해 좀 더 생각해보자. 이 activation function의 1st derivative는 아래 slide의 bell curve 처럼 생겼기 때문에, activation function output값이 매우 큰 양수이거나 음수라면 그 값이 0이되어 더 이상 iterative optimization을 진행 하더라도 weight update가 일어나지 않게 된다.
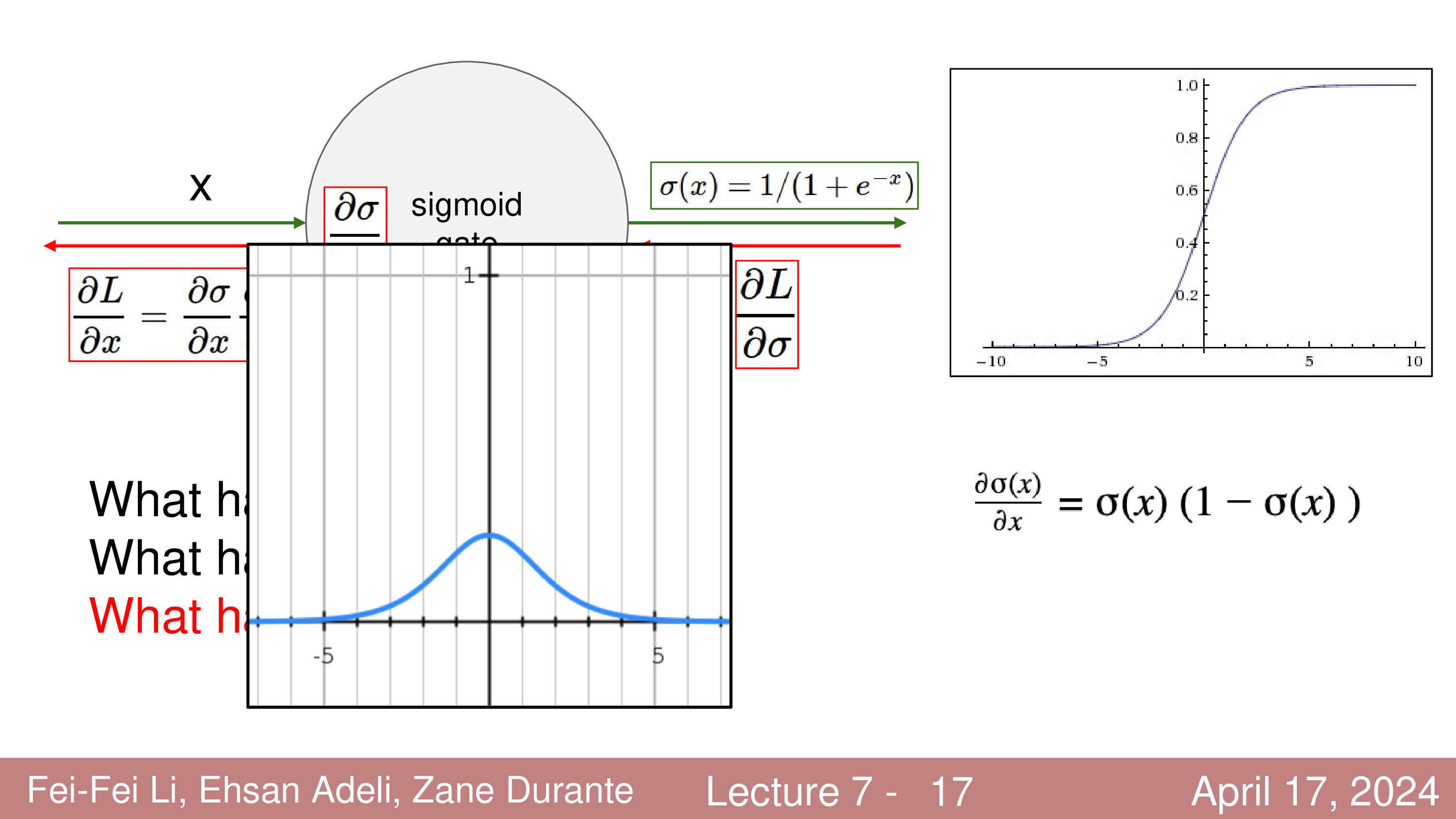 Fig.
Fig.
그래서 sigmoid는 먼저 gradient vanishing problem를 겪게 되는데,
이것 말고도 아래 slide의 3가지를 주된 문제점으로 꼽을 수 있다.
 Fig.
Fig.
이 중 두 번째 문제인 sigmoid outputs are not zero-centered는 또 다른 문제인데,
이는 진짜 말 그대로 모든 sigmoid activation function의 output이 0을 기준으로 대칭(?)인 것이 아니라 항상 양수라는 데서 온다.
앞서 얘기했던 것 처럼 어떤 임의의 layer의 weight matrix의 loss에 대한 gradient는 layer input과 upstream gradient의 outer product로 계산이 되는데,
layer input은 곧 이전 layer의 activation output이므로 이것이 모두 양수라는 것은 upstream gradient의 부호가 항상 유지된다는 것과 같다.
(all positive or all negative)
 Fig.
Fig.
그렇기 때문에 만약 아래 slide에서 처럼 optimal point로 이동하기 위해서는 가장 이상적인 direction이 4사분면 방향일지라도 zig-zag로 갈 수밖에 없게 되는 것이다.
 Fig.
Fig.
하지만 이건 mini-batch를 사용하거나 BatchNorm을 사용하는 것으로 어느정도 문제를 회피할 수 있다고 한다.
 Fig.
Fig.
마지막으로 practical하게 exponential operation을 적용해야 하는데, 이것이 그렇게 싸기만 한 연산은 아닐 것이다. 사실 sigmoid는 가장 원시적인 (?) activation function이고 실제로는 tanh, ReLU등이 기본적으로 많이 쓰이는데, 요즘은 GELU나 Swish activation function이 거의 기본적으로 쓰이고 있다.
 Fig.
Fig.
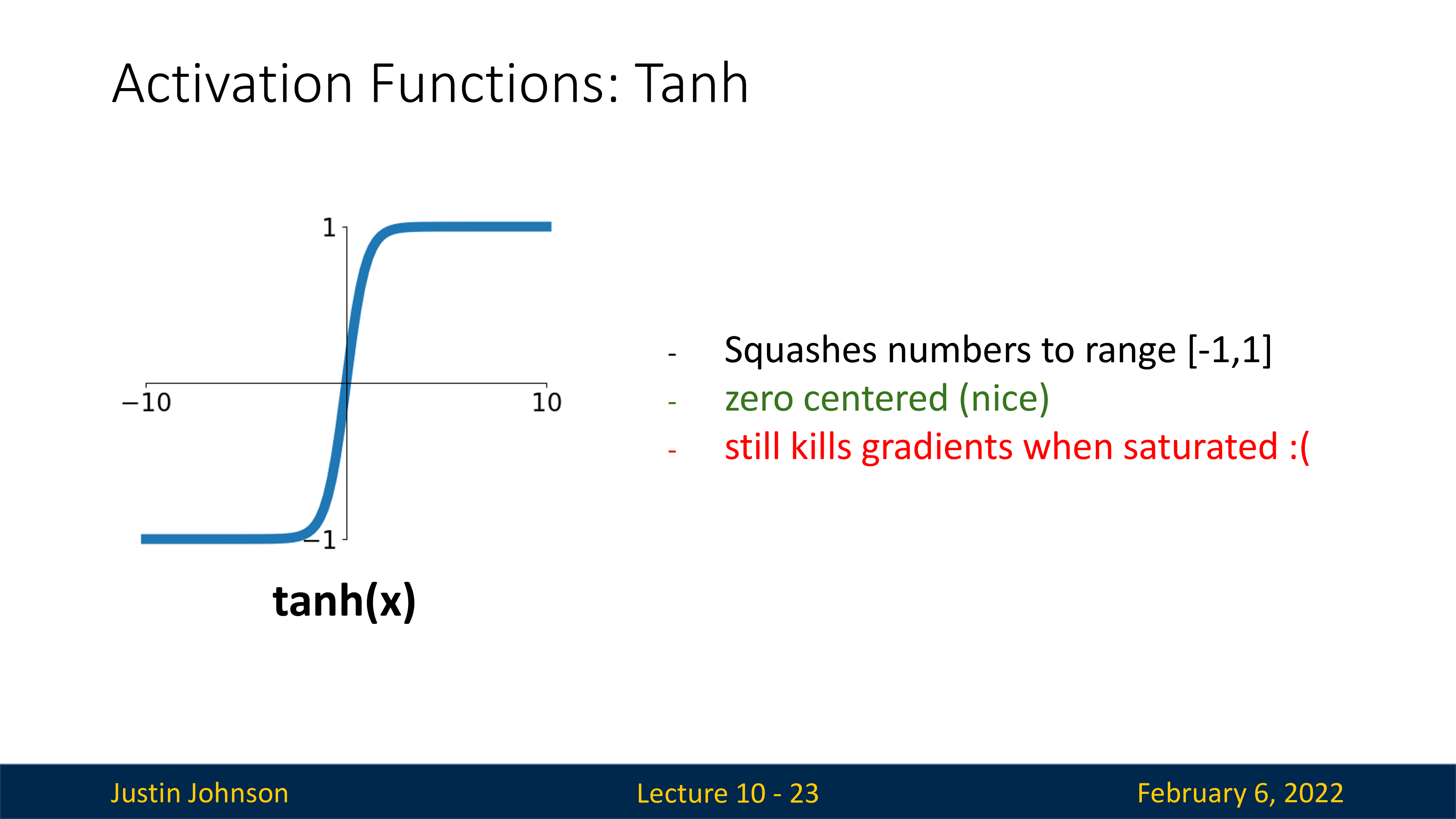 Fig.
Fig.
 Fig.
Fig.
 Fig.
Fig.
 Fig.
Fig.
 Fig.
Fig.
Modern Activation Functions
Gaussian Error Linear Units (GELUs)
Gaussian Error Linear Units (GELUs)는 ReLU와 비슷하게 생겼으나 0 부근에서 더 부드러우며 매우 큰 negative input이 아닌이상 0 gradient를 return하지 않으며, 무엇보다 probabilistic property를 가지고 있다.
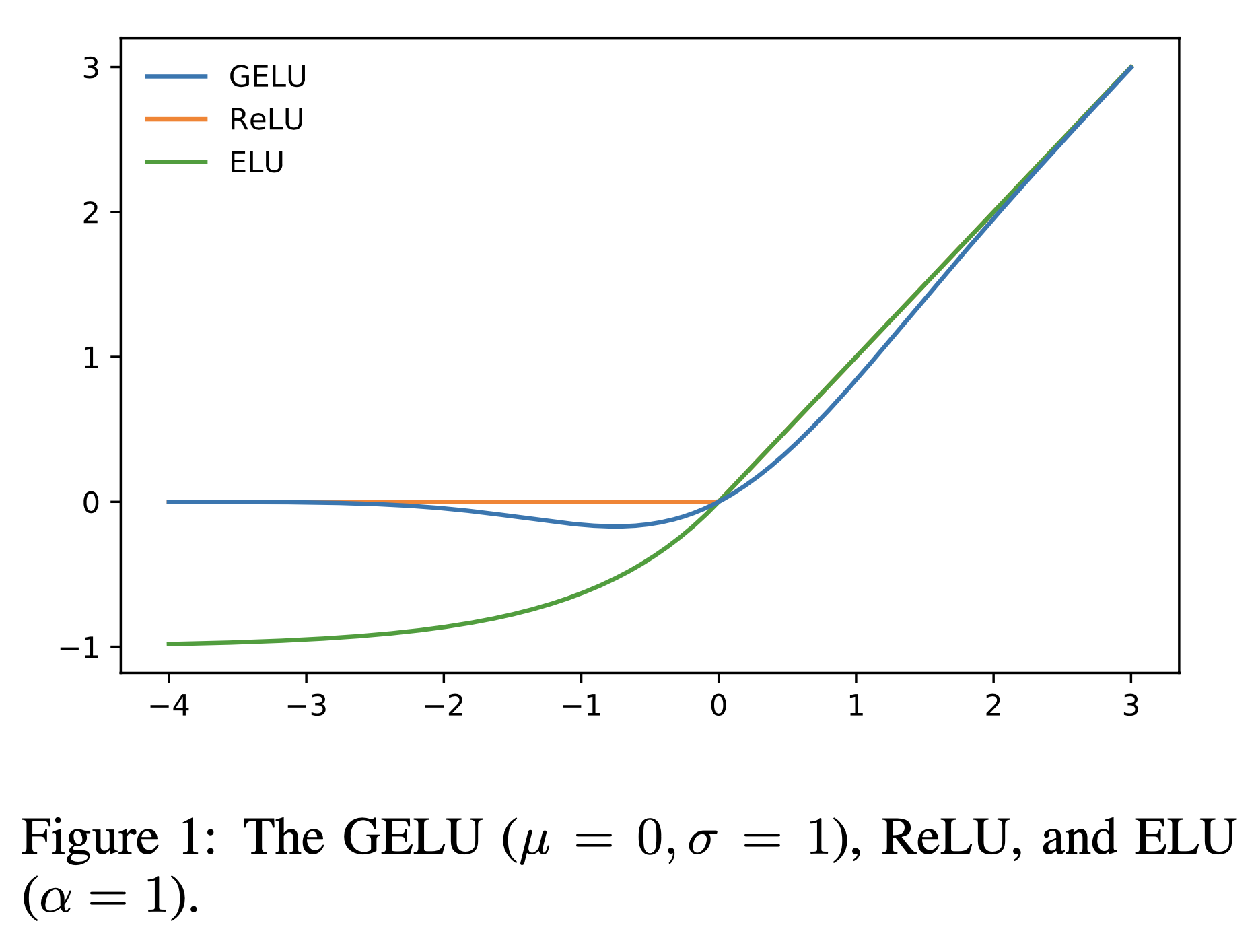 Fig.
Fig.
이게 무슨 소리냐면 GELU activation은 아래와 같은 수식으로 이루어져 있는데, 여기에 \(P(X \leq x)\) term이 들어가 있다.
\[\text{GELU}(x) = xP(X \leq x) = x \Phi(x) = x \cdot \frac{1}{2} [1 + erf (x/\sqrt(2))]\]여기서 random variable, \(X\)는 \(X \sim \mathcal{N}(0,1)\)을 따르는데,
직관적으로 sampling된 \(X\)가 layer input \(x\)보다 작을 확률이 반영되므로 \(x\)가 작을수록 0이 곱해질 확률이 높아지고 클수록 1이 곱해져 ReLU처럼 동작할 가능성이 커진다.
즉 dropout 처럼 작동하는 것을 생각할 수 있기 때문에 data-dependent dropout라고 부르기도 한다고 한다.
(\(X\)가 sampling된다고 표현했으나 어차피 fixed mean, variance로 표현되는 normal distribution에 대한 CDF, 즉 적분 값을 쓰기 때문에 deterministic한 값을 return한다.)
그런데 GELU는 exponential 연산이 들어가기 때문에 large scale NN에서 이를 줄이기 위해 근사 (approximate)한 수식을 쓰게 되는데 (적당히 taylor expansion등을 쓴다는 것 같은데), 이는 다음과 같다.
\[\begin{aligned} & \text{GELU}(x) = 0.5x (1+ \tanh[\sqrt{2/\pi} (x + 0.044715 x^3)]) & \\ & = x \sigma(1.702x) & \\ \end{aligned}\]GELU의 derivative는 CDF, \(\Phi\)를 미분하면 PDF, \(\phi\)가 되기 때문에 아래처럼 간단히 계산할 수 있다.
\[\begin{aligned} & \frac{\partial}{\partial x}\text{GELU}(x) = \Phi(x) + x \phi(x) & \\ & \text{where } \phi(x) = \frac{1}{\sqrt{2 \phi}}\exp(-\frac{1}{2}\frac{(x-\mu)^2}{\sigma^2}) & \\ \end{aligned}\]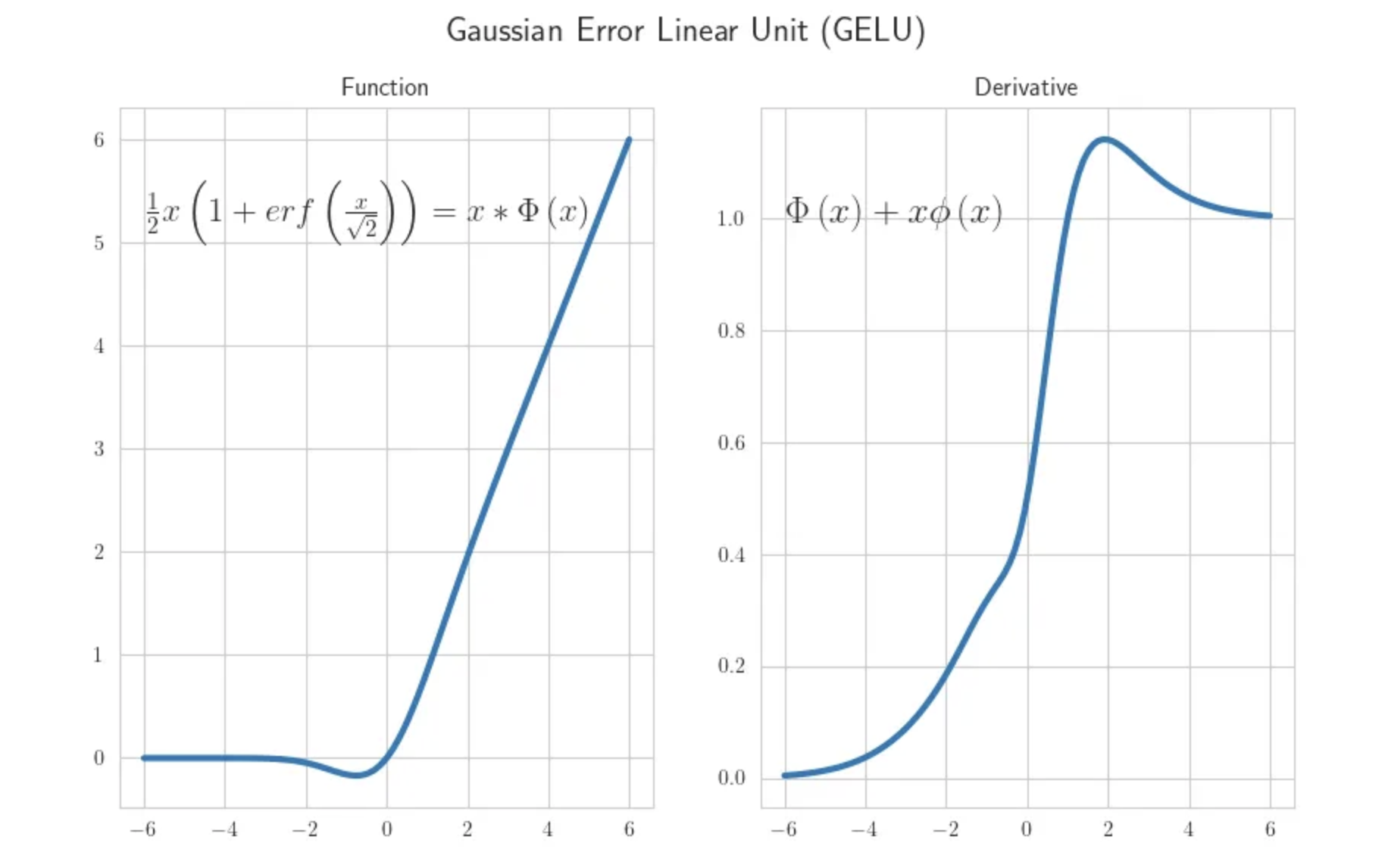 Fig. Source from link
Fig. Source from link
여기서 당연히 \(\mu, \sigma\)가 보통 \(0,1\)이지만 이것도 정하기 나름이며, learnable parameter로 두고 학습할 수도 있다고 한다. 실제 구현은 아래도 approximation을 쓰는 것 같은데, sigmoid 버전은 정확도가 좀 떨어지기 때문에 tanh version을 주로 쓰는 것으로 보인다.
 Fig.
Fig.
Self-Gated Activation Function (Swish) (a.k.a Sigmoid-Weighted Linear Units (SiLU))
그 다음은 SiLU인데, swish activation과 거의 같은 work으로 생각하면 될 것 같다. swish activation의 형태는 아래와 같은데,
\[\begin{aligned} & f(x) = \text{Swish}_{\beta}(x) = x \cdot \sigma( \beta x) & \\ & \text{where } \sigma(x) = \frac{1}{1 + \exp^{-x}}, \text{ usually } \beta=1 & \\ \end{aligned}\]사실 이는 GELU의 approximation version에서 \(\beta=1.702\)인 것과 같다고 볼 수 있다.
\[\begin{aligned} & f'(x) = \sigma(x) + x \cdot \sigma(x) (1-\sigma(x)) & \\ & = \sigma(x) + x \cdot \sigma(x) - x \cdot \sigma(x)^2 & \\ & = x \cdot \sigma(x) - \sigma(x) (1 - \sigma(x)) & \\ & = f(x) + \sigma(x) (1-f(x)) & \\ \end{aligned}\]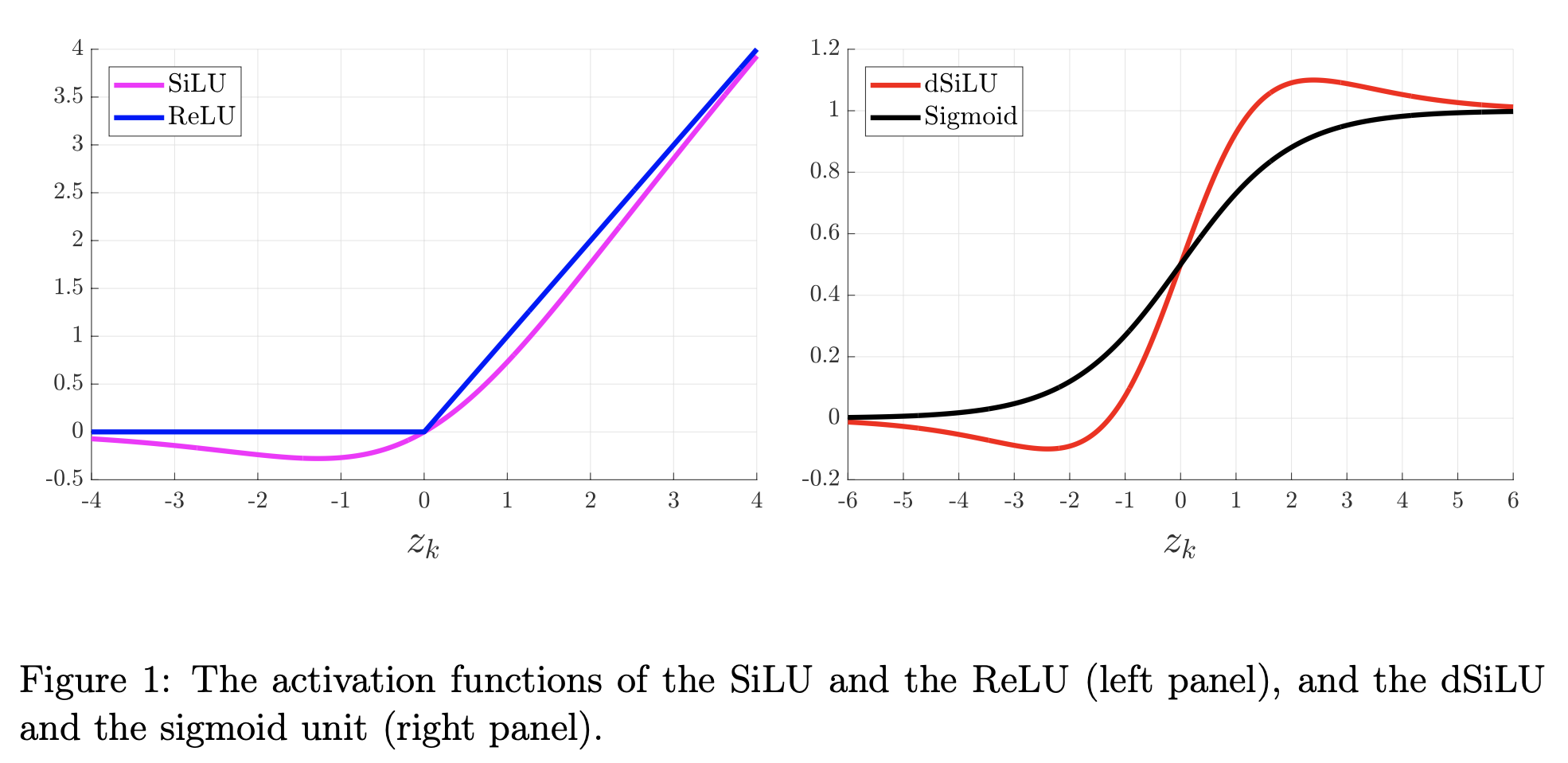 Fig.
Fig.
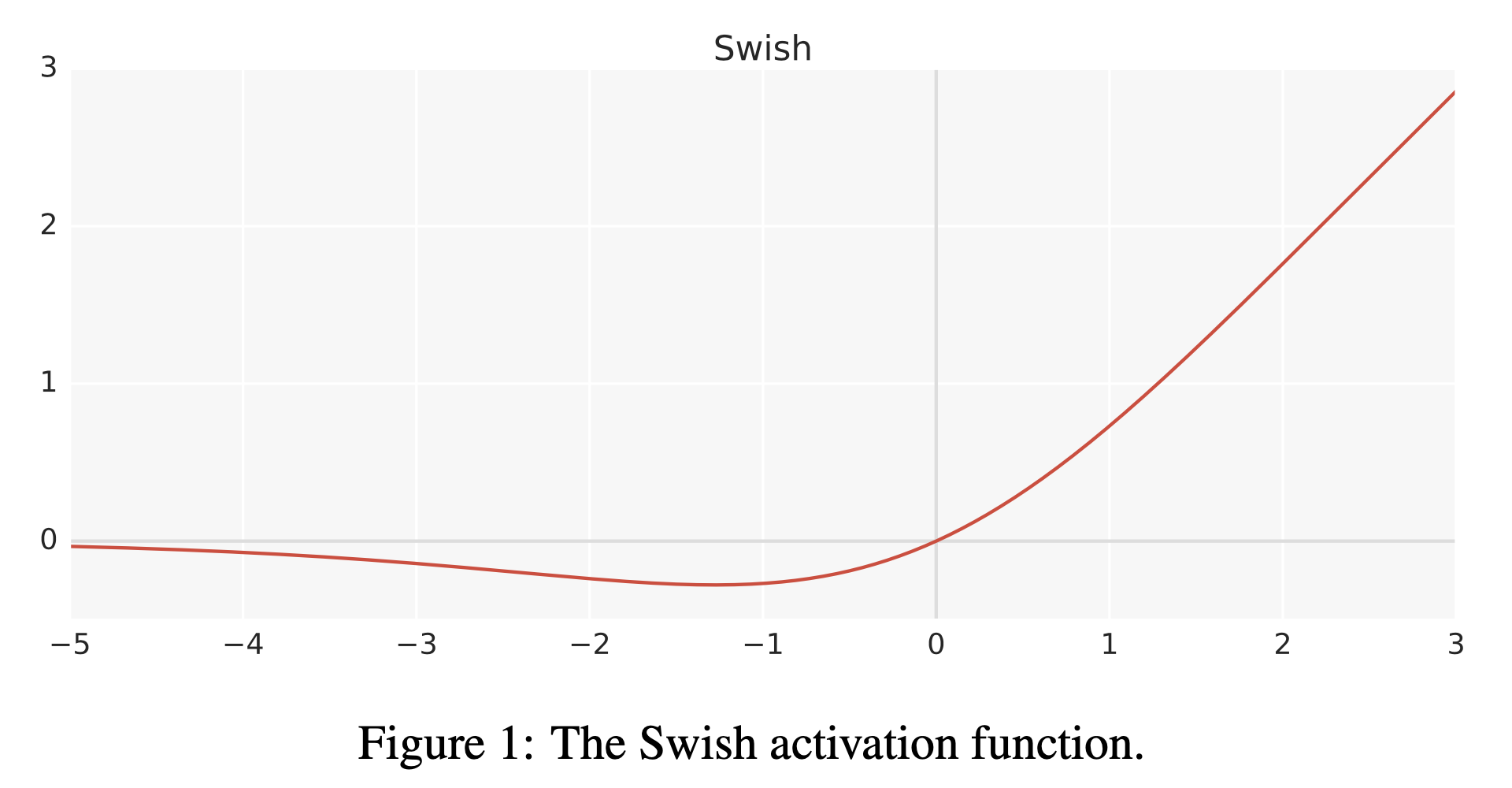 Fig.
Fig.
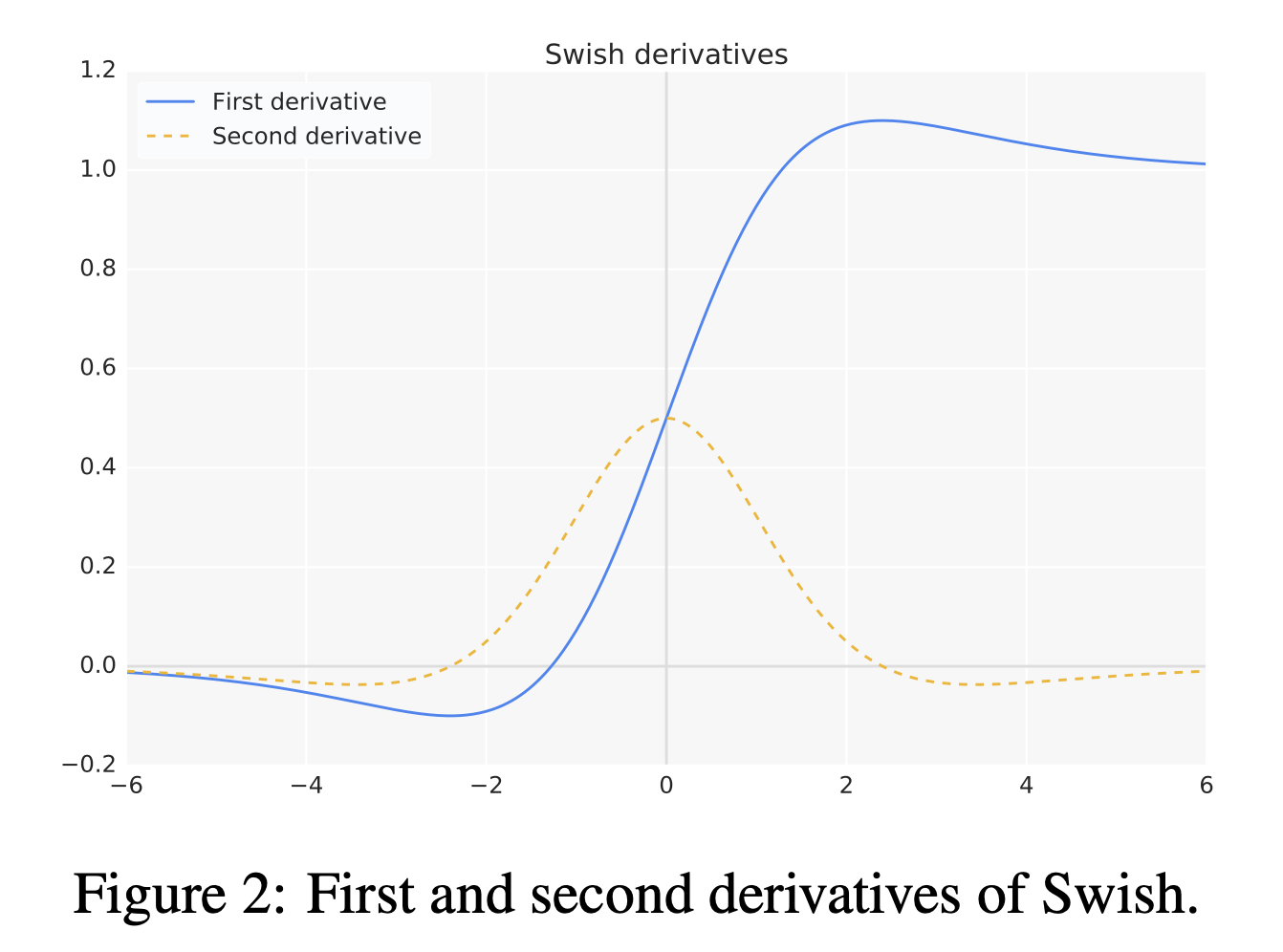 Fig.
Fig.
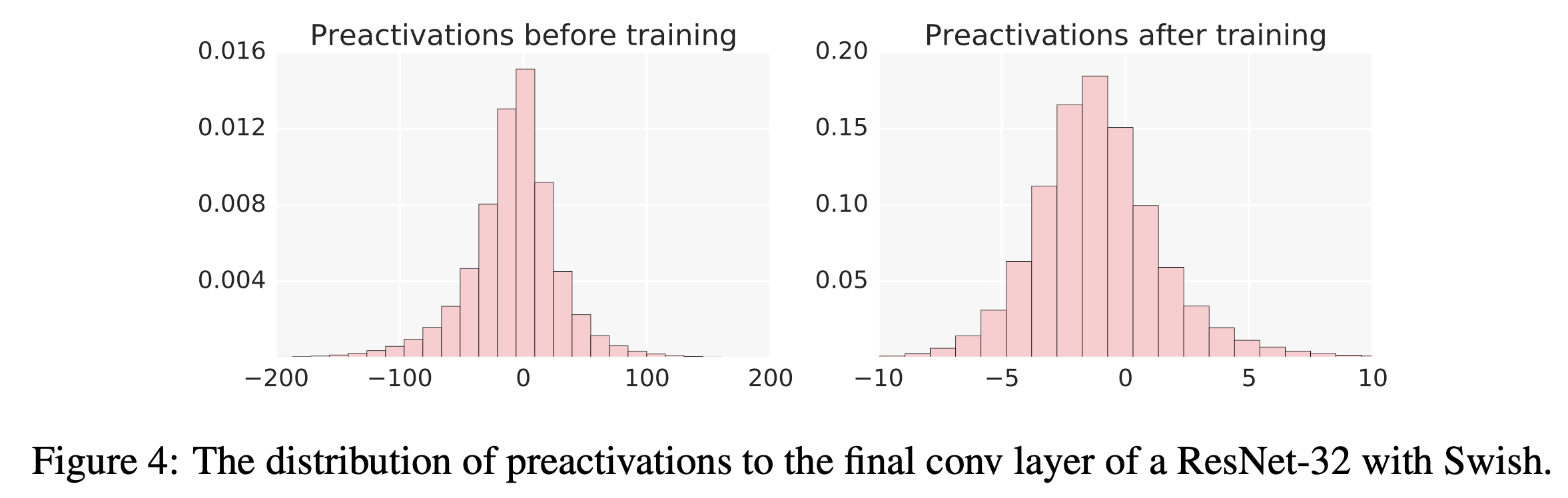 Fig.
Fig.
 Fig.
Fig.
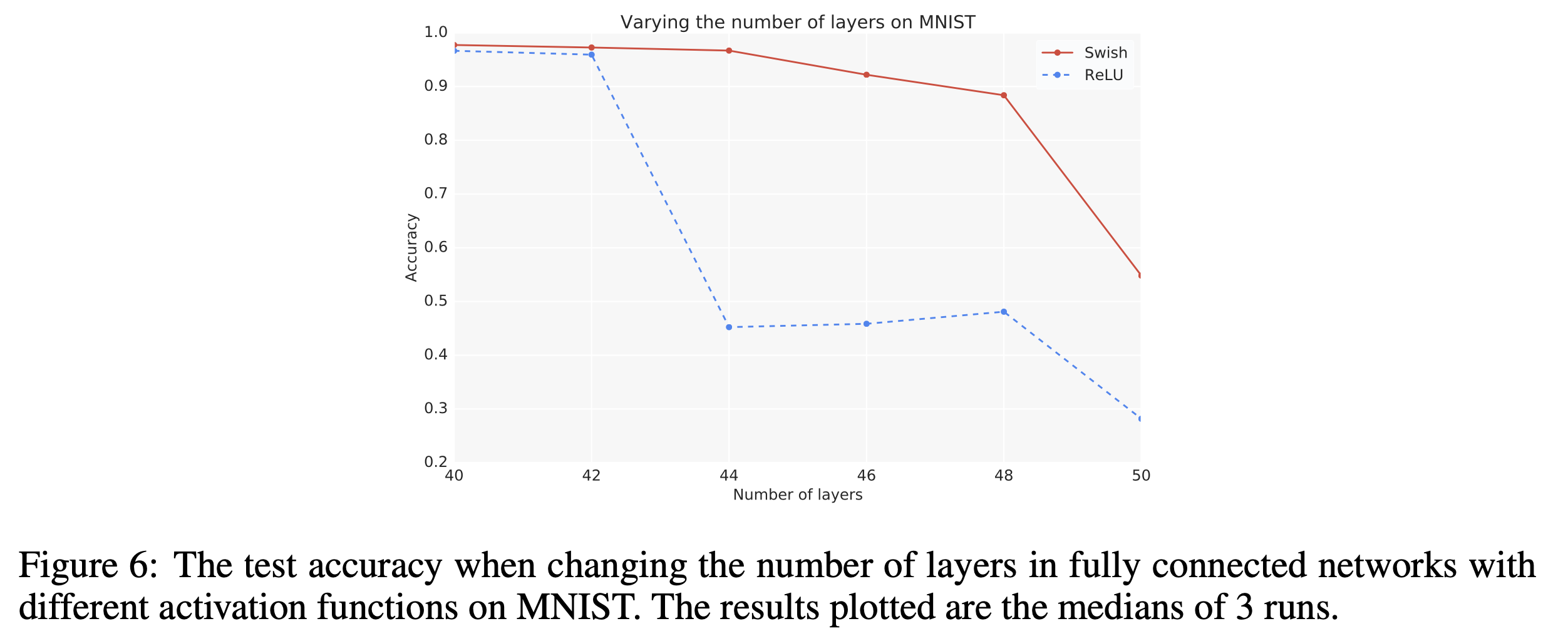 Fig.
Fig.
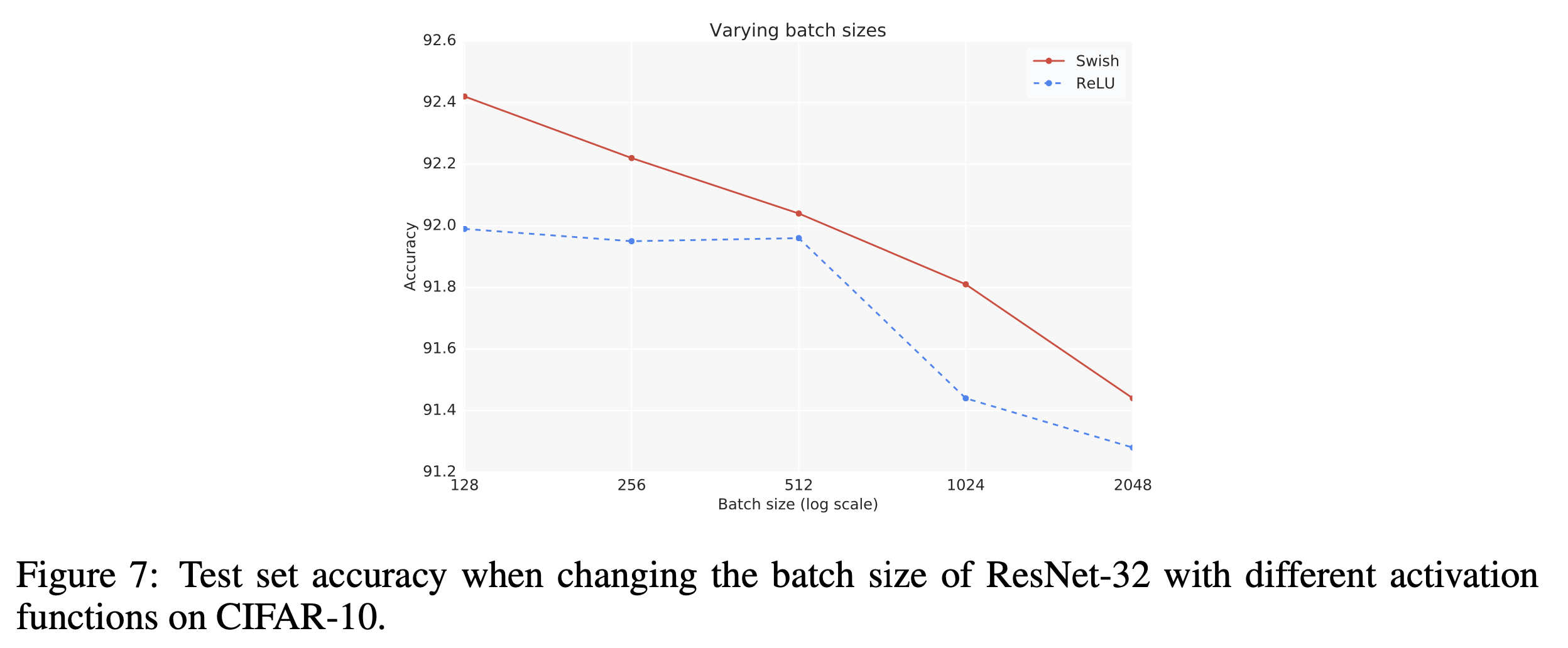 Fig.
Fig.
Gated Linear Unit (GLU)
그런데 사실 modern Large Language Model (LLM)들은 activation을 그냥 쓰지 않는다. Vanilla Transformer layer에는 nonlinear activation function이 들어가는 곳이 두 군데 있는데, 하나는 self attention의 softmax function이며, 다른 하나는 feed forward module의 중간에 들어가는 것이다.
\[\begin{aligned} & y = \text{FFN}_2 (f ( \text{FFN}_1(x) )) & \\ & \text{FFN}(x, W_1, W_2, b_1, b_2) = f(xW_1 + b_1)W_2 + b_2 & \\ \end{aligned}\]llama를 비롯한 modern llm들은 Gated Linear Unit (GLU)이라는 걸 쓰는데,
\[\begin{aligned} & \text{GLU}(x, W_1, V) = f(xW_1) \otimes f(xV) & \\ & \text{GELU}(x, W_1, V) = \text{GELU}(xW_1) \otimes f(xV) & \\ & \text{SwiGLU}(x, W_1, V) = \text{Swish}(xW_1) \otimes f(xV) & \\ \end{aligned}\]이를 사용해서 FFN을 아래와 같이 변형할 수 있다.
\[\begin{aligned} & \text{FFN}_\text{GLU}(x, W_1, V, W_2) = (f(xW_1) \otimes f(xV))W_2 & \\ & \text{FFN}_\text{GELU}(x, W_1, V, W_2) = (\text{GELU}(xW_1) \otimes f(xV))W_2 & \\ & \text{FFN}_\text{SwiGLU}(x, W_1, V, W_2) = (\text{Swish}(xW_1) \otimes f(xV))W_2 & \\ \end{aligned}\]이렇게 하면 훨씬 더 좋은 성능으 얻을 수 있다고 하는데,
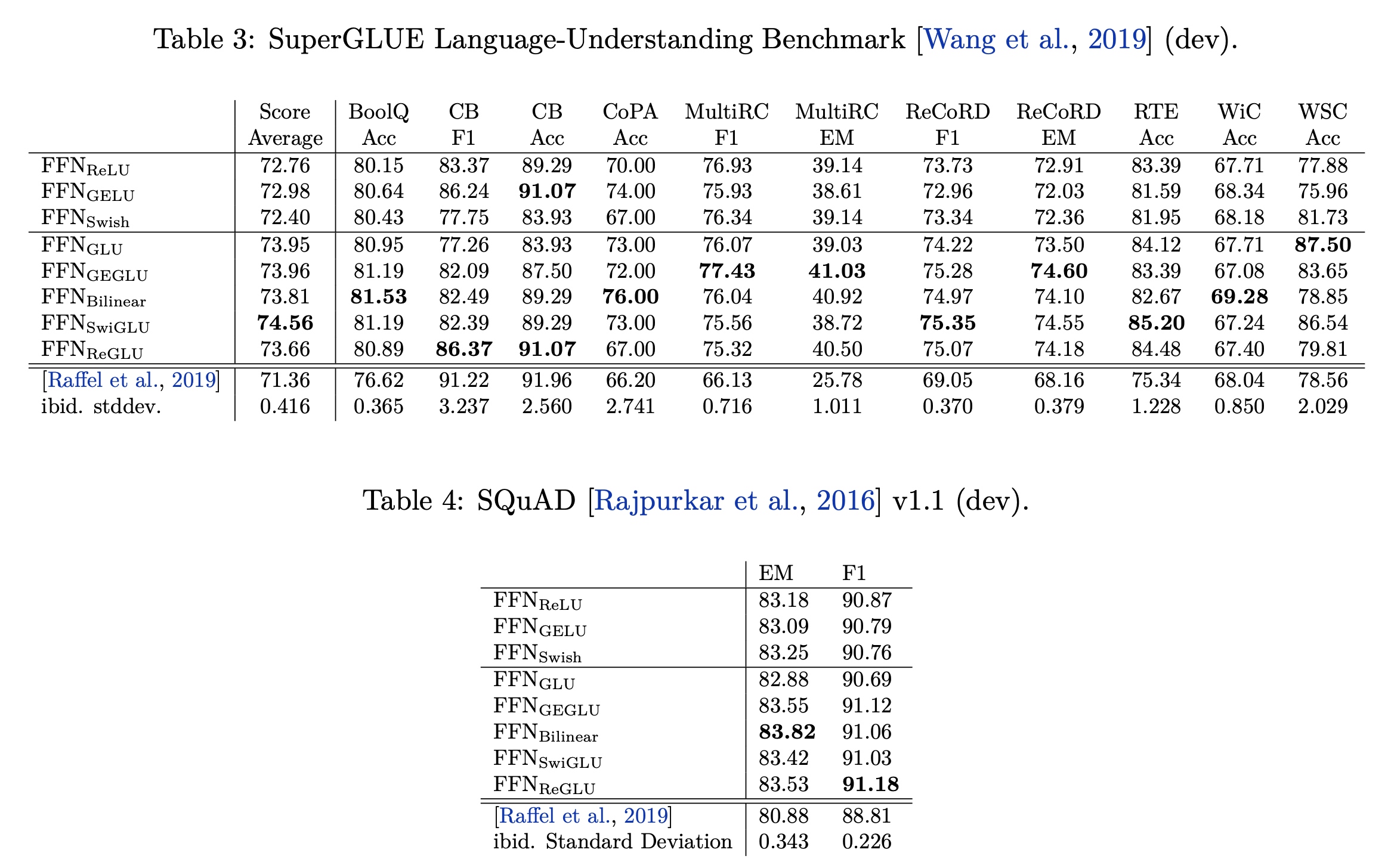 Fig.
Fig.
왜 이게 잘 되는지에 대해서는 Attention Is All You Need의 저자인 Noam Shazeer도 그 이유를 모르겠다고 적어놨다.
 Fig.
Fig.
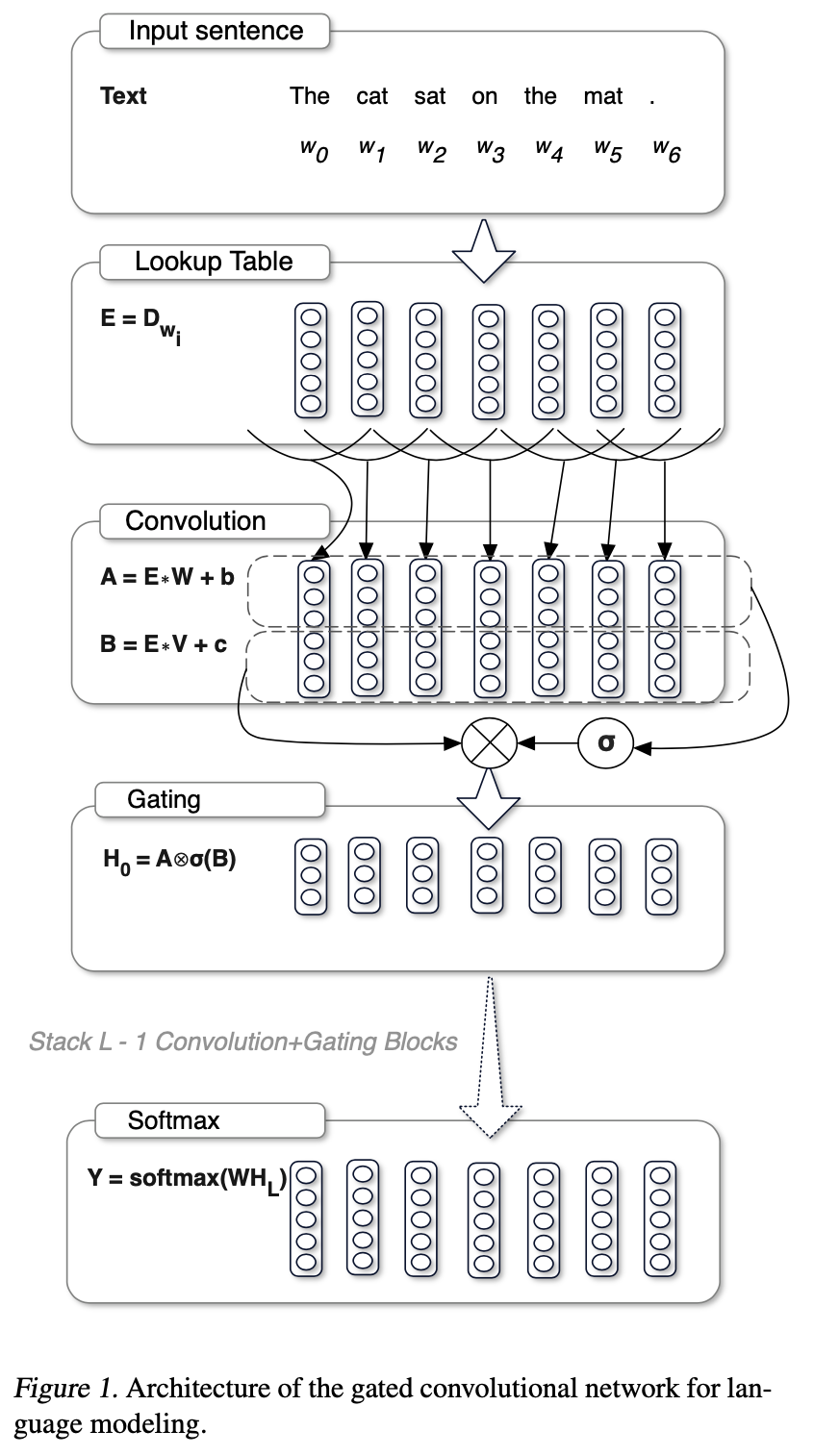 Fig.
Fig.
 Fig.
Fig.
 Fig.
Fig.
References
- Papers
- Gaussian Error Linear Units (GELUs)
- Sigmoid-Weighted Linear Units (SiLU) - Sigmoid-Weighted Linear Units for Neural Network Function Approximation in Reinforcement Learning
- Swish: a Self-Gated Activation Function
- Mish: A Self Regularized Non-Monotonic Activation Function
- Language Modeling with Gated Convolutional Networks
- GLU Variants Improve Transformer
- Lectures
- EECS 498/598 (Winter 2022) from Justin Johnson
- cs231n (Spring 2023)
- cs182
- cs224n
- Others