Notes

(WIP) Iterative Optimization Algorithms for ML (3/4) - Higher Order Methods For Deep Learning (K-FAC, Shampoo and so on)

10 Sep 2024

< 목차 >

Motivation and Introduction

앞서 Newton method와 같은 2nd order method가 1st order method보다 훨씬 좋은 이유에 대해 설명했다. 1st order는 접선의 기울기만을 계산하는 것이며, 2nd order method는 loss function이 어떻게 생겼는지를 근사할 수 있는데, 이는 given weight point에서의 loss surface가 어떤 모양일지를 taylor expansion으로 근사할 때 차수가 더 많으면 true function에 더더욱 가까워지기 때문이다.

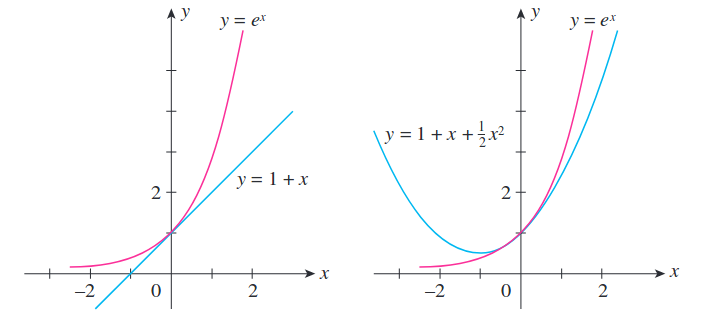taylor_1st_and_2nd_approx Fig.

즉, 2nd order method는 loss surface의 기울기만 측정하는 1nd order method와 다르게 2nd order taylor approximation을 통해 loss surface의 곡률 (Curvature)를 측정하며, 그렇기 때문에 step size를 더 정확하게 계산할 수 있게 되고, 따라서 수렴도 훨씬 빠르게 할 여지가 있다.

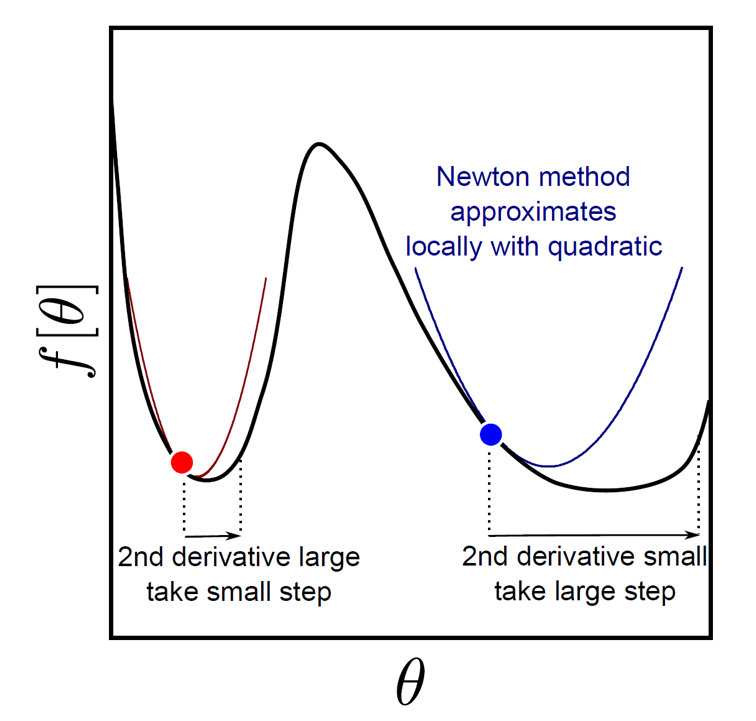classification1_newton_fig1 Fig.

하지만 2nd order method를 Deep Learning (DL)에 적용하기란 쉽지 않다고 했다. 그 이유는 2nd order approximation, Hessian의 계산이 너무 오래 걸리고 (intractable), 이를 저장하는데 memory도 많이 필요하기 때문인데, 아래 figure를 보면 \(N\)개 layer로 이뤄진 model의 \(N-1\)번째 layer같은 임의의 layer의 weight parameter 갯수가 \(d\)개일 때 Hessian, \(H\)는 \(d \times d\)만큼의 계산량과 memory를 요구한다는 걸 알 수 있다.

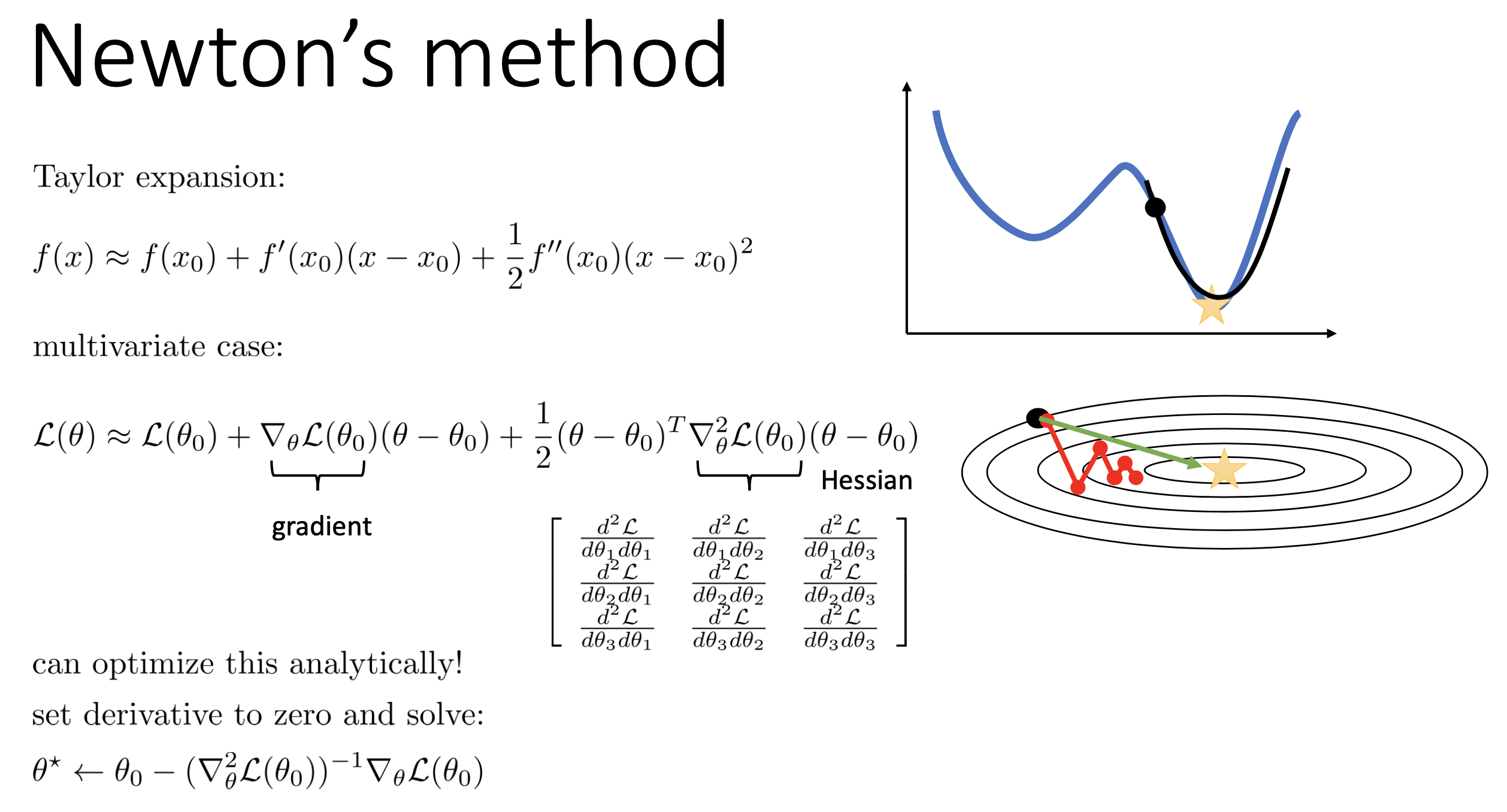cs182_lec5_fig16 Fig.

그래서 modern DL model들 중 hessian을 그대로 사용하여 학습된 model은 존재하지 않는다. RMSProp, AdaGrad, Adam같은 adaptive optimizer들을 사용하는데,

\[\theta \leftarrow \theta + \eta \cdot \color{red}{S^{-1}} \cdot \nabla_{\theta} L(\theta)\]

위의 수식에서 \(S^{-1} = I\)면 vanilla gradient descent를 의미하고, \(\eta=1\)이며 \(S = H\), Hessian이면 Newton's Method가 되며, mini batch의 gradient vector, \(g\)에 대해서 \(H \approx g g^T\)이면 AdaGrad같은 Adaptive Optimizer가 된다. 여기서 full matrix, \(g g^T\)를 쓰는 것은 비싸기 때문에 보통 adaptive optimizer들은 \(g\)를 elementwise product한 값을 쓰는데, 이는 approximate Hessian의 diagonal vector를 사용해 한번 더 approximation을 하겠다는 의미이다 (\(diag(H) = g \odot g\)).

여기서 \(S^{-1}\)은 Preconditioner라고 부르는데, 이는 기하학적으로 loss surface를 rotation 혹은 scaling 하여 optimization problem을 쉽게 만든다고 이해할 수 있다.

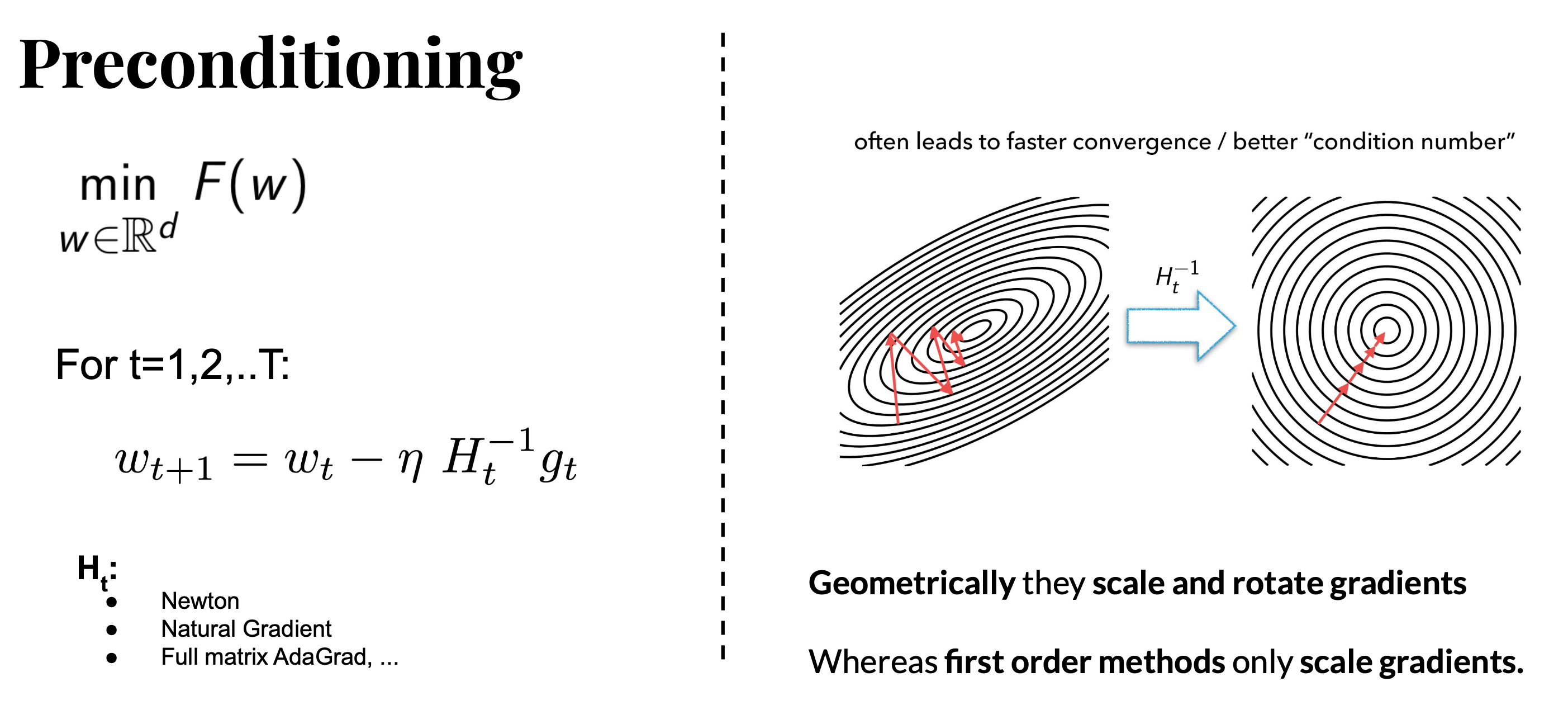preconditioning Fig. Slide adapted from Author of Shampoo, Rosanne Liu. 앞으로 Shampoo optimizer는 저자인 Rosanne Liu의 slide를 사용해 설명하도록 할 것

Parameter size가 더 커지고, model이 더 깊어질수록 발생하는 DNN training의 문제를 해결하고 같은 시간동안 더 빨리 수렴할 수 있게 하기 위해 고안된 대부분의 normalization, optimizer 등 training technique들은 보통 parameter간 optimization 불균형을 해결하기 위해 제안되었다고 생각할 수 있다. 어떤 parameter는 step size를 크게가기엔 너무 민감하지만 어떤 parameter는 둔감해서 step size를 크게 가져가도 되는데 나머지들 때문에 그렇게 하지 못하는 것이다. 즉 gradient를 잘 계산했음에도 learning rate을 키울 수 없어 수렴이 늦어지는 것이고, 대부분의 Adam같은 adaptive optimizer들은 수식에서도 알 수 있듯이 gradient를 parameter별로 scaling 해주기 때문에 (per parameter scaling) 수렴이 잘 되는 것이다.

하지만 이것만으로는 부족하다는 관점이 이번 post에서 알아볼 2nd order method들의 주장인데, 이는 hessian matrix가 어떻게 구성됐는지를 생각해봐야 할 것이다. Hessian matrix는 아래처럼 paramter간의 correlation을 modeling하게 되어있다.

\[H = \begin{bmatrix} \frac{\partial^2 L}{\partial \theta_1 \partial \theta_1} & \frac{\partial^2 L}{\partial \theta_1 \partial \theta_2} & \frac{\partial^2 L}{\partial \theta_1 \partial \theta_3} \\ \frac{\partial^2 L}{\partial \theta_2 \partial \theta_1} & \frac{\partial^2 L}{\partial \theta_2 \partial \theta_2} & \frac{\partial^2 L}{\partial \theta_2 \partial \theta_3} \\ \frac{\partial^2 L}{\partial \theta_3 \partial \theta_1} & \frac{\partial^3 L}{\partial \theta_1 \partial \theta_2} & \frac{\partial^2 L}{\partial \theta_3 \partial \theta_3} \\ \end{bmatrix}\]

이렇기 때문에 weight matrix 크기가 \(1000\)차원이라면 \(1000 \times 1000\)의 크기를 차지하는 matrix가 필요한 것이다. Hessian matrix의 inverse를 gradient에 곱해주겠다는 것은 loss surface를 scaling하는 걸 넘어 rotation 해준다고 앞서 얘기했는데, 직관적으로 이는 paramter간의 상관관계를 없앤다는 의미로 해석할 수 있다.

왜 이것이 상관관계를 modeling하는가? 위 hessian matrix는 다시쓰면 아래처럼 쓸 수 있는데, 이는 즉 예를 들어 parameter, \(\theta_1\)이 변화할때 그 변화가 \(\theta_2, \theta_3\)에 어떤 변화를 주는지를 의미하는 것이 된다.

\[H = \begin{bmatrix} \frac{\partial (\frac{\partial L}{\partial \theta_1})}{\partial \theta_1} & \frac{\partial (\frac{\partial L}{\partial \theta_1})}{\partial \theta_2} & \frac{\partial (\frac{\partial L}{\partial \theta_1})}{\partial \theta_3} \\ \frac{\partial (\frac{\partial L}{\partial \theta_2})}{\partial \theta_1} & \frac{\partial (\frac{\partial L}{\partial \theta_2})}{\partial \theta_2} & \frac{\partial (\frac{\partial L}{\partial \theta_3})}{\partial \theta_3} \\ \frac{\partial (\frac{\partial L}{\partial \theta_3})}{\partial \theta_1} & \frac{\partial (\frac{\partial L}{\partial \theta_3})}{\partial \theta_2} & \frac{\partial (\frac{\partial L}{\partial \theta_3})}{\partial \theta_3} \\ \end{bmatrix}\]

예를 들어 원래 roatation이 되기 전에는 \(\theta_1\)을 update하는 것이 \(\theta_2\)에도 영향을 끼칠 수 있기 때문에 optimization을 하는데 어려움을 겪을 수 있는 상황을 없애주는 것이라고 할 수 있겠다. 그러나 앞서 얘기한 것 처럼 weight matrix 크기가 \(n=1000\)차원이라면 \(n^2 \approx 1000 \times 1000\)의 크기의 hessian matrix, \(H\)가 필요하며, parameter update시에 우리가 진짜 필요한 연산은 \(H^{-1} \nabla_{\theta} L\)이기 때문에 이는 \(O(n^3)\)의 연산이 필요하게 된다. 이렇듯 hessian matrix를 사용하는 optimization도 연산량, 공간복잡도가 크다는 문제와 함께 변곡점에서 SGD보다 탈출이 어렵다는 단점같은게 존재하긴 하지만 여러가지 trick들을 곁들이면 1st order method들보다 훨씬 빠른 수렴이 이론적으론 가능하다고 한다.

한 편, parameter size가 매우 큰 DL에도 2nd order method를 적용하기 위한 approach들이 있었는데, 대표적으로 Kronecker-Factored Approximate Curvature (K-FAC)나 Shampoo들이 Kronecker-factored approximation을 사용해서 2dn order method의 연산량을 줄여 DL에 쓰도록 개발된 algorithm 들이다 (approx는 했지만 1st order는 아님).

kfac_and_shampoo Fig.

Kronecker-Factored Approximate Curvature (K-FAC)은 University of Toronto의 James Martens와 Roger Grosse가 제안한 method이며, Shampoo는 Google에서 2018년에 제안한 method로 24년 8월 현재 Training Algorithms Competition (AlgoPerf)라는 optimization algorithm 경진대회에서 2등보다 28%나 빠르게 NN training을 하게 되어 Nesterov Adamd을 제치고 1등을 했다고 한다.

하지만 Shampoo는 더 정교한 preconditioner 를 쓰는 대신 GPU device 여러개를 사용해 학습하는 distributed training 환경에서 사용하기에 Adam보다 훨씬 까다롭다는 단점이 있다고 한다. 즉 approximation을 했음에도 불구하고 여전히 scalable 한가에 대해 의문이 있는데, 여기서 scalable하다는 것은 “model size가 커지고 GPU같은 accelerater 수가 늘어날 때 초당 토큰 처리량 (throughput; tokens/sec)등을 손해보지 않을 수 있는가?”를 의미한다고 할 수 있다. 즉 동일 step에서의 성능은 좋지만 동일 step까지 가는데 wall clock time이 더 들기 때문에 의미가 퇴색된 것이다. Shampoo를 distributed training에 적용하는건 쉽지 않기 때문에 Distributed Shampoo라는 paper가 따로 publish될 정도로 난이도가 있다고 하는데, 그렇기에 개념 자체는 2018년에 처음 제안되었지만 이제서야 빛을 발하게 된 것 같다.

확실하지는 않지만 Gemini 1.5 Flash는 AdamW같은 1st order가 아니라 higher order가 쓰였다는 걸 보면 아마 shampoo가 production level에서 검증이 된 것으로 보인다.

gemini_flash_shampoo Fig.

DeepMind의 distributed training engineer인 Rohan Anil는 최근 한 tweet을 남겼는데, 그녀는 Non-diagonal preconditioning optimizer인 Shampoo가 드디어 인정을 받게 되어 (scalable해져서 라고 할 수 있을듯?) 너무 기쁘고 이 순간을 AlexNet moment for optimization for deep learning이라고 묘사했다.

Preliminaries

이 post의 목적은 second-order optimizer를 제대로 이해해 보는 것이다. 그러기 위해서는 당연히 hessian matrix가 무엇인지 알아야 하며, hessian, \(H\)의 eigenvalue와 eigenvector가 의미하는 바가 무엇인지 알아야 한다. 그리고 나아가 실제 hessian matrix를 iterative optimization 하는데 쓸 수 없으니 이를 근사한 방법들에 대해 알아야 하며, 그 중에는 Gauss Netwon method를 위한 \(G\)와 Fisher Imformation Matrix (FIM) method를 위한 \(F\)가 있다. 당연히 hessian을 곱해서 언션하는 행위를 근사한 것이기 떄문에 matrix H, G, F는 모두 loss surface의 곡률 (curvature)을 측정하는 것과 관련이 있다. 그리고 우리는 H -> G -> F로 발전하게된 history에 대해 이해 해야 한다. 하나 더, FIM에서 Empirical Fisher, \(F_{emp}\)가 파생되는데, 이는 우리가 자주 사용하는 Adagrad, RMSProp 그리고 Adam등의 adaptive optimizer들과 깊은 연관이 있다.

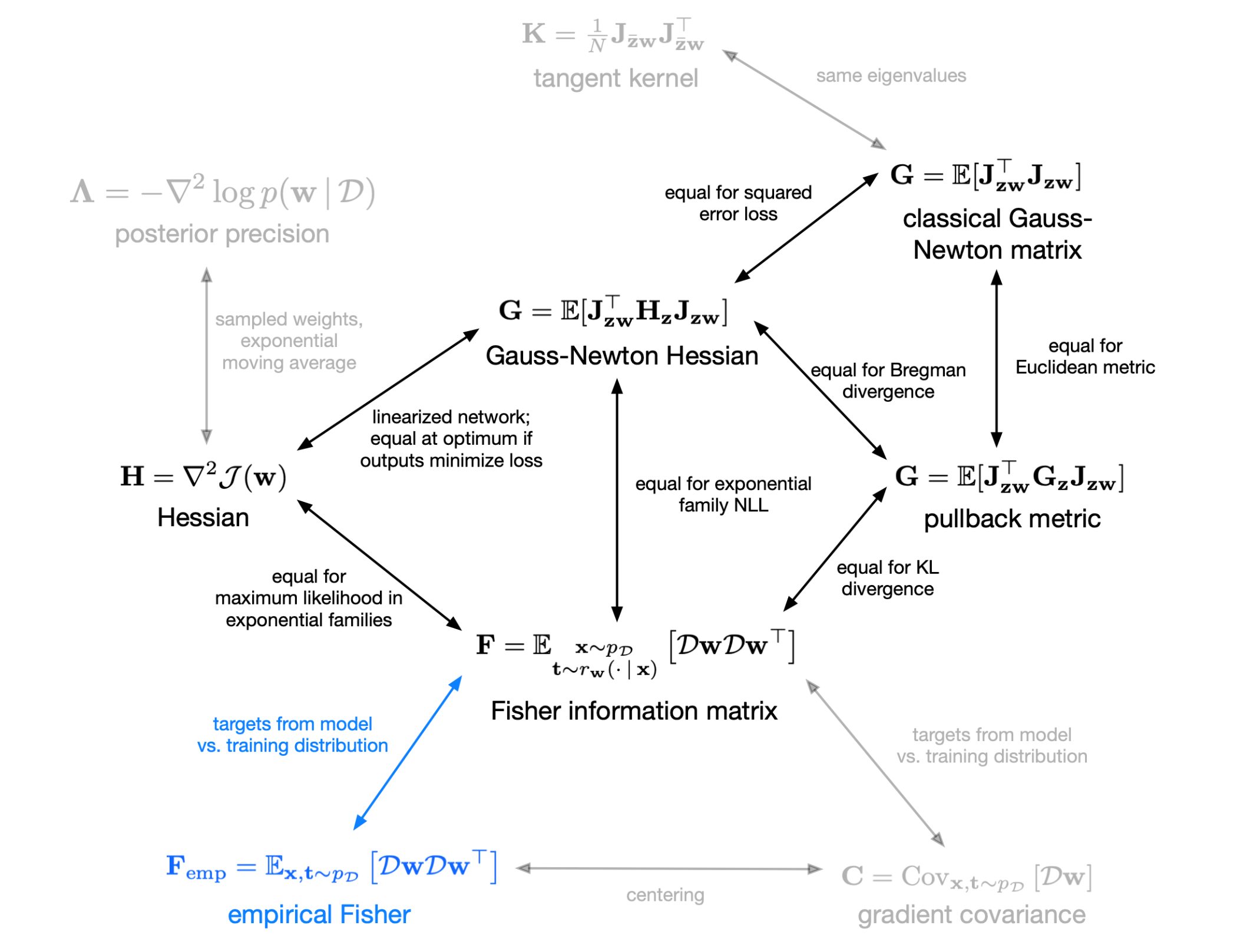NNTD_chapter_5_fig1 Fig. Source from CSC2541 Winter 2022 from Roger Grosse

최종적으로는 K-FAC과 Shampoo를 이해하는 것이 이 post의 목표이긴 한데, 2nd order method를 이해하기 위해서는 H, G, F를 이해하는 것이 먼저이다.

NNTD_chapter_4_intro

Hessian Matrix

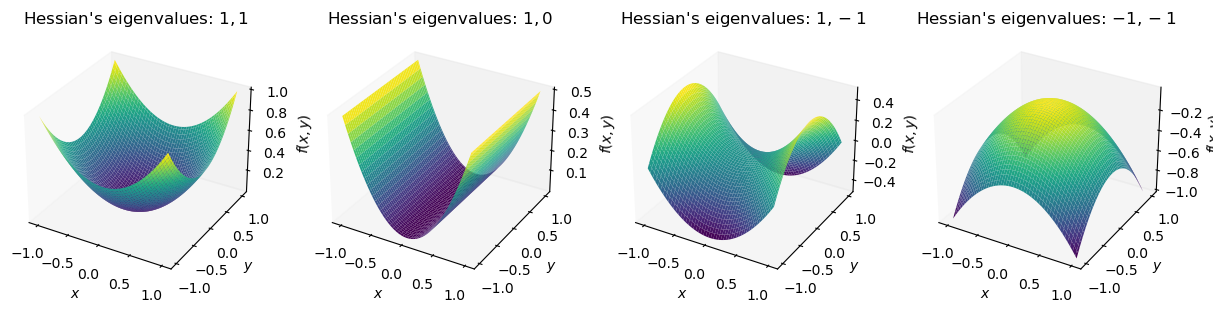hess_eig Fig.

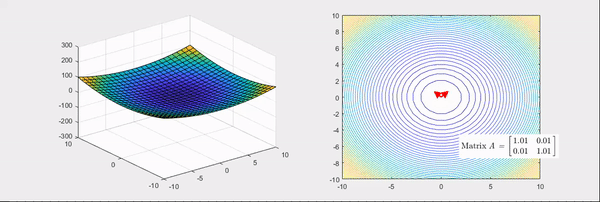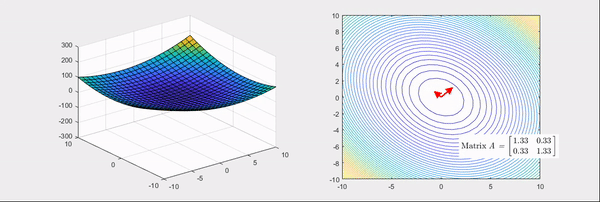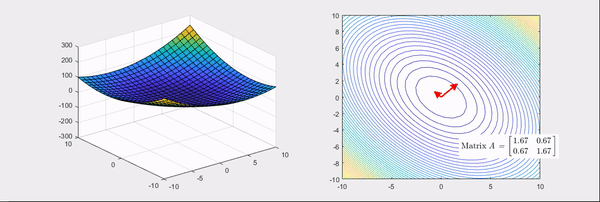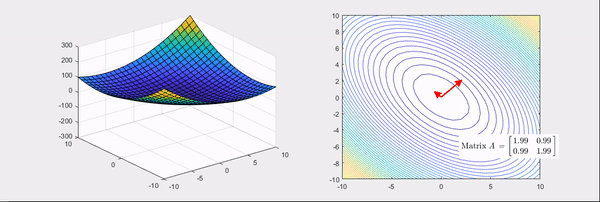hessian_animation1 Fig. Source from link

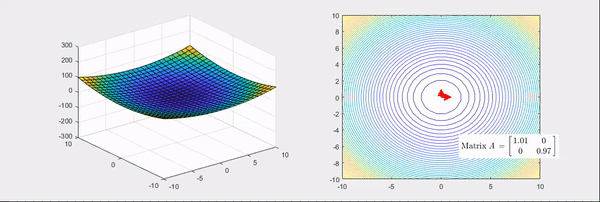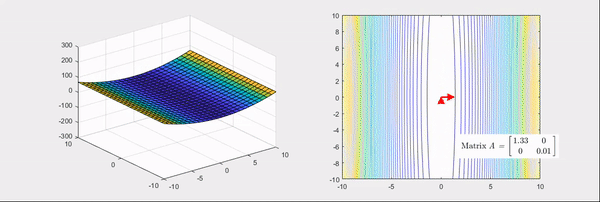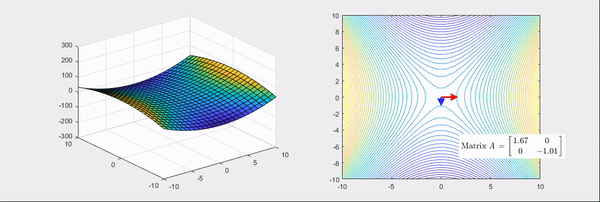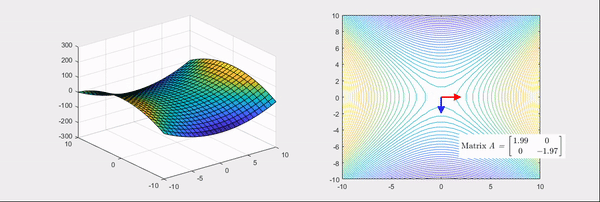hessian_animation2 Fig. Source from link

Newton's Method

\[\theta_{t+1} = \theta_{t} - H^{-1} \nabla L(\theta_{t})\] \[\begin{aligned} & \theta_{t+1} = \theta_{t} - H^{-1} \nabla L(\theta_{t}) & \\ & = \begin{bmatrix} w_2 \\ w_1 \\ \end{bmatrix} - \begin{bmatrix} \color{orange}{\frac{\partial^2 L}{\partial w_1^2}} & \color{purple}{\frac{\partial^2 L}{\partial w_1 \partial w_2}} \\ \color{purple}{\frac{\partial^2 L}{\partial w_1 \partial w_2}} & \color{green}{\frac{\partial^2 L}{\partial w_2^2}} \\ \end{bmatrix}^{-1} \begin{bmatrix} \color{red}{\frac{\partial L}{\partial w_1}} \\ \color{blue}{\frac{\partial L}{\partial w_2}} \\ \end{bmatrix} & \\ & = \begin{bmatrix} w_2 \\ w_1 \\ \end{bmatrix} - \frac{1}{ \color{orange}{\frac{\partial^2 L}{\partial w_1^2}} \color{green}{\frac{\partial^2 L}{\partial w_2^2}} - (\color{purple}{\frac{\partial^2 L}{\partial w_1 \partial w_2}})^2 } \begin{bmatrix} \color{green}{\frac{\partial^2 L}{\partial w_2^2}} & - \color{purple}{\frac{\partial^2 L}{\partial w_1 \partial w_2}} \\ - \color{purple}{\frac{\partial^2 L}{\partial w_1 \partial w_2}} & \color{orange}{\frac{\partial^2 L}{\partial w_1^2}} \\ \end{bmatrix}^{-1} \begin{bmatrix} \color{red}{\frac{\partial L}{\partial w_1}} \\ \color{blue}{\frac{\partial L}{\partial w_2}} \\ \end{bmatrix} & \\ & = \begin{bmatrix} w_2 \\ w_1 \\ \end{bmatrix} - \frac{1}{ \color{orange}{\frac{\partial^2 L}{\partial w_1^2}} \color{green}{\frac{\partial^2 L}{\partial w_2^2}} - (\color{purple}{\frac{\partial^2 L}{\partial w_1 \partial w_2}})^2 } \begin{bmatrix} \color{green}{\frac{\partial^2 L}{\partial w_2^2}} \color{red}{\frac{\partial L}{\partial w_1}} - \color{purple}{\frac{\partial^2 L}{\partial w_1 \partial w_2}} \color{blue}{\frac{\partial L}{\partial w_2}} \\ \color{orange}{\frac{\partial^2 L}{\partial w_1^2}} \color{blue}{\frac{\partial L}{\partial w_2}} - \color{purple}{\frac{\partial^2 L}{\partial w_1 \partial w_2}} \color{red}{\frac{\partial L}{\partial w_1}} \\ \end{bmatrix} & \\ \end{aligned}\]

Hessian Free (HF) Method

Gauss-Newton Method

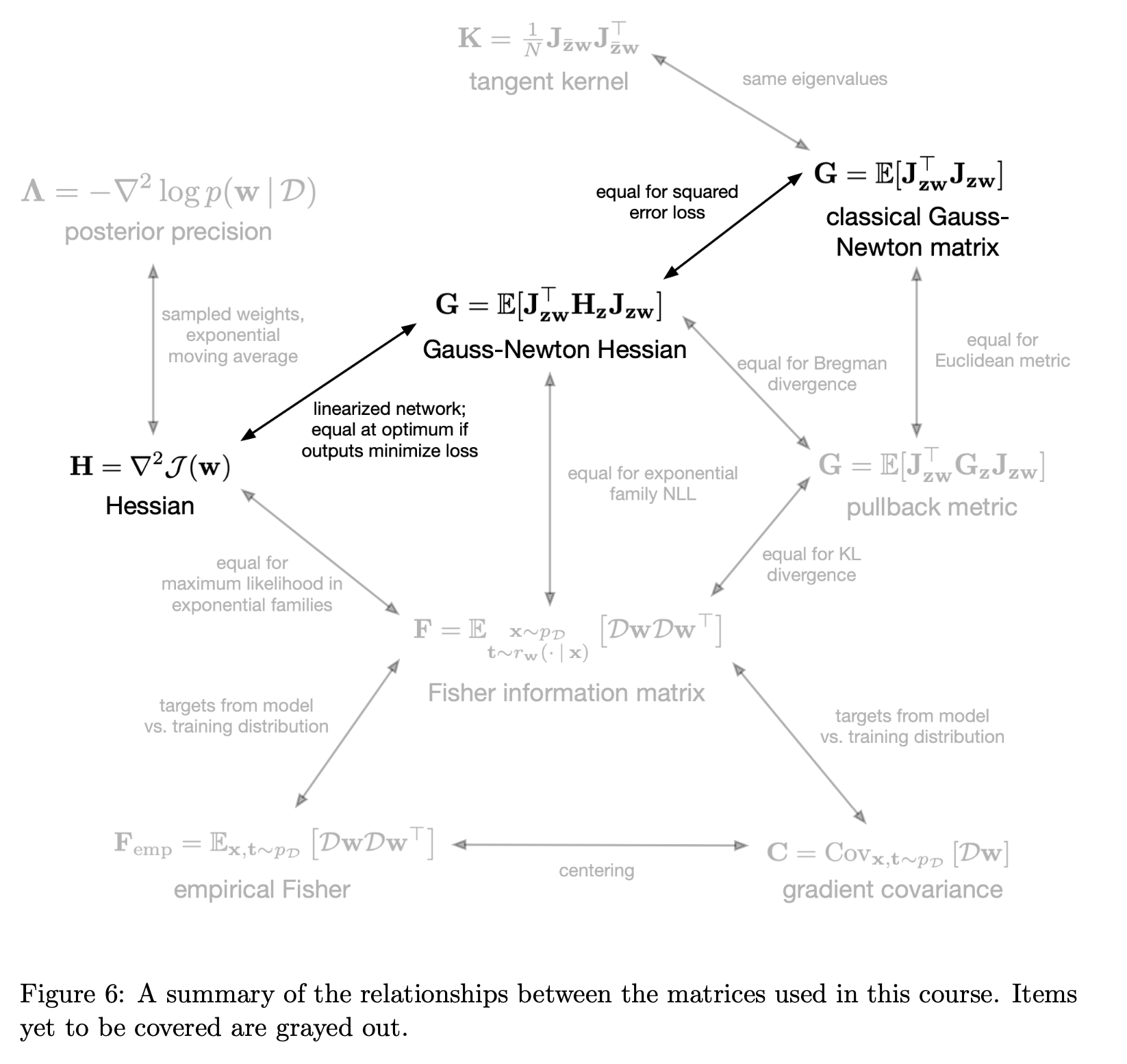NNTD_chapter_2_fig6 Fig.

Empirical Fisher Matrix (EF) Method and Adaptive Optimizers

NNTD_chapter_5_fig1 Fig.

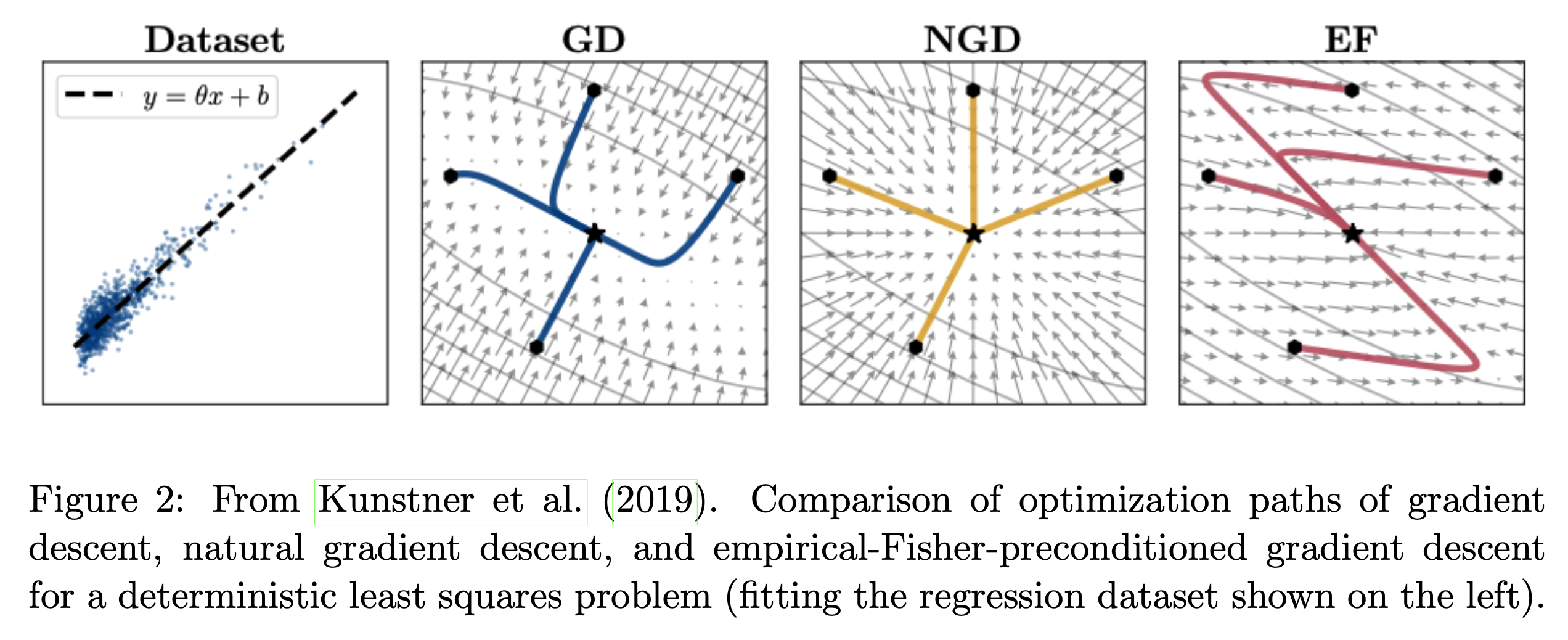NNTD_chapter_5_fig2 Fig.

(2015) Optimizing Neural Networks with Kronecker-factored Approximate Curvature (K-FAC)

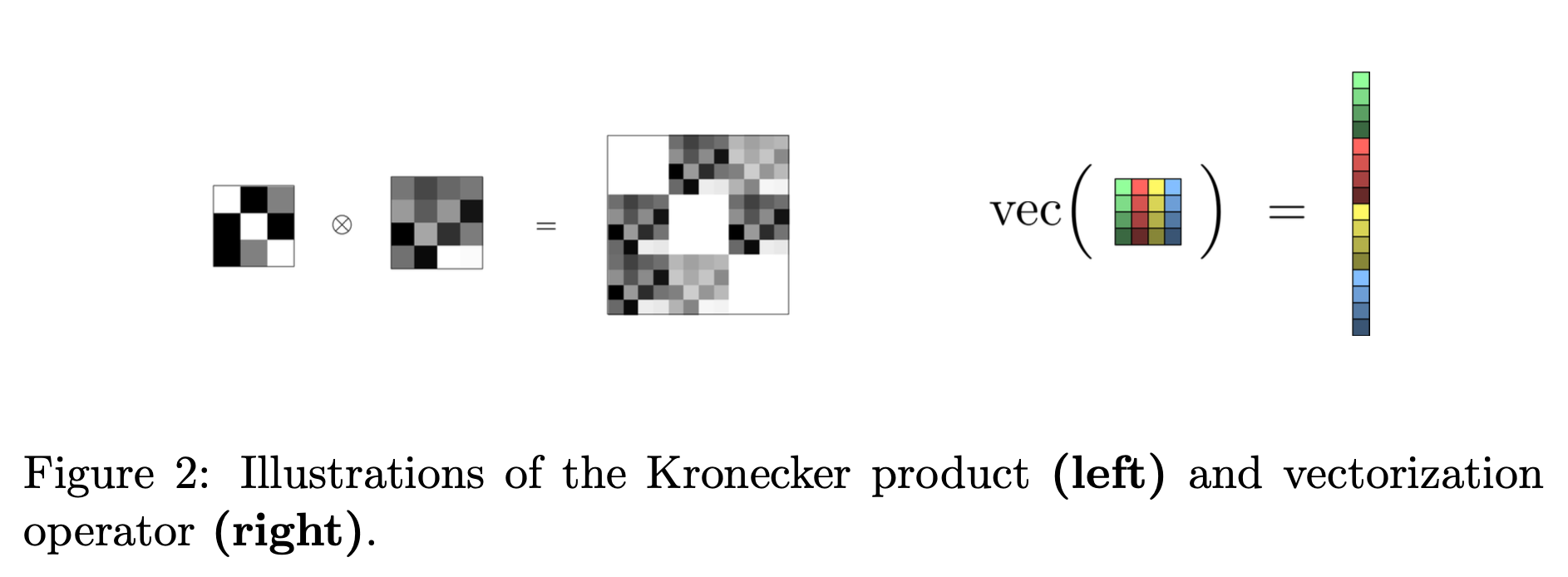NNTD_chatper_4_kfac_fig1 Fig.

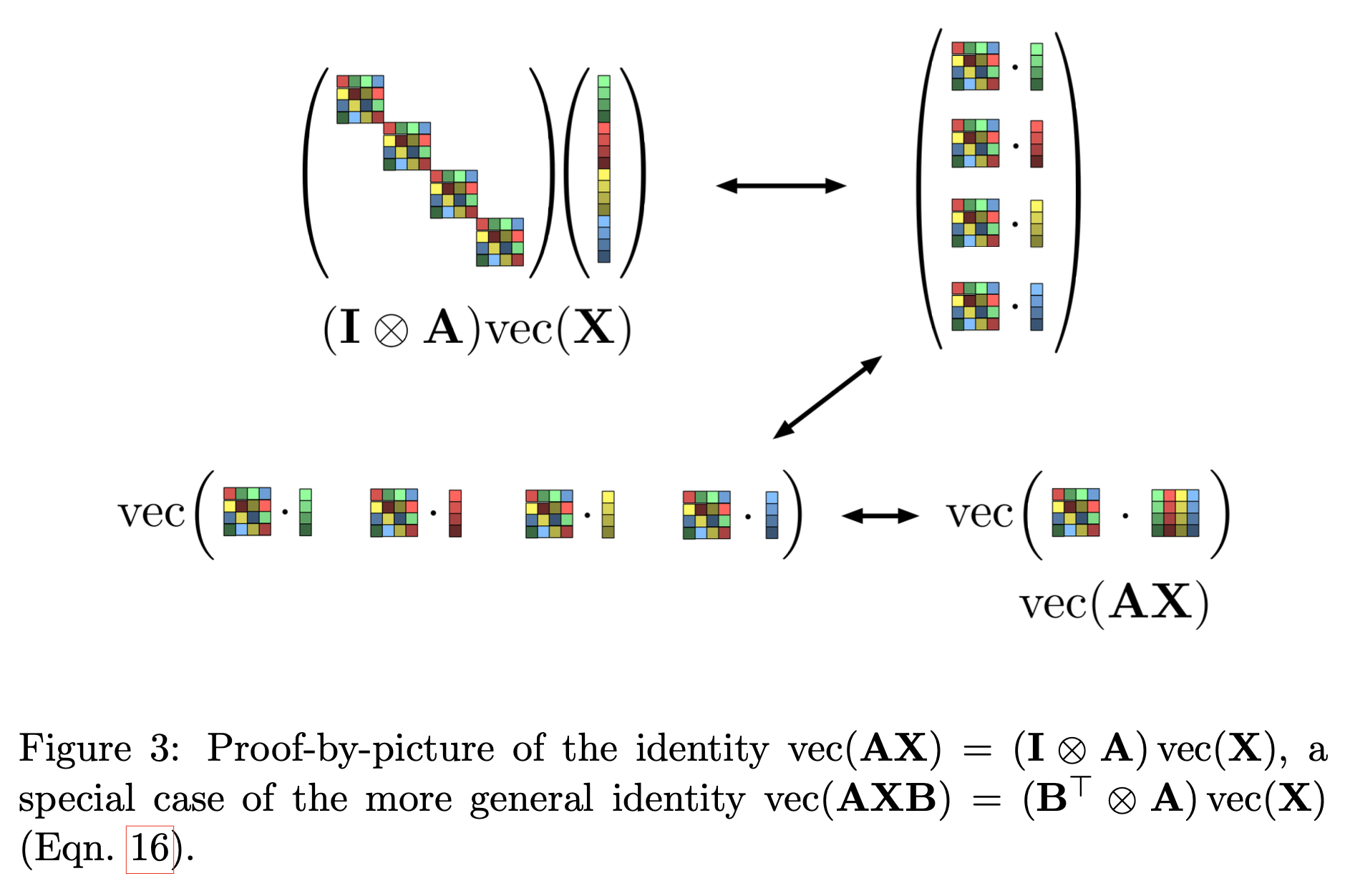NNTD_chatper_4_kfac_fig2 Fig.

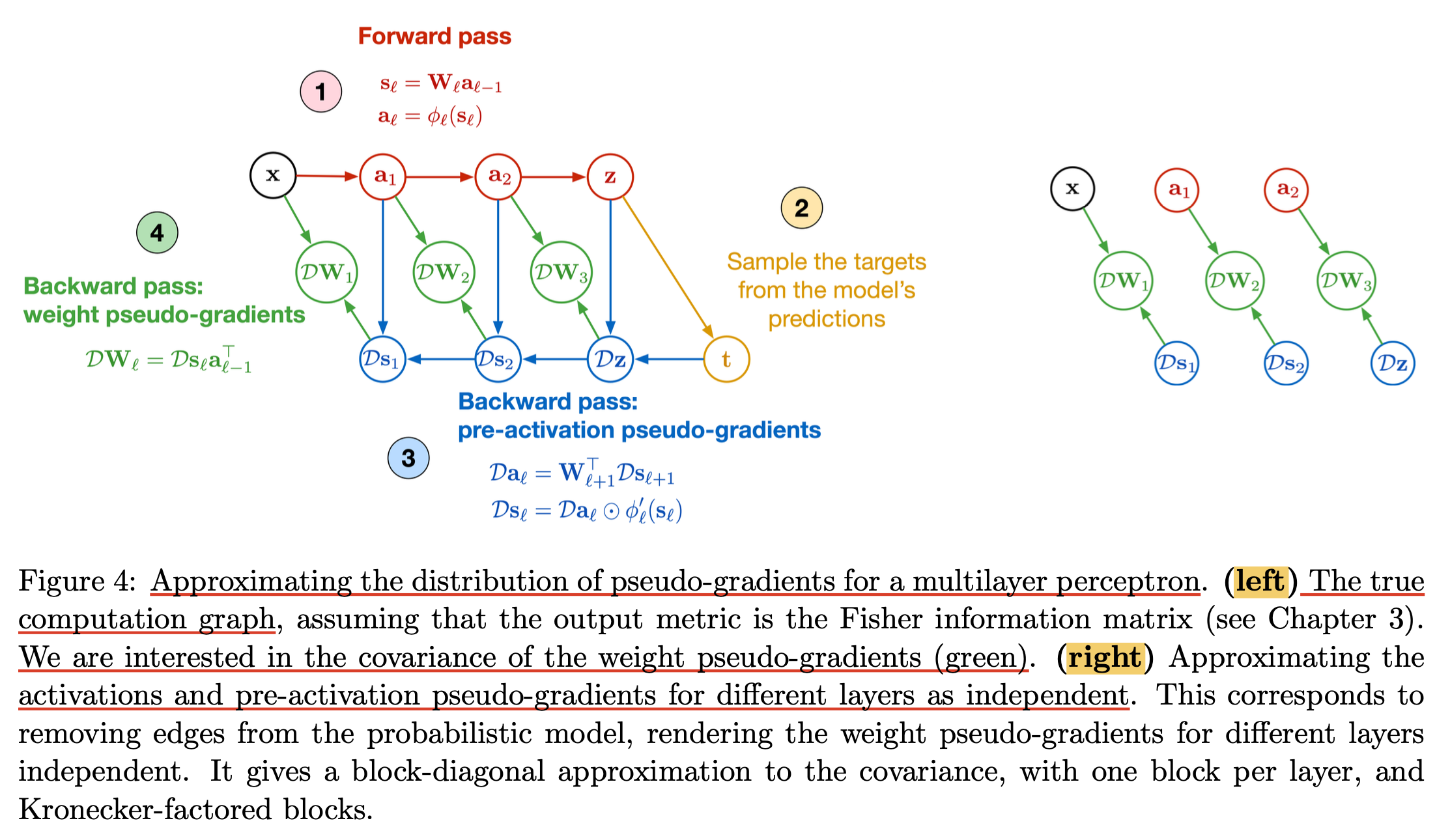NNTD_chatper_4_kfac_fig3 Fig.

NNTD_chatper_4_kfac_fig4 Fig.

(2018) Shampoo: Preconditioned Stochastic Tensor Optimization

Shampoo Optimizer는 사실 아래의 algorithm만 알면 될 정도로 간단하다. (distributed training을 고려하지 않는다면)

shampoo_paper_algorithm1 Fig.

Adam과 비교해서 생각해보자. Adam은 parameter size와 동일한 1st moment, 2nd moment를 계속 tracking했어야 했다. 그리고 1st moment, 2nd moment를 사용해서 아래처럼 연산해주면 됐다.

\[W_{t+1} = W_t - \eta \underbrace{\frac{s_t}{\sqrt{v_t} + \epsilon}}_{\text{Adam preconditioner}} G_t\]

Shampoo는 위 algorithm을 보면 preconditioner가 2개이다. 그리고 Left and right preconditioner 각각은 gradient tensor의 outer product, \(G_t G_t^T, G_t^T G_t\)를 계속 더해서 tracking한다. 그리고 Update를 할 때 양쪽 preconditioner를 모두 \(-1/4\)승을 해줘 update quantity를 계산하게 된다. (왜 -1/4인가에 대해서는 저자들이 분석한 결과 값이 그렇게 나왔다고 한다.)

shampoo_exponent

여기서 주의할 점은 각 preconditioner를 계산하기 위한 cost이다. Adagrad의 경우, diagonal preconditioner를 쓰는 것이 아니라 full matrix preconditioner를 쓴다면 원래 weight matrix와 같은 size인 gradient를 flatten한 \(g_t \in \mathbb{R}^{mn}\)를 outer product 해야한다. 그러므로 \(g_t g_t^T\)에서 \(g_t\)는 pararmeter size가 \(W_t \in \mathbb{R}^{m \times n}\)일 경우 \(g_t g_t^T \in \mathbb{R}^{mn \times mn}\)이어야 하며 이는 매우 큰 memory와 연산량을 요구한다.

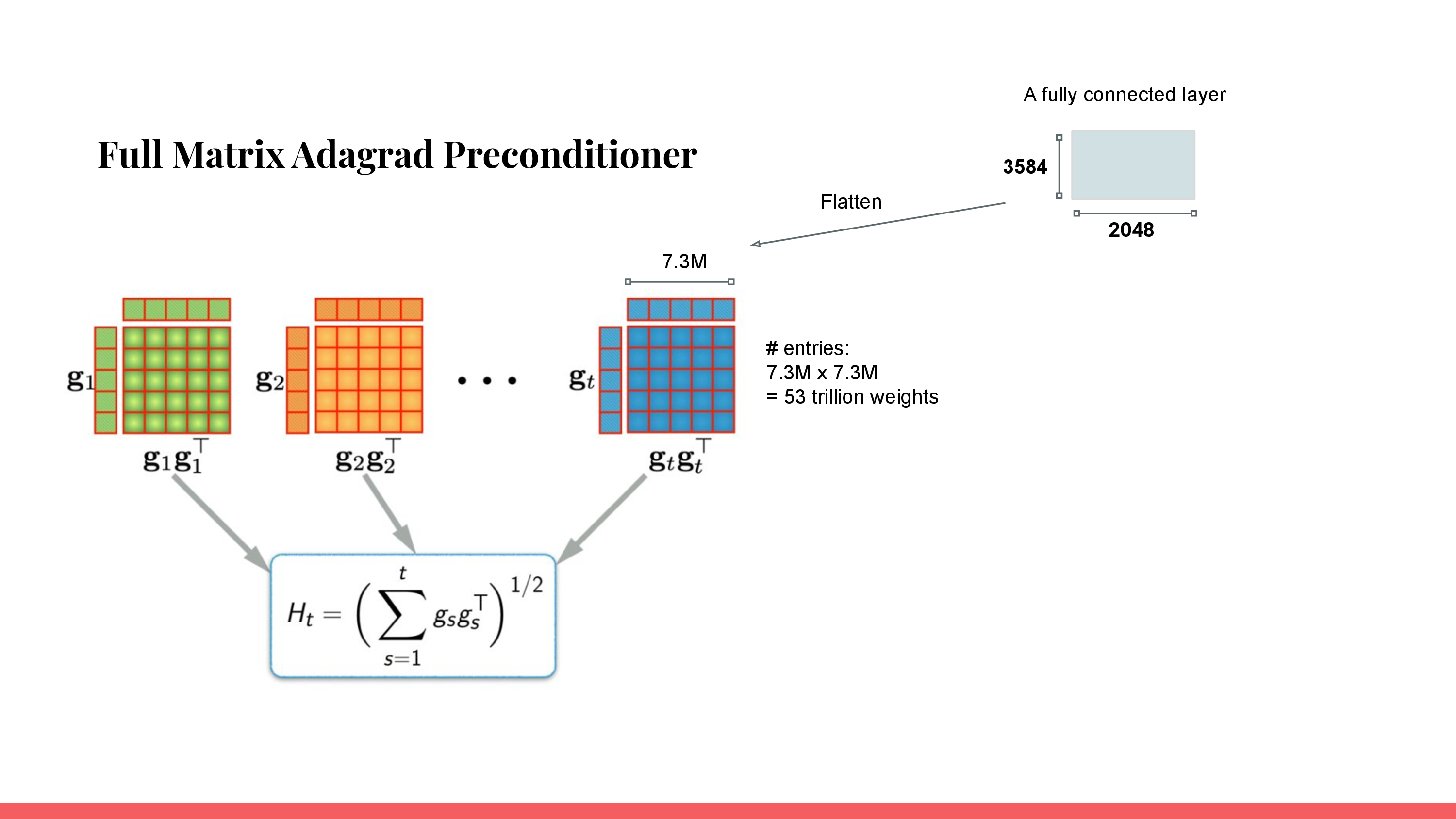distributed_shampoo_from_rohan_anil_slide_012 Fig.

그래서 Adagrad나 Adam등이 outer product의 diagonal vector만 사용했던 것인데,

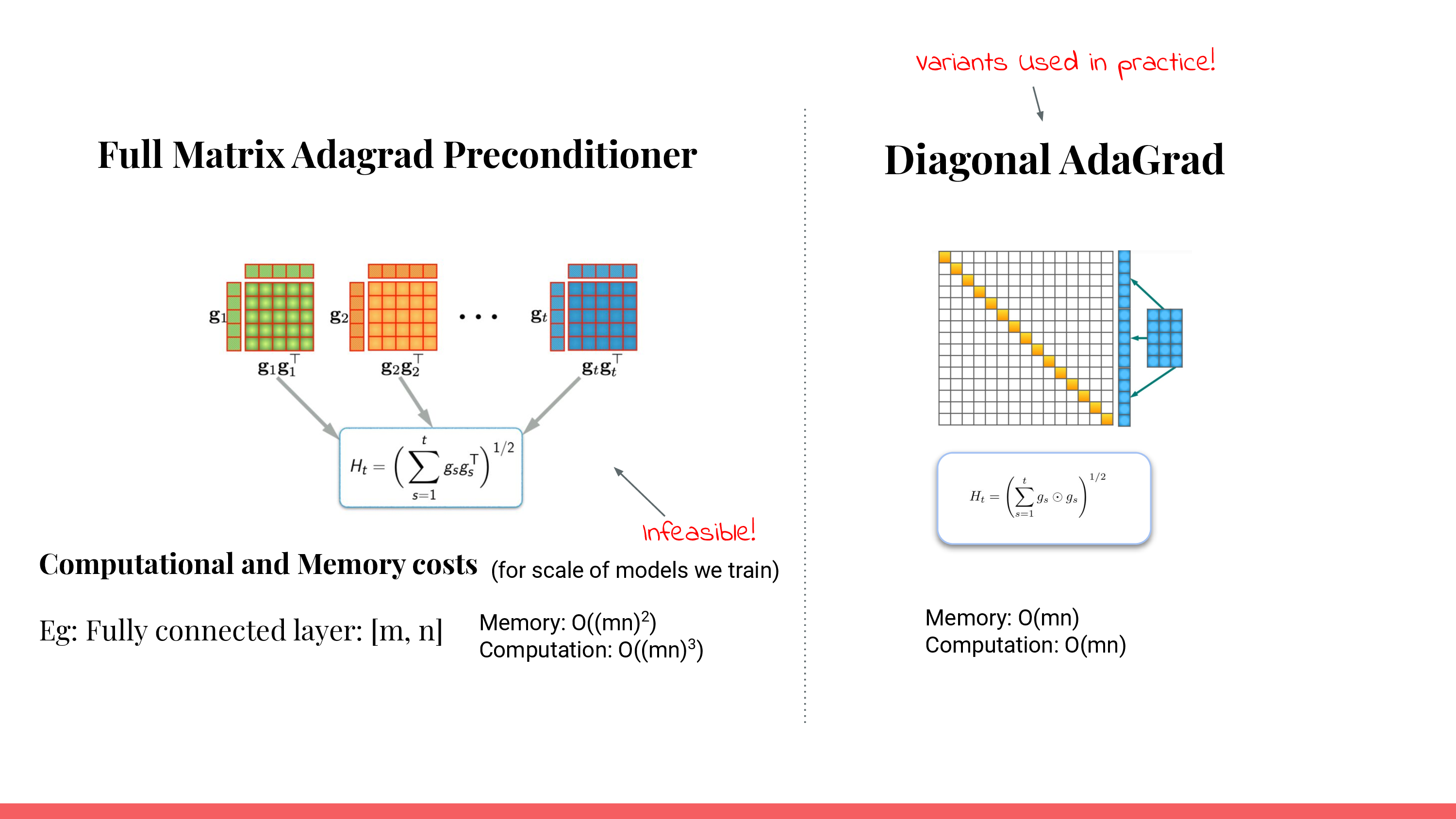distributed_shampoo_from_rohan_anil_slide_013 Fig.

실제 code를 보면 gradient matrix, \(G_t\)를 그냥 elementwise로 스스로와 곱한 뒤 (제곱한 뒤) sqrt한 값에 epsilon을 더해서 gradient에 나눠주는 것을 알 수 있다.

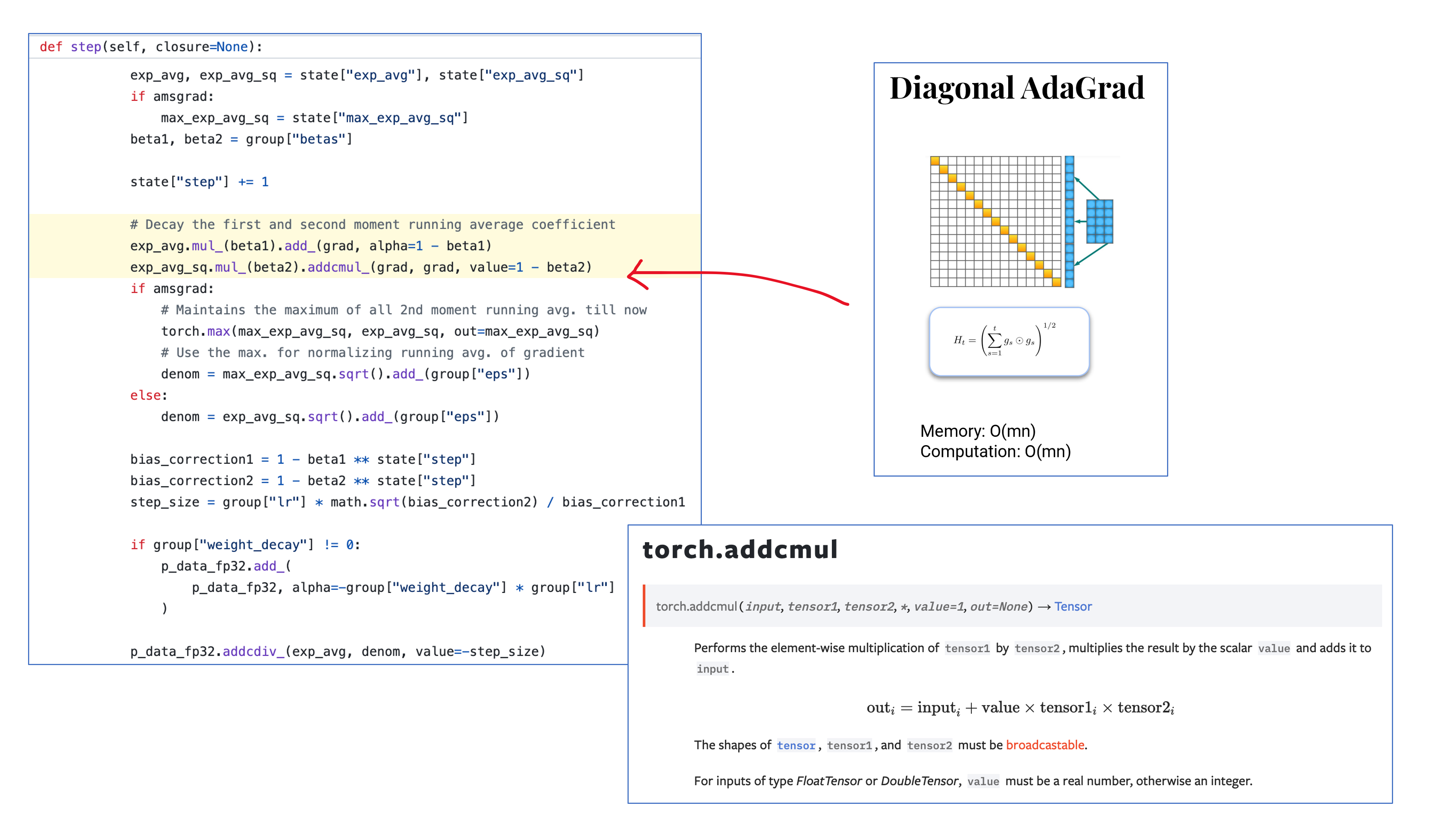adam_code_snippet Fig.

하지만 앞서 말했다시피 이는 parameter간의 corrlation 정보가 없다. Shampoo도 전체 parameter간의 correlation 계산하는 것은 아니지만 block diagonal 정도는 해주기 때문에 어느정도 parameter간 정보는 갖게 된다.

kfac_and_shampoo Fig.

Shampoo에서 각 preconditioner는 \(\mathbb{R}^{mn \times mn}\)이 아니다. 이들은 각각 \(L_t \in \mathbb{R}^{m \times m}, R_t \in \mathbb{R}^{n \times n}\)의 dimension을 가지게 되고, gradient 앞 뒤로 left, right preconditioner를 각각 곱해주게 된다. (딱 봐도 뭔가 유도할때 Singular Vector Decomposition (SVD)같은 technique을 이용해 hessian inverse를 gradient와 곱하는 것을 dimension-wise로 근사하는 것이 아닌가 하는 의심을 해볼 수 있다) 그렇기 때문에 space complexity도 더이상 \((mn)^2\)가 아니라 \(m^2+n^2\)가 되며, computational amount도 더이상 \(O(m^3n^3)\)가 아니라 \(O(m^3 + n^3)\)가 된다. (Adagrad같은 경우 elementwise로 계산만 하면 되기 때문에 memory \(O(mn)\), computation \(O(mn)\)이다)

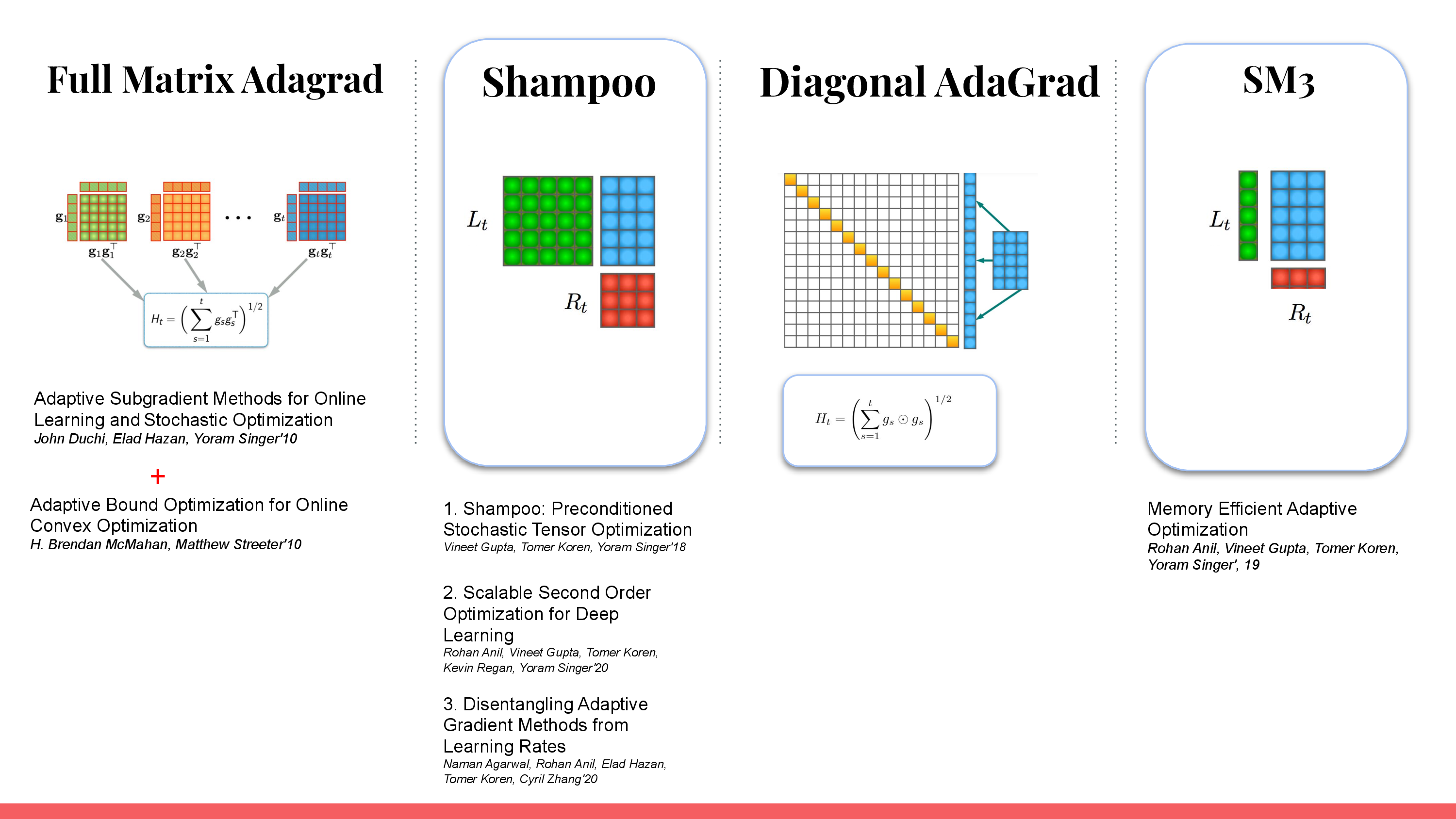distributed_shampoo_from_rohan_anil_slide_015 Fig.

아래는 Shampoo paper에 있는 3d tensor에 대해 shampoo를 적용한 것인데, 차원이 하나 더 늘어남으로써 preconditioning을 세 번 하는것으로 늘어났음을 알 수 있다. (근데 사실 weight matrix중에 2차원을 넘어갈 matrix가 존재하는 이유를 모르겠다.)

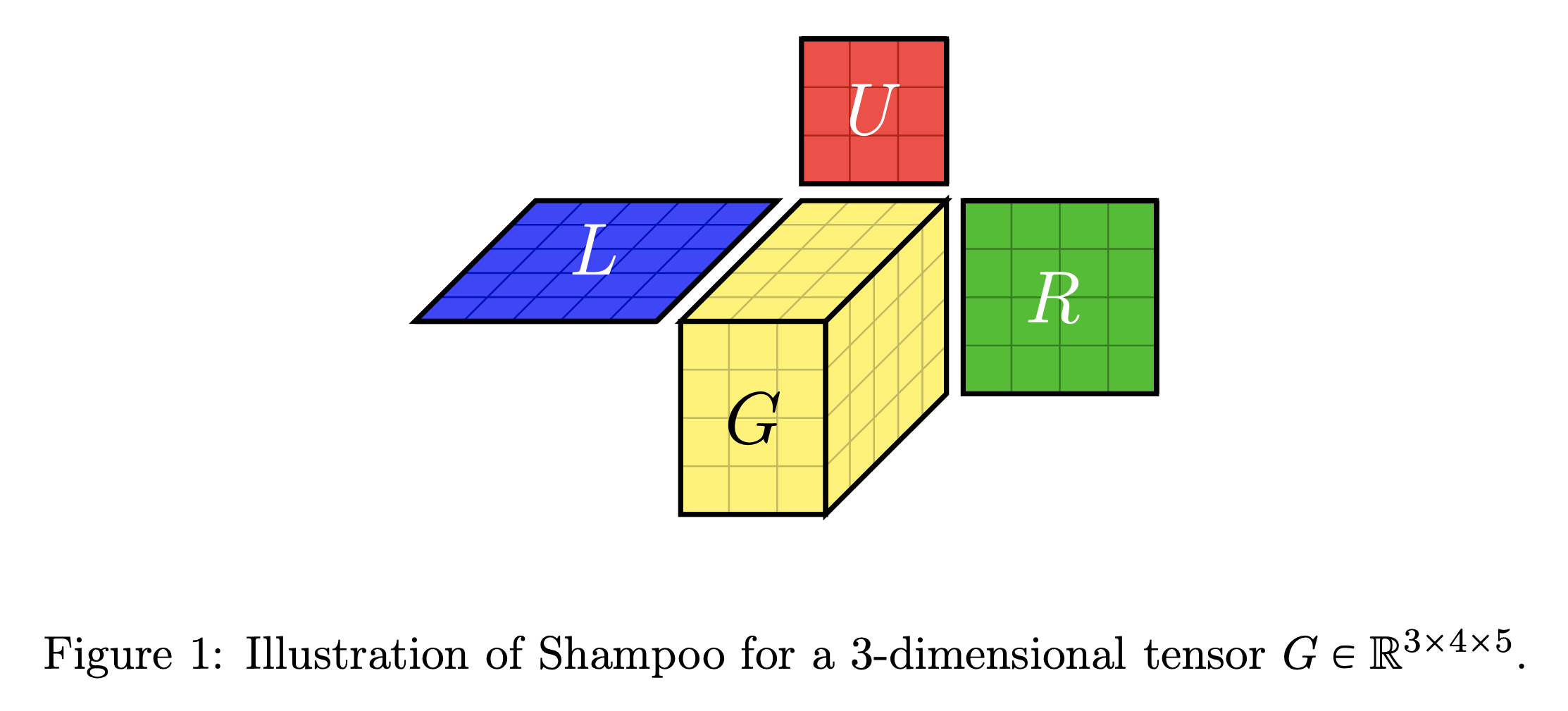shampoo_paper_fig1 Fig.

한 편, shampoo라는 이름은 preconditioning 때문에 붙은 거라고 한다 (…). 다른 adaptive optimizer들도 preconditioning을 하긴 하지만 제대로 된 preconditioning 했다는 의미에서 그런거 같다.

distributed_shampoo_from_rohan_anil_slide_006 Fig.

Derivation (Analysis of Shampoo for (2D) matrices)

Shampoo paper를 보면 optimization 분야의 paper답게 수학적인 tool을 많이 쓴다는걸 볼 수 있다. 앞서 살펴본 Kronecker products를 포함해서 아래 네 가지를 이해해야 하며,

  • Online convex optimization (OCO)
  • Adaptive regularization in online optimization
  • Kronecker products
  • Matrix inequalities

이를 이해했으면 page 6부터 9까지 Theorem 7과 Lemma 8, 9를 이해하면 왜 \(G_t \in \mathbb{R}^{m \times n}\)에 대해서 각각 \(\mathbb{R}^{m \times m}, \mathbb{R}^{n \times n}\)의 left, right conditioner를 곱하는 것 만으로 2nd order optimization을 근사할 수 있는지 이해할 수 있게 된다.

shampoo_paper_algorithm1 Fig.

(3D tensor에 대한 얘기도 있는데 이거는 일단 생략하겠다)

Experimental Results

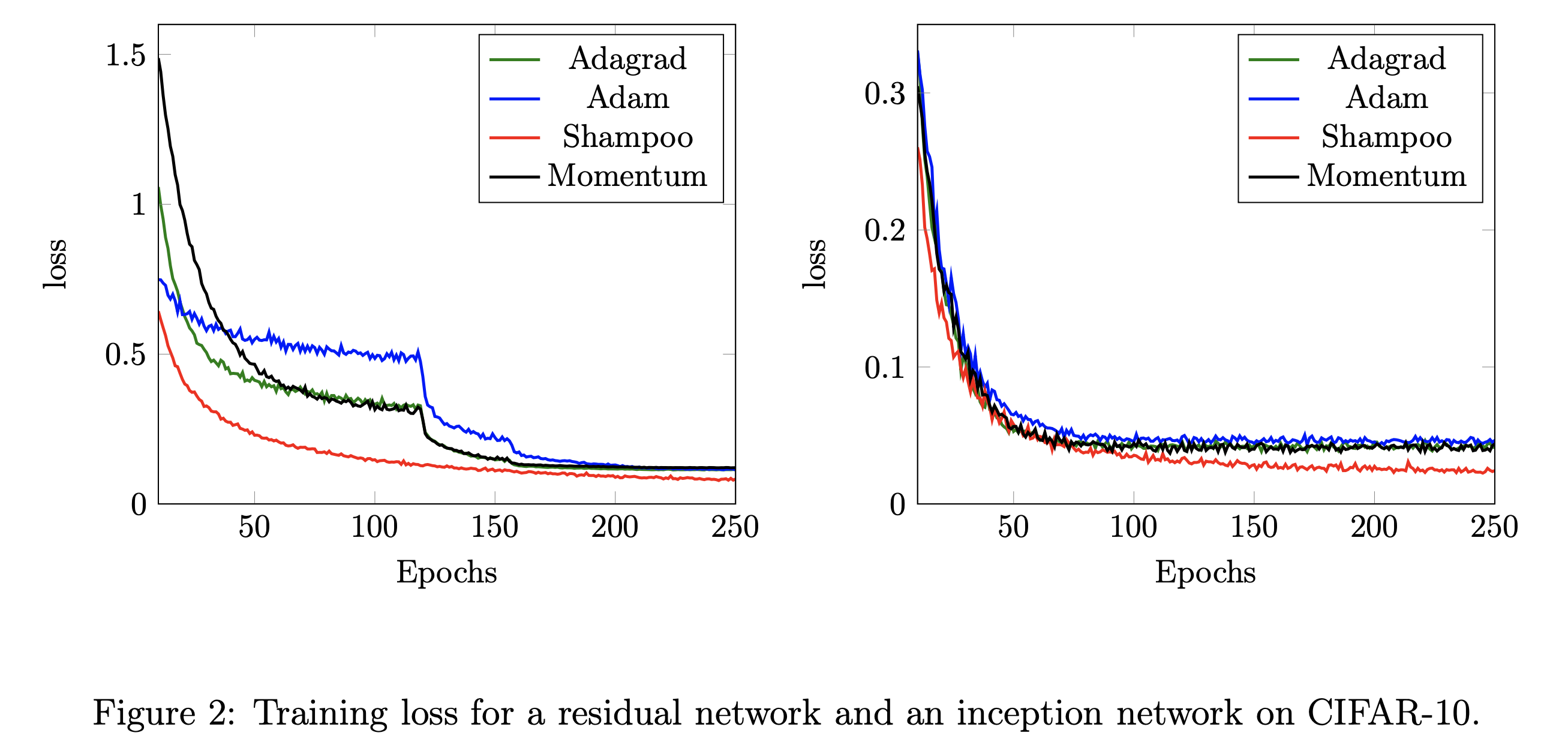shampoo_paper_fig2 Fig.

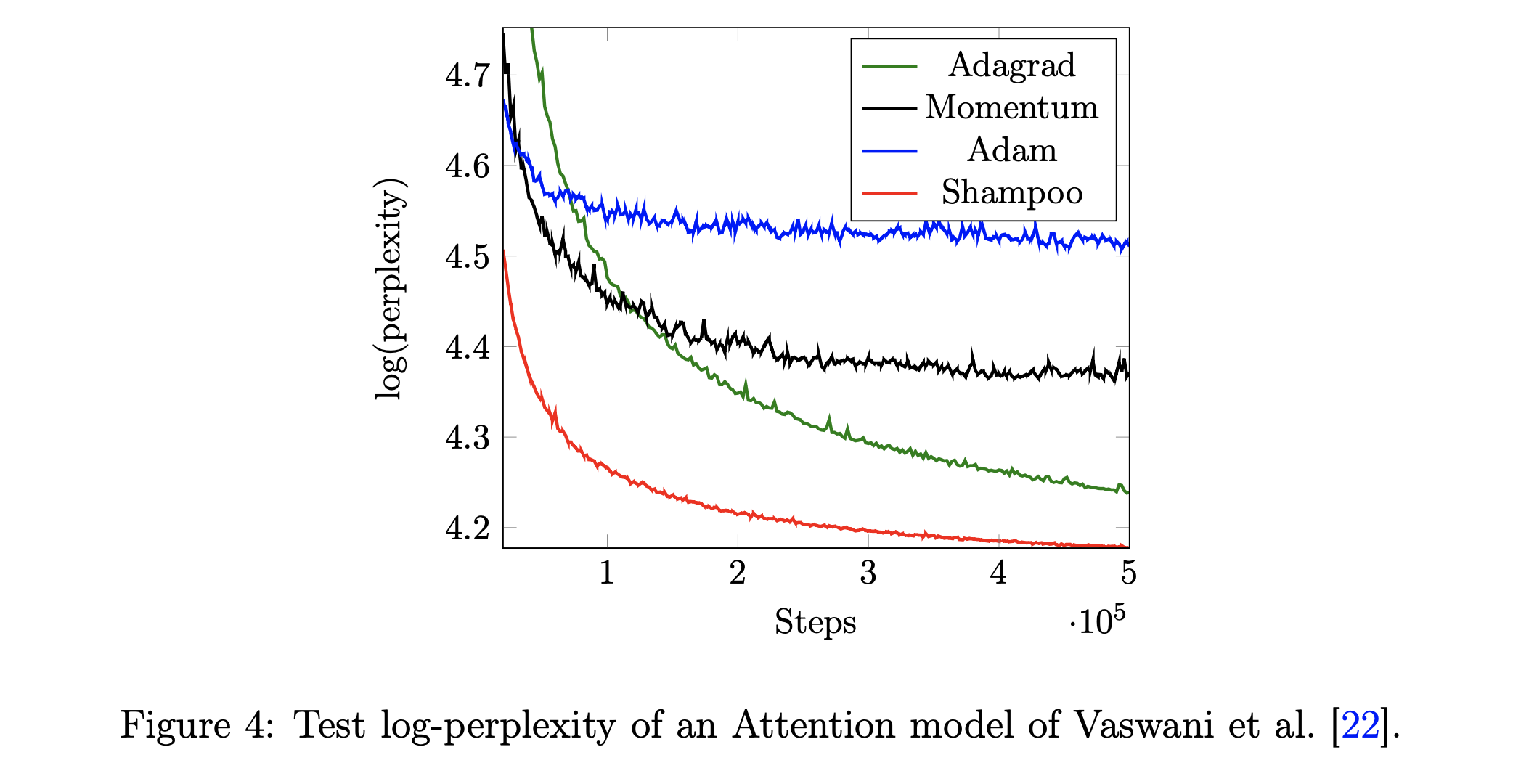shampoo_paper_fig4 Fig.

Scalable Distributed Shampoo

(2020) Scalable Second Order Optimization for Deep Learning

(2023) A Distributed Data-Parallel PyTorch Implementation of the Distributed Shampoo Optimizer for Training Neural Networks At-Scale

그다음은 FB team에서 publish한 distributed shampoo이다. Google이 지적했던 문제들을 비슷하게 지적하고 분석하긴 했으나, ZeRO-1 (deepspeed의 zero, pytorch의 fsdp)과 같은 distribute optimizer가 모든 optimizer state를 모든 worker가 똑같이 들고있는것이 아니라 (replicate) 각 worker가 나눠서 소유하는 것 처럼, 각 worker가 each parameters의 search direction을 계산하고 이를 collection한다는 점에서 차이가 있다.

그리고 pytorch에 integration 하고 그 implementation을 공개했다는 점이 또 하나의 가장 큰 contribution points이며, 그 외에도 Learning Rate Grafting이나 기존 adaptive optimizer들이 사용하던 Exponential Moving Average (EMA)나 weight decay등을 추가로 구현해 실험했다점이 중요 내용이다. 여기서 Learning Rate Grafting은

tmp

(2024) Can We Remove the Square-Root in Adaptive Gradient Methods? A Second-Order Perspective

(2024) ShampoO with Adam in the Preconditioner’s eigenbasis (SOAP): Improving And Stabilizing Shampoo Using Adam

References