(Re) Your mu-Transferred LR Could Not Be Optimal
27 Aug 2024< 목차 >
- Power Scheduler: A Batch Size and Token Number Agnostic LR Scheduler
- Scaling Optimal LR Across Token Horizons
- Time Transfer: On Optimal Learning Rate and Batch Size In The Infinite Data Limit
Power Scheduler: A Batch Size and Token Number Agnostic LR Scheduler
Motivation
Tensor Program V (TP-V)에 따르면 Maximal Update Parameterization (mu-P)로 standard deviation, per layer Learning Rate (LR), multiplier를 weight matrix마다 설정해줄 경우,
예를 들어 hidden size (width)가 64인 small scale transformer의 optimal LR이 width가 4096인 large scale model로 transfer가 되며 이를 mu-Transfer라고 부른다.
사실 TP-IV, V에서 수학적으로 제대로 유도한 것은 width가 늘어날 때 training stability, feature learning이 유지될 수 있도록 하는 것이었기 때문에,
실제로 확실히 transfer가 가능한 dimension은 width 뿐인데,
empirical하게는 depth가 증가할 때 (layer수가 늘어남)도 어느정도 유지가 되고,
batch size를 키울때도 유지가 된다고 한다.
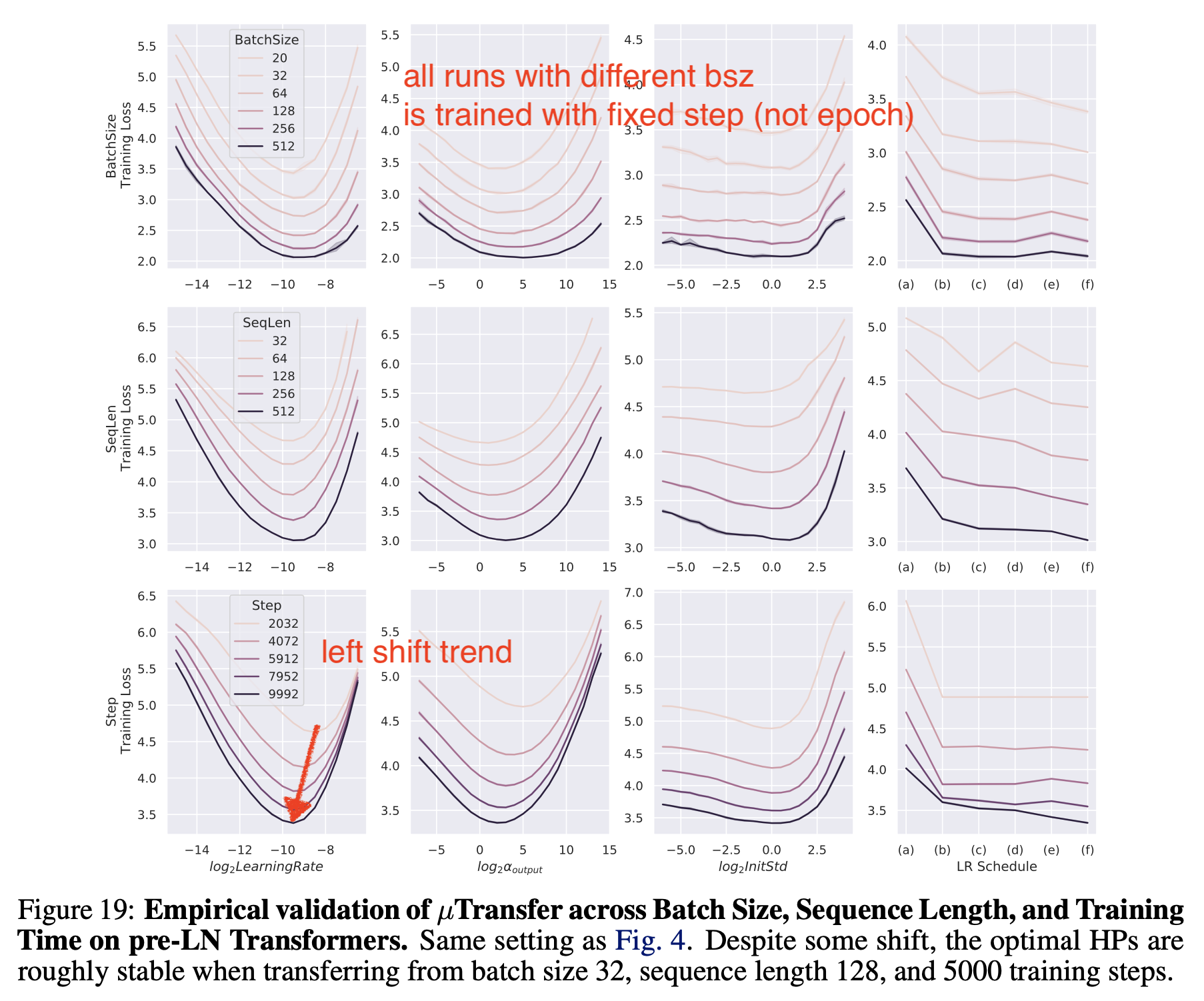
하지만 batch size에 대한 실험에 큰 맹점이 있는데, 이는 바로 batch size가 커질 때 training step가 줄어들지 않는 상황에서 실험을 했다는 것이다. 무슨 말이냐면 원래 batch size를 늘리면 1 epoch의 sample은 정해져 있으므로 optimization step수가 줄어들게 된다. 당연히 gradient estimiation에 쓰인 sample이 많아졌으므로 gradient는 보다 정교해질테고, step수가 줄어든 것은 어쩔 수 없으니 더 정교한 gradient가 됐다는 가정하에 LR을 키워줘야만 정해진 epoch동안 같은 valid loss에 도달할 수 있게 되는데, TP-V에서는 step수를 고정했다. 즉 batch size가 큰 실험은 epoch을 더 쓴 것이고 이 경우 optimal LR이 transfer됐다는 것이다.

그리고 TP-V에서 알려진 대로 small scale model로 Hyperparameter (HP) search를 해서 large scale로 transfer를 하려면 학습량, 즉 training tokens도 small scale에선 훨씬 적을 것인데, 이게 늘어나는 실제 large scale에서도 optimal LR은 transfer되지 않을 것이다. 위 TP-V의 figure를 보더라도 step수 (training tokens)가 늘어날 때도 자세히 보면 다른 transferred Hyperparameters (HPs)들과는 확연히 다르게 왼쪽으로 optimal LR이 이동하는 trend가 있다는 걸 확인할 수 있다. 이는 training tokens가 늘어나면 그만큼 많이 optimization을 한다는 것이고, LR scheduling을 할 경우 LR을 decay되는 량이 small scale과 비교해서 window?가 훨씬 길 것이므로 peak LR에서 학습되는 시간이 더 길 것이기 때문에 직관적으로 LR을 줄여야 한다고 할 수 있을 것이다. 이는 Scaling Exponents Across Parameterizations and Optimizers에도 잘 나와있다. 하지만 위 paper에서는 model size, \(N\)가 커질 때 chinchilla optimal에 따라 training tokens는 \(20N\)으로 균일하게 커진다고 가정해서 실험적으로 얼만큼 LR을 낮춰야 하는지 알아냈다.
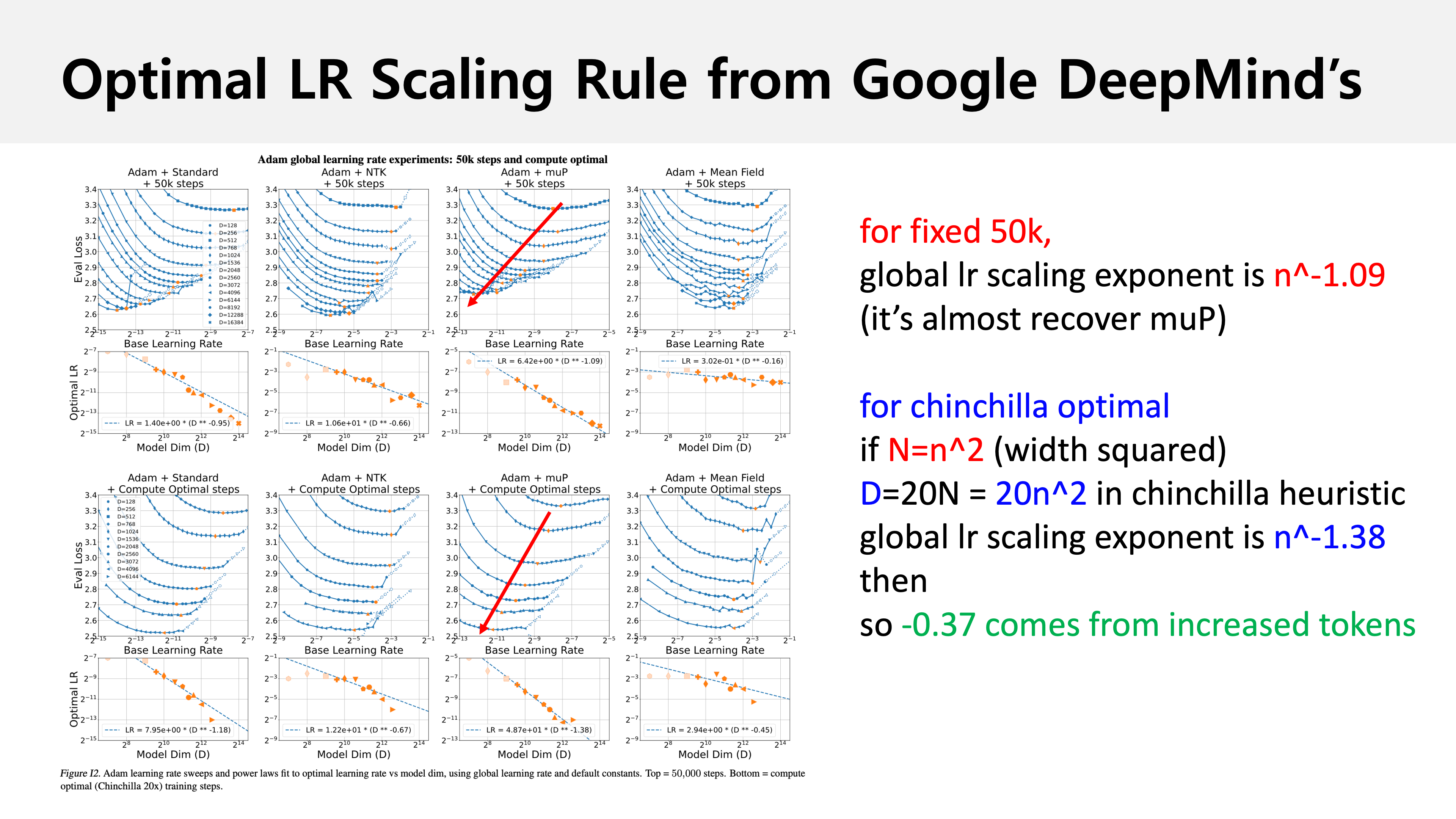
그런데 real-world scenario에서 compute optimal로 training하는 기관은 아마 없을 것이다.
7B model을 학습하는데 예를 들어 7e9*20/1e9=140B만큼만 필요하다고 생각할 사람은 없기 때문이다 (the more, the better).
그러니까 이런 realworld case에선 얼만큼 lr을 줄여줘야 하는지? batch size와의 관계를 고려하면 또 얼만큼 scale up해줘야 하는지?에 대한 것은 user가 알아내야 하는 것이다.
Power Scheduler, A Batch Size and Token Number Agnostic LR Scheduler라는 paper의 main research question는 small scale 보다 batch size, training tokens 가 증가할 때 과연 어떻게 LR scaling을 해야할까? 혹은 LR scheduler의 구간을 설정해줘야 할까?인 것이다.
물론 muP user들이라면 실험적으로 알고있던 내용일 수 있겠으나,
새로운 LR scheduler을 제안해줬다는 점에서 contribution이 확실히 있는 가뭄의 단비같은 paper라고 할 수 있겠다.
TL;DR하자면 batch size가 커지면 LR은 키워줘야하고 training tokens를 늘리면 줄여줘야 하는건 맞다.
하지만 이럴 경우 muP의 특성상 model size가 커질수록 base LR이 너무 작아지는 문제가 생기는데,
저자들은 새로운 LR scheduler, Power Scheduler를 제안했으며 이는 아래와 같이 생겼다.
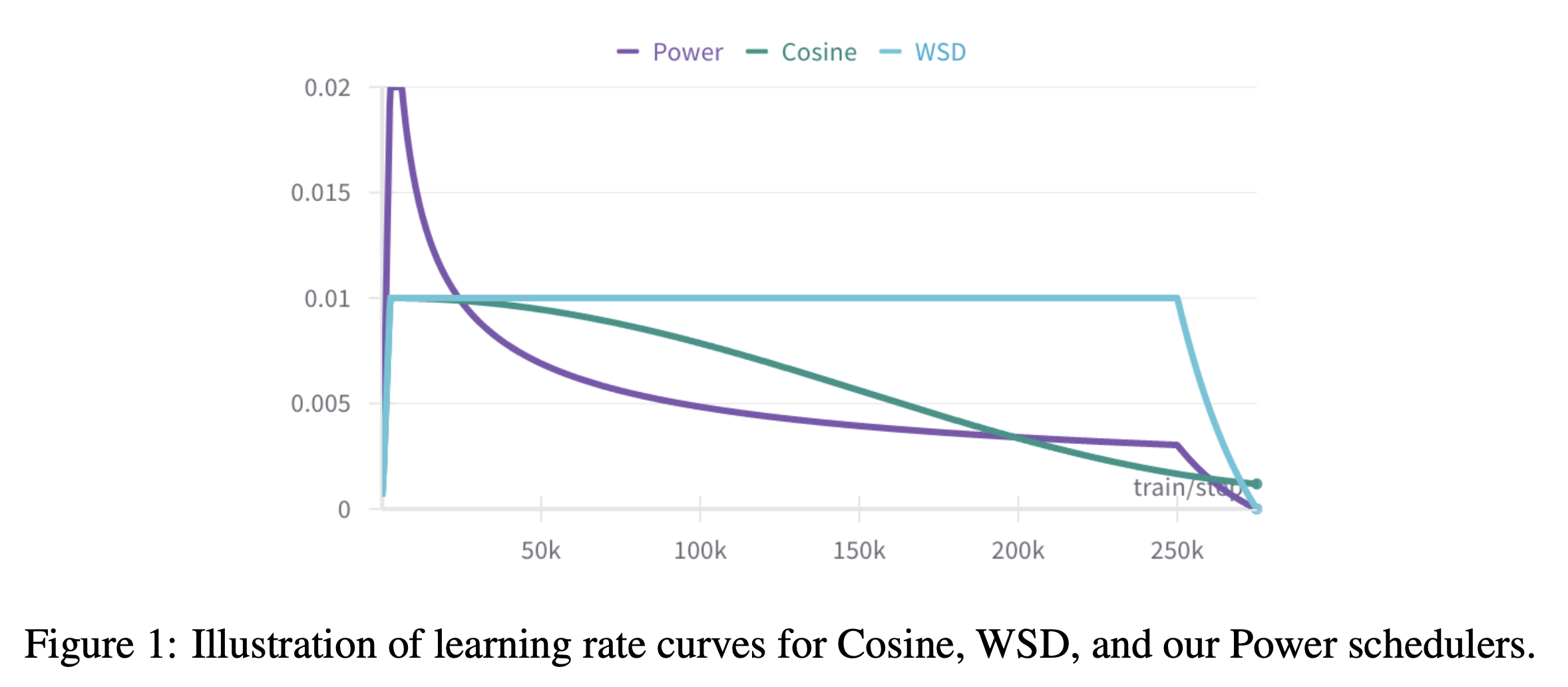 Fig.
Fig.
Preliminaries
Training tokens, batch size와 optimal LR간의 관계에 대해 분석하기 전에 먼저 preliminaries를 알아보자.
Maximal Update Parameterization (muP)
muP를 처음 접하는 이들은 TP-4, 5, 6를 읽고 와야겠으나, concept만 먼저 이해하고 싶은 이들을 위해 TL;DR하자면 width가 늘어날때 matmul output matrix의 element, 즉 activation의 크기가 커지지 않도록 initialization std를 설정해주고, gradient descent를 통해 weight matrix가 update되고 난 후에도 이를 유지하기 위해 learning rate도 1/width_scaling을 해주면 width가 무한히 커지는 large-scale 상황에서 (infinite width limit) training stability를 유지하고, feature learning을 maximize 할 수 있게 된다. muP는 feature learning을 maximize 하는 것이 핵심인데 (그래서 maximal update ~ 인 것), 모든 layer가 균일하게 학습이 되기를 원하기 때문에 gradient가 너무 큰 lm head (readout)의 gradient는 대충 1/10 해주고, 맨 앞의 embedding layer는 대충 10배 해주게 된다.

자연스럽게 width가 늘어남에 따라 training dynamics가 small scale과 유사하도록 setting한것과 다름 없기 때문에 (완전히 그렇지는 않다), 직관적으로 small scale의 optimal LR이 transfer된다는 것을 받아들여볼 수 있다.
Recap: Warmup-Stable-Decay (WSD)
Warmup-Stable-Decay (WSD)는 constant, linear, cosine 등의 LR scheduler의 한 종류이다.
일반적으로 Large Language Model (LLM)을 학습할 때에는 cosine decay를 많이 써왔는데,
요즘은 MiniCPM, DeepSeek LLM등에서 WSD가 ablation하기 좋다는 얘기를 하면서 WSD가 많이 쓰이는 추세인 것 같고 이를 비교대상으로 삼은 것 같다.
WSD는 figure만 봐도 이해할 수 있겠지만 굳이 설명하자면 여느 LR scheduler처럼 warmup phase가 존재하고, 그 뒤로는 peak LR을 유지하는 구간이 60~80%정도 되고, 그 이후 decay를 하게 되는데 식으로 쓰면 아래와 같다.
WSD의 장점은 cosine scheduler와 다르게 맨 처음부터 training step을 정해둘 필요가 없고,
monitoring을 하다가 언제든지 cooldown 하는 지점을 정할 수 있다는 것이라고 한다.
왜냐면 cosine LR scheduler같은 경우는 training step이 정해지면 그 시점에서 이미 LR이 0이 돼버린다거나 해서 돌이킬 수 없기 때문이다.
Analysis on Optimal LR according to Training Tokens and Batch Size
저자들은 먼저 width가 커짐에 따라 mutransferred optimal LR이 training tokens, batch size가 늘어날때도 유지되는지 실험하기 위해 아래 두 가지를 3 가지 model size에 대해서 반복한다.
- batch size를 고정하고 training tokens를 다양하게 하여 학습
- training tokens를 고정하고 batch size를 다양하게 하여 학습
Model configuration, optimizer hyperparameter는 아래와 같은데, 36M model이 width이 \(m_{\text{width}}=1\)인 걸 보니 정해진 training tokens, batch size에 따라서 LR sweep을 한 small scale proxy가 36M이었고, 이를 각각 scale down, scale up한 model이 12M, 120M인 것임을 알 수 있다. (depth는 여기서 안늘림)
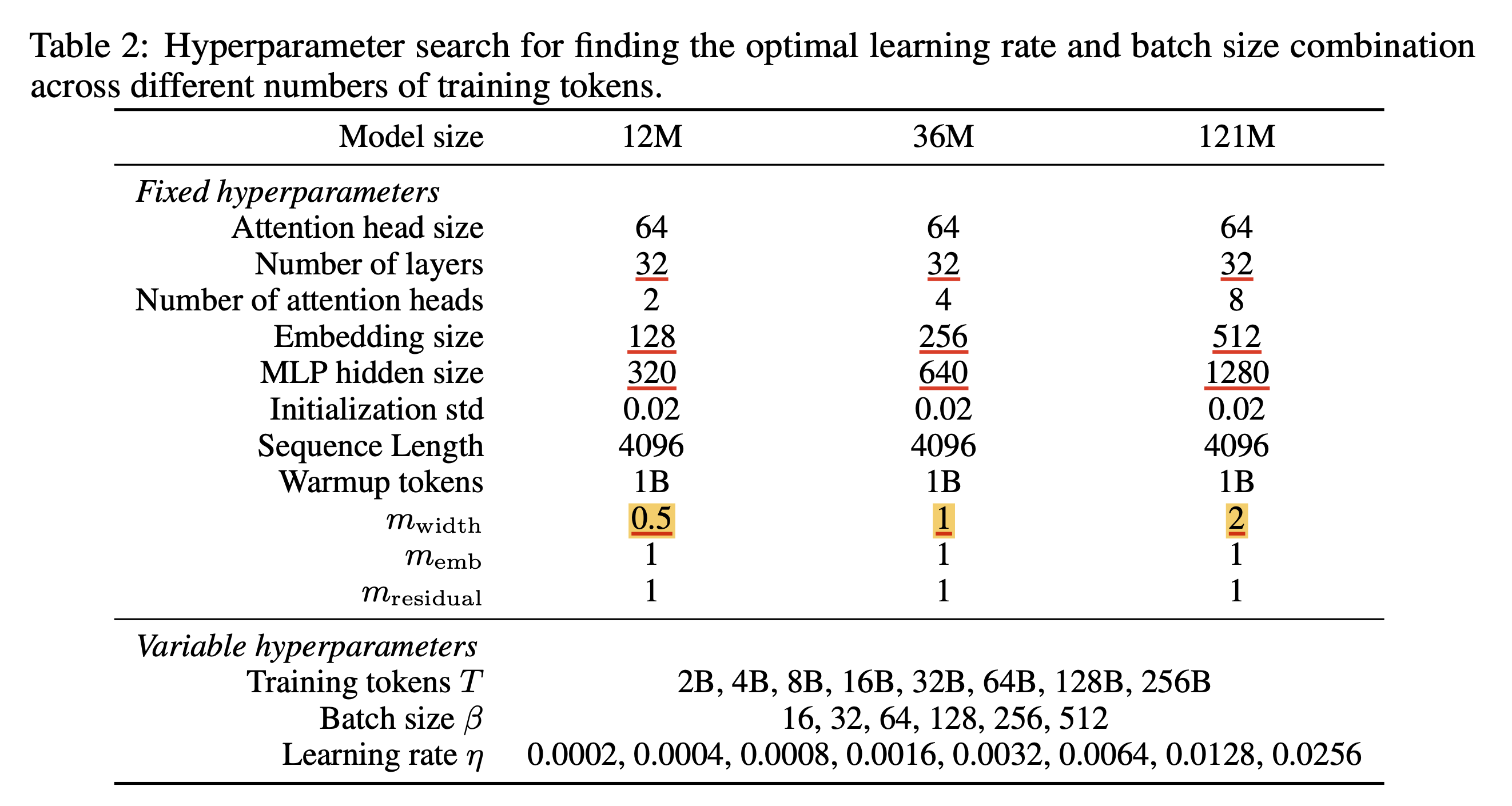
그 결과 아래와 같은 figure를 얻을 수 있었는데,
training tokens이 늘어나면 optimal peak LR이 감소하는 trend를 보인다는 것이 첫 번째 observation이다.
직관적으로 상대적으로 짧은 training tokens을 학습할 때 보다 긴 training horizon동안 LR이 천천히 decay될 테니 peak LR이 낮아져야 하는 것으로 생각해도 된다.
반면 training tokens를 고정하고 batch size가 커질 경우에는 optimal peak LR이 증가하는 trend를 보이는데, 이는 batch size가 커지면 estimated gradient가 정교해지지만 그 반동으로 total optimization step이 감소하기 때문에 똑같은 test error에 도달하기 위해서는 LR을 적절히 늘려줘야 하는 것은 당연하다고 할 수 있다.
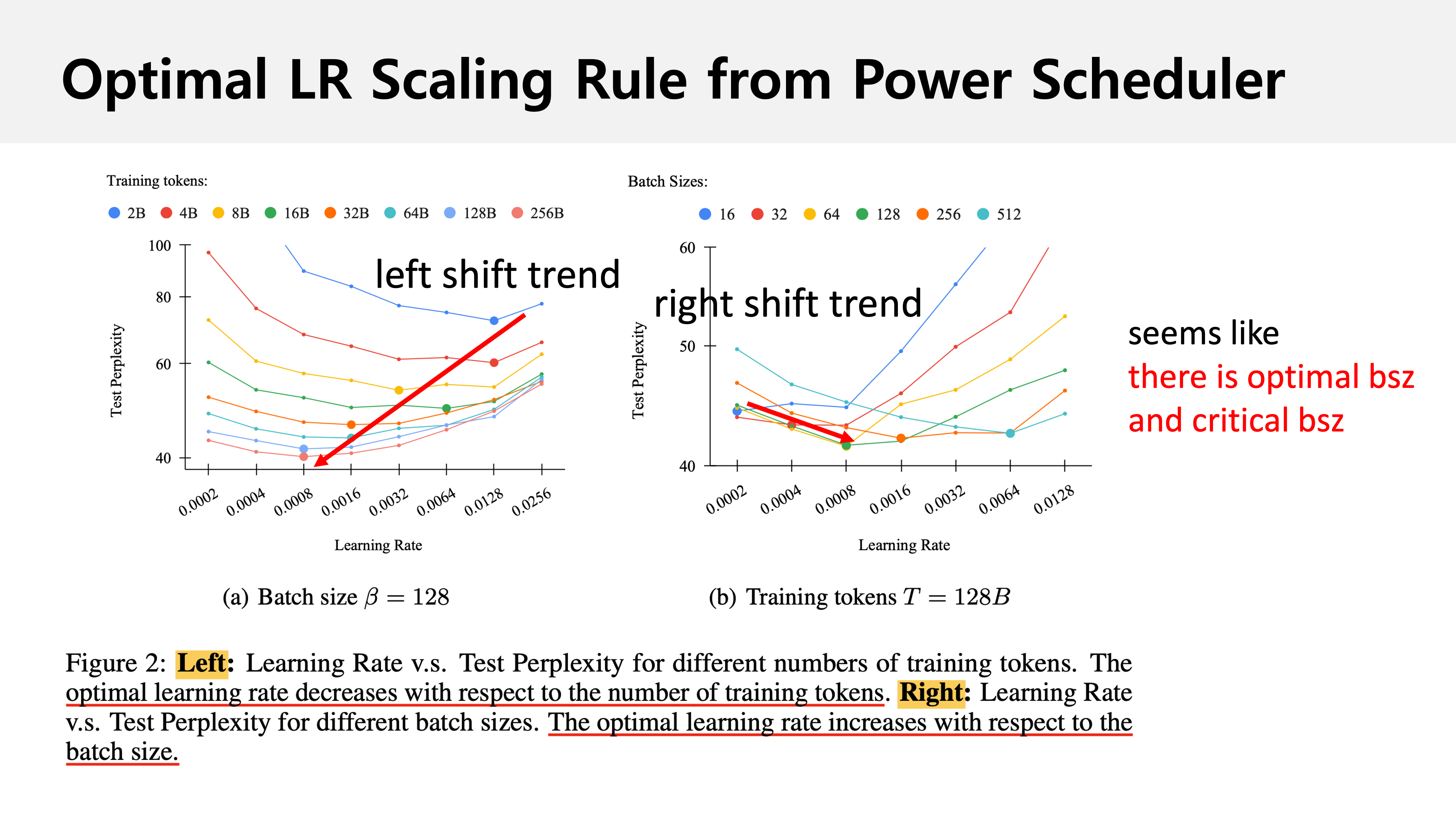
Paper에 별다른 언급은 없지만 또 하나의 observation이 있다면 어딘가 test error를 가장 낮게 하는 optimal batch size가 존재한다는 것이다.
사실 batch size가 성능을 좌우하는 요소가 되선 안된다는 얘기가 많은데 나는 동의하기 때문에 Adam optimizer의 weight decay, beta1, 2를 batch size에 따라 적절히 조절해주지 못한것이 문제일 것 같다.
그리고 optimal batch size로 보이는 점을 지나 batch size가 더 커지게 되면 test error가 올라가는 걸 볼 수 있는데,
이는 batch size가 어떤 지점을 지나면, 즉 너무 커지면 optimization step수가 충분하지 않아 LR을 보상해줘도 결국 똑같은 error에 도달할 수 없다는 걸 의미하며 이 어떤 지점을 critical batch size라고 부른다.
Relationship between Optimal LR, Batch Size and Training Tokens
그래서 optimal LR과 batch size, the number of training tokens와의 상관관계는 어떻게 된다고 할 수 있을까.
아래 figure는 위에서 했던 batch size, training tokens에 따른 실험을 다르게 plot한 것으로 보이는데, 우리는 여기서 같은 batch에서는 training tokens가 늘어날 때 LR을 줄여야 한다는 것과 더불어 optimal LR과 batch size의 ratio가 각 training tokens에 대해서 상대적으로 stable하게 유지된다는 것을 알 수 있다. (라고 저자들이 얘기하는데, 일단 적어도 trend는 유지되는 것으로 보인다)
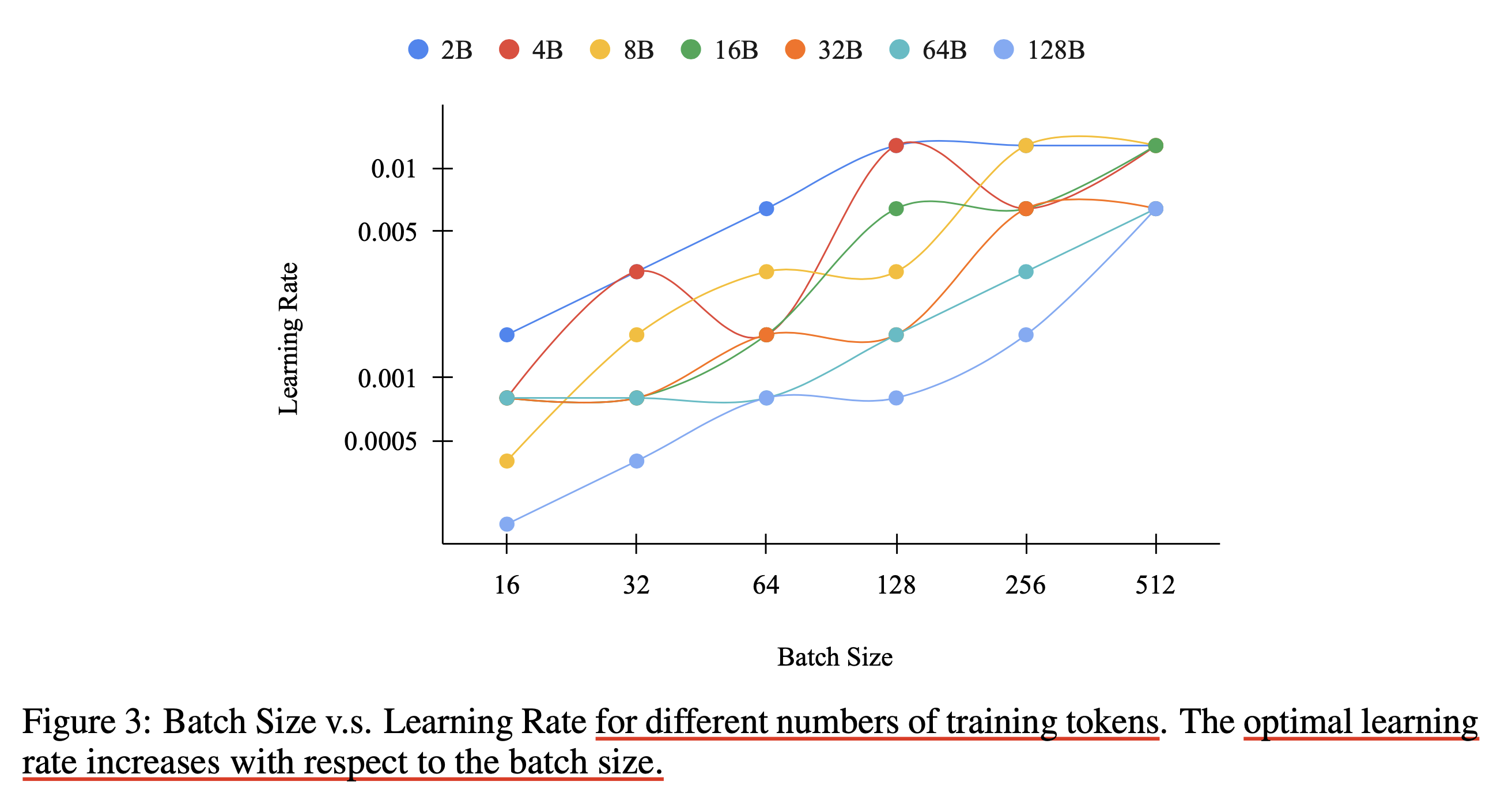
그래서 저자들은 가설을 2개 세워 검증하기로 하는데, 첫 번째는 “주어진 batch size와 training tokens pair \((\beta,T)\)와 WSD scheduler에 대한 optimal LR, \(\eta_{\text{opt}}\)는 batch size, \(\beta\)와 비례한다” 이다. 저자들은 먼저 아래 ratio, \(\gamma\)를 새롭게 정의했다.
\[\gamma = \frac{\eta_{\text{opt}}}{\beta}\]그리고 3개의 model size, \(12M, 36M, 121M\)에 대해서 extensive HP search를 진행했다. 이들은 가능한 모든 \((T, \beta, \text{model size})\) 조합에 대해서 optimal LR을 찾은 뒤, best three batch size만 남겨서 plot했다고 하며 (why?) 결과는 아래와 같다.
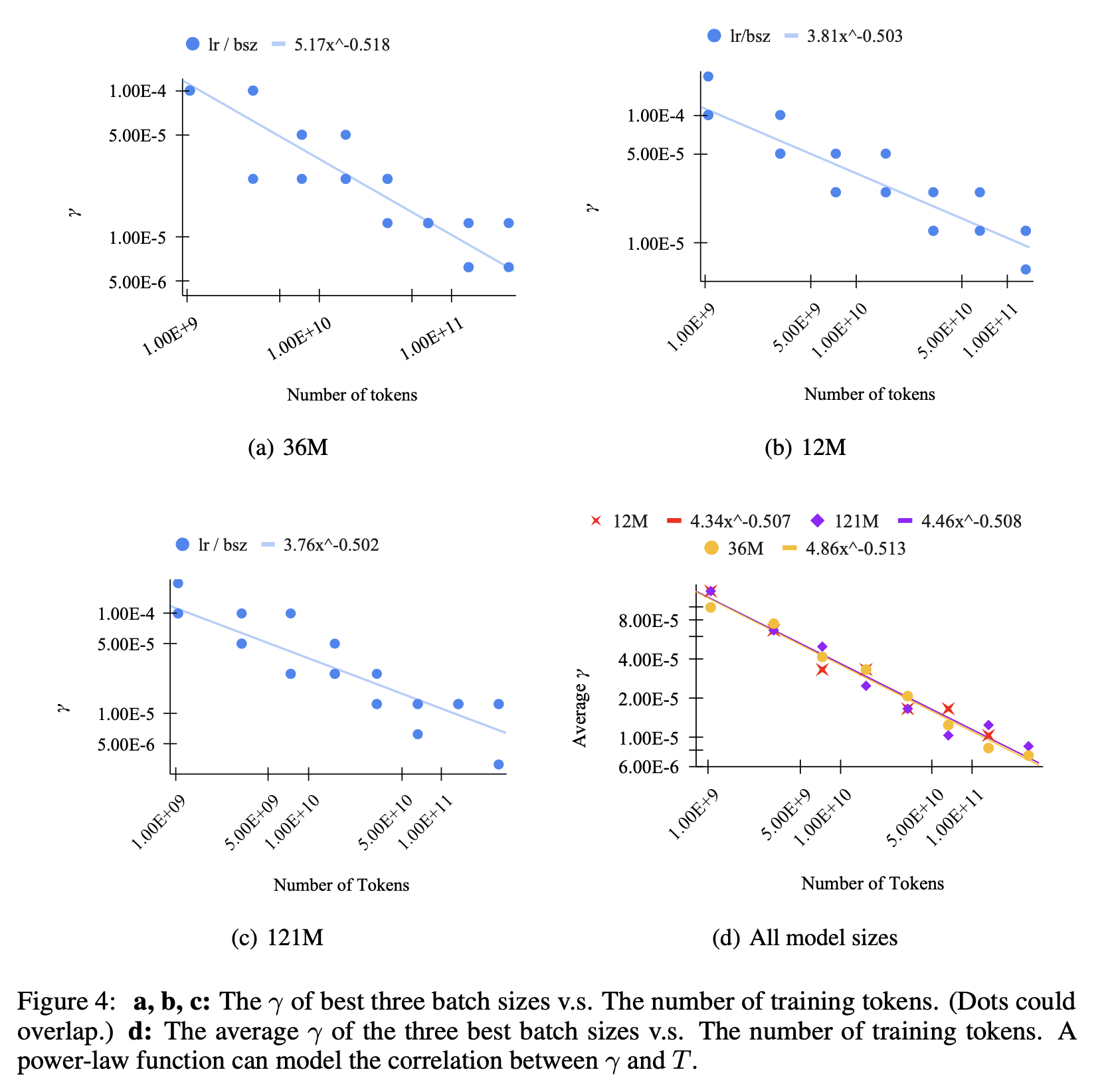
실험으로 부터 얻을 수 있는 결론은 “fixed training tokens, \(T\)가 주어졌을 때, ratio, \(\gamma\)는 어떤 작은 영역 (small region)에 떨어진다”는 것이었다고 하는데, 위 plot은 간단하게 말하면 model size에 상관없이 (왜냐면 muP쓰긴 하니까) training tokens가 늘어날수록 batch size - optimal LR scaling ratio가 줄어든다는 것으로, batch size가 커지면 step이 줄어들기 때문에 peak LR을 scaling해줘야 하지만 training tokens가 늘어나면 peak LR에서 천천히 decay되는 값으로 오래 학습되므로 batch가 증가할수록 LR을 scaling해주는 비율이 줄어드는 것이라고 할 수 있으며 서두에 얘기했던 직관과 일치한다고 할 수 있다.
저자들은 추가로 “ratio, \(\gamma\)는 \(T\)에 대해 power law 관계에 있을 것이다”라고 주장하고 이를 fitting한다.
\[\gamma = a T^b\]저자들은 실험 결과를 종합한 결과 \(\gamma = 4.6 T^{-0.51}\)의 power function을 얻을 수 있었다고 한다.
마지막으로 수식을 정리하면 optimal LR과 batch size는 \(\gamma\)의 관계에 있기 때문에 WSD를 쓸 경우 batch size, training tokens에 따라서 아래의 관계를 갖는다고 할 수 있으며, 저자들은 \(a, b\)는 small scale에서 쉽게 찾을 수 있다고 한다.
\[\eta_{\text{opt}} = \beta \cdot a T^b\]흠… 여기서 \(T\)가 바뀌지 않는다면 Adam optimizer에 대해서 batch size와 LR의 관계는 linear하다는 점에도 주목해야 한다. 이에 대한 많은 논문이 있고 그들은 보통 \(\sqrt{n}\)배냐 \(n\)배 사이의 결론을 내긴 하는데 이번 paper에서는 linear relationship인 것으로 가정하고 (figure 3를 보면 대충 linear이지만 완전 그런지는 솔직히 모르겠다) curve fitting을 해서 그런 것 같다.
Power Scheduler
그런데 위의 training tokens 수와 optimal LR의 관계는 몇가지 문제점이 있다고 한다. 첫째는 training steps을 training 전에 정해야 한다는 것이고, 두 번째는 muP가 optimal LR을 너무 많이 discount한다는 것이다.
예를 들어 10T tokens, 1024 batch size로 학습 시 optimal LR은 0.0011정도 되는데, 가장 작은 모델의 hidden size를 128로 설정하고 요즘 나오는 8B model들의 width가 4096라면 muP로 실험할 경우 width scaling factor가 32가 되고, hidden matrix들의 optimal LR은 이 경우 \(1/m_{\text{width}}\)로 discount 되므로 LR은 \(0.0011/32=0.000034375\)가 된다. 여기에 \(\gamma = 4.6 T^{-0.51}\)를 적용해주면 dataset이 \(10T\)이고, batch size가 \(\beta=1024\) (tokens량은 iter당 4M)라면 \(1024 \cdot 4.6 \cdot (10e12)^-0.51=0.0011\)배가 되므로 \(0.000034375*0.0011=0.0000000378125\)가 된다. Llama-3에서 8B model을 15T 학습하는데 쓴 global LR은 (muP아님) 3e-4정도 되기 때문에 이것보다도 1000배 작은 scale이 되는 것이다 (llama-3의 batch size는 모른다). (사실 llama-3에 대해서는 llama-2가 2T 학습할 때도 3e-4를 썼는데 15T 할 때도 3e-4를 썼기 때문에 이 LR이 search가 된 near-optimal이 맞는지 조차 의심이 든다)

저자들은 small LR이 나중에 convergence 하는 데에는 좋지만 early training phase에서 충분히 optimization space를 exploration 할 가능성을 줄이기 때문에 초반에는 large LR이 할당도리 필요가 있다고 주장했다.
사실 이 부분에 대해서 왜 fitted power curve로 scaling해주면 말도 안되는 LR이 나오는지 모르겠다. optimal bsz-LR scaling은 deepseek-LLM이나 miniCPM 등에서도 많이 하는 방법이고 deepseek 에서는 flops가 증가할때 power law exponent가 \(-0.125 (1/8)\)정도가 나왔었다.
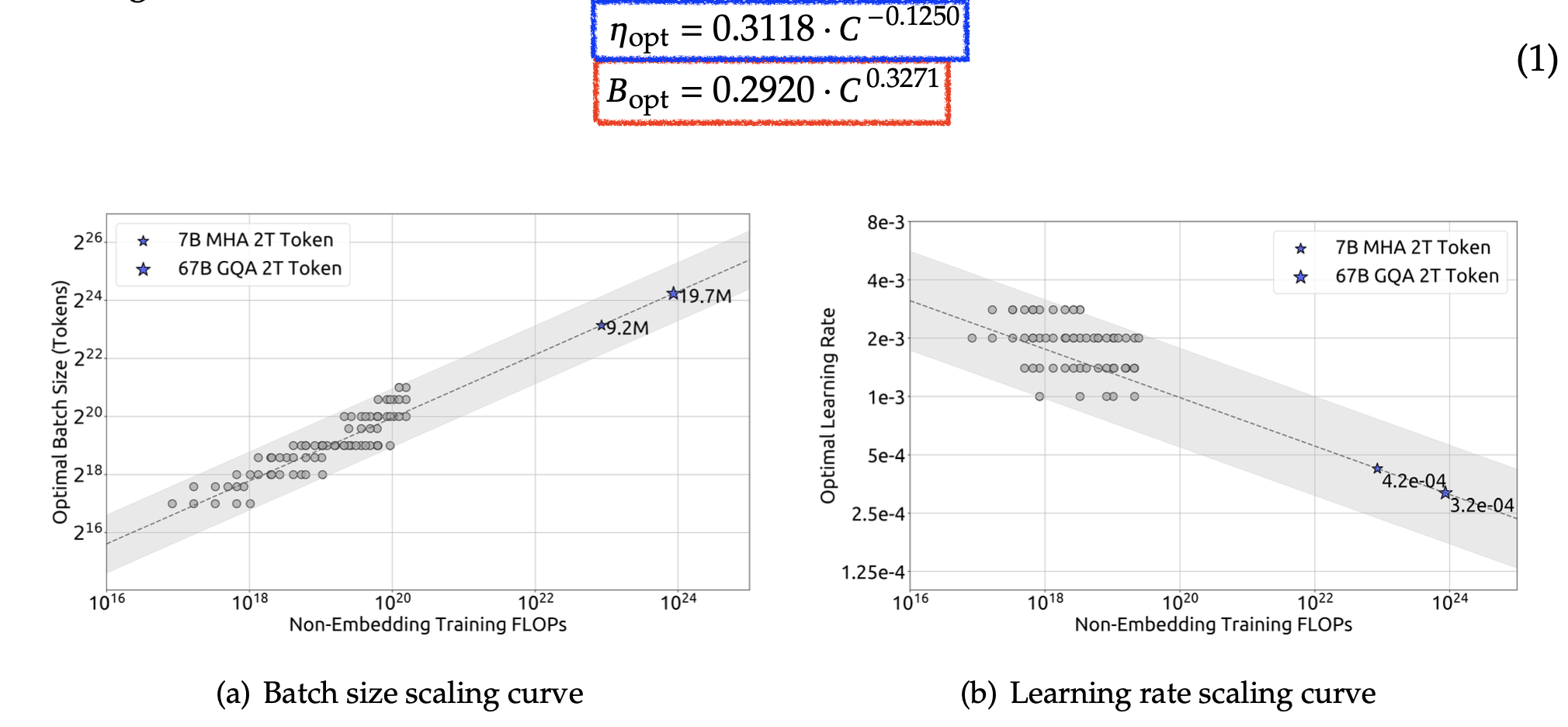
아무튼 저자들은 power scheduler를 제안했는데,
이는 아래 수식으로 정의된다.
 Fig.
Fig.
여기서 \(\beta\)는 batch size, \(n\)은 현재 timestep까지 학습된 token량, \(a\)는 LR의 amplitude, \(b\)는 학습이 됨에 따라 decaying되는 LR의 power-law exponent값, 그리고 \(\eta_{\text{max}}\)는 peak LR이다.
주의할점은 이제 HP search 기준 등이 기존의 muP와 꽤 달라진다는 것이다. 앞서 muP는 small scale에서 peak optimal LR 하나만 찾으면 그대로 optimal LR transfer할 수 있었지만 (batch size, training tokens가 바뀌지 않는 다면), 이제 \(\eta_{\text{max}}, a, b\)를 찾아야 한다. 저자들은 \(\eta_{\text{max}}=0.02\)로 두고 \(a,b\)를 search한 것으로 보이며, 결과는 아래와 같다.
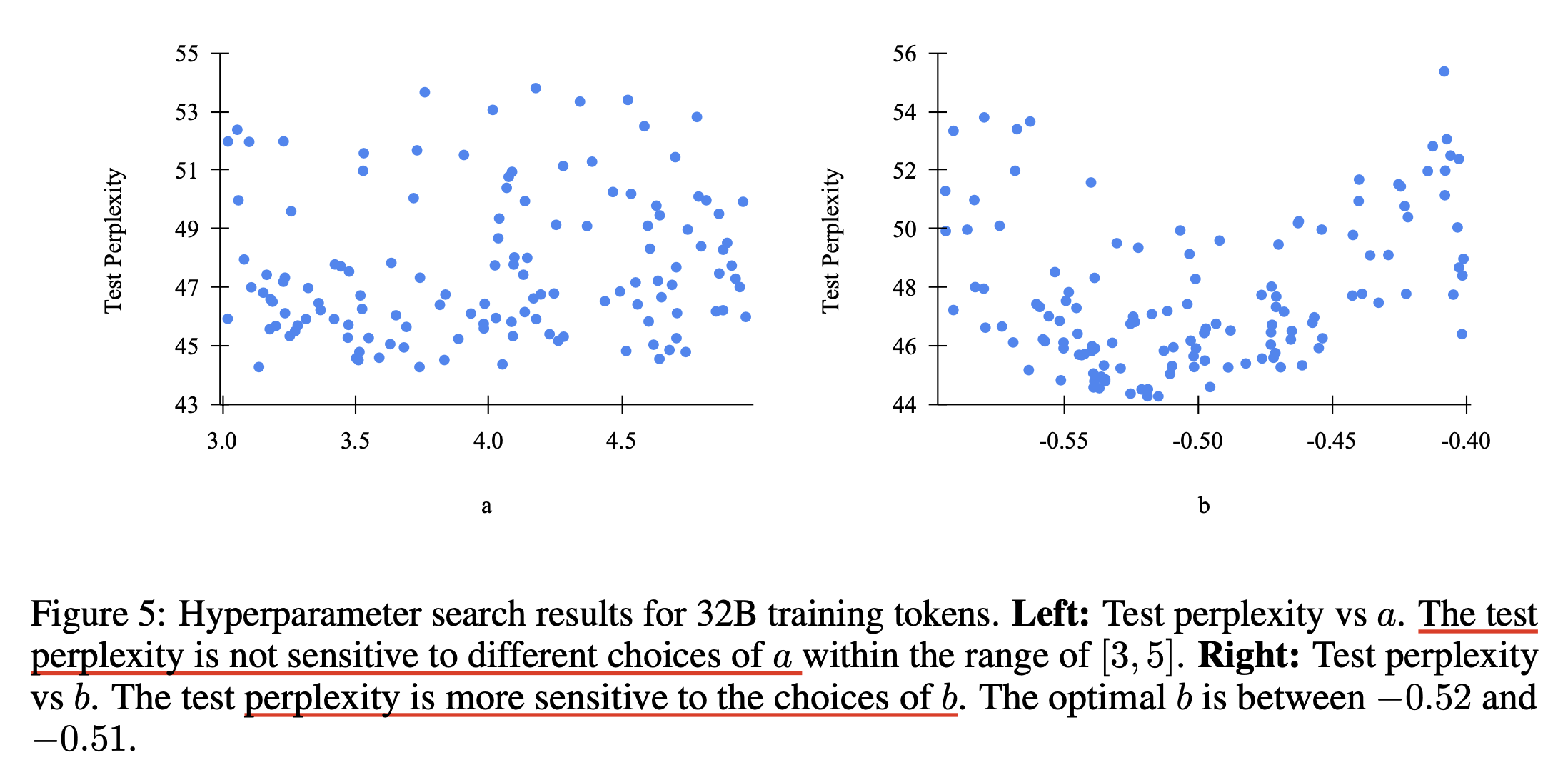
한눈에봐도 test error는 \(a\)보다 \(b\)에 더 민감한 것을 알 수 있으며, 최종적으로 아래와 같이 HP를 설정했다고 한다. (32B tokens에 대해 test됨)
\[a=4, b=-0.51, \eta_{\text{max}}=0.02\]그리고 다양한 batch size, the number of training tokens에 대해 실험한 아래 figure를 봐도 대부분의 session의 optimal b 값이 \([-0.49, -0.53]\)안에 떨어졌다고 한다. (power scheduler를 실험해볼 사람이 있다면 대충 이 값 쓰라는 소리)
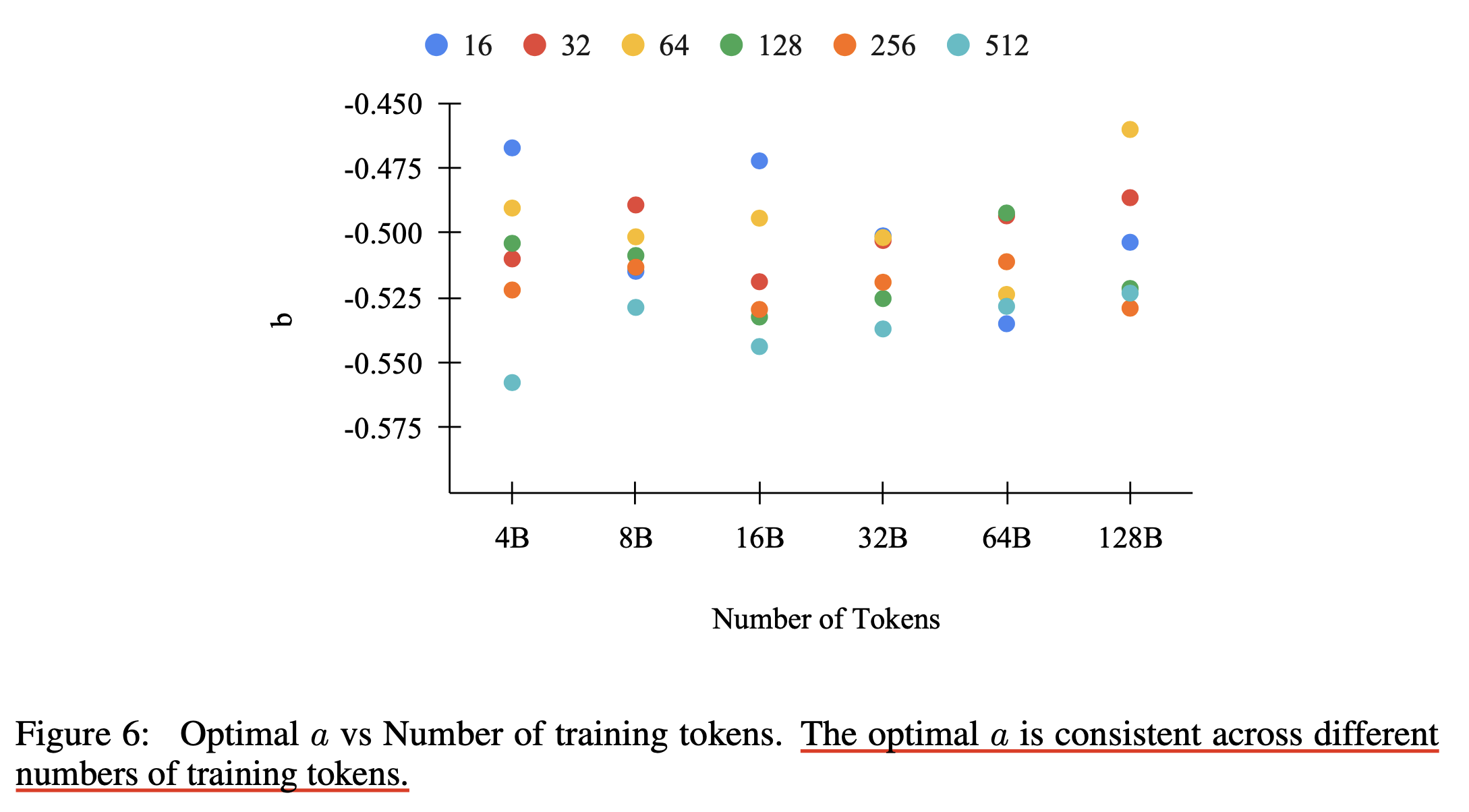
Experimental Results
실험 결과는 분석이 많이 없어서 생략하도록 하겠다.
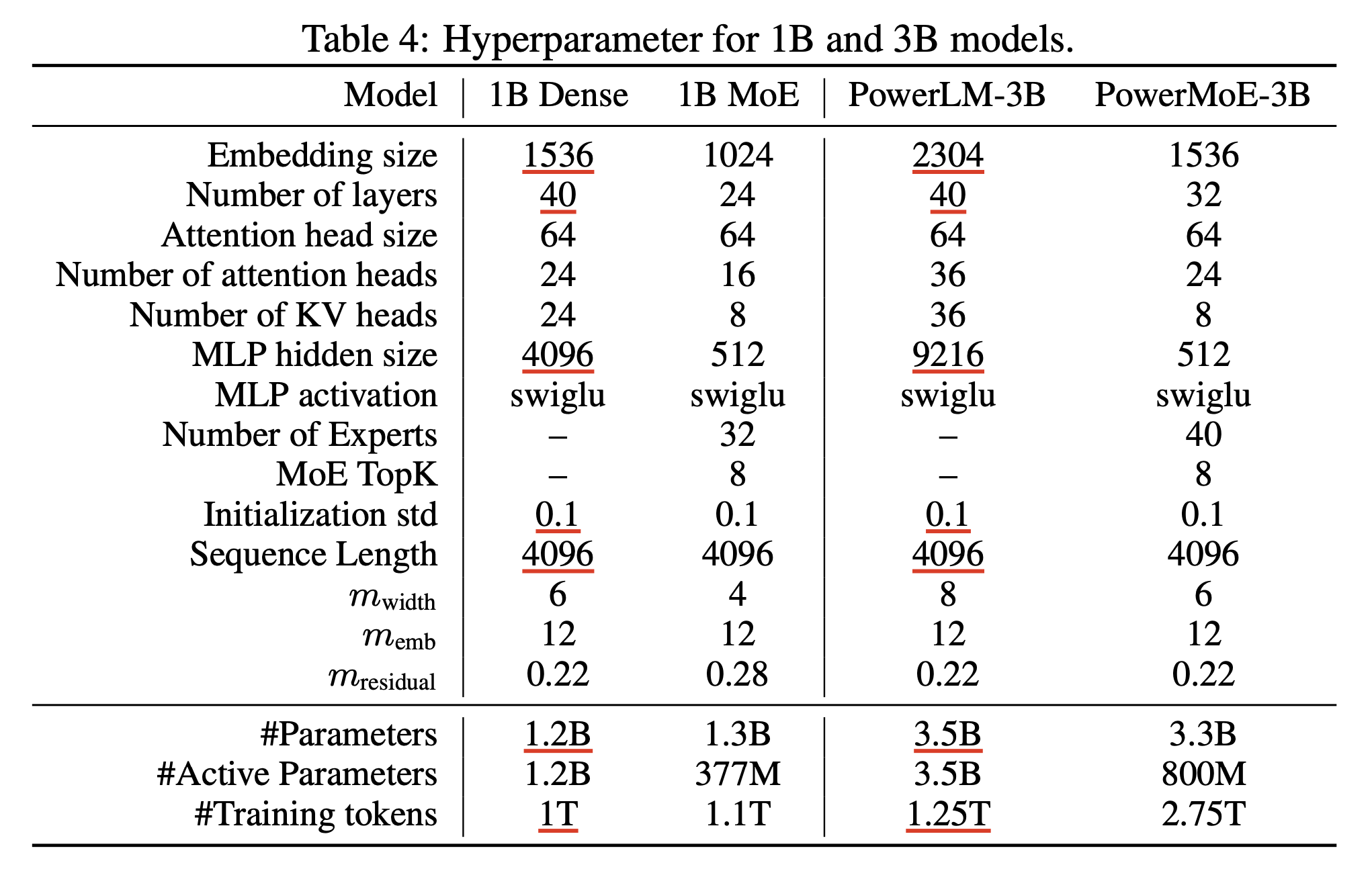
Depth가 좀 깊은데, 요즘 말이 나오는 reasoning 성능을 올리기 위해 architecture search를 한 건지는 모르겠다.
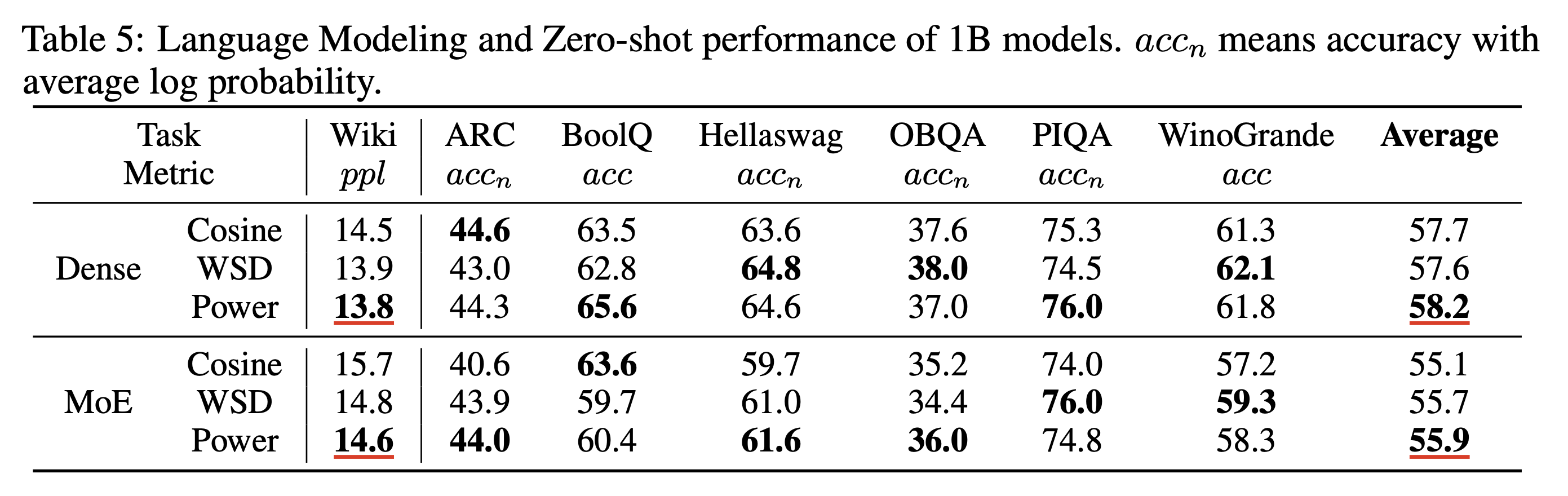
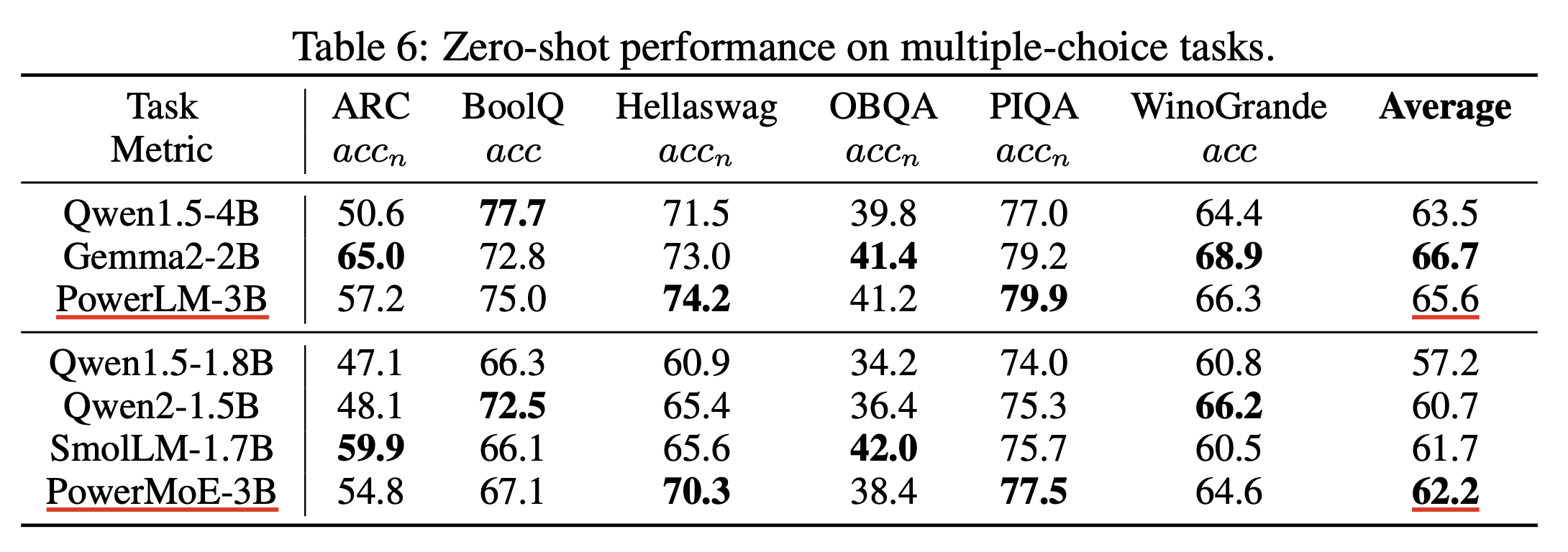
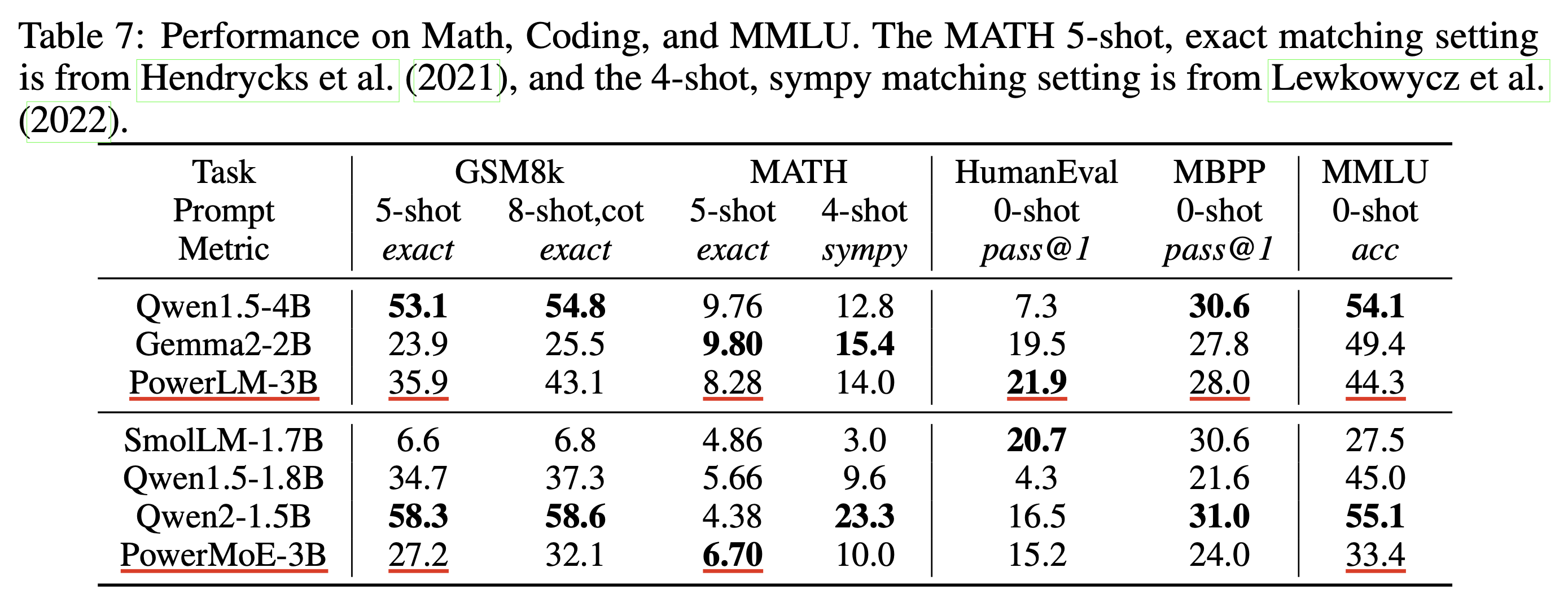
Scaling Optimal LR Across Token Horizons
최근 Scaling Optimal LR Across Token Horizons라는 paper가 arxiv에 올라와 관련 내용까지 추가하여 post를 연장하기로 했다. Microsoft 연구진이 공유한 실험 내용은 TL;DR하자면 아래와 같다.
- (bsz는 고정이고) training tokens가 증가할 때, optimal LR은 muP 적용 여부와 상관 없이 left shift (작아지는) trend를 보인다.
- 이는 model size와 관계가 없이 같은 trend를 보이며, 대충 training tokens가 N배 증가하면 \(\eta_{\text{new}} \propto \eta \cdot N^{-0.3}\)정도의 scaling trend를 보인다.
- bsz가 커지면 (아마 당연히 critical bsz에 도달하지 않았다면) optimal LR은 그만큼 증가할 것이라는 가설을 재검증했으며, 이 때 각 bsz에 대해서 training tokens 증가에 따른 optimal LR scaling trend는 거의 같았다 (parallel)
- 즉 \(LR(BS, D) = f(BS)D^{-\beta}\) (보통 adam이면 \(f(BS) \approx B^{0.5} \sim B^{1.0}\))
- llama-1는 1T tokens로 학습하는데 3e-4 LR을 썼지만, 추정결과 이는 너무 큰 값이고 1e-4정도를 썼어야함.
 Fig.
Fig.
 Fig.
Fig.
근데 다른건 그렇다 치고 llama에 대해서는 개인적으로 최종 성능이 llama-1보다 좋았는가?에 대한 결과가 없기 때문에 이게 맞는지 모르겠다. dataset이 공개가 아니어서 그랬을 수도 있지만 말이다.
 Fig.
Fig.
실제로 이들의 주장이 맞다고 생각해보면 llama는 시리즈를 통틀어 dataset size가 1T -> 2T -> 15T++로 늘어난 상황에서도 7B~8B model size에서 3e-4를 사용했는데, 1T에서 \((D_{\text{scaled}}/D_{\text{proxy}})^{-0.3}\)에 따라 1e-4가 도출됐으므로 15T로 늘어난 llama-3의 경우 \(15^{-0.3}=0.44\)배 더 작은 4.4e-5를 써야 하는 것이다. 이는 power scheduler에서 얘기하는 것 처럼 너무 작은 값일 수도 있고 아닐 수도 있다. 과여 이렇게 학습했을 때 저자들은 성능을 보장할 수 있을까? meta에서 어떤 scaling rule을 사용했는지 모르겠지만 그들도 바보는 아니기 때문에 진실이 궁금하다.
또 한가지 유의해야 할 점은 보통 training FLOPs가 증가하면 optimal bsz, critical bsz가 증가하는데 이들은 bsz를 고려하지는 않았다는 점과 small scale에서 sweep을 할 때도 1T tokens를 학습할 때 쓴 bsz=4M을 그대로 썼다는 점과 (즉 small scale에겐 너무나 큰 bsz) llama의 parameterization이 무엇인지 모른다는 점에서 성능 비교 결과도 없이 llama-1이 잘못됐다고 주장하는 것은 비약이 있을 수 있다는 것이다.
 Fig.
Fig.
Time Transfer: On Optimal Learning Rate and Batch Size In The Infinite Data Limit
(241011) Another one.
Time Transfer: On Optimal Learning Rate and Batch Size In The Infinite Data Limit라는 paper가 나왔다. muP를 적용했음에도 불구하고 batch size와 training tokens가 증가함에 따라 optimal LR이 shift되는 경향 자체는 존재하지만, 이 두개가 joint하게 scaling될 경우 둘 간에 상호작용이 있기 때문에 더 복잡한 현상이 있기 마련이기 때문에 만약 그냥 muTransfer하지 않고 bsz, tokens 증가에 따라 optimal scaling을 하기 하려고 마음먹었다면 엄밀한 rule을 써야만 한다. 왜냐면 어설프게 scaling law를 찾았다간 power scheduler의 저자들이 얘기한 것 처럼 너무 LR이 작아질 수도 있기 때문이다.
사실 Scaling Optimal LR Across Token Horizons에서는 bsz를 고정하고 학습량 증가에 따라 LR이 어떻게 변하는지만 봤기 때문에 bsz, training tokens를 jointly incresaing하면서 optimal bsz, critical bsz등이 어떻게 변하는지에 대해서는 알 수가 없는데 (보통 따로 따로 scaling rule을 정립하고 합침), 실제 LLM을 학습할 때는 small scale proxy 대비 bsz, tokens가 jointly 증가하기 때문에 이에 대한 자료를 공개해줘서 고맙다고 할 수 있겠다. 그리고 LR sensitivity는 어떻게 변하는지에 대해 자세히 실험적으로 분석했다.
먼저 첫 번째 figure를 보자.
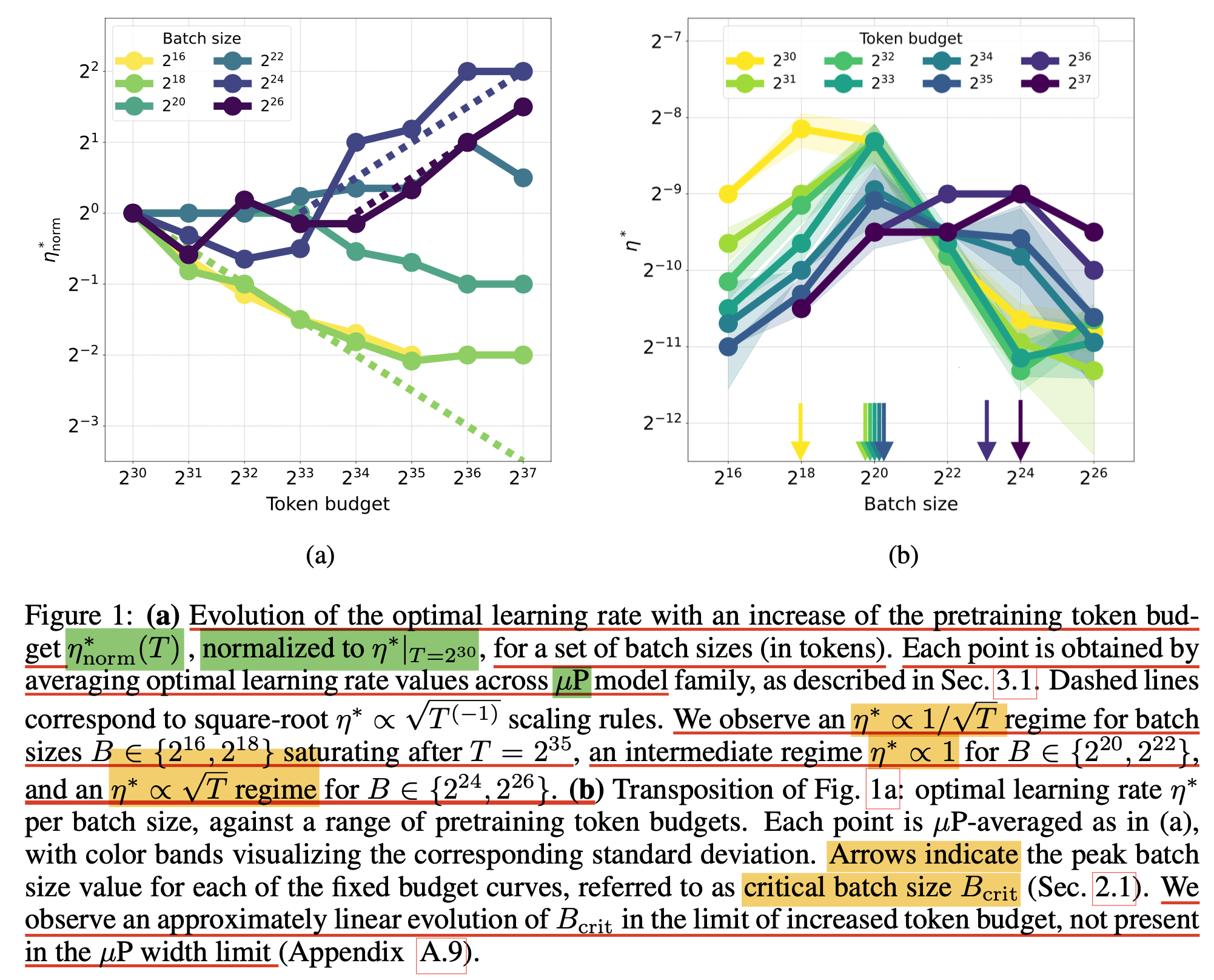 Fig.
Fig.
1(a)는 서로 다른 bsz, 65k~67M에 대해 token budget (training tokens)를 1B~137B까지 변화시키면서 token budget이 1B일 때의 optimal LR에 비해 얼마나 optimal LR이 변하는지를 관측한 것인데, bsz가 작은 경우에는 token budget이 증가할수록 optimal LR이 sqrt만큼 감소하는 \(\eta \propto 1/\sqrt{T}\) regime을 따르다가 34B정도의 token량 쯤 되면 saturation되어 더이상 LR을 scaling 하지 않는 regime에 진입하게 된다. (근데 여기서 주의할점은 optimal LR이 그렇다는 것이지 validation ppl이 어떻게 변하는지는 반영이 안됐다는 것이다. 아마 token budget이 증가할수록 성능이 좋아지긴 하겠지만 말이다)
반면 bsz가 너무 작지도 크지도 않은 1M, 4M에 대해서는 학습량이 늘어도 LR이 shift되지 않는 intermediate regime, \(\eta \propto 1\)에 있게 되고,
매우 큰 bsz인 16M, 67M에 대해서는 학습량이 증가하면 optimal LR이 sqrt만큼 증가하게 된다고 하는데 \(\eta \propto \sqrt{N}\),
사실 이 부분에 대해서는 이게 무슨 현상인지를 잘 모르겠다.
일단 \(2^{30}\) token budget에 대해서 bsz가 \(2^{24}, 2^{26}\)인 경우 optimization step이 각각 \(64,16\)밖에 되질 않는 기괴한 config들이 있는데,
아마 오른쪽 1(b)에 있는 token budget마다의 critical bsz를 넘지 않는 실험들에 대해서만 믿을 수 있지 않을까 싶다.
그 다음은 token budget 증가에 따른 optimal batch size 변화 양상인데,
miniCPM이나 deepseek에서 관찰된 것 처럼 학습량이 늘어날수록 optimal batch size가 증가하는 것을 또 다시 증명했다고 볼 수 있겠다.
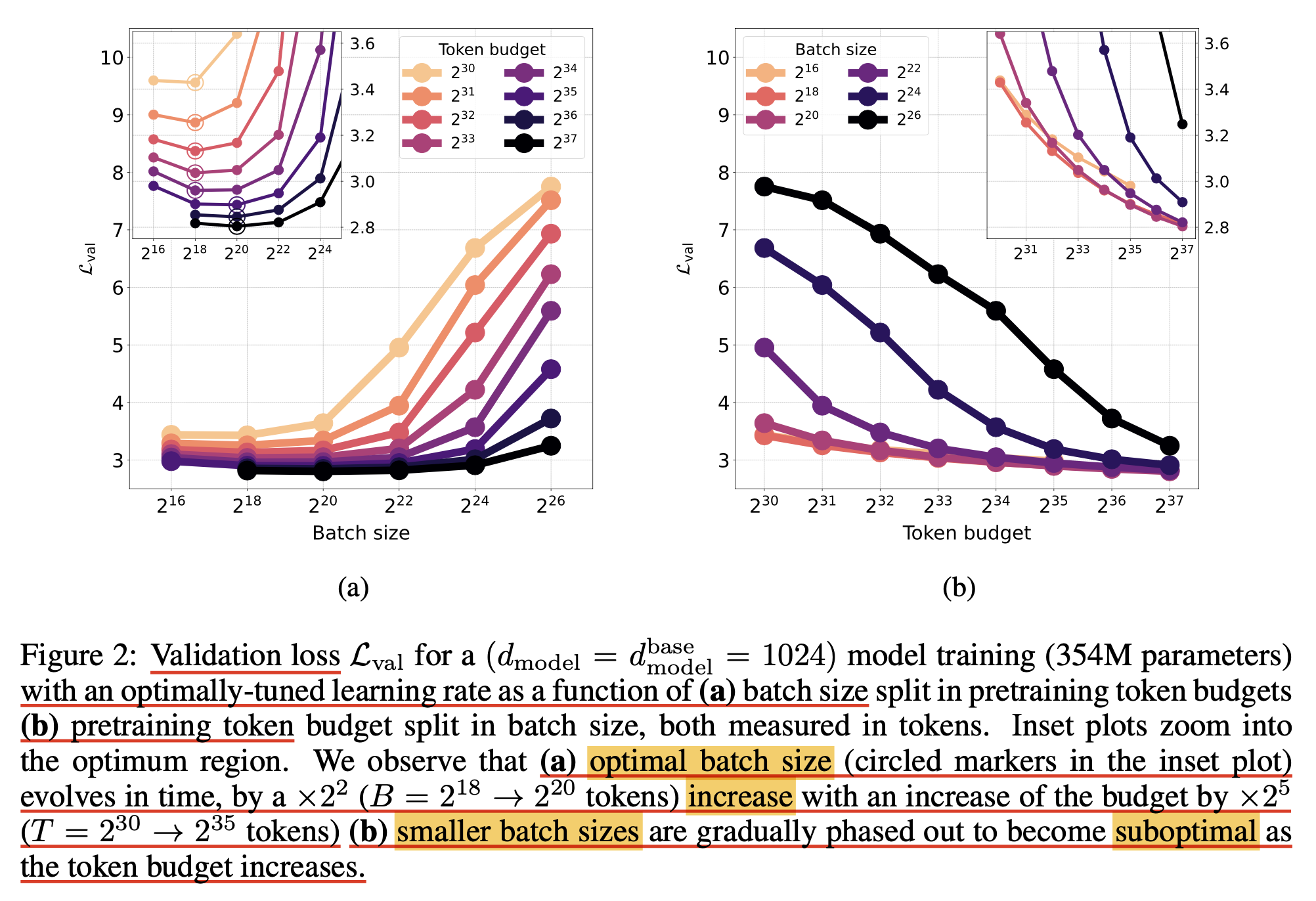 Fig.
Fig.
그런데 이는 여전히 갑론을박할 수 있는 주제라고 생각하는 것이, 왜냐하면 LR과 adam moment factor, weight decay등을 jointly 조절해주지 않으면 이럴 수도 있기 때문이다.
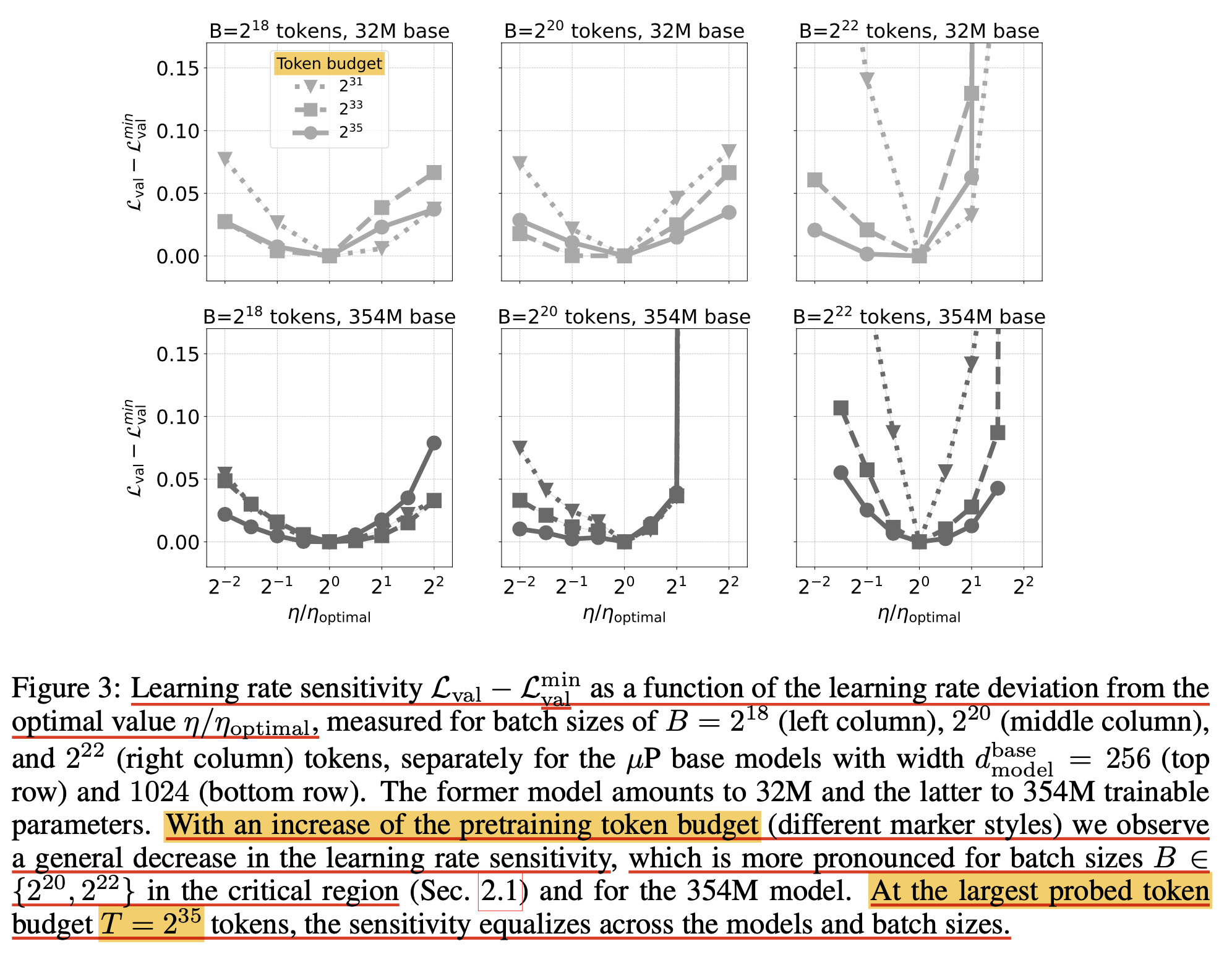 Fig.
Fig.
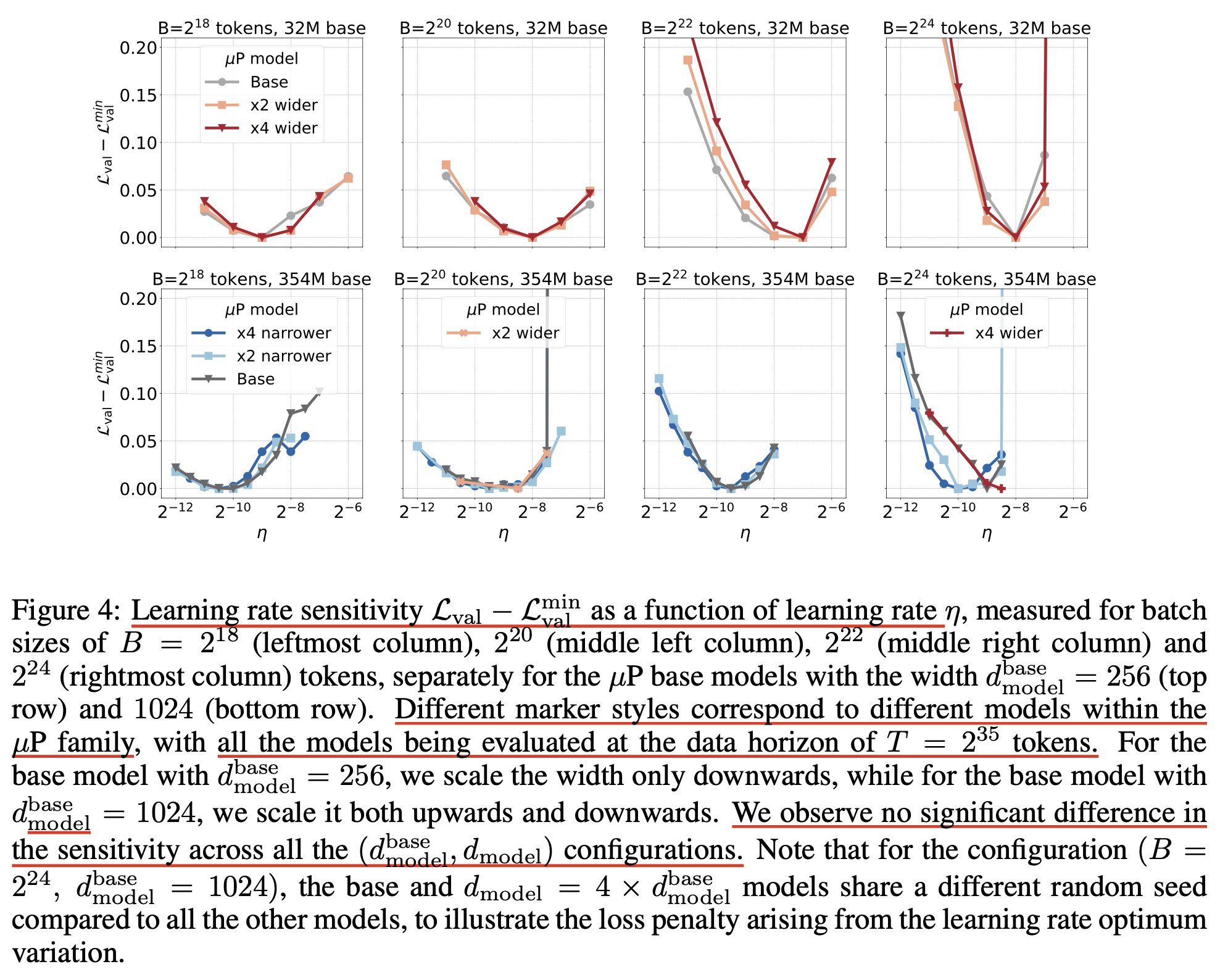 Fig.
Fig.