(WIP) (Paper) Scaling Exponents Across Parameterizations and Optimizers

< 목차 >

• Overview
• Background
  • Parameterizations and Optimizers
  • Stability, nontriviality and feature learning
  • Alignment
  • Summary of The Paper's Results
• 3. Theoretical Contributions
  • 3.1. Model and Notation
  • 3.2. Equivalence classes
  • 3.3. Alignment-General Space of Parameterizations
    • First Forward Pass: Stability At Initilization
    • Gradients At Initialization
    • Optimizer Update Rules
    • First Backward Pass
    • Defining The Activation Update Residual
    • Defining Alignment Variables
    • Second Forward Pass: Stability During Training
    • Third And Subsequent Passes: Stability During Training
    • Nontriviality
    • Summary of Constraints
    • Prior Work (muP) As A Special Case
    • Maximum Stable LR Exponents For All Parameterization
  • 3.4. Alignment Ratio
• 4. Experiments
  • Experimental Details
  • 4.1. Alignment Experiments
  • 4.2. Per-layer Learning Rates
    • Adam
    • SGD and Adam + Parameter Scaling
  • Epsilon Underflow in Adaptive Optimizers
  • Weight Decay Experiments
  • Fixed Step vs Compute Optimal experiments
• References

Overview

그동안 Transformer (주로 LLM)을 scaling up을 하기 위한 parameterization method가 많이 제안되어 왔는데, 이 paper는 말 그대로 large Neural Network (NN) training을 위한 paramterization과 각종 optimizer들의 조합을 다 실험해본 정신나간 paper라고 할 수 있다.

Our extensive empirical investigation includes tens of thousands of models 
trained with all combinations of three optimizers, four parameterizations, 
several alignment assumptions, more than a dozen learning rates, 
and fourteen model sizes up to 26.8B parameters.

탐색한 parameterization, optimizer는 다음과 같고, 각 조합에 대해 model size별로 learning rate, weight decay를 싹다 sweep해서 어떤 방법이 가장 stable한지? optimal한지?에 대한 결론을 냈다고 보면 된다.

• parameterization
  • Standard Parameterization (SP)
  • Neural Tangeng Kernel (NTK)
  • Mean Field Theory (MFT)
  • Maximal Update Parameterization (muP)
• Optimizer
  • SGD with momentum
  • AdamW (truly decoupled, not pytorch version)
  • Adafactor

Background

Parameterizations and Optimizers

이 글을 읽는 이 중에는 Parameterization이 생소한 이도 있을 수 있다고 생각한다. 간단하게 recap하자면 이는 NN training을 위한 Hyperparameters (HPs) 들로, 주로 아래 3가지 factor를 얘기한다.

• 각 layer별로
  • (1) the init variance for parameters (weight, bias, embedding …)
  • (2) a parameter multiplier
  • (3) ther learning rate

이 paper에서는 parameterized quantities에 대한 recipe로 아래 수식을 정의했는데,

Fig.

여기서 parameterized quantities와 scaling dimension은 다음과 같다.

• parameterized quantities
  • initialization scale
  • parameter multipliers
  • learning rate
• scaling dimensions
  • model width
  • model depth
  • context length
  • batch size
  • training horizon (steps)

이 때 parameterized quantities를 경정하는 요소인 width에 대해서 한 번 생각해보자. 예를 들어서 일반적인 He init같은 Standard Parameterization (SP)의 경우, global learning rate가 모든 parameter에 같은 값으로 똑같이 적용되고, 이는 model width가 증가하더라도 변하지 않는다. 즉 이는 width라는 scaling dimension, \(n\)에 대해 모든 parameter의 lr이 아래가 성립하는 것이다.

하지만 예를 들어 muP의 경우는 model의 frontend에 해당하는 (1) embedding matrix, backend에 해당하는 (2) lm_head (or unembedding matrix) 그리고 중간 (3) hidden weight의 각 layer 별로 이 exponent가 다르게 주어진다. 즉 muP는 embedding, hidden, lm_head 와 중간에 있는 transformer body의 QKVO projection, FFN1, 2 로 optimizer group이 그룹이 나눠지는 것이다.

즉 initialization variance에 대해서도 이 세 그룹에 대해서 width가 증가할수록 scaling이 되는데 이 exponent가 얼마인지를 이해해야 한다. 여기서 parameter별로 있는 multiplier에 대해 언급하고 싶은데, 이 값은 보통은 1.0이지만 1.0이 아니더라도 (보통 embedding에 3.0~10.0을 씀) 이 값은 trainable (learnable)한 nn.parameter가 아니다. 이는 weight matrix와 input activation이 곱해질 때 추가로 곱해지는 값으로 gradient scale을 조정하는 목적으로 쓰이는데, 이에 대해서는 곧 얘기하도록 하겠다.

Fig.

Fig.

Stability, nontriviality and feature learning

muP에서는 아래 3가지 constraint을 정의해서 이를 만족하는 parameterization를 유도했다.

• Stability: the activations are exactly constant scale and the logits are no more than constant scale
• Non-Triviality: the change in logits after the initialization is at least constant scale
• Feature Learning: the latent representations change and adapt to the data during training, as a constant scale change after initialization in the activations directly before the readout layer
  • features from each layer can be used for downstream task (like BERT)

먼저 Stability라는 것은 모든 layer의 acitvation이 특정 step에서 bound된 일정한 크기만큼 변화하는 것을 의미한다. 그리고 NN의 output logit은 일정한 크기 이하여야 한다.

두 번째 Non-Triviality는 logits이 random init한 시점부터 최소한 어느 정도 이상의 변화가 있어야 한다는 것을 의미한다. 아예 parameter가 변하지 거의 않아서 logits도 거의 움직이지 않는다면 이는 좋은 solution이 아니라 trivial solution이 된다.

마지막으로 Feature Learning은 모든 NN의 layer parameter들이 random init된 시점으로 골고루 변하여, 모든 layer가 input feature로 부터 유의미한 statistics를 뽑아낼 수 있다는 것으로 생각하면 될 것 같다. 이는 NTK같은 것들이 못하는 것이라고 Yang et al.이 실험적으로 밝혀냈는데, NTK등은 거의 모든 layer, 특히 중간 layer의 weight이 거의 움직이지 않기 때문에 유의미한 feature를 뽑을 수가 없어서 downstream task에서 좋지 못한 성능을 보였다.

위의 constraint들을 만족해야 하는 이유는 뭘까? 이렇게 되면 model width가 늘어나는 것에 관계 없이 activation이 constant scale로 커지므로 안정적이고, feature learning을 모든 layer별로 유의미하게 하며 non-trivial solution을 return하기 때문에 small model의 dynamics를 large model로 transfer 할 수 있다. 즉 Optimal Learning Rates (LR)같은 것들이 전이 (transfer) 되는 것이다.

Alignment

Paper에서는 alignment (정렬)이라는 keyword가 계속해서 등장한다. 이는 Reinforcement Learning form Human Feedback (RLHF) 같은 training process가 자유분방한 LLM을 사람의 의도에 맞게 정렬 시킨다는 맥락에서 alignment learning 이라고 불리우는 것과 같다. 또한 음성 인식 (Automatic Speech Recognition; ASR)에서도 어디서부터 어디까지의 음성 segment의 feature가 정답 text에 mapping되는지에 대해 (monotonic) alignment라는 말을 사용한다.

Fig. Speech Alignment Example. Source from Listen Attend and Spell

이 paper에서 alignment라는 단어가 나온 맥락은 앞서 얘기한 stability에 대한 condition이 첫 번째 forward, backward step, 두 번째 forward, backward step … 등 learning process가 진행될수록 달라지며, 특히 맨 처음 step의 random init parameter와 data의 matmul과 다르게 다음 optimization step 부터는 parameter가 update되면서 data에 대한 infromation을 담기 때문에 correlation이 생기고, 그 결과 parameter와 activation간의 "alignment"를 유발한다고 주장한다. Alignment는 여기서 vector들이 유사한 방향 (similar direction)을 가리키는 것을 의미한다고 한다.

한 편, 주어진 layer을 통과한 뒤의 acitvation의 norm은 다음 세 가지 quantity에 의해서 결정된다.

• the scale of the input to the layer
• the scale of the parameters in the layer
• the alignment between the parameters and the input or “data”

여기서 alignment의 contribution에 대해 no alignment, significant alignment인 경우가 있을 수 있는데, 각각의 경우 model width가 \(n\)일 경우 norm의 scale에 아래와 같이 영향을 주게 된다.

• no alignment: \(O(\sqrt{n})\)
• significant alignment: \(O(n)\)

왜 그럴까?

일단 우리는 input vector와 2D weight matrix multiplication (matmul)에 대해 생각할 때, 이 matmul의 output vector는 input vector와 weight matrix의 column vector간의 내적 (inner-product)의 결과물들이라는 사실로부터 출발해야 한다.

그렇다면 output vector의 각 element (coordinate)값은 각 vector의 길이 (NN width)가 \(n\)일 경우 \(n\)번의 elementwise product과 summation이 되기 때문에 element의 scale은 alignment가 없으면 \(O(\sqrt{n})\)가 되고, alignment가 충분한 경우 \(O(n)\)이 된다.

• when two vectors are zero mean and i.i.d sampled from random gaussian, inner products scales like \(\color{red}{O(\sqrt{n})}\)
  • by Central Limit Theorm; CLT
• when two vectors are correlated or worst case are identical, inner products scales like \(\color{blue}{O(n)}\)
  • by Law of Large Numbers; LLN

이는 Central Limit Theorm; CLT과 Law of Large Numbers; LLN에 의해 수렴하는 통계적 특성 때문인데, CLT는 동일한 확률 분포를 가진 독립 확률 변수 (i.i.d) n개의 평균의 분포는 n이 적당히 크다면 정규 분포 (normal distribution)에 가까워진다는 정리로 어떤 모집단에서 sampling을 하던 (binomial이던, gaussian이던) 그 sample들의 mean 값인 sampled mean의 분포가 정규 분포로 수렴한다는 것이다. 그런데 NN이 random init된 초기 상황에 matrix, \(W\)는 \(\mathcal{N}(0,\sigma_W)\)에서 sampling된 것이고, layer의 input또한 standardization 이 된 경우 zero mean을 갖게 되므로, 맨 처음 forward를 한 경우, 둘의 곱은 CLT에 따라 \(\mathcal{N}(0,n \sigma^2)\)이 된다. 즉 matmul의 결과물인 outgoing activation의 norm은 variance에 dominate 되어 \(O(\sqrt{n})\) scale이 되는 것이다.

반면에 두 vector가 correlation이 생기게 되거나 아니면 최악의 경우 identical해진다면 outgoing activation의 norm은 양상이 달라진다. 예를 들어 first forward pass는 CLT에 따라 norm의 scale을 계산했으나, first backward pass를 생각해보면 parameter, \(W\)의 update quantity, \(\Delta W\)는 first batch의 function으로 으로 표현되기 때문에 data distribution과 correlation이 생긴다. 그러면 다음 second forward pass부터는 inner product는 \(O(\sqrt{n})\)이 아닌 \(O(n)\)으로 scale되게 된다. 따라서 우리는 stability 관점에서 activation이 항상 constant scale 되기를 원했으므로, updated parameter, \(W + lr \cdot \Delta W\)가 data distribution과의 correlation이 생기는 것을 감안해서 LR을 보정해줘야 (counteract) 한다. 지금의 경우 우리는 activation의 norm을 나타내는 점근 표기법 (asymptotic notation), \(O\)가 \(n\)에 대한 것이 아니라 \(\sqrt{n}\)에 대한 것이었으면 좋겠으므로 significant alignment가 있다면 maximal stable LR은 \(O(\sqrt{n})\)배 작아야 할 것이다.

Summary of The Paper's Results

여태까지의 내용을 한 장의 slide로 정리한다면 아래와 같을 것이다.

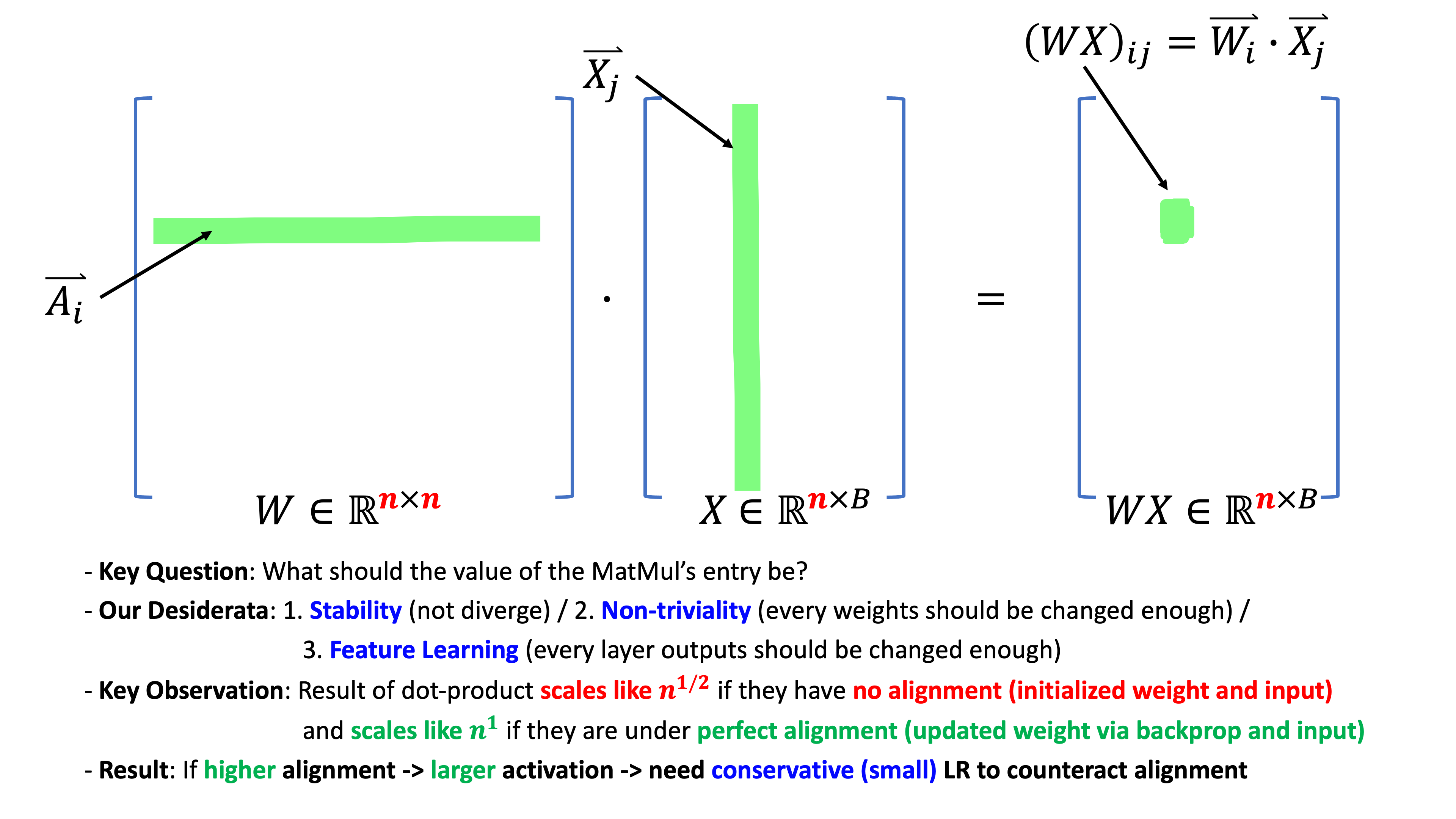Fig.

이는 현재 다루는 paper뿐 아니라 muP에서의 핵심 내용이기도 하다. Greg Yang이 lead한 muP, Tensor Programs VI: Feature Learning in Infinite-Depth Neural Networks와 Spectral muP, A Spectral Condition for Feature Learning paper를 같이 읽기를 매우 추천하며, 아래 paragraph도 현재 우리가 해결하고자 하는 바를 잘 설명한 것 같아 추가로 첨부한다.

Fig.

아래 table은 Scaling Exponents~ paper에서 제안하는 각 parameterization 별로 서로 다른 alignment assumption에 따라서 어떻게 per layer LR을 설정해줘야 하는지를 요약한 것이며, 우리가 앞으로 수학적으로, 실험적으로 측정하여 얻은 값들의 최종 결과이다.

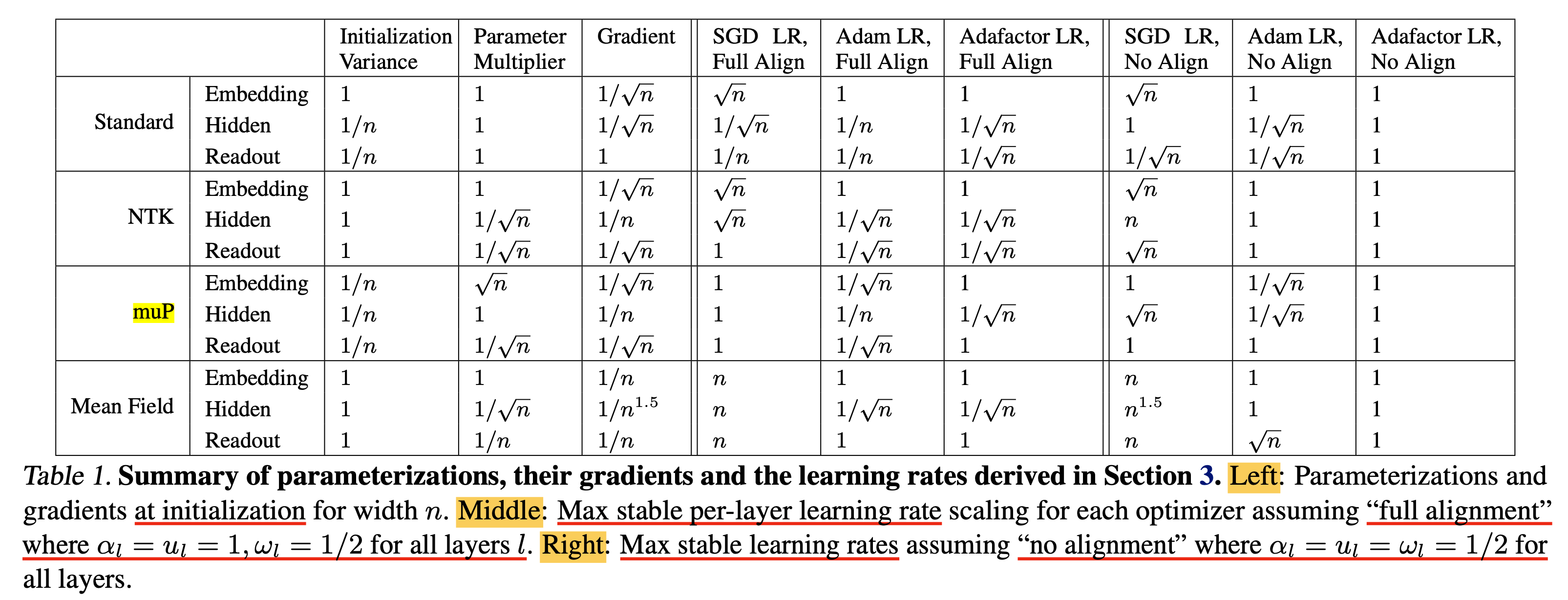Fig.

3. Theoretical Contributions

이제 이론적으로 Table 1의 maximal stable LR을 유도해보려고 한다.

3.1. Model and Notation

먼저 notation을 아래와 같이 정의한다.

• num hidden layers: \(L\)
• input and output dim: \(d\)
• hidden layer dim: \(n\)

• nonlinearity: \(\phi: \mathbb{R} \rightarrow \mathbb{R}\)

• Model
  • embedding layer: \(W_1 \in \mathbb{R}^{n \times d}\)
  • hidden layers: \(W_2, \cdots, W_L \in \mathbb{R}^{n \times n}\)
  • readout layer: \(W_{L+1} \in \mathbb{R}^{d \times n}\)

이제 각 layer, \(l\)별로의 parameterization을 아래와 같이 정의하는데, 이는 앞서도 나왔던 표현으로 소위 abc-parameterization이라고 부른다.

• param multiplier: \(n^{-a_l}\)
• param init: \(W_l \sim \mathcal{N}(0, n^{-2b_l)}\)
• lr \(\eta_l \propto n^{-c_l}\) with width-independent constant of proportionality that we omit here

이제 input, \(x \in \mathbb{r}^d\)에 대해서 model은 \(z_1, \cdots, z_l\)의 layerwise activation을 갖게 되고, 최종적으로 Loss를 계산하기 전의 logit, \(z_{L+1}\)을 얻게 된다.

• change in params in layer l between initialization and step t: \(\Delta W_{l}^t\)
• change in activations in layer l between initialization and step t: \(\Delta z_{l}^t\)

3.2. Equivalence classes

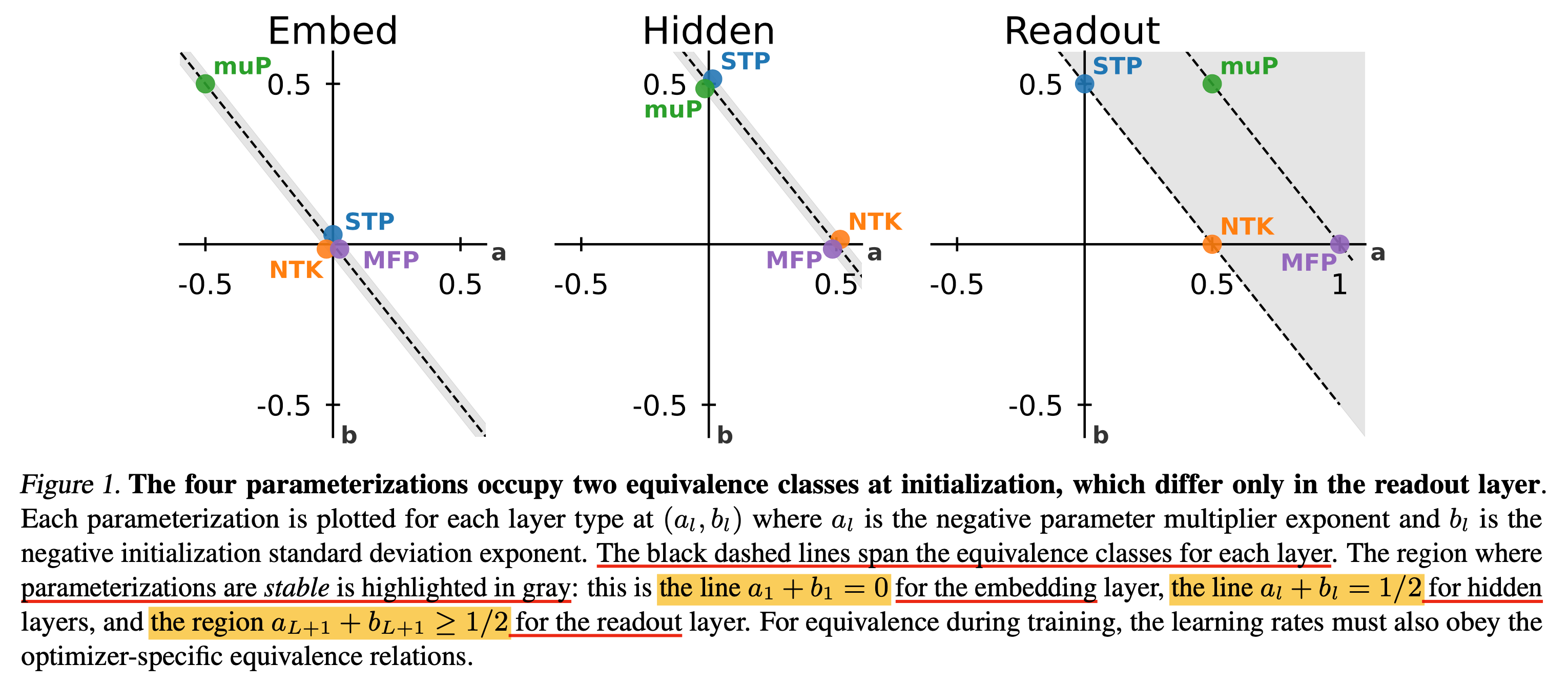Fig.

3.3. Alignment-General Space of Parameterizations

앞서 얘기한 것 처럼 first forward pass를 넘어 second forward pass가 되면 \(l\)번째 layer의 actiation은 아래처럼 계산이 된다.

여기서 첫 번째 term인 \(W_l z{l-1}\)은 둘 다 normal dist로부터 i.i.d sampling 된 init param과 roughly i.i.d인 init activation이기 때문에 전혀 align되어있지 않을 것이다. 결국 이 summation에서 나머지 세 가지 term은 parameter update가 data distribution이나 model의 다른 parameter와 align될 것이기 때문에 alignment를 가지게 될 것이다. 그래서 저자들은 다음의 alignment exponent를 정의하게 되는데,

• alignment exponent for \(\Delta W_l z_{l-1}\): \(\alpha_l\)
• alignment exponent for \(W_l \Delta z_{l-1}\): \(\omega_l\)
• alignment exponent for \(\Delta W_l \Delta z_{l-1}\): \(u_l\)

First Forward Pass: Stability At Initilization

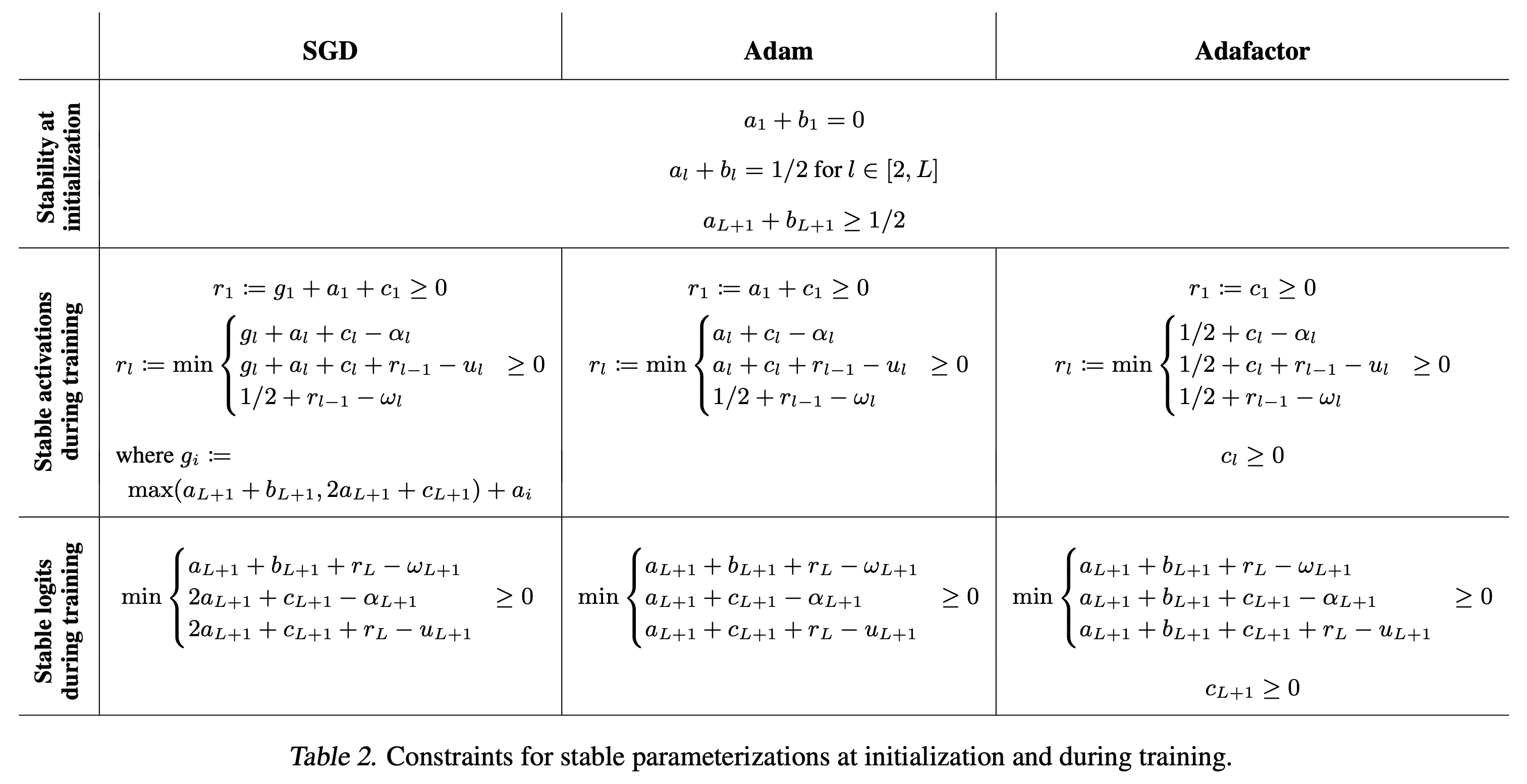Fig.

Gradients At Initialization

Optimizer Update Rules

First Backward Pass

Defining The Activation Update Residual

Defining Alignment Variables

Second Forward Pass: Stability During Training

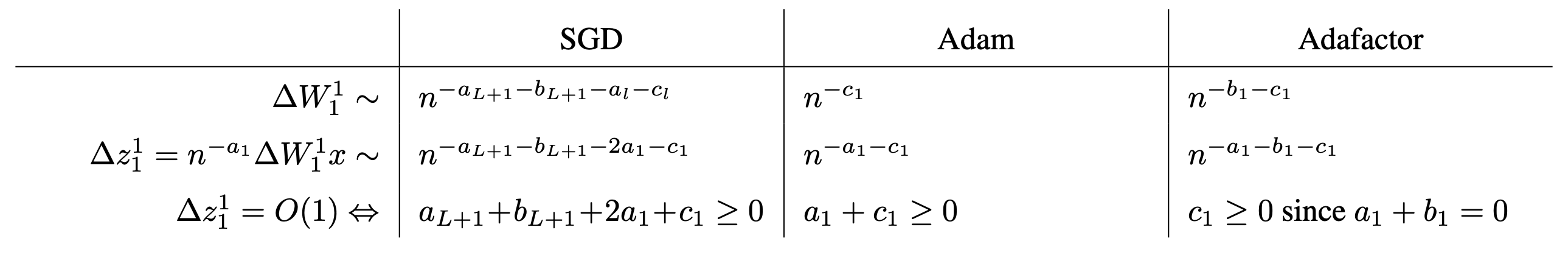Fig.

Fig.

Fig.

Third And Subsequent Passes: Stability During Training

Nontriviality

Fig.

Summary of Constraints

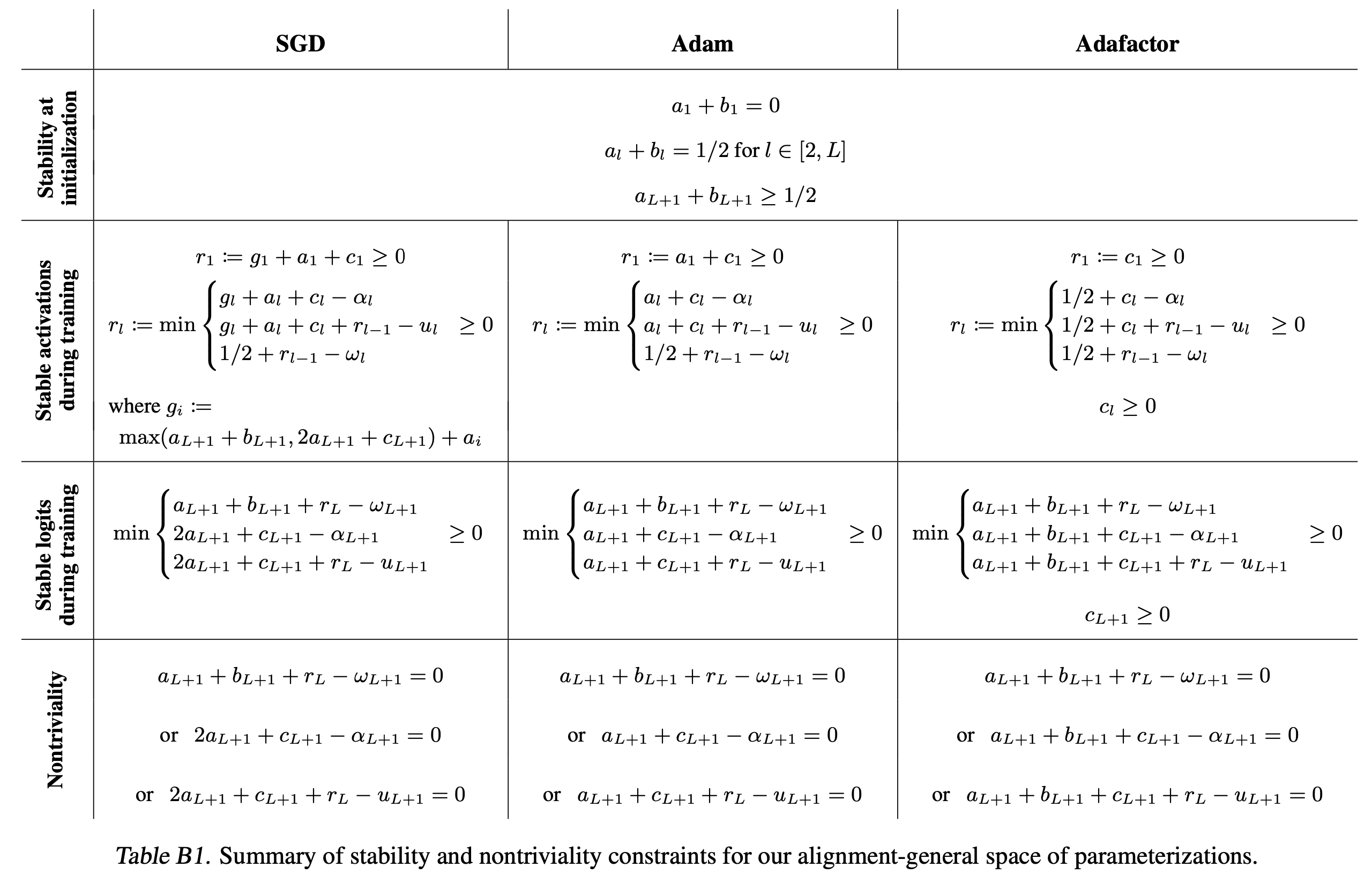Fig.

Prior Work (muP) As A Special Case

여기서 모든 layer에 대해 \(\alpha_l = 1\)로 둔 이유는 parameter updates와 data distribution의 alignment 때문에 \(\Delta W_l\)과 activation \(z_{l-1}\)가 align된다는 가정 때문이다.

Maximum Stable LR Exponents For All Parameterization

이제 alignemnt assumption에 따른 \((\alpha_l, \omega_l, u_l)\)로 이루어진 두 가지 set을 정의하고, 아래 Table 1의 각 layer, parameterization과 assumption에 따른 maximum stable LR을 유도하려고 한다.

Fig.

이를 유도하기 위해서는 먼저 앞서 정의했던 alignment type에 대해서 생각해봐야 한다.

• alignment between the parameter updates and data distribution: \(\Delta W_l z_{l-1}\)
• the alignment occurs not between parameters and data, but between the updates to parameters in earlier layers and the initialization parameters in the later layer: \(W_l \Delta z_{l-1}\)
• may contain both kinds of alignment, between the parameters and data or between parameters in different layers: \(\Delta W_l \Delta z_{l-1}\)

3.4. Alignment Ratio

우리는 앞서 \(l\)번째 layer의 activation, \(z_l\)에 contribute하는 alignment variables, \(\alpha_l, \omega_l, u_l\)를 정량화 (quantify) 했으며, 이는 특히 아래 expanded sum의 개별적인 term에 기여를 했다.

하지만 실제 training 이 시작되면, 이 sum안의 각 term들의 alignment정도는 서로 간섭을 받게 된다 (interfere constructively or destructively). 그렇기 때문에 실제로는 \((W_{l} + \Delta W_{l})\)와 \((z_{l-1} + \Delta z_{l-1})\)사이의 single alignment quantity만이 activation, \(z_l\)의 scale을 결정하게 된다.

그래서 저자들은 log alignment ratio라는 metric을 새로 정의하게 된다. 이는 실험적으로 training동안 얼마나 누적되는 alignment (accumulated alignment)가 activation scale에 얼마나 contribution하는지를 이해하기 위해 쓰일 수 있다.

여기서 norm은 Frobenius norm이다.

4. Experiments

Experimental Details

Fig.

Fig.

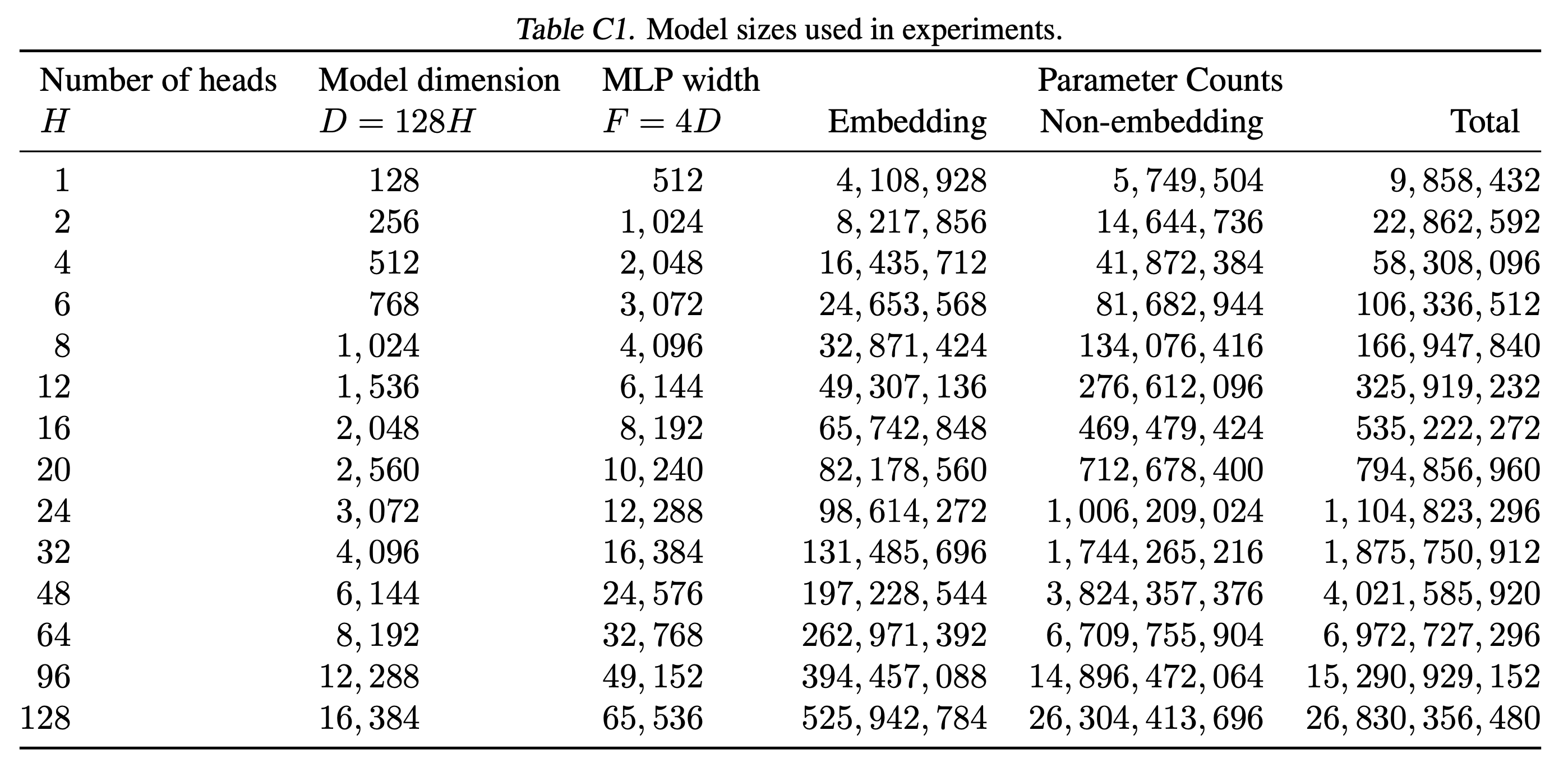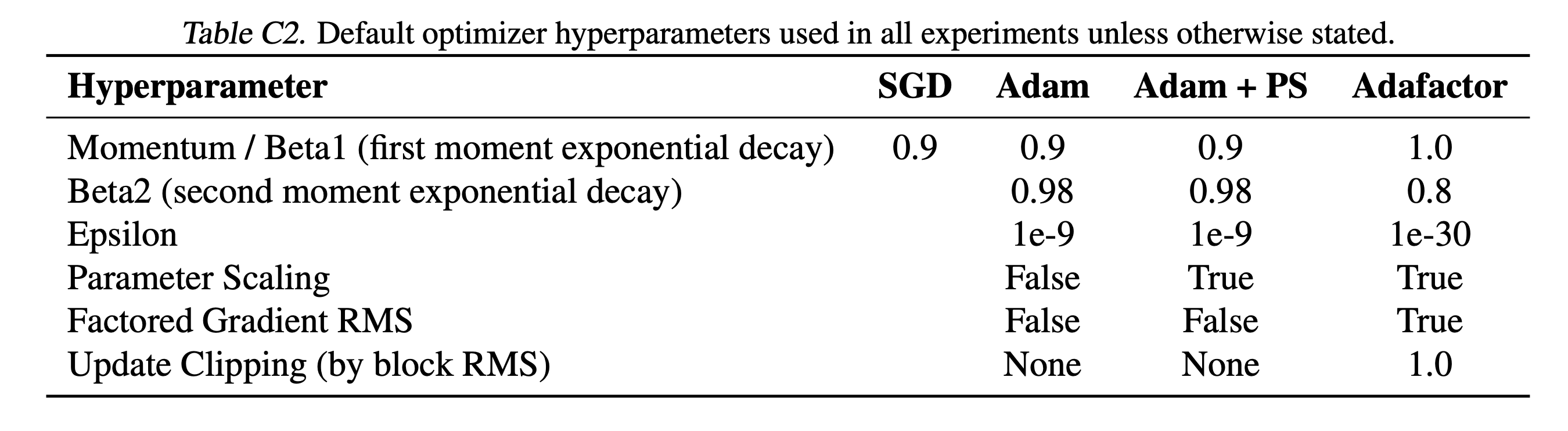Fig.

Fig.

Fig.

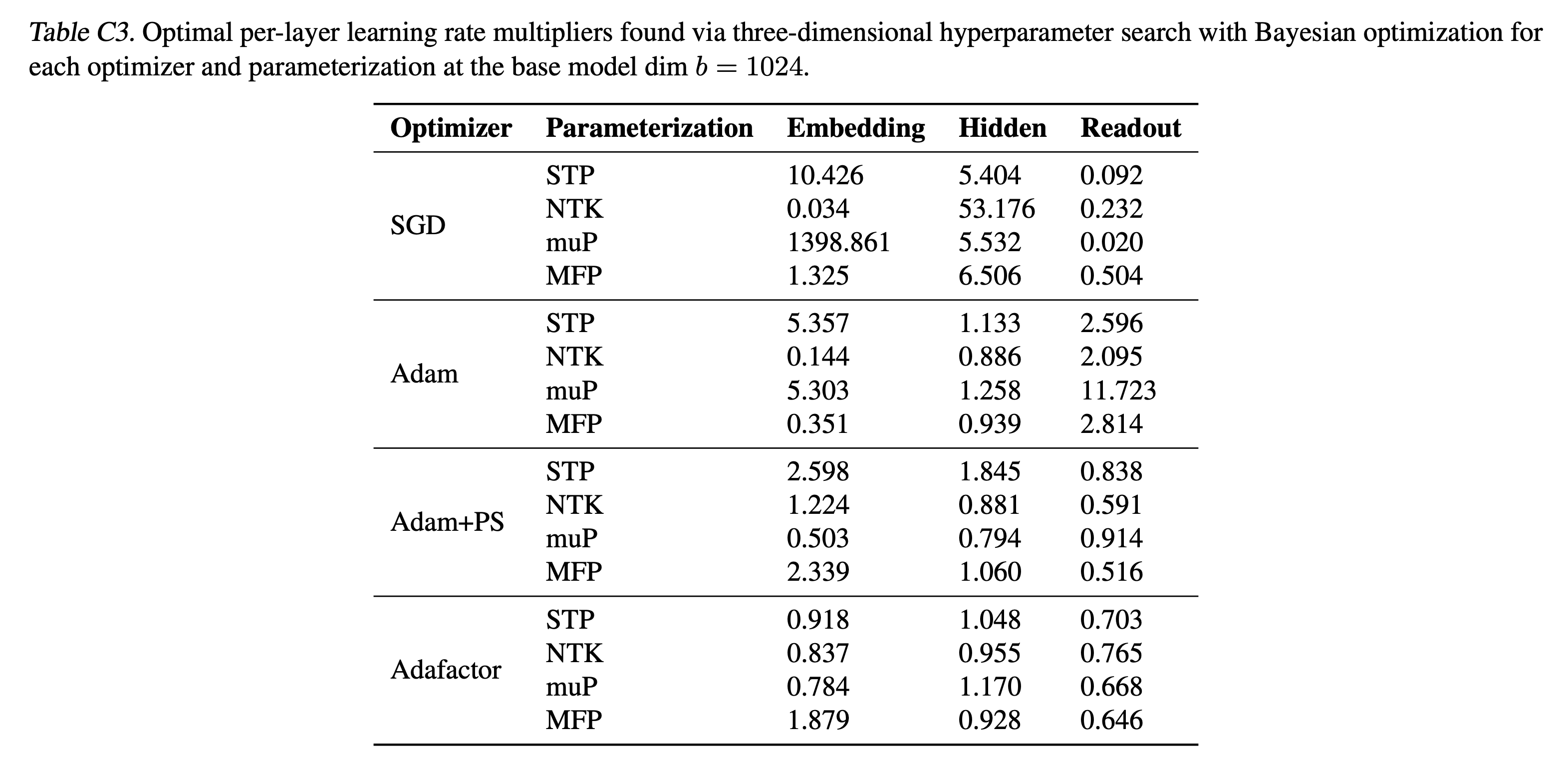Fig.

Fig.

4.1. Alignment Experiments

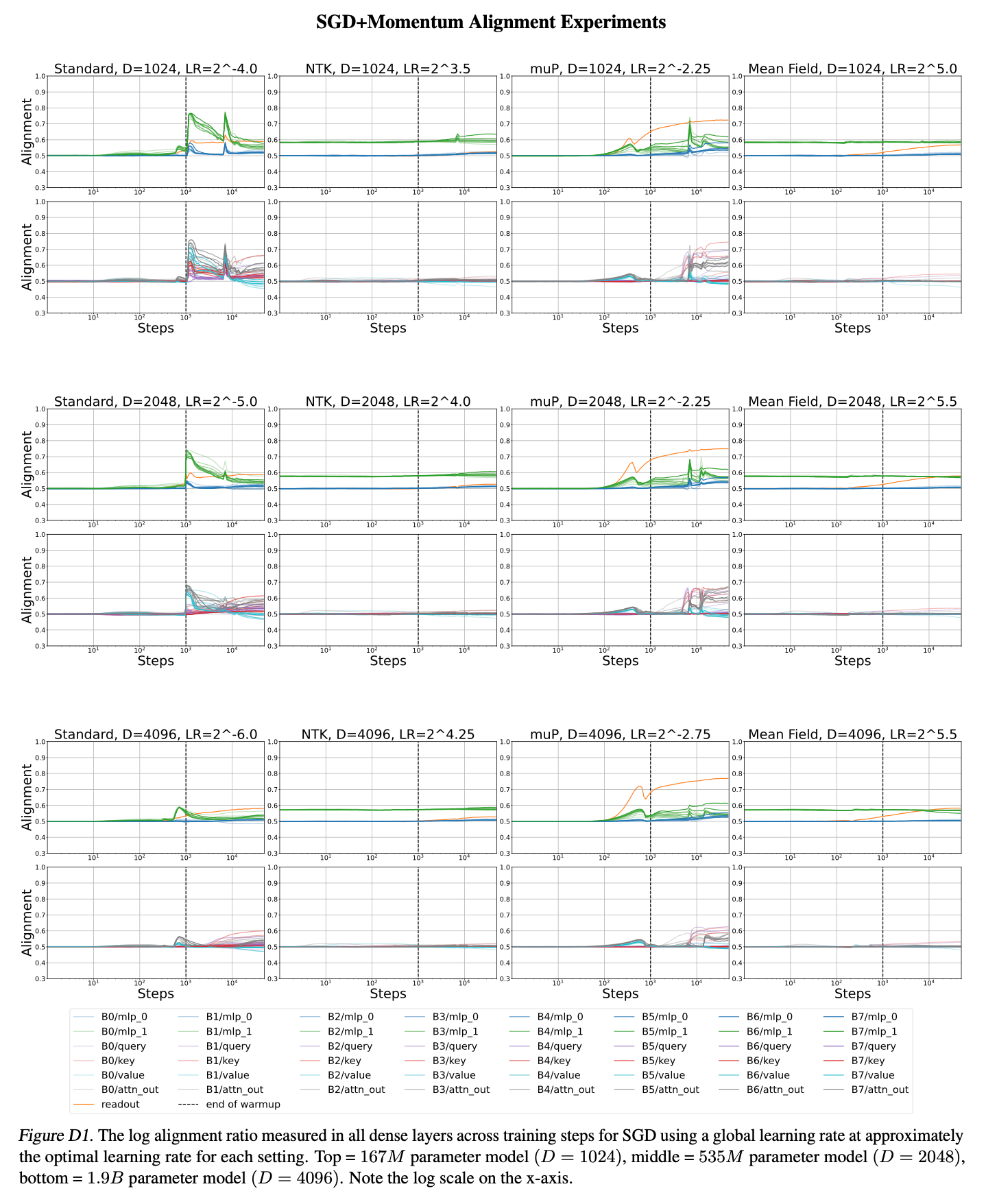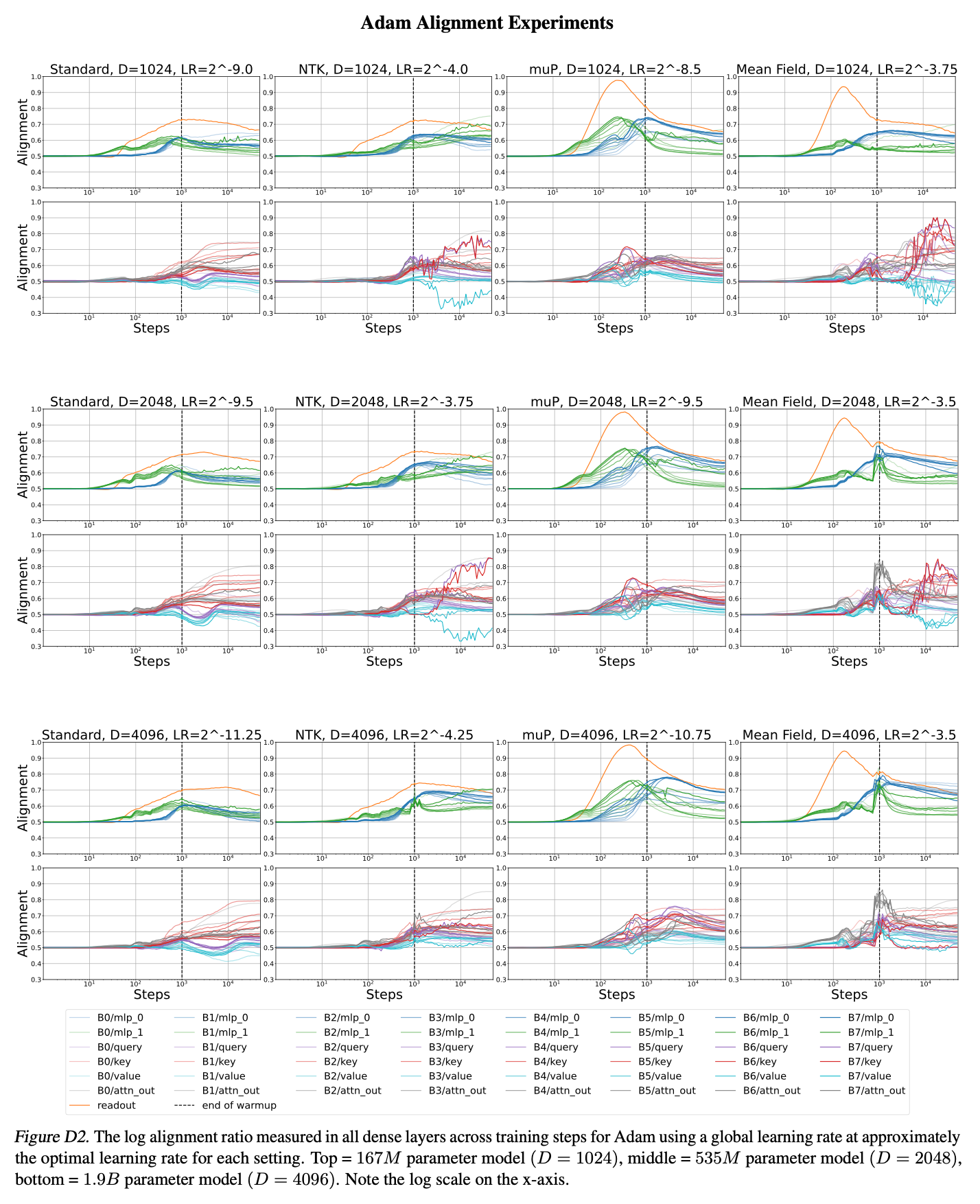Fig.

Fig.

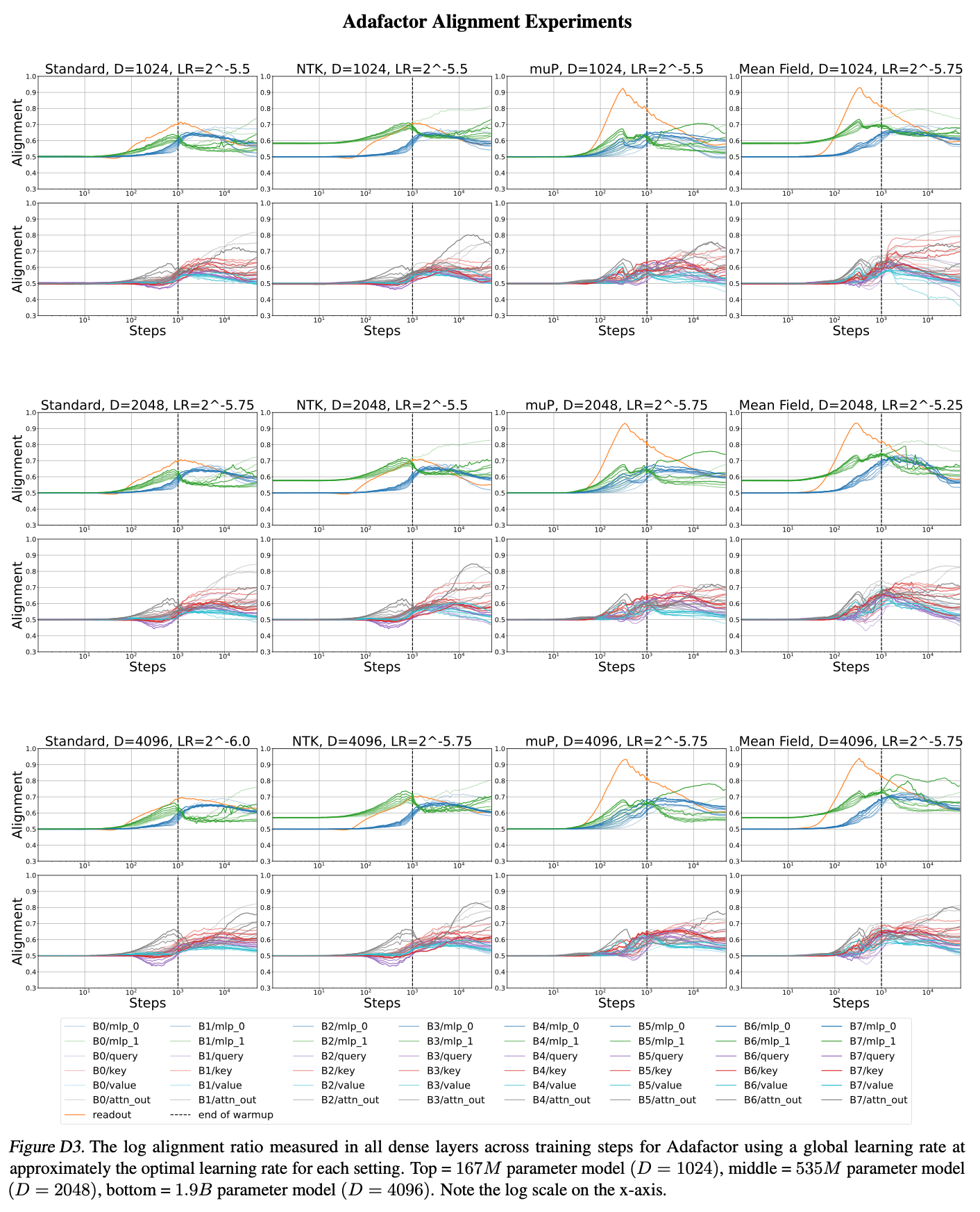Fig.

Fig.

4.2. Per-layer Learning Rates

저자들은 위에서 정리한 table 1의 aligment assumption와 optimizer별로의 per layer LR exponents를 global LR baseline과 비교해 얼마나 좋은지를 실험적으로 보였다.

Fig.

하지만 global LR baseline이 좋은 결과를 보일 때가 있는데, 이는 theoretical prescription과 우연하게도 매칭될 때이다. 그리고 이런 경우에는 mup + SGD + full alignment나 adafactor + any parameterization + no alignment가 있다고 얘기한다.

Adam

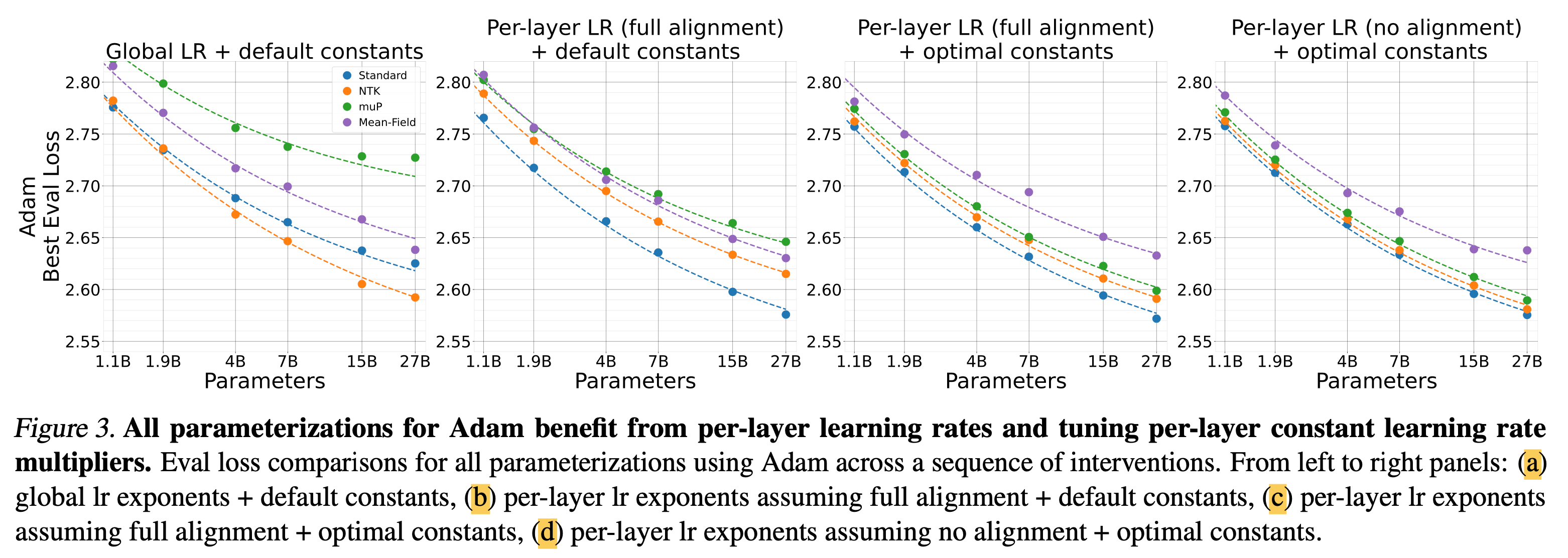Fig.

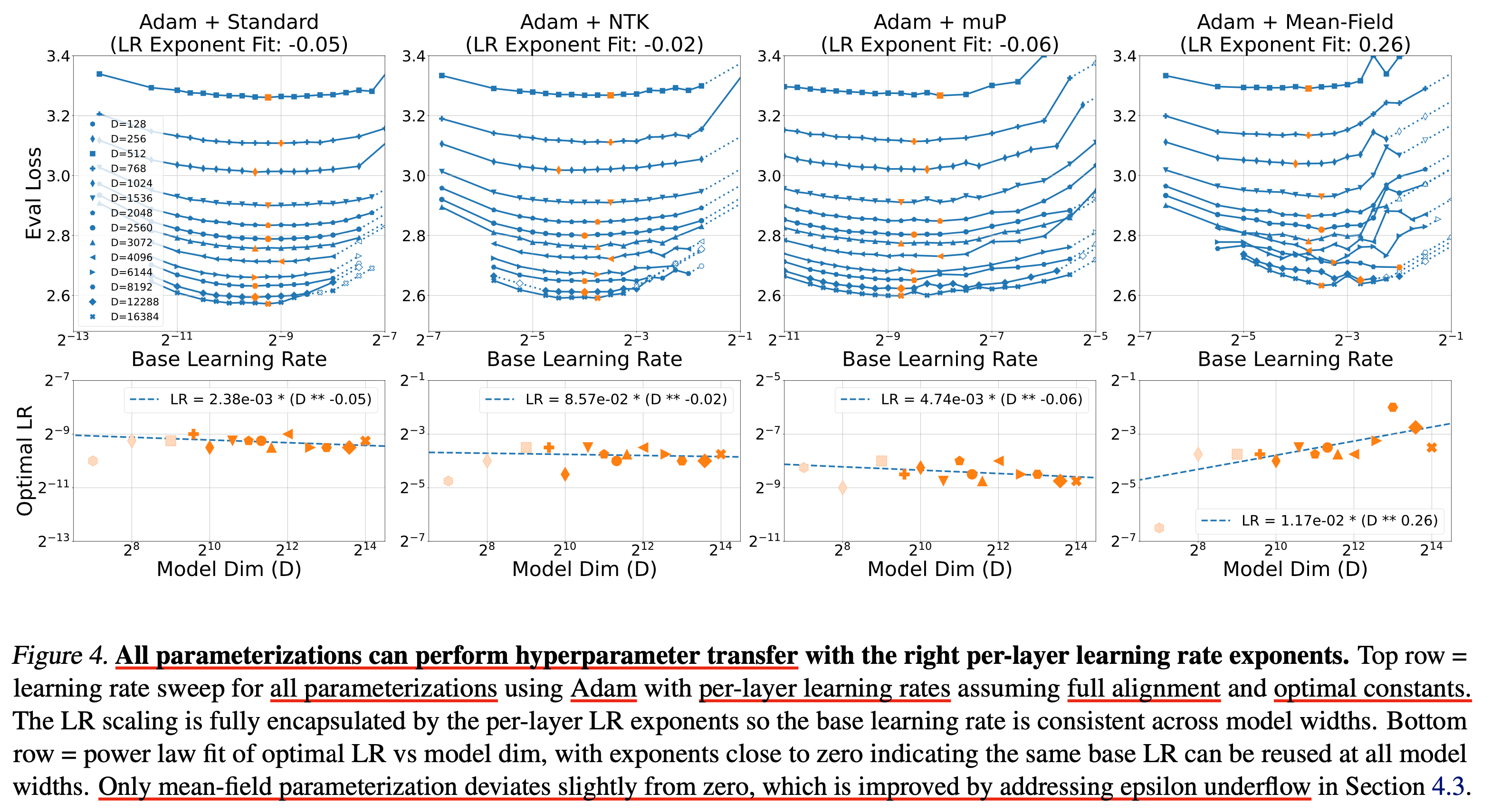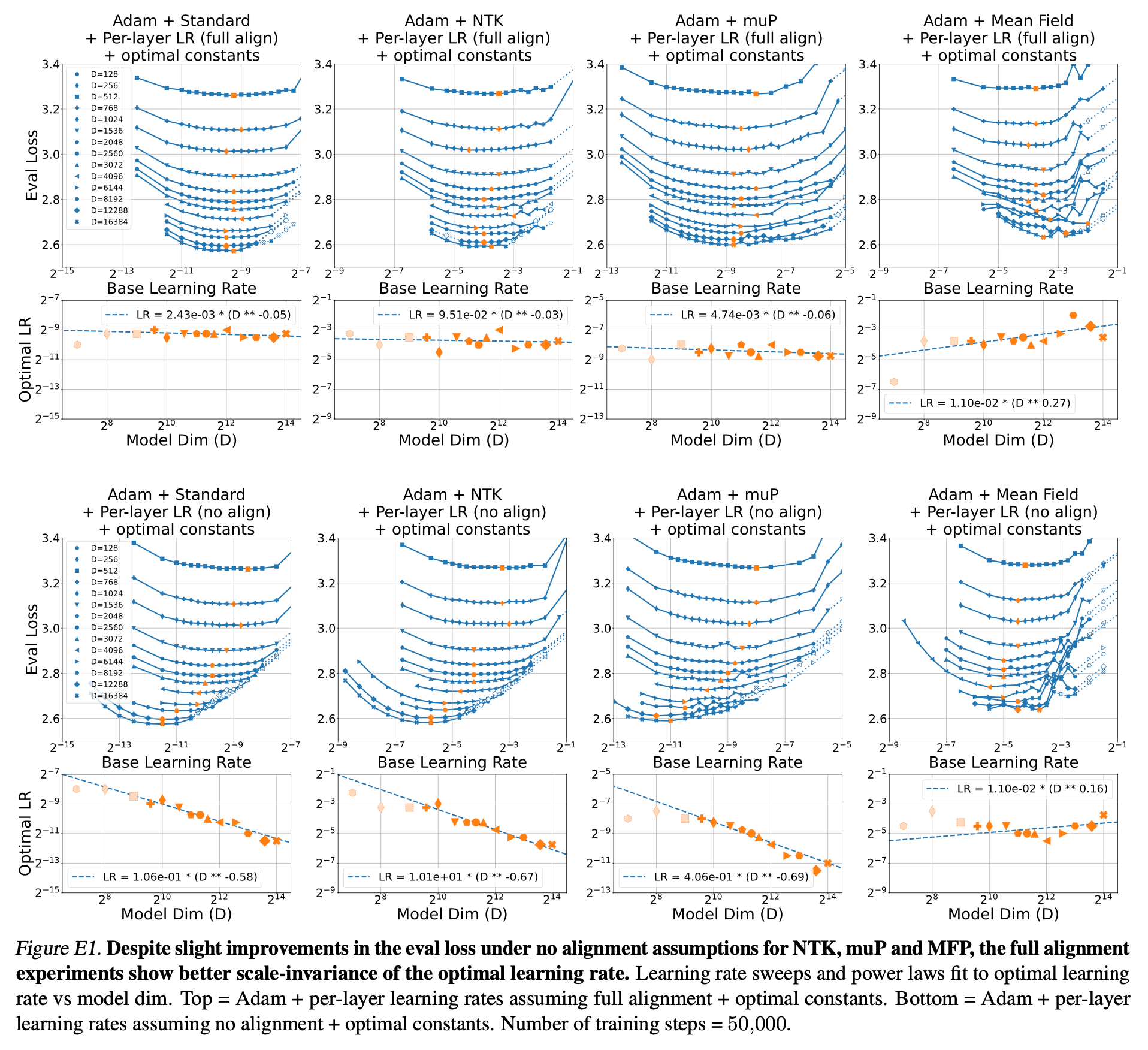Fig.

Fig.

SGD and Adam + Parameter Scaling

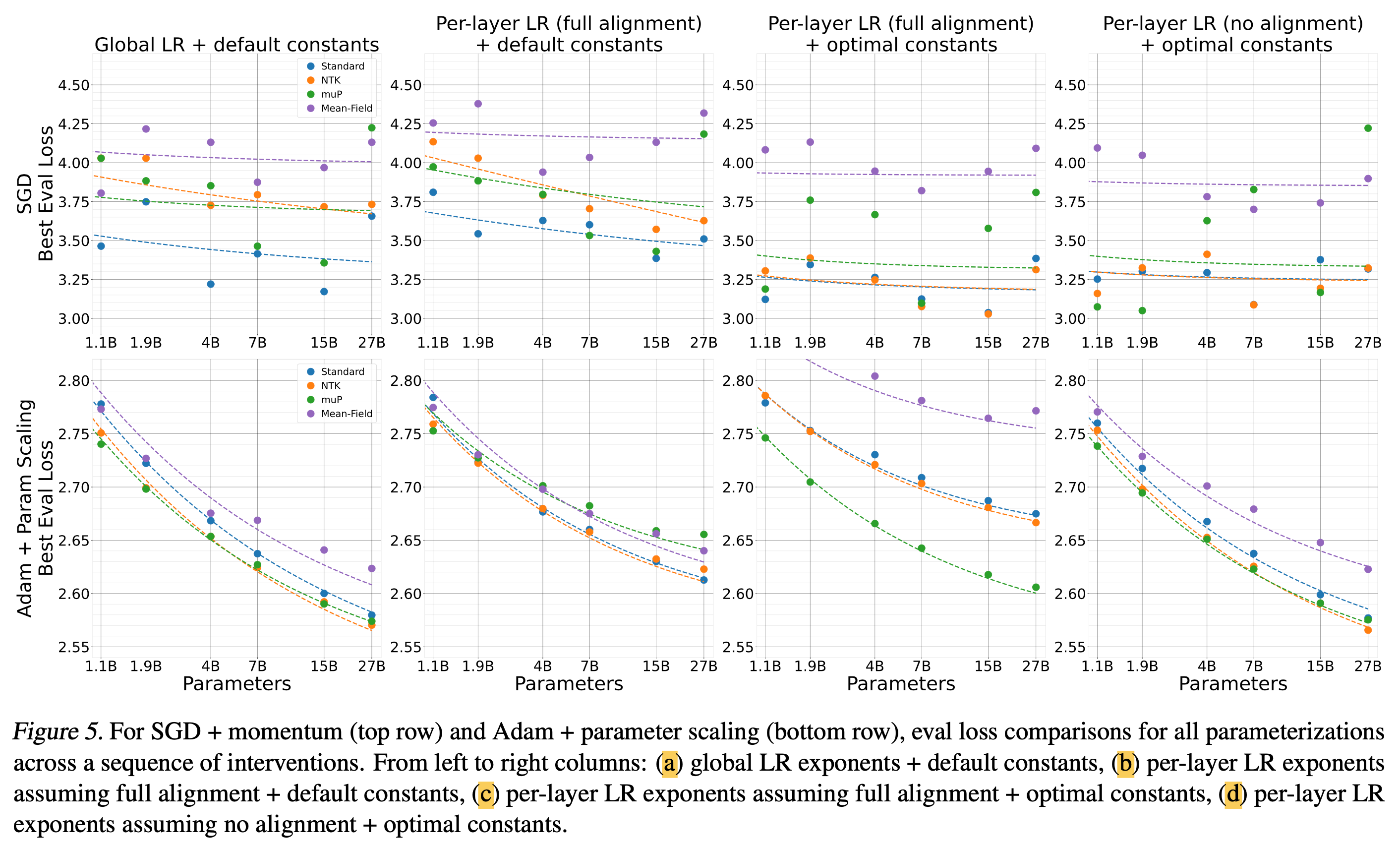Fig.

Epsilon Underflow in Adaptive Optimizers

Fig.

Fig.

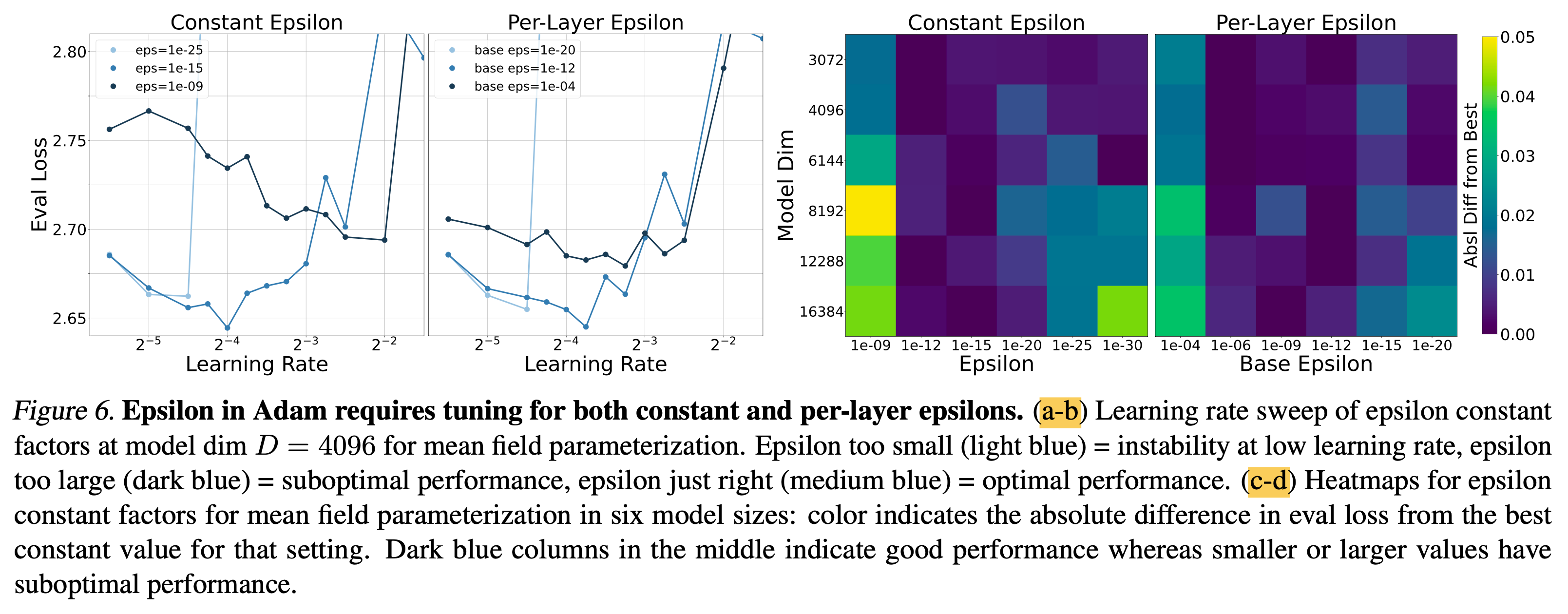Fig.

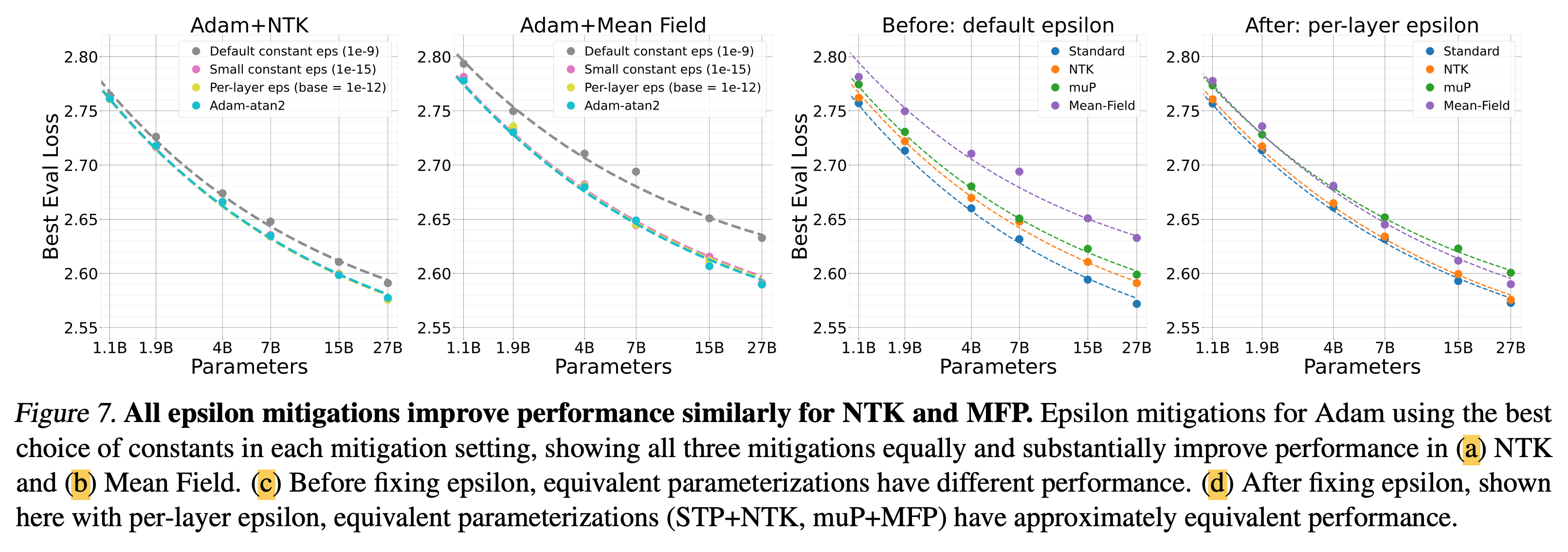Fig.

Fig.

Weight Decay Experiments

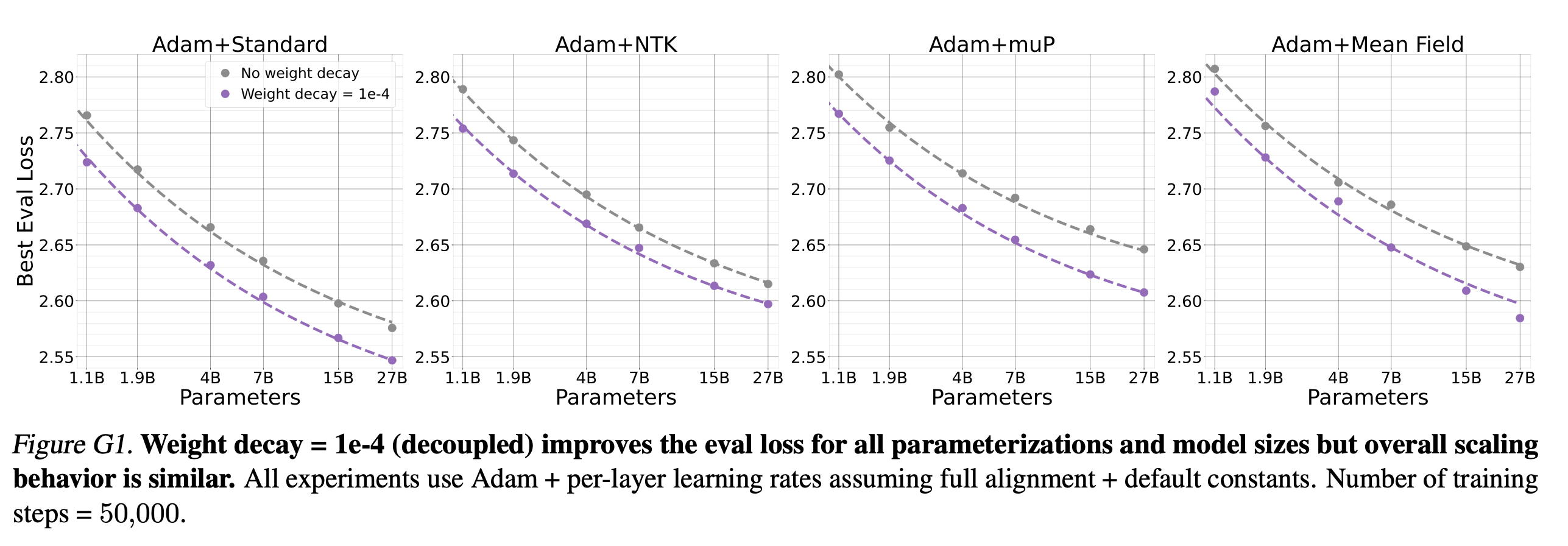Fig.

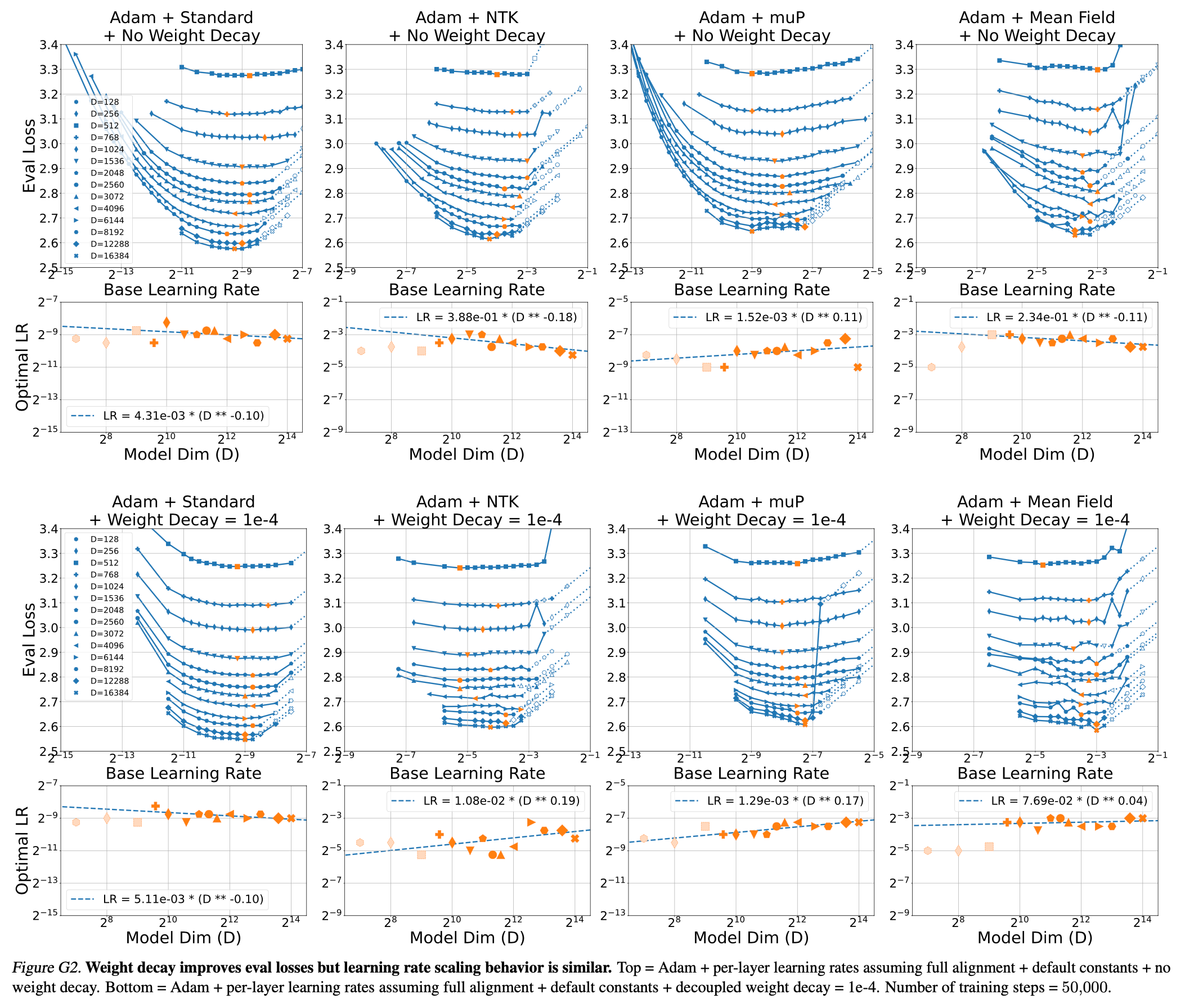Fig.

Fig.

Fixed Step vs Compute Optimal experiments

마지막으로 practically 중요한 내용인데, TP-V에서 실험된 muTransfer는 fixed training step에 대해 실험됐기 때문에 dataset size가 커지는 realistic scenario에서는 양상이 다를 수 있다는 것이다. 사실 이는 wikitext를 Transformer decoder에 학습한 경우에 대해서는 사실이라고 할 수 있겠으나, 실제 GPT-3를 학습한 경우는 아래의 setting으로 실험했기 때문에 dataset size가 아예 안바뀌었던 것은 아니다.

• Small scale proxy model
  • width: 256
  • layers: 32
  • total num. params: 0.04B (40M)
  • num. training tokens
    • short horizon: 4B
    • short horizon: 16B
  • batch_size: ???
• Target model
  • width: 4096
  • total num. params: 6.7B
  • num. training tokens: 300B
  • batch_size: ???

즉 TP-V에서 GPT-3에 대해 40M to 6.7B transfer한 내용은 그렇게 문제가 되지 않는 것이다 (fp32로 학습하고 relative Positional Embedding (PE)를 썼다는 것 빼고).

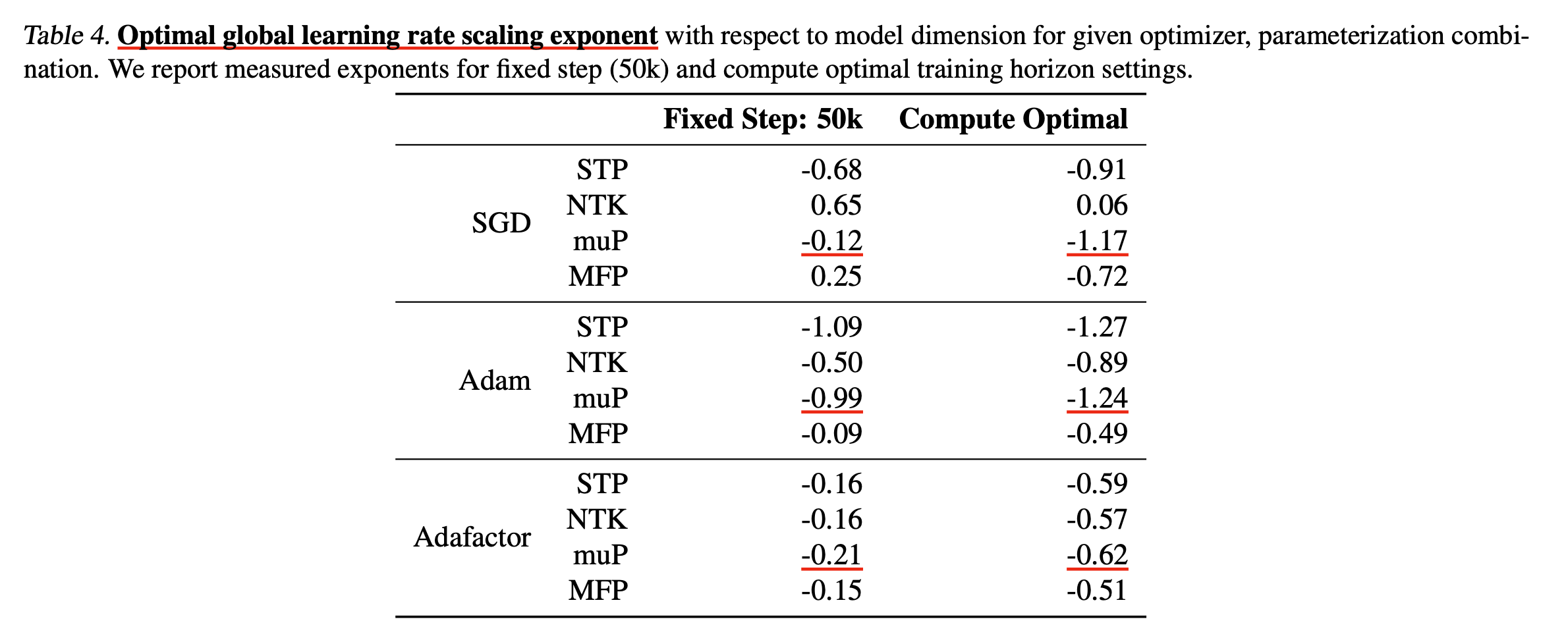Fig.

Fig.

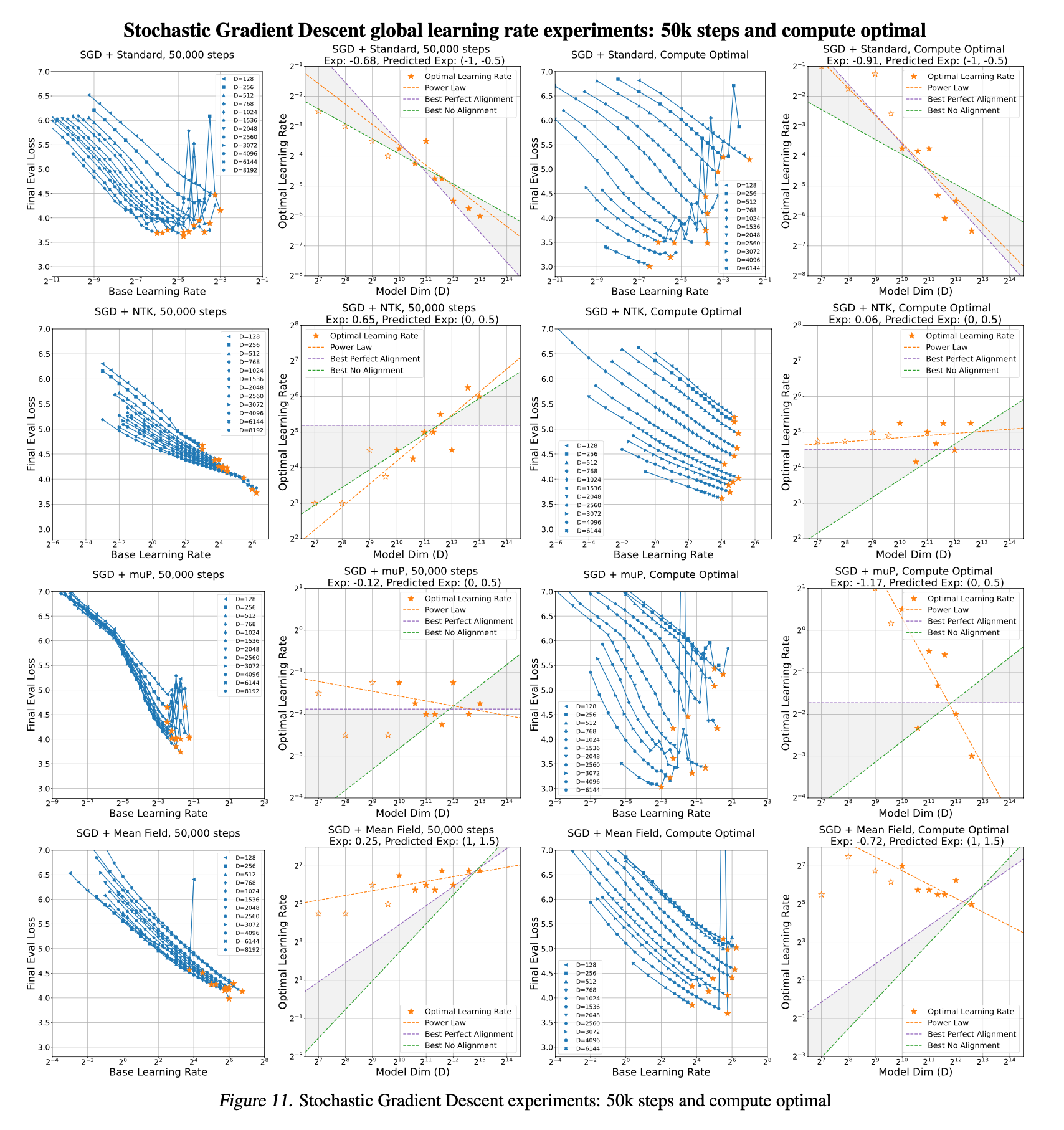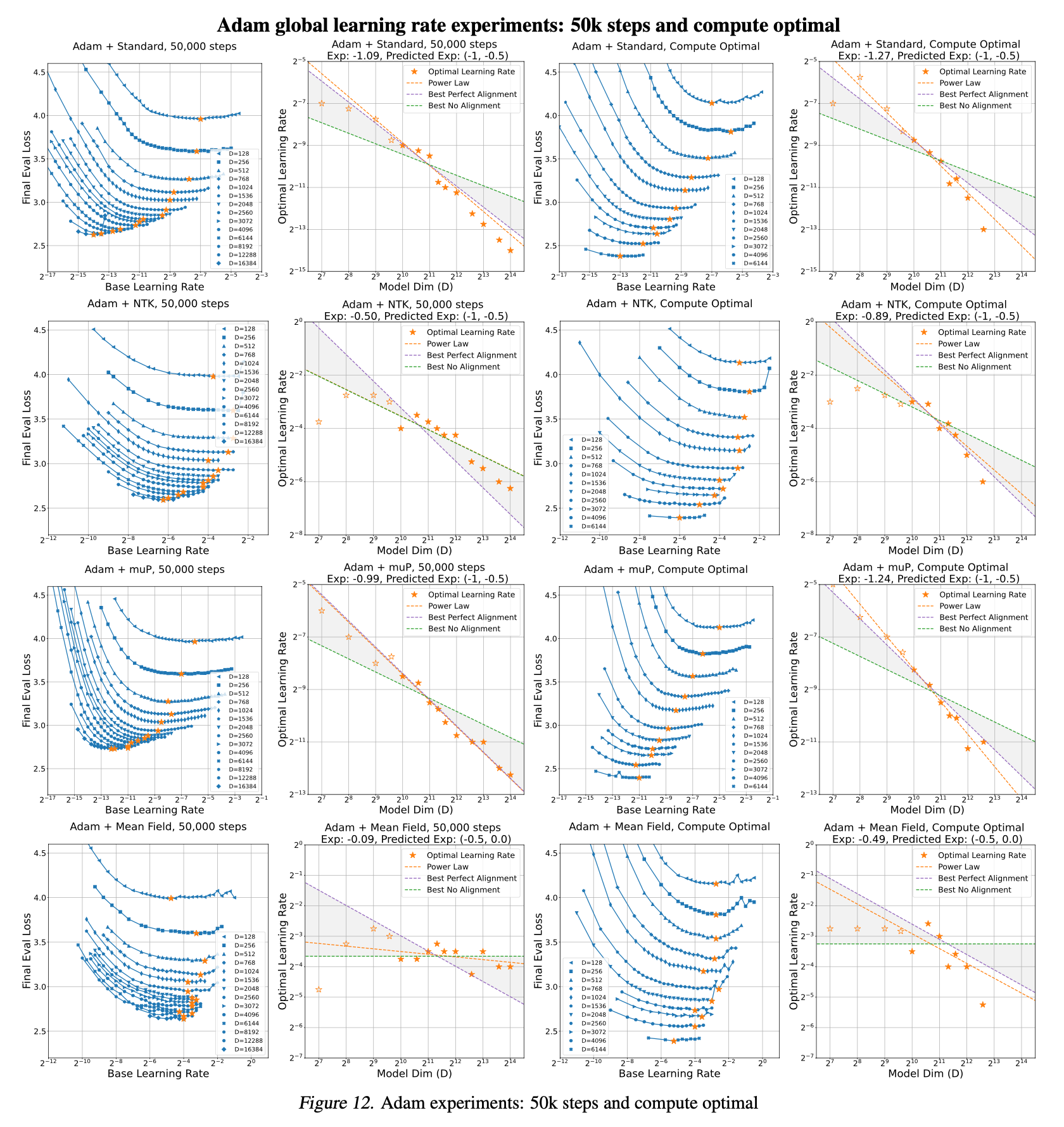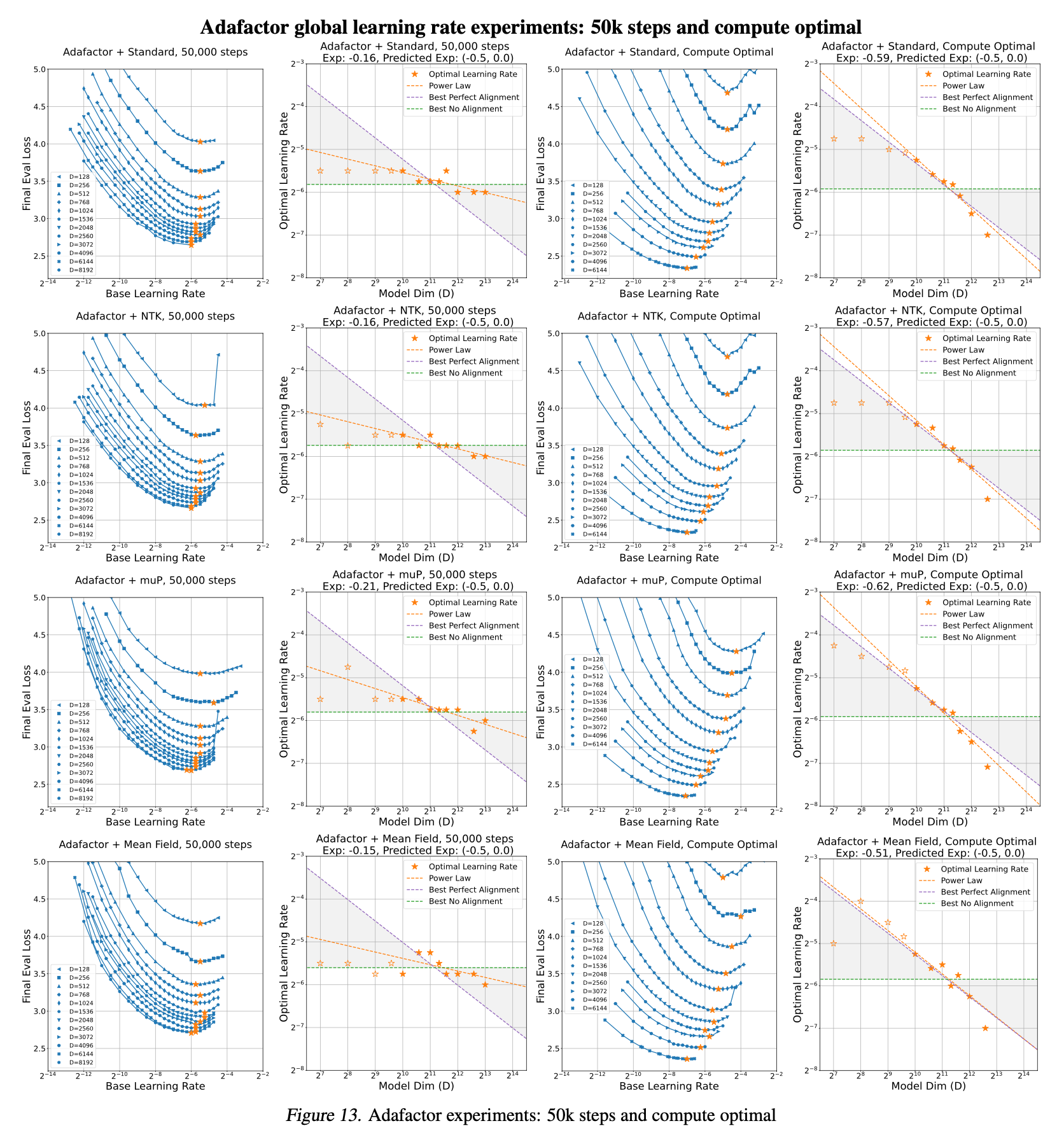Fig.

Fig.

References

• Papers
  • Scaling Exponents Across Parameterizations and Optimizers
    • arxiv version
    • Author’s tweet
  • Compute Better Spent: Replacing Dense Layers with Structured Matrices
  • Tensor Programs V: Tuning Large Neural Networks via Zero-Shot Hyperparameter Transfer
  • Feature Learning in Infinite-Width Neural Networks
  • A Spectral Condition for Feature Learning
• Blogs and Others
  • July Papers: All About Scaling from GraphCore