(WIP) Scaling Law for Autoregressive Transformer based Language Model
13 Jun 2024< 목차 >
- Key Papers of Scaling Law for Large Scale Neural Network (NN) Training
- Overview
- (2020 Jan) Scaling Laws for Neural Language Models (Kaplan et al.)
- Basic Notation And How To Compute FLOPs Per Token
- Summary of Key Findings
- Summary of Scaling Laws
- Training Setup
- Approximate Transformer Shape and Hyperparameter Independence
- Performance with Non-Embedding Parameter Count N
- Comparing to LSTMs and Universal Transformers
- Generalization Among Data Distributions
- Charting the Infinite Data Limit and Overfitting
- Critical Batch Size
- Optimal Performance and Allocations
- Some Potential Caveats to Paper's Analysis
- Emergent Ability and Grokking
- (2020 Oct) Scaling Laws for Autoregressive Generative Modeling (Kaplan et al.)
- (2021 Feb) Scaling Laws for Transfer (Kaplan et al.)
- (2022 Mar) Training Compute-Optimal Large Language Models (a.k.a Chinchilla Optimal)
- Approach 1: Fixing model sizes and vary number of training tokens
- Approach 2: IsoFLOP profiles
- Approach 3: Fitting a parametric loss function
- Optimal Model Scaling Results (Gopher (280B) vs Chinchilla (70B))
- Consistency of scaling results across datasets
- Compared to Kaplan et al.
- Curvature of the FLOP-loss frontier
- Other differences between Chinchilla and Gopher
- Limitations
- A Replication Attempt for Chinchilla Scaling Approach 3
- It is Compute Optimal! Not Optimal!
- Some Papers of Large Language Model (LLMs) Exploring Scaling Exponents in Realistic Scenario
- Additional Litreatures
- (2024 June) Resolving Discrepancies in Compute-Optimal Scaling of Language Models
- (2023 Dec) Beyond Chinchilla-Optimal: Accounting for Inference in Language Model Scaling Laws
- (2024 May) Scaling Laws and Compute-Optimal Training Beyond Fixed Training Durations
- (2023 May) Scaling Data-Constrained Language Models
- (2024 July) Scaling Laws with Vocabulary: Larger Models Deserve Larger Vocabularies
- +Updated) (2024 July) Cross-Lingual Continual Pre-Training at Scale
- References
Key Papers of Scaling Law for Large Scale Neural Network (NN) Training
Overview
이번 post에서는 Cross-Entropy Loss로 학습되는 Autoregressive Transformer based Langugage Model의 Scaling Law의 detail들에 대해 알아보려고 한다.
Scaling Law란 쉽게 말해서 Training or Evaluation Loss가 감소하는 경향이 Model Size (M)나 Dataset Size (D)같은 quantity와 멱법칙 (power-law) 관계에 놓여져 있다는 것이다.
\[\begin{aligned} & \text{A Power Law: }y = (cx)^a & \\ \end{aligned}\]실제로 어떤 관계에 놓여져 있는지 곧 자세히 얘기하겠으나, 살짝만 먼저 얘기해보자. 아래는 (2020 Jan) Scaling Laws for Neural Language Models의 figure인데,
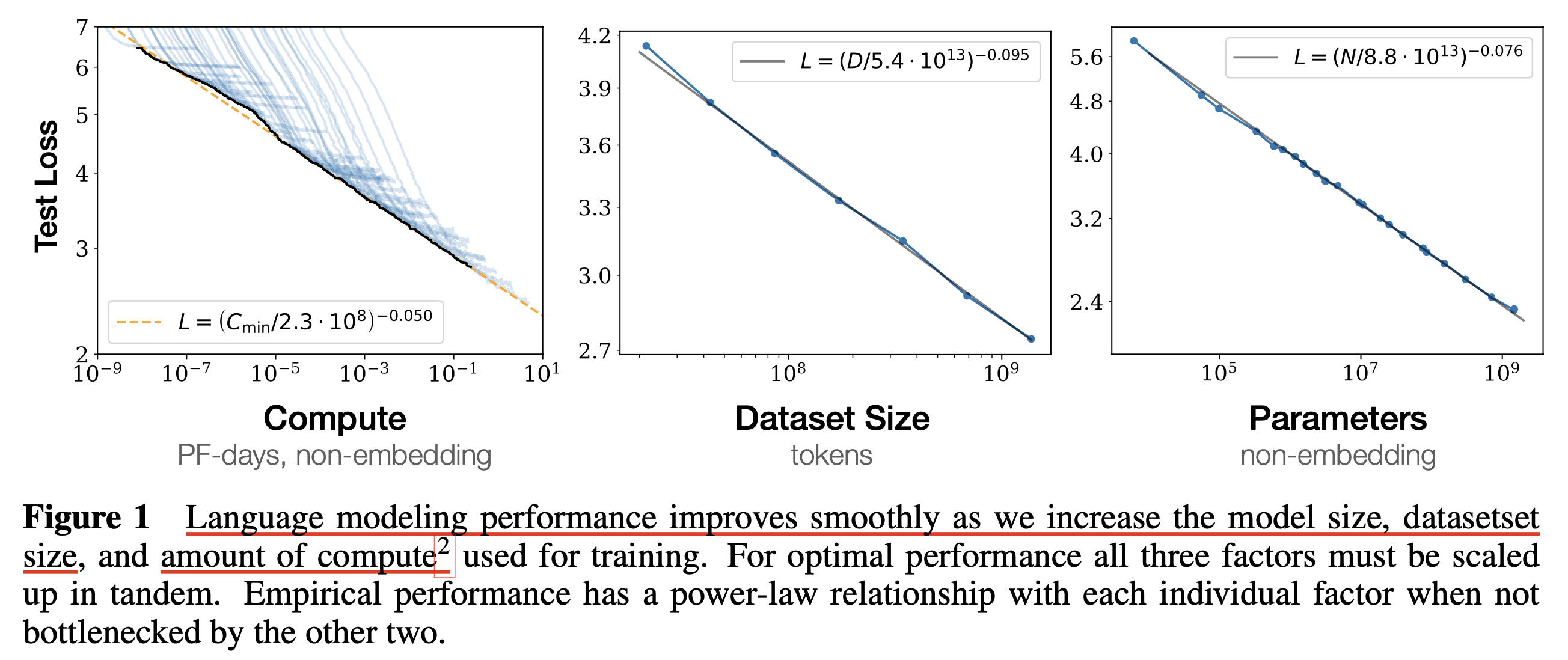 Fig.
Fig.
여기서 C는 얼마나 “학습하는 데 GPU resource를 사용했는가?”를 의미하는 Compute Budget이며, N이나 D가 커질수록 부동 소수점 연산 횟수 (FLOPs)가 증가하므로 C가 증가하기 때문에 C는 M, D와 다음의 관계가 있으며,
\[\begin{aligned} & C \approx N \cdot D & \\ & \text{ where } D \text{ is Dataset Size and } N \text{ is Model Size} &\\ \end{aligned}\]Autoregressive Transformer를 Language Modeling (LM) task로 학습했을 때, OpenAI의 dataset을 따를 경우 \(L=2.57 C^{-0.048}\)을 따른 다는 것을 알 수 있다. 물론 dataset size나 model architecture가 달라지면 이 값은 달라질 수 있다.
결과적으로 수백~수천 번의 실험을 통해 power law 관계를 찾아낸 OpenAI는 GPT-3를 학습하기 위한 가장 모양이 좋은 (기울기가 좋은) function에 맞춰 175B scale의 Transformer based LM을 학습하는데 성공했다.
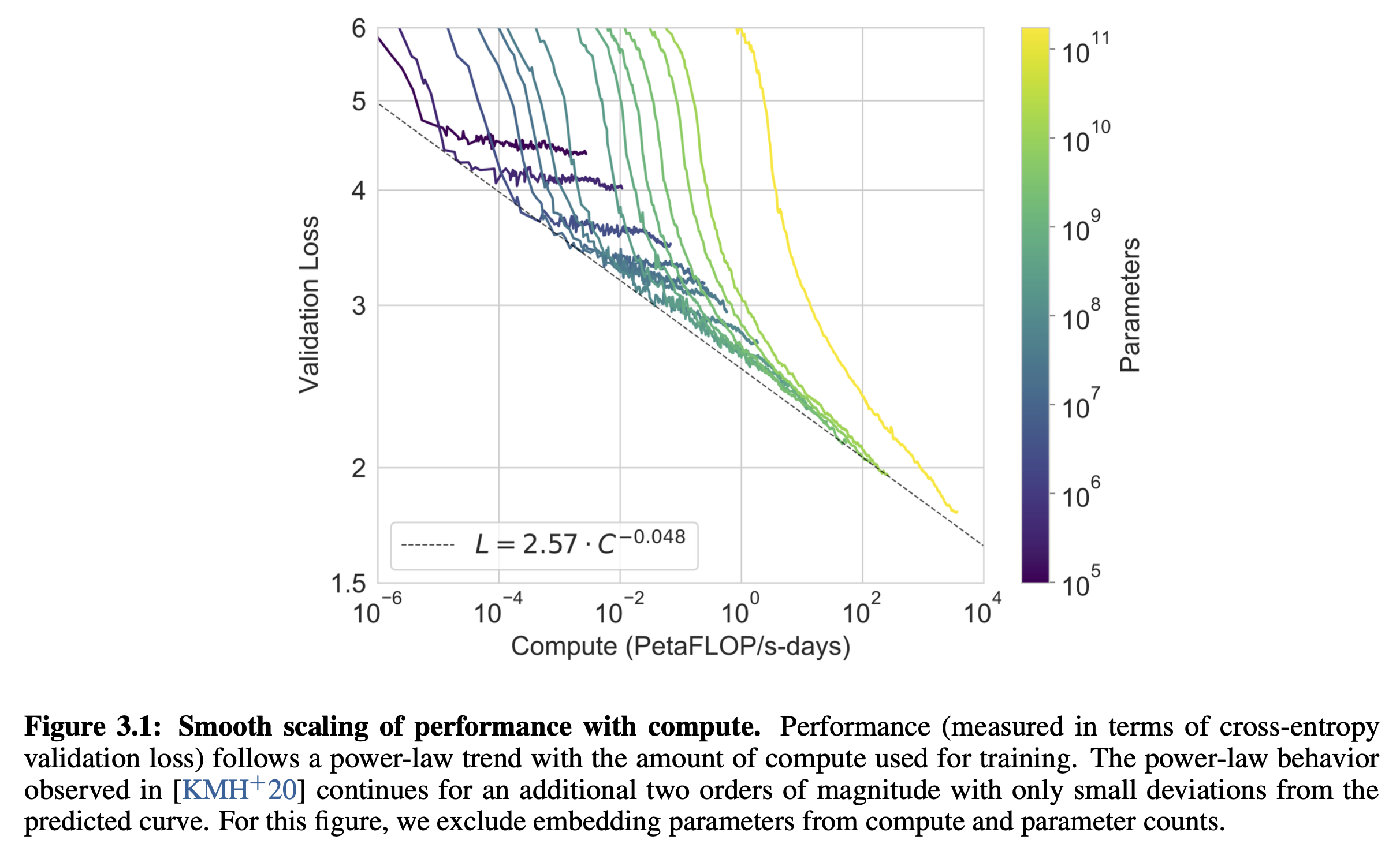 Fig.
Fig.
사실 2024년 현재 Deep Learning (DL)을 하는 사람 중 이에 대해 못 들어본 사람은 없을 것이다.
그리고 이미 많은 research group이 증명했기에 결과론적이지만 “model이 커지면 성능 좋아지는건 당연한거 아니야?”라고 생각할 수 있겠으나,
paper 내용들을 자세히 보고 고민해보지 않으면 real world에서 Scaling Law prediction을 하려면 어떤 setting으로 실험을 진행해야 하는지에 대해 어려움을 겪을 수 있다.
왜냐면 Scaling Law를 하는 이유가 실제 70B model을 학습하는 것이 목표라면 40~500M정도 되는 small scale model들로 loss를 찍어보고,
각 dataset이나 model architecture별로 power function을 그려본 뒤, target하는 valid loss에서 가장 좋은 case를 골라 sacling up하고 GPU 수천장을 태울 수 있기 때문이다.
하지만 이 경우 "small model과 large model의 경향이 다르면 어떡하지?", "small model과 large model에 필요한 batch size가 다를텐데 이건 어떻게 설정하지?", "small model을 얼마나 길게 (충분히) 학습해야하지?"같은 부분이 고민이 될 수 있다.
실제로 (2022 Jun) Emergent Abilities of Large Language Models같은 paper를 보면 Large Language Model (LLM)의 경우에도 pre-training이 진행되는 과정에서 갑자기 model에 없던 능력이 발현되는 경우 (emergent ability)가 있다. 즉 충분히 큰 large model 중에서도 model size에 따라 이 경향이 다르고, small model에서는 아무리 길게 학습해도 이런게 발현되지 않을 수도 있는데 Scaling Law가 안정적일 수 있느냐? 같은 문제는 당연히 던져봐야 하는 질문이기 때문이다.
 Fig. GPT-3 paper를 다시 보니 얼마나 OpenAI가 insight가 있었는지, 그리고 그걸 증명했는지 새삼 대단하다고 느낀다.
Fig. GPT-3 paper를 다시 보니 얼마나 OpenAI가 insight가 있었는지, 그리고 그걸 증명했는지 새삼 대단하다고 느낀다.
본 post에서는 LLM에 대한 Scaling Law를 다룬 유명 paper들을 참고해 이런 부분들을 집중적으로 알아보려고 한다. Paper list는 2020년에 OpenAI에서 발표된 Kaplan et al. 의 seminal paper, (2020 Jan) Scaling Laws for Neural Language Models를 시작으로 아래와 같다.
- (2020 Jan) Scaling Laws for Neural Language Models
- (2020 May) Language Models are Few-Shot Learners (a.k.a GPT-3)
- (2020 Oct) Scaling Laws for Autoregressive Generative Modeling
- (2021 Feb) Scaling Laws for Transfer
- (2022 Mar) Training Compute-Optimal Large Language Models (a.k.a Chinchilla Optimal)
- (2023 Dec) Beyond Chinchilla-Optimal: Accounting for Inference in Language Model Scaling Laws
이 외에도 MAmmoTH등으로 유명한 Tiger Lab의 Wenhu Chen의 LLM Lecture인 CS 886를 많이 참고했으므로 이 post와 함께 같이 참고하길 바란다.
(2020 Jan) Scaling Laws for Neural Language Models (Kaplan et al.)
먼저 가장 가장 유명한 Kaplan et al.의 Autoregressive Transformer based Language Model (LM)에 대한 Scaling Law paper를 살펴보자.
앞서 서술한 것 처럼 main research question은 "model performance (loss)와 model size, dataset size는 어떤 관계가 있을까?"이다.
Basic Notation And How To Compute FLOPs Per Token
Scaling Law에 대해 본격적으로 까보기 전에 기본적인 Notation과 Token당 필요한 초당 부동 소수점 연산 (Floating point operations per second; FLOPS, flops or flop/s)에 대해 알아야 하기 때문에 이들에 대해서 먼저 알아보려고 한다.
 Fig.
Fig.
Notation은 어려운 것이 없다. Number of model parameters, \(N\)는 말 그대로 model size를 말하는 것이지만 특이한 점이 있다면 embedding matrix와 positional embedding matrix는 포함하지 않는다. 그리고 embedding은 count안하기로 했으니 non-embedding parameter와 학습에 쓸 training tokens를 곱해 training compute, \(C\)라는 값을 쓰는데, 실제로는 batch size, \(B\)와 training step, \(S\)를 곱해서 \(C \approx 6NBS\)라고 쓴다. 대충 batch size, training steps, 그리고 sequence length를 곱하면 이들은 비례관계가 되니 신경쓰지 않아도 될 것 같다.
그리고 training compute budget, \(C\)의 단위(?)로 PF-days를 인용한다 (쓴다)고 하는데, 이는 다음과 같은 의미를 가진다.
A petaflop/s-day (pfs-day) consists of performing 1015 neural net operations per second for one day,
or a total of about 1020 operations
그리고 내가 녹색으로 표시한 critical batch size, \(B_{\text{crit}}\)과 \(C_{\text{min}}, S_{\text{min}}\)이 있는데, 이것들은 모두 critical batch size와 관련되어 있는 term들이다.
Critical Batch Size, \(B_{\text{crit}}\)이라는 것이 익숙하지 않을 수 있어 짧게 설명하겠다. 이는 2018년에 나온 paper로, 짧게 요약해서 parallelism으로 batch size를 늘려봐야 gradient가 더 정교해지기 어려워 training time을 줄여주는 효과가 없는 지점을 말한다. (Blog내에 관련 post가 있으니 참고해도 좋다)
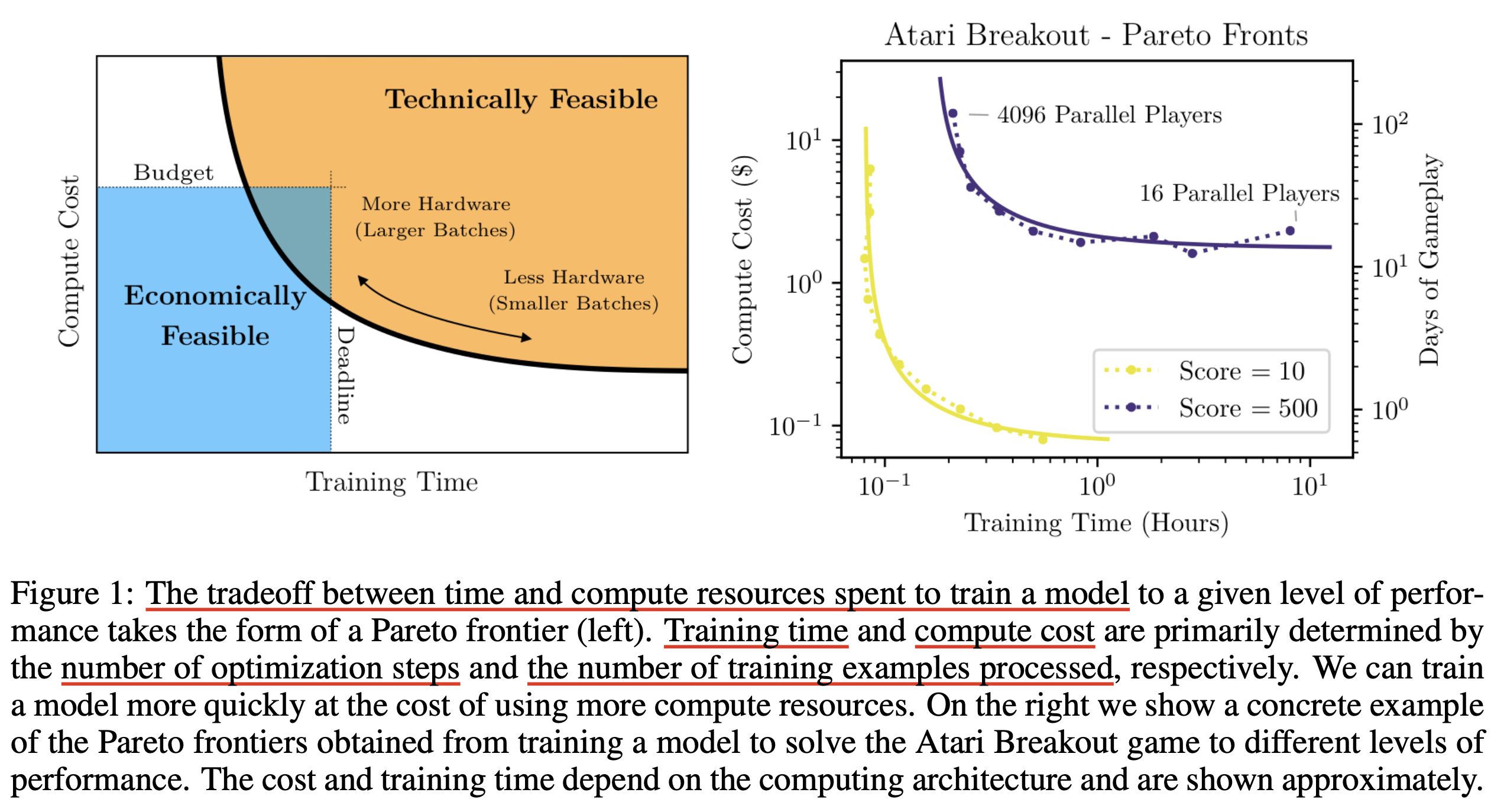 Fig.
Fig.
위 figure를 보면 예를 들어 Atari를 play하는 agent가 10점을 달성하기 위해서 필요한 training time vs compute cost curve (band)가 있는데,
오른쪽 부분을 보면 이 band가 휘어지기 전에는 training time를 줄이기 위해서는 compute cost가 더 필요하거나 덜 필요하지 않다는 것을 알 수 있다.
여기서 training time이 줄어드는데 compute cost가 줄어들지 않는 이유는 예를 들어 GPU 8개를 parallelize한 경우 training step이 1000 필요한데,
GPU를 16개 parallelize하면 gradient가 정교해져서 training step을 500번 으로 줄여도 되기 때문이다.
이 경우 GPU를 16개 더 쓰더라도 computing을 1/2번 하기 때문에 compute cost가 같은 것인데,
단 앞서 말한 것 처럼 gradient가 더 정교해질 여지가 없다면,
즉 bend가 구부러지는 지점에서는 더 이상 이것이 성립하지 않는다.
이 batch size가 바로 Critical Batch Size, \(B_{\text{crit}}\)인 것이다.
이제 \(C_{\text{min}}, S_{\text{min}}\)가 남았는데, 이들은 각각 특정 loss값에 도달하기 위해서 필요한 최소 non-embedding computes와 minimal number of steps를 의미한다고 한다. 이 때, \(C_{\text{min}}\)는 critical batch size보다 훨씬 작은 batch size를, \(S_{\text{min}}\)는 훨씬 큰 batch size를 사용해 학습된 경우를 말한다고 한다.
그리고 power function의 exponent는 \(\alpha\)로 표현된다.
그 다음으로 token을 하나 계산하는데 필요한 FLOPs를 계산하는 법에 대해 알아보자. 먼저 계산에 사용될 notation들은 다음과 같다.
- model size: \(N\)
- number of layers: \(n_{\text{layer}}\)
- hidden size: \(d_{\text{model}}\)
- intermediate hidden size: \(d_{\text{ff}} = 4 d_{\text{model}}\)
- attention output dim size: \(d_{\text{attn}} = d_{\text{model}}\)
- number of attention heads per layer: \(n_{\text{heads}}\)
- context length: \(n_{\text{ctx}}\)
이제 이 term들을 따라서 model size, \(N\)과 model을 forward하는데 필요한 FLOPs는 다음 table과 같이 정리가 된다.
 Fig.
Fig.
대부분은 Feed Forward Network (FFN)의 intermediate dim, \(d_{\text{ff}}\)는 \(d_{\text{model}}\)의 4배로 설정되고, attention output hidden size, \(d_{\text{attn}}\)는 \(d_{\text{model}}\)와 같은게 일반적이므로, model size는 다음과 같이 쓸 수 있다.
\[\begin{aligned} & N \approx 2 d_{\text{model}} n_{\text{layer}} (2 d_{\text{attn}} + d_{\text{ff}}) & \\ & = 12 n_{\text{layer}} d_{\text{model}}^2 & \\ \end{aligned}\]여기서 bias등은 model size에 contirubte 하지 않는데 (제외되는데), 이것 말고도 embedding matrix, \(n_{\text{vocab}} d_{\text{model}}\)과 positional embeddings, \(n_{\text{ctx}} d_{\text{model}}\)도 제외된다. 이는 Kaplan et al.이 Scaling Law prediction을 할 때 더 부드러운 plot을 얻기 위해서라고 paper에 쓰여있다.
Transformer의 forward pass, \(C_{\text{forward}}\)는 대략적으로 다음과 같이 계산되는데,
\[C_{\text{forward}} \approx 2 N + 2 n_{\text{layer}} n_{\text{ctx}} d_{\text{model}}\]여기서 model size에 계수가 2 붙는 이유는 matmul을 할 때 multiply-accumulate (아마 multiply-add 얘기하는듯) operation이 사용되기 때문이다.
FLOPs에 대해 헷갈릴 수 있어 recap하자면 \(K \times M\), \(M \times N\) matrix 두 개를 곱할 때 총 \(M * N * K\)의 Fused Multiply-Adds (FMAs)가 발생하고 (link 참고), 각각 FMA는 덧셈과 곱셈 2개의 operation으로 이루어져 있으므로 총 \(2*M*N*K\) FLOPs가 필요하게 된다. 그렇기 때문에 여기서 한 token에 대해서 QKV attention projection을 하려면 Transformer는 self attention이 residual block마다 있으니 layer 갯수만큼 곱해주고, 한 token vector \(1 \times d_{\text{model}}\)과 \(d_{\text{attn}} \times d_{\text{attn}}\)의 weight matrix 3번이 곱해지므로 \(2 n_{\text{layer}} d_{\text{model}} 3 d_{\text{attn}}\)이 되는 것이다.
이 table에서 아마 다른 건 다 이해가 갈텐데,
attention: mask라는 operation에 대해서는 따로 설명이 쓰여있지 않다.
이 연산은 \(2 n_{\text{layer}} n_{\text{ctx}} d_{\text{attn}}\)이고,
sequence length (context length)에 비례하는 것으로 보아 \(QK^T\)를 의미하는 것 같다.
아무튼 Kaplan et al.에서의 총 forward 연산은 \(C_{\text{forward}} \approx 2 N + 2 n_{\text{layer}} n_{\text{ctx}} d_{\text{model}}\)가 되는데, Kaplan은 \(d_{\text{model}} > n_{\text{ctx}}/12\)인 경우 \(C \approx 2N\)로 근사할 수 있다고 하는데, GPT-3를 학습하던 시절에는 이게 성립하기 때문에 무시할 수 있었던 것으로 보인다. 여기에 backward가 보통 forward의 2배라는 점을 고려하면 non-embedding compute는 \(C \approx 6N\)이 되는 것이다. 이것이 한 token당의 forward + backward FLOPs가 되므로 한 iteration step에 쓰인 token갯수를 곱하면 우리는 \(6ND\)라는 수식을 얻게 된다.
Summary of Key Findings
이제 paper의 주된 결과를 요약해서 알아보자. Key finding는 다음과 같은데,
- Performance depends strongly on scale, weakly on model shape
- Smooth power laws
- Universality of overfitting
- Universality of training
- Transfer improves with test performance
- Sample efficiency
- Convergence is inefficient
- Optimal batch size
이를 하나씩 해석해보면 다음과 같다.
Smooth power laws: model performance는 다른 두 요소에 의해 bottleneck이 생기지 않는 한, 세 가지 scale factor인 C, N, D 각각의 power law relationship을 가지며, 그 trend는 6배 이상의 크기에 걸쳐있음.Universality of training: Training curves 또한 predictable scaling law를 따르는데, 이 때 scaling law의 parameter는 model size와는 무관함. Training curve의 초기 구간 (early part)를 extrapolate 함으로써 훨씬 길게 학습했을 경우의 loss를 예측할 수 있음.Sample efficiency: Sample efficiency란 “같은 성능에 도달하기 위해 얼마나 많은 data sample이 필요한가?”를 의미하는 metric이며 강화 학습 (Reinforcement Learning; RL)에서 특히 많이 쓰이는 term인데, model이 클수록 sample efficiency가 더 좋기 때문에 더 적은 optimization step, sample들로도 같은 성능에 도달함.
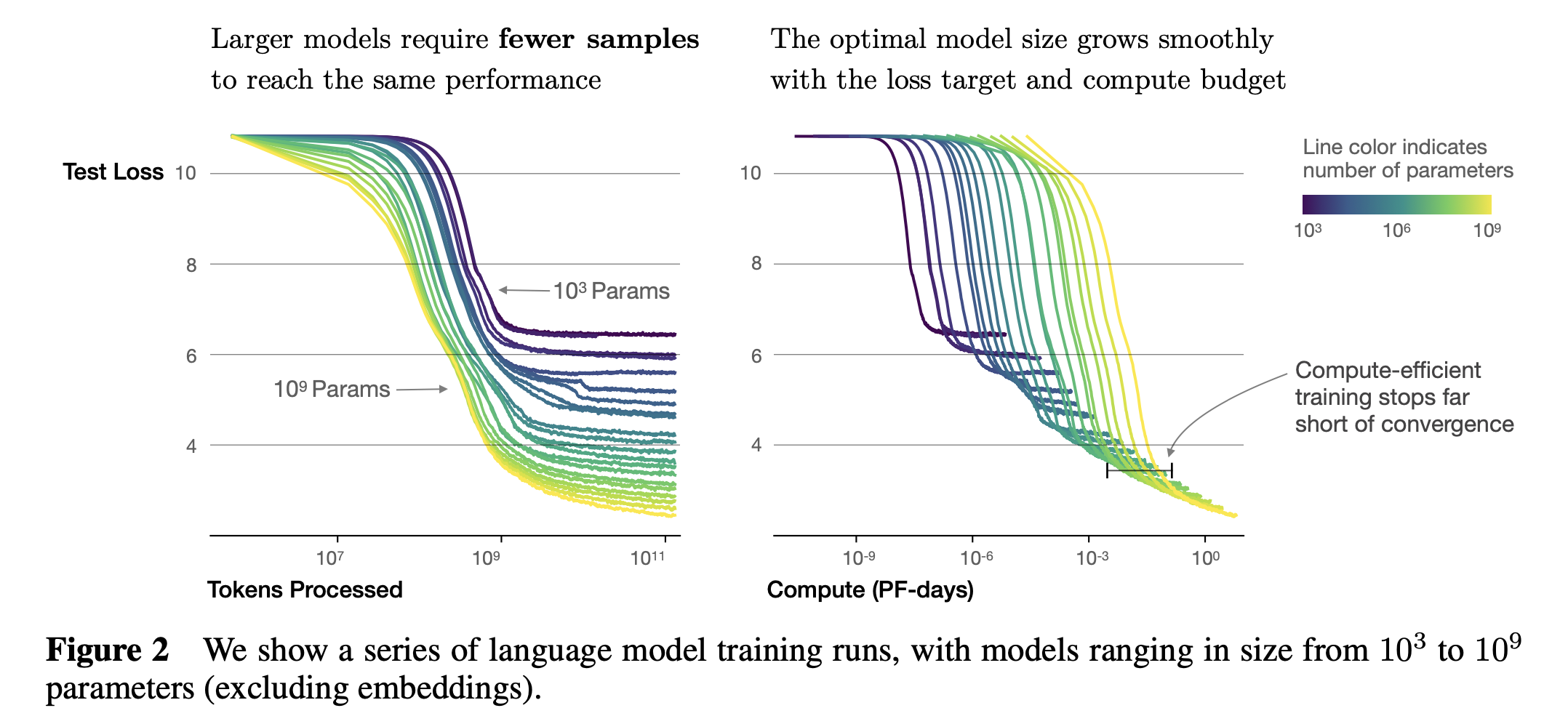 Fig. large model은 더 적은 optimization step과 data sample로 원하는 성능에 도달하기 쉬움 (1)
Fig. large model은 더 적은 optimization step과 data sample로 원하는 성능에 도달하기 쉬움 (1)
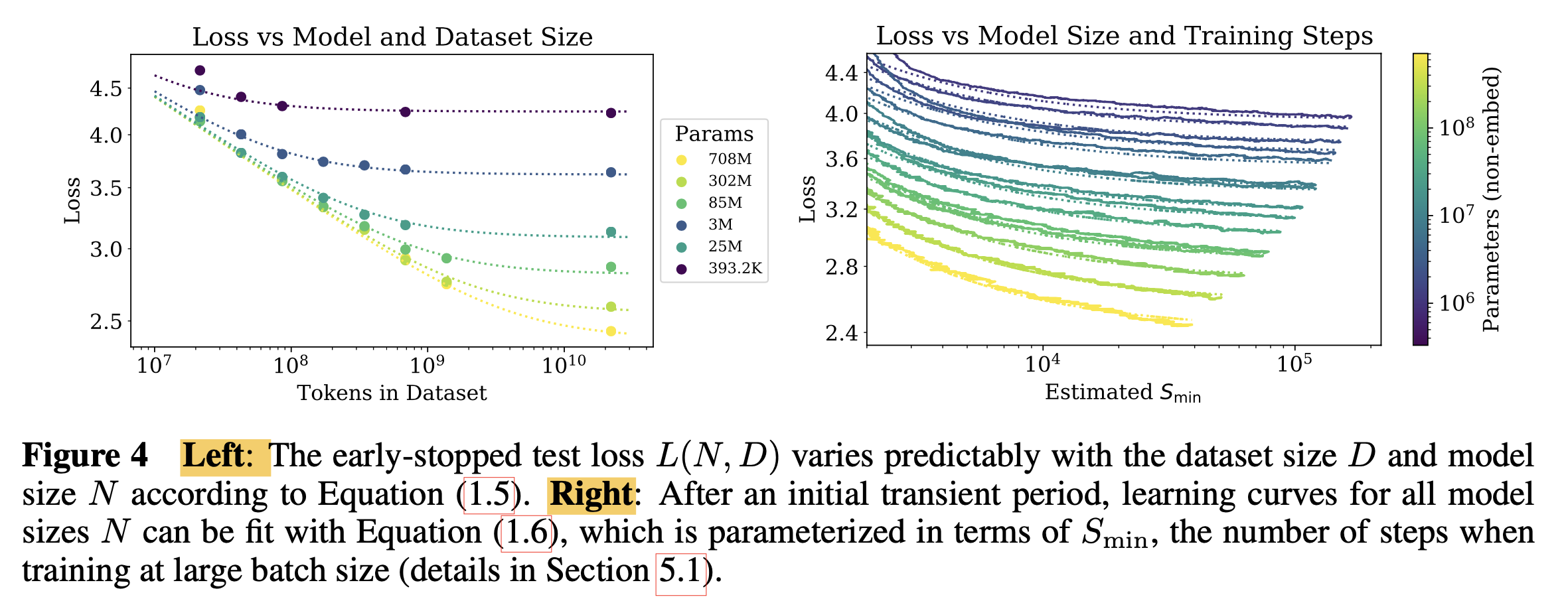 Fig. large model은 더 적은 optimization step과 data sample로 원하는 성능에 도달하기 쉬움 (2)
Fig. large model은 더 적은 optimization step과 data sample로 원하는 성능에 도달하기 쉬움 (2)
Convergence is inefficient: Sample efficinecy와 연관되어 있는 내용인데, 만약 fixed budget, C에 대해서 model size, N과 dataset size, D에 제한이 없다면 매우 큰 model을 수렴하지 못하는 지점까지라도 학습하는 것이 작은 model을 수렴할 때 까지 돌리는 것 보다 성능이 좋음
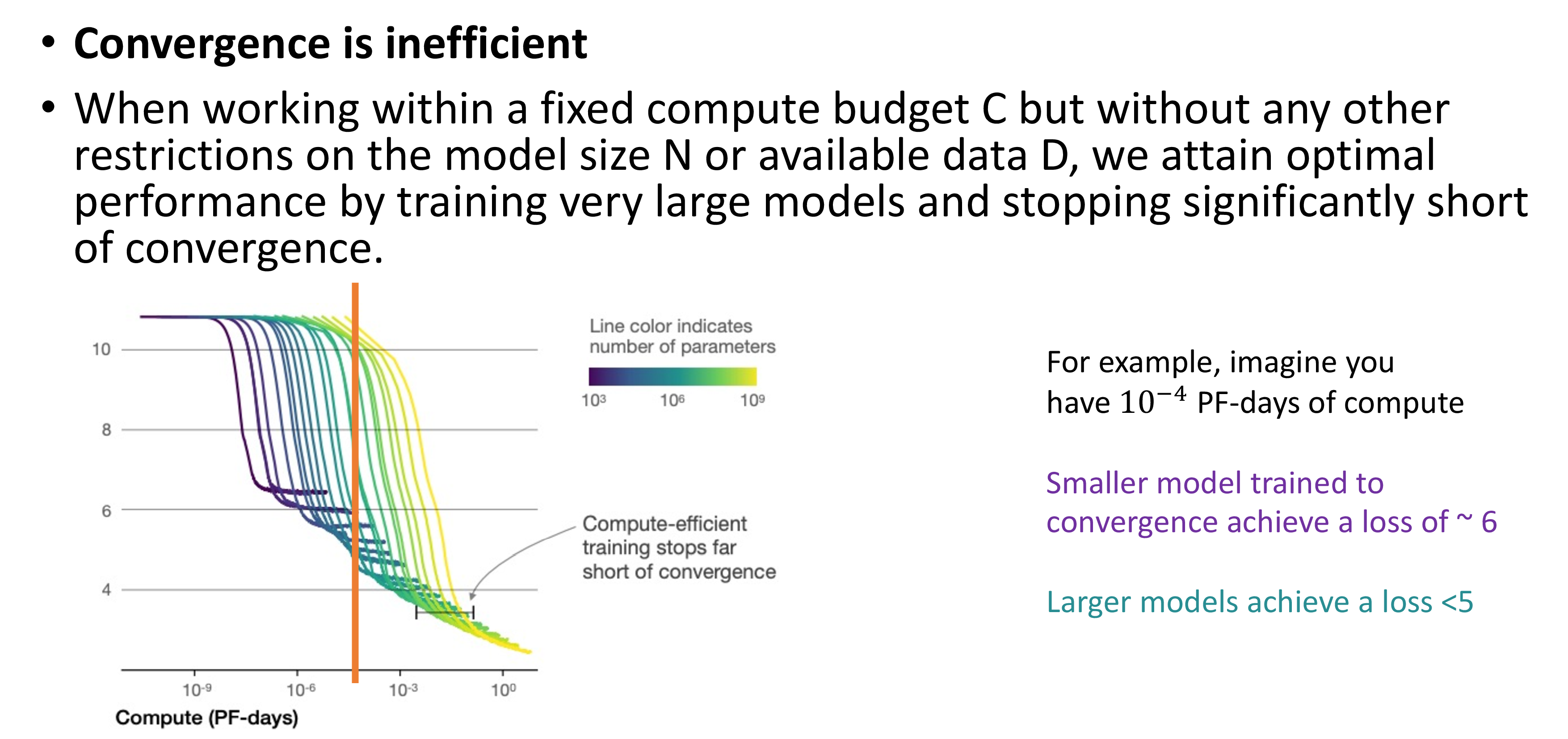 Fig. 같은 성능을 도달하기 위해 작은 model을 수렴할 때 까지 돌리는 것 보다 큰 model을 적당히 돌리는게 더 나을 수 있음.
Fig. 같은 성능을 도달하기 위해 작은 model을 수렴할 때 까지 돌리는 것 보다 큰 model을 적당히 돌리는게 더 나을 수 있음.
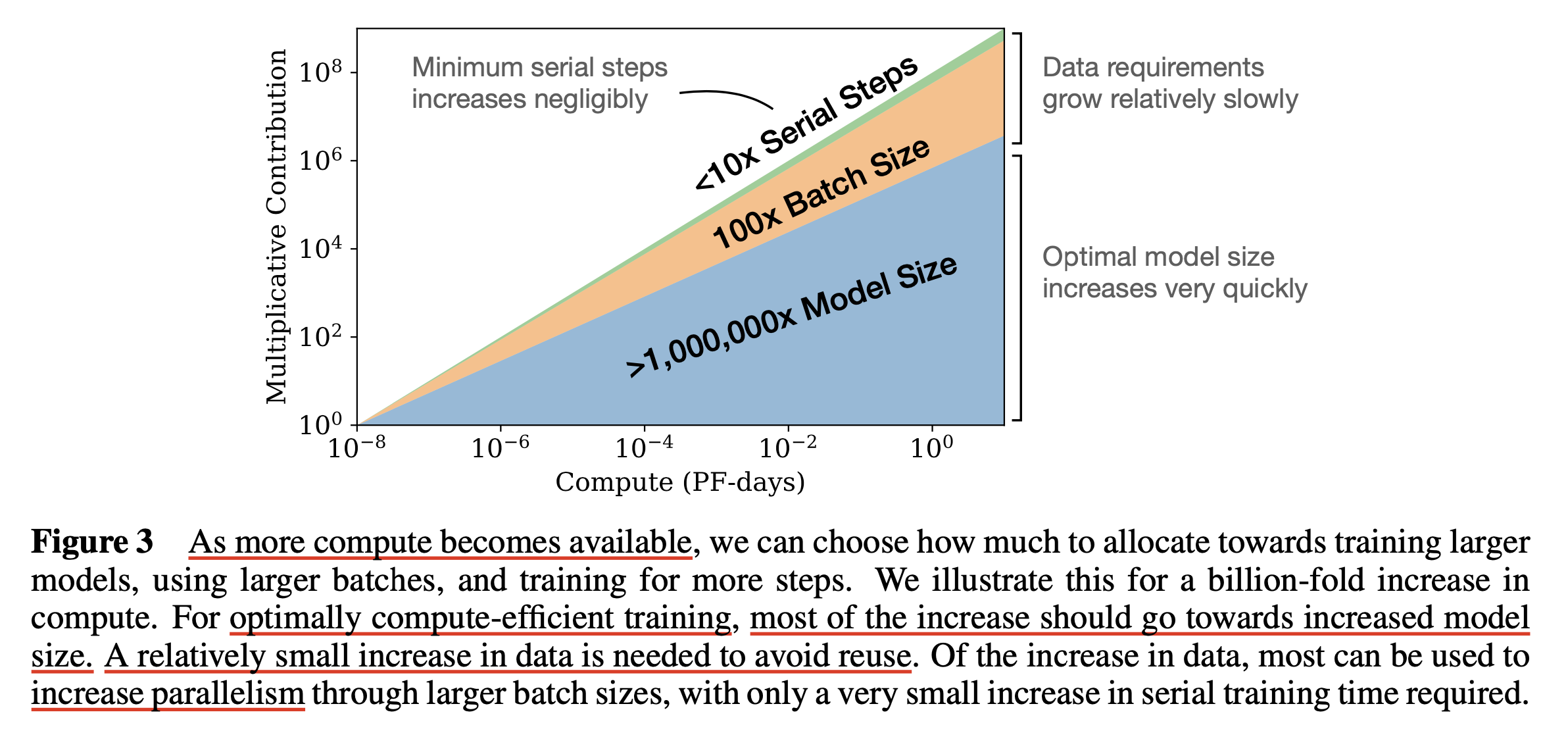 Fig. Model size를 키우는 것에 대부분의 compute를 투자하는 것이 가장 효율적으로 원하는 성능에 도달할 수 있는 방법이라 할 수 있음.
Fig. Model size를 키우는 것에 대부분의 compute를 투자하는 것이 가장 효율적으로 원하는 성능에 도달할 수 있는 방법이라 할 수 있음.
Performance depends strongly on scale, weakly on model shape: model performance는 scale과 강한 상관관계가 있으며 model architecture shape와는 크게 상관이 없었다. 예를 들어 model size, N이 같다면 deep narrow인지? wide shallrow인지는 크게 중요하지 않다는 것.Universality of overfitting: LM의 Performance는 power law를 따라 예측 가능하다고 했지만, 이는 model size, N과 dataset size, D가 같이 scaling up될 경우고, 둘 중 하나가 fixed인 경우 overfitting이 발생함. overfitting에 의한 performance penalty는 \(N^{0.74}/D\)를 따르기 때문에 이를 피하기 위해선 N이 8배 커질 경우, D도 5배 커져야 함 (dataset reuse하면 안됨).Transfer improves with test performance: 얼마나 model이 OOD data distribution에서 좋은 성능을 보일 것인지는 validation loss를 측정함으로써 예측할 수 있음.Optimal batch size: Model size나 dataset size와 optimal batch size는 관계가 없음. 다만 loss와 관련된 power function으로 표현될 뿐임. 즉, 도달하고자 하는 loss가 낮으면 batch size를 키워야 하며 해당 paper에서는 가장 큰 model size에 대해서 1~2M tokens를 batch size로 씀.
 Fig. Takeaways
Fig. Takeaways
Summary of Scaling Laws
그래서 어떤 공식과 값들이 도출되었는가? Appendix를 보면 아래와 같은 요약본을 얻을 수 있다.
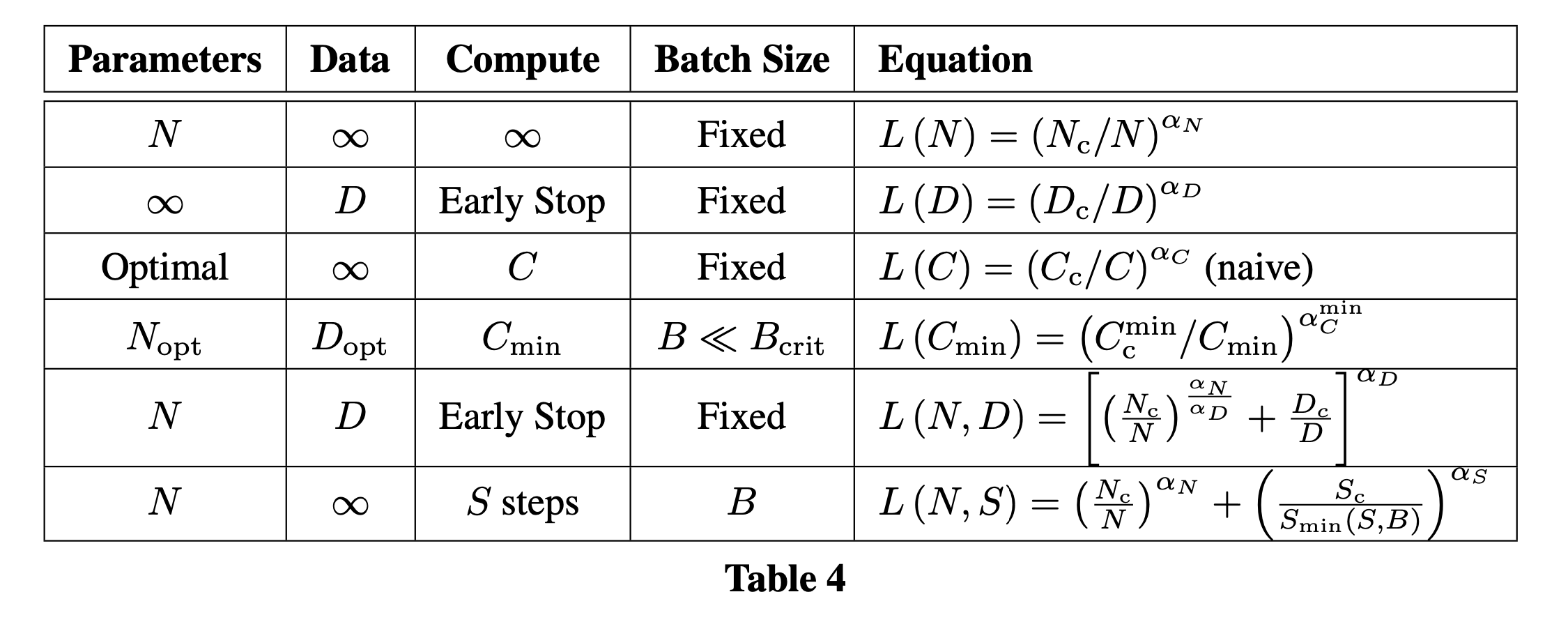 Fig.
Fig.
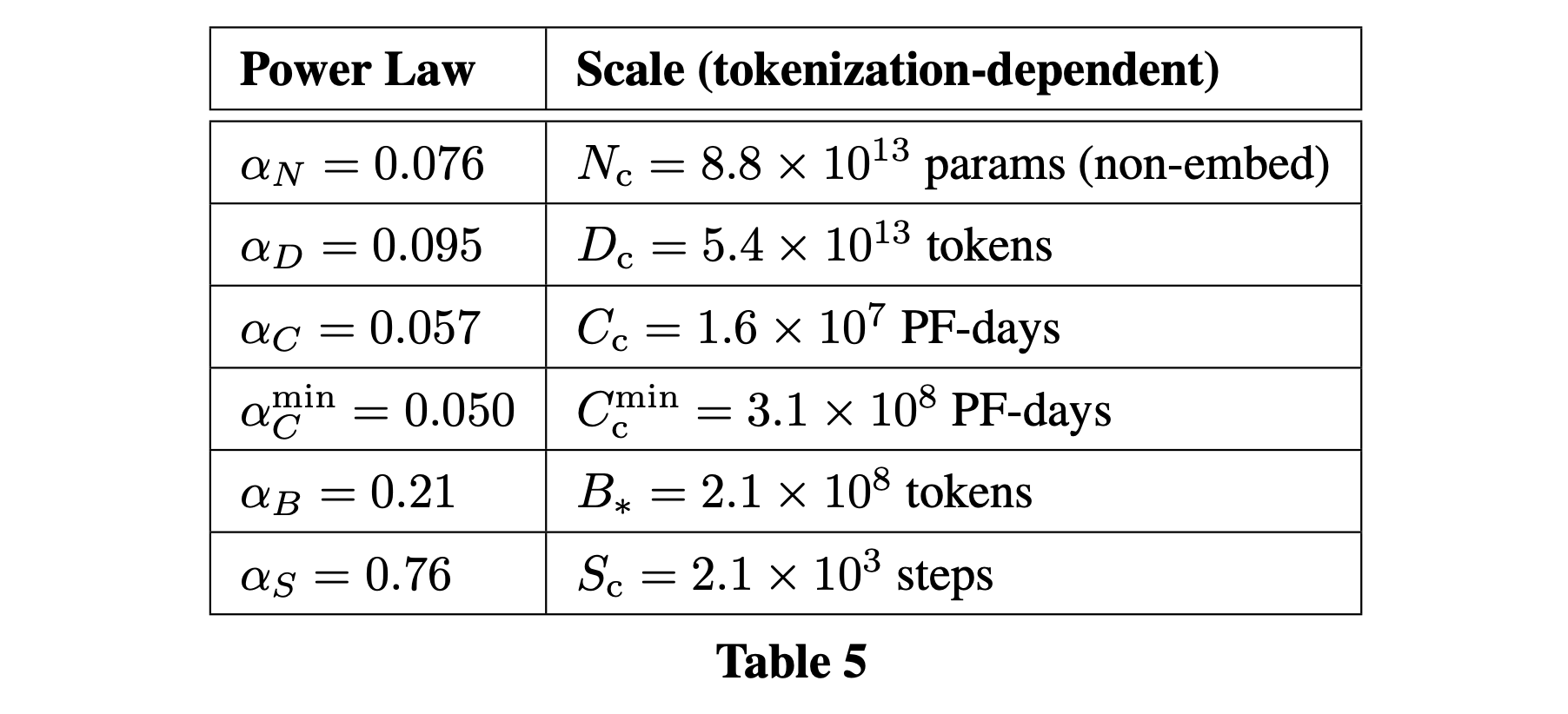 Fig.
Fig.
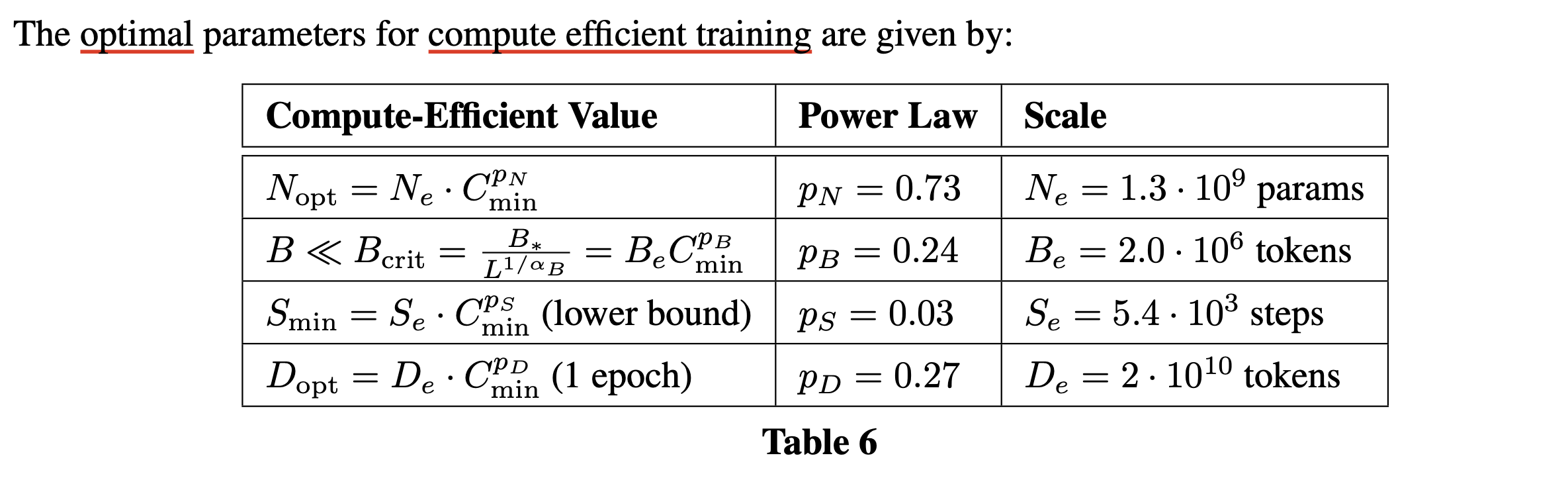 Fig.
Fig.
Training Setup
 Fig.
Fig.
 Fig.
Fig.
 Fig.
Fig.
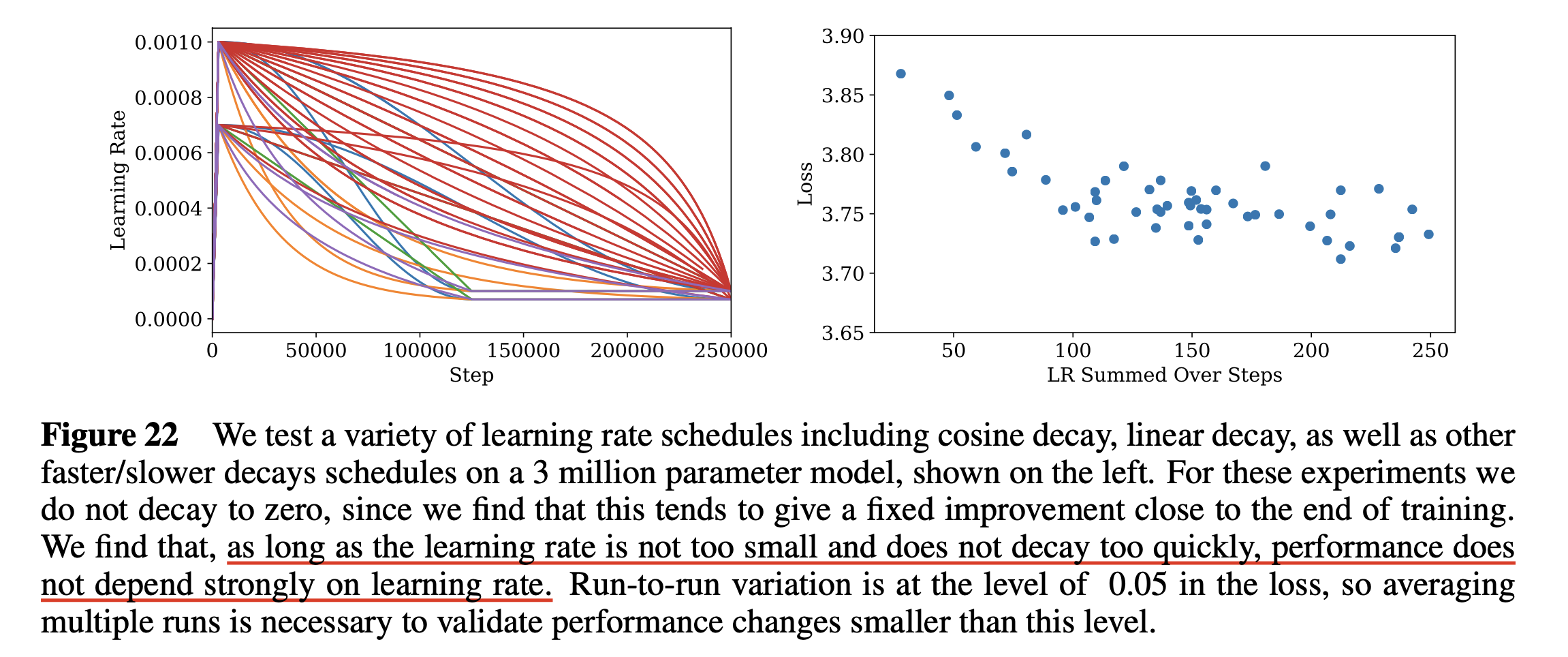 Fig.
Fig.
이제 주요 figure와 실험 결과의 detail에 대해 좀 더 알아보자.
Approximate Transformer Shape and Hyperparameter Independence
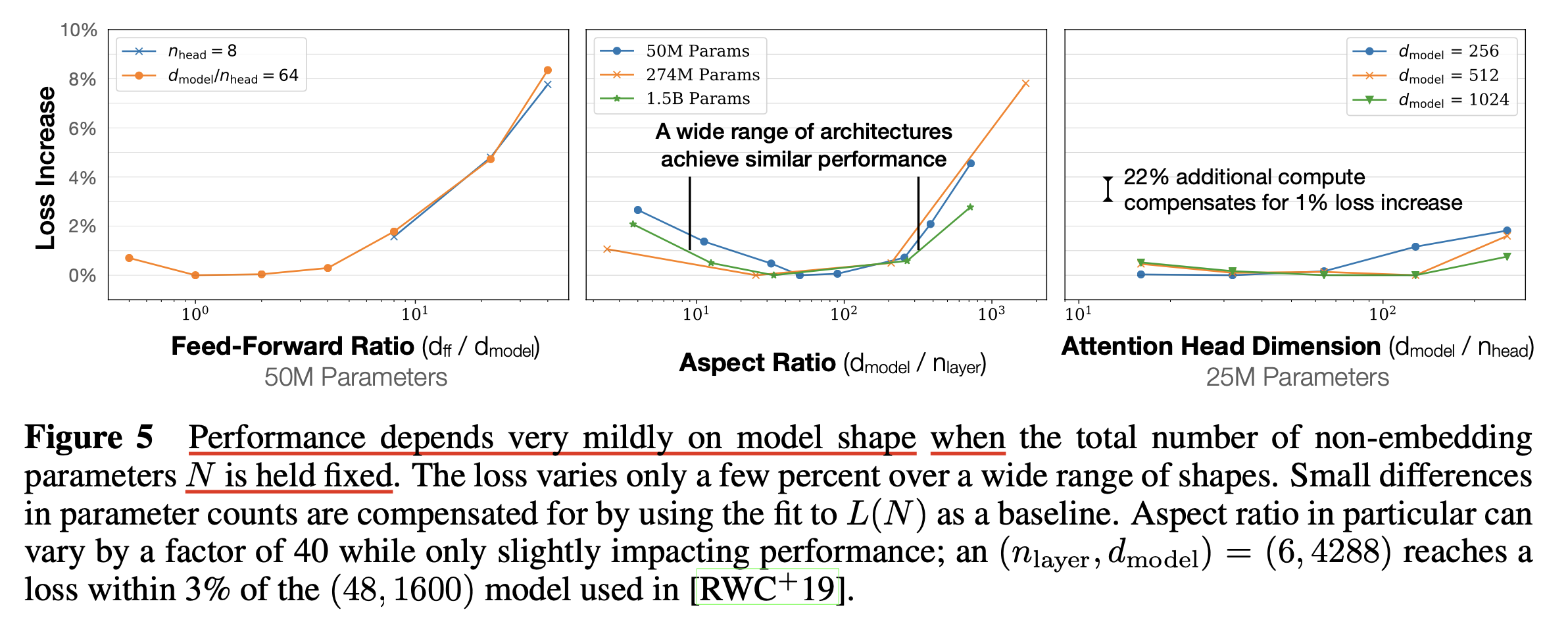 Fig.
Fig.
Performance with Non-Embedding Parameter Count N
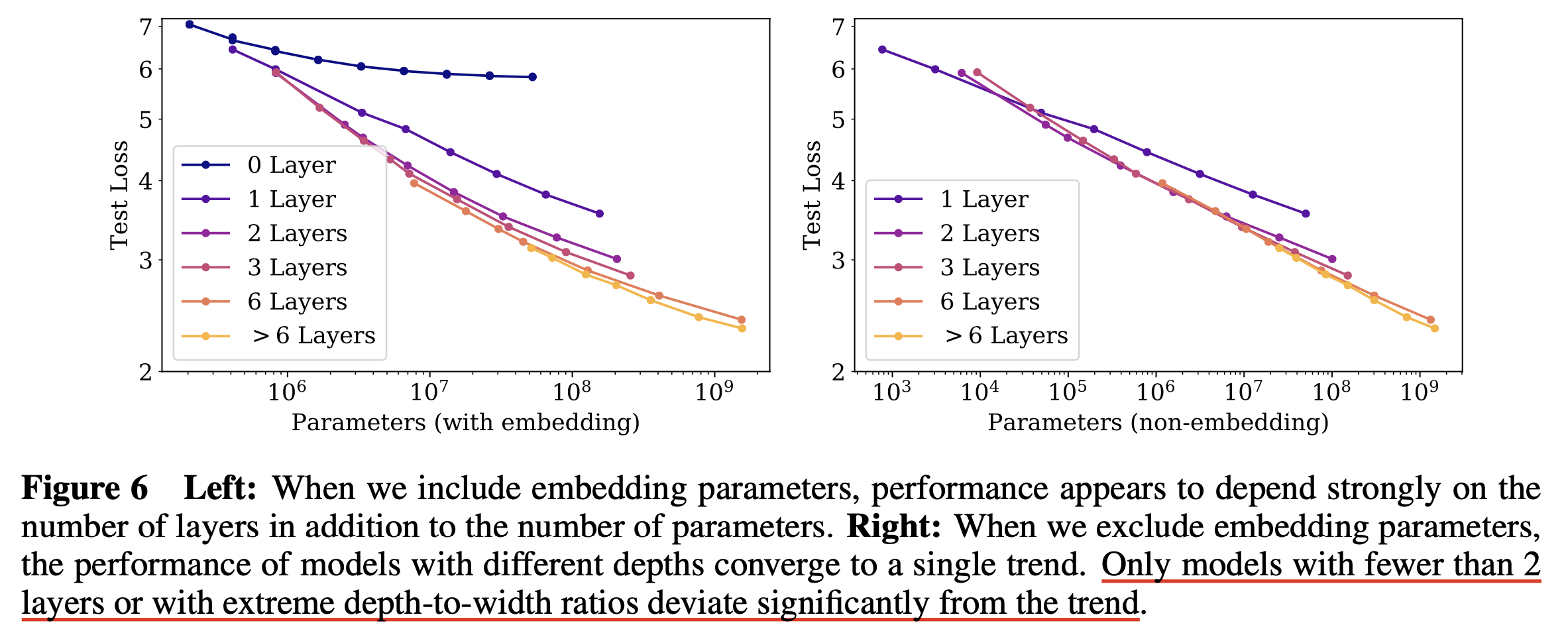 Fig.
Fig.
Comparing to LSTMs and Universal Transformers
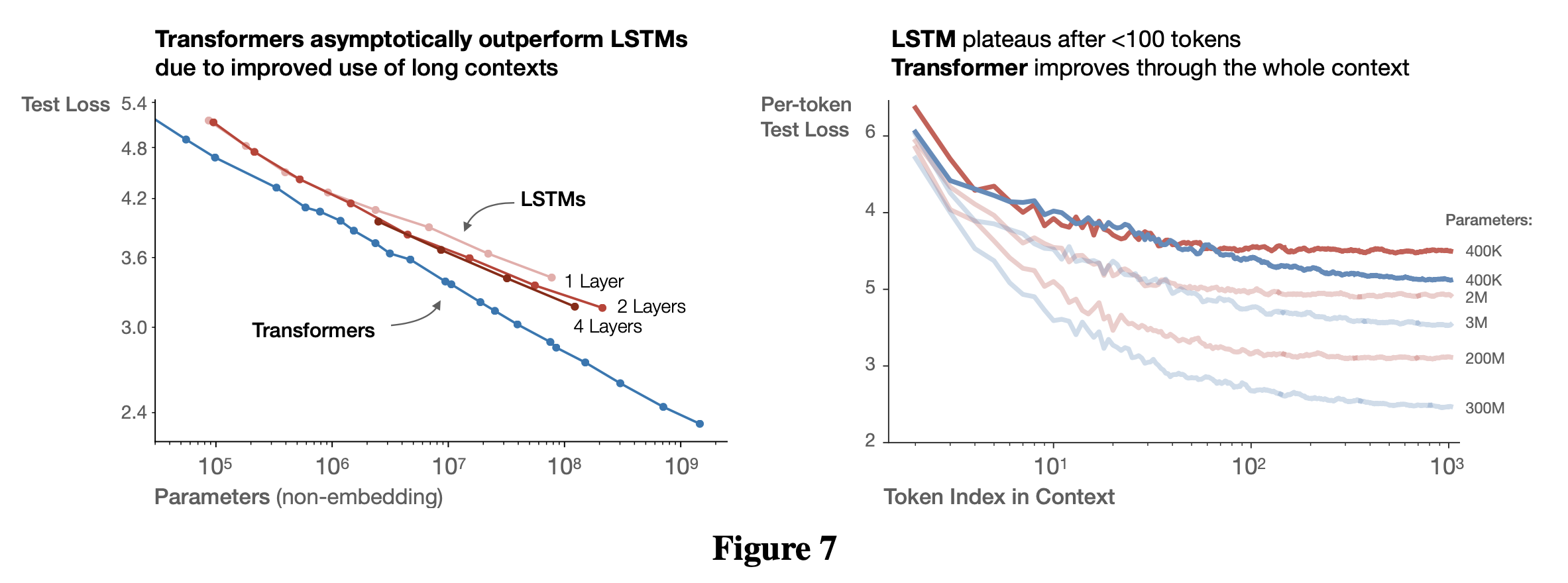 Fig.
Fig.
Generalization Among Data Distributions
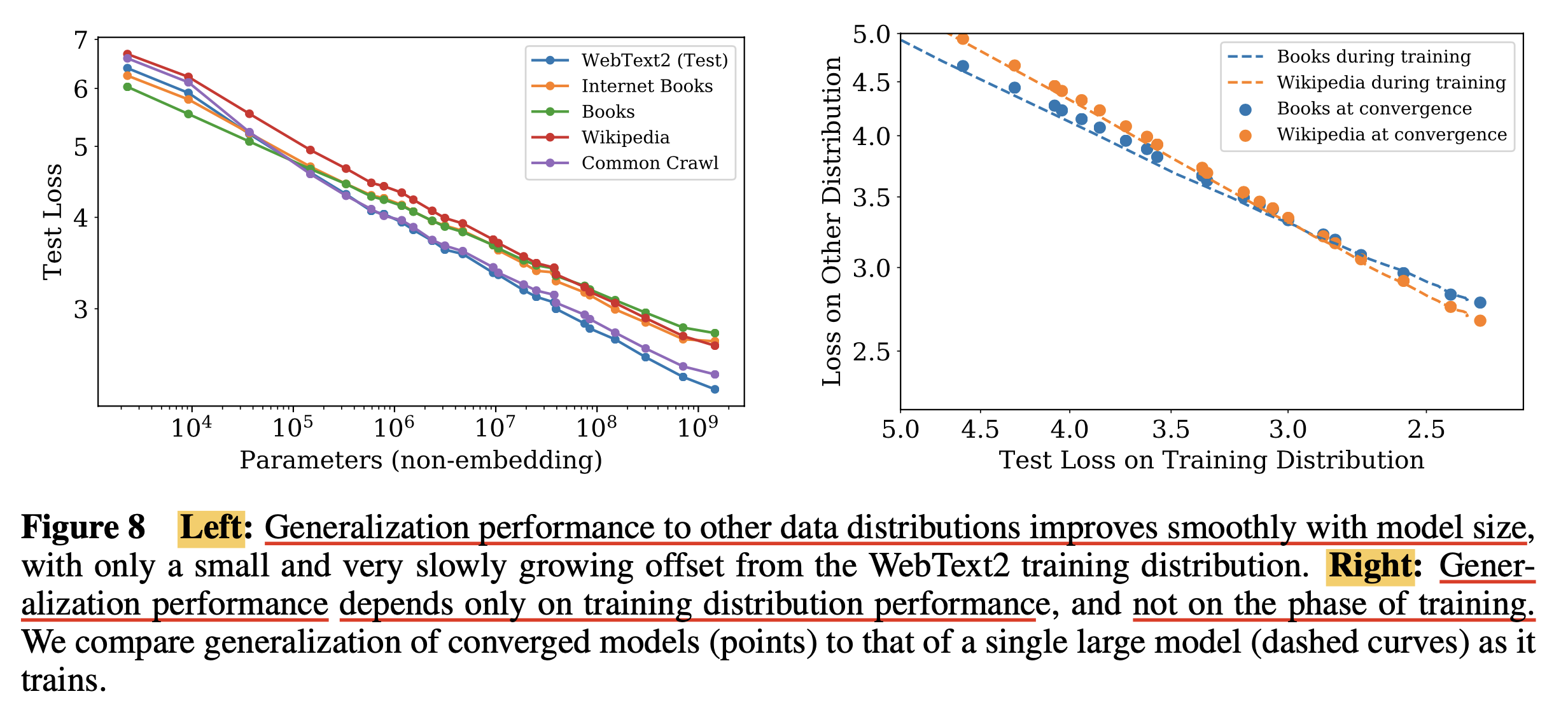 Fig.
Fig.
Charting the Infinite Data Limit and Overfitting
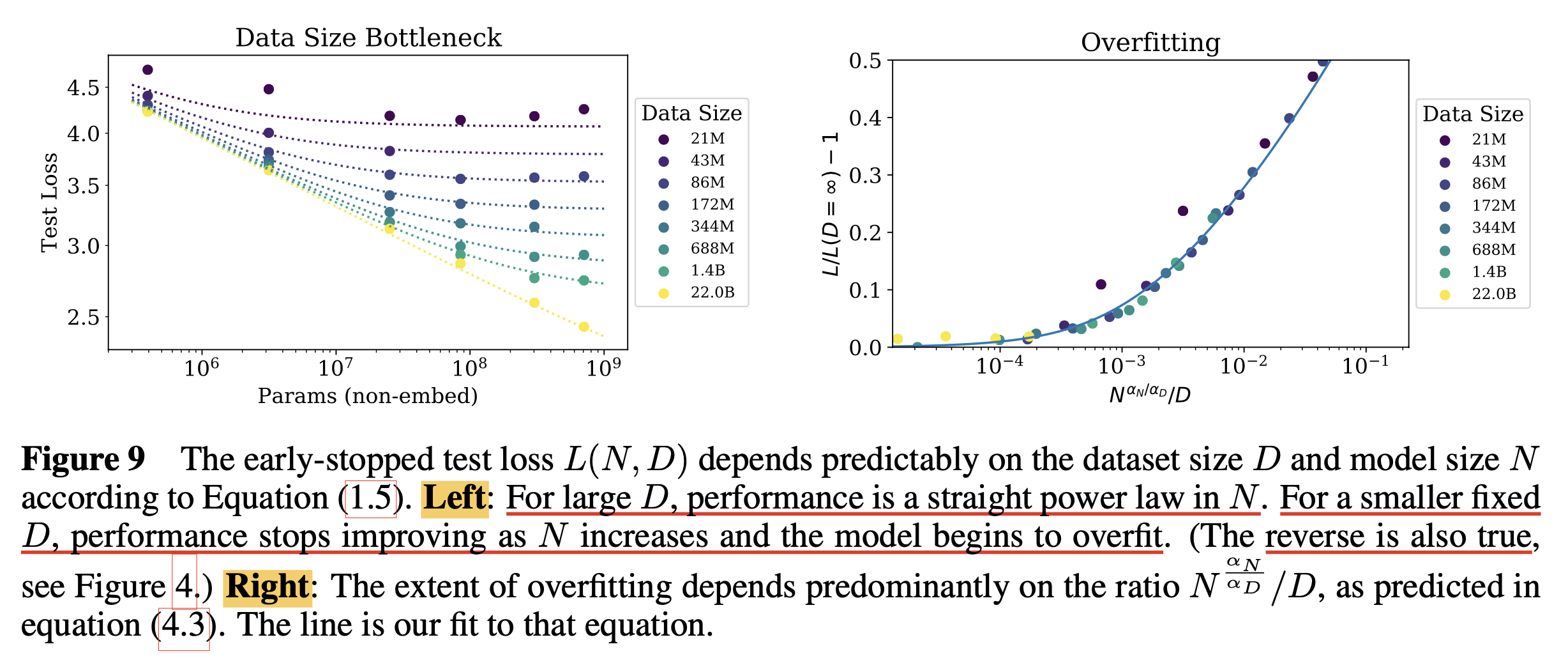 Fig.
Fig.
 Fig.
Fig.
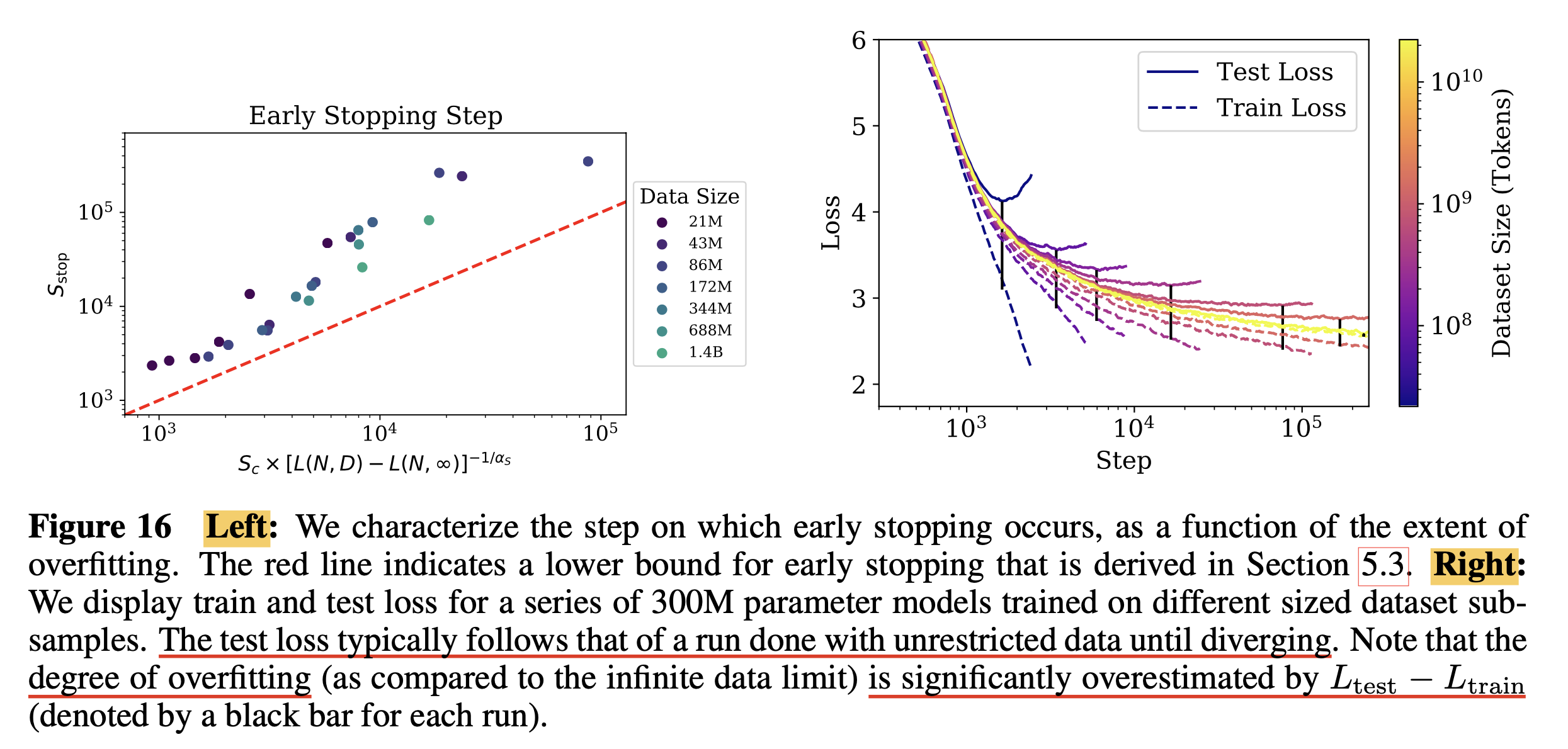 Fig.
Fig.
Critical Batch Size
한 편 Kaplan et al.의 paper에 나와있는 critical batch size에 대해서 알아보자.
"model size, dataset size 별로 critical batch size는 어떻게 정해야 할까?"
Kaplan et al.은 놀랍게도 model size와 critical batch size, \(B_{\text{crit}}\)은 관계가 없으며, 오직 관계가 있는 factor는 도달하고자 하는 loss, \(L\)이었다고 한다.
\[B_{\text{crit}} = \frac{B_{\ast}}{L^{1/\alpha_B}}\] Fig.
Fig.
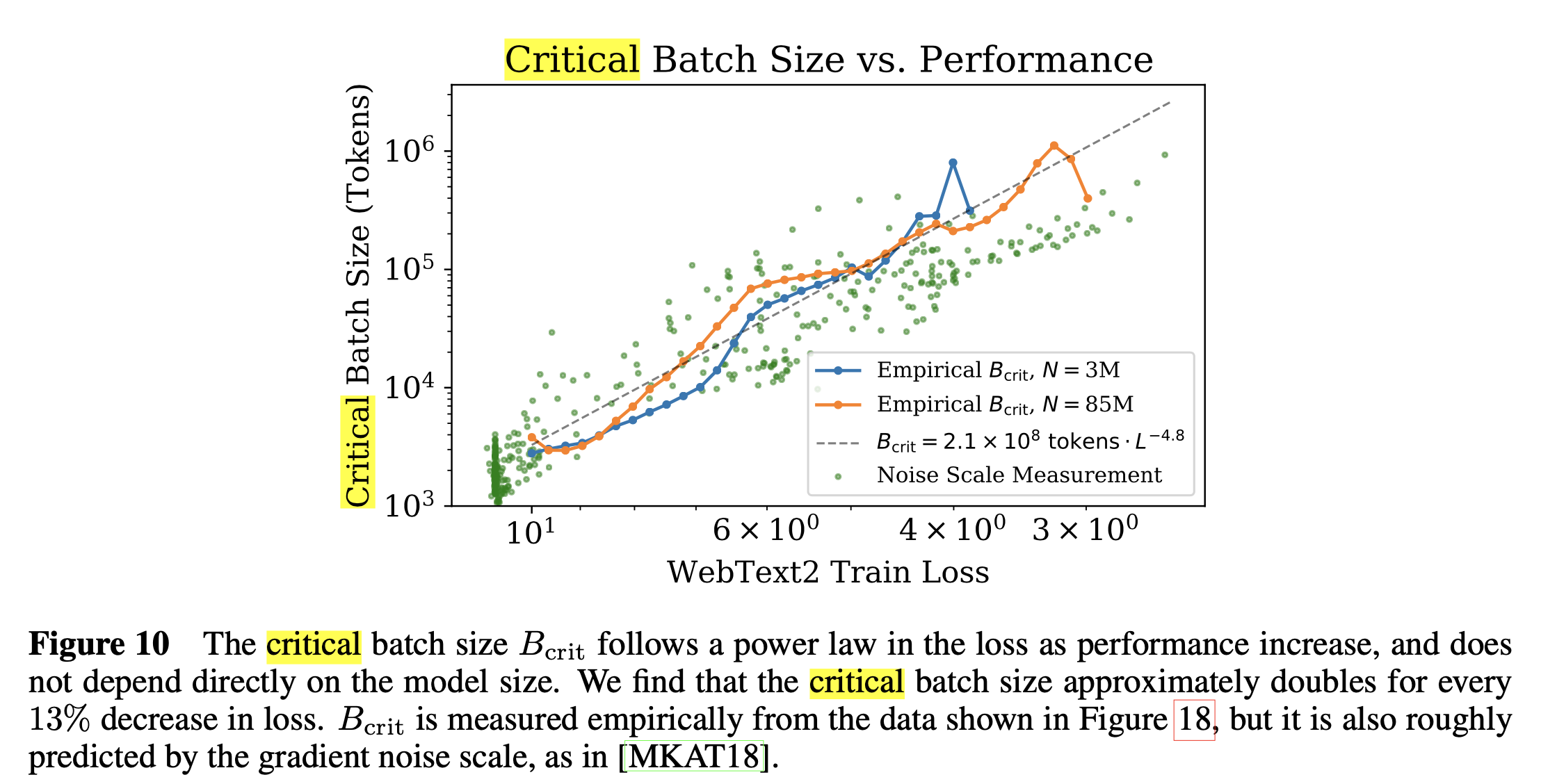 Fig.
Fig.
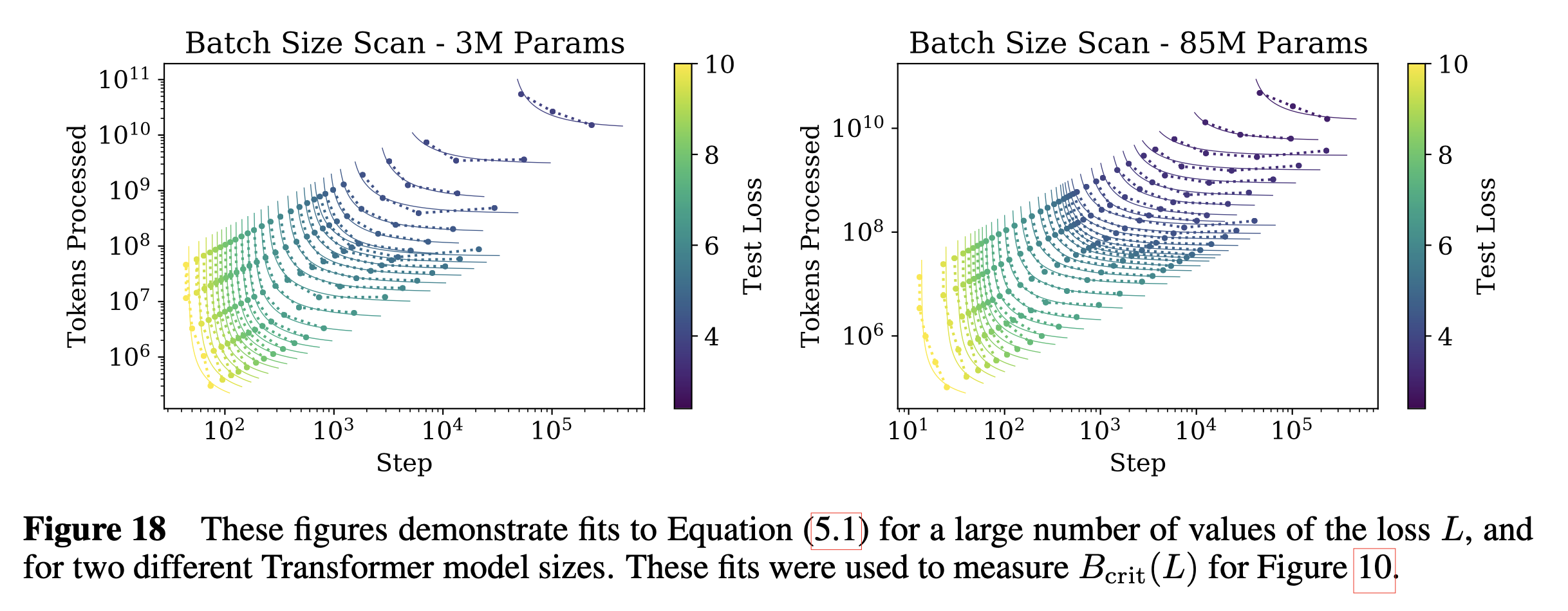 Fig.
Fig.
그래서 몇달 뒤 나온 GPT-3는 어떻게 batch size를 정했을까.
 Fig.
Fig.
GPT-3는 Kaplan et al.을 통해 model size가 커질수록 더 큰 batch size, 더 작은 LR를 써야한다는 것을 실험적으로 알아냈다고 한다.
아래 Table 2.1은 실제로 model size별 batch size, LR이다.
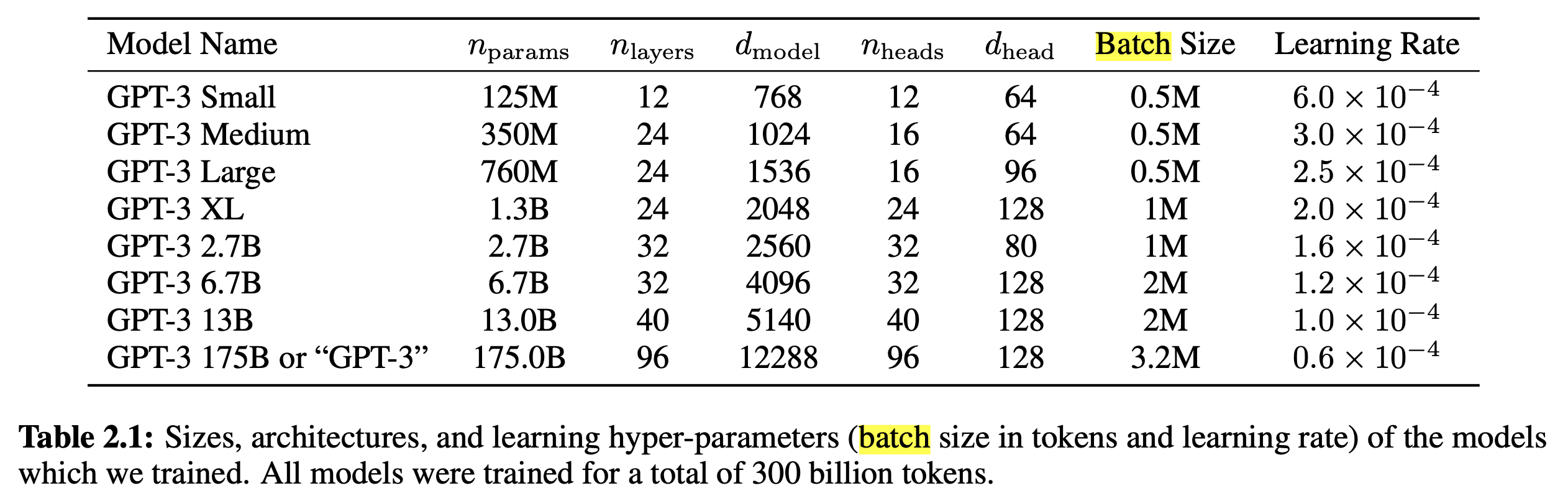 Fig.
Fig.
나머지 training detail은 다음과 같은데, 총 training tokens가 300B일 때, early training stage인 4~12B 까지는 LR warm up을 하듯, 굉장히 작은 batch size인 32K tokens부터 feeding했다고 한다.
 Fig.
Fig.
이는 critical batch size가 제안된 An Empirical Model of Large-Batch Training에서 training 후반부로 갈수록 더 어려운 feature를 배워야 하기 때문에 batch size가 많이 필요하다고 한 것과 동일한 철학이라고 할 수 있다. (즉 반대로 training 초기에는 gradient diversity가 낮기 때문에 sample이 많아봐야 정교해지지 않기 때문에 최대한 이를 활용한 것)
Optimal Performance and Allocations
사실 본 논문에서 아래 Figure (right)은 fixed batch size에 대해서 N을 바꿔가며 실험했다고 한다. 그런데 우리는 critical batch size라는게 존재하므로 more computationally efficient training을 할 수 있음을 안다.
One might ask why we did not simply train at Bcrit in the first place.
The reason is that it depends not only on the model but also on the target value of the loss we wish to achieve,
and so is a moving target.
 Fig.
Fig.
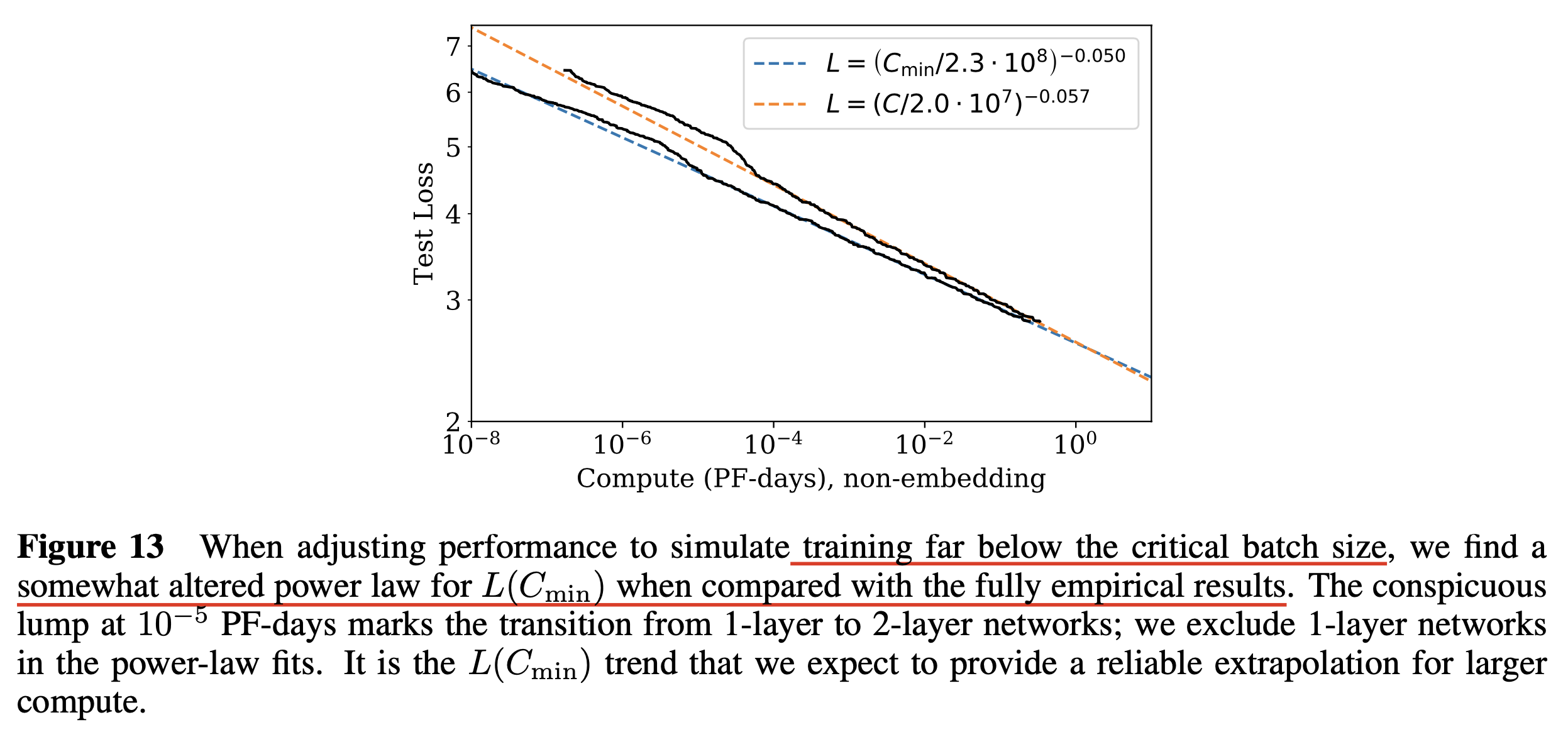 Fig.
Fig.
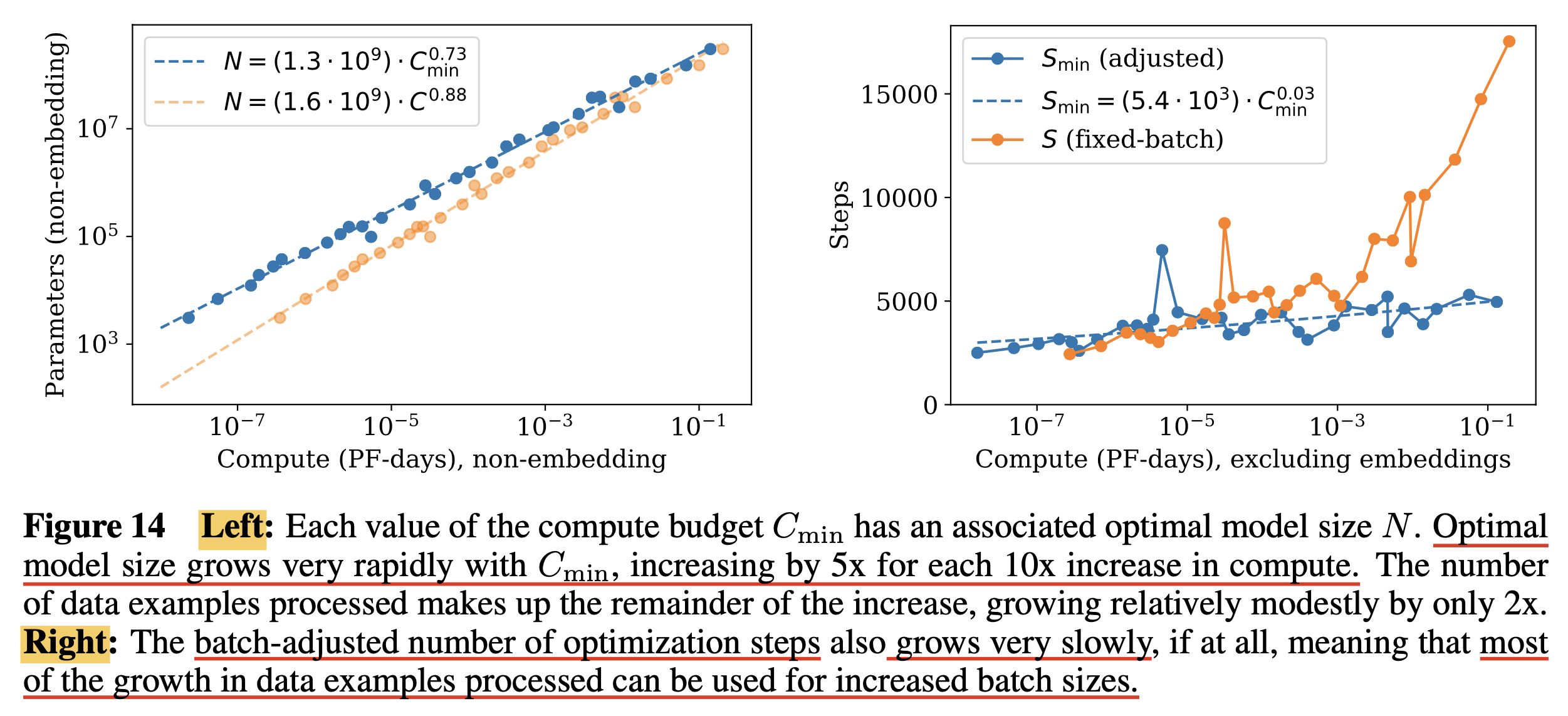 Fig.
Fig.
 Fig.
Fig.
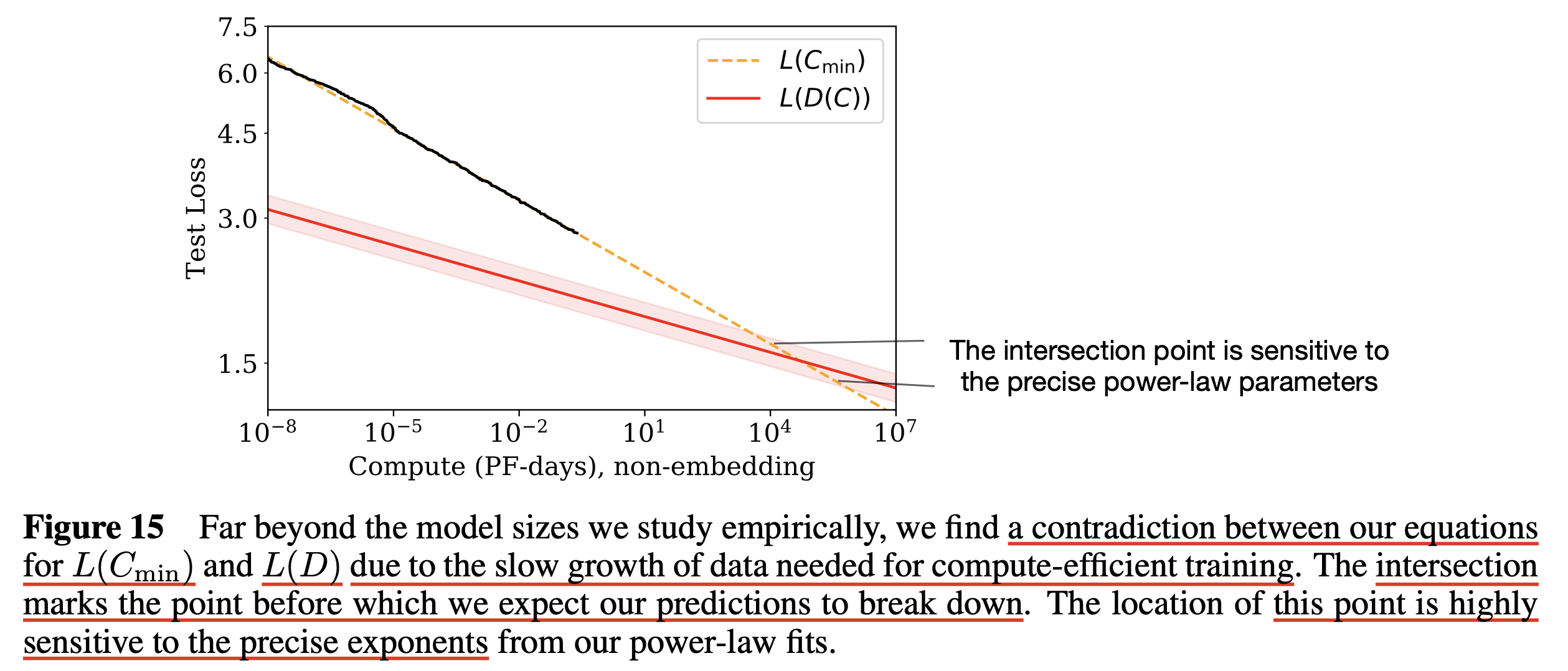 Fig.
Fig.
Some Potential Caveats to Paper's Analysis
 Fig.
Fig.
Emergent Ability and Grokking
한 편, Scaling Law로 예측이 어려운 성능 지표들도 있다. Curve가 비연결적 (discontinuous) 하다고 해야하나? Anthropic의 post를 보면 이에 대한 요약이 있는데,
 Fig.
Fig.
다들 유명한 얘기들인데,
첫 번째 얘기는 GPT-3 paper에 있는 내용으로, Wei et al.의 Emergent Ability paper와도 관련이 있는 내용이다.
Emergent Ability란 어떤 추론 능력등이 training 내내 발현되지 않다가 어느 순간 발현된다는 것인데,
아래 figure를 보면 training FLOPs가 특정 지점을 경과하기 전에는 여러 size의 model의 각 task별 accuracy가 random guess 수준을 넘지 못하다가 갑자기 넘는 것을 볼 수 있다.
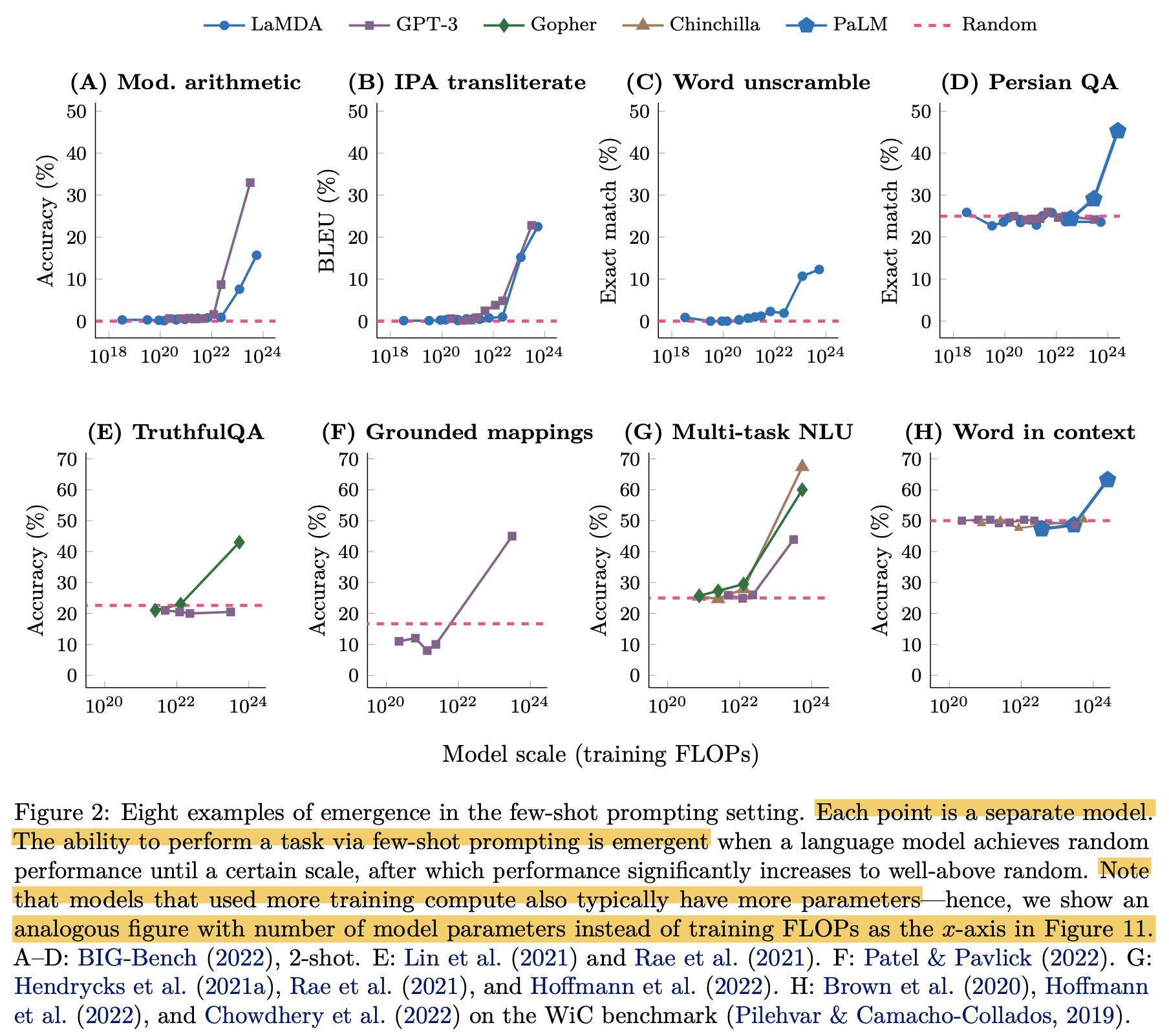 Fig.
Fig.
이를 model size별로 구분한 아래 figure를 보면, model을 길게 학습할수록, model size를 키울 수록 이런 현상이 나타나는 것을 알 수 있다.
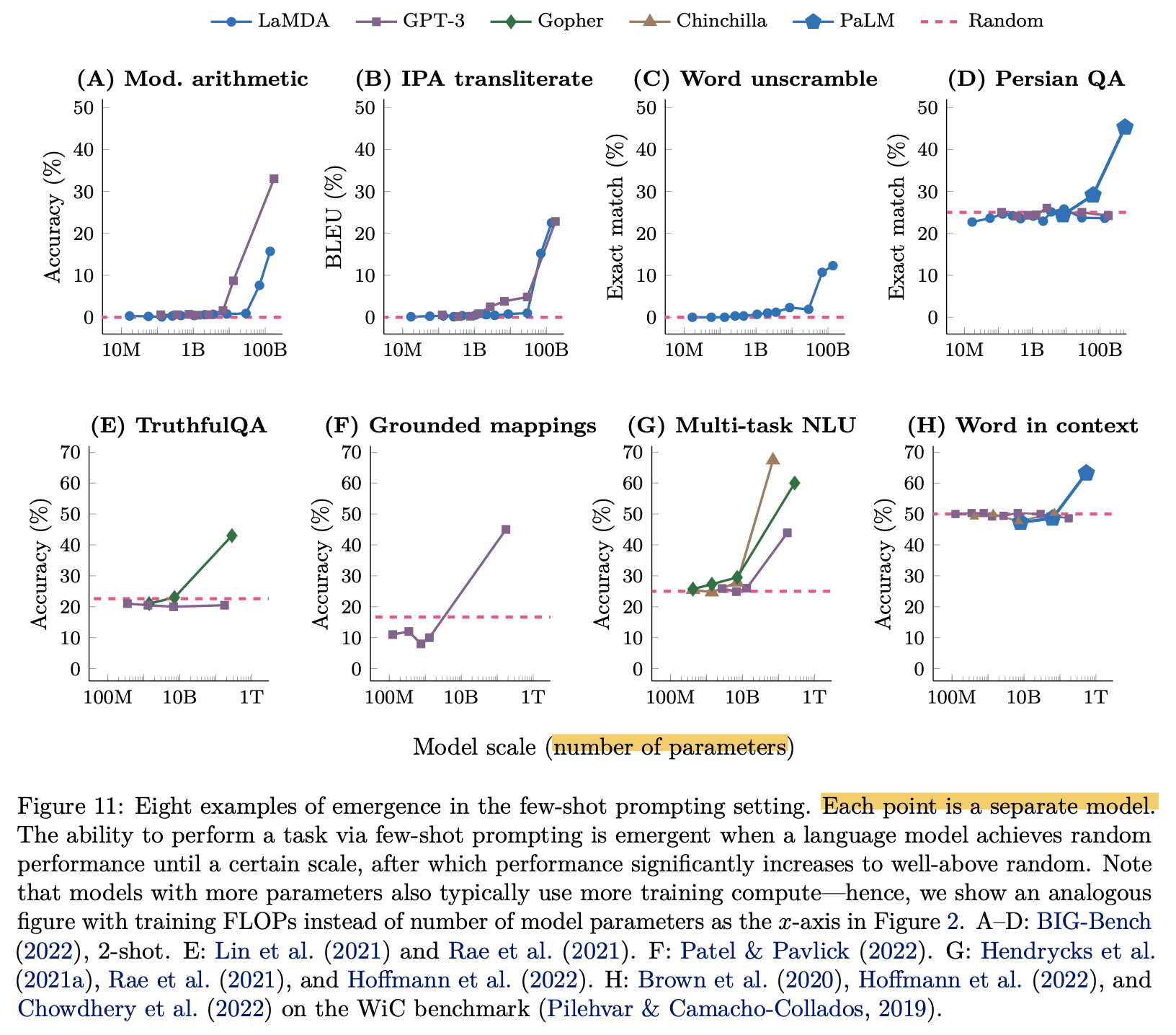 Fig.
Fig.
(GPT-3는 Kaplan et al.의 scaling law를 따라 학습되었을 것이고, figure의 Chinchilla라는 model은 곧 살펴보게 될 것이다)
이런 현상은 OpenAI에서 나온 Power et al.의 Grokking라는 현상과도 관련이 있다고 할 수 있을 것 같은데,
Grokking은 model이 overfitting하다가 갑자기 generalize하는 현상을 말한다.
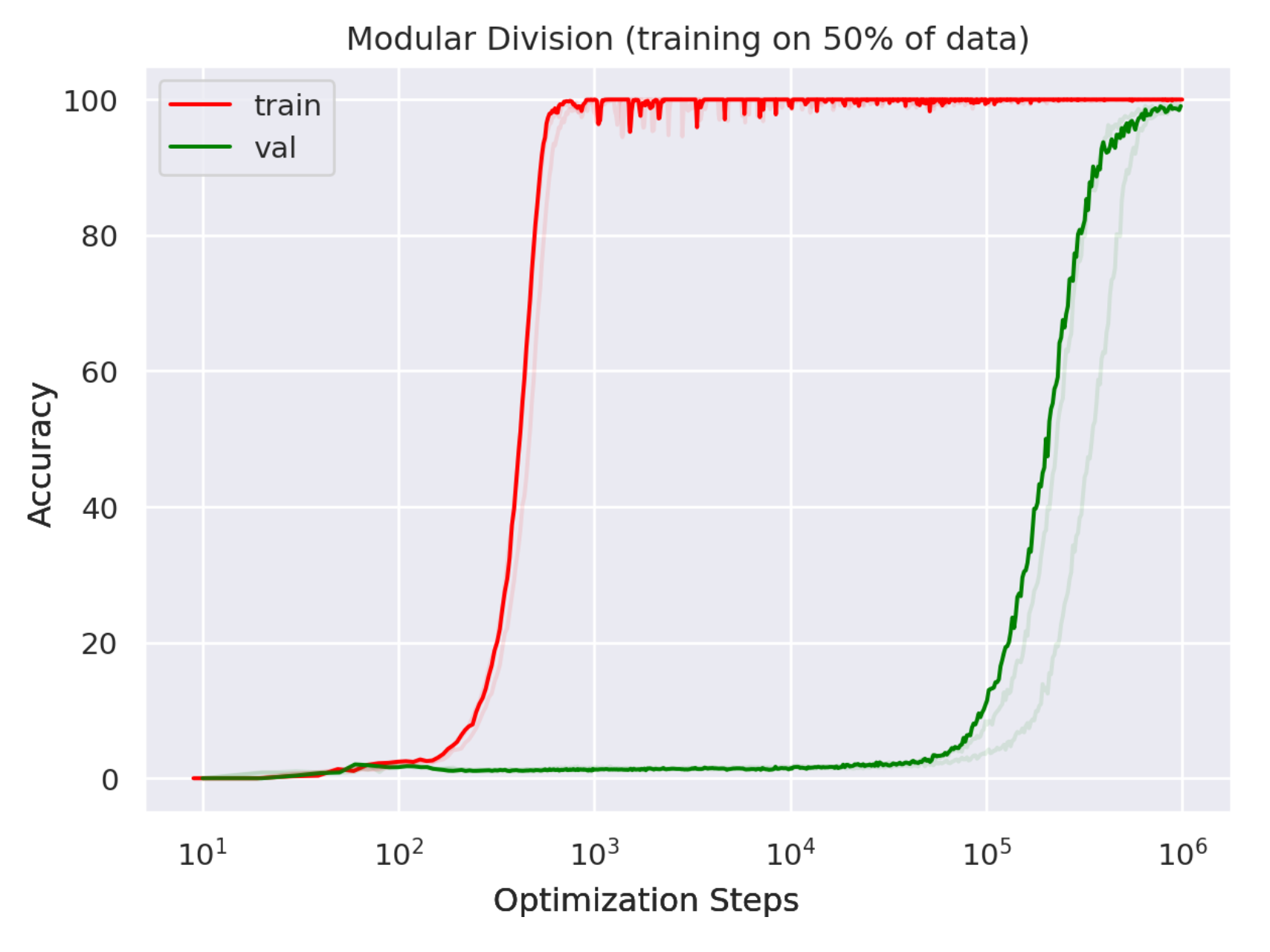 Fig.
Fig.
이렇듯 과거의 관점 (classic regime)에서는 overparameterized model이 overfitting하기 쉽다고 생각했으나, 현대의 관점 (modern regime) dataset size, model size, 그리고 compute budget이 커지면 갑자기 generalize를 한다거나 능력 발현이 된다고 얘기하는데, Scaling Law는 loss prediction은 매우 부드럽게 할 수 있지만 이런 task별 accuracy에 대해서는 약간 예측력이 부족하다고 할 수 있을 것 같다.
(2020 Oct) Scaling Laws for Autoregressive Generative Modeling (Kaplan et al.)
다음으로 알아볼 paper도 OpenAI에서 2020년에 낸 Scaling Laws for Autoregressive Generative Modeling라는 paper이다. 이는 LM처럼 Autoregressive 하게 next token generation을 하도록 objective function을 정의했다면, 그 task가 LM이던 image generation이나 video generation이던 상관없이 scaling law를 따른 다는 것을 보인 paper이다.
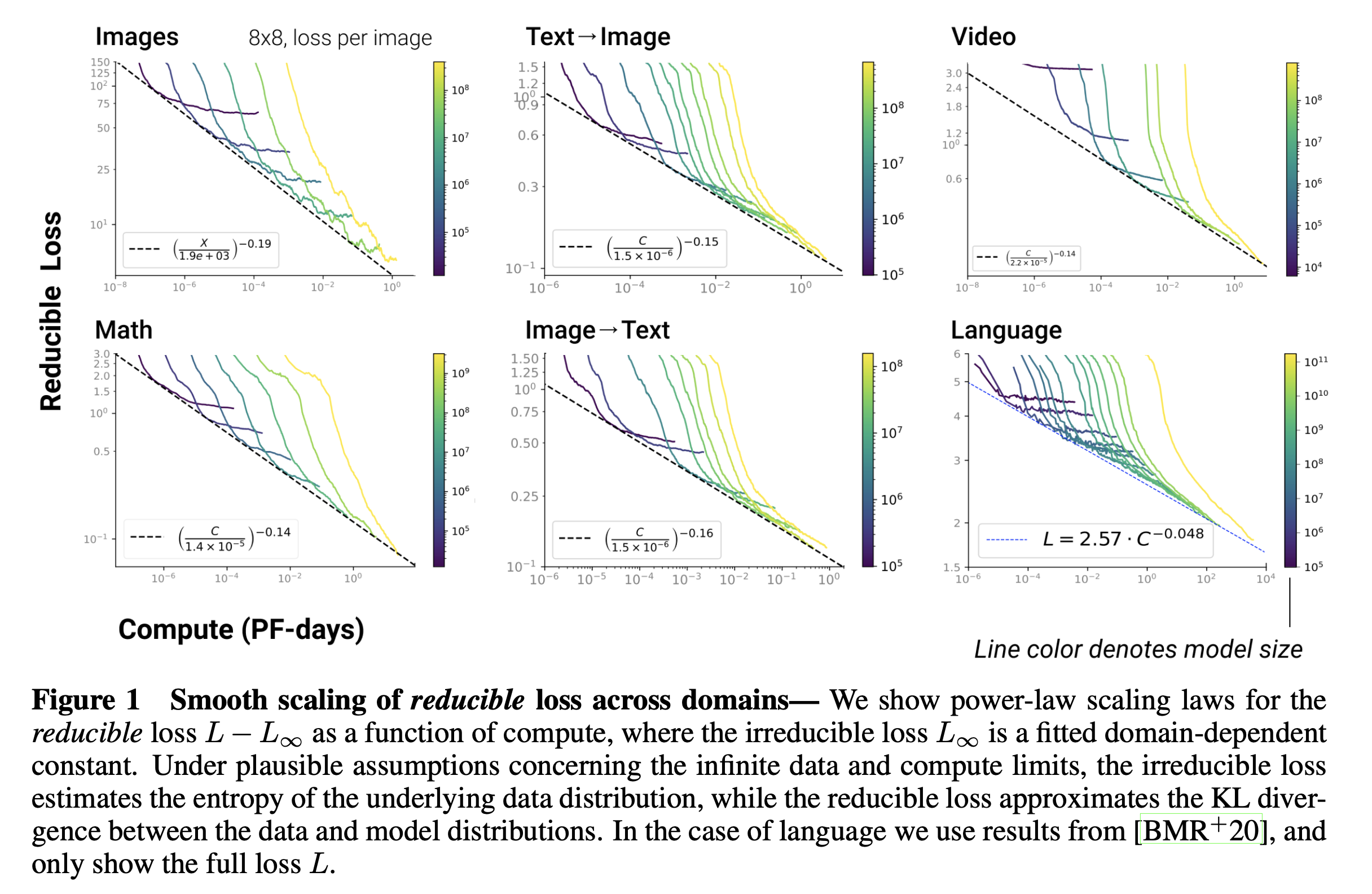 Fig.
Fig.
사실 이번 post의 target은 LM 뿐이기 때문에 이 paper는 언급만 하고 간단하게 넘어가려고 하는데, 새삼스럽게 이런 scaling에 대한 연구를 이미 잔뜩 해놓고 결국 2022년에 증명해버린 OpenAI가 너무 대단한 것 같다.
Summary of Results
여기서 다룬 task는 다음과 같은데,
- generative language modeling
- image and video modeling
- multimodal modeling of text-image correlations
- mathematical problem solving
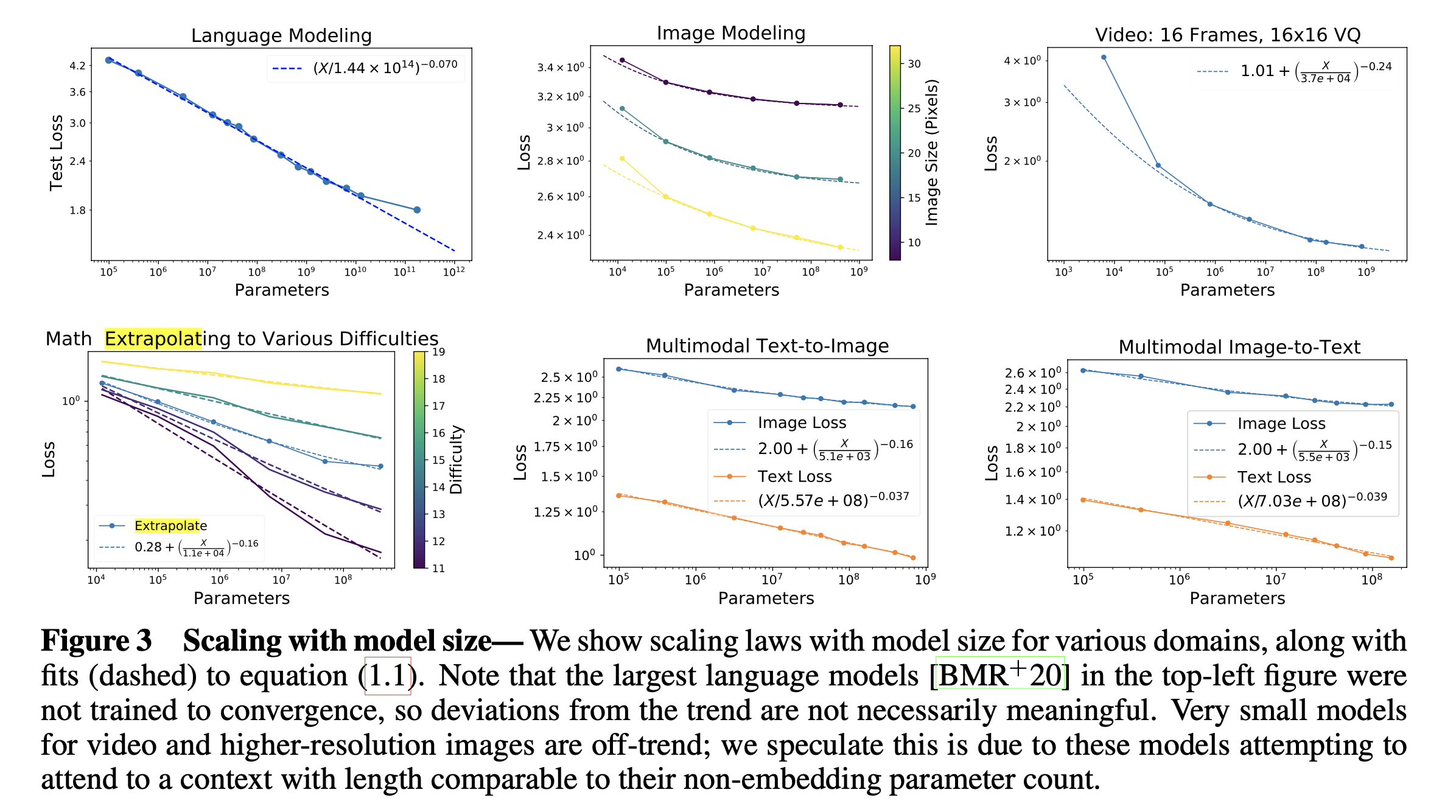 Fig.
Fig.
Mathematical Problem Solving and Extrapolation
Mathematical problem solving는 Autoregressive Transformer model이 말 그대로 수학 문제를 풀 수 있는지를 측정하는 task이다. Text 형태의 수학 문제를 input으로 답변을 생성해 accuracy를 측정하면 되는데, DeepMind가 제안한 Math problem generator를 통해 example들을 보면 다음과 같다.
 Fig.
Fig.
(대부분이 산수, 인수분해 등 쉬운 난이도임을 알 수 있지만 요즘 나오는 LLM들도 이런걸 완벽히 해내지 못하는 걸 보면 당시 (2019)년에는 이게 거대한 challenge였음을 알 수 있을 것이다)
이 paper의 contribution에 보면 수학적 추론 성능 (mathematical reasoning ability)를 측정하기 위해서 interpolation, extrapolation을 모두 측정할 수 있도록 data를 만들어서 공개했음을 알 수 있는데,
 Fig.
Fig.
여기서 interpolation이란 training set에 있는 문제들과 비슷한 형태, 난이도를 갖는 test set을 의미한다. 예를 들어 2차 방정식의 근을 구하는 것의 숫자만 바뀌는것은 interpolation에 해당하지만, 만약 5차 방정식의 근을 구해야 한다면 이것은 extrapolation에 해당하게 된다.
 Fig.
Fig.
우리가 ML model에 기대하는 것은 dataset이 sampling된 true distribution을 찾아내는 것인데, 사실 주어진 training sample들만 가지고 extrapolation을 하기란 되게 어려운 일이라고 할 수 있다.
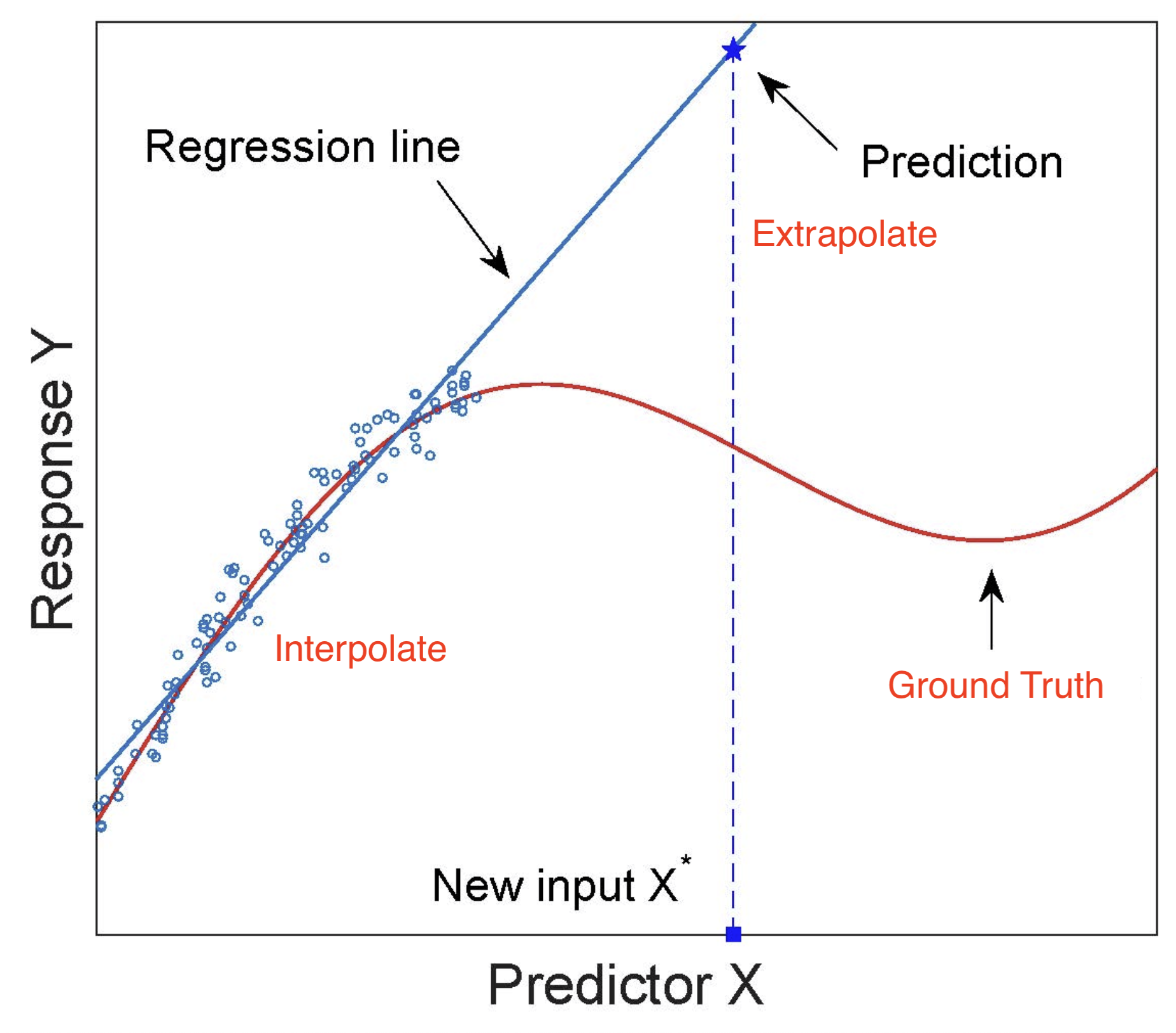 Fig. Source from here
Fig. Source from here
Kaplan et al.은 주로 extrapolation과 model size, dataset size간의 scaling law를 찾으려고 했는데, 결과는 다음과 같았다.
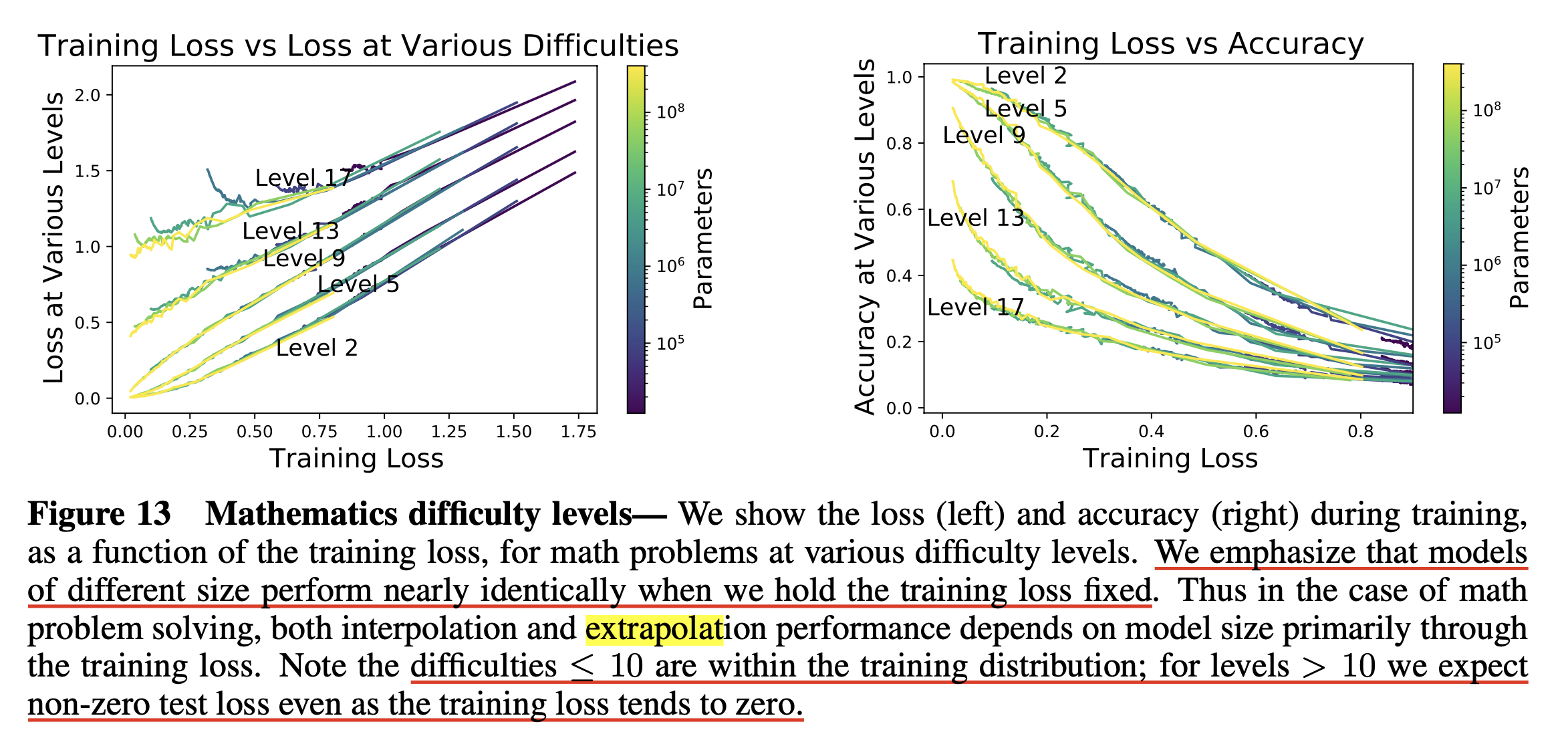 Fig.
Fig.
결과를 보면 model size가 커진다고 해서 난이도 (difficulty)가 높은 문제를 풀 수 있는 것은 아니었다는 것을 알 수 있는데, 다시 말해서 extrapolation 능력은 model size에 dependent하지 않는다는 것이다.
 Fig.
Fig.
그러니까 만약 우리가 수학적 추론 성능을 올리고 싶다면 최대한 다양하고 좋은 data를 수집하는 것이 key가 되는 것이라는 내용이다.
(2021 Feb) Scaling Laws for Transfer (Kaplan et al.)
Key Results
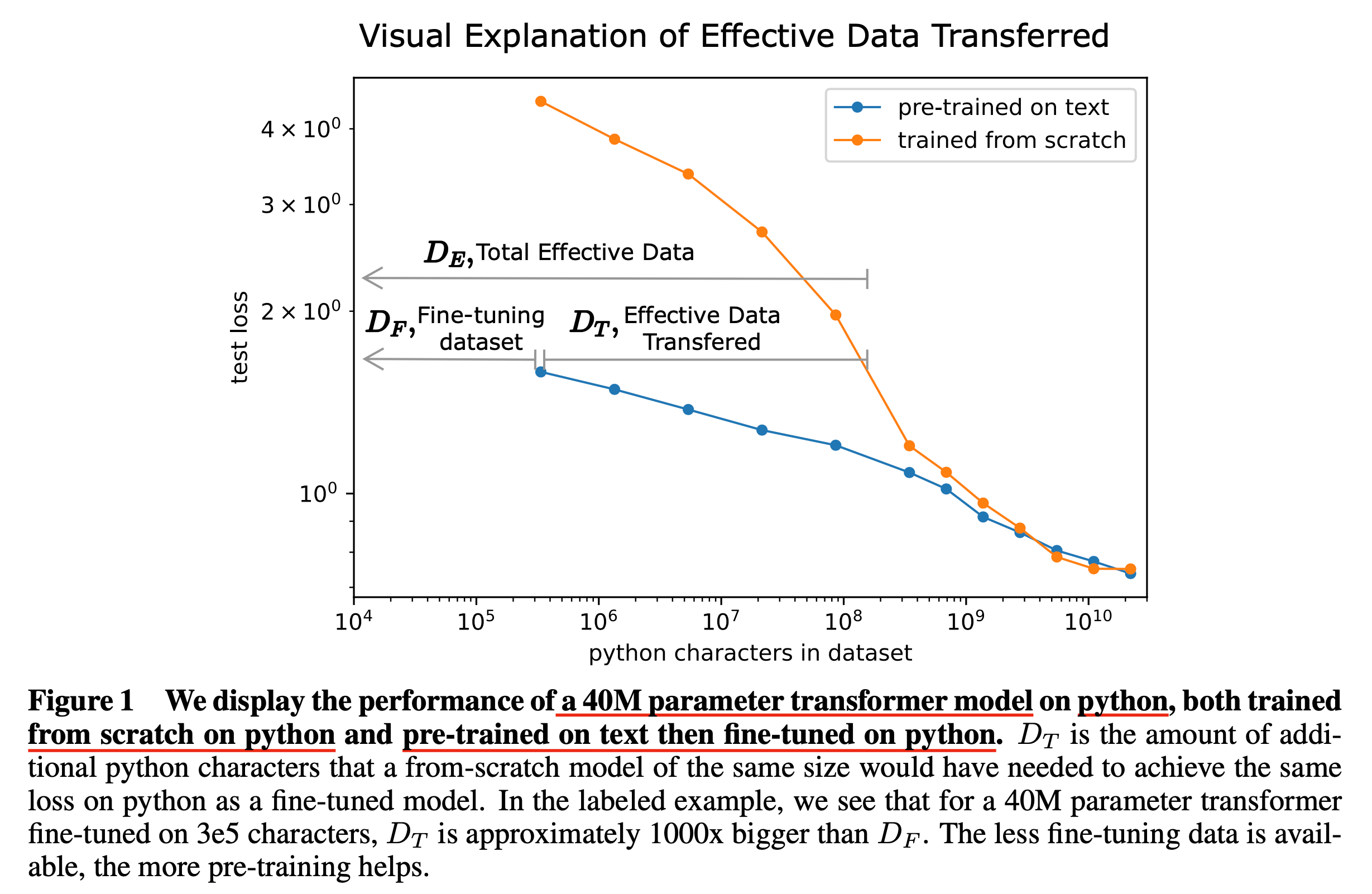 Fig.
Fig.
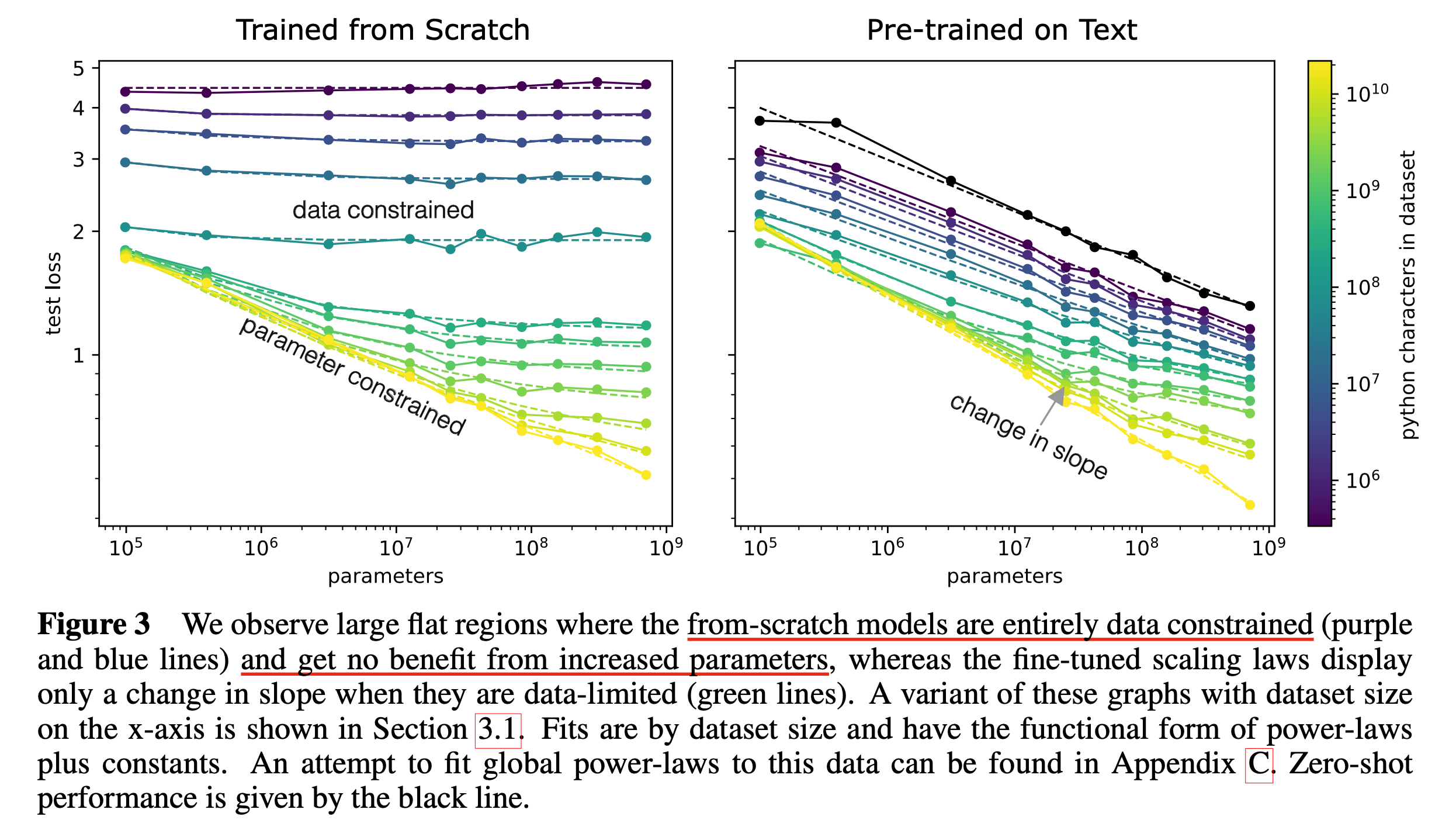 Fig.
Fig.
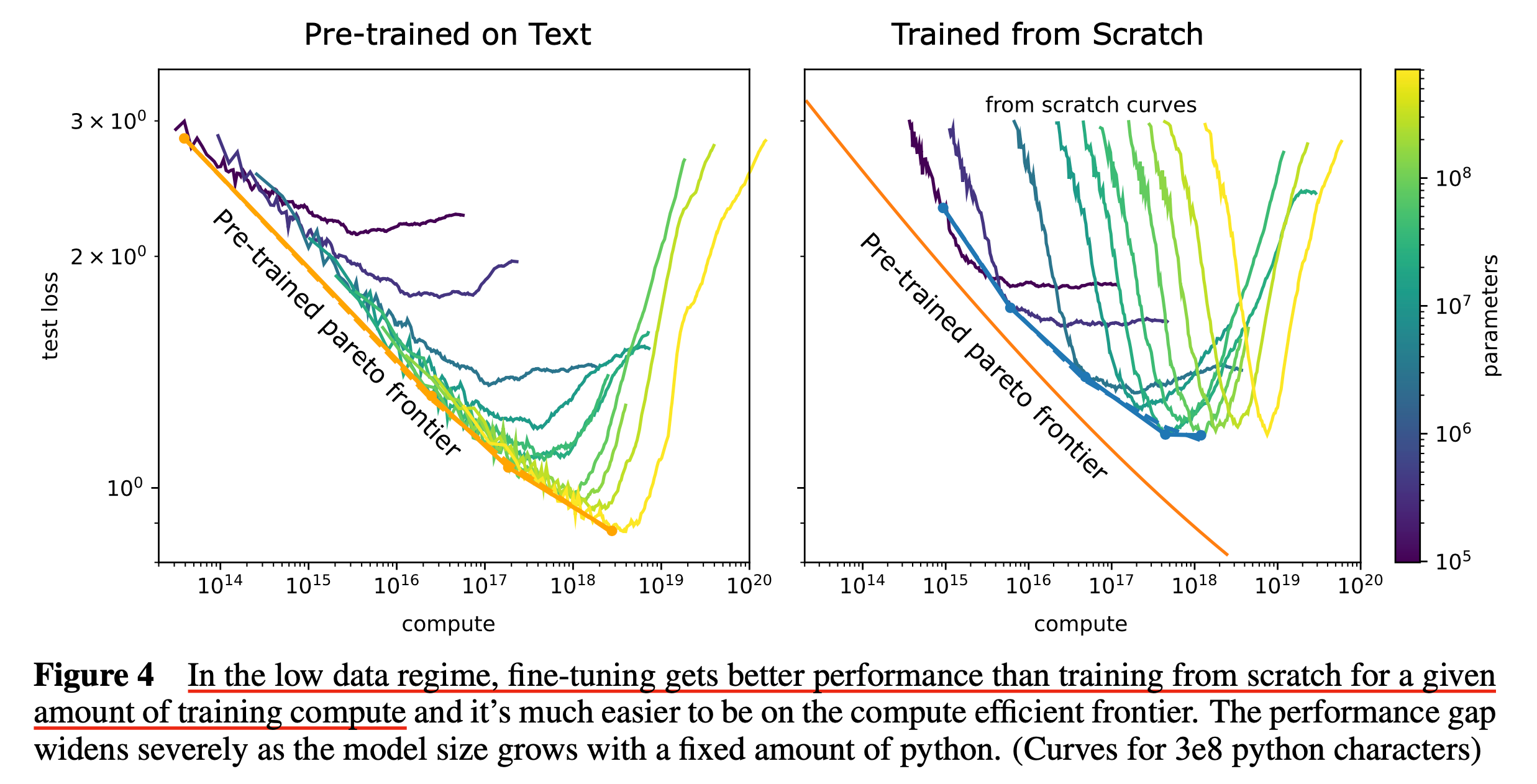 Fig.
Fig.
Ossification – can pre-training harm performance?
Fine-tuning is usually compute efficient (ignoring pre-training compute)
Limitations and Discussion
(2022 Mar) Training Compute-Optimal Large Language Models (a.k.a Chinchilla Optimal)
이제 Hoffmann et al.의 Training Compute-Optimal Large Language Models에 대해서 알아보자.
이는 Chinchilla Optimal이라고도 알려져 있으며,
Scaling Law prediction for LLM 분야에서는 2020 Kaplan et al.과 쌍두마차인 paper라고 할 수 있다.
Hoffmann et al.과 Kaplan et al.은 compute budget이 증가하면 model size와 dataset size를 얼만큼 scaling up 해야 하는가?에 대해 서로 다른 결론을 도출했는데,
즉 \(N_{\text{opt}}(C) \propto C^{a}, D_{\text{opt}}(C) \propto C^{b}\)의 exponent, \(a,b\)가 다른 것이다.
결과적으로 Chinchilla optimal이 하고싶은 얘기는 아래 Figure 1과 같은데,
compute budget이 정해지면 그 budget에 대해서 가장 좋은 성능을 내려면 이전 paper들의 model들과 비교해서 model size는 좀 더 작아야 하고, dataset size는 좀 더 커야, 즉 더 길게 학습해야 한다는 결론에 이르렀다.
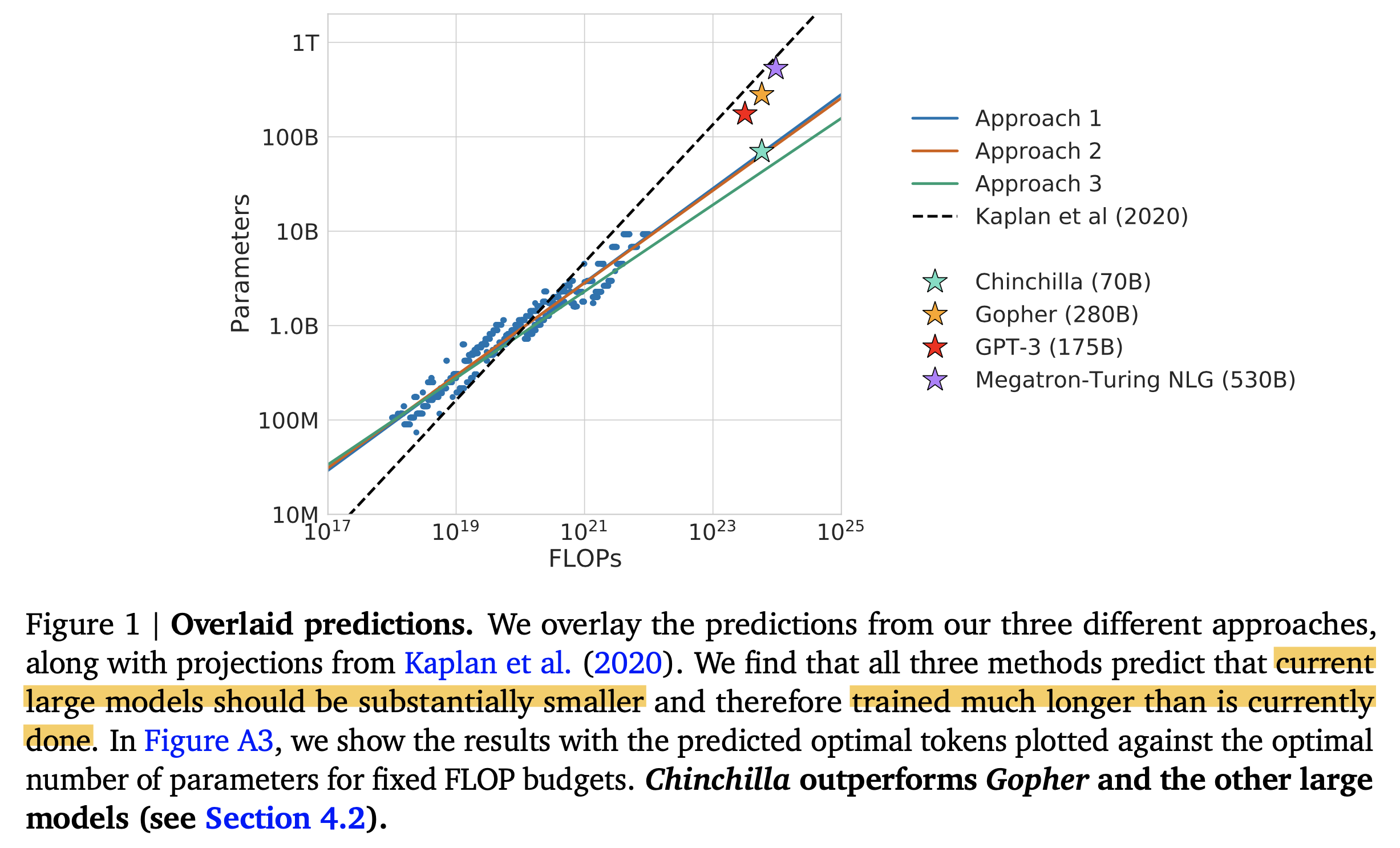 Fig. GPT-3, Kaplan et al.등은 Chinchilla 입장에서는 너무 inefficient하게 학습됐다. 즉 더 작은 model size를 더 길게 학습했어야 한다.
Fig. GPT-3, Kaplan et al.등은 Chinchilla 입장에서는 너무 inefficient하게 학습됐다. 즉 더 작은 model size를 더 길게 학습했어야 한다.
GPT-3는 170B, NVIDIA의 Megatron Turing Neural Language Generator (MT-NTG)는 530B에 달하는 model size를 갖는 등, chinchilla가 등장하기 전 까지만 해도 model size를 키우는 것이 이득인 것처럼 보였으나 chinchilla는 이를 부정한다.
 Fig. 현재 model size를 너무 키우는 trend는 잘못됐다. model size가 더 작다면 inference시에도 더 이점이 있다.
Fig. 현재 model size를 너무 키우는 trend는 잘못됐다. model size가 더 작다면 inference시에도 더 이점이 있다.
저자들은 \(N_{\text{opt}}(C) \propto C^{a}, D_{\text{opt}}(C) \propto C^{b}\)의 exponent값을 구하길 원했는데, 이는 아래 objective function을 minimize하는 것으로 풀 수 있다.
\[N_{\text{opt}}(C), D_{\text{opt}}(C) = \argmin_{N,D \text{ s.t. } FLOPs(N,D)=C} L(N,D)\] Fig.
Fig.
앞서 얘기한 것 처럼 이 paper의 결과는 Kaplan et al.의 그것과 다르다.
결과적으로 Chinchilla라는 이름의 model을 학습할 수 있었는데,
이는 Compute Optimal Model로 model size가 4배나 크지만 훨씬 적게 학습한 Gopher 등에 비해서 월등히 좋은 성능을 보인다고 주장한다.
 Fig.
Fig.
Approach 1: Fixing model sizes and vary number of training tokens
이제 Chinchilla optimum를 계산하는 방식에 대해 알아보자. 저자들이 제안한 approach는 총 3개가 있지만, 결과적으로 다 비슷한 결론에 도달했다고 한다. 즉 compute budget이 늘어나면 model size는 얼만큼? dataset size는 얼만큼? 늘려야하는지를 의미하는 exponent가 거의 비슷했다는 것이다.
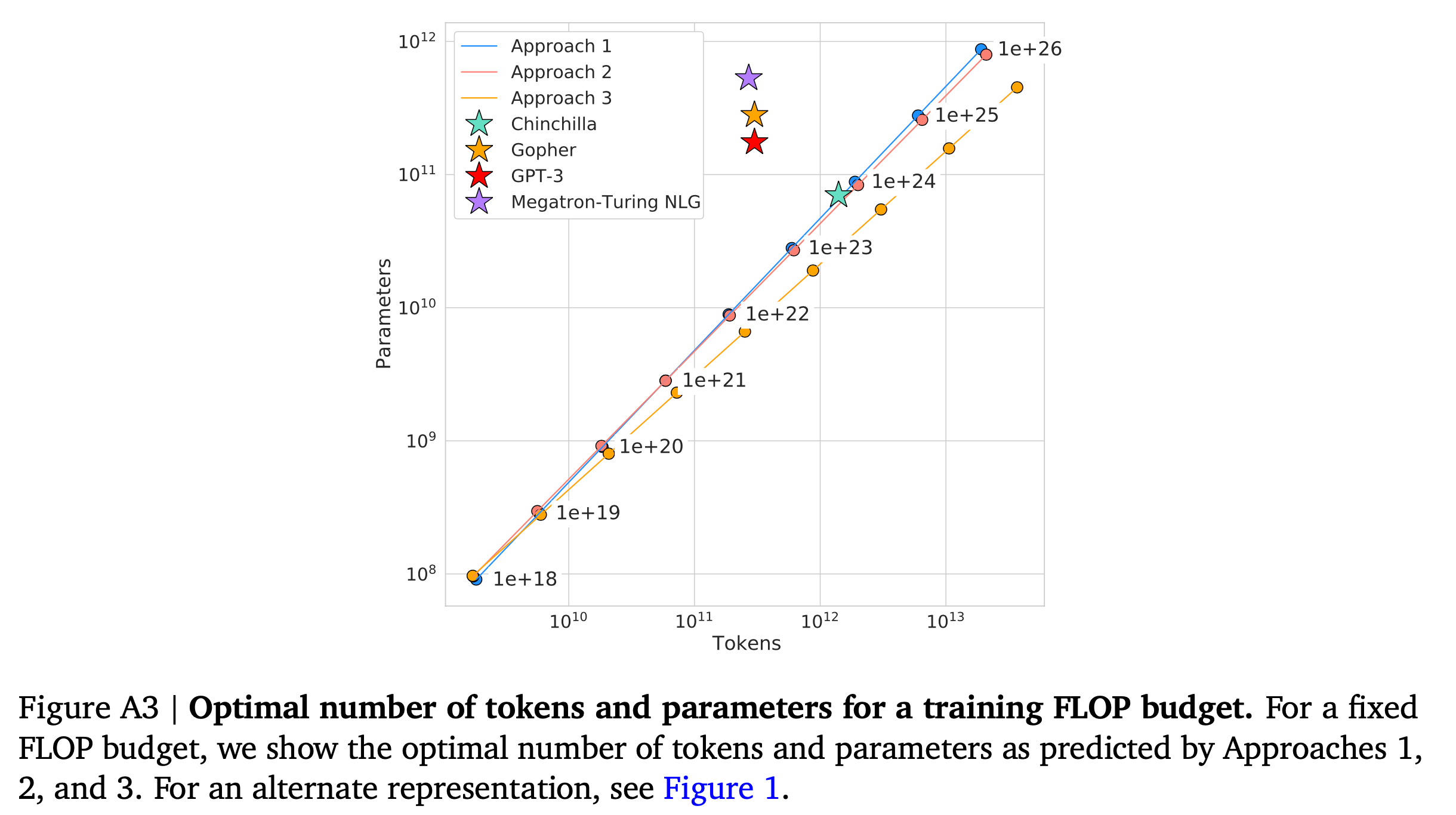 Fig. 사실 Approach 3는 살짝 deviate한 것 처럼 보인다.
Fig. 사실 Approach 3는 살짝 deviate한 것 처럼 보인다.
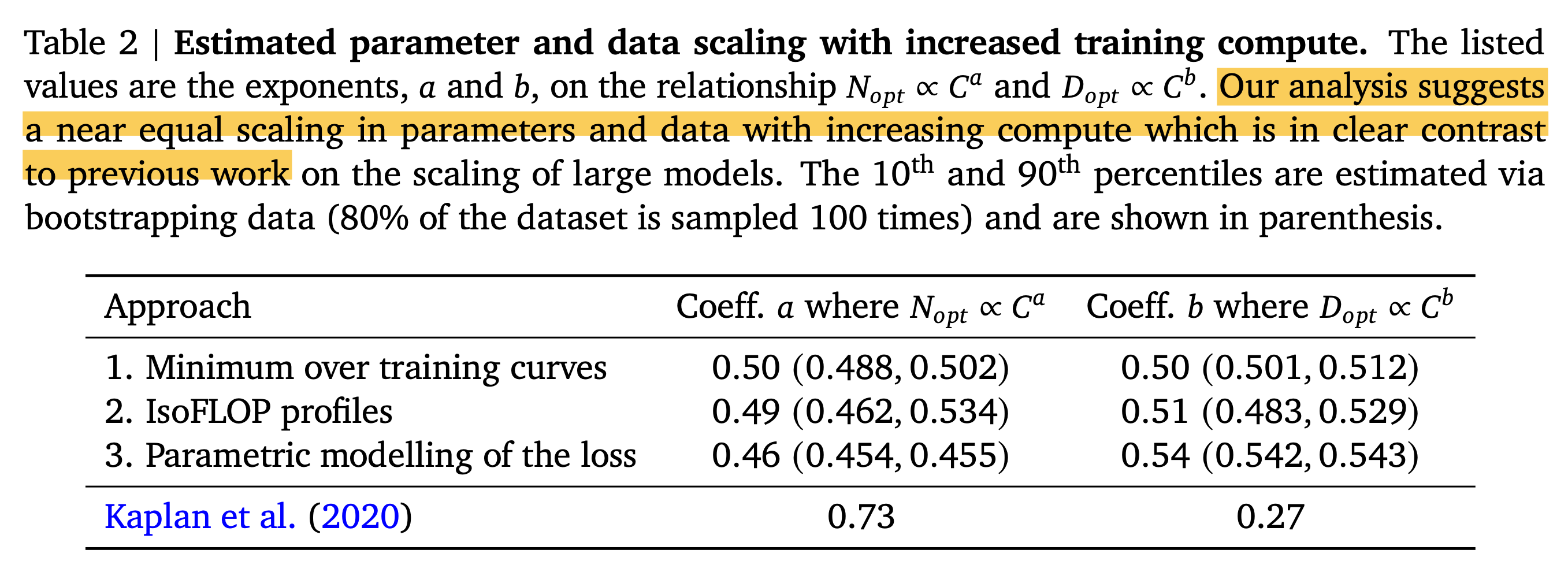 Fig. 실제로 Approach 3의 exponent는 값이 좀 다르다.
Fig. 실제로 Approach 3의 exponent는 값이 좀 다르다.
먼저 Approach 1에 대해서 알아보도록 하자.
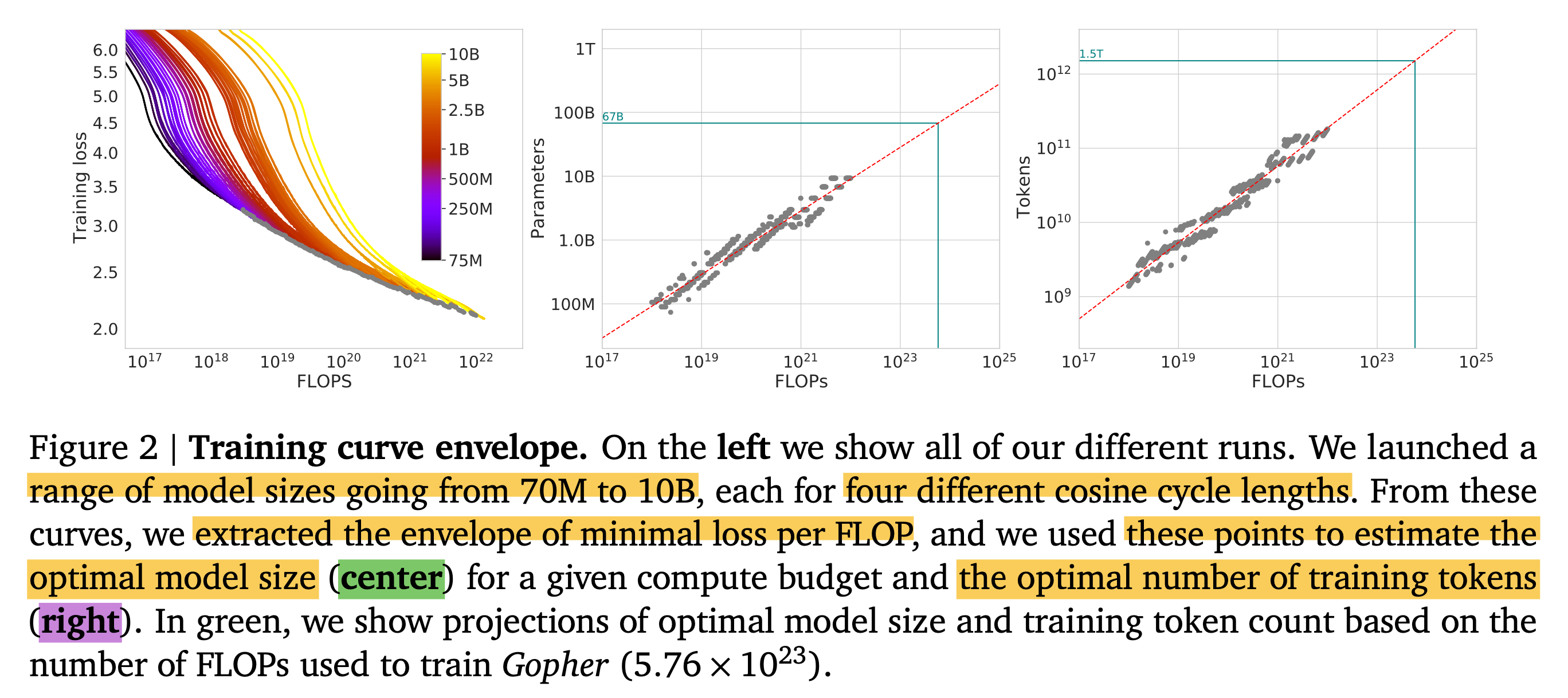 Fig.
Fig.
Approach 1에서는 70M부터 10B 정도 size의 model들에 대해서 각각 model size를 fix하고 4개의 다른 number of training sequences, dataset size에 대해서 final loss가 어떻게 찍히는지 관측하고, power function을 fitting했다. 그 결과 compute budget, \(C\)와 그 때의 optimal model size, dataset size를 의미하는 \(N_{\text{opt}}, D_{\text{opt}}\)에 대해서 아래의 관계 식의 exponent를 얻을 수 있었다고 한다.
\[\begin{aligned} & N_{\text{opt}} \propto C^a = C^{0.5} & \\ & D_{\text{opt}} \propto C^b = C^{0.5} & \\ \end{aligned}\]Approach 2: IsoFLOP profiles
Approach 2는 IsoFLOP이라고 알려져 있는데,
이는 고성능 컴퓨팅 (High Performance Computing; HPC) 분야에서 사용되는 말이다.
Iso-라는 접두사는 그리스어 isos 에서 유래했다고 하며, “동일한” 이라는 의미를 같는다.
즉, 같은 부동 소수점 연산 횟수 (FLOP)를 갖는다면 model size가 얼마든지 같이 묶이는 것이다.
이를 위해서 먼저 9개의 서로 다른 fixed FLOP (ranging from \(6e18 \sim 3e21\) FLOPs)마다 십 수번의 \((N,D,L)\)조합을 실험한다 Figure-3(left).
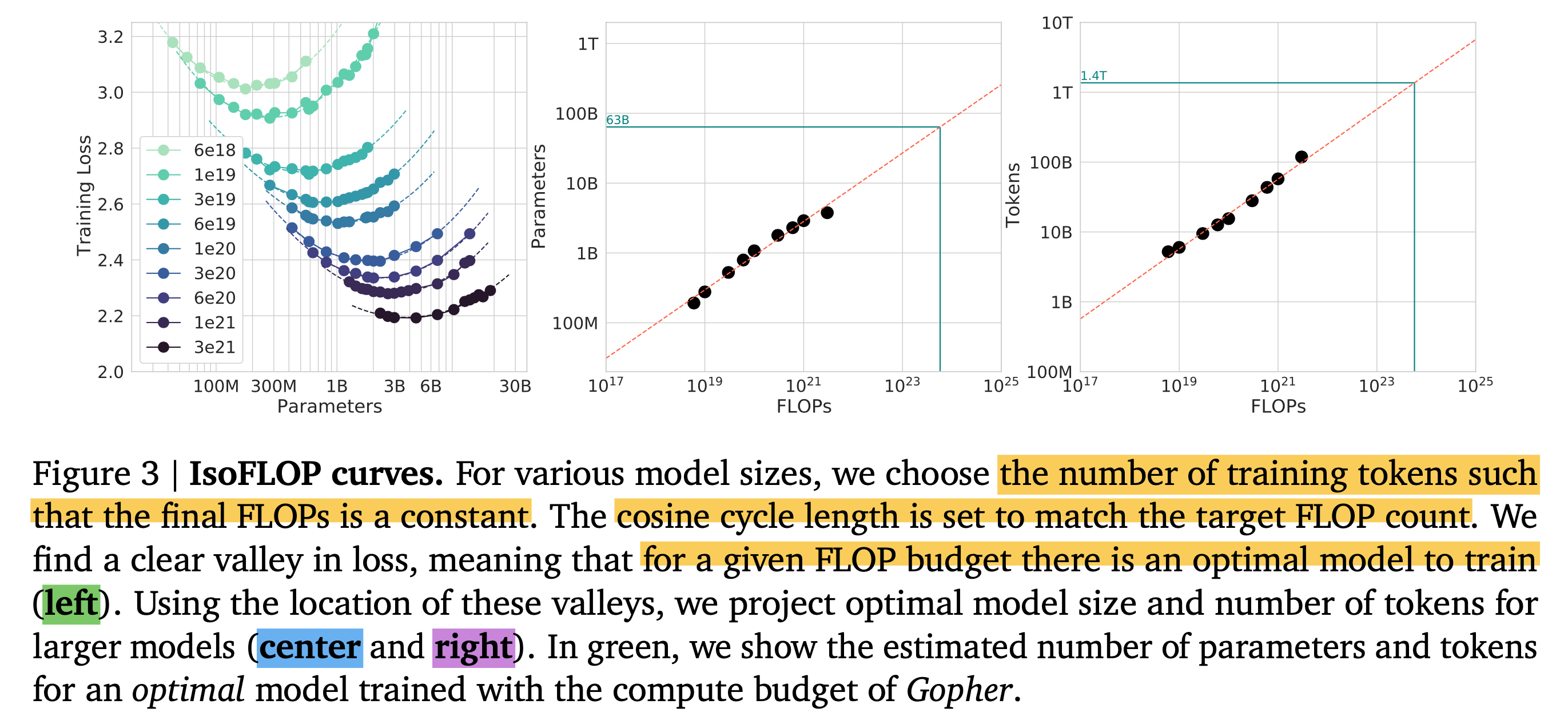 Fig.
Fig.
그리고 각 fixed budget 가운데 가장 loss가 낮은 \((N,D,L)\)에 대해서 power function fitting을 진행하여 Figure-3(center, right)를 얻는다. 그 결과 아래의 exponent를 얻을 수 있었는데, approach 1과 크게 차이가 안난다는 점을 알 수 있다.
\[\begin{aligned} & N_{\text{opt}} \propto C^a = C^{0.49} & \\ & D_{\text{opt}} \propto C^b = C^{0.51} & \\ \end{aligned}\]Approach 3: Fitting a parametric loss function
Approach 3는 parameteric approahc이다. 말 그대로 linear regression을 하듯 given parameter를 fitting하는 것이다. 이에 사용될 functional form은 다음과 같으며,
\[\hat{L}(N,D) \triangleq E + \frac{A}{N^\alpha} + \frac{B}{D^\beta}\]우리는 아래 objective function을 optimize할 것이다.
\[\min_{A,B,E,\alpha,\beta} = \sum_{\text{Runs } i} \text{Huber}_{\delta} (\log \hat{L} (N_i, D_i) - \log L_i)\]이는 predicted log loss와 observed log loss사이의 Huber loss를 최적화 하는 것이 되는데,
observed loss야 우리가 실험을 통해서 얻을 값이고,
predicted loss는 위에 정의한 것 처럼 총 세 가지 term으로 이루어져 있다.
먼저 \(E\)라는 term은 natrual language의 entropy라고 되어있는데,
쉽게 말해서 infinitde size의 model을 infinite data에 대해 학습할 경우를 얘기한다.
즉 아무리 학습해도 넘을 수 없는 gap을 의미하는 것이라 할 수 있다.
2nd term, \(\frac{A}{N^\alpha}\)는 \(N\)에만 의존하는 term으로,
완벽하게 학습된 \(N\) size의 transformer가 보일 수 있는 ideal performance보다 얼마나 떨어지는지를 포착하고,
마지막 3rd term, \(\frac{B}{D^\beta}\)는 \(D\)에만 의존하는 term으로,
우리가 보통 model이 정해진 size의 dataset만을 학습하기 때문에 실제로는 convergence할 때 까지 학습할 수 없다는 사실을 포착하는,
즉 얼마나 undertraining 되었는지를 포착하는 term이라고 할 수 있다.
다르게 말하면 E는 kaplan et al.에서도 irreducible loss라는 표현을 쓰는데,
이를 의미하는 것이고, 2nd and 3rd term은 각각 model과 data가 유한할 경우를 내포하고 있다고 할 수 있다.
저자들은 실제로 정의한 Huber loss와 LBFGS 라는 optimization algorithm을 통해 아래의 결과를 얻었는데, (자세한 내용은 paper와 appendix 참고)
\[L(N,D) = \underbrace{1.69}_{E} + \frac{406.4}{N^{0.34}} + \frac{410.7}{D^{0.28}}\]여기에 Gopher (280B)와 Chinchilla (70B)의 model size와 trained tokens를 대입하면 우리는 아래와 같은 결과를 얻을 수 있다.
\[\begin{aligned} & \underbrace{L(280 \cdot 10^9, 300 \cdot 10^9)}_{\color{blue}{Gopher}} = 1.69 + 0.052 + 0.251 = 1.993 & \\ & \underbrace{L(70 \cdot 10^9, 1400 \cdot 10^9)}_{\color{red}{Chinchilla}} = 1.69 + 0.083 + 0.163 = 1.936 & \\ \end{aligned}\]그니까 우리는 주어진 data distribution과 model architecture에서 얼마나 Gopher가 비효율적으로 크고 적게 학습됐는지를 알 수 있는 것이다.
아래 figure는
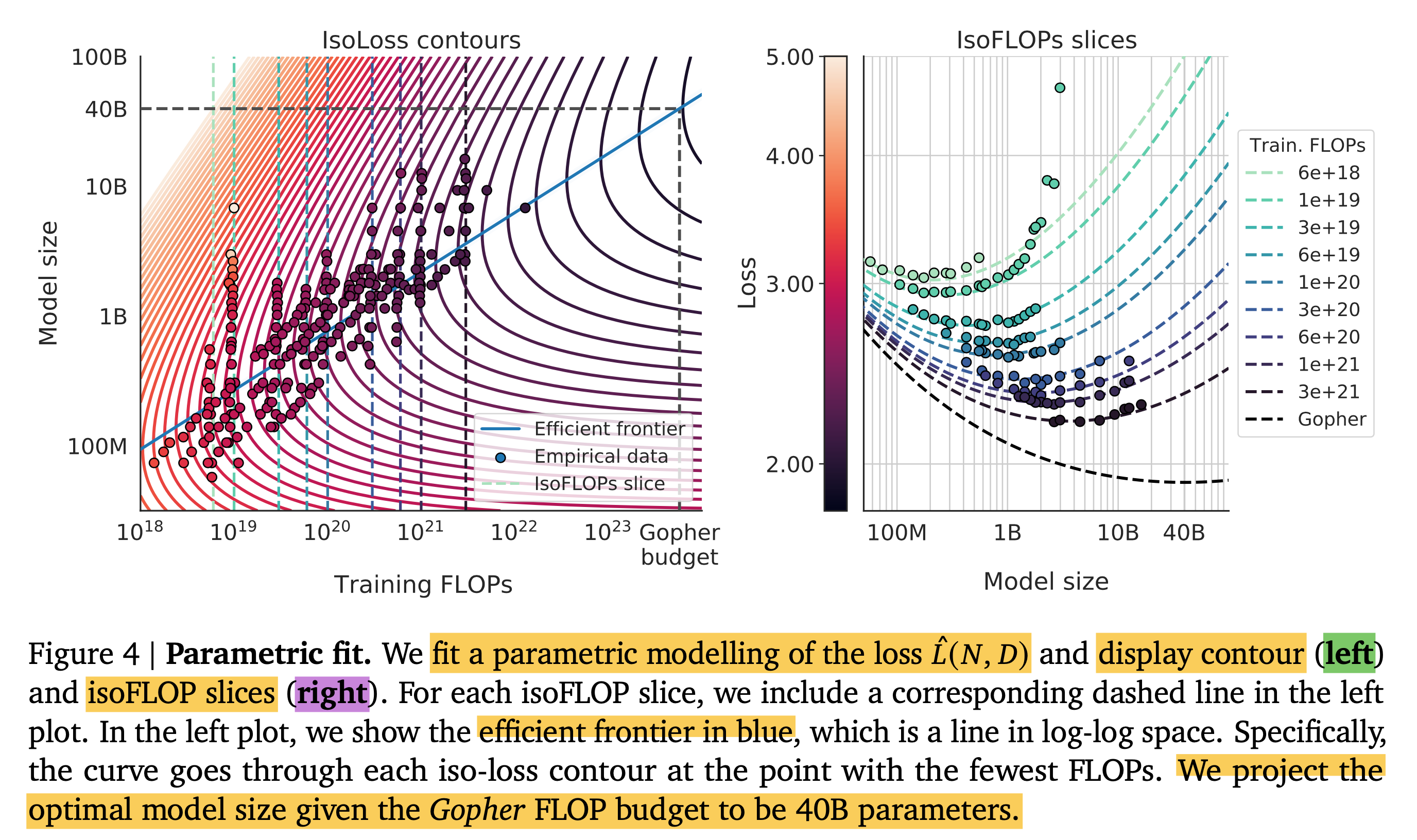 Fig.
Fig.
Optimal Model Scaling Results (Gopher (280B) vs Chinchilla (70B))
 Fig.
Fig.
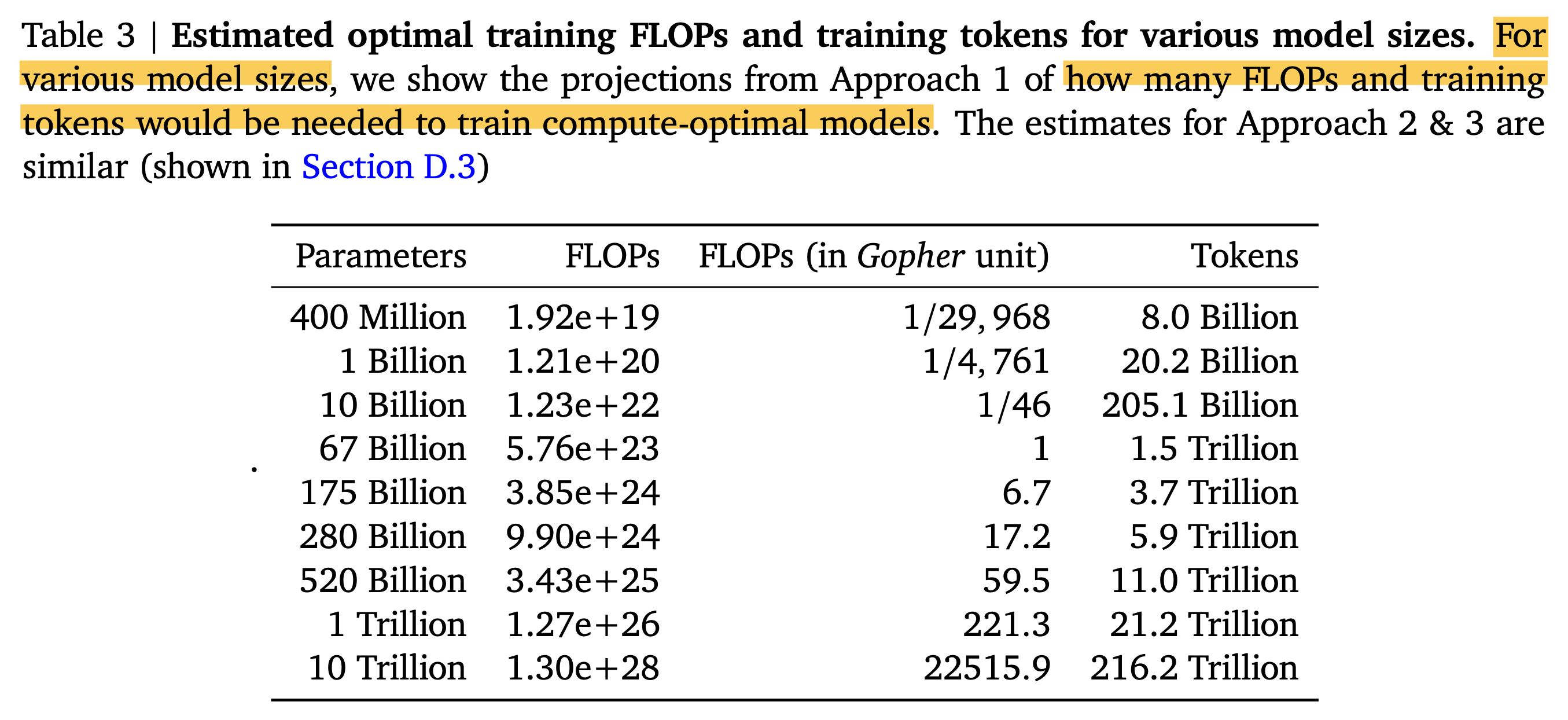 Fig.
Fig.
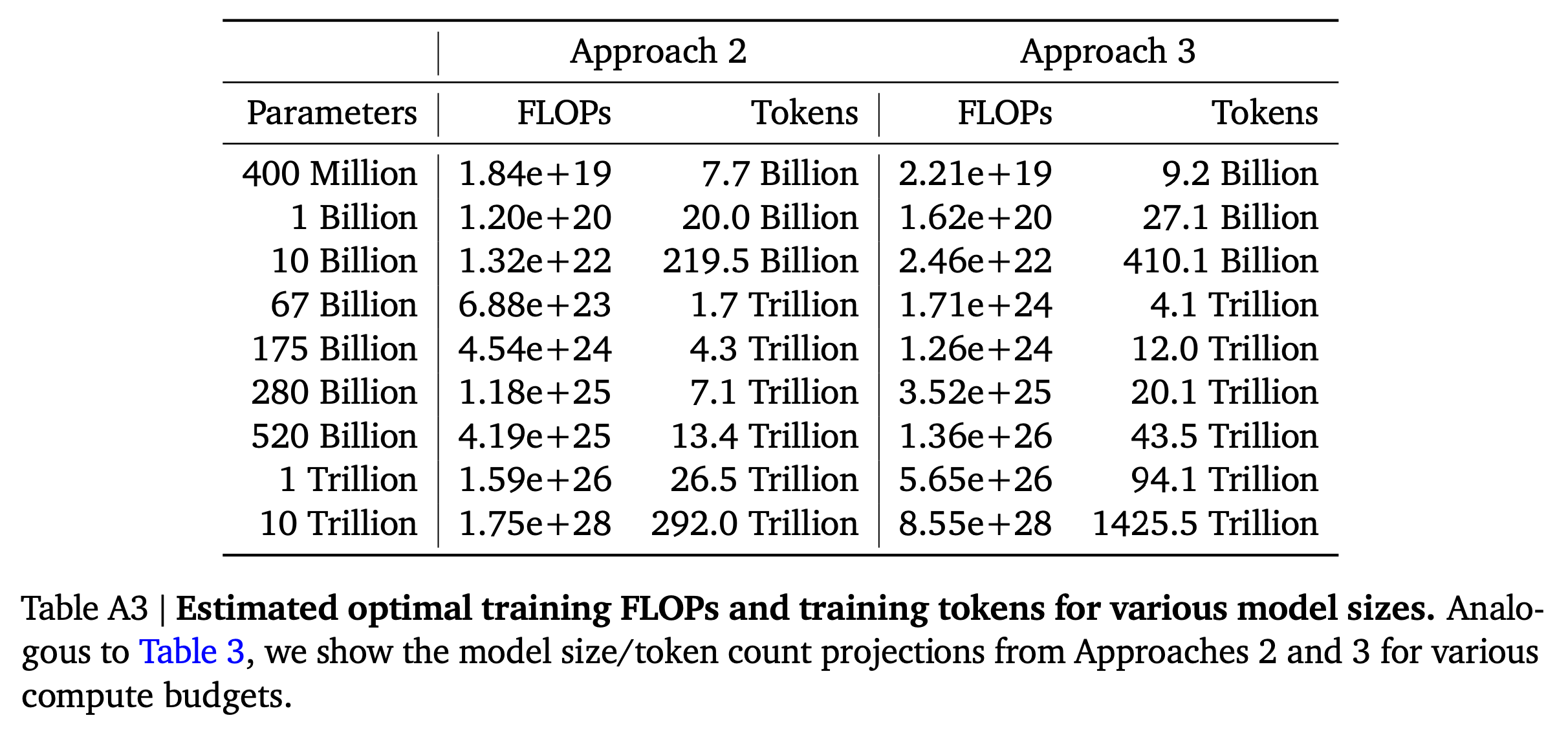 Fig.
Fig.
 Fig.
Fig.
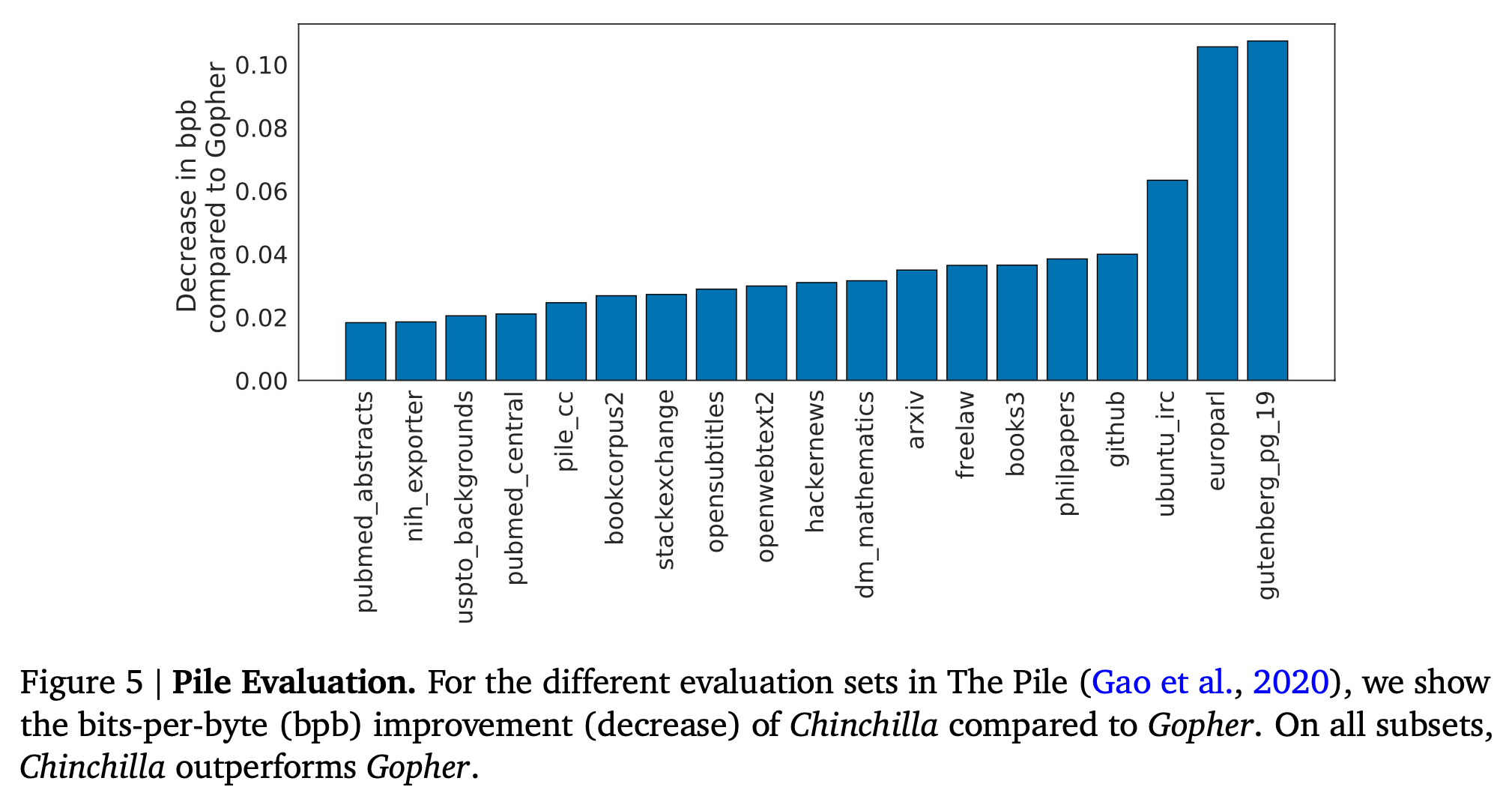 Fig.
Fig.
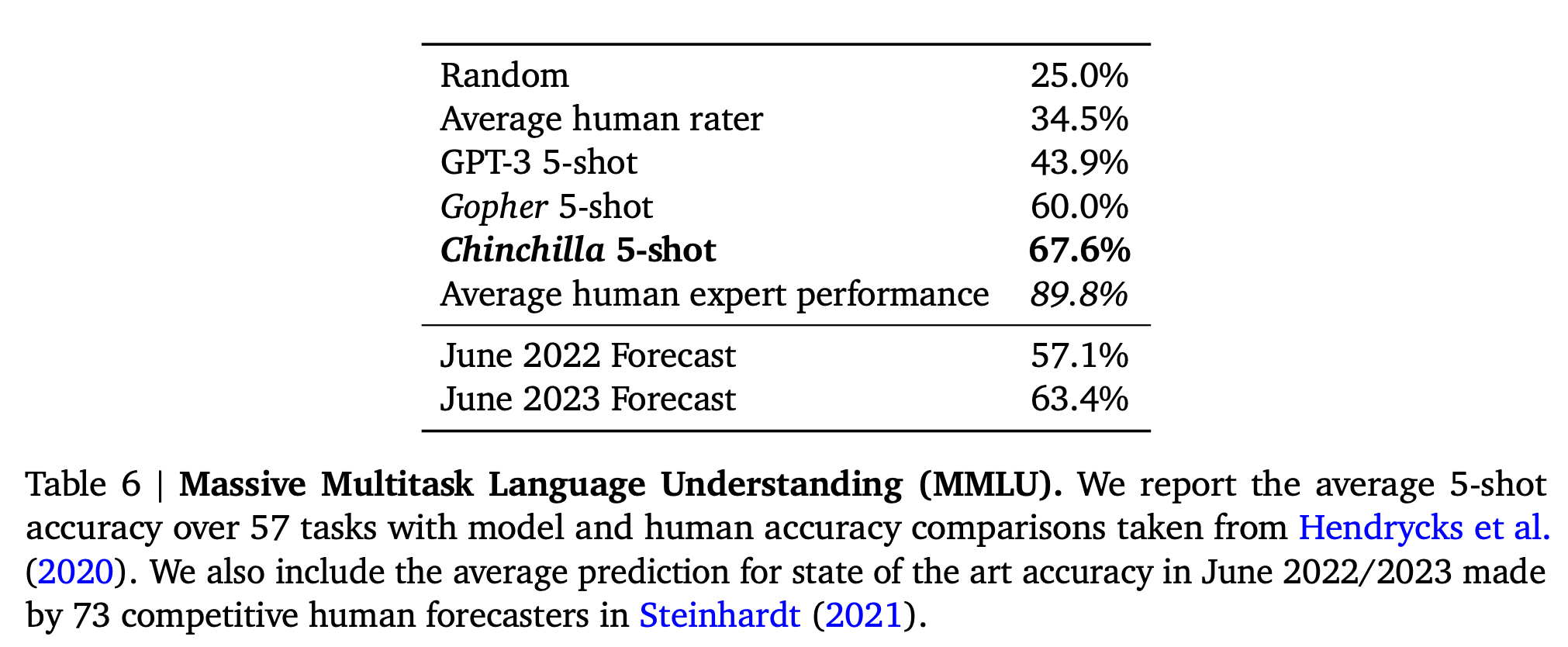 Fig.
Fig.
Consistency of scaling results across datasets
 Fig.
Fig.
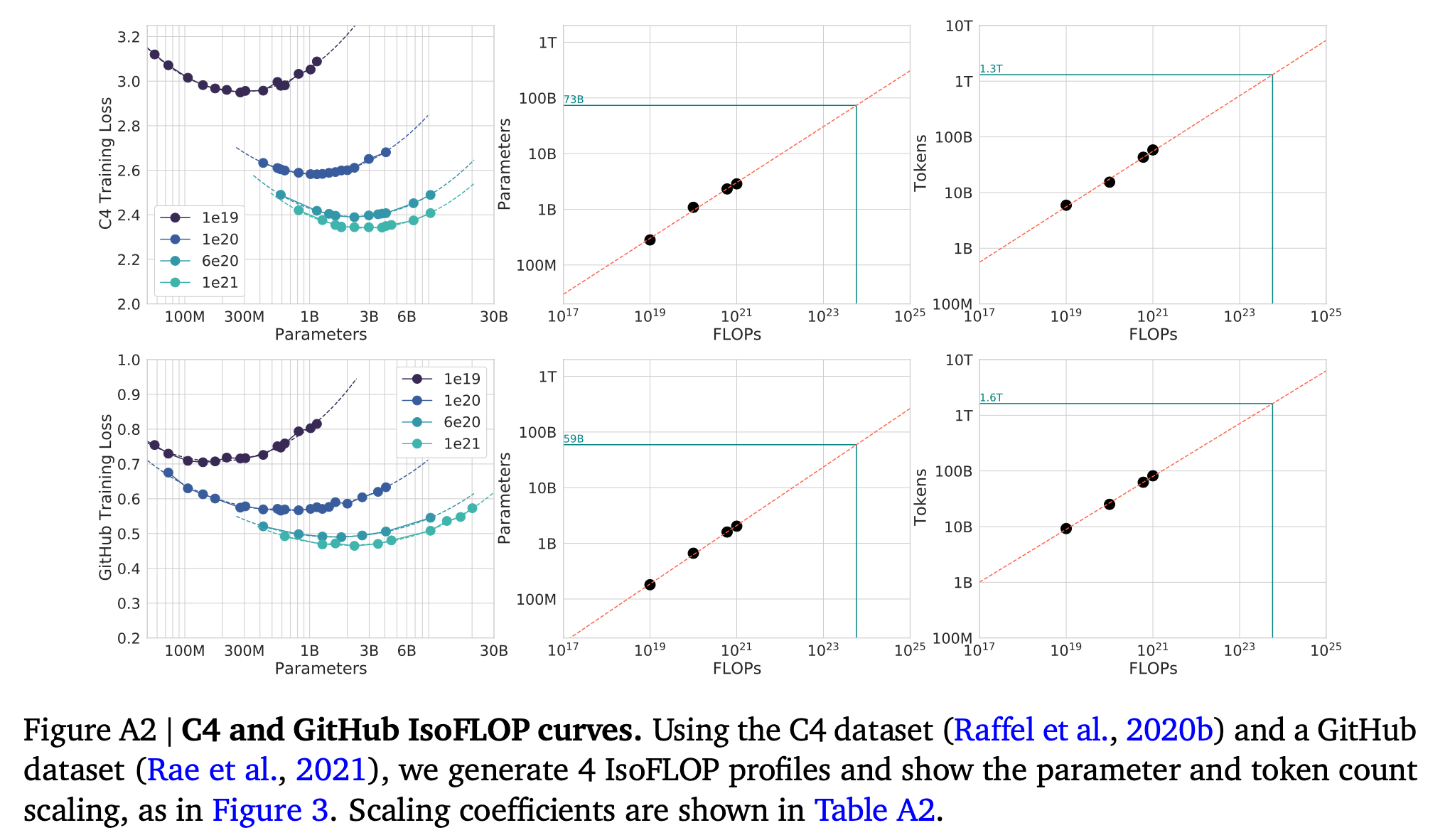 Fig.
Fig.
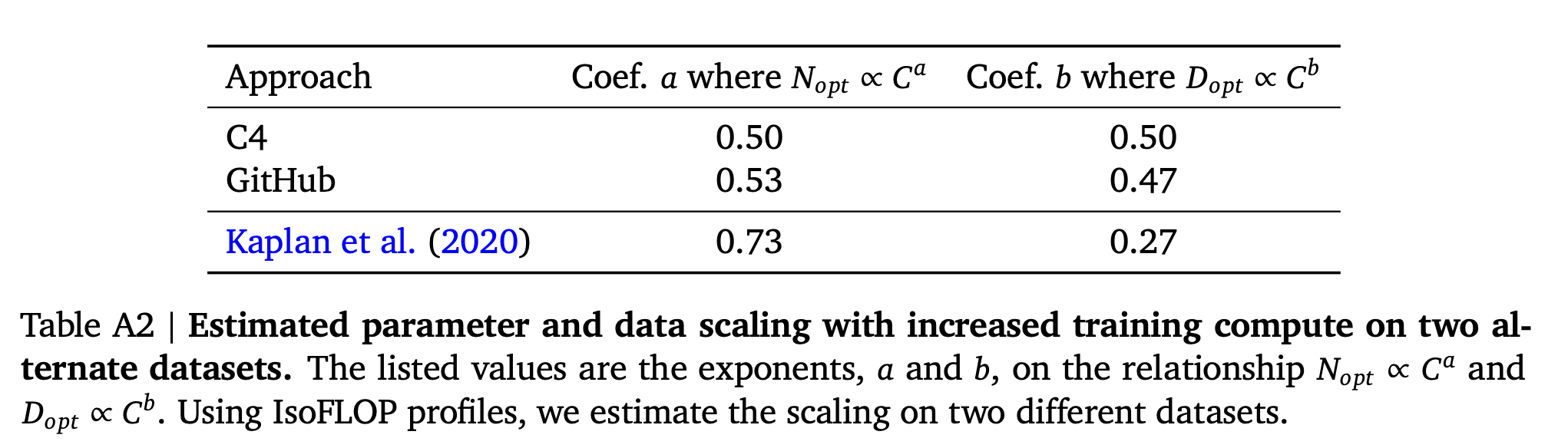 Fig.
Fig.
Compared to Kaplan et al.
 Fig.
Fig.
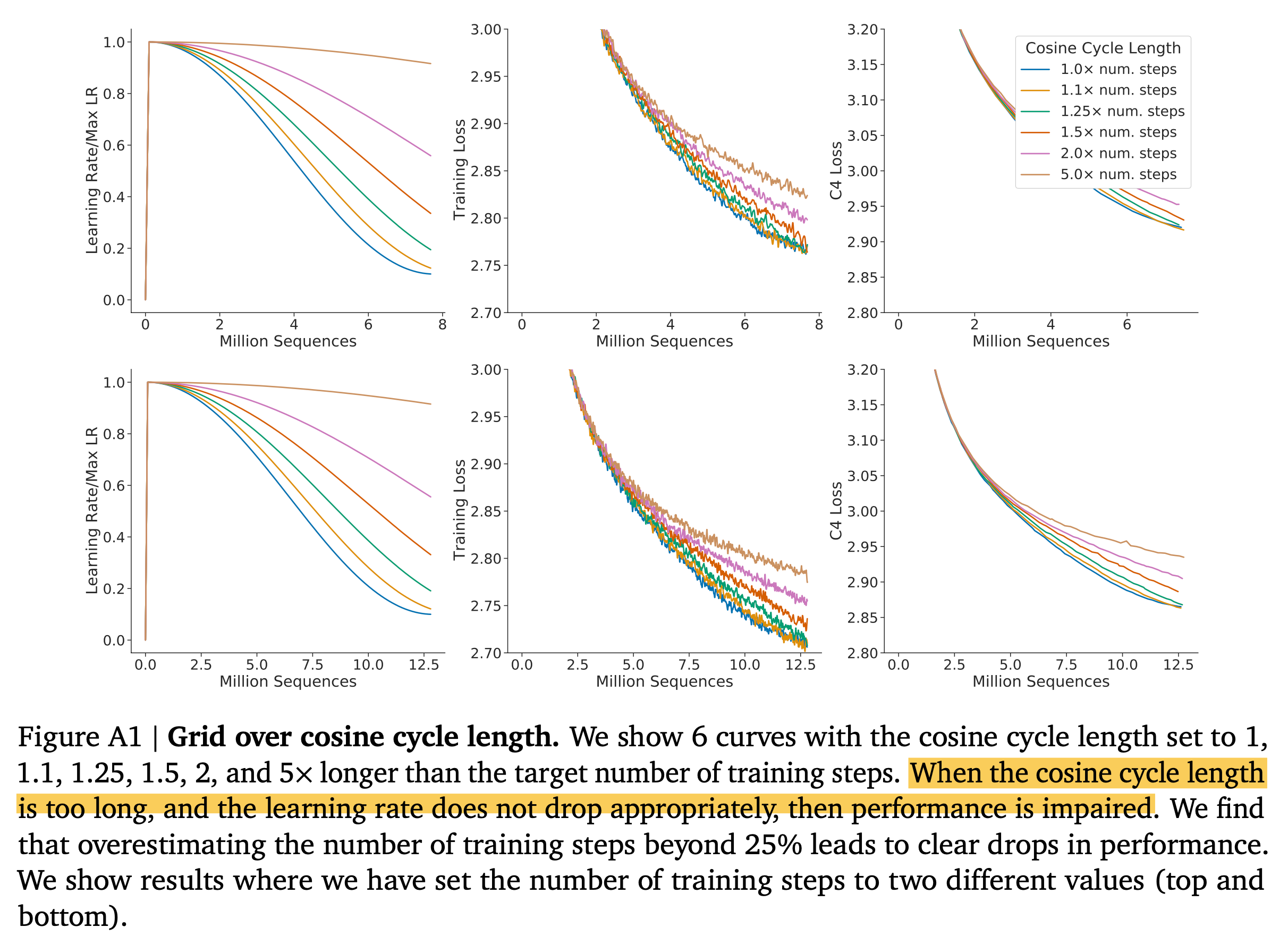 Fig.
Fig.
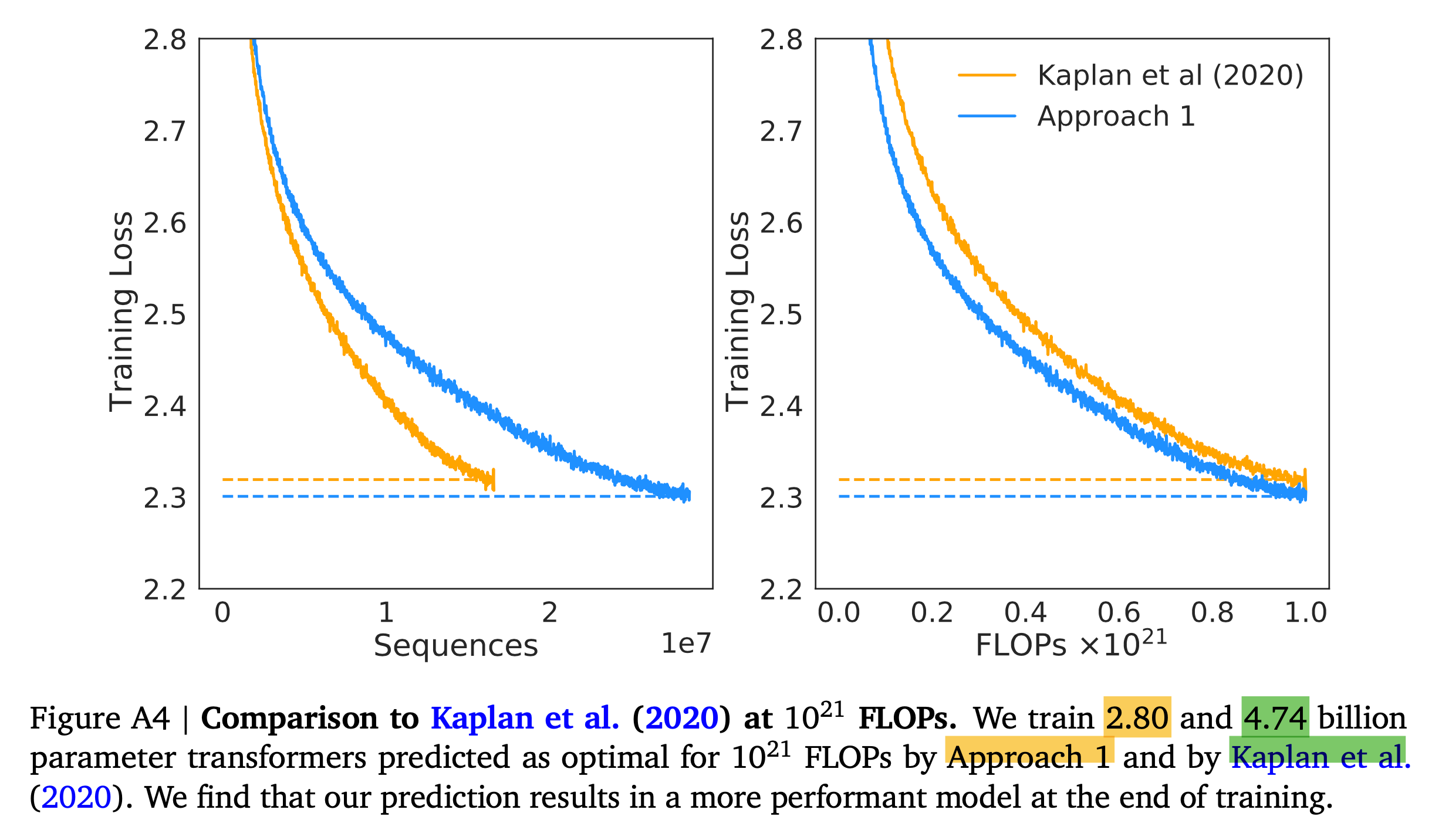 Fig.
Fig.
Curvature of the FLOP-loss frontier
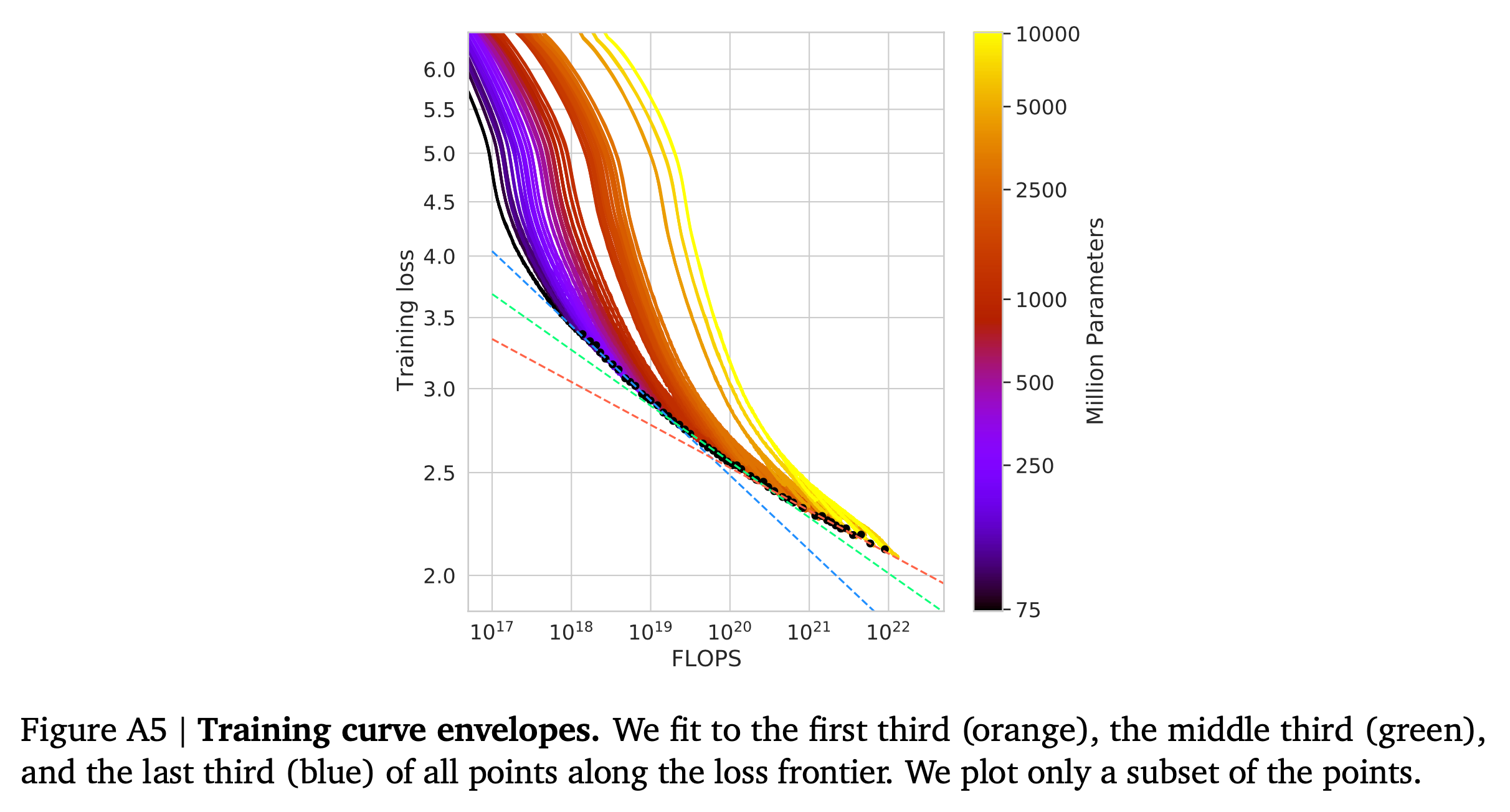 Fig.
Fig.
Other differences between Chinchilla and Gopher
사실 Gopher와 Chinchilla는 compute budget에 따른 model size, dataset size allocation만 다른 것은 아니다. Chinchilla는 AdamW Optimizer를 썼는데 반해 Gopher는 Adam을 썼고, Chinchilla는 optimizer state에 대해서 higher precision copy를 썼고 Gopher는 아니라고 하는데, 아마 이는 mixed precision 얘기를 하는 것 같다.
 Fig. 아니 아무리 bf16을 쓰더라도 Adam update시 mixed precision은 써야하는 것 아닌가?
Fig. 아니 아무리 bf16을 쓰더라도 Adam update시 mixed precision은 써야하는 것 아닌가?
아래 figure를 보면 간단히 해석이 가능할텐데, 결과적으로 AdamW, higher precision을 쓴게 더 좋았다는 것이다.
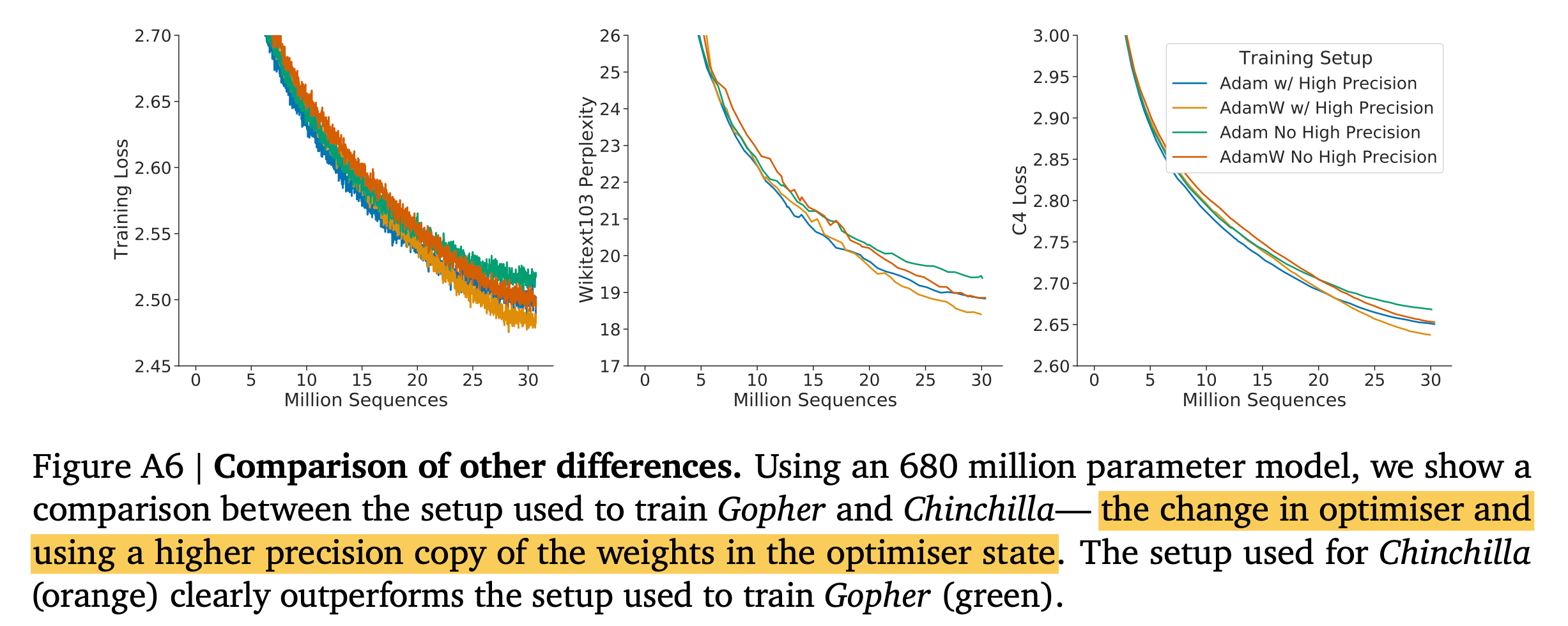 Fig.
Fig.
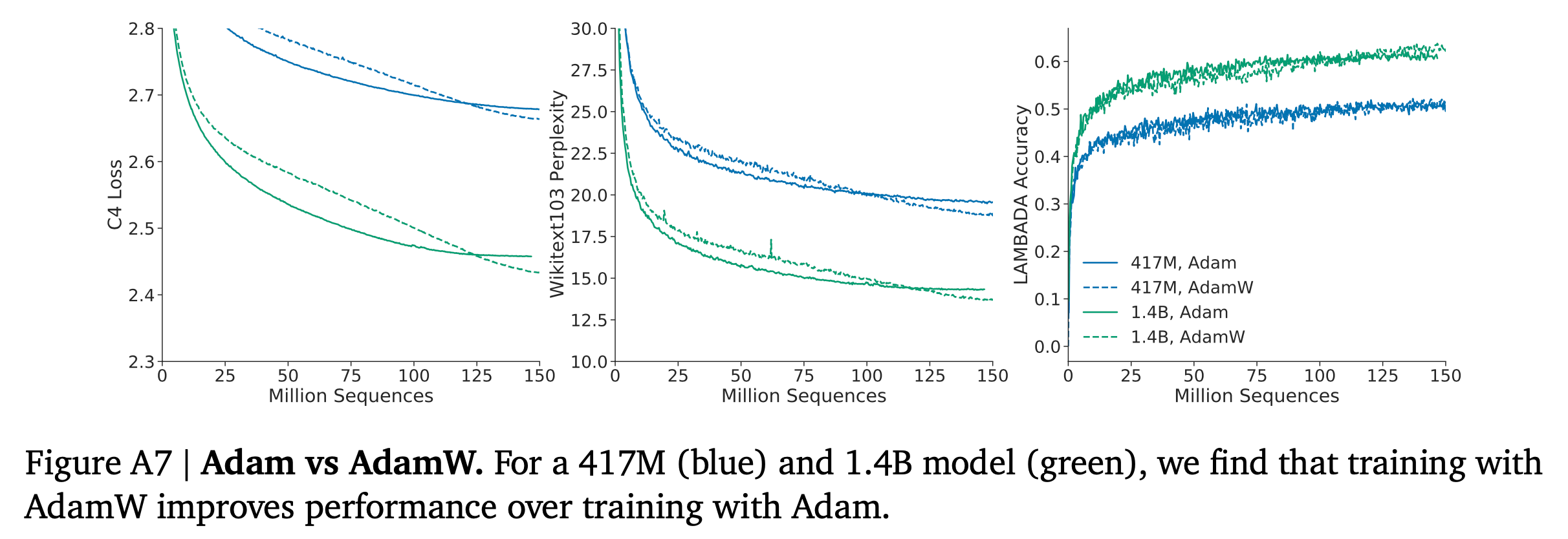 Fig.
Fig.
아마 이런 issue 때문에 280B를 이겼다고 할 순 없을 것 같고, 우리는 AdamW와 mixed precision을 써야한다는 takeaway만 기억하면 될 것 같다.
Limitations
 Fig.
Fig.
 Fig.
Fig.
A Replication Attempt for Chinchilla Scaling Approach 3
It is Compute Optimal! Not Optimal!
사실 왜 Kaplan et al.과 Hoffmann et al.의 결과에 차이 (discrepency)가 있는지,
어떤게 맞는지 결론을 내기 어렵다.
게다가 매몰되지 말아야 할 것이 있는데,
Kaplan et al.이나 chinchilla의 compute optimal은 말 그대로 Model Size가 70B일 경우 Compute Optimal에 따르면 training tokens를 그렇게 배정해야 한다는 것이지, 이것이 70B Model의 최고의 성능은 아니라는 것이다.
예를 들어 한 번 compute budget이 정해지면 7B를 10T tokens할 바에야 70B를 더 적게 (1.4T 정도?) 학습하는게 더 computationally efficient 하다고 할 지언정,
모종의 이유로 (대부분 inference비용 문제일듯) model size를 7B로 정했다고 해도 7B의 compute efficient training tokens는 2T일 수 있지만 그보다 더 길게학습해도 문제는 없는 것이다.
오히려 model performance는 거의 대부분의 경우에 무조건 좋아지기 마련이다.
아마 같은 data를 one epoch 이상 보는것이 아니라면 그럴 것이다
최근 나오고있는 SOTA model들은 거의 다 Over-Training되고 있다.
(GPT-4, Claude 제외, 이들은 어떻게, 얼마나 학습되었는지 알려져있지 않지만 아마 그러지 않았을까)
 Fig.
Fig.
실제로 아래 tweet을 보면 Eluther AI의 한 researcher는 Chinchilla optimal에 대해서 많은 사람들이 오해하고 있다고 얘기한다. 요약하자면 Chinchilla optimal이란 “Fixed budget에 대해서 어떻게하면 가장 낮은 loss를 달성할 수 있을까요?”에 대한 내용을 다루고 있으며, 만약 당신이 fixed model size 혹은 fixed dataset size를 가지고 있다면 더이상 optimal이 아닐 것이라는 것이며, 예를 들어 fixed model size를 학습할 것이라면 언제나 over-training하는 것이 성능상 제일 좋을 것이라는 말이다.
 Fig. Source from here
Fig. Source from here
 Fig. Source from here
Fig. Source from here
그러니 Compute optimal이라는 말에 너무 매몰되지 말도록 주의해야 할 것이다.
Some Papers of Large Language Model (LLMs) Exploring Scaling Exponents in Realistic Scenario
DeepSeek LLM: Scaling Open-Source Language Models with Longtermism
2024년에 나온 꽤 유망한 LLM중 하나인 DeepSeek의 Technical Report에는 요즘 opensource community에서는 Scaling Law를 무시하고 fixed size의 high quality model을 학습하려고 하는 경우가 많다며 이를 비판하는 다음과 같은 문구가 있다.
 Fig.
Fig.
DeepSeek은 Scaling Law를 분석하고 최적의 model size, batch size, LR 등과 compute budget간의 relationship을 밝혀냄으로써 매우 좋은 model을 손에 넣을 수 있었는데, 이 paper의 핵심 contirubition은 다음과 같다.
- Compute budget, C 와 optimal batch size, LR 간에 power law 관계가 성립한다는 것을 보임
- kaplan, Hoffmann 이 주장하는 Scaling Law는 서로 model size가 커질경우 dataset size가 얼마나 커져야 하는지에 대해서 다른 결과를 도출했는데, 그 이유는 (kaplan의 경우) embedding을 포함하지 않았거나 했기 때문이므로, 아예 정확하게 token당 필요한 FLOPs 라는 factor, M을 정의해서 C=6ND가 아닌 C=MD를 정의해서 7B, 67B model에 대해서 정확히 Scaling Law를 예측함
 Fig.
Fig.
여기서 첫 번째의 경우, model size, N 등이 달라질 때 마다 optimal HP로 tuning된 성능을 기준으로 Scaling Law prediction을 해야 하는데, kaplan, Hoffmann 등 주요 논문에서 이 부분이 빠져있기 때문에 이 관계에 대한 empirical study를 한 것은 실제로 Scaling Law를 적용할 이들에게 좋은 insight를 줄 것이다.
 Fig.
Fig.
Power Law Relationship between Compute Budget, C and optimal batch size and LR
그래서 어떻게 batch size, LR에 대한 power law를 fitting했을까. 우선 이들이 batch size, LR의 power law만 찾는 이유는 다른 HP들은 model size등이 변할 때 경험적으로 값들이 크게 변하지 않기 때문이었다고 한다.
 Fig.
Fig.
저자들은 \(C\)가 증가하면 batch size, LR이 어떻게 변하는지에 대한 power function을 찾기 위해서 먼저 \(1e17\)의 fixed compute buedget과 \(177M\) Flops/token의 model size를 정하고 (그렇다면 \(D=C/M\)으로 정해질 것) 정해진 범위 내의 batch size, LR을 grid search 했다.
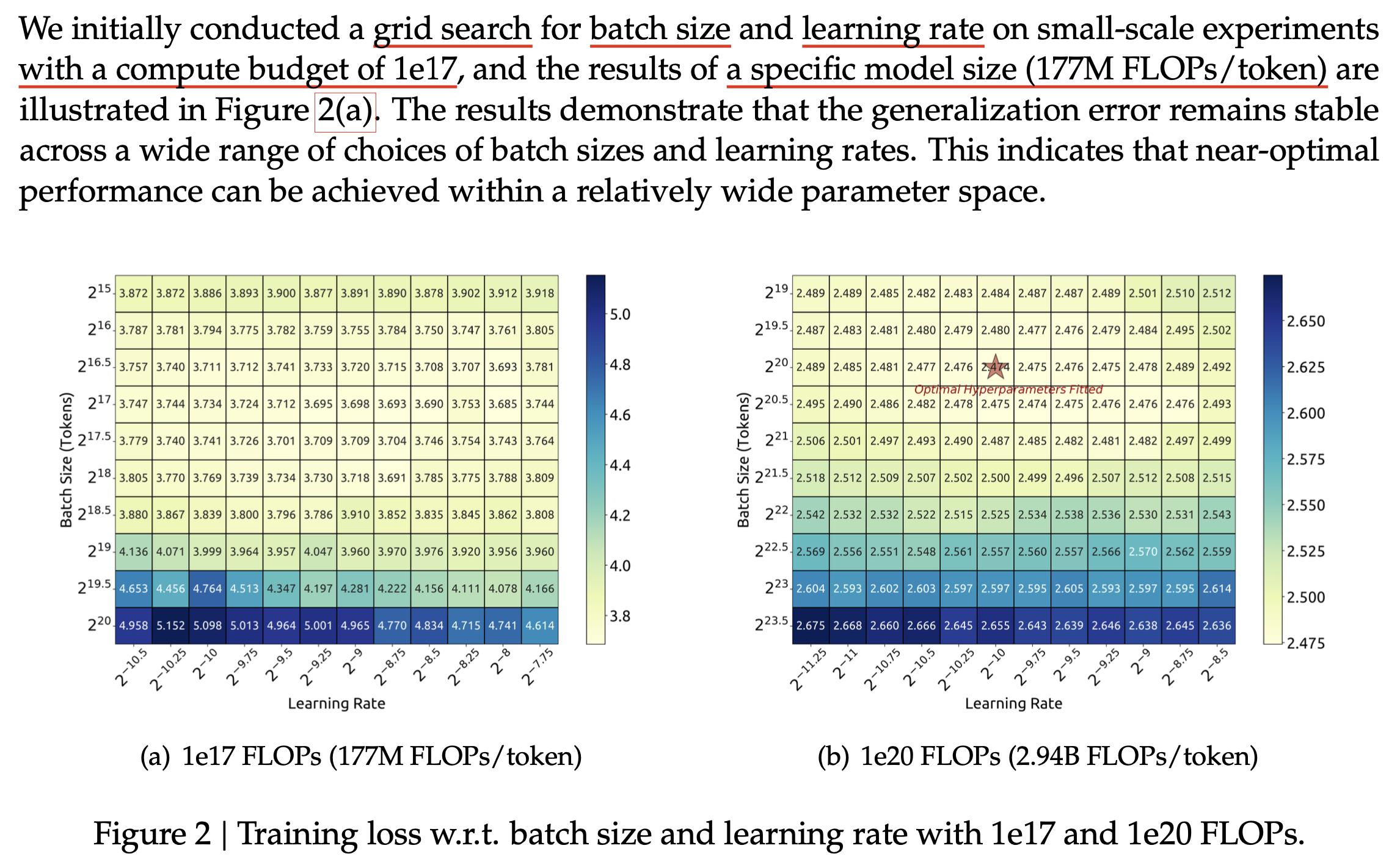 Fig.
Fig.
그리고 \(C\)를 \(1e17 \sim 2e19\)까지 늘려가면서 (즉 model size는 고정이므로 dataset size, \(D\)를 늘려가면서) minimum loss의 \(0.25\%\)수준을 보이는 near optimal value들을 좌표계에 다 찍어서 curve fitting을 한 결과 아래의 power function을 얻을 수 있었다고 한다.
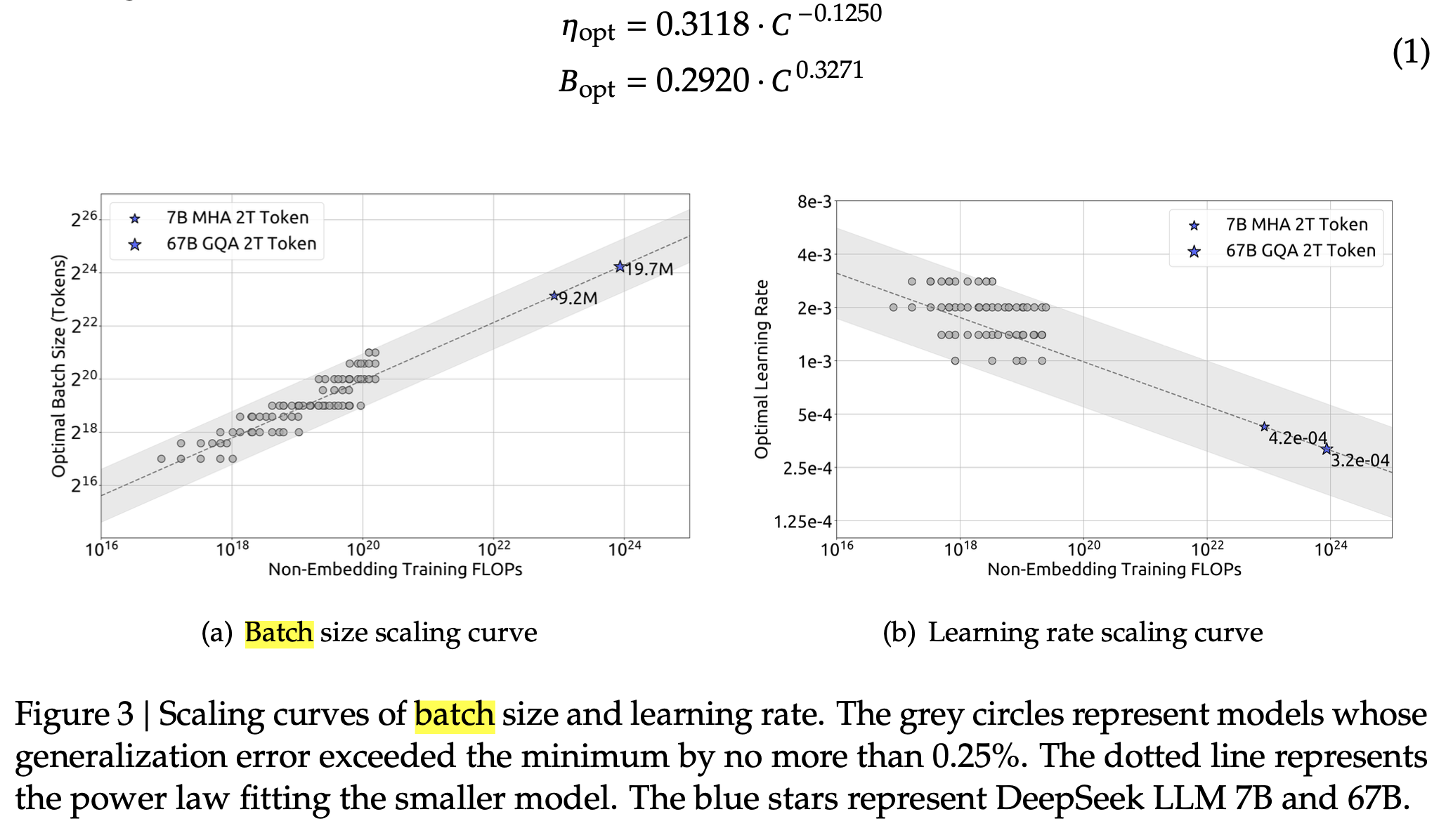 Fig.
Fig.
즉 Compute Budget, C가 증가할수록 batch size는 키워야 하고 LR은 줄여야 한다는 결론에 다다랐으며,
얼만큼 줄여야 하는지도 알아낸 것이다.
그 결과 Figure 2(b)의 \(C=1e20\), \(M=2.94B\) FLOPs/tokens model size에 대해서 batch_size, LR을 찾아 fitting을 한 것이 grid search 한 것 중 optimum인 것과 정확히 일치한다는 결과를 보였다.
 Fig.
Fig.
하지만 이는 \(C\)에 대한 optimal batch size, LR의 power law로 Kaplan et al.의 target loss, \(L\)에 대한 critical batch size과는 차이가 있으니 잘 생각해서 받아 들여야 할 것이다. 그리고 이 결과는 DeepSeek에서 제안하는 multi step LR scheduler를 쓴 것이고 dataset이나 model arch에 따라 달라질 수 있으므로 맹신하면 안된다. 그리고 batch size warming up같은 것도 고려가 되어있지 않다.
개인적으로는 \(C\)가 같다면 model size가 7B거나 70B거나 같은 batch size, LR을 쓰는 것이 optimal이라는 것에 거부감이 들기는 한다.
Estimating Optimal Model and Data Scaling
저자들은 Compute Budget, \(C\)에 대해 찾은 optimal batch size, LR을 통해 \(C\)가 증가하면 model size, dataset size를 얾나큼 늘려야 하는지에 대한 model/data scaling-up strategy를 찾는 실험을 했다.
즉 아래 scaling exponent를 찾는 것이다.
여기서 \(C\)는 대략적으로 \(C=6ND\)관계를 따른다고 앞서 Kaplan et al.에서 밝혔는데, kaplan은 \(N=N_1\)을 따르며 이는 embedding matrix를 포함하지 않은 parameter의 수를 의미했고, Hoffmann et al.은 embedding을 포함한 \(N=N_2\)를 썼다. 하지만 DeepSeek의 저자들은 이들 모두 잘못됐다고 얘기한다.
 Fig.
Fig.
왜냐하면 둘 다 attention opeation의 computational overhead를 고려하지 않았고, Hoffmann et al.의 경우 embedding matrix는 compute에 기여하는 데 비해 너무 방대한 model size를 갖는다고 주장한다. (아마 embedidng layer는 look up만 하는 데 반해서 vocab_size * hidden_size 만큼의 크기를 갖기 때문인 듯 하다. 실제로 대부분의 LLM에서 embedding matrix가 같는 portion은 매우 크다.)
그래서 본인들은 실제 token당 FLOPs를 아래와 같이 attention operation overhead를 포함해서 계산했다고 하는데, 이것이 \(M\)이다.
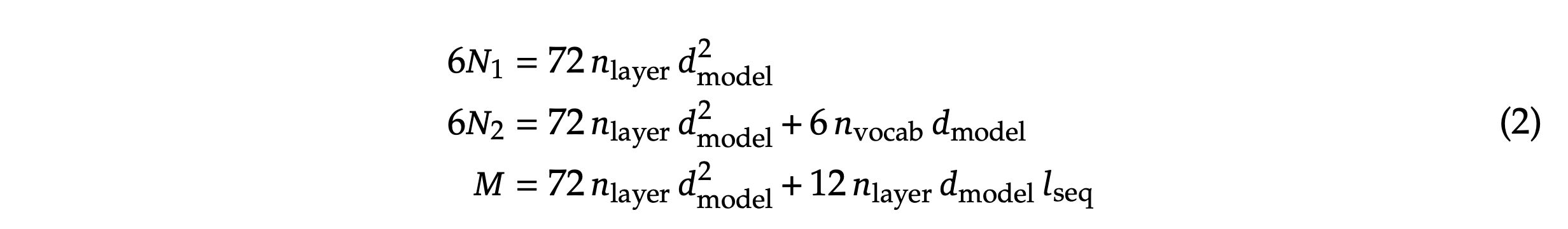 Fig.
Fig.
Transformer의 layer 수와 model size별 각 approach의 \(N\) 차이는 다음과 같다.
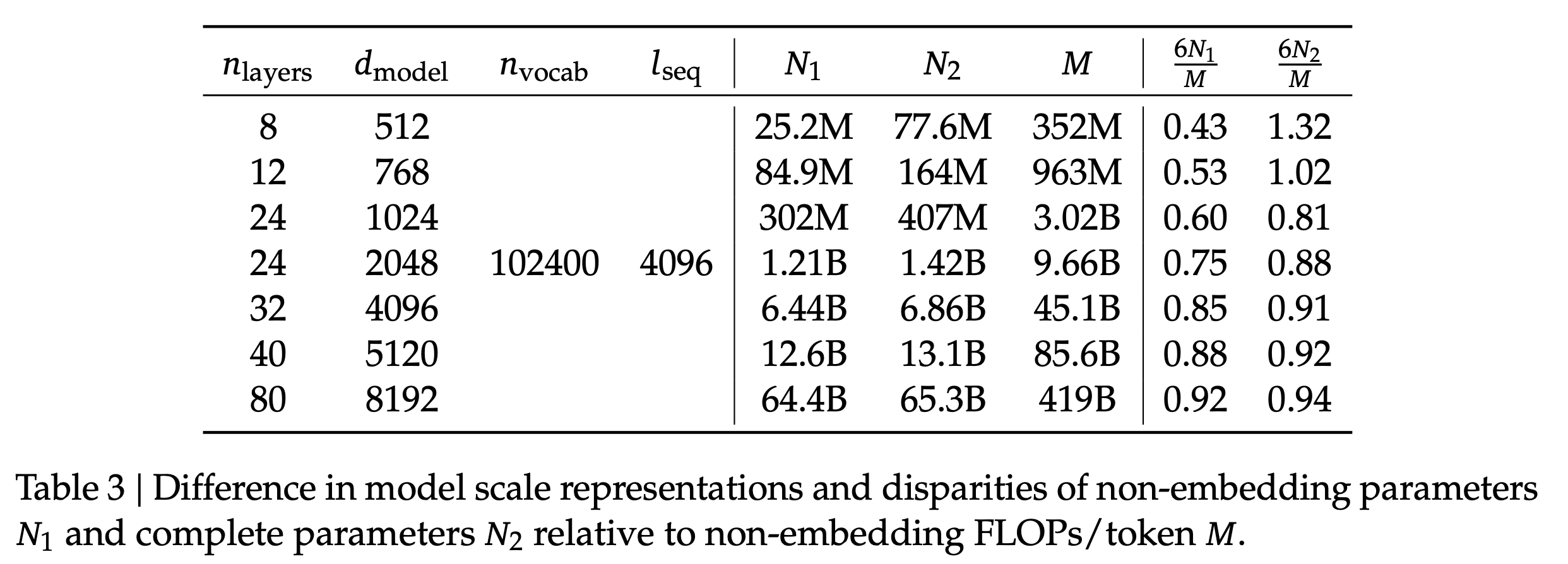 Fig.
Fig.
이제 우리가 찾고 싶은 것은 \(C\)가 주어졌을 때 loss를 최소로 하는 scaling exponent, \(a,b\)를 찾는 것으로, 아래 objective function을 minimize하는 exponent를 찾는 것이다.
 Fig.
Fig.
저자들은 Hoffmann et al.의 IsoFLOP curve를 이용해서 8개의 다른 fixed compute budget를 갖는 경우에 대해 10개의 서로 다른 model size, dataset size를 같는 case들을 실험했다. 즉 80번의 실험을 해서 아래 Figure 4(a)의 IsoFLOP curve를 얻은 것인데, 이 때 사용된 metric은 training set과 비슷한 distribution으로 이루어진 validation set에 대해 측정한 Bits-Per-Bytes (BPB)이다.
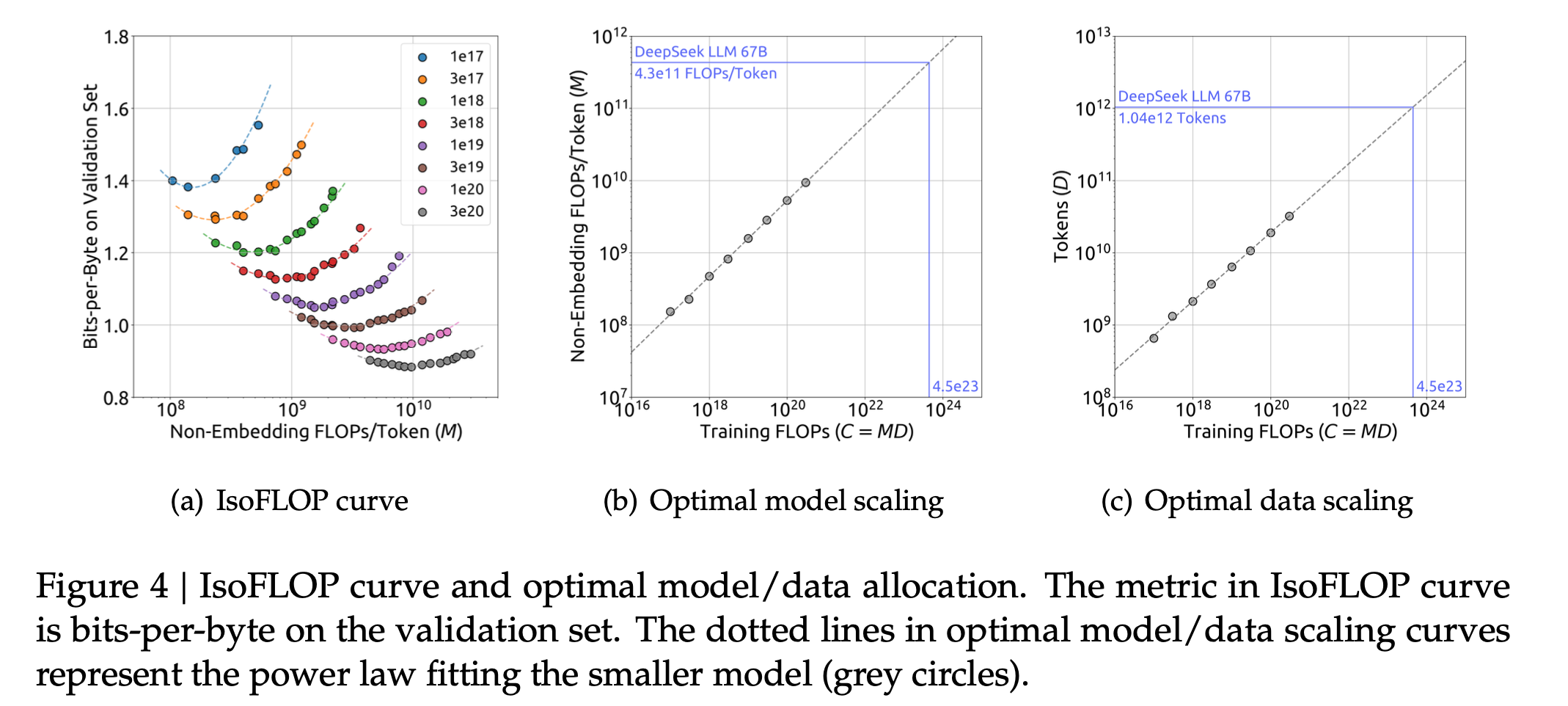 Fig.
Fig.
그리고 이 때 각 budget, \(C\)별로 사용된 optimal batch size, LR은 앞서 계산한 \(C\)에 대한 power function을 사용했다.
이들은 각 budget에서 얻은 best \(M,D\)를 통해서 base model의 model size, dataset size 에서 compute budget을 x배 태우려면 model size, dataset size는 각각 얼마나 (y배, z배) 키워야 할까?를 의미하는 exponent를 아래와 같이 구하게 된다.
 Fig.
Fig.
이는 Kaplan et al.의 exponent와 비교해서는 dataset size, model size를 꽤 비슷한 규모로 키우는 결론이라고 할 수 있다. 최종적으로 이들은 주어진 dataset과 target model size, \(7B, 67B\)에 대해서 BPB prediction을 거의 완벽하게 해낼 수 있었다.
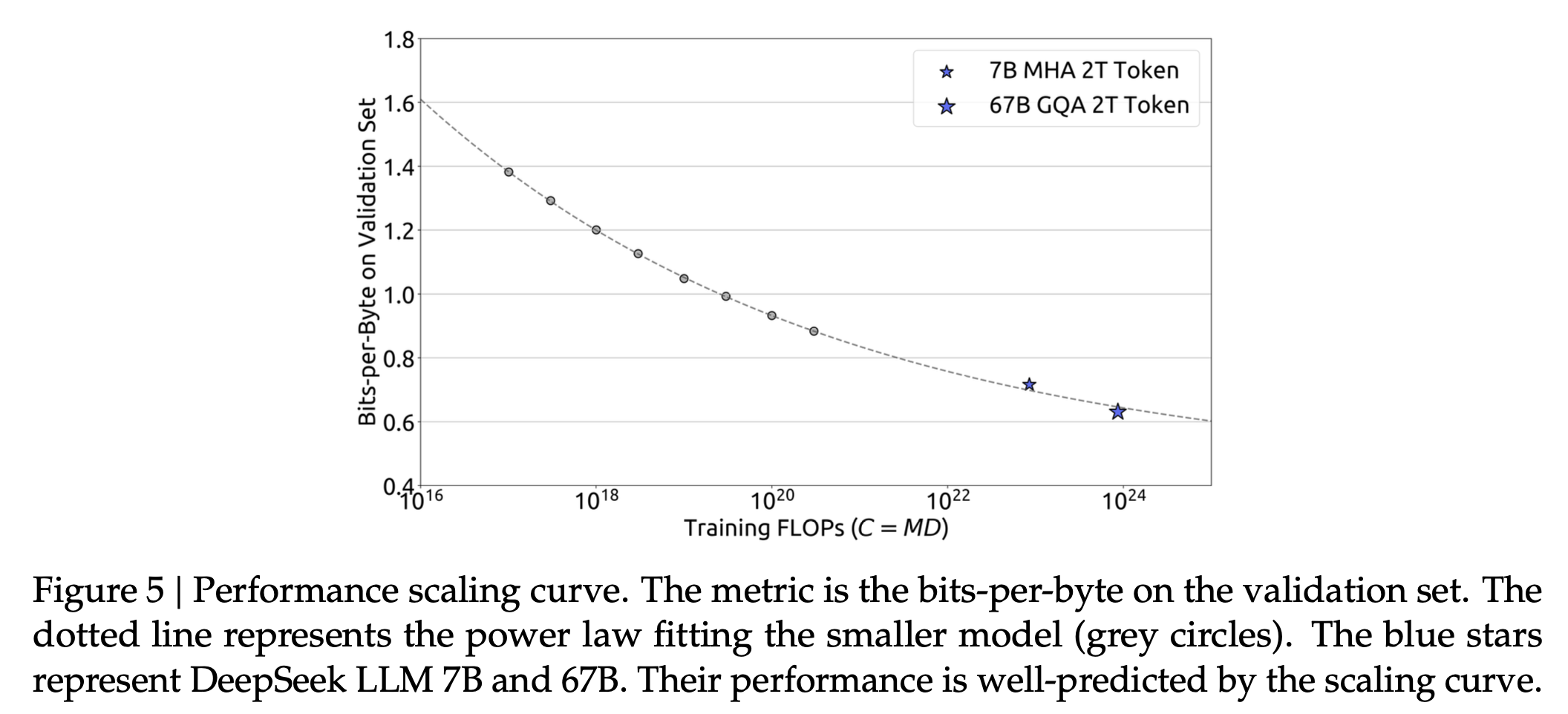 Fig.
Fig.
이들은 budget, \(C\)를 계산할 때 kaplan과 Hoffmann approach를 사용해서 re-fitting해보기도 했는데, budget이 충분히 커지면 결과가 비슷했으나, lower budget의 경우에 대해서는 꽤 큰 차이를 보였다고 한다.
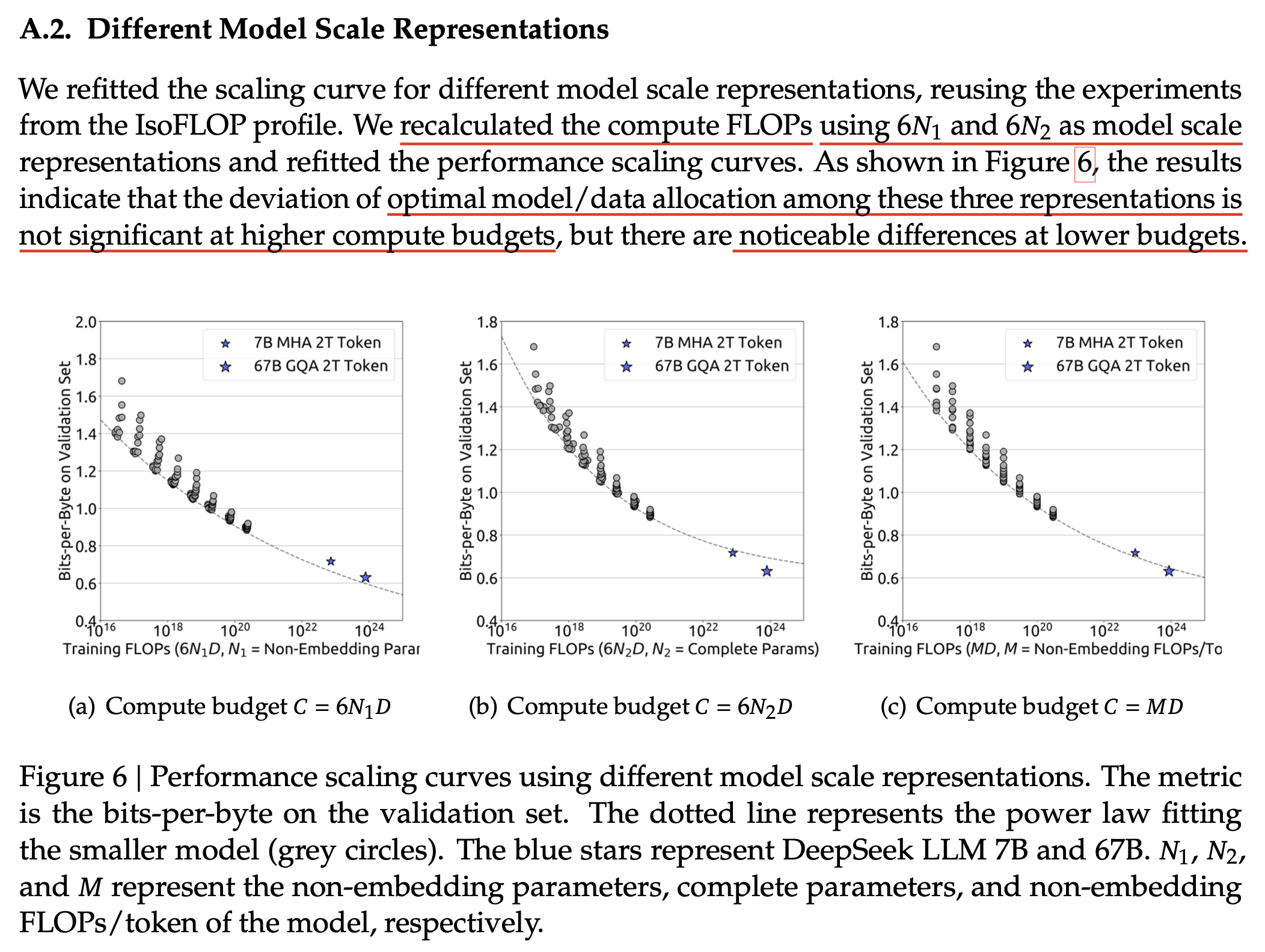 Fig.
Fig.
kaplan의 \(6N_1\)을 사용할 경우 large scale model의 performance를 overestimate 하는 경향을 보이고, Hoffmann의 \(6N_2\)를 사용할 경우에는 그 반대였다고 한다.
Over-Training
한 편, DeepSeek LLM의 경우 target model size, \(7B, 67B\)에 대해서 같은 dataset size, \(D\)를 사용했다는 점에 주의해야 한다. 둘 다 2 Trillion (T) tokens을 사용했다.
 Fig.
Fig.
Fixed dataset size를 사용하는것은 Scaling Law를 할 때 꽤 주의해야 하는 요소인데, Kaplan et al.에 나와있듯 Scaling Law prediction은 \(N(M), D\)가 조화롭게 scaling될 경우에만 performance degradation을 최소화 할수 있기 때문이다.
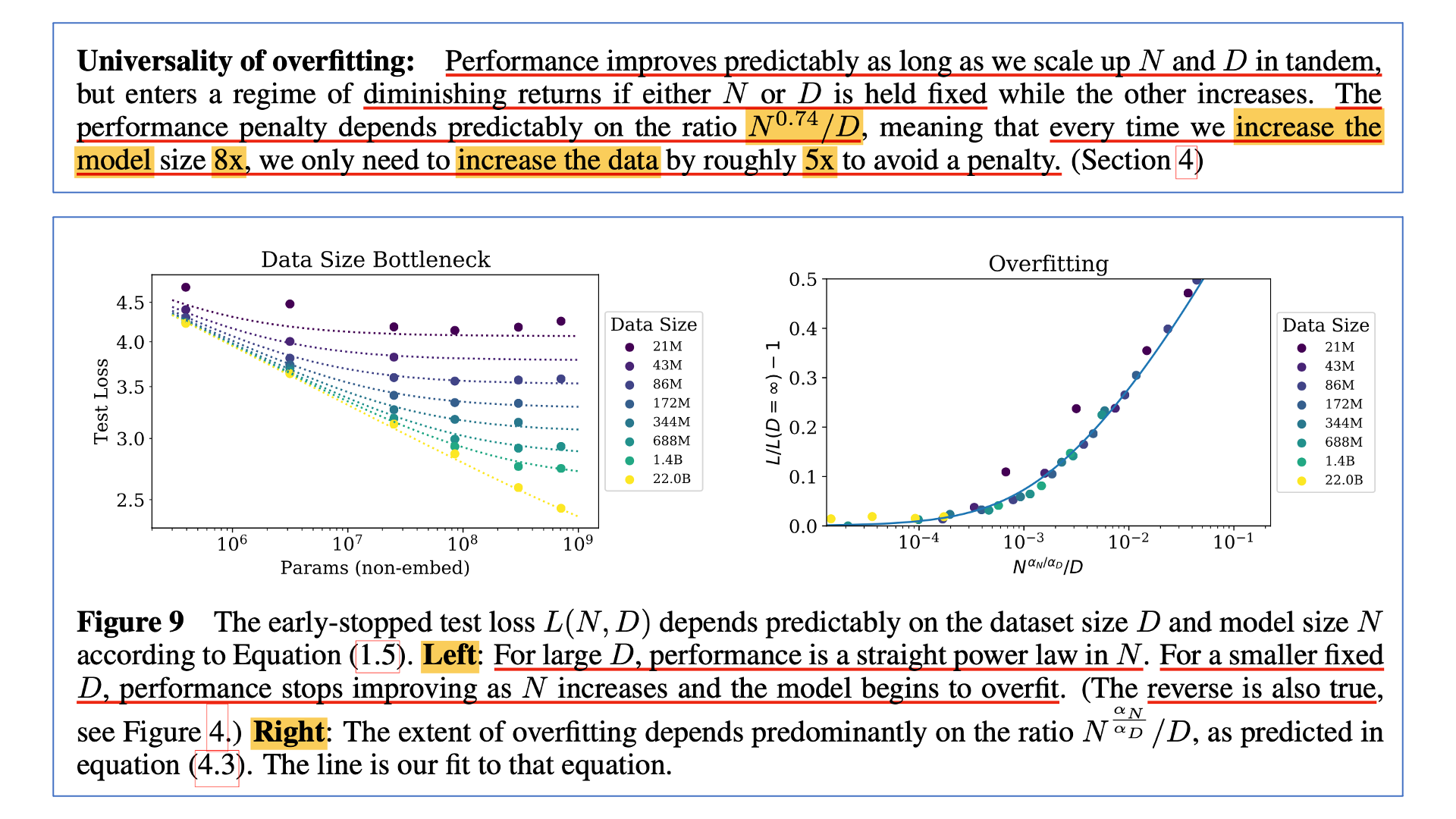 Fig.
Fig.
그런데 2T token이 \(7B, 67B\)의 compute optimal보다 좋다면 상관은 없을 것이다. 성능이 더 좋아지면 좋아졌지 안좋아질리는 없을 것이기 때문이다. 실제로 \(67B\)에 대해서 optimal dataset size는 \(1T\)밖에 되질 않는데,
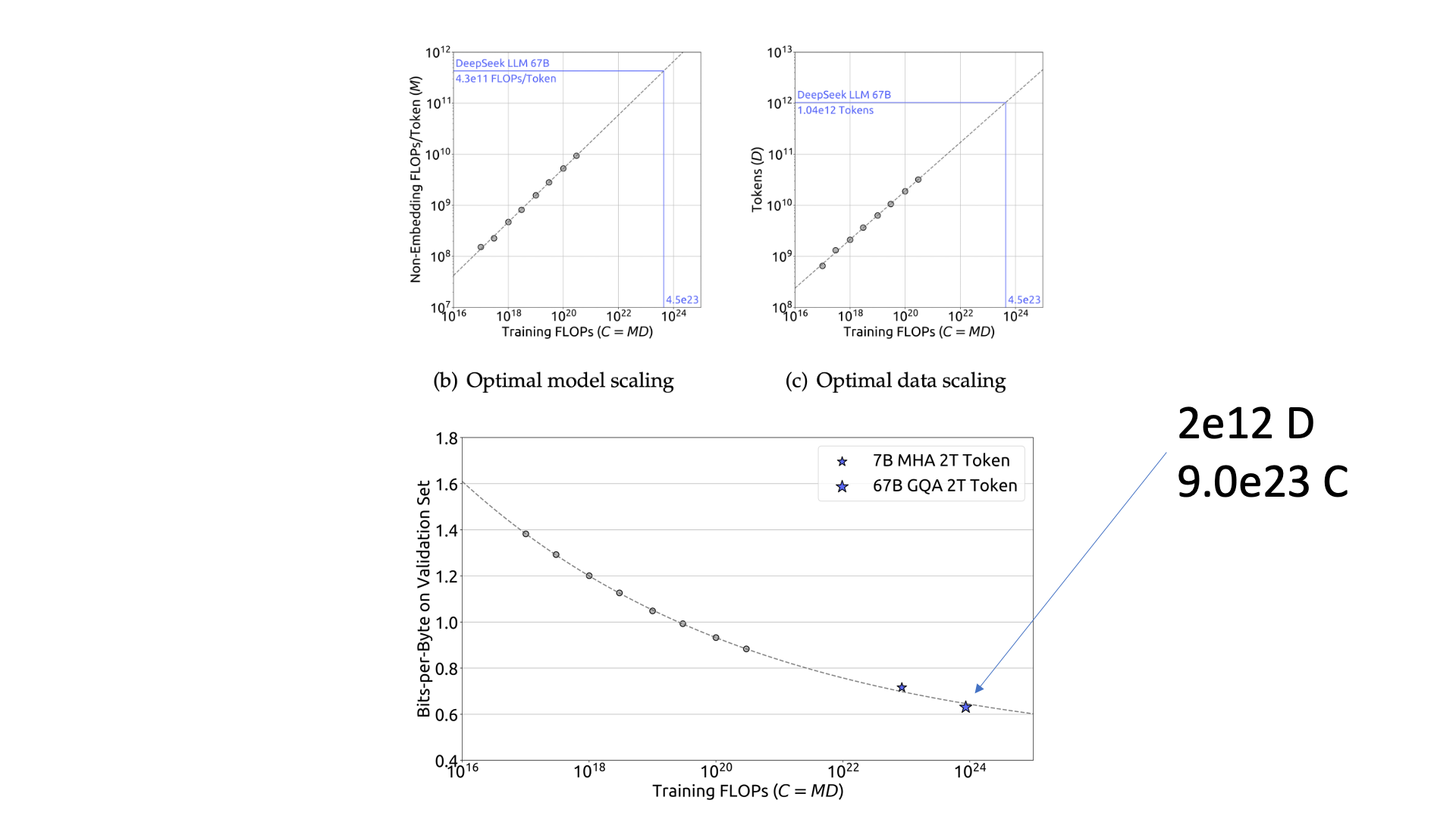 Fig.
Fig.
Scaling Components according to Dataset Quality
DeepSeek에서는 또한 quality 별로 3개의 dataset에 대해서 같은 작업을 반복해서 exponent를 찾았다고 하는데, 결과적으로 dataset quality가 좋을수록 budget이 증가할 때 model size를 좀 더 키우고, dataset size는 덜 키우는 경향을 보였다고 한다.
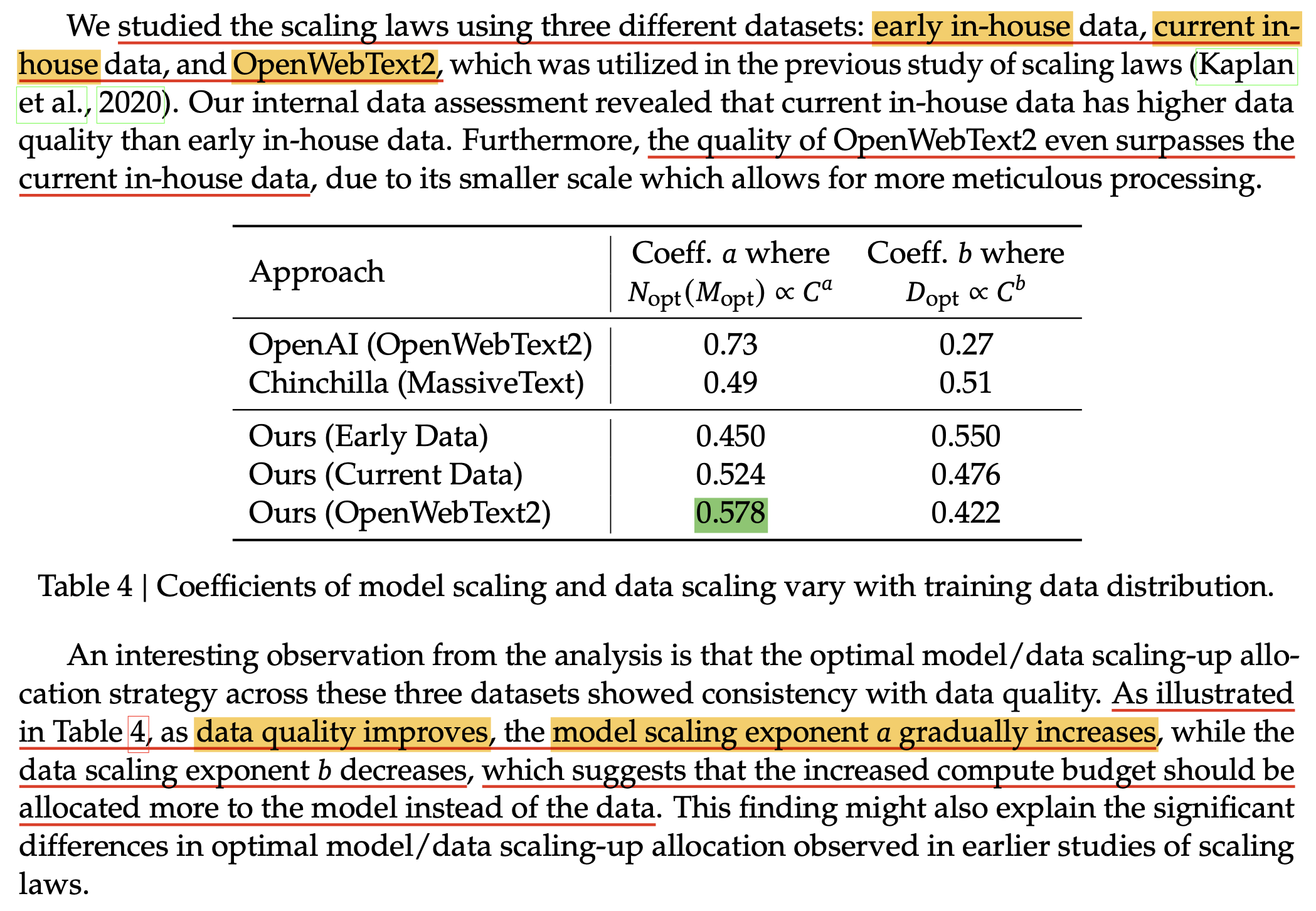 Fig.
Fig.
직관적으로 data sample하나하나의 quality가 좋으면 그 data로부터 더 많은 정보를 배울 수 있기 때문에 말이 된다고 생각할 수 있을 것 같다. 사실 우리가 target하는 task들에 대해서 fixed validation set을 정하고, 이에 대한 loss (or accuracy)의 Scaling Law를 그려 기울기가 어떤지를 보고 dataset을 정하면 제일 좋을테지만, 이런 방식으로 dataset quality를 판단하는 것도 시도해 볼 만 한 것 같다.
MiniCPM: Unveiling the Potential of Small Language Models with Scalable Training Strategies
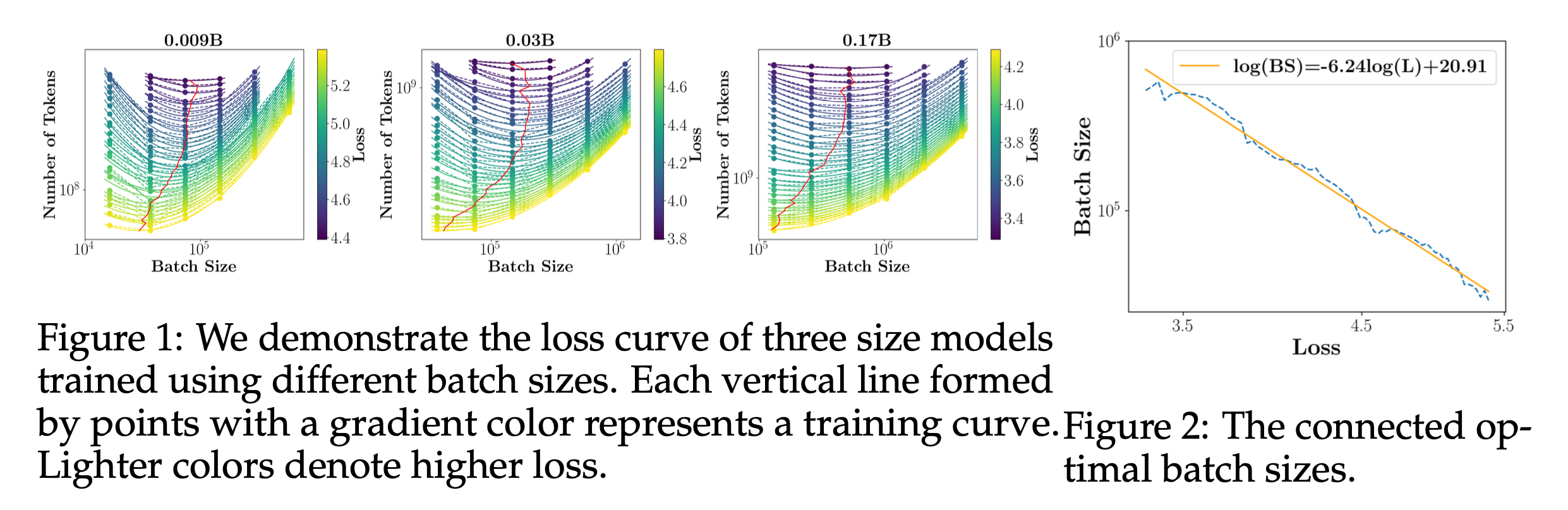 Fig.
Fig.
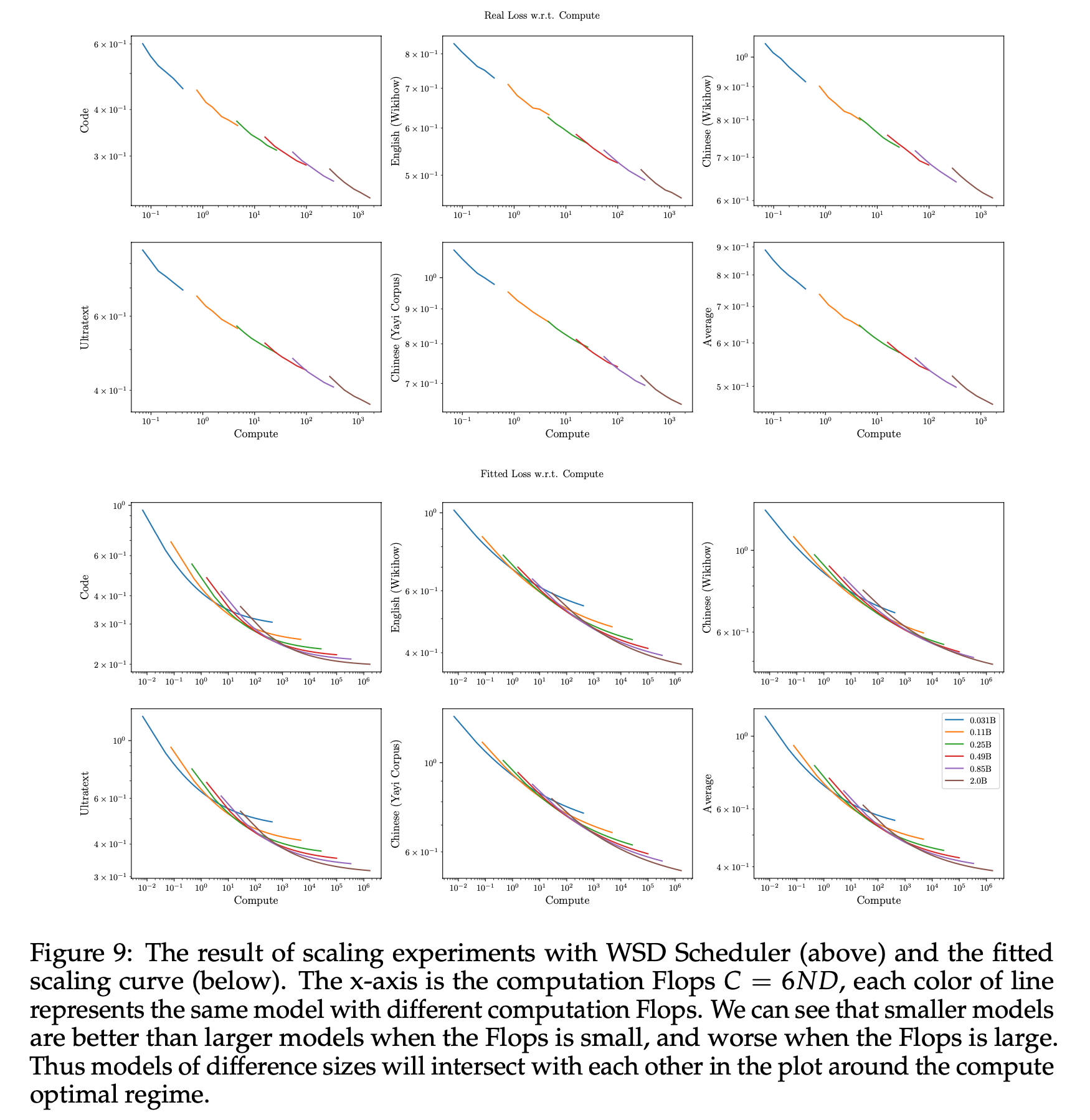 Fig.
Fig.
Additional Litreatures
(2024 June) Resolving Discrepancies in Compute-Optimal Scaling of Language Models
(2024 June) Resolving Discrepancies in Compute-Optimal Scaling of Language Models는 Kaplanr et al.과 Hoffmann et al.의 scaling exponent 차이가 어디서 발생하는지 분석한 paper이다. 사실 dataset이 같다면 compute budget이 증가할 때 model size, dataset size를 얼만큼 scaling해야 하는지를 의미하는 exponent 값은 같아야 하는데, 신기하게도 이 두 paper의 결과는 달랐다. Kaplan et al.은 scaling 시에 model parameter를 더 키우라는 결론이 나왔고, Hoffmann et al.은 equally scaling하라는 결론이 나왔었다. 이 둘간에 차이가 나는 이유에 대해서 해당 paper는 아래와 같은 flow로 Kaplan et al.의 문제를 해결해나갔다.
- training setup은 아래와 같음
- dataset
- OpenWebText2 (30B)
- WebText2
- RefinedWeb (600B)
- MassiveText
- model (대충 Noam architecture)
- bf16
- SwiGLU
- depth-scaled init
- RoPE
- qk-layernorm
- z-loss
- 50K vocab size
- dataset
- Kaplan et al. 에서 출발
- 1.Kaplan et al. 의 model size counting method는 non-embedding parameters만 측정하는 것인데, small scale model에서 embedding weight의 contribution은 크기 때문에 간과하면 안됨
- embedding weight tying을 할 경우 차이가 더 벌어짐
Solution: counting the head FLOPs
- 2.LR warmup stage가 모든 compute budget에서 같아서 small model들인 undertraining 됐을 확률이 큼
- Kaplan et al.에서는 Scaling Law 실험을 할 때 모든 scale에서 batch size를 고정하고 (이 논문도 reproduce를 위해 \(2^{19}=524,288\)로 고정), warmup stage를 3000 step으로 고정함
- 즉 작은 compute budget 에서 batch size가 상당히 클테니 어떤 경우는 warmup 이후 LR decay iteration이 있어야 하는데 warmup만 하다 끝날 수 있음
Solution: we set the number of warmup tokens to be identical to the model size N
- 3.Hoffmann et al.이 주장한 Kaplan et al.과 본인들의 결과가 차이나는 이유인 cosine LR scheduler의 length를 실험해봤는데 1, 2번이 충족돼서 그런지 큰 차이 없음.
- 4.Scale마다 batch size, LR, AdamW beta2 가 잘 tuning되어야 함
- TBD
 Fig.
Fig.
Correcting Batch Size, Learning Rate and AdamW Beta2
(2023 Dec) Beyond Chinchilla-Optimal: Accounting for Inference in Language Model Scaling Laws
(2023 Dec) Beyond Chinchilla-Optimal: Accounting for Inference in Language Model Scaling Laws는 2023년 MosaicML에서 publish한 paper이다.
이 paper의 main reseqrch question은 "Chinchilla optimal은 다 좋은데 inference에 대한 dimension이 빠져있다"는 것이다.
주된 주장은 fixed compute budget에서 model size가 7B가 optimal일지라도,
미래에 service를 하면서 얼만큼의 token을 inference할 건지에 따라서 5B가 optimal일 수도 있다는 것이다.
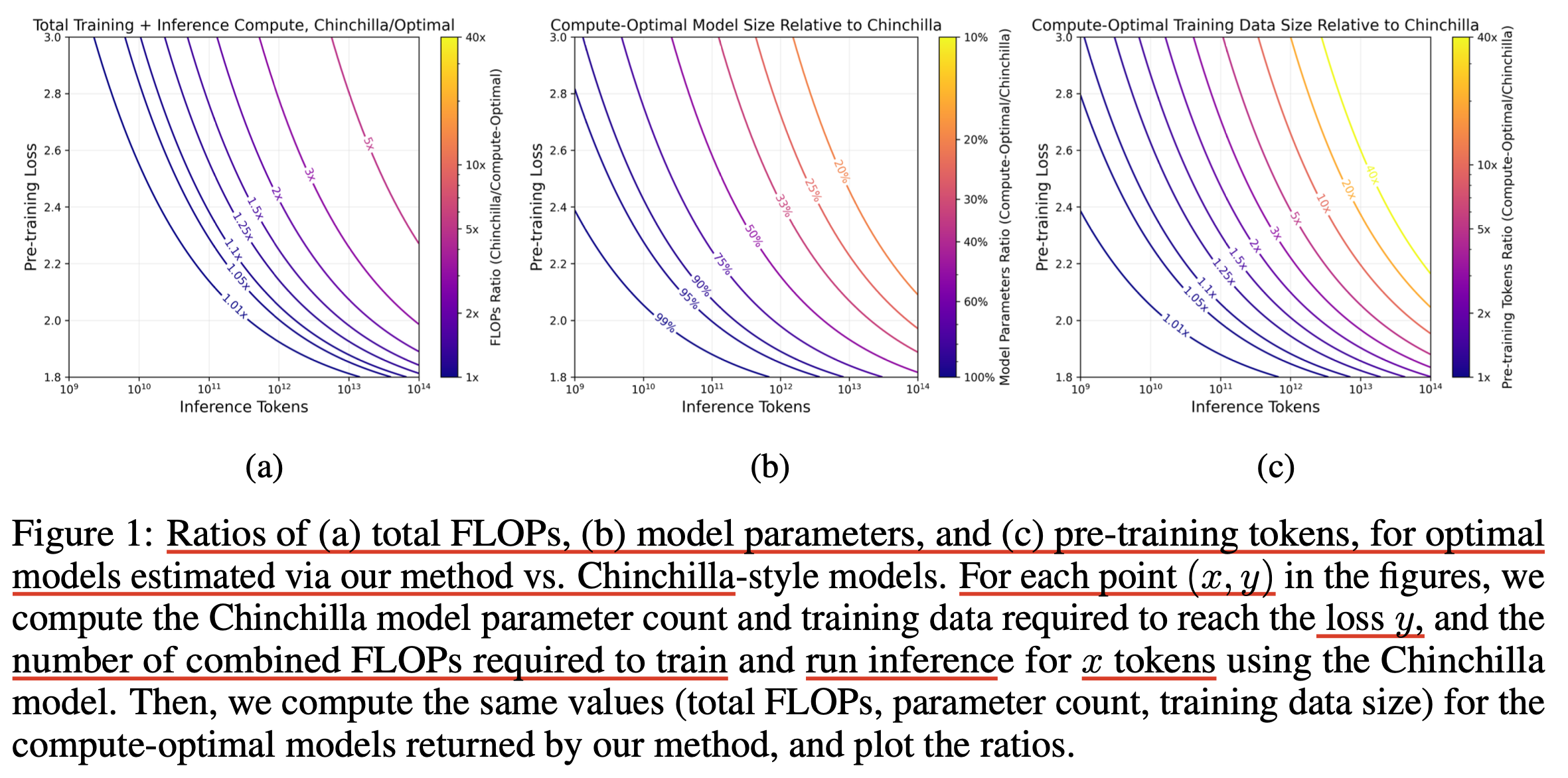 Fig.
Fig.
이 paper는 크게 다루지 않을 것이므로 관심있는 사람들은 paper를 찾아 보면 되는데, 확실히 요즘 llama3나 phi-3 등을 보면 service scenario에 맞게 model size를 fix해놓고 매우 길게 training을 하는 것이 추세인 걸 보면 공감이 가는 내용이라고 할 수 있다. 이는 model size가 3B, 7B 등으로 고정인 경우 이를 길게 학습하는 것이 compute optimal은 아닐지언정 compute optimal 30B model보다 좋을 수 있기 때문에 성능상 issue도 딱히 없어보인다.
(2024 May) Scaling Laws and Compute-Optimal Training Beyond Fixed Training Durations
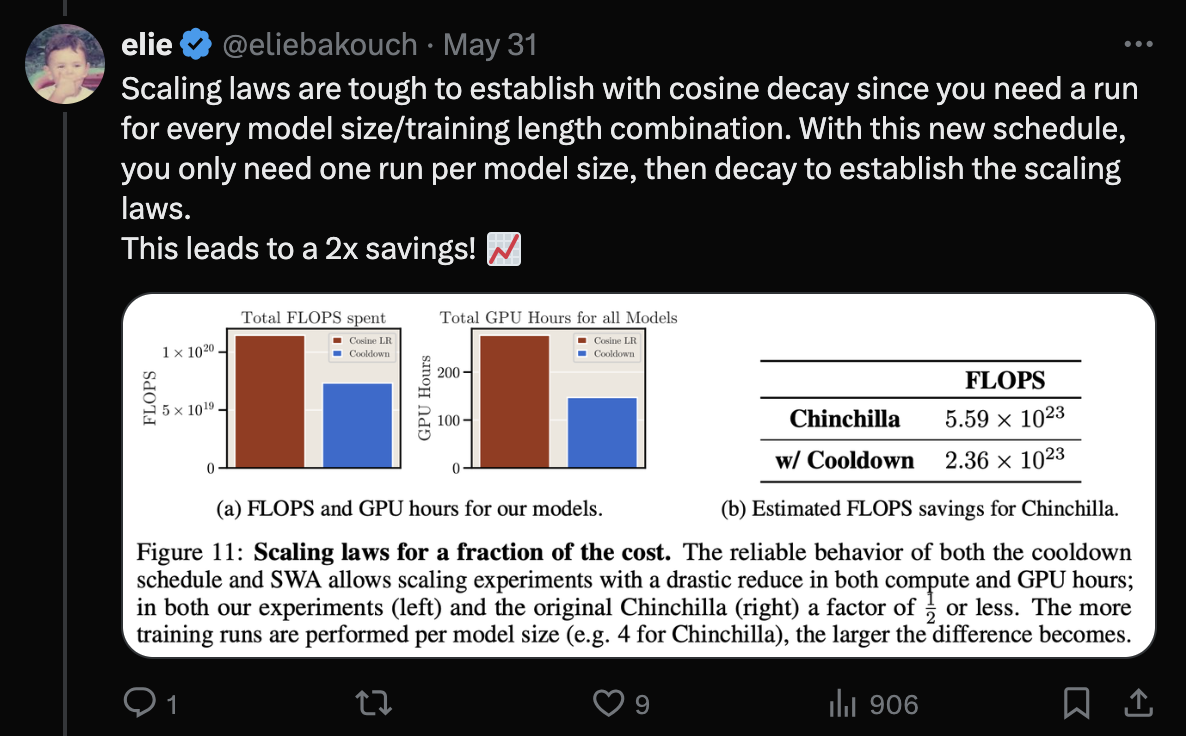 Fig.
Fig.
(2023 May) Scaling Data-Constrained Language Models
2023년 10월에 publish된 Scaling Data-Constrained Language Models는 dataset size가 제한되어 있을 때, 즉 2T, 3T도 안될 때 LM은 어떤 Scaling Law를 갖게 되는지에 대해 탐색한 paper이다.
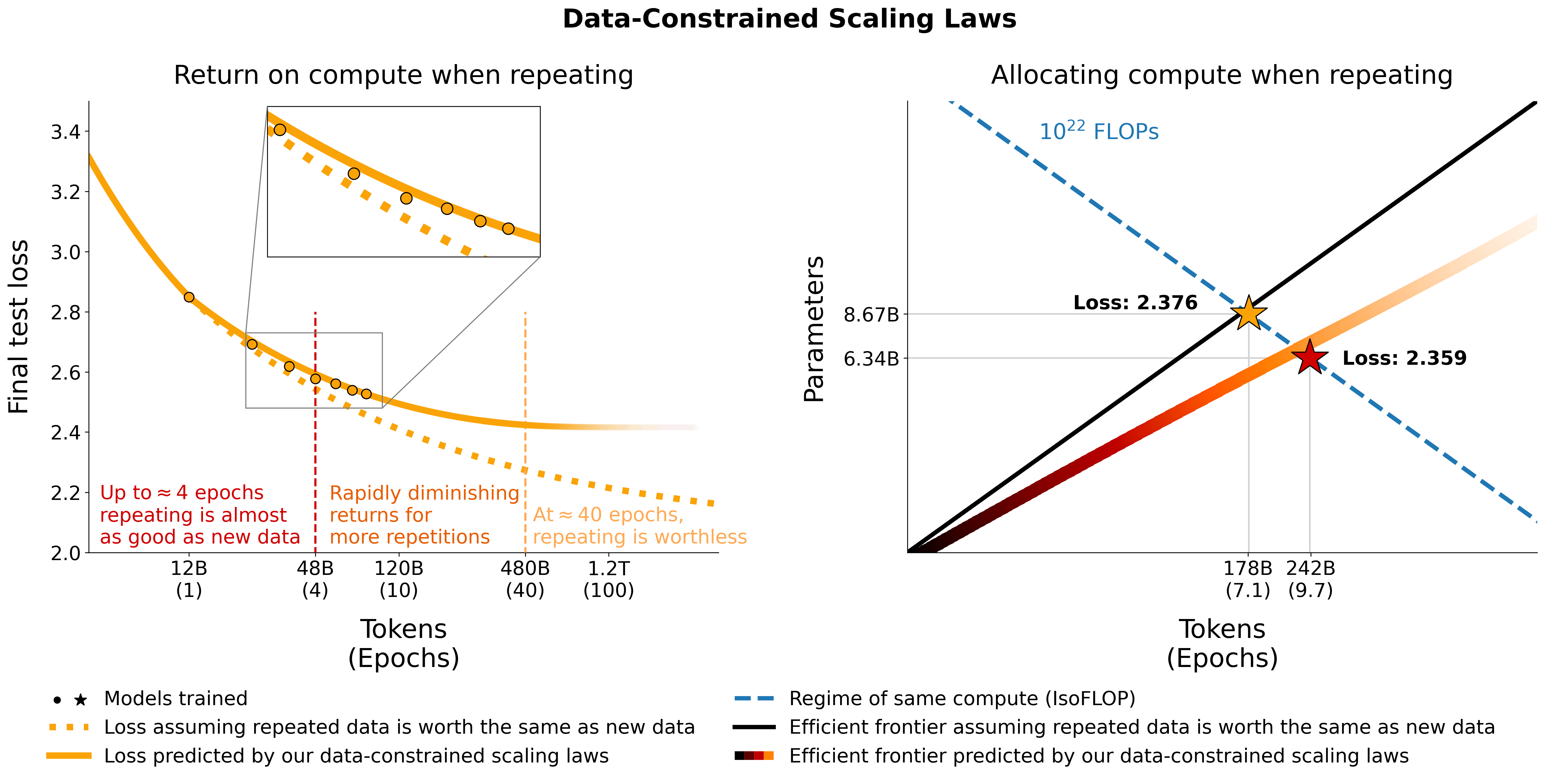 Fig.
Fig.
(2024 July) Scaling Laws with Vocabulary: Larger Models Deserve Larger Vocabularies
정말 마지막으로 (이제 그만하고싶다), vocab size에 대한 Scaling Law도 있다.
Scaling Laws with Vocabulary: Larger Models Deserve Larger Vocabularies에서는 non-embedding parameter size가 커질수록, embedding parameter size는 어떻게 scaling되어야 하는가?에 대해 empirical study를 했으며,
아래의 power law를 얻게 됐다.
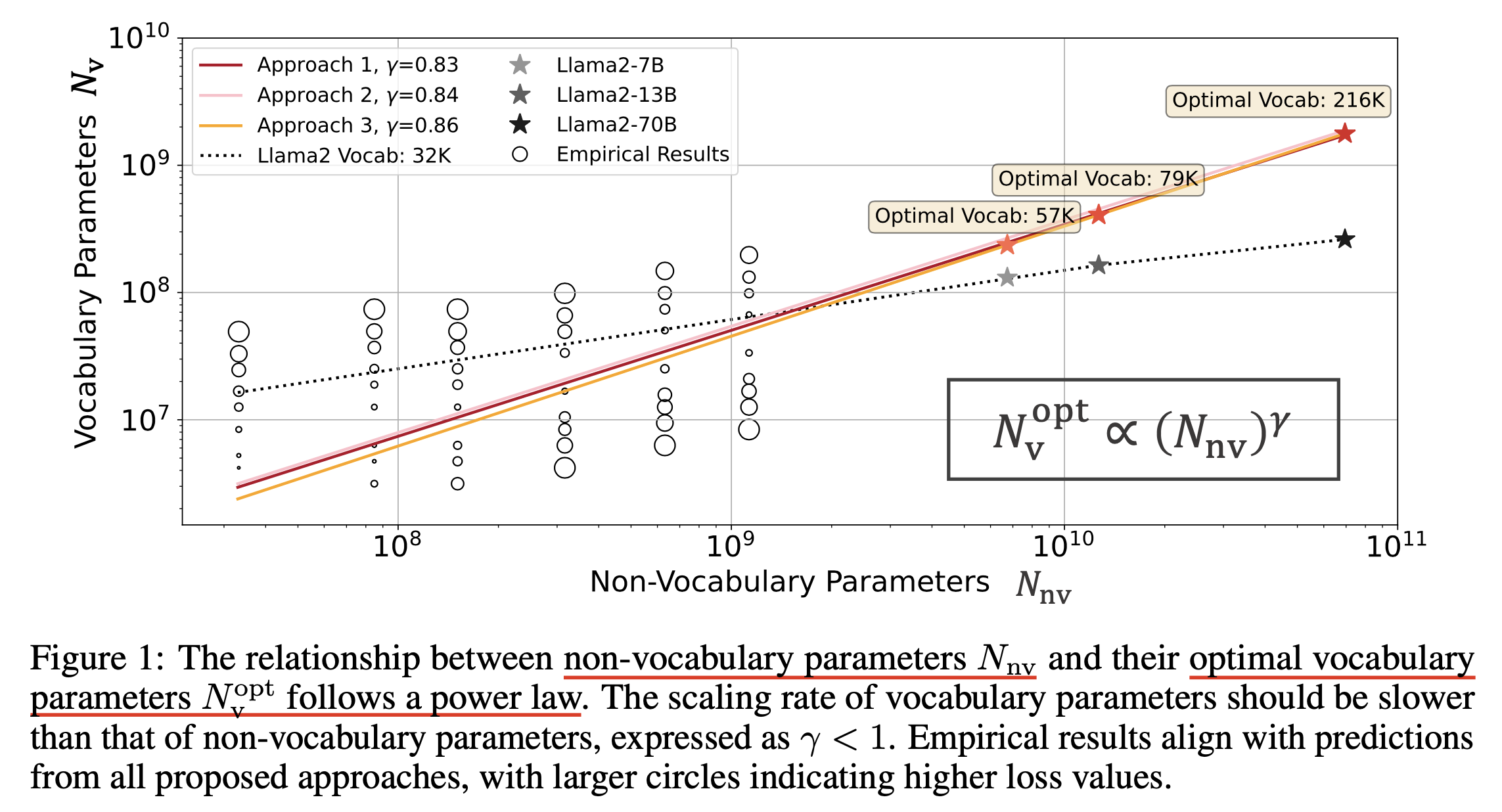 Fig.
Fig.
Motivation은 다음과 같은데, 같은 7B LLM에 대해서 왜 LLaMa-2는 32k vocab을 썼고, Gemma-2는 200k가 넘는 vocab size를 썼냐는 것이다. 그리고 Gemma-2가 성능이 더 좋기 때문에 vocab size에 대해서 크면 클수록 좋다고 생각할 수 있지만, 둘의 architecture 차이도 있겠고 무엇보다 training tokens (FLOPs)를 gemma가 훨씬 더 썼기 때문에 동등 비교가 되는건 아니지만 어쨌든 둘간의 7배달하는 embedding size 차이가 있다. (Kaplan et al.은 embedding matrix가 FLOPs에 contribution하는게 적다고 하여 배제하긴 했지만 포함했어도 이 둘을 나눠생각한 것은 이 paper가 처음인 것 같다)
 Fig.
Fig.
저자들은 대부분의 LLM들이 본인들이 찾은 compute-optimal vocab size보다 작은 vocab size를 갖는다고 한다.
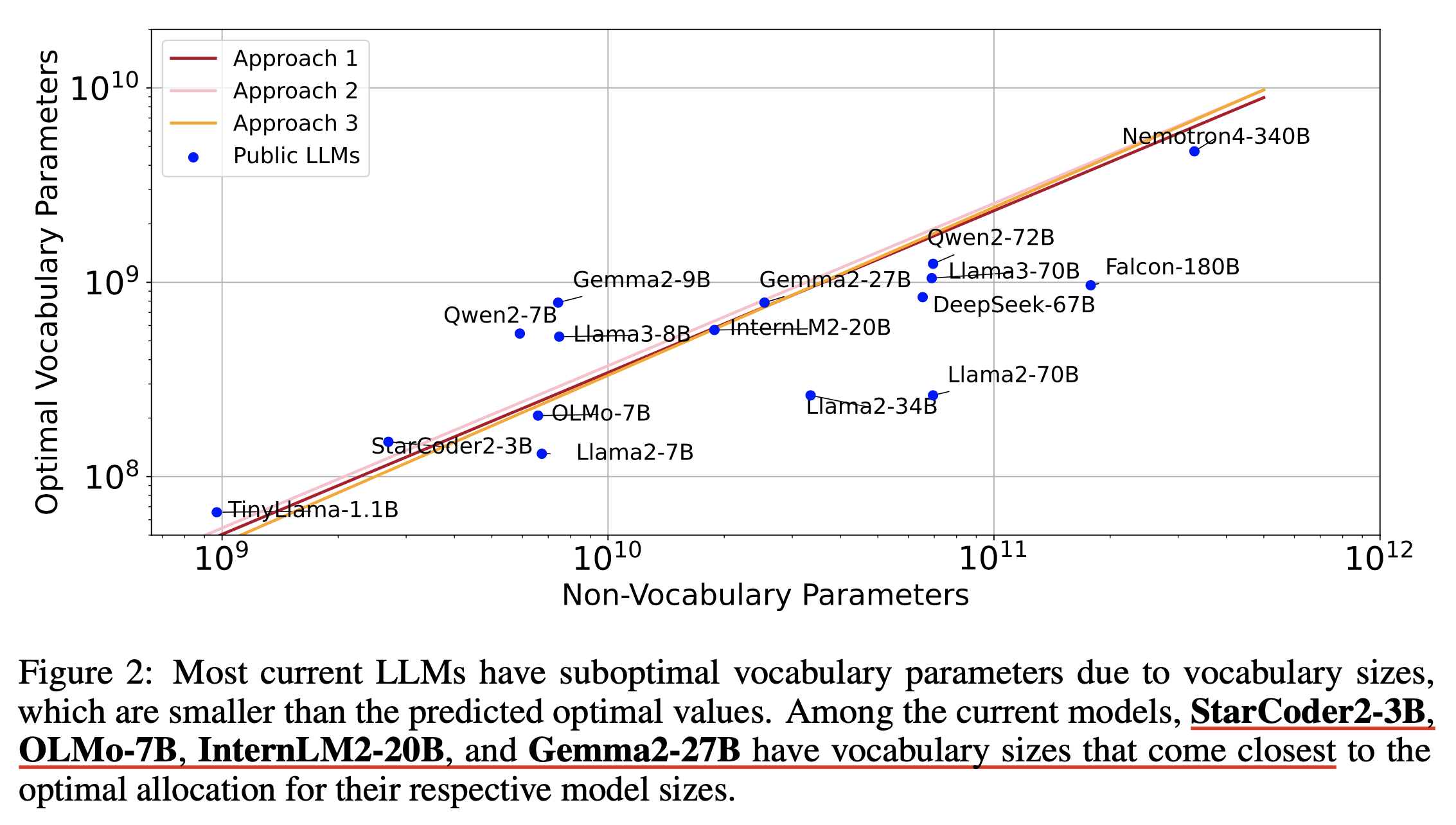 Fig.
Fig.
하지만 우리가 앞서 몇번 얘기했던 것 처럼 이번에도 compute-optimal vocab size일 뿐이라는 점에 주의해야 한다. 이 vocab size로 학습하지 않으면 optimal performance가 안나오는 것은 아닐 것이다. 다만 비효율적으로 학습될 뿐이라고 생각할 수 있겠다. (그럼에도 vocab size가 같이 scaling돼야 한다는 점은 나로서는 처음 보는 dimension이기 때문에 앞으로 design을 할 때 고려해야 할 것 같다)
How To Find Power Law? (Define metric first)
그래서 어떻게 했는가?
chinchilla optimal의 IsoFLOPs같은 approach를 썼는데, 이렇게 하기 위해서는 vocab size가 다를 때도 측정이 가능한 fair metric이 필요하며, 기존의 CE loss나 perplexity를 사용할 수는 없다.
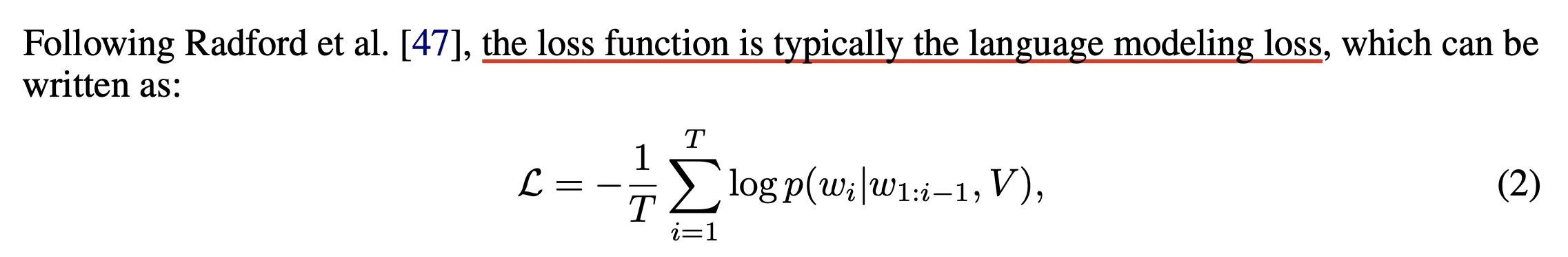 Fig.
Fig.
저자들은 Bits Per Character (BPC)이랑 살짝 다른 metric을 제안하는데, 사실 BPC와 비교해서 그냥 normalization을 unigram token prob으로 대체했다 정도의 차이만 있다.
 Fig.
Fig.
 Fig.
Fig.
 Fig. Source from Chip Huyen’s post
Fig. Source from Chip Huyen’s post
 Fig.
Fig.
 Fig.
Fig.
Key Analysis
 Fig.
Fig.
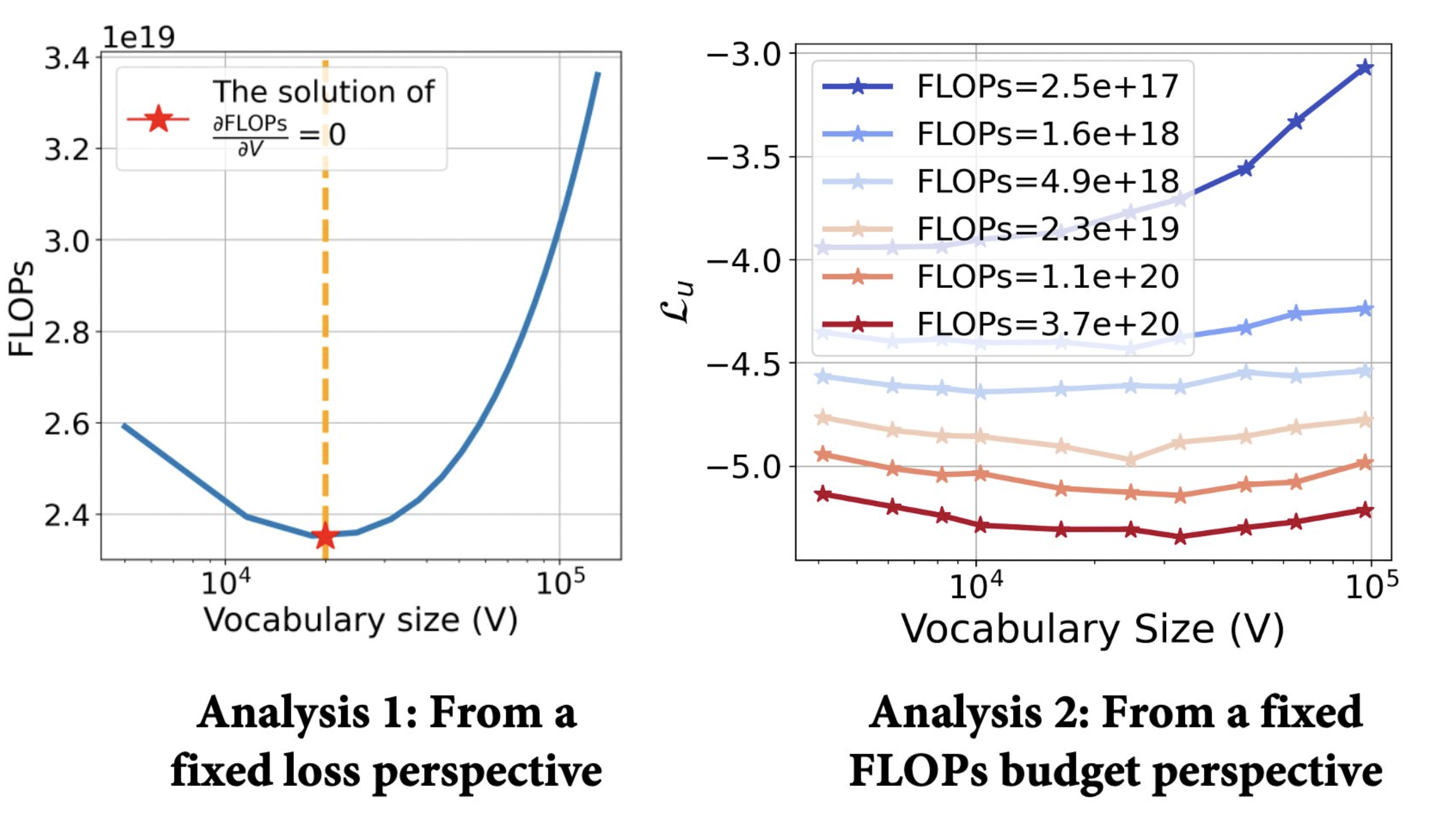 Fig.
Fig.
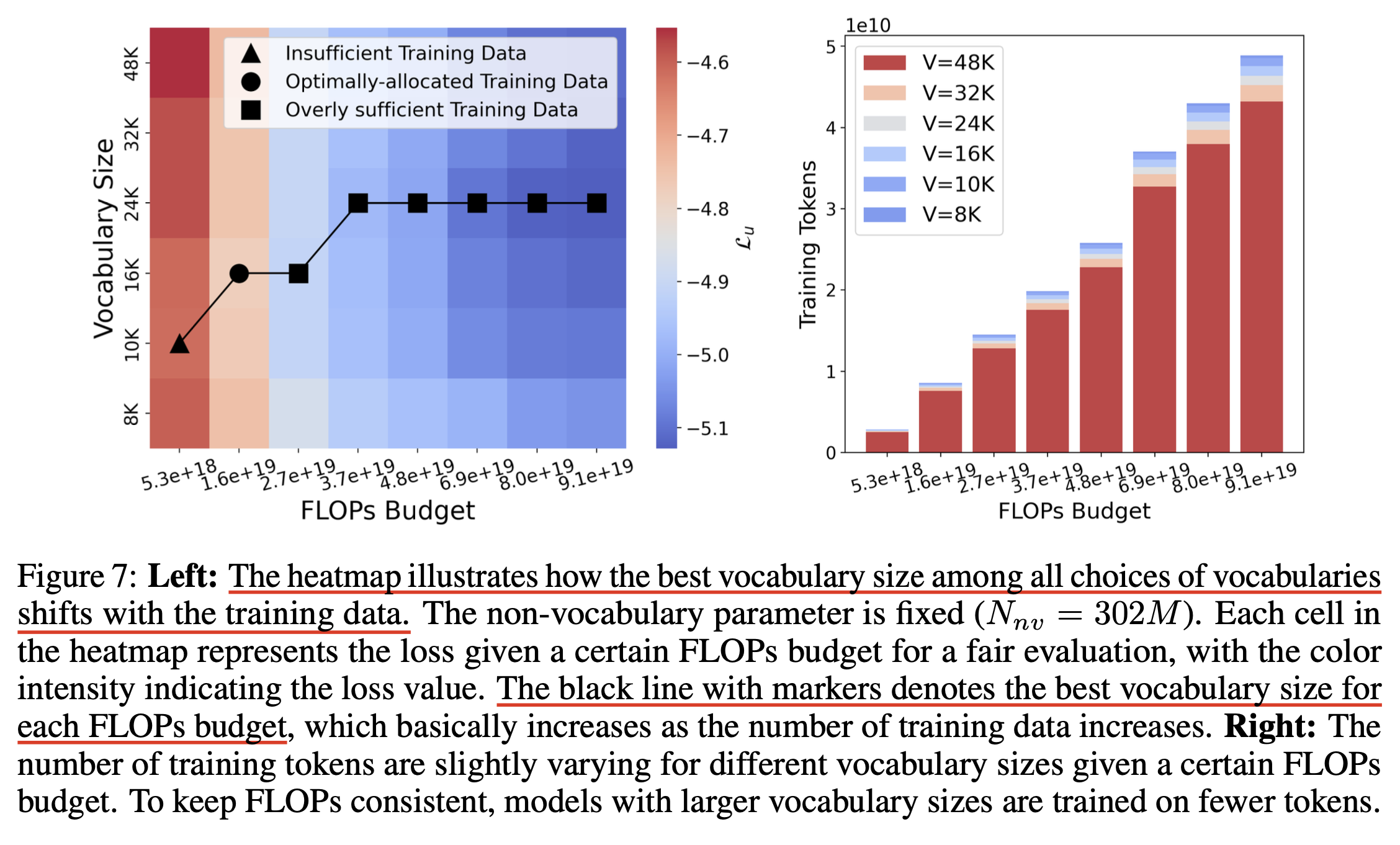 Fig.
Fig.
Scaling Law
tmp
for 3 Different Data Constrained Condition
- under-training
- compute-optimal allocated
- over-training
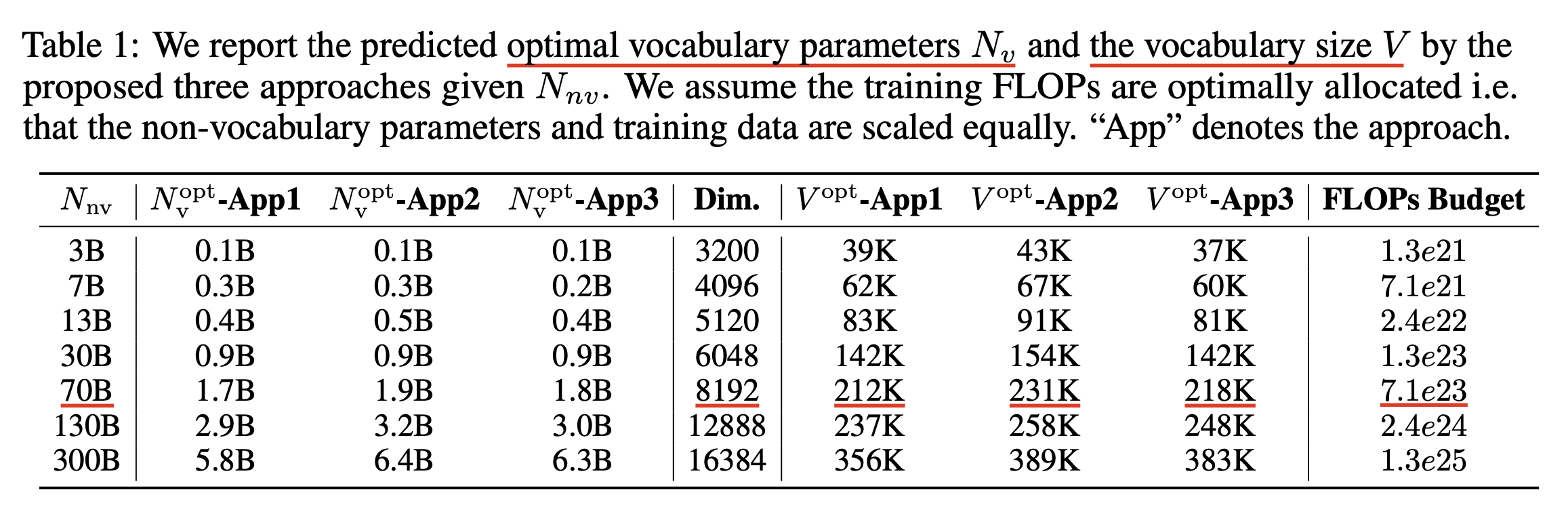 Fig.
Fig.
 Fig.
Fig.
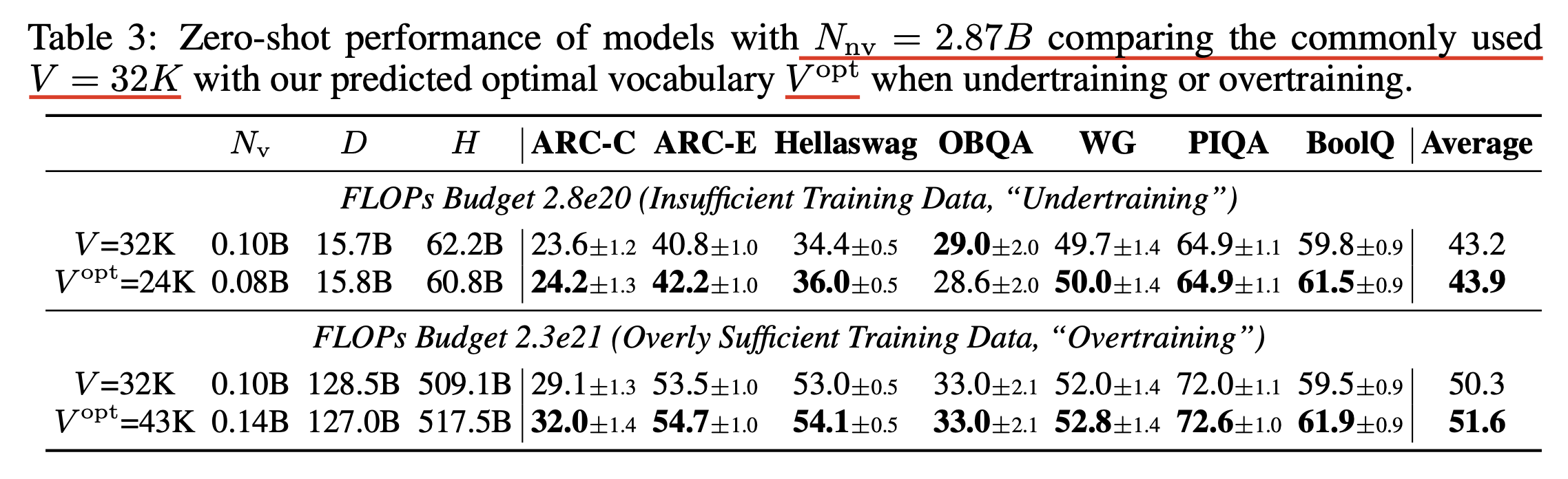 Fig.
Fig.
 Fig.
Fig.
+Updated) (2024 July) Cross-Lingual Continual Pre-Training at Scale
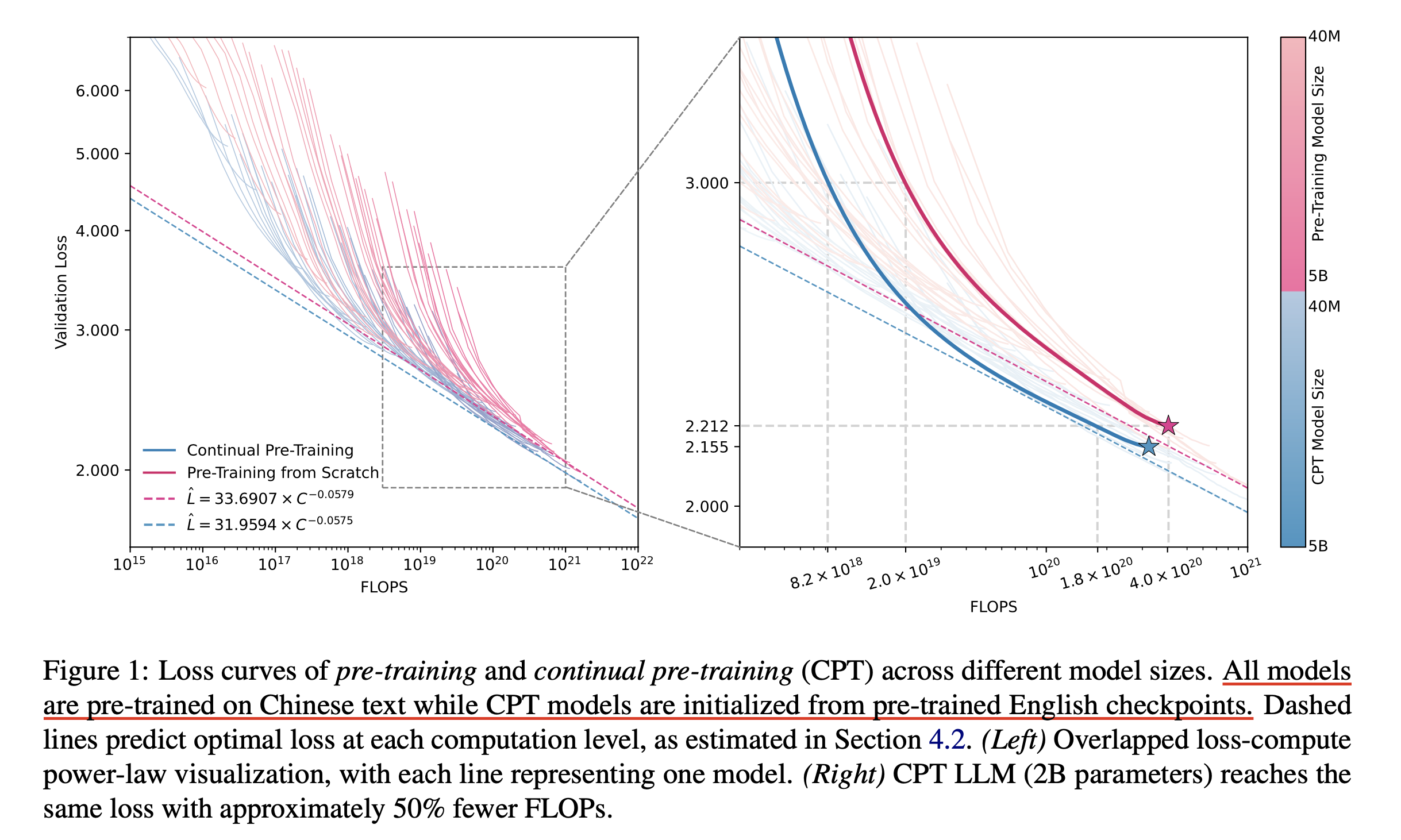 Fig.
Fig.
 Fig.
Fig.
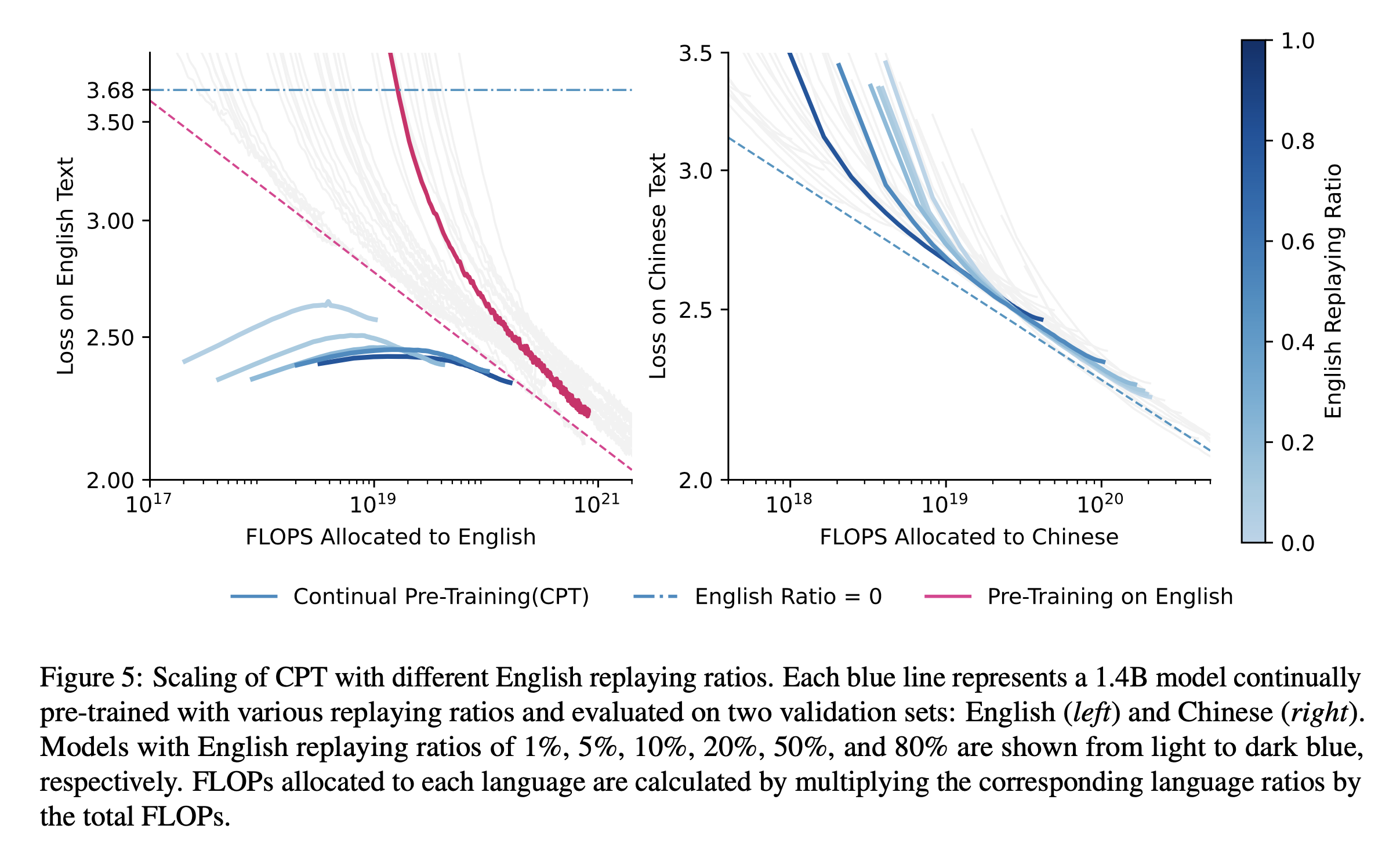 Fig.
Fig.
References
- Wiki
- Papers
- Core
- (2020 Jan) Scaling Laws for Neural Language Models
- (2020 Oct) Scaling Laws for Autoregressive Generative Modeling
- (2021 Feb) Scaling Laws for Transfer
- (2022 Mar) Training Compute-Optimal Large Language Models (a.k.a Chinchilla Optimal)
- (2023 Dec) Beyond Chinchilla-Optimal: Accounting for Inference in Language Model Scaling Laws
- (2024 June) Resolving Discrepancies in Compute-Optimal Scaling of Language Models
- Additional
- (2020 May) Language Models are Few-Shot Learners (a.k.a GPT-3)
- (2022 Jun) Emergent Abilities of Large Language Models
- (2023 Mar) GPT-4 Technical Report
- (2024 Jan) DeepSeek LLM: Scaling Open-Source Language Models with Longtermism
- (2024 Apr) MiniCPM: Unveiling the Potential of Small Language Models with Scalable Training Strategies
- (2024 May) Scaling Laws and Compute-Optimal Training Beyond Fixed Training Durations
- (2024 May) DataComp-LM: In search of the next generation of training sets for language models
- (2024 Jun) Reconciling kaplan and Chinchilla Scaling Laws
- Breaking Language Barriers: Cross-Lingual Continual Pre-Training at Scale
- Chinchilla Scaling: A replication attempt
- Scaling Vision Transformers to 22 Billion Parameters
- Scaling Data-Constrained Language Models
- Scaling Laws with Vocabulary: Larger Models Deserve Larger Vocabularies
- Core
- Lectures and Videos
- Blogs and Others
- Scaling Laws
- Grokking
- FLOPs
- Critical Batch Size