(WIP) Deep Dive into Normalization Modules (Layer Normalization (LayerNorm; LN), Root Mean Squared (RMS) Normalization (RMSNorm), and Weight Normalization (WN))

< 목차 >

• Introduction
• Layer Normalization (LayerNorm)
• Root Mean Squared (RMS) Norm (RMSNorm)
  • Invariance Analysis
  • Gradient Analysis
    • Let's think bout Backprop through Vanilla LayerNorm and w/o LayerNorm
    • RMS Norm
  • partial RMSNorm (pRMSNorm)
  • Experimental Results
    • CIFAR-10 Classification
• Geometry of parameter space during learning
  • Riemannian metric
  • The geometry of normalized generalized linear models
    • Implicit learning rate reduction through the growth of the weight vector
    • Learning the magnitude of incoming weights
• Further Things to read
  • Weight Normalization (WeightNorm)
  • Non-Parametric LayerNorm from OLMo
• References

Introduction

Layer Normalization (LayerNorm)은 2016년에 publish 된 paper로 training stability를 개선함에 따라 같은 wall clock time 동안 더 빨리 model convergence를 할 수 있게 도와주도록 설계되었다. LayerNorm 이전 2015년에는 Batch Normalization (BatchNorm)이라는 것이 있었고, LayerNorm이 제안되던 시기에 Weight Normalization (WeightNorm)도 제안되었으며 이 세 가지가 가장 근본적인 normalization method라고 할 수 있고 그 이후 group norm, instance norm 등이 제안되었다. 대부분의 normalization, Adam등의 adaptive optimizer, 그리고 architecture design 등은 얼마나 깊은 model을 얼마나 효과적으로 (주어진 training step, wall clock time 동안 더 빠르게 학습) 학습할 수 있는지를 주안점에 두고 연구되어 왔으며 이 세 가지 normalization module의 목적도 그렇다고 할 수 있다.

한 편, Root Mean Square (RNS) Layer Normalization (RMS Norm)은 2019 NIPS에 publish 됐는데, RMS Normalization Module 이라고 해서 기존의 LayerNorm과 목적에서 큰 차이가 있지는 않고 대부분의 Standardization나 Normalization 처럼 layer가 많아질수록 gradient가 exploding or vanishing하는 문제를 막기 위해 layer의 input, output 크기를 유지하는 것이 목적이다. 하지만 RMSNorm은 일반 LayerNorm보다 속도가 더 빠르다고 알려져 있다.

Fig. 단순히 수렴 속도를 말하는 것이 아니라 1000번 fwd+bwd+opt_step을 할 동안 걸린 wall clock time이 더 빠르다.

이는 LayerNorm의 주된 contribution points 라고 알려진 것들 중 실제로 기여하지 않는 일부를 제거하여 computational overhead를 실제로 줄임으로써 달성한 것인데, 그렇기에 근 2~3년 사이 나온 대부분의 modern Large Language Model (LLM)에는 기본적으로 LayerNorm 대신 RMSNorm이 들어간다. 이렇게 RMSNorm, Gated Linear Unit (GLU), Grouped Query Attention (GQA)등이 들어간 Transformer variant 들에는 대표적으로 LLaMa-3나 Qwen 같은 것들이 있는데, Noam Shazeer 등 google 개발진들이 개발했다고 해서 Noam Architecture라고 부르기도 한다.

이번 post에서는 LayerNorm과 RMSNorm에 어떤 차이가 있으며, 왜 RMSNorm을 써야하는지에 대해서 생각해보려고 한다.

Layer Normalization (LayerNorm)

LayerNorm은 input feature의 통계량, mean, variance를 사용해 feature의 수치를 조정해준 뒤, learnable parameter인 \(\gamma, \beta\)를 곱해 scale and shift하게 되어있다. (weight, \(\gamma\)는 gain이라고 부르기도 한다.)

즉 주어진 data에 mean을 빼서 zero centering을 하고, variance로 나눠 distribution range를 줄이는 일을 모든 layer 마다 하는 것이다 (보통 모든 layer마다 LayerNorm이 들어가므로).

LayerNorm 이전에 BatchNorm이 있었는데, batch dimension을 따라 normalization 하는 BatchNorm과 다르게 channel dimension으로 normalization을 한다는 차이가 있으며, 통계량에 대한 running average를 저장하고 있다가 test time에 써야하는 BatchNorm의 문제점도 없다는 장점이 있다.

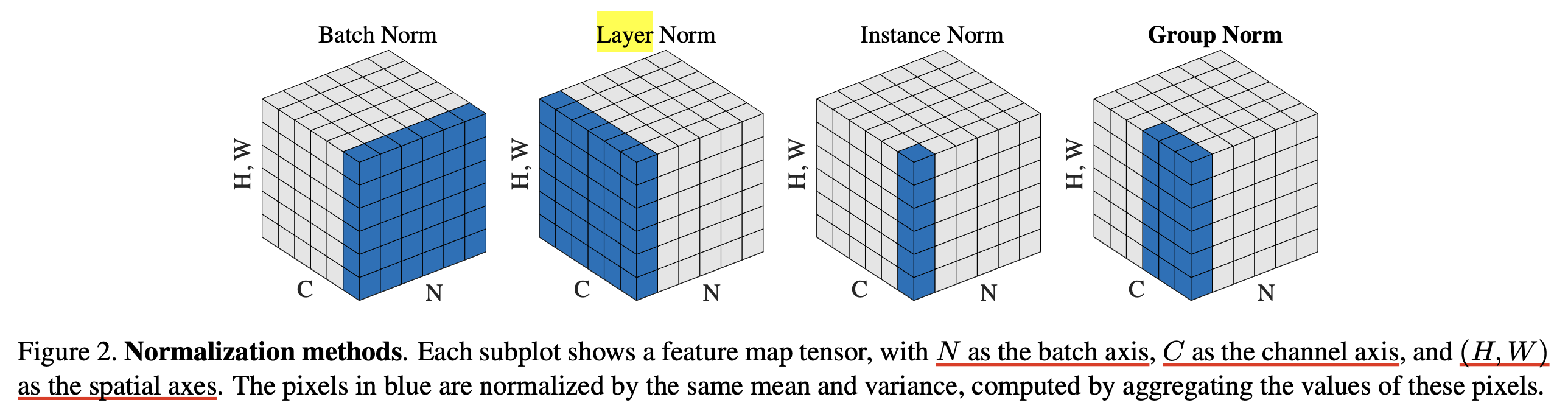Fig. Source from Group Normalization

BatchNorm은 본래 내부 공변량 변화 (Internal Covariate Shift; ICS)라는 현상을 완화하여 DNN training에 기여한다고 알려져 있었는데, 이는 어떤 i번째 layer의 input distribution이 i-1번째 layer의 weight의 update에 따라 변하는 현상을 의미한다. 하지만 BatchNorm은 mini-batch size가 작으면 그 통계량을 믿을 수 없다는 점과 가변 길이 (variable length)를 갖는 input에 대해서 제대로 working하지 않을 수 있다는 단점 때문에 language modeling (LM)등의 sequence modeling에서는 LayerNorm이 dominant하게 쓰인다고 할 수 있다.

(현대에 와서는 ICS가 BatchNorm이 working하는 주된 원인이 아니라는 말이 많은데, 이에 대해서는 How Does Batch Normalization Help Optimization?등을 찾아보면 좋을 것 같다)

Fig. footnote about ICS

앞서 얘기했던 것 처럼 BatchNorm이나 LayerNorm이 개발된 목적은 주어진 시간 동안 optimization을 더 잘해서 좋은 point로 도달하기 위함인데, 직관적으로 input을 normalization (정확히는 standardization) 하지 않으면 backprop시 layer input과 upstream gradient가 outer product되는 과정에서 매우 큰 gradient가 발생하므로 LR을 균일하게 쓸 수 없는 문제가 발생한다. (이를 보통 training stability를 개선한다고 표현한다)

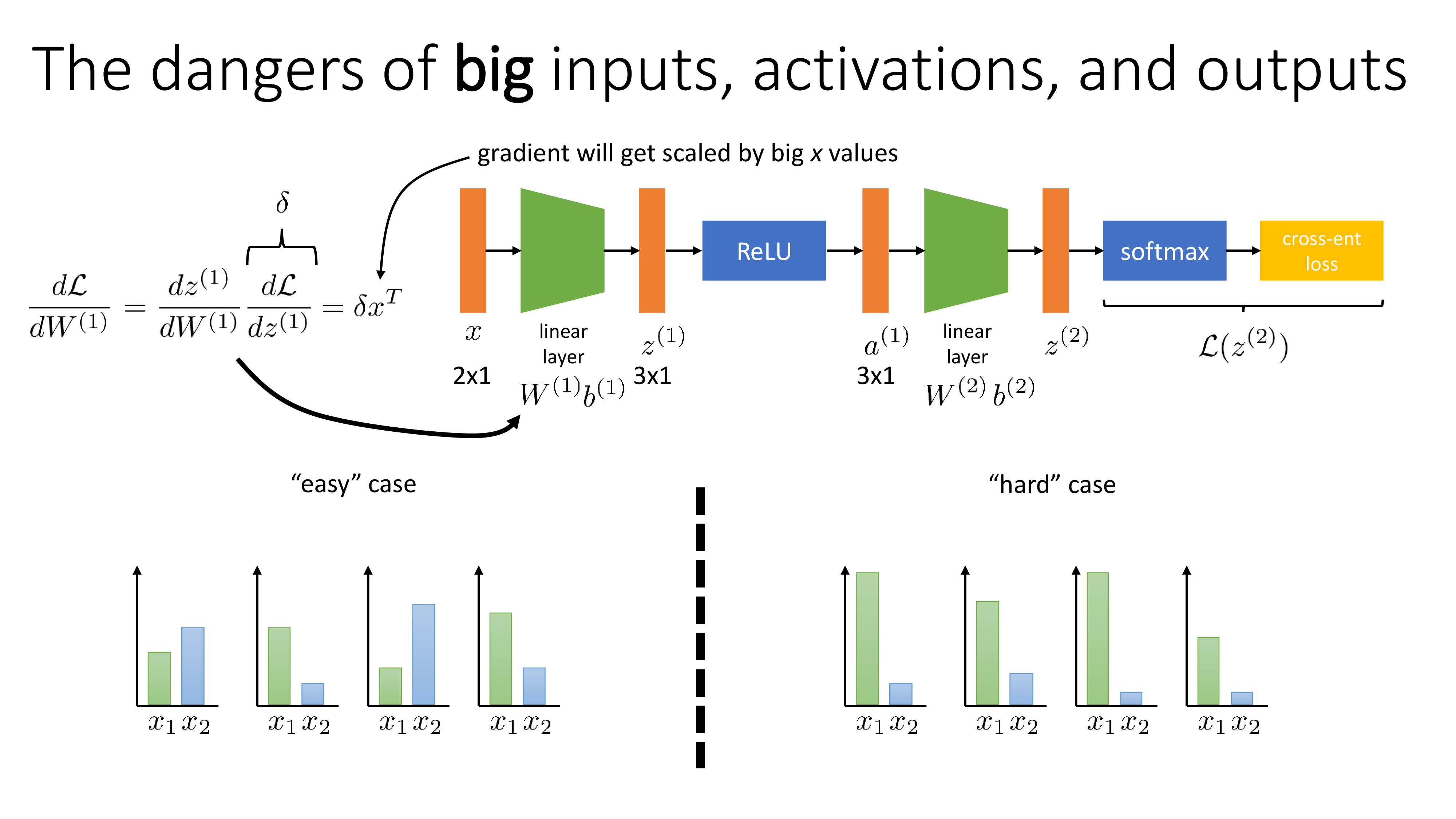Fig. Source from Sergey Levine’s Lecture, CS182

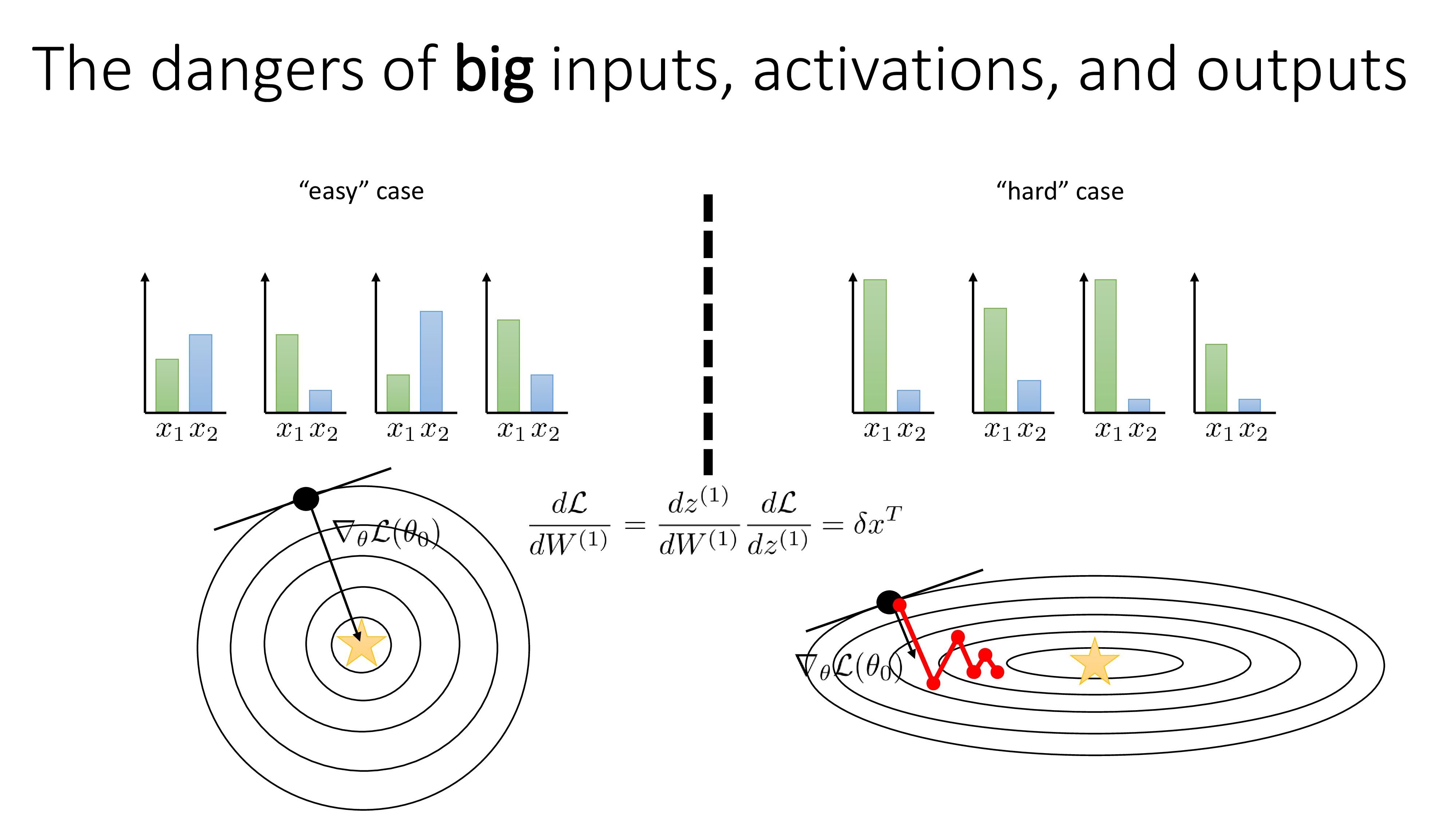Fig. Source from Sergey Levine’s Lecture, CS182

그렇기에 big inputs (activations)에 대한 문제를 해결하고자 Transformer를 포함해 대부분의 NN model들이 매 layer마다 normalization module을 가지고 있는 것이라고 할 수 있다.

Fig. Source from Sergey Levine’s Lecture, CS182

Fig. Source from Sergey Levine’s Lecture, CS182

Root Mean Squared (RMS) Norm (RMSNorm)

그래서 왜 RMSNorm을 써야 하는가? 왜 이것은 LayerNorm보다 더 빠른가? 이제 RMSNorm가 LayerNorm과 비교해서 어떤 차이가 있는지 알아보자.

먼저 RMSNorm paper의 notation대로 다시 LayerNorm을 써보자. 어떤 Feed-Forward Network (FFN)이 존재할 때, input vector, \(x \in \mathbb{R}^{m}\), 그리고 이 FFN의 output vector, \(y \in \mathbb{R}^{n}\)에 대해서 다음이 성립하며,

여기서 \(w_i, b_i\)는 \(y_i\) element를 만드는 weight and bias 이며, \(f(\cdot)\)는 non linear activation function이며, 마지막으로 \(a \in \mathbb{R}^{n}\)은 weighted summed inputs to neurons으로, 즉 normalization module의 target을 의미한다.

Vanilla LayerNorm은 앞서 얘기한 것 처럼 주어진 summed input, \(a\)로부터 mean, variance 를 계산한 뒤 아래와 같이 normalization을 수행한다.

여기서 \(g_i\)는 learnable weight, 즉 gain 이며, initialization은 1로 setting 되며 standardized summed input에 대해서 re-scale 하는 역할을 한다. (당연하게도 i번째 output vector element에 곱해지므로 이는 scaling이다)

반면 RMSNorm은 다음과 같이 formulation 되는데, 보면 LayerNorm과 비교해서 \(\mu\) term이 빠졌다는 걸 알 수 있다. (즉 중요한 두 가지 statistic 중에서 mean을 제외함)

이 부분이 point인데, 사실 LayerNorm은 layer의 input, weight에 대해서 re-centering invariant, re-scaling invariant 하다는 특성을 갖는 것이 LayerNorm의 core contribution이라고 알려져 있는데, RMSNorm의 저자들은 mean을 사용해 re-centering 하는 것이 주효하지 않았다고 보고 이를 뺀 것이다.

Invariance Analysis

이에 대해 분석하기 위해서 RMSNorm의 저자들은 input,

Gradient Analysis

이번에는 backprop시 RMSNorm이 gradient에 미치는 영향을 보려고 한다. 사실 이 부분은 되게 중요하다고 할 수 있는데 그 이유는 다음과 같다.

• 1.Backward시 gradient outlier를 완화할 수 있는지 미리 알 수 있음
• 2.High performance fused kernel을 작성할 때 backward를 직접 구현해야함
  • llm.c, Triton

Fig. Source from cudamode IRL meetup

Fig. Source from cudamode IRL meetup

Fig. Source from cudamode IRL meetup

물론 이 post에서 triton kernel 구현체에 대해서도 짧게 살펴볼 것이기 때문에도 중요하긴 하지만 지금 더 중요한 것은 1번이다.

Let's think bout Backprop through Vanilla LayerNorm and w/o LayerNorm

RMSNorm의 gradient를 분석하기 전에, 먼저 LayerNorm의 backprop을 계산해보자.

그 전에 편하게 수식을 정히하기 위해서 아래와 같이 notation을 재 정의 할건데, 각 input vector, scale and shift parameter 들과 우리가 구하고자 하는 gradient들은 다음과 같다.

• variables
  • input: \(x \in \mathbb{R}^{N}\)
  • scale param (weight): \(g \in \mathbb{R}^{N}\)
  • shift param (bias): \(b \in \mathbb{R}^{N}\)
• target gradients
  • input: \(\frac{\partial L}{\partial x} = [\frac{\partial L}{\partial x_1}, \frac{\partial L}{\partial x_2}, \cdots, \frac{\partial L}{\partial x_N}]\)
  • weight: \(\frac{\partial L}{\partial g} = [\frac{\partial L}{\partial g_1}, \frac{\partial L}{\partial g_2}, \cdots, \frac{\partial L}{\partial g_N}]\)
  • bias: \(\frac{\partial L}{\partial b} = [\frac{\partial L}{\partial b_1}, \frac{\partial L}{\partial b_2}, \cdots, \frac{\partial L}{\partial b_N}]\)

이제 LayerNorm을 적용하면 우리는 아래와 같은 수식을 얻을 수 있는데,

먼저 input, LayerNorm param, 그리고 layer의 weight matrix에 대한 gradient를 계산하기 위해서는 당연히 upstream gradient를 알아야 하고, 이를 \(\partial L / \partial y \mathbb{R}^{n}\)라고 하겠다.

사실 LayerNorm module weight, bias는 Efficient Backprop에 의해서 매우 간단하게 구할 수 있다.

RMS Norm

먼저 normalization module의 weight and bias인 \(g, b\)에 대한 gradient는 upstream gradient를 \(\frac{\partial L}{\partial v}\)라고 할 때, 아래와 같이 간단한게 계산할 수 있다.

하지만 weight matrix, \(W\)에 대한 gradient는 훨씬 복잡하다고 하는데, 이는 RMS에 있는 quadatic computation 때문이라고한다.

Kronecker product는 아래와 같이 계산되는 operation인데, matrix, \(A\)가 \(m \times n\)이고, matrix, \(B\)가 \(p \times q\)라면, Kronecker product의 결과는 \(pm \times qn\) matrix가 된다.

이제 R’을 \(\partial L / \partial W\)수식에 다시 넣으면 우리는 weight에 대한 gradient가 input scaling에는 invariant하지만 weight matrix scaling에 대해서는 계속해서 negative correlation을 갖는 다는 것을 알 수 있으며, input scaling에 대한 gradient의 sensitivity를 줄인 RMSNorm은 training stability를 높히는데 기여할 수 있게 되는 것이다. 반면에 negative correlation은 implicit LR adoptor 역할을 하며 weight matrix에 large-norm이 생기는 것을 피하게 함으로써 model convergence에 도움을 준다고 볼 수 있다.

partial RMSNorm (pRMSNorm)

Experimental Results

과연 mean term을 제외해도, 즉 re-centering을 하지 않아도 괜찮은 걸까?

사실 이에 대한 가장 좋은 방법은 실험으로 증명하는 것일 수 있다 (empirically).

CIFAR-10 Classification

그 다음은 10개 iamge class를 분류하는 CIFAR-10에 대한 performance 비교이다. 보통 image domain에서는 BatchNorm이 더 잘 작동한다고 알려져 있기 때문에 LayerNorm, RMSNorm과 더불어 BatchNorm도 같이 비교했는데 (WeightNorm도 포함), BatchNorm이 가장 성능이 좋았고 LayerNorm 류에서는 test error자체는 비등비등했으나 test error 자체에서는 RMSNorm이 더 좋았다. 즉 generalization에 대해서는 RMSNorm이 더 좋았던 건데, 이에 대한 자세한 분석은 없다.

Fig.

BatchNorm이 더 좋은 이유에 대해서는 자세한 reference가 기억나지 않지만, 아마 같은 channel dimension에 대해서 normalization을 하는 LayerNorm과 비교해서 channel-wise information이 중요한 image domain에서는

Fig. Source from Group Normalization

Geometry of parameter space during learning

Riemannian metric

The geometry of normalized generalized linear models

Implicit learning rate reduction through the growth of the weight vector

Learning the magnitude of incoming weights

Further Things to read

Weight Normalization (WeightNorm)

여기서 \(v \in \mathbb{R}^{k}\)는 k dim vector이고, \(g \in \mathbb{R}^1\)는 scalar이며, \(\parallel v \parallel\)는 \(v\)의 euclidean norm을 의미한다. 즉 이제 weight vector, \(w\)의 크기 (norm)은 \(\parallel w \parallel=g\)가 되는 것이다. 이러한 reparameterizaton 때문에 이를 WeightNorm이라고 하는 것이다.

Non-Parametric LayerNorm from OLMo

OLMo

code

References

• Papers
  • Core
    • Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
    • Layer Normalization
    • Weight Normalization: A Simple Reparameterization to Accelerate Training of Deep Neural Networks
    • How Does Batch Normalization Help Optimization?
    • Root Mean Square Layer Normalization
  • Further
    • Understanding and Improving Layer Normalization
    • Pre-RMSNorm and Pre-CRMSNorm Transformers: Equivalent and Efficient Pre-LN Transformers
    • LayerNorm: A key component in parameter-efficient fine-tuning
• Others
  • Backprop Ninja from Andrej Karpathy
  • Triton Tutorial on LayerNorm
  • Layer Normalization, and how to compute its Jacobian for Backpropagation? from neuralthreads
  • CUDA MODE Lecture 28: Liger Kernel - Efficient Triton Kernels for LLM Training
  • tweet from NYRE
  • (Reddit) Why does it matter that RMSNorm is faster than LayerNorm in transformers?