(WIP) Right Way To Scale Neural Networks. (Tensor Program 4 and 5; Maximal Update Parametrization (muP) and Hyperparameter Transfer (muTransfer))
04 Jan 2024< 목차 >
- Introduction
- War-muP
- Recap) Standard Parameterization (SP) for Nerual Network
- Weight Initialization Case Study
- The Basic Math in muP and It's Desiderata
- Why SP Sucks?
- Transformer with muP
- muP is more than just predicting the optimal LR of wide SP models
- A Very Basic Primer on Why The Correct Parametrization Can allow HP Transfer Across Width
- Experimental Results
- More Details for Implementing muP
- Dive Deeper into muP (in Theory)
- Behaviors of Gaussian Matrices vs Tensor Product Matrices
- Preparation for the Derivations
- Linear Tensor Product Matrix (e.g. SGD Updates)
- NonLinear Tensor Product Matrix (e.g. Adam Updates)
- Vector Case (e.g. Readout Layer)
- Deriving muP for Any Architecture
- Why Other Parametrizations Cannot Admit Hyperparameter Transfer
- Something Interesting (Things to think about)
- Pytorch Implementation of muP
- References
Introduction
Motivation (from GPT-4)
OpenAI는 어떻게 GPT-4를 학습시켰을까?
Learning algorithm 을 말하는 것이 아니라 어떻게 안정적으로, 그리고 경제적으로 model을 잘 학습했느냐는 것이다. 모르긴 몰라도 model size가 수백 billion (B)에 달하는 modern Large Language Model (LLM)에 대해서 가장 성능을 잘 낼 수 있는 LR 등의 Hyperparameters (HPs)를 exhaustive search 하는 노가다를 뛰진 않았을 것이고 뭔가 비밀이 숨어 있을 것이라고 생각해 볼 수 있다.
우리는 그 hint를 GPT-4의 Technical Report에서 찾을 수 있는데,
사실상 이 report paper는 우리는 scaling prediction을 잘 했어요와 우리 model이 이런것도 돼요만 얘기하고 있다.
Scaling law는 Model Sizes를 \(N\), Compute Budgets를 \(C\), 그리고 Dataset Sizes를 \(D\)라고 할 때, 어떤 Autoregressive Model의 Loss, \(L\)는 다음의 법칙을 따른다는 내용을 담고 있는데,
OpenAI 연구진들이 2020년에 이미 실험적으로 검증한 바 있다.
여기서 미지수, \(x\)는 \(N,C,D\) 모두가 될 수 있으며 \(L_{\infty}\)는 irreducible loss로,
이는 reducible loss와 다음과 같은 차이가 있다.
다시 말하면 irreducible loss는 실제 dataset의 distribution의 entropy를 말하며, reducible loss는 model이 예측하는 distribution과 true dataset distribution간의 KL Dirvergence (KLD)이다. 이것은 당연하게도 우리가 사용하는 learning objective인 Cross Entropy (CE) loss가 두 분포간의 KLD를 의미하는 것과 같은 맥락이다.
다시, 결국 OpenAI가 증명하고자 하는 수식인 \(L(x) = L_{\infty} + (\frac{x_0}{x})^{a_x}\)가 의미하는 바는 CE loss를 사용하는 Autoregressive Transformer model은 model size, compute budget이 증가할수록 performance가 증가하는데, 이것이 멱법칙 (power-law)를 따른다는 것을 의미한다.
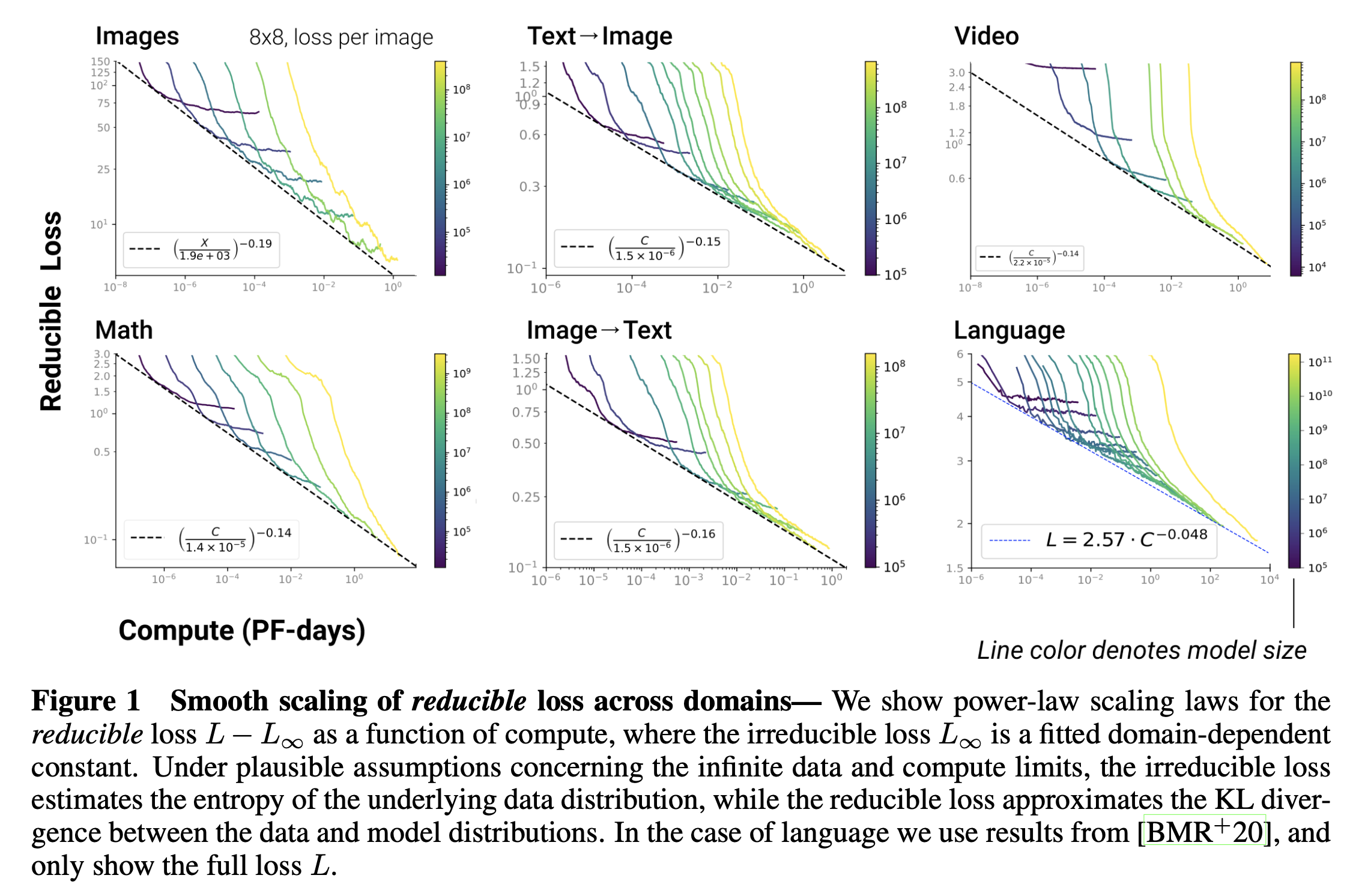 Fig.
Fig.
여기서 GPT-4는 Image-to-Text와 Text-to-Text (Language Modeling; LM)인데, 이들은 다음의 법칙을 따른다.
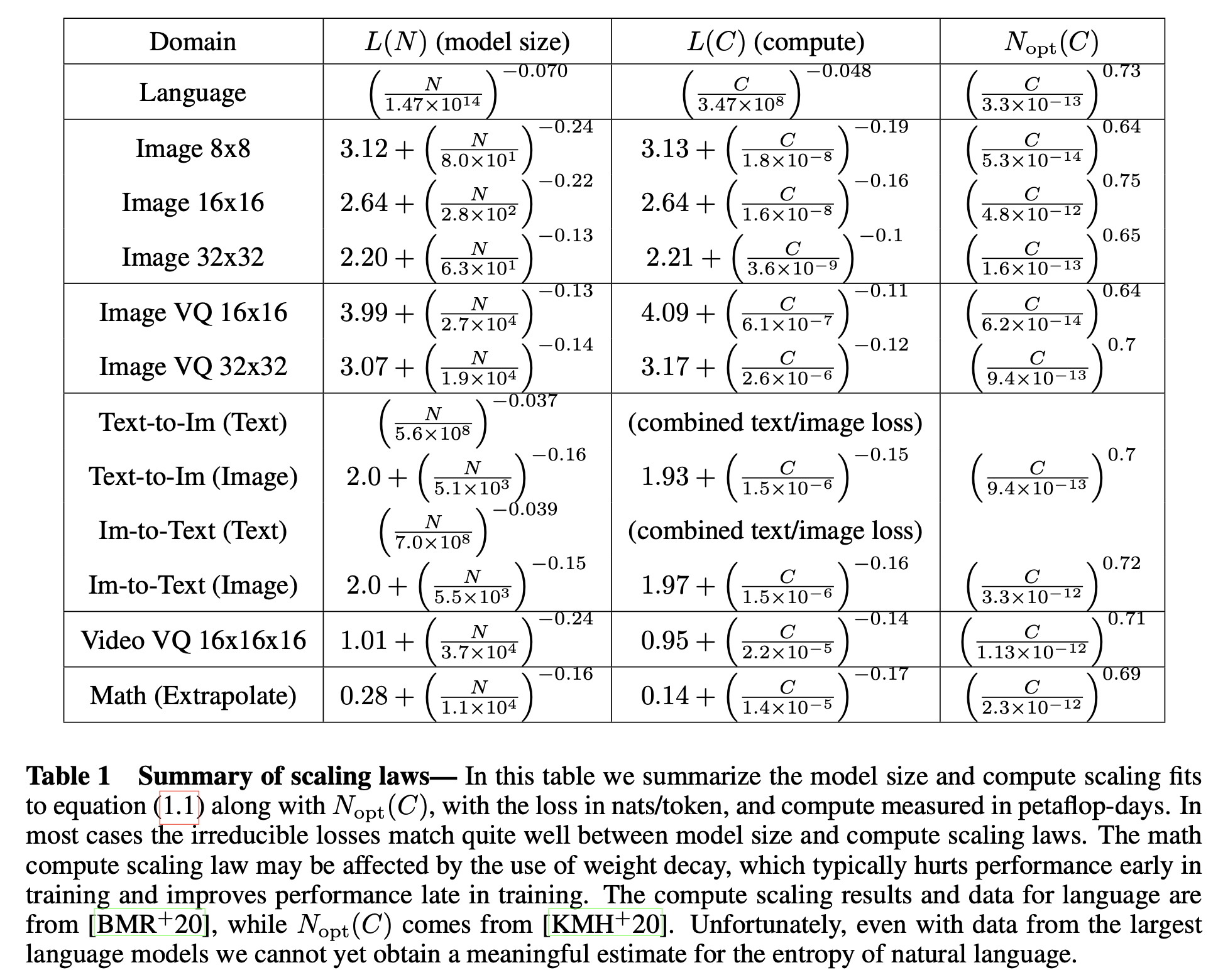 Fig.
Fig.
GPT-4의 report에서도 이 scaling law를 정확하게 언급하고 있는데, section 3에서 실제로 이들은 model이 커짐에 따라서 loss predicion을 거의 오차없이 해냈음을 자랑하고 있다.
 Fig.
Fig.
OpenAI는 next token prediction (Perplexity; PPL 같은 것)과 humaneval 지표에서 모두 매우 높은 정확도로 loss (accuracy) predicion을 할 수있었다고 얘기한다.
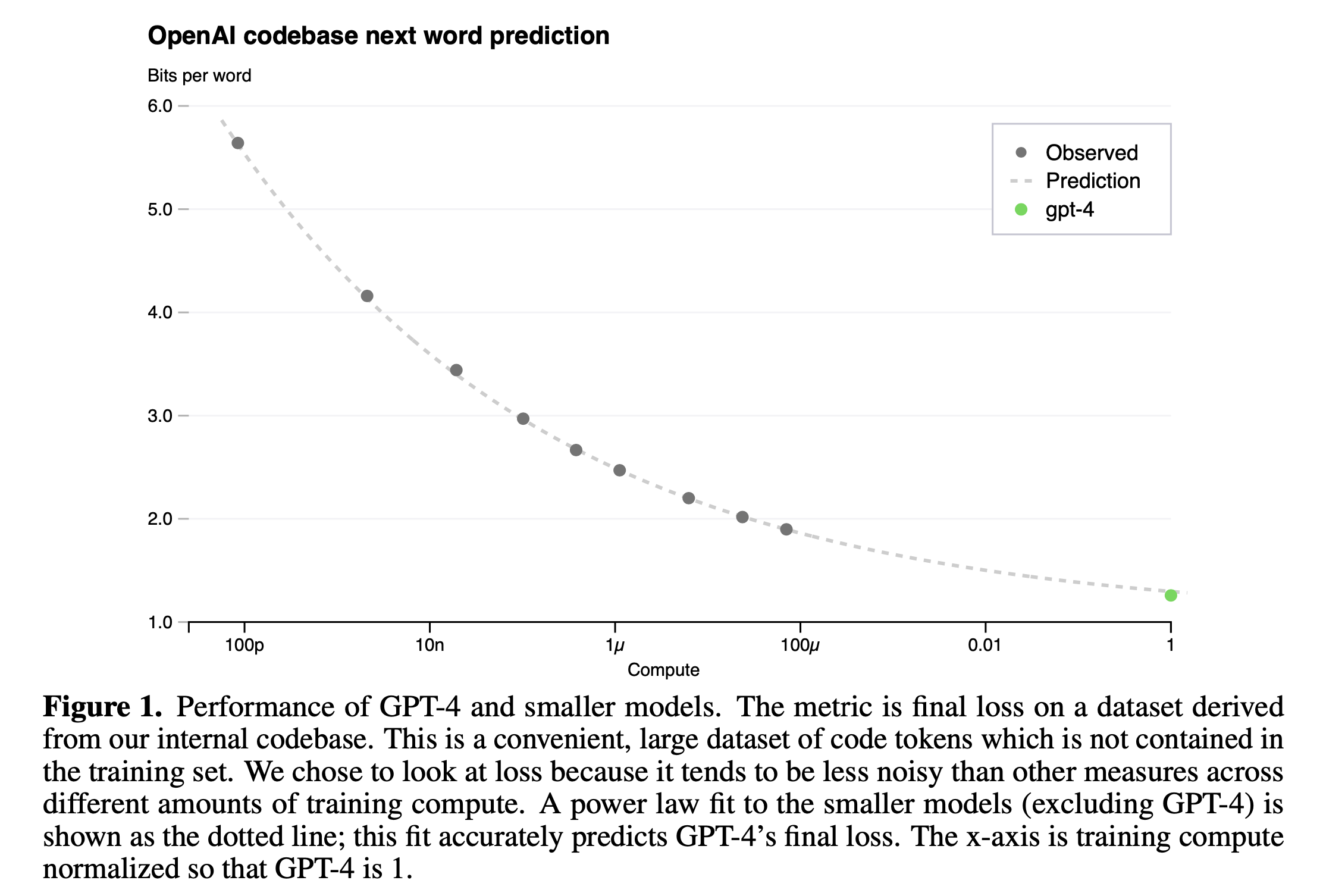 Fig.
Fig.
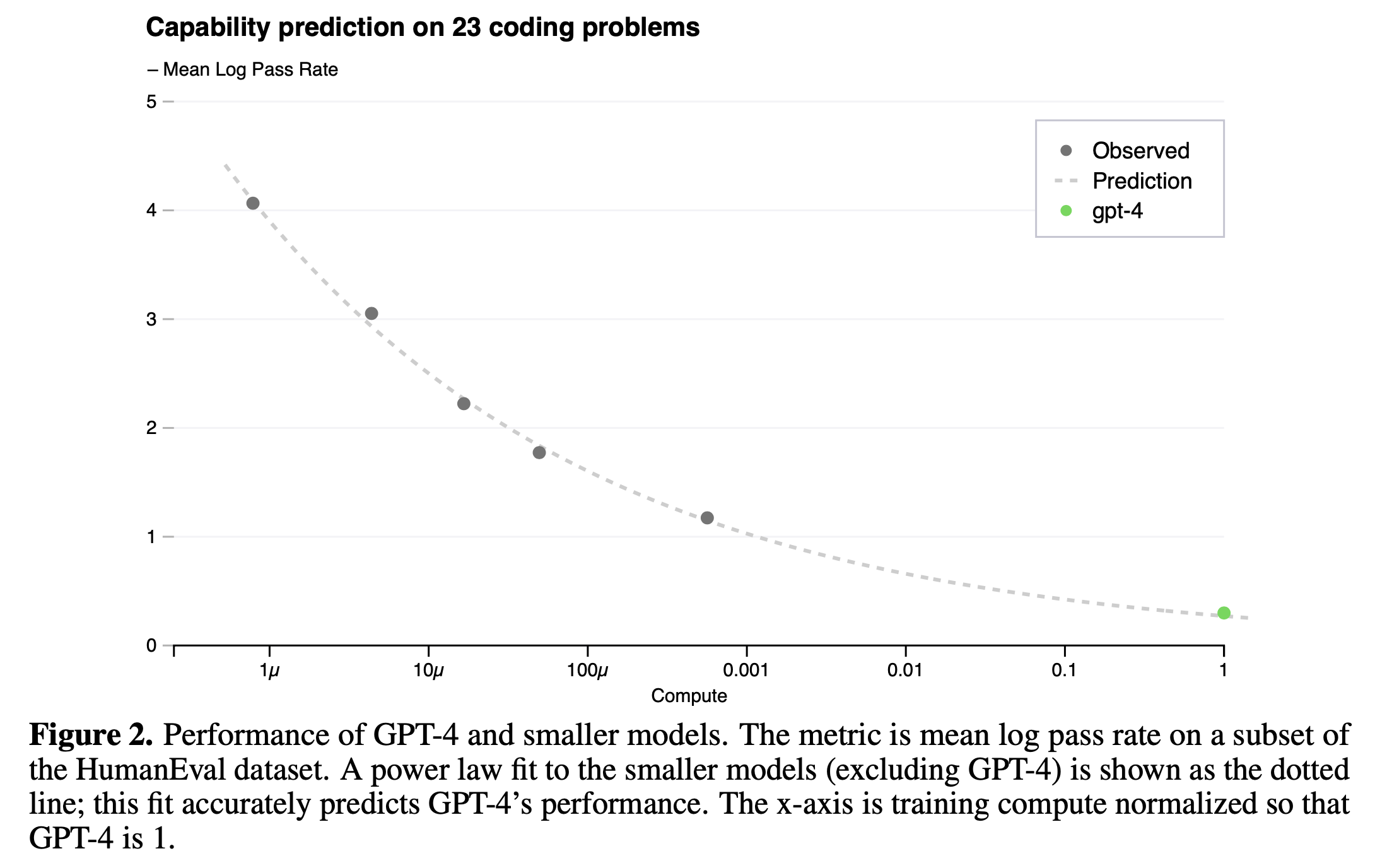 Fig.
Fig.
GPT-4 논문에는 architecture가 어떻게 생겼는지? 어떤 data sample들을 사용해서 얼만큼 학습했고 learning objective가 어떻게 되는지? 에 대한 얘기는 없지만 제일 중요한 Scaling Prediction을 어떻게 했는지?에 대한 내용도 빠져있다. 솔직히 learning algorithm이야 PPO가 좋니 DPO가 좋니 하면서 여러 algorithm들이 publish되고 있고, GPT-4의 architecture는 Mixture of Expert (MoE)로 학습되었다는 것이 ground truth처럼 여겨지고 있는데, 여타 수많은 실리콘밸리 기업들이 만드는 SOTA opensource model들이 MoE인 것을 보면 소문이 사실인 것으로 보이지만 지금 우리가 눈여겨 볼 것은 Scaling Law prediction이다.
게다가 Scaling Law 를 하려면 또 중요한 부분이 있는데,
바로 model size에 대한 function을 그릴 때 model size가 커질 때 마다 최적의 HP를 찾고 loss를 찍어야 한다는 것이다.
그래야 law를 제대로 구할 수 있는데,
그렇기 때문에 우리는 추가로 신경 써야 할 것은 dataset, model architecture가 있을 때, Scaling Law를 위해 각 setting별 HP을 찾아내려면 얼마나 많은 computing resource를 태워야 할까?라는 것이다.
muP and muTransfer
사실 GPT-4 technical report를 잘 살펴보면 introduction에 인용한 paper들 중 Maximal Update Transfer (muTransfer)라는 것이 있다. 이는 Maximal Update Parameterization (muP)이라는 work의 확장판으로, 요약하자면 작은 model에서 LR, layer initialization, 그리고 layer 별 scaling factor등의 HP를 찾고, 예를 들어 작은 model의 optimal setting을 찾았으면 이를 1000배, 10000배 큰 model로 그대로 확장하여도 (transfer) 그것이 큰 model의 optimal HP가 된다는 것이다. 다시 말해 작은 model에서 search만 하면 그대로 2배, 3배, 10배 큰 model의 optimal HP을 찾은 셈이고, 이들의 loss를 찾으면 100배 큰 target model에 대한 loss를 정확히 예측할 수 있을 것이라는 거다.
muP, muTransfer는 Microsoft에서 large neural networks training에 대해 연구하던 수학과 출신 Greg Yang과 마찬가지로 Microsoft에서 같이 연구하며 LoRA를 제안한 Edward Hu가 공동연구한 작업물이다.
(Edward가 초기 OpenAI-Microsoft parternership onsite engineering team 멤버 8명 중 한명이며 GPT-4 technical report에도 reference가 달려있기 때문에 아마 GPT-4를 학습하는데 반드시 쓰였을 것으로 보인다)
 Fig. Edward의 video에 따르면 Cerebras와 DeepMind의 LLM에도 사용된 것으로 보인다.
Fig. Edward의 video에 따르면 Cerebras와 DeepMind의 LLM에도 사용된 것으로 보인다.
사실 muP와 같은 것들은 모두 Greg Yang이 연재하는 Tensor Program (TP)라는 serires로 묶이는데, muP와 muTransfer는 각각 TP4와 TP5에 해당한다.
 Fig. Greg Yang은 2019년 2월부터 혼자 paper를 내는 또라이다.
Fig. Greg Yang은 2019년 2월부터 혼자 paper를 내는 또라이다.
Greg의 궁극적인 goal은 NN을 scaling up 하는 optimal한 방법과 그러한 모델들에 대한 robust undertanding을 제공함으로써 safety와 alignment를 하는 데 도움이 되는 Large Scale Deep Neural Network (NN) training을 위한 모든 것의 이론을 정립하는 것이라고 한다. 왜냐하면 Richard Sutton의 Bitter Lesson에도 나와있듯 결국 computing resource를 쏟아붇는 것만이 답인데, 뉴턴이 고전 물리학을 제대로 정립하고 이를 scale-up해서 소련이 우주발사체를 성공시킨 것 처럼 scale-up하는 것에 대한 이론 정립을 하는 것이 매우 중요하다고 믿기 때문인 것 같다.
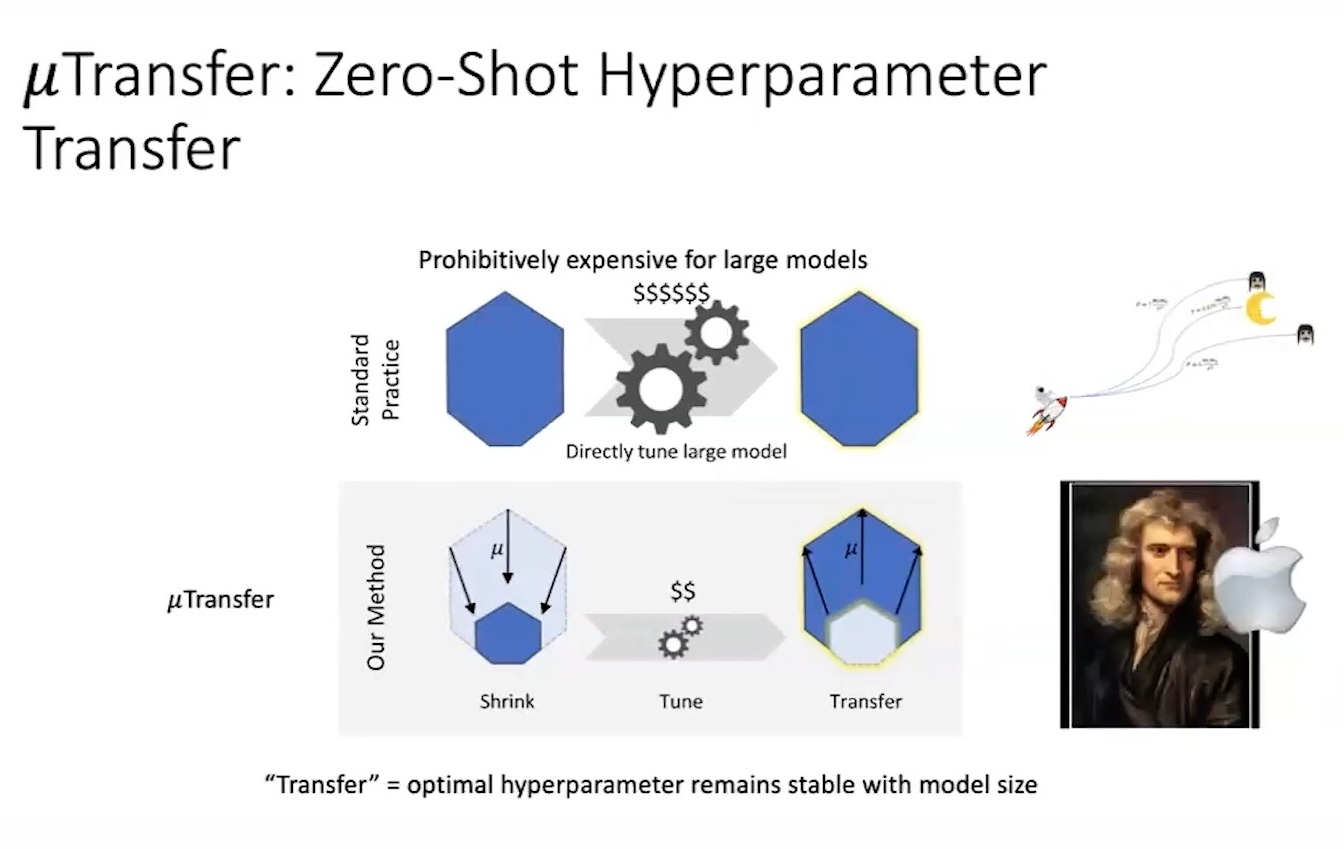 Fig.
Fig.
그래서 muP와 Mu transfer는 정확히 무엇인가.
muP는 NN이 어떻게 parameterization 되어야 하는가?에 대한 work인데,
NN parameterization이란 model의 width에 따라서 각 layer의 weight initialization과 그에 맞는 LR를 어떻게 정할지? 등을 의미한다.
그전에 모두가 쓰고있던 Lecun, Kaming Init같은게 존재하는데 왜 또 이게 필요한걸까? Greg과 Edward는 그 이유로 pytorch의 weight initialization이 training dynamics를 고려하지 않았기 때문이라는 점을 지적한다.
 Fig.
Fig.
muP는 말 그대로 training dyanmics를 고려해서 parameterization을 제대로 하자는 것인데,
이를 위해선 parameterization이 정확히 무엇인지 부터 알아야 한다.
후에 제대로 설명하겠지만 내용이 길기 때문에 간단하게만 먼저 설명하자면 muP가 처음 제안된 TP-4에서는 아래 세 가지를 parameterization으로 규정한다.
a: per weight Multiplierb: per weight Initalization Variancec: per Learning Rate (LR)
이 3개로 구성된 parameterization을 abc-parameterization이라고 한다.
 Fig.
Fig.
위 수식이 복잡해 보이지만, L개의 layer depth를 갖는 MLP에 대해서 각 layer의 weight matrix의 random Gaussian initialization의 variance는 NN의 width, \(n\), 즉 hidden layer의 역수인 \(n^{-2b_l}\)꼴로 표현되며, 해당 weight의 LR은 \(n^{-c}\)로 scaling해주며, 생소하겠으나 \(n^{-a_l}\)가 붙는 것의 의미는 해당 layer의 output tensor (pre-activation)에 곱해주는 factor를 의미한다. 곧 example을 통해 왜 이렇게 해야 하는지 알아보겠으나 이렇게 하면 우리는 gradient를 control할 수 있고 나아가 layer 별 acivation output이 일정한 크기가 되도록 유지할 수 있다.
그런데 이 모든 abc-parameterization은 \(n\)에 대한 term이지 않은가? 즉 우리가 원하는 것은 hidden size가 늘어날 때, 즉 model size가 커질 때도 똑같이 activation의 크기를 일정 수준으로 유지하여 small model과 large model의 training dynamics gap을 줄이는 것이 목표이다. 그러니까 TP-4의 goal은 weight type별로 (input, hidden, output) 어떻게 이 \(a,b,c\)를 구하는지 계산하고 정립하는 것이었다고 할 수 있다.
 Fig. width에 대한 function으로 LR, init variance등이 control 되어야 함.
Fig. width에 대한 function으로 LR, init variance등이 control 되어야 함.
직관적으로 muP를 따라 parameterization을 할 경우,
model size가 커지더라도 커진 width에 따라 LR, init std등이 보정되므로 우리는 비슷한 optimization process를 겪을 것이라는 걸 예상해 볼 수 있다.
그 결과 LR같은 Hyperparameter (HP)가 전이 (transfer)된다는 내용이 있는데,
이것이 바로 TP-5에서 다루는 내용이다.
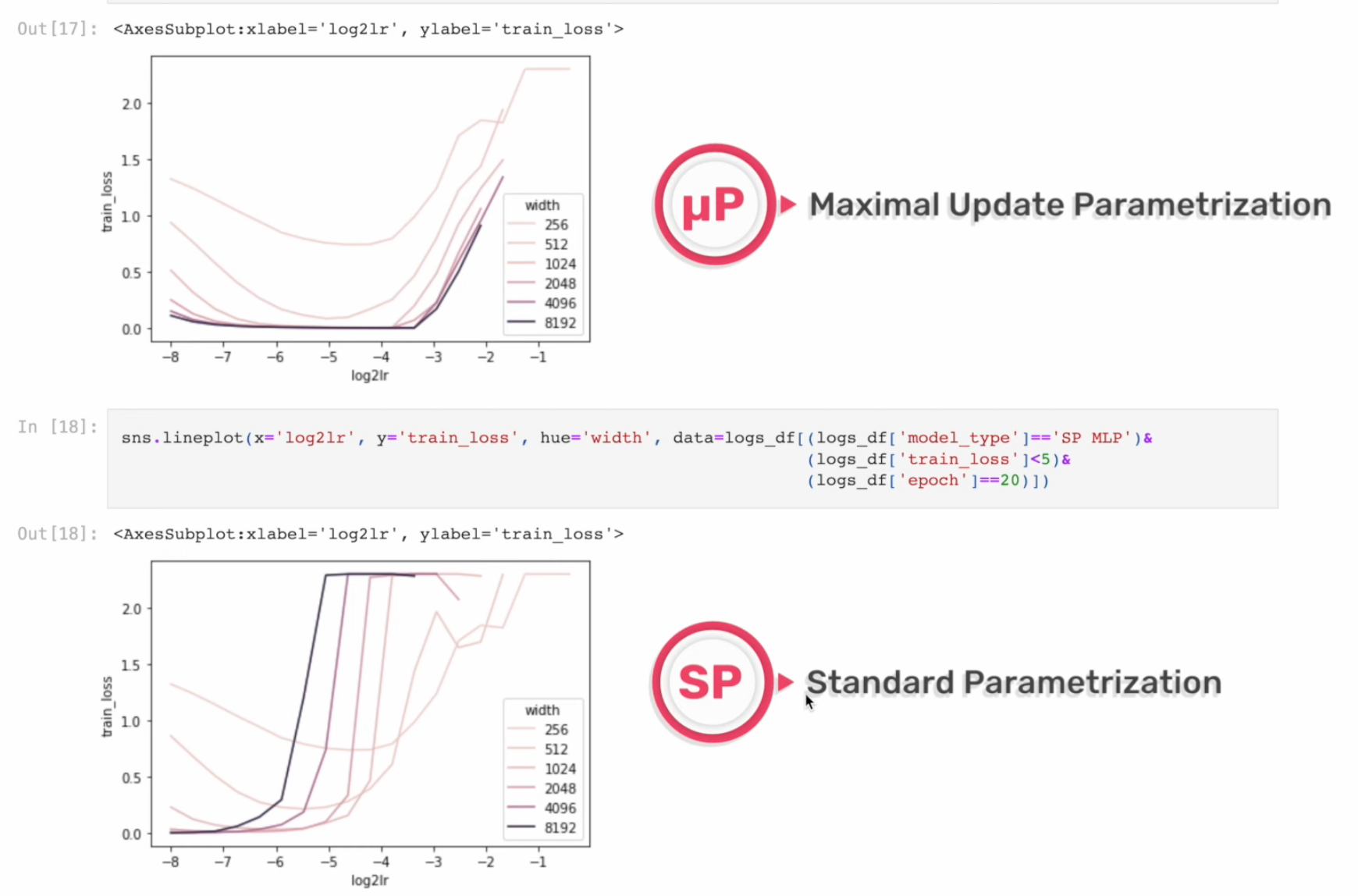 Fig.
Fig.
위 figure처럼 pytorch의 Standard Parameterization (SP)을 따를 시에는 model의 width가 다를 때 (지금은 MLP 얘기하는데 Transformer도 같음) optimal LR로 보이는 지점이 다른 것을 알 수 있다 (각 training curve는 다른 width를 의미한다).
반면에 muP를 적용한 경우 training loss가 0에 수렴하는 toy example이라서 잘 안보이지만 거의 비슷한 LR를 사용해도 그것이 곧 optimal LR이 되는 것을 볼 수 있다.
이말인 즉 muP를 사용해서 model init을 하면 small scale model에서 HP tuning을 빡세게 한 뒤,
그대로 model을 수십배 scale up해도 HP tuning을 할 필요가 없다는 것을 의미한다.
말 그대로 muP를 사용해서 학습할 model들에 대해서는 HP가 전이 (transfer)가 된다는 것이다.
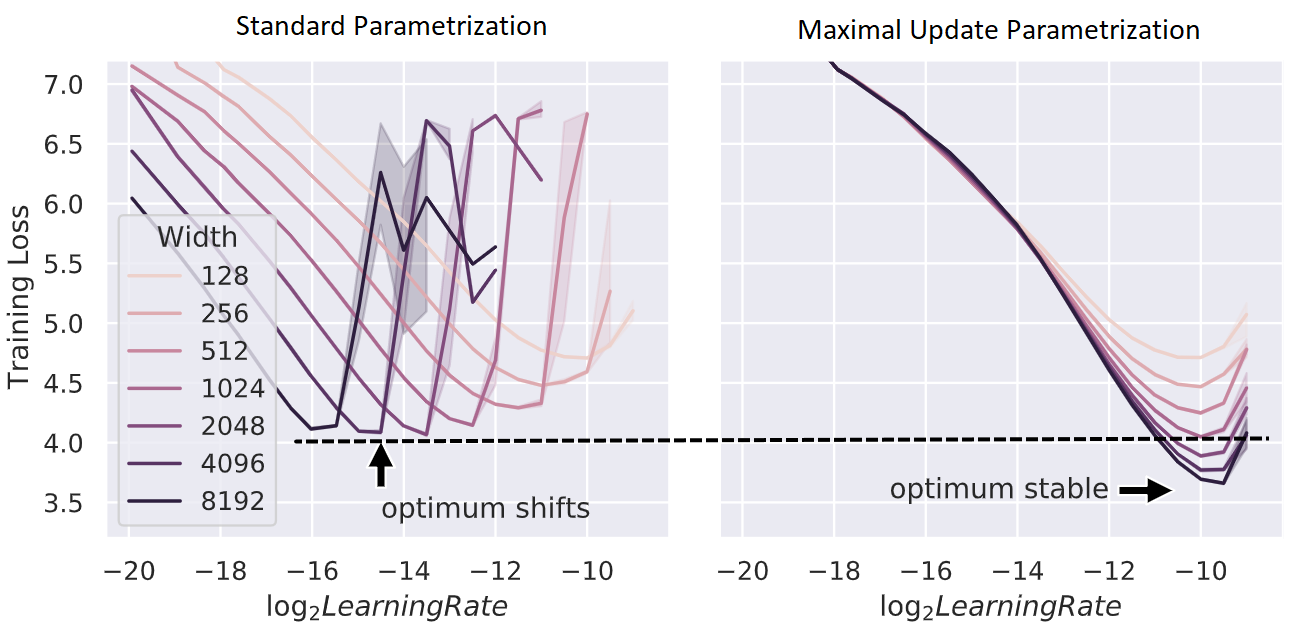 Fig.
Fig.
저자들은 SP와 muP를 interpolation해서 parameterization 해 본 결과, muP가 거의 유일한 (unique) parameterization transfer가 된다는 것을 보였다.
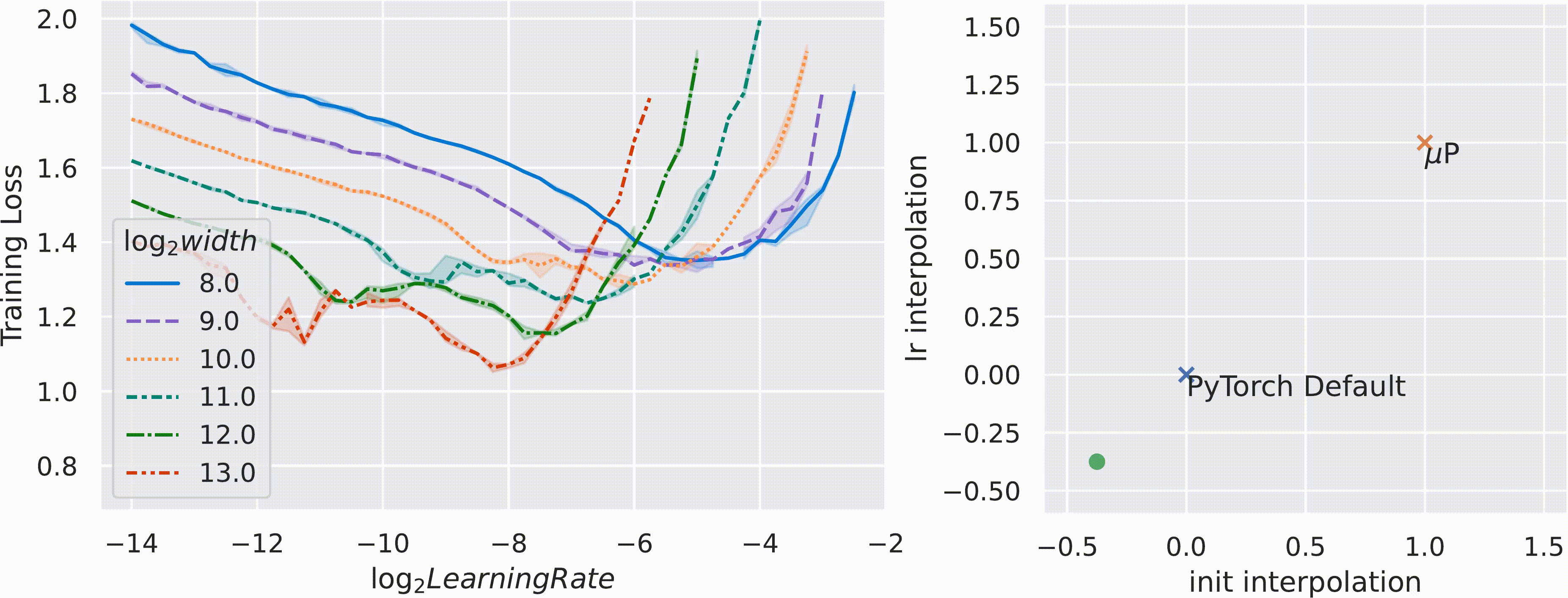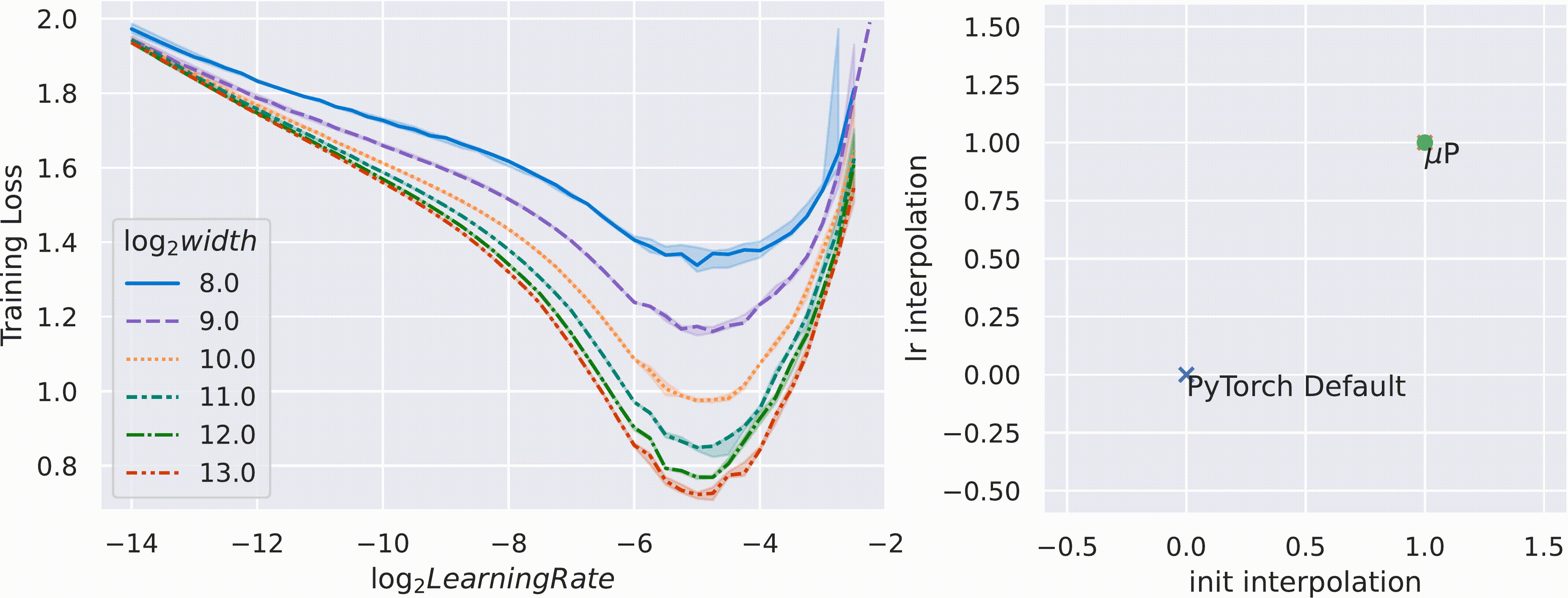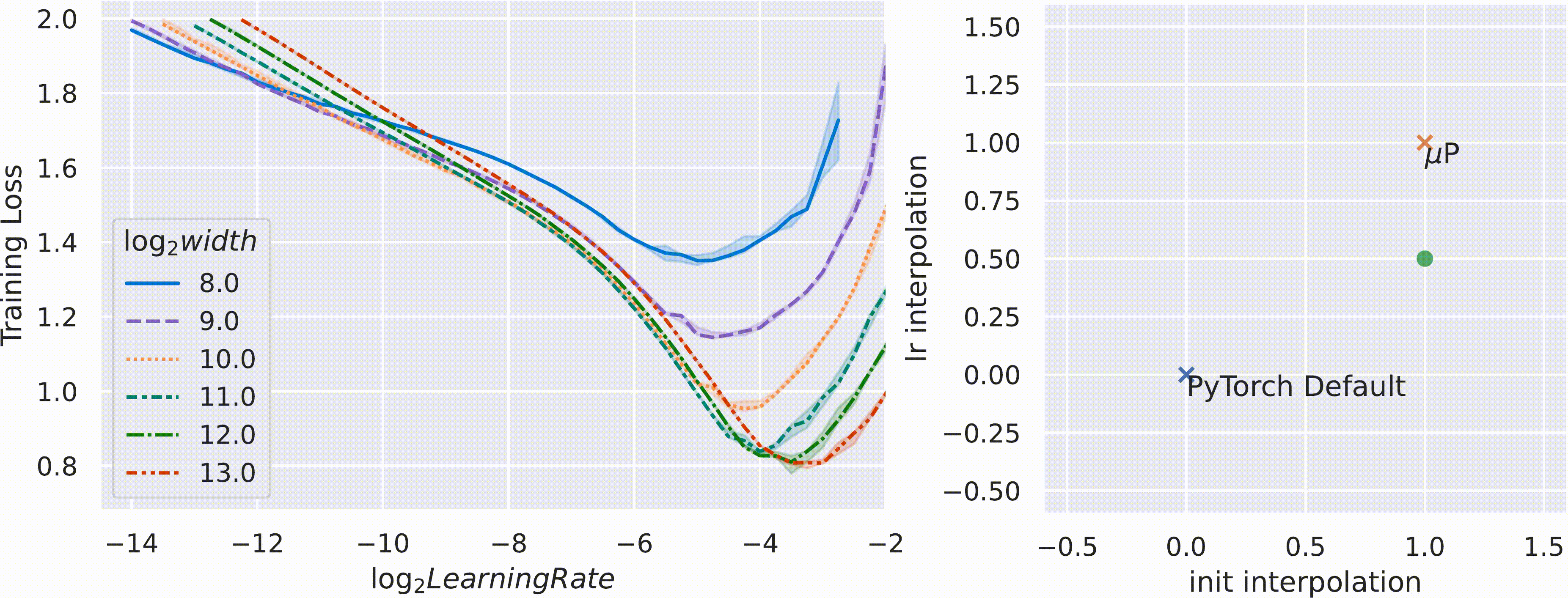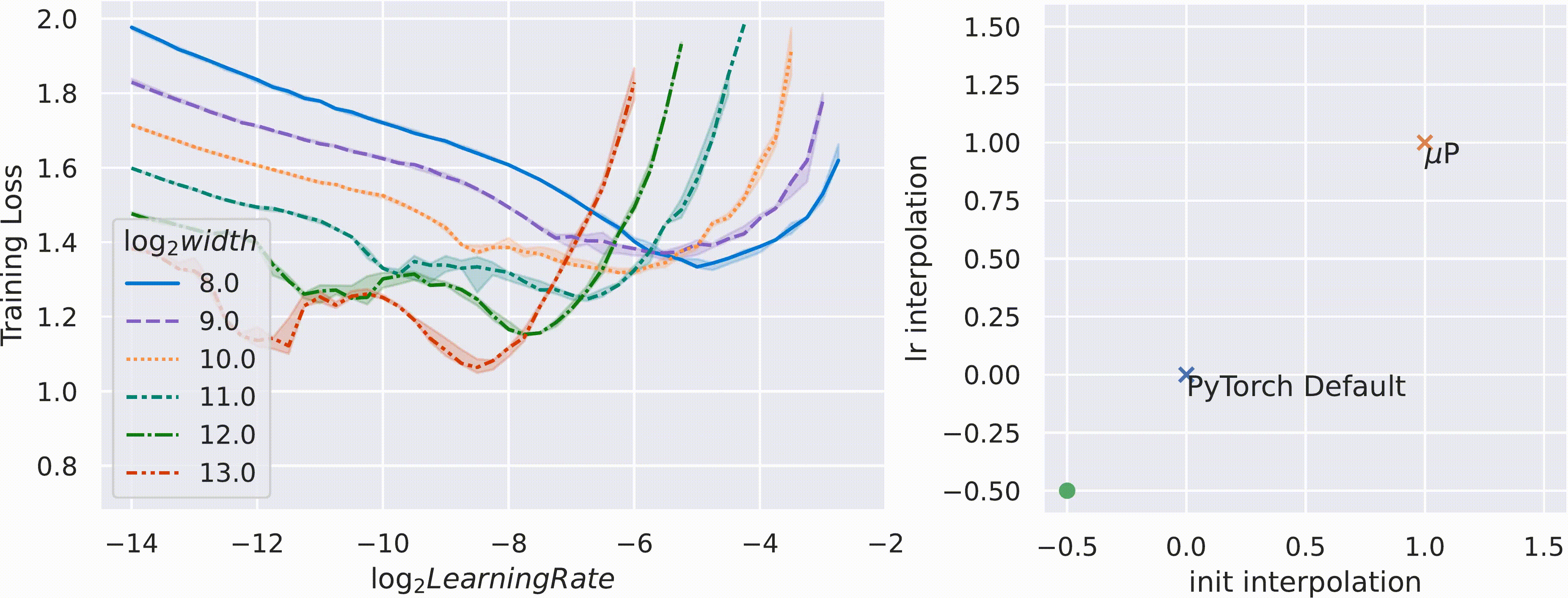 Fig.
Fig.
저자들이 말하고 싶은 것은 정리하자면 model을 scaling up할 때,
"음 이 model size의 optimal LR은 이 값이군"하고 size별로 optimal HP를 찾을 생각을 하는 것이 아니라,
 Fig.
Fig.
 Fig. 예를 들어 한 module (layer)에 대해서는 width가 2배 늘어나면 lr을 1/2배 해야겠다. 같은 공식이 TP4에서 유도된다.
Fig. 예를 들어 한 module (layer)에 대해서는 width가 2배 늘어나면 lr을 1/2배 해야겠다. 같은 공식이 TP4에서 유도된다.
어떻게하면 small scale model의 HP을 transfer할 지를 생각하는 것이 훨씬 싸고 심지어 성능도 좋다는 것을 이해해야 한다는 것이다.
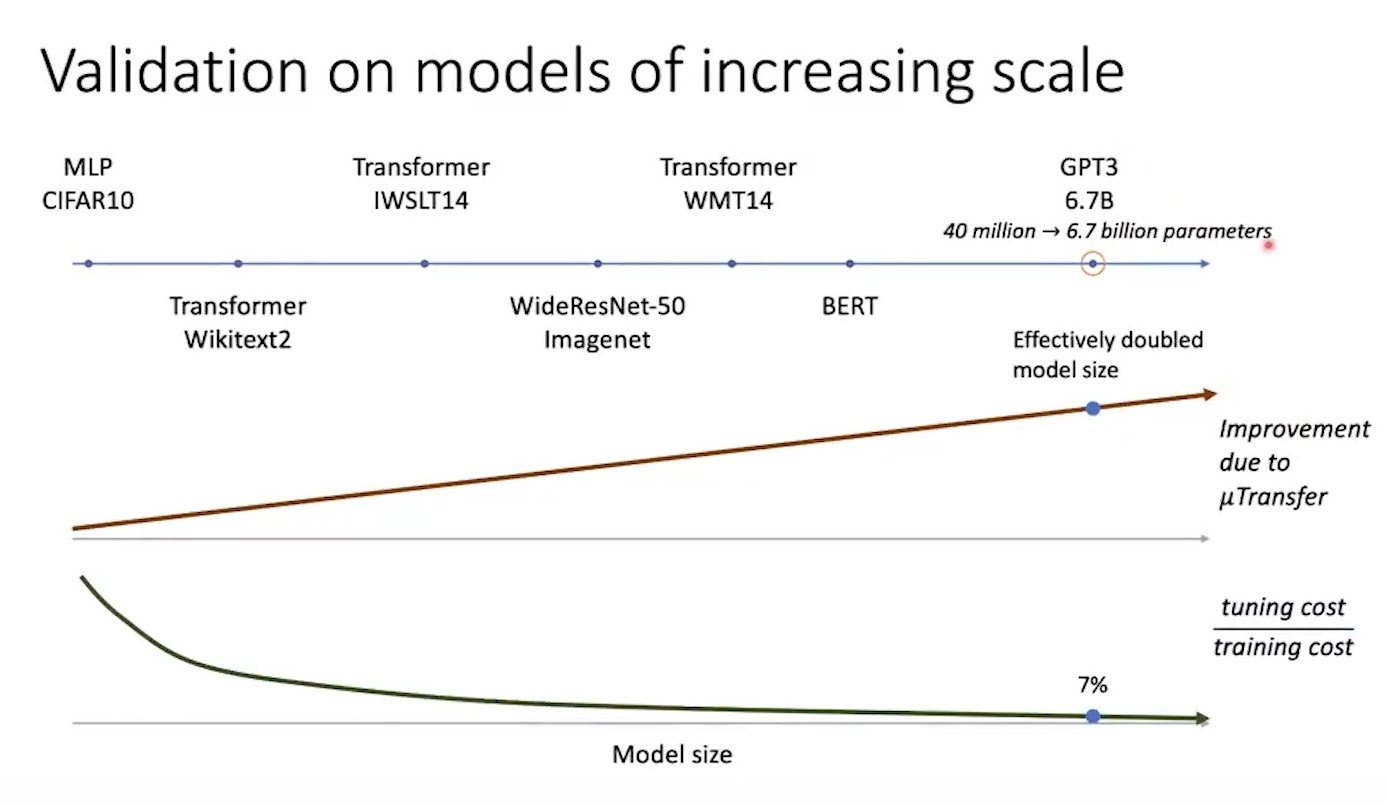 Fig.
Fig.
물론 Kaming init 같은 SP를 사용하는 경우에도 model size가 커질때 LR을 width, \(n\)에 대해서 \(1/n\)배 scaling하라는 heuristic 하는 방법을 쓸 수도 있다. 하지만 Greg은 이는 muP와 비교해서 global LR을 scaling한다는 점 때문에 maximal feature learning 이 안 되기 때문에 올바른 방법이 아니라고 주장한다. (이게 무슨 내용인지는 곧 다시 얘기하게 될 것)
아래 figure를 보면 보통 width가 커질 때 LR을 포함한 HP들의 optimum은 보통 shift 되기 마련인데, unstable한 것을 볼 수 있다.
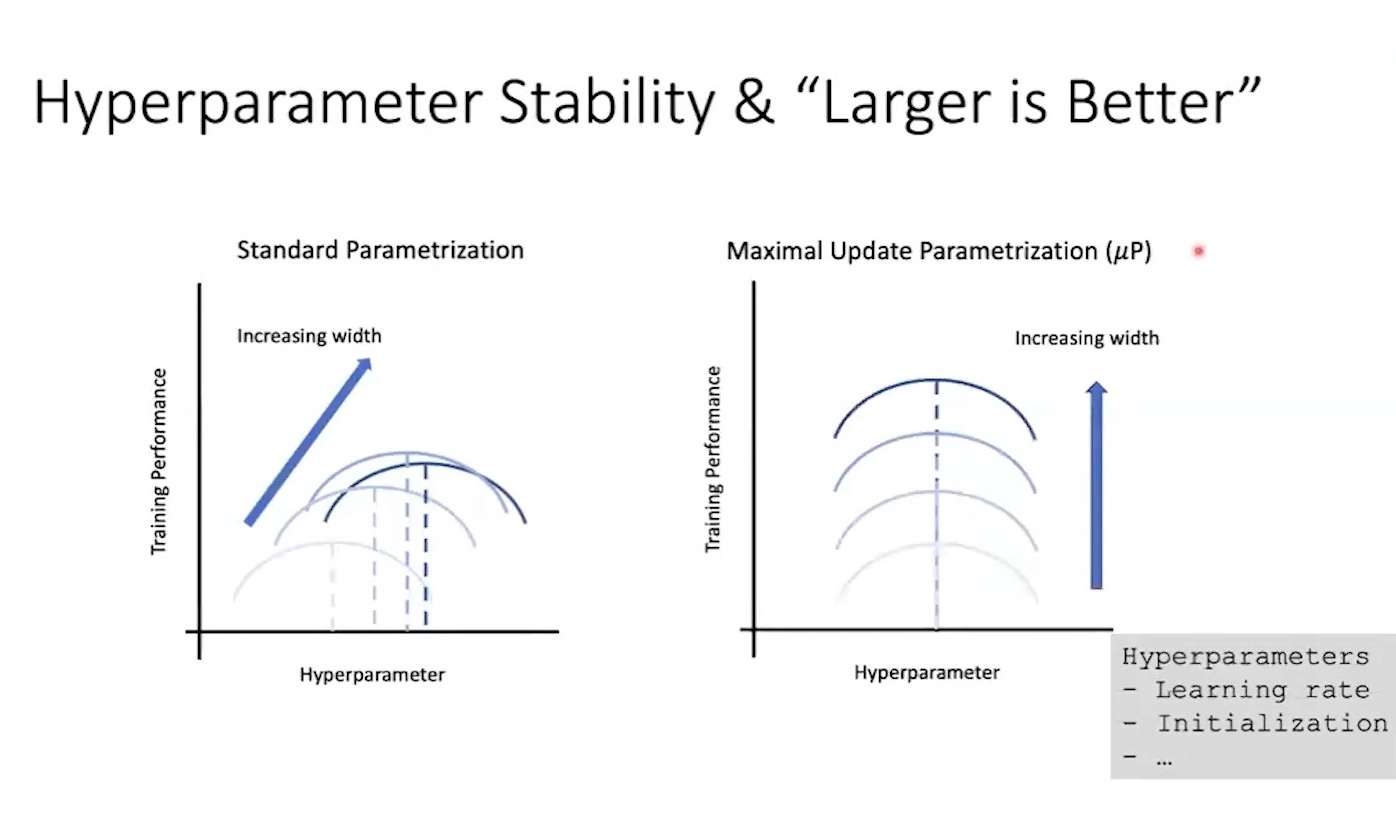 Fig.
Fig.
그래서 어떻게 muP를 하면 되는가? 우리는 아래 table을 채워야 할 것이다. 모든 abc-paramterization의 값들은 width, \(n\)에 대해 power of n 형태를 띄고 있다.
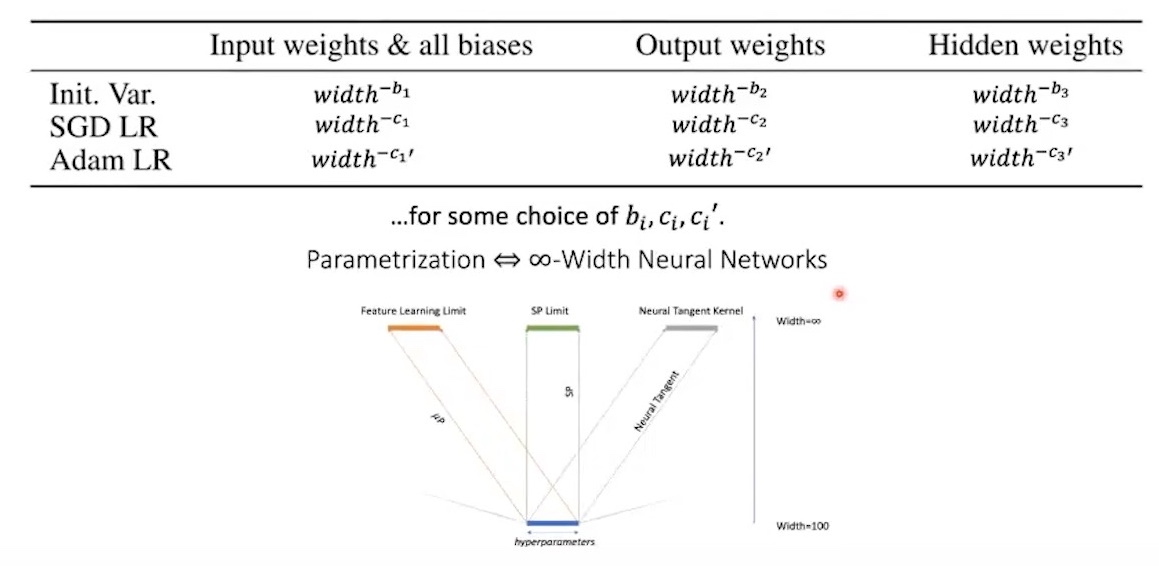 Fig.
Fig.
결과적으로 TP-4에서는 아래 table을 유도하게 되는데,
여기서 fan_in은 layer의 input size를 의미하며,
fan_out은 layer의 output size을 의미한다.
 Fig. Maximal Update Parameterization Table
Fig. Maximal Update Parameterization Table
이 post에서는 어째서 이런 rule이 유도됐는지에 대해서 직관적으로, 가능하다면 수학적으로 엄밀히 알아볼 것이다.
+) 물론 parameterization에 muP와 SP만 있는 것은 아니다. Neural Tangent Kernel (NTK)라는 paper에서 얘기하는 parameterization인 Neural Tangent Parameterization (NTP)도 존재하고 Mean Field Theory (MFT)같은 다른 것도 있다. 하지만 곧 SP와 NTP 모두 문제가 있다는 점을 보일 것이다.
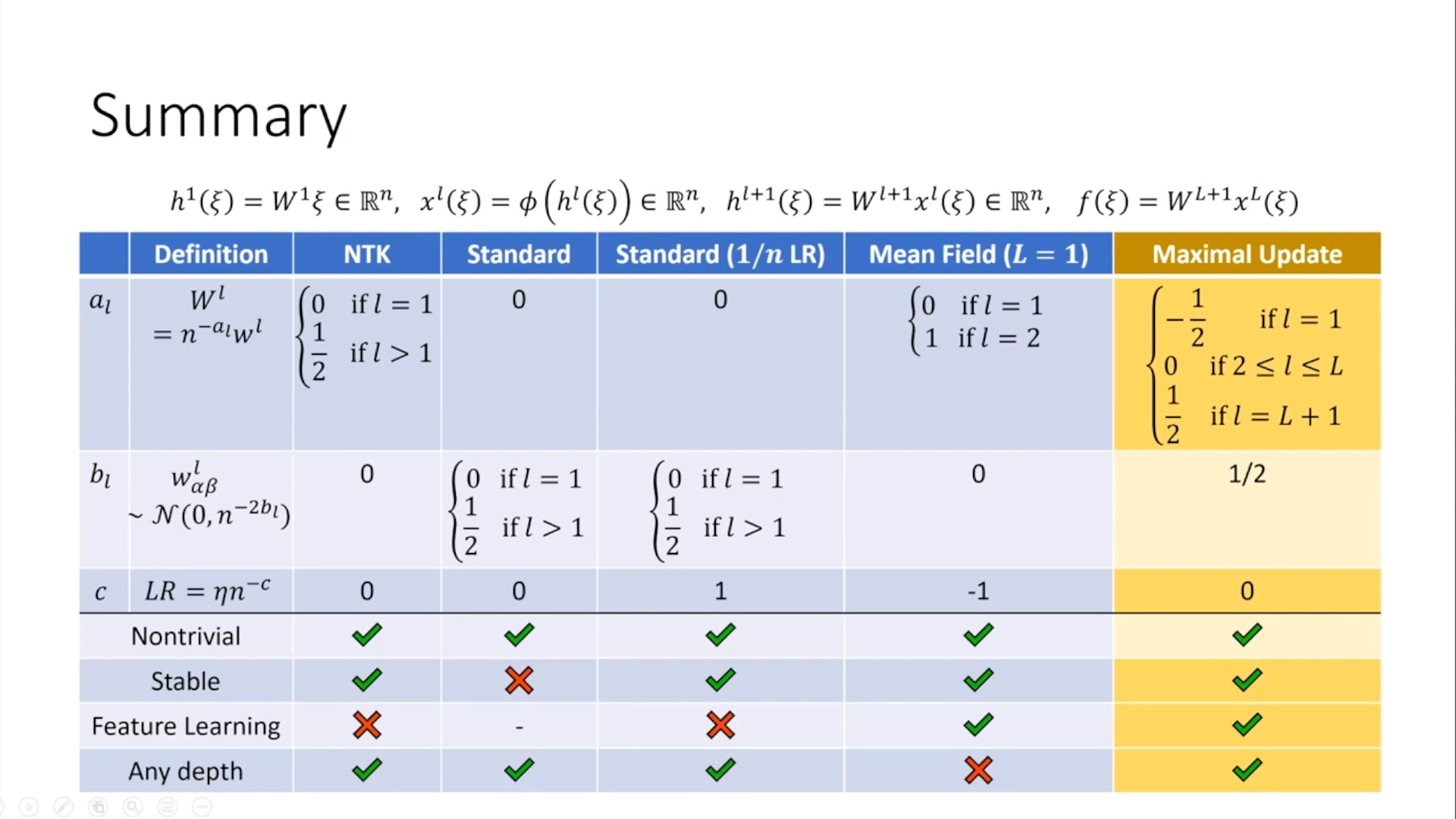 Fig. table의 값이 바로 TP-5 table3와 다른 점은 abc-symmetry 때문이다.
Fig. table의 값이 바로 TP-5 table3와 다른 점은 abc-symmetry 때문이다.
'Mu' means Maximal Update !
그런데 muP란 이름의 P가 Parameterization이라는 건 알겠는데 Mu (Maximal Update)란 무슨 의미를 가지고 있는 걸까?
이는 TP4의 paper title이 Feature Learning in Infinite-Width Neural Networks인 것과 관련이 있는데,
말 그대로 training 과정에서 모든 layer의 parameter들이 최대한 update되는 되는방향으로 update (maximul update) 되기 위한 parameterization을 제공하겠다는 것이다.
아래 abc-parameterization의 공간을 2차원에 projection하여 그린 (원래는 6차원이라고 한다) figure를 보자. Pytorch SP (보통 Kaming or Xavier Init), NTP 등이 어떤 공간에 놓여지는지를 볼 수 있는데,
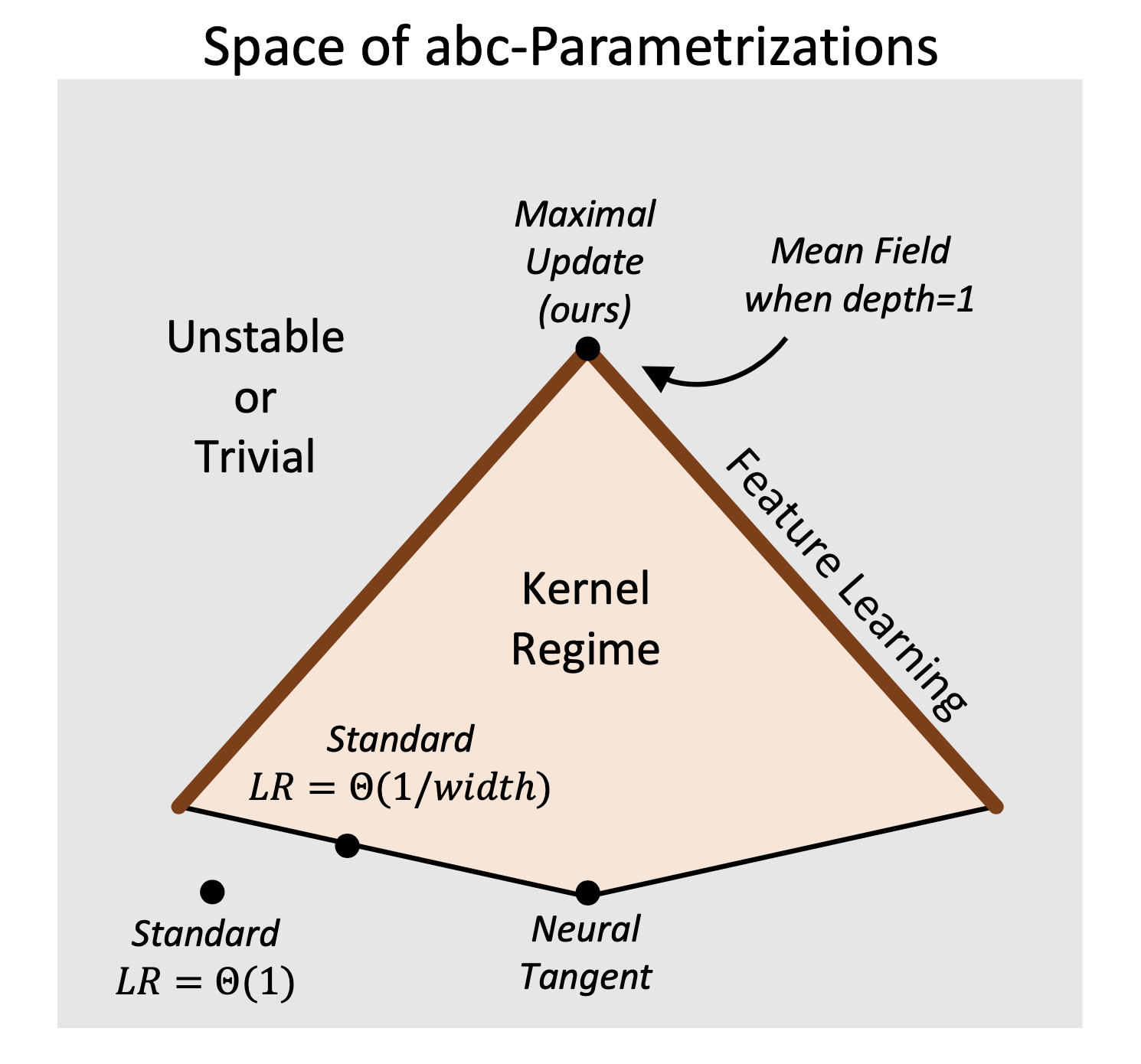 Fig.
Fig.
여기서 Trivial이란 model이 맨 처음 weight initialization 상태에 남아있다는 것을 의미하며,
Unstable이란 model이 학습 도중 결국 발산해버린다는 의미를 가지고 있다.
그리고 Kernel Regime이란 NTK라는 paper에 대해서 더 깊게 얘기해야 하므로 넘어가겠으나,
대충 NTK나 LR을 잘 정한 SP의 경우에도 잘 해봐야 Kernel Regime의 일부에 속하며 Feature Learning을 의미하는 갈색 선에 포함되지는 못한다는 것을 볼 수 있다.
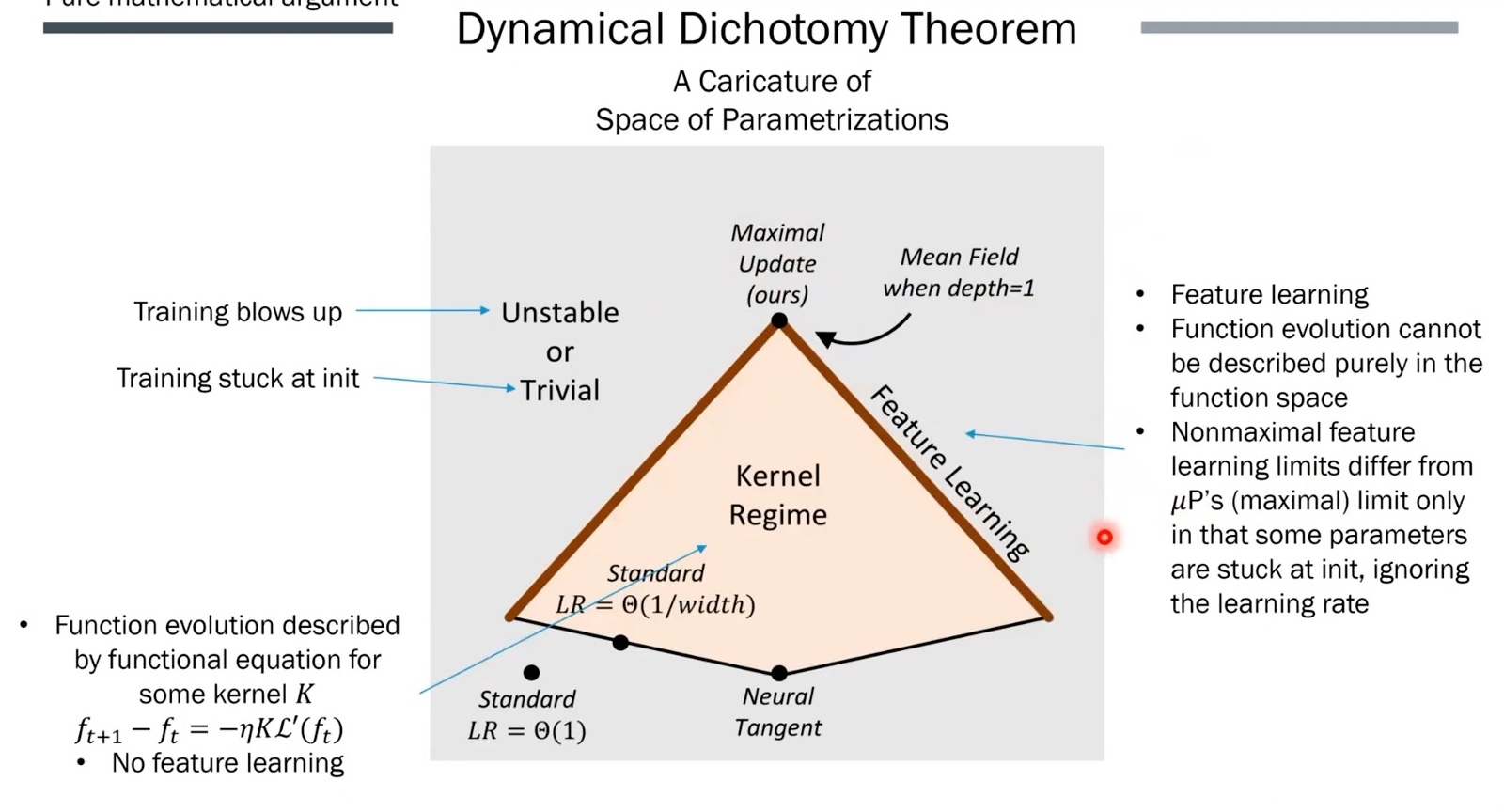 Fig.
Fig.
이게 무슨 말이냐? 이는 수학적으로 NN의 width가 무한대에 가깝게 넓어질 때 NN training의 양상이 어떻게 변한는지 아름답게 정의한 NTK조차 이론상으로는 그렇지만 가장 중요한 Feature Learning이라는 관점에서는 그렇지 않다는 점을 시사한다.
무슨 말이냐면 예를 들어 NTK로 Word2Vec을 하습한 뒤, 이를 downstream task에 대해서 Word2Vec embedding을 PCA해서 top US cities, states 의 feature를 2d space에 뿌려보면 거의 random feature 수준의 결과를 보여준다는 점이다.
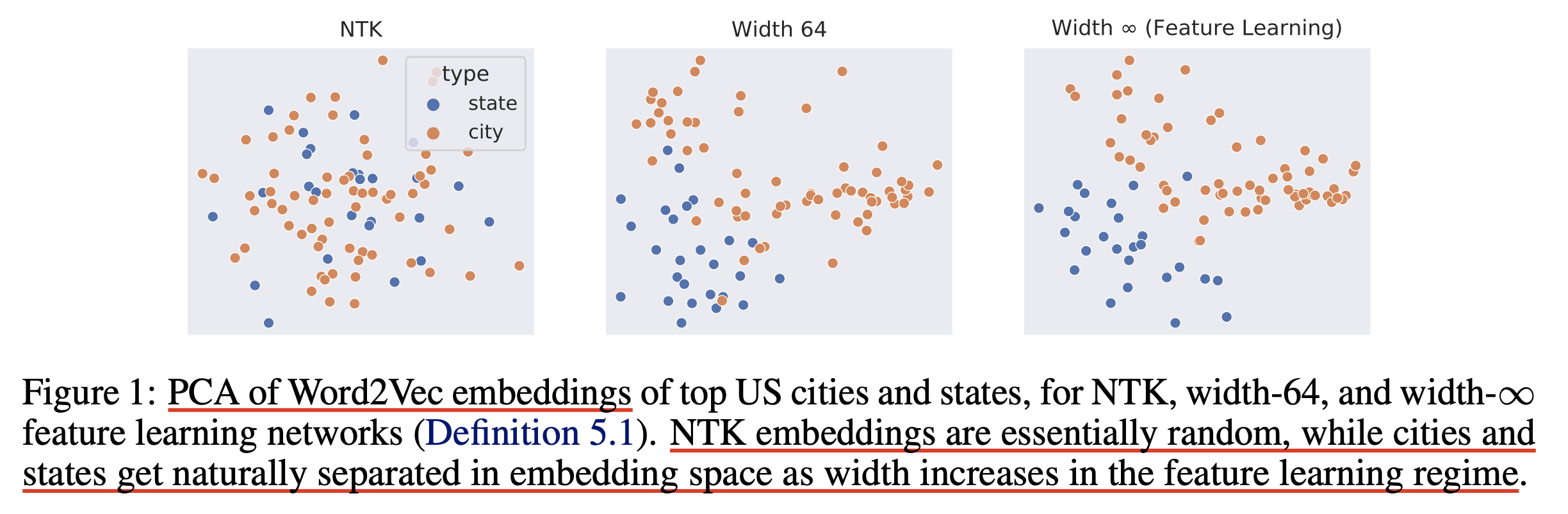 Fig.
Fig.
LR을 잘 설정한 SP는 상황이 조금 다를 수 있겠으나, 잘 정의되지 못한 parameterization이 얼마나 feature learning을 고려하지 못했으며 이런 점들이 BERT같이 pre-training을 하고 transfer learning을 하는 경우에 대해 매우 치명적인지 알 수 있는 부분이다.
또 이런 예시가 있을 수 있는데, 아래는 Wav2Vec 2.0이라는 speech domain의 BERT같은 model을 pre-training하고 fine-tuning하는 경우에 대한 얘기이다. 여기서 우리가 원하는 점은 pre-training을 통해 음소 정보를 포함한 acoustic feature를 model이 잘 배워 음성 인식 (Automatic Speech Recognition; ASR)에서 좋은 성능을 보이는 것인데, 실상은 fine-tuning을 하기 전과 후의 layerwise feature similarity를 비교해보면 가장 깊은 layer들의 feature는 pre-training으로부터 매우 많이 멀어진다는 것 (deviate)을 확인할 수 있다.
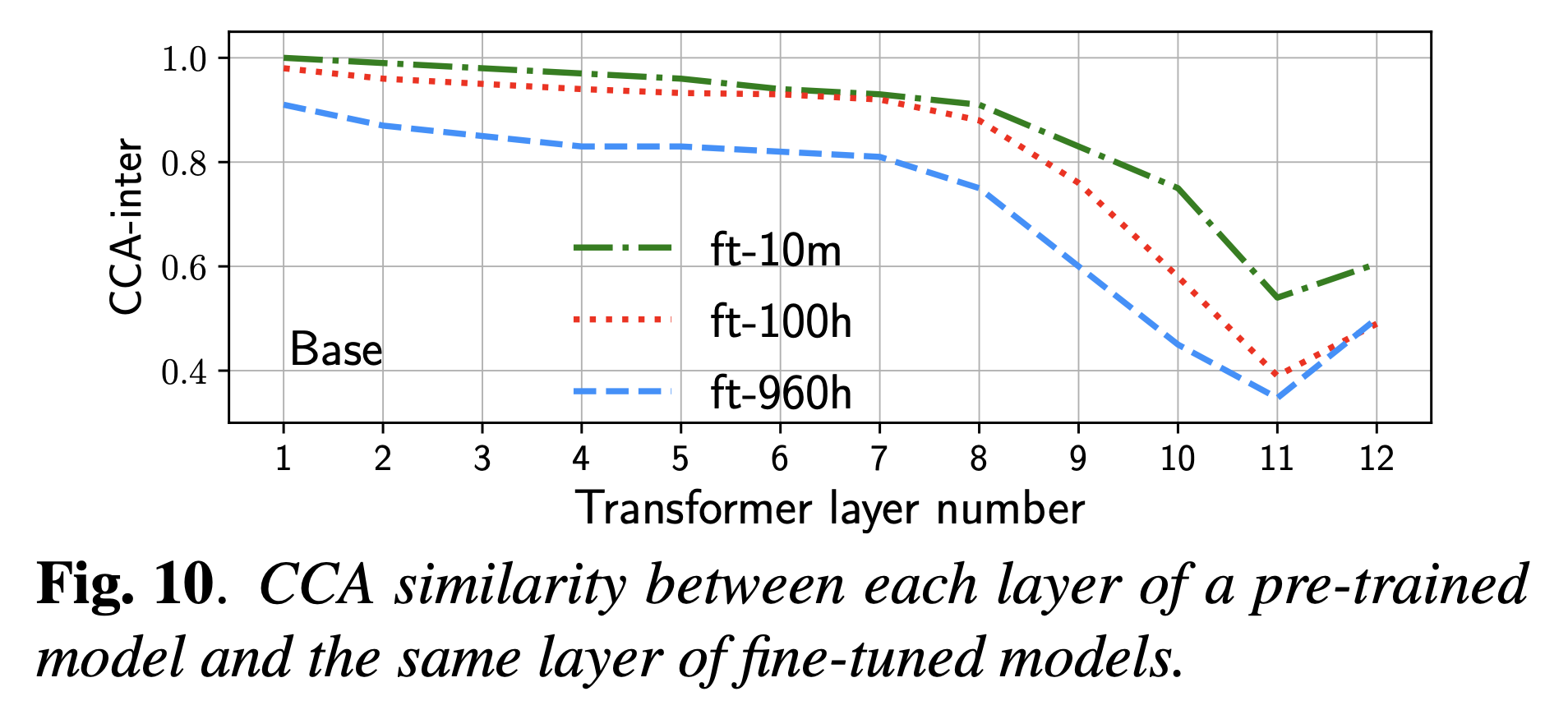 Fig. Source from here
Fig. Source from here
즉 위 figure의 quote에도 잘 나와있지만 마지막 3개 layer는 사실상 random init한 것 보다 좋을게 없는 feature를 배운 것이기 때문에 차라리 random init을 하거나 3개 layer를 제거하고 학습하는것이 사실상 낫다는 결론을 낼 수도 있는 것이다. 물론 이것이 ASR에 적합하지 않은 feature였다는 것이며 NN training입장에선 열심히 feature learning을 했을 수도 있겠지만… 이런 현상은 비단 Wav2Vec 2.0 뿐만의 문제가 아니며 AutoEncoder style인 BERT등에서 많이 관측되어온 문제라고 할수 있다.
muP는 사실 maximal feature learning이 가능하도록 parameterization 하는 것을 의미하는 것이다.
NN을 학습할 때 (특히 큰 model) gradient가 각 layer별로 vanishing 혹은 exploding되는 문제가 존재할 수 있는데,
제대로 parameterization을 하지 못하고 “음 loss 터지니까 lr 낮춰야지”하는 판단을 내리면 특정 layer들은 training time 동안 의미있는 feature learning을 하지 못하는 경우가 있을 수도 있다.
즉 model size가 변하더라도 activation 값들의 scale을 유지함으로써 stability, feature learning이 유지될 수 있도록 width에 대한 function으로 paramterization하는 것이 TP-4,5의 key intuition인 것이다.
 Fig.
Fig.
실제 DNN을 학습할 때 연구자들은 edge of stability에 다다라서야 가장 좋은 성능을 내는 solution을 얻을 수 있다는 말을 종종 하곤 하는데, 이를 위해서 모든 layer의 lr을 최대한 크게 가져가기 위해서는 반드시 muP같은 장치를 해줘야할 필요가 있는 것이다. 아마 꼭 muP가 아니더라도 (모든 layer가 균일하게 학습되지 않더라도), per layer LR scaling만이라도 해줘야 할 것이다
 Fig. Source from tweet thread
Fig. Source from tweet thread
 Fig. Source from tweet thread
Fig. Source from tweet thread
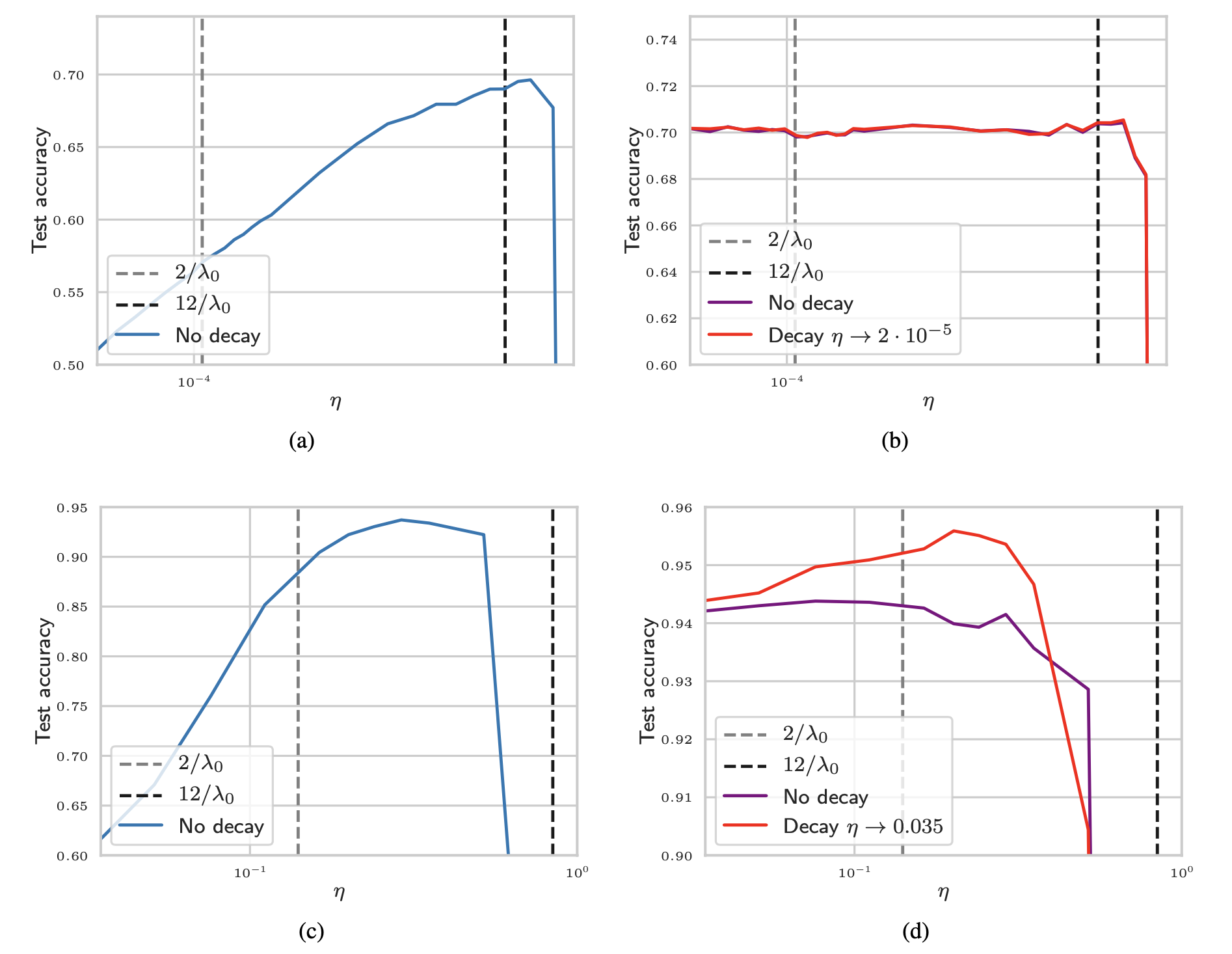 Fig. Source from paper
Fig. Source from paper
가끔 muP는 HP transfer를 목적으로 개발된 것이라고 하는 사람도 있는데,
여기에 매몰되면 안된다.
Greg과 Edward가 TP-IV를 정의할 때 목표로한 것은 Feature Learning을 최대화 하는 것이라는 점을 잊어서는 안된다.
(p.s. 아래 TP-5 paper에 대한 Openreview를 보자.
Greg과 Edward는 reviewer들이 “muP가 TP-4에서 이미 유도됐기 때문에 novelty가 없다”던가,
“muP는 HP transfer를 의도하고 만들어진 parameterization”라고 하며 TP-5의 contribution을 misunderstanding하는 것 같아 안타까워 하는걸 볼 수 있다)
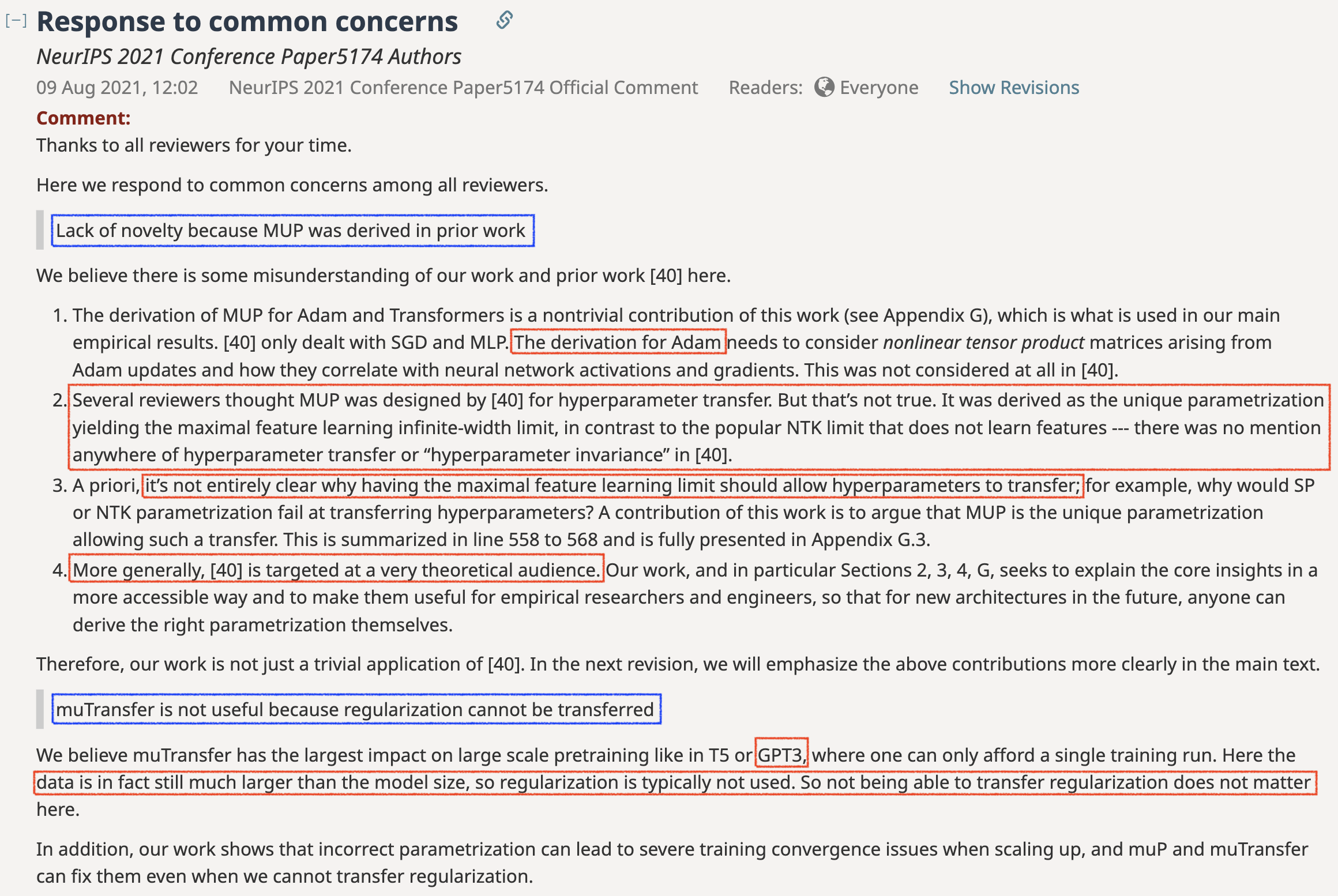 Fig. Source from Openreview
Fig. Source from Openreview
Other Methods Can Predict Scaling Law but...
앞서 충분히 전달이 됐을 것으로 보이지만 muP를 하는 것이 단순 parameterization을 잘하는 것으로 그쳐서는 안된다는 점을 한번 더 강조 하고 싶다. 우리는 작은 model (small scale proxy model)로 더 큰 model의 loss를 단 한번의 HP tuning 없이 예측할 수 있어야 한다. 즉 zero-shot Scaling Law prediction을 하는 것이다.
 Fig.
Fig.
앞서 설명한 것처럼 NanoLM에서도 GPT-4가 loss를 정확히 예측했다고 자랑하긴 하나 그것은 unpublished method이다. 원래대로라면 작은 model들로 scaling law를 찾았다 하더라도 큰 model이 그 loss를 찍기 위해서는 researcher들이 HP tuning을 해야한다. 아래 figure에 나오는 구절은 NanoLM라는 paper에서 발췌한 것인데, 각 model, dataset size 그리고 computing budget이 있을 때 optimal loss값이 scaling law를 따른 다는 것은 이미 검증된지 오래이긴 하지만 대다수의 scaling law paper에서 어떻게 이 HP을 찾을것인가에 대한 얘기는 없다는 점을 언급한다.
 Fig.
Fig.
NanoLM에서는 muP와 scaling law를 결합했을 때 muP zero-shot transfer를 할 경우 loss가 power function에 fitting 된다는 것을 실험적으로 보였다. 당연하게도 muP를 쓸 경우 model size가 커짐에 따라 HP가 zero shot transfer되므로 더 쉽게 scaling law를 그릴 수 있다는 점은 받아들이기 쉬울 것이다 (아마 GPT-4가 이렇게 했으리라고 강력히 의심이 되는 바 이지만 정확하게 알려진 바는 없다)
하지만 scaling law를 편하게 찾기 위한 방법이 꼭 muP만 있는 것은 아니다. 당연히 노가다를 해도 되고, 아니면 model size별 batch_size와 LR (lr)의 관계식 또한 찾거나, lr에 민감하지 않은 구조체를 쓴다거나 할 수도 있다.
예를 들어 DeepSeek LLM이라는 paper에서는 말한 것 처럼 model size가 커지면 작은 model에서 찾은 optimal batch_size, lr이 얼만큼 커져야 하는지?에 대한 batch_size에 대한 scaling law와 lr에 대한 scaling raw 함수를 아예 찾았다.
아래는 DeepSeek LLM의 model size별 LR과 batch_size인데,
 Fig.
Fig.
저자들이 말하길 Scaling Law는 compute budget, \(C=6ND\) (where C is compute budget, N is model scale and D is dataset scale)가 커질 수록 성능이 기하급수적으로 좋아지는 건 맞지만,
model scale이 커질 때 HP setting를 어떻게 해야되는지 알려져 있지 않기 때문에 누군가는 "model size 커졌는데 좋아진거 맞아?"라고 생각할 수 있는 불확실성이 존재했다고 한다 (당연히 HP를 잘 못찾으면 optimal performance가 아니므로 power function에 fitting되지 않아 보일 수 있기 때문).
 Fig.
Fig.
저자들은 위 figure에서처럼 compute budget C와 batch_size, lr간의 scaling law를 찾았는데,
 Fig. weight init std, adamw beta1, beta2, weight decay 등 기본적인 hyperparmeter값. batch_size, lr만 다른듯하다.
Fig. weight init std, adamw beta1, beta2, weight decay 등 기본적인 hyperparmeter값. batch_size, lr만 다른듯하다.
이를 위해 먼저 small-scale model에 대해서 아래처럼 가능한 범위내의 HP를 sweep해서 grid search를 한다. (이 중 weight decay등 어지간한 HP들은 각 model size에서 optimal point가 비슷했다고 하며 바로 위의 figure와 같은 값을 쓴 것 같다)
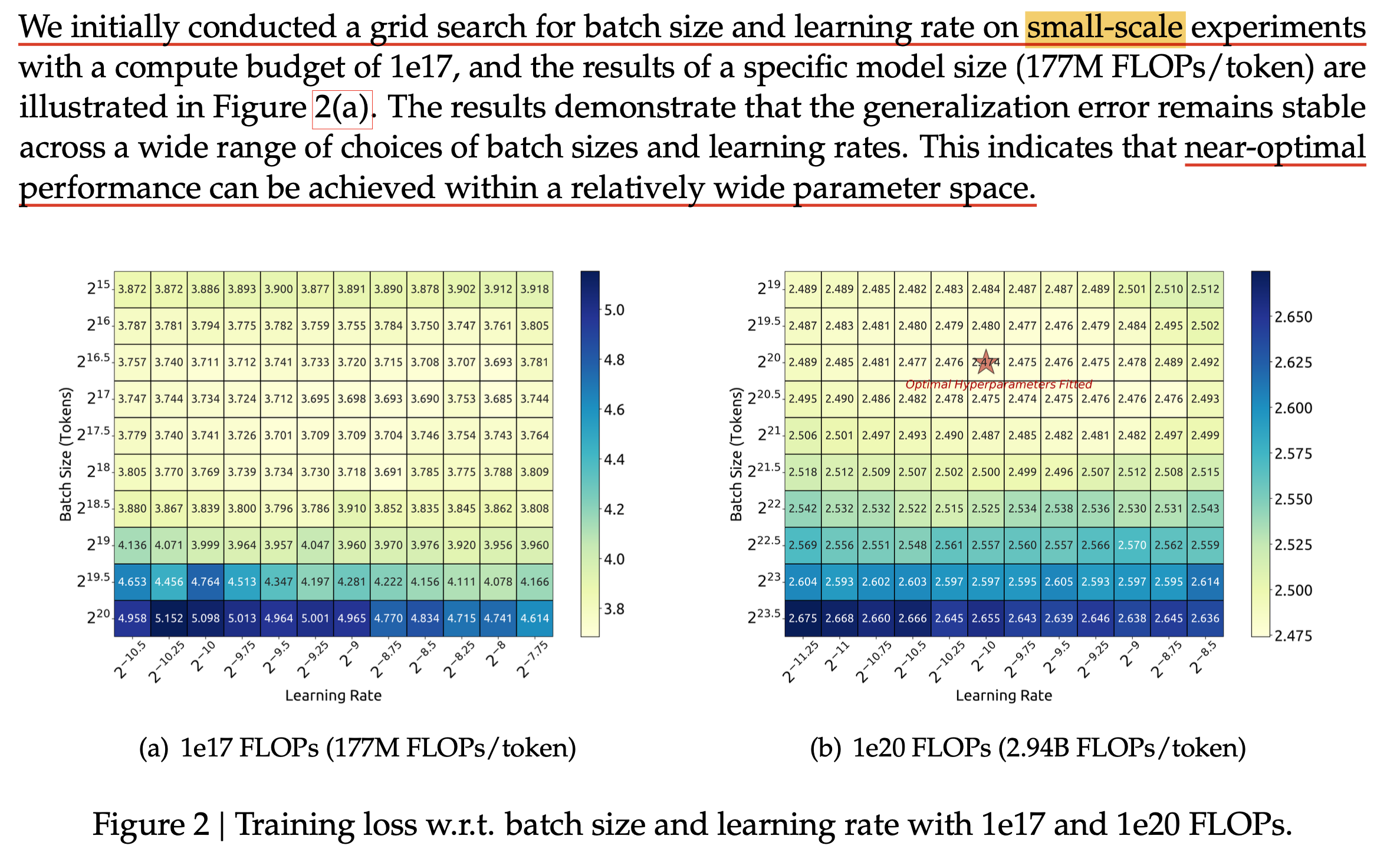 Fig.
Fig.
그리고 optimal setting에서의 (minimum인셈) generalization error (train error? 혹은 valid error)보다 0.25% 내외에 있는 점을 모두 찍어서 regression을 한다.
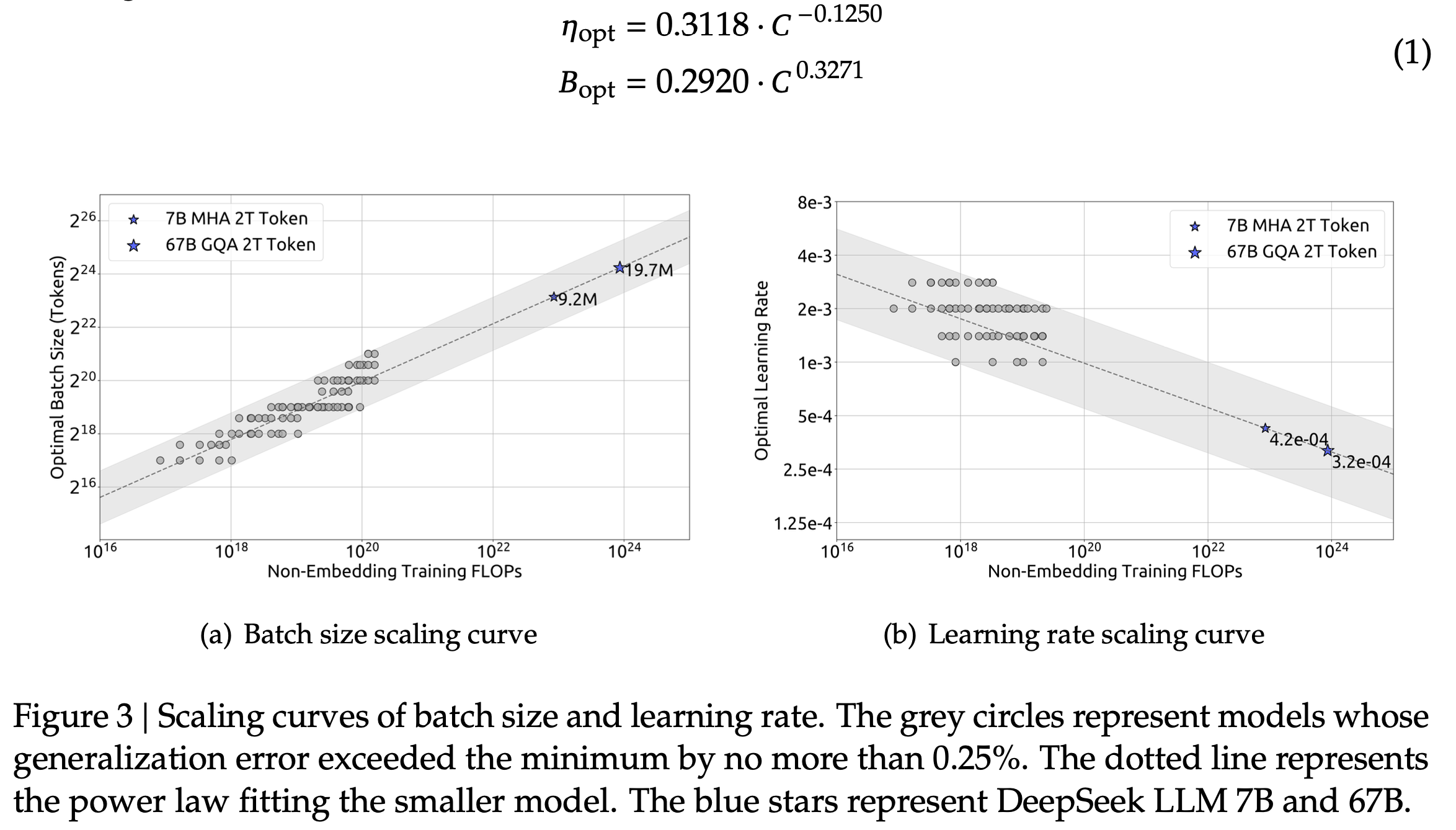 Fig.
Fig.
이렇게 해서 lr, batch_size와 compute budget에 대한 power function을 구해서 (위 figure에서 음영 가운데 있는 점선) 학습을 했을 때 optimal HP와 거의 근접한 수치를 얻을 수 있었다고 한다. (target model size에 대해서도 예측한 값 근처의 near optimal이라 생각되는 지점을 다 찍어봤을듯)
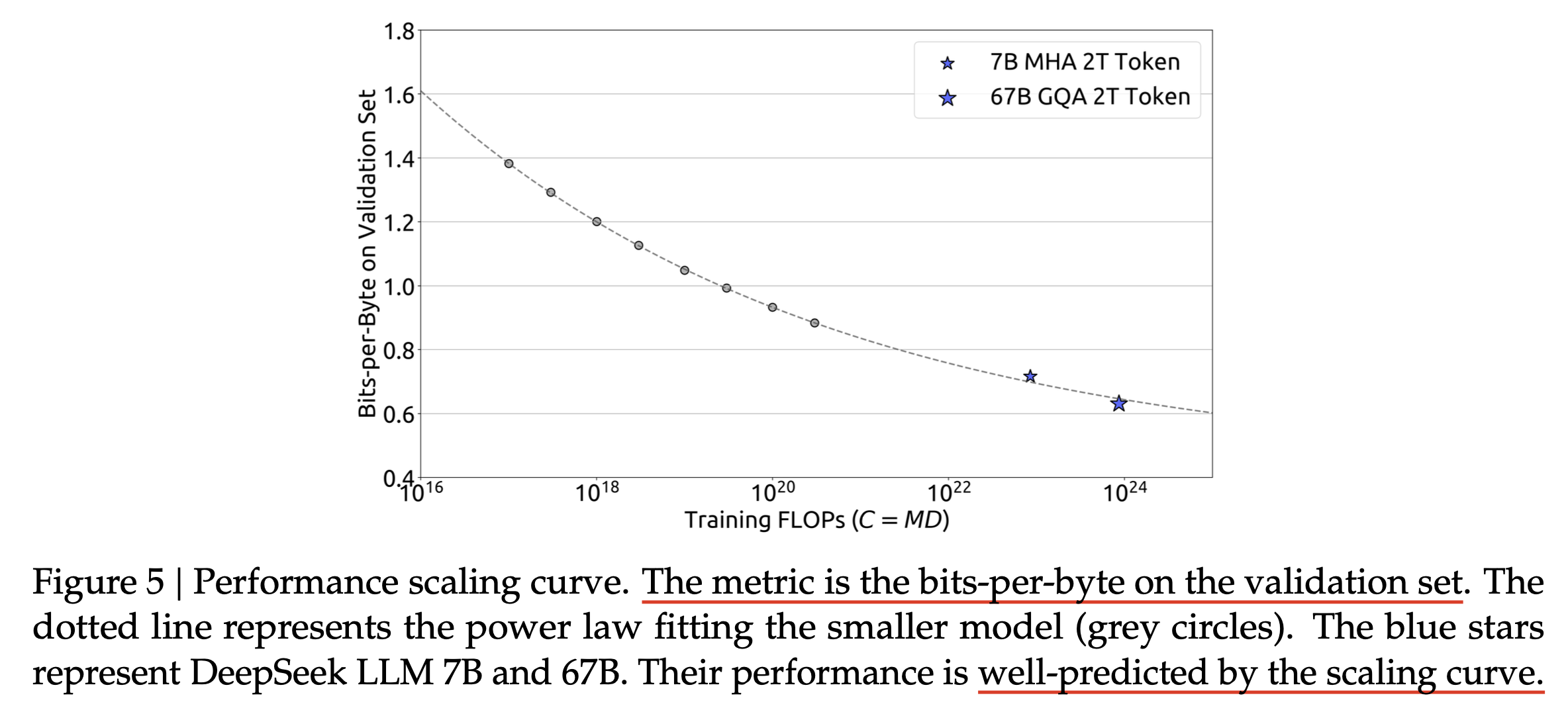 Fig.
Fig.
그 다음으로 lr에 민감하지 않도록 architecture를 수정할 수도 있다고 얘기했는데, 최근에 나온 cmd r+같은 model은 Transformer의 저자진들이 창업한 Cohere라는데서 만든 model이며 query, key projection layer 전에 각각 서로 다른 normalization layer를 쓴다.
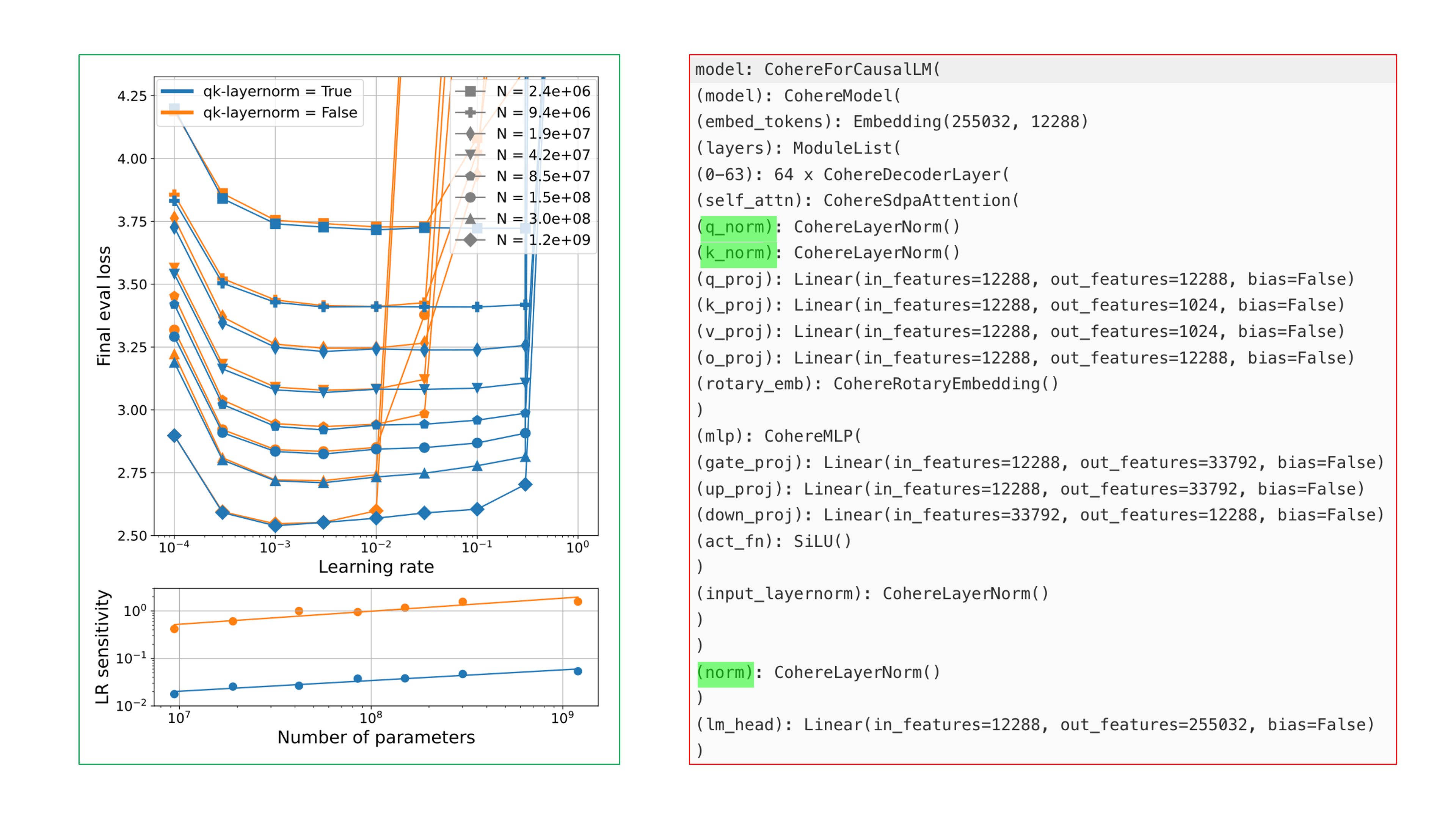 Fig.
Fig.
이는 Small-scale proxies for large-scale Transformer training instabilities라는 paper에서 다루고 있는 내용으로, 우리가 normalization을 하는 것이 gradient exploding, vanishing 등을 방지해서 training stability를 높히는 데 기여하는 것과 같은 맥락이라고 볼 수 있을 것 같다. 이런 구조를 쓸 시 model size가 커짐에 따라 lr이 크게 다르지 않다면 우리는 lr 변경없이 scaling law prediction을 한 뒤 target size의 model도 같은 lr을 쓸 수도 있을 것 같다. 하지만 이런 방법은 가뜩이나 비싼 layernorm을 매 layer마다 추가하는 비용이 발생하며, model scale이 커져도 LR sensitivity가 크지 않다는 것이지 그게 optimal일 것이라는 보장은 없다는 단점이 있다.
마지막으로 muP를 사용하는것도 Scaling Law의 비용을 줄이는데 좋은 방법론일 수 있는데, NanoLM에서는 GPT뿐 아니라 Llama, BERT 구조체에서도 muP + scaling law가 통한다는 것을 보여준다.
 Fig.
Fig.
어쨌든 muP와 Scaling law prediction을 결합하는 것은 model size별로 HP을 다시 찾지 않으면서도 power function을 그릴 수 있게 해주는 매우 강력한 조합이 될 것이고,
이 pipeline에 bug가 없다는 걸 검증했다면 이제 남은 일은 model architecture는 어떤게 좋은지? pretraining을 위한 dataset의 subset별 mixture ratio는 어떤게좋은지? 등등 predicted loss가 제일 낮은지를 확인해서 그 조합으로 scaling up을 하기만 하면 된다.
War-muP
Recap) Standard Parameterization (SP) for Nerual Network
muP로 본격적으로 diving하기 전에 먼저 Deep NN training에 사용되는 weight random initiazliation, Pytorch의 Standard Parameterization (SP)에 대해 recapitulate 해보자.
Lecun Init이나 Xavier Init, He init같은 initialization method는 그 방법마다 차이가 있겠으나 동기는 모두 학습을 안전하게 (stable) 하기 위해서로 같다.
보통 학습이 불안정 (unstable) 하다는 것은 gradient가 너무 커서 exploding 하거나 (결국 발산으로 이어짐),
너무 작아서 (0이 됨) vanishing되는 것을 말한다.
Initalization method는 NN의 input, output 을 정규화 (normalization)하는 것과도 유사한 철학이라고 할 수 있다.
핵심은 NN training시 layer output (activation)들을 reasonable scale로 떨어지게끔 보장함으로써 gradient를 균일하게 만들어 문제를 해결하는 것이다.
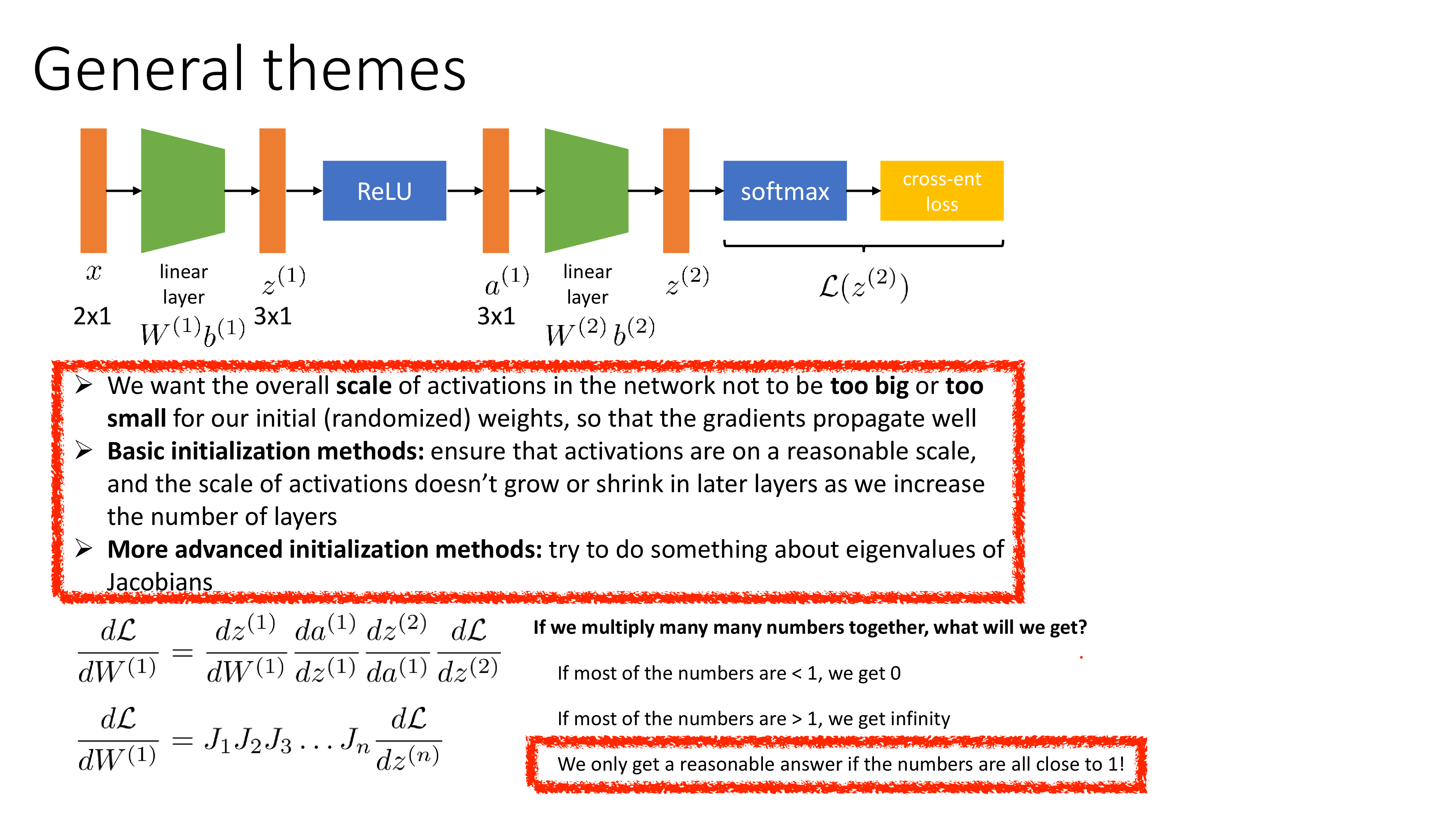 Fig. Source from Sergey Levine’s ML Lecture (CS182)
Fig. Source from Sergey Levine’s ML Lecture (CS182)
Init에 대한 직관을 얻기 위해 Sergey Levine의 CS182 Lecture를 이용해 간단하게 init method들을 recap해보자. 먼저 매우 작은 값으로 initialization을 하는 간단한 method이다. 이는 \(\mathcal{N}(0,0.0001)\)같은 gaussian distribution에서 sampling한 값으로 초기화 하는 것으로, 매우 작은 random value들을 사용하는것이다. 하지만 이 경우 network가 deep 해질 수록 문제를 일으키는데, 당연하게도 이전 layer output에 매우 작은 값으로 이루어진 matrix를 곱하면 그 다음 layer의 output은 더 작아지기 때문이다 (activation을 하더라도).
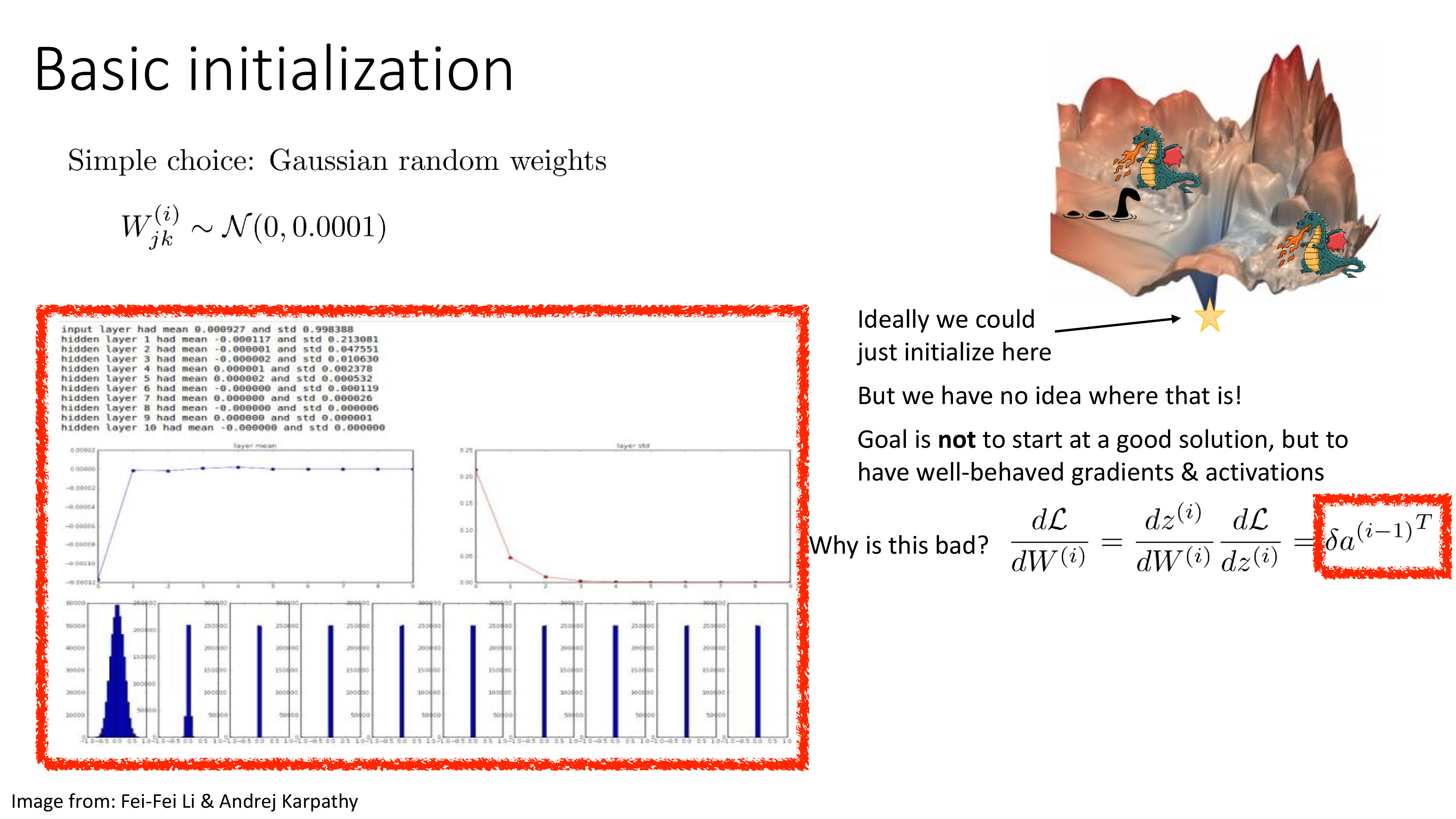 Fig. Source from Sergey Levine’s ML Lecture (CS182)
Fig. Source from Sergey Levine’s ML Lecture (CS182)
위 figure의 왼쪽 subfigure는 layer별 activation output의 distribution을 나타낸 것인데, 보면 propagate이 될 수록 mean은 0에 수렴하고 standard deviation (std)는 매우 작아지는 것을 볼 수 있다. 그런데 backprop에서 어떤 weight의 loss에 대한 미분 값 (derivative), \(\frac{\partial L}{\partial W_i}\)는 upstream gradient와 current layer input의 곱으로 나타나지 않는가? 이러면 weight의 gradient는 0이 되므로 아무런 학습이 진행되지 않을 것이다.
Gradient가 0이되는 지점은 과연 어디일까? 그렇다 우리는 그 고차원에 널린 수많은 strating point들 중 가장 최악이라 할 수 있는 plaetau에서 시작을 하는 셈이 되는 것이다.
 Fig. Source from Sergey Levine’s ML Lecture (CS182)
Fig. Source from Sergey Levine’s ML Lecture (CS182)
이제 이를 고쳐보자. 먼저 normal distribution을 따르는 것은 그렇게 문제가 아닐 것이라 생각하고, gaussian의 variance를 다르게 주면 어떨까?
\[W_{ij} \sim \mathcal{N}(0, \sigma_W^2)\]이 soltuion에 대한 idea는 단순한 linear layer 한 개에 대해 forwarding해서 얻은 output의 variance를 측정함으로써 이해할 수 있는데, 먼저 bias, \(b\)의 elements는 거의 0이라고 가정하고, input vector, \(a\)와 weight matrix, \(W\)로 부터 output, \(z\)는 다음과 같이 쓸 수 있다.
\[z_i = \sum_j W_{ij} a_j + b_i = \sum_j W_{ij} a_j + 0\]만약 어떤 초기 input, \(x\)를 0 mean, 1 variance가 되도록 \(x\)의 standard deviation (std)로 standardization 했다면, layer input, \(a\)는 \(\mathcal{N}(0, \sigma_a)\)를 따를 것이고, 이 때 layer output의 한 element인 \(z_i\)의 variance는 다음과 같이 계산될 수 있다.
\[\begin{aligned} & \mathbb{E} [z_i^2] = \sum_j \mathbb{E} [W^2_{ij}] \mathbb{E} [a^2_j] = D_a \sigma^2_W \sigma^2_a & \\ & \text{where } D_a \text{ is dimension of input vector (tensor)} & \\ \end{aligned}\]이렇게 variance가 계산이 되는 이유는 직관적으로 layer output이란 결국 layer input과 weight matrix의 한 row를 dot product한 것이며 각 elements들은 서로 iid이기 때문에 rought하게 두 random variable의 variance, \(\sigma_W^2 \sigma_a^2\)가 element 갯수, \(D_a\)만큼 scaling된 값이라고 생각할 수 있기 때문이다.
 Fig. cs231n의 slide. notation이 조금 다르지만 같은 얘기.
Fig. cs231n의 slide. notation이 조금 다르지만 같은 얘기.
여기서 우리가 원하는 건 뭘까?
직관적으로 우리는 layer의 입출력의 variance가 유지되길 원한다.
\[Var(z_i) = Var(a_i)\]왜냐하면 \(D_a \sigma^2_W\)가 1보다 커지면 layer를 거듭할 수록 layer output의 element들의 커질 너무 커질 것이고, 반대로 1보다 작다면 작아질 것이다. 그러므로 이 값을 1에 가깝게 되도록 \(\sigma_W^2\)를 선택하는 것이 좋은 선택이 될 것이고, 이를 Xavier Init이라고 부른다.
\[\sigma_W^2 = 1 / D_a\]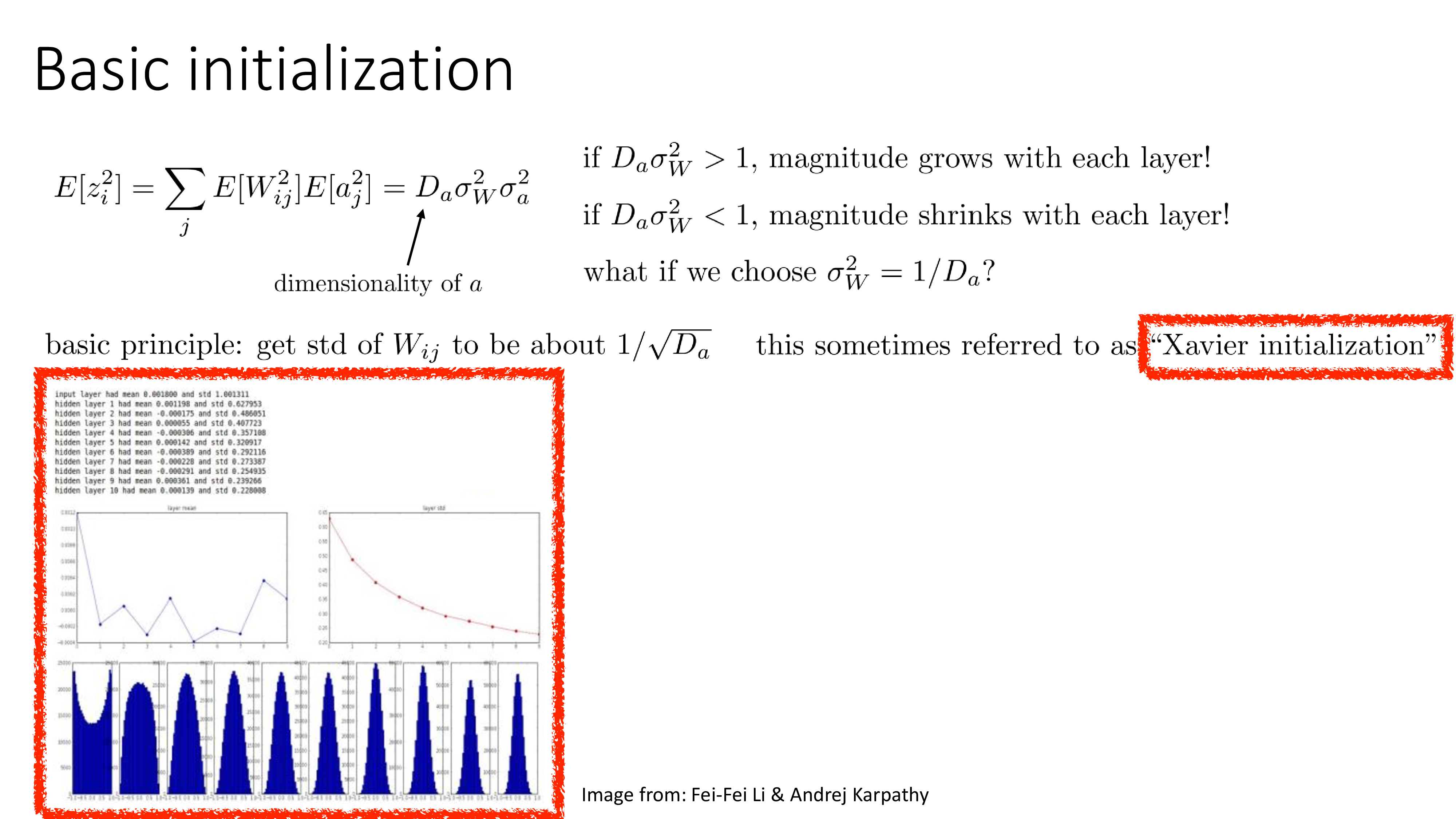 Fig. Source from Sergey Levine’s ML Lecture (CS182)
Fig. Source from Sergey Levine’s ML Lecture (CS182)
물론 위 figure를 보면 layer를 거듭할수록 magnitude가 여전히 줄어드는 것을 볼 수 있긴 하다 (정확히는 mean, std). 그렇지만 전보다 훨씬 나아졌고, 이는 modern deep learning에서 많이 쓰이는 init method이지만 왜 여전히 std가 줄어드는지에 대해서는 한 번 생각을 해 봐야 한다.
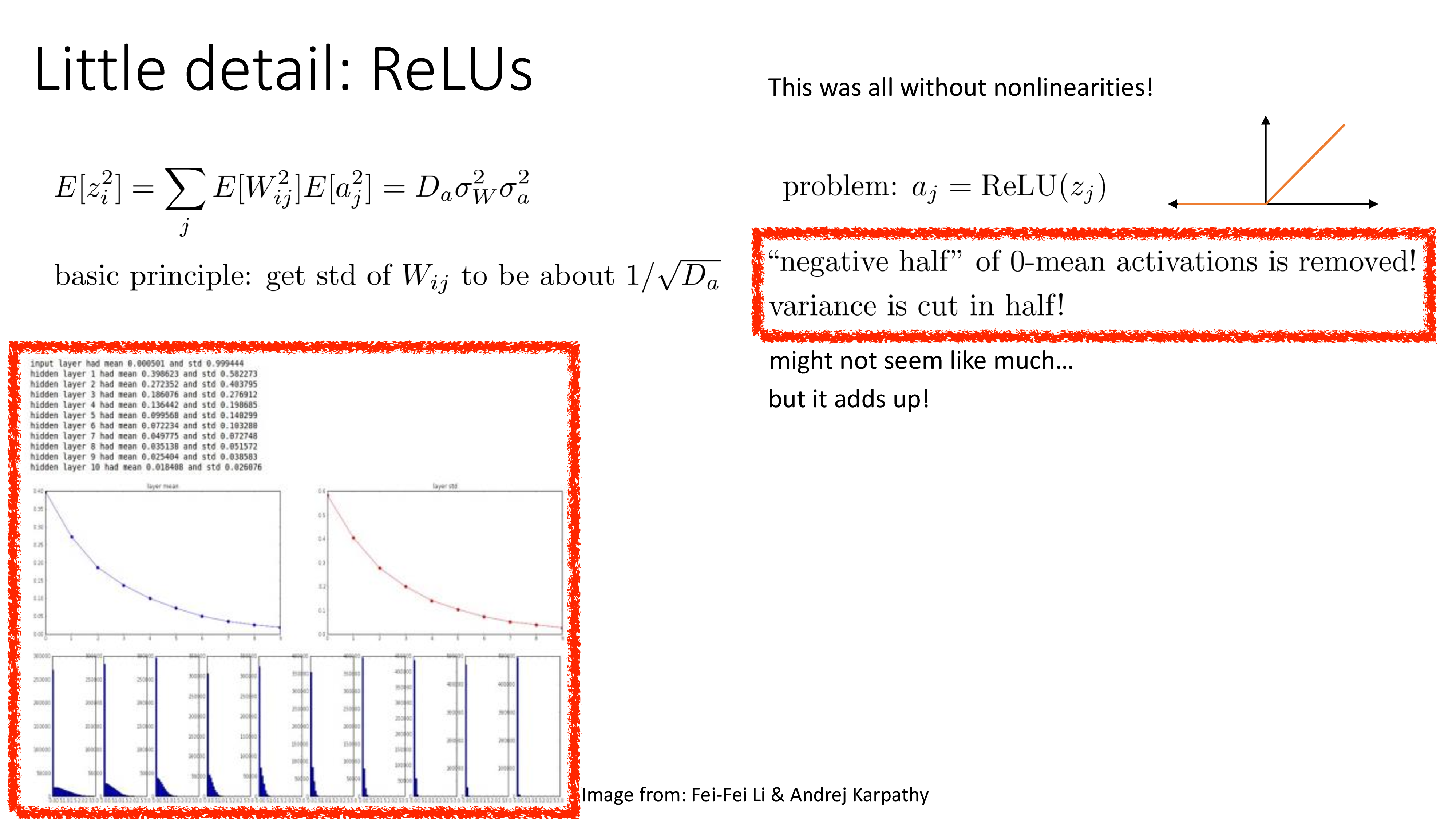 Fig. Source from Sergey Levine’s ML Lecture (CS182)
Fig. Source from Sergey Levine’s ML Lecture (CS182)
그 이유는 바로 ReLU같은 activation function 때문인데,
이를 고려하지 않았을 때는 input이 정말로 normally distributed 할 수 있었을지 몰라도 ReLU가 들어가면 음수를 갖는 pre-activation의 element들은 모두 0으로 zero out 된다.
즉 pre-activation이 normally distributed 라면 절반은 날아가는 셈이고,
이것이 variance를 줄이게 되는 것이다.
이 상황을 해결할 수 있는 가장 간단한 발상은 "음... 절반 정도 날아갈 테니 2배 정도 scaling 해주면 되지 않을까?"이다.
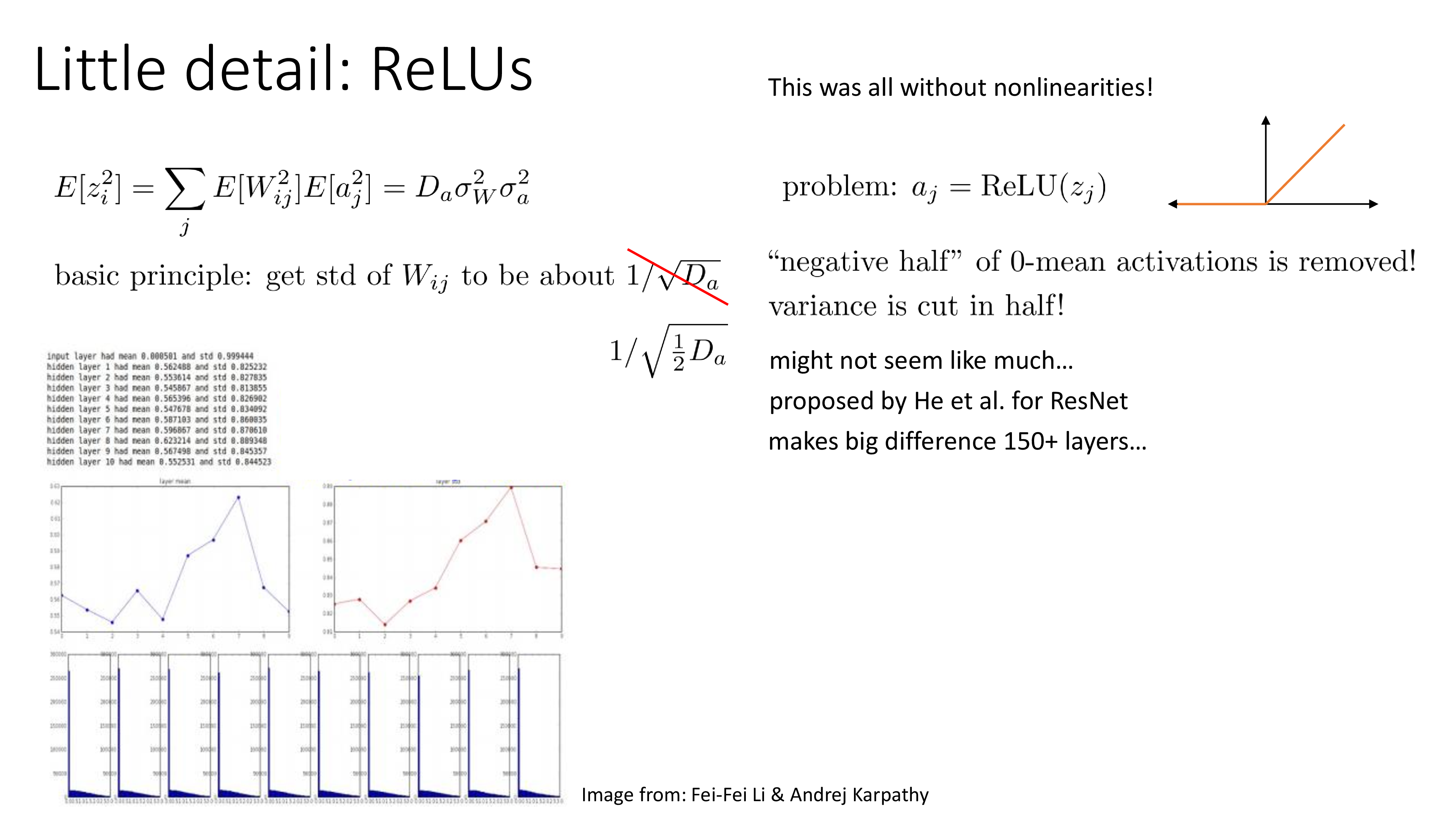 Fig. Source from Sergey Levine’s ML Lecture (CS182)
Fig. Source from Sergey Levine’s ML Lecture (CS182)
이것이 바로 He init이며, ResNet에 이를 적용하는 것 만으로도 엄청난 차이를 만들수 있었다고 한다. (요즘은 잘 안 쓰는 activation function들 이지만 sigmoid, tanh냐 ReLU냐에 따라서 더 잘 듣는 init method가 있다는 걸 알 수 있다)
Advanced Initialization (for intuition)
그 밖에 Sergey는 좀 더 진보된 (?) 방법을 소개하는데, 내 생각에 이게 muP를 이해하는데 도움이 될 것 같아서 짧게 언급하려고 한다.
 Fig. Source from Sergey Levine’s ML Lecture (CS182)
Fig. Source from Sergey Levine’s ML Lecture (CS182)
우리는 학습만 안정적으로 잘 된다면 어떤 init method를 쓰던 상관이 없다. 다만 layer가 깊어질수록 중간이하나 저층부의 layer들의 weight matrix의 gradient는 jacobian을 무수히 많은 곱한 형태일 것이다. 그리고 이것이 평균적으로 1보다 크다면 gradient가 폭발할 것이고, 아니면 0이 되어 사라질 것이다. 우리는 jacobian들이 1에 가까운 값이길 원하는데, 그렇다면 이를 Singular Vector Decomposition (SVD)해서 중간에 있는 \(\color{red}{\Lambda}\) matrix를 날려버리면 될 것이다.
왜 그런가? SVD의 결과물의 right hand, \(U\)와 left hand matrix, \(V\)는 orthonormal matrix이다. 즉 크기가 1인 basis들의 집합이고, 이는 어떤 vector와 곱해질 때 rotation을 하는 일만을 한다. 중요한 것은 가운데 있는 \(\color{red}{\Lambda}\)인데, 이것은 vector를 scaling 해주는 역할을 하는 diagonal matrix이다. 즉 이 matrix의 성분이 모두 1이면 되는데, 그렇다는 것은 identity matrix가 된다는 것이고 따라서 \(\color{red}{\Lambda}\)를 없는 셈 치면 되는 것이다.
 Fig. Source from Sergey Levine’s ML Lecture (CS182)
Fig. Source from Sergey Levine’s ML Lecture (CS182)
물론 학습 중간에 튀어나올 jacobian을 SVD할 수는 없다. 우리가 할 수 있는 일은 weight init일 뿐이다. 하지만 계속해서 곱해질 jacobian는 결국 loss 부터 역전파되어오는 upstream gradient에 weight matrix를 transpose해서 곱할 뿐이므로 weight matrix를 어떤 방법으로든 init하고 SVD를 취한 뒤 \(\color{red}{\Lambda}\)를 버리기만 하면 된다. (잘 안쓰이는 방법인듯하지만 앞으로의 내용들을 이해를 하는데 도움이 될 것이다)
Weight Initialization Case Study
nn.Linear
그래서 Pytorch에서 쓰는 Standard Parameterization (SP)은 무엇인가? nn.init docs를 보면 앞서 말한 다양한 init method가 구현되어 있다는 것을 알 수 있다.
 Fig. Xavier Init. 왜 (fan_out + fan_in) 으로 나누는지는 잘 모르겠다.
Fig. Xavier Init. 왜 (fan_out + fan_in) 으로 나누는지는 잘 모르겠다.
 Fig. He Init.
Fig. He Init.
 Fig. normal dist가 아닌 uniform dist version도 있다.
Fig. normal dist가 아닌 uniform dist version도 있다.
torch.nn.Lienar는 사실 kaiming init의 uniform version을 쓰고 있다. Linear는 이렇고 각 nn.Module들은 각기 다른 이유로 (theoritical or empirical) 다른 init을 쓰는 것 같다.
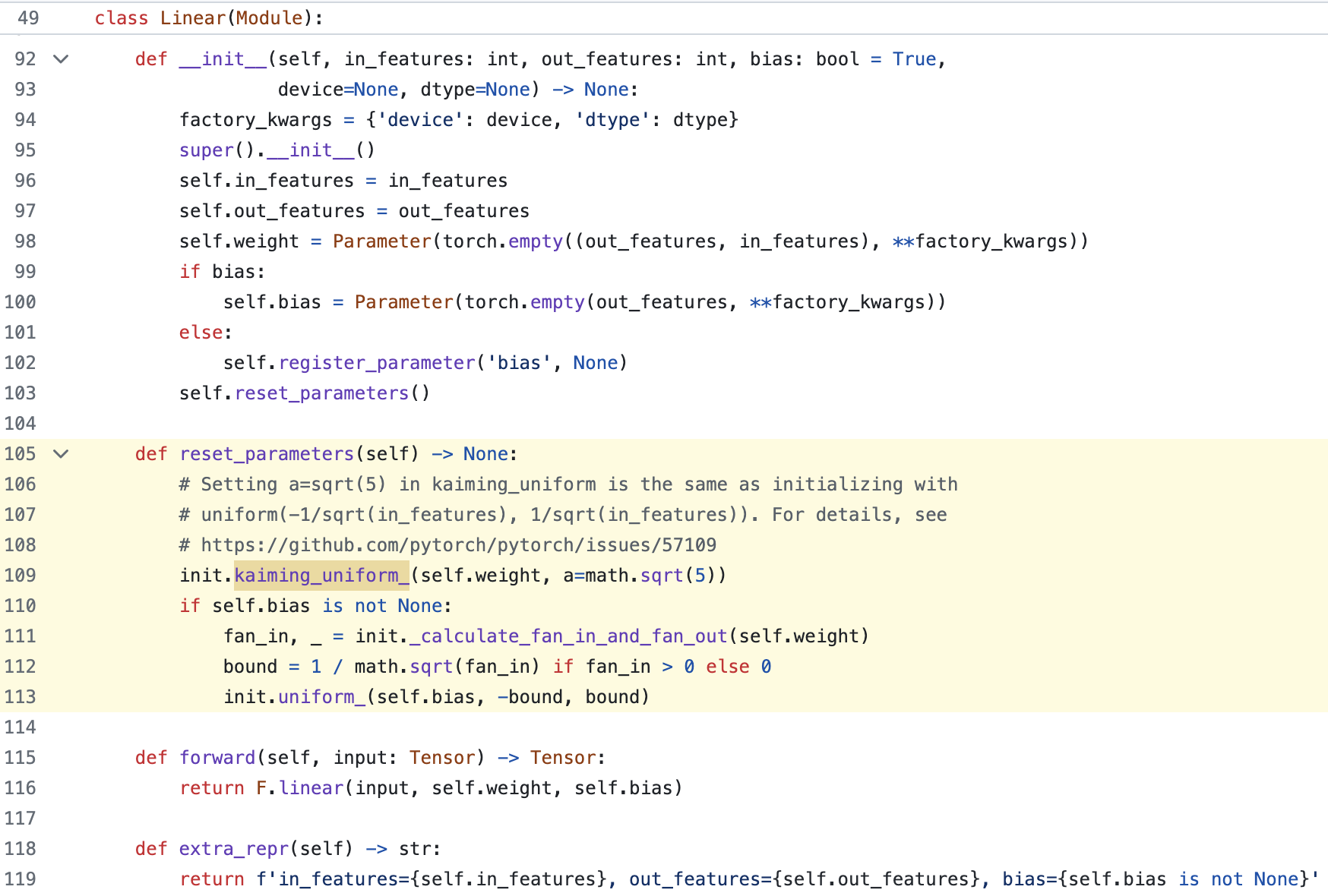 Fig. Source from here
Fig. Source from here
 Fig. Kaming He Init 의 uniform version을 씀.
Fig. Kaming He Init 의 uniform version을 씀.
GPT-2
당연히 module별 pytorch default init은 부족할 수가 있는데, 왜냐하면 (내생각에) 모든 training dynamics 등을 고려한 것이 아니고 일반적으로 알려진 것들 중 가장 안전한 방법만 구현해놨을 수가 있기 때문이다. 그래서 실제 model 학습에 쓰인 구현체를 봐야하는데, 예를 들어 huggingface에 구현된 GPT-2의 weight init method이며, bias는 0으로 init하고 다른 linear (conv도 linear 역할) weight matrix들은 정해진 std내의 norm dist로, embedding matrix도 마찬가지이지만 pad token은 0으로 embedding 하며, layernorm에 대한 init도 따로 model 구성에 따라 적용해준다.
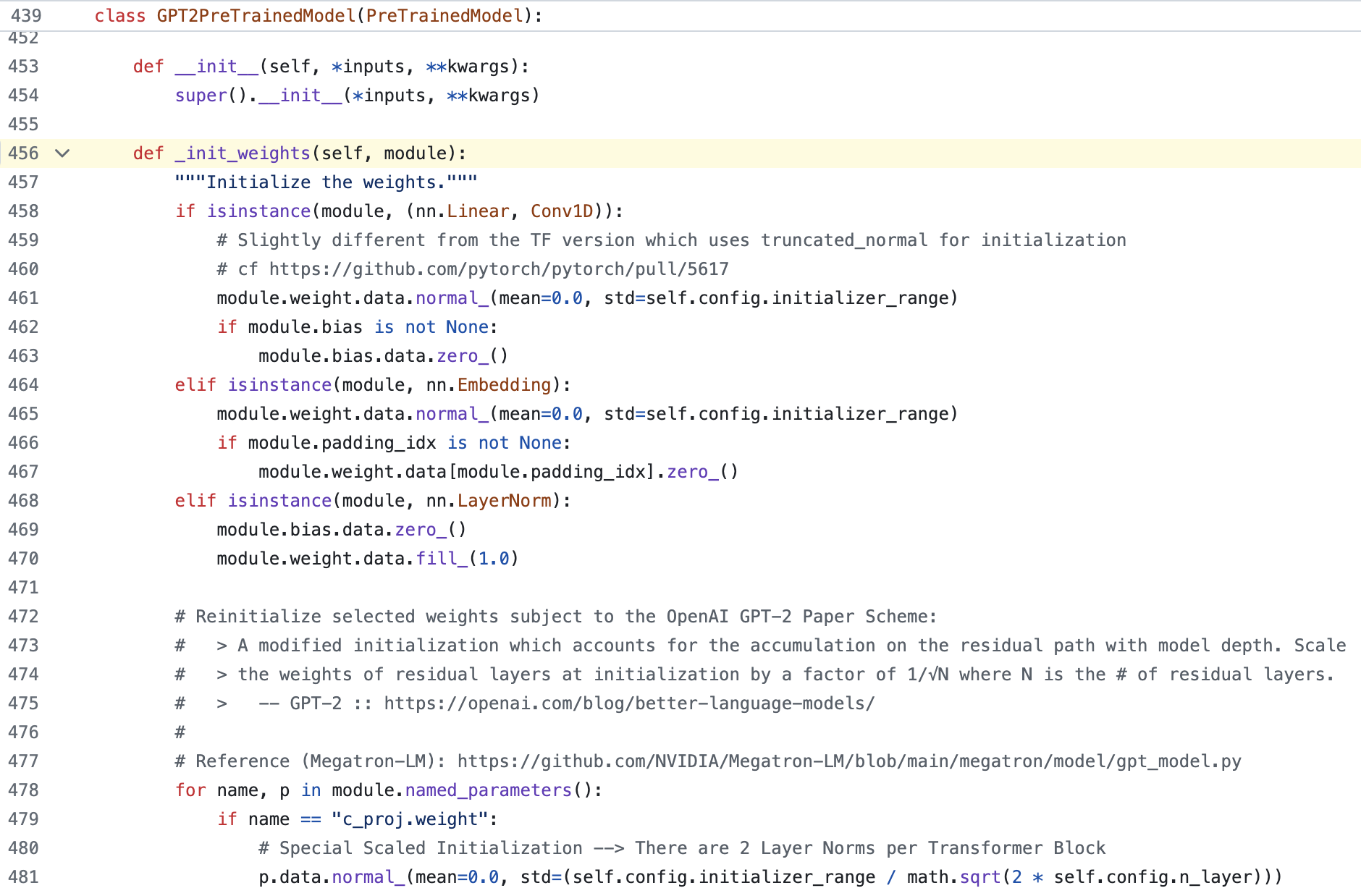 Fig. Source from here
Fig. Source from here
GPT-2의 정해진 std는 보통 0.02이며 layernorm은 1로 초기화, bias는 0으로 둔다. 위 코드에도 나와있고, GPT-2 official implementation에도 나와있지만, 예외적으로 GPT-2의 각 residual block의 마지막 layer 들에 대해서는 \(0.02/\sqrt{2 \cdot n_{layers}}\)를 쓴다고 한다.
 Fig. Source from Cerebras-GPT
Fig. Source from Cerebras-GPT
왜 그럴까?
사실 GPT-2 paper에는 이에 대해서 이렇다할 theoritical explanation이 없다. 다만 Andrej Karpathy의 video에 이 \(0.02\) hard coding에 대한 해석이 있는데, 이 내용이 꽤 맞는 것으로 보인다. 요지는 결과적으로 GPT-2도 Xavier를 따른다는 것인데, 만약 hidden dim인 \(768\)에 대해서 앞서 설명한 것 처럼 \(1/\sqrt{768}\)을 하면 대충 \(0.036\)이 나오며, dim이 \(1600\)인 경우 \(0.025\)가 나오기 때문이다.
\[\begin{aligned} & 1/\sqrt{768} = 0.036 & \\ & 1/\sqrt{1600} = 0.025 & \\ & 1/\sqrt{4096} = 0.016 & \\ \end{aligned}\]그러니까 대충 GPT-2를 안정적으로 학습하기 위한 값이 0.02인 것이 얼추 들어맞는 것이다. 그럼 여기서 model depth가 \(N\)일 경우, 즉 residual block 갯수 (layer 갯수)가 \(N\)일 경우 매 residual 연산을 해주는 부분의 바로 직전 layer를 \(1/\sqrt{N}\)배 해 주는 이유는 뭘까?
그 이유는 residual connection을 통해서 input activation이 더해질 경우 계속해서 variance가 커지기 때문이라고 하는데, 예를 들어 아래 karpathy video의 figure를 보면 768 dim의 zero init vector를 input으로 시작했을 때 torch.randn 함수를 통해 zero mean unit variance인 768 dim의 vector를 만들어 100번 residual connection 을 수행할 경우 최종 output vector의 standard deviation은 \(\sqrt{100}=10\)이 되는 것을 볼 수 있다.
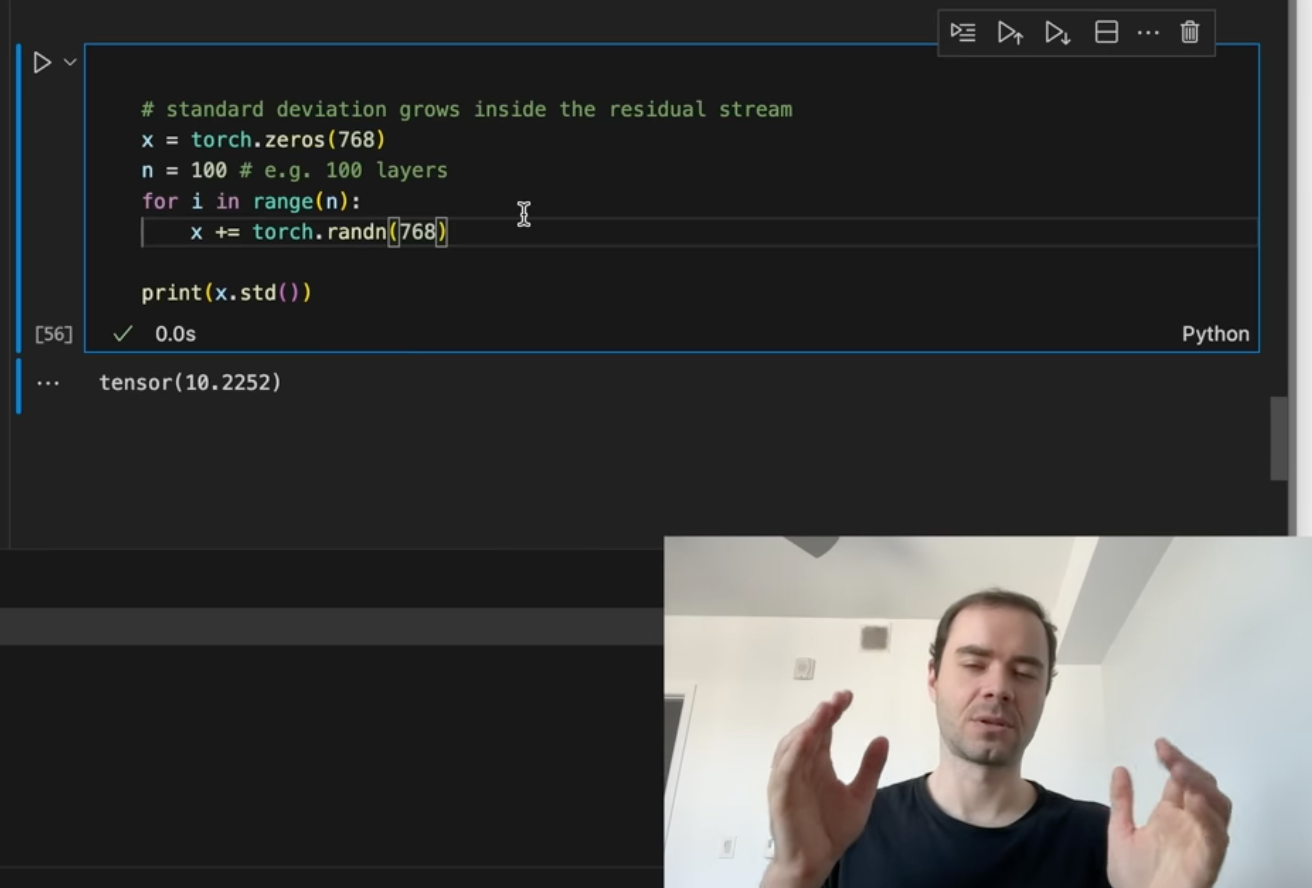 Fig.
Fig.
n이 16이어도 마찬가지인데,
import torch
x = torch.zeros(768)
n = 16
for i in range(n):
x += torch.randn(768)
print(x.std())
tensor(1.0433)
tensor(1.4609)
tensor(1.8082)
tensor(2.0788)
tensor(2.2850)
tensor(2.5260)
tensor(2.7856)
tensor(2.9724)
tensor(3.1985)
tensor(3.3561)
tensor(3.4583)
tensor(3.5661)
tensor(3.7218)
tensor(3.8444)
tensor(3.9327)
tensor(4.0394)
여기에 residual path의 갯수의 sqrt만큼 scaling해주면 (지금은 100이므로 10) output vector distribution은 1로 떨어지게 된다.
import torch
x = torch.zeros(768)
n = 16
for i in range(n):
x += n**-0.5 * torch.randn(768)
print(x.std())
tensor(0.2496)
tensor(0.3496)
tensor(0.4313)
tensor(0.4918)
tensor(0.5513)
tensor(0.6096)
tensor(0.6565)
tensor(0.7212)
tensor(0.7646)
tensor(0.8178)
tensor(0.8478)
tensor(0.8758)
tensor(0.9182)
tensor(0.9676)
tensor(0.9963)
tensor(1.0464)
Transformer에는 residual block별로 2개의 residual connection이 있으므로 우리는 residual path 별 output projection layer weight들에 대해서는 \(1/\sqrt{2 N}\)배 해줘야 최종적인 network output의 standard deviation이 1로 유지될 수 있는 것이다.
class Block(nn.Module):
def __init__(self, config):
super().__init__()
self.ln1 = nn.LayerNorm(config.n_embd)
self.attn = FlashAttn(config)
self.ln2 = nn.LayerNorm(config.n_embd)
self.mlp = MLP(config)
def forward(x):
x = x + self.attn(self.ln1(x))
x = x + self.mlp(self.ln2(x))
return x
여기서 또 하나 Transformer는 residual connection을 다수 사용하기 때문에 위의 simple example처럼 activation의 std가 점점 늘어날 것이고 이것이 학습에 안좋은 영향을 끼치진 않을까? 하는 생각을 할 수도 있는데, 실제 상황에서는 normalization layer가 존재하며 여러가지 변수가 있기 때문에 실제로 그렇지는 않을 것 같다. (일단 지금은 그렇게 생각하는데 나중에 생각나면 보충하겠다)
이런식으로 꽤 커다란 Transformer를 학습할 때에는 Xavier, Kaming init의 기본 철학에서 벗어나지는 않지만 model architecture의 특수성에 따라 layer별로 detail하게 init method를 설정해줘야 한다는 점이 매우 중요하다고 할 수 있다.
GPT init in Megatron-LM
NVIDIA의 Megatron에서는 어떻게 GPT model을 init하고 있을까.
NVIDIA는 Megatron-LM framework을 사용해서 Megatron-Turing Natural Language Generation model (MT-NLG)을 학습한 전력이 있는데,
model 크기가 무려 530B에 달한다.
Megatron의 key contribution은 vertical로 쪼개는 (partition) mechanism인 Tensor Parallelism (TP)를 사용해서 매우 큰 Trasnformer를 학습시켰다는 것인데,
살펴보면 실제 구현 자체는 GPT-2를 거의 따르는 것으로 보인다.
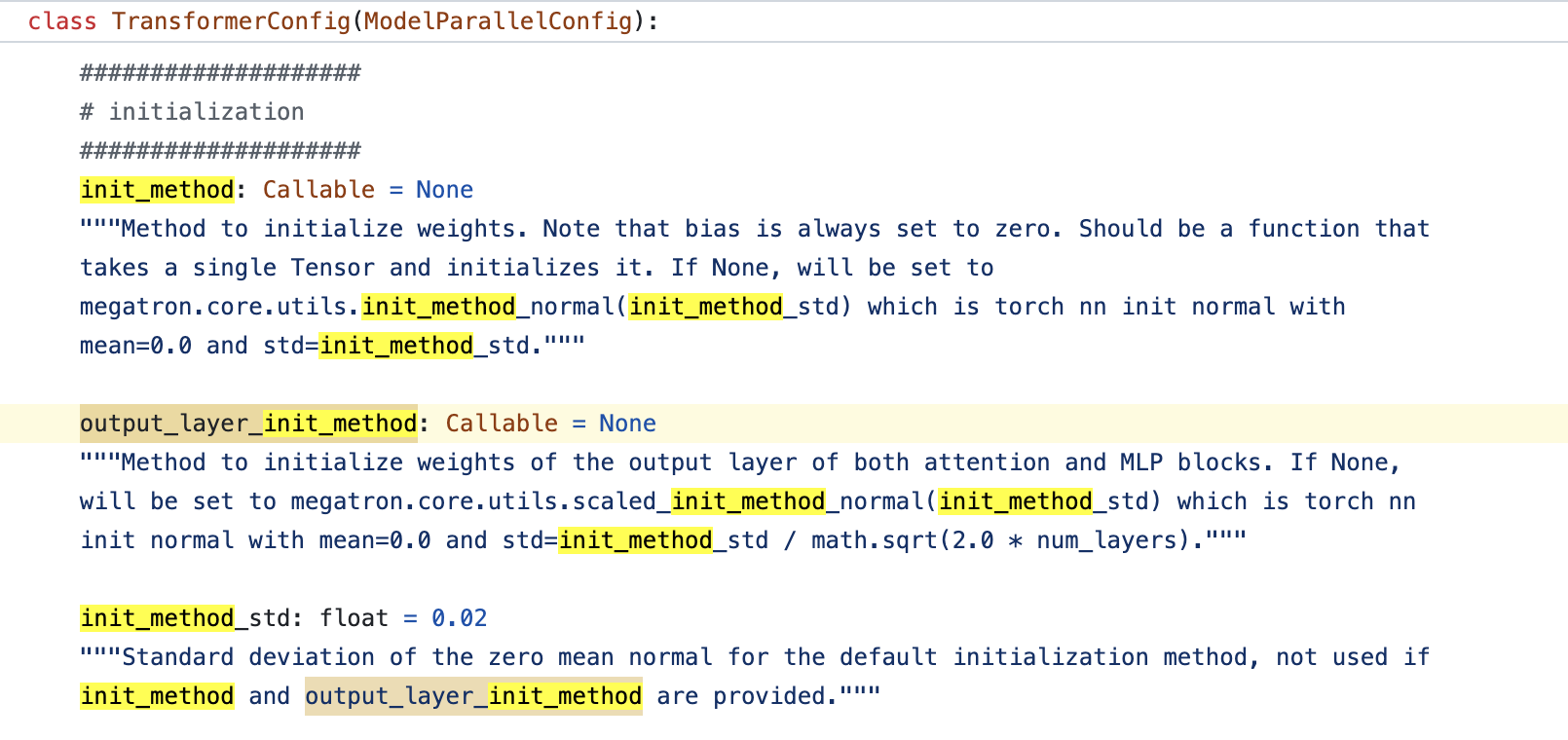 Fig.
Fig.
위 model config에 나와있는 것 처럼 init_method를 정의할 수 있는데, 기본적으로 zero mean의 normal distribution을 따르며, 이 때의 std만 따로 옵션으로 줄 수 있다. (code를 더 살펴보면 TP라고 다른 부분은 없다, 그냥 다른 module class를 쓸 뿐)
그리고 보통 self attn block이나 FFN의 input은 std=\(0.02\)를 따르지만 residual block의 output layer들은 기본 std에 layer 갯수의 sqrt로 discount해줬던 GPT-2처럼 다르게 설정해준다. model configuration을 따로 설정해주지 않으면 대부분의 weight matrix들은 default std범위로 (아마 \(0.02\)), output layer들은 \(0.02/\sqrt{2 \cdot n_{layers}}\)로 초기화 해주는데, 사실 530B를 이렇게 학습할 수 있다고 생각하면 오산이다. Using DeepSpeed and Megatron to Train Megatron-Turing NLG 530B, A Large-Scale Generative Language Model라는 paper를 보면 training setup에 대한 detail이 아래와 같이 적혀있는데, 당연하게도 \(0.02\)는 530B의 hidden dimension으로 계산한 값과 한참 동 떨어진 값이기 때문에 이를 쓰는 것 자체가 nonsense이지만, 저자들은 여기에 더불어 \(1/\sqrt{3}\)만큼 더 discount한 값인 \(\sqrt{1/(3*\text{hidden-size})}\)를 사용했다.
 Fig. Source from MT-NLG
Fig. Source from MT-NLG
그러니까 variance가 큰 것을 억제하기 위해서 LR나 다른 값들을 hard하게 조정할 것이 아니라면, 절대로 \(std=0.02\)를 쓰면 안되는 것이다.
LLaMa
이번에는 opensource LLM중 가장 유명하고 최근 version 3에서 어마어마한 성능을 보여주고있는 LLaMa에 대해 알아보자. llama가 opensource이지만 사실 완전 opensource는 아닌 것이 training code등이 공개되지 않았다. meta-llama/llama3/llama/model.py가 공식 repo인데, 이는 inference를 위해 model을 loading하고 generate할 수 있는 코드가 있지 (그마저도 최적화 되지 않았음) 다른 흔적은 없다. 이 repo에 있는 흔적이라곤 그냥 vanilla init밖에 없다.
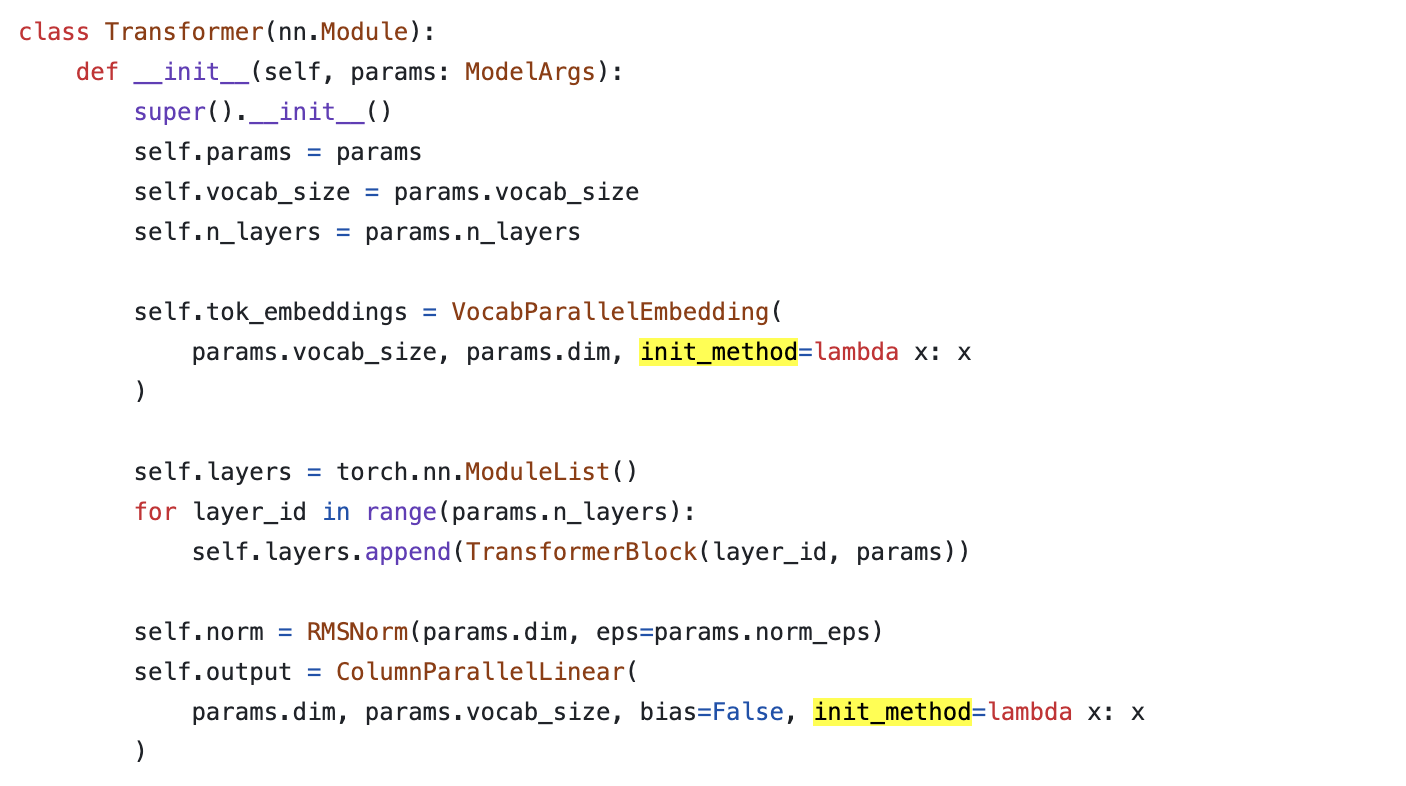 Fig.
Fig.
왜냐면 어차피 llama model weight을 loading하는 end-user입장에서 이딴건 알 필요도 없을 뿐더러, 이는 meta 연구진의 진귀한 보물 같은걸 알려주는 것이나 다름 없기 때문이다.
그럼에도 위의 init_method는 어떻게 작동하는지 궁금할까봐 얘기하자면 Megatron-LM과 똑같다.
LLaMa에는 아무래도 TP가 똑같이 적용된 것 같은데 (fairscale의 TP, torch FSDP 사용해서 학습한듯),
init_method가 lambda x: x라는 건 그냥 weight을 입력으로 받으면 normal dist로 초기화 하는것이 아니라 그냥 뱉겠다는 의미다.
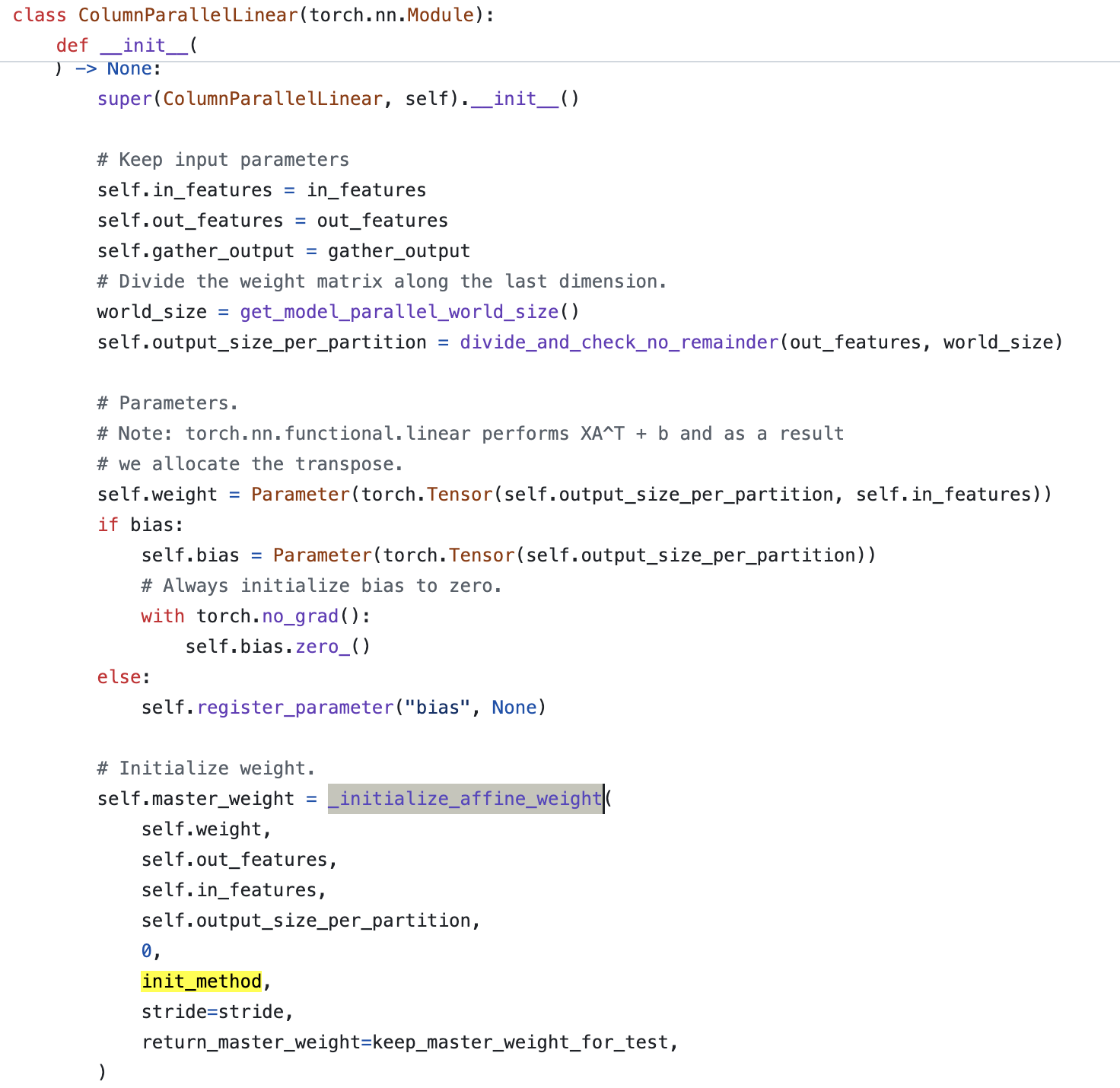 Fig.
Fig.
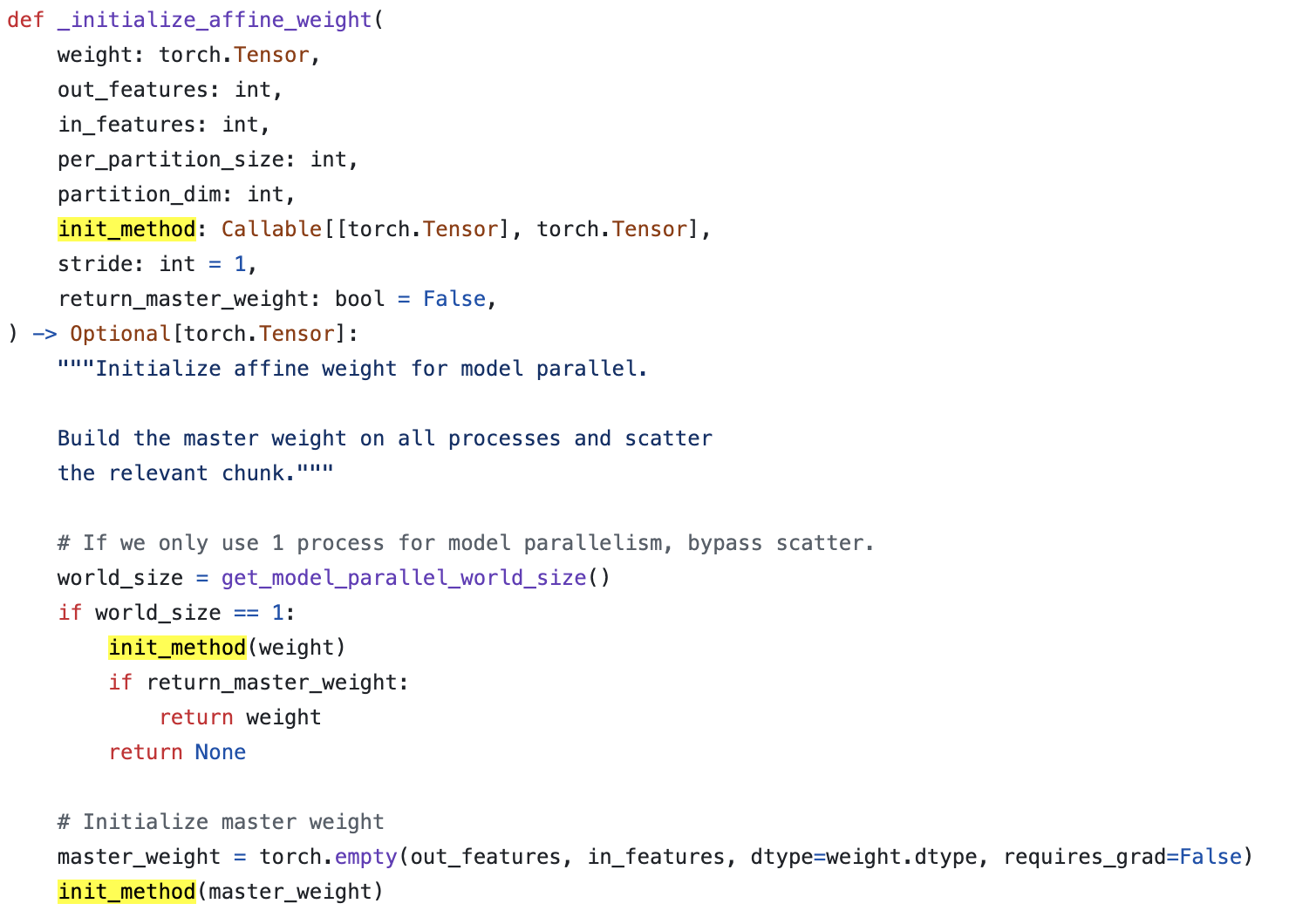 Fig.
Fig.
한마디로 초기화 하는방법은 안알려주는 것이다. 어떤이들은 training source code까지 공개하는 opensource model과 model weight만 공개하는 open weight model을 구분 지어야 한다고 얘기하는데, llama가 정확히 후자에 해당하는 것이다. (거기에 license도 제약이 있으니 truly open은 아니다)
한 편, Meta의 새로운 opensource project인 torchtitan이라는 최근에 meta에서 공개한 opensource에서는 llama를 from scratch로 학습할 수 있는 code를 제공한다.
이 repo는 pytorch의 새로운 feature (TP라던가)를 test하는 실험실정도로 생각하면 되는데,
매우 active하게 commit이 이뤄지고 있으며 LLaMa를 주어진 dataset에 대해서 pytorch의 새로운 distributed training technique들을 사용해 매우 빠르게 학습할 수 있는 sample을 제공한다.
바로 이 sample trainer에 2가지 model init meethod가 존재하는데,
하나는 우리가 이미 알고있는 방법이고 나머지 하나는 depth_init이라는 것이다.
 Fig.
Fig.
이는 layer_id에 따라서 residual block 내의 output layer의 std를 조절하는 방법으로,
front-end에 가까운 layer일 수록 std의 범위가 커지고 (역수이므로),
back-end에 가까울수록 std가 작아지게 된다.
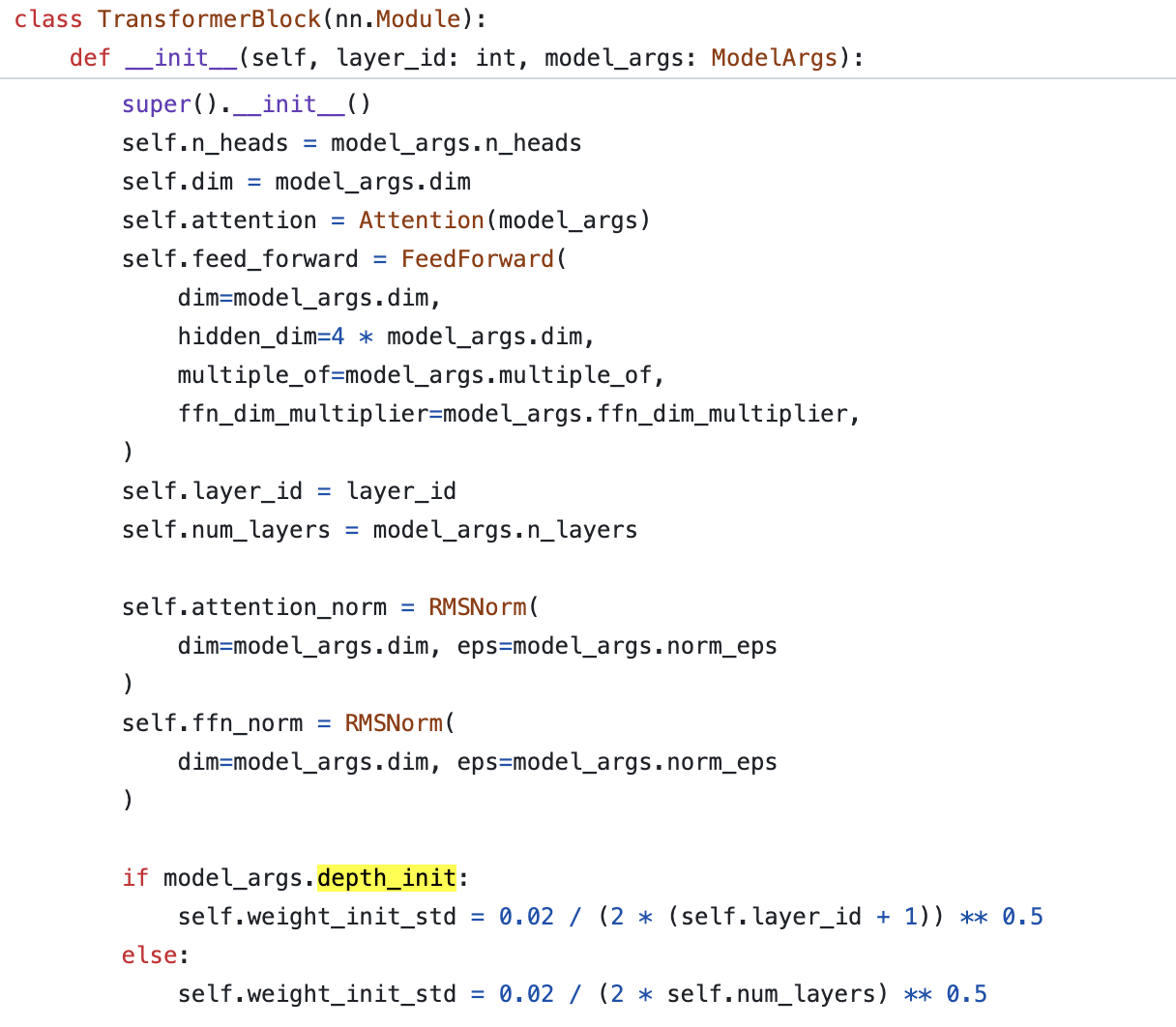 Fig.
Fig.
뭐 depth_init을 쓸 것이 아니라면 residual path의 마지막 weight들의 init_std는 \(0.02/\sqrt{2 \cdot n_{layers}}\)를 따르게 되는데, GPT-2의 철학과 같다.
 Fig.
Fig.
Attention의 예시를 보면 아래와 같은데,
 Fig.
Fig.
torch.nn.init.trunc_normal_이라고 해서 기본적으로 -2~2를 벗어나지 않는 값을 normal dist로부터 sampling한다.
 Fig.
Fig.
하지만 GPT-2가 성공했고 GPT-3또한 GPT-2의 init method를 그대로 따랐다고는 해도 GPT-2 init method는 너무 오래됐으며, 2024년 현재 llama3까지 오면서 model size나 architeture design 자체가 많이 변했기 때문에 init method에 변화가 생기는 건 자연스럽다고 할 수 있겠다.
 Fig. Source from GPT-2. GPT-2는 최대 1.5B 크기다.
Fig. Source from GPT-2. GPT-2는 최대 1.5B 크기다.
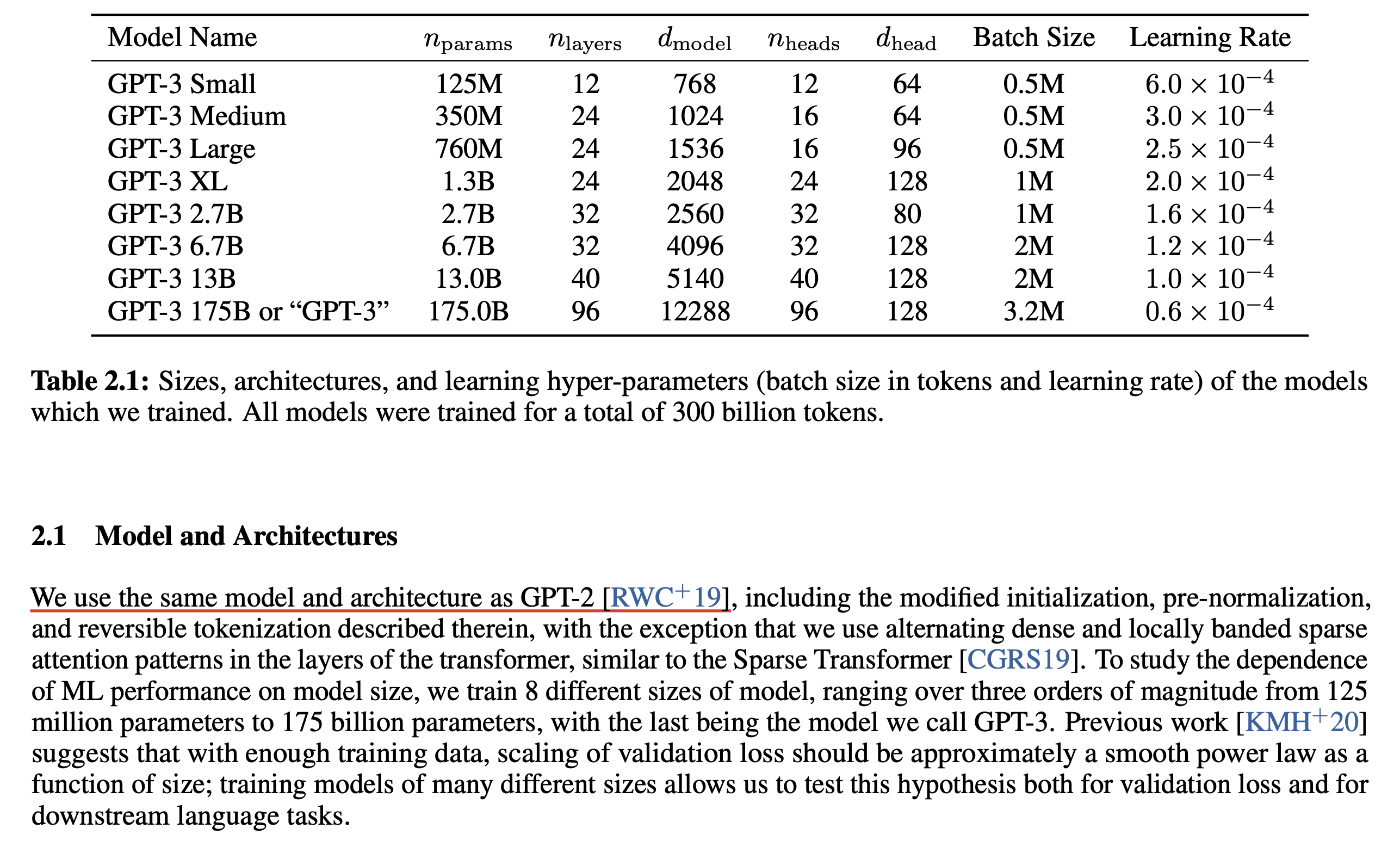 Fig. Source from GPT-3. GPT-3또한 GPT-2의 init method를 똑같이 따랐으며 GPT-3까지 잘 scale up을 할 수 있었다.
Fig. Source from GPT-3. GPT-3또한 GPT-2의 init method를 똑같이 따랐으며 GPT-3까지 잘 scale up을 할 수 있었다.
아래는 최종적으로 llama init을 하는 부분인데,
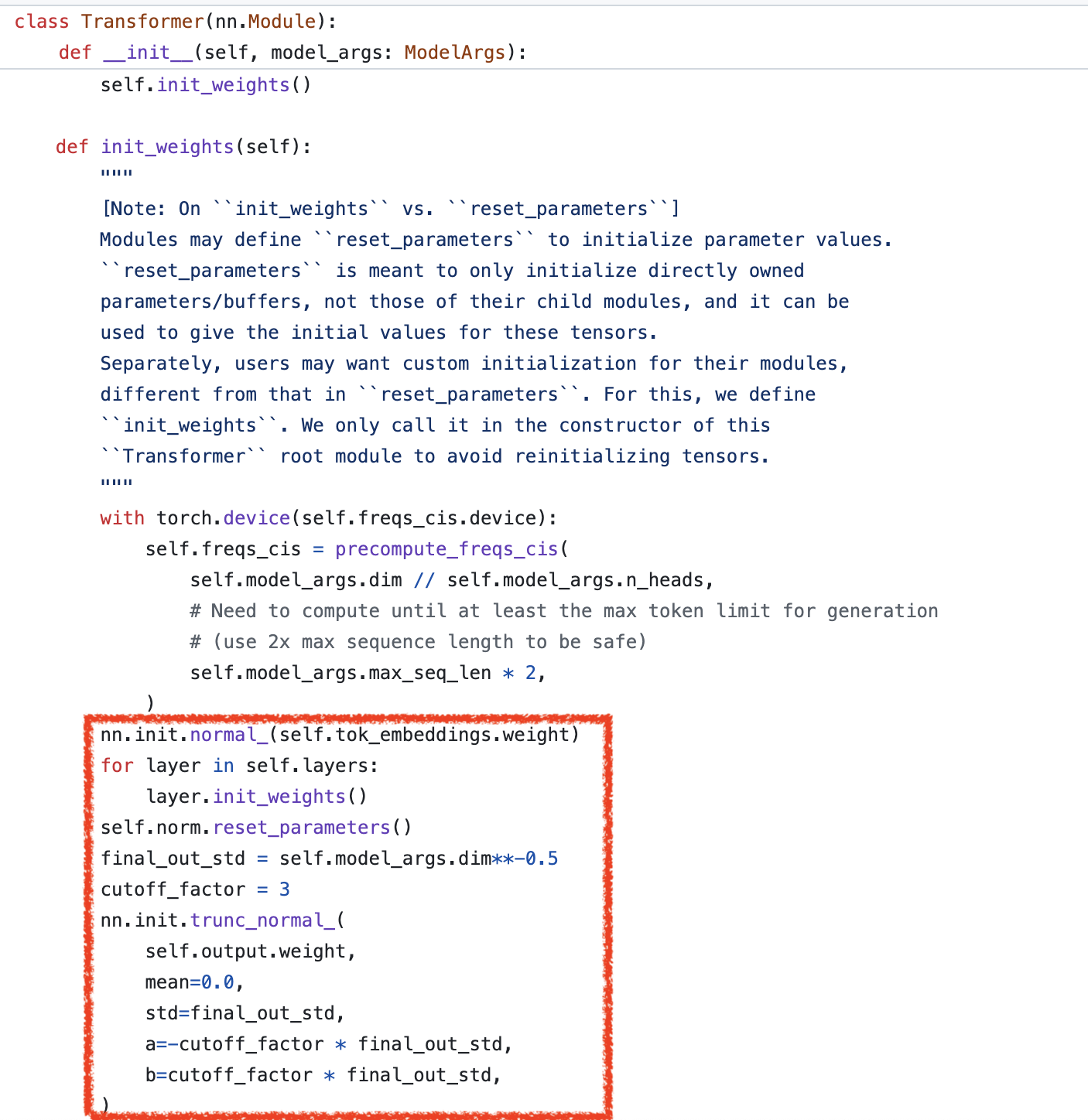 Fig.
Fig.
layernorm들은 전부 reset_parameters를 따르며 그냥 weight은 1로, bias는 0으로 설정하는 것이다. 위 figure에서 NN의 가장 앞, 뒤를 담당하는 embeding layer와 unembedding layer의 init method도 확인할 수 있는데, GPT-2와 다르게 우선 llama는 embeddig weight을 0.02가 아닌 1로 초기화 한다. 그리고 unembedding layer는 hidden dim의 역수를 variance로 쓴다. 이럴 경우 하면 GPT-2와는 다르게 embedding, unembdding layer가 매우 다른 분포를 갖게됨을 볼 수 있다.
>>> import torch
>>> emb = torch.nn.Embedding(128000,4096)
>>> torch.nn.init.normal_(emb.weight)
Parameter containing:
tensor([[ 1.8772, -0.1578, 0.8438, ..., -1.9624, 2.0276, 1.1533],
[ 1.4098, -0.6993, -0.7098, ..., -0.1006, 1.4068, 0.6409],
[-1.2407, 0.3933, -1.1777, ..., -0.1205, 0.4230, -0.8709],
...,
[ 0.3169, 1.8465, -2.8221, ..., -0.1374, -0.3028, -1.4693],
[-0.8811, -0.5013, 1.2798, ..., -0.2936, 0.4156, -0.6553],
[ 0.3806, 0.3108, -2.5151, ..., 1.2739, -1.2262, 0.9775]],
requires_grad=True)
>>> emb.weight.mean()
tensor(8.2497e-05, grad_fn=<MeanBackward0>)
>>> emb.weight.std()
tensor(0.9999, grad_fn=<StdBackward0>)
>>> unemb = torch.nn.Linear(4096,128000)
>>> cutoff_factor = 3
>>> final_out_std = 4096**-0.5
>>> torch.nn.init.trunc_normal_(
unemb.weight,
mean=0.0,
std=final_out_std,
a=-cutoff_factor*final_out_std,
b=cutoff_factor*final_out_std
)
Parameter containing:
tensor([[ 0.0045, -0.0133, -0.0185, ..., 0.0022, -0.0039, 0.0007],
[ 0.0116, -0.0042, 0.0021, ..., -0.0042, 0.0022, -0.0060],
[ 0.0275, -0.0002, 0.0087, ..., -0.0050, -0.0144, -0.0259],
...,
[-0.0044, -0.0201, 0.0044, ..., -0.0346, 0.0185, 0.0050],
[-0.0011, 0.0103, -0.0093, ..., 0.0195, -0.0128, -0.0041],
[ 0.0157, 0.0071, -0.0284, ..., -0.0178, -0.0069, 0.0201]],
requires_grad=True)
>>> unemb.weight.mean()
tensor(1.0176e-06, grad_fn=<MeanBackward0>)
>>> unemb.weight.std()
tensor(0.0154, grad_fn=<StdBackward0>)
당연히 llama는 weight tying을 하지 않았으니 이런 선택이 가능하지만 그럼에도 너무 값 차이가 많이나서 weight이 update되는 양상이 GPT-2와는 매우 다를 것으로 예상된다.
+Updated) depth_init에 대해서 torchtitan에 issue를 남겼더니 답변이 왔다.
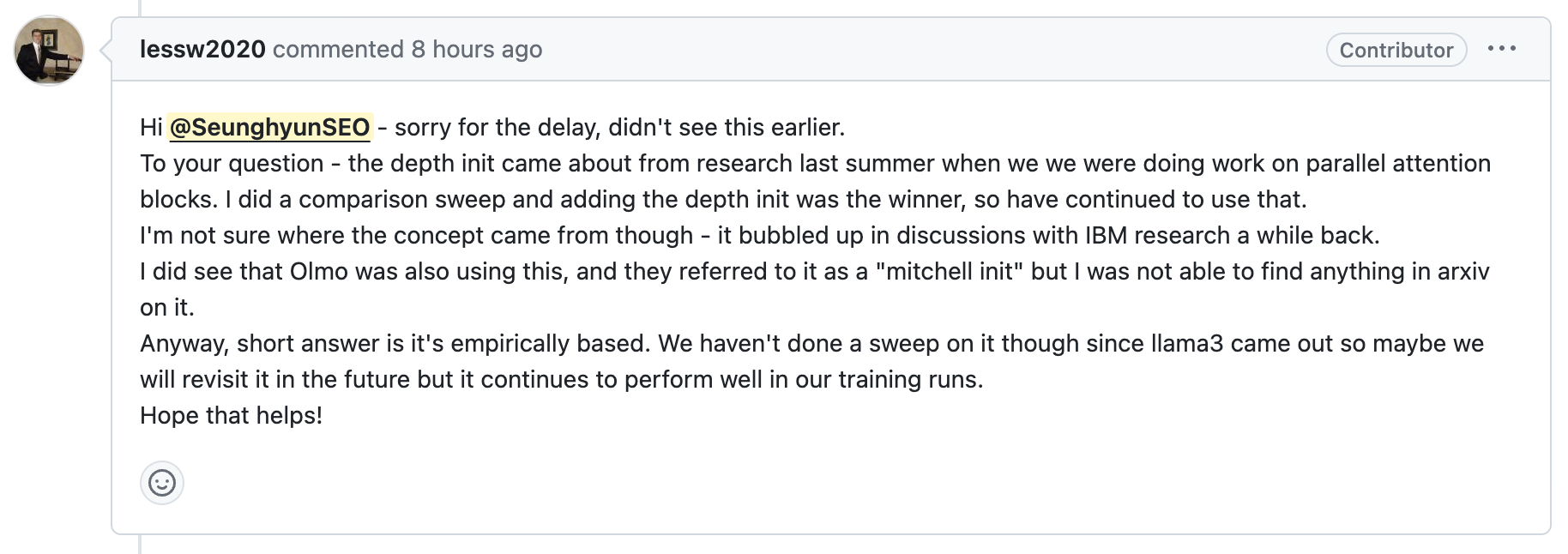 Fig.
Fig.
답변의 내용은 IBM과 협업하던 도중 (torchtitan이 IBM과 합작해서 실험하다 나온 project인듯) 갑자기 아이디어가 떠올랐고,
실험 결과 경험적으로 이게 제일 좋았다는 것이다.
그리고 AI2의 OLMo에서 이를 먼저 도입했다고 하는데,
AI2에서는 이를 Mitchell Init이라고 부르며,
llama-3가 나온 뒤로 더 비교해본 적은 없지만 경험적으로 좋았던 init method를 open했다는 얘기다.
(llama-3가 어떻게 init되었는지 leak 된 줄 알았지만 그게 아니라는 소리며,
이보다 더 좋은 method를 탐구했다는 얘긴데 어쩌면 muP일지도…?)
한 편, Huggingface의 LlamaPreTrainedModel class의 init method는 아래와 같은데, 당연히 이는 llama의 init method가 알려지지 않아서 대충 작성한 것 처럼 보이니 이걸 사용해서 pre-training을 시도하는 사람도 없겠지만 만약 당신이 그렇다면 재고해보도록 하자.
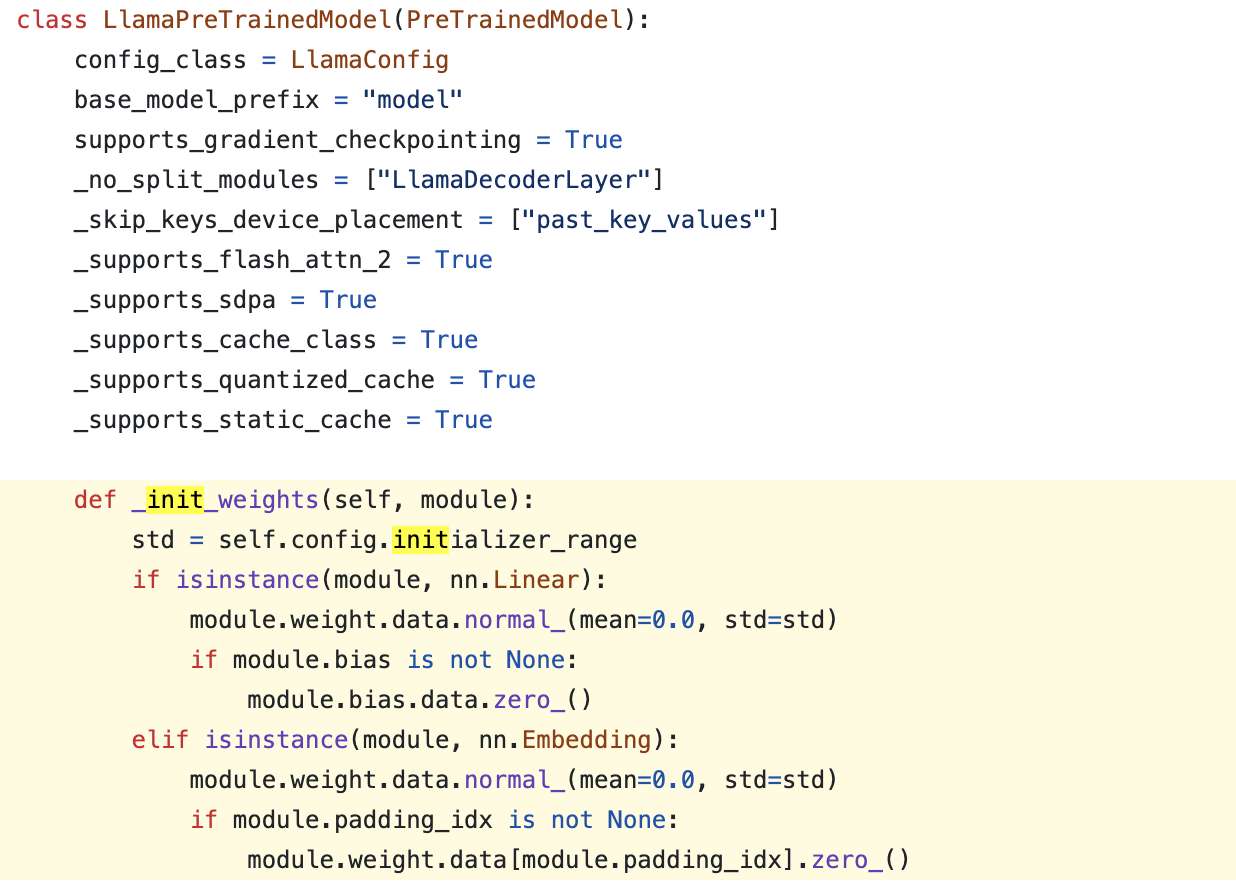 Fig. huggingface llama-3 init method (don’t use this for pre-training)
Fig. huggingface llama-3 init method (don’t use this for pre-training)
OLMo and BigCode
말이 나온 김에 OLMo의 init method들도 확인해보자. OLMo는 앞서 말한 것 처럼 llama가 weight만 공개하고 training code는 공개하지 않은 open weight model인 것과 다르게 training code와 training log까지 싹 다 공개한 완전한 opensource 라고 할 수 있다. 앞서 depth_init이 OLMo에서는 Mitchell Wortsman의 이름을 딴 만든 mitchell_init이라 부른다고 했는데, mitchell은 앞서 scaling law prediction을 얘기하며 잠깐 언급했던 Small-scale proxies for large-scale Transformer training instabilities의 1저자로 현재 Anthropic에서 pre-training team에 속해있는 researcher이다.
 Fig.
Fig.
즉 그만큼 pre-training에 대한 조예가 깊다는 뜻으로 이해하면 될 것 같고, OLMo의 init method는 mitchell_init을 포함해 4가지 정도가 있다.
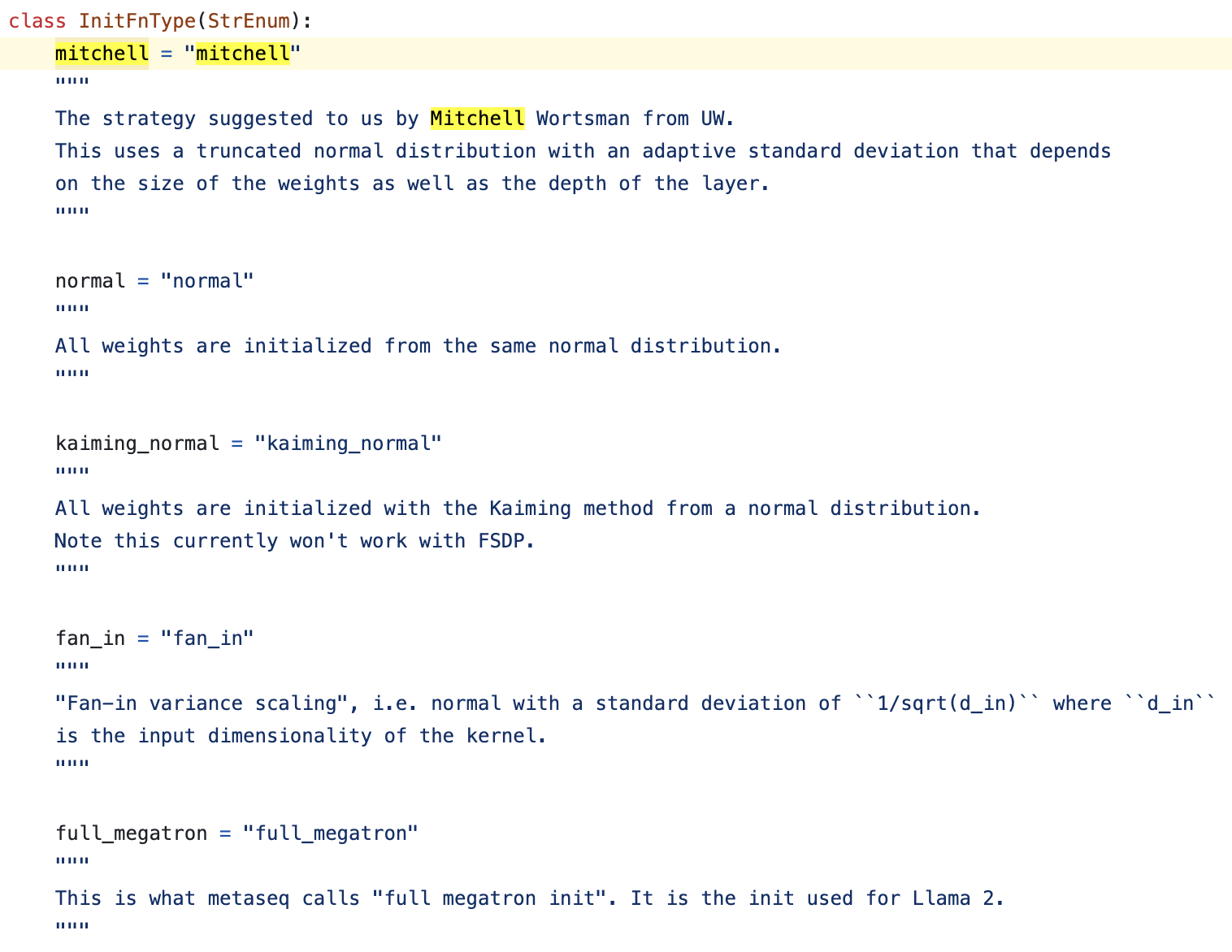 Fig.
Fig.
살펴보자면 다음과 같은데,
mitchel_init- normal_init: 정해진 init_std_range로 모든 weight을 init함
- kaming_normal: torch.nn.init의 kaming을 따를 것 같은데 \(2/\sqrt{\text{fan-in}}\)으로 init 할 듯 함
- FSDP랑 충돌나서 구현 안해둔 듯
- fan_in: 비슷하게 network input feature dim인 \(1/\sqrt{text{fan-in}}\)로 init함
- full_megatron: GPT-2스러운 것으로 보이는데 llama-2에서 이를 썼다고함 (오…)
먼저 embedding weight부터 살펴보자면 아래와 같다.
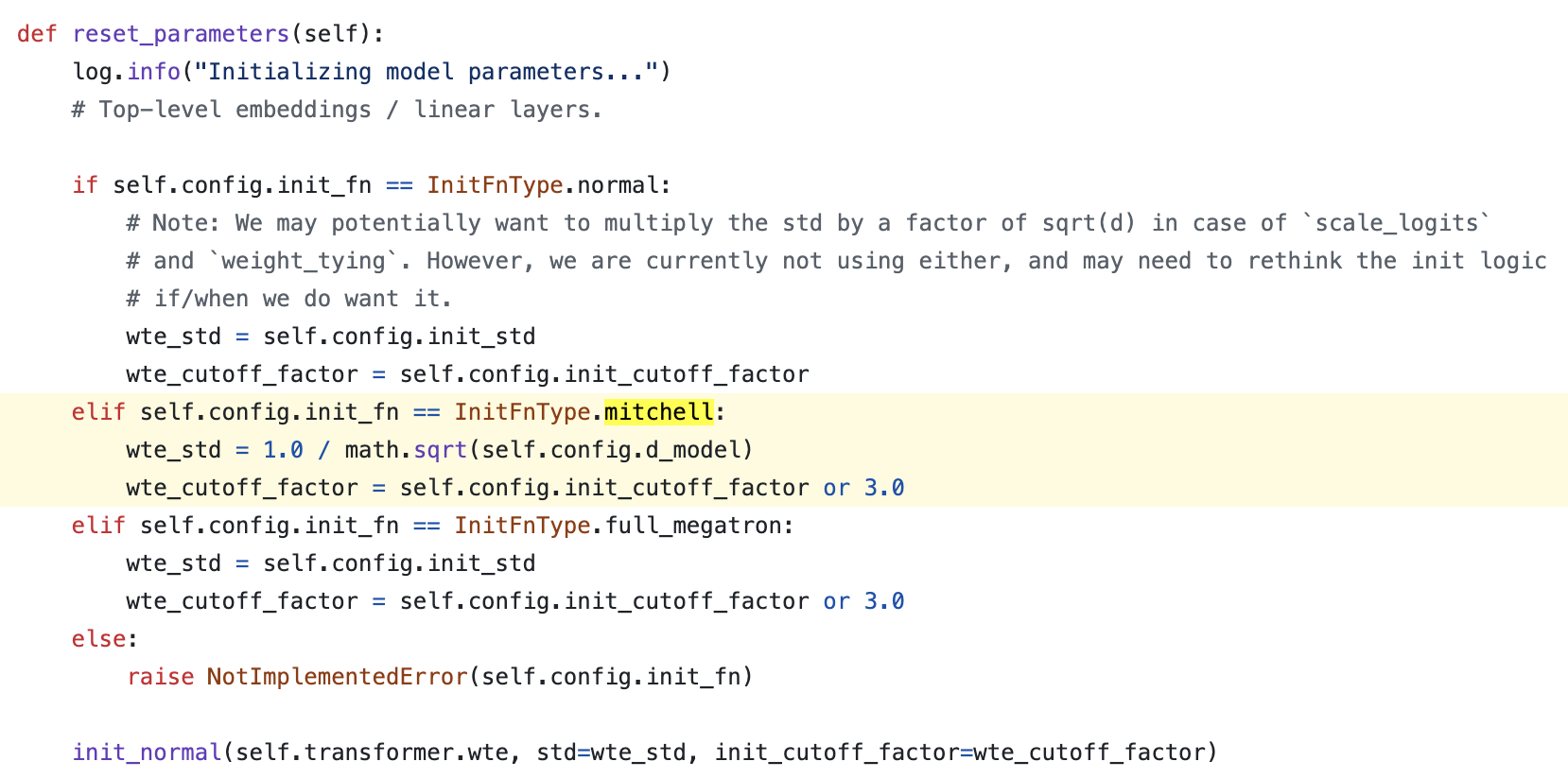 Fig.
Fig.
full_megatron과 normal init은 모두 정해진 std range의 값으로 초기화 하는 걸 택했으나 mitchell_init은 hidden_size (embedding dim)으로 init한다. 사실 앞서 살펴본 것 처럼 정해진 std가 0.02라면 이는 7B의 hidden size를 \(1/\sqrt{\text{hidden size}}\)한 것과 다름 없는 수준이기 때문에 같다고 볼 수 있다.
다음은 unembedding layer인 lm_head인데 이것도 다 비슷하다고 할 수 있다.
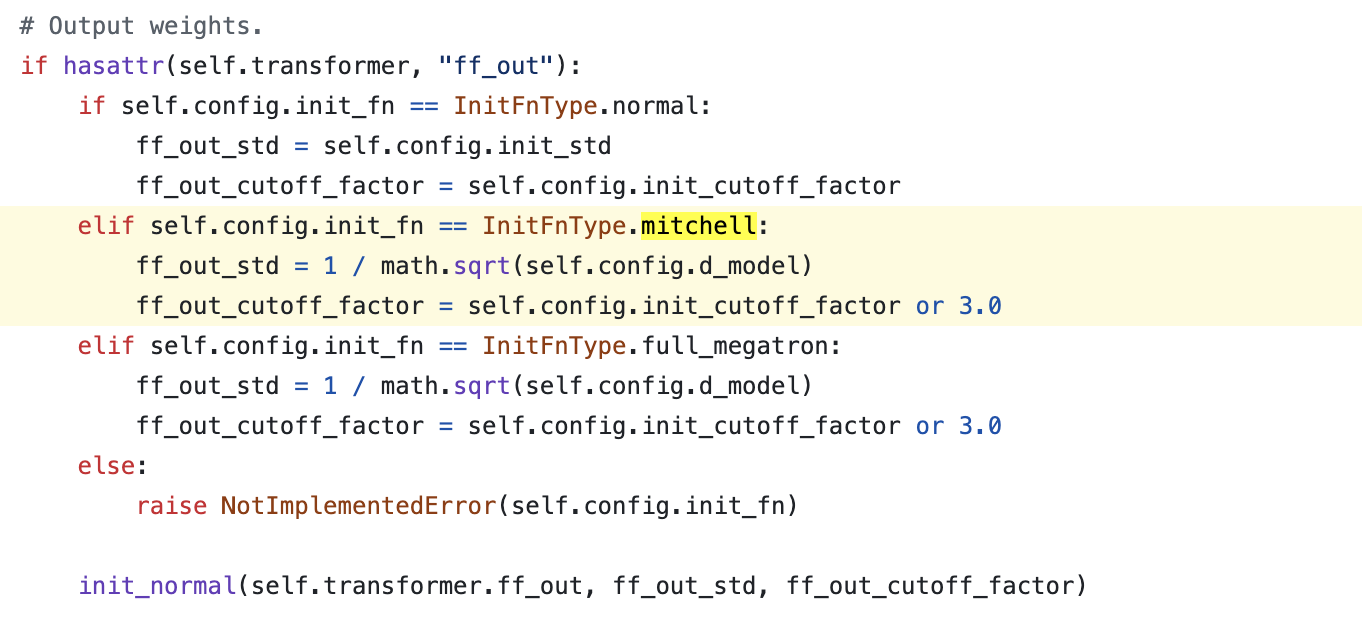 Fig.
Fig.
이제 residual block내에 있는 attn QKVO, ffn in/out 부분인데, 이것도 사실 GPT-2스럽거나 mitchell의 경우 layer index의 역수를 사용하는 것으로 딱히 특이할게 없다.
 Fig.
Fig.
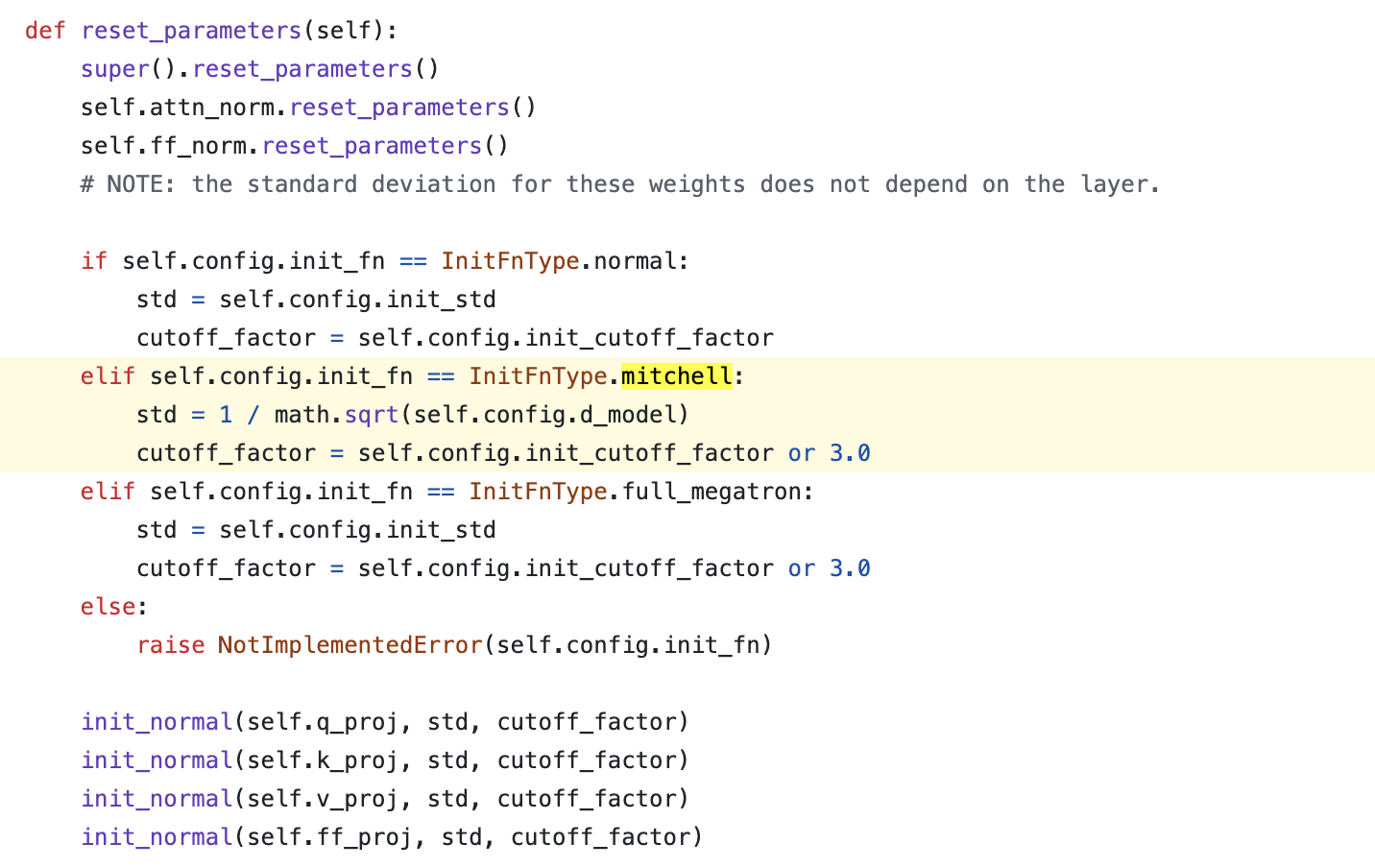 Fig.
Fig.
딱히 OLMo라고 흥미로운게 있진 않았는데, repo의 commit/PR history를 보다가 이런 issue를 보게 되었다.
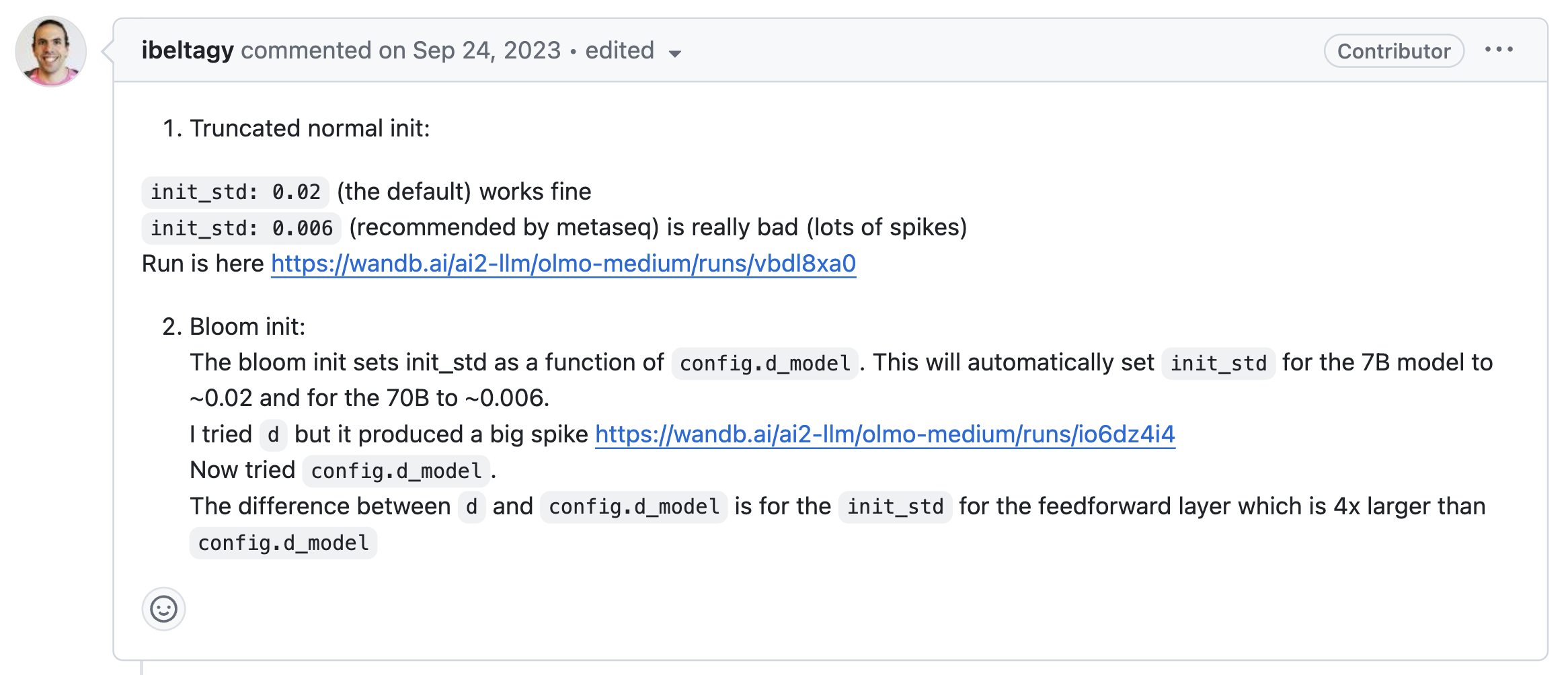 Fig.
Fig.
내용은 BigCode (BigScience 같은 그룹인듯?)에서 사용하는 init method에 대한 실험을 해봤다는 것인데, 이분의 실험결과는 그렇다 치고 bigcode에서는 pre-training stability에 있어서 \(std=2/\sqrt{\text{hidden size} * 5}\)로 init하는게 주요했다는 것이다.
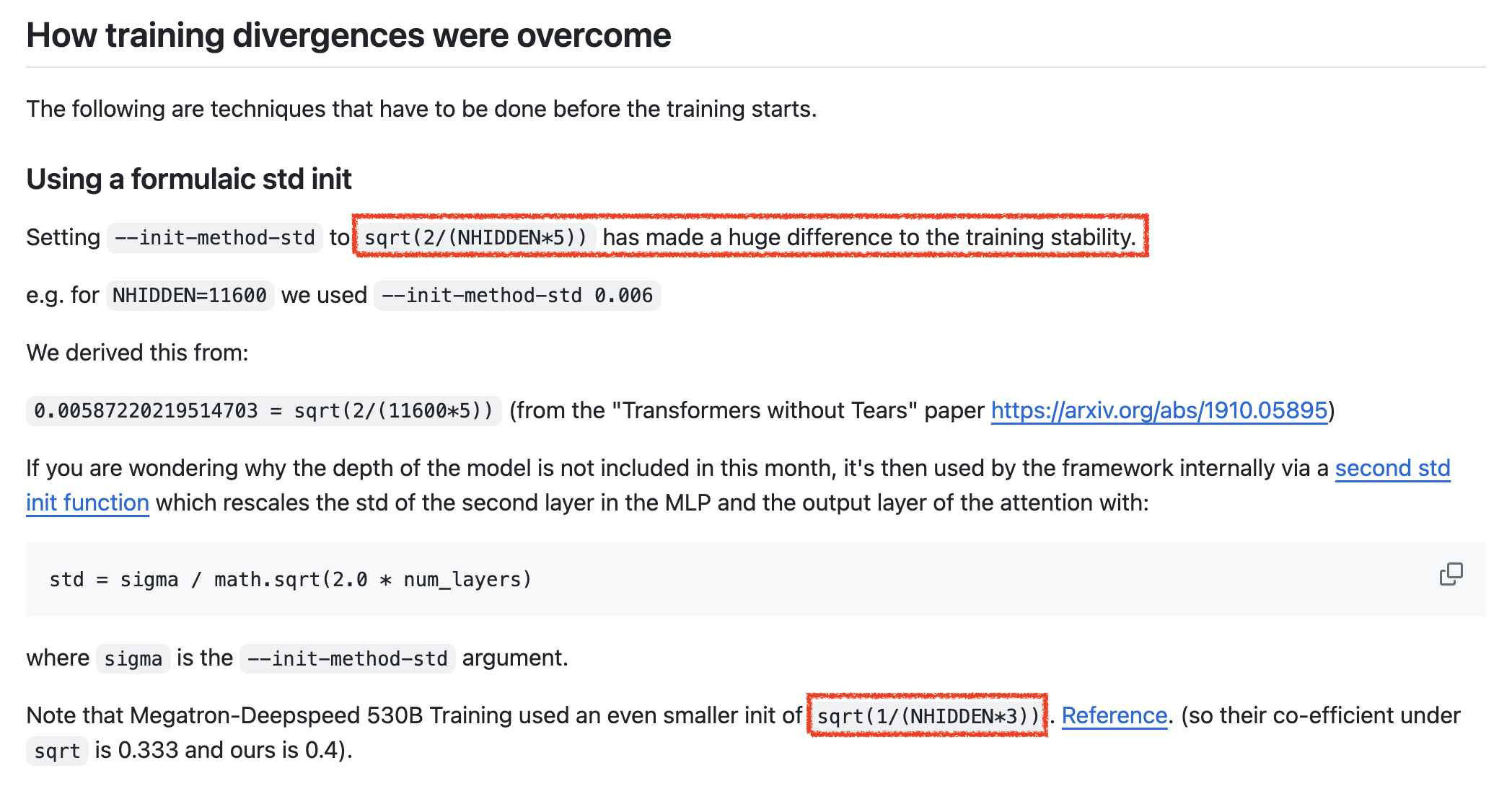 Fig.
Fig.
위 AI2 researcher가 실패했다는 init method는 좀 특이한데, 모든 layer를 fan_in으로 초기화 하는 것이다. 특이하다기보다는 xavier, kaming 혹은 OLMo의 fan_in init같은건데 GPT-2같은 init method를 쓰는 대부분의 modern LLM과 달리 FFN layer는 사실 xavier를 따르려면 ffn output projection layer의 경우 fan_in인 intermediate hidden size가 보통 기본 hidden size의 4배에 달하기 때문에 매우 큰 차이가 나는데 이것이 실패했다는 것이다. (하지만 muP에서는 이와 비슷하게 ffn out을 init한다… 곧 revisit할 것)
Pathway LM (PaLM) Init
정말 마지막으로 Google의 PaLM의 init method에 대해서 알아보자. 2022년에 나온 paper이고 PaLM을 기반으로 한 Gemini를 써보면 구리기 때문에 이를 따르는 것이 맞나 싶지만, 나는 PaLM paper자체에는 매우 많은 정보가 있고 (MFU라던지) 방법론 자체가 틀린 것이 아니라 학습량 등이 문제인 것으로 생각하기 때문에 paper를 한 번 보는 것 자체는 좋다고 생각한다.
 Fig.
Fig.
PaLM은 init method로 fan_in variance를 택했는데, 여기에 추가적으로 Adam이 아닌 Adafactor Optimizer를 사용했다고 한다. 왜 Optimizer얘기를 하나 싶겠지만 사실 optimizer는 init variance와 같은 parameterization과 큰 관련이 있다. 곧 muP에서도 다루겠지만 이는 gradient를 계산해서 LR을 곱해 parameter를 update하는 rule 자체를 정의하기 때문이며, training이 진행될수록 그 parameter를 통과하는 activation의 variance는 optimizer도 크게 기여하기 때문이다. 이런 부분에서 Adam과 다르게 Adafactor는 gradient를 weight norm으로 scaling 해주는 부분이 다른데, 이는 muP의 철학과도 관련이 있다 (말미에 살펴볼 예정)
그 밖에 눈에 띄는 점은 residual path, \(N\)개에 대해서 output projection weight 마다 \(1/\sqrt{2N}\)배 해주지는 않았다는 점과, embedding, unembedding layer를 \(\mathcal{N}(0,1)\)로 init한 뒤, 이 둘을 tying했기 때문에 특별한 조치를 취해줬다는 것인데, 바로 logit에 vocab size, \(n\)에 대해서 \(1/\sqrt{n}\)만큼 scaling해줬다는 것이다.
이렇게 한 이유는 아무래도 embedding weight은 backprop시 backend에서 한 번, frontend에서 한 번, 총 두 번 update될텐데 이 둘이 받는 gradient의 양이 아마 다르기 때문인 것으로 보인다. 그래서 training stability를 위해서 gradient를 discount한 것으로 보인다.
예를 들어 아래 처럼 output layer의 input을 \(x\), unembedding weight을 \(W_{emb}\), 그리고 logit을 \(z\), scaled logit을 \(\tilde{z}\)이며 bias는 없다고 생각하자.
\[\begin{aligned} & z = W_{emb} x, & \\ & \tilde{z} = \frac{1}{\sqrt{n}} z & \\ \end{aligned}\]True label을 \(\hat{y}\)라고 할 때 XEntropy loss, \(L=\sum_{i}\hat{y_i} \log y_i\)의 unscaled logit, \(z\)에 대한 gradient는 먼저 아래처럼 구할 수 있다.
\[\begin{aligned} & \frac{\partial L}{\partial z} = \frac{\partial L}{\partial \tilde{z}} \frac{\partial \tilde{z}}{\partial z} & \\ & = \frac{\partial L}{\partial \tilde{z}} \frac{1}{\sqrt{n}} & \\ & = (y-\hat{y}) \frac{1}{\sqrt{n}} & \\ \end{aligned}\]이제 각 weight, input에 대한 gradient를 계산하면 아래와 같은 값을 얻을 수 있다.
\[\begin{aligned} & \color{red}{ \frac{\partial L}{\partial W_{emb}} } = \frac{\partial L}{\partial z} x^T & \\ & = (y-\hat{y}) \frac{1}{\sqrt{n}} x^T & \\ & \color{blue}{ \frac{\partial L}{\partial x} } = W_{emb}^T (y-\hat{y}) \frac{1}{\sqrt{n}} & \\ \end{aligned}\]그런데 여기서 잊으면 안되는 것이, 우리는 logit을 scaling down 해서 softmax를 취했기 때문에 이는 사살싱 temperature를 키운 softmax를 한 것이나 다름이 없다는 것이다.
\[\begin{aligned} & \color{red}{ \frac{\partial L}{\partial W_{emb}} } = (Softmax(\frac{W_{emb}x}{\sqrt{n}}) - \hat{y}) \frac{1}{\sqrt{n}} x^T & \\ & \color{blue}{ \frac{\partial L}{\partial x} } = W_{emb}^T (Softmax(\frac{W_{emb}x}{\sqrt{n}}) - \hat{y}) \frac{1}{\sqrt{n}} & \\ \end{aligned}\]즉 이는 원래 softmax보다 prob을 줄여서 loss를 계산하기 때문에 기존보다 더 큰 loss를 받지만 그 gradient 자체는 또 \(1/\sqrt{n}\)만큼 discount되는 효과를 낳게 된다.
The Basic Math in muP and It's Desiderata
이제 muP를 이해하기 위한 key concept과 basic math에 대해서 먼저 알아보고 어떻게 이를 general NN에 적용할 수 있는지 알아보자. Greg의 muP video를 보면 결국 muP와 SP의 차이는 다음의 한 slide로 요약할 수가 있다.
 Fig.
Fig.
가장 큰 변화 두 개는 Transformer model을 학습한다고 할 때 다음과 같다.
- logit을 만드는 last layer의 output에 NN의 width, \(n\)의 sqrt의 역수, \(1/\sqrt{n}\)를 곱해줌
- 입력단의 embedding layer output에 \(\sqrt{n}\)만큼을 곱해줌
- Embedding layer가 원래 SP를 따른다면 fan_in이 아닌 fan_out, 즉 transformer의 model dim으로 init을 해줌
먼저 last layer의 경우 SP를 따를 경우 너무 큰 값으로 init되어 너무 많은 gradient가 흐르기 때문에 discount를 해주는 것이고, first layer는 반대로 gradient가 너무 작기 때문에 \(\sqrt{n}\)만큼 scaling 해줘야 한다는 것이 Greg의 설명이다.
사실 바로 직전에 얘기한 PaLM의 logit scaling과 결이 맞다는 점에서 google도 비슷한 관찰을 했던 것 같은데,
위 slide의 내용을 보면 first layer (embedding layer)에 대해서 "embedding output을 scaling 해줌으로써 gradient를 scaling하는 효과를 갖는다"라고 되어있어 반대로 last layer는 gradient가 작게 보정될 것이라는 걸 쉽게 유추할 수 있다.
이렇게 하는 이유는 여러번 얘기한 것 처럼 muP의 이름이 Maximal Update (Mu)인 것에서 알 수 있는데,
TP-4, muP의 목적이 NN의 width, \(n\)이 늘어남에 따라 training dynamics가 괴랄하게 바뀌지 않으면서,
즉 같은 order of magnitude로 변하는게 보장되게 하여 모든 layer에 대해 gradient가 vanishing하거나 exploding하지 않는 선에서 최대한 많이 update 되어 결국 feature learning을 maximize 하는것이 목표이기 때문이다.
 Fig. width가 무한대로 가는 경우에도 모든 layer에서 유의미한 feature learning을 보장하는 것이 muP
Fig. width가 무한대로 가는 경우에도 모든 layer에서 유의미한 feature learning을 보장하는 것이 muP
SP와 muP의 차이는 또 layer별로 LR을 다르게 주는 것,
즉 per layer LR를 사용한다는 점에도 있다.
이것 또한 "layer별로 weight init시 std, LR를 다르게 줘서 training stability를 높히고 feature learning을 maximize하겠다"라는 목적은 같다.
위 slide에는 이 부분에 대한 언급은 없는데,
사실 per layer LR를 보통 muP에서 per layer라고 해 봤자 input layer (embedding), hidden, output layer (unembedding) 이렇게 세 부류로 나누는데 per layer LR을 준다는 점이 곧 gradient를 scaling 한다는 것과 같은 의미를 가지기 때문에 이미 반영된거라고도 볼 수 있다.
"목적은 같은데 왜 구현이 다른가요?"에 대해서는 구현의 편의성 때문이라고 할 수 있는데,
이것 또한 곧 살펴보게 될 것이다.
아래는 microsoft가 release한 mup package의 문서의 일부분으로,
muP가 뭘 바라고 만들어 졌는지 (desiderata; 사전적 의미로 ‘간절한 열망’, ‘바램’)가 간단하게 적혀 있다.
(paper에도 있는 내용)
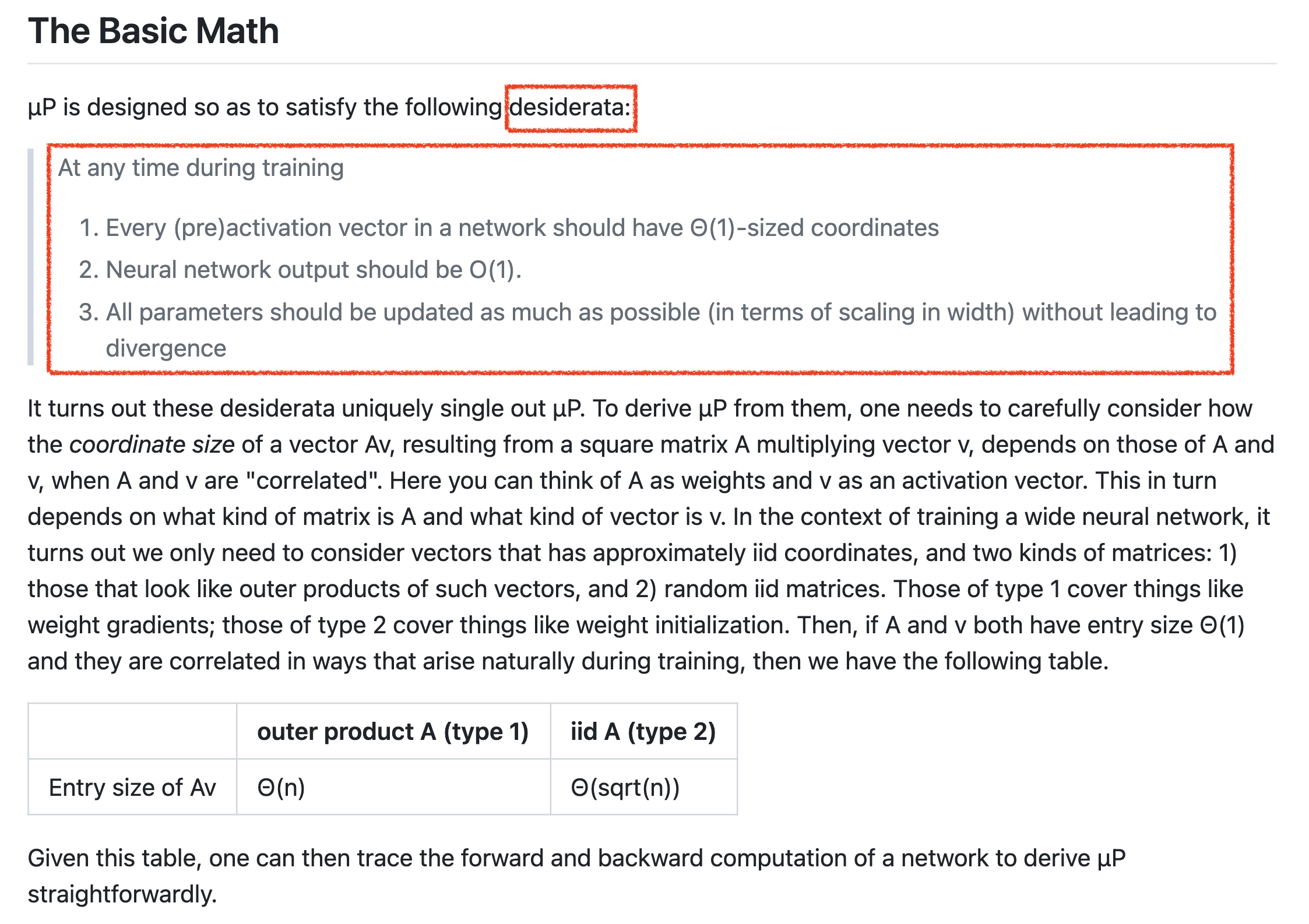
위 table의 desiderata는 저자들이 바란 NN의 scale이 커질 때 이상적으로 지켜져야할 것이라고 할 수 있는데,
이는 요약하자면 다음과 같다.
Stability: 각 layer별 activation 값이 정확히 constant scale이어야 하고 output logit은 특정 constant scale을 넘어선 안됨 (the activations are exactly constant scale and the logits are no more than constant scale)Non-Triviality: 학습이 시작된 이후부터 logit값은 최소한 특정 constant scale이상으로 변화해야함 (the change in logits after the initialization is at least constant scale)Feature Learning: 학습이 시작된 이후부터 모든 layer의 activation, 즉 feature는 발산하지 않고 최대한 크게 update되어야함 (the latent representations change and adapt to the data during training, as a constant scale change after initialization in the activations directly before the readout layer)- features from each layer can be used for downstream task (like BERT)
저자들은 NN이 training을 통해 non-trivial solution을 얻고 maximum feature learning을 하기 위해서 위 세 가지 조건이 꼭 성립해야 한다고 얘기하는 것이고,
이를 실제로 계산해 수식을 유도하다보면 layer (weight)별로 LR, init_std를 잘 설정해야 해야만 한다는 muP가 유도된다고 한다.
여기서 \(\Theta( \cdot ), O(\cdot)\)는 점근 표기법 (asymptotic notation) 혹은 Big O notation이라고 하는데, CS 분야에서도 많이 쓰이지만 수학자들이 많이 쓰는 표현이다 (Greg Yang이 수학자 출신이다). 조금 recap 해보면, 보통 CS에서 Big O notation이 사용되는 맥락을 보면 어떤 list의 element 수가 n개일 때, 어떤 작업을 수행하는 데 있어 실행 시간 (시간 복잡도)가 n이 늘어남과 관계없이 유지될 때 constatnt라고 하며 (hash table access등이 이에 해당됨) 이를 \(O(1)\)으로 표기하곤 한다. unsorted list에서 어떤 item을 찾느 경우 같이 n이 2배가 되면 실행시간은 선형적으로 (linear) 2배가 되는 경우 \(O(n)\)으로 쓰며, burble sort같이 제곱으로 증가하면 \(O(n^2)\)으로 쓰며 quadratic하다고 한다.
그런데 위 문서 내용을 보면 \(O, \Theta\)가 같이 사용되고 있다.
사실 점근 표기법에는 \(O, \Omega, \Theta\) 등 다양한 기호를 사용해 쓸 수 있는데,
각각은 worst case (상한; upper bound), best case (하한; lower bound) 그리고 tight Bound를 의미한다.
그러니까 \(O(1)\)은 실행 시간을 예시로 생각했을 때 constant인 상한을 갖는 것인데,
비유를 하자면 하루에 최대 8시간 까지 일 할 수 있다고 하는 경우와 같기 때문에 매일 8시간 일을 하거나 그보다 적은 시간동안 일을 해도 된다.
하지만 \(\Theta(1)\)은 실행 시간이 constant와 같다는 걸 의미하며,
매일 정확히 8시간의 일을 해야 하는 것과 같다.
그러니까 \(\Theta(n)\)은 n이 커지면 정확히 실행 시간이 n만큼 커진다는 걸 의미하고, \(O(n)\)은 그의 상한이 n배 커지는 것이기에 실제 실행 시간을 그렇지 않을 수 있다.
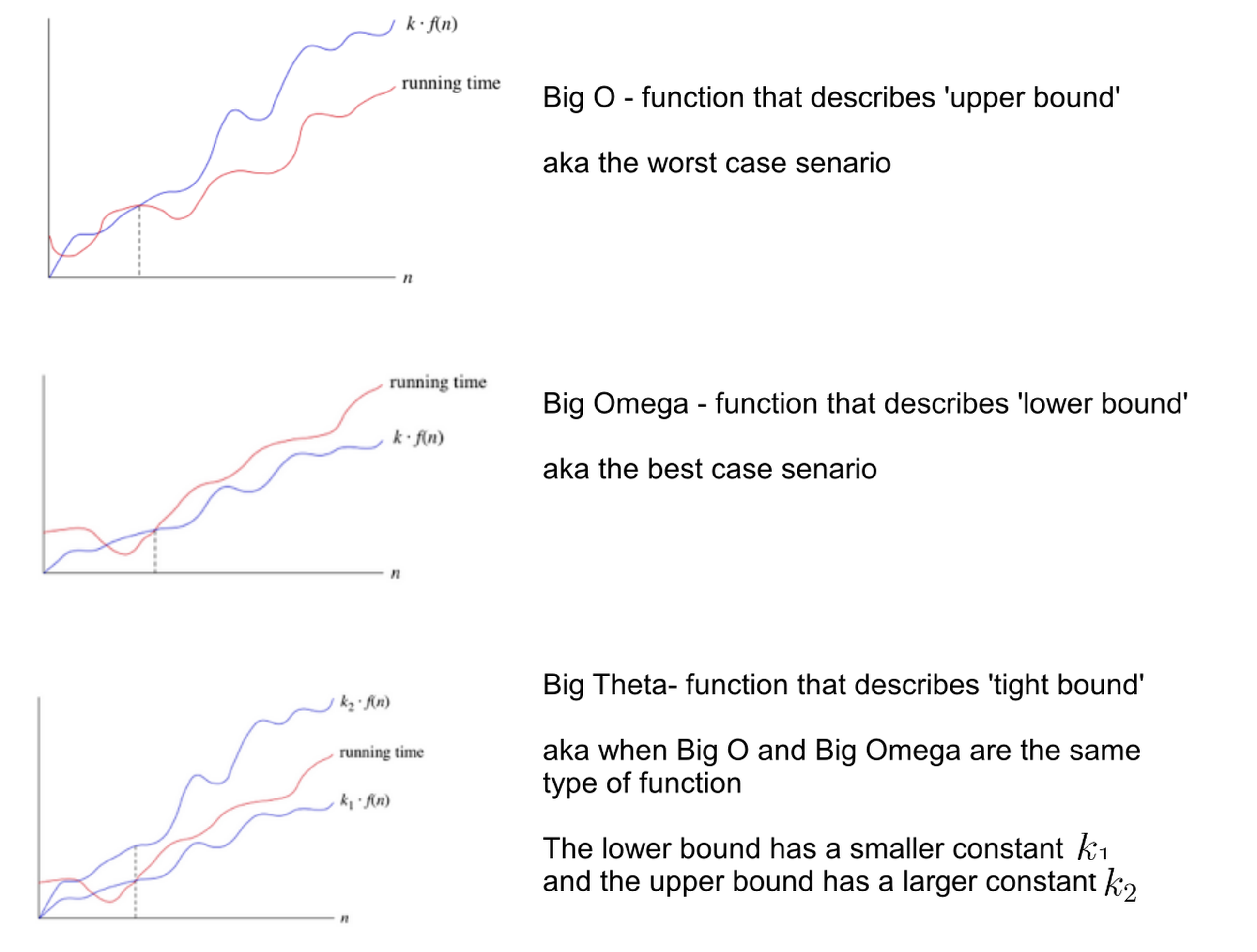 Fig. Source from here
Fig. Source from here
그러니까 muP의 바램은 다음과 같은 것이다.
- NN training 동안 어떤 시점에라도
- NN내의 모든 (pre)activation vector 들이 가 \(\Theta(1)\) sized coordinates을 가져야 하고 (즉 NN의 중간 결과물들의 각 성분의 크기가 width와 관계없이 일정하게 유지돼야 함)
- NN의 output 은 \(O(1)\)이어야 하며 (NN의 output이 일정한 상한을 가지며 width와 무관하게 일정함)
- 모든 parameter 들은 발산하지 않는 선에서 가능한 최대로 update 되어야 (변해야) 한다.
다시 말해서 muP가 원하는것은 학습이 진행되는 동안 어느 timestep에서도 (pre)activation vector의 각 coordinate별 값의 크기가 width, n과 무관하게 constant하게 유지되어야 하며, NN의 output (logit 인듯)이 항상 O(1)을 만족해야 하며, 따라서 어느 timestep에서나 모든 layer가 유의미한 feature learning이 보장되어야 한다라고 할 수 있다.
그리고 저자들은 이를 모두 만족하는 유일한 solution은 muP라고 주장한다.
Size가 \(\Theta(1)\)로 유지되어야 한다는 건 무슨의미일까?
곧 다시 언급하겠으나, 내가 이해한바가 맞다면 이는 어떤 vector가 N차원이라면 N개 element가 모두 크기가 1이어야 된다던가,
전체 vector의 norm이 1이어야 한다던가? 이런건 아니다.
width가 증가하거나 감소하는 것과 상관 없이 유지된다라는 것이 point이다.
아래는 GPT-2 architecture이지만 size가 아주 작은 model에 대해서 내가 직접 coordinate check을 한 결과이다.
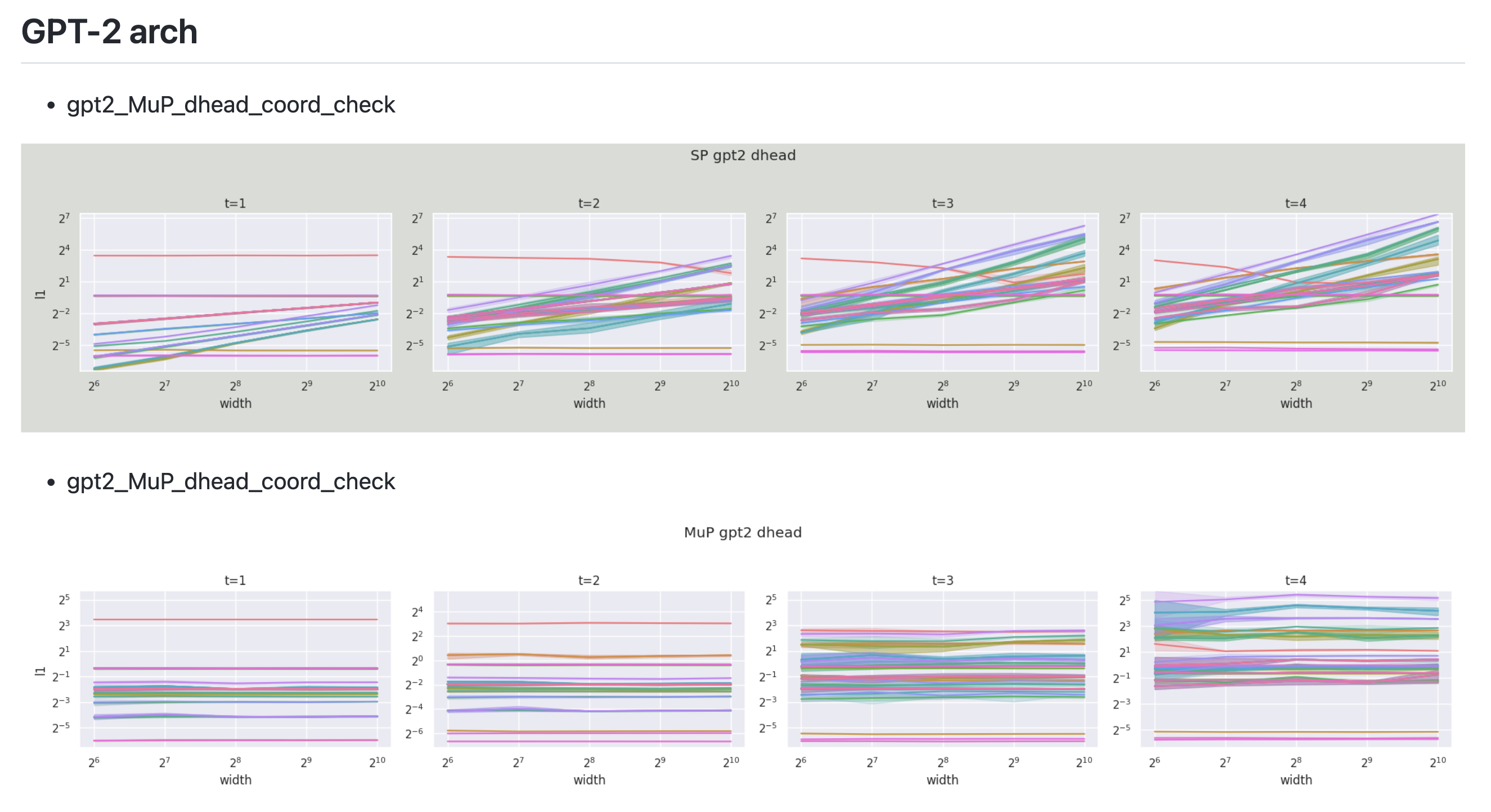 Fig.
Fig.
Figure를 보면 어떤 동일한 width에 대해서 optimization timestep이 경과할 때 y축 값이 살짝 변할 수도 있다는 걸 알 수 있다. 여기서 y value는 모든 pytorch의 layer (module)에 hook을 걸어서 layer별 activation output을 뽑아 l1 norm을 측정한 것이라고 보면 된다. 그런데 여기서 눈여겨 봐야할 점은 이 값이 조금 변하는게 아니다. 당연히 timestep이 경과할수록 이 값이 변할 수는 있지만 width에 상관없이 예를 들어 t=1에서 t=2로 갈 때 변화량이 균일하며 그렇게 크게 변하지 않았다는 것이다. 이것이 바로 muP의 핵심이며 \(\Theta(1)\)가 의미하는 바라고 나는 이해했다. Figure를 통해 우리는 muP를 적용한 것은 이 변화량이 width에 상관없이 유지되지만 SP를 사용한 경우는 width가 증가함에 따라 폭발하는 것을 알 수 있다.
아래는 llama3 model에 대해 muP를 구현하고 coordinate check을 한 것인데, 이것 또한 잘 유지되는 것으로 보인다.
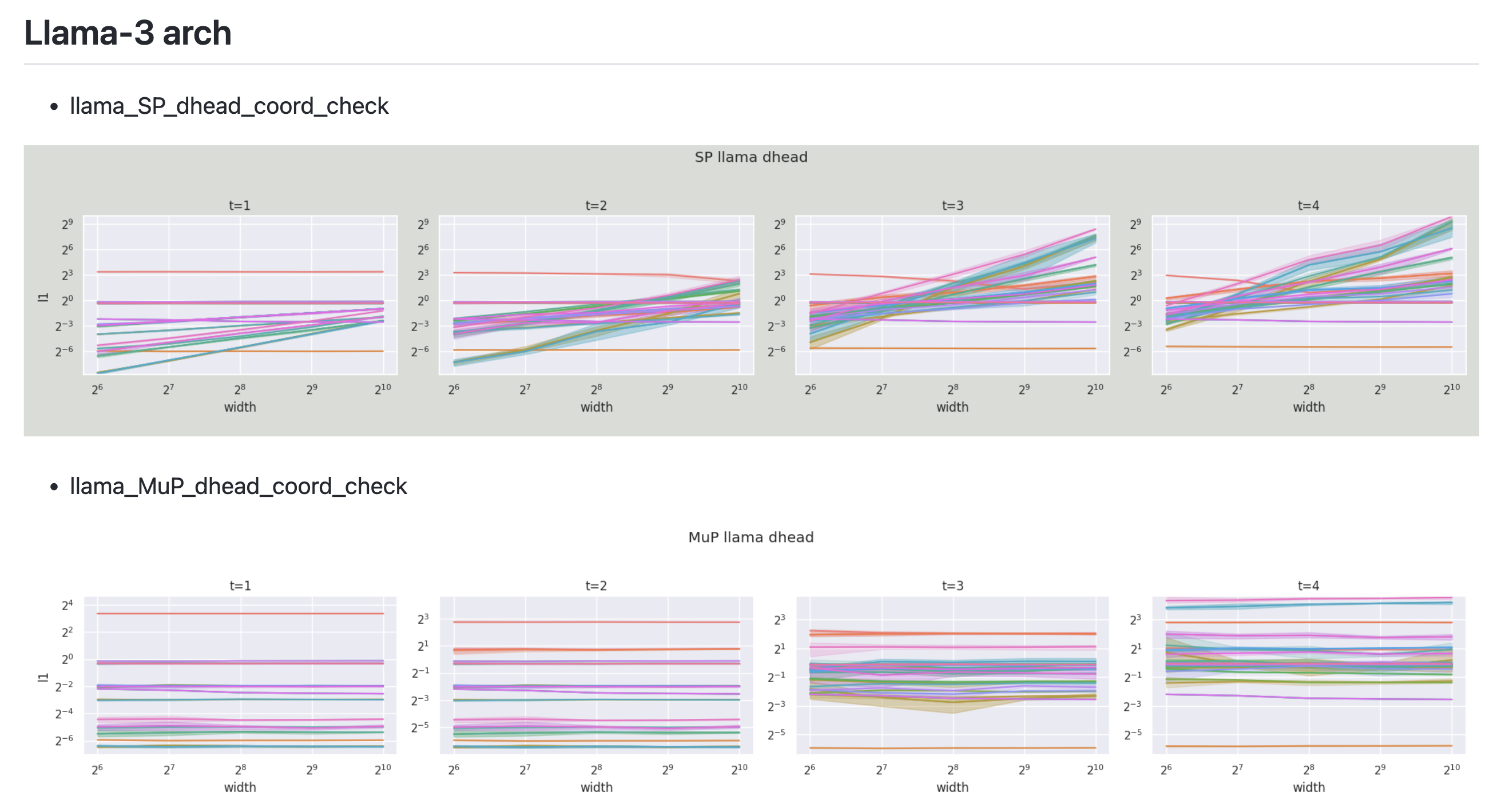 Fig.
Fig.
그래서 muP를 이제 어떻게 유도하면 되는가?
저자들은 어떤 matrix, \(A\)와 vector, \(v\)를 곱한 \(\color{red}{Av}\)의 각 coordinate size가 \(A,v\)가 서로 correlation이 있을 때 \(A,v\) 각각의 coordinate size가 어떻게 달라지는지를 주의 깊게 고려해야 한다고 한다. 당연히 여기서 \(A\)는 NN의 어떤 weight matrix이며, \(v\)는 activation vector로 생각할 수 있으며, \(A\)가 어떤 종류의 matrix이고 \(v\)가 어떤 종류의 vector인지에 따라 \(Av\) entry의 변화양상 (?)이 다르다고 한다. 그런데 NN에서 \(A\)는 사실상 두 가지로 밖에 안 나뉜다.
- (type 1) 이런 vector들의 outer product로 만들어진 matrix
- (type 2) iid sampling된 matrix
이 중에서 type 2는 initialized weight matrix임을 바로 알겠다.
그런데 type 1은 뭘까?
이는 weigth matrix의 gradient을 의미한다.
그런데 wegiht matrix의 gradient가 activation 같은 vector와 외적 (outer product)하는 경우가 왜 존재하는걸까?
이는 backpropagation을 하면 weight의 gradient는 결국 upstream gradient와 layer input의 outer product로 계산이 되기 때문이며,
우리가 nn을 학습하게 되면 weight matrix, \(W\)를 gradient descent에 따라 update하게 되는데,
예를 들어 한 번 SGD를 하게 되면 \(W + \eta \cdot \color{red}{\Delta W}\)가 되므로 (\(\eta\)가 lr),
weight gradient와 activation을 곱하는 일도 발생할 수가 있는 것이다.
여기서 만약 \(A,v\)의 각 entry들이 모두 \(\Theta(1)\)이고, training 중에 자연스럽게 발생하는 방식으로 correlation이 있다면 아래 table을 비로소 얻을 수 있다는 것이 저자들의 주장이다.
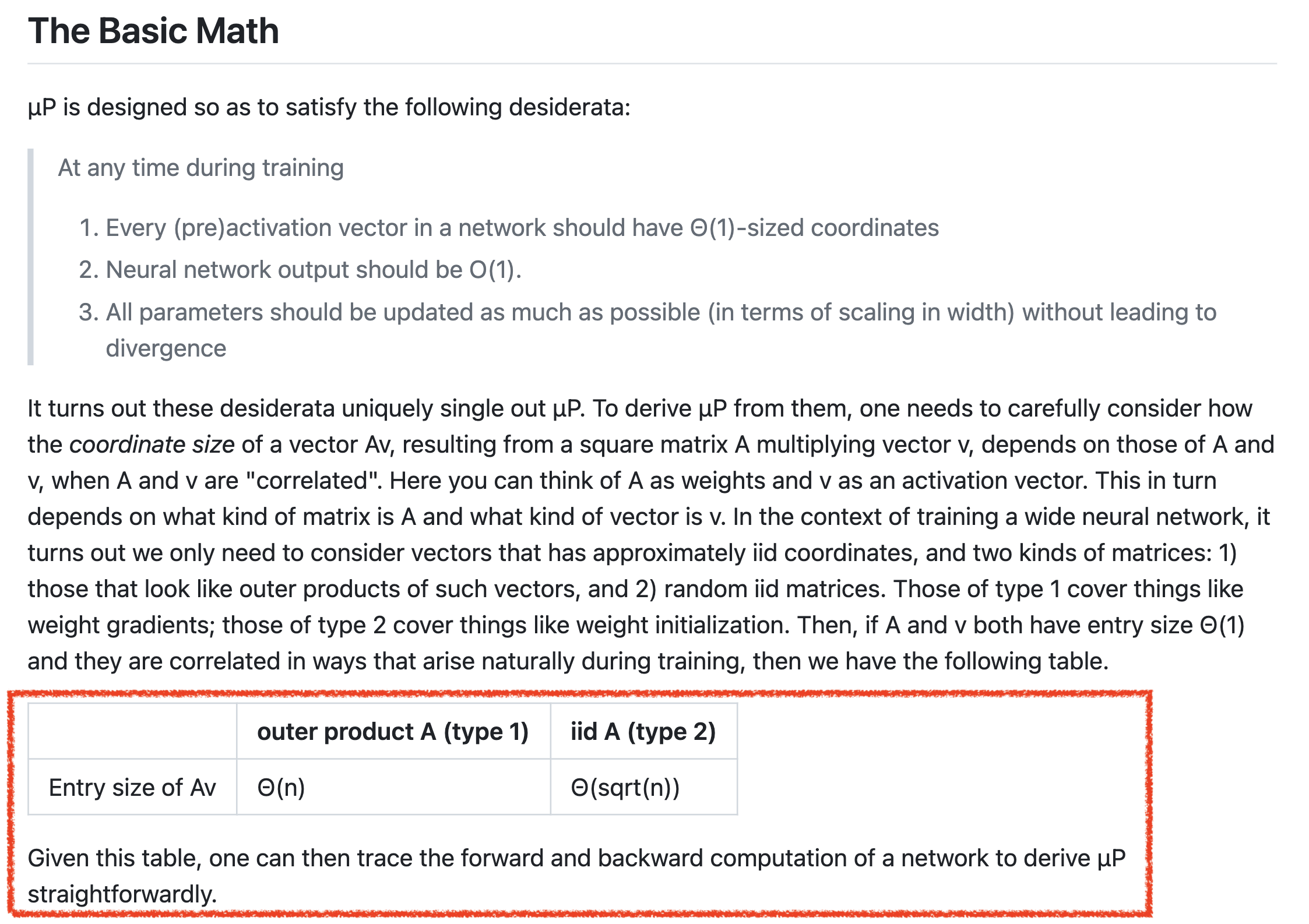
그리고 저자들은 이 table 을 가지고 NN forward, backward 계산을 직접 해보면 muP를 쉽게 유도해낼 수 있을거라고 한다.
Central Limit Theorm (CLT) and Law of Large Numbers (LLN)
이제 entry size of \(Av\)가 \(A\)의 type에 따라서 \(\Theta(n), \Theta(\sqrt{n})\)이 되는이유에 대해 생각해보자. 이를 이해하기 위해서는 두 가지 수학적 (통계적) convergence theorm이 중요하게 쓰이는데, 이 두 가지는 각각 큰 수 (대수)의 법칙 (Law of Large Numbers; LLN)와 중심 극한 정리 (Central Limit Theorem; CLT)이다.
먼저 LLN은 무작위로 뽑은 n개의 sample, 즉 n개의 random variable의 mean은 n이 매우 클 때 (무한대에 가까워 질 때) 모집단의 mean과 같아진다는 통계와 확률 분야의 기본 개념이다.
\[\frac{1}{n} \sum_{i=1}^n x_i \rightarrow \mathbb{E}[X], \text{as } n \rightarrow \infty\]여기서 각 sample은 서로에게 영향을 받지 않고 같은 distribution에서 sampling되어야 한다는 independent identical distributed (iid) assumption이 있는데, 쉽게 말해서 동전을 1000번 던질 때 550번째 동전의 확률은 이전 1~549번의 동전 던지기의 결과와 무관하며, 매 시행시 동일하게 1/2의 bernoulli distribution을 갖는다는 것이다.
CLT는 마찬가지로 iid sample에 대한 convergence theorm로, n개 sample의 mean의 분포는 n이 적당히 크다면 (마찬가지로 무한대에 가까우면) 정규 분포 (normal distribution)에 가까워진다는 것으로, 매우 불규칙한 분포도 충분히 많은 수를 더하면 결국 정규 분포로 수렴한다는 내용이다. 즉 어떤 \(\mathcal{N}(\mu, \sigma^2)\)에서 \(n\)개를 뽑아 이 \(n\)개의 mean값인 \((\sum_{i=1}^n x_n) /n\)의 분포를 찍어보면 이는 \(\mathcal{N}(\mu, \sigma^2 / n)\)을 따르게 된다. 종종 CLT를 햇갈리는 경우가 있는데, 이는 어떤 모집단에서 sampling을 하던 (binomial이던, gaussian이던) 그 sample들의 mean 값인 sampled mean의 분포가 정규 분포로 수렴한다는 것이지, sample을 여러개 뽑으면 그 sample들의 분포가 정규 분포가 되는건 아니다.
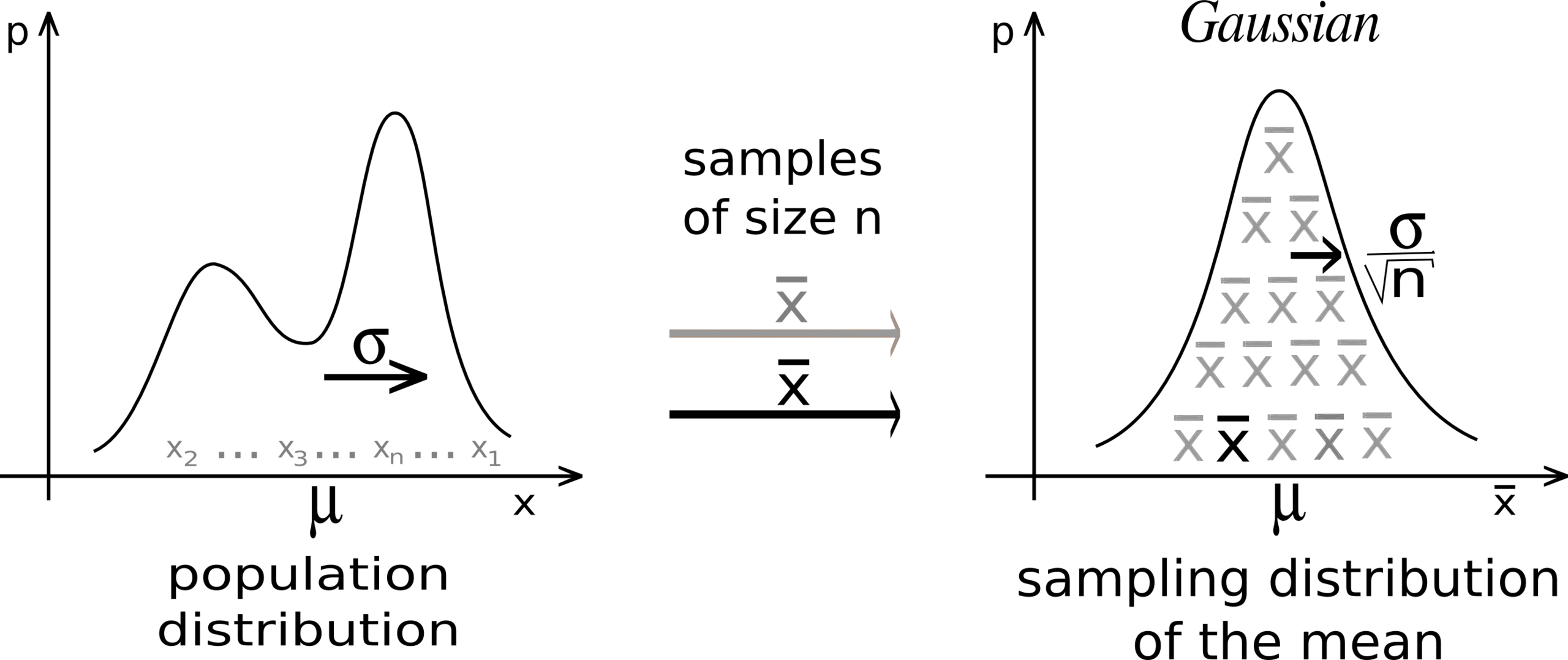 Fig. Source from wiki
Fig. Source from wiki
CLT는 \(x_1, \cdots, x_n\)의 mean이 \(0\)이라고 가정하면 다음과 같이 쉽게 쓸 수 있다.
\[\begin{aligned} & \frac{1}{\sqrt{n}} \sum_{i=1}^n x_i \rightarrow \mathcal{N}(0, \sigma^2), \text{as } n \rightarrow \infty & \\ & \text{where } \mathbb{E} [x_1^2] = \sigma^2 & \\ \end{aligned}\] \[\begin{aligned} & \frac{1}{\sqrt{n}} \sum_{i=1}^n (x_i - \mathbb{E}[X]) \rightarrow \mathcal{N} (0, \sigma(X)^2), \text{as } n \rightarrow \infty & \\ \end{aligned}\]여기서 만약 mean값이 \(0\)이 아니라 (non-zero) \(\mu\)인 더 일반적인 상황을 가정하면 sasmple들의 합인 \(\sum_{i=1}^n x_i\)는 다음과 같다.
\[\begin{aligned} & \sum_{i=1}^n x_i = \underbrace{n \mu}_{\text{by LLN}} + \underbrace{\sqrt{n} \sigma \mathcal{N}(0, 1)}_{\text{by CLT}} + \text{ low order terms ...} & \\ & \text{where } \mathbb{E}[x_1] = \mu \text{ and } \mathbb{E} [x_1^2] = \sigma^2 & \\ \end{aligned}\]여기서 아래 두가지 사실이 쓰였다.
\[\begin{aligned} & \text{Fact: if } X, Y \text{ are independent}, Var(X+Y) = Var(X) + Var(Y) & \\ & Var(cX) = c^2 Var(X) & \\ \end{aligned}\]직관적으로 위 수식은 \(\mathcal{N}(\mu, \sigma)\)에서 sampling된 sample 1개는 \(\mu+\sigma \mathcal{N}(0,1)\)의 값을 크게 벗어나지 않을테니 당연하게 받아들일 수 있을 것이다. 위 수식이 말하는 바는 정리하자면 n개 sample의 합은 non-zero mean을 가질 경우 LLN에 의해 dominant하고, 그 다음으로 CLT에 의해 variance에 subdominant하다고 할 수 있다.
곧 나오겠지만 우리는 어떤 term이 NN연산에 가장 크게 contribute하는지에 따라서 \(1/n\) or \(1/\sqrt{n}\)로 scaling할지를 정하게 될 것이다.
from CLT and LLN to muP (Type 1 (Comfort Zone) vs Type 2 (Unfamiliar Territory))
그런데 왜 LLN과 CLT 얘기를 하는 걸까?
아마 눈치를 챘겠지만 (pre-)activation vector와 weight matrix의 multiplication 결과물인 \(Av\)는 사실상 매우 많은 vector간 dot product를 병렬화 한 것이나 다름이 없고, 두 \(n\) size의 vector를 dot product 하는 것은 각각의 element를 곱해서 \(n\)번 더한 것이기 때문이다.
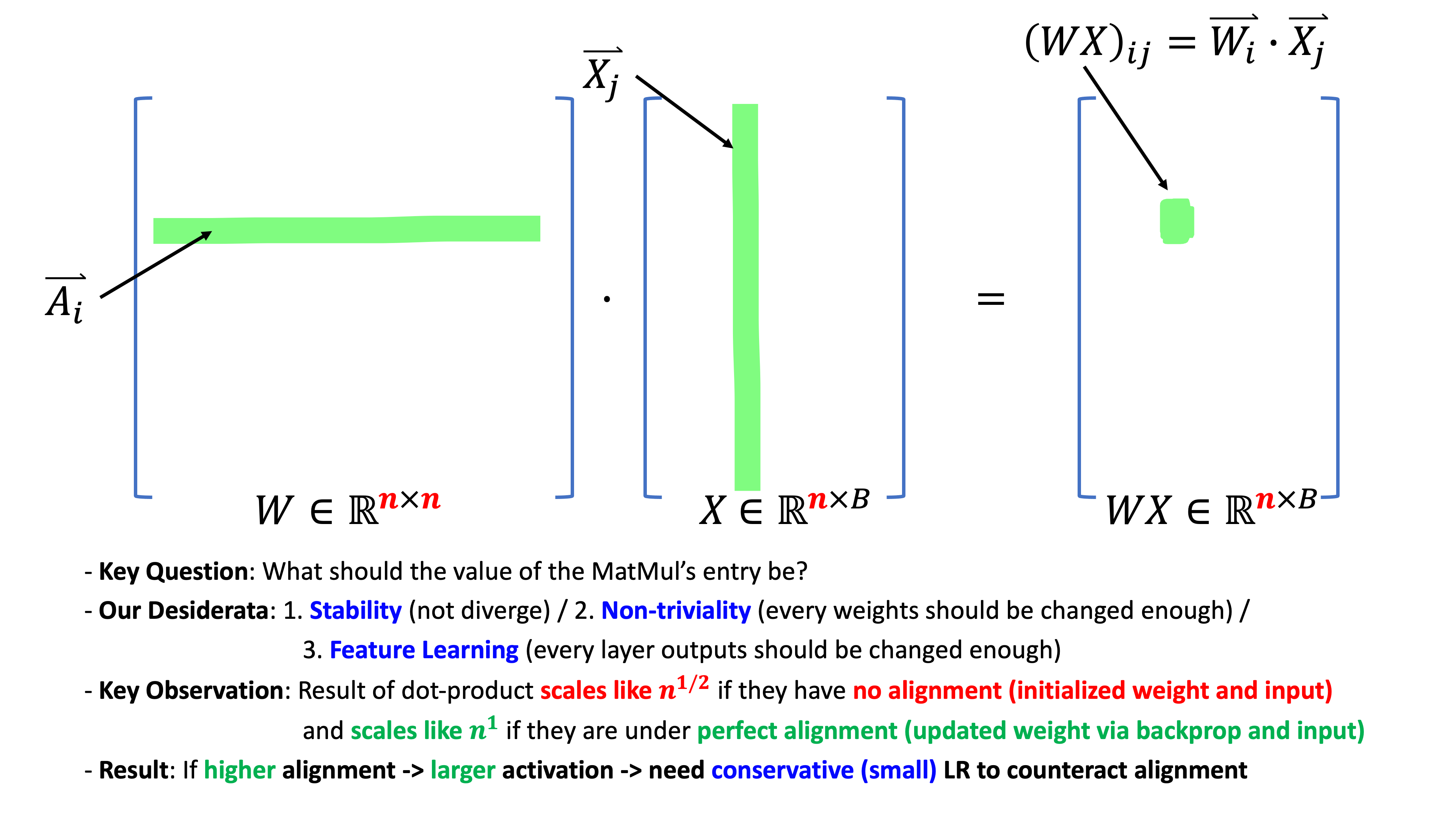 Fig. TL;DR of muP
Fig. TL;DR of muP
보통 NN의 layer별 weight matrix, \(A\)는 zero mean, \(\sigma\) variance인 gaussian로부터 iid sampling 된 값들로 initialization 된다.
즉 \(A\) matrix의 첫 번째 row vector는 iid인 셈이고 input vector는 어떤 값이 될지는 모르겠지만,
우선 적당히 큰 width의 NN에 대해서 모든 (pre-)activation은 대략적으로 iid coordinate을 가질 것이라는 직관이 있다.
(이에 대한 증명은 TP-3, 4에 나와있다고 한다. 어떤 N번째 layer의 input, pre-activation은 이전 N-1번째 layer의 activated output일텐데 이 값이 infinity나 zero로 발산하거나 수렴하지 않는다고 한다.)
 Fig. training time 어느 시점 (any time)에서도 (pre-)activation vector와 이것의 gradient vector (즉 previous layer 시점에서는 upstream gradient)는 width가 충분히 크다면 roughly iid 이다.
Fig. training time 어느 시점 (any time)에서도 (pre-)activation vector와 이것의 gradient vector (즉 previous layer 시점에서는 upstream gradient)는 width가 충분히 크다면 roughly iid 이다.
이제 \(Av\)를 계산해보자. Matrix, \(A\)의 entry들이 \(\mathcal{N}(0, \sigma^2)\)에서 sampling 됐다고 할 때, Matrix, \(A \in \mathbb{R}^{m \times n}\)와 이전 layer의 output activation, \(v \in \mathbb{R}^{n \times 1}\)에 대해 matrix multiplication을 하면 \(Av \in \mathbb{R}^{m \times 1}\)가 되는데, 이 output vector의 entry는 다음과 같이 쓸 수 있다.
\[(Av)_i = \sum_{j=1}^n A_{ij} v_j\]즉 matrix, \(A\)의 row와 vector, \(v\)의 dot product가 element 하나를 만들게 되는 것이다. 여기서 CLT가 쓰이게 되는데, 직관적으로 NN의 width, \(n=j\)이 커짐에 따라 \(Av\)의 entry 값 하나는 CLT에 따라 아래의 normal distribution으로 수렴하게 된다.
\[\frac{1}{\sqrt{n}} (A_{i1}v_1 + \cdots + A_{in}v_n) = \mathcal{N} (0, \sigma^2)\]왜냐하면 우리의 바람 대로라면 \(v\)의 각 성분 \(v_j\)는 \(\Theta(1)\)이며, 두 vector는 모두 zero mean distribution에서 iid sampling 됐기 때문이다. 이 말인 즉 \(A_{i1} v_1 \in \mathbb{R}^{1 \times 1}\)의 std가 \(\sqrt{n}\sigma^2\)이므로, matrix의 각 entry들은 통계적으로 std의 범위를 크게 벗어나지 않게 되기 때문에, output, \(Av_{i}\)는 \(\Theta(\sqrt{n})\)에 bound되어 있다는 말이 되는데, 앞서 말한 LLN vs CLT에서 덧셈을 하는 값이 zero mean, iid이기 때문에 variance가 dominant해지는 것이다.
이는 앞서 He init과 같은 상황으로 우리가 init 시점에서 forward pass의 activation을 \(\Theta(1)\)로 만들려면 \(\sigma=\frac{1}{\sqrt{n}}\)으로 설정하면 될 것이다.
반면에 만약 \(A,v\)가 non-zero mean을 갖거나 correlation이 강하게 생기면 이들의 element-wise multiplication의 합은 더이상 CLT를 따르지 않게 되고 LLN을 따르게 된다고 하는데, 이는 matmul type이 type 1인 경우를 의미한다. type 1 (outer product)가 LLN을 따르는 이유는 backpropagation과 gradiet descent 때문에 weight gradient와 (pre-)activation이 곱해지기 때문이다. 이 때 이전 training timestep에서의 weight gradient, \(\Delta A_{t}\)는 아래와 같이 계산된다.
\[\begin{aligned} & A_{t+1} v' = (A_{t} + \eta \Delta A_{t}) v' & \\ & = (A_{t} + \eta \frac{\partial L}{ \partial A_{t}}) v' & \\ & = (A_{t} + \eta \color{blue}{g_t v^T}) v' \text{ where } g_t \text{ is upstream grad} & \\ & = A_{t} v' + \eta g_t ( v^T v') & \\ & = A_{t} v' + \color{red}{n} \eta g_t \underbrace{\frac{( v^T v')}{\color{red}{n}}}_{\text{type 1: LLN}} & \\ \end{aligned}\]여기서 NN이 training 될 때 LR이 매우 크지 않다면 weight update 되는 량은 작을 것이고 (\(\Delta A \approx 0\)),
더군다나 width가 충분히 큰 NN 부터는 weight update도 크게 되지 않기 때문에 (lazy training regime) 어떤 layer의 ouptut은 같은 data distribution의 서로 다른 sample에 대해서 크게 다르지 않은 vector를 return할 것이다.
즉 NN의 mini-batch가 다르더라도 \(n\)번째 layer의 이전 timestep에서의 input feature, \(v=v_{t+1}\) 는 \(v'=v_t\)와 correlation이 매우 클 것이다.
이제 우리는 LLN에 따라서 \((v^T v' / n)\)는 deterministic scalar, \(R\)로 수렴한다고 생각할 수 있다.
즉 이 경우는 random gaussian matrix와 input vector간의 matmul가 CLT를 따라 수렴한 값 보다 \(\sqrt{n}\)배 크다는 결론에 도달할 수 있는 것이다.
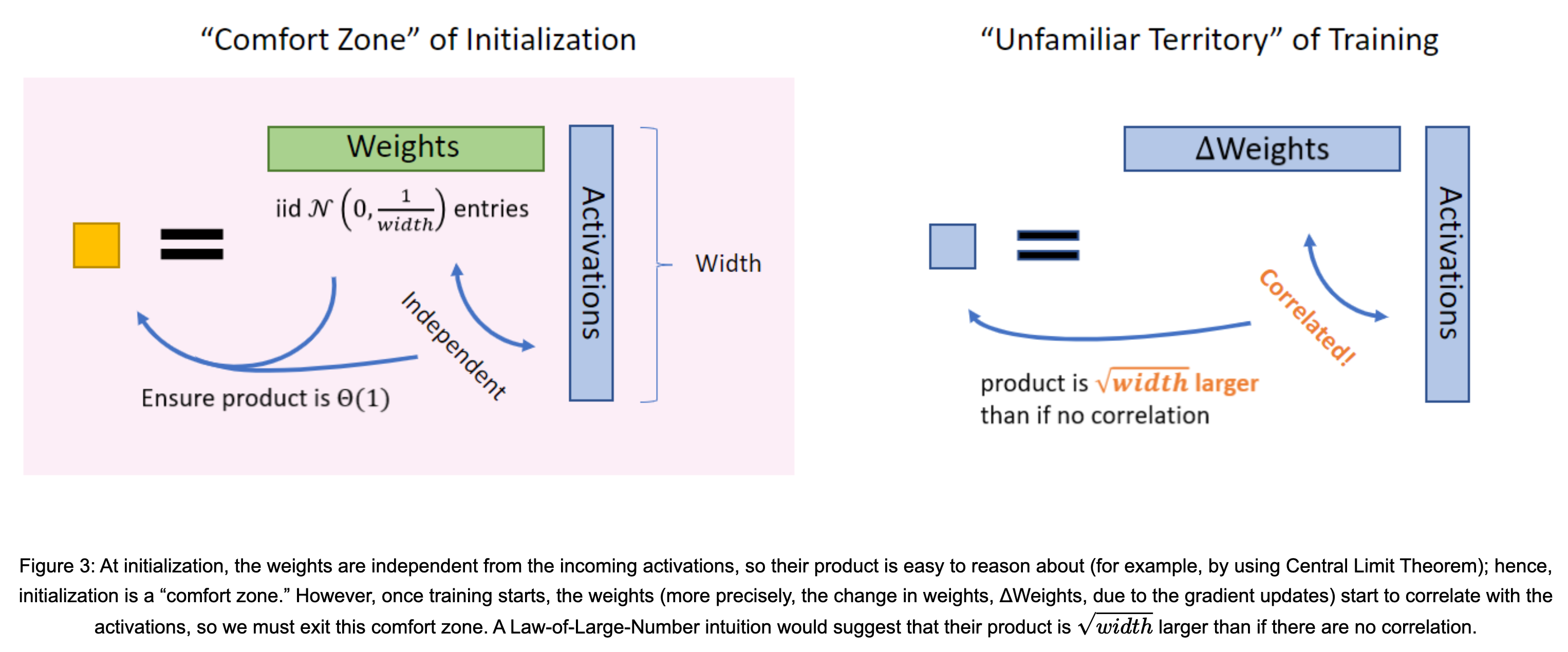 Fig. Type 1 (Comfort Zone) vs Type 2 (Unfamiliar Territory). Source from Microsoft Blog for muP
Fig. Type 1 (Comfort Zone) vs Type 2 (Unfamiliar Territory). Source from Microsoft Blog for muP
그런데 activation들이 iid sampled vector인 것도 장담할 수 없는데 LLN이 통하는걸까? 그리고 iid라고 해도 dot product는 iid vector간의 element wise product를 sum한 값이지 않은가? 그 이유는 수많은 실험을 통해 분석한 결과 roughly iid가 성립하고, stable parameterization 이라면 두 vector 모두 \(\Theta(1)\) coordinates을 가지기 때문이라고 한다. (더 자세한 내용과 수학적인 엄밀함은 TP-4, 5를 자세히 읽어도 좋고 이 post의 후반부에서도 다루기도 할 것)
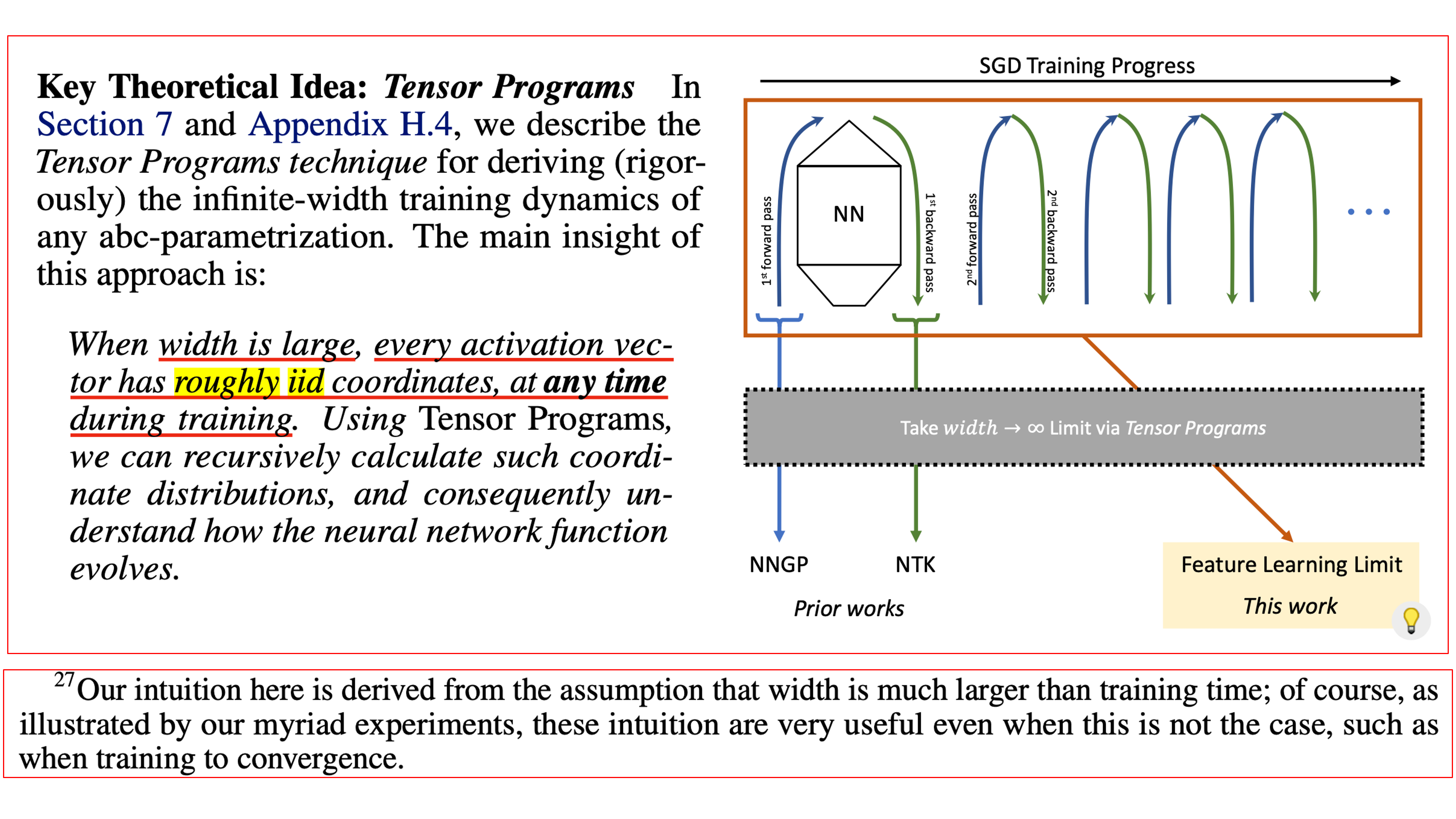
TP-5의 appendix에는 아래와 같은 내용도 있다.
 Fig. LLN and CLT for “look like” random independent samples (1)
Fig. LLN and CLT for “look like” random independent samples (1)
 Fig. LLN and CLT for “look like” random independent samples (2)
Fig. LLN and CLT for “look like” random independent samples (2)
정리하자면 large scale NN training의 수많은 matmul의 output scale을 muP에서는 weight matrix의 type에 따라 총 2가지 convergence theorm, CLT and LLN을 이용해 아래 table로 정리했다.

그런데 "우리가 궁극적으로 원하는 것은 모든 (pre-)activation들이 constant scale, \Theta(1)을 가져게 만들어 training stability를 높히고 나아가 maximal feature learning까지 달성하는 것"이지 않는가?
이제 우리는 matrix type이 어떤 것이냐에 따라서,
즉 matmul output의 entry가 LLN과 CLT중 무얼 따라 결정되느냐에 따라 weight init std, LR 그리고 multiplier 까지 정할 수 있게 되었고 이것이 muP의 핵심이다.
 Fig.
Fig.
 Fig.
Fig.
Why SP Sucks?
이제 muP를 위한 기본 concept과 basic math에 대해 이해하게 됐으니 왜 SP가 안좋은지에 대해 생각해보자. 먼저 1 hidden layer를 갖는 linear perceptron를 SGD update하는 경우에 대해 생각해보자.
\[f(x) = V^{\top}U x\]이는 non linearlity가 없고 scalar input, scalar output을 갖는 form이며, 각 weight matrix는 \(V, U \in \mathbb{R}^{n \times 1}\)이 된다.
SP를 따르면 각각의 alpha, \(\alpha \in [n]\)에 대해서 \(V_{\alpha} \sim \mathcal{N}(0,1/n), U_{\alpha} \sim \mathcal{N}(0,1)\)을 갖게 된다. 이러한 sampling은 초기화 시점에는 network output, \(f(x) = \Theta(\vert x \vert)\)를 보장한다고 한다.
이제 1 step SGD를 한다고 생각해보자. 그럼 각 weight matrix는 다음과 같이 update 될 것이다.
\[\begin{aligned} & V' \leftarrow V + \theta U & \\ & U' \leftarrow U + \theta V & \\ \end{aligned}\]여기서 \(\theta\)는 여기서 θ는 input, label, objective function에 따라 결정되는 크기가 \(\Theta(1)\)인 scalar 라고 하는데, 이는 loss로부터 propagate되는 upstream gradient 등을 의미하는 것으로 정확히는 아래처럼 계산할 수 있을 것이다.
\[\begin{aligned} & V' \leftarrow V + \eta \frac{\partial L}{\partial V} = V + \eta \frac{\partial L}{\partial f} \frac{\partial f}{\partial V} = V + \underbrace{\eta \frac{\partial L}{\partial f} Ux}_{\theta U} & \\ & U' \leftarrow U + \eta \frac{\partial L}{\partial U} = U + \eta \frac{\partial L}{\partial f} \frac{\partial f}{\partial U} = U + \underbrace{\eta \frac{\partial L}{\partial f} Vx}_{\theta V} & \\ \end{aligned}\]아마 서로 다른 두 weight matrix가 서로의 학습에 관여한다는 얘기를 하고 싶었던 것 같은데, 이제 lr, \(\eta=1\)에 대해 1 step param update를 하고 난 뒤의 network output은 다음과 같이 계산할 수 있다.
\[\begin{aligned} & f(x) = V'^{\top}U' x & \\ & = (V^{\top}U + \theta U^{\top}U + \theta V^{\top}V + \theta^2 U^{\top} V) x & \\ \end{aligned}\]여기서 문제가 생기는데, \(n \rightarrow \infty\)인 경우 1 step SGD update를 한 것 만으로도 network output이 blow up하게 되는데 그 이유는 LLN에 따라 \(U^{\top} U = \Theta(n)\)이기 때문에 \(n\)에 비례해서 output 또한 \(\infty\)로 발산하기 때문이다. (\(U_{\alpha} \sim \mathcal{N}(0,1)\)에 대해 \(U^{\top} U= \sum_{i=1}^n U_i^2\)이므로 \(\Theta(n)\)는 당연해 보인다)
How muP Fixes Problem
이제 여기에 muP를 적용하자.
현재 1 layer perceptron 상황에서 muP를 따르려면 output layer, \(V_{\alpha}\)는 SP와 다르게 \(\mathcal{N} (0,1 / \text{fan-in}^2) = \mathcal{N}(0, 1/n^2)\) 분포를 따라 sampling하고, input layer인 \(U_{\alpha}\)는 SP처럼 \(\mathcal{N} (0,1 / \text{fan-in}) = \mathcal{N} (0,1)\)을 따르게 된다. (hidden layer는 없음)
그리고 SGD를 쓰는 경우 모든 layer에 \(\eta=1\)만큼의 LR이 적용되던 것과 달리 (only global LR), 각각 \(\eta_V = \eta \cdot 1/n = 1/n, \eta_U = \eta \cdot n = n\)의 LR이 각각 적용될 것이다. 이제 마찬가지로 1 step SGD를 하면 update 수식이 조정된 LR을 따르므로
\[\begin{aligned} & V' \leftarrow V + \frac{\theta}{\color{red}{n}} U & \\ & U' \leftarrow U + \color{red}{n} \theta V & \\ \end{aligned}\]network output은 다음과 같이 변하게 된다.
\[\begin{aligned} & f(x) = V'^{\top}U' x & \\ & = (V^{\top}U + \theta \color{red}{n^{-1}} U^{\top}U + \theta \color{red}{n} V^{\top}V + \theta^2 U^{\top} V) x & \\ \end{aligned}\]똑같이 LLN을 따라 생각해보면 \(U^{\top} U\)는 여전히 \(\Theta(n)\)이지만 width, \(n\)만큼 discount 되므로 \(\Theta(1)\)이 되어 blow up 하지 않는다 (stable 해진다) 그리고 \(V^{\top}V = \sum_{i=1}^n V_i^2 = \Theta(1/n)\)이지만 \(n\)이 이를 counter하게 된다.
Simple MLP Example with muP
이제 simple 2 layers Multi Layer Perceptron (MLP)를 gradient descent로 학습하는 경우에 대해서 생각해보자. 이 내용은 TP-5에 나와있는데, TP-4가 훨씬 내용이 복잡해 보이기 때문에 앞으로 TP-5를 위주로 설명하고 detail이 필요할 경우 TP-4의 내용을 가져오도록 하겠다. SP를 따르는 MLP를 수식으로 쓰면 다음과 같다.
\[\begin{aligned} & \text{for } n = \text{width}, d_{in} = \text{data dimension} & \\ & f(\xi) = W^{3\top} \phi (W^{2\top} \phi(W^{1\top} + b^1) + b^2) & \\ & \text{with init. } W^1 \sim \mathcal{N}(0, \frac{1}{d_{in}}), W^{\{2,3\}} \sim \mathcal{N}(0, \frac{1}{n}), b^{\{1,2\}} = 0, Lr = \eta & \\ \end{aligned}\]Greg은 이런 SP init method들의 문제점은 NN의 training dynamics를 전혀 고려하지 않는다고 하는데, 여기서 말하는 training dynamics는 일련의 gradient 같은걸 말한다 (gradient sequence?). 즉 어떻게 이 gradient가, optimization process가 흘러야 하는지에 대한 고려가 없다는 것이다. 즉 앞서 살펴봤던 type 1, 2 matrix에 따르면 type 2에 대한 고려는 있지만 type 1에 대한 고려는 없다는 말을 하고싶은 것이다.
이 MLP 문제에서 muP을 사용하는 것 만으로도 width가 넓어짐에 따라 무조건 좋은 성능 (the wider the better)을 같은 optimal HP에서 보일 수 있다고 하는데,
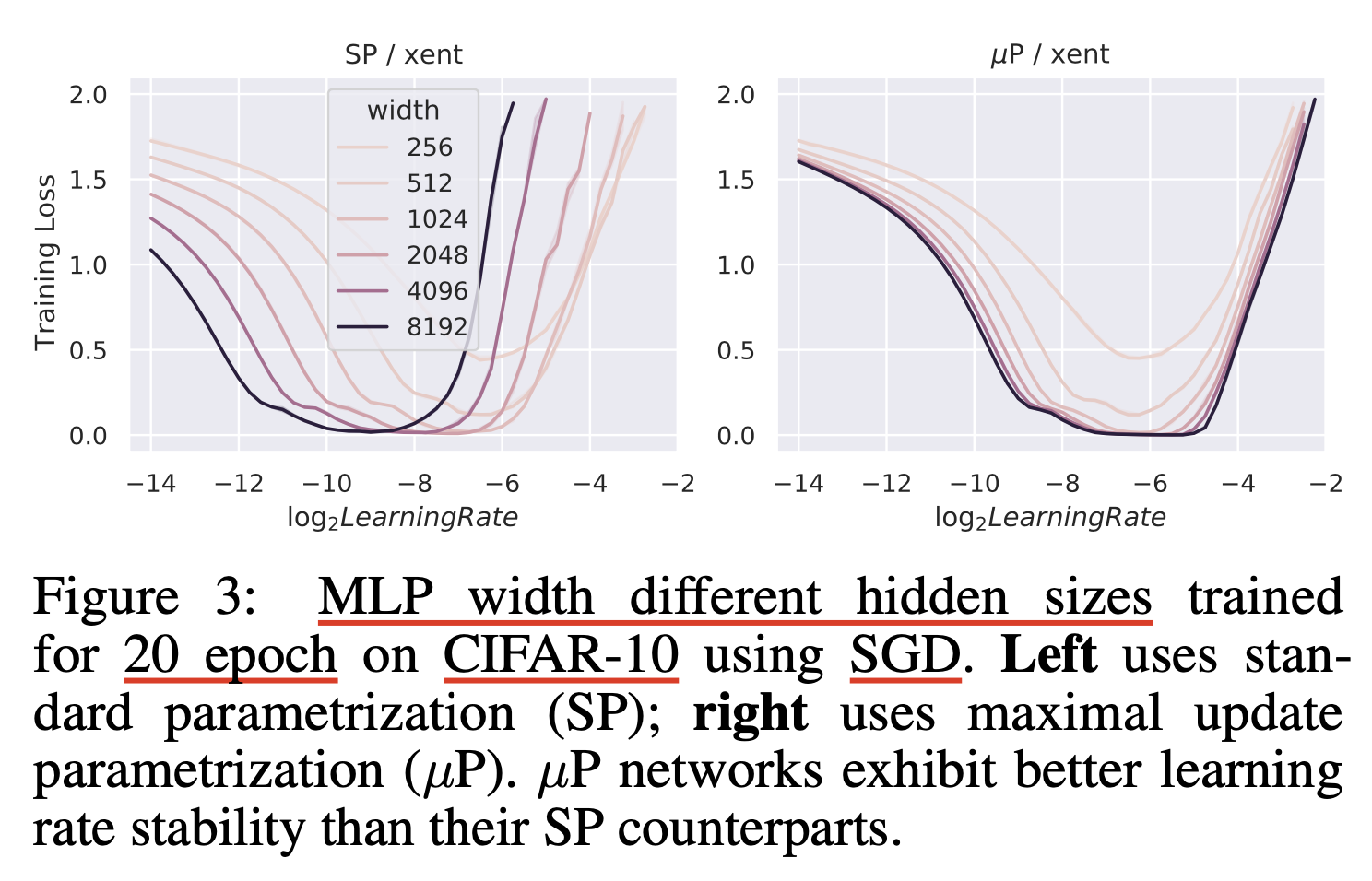 Fig.
Fig.
muP를 사용할 경우 아래와 같이 parameterization이 된다.
\[\begin{aligned} & \text{for } n = \text{width}, d_{in} = \text{data dimension}, & \\ & W^{1} \in \mathbb{R}^{d_{in} \times n}, W^{2} \in \mathbb{R}^{n \times n}, W^{3} \in \mathbb{R}^{n \times d_{out}}, b^{\{1,2\}} \in \mathbb{R}^{n}, & \\ & \phi = ReLU, \text{Loss fct} = \text{X-entropy} & \\ & f(\xi) = W^{3\top} \phi (W^{2\top} \phi(W^{1\top} + b^1) + b^2) & \\ & \text{initialize } W^{1} \sim \mathcal{N}(0,\frac{1}{d_{in}}), W^{2} \sim \mathcal{N}(0,\frac{1}{n}), W^{3} \sim \mathcal{N}(0,\frac{1}{\color{red}{n^2}}), b^{\{1,2\}} = 0 & \\ & \text{with SGD Lr } \eta_{W^1} = \eta_{b^1} = \eta_{b^2} = \eta \color{red}{n}, \eta_{W^2} = \eta, \eta_{W^3} = \eta \color{red}{n^{-1}} & \\ \end{aligned}\]여기서 \(\eta\)는 master LR (lr)이라고 하며,
빨간색으로 표시된 부분이 SP와 muP간의 key difference이다.
보면 SP에서는 \(W^2, W^3\)가 input dimension의 역수를 std로 갖는 gaussian distribution을 따라 init되었지만,
muP에서는 \(W^3\)가 input dimension의 sqrt의 역수가 된 것을 알 수 있고,
모든 layer에 동일한 master lr이 적용되던 것에서 bias와 weight의 lr이 다르게 적용되고,
hidden layer의 weight과 input 쪽, output 쪽 layer의 lr은 모두 다르다는 것을 알 수 있다.
이것이 muP의 가장 Basic Form이다.
아래는 앞서 introduction에서 살짝 언급한 muP를 위한 table 이며,
방금 MLP에 적용된 parameterization rule이 summarize되어있다.
 Fig.
Fig.
이 table은 방금 말한 것 처럼 NN이 학습되는 동안 어느 시점의 weight matmul의 결과값이 width에 따라 크게 달라지지 않도록 하기위한 처리를 한 것이라고 보면 된다.
저자들은 table 3, basic form을 추가적으로 변형할 수 있다고 하는데,
예를 들어 매 \(n\)이 등장할 때 마다 (tune-able) multiplicative constants (multiplier)를 곱해줄 수 있다고 한다.
여기서 tuna-able이라는 의미는 lr 처럼 우리가 최적의 multiplier를 search해야 한다는 걸 의미한다.
(learnable과 헷갈리지 말자)
예를 들어서 \(\tilde{n} \stackrel{\mathrm{def}}{=} n / n_0\)라는 constant를 도입하면 위의 수식은 아래처럼 변형될 수 있는데,
\[\begin{aligned} & \text{initialize } W^{1} \sim \mathcal{N}(0,\frac{1}{d_{in}}), W^{2} \sim \mathcal{N}(0,\frac{1}{n}), W^{3} \sim \mathcal{N}(0,\frac{1}{n \cdot \color{blue}{ \tilde{n}}}), b^{\{1,2\}} = 0 & \\ & \text{with SGD Lr } \eta_{W^1} = \eta_{b^1} = \eta_{b^2} = \eta \color{blue}{\tilde{n}}, \eta_{W^2} = \eta, \eta_{W^3} = \eta \color{blue}{\tilde{n}^{-1}} & \\ & \text{where } \tilde{n} \stackrel{\mathrm{def}}{=} n / n_0 & \\ \end{aligned}\]여기서 \(\tilde{n} \stackrel{\mathrm{def}}{=} n / n_0\)이기 때문에 \(n\)이 base width, \(n_0\)인 경우 파란색으로 표시된 \(\tilde{n}=1\)이 되므로 완전히 SP와 같아지게 된다. 조금 헷갈리 수 있는데, \(n\)이 들어갈 수 있는 자리마다 multiplier를 끼워넣을 수 있는 것이므로 output weight의 경우 \(n^2\)이지만 하나만 \(\tilde{n}=n/n_0\)로 치환이 된 것이다. 하지만 당연하게도 \(n\)이 커지면 SP의 수식과 매우 빠르게 달라지게 된다 (deviate).
즉 이부분이 시사하는 바는 \(n_0 = 128\) width의 Transformer나 ResNet model을 학습해서 좋은 결과를 얻는 것은 SP나 muP 모두 같을 수 있지만, 이를 scaling up 하는 방법 자체가 아예 다르다는 것을 의미한다.
또 오해하지 말아야 할 것이 지금의 경우 multipler는 \(1/n_0\)인 것이며, 만약 base width가 256이면 \(1/256 \approx 0.0039\)가 된다. 물론 꼭 이럴 필요는 없다. 이는 SP로 setting된 base model의 optimal HP를 muP를 이용해서 잘 scaling up하기 위해 좋은 setting인 것이지, multiplier가 0.5이든 10이든 상관없다.
Transformer with muP
이제 toy problem에서 Transformer로 넘어가보자. 저자들은 Transformer에 muP를 적용하는 것은 MLP와 기본적으로 같은데 한 가지가 더 추가되어야 한다고 한다.
 Fig.
Fig.
바로 Scaled Dot Product Attention (SDPA) logit 을 계산할 때 attention dimension, \(d\)의 square root, \(\sqrt{d}\)로 나눠주는 게 아니라 \(d\)로 나눠주는 것이라고 한다.
 Fig.
Fig.
그 이유는 original Transformer paper, Attention Is All You Need에서는 model이 처음 학습될 시점에 q와 k가 서로 관련이 없는 vector들로 이뤄진 matrix일 것이기 때문에 CLT를 가정해서 \(\frac{1}{\sqrt{d}}\)만큼 scaling해 줘야 한다고 쓰여있으나, 실제로 training이 시작되면 두 tensor는 correlation이 생기기 때문이라고 한다. 즉 attention logit도 LLN을 따라 \(d\)로 나눠줘야 한다는게 TP-V 저자들의 주장이다.
 Fig. q, k는 서로 같은 input을 projection하므로 correlation이 생기기 때문에 LLN을 따라야 한다는 주장
Fig. q, k는 서로 같은 input을 projection하므로 correlation이 생기기 때문에 LLN을 따라야 한다는 주장
Attention Is All You Need에 보면 SDPA의 origin에 대한 note가 있다.
 Fig. dot product attention이 훨씬 빠른 연산이지만 head dimension이 커질 수록 additive attention에 비해 성능이 안나오는데, 그 이유를 Attention Is All You Need의 저자들은 logit scaling을 해주지 않아 gradient가 작아졌기 때문이라고 한다. 그렇기 때문에 init 시점에서 CLT에 따라 sqrt(d_k)로 나눠줘야 한다고 주장했다.
Fig. dot product attention이 훨씬 빠른 연산이지만 head dimension이 커질 수록 additive attention에 비해 성능이 안나오는데, 그 이유를 Attention Is All You Need의 저자들은 logit scaling을 해주지 않아 gradient가 작아졌기 때문이라고 한다. 그렇기 때문에 init 시점에서 CLT에 따라 sqrt(d_k)로 나눠줘야 한다고 주장했다.
Attention logit의 scale에 따른 gradient scale에 대해 간단하게 계산해보자. Logit vector, \(z \in \mathbb{R}^{1 \times n}\)에 대해서 softmax output, \(s \in \mathbb{R}^{1 \times n}\)는 다음과 같이 게산된다.
\[s_i = \frac{\exp(z_i)}{\sum_j \exp(z_j)}\]이제 backpropgation을 위한 softmax function의 gradient를 계산해보자.
\[\frac{\partial s_i}{\partial z_k} = \left\{\begin{matrix} s_i (1-s_i) & \text{ if } i = k \\ -s_i s_k & \text{ if } i \neq k \end{matrix}\right.\] \[J_{ik} = \begin{pmatrix} \frac{\partial s_1}{\partial z_1} & \frac{\partial s_1}{\partial z_2} & \cdots & \frac{\partial s_1}{\partial z_n} \\ \frac{\partial s_2}{\partial z_1} & \frac{\partial s_2}{\partial z_1} & \cdots & \frac{\partial s_2}{\partial z_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial s_n}{\partial z_1} & \frac{\partial s_n}{\partial z_2} & \cdots & \frac{\partial s_n}{\partial z_1} \\ \end{pmatrix}\] \[J_{ik} = \frac{\partial s_i}{\partial z_k} = y_i (\delta_{ik} - y_k)\] \[J_{ik} = \begin{pmatrix} s_1 (1-s_1) & -s_1 s_2 & \cdots & -s_1 s_n \\ -s_2 s_1 & s_2 (1-s_2) & \cdots & -s_2 s_n \\ \vdots & \vdots & \ddots & \vdots \\ -s_n s_1 & -s_n s_2 & \cdots & s_n (1-s_n) \\ \end{pmatrix}\]우리는 scaled softmax를 계산할 것이기 때문에 \(\alpha\)로 scaling을 해줄 것이다.
\[s_i = \frac{\exp(z_i/\alpha)}{\sum_j \exp(z_j/\alpha)}\]muP is more than just predicting the optimal LR of wide SP models
muP의 저자들은 muP가 단순히 small proxy model로 hyperparam tuning을 한 뒤 large target model로 transfer하는 것 이상의 의미가 있다고 한다.
 Fig.
Fig.
앞서 얘기했지만 HP transfer를 가능하게 한 것은 바로 같은 timestep에서 width-invariant한 activation scale을 보이도록 paramterization을 강제했기 때문이다.
그르고 이것을 만족하면 우리는 gradient exploding or vanishing 현상이 일어나지 않는 선에서 모든 weight matrix, bias, embedding layer들을 가능한 크게 update 할 수 있는 lr을 설정할 수 있게 된다.
즉 모든 layer가 동일한 속도로 최대한 update 되도록 만들 수 있는 것이다.
실제로 SP를 따를 경우 어떤 layer는 너무 빨리 update되며 일부는 너무 느리게 update되기도 한다고 하는데,
특히 embedding matrix가 매우 느리게 update된다고 한다.
 Fig.
Fig.
특히 Transformer architecture에 대해서는 attention logit같은 hidden quantity는 1 step param update만 하더라도 blow up하기 시작하는데,
이를 막기 위해 lr을 애초부터 작게 주거나 scheduling을 하는 전략을 떠올리는게 보통이겠지만 이는 좋은 방법이 아니라고 한다.
왜냐하면 word embedding 같은 경우는 학습이 진행되더라도 width와 무관한 어떤 amount에 따라 update 되기 때문에 lr을 작게 주는 것은 매우 큰 model에서는 word embeddings을 충분히 학습하지 않는 상황을 초래할 수 있기 때문이다.
하지만 아래 figure를 보면 muP를 적용할 경우 layer별로 lr과 weight init, multiplier 전략이 모두 잘 설정되어 있기 때문에 안정적으로 학습을 할 수 있었다고 한다.
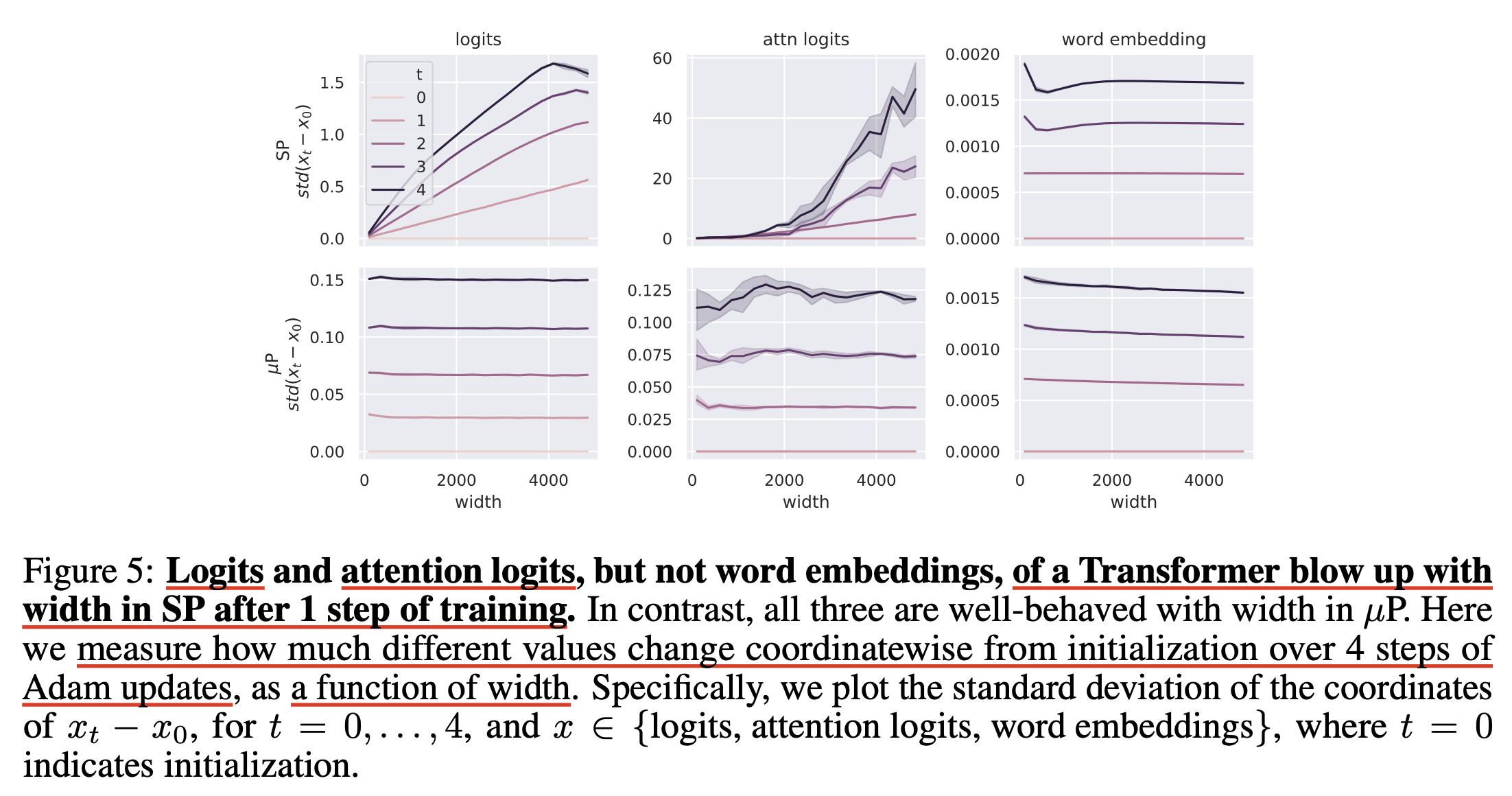 Fig.
Fig.
위 figure는 TP-5의 저자들이 제안한 coordinate checking이라는 것인데,
이는 마치 Autograd engine을 검증하기 위해서 manually gradient를 계산해 보는 것과 같다고 한다.
방법은 먼저 4 step 정도 Adam optimizer등을 사용해 parameter update를 한다. 그리고 각 timestep 마다 (pre)activation vector의 차원(or 좌표, coordinate)마다의 value 변화를 추정하는데, 다시 말해서 initial value와의 차이를 계산해서 얼마나 원래 value로부터 이탈했는지 (deviate) 했는지 (standard deviation)를 측정한다. 간단히 말해서 layer output마다의 l1 norm을 측정한다고 보면 되고, 이걸 model width를 늘려가면서 측정하면 되는데, 학습을 안정적으로 하기 위해서는 이 값이 width가 증가함에 따라 커지거나 0으로 줄어드는 것이 아니라, 균일한 모양 (flat)을 보여야 한다.
이 부분에 대해서 헷갈리는 사람들이 있는데,
이를 해석할 때 training step이 달라져도 이 값이 같을 필요는 없다는 점에 주의해야 한다.
당장 위의 figure만 보더라도 같은 color의 값이 step이 경과될 수록 움직인다.
중요한 점은 같은 timestep에서 width에 의해 scale이 변동되지는 말아야 한다는 것이고,
이것이 muP의 desiderata이다.
Coord check을 위한 tip으로는 실제 training에 쓸 lr보다 훨씬 큰 값으로 potential issue를 감지하는 것이 중요하다는데, 자세한 사항은 repo의 implementation을 참고하면 될 것 같다.
A Very Basic Primer on Why The Correct Parametrization Can allow HP Transfer Across Width
그래서 왜 muP가 HP Transfer를 가능케 할까?
먼저 CLT를 따라서 만약 \(x_1, \cdots, x_n\)이 어떤 zero-mean unit variance gaussian distribution으로 부터 iid sampling 됐으면 \(\frac{1}{\sqrt{n}} (x_1 + \cdots + x_n)\)는 \(n \rightarrow \infty\)일 경우 \(\mathcal{N} (0,1)\)로 수렴한다. 이 때, 각 sample의 합에 붙는 scaling factor를 \(\color{red}{c_n}\)이라 생각해보자.
\[\color{red}{c_n} (x_1 + \cdots + x_n)\]여기서 \(c_n = \frac{1}{\sqrt{n}}\)인 경우 우리는 이 sample들의 합이 zero mean unit variance normal distribution를 따르는 한 값이 된다.
하지만 \(c_n = 1/n\)이라면 어떨까? 이는 \(n\)이 무한대로 커질 경우 0으로 수렴한다. 그리고 \(c_n = 1\)일 경우에는 무한대로 발산해 버린다. 그러니까 여기서 우리는 \(n \rightarrow \infty\)에 대해서 발산하거나 0이되지 않으며 non trivial solution을 제공하는 올바른 order를 갖는 scaling factor는 \(c_n = \frac{1}{\sqrt{n}}\)뿐이라는 것에 동의 할 수 있다.
이제 우리는 아래의 function을 minimize하고 싶다.
\[\begin{aligned} & F_n (c) \stackrel{\mathrm{def}}{=} \mathbb{E}_{x_1, \cdots, x_n} f(c(x_1 + \cdots + x_n)) & \\ & c \in \mathbb{R}, f: \mathbb{R} \rightarrow \mathbb{R} \text{ is bounded contiuous function} & \\ \end{aligned}\]만약 우리가 \(\alpha \in \mathbb{R}\)에 대해서 \(c=\alpha / \sqrt{n}\)로 reparameterize 한다면, CLT에 의해서 \(n \rightarrow \infty\)일 때, function \(G_n(\alpha) \stackrel{\mathrm{def}}{=} F_n(c) \rightarrow \mathbb f(\mathcal{N}(0,\alpha^2))\)는 \(\alpha\)의 function으로 안정화 된다.
그러면 충분히 큰 n에 대해서 optimal \(\alpha_{n}^{\ast} \stackrel{\mathrm{def}}{=} \arg \min_{\alpha} G_n(\alpha)\)는 \(N >> n\)인 \(\alpha_{N}^{\ast}\)에 가까워져야 한다고 할 수 있으며, \(N=\infty\)인 경우에 대해 small problem, \(F_n\)에서 구한 optimal solution \(c_{n}^{\ast}\) or \(\alpha_{n}^{\ast}\)를 정확하게 large problem인 \(F_N\)으로 전이 (transfer) 할 수 있다고 한다.
다시 말해서 \(G_n\)는 \(\alpha_{n}^{\ast}\)에 의해 근사적으로 최적화 될 수 있으며, \(F_n\)은 \(c_n^{\ast} \sqrt{n/N}\)에 의해 근사적으로 최적화 될 수 있는 것다고 한다.
저자들은 Transfer algorithm이란 \(\alpha\)를 그대로 large problem에 copy하는 것이므로, \(c=\alpha/\sqrt{n}\)이 올바른 parameterization이라고 할 수 있다고 한다.
이제 이를 NN training의 scenario에 대입해보자. 우리는 각각의 변수들을 아래와 같이 생각할 수 있는데,
- \(n\): width of NN
- \(c\): HP such as LR
- \(x_1, \cdots, x_n\): randomly initialized parameters of width-\(n\) NN
- \(f\): test-set performance of NN
after training - \(F_n\): expectation over random initializations’ test-set performance
이에 따라서 우리가 parameterization을 잘 한다면 충분히 큰 width를 갖는 model size중 가장 작은 model size에서 찾은 optimal LR는 매우 큰 large model로 transfer 된다고 할 수 있다고 한다.
이를 바로 zero-shot transfer라고 부르는 것이다.
물론 저자들이 주장하는 바는 muP는 잘 정의된 infinite-width limit를 갖고있는데 반해 SP는 그렇지 못하다고 한다. TP paper에 종종 ~limit 이라는 표현이 나오는데, 이는 특정 조건이 무한히 커질 때의 동작을 의미한다. 예를 들어 NN의 무한 폭 한계 (infinite-width limit)는 NN의 width가 무한히 커질 때 어떤 값으로 수렴한다 같은 의미를 가진다. 당연히 muP의 저자들은 SP는 잘 정의되지 못하는 infinite-width limit을 갖는다고 하는데, 다른 말로는 어떤 distribtuon으로 수렴하지 않고 발산한다는 말이다. Greg은 여기서 수학을 좀 치는 사람들은 (일단 난 아니다) lr을 잘 정의하면 잘 정의된 infinite-width limit가 있을 수도 있다고 하지만 어쨌든 muP만큼의 좋은 parameterization은 아니라고 한다.
 Fig.
Fig.
Experimental Results
Main Results from TP-5
이제 TP-5에서의 muTransfer 실험 결과를 보도록하자.
Paper에는 ResNet, BERT, NMT task 그리고 GPT-3를 포함한 Autoregressive Language Modeling (LM) task에 대한 결과가 있다. 나의 main interest는 LLM이기 때문에 이번 post에서는 LM에 대해서만 알압도록 하고, 덧붙혀 muP를 써서 pre-training을 한 다른 paper들도 살짝 소개하려고 한다.
LM on WikiText-2
먼저 WikiText-2라는 유명한 dataset에 decoder only Transformer model을 학습한 경우이다.
기본적인 model arch setting은 다음과 같다.
- muP applied decoder only Transformer
- pre-layernorm
- 4 attention heads (fixed)
- base width: 128
- base depth: 2
먼저 이 setting에서 살펴볼 것은 나머지는 다 고정하고 아래 parameterization 변수들을 sweep하여 width나 depth이 커질 때 어떻게 loss가 변하는지 살펴보는 것이다. (5번 random seed를 달리해서 실험한 뒤 평균 냄)
- LR
- init_std == init_variance
- multiplier
- LR scheduler
나머진 다 친숙하겠으나 LR scheduler에서 “이게 그렇게 중요한가?”라는 생각이 들 수 있는데, LLM같이 큰 model을 매우 길게 학습하는 경우, 이에 따라서 성능이 크게 갈릴 수 있으니 유념해서 볼 필요가 있다. 아래 figure의 마지막 column에 나와있는 (a), (b), (c) …는 linear decay, stepLR, inverse sqrt 등 서로 다른 scheduler를 쓴 경우에 대해서 model param이 증가하면 성능이 일관되게 좋아지는가?를 확인했다고 보면 된다.
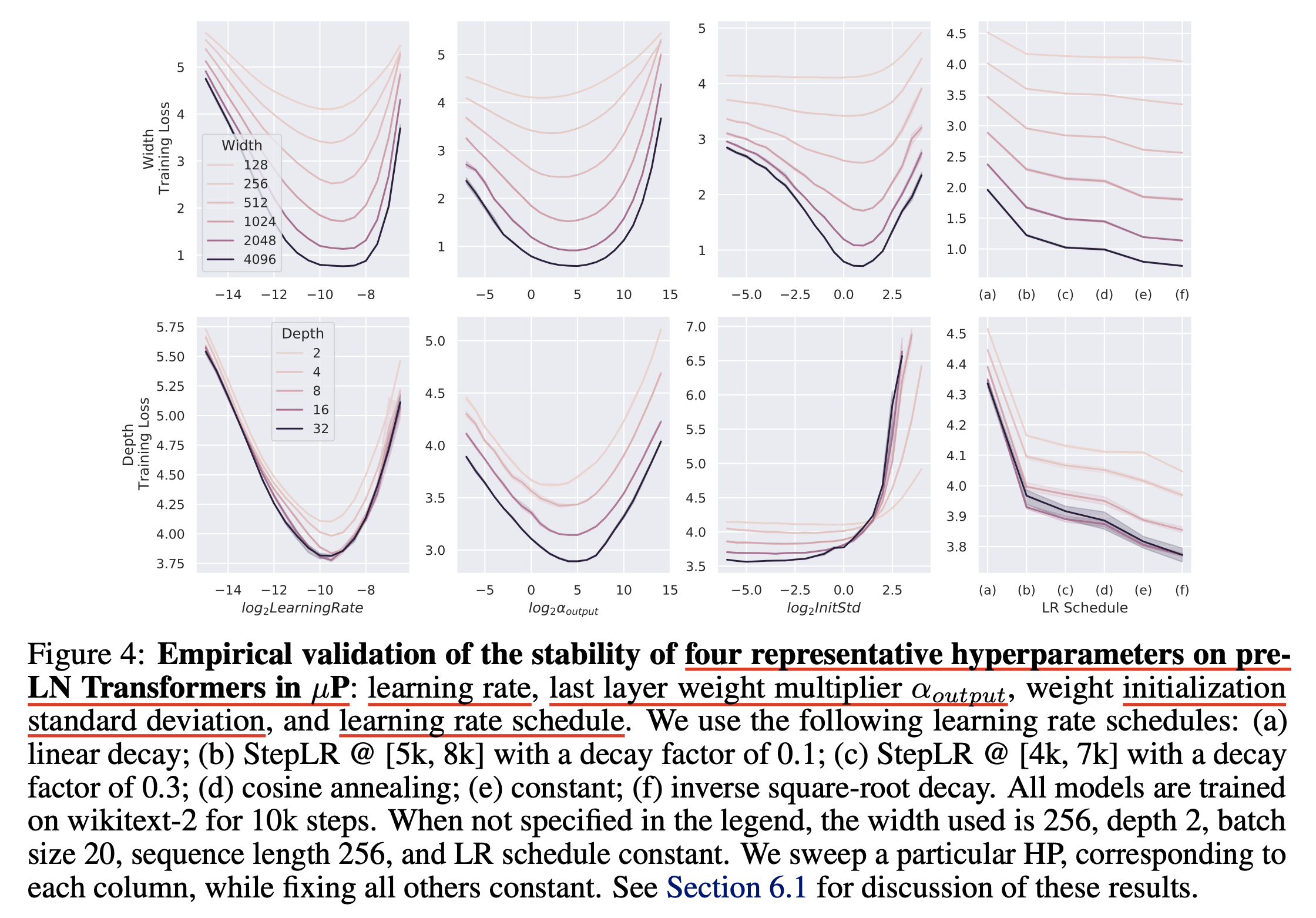 Fig.
Fig.
Figure caption에 나와있는 것 처럼 모든 model은 wikitext-2에 10k step만큼 학습되었는데, 아무래도 어느정도 충분히 param update가 되어야 하기 때문에 당연하게 생각할 수 있을 것 같다. 실제로 저자들은 LM pre-training의 경우, 경험적으로 아래의 값들만 충족되면 transfer가 안정적으로 된다고 언급했다.
- minimum width: 256 (num_head: 4, 즉 dim_head:64)
- depth: 4
- batch_size: 32
- seq_len: 128
- training_step: 5000
target scale is within the “reasonable range”
즉 위 실험은 wikitext-2에 대해 10k 했으니 큰 문제가 없을 것이고, 결과물을 보면 depth를 고정하고 width를 늘릴 때는 optimum transfer가 잘 되는 것으로 보이지만 exact optimum는 살짝 다를 수 있다고 한다. 하지만 이는 SP와 비교해서는 무시할만한 수준이라고 한다.
그런데 depth scaling을 할 때는 특히 best init_std가 잘 transfer되지 않는 것을 볼 수 있다 (2nd row, 3rd col). 다른 HP는 어느정도 transfer가 되는 걸 볼 수 있지만 사실 TP-4, 5에서는 depth scaling 에 대해 증명한 바가 없다. 이 부분에 대해서 더 궁금한 사람은 Tensor Programs VI: Feature Learning in Infinite-Depth Neural Networks를 봐야 할 것이다.
Transferability across Batch Size, Sequence Length and Training Steps
아래 figure는 appendix에 추가적으로 있는 것인데, width나 depth같이 model param을 변화시키는 것 뿐만 아니라 아래 세 가지에 대해서 변화를 주면서 loss를 측정해 본 것이다.
batch_sizeseq_lentraining steps
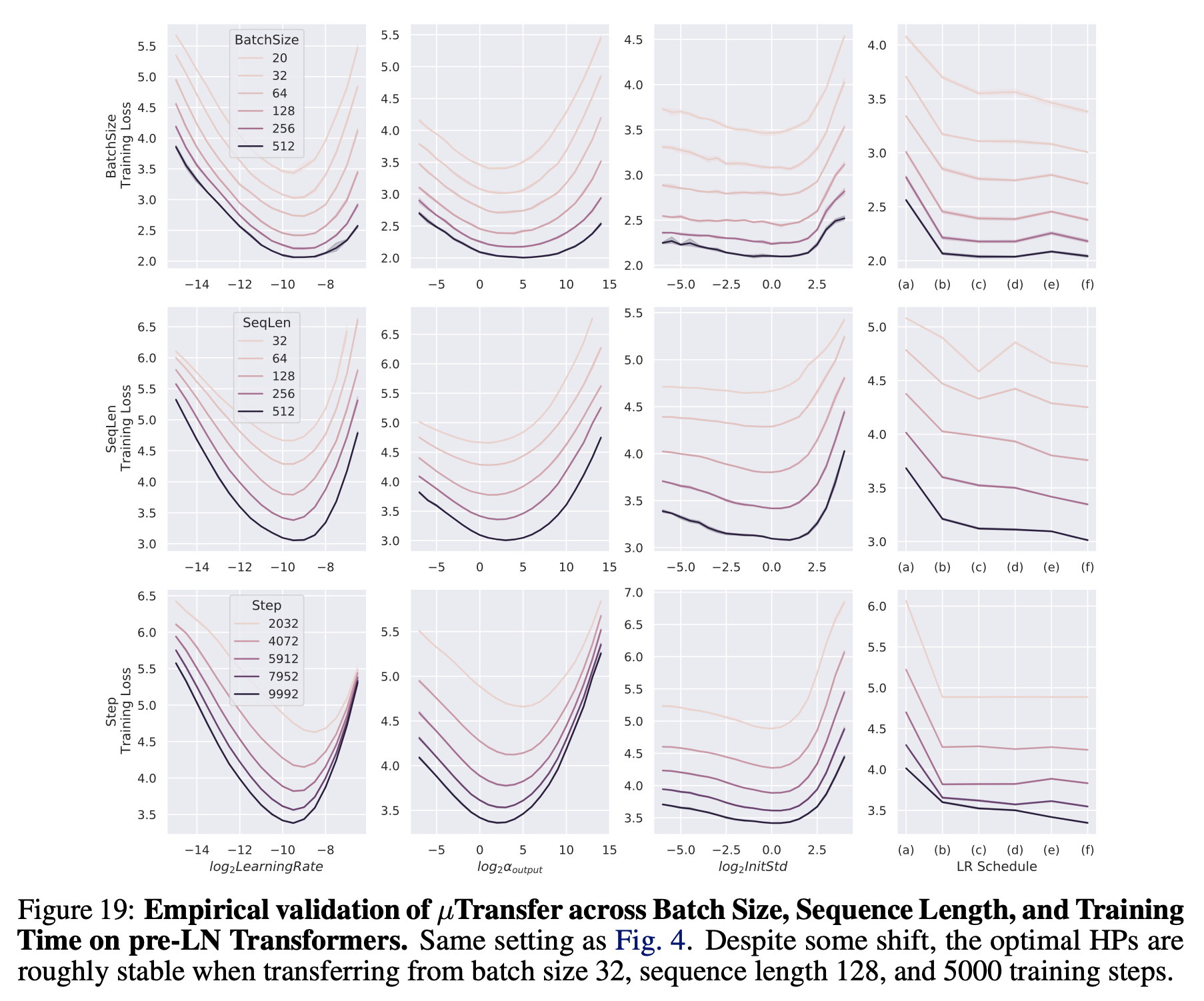 Fig.
Fig.
실험 결과 batch_size가 증가할수록 optimal LR 등에 약간의 shift가 있지만 꽤 잘 transfer되는 것을 볼 수 있다고 한다.
아마 이는 같은 Model size에 대해서,
예를 들어 100M으로 고정하고 실험한 것인 것으로 보이며 batch_size가 커질수록 성능이 좋아지지만 optimal LR등이 transfer된다고 이해할 수 있을 것 같다.
이는 당연히 minimum batch_size, seq_len, training steps (5k) 를 넘긴 시점부터 안정적일 것이다.
좀 더 discussion을 하자면 batch_size sweep의 경우 아무래도 LR이 고정인데 batch_size가 증가할수록 성능이 좋아진다는 걸 보면 똑같은 training step을 돌린 것 같다. 아무래도 batch_size가 커지면 sample들로 부터 얻는 gradient가 더 정교해져 더 optimal로 향할 가능성이 높아지긴 하지만, 이 경우 batch_size가 예를 들어 2배 커지면 training step이 1/2배로 작아지기 때문에 global LR이 transfer될 지언정 대략 \(\sqrt{2}\)정도 LR을 키워주지 않으면 안된다. 그리고 이것이 critical batch_size를 성립이 되는지? 등에 대한 의문이 있다.
+Updated) paper를 다시보다가 아래와 같은 footprint를 발견했는데, 저자들은 batch_size를 늘려도 optimal LR이 transfer되는지 보는 실험 등에서는 FLOPs를 고정하지 않았다고 한다.
즉 batch_size가 2배 커져도 training steps는 예를 들어 10000으로 고정인 것이다.
이 경우 batch_size가 2배가 됐으니 실제 consume하는 token량은 2배가 되므로 FLOPs는 2배가 된 셈이지만 greg은 batch_size나 training steps가 증가할 때 LR을 어떻게 scaling 하는 것이 올바른가?에 대한 것,
즉 optimlly scaling하는지는 관심이 없었다고 하니,
실제로 muP를 적용해 LLM을 학습하려고 할 때에는 이를 반드시 고려해야 할 것이다.
 Fig.
Fig.
seq_len에 대한 실험은 같은 batch_size에서 seq_len가 늘어나는 것은 사실상 batch_size가 늘어나는 것 처럼 token 수가 늘어나므로 gradient가 다양해져 summed gradient가 더 정교해져서 그런 것 같은데,
batch_size와 연결지어 생각해본다면 예를 들어 seq_len=128일 때 batch_size를 키우는 것은 서로 다른 문장에서의 gradient를 받으므로 더 다양한 gradient를 얻을 수 있지만,
batch_size=32로 두고 seq_len를 512로 늘리는것은 한 문장 내에서의 token이 증가하는 것이기 때문에 correlation이 있어 gradient가 덜 다양해서 효과가 크지 않은 것 같다.
Training steps에 대해서도 당연히 transfer가 되는데,
1 epoch이 2~3 Trillion (T)를 당연하게 넘어가는 modern LLM에는 overfitting이라는 개념이 없기 때문에 당연하다고 생각할 수 있을 것 같다.
사실 batch_size, seq_len, 그리고 training steps 세 가지에 대해서도 transfer된다는 발견은 그냥 그렇구나 하고 넘어갈 것은 아니다. 왜냐면 우리가 GPT-4 size의 LLM을 학습할 경우 small scale proxy로 HP를 예측하려면 보통 학습량 (dataset size)와 과 model size를 작게 주기 때문이다. 예를 들어 아래 그림을 보자 가장 작은 small scale proxy는 Computing Budget, \(C=100p=100\text{e-}12=1\text{e-}10\)이고, target compute budget은 \(C=1\)이다.
 Fig.
Fig.
즉 가설을 세워보자면 OpenAI는 GPT-4 학습을 위해서 먼저 10배 작은 budget으로 HP search를 하고, 조금씩 budget을 키우면서 (보통 model size를 키움) 위해 8개의 실험을 더 돌려 scaling power function의 계수인 exponent를 찾는 일을 dataset 후보군 10개에 대해서 진행하여 가장 좋은 exponent를 갖는 training setting을 고른 것이다. 만약 10배 작은게 사실이라면 budget은 보통 \(C=6ND\)로 표현되며, 여기서 \(N\)은 model size (embedding weight matrix를 제외한 나머지 param 수), \(D\)는 dataset size (token 수)를 의미한다. 즉 만약 GPT-4의 model size가 세간에 알려져 있는 것 처럼 대략 \(N=200B=200e9\)이고, dataset size는 \(D=20T=20e12\)라고 생각해보면, smallest scale proxy는 \(C\)가 10배 작을 경우 \(N,D\)가 fair하게 5배씩 작을 경우 \(N=200e4=0.002e9=0.002B\), \(D=20e7=0.2e9=0.2B\)가 된다. 하지만 저자들은 muP로 HP transfer를 하기 위해서는 model size가 최소 width=256 (num_head=4), depth=4를 넘어야 한다고 했기 때문에 적당히 model spec을 키워 대충 \(N=0.02M=20M\)정도로 잡는다면 \(N=0.02B\)가 될 수도 있다.
Post-Norm
마지막으로 post-layernorm에 대한 실험이 있는데, 꽤 transfer가 되는 것 같지만 저자들은 post-norm이 훨씬 더 HP에 sensitive하기 때문에 muP효과가 더 두드러진다고 얘기한다. post-norm이 왜 불안정한지에 대해 생각하는 것 자체가 large scale NN training에 대한 이해도를 높혀줄 수 있을 것 같긴 하지만, 요즘 pre-norm을 쓰는 곳은 없으니 넘어가도록 하겠다.
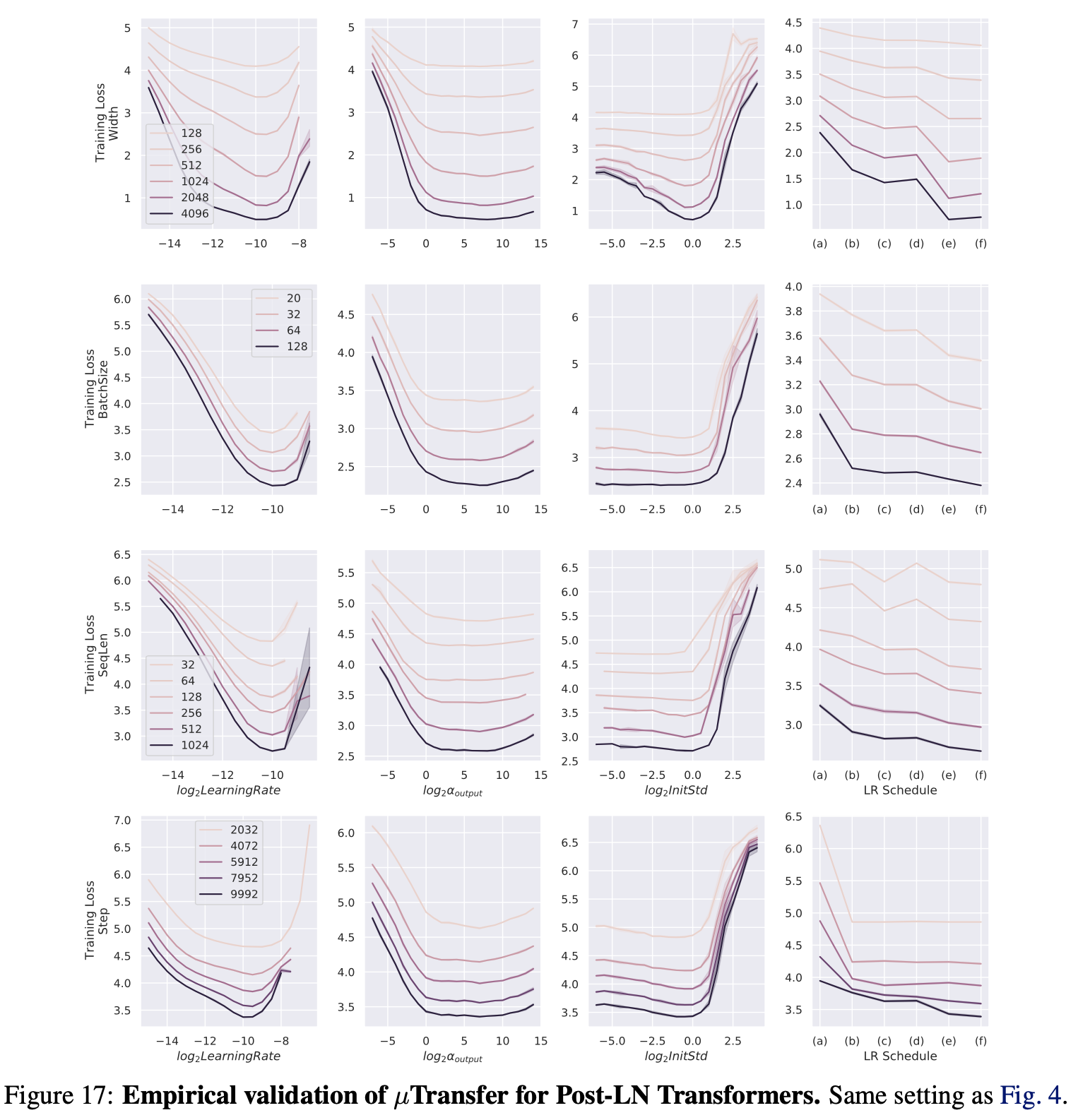 Fig.
Fig.
이렇게 muP라고 만능은 아니며 어떤 HP는 transfer가 잘 되고 (잘 되더라도 오차 조금이라도 존재),
어떤 것은 잘 안되기도 하며 심지어 아예 안되는 것도 있다고 하는데,
곧 Which HP Can Be Transferred?라는 section에서 더 자세히 알아보도록 하겠다.
GPT-3
이번에는 GPT-3 scale의 LM pre-training 결과이다.
Optimal HP search를 위한 small scale proxy model와 target GPT-3 model의 configuration과 training에 사용된 token량은 다음과 같다.
Small scale proxy model- width: 256
- layers: 32
- total num. params: 0.04B (40M)
- num. training tokens
- short horizon:
4B - short horizon: 16B
- short horizon:
- batch_size: ???
Target model- width: 4096
- total num. params: 6.7B
- num. training tokens:
300B - batch_size: ???
Small scale proxy model은 target model에 비해 168배 작은 model이었기 때문에 여기에 들어간 HP tuning cost는 전체 pre-training의 7%밖에 되지 않았다고 하는데, 이 값은 아래 수식에 따라 도출되었다.
\[\begin{aligned} & \frac{ s(t_1 N_1 + t_2 N_2) } { ST } \approx 0.07 & \\ & \text{where } s=40M \text{ is num.param for small scale model} & \\ & S=6.7B\text{ is num.param for target model} & \\ & t_1=4B \text{ is num. training tokens for short horizon HP search} & \\ & N_1=350 \text{ is num. trials for short horizon HP search} & \\ & t_2=16B \text{ is num. training tokens for long horizon HP search} & \\ & N_2=117 \text{ is num. trials for long horizon HP search} & \\ & T=300B \text{ is num. training tokens for training target model} & \\ \end{aligned}\]여기서 small scale model이 더 적은 training tokens를 사용해 학습되었는데, 저자들은 이렇게 해도 HP transfer에 아무런 큰 영향이 없을 것이라고 믿고 실험을 진행 했으며, token수에 따라서 얼마나 optimal HP가 차이나는지 확인하기 위해 각각 short, long horizon dataset을 구성해 실험하였다.
그래서 실제 target model 대비 4/300=0.013, 16/300=0.053배의 dataset만 쓰고 HP transfer를 한 결과는 어떨까? 먼저 muP로 tuning할 HP의 search space는 아래와 같았다.
 Fig.
Fig.
그리고 HP sweep을 한결과는 아래와 같았는데, 보다시피 short horizon, long horizon에서 찾은 HP값이 크게 다르지 않음을 알 수 있다.
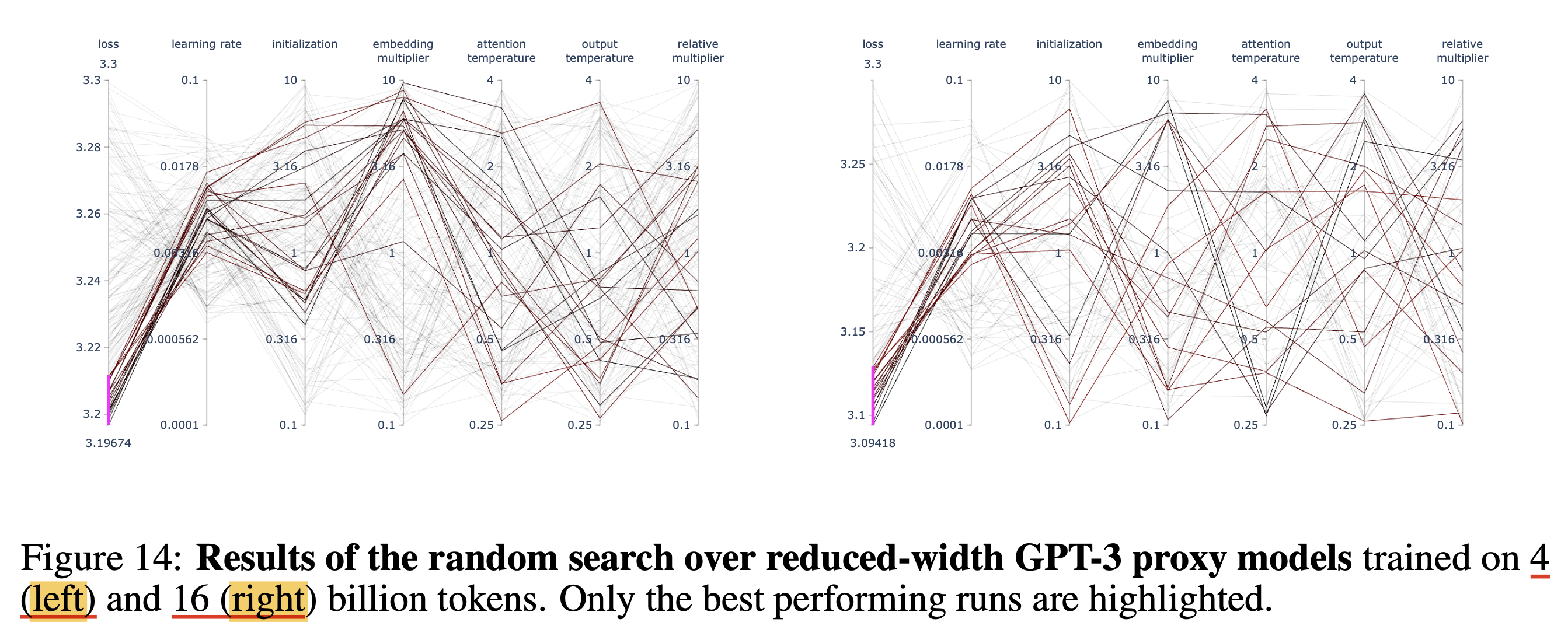 Fig.
Fig.
저자들이 분석하기를 총 467 training session run했을 때 366 session이 발산하지 않았고, 결과를 분석해봤을 때 아래 나머지 HP들은 큰 impact가 없어서 1로 setting했지만 아래 세 가지는 크게 중요했다고 얘기한다.
- LR
- init scale (아마 init_std)
- embedding _scale (아마 input embedding multiplier)
 Fig.
Fig.
저자들은 40M으로 찾은 optimal HP를 6.7B target model로 zero shot transfer 하는데 성공했고, 그 결과 일반 SP 6.7B model보다 거의 모든 task에서 좋은 performance를 보였으며 심지어 13B와 비교했을 때도 비빈다는 결과를 얻을 수 있었다고 한다.
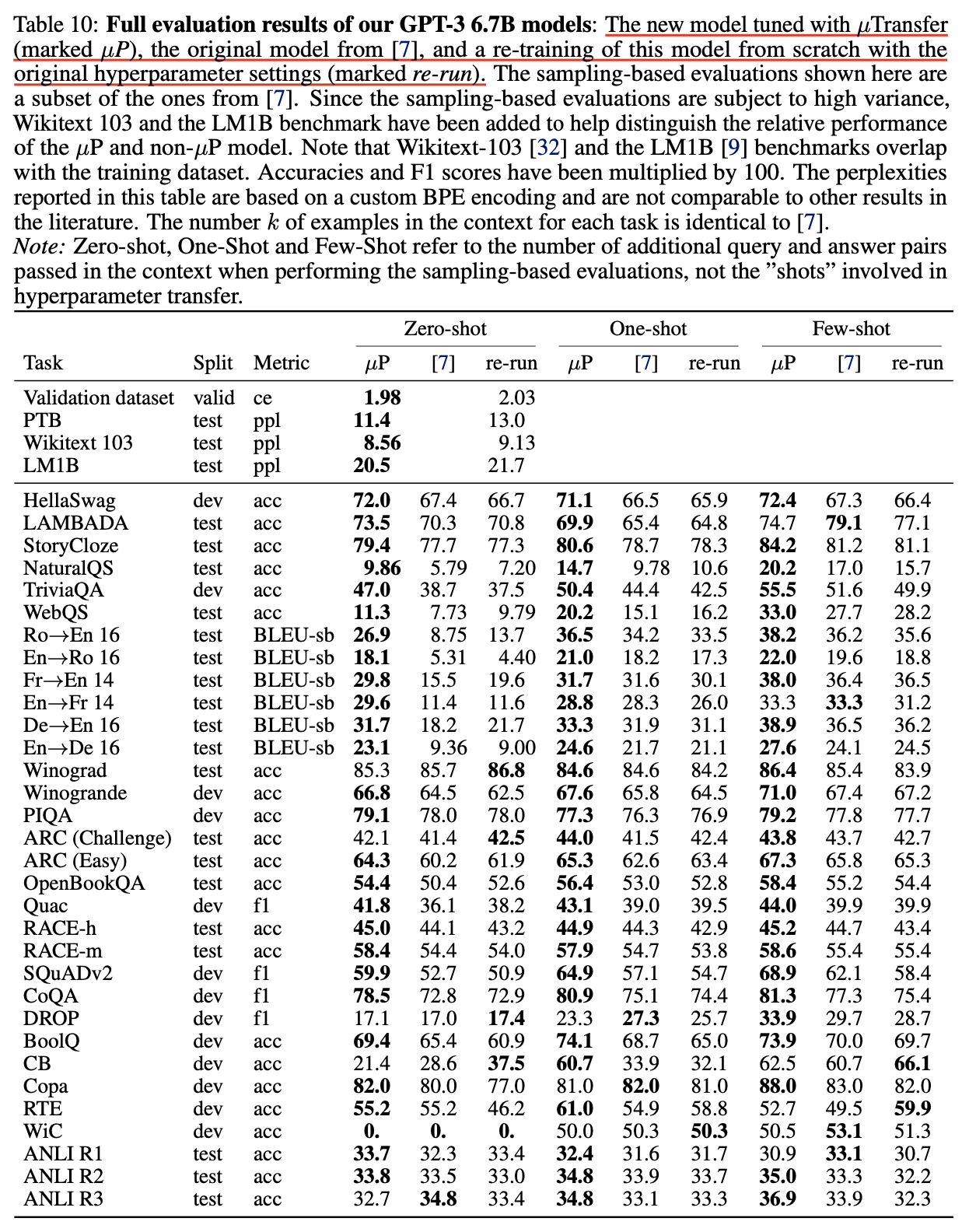 Fig. SP vs muTransfered in 6.7B
Fig. SP vs muTransfered in 6.7B
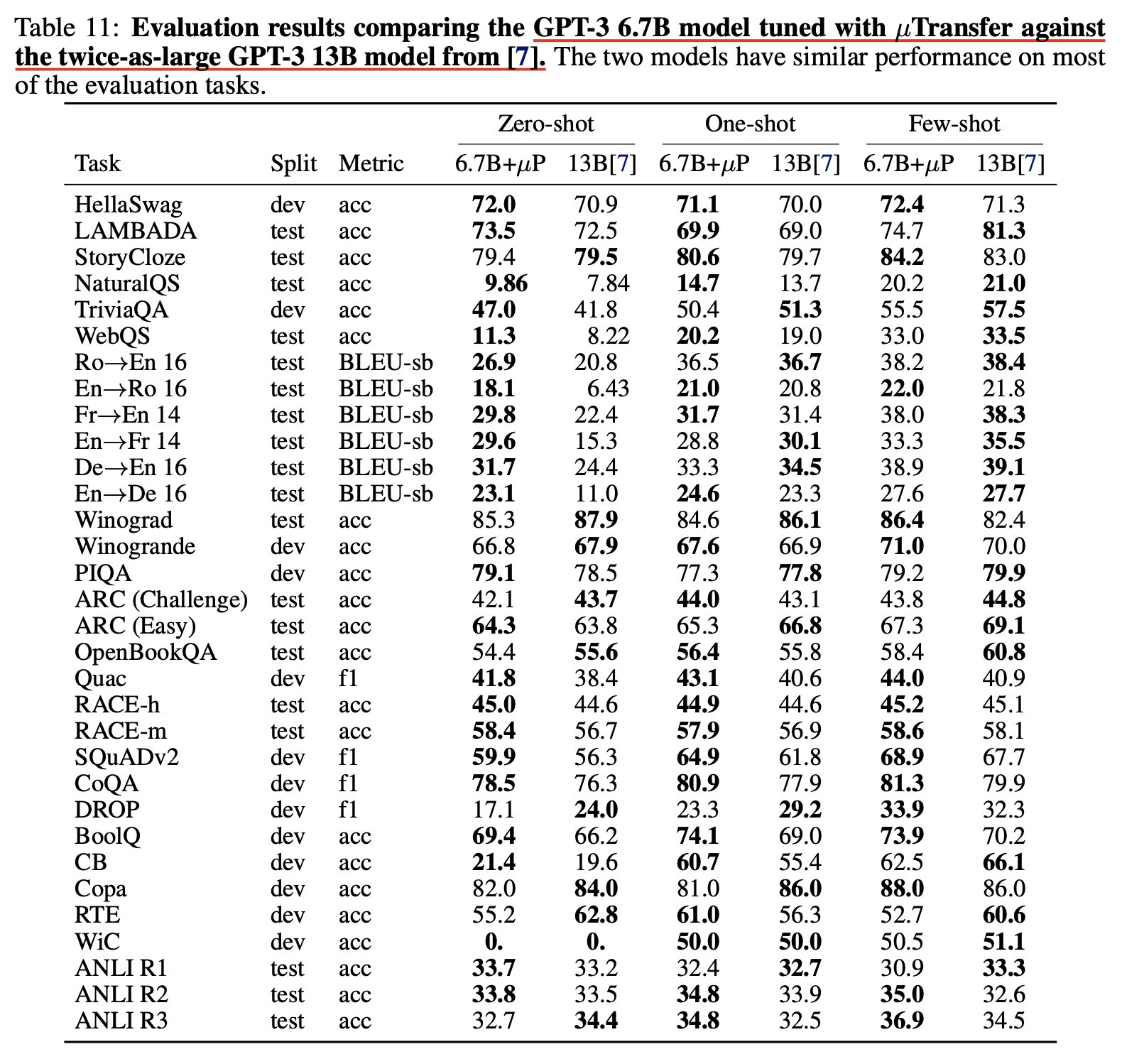 Fig. muTransfered 6.7B vs 13B
Fig. muTransfered 6.7B vs 13B
하지만 이는 아주 완벽한 comparison은 아니긴 하다.
Paper에는 GPT-3 original paper와의 code 차이를 최대한 배제하기 위해 다시 baseline 학습을 하다가 model configuration을 잘못 줬다고 한다 (?).
즉 SP 6.7B re-run baseline에는 실수로 absolute Positional Embeding (PE)를 사용했으며,
6.7B muP applied target model에는 relative PE를 썼다는 것이다 (…).
여기에 custom tokenizer까지 썼기 때문에 original paper와의 직접적인 ppl comparison은 아예 불가능한 수준이다.
당연히 original paper와는 ppl이 아니라 task별 accuracy를 비교했으니 문제가 없을 것으로 생각할 수도 있지만,
tokenizer만 달라져도 성능이 천차만별로 달라질 수 있기 때문에 이것이 fair comparison이 맞는지는 모르겠다.
 Fig.
Fig.
근데 뭐 re-run baseline과 Mu-transfered model만 비교하면 PE빼고는 다른게 없긴 한데, 보통 PE라는 것이 training dataset에서 보지 못한 sequence length의 data에 generalize를 하냐 마냐 이기 때문에 long context를 다루는 valid set이 아니라면 납득이 가능하다고 생각할 수도 있다.
그런데 re-run vs muP에 대해서 또 다른 차이가 있는데, 저자들은 muP로 학습을 하다가 lowered precision training을 했는데, FP16을 사용할때 흔히 발생하는 numerical issue인 underflow를 겪었다고 했다. FP16 으로 학습할 경우 보통 mixed precision을 사용해야 하고, 이 경우 제일 핵심적인 요소 중 하나가 loss를 scaling해서 underflow가 나지 않도록 방지 해주는 것인데도 muP에서 이것이 발생했다는 것은 loss가 정상 범주를 벗어났다는 것을 의미하고, 더 안정적인 학습을 하게 해준다고 주장하는 muP가 SP와 다르게 발산해버렸다는 것이 우연인지 이 방법론을 증명하는데 실패한건지는 잘 모르겠다 (…).
저자들이 issue tracking을 한 결과 underflow는 backawrd pass에서 발생했다고 하는데, 추측하길 muP를 사용하면 linear weight에 more aggressive HP가 할당되기 때문에 divergence하기 더 쉬운 것이라고 얘기한다.
 Fig.
Fig.
결국 저자들은 결국 muP model에 대해서만 FP32로 학습을 진행했다고 한다.
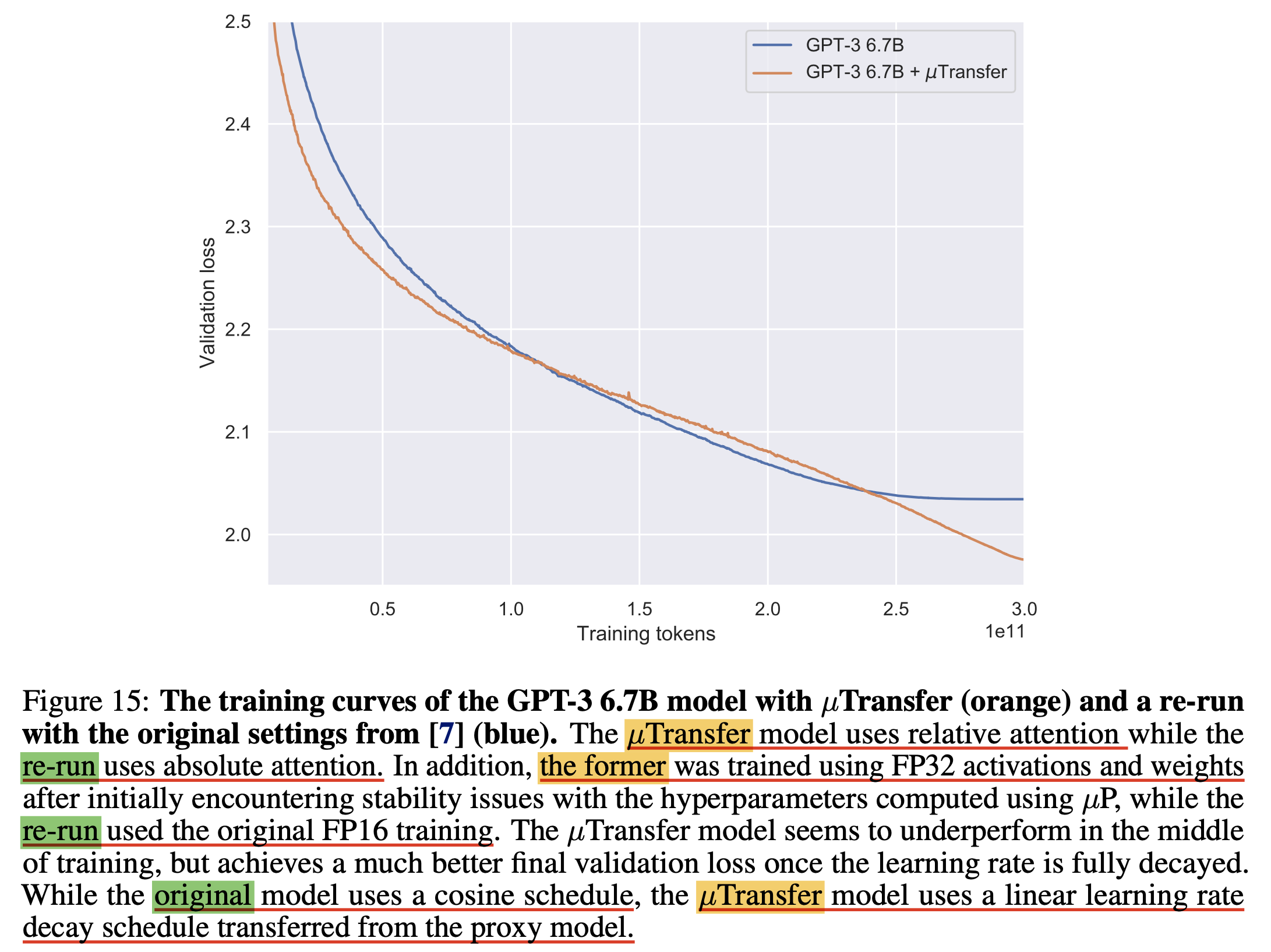 Fig. SP re-run vs muP. 이걸 믿어도 되는가?
Fig. SP re-run vs muP. 이걸 믿어도 되는가?
GPT-3에 대한 결과를 믿어도 되는지 모르겠지만
어쨌든 실험 결과 저자들은 Wider Is Always Better를 실험적으로 증명할 수 있었다고 얘기한다.
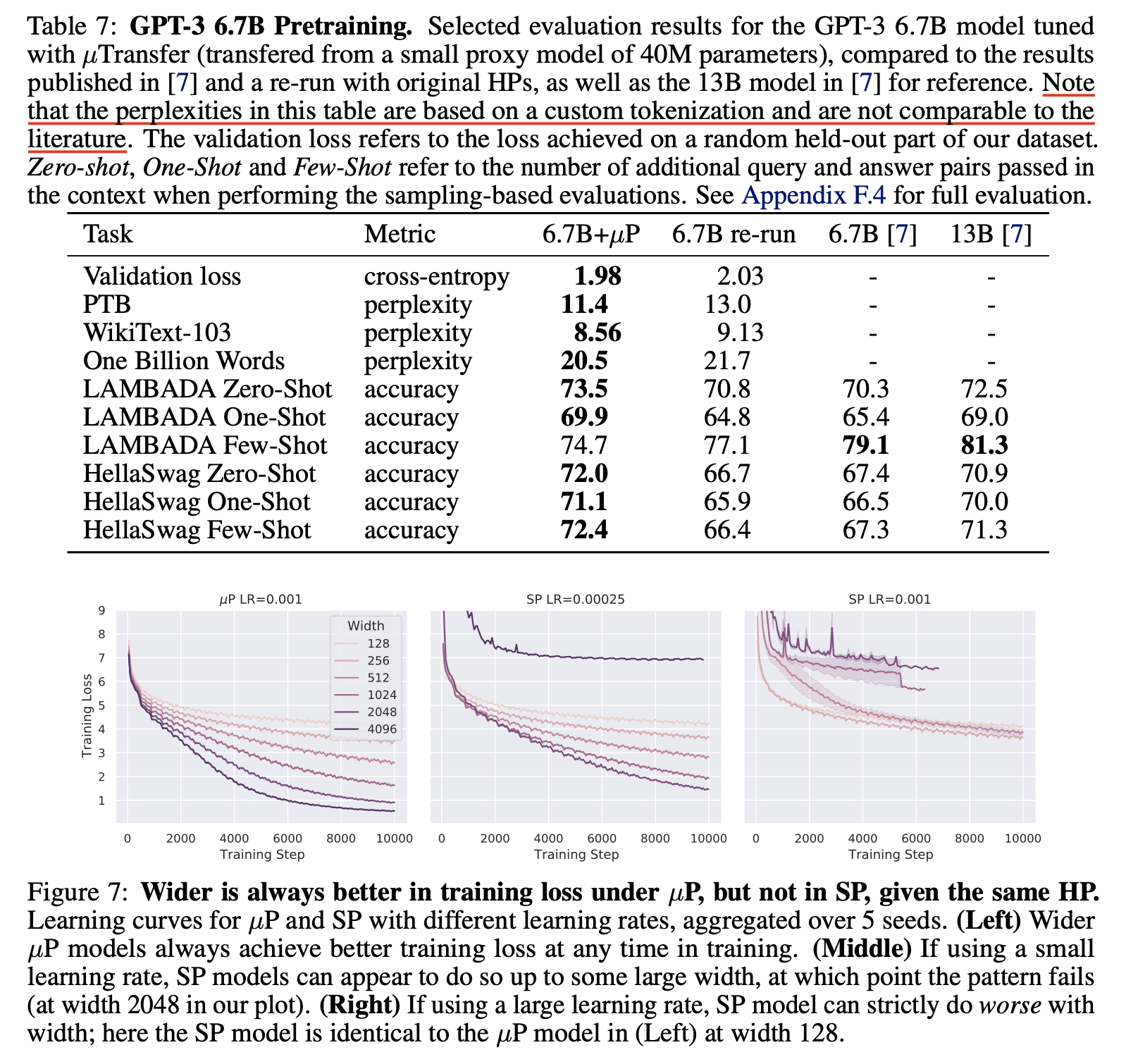 Fig.
Fig.
저자들은 muP를 custom model에 대해서 제대로 구현했는지 확인하려고 할 때, coordinate check와 더불어 width가 늘어날 때 항상 loss curve가 아래있는지를 확인하는 것으로 쉽게 sanity check을 할 수 있을거라고 얘기한다.
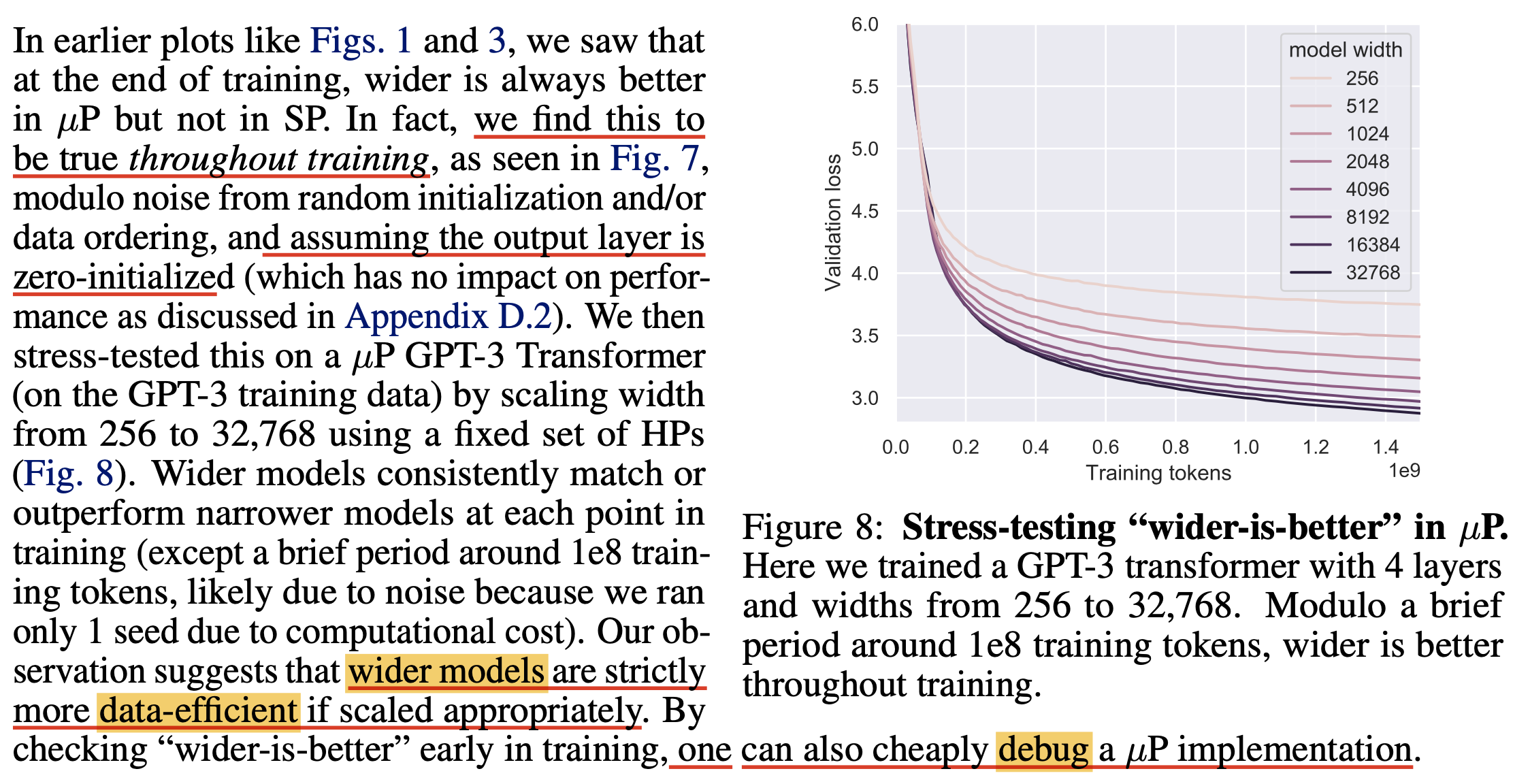 Fig.
Fig.
Other LLMs Trained with muP
앞서 살펴본 것 처럼 사실 TP-5의 GPT-3 실험에는 신뢰가 안가는 구석이 몇군데 있다. 서로 다른 PE를 썼다던가, numerical issue로 FP32를 썼다던가. 그래서 추가적으로 muP를 사용해서 LLM을 학습했다는 다른 paper들의 결과들을 같이 보려고 한다.
(2023 March) Observations from Cerebras-GPT
먼저 Cerebras-GPT의 내용을 보자.
Edward가 말한 것 처럼 공식적으로 muP를 사용했다고 밝힌 case들 중 유명한 기관이 Cerebras인데,
여기서 test해봤을 때 model size별 FLOPs와 loss의 Scaling Law는 아래와 같았고 실제로 muP를 했을 때 훨씬 안정적인 scaling prediction을 할 수 있었다고 얘기한다.
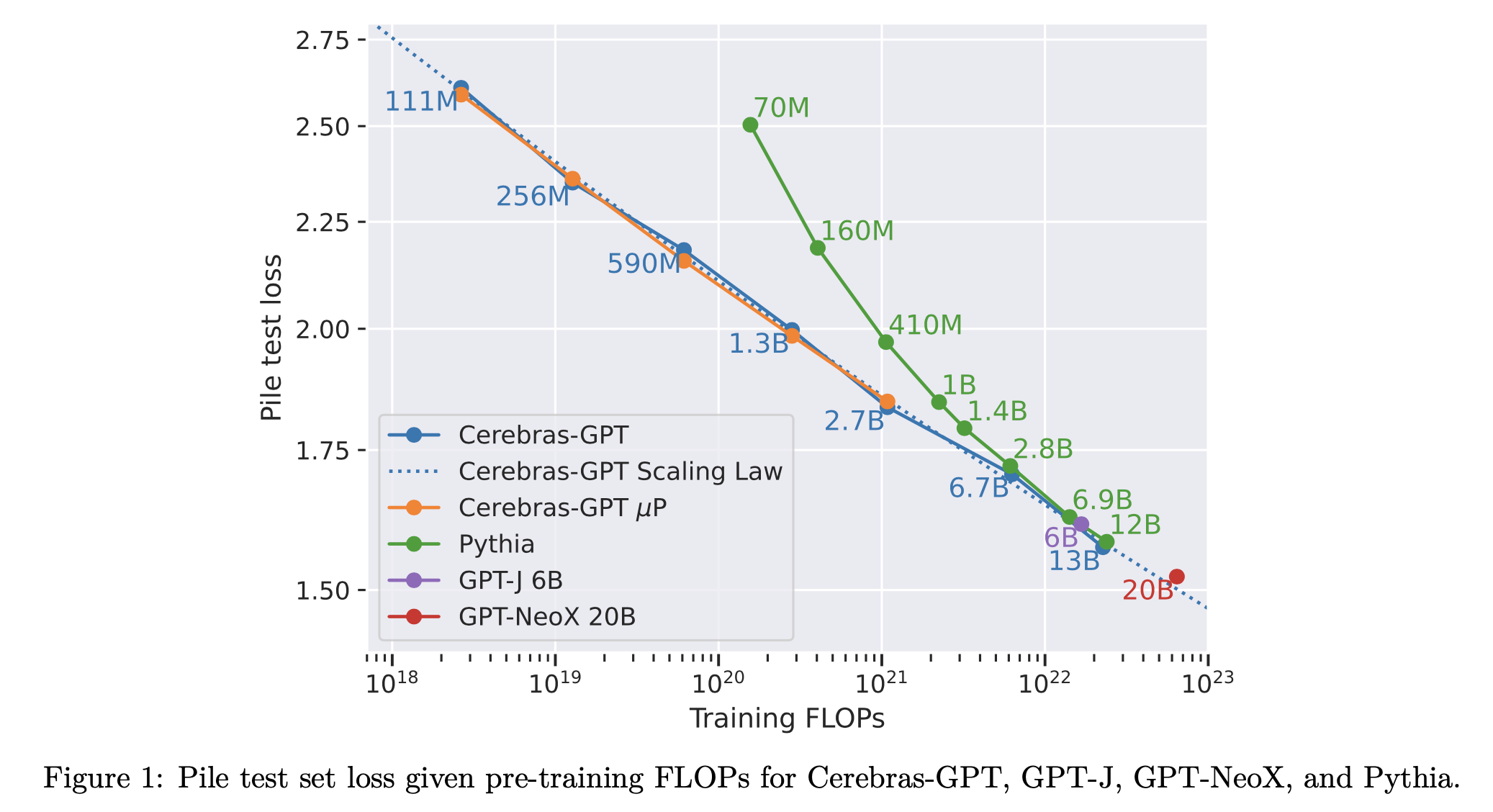 Fig.
Fig.
muP를 쓴 경우 (orange)와 위 graph를 SP를 쓴 경우 (blue)의 scaling law curve가 크게 다르지 않은 것을 확인할 수 있는데, 당연하게도 muP가 scaling law를 정교하게 해준다거나 이런건 아니고 SP도 뇌 비우고 HP search를 하면 optimal scaling law를 찾을 수 있기 때문에 이 둘의 차이가 없다는 건 더 적은 비용으로 muP가 grid search등으로 각 computing budget에서 HP를 찾아 scaling law를 만든 것과 동일한 curve를 얻게 됐다는 점에 주목해야 할 것이다.
하지만 curve를 보면 muP와 SP를 비교했을 때, target size인 2.7B에서 (muP를 2.7B까지만 했으니) SP가 test loss가 더 낮긴 했는데, 저자들은 lucky해서 그렇다고 믿고있다고 한다. 혹은 내가 생각하기에는 optimal HP를 제대로 찾지 못했다거나, 앞서 batch_size, training steps transferability에서 논했던 것 처럼 실제 LLM training scale에서는 batch_size 등이 변하기 마련인데 이를 제대로 고려하지 않은 것이 원인이지 않을까 싶다.
 Fig.
Fig.
저자들은 우연히 SP가 더 좋았던 것과 별개로 여전히 downstream에서는 muP가 좋았다는 얘기를 한다. 이 부분에 대해서는 TP에서도 실제로 LR을 1/width sacling한 SP도 좋은 solution을 찾을 수 있다고 얘기하긴 했지만 이것이 maximal feature learning regime이 아니기 때문에 fine-tuning task에서 차이가 나는것이 아닌가 하는 생각이 든다.
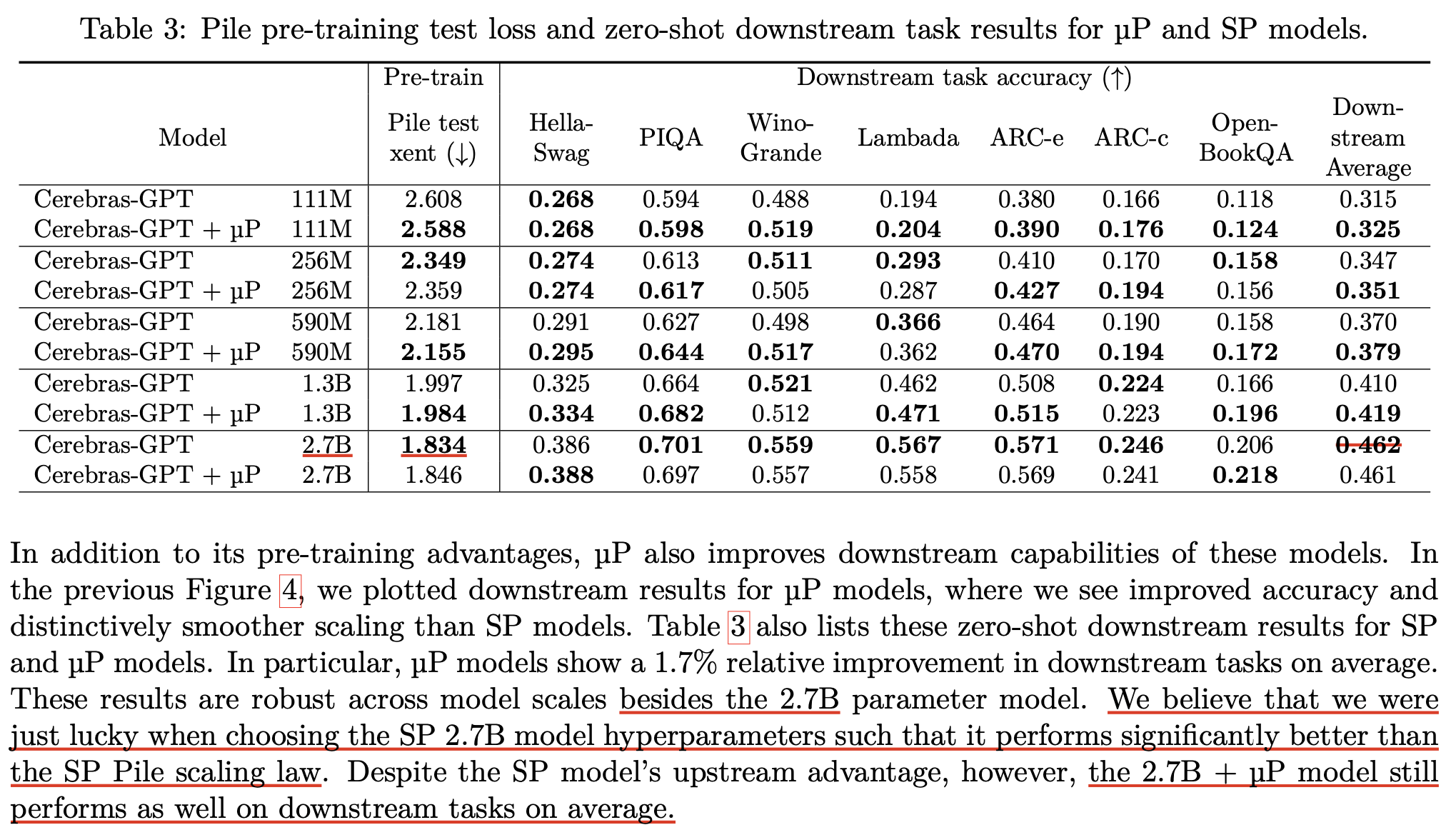 Fig.
Fig.
Cerebras에서는 또한 muP를 하지 않았을 경우 pre-training을 하면서 lowered precision으로 인한 underflow issue나 이로인한 weight 이 증가하는 문제 등이 있었음을 appendix에 자세히 적어두었는데, muP가 이를 완전히 해결해주었는지는 모르겠으나 별 다른 얘기가 없는 것으로 보아 도움이 되었던 것 같다. 왜냐면 muP 저자들이 주장하듯 muP는 zero-shot transfer를 가능케 하는 것을 넘어서 학습 안정성에 기여하는 유일한 방법론이기 때문이다. 하지만 사실 TP-5에서 muP가 fp16 mixed precision issue가 있었다고 했기 때문에, 이 부분은 믿기가 어려운 것 같다. 차라리 “muP는 backprop시 underflow issue가 있지만 bf16 precision은 dynamic range이 fp32와 같아서 modern LLM training에선 문제가 없어요”라고 하면 모를까.
 Fig.
Fig.
그 밖에 Cerebras-GPT는 실제 muP로 실험을 하려는 사람을 위해 본인들의 training setup을 공개했다는 점에서 매우 고마운 paper인데, 그들의 실험을 보면 small scale proxy model들과 2.7B scale의 target model에 사용된 batch_size와 training에 사용된 tokens 수 (training steps)가 다르다는 걸 알 수 있다.
 Fig.
Fig.
물론 TP-5에서도 batch_size, training steps가가 커져도 optimal LR이 transfer 보이긴 했으나 실제 GPT-3실험에서는 같은 batch_size를 썼기 때문에 실제 training setting을 어떻게 해야할지 궁금한 사람이 많았을 것이다.
Cerebras-GPT 저자들은 다행히 small scale을 학습할 때 더 적은 training tokens와 batch_size를 사용해도 큰 문제가 없었다고 하며,
batch_size가 현재 computing budget에 대해서 충분히 크다면 target setting의 batch_size와 같지 않아도 된다고 얘기한다.
 Fig.
Fig.
여기서 특정 computing budget에 대해서만 batch_size가 충분히 크면 된다고 하는 내용은 Critical Batch Size를 의미하는데, 이 값보다만 크면 된다고 얘기한다. 아마 이 내용은 TP-5에서 batch size가 증가함에 따라 LR을 어떻게 scaling하는지에 대해 얘기하면서 Critical batch size paper의 equation을 따르면 batch size가 클 경우 더 이상 LR이 늘어나지 않기 때문에 transfer가 더 잘 된다고 했는데, 이 얘기를 하는 것 같다.
Critical batch_size란 해당 computing budget를 사용해 달성할 수 있는 loss에 대한 power function으로 나타나기 때문에 budget이 늘어날수록 커진다. 즉 model size, dataset size가 커지면 budget이 커지는 것은 당연하고, 이 때 loss값도 exponentially decreasing하기 때문에 critical batch_size는 커지기 떄문에 저자들의 주장이 맞다면 target model training setup으로 갈 수록 batch_size를 적당히 키워주면 (왕도는 없어보인다), 안정적인 HP transfer를 하는 데는 문제가 없다는 것 같다.
(2024 April) Observations from Tele-FLM
그 다음은 Tele-FLM Technical Report라는 중국 기관에서 PLM 학습에 muP를 사용한 것에 대한 내용이다. 먼저 연구진은 small scale proxy model을 target model과 대비해 head 갯수, hddein size, FFN hidden size만 다르게 설정하고 나머지 layer 갯수와 context length, vocab size등은 똑같이 유지했다.
 Fig.
Fig.
 Fig.
Fig.
여기서 identical dataset에 대해서 trasnfer가 된다는 것은 좀 잘못된 얘기 같은데, 정확히는 identical data distribution이라고 해야 할 것 같다. 왜냐면 TP-5에서도 GPT-3를 실험할 때 dataset의 일부 (subsampled dataset)만 사용해 학습한 model로 transfer를 헀기 때문이다.
 Fig.
Fig.
여기서 small scale model로 grid search한 HP는 다음 figure에 나오는 7개 인데,
 Fig.
Fig.
최종 9개의 후보군에 대해서 시간에 따른 training loss curve와 grad norm curve를 그린 것이 바로 아래의 figure이다.
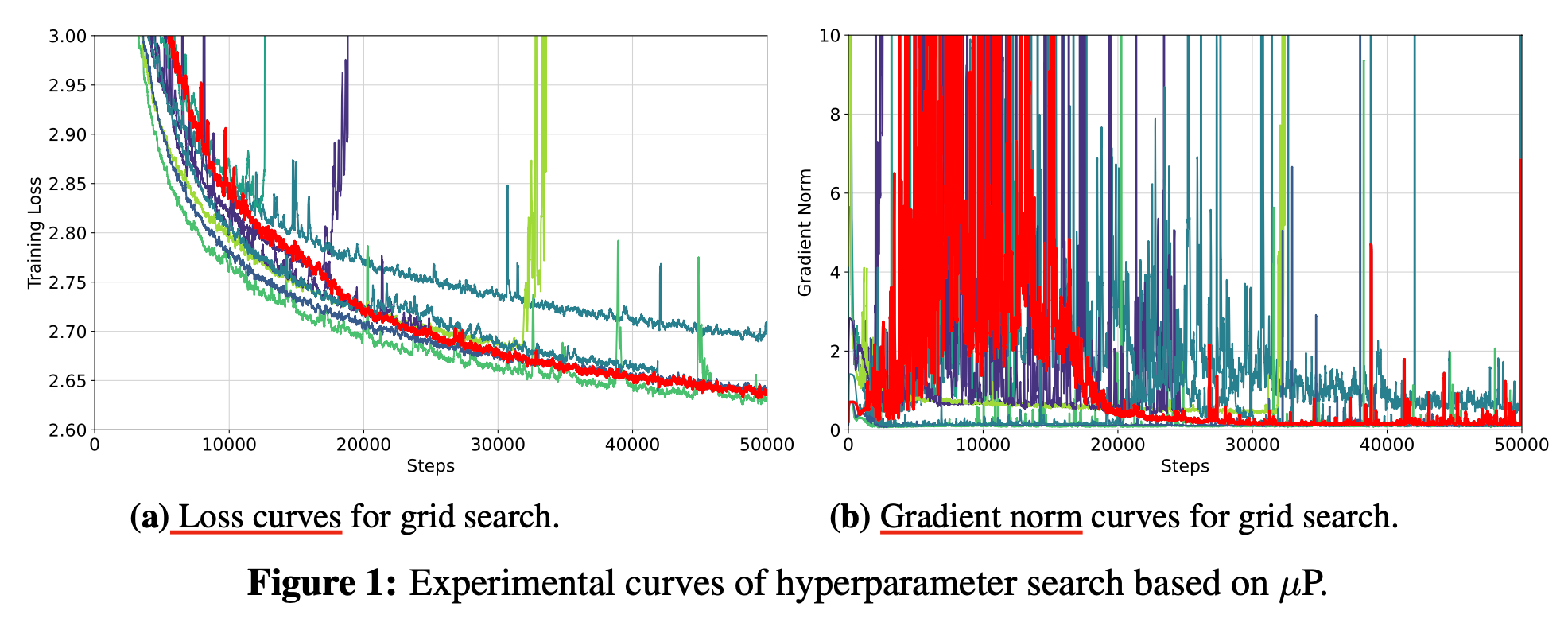 Fig.
Fig.
여기서 가장 좋은 curve가 red curve였기 때문에 이것의 HP를 traget model인 52B size model로 transfer했다고 한다. (앞서 TP-5의 numerical instability에서도 느꼈겠지만 muP를 쓴다고 grad norm이 튀지 않는 것은 아니다. 왜냐면 muP는 어떤 optimization timestep에서 activation output의 norm이 width에 상관없이 constant scale이 되도록 parameterization하는 것일 뿐이기 때문이다. 즉 이 값이 엄청 크다거나, optimization steps가 늘어날수록 점점 커진다던가 하는건 알 바가 아니다)
어쨌든 Tele-FLM team은 아래 table 4처럼 master lr을 비롯한 multipler, std를 얻게 되었다. 물론 다 얻은 건 아니고 어떤 scheduler를 써야하고 batch_size를 써야하는지 등등은 찾지 못했다.
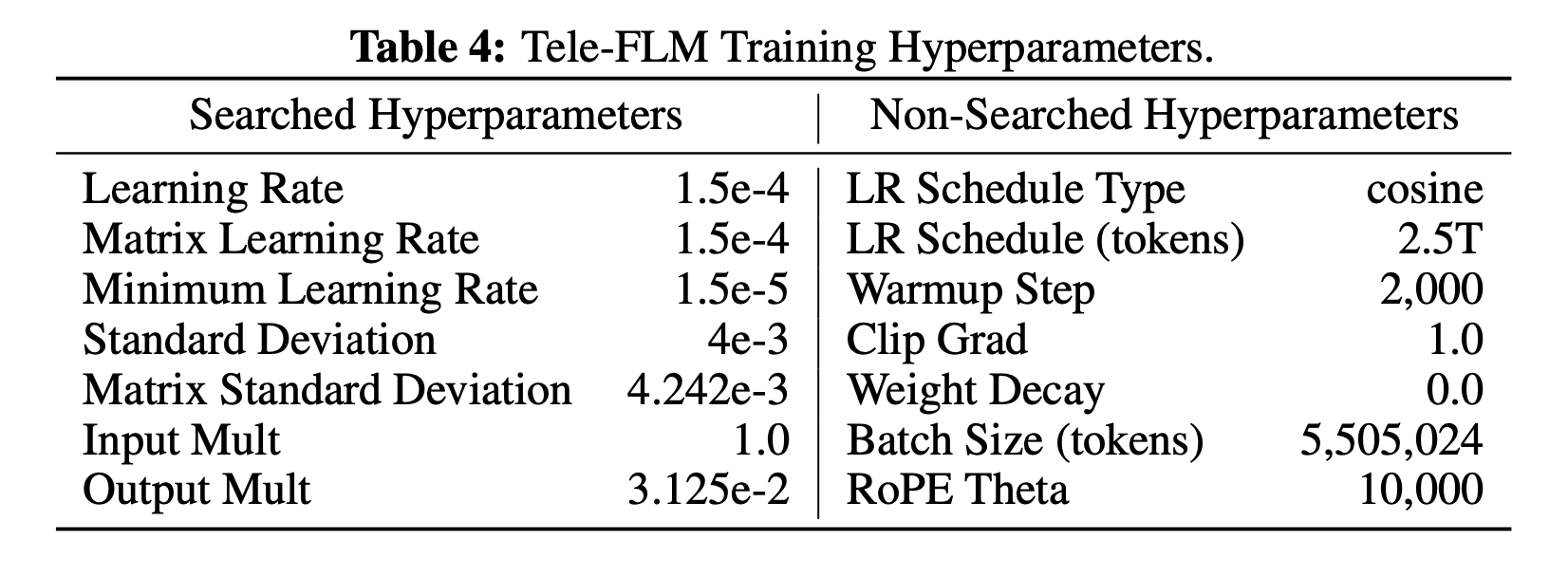 Fig.
Fig.
실제로 muP를 적용하려는 practitioner들은 Table 4의 HP value들과 앞서 소개한 Cerebras-GPT의 HP value들, 그리고 뒤이어 소개할 muP를 적용한 paper들에서의 HP search space와 optimal value값들을 잘 참고하길 바란다. 아마 구현 방법과 model architecture, dataset distribution에 따라서 value는 천차 만별일 수 있기 때문에 어느 하나를 맹신하기 어려워 보인다.
아무튼 이렇게 얻은 HP를 통해서 52B model을 학습하면서 단 한번도 loss가 발산 (divergence)하지 않았으며, validation loss도 saturation 되거나 overfitting해서 올라가지 않았다고 한다.
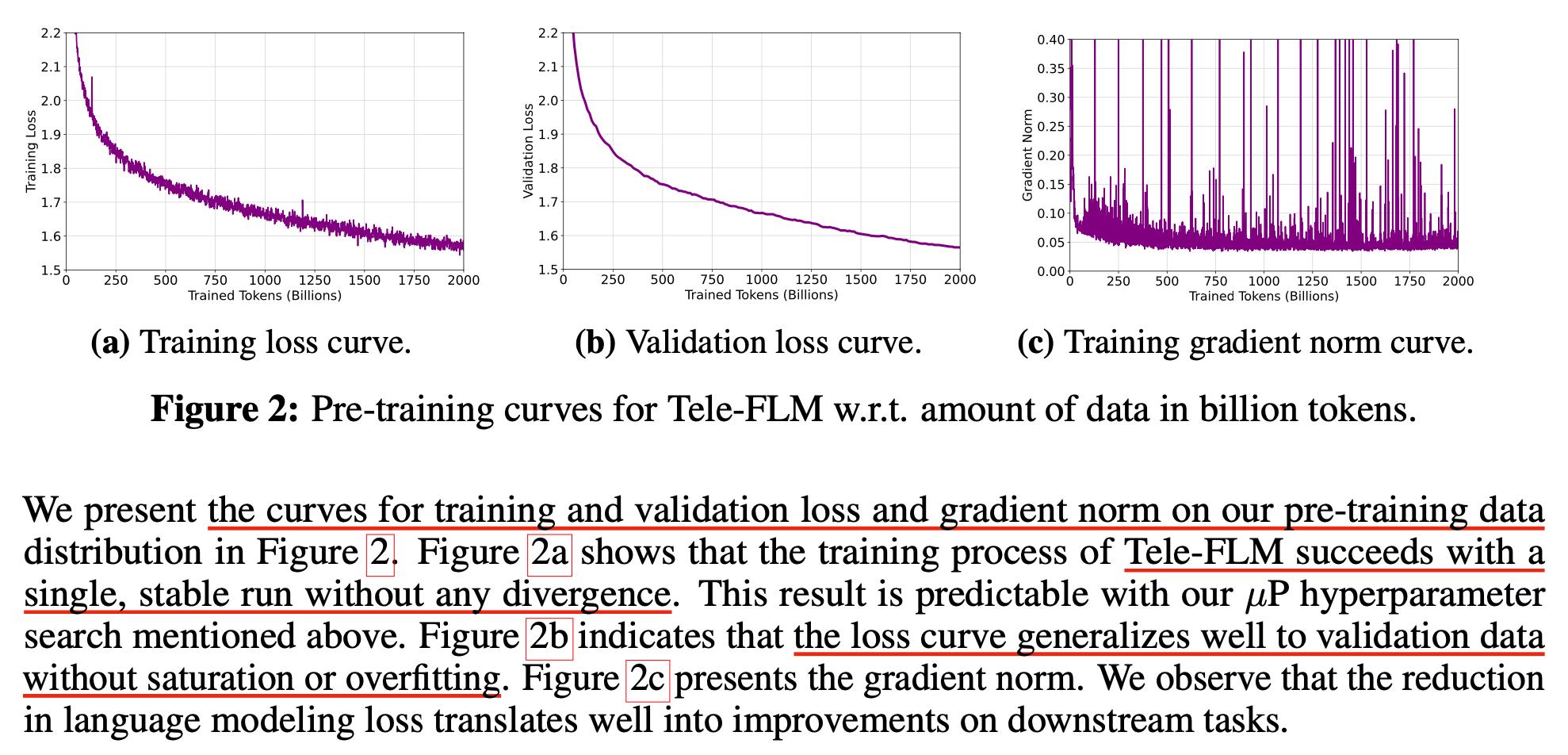 Fig.
Fig.
Tele-FLM은 en-zh (영중) 모델이기 때문에 english, chinese benchmark를 둘 다 평가했는데, corpus의 비율때문인지 model size gap 때문인지 정확히는 모르겠으나 MMLU같은 점수는 llama-3 70B에 못미치고
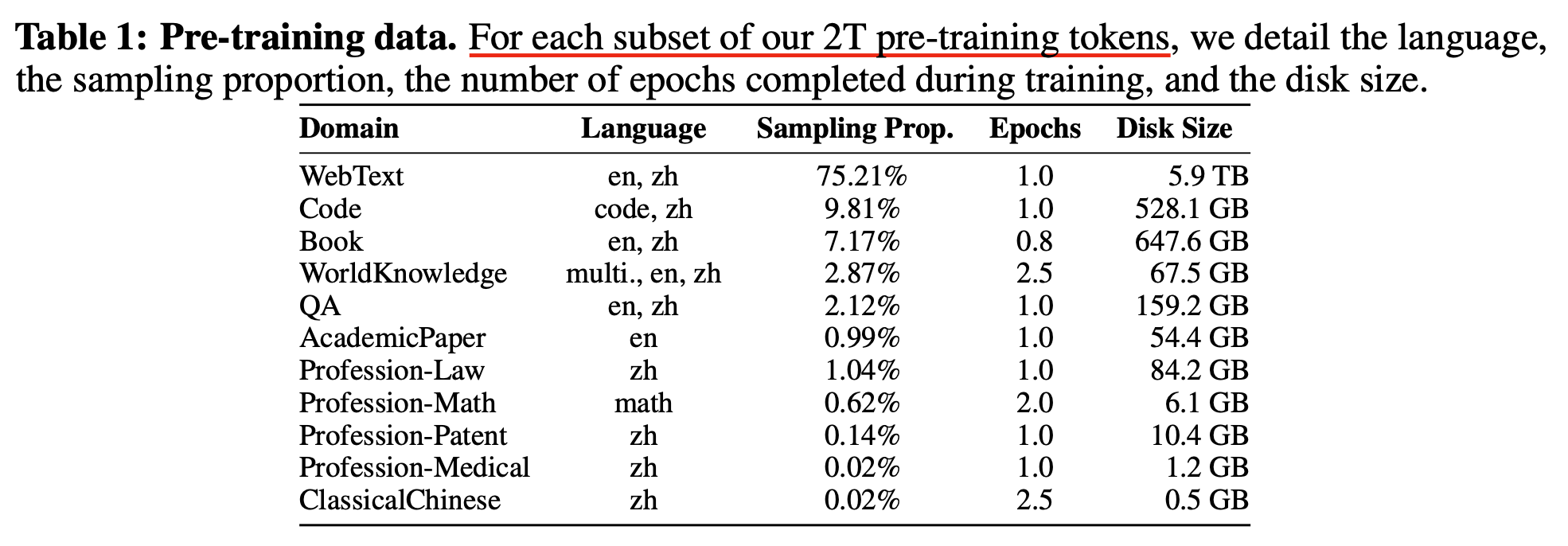 Fig.
Fig.
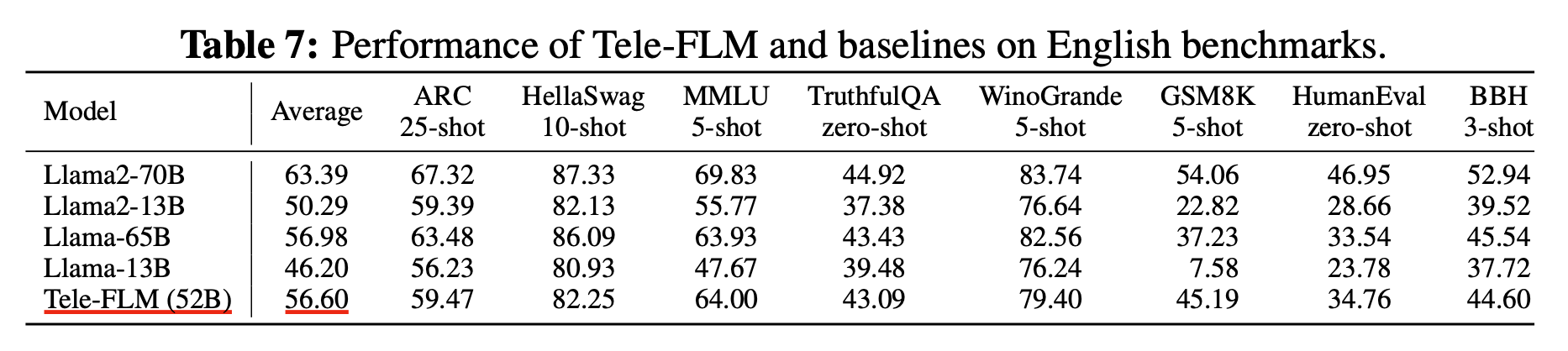 Fig.
Fig.
Chinese MMLU (C-MMLU)를 비롯한 chinese benchmark도 Qwen에 비해 떨어지는 모습을 보여줬다. (내가 성능까지 확인하는 이유는 muP가 주장하는 것 처럼 maximal feature learning을 하는 것이 width에 따른 herustic LR scaling을 한 SP보다 좋은게 보장되는지 궁금하기 때문이다.)
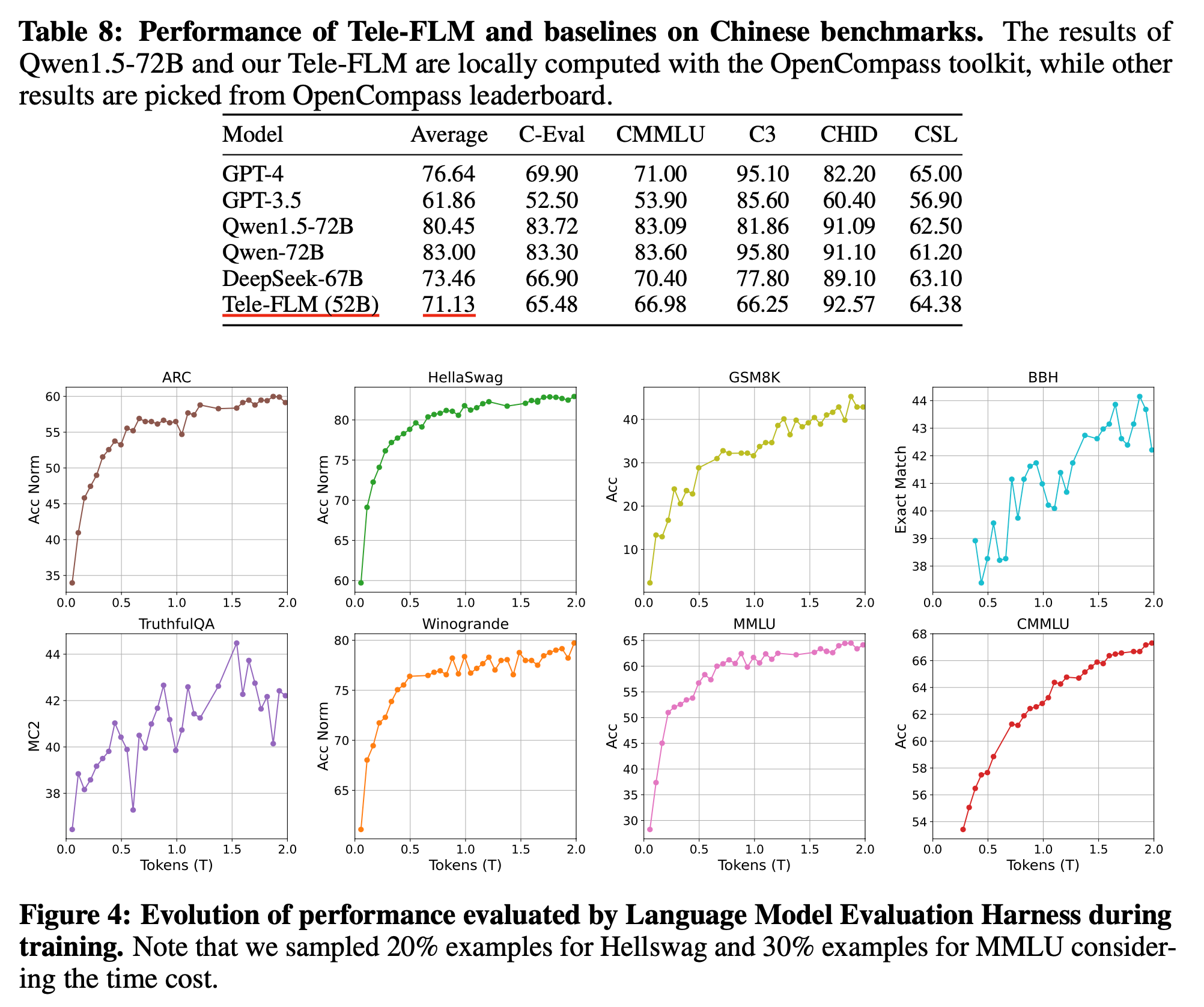 Fig.
Fig.
그런데 또 LLM 분야에서 쓰는 metric 중 PPL (Perpleixty)같이 쓰이지만 살짝 다른 Bits-Per-Bites (BPB)에서는 chinese에서 Tele-FLM이 더 좋은 성능을 보이긴 했다고 한다.
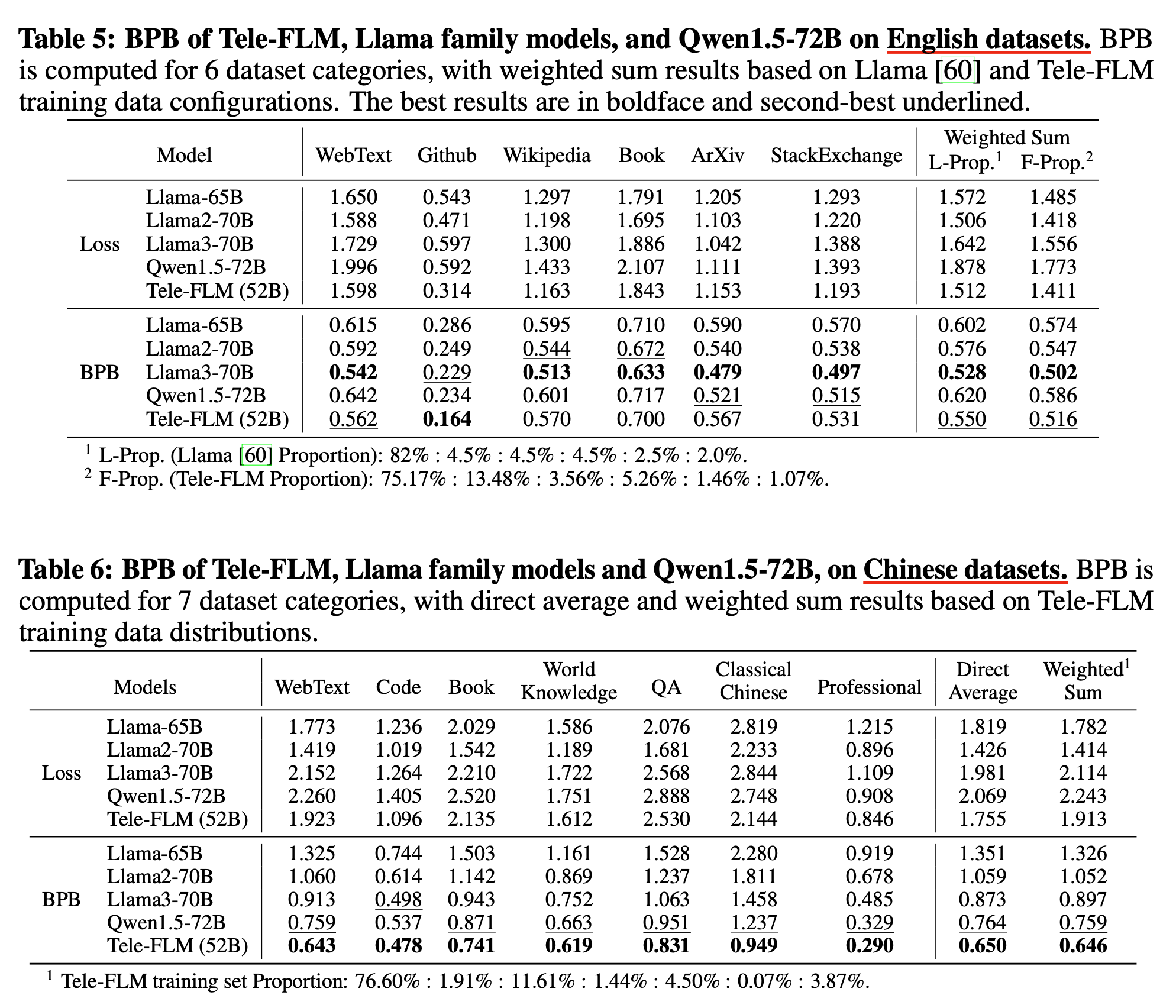 Fig.
Fig.
(2024 April) Observations from MiniCPM
이번에는 MiniCPM의 내용을 보자. 이것도 muP를 reference한 몇 안되는 paper 중 하나로 꽤 재미있는 결과가 많은 paper이다. 이 paper에서도 muP를 사용해 training stability를 높혔다고 하는데, 실험은 model size, \(N=0.009B\)에 대해서 실험했고 dataset 크기는 \(\vert D \vert = 10N = 0.09B\)에 대해서 했다. MiniCPM의 target model size와 dataset size (token 수)는 다음과 같은데,
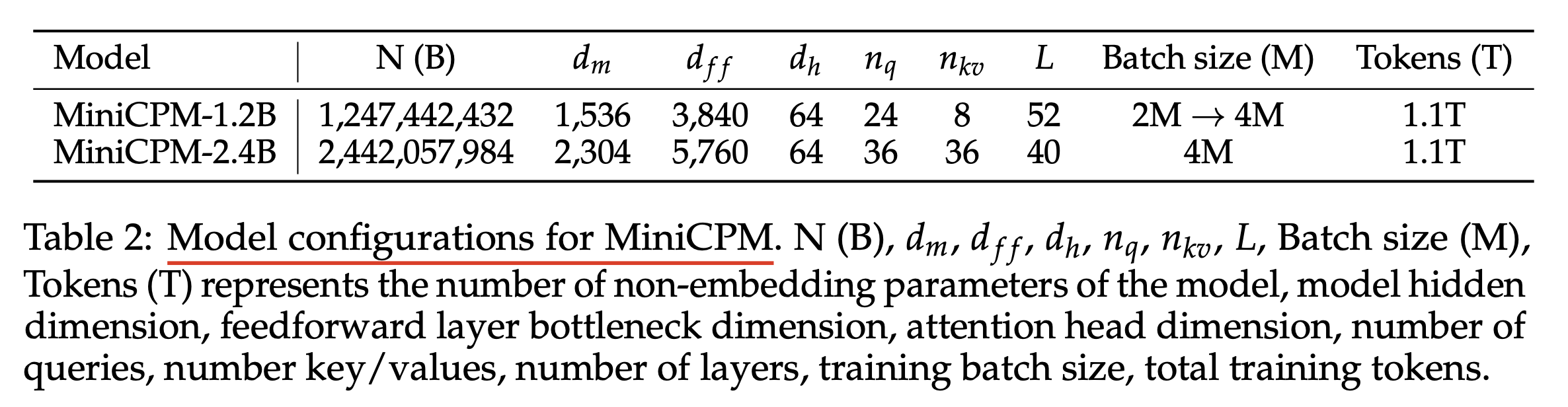 Fig.
Fig.
실제 \(1.1T\) tokens에 대해 학습해야 하지만 proxy model을 학습할 때는 그의 \(1/100\)정도 되는 \(0.09B\)로 down sampling 해서 HP search를 해도 문제가 없다는 것이다 (실험 결과). (사실 muP에서는 전체 dataset의 몇%로 proxy model을 학습해야 하는지? proxy와 target model의 batch_size를 어떻게 해야하는지? 등등에 대한 언급은 잘 없었다)
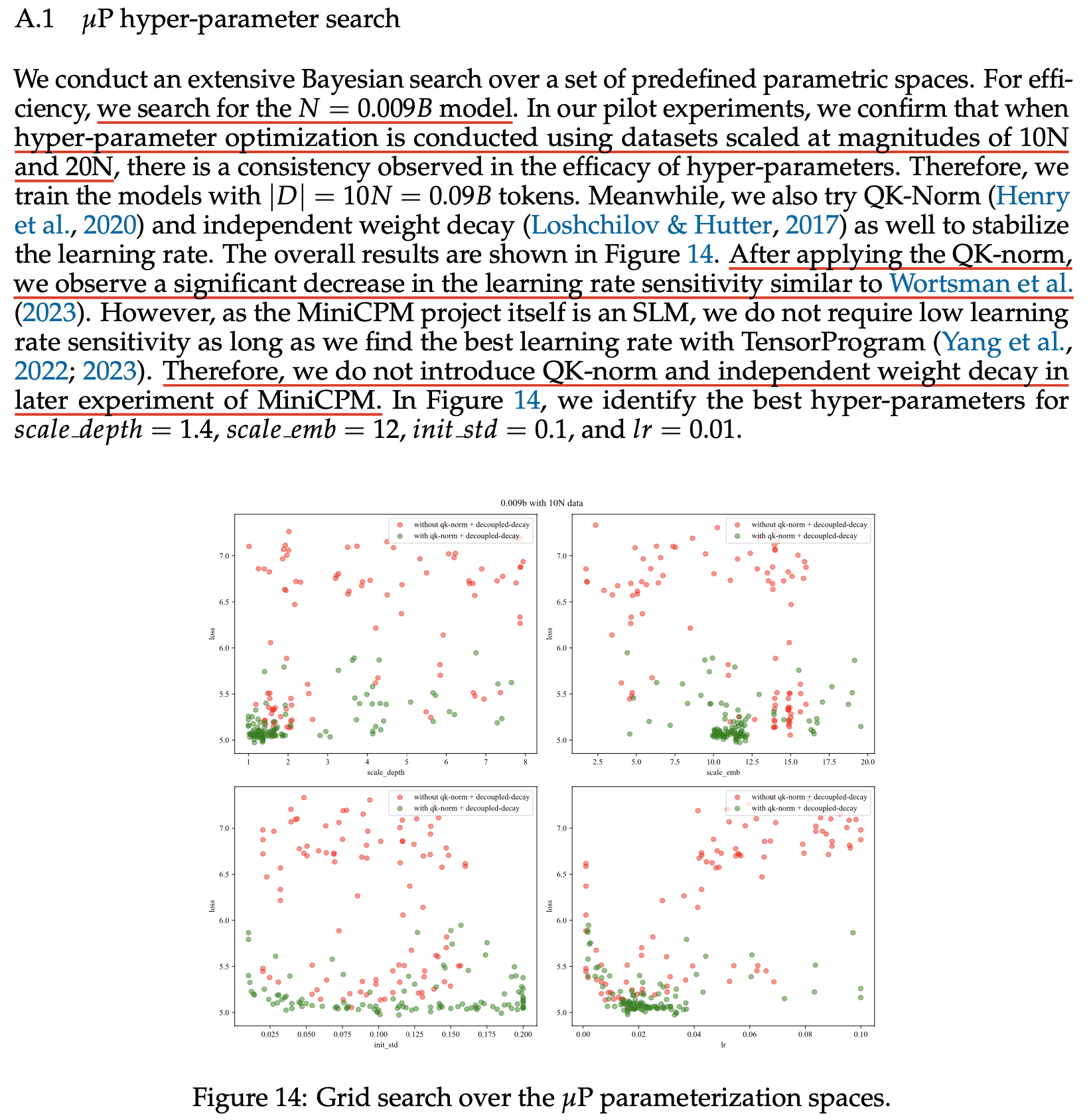 Fig.
Fig.
MiniCPM에서는 추가적으로 QK Norm와 AdamW도 적용해서 실험해봤는데, 이것들도 모두 training stability를 위한 것들이다. Pre-training에서 가장 중요한 것은 gradient가 exploding하거나 vanishing하지 않으면서 loss가 계속 떨어지는, 즉 feature learning을 하는 것인데, 이를 달성하기 위해서는 muP든 뭐든 필요한건 다 해야 하는 것이다. 결과적으로 paper에서는 muP를 적용하면 QK norm은 별로 효과가 없다는 것이 증명되었는데, 이는 QK Norm paper에도 증명된 것이다. 별개로 요즘 핫한 LLaMa-3같은 model은 QK norm도 적용되었고, QKV layer에 bias도 stability를 위해 제거했다 (요즘 거의 국룰인듯함).
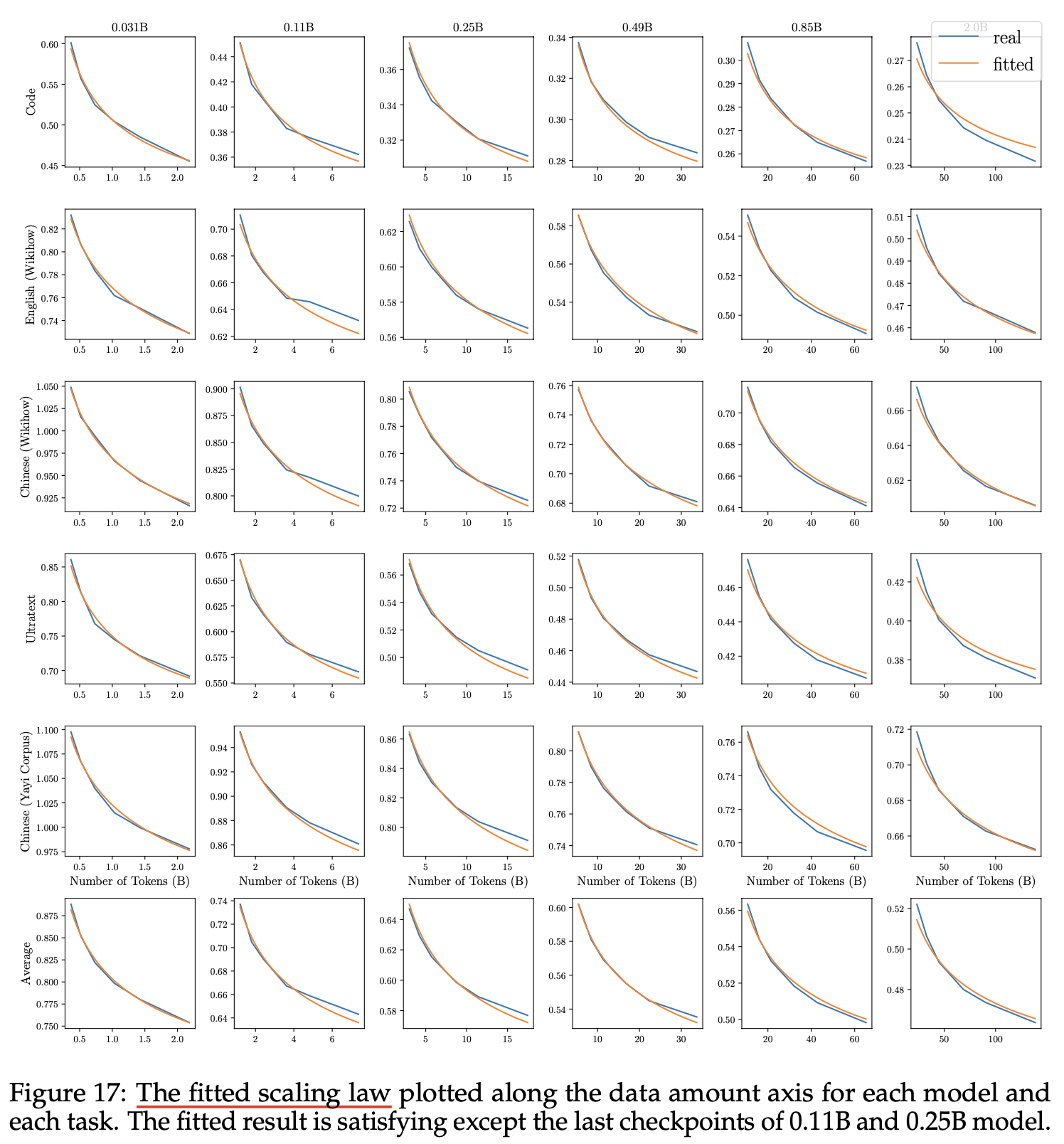 Fig.
Fig.
여기서 scale_depth는 TP-6에 등장하는 개념인데, 여기서는 depth scaling을 할 때 residual block별로 std를 어떻게 설정해줘야 하는지에 대한 내용이 있으며 MiniCPM은 이것까지 적용했다고 볼 수 있다. 이를 위해서 다른 muP를 적용한 paper들과 다르게 attention logit을 \(d_k\)가 아닌 \(\sqrt{d_k}\)로 scaling했다고 한다.
 Fig.
Fig.
이번에는 TP-6까지 cover할 생각이 없기 때문에 넘어가도록 하겠다. (관심있는 사람들은 MiniCPM과 TP-6를 보도록)
(2024 April) A Large-Scale Exploration of muTransfer
A Large-Scale Exploration of μ-Transfer에는 LLaMa와 같은 Noam architecture (GLU variants, RoPE, pre-norm, RMSNorm, no bias)에 대한 muP transfrability 정보가 많이 담겨있다. 그리고 batch size나 weight decay에 대한 내용도 포함되어 있다.
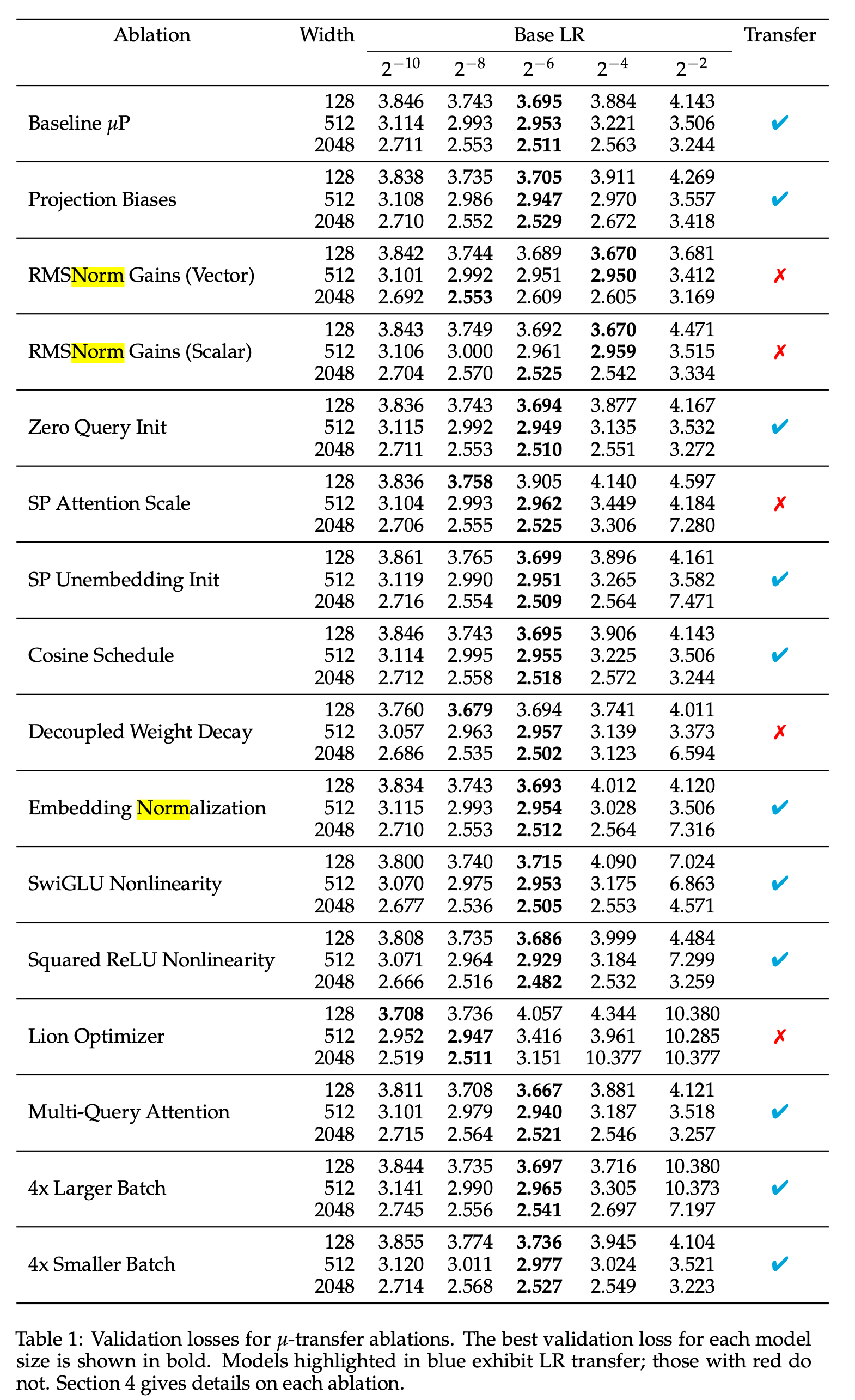 Fig.
Fig.
자세한 내용은 paper를 참조하길 권하고 이 중에서 몇 가지만 살펴보려고 한다.
모든 실험은 GLU variants를 사용하지않은 (2 layer FFN) Noam architecture를 사용했고, hidden size, width를 \(M=HD\)로 정의했으며 \(H\)는 the number of head, \(D\)는 head dimension이고 \(D=128\)로 고정했으며, FFN size는 \(F=4M\)이다. 여기에 proxy model의 width는 \(P=128\)로 고정했고, bfloat 16 activation, gradient를 썼으며 default optimizer setting으로는 \(2^{18}=262K\) batch size와 \(125K\) total steps, \(10K\) warmup steps를 가졌으며, weight decay는 0으로 설정하고 \((\beta_1, \beta_2)=0.9, 0.98\), \(\epsilon=1\text{e-}9\)인 AdamW를 썼다. 모든 실험은 아마 C4 dataset와 T5 tokenizer, sequence length=256으로 setting된 것 같다.
해당 paper에는 batch size를 4배 키운 실험과, 1/4배로 줄인 실험을 하는데, 이는 TP-5의 LR transfer across batch_size 실험이 batch size는 바꿨으나 fixed training steps은 유지한 것과 다르게 realistic scenario에 맞게 training tokens를 유지했다. 즉 batch를 4배 늘렸으면 training steps가 4배 줄어든 것이다. 따라서 batch_size가 \(n\)배 늘어나거나 줄어들면 이에 따라 LR도 \(\sqrt{n}\) scaling하는 heuristic을 적용했고,

결과적으로 transfer가 됐다.
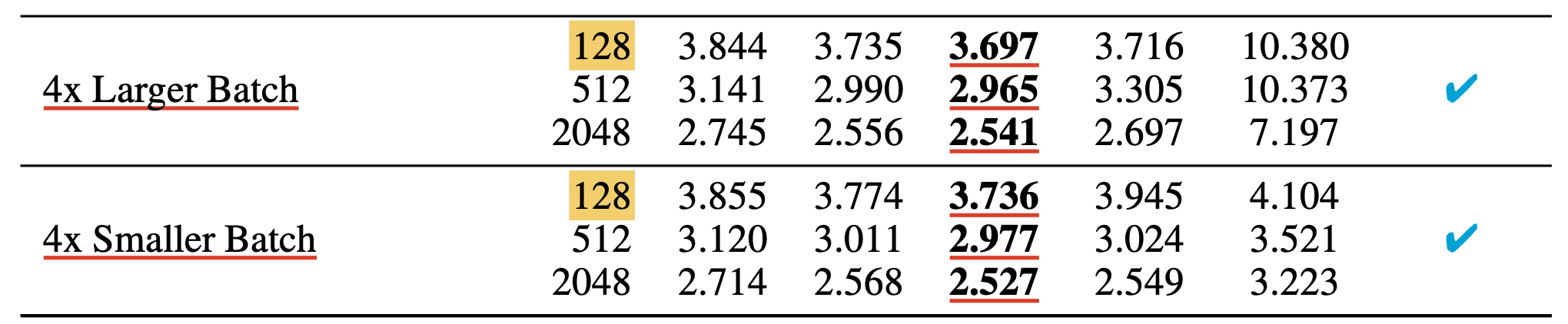
아마 많은 이들이 이 부분이 궁금했을텐데 실험결과가 늘어 도움이 될 것 같다. 하지만 realistic scenario에서는 batch size scaling은 물론 training tokens까지 scaling되기 때문에 이 실험까지 있으면 좋았겠지만 하는 생각이 든다. (최근 제안된 DeepMind paper등에서는 training tokens가 늘어나면 LR을 그만큼 줄여줘야 한다고 주장하는데 이에 대해 따로 이론은 없고 empirical result만 있다)
Lion optimizer에 대한 실험도 있는데, Adafactor와 마찬가지로 Adam variant를 쓸 때는 LR scaling rule을 더 신경써야 한다는 걸 알 수 있고, 아쉽지만 smallest model에서의 optimal LR은 transfer되지 않았으나 그럭저럭 되긴 한다는 것 같다.

이 밖에도 많은 실험이 있으니 참고하면 좋을 것 같지만 해당 paper는 LR sweep range를 \(2^{-10}~2^{-6}\)까지 4배씩 하면서 값을 찍어봤다던가 (LR에 대해서만 sweep) 하는 limitation이 있으니 이런 점을 감안해야 할 것 같다. AdamW optimizer의 weight decay term에 대한 얘기가 있는데, 이 부분은 muP를 사용한 후속 연구들과 상충되는 내용이어서 다루지 않으려고 한다. 요약하자면 pytorch 같은 library의 구현체는 weight decay에 parameter의 LR이 곱해지게 되는데 (구현 문제나 Adam과의 consistency 등 여러가지 이유로), muP는 LR이 1/width scaling되기 때문에 이를 피해야 하는게 정상이지만 (왜냐면 decay는 transfer가 안됨) 해당 paper에서는 pytorch default가 더 좋았다는 것이다. 사실 small scale에서는 weight decay를 쓰지 않고 target scale에서만 쓰면 되므로 이 부분은 무엇이 참인지 가리지 않더라도 넘어갈 수 있기도 하다.
Grok
Greg Yang은 Microsoft에서 muP, muTranfer에 대해 연구하고,
OpenAI와 cowork을 한 뒤 현재는 x.ai에 있다.
그리고 x.ai는 얼마전 Grok이라는 314B 크기의 LLM을 공개했는데,
당연히 나의 관심사는 "그래서 Grok에도 muP 썼겠지?"이다.
그리고 정답은 yes이다. Unsloth Co-founder Daniel Han은 open weight model이 공개될 때 마다 이를 분석하는 tweet thread을 쓰는데, 여기를 보면 다음과 같은 detail들이 있음을 알 수 있다.
- Mixture of Expert (MoE)를 사용
- Tie Embedding
- QKV 에 bias가 있고 MLP에는 bias가 없음
- Grouped Query Attention (GQA) 사용
- muP like input, output, attention logit scaling
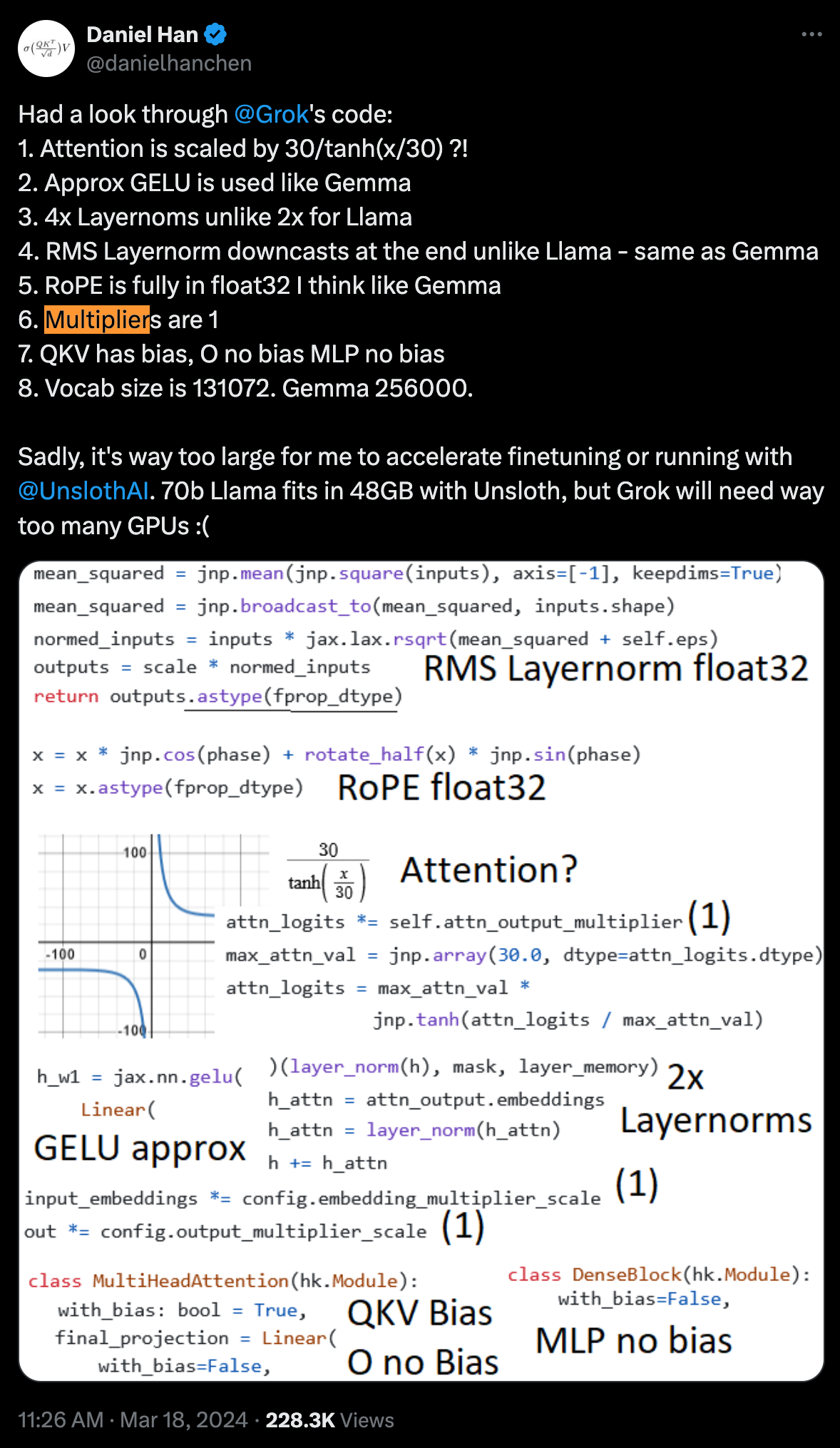 Fig. Source from tweet thread
Fig. Source from tweet thread
그리고 input, attn, logit multiplier가 설정되어 있는 걸 알 수 있는데, 이들은 muP를 적용한 흔적이라고 유추할 수 있을 것 같다. (다만 GQA, depth scaling이 고려된 값일 수 있다)
 Fig. Source from tweet thread
Fig. Source from tweet thread
또 특이한 점은 logit 값을 특정 range에 bound되도록 처리해줫다는 것인데, 아마 qk-norm처럼 logit이 blow up 하는걸 방지하기 위해서 그런 것 같다.
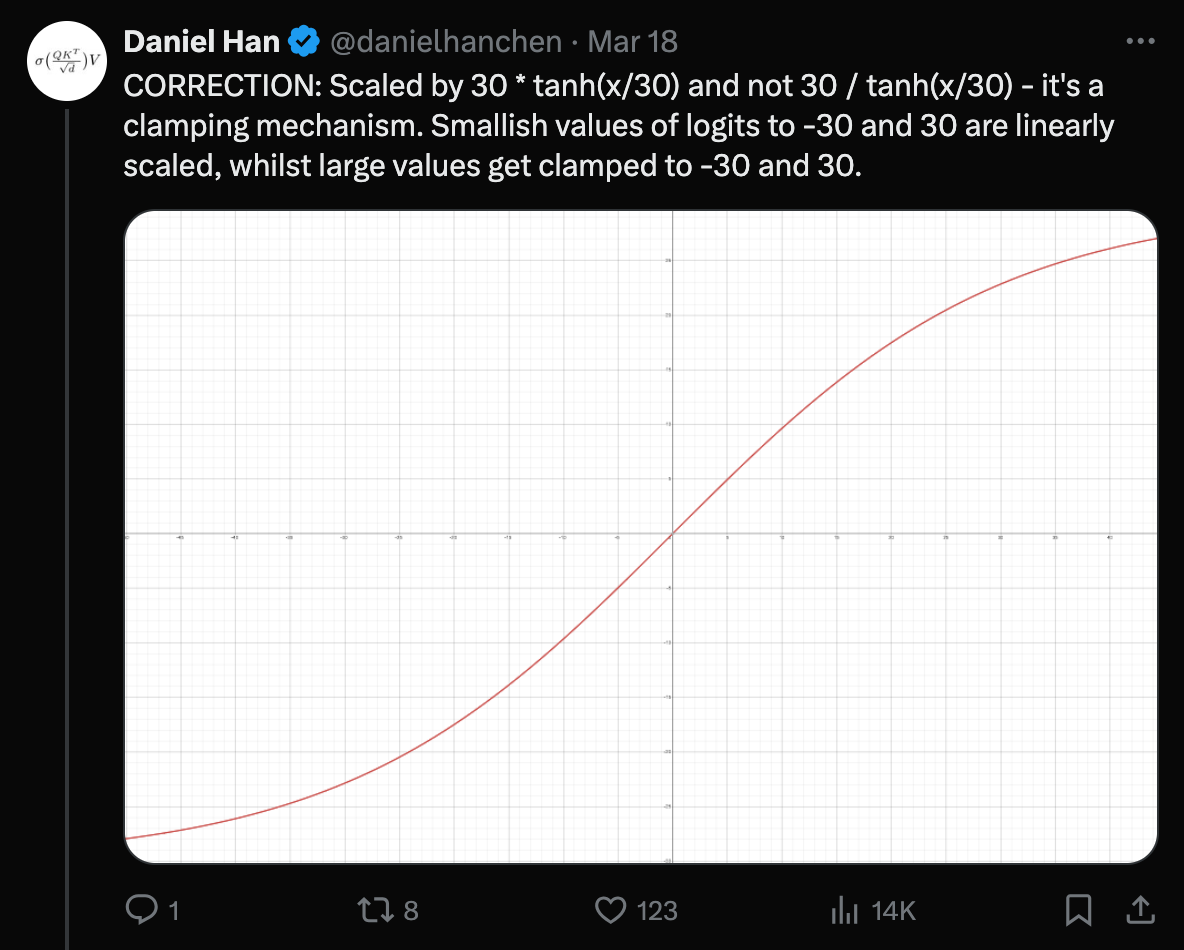 Fig. Source from tweet thread
Fig. Source from tweet thread
Open weight model들이 그러하듯 init_method는 어차피 weight을 제공하기 때문에 따로 code를 공개하지 않았다.
+Updated) 오늘 (28th Jun 2024) drop된 Google의 GEMMA 2를 보면 Grok과 비슷한 attn logit scaling trick을 쓴 것 같다.
 Fig.
Fig.
아마 training stability를 위한 아래 세 가지는 orthogonal하여 다 같이 적용해도 될 것으로 보인다.
- qk-norm
- muP
- (attn, output) logit soft scapping
하지만 나는 아직 실험을 안해봐서 어떤 부분에서 충돌이 있을지는 모르겠다.
+Updated) (2024 April) Phi-3
Open weight Small LLM (SLM) model중 가장 강력한 Phi-3에서도 muP를 사용한 흔적이 발견되었다. Phi-3가 Greg, Edward가 있던 Microsoft이므로 당연한 것 같지만, 다시 한 번 효과가 증명이 됐다고 볼 수 있을 것 같다.
 Fig.
Fig.
(Technical report에는 짧게 언급만 있을 뿐 별다른 training detail은 없음)
+Updated) (2024 July) Apple Foundation Model (AFM)
Another day, another muP.
오늘 publish된 Apple Intelligence Foundation Language Models에도 muP가 사용됐다. Apple Foundation Model (AFM)에는 on-device용 2.5B non embedding parameter size model과 server side의 model에 대한 pre-training setupt등을 공개했는데,
 Fig.
Fig.
Small-scale proxies for large-scale Transformer training instabilities에서 사용한 simple muP를 사용했다.
이는 muP에서 hidden weight의 optimizer LR만 base model 대비 width, \(1/n\)배 scaling 해준 것이고,
small scale proxy model에서 LR sweep만 했는데 (당연하게도 LR만 바꿨으니 multiplier는 없다) optimum LR이 \(0.01 \sim 0.02\)정도로 나왔기 때문에 보수적으로 \(0.01\)을 썼다고 한다.
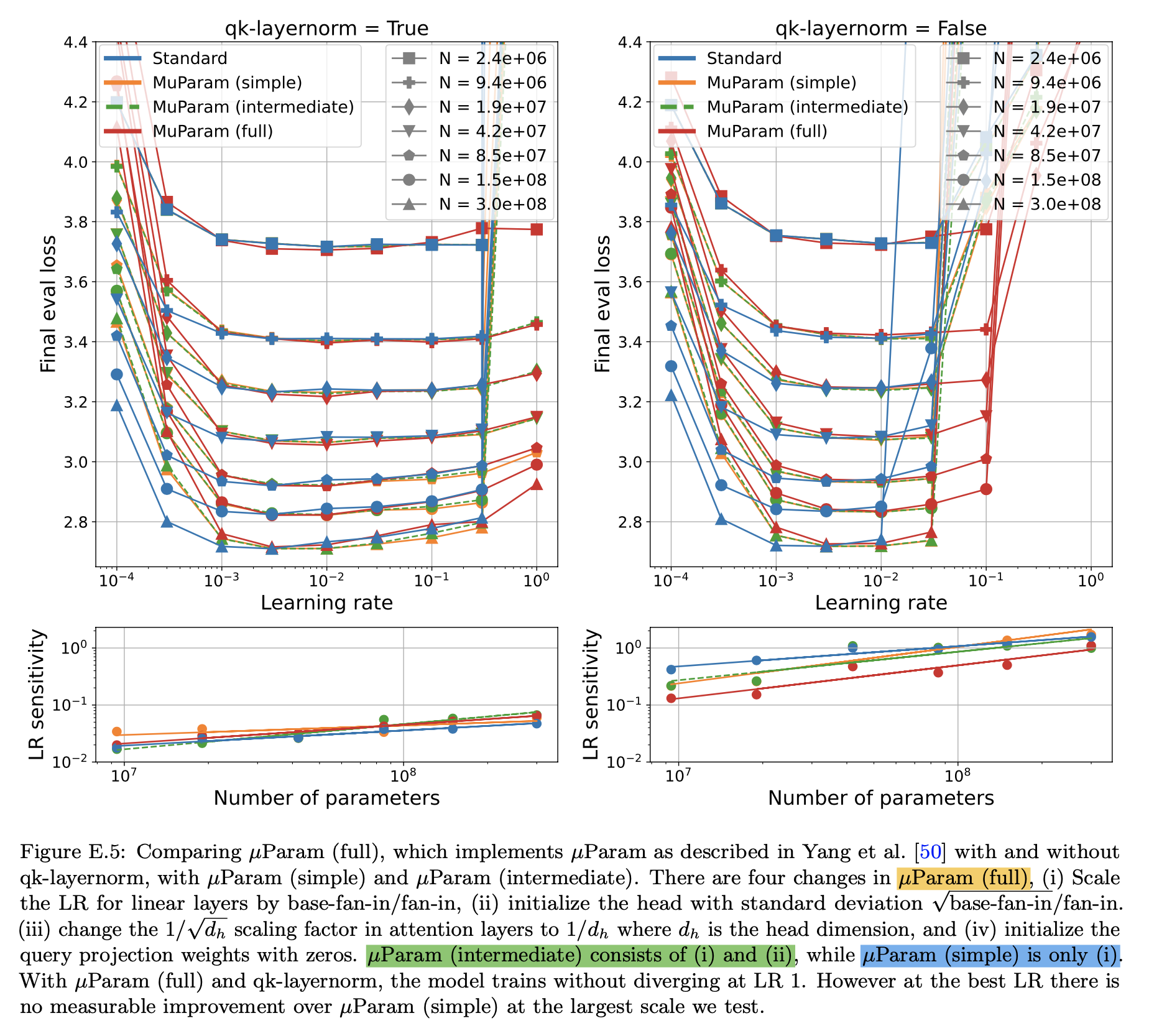 Fig.
Fig.
보수적으로 \(0.01\)을 쓴 것은 muP를 사용하는 후속 paper들에서 주장하길 optimum transfer는 fixed dataset에 대해서 성립하고 training tokens가 늘어나면 작은 값으로 left shift하는 경향이 있다고 하는 것을 생각해 보면 맞는 선택이었던것 같고, 저자들은 muP에 의해 hidden weight이 base LR 대비해서 \(0.1\)배 scaling됐다고 하니 width는 대략 \(10\)배 정도 큰 것으로 생각하면 된다. 즉 AFM이 small scale로 \(768\) hidden dimension을 선택했으니 \(\frac{1}{(8192/768)}\approx 0.1\)이므로 \(8192\) hidden을 썼다면 MMLU 성능과 함께 유추해 봤을 때, AFM-server의 model size는 대략 70B지 않을까 싶다. 여기에 Adam optimizer를 쓴 것이 아니라 RMSProp variant를 썼다고 하니 muP와의 정합성 문제가 있을 수 있지만 QK-layernorm 등을 사용했으니 큰 문제가 없었던 게 아닐까 싶다.
 Fig.
Fig.
좀만 더 얘기해보자면 llama-3 등 modern llm 들의 training setup reference들을 보면 대충 8B는 3e-4, 70B는 1.5e-4정도를 쓴다. 그런데 hidden weight에 대해서 AFM은 \(0.01 \times 0.1 = 0.001\)이 되므로 llama-3 70B가 near optimal일 것이라는 가정을 해보면 이것보다 6~7배는 큰 LR을 썼음에도 학습에 성공한 것이다. 이 부분에 대해서는 아마 QK layernorm 덕이 크지 않았을까 싶다. 그리고 batch size를 deepseek style로 power curve fitting했다고 하는데, chip utilization 때문에 optimal batch size보다 성능을 조금 손해보더라도 큰 batch를 썼다고 한다 (이게 MFU는 아닐거같고 그냥 빨리 끝내려고 한게 아닐까 싶다). 이 대목에서 왜 small scale proxy의 hidden size를 128같은걸 쓰지 않았는가?에 대한 힌트를 얻을 수 있을 것 같은데, 보통 vocab size가 커지면 model이 작아도 batch size를 크게 늘릴 수 없고, 이에 따라 model size를 키워 utilization을 채우는 것이 target model size와의 discrepency gap도 줄일 겸 좋기 때문에 그런 것 같다.
Apple은 muP vs SP (+로 optimizer 비교) 검증하기 위해 on-device model을 3.1T tokens 학습하여 benchmark performance를 비교했다.
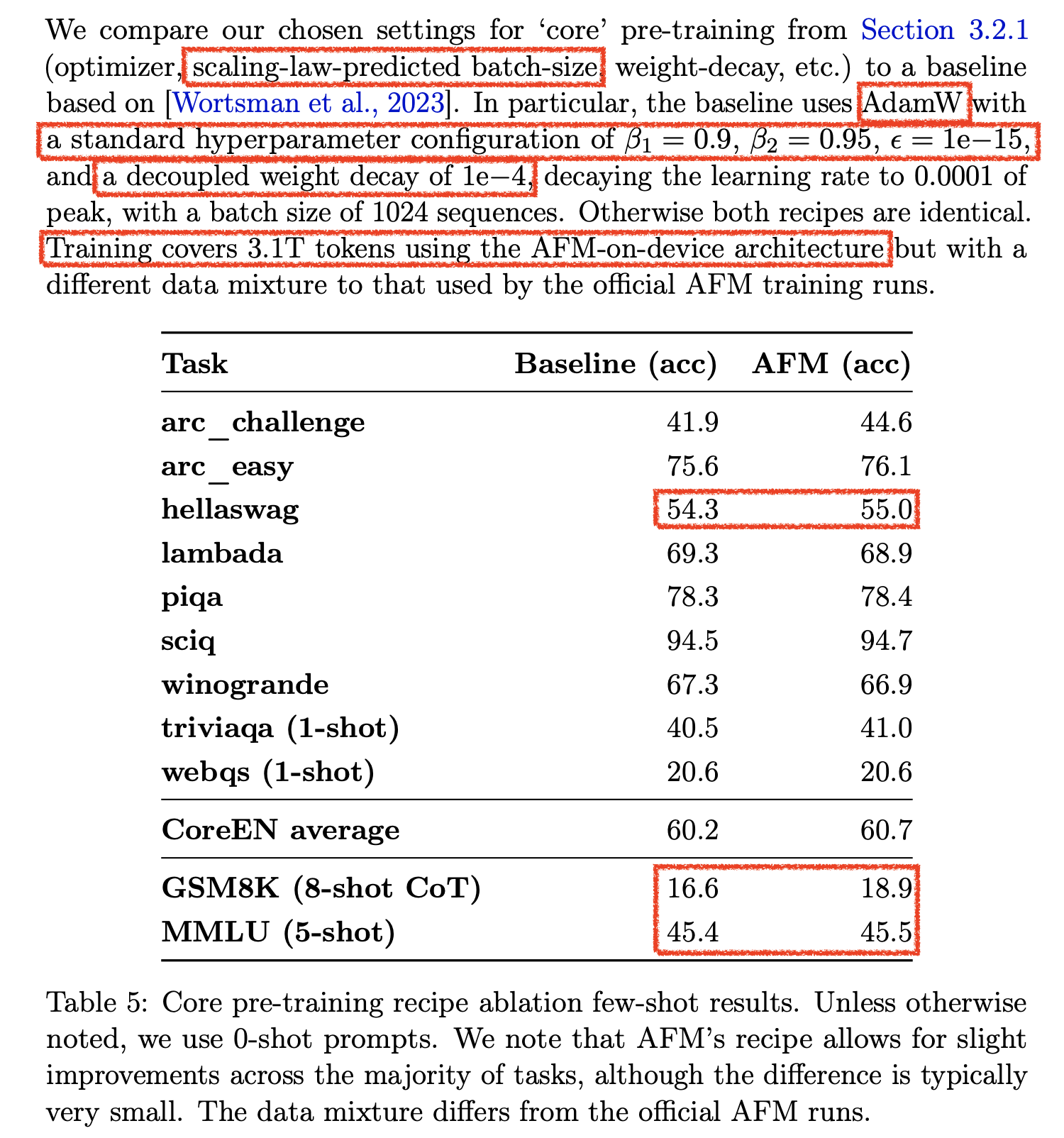 Fig.
Fig.
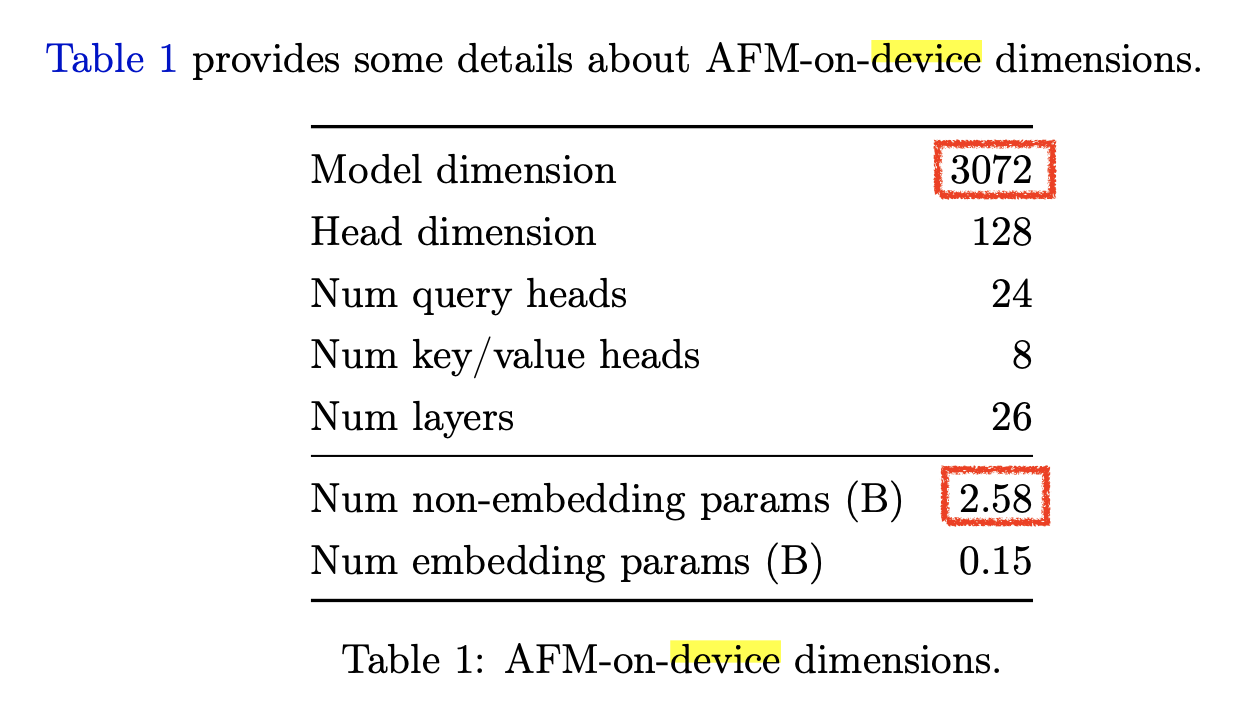 Fig. on-device model size
Fig. on-device model size
Llama-3 얘기가 나온김에 얘기를 조금 해보자면,
llama-3는 8b, 15T scale에 3e-4, 70b, 15T scale에 1.5e-4를 썼다.
사실 llama-3는 어떤 paramterization을 사용했는지 알려진 바가 없으며,
llama-2에 비해 학습량이 8배 이상 증가했음에도 불구하고 lr은 그대로 3e-4를 썼기 때문에 이것이 optimal인지 조차 의심스럽지만 조심스럽게 유추해볼 수 있는 부분은 width가 8b에서 70b로 갈 때 4096 -> 8192가 됐기 때문에 2배 증가했고, 이에 따라 lr이 1/2배 됐다는 것이다.
이는 width가 늘어남에 따라 global LR을 1/n 했다는 것은 muP의 핵심이 hidden weight에 대해서 1/n LR scaling을 해주는 것이기 때문에 어느정도 반영은 됐다고 볼 수 있고,
embedding에 특별히 scaling을 해주지 않았더라도 embedding이 다른 hidden weight과 training time동안 균일하게 학습되진 않더라도 lazy training될 것이기 때문에 어느정도 학습된 결과는 비슷할 수 있을 것 같다.
별개로 앞서 말한 것 처럼 embedding이나 readout에 대해서는 아마 scaling을 해주거나 fanout init을 해줬을 것 같은데, 그 이유는 fairseq에 이미 이런 technique들이 적용되고 있기 때문이다.
 Fig.
Fig.
More Details for Implementing muP
Parametrization Terminologies abd Further Explanations of the muP tables
이번 section에서는 앞으로 모든 새로운 model architecture 에 대해서 muP를 잘 적용하고 학습하기 위해서 parameterization이란 무엇인지?,
multiplier란 정확히 무엇인지? 등에 대해 한 번 더 용어를 짚고,
특히 실제와 같은 Transformer based LM을 SGD가 아니라 Adam으로 학습하는 상황에 적용하기 위한 주의할 점 등에 대해 알아보려고 한다.
모든 내용은 주로 Appendix에 나와있다.
먼저 multipler는 말 그대로 weight matrix에 곱해지는 값인데 정확히는 다음과 같은 의미를 가지고 있다.
 Fig.
Fig.
먼저 multipler, \(c\)는 학습이 되는 값이 아니다.
어떤 NN의 parameter tensor, \(W\)에 대해서든 \(W\)는 \(cW\)처럼 scaling될 수 있다.
구체적으로 이를 parameter multipler라고 부른다.
예를 들어 attention logit은 sequence length가 \(L\)일 때 \(q, k \in \mathbb{R}^{L \times dim}\)에 대해서 \(q^{\top} k \in \mathbb{R}^{L \times L}\)가 되도록 내적하고 \(\sqrt{d_{head}}\)로 나눠주는 scaled dot product 를 하게 되는데, 이 \(<k,q> / \sqrt{d_{head}}\)는 \(q = Wx\)인 weight matrix, \(W\)에 multipler, \(1 / \sqrt{d_{head}}\)를 적용한 것과 같다.
중요한점은 multiplier 는 일반적으로 initialization에 합쳐질 경우 backprop에 영향을 주기 때문에 흡수 될 수 없지만, 그럼에도 불구하고 학습이 끝나면 weight에 합쳐질 수 있다.
그 다음은 parameterization이라는 term인데,
이는 NN의 width가 변할 때 어떻게 HP가 변해야 하는지를 의미한다.
 Fig.
Fig.
즉 우리는 “1024 width에서는 lr을 0.0001로 하고 128 width에서는 0.01로 해야 돼”, 라고 생각할 것이 아니라 “width가 8배 늘었으면 weight init 혹은 lr을 ~~배 해줘야 해”라고 생각해야 한다는 것이고 이것이 parameterization 인 것이다. parameterization 은 아래 세 가지로 구성되는데,
a: per weight multiplierb: per weight initalizationc: per LR
이를 TP-4에서 이 3개를 abc-parameterization이라 부른다고 앞서 post의 introduction에서 얘기했다.

그리고 이 abc-parameterization 공간에서 SP, Neural Tangent Kernel (NTK)라는 paper에서 제안하는 Neural Tangent Parameterization (NTP) 등이 어떤 공간에 놓여지는지가 TP-4에 자세히 나와있는데,
 Fig.
Fig.
대충 SP는 보통 global lr을 모든 layer에 균일하게 적용하는데, 이 경우 trivial하거나 (init weight로부터 거의 움직이지 않음) unstable한 solution (하습 도중 diverge)을 제공할 수 있으며, NTP를 사용할 경우 커널 영역 (kernel regime)에서 NN학습을 해석할 수 있지만 이는 모든 layer들이 유의미한 Feature Learning을 한다는 관점에서는 동 떨어져 있으며, 이 모든걸 충족하는 유일한 solution은 muP뿐이다.
Matrix-Like, Vector-Like, Scalar-Like Parameters
TP-4, 5에서 저자들은 NN에 있는 parameter들의 dimension을 2 가지로 구분한다.
width, \(n\)이 증가할수록 차원이 증가하면 infinite라고 부르고 그게 아니면 finite이라고 하는데,
NN의 모든 layer들은 크게 세 가지로 나눌 수 있다.
Matrix-LikeVector-Like- Scalar-Like
이는 weight tensor에 width가 늘어나면 infinite로 향하는 차원이 몇개 있느냐?를 기준으로 삼은 것이다.
즉 weight matrix가 2차원이라고 생각할 때,
가령 MLP layer의 hidden layer가 \(W_{\text{hidden}} \in \mathbb{R}^{n \times n}\)이면 무한대로 늘어나는 차원이 2개이므로 matrix-like인 것이고,
front-end쪽 matrix는 input vector가 \(\mathbb{R}^{B \times d}\) (B=batch size, d=input dim)일 때,
n이 늘어나도 d는 유지되기 때문에 이 경우 \(W_{\text{emb}} \in \mathbb{R}^{n \times d}\)는 1개 차원만 무한대로 늘어나므로 vector-like이다.
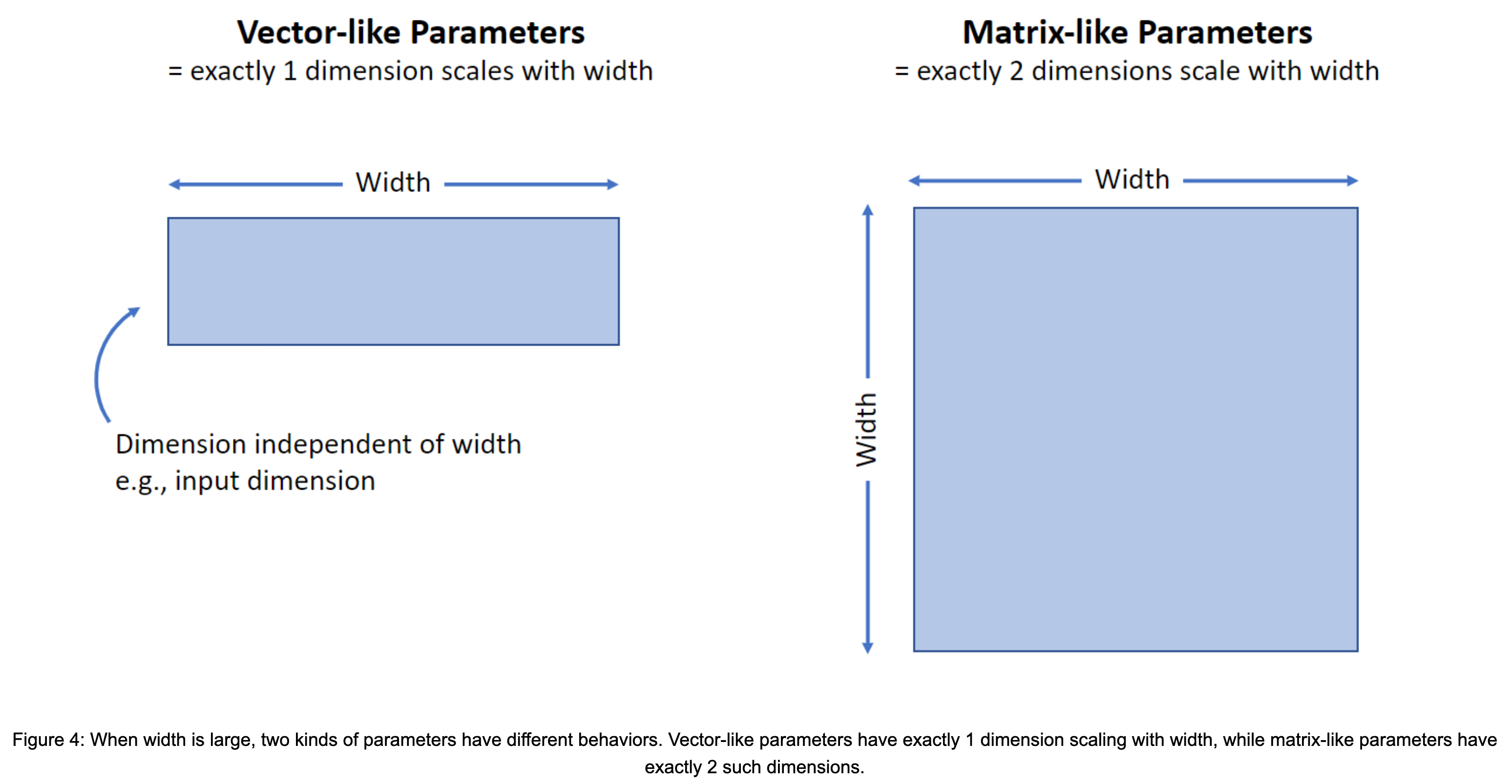 Fig.
Fig.
예를 들어 Transformer에서 \(d_{model}, d_{ffn}, d_{head}, n_{head}\)는 width에 따라 변하는 값들이지만, vocab size와 context size (?) 등은 변하지 않는다. 다시 이 셋은 다음처럼 표현할 수 있다.
- Matrix-Like : width에 따라 변하는 차원이 2개인 것
- 아래 vector-like를 제외한 모든 hidden weights
- Vector-Like : width에 따라 변하는 차원이 1개인 것
- 예를 들어 input weights (embedding layer weight), all biases, output weights
- Scalar-Like : width의 변화와 무관한 것 (0차원)
- 이 경우에 해당하는 weight은 거의 없지만 몇 가지가 있다.
 Fig.
Fig.
asdasdasd
3 tables of Implementing muP
앞서 muP를 구현하기 위해 각 weight tensor가 matrix-like냐 vector-like냐를 구분해야 한다고 했다. 그리고 이를 이용해서 예를 들어 Transformer architecture의 weight을 구분짓고 table을 아래처럼 만들 수 있었다.
 Fig.
Fig.
앞선 subsection에서 위를 basic form이라고 불렀는데,
이는 layer output에 곱해줄 tunable (not learnable) multiplier가 존재하지 않았다.
여기에 multiplier를 추가하면 아래처럼 table 8를 만들 수 있는데,
이를 사용해서 학습해도 table 3와 같은 결과가 나와야 한다.
 Fig.
Fig.
위 두 table에서 input weights, all biases 그리고 output weights는 모두 width가 늘어날 infinite dimension으로 가는 dimension이 1개인 vector-like이고, 중간에 들어가는 hidden weights들은 모두 matrix-like에 해당된다. 그리고 embedding, unembedding layer들은 fixed vocab size를 hidden dim으로, hidden dim을 fixed vocab size로 변환하는 infinite-to-finite type이므로 vector-like 이며, bias들도 모두 infinite로 팽창하는 dim이 존재하지만 차원 하나는 언제나 1차원이므로 vector-like이다 (여기서 bias는 항상 fan-in이 1이다). 그리고 multiplier는 우리가 한 번 이 값을 찾았으면 width를 키우더라도 계속 똑같은 값을 유지하고 각 layer output에 곱해줘야 하는 상수이다.
여기에 table 9까지 muP를 구현할 수 있는 table은 총 세 개가 되는데,
 Fig.
Fig.
이 셋은 모두 같다는 점을 우리는 이해해야 한다.
왜냐하면 앞서 말한 것 처럼 muP가 처음 제안된 TP-4에서는 abc-parameterization라는 것을 정의하는데,
우리가 forward, backward pass를 통해 parameter가 update되어 activation이 어떻게 변하는지를 유도해보면 layer output에 multipler를 적절히 해주거나 param update양을 조절하기 위해 lr에 어떤 값을 곱해주거나, init_std를 특정 범위로 정하는 것은 모두 같다는 결론에 이를 수 있기 때문이다.
즉 embedding weight, hidden weight, bias, unembedding weight 등에 대해서 위 세 가지 값이 다 다르다고 할 수 있다는 말인데,
여기서 multiplier를 모두 1로하면 그 반동으로 weight init variance와 LR에 scale 해줘야 하는 값이 변해야 한다.
table 3는 multiplier가 없는 가장 단순한 form이고,
table 8, 9는 abc-parameterization에 따라 multiplier를 이리 저리 바꾼 table이 되는 것이다.
여기서 "왜 이런 짓을 할까? 그냥 table 3 쓰면 안될까?"라는 생각을 할 수 있는데,
우리가 table 8, 9를 눈여겨봐야 하는 이유는 우리가 embedding, unembedding의 weight을 묶는 경우 (tie)를 고려했기 때문이다.
이는 transformer 에서 흔한 approach인데,
특히 vocab size가 큰 LLM의 경우 (예를 들어 llama-3는 거의 125k) embedding weight matrix는 [vocab_size X hidden]의 크기를 갖게 되는데 이 값이 매우 크기 때문에 model deployment 측면에서 손해가 막심하기 때문이다.
Embedding weight이 차지하는 비율은 model size가 적당히 큰 small LLM에서 더 크기 때문에 최근 나오는 Phi-3같은 2.7B수준의 model에서는 필수적이다.
또한 memory 관점이 아니더라도 one-hot vector를 embedding space로 보내는 것과 last hidden을 다시 vocab dimension으로 보내는 것은 기능이 같기 때문에 weight tying은 자연스러운 발상이지만,
이 경우 table 3를 사용할 수 없다.
그 이유는 당연하게도 embedding, unembedding weight matrix를 서로 다른 init_std로 init하기 때문인데,
table 8, 9의 경우 embedding, unembedding weight matrix 모두 init_std를 같은 값으로 준다는 걸 알 수 있다.
width scaling을 해주더라도 같은 값으로 scaling해주기 때문에 이 경우 embedding, unembedding은 같이 묶일 수 있게 된다.
그리고 당연하게 같은 weight matrix에 대해서는 optimizer group을 하나 밖에 할당할 수 없기 때문에 LR도 똑같이 흘러야 하는데,
이 것도 성립한다.
(여기서 front-end의 embedidng의 경우 fan_out은 vocab_size를 의미하고 fan_in은 1을 의미한다는 것을 알아야 한다.
그 이유는 embedding layer의 vocab_size는 변하지 않고 고정된 값이기 때문에 scaling해주지 않고,
실제로 이 layer가 하는 일은 one-hot vector를 hidden_size의 soft embedding으로 변환해주는 것이기 때문에 fan_out은 hidden_size가 되는 것)
그런데 우리는 unembedding weight의 gradient는 너무 크기 때문에 discount해주고,
embedding weight의 gradient는 너무 작을 것이기 때문에 boosting해줘야 한다는 철학은 유지해줘야 한다.
그렇기 때문에 multiplier를 곱해서 이를 해결하는 것이다.
예를 들어 어떤 NN의 맨 앞단 (embedding 부근)의 init이 아래와 같을 때,
\[h^{1}(\xi) = W^1 \xi, \text{ where } W^1 \sim \mathcal{N}(0, \sigma^2), \text{ lr } = \eta\]weight, \(W^{1}\)의 1 step SGD weight update는 loss, \(L\), input \(\xi\)에 대해서 아래와 같다.
\[W^{1}_{new} = W^{1} + \eta \cdot \frac{\partial L}{\partial z} \xi\]우리는 embedding layer의 update량을 키우고 싶은 것인데, 직관적으로 lr을 키우는 것과 embedding output의 init_std 자체를 키우고 (그럼 큰 값으로 init됨), embedding output vector를 scaling하는것은 동일한 효과를 가져올 수 있음을 알 수 있다.
\[\begin{aligned} & h^{1}(\xi) = W^1 \xi, \text{ where } W^1 \sim \mathcal{N}(0, \sigma^2), \text{ lr } = \eta \cdot \color{red}{n} & \\ & h^{1}(\xi) = \color{red}{\sqrt{n}} W^1 \xi, \text{ where } W^1 \sim \mathcal{N}(0, \sigma^2 \cdot \color{red}{\frac{1}{n}}), \text{ lr } = \eta & \\ \end{aligned}\]이를 변형하면 우리는 어떤 layer에는 table 3를 적용하고, 어떤 layer는 table 4를 적용할 수도 있게 되는데, 구체적으로 아래의 appendix J 내용처럼 abc parameterization 에 대해서 \(\theta\)를 무엇으로 설정하느냐에 따라서 구현에 변형을 줄 수 있다.
 Fig.
Fig.
아래 code snippet을 직접 실행해보면 큰 도움이 될 것 같은데, 주석 처리된 두 HP set에 대해서 backprop결과는 같다는 걸 알 수 있다.
from torch import manual_seed, nn, optim, randn
manual_seed(1234)
### Uncomment one of these lines -> in both cases y2 comes out the same!
lr = 1; mult = 1e-3; init_std = 1 / mult;
# lr = 1e-3; mult = 1; init_std = 1
l = nn.Linear(1024, 2048, bias=False)
nn.init.normal_(l.weight, std=init_std)
model = lambda x: l(x) * mult
opt = optim.Adam(l.parameters(), lr=lr, eps=0)
x = randn(512, 1024).requires_grad_()
y1 = model(x).mean()
print(y1)
y1.backward(); opt.step()
y2 = model(x).mean()
print(y2) # Comes out the same, regardless of LR
즉 구현의 편의성에 따라서 abc param을 swtich할 수 있는 것인데, Table 3, 8, 9를 섞어서 embedding은 table 3을 따르고 hidden은 8을 따르고 bias는 9를 따르고 이런식으로 해도 된다.
Table 8의 장점으로는 직접 봐도 알 수 있듯이 vector-like에는 모두 init에 대해서 uniform scaling rule이 적용된다는 편리함이 있으며 infinite to finite mapping을 하는 vector-like에 대해서는 \(1/\text{fan-in}\)만 항상 적용해주면 되는 편리함이 있다고 한다.
 Fig.
Fig.
그리고 이 것이 attention logit을 \(1/\sqrt{d_k}\)가 아닌 \(1/d_k\)로 scaling하는 이유를 설명하기도 한다고 하는데, attention logit은 \(d_k\)와 상관없이 항상 sequence length, \(T\)에 대해서 \(T \times T\)의 차원을 갖기 때문이다. 추가로 appendix B에는 아래의 content들이 포함되어있는데,
- Initialization Mean
- Zero Initialization Variance
- What Are Considered Input Weights? Output Weights?
- What Counts As a “Model”? Does the MLP in a Transformer Count As a “Model”?
먼저 weight init시 mean은 어떻게 할 거냐?에 대한 것은 어떤 table에도 없고 기본적으로 0으로 생각하지만 layernorm 같은 경우는 1로 둘 수 있다 (보통 그렇다).
그리고 어떤 weight은 zero variance로 init을 할 수 있다고 한다 (하는 것이 좋다)는 내용도 있다.
즉 weight matrix가 처음에 0이 되는 것인데,
이는 query projection layer와 unembedding layer같은 infinite dim이 finite dim으로 가는 경우애 width가 커짐에따라 0으로 vanishing 하기 쉽기 때문에 transfer를 더 잘하기 위해서 사용하는 technique이라고 한다 (appendix D.2).
 Fig.
Fig.
이를 제거해야 small scale proxy model을 target model로 더 잘 transfer할수 있기 때문에 zero init을 하게 된다고 하는데, 아마 이 경우 weight matrix가 0이지만 여전히 input matrix와 이후 activation function (softmax 등)의 영향을 받아 gradient가 전파되기 때문에 update가 되므로 걱정하지 않아도 될 것이다. 다만 width와 상관없이 0으로 init되어 점진적으로 update되는 것이다. (이 부분에 대해서는 곧 따로 더 논의해 볼 것이다)
Detailed Implementation of Transformer with muP
이번에는 실제 Transformer model을 pre-training 하기 위해 각 module별로 detail을 조금 더 알아보자. 아래 table은 muP를 사용해서 안정적으로 PLM학습에 성공했다는 Cerebras-GPT의 appendix의 table인데, TP-5의 table 8를 extension해서 Transformer에 맞게 정리한 것이다.
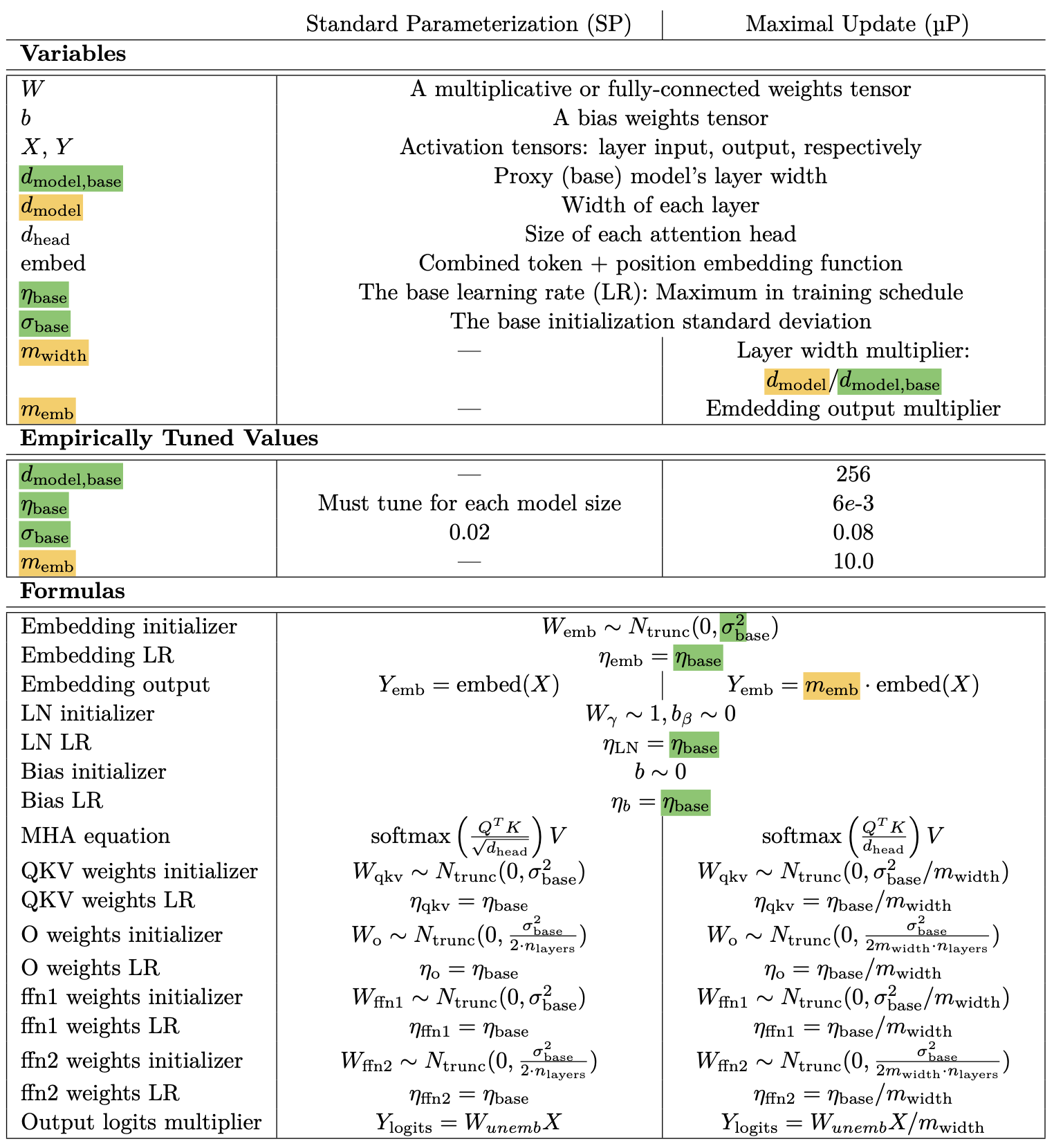 Fig.
Fig.
어떻게 이 table이 나오게 됐는지는에 대해서 몇 가지만 짚고 넘어가도록 하겠다.
Embedding (Input Weights)
먼저 Transformer LM의 frontend인 embedding layer이다. 아래 paragraph를 보면 embedding과 unembedding의 fan_in, fan_out은 다음과 같다.
- embedding
- fan_in: vocab_size
- fan_out: d_model
- unembedding
- fan_in: d_model
- fan_out: vocab_size
Embedding weight의 init_std는 table 8을 따를 경우 \(1/\text{fan-in}\)이 되어야 하는데, vocab_size는 width가 커짐에 따라서 변하지 않기 때문에 \(1/\text{fan-in}=1\)이 된다.
 Fig.
Fig.
위 Figure에서 좀 헷갈릴만한 내용이 있는데, word embedding에 대해서 embedding은 one-hot이기 때문에 init variance를 1로 설정하는것이 더 자연스러울 것이라는 거다. 하지만 1은 사실 너무 크다고 할 수 있다. 내가 이해한 것은 init_std scaling이 \(\Theta(1)\)이라는 거지 std를 exactly 1로 설정하라는 것은 아닌데 좀 헷갈리게 쓴 것 같다. 실제로 다른 muP로 실험한 LLM들의 paper, code등을 보면 \(0.01 \sim 0.08\)정도의 값을 줬다는 걸 알 수 있다. 오해하지 말아야 할 것이 table 8을 따를 경우 그렇다는 것이고, 구현에 따라서 multiplier, LR등을 잘 설정해주면 \(0.5 \sim 1\)을 줄 수도 있는 것 같다.
Embedding weight parameterization을 할 때 잊지 말아야 할 것이 있는데, unembedding은 multipler를 HP로서 잘 언급해놓고 embedding에 대해서는 언급을 하지 않았기에 이를 놓칠 수 있지만 embedding multiplier는 매우 중요한 parameter이기 때문에 꼭 search를 해줘야 한다. 실제로는 input embedding vector에 곱해주는 muliplier가 있으며 값은 \(3 \sim 10\)정도로 꽤 큰 값이기 때문에 빼먹으면 안된다.
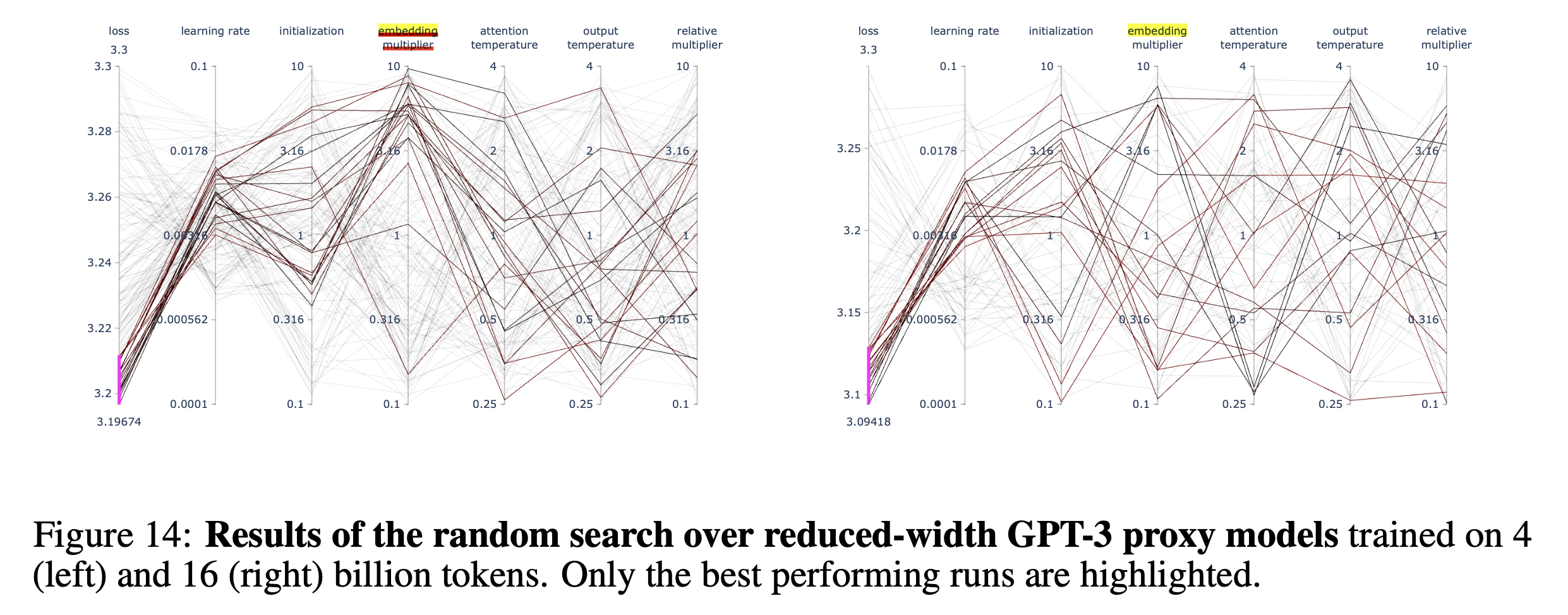 Fig.
Fig.
어떤 layer의 output tensor에 \(\sqrt{n}\)배를 하면 backprop을 통해 얻는 해당 weight matrix에 대한 gradient도 \(\sqrt{n}\)배가 됨을 보였으므로 이것이 gradient scale을 키워 궁극적으로 \(W_{emb}x\)가 \(\Theta(1)\)을 유지하게 하려는 strategy임은 쉽게 받아들일 수 있을 것이다.
 Fig. 이런 방법은 fairseq에도 이미 적용되어 있었다고 한다.
Fig. 이런 방법은 fairseq에도 이미 적용되어 있었다고 한다.
한 편 embedding parameterization이 이렇게 유도되는 이유에 대해 다뤄본 적이 없는 것 같으니 간단하게만 생각해보자. 먼저 embedding (input) weight의 shape은 \(n \times d\)로 input feature의 dimension \(d\)는 width가 커질 때 같이 증가하지 않는다는 점을 이해해야 한다. 즉 \(n\)에 따라 infinity로 커지는 차원이 1개이므로 vector-like type이다.
\[\begin{aligned} & \underbrace{W_{1} \xi'}_{\text{should be } \Theta(1)} = \underbrace{W_{0}}_{\Theta(1)} \xi' + \underbrace{\eta \cdot \Delta W_{0}}_{\Theta(1)} \xi' \text{ where } W \in \mathbb{R}^{n \times d}, \xi \in \mathbb{R}^{d \times 1} & \\ & = W_{0} \xi' + \eta \cdot \color{red}{n^{-c}} \cdot \underbrace{(g_0 \xi^T)}_{?} \xi' \text{ where } g_0 \in \mathbb{R}^{n \times 1} \text{ is upstream grad} & \\ \end{aligned}\] Fig.
Fig.
UnEmbedding (Output Weights)
그 다음 unembedding weight에 대해서는 Table 3, 8 중 어떤 구현을 따를건지에 따라 아래 처럼 init std, LR scaling을 해주면 된다.
 Fig.
Fig.
 Fig.
Fig.
여기서 logit scaling의 구현에 대해 짧게 얘기하고 넘어가겠다. 왜 그러냐면 paper의 notation상으로는 logit을 만들고 multiplier를 곱해야 할 것 같은데, Greg의 official code는 그렇지 않기 때문이다.
구현 방법은 아래 muP official repo의 방식처럼 input scaling을 하는 것과,
 Fig.
Fig.
unembedding weight matrix와 input을 곱해 logit을 구한 뒤에 scaling을 하는 logit scaling,
이렇게 크게 두 가지가 있을 수 있는데 Greg을 제외하고 대부분의 경우 후자를 사용한다.
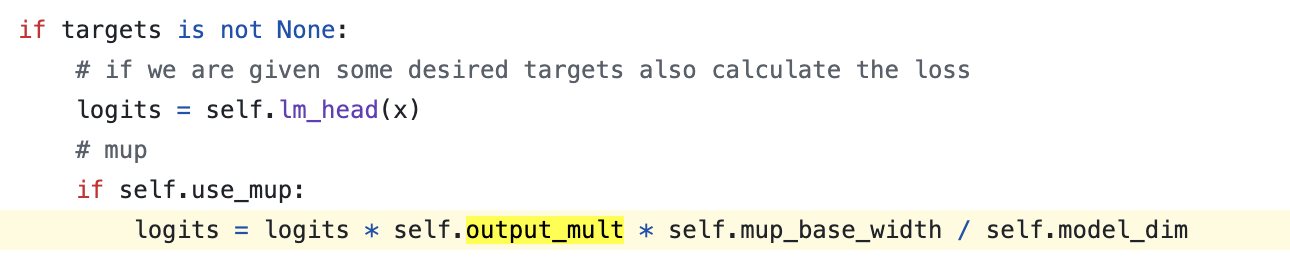 Fig. Source from NanoLM
Fig. Source from NanoLM
 Fig. Source from Microsoft/Phi-3
Fig. Source from Microsoft/Phi-3
사실 backprop을 유도해보면 이 둘간에 차이는 없어야 한다. 왜냐하면 input element들을 예를 들어 \(1/\sqrt{n}\)하고 embedding vector들과 dot product해서 weighted sum하는 것과, weighted sum을 한 뒤 \(1/\sqrt{n}\)하는 연산은 linear하기 때문이며 backprop 수식을 유도해보면 이 둘은 수학적으로 같기 때문에 gradient도 같아야 한다. 실제로 아래 연산을 수행해도 같은 값이 나온다.
import torch
import torch.nn as nn
import torch.nn.functional as F
vocab_size = 128000
d_embd = 4096
bias = False
unemb = nn.Linear(d_embd, vocab_size, bias=bias).cuda().bfloat16()
nn.init.normal_(unemb.weight, mean=0.0, std=1.0)
input = torch.randn(d_embd).cuda().bfloat16()
logit_scaled_logit = unemb(input) * d_embd**-0.5
input_scaled_logit = unemb(input * d_embd**-0.5)
logit_scaled_softmax = F.softmax(logit_scaled_logit, dim=-1)
input_scaled_softmax = F.softmax(input_scaled_logit, dim=-1)
logit_allclose = torch.allclose(logit_scaled_logit, input_scaled_logit, atol=1e-6)
softmax_allclose = torch.allclose(logit_scaled_softmax, input_scaled_softmax, atol=1e-6)
print(f"logit allclose? {logit_allclose}")
print(f"softmax allclose? {softmax_allclose}")
print(f"logit max diff: {torch.max(torch.abs(logit_scaled_logit - input_scaled_logit)).item()}")
print(f"softmax max diff: {torch.max(torch.abs(logit_scaled_softmax - input_scaled_softmax)).item()}")
logit allclose? True
softmax allclose? True
logit max diff: 0.0
softmax max diff: 0.0
물론 bias term이 있다면 주의해야한다. 이 경우 logit은 weighted sum + bias 이기 때문에 bias를 더한 뒤 scaling하는 것이 weighted sum에만 scaling하는 것과 다르기 때문이다.
logit allclose? False
softmax allclose? False
logit max diff: 0.0166015625
softmax max diff: 3.814697265625e-06
하지만 같을 것 같은 연산도 실제 상황에서는 말이 다를 수가 있다. 아마 n개 element를 더해서 나누는 것과, scale down한 n개 element를 더하는 것은 이론적으로 같아보이지만 numerical error가 있을 수 있기 때문에 주의해야 할 것 같다.. (사실 큰 차이는 없지만 large scale, lowered precision에서 어떻게 될 지는 잘 모르겠다)
실제로 training loss curve를 보면 거의 같으니 넘어가도 될 것 같긴 하다.
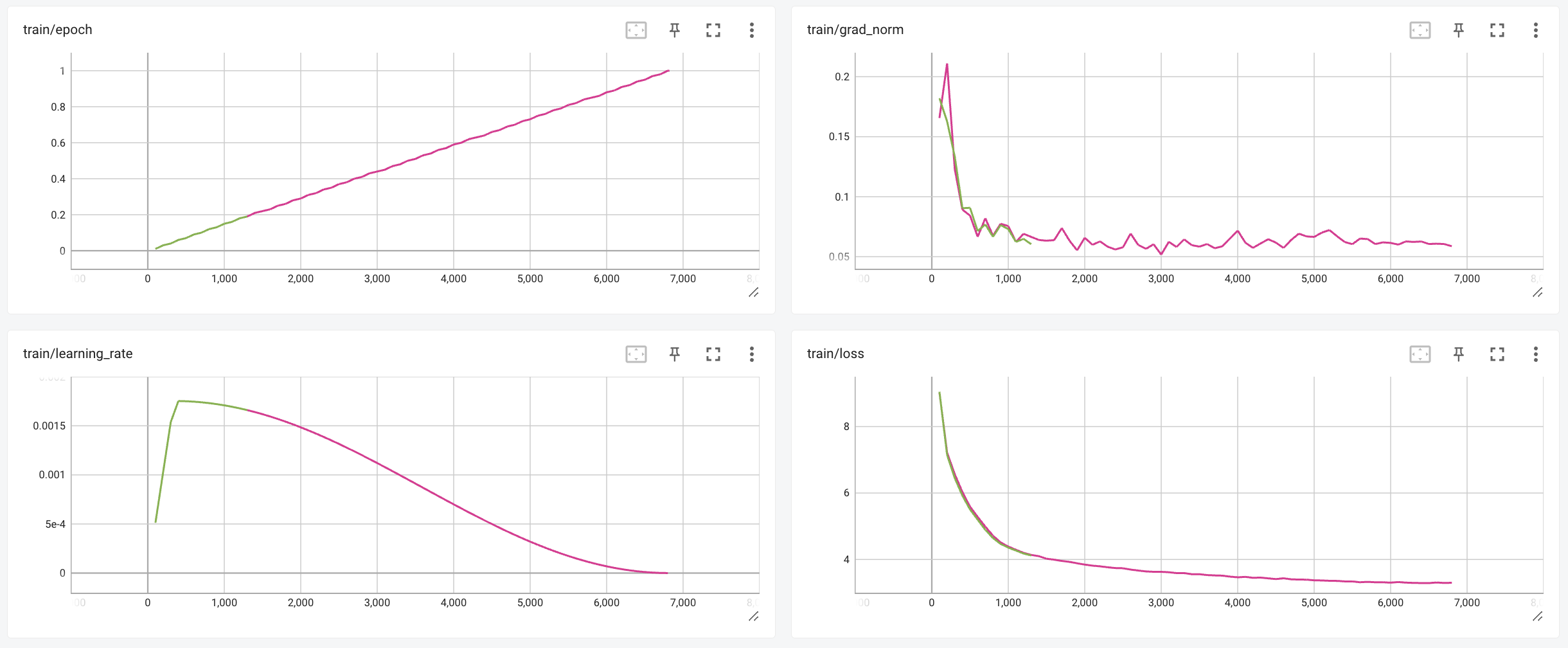 Fig. The Comparison of Training Loss Curve between Input Scaling and Logit (Output) Scaling
Fig. The Comparison of Training Loss Curve between Input Scaling and Logit (Output) Scaling
하지만 llama3 model에 muP를 구현해 coordinate check을 한 경우를 보면 어떤 layer output 하나가 width가 커짐에따라 exploding하는 (pre-)activation이 보이는데,
이건 사실 logits = scale * lm_head(x)이라고 치면 lm_head가 multiplier를 곱해지지 않으면 width에 대한 고려가 없는 init_std를 가지기 때문에 logit norm이 커진다고 보면 될 것 같다.
Logit scaling을 할 시 coordcheck에 반영이 안 돼서 그렇지 어차피 scaling을 \(1/width\)해줄 것이니 그냥 쓰면 된다.
(아마 coordcheck method가 weight이 곱해지기 전의 결과를 plot하기 때문에 이를 맞춰주기 위해 Greg이 처리를 한 것으로 보인다)
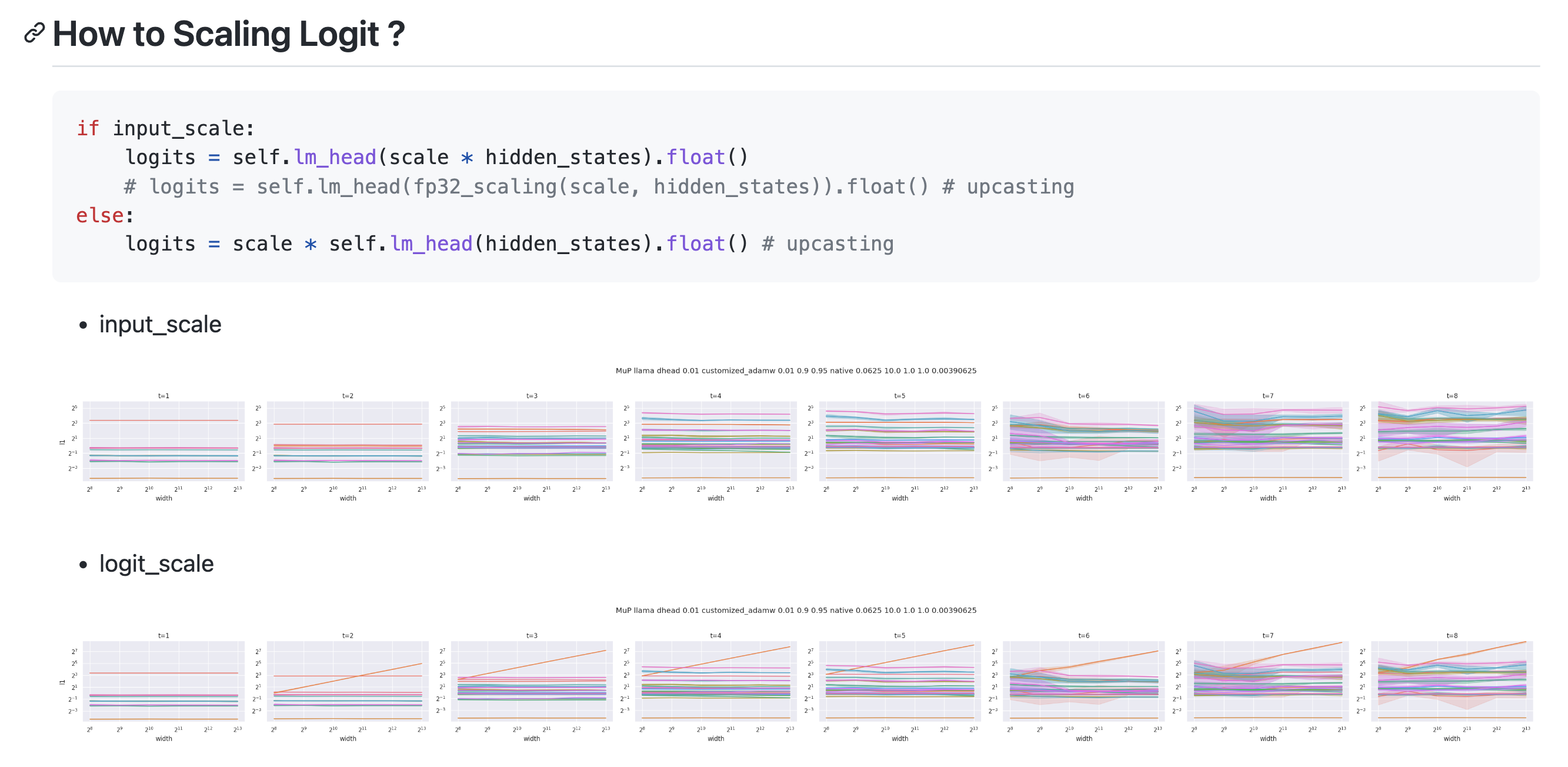 Fig. The Comparison of Coord Check between Input Scaling and Logit (Output) Scaling
Fig. The Comparison of Coord Check between Input Scaling and Logit (Output) Scaling
Other Parameters
저자들은 아래와 같은 module들에 대해서도 어떻게 처리해야 하는지 간단히 적어놨다.
- Learnable scalar multipliers
- Positional Bias
- Spatial MLPs
Positional Bias에 대해서만 간단히 얘기하고 넘어가자면, 이는 ALiBi같은 algorithm을 의미한다고 보면 될 것 같다. 이런 류의 PE는 일단 context length, \(T\)에 대해서 \(Q^TK \in \mathbb{R}^{T \times T}\)의 score map가 만들어지면, 여기에 relative position 정보를 주입하기 위해 마찬가지로 \(T \times T\)크기의 learnable parameter를 더해준다. TP-5에서는 이런 learnable positional bias는 infinity width limit에서 무한대로 가는 차원이 없는 것으로 인식되기 때문에 간단히 zero init을 해주면 된다고 한다. (나머지 내용은 paper참고)
Optimizer Variants and HP
이번에는 Adam, SGD가 아닌 다른 optimizer varaints들을 사용할 땐 어떻게 해야하는지, Adam variants들의 HP는 어떻게 scaling해야 하는지에 대해서 알아보자.
AdamW
 Fig.
Fig.
Adafactor
\[\begin{aligned} & g \leftarrow \frac{\parallel w \parallel_F}{\parallel g \parallel_F} g & \\ & \text{where } w \text{ is param and } g \text{ is update} & \\ \end{aligned}\]다시 Google의 PaLM의 init method를 보도록 하자. muP를 대충 보고나니 어째 닮은 구석이 있어 보이지 않은가?
 Fig.
Fig.
epsilon, Gradient Clipping, Weight Decay and Momentum
Practical Considerations
Verifying muP Implementation via Coordinate Checking
앞서 모든 layer의 (pre-)activation vector들에 대해서 timestep별로 어떤 변화가 있는지 L1 norm 같은걸 재는 coordinate checking이라는게 있다고 했다.
timestep별로 actiation scale은 변할 수 있지만 이것이 width invariant하지 않으면 구현을 잘 못한 것이다.
사실 muP를 알고나면 당장 구현해서 쓰는 것 자체는 쉽기 때문에 엄밀히 check하지 않고 넘어갈 수 있는데,
muP는 GPT-2 architecture에 대해서 실험한 것이기 때문에 modern LLM에서 가장 많이 쓰이는 Noam architecture (LLaMa architecutre; pre-norm, RMS norm, no bias, rope, swiglu)에서는 예상 못한 bug가 있을 수도 있기 때문에 주의해야 한다.
물론 muP는 모든 NN layer에 적용될 수 있도록 general rule을 만들어놨지만 이를 확인하는 것은 manual backprop을 해보는 것 처럼 매우 중요하기 때문에 다시 한 번 언급한 것으로 보인다.
Zero Initialization for Output Layers and Query Layers in Attention
저자들은 output layers를 zero init할 경우 optimal HP transfer가 더 잘된다고 주장한다. 사실 이부분 내용이 좀 어려운데, 갑자기 Gaussian Process (GP)얘기를 꺼낸다. 아마 Neural Network Gaussian Process (NNGP)를 의미하는 것 같은데, Greg의 Tensor Program series의 첫 번째인 TP-1이 관련 내용을 다루기 때문인 것으로 보인다.
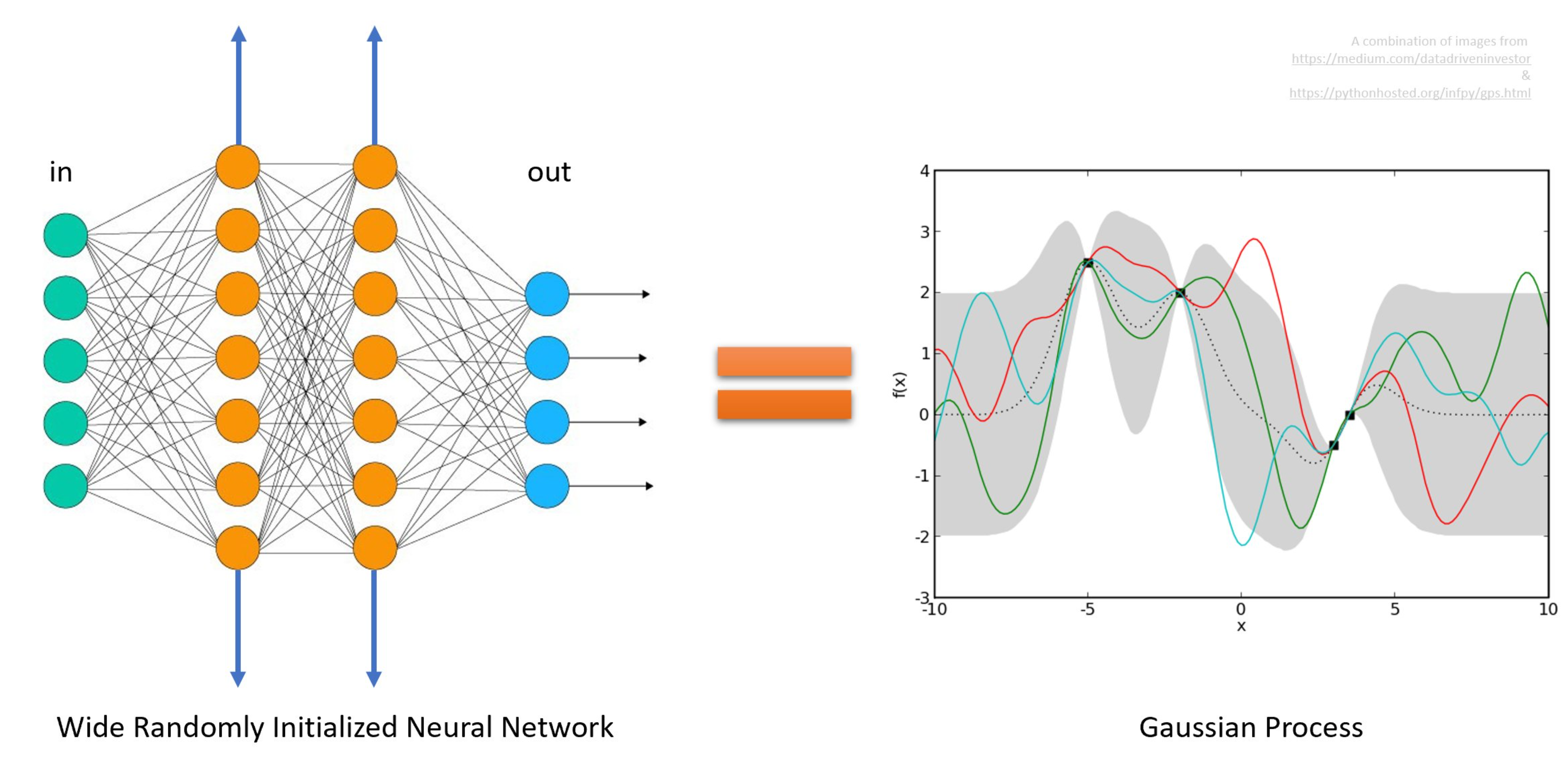 Fig.
Fig.
Activation Functions
과연 activation function에 대해서도 muP robust할까?
이에 대한 답은 ReLU대신 tanh를 써도 transfer가 되긴되지만 (논문이 나올 당시만 해도 GLU variants인 swiglu, geglu가 아니라 ReLU로 실험한듯 함), tanh나 softmax같은 squashing activation function은 (아마 value들이 한쪽으로 쏠리는 의미같다) narrower network가 activation value들을 saturate시키는 현상이 wider model보다 심하기 때문에 small gradient를 만들기 쉽고, 결과적으로 HP landscape을 망가뜨릴 수 있다고 한다.
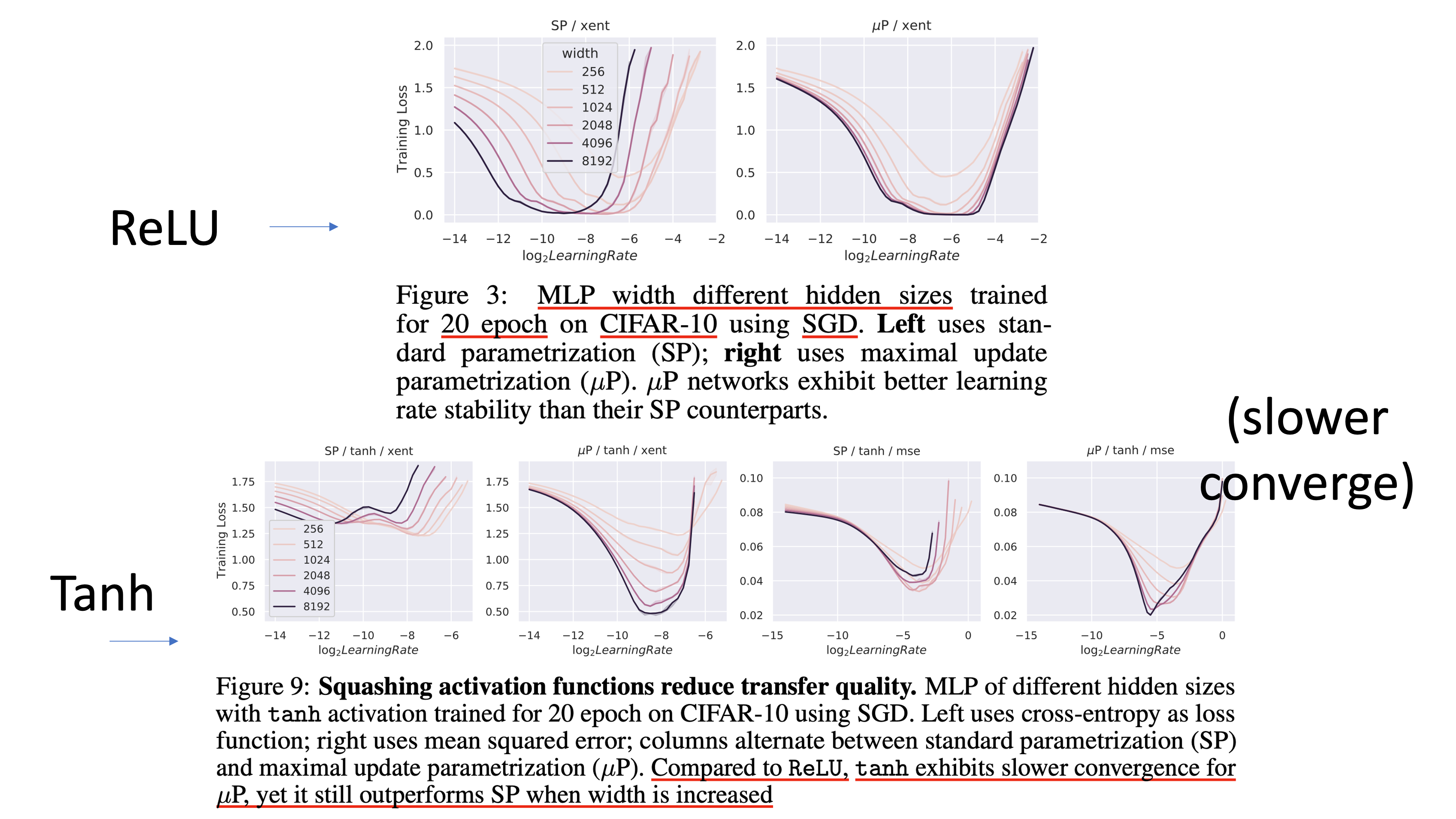 Fig.
Fig.
(심심하신분들은 유도해보길 바란다)
Enlarge d_k
muP를 할 때 또 주의해야 할 사항 중 하나는 \(d_{\text{head}}=d_k\)를 충분히 크게 유지해야 한다는 것이다. 그렇지 않으면 small scale proxy model의 random HP search의 quality 자체가 떨어지고 transfer도 잘 되지 않는다고 하는데, 아마 후자의 경우 \(n\)이 충분히 커야 convergence theorm이 성립하기 때문인 것 같다. 앞서 wikitext를 사용한 LM training시 최소 width=256, num_head=4를 유지해야 한다고 했는데, 이 경우는 \(d_k=64\)이 되지만 저자들은 \(d_k=32\)면 충분하다고 얘기한다. 아래 figure를 보면 \(d_k=8\)의 attention logit multiplier, \(c_{\text{attn}}\)를 \(d_k=128\)로 transfer 했을 때는 optimum 자체도 noisy하고 transfer도 잘 안되는 걸 확인 할 수 있다.
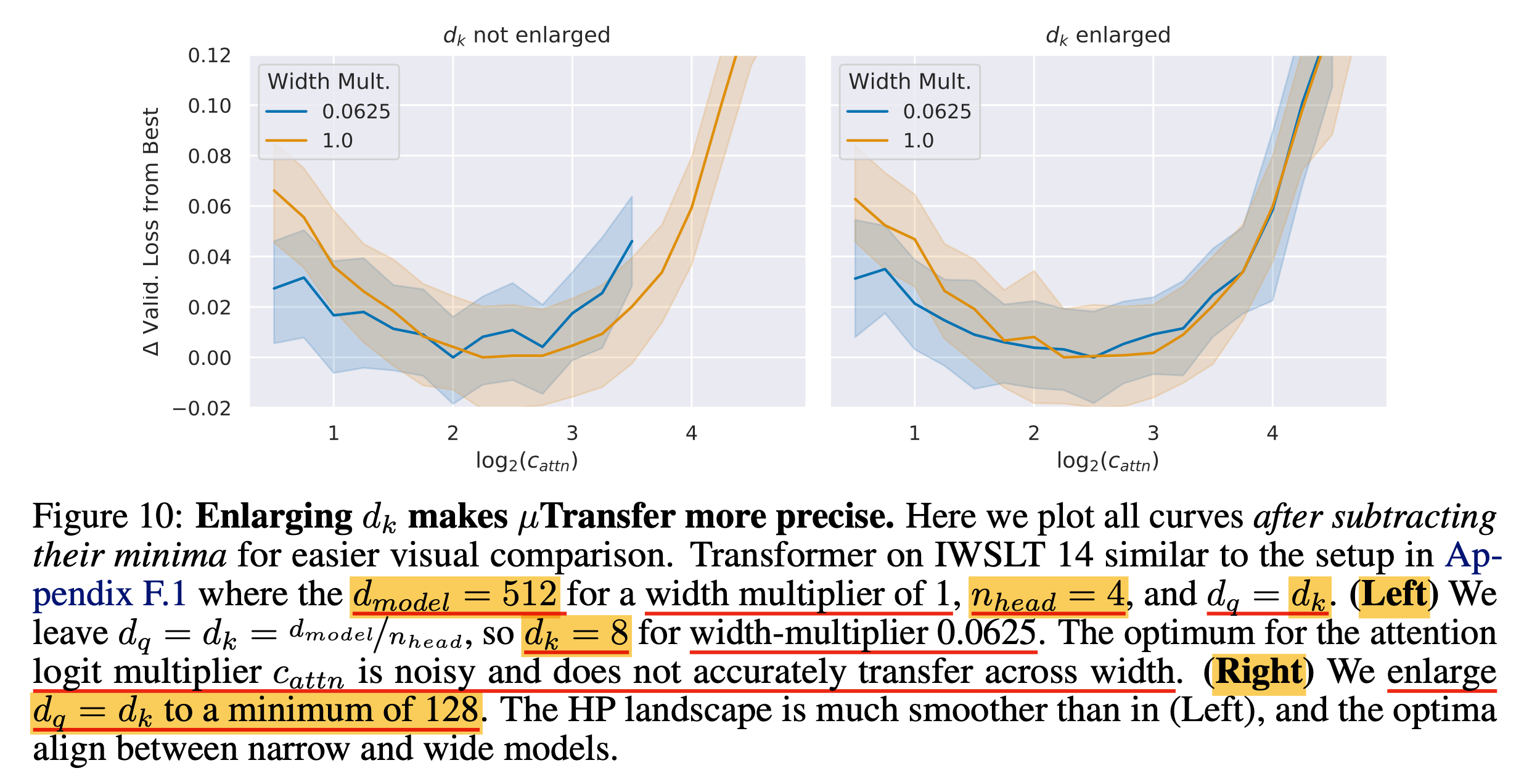 Fig.
Fig.
Using a Larger Sequence Length
Transformer에 대해서 larger sequence length를 쓰는 경우 init std transfer가 더 잘 됐다고 하는데, 그 이유는 잘 모르겠다고 한다. (아마 같은 문장 내의 token들이 gradient diversity가 비슷하기 때문에 다른 behavior가 있는 것 아닐까?)
Tuning Per-Layer HP
Best performance를 위해서라면 모든 layer (weight)의 LR, init std등을 다 탐색할 수도 있겠지만, 실제로 muP를 사용할 때는 아래의 항목들만 고려해도 좋은 result를 보인다고 한다.
- global LR
- global init std
- input mult
- output mult
- attention mult
Which HP Can Be Transferred?
Table For Transferable And Not Transferable HPs
앞서 몇몇 case들에서 어떤 HP가 어떤 factor에 invariant하게 transfer가 되는지, 혹은 어떤 HP가 안되는지에 대해서 이미 알아봤다.
 Fig.
Fig.
먼저 위 table에 정리된 것 처럼 대부분의 LR을 포함한 optimization related factor, init std 그리고 multiplier 등은 다 transfer가 되지만 dropout이나 weight decay같은 overfitting을 막아주는 regularization들은 transfer가 되질 않는다고 쓰여있다.
그리고 마지막으로 muTransfer across라는 항목이 있는데,
여기 width같은게 있는 걸 보면 width에 따라 (across width) transfer가 된다는 걸 의미한다고 생각할 수 있다.
그리고 나머지들은 wikitext 실험에서 충분히 얘기했지만 empricially transferable하다는 것이지 width limit처럼 이론적으로 정립이 된 것은 아니다.
(그래서 asterisk가 붙어있는 것)
저자들은 특히 multiplier라는 HP는 SP만 쓰던 이들에게는 생소할 수 있는데, 이는 same width에서 SP와 muP를 이어주는 bridge역할을 하기에 중요하다고 얘기한다. 만약 이값이 잘 setting되면 둘의 training dynamics는 아예 같아진다고 (identical) 한다.
HP That Don’t Transfer Well
그런데 왜 regularization을 위한 HP들은 transfer되지 않는걸까? 이에 대한 해답이 appendix E.1에 적혀있는데, overfitting을 막기 위한 dropout, weight decay등은 보통 dataset size를 알아야 하는데, muP는 이를 전혀 모르기 때문이라고 한다.
 Fig.
Fig.
그런데 어떤 HP가 regularization을 위한 HP라고 할 수 있는지도 사실 의문일 수 있다고 한다. 저자들은 엄밀히 말하면 이들을 정확히 나누는 경계선은 없다고 한다. 다만 dropout이나 weight decay가 통상적으로 그렇게 여겨질 뿐이고 (실험적으로도 그렇고), batch_size나 LR도 때때로 training을 regularize하긴 하지만 dynamics에 더 영향을 끼친다고 한다. (실제로도 LR은 transfer가 되지 않는가?)
저자들은 전자에 대한 transferability (regularization HP)는 후속 연구로 남겨둔다고 하는데, 사실 modern LLM은 dataset size가 워낙에 크기 때문에 (model이 워낙 크지만 dataset size가 훨씬 크기 때문에 overparameterized라고 부르기도 민망한 것 같다) overfitting이란 개념이 없어 regulaization은 신경쓰지 않아도 될 것 같다. (openreview에도 언급되어 있다)
(Learning Rate, Batch Size) Scaling
저자들은 후자 (LR transferability across batch_size)에 대해서 좀 더 언급하는데, 앞서 말한 것 처럼 TP-5에서 LR이 batch_size가 커짐에 따라 transfer가 되는 것을 보이긴 했으나 이것이 optimal scaling을 의미하는 것은 아니었다는 점을 한번 더 언급한다. 즉 원래는 batch_size가 \(n\)배 커지면 gradient가 정교해지고 training steps가 줄어들기 때문에 LR을 \(\sqrt{n} \sim n\)배 scaling해줘야 하는데, TP-5에서는 이를 전혀 고려하지 않은 것이다. (그러나 앞서 필자가 말한 것 처럼 muP를 실무에 적용할 누구라도 이를 간과해서는 안된다. 그러면 경우에 따라 매우 underfitting한 target model을 얻게 될 것이다)
 Fig.
Fig.
그리고 저자들은 batch_size에 따른 LR transferability result가 30번 reference의 결과를 recap (반복) 한다고 하는데, 이 paper가 바로 앞서도 짧게 언급했던 Critical Batch Size를 정의한 paper이다. 뭔소린가 하고 section 10.3을 보니 batch_size에 따른 optimal LR scaling을 연구한 work들과의 관계를 설명하는데,
 Fig.
Fig.
여기서 critical batch_size paper에 따라서 LR을 \(\frac{a}{(1+b/batchsize)}\)하기 때문에 batch_size가 충분히크다면 LR은 더이상 scaling되지 않기 때문에 충분히 큰 batch_size에 대해서는 optimal LR은 대략적으로 상수가 된다고 얘기한다. 즉 안정적으로 transfer된다는 얘기를 하고 싶은가본데 (아마 Cerebras-GPT의 critical batch size관련 내용이 여기서 나온 것 같다), 사실 sufficiently large batch_size란 critical batch size를 넘는 시점을 의미할 것이기 때문에, 실제로는 서로다른 (model size, dataset size) 조합의 small scale proxies에 대해서 이 값들은 모두 다를 것이기 때문에 (왜냐면 critical batch size는 computing budget, \(C=6ND\)에 의해 도달할 수 있는 loss에 대한 power function 꼴이기 때문) 이 값을 찾는 것 자체가 문제가 될 수 있다. 그리고 muP 하나 잘 하겠다고 critical batch size이상의 batch size를 사용하게 되면 underfitting될 우려가 있기 때문에 그렇게 batch_size를 가능한 한 크게 잡는 것은 좋은 방법은 아닌 것 같다.
On the Definitions of Width
Dive Deeper into muP (in Theory)
이제 본격적으로 muP의 이론적 근거에 대해서 좀 더 파고들어보자.
Behaviors of Gaussian Matrices vs Tensor Product Matrices
Key Insights
Preparation for the Derivations
Linear Tensor Product Matrix (e.g. SGD Updates)
NonLinear Tensor Product Matrix (e.g. Adam Updates)
asdasdasd
Vector Case (e.g. Readout Layer)
Gaussian Matrix (e.g. Hidden Weights Initialization)
이제 \(A \in \mathbb{R}^{n \times n}\)이 \(A_{\alpha \beta} \sim \mathcal{N}(0,1/n)\)을 따르는 random gaussian matrix이며 \(x \in \mathbb{R}^n\)는 근사적으로 \(Z^{x}\) distribution을 갖는 iid coordinates을 갖는 상황에 대해 고려해보자.
Deriving muP for Any Architecture
Output Weights
 Fig.
Fig.
Hidden Weights
 Fig.
Fig.
Input Weights and Biases
 Fig.
Fig.
Attention
Why Other Parametrizations Cannot Admit Hyperparameter Transfer
Standard Parametrization (SP)
Neural Tangent Parameterization (NTP)
NTP는 Neural Tangent Kernel (NTK)에서 제안된 parameterization method이다. NTK는 말 그대로 kernel인데, NN이 gradient descent로 training 되는 경우 어떻게 진화 하는지 (evolve)를 설명하는 kernel 이며, ‘왜 deep learning model은 random initialization을 하더라도 결국 좋은 minima로 수렴하는가?’, ‘왜 trainset 뿐 아니라 testset에서도 좋은 성능을 보이는가?’, 즉 ‘Convergence and Generalization in Neural Networks’에 대한 내용을 다룬다.
NTK는 NN이 non linearity를 갖는 model이지만 너비가 무한하게 넓은 (infinite width) NN에 대해서 이를 linear 하다고 생각하고 문제를 풀 수 있다고 얘기하는데, 이 paper에서 얘기하는 어떤 weight parameterization 방법이 바로 NTP이다. NTK에 대한 내용을 다 다루기엔 너무 양이 많기 때문에 NTK에 대한 post를 따로 작성했으니 이를 보고 오면 될 것 같다.
TP 저자들은 NTK에 문제가 있다고 지적했는데,
바로 NTK는 Feature Learning을 전혀 고려하지 않았다는 것이다.
아래 Word2Vec 을 NTK를 따라 학습한 예제를 보자.
 Fig.
Fig.
NTK는 top US cities, states의 Word2Vec embedding을 PCA했을 때 거의 random에 가까운 결과를 보여주는데, NN의 width를 64혹은 무한대에 가깝게 늘리면서 일반적으로 학습한 경우 도시 이름들의 embedding들이 잘 분리되는 것을 볼 수 있었다고 한다. 특히 NTK의 경우 분석결과 NN의 마지막 layer들이 거의 random에 가까웠다고 하는데, 이는 BERT같이 pre-training을 하고 transfer learning을 하는 경우 매우 치명적이라고 할 수 있다고 한다.
 Fig.
Fig.
 Fig.
Fig.
NTK의 문제점은 output layer, 즉 readout layer의 gradient가 너무 큰 것이라고 Greg은 얘기한다. 그렇기 때문에 중간 layer들은 충분히 update되지 않는데, 그렇다고 LR을 키우면 output layer가 blow-up하기 때문에 그럴 수 없는 것이다.
Other Parametrizations
Something Interesting (Things to think about)
(2022) muP's LR Sensitivity Exp from "Small-scale proxy..." Paper
이번 Section에서는 “muP를 사용해서 학습하니 좋았어요, muP detail은 이랬어요”하는 paper들을 다루진 않는다. 다만 muP와 관련된 흥미로운 내용들이 있어 같이 더 생각해보자는데서 작성하게 되었다.
Updated) Small-scale proxies for large-scale Transformer training instabilities는 너무 중요한 정보를 많이 담고 있어서 따로 post를 만들었으니 link를 참고하길 바란다.
Rethinking LoRA
“muP가 LoRA도 개선할 수 있을까?”
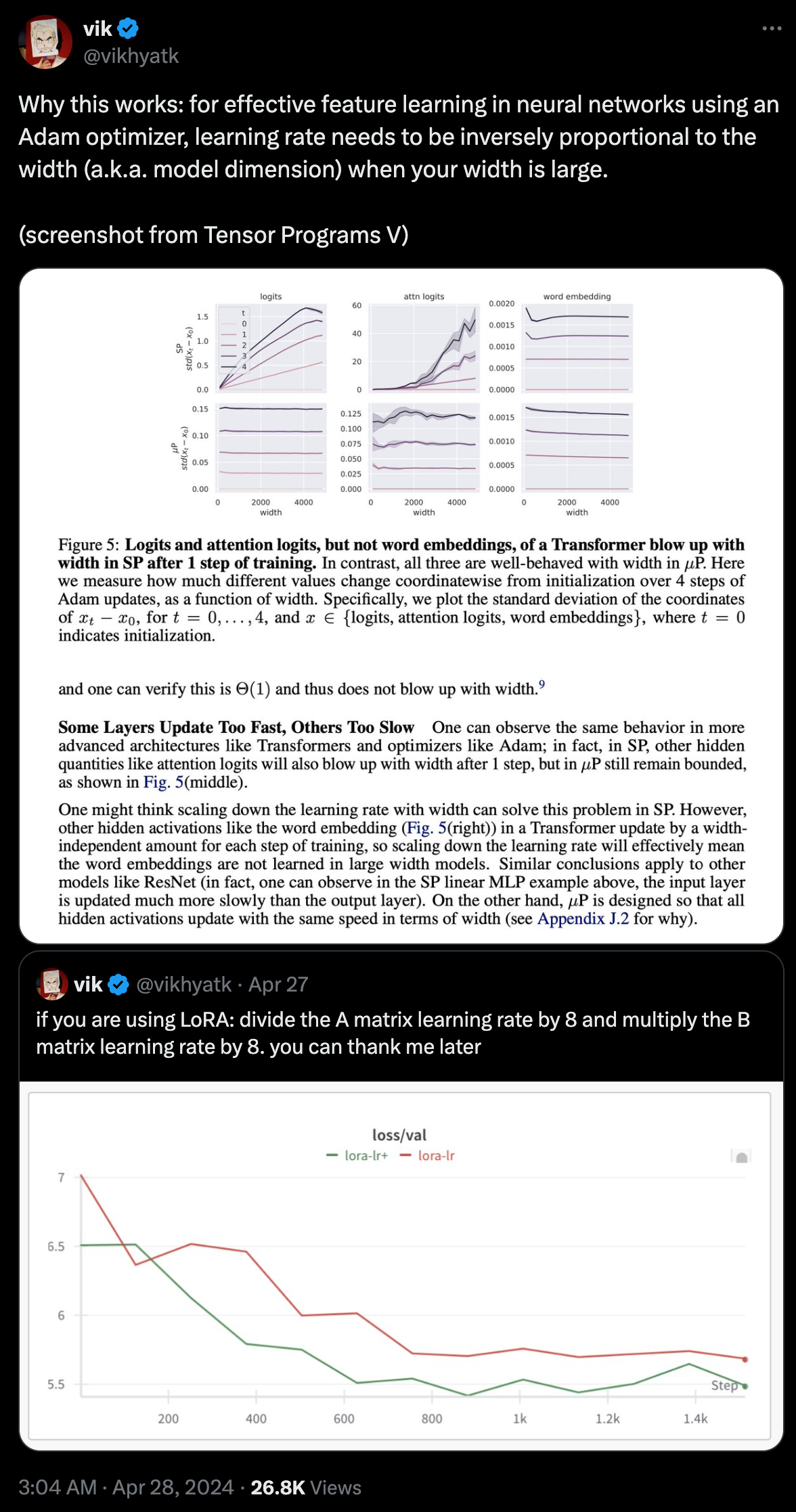 Fig. Source from tweet thread
Fig. Source from tweet thread
위 tweet thread에 따르면 LoRA는 pretrained model weight을 freezing 하고 learnable한 weight matrix \(A, B\)를 사용해서 낮은 차원에서의 optimization을 하는 method인데, 이것도 muP에서 얘기한 feature learning 관점에서 보면 A와 B layer들의 LR은 각각 달라야 한다는 주장 같다.
\[\begin{aligned} & layer_{out} = (W_0 + AB) layer_{in} & \\ & A \in \mathbb{R}^{n \times r}, B \in \mathbb{R}^{r \times n} & \\ \end{aligned}\]A와 B weight matrix의 dimension은 width가 \(n\)이고 LoRA rank가 \(r\)일 이들 또한 width에 영향을 받는 vector-like matrix이기 때문이라는 논리 같은데, 사실 별로 맞는 말인지는 모르겠다만 이런 LoRA 학습에도 parameterization을 고려해볼만 하다 라는 부분만 생각해보면 좋을 것 같다.
About Grad Norm
사실 이 부분에 대해서는 딱히 답이 없는데, TP-5의 GPT-3 실험에서도 backward시 underflow issue가 있었기 때문에 gradient에 대한 얘기를 좀 해보려고 한다.
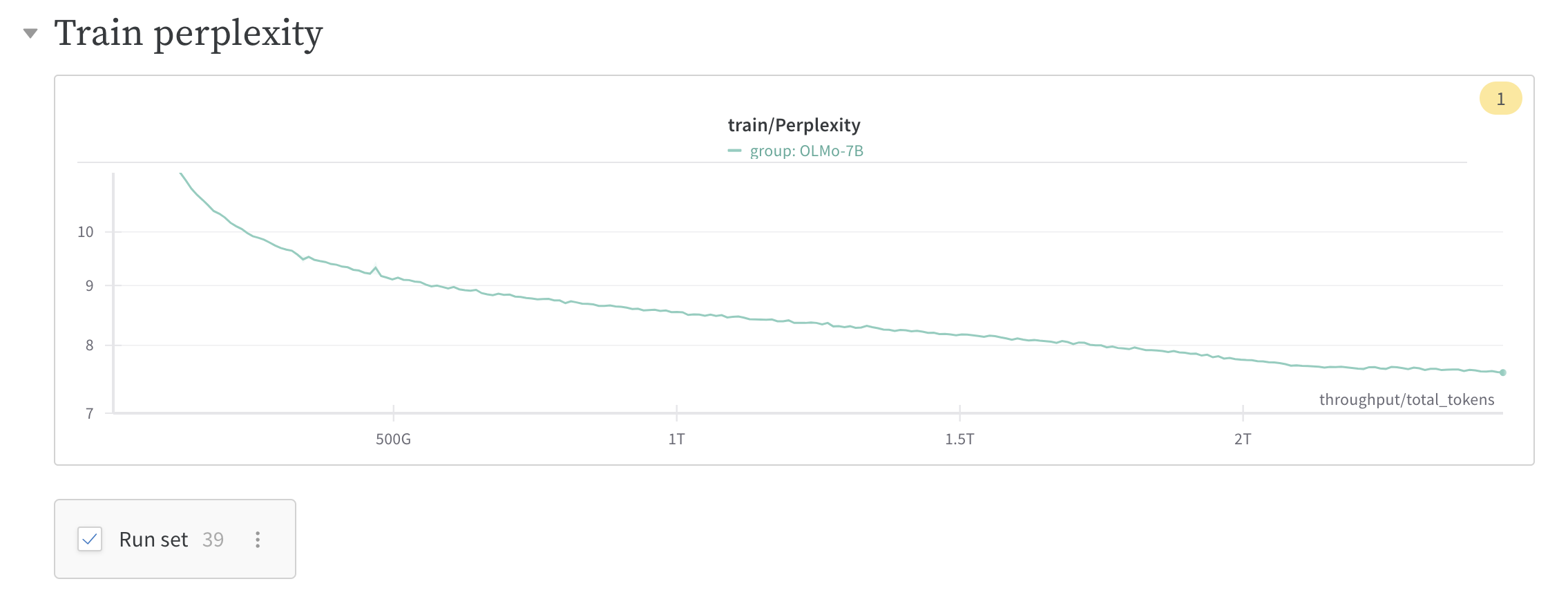 Fig. Source from here
Fig. Source from here
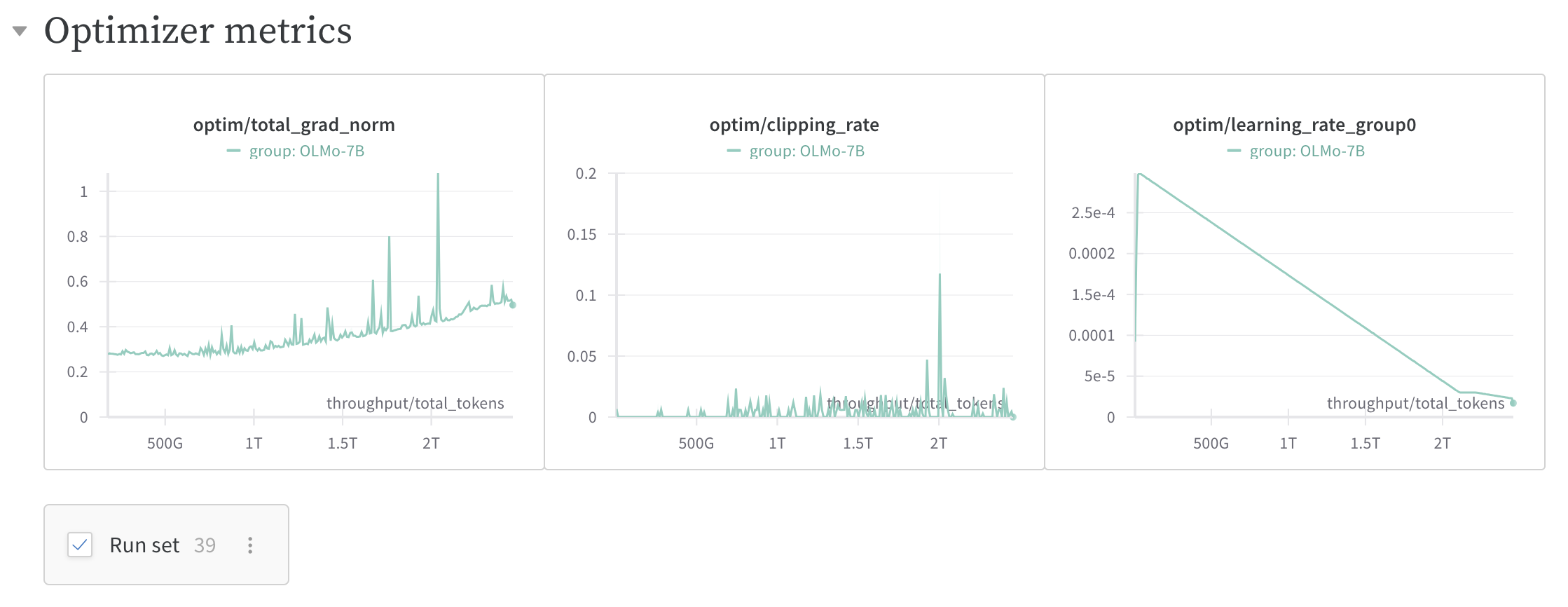 Fig. Source from here
Fig. Source from here
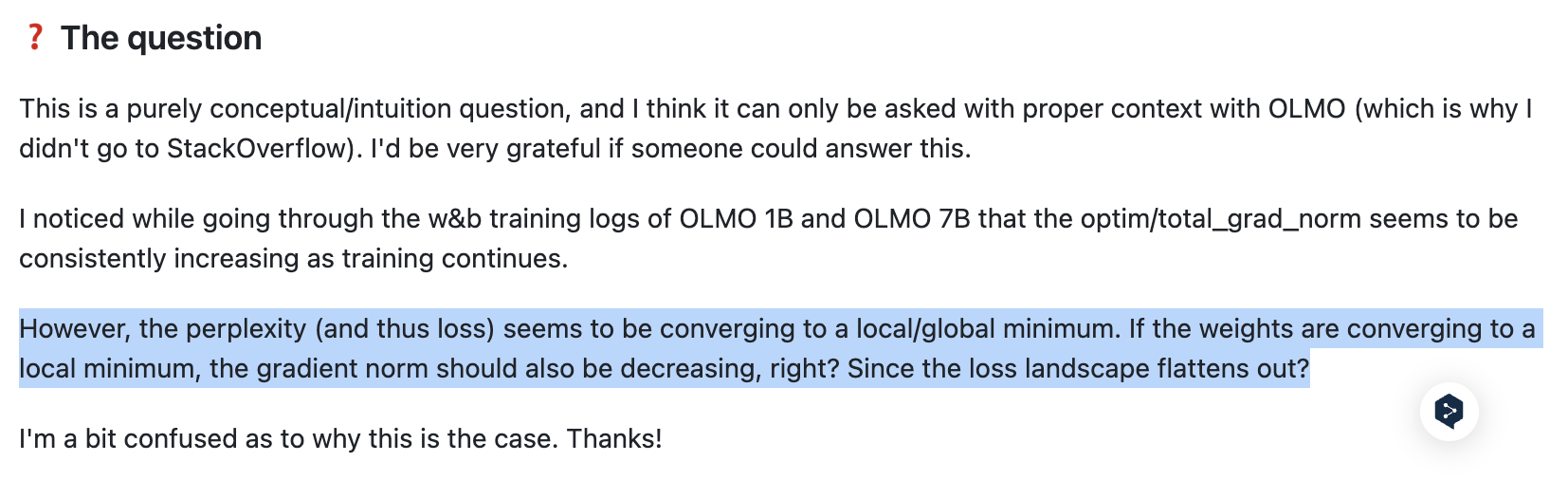 Fig. Source from here
Fig. Source from here
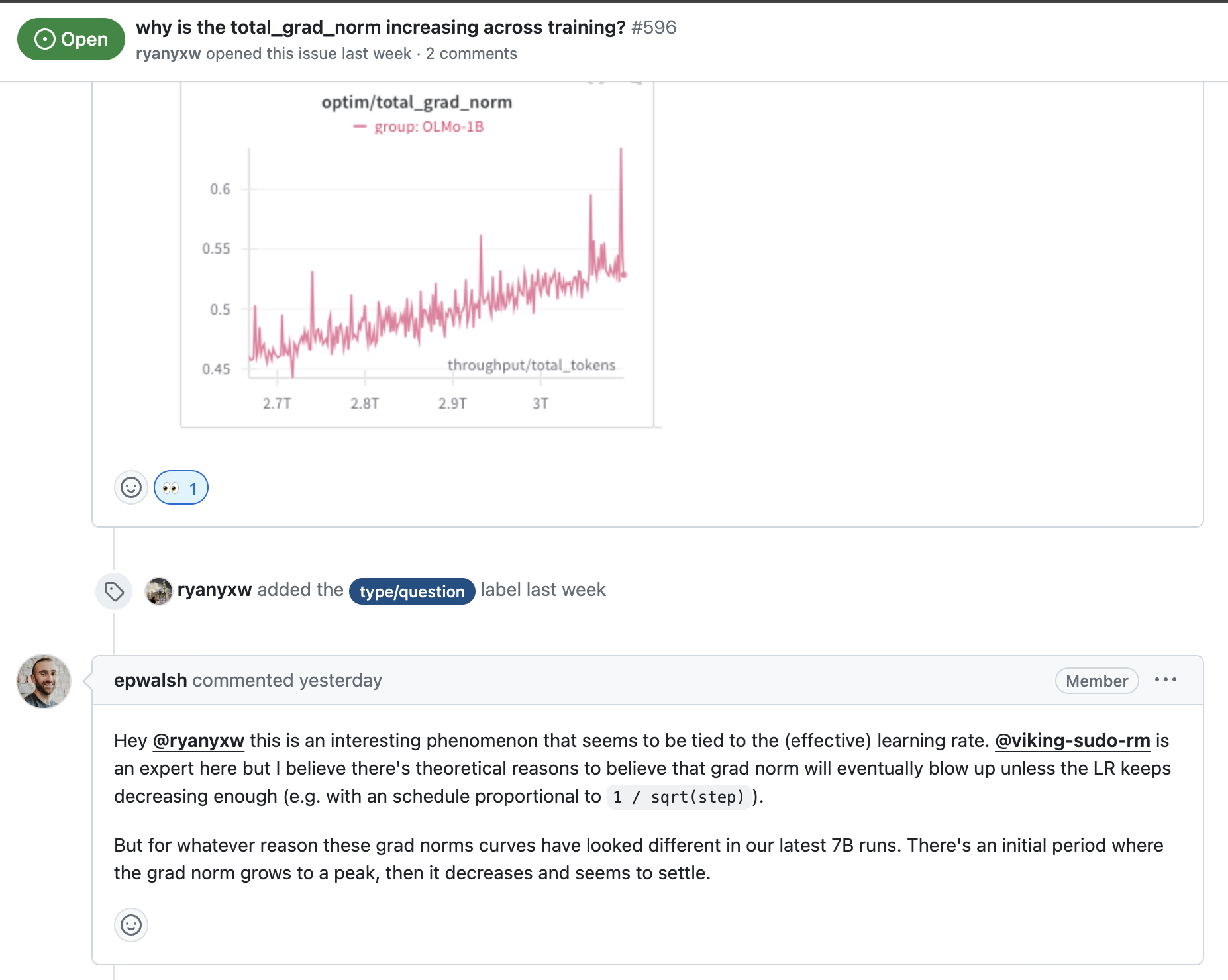 Fig. Source from here
Fig. Source from here
Pytorch Implementation of muP
그래서 구현을 어떻게 하느냐?
muP의 결론은 한 문장으로 "training time동안 모든 layer가 균일한 속도로 학습되게 하기 위해서 (모든 layer가 유의미한 feature를 배우도록) layer별로 LR, initatlization 그리고 multiplier를 다르게 해주자"로 요약할 수 있다.
그러니까 사실 pytorch framework로 이걸 구현하는건 그렇게 어렵지 않다.
Optimizer에 parameter list를 넘겨줄 때 LR module별로 다르게 주고,
transformer일 경우 attention scale을 다르게 주고… 등등만 해주면 된다.
이제 아래 official repo에서 중요한 부분들만 따로 살펴볼 것이다.
Original Impl
Overview
먼저 original implementation을 보자. mup pakcage는 pypi install이 가능하고, torch의 nn.Module을 상속받는 모든 model subclass에 사용이 가능하지만 huggingface transformer에 적용한 버전을 보자. 사용법은 간단한데 다음과 같다.
- 먼저
base_model과 여기서 width가 변한delta_model을 정의해준다. mup.make_base_shapes라는 함수를 통해 어떤 weight이 matrix-like, vector-like… 인지 파악한다.- 다음으로 실제 target model을 만든 뒤
mup.set_base_shapes를 통해 model의 각 layer weight, bias 등에 attribute으로 infinite dim이 몇개인지등을 등록해준다. - huggingface model의 수정된 _init_weights()을 call하여 각 weight별 standard deviation을 사용해 param init을 한다.
- 마지막으로 optimizer를 선언하는데, weight별로 lr이 달라야 하며, 이는
mup.MuAdam, mup.MuSGD 등을 사용해서 얻는다.
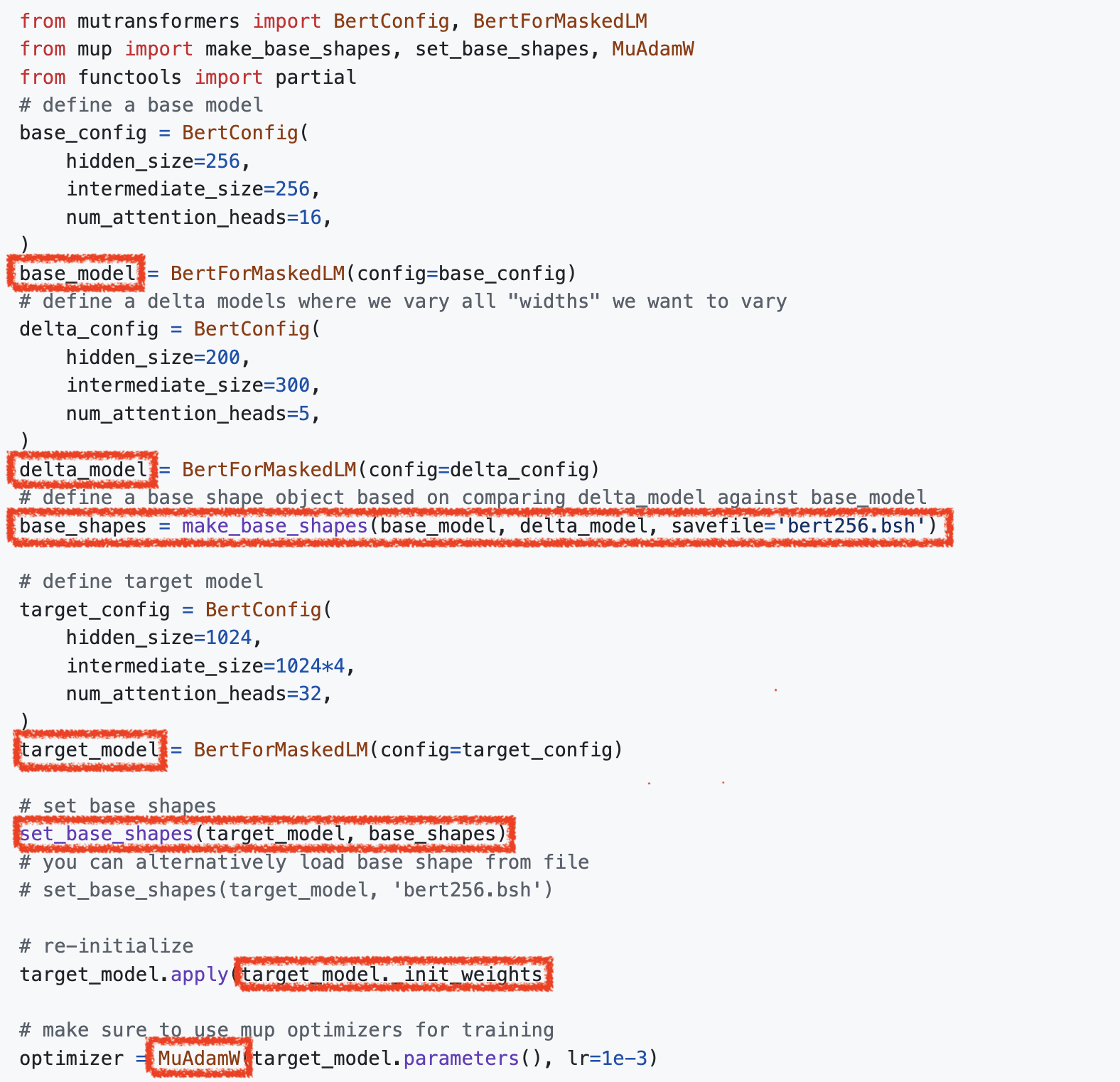 Fig.
Fig.
Weight Initialization
 Fig.
Fig.
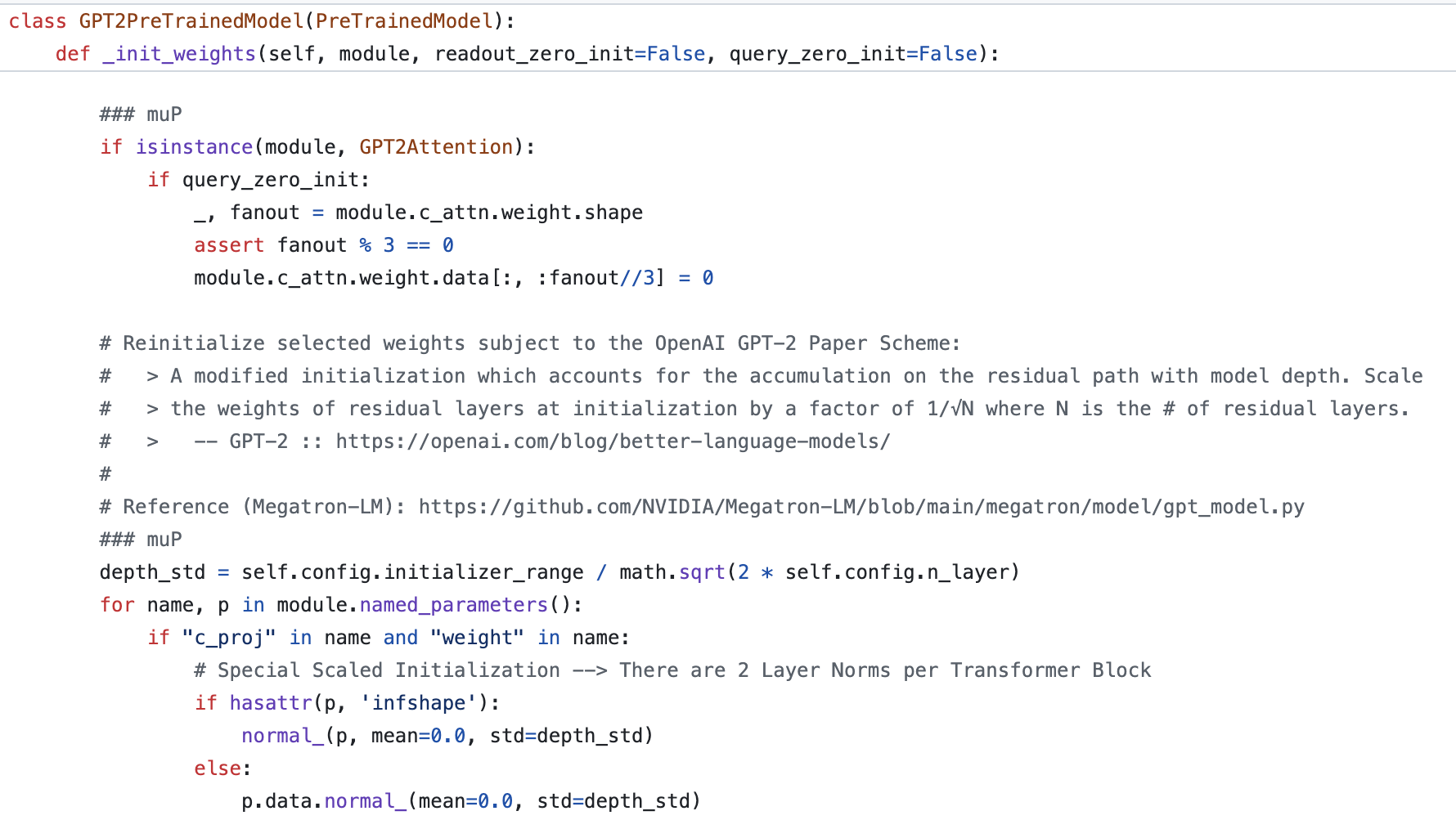 Fig.
Fig.
Set Attention Multiplier
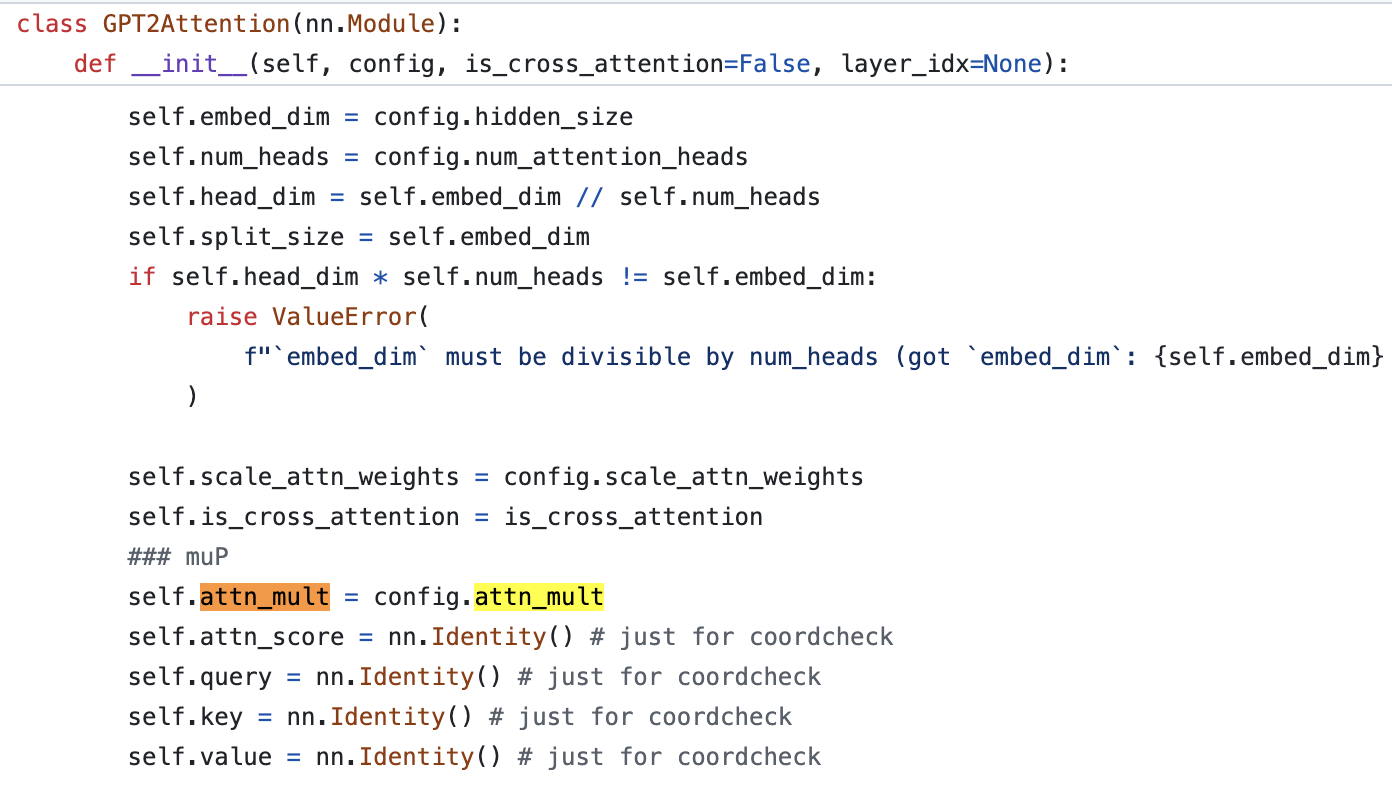 Fig.
Fig.
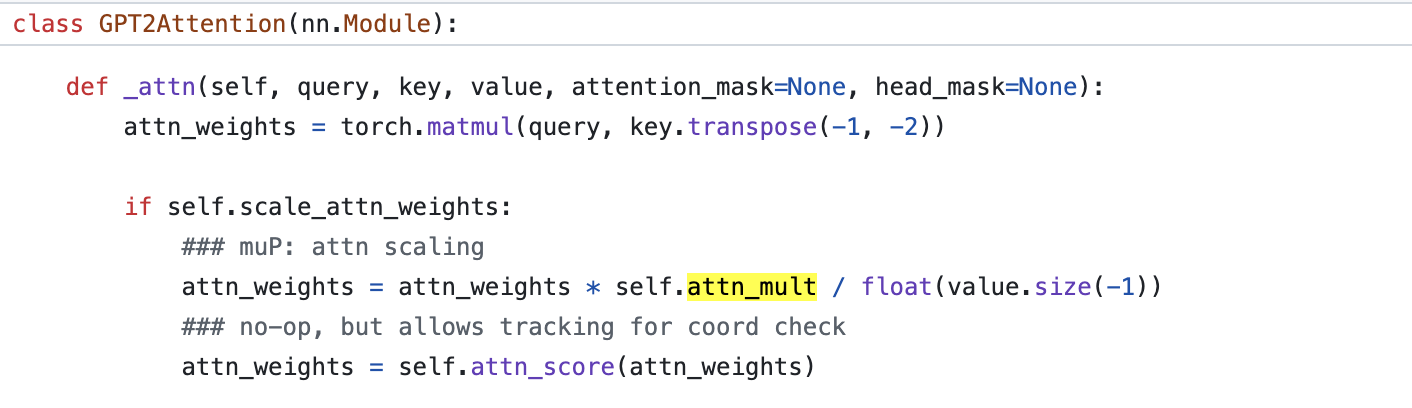 Fig.
Fig.
Get Layerwise LR Scaled Optimizer
Caveats
Don't Believe Other's muP HPs and Always Check Coordinates
사실 nn.module을 종류별로 나눠서 init_std를 잘 설정해주고 (module type이 많아봐야 3~4종류), lr도 per layer lr만 설정해주면 큰 어려움은 없어보인다. 물론 deepspeed, megatron같은 distributed package를 쓴다면 param, optimizer state가 sharding이 되기 전에 이를 잘 적용해줘야 한다던가 하는 디테일이 있지만 그것도 난이도가 높지는 않다.
하지만 이를 제대로 구현해서 scaling up하다보면 HP transfer에 실패하거나 아예 발산해버릴 수도 있다. 이 issue에서는 coordinate check을 통해 optimization step이 경과하더라도 width별로 layer output vector들의 norm이 flat하게 유지되는 걸 확인했음에도 megatron으로 1.3B model학습을 하는데 실패했다. NaN이 뜬다는 걸로 봐서 TP 저자들이 경험한 mixed precision issue인 것 같은데, 여전히 왜 (pre-)activation 의 크기가 width에 상관없이 constant로 유지되고 Transformer 최종 output이 O(1)인데 이게 발산해버리는지 잘 모르겠다.
그 밖에 또 필자가 muP를 새로운 architecture에 구현하는데 어려움이 있었는데,
그 이유는 참고할만한 muP 구현체들이 서로 다르기 때문이다.
물론 논문을 보고 구현하는것이 가장 뒤탈이 없겠으나,
논문에도 muP를 구현하는 방법이 table 3, 8, 9로 세 가지나 있으니 헷갈리는 것이다.
철학 자체는 "embedding은 update시 gradient를 커진 width만큼 boost, unembedding은 discount"으로 모두 같으나 나는 꽤 헷갈렸다.
또한 TP-5 저자진들의 official code에도 이런저런 이슈가 있다. 그 중 하나는 앞서 embedding layer parameterization 부분에서 설명했던 것 처럼 embedding tokens에 곱해줄 input multiplier가 아예 구현에 빠져있다는 것인데, 다른 paper들에서는 이 값을 매우 크게 주고 있고 TP의 철학에서도 가장 front-end에 있는 embedding layer는 lr을 크게 주던가 weight init을 크게 하던가 multiplier를 곱해주던가 뭐는 하나 해줘야 하는 것으로 보이는데 official repo에 이것이 빠져있는 것이다.
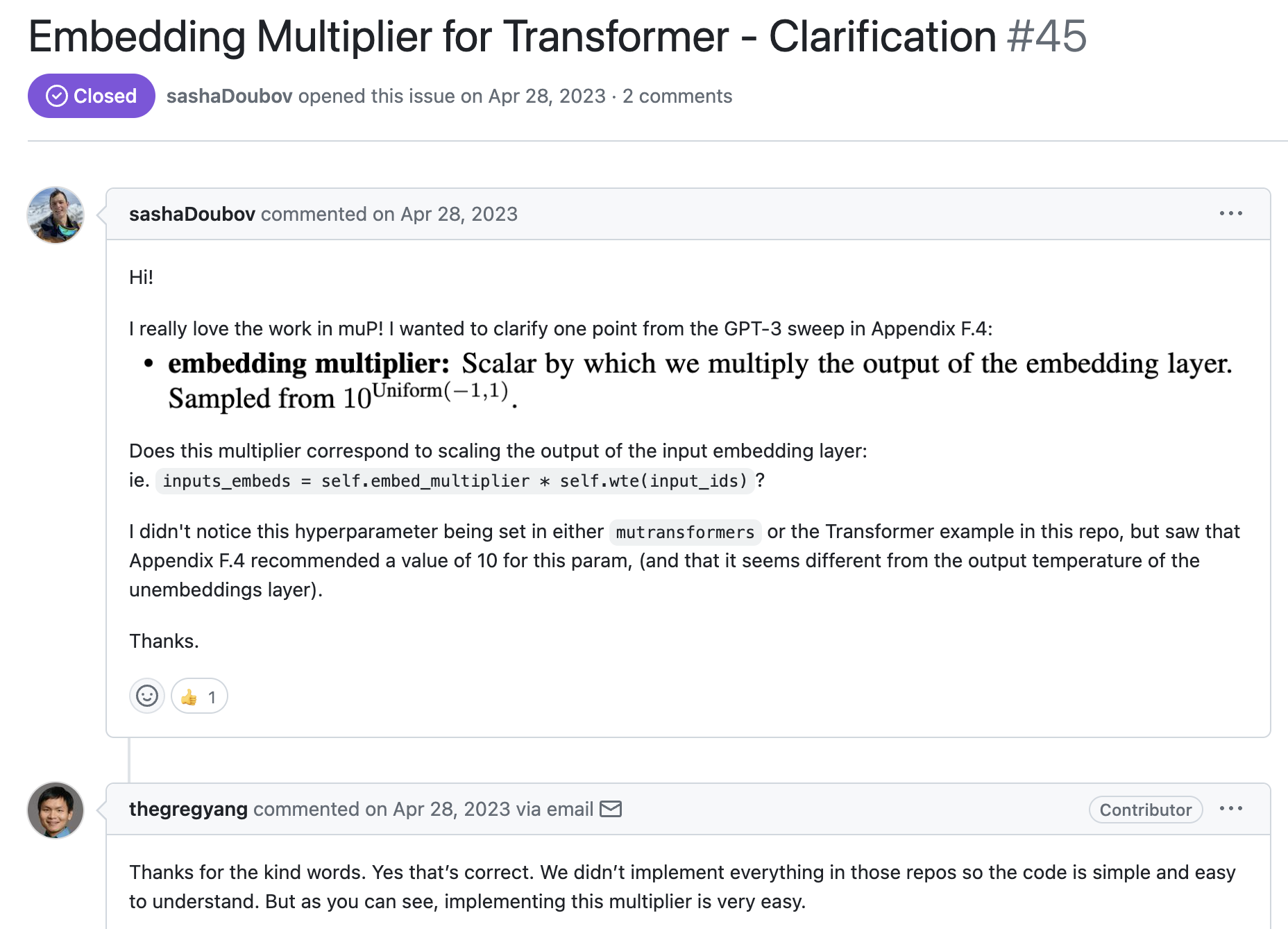 Fig. 실수가 맞다고 하는 Greg Yang. issue
Fig. 실수가 맞다고 하는 Greg Yang. issue
그리고 구현이 다르면 small scale에서 sweep한 HP space자체도 달라지는데, 경험상 muP를 쓴 MiniCPM, TeleFLM, nanoLM, Cerebras-GPT 등이 모두 detail이 달라서 그들의 search space가 내 구현과 들어맞을 거라는 보장이 없다. 예를 들어 누구는 lr을 1e-3부터 1e-1까지 탐색해서 1e-2 수준의 lr을 최종적으로 썼지만 누구는 더 작은 lr 범위를 찾아 6e-3을 쓰기도 하는데, 대신 multiplier를 다르게 준다던가 할 수도 있는 것이다.
| paper | param | optimal | search space (approximatly) | note |
|---|---|---|---|---|
| cerebras (40M GPT-2) | master lr | 0.006 | 0.004~0.012 | for matrix-like, scale lr by 1/(d_m/d_base) |
| init_std | 0.08 | 0.05~0.18 | for matrix-like, scale lr by 1/sqrt(d_m/d_base). (see paper for more detail of output layers) | |
| input_mult | 10.0 | 1~10 | ||
| attn_mult | 1 | - | scale attn logit by d_k | |
| output_mult | 1 | - | scale logit by 1/(d_m/d_base) | |
| minicpm (0.009B) | master lr | 0.01 | 0~0.1 | for matrix-like, scale lr by 1/(d_m/d_base) |
| init_std | 0.1 | 0.01~0.2 | for matrix-like, scale lr by 1/sqrt(d_m/d_base) | |
| input_mult | 12 | 2.5~20 | - | |
| attn_mult | 1 | - | scale attn logit by sqrt(d_k) (not following TP-5) | |
| output_mult | 1 | - | scale logit by 1/(d_m/d_base) | |
| scale_depth (from TP-6) | 0.01 | 1~8 | see TP-6 | |
| teleflm (64-layer GPTs) | vector-like lr | 1.5e-4 | - | - |
| matrix-like lr | 1.5e-4 | - | - | |
| vector-like init_std | 4e-3 | - | - | |
| matrix-like init_std | 4.242e-3 | - | - | |
| input_mult | 1.0 | - | - | |
| attn_mult | ? | - | - | |
| output_mult | 3.125e-2 | - | - | |
| nanolm (64-layer GPTs) | master lr | 0.001 | 0.0001~0.01 | - |
| init_std | 0.01 | - | - | |
| output_mult | 1.0 | - | - |
(자세한 내용은 reference에서 각 paper들 참고)
그래서 구현이 맞는지 coord check 을 다양한 condition에서 확인하고, search할 HP space도 잘 설정해서 실험을 무수히 많이 돌려 이를 검증해야 한다. 추가로 언급하자면 Tele-FLM의 경우 init_std값이 다른 paper들보다 훨씬 작은 걸 알 수 있는데, 이는 다른 work들의 base model spec이 40M +- 인 것 (대충 hidden size 64~128)에 비해서 꽤 큰 hidden size를 썼기 때문이다. 즉 base model이 512인 상황에서 base model은 사실상 SP와 다를게 없고, 보통 Lecun init을 따를 경우 model size가 클수록 init_std가 작으니 이는 어쩔 수 없는 것이다.
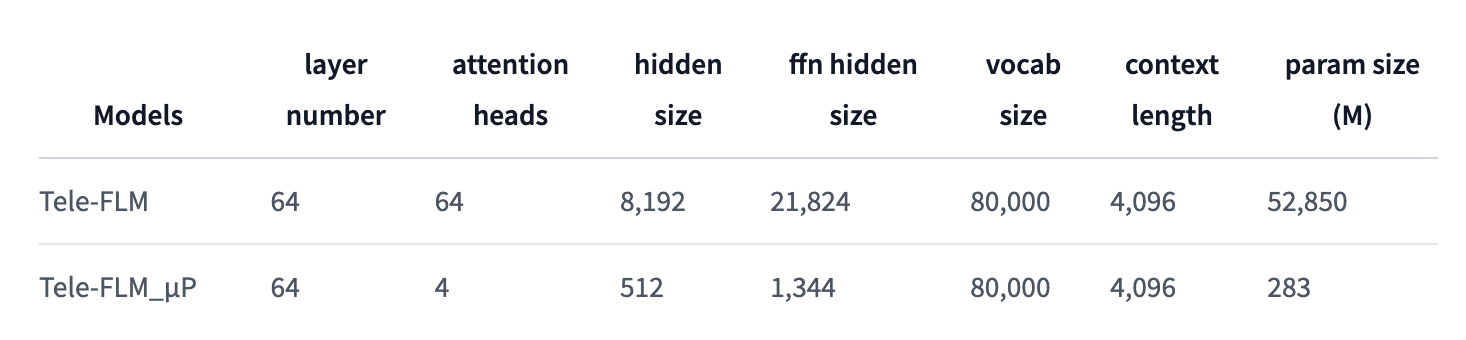
또한 training step이 부족하거나 하면 또 transfer가 안되는 것 처럼 보일 수도 있으므로 이것도 신경써야 하고, loss가 local minima에 수렴하는 HP 구간인 loss basin을 벗어나면 wider is always better이나 scaling law가 실패할 수 있다는 점도 주의해야 한다.
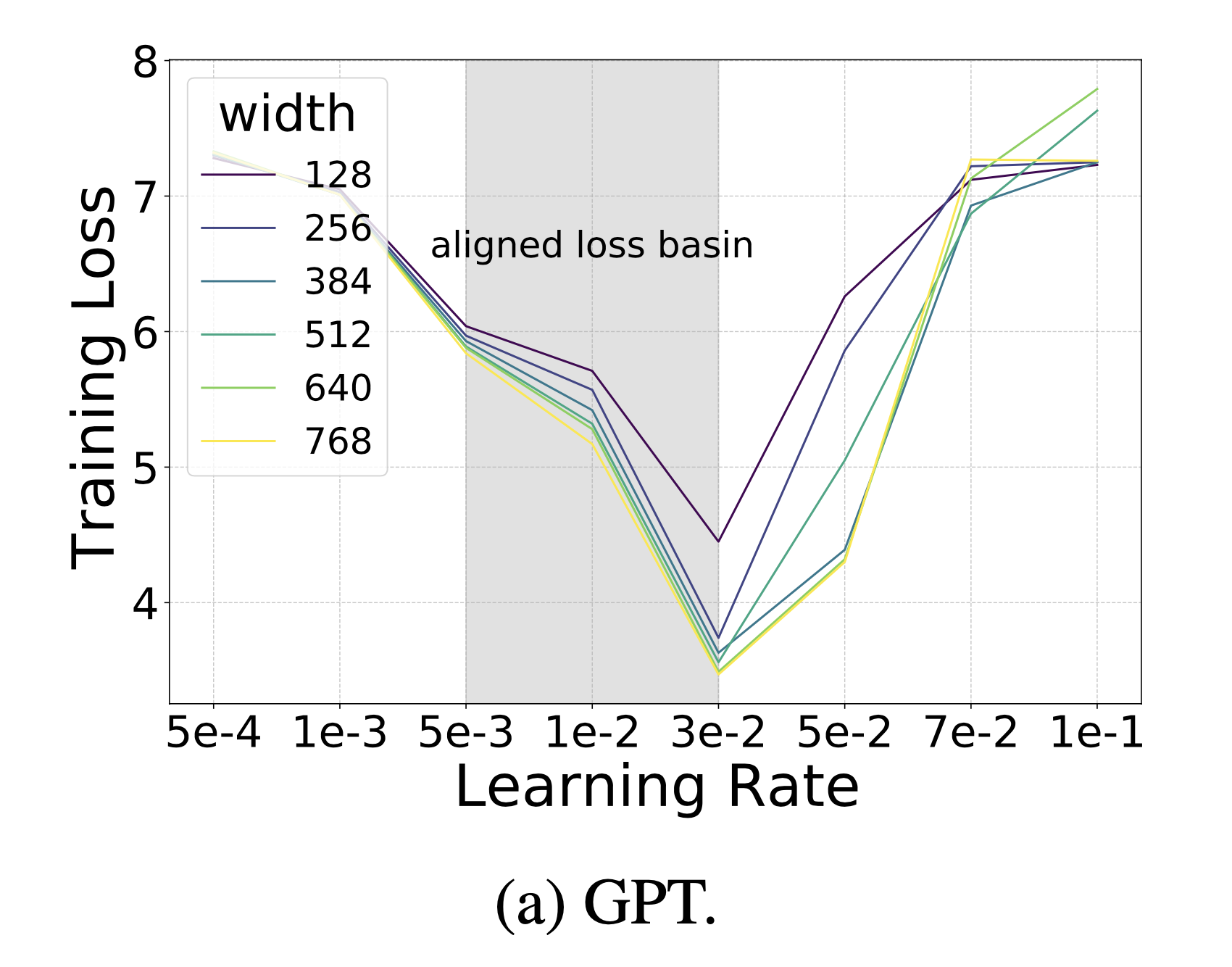
그리고 너무 작은 model들에서 scaling law prediction 하는 것은 noisy할 수 있기 때문에 서로다른 HP의 값을 average하는 방법도 생각해보면 좋을 것 같다는 내용이 NanoLM에 나와있으니 참고하면 좋을 것 같다.
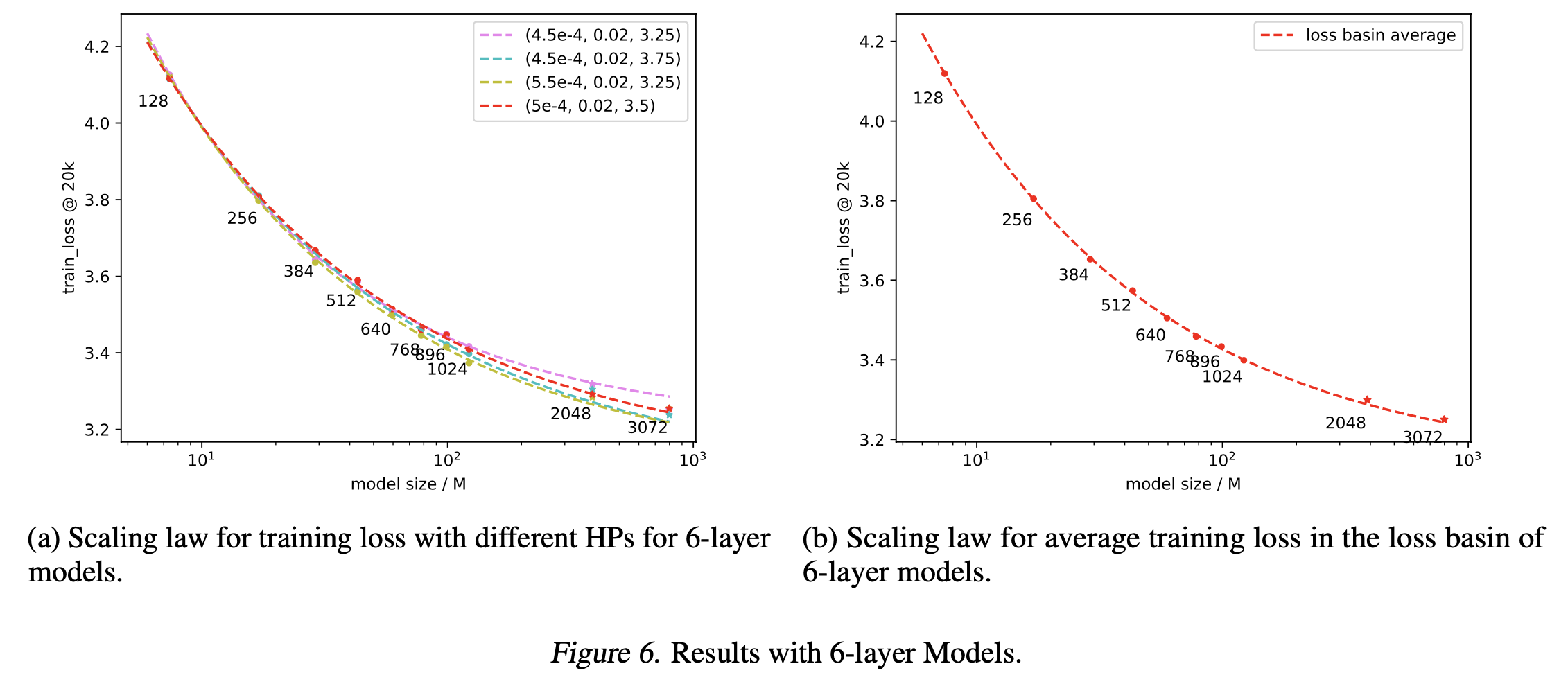
+Updated) Absorbing Multiplier
추가로 muP를 적용한 codebase로 pre-training을 한 model을 배포할 때 주의해야 할 점이 있다. 당연히 model class를 새로 정의해서 이를 사용하면 좋겠지만 예를 들어 llama-3 architecture로 학습한 weight을 huggingface에 배포한다고 생각해보자. huggingface model에는 당연히 muP 구현이 없기 때문에 multiplier가 존재하지 않고 optimizer도 새로 정의해야 한다. 근데 그냥 배포만 한다면 weight init method, optimizer lr scaling등은 신경쓰지 않아도 되지만 (이미 학습이 됐으니까) multiplier를 layer output에 곱해주지 않으면 inference자체가 이상하게 된다. 그러므로 이 경우 multiplier를 weight matrix에 흡수 시켜줘야 (absorbing)하고 이는 inference에 아무런 영향도 주지 않는다.
 Fig.
Fig.
하지만 당연히 이 model class를 사용해 fine-tuning을 한다면 얘기가 달라진다. 왜냐하면 ABC-symmetry에 따라서 multiplier를 weight에 포함시키려면 gradient크기가 달라지고 이는 TP를 break할 수 있기 때문이다.
p.s. Noam Shazeer의 Fast Transformer Decoding: One Write-Head is All You Need에도 비슷한 내용이 있다.
 Fig.
Fig.
+Updated) Your muTransferred LR may not be optimal
추가로 muP 실험을 할 때 주의해야 할 점이 있는데, 실제 target model로 scale-up할 때 보통 batch size, the number of training tokens도 증가하기 마련이지만 TP는 이를 고려하지 않았다는 점이다. GPT-3 HP search를 할 때 greg은 batch size를 실제 target model에서 쓸 것으로 고정한 것으로 보이고 (아마도), training step은 4B tokens에서 search를 하고 실제로는 300B 학습을 한 것으로 보이는데, 이는 75배 밖에 차이가 안나지만 요즘 실제 학습되는 LLM들은 5~15T는 우습기 때문에 수천배에 달하는 학습량 discrepency가 발생할 수 있다. 이 경우 아마 muTransferred LR은 더 이상 optimal이 아니게 될 가능성이 높다. 그러므로 반드시 학습량과 batch size에 따른 optimal LR scaling을 고려해야 학습에 성공할 수 있을 것이니 이에 주의해야 할 것이다.
References
- Papers
- Tensor Program Core Materials
- Tensor Programs IV: Feature Learning in Infinite-Width Neural Networks
- Tensor Programs V: Tuning Large Neural Networks via Zero-Shot Hyperparameter Transfer
- Tensor Programs VI: Feature Learning in Infinite-Depth Neural Networks
- A Spectral Condition for Feature Learning
- Steering Deep Feature Learning with Backward Aligned Feature Updates
- Why do Learning Rates Transfer? Reconciling Optimization and Scaling Limits for Deep Learning
- Sparse maximal update parameterization: A holistic approach to sparse training dynamics
- How to set AdamW’s weight decay as you scale model and dataset size
- Scalable Optimization in the Modular Norm
- Papers about LLM trained with Tensor Program
- Cerebras-GPT: Open Compute-Optimal Language Models Trained on the Cerebras Wafer-Scale Cluster
- MiniCPM: Unveiling the Potential of Small Language Models with Scalable Training Strategies
- Tele-FLM Technical Report
- NanoLM: An Affordable LLM Study Benchmark via Accurate Loss Prediction Across Scales
- A Large-Scale Exploration of μ-Transfer
- Phi-3 Technical Report: A Highly Capable Language Model Locally on Your Phone
- Apple Intelligence Foundation Language Models
- NTK Related
- Others
- Disentangling feature and lazy training in deep neural networks
- Measuring the Effects of Data Parallelism on Neural Network Training
- Scaling Limit of Neural Networks with the Xavier Initialization and Convergence to a Global Minimum
- Small-scale proxies for large-scale Transformer training instabilities
- Training Compute-Optimal Large Language Models
- DeepSeek LLM: Scaling Open-Source Language Models with Longtermism
- Scaling Laws and Compute-Optimal Training Beyond Fixed Training Durations
- Large Batch Training of Convolutional Networks
- Tensor Program Core Materials
- Blogs and Others
- Tensor Program Related
- On infinitely wide neural networks that exhibit feature learning
- µTransfer: A technique for HP tuning of enormous neural networks
- MiniCPM: Unveiling the Potential of End-side Large Language Models
- A Gentle Introduction To Weight Initialization for Neural Networks from WandB
- Greg’s tweet thread for NNGP
- Reduce Model Tuning Costs with muP from Theo Clark
- NTK reltated
- Common LLM’s Pre-training Setting
- What to do to scale up? from Simo Ryu
- Tensor Program Related
- Video
- Tensor Program Related Videos from Creators
- μTransfer: Tuning GPT-3 HPs on one GPU, Explained by the creator
- (2022 June) Greg Yang - “Tuning Large Neural Networks via Zero-Shot Hyperparameter Transfer”
- (2021 Mar) Greg Yang — Feature Learning in Infinite-Width Neural Networks
- (2020 Dec) Feature Learning in Infinite-Width Neural Networks from Greg Yang
- (2023 Jan) Large N Limits: Random Matrices & Neural Networks from Greg Yang
- (2023 Sep) Greg Yang: The unreasonable effectiveness of mathematics in large scale deep learning
- (2022) Tuning GPT-3 on a Single GPU via Zero-Shot Hyperparameter Transfer
- Tensor Program Explained from Others
- NTK Related
- Illustration of NTK from Author (Arthur Jacot)
- Videos from CS229M: Machine Learning Theory
- Neural Tangent Kernel Analysis of Deep Narrow Neural Networks from 류경석 교수님
- 수리과학부 류경석 교수 - Training Dynamics and Complexity of Infinitely Wide WGAN and Minimax
- Recent Developments in Over-parametrized Neural Networks, Part I
- SNU 류경석 - Neural Tangent Kernel Analysis of Deep Narrow Neural Networks
- Lecture 7 - Deep Learning Foundations, Neural Tangent Kernels
- Deep Learning Foundations by Soheil Feizi : Large Language Models
- On the Connection between Neural Networks and Kernels: a Modern Perspective -Simon Du
- Linalg, Backprop and GPT-2 from scratch
- LLM Pre-training and Scaling Law
- Tensor Program Related Videos from Creators
- Codes
- Backpropagation Through Softmax Activation
- The Softmax function and its derivative from Eli Bendersky
- Transformer Networks: A mathematical explanation why scaling the dot products leads to more stable gradients from Thomas Kurbiel
- Derivative of the Softmax Function and the Categorical Cross-Entropy Loss from Thomas Kurbiel
- Temperature check: theory and practice for training models with softmax-cross-entropy losses
- Regularizing Neural Networks by Penalizing Confident Output Distributions
- Softmax Gradient Tampering: Decoupling the Backward Pass for Improved Fitting
- tmp