(WIP) Relationship between Logit Growth Problems of Deep NN and LayerNorm

< 목차 >

• Motivation
• Preliminaries) Backprop Through Softmax Activation
• Analysis
  • Attention Logit Growth Problem and QK Layernorm
  • Last Layer's Logit Growth Problem and Z-Loss
• Connection to muP
• Caveats and FAQ
  • Do We Need Z-Loss ?
  • Latency
  • Non-trivial Tips for Implementation
• +Updated) Lessons from Chameleon
• +Updated) Lessons from Gemma 2
• +Updated) Lessons from LLaMa-3.2 (multimodal llama-3)
• +Updated) Methods of improving LLM training stability
  • Method w/o introducing additional modules
  • Method w/ introducing additional modules
  • Caveats
• References

Motivation

이번 post에서는 Small-scale proxies for large-scale Transformer training instabilities라는 paper를 분석해볼 것이다. 이 paper에서는 어떨 때 loss가 발산해버리는지를 softmax activation을 통과하기 전의 logit들, 즉 각 transformer의 각 residual block들의 attention logit과 last layer의 logit과 관련되어 있다고 보고 이를 분석 한 뒤, ViT-22B paper에서 제안된 QK normalization layer과 PaLM에서 제안된 Z-loss라는 module이 Learning Rate (LR) sensitivity에 어떤 영향을 주는지에 대해 분석한다.

QK layernorm은 보통 Transformer가 self_attn 전에 input norm 한 번만 하는 것과 다르게, Q, K space로 projection한 뒤 dot product attention을 하기 전 Q, K tensor를 각각 normalization 함으로써 training stability를 높히는 technique을 말한다.

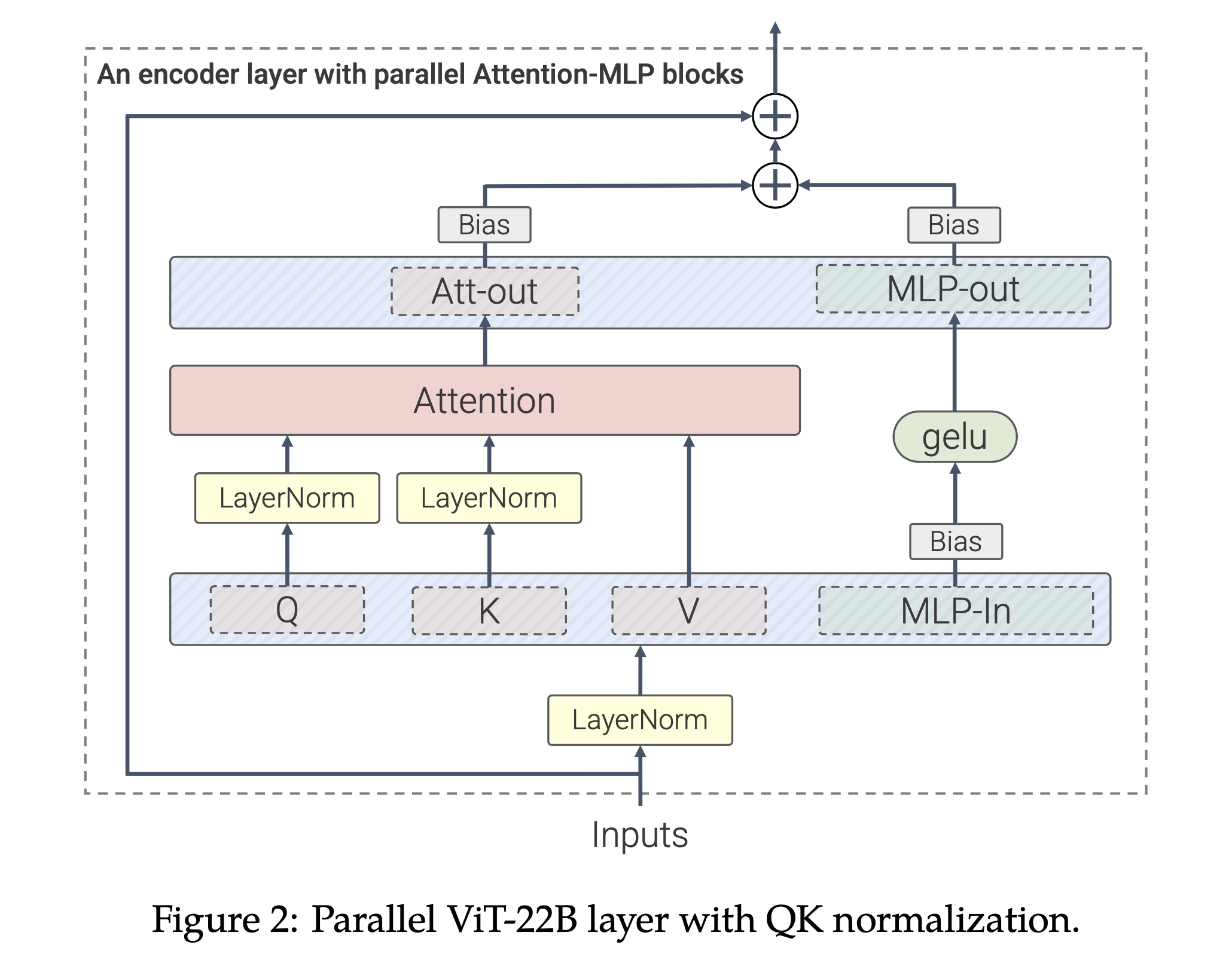Fig.

Scaling Vision Transformers to 22 Billion Parameters에서는 QK layernorm이 working하는 이유를 attention logit tensor의 element가 불균형하게 학습되면서 element 하나가 매우 커지게 되면, softmax output이 softmax activation dimension에 대해서 one-hot vector 처럼 되어 문제가 발생한다고 report했다. 즉 entropy가 0에 가까워지면 training instability가 일어나는 것이다.

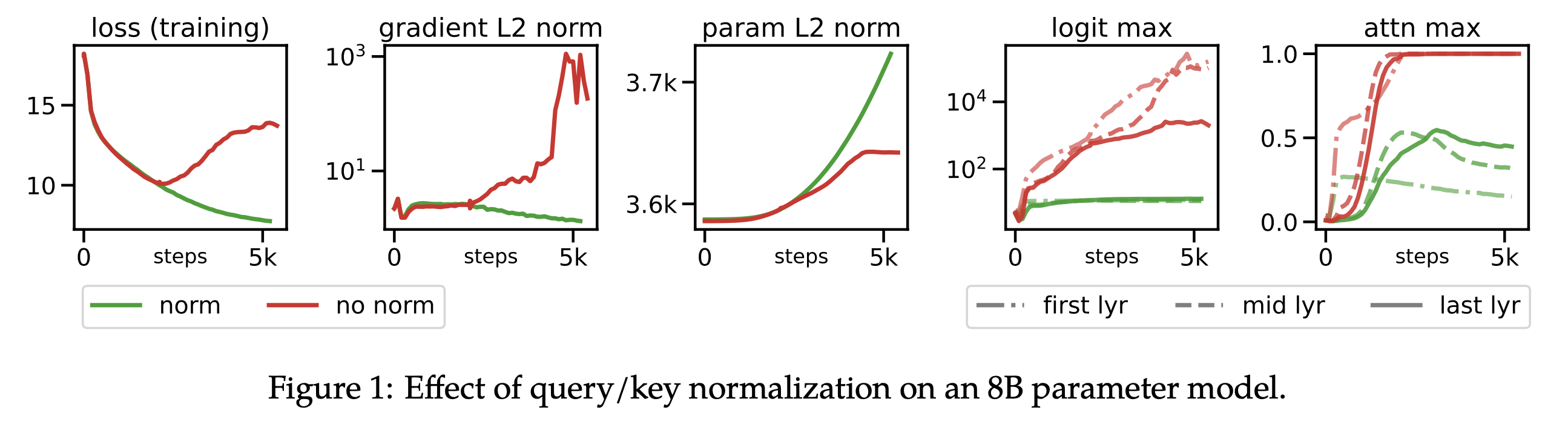Fig.

바로 위 figure를 보면 Vision Transformer (ViT)의 attention logit tensor의 max value가 커지면 gradient norm이 커지게 되고, 이에 따라 loss가 발산 (diverge) 해버리게 된다. 하지만 paper에서는 왜 logit max가 커지면 loss가 발산하는지? 에 대한 분석이 부족하다. 나는 softmax 전 logit tensor가 one-hot에 가까워지면 logit, \(Z\)에 대한 gradient, \(\partial L / \partial Z\)는 0에 가까워져 gradient vanishing이 일어나는 것으로 알고있는데, 이번 post에서 small scale proxy~ paper와 backpropagation 등을 고려해 그 이유에 대해 생각해 볼 것이다.

결과적으로 QK layernorm을 사용할 경우 아래와 같이 LR sensitivity를 크게 개선할 수 있었다고 하는데, LR sensitivity는 optimal validation performance를 보이는 optimal LR point를 벗어나면 validation performance가 나빠지기 마련인데, optimal point에서 얼마나 벗어나야 valid error가 나빠지는지?를 의미한다고 할 수 있다. 즉 LR sensitivity 가 개선됐다, 즉 둔감해졌다는 말의 의미는 optimal LR과 비슷한 performance를 내는 LR 분포의 범위가 넓어졌기 때문에 대충 LR을 찍기만 해도 너무 터무니 없는 값이 아니면 near optimal performance를 얻을 수 있다는 것이다.

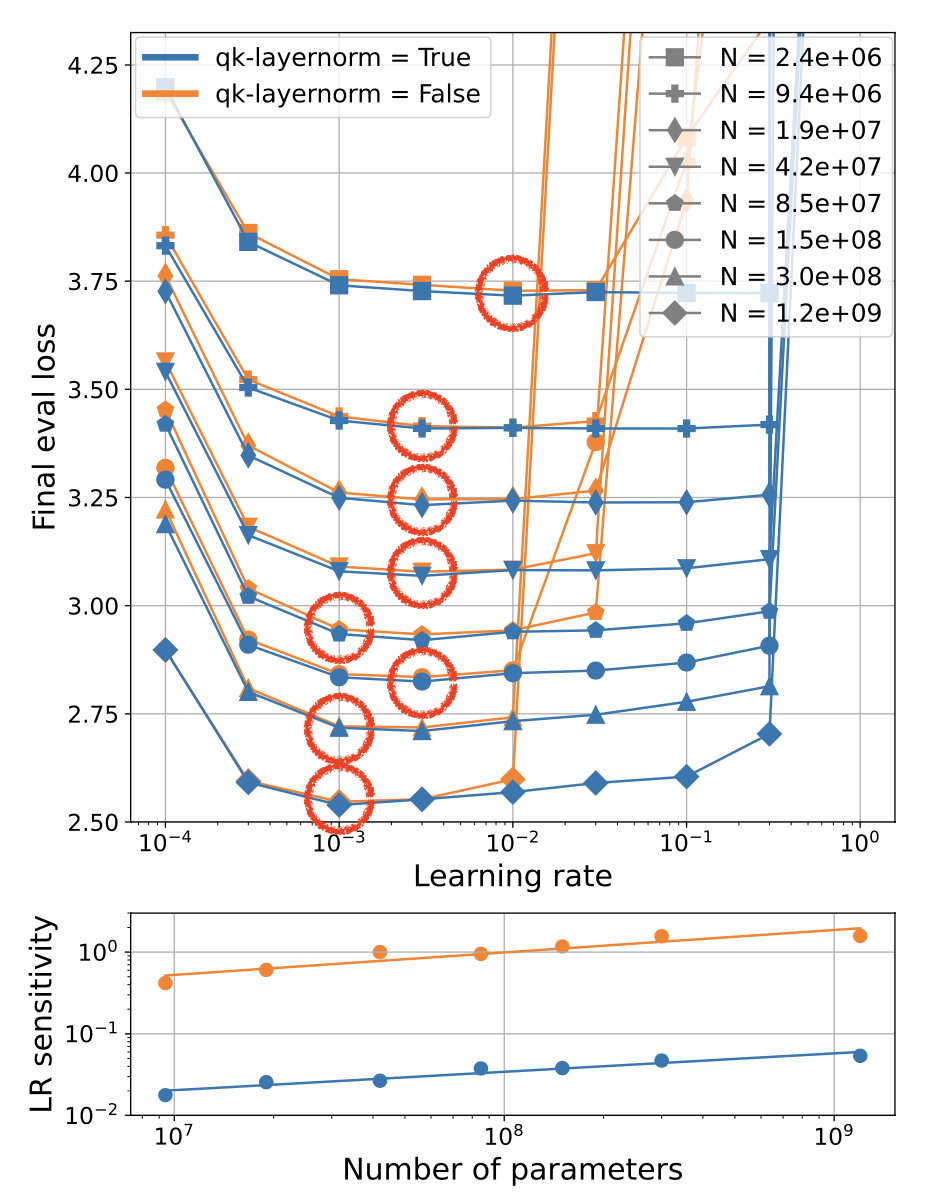Fig.

Preliminaries) Backprop Through Softmax Activation

본격적으로 paper의 findings에 대해 얘기하기 전에, softmax activation을 통해 logit으로 전파되는 gradient를 유도하여 logit의 scale에 따른 gradient scale에 대해 생각해보자.

Logit vector, \(z \in \mathbb{R}^{1 \times n}\)에 대해서 softmax output, \(s \in \mathbb{R}^{1 \times n}\)는 다음과 같이 계산된다.

Softmax activation function의 backprop 결과는 아래와 같은데, 여기서 \(i=k\)인 경우와 아닌 경우에 대해서 derivative 값이 달라지는 것에 유의해야 한다.

각각 \(i=k, i \neq k\)인 경우에 대한 미분 결과는 chain rule을 사용하면 아래와 같이 간단하게 얻을 수 있는데,

이는 두 변수가 같은 값을 가지면 1, 아니면 0이 되는 Kronecker delta를 사용해서 아래와 같이 표현할 수도 있다.

가끔 헷갈리는 사람들이 있는데, softmax activation output의 미분체는 모든 input을 normalizer로 썼기 때문에 jacobian의 off-diagonal elements가 0이 아니라는 점에 주의할 필요가 있다.

보통 softmax가 Cross Entropy (CE) loss와 같이 사용되기 때문에 loss에 대한 미분체인 \(\frac{\partial L}{\partial z}\)도 같이 언급 되는 경우가 많은데, CE loss는 Negative Log Likelihood (NLL)이기 때문에 log에 대한 미분과 위에서 구한 softmax activation의 미분 결과와 ground truth label이 one hot vector라는 점을 이용하면 아래와 같이 쉽게 계산할 수 있다.

이제 logit이 커지는 것과 softmax activation에 대한 jacobian, 그리고 training stability에 대해 생각해보자. 먼저 간단하게 생각할 수 있는 부분은 아래 jacobian matrix에서 logit이 커질 경우 softmax vector, \(s_1, s_2, \cdots\)의 값은 one-hot vector에 가까워 질 것이고, 이에 따라서 vector간 dot-product 결과는 0에 가까워질 것이므로 gradient가 사라질 수 있다는 것 (gradient vanishing)이다.

이는 Attention Is All You Need에서도 유사하게 언급되는 내용으로, transformer의 self attention module에서 단순 dot product를 하는 것이 아니라 scaled dot product를 하는 이유 또한 small gradient problem 때문이다.

Fig.

Analysis

Attention Logit Growth Problem and QK Layernorm

Attention logit뿐 아니라 output logit scale이 어떠냐에 따라서 Transformer의 training stability가 달라진다는 얘기는 이전부터 있었던 것으로 알고 있다. fp16에서의 numerical instability issue도 있었던 것으로 기억하는데, fp16에서 under- or over-flow issue가 있다는 것 자체가 logit값이 너무 커지거나 작아져 문제가 있다는 것이고, 이는 fp16이 아니더라도 gradient를 vanishing or exploding 시킬 수 있다는 문제로 생각해볼 수 있겠다.

Fig.

Attention Logit Growth라는 term 자체는 Scaling vision transformers to 22 billion parameters라는 paper에서 처음 정의됐다고 한다.

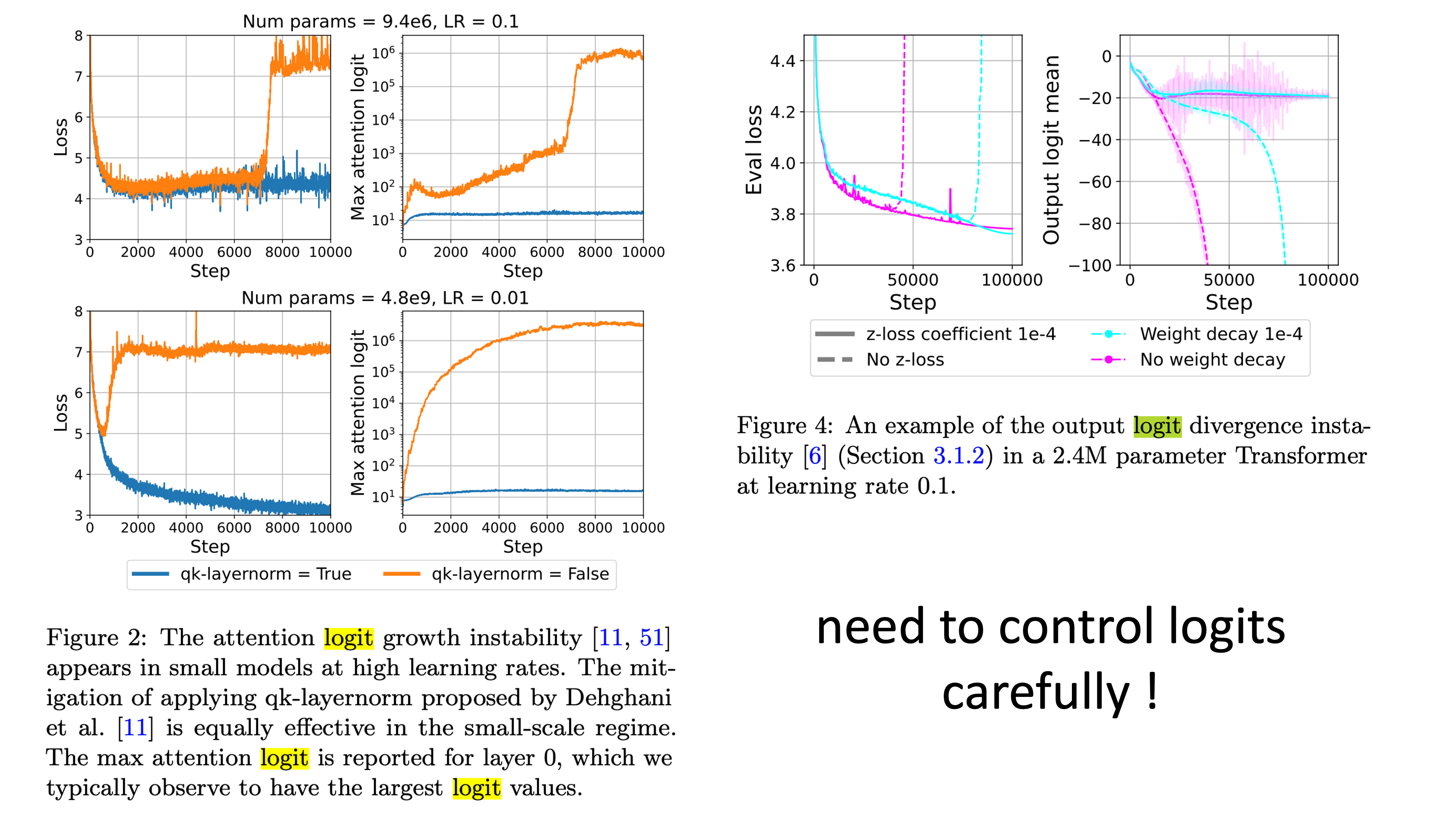Fig.

Fig.

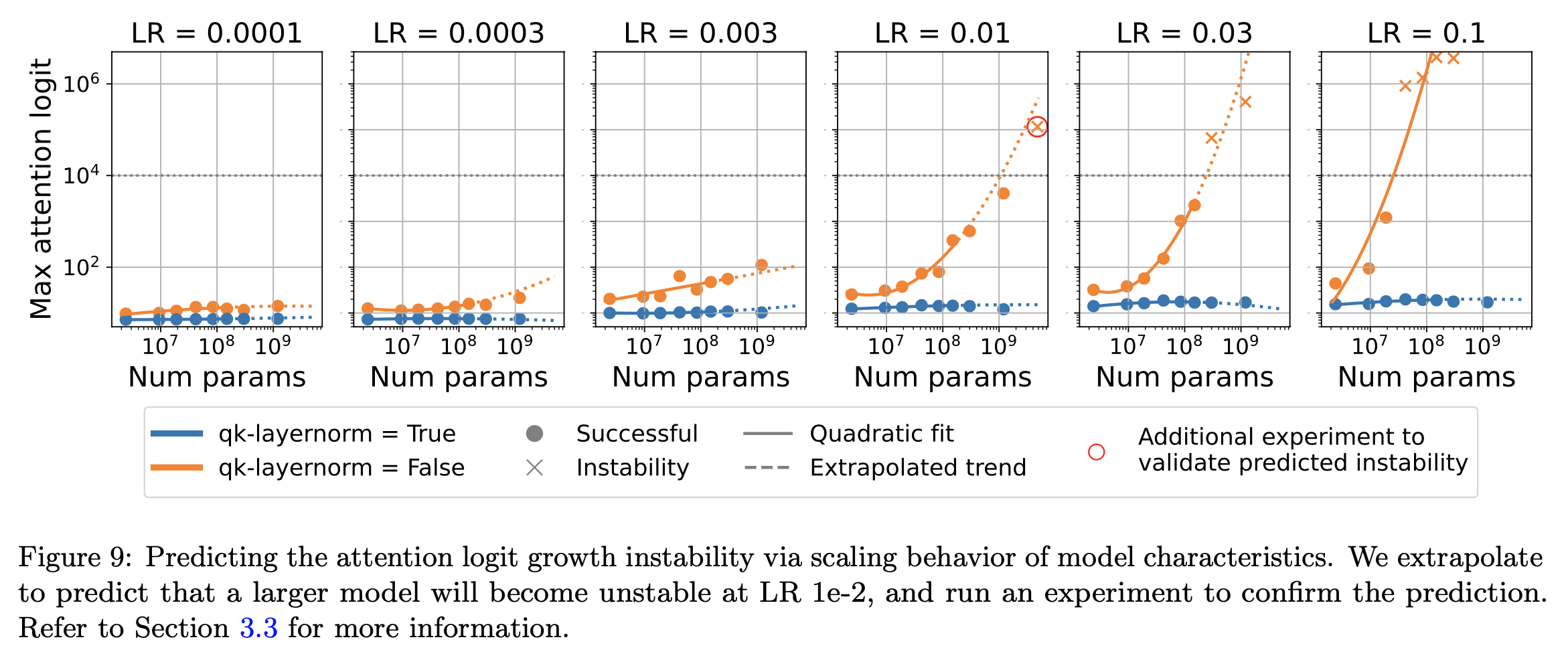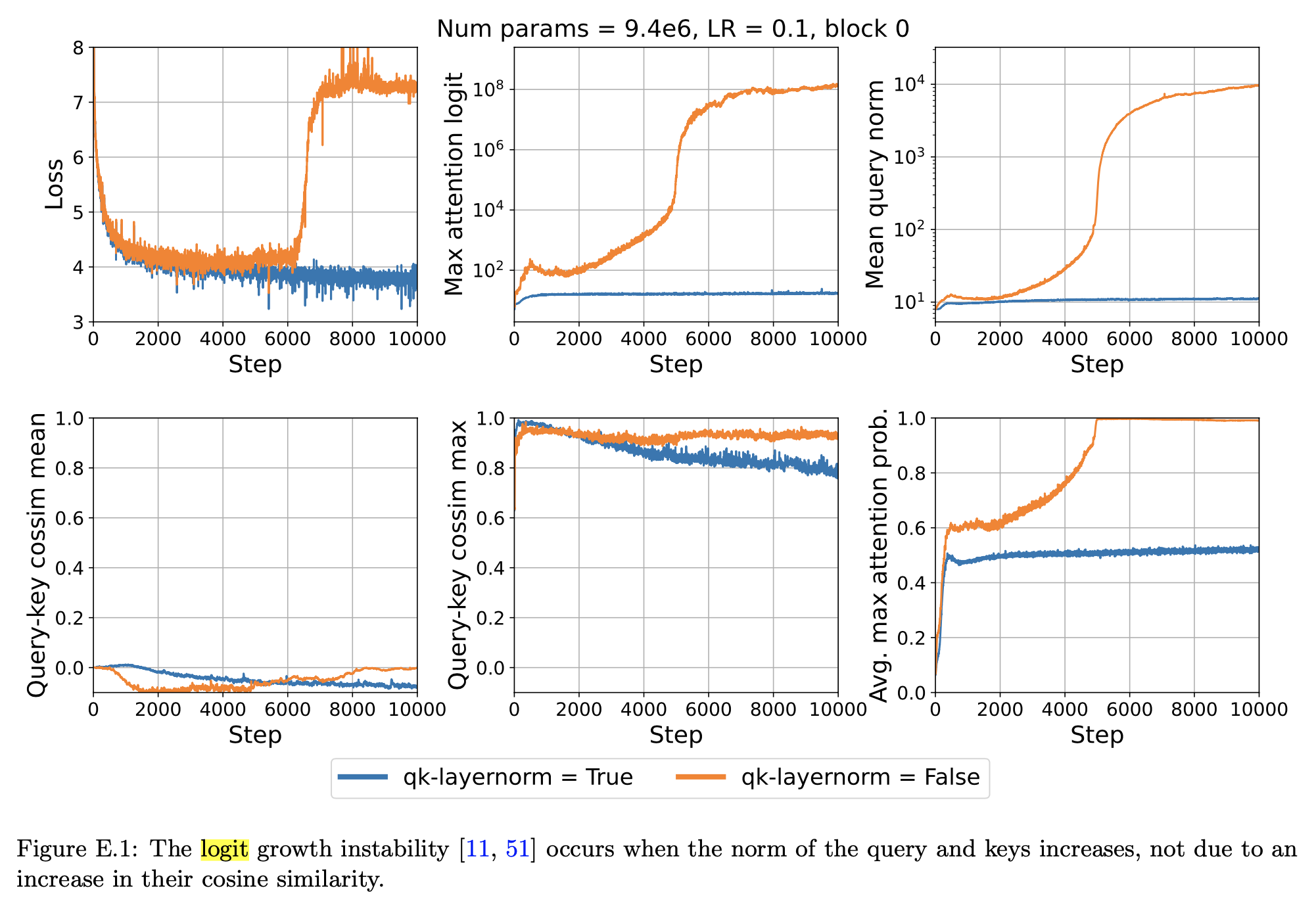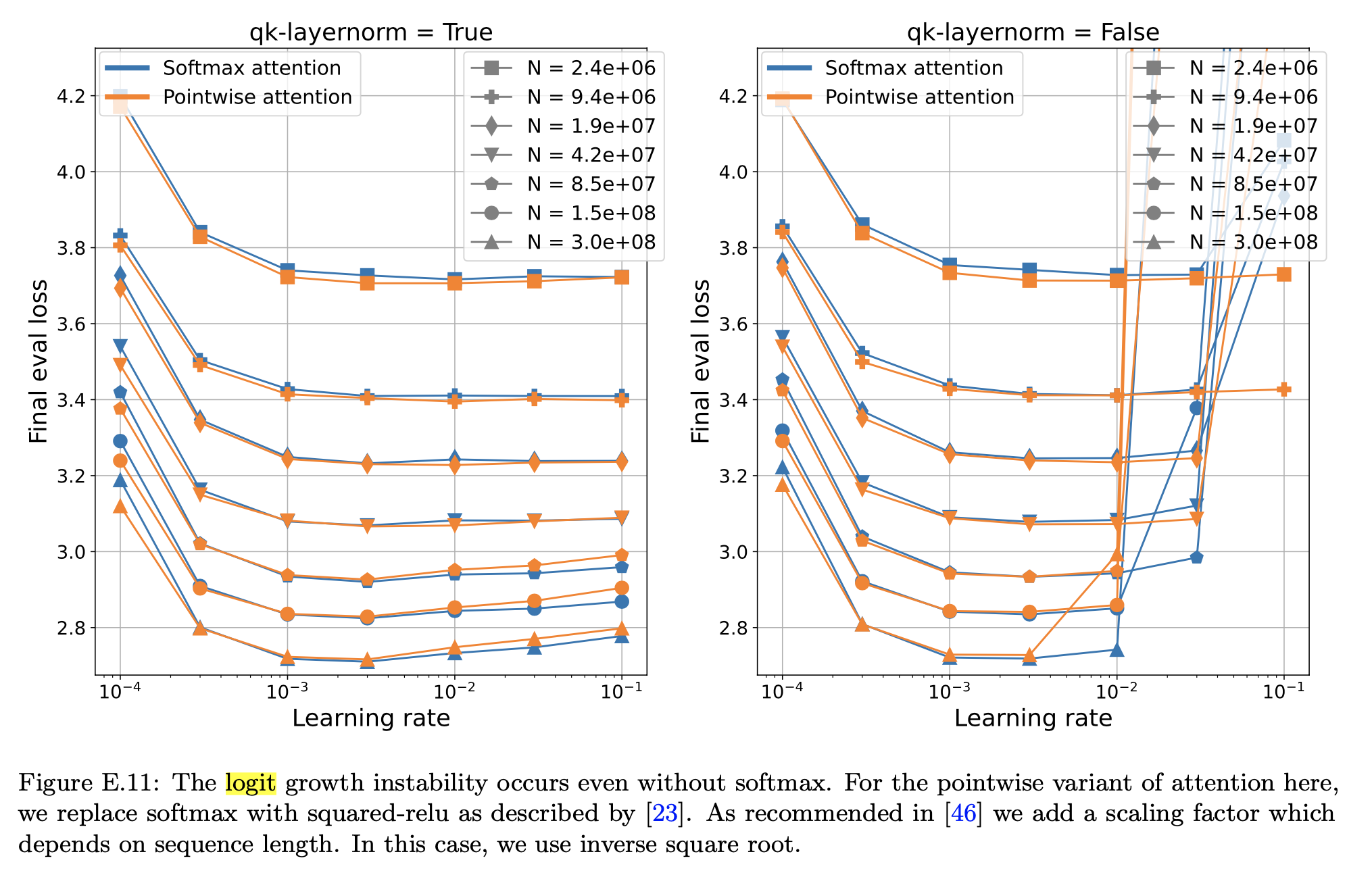Fig.

Fig.

Last Layer's Logit Growth Problem and Z-Loss

Connection to muP

아래 figure를 보면 width가 커질 수록 QK layernorm을 적용하지 않은 경우, 좋은 LR range를 벗어나면 발산해버리기 쉽다는 걸 보여주지만 QK layernorm을 사용하면 LR을 optimal value로부터 크게 벗어나도록 설정해도 performance가 많이 떨어지지는 않다는 걸 확인할 수 있다. 즉 LR sensitivity가 낮아진 것이다.

Fig.

하지만 paper의 exp setting은 아래와 같이 xavier like fan-in variance를 썼다는 걸 알 수있는데, embedding weight은 fan-out을 썼다는 점에 주의해야 한다 (즉 완전 Standar Parameterization (SP)는 아니다).

Fig.

또 하나 눈여겨 볼 만한 점은 QK layernorm을 쓰면 sensitivity는 줄어들지만 SP에 대해서 optimal LR은 왼쪽으로 shift되는 trend를 보인다는 것이다. 이 부분에 대해서 "음 model size, N이 커지면 LR이 감소하는 경향이 power function 꼴인데 이걸 찾아볼까?"라고 생각할 수 있는데, 이것이 정확히 DeepSeek LLM이 한 것이라고 볼 수 있다. 그런데 사실 이는 model width가 \(n\)배 커지면 lr은 \(1/\sqrt{n}\)배 scaling 해주는 Tensor Program (TP) IV, V의 Maximal Update Parameterization (muP)의 철학과도 부합한다고 할 수 있다. 여기에 muP는 unembdding, embedding에 scaling을 조금 해주고 attn logit을 좀 더 수정했을 뿐, 대부분의 scaling method들이 사실상 거의 다 같은 경향을 보여준다는 것이라 할 수 있다. (사실 이 post는 muP에 대한 post를 작성하다 만들었으니 muP가 뭔지 궁금한 이들은 해당 post나 TP-V 논문을 보도록 하자)

Paper에서는 SP와 비교해서 muP도 실험해봤는데, goal은 "muP도 QK layernorm이 필요할까?"를 확인하는것 이었고 답은 “LR sensitivity를 낮추는게 목적이라면 yes”이긴 하다. 하지만 muP의 경우 어차피 HP가 transfer되기 때문에 QK layernorm이 없어도 된다는게 저자들의 의견이다.

Fig.

이 부분에 대해서는 매 residual block마다 layernorm을 추가하는 것이 computing resource가 추가되는 단점이 있기도 하고, 저자들이 muP를 respect하는 차원에서 얘기한 것 같자만 실제로 muP를 통해 small scale의 optimal LR을 \(n\)배 큰 target model로 transfer하는 경우 real-world에서는 width뿐 아니라 batch size, the number of training tokens도 같이 scaling하기 때문에 이런 경우 optimal LR이 조금 shift되는 trend를 맊기 위해서 LR sensitivity는 낮추면 낮출수록 좋다는게 내 의견이다.

Caveats and FAQ

Do We Need Z-Loss ?

사실 paper를 대충 봤을 때, training instability를 해결하기 위해서 QK layernorm과 Z-loss를 모두 구현해야 되는 것이 아닌가 하는 생각을 했다. 왜냐하면 결국 attention logit이 발산하지 않게 막더라도 last layer의 logit은 발산할 가능성이 있기 때문이다. 이러면 결국 LR sensitivity를 낮출 수 없을 것이다. 하지만 자세히 읽어보면 paper Figure 3 등을 봤을 때 Z-loss가 없어도 QK layernorm과 weight decay만으로 이는 어느정도 달성 되는 것으로 보인다. 본래 Z-loss를 쓰려면 hyperparameter tuning을 해야 하므로 LR의 search space가 낮아지는 대신 다른 search dimension이 생기는 것이 아닌가 해서 조삼모사 일 수 있겠다고 생각했으나, 그냥 QK layernorm만 쓰면 괜찮을 것으로 보인다.

Latency

Google의 computer vision researcher인 Lucas Bayer의 tweet를 보면 왜 사람들이 (특히 다른 domain) 이런 free lunch를 간과하는지 모르겠다고 한다. 덧붙혀 누군가 "layer마다 layernorm를 끼워넣는게 latency에 큰 영향을 끼치지는 않나요?"라는 질문에, "1.6%의 latency와 big model에서의 training stability or training optimality 중에 뭐가 더 가치 있을까?"라는 답을 단다.

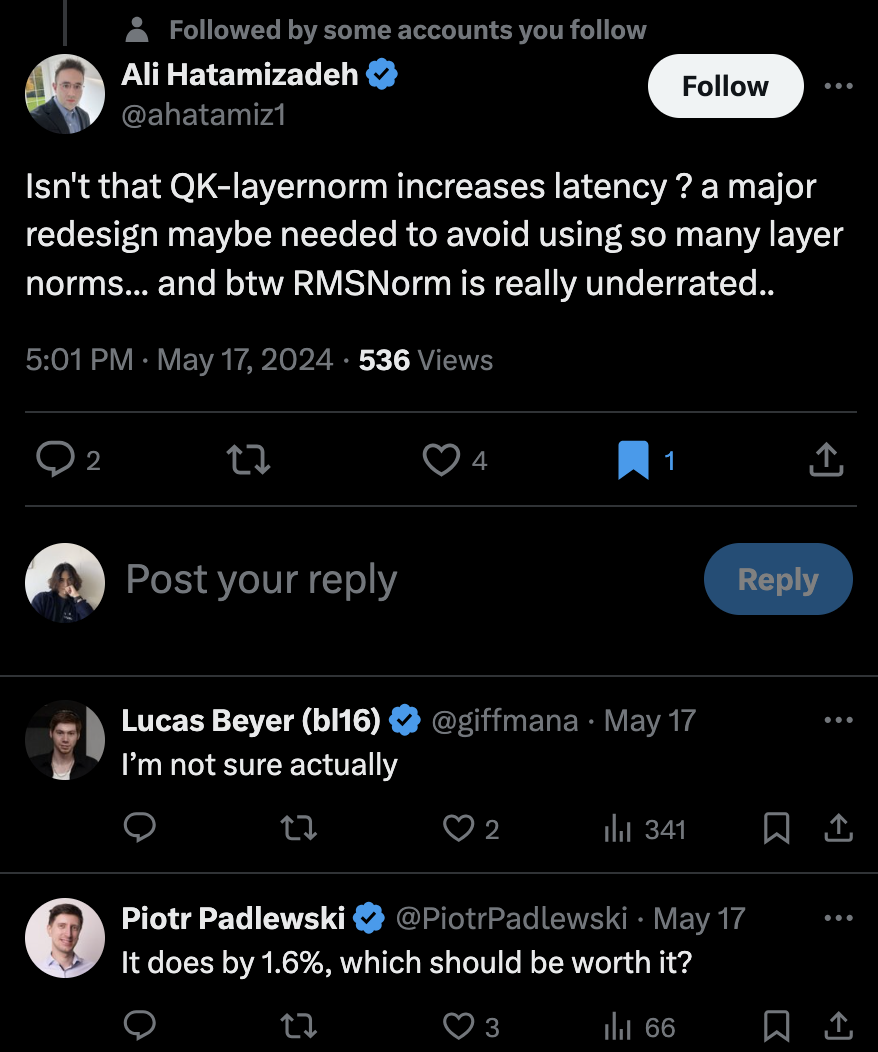Fig. about latency

위 tweet thread에 답변을 단 researcher는 Reka.ai 소속이며, 사실 Cohere의 cmdr+에도 매우 큰 model (100B수준)에 QK layernorm이 들어간 것을 보면 Google 출신들의 startup들에 모두 들어간 기술이라고 볼 수 있는데, 이는 z-loss나 logit scaling 등과 함께 ‘그들은 다 알고있는’ scaling technique이 아닌가 싶다.

Fig.

Fig.

(logit의 gradient를 discount하려는 부분은 Tensor Program과 PaLM 등 large scale transformer를 학습하기 위한 paper들에 몇 번 나온 적 있다.)

Non-trivial Tips for Implementation

다음은 구현에 대한 얘기를 잠깐 해보겠다. 사실 QK layernorm는 Q projection layer와 K projecton layer를 통과한 tensor에 nn.LayerNorm 혹은 RMSNorm를 적용하기만 하면 되므로 구현이 그리 어렵지 않다. 여기에 bias는 보통 넣지 않으니 bias=False로 두는 등의 사항만 결정하면 된다. 하지만 놀랍게도 당연하게 모두가 거의 똑같이 구현을 해야할 정도로 자유도가 없어보이는 QK layernorm은 Tensor Parallel (TP)를 고려하면 얘기가 좀 달라진다.

Fig.

TP는 model이 너무 클 경우 linear layer의 weight matrix를 쪼개서 (partition) 연산하는 방법으로 Data Parallel (TP)과는 구분되는 technique이다. 그런데 TP를 적용하면 self attention module에서 Q tensor와 K tensor가 기존에 [B, T, C]의 크기를 갖는 것과 달리 channel dimension이 TP degree만큼 분산된 형태인 [B, T, C/TP_degree]로 나눠지게 된다. 그 후 the number of head와 head dimension 으로 표현되는 4D tensor로 변환하게 되면, 이는 [B, T, nhead/TP_degree, dhead]가 된다.

즉 여기서 projected tensor의 channel dimension이 나눠져 있기 때문에 우리는 모든 head 별로 다르게 layernorm을 적용하는 head-wise layernorm을 적용하는데 문제가 생기게 된다. 보통 TP를 할 경우 layernorm weight은 나누지 않기 때문에 일반적으로 구현하게 되면 model이 같은 weight을 공유하게 되므로 서로다른 head가 서로 다른 stat을 배우지 못하게 된다.

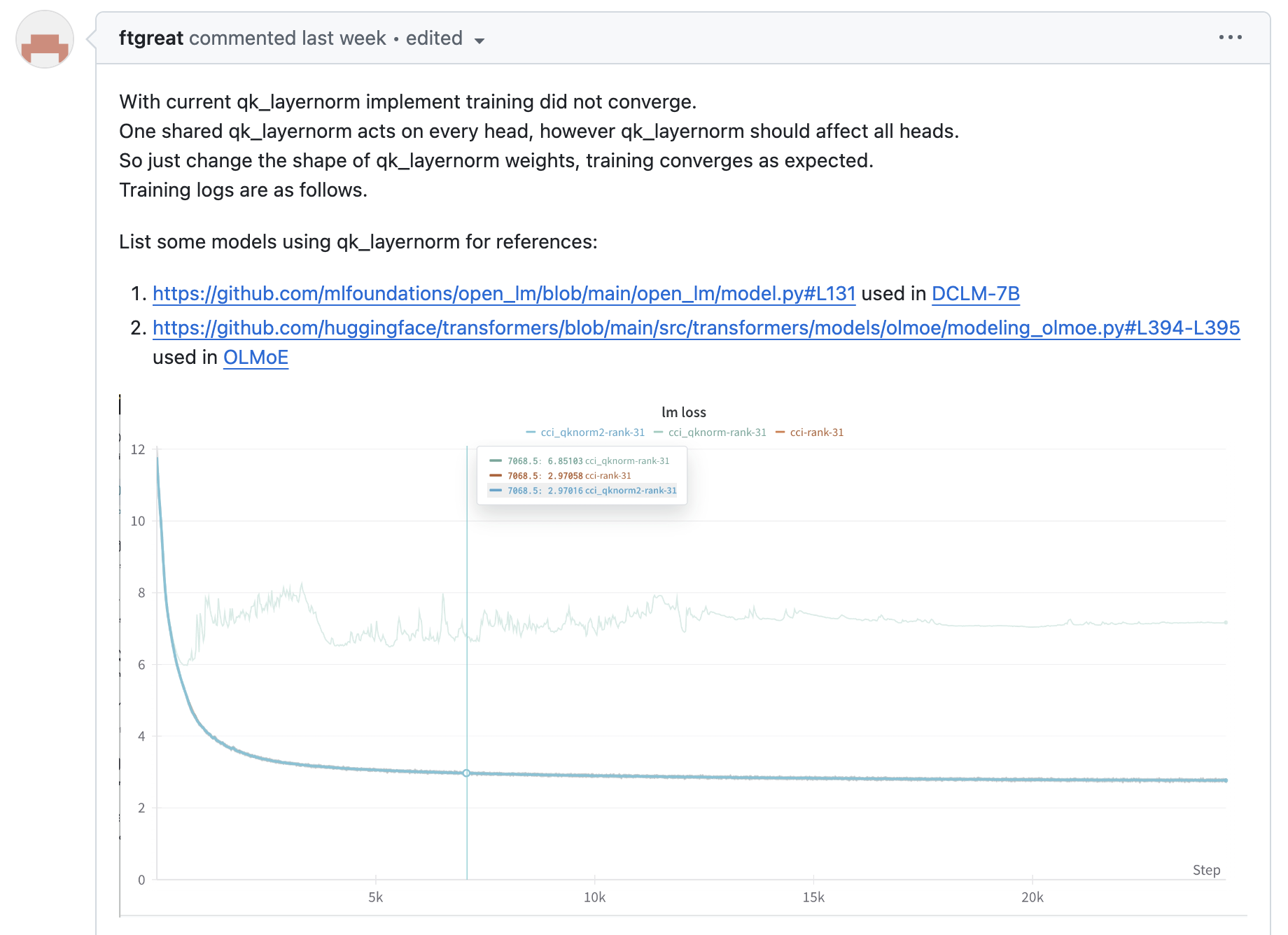Fig. issue 2

그리고 이는 어떤 baidu의 llm engineer가 말하길 model convergence issue를 야기한다고 한다. 그래서 이 user는 megatron-LM에 PR을 날렸는데,

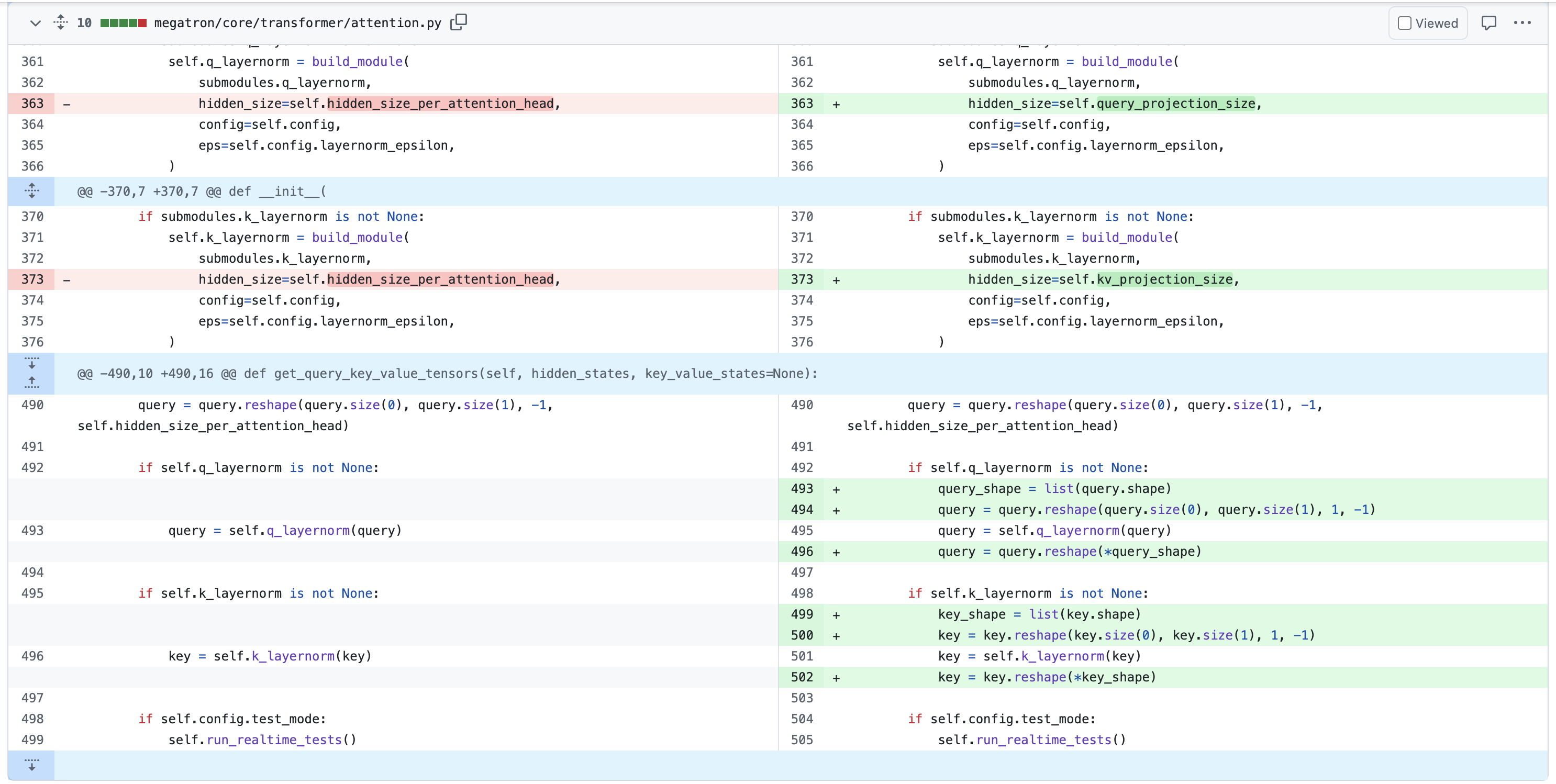Fig.

이 방법을 쓰면 layernorm weight을 dhead dimension만큼만 만들지 않고 nhead*dhead = hidden_size 만큼 만들게 되면서 문제를 해결해 줄 수 있다. 가 아니라 사실 이 PR은 TP를 고려하지 않았기 때문에 TP를 적용하는 순간 에러가 날 것이다. 이미 쪼개진 query, key tensor에 대해서 이렇게 구현해봤자 도움이 되지 않는다.

이제 남는 방법은 두 가지가 있을 수 있는데, 하나는 hidden_size 만큼의 weight을 갖지만 TP를 적용하면 device별로 쪼개진 Q, K를 갖기 때문에 이를 all-gather해서 layernorm을 적용한 뒤에 다시 scatter하는 것인데, QK layernorm을 위해서 all-gather를 해야 한다면 반기는 사람은 아무도 없을 것이다. 두 번째 방법은 각 device별로 dhead만큼의 weight을 갖기는 하지만 backprop시 QK layernorm에 대해서는 gradient all-reduce를 하지 않는 것이다. 이럴 경우 model checkpoint를 save or load할 때 처리를 좀 해줘야 겠지만 device 별로 서로 다른 weight을 학습할 것이기 head-wise QK layernorm이 될 것이다.

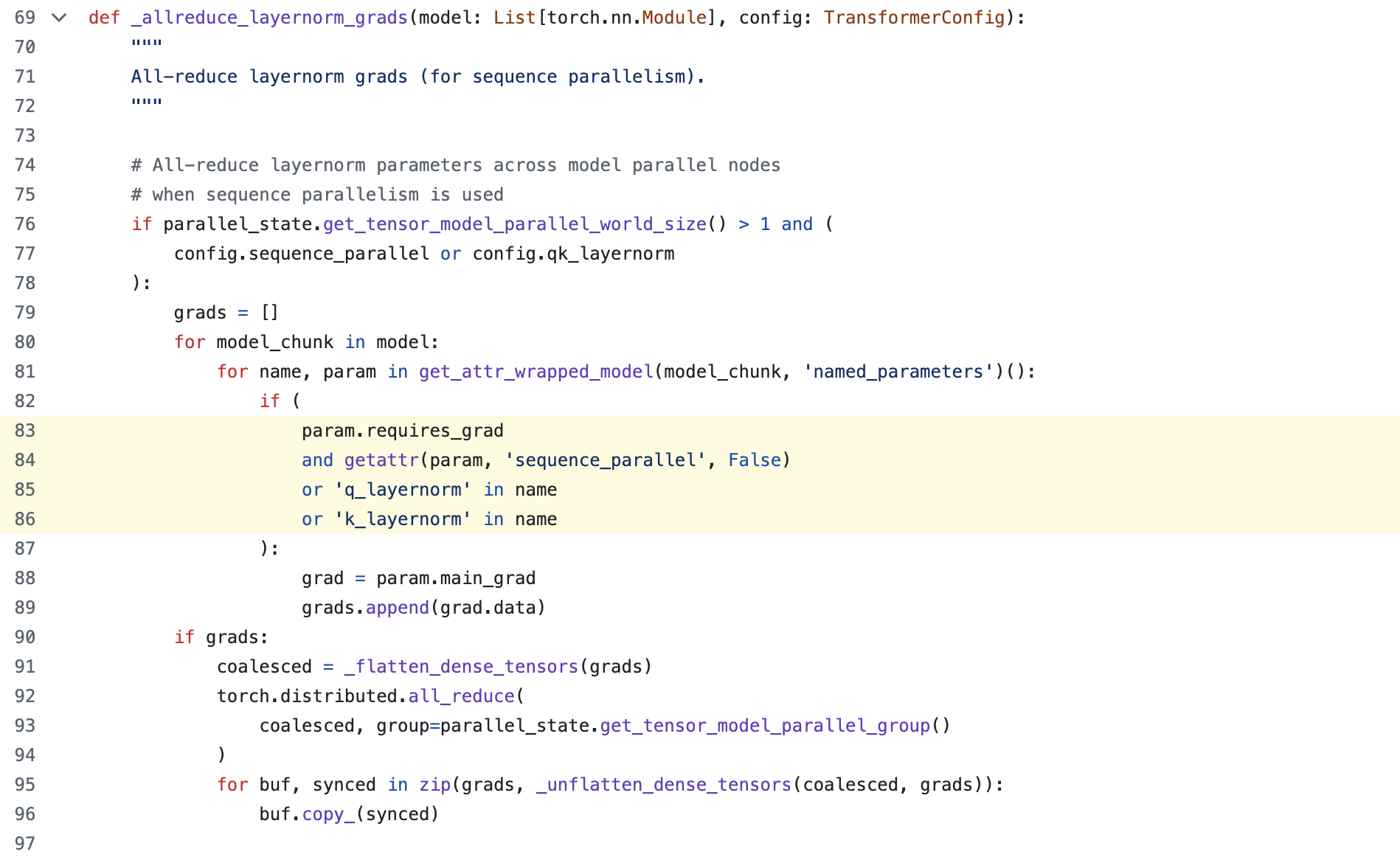Fig. 여기서 QK norm 일 때 all-reduce를 안하면 된다. Source

Huggingface transformers에 있는 QK layernorm들의 구현을 보면 cohere의 cmdr+의 경우 아래처럼 bias가 없는 nn.LayerNorm을 사용하고, 구현도 headwise norm로 되어 있는 것을 알 수 있는데,

Fig.

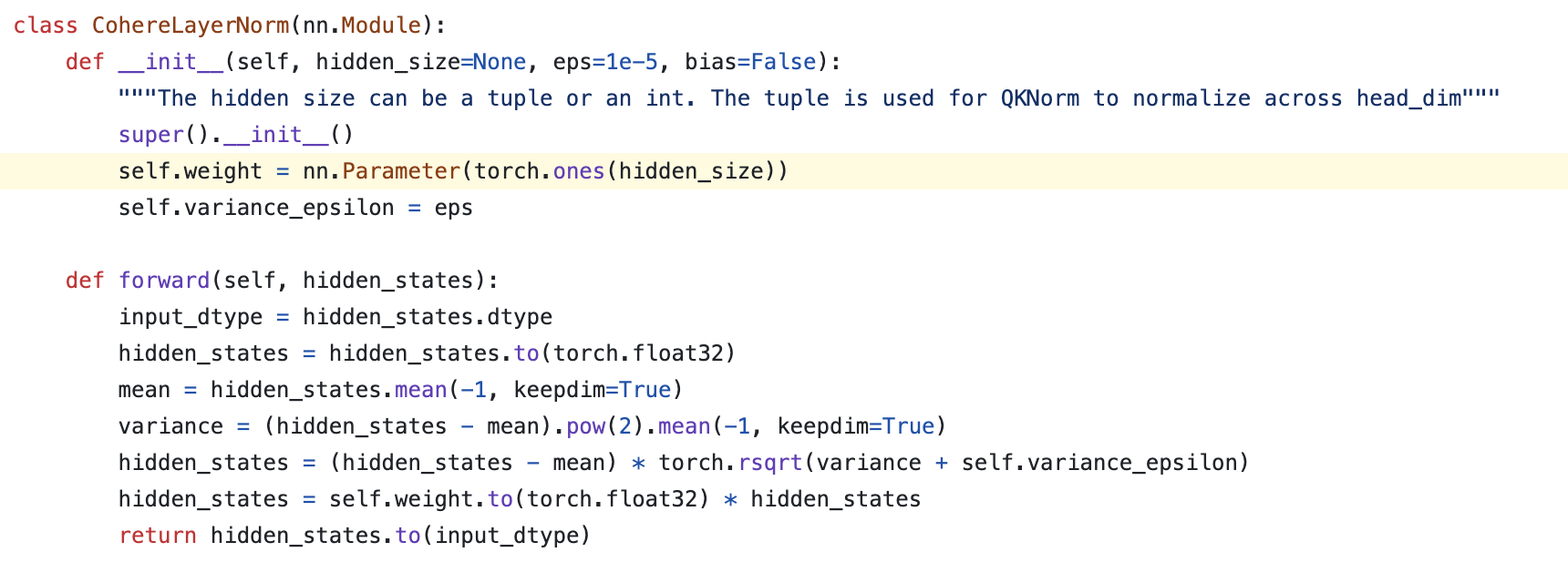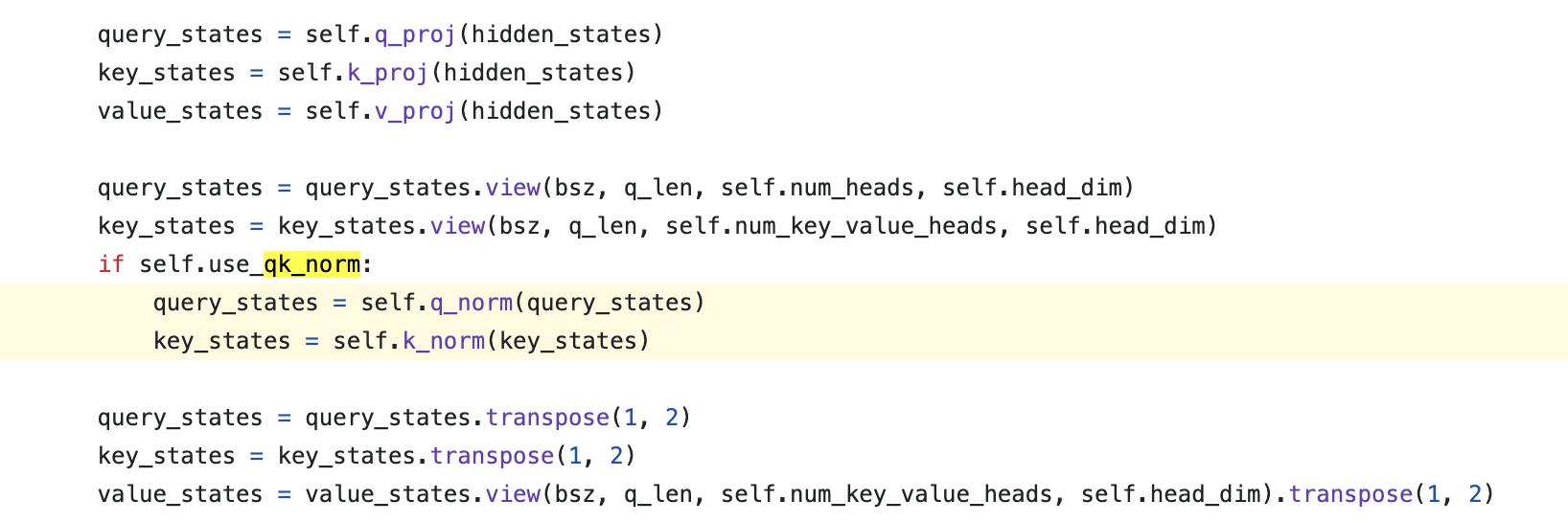Fig.

Fig.

code author도 TP를 사용할 때에는 주의해야 한다고 적어뒀다. 반면에 microsoft의 phi는 아래처럼 dhead size의 weight을 갖게되는데, 이는 shared stat을 쓰겠다는 의미이다.

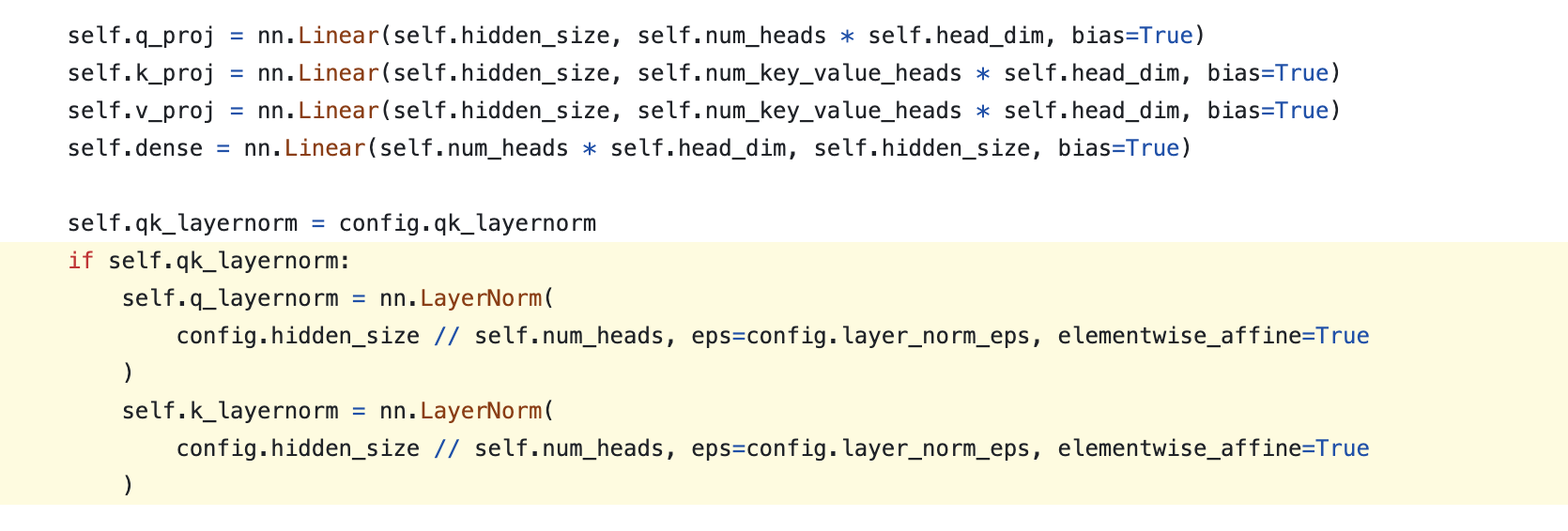Fig.

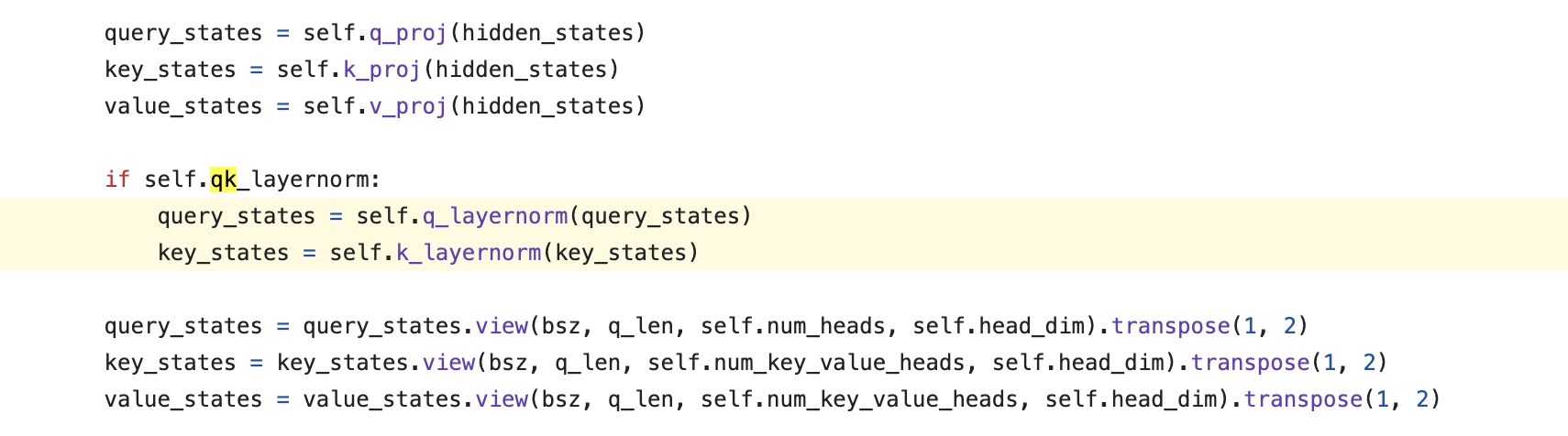Fig.

하지만 내가 megatron-LM을 test해본 결과 이렇게 head-wise로 구현을 한 경우에도 convergence test에 문제가 있었다. 이는 NVIDIA의 fused kernel library인 Transformer Engine (TE)의 numerical issue인 것으로 보이는데, megatron의 maintainer도 이를 알고있는지 NVIDIA의 또다른 large scale distributed training을 위한 library, Apex의 fused norm을 사용하는 PR을 했다.

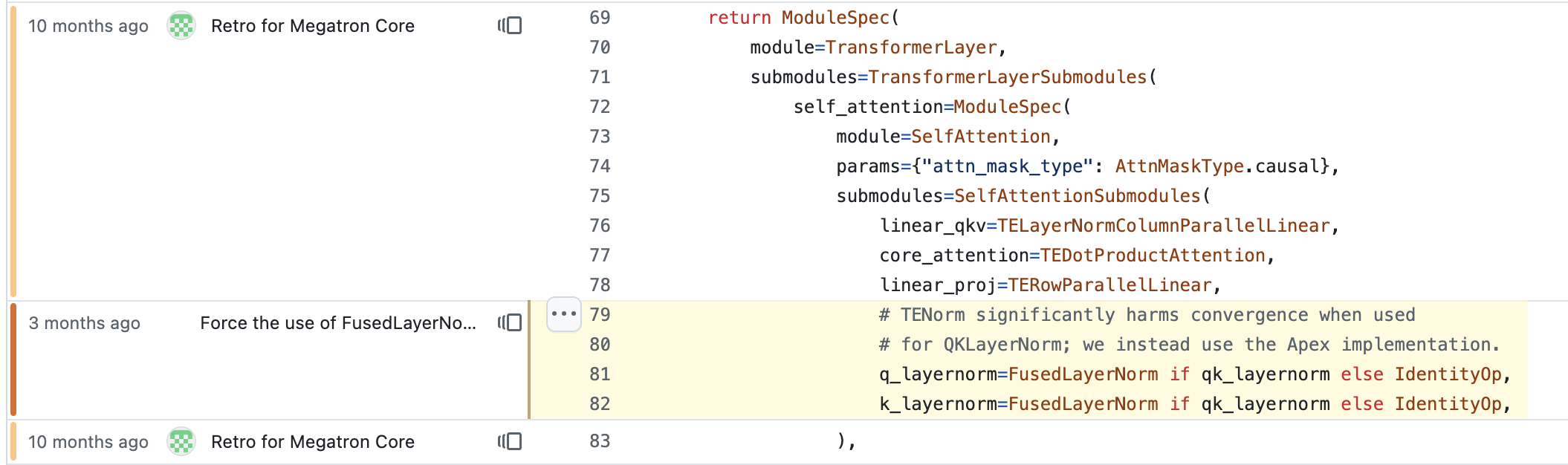Fig.

아래 figure는 convergence test 결과인데, 실험은 width (hidden_size) = 512인 transformer language model에 대해서 262k batch tokens로 20k step 학습한 경우이고, bf16 precision에 TP는 사용하지 않았다 (단순히 kernel만 test하는 것이므로).

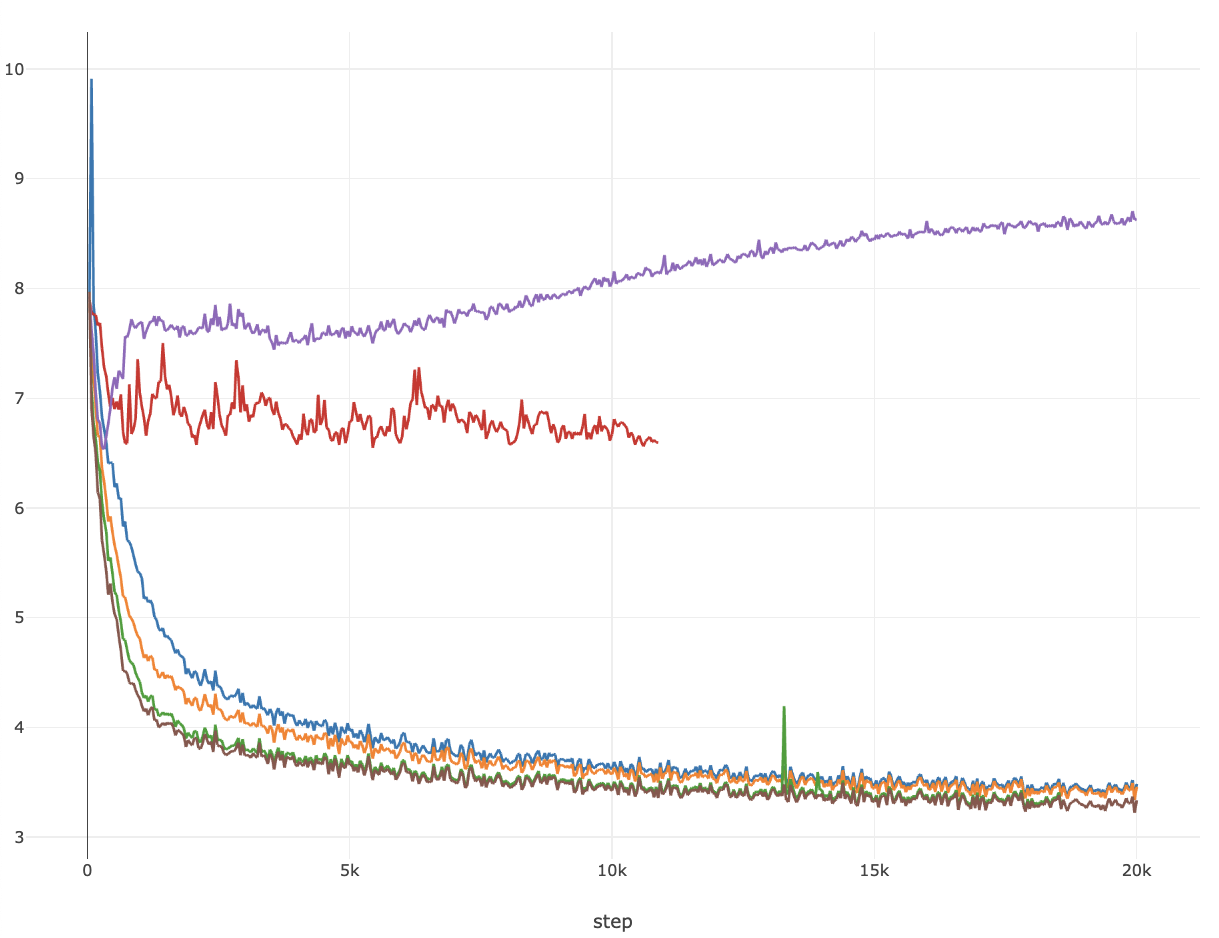Fig.

• purple: lr=0.0625, w/o qk_layernorm
• red: lr=0.0625, w/ qk_layernorm, TENorm
• blue: lr=0.0625, w/ qk_layernorm, FusedNorm, headwise
• orange: lr=0.0625, w/ qk_layernorm, FusedNorm, shared
• green: lr=0.00552, w/ qk_layernorm, FusedNorm, headwise
• darkbrown: lr=0.00552, w/ qk_layernorm, FusedNorm, shared

신기하게도 shared가 headwise보다 성능이 좋았는데, 이는 좀 더 살펴봐야할 것 같다.

+Updated) Lessons from Chameleon

최근 meta에서 공개한 multimodal foundation model, Chameleon: Mixed-Modal Early-Fusion Foundation Models의 technical report에 대해서 잠깐 얘기를 해보자. 물론 Chameleon에 대해서 다루는 이유는 QK layernorm과 함께 training stability에 대한 내용이 담겨져 있기 때문이다. 먼저 Chameleon은 아래와 같이 생긴 autoregressive model이지만 text만 다루는 LM과 다르게 image-text pre-training을 같이 진행했다. (Image token이 vocab에 추가된 것을 제외하고는 LM과 똑같은데, 주어진 fixed size image에 대해서 discretaztion을 하는 image encoder와 이를 decoding하는 module은 paper를 참고하길 바란다)

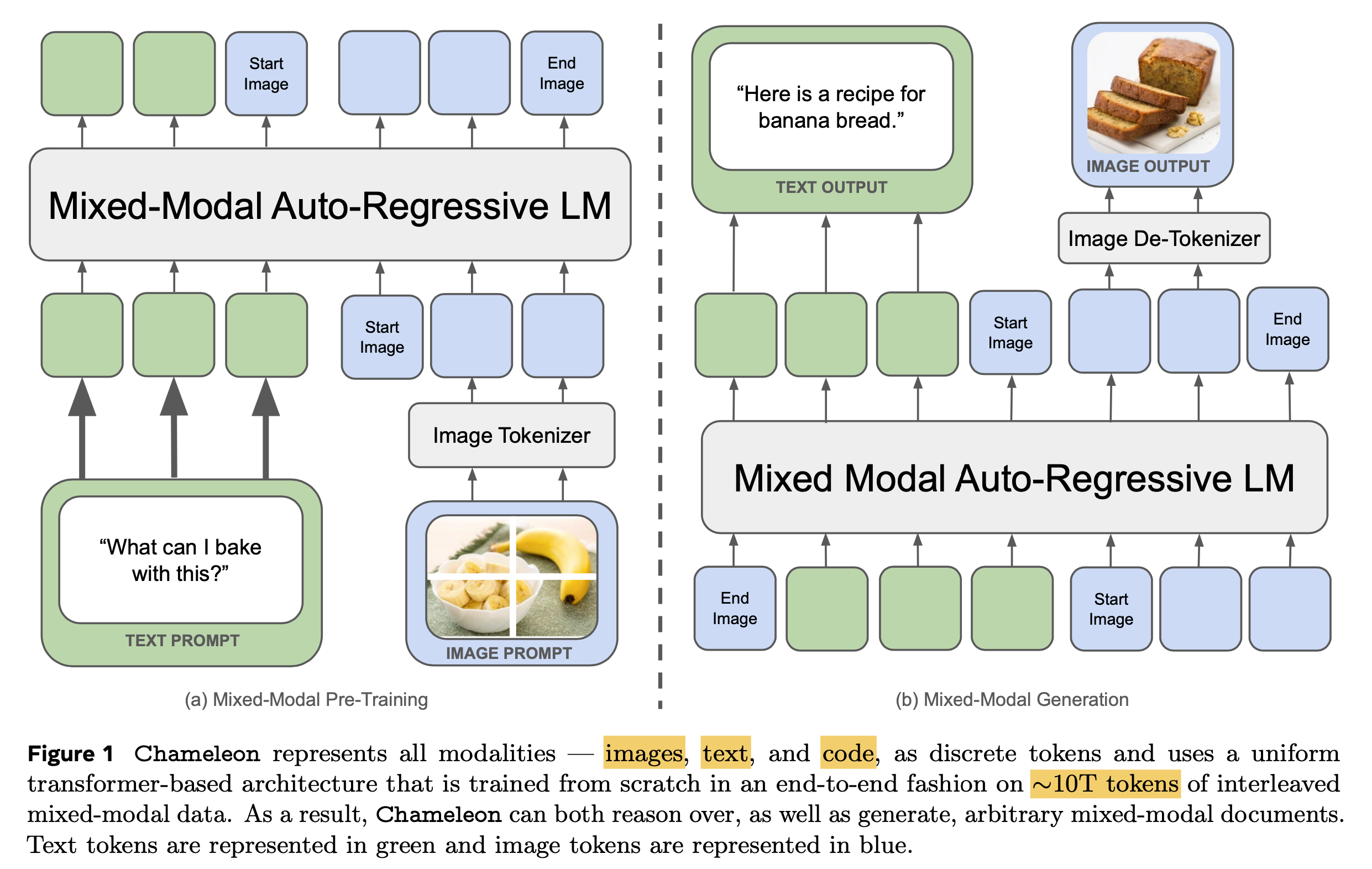Fig.

Fig.

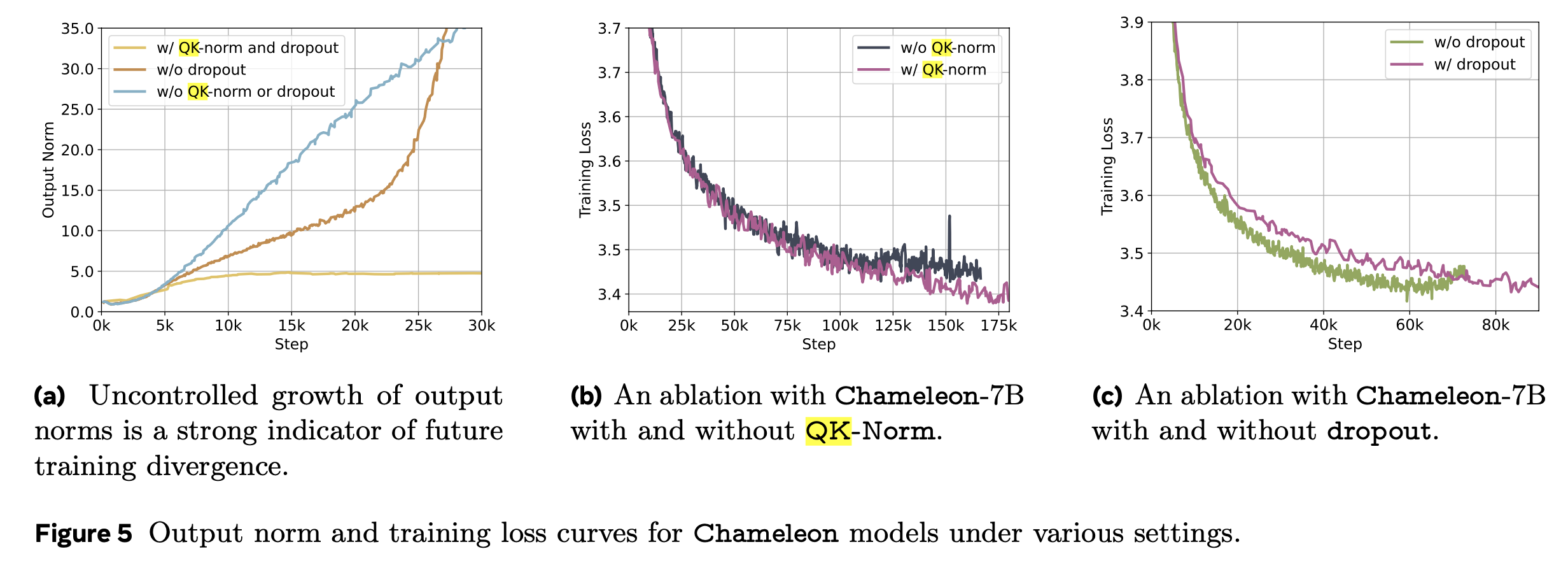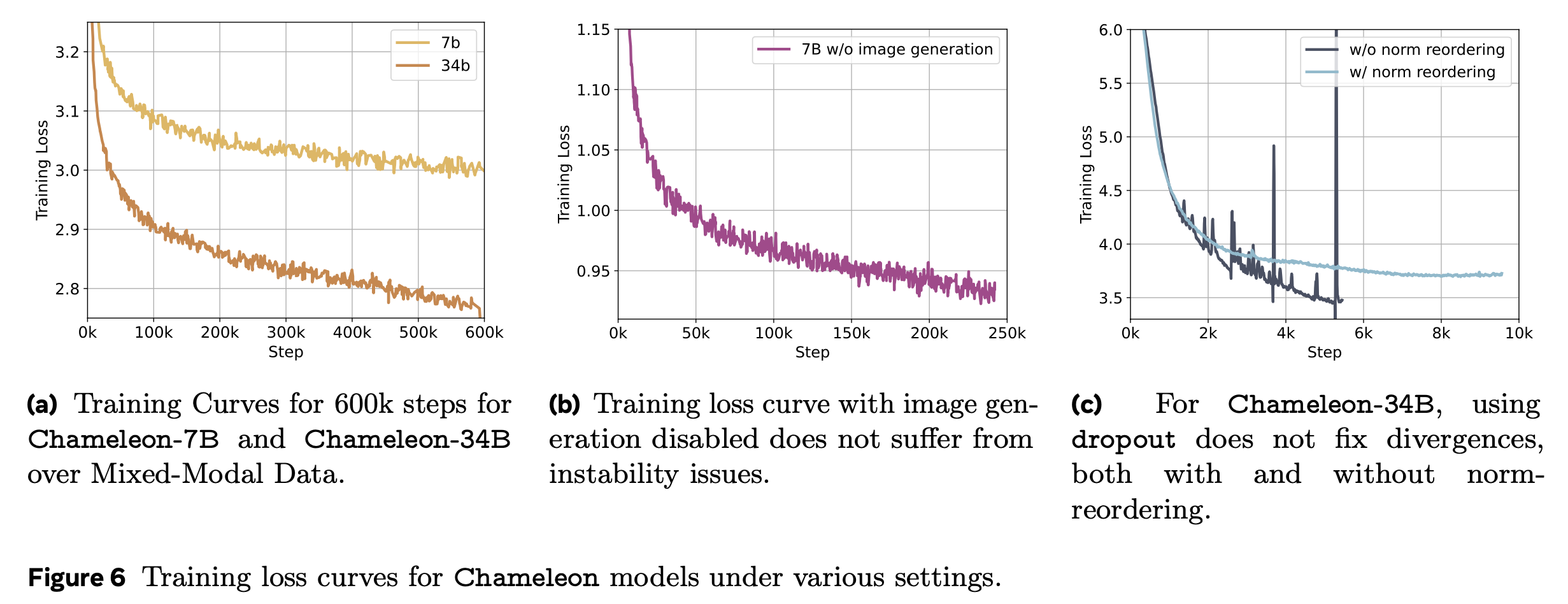Fig.

Fig.

Fig.

여기서 normalization re-ordering 얘기를 하면서 Shifted window (Swin) Transformer를 citation하는데, 사실 post norm 얘기를 하고싶은걸로 봐서 Swin Transformer v2를 refer할 것을 v1으로 잘못 한 것 같다.

• Swin Transformer: Hierarchical Vision Transformer using Shifted Windows
• Swin Transformer V2: Scaling Up Capacity and Resolution

Swin Transformer v1에는 사실 training stability 얘기도 없을 뿐더러 pre-norm을 그대로 사용했으며 model scale up 얘기는 v2에서 나오기 때문에 v2가 맞는 것 같다.

그래서 Swin Transformer의 post-norm에 대해서 알아볼 건데, 사실 이는 Attention Is All You Need의 original post-norm를 조금 변형한 res-post-norm라는 걸 도입했으며, 이는 아래 figure를 따른다.

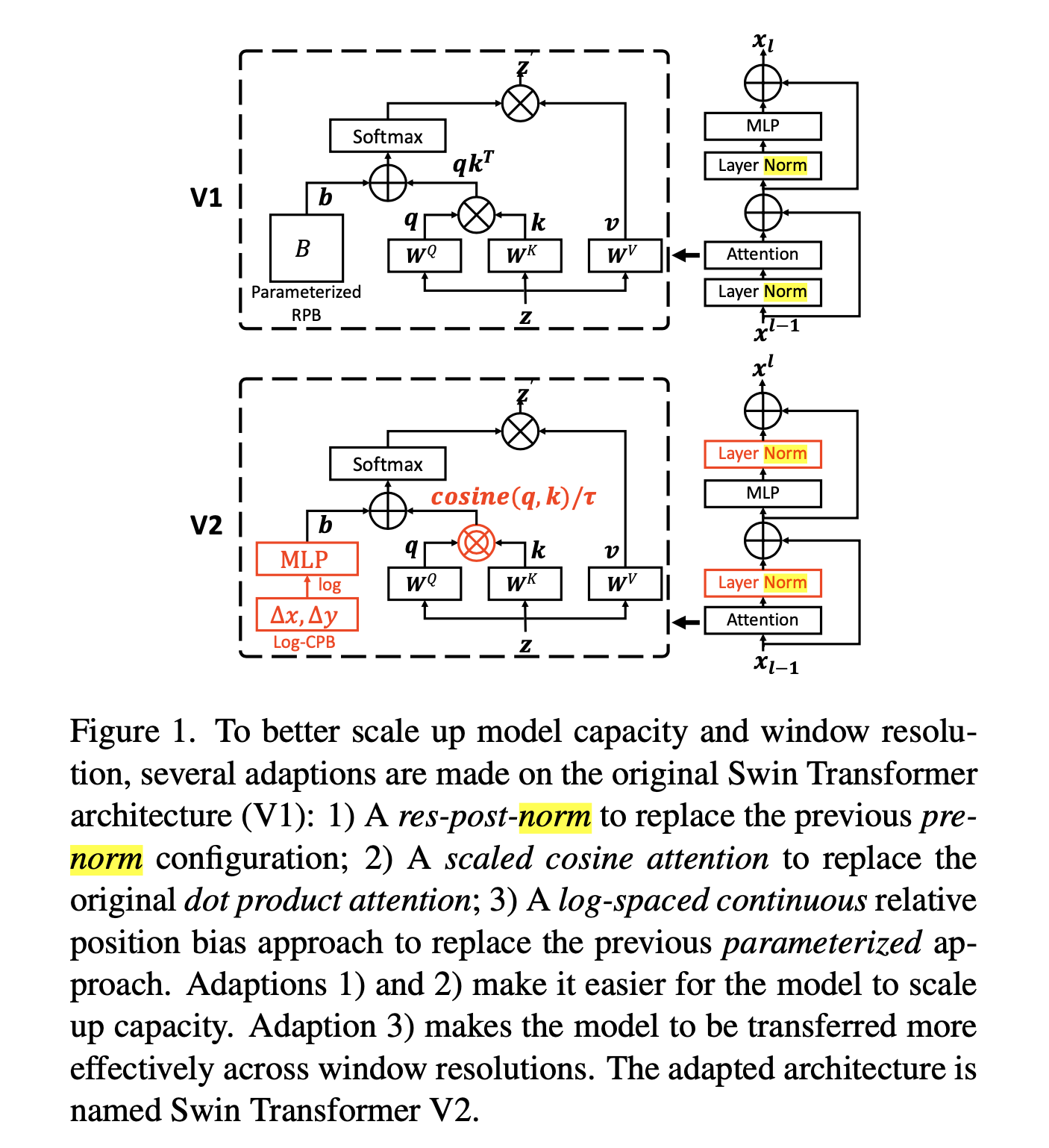Fig.

Caption에 쓰여있듯 Swin Transformer v2는 v1과 비교해서 3가지가 다른데 이는 다음과 같다.

• pre-norm 이 아닌 res-post-norm 도입
  • activation output에 적용
• 일반적인 SDPA가 아닌 scaled cosine attention 사용
  • normalized similarity에 learnable value를 temperature로 사용
• log-spaced continuous relative position bias

먼저 pre-norm, post-norm에 대한 깊은 고찰은 On Layer Normalization in the Transformer Architecture를 참조하면 되는데 (이들이 먼저 pre-norm을 제안한 것은 아니고 google이 paper에는 post-norm으로 표기했지만 code-base에서는 이미 pre-norm을 쓰고 있었다고 알고 있다),

Fig.

원래는 residual을 activation output과 함께 더한 뒤, 이 값을 normalization하는 것이 바로 post-norm이었다. 이것 말고도 sandwitch layernorm이 있는데, 이는 pre-norm과 post-norm을 같이 쓰는 전략을 의미하는데,

Fig.

swin transformer의 footnote를 보면 알 수 있듯, post-norm은 training stability에 좋지 않다는 단점이 있고 sandwitch norm은 represnetation power가 줄어들어 성능이 감소한다고 볼 수 있다. Original post-norm에 대해서 간략하게 좀만 더 서술하자면 (paper를 읽기를 권하지만), 해당 paper의 저자들은 pre-norm과 post-norm을 각각 적용할 경우 NN initialization 시점에서 어떻게 gradient norm이 layer를 거듭할수록 (층이 깊어질수록) 커지는지?에 대해 theoritical, empirical study를 모두 진행하여 post-norm은 layer를 거듭할수록 gradient norm이 커지기 대문에 높은 lr로 학습될 수 없고, 높은 lr로 학습을 원한다면 warm-up을 강제할 수 밖에 없다는 점을 보였다.

Fig.

그런데 왜 Swin Transformer는 하필 residual을 더한 후 norm을 하는 일반적인 방식을 쓰지 않은 걸까? 둘의 차이는 과연 무엇일까?

Paper에는 별다른 언급이 없지만 우리가 residual connection의 원래 도입 배경을 생각해보면 왜 이것이 작동하는지 생각해볼 수 있을 것 같은데, 원래 residual learning이란 Identity Mapping을 가정하고 만들어진 것으로, layer의 output이 될 full representation을 학습하는 것 보다 이전 layer의 output과 현재 layer의 output간의 차이 (residual)를 학습하는것이 훨씬 쉬울 것이라 가정한 것이다.

• Deep Residual Learning for Image Recognition
• Identity Mappings in Deep Residual Networks

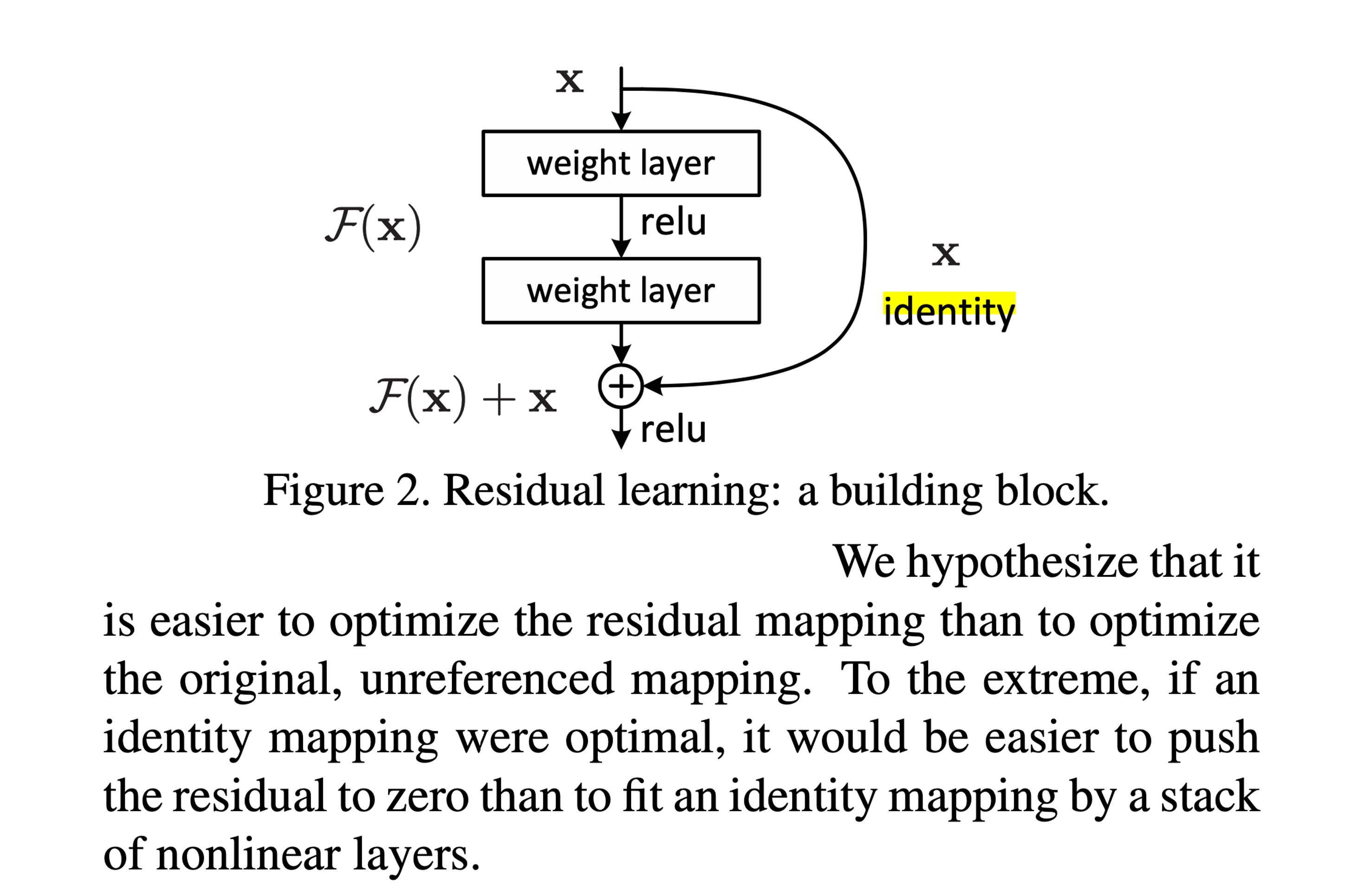Fig.

그렇기 때문에 \(f(x) = x' - x\)의 형태가 되는 것인데, 여기서 weight이 zero matrix라면 residual이 0이 되는 것이다. 보통 weight matrix는 아예 0은 아니고 input feature dimension의 역수를 standard deviation으로 갖도록 initialization 되기 때문에 training이 잘 된다면 유의미한 통계량을 배우게 된다. Residual connection은 본래 NN이 deep해졌을 때 gradient가 vanishing or exploding하는 것을 막아준다고 볼 수도 있는데, 이는 backprop을 유도해보면 아래와 같기 때문에 gradient vanishing등이 일어나더라도 residual path가 존재하기 때문에 gradient가 그대로 흐르기 때문이라 할 수 있다.

직관적으로 기존의 post-norm은 residual까지 더한 뒤 normalization을 하기 때문에 residual path의 기울기도 영향을 받을 것이고, Swin Transformer의 res-post-norm은 residual에 대해서 gradient가 온전히 흐르기 때문에 gradient가 더 잘 보존되는 것이 아닌가 싶다.

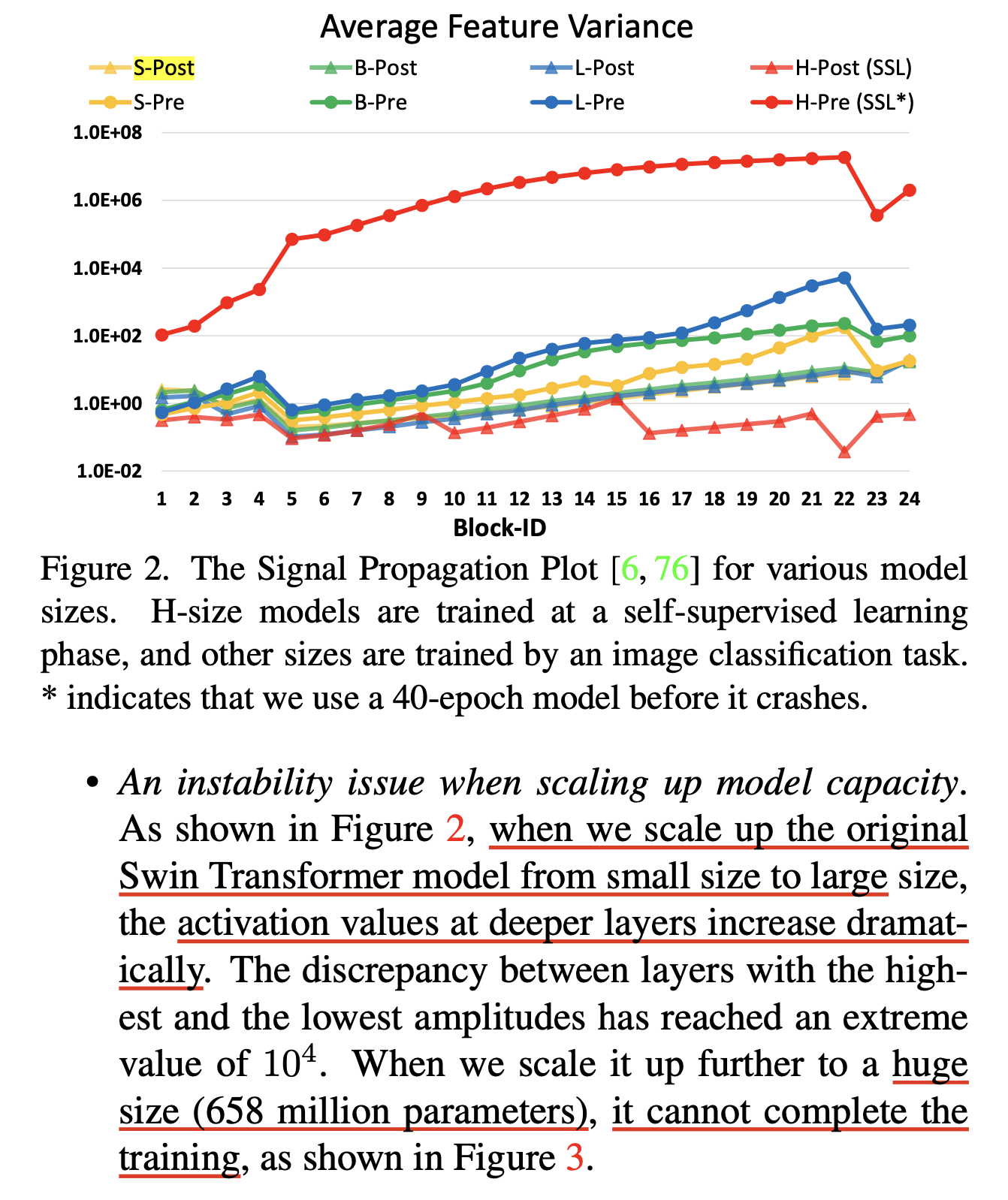Fig.

결과적으로 위 figure에서 pre-norm이라고 쓰여있는 기존의 method의 경우 model size가 커질 수록 depth가 깊어질수록 activation norm이 증가하는 trend를 보였는데 반해, res-post-norm을 쓴 경우에는 그렇지 않았다고 얘기한다. (그런데 여기에는 cosine qk dot product 등 swin transformer v2에서 새롭게 들어가는 feature가 들어간 건지는 모르겠으며, init method를 봤을 때 large LM 학습 시 residual branch의 std를 layer의 수로 나눠주는 등의 처리를 안해준 것으로 보아 이 문제도 있었던 것 같다는 생각이 든다)

Fig.

Fig.

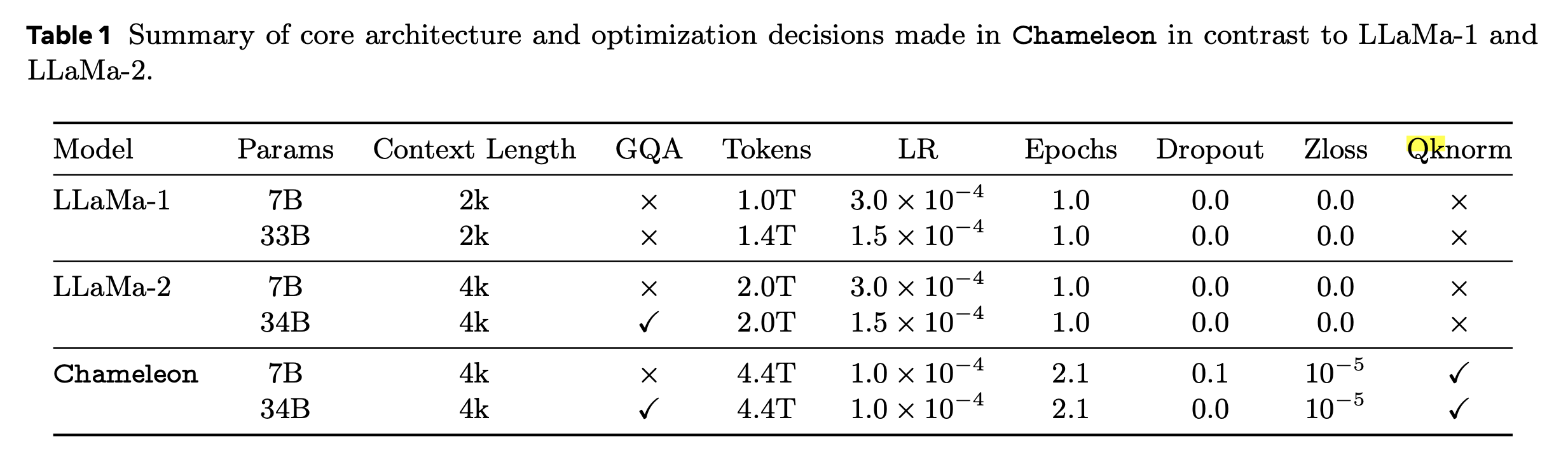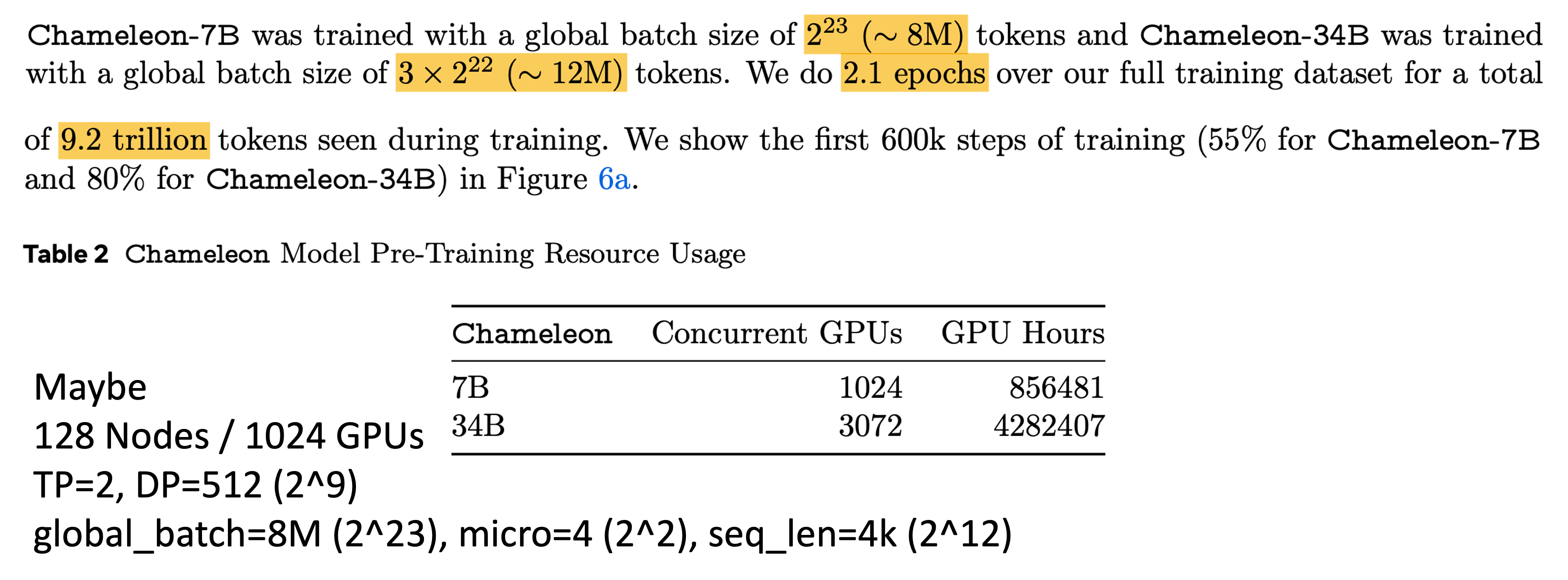Fig.

Fig.

+Updated) Lessons from Gemma 2

한 편, 최근에 공개된 Gemma 2에서는 QK norm이나 z-loss에 대한 언급은 없으며, pre-norm과 post-norm을 같이 사용했으며 Logit Soft-Capping이라는 것이 도입됐다.

Fig.

Fig. Source from Daniel Han

여기서 post-norm은 training stability를 위해 도입된 것이 확실하지만, soft-capping도 정황상 그래보이나 확실한건지? 아니면 post-norm을 추가 도입함으로써 생기는 convergence issue를 해결하기 위해 넣은 것인지?에 대해서 생각을 해보게 된다.

왜냐하면 Gemma 2의 soft-capping은 Neural Combinatorial Optimization with Reinforcement Learning라는 paper를 reference 삼고 있는데, soft-capping은 다르게 말하면 logit clipping이라고 할 수 있는 것 같아 보이며, 본래 Reinforcement Learning (RL) task에서 last NN layer의 output prob을 normalize 함으로써 (logit을 clipping한 것이 softmax되는 효과가 있음) agent가 더 많은 exploation을 하게 하여 (즉 entropy를 키우고 mode collapse를 줄임) 성능향상에 기여 했다고 서술되어 있다. 아마 label smoothing이나 confidence penalty가 generalization에 기여하는 효과를 생각하면 될 것 같다.

Fig.

Training stability 관점에서는 transformer last layer의 logit에 대해 soft capping을 하는 경우 loss에 대한 logit의 derivative를 유도해보면 아래와 같은데,

여기에 logit scaling을 하는 경우까지 추가하면 (cohere의 cmdr이 이렇게 학습됨),

아래와 같이 마지막 layer의 loss에 대한 input gradient를 유도할 수 있다.

이는 직관적으로 너무 큰 logit값에 대해서 gradient를 줄여주는 역할을 하며 (tanh backprop은 logit이 크면 gradient가 0에 가까워짐), 보통 logit scaling도 1보다 작은 값이 설정되기 때문에 두 feature 모두가 gradient가 너무 커지지 않도록 조정해주는 역할을 함으로써 training stability에 기여햔다고 볼 수 있다.

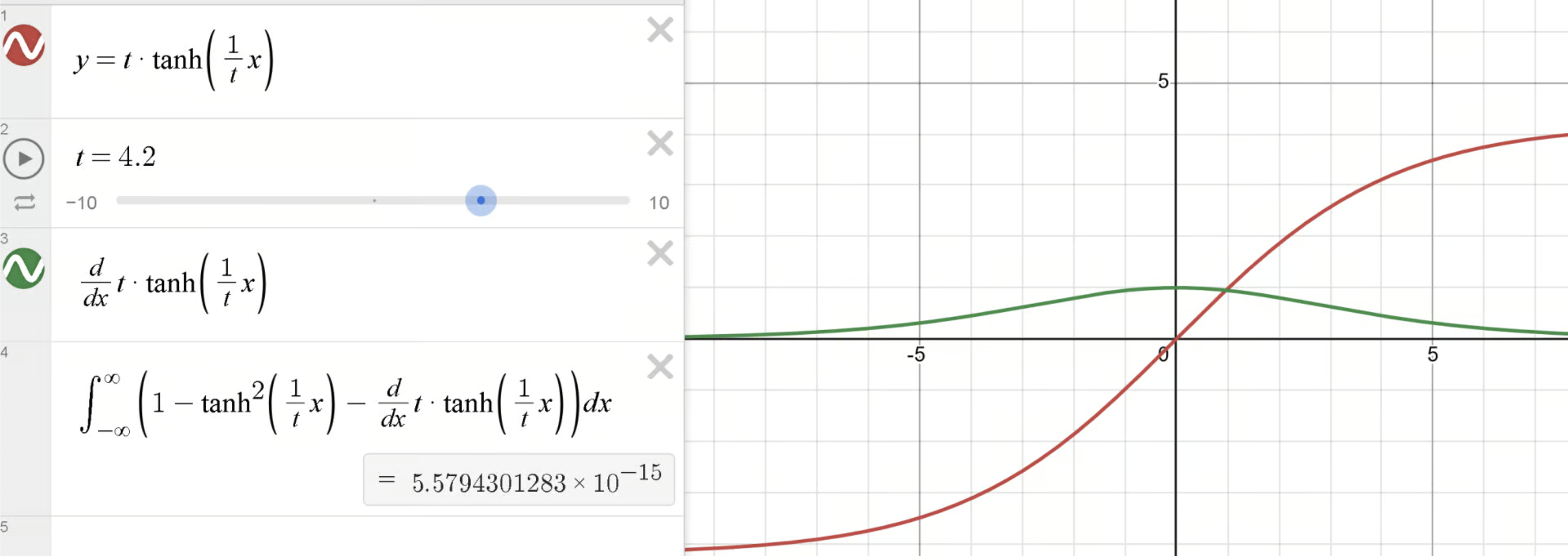Fig. Source from Unsloth Blog

사실 sigmoid, tanh activation을 사용하는 경우 gradient가 0에 가까워져 더이상 param update가 진행 되지 않는 gradient vanhishing문제가 일어나기 마련인데, 이는 softmax와 결합돼서 사용되기 때문에 큰 문제는 아닐 것으로 보인다. 즉 예를 들어 FFN layer의 activation으로 gelu나 silu대신 tanh를 쓰는 것이 아니기 때문에 큰 문제는 없을 것으로 보인다.

아래는 Unsloth의 codebase를 참고하여 pytorch로 변환한 경우이다.

def backward_pass(upstream_grad, logits, labels, logits_transformed, log_sum_exp, logit_softcapping=0, logit_scaling=0):
    """
    Arguments:
        upstream_grad: Tensor of shape (batch_size,), upstream gradient (usually ones)
        logits: Tensor of shape (batch_size, num_classes), original logits
        labels: Tensor of shape (batch_size,)
        logits_transformed: Tensor of shape (batch_size, num_classes), transformed logits from forward pass
        log_sum_exp: Tensor of shape (batch_size, 1), from forward pass
        logit_softcapping: float, softcapping parameter
        logit_scaling: float, scaling parameter
    Returns:
        dL_dx: Gradient with respect to the original logits, shape (batch_size, num_classes)
    """
    # Ensure upstream_grad has shape (batch_size, 1)
    upstream_grad = upstream_grad.unsqueeze(1)

    # Compute softmax probabilities
    exp_logits = torch.exp(logits_transformed - log_sum_exp)
    sum_exp_logits = torch.sum(exp_logits, dim=1, keepdim=True)
    p_ij = exp_logits / sum_exp_logits  # Softmax probabilities

    # Create one-hot encoding of labels
    batch_size, num_classes = logits.shape
    y_ij = torch.zeros_like(logits)
    y_ij.scatter_(1, labels.unsqueeze(1), 1.0)

    # Handle ignore index (-100)
    mask = labels != -100
    mask = mask.unsqueeze(1).float()

    # Compute gradient with respect to z_i: dL/dz_i = p_i - y_i
    dL_dz = (p_ij - y_ij) * mask

    # Compute derivative of z_i with respect to x_i
    dz_dx = torch.ones_like(logits)

    # Apply logit scaling derivative if enabled
    if logit_scaling != 0:
        dz_dx *= logit_scaling

    # Apply logit softcapping derivative if enabled
    if logit_softcapping != 0:
        # Need to recompute s_i_j (scaled logits before softcapping)
        if logit_scaling != 0:
            s_ij = logit_scaling * logits
        else:
            s_ij = logits.clone()

        tanh_term = torch.tanh(s_ij / logit_softcapping)
        derivative_tanh = 1.0 - tanh_term ** 2  # Derivative of tanh(u) is 1 - tanh^2(u)

        # Multiply by derivative of tanh
        dz_dx *= derivative_tanh

    # Compute gradient with respect to x_i: dL/dx_i = dL/dz_i * dz/dx_i
    dL_dx = upstream_grad * dL_dz * dz_dx

    return dL_dx  # Gradient with respect to logits

Daniel han의 실험에 따르면 9B의 경우 (last layer의) logit soft-capping만으로 training stability (혹은 convergence)가 개선되었지만 (사실 아무거도 안 쓴 것도 괜찮아 보임), model size가 커져 27B가 될 경우 attention logit soft-capping이 필수였다고 한다. (근데 이게 fine-tuning 얘기인지 pre-training 얘기인지 잘 모르겠긴 하다. Unsloth는 PEFT 전문 startup이니 fine-tuning에도 중요하다는 얘기 아닐까)

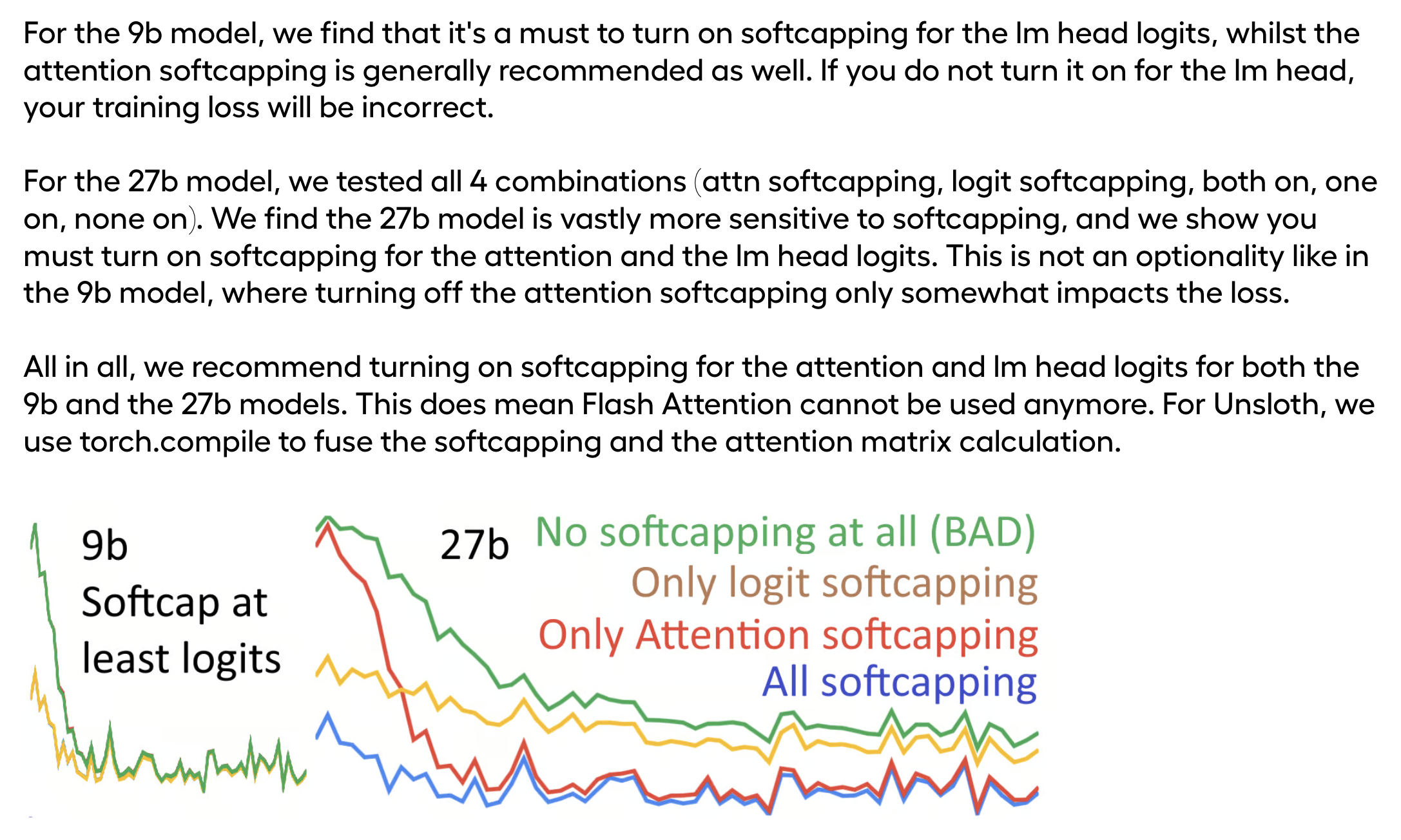Fig.

한 편, HF transformers code-base를 통해 아래와 같이 구현되어 있음을 확인할 수 있는데, gemma 2의 post-norm도 residual branch가 다 끝나고 되는 것이 아니라 swin transformer 처럼 activation out에 norm을 적용한 후에 residual을 더하는 것을 볼 수 있다.

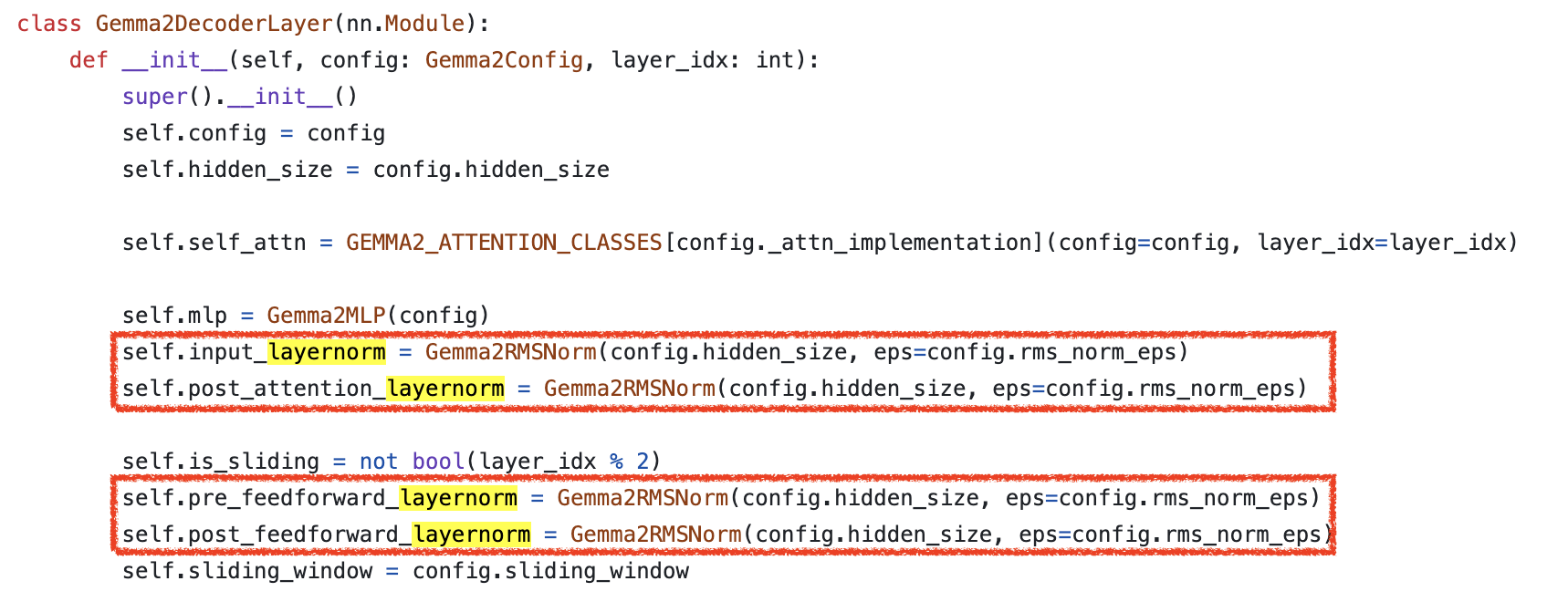
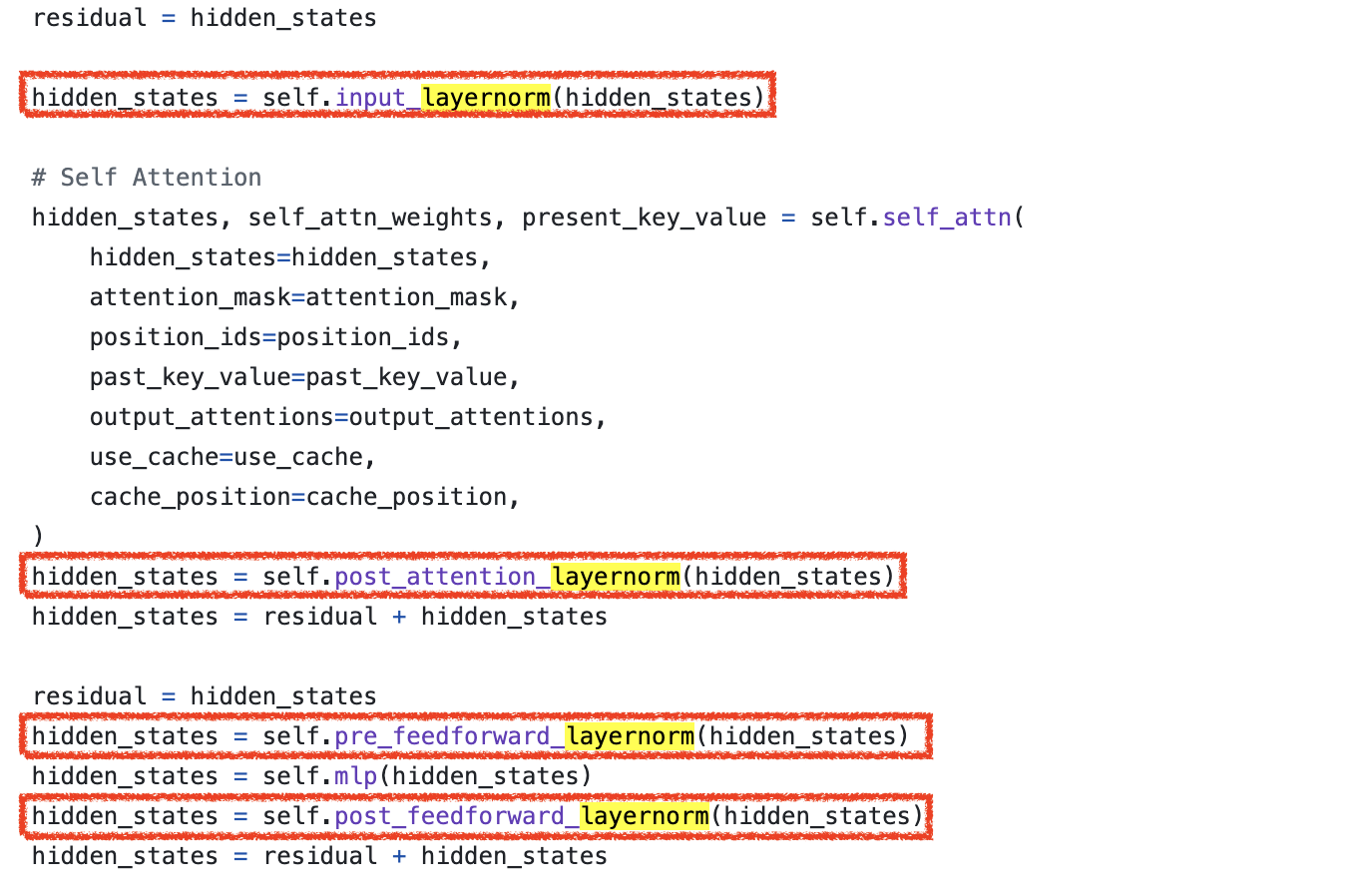
Attention logit soft-capping에 대해서는 아래처럼 구현이 되어있는데, 사실 글을 처음 쓰기 시작한 시점만 해도 flash attention 같은 CUDA base fused kernel에 soft-capping이 구현되어 있지 않았으나 지금은 구현되었기 때문에 편하게 FA를 쓰면 된다 (torch sdpa는 아직).

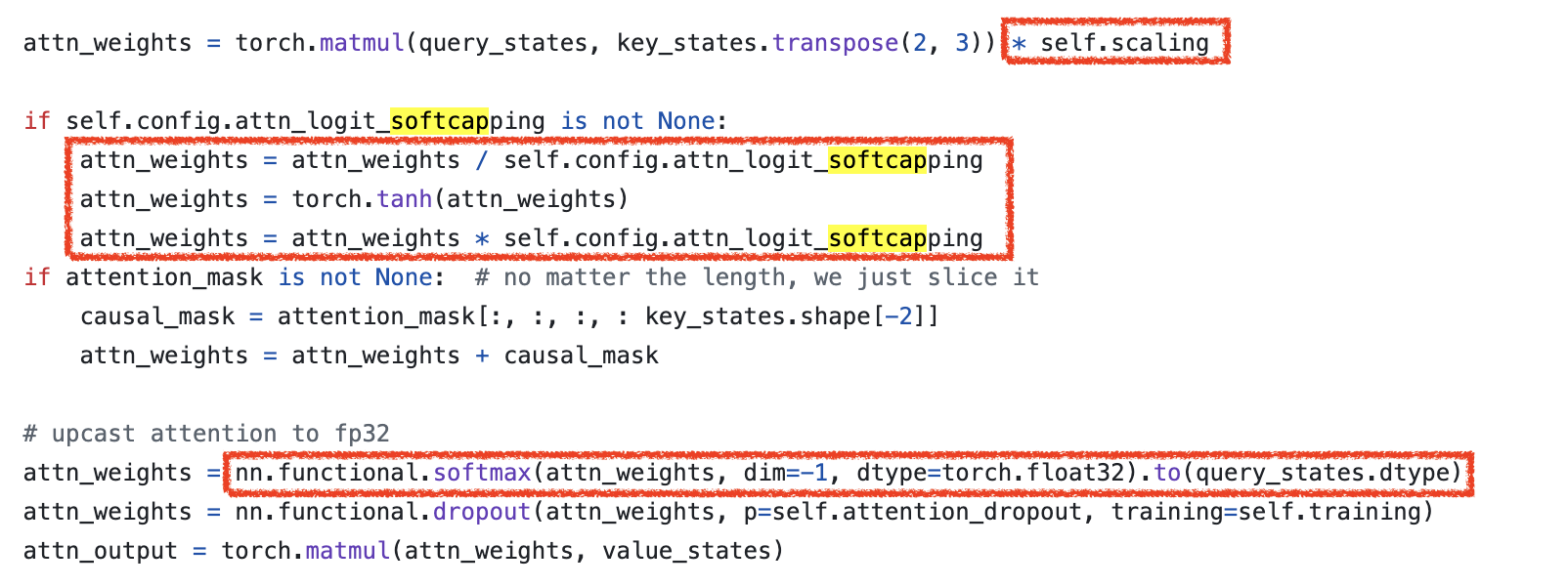
여기에 추가로 남는 의문은 왜 SDPA를 해야하는가 (즉 왜 scaling을 더 해줘야 하는가)이다. 본래 SDPA를 하는 이유는 dhead 차원의 vector 두 개가 내적이 된 결과값이 dhead가 커질수록 커지는 것을 방지하기 위해 이를 counter하는 것이었는데, tanh가 어느정도 이를 해주는 것 아닌가 싶었기 때문이다. 게다가 gemma2는 \(\sqrt{d_k}\)를 쓰지도 않고 이것보다 더 애매하게 작은 수치를 쓴다 (9B에 대해서 \(\sqrt{224}\)). 이는 나중에 생각해보도록 하고,

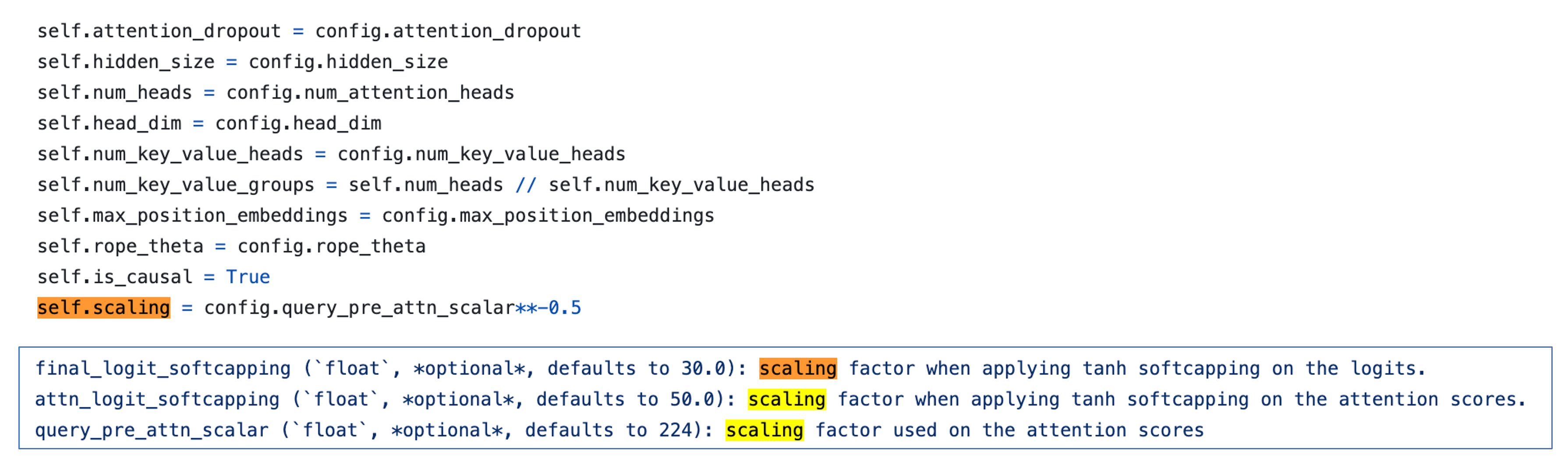
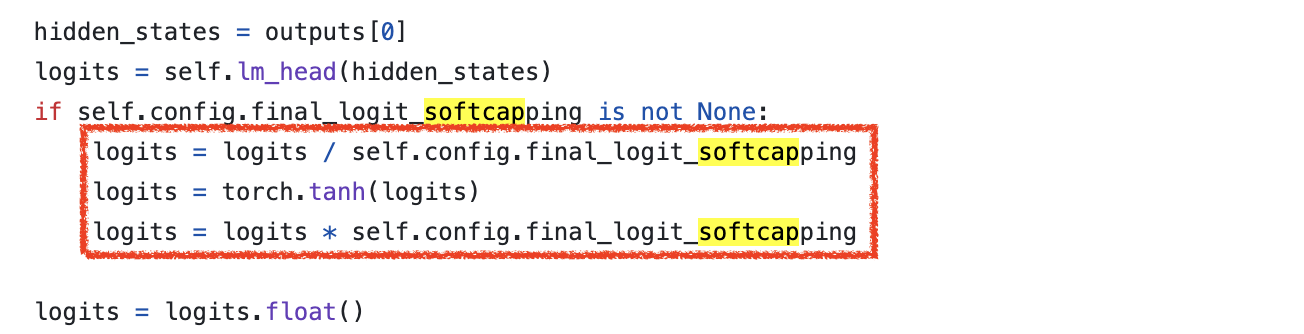
마지막으로 last layer의 logit soft-capping도 아래처럼 구현하면 된다.

+Updated) Lessons from LLaMa-3.2 (multimodal llama-3)

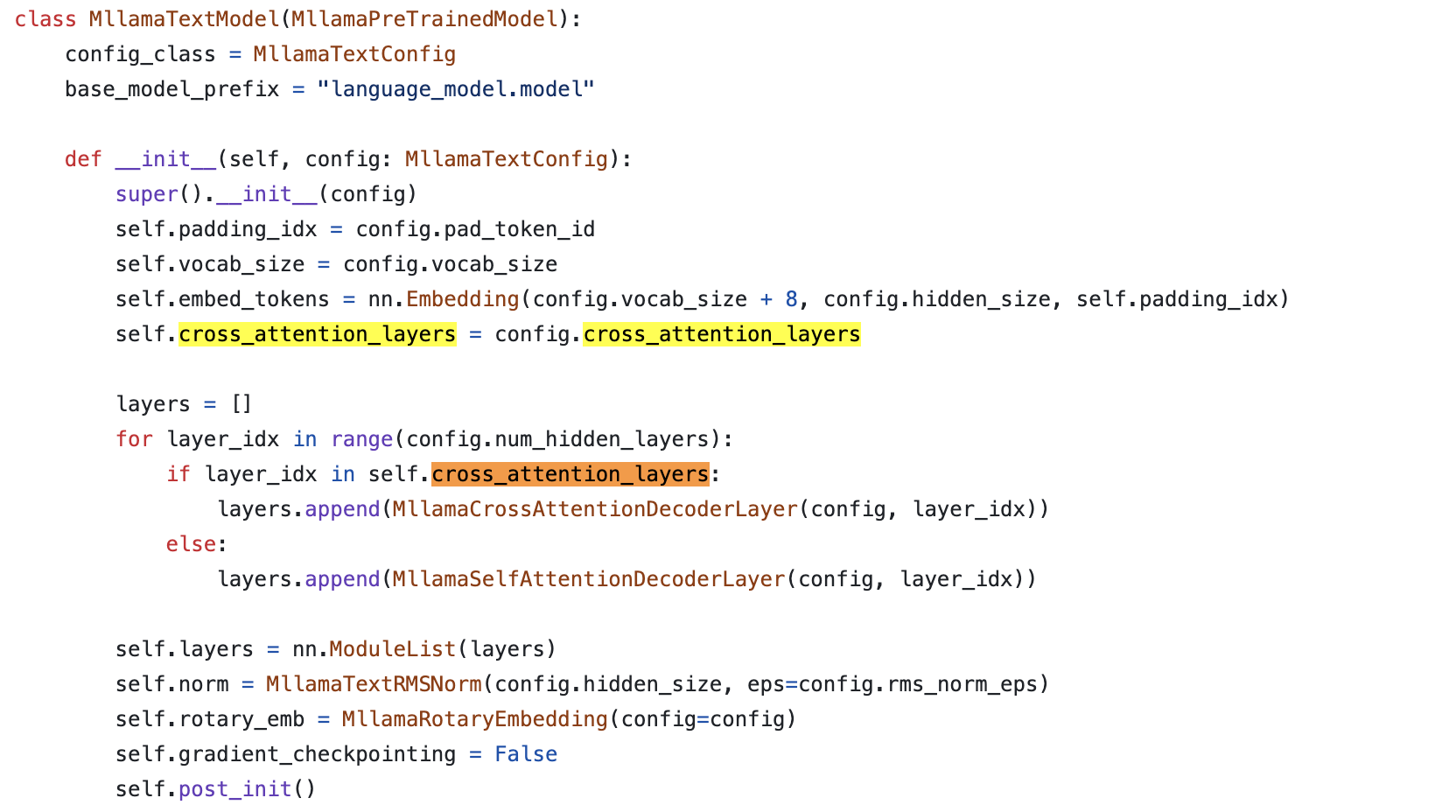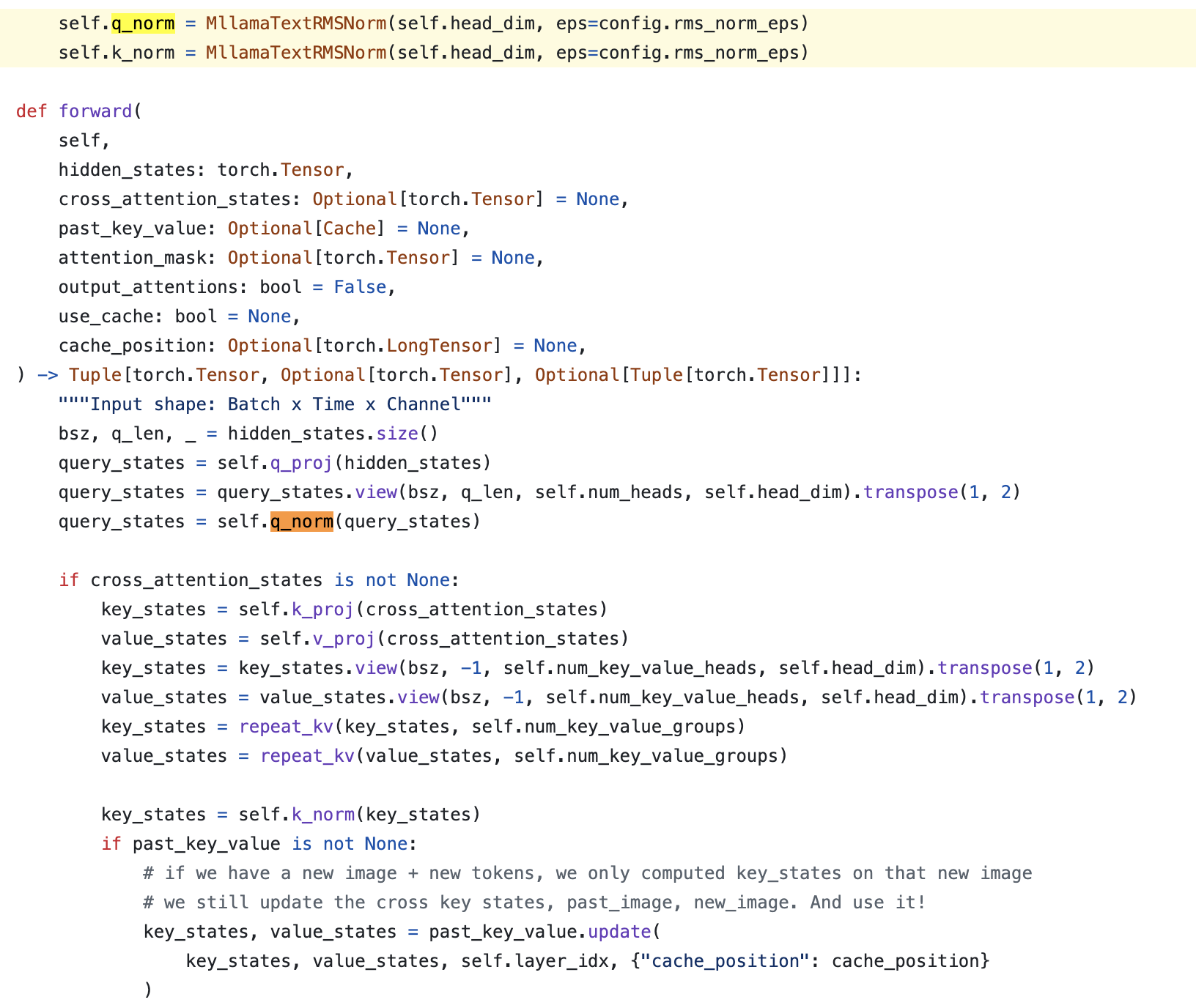Fig. Fig. Fig. Fig.

+Updated) Methods of improving LLM training stability

며칠 전 Methods of improving LLM training stability라는 paper가 올라와서 조금 더 작성해보기로 한다. 이 paper는 앞서 얘기한 모든 technique들을 다 실험해본 report라고 볼 수 있다.

• LR sensitivity (==stability) 가 개선되는가?
• 성능 개선에도 도움이 됐는가? (minimal valid loss는 몇인가?)

이 두 가지를 중점적으로 봤고, 그 결과 qk norm이 가장 좋았음을 확인할 수 있었다.

저자들은 앞에 paper들이랑 거의 동일하게 logit의 l2 norm이 커지면 softmax가 one-hot처럼 되는 것에 대해 분석하기 위해 uniform sampled vector를 softmax 할 때 input vector를 10배, 40배 … scaling 해가면서 output distribution을 비교했는데, one hot encoding처럼 되면 gradient propagation에 문제가 생긴다고 써놓긴 했으나 왜그런지 제대로 분석을 하진 않은 것으로 보인다.

gradient에 대한 분석은 크게 없고, 단순히 터진 모델과 (diverge) 그렇지 않은 모델 (converge)을 비교했을 때, attn QKV proj, attn out proj, ffn fc2 proj 의 l2 norm값이 2배 이상 컸다는 걸 관찰했다는 table만 첨부했다. (logit growth와 training stability를 설명하는 요즘 paper들은 대부분 theoritical analysis가 부족한게 많은 것 같아 아쉽다)

Method w/o introducing additional modules

어쨌든 목표는 qkv proj, attn out proj, ffn fc2 proj의 output tensor의 l2 norm을 줄이기 위한 방법들을 다 적용해보는 것이고, 그러기 위해 NVIDIA team은 layernorm을 추가로 넣는 방법과 아닌 방법을 모두 탐색했다. 나는 이를 구분하기 위해서 subsection을 두개로 쪼갰다.

• 1.\(\alpha\)-Reparam
• 2.soft_temp (softmax temperature)
• 3.soft_cap (softmax capping)
• 4.soft_clip (softmax clip)

먼저 \(\alpha\)-Reparam은 Stabilizing Transformer Training by Preventing Attention Entropy Collapse라는 Apple의 paper에서 제안된 방법론으로,

여기서 \(\sigma (W) \in \mathbb{R}\)는 임의의 linear layer의 weight matrix W의 spectral norm을 의미하며, learnable parameter \(\gamma \in \mathbb{R}\)는 1로 초기화 되어있다. 저자들은 아래 vanilla transformer block의 모든 linear layer에 이를 적용했다고 하는데,

이는 마치 Kingma et al.의 weight normalization (WN)과 유사한 형태를 띄고 있다.

그 다음으로 softmax_temp는 너무 간단한건데, (learnable) temperature param인 \(\beta\)를 logit에 곱해서 logit scale을 relaxation 하는 것이다. 아래와 같은 꼴에서는 temperature가 0.5, … 낮아질수록 attention entropy가 커진다 (평평해진다).

soft_cap은 앞서 설명했으니 넘어가도록 하고, soft_clip은 아래처럼 정말 일정 값이 넘어가면 clip하겠다는 전략인데, 이 method의 문제는 clip된 값에는 backprop이 안된다는 것이다.

Method w/ introducing additional modules

이제 layernorm (or rmsnorm)등의 nn module을 추가로 넣는 방법론들인데,

• 5.Layerscale
• 6.qk_norm
• 7.qk_norm_cap
• 8.qkv_norm
• 9.qk_fc2_norm (== gemma, chameleon)

여기서 layerscale은 layer output을 scale해주는 trainable parameter를 넣는 것이고,

나머지 qk_norm이나 qk_norm + softcap, qk_fc2_norm (residual post norm 추가) 등은 앞서 많이 설명했으니 생략하겠다.

결론적으로 저자들은 layerscale, alpha-reparam등은 쓸모가 없으며, softmax clip이나 temperature같은 것들도 lr sensitivity를 개선하지 못했으며, qk norm에 추가로 attn out proj, fc2 norm 등을 추가하는것은 computational overhead를 증가시키는 것에 반해 성능이 개선된다거나 LR sensitivity가 개선된다거나 하지 않았기 때문에 qk norm에 softcapping등을 추가하는 걸 중점적으로 더 보게 됐다고 한다. (qk_norm 베이스에 softcap등을 추가하는 것 위주로)

Caveats

여기서 qk norm과 qk norm + FC norm에 대해서 생각해볼 점이 있는데, attn out proj와 fc2 layer에 normalization을 적용해서 residual에 더해지기 전의 값을 줄이는 것이 training stability에는 큰 도움이 되지 않는다는 결론 자체는 받아들일 수 있겠으나, quantization 등의 task를 고려해서 생각하면 얘기가 다를 수 있으니 이 점에 대해서는 생각해봐야 할 것이다.

References

• Papers
  • Small-scale proxies for large-scale Transformer training instabilities
    • tweet thread from author
  • ST-MoE: Designing Stable and Transferable Sparse Expert Models
  • Scaling Vision Transformers to 22 Billion Parameters
    • blog
  • Intriguing Properties of Vision Transformers
  • A Theory on Adam Instability in Large-Scale Machine Learning
  • Stable and low-precision training for large-scale vision-language models
  • Stabilizing Transformer Training by Preventing Attention Entropy Collapse
  • Chameleon: Mixed-Modal Early-Fusion Foundation Models
  • On Layer Normalization in the Transformer Architecture
  • Methods of improving LLM training stability
• Code Implementations
  • modeling_cohere.py
  • modeling_phi.py
  • modeling_olmoe.py
  • Convergence issue from megatron
    • issue 1
    • issue 2
• Backpropagation Through Softmax Activation
  • The Softmax function and its derivative from Eli Bendersky
  • Transformer Networks: A mathematical explanation why scaling the dot products leads to more stable gradients from Thomas Kurbiel
  • Derivative of the Softmax Function and the Categorical Cross-Entropy Loss from Thomas Kurbiel
  • Temperature check: theory and practice for training models with softmax-cross-entropy losses
  • Regularizing Neural Networks by Penalizing Confident Output Distributions
  • Softmax Gradient Tampering: Decoupling the Backward Pass for Improved Fitting
• Gemma 2
  • Gemma 2: Improving Open Language Models at a Practical Size
  • 4.44 HF modeling_gemma2.py
  • details from Daniel Han
  • details from Daniel Han 2