(WIP) Neural Tangent Kernel (NTK) and Mean Field Theory (MFT)
04 Jan 2024< 목차 >
- (Motivation) Why Neural Tangent Kernel (NTK) and Mean Field Theory (MFT) ?
- From Linear Regression to Neural Network Gaussian Process
- Neural Tangent Kernel (NTK)
- Mean Field Theory (MFT)
- References
(Motivation) Why Neural Tangent Kernel (NTK) and Mean Field Theory (MFT) ?
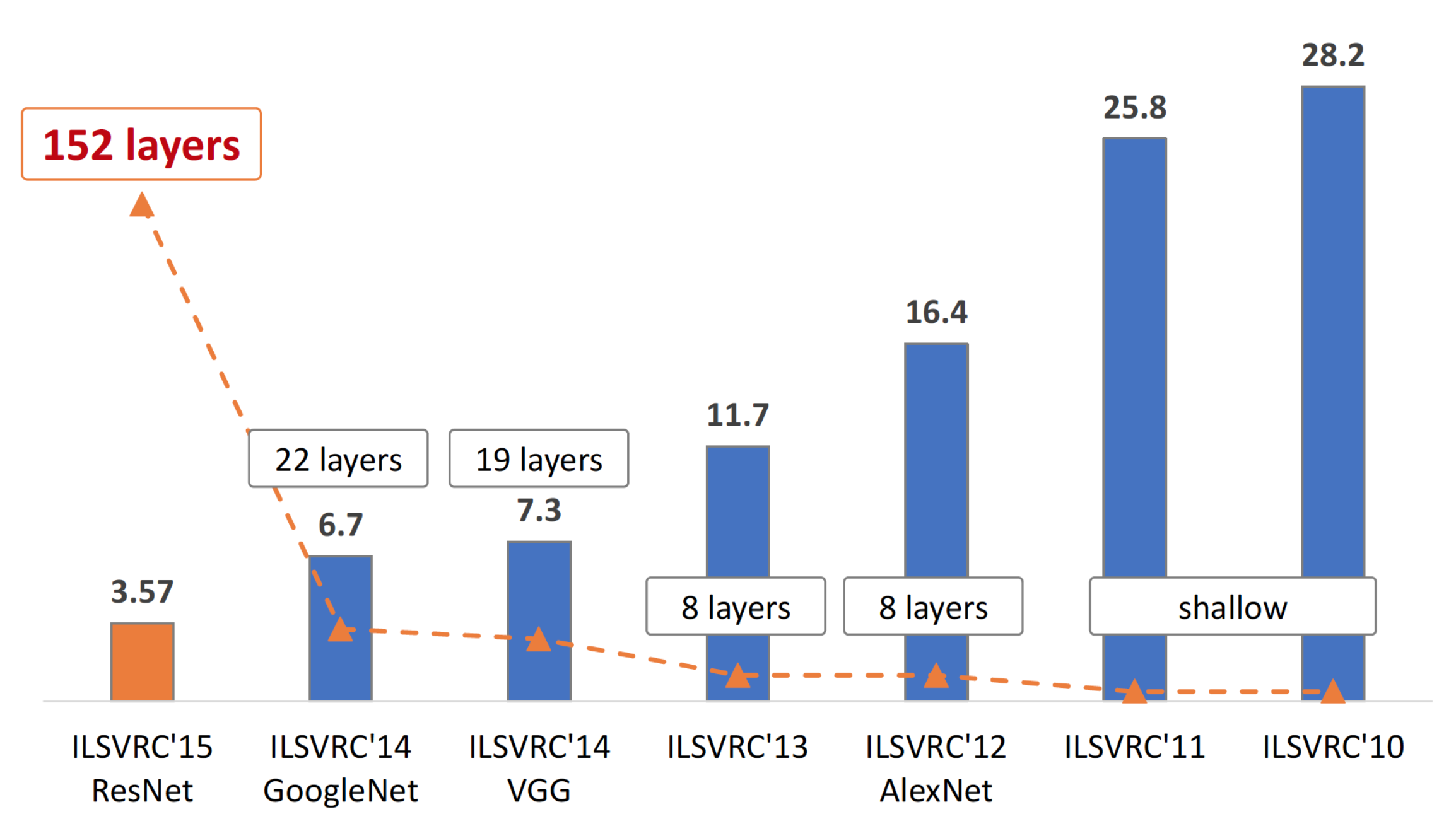 Fig. Source from here
Fig. Source from here
 Fig. Source from here
Fig. Source from here
 Fig. Source from here
Fig. Source from here
From Linear Regression to Neural Network Gaussian Process
NTK에 대해서 intuition을 얻기 위해서는 먼저 Kernel Method에 대해 알아야 한다. 이를 위해 고전 ML의 Linear Regression부터 Kernel Regression, 그리고 Gaussian Process (GP)와 이것들의 Neural Network (NN)간의 관계에 대해 알아보자.
- Linear Regression
- Non-Linear Regression
- Kernel Regression
- Gaussian Process (GP) Regression
- Neural Network Gaussian Process (NNGP)
1. Linear Regression
먼저
2. Non-Linear Regression and Kernel Regression
하지만 linear regression에는 real world dataset에 curve fitting을 하는데 있어 한계가 존재한다.
Kernel은 예를 들어 아래의 figure처럼 2차원에서는 linearly separable하지 않은 dataset을 3차원으로 lifting시켜 linear hyperplane을 그어 문제를 푸는 경우에 사용된다.
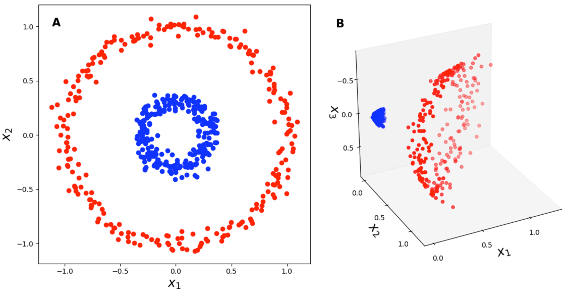 Fig. from 2-dim to 3-dim
Fig. from 2-dim to 3-dim
고차원으로 lifting시켜주는 mapping function을 \(\phi(\cdot)\)라고 하고 \(\phi(x_i)\)는 3차원을 넘어서 10차원, 20차원… 무한차원이 될 수도 있다고 치자. 원래차원의 data point들을 명시적으로 (explicitly) 어떤 고차원의 어떤 형태로 변환을 해서 regression, classification 하는 것은 직관적이지만 conputationally inefficient하다. 그런데 non-linear regression이나 SVM등의 solution은 수식을 풀어보면 각 data-point들의 similarity, \(\phi^T \phi\)를 계산하는 term으로 표현된다는 점을 알아차릴 수 있다.
바로 이부분에 주목해서 실제 고차원으로 maapping된 data point들간의 inner product는 사실상 어떤 함수 (kernel) 값과 같다는 점을 이용해 실제 해당 차원으로 명시적으로 data point를 변환하지 않더라도 문제를 풀 수 있는 경우가 있는데, 이 때 사용되는 원래 data point들 간의 similarity를 measure하는 function?을 Kernel이라고 부르며, 이를 Kernel Trick이라고 부른다.
심지어 무한 차원에서의 inner product도 이에 대응하는 kernel이 있는데, 이를 Radial Basis Function (RBF) 혹은 Gaussian kernel이 바로 그것이다.
Kernel Regression에 대해서도 살짝 recap 해보도록 하자.
3. Gaussian Process (GP) Regression
4. Neural Network Gaussian Process (NNGP)
Neural Network Gaussian Process (NNGP)는
Neural Tangent Kernel (NTK)
Intuition of NTK
Neural Tangent Kernel (NTK)도 이름에서 알 수 있듯 Kernel이다. 고전 ML의 그것과 컨셉 자체는 다를 바가 없다는 점을 받아들이고 얘기를 해보자.
NTK에서는 Neural Network (NN)의 width (hidden dimension)가 무한히 넓어지는 경우에 대해서 (width limit), Neural Network (NN) training은 linearized model을 다루는 것과 같다는 것을 보인다. 무슨 말일까?
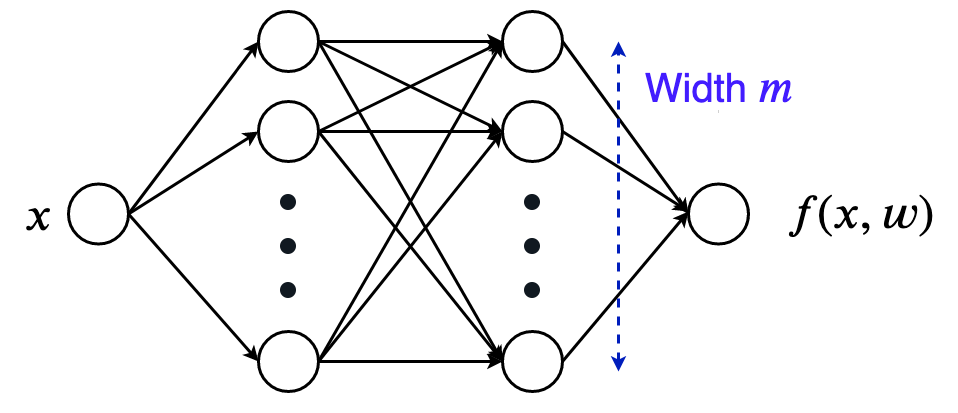 Fig. Source from here
Fig. Source from here
이를 직관적으로 이해하기 위해서 relu를 activation function으로 쓰는 간단한 2-layer MLP를 예시로 들어보자.
이 model로 regression 문제를 풀 건데, 이런 NN을 이루는 weight을 randomly initalization 해보면 아래같이 다양한 function을 얻을 수 있다.
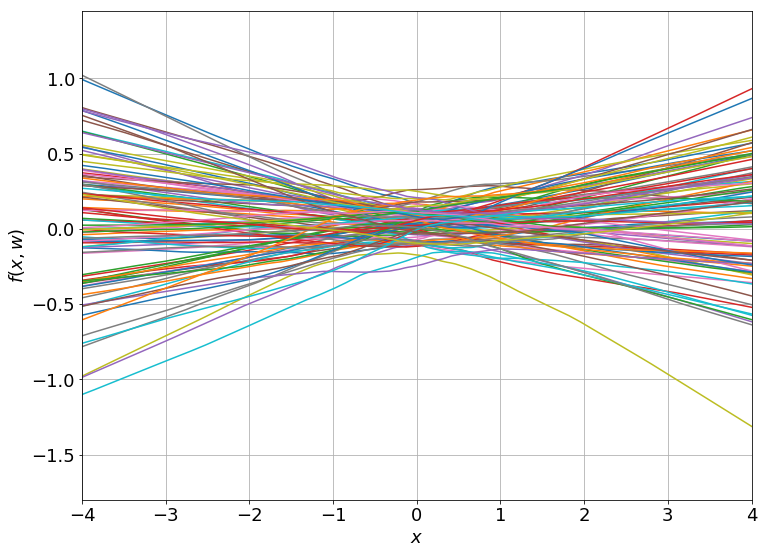 Fig. Source from here
Fig. Source from here
이제 이를 아래의 objective function으로 학습시켜보자. (full batch gradient descent)
\[L(w) = \frac{1}{N} \sum_{i=1}^N \parallel f(\bar{x_i}, w) - y_i)^2\parallel\]여기서 \(w, \bar{x_i}, \bar{y_i}\)는 각각 NN weight, input, ground truth label 이다. 그리고 이 NN은 gradient descent로 optimization을 할 경우 시간에 따라 아래와 같이 변하는 것을 볼 수 있다.
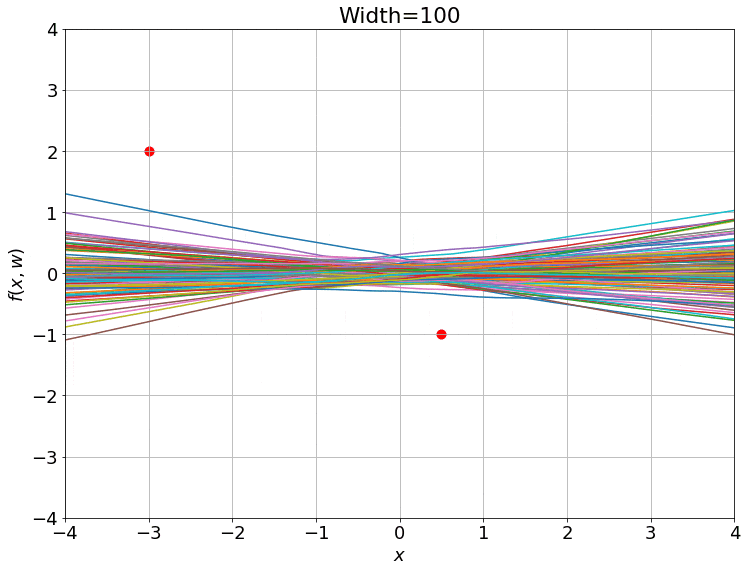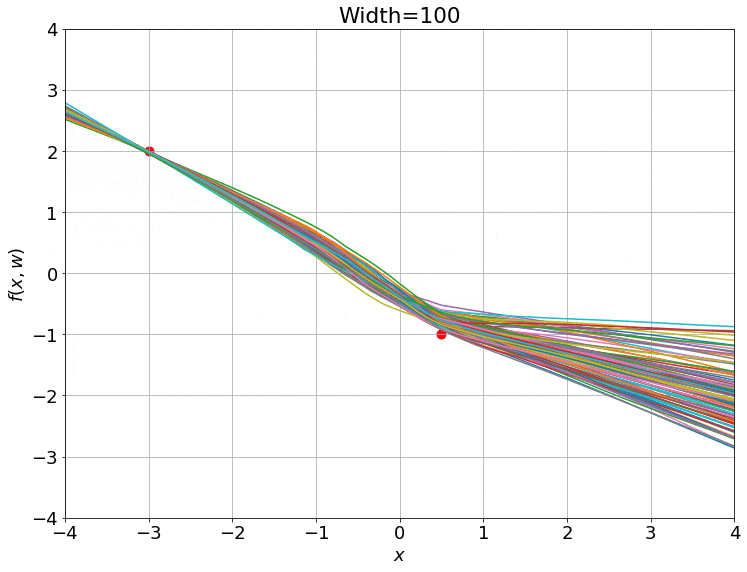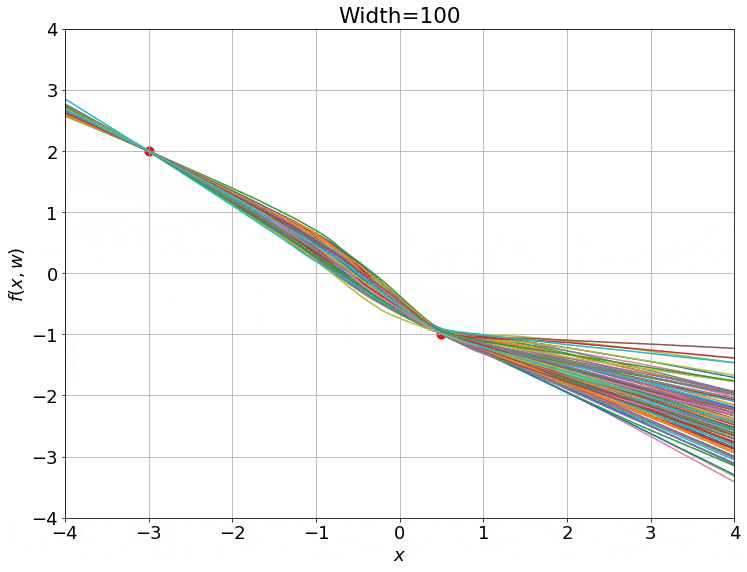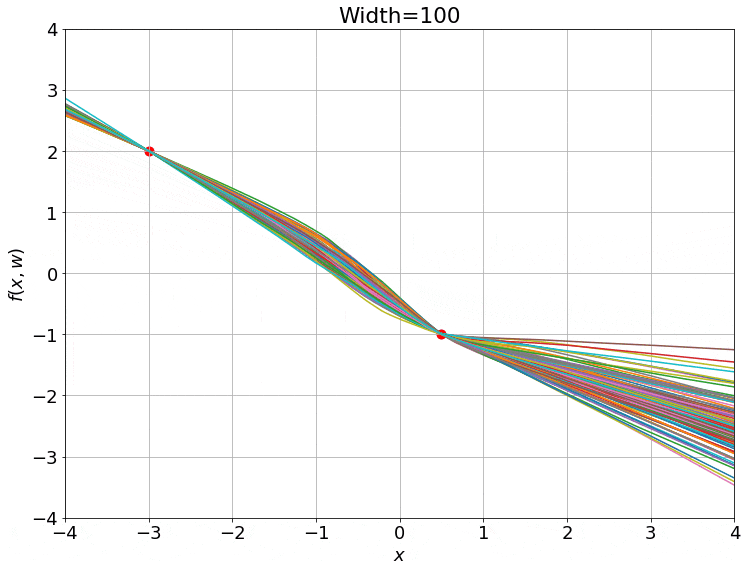 Fig. Training 100 ReLU nets using gradient descent on square loss. Source from here
Fig. Training 100 ReLU nets using gradient descent on square loss. Source from here
여기서 재밌는 점은 NN을 학습하기 위해 맨 청므 randomly initialization한 weight과 updated weight이 크게 다르지 않다는 점이다.
그리고 이 현상은 NN의 hidden width가 커질수록 (weight matrix의 크기가 커질 수록) 두드러진다.
실제로 initialization point 로 부터 서롣 다른 width에 대해서 weight이 변하는 것을 animation으로 나타냈을 때 거의 animation이 변화하지 않는다는 것을 아래 figure에서 확인할 수 있다.
이를 Lazy Training현상이라고 한다.
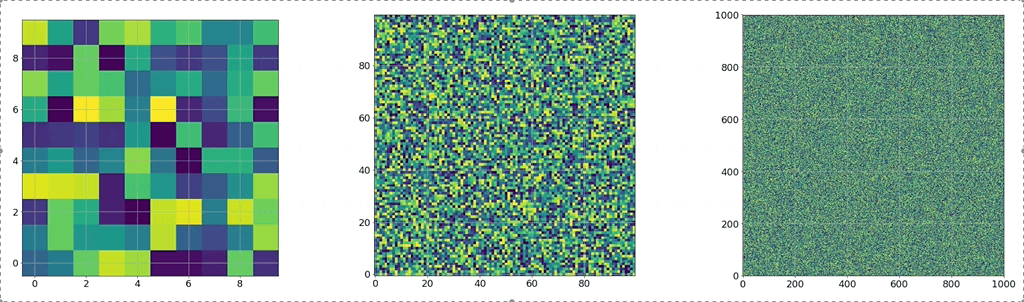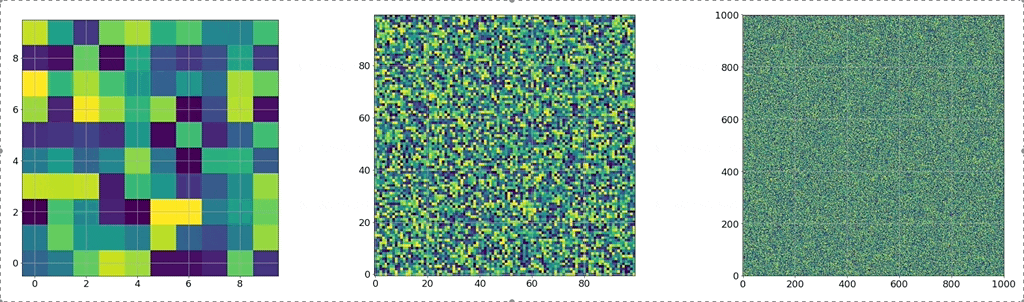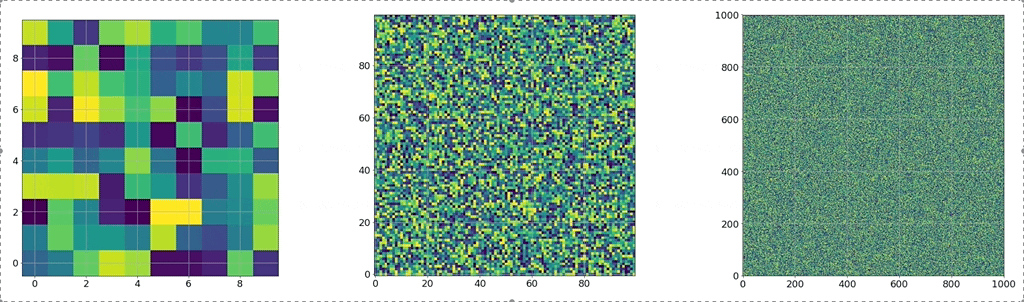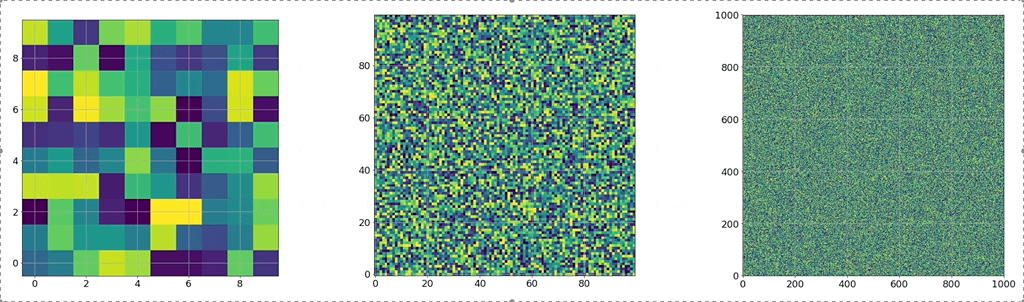 Fig. width에 따른 weight 변화량 2배속. Source from here
Fig. width에 따른 weight 변화량 2배속. Source from here
그리고 init weight으로부터 optimization step이 경과할 때 마다 weight vector의 L2 nore을 init weight과 비교해서 상대적인 변화 (relative change)를 측정했을 때,
\[\frac{ \parallel w(n) - w_0 \parallel_2 }{ \parallel w_0 \parallel_2 }\]width가 늘어늘 수록 weight이 거의 움직이지 않는다는 것을 아래 animation을 통해 알 수 있다.
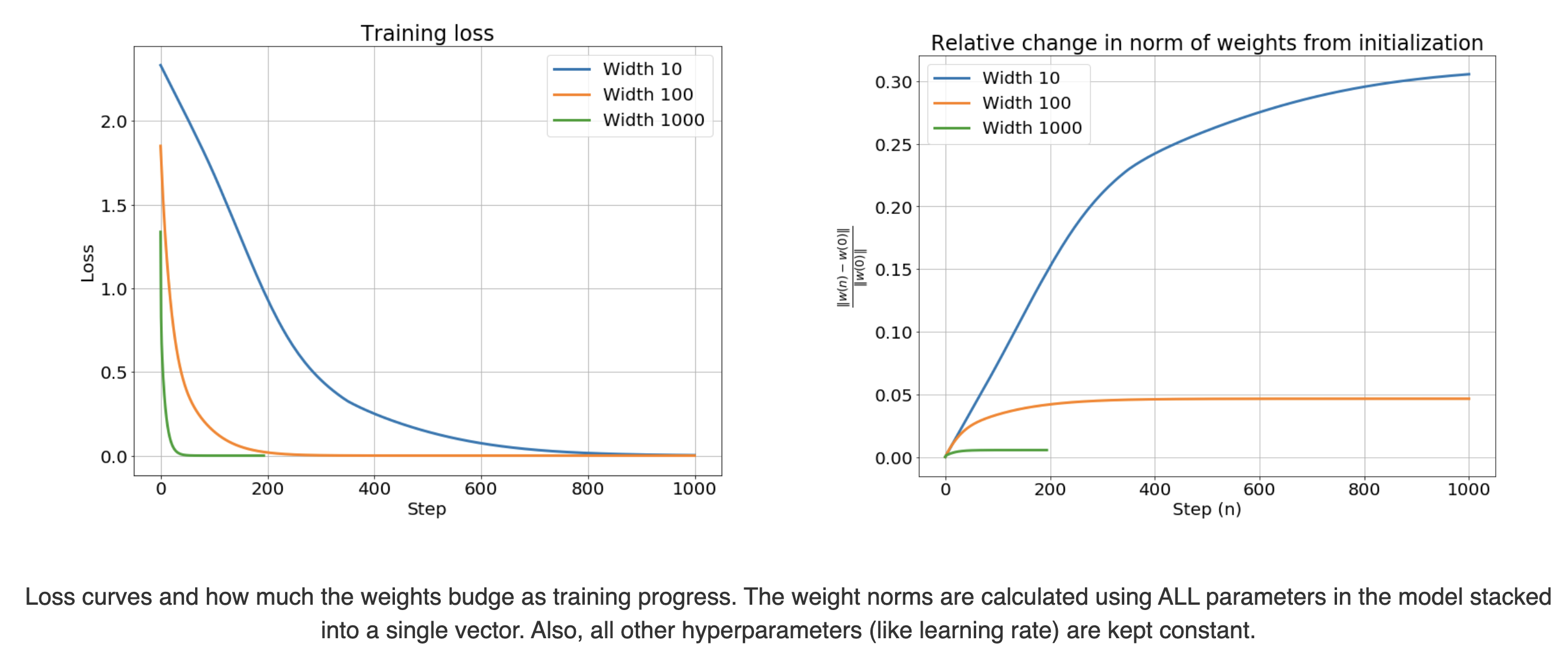 Fig.
Fig.
width가 2배 커지면
Taylor Expansion Of The Network Function With Respect To The Weights Around Its Initialization.
이제 NTK를 유도할 것이다.
이를 위해서 우리는 weights, \(w\), inputs, \(x\)에 대해서 network output \(f(x,w)\)를 표현할 것인데, 앞서 우리는 weight matrix가 충분히 크다면 matrix entry들은 (random) initialization으로 부터 거의 멀어지지 않는 다는 것을 관찰했다. 그렇기 때문에 이 function output은 initialized weight, \(w_0\)부근에서 1st order taylor approximation (1차 테일러 근사)를 할 수 있게 된다.
\[\begin{aligned} & f(x,\color{red}{w}) \approx f(x,w_0) + \nabla_w f(x, w_0)^T (\color{red}{w} - w_0) & \\ & y(\color{red}{w}) \approx y(w_0) + \nabla_w y(w_0)^T (\color{red}{w} - w_0) & \\ \end{aligned}\]당연하게도 taylor 근사는 \(w_0\)의 작은 부근 (small region)에서는 원래 function과 유사한 모양을 갖지만 region을 벗어나면 다른 function이 되어버리는데, 이는 곧 다시 얘기하겠다.
 Fig.
Fig.
어쨌든 우리는 network output을 아래처럼 얻게 되었는데,
\[\begin{aligned} & y(\color{red}{w}) \approx y(w_0) + \nabla_w y(w_0)^T (\color{red}{w} - w_0) & \\ \end{aligned}\]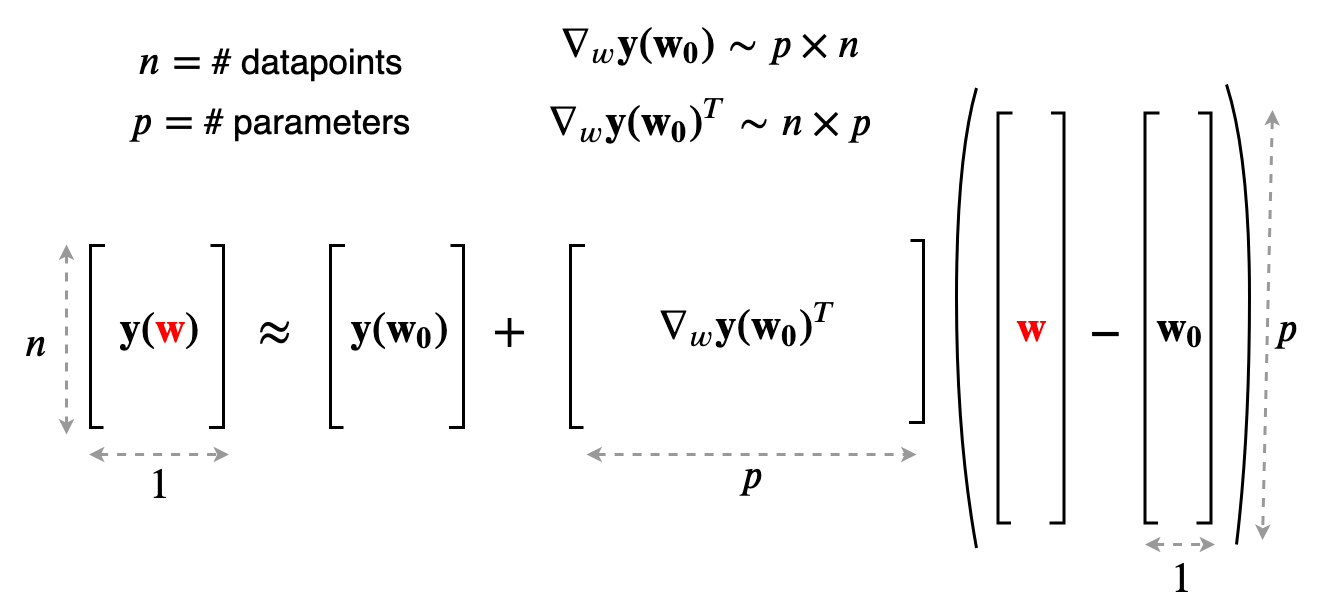 Fig.
Fig.
여기서 \(y(w_0)\), \(\nabla_w y(w_0)^T\)같은 것들은 모두 input을 넣으면 결정되는 상수이므로, 이는 \(w\)에 대해서 linear regression을 하는 것과 같다고 할 수 있다. 하지만 model function은 여전히 input에 대해서는 여전히 non linear하다고 할 수 있는데, 왜냐하면 model의 gradient를 계산하는 것은 여전히 linear operation이 아니기 때문이다.
그런데 사실 이는 initalized weight부근에서의 gradient vector인 feature map, \(\phi(x)\)를 사용하는 linear model이라고 할 수 있다고 한다. 왜냐면 이것도 어차피 input을 어떤 정해진 function을 사용해서 (init weight은 변하지 않으므로) lifting하는 것과 같기 때문이다.
\[\phi(x) = \nabla_w f(x, w_0)\]당연히 feature map이 나왔으니 kernel trick이 떠오를 테고, 이것이 곧 NTK로 발전하는 것이다.
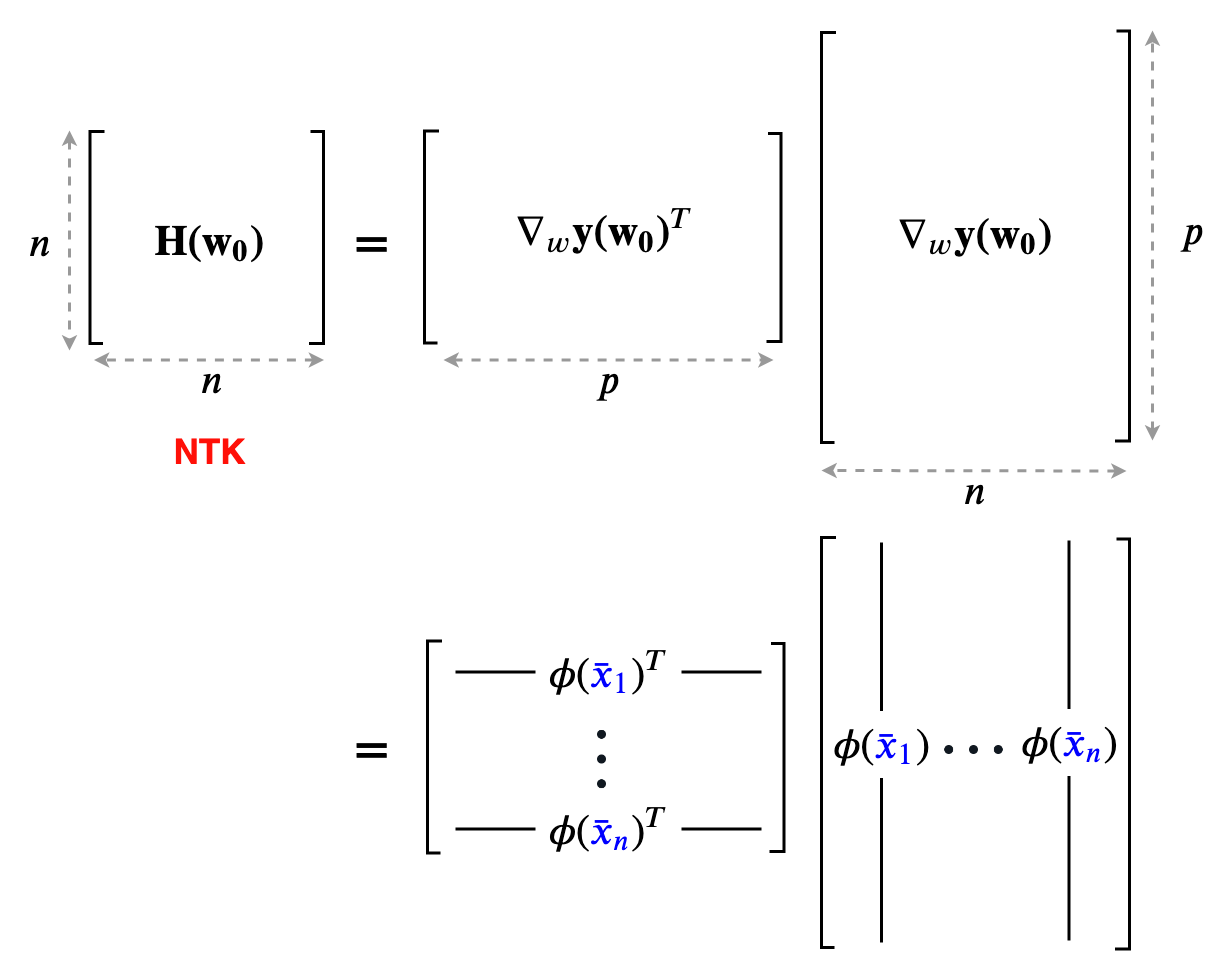 Fig.
Fig.
이를 위해서는 gradient flow등에 대해서 이해해야 하는데, 그 전에 먼저 1st order taylor approximation이 어떤상황에서, 얼마나 믿을만한 지에 대해서 얘기하도록 하자.
When is the Approximation Accurate?
항상 뭔가를 근사할 때에는 이것이 왜? 언제? 원함수와 비슷한지를 고려해봐야 한다. 앞서 samll region에 대해서 lienarized function과 original function은 갖다고 했는데, NN의 model output은 언제 linearization할 수 있는지 보자.
간단히 생각하기 위해서 먼저 hidden layer가 1층인 단순한 NN에 대해서 생각해보자. Inputs, outputs는 모두 1차원이며 bias는 생략한다.
\[f(x, w) = \sum_{i=1}^m b_i \sigma(a_i,x)\]여기서 \(\sigma\)는 twice diffentiable activation function이며 (ReLU는 그렇지 않다), weight vector, \(a_i, b_i\)는 parameter vector, \(w \in \mathbb{R}^{2m}\) 하나로 stack해서 생각한다. 여기에 \(a_i, b_i\)는 LeCun Initialization을 적용한다. 즉 input feature dim의 역수를 standard deviation으로 사용해서 layer가 거듭될수록 activation의 variance가 커지지 않도록 해주는 것이다.
\[\begin{aligned} & a_i \sim \mathcal{N}(0,1) & \\ & b_i \sim \mathcal{N}(0,\frac{1}{N}) & \\ \end{aligned}\]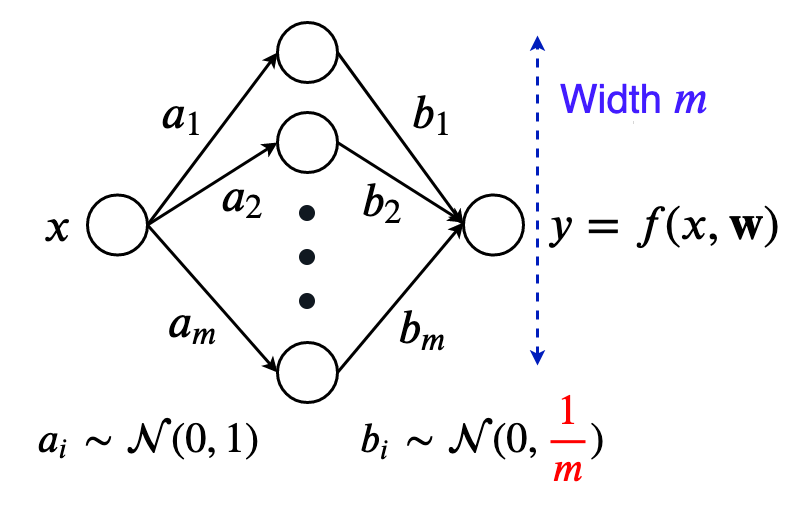 Fig.
Fig.
이제 우리는 이 NN의 width, \(m\)이 무한대로 갈 때 (as width goes to infinity), linear approximation이 얼마나 정교해지는지에 대해서 확인할 것이다.
먼저 width asymptotics, \(\kappa(w_0)\)를 분석하기 위해서, 우리는 model Jacobian과 Hessian을 찾아야한다. 일반적으로 이들은 각각 matrix와 rank-3 tensor이다.
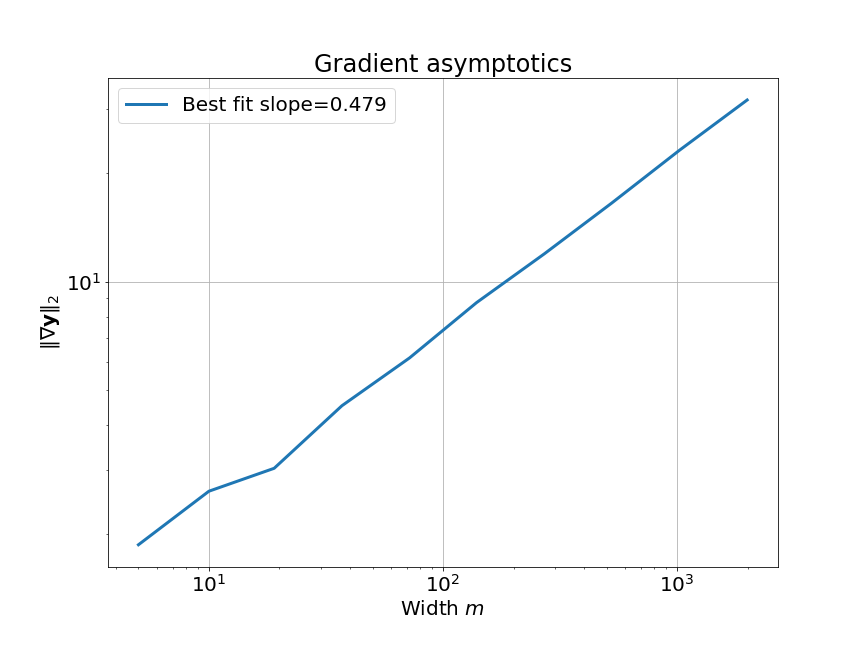 Fig.
Fig.
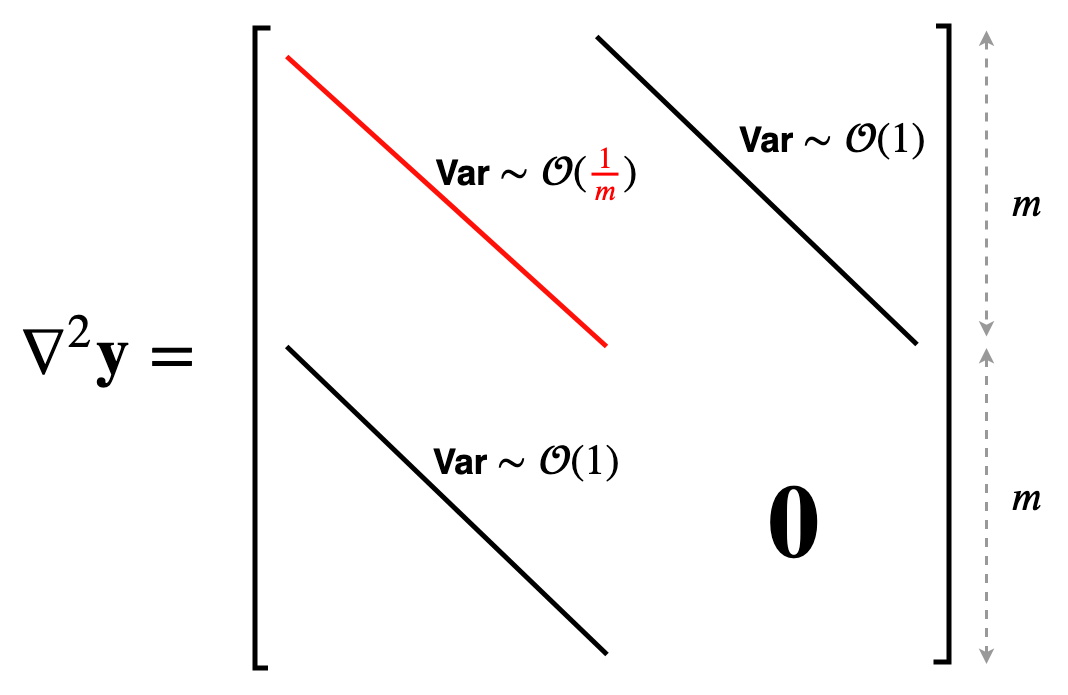 Fig.
Fig.
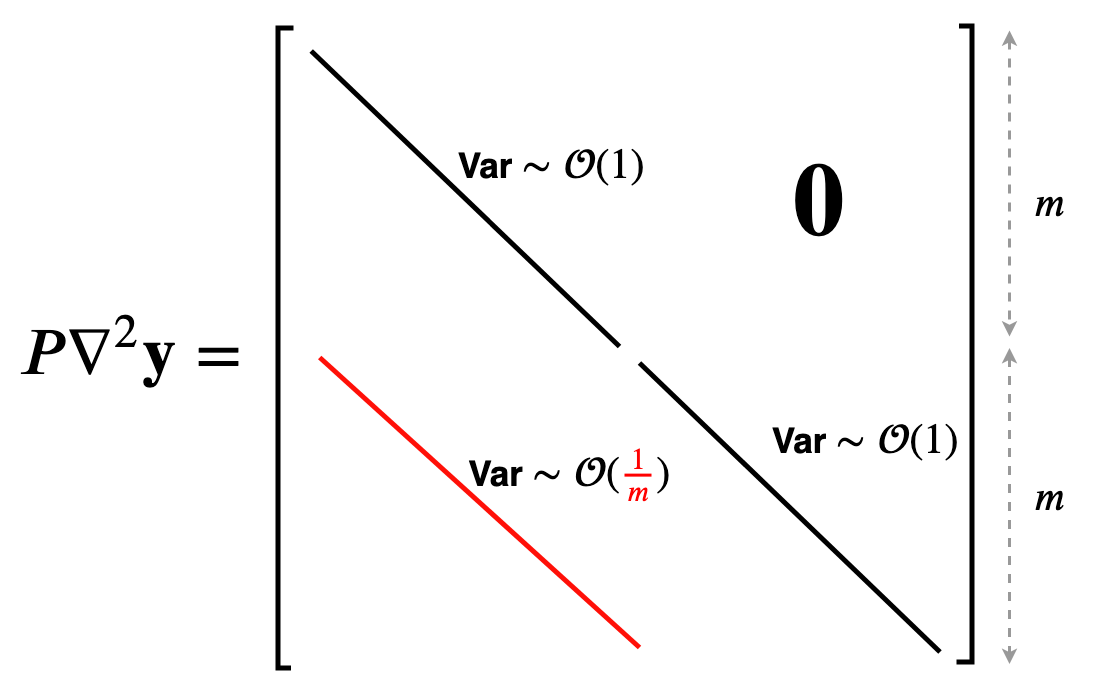 Fig.
Fig.
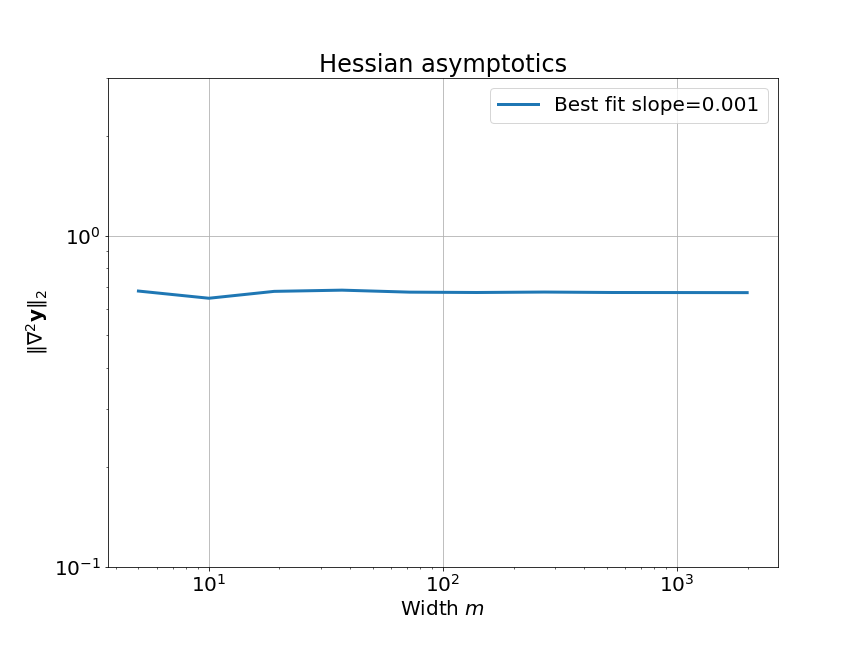 Fig.
Fig.
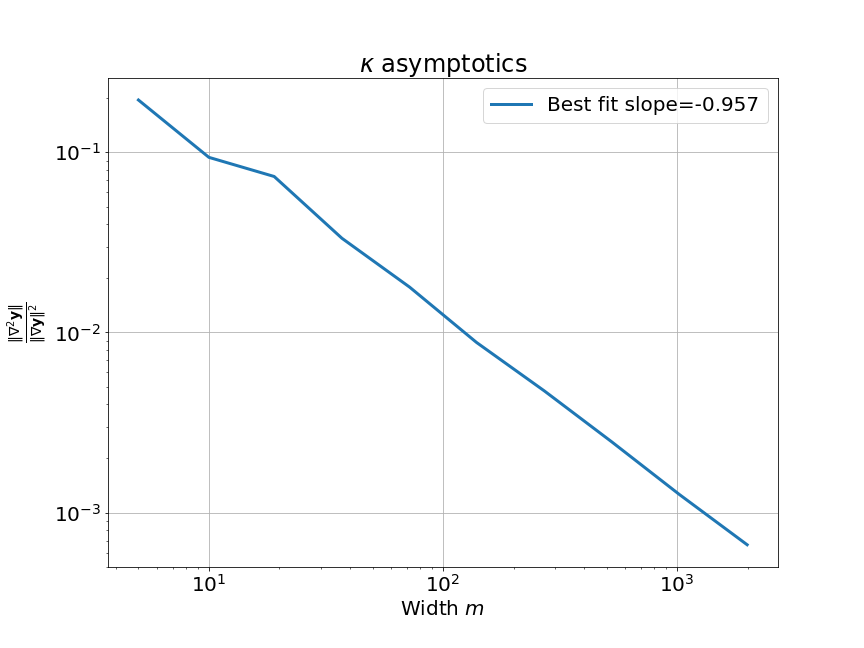 Fig.
Fig.
Scaling the Output
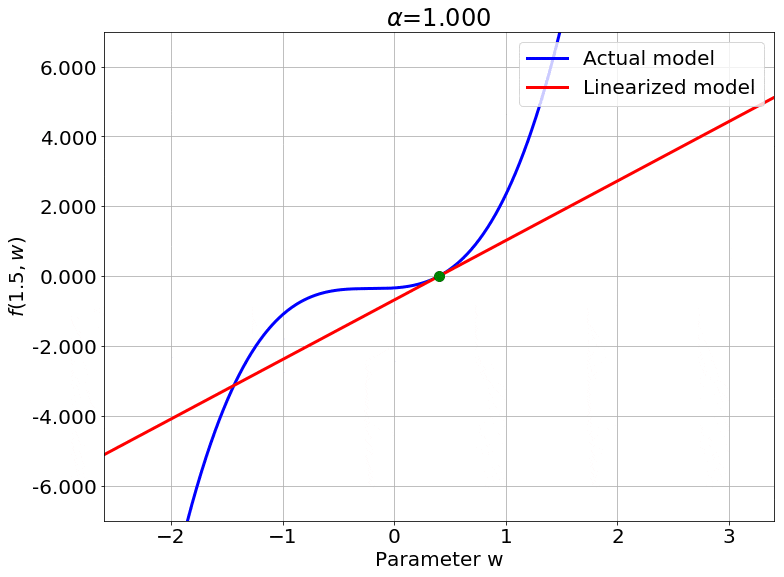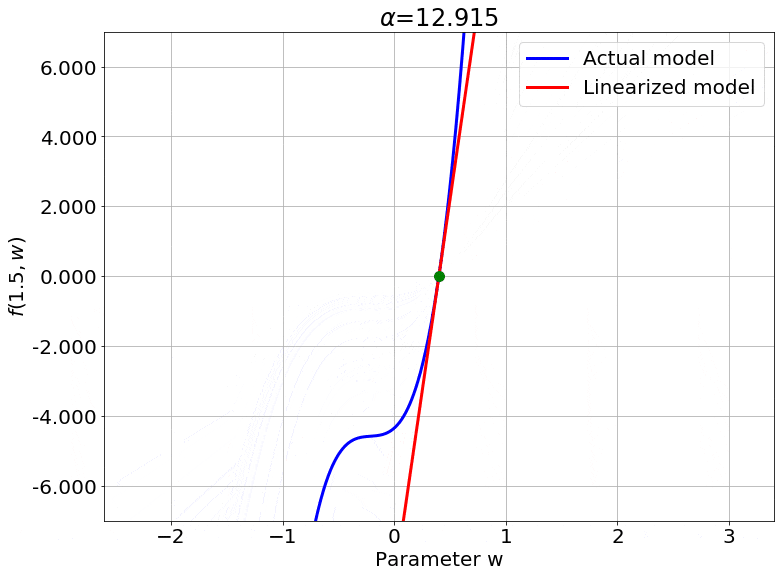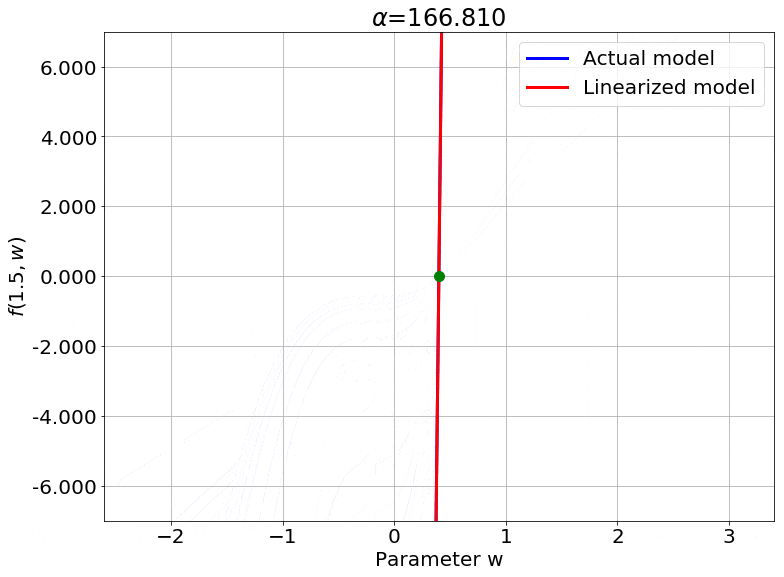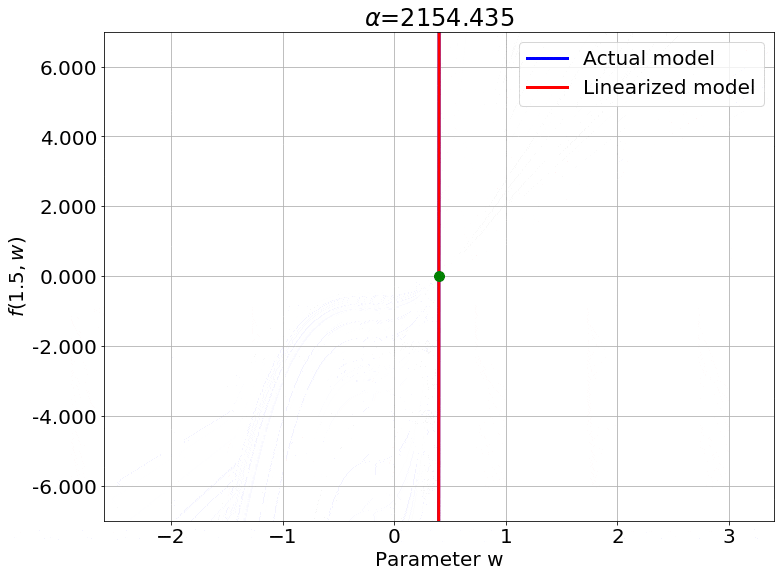 Fig.
Fig.
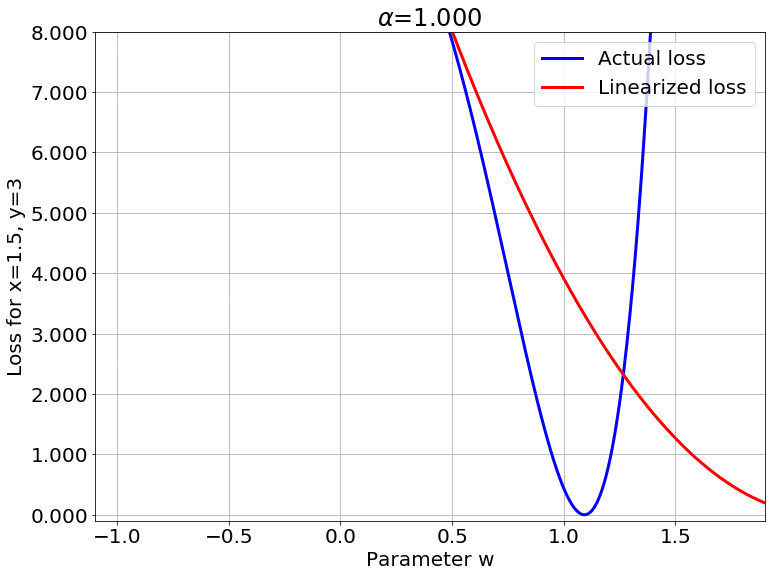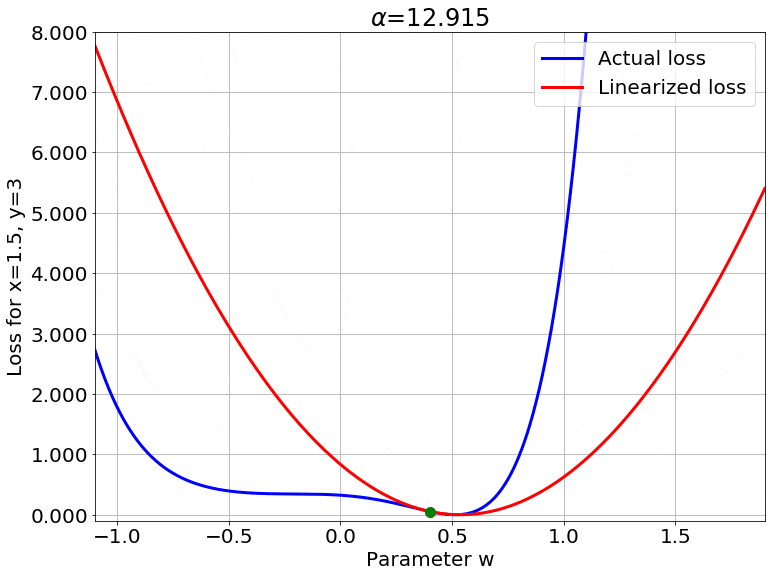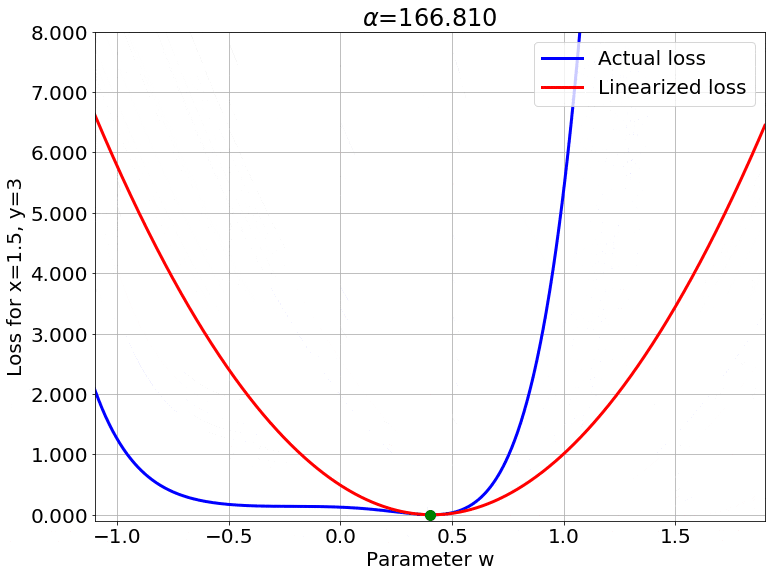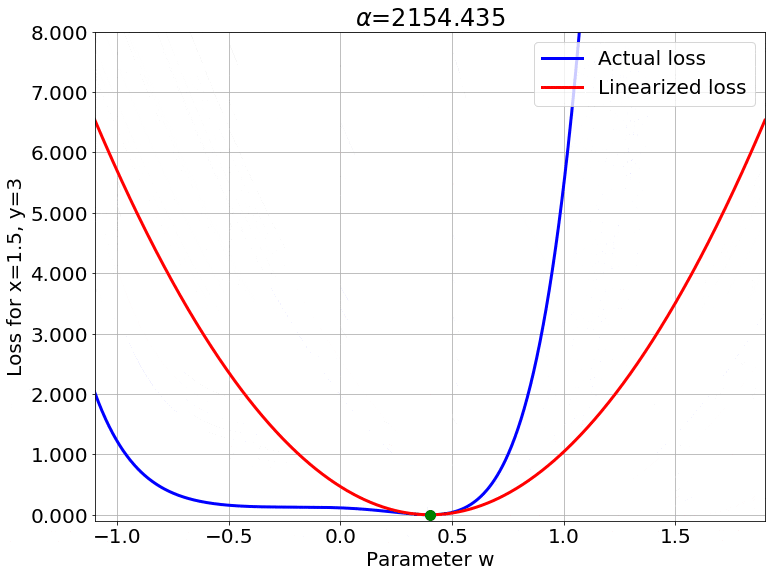 Fig.
Fig.
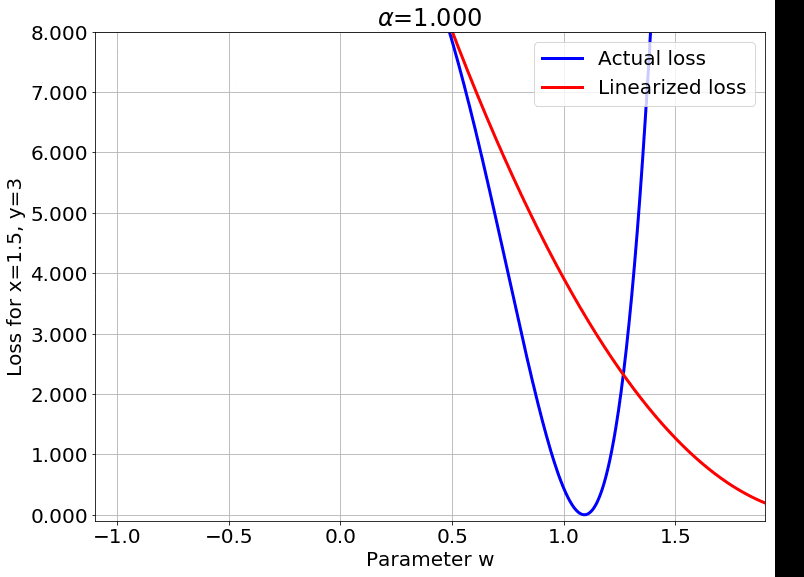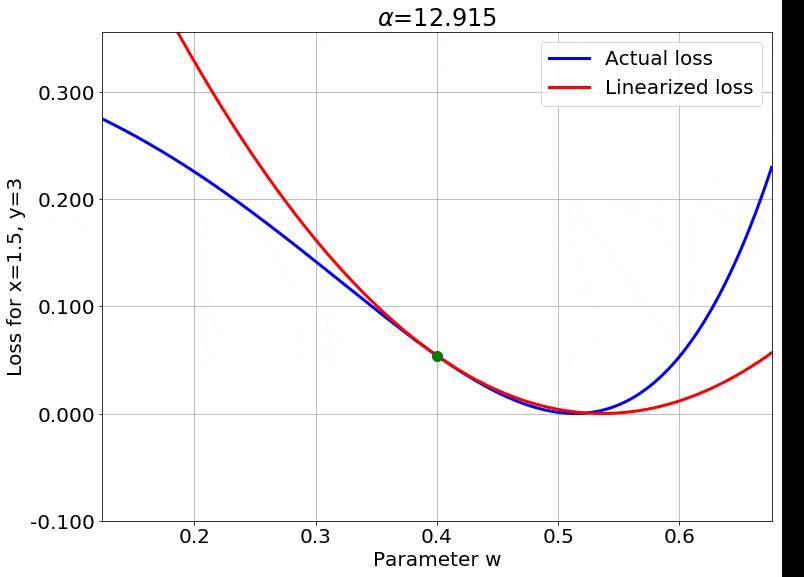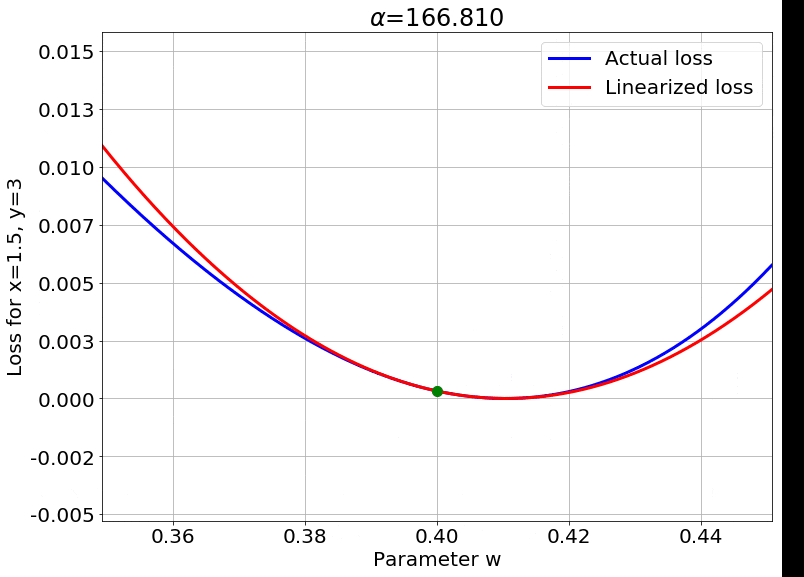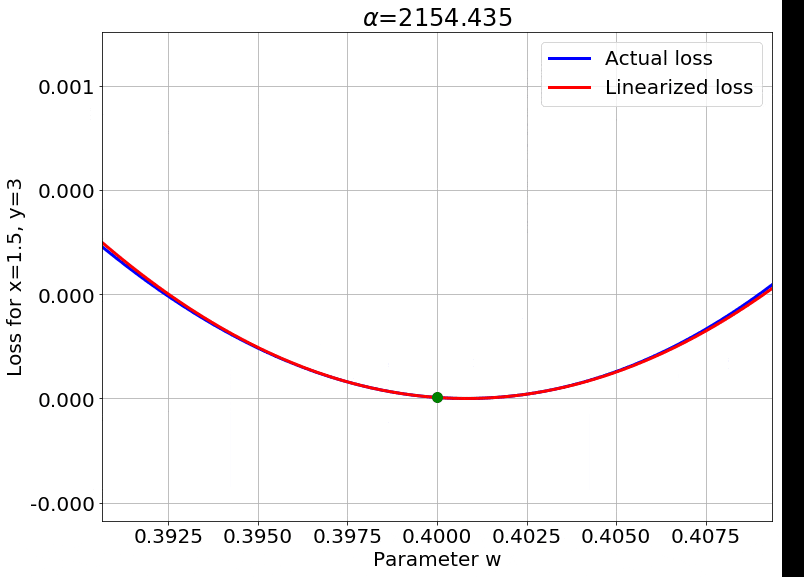 Fig.
Fig.
Gradient Flow
\[w_{k+1} = w_k - \eta \nabla_w L(w_k)\] \[\frac{w_{k+1} - w_k}{\eta} = - \nabla_w L(w_k)\] \[\frac{dw(t)}{dt} = - \nabla_w L(w(t))\] Fig.
Fig.
Seeing the Kernel Regime
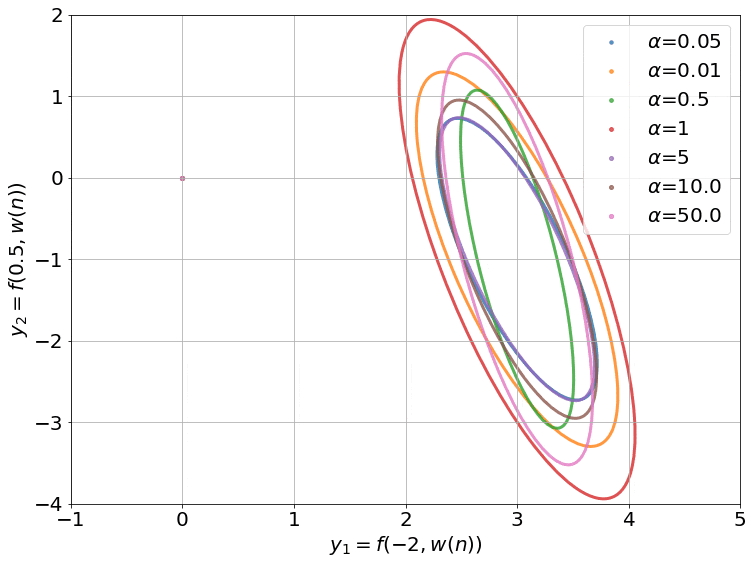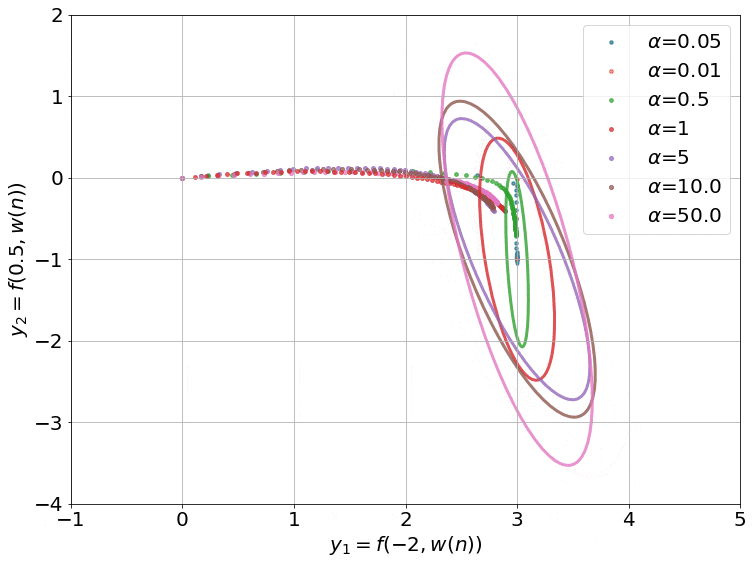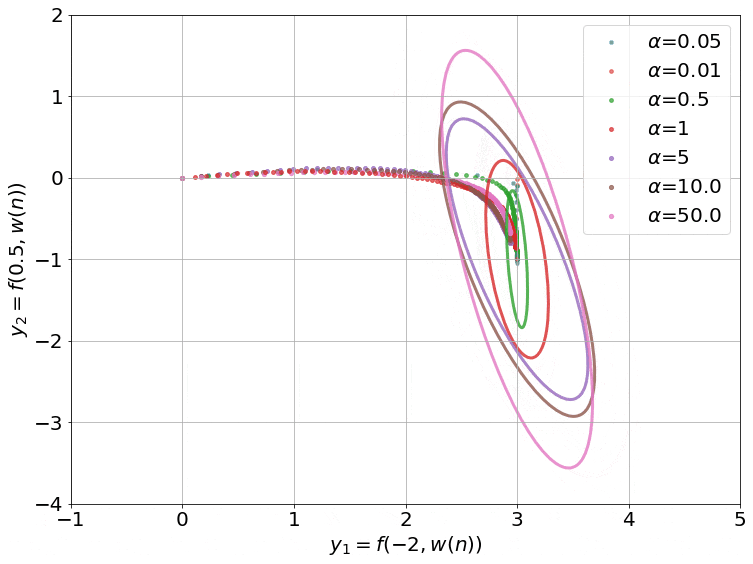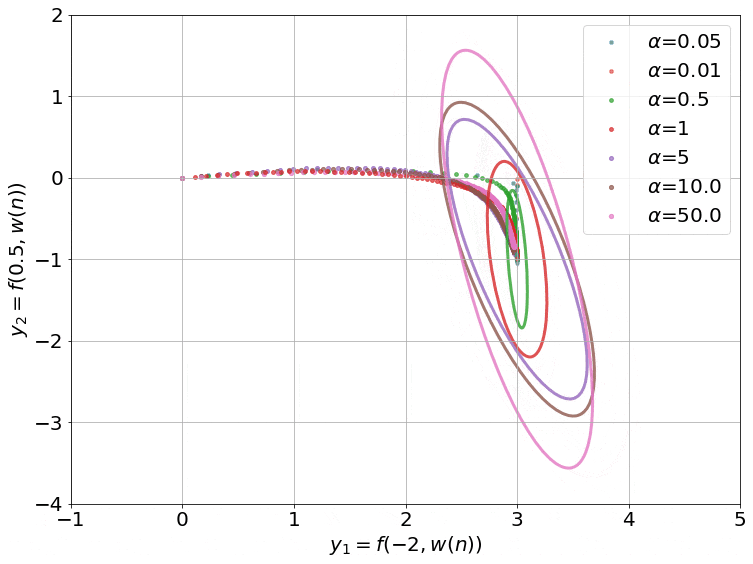 Fig.
Fig.
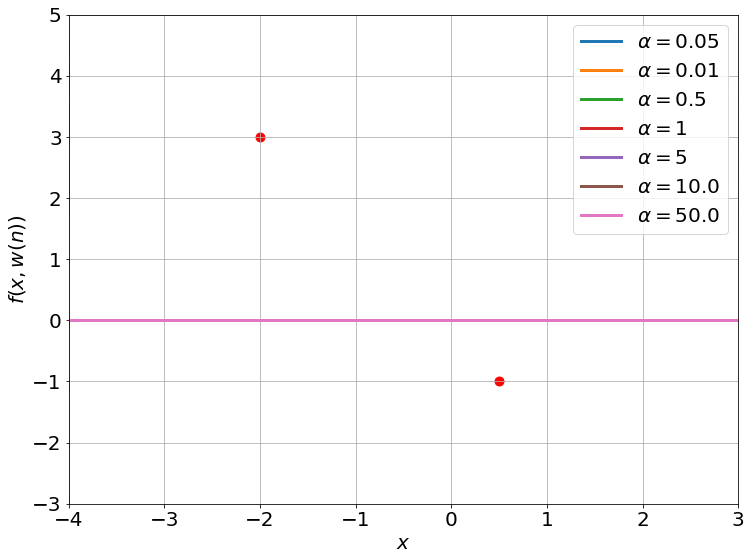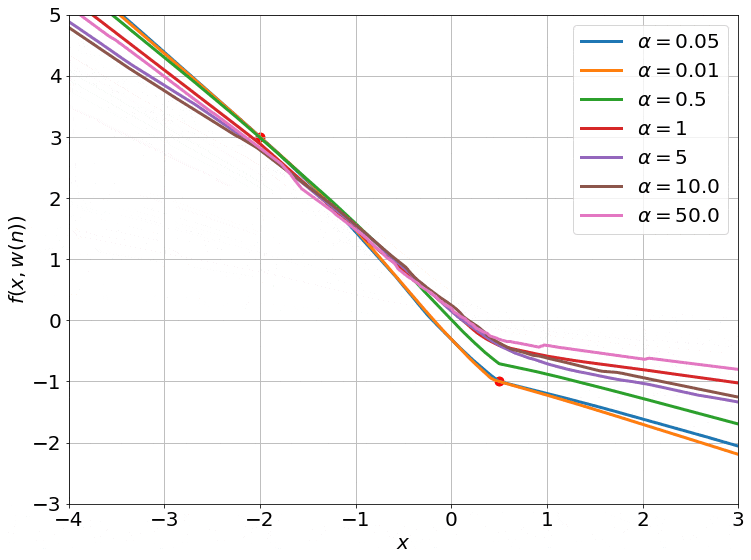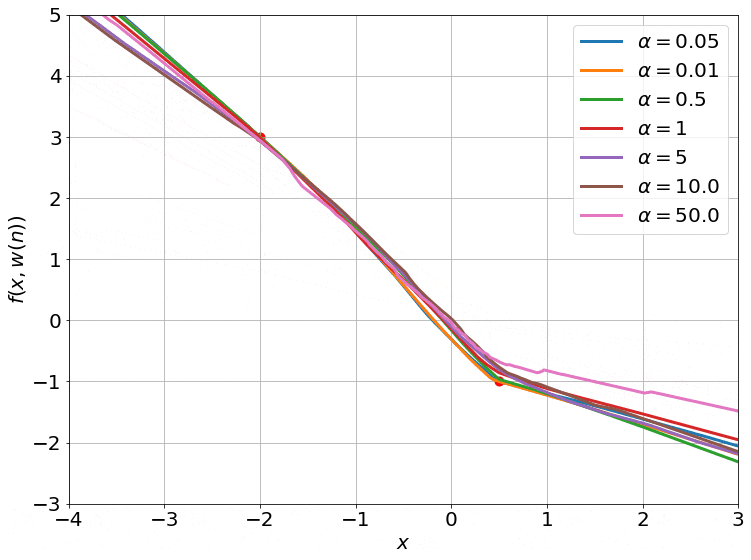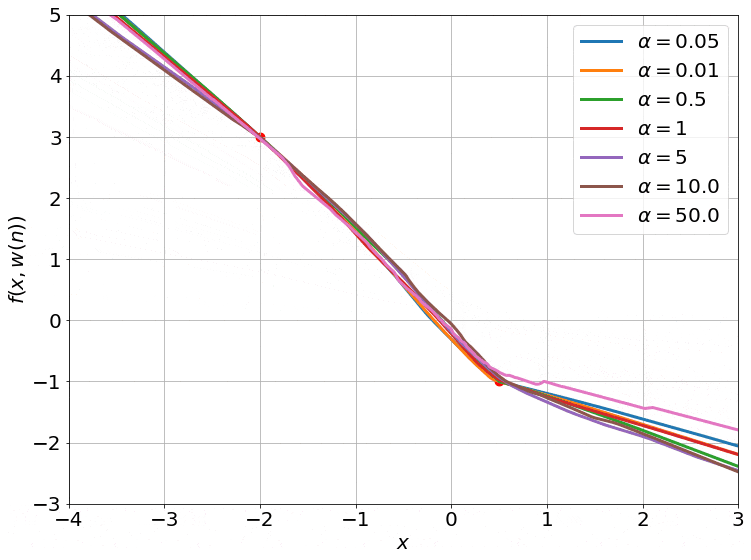 Fig.
Fig.
What is NTK Framework ?
(맨 마지막에 작성할 것)
Mean Field Theory (MFT)
What is MFT?
References
- Papers
- Neural Tangent Kernel: Convergence and Generalization in Neural Networks
- Wide Neural Networks of Any Depth Evolve as Linear Models Under Gradient Descent
- Neural Tangent Kernel Analysis of Deep Narrow Neural Networks
- On Lazy Training in Differentiable Programming
- Understanding the Generalization of Adam in Learning Neural Networks with Proper Regularization
- Identifying good directions to escape the NTK regime and efficiently learn low-degree plus sparse polynomials
- Infinite Width Models That Work: Why Feature Learning Doesn’t Matter as Much as You Think
- LoRA Training in the NTK Regime has No Spurious Local Minima
- Analyzing Finite Neural Networks: Can We Trust Neural Tangent Kernel Theory?
- Blogs
- Videos and Lectures
- Illustration of NTK from Author (Arthur Jacot)
- Lecture 7 - Deep Learning Foundations: Neural Tangent Kernels by Soheil Feizi
- Deep Learning Foundations by Soheil Feizi : Large Language Models
- Neural Tangent Kernel Analysis of Deep Narrow Neural Networks from 류경석 교수님
- 수리과학부 류경석 교수 - Training Dynamics and Complexity of Infinitely Wide WGAN and Minimax
- Recent Developments in Over-parametrized Neural Networks, Part I
- SNU 류경석 - Neural Tangent Kernel Analysis of Deep Narrow Neural Networks
- On the Connection between Neural Networks and Kernels: a Modern Perspective - Simon Du
-
From Neural Tangent Kernel to Mean-field Analysis from Quanquan Gu
- (UnderstandingDL) Virtual Lecture Series hosted by Data ICMC
- CS229M: Machine Learning Theory
- Analyzing Finite Neural Networks: Can We Trust Neural Tangent Kernel Theory?