Critical Batch Size (Large Batch Training Difficulties)

< 목차 >

Motivation
Critical Batch Size By Measuring Gradient Noise Scale
Solution Quality (Generalization Gap)
LR Scaling According to Batch Size
Summary
References

Motivation

보통 Deep Learning (DL)을 할 때 large batch size로 training 할 수만 있다면 마다할 사람은 없을거다. Resource만 된다면 말이다.

우리는 정해진 objective function 에 대해서 non-linear operator가 포함된 거대한 Neural Network (NN) model의 optimal solution을 close-form으로 찾을 수 없기 때문에 gradient descent라는 optimization algorithm을 통해 parameter를 iterative하게 update 하며 optimal solution을 찾아간다. 이 때 우리가 estimate한 gradient는 전체 sample들 중 일부를 사용해서 얻은 것으로 부정확한데 (noisy), batch size를 키울 경우 이 값이 더욱 정교해진다.

하지만 이럴 경우 한 step당 보는 sample이 많아지게 되고, 그 결과 한 epoch당 optimization을 수행하는 step 수가 줄어들게 된다. 그렇기 때문에 이를 보상하기 위해서 step size (LR; LR)를 적당히 키워야 batch size가 작은 경우와 비슷한 지점에 도달할 수 있을 것이다.

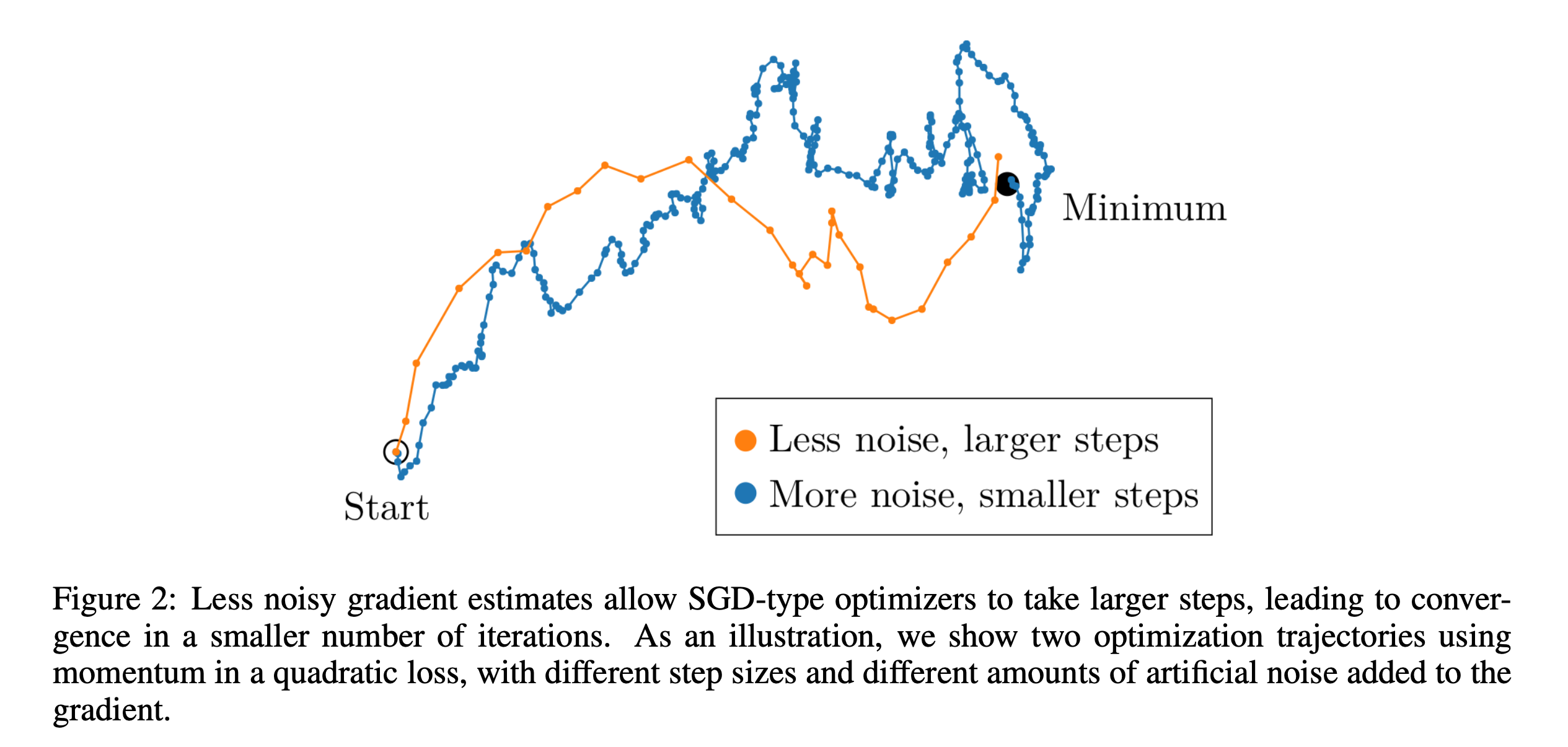gradient_noise_fig3 Fig.

Batch size를 키움으로써 얻을 수 있는 이득은 크게 몇 가지가 있을 수 있는데, 그 중 하나가 바로 training time을 줄이는 것이다. 그 이유는 iteration 수가 줄어들기 때문이다. 하지만 이는 특정 지점에 도달할 때 까지만 유효한 이야기 일 수 있다. 우리가 한 개 node에 배치할 수 있는 최대 8개의 GPU device를 넘어 수십, 수백개의 node를 연결한 multi-node 상황에 놓여있다고 생각해보자. ZeRO-DP라는 method로 Data Parallelism (DP)처리를 해서 매우 많은 sample을 볼 수 있게 되었다. Device가 늘어날수록 batch size가 커져 너무 큰 지경에 이를 수 있다. 그래서 이게 뭐가 문제가 되는가? 크면 클수록 좋은게 아닌가?

아래 ZeRO-DP paper의 주석을 보자. Prior work 라고 언급된 것은 OpenAI에서 개발한 human level의 Dota2 를 play 하는 agent에 대한 technical report, Dota 2 with Large Scale Deep Reinforcement Learning이다.

zero_large_batch_dota Fig.

Dota2 라는 게임을 play하는 agent를 학습하면서 어떤 batch size가 가장 가성비가 좋은지?를 연구했었는데, 특정 지점을 지나면 더이상 device를 많이 쓰는 것이 같은 성능을 달성하기 위한 training time을 줄여주지 않는다는 것을 발견했다고 한다. 이는 또 다른 표현으로 slow convergence라고도 한다.

이게 무슨말일까?

Critical Batch Size By Measuring Gradient Noise Scale

An Empirical Model of Large-Batch Training라는 paper는 OpenAI DOTA2 team이 OpenAI Five Agent를 학습하기 전 선행으로 한 연구이다. 여기서 어떻게하면 주어진 task에서 가장 효율적인 (가성비가 잘 나오는) batch size인 Critical Batch Size를 알 수 있는가? 라는 질문을 한다. (OpenAI는 이미 2018~2019년 부터 large scale training에 진심이었다고 볼 수 있다. 하긴 이들이 만들고자 하는 것은 Artificial Generatl Intelligence (AGI)이기 때문에 효율적인 scale up을 위해 반드시 필요한 과정이었으리라 생각된다)

Critical batch size란 뭘까?

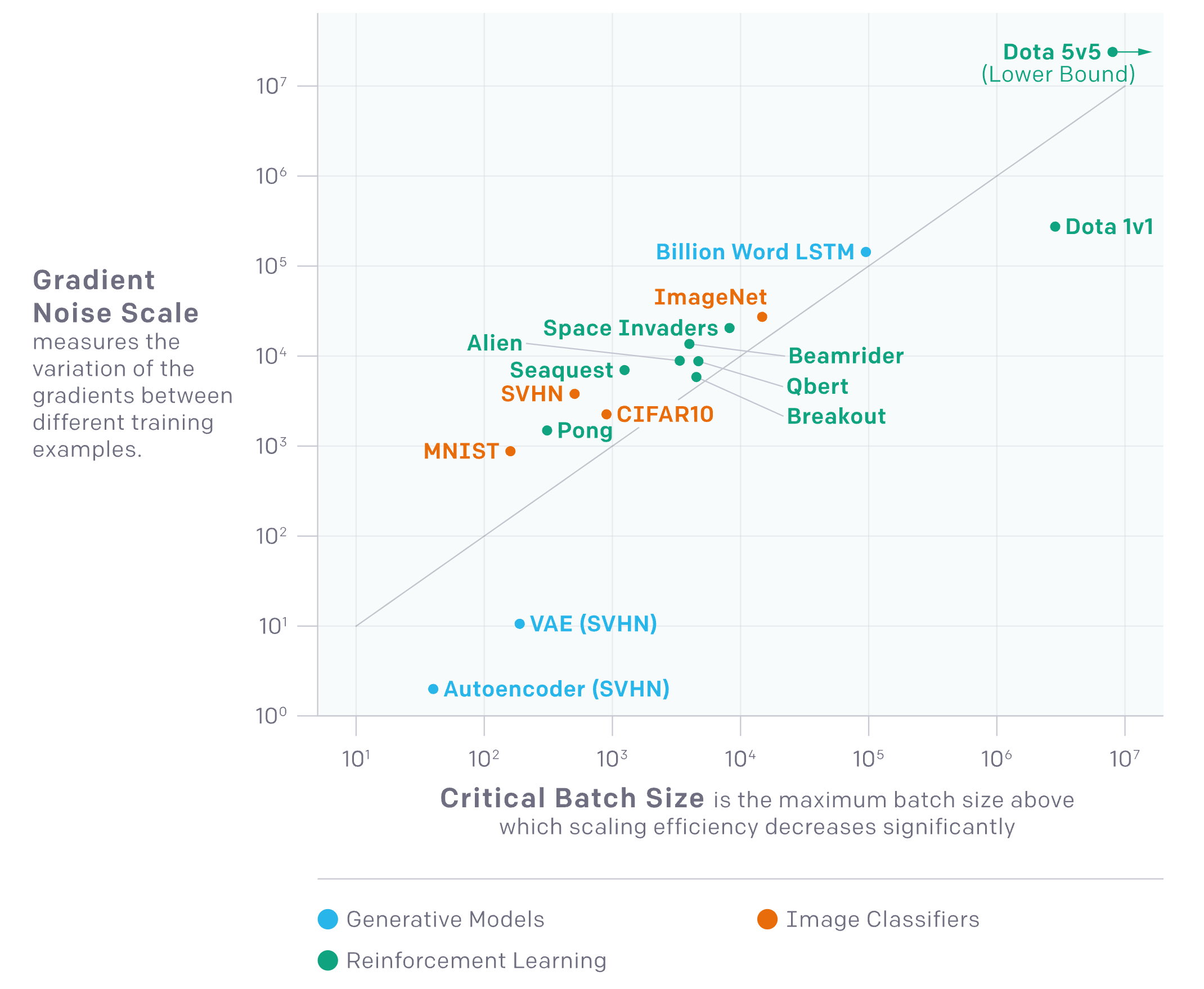gradient_noise_fig1 Fig.

위의 figure를 보자. 먼저 여기서 좌측의 Gradient Noise Scale이란 서로 다른 training sample 에 대한 gradient의 변화율을 measure한 것이다 (정확히는 network gradients의 Signal-to-Noise Ratio (SNR) 라고 한다). 그리고 좌표 평면상에 놓여진 task들을 살펴보면 어려운 task일 수록 (5:5 AOS게임인 Dota2를 푸는 것이 MNIST 분류를 하는것 보다 어렵다) Gradient는 훨씬 더 noise하다는 걸 알 수 있고, 그에 따라서 Critical Batch Size라는 것이 매우 커진다는 걸 알 수 있다. Critical batch size란 scaling efficiency가 확 떨어지기 직전의 어떤 순간, 즉 이 task를 푸는 데 있어 maximum batch size를 의미한다. 이 말은 예를 들어, MNIST같은건 batch size를 키워봐야 낭비가 된다는 것으로 (redundant), 아무리 device가 많아봐야 병렬 처리를 많이 하는 것이 아무런 득이 되지 않는다는 것이다.

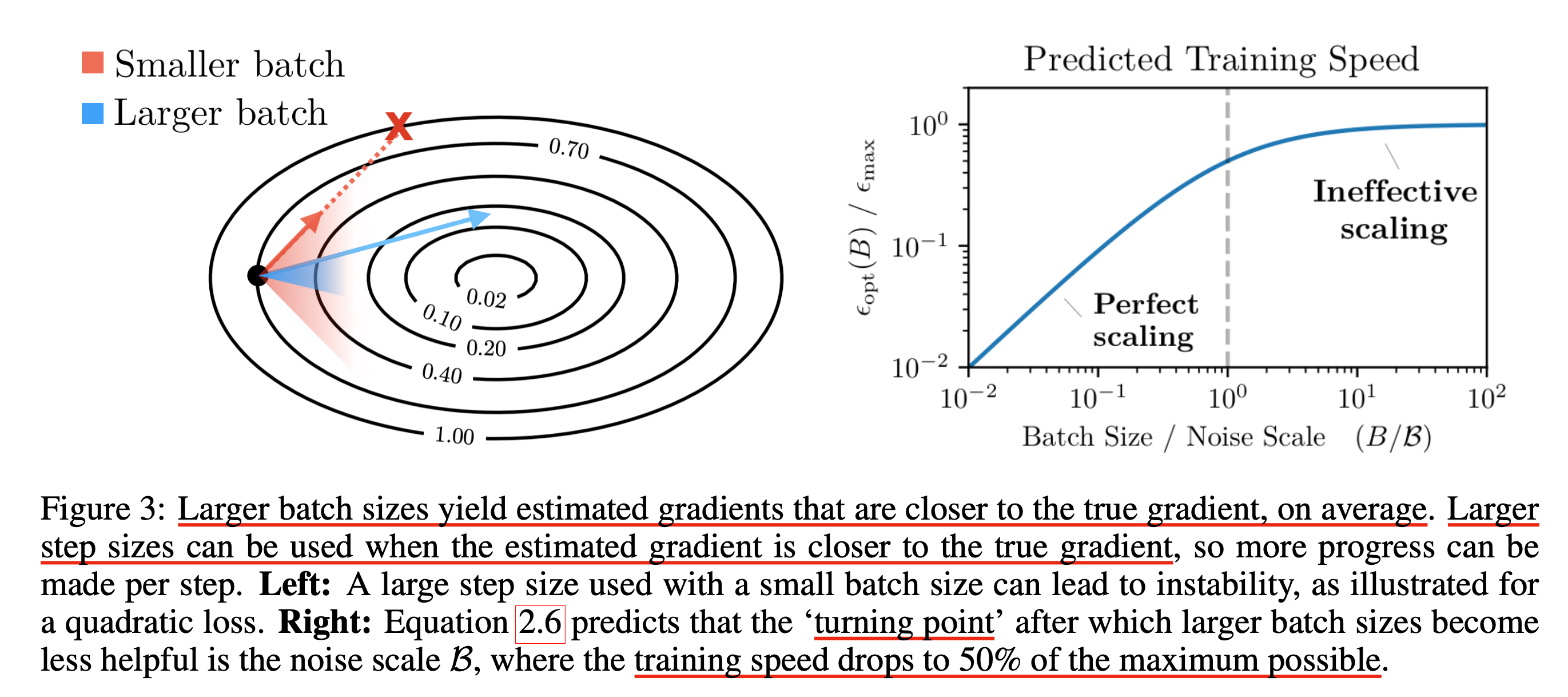gradient_noise_fig4 Fig.

왜 그럴까? 이는 직관적으로 task가 어렵지도 않은데, 많은 sample을 쓴것과 아닌것의 estimated gradient가 비슷비슷 하기 때문이다. 앞서 SGD의 예시를 들었던 것 처럼 MNIST data 10개를 보고 만든 gradient나 1000개를 본 것이나 그놈이 그놈이라는 것이다.

gradient_noise_fig3 Fig.

연구진들이 실험적으로 찾아낸 것은 바로 위의 figure에서 언급한 Ineffective한 scaling point를 찾는 것이다. 이 지점을 넘어가면 최대로 효율적으로 training할 경우의 50%정도나 training speed가 감소할 수 있다고 한다.

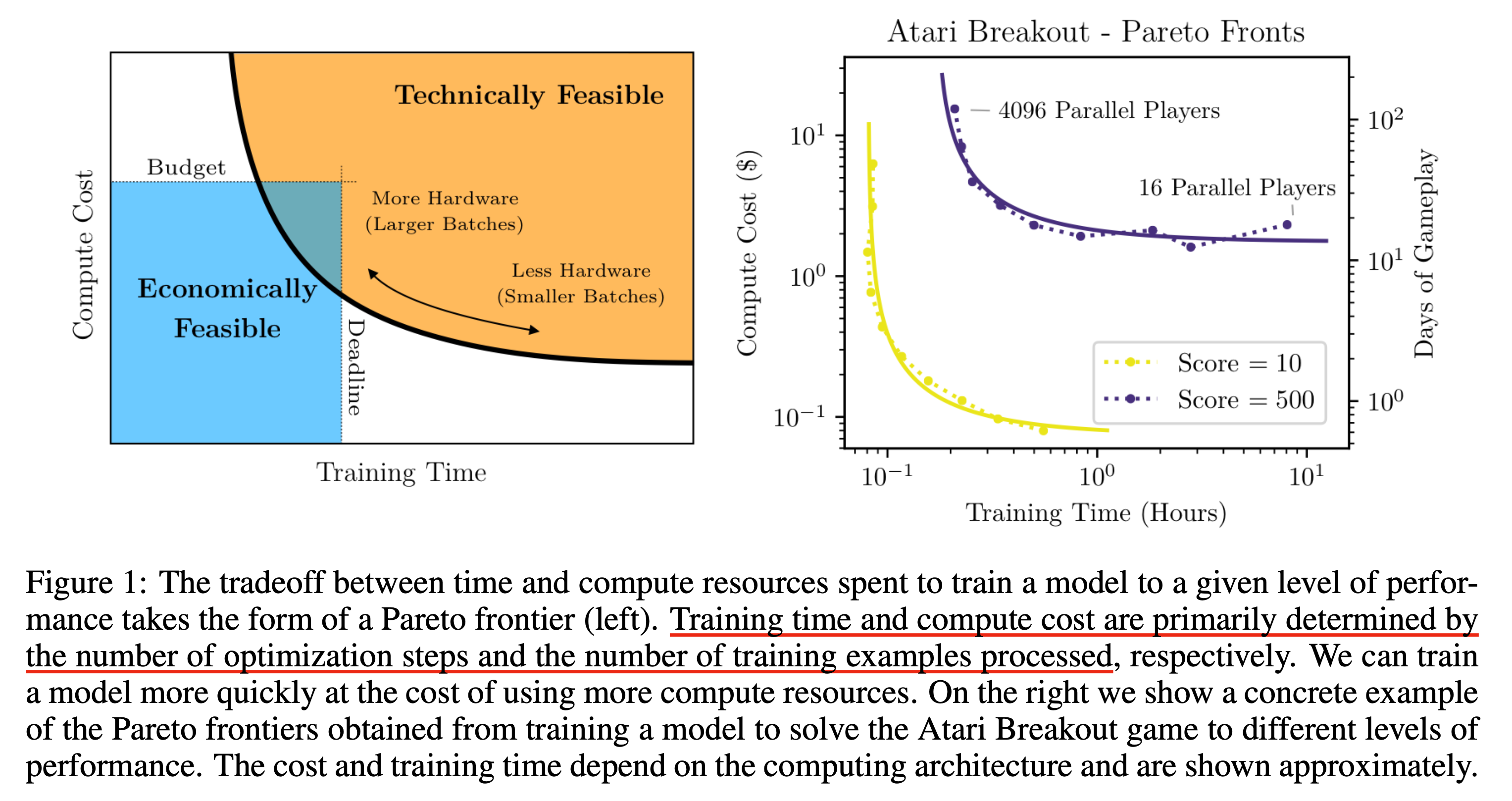gradient_noise_fig2 Fig.

위의 figure의 오른쪽 sub figure는 Atari 라는 어떤 콘솔 게임을 play하는 agent를 학습하는 task가 특정 점수를 달성하기 위해서는 어떤 얼만큼의 resource로 얼만큼의 training time을 써야 하는지를 의미한다. Parallel player 가 작은 것이 batch size가 작은것이고 그 반대는 큰것이다.

여기서 우리가 알 수 잇는것은 매우 batch size가 작은 very small batch size의 경우에는 batch size를 2배 키우는 것에는 아무런 risk가 없다는 것인데, 다시 말해 computational cost를 추가로 들이지 않고도 training wall clock time을 반으로 줄일 수 있다는 것이다. 누군가는 이에 대해서 “아니 batch size를 키운다는 것은 (GPU) chip을 2배나 더 쓴다는 것인데 이게 왜 computational cost가 늘어나는게 아니야?”라고 생각할 수 있다.

하지만 늘어난 matmul 연산 횟수; 즉 FLOPs만큼 iteration 수도 절반이 되기 때문에 전체 cost가 같다는 것이고, 실제로 병렬처리를 2배로 해줌으로써 iteration이 절반이 되더라도 달성하는 validation loss가 같다.

반대로 very large batch size에서는 아무리 compute resource를 늘려도 training time은 줄어들지 않는다. 이말인 즉 512개 GPU로 병렬처리한 것이 loss 10에 수렴하는데 10시간이 걸렸는데, 1024개 GPU를 쓰면 5시간이 걸리는 것이 아니라 비슷하게 9시간 걸리면 이는 cost를 추가로 들여야 하는 것이 된다.

즉 우리가 알고 싶은 것은 bend (curve)의 구부러지는 지점이며, Gradient noise scale은 바로 이 bend를 예측하기 위한 metric 이 된다.

한 편, 우리에게 주어진 budget (computing resource)와 time (deadline)이 주어져있다고 할 때, 경제적으로 그럴싸한 (Economically Feasible)한 구간에 이 technically feasibility를 의미하는 region이 안 들어올 수도 있다. 이 bend는 더 높은 점수를 달성하려고 할수록 (즉 더 높은 난이도의 task를 해결하려고 할 수록) 더 위로 이동하기 때문에 ecnomically feasible하지 않게 된다. 그러면 어떻게 해야 할까?

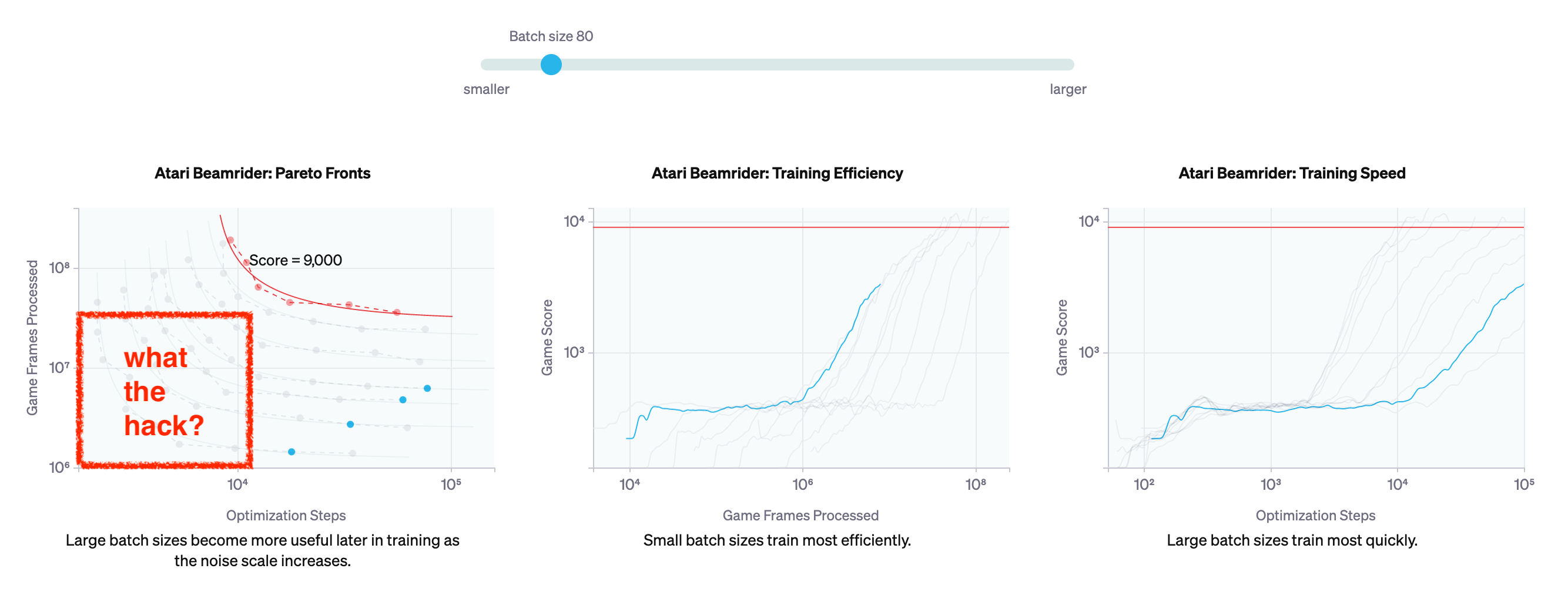feasibility Fig. 가령 일정 수준 이상의 computing power를 쓰지 않으면 (batch size가 작으면), 영겁의 세월을 학습에 써야하거나 아예 그 성능에 도달하지 못할 수도 있다.

아마 budget과 time을 늘리는 것 말고는…?

아무튼 여기서 우리가 이해해야 하는 것은 batch size를 무작정 늘려서 GPU util을 높히는것이 마냥 좋은 것은 아니라는 것이다.

Patterns in the gradient noise scale

일반적으로 gradient noise scale에는 몇 가지 패턴이 있다고 한다. 바로 학습이 진행되면서 noise scale이 수십 배 수준으로 증가한다는 것이다.

Image classification을 하는 경우에 대해서 생각해보자. 맨 처음에는 edge 같은 small-scale의 obvious feature를 학습하는 데 시간을 쓸 것이라고 한다. NN 입장에서도 사물을 인식하는 것이 먼저라는 것은 직관적으로 받아들이기 쉬울 것이다. 그 다음엔 더 복잡한 intricate feature를 배우게 된다고 하는데, 이는 점점 noise scale이 커지는 것을 의미한다.

연구진은 이런 현상이 여러 task, 여러 model에서도 비슷하게 나며, 더 powerful한 model이 더 큰 gradient noise scale을 갖게되고 이는 더 낮은 loss로 이어진다고 했는데 (아마 더 detail한 걸 배울 수 있는 capacity가 생기고 optimization space가 더 복잡해진다거나 하기 때문에 더 좋은 solution을 찾을 순 있겠지만 그만큼의 noise scale이?), 그러므로 우리가 large model을 학습할 때는 small model을 학습할 때 보다 더 많은 병렬 처리를 해야한다고 얘기한다. 하지만 large model을 학습하는 경우에도 이것이 모든 training phase에서 옳은 것은 아니다.

In DOTA2 Experiment

OpenAI의 DOTA2 실험을 살펴보자. DOTA2는 MNIST와 비교도 안되는 어려운 task이다. 아래의 figure는 batch size에 따른 달성 가능한 skill 점수와 (높을수록 더 DOTA를 잘한다고 보면 된다), speed up 에 대한 관계를 나타낸다.

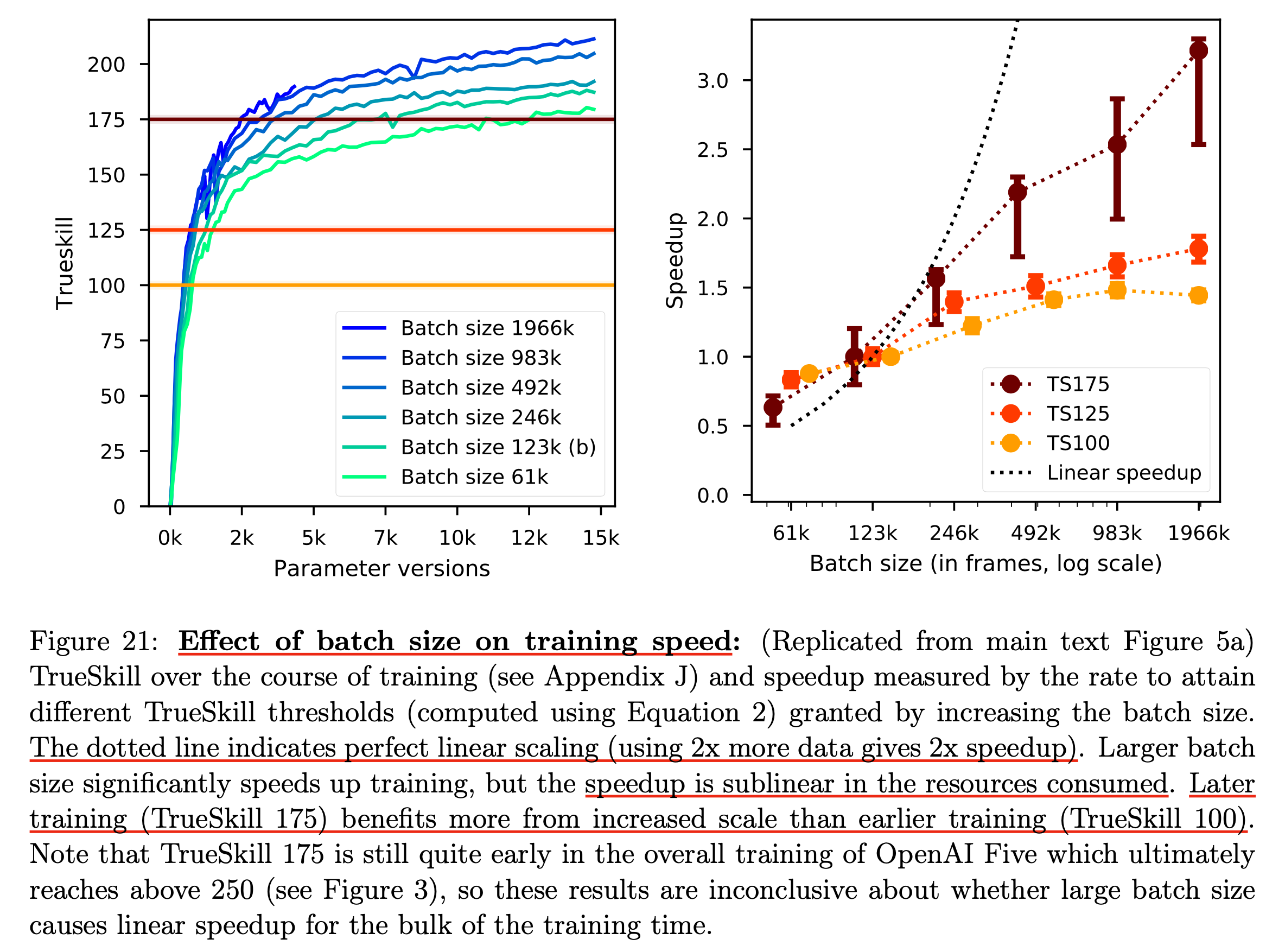dota2_scale_fig1 Fig.

여깃 주목해야 할 점은 batch size가 클 수록 결국에 수렴하는 지점은 좋을 수 있지만 오른쪽의 speedup과 batch size의 관계가 linear하지 않다는 것이다. 즉 2배 computing resource를 더 쓰면 1/2배 시간이 줄어들어야 하는데 (speed up), 실제로는 batch size를 매우 크게 키우게 되면 점점 같은 성능에 도달하기 위해서 sublinear한 성능을 갖게 된다는 점이다.

그렇다는 말은 우리가 batch size를 키우면서 iteration이 반으로 줄어들게 될 텐데, 이를 늘려서 학습을 더 해줘야 한다는 것이다. 그럼에도 speed up은 있긴 있기 때문에 이득이 없지는 않다만 가성비가 안나온다는 것이다.

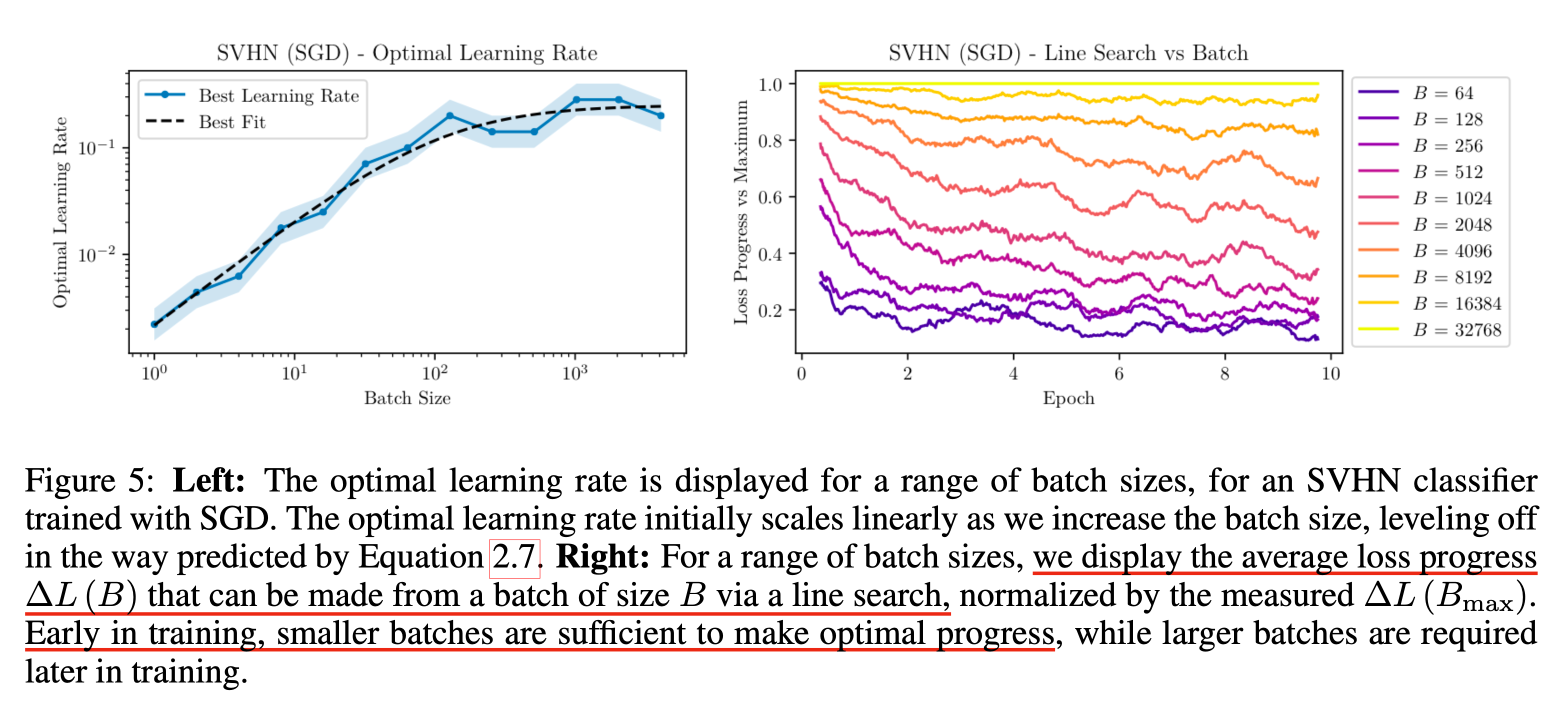gradient_noise_lr2 Fig. 오른쪽의 sub figure를 보면 Street View House Numbers (SVHN) dataset에 대한 분류 문제를 풀 때 학습 초기는 작은 batch size로도 충분하다는 걸 알 수 있다.

이는 앞서 살펴본 critical batch size와 같은 결과인데, 우리가 병렬처리를 많이한다 한들 학습 초기의 optimiation은 난이도가 쉽기 때문에 병렬처리를 한것에서 이득을 볼 수가 없는 것이다. 그러니까 우리는 학습 초기에는 batch_size를 적게 주다가 나중에 batch_size를 키우는 일종의 curriculum learning을 하는게 나은 선택일 수 있는 것이다.

하지만 TS175 조차도 굉장히 학습 초반에 관한 것이며 (물론 resource가 한정되어있으니 scaling law?를 밝혀내기 위해 early phase만 가지고 한 것이다), pro level에 도달하기 위해서는 아무리 batch size를 키워도 아득한 시간만큼 학습을 해야 할 수 있다.

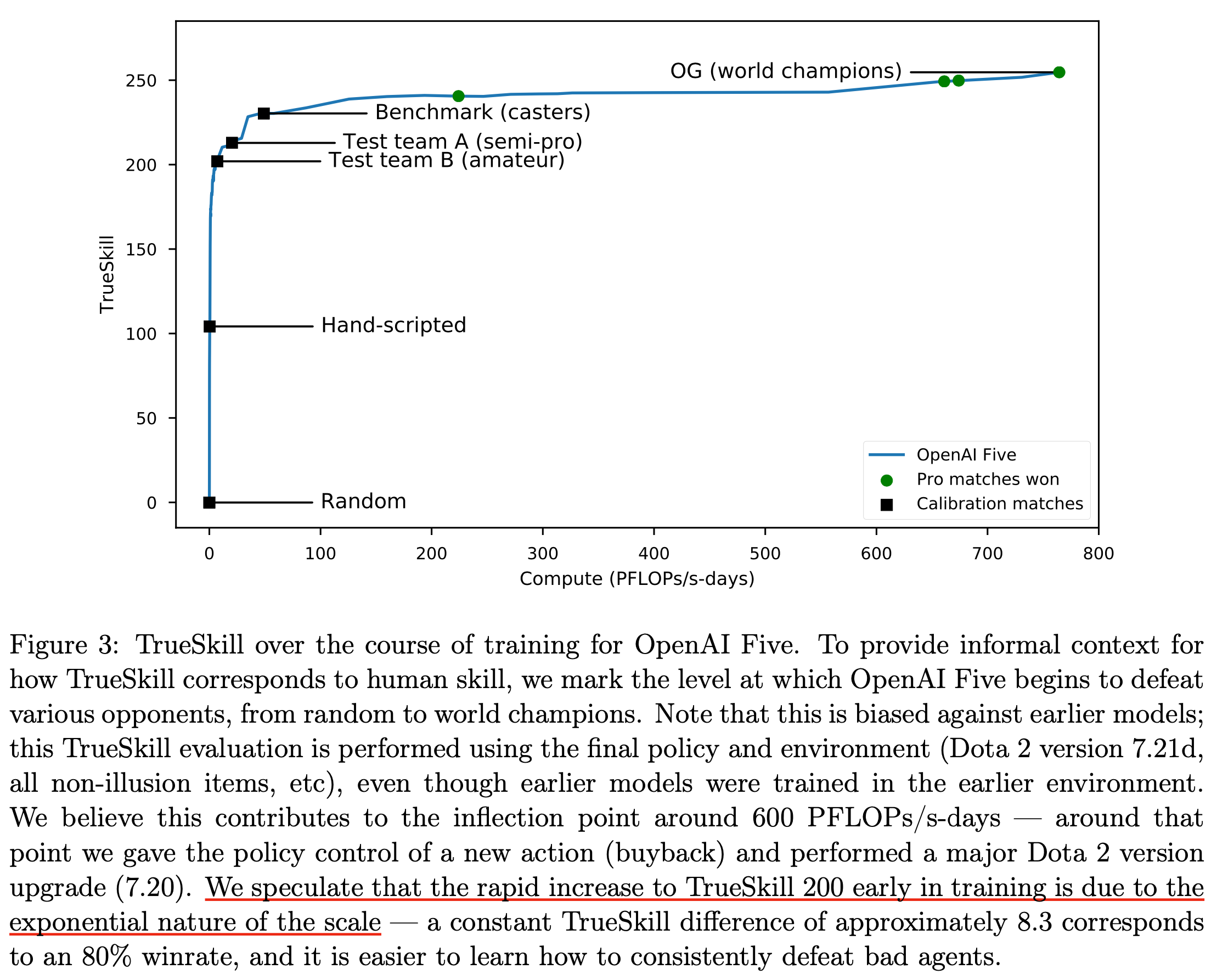dota2_scale_fig2 Fig.

Learning Rates Tuning

한 편, 우리가 batch size를 n배 늘려 gradient를 더 정교하게 만들려고 했다면, 전체 dataset이 늘어날 일이 없으므로 training steps는 자연스럽게 n배 줄어든다. 그렇기 때문에 이를 보상하기 위해서 LR을 늘려줘야 한다.

empirical_batch_size_paper_lr_tuning_fig2

Paper에서는 noise scale에 대한 mathematically derivation을 할 때 batch size가 증가할 때 optimal lr를 쓴다는 가정이 깔려있다고 한다. 하지만 실전에서는 이는 불가능에 가까운데, near optimal이면 가정이 그렇게 깨지진 않는 것 같다.

저자들은 SGD에 대해서는 batch size가 n배 늘어날 때마다 n배 해주고 Adam에 대해서는 \(n^{0.5} \sim n^{1.0}\)배 해줘야 하고, optimizer에 상관없이 batch size가 늘어나다가 특정 지점을 지나면 constant해진다는 function을 정의했다.

empirical_batch_size_paper_lr_tuning_fig2

그리고 Street View House Numbers (SVHN) Dataset에 대한 image classification task로 실험적을 통해 batch size가 증가함에 따라 optimal LR이 예상한 바와 같은 경향을 보인다는 것을 증명했다. (아래 figure의 왼쪽 subfigure)

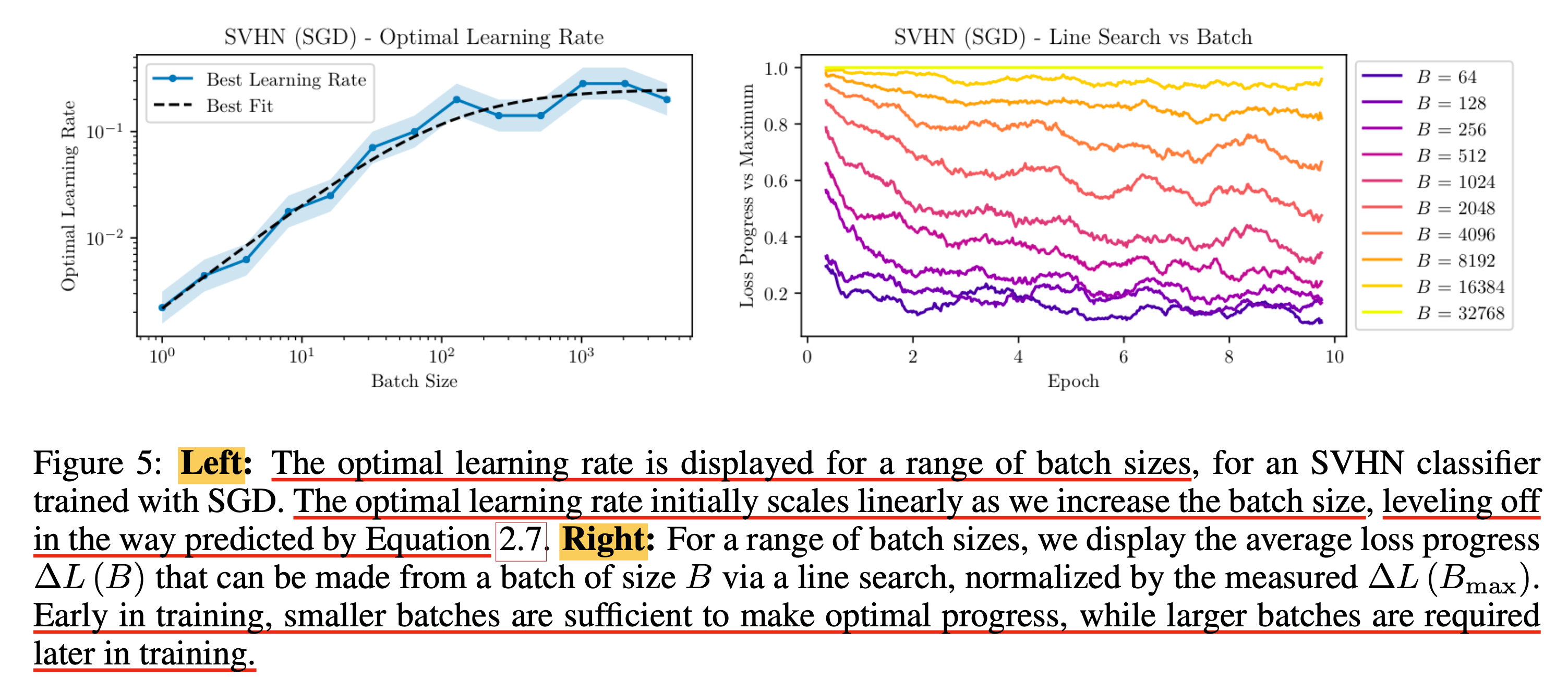
empirical_batch_size_paper_fig5

직관적으로 batch size가 critical batch size부근을 지나면 더이상 gradient는 정교해지지 않을 것이고, 더 정교해지지 않는다면 LR을 키워줄 이유가 없다. 만약 키워준다면 overshoot해서 diverge해버리는 경우 밖에 없을 것이다.

empirical_batch_size_paper_lr_tuning_fig3

사실 \(\sqrt{n}\)배 해주느냐, \(n\)배 해주느냐는 같은건 새로운 발견은 아니긴 하지만, paper에서는 이를 이론적으로 정립하고 좀 더 검증했다고 할 수 있다.

Model Size Dependence

누군가에게는 "model size가 증가할수록 critical batch size가 늘어나는 것 아닐까?" 하는 생각이 들 수 있다. 하지만 저자들은 critical batch size는 model size와 거의 관계가 없다고 한다. 다른 말로 하면 critical batci size는 model size로 표현되는 function이 아닌 것이고, 다만 달성하려는 loss에만 관련이 있다고 한다.

empirical_batch_size_paper_model_size

하지만 역설적(?)이게도 실제로는 간접적으로 관련이 있다고 할 수 있다. 왜냐하면 model size가 크다는 것은 더 좋은 loss에 도달한다는 것이고, 더 좋은 loss에 도달하려면 task 난이도가 올라가는 것이기 때문에 noise scale이 커져 batch size를 키워야 하는 것이다. 다른말로 하면 작은 model은 절대로 그 loss에 도달할 일이 없기 때문에 (model capacity 때문에?) batch size를 키워도 그 loss에 도달할 일은 거의 없을 것이다.

아래 figure를 보자.

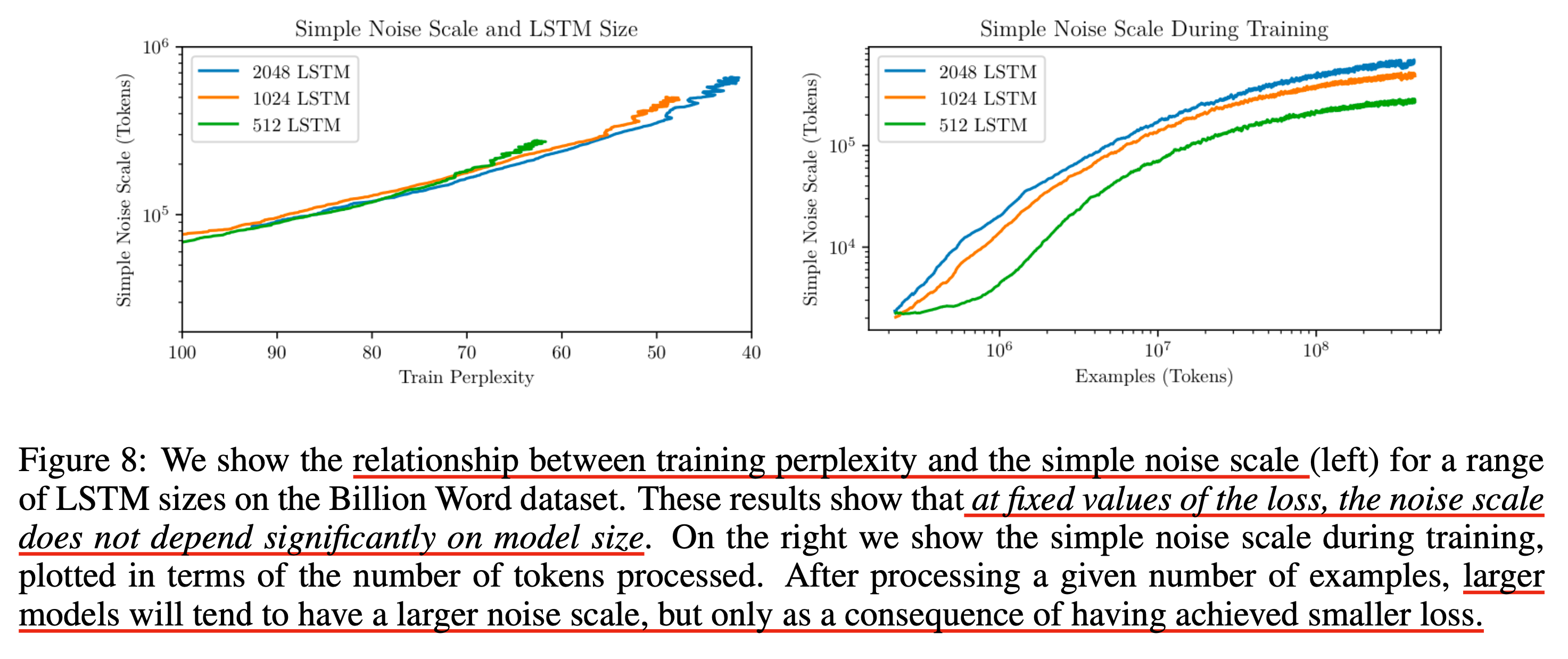
empirical_batch_size_paper_fig8

왼쪽 subfigure를 보면 Language Modeling (LM) task에 대해 LSTM를 학습했을 경우 hidden size에 관계없이, 즉 model size에 관계없이 perplexity가 같다면 noise scale은 거의 같다. 하지만 큰 model은 특정 tokens를 학습하고 나면 더 낮은 loss를 향해 가기 시작하면서 작은 model과의 차이가 벌어지게 된다. 바로 이러한 mechanism에 의해서 critical batch size가 증가한다고 볼 수 있다.

Pareto Frontiers

그 다음은 Pareto frontier에 대한 얘기이다. 저자들은 batch size에 대해서 해당 eval loss에 도달하기 위한 optimization steps, the number of data samples를 측정함으로써 pareto frontier를 형성할 수 있었다고 한다. 그리고 critical batch size를 넘지않는 training run들은 per training examples 마다 비슷한 behavior를 보였고, critical batch size를 넘는 training run들은 per optimization steps 마다 비슷한 behavior를 보였다고 한다.

empirical_batch_size_paper_pareto_frontier_fig1

만약 ritical batch size가 64였다고 생각해보자. 그렇다면 전자에 대해서 batch size, B=2와 B=4인 경우에 대해서 4 batch를 봤을 때 behavior가 거의 같았다는 것이다. 이 때 당연히 LR은 SGD라면 2배, Adam이라면 \(\sqrt{2}\)배 정도 됐을 것이다. 즉 consumed batch에 대해서 비슷한 behavior를 보였다는 것은 정확히 B=2가 1000step, B=4가 500step 갔을 때 eval loss가 같았다는 것이고, 실제로 도달한 결과도 같다. 이것이 아래 figure의 오른쪽에 해당하는 내용이다.

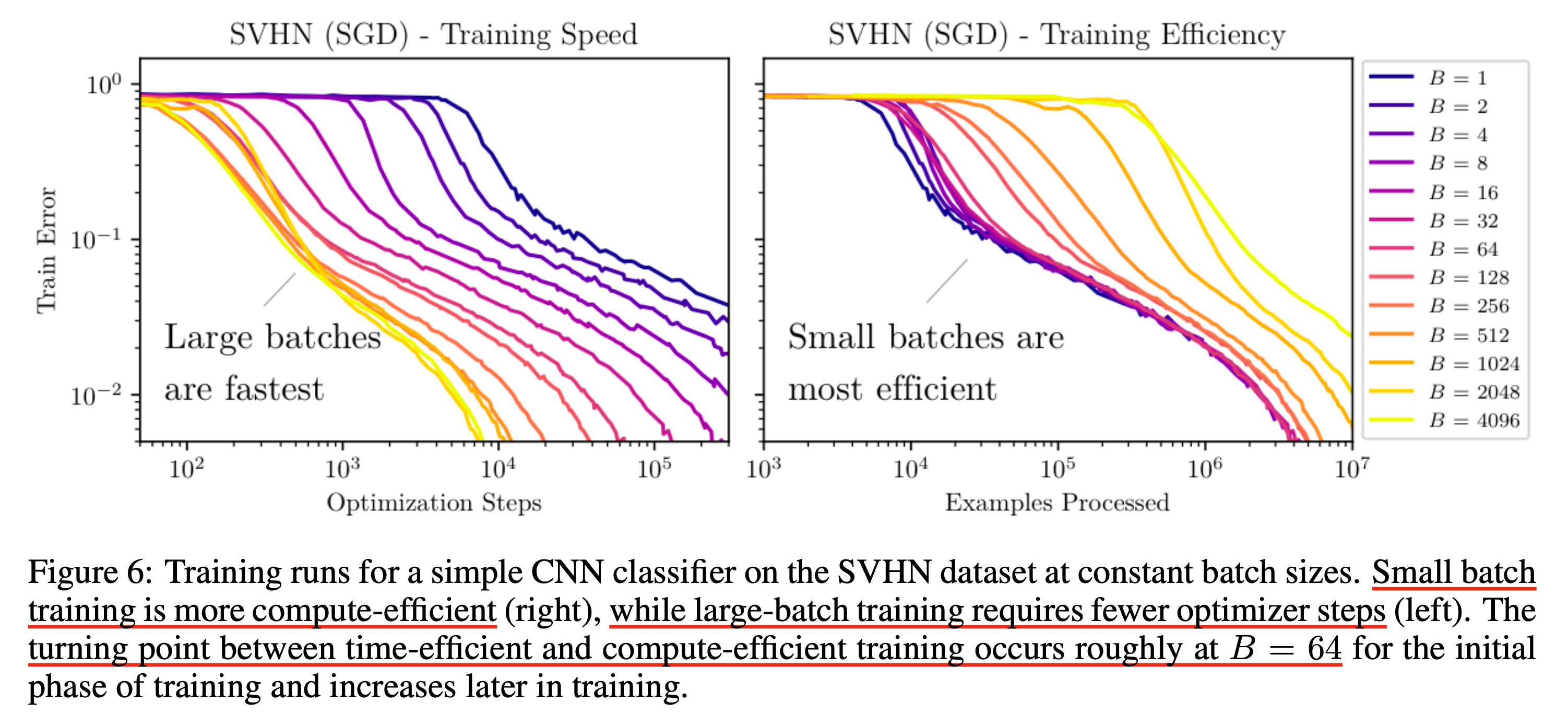
empirical_batch_size_paper_fig6

그런데 위 figure의 오른쪽 subfigure를 보면 B=64를 넘어가는 training run들은 갑자기 Examples processed가 급증한다. 이는 B가 커짐에 따라 gradient가 정교해지지 않고, 그에 따라 LR도 늘어나지 않았기 때문에 한 번에 더 많은 example을 봤음에도 B=64의 한 step과 결과가 같았기 때문이다. 이 내용이 왼쪽 subfigure에 나와있는데, 이번에는 B가 매우 큰 지점부터 역으로 B=64인 지점까지 필요한 optimization steps가 거의 비슷하다. 다행히 critical batch size, B=64보다 큰 batch를 쓸수록 조금이나마 필요한 step수가 아주 조금이라도 줄어들기는 한다. 주의할 점은 training step당 batch size가 말도 안되게 큰 것에 비해서 step은 비슷하기 때문에 실제로 학습량은 매우 큰 것이지만 물리적으로 training time은 줄어들지 않았다는 것이다. 앞서 우리가 계속 얘기했던 내용이다.

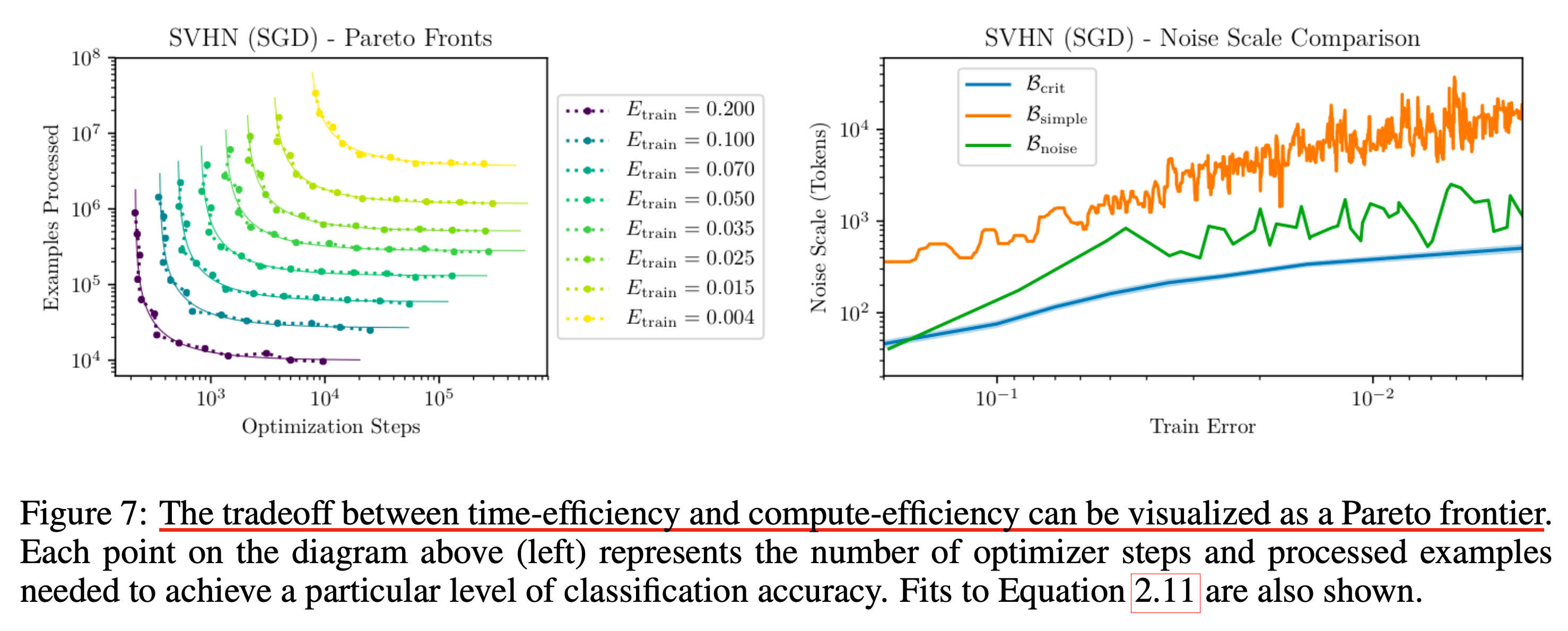
empirical_batch_size_paper_fig7

이제 이에 대해서 위 figure의 왼쪽 subfigure처럼 각 도달하고자 하는 loss별로 Optimization Steps VS Exampled Proceesed plot을 얻을 수 있었다. (여기서 오른쪽 subfigure의 quantity들은 아래와 같은데, 자세한 내용은 paper를 참고하자.)

Critical Batch Size (\(B_{\text{crit}}\))
Simple noise scale (\(B_{\text{simple}}\))
Full noise scale (\(B_{\text{full}}\))

이는 앞서 가장 먼저 봤던 Compute Cost vs Wall Clock Time plot과도 같다고 할 수 있다.

gradient_noise_fig2 Fig.

그러니까 우리는 특정 model과 tokens량을 학습하기 위해서 (예를 들어 LLM), 아무리 빨리 해당 성능에 도달하고 싶어 GPU resource를 들이 부어도 물리적으로 그 성능에 도달할 수 있는 한계가 존재하기 때문에 이를 거스를 수가 없는 것이다. 만약 GPU가 2048장이 있다면 2048장을 다 투자한다고 loss=3.5를 달성하는데 걸리는 시간이 줄지 않을 것이므로, 512장씩 LR, weight decay등 HP search ablation하는 데 병렬 처리를 하는 것이 더 도움이 될 것이다.

Measuring Effect of Batch Size according to Model and Task

다음은 Measuring the Effects of Data Parallelism on Neural Network Training의 실험 내용이다. 앞서 OpenAI의 paper처럼 task별로 critical batch size는 다르지만, 모두 일관되게 batch size가 커짐에 따라 필요한 optimization step 수가 linear하지만 중간에 이탈해서 sub linear 해지는 것을 볼 수 있다.

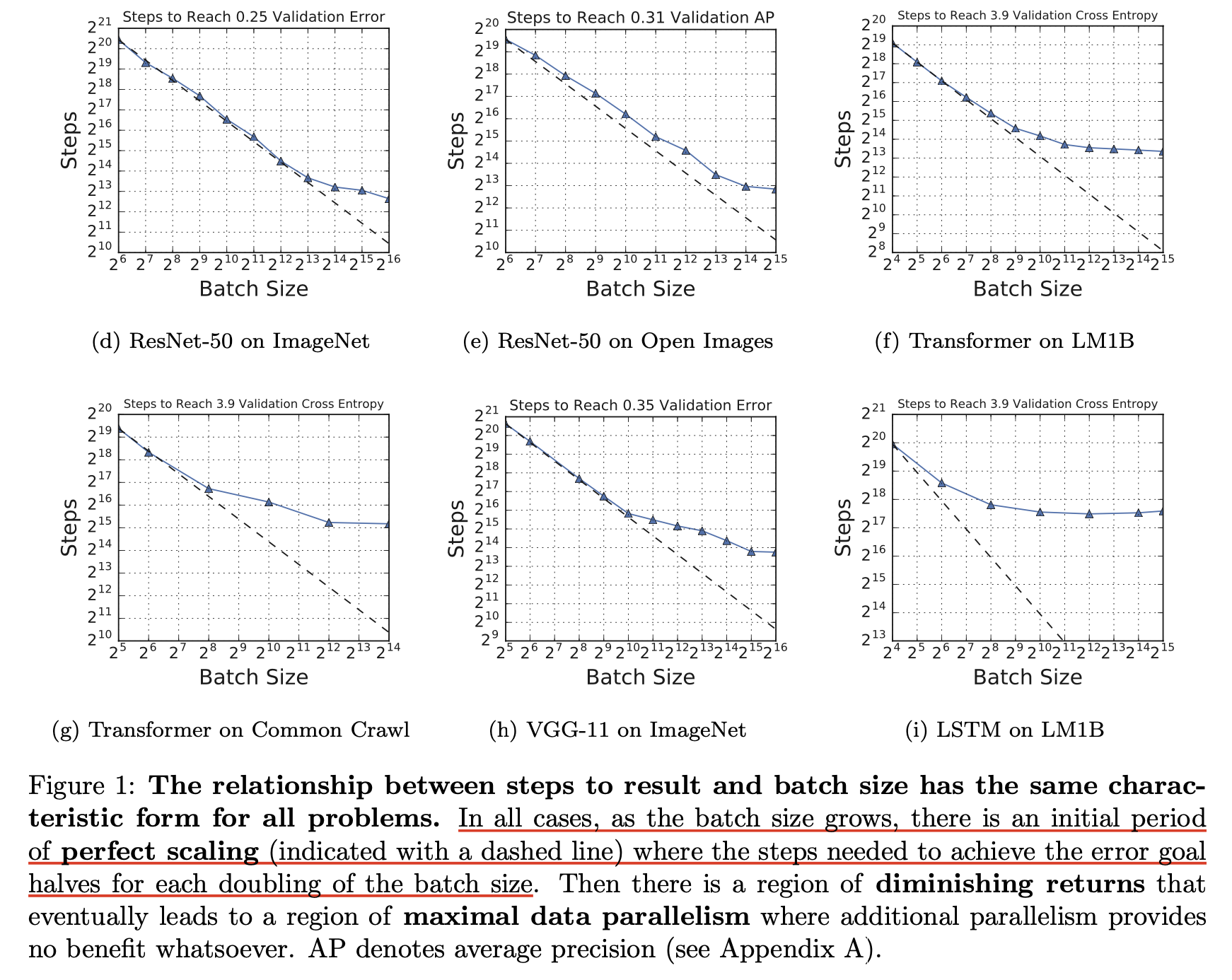measuring_effcet_of_dp_task Fig.

보통 batch size를 키우면 LR을 같이 키워줘야 한다고 했는데, 이 실험은 Learning Rate (LR) tuning을 한 것으로 보인다.

measuring_effcet_of_dp_exp_lr Fig.

그럼에도 불구하고 앞서 살펴본 사례들 처럼 excessively large batch size는 training wallclock time을 줄이는데 크게 도움이 안 되는 것으로 보인다.

그리고 다음은 되게 중요한 observation 중 하나인데, 어떤 model들은 특히 더 scale up 하기가 좋은데 예를 들어 Transformer는 LSTM같은 architecture와 비교해서 훨 씬 더 좋았다는 것이다.

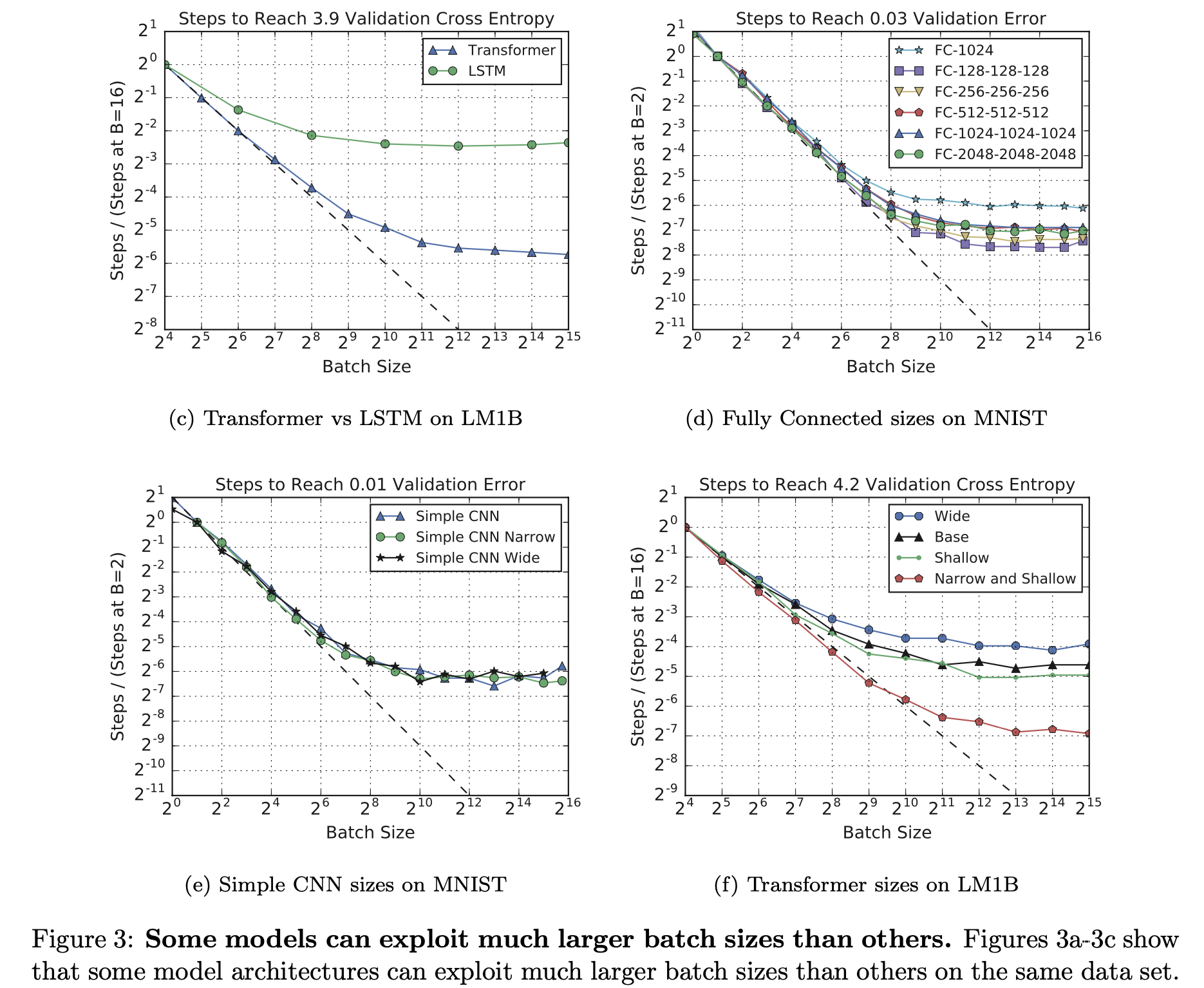measuring_effcet_of_dp_model Fig.

Transformer를 쓰는 이유가 Scale Up하기 좋아서 라는게 다시 증명되는 부분이라고 할 수 있겠다.

Language Modeling Task and Modern LLM (>2023)'s Batch Sizes (Case Study)

저자들은 VAE같은 generatvie model < classification, spacebader 등 < language modeling < dota 5v5 등의 순서대로 task 난이도가 어렵다고 했다. 즉 graident noise scale이 크고 이에 따라 critical batch size가 크기 때문에 parallelism으로 wall clock time을 줄이기 쉬운 것이다.

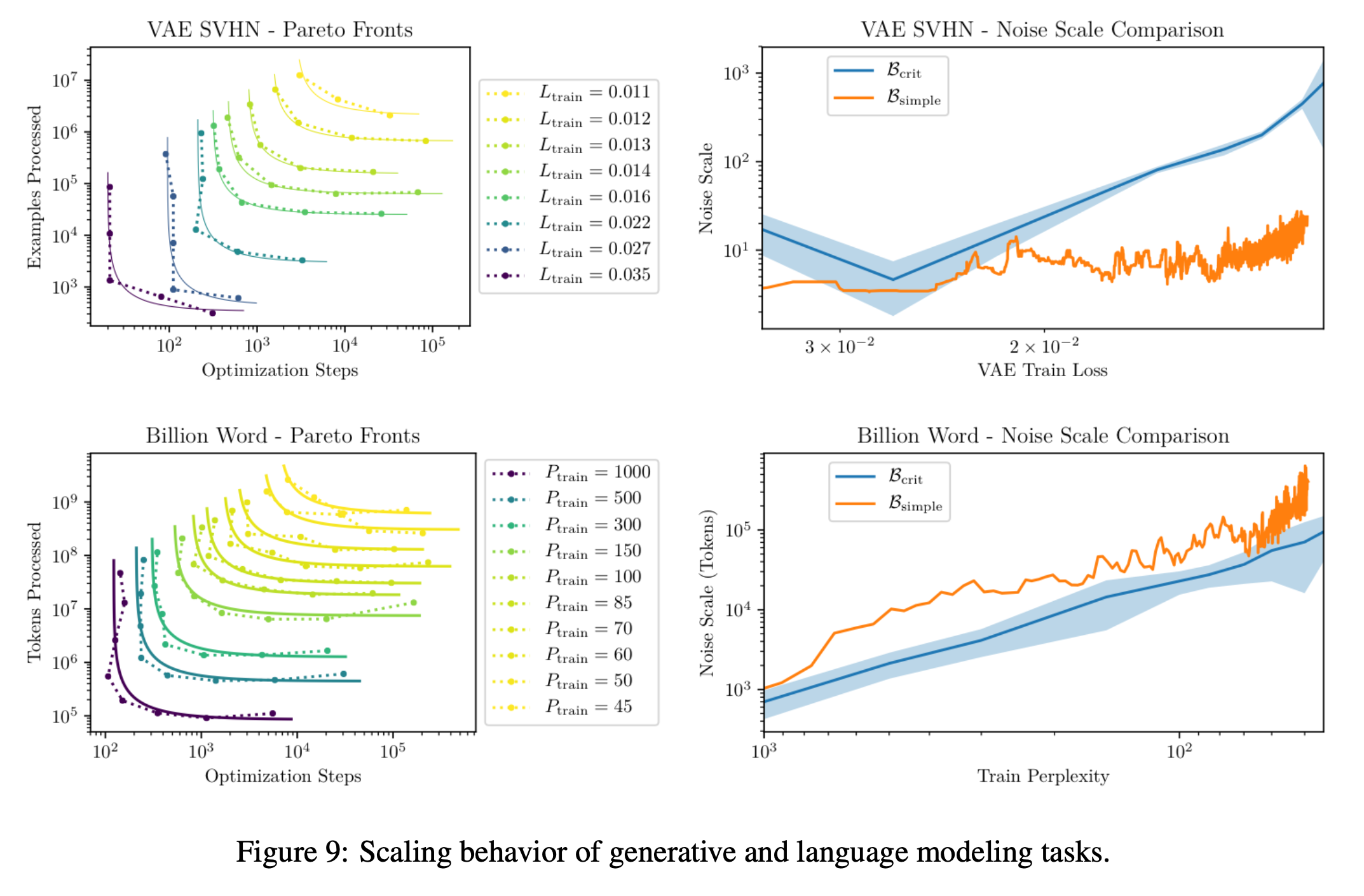empirical_batch_size_paper_fig9 Fig.

위 figure를 보면 달성하고자 하는 training ppl이 낮으면 낮을 수록 더 큰 scale로 critical batch size가 증가하는 것을 알 수 있다. 그리고 가장 좋은 performance를 보이는 아래 subfigure의 yellow band를 보면 flops를 투자할수록 optimizer steps가 줄어드는 경향이, 즉 wall clock time이 줄어드는 경향이 위의 VAE보다는 훨씬 큰 것으로 보인다.

한 편, OpenAI의 유명한 Work중 하나인 Kaplan et al.의 scaling law for LM에서 또 한번 critical batch size는 model이 달성하고자 하는 loss, performance에만 depend하지 model size와는 상관이 없다는 얘기를 한다.

kaplan_scaling_law_paper_critical_batch_size_fig1 Fig.

실제로 아래 figure를 보면 3M, 85M에 대해서 실험적으로 측정한 critical batch size와 \(B_{crit}(L)\) curve fitting을 한 결과가 거의 align되고, model size는 큰 상관이 없다는 걸 An Empirical Batch Size~~에 이어 다시 보였다. (둘 다 OpenAI’s work)

kaplan_scaling_law_paper_critical_batch_size_fig2 Fig.

그래서 실제로 modern LLM들은 어떤 batch size를 썼을까? 이 때 이 수치들을 종합해서 내 실험에 적용하려고 할 때 주의해서 봐야할 점이 있다.

batch size를 볼 때 model size를 보지 말 것
model size와 processed tokens (총 학습량)를 통해 어떤 loss를 얻을 수 있는지를 기준으로 batch size를 판단할 것
critical batch size에 반드시 도달하지 않아도 됨 그 지점을 넘지 않는다면 성능상 이슈가 없을 것임.
다만 가용 GPU 수가 많아서 resource를 전부 투자해 실험을 빨리 끝내고 싶어 parallelism degree를 늘리려고 할 때, critical batch size를 넘는지?가 성능에 영향을 끼칠 수 있기 때문에 이를 알아보는 것임
batch size를 \(n\)배 늘릴 경우 critical batch size를 넘지 않았다면 이전 optimal global LR을 \(\sqrt{n}~n\)배 늘려주는 것이 동반되어야 투자한 compute resource대비 target valid loss에 도달할 수 있는 wall clock time을 줄일 수 있음.

앞서 대부분 설명한 것들이지만 누군가 아래 table들을 보고 batch size를 임의로 정할 수도 있을 것 같아 다시 정리했다. 아래 소개할 table들은 모두 2023년 LLaMa-2 이후로 paper에서 batch size를 비롯한 training detail이 공개된 것들이다.

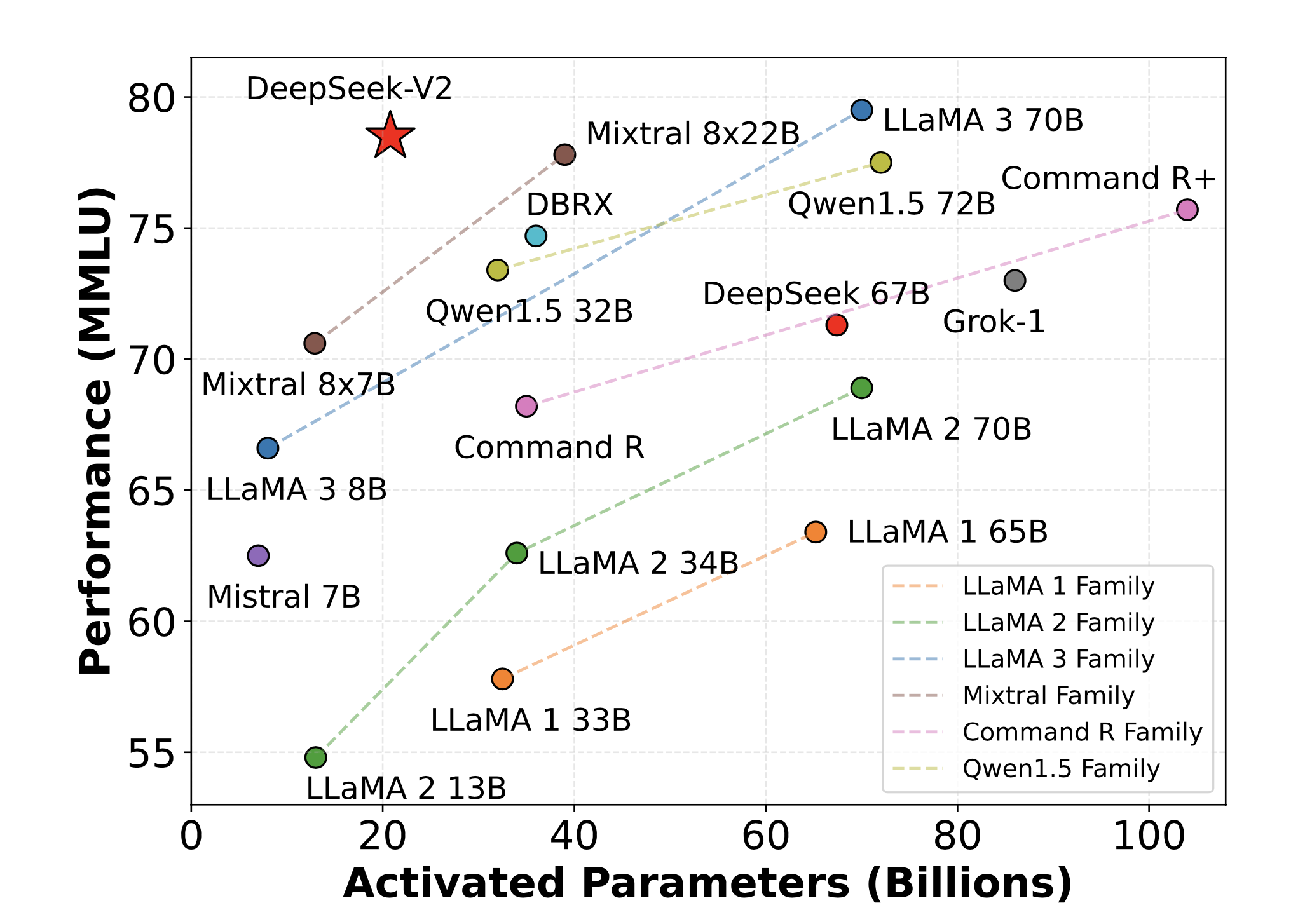deepseek_v2_model_vs_performance_plot Fig. Model size vs Performance Plot

먼저 LLaMa부터 qwen, teleflm, mincpm이다.

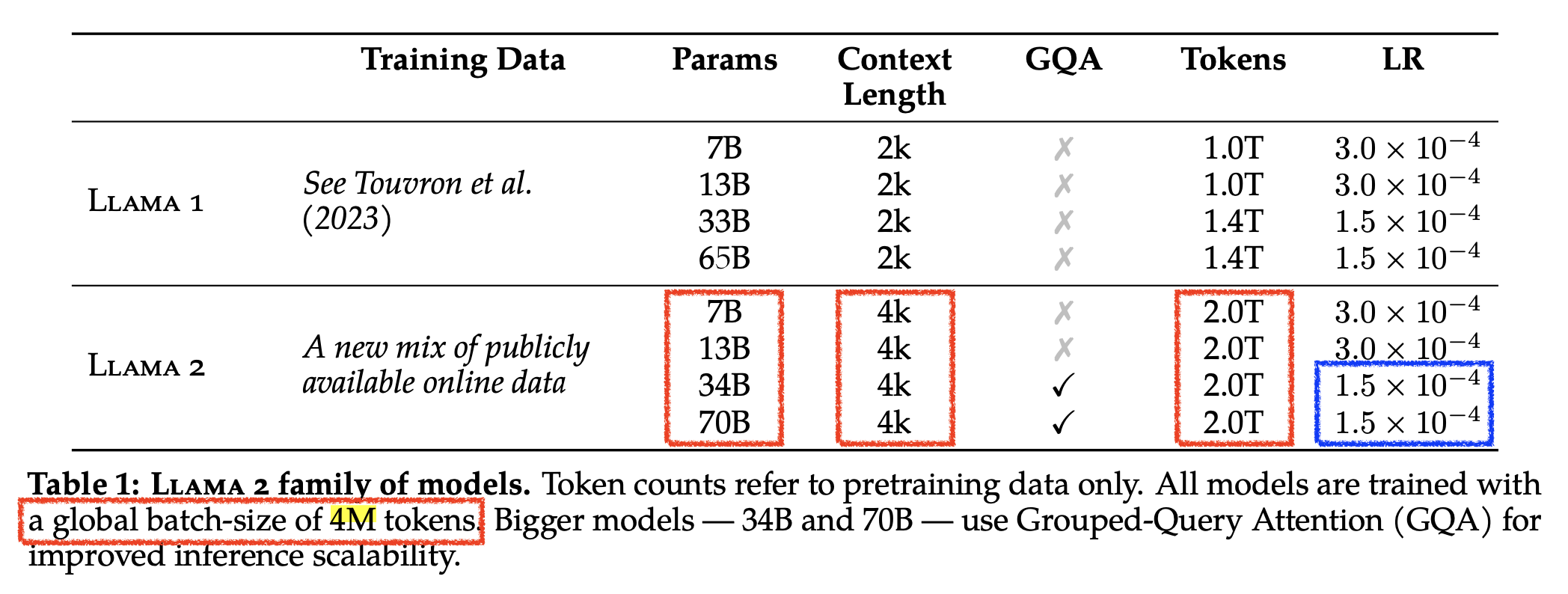bsz_llama2 Fig. LLaMa-2

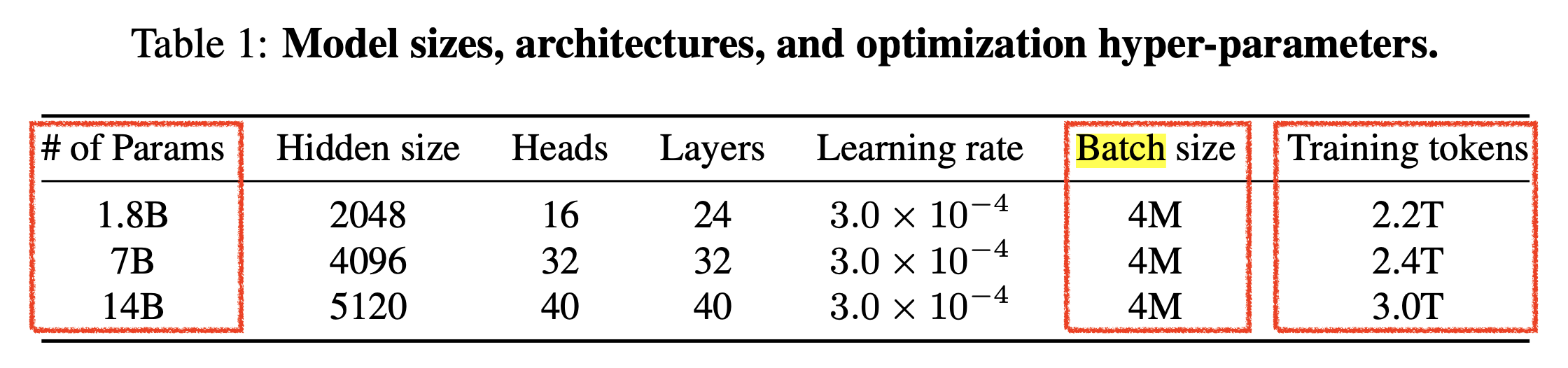bsz_qwen1 Fig. Qwen-1

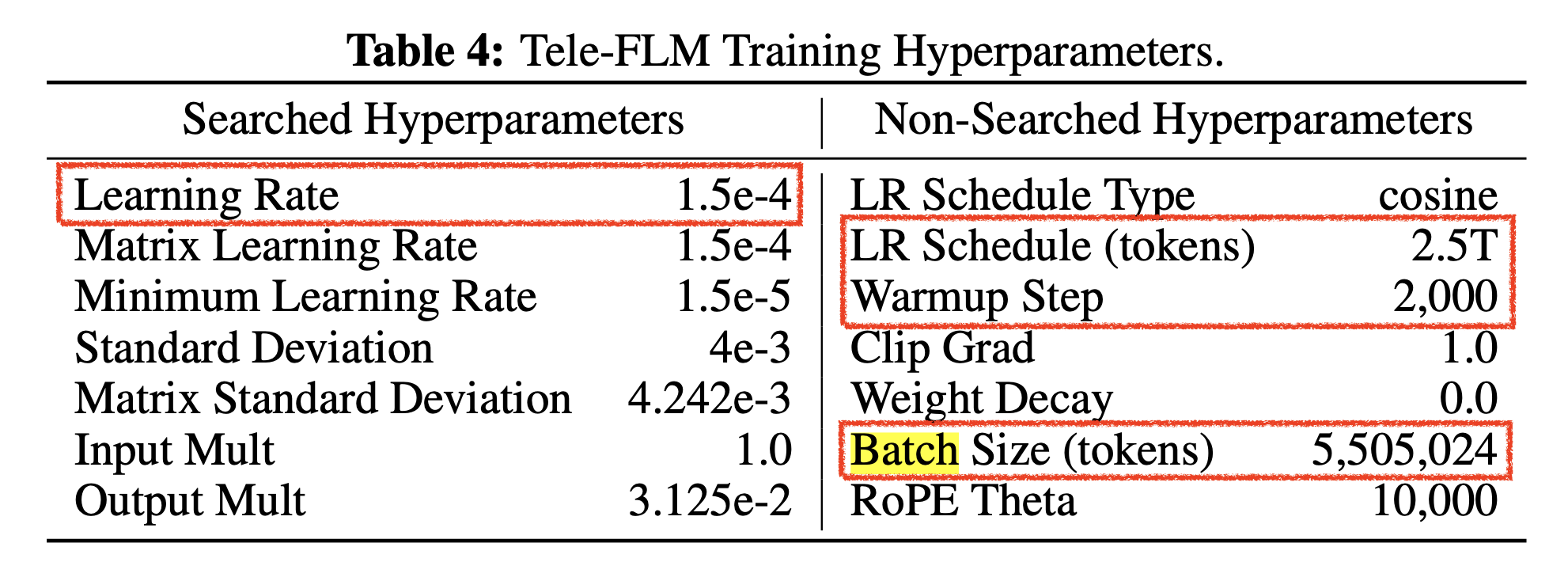bsz_teleflm Fig. Tele-FLM

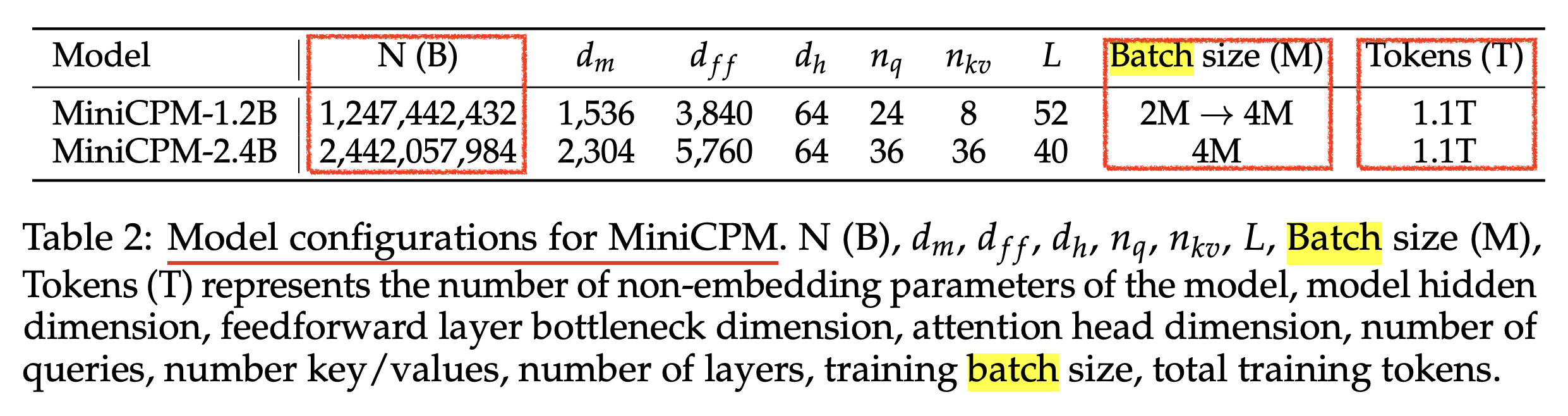bsz_minicpm Fig. MiniCPM

다시 한 번 강조하자면 “model size가 7B라면 이정도 batch size를 쓰면 되겠군”이라고 판단해서는 안된다. Model은 transformer architecture를 쓰고 internet scale web dataset을 써서 LM task를 학습할 때, model size와 총 training steps을 동시에 고려해서, 즉 투입된 compute resource에 따라 도달할 수 있는 valid performance에 따라 critical batch size가 결정 될 것이다. 그리고 위 table에 있는 값들은 critical batch size는 아닐 것이다. 다만 critical batch size를 넘지 않거나 그 근처의 값일 것이라고 추측할 뿐이다.

DeepSeek LLM v1에서는 아래와 같은 batch size가 쓰였는데,

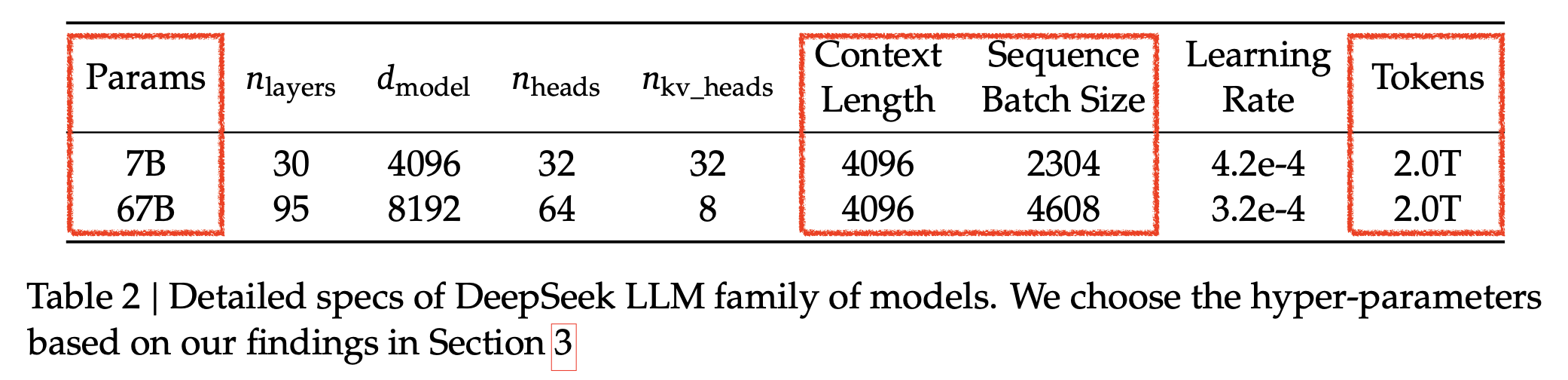deepseek_v1_bsz Fig. DeepSeek-v1

이들은 투입된 compute resource (보통 6 * model size * training tokens에 비례함)에 비해 loss를 예측할 수 있고, 이에 따라서 어떤 batch size, learning rate가 optimal인지 예측했다. (자세한 내용은 paper 참고)

즉 이것도 critical batch size라고 할 수는 없고 그 근처의 값이거나 더 낮은 값이라고 예상할 수 있는데 (낮으면 성능상 이슈는 없을 거니까), Compute budget, C에 대해서 C=6*7*2=84가 투입됐을 때 도달 가능한 loss에 대해서 batch size가 4096*2304=9.4M tokens쓰인 것이다. 그런데 만약 우리가 6T만큼의 token량을 더 학습하고 싶다면 어떻게 해야할까? 바로 3배 할 수는 없는 것이, compute cost는 3배 증가했지만 이에 따른 valid loss는 linear하게 떨어지지 않을 것이기 때문이다. 우리는 아래있는 C=6*67*2를 통해서 compute resource가 67/7=9.7배 증가했을 때 valid loss가 어떻게 예측될 지는 모르겠으나 optimal batch size가 대충 67B*2T에 대해서 18.8M이므로 안전하게 3배 증가했을 경우는 14M정도 쓰는 것이 안전할 것이다. (critical batch size와 optimal batch size가 왔다 갔다 하니 해석에 주의하길 바란다)

DeepSeek LLM v2에서는 아래와 같은 HP를 썼는데, 여기서 중요한 점은 DeepSeek v2는 Dense model이 아니라 MoE model이며, 총 model size는 236B이고 inference시 activate params는 21B이다.

deepseek_v2_training_details_fig2 Fig.

보통 MoE를 하면 inference시 21B만 써도 dense 21B 보다 훨씬 좋은 성능을 내기 마련이며, 이들은 8.1T tokens 학습했다. 그러니 desne 21B를 8.1T tokens학습한 것보다 훨씬 도달할 수 있는 valid loss가 적을 것임에도 불구하고 batch size는 9216*4096=37.7M이 쓰였다.

그렇다면 DeepSeek v2의 performance gain은 어땠을까? 아래 table을 보면 DeepSeek v1에 비해서 MMLU가 7.2점 올랐다. 물론 MMLU는 loss와 아예 직접적으로 연관이 있지는 않다. 전반적인 pre-trained LLM의 performance의 하나의 proxy일 뿐이지만 이를 통해서 사용된 batch size가 reasonable 한지 추론해 볼 수 있을 것이다.

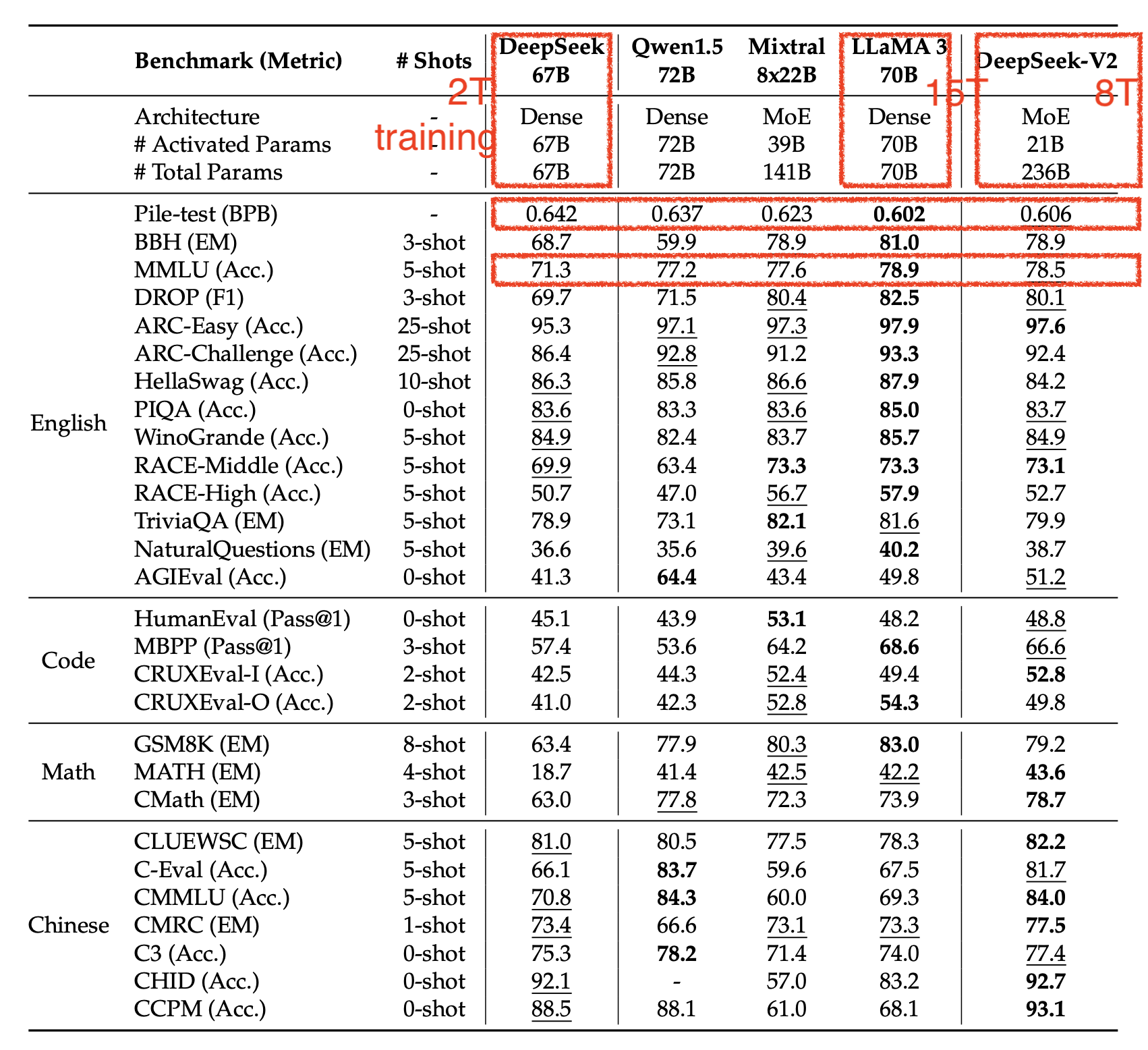deepseek_v2_model_vs_performance_table Fig.

하지만 MoE의 경우 batch size가 이렇게 큰 것에 대해서 추론하기가 어려울 것 같은데, 왜냐하면 training tokens의 일부만 각 expert에 할당되도록 학습되기 때문이다. 여러 가령 128개 tokens이 expert 64에 대해서 학습된다면 공평하게 2개 tokens만 학습될 경우 expert에 대해서는 batch size가 분산되는 효과가 있다.

deepseek_v2_training_details_fig1 Fig. (그런데 왜 이렇게 낮은 std를 썼을까…?)

위 table에 LLaMa-3 얘기도 있는데, 이는 70B dense model임에도 불구하고 DeepSeek v2 MoE보다 성능이 좋다. 하지만 LLaMa-3의 training tokens는 15T라고 알려져 있는 가운데, 아쉽게도 batch size등의 details는 없다.

llama3_chinchilla Fig.

Dense model인 DeepSeek v1과 LLaMa-3만 비교해보자면 computation 자체는 6*70B*15T/6*67B*2T=7.83배 더 쓰였다고 계산할 수 있지만, 사용된 dataset도 다르고 MMLU는 loss와는 다른 것이며 loss가 알려져있다 해도 (BPB가 있지만) 직접 비교가 어렵기 때문에 critical batch size를 논하기가 어렵다. 하지만 앞선 paper들을 따랐을 때 대충 30~40M정도 썼다고 유추해볼 수 있지 않을까 싶다.

Batch Size Considering Throughput

InstructGPT에서도 Proximal Policy Optimization (PPO)의 minibatch size를 정하는 데 있어 32가 가장 좋았지만 성능 감소를 감안하더라도 학습 효율을 위해 64를 골랐다고 한다 (아마 device당 수치인 것으로 보인다).

instruct_gpt_batch_size_ppo_fig Fig. from InstructGPT

Pre-training은 아니지만, 이렇듯 batch size를 정할 때 효율이 가장 좋은 critical batch size나 성능이 가장 좋은 optimal batch size를 넘기더라도, parallelism의 efficiency를 고려해서 이보다 큰 batch size를 고르는 일도 있으니, 경우에 맞게 batch size를 정할 수 있어야 할 것이다.

Increasing Batch Size During Training (In PaLM)

Pathway LM (PaLM)에는 앞서 얘기한 "Training 동안 초반에는 task 난이도가 쉽고 점점 난이도가 올라가서 batch size를 올려주는 것이 좋다"라는 언급이 있다. PaLM은 Google의 Large Language Model (LLM)인데, 이들도 학습을 할 때 early training phase에서는 더 낮은 batch size를 쓰다가 점점 batch size를 키우게 됐다고 한다.

palm_batch_size Fig. from PaLM

이는 GPT-3, PaLM에 모두 쓰인 approach인데 2019, 2022년이면 outdate되었다고 할 수 있겠지만 DeepSeek V2나 MiniCPM등에서도 언급된 것 처럼 2024년에 나온 LLM에서도 batch size ramp up등은 흔히 쓰이는 technique인 것 같다.

"The batch size should not be treated as a tunable hyperparameter for validation set performance"

한 편 Google의 Tuning Playbook에는 batch size를 포함해서 어떻게 HP tuning을 해야하는지에 대한 pro tip들이 있는데, batch size는 validation performance를 tuning하는데 tunable factor여서는 안된다는 말이 있다. 즉 batch size는 training time과 computing resource consumption간의 tradeoff를 결정하는 것이지, LR, optimization steps등이 맞춰진다면 batch size를 tuning하는 것으로 성능이 변해서는 안된다는 것이 핵심 논리이다.

google_tuning_playbook_fig1 Fig. Source from Google’s Tuning Playbook

여기서 저자들은 보통 ideal batch size는 가용 hardware에서 쓸 수 있는 가장 큰 batch size이다라고하는데, 우리가 앞서 critical batch size에서 얘기한 바에 따르면, 이는 보통 그렇다는 것이지 언제나 그런 것은 아닐 것이다. Critical batch size를 넘어가면 optimization steps가 마찬가지로 늘어야 할 것이다.

Solution Quality (Generalization Gap)

한 편, large batch size를 사용하는 것이 redundant한 것을 넘어서 실제로 수렴하는 지점이 다르지 않을까? 라는 생각이 들 수도 있다. 이번에는 아래 Large-Scale Deep Learning Optimizations: A Comprehensive Survey의 한 구절을 보자.

large_batch_survey_section4 Fig.

실제로 batch size가 너무 커져서 어떤 특정 spot을 careful optimization scheme없이 넘기게 되면 test accuracy이 확 떨어질 수 있다는 것이다. 다시 말해서 train sample과 다른 새로운 sample들에 대해서 전혀 generalize를 못할 수도 있다는 것인데, 이를 paper에서는 generalization gap이라고 부른다.

저자들은 Batch size를 키우면 안정적인 학습 (stable training)을 위한 LR의 range 가 급격히 줄어든다고 paper는 주장하는데, 어떤 reference paper에 따르면 이것이 large batch method가 sharp minimizer에 빠지기 때문이라고 주장한다. (하지만 이 이론이 딱 들어맞는지는 모르겠다. 왜 batch size를 키우는것만으로 sharp minima에 빠질 확률이 높아지고, 빠지면 다시 recover가 안되는지에 대해서 설득이 되지 않았는데, 아무래도 SGD에 가까울수록 variance가 커서 saddle point같은걸 탈출할 확률이 높다는 것과 같은 논지인 것 같다.)

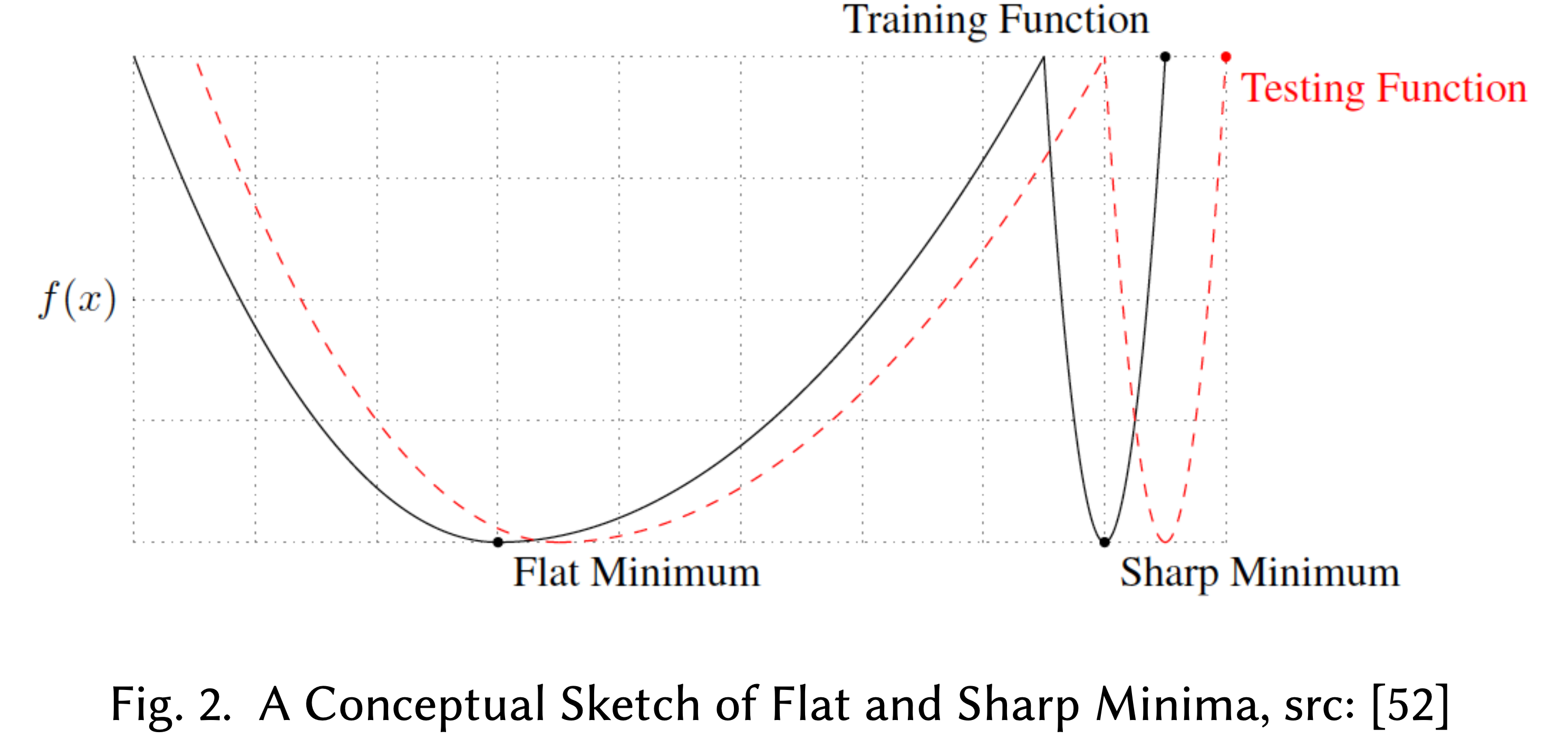sharp_minimizer Fig. Sharp Minimizer. Source from here

반면에 small batch method는 flat minima로 수렴하기 쉽다는 것이 알려져 있다고 한다. 위의 figure에서 직관적으로 flat minima는 test data point들에 대해서 objective function이 실제 training objective function과 다르다 해도 이들은 크게 다르지 않을 것이며, flat minima의 solution의 경우 이동한 objective function에도 잘 맞는 걸 볼 수 있다.

하지만 이를 반박하는 paper도 많은 것 같다. 앞서 얘기한 것 처럼 optimization step size를 늘리면 해결된다고 주장하는 이들도 있고, heuristic하게 warmup stage를 동반한 LR scaling을 하거나 layer별로 다르게 LR을 주는 것으로 해결이 가능하다고도 했다. Accurate, Large Minibatch SGD: Training ImageNet in 1 Hour에 따르면 적어도 ImageNet에 대해서는 성능 감소 없이 large batch training을 이뤄냈다고 한다.

about_solution_quality Fig. Large batch size가 solution quality를 해치는가?에 대한 갑론을박.

LR Scaling According to Batch Size

Linear or Square Root LR Scaling

앞서 critical batch size를 제안한 paper에서도 SGD냐 Adam이냐, 그리고 Task에 따라서 대략 \(n\)배 batch size를 키우면 LR은 \(n^{0.5} \sim n^{1.0}\)정도 scaling해주면 된다고 했다. (critical batch size에 도달하기 전까지)

이에 대해서 조금만 더 생각을 해 보자면, 먼저 LR을 선형적으로 키워주는 것에 대해서는 plain SGD를 생각할 경우, k 번의 optimization step을 한 큐에 처리하는 것이나 다름 없기 때문에 (대신에 더 정교한 방향으로 한 step 갈 것) k배 크게 이동하는 것이 직관적으로 맞을 것이다. 하지만 SGD에서 update 될 \(\Delta \theta\)의 co-variance matrix는 다음과 같다. (N개 sample에 대해 gradient의 평균을 구하던 원래의 case를 B배 batch size 키웠다고 생각)

\[\Delta \theta \approx \frac{\alpha^2}{\vert B \vert} (\frac{1}{N} \sum_{n=1}^N g_n g_n^T)\]

이 경우 서로다른 parameter들 간의 변화량을 의미하는 covariance를 동일하게 유지해주는 방법은 LR, \(\alpha\)를 square root 배 해주는 것일 수 있다고 한다.

사실 이것들 말고도 여러 주장이 있는것으로 아는데, OpenAI의 수많은 실험에 따라 task에 따라서 \(n^{0.5} \sim n^{1.0}\)배 해주면 된다는 것은 충분히 증명이 됐으니 resource를 좀 써서 scaling law를 찾는 것이 가장 맘 편할 것을 보인다.

아래의 figure를 좀 더 보자. 이는 Measuring the Effects of Data Parallelism on Neural Network Training.의 plot으로, Trasnformer를 common crawl dataset에 학습한 경우 같은 validation error에 도달하기 위해서 batch size가 증가에따라 LR scaling해주는 것이 sqrt scale도 못따라가는 것을 볼 수 있다.

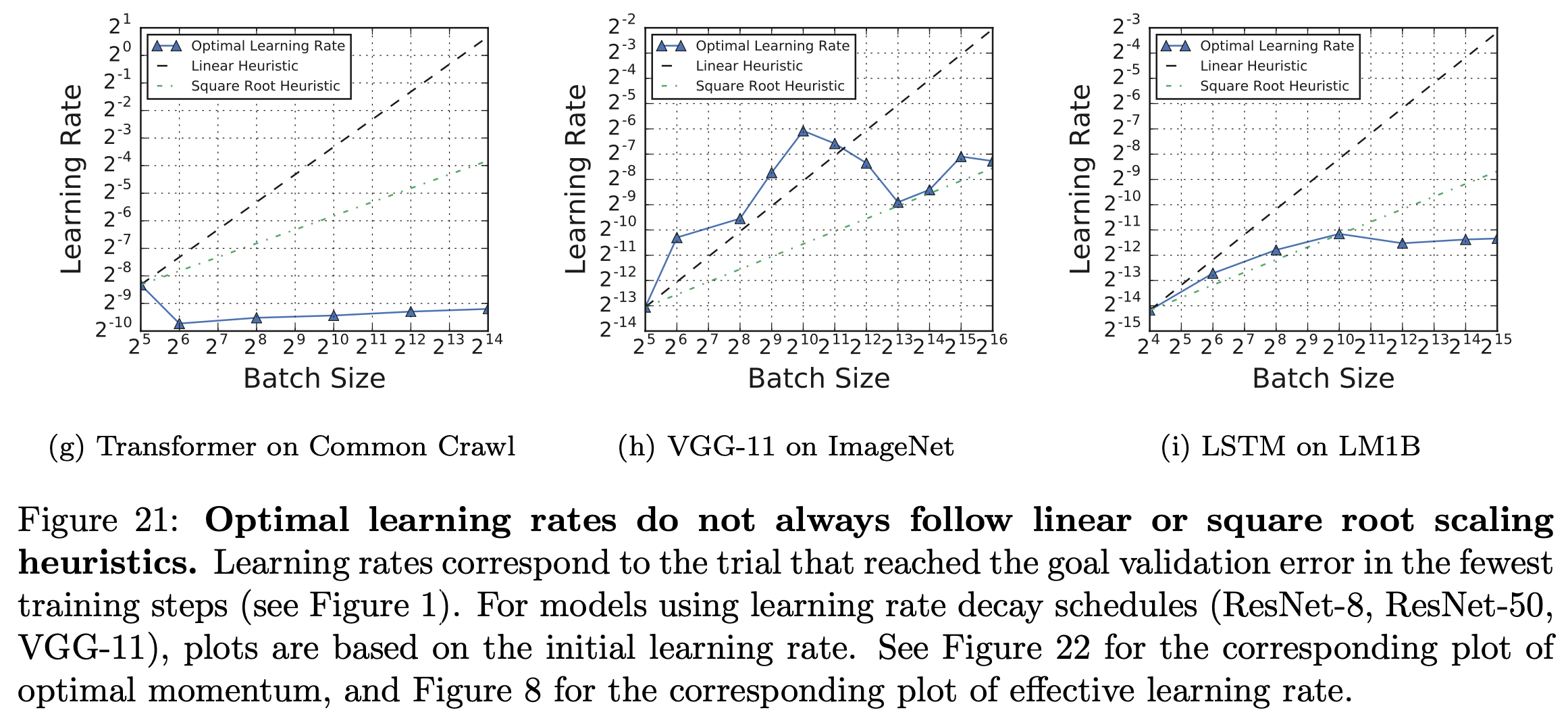measuring_effcet_of_dp_fig21 Fig.

그리고 이 때의 optimal momentum은 아래의 plot에 대응한다.

measuring_effcet_of_dp_fig22 Fig.

이 둘을 같은 plot에 표현하면 다음과 같다.

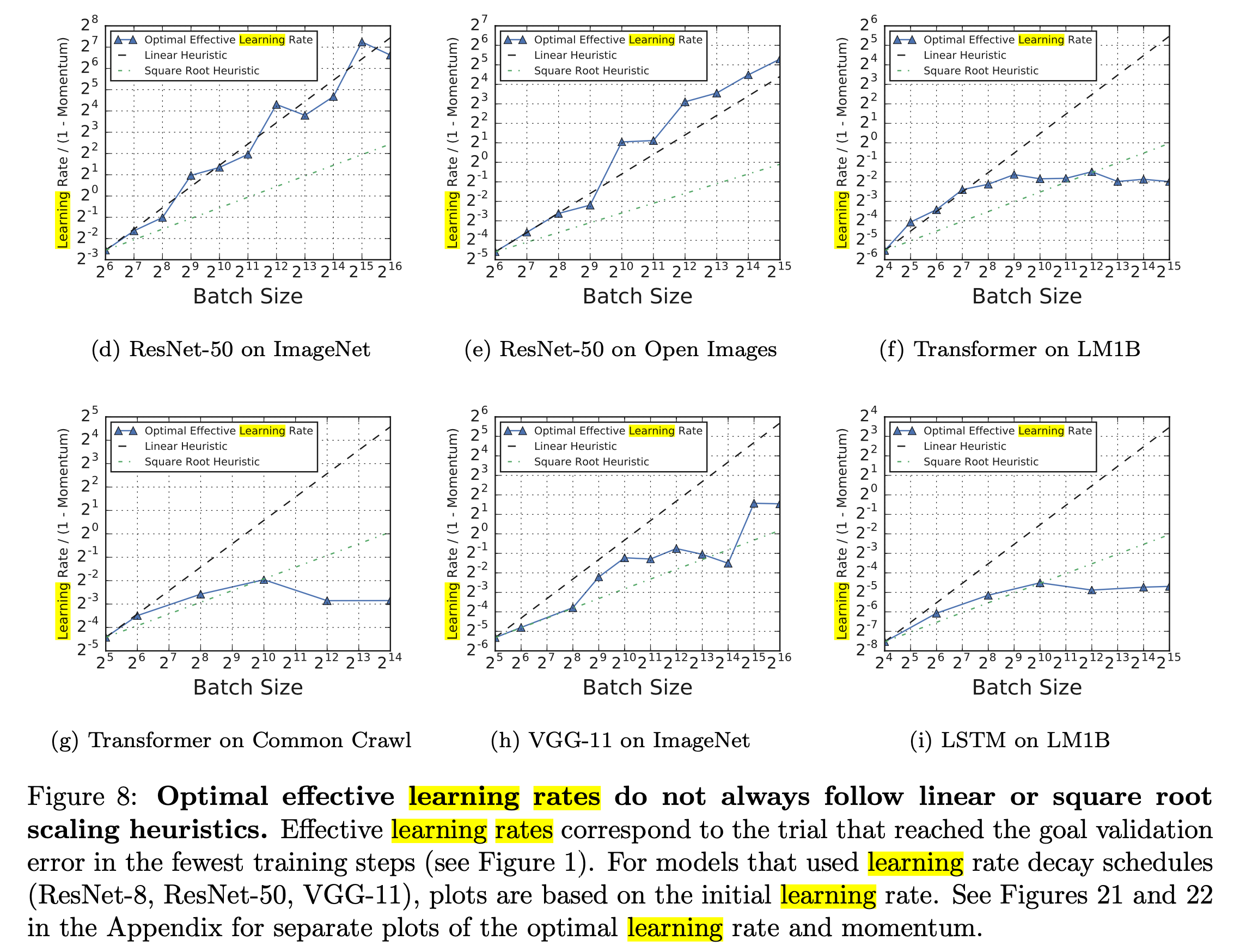measuring_effcet_of_dp_fig8 Fig.

그럼 LR이나 momentum이 얼마나 sensitive한가? 이는 아래의 plot을 보면 또 알 수 있다.

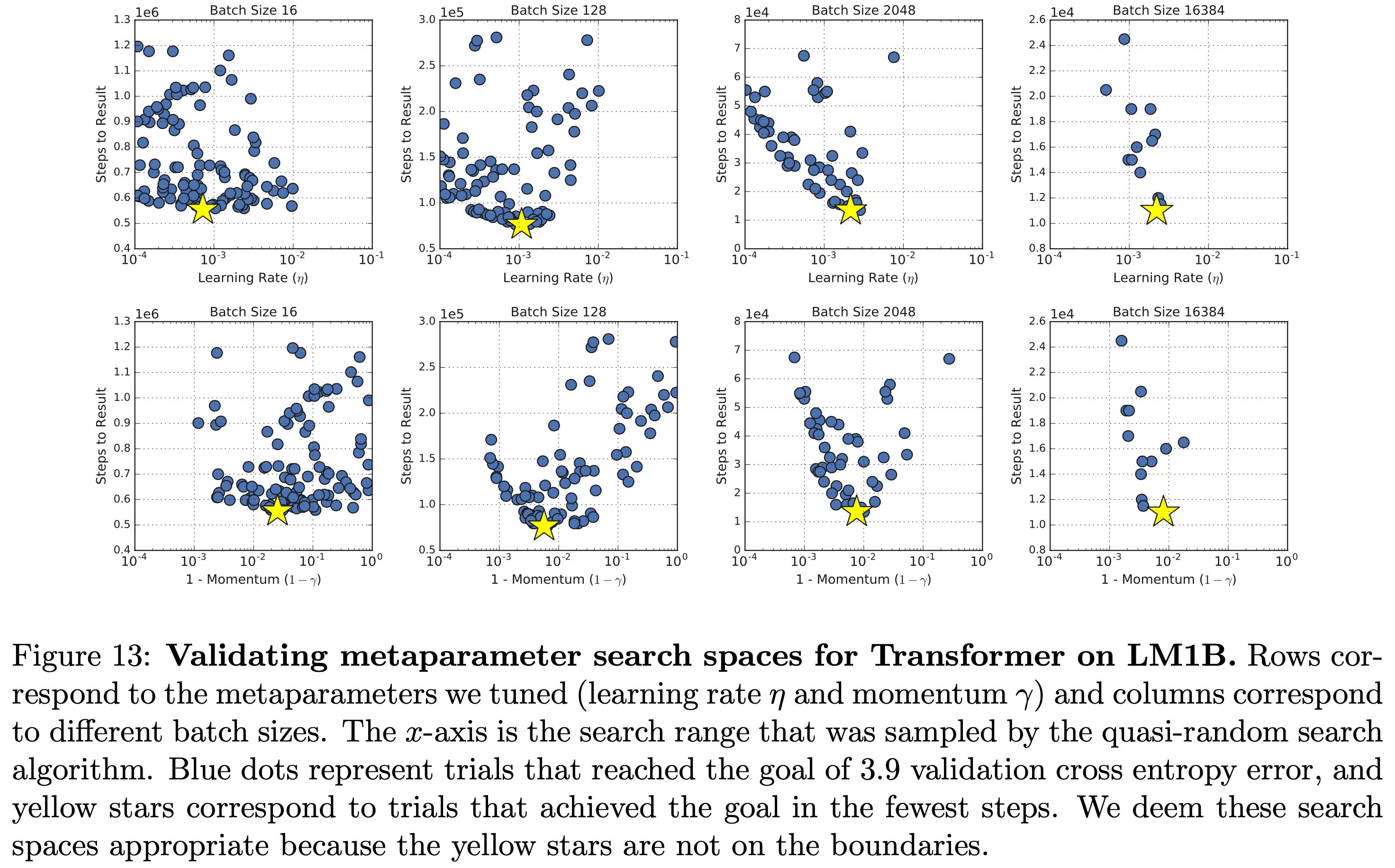measuring_effcet_of_dp_fig13 Fig.

이런 empirical result들을 볼 때, LR은 결국 사람이 튜닝을 할 수 밖에 없는 것 같기도 하다.

TBC) Understanding Optimization using Stochastic Differential Equations

How to Scale Hyperparameters as Batch Size Increases

Learning Rate Range Test (LRRT)

Learning Rate Range Test (LRRT)라는 method는 model이 diverge하지 않는 선에서 쓸 수 있는 가장 큰 LR을 찾는 method라고 한다. (이에 대한 MS Deepspeed team의 blog post를 참고하면 좋을 것 같다)

Device당 512 batch size를 갖는 경우에 대해 device를 4배로 늘려 2048 batch size를 쓰는 경우를 생각해보자. 이 경우 slow convergence 현상이 발생하는데, 앞서 말한 것 처럼 늘어난 batch 만큼 iteration 수가 줄어들겠으나 이런 setting으로는 baseline 과 같은 성능을 낼 수 없는 것을 말한다. 즉 LR을 키우거나 step수를 늘리거나… 해야 되는데, 이 경우에는 늘어난 batch size만큼 무지성으로 sqrt를 씌우지말고 실제로 어디가 upper bound인지 search를 한다.

lrrt

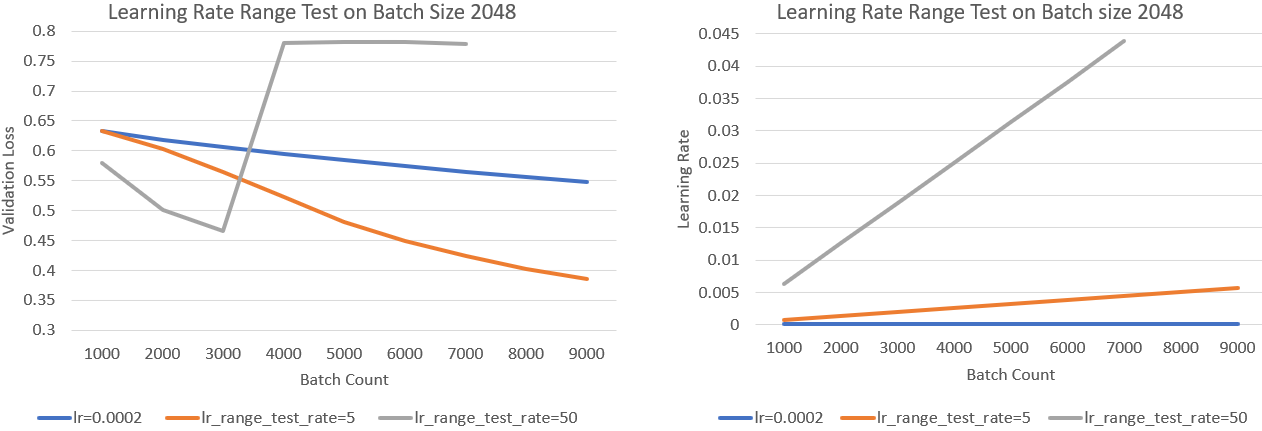
위 figure에서 왼쪽 sub figure는 첫 training batch 9000개에 대한 validation loss 를 의미한다. Grid search로 2048 batch size에 대한 best fixed lr을 0.0002로 찾았다고 치자. 이제 이를 기준으로 lr을 서서히 키우는데 변화율을 다르게 해서 관찰해보자. 너무 급격하게 키운 gray line은 중간에 발산했으나 적당히 증가시킨 orange line은 best fixed lr을 쓴 blue line보다 훨씬 loss가 잘 떨어지는 걸 볼 수 있다. 즉 이 model이 현재 batch size로는 최대 키울 수 있는 LR이 0.005정도이니 이 안에서 scheduling을 해주겠다는 매우 simple한 method이다.

사실 training step이 경과할수록 parameter가 update되므로, 초반에 문제없는 lr이 나중에도 문제가 없다는 보장이 있는지는 모르겠다. 게다가 터지기 직전의 LR이 optimal LR일 것이라는 설(?)은 많이 언급되지만 사실인지 아닌지 모르겠기 때문에 안전한 방법은 아닌 것으로 보인다.

Summary

Motivation에서 얘기했던 주석은 어떤 맥락에서 나왔는가?