(WIP) How to measure feature learning ? Canonoical Correlation Analysis (CCA) and Centered Kernel Anaylsis (CKA)
27 Feb 2023< 목차 >
Singular Vector Canonical Correlation Analysis (SVCCA)
Canonical Correlation Analysis (CCA)는 layer 별 neuron 들의 representation 이 얼마나 유사한지를 비교하게 해주는 algorithm이다. 여기에 Singular Vector Decomposition (SVD) 를 더한 것이 SVCCA이며, 이는 Google brain이 2017년에 publish한 Neural Network (NN) 분석 tool이다.
정준상관분석 (Canonical Correlation Analysis; CCA)이라고 하는 방법론의의 어원을 살펴보면, ‘Canonical’이라는 용어는 ‘규범적인’을 뜻하는 것으로, CCA는 두 개 이상의 집합 간에 존재하는 관계의 규범적인 (가장 대표적인) pattern을 찾는것을 의미한다. CCA는 여러 개의 변수가 있는 두 집합 사이의 상관 관계를 분석해, 각 집합이 상대 집합과 최대한으로 상관되는 선형 조합을 찾아내는데, 두 집합에 대해서 그들 사이의 최대 상관을 나타내는 선형 조합을 찾아내는 것이라고 한다.
예를 들어 \(X \in \mathbb{R}^{m},Y \in \mathbb{R}^{n}\)가 각각 \(X\)는 지능 검사 결과를 나타내는 변수들이고 \(Y\)는 학업 성적을 나타낸다고 칠때, 먼저 \(a=(a_1, a_2, \cdots, a_m), b=(b_1, b_2, \cdots, b_n)\)이라는 weight vector를 정의해서 각각의 집합과 선형 결합을 한다.
\[U=a^TX, V=b^TY\]여기서 \(U, V\)를 각각 대표적인 (canonical) 조합으로 볼 수 있고, 우리는 objective를 아래와 같이 설정하고 optimize를 하면 된다.
\[\begin{aligned} & \rho = \max corr (U,V) & \\ & \text{where } corr(U,V) = \frac{ Cov(U,V)}{ \sqrt{Var(U) \cdot Var(V)}} & \\ \end{aligned}\]이는 두 개의 matrix가 주어졌을 때 이들이 어떤 bases에 projection 됐을 때 두 correlation이 maximize 되는가?를 의미하는 bases를 찾아내는 것과 같고, correlation이 가장 큰 bases를 일단 찾았으면 그 뒤로 또다른 bases를 찾을 때 이전에 찾은것과 중복되지 않도록 각 canonical variable끼리는 orthogonality하다는 constraint를 걸어줘야 한다.
\[\begin{aligned} & \rho_i = \max_{W_X^i, W_y^i} corr (X W_X^i, Y W_Y^i) & \\ & \text{subject to } \forall_{j < i} X W_X^i \perp X W_X^j & \\ & \forall_{j < i} X W_Y^i \perp X W_Y^j & \\ \end{aligned}\]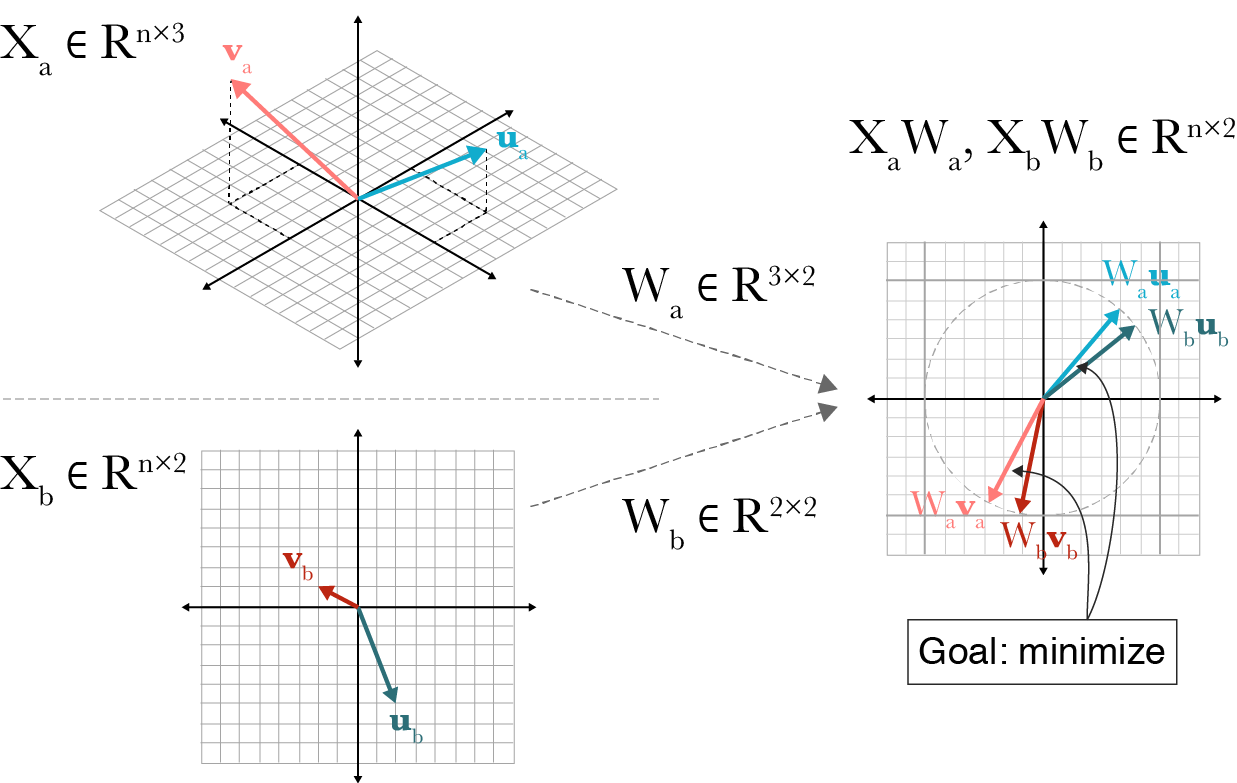 Fig. Intuitive visualization of CCA. observation, n=2일 때 3차원 feature X_a와 2차원 feature, X_b간의 상관관계를 maximize하는 linear projection weight, W_a, W_b를 찾는 것이 CCA의 목적. Source from link
Fig. Intuitive visualization of CCA. observation, n=2일 때 3차원 feature X_a와 2차원 feature, X_b간의 상관관계를 maximize하는 linear projection weight, W_a, W_b를 찾는 것이 CCA의 목적. Source from link
CCA는 variance를 maximize하는 projection weight을 찾는 Principal Component Analysis (PCA)같은 고전 statistics, machine learning 기법과 유사하다고 생각할 수 있으며, 당연히 PCA처럼 analytic solution이 존재하는 것으로 보이며 이는 standard eigenvalue method를 사용해서 풀 수 있다고 한다. (사실 여기까진 자세히 안봐서 궁금하면 찾아보길 바란다)
이제 이를 NN의 feature로 확장해보자. 이 과정에서 SVCCA의 저자들은 각 layerwise feature에 대해서 SVD를 적용해서 dimensionalty reduction을 먼저 한 뒤에 CCA를 해야 한다고 주장하는데, 뭐 직관적으로 너무 feature dimension이 커서 noise가 많기 때문에 이를 제거한다고 할 수 있는데, 관련 자료들을 보면 CCA의 sensitivity에 대한 얘기들이 좀 있다. (하지만 SVD를 하고 CCA를 한다고 해도 결국엔 선형 CCA를 하기 때문에 kernel CCA같은게 필요할 것)
SVCCA를 하려면 아래 3가지 step을 하면되는데,
- Step 1: m개의 data points를 NN에 넣어 원하는 layer들의 outputs를 뽑는다.
- Step 2: SVD를 수행하여 중요한 direction들만 남긴다.
- Step 3: CCA를 수행한다.
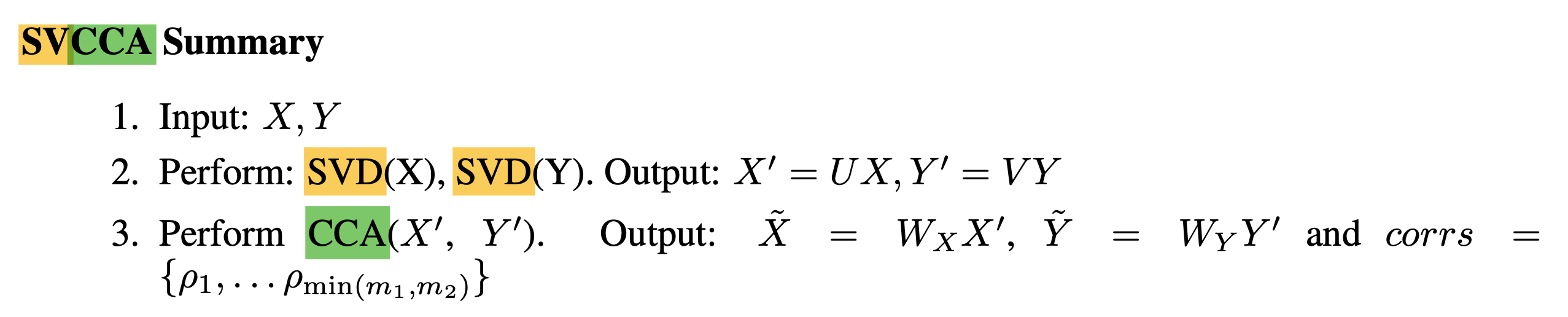
Distributed Representations
Why the two step SV + CCA method is needed.
Applications of SVCCA
SVCCA를 사용하면 아래처럼 NN training을 분석할 수 있게 되는데,
- 같은 구조를 가진 두 개의 네트워크 net1, net2 끼리 같은 layer 의 similarity 계산
- 한 네트워크 내의 서로 layer output들간에 similarity 계산
1번같은 경우 model이 training되면서 (epoch 10, 20, … 100) 어떤식으로 각 layer의 출력값들이 변하는지를 시간에 따라 분석하는 feature learning dynamics를 파악할 수 있게 해주고, 2번의 경우 어떤 layer들이 비슷한 역할을 하는지에 대한 힌트를 제공하기도 한다.
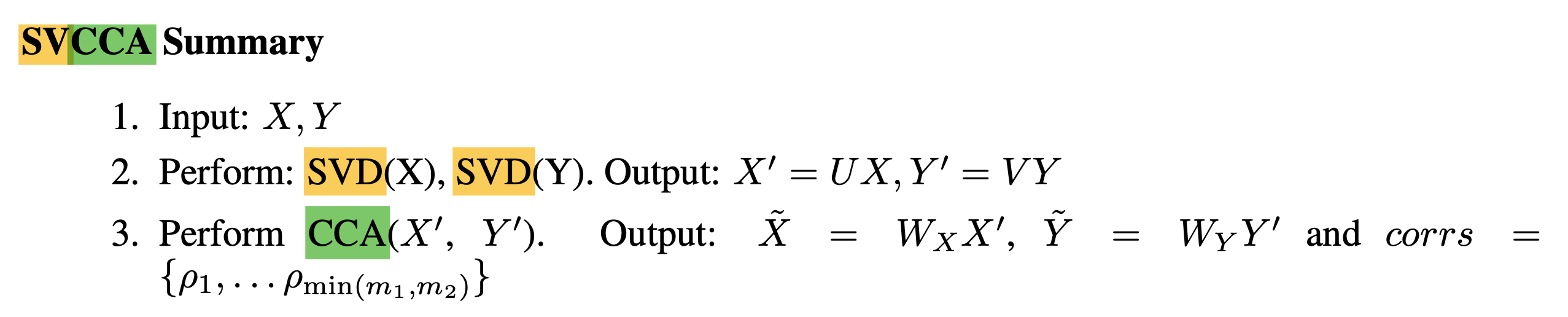 Fig.
Fig.
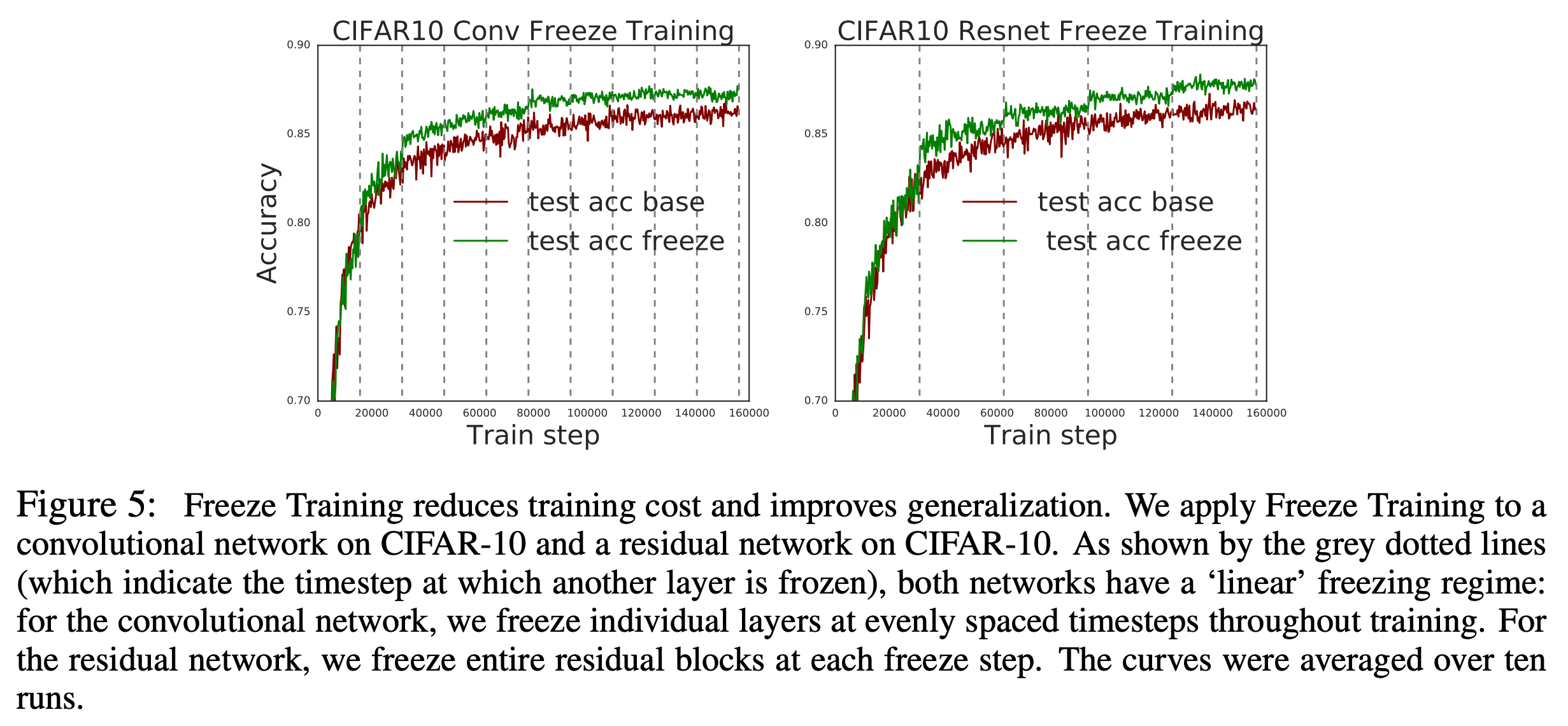
예를 들어 아래 image classification을 위한 convnet, resnet의 학습 추이를 보자.

저자들은 lower layer들은 training process에서 크게 변하지 않는다고 판단, lower layer들을 전부 freezing해서 학습했고, 이는 working했다고 한다.
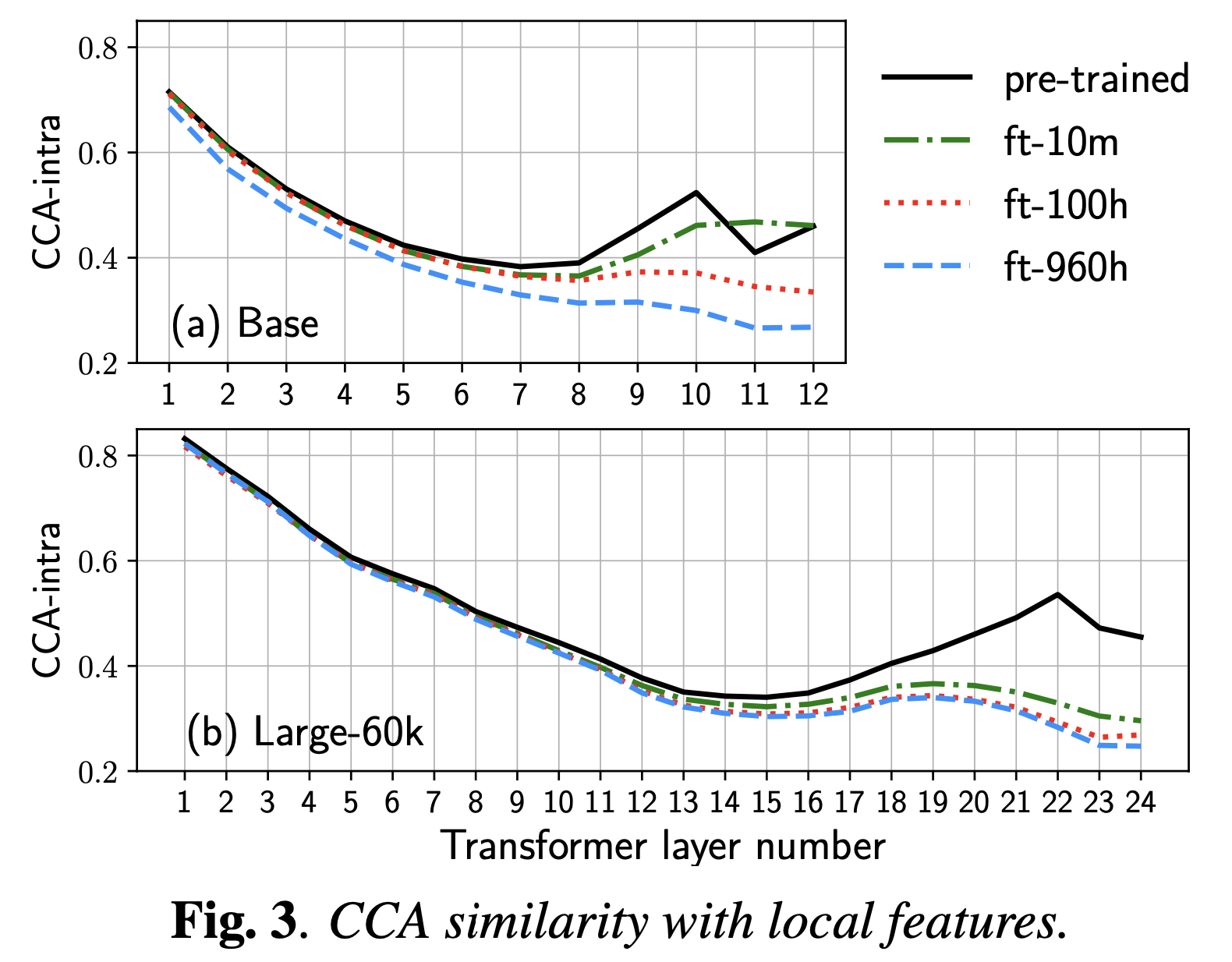
이는 Layer-wise Analysis of a Self-supervised Speech Representation Model라는 paper나 다른 BERT관련 paper들에도 나오는 내용인데, 해당 paper에 등장하는 Wav2Vec 2.0은 contrastive learning으로 pre-training되어 1d wave signal을 받아 speech representation을 뽑도록 학습된 transformer 기반 architecture로 NLP의 BERT같은 것이라 보면 된다.
저자들은 pre-training model과, 음성 인식 (Automatic Speech Recognition; ASR) task로 fine-tuning한 model들 간 CCA analysis를 했을 때 (SVCCA는 아닌가?), 아래 layer들의 feature는 거의 변하지 않은 것을 확인했다.
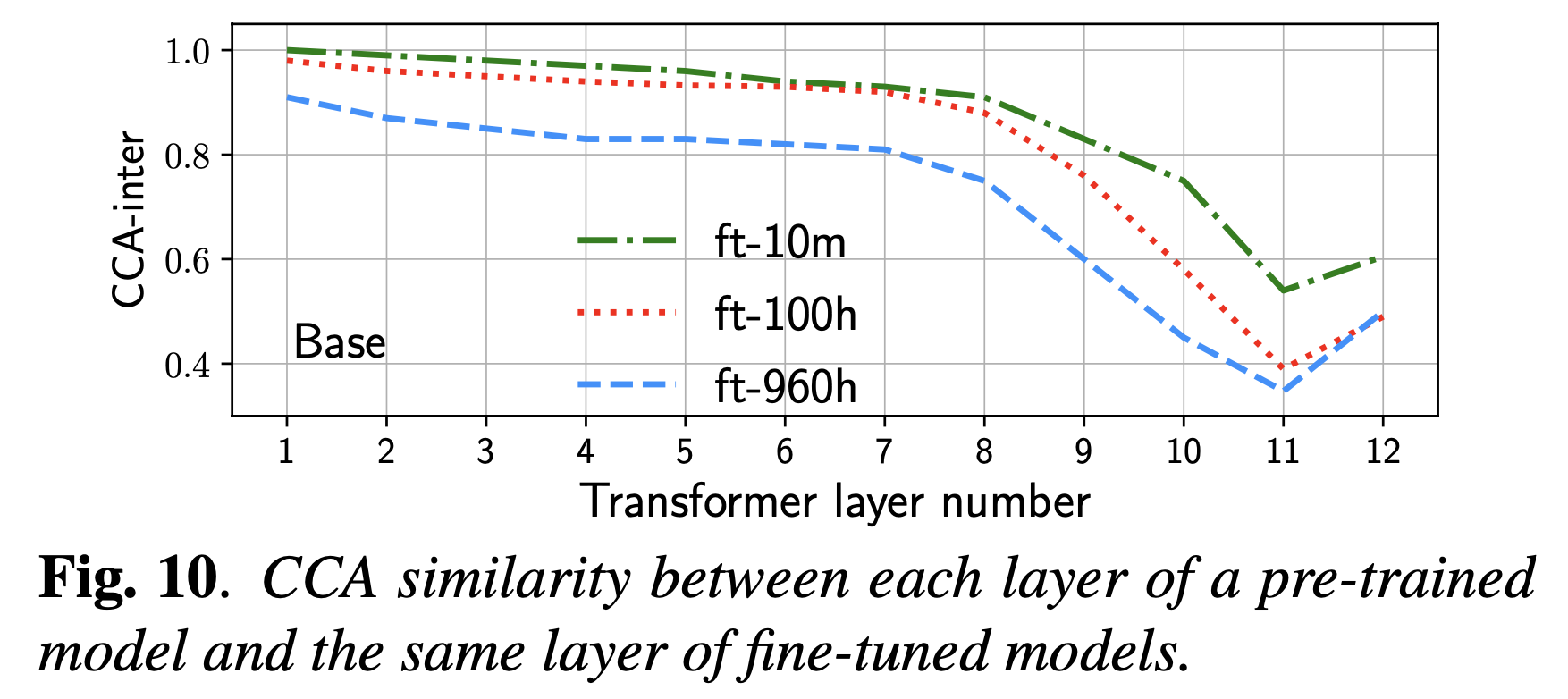
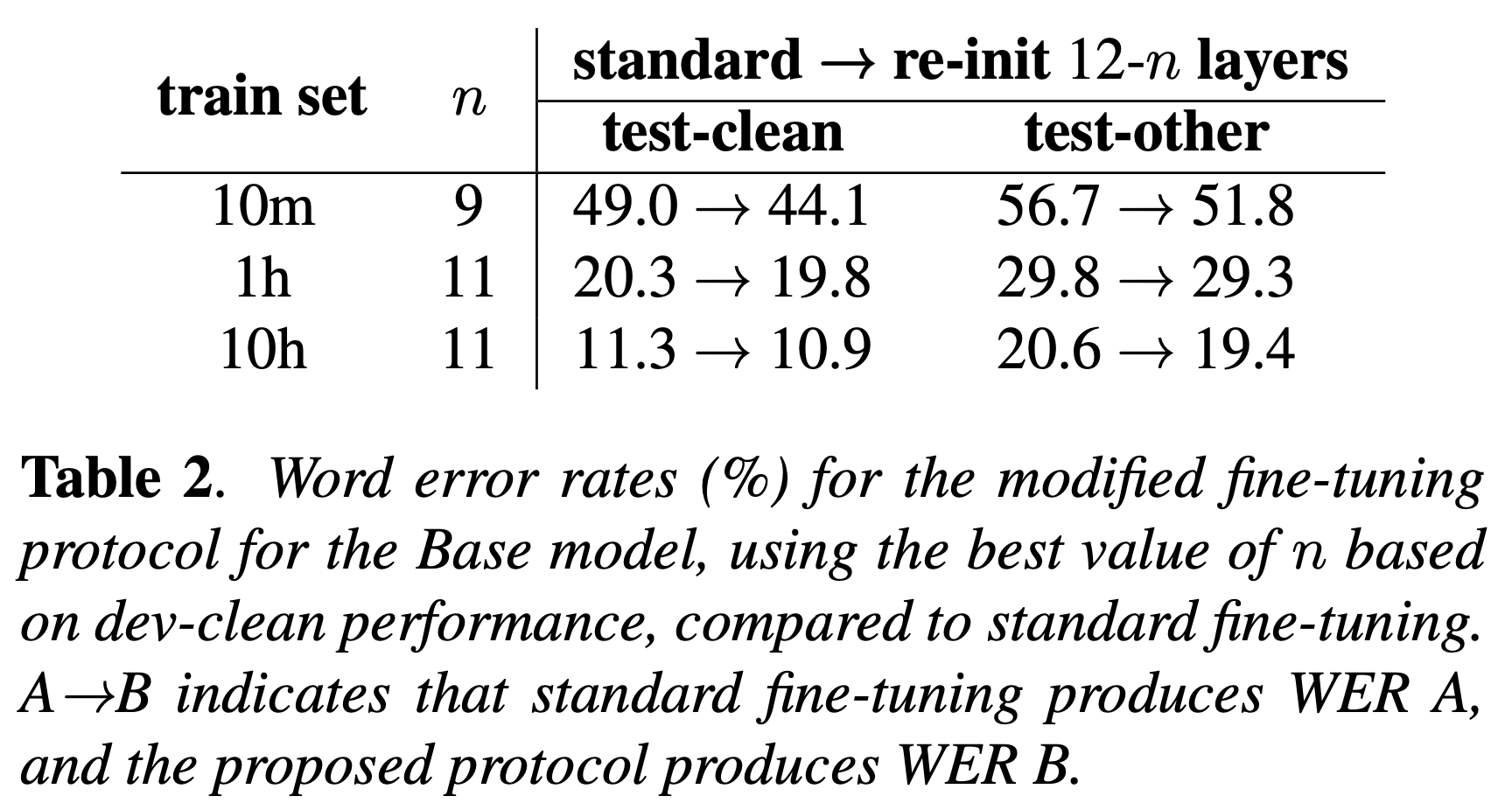
하지만 여기서 저자들은 이것이 pre-training 단계에서 last layer는 별로 좋은 representation을 학습하지 못한 것이라 판단하고, 마지막 n(3)-layer를 re-init하는 방법을 택했으며 결과적으로 performance improvement가 있었다.
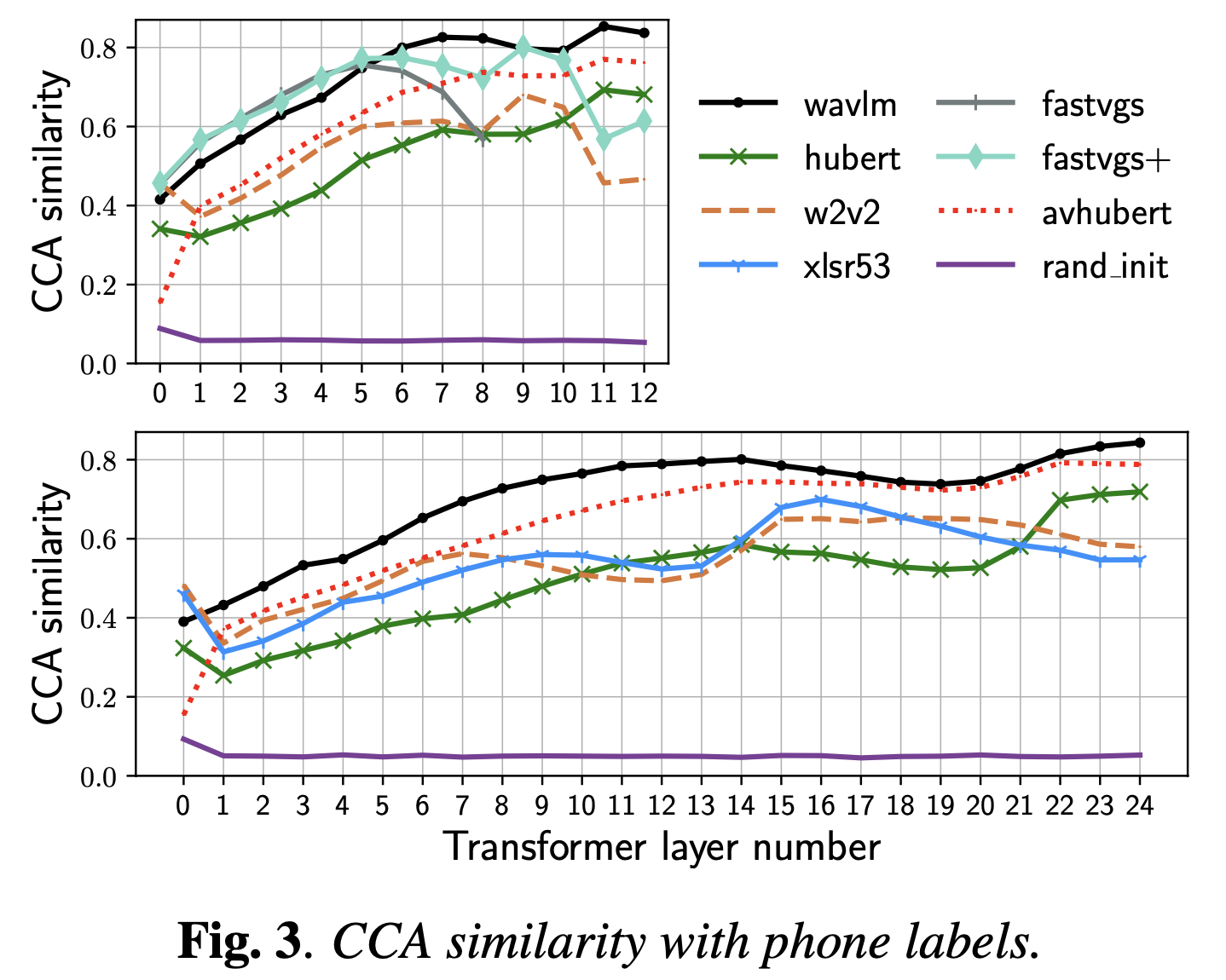
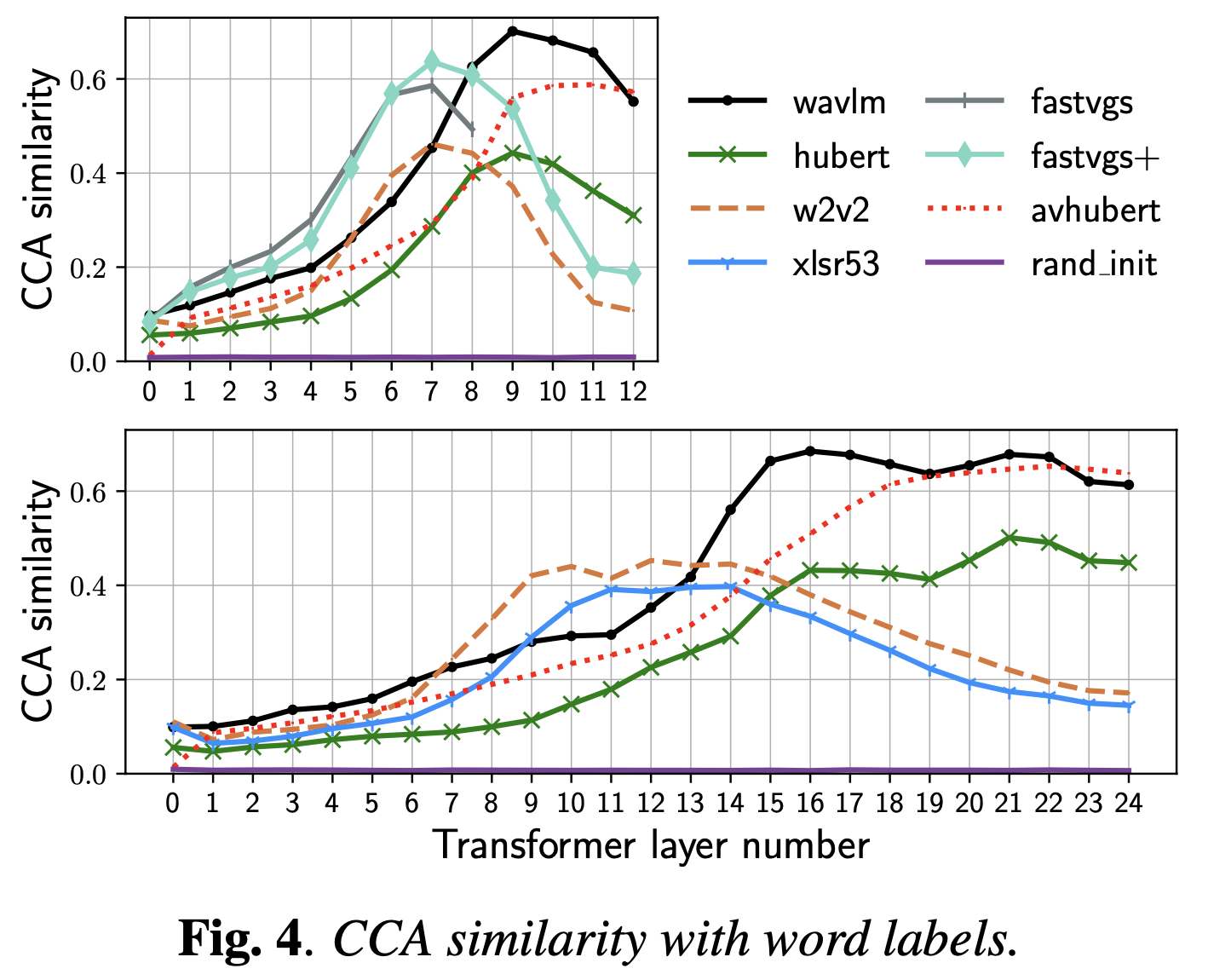
이 논문들은 그밖에도 재밌는 분석이 많은데, 앞서 CCA가 서로 다른 feature dimension에 대해서도 적용이 가능한 기법인 것을 이용해 speech representation에서 음소 정보 (phonetic information), semantic imformation 등을 어떤 layer가 배우게 되는지에 대해 분석하기도 했다.
그리고 보통 연속해서 등장하는 feature들이 비슷한 speech data의 특성이 실제로도 반영되는지 확인하기 위해 local feature간 CCA를 계산하는 등의 분석도 거쳤다.
그 밖에도 SVCCA의 저자들은 cross model comparison, compression등이 가능하며, interpretability에서도 장점을 보인다고 서술했는데 더 궁금한이들은 paper를 참고하길 바란다.
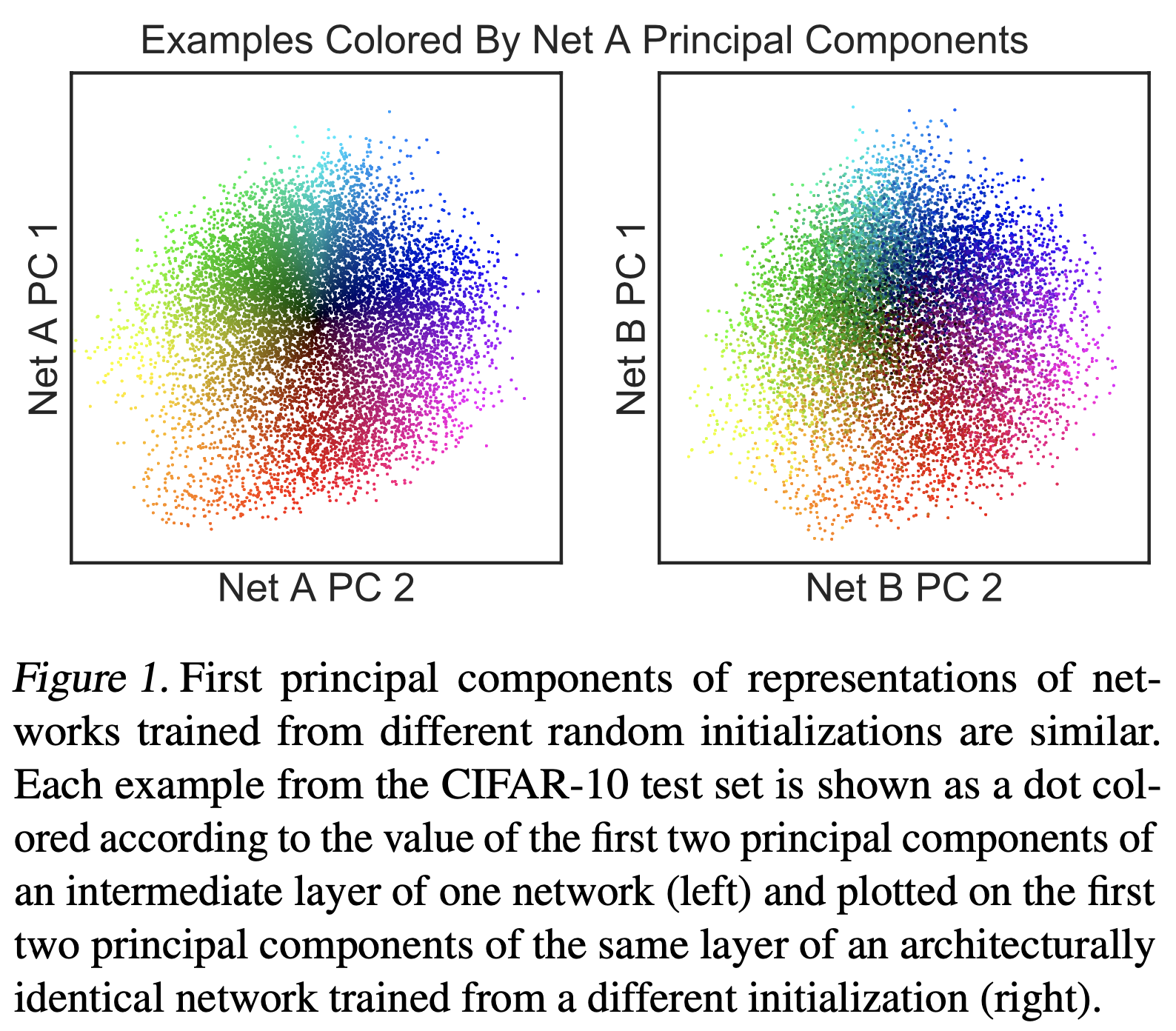
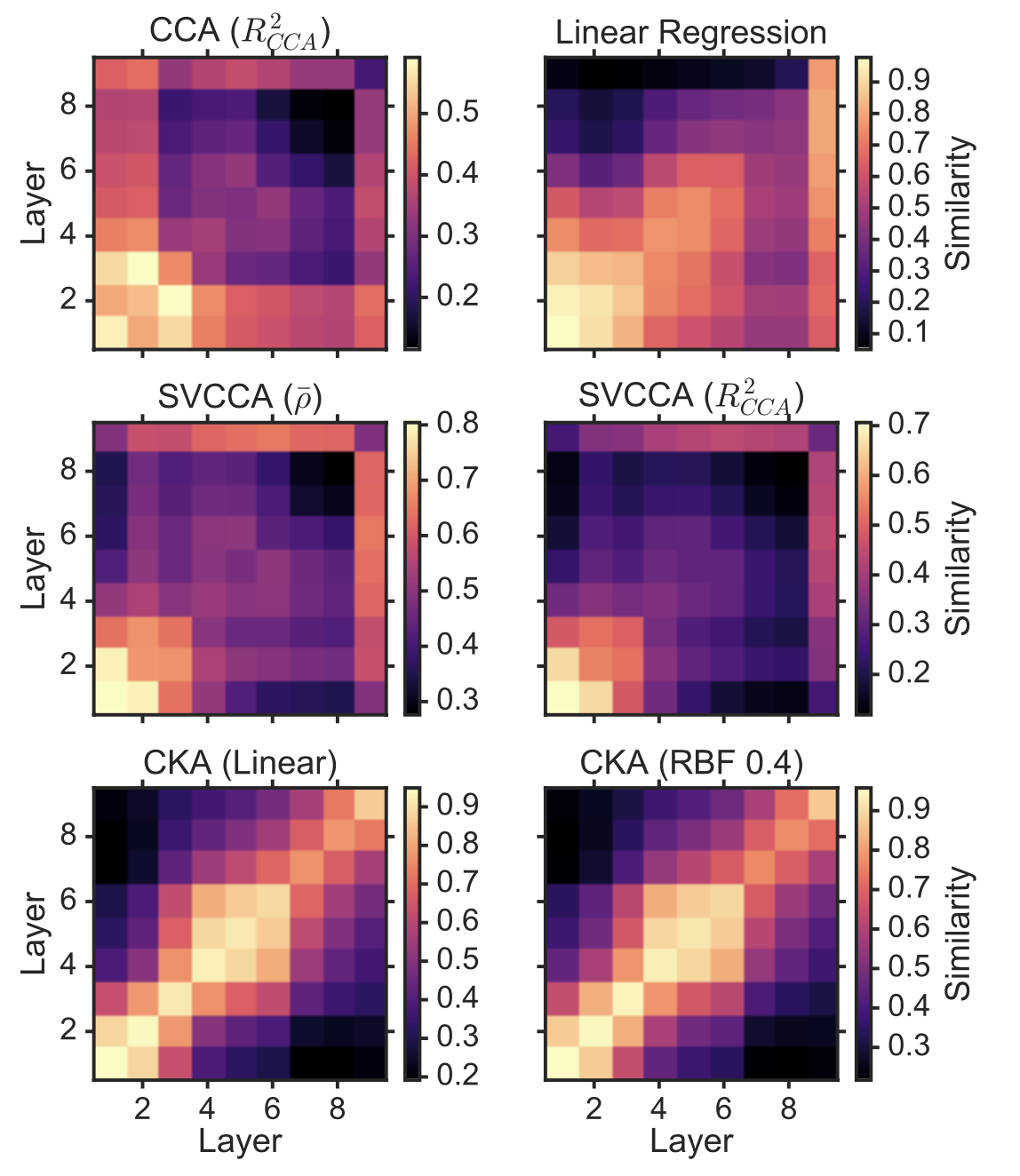
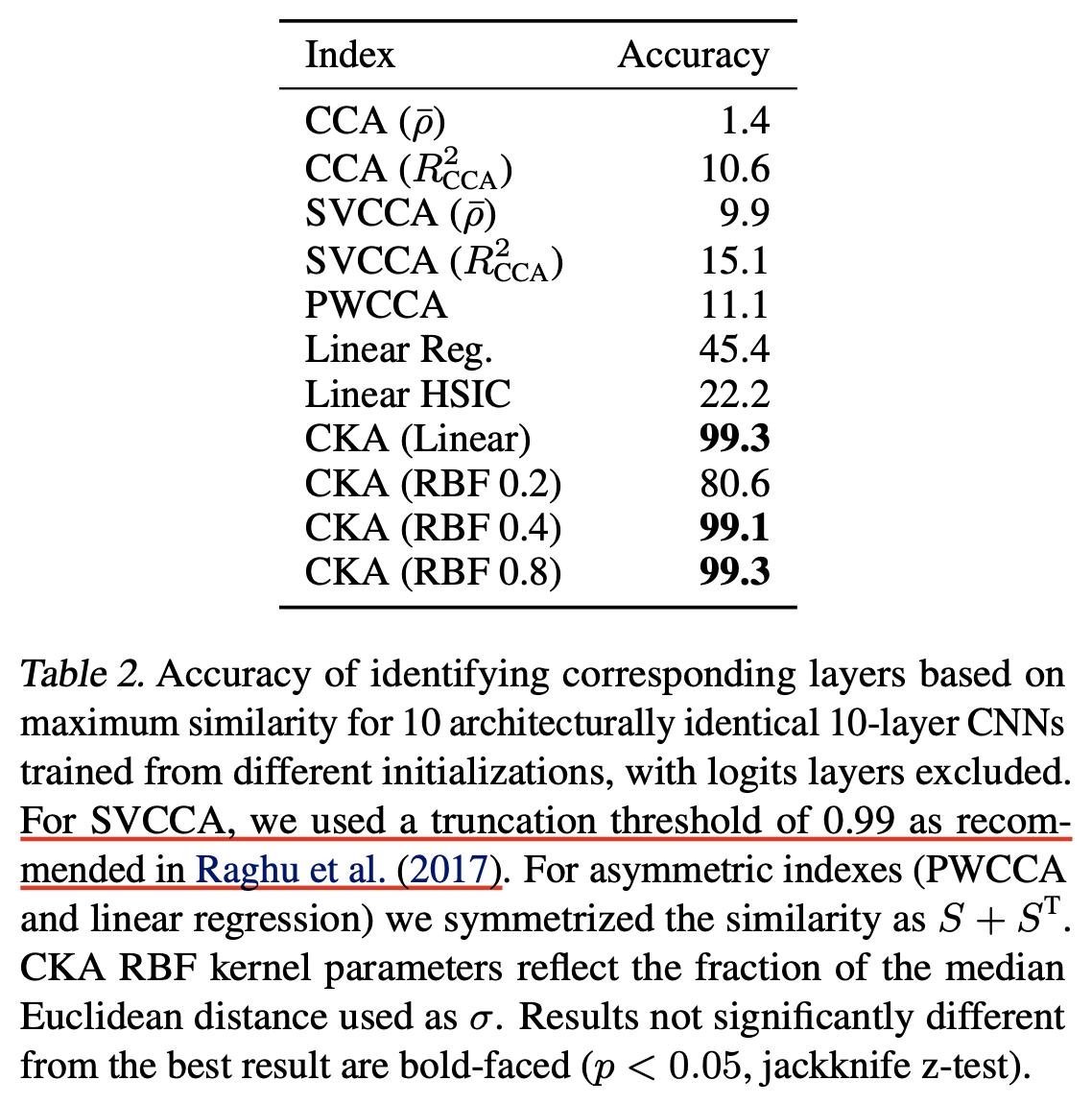
Centered Kernal Analysis (CKA)
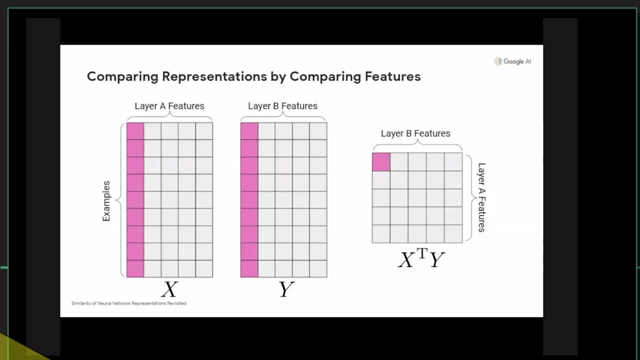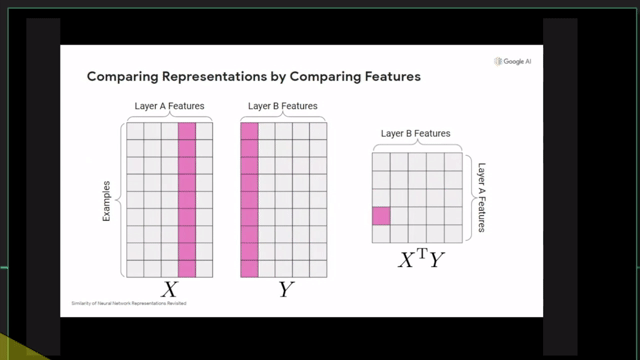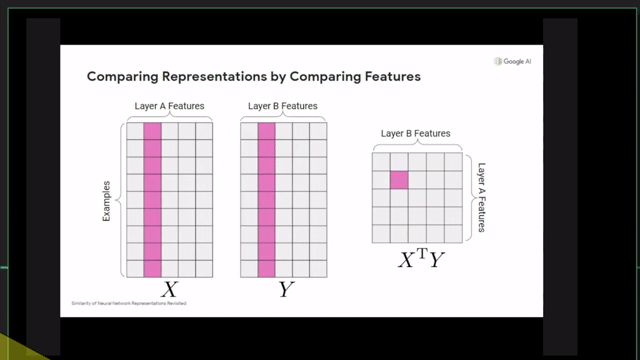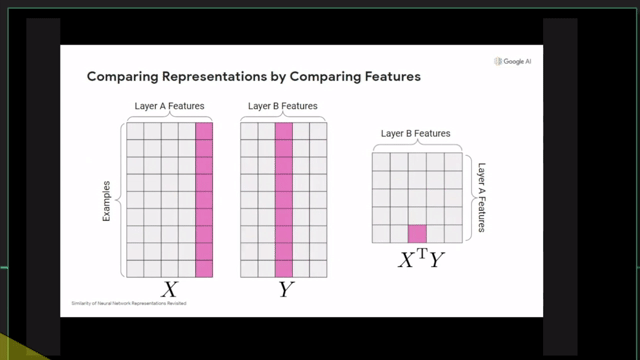
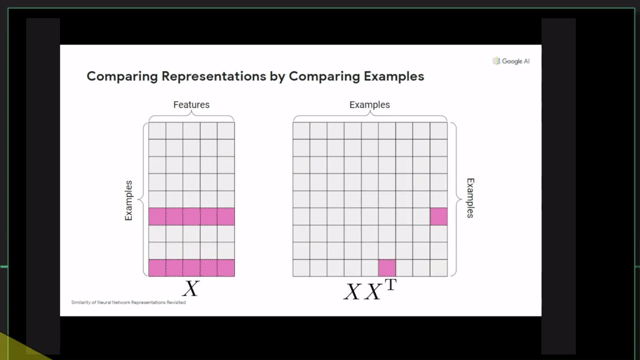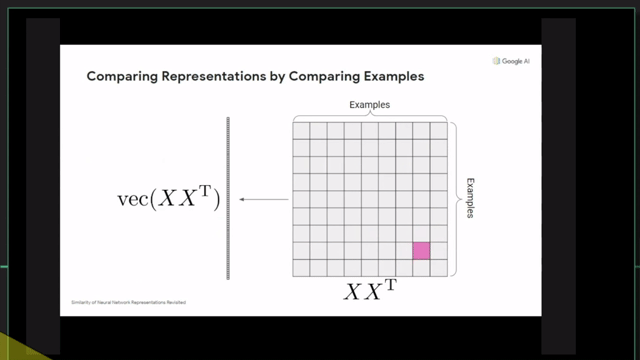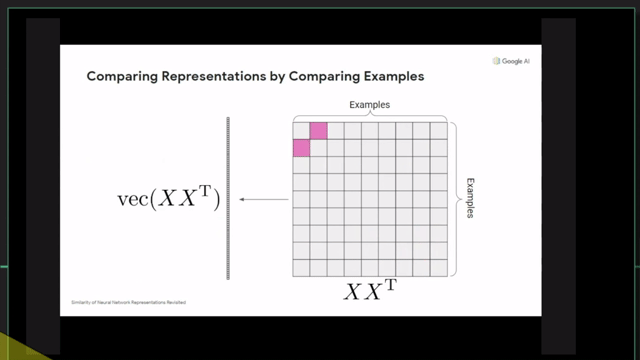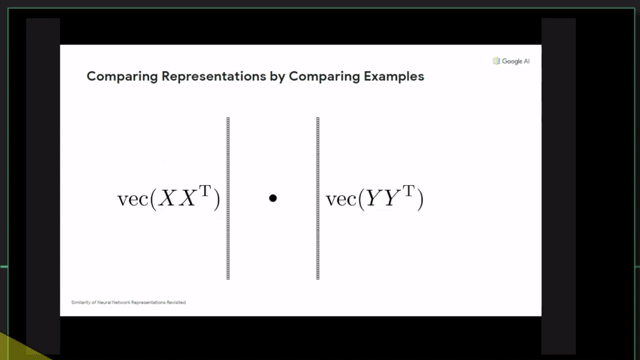

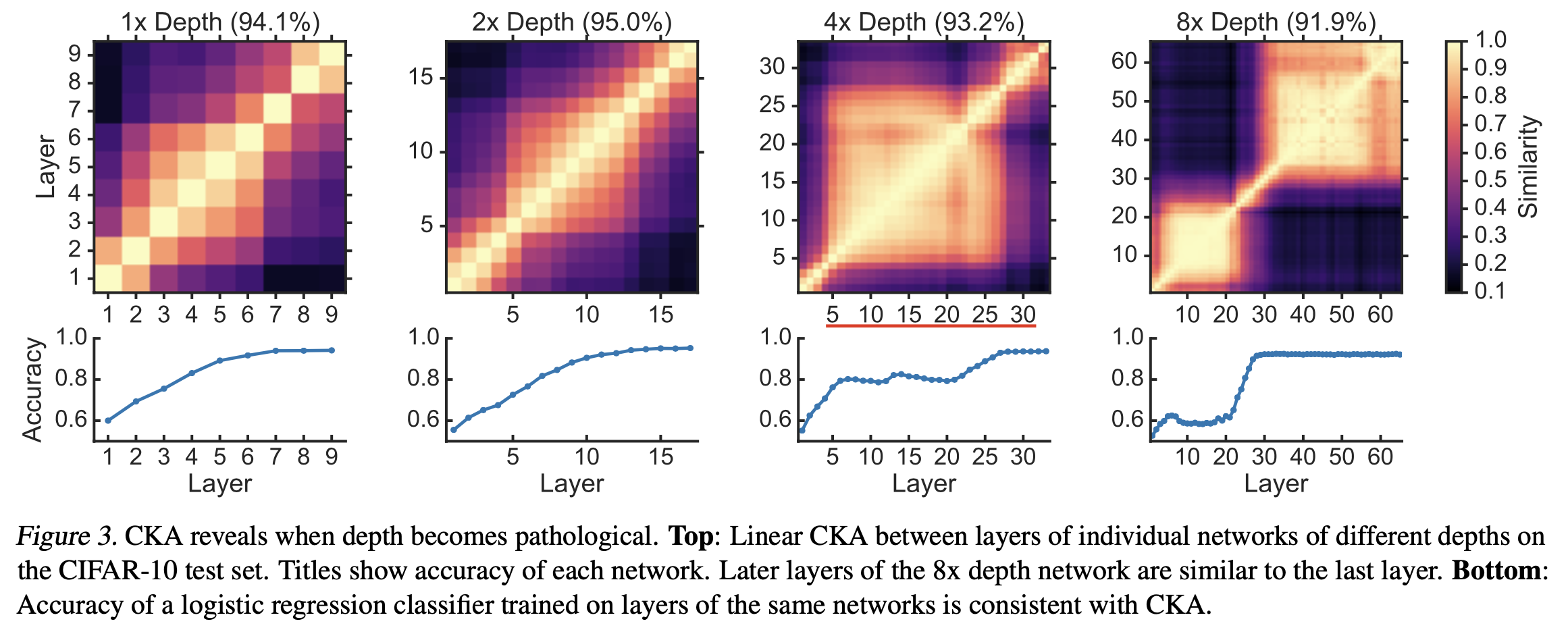

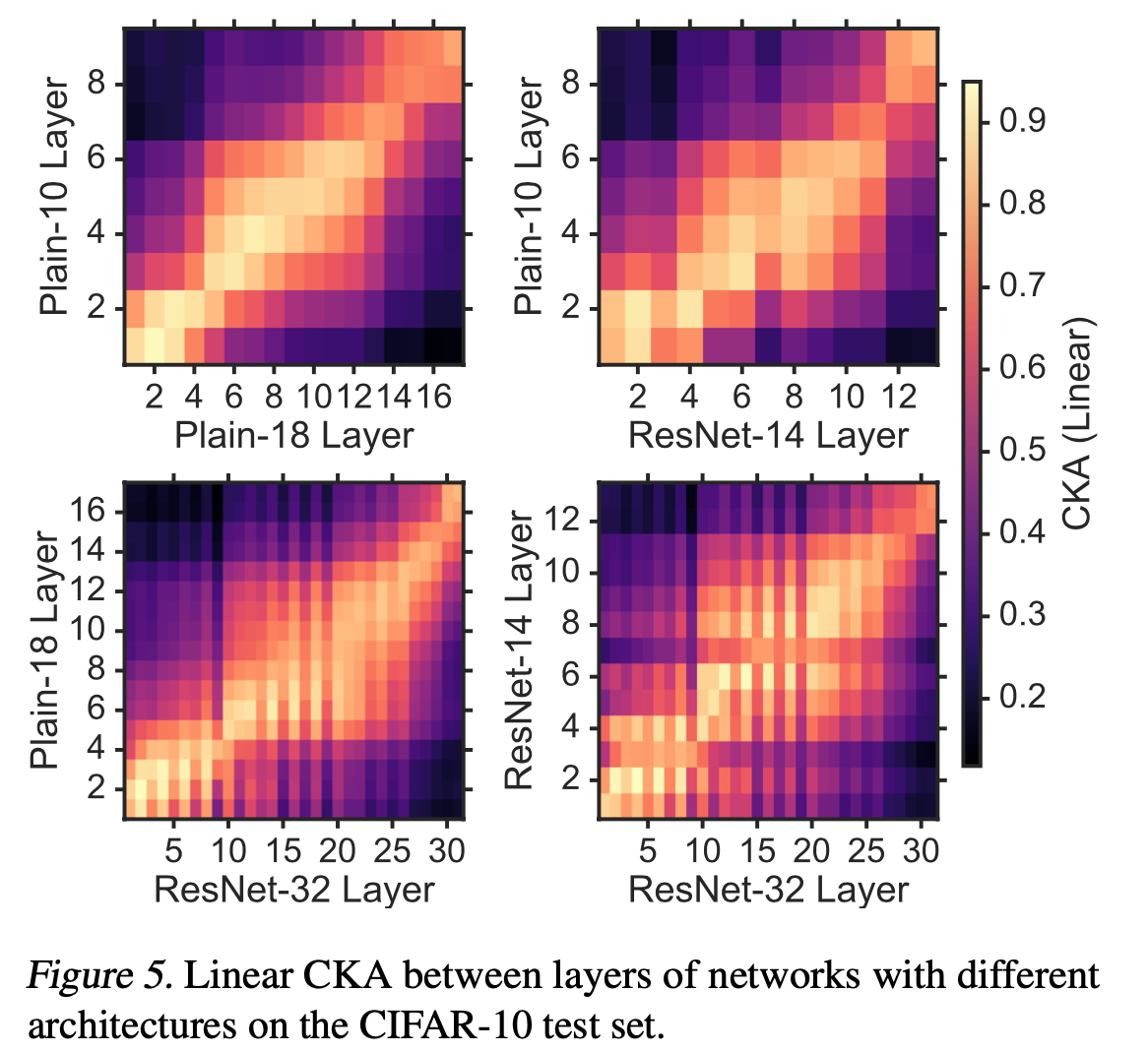
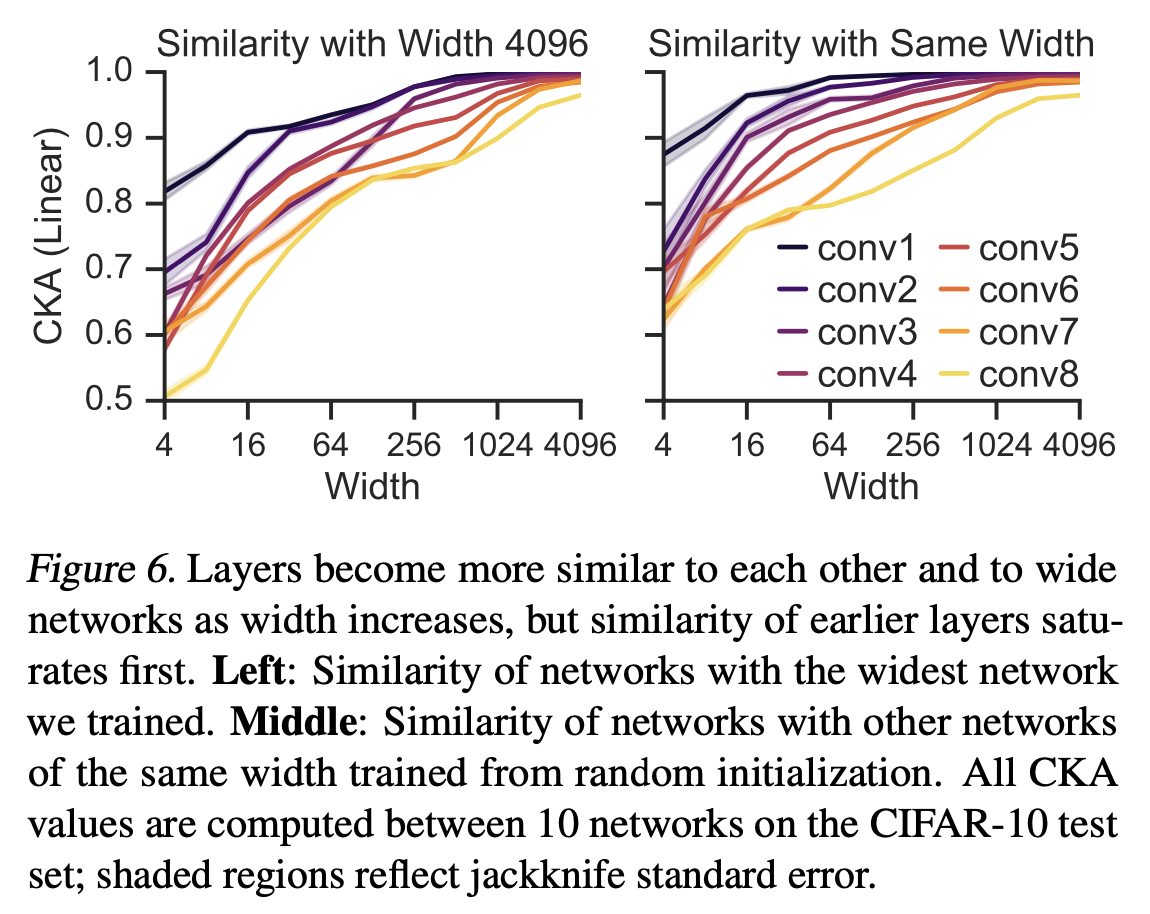
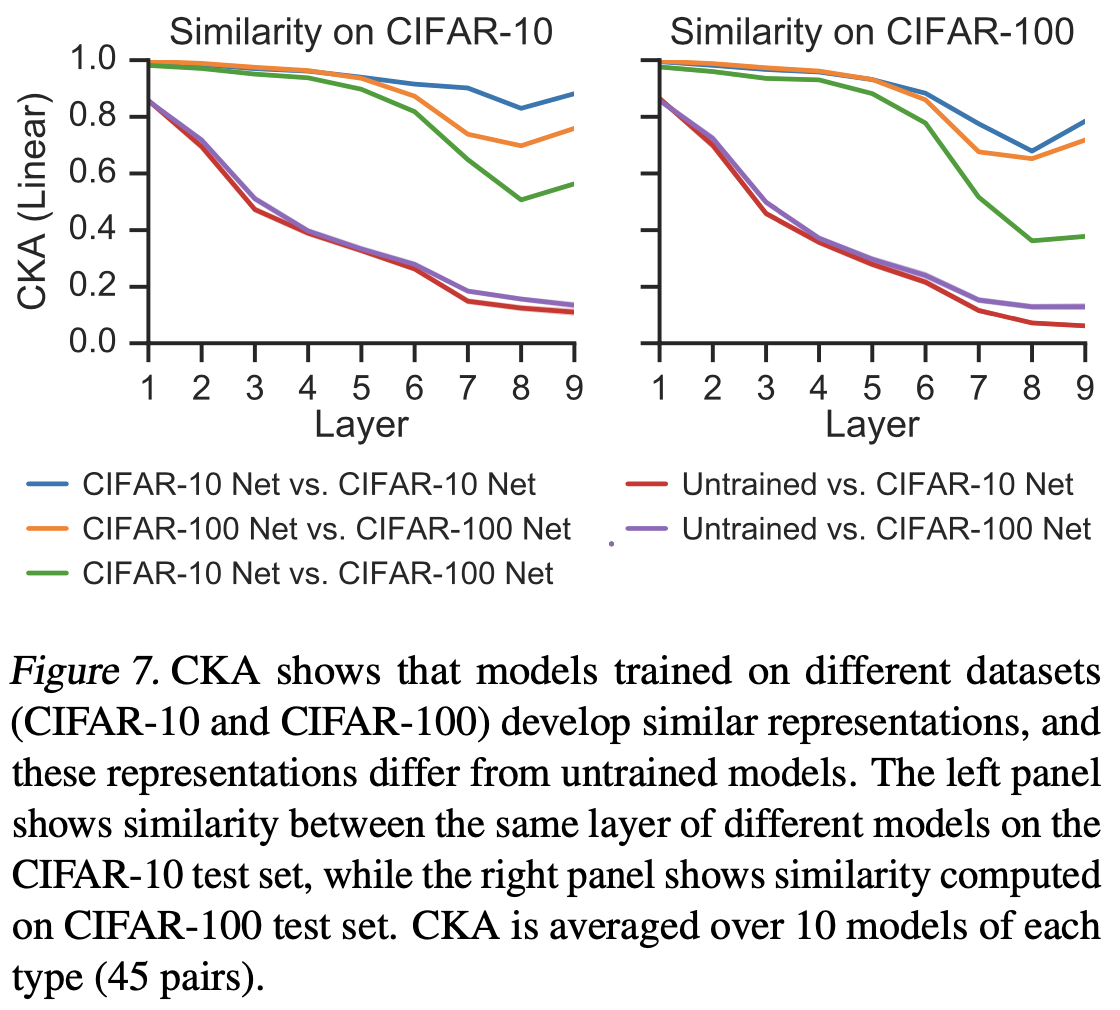
References
- Papers
- SVCCA: Singular Vector Canonical Correlation Analysis for Deep Learning Dynamics and Interpretability
- Similarity of Neural Network Representations Revisited (CKA)
- Insights on representational similarity in neural networks with canonical correlation
- Layer-wise Analysis of a Self-supervised Speech Representation Model
- Comparative layer-wise analysis of self-supervised speech models