Notes

Deep Dive into Low Rank Adaptation (LoRA)

28 Dec 2022

< 목차 >

Motivation

Low Rank Adaptation (LoRA)은 Pre-training 된 Model 을 downstream task 로 fine-tuning (adaptation) 하는 전이 학습 (Transfer Learning) 방법 중 하나이다. LoRA는 model parameter 전체를 update하지 않고 일부분만 update 함으로써, 더 적은 GPU resource로 효율적으로 학습하는 Parameter Efficient Fine-Tuning (PEFT)method로 분류된다.

PEFT method들은 최근 pre-trained model 의 규모가 더 커지면서 (Large Scale) 더욱 대두되고 있는데, 학습에 필요한 GPU 에 올라가는 memory 와 training time, 그리고 학습된 model의 저장 용량 등이 효율적이기 때문에 여러개의 customization 을 만들고 관리해야 하거나 end-user 들이 customization, personalization 하기 용이하다는 것이 장점이다. 또한 pre-trained model 이 가지고 있던 좋은 generalization 능력을 학습을 하면서 잃어버리는 catastrophic forgetting이 일어나는 경우가 많은데, PEFT를 쓰면 방지할 수도 있지만 이는 pessimistic하게 생각하면 underfitting한다고도 볼 수 있다.

Parameter Efficient하다는 것은 몇 가지 의미가 있을 수 있는데, 주로 쓰이는 의미는 실제로 학습시에 미세 조정되는 parameter의 수 (Trainable Parameter) 가 전체 모델의 사이즈와 비교해서 1~2% 밖에 안된다는 의미로 쓰인다. 혹은 저장되는 모델의 parameter가 마찬가지로 1~2% 로 학습된 parameter들만 저장되기 때문에 그 부분에서도 parameter efficient 하다고도 할 수 있다.

한 편, PEFT 방법들 중에서도 LoRA가 특히 주목을 많이 받는데, 그 이유 중 또다른 하나는 아래처럼 model arcitecture 에 module을 끼워넣어 구조 자체를 바꿔버리는 것이 아니라는 것 때문이다. 실제로 Inference 시에 연산 속도에서 손해를 보는 adapter 계열과 다르게 구조를 바꾸지 않기 때문에 속도가 저하되지 않는다.

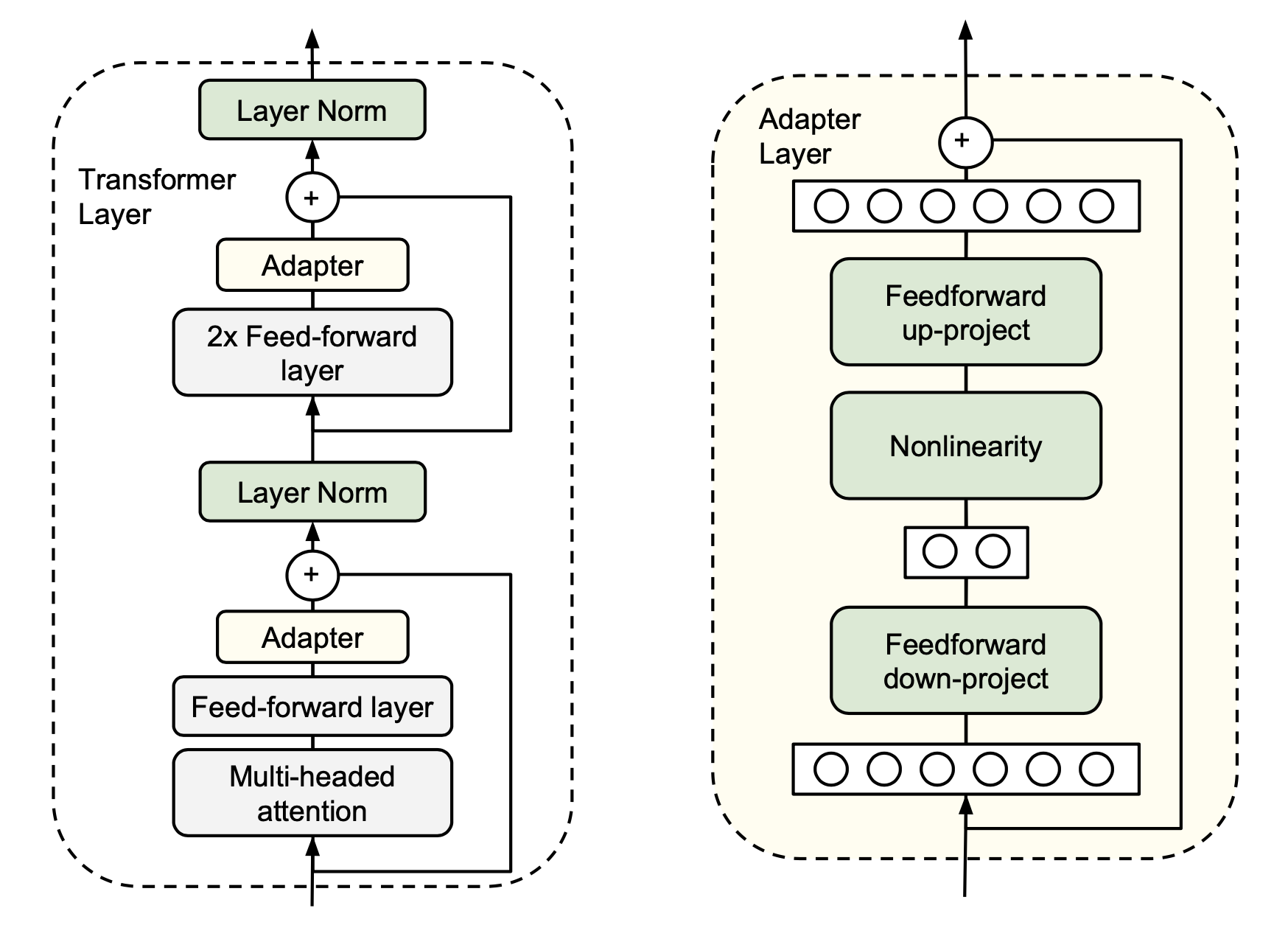houlsby_fig2 Fig. Adapter 계열에서 가장 유명한 Houlsby Adapter는 MHA와 FFN module뒤에 adapter가 추가되면서 logic을 바꾼다

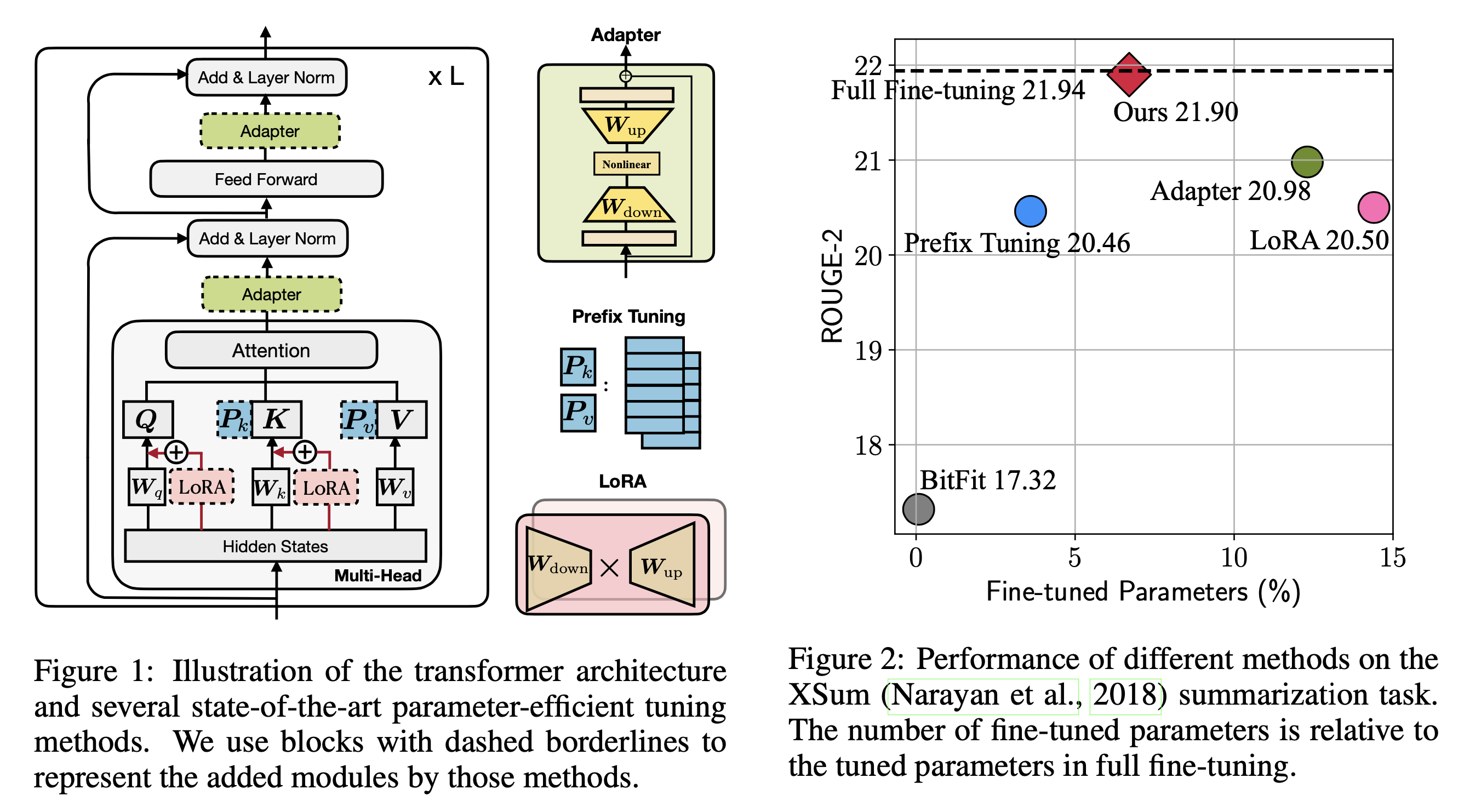towards_fig1 Fig. Well-Known PEFT methods of NLP domain. Source From Towards a Unified View of Parameter-Efficient Transfer Learning

LoRA 의 장점을 좀 더 정리해보자면 다음과 같은 것들이 있겠다.

  • Reasonable and simple approach based on theory (low intrinsic dimension) and diverse experiments
  • Require low VRAM, faster training time, low storage
    • 특히 end-user 나 모델을 개인화 (custom, personalization) 해주는 서비스에 매우 좋음
  • LoRA does not change inference logic (throughput remains same)
  • Applied on various domain and tasks successfully
    • model 구조, domain, task를 막론하고 adaptation 이라면 잘 됨

마지막에 언급한 것 처럼 원래는 NLP 분야에서 먼저 적용됐지만 최근에는 주어진 prompt 로 부터 image 를 만들어내는 text-to-image task의 Diffusion-based Model에 대해서도 LoRA 와 같은 PEFT 를 하는것이 굉장히 잘 먹힌다는것이 밝혀져 더더욱 주목을 받고 있는 중이다.

lora_character Fig. Stability AI 의 Latent Diffusion Model (LDM) 구조 중 Unet 에 대해 LoRA 를 적용해서 몇개 되지도 않는 이미지로 단시간 adaptation 을 했을 때의 결과물. Backbone model 은 Joker 라는 character를 생성해달라고 했을 때, 원작인 cartoon 풍의 image를 많이 봤기에 그 style로 만들지만 LoRA로 Joaquin Phoenix가 연기한 2019년에 개봉작 Joker의 이미지를 학습시킨 경우 generated image style이 확 바뀐걸 느낄 수 있다. Source from link

하지만 필자가 나열한 장점들 중에서 update 해야 하는 parameter 수가 적기 때문에 학습 속도가 빨라진다라는 것은 사실 틀린 이야기 일 수도 있다. 왜냐하면 한 epoch당 걸리는 시간은 모델의 크기에 따라 2배 이상 차이가 나기도 하지만 (Full ft vs LoRA), 실제 수렴하는 지점까지의 training time을 비교해보면 비슷하기 때문이다. 즉 LoRA는 속도가 빠른대신 더 큰 lr로 더 full ft보다 2~3배의 epoch을 학습해야 하는 것이 일반적이다. 그리고 model의 generalization 능력을 유지한다는것은 어떻게 보면 그냥 under-fitting했다고 할 수도 있기 때문에 target 하는 task 가 성능이나 task fitting 정도가 더 중요하다면 LoRA를 쓰는 걸 심사숙고 해봐야 할 것이다.

LoRA 의 처음 시작은 원 논문에서처럼 RoBERTa, DeBERTa 등 BERT 계열의 pre-trained model을 Natural Laugnage Understanding (NLU) task로 fine-tuning 을 하는 것이었다.

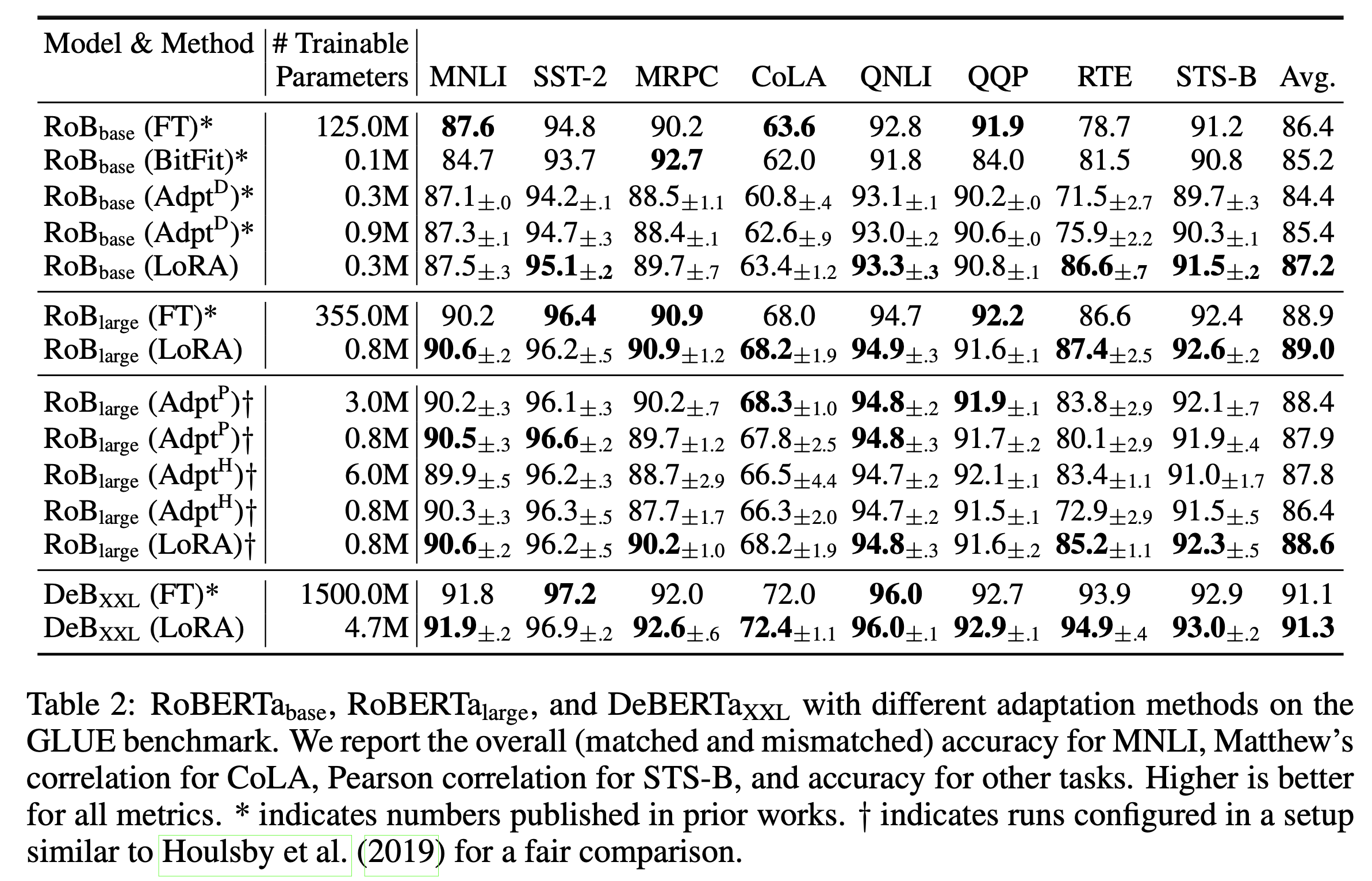lora_paper_table2 Fig. NLU Task Benchmark Table

RoBERTa Large model의 경우 전체 parameter의 개수가 355,000,000 (350M)정도 되는데, 이 중에서 LoRA는 오직 0.8M만 tuning에 사용했다. 그럼에도 LoRA는 Full Fine-tuning 을 앞서는 성능을 보여주기도 했는데, 이는 NLU Task가 너무 간단해서 그런면도 있습니다. 즉 이런 간단한 task 의 경우에는 LoRA가 특별한게 있다기 보단 task특성상 오히려 underfit한게 좋은거 라고 생각할 수도 있는 것이다.

그리고 실제로 제가 속도를 비교하기 위해 LoRA 를 구현해서 RTE Task에 대한 튜닝을 했을 때는 성능이 Full Fine-tuning 이 더 좋았습니다만 epoch당 속도는 2배이상 LoRA가 빨랐습니다. (hyperparameter를 많이 찾아보진 않았음)

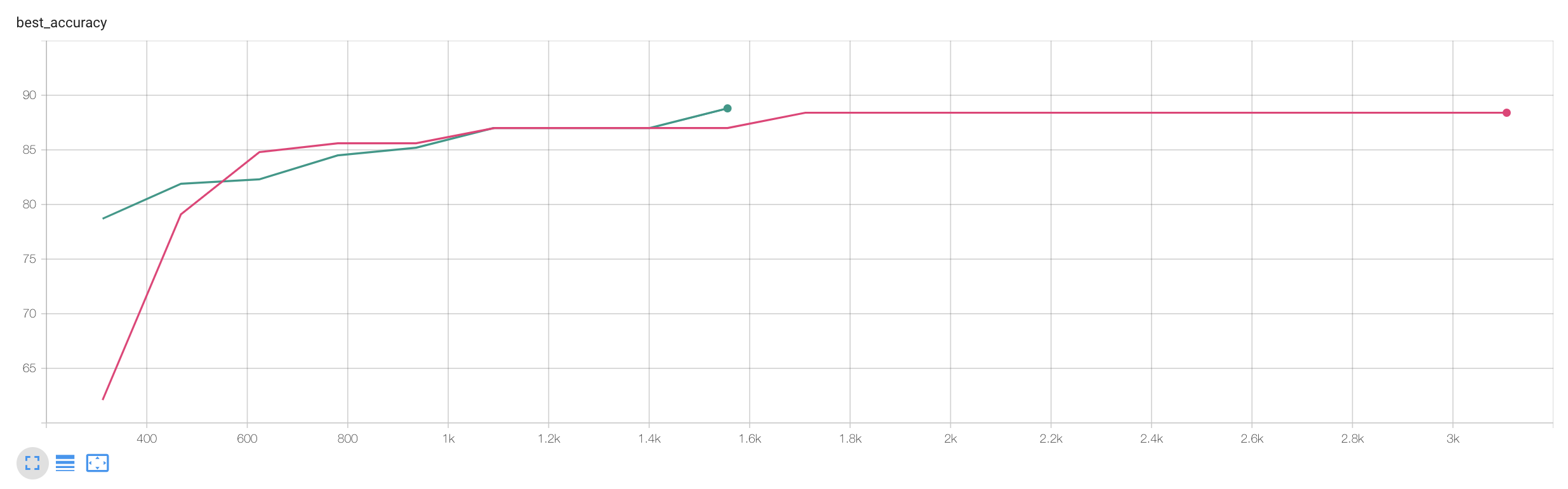roberta_rte_ft_vs_lora_fig1 Fig. 실제로 필자가 NLP의 GLUE task로 model을 Full Fine-tuning VS LoRA를 해본 결과, 근소하게 Full Fine-tuning의 성능이 더 좋았다.

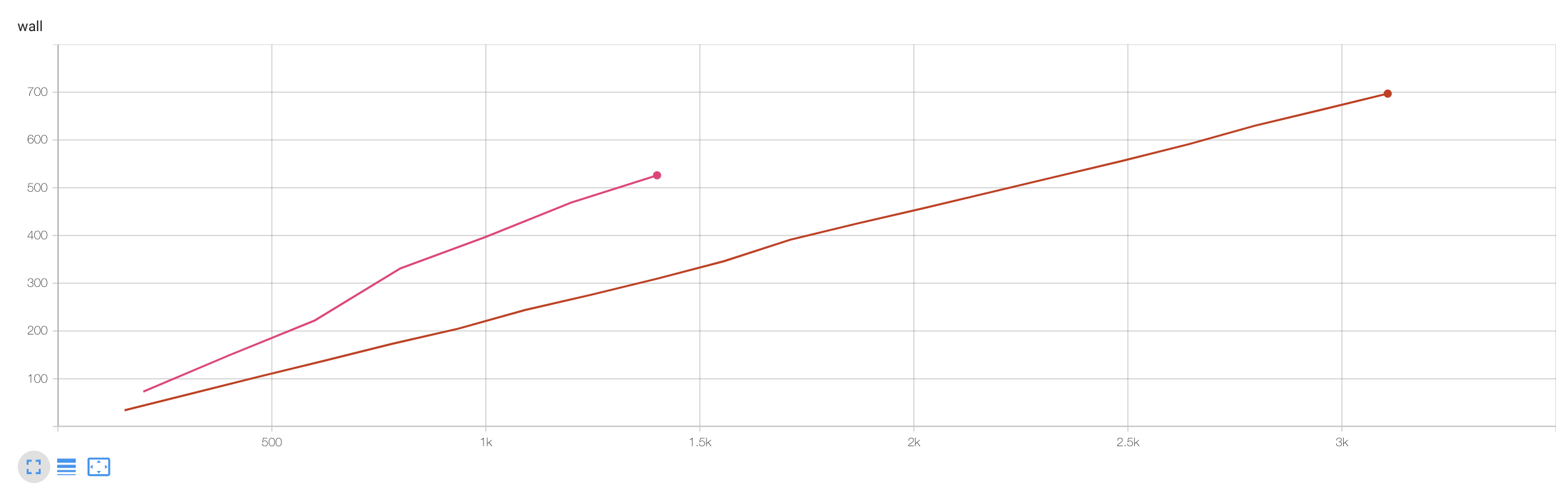roberta_rte_ft_vs_lora_fig2 Fig. 논문에서 주장한 hyperParameter 에 따르면 특정 task 에 대해 Full ft 는 10epoch, LoRA 는 30epoch을 학습했다고 한다. 실제로 필자가 NLP의 GLUE task로 model을 학습했을 때 두 실험 중 LoRA의 training wall clock time(y축)이 더 길었다.

이후 개정된 Arxiv version에는 GPT-3 같이 거대한 모델에 대해 실험을 해서 역시 Full Fine-tuning 에 버금가는 성능을 보여줌으로서 PEFT의 효율성에 대해 추가적인 언급이 있었다.

이제 LoRA가 왜 이게 작동하는지? 정확히 무엇인지? 에 대해 알아보자.

Low Rank Adaptation (LoRA)

LoRA의 구현 자체는 굉장히 간단하다. 아래의 figure 가 LoRA를 설명하는 전부이다.

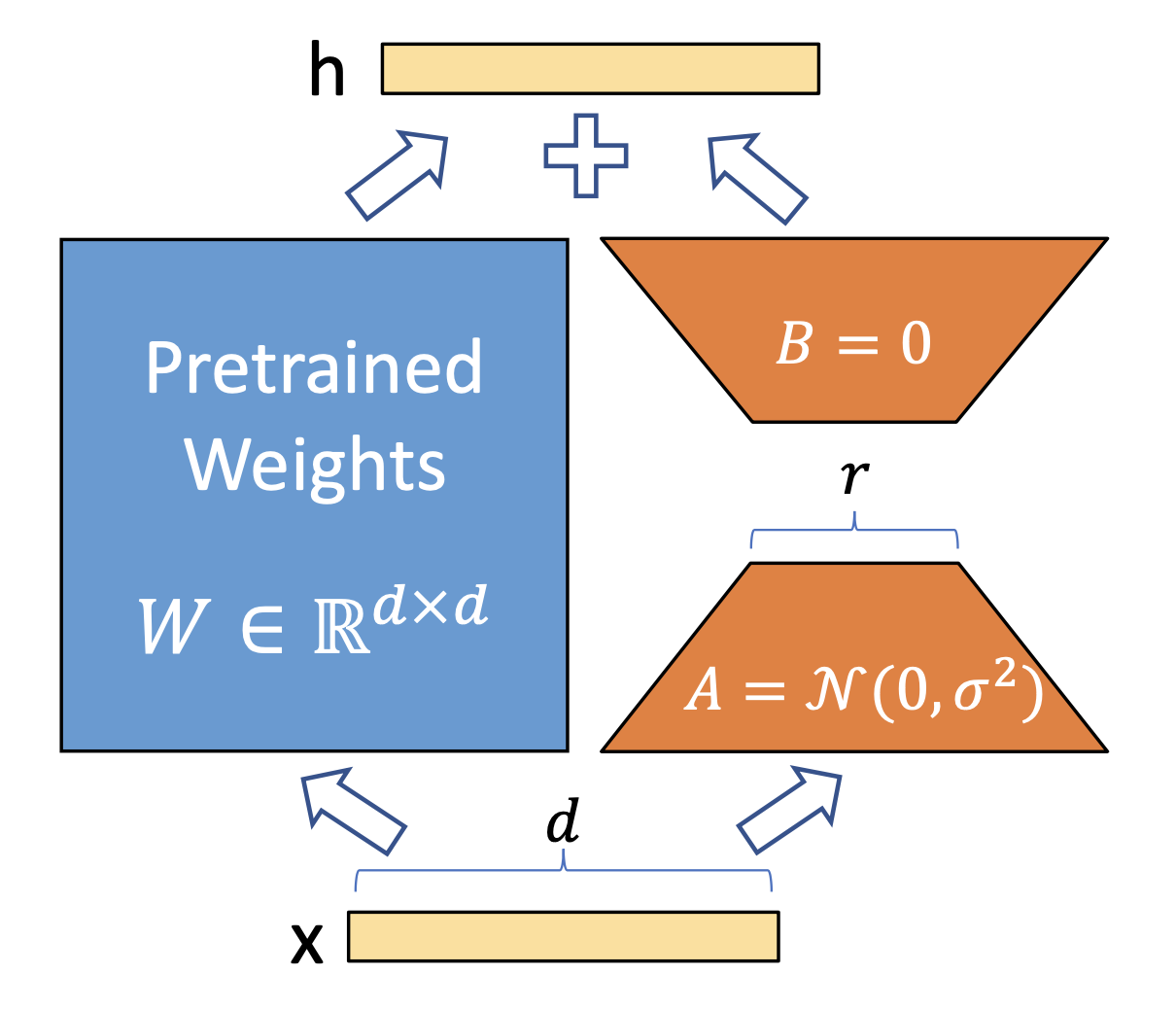lora_paper_fig1 Fig. Diagram of LoRA

어떤 pre-trained model 의 특정 layer 의 weight matrix 가 \(W_0 \in \mathbb{R}^{d \times d}\)라고 할 때, 이 layer 에 입력 x 를 넣었을때 output, \(h\)는 다음과 같을 것이다 (no bias일 경우).

\[h = Wx\]

여기서 pre-trained weight 을 특정 task 에 대해서 adaptation 한다면 weight이 gradient descent로 update 될 것이다. Update되는 변화량을 \(\Delta W\)라고 하면 최종적으로 우리가 얻게되는 fine-tuned model의 weight은 다음과 같다.

\[W^{\ast} = W_0 + \Delta W\]

그렇다면 fine-tuned model 로 forwarding 을 한 경우 layer output hidden, \(h\)은 다음과 같이 변하게 되는데,

\[h = W^{\ast}x = (W_0 + \Delta W)x\]

LoRA는 initial weight matrix, \(W_0\)는 update 하지 않고 (freezing), update 되는 \(\Delta W\)를 저차원 (Low Rank)으로 행렬 분해 (Matrix Decomposition)하고, 이 분해된 layer들만 update를 하게 된다.

\[h=W_0 x+\Delta W x=W_0 x+B A x\]

무슨말이냐면 원래 update될 parameter, \(\Delta W\)는 \(W_0\)와 같은 size여야 하는데, 이 detla가 원래는 full rank일지 rank가 3일지 몰라야 하지만 인위적으로 low rank parameterization하여 고정시킨 후 학습하겠다는 것이다. 이는 모든 linear layer라면 다 적용이 가능한 technique이지만 일반적으로 transformer block 의 일부분인 Q, V projection layer에 적용한다.

lora_fig_custom Fig. LoRA paper 에서는 Transformer 각 Layer 의 Q, V Weight Matrix 에만 적용된 결과가 report 되어 있다. Source from link

Diffusion-based model의 경우에는 conv layer, Q, K, V, O layer 모두에 LoRA를 쓰는 것이 일반적이다.

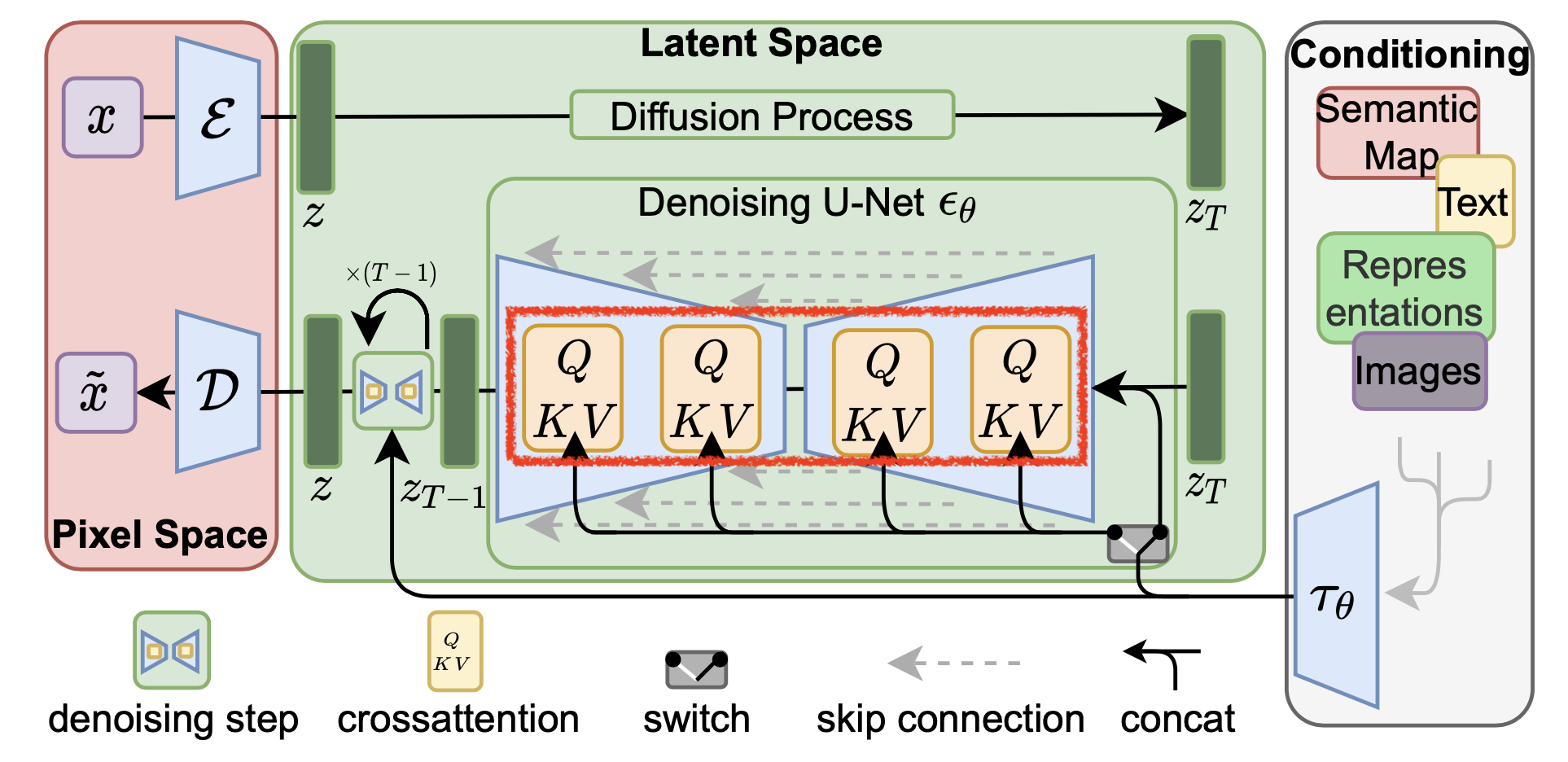lora_ldm Fig. Diffusion Model 에 적용된 LoRA 는 보통 UNet 의 Cross Attention 에 적용할 수 있지만 Bias, Conv2D 등 모든 곳에 적용되기도 한다.

Why does it work? : Over-parametrized Models have Low Intrinsic Rank

왜 LoRA 가 working 하는 걸까? 왜 하필 이런 low rank parameterization을 했을까?

그 배경에는 Over-parametrized model이 경우 (데이터셋의 개수보다 모델 parameter의 수가 더 큰 경우), gradient based optimization을 통해 찾은 solution이 실제로는 Low Intrinsic Rank를 가지고 있으며, 그렇기 때문에 ‘adaptation (fine-tuning)을 할 때의 update weight, \(\Delta W\)도 마찬가지로 Low Intrinsic Rank 를 가질 것이다’라는 가정이 깔려있기 때문이다.

(In Paper)

We take inspiration from Li et al. (2018a); Aghajanyan et al. (2020) 
which show that the learned over-parametrized models in fact reside on a low intrinsic dimension. 
We hypothesize that the change in weights during model adaptation also has a low “intrinsic rank”,
leading to our proposed Low-Rank Adaptation (LoRA) approach. 
LoRA allows us to train some dense layers in a neural network indirectly 
by optimizing rank decomposition matrices of the dense layers’ change during adaptation instead, 
while keeping the pre-trained weights frozen.

LoRA의 철학을 이해하기 위해서는 intrinsic rank (dimension)이 무엇인지 알아야 한다. Measuring the Intrinsic Dimension of Objective Landscapes (Li et al.)라는 paper가 가장 먼저 Deep Learning (DL)의 objective function 에 대해서 intrinsic dimenstion을 계산하는 방법을 제안했고 Intrinsic Dimensionality Explains the Effectiveness of Language Model Fine-Tuning (Aghajanyan et al.)에서 이를 NLU task 로 확장해 Pretrained Langugage Model (PLM) 들도 low intrinsic rank 를 가지고 있다는 것을 실험적으로 보여주기 때문에 이 두 paper를 잘 봐야 한다.

What is Intrinsic Dimesnion ?

Intrinsic Dimension 이란 wiki 를 찾아보면 어떤 dataset을 표현하는데 필요한 최소한의 variable을 의미한다고 나와있다. 이와 유사하게 Digital Signal Processing (DSP)에서도 어떤 function을 approximation하기 위해 표현한 최소한의 변수는 얼마인가? 같은 의미로 사용된다고 한다. 이게 무슨소리일까?

예를 들어서 어떤 dataset의 feature가 3차원 이라고 생각해 보자. 원래 각 data point 를 표현하기위해서는 3차원 좌표가 모두 필요하지만 우연히 이 데이터들이 어떤 평면 위에 놓여져 있다면 어떨까?

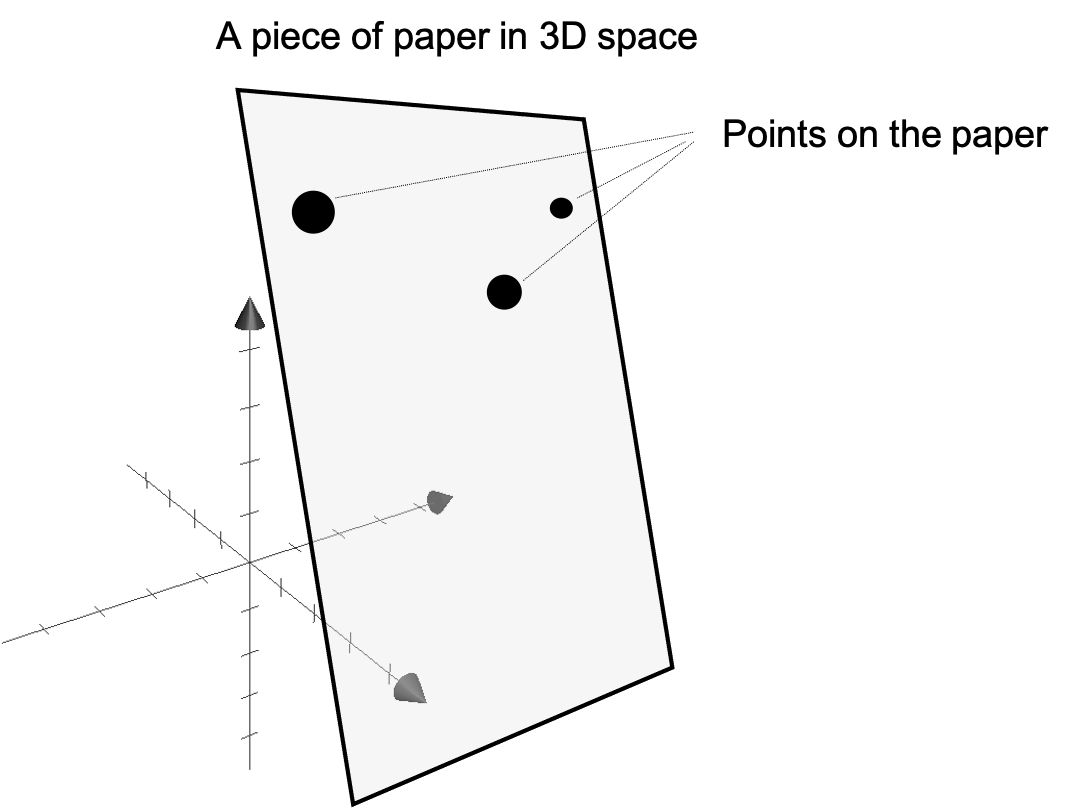intrinsic_example_fig1 Fig. Source From Matthew N. Bernstein’s post

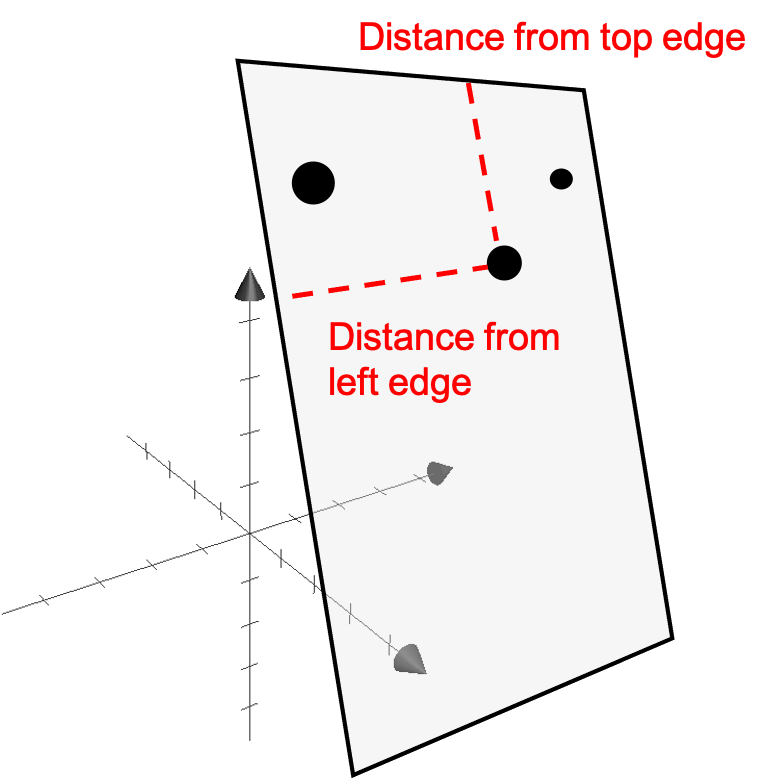
실제로 이 dataset 전체를 표현하기 위한 변수들은 x,y,z 까지 세개의 basis vector가 필요한 것이 아니라 data points들이 놓여져 있는 plane의 basis vector 2개만 있으면 될 것이다.

intrinsic_example_fig2

이제 DL의 objective landscape의 intrinsic dimension에 대해 이해하기 위해 Li et al. 에서 나온 toy problem 실험에 대해 살펴보도록 하자. 먼저 다음과 같이 D 차원의 parameter를 갖는 model이 있다고 치자.

\[\theta^{(D)} \in \mathbb{R}^D\]

모델은 randomly initializtion 되었고, gradient based optimization을 통해 우리가 얻은 최종 solution은 다음과 같다.

\[\theta_{\ast}^{(D)}\]

이제 $D=1000$이며, \(\theta^{(D)}=[\theta_0,\theta_1,\cdots,\theta_D]\) 첫 100개 elements는 합이 1이되도록, 그 다음 100개는 2가 되도록 … 이런식으로 10개 그룹으로 나눠져서 squared error cost function 을 최소화 하는 방향으로 학습되는 경우에 대해 생각해보자. (지금의 setting은 일반적인 DL setting과는 조금 다르다)

이 문제의 solution 들을 구해보면 실제로 굉장히 redundant 하다는 것을 알 수 있다고 하는데, linear algebra 조금만 알고있으면 soultion들의 manifold 가 990 차원의 초평면 (hyperplane)이 된다는 것을 알 수 있다고 한다. 이 말의 뜻은 cost (loss) 가 0인 어떤 point 에 대해서 여전히 zero cost 를 유지하면서 이를 움직일 수 있는 orthogonal direction이 990개나 된다는 뜻이라고 하는데 이를 수식으로 표현하면 다음과 같으며, 이 때 D가 원래차원, s가 solution set 의 차원, 그리고 \(d_{int}\) 가 바로 intrinsic dimensionality라고 한다고 한다.

\[\begin{aligned} & D = \color{red}{d_{int}} + s & \\ & 1000 = 10 + 990 & \\ \end{aligned}\]

사실 필자는 이 실험이 잘 와닿지 않아서 더 간단한 example을 떠올려 보기로 했다. 이번에는 3차원 parameter space 에서 optimization을 한다고 생각해보자.

\[\theta \in \mathbb{R}^3\]

아래와 같이 initial point, \(\theta_0\) 에서 출발하는데, 우리는 \(\theta\) 의 한 element 인 \(\theta_3\) 가 0이 되도록 optimization을 하는 것이 목표이다.

intrinsic_dim_toy_example_fig1

우리는 지금 intrinsic dimension 이고 뭐고 모르기 때문에 3차원에서 \(\theta\)를 이리저리 움직이면서 objective 를 만족하는 parameter 를 찾아야 한다. Solution은 \(z\)가 0이기만 하면 되기 때문에 \(\theta_3\) 가 0이기만 하면 되니까 \((\theta_1,\theta_2,\theta_3)\) set으로 봤을때 (1,2,0), (4,7,0), (999,1213,0) 어떤 값이어도 된다. 여기서 gradient base optimization을 하려면 loss function, dataset, model parameter 이 세 가지 요소를 가지고 landscape을 그린 뒤 전체 공간에서 parameter를 움직여야 하는데, model param이 3차원이기 때문에 3차원에서 이리저리 움직여야 한다.

intrinsic_dim_toy_example_fig2

하지만 지금의 경우 직관적으로 이런 생각이 들 수 있다. ‘3차원에서 이 parameter 를 조정할 필요가 있을까?’, '그냥 z축에 대해서 최적화를 하면 되지 않을까?'

intrinsic_dim_toy_example_fig3

즉 어떤 경우에는 우리가 optimization을 하는데 \(\theta\)를 움직여봐야할 공간은 움직여야할 공간이 아주 운좋게도 1차원에 있을수도 있는 것이다. 이렇게 우리가 바로 알 수는 없지만 full parameter space가 아니라 그 보다 작은 sub-space space에서도 full parameter space에서 search를 한 것과 거의 같은 성능 (solution)에 도달할 수 있는 최소한의 dimension을 바로 DL의 loss landscape의 (paprameter space의) intrinsic dimension이라고 paper는 정의한 것이다.

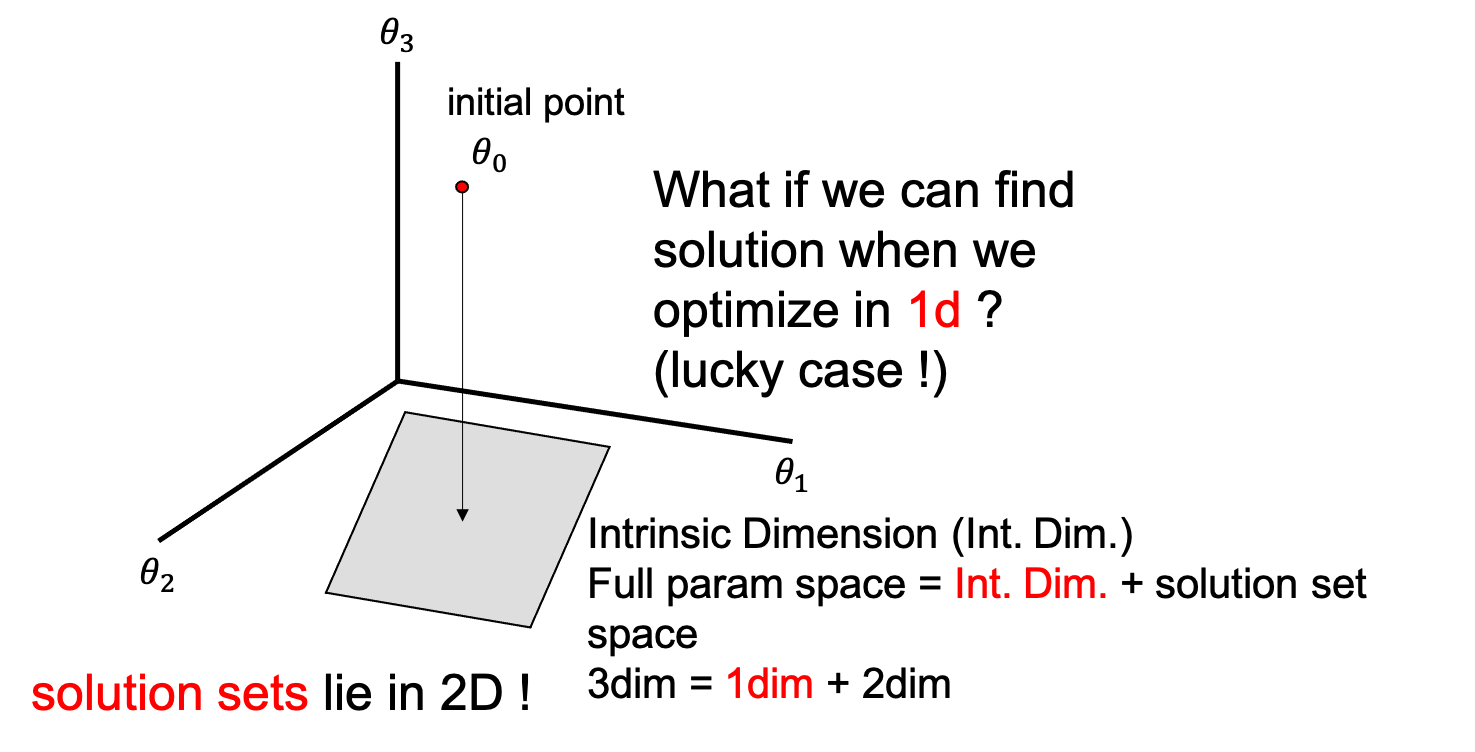
그리고 intrinsic dimension을 알면 우리는 solution space까지 정의할 수 있는데, 지금의 경우 solution space는 2차원이다. 왜 2차원인지에 대해서는 full parameter space가 \(D=3\)이지만 현재 intrinsic dimension은 \(d_{int}=1\)이기 때문에, 그 나머지 space가 모두 objective를 만족하는 solution set이 되기 때문이다.

\[\begin{aligned} & D = d_{int} + s & \\ & 3 = 1 + 2 & \\ \end{aligned}\]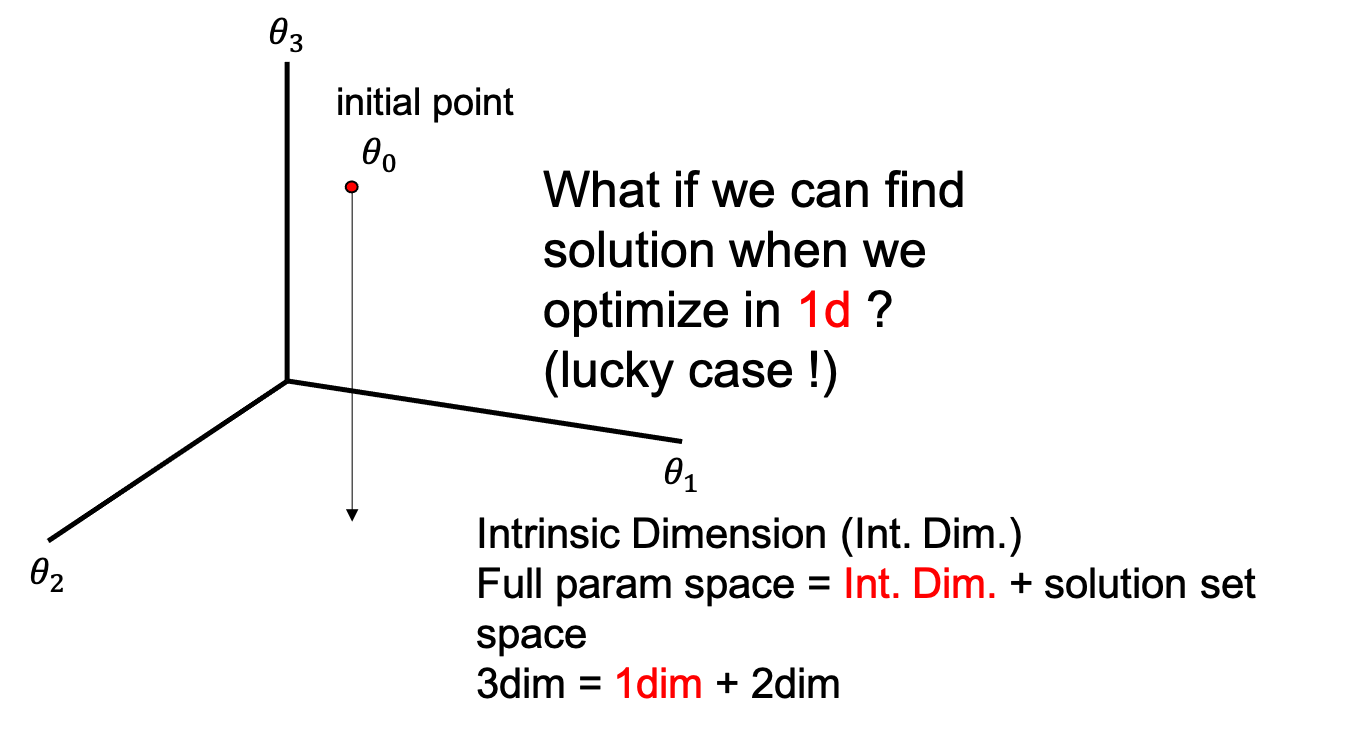

intrinsic_dim_toy_example_fig4

지금의 toy example은 \(\theta_3\)가 0이기만하면 어떤 parameter set도 solution이 될 수 있기 때문이며, 그 공간은 아래 figure에 나와있는 것 처럼 \(\theta_1,\theta_2\)가 span하는 공간을 전부 포함한다.

intrinsic_dim_toy_example_fig5

Intrinsic Dimension of Deep Neural Network

이제 toy problem이 아닌 실제 경우에 대해 생각해 보려고 한다. 이 paper의 key는 우리가 실제로 학습하는 Deep Neural Network (DNN)의 parameter space는 실제로는 너무 과하고 (over-parameterized), 실제로 optimization은 그보다 더 작은 sub-space에서 해도 된다는 것이 핵심이다. (당연하게도 paper가 주장하는 바는 intrinsitc dim이 낮기 때문에 optimal solution은 많다는 것이며 이것이 DNN이 잘 되는 이유가 될 것이다)

그래서 paper에서는 full model param space가 \(D >> 10\)일 때, 10차원 쯤 되는 작은 제약된 공간에서만 움직여도 solution을 찾을 수 있을까?를 실험해 보았다. 어떤 \(D \times d\) 차원을 갖는 행렬 \(P\) 가 존재하고 d 차원 parameter vector 인 \(\theta^{(d)}\)가 있다고 생각해보자 (\(d\)는 \(D\)보다는 훨씬 작다). 이제 \(\theta^{(D)}\)를 아래의 수식으로 다시 정의할 수 있다.

\[\theta^{(D)} = \theta_0^{(D)} + P \color{red}{\theta^{(d)}}\]

여기서 \(\theta_0^{(D)}, P\)가 고정 (frozen) 되어있고, \(\theta^{(d)}\)만 학습된다면, 이제 원래의 parameter 차원보다 훨씬 작은 어떤 \(d\)차원의 자유도만을 갖는 random subspace에서 학습을 하는 경우가 된다.

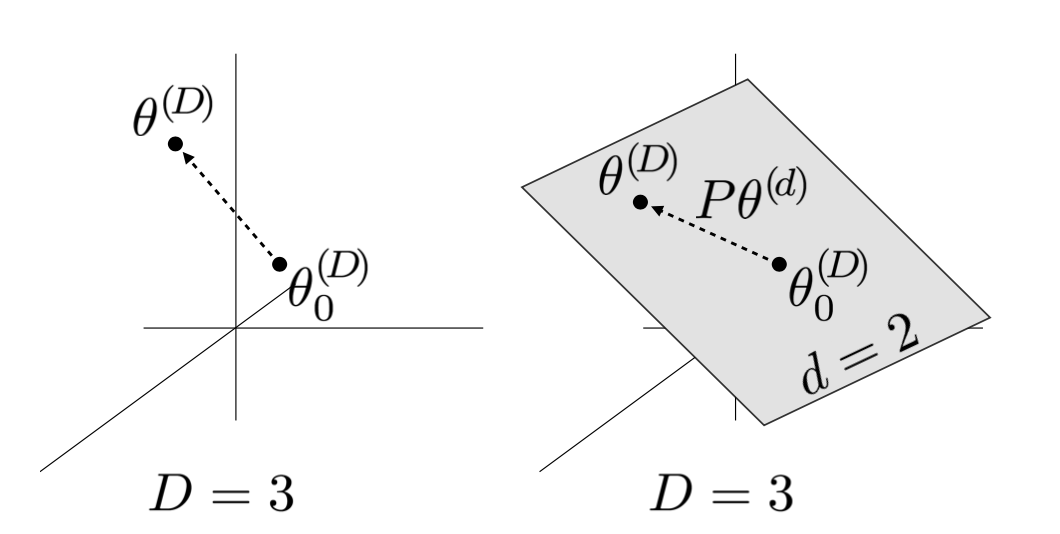2018_low_intrinsic_fig1a Fig. 실제로는 3차원에서 (좌) 최적화 되어야할 것이 2차원 (평면) 에서 최적화 될 수 있음 (우).

즉 위의 figure의 경우에서 3차원이 전체 parameter space지만 optimize는 2차원 평면에서만 진행 되는 것이 된다. 이 때 \(\theta^{(d)}\)는 모든 값이 0 으로 초기화되므로 맨 처음 값은 \(\theta^{(D)} = \theta_0^{(D)}\)가 된다. 몇가지 덧붙히자면 \(d=D\) 로 크기가 같고 \(P\) 행렬이 모든 대각 행렬이 1 이고 나머지는 0인 Identity Matrix 라면 원래의 optimization 을 recover 하게 된다. 이런 일반적인 방식의 optimization을 paper에서는 direct optimization이라고 한다. 또한 마찬가지로 크기가 같고 \(P\) 행렬이 모든 \(\mathbb{R}^D\)에 대해서 random orthonormal basis라면 direct optimization 의 rotation 버전이 된다고 한다.

이제 실제로 NN을 학습해보자. 논문에서는 간단한 Fully Connectied (FC) Network와 Convoluation Network로 이루어진 LeNet등에 대해 direct optimization을 한 경우의 \(90%\) 성능에 달하는 \(d_{int90}\)지점을 측정하기 위해 \(d\)를 작은 값 부터 천천히 증가시켜 eval accuracy를 측정했다..

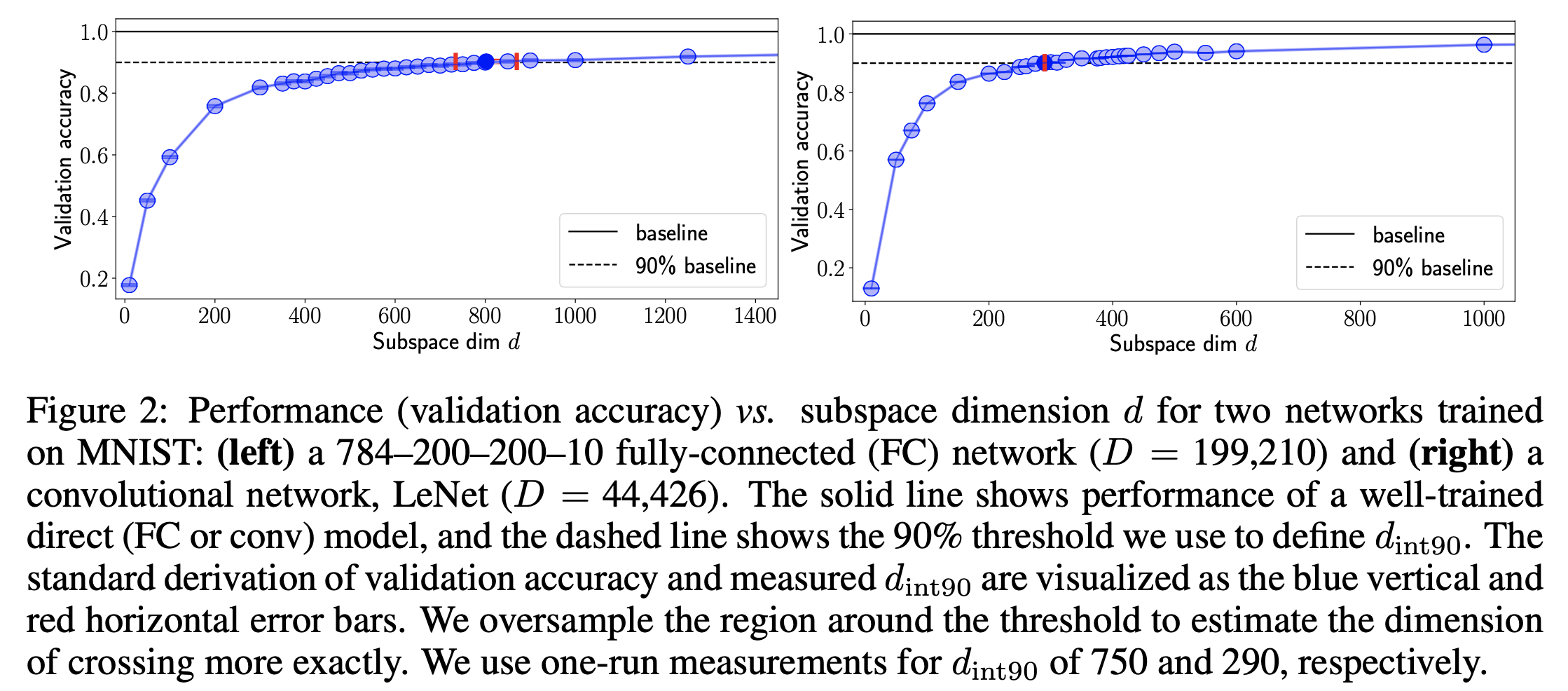
2018_low_intrinsic_fig2

그리고는 위와 같은 결과를 얻었는데, 실제로 NN의 크기에 비해 \(90%\) 성능에 도달할 수 있는 intrinsic dimension 은 꽤 작았음을 알 수 있었다고 한다. 이는 NN parameter가 실제로는 그렇게까지 많이 필요 없다는 말과 같고 논문에서는 결과적으로 압축할 여지가 많다 (compressible) 하다고 표현하기도 한다. FC Network 의 경우 750 밖에 필요하지 않았고 LeNet에 대해서는 이보다 훨씬 작은 값이 필요했다고 합니다. (MNIST, CIFAR 모두에서)

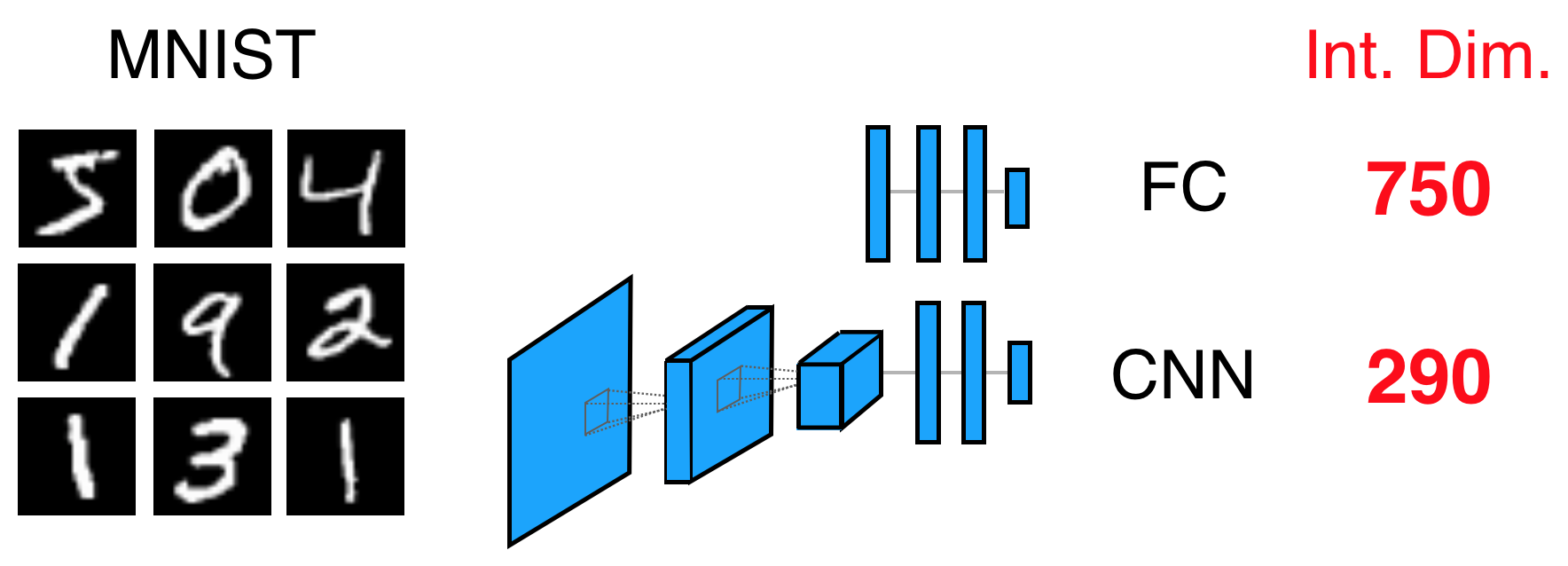intrinsic_blog_fig1 Fig.

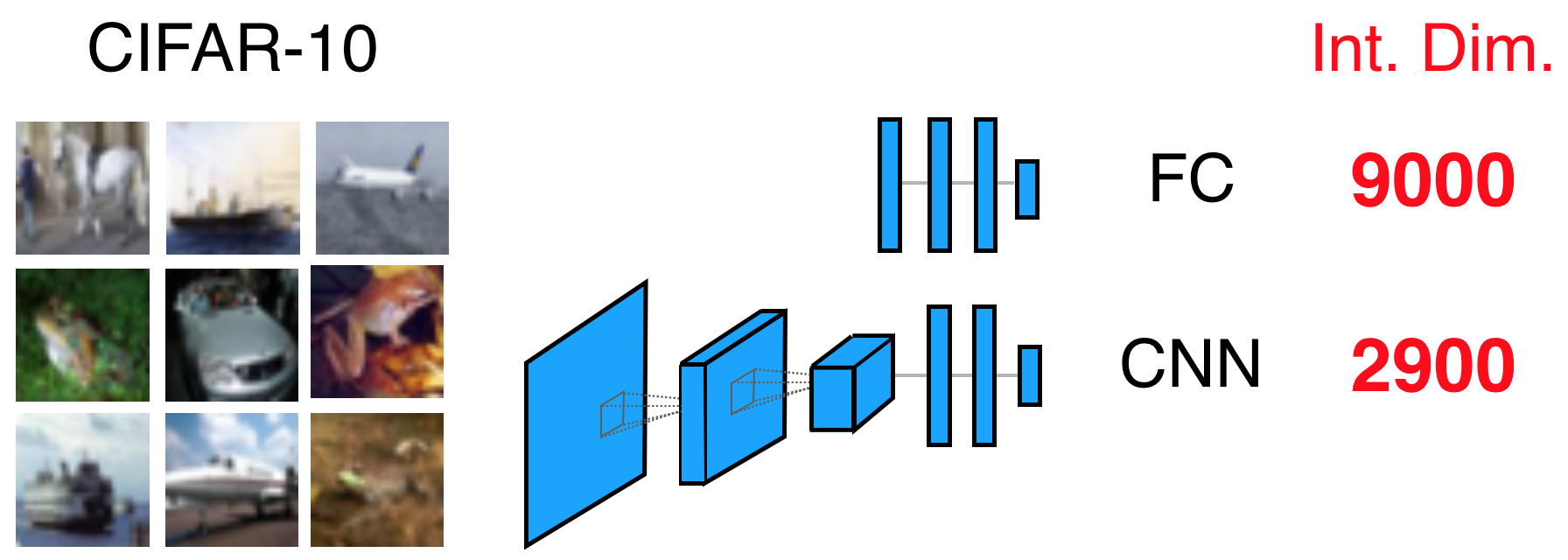intrinsic_blog_fig3 Fig.

또 간단한 pong, humanoid task를 Reinforcement Learning (RL)로 학습했을 때에도 NN은 본래의 parameter size보다 훨씬 더 작은 intrinsic dimension을 갖고있음을 확인할 수 있었다고 한다.

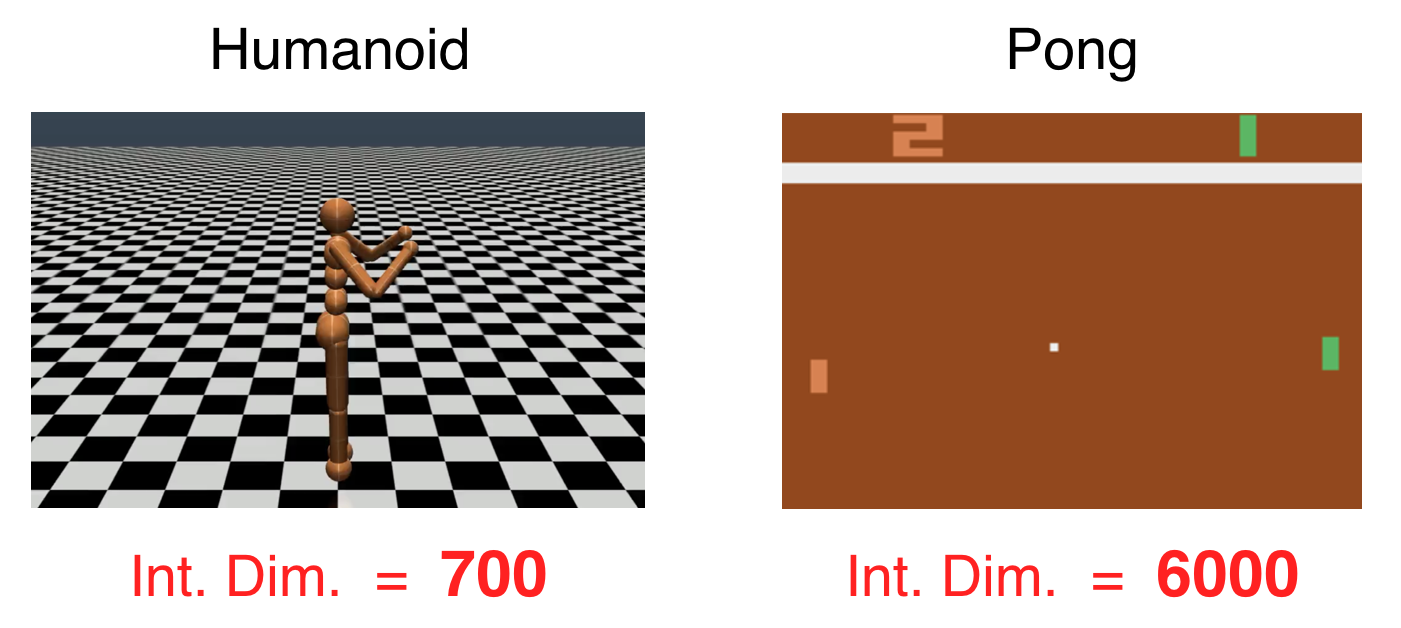intrinsic_blog_fig4 Fig.

Aanlysis on Wider and Deeper (Taller) Network

추가적으로 아래와 같이 intrinsic dimension이 750 인 FC Network 의 hidden size를 늘려보고 (make model wider), 레이어를 더 쌓는 (make model deeper (taller)) 실험을 했을때 재밌는 결과가 있었다고 하는데,

intrinsic_base Fig. baseline FC Network

바로 어떻게 해도 모델의 intrinsic dimension이 750 으로 유지되었다는 것이다.

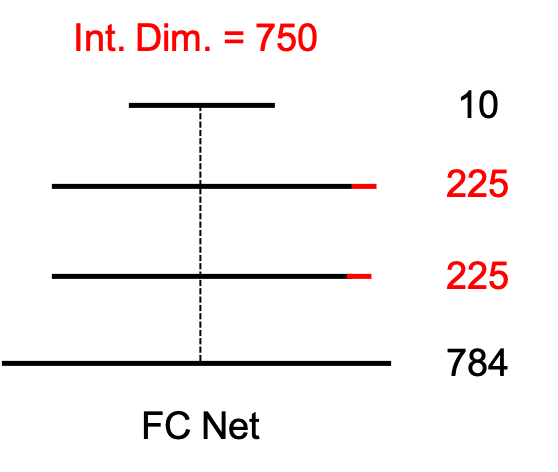intrinsic_wider Fig. wider model

intrinsic_deeper Fig. deeper model

저자들은 이로부터 Deep Learning을 할 때에는 더 큰 model 을 학습하는게 쉽다는 일반적인 특성이 이 때문일 수 있다고 주장했다. 물론 dataset, task, model architecture 구조에 따라 다르긴 하겠으나, 그 이유는 FC를 예로 들어볼 때 784–200–200–10 FC Network의 full parameter size가 199,210 (bias 포함)에서 229,735이 되었음에도 여전히 intrinsic dimension은 750 이므로 결과적으로 solution set이 존재하는 공간이 더 늘어난 것이 되기 때문이다. 즉 모로가도 서울로 가기만 하면 100점을 받는 상황에서 goal인 지점이 훨씬 늘어난 것이다.

\[\text{Full Param Space} = \text{Int. Dim} + \text{Solution Space}\] 
(In paper)
This latter result has the profound implication that once a parameter space is large enough to solve a problem, 
extra parameters serve directly to increase the dimensionality of the solution manifold.

Some networks are very compressible

Paper에는 더 많은 discovery 와 application이 있지만 하나만 더 얘기하고 넘어가려고 한다. Intrinsic dimension을 측정함으로써 한가지 얻어갈 수 있는 것은 model을 performance degradation이 거의 없는 선에서 압축해 결과적으로 저장 공간을 줄일 수 있다는 것이다.

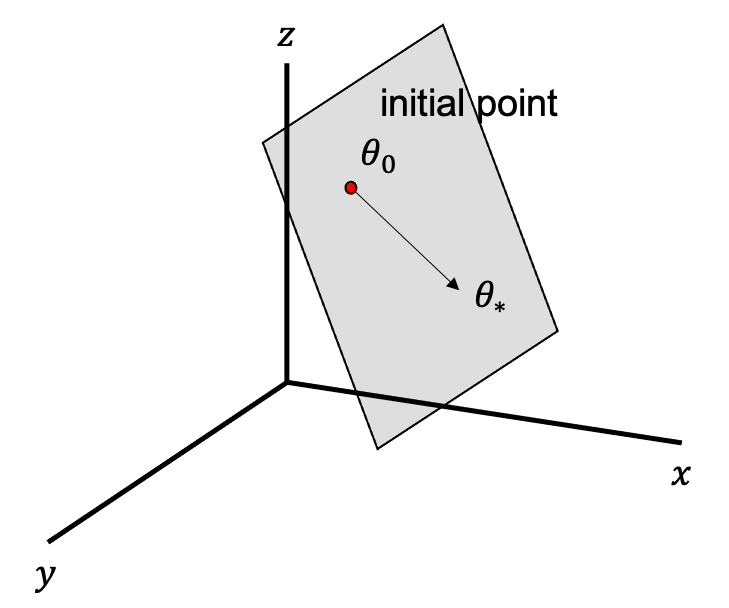subspace_fig1 Fig.

위와 같이 실제로 우리에게 필요한 것은 intrinsic dimension과 \(P \in \mathbb{R}^{D \times d}\)공간으로 Projection 될 \(\theta^{(d)} \in \mathbb{R}^{d \times D}\)이므로 P를 나타낼 random seed와 (P는 학습 안됨), learned parameter, \(\theta^{(d)}\)만 정의하는 것으로 model을 정의할 수 있기에 저장 공간을 수십배 절약할 수 있는 것이 된다. 여기서 주의할 점은 저장 공간이 줄어들엇다는 것이지 model의 속도가 개선되었다거나 하는 점은 없다는 것이다.

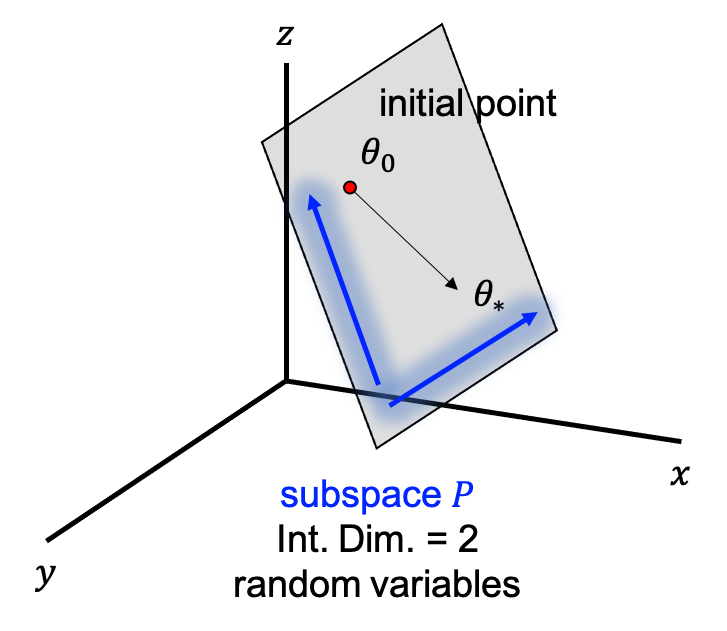subspace_fig2 Fig. random generated variable 2 개로 subspace 를 나타낼 수 있다.

Analysis of Intrinsic Dimension in NLU Tasks

이제 LoRA의 intrinsic dimension에 대한 reference 중 다음으로 넘어가자. Paper title은 Intrinsic Dimensionality Explains the Effectiveness of Language Model Fine-Tuning이다.

저자들의 첫 번째 observation은 model size가 클수록, 학습이 더 잘 될수록 (RoBERTa가 BERT보다 좋다고 할 수 있음), full fine-tuning의 \(90%\)성능을 낼 때의 supspace dimension인 \(d_{90}\)가 점점 작아진다는 것이다. 이는 pre-training한 model에 대해서 NLP task로 fine-tuning할 경우에 대해 측정한 것이다.

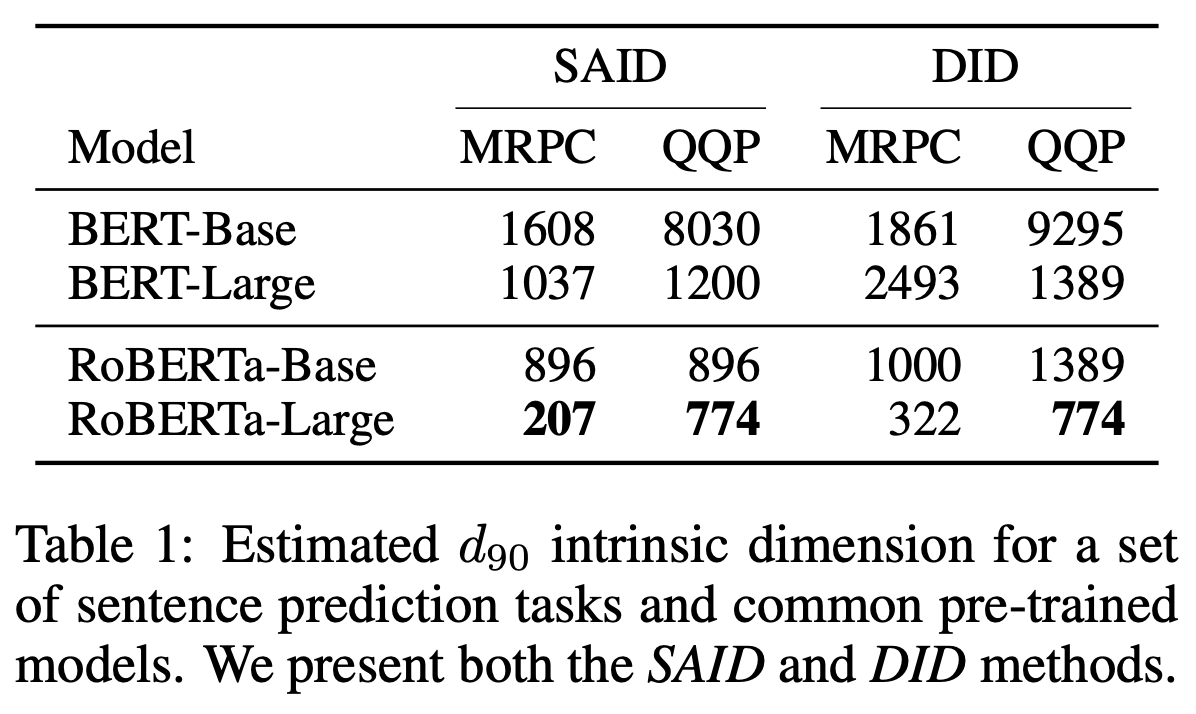2020_low_intrinsic_table1 Fig.

그 다음은 RoBERTa-Base를 from scratch로부터 pre-training할 때 매 10k update step마다 \(d_{90}\)을 측정한 것으로, training이 진행 될 수록 이 값이 낮아지는 걸 알 수 있었다고 한다.

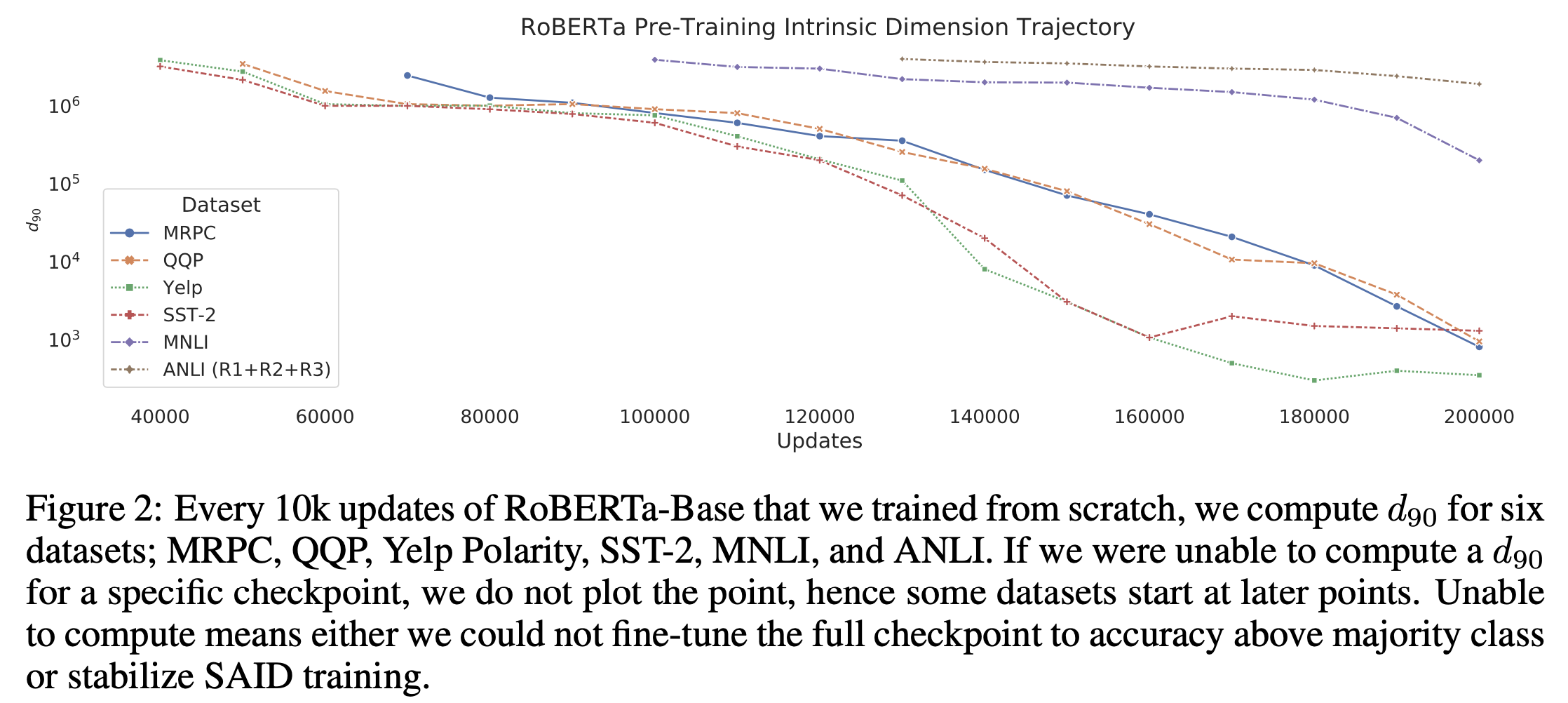2020_low_intrinsic_fig2 Fig.

저자들은 또한 parameter size가 커질수록 intrisinc dimension이 더 낮아진다는 것도 보였다.

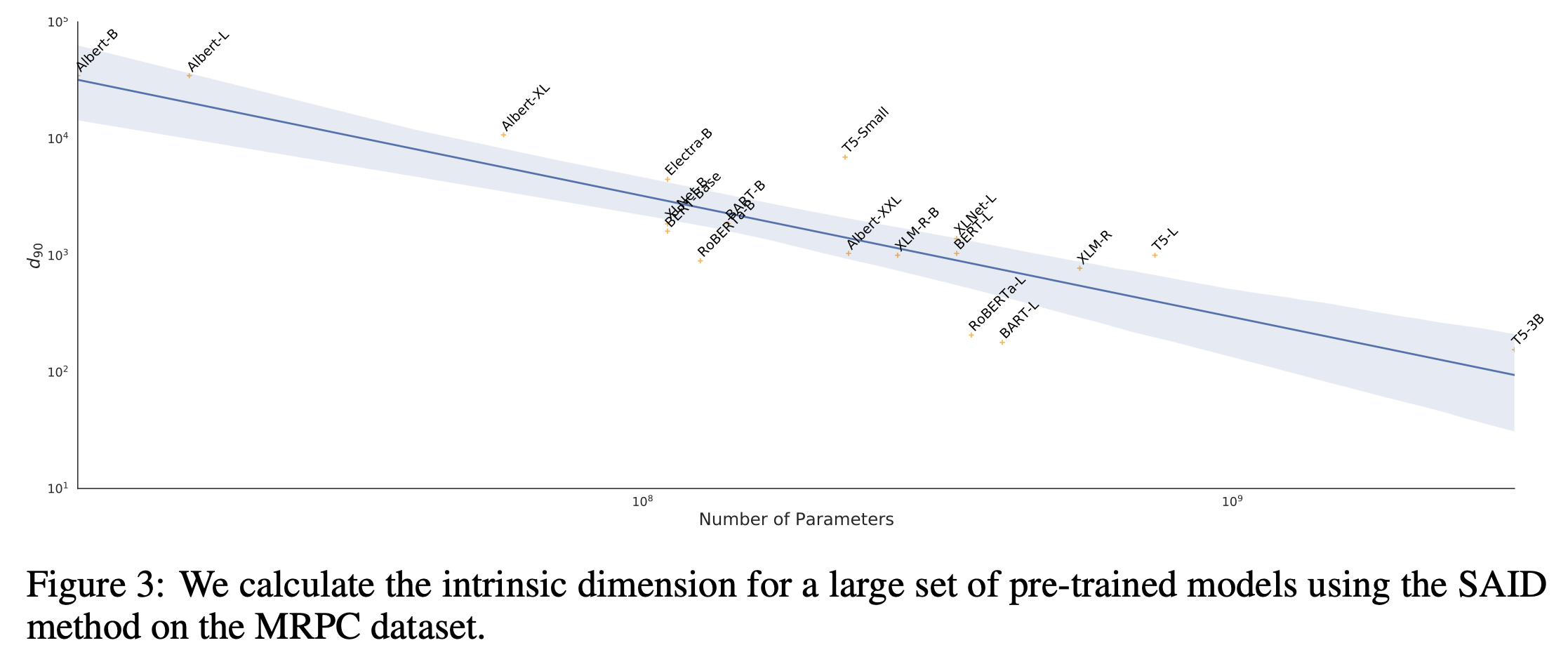2020_low_intrinsic_fig3 Fig.

결과적으로 여러 NLP task에 대해 pre-training이 잘 되면 adaptation (fine-tuning)을 할 때 필요한 sub-space가 점점 낮아진다는 걸 밝힌 셈이다. LoRA도 NLP task에 대해 adaptation을 하는 행위의 intrinsic dimension이 낮을 것이라는 가설을 가지고 있는데, 기존에 이미 study된 내용과 다를바가 없다고 할 수도 있겠으나 pre-trained weight을 frozen하고 (Aghajanyan et al. (2020) 은 pre-trained weight을 frozen하지 않음)해서 효율적으로 학습하는 algorithm을 design한 것이 noverlty라고 할 수 있다.

lora_measuring_fig4 Fig. adaptation에 이런 개념을 적용한 것은 처음이 맞다

Back to LoRA

이제 다시 LoRA로 돌아와보자. 앞서 Measuring the Intrinsic Dimension of Objective Landscapes paper에 대입해보면 우리가 필요한것은 아래 3가지가 된다.

  • (random) initial point
  • (random) sub-space projector
  • trainable parameter

그런데 우리는 random initial point가 필요하지는 않다. 이것보다 더 좋은 initialization point가 있다면 거기서부터 update를 하면 되는데, pre-trained Language Model (LM)같은걸 쓰면 된다.

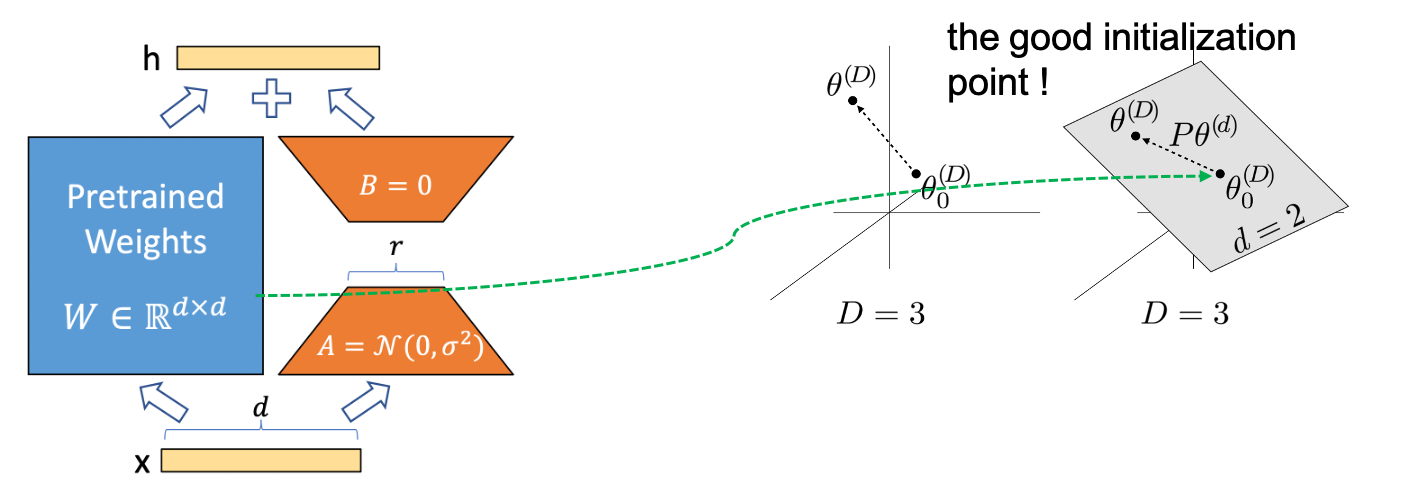lora_measuring_fig1 Fig.

그리고 sub-space projector를 정의해야 하는데, 원래 paper에서는 이것이 random sub-space로 한 번 정의되고나면 고정되어 학습이 되지 않았으나 LoRA는 parameterize된 이후 학습이 된다는 점에 주의해야 한다.

\[h = Wx + BAx\]

그리고 LoRA의 AutoEncoder (AE)스러운 bottleneck구조의 B가 한눈에 봐도 sub-space를 나타내는 것임을 알 수 있고, A는 input을 그 space로 보내는 module이라는 것을 알 수 있다.

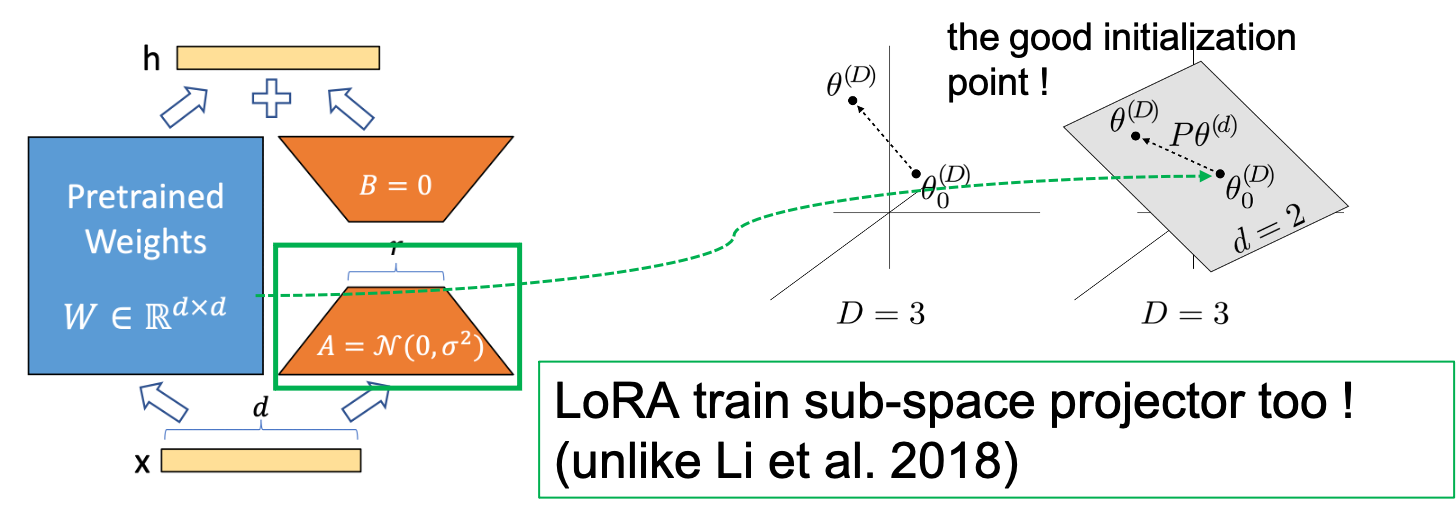lora_measuring_fig2 Fig.

후술하겠으나 \(B, A\)는 맨처음에 matrix multiplication을 해서 \(W\)와 같은 크기의 matrix로 만들면 모든 element가 0이 되도록 initialization되는데, 이는 맨 처음에는 pre-trained weight point의 activation output부터 학습이 진행되어야 하기 때문이다.

Connection to Traditional Low Rank Approxmiation (LRA)

한 편, Low Rank Adaptation (LoRA)와 비슷한 term으로 Low Rank Approximation (LRA)가 있다. 아마 ML을 하는 사람들은 모두 '이거 LRA하겠다는 건가?'라는 생각을 할 것 같다. 하지만 paper 자체에 approximation 이라는 표현을 쓰고있지는 않으며 이는 정확히는 update될 weight matrix, \(\Delta W\)를 애초에 low rank로 분리 (factorization)해서 학습하는 것이지 이미 학습된 delta의 rank를 줄이는 방향으로 approximate하는 것이 아니기 때문에 필자는 LoRA와 LRA가 구분된다고 생각한다. (저자들이 의도적으로 구분지은것이라고 생각한다)

lora_measuring_fig3 Fig. LoRA를 제대로 알기위해선 LRA를 이해해야하는게 맞을까? 아니면 Intrinsic Dim을 이해하는게 맞을까?

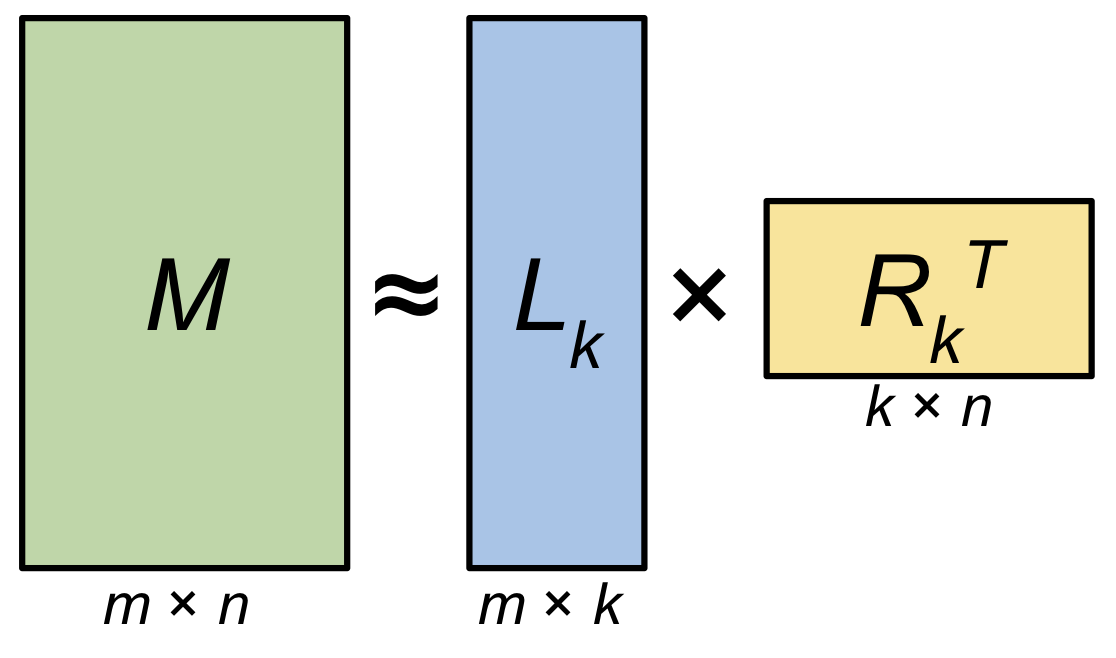matrix_lra_fig2 Fig. rank n인 matrix를 (full rank일 경우를 가정), rank k 로 matrix를 decompose하는 예시

Experimental Results of LoRA

이제 experimental result와 analysis를 보도록 하자. Main table은 아래와 같은데, 요약하자면 LoRA가 backprop으로 gradient가 흘러 update되는 trainable parameter size가 full fine-tuning보다 훨씬 적음에도 불구하고 competitive performance를 보여준다던가 심지어 더 좋은 성능을 보여주기도 한다는 것이다.

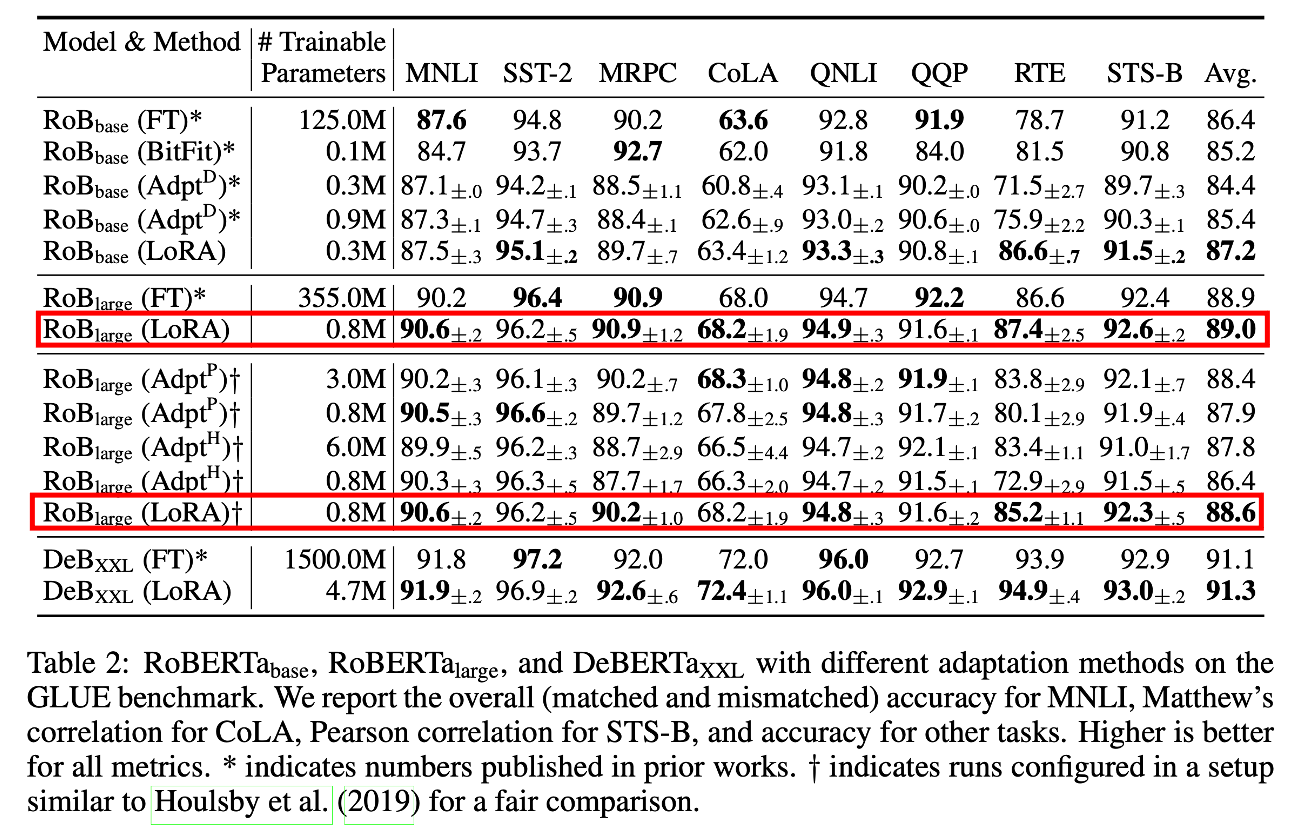lora_nlu_table Fig.

그리고 latest arxiv version에는 autoregressive model 인 GPT-3에 대한 adaptation 성능 비교도 있는데, 여기서도 LoRA가 더 잘나오는 경우도 있었다.

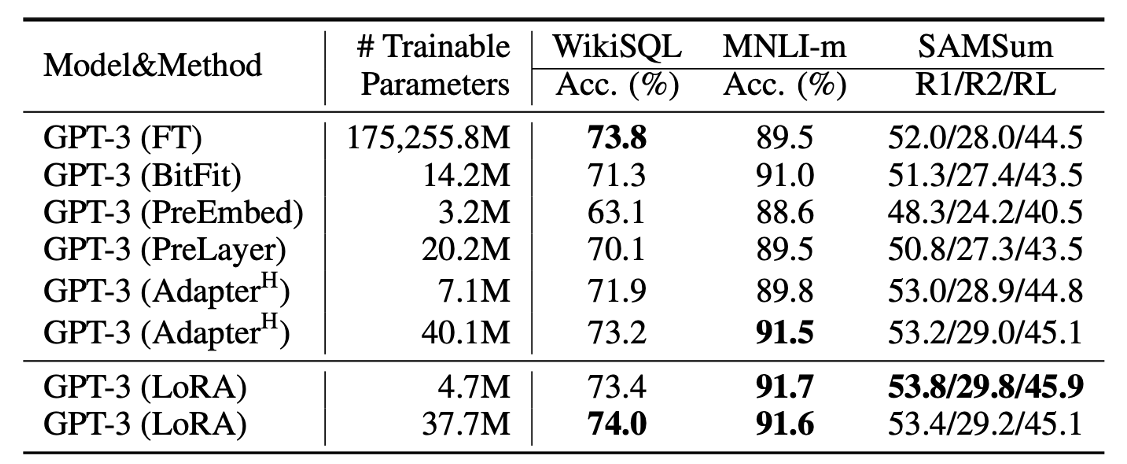lora_gpt3_table Fig.

What is Generalized Language Understanding Evaluation (GLUE)

NLP 도메인이 아닌 독자들은 (본인 포함) Generalized Language Understanding Evaluation (GLUE)를 이번에 처음 접해봤을 수도 있기에 짧게 소개해보려고 한다. 가장 유명한 NLU Benchmark 중 하나인 GLUE 는 아래의 8개 task 들을 포함하는데, 보통 각 task 별로 정확도를 측정한 뒤에 평균을 내서 report한다.
(이미 알고 있는 사람들은 skip하면 된다)

  • Single-Sentence Tasks
    • CoLA (2 class) : The Corpus of Linguistic Acceptability is a set of English sentences from published linguistics literature. The task is to predict whether a given sentence is grammatically correct or not.
    • SST-2 (2 class) : The Stanford Sentiment Treebank consists of sentences from movie reviews and human annotations of their sentiment. The task is to predict the sentiment of a given sentence: positive or negative.
  • Similarity and Paraphrase tasks
    • MRPC (2 class) : The Microsoft Research Paraphrase Corpus is a corpus of sentence pairs automatically extracted from online news sources, with human annotations for whether the sentences in the pair are semantically equivalent.
    • QQP (2 class) : The Quora Question Pairs dataset is a collection of question pairs from the community question-answering website Quora. The task is to determine whether a pair of questions are semantically equivalent.
    • STS-B (1 class) : The Semantic Textual Similarity Benchmark is a collection of sentence pairs drawn from news headlines, video, and image captions, and natural language inference data. The task is to determine how similar two sentences are.
  • Inference Tasks
    • MNLI (2 class) : The Multi-Genre Natural Language Inference Corpus is a crowdsourced collection of sentence pairs with textual entailment annotations. Given a premise sentence and a hypothesis sentence, the task is to predict whether the premise entails the hypothesis (entailment), contradicts the hypothesis (contradiction), or neither (neutral). The task has the matched (in-domain) and mismatched (cross-domain) sections.
    • QNLI (2 class) : The Stanford Question Answering Dataset is a question-answering dataset consisting of question-paragraph pairs, where one of the sentences in the paragraph (drawn from Wikipedia) contains the answer to the corresponding question. The task is to determine whether the context sentence contains the answer to the question.
    • RTE (2 class) : The Recognizing Textual Entailment (RTE) datasets come from a series of annual textual entailment challenges. The task is to determine whether the second sentence is the entailment of the first one or not.

이 중에서 STS-B 만 regression 이며 나머지는 모두 classification task이다. 모든 benchmark는 보통 binary class를 가지고 있으며, 가장 학습시간이 오래걸리는 MNLI task 만 class 가 3개이다. 그리고 CoLA와 STS-B는 correlation을 측정한다.

Quantative Results

대부분의 GLUE task 들이 pre-trained model을 adaptation하는 관점에서는 쉽기 때문에 (이미 문장을 이해하는 능력이 있음), RoBERTa 논문에서는 모든 task 들이 10epoch 학습된 결과만 report 했다. 하지만 LoRA는 특정 task들에 대해서 30epoch을 학습한 경우도 있었다. 이는 trainable parameter가 적기 때문인데, 앞서 말한 것 처럼 epoch당 LoRA가 2배 빠르고 GPU resource도 덜 먹는다 쳐도 epoch을 3배 더 돌린다는 점에서 training wall clock time측면에서 LoRA가 더 느리다는 걸 의미한다.

아래는 RTE라는 task에 대해서 필자가 구현한 code로 실험한 결과이다. Fair comparison을 위해 RoBERTa 를 제안한 facebook 의 library Fairseq을 사용해 V100 장비 1대로 Full Fine-tuning 학습을 했으며 비교를 위해 LoRA official implementation code를 직접 구현해 paper와 같은 linear layer에 LoRA injection을 했으며, adaptation을 위한 classifier weight을 같은 random seed로 초기화 해 학습했다.

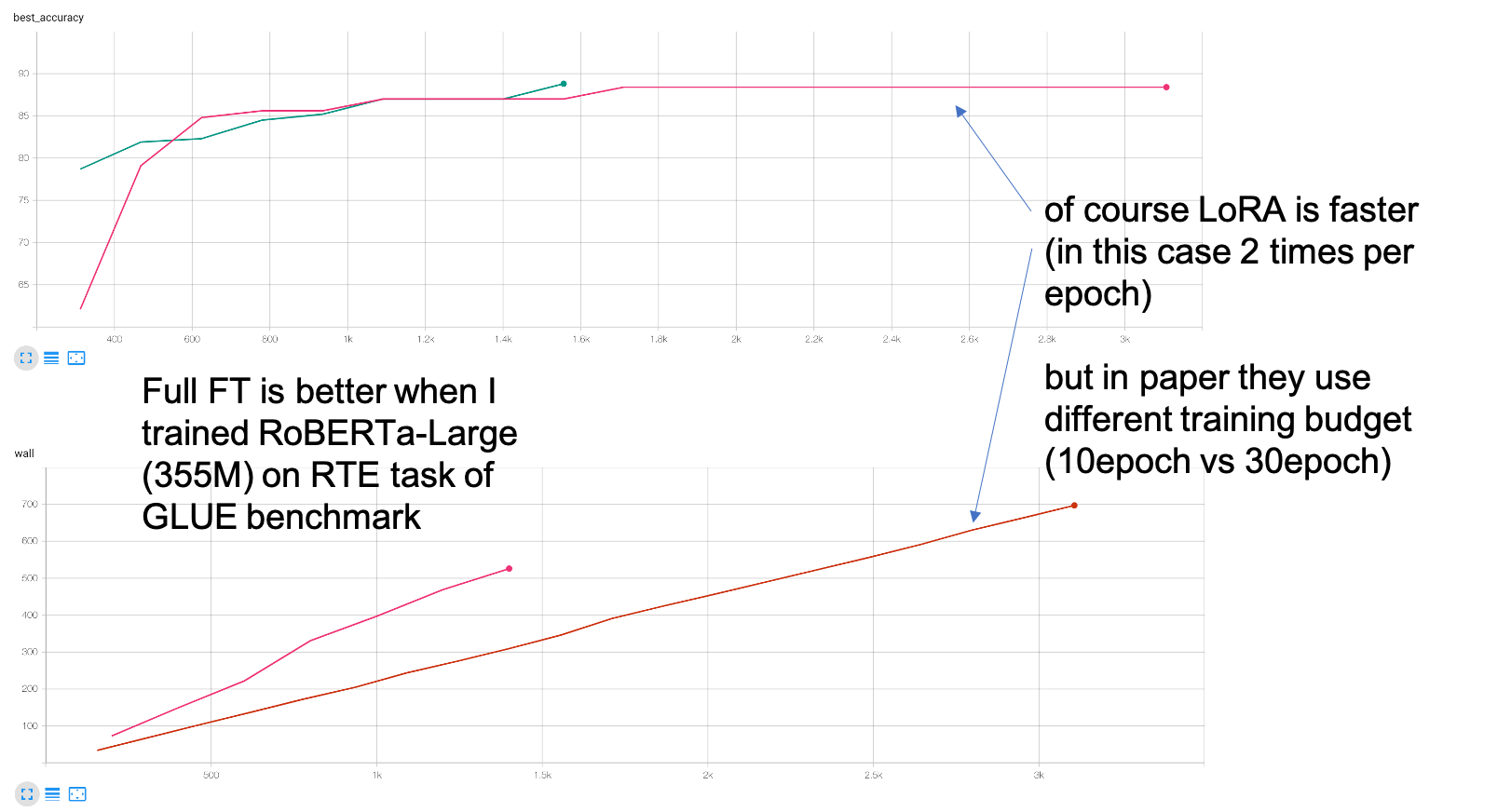lora_nlu_my_exp_fig1 Fig. Best Accuracy (위), Training Wall Clock (아래)

위의 figure에서 보여지는 바와 같이 training wall clock을 봤을 때 LoRA가 2배정도 빠르긴 했으나 LoRA paper의 recipe 대로 30 epoch을 돌렸을 경우는 오히려 LoRA가 더 오래걸린다는 걸 알 수있고 accuracy 또한 full fine-tuning이 근소 우위에 있음을 알 수 있다. 사실상 LoRA paper 에서 주장하는 LoRA가 더 좋다는 것은 ‘random seed 차이라고도 할 수 있지 않을까?’ 라는 생각이 들기도 하는데, paper 에서도 여러번 실험을 해 standard deviation 을 report 하기는 했다.

lora_nlu_table Fig.

또한 RoBERTa paper 자체는 얼마나 Pre-training 이 잘 됐는가? 를 주장하기 위해서 NLU 실험을 했기 때문에 fine-tuning을 할 때 hyperparameter sweep을 적게했기 때문에 best performance가 아닌 상황에서 LoRA와 비교를 하려니 (LoRA는 sweep을 꽤 한것으로 보인다) LoRA가 더더욱 좋아보이는 것이 아닌가? 하는 생각도 들었다. (GPU, torch version등이 달라서 그런지 필자가 했을 때는 full fine-tuning이 근소하게 더 좋은 결과를 냈다)

RTE같은 task가 얼마나 간단한 것인지에 대해서는 아래의 learning curve 를 보면 또 알 수 있는데,

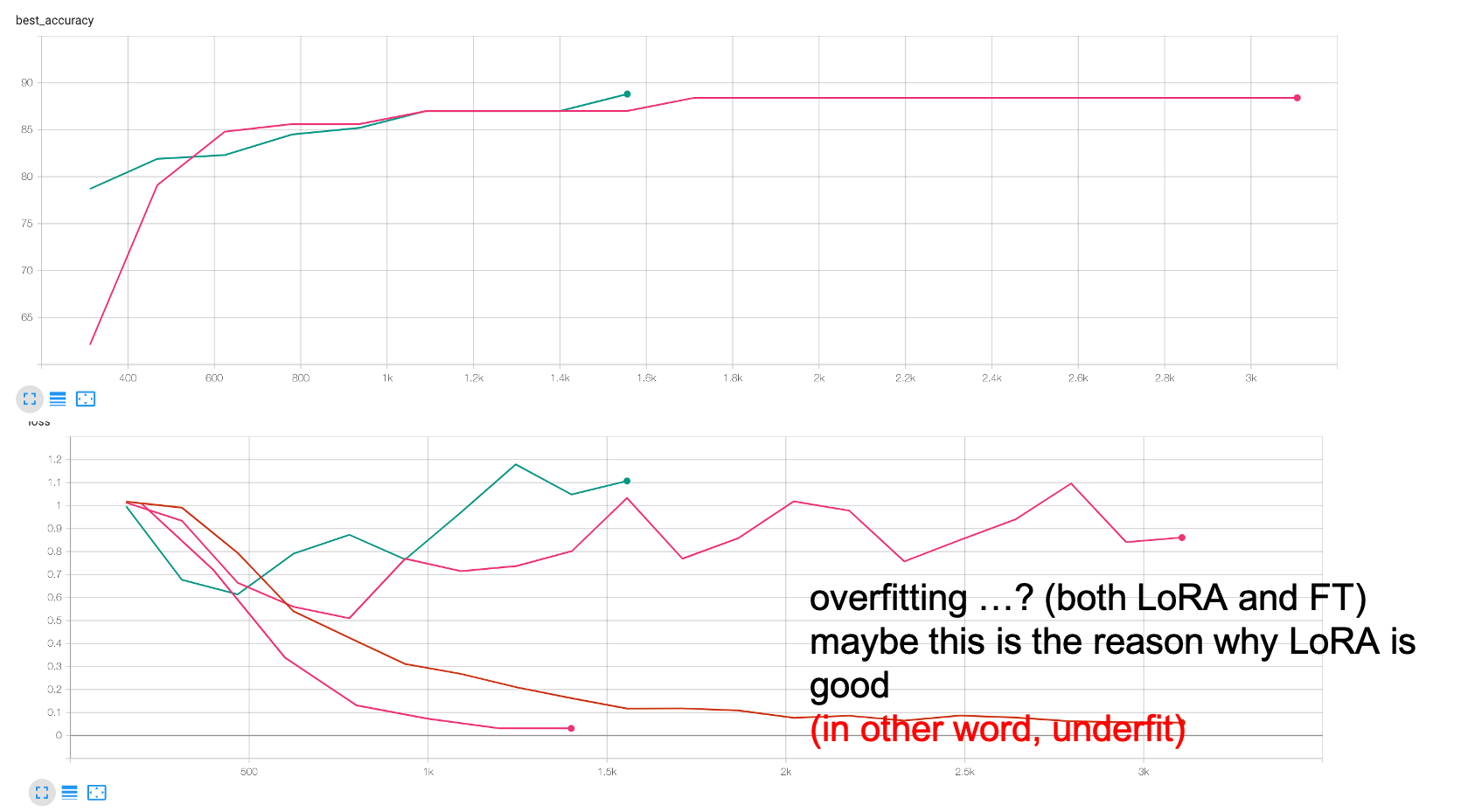lora_nlu_my_exp_fig2 Fig. Best Accuracy (위, not Accuracy), Loss (아래)

validation curve 가 LoRA, Full FT 할 것 없이 위로 치솟는걸 보면 애초에 overfitting 을 하는 task인 것이라고 할 수 있다. 이런 관점에서 LoRA는 degree of freedom이 제한된 optimization을 하기에 underfitting이 되는 것이 오히려 도움이 됐던게 아닌가? (좋게 말하면 generalization capability가 유지됨) 하는 추측도 할 수 있겠다. 이는 MNLI같이 training이 오래 걸리는 high resource task에 대해서도 마찬가지였는데, 여기서 또 주목할만한 점은 MNLI는 epoch 당 속도가 full fine-tuning에 비해 그렇게 높지도 않았다는 것이다. (이 경우엔 10 epoch (Full) vs 10 epoch (LoRA))

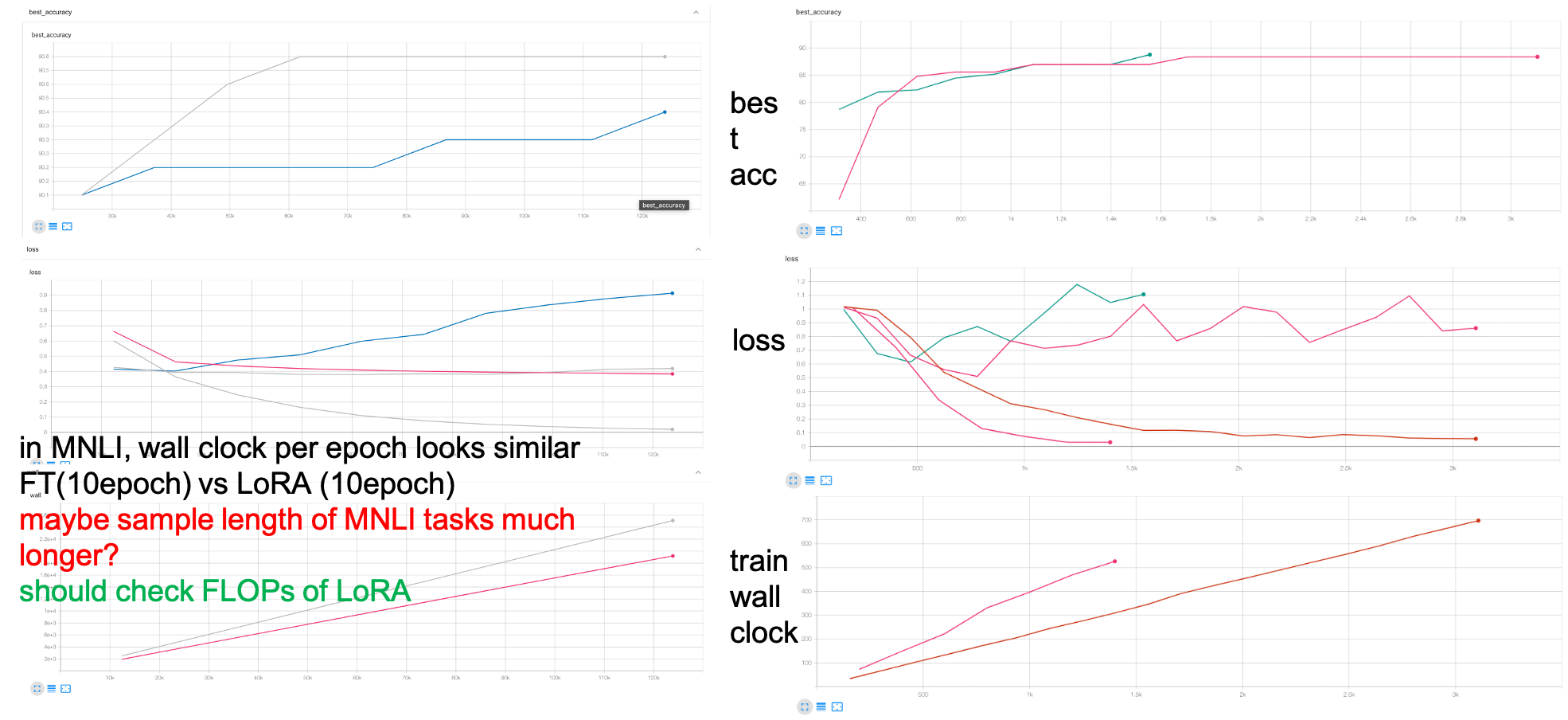lora_nlu_my_exp_fig3 Fig.

Why LoRA faster and memory efficient?

LoRA를 적용하면 FT 대비 training에 필요한 GPU 의 VRAM memory를 4배 정도 절약할 수 있으며, training speed도 가속화 할 수 있다고 알려져 있다. Training speed 는 2배까지 차이가 나는 경우도 있으나 경우에 따라 다르고 (정확히 FLOPs 를 계산해봐야겠으나), GPU에 올라가는 model의 memory는 같겠으나 forward, backward시 필요한 memory가 거의 1/4 수준으로 줄어든다. 실제 논문에서는 GPT-3 175B 기준으로 training speed 는 25% 향상 되는 등 정량적인 수치가 기재되어 있다.

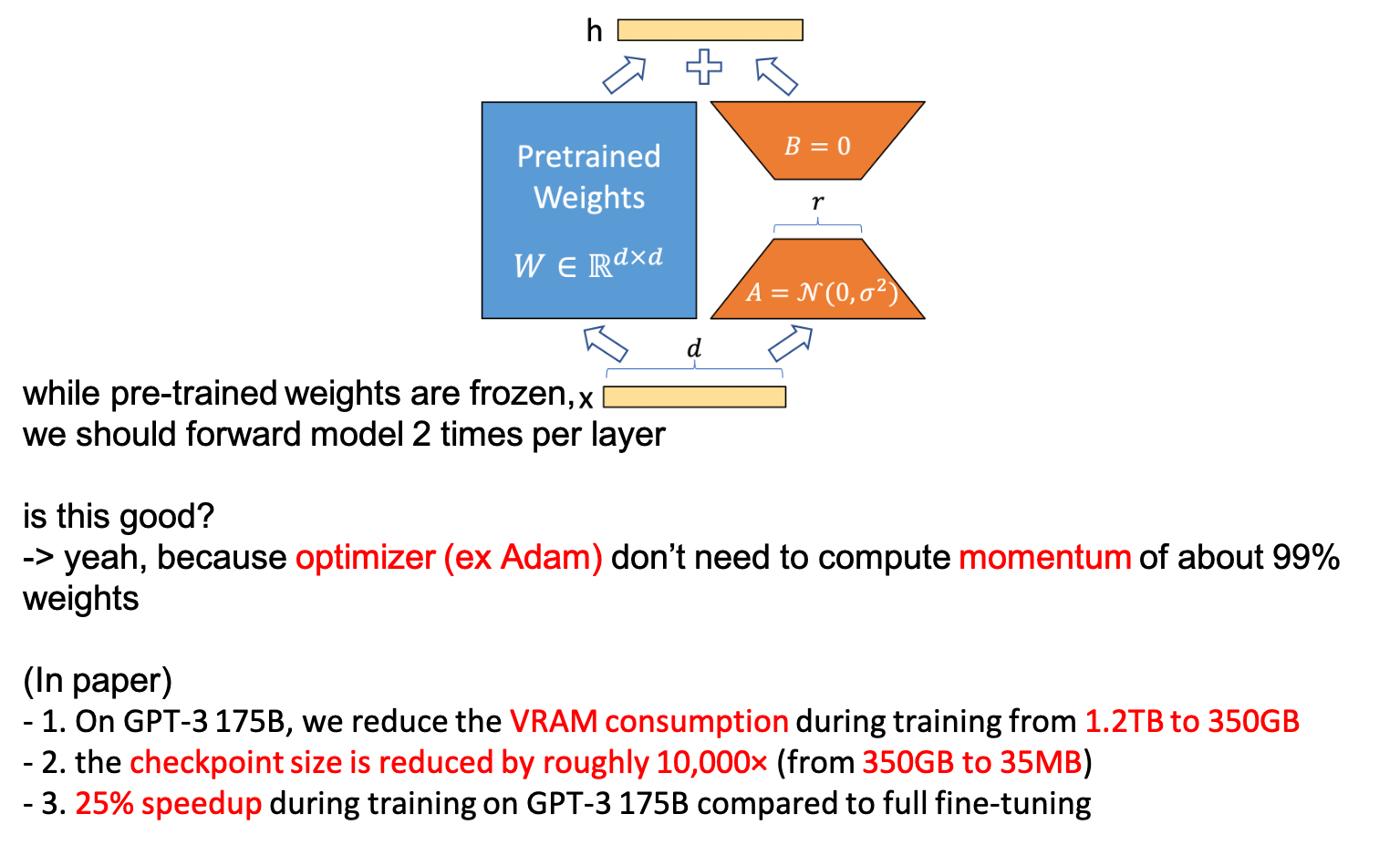lora_flops Fig.

먼저 forward computation을 할 때 memory가 줄어드는 것에 대해 생각해보자. 첫 번째로 backward를 위해 저장할 activation의 양이 줄어든 부분이 기여를 했을 것이다. 그리고 두 번째는 paper에 언급이 되어있느 것인데, 바로 Adam optimizer (momentum method)를 쓸 경우 저장해야하는 parameter가 전체 parameter size의 몇 배가 필요한데, 이것이 확줄어들었기 때문이다. Adam같은 경우 momentum을 따로 계산하고 또 그만큼 이전 update했던 state를 저장하고 있어야 하는데, 이것들은 모두 trainable parameter에 대해서만 해당된다.

adam_algorithm

LoRA는 99% 이상의 prarameter를 update 하지 않기 때문에 계산해야하는 momentum 같은것이 확 줄어들어 memory save를 한 것이다.

이제 backward computation에 대해 생각해보자. 아래의 official implementation를 보면 rank, r을 제대로 설정할 경우 forward pass가 아래처럼 2번 따로 연산되어 합쳐진 것을 한 layer의 결과물로 정의하는 것을 알 수 있다.

h = Wx + A@B^Tx * scaling

여기서 2번 연산하는 것에 거부감이 자연스럽게 들 수 있다. '아니 결국 결과물을 합칠 거면 (W+A@B^T)로 weight 을 합친다음 x와 연산하면 1회만 하면 되는 것 아닌가?'라는 생각이 들 수 있고 실제로 이렇게 해도 학습은 잘 될 수도 있다. 왜냐하면 이렇게 합치더라도 optimizer에 pre-trained model은 제외하고 각 linear layer별 LoRA A, B만 optimizer에 정의해주면 되기 때문이다. 그렇다면 training시 이 둘을 나눈 것은 실수일까?

def train(self, mode: bool = True):
    def T(w):
        return w.transpose(0, 1) if self.fan_in_fan_out else w
    nn.Linear.train(self, mode)
    if mode:
        if self.merge_weights and self.merged:
            # Make sure that the weights are not merged
            if self.r > 0:
                self.weight.data -= T(self.lora_B @ self.lora_A) * self.scaling
            self.merged = False
    else:
        if self.merge_weights and not self.merged:
            # Merge the weights and mark it
            if self.r > 0:
                self.weight.data += T(self.lora_B @ self.lora_A) * self.scaling
            self.merged = True       

def forward(self, x: torch.Tensor):
    def T(w):
        return w.transpose(0, 1) if self.fan_in_fan_out else w
    if self.r > 0 and not self.merged:
        result = F.linear(x, T(self.weight), bias=self.bias)
        if self.r > 0:
            result += (self.lora_dropout(x) @ self.lora_A.transpose(0, 1) @ self.lora_B.transpose(0, 1)) * self.scaling
        return result
    else:
        return F.linear(x, T(self.weight), bias=self.bias)

그렇지않다. 왜냐하면 error backpropagation시 downstream gradient는 upstream gradient와 layer input의 outer product이기 때문이다.

\[\begin{aligned} & \frac{dL}{dh_i} = \frac{dL}{dh_{i+1}} & \\ & \frac{dL}{dW_i} = h_i^T \frac{dL}{dh_{i+1}} & \\ \end{aligned}\]

여기서 LoRA는 뒤에 있는 weight matrix에 대한 derivative를 구하는 부분에서 이점이 있는데, 어떤 layer의 wegith matrix의 derivative를 구하기 위해 서로 곱해줘야 하는 upstream gradient의 tensor size와 layer input의 tensor size가 LoRA의 bottleneck구조를 쓰는것이 merge를 해서 forwarding하는 것 보다 훨씬 작다는 것을 직관적으로 알 수 있다.

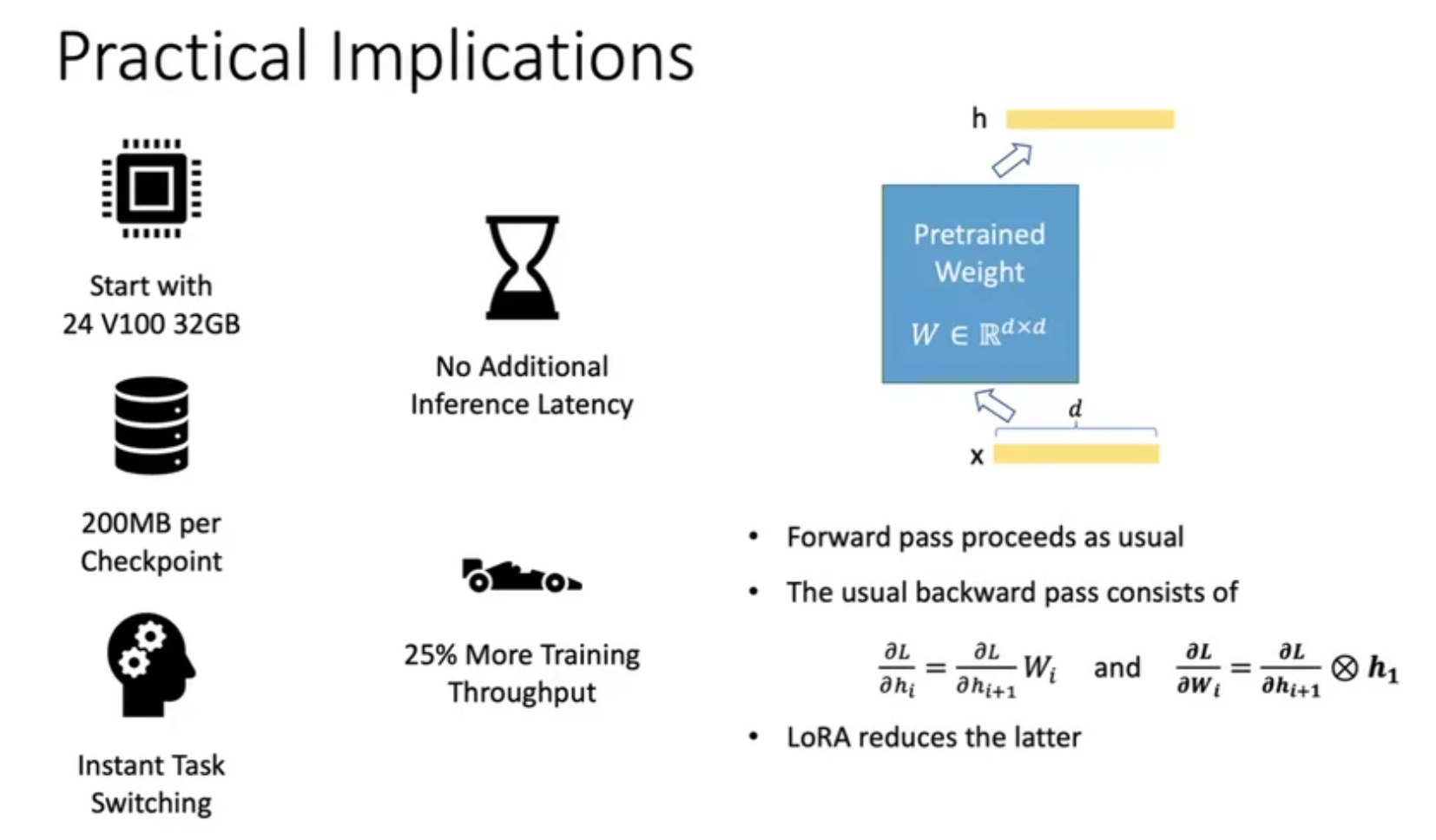lora_backward Fig. Slide adopted from the presentation of LoRA at ICLR 2022.

Further Analysis and Ablation Studies

Which Weight Matrices Should We Apply LoRA to ?

그 다음으로 LoRA 논문에 있는 몇가지 분석과 고찰에 대해 알아보자. 먼저 첫 번째는 '그래서 어떤 linear layer 에 LoRA 를 inject 해야하는걸까?'이다.

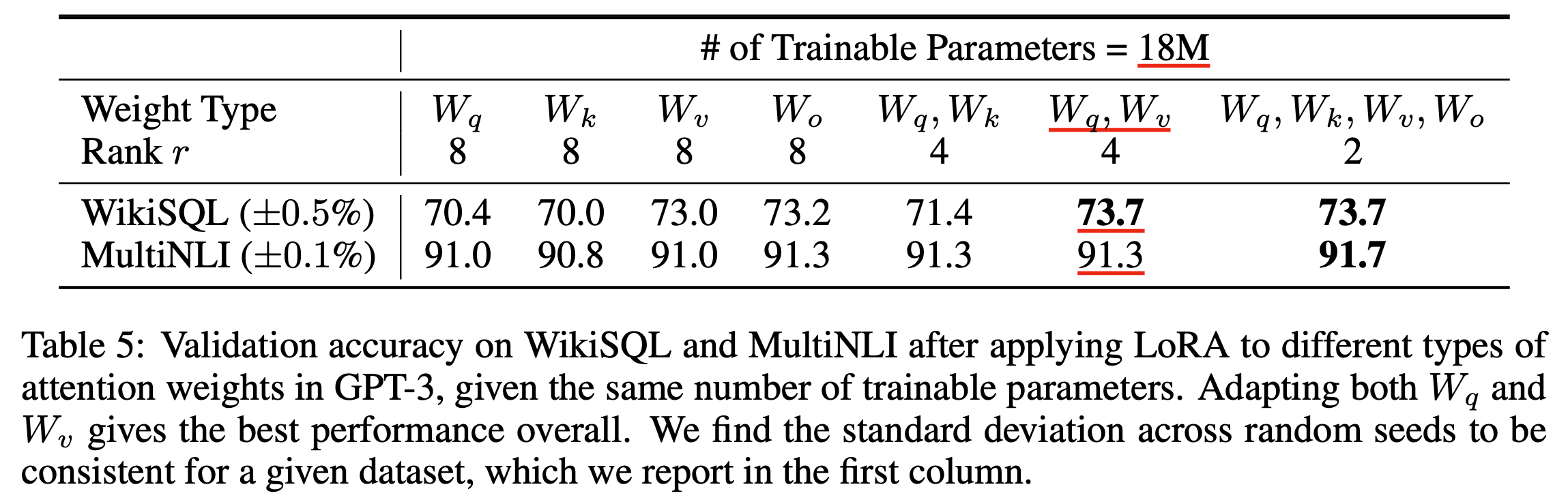lora_paper_table5 Fig.

사실 정답은 없다. Paper에서는 Q, V layer에만 적용하거나 Q, K, V, O 모두에 적용하는것이 가장 좋았다고 하는데, 성능 차이가 그다지 크지않기는 했다. 따라서 adaptation을 하려는 task, training budget에 따라 (많이 적용할수록 cost올라감), 혹은 prior knowledge에 따라서 layer를 정하면 되겠다.

Optimal Rank r for LoRA

두 번째는 '그럼 optimial rank 는 몇인가?'이다.

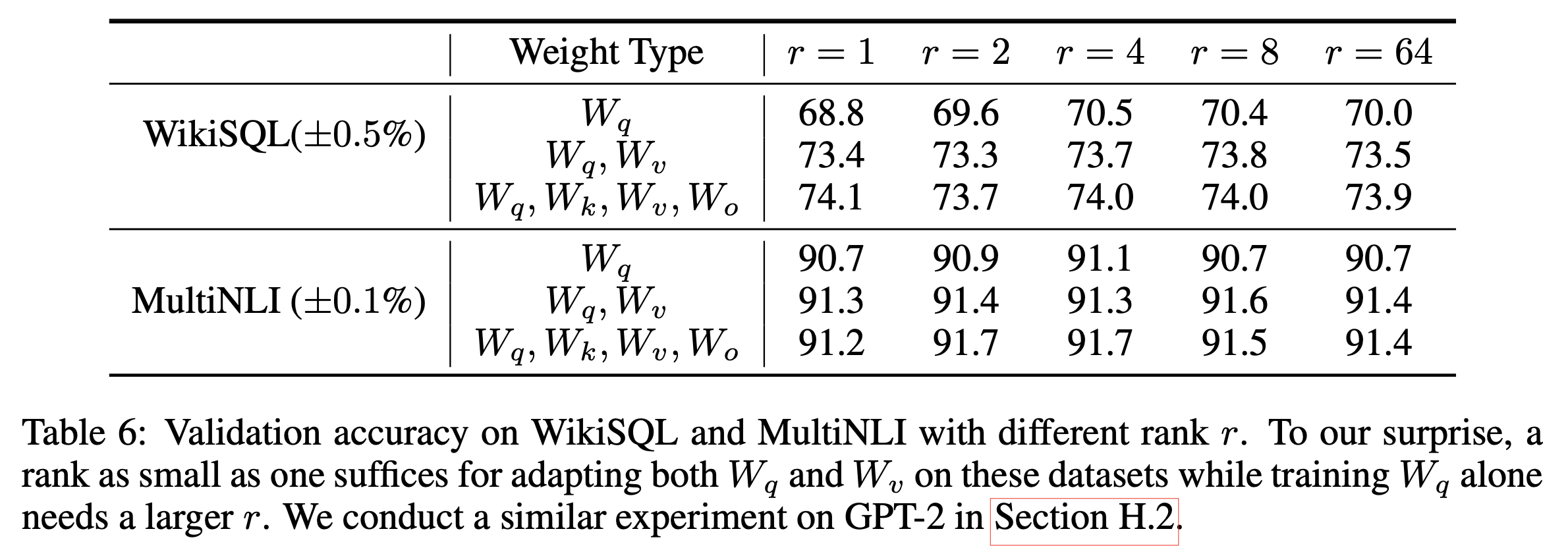lora_paper_table6 Fig.

이것도 정답은 없다. 일단 rank, \(r\)값이 sub-space 의 크기를 정하는 것은 알겠으나 어느 정도가 적당한지는 intrinsic dimension, \(d_{int}\) 를 측정할때처럼 해보는 수 밖에 없는 것 같다. 보통 \(r=4,8,16\)정도로 정하므로 몇 가지 실험을 통해 결정하는 수 밖에 없을 것 같다.

Scalar Factor

세 번째는 'scaling factor는 몇으로 정해야할까?'이다. Scaling factor는 \(\frac{\alpha}{\alpha}\)로 정의되는데, paper에서는 NLU 를 할 때 \(\frac{\alpha}{r} = \frac{16}{8} = 2\)로 정했다. 이 \(\alpha\)값은 training 때도 사용되는 값인데 사실상 learning rate 와 같은 역할을 한다고 하며, 추론시에 사용될 때는 adaptation 된 정도를 조절하는 용도로 쓰일 수도 있다고 한다. 즉 \(\alpha\)를 16으로 해서 학습했다고 하더라도 adaptation을 하고 보니 너무 parameter가 많이 변했다 싶으면 8로 낮출 수도 있다는 것이다.

Subspace Similarity between Different r and Random Seed

그렇다면 \(r\) 값이 다르면 추가로 \(r\) 이 같더라도 random seed 가 다르면 학습된 sup-space가 서로 많이다를까? Paper에서는 실제로 학습된 \(\Delta W\)의 sub-space를 비교 분석했다.

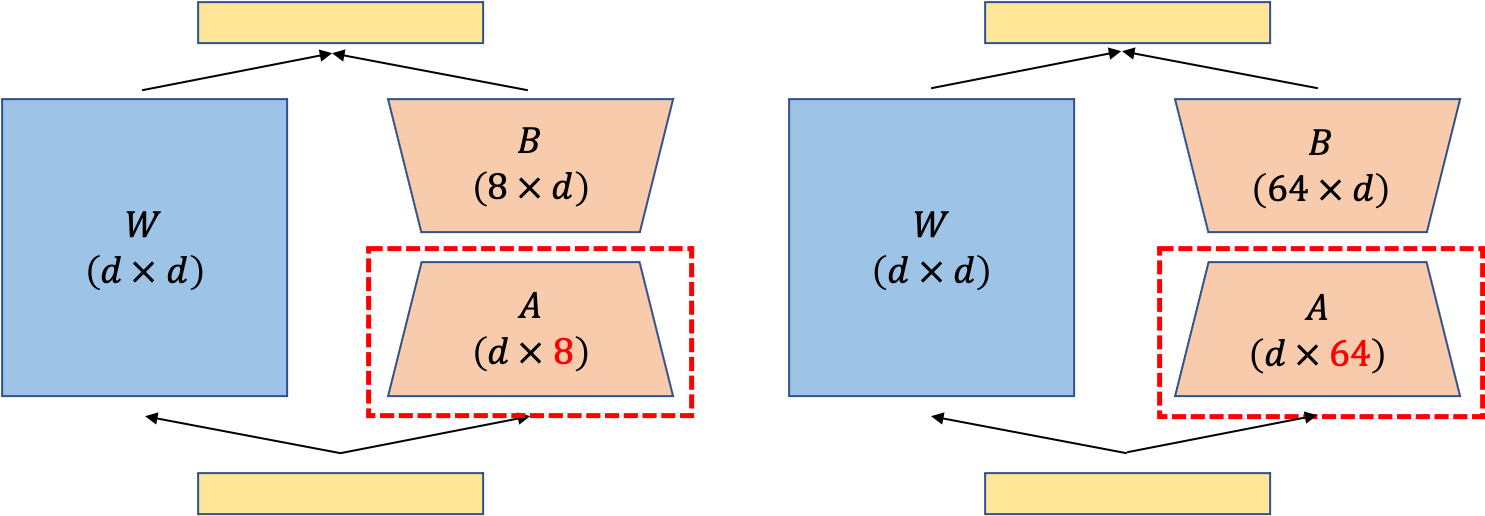subspace_sim_fig Fig.

LoRA에서 sub-space을 의미하는 layer는 \(A\) layer 였다. 이를 서로다른 rank, seed 에 대해서 학습하고 비교분석을 했는데, paper에서는 같은 pre-trained weight에서 출발해 학습된 \(A_{r=8}, A_{r=64}\)를 비교한다. 먼저 Singular Value Decomposition (SVD)를 통해 right singular unitary matrices, \(U_{A_{r=8}}, U_{A_{r=64}}\)를 뽑느다. 당연히 얻은 matrix는 \(r=8\), 일경우 \(d \times 8\)차원이 되고, \(r=64\)일 경우 \(d \times 64\)가 되어 column 수가 다르다. 이들이 full rank를 갖는다면 sub-space는 다른 것일 수 있지만, 만약 \(U_{A_{r=8}}\)의 상위 i 개 (\(1 \leq i \leq 8\))가 span하는 공간이 얼마나 \(U_{A_{r=64}}\)의 상위 j 개 (\(1 \leq j \leq 64\))에 포함되어 있는가를 확인해서 비슷하다면 이 둘은 거의 같다고 볼 수 있다. 'sub-space 가 얼마나 유사한가?'를 측정하는 것은 아래의 수식을 사용했다.

\[\phi(A_{r=8}, A_{r=64}, i, j) = \frac{ \parallel U_{A_{r=8}}^{iT} U_{A_{r=64}}^{j} \parallel^2_F }{min(i,j)} \in [0,1]\]

이는 Grassmann distance라는 method 에 근거한 metric이며 값은 0~1 사이 값으로 1이면 굉장히 유사한 것이라고 한다. 아래는 96개 layer 중 48번째 layer 에 대해서 실험한 것인데 (더 자세한 내용은 paper 의 appendix 참고), 결과적으로 layer 별로 sub-space는 비슷했다고 한다.

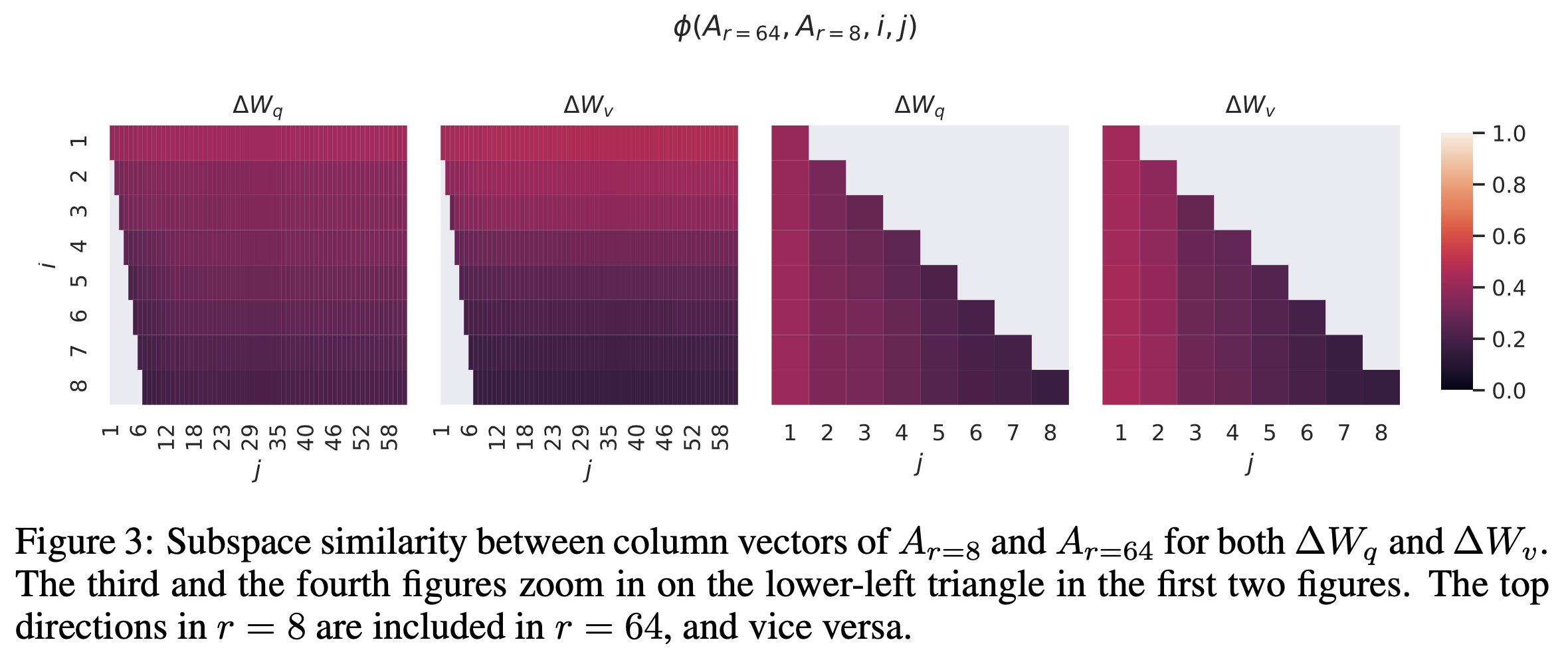lora_paper_fig3 Fig.

이 실험에서 알 수 있었던 것은 figure에 나타나는 바와 같이 rank 가 늘어나도 상위에 있는 singular vector 들의 direction 은 꽤 겹치더라는 것이다. 특히 최상위 1개의 경우 similarity 가 0.5 이상으로 밝혀져 왜 GPT-3 에서 rank 1 LoRA 학습이 잘 되는지를 알 수 있었으며, 학습이 되면서 상위 몇개를 제외하고 나머지들은 direction이 제각각으로 변하는 것을 볼 때 나머지 basis들은 noise나 다름없다는 주장을 한다. 즉 adaptation weight 은 예상했던대로 굉장히 low rank 였던 것이라고 할 수 있는 것이다. 그렇다면 같은 pre-trained weight, 같은 rank 일때 random seed 가 다른 경우에는 어떨까?

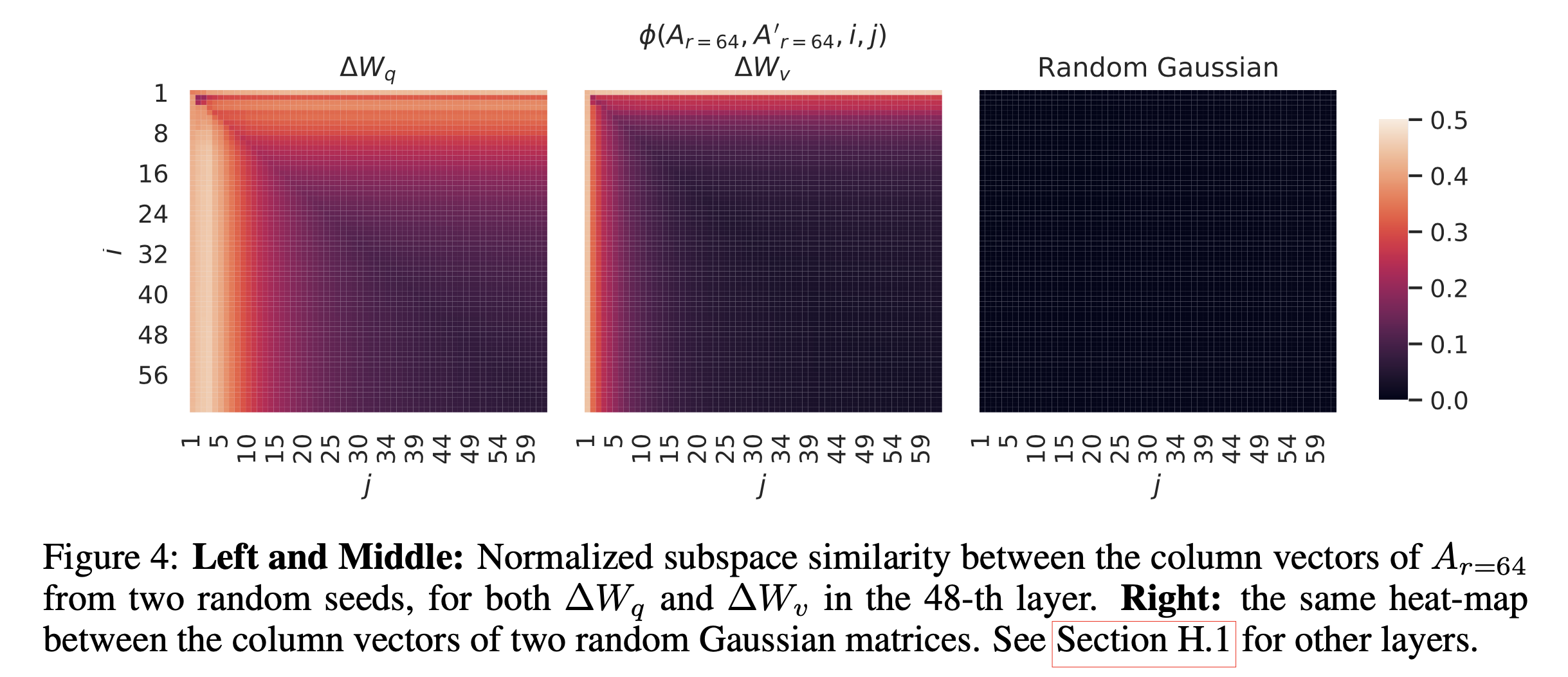lora_paper_fig4 Fig.

이런 경우 seed가 달라도 결국 상위 direction은 같은 곳으로 align 되는 것을 확인할 수 있었다고 한다.

How Does The Adaptation Matrix compared to Pre-trained Matrix W

마지막은 \(W_0, \Delta W\)의 관계에 대한 것이다. 얼마나 이 둘은 관련이 있을까? (혹은 수학적으로 \(\Delta W\)의 대부분이 \(W\)의 top singular direction에 포함될까?)

lora_paper_table7 Fig.

저자들은 \(W\)를 \(\Delta W\)의 r차원 sub-space로 projection했다. 이는 \(U^T W V^T\)로 계산할 수 있는데, \(U,V\)는 각각 detla의 left, right singular matrix이다. 그리고 이들의 Frobenius norm, \(\parallel U^T W V^T \parallel_F\), \(\parallel W \parallel_F\)을 계산했다고 한다. 또한 pre-trained weight, \(W\)의 상위 몇개의 rank만으로 low rank approximation한다거나 random matrix의 SVD 결과를 써서 실제로 얼마나 각 matrix들과 correlation이 있는지를 봤다.

결과적으로 3가지 observation이 있었는데, 첫 번째는 \(\Delta W_q\)가 random matrix와 비교해서 \(W_q\)와 correlation이 훨씬 높았다는 것인데, 이는 \(W\)에 이미 존재하는 몇가지 feature들을 증폭 (amplification)했다는 걸 의미한다고 한다. (당연하게도 \(W\)의 top direction들을 사용한 경우는 값이 \(21.67\)로 매우 컸음)

둘째로, LoRA 학습된 \(\Delta W\)가 \(W\)의 상위 singular direction을 단순히 반복하는 것이 아니라 \(W\)에서는 강조되지 않은 (not emphasized) direction들을 증폭시켰다는 것이다. 즉 LoRA로 학습된 것이 pre-trained weight과 아예 동떨어진 것도 아닌데 아예 redundant한 것도 아니라는 것이다.

마지막으로 amplification factor가 \(r=4\)인 경우가 \(r=64\)인 경우보다 꽤 크다는 것이었다고 하는데, 이는 rank가 늘어나봐야 별 도움 안된다로 이해할 수 있을 것 같다.

결과적으로 LoRA matrix는 general pre-trained model에서 강조되지 않았으나 특정 task를 배우는데 있어 중요한 feature들을 증폭시키는 매우 직관적이면서 중요한 일을 했다는 것이 된다.

Adaptive LoRA (AdaLoRA)

Motivation

한 편, LoRA가 simple하면서도 full fine-tuning대비 더 적은 gpu resource를 가지고도 비슷한 성능을 냈기에 각광받게 되었지만 rank를 어떤 layer에 얼만큼 할당할지? 같은 hyperparameter tuning은 known issue로 여러 연구자들의 target이 되었다. 실제로 Adaptive Budget Allocation for Parameter-Efficient Fine-Tuning라는 ICLR 2023 에 발표된 논문에서는 이를 분석하고 solution을 제시했다. 논문에서는 Multi Head Attention (MHA)Block 에서 어떤 linear layer 들이 중요한지? 그리고 전체 model architecture에서 어떤 층의 layer 들이 중요한지? 를 분석했다. 이를 위해 일부분만 trainable하게 두고 나머지는 전부 freezing 하는 실험을 여러 경우에 대해 진행했는데, 가장 난이도가 있는 GLUE benchmark subset인 MNLI를 통해 분석을 진행했으며, 이는 어떤 layer에 더 많은 resource (rank) 가 할당되어야 하는지를 알아보기 위한 실험이었다.

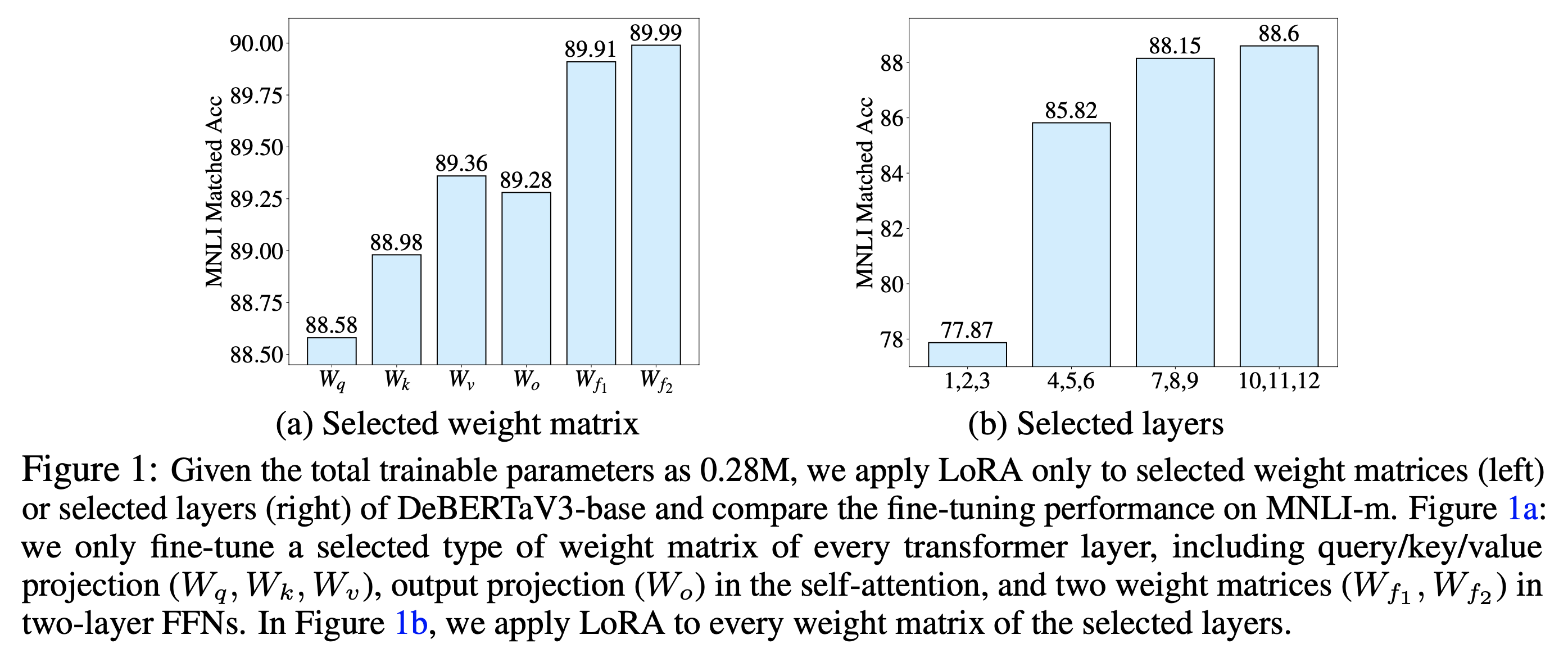adalora_fig1 Fig.

결과를 보면 LoRA 에서 언급한 Q, K, V, O projection layer 외에도 feed forward layer 들도 중요한 것으로 보이며, 1,2,3층 같은 저층부 보다는 고층부로 갈수록 중요도가 더 높아지는걸 알 수 있었다. AdaLoRA의 철학은 처음에는 같은 rank의 LoRA로 시작했지만 시간이 흐를수록 loss를 줄이는데 기여를 덜 하는 layer들은 rank를 감소시키는 것 (심하면 0으로 만듦)이다.

한편 이런 layer-wise analysis는 AdaLoRA 에만 있었던건 아니다. Custom Diffusion이라는 논문에서도 LDM 모델구조에서 U-Net 부분의 Cross Attention 부분 중 어떤 layer가 중요할까?를 분석했었다. 결과적으로 일부분만 학습하는 효율적인 방법을 채택할 순 없을까?를 분석했는데,

lora_ldm Fig.

fine-tuning시 각 layer들의 weight matrix가 얼마나 변했는가?를 의미하는 normalized distance (norm)를 측정했다.

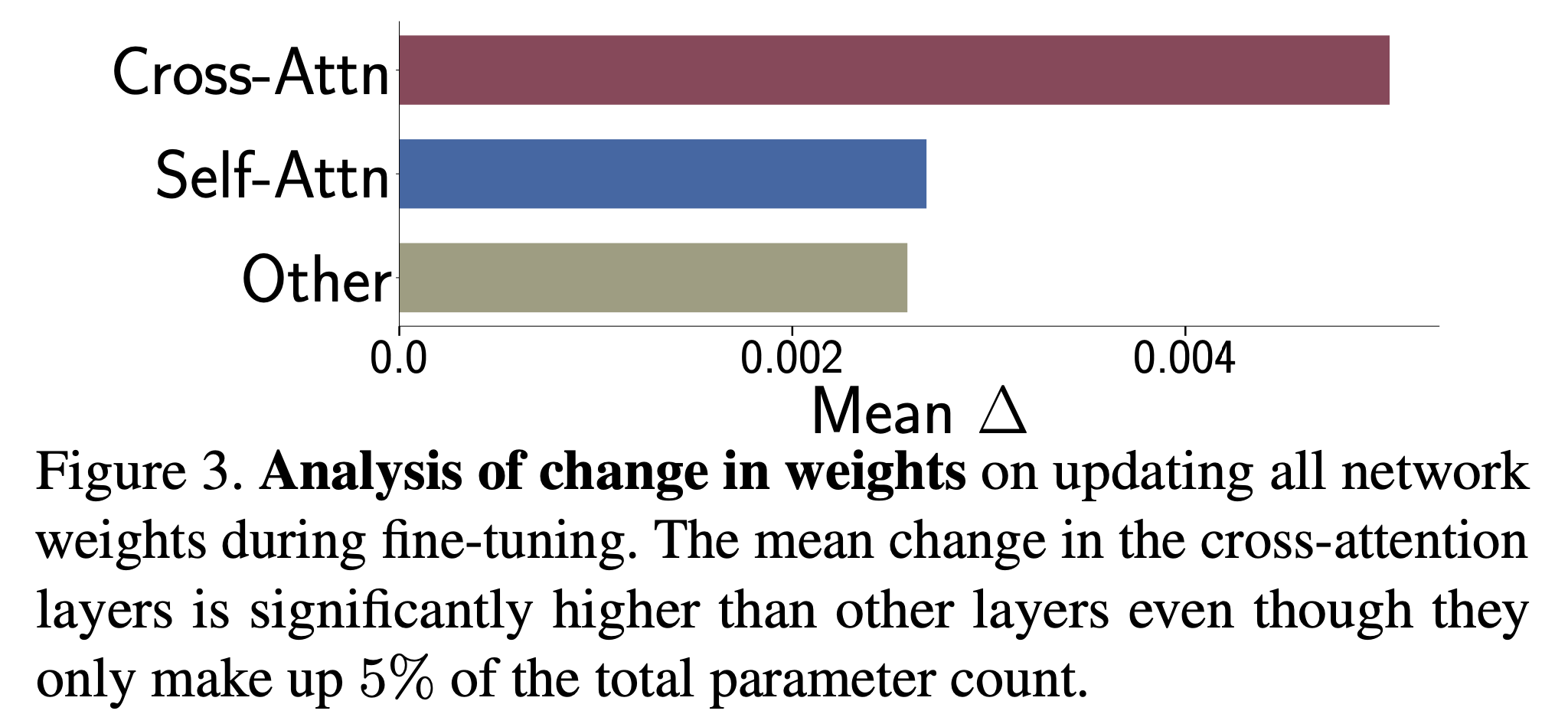custom_diffusion_fig1 Fig.

결과적으로 K, V projection layer가 가장 많이 변한다는 점을 확인해 이 부분만 tuning하는 방법을 제안했다.

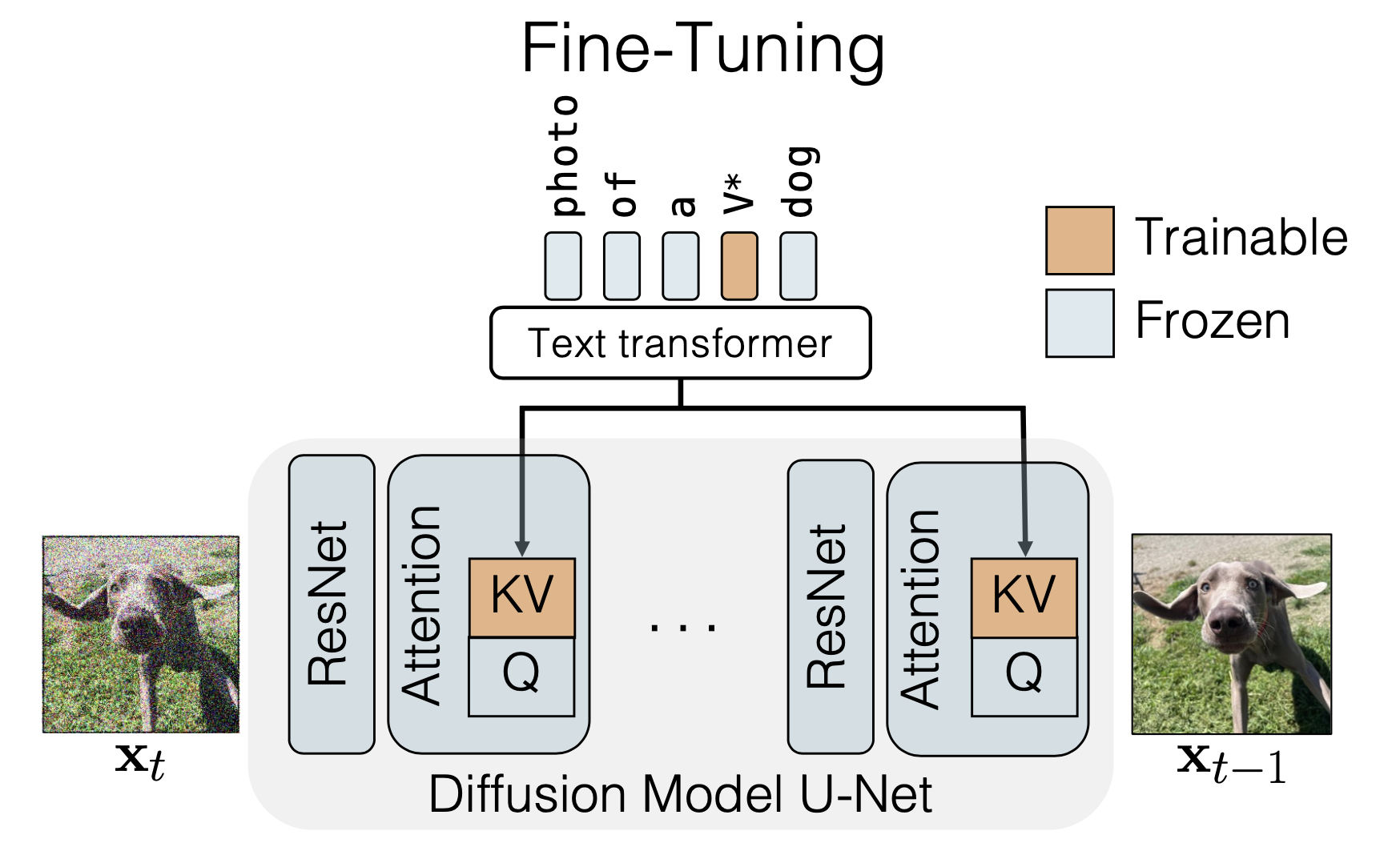custom_diffusion_fig2 Fig.

추가) 이 부분에 대해서는 필자가 반대로 K, V는 freezing 하고 Q 만 tuning하는 실험을 해봤는데, 학습이 잘되는걸 봐서는 크게 의미가 있는 분석은 아니었던 것 같다. SVCCA 나 CKA 등 layer의 activation output들이 fine-tuning 전후로 얼마나 변했는가?를 measure하는 tool을 썼을때도 사실 K,V 는 큰 변화가 없었다. 차라리 실제로 module별로 freezing 해보고 evaluation을 했던 낸 AdaLoRA가 더 나은 방식이었던 것 같다.

Methods

SVD-based Adaptation

어떤 layer 가 중요한지? 그래서 얼마만큼의 rank 가 필요한지? 를 알기위해선 어떻게 해야할까? 간단한 방법으로 square matrix 에 대해 SVD를 해서 singular value를 측정할 수 있겠다. 정확히 말해서는 우리는 LoRA 처럼 pre-trained weight (good initialization point)는 그대로 두고 adaptation이 될 \(\Delta W\)에 대해 학습 중간 중간 SVD를 취해서 상위 몇개만 남겨두는 것이다.

\[\begin{aligned} & W=W^{(0)}+\Delta=W^{(0)} + \underbrace{B A}_{\text{LoRA}} & \\ & W=W^{(0)}+ SVD(\Delta) = W^{(0)} + UDV & \\ \end{aligned}\]

하지만 이렇게 하면 매 optimization step 마다 SVD 를 해야하는데 SVD 계산 비용이 비싼편이기 때문에 training time이 매우 느려질 수 있다. 그래서 SVD 스타일을 따르되, 매 번 SVD를 하지는 않고 이 factorized matrix모양을 그대로 학습하는 방법을 택한다.

\[W=W^{(0)}+\Delta=W^{(0)}+P \Lambda Q\]

여기서 \(P \Lambda Q\)가 SVD 와 다름 없기 때문에 각각은 다음과 같다.

  • Left Singular Matrix : \(P\)
  • Diagonal Matrix : \(\Lambda\)
  • Right Singular Matrix : \(Q\)

SVD를 할 때 diagonal matrix 는 singular value 들이 크기순으로 정렬되어있고 left, right singular matrices는 각자의 column vector 들이 orthogonal 한 특성을 갖고 있기 때문에 우리가 SVD 를 한것과 같은 효과를 내면서 singular value 기준으로 rank 를 늘렸다 줄였다 하기 위해서는 이 특성이 성립해야 하므로 아래와 같은 regularization term 을 추가로 넣어준다.

\[R(P, Q)=\left\|P^{\top} P-I\right\|_{\mathrm{F}}^2+\left\|Q Q^{\top}-I\right\|_{\mathrm{F}}^2\]

AdaLoRA vs LoRA

그런데 이 쯤에서 '아니 LoRA 랑 AdaLoRA 랑 AB 에서 AXB 꼴로 된 것 밖에 없잖아? term 만 1개 늘었네?'같은 생각이 들 수 있다. 말 그대로 \(A, B\) matrix 형태는 유지하되 쓸모없는 vector들을 그냥 제거해버리면 되는데 굳이 3개로 decomposition 을 할 이유가 있을까? 저자들은 이런식으로 원래 LoRA 에서 필요없는 vector쌍 (doublet)을 아예 제거해버리는 Structed Pruning 을 할 수도 있지만 이렇게하면 아주 낮은 가능성이지만 (논문에 있는 표현) 다시 이 vector가 필요해질 때 이를 recover 할 수 없다는 점, 기존의 LoRA는 orthogonal 가정이 없기 때문에 doublet 이 서로 의존성이 있으므로 함부로 제거하기에는 original matrix 가 많이 변할 수 있다는 점을 문제삼았다.

(In Paper)

First, when a doublet is measured as unimportant, we have to prune all of its elements. 
It makes scarcely possible to reactivate the pruned doublets as their entries are all zeroed out 
and not trained. 
In contrast, AdaLoRA only masks out the singular values based on (3) 
while the singular vectors are always maintained. 
It preserves the potential of future recovery for the triplets dropped by mistake. 

Second, A and B of LoRA are not orthogonal, meaning the doublets can be dependent with each other. 
Discarding the doublets can incur larger variation from the original matrix than truncating 
the smallest singular values. 
Therefore, the incremental matrices are often altered dramatically after each step of rank allocation,
which causes training instability and even hurts generalization.

Importance-Aware Rank Allocation

이제 \(\Lambda\) 에서 중요도를 측정한 뒤에 학습을 하면서 제거를 하면 되는데, 사실 official implementation 이 없어 실제로 지우는건지 아니면 어떻게 처리하는지는 잘은 모르겠다.

\[W=W^{(0)}+\Delta=W^{(0)}+P \Lambda Q\]

논문에는 masked out한다고 되어있어서 덕분에 나중에 중요도가 올라가면 recovery 하는 것 같은데, 이는 나중에 기회가 되면 다시 revisit하도록 하겠다.

\[\tilde{\Lambda}_k^{(t)}=\Lambda_k^{(t)}-\eta \nabla_{\Lambda_k} \mathcal{L}\left(\mathcal{P}^{(t)}, \mathcal{E}^{(t)}, \mathcal{Q}^{(t)}\right)\] \[\Lambda_k^{(t+1)}=\mathcal{T}\left(\tilde{\Lambda}_k^{(t)}, S_k^{(t)}\right), \text { with } \mathcal{T}\left(\tilde{\Lambda}_k^{(t)}, S_k^{(t)}\right)_{i i}= \begin{cases}\tilde{\Lambda}_{k, i i}^{(t)} \quad S_{k, i}^{(t)} \text { is in the top-b } b^{(t)} \text { of } S^{(t)}, \\ 0 \quad \text { otherwise, }\end{cases}\]

Magnitude of Singular Values

그 다음은 어떤 값을 기준으로 pruning을 할 것인가?에 대한 내용이다. 가장 간단한 방식은 우리가 SVD 를 모방했기 때문에 singular value 의 크기를 기준으로 하는것이다.

\[S_{k,i} = \vert \lambda_{k,i} \vert\]

이 방식은 학습도 꽤 안정적으로 잘 되지만 어떤 parameter가 모델의 성능에 기여했는지에 대해서 정량화하기에 최적이지는 않았다고 한다.

Sensitivity-based Importance

그 대안으로 논문에서 제시한 것이 바로 Sensitivity-based Importance Score이다. (AdaLoRA에서 처음 제시한건 아니고 reference들을 찾아보면 prior work들에 대해 찾을 수 있다)

\[S_{k, i}=s\left(\lambda_{k, i}\right)+\frac{1}{d_1} \sum_{j=1}^{d_1} s\left(P_{k, j i}\right)+\frac{1}{d_2} \sum_{j=1}^{d_2} s\left(Q_{k, i j}\right)\]

위의 수식에서 \(s(\cdot)\) 함수는 각각의 single entry 들에 대한 특정 importance function 인데, 논문에서는 이를 magnitude of the gradient-weight product로 정의했다.

\[I\left(w_{i j}\right)=\left|w_{i j} \nabla_{w_{i j}} \mathcal{L}\right|\]

여기서 \(w_{ij}\)는 trainable parameters이다. 위의 함수가 나타내는 바는 바로 해당 parameter 가 제거되면 loss 가 얼마나 변하는지? 에 대한 변화량을 정량화한 것이 된다고 한다. 즉 이게 크면 model performance 에 기여를 많이 하는 것이 되므로 남겨야 되는거고 이것이 미비하면 pruning하면 되는 것이다. 추가적으로 paper에서는 PLATON: Pruning Large Transformer Models with Upper Confidence Bound of Weight Importance라는 논문의 실험결과를 근거로 들어 좀 더 개선된 algorithm을 제시했다. 요약하자면 우리가 deep learning을 할 때 mini-batch sampling을 하기 때문에 sensitivity를 위의 수식으로 측정하기에는 uncertainty 가 크다는 것이다. 그래서 이를 고려해서 아래의 수식을 사용했다고 한다.

\[\begin{aligned} & \bar{I}^{(t)}\left(w_{i j}\right) =\beta_1 \bar{I}^{(t-1)}\left(w_{i j}\right)+\left(1-\beta_1\right) I^{(t)}\left(w_{i j}\right) & \\ & \bar{U}^{(t)}\left(w_{i j}\right) =\beta_2 \bar{U}^{(t-1)}\left(w_{i j}\right)+\left(1-\beta_2\right)\left|I^{(t)}\left(w_{i j}\right)-\bar{I}^{(t)}\left(w_{i j}\right)\right| & \\ \end{aligned}\]

즉 가장 고도화된 \(s(\cdot)\)은 다음과 같게 된다고 한다.

\[s^{(t)}\left(w_{i j}\right)=\bar{I}^{(t)}\left(w_{i j}\right) \cdot \bar{U}^{(t)}\left(w_{i j}\right)\]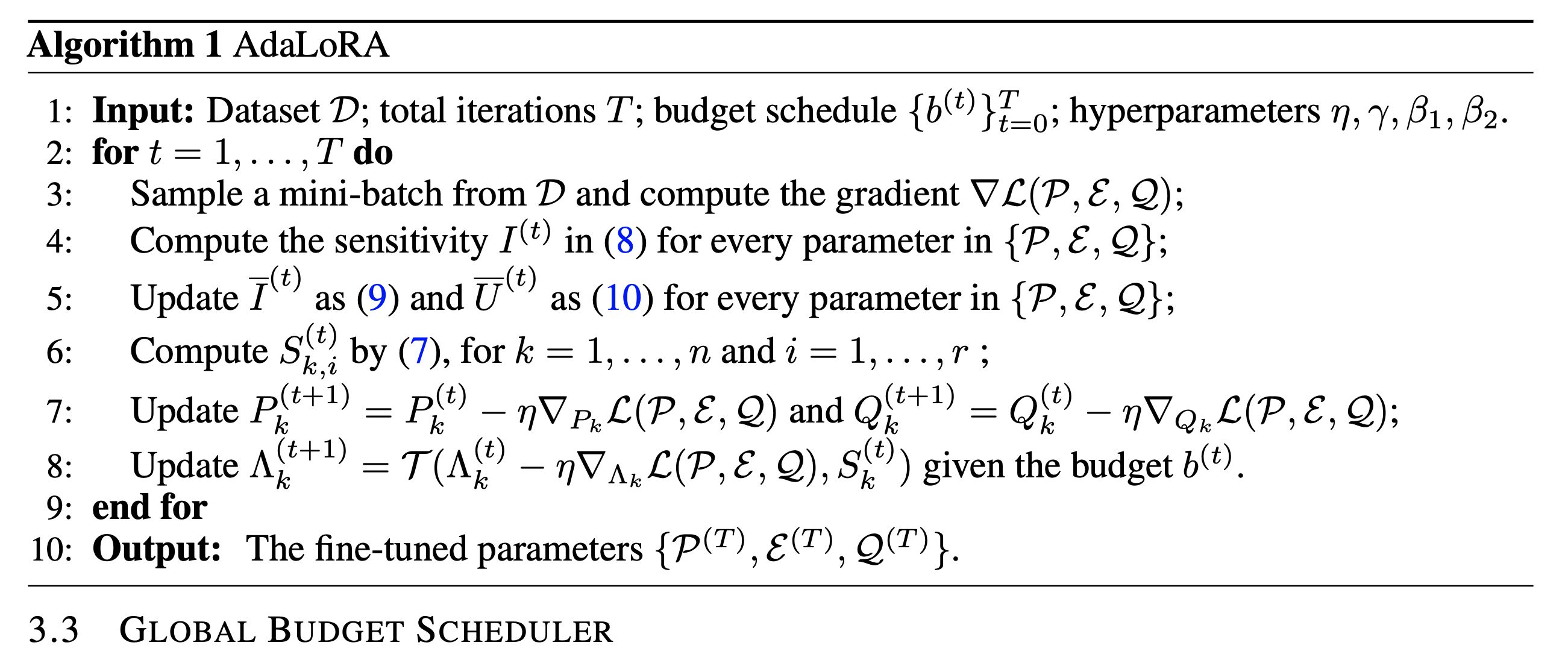

adalora_algorithm1 Fig.

Results

몇 가지 detail과 global budget scheduler같은 것들이 있지만 해당 post에서는 생략할테니 관심있는 사람들은 paper를 확인하길 바란다. 중요한 것은 AdaLoRA를 적용하면 그래서 좋아지는가?인데, 앞서 LoRA 결과를 얘기하며 밝혔던 것처럼 개인적으로는 NLU task (GLUE benchmark) 자체가 너무 쉬운 benchmark가 아닌가 싶다. 그치만 AdaLoRA가 outperforming했다니 그런가 보다 싶고,

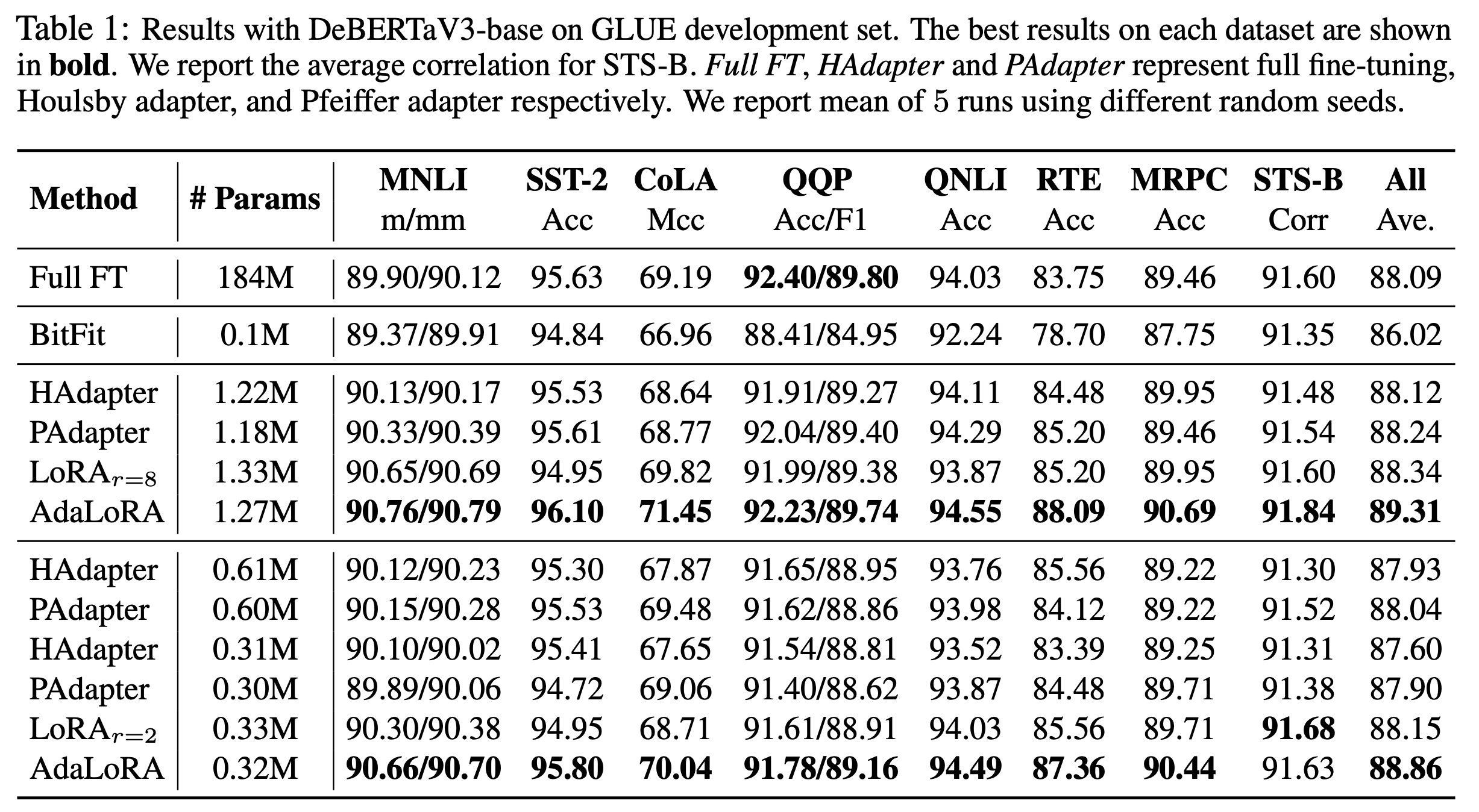adalora_table1 Fig.

학습이 다 된 DeBERTa에 대해서 rank budget은 각 layer별로 아래처럼 할당되었다고 한다.

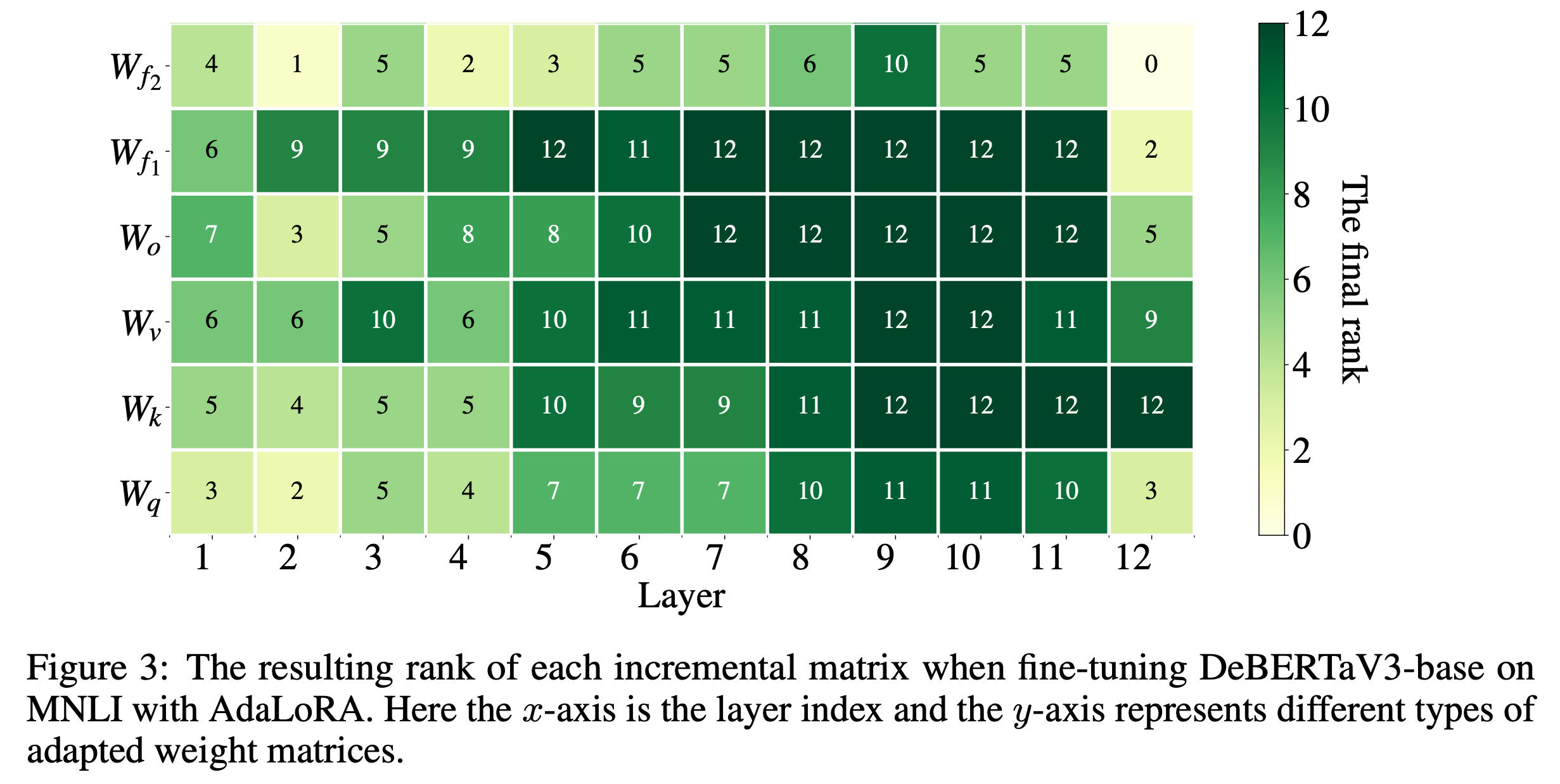adalora_fig3 Fig.

여기서 ‘importance score 계산하다보면 step 당 걸리는 시간과 메모리가 더 들겠지?’같은 생각을 할 수 있는데, SVD를 매 step하는 것이 아니며 학습이되면서 rank가 줄어들어서인지 생각보다 큰 차이가 나지는 않았다고 한다.

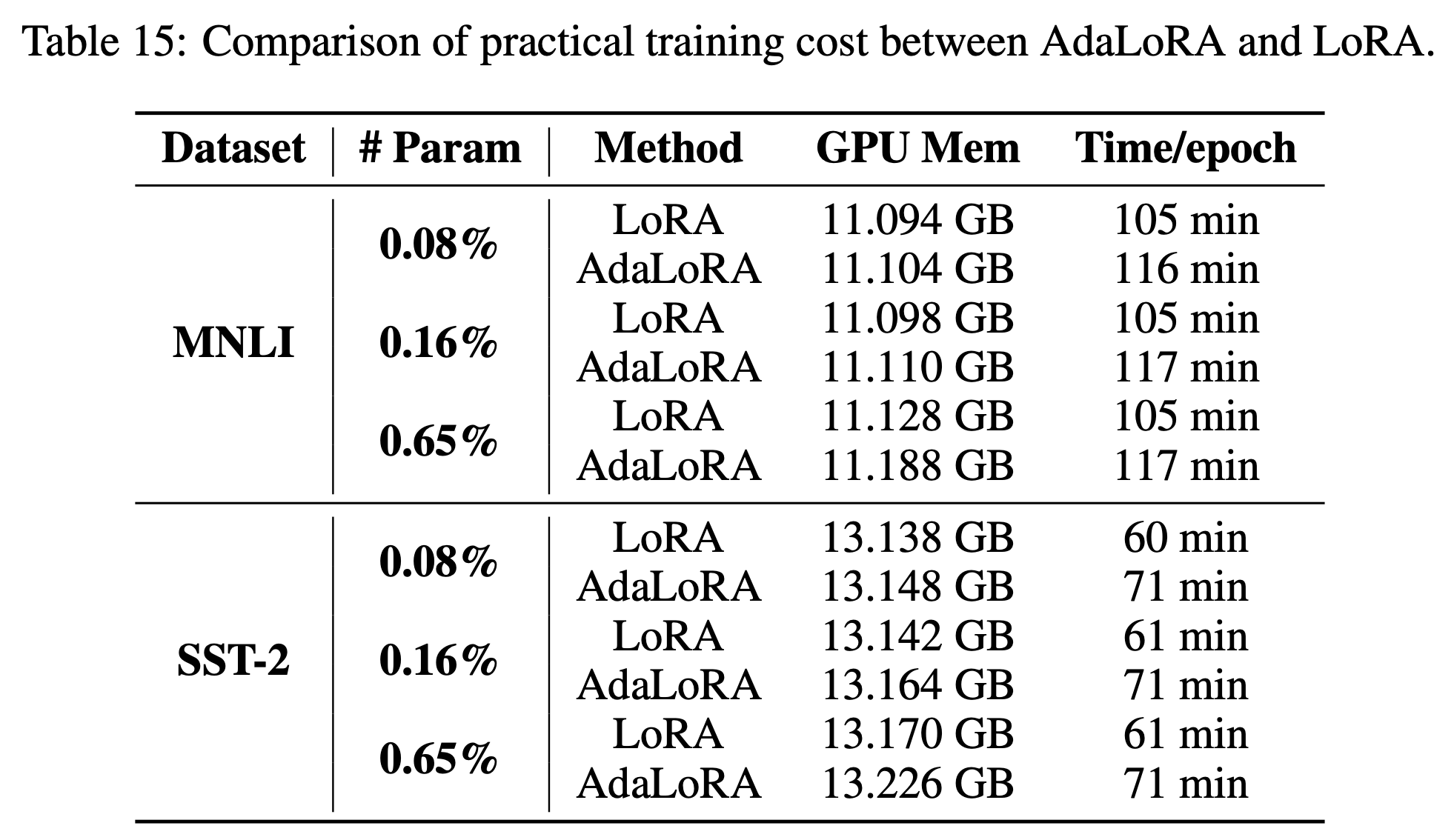adalora_table15 Fig.

LoRA on Other Domains

Image Generation

Image generation 분야에서 LoRA를 적용한 것은 딱히 white paper reference는 없다. 다만 cloneofsimo/lora라는 repo 에서 가장 먼저 LoRA 를 diffusion-based model 의 conv2d, unet 의 linear layer 들에 적용했다. 그리고 이것이 훗날 huggingface 의 PEFT library에도 붙게 되었고, 서두에 motivation하면서 보여준 것처럼 image generation + PEFT는 굉장히 잘된다.

lora_character Fig.

하지만 사람 얼굴을 학습하는 등의 어려운 adaptation 에서는 extremely low rank 로는 한계가 있다는 report 가 꽤 있는 것 같다. 그렇기에 이 분야는 LoRA 말고도 다른 PEFT 기법들을 제시한 논문들이 우후죽순으로 쏟아지고 있으니 관심이 있다면 더 찾아보면 좋을 것 같다.

Speech (Recognition, Understanding)

Speech 분야에서도 PEFT 를 적용하려는 시도가 있었다. 주요 reference로는 Exploring Efficient-tuning Methods in Self-supervised Speech Models 라는 paper가 있다. 이는 Self Supervised Learning (SSL) 로 pre-training 한 speech encoder를 음성 인식 (Automatic Speech Recognition; ASR), 감정 인식등 (Spoken Language Understanding; SLU 류)의 downstream task 로 adaptation 할 때 PEFT methods를 써 성능을 비교하는 실험을 했다.

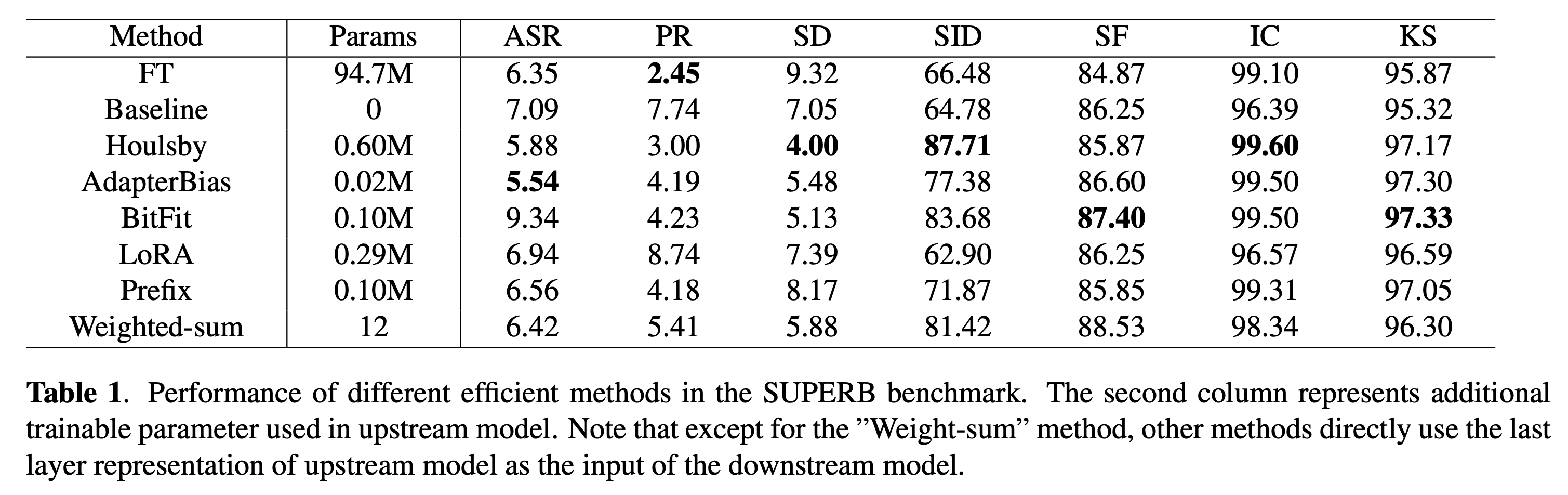efficient_finetuning_methods_table1 Fig.

여기서 필자가 가장 관심있는 것은 ASR이었는데, Full Fine-tuning 을 하는 것 보다 adapter base method가 더 좋다고 하는데 사실 detail이 많이 없고 필자의 경험과도 align이 되지 않아 별로 믿음이 가지는 않았다. 심지어 NLP, image generation 등 PEFT가 잘 먹히는 분야에서도 training budget만 충분하다면 full fine-tuning이 좋은 성능을 내는 경우가 많기 때문에 LoRA등을 하지 않는데, ASR이 adapter보다 못하다는건 hyperparameter search를 제대로 못한것이 아닌지 의심이 되기도 했다.

또한 PEFT로 ASR을 하기에는 ASR은 adaptation이라고 보기 어렵다는 의심때문에 그런 것도 있는데, image generation 은 원래도 prompt 를 given 으로 image 를 생성하던 능력에 어떤 특정 image의 detail을 adaptation하는 것이고, NLP 도 비슷한 수준인데 반해 pre-trained speech encoder는 그정도의 capa는 없을 수 있다. 보통 SSL trained speech encoder는 발음열로 추정되는 representation을 학습하게 되는데, ASR은 이를 완벽히 text로 mapping할 능력을 학습해야 하므로 난이도 자체가 PEFT로 하기에는 어려운 것이 아닌가 하는 것이 내 생각이다. 하지만 처음으로 이런 PEFT 기법을 다양한 speech task 에 적용해봤다는 데 논문의 contribution이 있다고 할 수 있겠으며, 아직 study할 room이 많이 존재하는 것 같다.

References