Notes

Predictive Uncertainty of Deep Learning based Models (Bayesian Deep Learning and Monte Carlo (MC) Dropout)

17 Dec 2022

< 목차 >

Bayesian Modeling and Model Uncertainty

머신러닝에서 Bayesian Approach는 무엇을 의미할까요?

일반적인 머신러닝, 딥러닝에서는 우리가 추정하고자하는 출력 분포의 파라메터를 ‘점 추정(Point Estimation)’ 하게 됩니다. 점 추정이란 예를 들어 Maximum Likelihood Estimation (MLE) 를 통해 Likelihood 가 가장클 때의 값을 딱 하나만 사용해서 추론 결과를 내는, 즉 예를 들어 Gaussian Distribution Target 분포라면 (\(\mu=4.5\), \(sigma=2.7\)) 같은 식으로 deterministic 한 결과를 내는걸 의미합니다.

이는 prior를 고려해서 posterior를 구한 뒤 계산하는 Maximum A Posterior를 사용해서 파라메터를 찾아도 마찬가지 입니다.

하지만 이런 방식의 결과는 결과가 Over Confident 하다는 문제가 발생할 수 있는데요, 과연 이는 어떤 문제 일까요?

MLE and Bayesian Inference for Regression

아래는 Maximum lieklihood Approach를 통해 likelihood를 크게 만드는 파라메터 하나만을 점 추정한 선형회귀의 결과입니다.

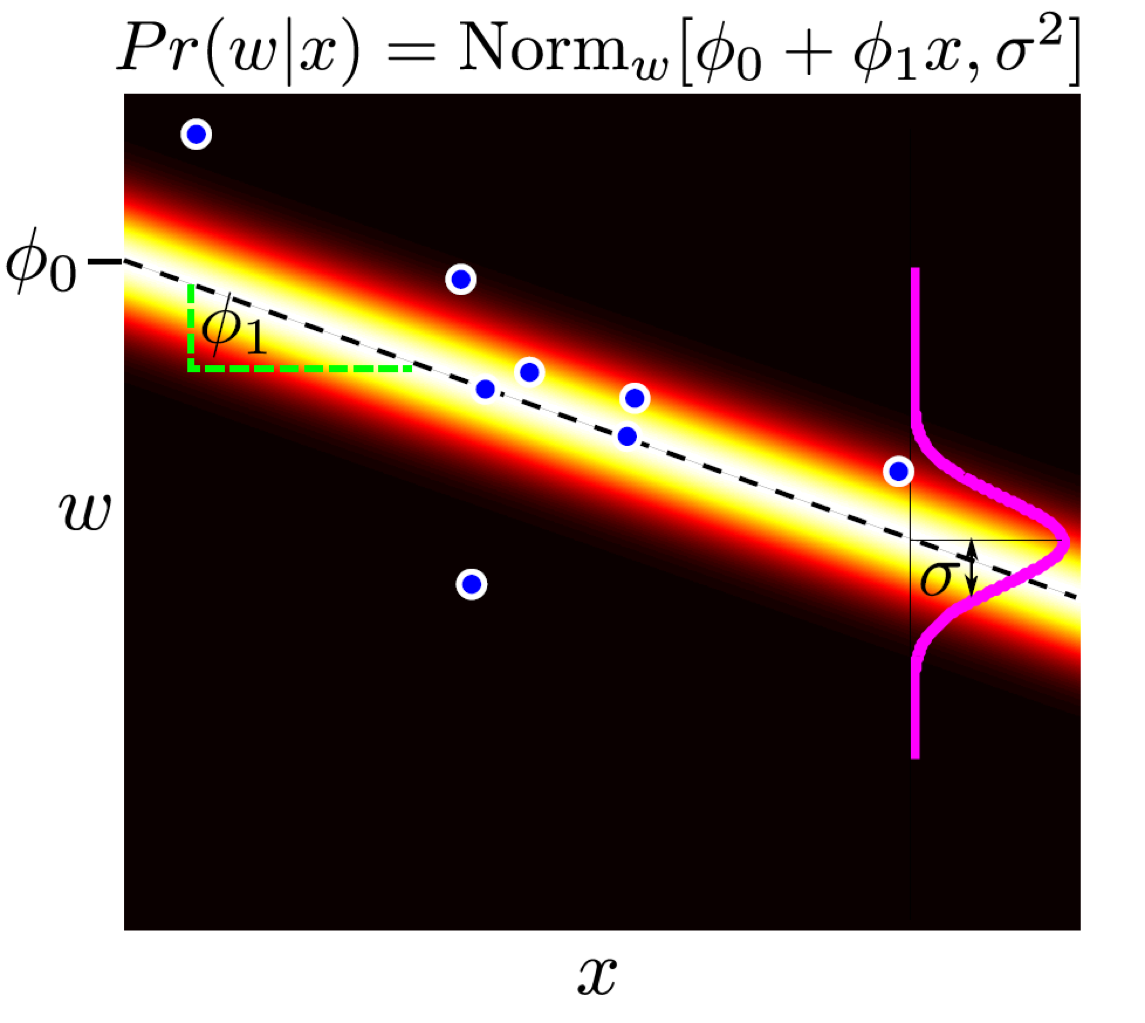linear_regression Fig.

아래는 Bayesian Approach 통해 Inference한 방법입니다.

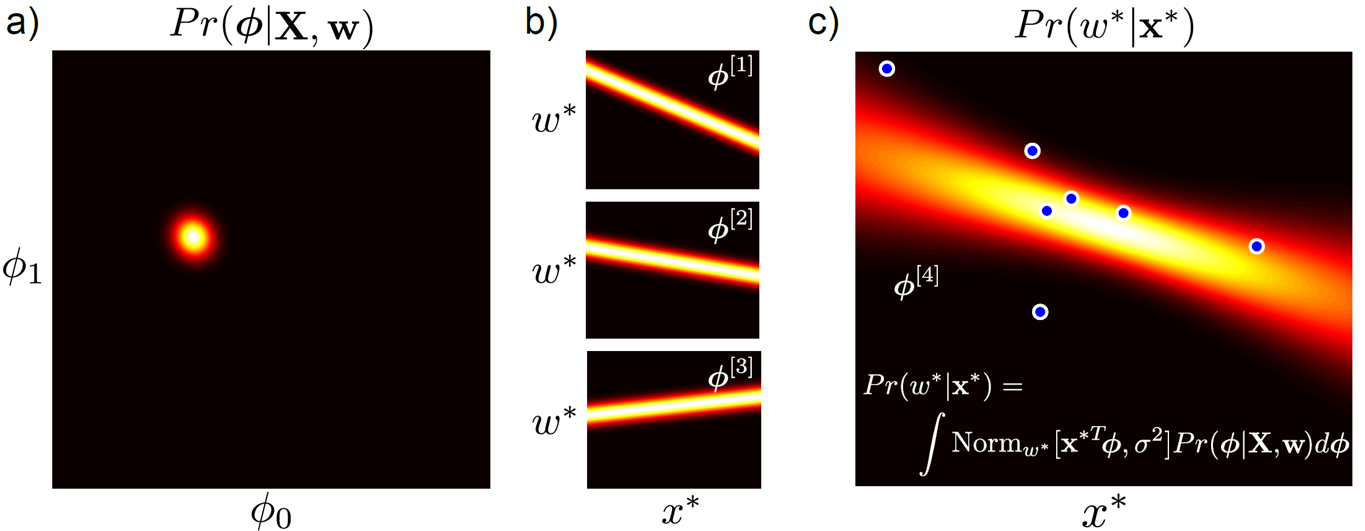bayesian_inference Fig.

Bayesian Inference 란 그림에서도 알 수 있듯이, 예를들어 Target 분포가 Gaussian Distribution 이라면 Parameter Space 가 \(\mu, \sigma\) 에 대한 2차원 공간으로 주어질 것이고 이 속에서 표현 가능한 모든 값들을 사용해 (적분해) 회귀 곡선을 그리겠다는 겁니다.

둘의 차이는 회귀 곡선이 데이터 포인트가 별로 없는 부분에 대해서는 variance가 엄청 크게 나타난다는 겁니다. 즉 모델이 데이터가 없는 부분에 대해서는 잘 모른다고 대답하는것과 같죠.

MLE vs Bayesian Inference for Classification

분류 문제에서도 볼까요? 아래는 Binary Classification의 결과 예시 입니다.

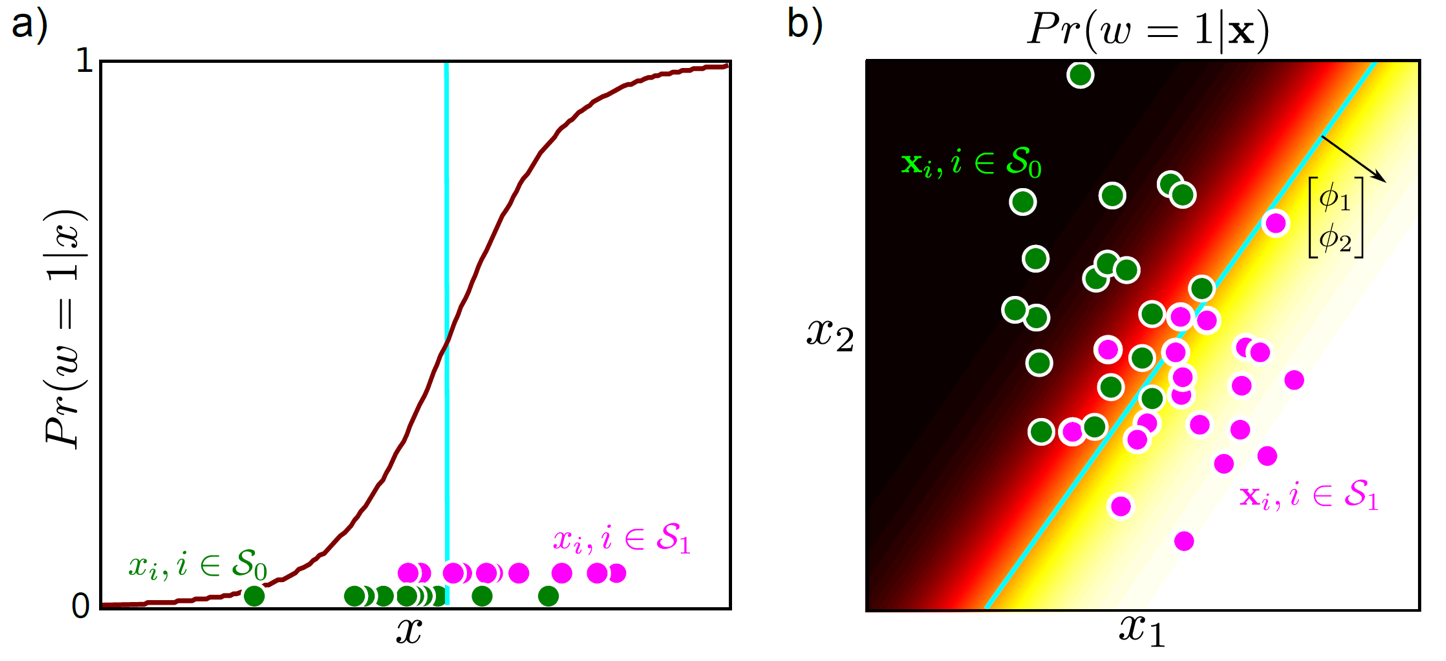mle_decision_boundary Fig.

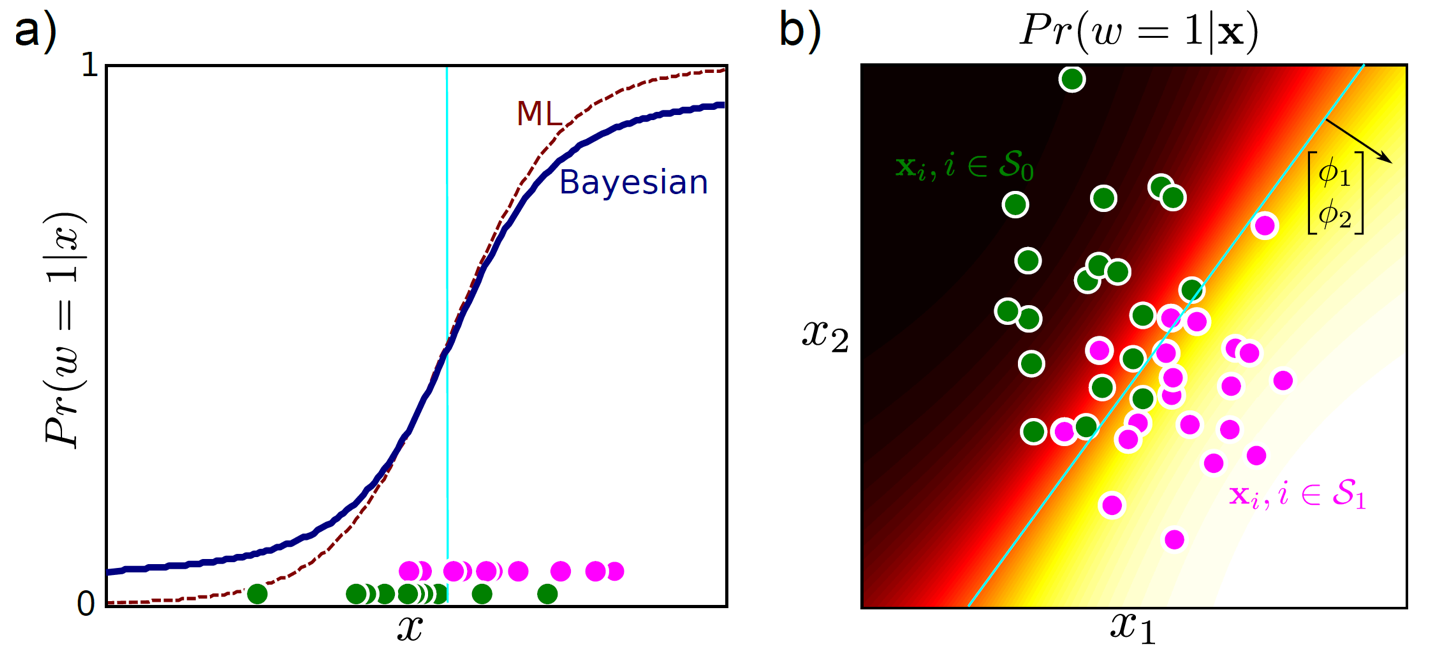bayesian_decision_boundary_2 Fig.

마찬가지로 MLE를 사용하면 Likelihood가 가장 클 때의 값만 취하는 점추정의 경우(위) Decision Boundary 가 데이터의 밀도와 상관없이 그어지는 걸 알 수있지만, Bayesian Inference 를 할 경우 데이터가 부족한 부분에 대해서는 Decision Boundary 가 옅어지는 (분산이 커지는) 걸 볼 수 있죠?

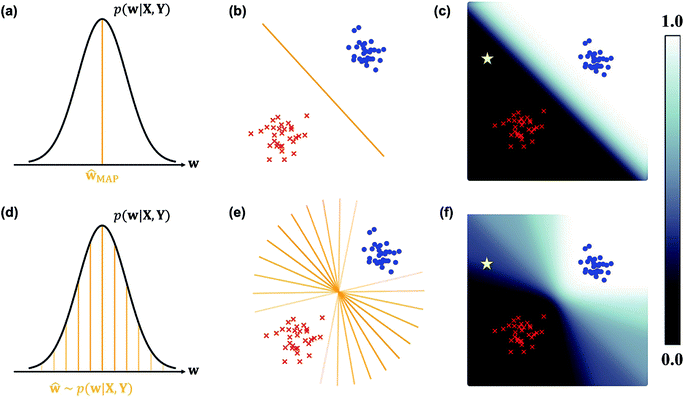bayesian_decision_boundary Fig. Source From link

MLE는 학습이 끝난 뒤 위의 그림처럼 별 모양의 데이터가 들어가면 (학습때 보지 못한 데이터, 즉 Out-of-Distribution (OOD) ?), 모델이 자신있게 ‘class1’이라고 분류하는 모습을 볼 수 있는데요, 이는 좋지 어떤 경우에는 굉장히 치명적일 수 있습니다.

가령 뇌 종양이나 녹내장 같은 병을 진단하는 Binary Classification Task 에서 모르면 모른다고 하는 편이 낫지 (분산이 크게 나옴) 이걸 데이터가 많은 부분과 같은 자신감 (Confidence) 로 아닌데요?하면 큰일이 날 수 있는거죠.

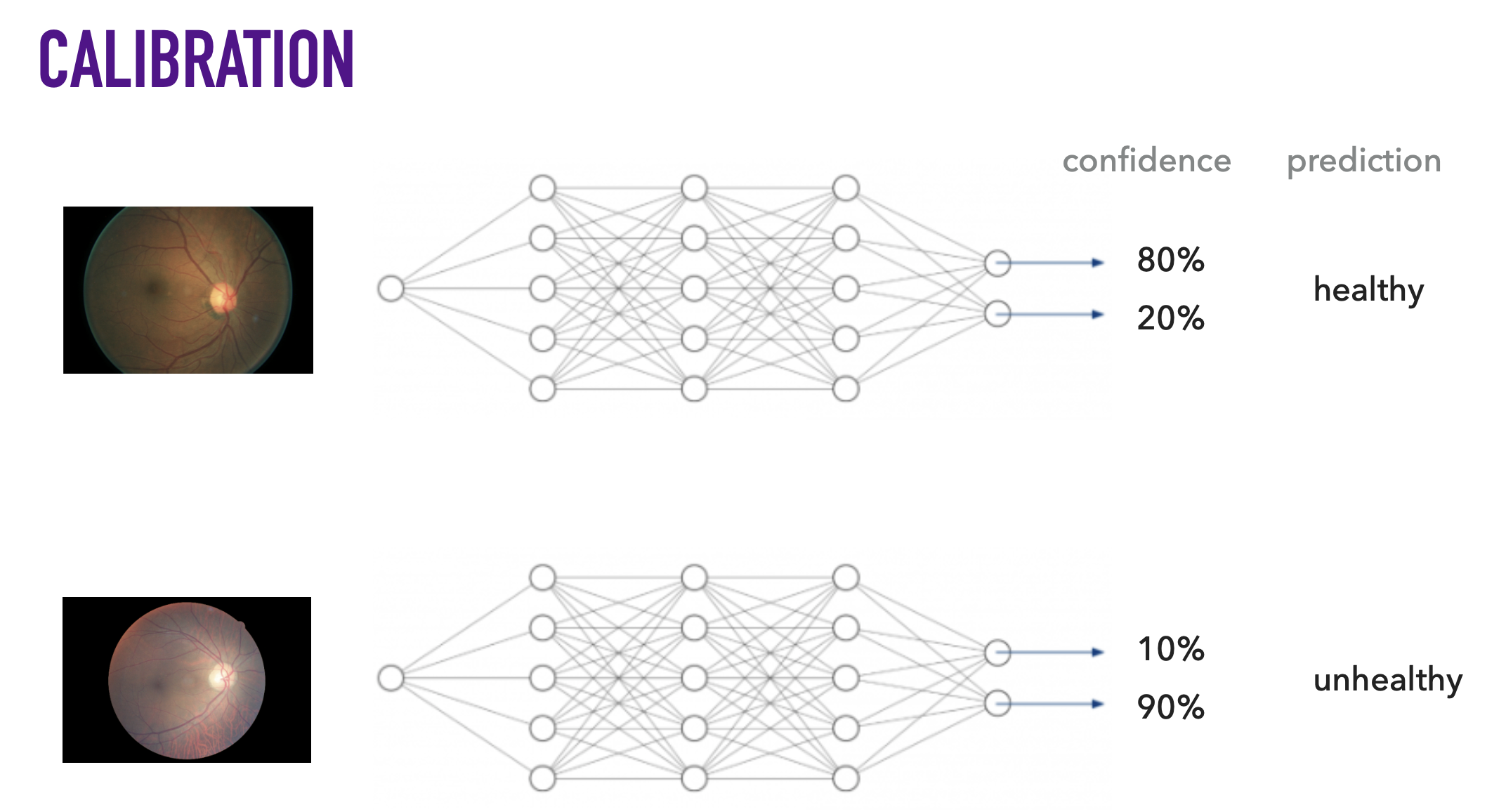calibration_fig1 Fig.

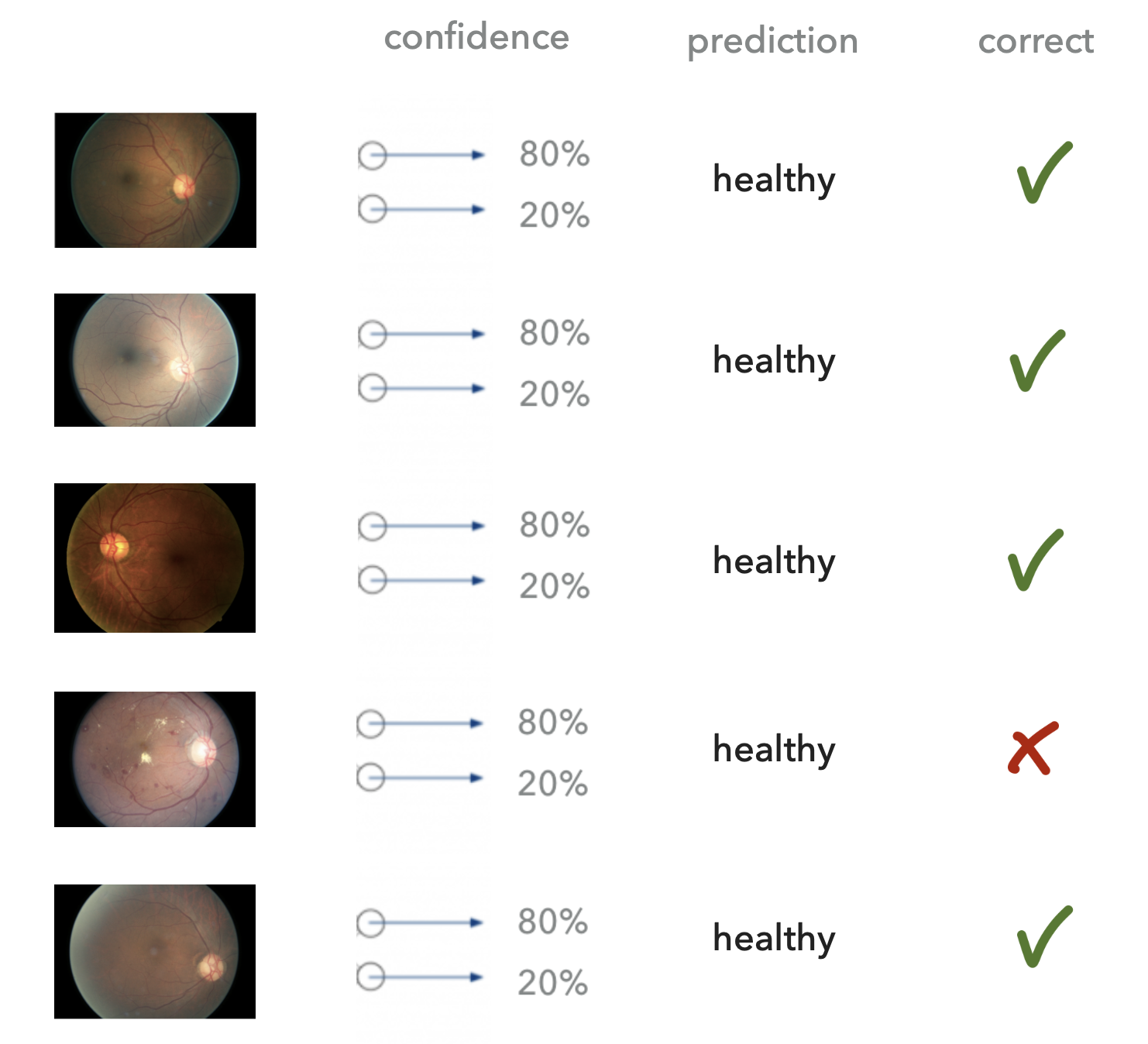calibration_fig2 Fig.

그런데 이런 Over Confidence 문제가 일반적인 머신러닝 Approach 에서도 문제인데, 현재 많이 쓰이는 Neural Network 에서는 더욱 두드러진다고 합니다.

neural_network_overconfidence Fig.

What is the Problem of Bayesian Approach?

우리는 앞서 모델이 어떤 부분을 모르는지를 나타내는, 즉 모델의 불확실성 (Model Uncertainty)을 나타내는 건 꽤 중요한 일임을 알게되었습니다. 그러면 Bayesian Approach 로 추론하는게 항상 제일 좋아보이는데 이 방법을 항상 쓰면 되지 않을까요?

사실 Bayesian Inference 를 한느것이 그렇게 값싼 연산은 아닙니다.

우리가 가장 흔하게 쓰는 MLE는 Target 분포를 Gaussian 쯤으로 정했을 때 Likelihood를 가장 높게 나타내는 \(\mu, \sigma\) 한 점만 고르면 된다고 했죠?

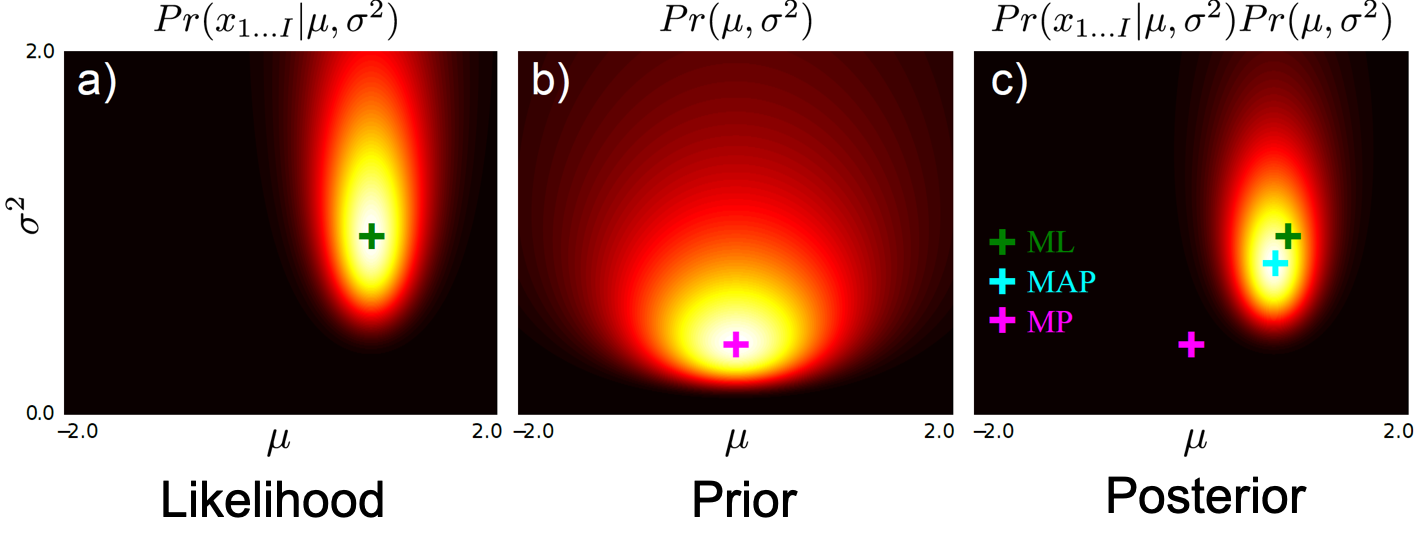map_and_bayesian_fig1 Fig.

여기서 \(\mu, \sigma\) 이 각각 음 대충 0 mean, unit variance 일 확률이 가장 높겠지? 라는 Prior가 들어가면 이 둘을 이용해 Posterior 를 구할수 있습니다.

\[\begin{aligned} & p(\theta \vert X) = \frac{p(X \vert \theta) p(\theta)}{p(X)} \\ & \approx p(X \vert \theta) p(\theta) \\ \end{aligned}\]

여기서 이 Likelihood 와 Prior 가 서로 Conjugate 관계이면 (Inverse Gaussian 이거나 Gaussian) Posterior 는 구하기 쉬울테고, Posterior 에서도 마찬가지로 이 값을 가장 크게해주는 점 하나만 추정한다면 그렇게 어렵지 않을겁니다.

(위의 그림을 보시면 MLE 와 MAP Solution 이 다르다는걸 알 수 있죠?)

여기서 Bayesian Inference 까지 하려면 이 Posterior 상의 모든 \(\mu, \sigma\) 와 각 점들의 확률값들을 사용해 이를 적분해야 하는데요,

\[\int_{\theta} p(x^{\ast} \vert \theta) p(\theta \vert X) d\theta = p(x^{\ast} \vert X)\]

즉 Posterior 를 학습한 다음에, 적분까지 취해야 한다는 겁니다.

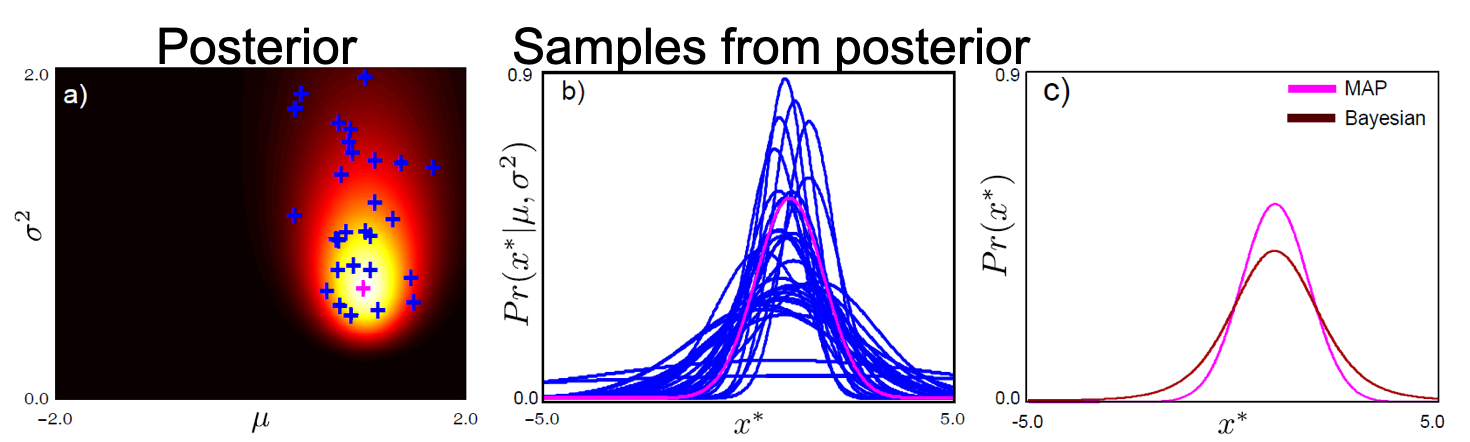map_and_bayesian_fig2 Fig.

하지만 이런 적분 연산은 간단한 머신러닝 보다 더 흥미로운 모델, 즉 현대 딥러닝에 쓰이는 모델들에서는 수행하기 어려운 연산이고, 일반적인 머신러닝의 경우에도 비싼 연산인데 Model Weight (Parameter) \(\theta\) 가 많게는 억단위가 넘어가는 요즘 모델들에 대해서는 거의 불가능한 수준의 연산이 되게 됩니다. (이를 Intractable 하다고 합니다.)

그래서 Bayesian Inference 를 할 때에는 Laplace Inference 나 Variational Inference 등 Posterior를 간단한 분포로 근사 (Approximation) 하는 방법을 사용하는 등 조치가 필요합니다.

Bayesian Linear Regression Example and Perspective of The Number of Data Points

우리가 앞서 Bayesian Inference 의 중요성에 대해서 얘기했지만 이게 항상 유효한가?, 비싼데 꼭 항상 할 필요가 있는가? 에 대해서도 생각해봐야 하는데요, 결론부터 말하자면 데이터가 충분히 많으면 Bayeisan Inference 나 MLE, MAP 나 거의 같은 Solution 을 제공하기 때문에 데이터가 충분히 많으면 그럴필요 없다 라고 할 수 있겠습니다.

선형 회귀를 한다고 생각해봅시다.

weight 는 일단 1차원이고,

\[y = wx + \epsilon, \text{where } \epsilon \sim N(0, \sigma^2)\]

이 때 Data Sample 은 3개밖에 없다고 생각합시다.

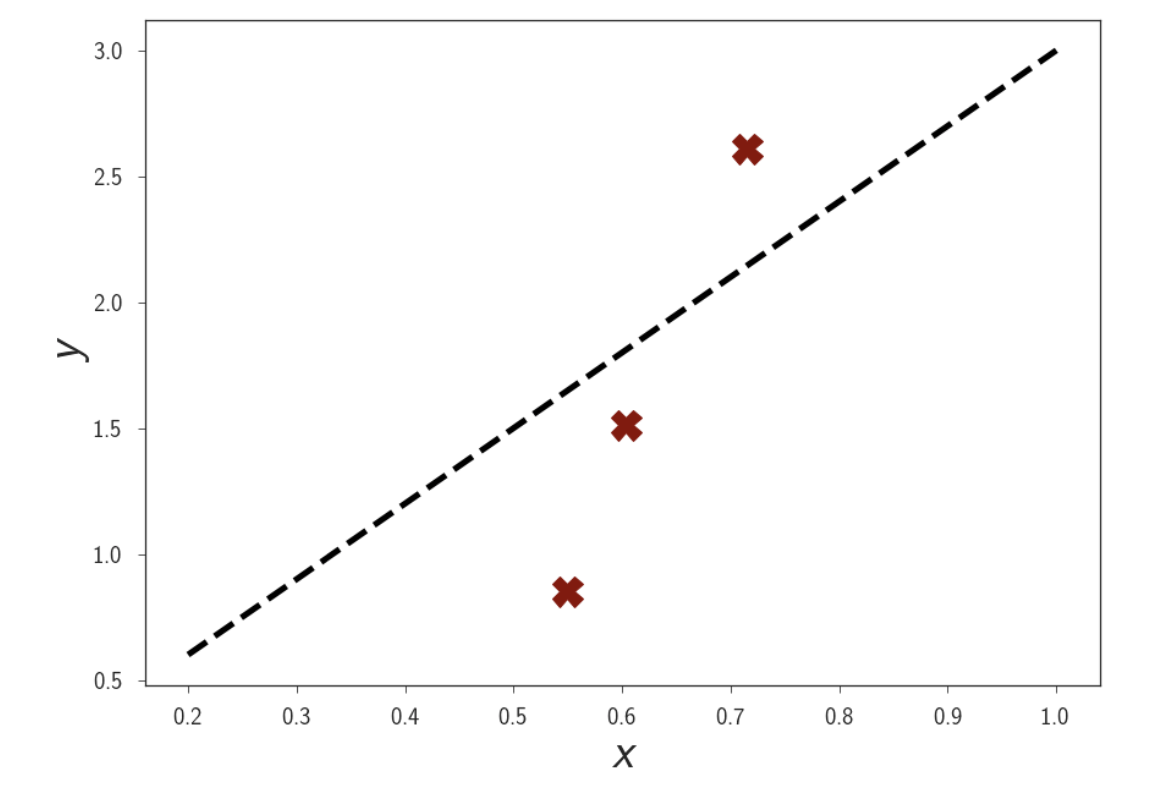nyu_linear_regression_fig1 Fig.

이 문제의 MLE Solution 은 다음과 같이 쉽게 구할 수 있겠죠?

\[\begin{aligned} & w_{MLE} = arg max_{w} log p(D \vert w) \\ & = arg max_{w} \sum_i log p(y_i \vert x_i, w) \\ \end{aligned}\] \[\max _w \sum_{i=1}^N \log \mathcal{N}\left(y_i \mid w x_i, \sigma^2\right) \Longleftrightarrow \min _w \frac{1}{N} \sum_{i=1}^N\left(y_i-w x_i\right)^2\]

데이터가 적기 떄문에 실제 데이터가 샘플링 된 Optimal Solution 인 \(w_{ture}\) 에 도달하지는 못했네요.

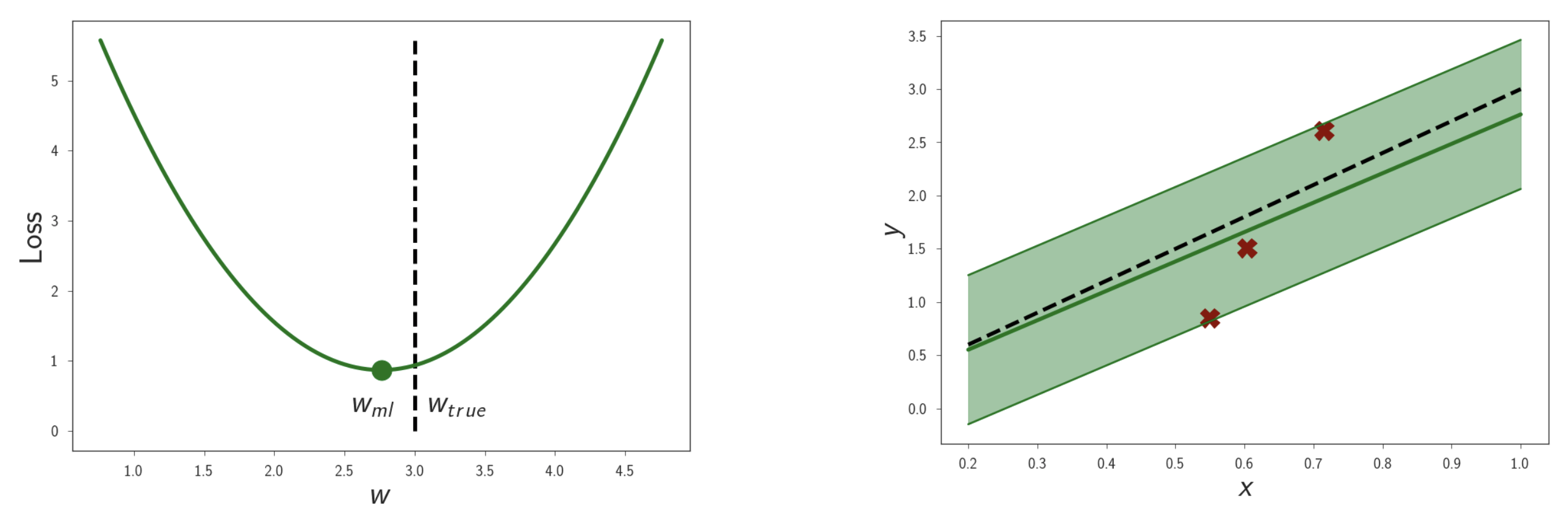nyu_linear_regression_fig2 Fig.

이제 MLE 로 구한 Solution 의 Uncertainty 는 얼마나 되는지 측정하기 위해 weight, \(w\) 의 prior distribution \(p(w)\) 를 도입합시다.

w 가 어떤 값이냐에 따라서 선이 다르게 그어지는 걸 알 수 있죠.

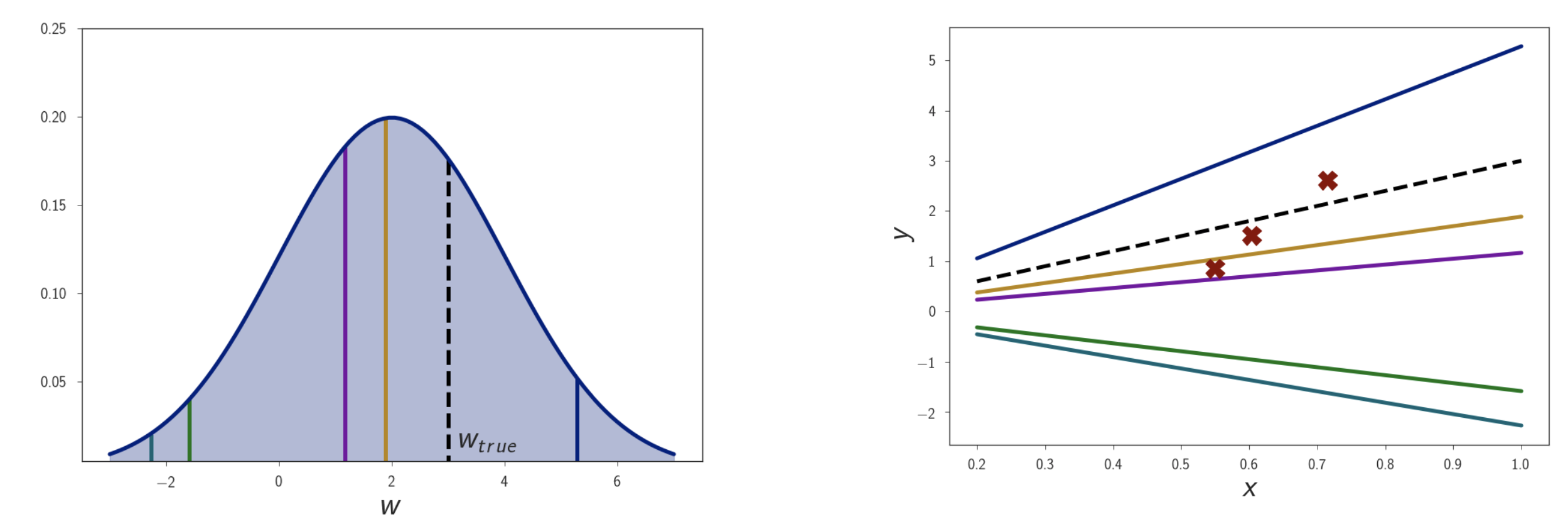nyu_bayesian_inference_fig1 Fig.

이제 Posterior 를 구하기 위해 Bayes Rule 에 따라 Likelihood와 Prior를 곱합시다.

\[\text{Posterior} \approx \text{Likelihood} \times \text{Prior}\] \[p(w \vert D) = \frac{p(D \vert w ) p(w)}{p(D)}\]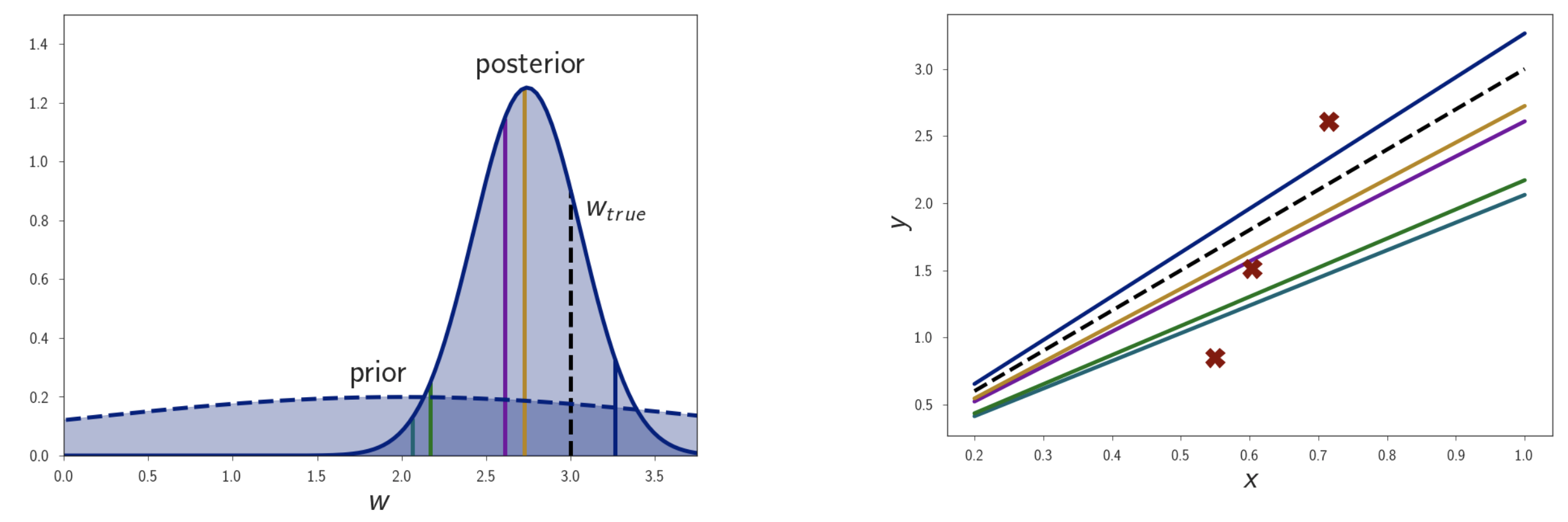

nyu_bayesian_inference_fig2 Fig.

그러면 실제로 우리가 weight 는 2.0에 있을 확률이 제일 높겠지? 라고 생각하고 만들었던 Prior 분포에 dataset의 정보가 주입되면서 만들어진 Posterior 분포가 위와 같이 만들어지고 여기서 제일 높은 값을 취한 MAP Solution 인 황색선 또한 MLE 처럼 \(w_{ture}\) 와 거리가 있는 것을 알 수 있습니다.

\[\begin{aligned} & w_{MAP} = arg max_{w} log p(w \vert D) \\ & = arg max_{w} log p(D \vert w) + log P(w) \\ \end{aligned}\]

(Prior 를 도입한 Solution, 즉 MAP 는 MLE + Regularization 임을 알 수 있다. P(w) 가 Gaussian 이면 \(L_2\) Norm, Laplace 이면 \(L_1\) Norm)

이제 이 Posterior 의 모든 weight 값들을 고려해서 적분해주면 Uncertainty 를 estimation 하는 결과를 낼 수 있는데요, 여기서 데이터를 늘려봅시다.

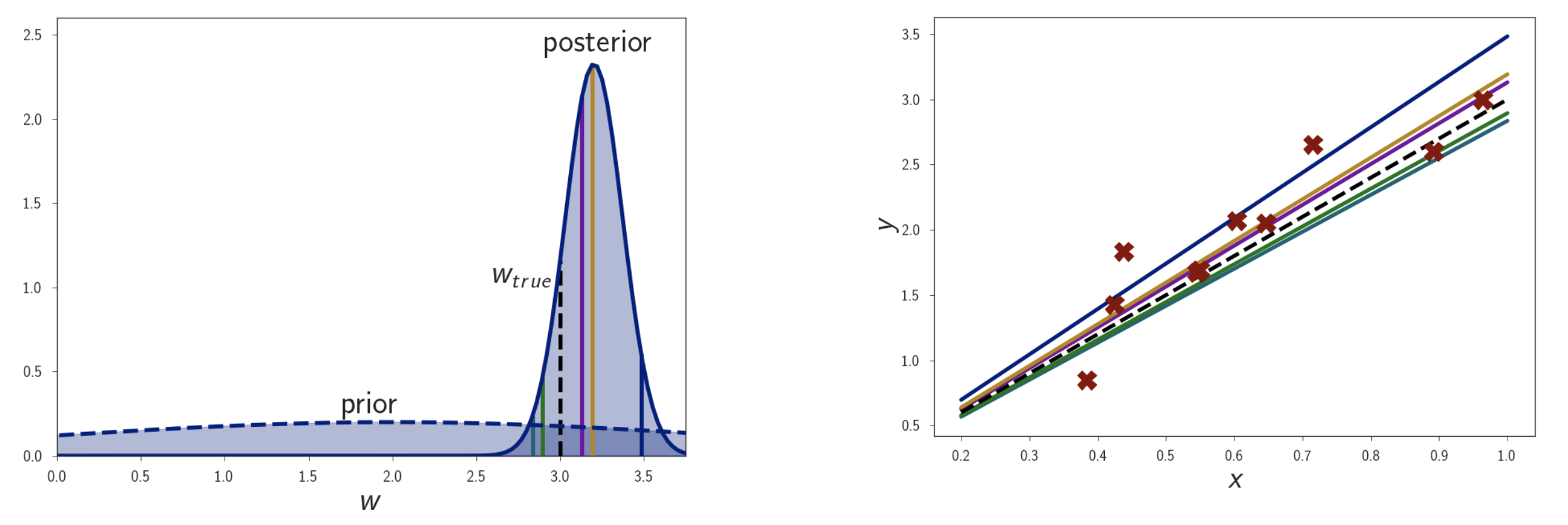nyu_bayesian_inference_fig3 Fig.

데이터를 늘릴수록 Likelihood 가 바뀌고, 그에 따라 Posterior 가 바뀌는 것을 볼 수 있죠.

더 늘려볼까요?

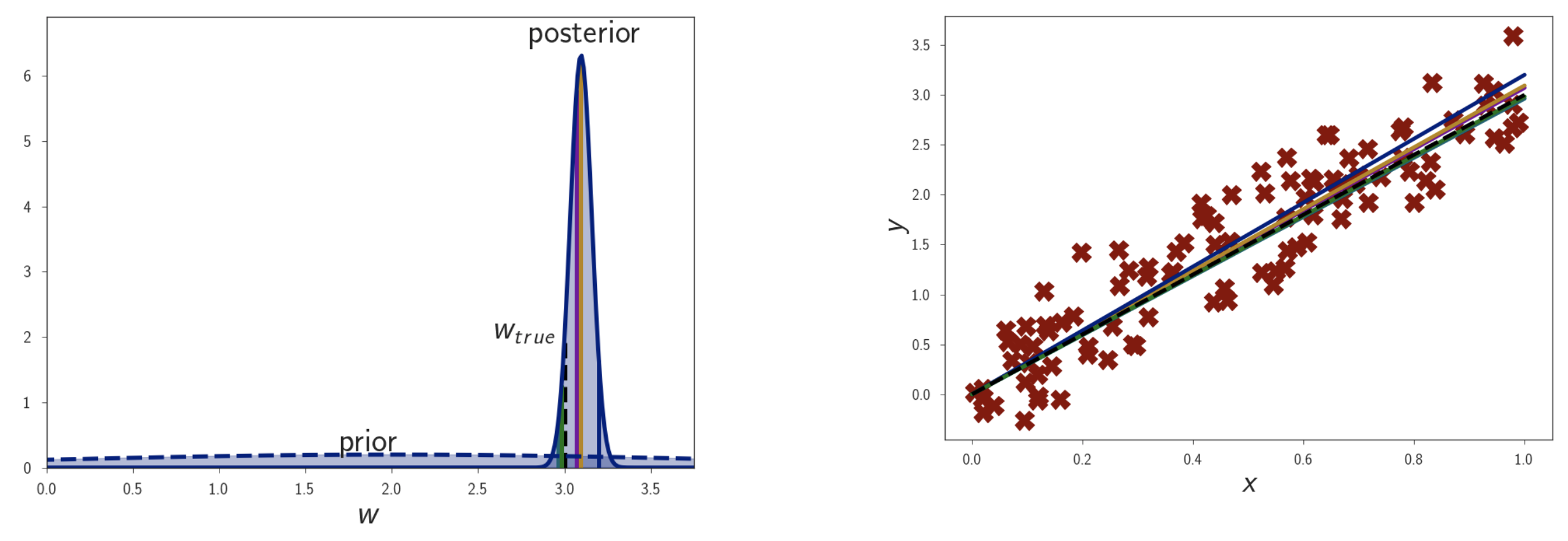nyu_bayesian_inference_fig4 Fig.

그렇습니다. 데이터가 많아질수록 Posterior 는 점점 Delta Function 에 가까운 모양을 하면서 결국에는

\[w_{\text{true}} \approx w_{\text{MAP}} \approx w_{\text{MLE}} \approx w_{\text{Bayesian Inference}}\]

가 되는것을 알 수 있습니다.

하지만 데이터와 파라메터의 Space 가 커질수록 이런 현상은 거의 없다고 봐야될 것 같습니다 (…)

Approximation

Variational Inference

그러면 어떻게 해야 복잡한 딥러닝 모델의 Posterior 를 계산하고 적분할 수 있을까요?

Notation 부터 다시 써봅시다. 앞으로 제가 쓸 수식의 기본 뼈대로 Yarin Gal 의 박사 학위 논문 (Thesis) 를 사용하겠습니다.

  • Label : \(Y\)
  • Input : \(X\)
  • Model Weight : \(w\)
  • Likelihood : \(p(y \vert x, w)\)
  • Posterior : \(p(w \vert X,Y) = \frac{ p(Y \vert X,w) p(w) }{ p(Y \vert X) }\)
    • Likelihood 와 Prior 의 곱이라고 생각할 수 있음.
  • Bayesian Inference : \(p( y^{\ast} \vert x^{\ast}, X,Y) = \int p(y^{\ast} \vert x^{\ast},w) p(w \vert X,Y) dw\)
    • Posterior 를 사용해서 적분함
  • Evidence (Normaliser) : \(p(Y \vert X) = \int p(Y \vert X,w) p(w) dw\)
    • Posterior 수식의 분모

여기서 우리가 구하기 힘든건 \(p(w \vert X,Y)\) 라는 Posterior 입니다. 이 구하기 힘든걸 True Posterior 라고 하겠습니다 (실제로 분모의 적분까지 써서 복잡하게 계산해야 하지만 계산할 수 없는 것).

근데 이 분포가 굉장히 간단한 분포를 가정해보면 어떨까요? 이를 \(q(w \vert \theta)\) 혹은 \(q_{\theta}(w)\) 라고 정의합시다. 만약 이 분포가 mode가 한개인 가우시안 분포라면 어떨까요? \(\theta = \mu, \sigma\)가 될 것이고 그렇다는 것은 mean, variance 값만 하나씩 구해주면 되겠죠?

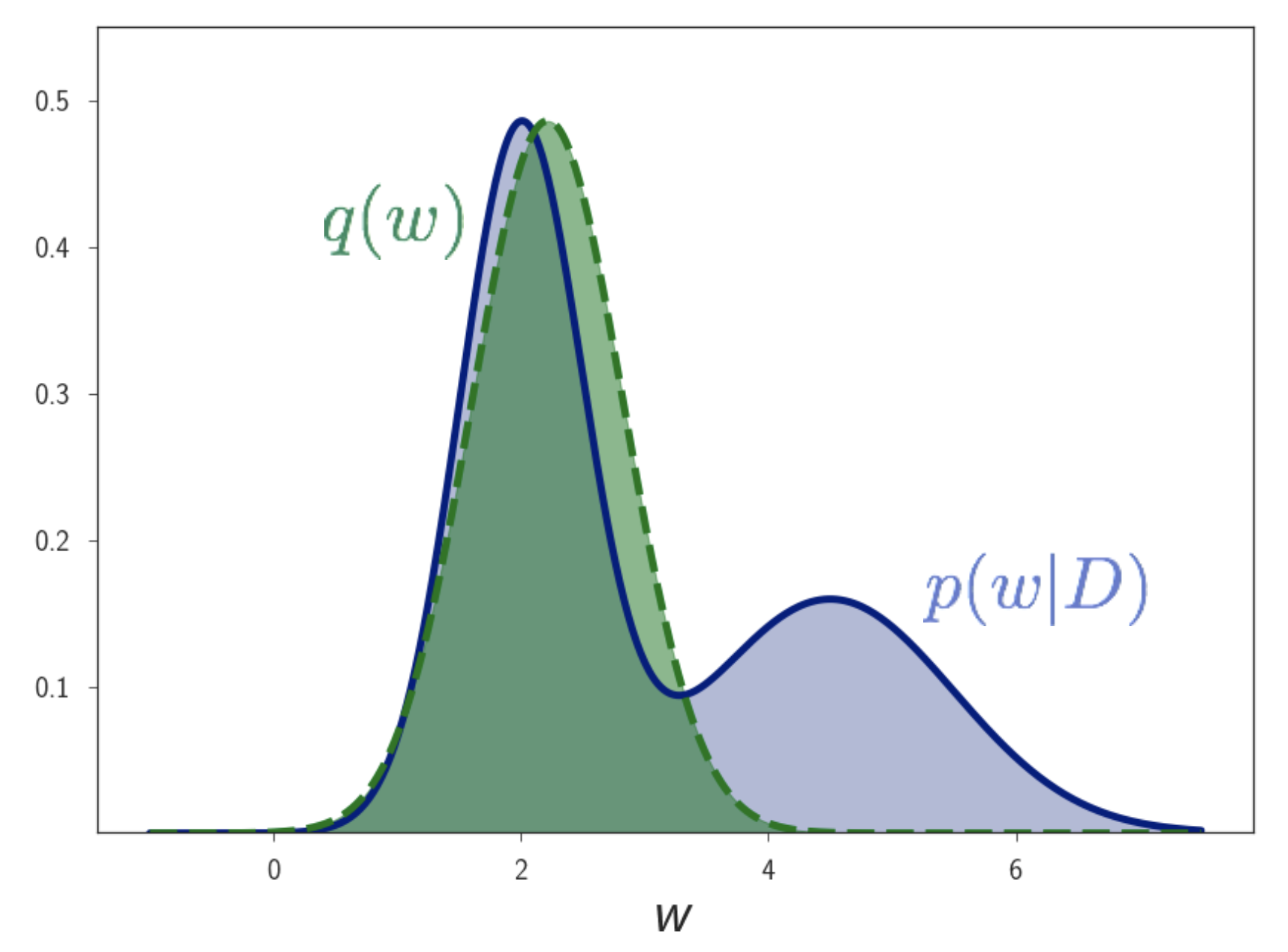nyu_variational_approximation_fig Fig.

물론 이게 실제 분포가 아니지만, mean 값을 posterior의 최대인 지점과 비슷하게 설정하고 variance 를 조절해가다보면 꽤나 비슷한 모양을 얻을 수 있지 않을까요? 중요한건 우리가 하고 싶은게 Bayesian Inference 이기 때문에 이게 어떻게 생겼는지는 크게 관심이 없고 다만 데이터를 잘 반영하는 분포 이기만 하면 충분할 것 같습니다.

우리가 해야될 일은 이 두 분포가 최대한 유사해지는 \(\theta\) 를 구하는 건데요, 이를 위해 서로 다른 두 확률 분포가 서로 얼마나 유사한지를 잴 수 있는 Kullback–Leibler Divergence (KLD) 를 이용할 겁니다.

\[KL(q_{\theta} \parallel p(w \vert X,Y)) = \int q_{\theta}(w) log \frac{ q_{\theta}(w) }{ p(w \vert X,Y) }\]

이 적분식은 \(q_{\theta}(w)\) 가 \(p(w \vert X,Y)\) 에 대해서 연속적일 때만 정의가 된다고 합니다. KLD 값이 0에 가까울 수록 두 분포가 유사한 것이되는데요, 그렇게 되는 \(q_{\theta} (w)\) 를 구했으면 Bayesian Inference 를 어떻게 바꿀 수 있을까요? 바로 아래처럼 바꿀 수 있습니다.

\[p( y^{\ast} \vert x^{\ast}, X,Y) = \int p(y^{\ast} \vert x^{\ast},w) p(w \vert X,Y) dw\] \[p( y^{\ast} \vert x^{\ast}, X,Y) \approx \int p(y^{\ast} \vert x^{\ast},w) q_{\theta}(w) dw = q^{\ast}_{\theta}(y^{\ast} \vert x^{\ast})\]

posterior 를 구하기 쉬운 가우시안으로 만들었기 때문에 할만해진 것 같습니다.

이제 어떻게 모델을 학습하느냐? Objective 는 어떻게 생겼느냐? 에 의문이 생기실 것 같습니다

이는 Evidence Lower BOund (ELBO) 라는 것을 유도해낸 뒤에 이를 최적화 하면 되는데요,

\[L_{VI}(\theta) = \int q_{\theta}(w) log p(Y \vert X,w) dw - KL (q_{\theta} \parallel p(w)) \leq log p(Y \vert X) = \text{log Evidence}\]

이를 같이 유도해보죠.

Evidence Lower Bound (ELBO)

ELBO 를 유도해야 하는 이유는 KLD 를 직접적으로 최적화 할 수 없기 때문이라고 알려져 있는데요, 이를 유도하기 위해서는 몇 가지 수학적인 연산자를 알아야 합니다.

  • Expectation <-> Integral : \(\mathbb{E}_q[p(x)] = \int_x q(x) p(x) dx\)
  • KLD : \(KL(q \parallel p) = \int q log \frac{q}{p} = \mathbb{E}_q [ log \frac{ q }{ p } ]\)
  • Entropy : \(H(p) = \int p log p = \mathbb{E}_p [log p]\)
  • Jensen’s Inequality : \(f (\mathbb{E} [X]) \geq \mathbb{E} [ f(X) ]\)

자 이제 첫 번째로 \(p(y \vert x)\) 라는 Evidence 에 대해 생각해 봅시다.

\[log p(y \vert x) = log \int_w p(y \vert x, w) p(w) dw\]

+) ELBO는 Variational Auto Encoder (VAE) 에서도 같은 방법으로 유도하는데요, VAE에서는 \(log p_{ \color{red}{\theta}}(x)\) 라고 하는 Log Likelihood 에 잠재변수 z 를 끼워서 Objective 를 유도하기도 합니다. 즉 이 때는 Evidence 에서 출발하지 않는데요,

지금의 경우는 model 이 주어지지 않았을 때, Evidence 에서 시작하는 것이고, VAE의 경우는 그 model이 deterministic 하게 주어졌다고 생각하고 시작하기 때문에, 거의 같은 수식을 전개하지만 시작할 때 다른 용어를 쓰는 것 같습니다.

지금의 경우는 Evidence 를 쓰는데요, Model Evidence 는 다른 말로 Marginal Likelihood 라고도 합니다. 이는 Model이 주어진 (parameter space 상의 한 점으로) 경우를 모든 parameter space 에 대해 적분 하는, 주변화 (Marginalization) 을 한게 Evidence 니까 모든 경우에서의 Likelihood 를 고려한 상위 ? 개념 이라고 할 수 있겠네요.

우변의 결합 분포는 w 에 대해 적분을 하면 \(p(y \vert x)\) 가 되기 때문에 아무 문제가 없고, 이제 여기에 \(\frac{q_{\theta}(w)}{q_{\theta}(w)}\) 라는 항을 곱해봅시다.

\[log p(y \vert x) = log \int_w p(y \vert x, w) p(w) \frac{q_{\theta}(w)}{q_{\theta}(w)} dw\]

여기서 \(\frac{q_{\theta}(w)}{q_{\theta}(w)}\) 는 1이기때문에 1을 곱하는건 아무 문제가 안됩니다.

위 수식은 적분 연산자를 기대값으로 바꿀 수 있으니 아래와 같이 식을 수정할 수 있습니다.

\[\begin{aligned} & log p(y \vert x) = log \int_w p(y \vert x, w) p(w) \frac{q_{\theta}(w)}{q_{\theta}(w)} dz \\ & = log ( \mathbb{E}_q [ \frac{p(y \vert x, w) p(w)}{q_{\theta}(w)} ] ) \\ \end{aligned}\]

여기에 Jensen’s Inequality 를 사용하면

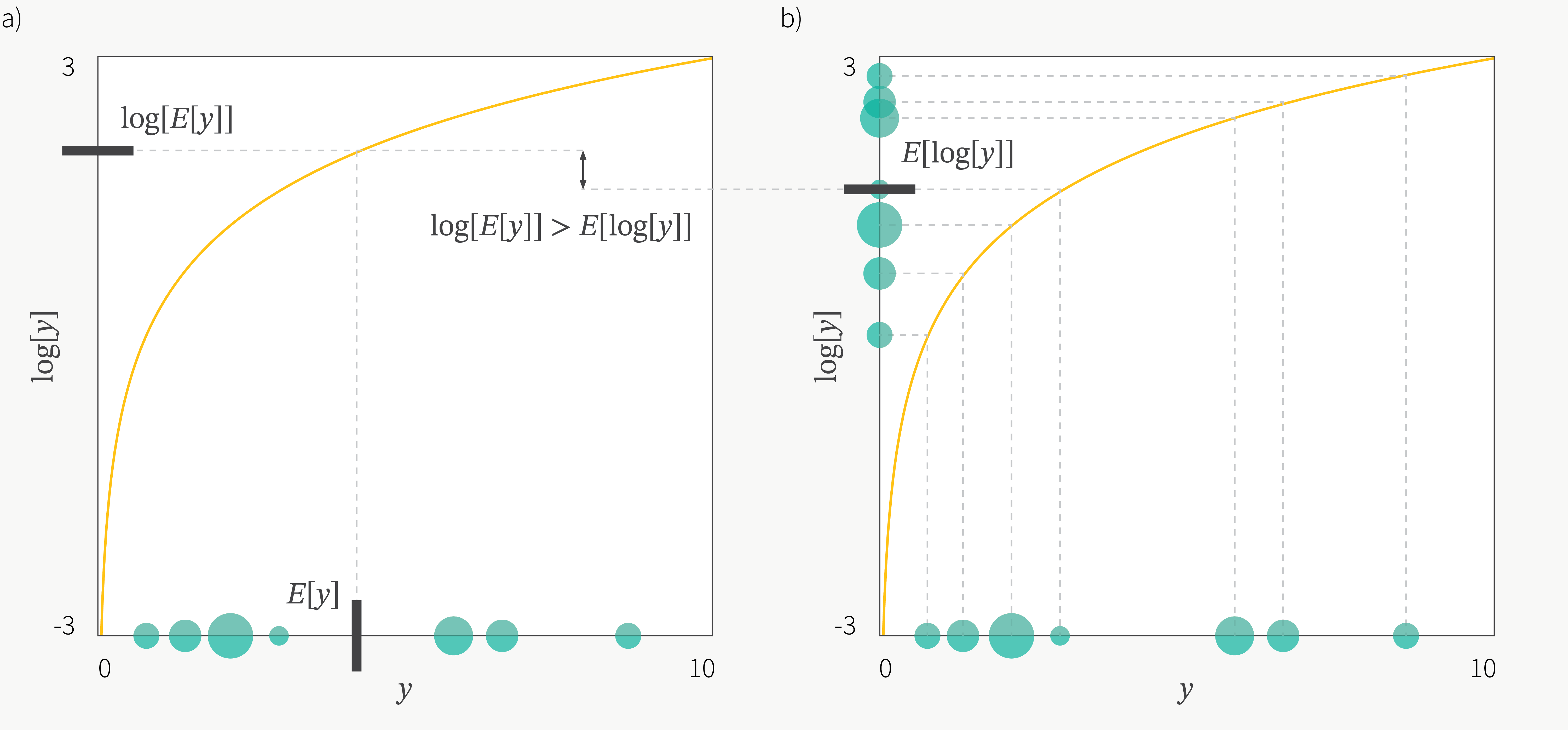
jensen

\[\begin{aligned} & log ( \mathbb{E}_q [ \frac{p(y \vert x, w) p(w)}{q_{\theta}(w)} ] ) \geq \mathbb{E}_q [ log (\frac{p(y \vert x, w) p(w)}{q_{\theta}(w)}) ] \\ \end{aligned}\]

가 됩니다.

여기서 우변의 분수는 log가 취해져 있기 분해를 할 수 있는데요, 이를 적당히 분해하면

\[\begin{aligned} & log ( \mathbb{E}_q [ \frac{p(y \vert x, w) p(w)}{q_{\theta}(w)} ] ) \geq \mathbb{E}_q [ log p(y \vert x, w)] + \mathbb{E}_q [ log \frac{ p(w) }{q_{ \theta}(w)} ] \\ & \geq \int q_{\theta}(w) p (y \vert x, w) dw - KL (q_{\theta} (w) \parallel p(w) ) \\ \end{aligned}\]

최종적으로

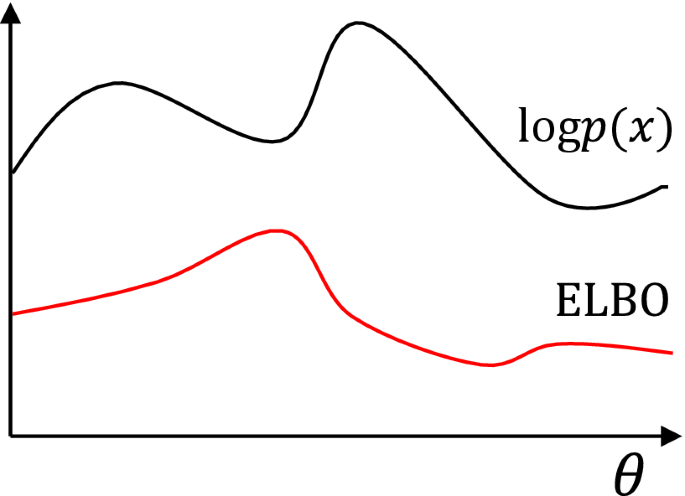
\[\text{Log Evidence} = log p(y \vert x) \geq \int q_{\theta}(w) p (y \vert x, w) dw - KL (q_{\theta} (w) \parallel p(w) )\]

라는 수식을 얻는데요, 여기서 좌변을 Log Evidence, \(log p(y \vert x)\) 라고 부르고 우변은 이 보다 작은 하계 (Lower Bound) 이기 때문에 이를 Evidence Lower BOund (ELBO) 라고 부릅니다.

How tight is the Bound?

추가적으로 그러면 Log Evidence 와 Bound 는 얼마만큼의 차이가 있는지 알아보겠습니다.

아까 우리가 정의한 근사 posterior 와 실제 posterior 와의 KLD 수식이 있었습니다.

\[KL(q_{\theta} (w) \parallel p(w \vert X,Y)) = \int q_{\theta}(w) log \frac{ q_{\theta}(w) }{ p(w \vert X,Y) }\]

KLD도 기대값으로 바꾸면

\[\begin{aligned} & KL(q_{\theta} (w) \parallel p(w \vert X,Y)) = \int q_{\theta}(w) log \frac{ q_{\theta}(w) }{ p(w \vert X,Y) } \\ & = \mathbb{E}_q [log \frac{q_{\theta}(w)}{p(w \vert X,Y)}] \\ \end{aligned}\]

가 됩니다.

여기서 Posterior 는 Bayes Rule 을 통해 Likelihood, Prior, Evidence 세 가지를 가지고 구한 값이었죠?

\[p(w \vert X,Y) = \frac{ p(Y \vert X,w) p(w) }{ p(Y \vert X) }\]

이를 사용하면

\[\begin{aligned} & KL(q_{\theta} (w) \parallel p(w \vert X,Y)) = \mathbb{E}_q [log \frac{q_{\theta}(w)}{p(w \vert X,Y)}] \\ & = \mathbb{E}_q [log \frac{q_{\theta}(w) p(Y \vert X)}{p(Y \vert X,w) p(w)}] \\ & = \mathbb{E}_q [ log p(Y \vert X) ] - \mathbb{E}_q [ log (\frac{p(Y \vert X, w) p(w)}{q_{\theta}(w)}) ] \\ \end{aligned}\]

가 됩니다.

아까 우리가 구한 ELBO 는 아래와 같았죠?

\[\begin{aligned} & \text{Log Evidence} = log p(Y \vert X) \\ & \geq \text{Lower Bound} = \mathbb{E}_q [ log (\frac{p(Y \vert X, w) p(w)}{q_{\theta}(w)}) ] \\ & = \int q_{\theta}(w) p (y \vert x, w) dw - KL (q_{\theta} (w) \parallel p(w) ) \\ \end{aligned}\]

즉 여기서 Bound 가 얼마나 Tight 한지는 실제로

\[\begin{aligned} & KL(q_{\theta} (w) \parallel p(w \vert X,Y)) = \mathbb{E}_q [ log p(Y \vert X) ] - \mathbb{E}_q [ log (\frac{p(Y \vert X, w) p(w)}{q_{\theta}(w)}) ] \\ & = \text{Log Evidence} - \text {Lower Bound} \\ \end{aligned}\]

가 되는 겁니다.

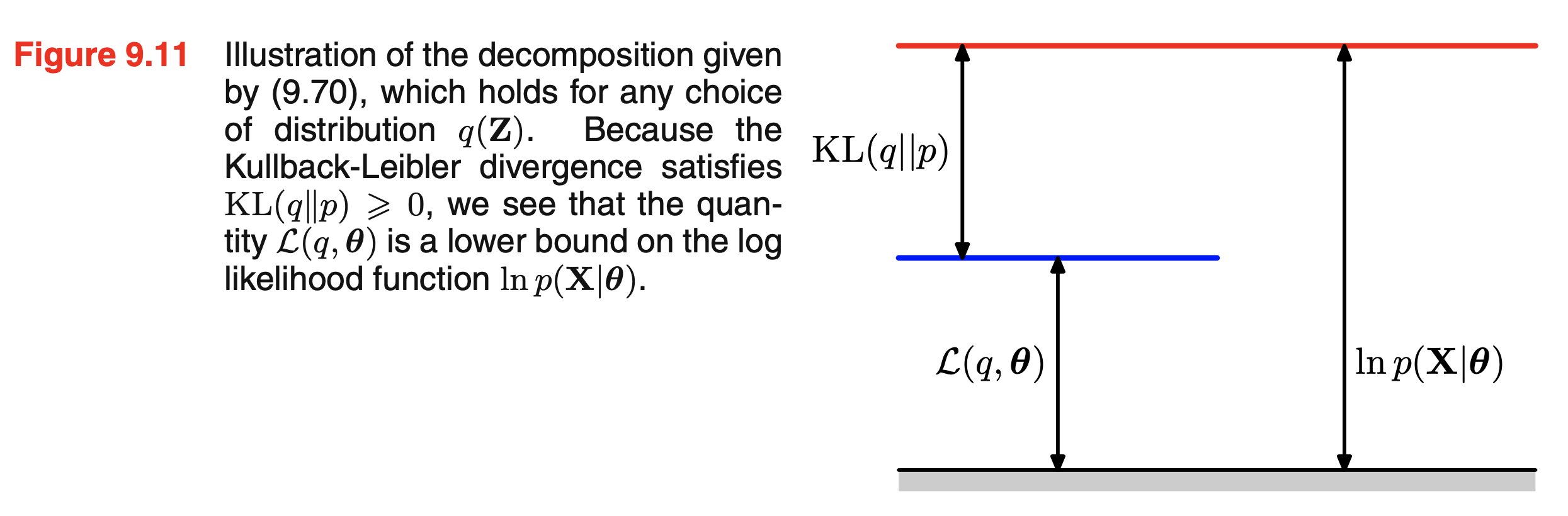bishop_elbo1 Fig. Log Evidence 의 한 점?인 Log Likelihood 를 ELBO 와 KLD 의 합으로 나타낸 그림. Bishop 책의 EM 알고리즘에 대한 그림이다.

evidence_elbo

How to train NN using VI ?

마지막으로, 이제 어떻게 모델을 학습하면 될까요?

\[log p(Y \vert X) \geq \int q_{\theta}(w) p (Y \vert X, w) dw - KL (q_{\theta} (w) \parallel p(w) )\]

Laplace Approximation

nyu_laplace_approximation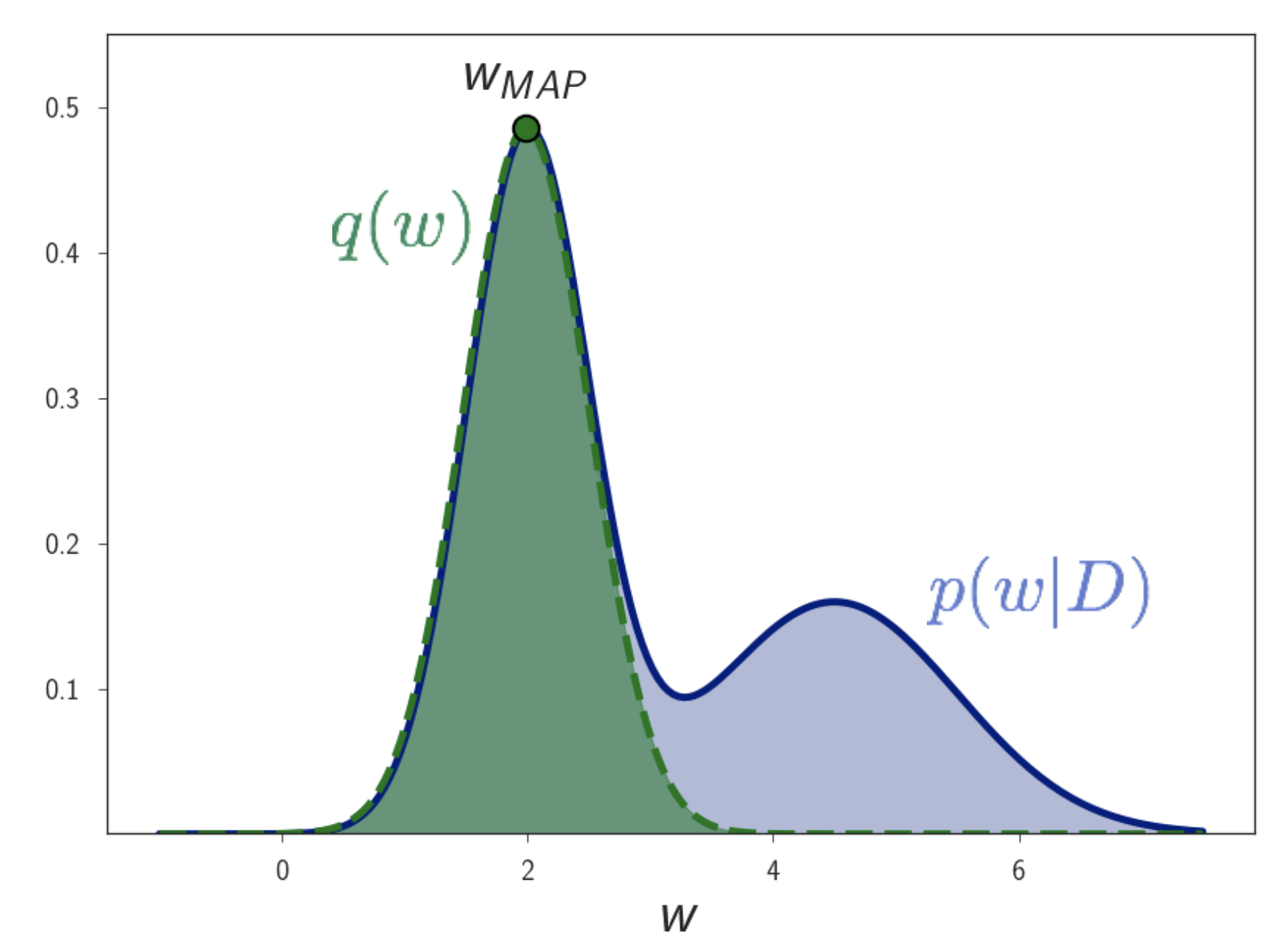_fig Fig.

MARKOV CHAIN MONTE CARLO

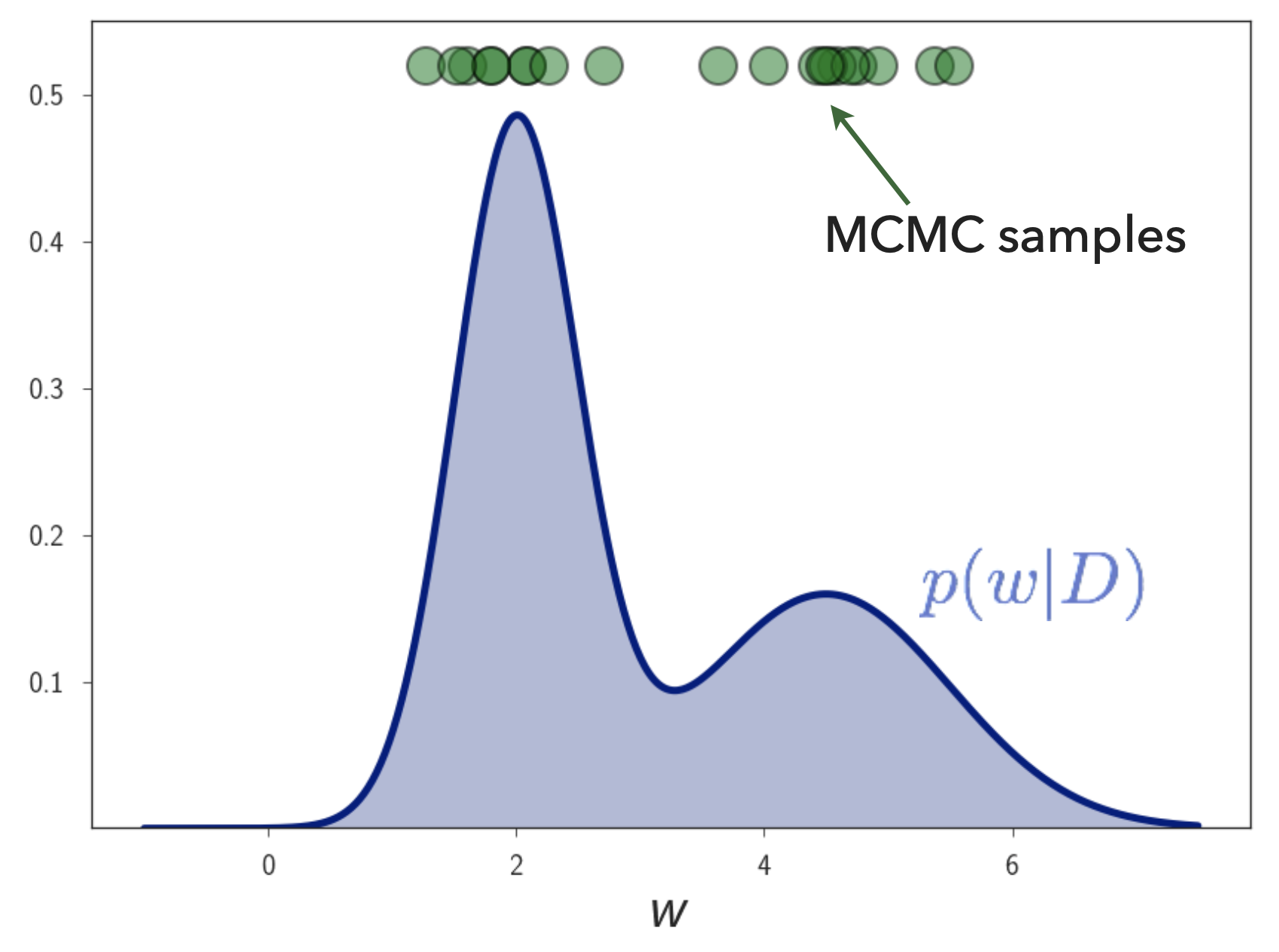nyu_mcmc Fig.

Dropout as a Bayesian Approximation

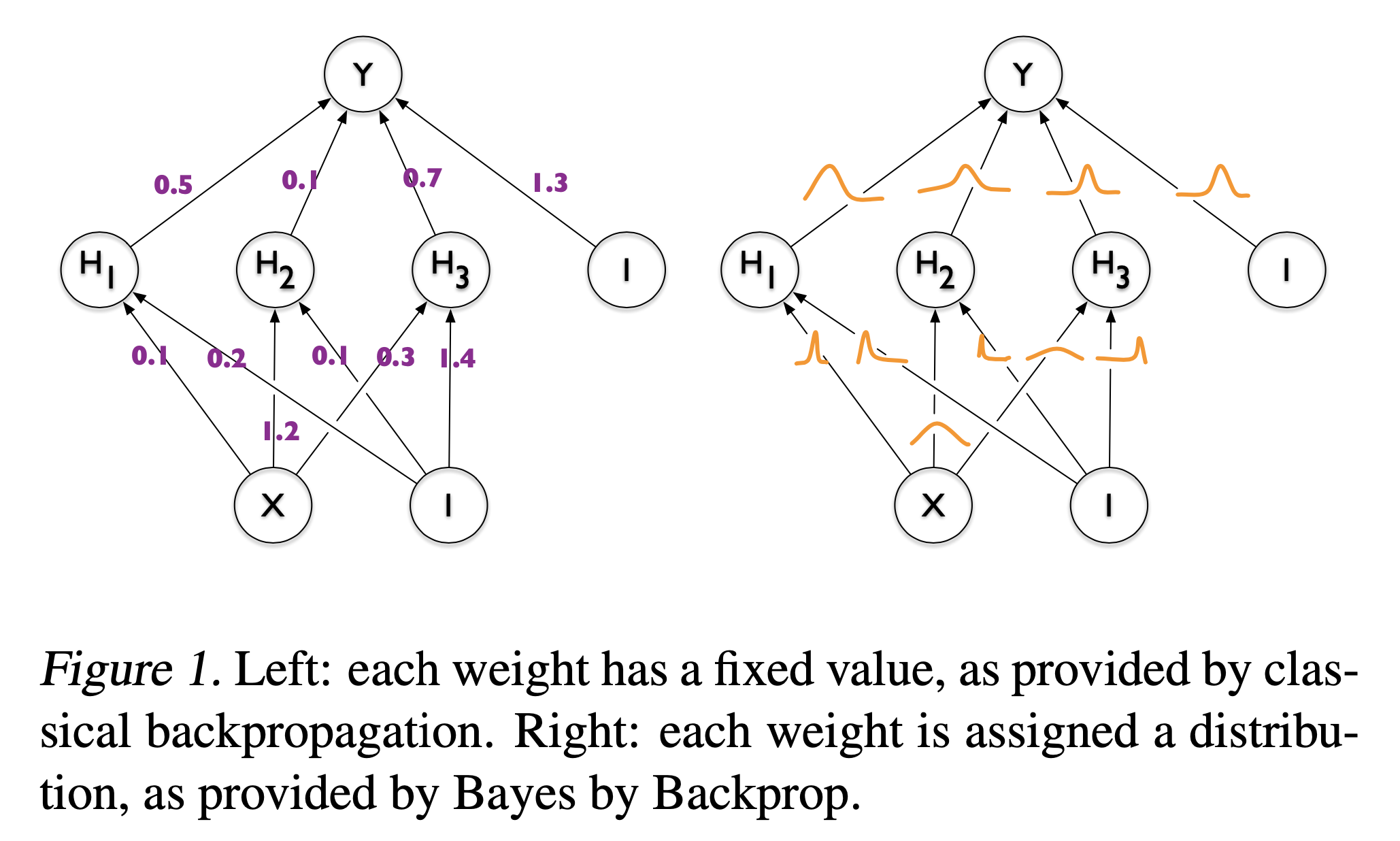bnn_fig Fig.

References