Notes

Convolution Families

21 Jun 2022

< 목차 >

Main credit for the figure resources goes to the lecture slides in cs231n and other resources are listed in the References.

Standard Convolution Layer in Convolutional Neural Networks (CNNs)

Convolution Neural Network (CNN) 는 90년대 Gradient-Based Learning Applied to Document Recognition라는 논문에서 처음 제안되었다.

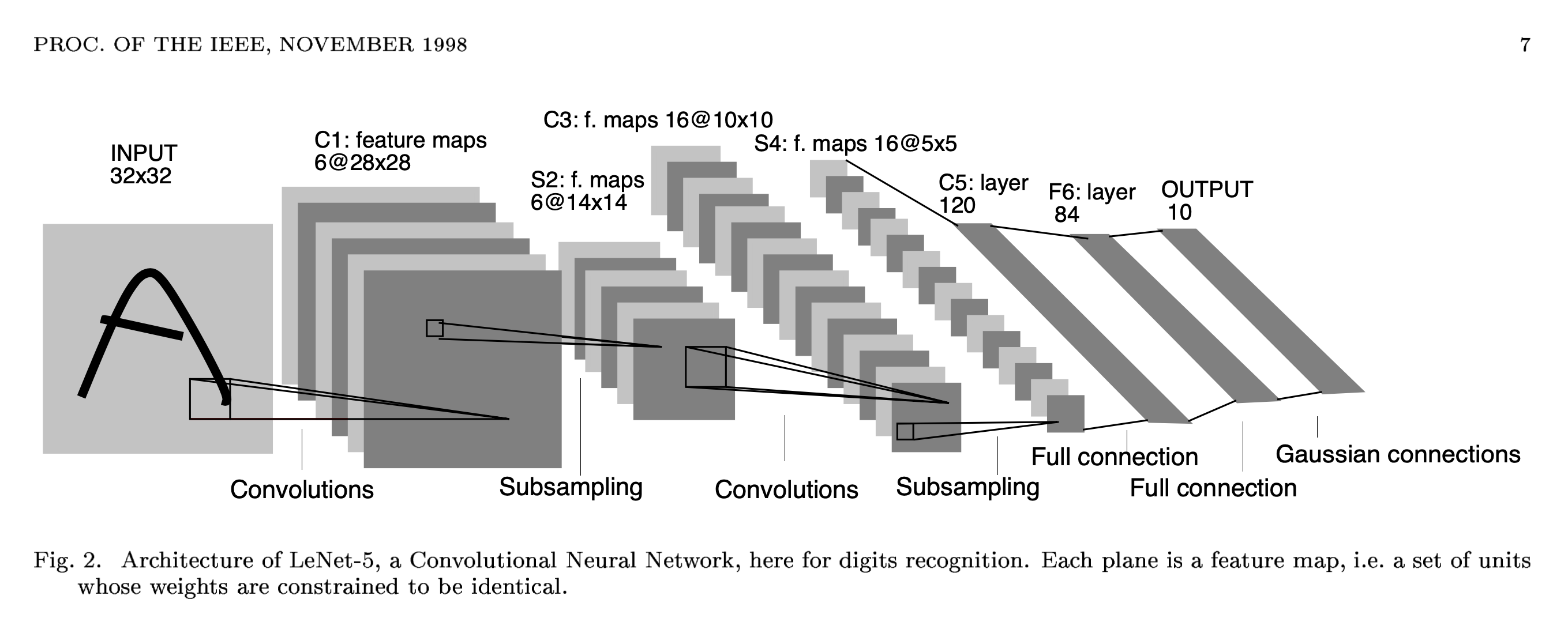lenet_5 Fig.

이는 Convolution Layer (Conv Layer), Pooling Layer 두 종류로 구성되어있는 간단한 Neural Network (NN) 인데 Yann Lecun은 이 네트워크를 필기체 (handwritten characters)를 인식하는데 사용했다.

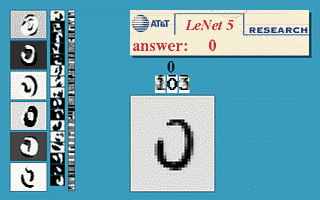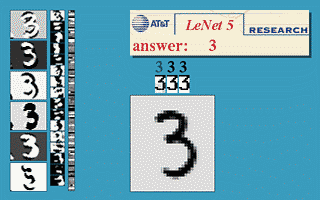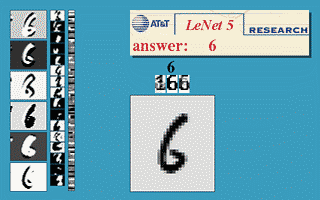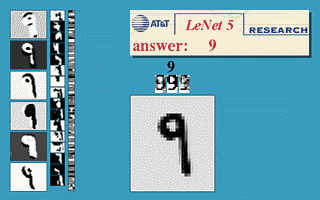asamples Fig. Legendary Animation from Yann Lecun’s website

Yann Lecun 이 제안한 LeNet 에 사용된 Conv Layer 는 이후 여러 논문에서 등장하는 변이체들의 가장 간단한 버전으로, 이산 신호 처리 (Digital Signal Processing; DSP) 에서 신호를 분석하고 필터링을 하는 등의 목적으로 사용되는 Convolution Operation 과 거의 유사하게 동작한다.

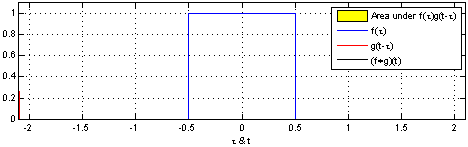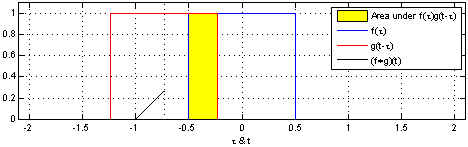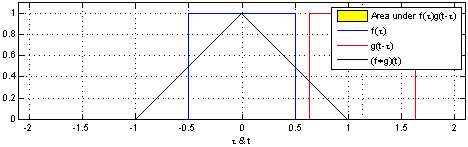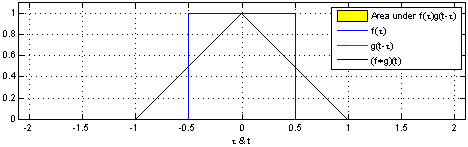wiki_conv.gif Fig. How Convolution Operation in DSP works

어떤 Filter (빨간색) 가 전체 입력 (파란색; 이미지라고 생각하시면 된다)를 쭉 훑으면서 (sliding) 새로운 feature (검은색)을 출력하는 mechanism 이 NN에 적용된 것이다.

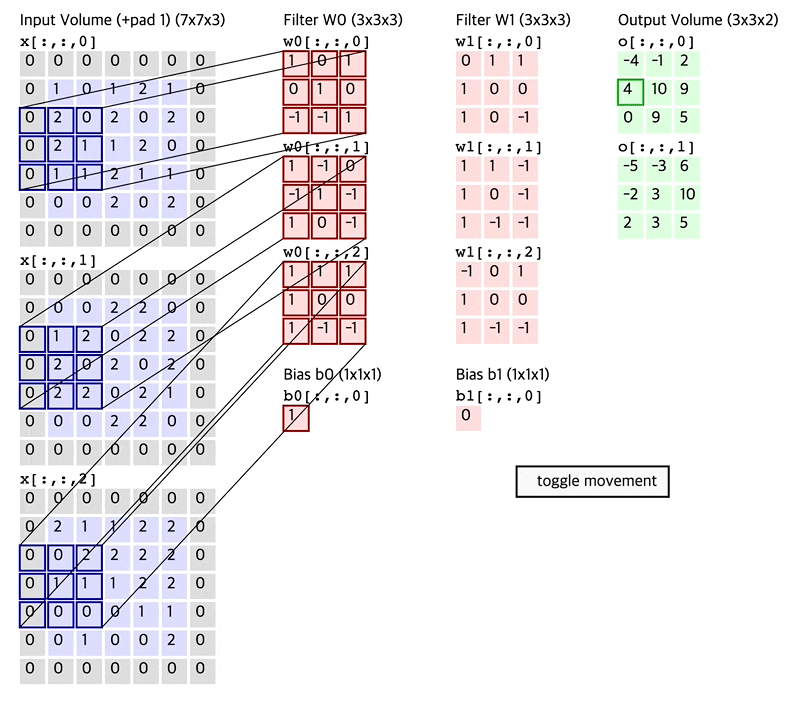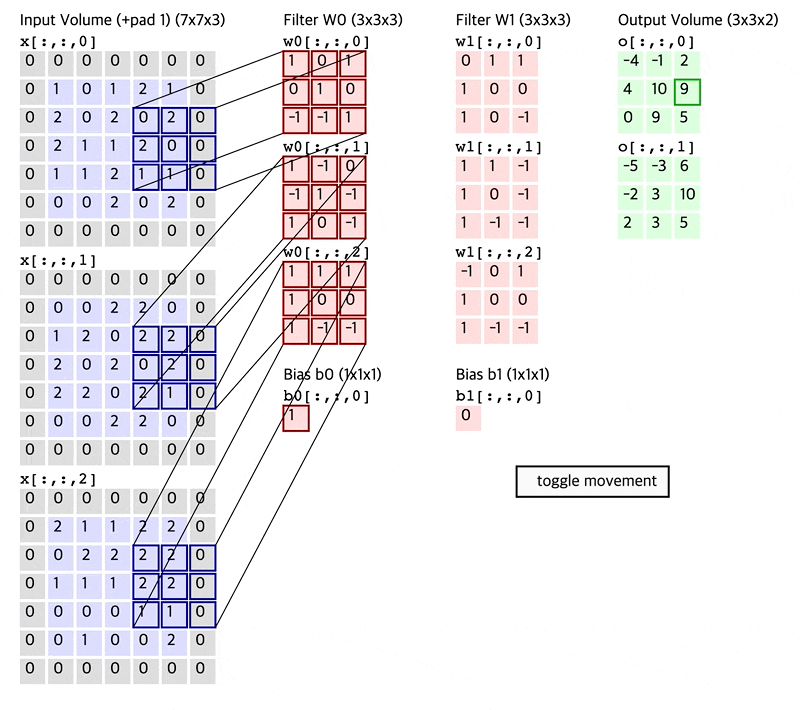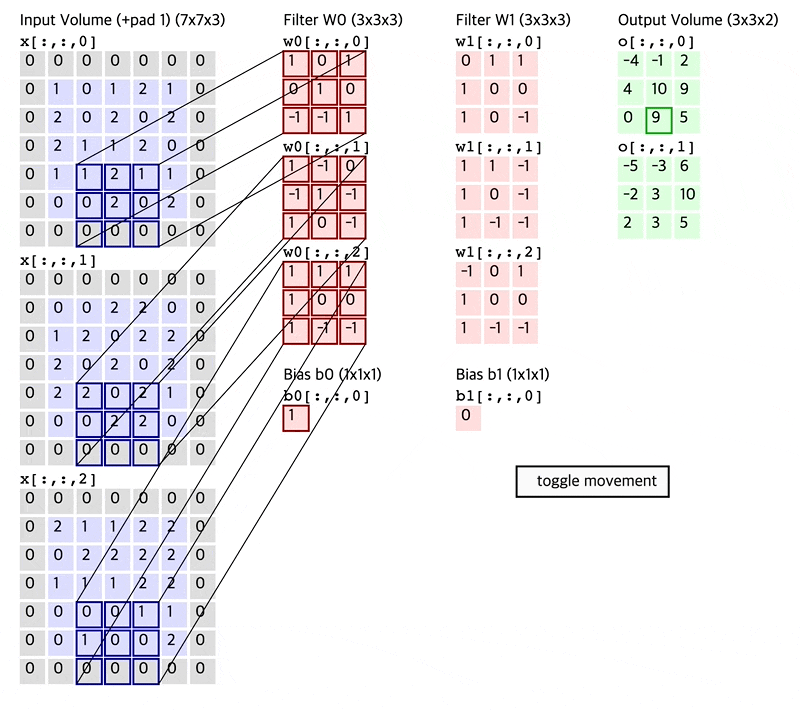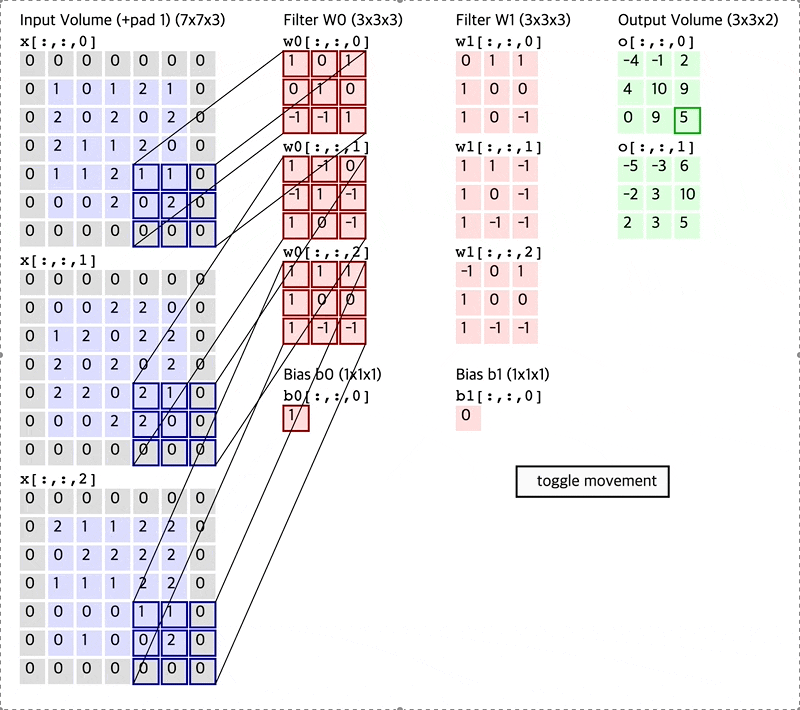conv_animation Fig. How Convolution Layer works

Fully Connected (FC) Layer VS Convolution Layer

CNN 은 입력 데이터가 이미지라는 명시적인 가정 (explicit assumption)을 깔고 간다. 왜 이미지를 처리할 때 FC Layer 가 아닌 Conv Layer 를 써야 하는걸까? 만약 우리가 어떤 이미지 가로 세로가 32 이고 컬러인 이미지 (3채널) 를 처리하고 싶다고 생각해 보자. 예를 들어 input matrix 의 차원은 \(\mathbb{R}^{32 \times 32 \times 3}\)가 될 것이다. 이걸 FC Layer 에 넣는다고 생각해보면 일단 이미지 전체를 쭉 펴서 (stretched, flatten), 3072 차원의 vector 로 만들어야 한다. 그러면 이를 FC Layer 에 넣을 수 있을 것이다.

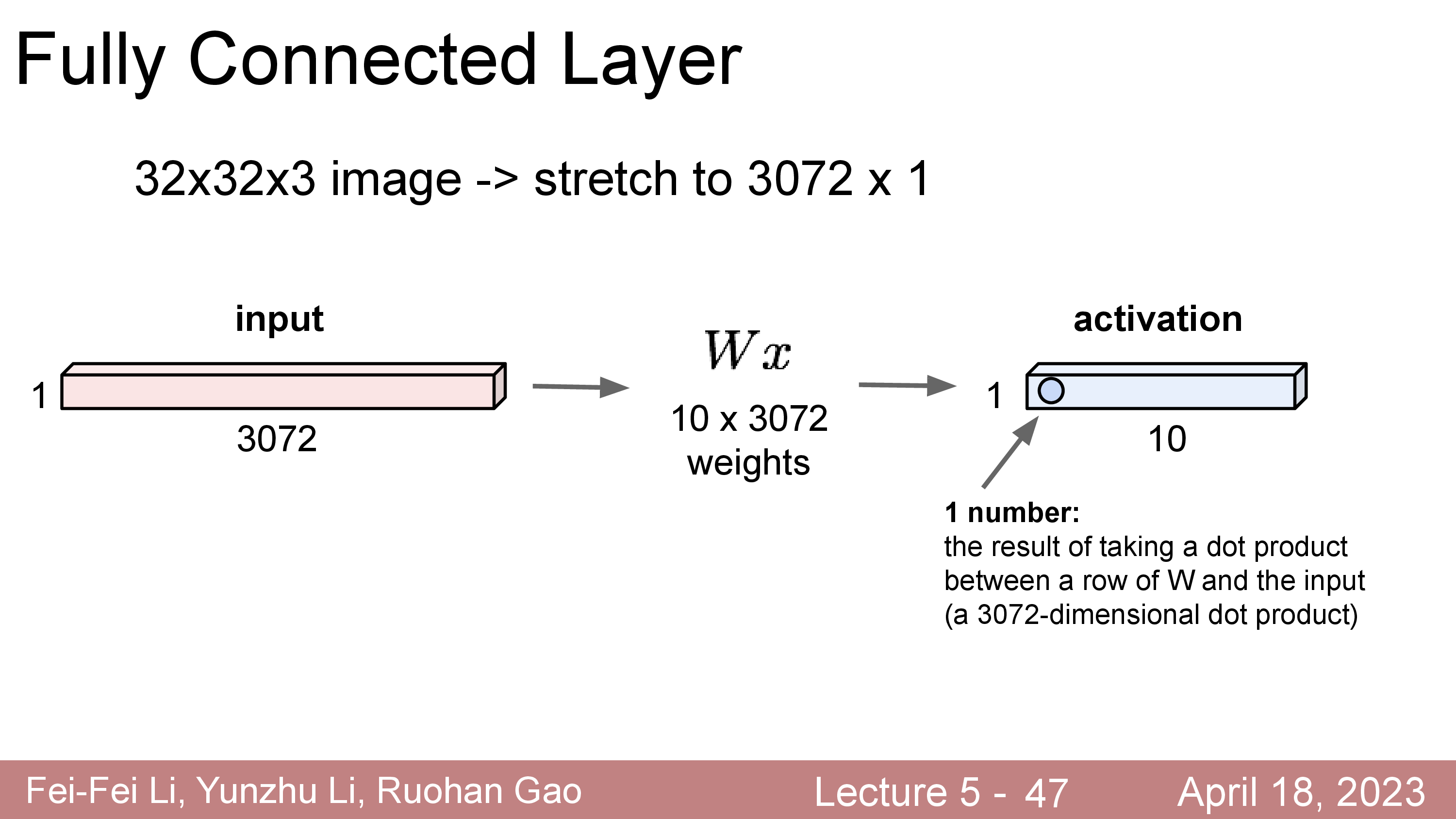
lecture_5_slide_047

하지만 이런식으로 image input 을 네트워크에 통과시키는것은 image는 인접한 pixel 끼리 높은 상관 관계 (correlation) 을 갖고 있다는 prior 를 반영하지 못한다. 그래서 공간 구조 (spatial structure) 를 보존 (preserve) 한 채 feature 를 뽑기 위해 설계된 Convolution Layer 가 CNNs 의 핵심적인 layer 로 Yann Lecun 에 의해 제안되었다.

lecture_5_slide_048

Convolution Layer 는 고정된 크기의 Filter (Kernel 이라고도 함)를 두고 이를 input matrix 를 쭉 훑으면서 (sliding or convolving)하며 연산한다.

lecture_5_slide_049

이 Filter 는 Standard CNN 에서는 input matrix 의 channel (ex RGB면 3, gray면 1)을 전부 cover 하는 식으로 되어있다.

lecture_5_slide_050

이 Filter 는 학습 가능 (Learnable) 하며 전체 image 를 쭉 순회하면서 연산하면 최종적으로 아래와 같은 결과물이 나온다.

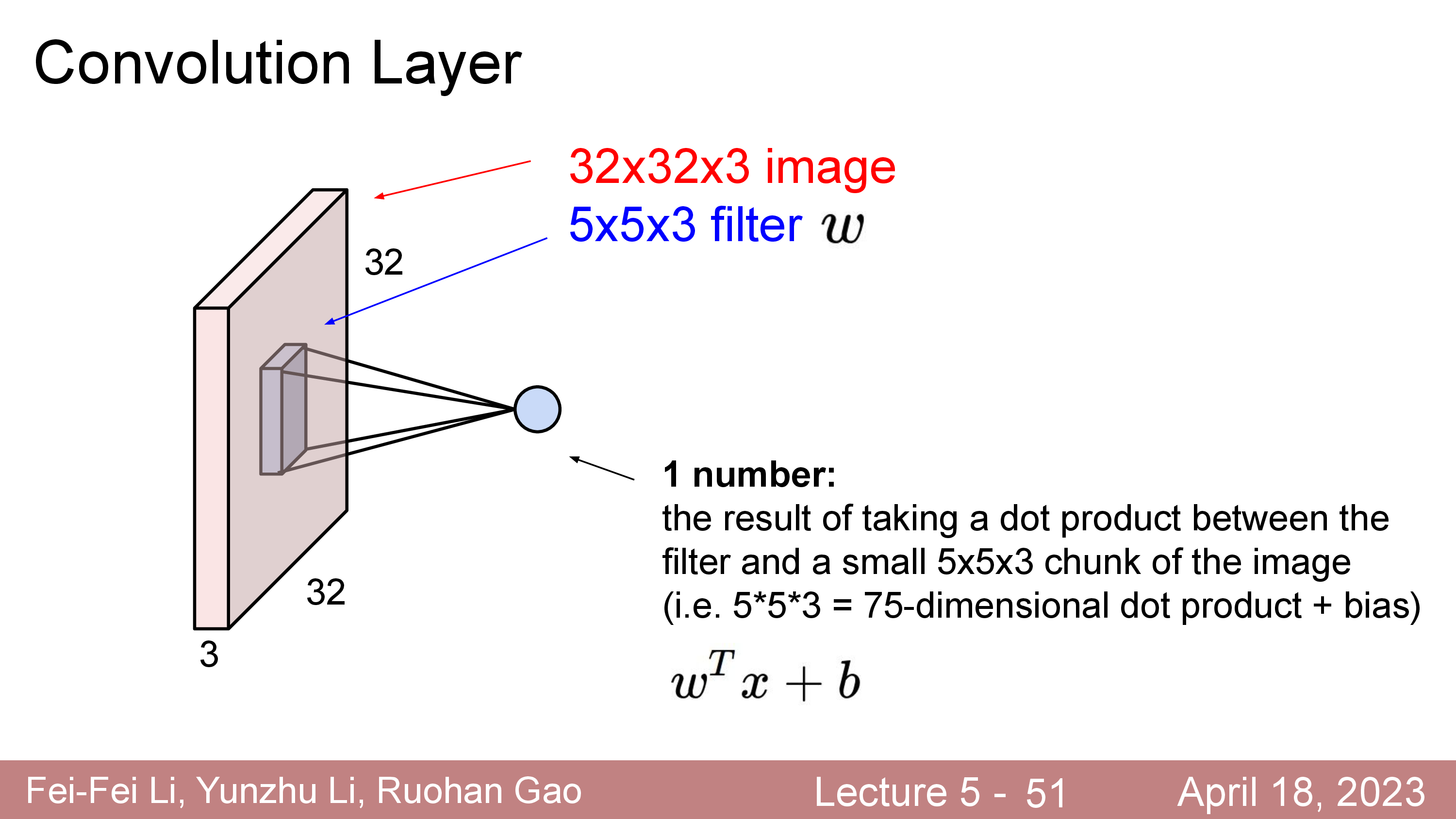
lecture_5_slide_051

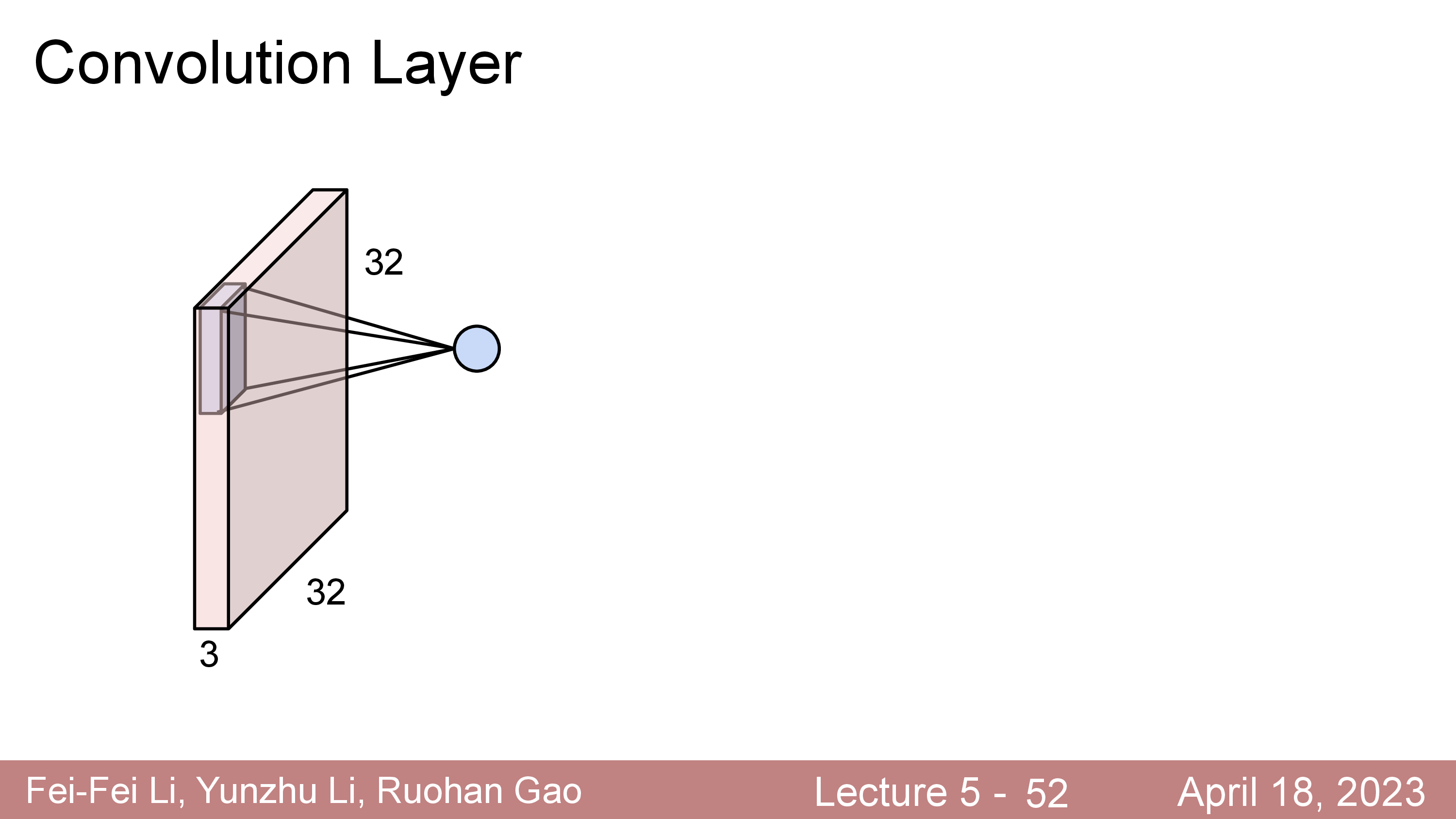
lecture_5_slide_052

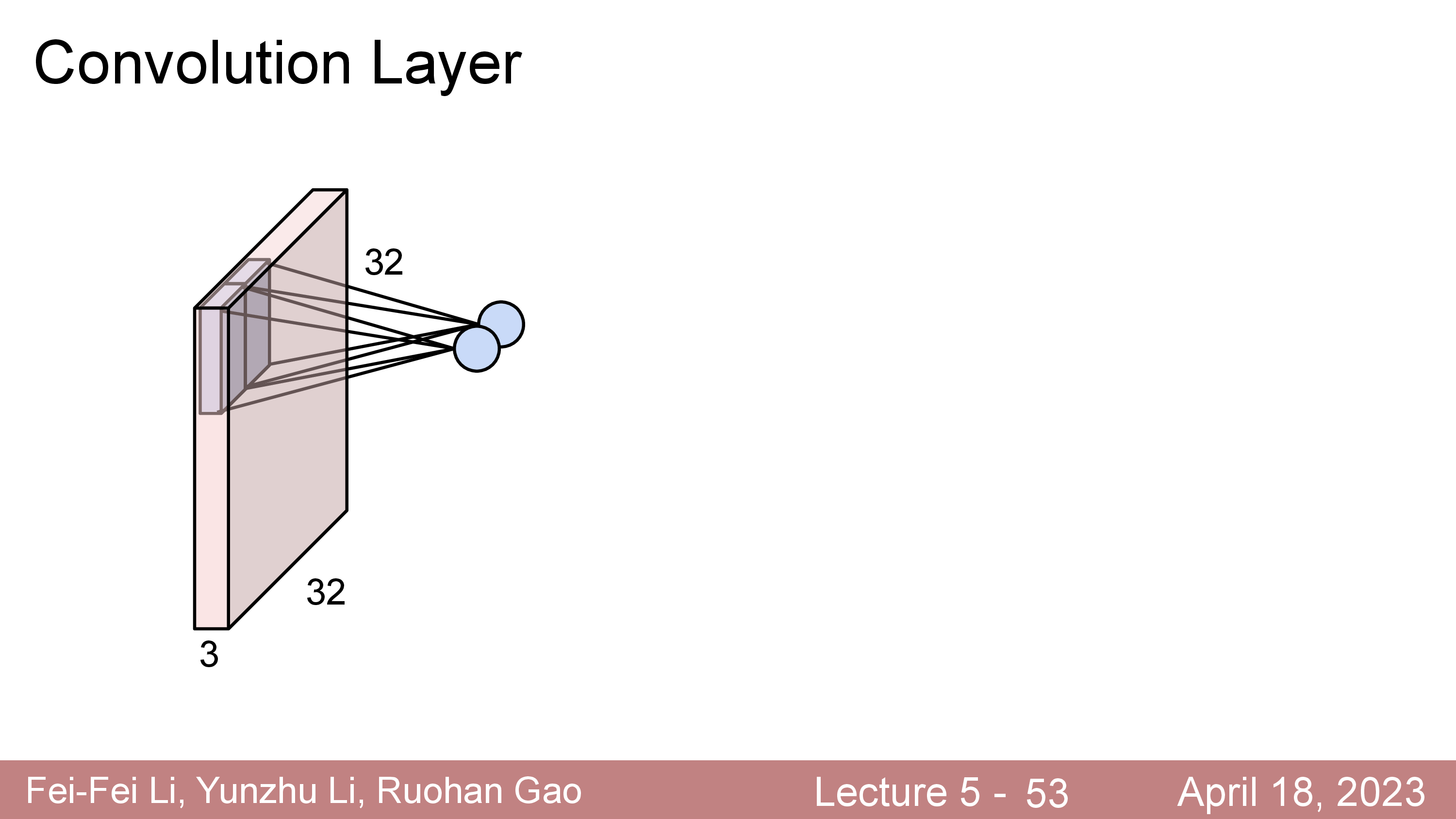
lecture_5_slide_053

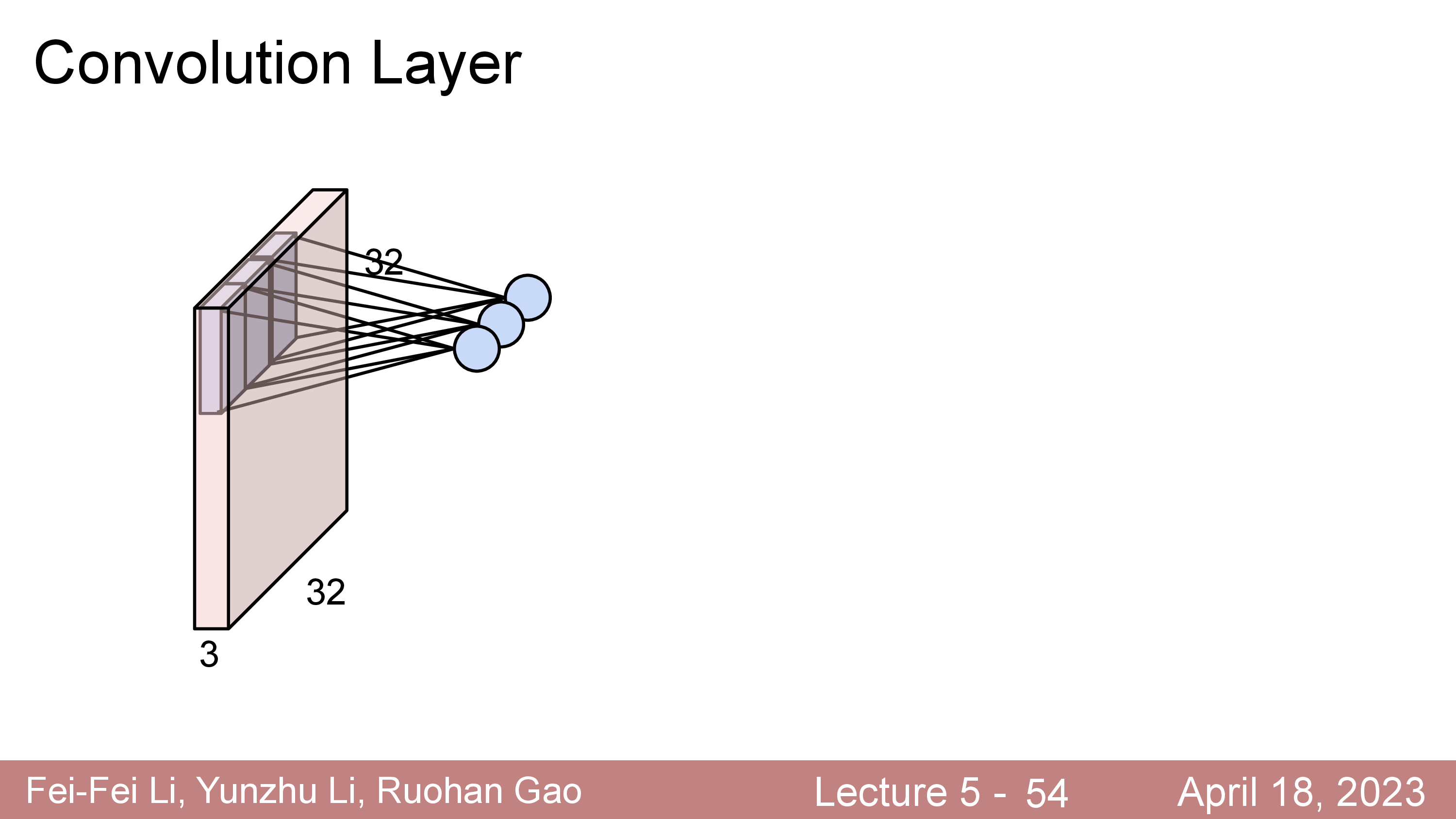
lecture_5_slide_054

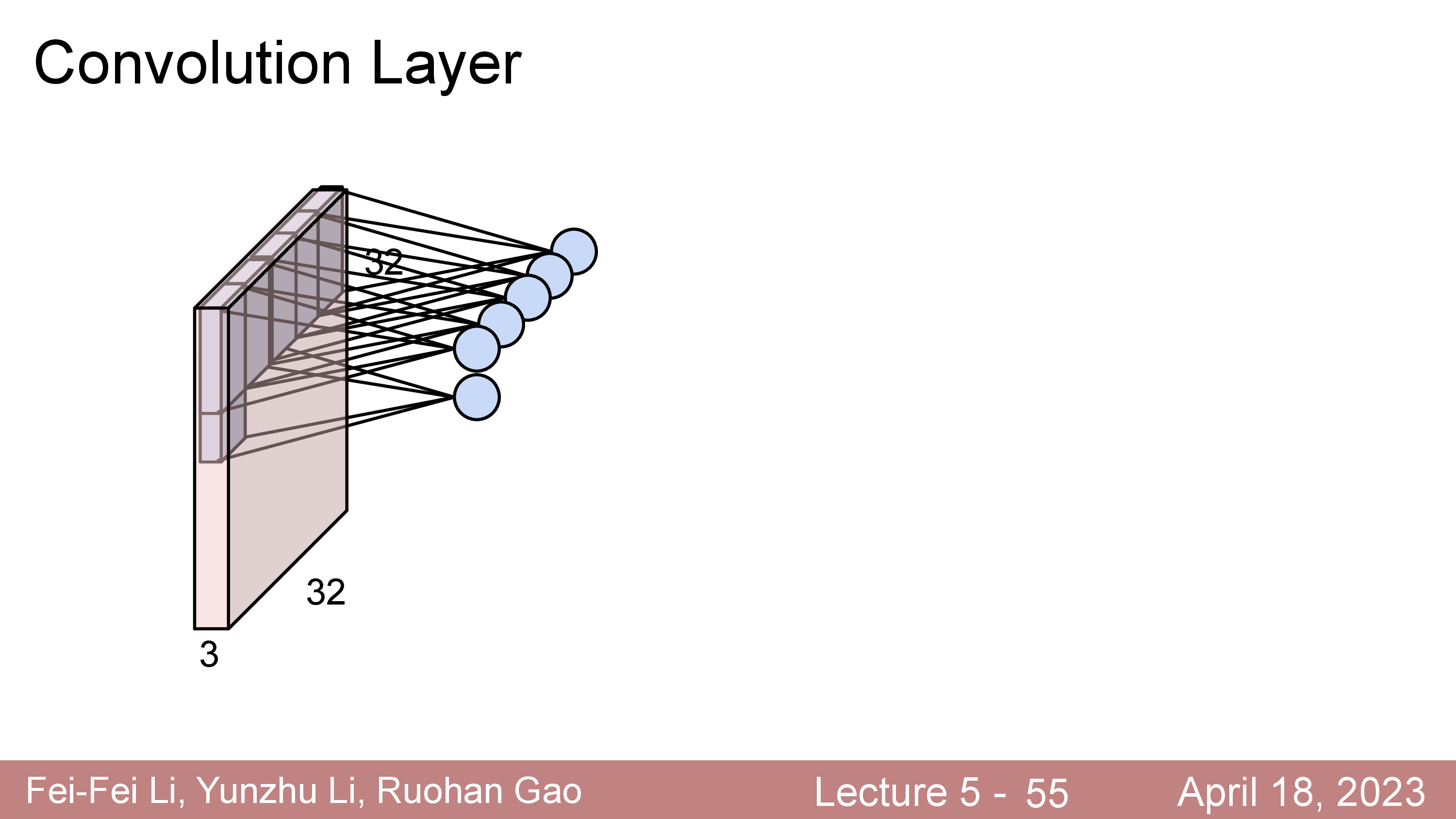
lecture_5_slide_055

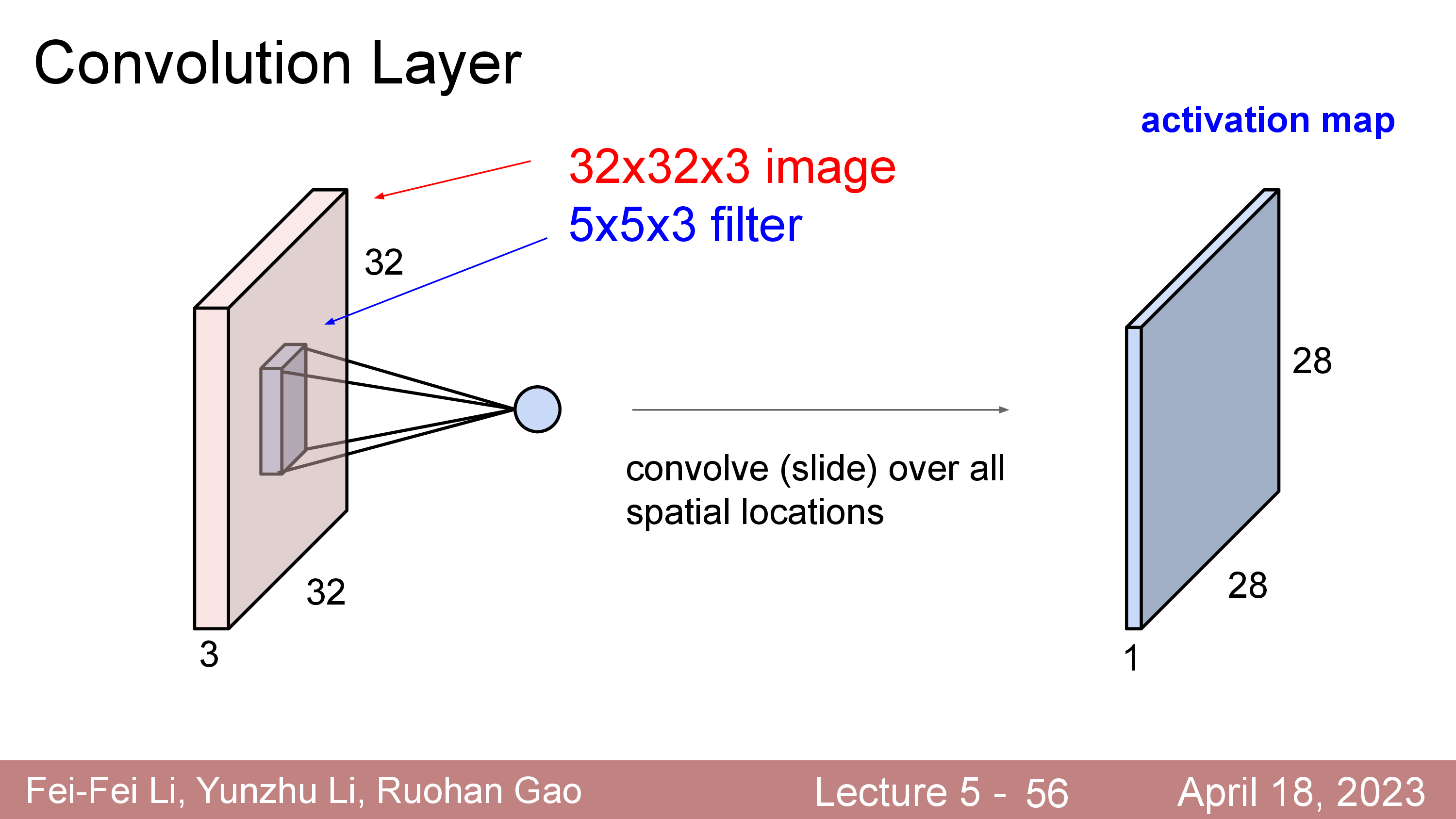
lecture_5_slide_056

원래 32x32x3 input image 의 channel depth 가 3이었으나 전체 depth 를 cover 하는 5x5x3짜리 filter 를 1개 쓸 경우 28x28x1 짜리 결과물이 나오는데 이를 activation map 이라고 부른다.

Output Size of Convolution Layer

당연히 output matrix 는 input matrix 의 5x5 영역을 연산해서 1개의 element로 출력하기 때문에 크기가 줄어들 수 밖에 없는데, 출력 크기가 얼마인지는 input matrix 의 크기와 filter 의 크기를 다음의 Notation 으로 정의할 때

  • input matrix 너비 : Width (W)
  • input matrix 높이 : Height (H)
  • input matrix 채널 : Channel (C)
  • filter 크기 : F
  • filter 의 convolve 연산을 하는 간격 (stride) : S

아래처럼 계산할 수 있다.

\[\begin{aligned} & \text{Output's Width } = (W-F) / S + 1 & \\ & \text{Output's Height } = (H-F) / S + 1 & \\ \end{aligned}\]

위의 예제의 경우 stride 가 1이고 filter size 가 5x5 이기 때문에 아래처럼 최종적으로 계산할 수 있다.

\[\begin{aligned} & \text{Output's Width } = (W-F) / S + 1 = (32-5)/1 + 1 = 28 & \\ & \text{Output's Height } = (H-F) / S + 1 = (32-5)/1 + 1 = 28 & \\ \end{aligned}\]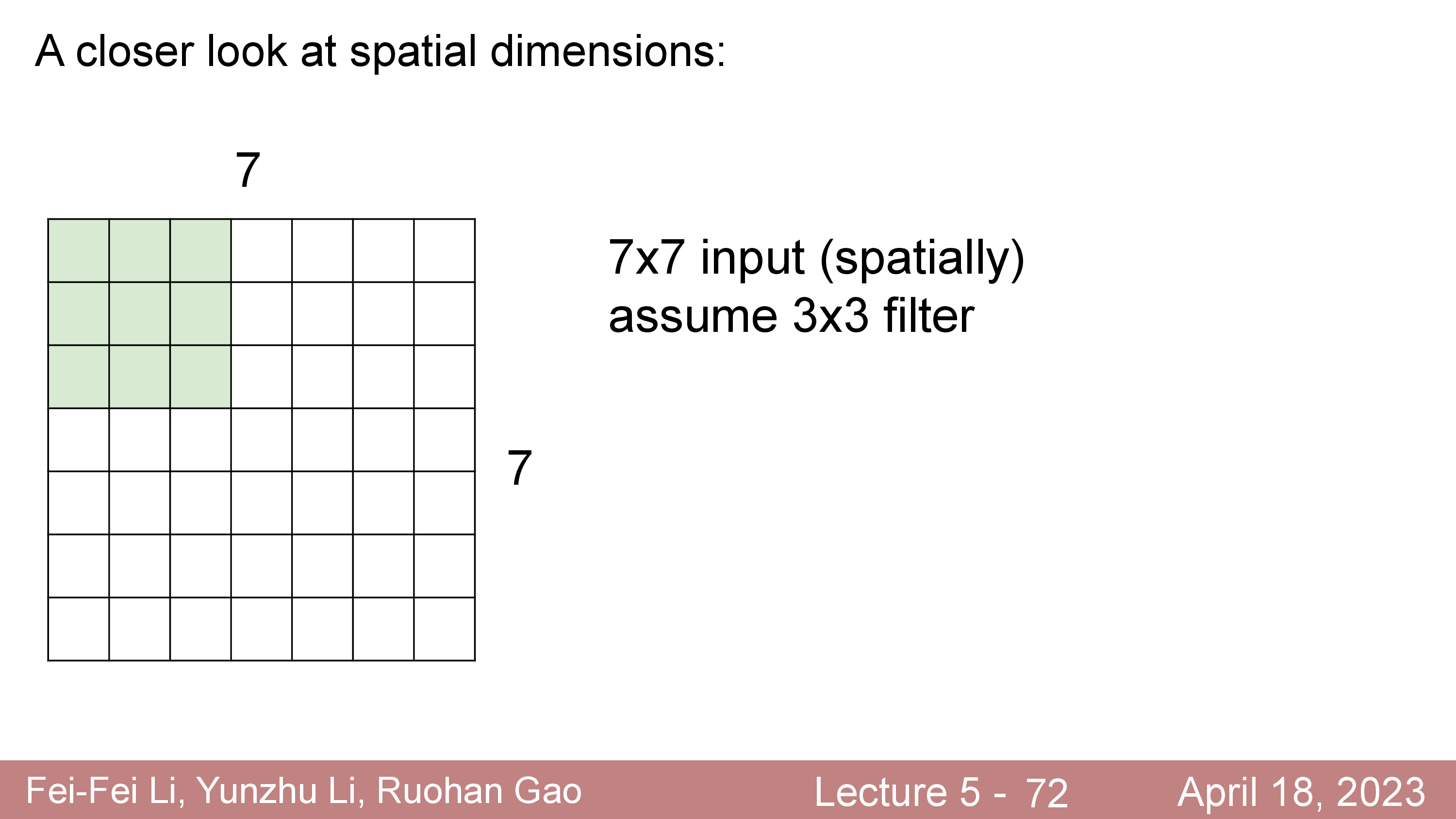

lecture_5_slide_072 Fig.

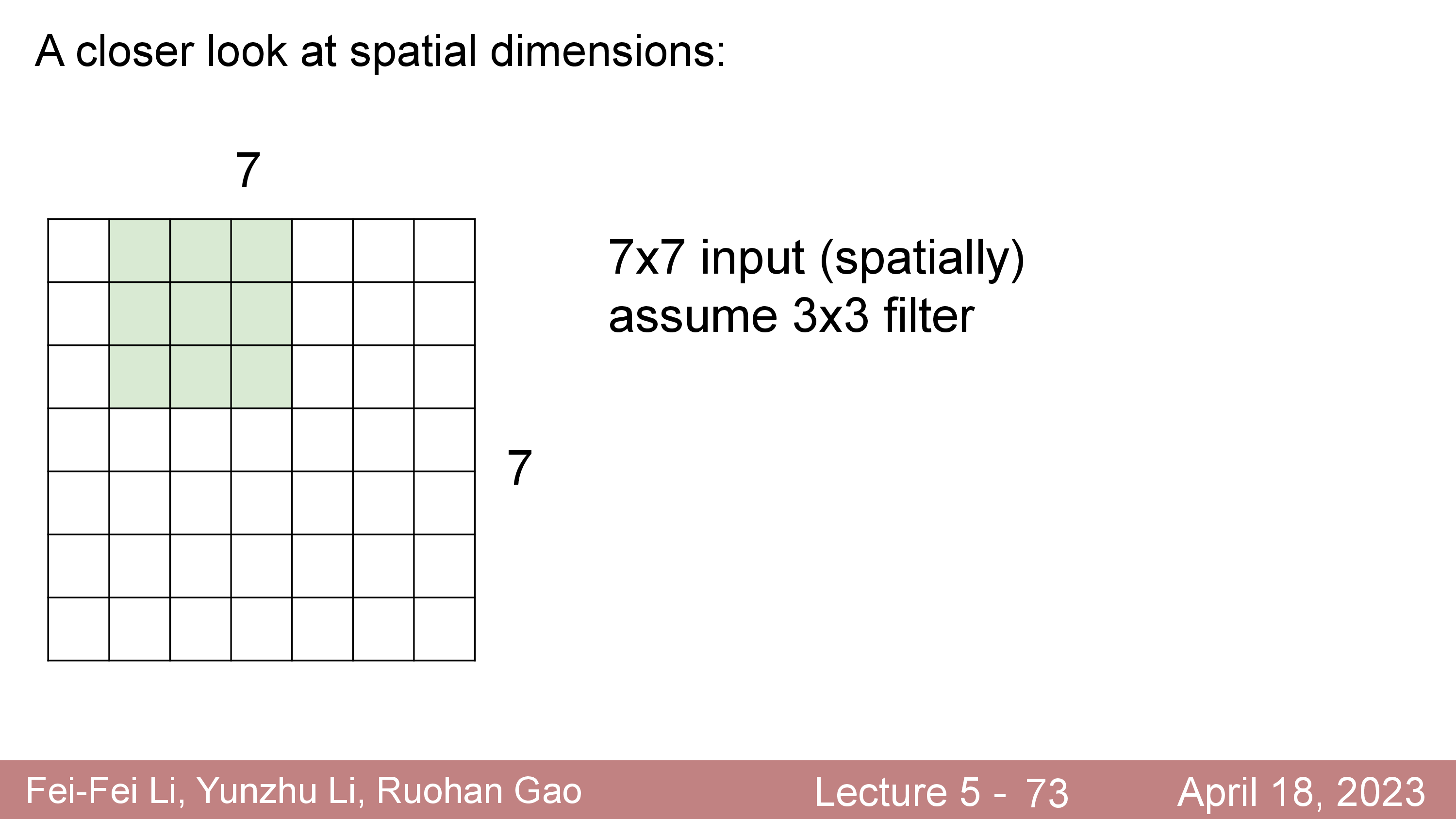lecture_5_slide_073 Fig.

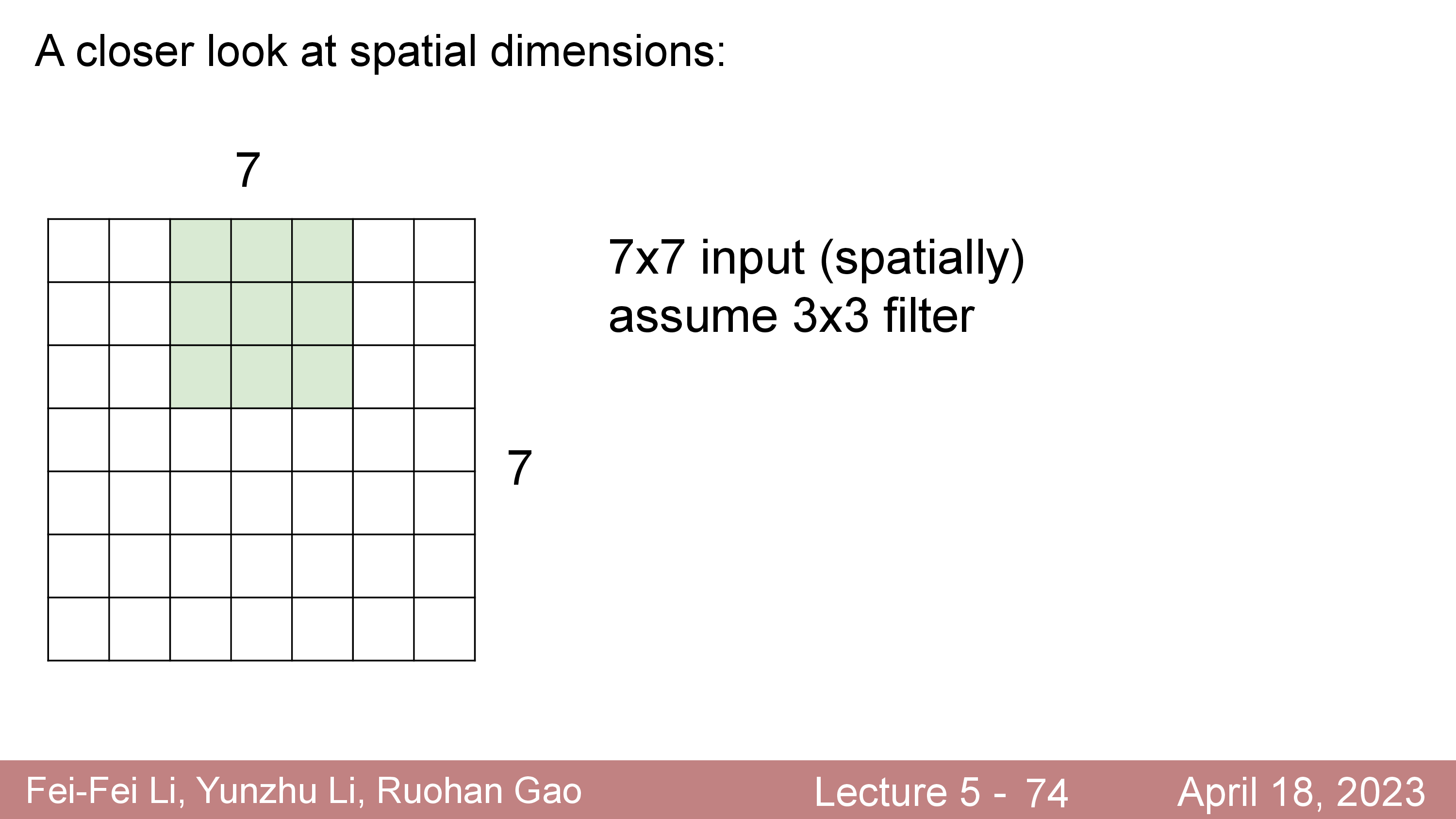lecture_5_slide_074 Fig.

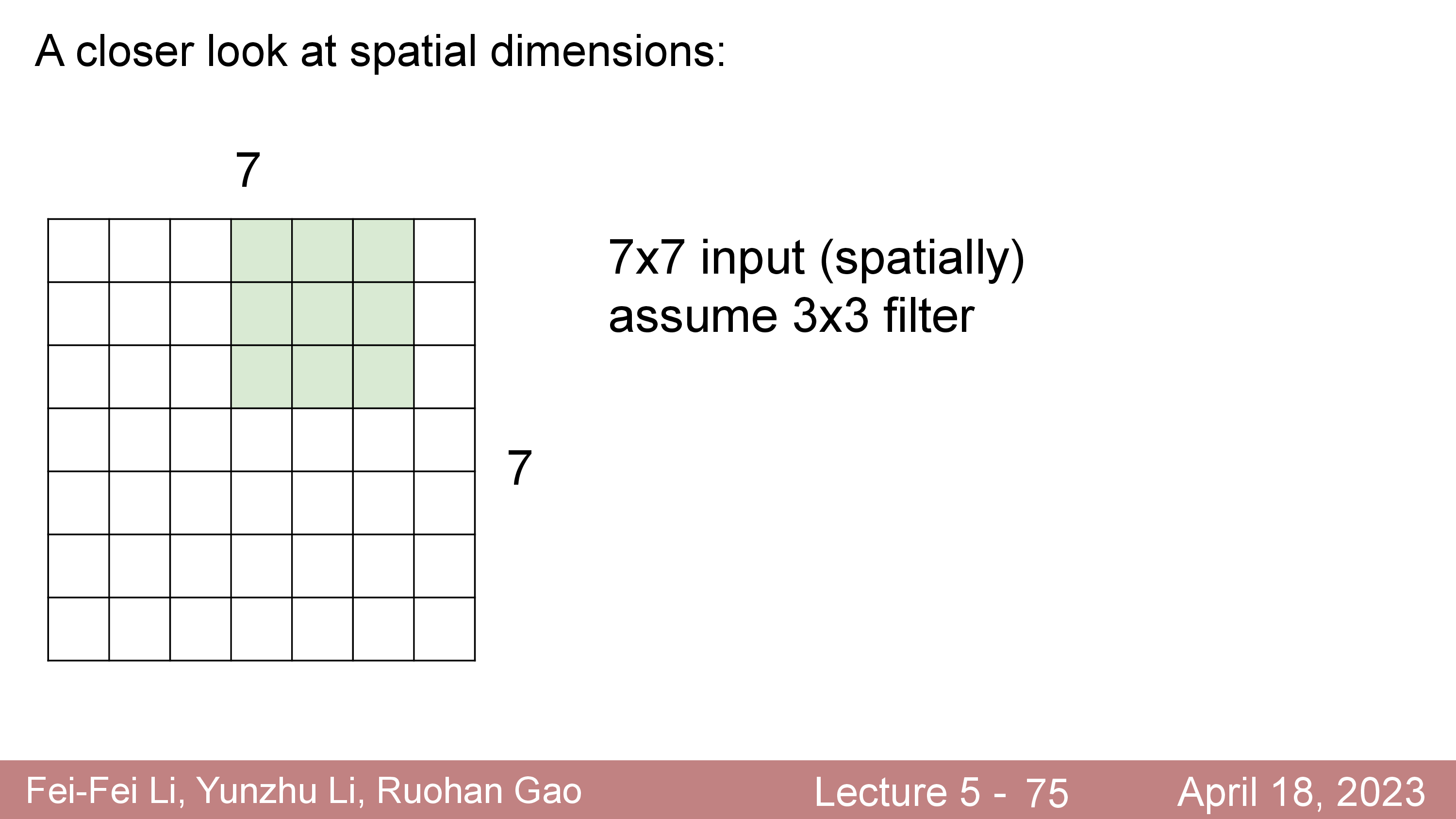lecture_5_slide_075 Fig.

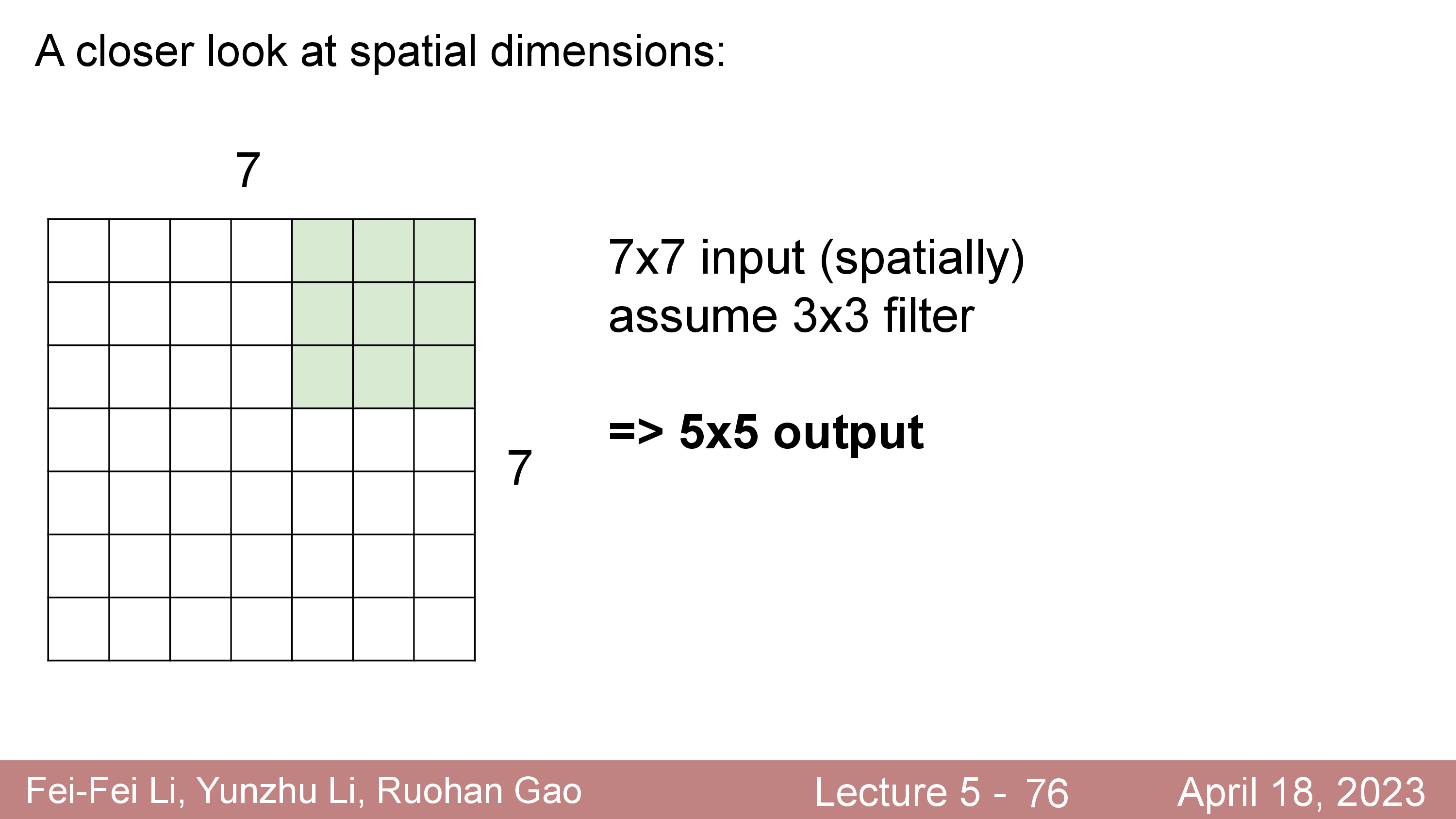lecture_5_slide_076 Fig.

Zero Padding

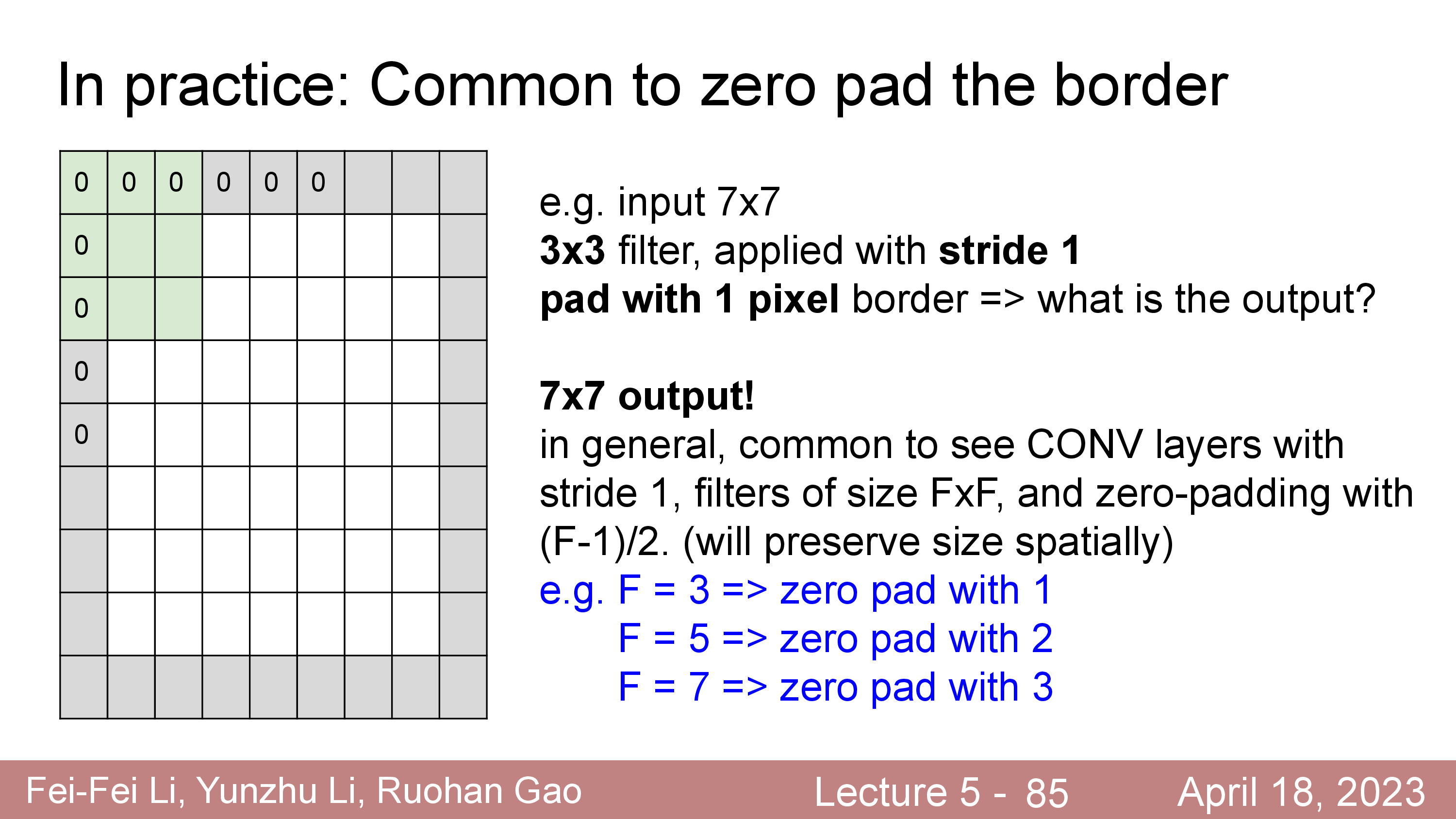
한편 stride=2,3 ... 같이 stride 를 설정할 수 있지만,

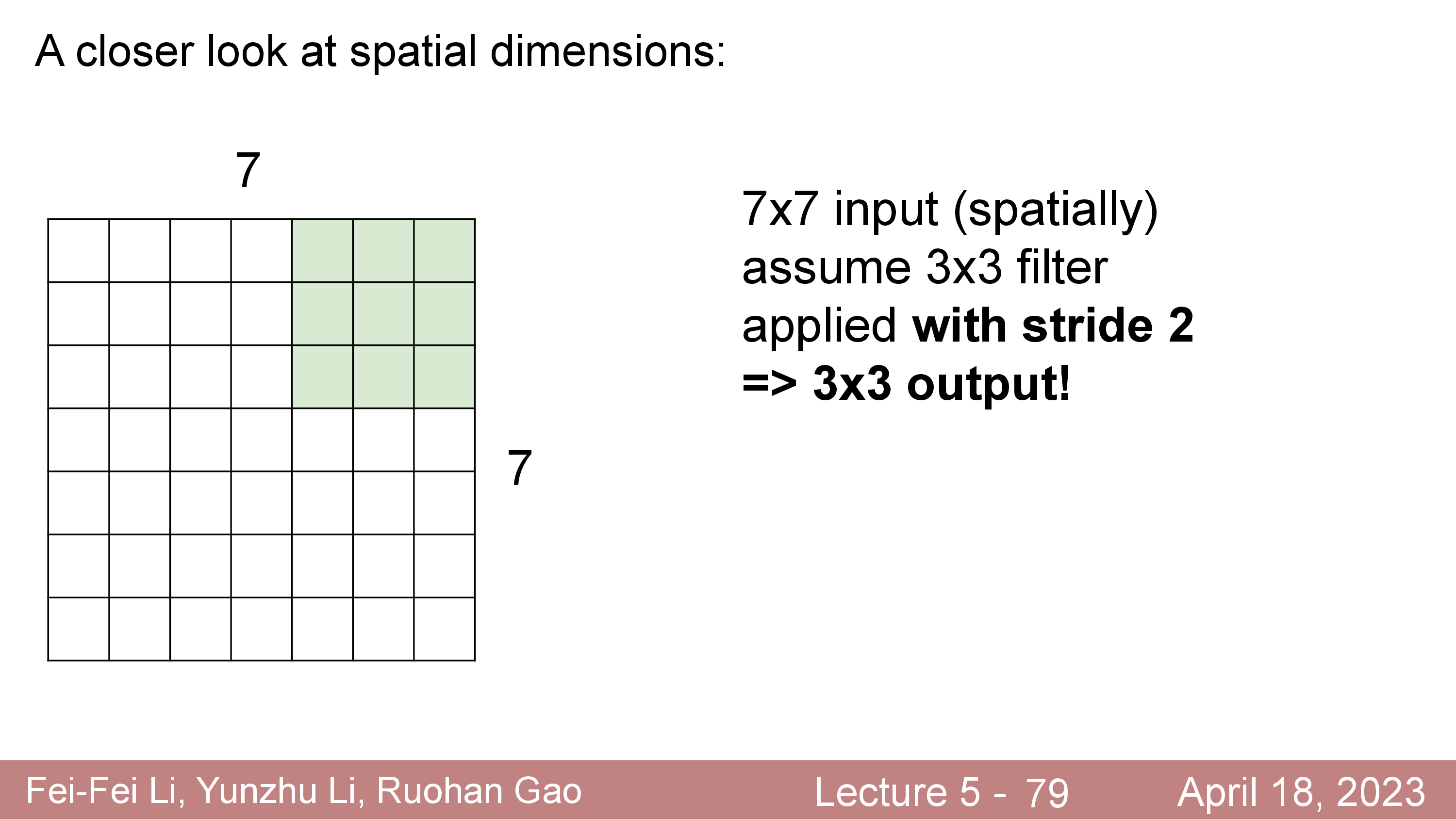
lecture_5_slide_079

7x7 같은 H,W 를 갖는 경우에 stride=3 를 적용하는 것과 같은 경우는 사용할 수 없다.

lecture_5_slide_080

lecture_5_slide_081

lecture_5_slide_082

이런 issue를 해결하기 위해서, 또는 input matrix 의 H, W shape 을 변화시키지 않기 위해 아무 의미 없는 0의 값을 갖는 Zero Padding 을 취해주는 것이 일반적이다. 이런 경우 input matrix 의 외곽에 값이 0 인 것들을 아래와 같이 추가해주는데, 이를 바로 padding 이라고 한다. (우리가 겨울에 오리털을 겉에 두르는게 padding이듯)

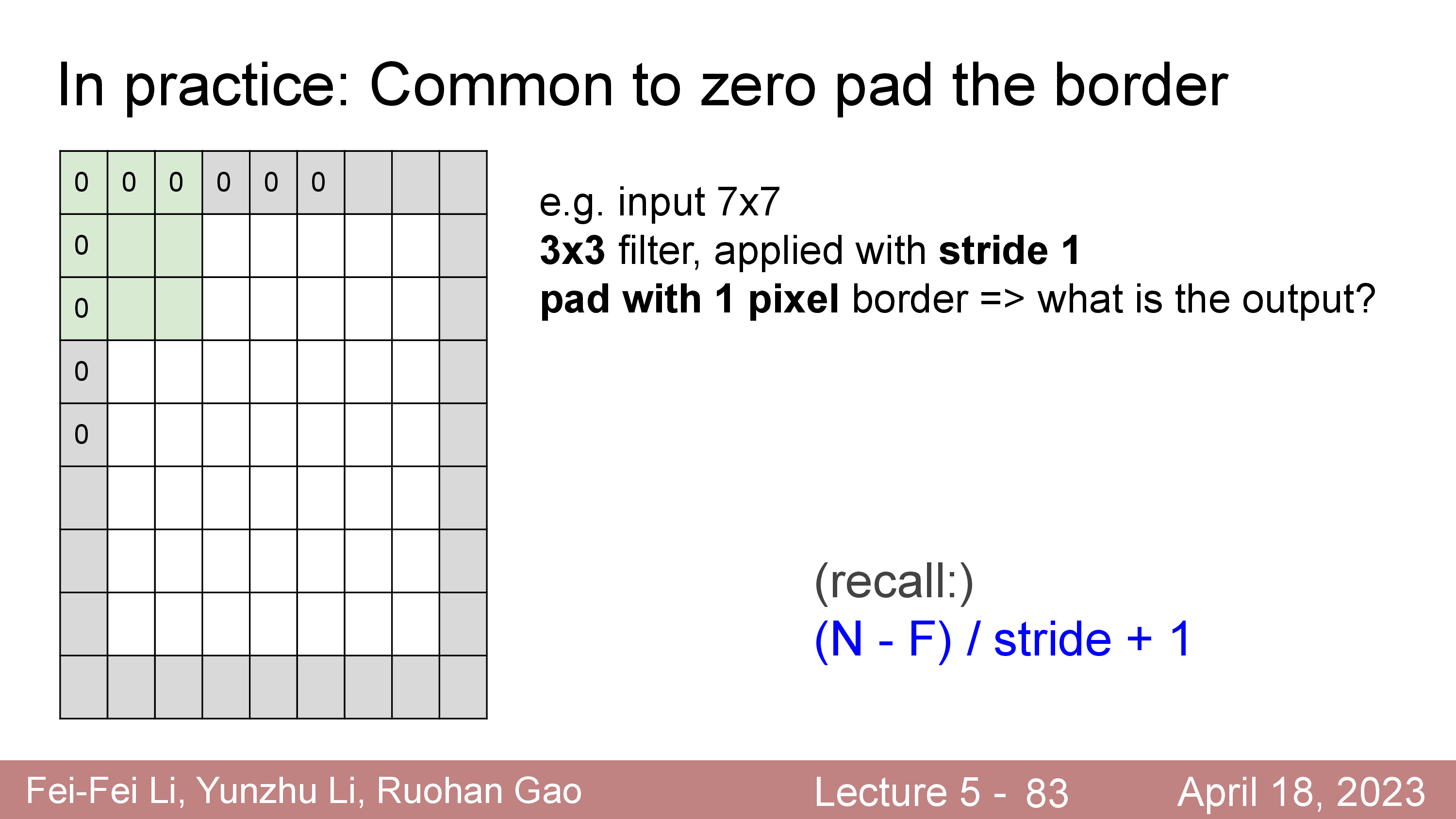
lecture_5_slide_083

그 뒤에 filter 를 convolve 하면 출력 matrix 는 아래처럼 계산된다.

\[\begin{aligned} & \text{Output's Width } = (W+2P-F) / S + 1 & \\ & \text{Output's Height } = (H+2P-F) / S + 1 & \\ \end{aligned}\]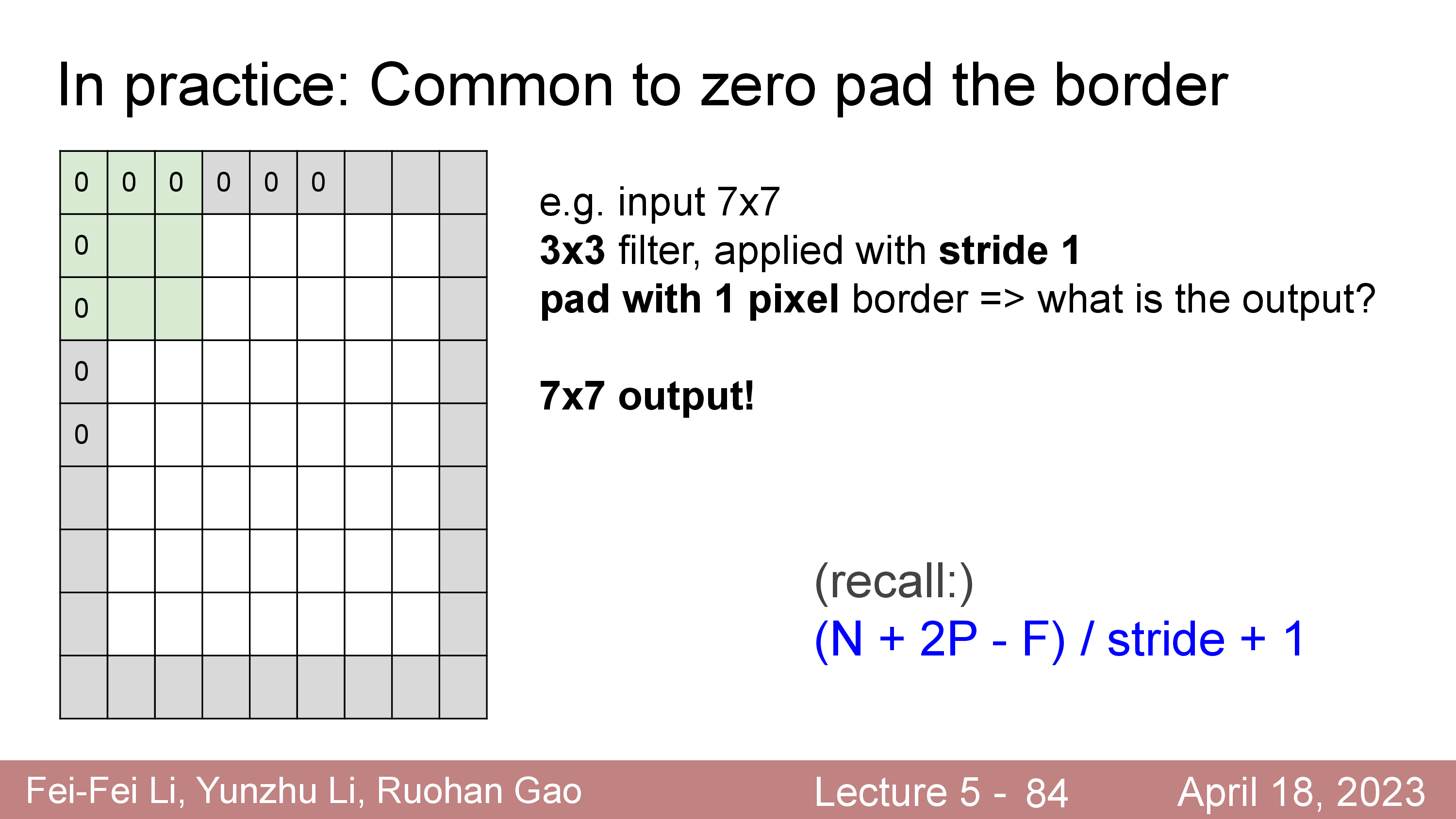

lecture_5_slide_084

일반적으로 filter size 에 따른 Padding 은 다음과 같이 해준다.

lecture_5_slide_085

Multiple Filter (Multiple Feature Maps)

한편 Convolution filter 한개를 가지고 연산하면 activation map 이 1개가 나오는데 이 filter 를 늘려보면 어떨까?

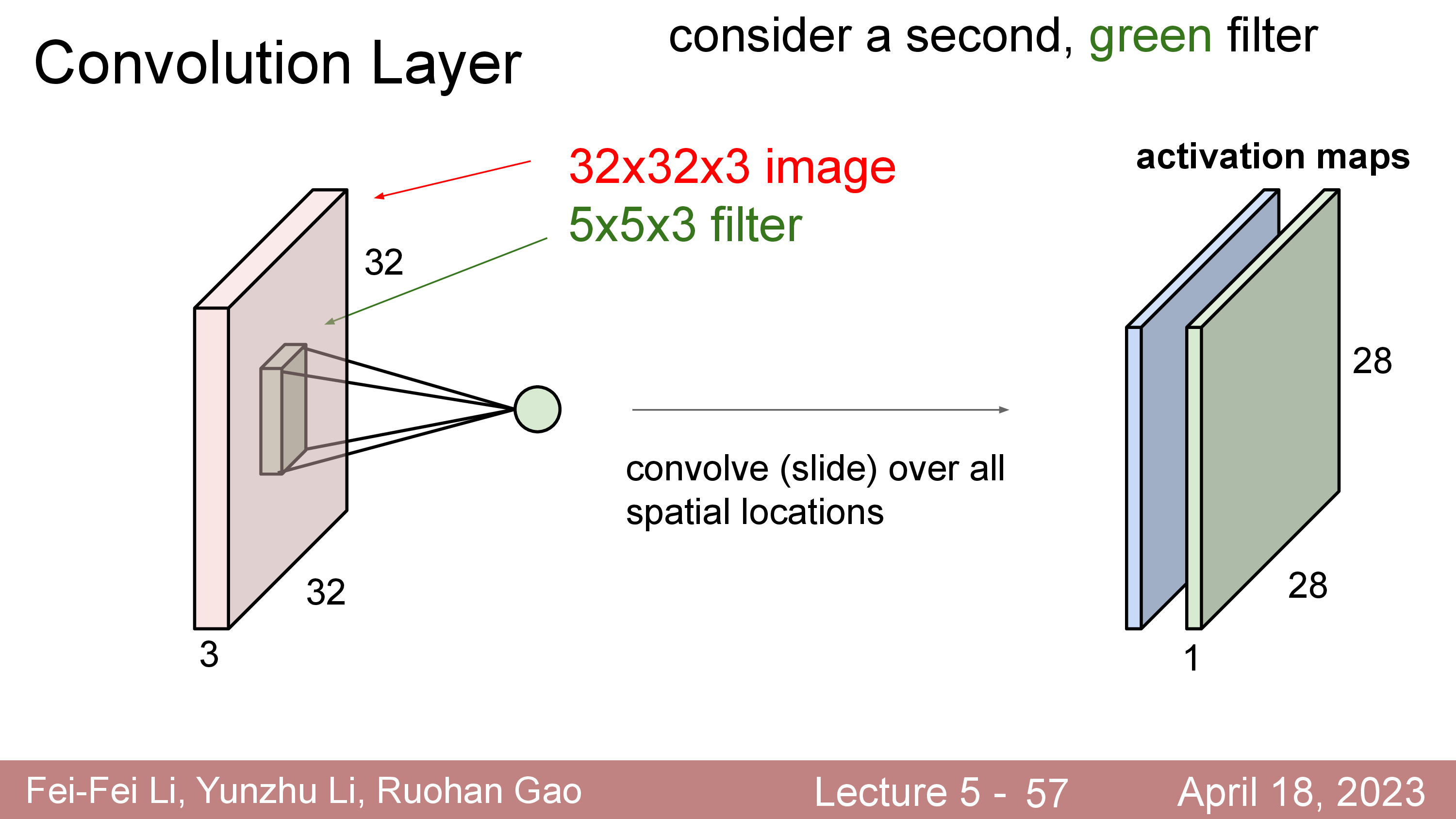
lecture_5_slide_057

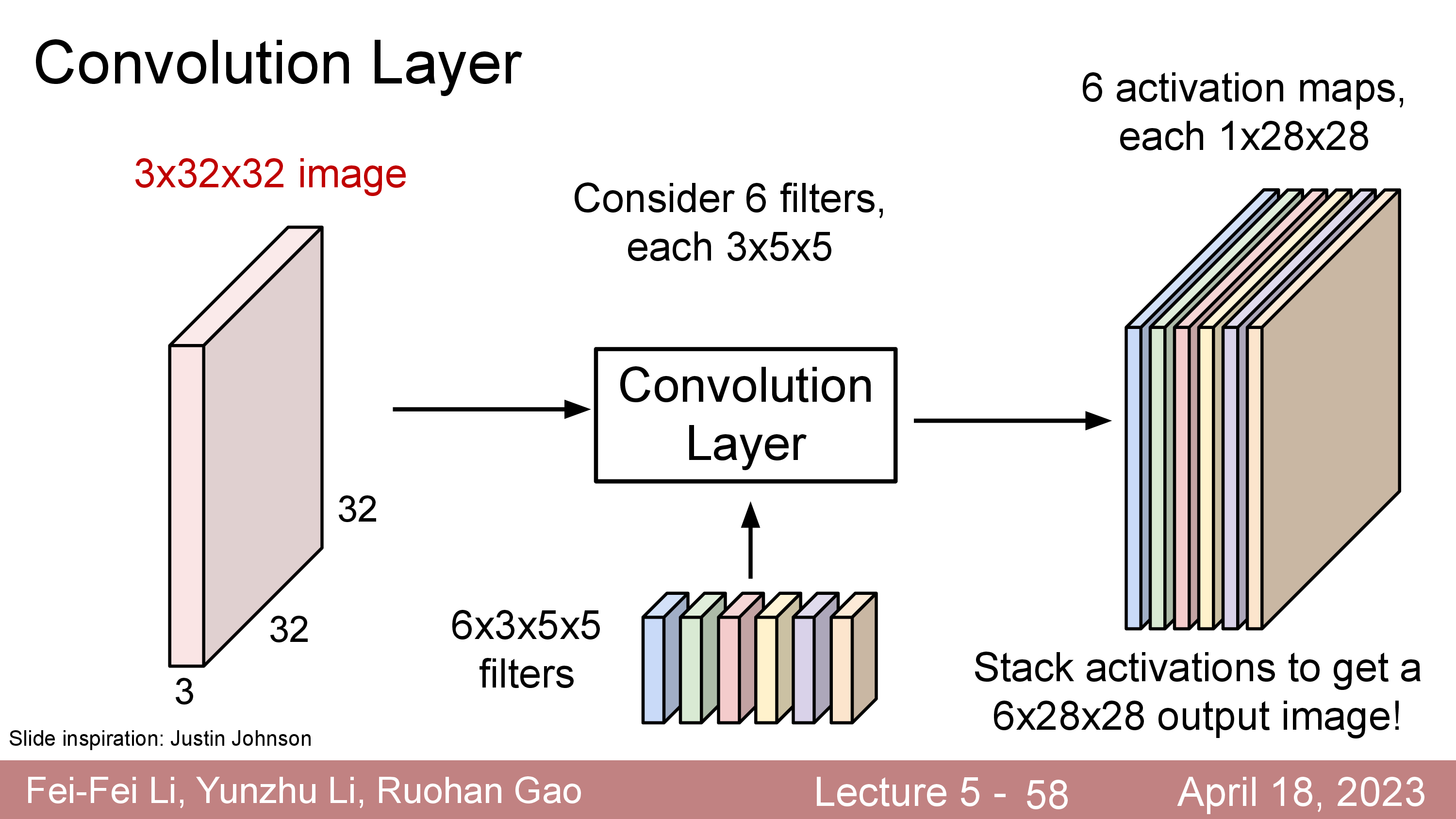
이를 6개까지 늘린다면 28x28x1 이 6개 이므로 28x28x6 의 matrix가 될 것이다.

lecture_5_slide_058

여기에 bias 까지 더해줄 수도 있다.

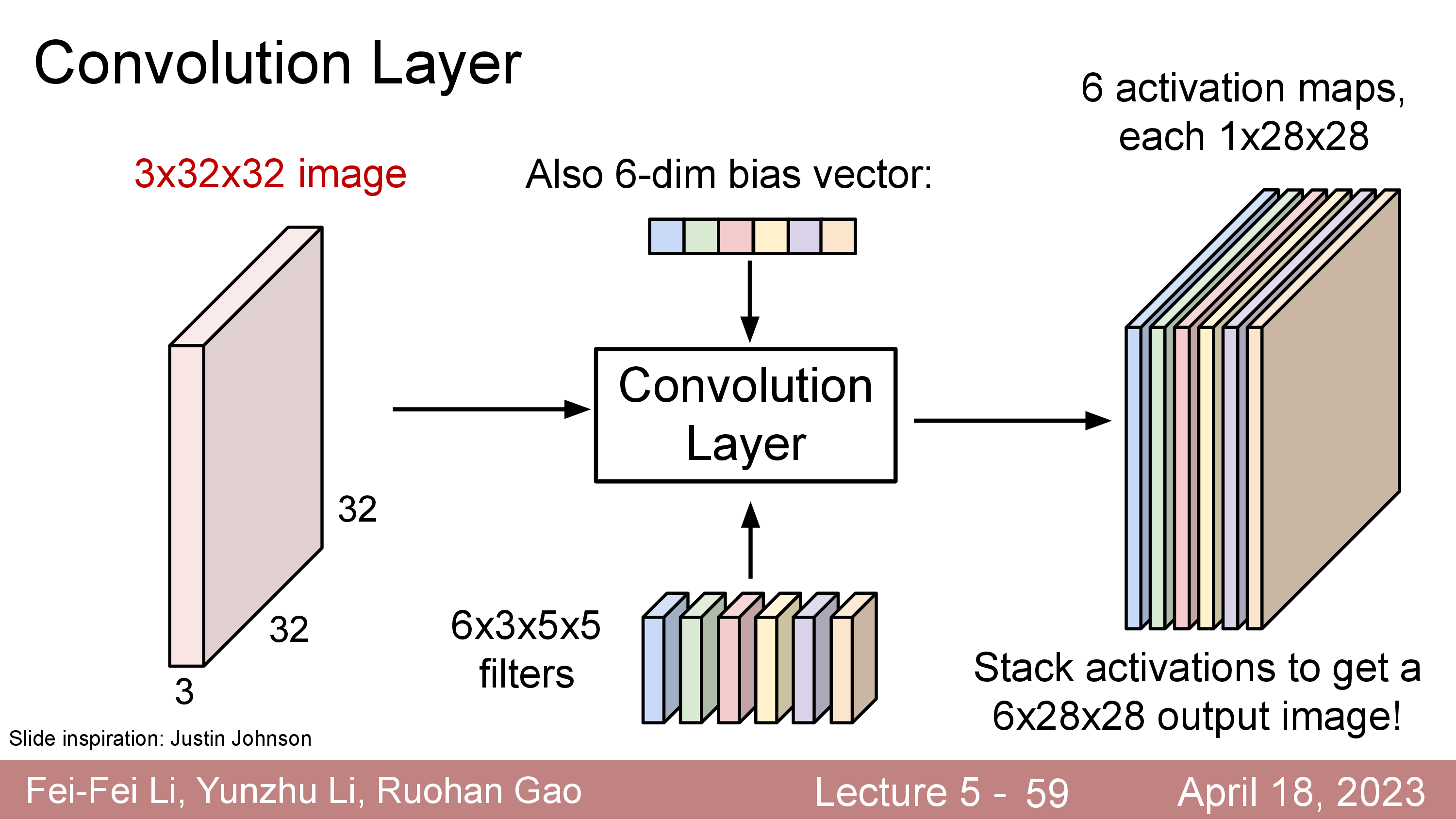
lecture_5_slide_059

이 경우에는 learnable filter 가 6배로 늘어나겠지만 여전히 FC Layer 를 사용할때과 비교해서 몇개 안되는 parameter size이다. 이렇게 filter 를 여러개 둠으로써 처음에는 한 pixel당 RGB 3차원의 정보만 가지고 있던 matrix 가 더 고차원 (ex 6차원) 의 정보를 갖는 matrix 로 바뀌게 된 것이나 다름 없게 된다. (Kernel, K=6)

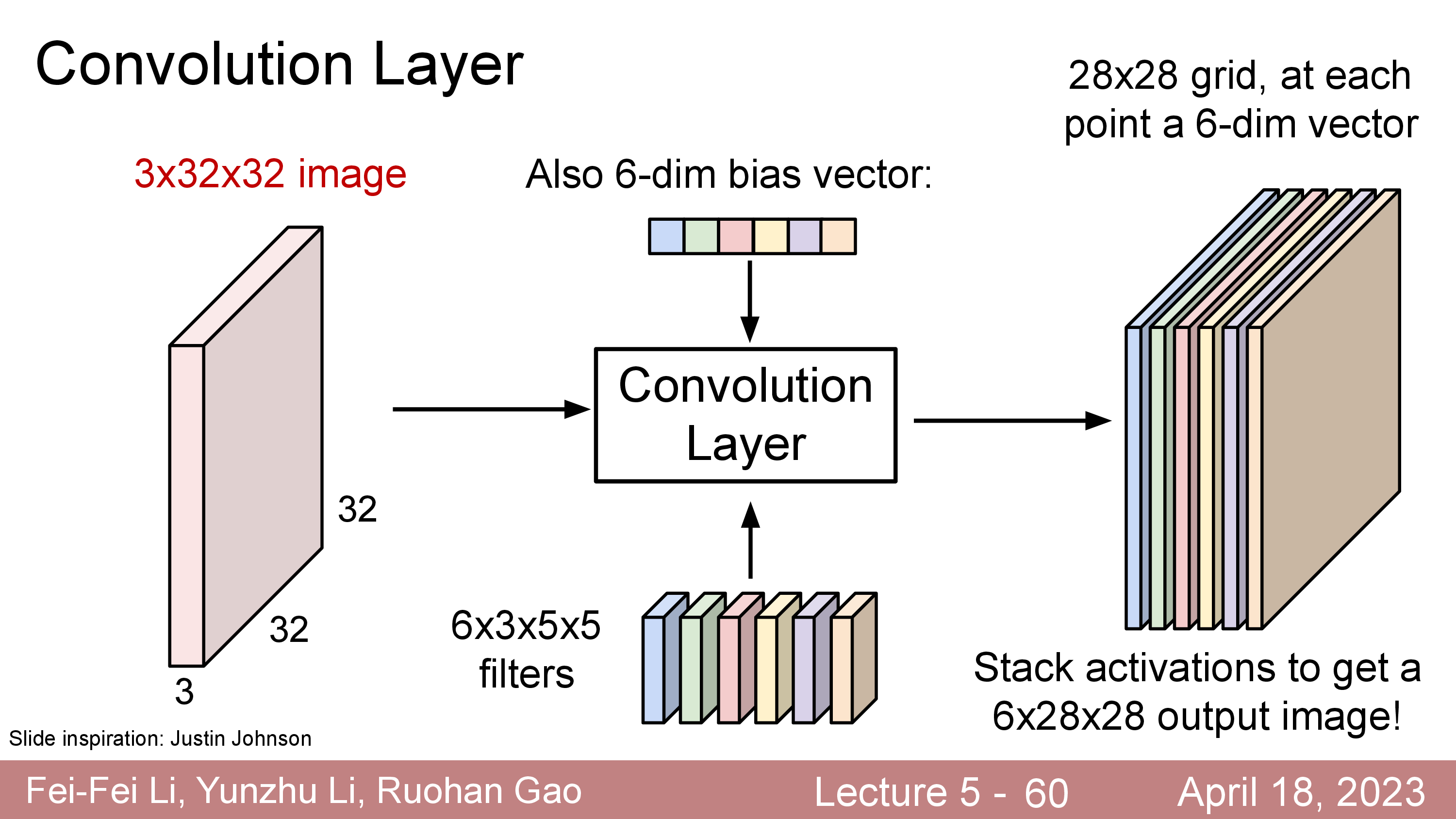
lecture_5_slide_060

한 이미지의 layer output 이 (HxWxC) 3차원 의 Tensor였는데, deep learning은 mini batch 만큼의 연산을 하기 때문에 실제로는 4차원 tensor 를 갖게 된다.

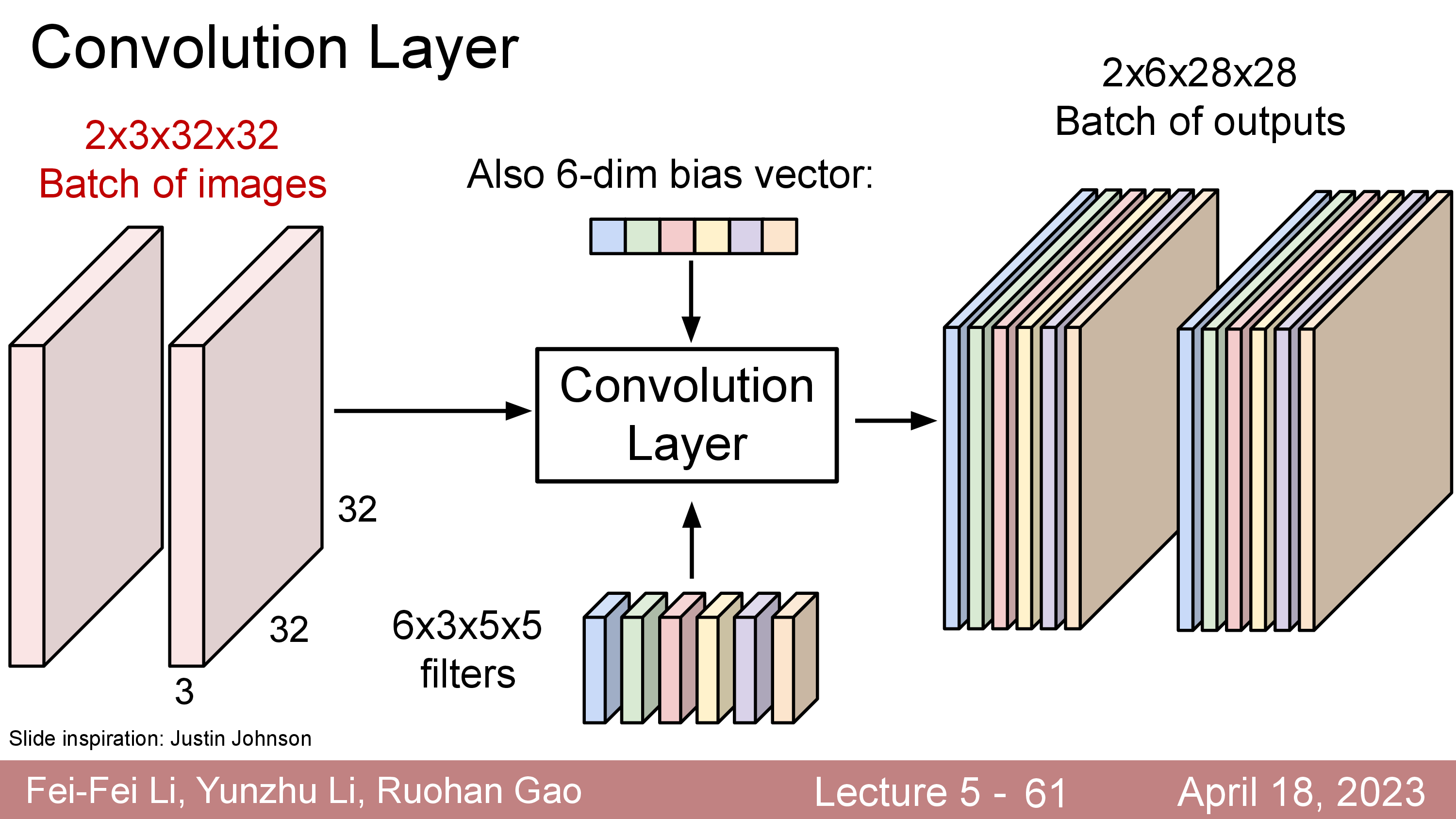
lecture_5_slide_061

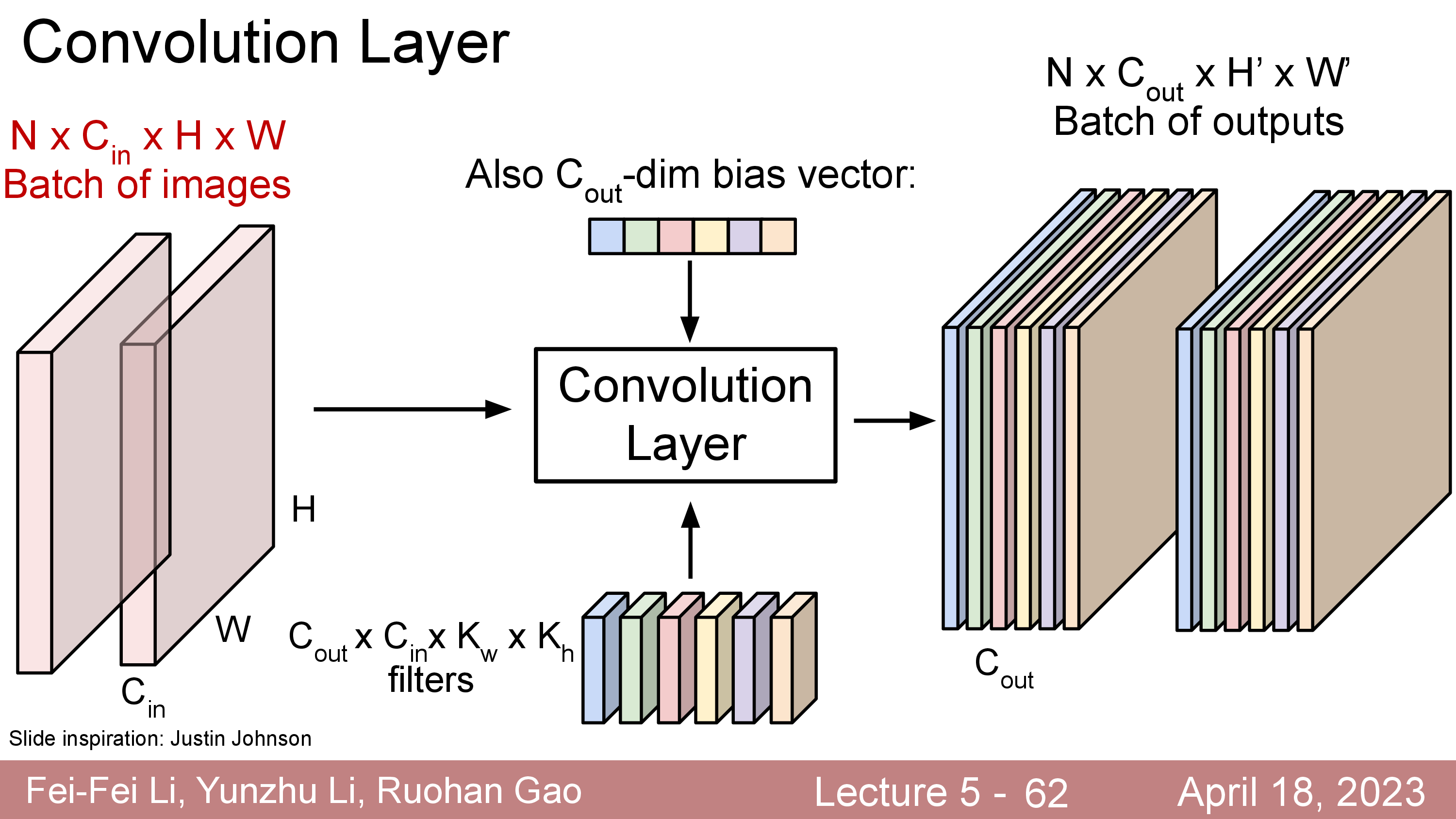
lecture_5_slide_062

CNN은 input image 가 이런 Convolution Layer 를 몇개씩 통과하게 디자인 되어 있고,

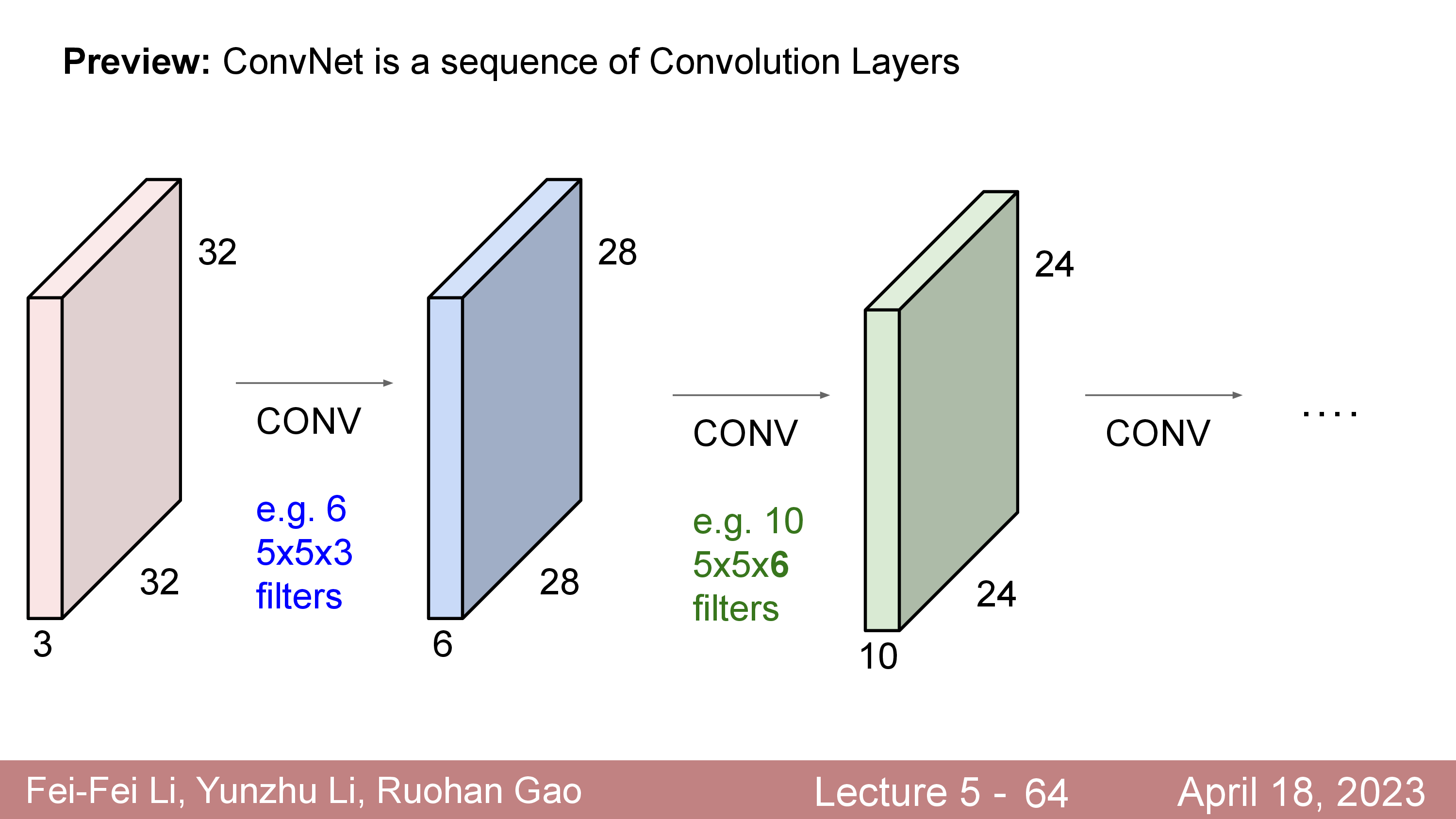
lecture_5_slide_064

이때 각 layer 를 통과한 elements 들은 non-linear activation function 을 통과하게 되어있다.

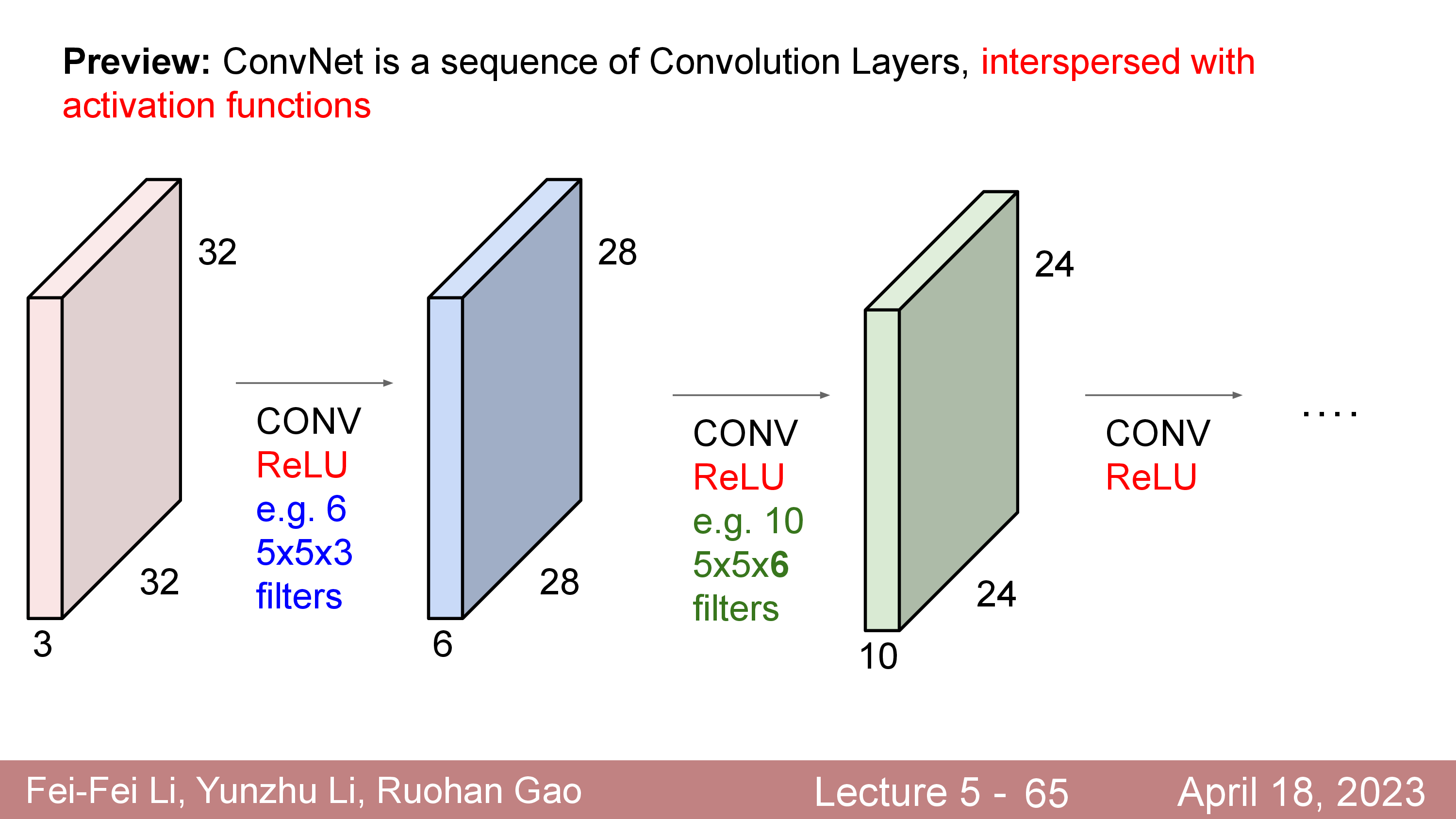
lecture_5_slide_065

What features are extracted ?

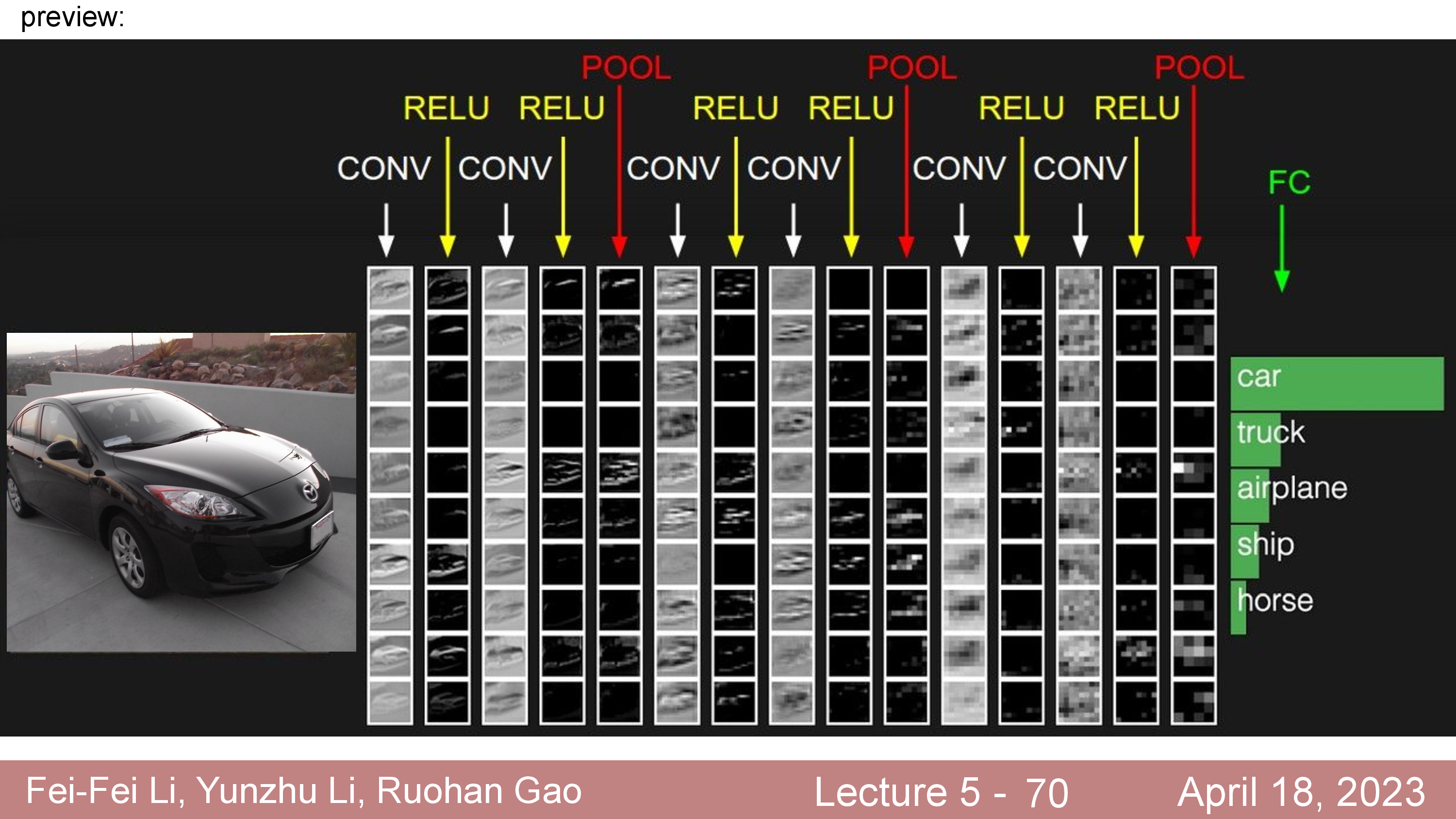
CNNs 은 이런 Convolution layer 가 몇개 쌓여있고 마지막에 FC Layer 와 Classifier 로 이루어져 있다 (아니면 Conv 와 Classifier 만 있거나). 이 때 input 쪽 부터 Convolution 을 통과하면서 어떤 feature 들이 나오는가?에 대해서는 입력단에 가까울수록 low level feature 를 뽑다가 마지막에 가서는 high level feature 를 뽑는다는 등의 분석들이 많이 있었다.

lecture_5_slide_070

사람의 얼굴을 인식하는 application 을 위한 CNNs 을 학습시켰다고 쳐 보자. CNNs 의 저층부 부터 고층부에 해당하는 Conv Layer 들은 아래처럼 저층부에서는 low level feature 인 edge나 명암 등을 파악하고

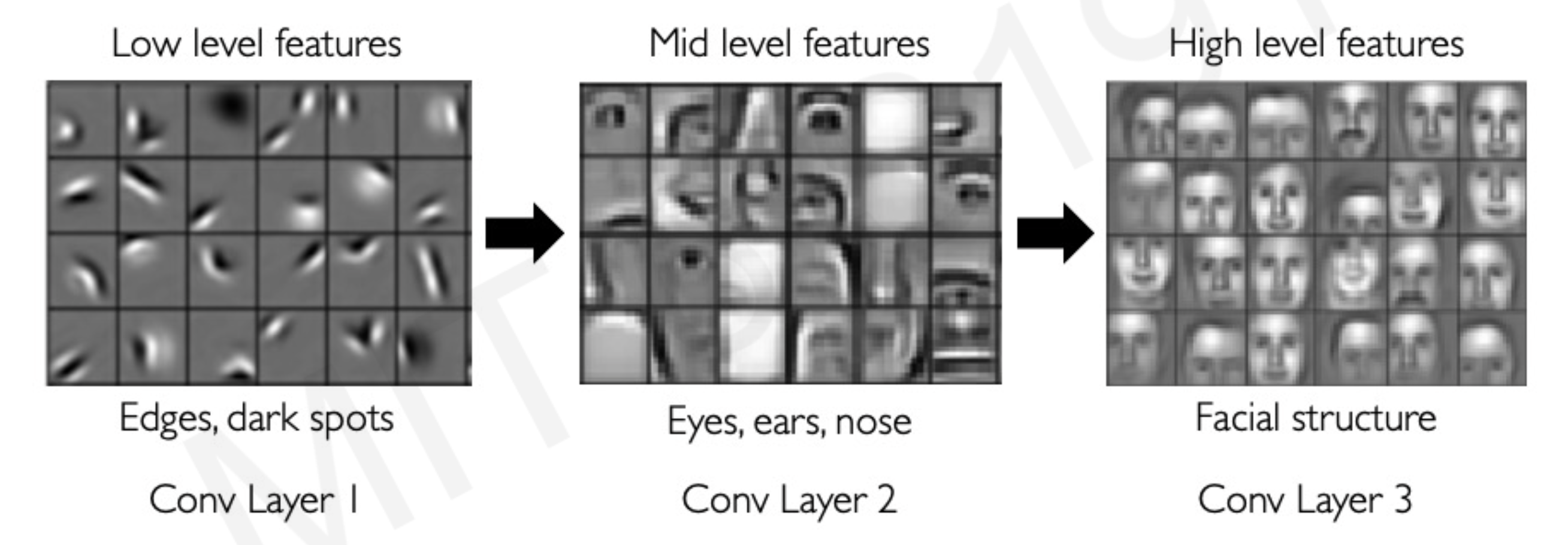
mit_feature_map_fig2

중간에서는 코와 눈 같은 mid level 의 feature를, 그리고 마지막쯤 되서는 얼굴의 전체적인 구조인 high level feature 를 뽑게 된다. 이는 image processing 분야에서 edge 등을 뽑기 위해 사람이 디자인한 (hand designed) 아래와 같은 filter 등을 사용해 convolution 연산한다는 것과 비교해 봤을 때 deep learning으로 학습한 filter weight도 충분히 어떤 layer 에서는 이런 식의 filter 로 학습되어있을 가능성이 있다는 것은 놀라우면서도 자연스러운 일일 수 있다.

mit_feature_map_fig1

우리가 의도하지 않았지만 필요에 의해 사람이 디자인한것과 같거나, 그 이상의 무언가 (사람이 생각하지못한)를 발견했으니 말이다. 이렇듯 CNNs 은 image input 에 대해 특화된 Neural Network 이며 다음과 같은 장점을 가지고 있다.

  • Image input 에 대한 강력한 inductive bias 가 있음
    • Local Connectivity : 어떤 pixel 이든 주변 pixel 들과 correlation 이 클 것임. 즉 공간 정보 (Spatial Information) 를 보존하면서 feature 를 뽑는게 좋음.
  • Parameter Sharing : FC 와 다르게 Filter size 만큼의 parameter 만 필요함. FC Network가 32x32x3 짜리를 처리하기 위해 3072x?? 크기의 커다란 weight 이 필요함.
  • Can be applied to any inputs with variable length : 가변길이의 Input 에 모두 사용할 수 있음. 예를 들어 32x32x3 이미지로 학습한 filter 도 256x256x3 이미지에 사용 가능함 (성능은 논외).

Pooling Layer

CNNs 에는 마지막으로 Pooling Layer 라는게 존재하는데, input tensor 의 일정 부분마다 가장 큰 값 (max pooling) 혹은 그 구역의 평균 (average pooling) 을 취해서 리턴해주는 layer이다. 이는 네트워크 전체의 parameter 수와 연산량을 줄여주는 역할과 더불어 overfitting 을 억제 해줄수도 있다고 하는데,

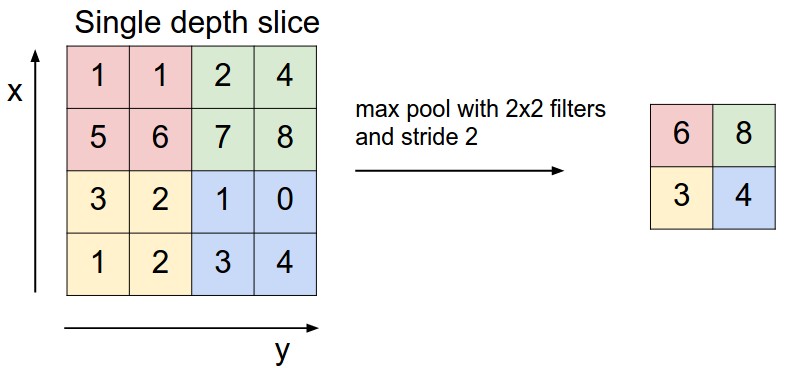
max_pool

Pooling Layer 의 filter size 를 F=2, stride 를 S=2 라고 하면 input tensor 가 위의 figure 에서처럼 H,W 가 절반으로 줄어드는걸 볼 수 있다. Average 와 Max pooling 중에서는 역사적으로 average 도 많이 사용되었지만 요즘은 사장되어 max 가 더 많이 쓰인다고 하지만, 누군가는 아니 그냥 stride 크게 한 Conv 쓰면 되지 굳이 이거까지 해줘야 하나? 라는 생각을 할 수 있다. 실제로도 pooling layer를 버리는것이 생성 모델을 학습하거나 하는 경우에는 더 좋기도 해서 딱히 성능개선이 없으면 굳이 temporal resolution 을 줄이기 위해서 가져갈 필요는 없는 layer 라고도 한다.

그 밖에 Normalization Layer 와 FC Layer 를 끝으로 이어붙히면 computer vision application 을 위한 일반적인 CNNs 을 하나 만든 셈이 된다.

Convolution Layer vs Fully Connected (FC) Layer Again

여기서 Standard Conv Layer 의 varient 들로 넘어가기 전에 마지막으로 짚고 넘어갈 것이 있다. 바로 Conv Layer 와 FC Layer 간의 관계다. 두 Layer 의 차이점이라면 Conv Layer 는 neuron 들이 지협적인 공간 (local region) 에만 연결되어 있다는 점과 parameter 를 공유한다는 점이고, 공통점이라면 두 layer 모두 여전히 dot product 연산을 한다는 것이다. 즉 어떤 상황에는 사실상 둘이 동치가 될 수 있다는 것이다.

예를 들어 어떤 image tensor 의 사이즈가 7x7x512라고 하자. 이를 flatten 하면 1x25088 의 vector가 된다. 25088x4096 크기의 FC Layer 를 쓴다면 1x4096 의 출력물이 나올텐데, 이번에는 Conv Layer 를 써보려고 한다. 마찬가지로 7x7 짜리 이미지에 F=7,P=0,S=1,K=4096 의 Conv Layer 를 쓴다면 어떨까? 결과는 1x1x4096으로 같다. 이는 반대로도 성립이 되는데요, 즉 어떤 Conv Layer 도 같은 기능을 하는 FC Layer 로 나타낼 수 있다.

그렇다면 FC Layer 를 Conv Layer 로 대체하는게 가능한데 이건 어떨때 쓸까? 사실 이는 실제 상황에서 유용하다고 하는데, 위의 예시에서 handwritten character 같은 문제를 풀기 위해서 Conv, Pooling layer들을 막 조합해서 이어붙힌 뒤에 마지막으로 FC Layer 를 쓰면 끝이라고 했었다. 이렇게 NN을 구성해도 되나 Yann Lecun이 제안한 LeNet 에는 사실 FC Layer 가 없다. 대신 이 역할을 하는 Conv Layer 만 존재할 뿐이다. 이렇게함으로써 얻을 수 있는 장점은 바로 CNNs 은 학습때보다 더 큰 사이즈의 image input 을 입력으로 써도 전혀 문제가 없다이다.

Yann Lecun 은 다음과 같은 post를 sns에 게시한 적이 있다.

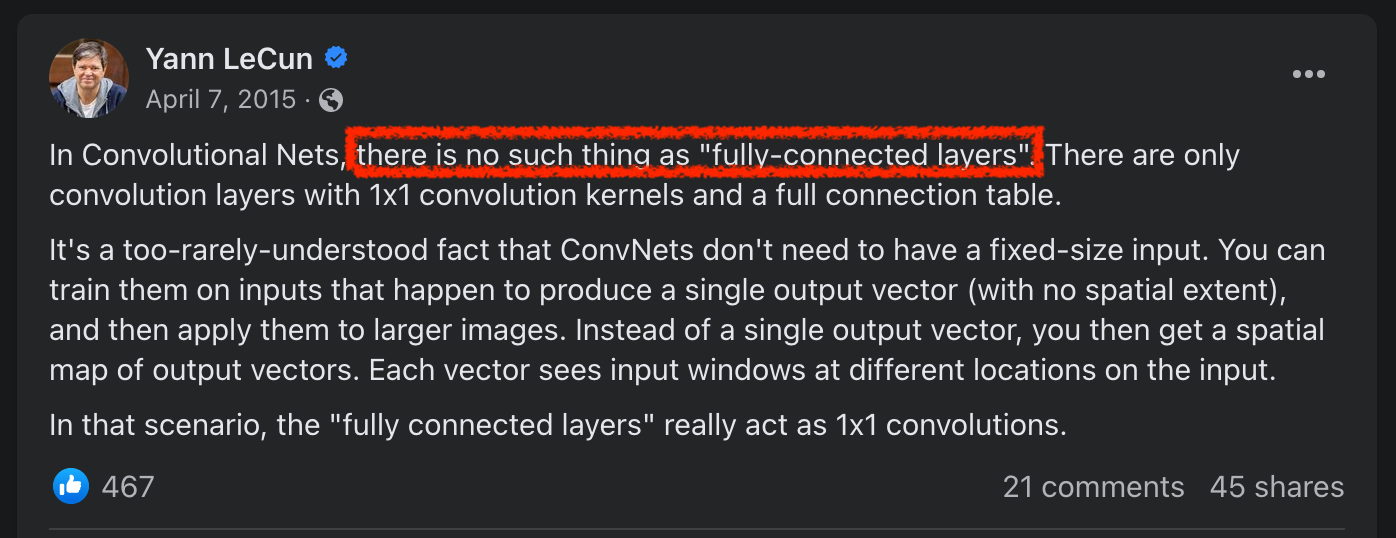yann_cnns_fc Fig. Yann’s FB post

TL;DR 하면 '사람들이 잘 모르지만 CNNs 에는 사실 FC Layer 가 없다. 1x1 Convolution 이 있을 뿐'이라는 것이다. 왜 이런말을 하는걸까?

CNN 에서 Conv Layer 들은 우리가 Filter 를 학습한 것이고 Filter 는 어떤 크기의 이미지가 들어와도 문제없이 연산을 해 출력 tensor를 return할 수 있다. Conv Layer는 문제가 안된다. 하지만 마지막에 class dimension 으로 projection 해주는 FC Layer 는 문제가 될 수 있다.

예를 들어 224x224x3 짜리 이미지를 받아서 학습된 CNNs 이 있다고 생각해 보자. 이는 Conv->Pool 로 구성된 layer 가 겹겹이 쌓여있을건데, CNNs 의 한 종류인 AlexNet 의 경우 5개의 Pooling Layer 덕에 224/2/2/2/2/2=7로 down sampling 이 된다. 즉 마지막 feature map 의 H,W 사이즈는 7x7 인거죠. AlexNet 의 마지막에는 FC Layer 가 3 개가 있는데 4096 차원으로 projection 하는 layer 2개와 마지막으로 image class 1000개에 대응하는 공간으로 projection 하는 layer가 한 개 있다. 이 FC Layer 를 Conv Layer 로 변환해보면 아래처럼 쓸 수 있다.

  • input tensor [7x7x512] 을 받아 [1x1x4096] 으로 출력하는 Filter size 7x7 짜리 Conv Layer
  • output 을 [1x1x4096] 로 뽑아주는 Filter size 1x1 짜리 Conv Layer
  • 최종 output 을 [1x1x1000] 로 뽑아주는 Filter size 1x1 짜리 Conv Layer

그렇다면 모델이 학습된 224x224 image 가 아니라 더 큰 image 인 384x384 라는 image 들어왔을때 모델은 이를 어떻게 처리해야 할까? FC Layer 로 마지막 출력단을 구성했을 때는 다음과 같은 방법이 있을 수 있다.

  • 1.384x384 이미지를 tool 을 이용해서 224x224로 resize 한다.
  • 2.일부분을 자른다 (crop).
  • 3.384x384 이미지를 convolution 연산하듯 224x224로 window 만큼 CNNs에 넣고 이를 sliding 하면서 반복한다.
  • 4.etc

이렇게 꼭 해야되는 이유는 FC Layer 는 고정된 (static) 입력을 꼭 받아야만 class 1000개 에 해당하는 output vector 를 만들어낼 수 있기 때문이다. 하지만 이를 Conv Layer 로 바꾼 시점에서 이점이 생기는데요, 384x384 image 를 그냥 넣어도 된다는 것이다. 이렇게 하면 출력단의 FC 처럼 작동하는 3개 Conv Layer 들이 뱉는 결과물의 모양이 조금 달라질뿐 logic 자체는 문제가 안생기는데,

  • 12x12x512 -> 6x6x4096
  • 6x6x4096 -> 6x6x1000
  • 6x6x1000 -> 6x6x1000

즉 우리가 학습때보다 더 큰 larger image 에 대해 sliding 하면서 각 구역마다의 class vector 를 뱉는 것 처럼 자동으로 된다는 것이다. FC Layer도 이런식으로 구현할 수 있지만 이렇게 하는거보다 Conv Layer 를 쓰는게 더 효율적이다. 왜냐하면 전체 CNNs 연산을 sliding 하면서 모든 구역마다의 input 을 CNNs 에 반복적으로 통과시키는거보다 낫기 때문이다 (대부분의 region이 겹침).

Evaluating the original ConvNet (with FC layers) independently 
across 224x224 crops of the 384x384 image in strides of 32 pixels 
gives an identical result to forwarding the converted ConvNet one time.

그러면 6x6 짜리 행렬은 어떻게 처리하느냐? 이때 각 구역의 class 들을 평균 취해서 쓰면 된다는 것이 되는데, 이게 꽤 효과가 있어 일부러 image 사이즈를 크게 늘려서 구간별로 class 를 일부러 보고 평균 내서 더 좋은 성능을 내기도 한다고 한다. 마지막으로 FC Layer 대신 Conv 를 사용하면 이를 object detection 이나 multiple character recognition 같은 것도 가능해 진다.

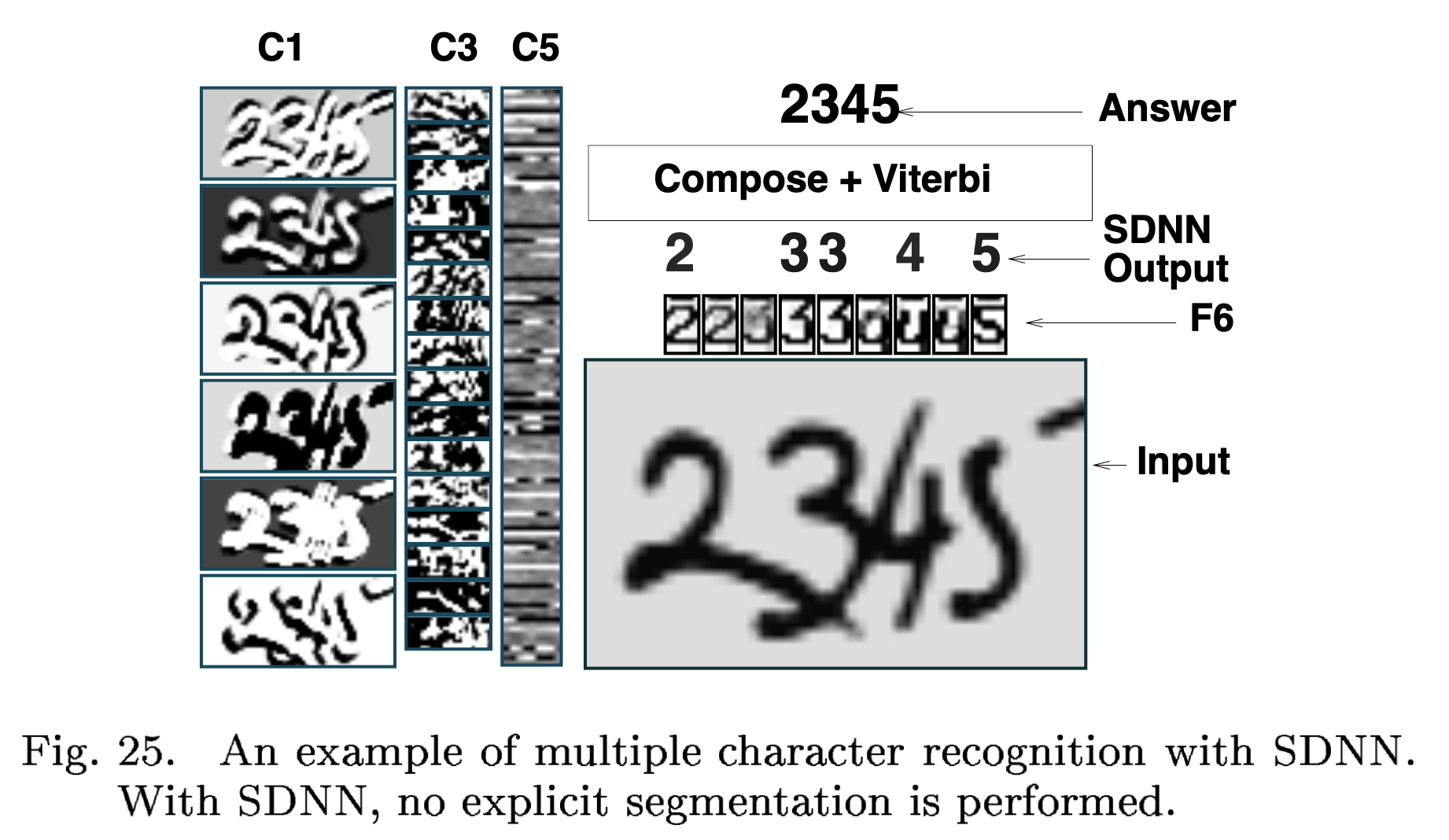multiple_recognition Fig. Yann Lecun 의 LeNet 에 나온 multiple character recognition 예시.

Number of Parameters and Computational Cost

앞서 FC Layer 보다 Conv Layer 를 쓰는 것의 장점으로 공간 정보를 유지한다는 점과 parameter 수가 적다는 (share 하므로) 점을 말씀드렸는데, 실제로 얼만큼의 memory 가 필요한지 보자. 아래의 예시를 보시면 한 Conv Layer 에 필요한 Parameter 수는 5x5 에 input tensor 의 channel 이 3이고 layer의 output tensor의 channel 이 10일 경우 5x5x3 + 1 (bias) = 76 가 10개 있으므로 760 이 됨을 알 수 있다.

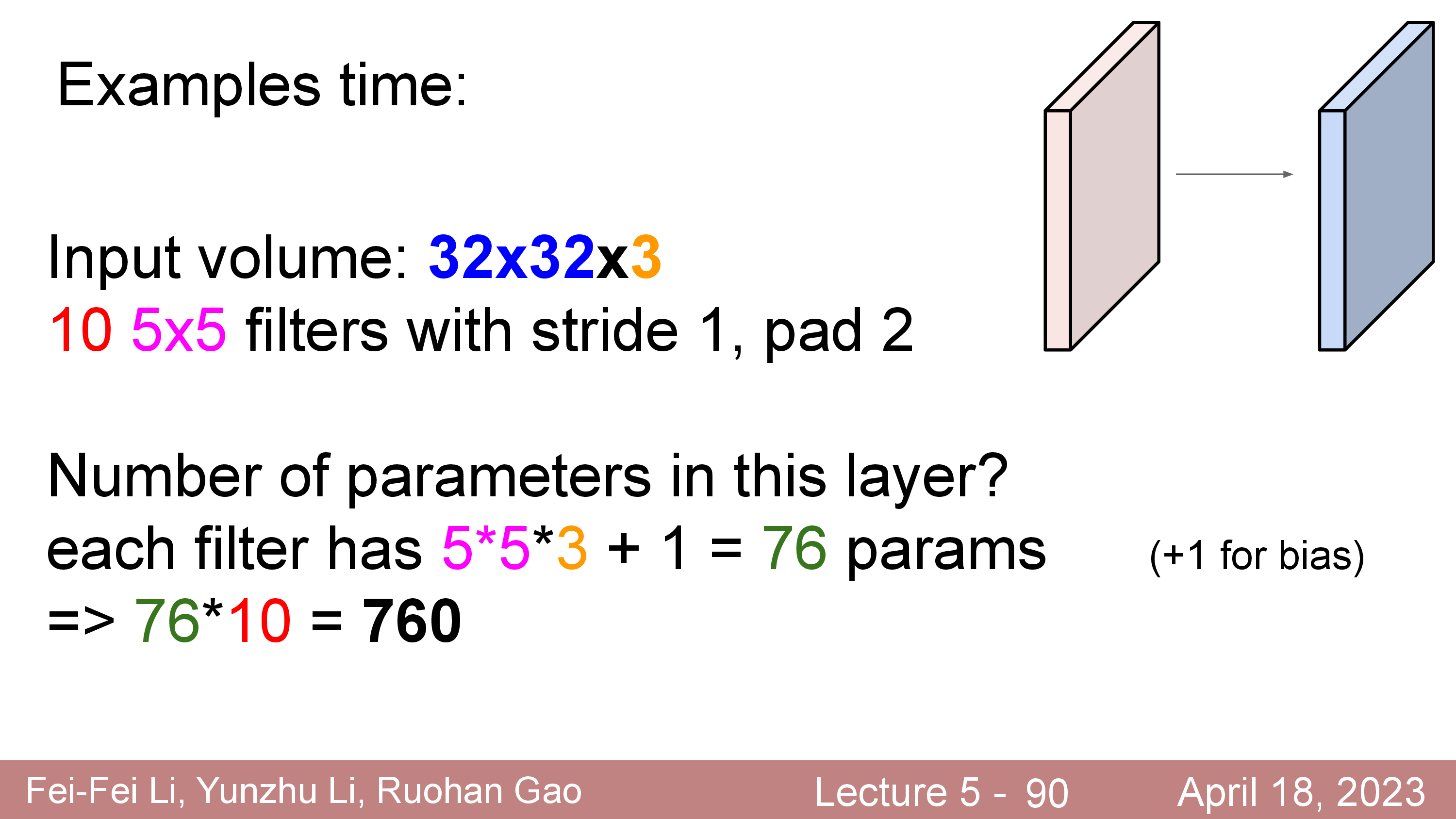
lecture_5_slide_090

즉 위에서처럼 notation 을 다시 아래와 같이 쓰면

  • input matrix 너비 : Width (W)
  • input matrix 높이 : Height (H)
  • input matrix 채널 : Channel (C)
  • filter 크기 : F
  • filter 의 convolve 연산을 하는 간격 (stride) : S
  • filter 의 개수 : K

Conv Layer 의 Parameter 수는 bias 까지 해서 \(F^2 C K + K\) 개가 된다. 이를 FC Layer 로 디자인한다고 치면 32x32x3 image 를 flatten 해서 3072 차원으로 만든 뒤에 3072x10240 의 weight matrix 와 연산하고 다시 32x32x10으로 reshape 해줘야 한다. parameter 수가 엄청 차이나는것을 알 수 있다.

Receptive Field

한 편, Conv Layer 를 Stack 해서 디자인한 NN에는 Receptive Field라는 개념이 있다. Conv Layer 라는 것이 현재 layer output tensor의 한 point 를 만들기 위해서 보는 input tensor 의 영역이 여러층을 지날 수록 더 늘어난다는 것이다. 실제로 한 point 를 만들기 위해 그 주변부인 KxK 영역만 보던 것이

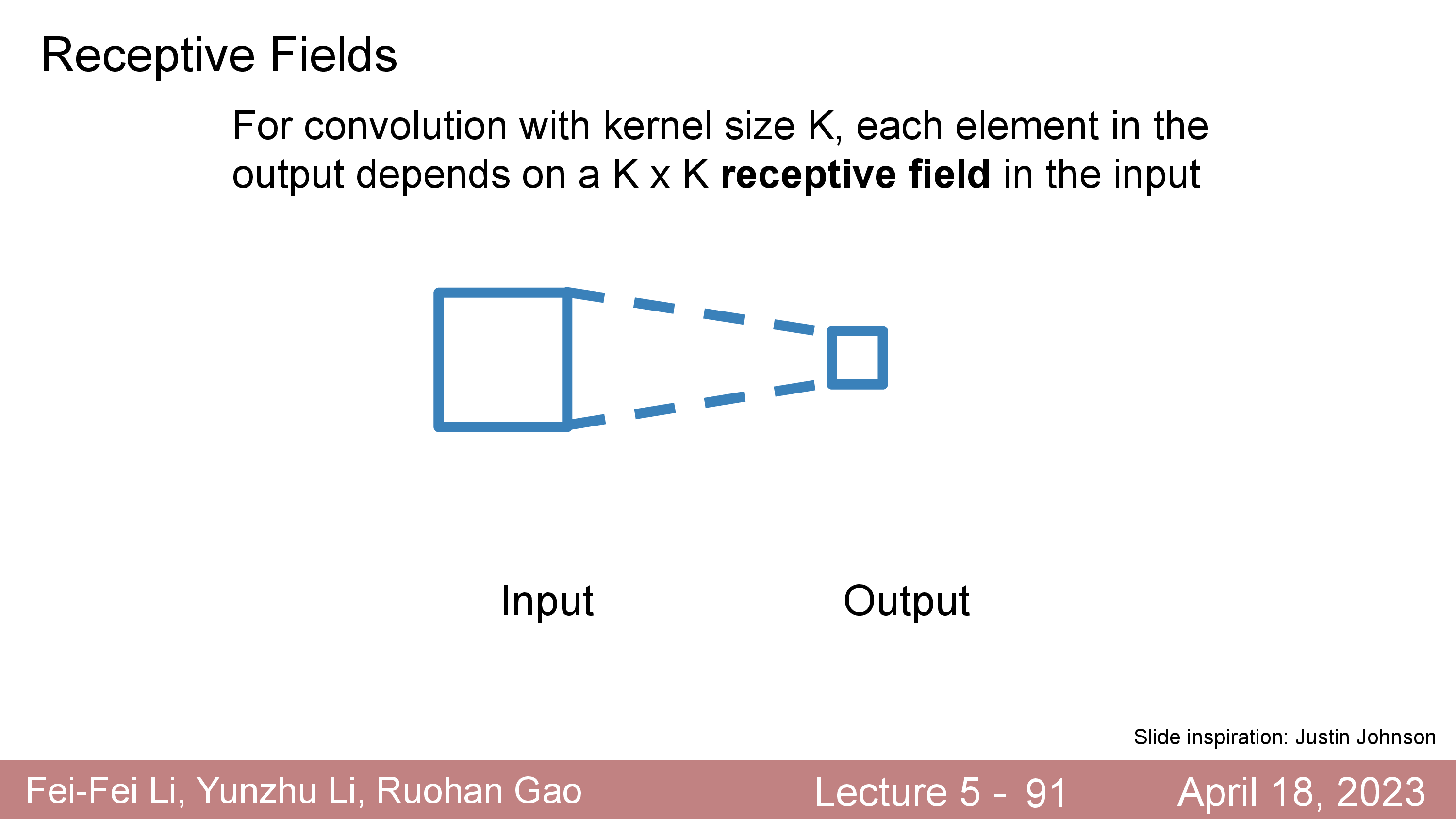
lecture_5_slide_091

L개가 쌓이면 1+L*(K-1) 만큼의 영역을 본 것이 되고 언젠가는 전체 image 를 다 보는 것이 되는 것이다.

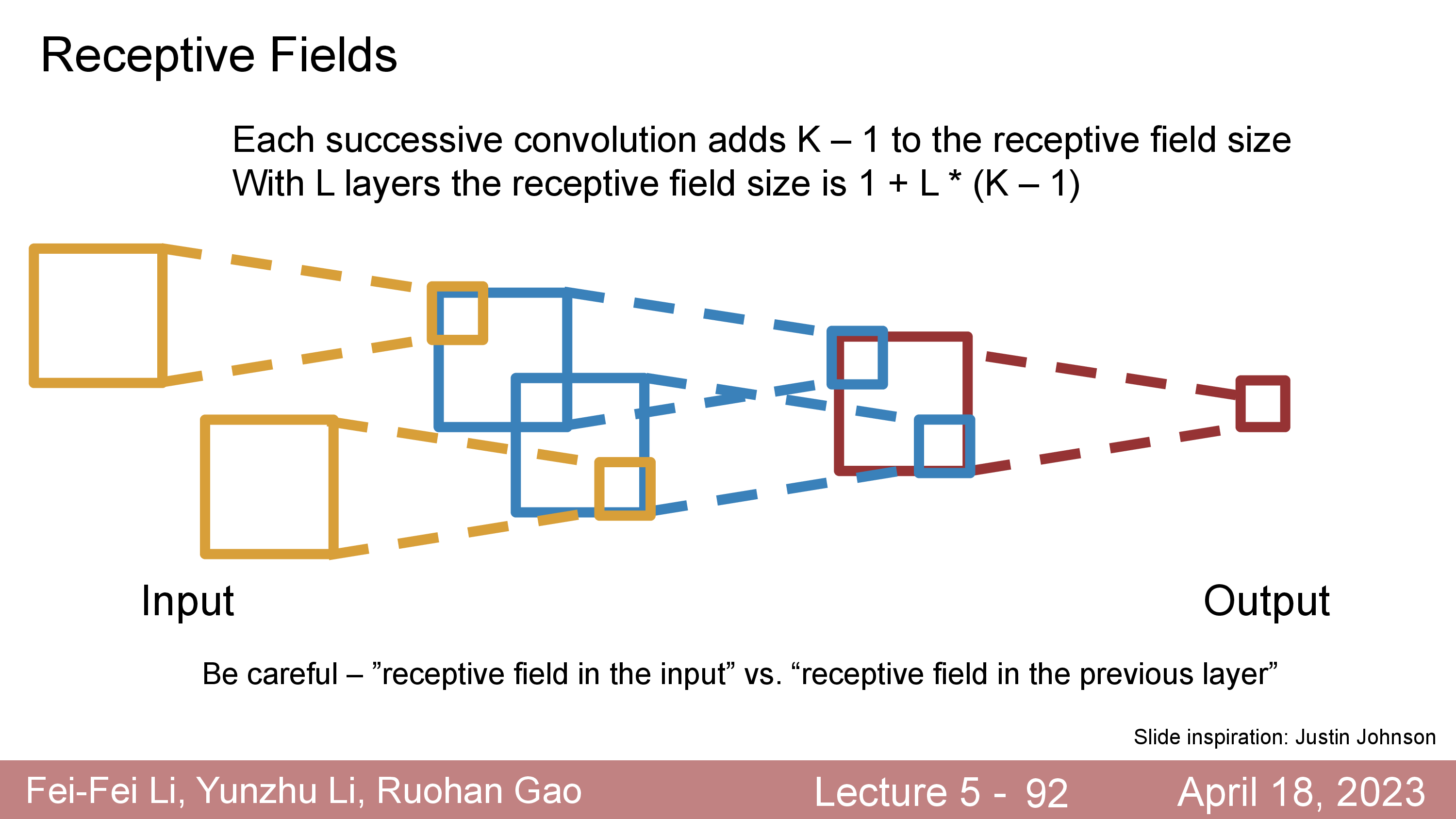
lecture_5_slide_092

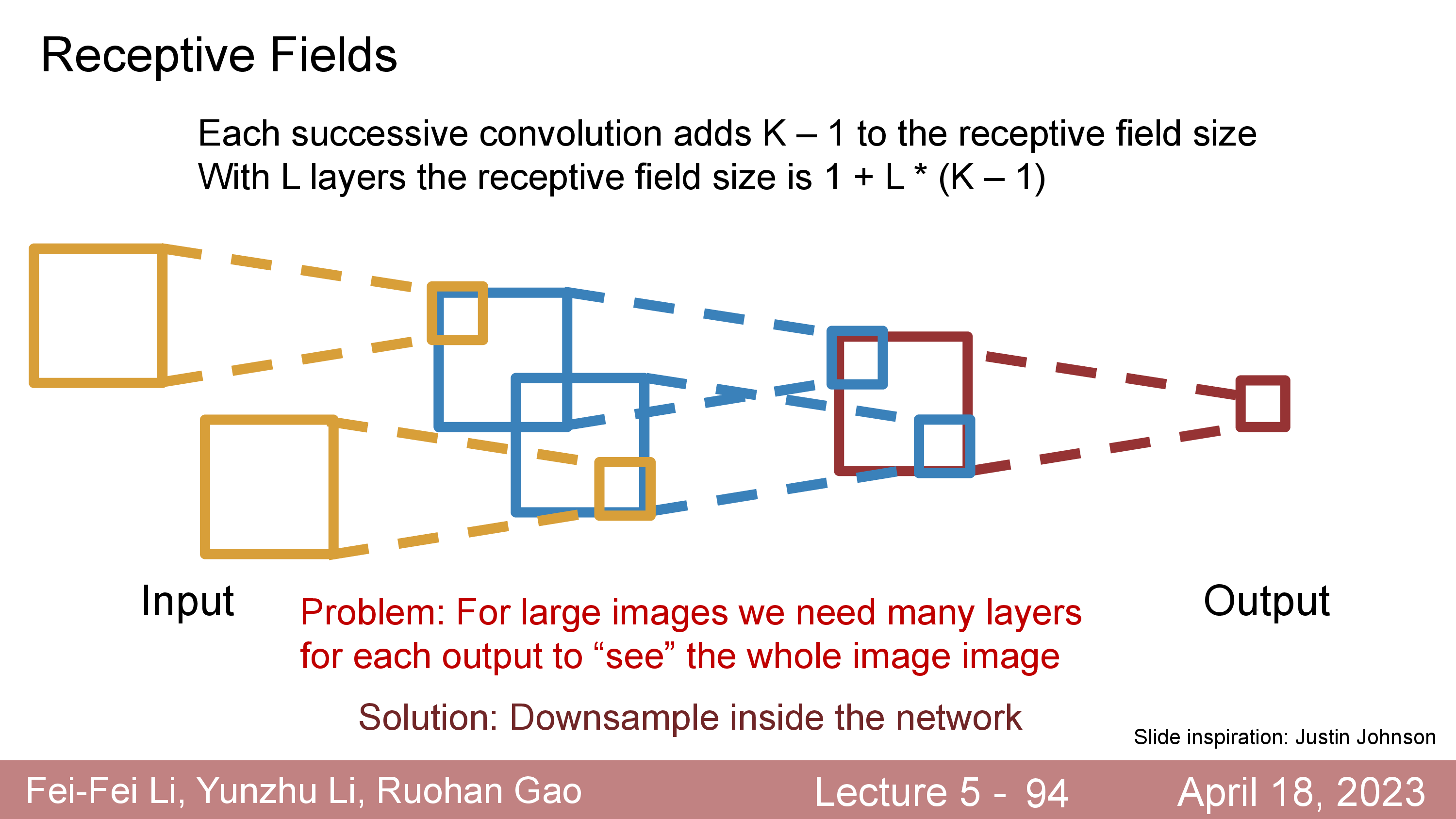
그러면 전체 image region 을 다 cover 했으면 좋겠는데, 그러기위해서는 층을 매우 깊게 쌓아야 할 수 있다. 이를 해결하기 위해서 좀 띄엄 띄엄 연산을 하는 Dilated Convolution 라던가 보폭이 더 큰 (larger stride) layer 를 사용하기도 한다.

lecture_5_slide_094

useful cheatsheet

  • Skip unless you are new to convolutional layers

lecture_5_slide_098

Milestone of CNNs

아래는 cs231n lecture note 에 있는 것으로, 몇 가지 유명한 Convolution Layer 를 이용한 모델들 이다.

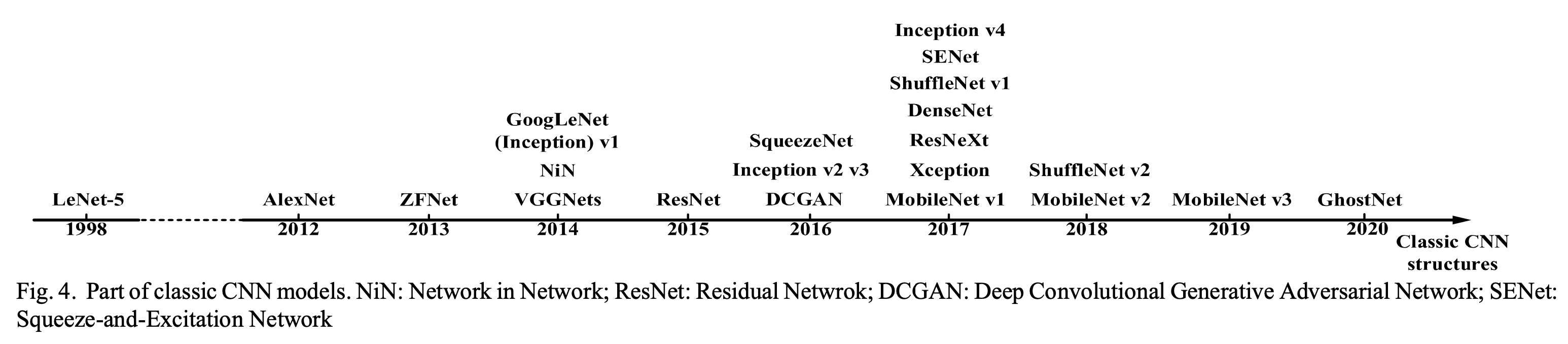survey_paper_milestone Fig. Source from A Survey of Convolutional Neural Networks: Analysis, Applications, and Prospects

  • LeNet: The first successful applications of Convolutional Networks were developed by Yann LeCun in 1990’s. Of these, the best known is the LeNet architecture that was used to read zip codes, digits, etc.

  • AlexNet: The first work that popularized Convolutional Networks in Computer Vision was the AlexNet, developed by Alex Krizhevsky, Ilya Sutskever and Geoff Hinton. The AlexNet was submitted to the ImageNet ILSVRC challenge in 2012 and significantly outperformed the second runner-up (top 5 error of 16% compared to runner-up with 26% error). The Network had a very similar architecture to LeNet, but was deeper, bigger, and featured Convolutional Layers stacked on top of each other (previously it was common to only have a single CONV layer always immediately followed by a POOL layer).

  • ZF Net: The ILSVRC 2013 winner was a Convolutional Network from Matthew Zeiler and Rob Fergus. It became known as the ZFNet (short for Zeiler & Fergus Net). It was an improvement on AlexNet by tweaking the architecture hyperparameters, in particular by expanding the size of the middle convolutional layers and making the stride and filter size on the first layer smaller.

  • GoogLeNet: The ILSVRC 2014 winner was a Convolutional Network from Szegedy et al. from Google. Its main contribution was the development of an Inception Module that dramatically reduced the number of parameters in the network (4M, compared to AlexNet with 60M). Additionally, this paper uses Average Pooling instead of Fully Connected layers at the top of the ConvNet, eliminating a large amount of parameters that do not seem to matter much. There are also several followup versions to the GoogLeNet, most recently Inception-v4.

  • VGGNet: The runner-up in ILSVRC 2014 was the network from Karen Simonyan and Andrew Zisserman that became known as the VGGNet. Its main contribution was in showing that the depth of the network is a critical component for good performance. Their final best network contains 16 CONV/FC layers and, appealingly, features an extremely homogeneous architecture that only performs 3x3 convolutions and 2x2 pooling from the beginning to the end. Their pretrained model is available for plug and play use in Caffe. A downside of the VGGNet is that it is more expensive to evaluate and uses a lot more memory and parameters (140M). Most of these parameters are in the first fully connected layer, and it was since found that these FC layers can be removed with no performance downgrade, significantly reducing the number of necessary parameters.

  • ResNet: Residual Network developed by Kaiming He et al. was the winner of ILSVRC 2015. It features special skip connections and a heavy use of batch normalization. The architecture is also missing fully connected layers at the end of the network. The reader is also referred to Kaiming’s presentation (video, slides), and some recent experiments that reproduce these networks in Torch. ResNets are currently by far state of the art Convolutional Neural Network models and are the default choice for using ConvNets in practice (as of May 10, 2016). In particular, also see more recent developments that tweak the original architecture from Kaiming He et al. Identity Mappings in Deep Residual Networks (published March 2016).

  • MobileNet: MobileNet was published in 2017 to implement CNNs in mobile setting. Depthwise saparable convolution is proposed.

Various Conv Layers

1D Conv (Compared to 2D Conv)

이제 Standard Convolution Layer 의 variant들을 알아보려고 한다. 이런 Convolution Layer 들은 주로 computational cost을 줄인다거나 (parameter 수를 줄인다거나), 저자들이 원하는 식으로 feature 를 뽑기위해 제안되어 왔다.

먼저 간단한 변형체인 1D Conv이다. Image 를 처리하기 위해 제안된 Standard Conv Layer 는 원래 H,W,C 로 이루어진 3D Tensor 를 처리하는데, Filter size 가 대부분 H,W 훨씬 작고 Convolve 를 하는 방식이 한쪽방향에서 다른 쪽으로 쭉 훑은 다음 그 다음 구역으로 (아래로) 가서 이를 전체 tensor 를 다 처리할때까지 반복한다. 즉 Channel, C 를 제외하고 2차원인 전체 image 의 H, W 부근을 커버함으로써 2D Conv 라고 불린다. (실제로는 ‘3차원이니까 3차원 아니야?’ 라고 할수 있지만 일반적으로 Conv Layer 의 Filter 하나는 input tensor 의 channel 전체를 커버하기 때문에 이를 2D Conv 라고 한다)

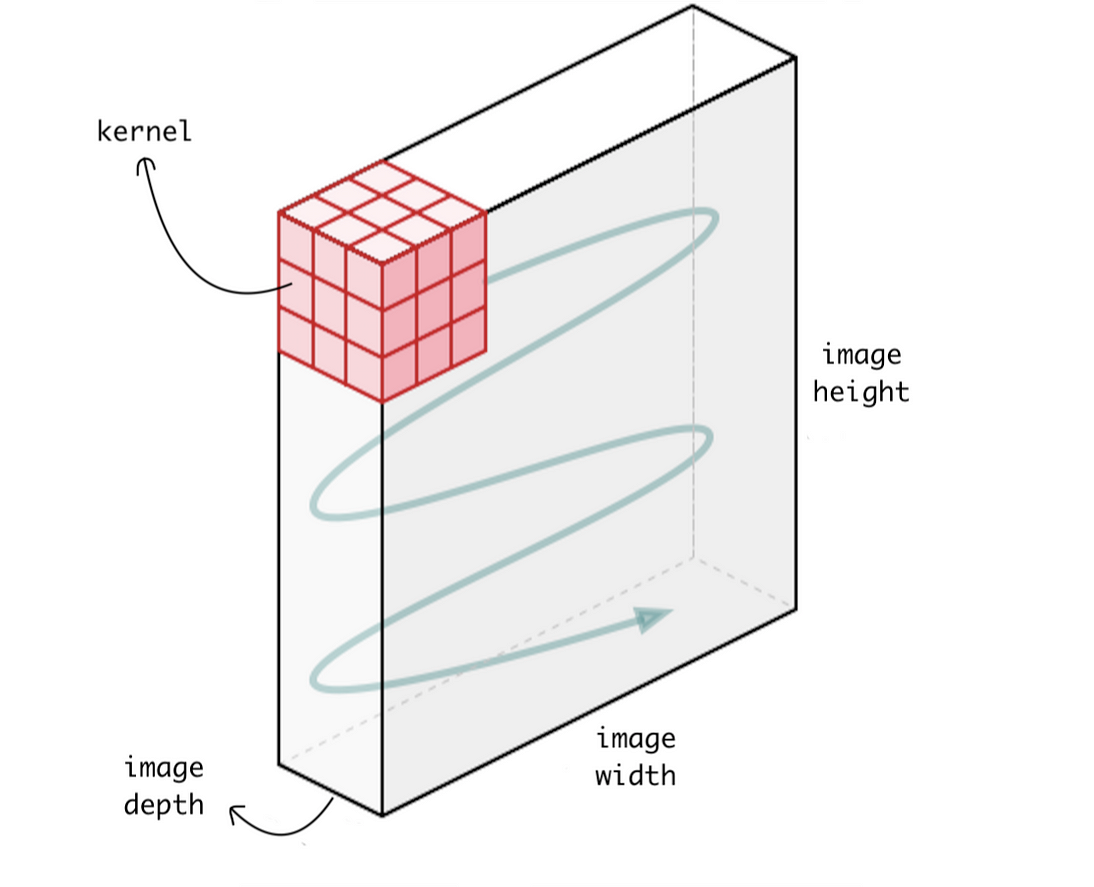2d_conv_example Fig. Standard 2D Conv Layer Example

1D Conv 는 자연어처리 (Natural Language Processing; NLP) 나 음성 분야 (Speech Domain) 같은 data 를 처리하는 Sequence Modeling에 사용된다. 왜 그럴까요? 이미지는 전체 HxW 크기의 2차원에서 Width 와 Height 모두 훑는게 의미가 있지만 Sequence Modeling 을 할 떄는 한 예를 들어 NLP 에서 text 문장, 즉 sequence 자체가 1차원 밖에 되질 않는다.

다시 정리해서 얘기하자면 이해를 돕기위해 image tensor 로 설명했었지만, image tensor 가 batch size B 를 포함해서 BxHxWxC의 4차원 Tensor 를 갖고있고 Filter 가 H,W 로 표현되는 2차원을 Convolve 했다면 sequence modeling 의 경우는 input tensor shape 을 batch size B, temporal resolution (time dim) T, Channel dim C 이렇게 BxTxC 로 표현되고, 이 때 T가 H나 W에 대응되면 나머지 한 차원은 없는 셈이 되는 것 이다. 한 문장이라는 것은 원래 1차원이기 때문이다. 여기서 1차원 Sequence 의 각 text token 들이 embedding layer 를 통과하면 각 token을 나타내는 vector 하나가 C 차원을 갖게되므로 BxTxC 가 되었던 것이다.

Yoon Kim의 Convolutional Neural Networks for Sentence Classification라는 paper를 보면 Conv Layer 로 Sequence Modeling 하는걸 찾아보실 수 있다.

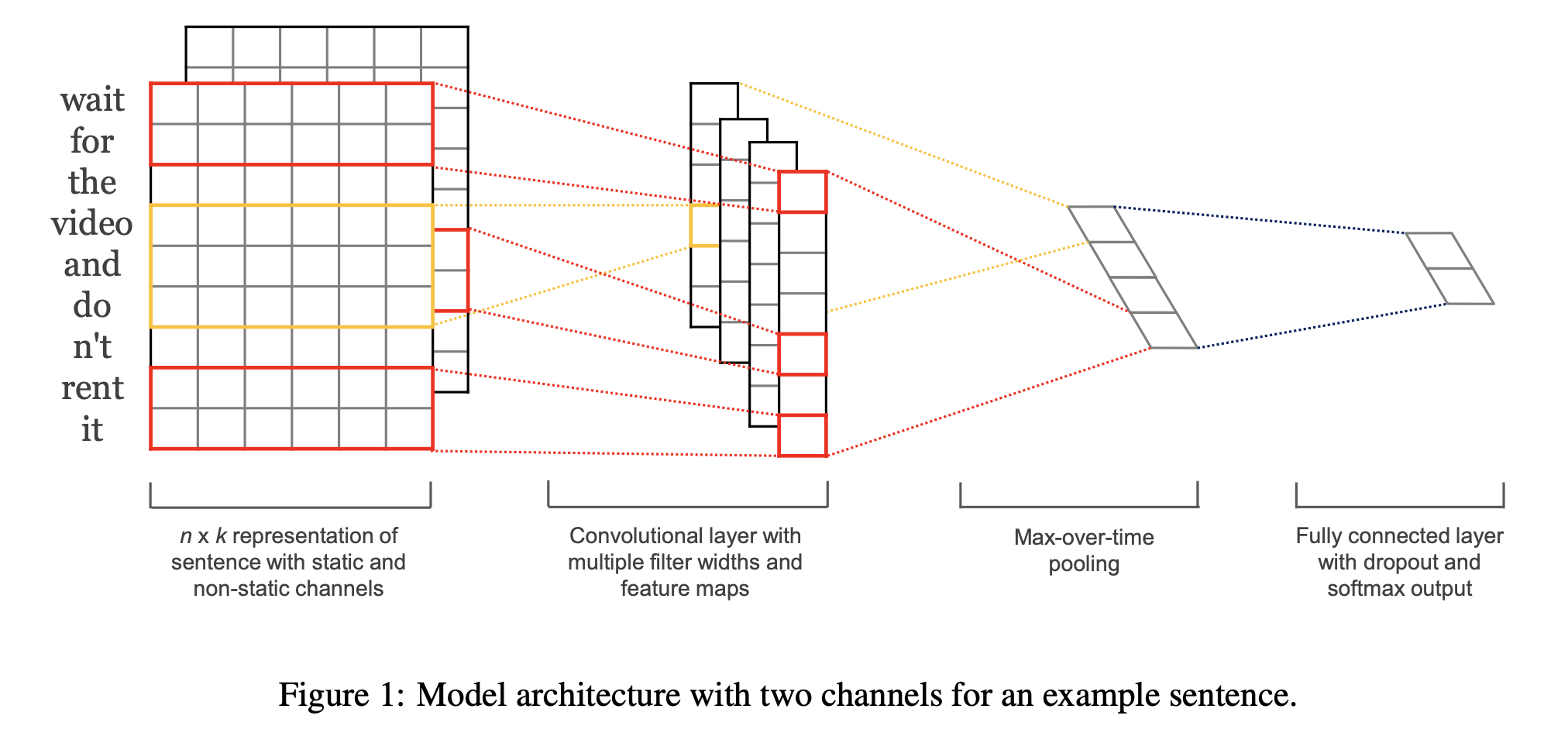
yoon_kim_1d_conv

이런 Sequence 에 그럼 2D 를 적용하는건 아예 불가능한가? 그건 아니다. 다만 어색할 수가 있는 것이라고 할 수 있다. 하지만 speech data의 경우 1d signal, BxTx1 을 모델이 처리하는 경우 1d cnn 을 사용하는, 즉 NLP와 상황이겠으나 1d signal 을 이산 신호 처리 (Digital Signal Processing; DSP) 의 Short Time Fourier Trnasform (STFT) 연산을 통해 BxTx256 같은 2d spectrogram matrix 의 덩어리로 만들 경우, 이를 BxTx256x1처럼 4차원으로 보고 2d conv 로 처리할 때도 있다. 물론 이때도 1차원으로 처리할 수 있다만 이 때 1d, 2d 를 쓰는건 관점의 차이다.

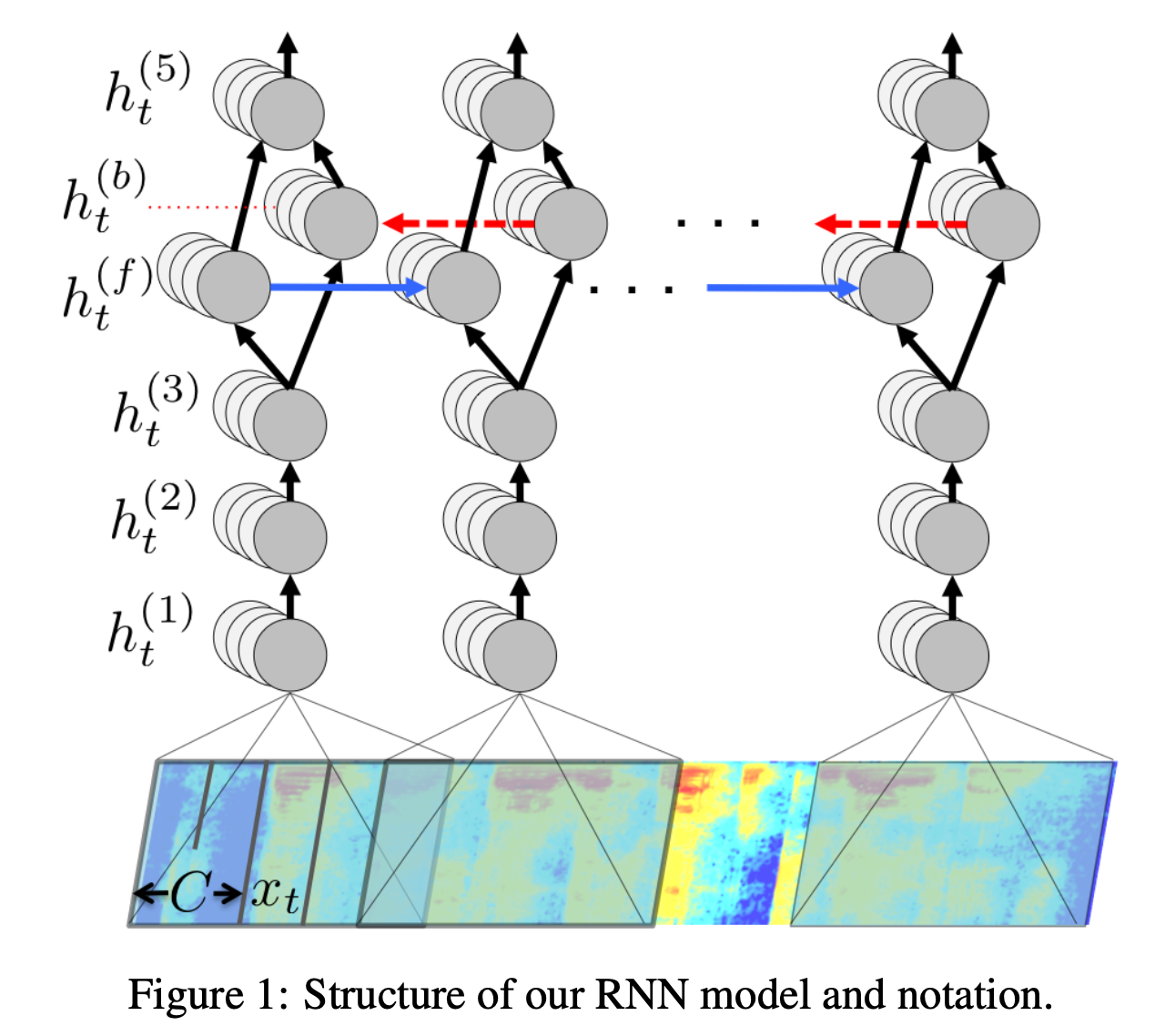
deepspeech

위의 그림에서 맨 아래있는 것이 spectrogram 인데요, 이를 이미지처럼 본다면 H,W 의 이미지 크기에 channel이 1인것으로 생각하고 2D Conv 를 하면 되는것이고, 그게 아니라 세로축이 Channel C 라고 본다면 1D Conv 를 하면 되는것이다. 이렇게 Sequence Modelign 시 사용되는 1d Conv 의 목적은 원래 Conv Layer 의 목적 처럼 Locality 를 capture 하면서 feature 를 뽑기 위한 목적도 있겠고, downsampling, 즉 temporal resolution 을 줄이려는 목적도 있다.

Speech data의 경우 후자의 목적도 꽤 강하다. 왜냐하면 음성 sequence 의 길이가 너무 길기 때문이다. 우리가 3초만 말을해도 컴퓨터입장애서는 sampling rate이 16000이라면 48000 길이의 sequence 가 되기 떄문에 stride 가 큰 Conv Layer 를 사용해서 이를 압축할 필요가 있는 것이다. 게다가 음성 sequence 는 인접한 frame feature 들끼리 correlation 이 굉장히 높아 (redundant)서 거의 필수로 NN 앞쪽에 꼭 Conv를 넣는 편이다.

Pointwise (1x1) Convolution

Pointwise Convlution, 혹은 1x1 Convolution 라고 불리는 Conv Layer 는 말 그대로 image tensor HxWxC 에서 한 pixel 에 대해서만 연산하는 filter 이다. 이런 kernel이 convolving 되기 때문에 image 를 다 커버하려면 HxW 만큼을 다 돌아야한다. 이는 앞서 살펴본 LeNet-5 에서 FC Layer 대신에 사용되기도 했으며 GoogLeNet라는 method에서 다음과 같이 다른 사이즈의 kernel 들과 Inception Module를 구성하기 위해 사용되었다.

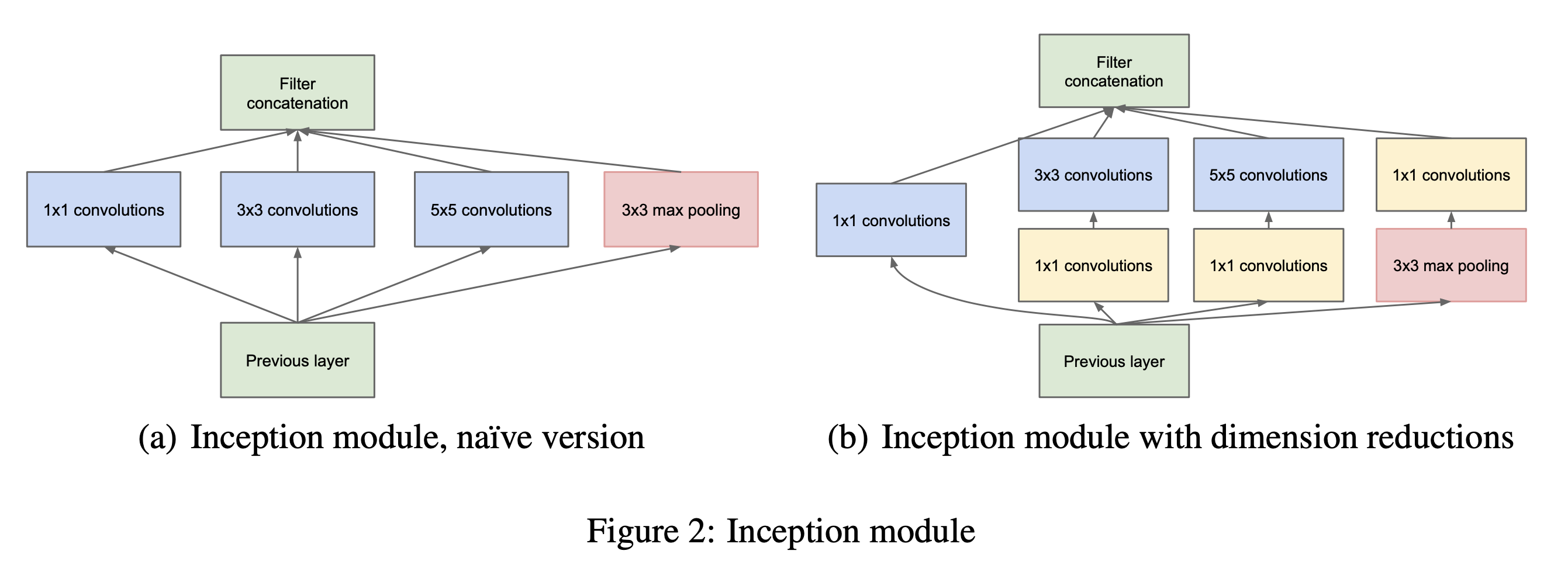
googlenet_paper_fig

이 module은 image 들이 촬영된 카메라와의 거리가 제각각 다르기 때문에 어떤 image는 가까이서 찍으면 object 가 사진의 대부분을 차지하고 그반대면 적은부분을 차지하기 때문에 필요한 kernel 의 사이즈가 다르게 되는 문제를 해결하기 위해 제안되었다고 한다. 서로다른 사이즈의 커널이 (각 1x1, 3x3 5x5) 뽑은 feature 들을 조합해서 쓰는건데, 여기서 오른쪽 (b) 를 보시면 모든 kernel size 별로 앞에 1x1 이 붙은걸 볼 수 있다. 1x1 Conv Layer는 일반적으로 input tensor 의 channel dim 이 클수록 Conv Layer 의 computational cost 가 증가하는걸 줄이기 위해서 channel 을 감소시키기 위해 하는 사용된다.

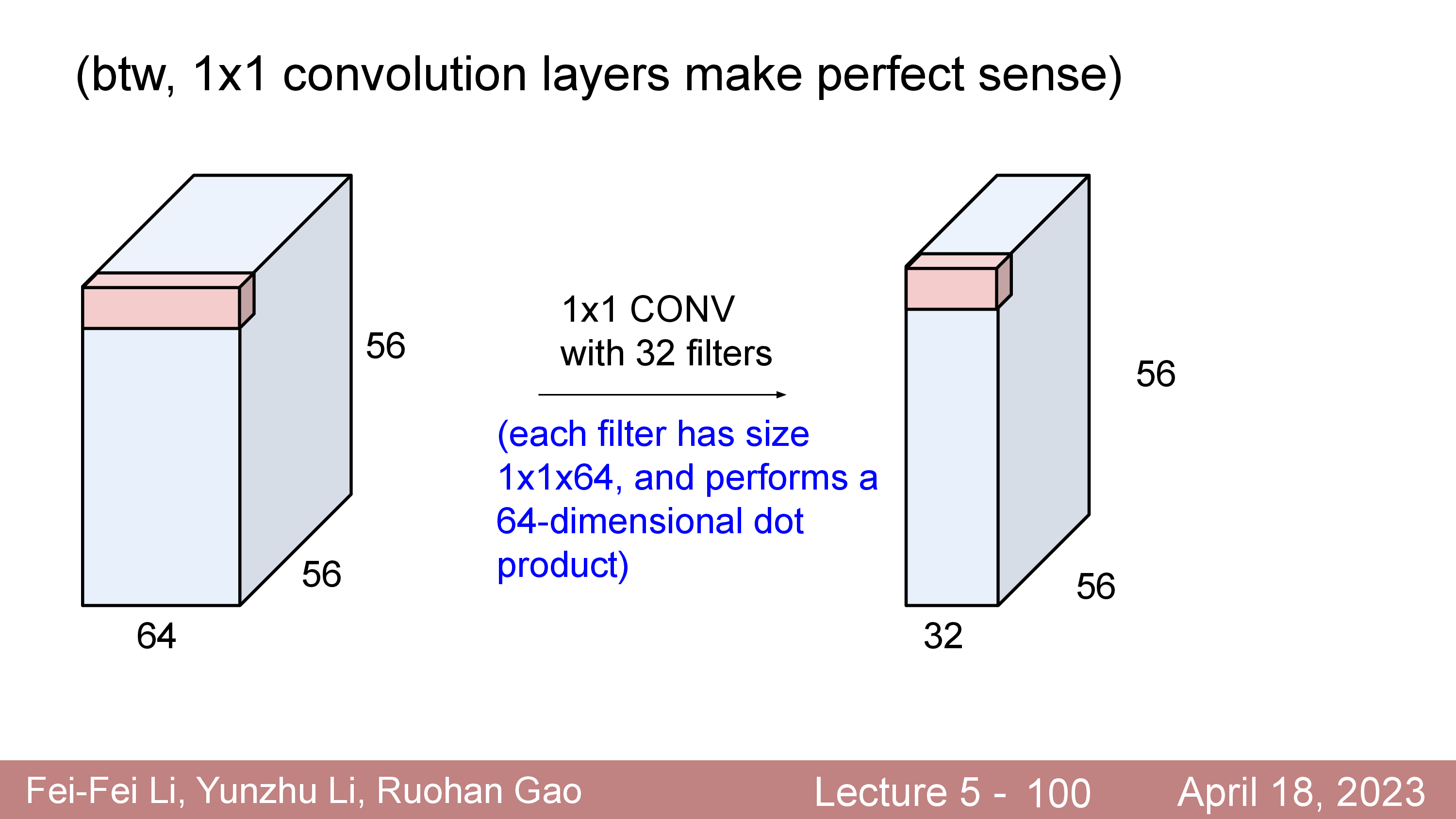
lecture_5_slide_100

그 밖에도 channel dim 을 유지한다고 하더라도 non-linearity 를 추가하기 위해서 같은 1x1 을 사용할 수도 있다.

Depthwise (Separable) Convolution

Depthwise Convolution layer 는 channel 별로만 convolution 을 해서 channel dimension 을 유지하는 layer 를 말한다. 아래의 standard convolution layer와 다르게,

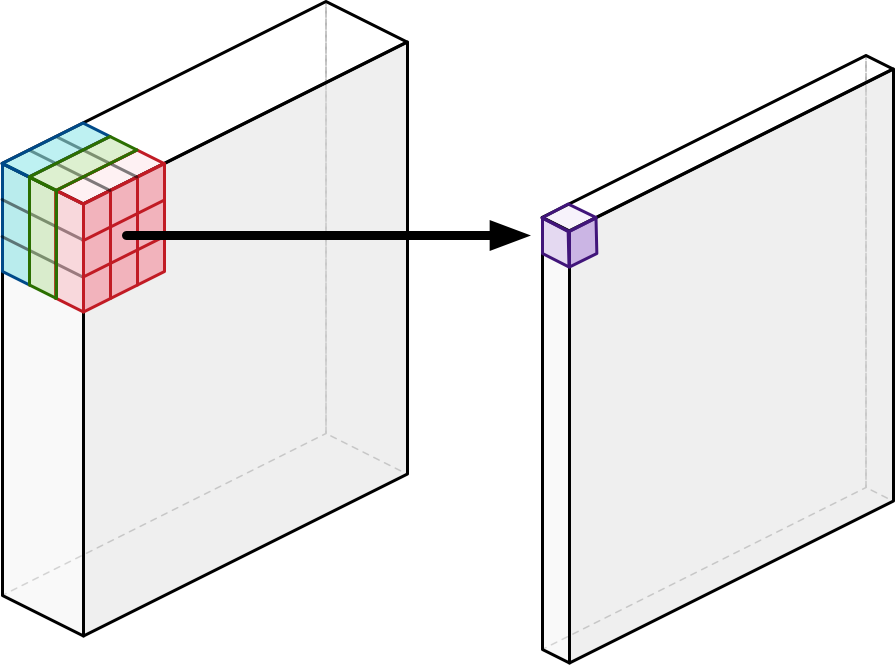matthjis_standard_conv Fig. Standard Convolution. Source from here

depthwise convolution은 원하는 channel 내에서만 convolving을 하기 때문에 channel 별 spatial information을 뽑을 수 있다고 한다.

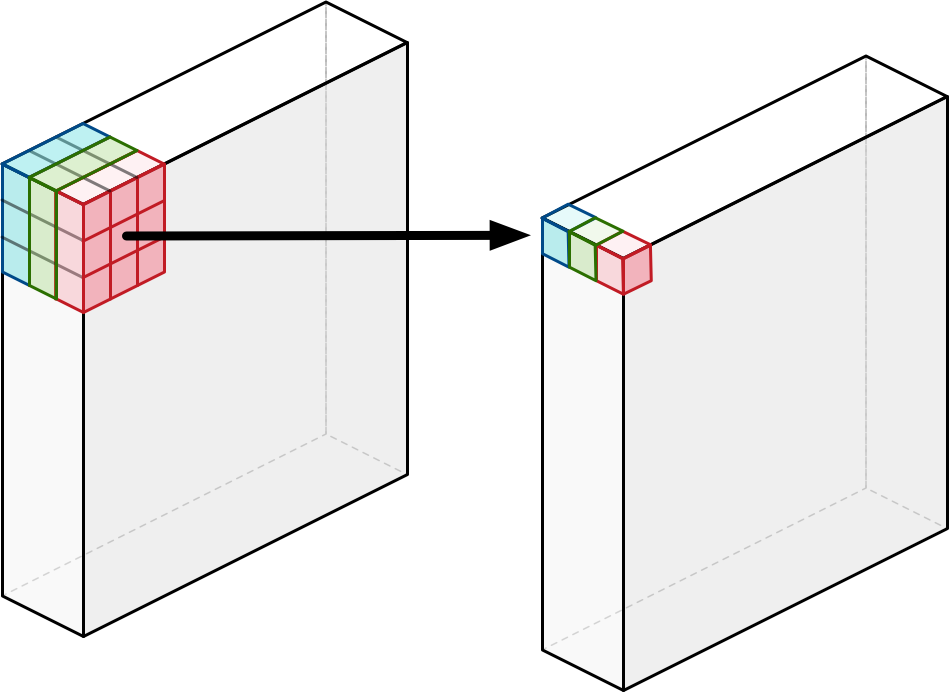matthjis_depthwise Fig. Depthwise Convolution. Source from here

이렇게 channel별로 convolution을 한 output의 channel 수는 input과 동일하게 유지되는데, 여기서 point wise convolution을 한 번 더 하면 비로소 기존의 convolution과 동일한 output을 내놓게 되는데 이를 Depthwise Separable Convolution이라고 한다.

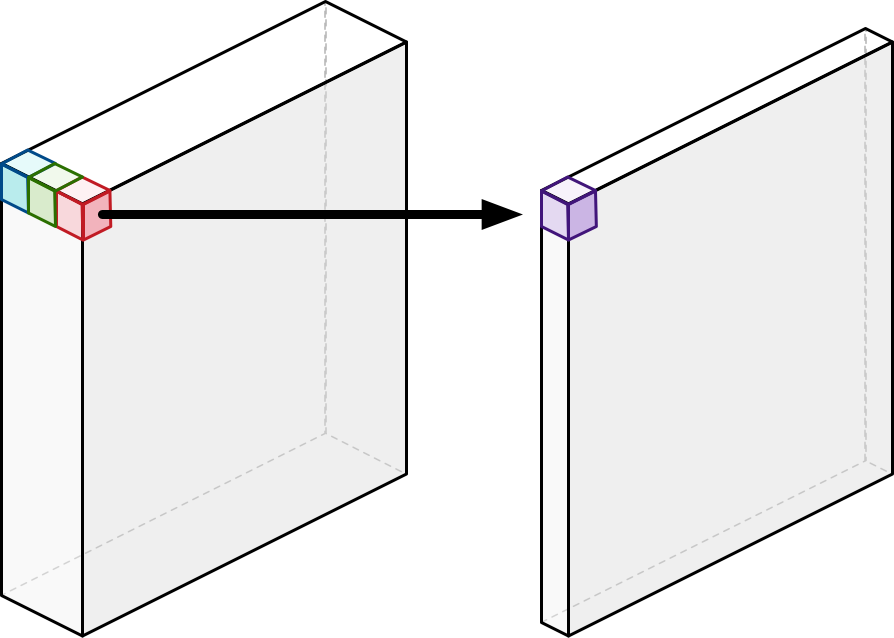matthjis_pointwise Fig. Pointwise Convolution. Source from here

Depthwise seperable convolution은 MobileNet에서 제안되었다고 알려져 있다. Mobile device라는 model 의 크기, 연산량 등이 제한된 환경 (limited budget)에서는 기존의 convolution operation이 비쌌기 때문에 이런 design을 한 것인데 (parameter 개수 == 용량 이기 때문에 이것도 문제),

mobilenet_paper_fig1 Fig. server가 아닌 개인의 mobile device에서 구동된다고 생각해보자.

witdh와 height를 각 \(H,W\) kernel size를 \(K\), input과 output channel dimension을 각각 \(C_1, C_2\)라고 할 때 각 convolution layer들의 parameter 수와 연산량은 (bias를 제외하면) 다음과 같다.

  • Standard
    • Num. param: \(K^2 C_1 C_2\)
    • Computational Cost: \(K^2 C_1 C_2 HW\)
  • Depth-wise
    • Num. param: \(K^2 C_1\)
    • Computational Cost: \(K^2 C_1 HW\)
  • Point-wise
    • Num. param: \(C_1 C_2\)
    • Computational Cost: \(C_1 C_2 HW\)
  • Depth-wise Separable
    • Num. param: \(K^2 C_1 + C_1 C_2\)
    • Computational Cost: \(K^2 C_1 HW + C_1 C_2 HW\)

이는 \(3 \times 3\) conv에 대해서 standard conv 대비 8~9배 줄어든 연산량으로도 비슷한 성능을 내는것을 가능하게 했다고 한다.

mobilenet_paper_fig2 Fig.

MobileNet 이 발전하면서 더 효율적이고 다양한 형태로 진화했다고 하니, 관심있는 분들은 더 찾아보시면 좋을 것 같다.

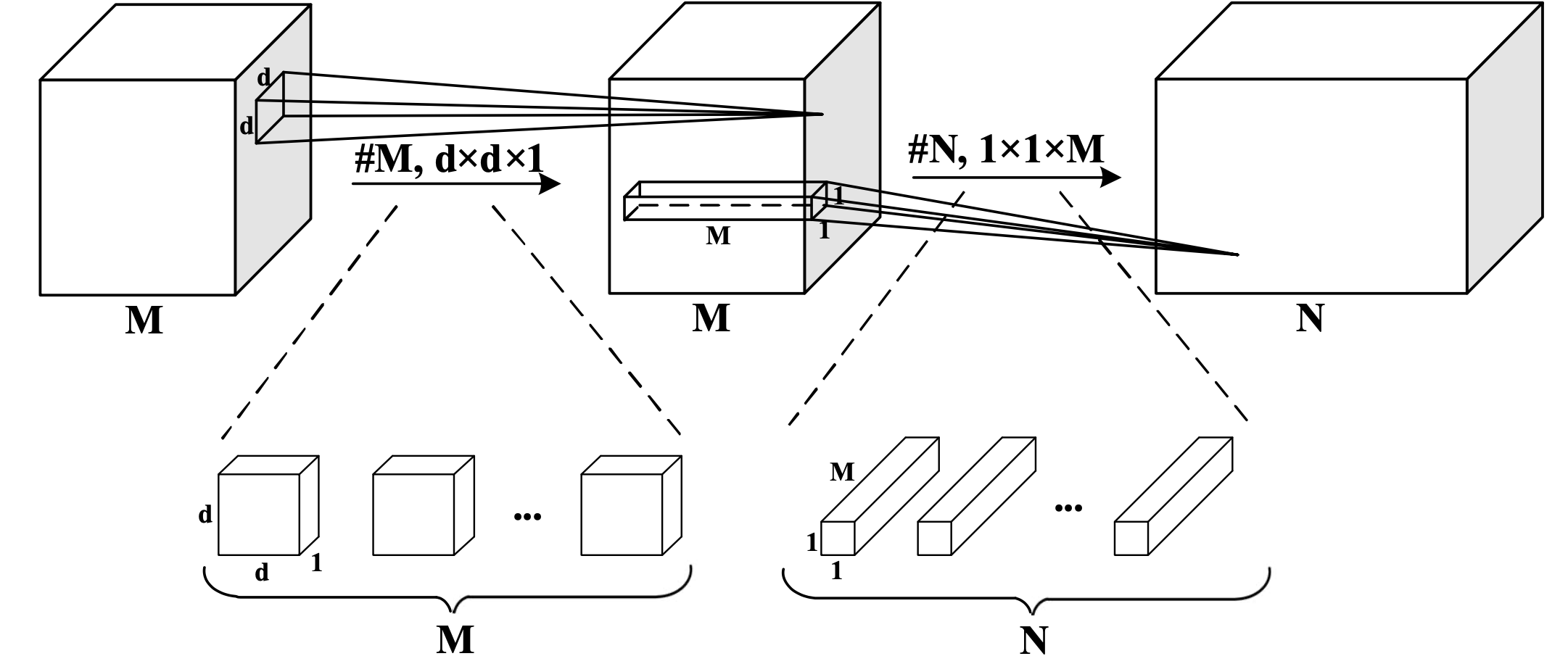survey_paper_mobilenet1 Fig. MobileNet v1. Source from here

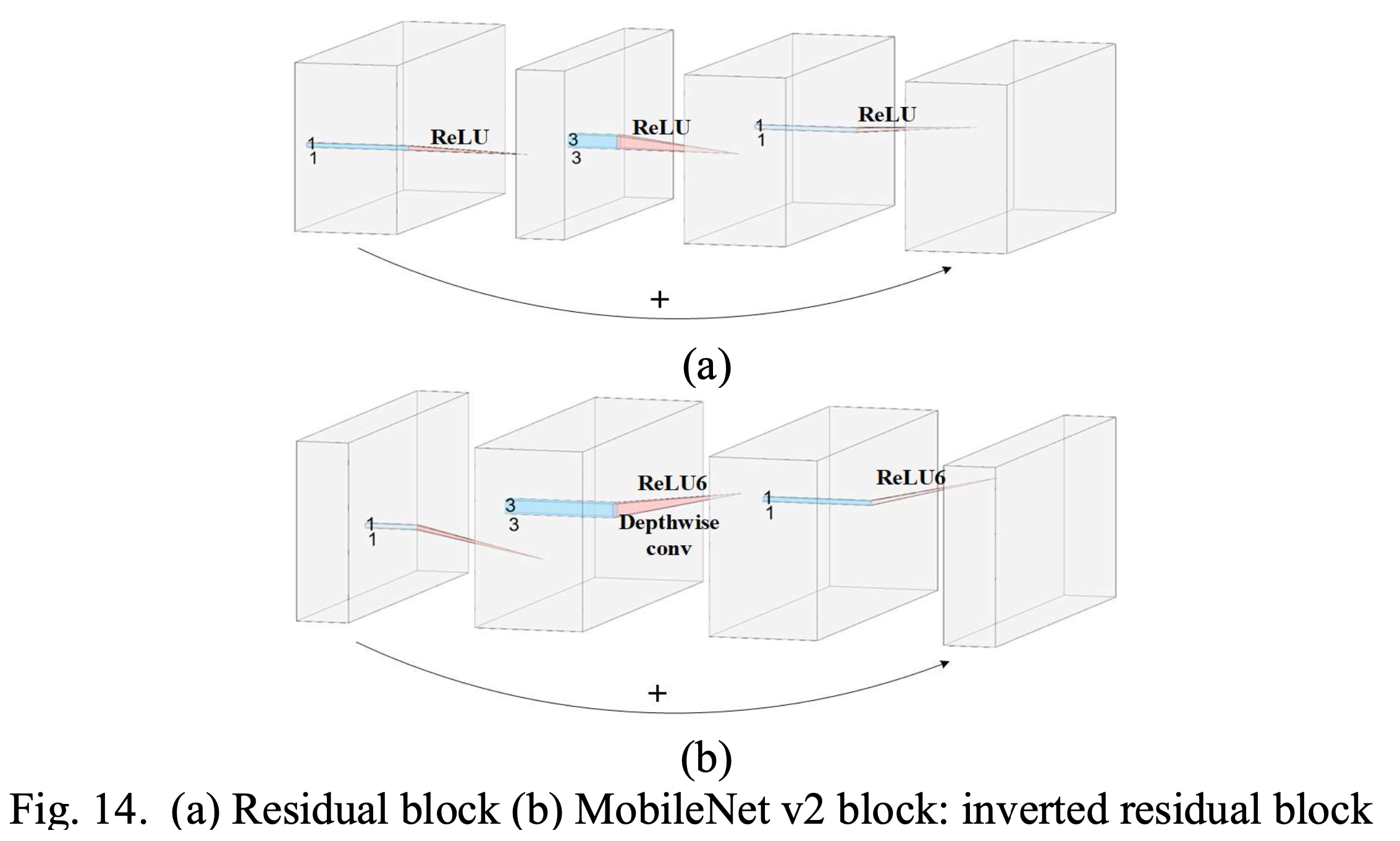survey_paper_mobilenet2 Fig. MobileNet v2. Source from here

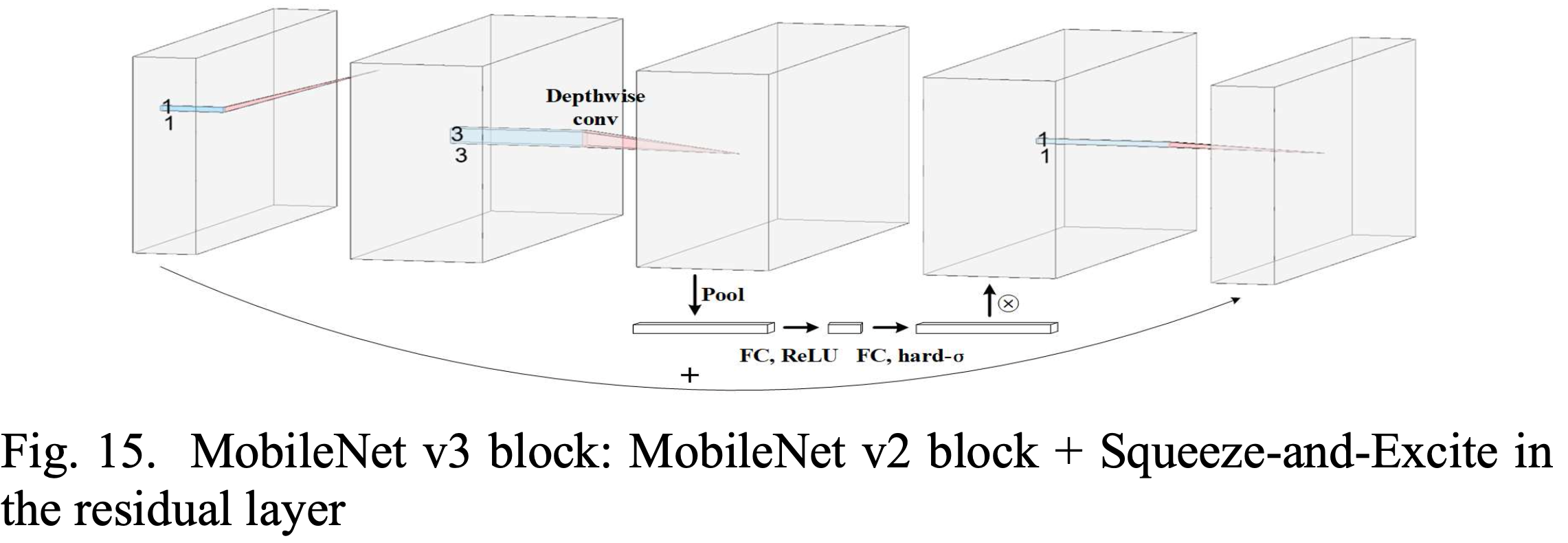survey_paper_mobilenet3 Fig. MobileNet v3. Source from here

Group Convolution

Filter Groups라고도 하는 Group Convolution 은 AlexNet 에서 처음 제안되었다고 알려져 있다. 이 구조의 motivation은 2개 이상의 GPU에서 효율적으로 연산하기 위해서 제안되었다고 한다.

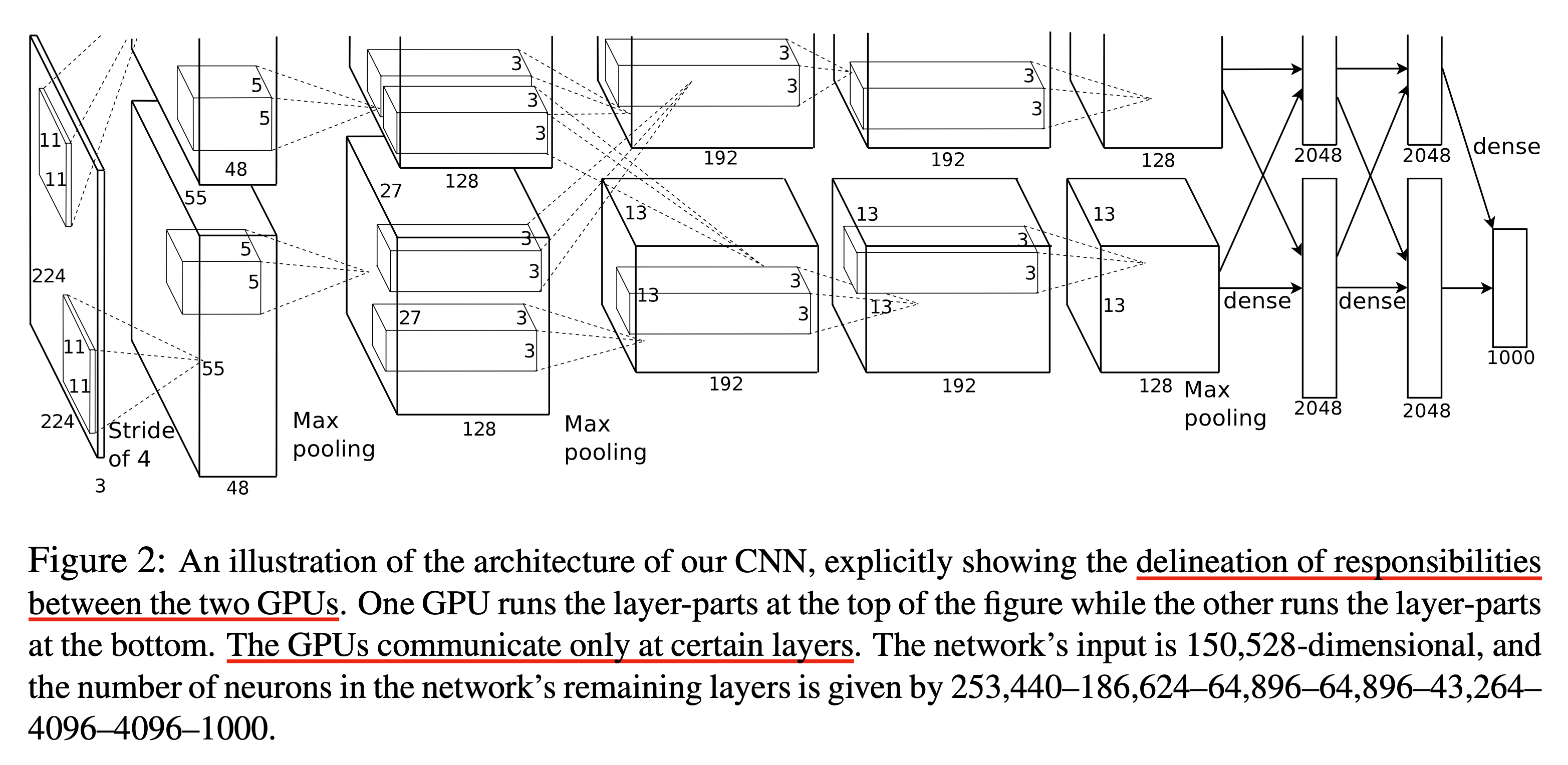alexnet_paper_fig2 Fig.

Group convolution는 아래의 figure와 같이 channel dimension을 나눠서 연산한다. Input tensor가 \(h \times w \times c_1\)의 dimension을 가질 때 2개의 filter group이 있는 경우에 대해 생각해 보자. 그러면 \(h \times w \times \frac{c_2}{2}\)로 mapping을 해주는 convlution filter group이 2개가 생긴다. 그리고 \(h \times w \times c_1\)의 tensor를 우선 이등분해서 각각에 convolution을 해준다. 그리고 이 둘을 이어붙히면 \(h \times w \times c_2\)가 되는 것이다. 이 filter group을 g개로 나누면 (이들은 모두 독립) 각 group에 의한 output tensor는 \(h \times w \times \frac{c_2}{k}\)로 일반화 할 수 있다.

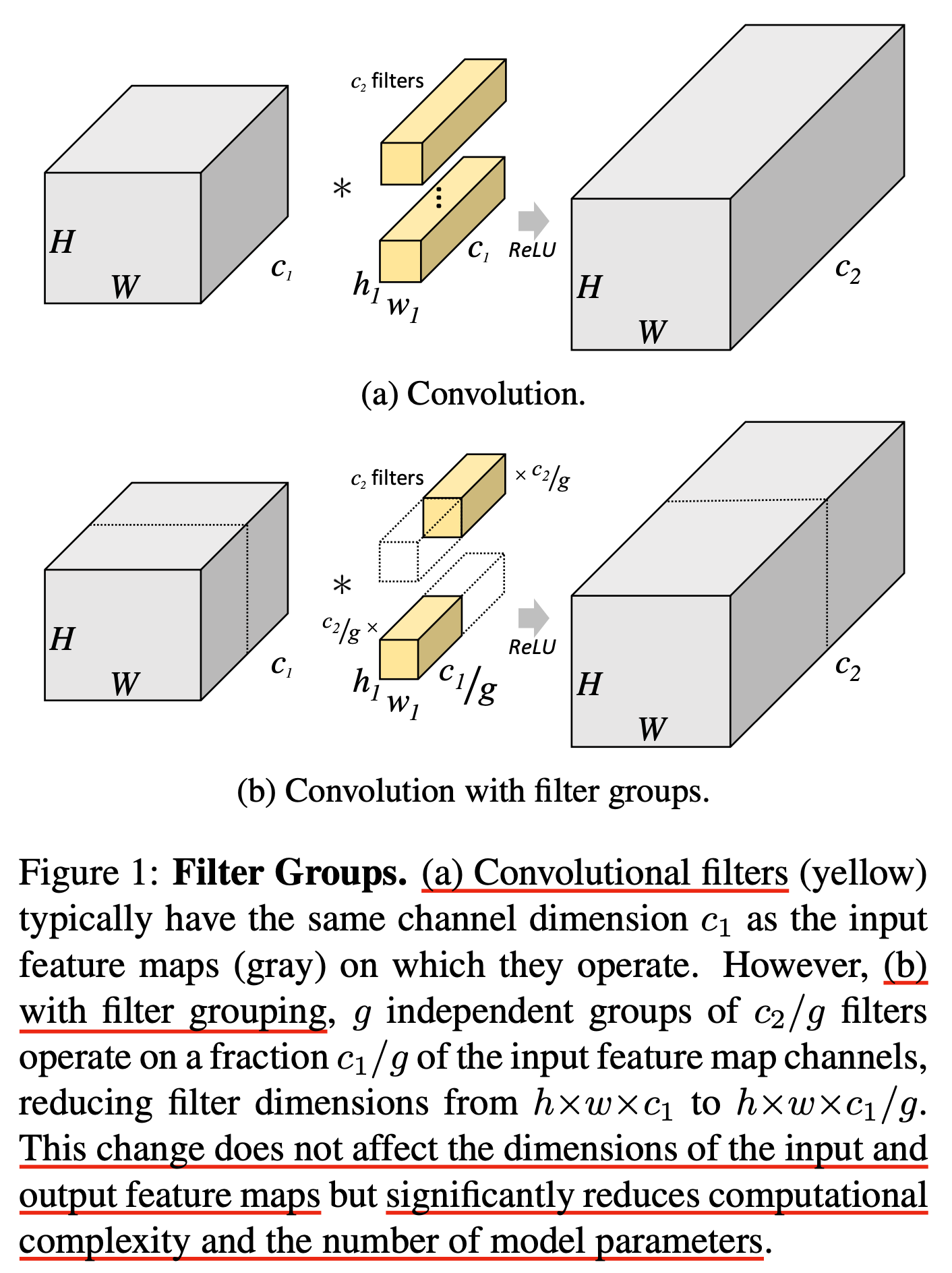deep_roots_paper_fig1 Fig. Source from Deep Roots: Improving CNN Efficiency with Hierarchical Filter Groups

위의 figure를 보시면 기본 convolution과 group convolution의 차이를 볼 수 있다. 이렇게 학습한 AlexNet은 더 적은 parameter를 computational cost를 줄일 수 있었다고 하는데, 예를 들어 위의 예시에서 convolution이 1x1이라고 가정했을 때 1x1 pixel에 대해 원래 convolution은 \(c_1 \times c_2\)의 connection을 갖는데 반해 group convolution은 \(\frac{c_1}{g} \times \frac{c_2}{g}\)을 각 group별로 갖게 된다. 그리고 이를 여러 GPU가 나눠서 연산하게 된다.

deep_roots_paper_fig2 Fig. Source from Deep Roots: Improving CNN Efficiency with Hierarchical Filter Groups

이에 따라서 group convolution은 더 작은 parameter와 computational cost를 갖게 되었는데 (GPU 별로 그렇다는 말 같다, 당시에는 distributed training이 민주화되지 않았기 때문에 더 획기적인 idea 였던 것 같다), 신기하게도 성능은 더 좋았다고 한다.

alexnet_paper_fig3 Fig.

그 이유는 alexnet의 저자들이 밝히길 아래와 같이 각 filter group들이 서로 다른 부분을 봄으로써 (group1은 색에 관계없는 (color-agnostic)을, group2는 색과 관련된 (color-specific)를 보는) 더 좋은 representation을 배우는 side-effect가 생겼기 때문이라고 한다.

deep_roots_paper_fig2 Fig. Source from Deep Roots: Improving CNN Efficiency with Hierarchical Filter Groups

(자세한 내용은 Yani loannou의 blog post를 참고해도 좋을 것 같다)

Dilated Convolution

Dilated Convolution 은 Filter 와 연산이 되는 point 의 수는 같지만 띄엄 띄엄 convolution 연산을 함으로써 cover할 수 있는 receptive field 를 늘린 것이다. 어떤 경우에 이게 필요할까?

survey_paper_dilated_conv_fig Fig.

예를 들어 어떤 녹음된 audio data를 처리한다고 생각해 보자. 보통 audio data는 1초를 16,000개의 값으로 표현한다 (sampling rate가 16,000이라고 함). 이럴 경우 인접한 feature들이 너무 correlation이 높을 것이다. 그리고 neural network model이 사실상 전체 음성을 cover하고 싶다고 치면 이 audio data를 띄엄띄엄 convolution 해야할 것이다. (왜냐면 어차피 인접한 feature를 더 보는게 거의 의미가 없을 수가 있기 때문이다)

Google의 대부분의 audio interface에 들어가있는 WaveNet의 경우 audio generatio을 위해서 input data가 예를들어 10초라면 160,000개에 달하는 vector를 처리해야 하는데, 이를 일반 convolution 을 쓸 경우 전체 data를 cover하기 위해서는 convolution을 사실상 무한히 쌓아야 했기 때문에

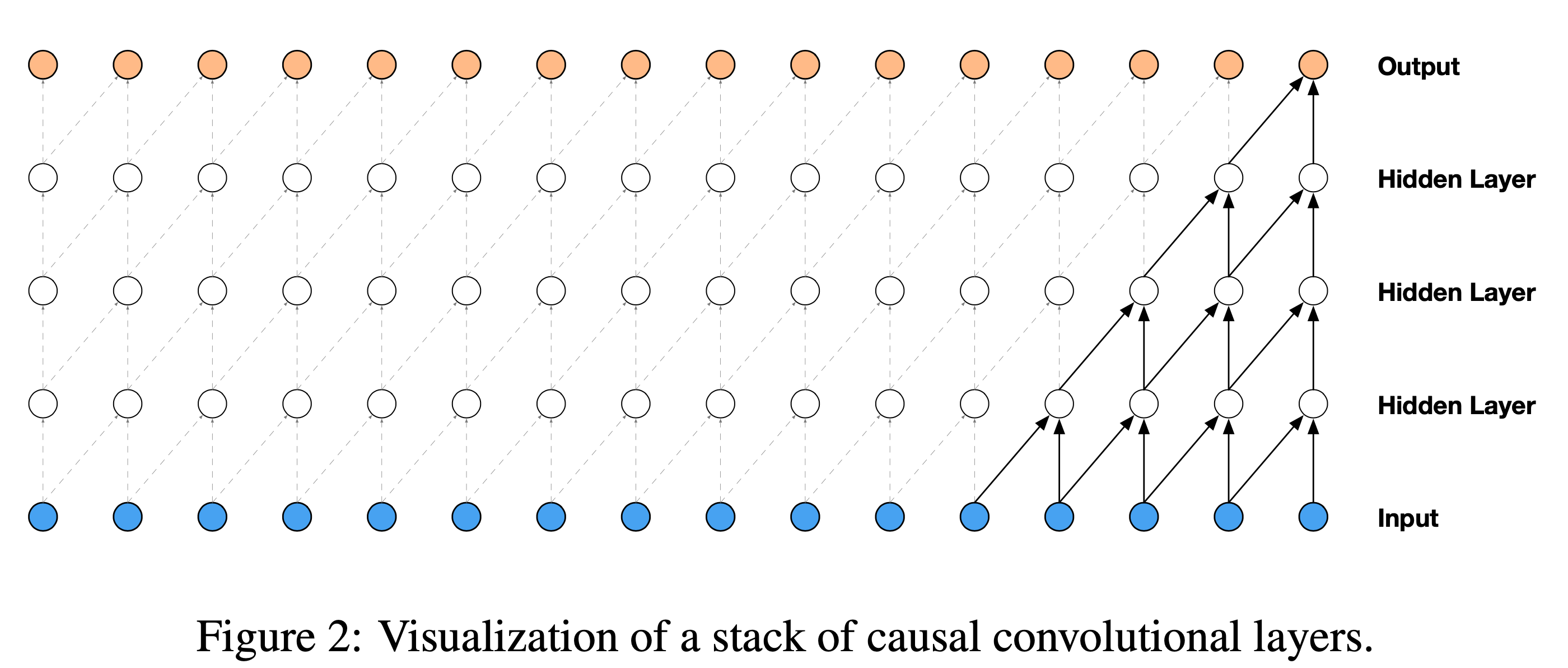
wavenet_paper_fig1

아래와 같은 design을 선택했고, 이것이 바로 dialeted convolution이다 (이 경우 1d dilated conv).

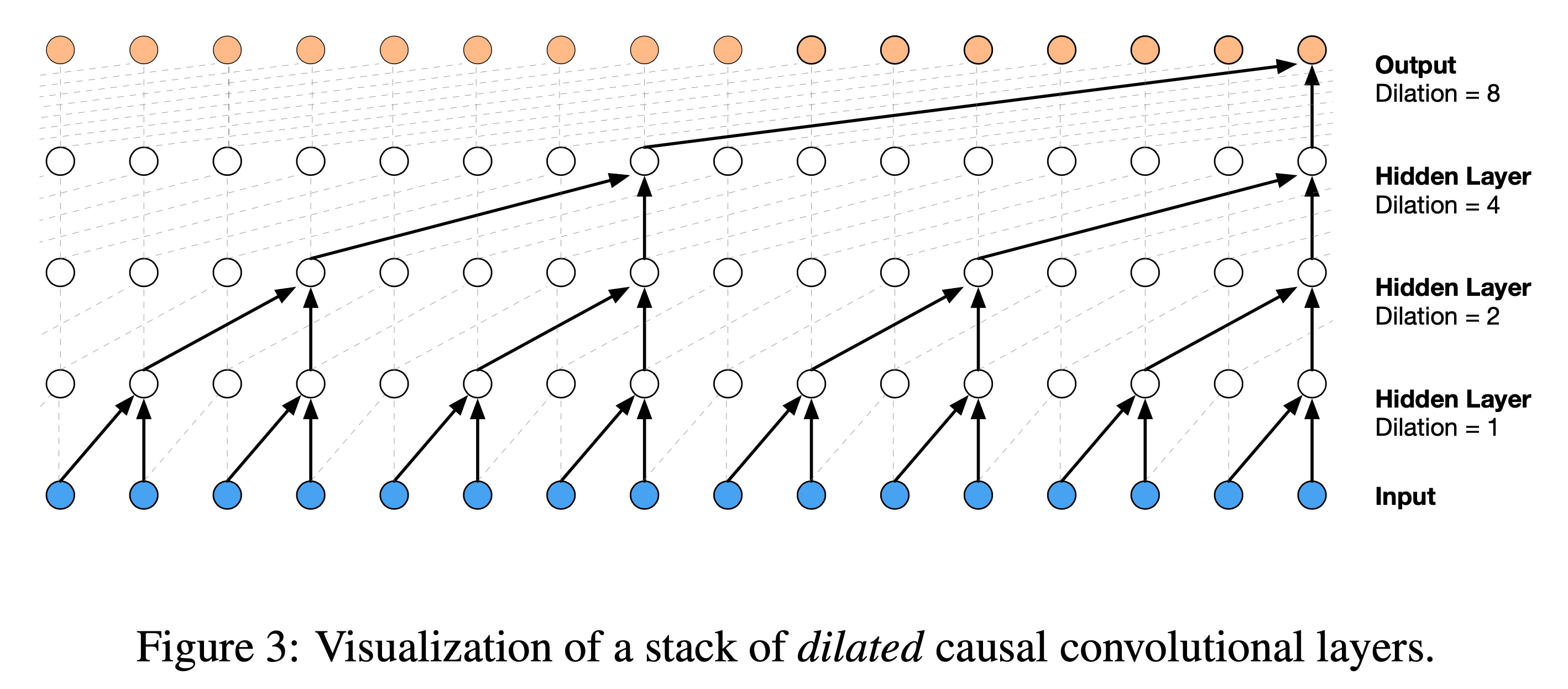
wavenet_paper_fig2

Dilated convolution을 할 경우 위로갈수록 점점 띄엄띄엄 보기 때문에 conv layer를 몇 층 쌓지 않고도 전체를 cover할 수 있었고, 이를 통해서 10초, \([160,000 \times 1]\) 차원 (time * channel)의 vector를 \([250 \times 256]\)으로 줄이는 이른 바 down sampling의 효과를 누려 그 뒤로 이어질 Recurrent Neural Network (RNN)의 computation cost를 확 줄일 수 있었다고 한다.

Conv Layer in Other Domain: Speech

이 밑으로는 다른 Domain, 특히 Speech Domain 에서 어떻게 Conv Layer 가 쓰이는지? 에 대해 추가적으로 다뤄보려고 한다. Transformer 에 대해 익숙하지 않은 분들은 이해하는 데 어려움이 있을 수 있고 관심 없으신 분들은 skip 하면 된다.

1D Conv as Fourier Transformer

위에서 1D Conv 를 소개해드리면서 Sequence Modeling 을 할 때 주로 1차원 Temporal resolution 을 줄이기 위한 (downsampling) 목적 등으로 1D Conv 를 쓴다고 얘기했는데요, 음성에서는 이게 좀 더 특별한 의미를 가질 수 있어서 이를 보충하려고 한다. 앞서 음성이 1차원 signal 이라고 얘기 했었다.

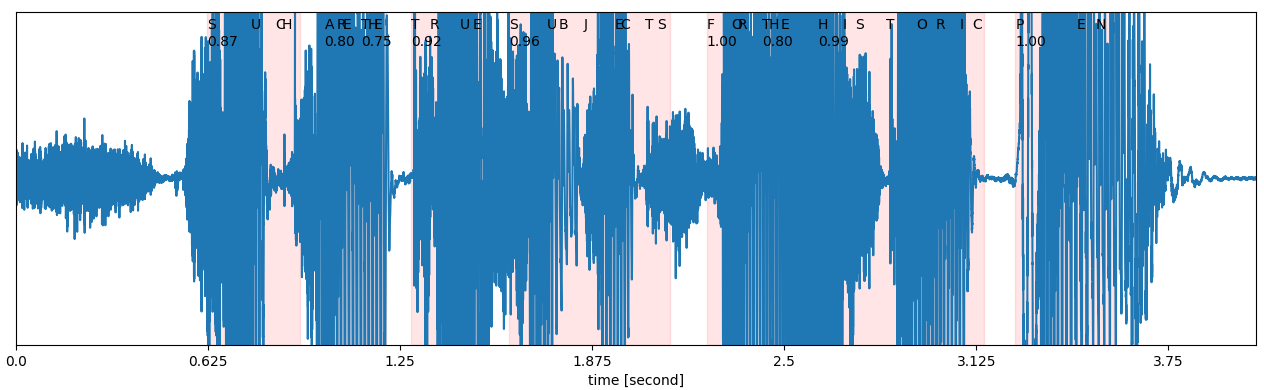1d_speech_signal Fig. Speech Signal 예시

이런 음성의 input shape 은 말그대로 Tx1 짜리 vector이다. 이 때 T 는 시간으로 발화된 음성의 길이이다. 우리는 이를 예를 들어 3초로 표현하지만, 컴퓨터 입장에서는 이를 이산적인 신호로 처리한다. 이 때 1초를 몇개로 표현할거냐? 를 sampling rate 으로 나타내는데, 굉장히 고품질이면 44,100 Hz (44.1k), 일반적으로는 16,000 Hz (16k), 통화할때의 품질이면 8,000 Hz (8k) 를 사용하곤 한다. 그니까 우리가 3초짜리 음성을 녹음했으면 뉴럴 네트워크 입장에서는 16k sampling rate 을 쓴다고 했을 때 48000x1 짜리 vector 를 입력으로 받아야 하는 상황이 되는 것이다. 그리고 이 vector 에는 정보가 많이 없다. 가령 우리가 발화를 할 때는 발화자의 음역대가 높은지? 낮은지? (주파수 대역), 크기 (pitch) 는 큰지? 등등의 정보가 있는데 일반적인 time domain 에서는 이것이 나타나지 않는 것이다.

그래서 이런 경우에는 DSP 분야에서는 Fourier Transform (FT) 을 사용해서 정보를 더 뽑아내곤 한다. Deep Learning 기반의 model들도 1d signal을 변환한 feature를 입력으로 쓰곤 한다 (그래서 어떤 관점에서는 고전 end-to-end ASR model들은 진정한 end-to-end라고 보기는 어렵다). FT 를 한다는 것은 간단히 말해서 어떤 정해져있는 coefficient set, 예를 들어 각 주파수 대역에 대응되는 filter 들이 있고 이를 원래 signal 과 연산해서 해당 정보들을 뽑아내는 것을 의미하게 되는데,

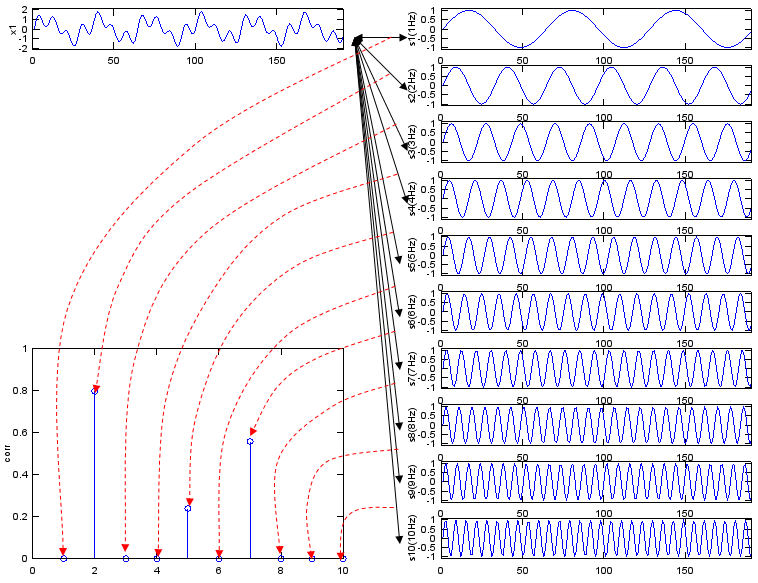fourier1 Fig. An Example of Fourier Transform. Source From link

이러면 또 중요한 시간축 정보가 전부 날아가기 때문에 이 FT 연산을 windowing 해서 일정 segment 에 대해서만 수행하고 이를 sliding 하면서 반복한다. 이렇게 하면 Window 내에 있는 한 segment 는 1개의 vector 를 뱉게 되고, 이 vector 에는 주파수 영역의 풍부한 정보가 담겨있게 된다. 이를 일정부분 겹치게 하면서 speech 의 끝까지 sliding 하면서 연산하면 꽤 temporal dimension이 줄어들 것이다.

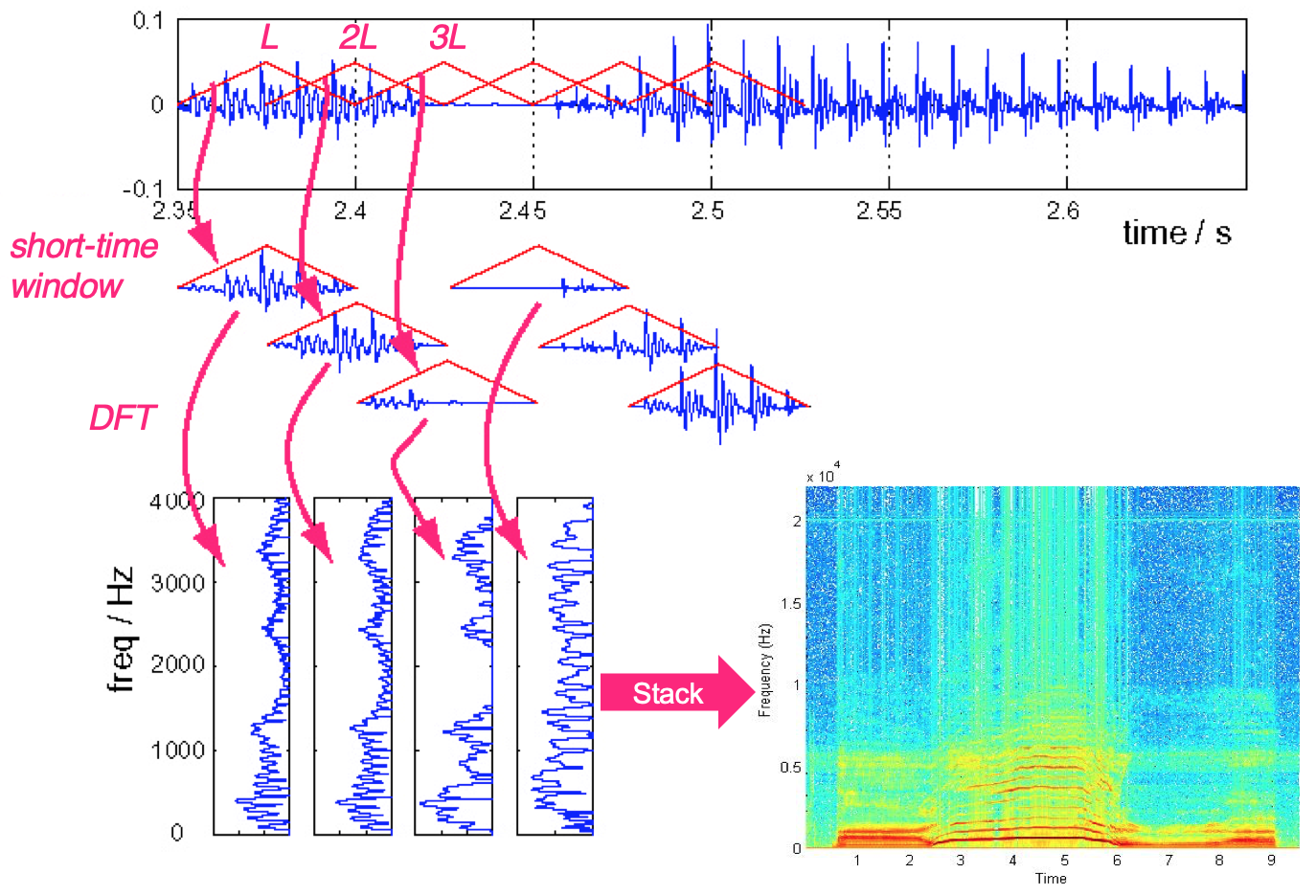stft_example2 Fig. Source from link

그러면 자연스럽게 한 시그널 당 2차원의 feature 가 생기는데 이를 Spectrogram이라고 부른다. 그런데 여기서 STFT 를 수행하는 것이 사실상 FT 를 위한 coefficient 를 1D Conv Layer 의 Filter 라고 생각하면 둘은 서로 같은 일을 하는거나 다름이 없다는걸 다들 느꼈을 것이다. 나아가 CNN Filter 를 FT Coefficient 로 초기화하고 서서히 학습해가면 사람이 디자인 한 것 보다 더 좋은 Filter 를 얻을 가능성도 있는 것이다.

nnAudio (Audio processing by using pytorch 1D convolution network) 같은 Repo 를 보시면 Audio Processing 을 1D Conv Layer 들로 구현한 구현체들을 살펴보실 수 있다. 그리고 Wav2vec 2.0이라는 speech domain의 유명한 architecture를 보면 1D Speech Signal 을 받아 1D Conv 7개를 사용해 Batch, Time, Channel, BxTxC 의 Spectrogram 스러운 Feature 를 뽑아내고 Transformer 에 이를 통과시키는 것을 볼 수 있다.

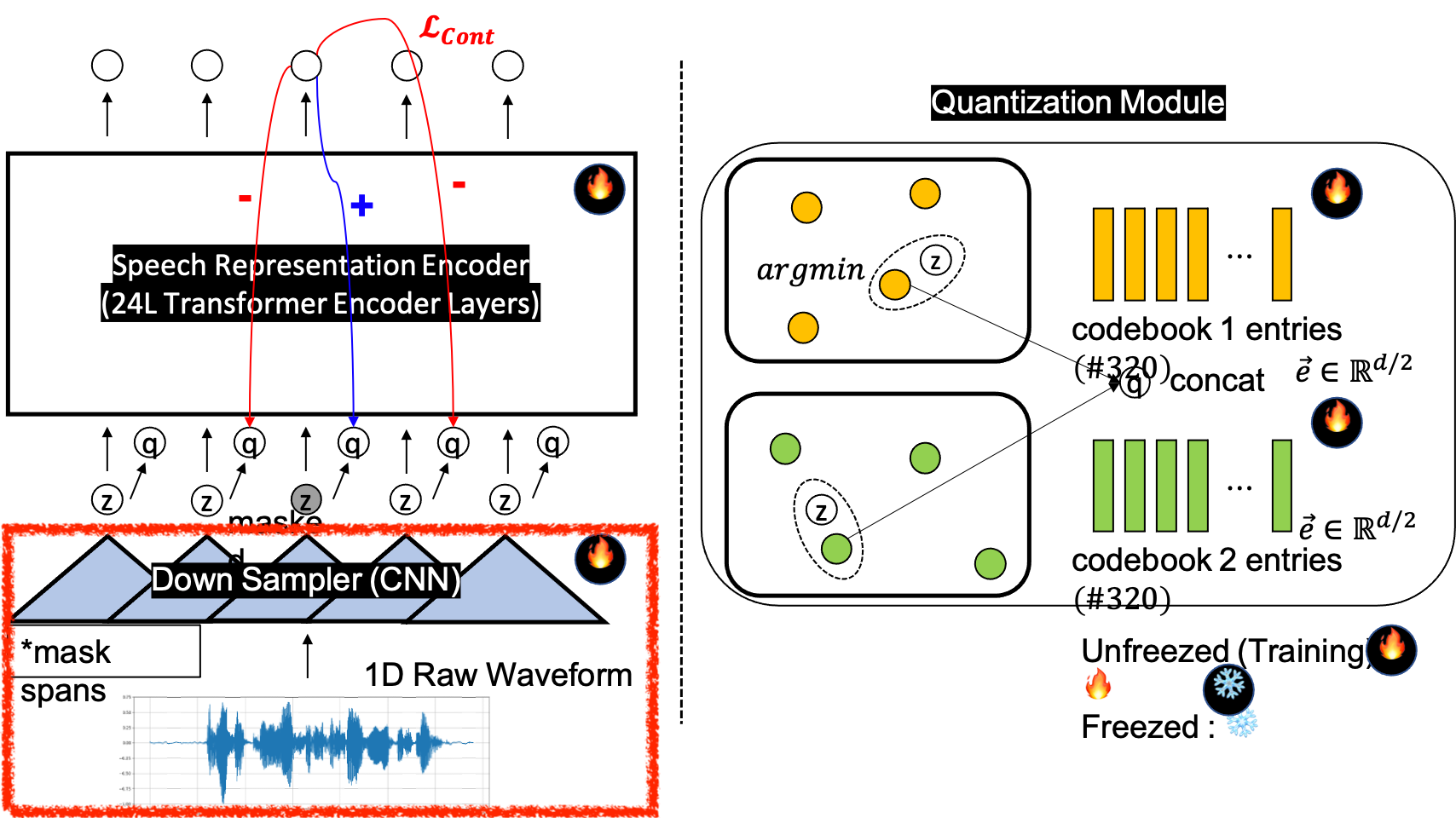
w2v2_arch

Paper에서는 7층 짜리의 다양한 kernel size, stride 를 갖는 1D Conv Layer 를 사용했는데 자세한 사항은 다음과 같다.

The feature encoder contains seven blocks and the temporal convolutions in each block 
have 512 channels with strides (5,2,2,2,2,2,2) and kernel widths (10,3,3,3,3,2,2). 

This results in an encoder output frequency of 49 hz with a stride of about 20ms between each sample, 
and a receptive field of 400 input samples or 25ms of audio. 

The convolutional layer modeling relative positional embeddings has kernel size 128 and 16 groups.

이렇듯 1d Conv Module은 음성 신호처리의 대체제로 사용되곤 한다. 그리고 이런 approach는 사람이 design한 fourier transform 에 쓰이는 cosine, sine filter 보다 더 강력한 kernel을 학습할 수 있다는 기대가 있다.

Convolution Module of Conformer Block

Transformer architecture 가 제안된 NLP 분야를 제외하고 CV 분야에서는 Vision Transformer, 그리고 speech domain 에서는 Conformer 라는 architecture가 현재 사실상의 기본 model (de facto)로 쓰이고 있다. 이들은 각각 Vanilla transformer 에 해당 분야의 inductive bias 가 들어가서 좀 변형된 형태를 가지고 있는데, Conformer 는 논문 제목에서도 알 수 있듯 Convolution-augmented Transformer for Speech Recognition 으로 Convolution Module 이 Multi Head Self Attention (MHSA) 바로 뒤에 stack 되어 speech sequence 에서 중요한 locality 를 잡아내는데 큰 도움이 되어 음성 인식을 포함한 수많은 음성 분야의 task 에서 State Of The Arts (SOTA) 성능을 내게 되었다.

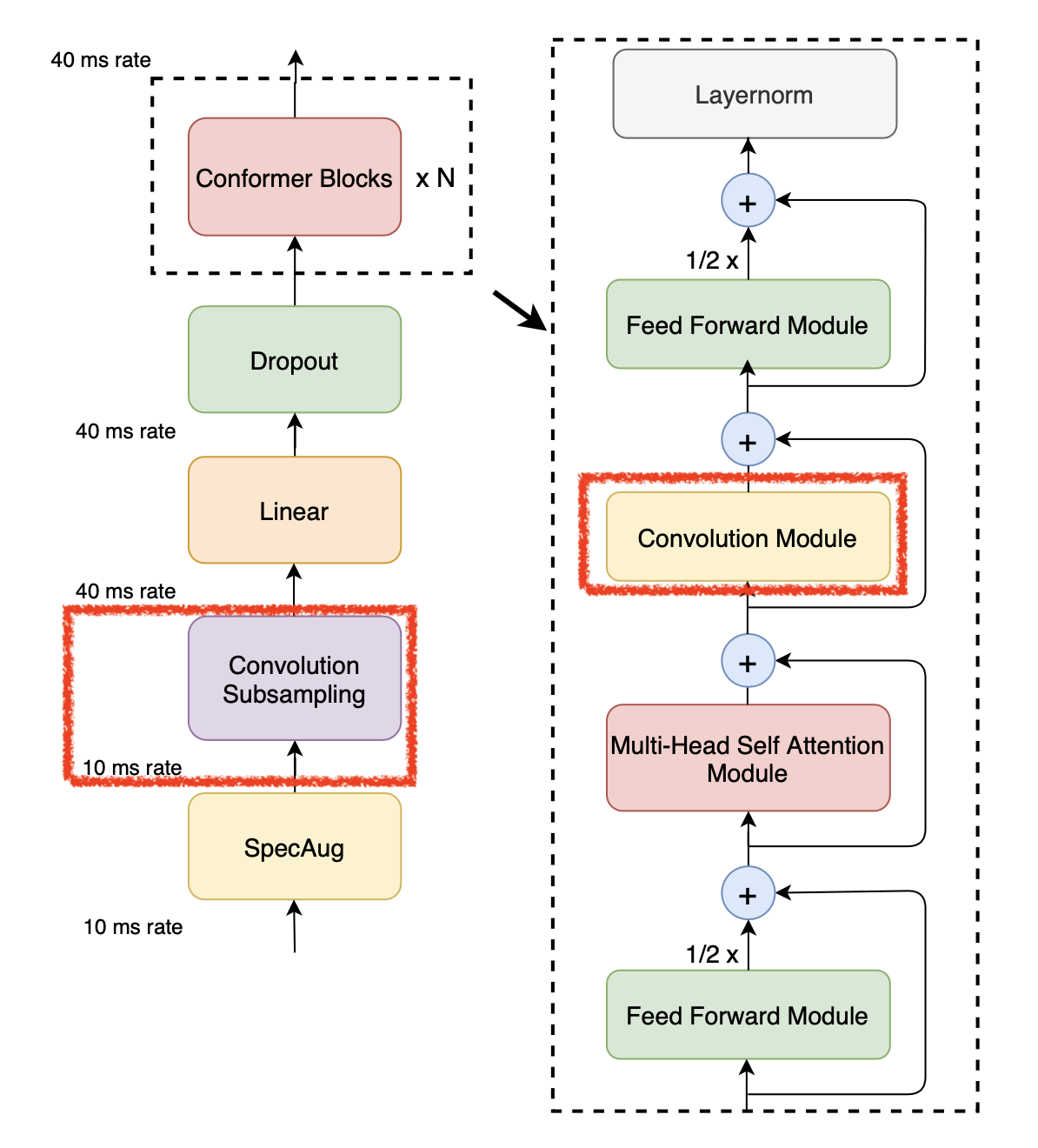conformer_arch Fig.

Conformer 는 (Mel) spectrogram 이라는 2D matrix (batch 까지 하면 3D tensor) 를 입력으로 받아 앞서 살펴본 것처럼 1D Conv Layer 가 한번 temporal resolution 을 확 줄여주는 과정이 있고 그 뒤로 이제 변형된 Transformer Block 인 Conformer Block 을 적게는 12번 (base size), 많게는 24 (L), 36번 (XL) 통과하게 된다. Conformer block에 들어간 Convolution Module 은 아래와 같이 생겼는데,

conformer_arch2 Fig.

기본적으로 1D Depthwise Conv 와 Pointwise Conv 로 결합되어 MobileNet 와 비슷한 구성이지만 Gated Linear Unit (GLU) 라는 모듈이 붙어있고, Normalization 과 Dropout 모듈들이 추가적으로 붙어있다.
이렇게 Conv 와 MHSA 를 명시적으로 구분지어 디자인 하는 아이디어는 Lite Transformer with Long-Short Range Attention 라는 paper 를 refer 하고 있는데,

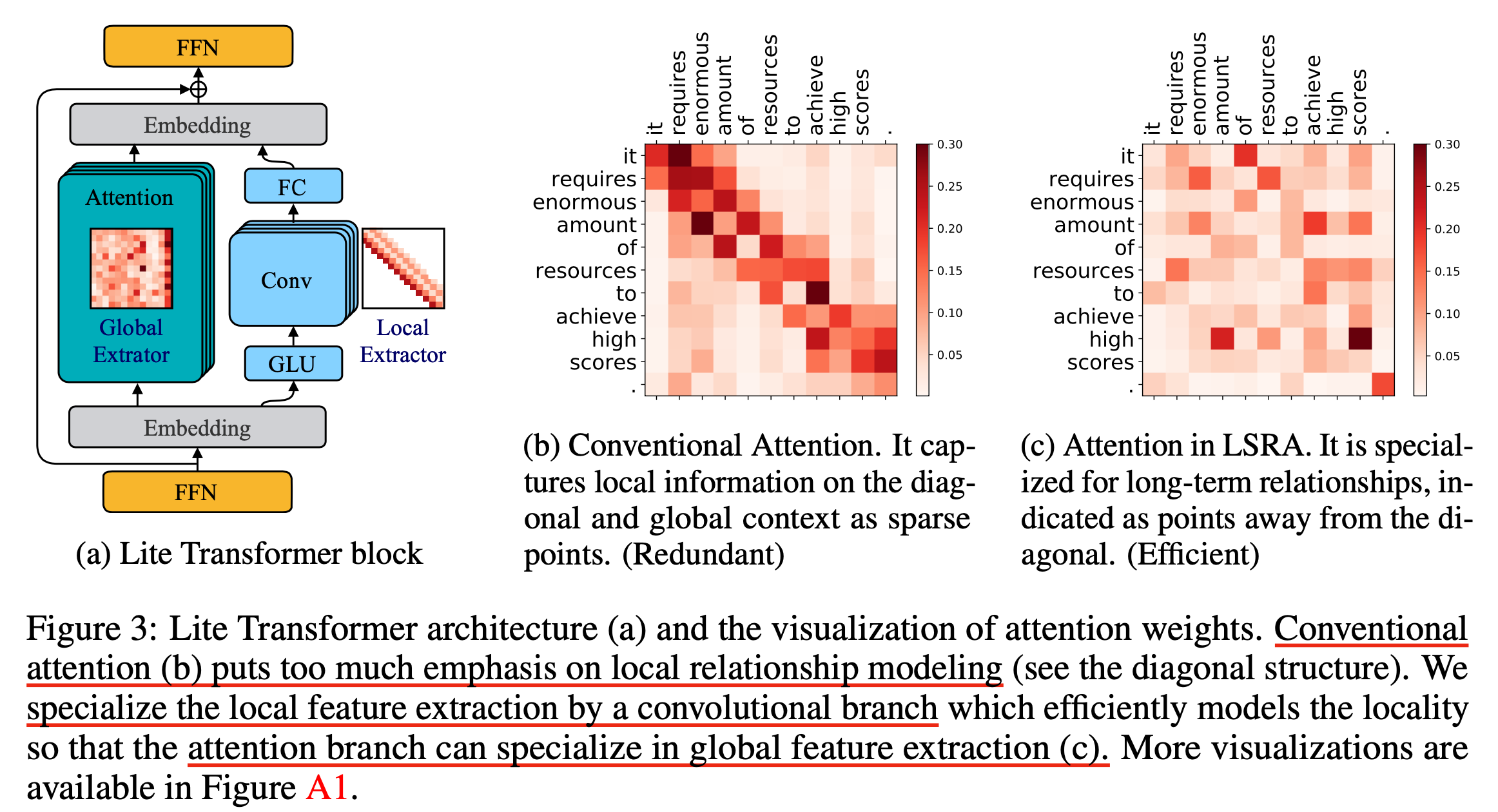lite_transformer_fig Fig.

원래 Transformer 의 각 Block 들의 MHSA 에는 여러 head 들이 존재하고 이들이 local feature 혹은 global feature 를 보는 것은 암시적으로 알아서 학습되어야 했으나 이 역할을 명시해서 나눠줌으로써 성능을 올리고 mobile 에서 구동 가능한 가벼운 architecture 를 만들었다는게 논문의 요지이다. (이런식으로 branch 를 나눠서 디자인하는 방법은 훗날 Branchformer로 발전되기도 했다)

(In branchformer paper ...)
Similar to this work, Lite Transformer (Wu et al., 2020) also adopts a two-branch architecture 
based on the standard self-attention and convolution to capture global and local dependencies. 

However, the motivation is quite different from ours.2 Lite Transformer uses specialized parallel branches 
to reduce the overall computation and model size for mobile NLP applications. 
In speech, convolutions play an integral role in its modeling due to the local correlations 
in continuous speech data, which Conformer has exploited.

Branchformer aims to re-design the architecture to make it more stable to train (Section 4.3), 
flexible to allow various attentions (Section 4.4), 
interpretable to present interesting design analysis (Section 4.6), 
and have different inference complexity in a single model (Section 4.7).

(사실 motivation 말고 크게 뭐가 다른지 모르겠음.)

여기서 GLU라는 Module이 추가적으로 쓰였는데 이는 FAIR의 Language Modeling with Gated Convolutional Networks라는 논문에서 제안되었다.

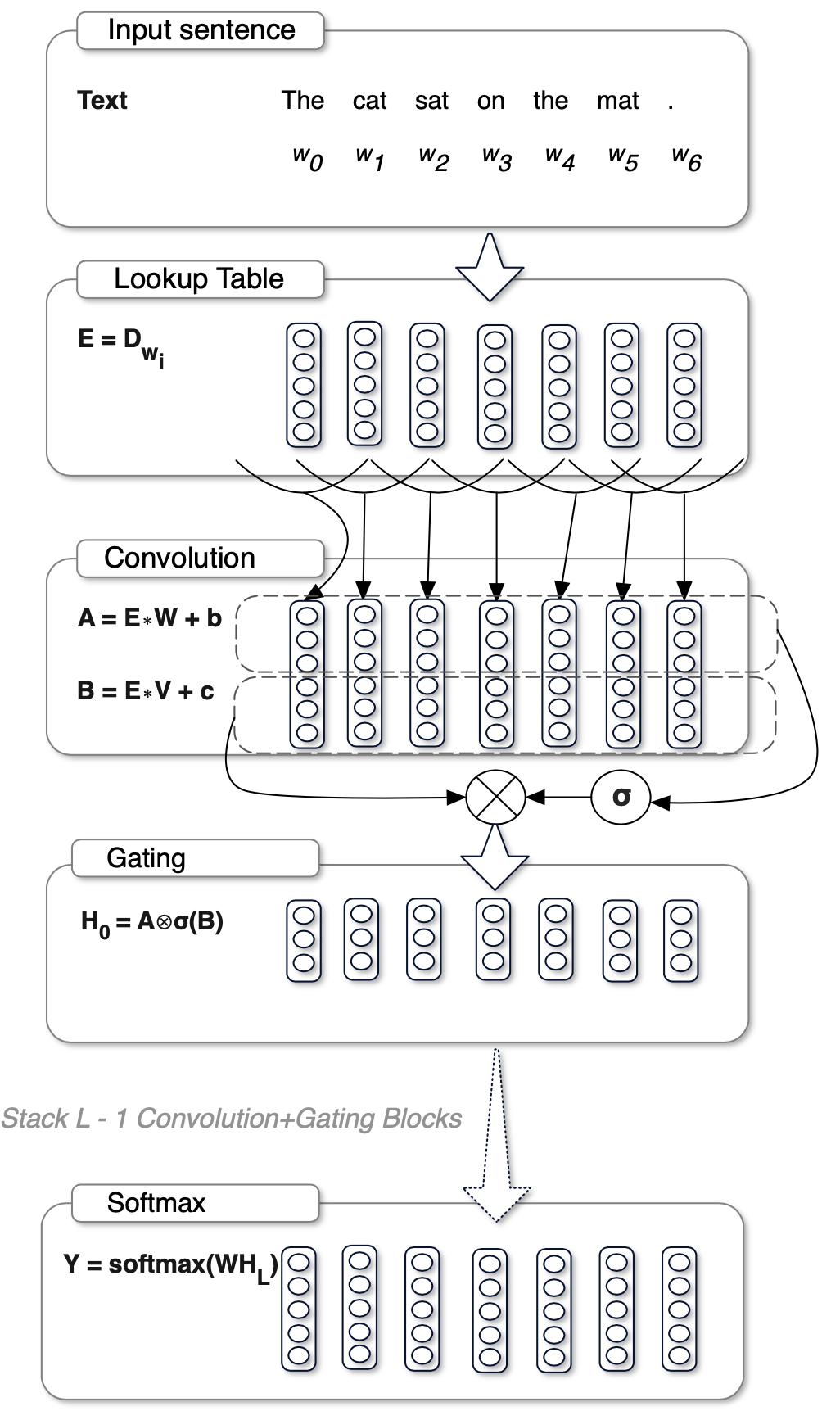glu_fig Fig.

Yann Lecun 이 head 로 있는 조직이어서 그런지 이상하리만치 Conv Layer 에 집착하는 FAIR는 모두가 Recurrent Neural Networks (RNNs) 으로 Language Modeling (LM)을 할 때도 Conv Layer만을 이용해 LM modeling한 적이 있는데, 자세한 사항은 paper를 확인해보면 될 것 같다.

Conv Layer for Relative Positional Encoding (RPE)

Conv Layer 를 Transformer 에서 사용하는 사례가 또 있으니 바로 Positional Infromation 을 만드는 데 사용하는 것이다. Transformer 는 RNN 과 비교해 병렬 처리로 인한 더 빠른 학습이 가능한 대신 input token 들의 position 정보가 추가로 필요한 구조이다. (RNN은 문장의 시작부터 한 방향으로 Context vector 를 생성하기 때문에 자연스럽게 position 정보가 들어갔다)

Positional Encoding (PE) 의 핵심은 position 정보를 넣어주는것도 있지만, 학습때 본 sequence 의 길이가 최대 250 같이 제한되어 있었어도 추론 시 350 개의 token 이 들어와도 이를 모델이 추론할 수 있게 잘 도와주도록 디자인 되어 있어야 한다는 건이다.

pe_relative_graph_figure Fig. Absolute PE vs RPE

일반적으로 transformer 원 논문에서 제안된 sine, cosine wave를 사용해서 position embedding을 만드는 absolute PE 보다 encoding 하려는 token 의 위치 기준으로 position 정보를 주입하는 Relative Positional Encoding (RPE) 이 더 성능이 좋다고 알려져 있다. 이렇게 상대적으로 위치 정보를 주입하는 RPE vector 들을 생성하는건 여러 가지 방식이 있을 수 있는데 대부분의 RPE 들은 Query (Q) 와 상호작용 (연산) 을 통해서 positional tensor를 만들어 내난드ㅔ, 앞서 소개했었던 음성 쪽의 BERT, Wav2Vec 2.0 architecture 에서는 Convolutional Positional Embedding 을 사용해서 positional tensor 를 modeling 했다. 이는 input을 1D Conv에 태워 position information을 뽑아내는 approach이다.

w2v2_pos

1D Conv 의 경우 Kernel 안의 Token 들만 보고 vector 만들어 내는데, 예를 들어 kernel이 [0.5, 1, 0.5] 의 weights을 갖는다고 치면 RPE 와 같은 일을 할 수 있게 된다. 즉 내가 현재 encoding하려는 기준 position에 가장 큰 weight을 할당 하고 window 밖에 있는 token 들은 무시하는 것이 Q에 따라 Relative Distance 를 나타내는 Vector 를 학습하는 것과 다를게 없게 된다.

shaw_conv Fig. Phrase in Shwa et al. paper

이렇게 만들어진 positional tensor 를 input tensor 와 더하는것으로 간단하게 position 정보를 input sequence에 주입할 수 있게 되는데, 이 idea 또한 Conv 를 좋아하는 FAIR의 Convolutional Sequence to Sequence Learning 라는 Paper 에서 제안되었다.

    x_conv = self.pos_conv(x.transpose(1, 2))
    x_conv = x_conv.transpose(1, 2)
    x = x + x_conv

Outro

Conv layer는 어떤 input tensor를 encoding을 할 때 공간정보를 보존하여 encoding하고 subsampling을 하여 연산 복잡도를 줄이거나 positional encoding역할을 하는 등 다양한 쓰임새가 있다. 본 post에서 다루지 않은 것들 중 VGGNet이나 ResNet같은 seminar paper들이 있으니 시간이 되면 꼭 따로 찾아보길 권장한다.

  • 1998, LeNet
  • 2012, AlexNet
  • 2014, GoogleNet
  • 2014, VGGNet
  • 2015, ResNet
  • 2017, MobileNets

References