(WIP) (CS285) Lecture 10 - Optimal Control and Planning
13 Oct 2024이 글은 UC Berkeley 의 교수, Sergey Levine 의 심층 강화 학습 (Deep Reinforcement Learning) 강의인 CS285를 듣고 작성한 글 입니다.
Lecture 10의 강의 영상과 자료는 아래에서 확인하실 수 있습니다.
- Fall 2020 ver.
< 목차 >
- Introduction to model-based reinforcement learning
- Open-Loop Planning
- Trajectory Optimization with Derivatives
- LQR for Stochastic and Nonlinear Systems
- Case Study and Additional Readings
- Reference
Introduction to model-based reinforcement learning
Lecture의 주제는 ‘Optimal Control and Planning’입니다.
 Slide. 1.
Slide. 1.
여태까지 cs285에서 배웠던 Deep RL의 흐름을 되짚어 봅시다.
- Lec 2, 4 : Supervised Learnign (SL)과 Reinforcement Learning (RL)은 어떻게 다른가?
- Lec 5, 6 : RL objective를 optimize 하기 위한 방법 중 Policy Gradient (PG) 에 대해서 알아보고, 이 alogirhtm의 문제점인 high variance를 해결하려면 어떻게 해야할까? Advantage Actor-Critic (A2C)
- Lec 7, 8 : Policy를 directly optimize 하지 말고 간접적으로 (implicitly) 학습할 순 없을까? -> Value-based method. 이 중에서 Dynamics (Transition Probability)를 몰라도 되는 model-free method이자 off-policy method인 Deep Q-Learning (DQN)에 대해서 알아봄.
- Lec 9 : Vanilla Policy Gradient (VPG) 는 잘못된 trust region에서 optimization을 하고 있었다 -> Natural Policy Gradient (NPG) and Trust Region Policy Optimization (TRPO)
지금까지 우리는 good policy를 얻기 위한 key algorithm들 을 거의 다 배웠다고 할 수 있습니다. TRPO를 정통으로 읽지는 않았지만 TRPO나 PPO도 concept은 같았습니다. 이제 Deep RL을 공부할 수 있는 뼈대를 다진 것이나 다름이 없습니다.
앞으로 배울 내용들은 다음과 같습니다.
- Lec 10 ~ 12 : Planning and Model-based RL (MBRL)
- Lec 13, 14 : Exploration
- Lec 15, 16 : Offline RL
- …
이 lecture들은 learning algorithm이 엄청나게 바뀐다기 보다는 여태까지 배운 것에 여러가지 option을 추가하는 것 쯤으로 생각하거나, policy를 얻는 것을 약간 다른 관점에서 보는 겁니다. Sergey는 잠깐 기어를 바꾼다는 표현을 씁니다 (shifting gear).
이번 lecture 10부터 당분간 알아볼 algorithm들은 더이상 transition dynamics (model)를 몰라도 되는 Model-free algorithm이 아닙니다.
 Slide. 4.
Slide. 4.
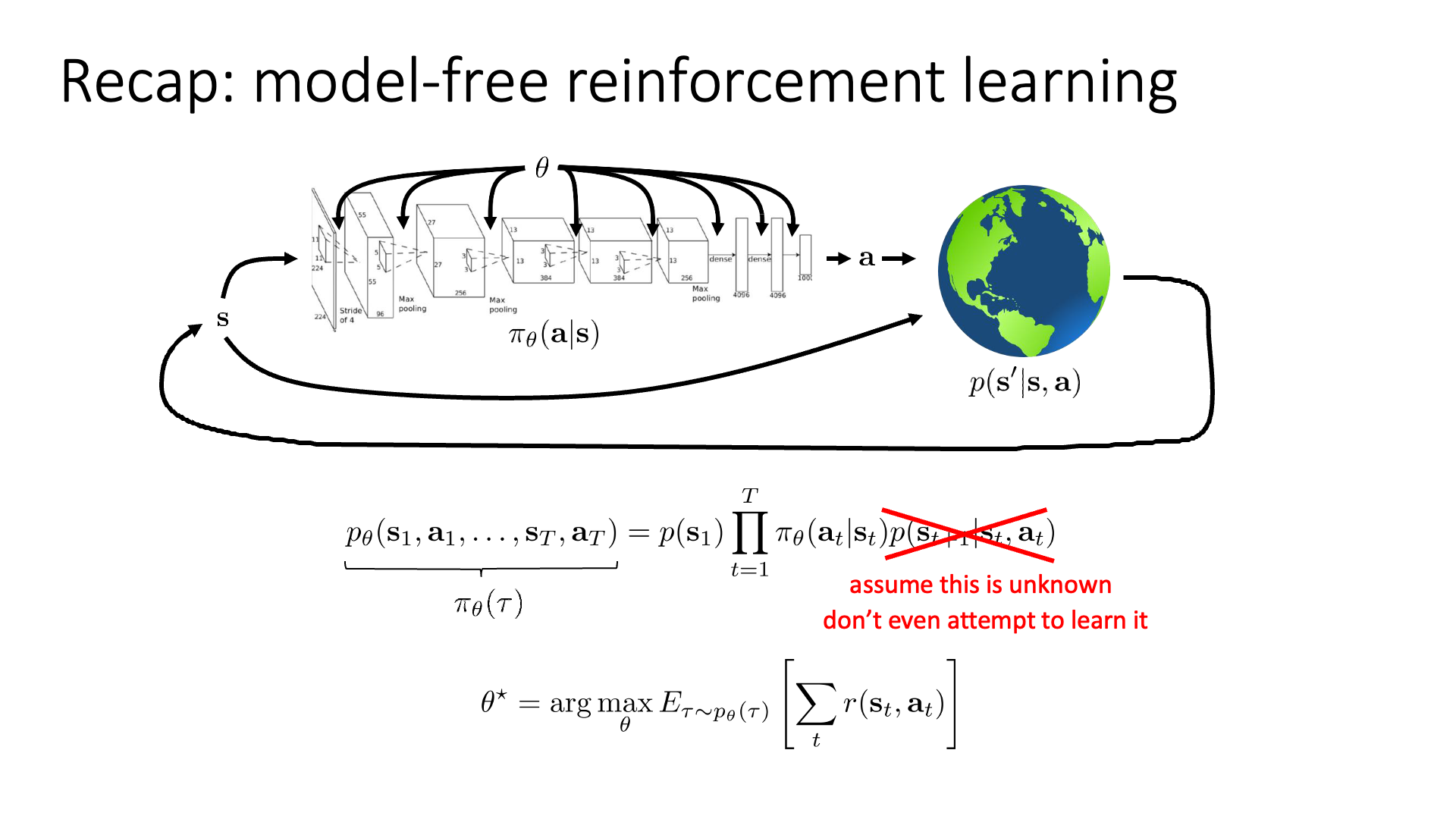
앞서 배운 algirhtm들은 Dynamic Programming (DP)으로 푸는 policy iteration 등을 제외하고는 dynmaics를 몰라도 됐습니다. 직접 agent가 environment와 interaction 하는 것으로 transition data를 쌓고 이를 evaluate해서 policy를 개선해왔습니다. Q-Learning은 이를 피하기 위해 Q값을 regress 했으며, policy optimization 계열들은 sampling을 여러번 하는 것으로 이를 대체햇죠.
하지만 앞으로는 배울 것은 transition dynamics (model)를 아는 경우에 대한 것들입니다.
혹은 dynamics를 Neural Network (NN)으로 학습해서 쓰는 algorithm들에 대해 알아볼 것인데,
이런 종류의 method를 Model-based RL (MBRL)이라고 합니다.
 Slide. 2.
Slide. 2.
만약 transition dynamics가 알면 어떤식으로 decision making을 할 수 있을까요? 더 좋은 decision을 내릴 수 있을까요?
 Slide. 5.
Slide. 5.
Slide 5를 보면 실제로 dynamics가 이미 주어져 있는 경우의 예시가 나와있습니다. Atari game이나 바둑 (Go)같은 경우 dynamcis가 알려져 있기 때문에 이를 활용할 수 있는 문제들인데, 이 중 DeepMind가 2015년 Nature에 publish한 Alphago는 Model-free와 model-based를 합친 것 입니다 (학습은 model-free로 하고 inference는 model-based로).
Robotics의 경우 특히 model (dynamics)를 학습하는 algorithm들이 많은데,
어떻게 동작하는지를 정의하는 것 자체는 쉬운데 (이미 알려져 있는데),
이 known model의 unknown parameter를 찾는 것을 하긴 해야합니다.
이를 system identification 라고 하는데, 대충 robot의 다리가 4개이니고 다리마다 관절이 있을 것인데 이것의 길이는 알지만 질량 (mass)이나 motor의 토크 (torque)같은건 모를 수도 있으니 이를 찾는겁니다.
여기서 중요하게 생각해볼 것은 아무래도 'dynamics를 아는게 실제로 RL을 학습하는 데 도움이 되는가?'이겠죠.
즉 조금이라도 더 좋은 policy를 얻는데 도움이 되는가 입니다.
당연히 대부분의 경우에는 도움이 된다고 하긴 합니다.
 Slide. 6.
Slide. 6.
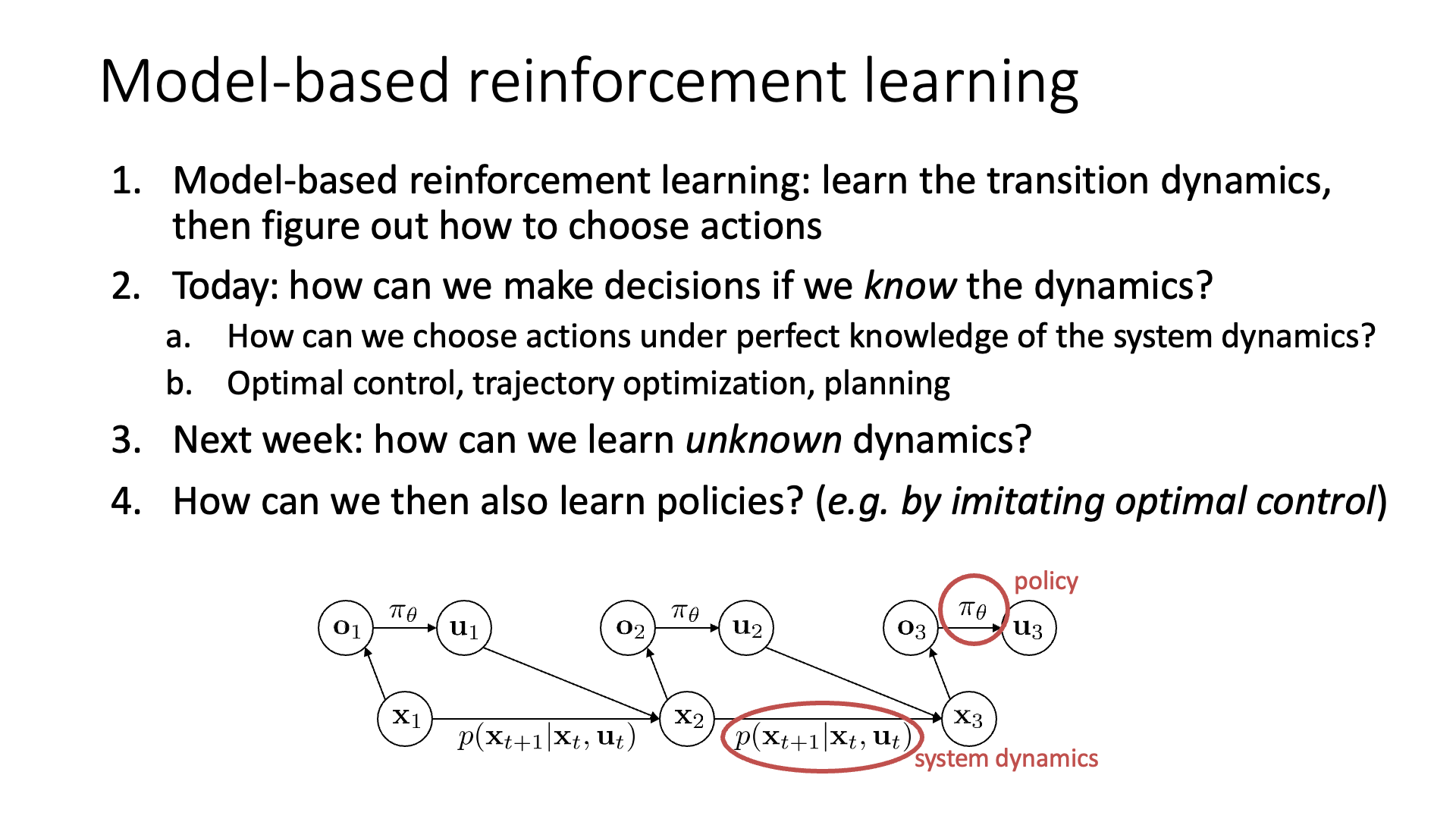
앞으로 lecture 10~12 까지 dynamics를 이미 알고 있는 경우, 혹은 학습해야하는 경우에 대해 알아볼 건데,
lecture 10에서 알아볼 것은 dynamics를 이미 알고 있는 경우에 해당하며 이런 경우에는 planning 또는 optimal control 한다고 얘기합니다.
lecture 11, 12에서는 이것이 주어지지는 않았지만 NN modeling을 합니다.
이제 planning이 무엇인지 알아보도록 합시다.
Motivating Example
사실 이 뒤로는 ‘나는 model-based RL에 전혀 관심이 없다’하는 사람은 생략해도 될 정도의 내용이 펼쳐지긴 합니다. Deep RL로 풀 수 있는 문제들에는 대표적으로 robotics, autonomous driving, 혹은 chatbot 같은 것들이 있습니다. 이중 human preference에 align된 chatbot을 만드는 Large Language Modeling (LLM) 분야가 요즘 핫하죠. 사실 planning 이쪽 계열은 robotics 같은데서 많이 쓰이고 LLM에선 주류도 아니기 때문에 혹시나 LLM을 위해 RL을 듣는 분들이 계시다면 이부분은 lecture 10~12 정도는 생략해도 괜찮습니다.
하지만 LLM을 하더라도 dynamics를 학습하는 MBRL 까지는 몰라도 되지만 planning 정도는 알아둬도 괜찮습니다. Deep Learning (DL)을 하는 사람이라면 모두가 알고있을 AlphaGO으로 planning에 대한 대략적인 개념을 소개드리고 이것이 어떻게 LLM같은 데에도 적용될 수 있는지 짧게 소개드려 보도록 하겠습니다.
AlphaGO는 바둑 (Go)을 두는 agent를 학습하는 것으로 아래와 같이 학습 됐습니다.
- 가장 먼저 프로 바둑기사의 기보로 Behavior Cloning (BC)을 먼저 해서 괜찮은 policy를 얻음.
- 꽤 바둑을 둘 줄 아는 learned policy 끼리 대전을 해서 trajectory를 얻고 agent를 강화함 (Model-free)
- 왜냐하면 바둑은 상대방이 있어야 하는 게임이라서 혼자 roll-out 할 수 없음
- 이 때 actor network와 critic network를 쓰는 Actor-Critic 구조를 썼음.
- 학습된 actor외에도 성능이 구리지만 rollout 하는데 문제가 없는 경량화된 actor를 하나 더 학습시킴
- 실제 사람과 대전할 때는 rollout actor와 critic network 등을 사용해 여러 가지 수를 simulation 해보고 최종 수를 둠
여기서 마지막에 simulation을 해보는 algorithm이 바로 Monte Carlo Tree Search (MCTS)라는 대표적인 planning algorithm 입니다.
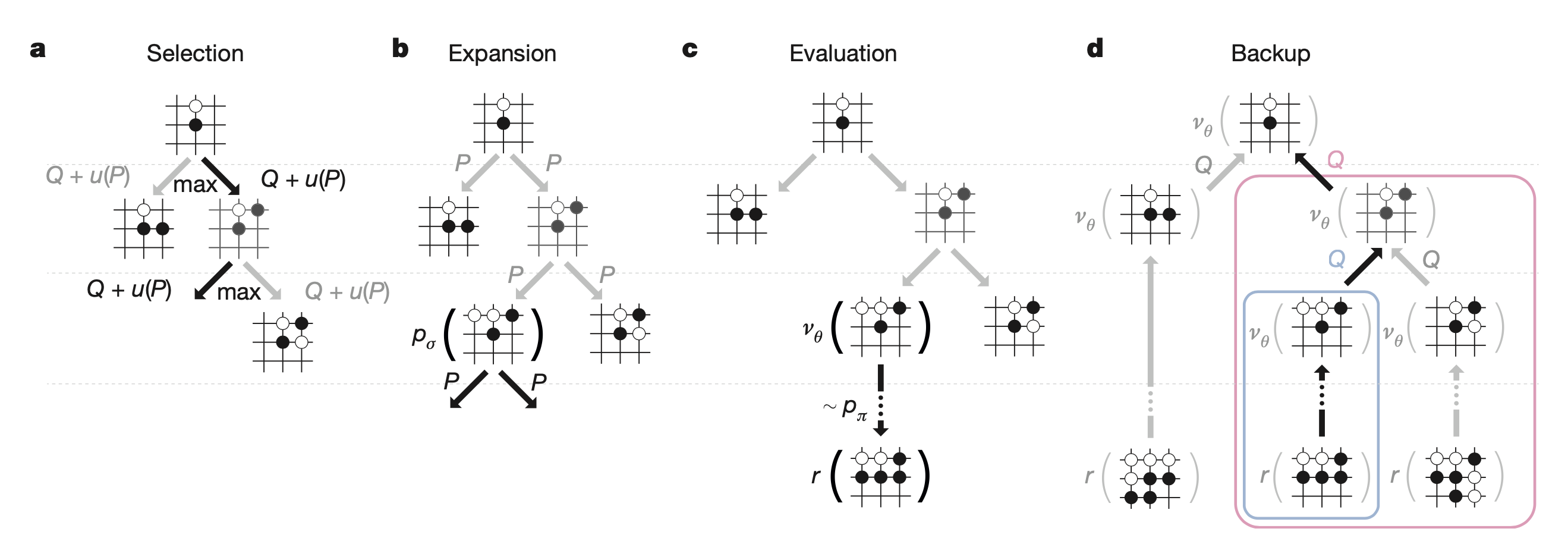 Fig. MCTS 예시
Fig. MCTS 예시
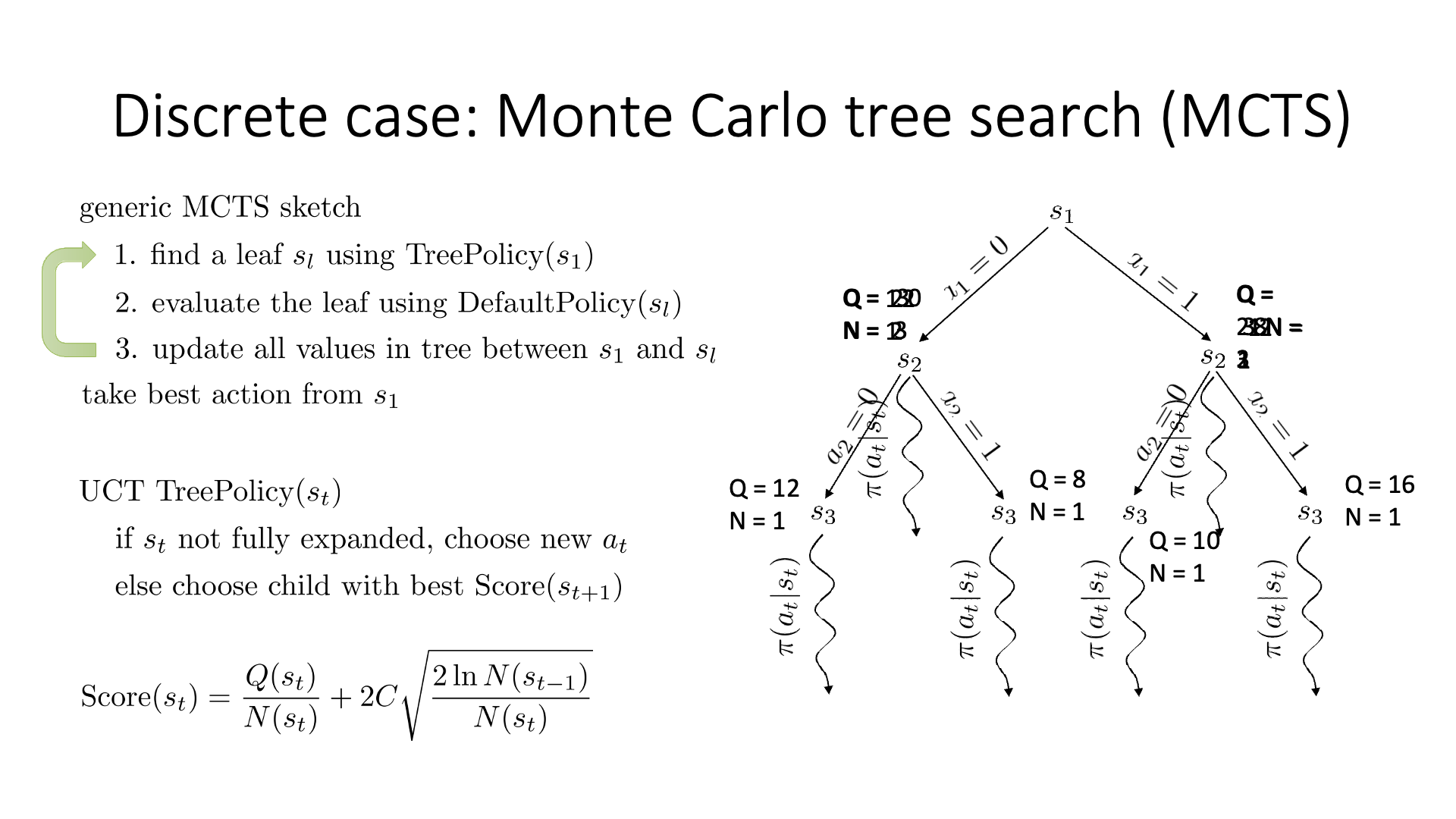
Planning이란 한줄로 요약하자면 action 하기 전에 머릿속으로 여러번 simulation 해본 뒤에 가장 좋은 action을 두는 것이라고 할 수 있습니다.
Monte Carlo 라는 이름에서 이를 유추할 수 있죠.
당연히 좋은 action이라면 더 많이 시행이 됐을 것이고 이에 따라 어떤 특정 state는 방문 횟수 (visit count)가 더 많이 찍힐겁니다. 곧 배울것이지만 tree search를 하고 나서, 최종 수는 내가 simulation 해서 얻은 실제 reward 값이나 Q값과 visi count를 종합해서 결정합니다. (마치 data structure의 tree를 traverse하는 것 처럼 경우의 수를 탐험합니다)
바둑 같은 경우 어떤 지점에 수를 두기로 했는데 이것이 실패하는 경우가 없죠. 우리가 어떤 수를 두면 그 다음 state가 어디로 갈 지 아는 것과 다름이 없으므로 dynamics를 아는 것이고, 그러므로 simulation (planning)이 가능한 것입니다. 물론 우리가 학습한 actor가 optimal policy라면 이런일을 할 필요는 없을지도 모르나 actor가 완벽하지 않다면 이런 inference 전략은 decision making을 하는 데 도움을 줄 수 있죠.
당연히 Neural Machine Translation (NMT)나 LLM쪽에서도 이런 시도가 있습니다. 왜냐하면 이런 task들도 action을 하면 바로 그 다음 state는 아는거나 마찬가지 이기 때문이죠. 아래는 NMT를 MCTS했을 때의 예시로 paper에서는 이것이 beam search보다 좋다고 얘기합니다.
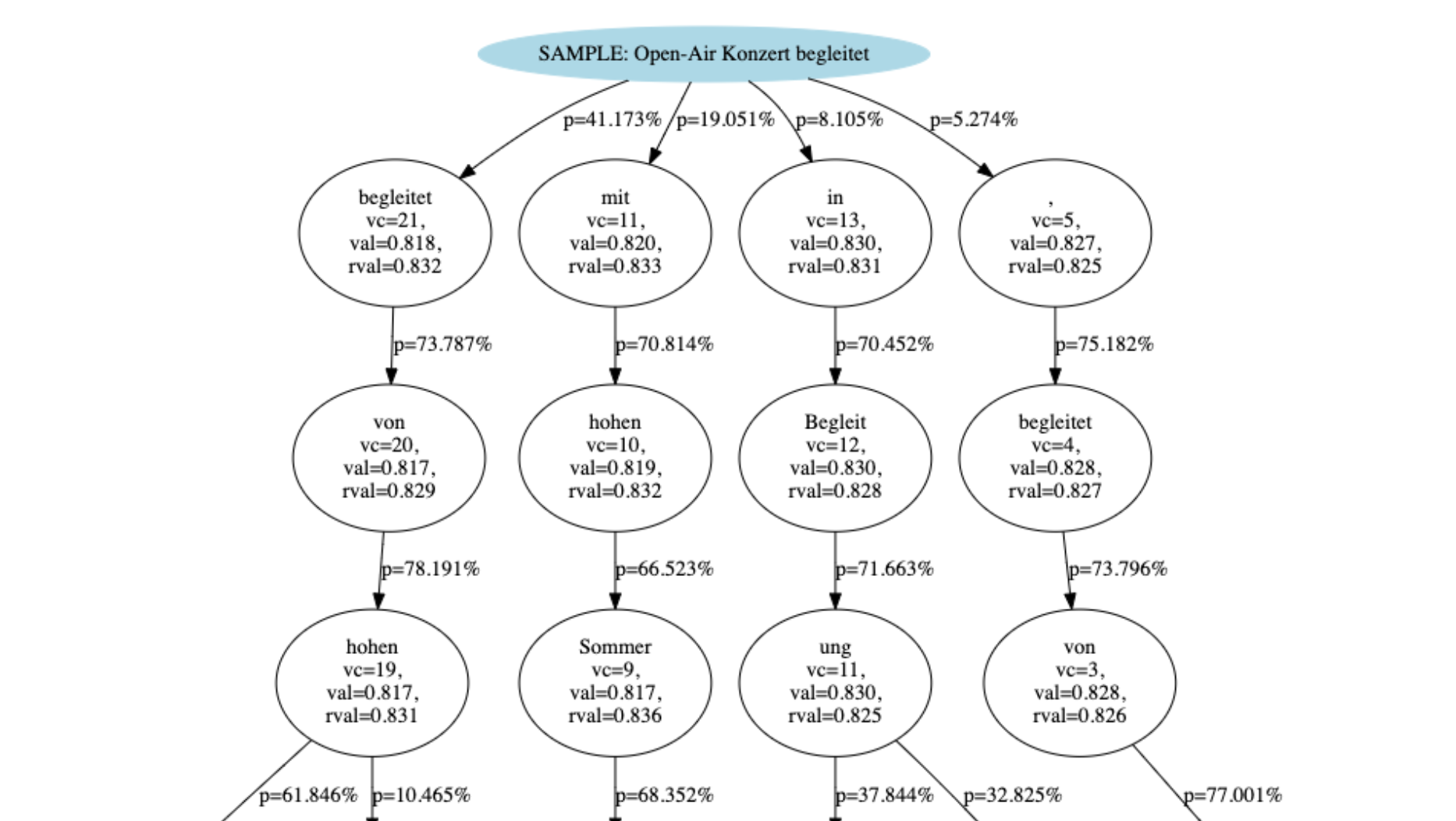 Fig. Source from Machine Translation Decoding beyond Beam Search
Fig. Source from Machine Translation Decoding beyond Beam Search
이런 motivation을 가지고 model-based RL에 대해 알아보도록 합시다.
Robotics Example Animation
 Fig.
Fig.
 Fig.
Fig.
tmp
Slide 7은 수식이 좀 깨졌는데 그냥 RL의 objective 수식을 recap한 것입니다.
\[\min_{a_1,\cdots,a_T} \log p(\text{eaten by tiger} \vert a_1, \cdots,a_T)\]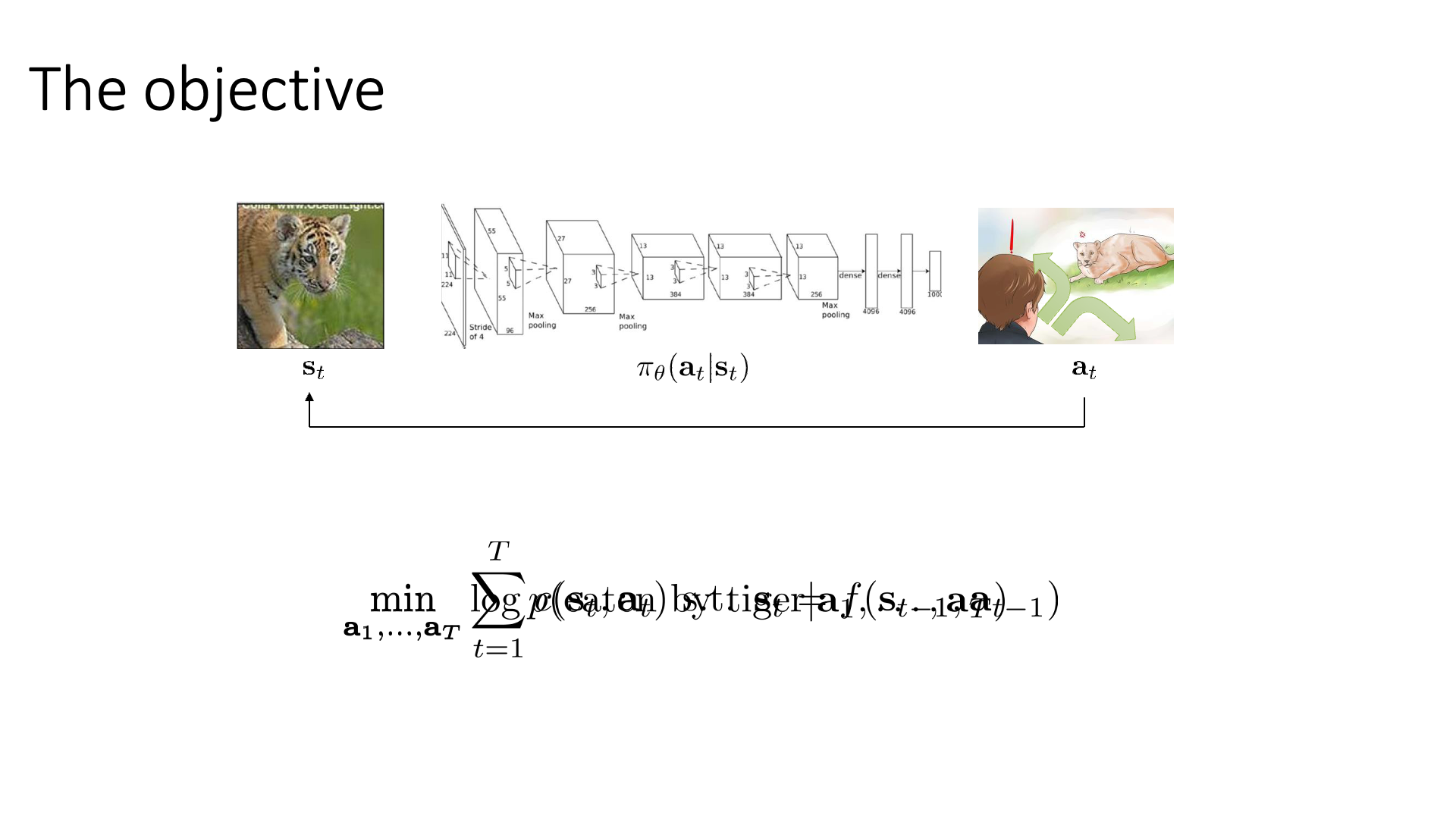 Slide. 7.
Slide. 7.
다만 이 수식에 parameterized policy, \(\pi_{\theta}\)는 없고 state와 action만 존재합니다.
당분간 explicit policy가 있다는 건 잊어버립시다.
왜냐하면 우리가 RL을 통해 결국 찾고 싶은 것은 어떤 state에 있을 때 최적의 action은 무엇인가?이고 그것을 modeling한 것이 policy이기 때문에,
위 figure를 예시로 들자면 딱히 policy가 없더라도 “현재 state에서 terminal state T까지 호랑이 한테 잡아먹히지 않기 위해서 어떻게 moving을 해야하는가?” 를 알기만 하면 됩니다.
즉 action sequence를 알기만 하면 되죠.
이를 위해서는 먼저 어떻게 행동할지에 대한 planning objective를 수식화해야 하는데, 별건 아니고 RL objective 같은 겁니다. Cost를 최소화 하거나 Reward를 최대화하는 거죠. (지금은 호랑이한테 뜯기기라도하면 (안좋은) cost가 발생)
\[\begin{aligned} & \min_{a_1,\cdots,a_T} \sum_{t=1}^T c(s_t,a_t) & \\ \end{aligned}\]그런데 위 수식은 future state가 past action에 영향을 받지 않는다는 것을 의미합니다. 따라서 우리는 아래의 constraint가 필요한데,
\[\begin{aligned} & \min_{a_1,\cdots,a_T} \sum_{t=1}^T c(s_t,a_t) \text{ s.t. } \color{red}{s_t = f(s_{t-1},a_{t-1})} & \\ \end{aligned}\]여기서 constraint, \(s_t = f(s_{t-1},a_{t-1})\)이 의미하는 바가 dynamics입니다.
이번에도 constrained optimization 를 풀어야 할 각오를 해야겠군요.
그런데 자세히 보면 \(f\)는 어떤 state에서 action을 했을 때 그 다음 state의 확률 분포를 return하지 않습니다.
‘다음은 어떤 state로 간다’ 라고 deterministic하게 알려줄 뿐이죠.
따라서 지금의 경우는 Deterministic Dynamics Case라고 부릅니다.
나중에는 Stochastic Dynamics Case에 대해서도 당연히 배울 겁니다만 언제나 그렇듯 special case인 deterministic case에 대해서 먼저 배울겁니다.
 Slide. 8.
Slide. 8.
Deterministic case에 대해서 조금 더 얘기해 봅시다. 위 figure가 의미하는 바는 environment로 부터 initial state, \(s_1\)를 얻었으면, 그 때 부터 agent는 reward를 maximize 하는 action sequence를 알아내서 한번에 쭉 action을 하는겁니다. 이 때, 어떤 state에서 어떤 action을 하면 그 다음 state는 deterministic하기 때문에 딱 하나로 정해져 있습니다.
\[a_1, \cdots, a_T = \arg \max_{a_1,\cdots,a_T} \sum_{t=1}^T r(s_t,a_t) \text{ s.t. } s_{t+1} = f(s_t,a_t)\](\(a_{t+1} = f(s_t,a_t)\)는 오타입니다. \(s_{t+1}\)가 맞습니다.)
Robot이 나와서 말인데 사람처럼 생긴 humanoid가 이족보행 하는 task를 생각해 봅시다. Robot이 걸을 때는 사실 현재 state에서 다음 action이 각 무릎 관절 (joint), 팔 관절의 각도를 몇도 회전한다 같은 것들이 될겁니다. 이를 달성하기 위해서 real time으로 계속 policy를 돌려서 joint를 움직이는 것 보다는 다리 관절을 5초 정도 움직일 것을 미리 planning하는 것이 더 효율적이고 자연스러울 겁니다 (이 경우 initial state 부터 terminal state까지 가는 것은 아니죠).
이번에는 stochastic case에 대해서 알아보겠습니다.
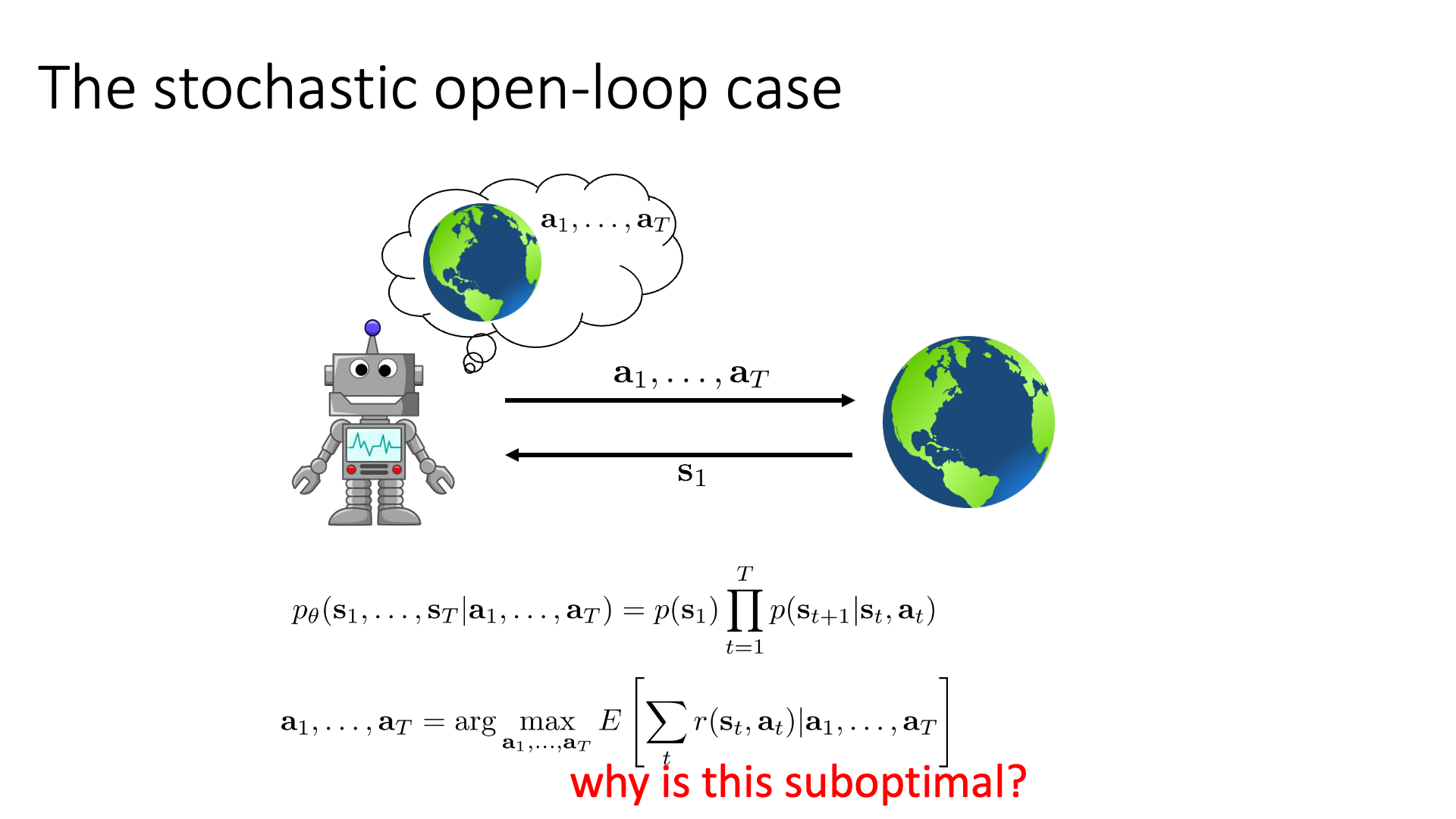 Slide. 9.
Slide. 9.
Deterministic case에서는 \(s_{t+1} = f(s_t,a_t)\) 처럼 다음 state가 그냥 정해졌는데, stochastic case의 경우에는 다음과 같이 action sequence를 조건으로 하는 state sequence 에 대한 distribution이 필요합니다.
\[p_{\theta}(s_1,\cdots,s_T \vert a_1, \cdots, a_T) = p(s_1) \prod_{t=1^T} p(s_{t+1} \vert s_t,a_t)\]주의할 점은 이 distribution은 여태까지 본 trajectory distribution과는 다르게 생겼다는 것입니다.
\[\begin{aligned} & \text{ - State Sequence Distribution of Stochastic Dynamic Case} & \\ & p_{\theta}(s_1,\cdots,s_T \vert a_1, \cdots, a_T) = p(s_1) \prod_{t=1}^T p(s_{t+1} \vert s_t,a_t) & \\ & \text{ - Original Trajectory Distribution} & \\ & \underbrace{p_{\theta}(s_1,a_1,\cdots,s_T,a_T)}_{p_{\theta}(\tau)} = p(s_1) \prod_{t=1}^T \color{red}{ \pi_{\theta}(a_t \vert s_t) } p(s_{t+1} \vert s_t,a_t) & \end{aligned}\]Plannig objective는 아래와 같이 쓸 수 있는데, deterministic case와 달리 expectation, \(\mathbb{E}\)가 수식에 포함되어 있습니다.
\[a_1, \cdots, a_T = \arg \max_{a_1,\cdots, a_T} \color{blue}{ \mathbb{E} } [ \sum_t r(s_t,a_t) \vert a_1,\cdots,a_T ]\]이런 approach가 stochastic environment에서 나쁘지는 않지만 어떤 경우에는 별로 좋지않은 sub-optimal한 결과를 내놓을 수 있다고 합니다. 이는 예를 들어 좋은 action을 하기 위한 critical information이 미래에 주어지는 경우라고 하는데, 만약 Sergey가 open-book 시험을 내준다고 하는데 무슨 문제를 낼지 안알려줬다면 생각하면 우리는 가능한 문제 (state) 에 대해서 다 생각해보고 이에 대해 답해보고 (action)를 해봐야 할겁니다. 나올만한 문제를 다 고려하는 경우 굉장히 suboptimal한 결과값을 내놓는 반면, closed-book 인 경우에도 어떤 문제를 낼 지 알려준다면 이런 경우가 훨씬 쉬울 거라고 합니다.
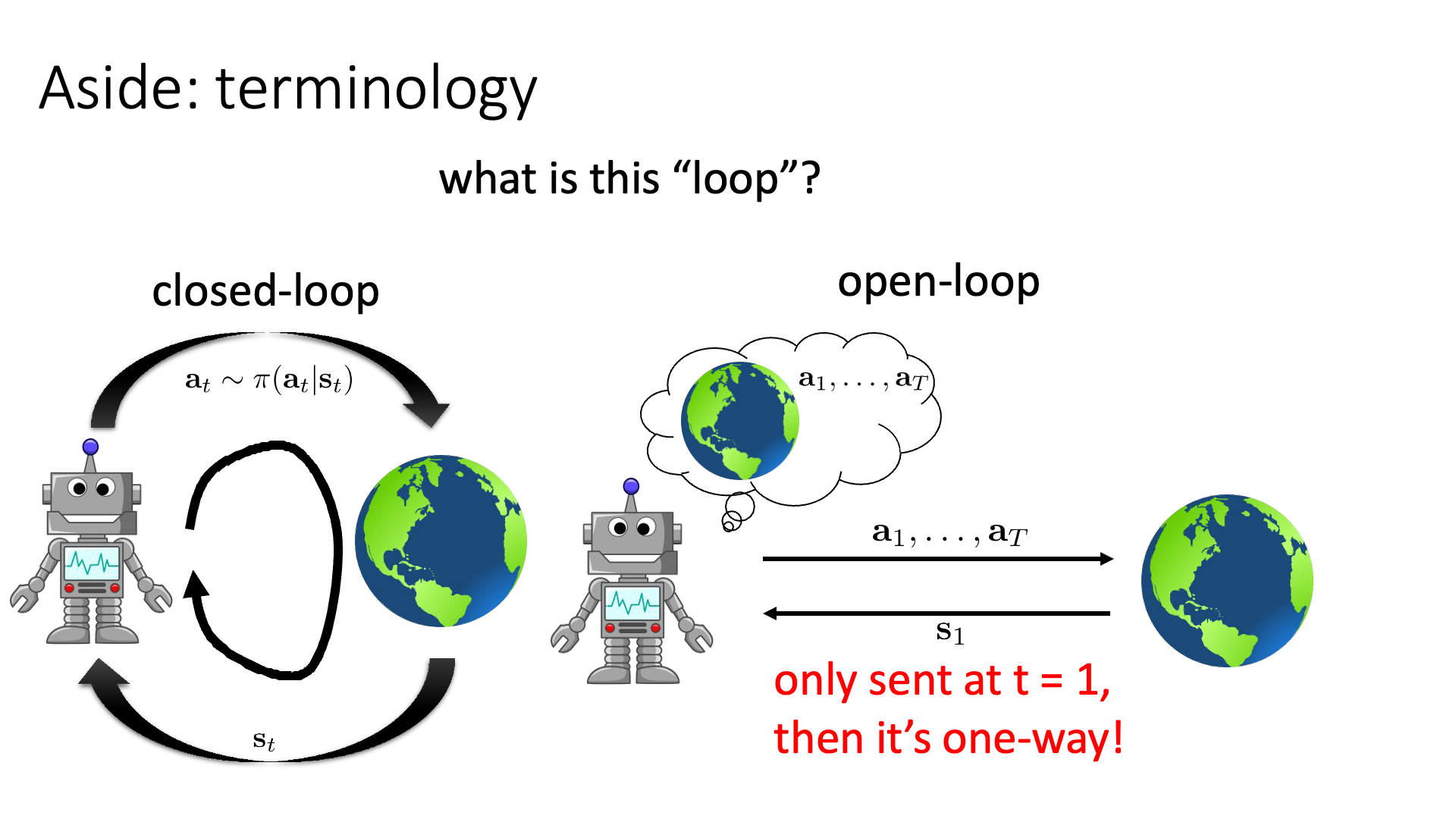 Slide. 10.
Slide. 10.
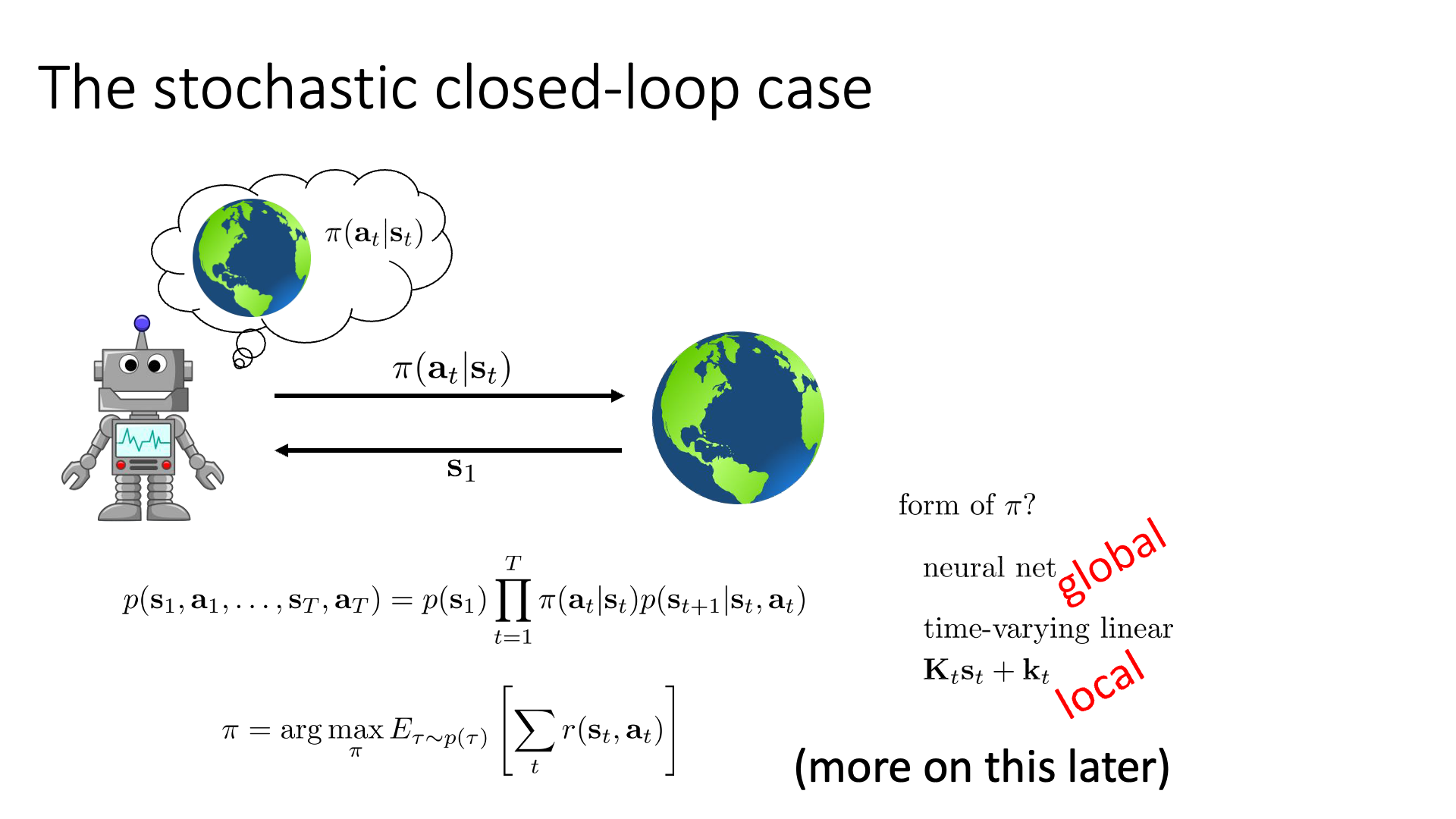 Slide. 11.
Slide. 11.
Open-Loop Planning
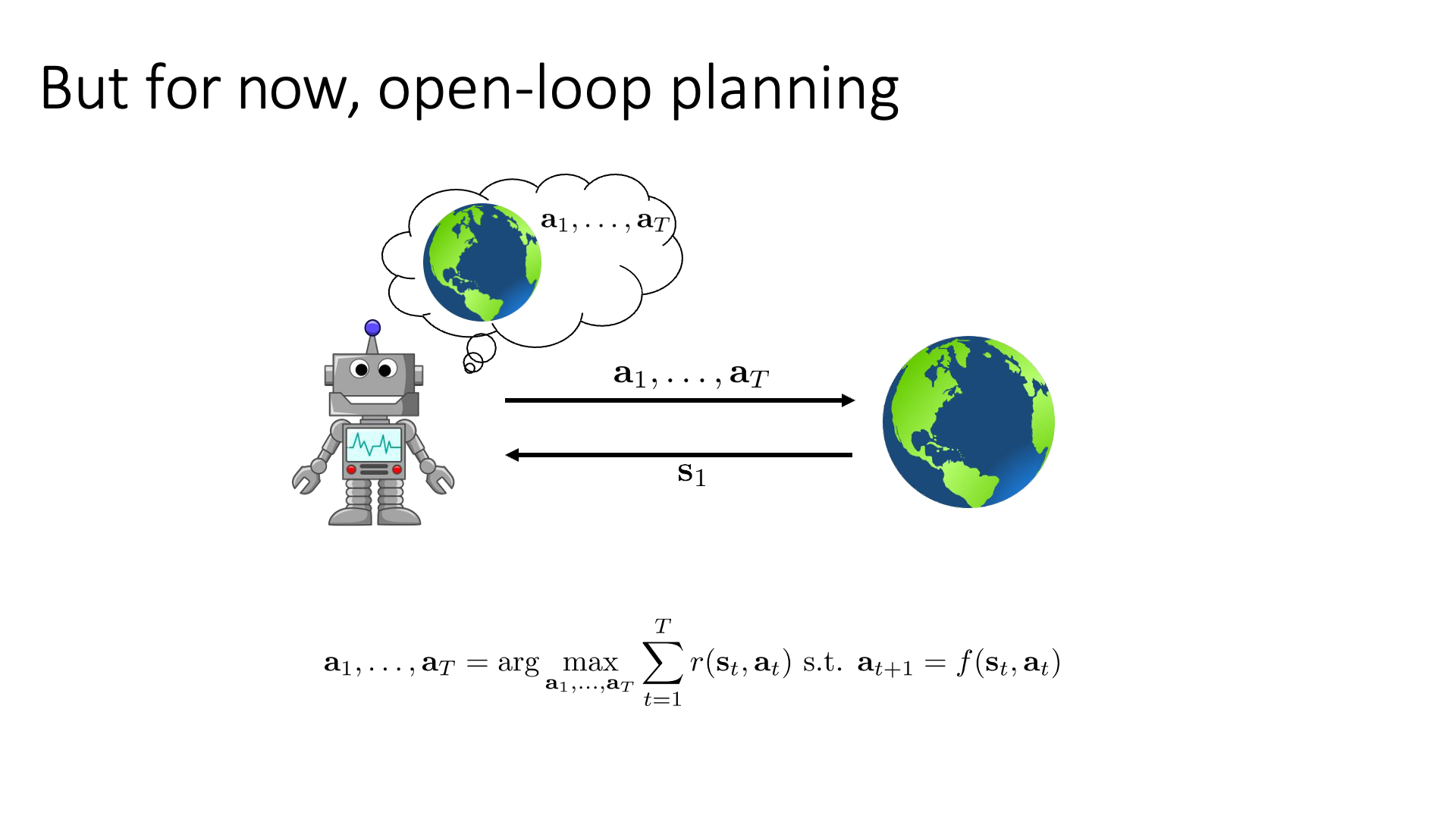 Slide. 13.
Slide. 13.
 Slide. 14.
Slide. 14.
Cross-Entropy Method (CEM)
Cross-Entropy Method (CEM)은 매우 간단한 algorithm 입니다.
우리가 하고싶은것은 \(A = (a_1, a_2, \cdots, a_{10})\)같은 일련의 (10개의) action sequence를 유추하고 싶은것이죠.
(아무 action이나 원하는건 당연히 아닐테죠)
먼저 10개 action으로 이루어진 sequence을 여러 번 뽑습니다.
\[A_1, A_2, \cdots, A_N\]예를들어 \(N=4\)라고 칩시다. 맨 처음에는 uniform하게 아무 action sequence만 뽑는겁니다. 이제 우리는 이 중에서 reward가 가장 높은 좋은 (elite) sequence를 2개 정도 뽑습니다.
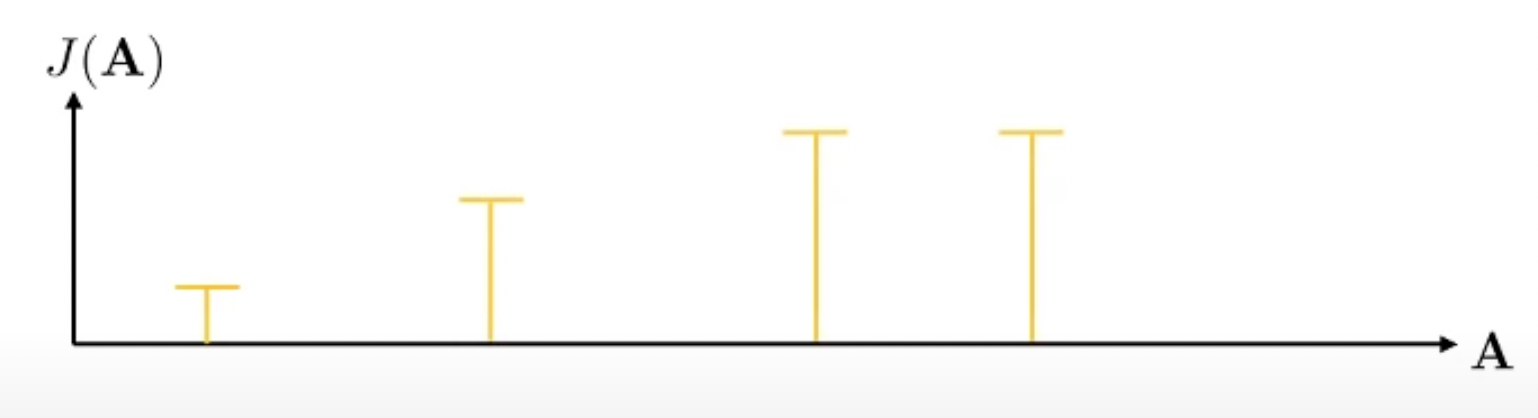 Fig.
Fig.
그리고 이 두 개 sample에 대해서 gaussian distribution을 fitting합니다.
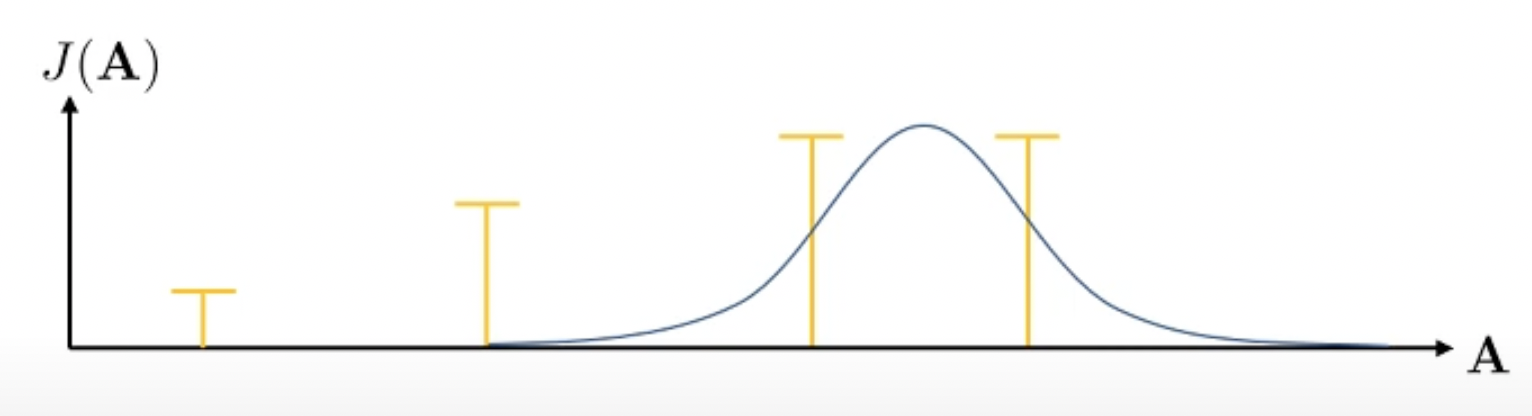 Fig.
Fig.
Maximum likelihood 문제를 풀면 되겠죠?
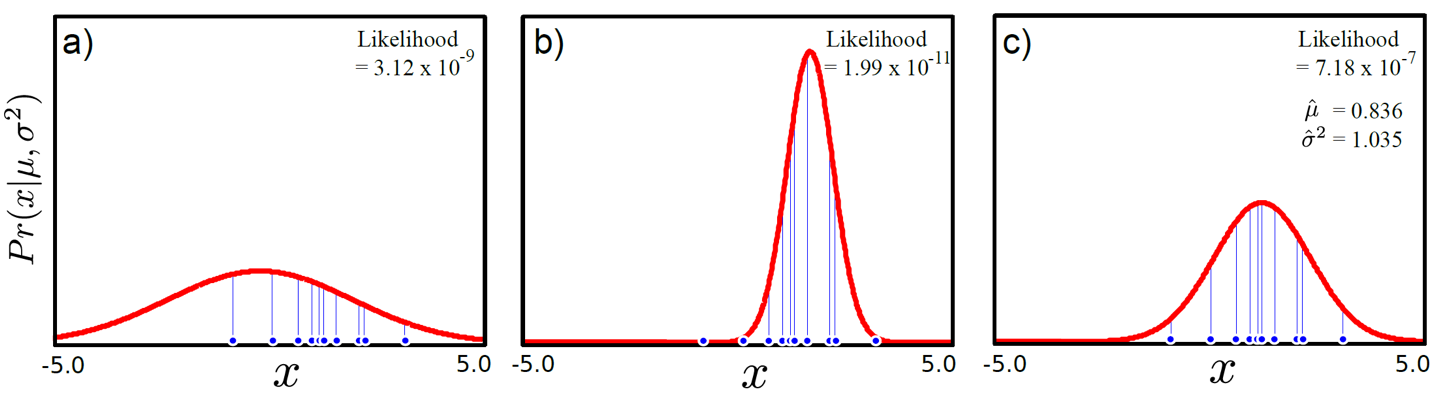 Fig.
Fig.
그 다음 fitting된 distribution으로 부터 action sequence를 더 뽑습니다. 당연히 더 likely 한 sequence가 많이 뽑히겠죠?
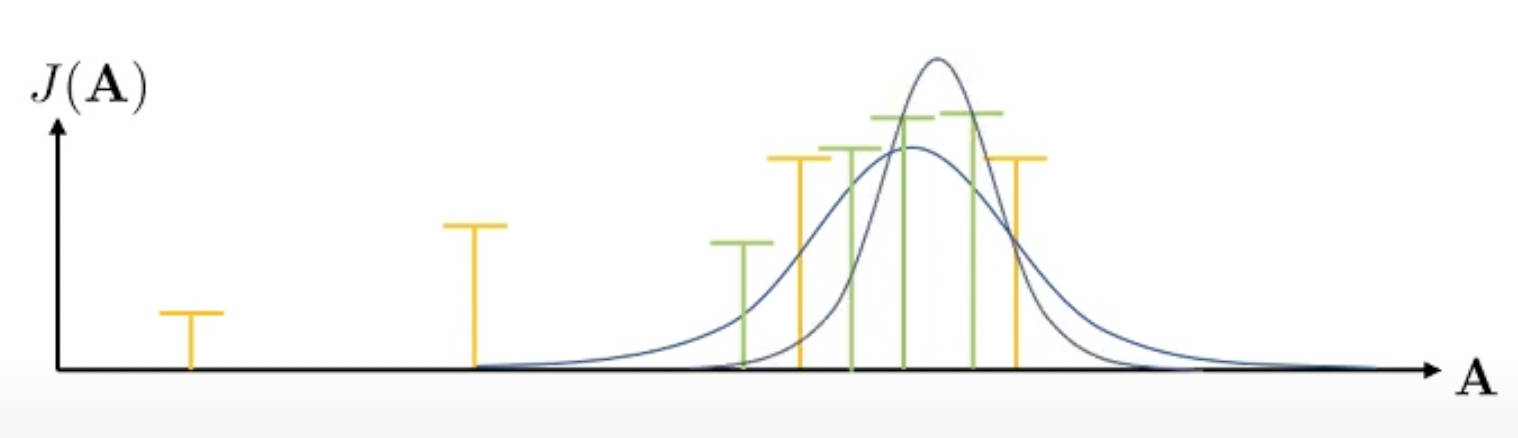 Fig.
Fig.
이제 또 이에 맞는 distribution을 구합니다. 이를 반복하는 것이 CEM 입니다.
 Slide. 15.
Slide. 15.
CEM의 장점은 매우 단순하며 parallization 되었다면 매우 빠르게 수행할 수 있는 것이라고 하는데, 당연히 성능은 뭐 별로 안좋겠지만 Sergey는 이론적으로는 optimal set을 구할 수 있다고 얘기하는 것 같습니다. 단점으로는 action space가 크면 아무래도 search space가 너무 크기때문에 문제가 될 것이고 (전혀 수렴하지 못하거나), open loop planning만을 위한 algorithm 이라는 겁니다.
 Slide. 16.
Slide. 16.
 Fig.
Fig.
 Fig.
Fig.
Monte Carlo Tree Search (MCTS)
 Slide. 17.
Slide. 17.
 Fig.
Fig.
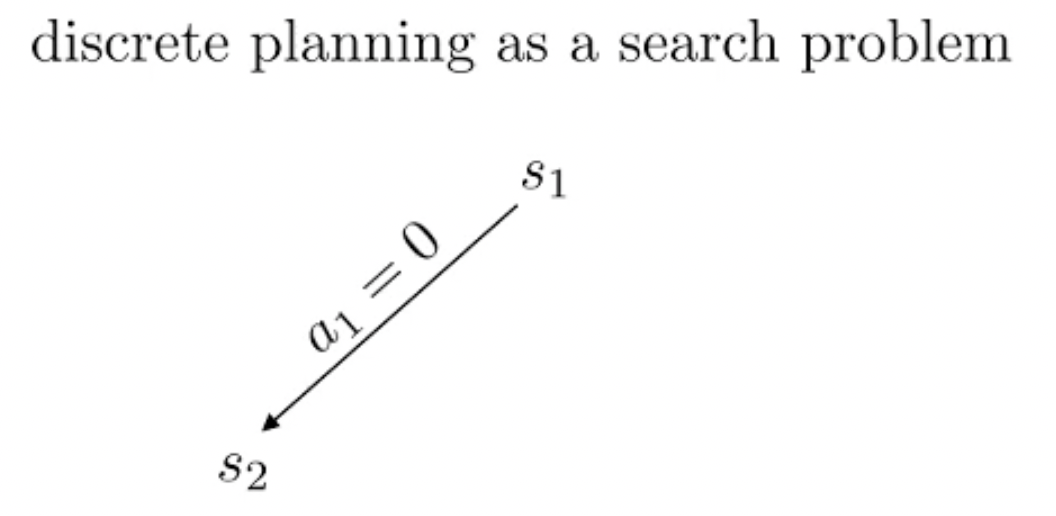 Fig.
Fig.
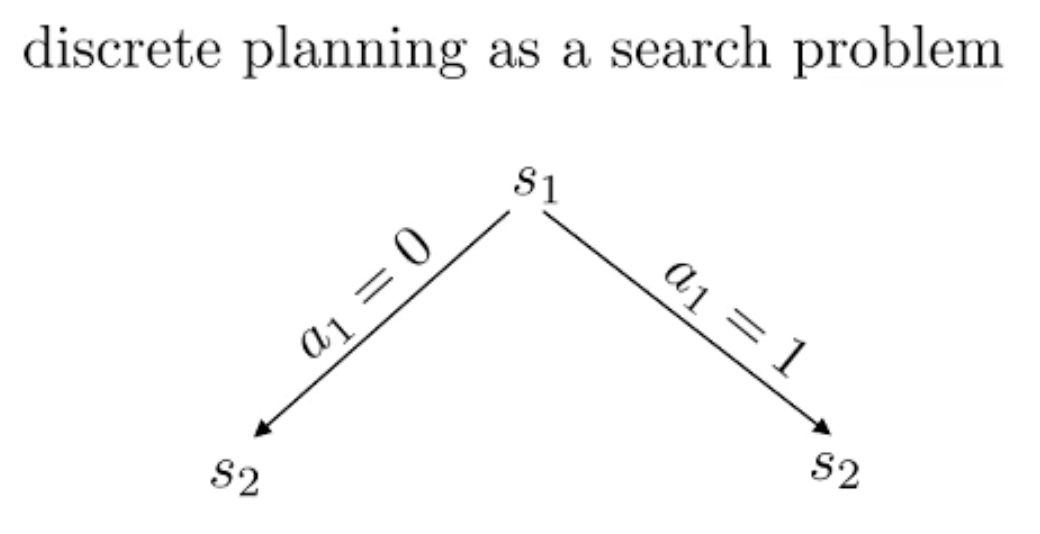 Fig.
Fig.
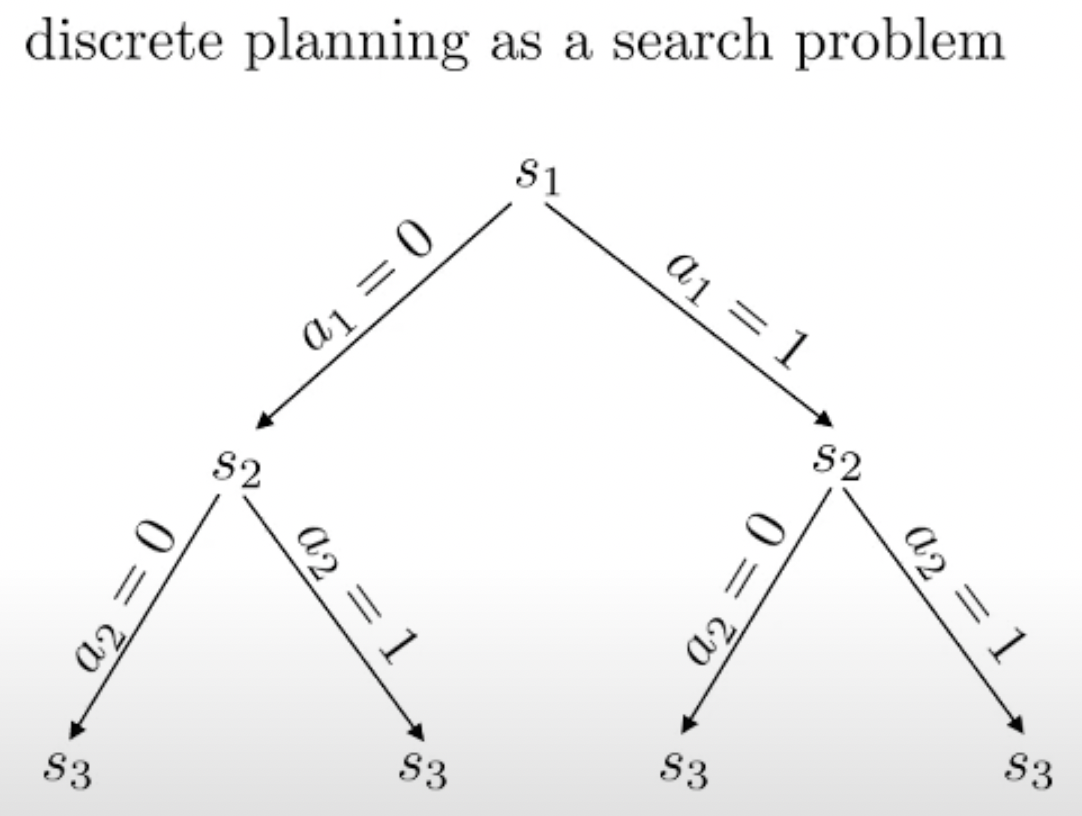 Fig.
Fig.
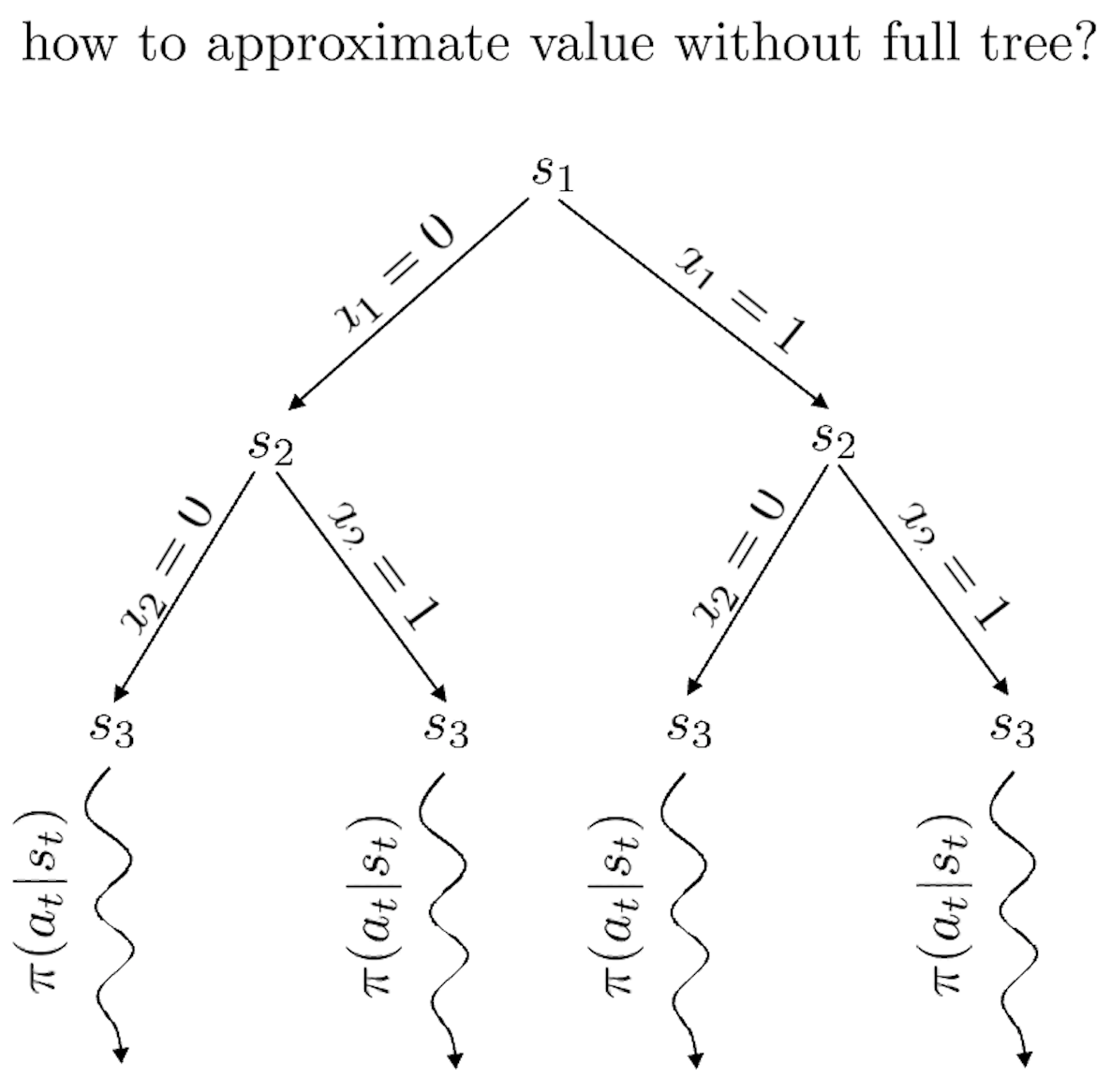 Fig.
Fig.
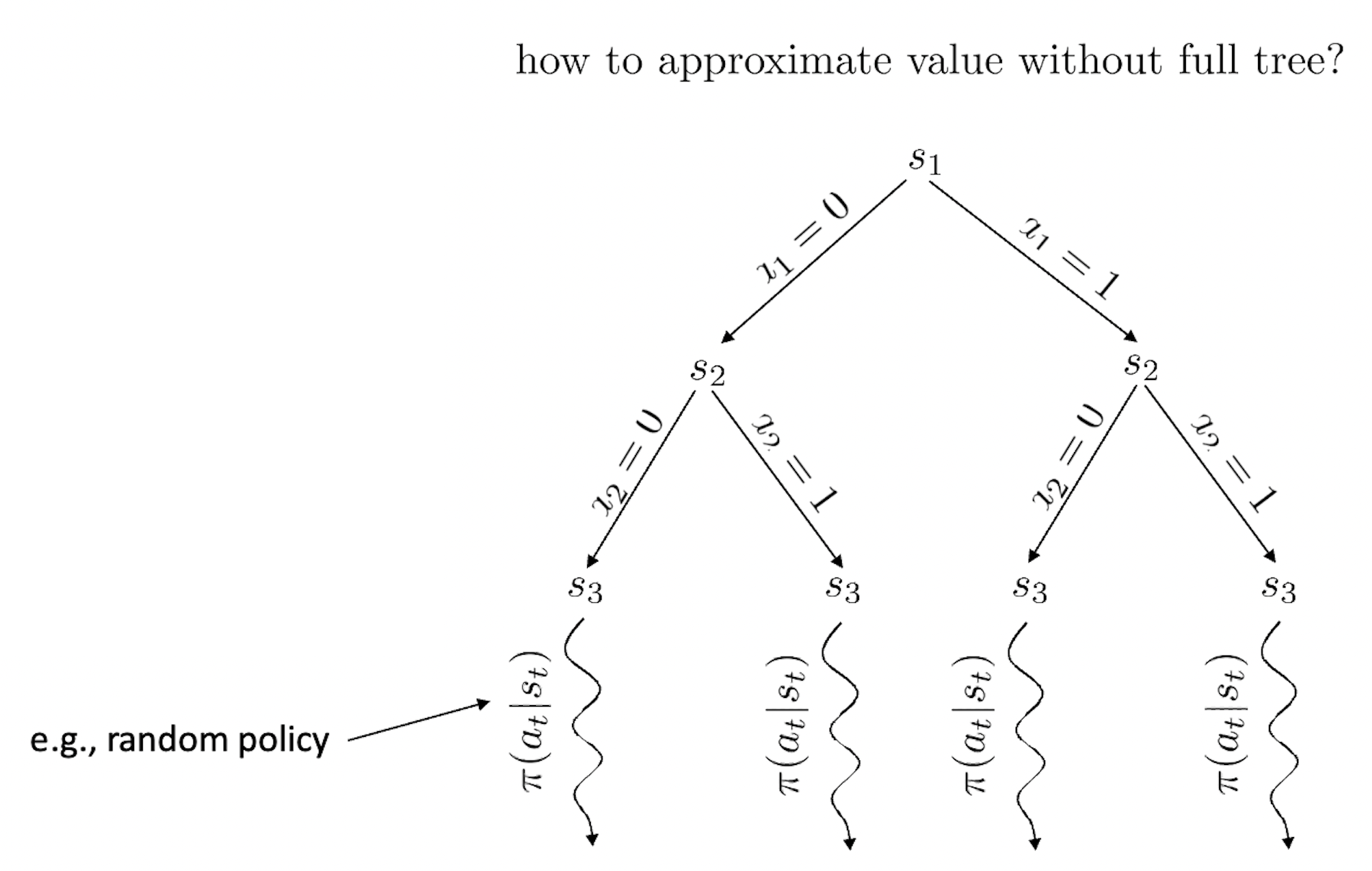 Fig.
Fig.
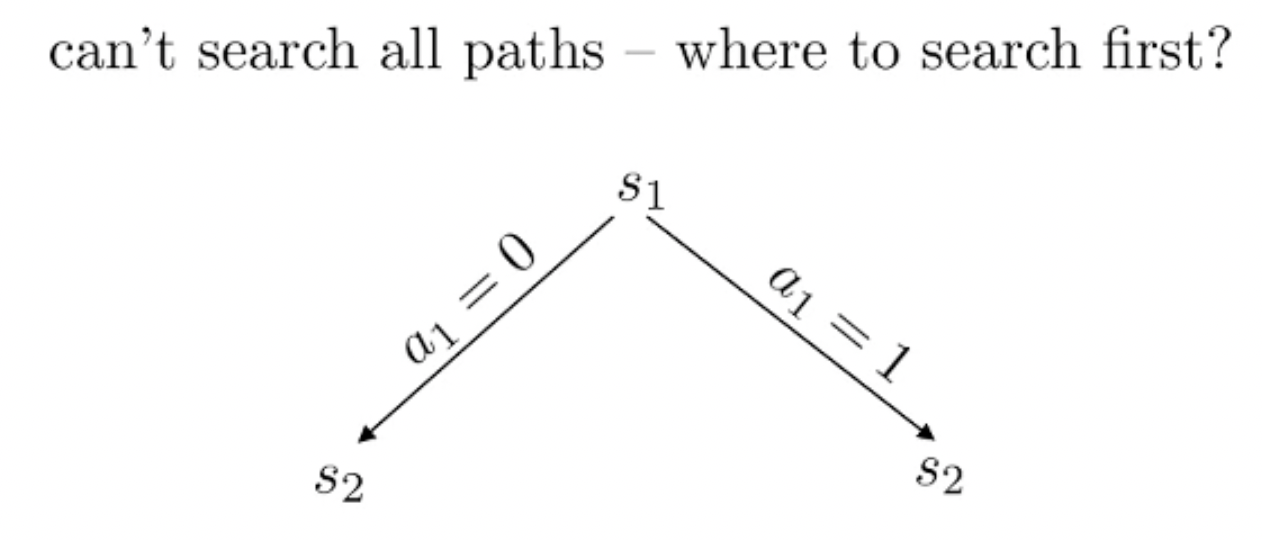 Fig.
Fig.
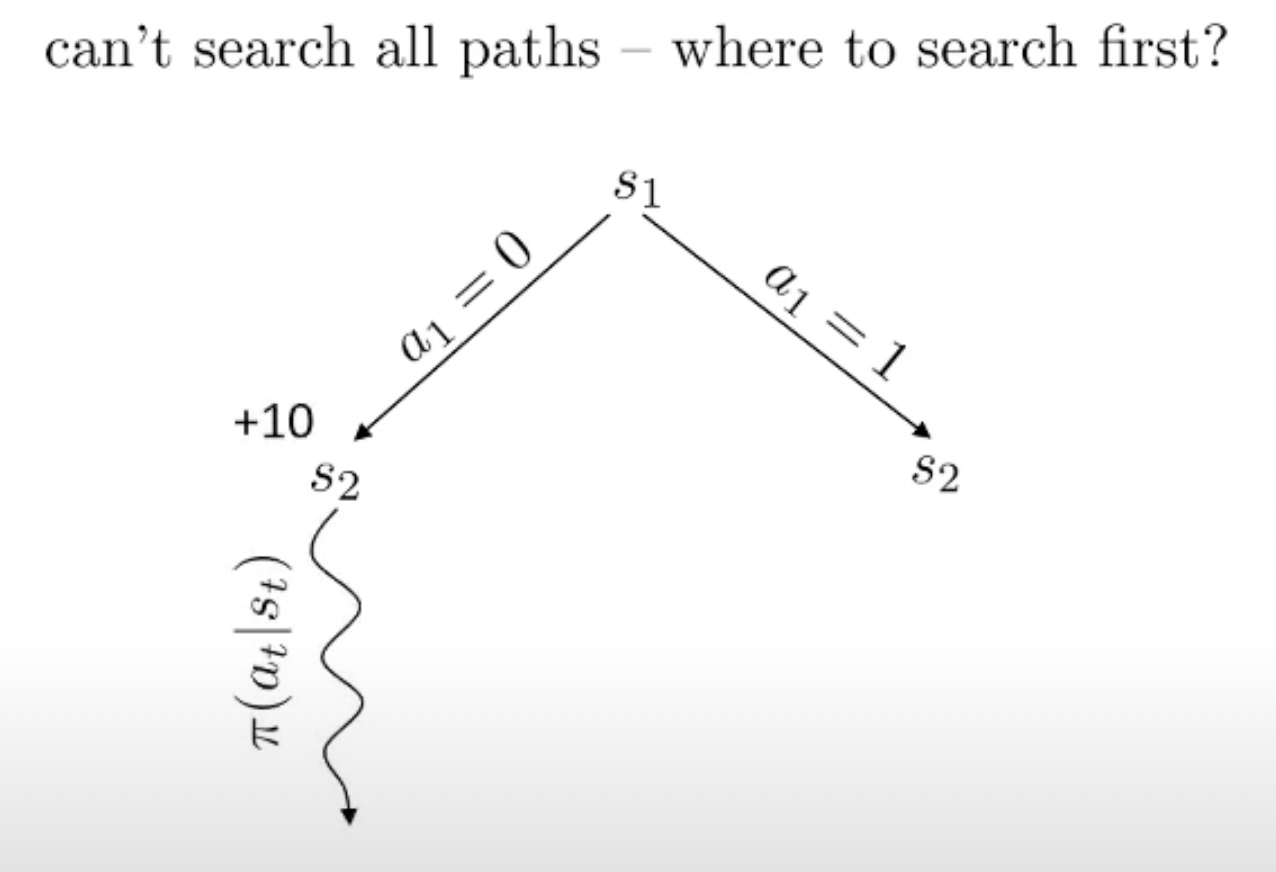 Fig.
Fig.
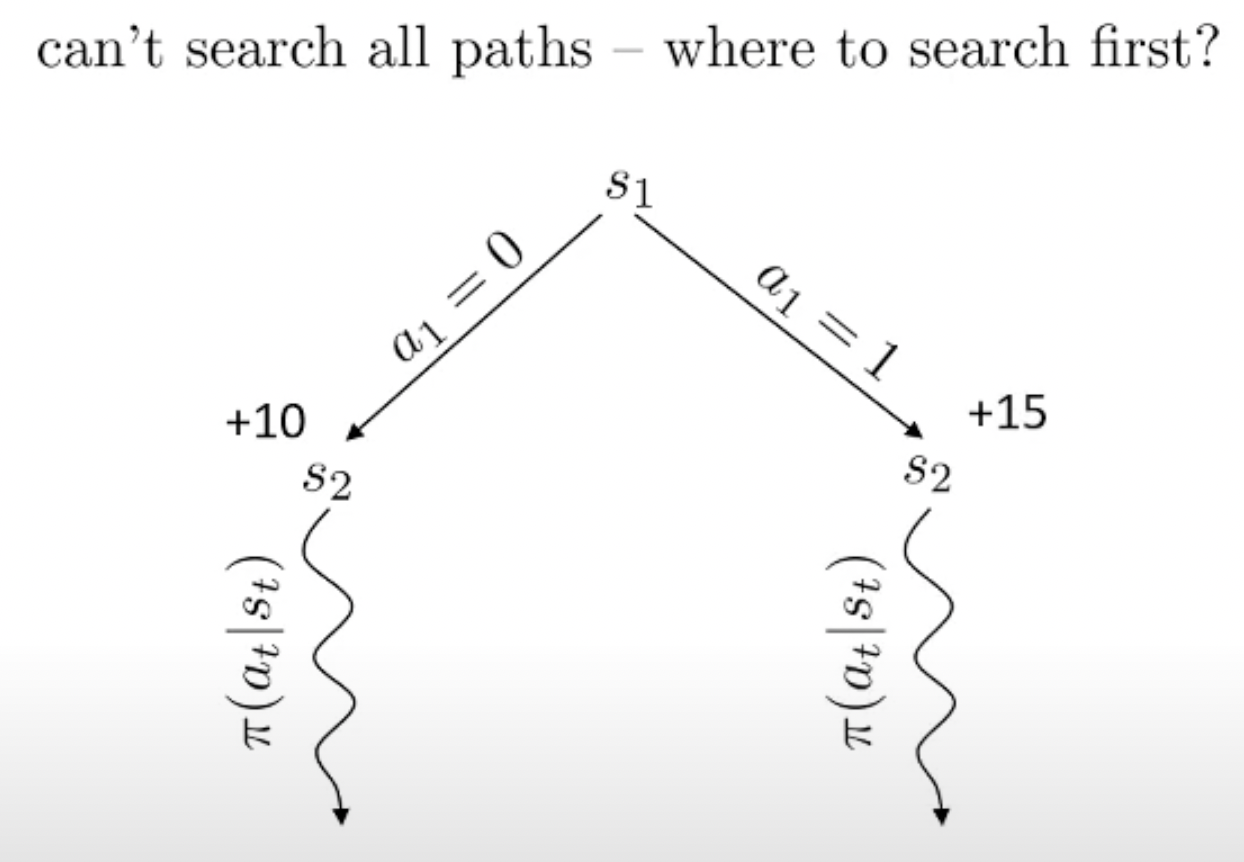 Fig.
Fig.
 Slide. 20.
Slide. 20.
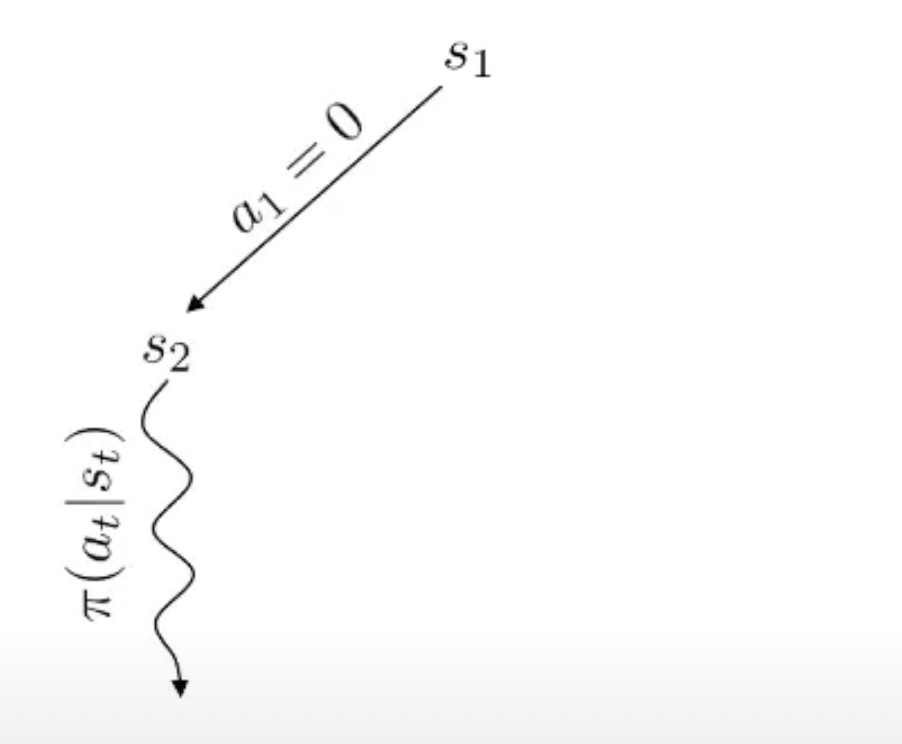 Fig.
Fig.
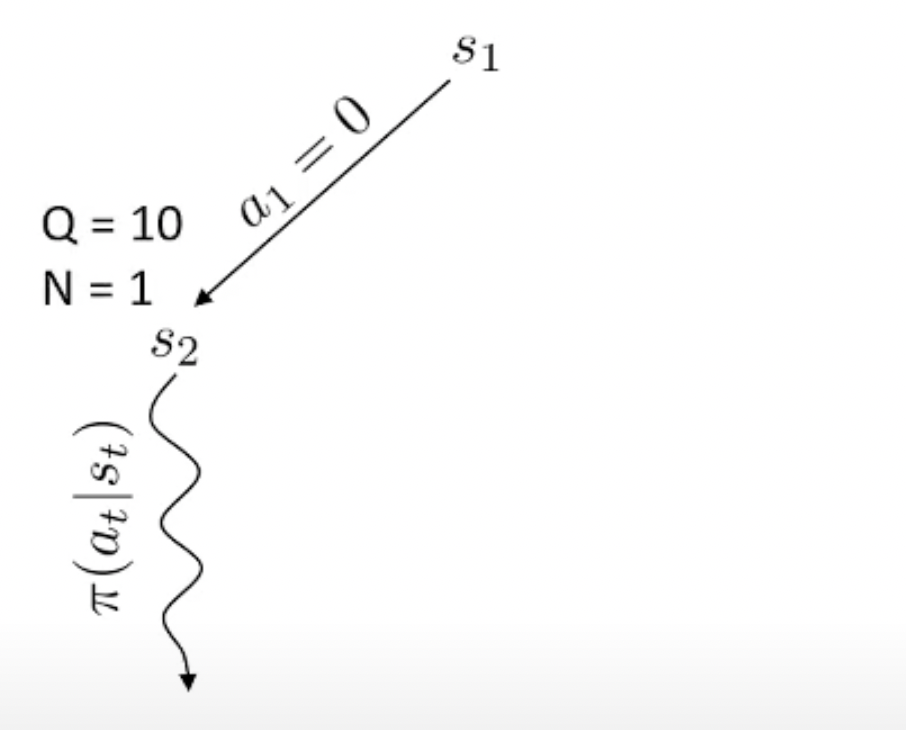 Fig.
Fig.
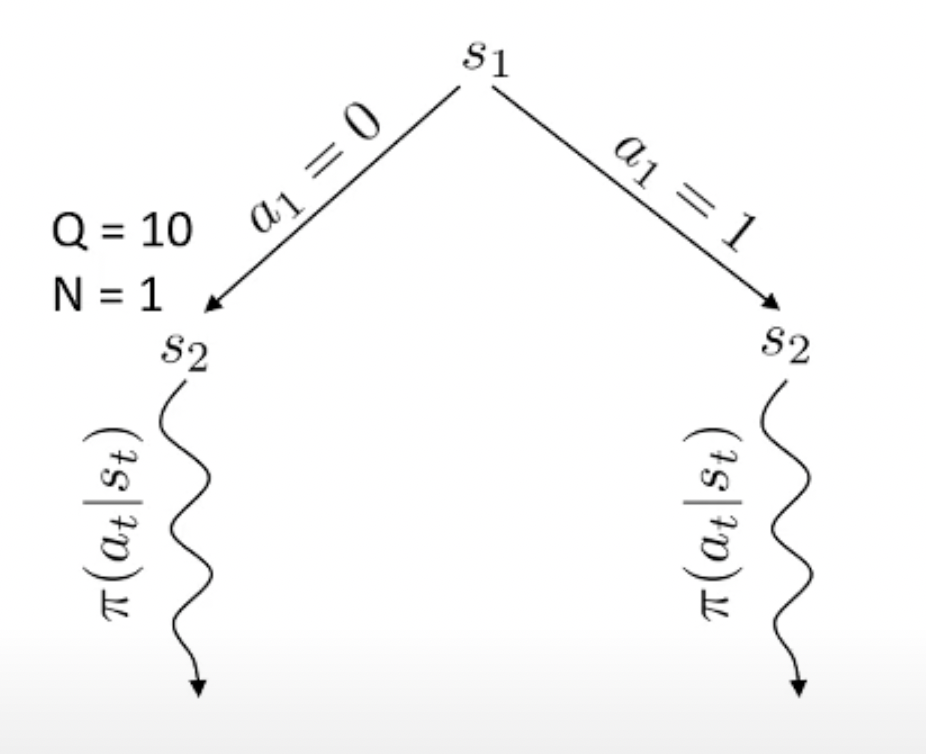 Fig.
Fig.
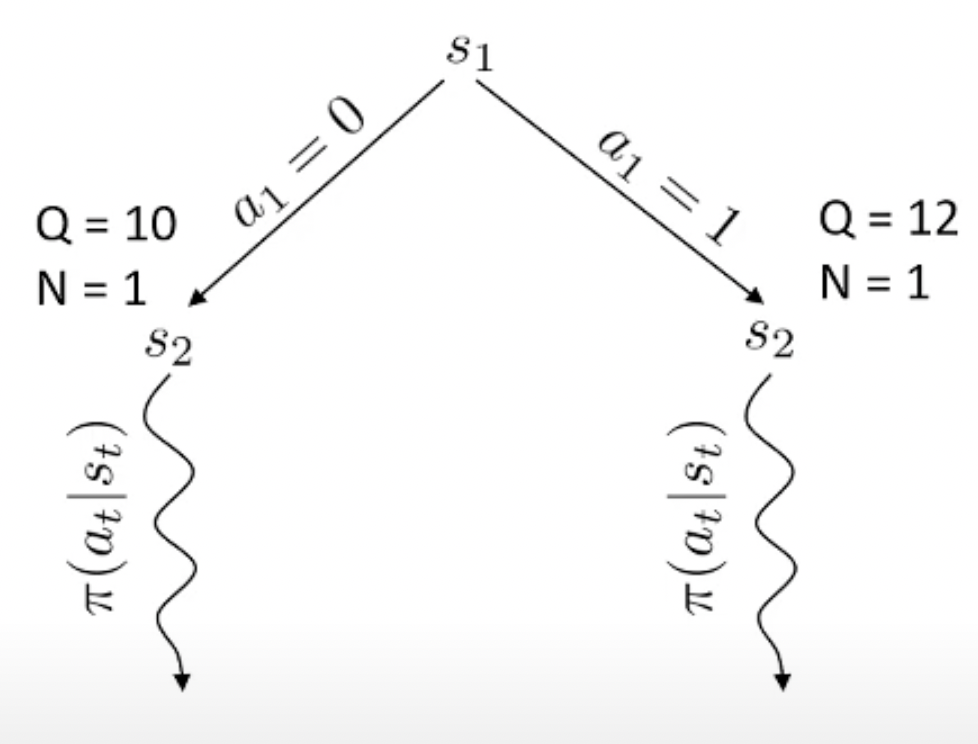 Fig.
Fig.
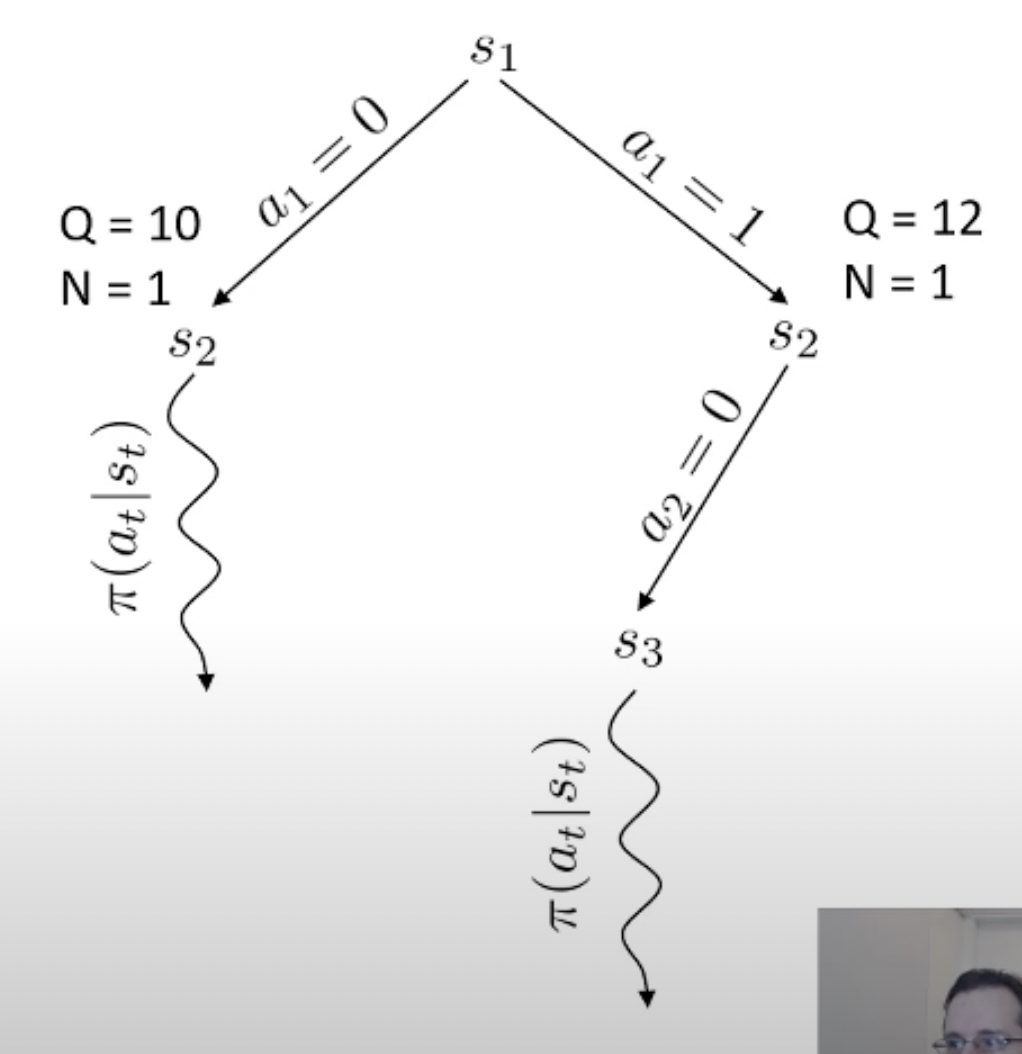 Fig.
Fig.
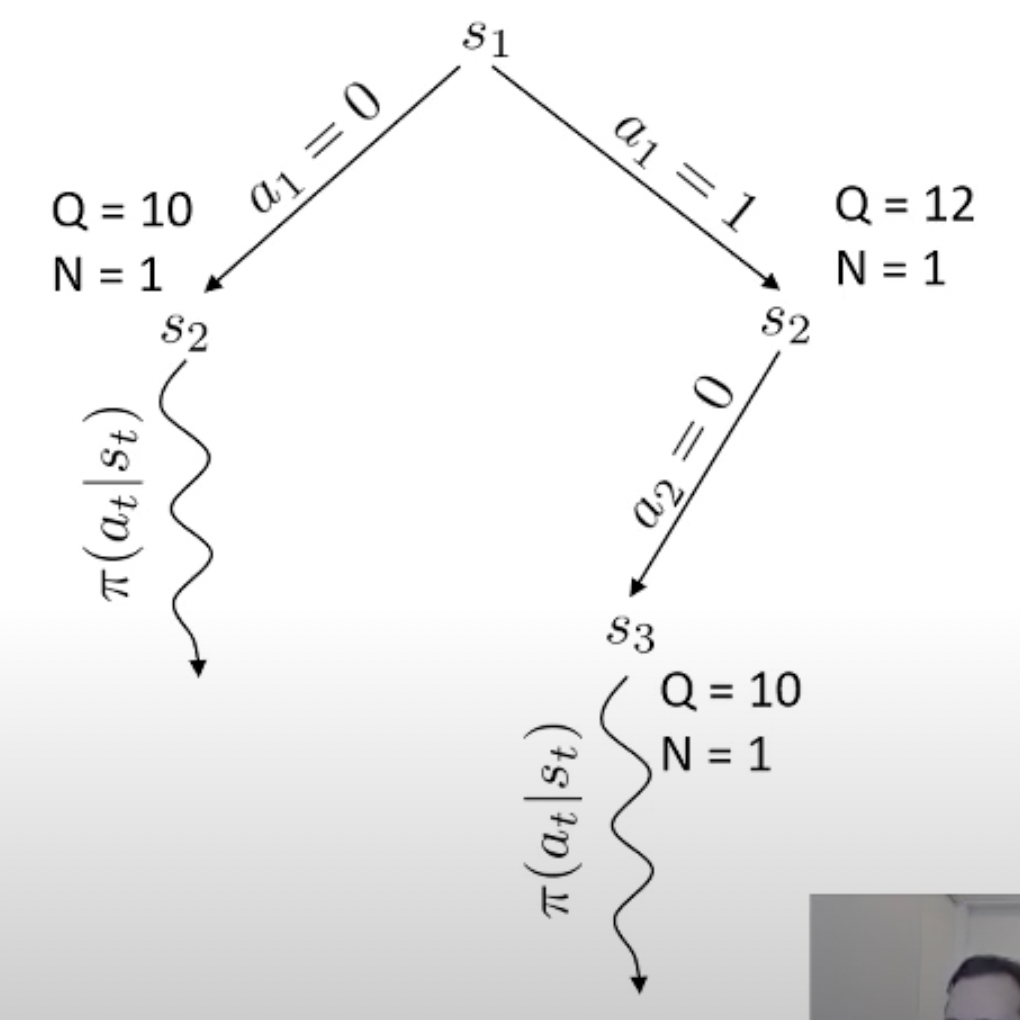 Fig.
Fig.
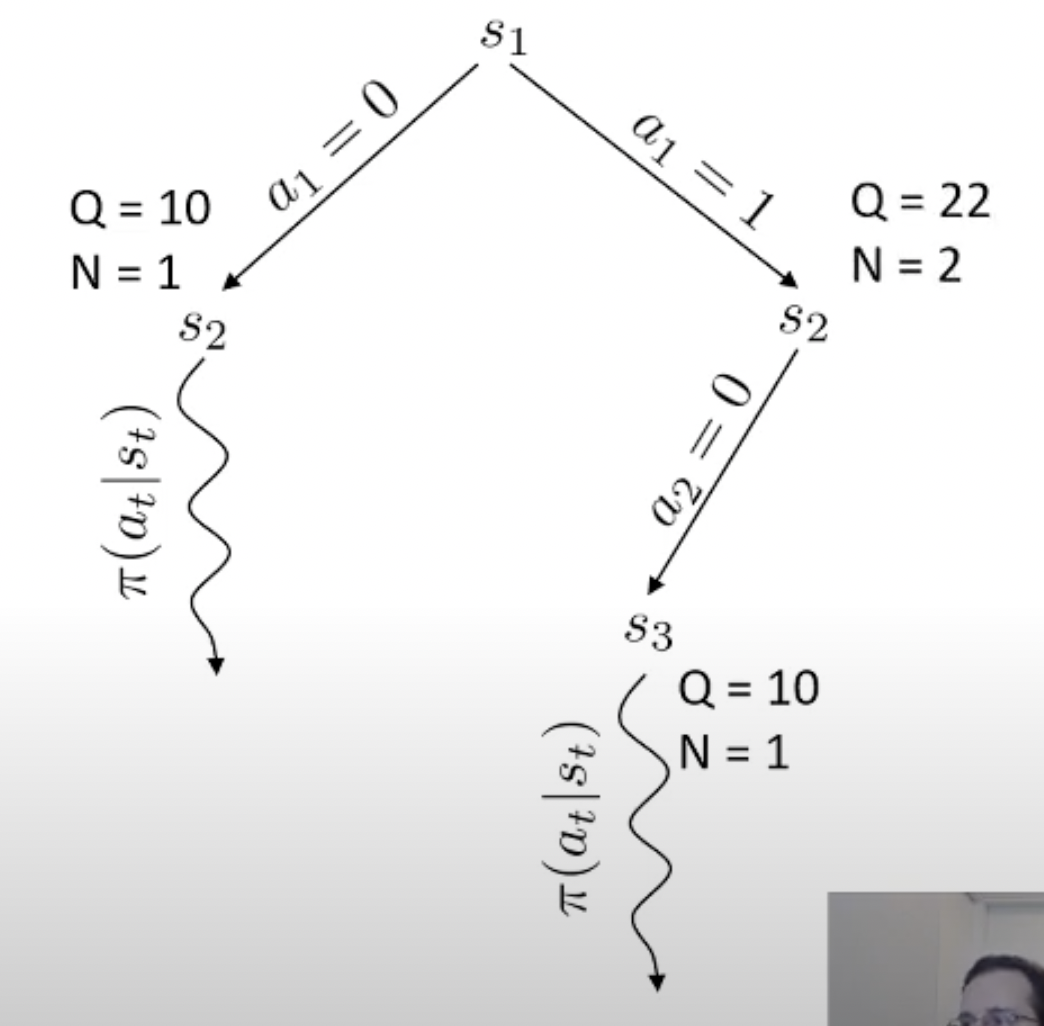 Fig.
Fig.
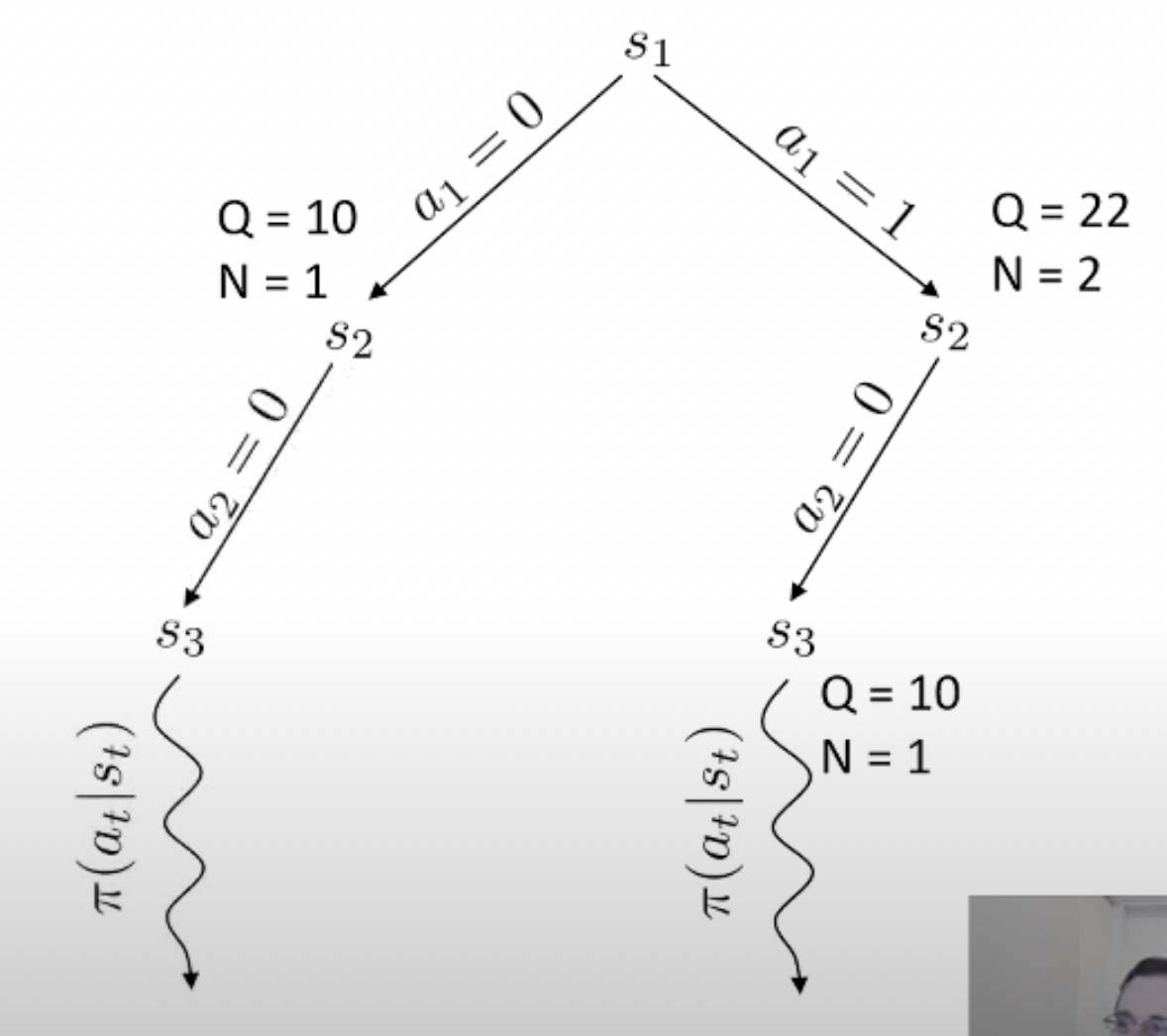 Fig.
Fig.
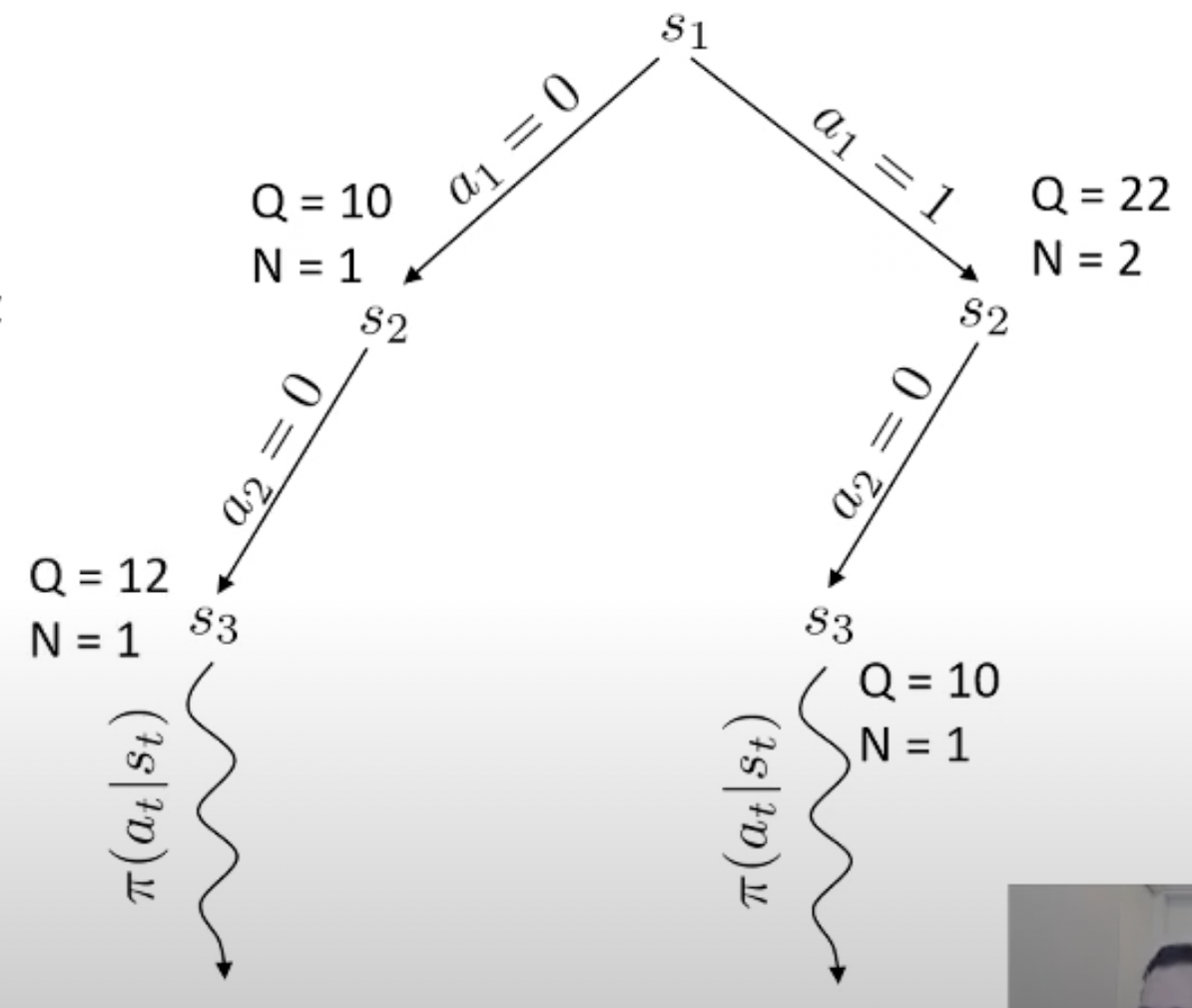 Fig.
Fig.
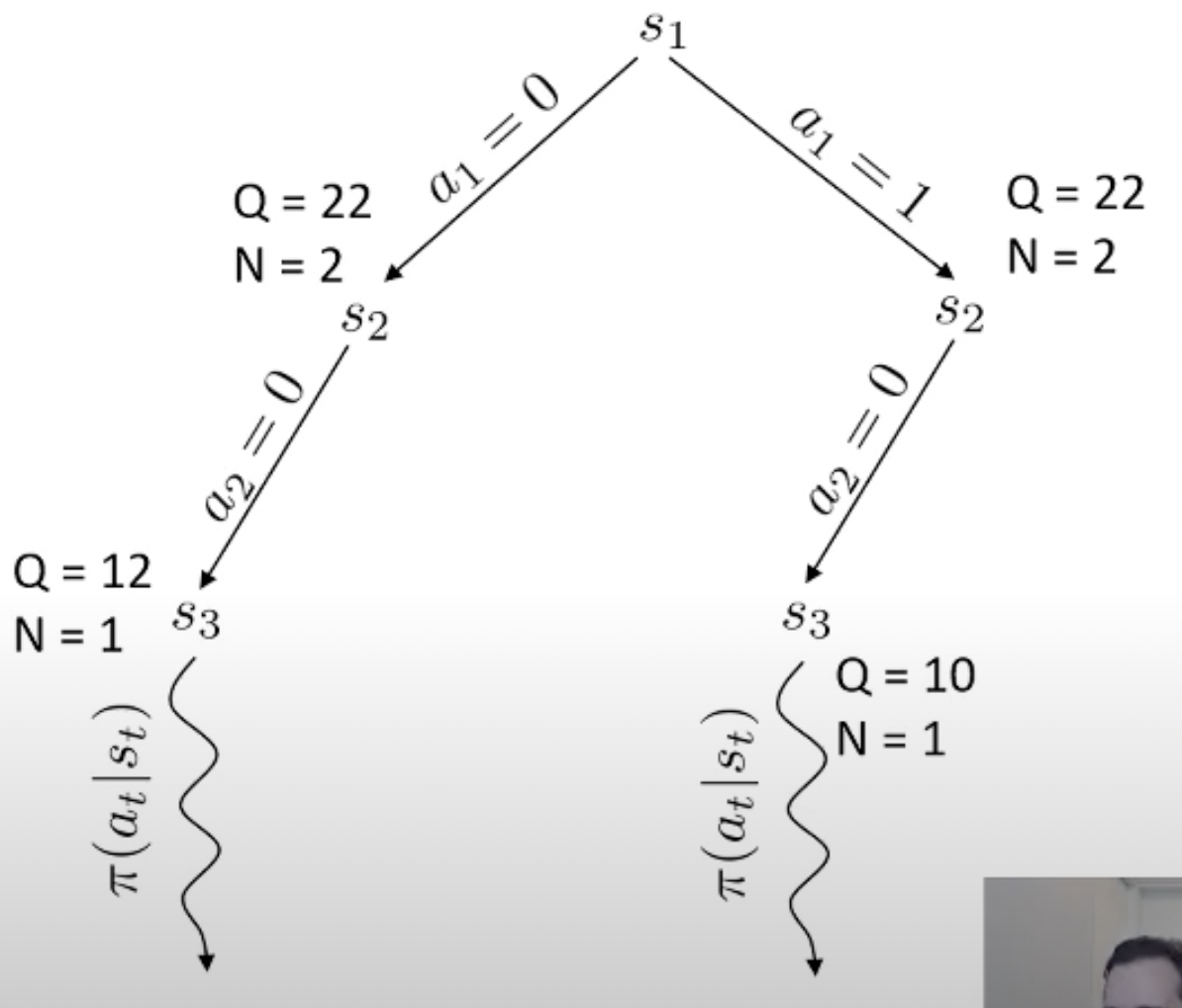 Fig.
Fig.
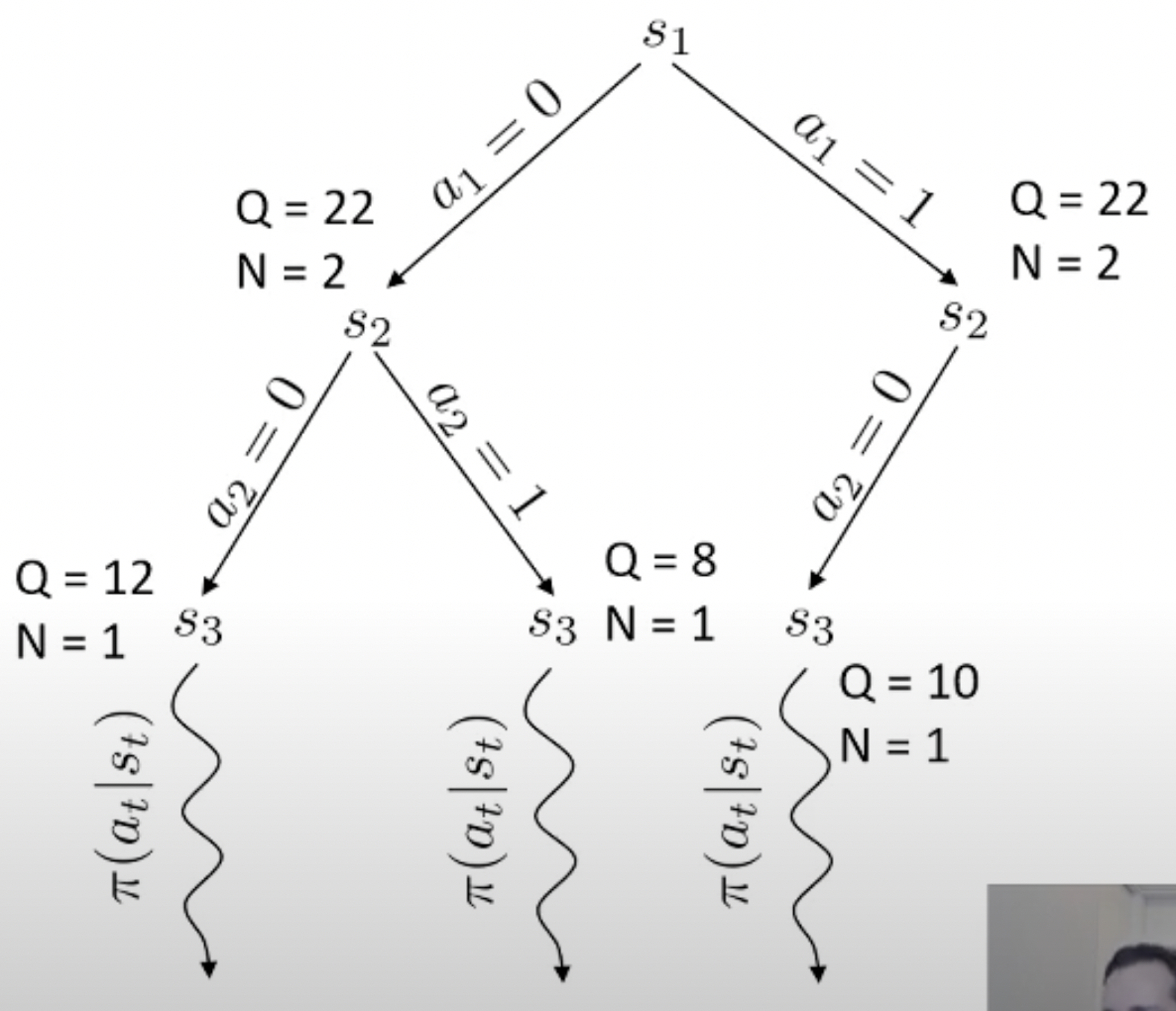 Fig.
Fig.
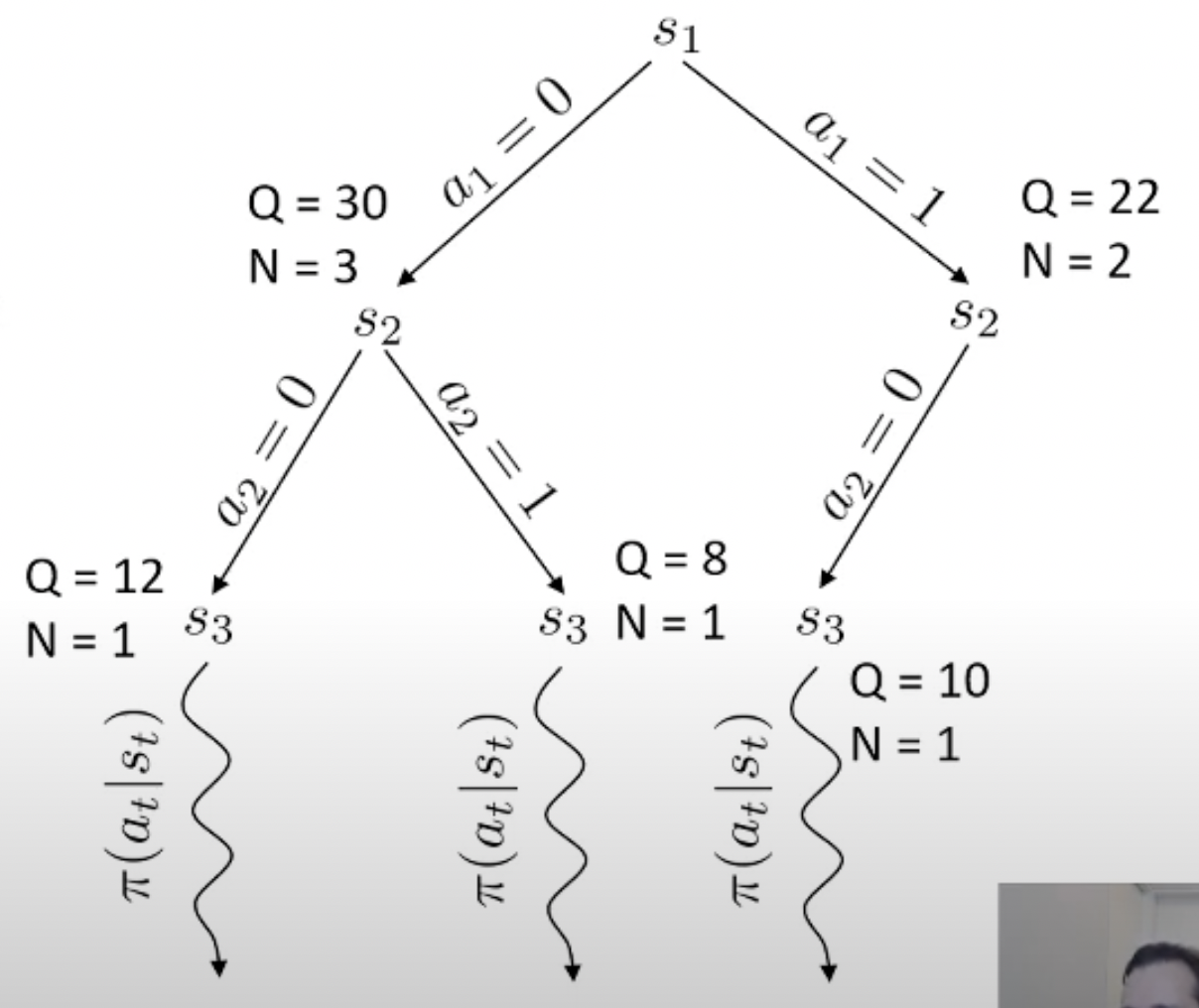 Fig.
Fig.
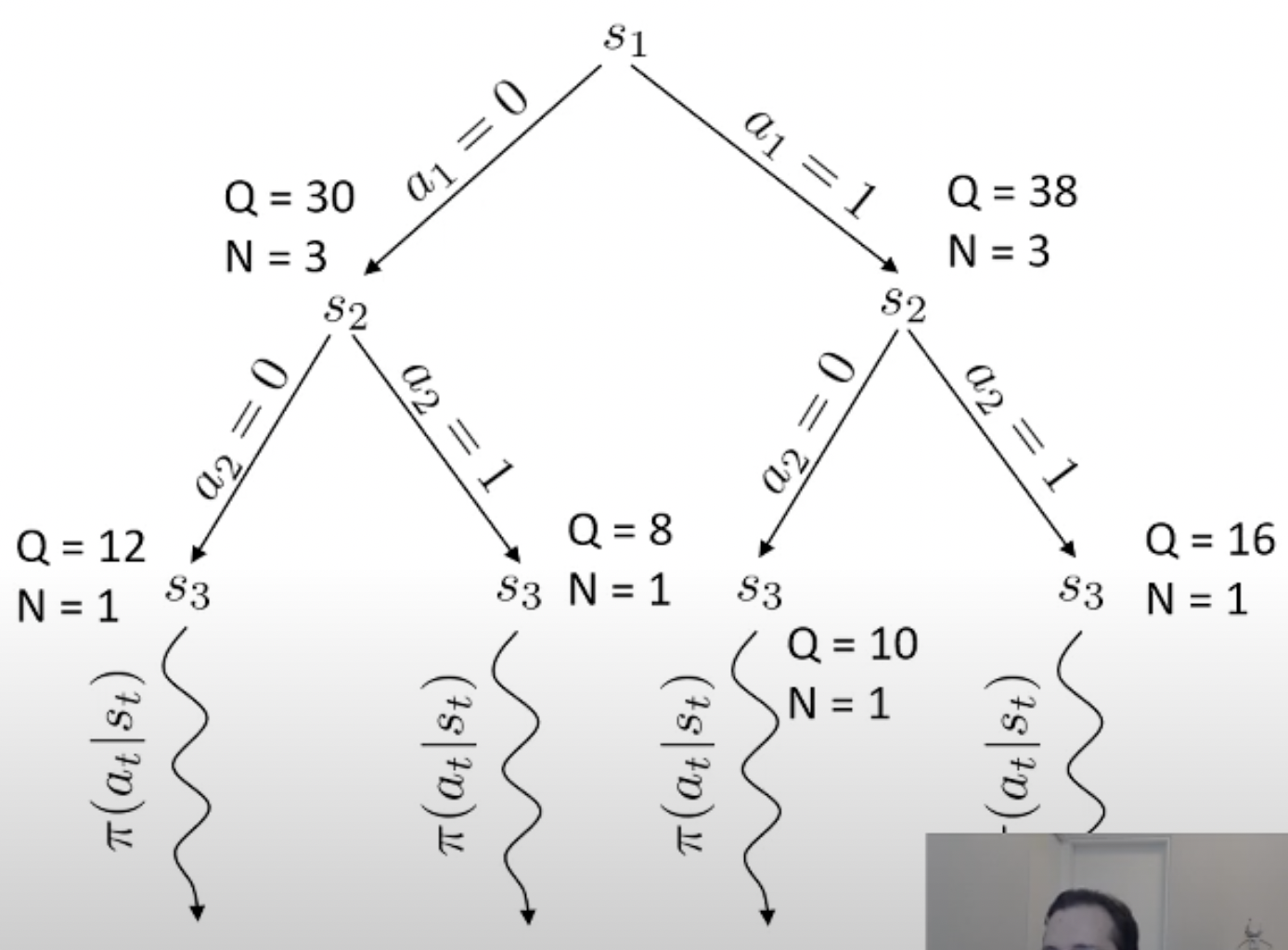 Fig.
Fig.
 Slide. 21.
Slide. 21.
Trajectory Optimization with Derivatives
 Slide. 23.
Slide. 23.
 Slide. 24.
Slide. 24.
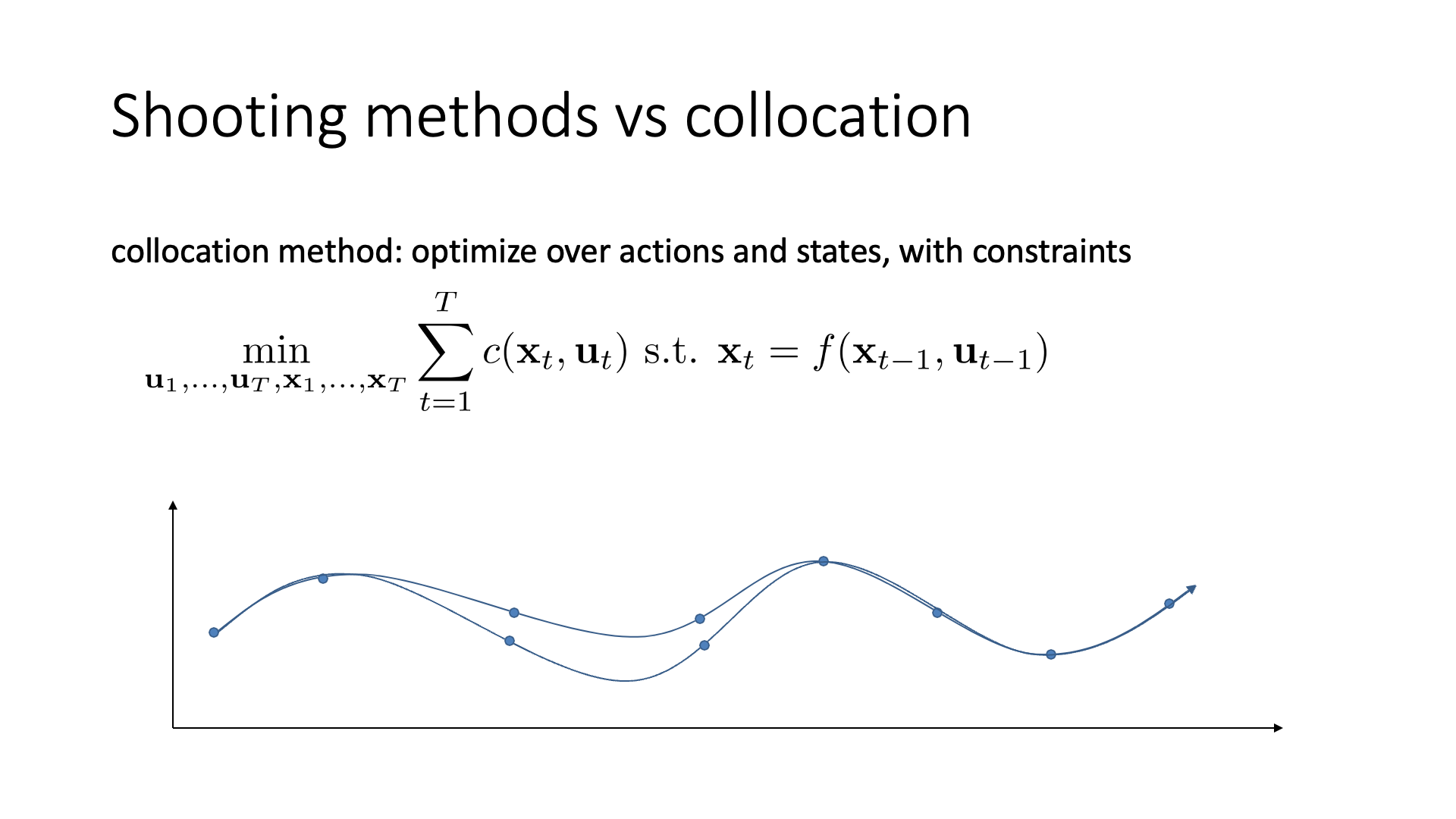 Slide. 25.
Slide. 25.
Linear Case : LQR
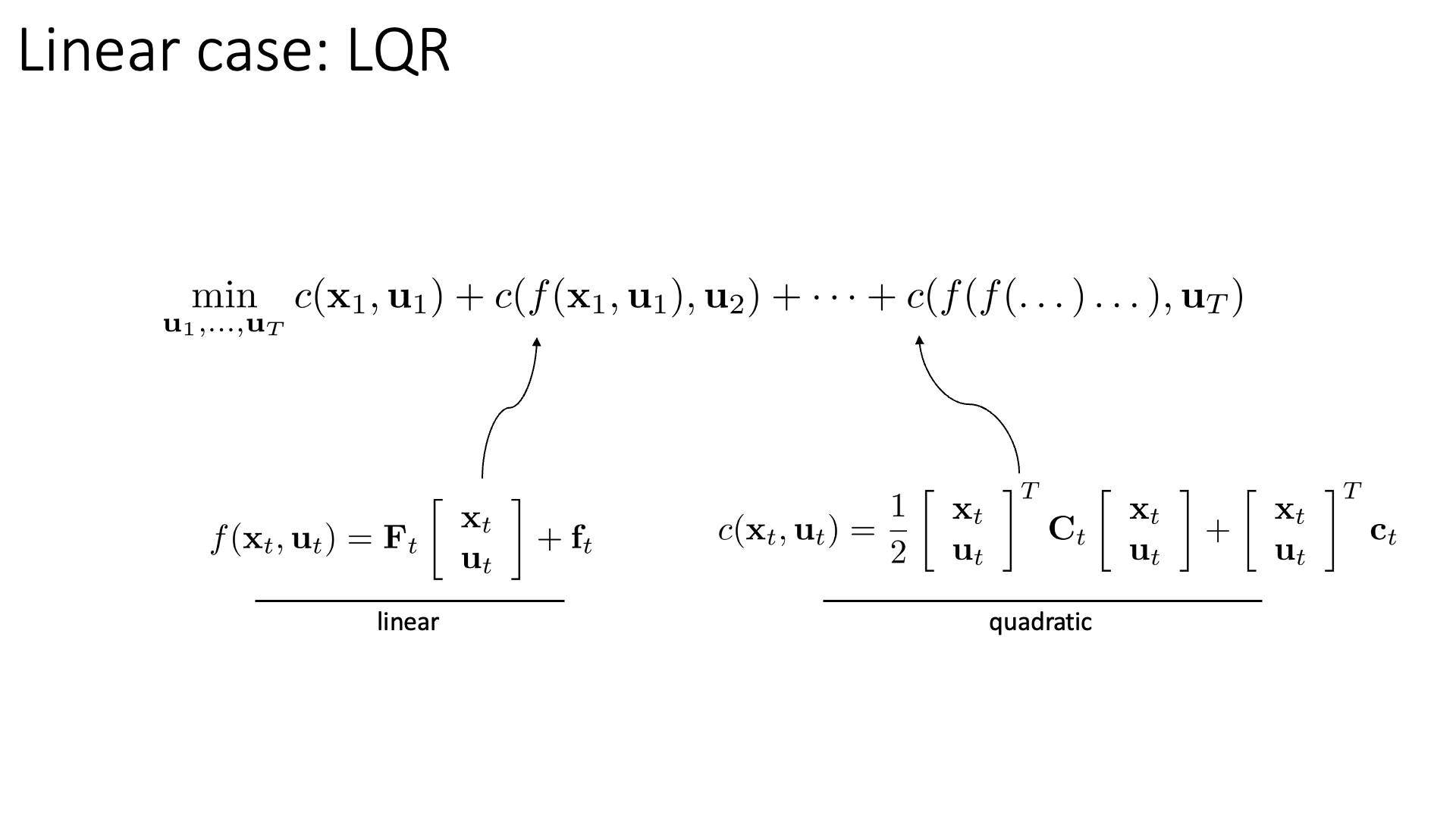 Slide. 26.
Slide. 26.
 Slide. 27.
Slide. 27.
 Slide. 28.
Slide. 28.
 Slide. 29.
Slide. 29.
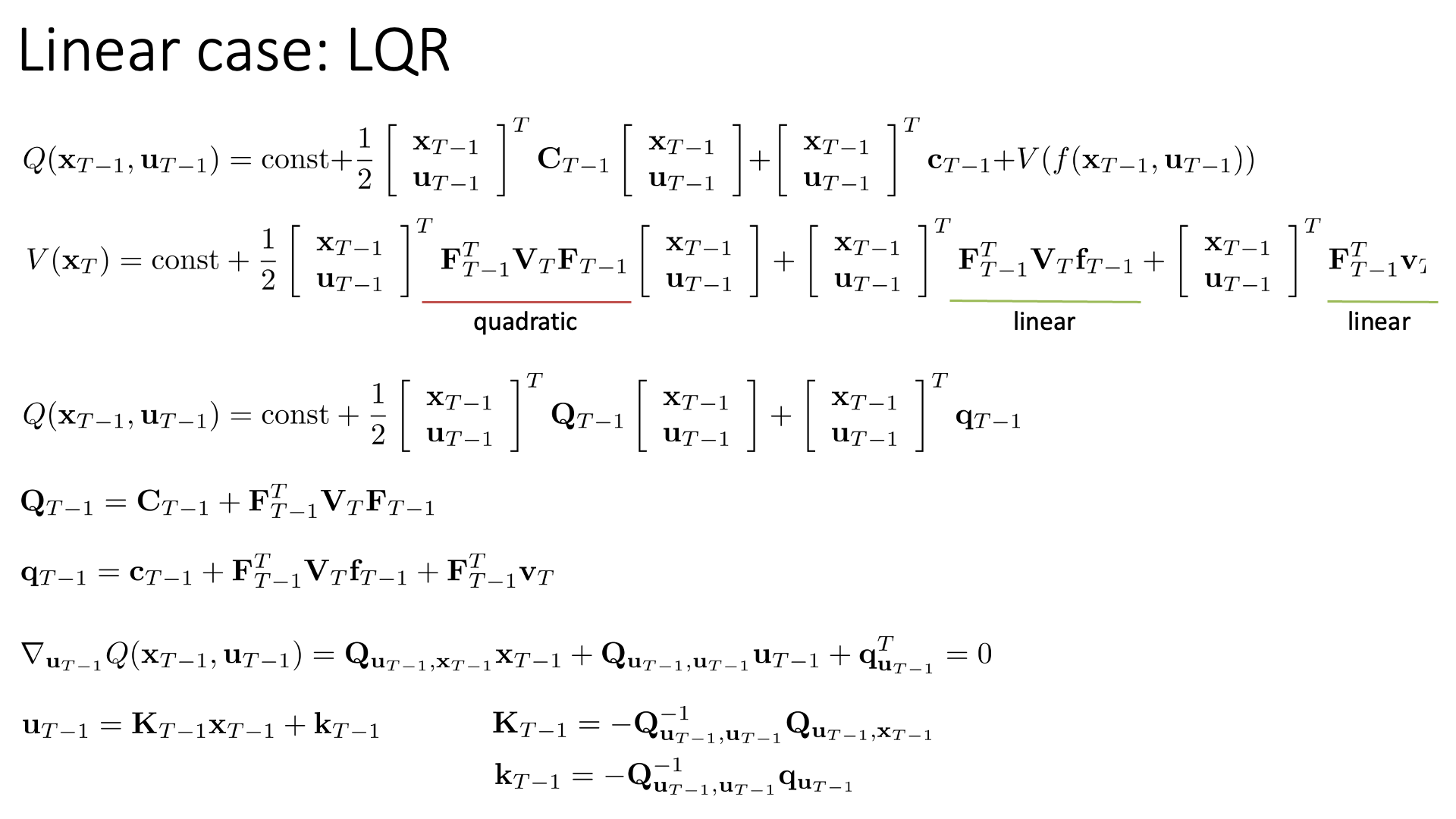 Slide. 30.
Slide. 30.
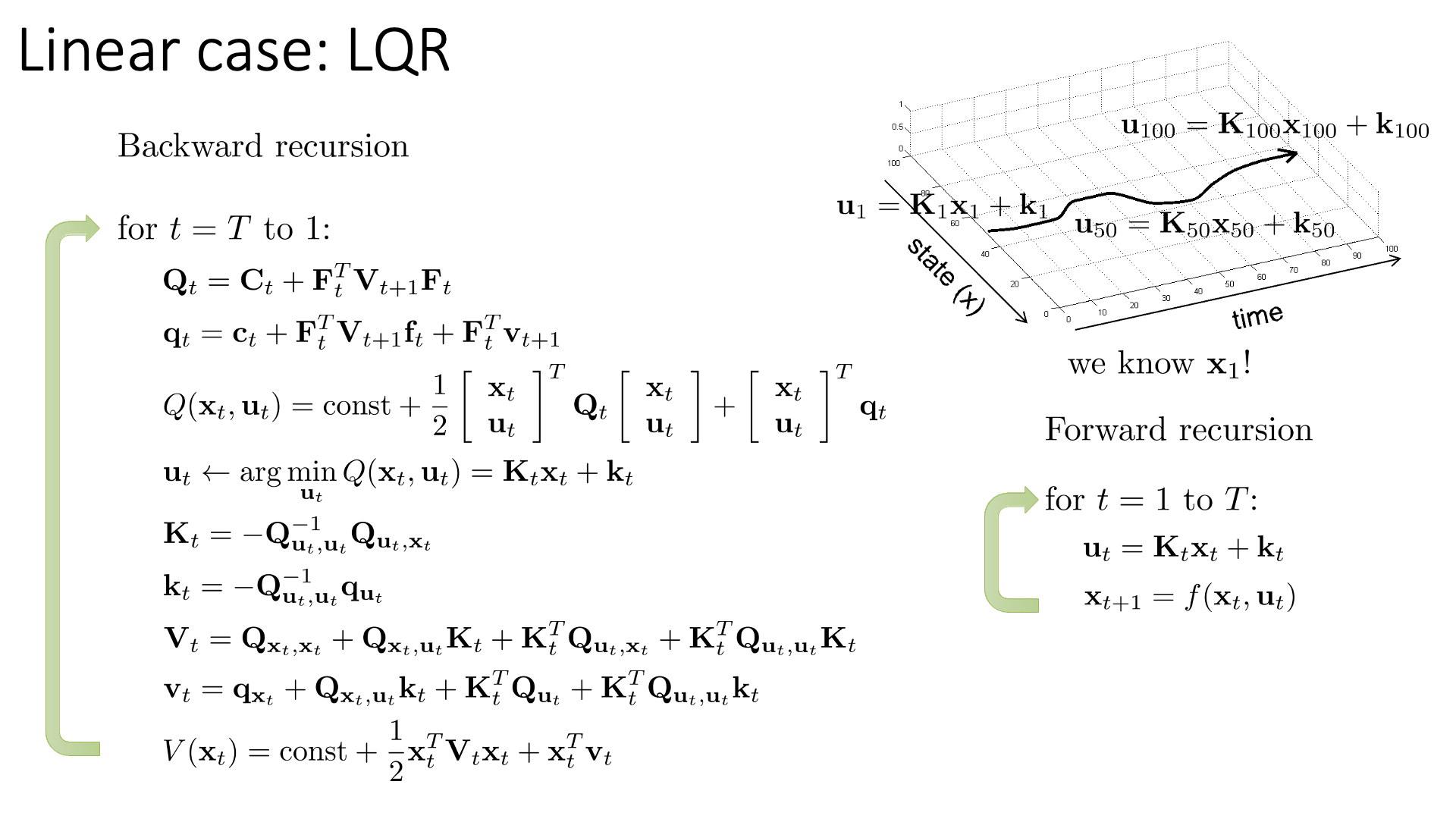 Slide. 31.
Slide. 31.
 Slide. 32.
Slide. 32.
LQR for Stochastic and Nonlinear Systems
 Slide. 34.
Slide. 34.
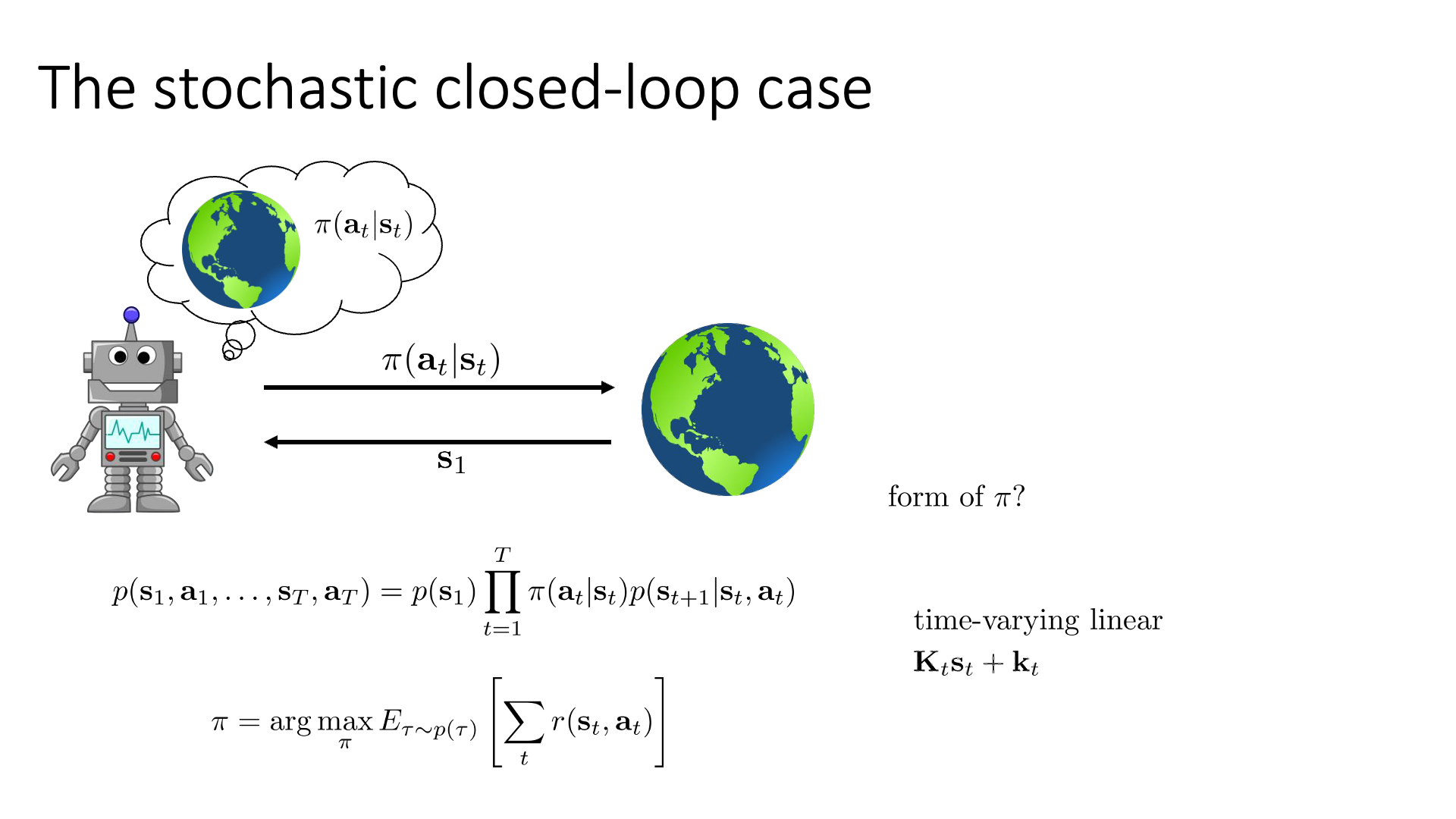 Slide. 35.
Slide. 35.
Non-Linear Case : DDP / Iterative LQR
 Slide. 36.
Slide. 36.
 Slide. 37.
Slide. 37.
 Slide. 38.
Slide. 38.
 Slide. 39.
Slide. 39.
 Slide. 40.
Slide. 40.
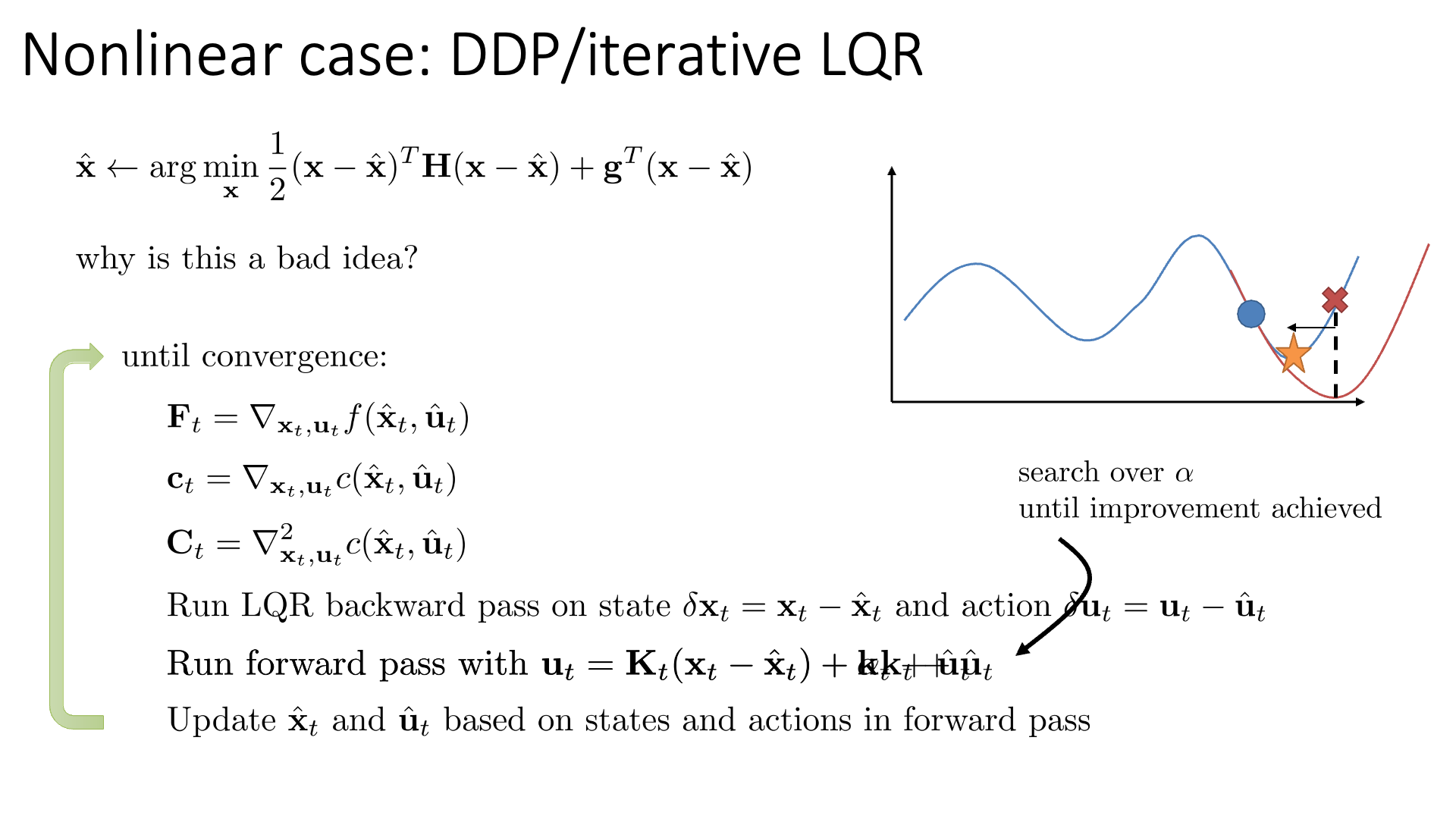 Slide. 41.
Slide. 41.
Case Study and Additional Readings
 Slide. 42.
Slide. 42.
 Slide. 43.
Slide. 43.
 Slide. 44.
Slide. 44.
 Slide. 45.
Slide. 45.
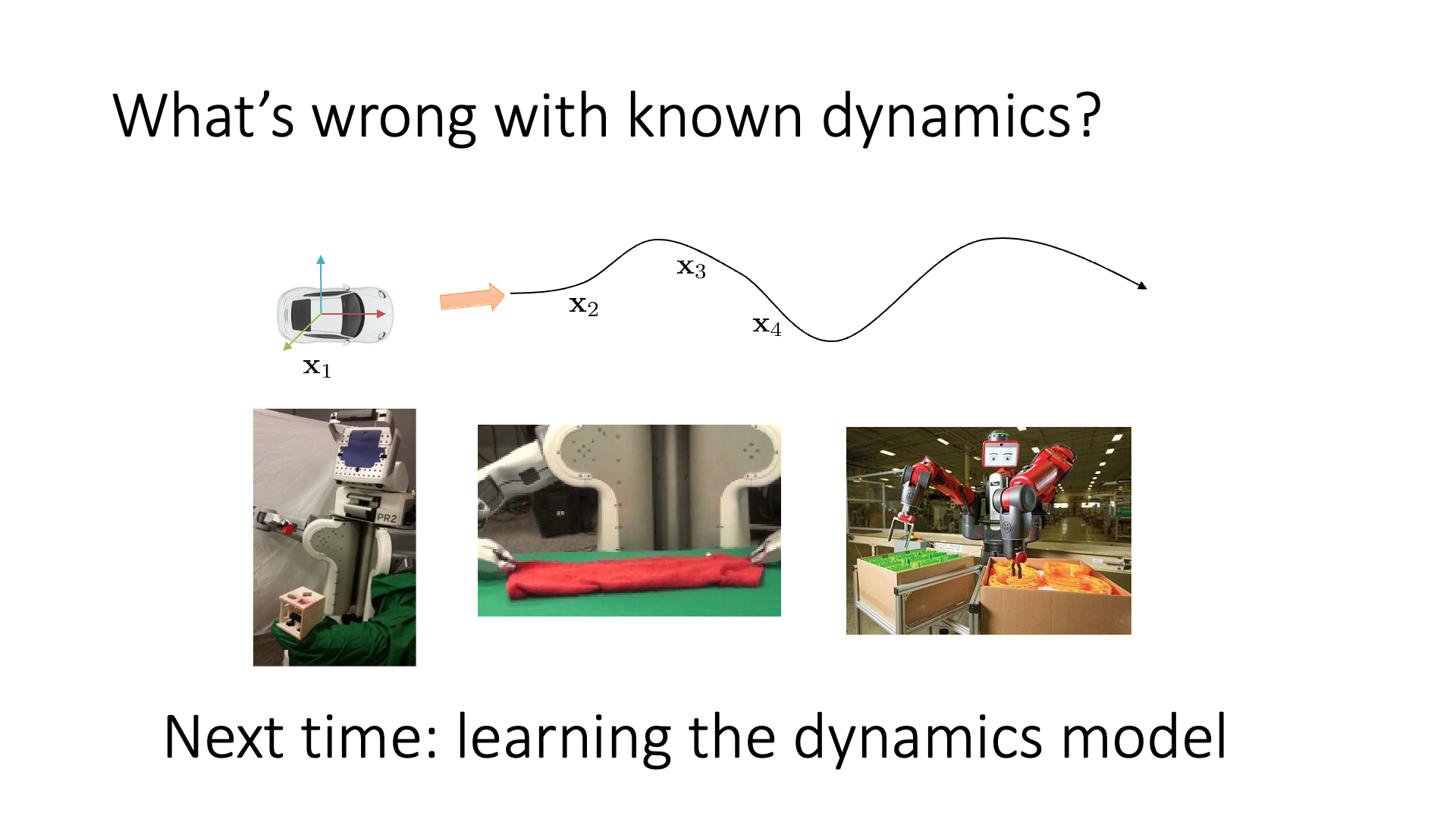 Slide. 46.
Slide. 46.
Reference
- Lectures
- CS 285 at UC Berkeley : Deep Reinforcement Learning
- Introduction to Trajectory Optimization from Matthew Kelly
- 10-703 Deep RL from Katerina Fragkiadaki
- slide for Planning, Monte Carlo Tree search
- slide for MBRL in explicit and observable low-dimensional state spaces
- slide for MBRL from sensory input, planning in sensory space, planning in a latent state space
- slide for MBRL (cont.) Stochastic latent dynamics models
- slide for AlphaGo, AlphaGoZero, AlphaZero
- Papers
- Deep Learning for Real-Time Atari Game Play Using Offline Monte-Carlo Tree Search Planning
- (AlphaGo) Mastering the game of Go with deep neural networks and tree search
- (AlphaGo Zero) Mastering the game of Go without human knowledge
- (AlphaZero) Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm
- (MuZero) Mastering Atari, Go, Chess and Shogi by Planning with a Learned Model
- Others