(WIP) (CS285) Lecture 20 - Inverse Reinforcement Learning

이 글은 UC Berkeley 의 교수, Sergey Levine 의 심층 강화 학습 (Deep Reinforcement Learning) 강의인 CS285를 듣고 작성한 글 입니다.

Lecture 20의 강의 영상과 자료는 아래에서 확인하실 수 있습니다.

• Fall 2020 ver.
  • Lecture Video Link (Youtube)
  • Lecture Slide Link 1

< 목차 >

• Introduction (Motivation)
• Why Inverse Reinforcement Learning?
  • The Imitation Learning Perspective
  • The Reinforcement Learning Perspective
  • So, Why IRL is good?
  • Formal Definition of IRL Problem
  • Feature Matching IRL
• Learning the Reward Function
  • Maximum Entropy IRL (MaxEnt IRL) ver 1
  • Maximum Entropy IRL (MaxEnt IRL) ver 2
• Approximations in High Dimensions
• IRL and GANs
  • Generative Adversarial Imitation Learning (GAIL)
• Suggested Reading Papers on IRL
• Reference

Introduction (Motivation)

Lecture 20의 주제는 Inverse Reinforcement Learning (IRL)입니다.

Slide. 1.

IRL의 역사는 굉장히 오래됐는데, Stanford University의 교수이자 Google Brain의 founding member인 Andrew Ng과 Berkeley의 교수이며 마찬가지로 ML업계의 living legend인 Stuart Russell이 거의 처음 제안한 방법론입니다.

Fig. IRL관련 자료들. Source from CS294-190

여태까지 우리가 policy를 학습하기 위해서 reward function이 정의되었다면 IRL은 reward function을 given data로부터 학습합니다. 그리고나서 policy나 value function을 학습하는 것이죠. 왜 사람이 직접 만든 (hand designed) reward function을 기준으로 policy를 하지 않는걸까요? 그 이유는 reward function는 잘 정의하는 것 자체만으로 상당히 어려운 일일 수 있기 때문입니다. Reward design에 따라서 학습 자체가 의도한 대로 되지 않을 수 있는데, 예를 들어 자율주행을 하는 agent를 학습하고 싶은데 사람을 죽일때마다 plus reward가 발생한다면 이 agent는 주행을 잘 하지는 못할겁니다.

혹은 주어진 context에 따라서 사람에게 도움이 되는 답변을 하는 chatbot을 만들고 싶은데, 이를 RL관점에서 보고 좋은 답변을 하면 plus reward를 주고 싶은데 좋은 답변을 정의하는 (design) 것 자체가 매우 어렵죠 현재 Deep Learing (DL)분야의 가장 핫한 topic인 Reinforcement Learnign from Human Feedback (RLHF)는 Large Language Model (LLM)을 human preference에 align된 chatbot 형태의 application으로 만들기 위해서 human preference (ranking) data를 수집하고 given trajectory들에 대해 무엇이 더 선호되는지를 Reward Model (RM)이 학습하고 최종적으로 이 RM이 주는 signal로 PPO를 한다는 점에서 IRL과 깊은 관련이 있습니다.

Fig. Preference based Learning. Source from CS294-190

Deep reinforcement learning from human preferences라는 2017년에 publish된 paper을 보다보면 아래와 같은 문구가 있는데, preference based RL이 정확히 IRL은 아니라는 뉘앙스를 확인할 수 있습니다. (Cooperative IRL과 관련이 있다고 하네요)

Fig.

Fig.

어쨌든 preference based RL은 IRL과 어느정도 관련이 있기 때문에 RL에 정통하지 않더라도 RLHF를 이해하고 이에 내재되어있는 문제점을 해결하기 위해서는 IRL에 대한 이해도가 필요할 것 같습니다.

Why Inverse Reinforcement Learning?

이번 강의에서 배우게 될 내용은 slide에 나와있는 것 처럼 다음과 같습니다.

• IRL의 문제 정의에 대해 이해하기
• IRL algorithm을 유도하기 위해서 어떻게 behavior에 관한 확률 모형 (probabilistic models of behavior)이 사용될 수 있는지 이해하기
• Practical IRL algorithm 알아보기

Slide. 2.

IRL은 imitation learning의 한 갈래로 볼 수도 있는데, human expert의 demonstration (demo)을 가지고 policy를 배우는 paradigm을 모두 imitation learning이라고 하기 때문입니다. Demo data를 directly learning하는, 즉 Supervised Learning (SL)을 사용하는 방식을 쓰면 lecture 2에서 다룬 Behaviour Cloning (BC)를 하는 것 이됩니다. 하지만 IRL의 경우에는 demo를 가지고 reward function을 먼저 학습하고 RL을 합니다. 즉 policy learning을 하는 flow에는 분명히 차이가 있지만 IRL도 demo trajectory를 사용해 reward function을 approximate하기 때문에 imitation learning으로 볼 수 있는 것이죠.

Inroduction에서 왜 IRL이 필요한지에 대해 잠깐 언급하긴 했지만 IRL의 필요성에 대해 논할 때에는 몇 가지 다른 관점 (perspective)가 존재할 수 있습니다.

The Imitation Learning Perspective

먼저 Imitation Learning perspective입니다. Behavior Cloning같이 human expert의 trajectory를 그대로 copy하는 것은 사실 현실과 괴리가 있다고 주장인데, 그 이유는 실제 사람이 다른 사람을 모방하는 과정은 그렇지 않기 때문이라고 합니다. 예를 들어, 어린아이는 어른의 행동을 보고 배울 때 정확히 그 동작들을 따라한다기 보다는 눈으로 그 task를 어떻게 수행하는지를 보고 이를 이해한 뒤 비슷하게 행동한다고 합니다.

Fig.

Slide. 4.

즉 slide의 문구처럼 'copy the actions performed by expert'가 아닌 'copy the intent of expert'가 맞는 것이죠. (lec20&t=5m28s 참고) 이런 방식으로 학습을 한 agent는 expert의 행동을 그대로 따라하는 것이 아니라 의도를 파악하기 때문에 expert data와는 전혀 다른 행동을 하게될 수 있다고 하는데, 이런 방식은 또한 아래와 같은 추가적인 이유로 (outcome이나 dynamics에 대한 추론이 전혀 없음, robot agent와 사람의 degree of freedom가 다름, data수집이 어려울 수 있음) BC방식의 direct imitation learning은 적절치 못하다고 얘기합니다.

Fig.

The Reinforcement Learning Perspective

그 다음은 RL perspective입니다. 결론부터 말씀드리자면 agent를 RL algorithm으로 학습할 때 reward design을 잘 해주지 못하면 의도와 다르게 agent가 학습될 수 있다는 것인데, 이런 문제는 Reward Hacking이나 Reward Exploitation라는 term으로 보통 정의됩니다. 이런 일이 발생하는 이유는 reward를 정의하기 어렵기 때문인데, 가령 atari에서 벽돌 깨기 (break)를 한다고 치면 score maximization하는 것은 자연스럽겠지만 자율 주행 (autonomous driving)에서는 어떤 주행이 좋은 주행인지 정의 하기 어렵습니다. Robotics나 chatbot의 reward function을 정의하는 것도 어렵죠.

Fig.

아래 animation이 reward hacking을 가장 직관적으로 나타내는 예시라고 할 수 있는데, boat racing 게임에서 1등을 하도록 agent를 학습하고 싶어 게임상의 score를 maximize하라고 reward function을 design했더니 agent가 score를 잘받기만 하면 되는것으로 오해해 제자리를 빙빙 돌면서 item만 먹도록 policy learning이 이루어 진 것입니다.

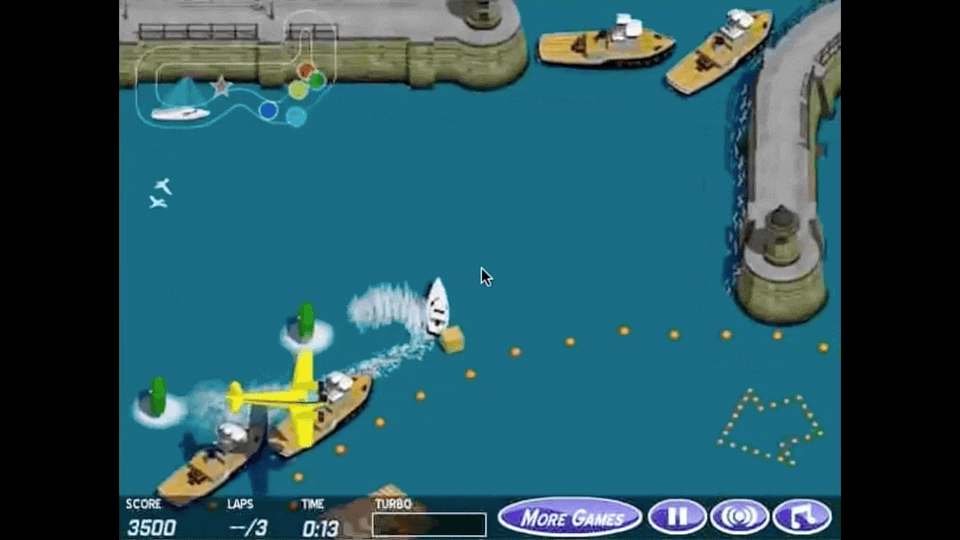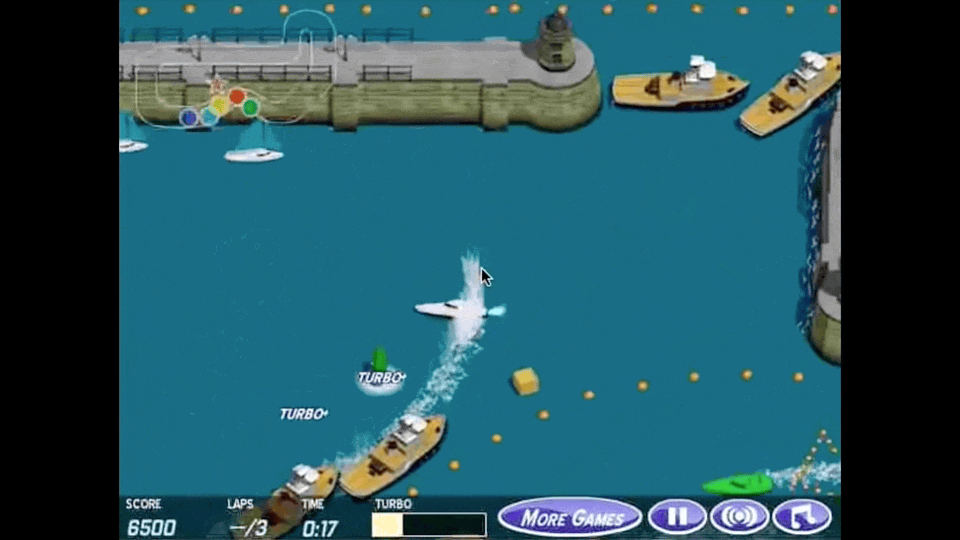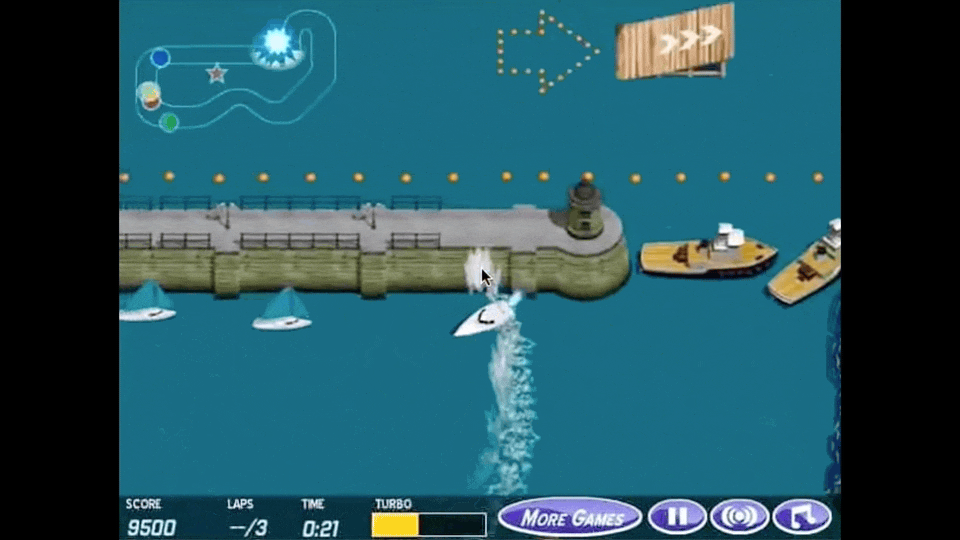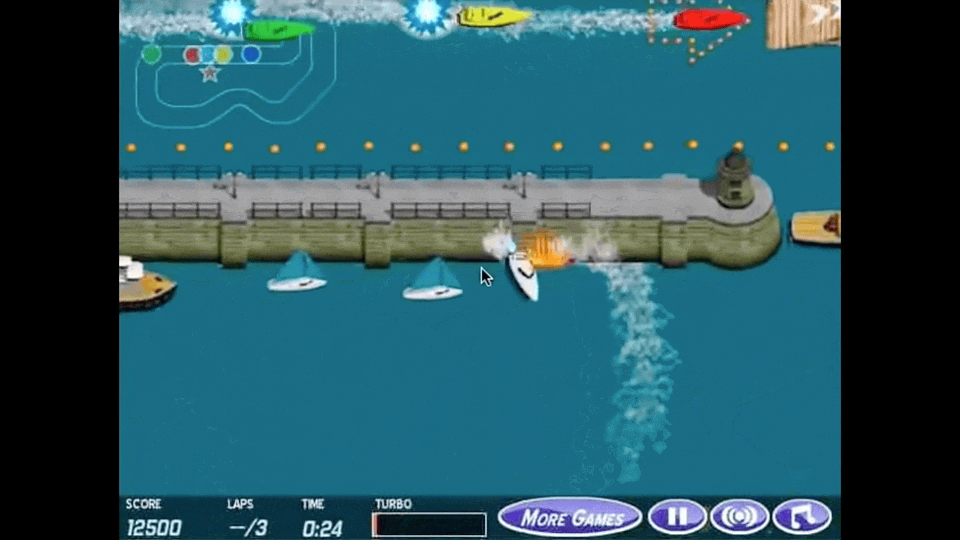Fig. Source from here

차로 autonomous driving을 한다고 쳐도 이런일은 쉽게 일어날 수 있으며, real world에서의 autonomous driving은 목적지에 도착한다거나 특정 속도로 달린다거나 교통법규를 준수해야하며, 다른 운전자들에 민폐를 끼치거나 사고를 내서는 안된다 등의 여러 factor들이 경쟁적으로 작용하므로 더더욱 문제가 어려워질 수 있습니다.

이를 해결하기 위해 IRL은 먼저 expert에게 어떻게 운전하는지 한번 보여달라고 하여 (demonstrate) trajectory sample들을 모읍니다. 그리고 어떤 reward function을 optimize하면 이 expert policy를 얻을 수 있는지를 유추합니다 (reward function 학습). 그리고 최종적으로 Actor-Critic등의 RL method와 learned reward function으로 policy를 학습하죠. 안타깝게도 naive version IRL은 underspecified problem이 될 수 있다고 합니다.

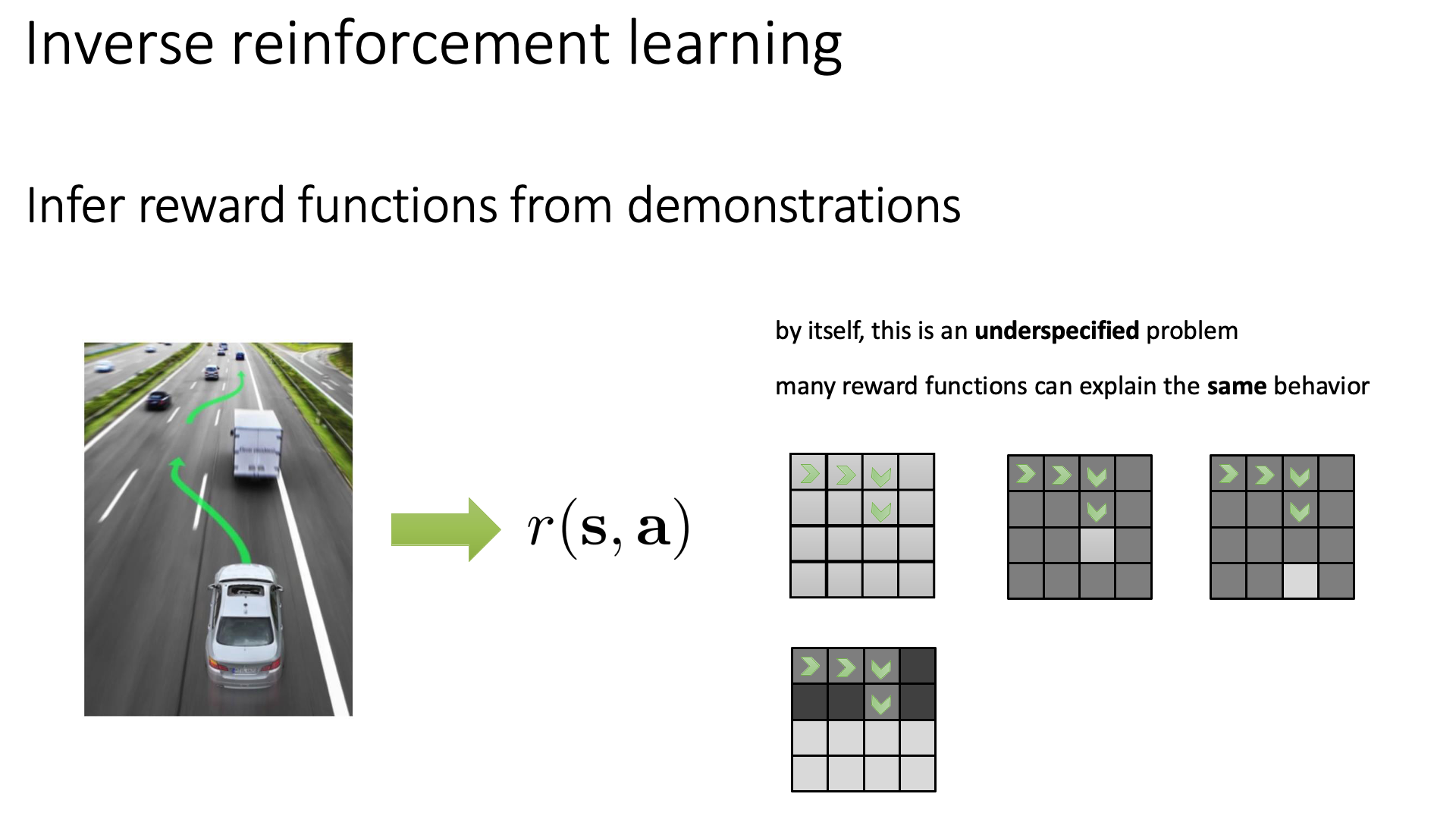Slide. 6.

이는 주어진 expert behavior를 설명할 수 있는 reward function은 안타깝게도 무수히 많을 수 있다는 걸 말합니다. 이를 위해 autonomous driving를 하는 경우를 생각해봅시다. 실제 autonomous driving을 할 때에는 신호등, 교통 표지판, 다른 차들 등 많은 semantic information이 존재하겠으나 지금은 toy example이므로 이런 정보는 무시하고 state, action만 존재하는 grid wrold를 생각하겠습니다. 아래와 같은 16x16 크기의 grid world에서 어떤 agent (expert)의 behavior trajectory가 화살표를 따라 주어졌을 때, 이 agent가 어떤 reward를 따라 이렇게 행동했을 지를 설명하려면 reward function은 어떻게 생겨야 될까요?

Fig. 16x16 Grid World Example

가장 간단한 경우는 특정 square에서 엄청나게 큰 plus reward를 받고 나머지 state에서는 minus reward를 받는 경우일 수 있습니다.

Fig. Possible Reward Function 1

그런데 만약 4 step을 observe하는 것을 하나의 trajectory로 정의한다면 아래 같은 경우도 되겠죠?

Fig. Possible Reward Function 2

아래의 경우도 물론 4개의 화살표로 이루어진 trajectory를 설명하는데 무리가 없을겁니다.

Fig. Possible Reward Function 3

혹은 매우 극단적인 경우 IRL을 했더니 주어진 trajectory이외의 state로의 transition을 할 시 \(-\infty\) reward를 주는 function을 얻을 수도 있습니다. 다시말해서 주어진 behavior data가 optimal behavior가 될 수 있는 reward function의 경우의 수는 \(\infty\)에 가깝다는 것입니다. (아마 여기까지 lecture를 들으신 분들이라면 직관적으로 expert의 data에 존재하지 않는 state에 대해서도 generalize 되는 reward function, policy을 얻기 위해 state에 대한 entropy term을 추가하는 것을 떠올리실 수 있을 것 같습니다)

So, Why IRL is good?

IRL을 하게되면 우리는 주어진 demonstration으로 부터 어떤 goal을 달성하기위한 reward function을 배우는 것이기 때문에, 주어진 demo의 condition과 다른 agent를 학습하는 것도 가능합니다. 예를 들어 ferrari로 만들어진 demo로 sonata를 학습할 수도 있는것인데, 만약 단순히 demo를 BC하려고 한다면 불가능 할겁니다.

Fig. Source from here

Formal Definition of IRL Problem

어떻게 이렇게 무수히많은 reward function 중에서 좋은 것을 가려낼 수 있는지?에 대해서 얘기하기전에 Sergey는 IRL 문제를 더 formal하게 정의하고 넘어가자고 합니다. Sergey는 ‘Inverse’ RL의 counterpart로 vanilla RL을 ‘Forward RL’이라고 정의합니다. 이 둘의 learning algorithm은 아래 slide에 잘 나타나 있습니다.

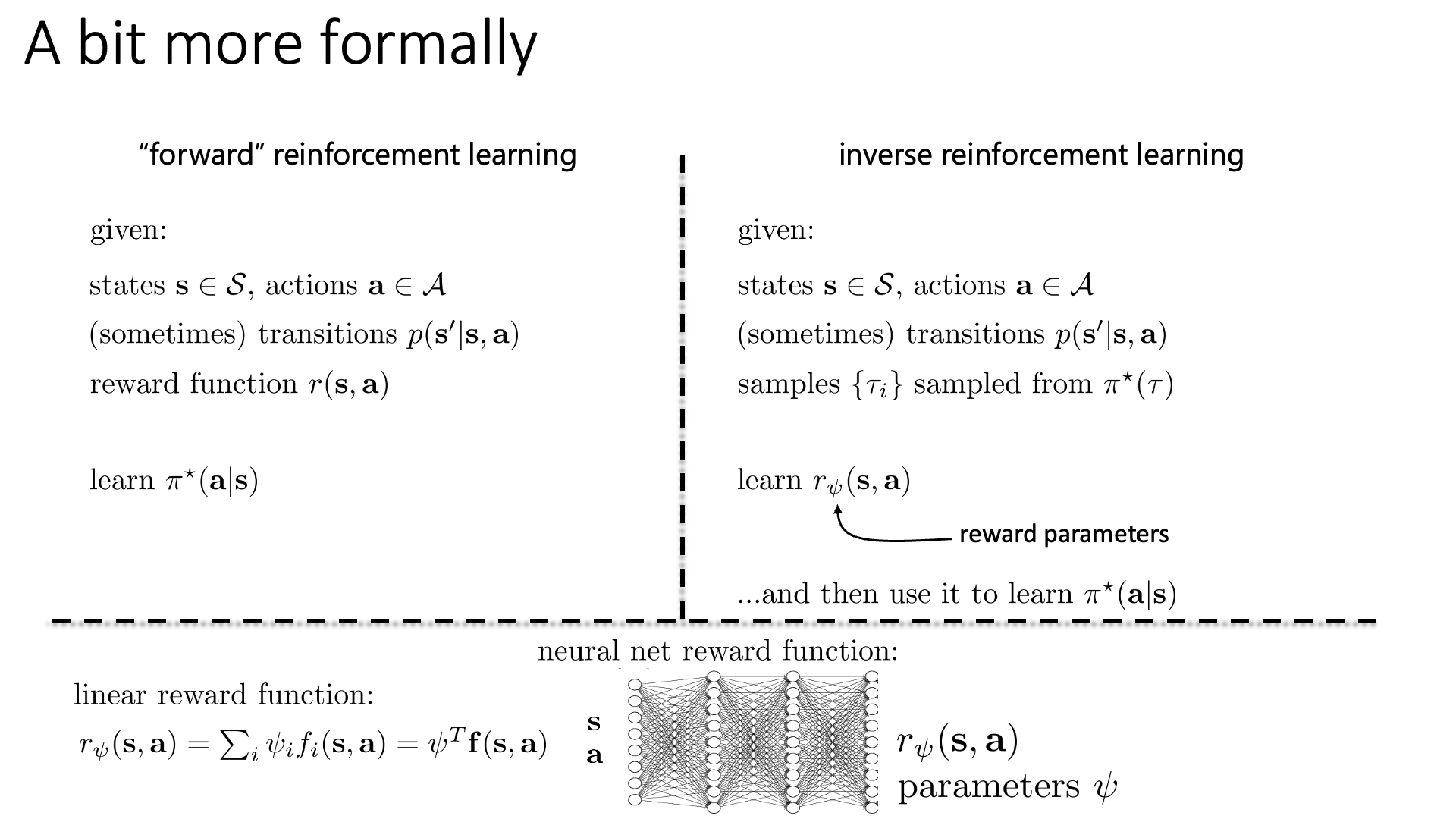Slide. 7.

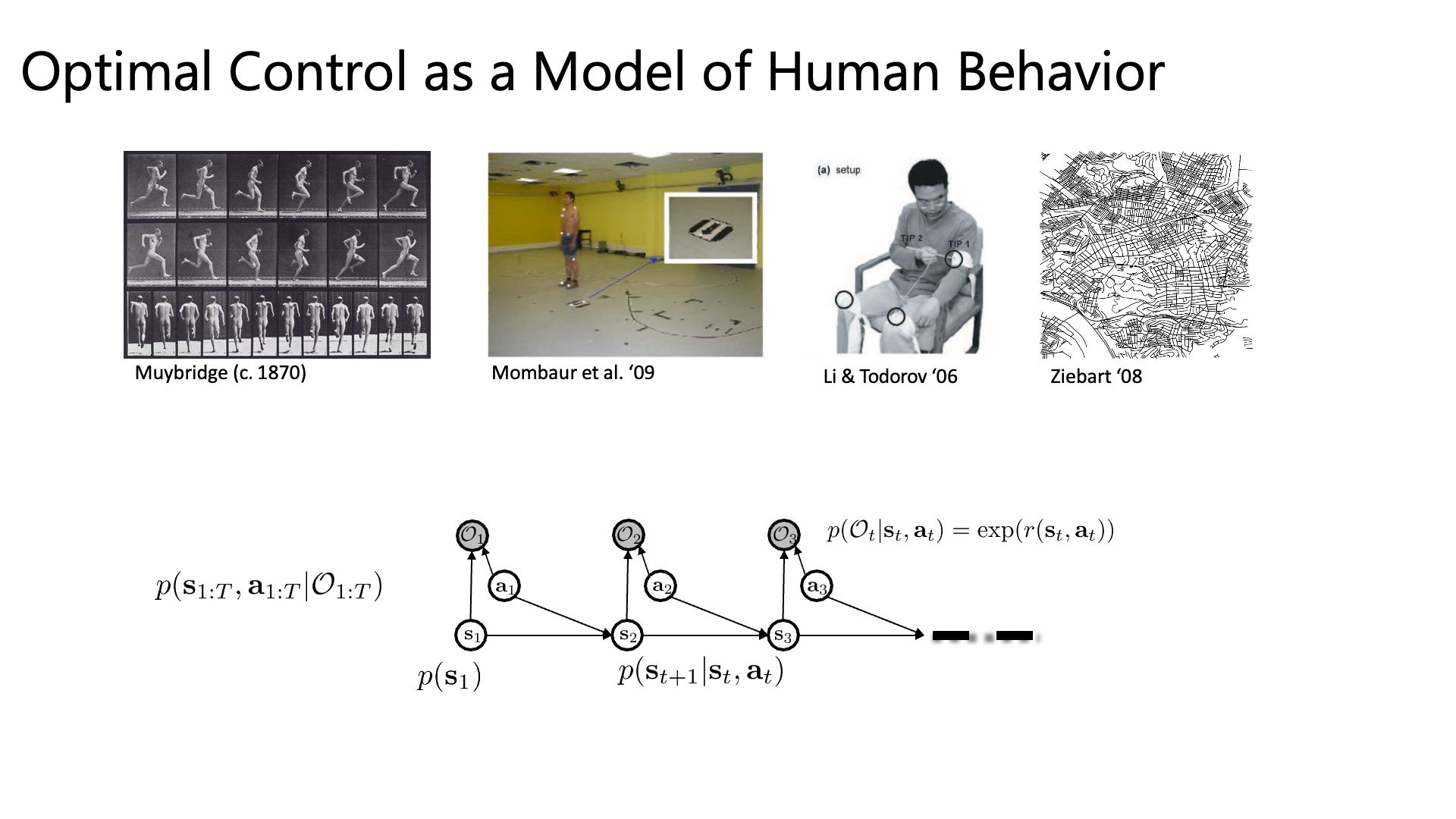
IRL을 잘 보면 reward learning phase가 추가되었다는 것 외에 우리가 가지고있는 human expert demo trajectory가 optimal policy, \(\pi^{\ast}(\tau)\)로 부터 sampling되었다고 표시했음을 알 수 있습니다. 물론 optimal policy가 뭔지, 어떻게 생겼는지 전혀 알 수 없습니다. 그냥 일단 optimal policy로부터 sampling되었다고 가정하는 겁니다.

IRL은 \(\psi\)로 parameterize된 reward function, \(r_{\psi}(s,a)\)을 학습하는데, 여기서 이 reward function을 구성하는 방법에는 여러 가지 방법이 있을 수 있지만 그 중 하나는 linear reward function이라고 합니다. 이는 feature들의 선형 결합 (linear combination)으로 reward function을 표현하는 것으로, weighted sum하는 것을 의미합니다.

여기서 \(\psi\)는 parameter vector이기때문에 feature, \(f\)와 dot product로 표현할 수도 있습니다. 당연히 deep RL에서는 이를 NN으로 design해서 학습할 수도 있습니다.

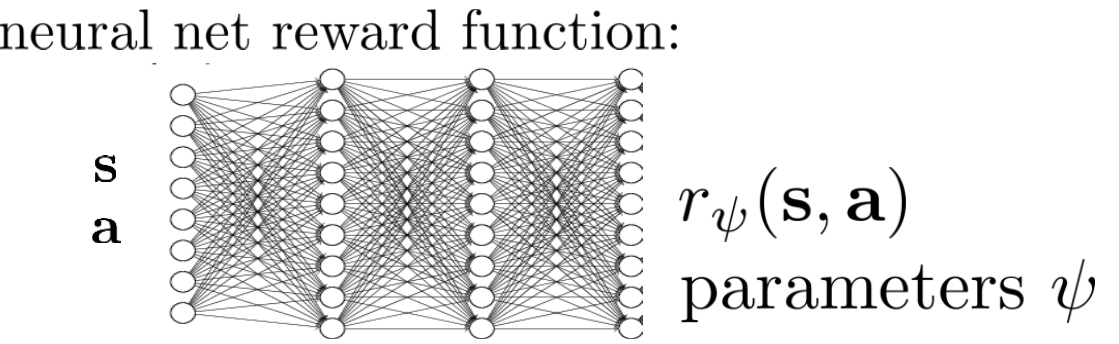Fig. Neural Network (NN) based Reward Function

그런데 우리는 feature를 weighted sum하는 method를 먼저 알아볼 것입니다. feature라는 것 \(s,a\)의 함수인데 과연 이것은 뭘 의미할까요?

Feature Matching IRL

Traditional IRL은 Feature Matching이라는 것에 집중했다고 합니다. 이는 modern IRL의 main topic인 Maximum Entropy (MaxEnt) method와는 상당히 다르다고 합니다. (MaxEnt는 이번 lecture의 main topic이며 probabilistic model임)

Fig. Feature matching은 2004년에 제안된 method이다.

Fig. MaxEnt RL은 2008년에 제안되었으니 이것도 그리 최신 기법은 아니다.

Feature matching를 하기 위해서는 먼저 내가 학습하려는 task 중에서 중요하다고 생각하는 feature를 정의해야 합니다. Autonomouse driving이라고 치면 아래와 같은 것들이 feature가 될 수 있습니다.

Fig. Example features

Feature matching의 key idea는 'reward는 s,a에 대한 feature와 관련이 있다 (의존한다)'라는 것인데, 이는 standard RL의 경우에도 비슷한 state에서 같은 action을하는 것이 유사한 reward를 줄 것이 예상되므로 직관적일 수 있습니다. 그러므로 어떤 \((s,a)\) pair에 대한 reward값을 그 state 이후 모든 state, action pair의 feature를 linear combination 한 것으로 표현하기로 한 것이죠.

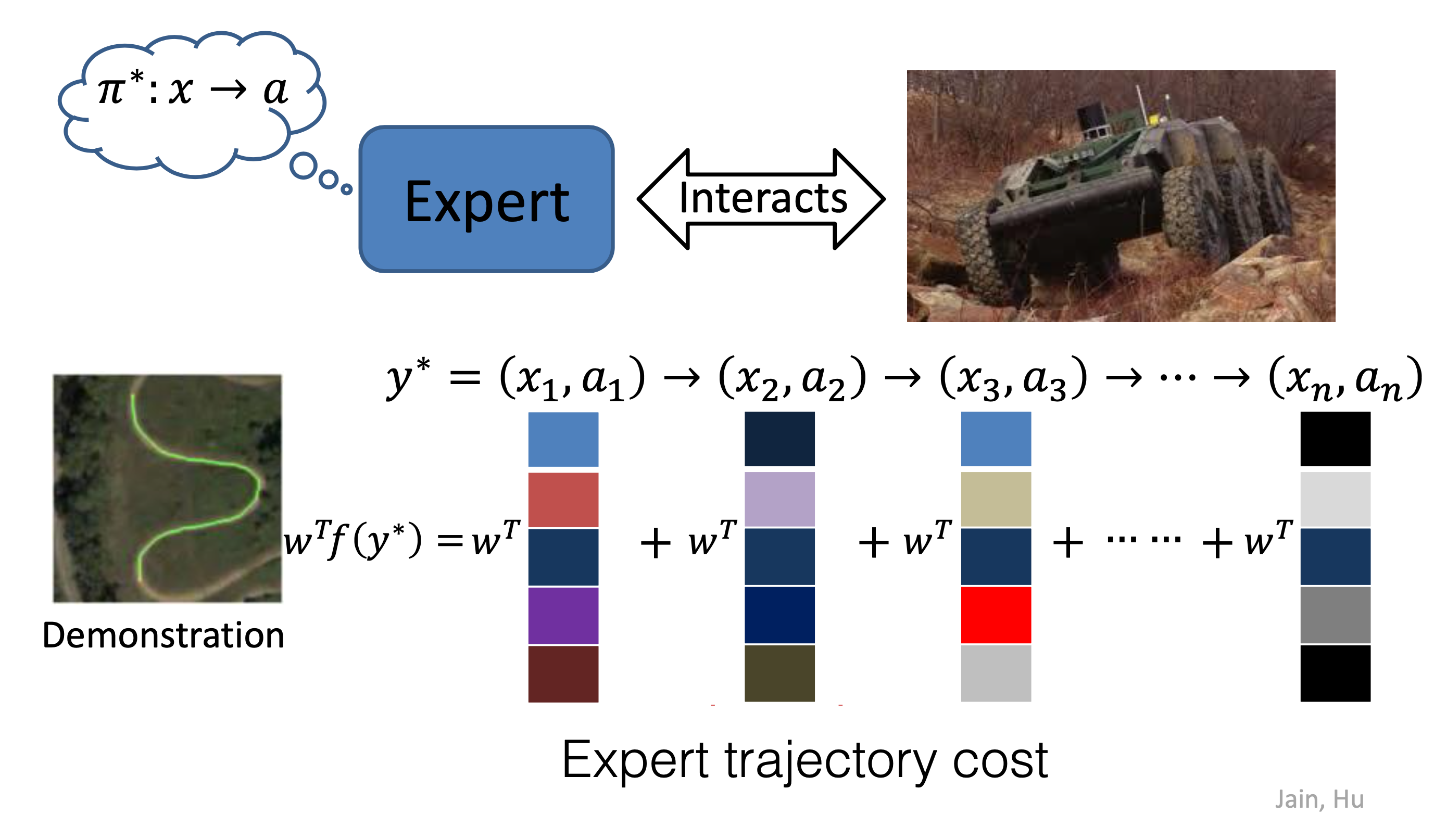Fig.

저는 이 시점에서 ‘이 feature를 고르는 것 자체 reward shaping을 하는 것이 아니냐?’라는 생각을 해보기도 했는데, 각 feature들에 대해서 어떤 점수를 줄지 정하지 않았으니 이는 온전한 reward function이라고 생각할 순 없을 것 같습니다.

이제 다음으로 할 것은 어떤 임의의 policy, \(\pi^{r_{\psi}}\)가 \(r_{\psi}\)를 따랐을 때의 optimal policy라고 한다면 이것의 모든 state action pair에 대한 feature의 기대값과 우리가 알 수 없지만 존재한다고 가정한 expert policy의 feature의 평균값을 (expectation) matching시키는 겁니다. 같아야 한다 라는 겁니다. 왜 이게 같아야 할까요?

직관적으로 이해가 될 수도 있지만 증명을 해봅시다. 지금 우리가 관심있는 quantity는 expert policy의 average feature count 이며 (여기서 \(n\)은 trajectory의 수),

주장하고자 하는 바는 다음과 같습니다.

먼저 reward function은 \(r_{\psi}(s,a) = \sum_i \psi_i f_i(s,a)\)로 정의했었습니다. 이제 trajectory만 가지고 다 표현하기 어렵기 때문에 그냥 이 policy를 따라서 sampling했을 때 state를 방문한 횟수를 의미하는 discounted state visitation frequency, \(\rho^{\pi}_{s_0} (s')\)를 다음과 같이 새로 정의합니다.

그러면 state value function, V를 우리는 다음과 같이 계산할 수 있습니다.

따라서 만약 어떤 state, \(s\)에서 임의의 policy와 expert policy의 average feature count가 같다면 (\(\mu^{\pi}(s) = \mu^{e}(s)\)), 해당 state에서의 value function값이 같게 됩니다. 그런데 여기서 문제가 있는데, 당연하게도 모든 \(w\)에 대해서 위의 수식이 성립한다는 겁니다. 이것이 바로 앞서 얘기했던 expert behavior를 optimal로 갖는 reward function은 무한대에 가깝다, 즉 모호함 (ambiguity)에 대한 얘기가 됩니다. 그러므로 좋은 \(w\)를 고른다는 것 자체가 무의미해지기 때문에 어떤 bias를 추가해야 하는데, 그것이 바로 아래 두 개가 되는 것입니다.

• Maximize Margin
  • (2004) Apprenticeship Learning via Inverse Reinforcement Learning (Pieter et al.)
  • (2006) Maximum Margin Planning (Ratliff et al.)
• Maximize Entropy
  • (2008) Maximum Entropy Inverse Reinforcement Learning (Ziebart et al.)

Slide. 8.

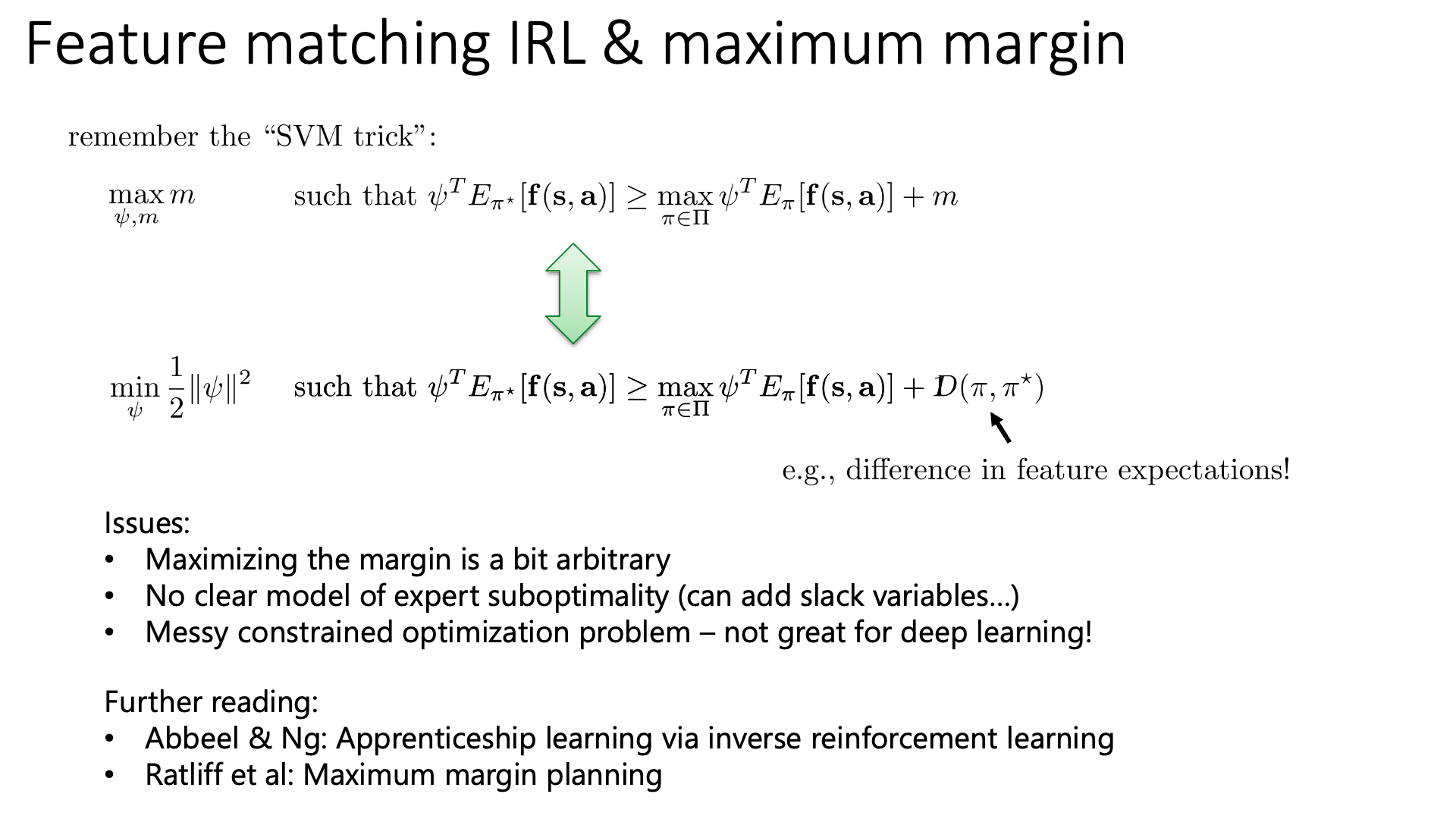
Maximum margin algorithm은 다음의 objective function을 최적화 하게 되는데,

사실 margin에 대한 term이 없어도 ‘모든 policy에 대해 average feature에 weight을 해준 것보다 expert의 average feature에 weight해준 것이 언제나 큰 weight을 찾는다’를 의미하므로 말은 될 것 같습니다. 여기에 margin까지 더한 maximum margin IRL이 원하는 바는 'expert의 value에 weight을 곱한 것이 다른 모든 policy의 value에 weight을 곱한 것보다 항상 같거나 커야 하며, 이들의 차이를 가장 크게 만드는 weight을 골라야 한다'가 됩니다. 혹은 ‘expert action과 다른 action들간의 Q value가 가장 크게 차이나는 reward function을 고른다’라고도 할 수 있죠. Sergey는 큰 margin을 갖는 weight vector를 고르는 것이 말이되긴 하지만 heuristic하다고 하긴 합니다. 어쨋든 이 objective function은 Support Vector Machine (SVM)의 trick을 사용해 아래처럼 표현할 수 있는데,

여기서 margin은 모든 policy에 대해서 항상 1로 유지하게 되지만 expert policy와 비슷한 경우에는 차이를 덜 벌리고 (심하면 reward가 같아도 되고), expert와 많이 다른 경우에는 차이를 더 크게 벌리기 위해 이를 두 policy의 divergence를 measure하는 것으로 바꿔도 된다고 합니다.

max margin method는 expert data가 suboptimal하다면 linearly seperable하지 않게 되고, 이러면 slack variable을 추가해야하고… maximum margin자체가 다소 arbitrary하다던가 … 등 몇 가지 issue가 있기 때문에 그다지 좋은 algorithm은 아니라고 합니다.

Slide. 9.

(이하 우리는 trajectory distribution의 확률에 관심이 있는 것이 아니라 실제로 working하는 sampling based learning algorithm에 관심이 있으므로 생략)

Slide. 10.

Slide. 11.

Learning the Reward Function

Maximum Entropy IRL (MaxEnt IRL) ver 1

Fig.

Fig.

Fig.

Fig.

Fig.

Fig.

Fig.

Maximum Entropy IRL (MaxEnt IRL) ver 2

Slide. 13.

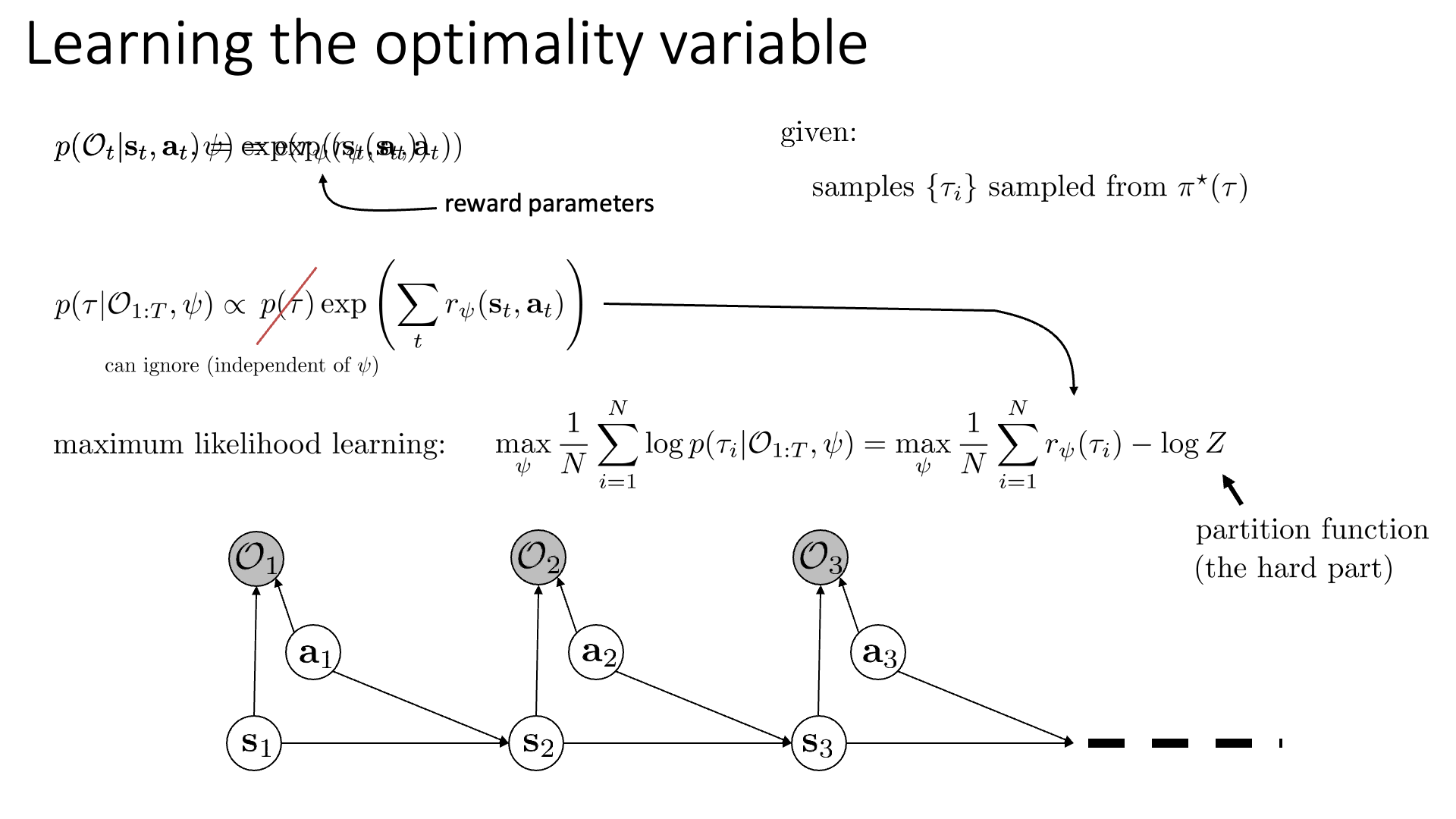
어떤 시점 time-step, t에서의 행동과 상태가 주어졌을 때, Optimality인 \(p\left(\mathcal{O}_{t} \mid \mathbf{s}_{t}, \mathbf{a}_{t}\right)\) 는 Reward에 \(\exp\)를 씌운 것과 같습니다. 이제 우리는 이 Reward를 \(r_{\psi}\)로 나타낼 겁니다.

우리의 목표는 파라메터 \(\psi\)를 찾아내는 거죠. 깔끔하게 수식에 \(\psi\) 를 추가해서 나타냅시다.

이제 Optimality와 \(\psi\)가 주어졌을 때 어떤 Trajectory \(\tau\)가 샘플링될 확률은 아래와 같이 나타낼 수 있는데요,

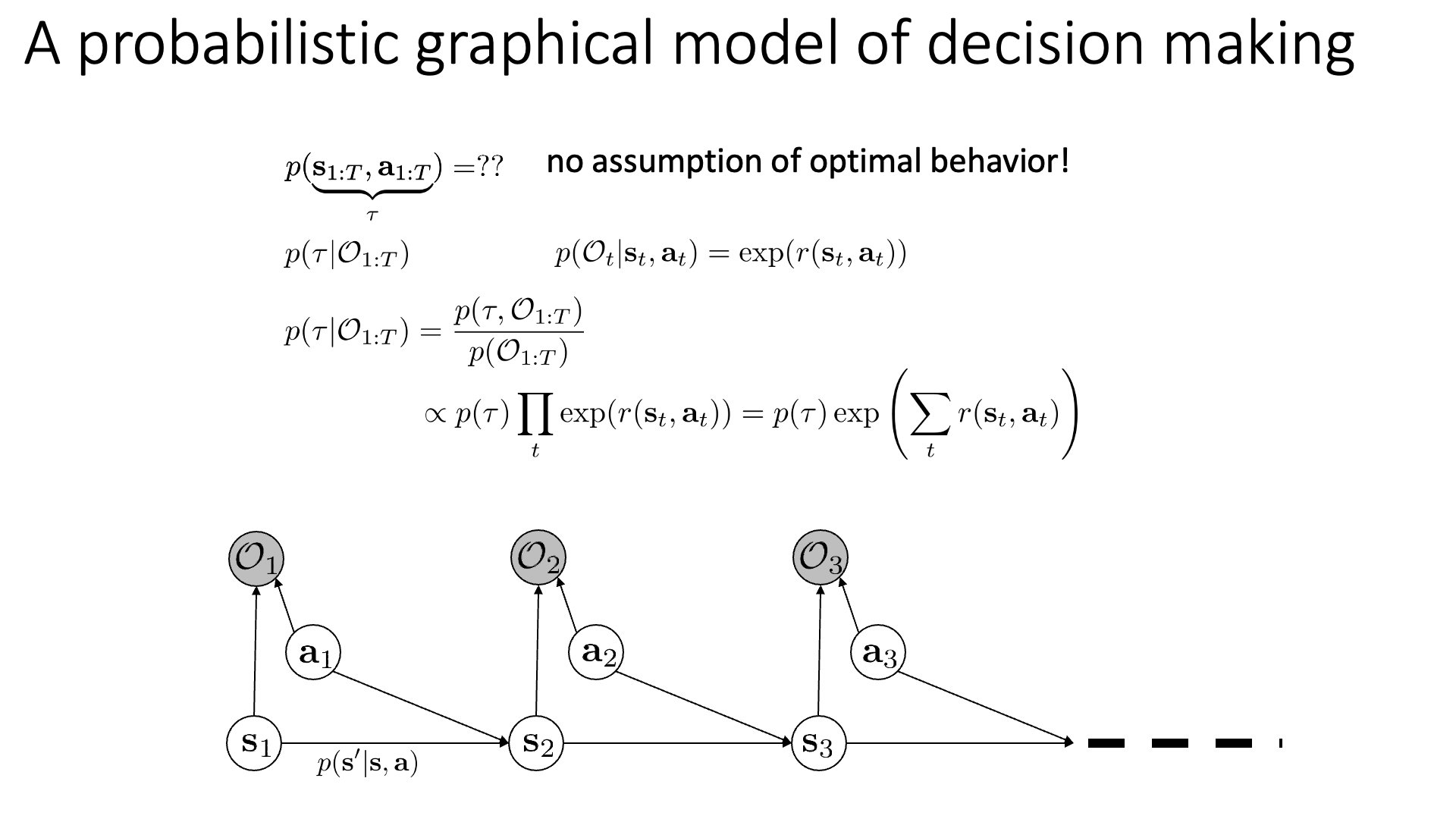
Trajectory의 확률과 Reward의 합에 exponential을 취한 값을 곱한 겁니다. IRL 세팅에서 우리는 어떤 Expert의 Behavior Trajectory 데이터가 알려지지 않은 Optimal Policy에서 뽑혔다고 생각 했죠.

최종적으로 우리가 Reward Function을 학습하는 방법은 Maximum Likelihood 방법이 되는데요, 수식으로 쓰면 아래와 같고,

Log Probability \(\log p\left(\tau_{i} \mid \mathcal{O}_{1: T}, \psi\right)\)를 최대화 하는, 그러니까 우리가 관측했던 Trajectory들의 확률 값을 최대화 하는 \(\psi\)를 찾는 것이 곧 Reward Function을 찾아내는 것이 됩니다. (ML에서 굉장히 많이 쓰는 방법이죠. Maximize Log Likelihood = Minimize Negative Log Likelihood)

여기서 아까 정의했던 수식의 \(p(\tau)\)는 파라메터와 관련 없는 term이기 때문에 제외하고 생각하면 아래의 식을 최대화 하는 것으로 바뀝니다.

여기서 \(Z\)는 Normalizer이며, 직관적으로 위의 수식이 나타내는 것은 우리가 샘플링하는 Sample Trajectory 들이 리턴하는 뭔지 모를 Reward의 평균 값을 크게 하는 \(\psi\)를 구하는 것이 됩니다.

여기서 Normalizer가 없으면 이 식은 굉장히 바보같은 식이 될 수 있다고 하는데요, 이 Normalizer가 없으면 위의 수식을 최대화 하는것은 단순히 모든 Trajectory가 리턴하는 Reward가 높게 되게 끔 학습을 하기 때문에 Expert 데이터와 다른 낮은 확률의 Trajectory들도 모두 높은 Reward를 얻게 되어 제대로 된 Reward를 얻을 수 없게 되기 때문입니다 (제대로 Trajectory를 평가할 수 있는 Reward가 아닌 것).

여기서 \(\color{red}{ \log Z }\) 는 Log Normalizer 혹은 Partition Function이라고 부르는데, 이것이 IRL 학습을 어렵게 만든다고 합니다.

Slide. 14.

이를 다시 수식에 대입하고 우리가 구하고자 하는 파라메터 \(\psi\)에 대한 그래디언트 까지 입히면 아래와 같이 쓸 수 있겠죠. (왜냐하면 우리는 Likelihood를 최대화 하는 방향으로 최적화를, 반대로 Loss를 최소화 하는 방향으로 최적화를 하기 위해서 Gradient를 구해야 하니까요)

위의 수식에서 우변의 2번째 항은 \(Log Z\)를 미분하는 것을 생각해보시면 금방 생각해내실 수 있을겁니다. 하지만 여기서 우변의 두번째 항인 모든 Trajectory에 대해서 적분하는 수식은 계산 불가능 (Intractable) 합니다. 그리고 이 수식에서 우변의 두 번째 term은 \(\frac{1}{Z} p(\tau) \exp(r_{\psi}(\tau))\) 가 \(p\left(\tau \mid \mathcal{O}_{1: T}, \psi\right)\) 이기 때문에 이를 이용해서 두 번째 term 자체를 \(p\left(\tau \mid \mathcal{O}_{1: T}, \psi\right)\) 분포 하의 기대값으로 표현할 수 있습니다.

여기서 첫 번째 term은 원본 수식을 보면 sampling을 해서 몇 개 Trajectory를 뽑아서 합친 (sum)걸로 근사할 수 있으며, 두 번째 텀은 적분 (Integral)한게 되죠.

위의 수식은 Optimal Policy \(\pi^{\ast}\) 하의 Reward를 미분한 것의 기대값과 현재 reward (파라메터)가 주어졌을 때의 \(\tau\) 분포 하의 Reward를 미분한 것의 기대값의 차이가 되는데, 즉 다시 해석하자면 우리가 구하고 싶은 gradient는 Expert Policy하에서의 gradient 값과 Current Reward하에서의 gradient 값의 차이 만큼이 됩니다.

이렇게 학습을 하면 우리는 가지고 있는 Expert Trajecotry에 대해서는 Reward를 증가시키도록, 그리고 그게 아닌, 즉 우리가 Current Reward로 샘플한 Trajectory에 대해서는 Reward를 감소시키도록 파라메터를 업데이트하게 됩니다.

Slide. 15.

Slide. 16.

Slide. 17.

Slide. 18.

Approximations in High Dimensions

Slide. 20.

Slide. 21.

Slide. 22.

Slide. 23.

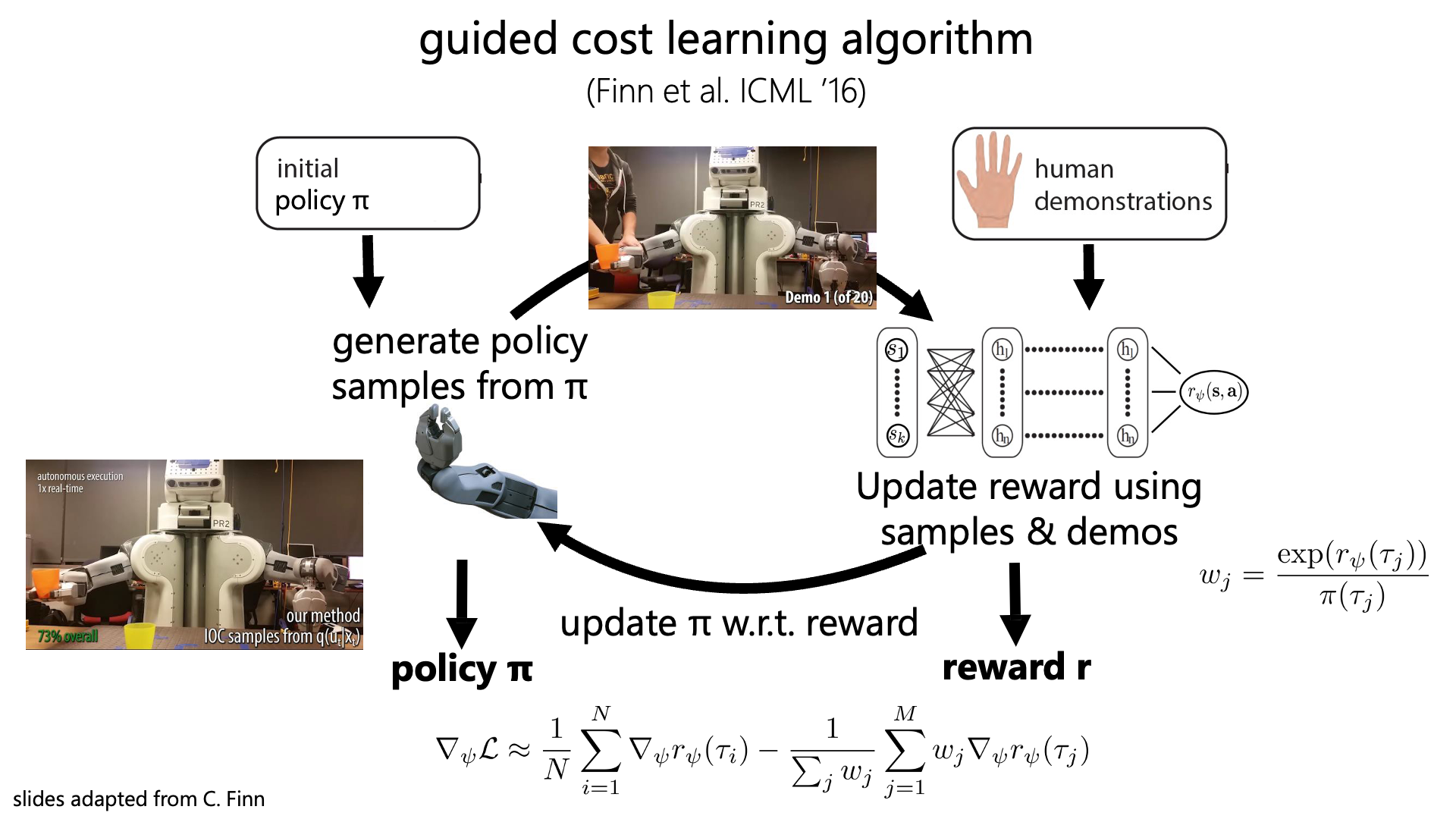Slide. 24.

IRL and GANs

한 편, IRL은 GAN과 연결지어 생각하는 paper들이 종종 제안되어 왔습니다. A Connection between Generative Adversarial Networks, Inverse Reinforcement Learning, and Energy-Based Models라는 paper가 그 중 하나인데, Chelsea Finn이라는 Stanford의 교수가 Berkeley에서 phd student로 재학하던 중 Sergey Levine, Pieter Abbeel과 같이 쓴 것입니다.

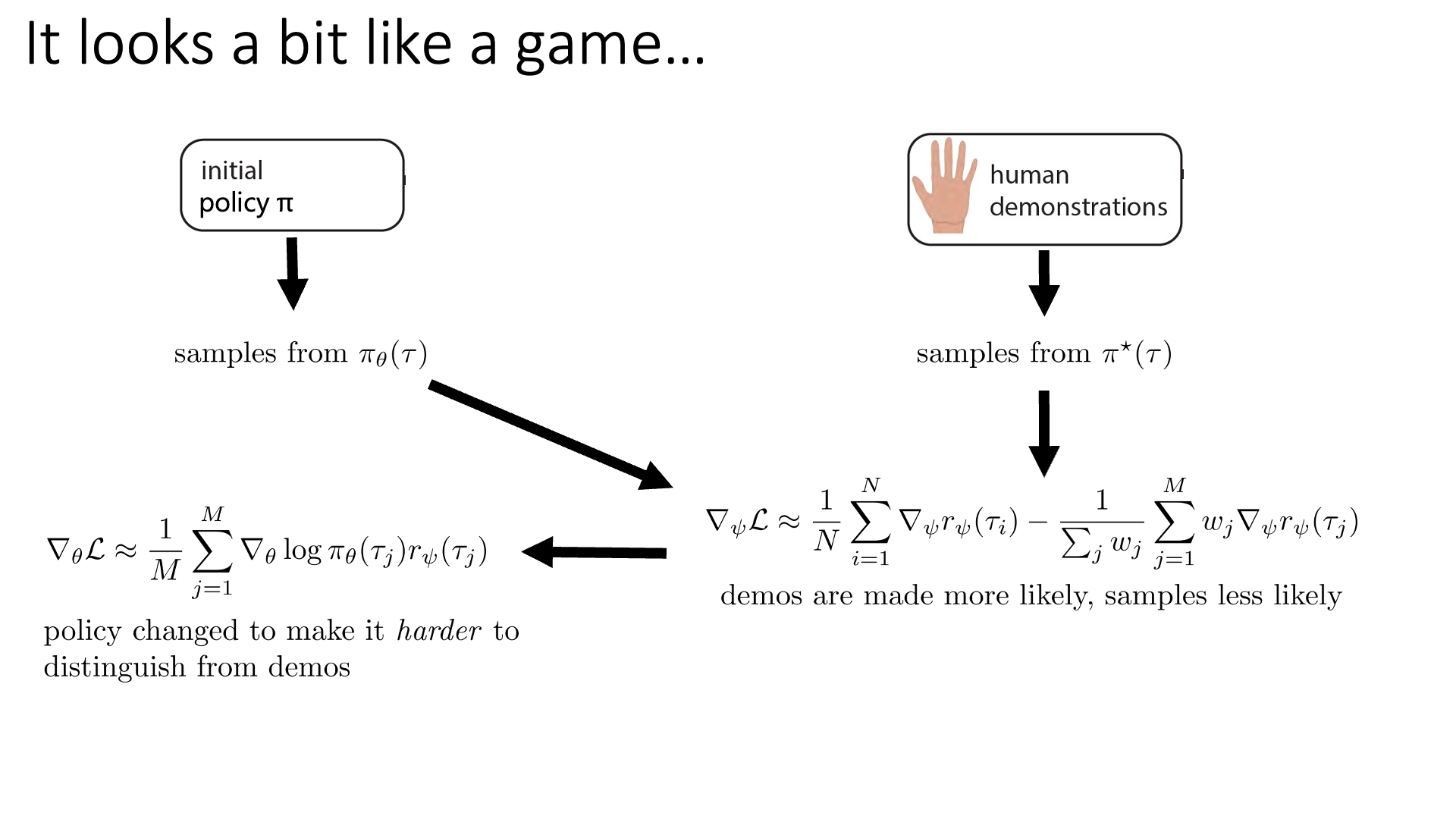Slide. 26.

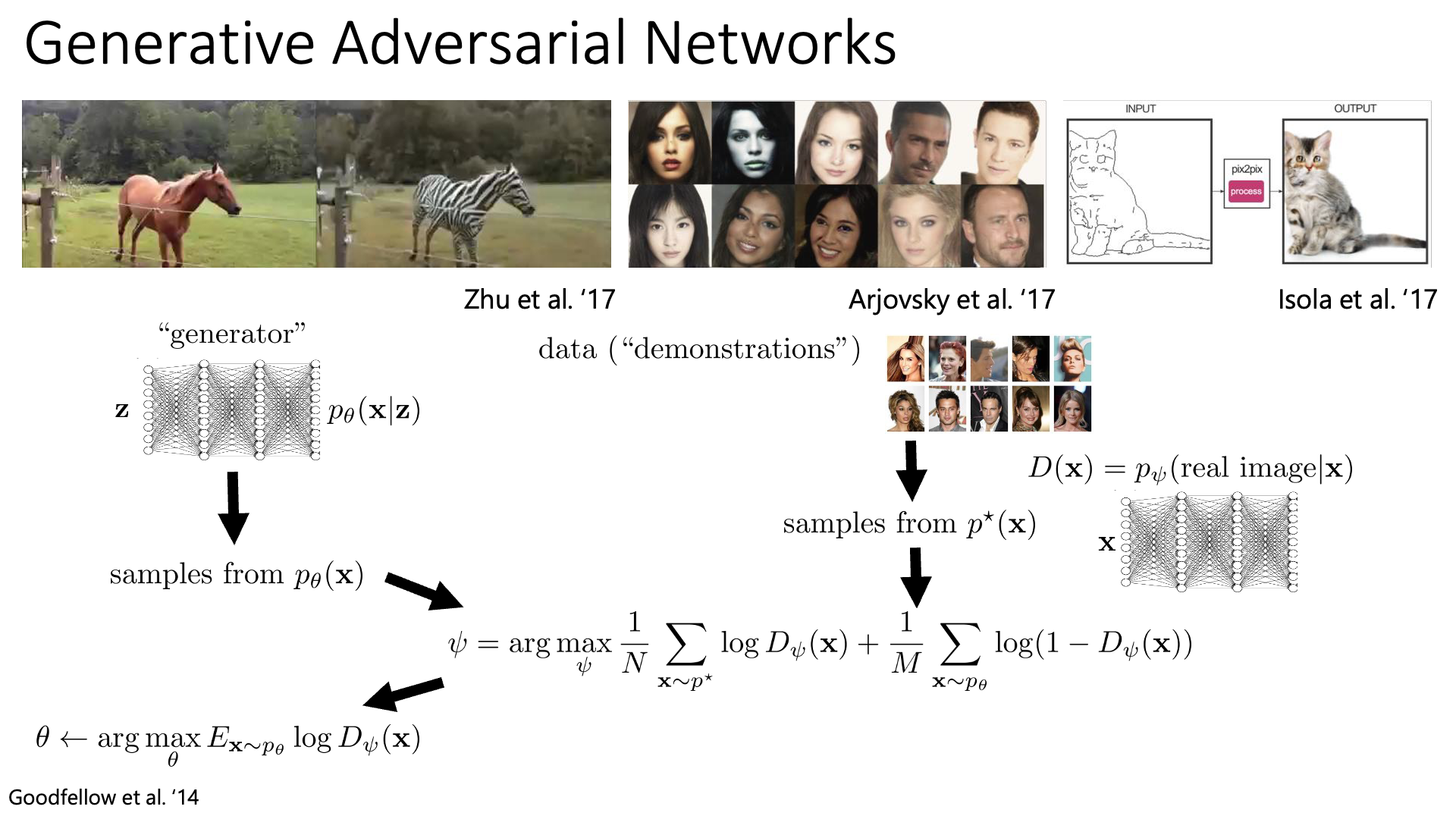Slide. 27.

Slide. 28.

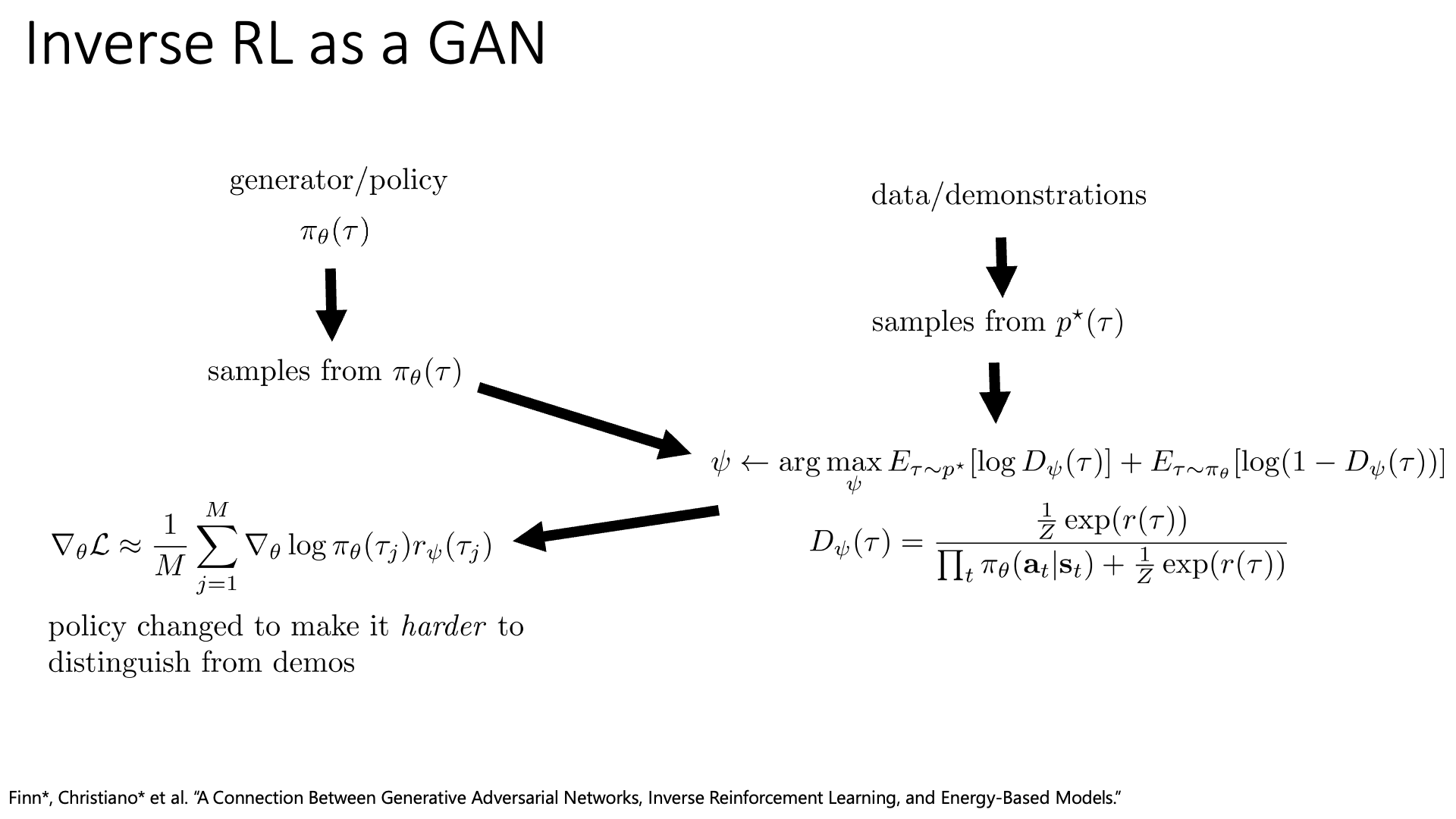Slide. 29.

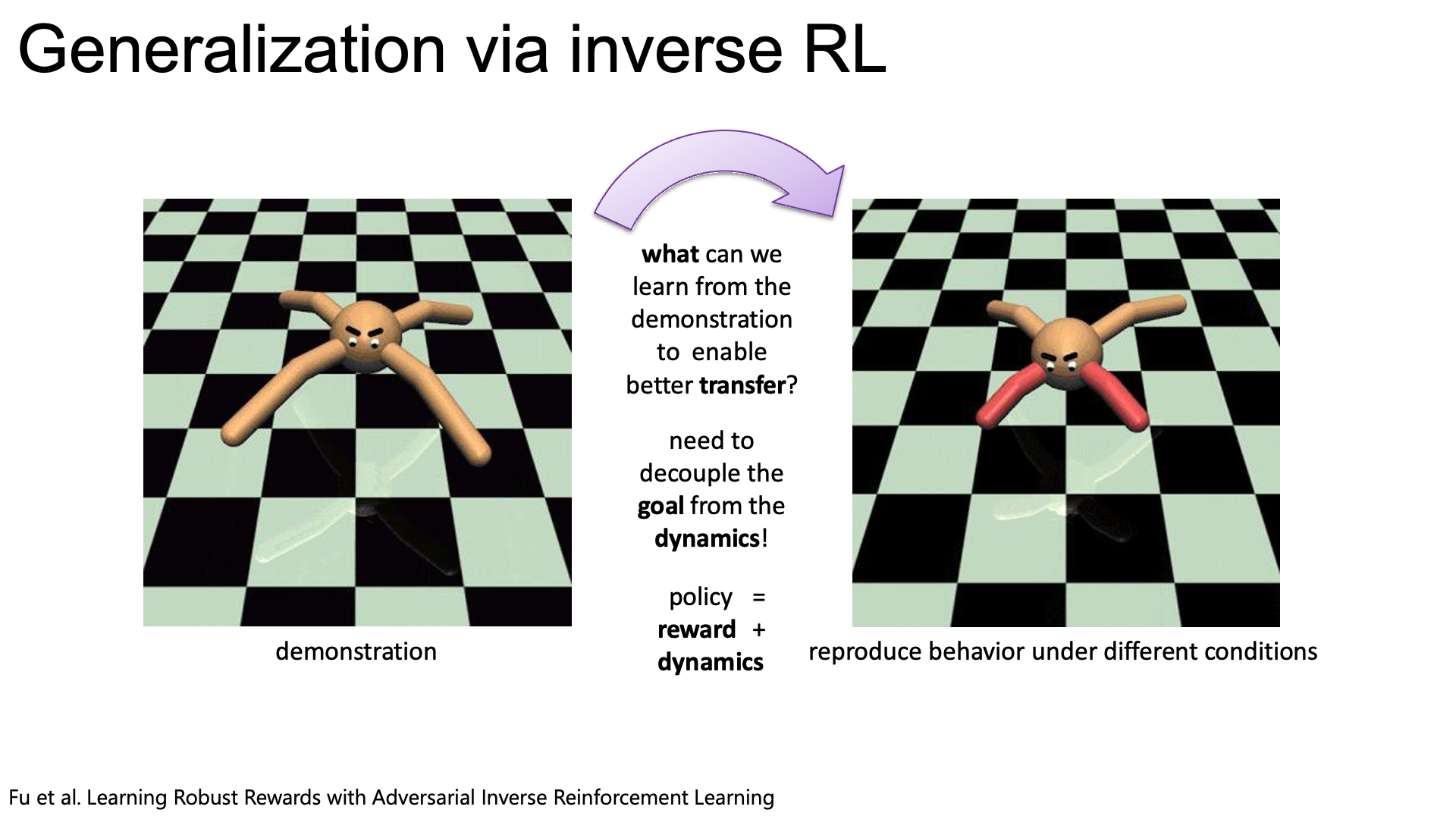Slide. 30.

Slide. 31.

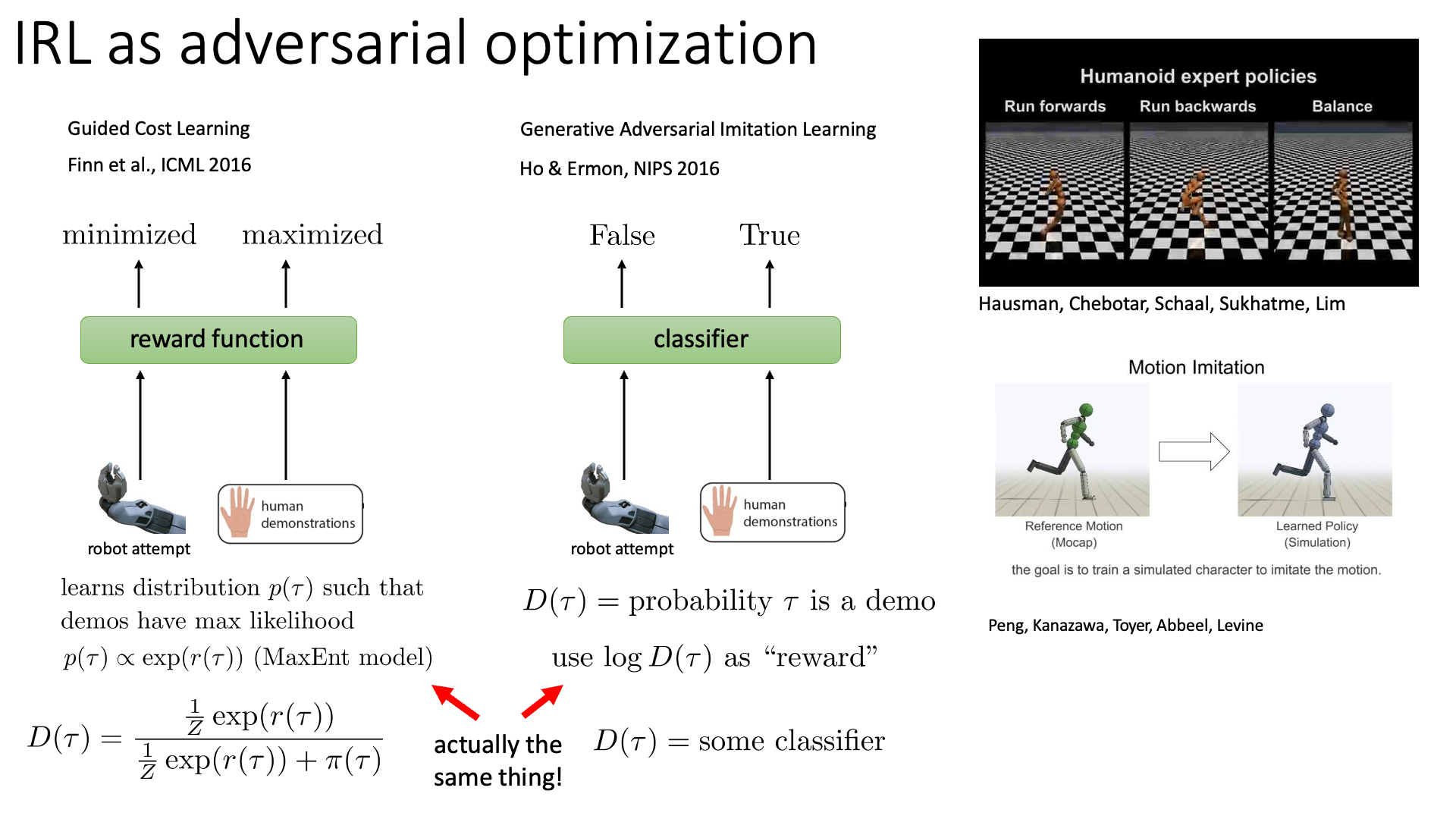Slide. 32.

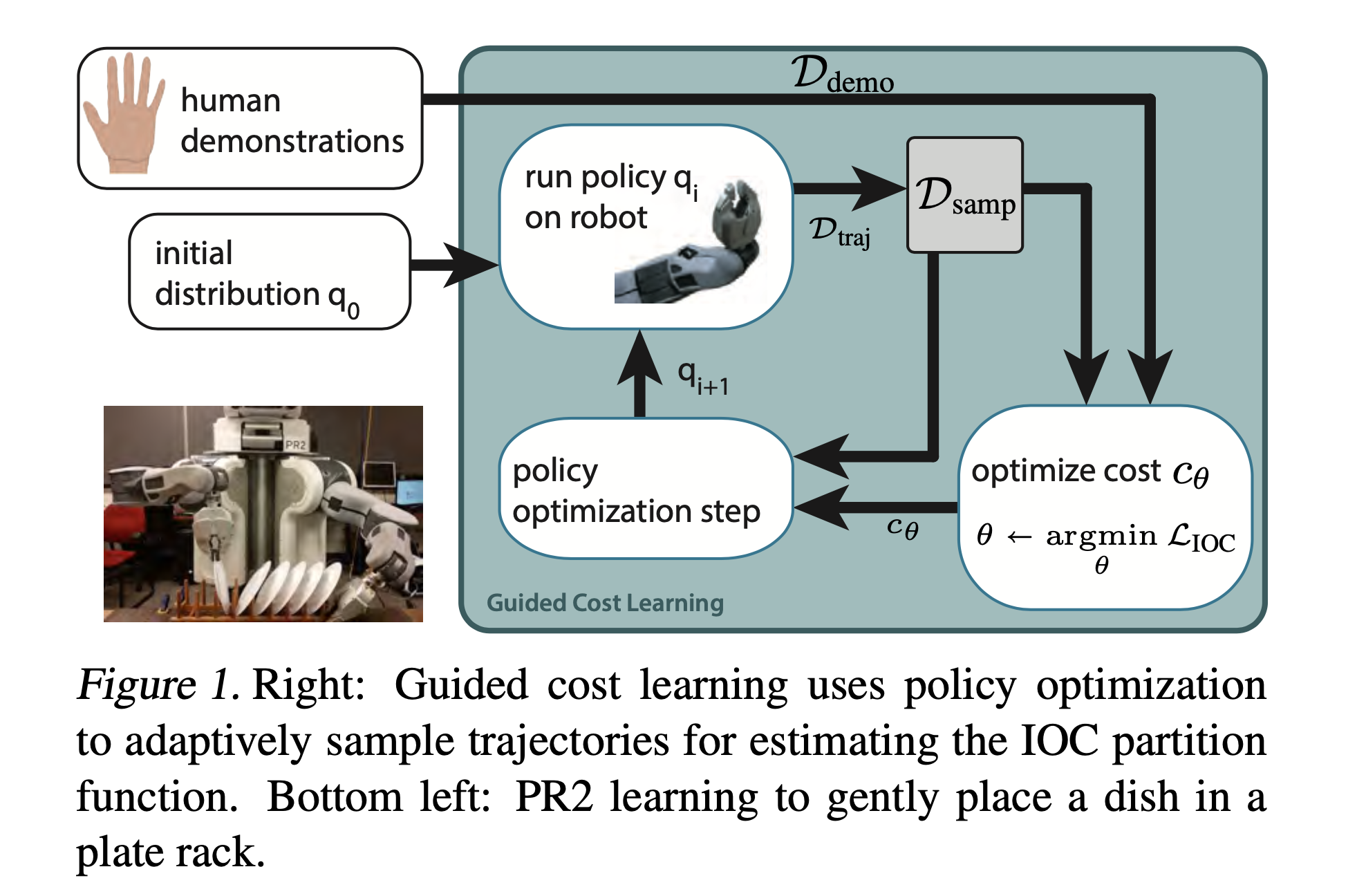Fig.

Fig.

Fig.

Generative Adversarial Imitation Learning (GAIL)

Generative Adversarial Imitation Learning (GAIL)은 2016년에 jonathan ho가 제안한 방법론입니다. 1저자인 Jonathan Ho는 Deep RL의 대가 Pieter Abbeel의 지도하에 phd를 받았으며 GAIL뿐 아니라 현재 Text-to-Image (T2I) generation 분야의 SOTA algorithm인 deep diffusion based algorithm의 가장 근본적인 paper라고 할 수 있는 (2015년에 하나 더 있지만) Denoising Diffusion Probabilistic Models (DDPM)를 제안하기도 했습니다.

Fig.

GAIL은

Fig.

Suggested Reading Papers on IRL

Slide. 33.

Reference

• Lectures
  • CS 285 at UC Berkeley : Deep Reinforcement Learning
    • Lecture 20, Inverse Reinforcement Learning
      • slide
  • CS294-190 Fa21 Advanced Topics in Learning and Decision Making
    • Week 5: Human-in-the-Loop RL (Preference-based Learning)
    • Week 6: Inverse RL (An Overview of Inverse RL)
    • Week 7: Assistance Games (Cooperative IRL)
  • CS885 Fall 2021 - Reinforcement Learning from Pascal Poupart
    • Imitation Learning
      • slide
    • Inverse Reinforcement Learning
      • slide
  • CMU 10-703 Deep RL 2023 Fall from Katerina
    • lecture 12: Imitation learning, behavior cloning
    • lecture 13: Imitation learning with generative models

    • lecture 14: Imitation learning with generative models (cond. ), multigoal imitation learning and reinforcement learning

    • IRL from Russ Salakhutdinov
  • Deep RL Bootcamp
    • Core Lecture 10b Inverse RL from Chelsea Finn
      • slide

  • CS 224R Week 4: Reward Learning from Chelsea Finn

  • Toward a Tractable Solution for Human-in-the-loop Reinforcement Learning: Algorithm and Benchmark from Kimin Lee