(WIP) Deep dive into TRPO and PPO

< 목차 >

• Overview
• 2015, Trust Region Policy Optimization (TRPO)
  • Monotonic Improvement Theorm and Result (Full Derivation)
  • Line Search
  • Conjugate Gradient Algorithm
  • Improved Sampling (Single Path vs Vine)
  • Limitation of TRPO
    • tmp
• 2017, Actor Critic using Kronecker-Factored Trust Region (ACKTR)
• 2017, Proximal Policy Optimization (PPO)
  • Clipped Objective
  • Adaptive KL Penalty
  • Final PPO Algorithm
  • Experimental Results
• Reference

Overview

본 post의 goal은 policy optimization 계열 algorithm의 꽃이라 할 수 있는 TRPO와 PPO에 대해서 알아보는 것이다.

• 2001, Kakade et al. Natural Policy Gradient (NPG)
• 2015, John Schulman et al. Trust Region Policy Optimization (TRPO)
• 2017, Yuhuai Wu et al. Scalable trust-region method for deep reinforcement learning using Kronecker-factored approximation (ACTKR)
• 2017, John Schulman et al. Proximal Policy Optimization (PPO)

2001~2년 NPG가 가장 먼저 제안이 되었다. TRPO는 NPG가 NN을 쓰는 경우 computational cost가 많이 들기 때문에 사용하기 어렵다는 문제를 해결하고 line search를 추가한 algorithm이다. 그리고 PPO는 TRPO의 Conjugate Gradient (CG)를 구현하는 것과 RNN, CNN을 쓸 때 성능 문제가 있으며 (atari 에서), multiple output을 요구하는 경우에 적용이 힘들다는 문제를 꼬집어 TRPO를 단순화한 version이다. 이들 셋은 다른 algorithm이지만 policy가 망가지지 않는 선에서 가장 크게 한 step update하는 것이라는 철학을 공유하고 있다.

앞서 CS285 lecture 9, Advanced Policy Gradient post에서 NPG까지 다뤘기 때문에 해당 post를 보면 대충 느낌은 오겠으나, 실제 TRPO paper는 많은 detail이 숨어있기에 (그래서 어렵다) 이를 제대로 이해해보려 한다. PPO는 TRPO와 크게 다르지 않고 empirical study이기 때문에 많은 이론적 근거가 있지는 않으나 이것도 CS285에서는 다루지 않았기 때문에 같이 다뤄보려고 한다.

2015, Trust Region Policy Optimization (TRPO)

TRPO는 Trust Region Policy Optimization라는 paper에서 제안된 것으로, NPG에 다음을 추가한 것이다.

• Monotonic Improvement Theorm
• Line Search
• Conjugate Gradient Algorithm

Fig.

Monotonic Improvement Theorm and Result (Full Derivation)

Fig.

Fig.

Line Search

NPG도 좋은 algorithm이지만 이는 2차 미분항 (hessian, fisher matrix)를 구하는 것이 비용이 많이 든다는 점, KLD를 2차 근사 함으로써 error가 생겨 KL constraint을 만족하지 못하거나 실제로 Surrogate Advantage를 improve 하지 못할 수 있다는 문제가 있다.

그래서 TRPO는 NPG에 약간의 변형을 주는데, 바로 optimization 분야에서 잘 알려진 backtracking line search를 추가하는 것이다. Algorithm은 단순한데, 개선이 있을 때 까지 gradient 부분에 \(\alpha, \frac{\alpha}{2}, \frac{\alpha}{4}, \cdots\)를 곱해보는 것이다. 이 때 \(\alpha\)는 \(0~1\) 사이 값이고, 이 중에서 제일 좋은 \(\alpha\)를 고른다.

이를 algorithm으로 작성하면 다음과 같다.

Fig.

Conjugate Gradient Algorithm

마지막으로 NPG의 2차 미분항을 계산하는 것이 비싸다는 점을 해결해 보자. 이것은 model이 커질 수록 (NN의 hidden dim이 커지고, layer수가 많아질 수록) 더 문제가 된다.

Conjugate Gradient Algorithm는

Improved Sampling (Single Path vs Vine)

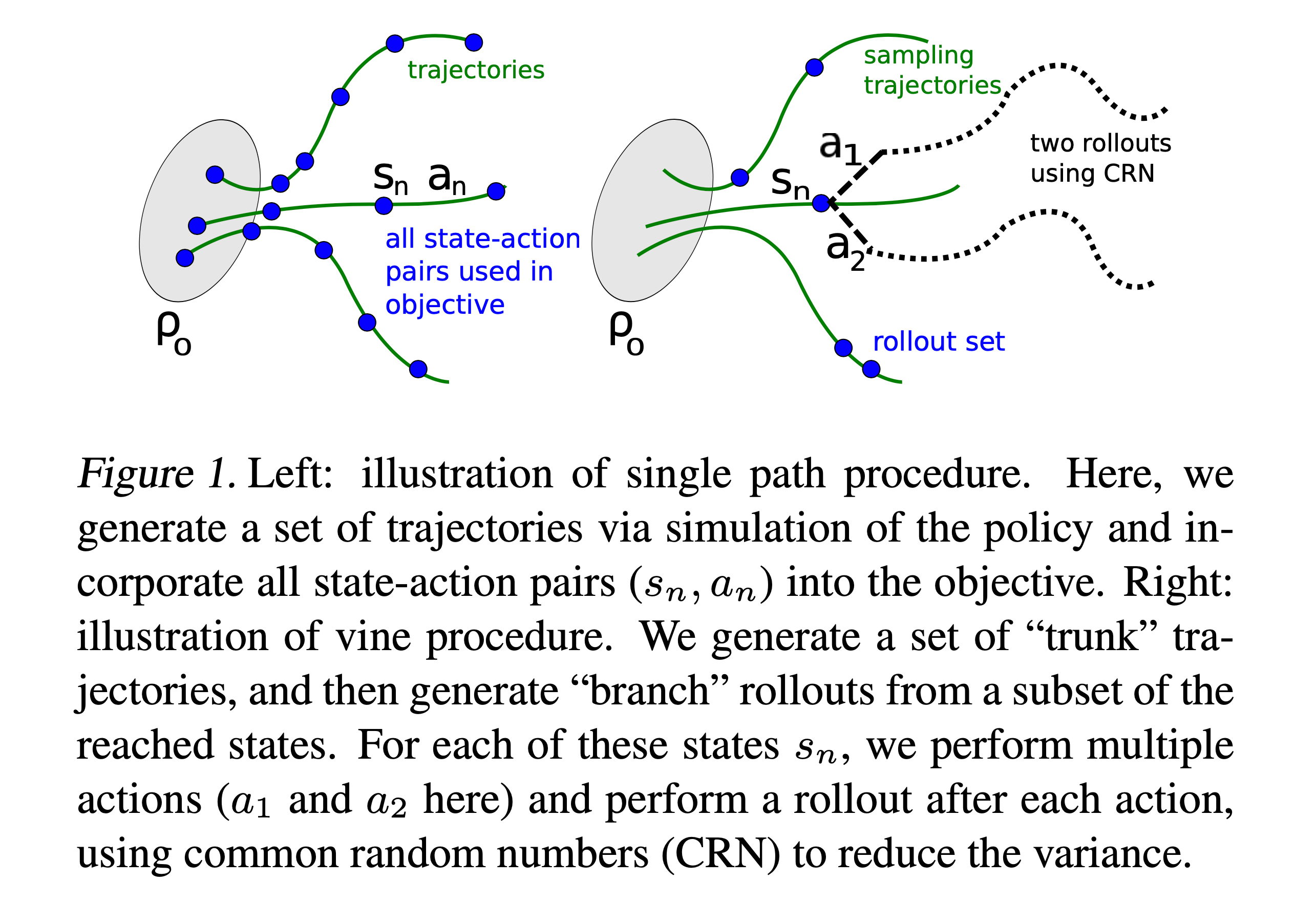Fig.

Limitation of TRPO

Fig.

TRPO는 dropout이나 shared network를 쓸 수 없다.

tmp

2017, Actor Critic using Kronecker-Factored Trust Region (ACKTR)

ACTKR은 Scalable trust-region method for deep reinforcement learning using Kronecker-factored approximation라는 2017년에 publish된 paper에서 제안된 것으로, KFAC Natural Gradient를 Advantage Actor-Critic (A2C)에 결합한 algorithm이다.

2017, Proximal Policy Optimization (PPO)

PPO는 Proximal Policy Optimization Algorithms라는 paper에서 제안되었다. 언급드렷다시피 John Schulman이 1저자이면서 NPG, TRPO를 단순화한 algorithm이다. 그럼에도 다양한 task에서 TRPO와 비슷하거나 더 좋은 performance를 냈다고 알려져 있다.

Fig.

어떻게 단순화 했는가? 바로 TRPO에서 언급됐던 것 처럼 두 policy간의 KLD term을 penalty term으로 주는 것이다.

Fig.

하지만 TRPO는 이 단순한 방식을 사용하지 않고 hard constraint optimization을 했었다. 그 이유는 penalty term의 coefficient를 단순히 constant로 정하기 어려웠기 때문이다. 그래서 PPO paper에서는 아래의 두 가지를 제안했다.

• Adaptive KL Penalized Objective
• Clipped Objective

Fig.

둘 다 TRPO가 conjugate gradient를 계산했던 것에 비하면 선녀라고 할 수 있는데, 각자 어떤 차이가 있는지 알아보도록 하자.

Clipped Objective

먼저 Clipped Objective이다. 이는 importance ratio를 기준으로 ratio가 특정 값을 지나가면 gradient clip 같은 걸 사용해 loss를 bound하는 것이다.

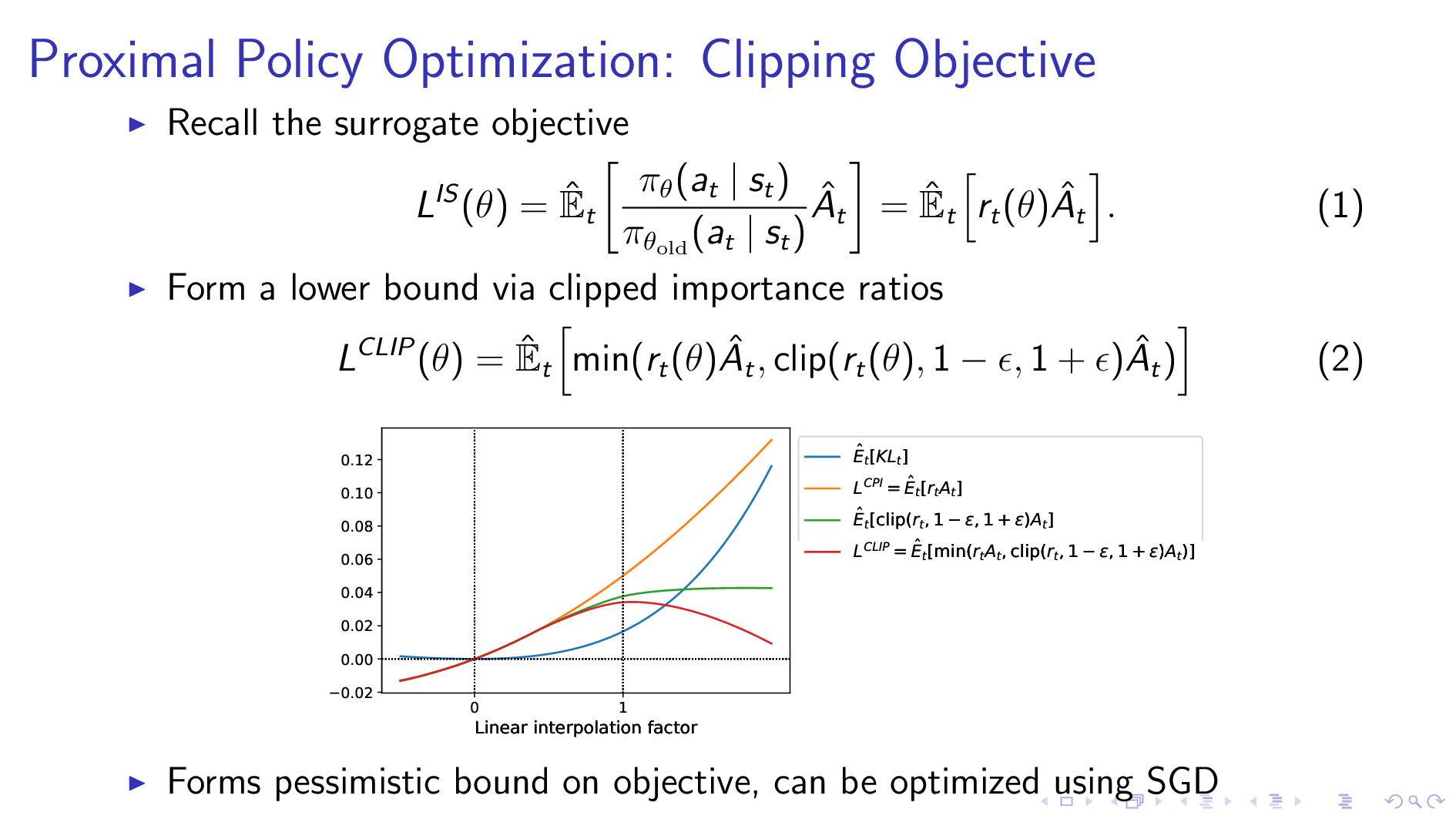Fig.

직관적으로 ratio를 기준으로 clip한다는 것은 'old policy와 너무 ratio 차이가 많이나는 방향으로는 update하지 말자'를 의미하기 때문에, 우리가 여태까지 얘기한 conservative update의 철학에 부합한다.

이제 Advantage 값과 ratio에 따라 objective와 gradient가 어떻게 바뀌는지에 대해 알아보자.

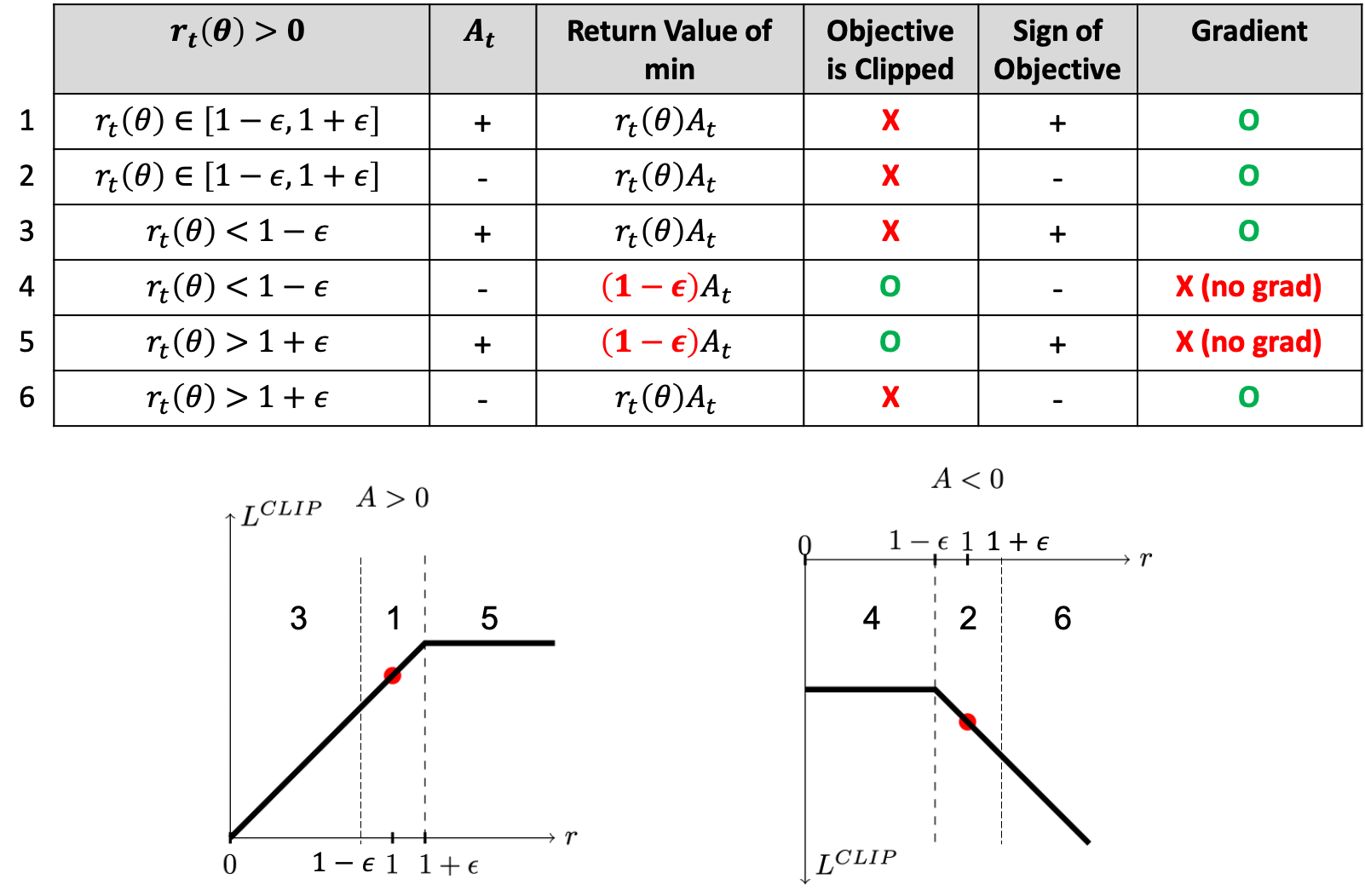Fig. Clipped objective에는 gradient가 흐르지 않는 구간이 있다. Source from link

PPO paper에도 나와있는데 clipped version은 advantage가 양수냐 음수냐에 따라서 다르게 작동한다.

A가 양수일 경우에 대해 먼저 생각해 보자. A가 양수라는 것은 이 action은 평균보다 좋았으니까 확률을 높히겠다는 것을 의미한다. 만약 old policy와 new policy의 ratio가 1인 경우라면 같은 state에서 같은 action을 확률이 정확히 같다는 것이다. 그러므로 확률을 높히는건 ok이다. 그런데 만약 ratio가 1보다 많이 크다고 생각해보자 (\(r_t(\theta) >1+\epsilon\)). 여기서 \(\epsilon=0.2\)는 hyperparameter이다. 그러면 이미 new policy의 해당 action에 대한 확률이 old policy보다 많이 큰데 (이미 policy가 많이 변했는데), 이걸 또 높히겠다는 꼴이 된다. 그러니까 이는 clip해서 필요이상으로 policy가 변하지 않게 막아야 한다. 반대로 ratio가 1보다 많이 작다고 생각해보자. 이는 문제가 별로 안되는게 new policy가 해당 action에 대한 확률이 old policy보다 작으니 그 action의 확률을 높히는 것은 두 policy의 gap을 줄이면 줄였지 늘리지는 않기 때문이다.

A가 반대인 경우에도 마찬가지다. A가 음수라면 해당 action의 확률을 낮추는것이 될텐데, 이미 ratio가 1보다 많이 작은 상황에서는 더 낮추는건 안된다. 그 반대인 ratio가 1보다 큰 경우는 ok.

하지만 여기서 눈에띄는 점이 하나 있다. 바로 clipping을 적용하면 더이상 gradient가 흐르지 않는다는 것이다.

Fig.

왜그러냐면 Actor의 parameter인 \(\pi_{\theta}(a_t \vert s_t)\)는 \(r_t(\theta)\)에 존재하는데, 이걸 \((1-\epsilon)\)으로 대체해버렸고, 이를 \(\theta\)에 대해 미분해도 아무런 일도 일어나지 않기 때문이다. 실제 유명한 PPO 구현체들을 봐도 대부분이 torch.clamp를 사용해서 clipping하는 부분이 구현되어있는데, 이 경우 gradient가 흐르지 않게 된다.

# https://github.com/DLR-RM/stable-baselines3/blob/a9273f968eaf8c6e04302a07d803eebfca6e7e86/stable_baselines3/ppo/ppo.py#L228C1-L231C75

# clipped surrogate loss
import torch as th
policy_loss_1 = advantages * ratio
policy_loss_2 = advantages * th.clamp(ratio, 1 - clip_range, 1 + clip_range)
policy_loss = -th.min(policy_loss_1, policy_loss_2).mean()

즉, threshold를 넘지 못하는 (state, action) tuple은 gradient계산에 쓰이지 못하고 버려지게 되는 것이다.

그래서 clipped PPO는 직관적으로 얼마나 괜찮은가? 아래 figure를 보자.

Fig.

아무튼 clipped PPO는 구현상 매끄럽지 못한 부분이 존재하지만 KLD를 직접 계산하지 않고도 pessimistic policy update를 할 수 있게 되었다.

Adaptive KL Penalty

이제 다시 Adaptive KL Penalized Objective로 넘어가 보자. 이는 TRPO에서 유도된 결과를 변형한 것이다. TRPO에서 원래 유도된 objective인 KL penalty term이 좋기는 한데 실제로 이걸 써보면 너무 policy update가 더디다고 한다. 그 이유는 KL term에 곱해주는 coeffcieint, \(\beta\)가 고정되어 있기 때문이다. 실제로 PPO로 학습을 해보면 서로 다른 여러 problem에 대해서 잘 working하는 \(\beta\)는 고사하고, 한 problem내에서도 학습하는 동안에도 변동이 있을 수 있다고 한다. 그래서 PPO paper에서는 coefficient, \(C\)를 매 step마다 adaptive하게 정한다. 그래서 이 첫번째 method의 이름이 Adaptive KL Penalty version가 되는 것이다.

Fig.

그래서 어떻게 \(\beta\)를 정하는가? 방법은 간단한데,

Fig.

Final PPO Algorithm

Fig.

Experimental Results

Fig.

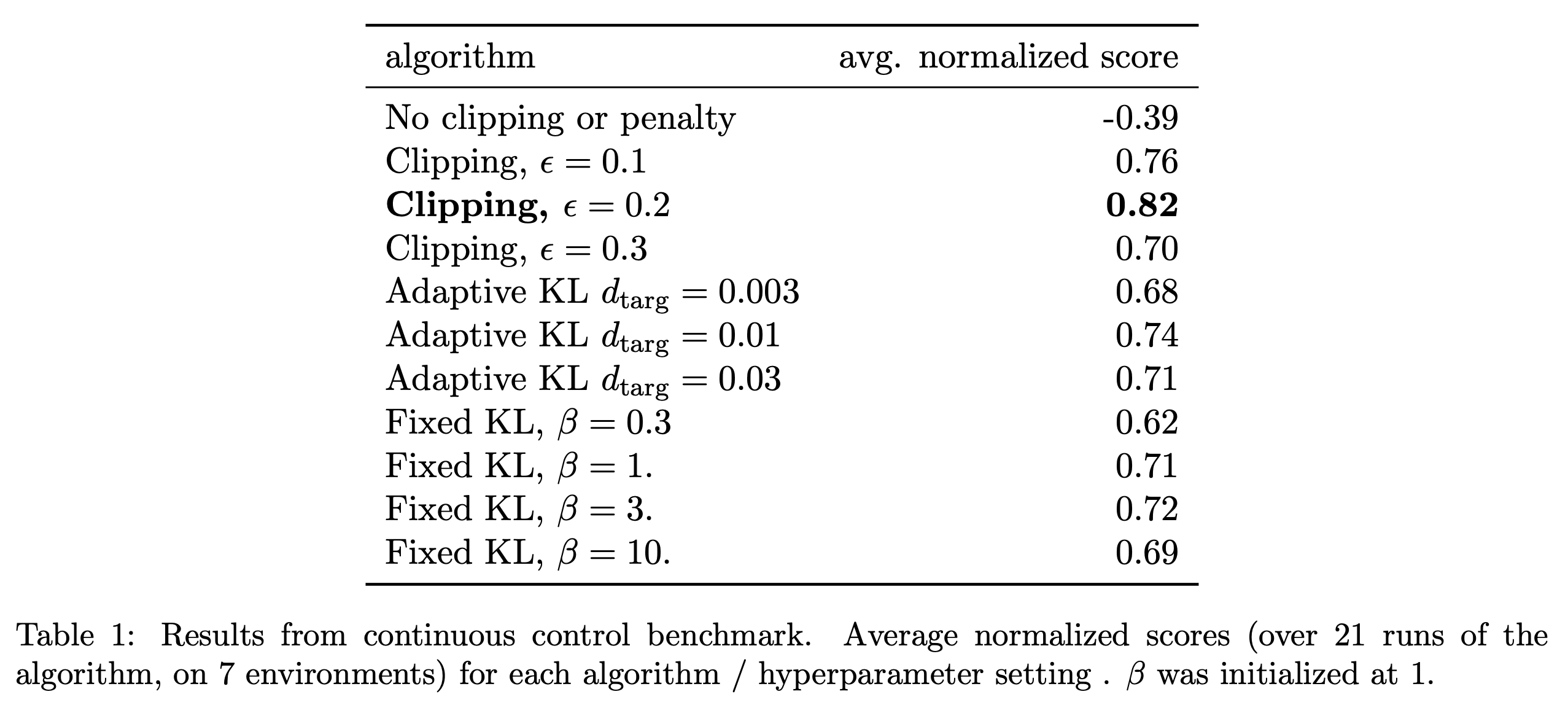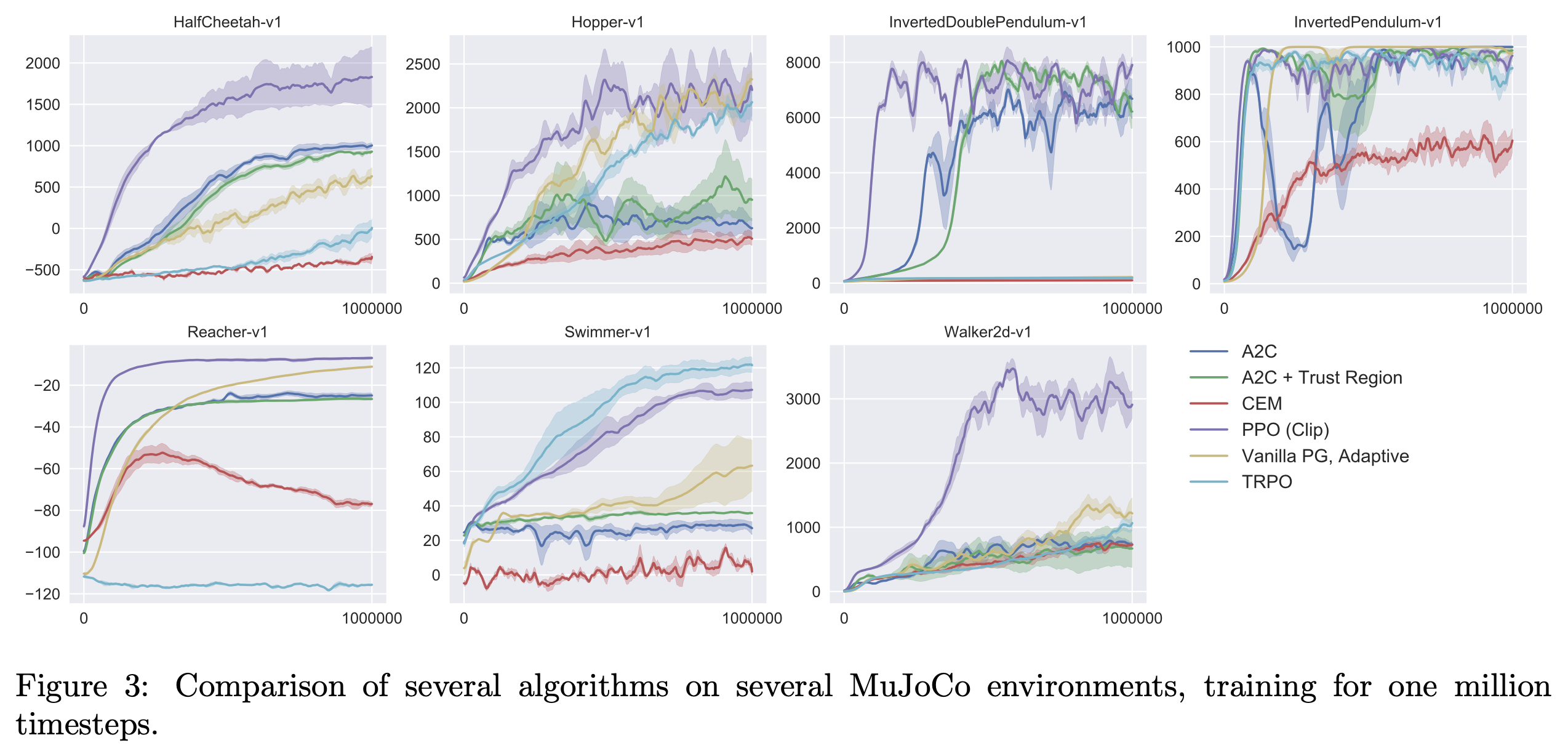Fig.

Fig.

Reference

• Papers
  • PhD Thesis of John Schulman
  • Trust Region Policy Optimization
  • Proximal Policy Optimization Algorithms
• Lectures, Videos, Notes and Talks
  • Deep RL Bootcamp
    • Deep RL Bootcamp Lecture 5: Natural Policy Gradients, TRPO, PPO from John Schulman
    • Deep RL Bootcamp Lecture 6: Nuts and Bolts of Deep RL Experimentation from John Schulman
  • CMU 10-703 Deep Reinforcement Learning from Katerina Fragkiadaki
    • 2023 Fall ver
      • Policy gradients, REINFORCE, Actor-Critic methods
      • Natural PG, PPO, TRPO
• Others
  • OpenAI Spinning Up
    • Vanilla Policy Gradient
    • Trust Region Policy Optimization
    • Proximal Policy Optimization
  • TRPO (Trust Region Policy Optimization) : In depth Research Paper Review
  • Policy Gradient Algorithms from Lilian Weng
    • korean version
  • Policy Optimization with Monotonic Improvement Guarantee from Runzhe Yang
  • TRPO 논문 리뷰 from 노승은님
  • Trust Region Policy Optimization (TRPO) 정리 from HiddenBeginner님
  • Trust Region Policy Optimization, Schulman et al, 2015 from Chris Ohk
  • Natural Policy Gradient 논문 리뷰 from Jangwon Kim
  • Trust Region Policy Optimization 논문 리뷰 from Jangwon Kim