(CS285) Lecture 4 - Introduction to Reinforcement Learning

이 글은 UC Berkeley 의 교수, Sergey Levine 의 심층 강화 학습 (Deep Reinforcement Learning) 강의인 CS285를 듣고 작성한 글 입니다.

Lecture 4의 강의 영상과 자료는 아래에서 확인하실 수 있습니다.

• Fall 2020 ver.
  • Lecture Video Link (Youtube)
  • Lecture Slide Link
• Fall 2023 ver.
  • Slide

< 목차 >

• What If There is no Human Label? Training with Reward !
  • Markov Decision Process (MDP)
  • Definition of MDP
  • Markov Process Examples
• The Objective for Reinforcement Learning
  • Re-interpret MDP as Markov Chain
  • Finite Horizon Case
  • Infinite Horizon Case
  • Why Expectations matter in RL
• Algorithms
  • The Anatomy of a RL Algorithm
  • Intuition of Training with RL
  • Which parts are Expensive?
• Value Functions
  • Q-Value Function and Value Function
• Types of Algorithms
  • Model-based RL
  • Value-based RL
  • Policy-based RL
• Tradeoffs Between Algorithms
  • Sample Efficiency
  • Stability and Ease of Use
  • Assumptions
  • Examples of Algorithms
• Reference

지난 lecture에서는 Behaviour Cloning (BC)에 대해서 배웠습니다. BC는 sequential decision making problem을 풀기 위한 가장 단순한 방법으로, Deep Learning (DL)의 Supervised Learning (SL)과 다를 바가 없었습니다. 다만 모든 sample이 i.i.d 가 아니라는 문제나 inference time의 state들은 우리가 학습한 data의 distribution인 \(p_{data}\)가 아니라 실제 학습된 policy가 만들어낸 \(p_{\pi}\)로 부터 sampling된다는 점 등이 naive BC로 사람의 행동을 모사하는 것을 어렵게 만든다는 것을 배웠습니다. Lecture 마지막에 우리는 log likelihood를 최대화 하는 것이 아니라 실제 좀 더 근본적인 목적 함수 (Objective Function)을 정의하고 이를 optimize해야 한다는 얘기를 했습니다.

이번 lecture부터는 어떤 objective function을 정의해야 하는지? 정의했으면 어떻게 optimize를 해야하는지? 등 본격적으로 강화 학습 (Reinforcement Learning; RL)에 대해서 배우게 될 것입니다.

Slide. 1.

What If There is no Human Label? Training with Reward !

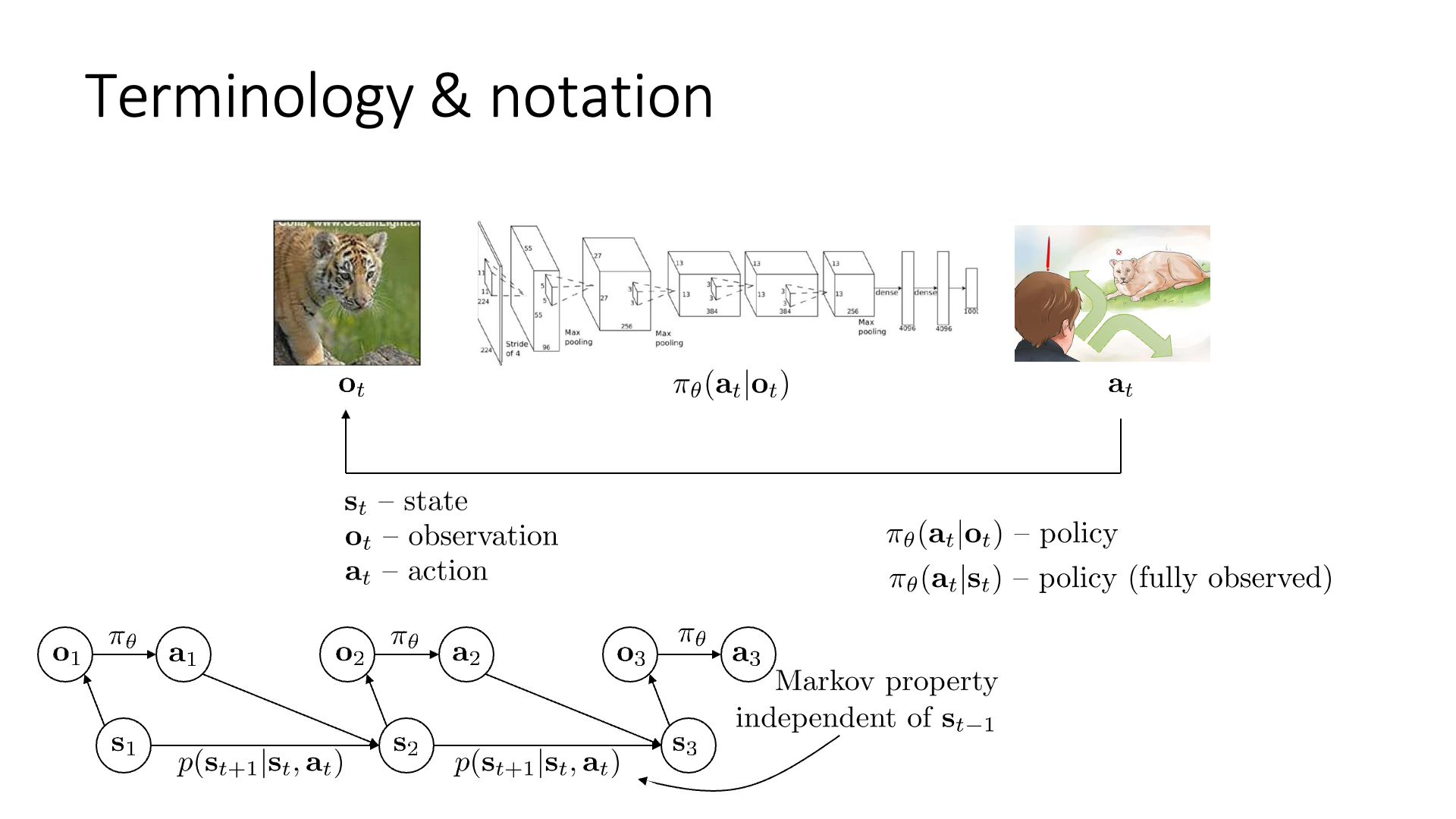Slide. 3.

Lecture 2의 에서는 RL의 기본적인 구성요소들과 BC에 대해서 알아봤습니다. RL의 goal은 어떤 state에서 어떤 action을 해야하는지를 알려주는, 두 state, action간의 mapping function인 정책 (Policy), \(\pi_{\theta}(a_t \vert s_t)\)을 학습하는 것 입니다. 그리고 좋은 policy란 Machine Learning (ML)을 할 때 log likelihood를 최대화 하는 parameter를 찾는 것 처럼 우리가 정의한 objective function을 최대화 하는 policy를 의미합니다.

이러한 정책을 하는 방법은 크게 두 가지로 나눌 수 있습니다.

• Policy based methods: explicit policy가 있고 이를 direct로 optimization 하는 방법
• Value based methods: explicit policy는 없지만 가치 함수 (Value Function) 라는 module을 만들고 이를 objective에 대해서 최대화하는 방향으로 학습한 뒤, 이로부터 policy를 정의하는 방법 (implicitly policy)

주의할 점은 value function을 학습하는 경우에도 결국에는 good policy를 얻는 것이 최종 목표라는 겁니다. (앞서 말씀드리자면 lecture 4,5,6,9 policy based methods에 대해서 배우고 lecture 7,8에서는 value based methods에 대해서 배웁니다.)

Lecture2에서 우리는 Markov Property에 대해서 배웠습니다. Slide 3에 나오는 것처럼 Graphical model로 Markove property에 대해서 설명했었는데 이는 아래의 5개의 element들로 이루어져 있었습니다.

• observation, \(o_t\)
• state, \(s_t\)
• action, \(a_t\)
• policy, \(\pi_{\theta}\)
• state transition probability, \(p(s_{t+1} \vert s_t, a_t)\)

State와 pbservation는 RL 연구자들이 많이 혼용해서 쓰지만 엄밀히는 다른 개념으로, state가 전체 물리계 정보 등을 포함하는 더 상위개념이었으며 observation은 이 state로 부터 얻을 수 있는 일부분으로 우리가 눈으로 볼 수 있는 image frame같은 것을 의미했습니다. State는 markov property를 만족하여 현재 encoding된 정보만을 가지고 그 다음 action, state를 완벽하게 알 수 있지만 observation는 그렇지 않았으며, observation은 full state를 추론 하는 데 필요한 정보를 모두 포함하고 있을 수도, 아닐 수도 있었습니다.

• Fully Observed Reinforcement Learning Algorithm (\(\pi_{\theta} (a_t \vert s_t )\))
• Partially Observed Reinforcement Learning Algorithm (\(\pi_{\theta} (a_t \vert o_t)\))

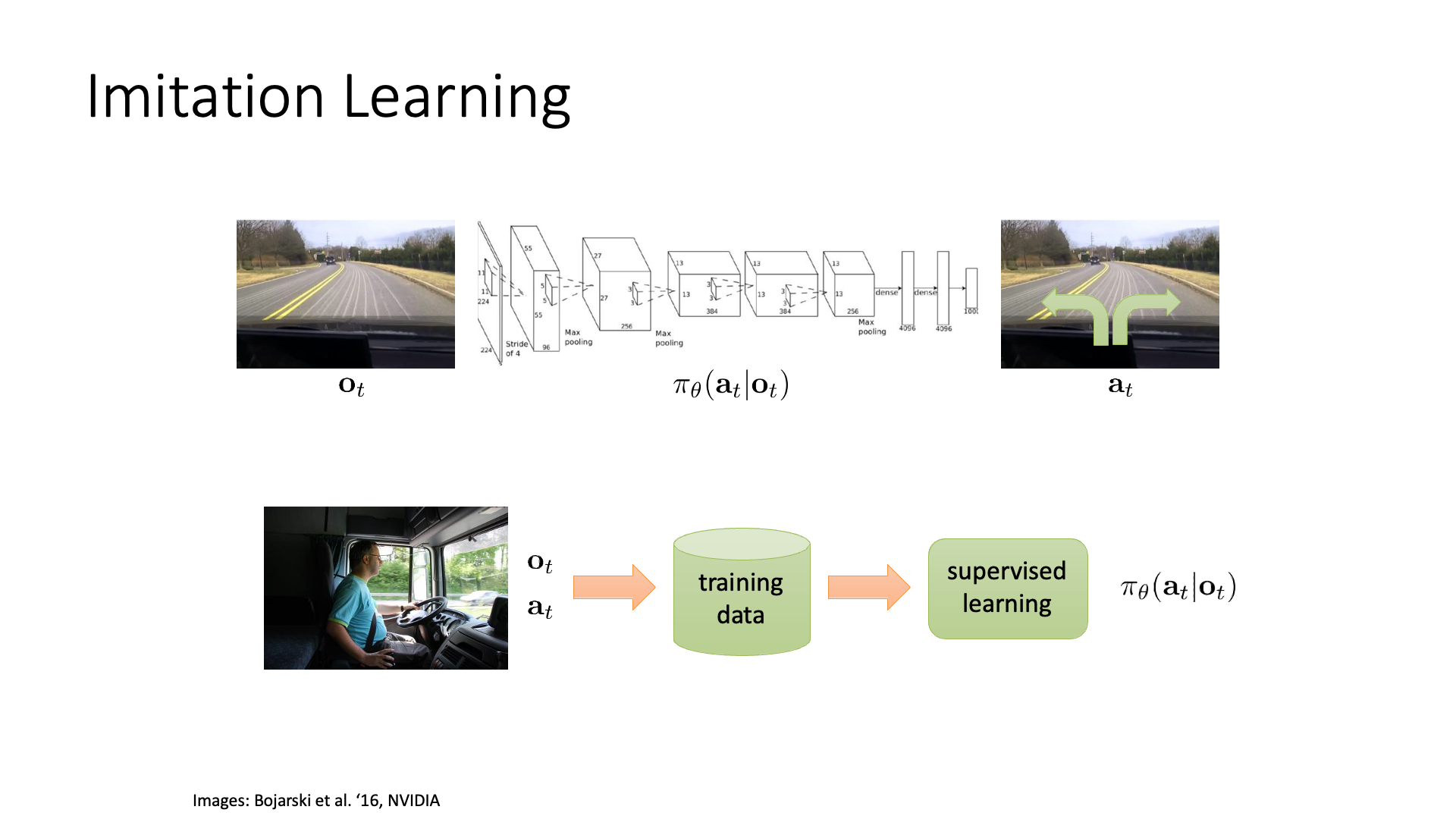Slide. 4.

Slide 4는 BC의 recap입니다. BC는 단순하지만 몇 가지 다음과 같은 문제점이 있었습니다.

• Human expert data를 모아야함 (SL이기 때문에)
• Distributional shift문제가 있음
  • 단순히 log likelihood를 최대화 하는 것은 실제 상황과 matching 되지 않음

Slide. 5.

특히 주어진 dataset에 대해서 Maximum Likelihood Estimation (MLE)를 하는 것은 실제 상황과는 맞지 않는 objective 였습니다. 이를 타개하기 위해서 우리는 어떤 우리가 원하는 objective, 예를 들어 자율 주행을 한다면 expert data의 likelihood를 최대화 하는 것이 아니라 실제로 agent가 이정도 주행을 했으면 ?점을 return 해줄 수 있는 objective function을 새롭게 정의하고, 이를 현재 optimization step의 policy로 부터 sampling한 data distribution 하에서 objective 값을 계산하여 optimization 해야 한다고 얘기 했습니다.

왜냐면 likelihood를 최대화 하는 것이 실제 우리가 목표하는 좋은 주행을 하기 위해서는 어떤 state에서 어떤 action을 해야하는지?를 알려주기는 어려울 수 있기 때문이며, 실제 policy distribution 하에서 optimization을 하는 것이 distributional shift를 덜 일어나게 해줄 수 있기 때문이죠.

그렇다면 objective function을 정의하기 위해서는 보상 함수 (Reward Function)라는 개념이 필요할겁니다. 그래야 ‘어떤 t 시점의 state, \(s_t\)에서 어떤 action, \(a_t\)이 몇점짜리 action이였는지’ 알 수 있을 것이며 이 reward 값들을 모아서 최종적으로 주행이 끝났을 때 ‘주행이 얼마나 좋았는지?’를 평가할 수 있을 것이기 때문입니다. 이를 \(s_t\)에서 \(a_t\)를 했을 때의 점수라고 해서 \(r(s_t,a_t)\) 라고 씁니다. (이 함수가 리턴하는 결과값은 vector가 아닌 scalar입니다)

RL은 BC와 비교해서 다음과 같은 특성이 있습니다.

• 매 action마다 정답 label이 없음
  • 대신 해당 action에 대한 reward가 주어짐
• 매 optimization step (iteration) 마다 dataset을 새로 만드는 것이 됨
  • 왜냐하면 policy가 update됐으면 trajectory distribution이 바뀌었으므로 그 distribution에서 새로 sampling해서 그 data들로 학습해야 하기 때문
• Objective function이 단순 log likelihood가 아님

Sergey는 이 reward function과 reward function을 가지고 정의한 objective function을 The heart of the decision making problems 혹은 The heart of the reinforcement learning problems 이라고 합니다. 왜 reward function이 그토록 중요할까요? 그 이유는 같은 자율 주행 agent를 학습한다고 하더라도 ‘빨리 도착할수록 가산점’으로 정의한 reward function으로 학습하는 것과 ‘교통 법규를 준수하면 가산점’으로 학습한 agent는 다를 것이기 때문입니다. 전자의 agent는 사람을 치고 가도 아무런 문제가 없는 agent가 되겠지만 후자는 그렇지 않겠죠. 그만큼 reward function design과 objective function design은 매우 중요한 것입니다.

이제 앞서 lecture 2에서 잠깐 설명하고 넘어갔던 Markov Decision Process (MDP)에 대해서 잠시 얘기해 보도록 하겠습니다.

Markov Decision Process (MDP)

Sergey의 Berkeley 직장 동료이자 Deep RL계의 쌍두마차 Pieter Abbeel의 Deep RL 입문 강의를 보면 이런 말을 합니다. (사실 Pieter가 훨씬 연식이 오래됐습니다.)

"만약에 당신이 풀고싶은 문제를 MDP로 mapping할 수 있다면, 그 문제는 RL algorithm으로 해결할 수 있다."

MDP에는 다음과 같은 instance들이 있습니다.

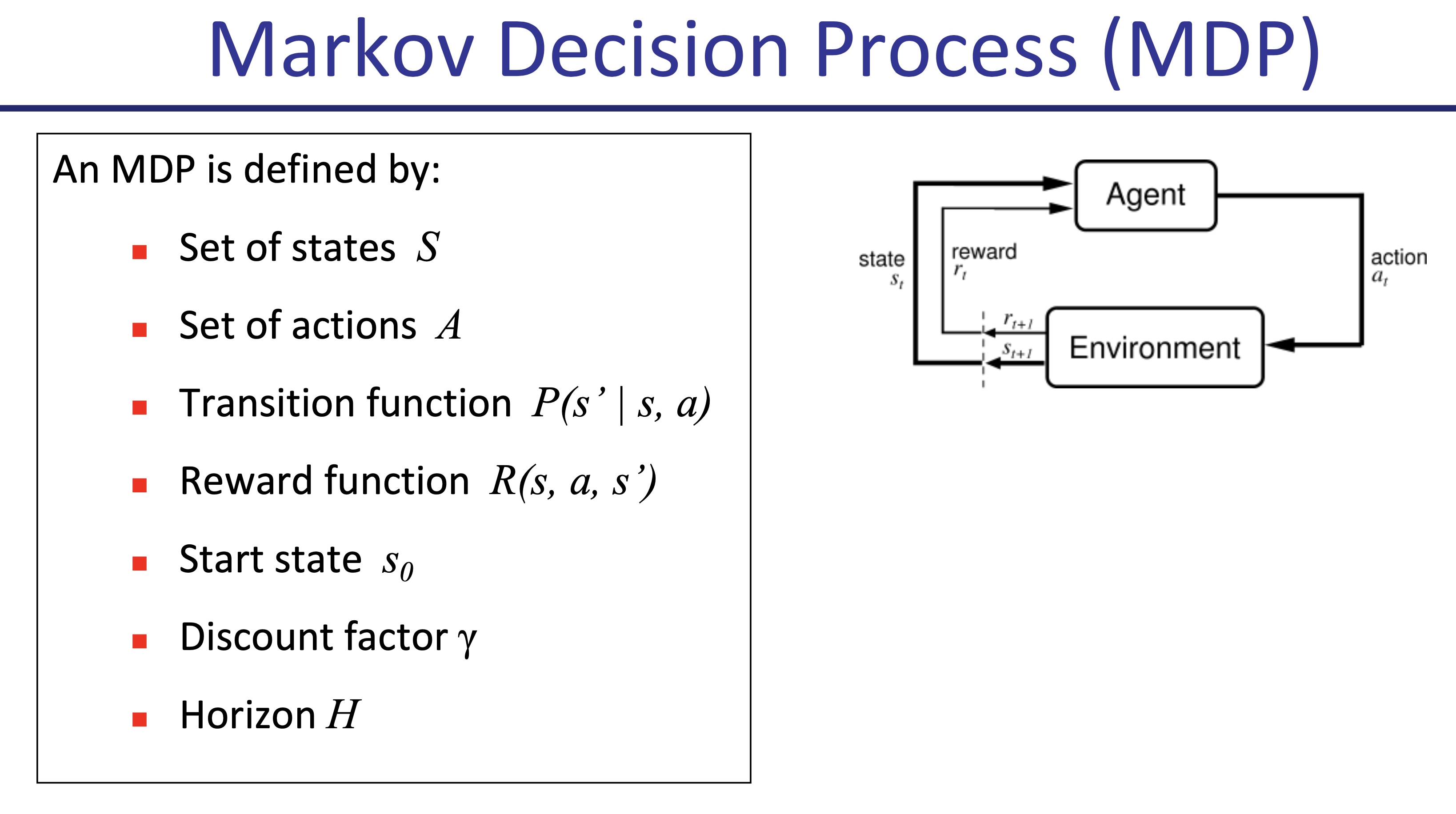Fig.

앞서 간단히 설명드린 것 처럼 어떤 t시점의 state \(s_t\)에서 어떤 \(a_t\)를 하면 어떤 reward, \(r(s_t,a_t)\)를 받고, 또 그 다음에는 어떤 상태, \(s_{t+1}\)로 내 상태가 변하는지? 등을 정의만 할 수 있으면 이 문제는 RL algorithm으로 풀 수 있는겁니다.

몇 가지 예시를 들어봅시다.

Fig.

로봇청소기의 경우 state는 내 집 구석구석이 될 테고 action은 상하좌우 움직이는 것이며 주어진 먼지를 먹을때 마다 +1점, 주어진 시간안에 먼지 한 톨 없이 청소했으면 +10점 … 등으로 정의 할 수 있으니까요. 이 밖에도 주식도 주어진 장 상황에서, position을 매입, 매수 정할 수 있고 따면 + 잃으면 - … 인데 이거는 사실 굉장히 어렵고 받아들이는 state 정보가 noisy하기 때문에 실패할 확률이 매우 높지만 어쨌든 RL로 할 수 있는겁니다.

한 편, 우리가 주어진 문제를 MDP로 mapping 해올 수 있으면 우리는 그 문제에 RL을 적용해서 풀 수 있다는 말은 반대로 말하면 모든 문제에 RL을 쓰지 말라는 것이 되기도 할겁니다. 앞으로 RL algorithm들에 대해 말씀드리겠지만 일반적으로 RL은 variance가 매우 큰 방법론으로 경우에 따라 수렴하지 않을 수도 (좋은 policy를 학습하지 못할 수도) 있기 때문에 아무데나 RL을 쓰면 시간낭비가 될 수도 있으니, MDP가 어떤것인지를 잘 이해해서 내 문제를 RL로 풀 수 있는 것인지?를 잘 가늠할 수 있는것이 좋을 것 같습니다.

Definition of MDP

이제 MDP에 대해서 제대로 정의를 해 봅시다.

Slide. 6.

먼저 Markov Chain부터 다시 봅시다. Markov는 Stochastic Processes 분야를 개척한 Andrey Markov라는 수학자의 이름을 따 왔다고 합니다. (Markov Chain, Markov Reward Process (MRP), Markov Decision Process (MDP) 모두 비슷하지만 조금씩 다른 개념 입니다)

Markov Chain의 개념은 굉장히 간단하며 구성 요소는 두 가지입니다.

• S: State space \(\rightarrow\) (states \(s \in S\))
• T: Transition operator \(\rightarrow\) \(p(s_{t+1} \vert s_t)\)
  • Transition probability, Transition Dynamics 라고도 부름

먼저 State space는 agent가 위치할 수 있는 모든 state를 포함하는 set입니다. 그리고 Transition operator는 \(s_t\)에서 \(s_{t+1}\)로 state가 바뀔 확률을 나타냅니다. 이것을 연산자 (operator)라고 하는 이유는 state distribution과 matrix multiplication 연산을 통해 다음 state의 distribution을 알려주기 때문입니다.

Markov chain의 graphical model은 Slide. 6.의 하단에 잘 나타나 있으며, 그래프의 edge가 나타내는게 바로 Transition probability가 입니다. 그리고 markov chain은 lecture 2에서 배운 markov property를 만족합니다.

하지만 markov chain에는 state의 개념만 있기 때문에 decision making problem을 해결할 수 없습닏. 문제를 풀기 위해서는 action, \(a_t\)에 대한 개념이 필요하죠.

Slide. 7.

MDP는 위의 markov chain 개념에 몇 가지 objects를 더 추가한 겁니다. 1950년대에 Richard Bellman에 의해 제안된 개념이라고 하네요.

Markov chain에 Action space 와 Reward function을 의미하는 \(A,r\)이 추가 되었습니다. (MDP이전에 Markov Reward Process (MRP)이라는 것에서는 또 A가 없이 r만 있는데, 여기서는 다루지 않는 것 같으니 생략하겠습니다)

Action이 추가됐기 때문에 transition operator에도 \(a_t\)가 추가로 condition되어야 합니다. 당연히 markov property를 만족해야 하니 \(s_t,a_t\) 에 의해서만 다음 상태 \(s_{t+1}\)이 결정되며, transition operator는 \(p(s_{t+1} \vert s_{t})\)가 아니라 \(p(s_{t+1} \vert s_{t}, \color{red}{a_{t}})\)가 추가된 형태로, 2D Matrix가 아닌 3D Tensor가 됩니다.

Reward function은 아래와 같이 나타낼 수 있으며,

Slide. 8.

이는 state와 action의 카티전 곱 (Cartesian Product)을 어떠한 real value number로 mapping해주는 함수라고 합니다.

즉 reward function의 input은 \((s_t, a_t)\)로 어떤 state에서 어떤 action을 하는 것이 얼만큼의 reward를 가진 action이었느냐?를 알려주는 함수라는 거죠.

MDP를 조금 더 확장하면 Partially Observed MDP (POMDP)가 되는데, state 외에 Observation space, \(O\), 그리고 \(S\)와 \(O\)사이의 관계를 나타내는 Emission probability, \(\varepsilon\)가 추가됩니다.

• S: State Space, state \(s \in S\)
• A: Action Space, action \(a \in A\)
• O: Observation Space, observation \(o \in O\)

Slide. 9.

Observation, \(o\)는 state에 depend하며 emission probability는 \(s_t\) 에서 \(o_t\)를 관측할 확률을 나타냅니다 (\(p(o_t \vert s_t)\)).

Lecture 2와 recap에서 말씀드린 것 처럼 state와 observation은 다릅니다. Observation은 encoding된 정보가 부족하여 markov property를 만족하지 않을 수 있습니다. 일반적으로 RL로 문제를 풀 때는 현재 state만 가지고도 그 다음 action, state를 다 알 수 있으므로 reward값을 state와 action에 의거해 산출합니다. POMDP의 경우 true state에 접근하지 않고 (못하고), observation에 근거해서 decision making을 해야 합니다.

Markov Process Examples

Markov Chain, MDP 그리고 배우진 않았지만 Markov Reward Process (MRP)의 몇 가지 example과 아직 배운적은 없지만 이제 곧 배우게 될 value function의 개념을 살짝 더해서 Markov Process와 우리가 앞으로 배우게 될 RL에 대해 insight를 얻어봅시다. 이하 모든 figure의 출처는 David Silver의 RL Lecture chapter 2: MDP 입니다.

• Markov Chain

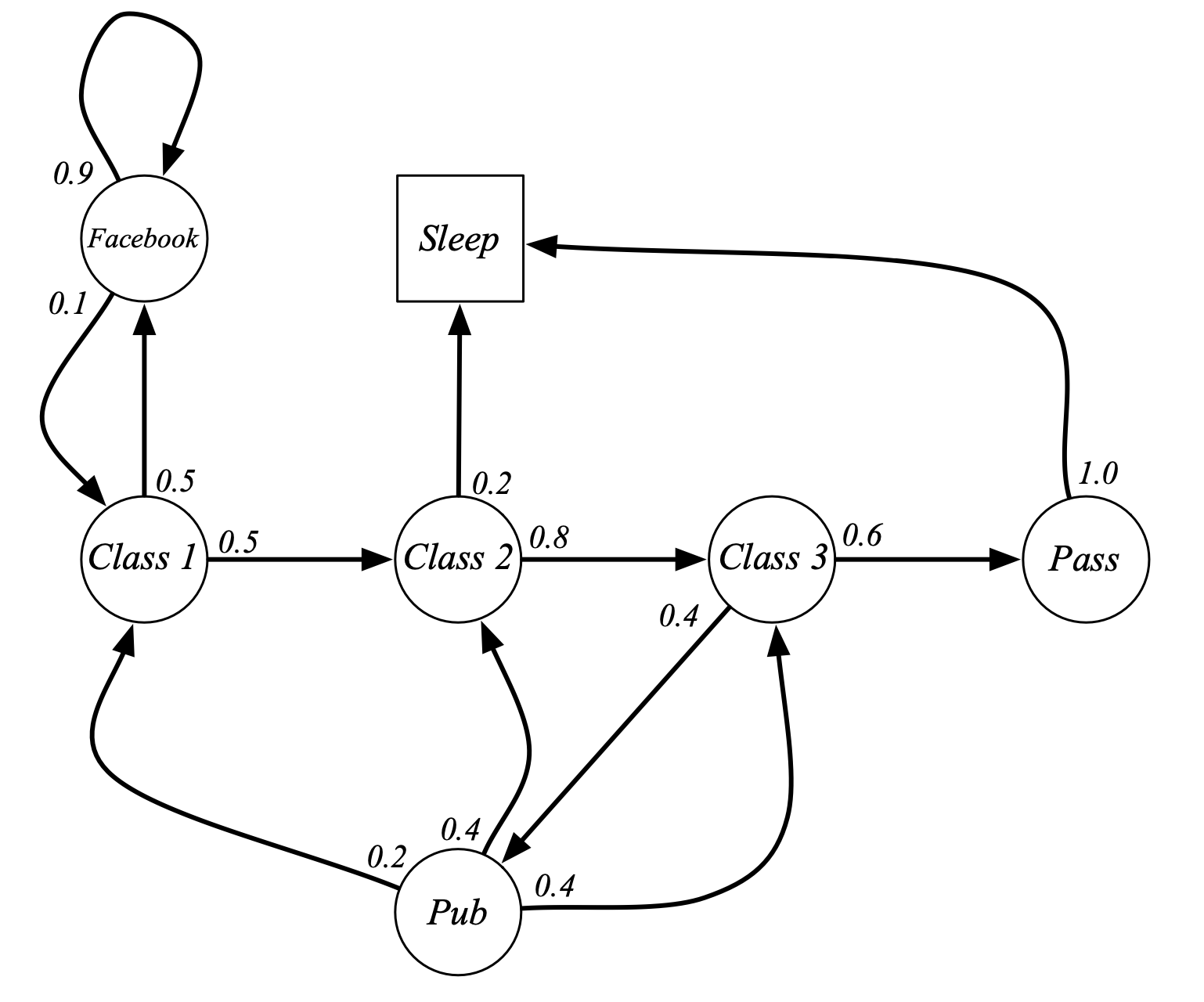Fig. Markov Chain Example: Student Markov Chain. 평범한 대학생의 동선을 markov chain으로 나타낸 예제 입니다. state과 state transition probability 만 있는 것을 알 수 있습니다. class 2를 듣다가 잠에 빠질 확률도 있고 facebook을 하는 state에 빠지면 헤어나오기 어렵다는 것도 알 수 있음.

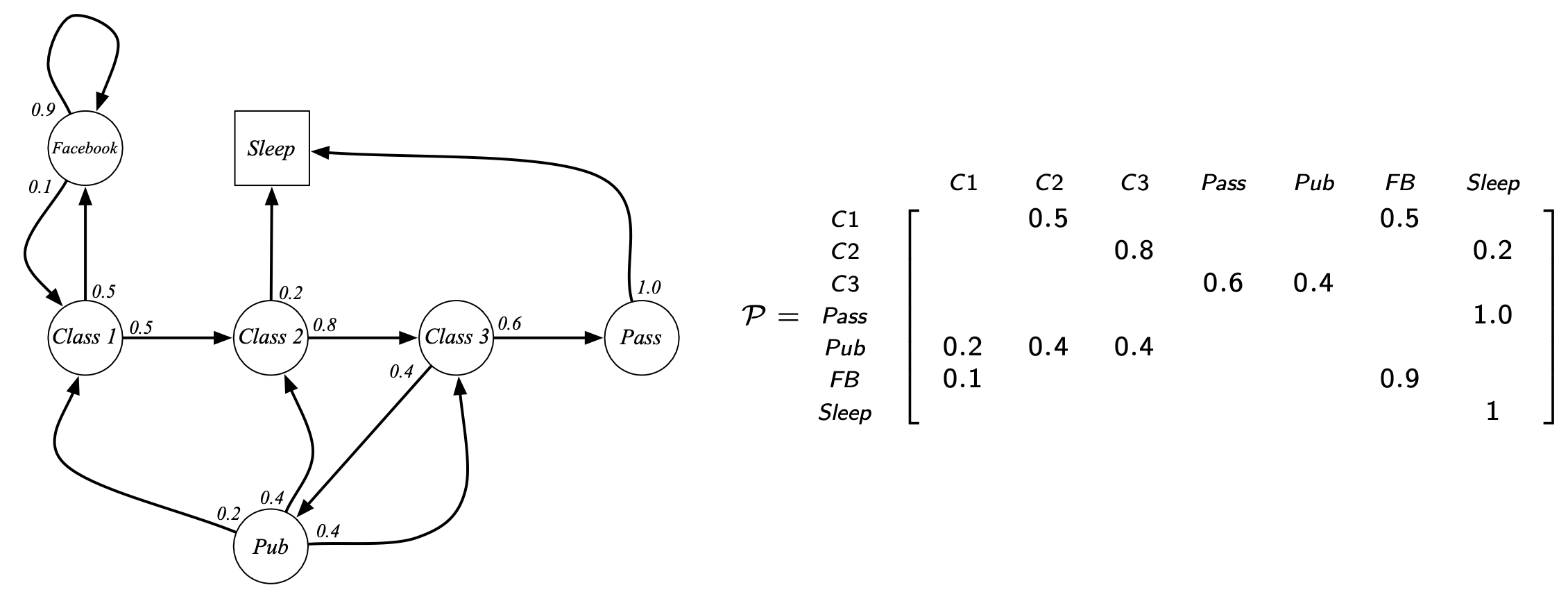Fig. Markov Chain의 Transition Probability Matrix (Operator) Example. 어떤 state끼리는 연결이 되어있지 않을 수도 있음.

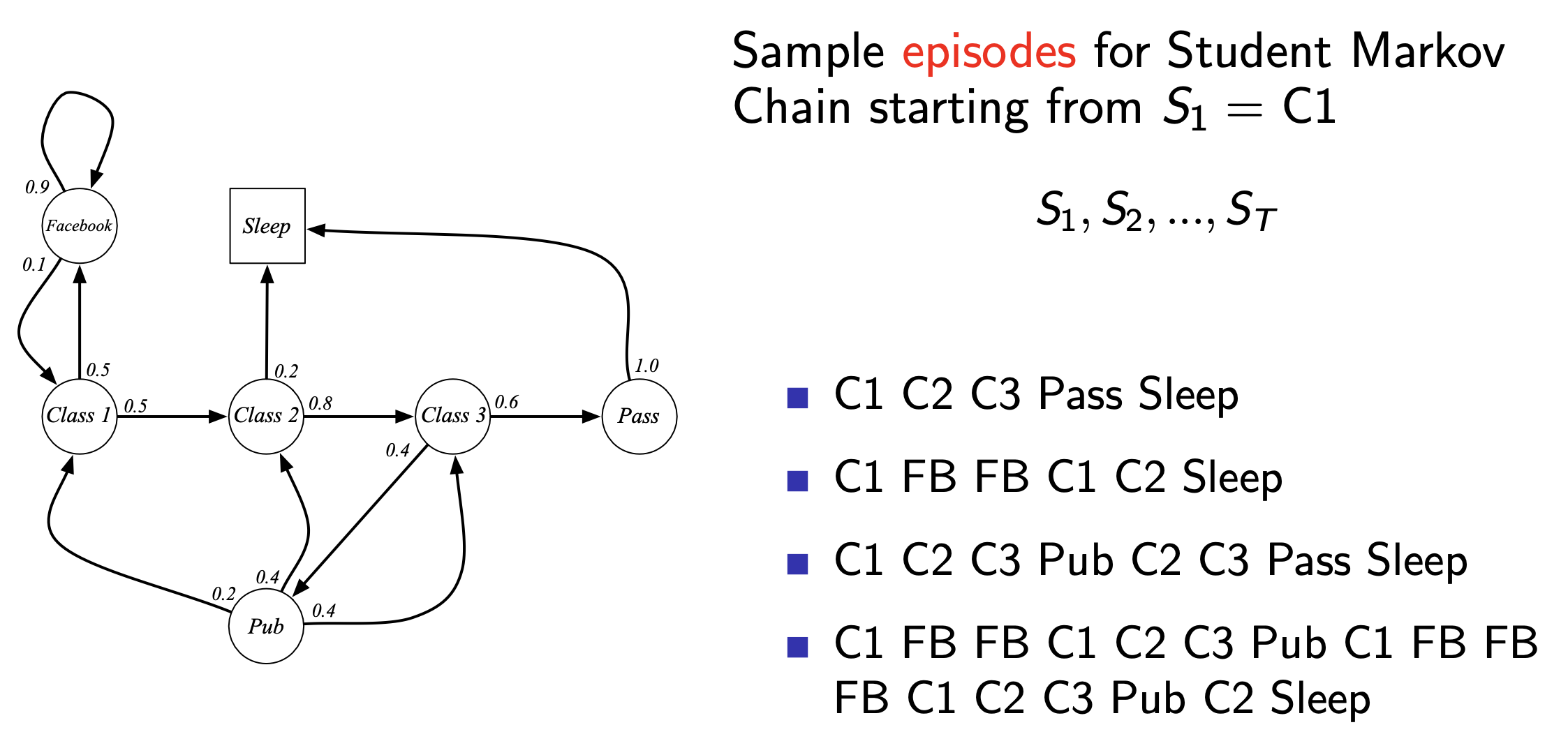Fig. Markov Chain을 통해서 일련의 episode를 몇 개 sampling 할 수 있음.

• Markov Reward Process (MRP)

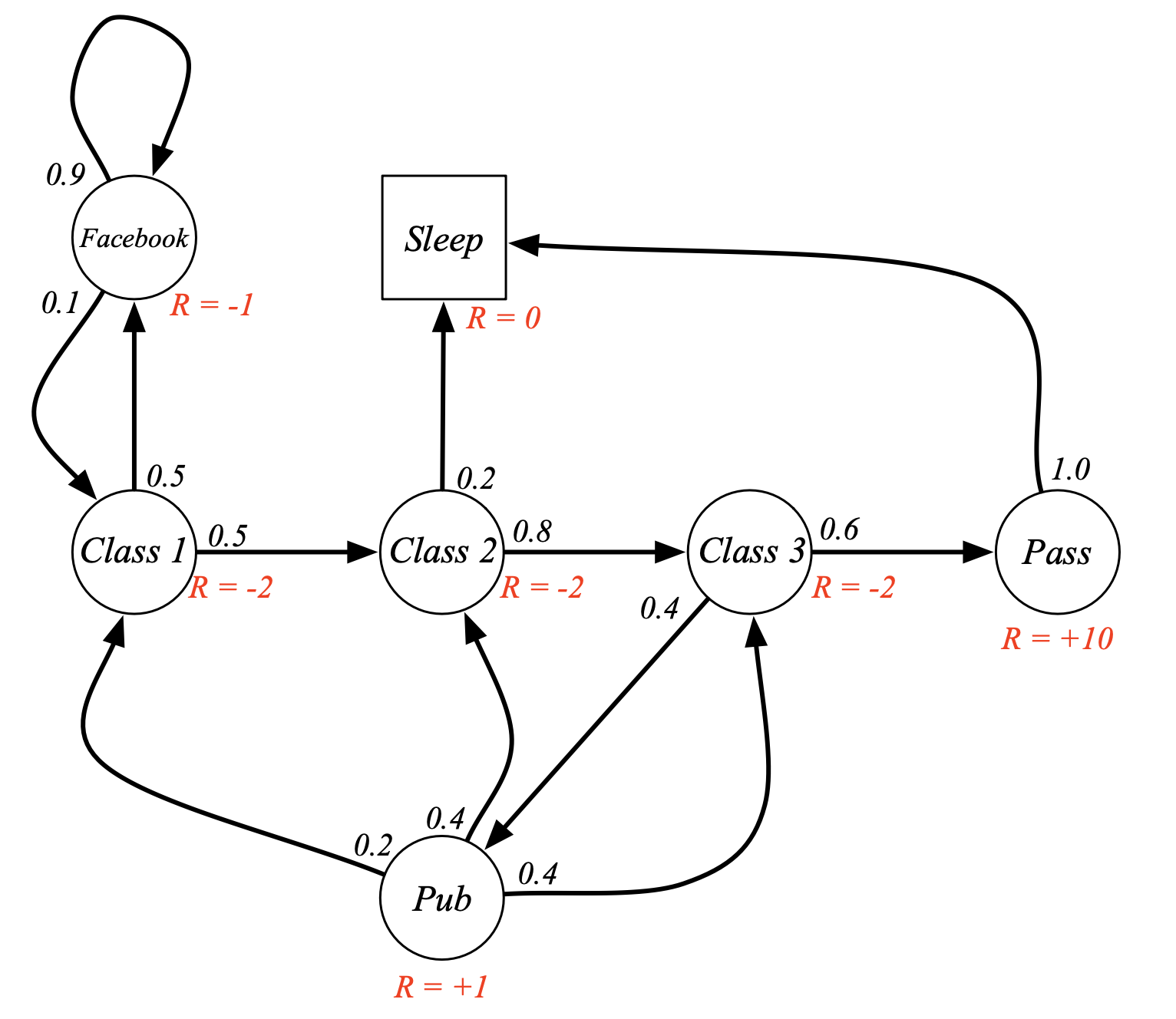Fig. MRP Example: Student MRP. 평범한 대학생의 동선을 MRP으로 나타냄. Markov Chain과 다르게 Reward가 추가됨. class1에 있는 것 만으로 -2의 reward를 받고 facebook을 하는 state로 빠지면 -1의 reward를 받거나 pass state로 가면 +10을 받음.

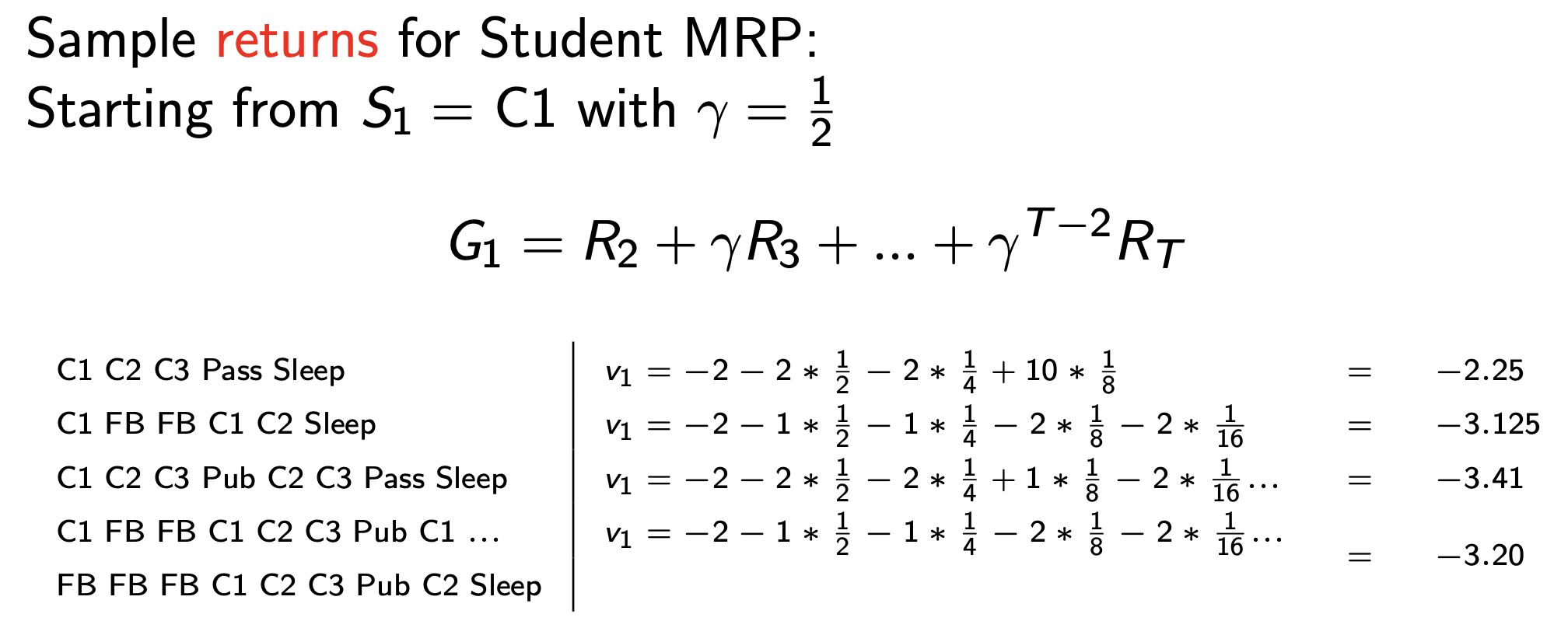Fig. MRP에서도 일련의 episode를 sampling할 수 있는데, 각 episode마다 reward의 합인 return을 계산해봄. 출발은 C1에서 하는데 우리의 목표는 일과를 끝내고 잠에 빠지는 것 (sleep state). sleep state는 terminal state로 이곳에 빠지면 무한 loop를 돌면서 이곳을 빠져나오지 못함 (게임 종료). 여기서 한 번 state를 옮길 때 마다 얻는 reward에 0.5씩 곱함. 이를 discount factor, \(\gamma\)라고 함.

Fig. 해당 state부터 state transtiion이 일어날 때 마다 받는 reward를 sum한 quantity를 이제 \(G_t\)라고 부름. discount factor가 0이냐 1이냐는 미래 얻게될 reward를 0~1로 scaling해주는 것으로 0에 가까울수록 근시안적 (myopic)으로 return을 계산하게 되고, 1에 가까울수록 원시안적 (far-sighted)으로 미래까지 고려해서 계산하게 됨.

Fig. discount factor의 insight. 가장 중요한 이유는 미래에 대한 불확실성이 존재하기 때문.

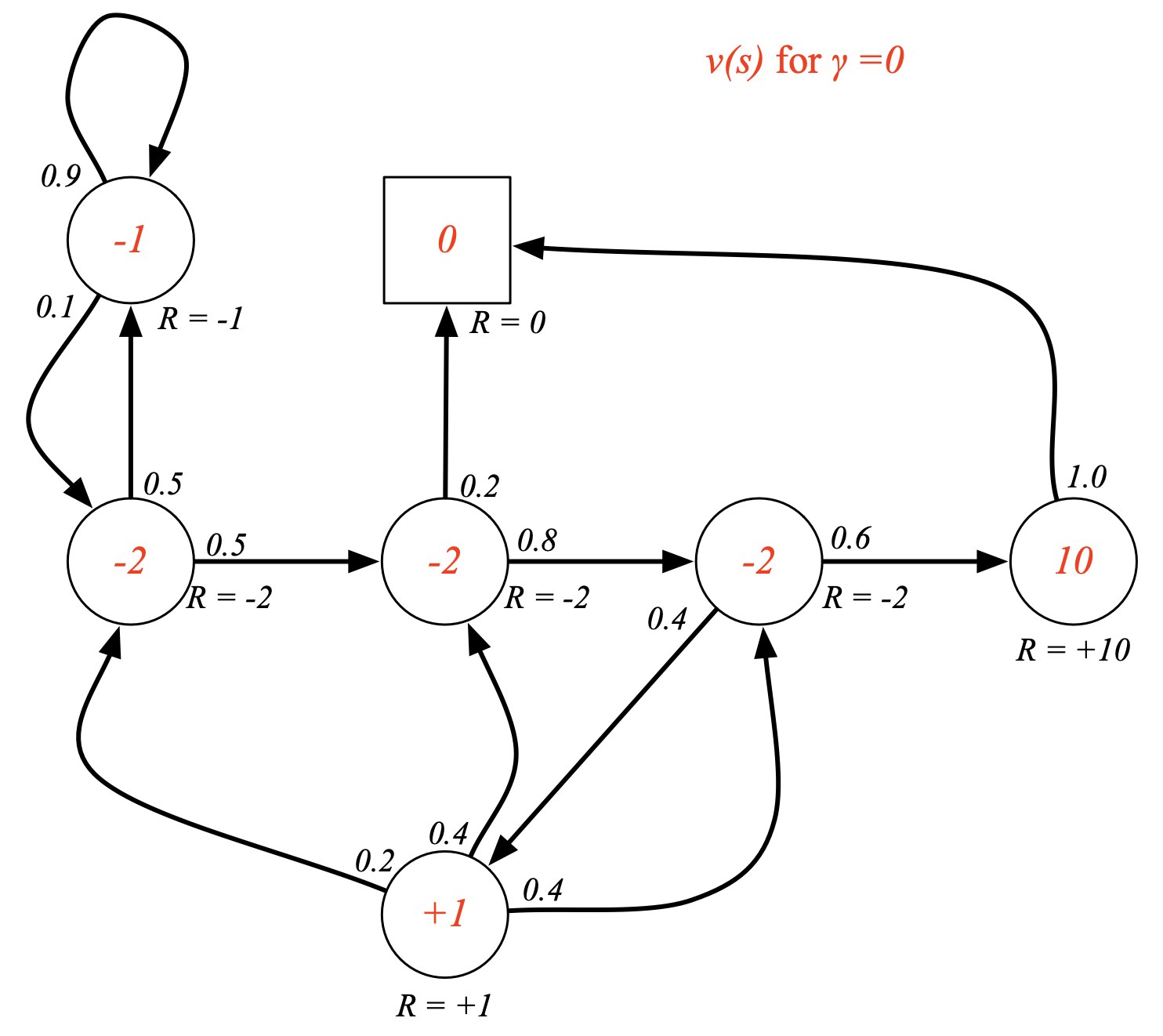Fig. 이제 각 state별로 “만약 여기서 출발한다면 얼마의 return을 받을 수 있을까?”를 계산함. 이를 이 state의 value라고 함.discount factor, \(\gamma\)이 0일 경우 현재 가치만을 고려하게 됨.

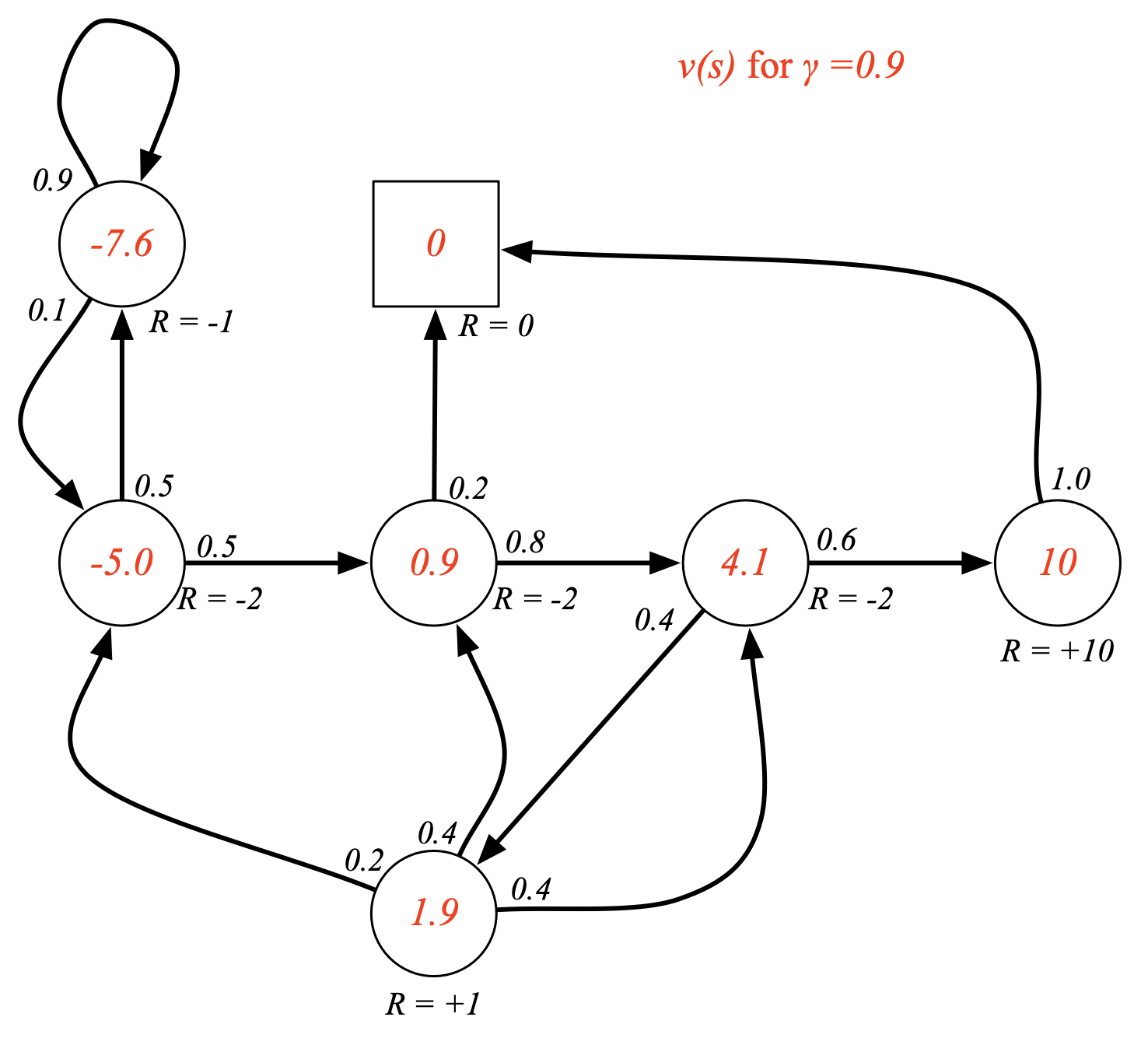Fig. discount factor, \(\gamma\)이 0.9일 경우 미래 가치를 적절하게 고려하게 됨.

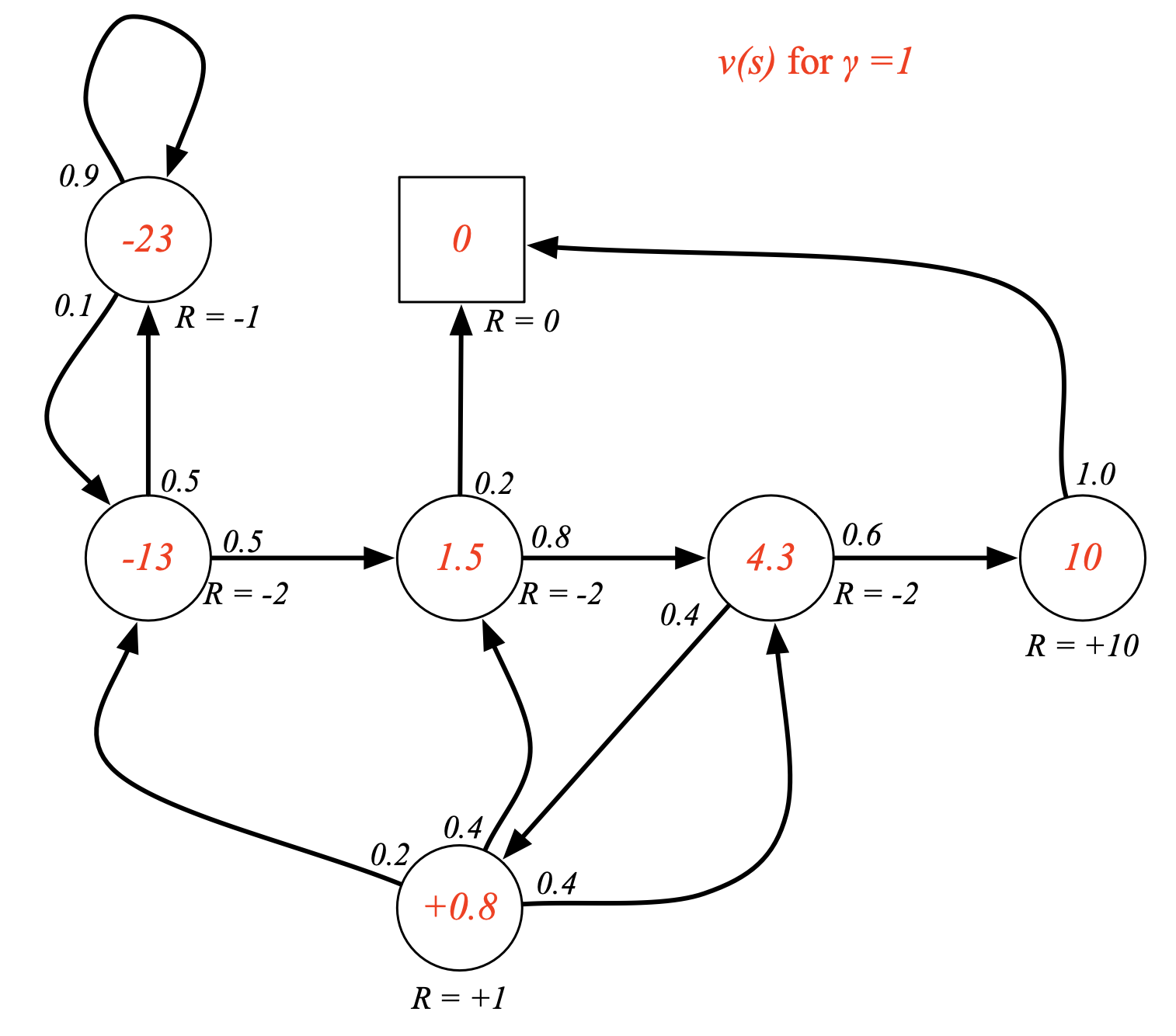Fig. discount factor, \(\gamma\)이 1일 경우.

Fig. 위의 \(\gamma\)가 0이 아닌 경우에 대한 state의 value는 어떻게 계산되었을까? 사실 그 state에서 갈 수 있는 next state선택지는 확률적으로 골라지기 때문에 가능한 모든 경우의수를 계산해야 함 (기대값)

Fig. 이 기대값을 쭉 전개하면 \(v(s) = \mathbb{E} [r + v(s_{t+1}) \vert s_t = s]\) 라는 신기한 수식을 얻게 되는데, 이를 bellman equation이라고 함.

Fig. bellman equation의 intuition. 다음 state (미래 state)의 value를 땡겨옴.

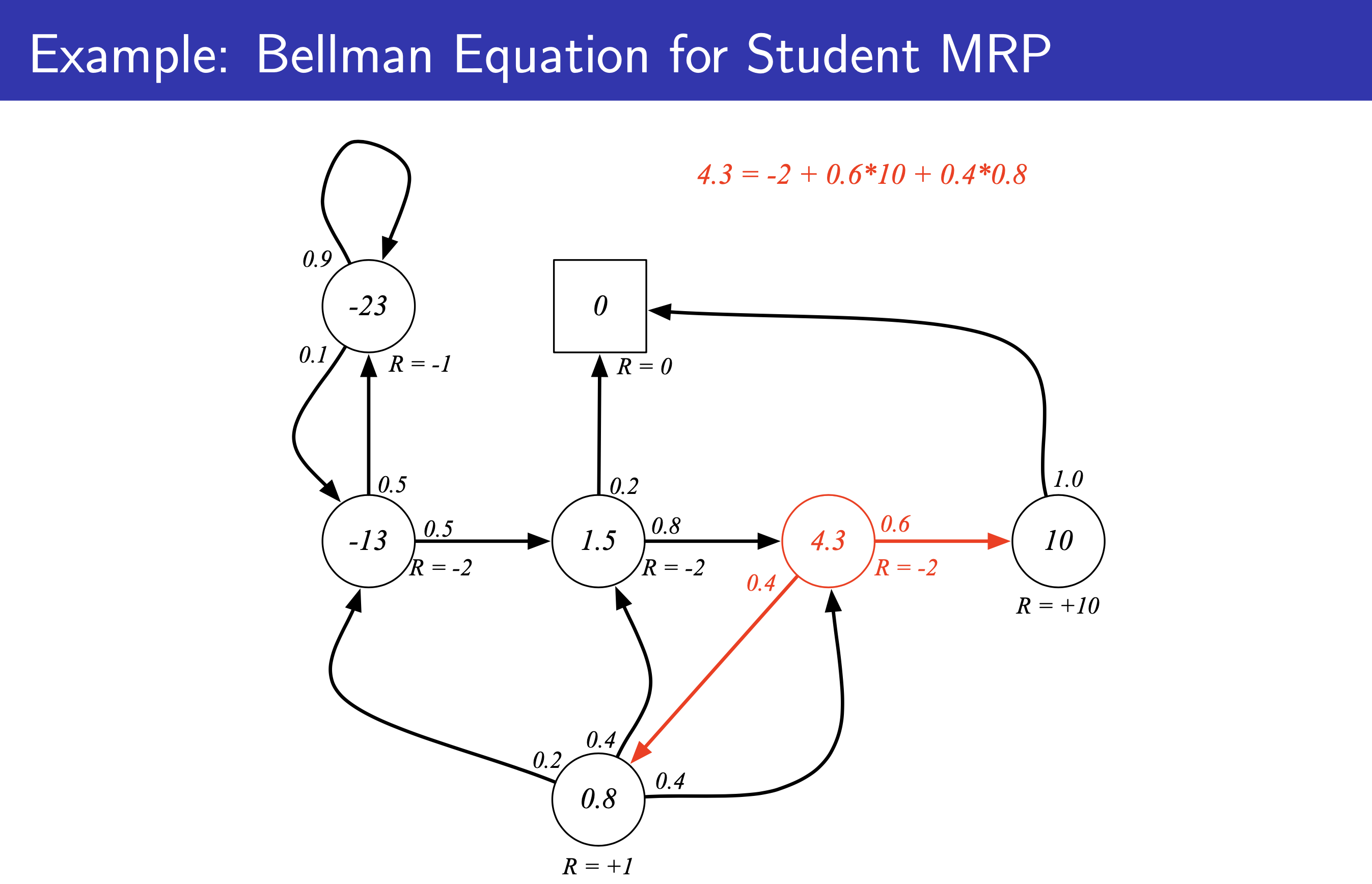Fig. discount factor가 1일 때 각 state의 value는 이렇게 계산된 것임.

• Markov Decision Process (MDP)

Fig. MDP의 full definition. 이제 action이 추가됨.

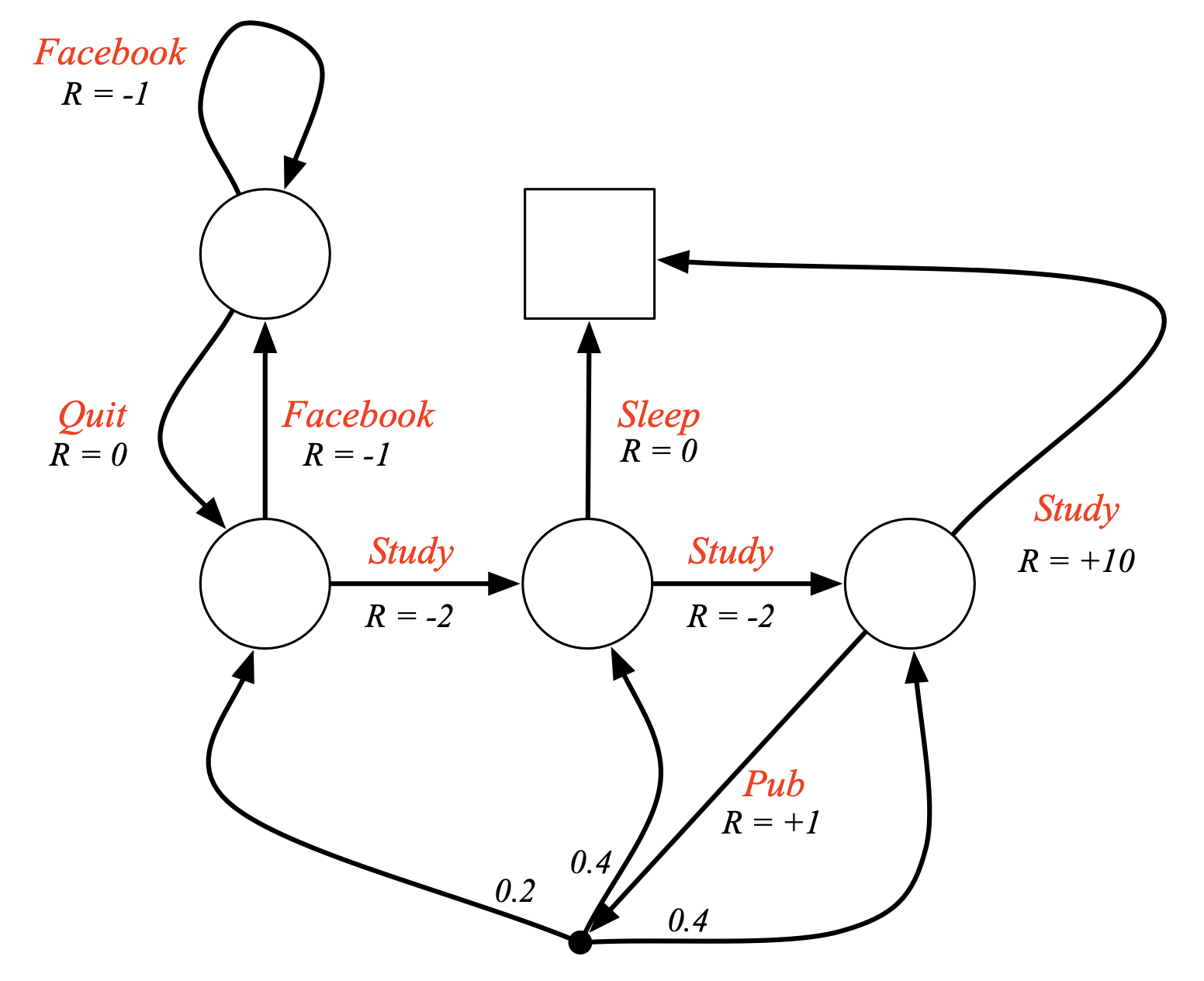Fig. MDP Example: Student MDP. 더 이상 state에 도달하면 reward를 받는 것이 아니라, state에서 어떤 action을 하면 그에 맞는 reward를 받음.

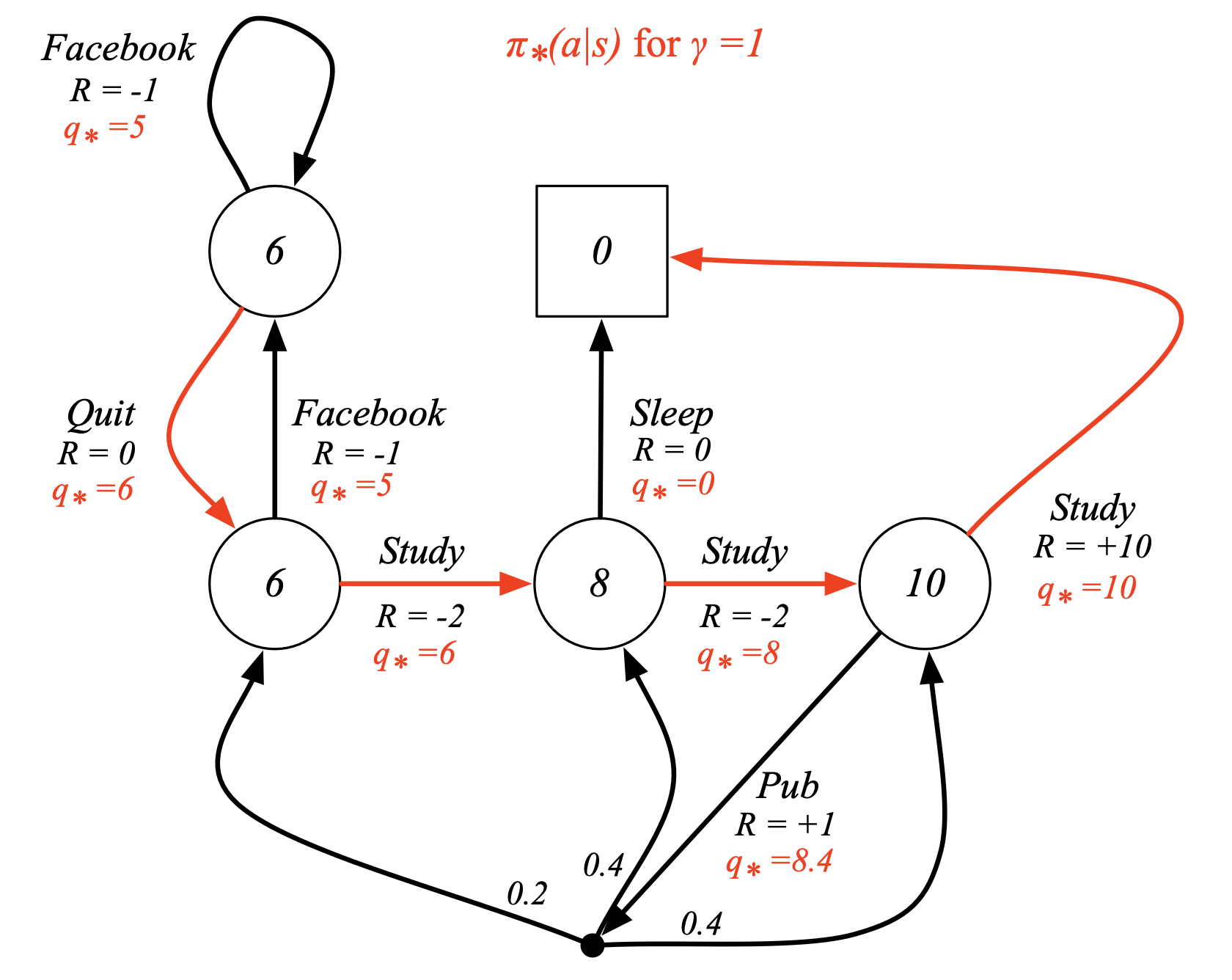Fig. Optimal Policy for Student MDP. 아직 이 내용은 다루지 않았지만 추가함. 어떻게하면 각 state의 value값을 계산할 수 있는지? state별로 value가 정해졌으면 어떤 state에서 어떤 action을 하는것이 (policy) 좋은 action인지? 에 대해서 곧 배울 것임.

Markov process에 대한 example을 소개해드리다 보니 RL에서 아주 핵심적인 개념 중 하나인 value에 대해서도 짧게 소개드리게 되었습니다. 이 example로 부터 insight가 생기셨으면 좋겠고 나중에 value에 대해 제대로 배워보도록 합시다.

The Objective for Reinforcement Learning

앞서 Likelihood를 최대화 하는 것만으로는 만족스러운 결과를 얻을 수 없다는 걸 알았습니다. 이제 정의한 MDP에 따라 강화 학습의 목적 함수 (The Objective for Reinforcement Learning)를 정의 해 보도록 하겠습니다.

RL은 결국 “어떤 상태에서 어떤 행동을 해야 하는가?” 를 잘 알려주는 good policy을 얻는 것이 목적입니다. Good policy란 어떻게 정의할 수 있을까요?

앞서 우리가 정의한 MDP에는 어떤 t시점의 state, \(s_t\)에서 어떤 action, \(a_t\)를 하면 reward를 받을 수 있었습니다. Policy라는 것은 \(s_t\)에서 가능한 Action space (set), \(A\)의 probability distribution을 알려주는 module입니다. Good policy는 reward가 높은게 좋다는 가정 하에 높은 reward를 받을 만한 action에 많은 확률값을 할당하는 policy가 될겁니다. 그리고 우리는 sequential decision making problem을 푸는 것이기 때문에 일련의 state들에 대해서 그 때마다의 action을 통해 얻을 수 있는 reward를 다 합친 값을 가장 크게 하는 policy를 good policy라고 할 수 있을겁니다. 즉 RL의 objective function은 현재의 parameter가 나타내는 policy가 얼마나 좋은 policy인가?를 measure해줄 수 있으면 되는데, 우리는 reward function이라는 매우 좋은 indicator가 있으니 현재의 policy를 따랐을 때 total reward값이 얼마인가?를 measure하면 되겠습니다.

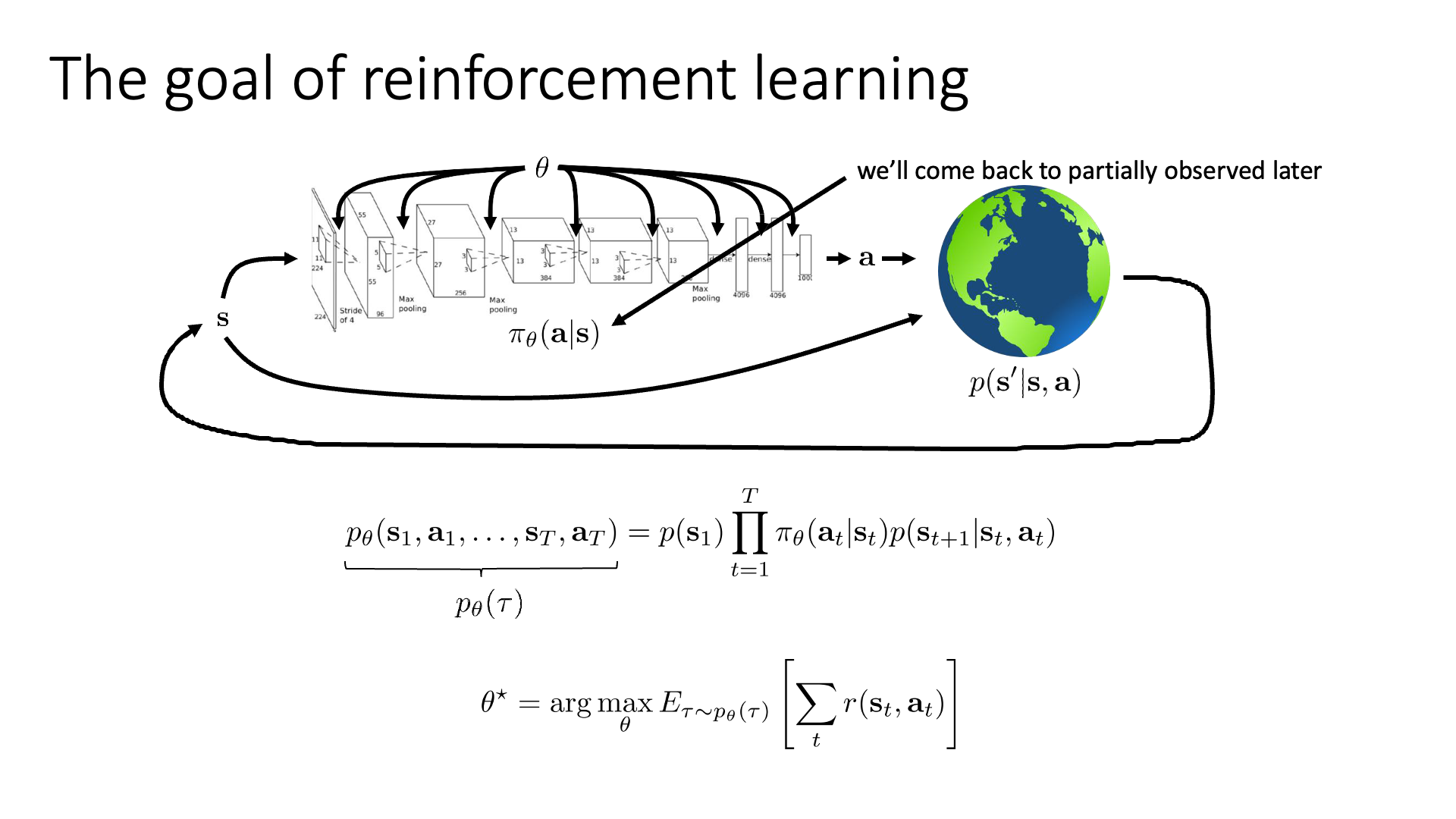Slide. 10. 이 Slide가 RL의 핵심을 모두 담고 있으므로 앞으로도 잘 기억해주시길 바랍니다

‘현재 policy를 따랐을 때 total reward가 얼마나 될 것이냐?’를 이제 수식적으로 표현해 봅시다.

먼저 일련의 (sequential) state, action 을 현재 policy를 따라서 쭉 sampling 합니다. lecture2 에서 이를 RL에서는 궤적 (Trajectory)라고 한다고 했습니다. 그런데 state, action은 모두 stochastic 합니다. 즉 probability distribution로 표현된다는 거죠. 우리가 어떤 t 시점 agent가 어떤 state에 있을 것인지? 그 state에서 어떤 action을 할 확률이 높은지? 가 모두 probability distribution이기 때문에 trajectory 또한 어떠한 probability distribution하에서 정의가 되는데, 이를 수식으로 표현하면 다음과 같습니다.

수식의 의미는 \(T\)라는 길이의 시간 동안 발생할 수 있는 state, action을 joint probability로 나타낸 것인데, 우변의 수식은 MDP 문제를 정의하는 것이기 때문에 markov property가 적용되어 복잡한 joint probability를 chain rule을 이용해 분해 (facorization)했다는 것을 의미합니다.

어떤 자율 주행을 하는 agent를 생각해 봅시다. 출발 선에서 agent가 현재 policy, \(\pi_{\theta}\)를 따라 주행을 하는데, \(p(s_1)\)는 맨 처음 agent가 있을 출발 선의 위치가 라는 probability distribution으로 표현된 겁니다. 그리고 첫 state (inital state), \(s_1\)에서 어떤 action을 할 지는 \(\pi_{\theta}\)가 알려주므로 이를 \(\pi_{\theta}(a_1 \vert s_1)\)라고 씁니다. Deep RL에서는 policy, \(\pi_{\theta}\)는 \(\theta\)로 parameteriz 된 Neural Network (NN)이고 \(\pi_{\theta}(a_t \vert s_t)\)는 NN에 input으로 \(s_t\)를 넣으면 \(a_t\)가 나온다는 것을 의미합니다. 그리고 action을 함으로써 해당 state에서 다음 state \(s_{2}\)로 갈 확률은 markov property에 의해서 \((s_1,a_1)\)로만 결정됩니다 (\(p(s_{t+1} \vert s_t, a_t\)). 이를 terminal timestep, \(T\)까지 반복해서 확률을 곱해서 우리는 위 수식의 우변을 얻을 수 있었던 겁니다.

이 때 \(T\)가 실수이면 finite horizon이라고 하고 \(T=\infty\)이면 끝이 없다고 해서 inifinite horizon이라고 합니다. 그리고 finite horizon case에 대해서 \(T\)시점까지 진행된 (만들어진) trajectory (sequence)를 하나의 episode라고 합니다. 앞으로 lecture에서는 별 말이 없으면 finite horizon case에 대해서 얘기할 것이며 어떤 trajectory, \(\tau\)가 sampling될 trajectory distribution을 \(p_{\theta} (\tau)\) 라고 표기하도록 하겠습니다.

이제 trajectory distribution을 정의했으니 아까 얘기했던 RL의 objective function을 써 봅시다. 우리가 원하는 것은 total reward를 최대화 하는 policy였죠? 그렇다면 현재 policy를 따를 때 total reward를 측정하고 이것을 높힐 수 있는 방향으로 parameter를 update해야 할겁니다. 그런데 어떤 sequence에 대해서 total reward를 재야 하는지를 모르죠. 어떤 한 두개의 trajectory에 대해서 이 값을 재면 정확하지 않을 수 있기 때문에 우리는 가능한 모든 trajectory에 대해서 이 값을 측정해야 합니다. 그러므로 우리는 현재 policy를 따르는 trajectory distribution하에서의 total reward에 대한 기대 값 (expectation)을 재면 되겠습니다.

그리고 이 objective를 최대화 하는 방향으로 policy (NN)을 optimization 하는 것이 우리의 최종 goal이 되겠습니다.

Sergey는 잠깐 여기서 video를 멈추고 수식의 의미를 곱씹어 봐야 한다고 합니다. 몇 가지 얘기를 해보자면 수식에서 trajectory distribution는 policy를 따른다는 겁니다. 이는 policy가 바뀔 때 마다 data의 distribution이 바뀔 수 있다는 걸 의미합니다. Data가 매 optimization step마다 바뀔 수 있다는 것은 대체 어떤 걸 의미하는 걸까요? 이런 식으로 학습하면 SL처럼 학습이 잘 될까요? 이 밖에도 다른 의문이 있을 수 있습니다.

앞으로 RL objective를 변형하고, 새로운 algorithm에 대해 설명하게 될텐데 이런 의문점들에 대해서 잘 생각해보면 좋을 것 같습니다.

Re-interpret MDP as Markov Chain

비록 우리가 정의한 objective function이 MDP상에서 정의되었지만 이는 markov chain으로도 해석될 수 있다고 합니다.

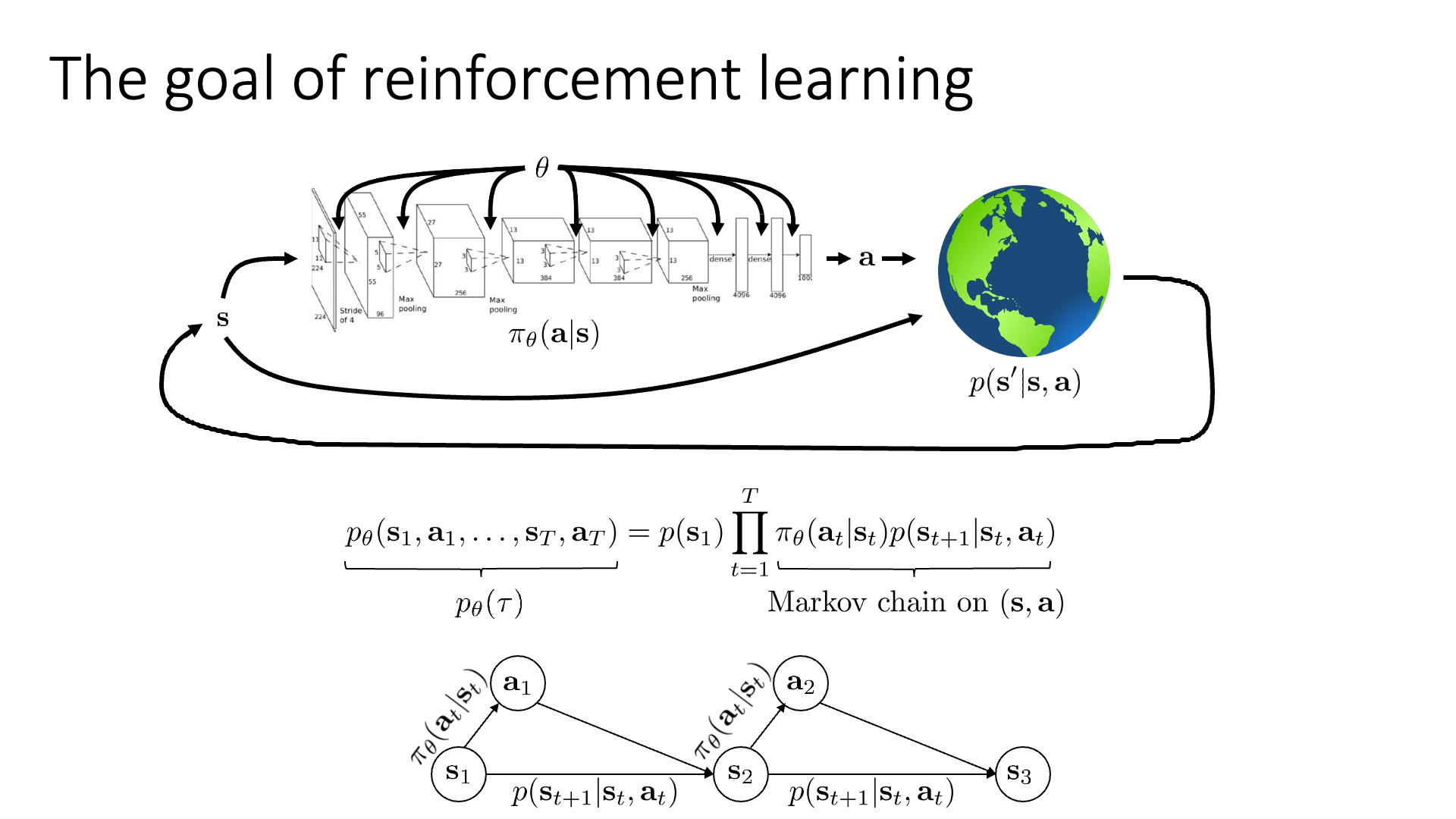Slide. 11.

그러기 위해서는 어떤 개념이 추가된 (Augmented) state space를 정의해야 한다고 합니다. 원래 markov chain은 state와 state transition probability만 존재했고

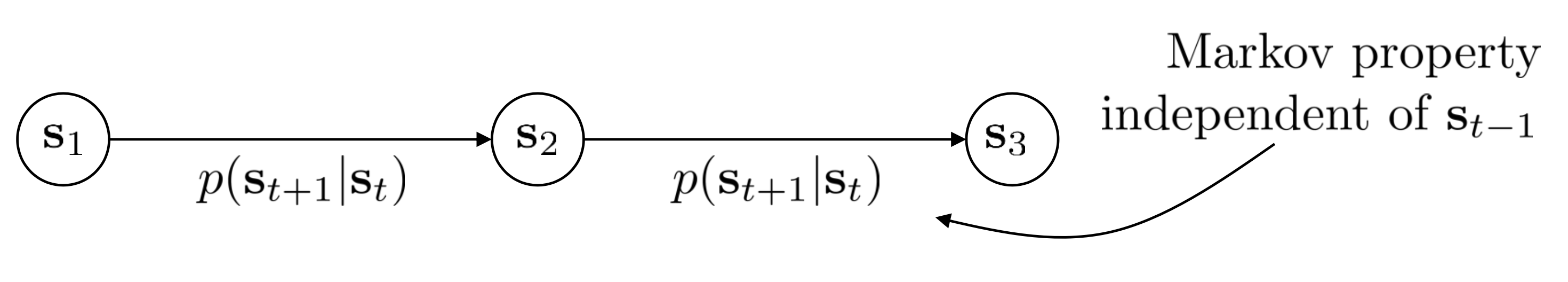
MDP에 와서는 action이 추가됐었습니다.

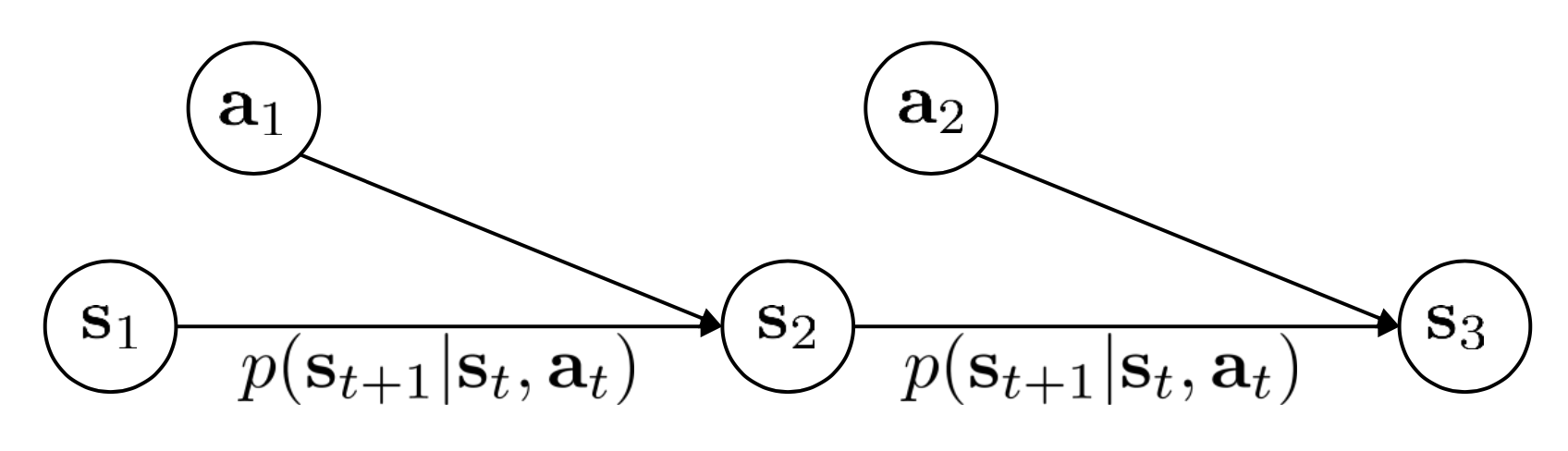
그런데 우리는 이 action이 state에 dependent 하다는 걸 (\(p_{\pi}(a_t \vert s_t)\)) 알고 있습니다.

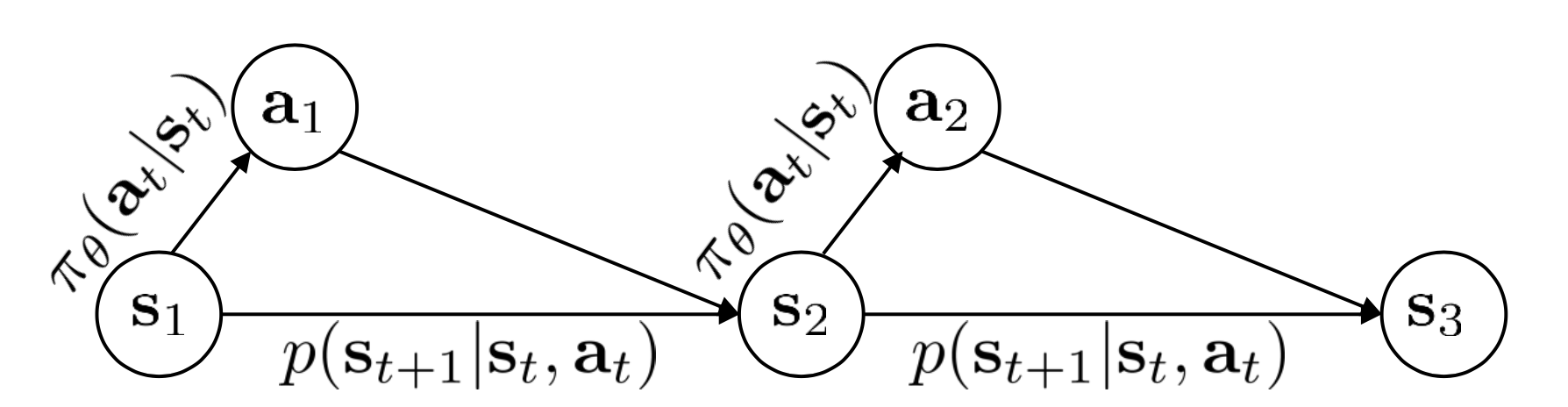
결국 state와 action은 group지어 생각할 수 있기 때문에 이를 markov chain 같은 형태로 바꾸면 (augmented markov chain) 다음과 같이 graph를 만들 수 있겠습니다. (Augmented state이 완벽하게 markov chain을 형성한다는 것을 알 수 있습니다)

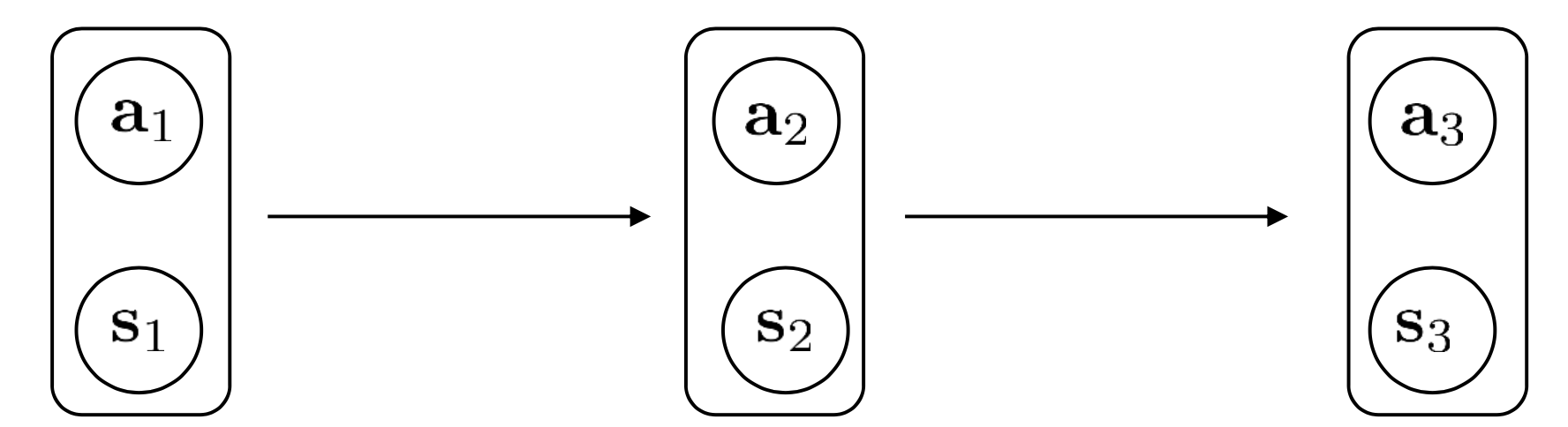
이에 따라 우리는 이제 transition operator를 \(p(s_t \vert s_t,a_t)\)가 아니라 \(p( (s_{t+1},a_{t+1}) \vert (s_t,a_t) )\)로 정의해야 하며, 이는 다음과 같이 MDP에서의 transition operator와 policy의 곱으로 나타낼 수 있게 되었습니다.

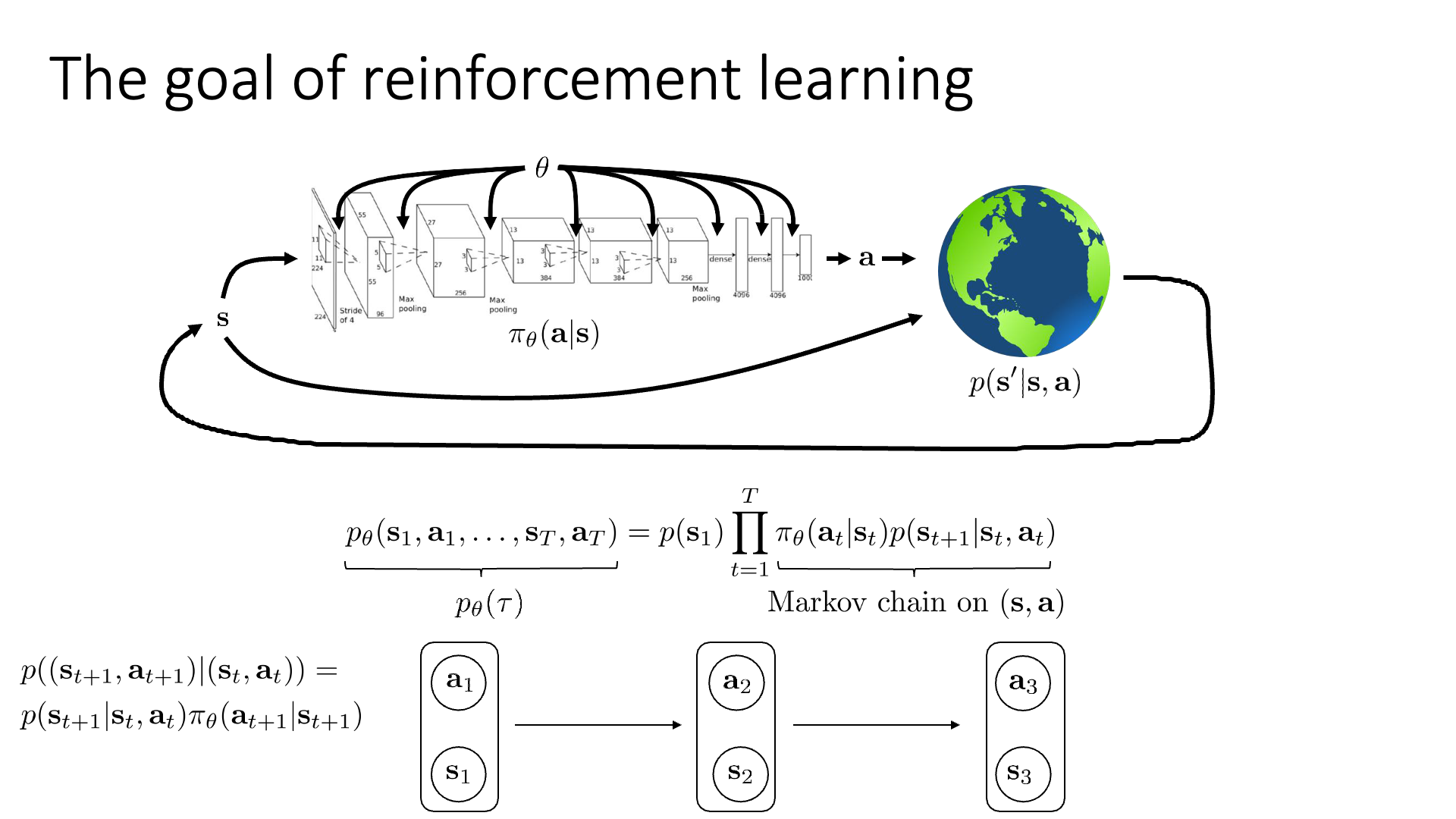Slide. 12.

아니 MDP에서 RL objective를 잘 정의했는데 왜 또 다르게 objective를 정의해야 하느냐? 그 이유는 후에 있을 공식을 유도하는 데 있어 이것이 더 편하기 때문이라고 합니다.

Finite Horizon Case

Finite horizon case의 objective function에 대해서 생각해 봅시다.

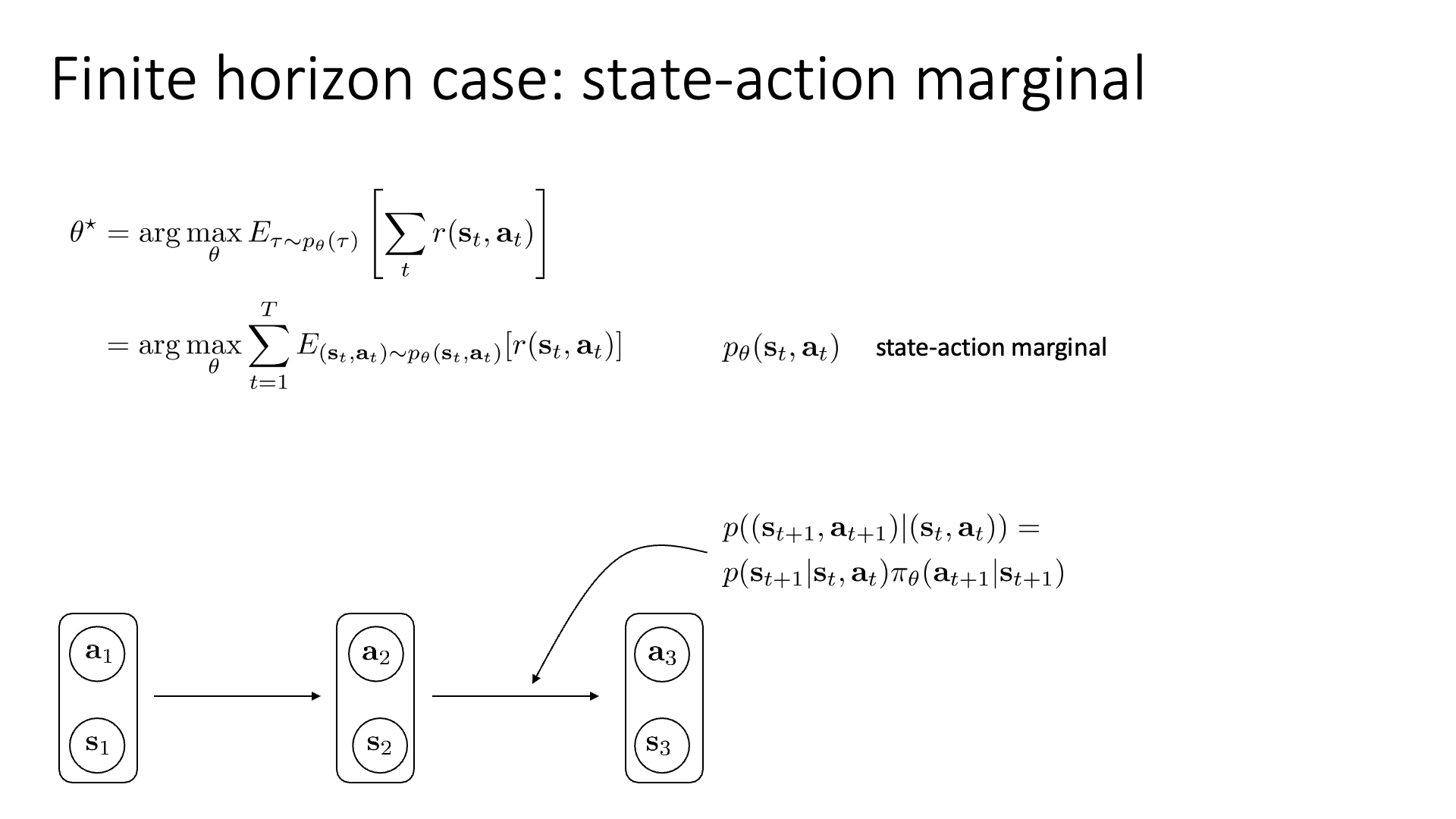Slide. 13.

RL objective function은 ‘현재 policy를 따르는 trajectory distribution 하에서의 total reward의 기대값’이었습니다.

우리는 앞서 augmented state space를 정의해서 markov chain을 형성했고, 이 수식에 기대값의 선형성 (linearity of expectation)을 이용해 \(\sum\)을 기대값 밖으로 빼면 수식을 아래처럼 쓸 수 있습니다.

여기서 \(p_{\theta}(s_t, a_t)\)를 state action marginal 이라고 부르는데 재배열 (re-written)된 objective는 state action marginal distribution 하에서의 기대값의 총 합을 의미합니다. 이런 수학적인 재배열이 쓸모없어 보일 수 있으나 우리가 finite horizon case가 아니라 infinite horizon case의 objective를 유도한다고 하면 꽤 유용하다고 합니다.

Infinite Horizon Case

Episode의 길이가 무한대인 상황 (\(T=\infty\))이 된다면 무슨 문제가 발생할까요? 첫 번째로는 앞서 정의한 objective function이 불분명 (ill-defined)해 질 거라는 겁니다. Infinite horizon case에서는 \(t=\infty\)가 되기 때문에 양수의 reward가 무한정 더해지는 상황이 발생할 수 있고, 이에 따라 objective 값 또한 \(\infty\)가 될 수 있습니다.

Slide. 14.

이런 경우 objective를 finite하게 만들기 위해서 사용되는 몇 가지 방법이 있습니다. 가장 단순한 방법은 보상의 총 합을 어떤 상수 time-step, \(T\)로 나누는 것입니다. 우리가 원하는 것은 주어진 total reward의 기대값을 maximize하는 parameter를 찾는 것인데 나눗셈은 이 결과를 바꾸지 않기 때문에 사용이 가능한 것이지만 이런 average reward formulation은 잘 사용되는 방법은 아니라고 합니다. 가장 많이 사용되는 방법은 후에 다시 언급하겠지만 1.0 이하의 감가율 (discount factor, \(\gamma\))를 reward에 적용하는 것입니다. (timestep이 경과할수록 1.0보다 작은 값이 누적되어 곱해지면서 (\(\color{red}{\gamma^t} \cdot r(s_t, a_t)\))가 결국 무한대로 발산하지 않는 것)

이렇듯 infinite horizon case의 objective값을 finite하게 만드는건 그다지 어려운 일은 아닙니다만 어떻게 하면 실제로 infinite horizon objective를 정의할 수 있는지에 대해서 더 얘기해 봅시다. 먼저 \((s_{t+1},a_{t+1})\)는 이전 augmented state인 \(p(s_t, a_t)\)에만 영향을 받는데, 이를 \(p(s_t, a_t)\)와 statec action transition operator, \(T\)를 곱해 표현할 수 있습니다.

더 일반화해서 쓰면 \(k\) timestep 뒤의 state action marginal에 대해서는 아래와 처럼 나타낼 수 있습니다.

여기서 Sergey가 질문을 하나 던집니다. 바로 “state-action marginal, \(p(s_t,a_t)\) 가 어떠한 고정된 분포, 즉 정상 확률 분포 (Stationary Distribution)으로 수렴할 수 있느냐?” 라는 겁니다.

이 질문은 markov chain의 정상성 (stationary)을 물어보는 것입니다. 이는 ‘각 state별로 이동할 확률이 정해져 있다면 동선에 특정한 pattern이 존재하지는 않을까?’라는 질문에서 출발합니다. 예를 들어 ‘100번 이동했다면 평균적으로 3번은 출발지점에 돌아올 것이다’ 같은 것이죠. 다만 항상 그런것은 아니고 ‘특정 조건’을 만족할 때 일정한 pattern이 나타난다고 하는데, 조건을 만족하면 어떤 지점에서 시작하더라도 state 사이를 충분히 많이 이동하게 되면 각 state의 방문횟수의 비율이 일정한 값으로 수렴 (converge)하게 된다고 합니다. 다시 말해 state들의 방문횟수의 비율이 특정 probability distribution으로 수렴하게 되고, 이때의 특수한 distribution을 바로 stationary distribution이라 부르는 거죠.

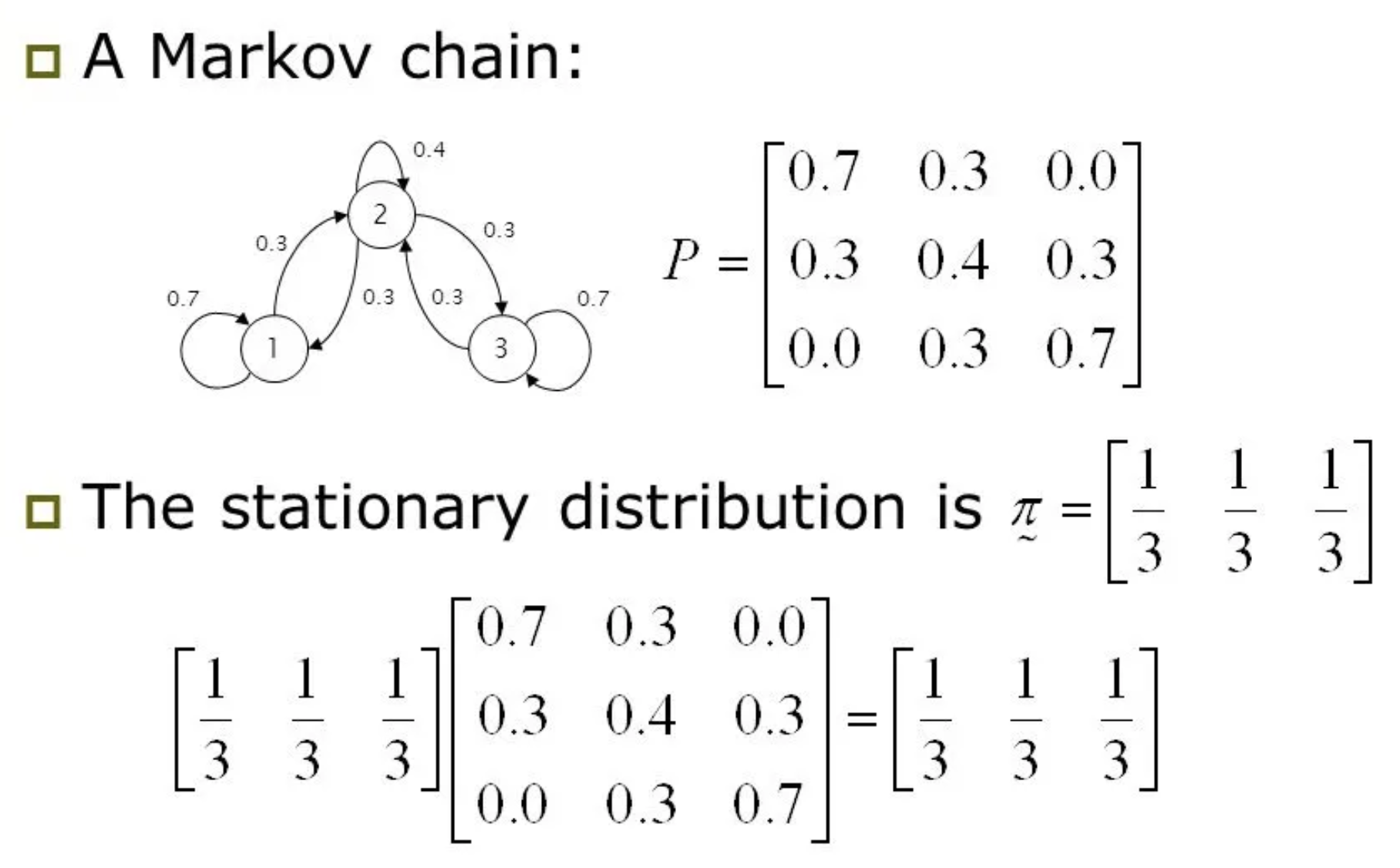Fig. An example of stationary distribution. (1/3, 1/3, 1/3)이라는 distribution은 transition probability를 몇번을 곱해도 (1/3, 1/3, 1/3)을 유지한다. Source from here

이를 수식적으로 나타내면 아래와 같은데,

이 때 \(\mu\)가 바로 stationary disribution입니다. 이 수식의 의미는 \(\mu\)라는 distribution에 \(T\)를 곱해도 여전히 \(\mu\)가 된다는 것으로 transition이 일어나도 distribution이 변하지 않는다는 걸 의미합니다. Sergey는 여기에 에르고딕성 (Ergodicity)나 chain의 비주기성 (Aperiodic) 특성 등 몇 가지 technique을 이용하면 stationary disribution이 존재한다는 것을 간단하게 보일 수 있다고 합니다. Chain이 aperiodic하다는 것은 그 일정 timestep이 지나면 원래 state로 돌아온다고 할 때 이 timestep의 최대 공약수가 1이라는 의미로, 주기가 없다는 걸 의미하고 ergodic하다는 것은 어떤 state도 다른 모든 state로 넘나들 수 있다는 가정으로, 만약 chain이 ergodic 하지 않을 경우 어디를 initial state로 삼느냐가 중요해지고 stationary distribution은 존재하지 않게 된다고 합니다.

어쨌든 몇 가지 가정을 깔면 stationary distribution이 존재한다는 것을 알 수 있고, 그 distribution이 무엇인지 해도 구할 수 있으며 (\((\color{blue}{T}-I) \color{green}{\mu}=0\)를 풀면 되는데 확률 값은 모두 음수가 아니며 이를 풀면 eigenvalue가 모두 1인 eigenvector를 구할 수 있게 된다고 함), 이는 agent가 어떤 initial state에서 출발하든 충분히 transition 하면 결국 stationary distribution \(\mu\) 로 수렴하게 된다고 합니다. 그렇기 때문에 \(t \rightarrow \infty\)면 objective function이 stationary distribution terms에 의해서 dominate 된다고 합니다.

여기서 \(p_{\pi}(s,a)\)가 policy, \(\pi\)하에서의 stationary distribution을 의미하는데, 자세히 보시면 아래첨자 (subscript), \(t\)가 없다는 걸 알 수 있습니다.

Slide. 15.

이렇게 우리는 stationary distribution하의 expectation을 사용해 infinite horizon case에 대한 objective를 정의할 수 있게 되었는데, 아마 transition probability \(\color{blue}{T}\)를 모르면 stationary distribution을 구할 수 없을 것이기 때문에 average reward method나 discount factor를 사용한 것으로 objective를 구해야 할 것 같습니다.

Why Expectations matter in RL

마지막 subsection의 내용은 “왜 우리가 정의한 RL objective는 expectation, \(\mathbb{E}\)를 포함하고 있는가?”에 대한 것입니다. 이는 수 많은 RL algorithm의 기저에 깔려있는 기본 원칙 (principle)을 이해하는 데 굉장히 중요한 개념이라고 합니다.

Slide. 16.

RL은 가장 높은 total reward의 기대 값을 얻기 위해 높은 reward를 주는 action들의 확률을 높히는 방향으로 policy를 optimize한다고 했습니다. 그런데 이 RL objective는 expectation \(\mathbb{E}\)가 취해져 있죠.

왜 그럴까요? 이는 모든 현재 policy를 따랐을 때 모든 trajectory의 total reward를 계산해야 엄밀한 값을 얻을 수 있기 때문도 있습니다만, reward function이 불연속 (discontinuous)하기 때문이라는 이유도 있습니다.

자율 주행을 하는 agent에 대한 toy example을 생각해 봅시다. Agent가 정상적으로 도로를 이탈하지 않으면 \(r=+1\), 아니면 (절벽으로 떨어지면) \(r=-1\)을 받습니다.

Fig.

이제 차의 위치 (position)에 대한 reward function, \(r(x)\)를 optimization을 한다고 칩시다. 이 reward function은 절벽의 경계선에서 갑자기 \(+1\)에서 \(-1\)로 변하기 때문에 불연속적 (not smooth)이며 따라서 미분 불가능 (non differentiable)합니다.

이번에는 action에 대한 policy를 probabilistic distribution으로 정의해 봅시다. Policy는 떨어진다 (fall)에 대한 확률 값, \(p_{\theta}(a=\text{fall}) = \theta\)을 return하고 확률의 전체 합은 1 이므로 안 떨어진다는 \(1-\theta\)를 return할 겁니다. (2가지 category에 대한 distribution이므로 Bernoulli distribution를 사용)

여기서 재밌는 점이 바로 \(\pi_{\theta}\)하에서 reward function의 expectation을 계산하게 되면 (\(\mathbb{E}_{\pi_{\theta}}[r(x)]\)), 이는 \(\theta\)에 대해서 매끄러워 (smooth)진다는 겁니다. (미분 가능 (differentiable) 해진다는 소리)

\(\mathbb{E}_{\pi_{\theta}}[r(x)] = \theta (+1) + (1-\theta)(-1)\).

이것이 왜 RL algorithm이 Gradient Descent (GD)같은 smooth optimization method를 사용해서 agent를 학습할 수 있게 해주며, reward signal이 매우 희박하게 발생하는 희박한 보상 문제 (sparse reward problem)에 대해서도 agent가 잘 학습이 될 수 있도록 해주는 RL algorithm의 key라고 할 수 있습니다. (바둑 같은 경우가 매 수를 둘 때마다 reward가 발생하지 않고 게임이 끝나야만 (보통 100수 이상) reward를 +1 (승) or -1 (패)로 주는 대표적인 sparse reward problem 입니다)

+) RL을 처음 접해보신 분들은 아직 와닿지 않을 수 있지만 바로 다음 chapter인 lecture 5에서 REINFORCE에 대해서 배우는데, 이를 gradients of the non-differentiable expected reward objective을 계산하는 Trick이라고 표현하기도 합니다. 최종적으로 유도되는 gradient의 수식은 우리가 아는 Cross Entropy (CE) Loss와 크게 다르지 않은데, 이는 reward function을 policy하에서의 expectation을 취한 수식을 수학적 tool을 사용해 유도하는 것으로 expectation 없이는 얻을 수 없는 것 입니다.

Algorithms

지금까지 objective function까지는 얻었지만 아직 어떻게 학습하는지 agent를 학습하는지는 모릅니다. Objective를 policy parameter, \(\theta\)에 대해서 미분하여 gradient descent를 해야 하는것인지? 학습 data는 어떻게 얻어야 하는 것인지? 등 아무것도 모르죠. 이제 본격적으로 RL algorithm들에 대해서 알아보도록 하겠습니다.

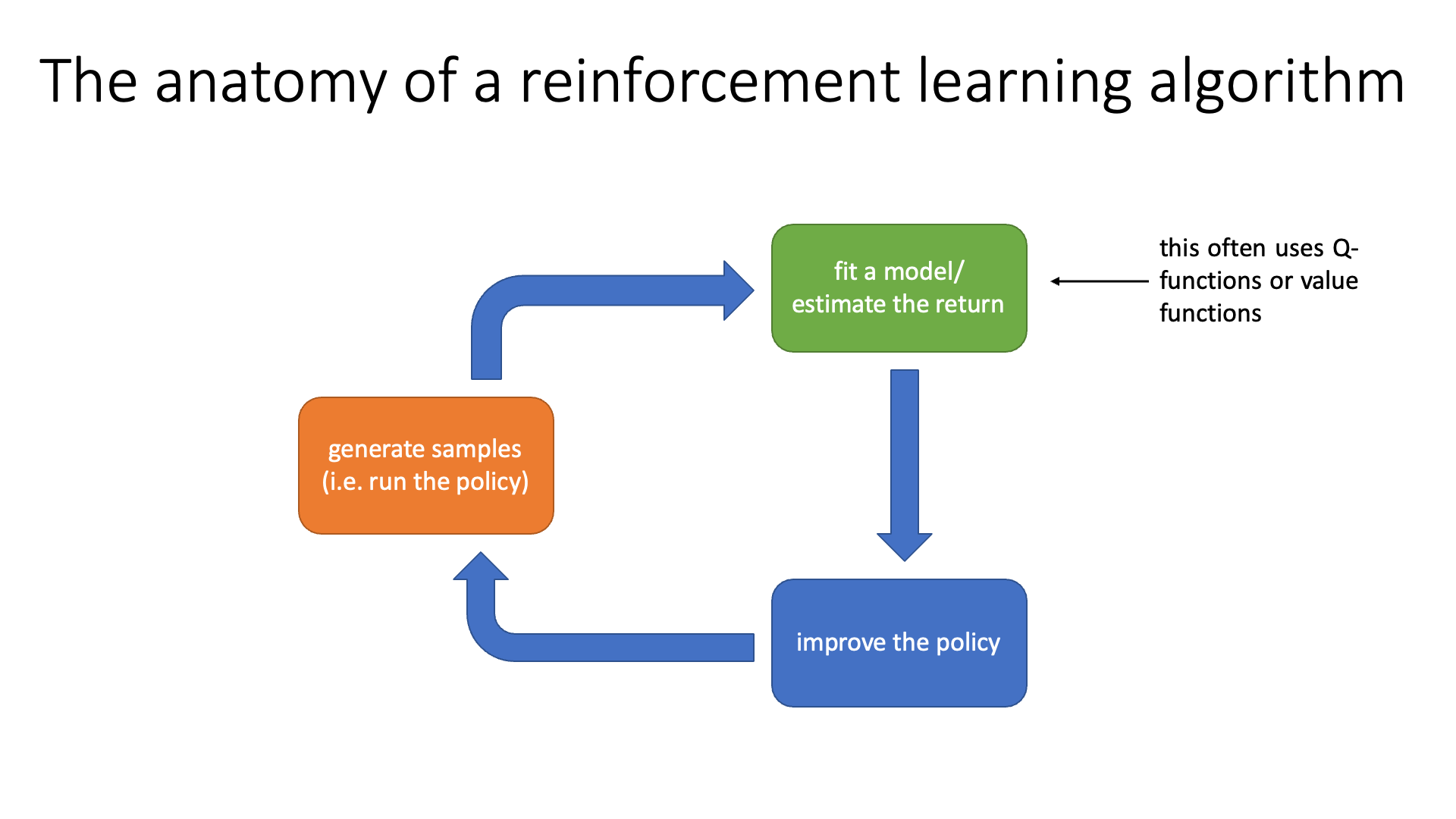
The Anatomy of a RL Algorithm

RL의 goal은 policy를 굴렸을 때 얻을 수 있는 total reward를 최대한 많이 받기 위해 높은 reward를 주는 action에 높은 확률을 할당하는 good policy를 얻는겁니다 (여러번 말할 만큼 매우 중요함). 사실 RL algorithm은 (철학은 같지만) 크게 두 가지로 나뉩니다.

• policy based method
• value based method

정책 기반 방법 (Policy based method)는 value-based method와는 다르게 policy를 parameterize 하는 명시적인 (explicit) NN을 정의합니다. 그리고 total reward의 기대값을 의미하는 RL objective funcion을 이 policy parameter에 대해서 직접 미분해 gradient를 구하고, DL에서 많이 쓰는 gradient descent처럼 update하면서 optimal policy를 찾는 method입니다.

반면에 가치 기반 방법 (Value based method)는 명시적인 policy가 없고 가치 함수 (Value Function)라는 module을 정의합니다. 이 value function은 모든 state에 value를 할당하는데 (학습이 되므로 점점 변함), 어떤 state에서 최적의 action은 현재 state에서 그 action을 함으로써 이동할 수 있는 다음 state들의 value값을 기준으로 가장 큰 값을 return하는 action이 됩니다. 이런식으로 policy를 얻기 때문에 vlaue based는 implicitly policy를 학습한다고 말합니다.

다시 말씀드리지만 학습 방법이 다른 value based와 policy based는 total reward를 최대한 많이 얻는 action을 하는 good policy를 얻는다는 데서 공통점을 가지고 있습니다. 그렇기 때문에 RL algorithm들은 학습 방법이 달라도 결국 비슷한 구조 (Anatomy)를 공유하게 되는데, 이는 아래 figure에 나와있는 것 처럼 세 가지 part로 이루어져 있습니다.

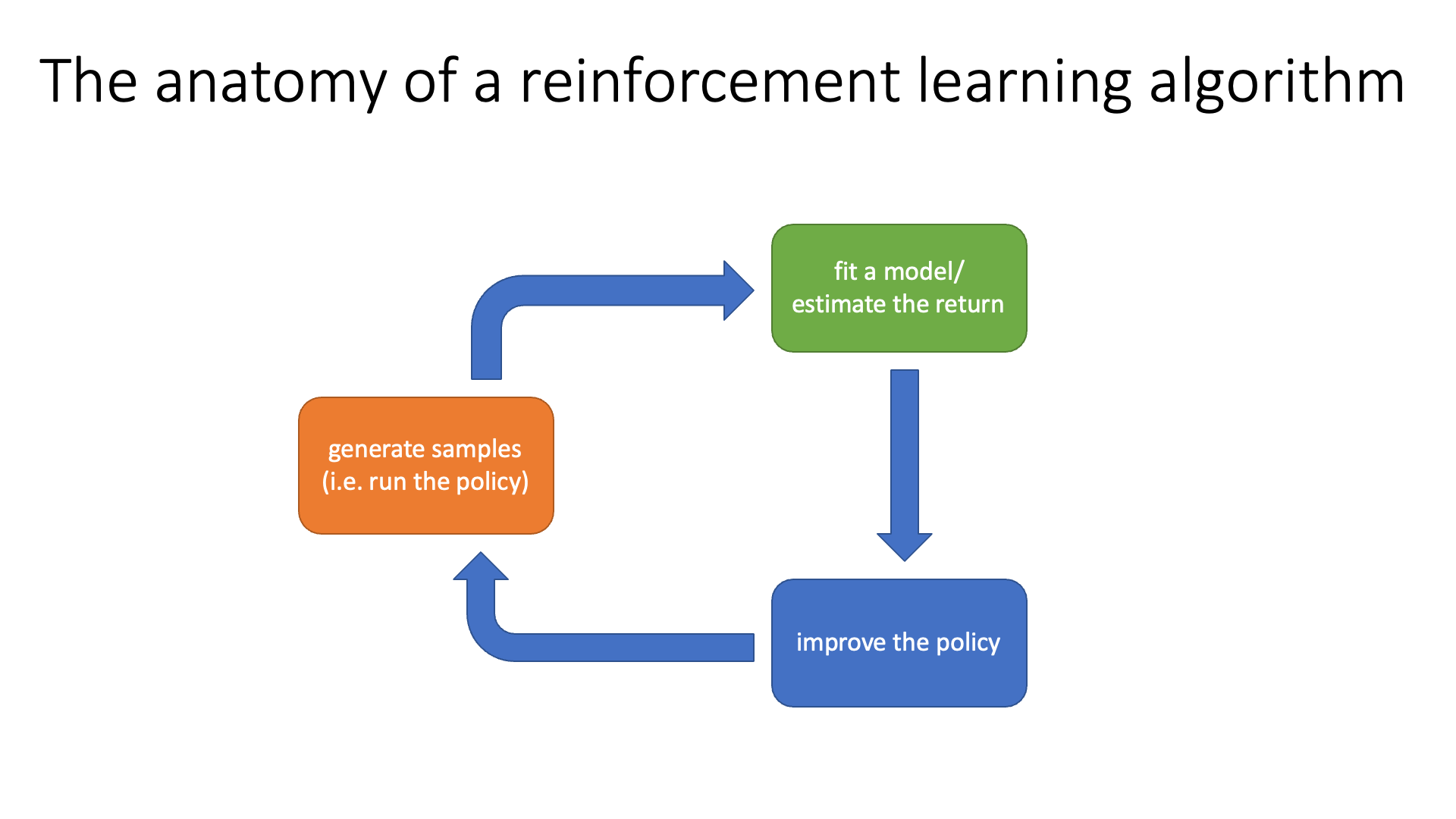Slide. 18.

RL algorithm들은 기본적으로 아래 3가지를 무한히 반복합니다.

• (Orange Block) 현재 policy를 따라서 state에서 action을 sampling하는 것을 T시점까지 반복해 길이 T짜리인 trajectory를 여러 개 만든다.
  • 이 때 각 state에서 action을 함으로써 enviroment가 reward를 준다.
• (Green Block) 각 trajectory의 누적된 reward (이를 return이라고 함)을 계산 (지금은 단순 덧셈) 해서 어떤 trajectory가 좋았는지 평가하거나 transition dynamics (model)을 학습하는 것이 될 수도 있습니다.
• (Blue Block) policy를 개선 한다 (policy의 parameter를 gradient descent같은 방법으로 update하여 더 좋은 action에는 더 높은 확률을 부여하도록 조정한다)

좀 더 얘기를 해보죠.

Orange block을 policy를 돌려서 sample을 만든다고 표현하는데, 그 이유는 RL objective function이 현재 policy를 따르는 trajectory distribution 하의 expectation이기 때문입니다. expectation은 실제로는 distribution 상의 모든 sample에 대해서 계산을 해야 하는데 그건 불가능하죠? 그러므로 우리는 practical하게 몇 개만 sampling을 하는겁니다. 그런데 핵심은 이 trajectory들을 통해 RL objective를 구하고 optimization을 한 step하면 또 policy가 변한 것이 되기 때문에 이 sample들은 버려야 한다는 겁니다. 이는 DL에서는 상상할 수도 없는 일인데, 매 optimization step마다 training data를 다시 만들어야 한다는 걸 의미합니다. Data를 알아서 만들고 평가해서 policy를 update하기 때문에 따로 자율 주행을 위해 어떤 state에서 어떤 action을 해야하는지?에 대한 human annotation이 필요가 없다는 장점이 있긴 합니다.
그래서 RL을 시행착오 (trial and error)를 통해 배우는 방법론이라 하기도 하죠.

두 번째 green block에 대해서 우리는 trajectory를 평가 (evaluate) 하는 것이라고 했습니다. 그런데 이는 사실 policy를 평가하는 것이기도 합니다. 왜 그럴까요? 만약 policy가 많이 학습돼서 꽤 좋은 policy가 됐다고 하면 어떤 state에서 좋은 action을 해서 결과적으로 total reward가 높아질 것이기 때문입니다. 그래서 이것은 policy evaluation이라고 얘기하기도 합니다.

앞으로 CS285에서는 이 anatomy가 자주 등장합니다. 이 기본적인 paradigm 안에서 각 algorithm들이 어떤 block에 장점이 있는지? 등에 대해 지속적으로 논하게 될 테니 잘 기억해 두시길 추천드립니다.

Intuition of Training with RL

RL objective로 agent를 학습한다는 것은 어떤걸 의미하는지 직관적으로 이해해봅시다. 먼저 orange block의 sample generation을 합니다.

Fig.

그리고 green block의 trajectory evaluation을 합니다. 분명히 이 중에는 좋은 trajectory가 있을 수 있고 아닌게 있겠죠? 좋은 trajectory라는 것은 정의하기 나름인데, 현재 trajectory들의 평균보다 좋은 걸의미할 수도 있고 절대적으로 +10점을 넘어야 좋은 trajectory라고도 할 수 있겠습니다.

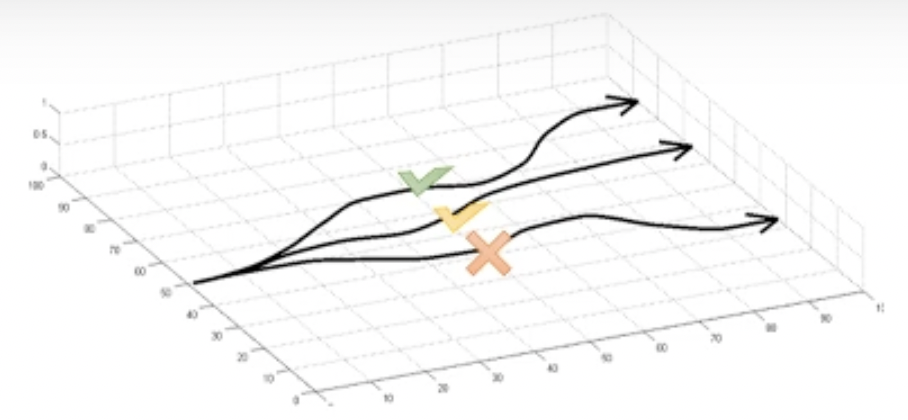Fig.

이 trajectory 들이 sampling될 확률은 trajectory distribution을 따랐죠. 그런데 trajectory distribution은 또 현재 optimization step, \(t\)시점의 policy, \(\pi_{t}\)를 따릅니다.

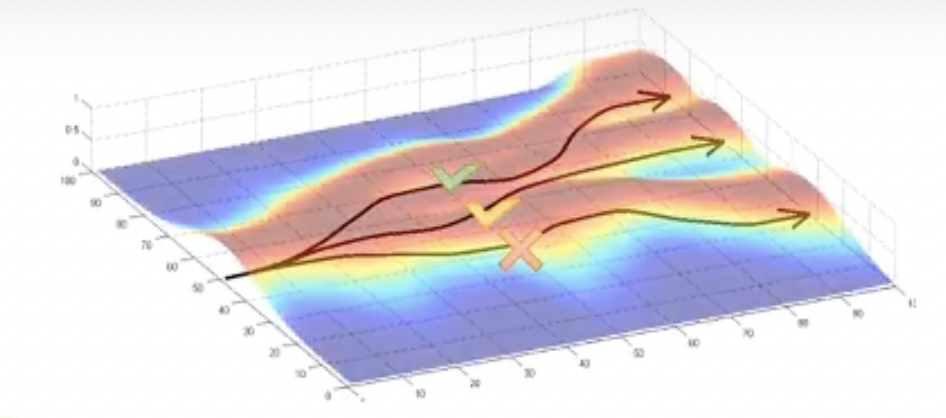Fig.

우리는 주어진 data sample중에서 좋은 sample이 무엇인지 알고있기 때문에 이 sample이 등장할 확률을 높히는 방향으로 policy를 한단계 update할 수 있습니다. 이것이 blue block이 하는 일입니다. 그러면 policy가 \(\pi_{t+1}\)로 바뀌었으니 당연하게도 trajectory distribution이 바뀔겁니다.

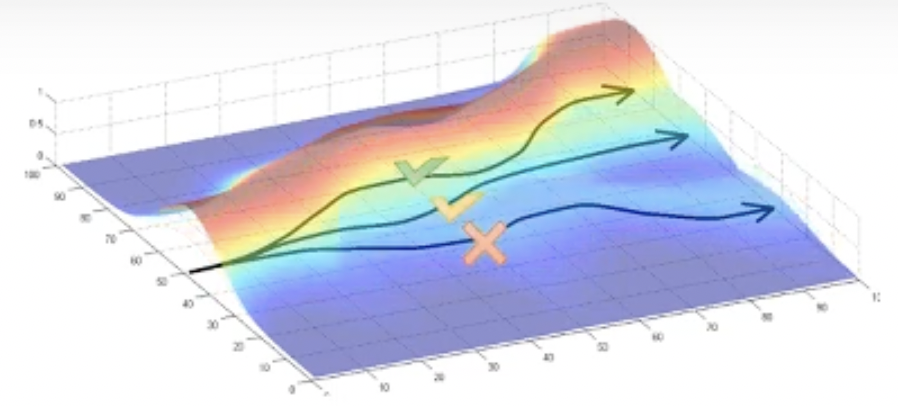Fig.

바뀐 distribution에서 또 sampling을 하면 이번에는 좀 더 괜찮은 trajectory들이 뽑힐것이고, 더 좋은 sample이 더 많이 뽑히도록 parameter를 또 조정하고… 이를 반복하게 될겁니다. 이것이 RL algotihm의 기본적인 mechanism 입니다. (설명드린 것은 RL algorithm들 중에서도 lecture 5에서 얘기할 policy gradient method의 overview입니다)

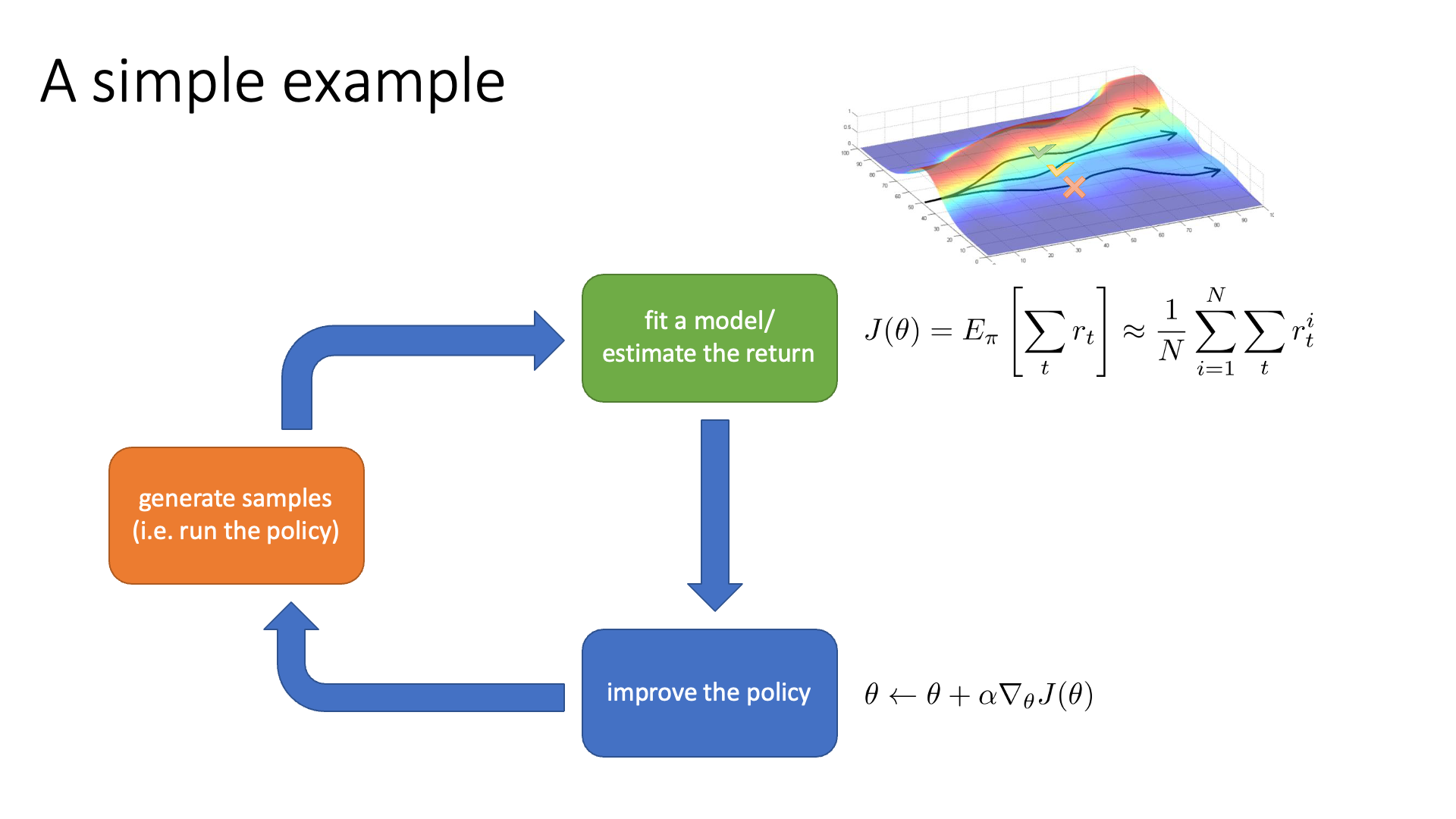Slide. 19.

이번에는 다른 example에 대해서 얘기해 봅시다. 바로 Model-based RL인데, Sergey는 이를 RL by Backpropagation이라고 표현합니다.

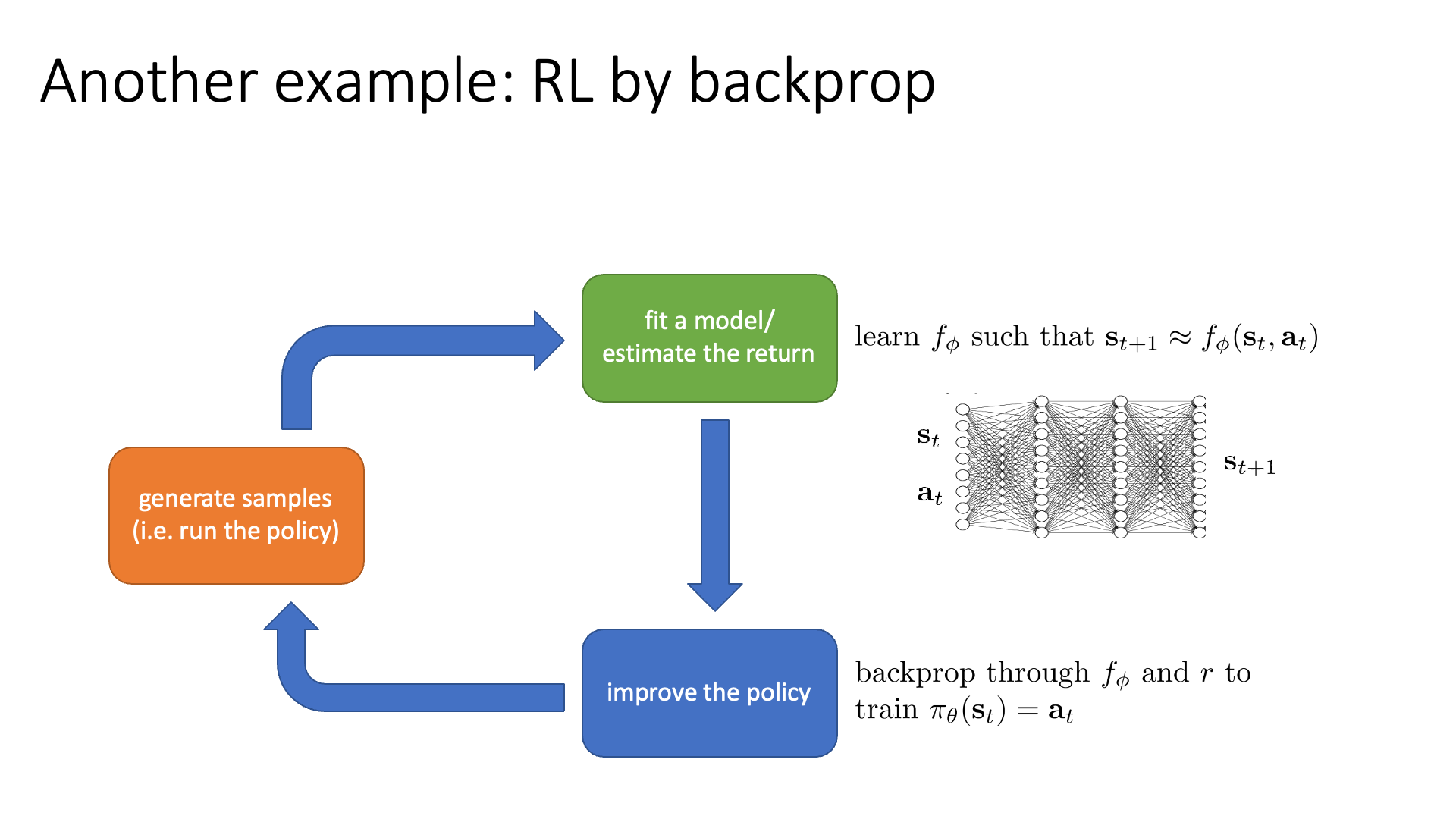Slide. 19.

Model-based RL이니까 transition dynamics를 NN으로 modeling해야겠죠?

Model, \(f_{\phi}\)는 \((s_t,a_t)\)를 given으로 다음 state, \(s_{t+1}\)을 추론하는 NN입니다. 이 module은 orange block에서 만들어진 training sample을 가지고 SL방식으로 학습됩니다. 원래 green block이 하는일은 environment로 얻었던 reward들을 memorize하고 있다가 단순히 sum연산을 함으로써 trajectory를 평가하는 것이었지만 이제 green block에서 optimization을 하게 됐으니 cost가 엄청 늘었습니다. 단순 sum operation은 몇 ms밖에 안걸리지만 training을 하는 것이니 수 분에서 수 시간 걸리는 것으로 바뀐 것이죠. 그리고 blue block에서는 \((\pi_{\theta}=a_t)\)를 학습하기 위해 \(f_{\phi}\)와 \(r\)을 통한 Error Backpropagation을 사용합니다. (사실 왜 굳이 이걸 RL by backprop이라고 하는지 모르겠습니다. 다른 RL들도 다 backprop 하는데 말이죠? 저도 RL newbie이기 때문에 detail을 몰라서 하는 말인데, Model-based RL은 lecture 11, 12에서 자세히 설명할테니 지금 잘 이해가 가지 않아도 너무 걱정 말라고 합니다.)

Which parts are Expensive?

RL anatomy의 전체 process 중 가장 cost가 많이드는 (expensive) part 는 어디일까?에 대해서 생각해 봅시다. 이는 우리가 풀고자하는 task에 따라서, 사용하려는 RL algorithm에 따라서 다릅니다.

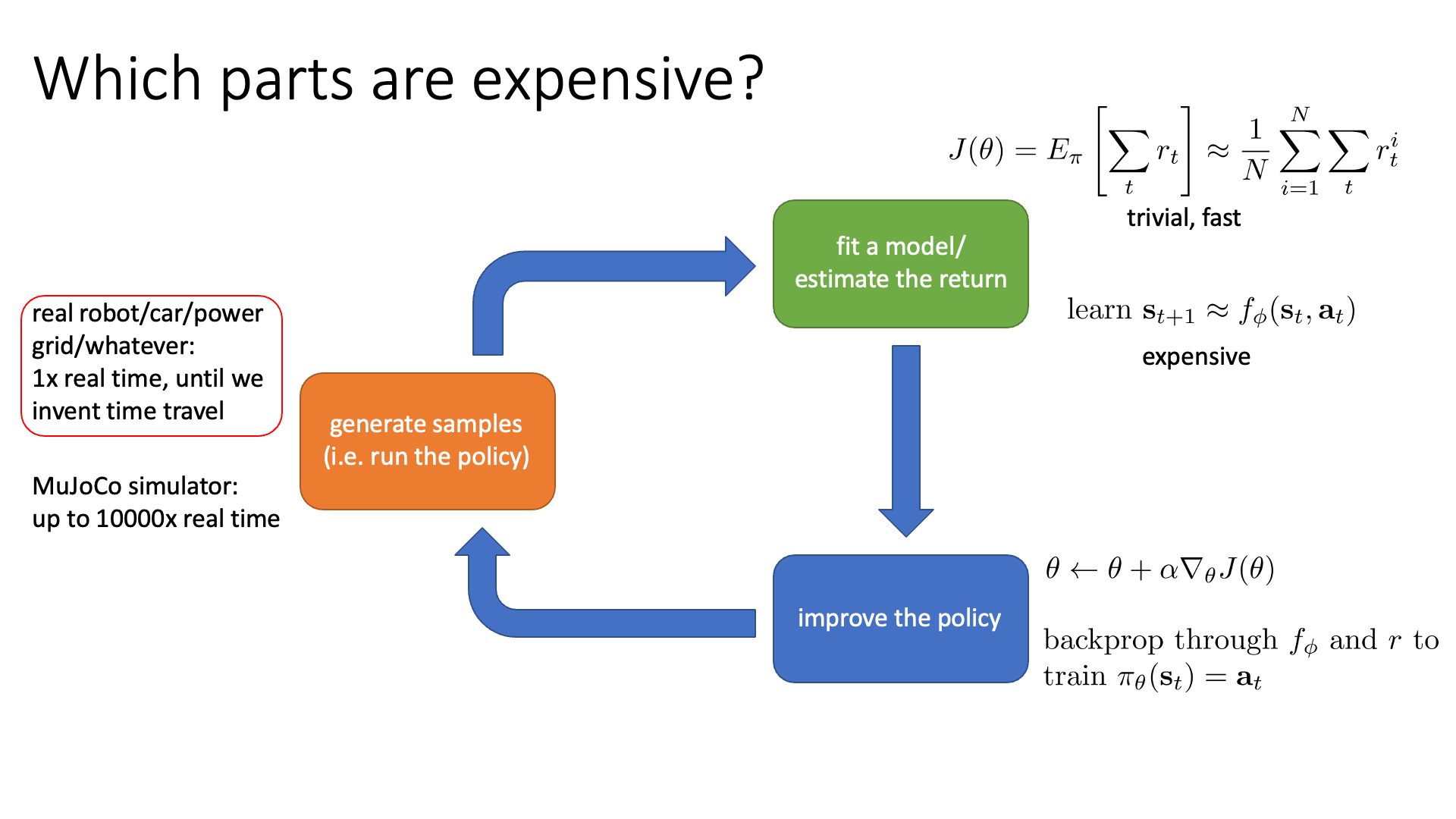Slide. 21.

우선 첫 번째로 orange block입니다. RL로 풀 수 있는 문제에는 자율 주행 (autonomous driving), 로봇 조작 (robot manimulation) 등이 있죠. 그런데 자율 주행을 위한 agent를 학습하기 위해 software를 실제 차에 내장하고 trial and error를 한다고 생각해 봅시다. 그런데 맨 처음 학습이 안된 random policy는 주행에 대한 개념이 없을 것이고 여기저기 들이받으며 사고를 많이 낼겁니다. 이럴 경우 차가 파손된 비용도 부담해야 하고 실제 주행을 하기 때문에 시간도 많이 걸릴 것입니다. 이런 경우를 sampling cost가 많이 든다 (expensive)고 하는 겁니다. 이를 해결하기 위해서는 simulation 환경에서 sampling을 하고 agent를 학습하는 방법을 써야합니다. OpenAI의 gym이나 MuJoCo등의 simulation을 위한 library를 사용하면 이는 더이상 문제가 되지 않을겁니다.

그 다음으로 green block인데, 이는 앞서 model-based RL에 대해 얘기하면서 살짝 눈치를 채셨을 것 같습니다. Dynamics를 modeling하는 경우, 더이상 green block은 cheap한 part가 아닐 수 있습니다. Bluew block에서도 마찬가지인데, 원래는 gradient를 계산하고 parameter update를 하는것은 그리 오래걸리는 연산이 아니겠으나 model-based RL같은 경우 비싸질 수 있다고 합니다.

곧 있으면 배우게 될 value based method 중 Q-Learning의 경우에는 green block에 resource를 몰빵하고 blue box는 그저 pytorch의 argmax operator를 수행하는 것으로 전혀 cost가 들지 않습니다. 이렇듯 algorithm이 무엇이냐에 따라서 우리가 집중적으로 봐야할 part가 달라집니다.

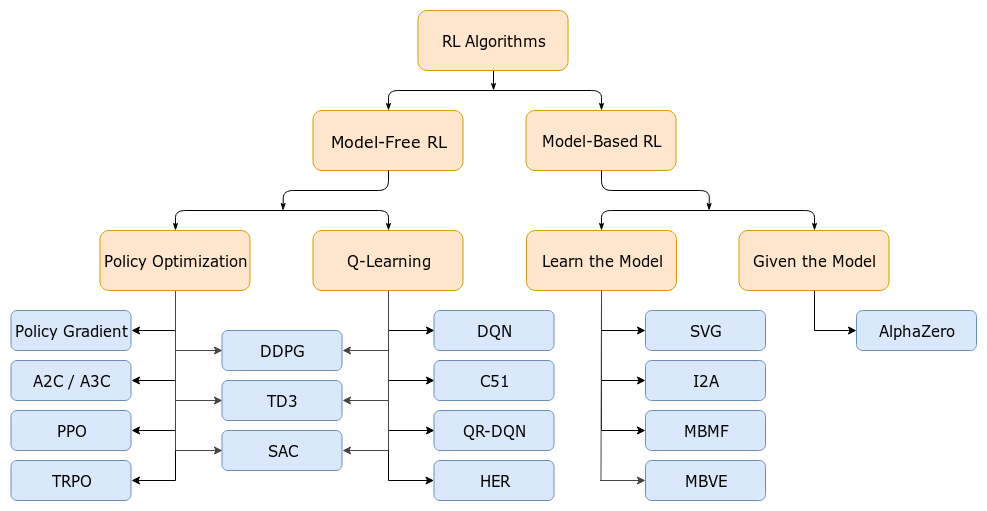
• Fig. A non-exhaustive, but useful taxonomy of algorithms in modern RL. 강화 학습 algorithm은 크게 Model-Free RL, Model-based RL로 나눌 수 있고 세부적으로 value based (Q-Learning)와 policy-based (Policy Optimization)로 나눌 수 있다. Q-Learning 계열은 green block이 expensive하겠구나라고 생각하고 이를 개선하기 위해서 어떤 노력들이 있었는지 찾아보는 것이 도움이 될 것 같다. Source from OpenAI Spinning Up.*

Value Functions

이번에는 가치 함수 (Value Function)에 대해 알아보려고 합니다. 이는 RL algorithm을 design하고 RL objective을 개념적으로 이해하는 데 있어 수학적으로 매우 유용한 module 이라고 합니다.

Slide. 23.

다시 RL Objective에 대해서 생각해 보도록 하겠습니다.

RL을 공부하다보면 이 수식을 다르게 표현하는 (re-writing)경우가 많습니다. 그 쓰는 과정에서 몇가지 trick이나 approximation을 추가해서 새로운 algorithm을 정의해기도 하죠. 이전에 trajectory distribution을 chain rule을 사용해 여러 distribution의 곱으로 표현했던 것이 기억이 나실 겁니다. 비슷하게 RL objective도 반복적인 (recursively) expectation으로 표현 (일련의 nested expectation)을 하려고 합니다.

RL objective를 1회 풀어 써봅시다. 아래처럼 가장 바깥쪽의 (outermost) expectation부터 만들어보는겁니다.

수식이 의미하는 바는 initial state distrubiton하의 가능한 모든 state들에 대해서, 또 각각의 state에서 할 수 있는 모든 action의 distrubiton하의 reward의 expectation을 의미합니다. 그니까 첫 state, 첫 action의 경우의수를 모두 고려해 각각의 reward를 계산해서 확률값만큼 곱해준 weighted sum인거죠.

이를 또 한 step 전개해서 두 번째 timestep에 대해서도 계산할 수 있습니다.

이를 teriminal state, \(s_T\) 까지 계속 반복합니다. 왜 이렇게 하는 걸까요?

Expeectation 안의 quantity를 다음과 같이 \(Q(s_t, a_t)\)라고 정의해봅시다.

그렇다면 우리는 RL objective를 아래처럼 간단하게 다시 쓸 수 있습니다.

여기서 \(Q(s_1,a_1)\)가 의미하는 바가 무엇이고, 만약 우리가 \(Q(s_1,a_1)\)을 안다면 어떤 일을 할 수 있을까요? 이는 \(s_1\)에서 어떤 \(a_1\)라는 action을 했을 때 즉시 받는 reward와 \(a_1\)이후 발생 가능한 trajectory에 대해서, 즉 \(s_2\)부터 또 trajectory distribution하의 total reward의 expectation을 더한 겁니다. 중요한 것은 \(a_1\)를 실제로 했을 때의 결과값이라는 겁니다. 실제로는 \(s_1\)에서 할 수 있는 action이 다양하겠죠? 그런데 \(Q\)라는 qunaitty는 각각의 action중 하나를 골라 실제로 한 번 하고 그 뒤로는 끝까지 모든 경우의 수를 탐색해서 이 action이 어떤 값을 return하는지를 알려주는 것이므로, 그 action이 몇점짜리 action인가?를 알려주는 indicator가 되는겁니다. 즉 우리는 \(s_1\)에서 할 수 있는 action이 (up, down, right, left) 4개로 discrete하다면 각각의 action을 해 보고 가장 Q값이 높은 action을 고르는걸 policy로 대체할 수 있는 겁니다. 이것이 바로 value-based method의 핵심입니다.

Q-Value Function and Value Function

Slide. 24.

이를 조금 더 일반화 해 봅시다. 큐 함수 (Q-function)는 slide 24의 상단에 있는 수식 처럼 나타낼 수 있습니다.

수식이 의마하는 바는 \(s_t\)에서 현재의 policy, \(\pi\)를 따라 \(a_t\)를 취함으로써 전개될 trajectory들이 terminal state, \(T\)까지 갔을 때 얻을 수 있는 total reward의 expectation (총 합)입니다. 이와 비슷한 개념으로 가치 함수 (Value function) 라는 것도 정의할 수 있습니다. (사실 둘 다 value function입니다. V function, Q function으로 나눠 부를 뿐인데 보통 V function을 value function이라 부르는 것 같기도합니다.)

이는 Q-function과 다르게 \(s_t\)에 대해서만 condition되어 있죠. 의미하는 바가 굉장히 clear한데, 이는 \(s_t\)에서 policy를 굴려 (roll-out) 얻을 수 있는 trajectory들이 terminal state까지 갔을 때 얻을 수 있는 total reward의 기대 값을 의미합니다.

눈치채셨겠지만 Q-function과 차이점은 action이 condition되어있느냐?라고 했는데, 이는 Value function, \(V\)는 그 state에서 취할 수 있는 action들을 모두 고려해서 expectation을 계산하는 것이고, Q-function은 \(s_t\)에서 policy를 굴려 \(a_t\)를 sampling했으면 이것은 정해진 것이고 (deterministic), 그 이후부터 expectation을 취한다는 겁니다. 그러니까 \(V\)는 \(Q\)의 평균이다 (action distribution 하의 Q값을 expectation한 것이다) 이렇게 말할 수가 있습니다.

사실 둘 다 value function이라고 하는데 같은 state, \(s_t\)를 기준으로 \(V\)는 state에만 의존하는, 모든 action을 고려하는 quantity이기 때문에 state value function이라고 하며 \(Q\)는 \(a_t\)까지 고려하기 때문에 state-action value function이라고 합니다.

마지막으로 굉장히 흥미로운 수식에 대해 말씀드리겠습니다. 우리의 RL objective는 사실 다음과 같이 표현할 수 있습니다.

현재 policy를 따라서 initial state, \(s_1\)의 value 값의 expectation을 구하는 것은 현재 policy를 따라는 trajectory distribution하의 total reward의 기대값을 구한다는 것과 같다는 거죠. 이 개념들은 나중에 RL algorithm을 유도하는데 굉장히 유용하게 쓰이므로 꼭 잘 이해를 하고 기억해주시길 바랍니다. (직관적으로나 수식적으로나 initial state에서의 value값이 RL objective와 같다는 것은 자명하기 때문에 더 설명드릴 것이 없습니다)

Slide. 25.

이는 실제로 value based method를 다루는 lecture 7, 8의 Policy Iteration과 Q-Learning라는 algorithm들의 기본 idea로, 모든 time-step에 대해서 Q or V 값을 계산한 뒤에 (혹은 NN으로 modeling해서 추론한 뒤에) 해당 state에서 가장 value가 높은 action에 확률 1을 부여해 (greedy) policy를 얻을 수 있습니다. 혹은 lecture 6의 Actor-Critic에서도 이 quantity가 사용되는데, 우리는 \(Q\)와 \(\)를 비교하는 것 만으로 어떤 action이 다른 action들보다 월등한지를 알 수 있기 때문에 (\(Q^{\pi}(s,a) > V^{\pi}(s)\)인 action은 모든 선택지의 평균보다 좋은 action임) 그 action의 확률을 높히는 방향으로 policy network를 optimize할 수도 있겠습니다. 이 idea는 Sergey가 very very very importatnt하다고 하니 꼭 곱씹어 보시길 바랍니다.

Slide. 26.

다시 RL algorithm의 anatomy를 revisit 해 봅시다. 앞서 여러 algorithm들은 각자의 강점이 있어 part별로 드는 cost가 다르다고 했습니다. Q-Learning의 경우에는 green block에 대부분의 resource를 투자하고 blue box는 그저 pytorch의 argmax operator를 수행해 전혀 cost가 들지 않는다고 했었는데, Q-function 값을 기준으로 policy를 update하기 때문에 이것이 매우 싼 part가 되는 것이었습니다.

Types of Algorithms

이번에는 RL algorithm의 여러 type들에 대해서 빠르게 훑어보는 시간을 갖겠다고 합니다.

Slide. 28.

먼저 정책 경사 (Policy Graidnet)류의 method은 RL bjective를 직접적으로 policy를 표현하는 parameter, \(\theta\)에 대해 미분해 gradient를 계산하고, 이를 경사 하강법 (gradient descent)같은 optimization algorithm을 통해 direct로 policy를 학습하는 algorithm들을 말합니다.

둘째로 가치함수 기반 (Value-based)류의 method는 value funciton이나 Q-value function을 NN으로 modeling하고 이를 토대로 policy를 emission해서 사용하는 것으로 implicitly policy를 학습하는 방법을 말합니다.

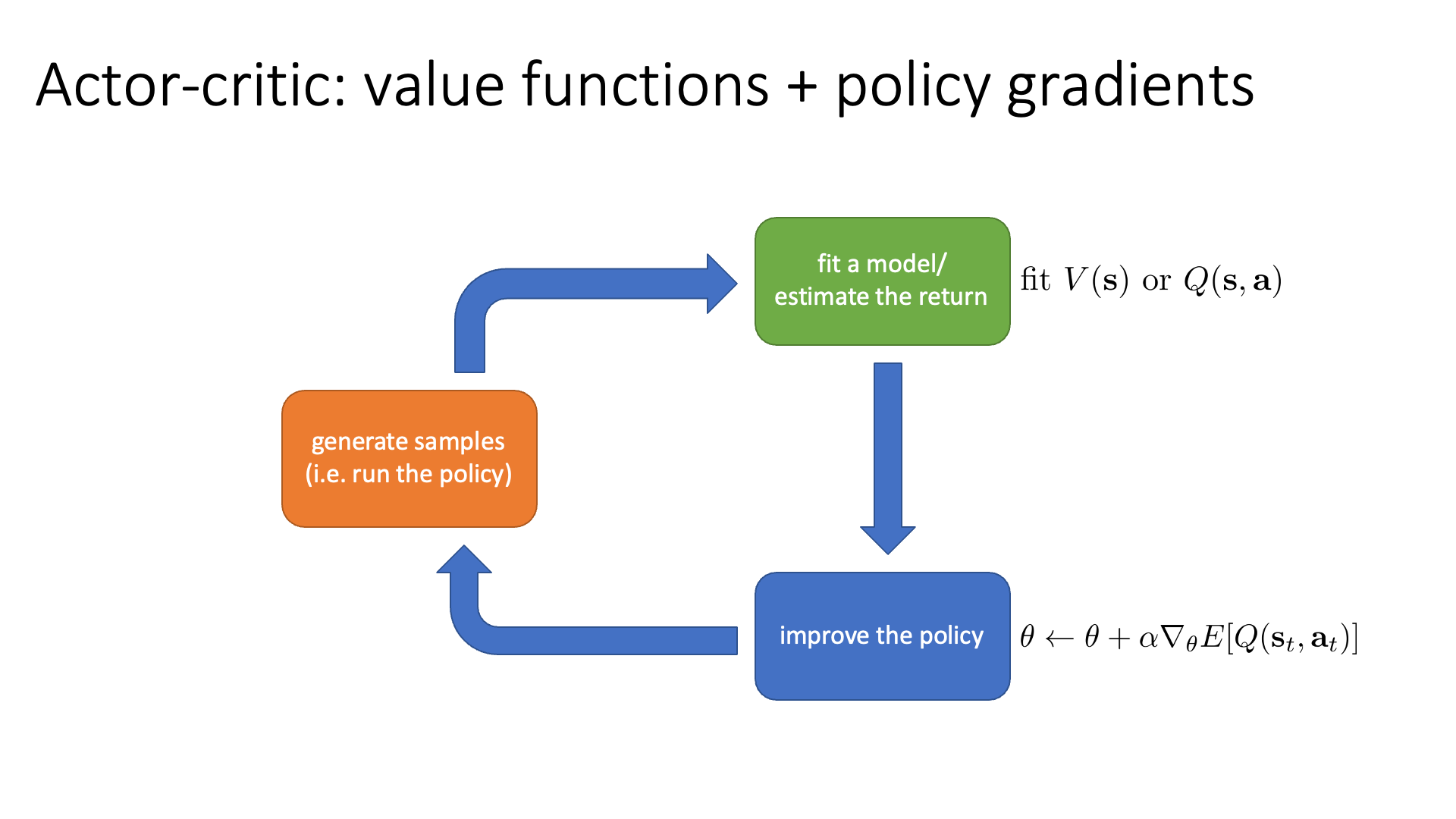
그 다음 Actor-Critic는 위의 두 algorithm의 hybrid version입니다. 이 algorithm은 value function과 policy network를 동시에 학습합니다. Lecture 5, 6에서 배우겠으나 policy gradient method는 일반적으로 gradient의 variance가 매우 큽니다. 그래서 불안정한 optimization을 할 가능성이 크죠. Actor-Critic은 policy가 어떤 state에서 어떤 action을 하면 그 action을 value functuio이 평가하여 이를 gradient를 계산하는 데 사용함으로써 더 정교한 gradient를 얻을 수 있게 됩니다. 이렇게 value값을 학습한 module을 action을 평가한다고 해서 비평가 (critic)이라고 부르며, policy를 Actor라고 부르기 때문에 Actor-Critic이라고 하는 것입니다.

마지막으로 Model-based RL method는 transition probability를 modeling하는 겁니다. 그리고 이를 explicit policy 없이 planning 하는 데 사용하거나, policy를 학습하는 데 사용한다고 합니다.

Model-based RL

Model-based RL Algorithm에 대해서 좀 더 얘기해봅시다.

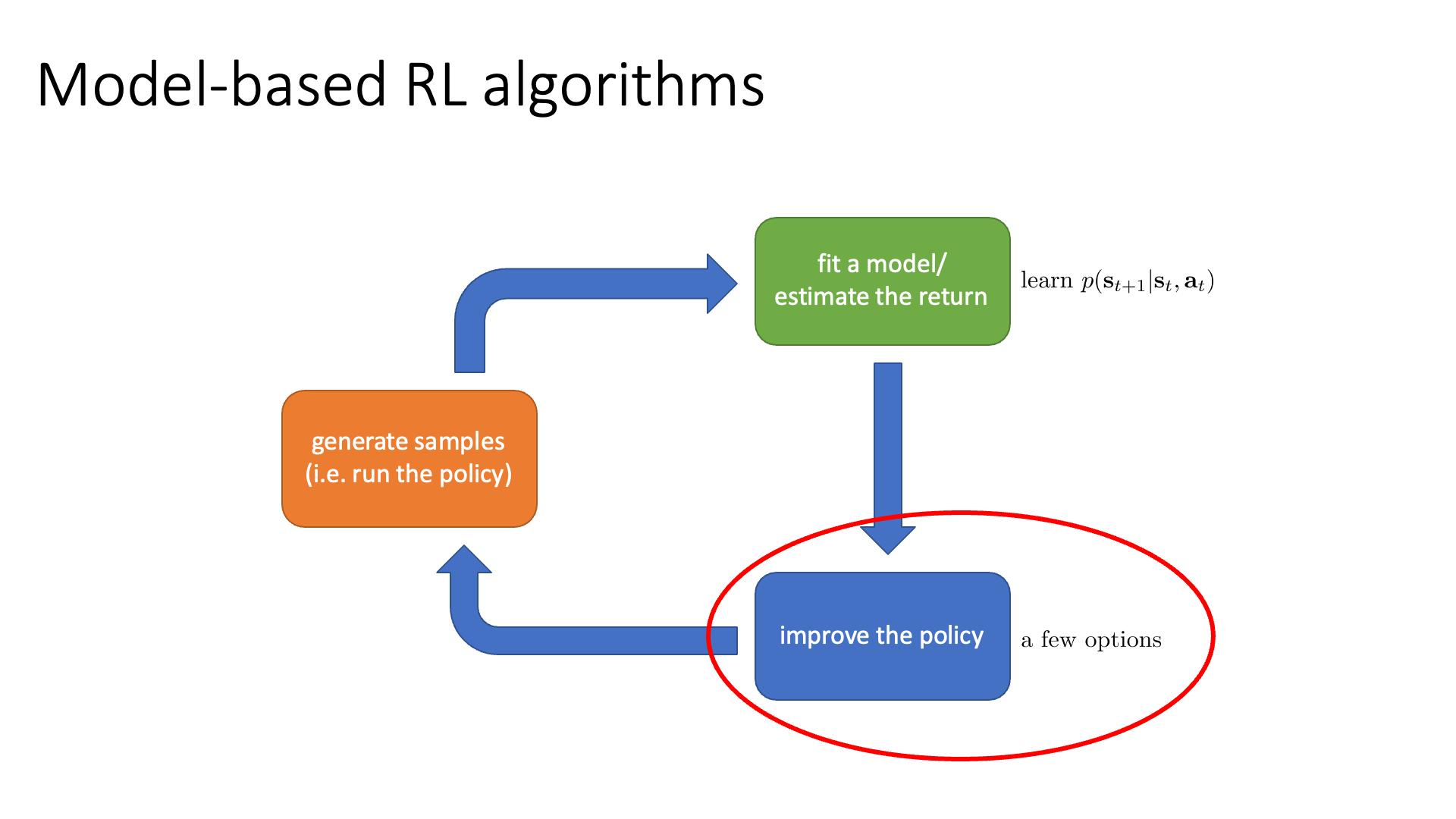Slide. 29.

Model-based RL은 dynamics를 추가로 modeling해야 한다고 여러 번 말씀드렸습니다. Dynamics를 근사한 NN은 \(s_{t+1}\)에 대한 distribution을 return하거나 deterministic model이라면 \(s_{t+1}\)를 그냥 return하게 됩니다. Blue box에 대해서 조금 더 얘기해 볼건데, 이는 세 가지로 분류됩니다.

• Just use the model to plan. (no policy)
• Backpropagate gradients into the policy
• Use the model to learn a value function

Slide. 30.

먼저 explicit policy가 없고 model을 사용해서 planning을 하는 경우입니다. Planning이라는 개념이 생소하실 수 있어 짧게 설명해드리면 AlphaGO에서 사용된 Monte Carlo Tree Search (MCTS)같은게 대표적인 planning method입니다. 우리는 policy는 없고 현재 state, \(s_t\)에서 어떤 action, \(a_t\)를 하면 어디로 가는지?를 알 뿐입니다 \((p(s_{t+1} \vert s_t, a_t))\). 그러니까 \(s_t\)에서 가능한 action들을 다 해보는 겁니다. AlphaGO를 예로 들면 agent가 현재 진행중인 흑/백돌이 놓여있는 state에서 끝까지 한번 다 둬보는 겁니다. 그 중에서 결국에는 게임을 이긴 \(s_{t+1}\)로 가는 \(a_t\)가 있겠죠? 그 action을 택하는 겁니다. 엄청 cost가 많이 들 수도 있고 continuous action space에서는 가능한 action이 무한대이기 때문에 쓸 수 없는 방법이지만 continuous action space에 대해서는 trajectory optimization이나 optimal control같은 method들이 있다고 합니다. 어쨌든 이런 식으로도 policy를 구할 수 있습니다.

그 다음은 policy가 있는 경우인데, learned dynamics model을 reward function의 policy에 대한 미분값을 구하는데 사용하거나, learned model을 value function을 학습하는데 사용하고, 이를 통해서 policy를 개선해 나가는 겁니다. (Sergey도 제대로 설명하지 않고 introduction의 범위를 벗어나기 때문에 더 이상의 설명은 생략하겠습니다. 궁금하신 분들은 lecture 11, 12를 참고하시기 바랍니다)

Value-based RL

Value-based method는 Q-function, V-function을 설명하면서 이미 조금 길게 서술했던 것 같습니다.

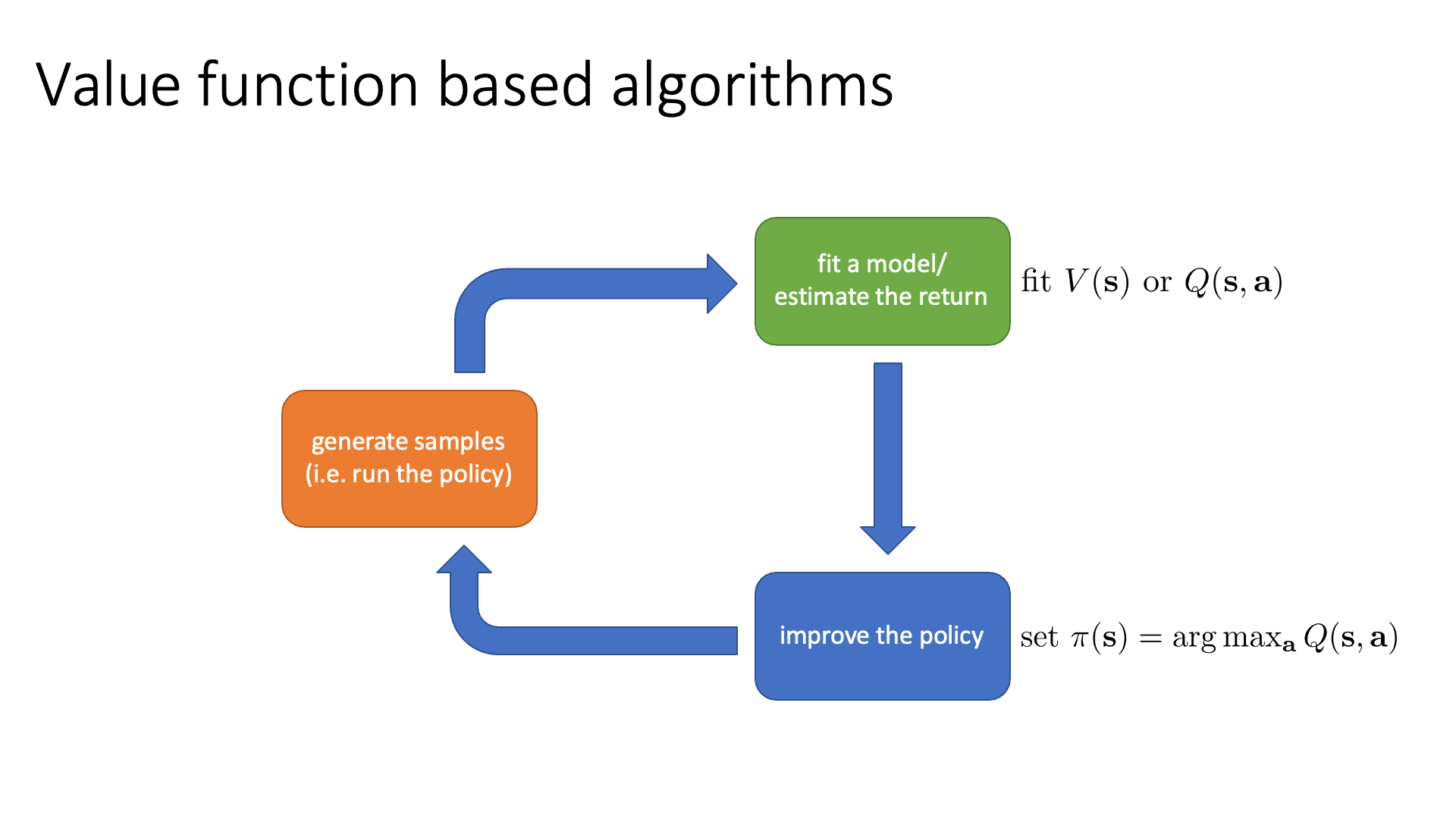Slide. 31.

원래같았으면 green block은 trajectory가 만들어지면서 발생한 reward들을 summation하는 것으로 아무런 cost가 들지 않았는데, 이걸 NN으로 modeling한다는 것은 Q or V를 학습한다는 겁니다. 어떻게 \(s_t\)에서 \(a_t\)를 하는것이 몇점짜리인지 알 수 있을까요? 모든 경우의 수 (\(s_t\)이후로의 trajectory들)을 다 돌려서 return을 얻은 다음 sum하는 방법이 있겠으나 이는 state space가 클수록 말도안되는 전략입니다. 따라서 이를 근사해야하는데, 자세한 내용은 lecture 7, 8에서 다루니 걱정하지 마시길 바랍니다.

어쨌든 green block에서 Q or V값은 NN으로 modeling을 하던지 말던지 scalar를 return합니다. 이는 사실 unimodal gaussian distribution을 modeling한다는 말이긴 한데, distributed RL이라고 해서 더 복잡한 distribution을 modeling하는 method들이 있습니다.

Policy-based RL

Policy-based RL은 여러 번 말씀드린 것 처럼 policy를 parameterize 한 explicit NN이 존재하고, RL objective를 policy parameter로 미분하여 objective를 maximize하는 방향으로 parameter update를 해나가는 방식입니다.

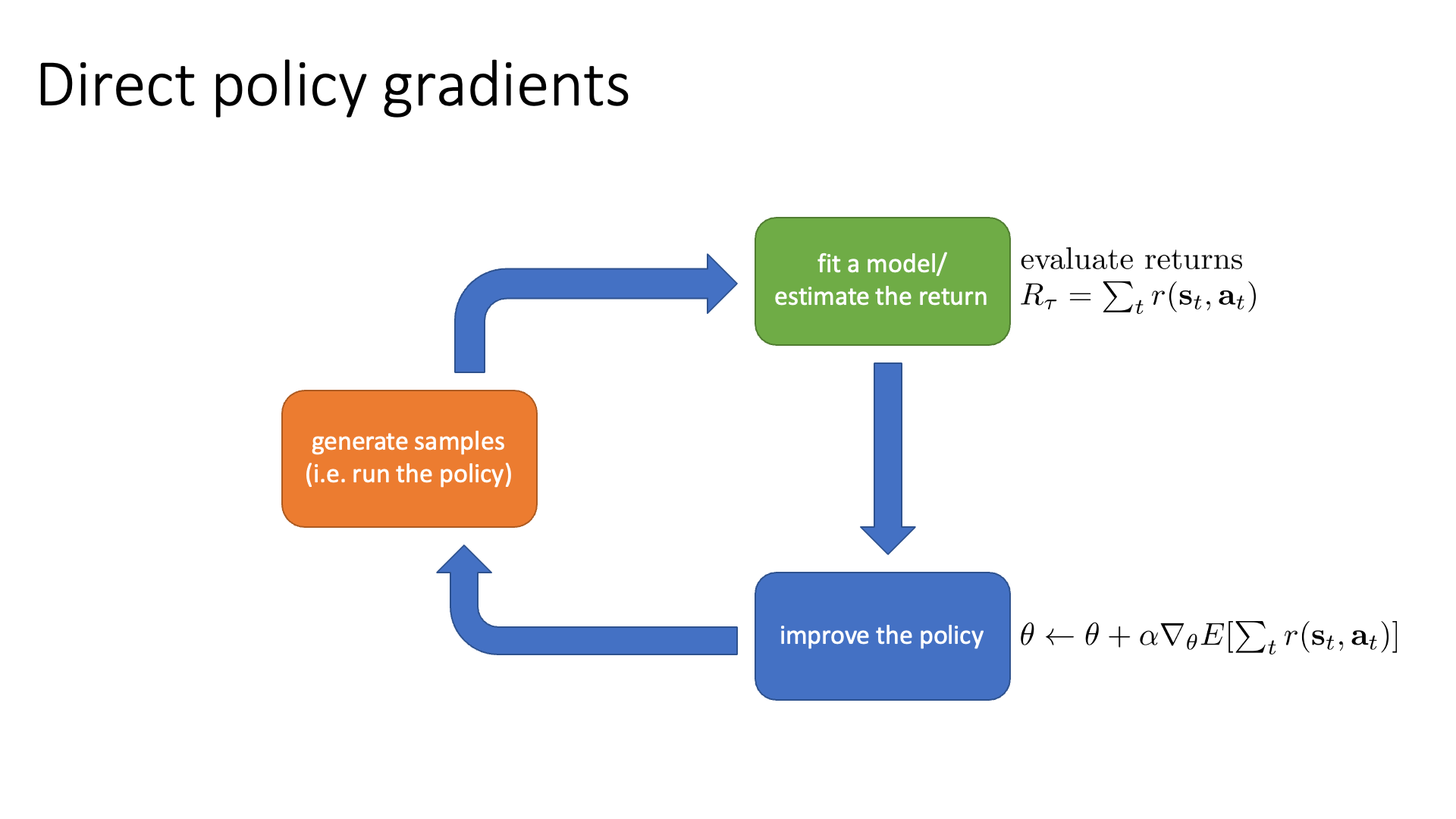Slide. 32.

이것 또한 Lecture 5에서 제대로 배울 것이기 때문에 생략하고, 여기에 value function을 같이 modeling하는 Actor-Critic도 6, 9장에서 머리가 아프도록 배울테니 넘어가도록 하겠습니다.

Slide. 33.

Tradeoffs Between Algorithms

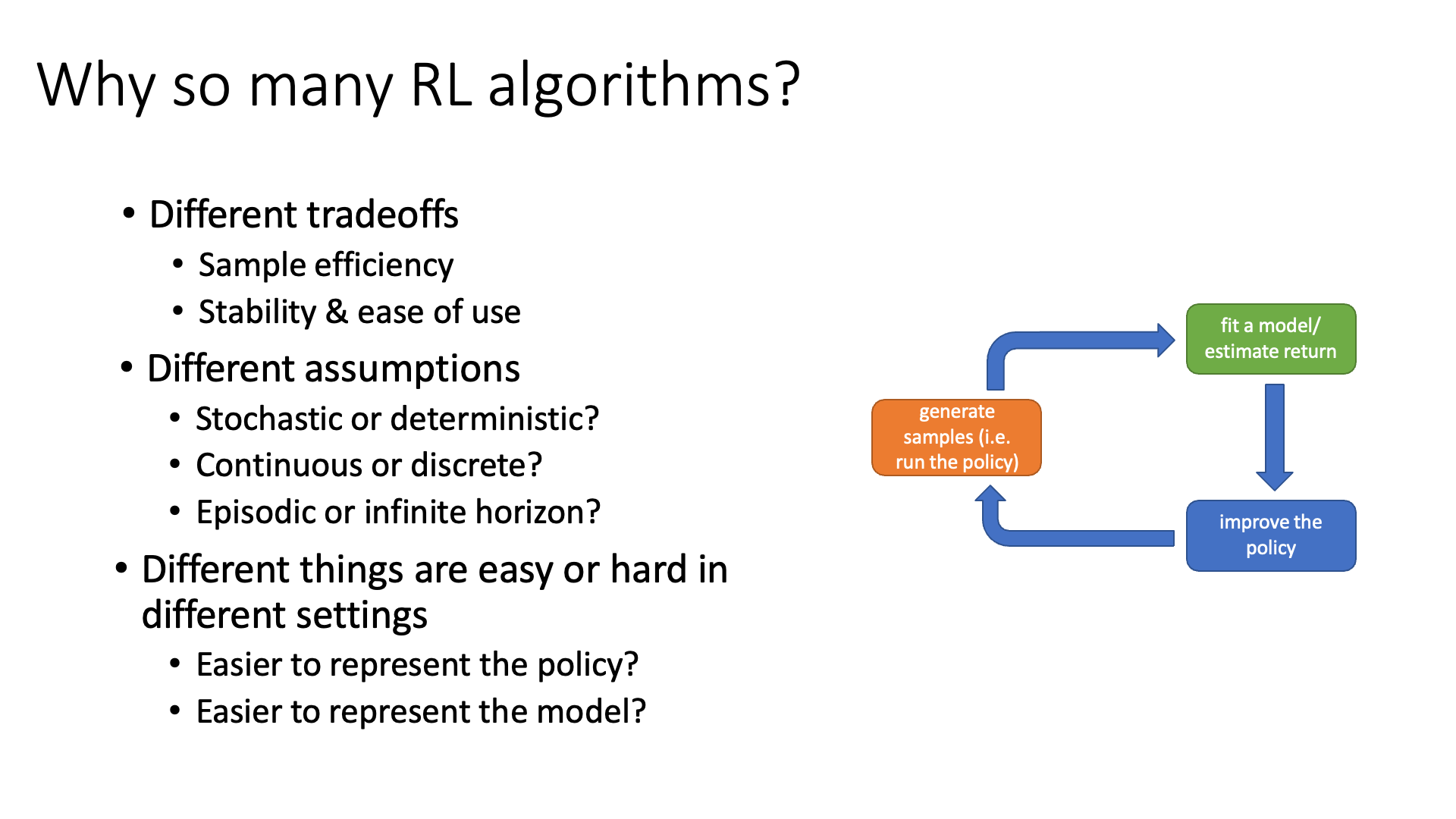
근데 우리가 이렇게나 다양한 RL algorithm들을 알아야 하는 이유는 뭘까요? 그냥 policy optimization 하는 algorithm하나만 파면 되는 거 아닐까요?

그 이유는 각 RL algorithm들의 장단점이 있는데, “내가 어떤 문제를 풀어야 하는가”에 따라서 성능과 효율성이 확연하게 차이가 날 수 있으며 푸는 문제에 따라서 가정을 해야 하는것이 다른데, 그에 맞는 method를 사용해야 하기 때문이라고 합니다.

Slide. 35.

서로 다른 RL algorithm에는 Trade-off가 존재하는데 대표적으로 다음의 두가지가 있습니다.

• Sample Efficiency
• Stability & Ease of Use

이들 중 첫 번째는 sample efficiency 입니다. 이는 “good policy를 얻기 위해서 얼마나 많은 양의 sample이 필요한가?”를 의미합니다.

또 다른 trade-off는 stability과 ease of use 인데, 가령 어떤 algorithm은 trajectory sampling은 매우 비쌀 수 있지만 inference시에는 NN model forward를 한 번만 하면 되기 때문에 사용성 측면에서는 훨씬 편한 경우도 있습니다. Stability 관점에서는 예를 들어 주어진 문제를 풀기 위해서는 “현재 문제를 풀기 위해 어떻게 sampling을 해야하는가??”, “어떻게 explore해야 하는가? (exploration vs exploitation)”, “어떻게 model을 fit해야 하는가?”, “어떻게 value function을 fit해야 하는가?”, “어떻게 policy update를 해야 되는가?”등을 고려해야 하고 각 issue마다 tuning해야하는 hyperparameter가 추가될텐데, 어떤 algorithm은 내가 정의한 문제 상황과 맞지 않아 비효율적일 수가 있다고 합니다.

또 한가지 이유는 각 algorithm이 가정하고 있는 것이 다른 것도 있다고 합니다.

• Stochastic envrionment를 다루는지, 아니면 deterministic envrionment를 다루는지?
• Continuous한 state, action space를 다루는지, 아니면 discrete한 space를 다루는지?
• Episodic problem 인지, 아니면 Iifinite horizon case인지?

예를 들어 어떤 task는 dynamics는 매우 복잡하지만 policy를 represent하는건 쉬울 수도 있고, 반대로 policy를 directly optimize하는 것 보다 dynamics를 modeling하는게 훨 씬 쉬울 수도 있습니다. 후자의 경우 그러면 Model-based RL이 적합하겠죠.

이제 각 trade-off에 대해서 조금 더 얘기해 보도록 합시다.

Sample Efficiency

Sample Efficiency에 대해서 먼저 얘기해보도록 합시다. 이는 우리가 good policy를 얻을 때까지 필요한 sample의 양을 의미한다고 했습니다.

Slide. 36.

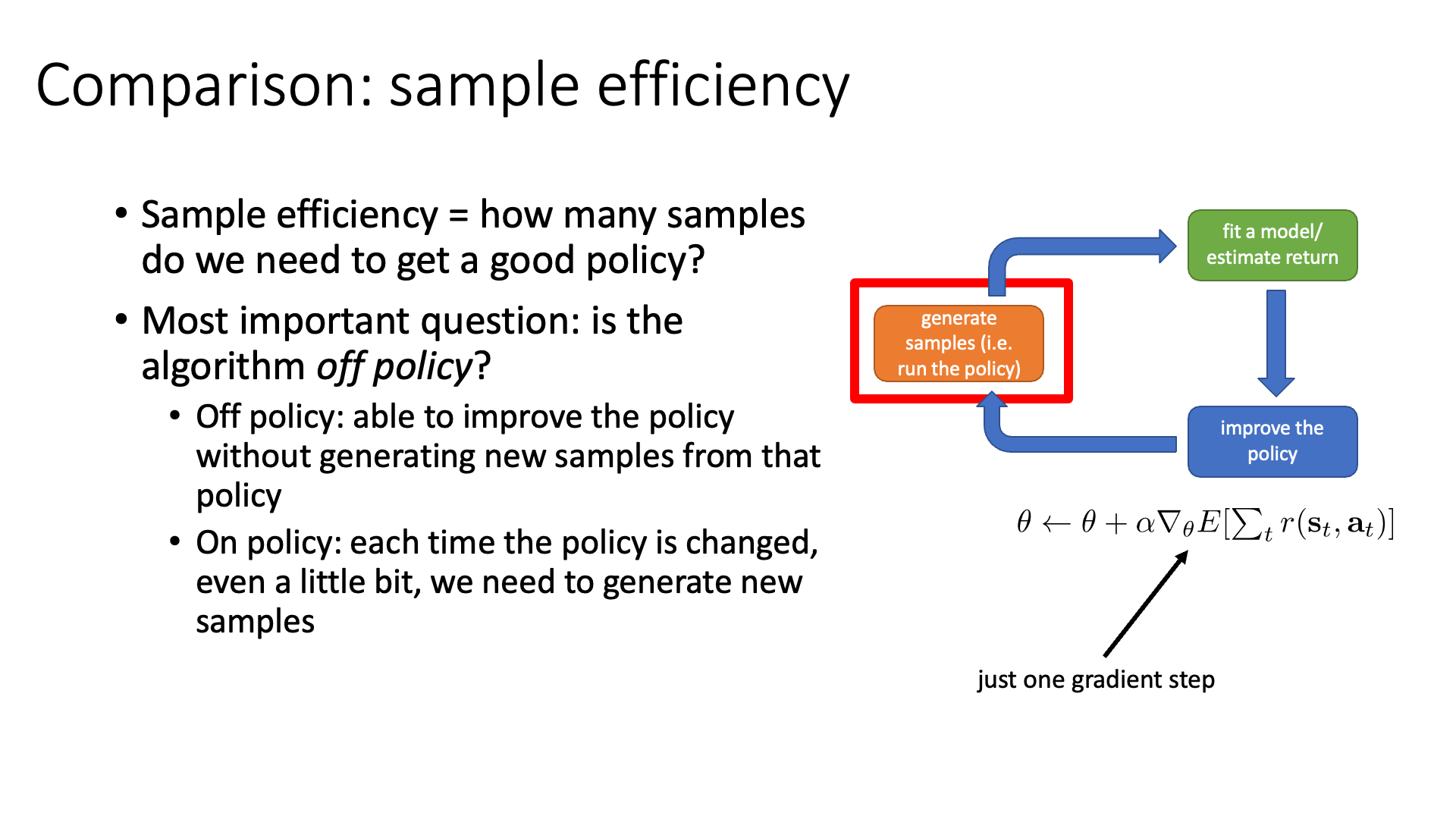
Sergey는 algorithm의 sample efficiency를 결정할 때 가장 중요한 질문 중 하나는 'algorithm이 Off-Policy 인가?라고 합니다. 이 개념도 곧 배울건데 기본적으로 RL algorithm은 on-policy 라고 합니다. 우리가 앞서 RL objective function을 현재 policy를 따르는 trajectory distribution하의 return의 기대값이라고 정의했습니다. 이 철학에 따라 policy가 바뀔 때 마다 trajectory distribution이 바뀌니 새로 data를 만들어야 한다고 했죠. Off-policy는 그런 제약조건에서 탈피 (off)를 했다고 표현할 수 있겠습니다. 이는 이전 optimization step에서 만들어진 sample을 활용해서 optimize를 할 수 있는 방식을 말합니다. 즉 매 번 data를 sampling하지 않아도 되는거. 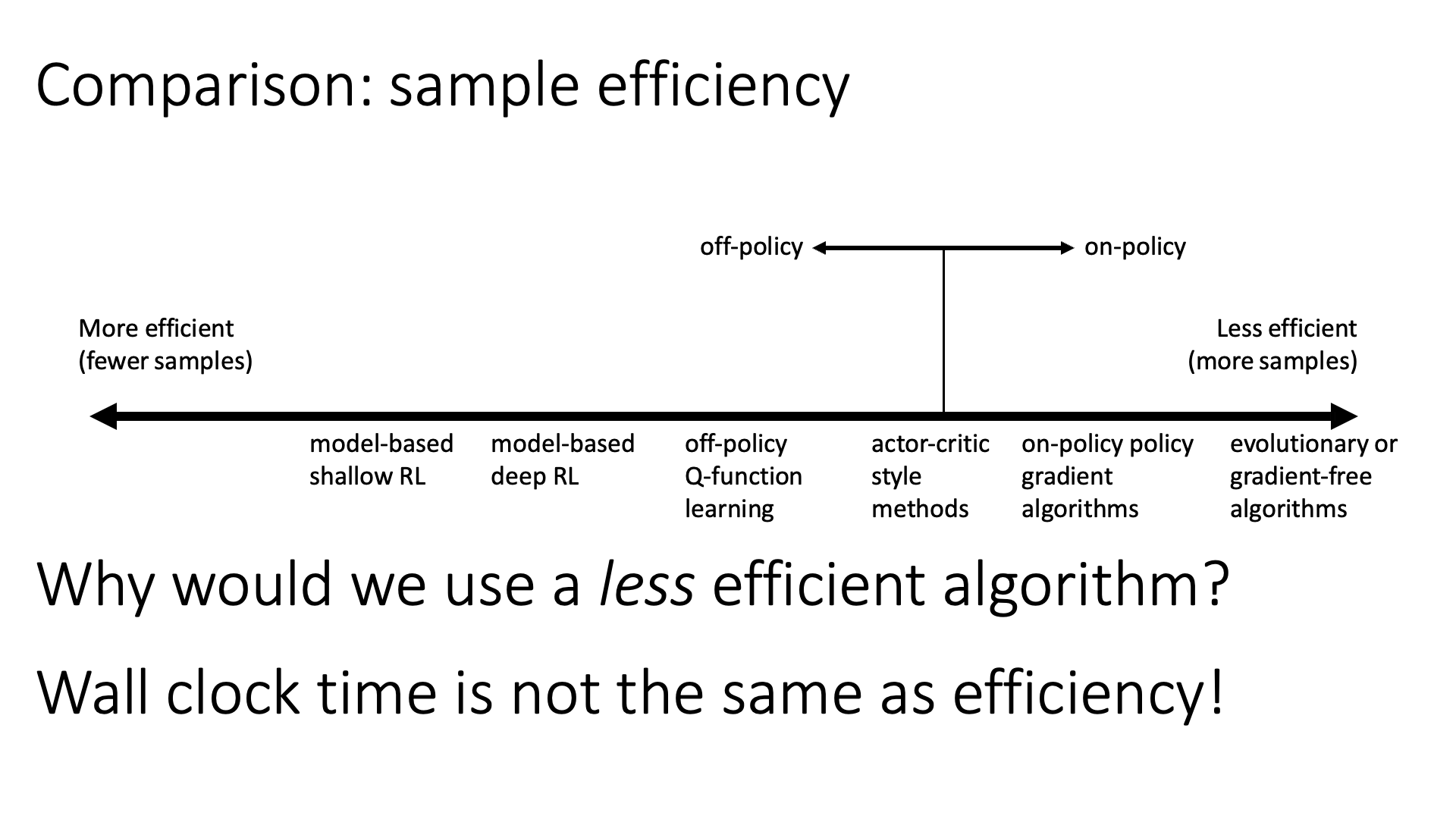아래 figure는 sample efficiency를 기준으로 RL algorithm들을 나열한 것입니다.

Slide. 37.

하지만 off-policy가 매 번 좋은 것은 아니며, 심지어 sample efficiency가 좋더라도 training에 총 걸린 시간 (wall clock time)은 efficient하지 않을 수도 있습니다. 가령 우리가 simulation 환경에서 agent를 학습한다고 할 때 trajectory 를 sampling하는 것이 그렇게 비싼 행위는 아닐 수가 있습니다. 이럴 경우 굳이 off-policy를 고집할 필요가 없죠. 왜냐면 모든 (RL을 포함한) algorithm들은 각자 trade-off가 있기 마련인데 off-policy가 가능하기 위해서 어떤 걸 포기했을 가능성이 높겠죠? 그러면 이제 optimization step을 얼마나 진행했는가?로 sample수를 얼마나 썼느냐가 나뉘어질 것이고, 이것이 곧 sample efficiency 일텐데, off-polciy로 같은 sample을 50 step씩 써서 50000 step을 간 것과 매 번 sampling을 다시 해서 1 step씩 10000 step을 간 것을 비교했을 때 후자가 성능이 더 좋다면 off-policy는 학습 시간이 더 걸린것이므로 더 안좋은 algorithm으로 평가 받을 수도 있습니다.

Stability and Ease of Use

두 번째는 algorithm의 Stability & Ease of Use입니다. 이 중, stability 는 algorithm이 optimal point로 수렴을 하는가? 수렴한다면 그 지점이 local minimum인지 optimal minimum인지?, 그리고 매번 학습할 때 마다 (seed가 다를 때 마다) 수렴을 하는지? 등을 의미합니다.

Slide. 38.

왜 이런것 까지 논해야할까요? 그 이유는 대부분의 RL algorithm들은 수렴을 보장하지 않기 때문이라고 합니다. 이는 lecture 9에서 제대로 다루는데 RL은 (특히 policy gradient method는) SL과 다르게 순수한 gradient descent를 사용하는게 아니기 때문입니다. Sergey는 대부분의 practical RL algorithm들은 fixed point algorithm이기 때문에 수렴성이 보장되지 않는다고 하는데, real-world problem과는 조금 동 떨어진 단순한 task인 tabular discrete state assumption 하에서만 그나마 수렴이 보장된다고 합니다. 잘 working하는 대표적인 RL algorithm 중 하나인 Q-Learning의 수렴성도 open problem이라고 합니다.

Model-Based RL의 경우 RL objective에 대한 optimization이 아니라 단순히 transition probability matrix를 학습하는 독특한 (peculiar) algorithm 이기 때문에 dynamics 를 학습하는 입장에서는 수렴할 수 있겠으나, 이것이 잘 학습됐다고 해서 이 것이 더 reward를 받는다거나 (수렴한다거나) 하는건 보장되어 있지 않는다고 합니다. 마지막으로 policy gradient의 경우 gradient descent 비스무리한 일을 하지만 가장 비효율적인 method라고 합니다.

Slide. 39.

Assumptions

Slide. 40.

앞서 우리가 푸는 문제에 따라 assumption이 다르고, 따라서 그에 맞는 RL algorithm을 골라야 한다고 말씀드렸습니다. 대부분의 경우 fully observable 한 상황을 가정하지만 (state에 access), real-world problem은 그렇지 않습니다. 특히 요즘 핫한 Large Language Model (LLM)도 RL을 쓰는데, Sergey는 lecture 21에서 이를 POMDP로 정의합니다. Context가 주어졌을 때 (state), 그 다음 단어 (action)는 무엇이 와야 하는가? 를 decision해야 하는데, context에는 발화자의 감정이나 의도같은게 나타나 있지 않아서 그렇게 얘기하는게 아닌가 싶습니다.

어쨌든 partially observed인 상황에서 우리는 RNN이나 transformer같은 history에 access할 수 있는 model을 써야한다고 앞서 lecture 2에서 배운적이 있습니다. 혹은 value function fitting method를 쓰는게 좋다고 sergey가 얘기하네요. LLM domain에서 보자면 Sergey lab에서 제안한 ILQL같은 것이 value based RL로 학습한 LLM인데, 관련된 얘기를 하는거 같습니다.

(나머지는 관련된 chapter에서 다루도록 하겠습니다)

Examples of Algorithms

마지막 subsection에서는 Deep RL algorithm과 example 몇 가지를 보여줍니다. 어차피 자세한 얘기는 안하기 때문에 이 subsection은 생략할 것이며, 궁금하신 분들은 Lecture 4의 part 6 video를 참고하시길 바랍니다.

Slide. 42. cs285에서 모든 algorithm을 다루지는 않는다. TRPO, SAC등은 언급은 하지만 관련 paper를 봐야한다.

Slide. 43. Playing Atari with Deep Reinforcement Learning

Slide. 44. End-to-End Training of Deep Visuomotor Policies

Slide. 45. High-Dimensional Continuous Control Using Generalized Advantage Estimation

Slide. 46. QT-Opt: Scalable Deep Reinforcement Learning for Vision-Based Robotic Manipulation

다음 lecture부터는 본격적으로 policy based method에 대해서 알아보게 될 것입니다.

Reference

• Lectures
  • CS 285 at UC Berkeley : Deep Reinforcement Learning
  • L1 MDPs, Exact Solution Methods, Max-ent RL (Foundations of Deep RL Series)
  • 2015 UCL Course on RL from David Silver
    • Lecture 2: MDP
      • slide
• Others
  • Markov Chain & Stationary Distribution from Hyungjun Kim
  • MCMC sampling의 마법 from Jyuno426
  • Reinforcement learning is supervised learning on optimized data