(CS285) Lecture 2 - Supervised Learning of Behaviors
26 Dec 2023이 글은 UC Berkeley 의 교수, Sergey Levine 의 심층 강화 학습 (Deep Reinforcement Learning) 강의인 CS285를 듣고 작성한 글 입니다.
Lecture 2의 강의 영상과 자료는 아래에서 확인하실 수 있습니다.
- Fall 2020 ver.
- Fall 2023 ver.
< 목차 >
- Summary and Motivation
- Terminology & notation
- Imitation Learning (Behavior Cloning)
- Addressing the problem in practice
- What's the problem of Imitation Learning ? (A preview of what comes next)
- Reference
Summary and Motivation
CS285는 강화 학습 (Reinforcement Learning; RL)에 대한 강의입니다.
Slide. 1.
이번 chapter의 주제는 Supervised Learning of Behaviors인데,
Lecturer Sergey는 RL을 처음 접하는 사람을 위해서 딥 러닝 (Deep Learning)의 지도 학습 (Supervised Learning; SL)이라는 개념을 사용해 아래와 같은 RL의 기본적인 요소들과 핵심 concept에 대해서 설명해 줍니다.
- Markov Decision Process (MDP)
- State, Action, Reward, Transition matrix 등
- Policy
- Value Function
- Bellman Equation
그러니 RL을 처음 접하시더라도 SL에 대해 아신다면 큰 문제 없이 강의를 보실 수 있습니다. (저는 Lecture 1을 건너뛰었는데 필요하시면 먼저 보셔도 됩니다.)
Terminology & notation
가장 먼저 Terminology에 대해서 알아봅니다.
Computer Vision 분야의 이미지 분류 (Image Classification) task 를 생각해 봅시다.
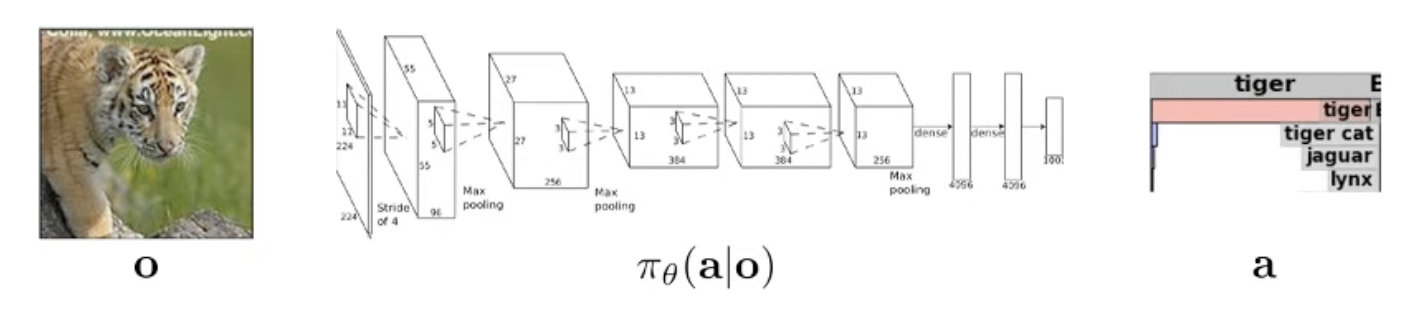Additive Fig.
우리가 문제를 풀기 위해서는 아래와 같이 image와 그에 대한 정답 label 을 의미하는 dataset과 mapping function을 정의하고 이에 대한 objective function을 정의해 likelihood를 최대화 하는 parameter를 찾아야 합니다. (이 때 mapping function은 보통 Neural Network 입니다.)
- Input : \(x\)
- Mapping Function : \(p(y \vert x)\) (\(f(x)\))
- Output : \(y\)
같은 문제에 대해서 RL은 아래와 같은 term을 씁니다.
- Input : \(o\) (observation)
- Mapping Function : \(\pi_{\theta} (a \vert o)\) (policy, function)
- Output : \(a\) (action)
RL이란 어떤 일련의 상황 정보 (지금은 이미지, observation)가 계속 들어오고, 그 때 마다 어떤 행동을 해야하는지 label (action)이 나와야 하는지를 알려주는 mapping function (정책, policy)를 찾는 (학습하는) 방법론으로, Notation에서 느껴지듯 사실 DL의 지도학습 (SL)과 RL은 별로 다른 바가 없습니다.
Additive Fig.
하지만 RL은 일련의 state 마다 decision을 하는 Sequential Decision Making Problem setting이 일반적입니다.
때문에 \(o \rightarrow a\) 같이 입력 (상태) 을 받아, 그 상황에서의 적절한 행동(행동)을 하는 것이 매 순간 일어납니다.
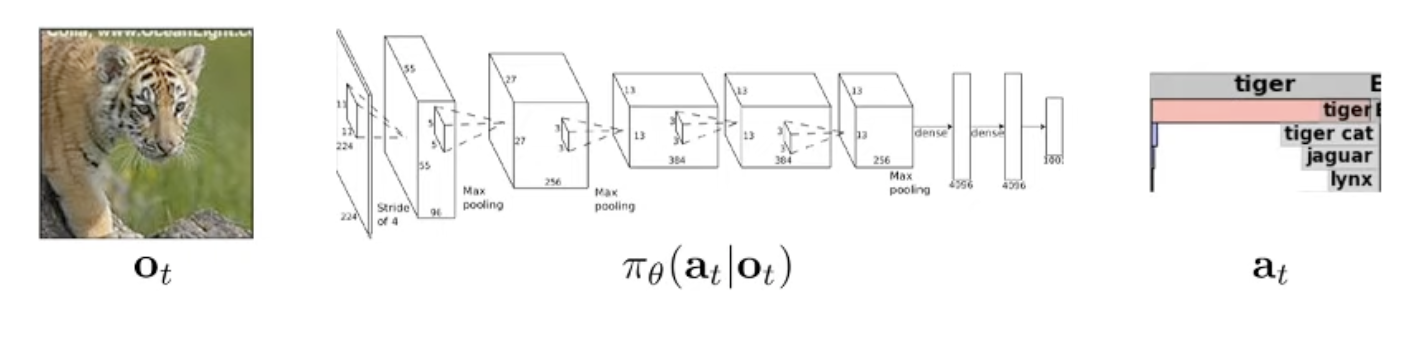
그래서 아래와 같이 시간 \(t\) 를 나타내는 아랫 첨자 (subscript)를 추가합니다.
(기본적으로 강화학습에서는 discrete time-step을 사용합니다).
- Input : \(o_t\) (observation)
- Mapping Function : \(\pi_{\theta} (a_t \vert o_t)\) (policy, function)
- Output : \(a_t\) (action)
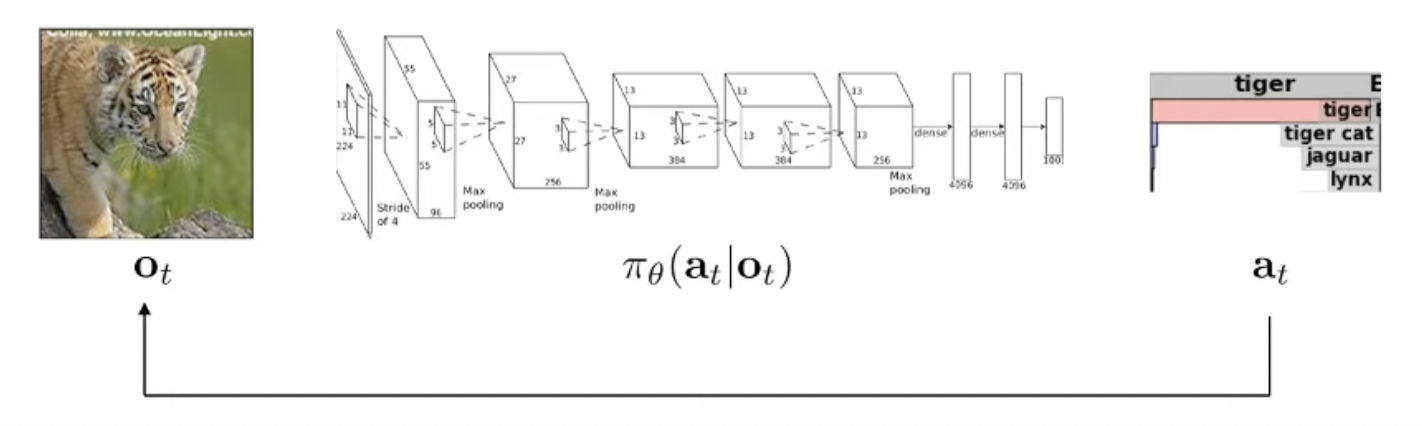
그리고 일반적인 SL과는 다르게 RL은 일련의 state에 대해서 계속 decision을 하기 때문에, 어느 시점의 output이 그 다음 시점의 input에 영향을 미칩니다. (\(a_t\)가 \(o_{t+1}\)에 영향을 줌).
예를 들어 위의 예시에서 호랑이라는 걸 제대로 인식하지 못하면 그게 영향을 미쳐서 그 다음엔 조금 더 나에게 가까워진 호랑이를 볼 (observe) 수 있는거죠.
그리고 input에 대한 output mapping function 을 RL에서는 정책 (policy)라고 부르고 \(\pi_{\theta}\)라고 많이 쓰는데,
정책이라고 부르는 이유는 이것이 매 input마다 어떤 선택 (행동)을 해야 하는지 알려주기 때문입니다.
문제를 좀 바꿔보겠습니다.
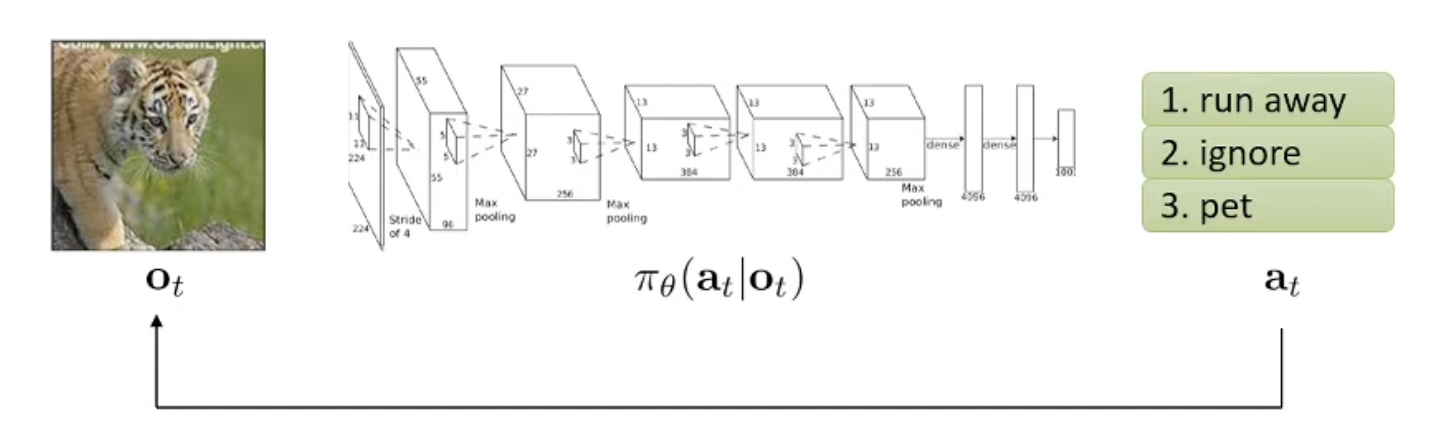
Mapping Function \(\pi_{\theta} (a_t \vert o_t)\) 가 출력하는 \(a_t\)가 object가 무엇인지를 나타내는 label이 아니라 action 이라고 생각해보겠습니다.
Additive Fig.
즉 호랑이를 봤으면 이제 policy가 왼쪽으로 갈지 오른쪽으로 갈지를 알려주는 것이죠. 그렇게 하는 편이 매 순간 어떤 결정 (행동)을 한다는 말에 더 어울리기 때문이죠.
Additive Fig.
Observation vs State
몇 가지 term을 더 추가해봅시다. observation, \(o_t\) 외에 상태 (state)라는 의미를 갖는 \(s_t\)와 이를 given으로 output을 출력해 주는 \(\pi_{\theta} (a_t \vert s_t)\)가 있습니다.
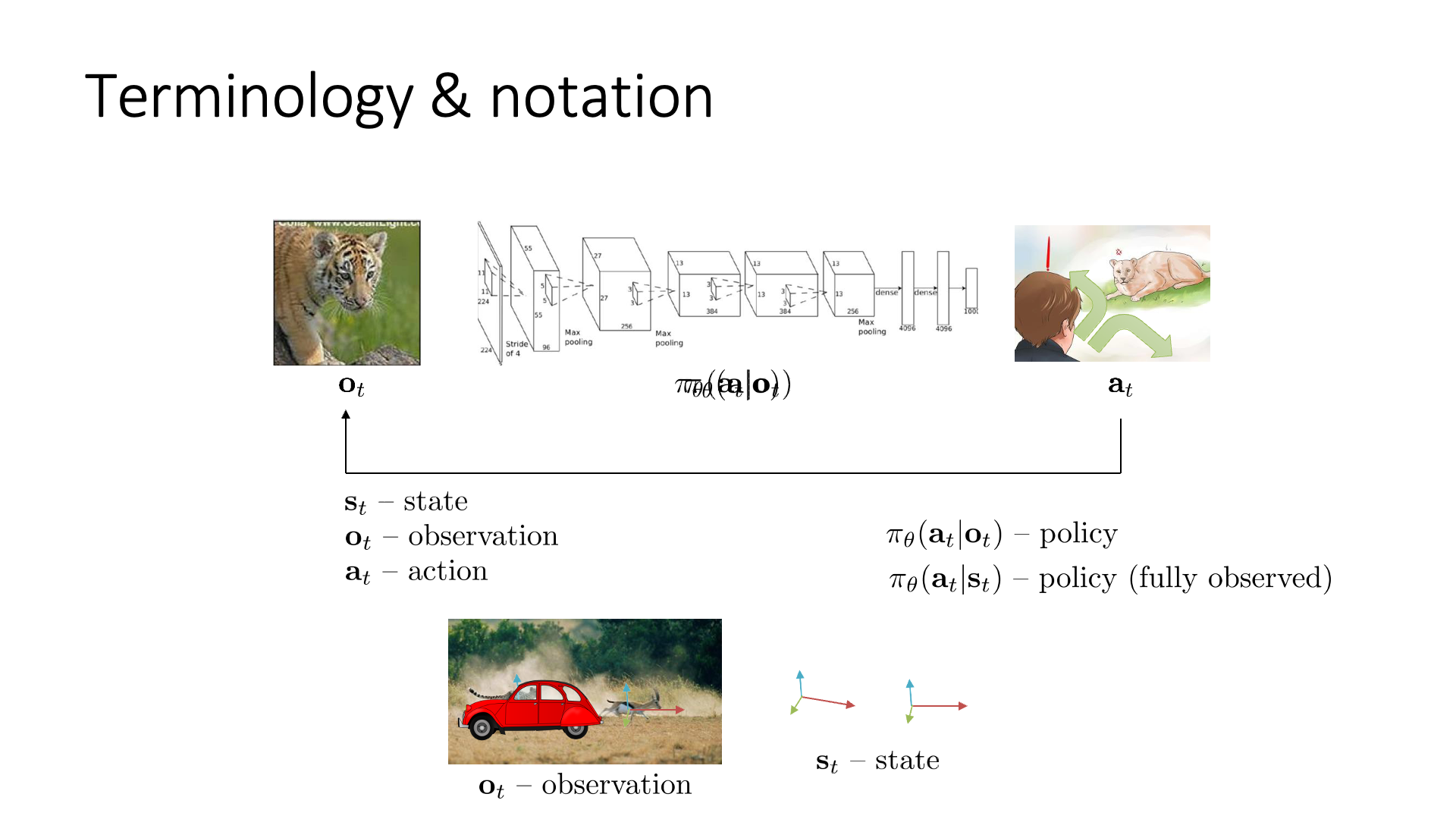Slide. 2.
Observation을 보고 action을 결정하는 것과 달리 state를 보고 action을 결정할 때는 fully observed 라는 것이 붙는데,
그 이유는 state가 observation의 상위 개념이기 때문입니다.
Observation이 놓치고 있는 정보를 state는 포함하고 있는거죠.
여기서 \(o_t\)와 \(s_t\)의 차이를 알아보기 위해서는 마르코프 상태 (Markov State)라는 것을 알아야합니다.
뒤에서 더 자세하게 다루겠으나 정의를 얘기하자면 “Markov state를 가정했을 때 Markov Graph의 노드를 나타내는 것이 상태 (state)라면, observation, \(o_t\)는 \(s_t\)로 부터 얻어지는 것”이라는 겁니다 (\(o_t\)가 더 작은 개념인것).
그래서 보통은 \(\pi_{\theta} (a_t \vert o_t)\)를 사용하지만 좀 더 엄격한 (restrictive) 상황에서는 \(\pi_{\theta} (a_t \vert s_t)\)를 사용하기도 한다고 합니다.
Markov State는 나중에 나오기 때문에 우선은 state와 observation의 차이에 대해 직관적으로만 이해해 봅시다. 예를 들어 치타가 가젤을 쫓아가는 이미지가 입력으로 들어왔다고 해보겠습니다. 이러한 이미지를 통해서 치타와 가젤의 위치가 각각 상대적으로 어디에 있으며, 이를 통해 치타가 가젤을 쫓아가는 것을 유추할 수 있죠.
Additive Fig.
이게 Observation 입니다.
Additive Fig.
Observation는 State로 부터 만들어지는데, state는 근본적인 물리계의 정보를 말합니다.
예를 들면 절대적인 위치 (position) 이나 물체의 속도 (velocity) 같은 것들이 되겠습니다.
지금은 두 가지의 차이가 명확해 보이지 않는데,
만약 어떤 자동차가 지나가면서 치타를 가렸다고 생각해보면 이야기는 달라집니다.
Additive Fig.
위의 경우에 observation에는 치타가 안 보이지만 state는 그렇지 않죠. 즉, state는 실제 정보 (true configuration)을 나타내는 것이고 Observation은 이것의 일부분 (image) 인 것입니다. (Observation은 State를 추론하기에 (deduce) 충분할 수도, 아닐 수도 있습니다.)
만약 우리가 observation만 본다면 치타가 안보여서 피할 생각을 안하겠지만, 치타의 gps 정보를 알고있다면 빨리 도망가야겠죠?
그렇다면 State를 이용해서 판단하는게 쉬울까?
Observation을 이용해서 판단을 하는게 쉬울까?
그리고 Observation은 많을수록 좋을까?
한 번 생각해봐야 한다고 Sergey는 얘기합니다.
우리가 앞으로 RL 얘기를 하면서 video game을 play하는 agent를 학습할 때 이런 agent는 computer simulation 상에서 작동할텐데, observation은 단지 computer 밖에서 game screen만 보는 우리처럼 agent가 image frame만 보는 것이 되고 state는 computer memory의 전체 상태를 보고 문제를 푸는것이 됩니다.
이를 간단한 Graphical Model로 생각해보자면 아래와 같은데 (Slide. 3.의 아래 부분)
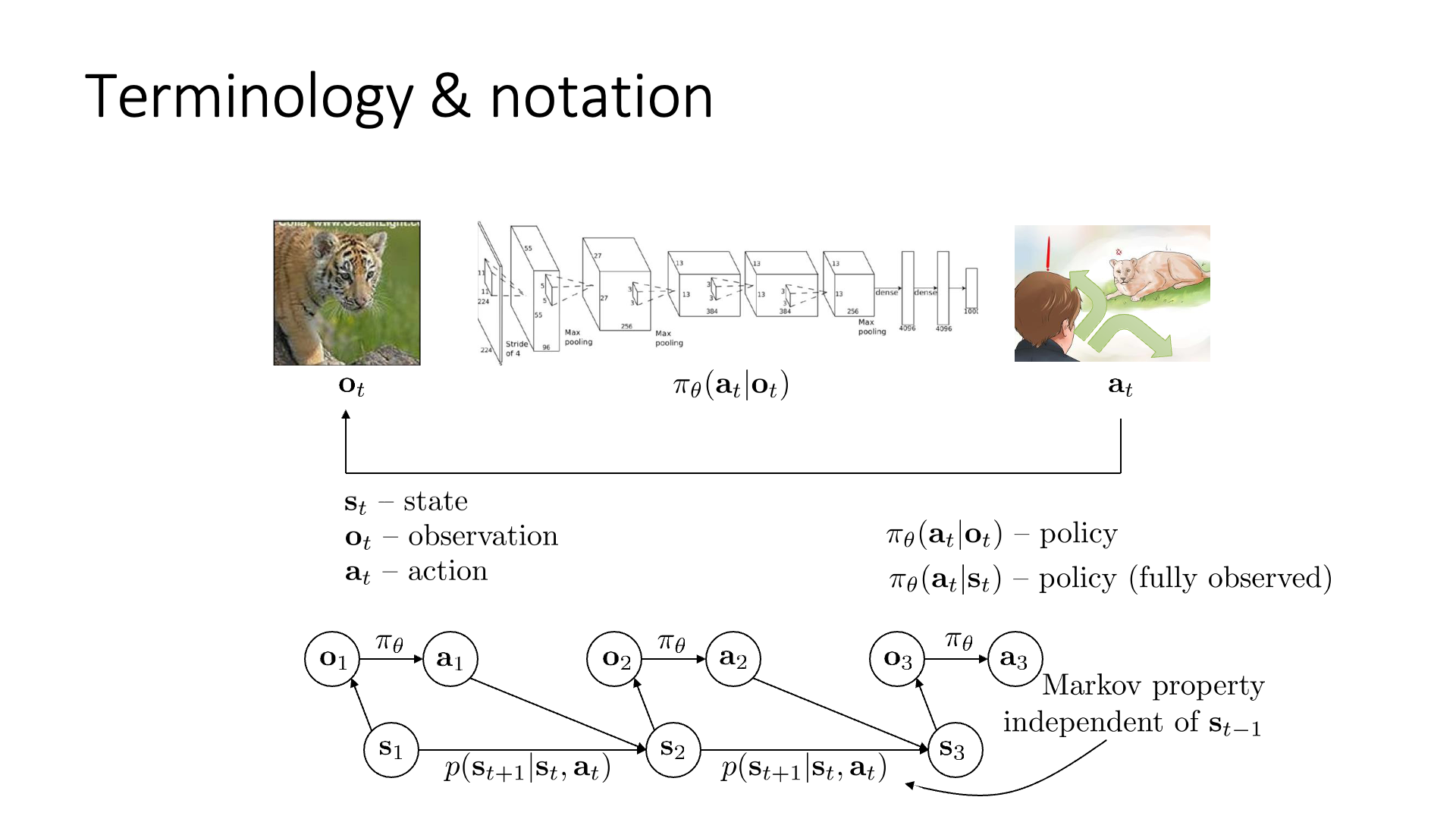Slide. 3.
이는 state, \(s_t\)에서 얻어낸 observation, \(o_t\)와 이를 given으로 어떤 행동, \(a_t\)을 할 지를 정하고, 이 행동의 영향으로 인해 다음 state가 바뀐다는 걸 나타냅니다.
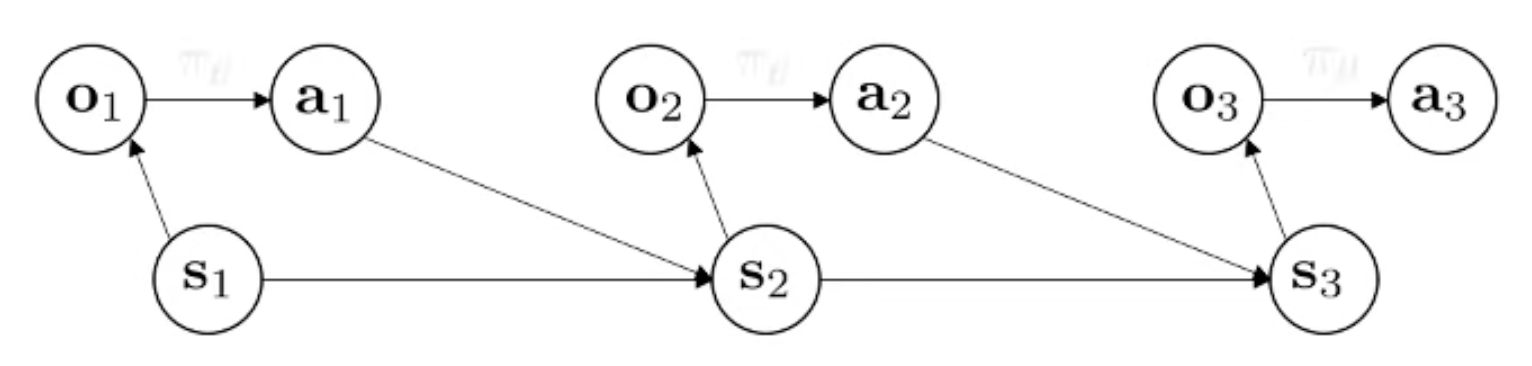Additive Fig.
이 때 다음 state가 어떻게 되느냐는 바로 직전의 state, action의 영향만 받는다는 것이 마르코프 가정 (markov assumption) 입니다.
즉 \(s_{t+1}\) 상태를 결정하는 데에는 \(s_{t}\) 이전의 상태인 \(s_{t-1}, s_{t-2}\)등은 영향을 끼치지 않고 (conditionally independent) 오직 \(s_t\) 만으로 모든 걸 합리적으로 결정할 수 있다는 겁니다.
그러니까 \(s_1\)은 \(s_3\)를 결정하는데 아무런 정보도 주지 못합니다.
하지만 내가 어떤 state에서 어떤 action을 하면 그 다음 state가 어떻게 될지는 확률적으로 정해집니다.
바로 \(p(s_{t+1} \vert s_t, a_t)\)라는 확률 분포에 따라 내 다음 state가 결정되는데요, 이를 상태 천이 행렬 (State Transition Probability)라고 합니다.
Additive Fig.
때로는 이 state transition probability를 dynamics라고도 합니다. 왜냐하면 state에는 observation이라고 할 수 있는 camera frame 정보 외에도 velocity 등의 정보가 있죠? 만약 agent가 치타인데 치타가 달리다가 오른쪽으로 꺾는 action을 하면 그 다음 state가 어떻게 될지가 치타의 속도를 포함한 여러 물리계의 요인에 따라 달라질 수도 있기 때문이죠.
Markov Property는 Sequential Decision Making을 하는 강화 학습에 있어 굉장히 중요한 특성이라고 합니다.
이러한 특성 (property)이 없이는 optimal policies를 정확하게 나타낼 (formulate) 수 없기 때문이라고 합니다.
특히 다음 chapter에서 본격적으로 RL을 배울 때 Markov Decision Process (MDP)라는 것을 배우게 될텐데 내가 풀고자 하는 task를 MDP로 끼워 맞출 (mapping) 수 있으면 앞으로 20장에 걸쳐 배울 RL algorithm을 다 적용해서 문제를 풀 수 있다는 것이 된다고 합니다.
(Source from this lecture’s comment))
Observation을 사용하냐 state를 사용하냐는 Markov Property를 만족하느냐 (과연 현재 (present) state만으로 미래 (future)를 제대로 판단할 수 있느냐) 하는 부분에 있어 차이가 있는데, 위의 치타가 가젤을 쫓는 경우를 생각해 봤을 때, 치타가 차에 가려진 어떤 시점에서는 그 시점의 observation 정보로는 제대로 된 판단을 내릴 수가 없습니다. 그렇기 때문에 이럴 경우에는 과거의 정보 (past Observation)를 기억해서 (Memorize) 사용 할 수 있다고 하는데, state를 사용하는 경우에는 Markov Property를 만족하기 때문에 그럴 필요가 없다고 합니다. (Sergey는 수많은 RL 연구자들이 observation과 state를 혼동해서 쓰는 나쁜 습관이 있다고 하는데 본인도 그럴 수 있으니 최선을 다하겠다고 합니다)
이 강의에서는 앞으로 state를 사용하는 상황을 가정할 것이라고 하며, Non-Markovian Observation를 사용하는 algorithm도 잠깐 소개할 예정이라고 합니다.
Slide. 4.
위의 slide는 어떤 term을 사용해도 상관 없다는 내용입니다. 왼쪽은 Bellman이라는 연구자에 의해 많이 연구된 Dynamic Programming (DP)의 term들인데, 이걸 써도 되고 오른쪽의 Robotics 분야의 term을 써도 된다고 하네요.
Imitation Learning (Behavior Cloning)
이제 정책 (Policy)이라는 것을 어떻게 학습 할 것인가에 대해서 간단하게 얘기하려고 합니다.
RL의 방법론들은 굉장히 복잡하고 어렵지만, 이번 chapter에서는 굉장히 직관적이고 간단한 방법만을 소개합니다.
이번에는 호랑이 한테서 도망가는 예제가 아닌, Autonomous driving task를 생각 해 보도록 하겠습니다.
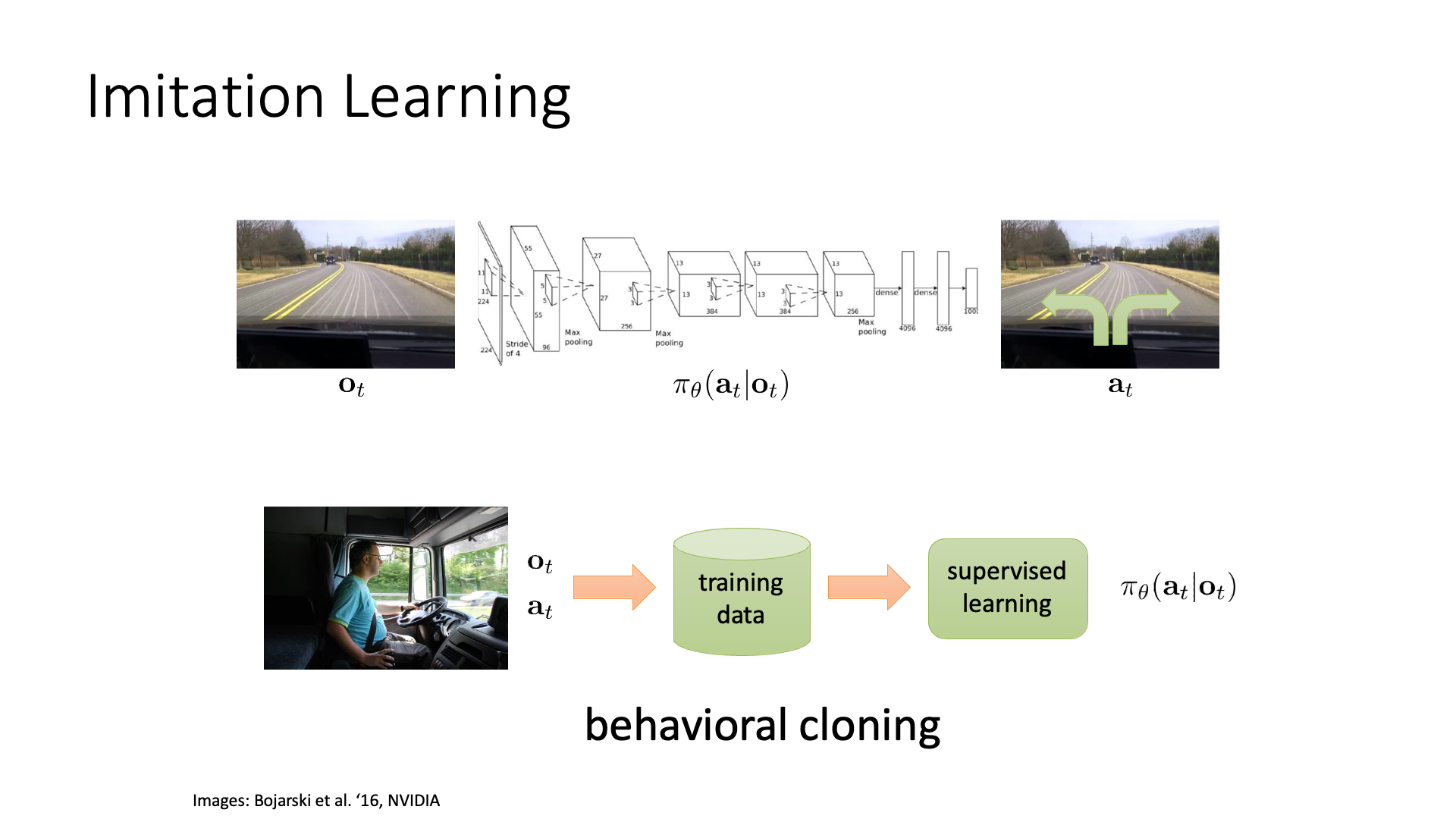Slide. 5.
Autonomous driving task에서는 카메라의 매 frame이 observation이 되겠고, 이에 따라 운전대를 어떻게 돌릴지 (action)를 결정하면 되겠습니다. Supervised Learning (SL)으로 문제를 풀어볼까요? 매 frame 마다 사람이 어떻게 운전대를 control 했는지에 대한 정답 label이 존재하다면 SL로 학습을 하면 될겁니다. 그리고 Neural Network (NN)가 곧 policy 가 되겠죠. Frame이 들어오면 그 frame을 기반으로 action label을 출력하는 그냥 image classifier, ResNet같은 겁니다.
이를 바로 Behavior Cloning (BC)이라고 합니다.
일반적으로 전문가 (Expert)의 행동을 모사 (Clone) 하기 때문입니다.
종종 이를 아예 Imitation Learning으로 퉁치는 경우가 있습니다만 제가 알아본 바로는 BC는 Imitation Learning의 한 방법론으로 나중에 나올 Inverse RL (IRL) 도 human expert의 지식을 전이하기에 Imitation Learning이라고 부르기도 합니다.
그러니까 BC를 Imitation Learning과 동치라고 설명하는 것은 잘못됐을 수 있습니다.
Does Imitation Learning works?
근데 이렇게 지도학습으로 자율주행 하는 것이 잘 working 할까요?
Slide. 6.
사실 이러한 방법은 (DNN 사용하기에 Deep Imitation Learning) 1989에 제안된 방법이며 그런대로 잘 작동해서 미 대륙 횡단을 해보려는 시도까지 했었다고 합니다.
Slide. 7.
하지만 이렇게 일반적으로 딥러닝의 지도 학습에서 사용되는 방법론이 대부분의 강화학습에서 잘 작용하지는 않는데,
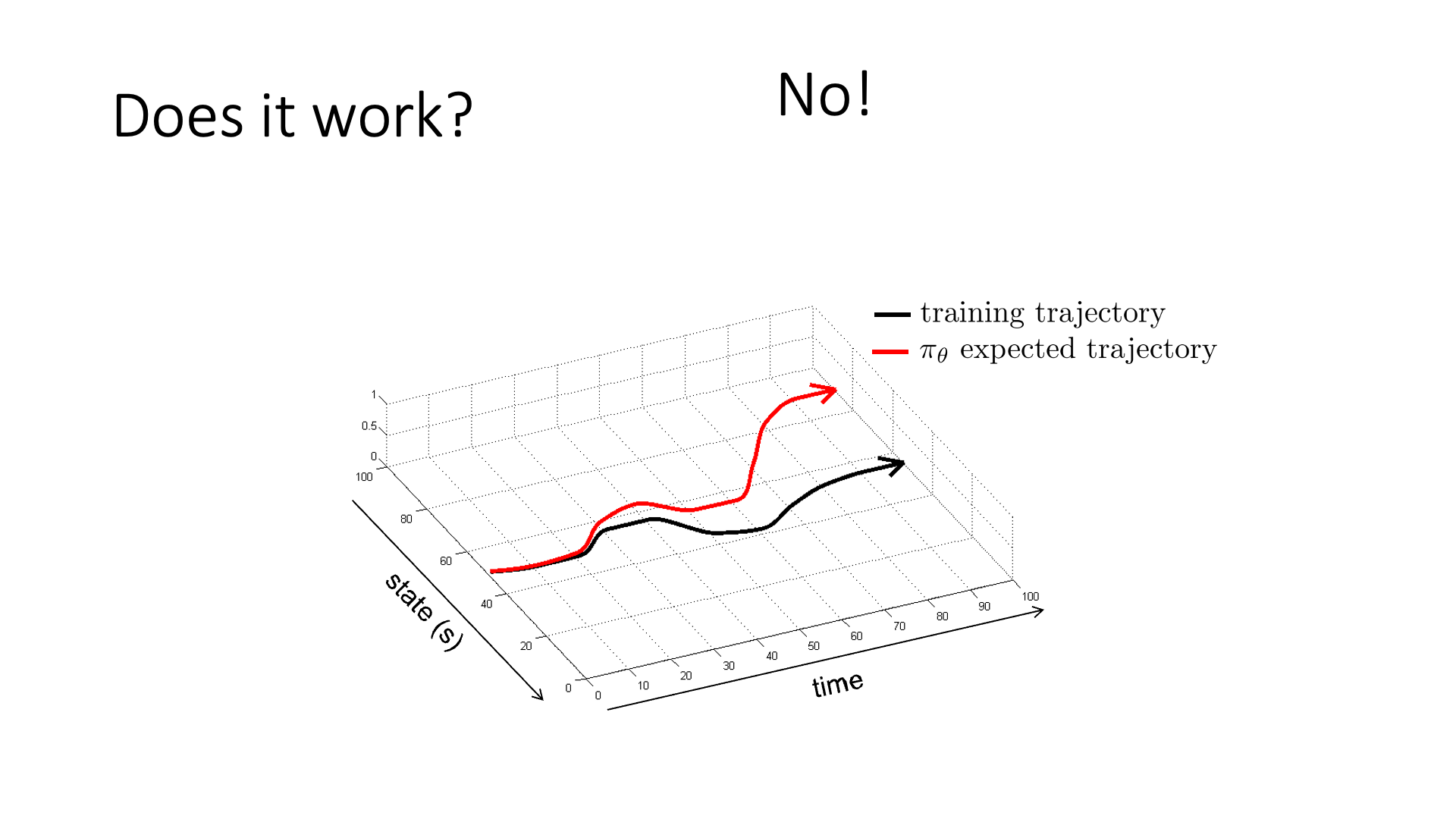
이는 Slide. 7.의 두 궤적 (trajectory)을 보면 알 수 있습니다.
Trajectory란 앞으로 RL 강의에서 주구장창 나올 terminology로 \((s_0, a_0, s_1, a_1, \cdots, s_t, a_t, \cdots)\)같이 시간 축에 따라 죽 늘어진 일련의 state, action을 의미합니다. 그래프가 의미하는 바는 시간에 따른 state의 변화인데, policy \(\pi_{\theta}\)를 학습하기 위한 training data의 실제 궤적 (training trajectory)이 (검은색)과 같을 때, 학습이 된 \(\pi_{\theta}\)가 예측한 기대 주행경로 (빨간색 궤적)가 시간이 흐를수록 굉장히 달라지는 걸 볼 수 있습니다. 즉 초반에는 궤적을 잘 따라가나 싶다가도 중간에 사소한 실수 (mistake)를 하게 되면 처음 보는 state에 빠지고, 그럼 또 이상한 action을 하고… 다시는 회복이 안되는 지경에 이르러 아예 주행을 망쳐버리는 겁니다. Sergey는 일반적인 SL에서는 이런 문제가 발생하지 않는다고 하는데, 그 이유는 training data sample들이 모두 i.i.d 가정이 깔려있기 때문으로 SL은 서로다른 두 data point가 서로에게 영향을 끼치지 않는 반면에 자율 주행을 하는 상황에서는 내가 현재 observation (혹은 state) 어떤 action을 하느냐에 따라서 그 다음 observation의 분포가 바뀌고 … 이런 일이 일어나기 때문입니다.
하지만 우려와 다르게 이는 practical하게는 잘 working하게 만들 수 있다고 하는데, 아래의 slide 처럼 서로 다른 곳을 응시하는 세 대의 카메라로 부터 정보를 받는 trick을 써 (그렇게 되도록 학습해야겠죠?) 서로가 실수들을 잡아주게 하고, data를 많이 투입해주면 (3000 mile의 training data (…?)) trajectory가 심하게 이탈할 일이 줄어들기 때문이라고 합니다.
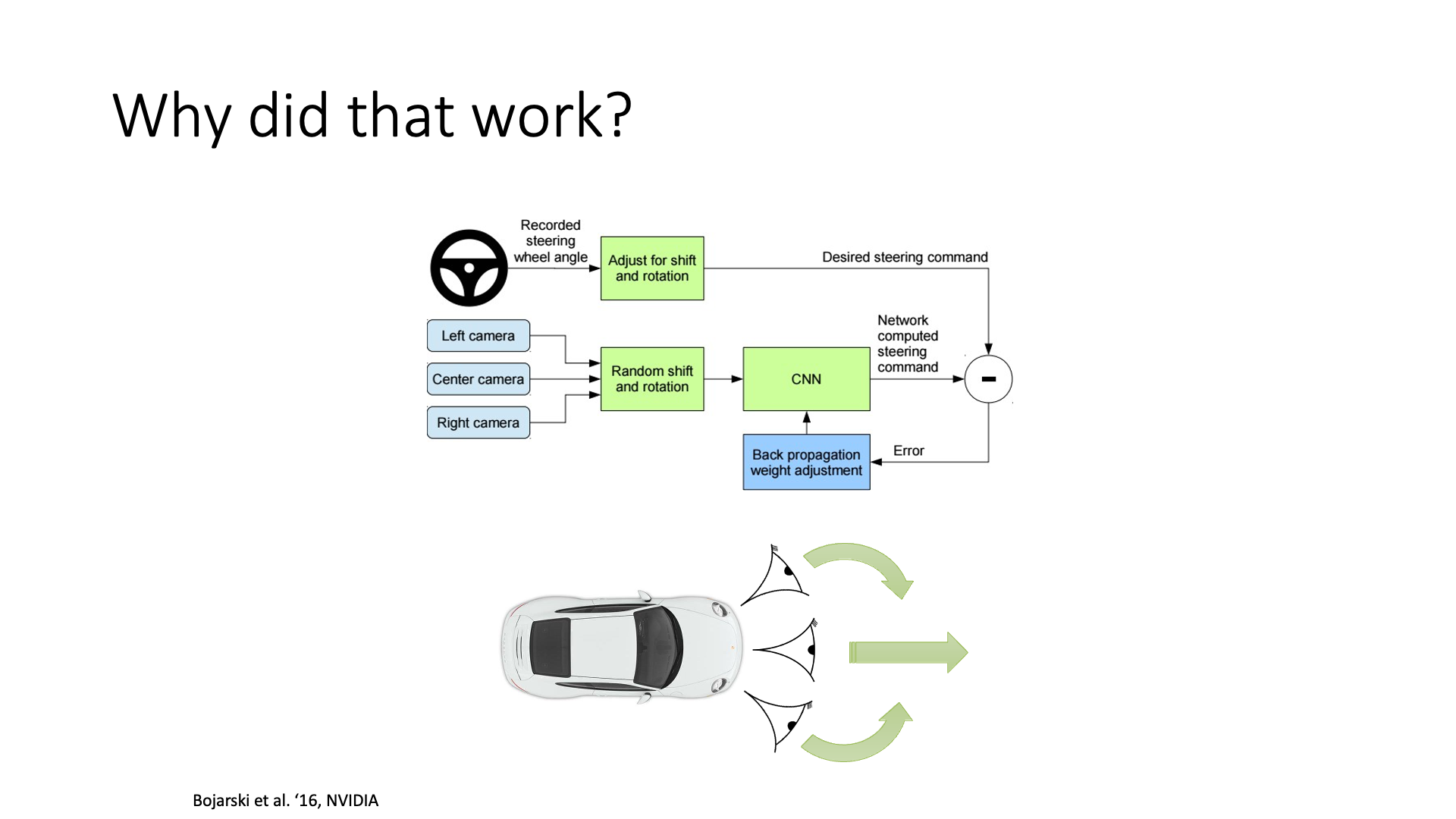Slide. 9.
아래 slide는 지금까지의 review 와 앞으로 배우게 될 개념들에 대한 얘기입니다. 왜 naive BC가 실패하는지에 대해서는 방금 i.i.d가 아니기 때문이라고 말했으며, lecture 말미에 실제로 얼마나 error가 누적되는지? 같은 것을 formulate할 것이며 어떻게 해야 BC를 성공적으로 할 수 있는지에 대한 몇가지 solution에 대해서 얘기할 것이라고 합니다.
Fig. 이 slide는 2023년 CS285에서 가져온 것인데, lecture 순서가 2020년에 비해서 조금 바뀌었습니다. 원래는 analysis를 맨 마지막에 했는데 먼저 analysis를 하고 DAgger 같은 해결책을 알려주네요
What's the Problem? : Distribution Shift
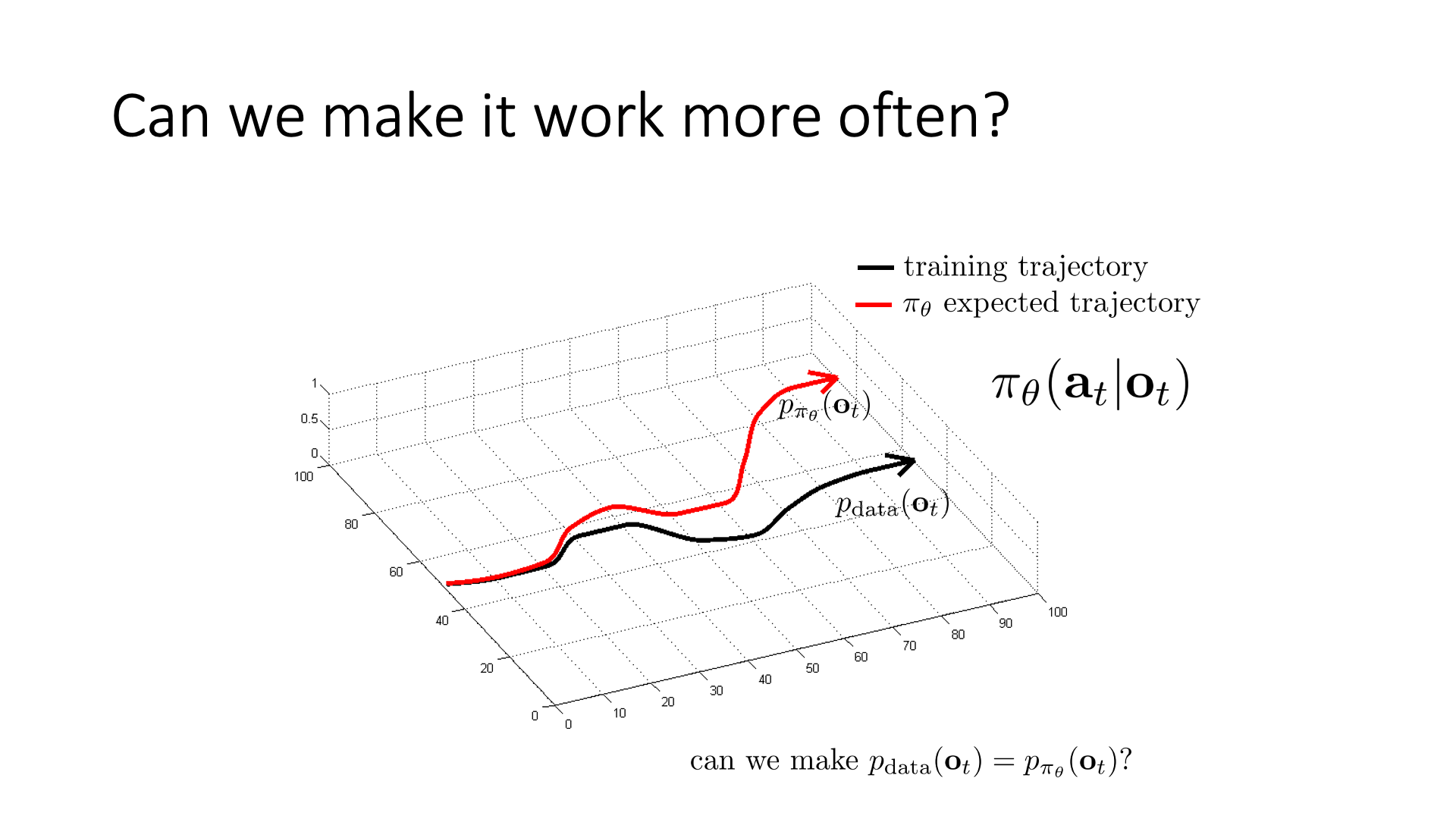
어디서부터 BC가 잘못된 건지 좀 더 분석을 해 봅시다. 일반적으로 SL은 training data의 분포 (training distribution), \(p_{data}(o_t)\)를 modeling하는 겁니다.
Slide. 11.
우리가 원하는 것은 policy를 잘 학습시켜 이를 완벽히 matching 시키는 거죠.
\[p_{\pi_{\theta}}(o_t) = p_{data}(o_t)\]하지만 생각만큼 잘 되지는 않습니다. 왜냐하면 우리는 \(p_{data}(o_t)\)로부터 sampling된 data를 가지고 Maximum Likelihood Estimation (MLE)을 하기 때문입니다.
무슨 소리냐? MLE는 observation (혹은 state, sergey가 지금 혼용하고있는데 미안하다고 합니다)이 \(p_{data}(o_t)\)으로 뽑혔을 때 그 observation에서의 정답의 확률을 1이 되도록 학습하는 겁니다. 그런데 우리가 실제 test하는 환경에서의 trajectory는 \(p_{\pi_{\theta}}\)에서 뽑힐것이므로 전혀 matching이 안되는거죠.
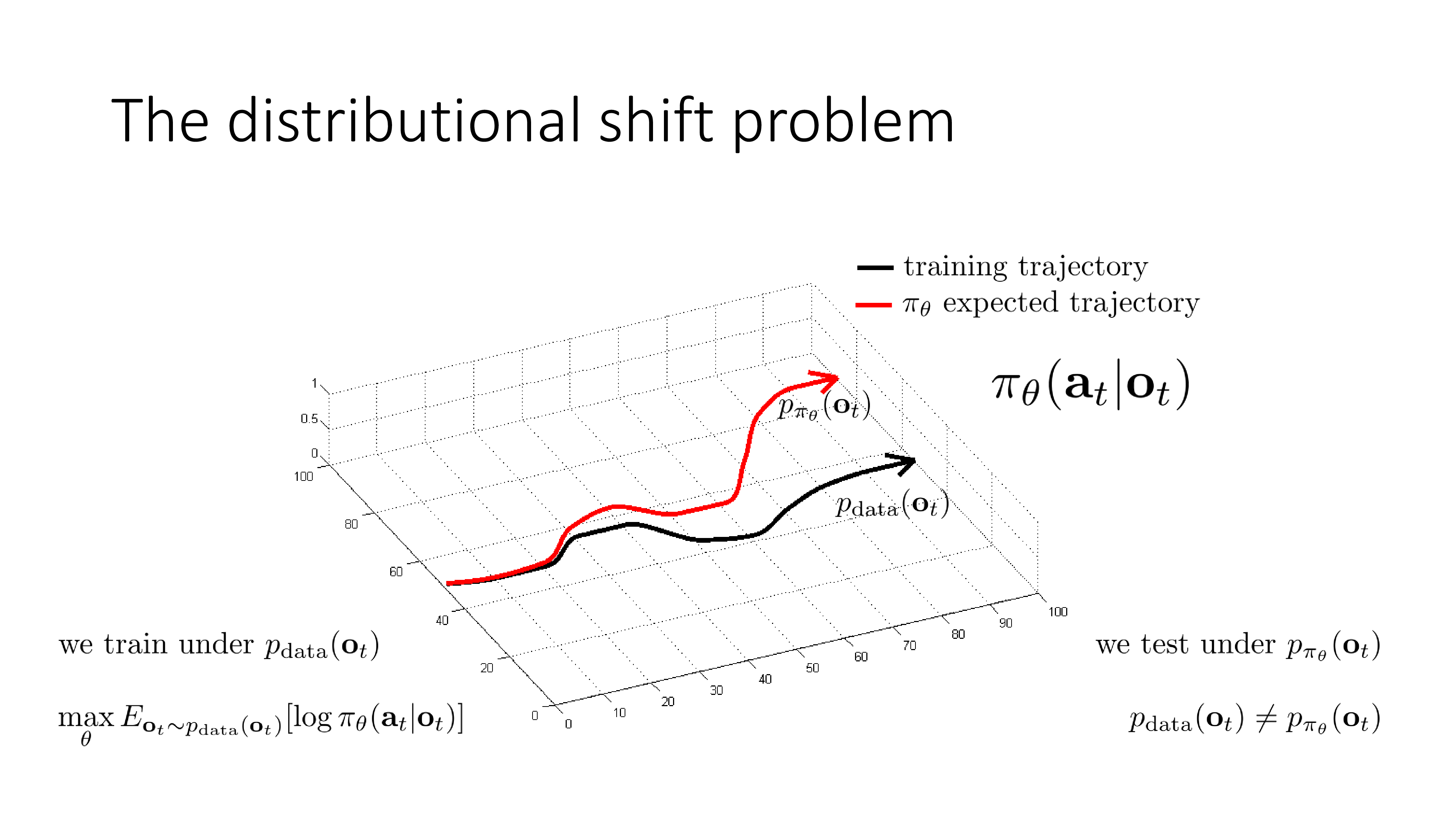
즉 i.i.d assumption 뿐만 아니라 objective function을 정의하는 것 부터 잘못된 겁니다. 우리는 주어진 training data distribution 하에서 MLE를 할 것이 아니라 다른 objective function이 필요한데, 예를 들어 학습된 (학습중인) policy \(\pi_{\theta}\)를 따라 observation, state를 만들고 그 때마다 정답이면 비용(cost)을 0 발생시키고, 틀렸으면 1 발생시키는 식으로 총 cost를 count하는 것을 objective로 정의하고 이를 minimize하는 방식으로 학습해보는 겁니다.
Fig. \(\pi^{\ast}\)가 human expert data이다. SL은 사실상 정답에 대한 one hot label이 있는것과 다름 없으므로 정답일 경우만 cost를 0으로 치는것은 자연스럽다.
즉 우리가 실제로 test할 policy를 가지고 objective를 정의하는 것이죠 (이것이 다음 lecture인 4장부터 우리가 새롭게 정의할 RL의 기본 objective function 입니다). (여기서 잠깐 question, 그럼 training을 하는 도중에 policty를 가지고 observation을 만들고 그에 맞는 label을 달아줘야 하는데, 이 pair가 없으면 어떡하죠? 이는 추후에 논의해봅시다.)
Variance Analysis of Imitation Learning
이번에는 BC가 최대 어디까지 나빠질 수 있는가?, 얼마나 error가 많이 누적될 수 있는가? 에 대해서 알아봅시다. (이 분석방법은 Lecture 9 Advanced Policy Gradients 에서 다시 등장합니다. RL에서 자주 쓰이는 것 같으니 이번 기회에 잘 알아두면 좋습니다.)
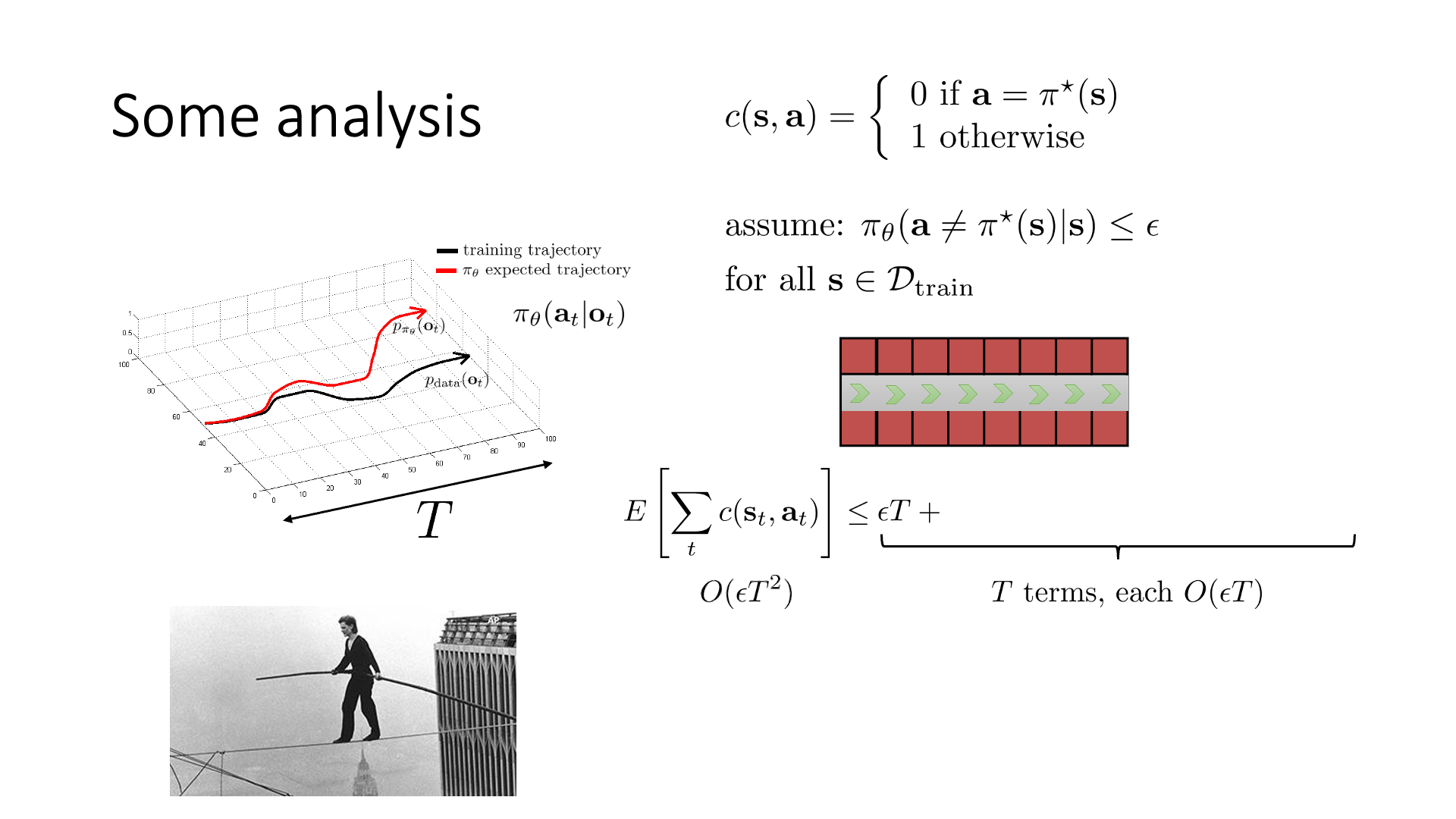Fig.
마천루 두개에 줄을 연결해서 외줄타기를하는 agent를 학습하려고 합니다. Trajectory의 총 길이를 \(T\)라고 하고, 아까처럼 cost function을 정의합니다. 맞으면 (외줄타기 전문가와 똑같이 행동하면) 비용이 0이고 틀리면 1 발생하는겁니다.
\[c(s,a)= \left\{\begin{matrix} 0 \space \text{if} \space a=\pi^{\ast}(s) \\ 1 \space \text{otherwise} \end{matrix}\right.\]매우 극단적인 example인데, 줄타기를 하다가 떨어질 경우 agent는 죽는 것이나 다름 없기 때문에 더이상 움직일 수 없어 그 뒤로는 계속 틀린 action을 하는거나 다름없게 됩니다. (당연하게도 expert는 떨어져 본 적이 없을 것이기 때문에 expert를 배운 agent는 어떤 action을 해야할 지 모르게 됩니다) 그리고 학습이 된 agent가 모든 state에 대해서 외줄타기 전문가와 다른 action을 할 확률이 매우 작은 값인 \(\epsilon\)이라고 합시다. 이제 우리가 궁금한 것은 학습이 된 agent가 timestep, T동안 얼마나 cost를 만들 것이냐? 입니다.
\[\mathbb{E}_{s_{1:T},a_{1:T}} [ \sum_t c(s_t,a_t)]\]먼저 시작하자마자 떨어졌다고 생각해 봅시다. 그러면 timestep T동안 계속 cost가 누적되는걸로 볼 수 있습니다.
\[\mathbb{E}[\sum_t c(s_t,a_t)] \leq \epsilon T\]그리고 실수를 하지 않는 경우는 \((1-\epsilon)\)이 되므로 식은 다음과 같이 전개됩니다.
\[\mathbb{E}[\sum_t c(s_t,a_t)] \leq \epsilon T + (1-\epsilon) (\qquad \qquad \qquad)\]이를 계속 전개하면 아래와 같은 수식이 됩니다.
\[\mathbb{E}[\sum_t c(s_t,a_t)] \leq \epsilon T + (1-\epsilon) (\epsilon(T-1) \qquad \qquad)\] \[\mathbb{E}[\sum_t c(s_t,a_t)] \leq \epsilon T + (1-\epsilon) (\epsilon(T-1) + (1-\epsilon)(\cdots))\]이 수식은 \(T\)개의 term으로 이루어져있고, 각 term들은 \(O(\epsilon T)\)를 가지게 되기 때문에 total bound는 \(O(\epsilon T^2)\)가 됩니다. 즉 BC의 cost는 \(O(\epsilon T^2)\)에 bound된 것인데, 최대로 못해도 이 정도의 cost가 든다는걸 의미합니다. 이 bound는 별로 좋은 것은 아닌데, 그 이유는 trajectory의 길이가 늘어날수록 (시간이 흐를수록) error가 제곱해서 (quadratically) 증가하기 때문입니다. Naive BC가 좋지 않다는 걸 정량적으로도 알 수 있게 되었네요. 하지만 이 analysis는 training Dataset에 포함된 State에 대해서만 생각했기 때문에 일반화된 분석이 아니었습니다. 좀 더 일반적인 분석을 해봅시다.
Fig. 2020년 version의 lecture에서는 DAgger라는 algorithm을 먼저 제안한 뒤에 analysis를 했기 때문에 slide에 DAgger라는 algorithm이 포함되어 있는데, 곧 배울테니 당황하지 마시길 바랍니다. DAgger의 경우 bound가 T에 대해 linear한 것으로 naive BC보다는 더 좋다는 걸 알 수 있습니다.
Training dataset에서 sampling된 data point들에 대해서만 analysis하는 것이 아니라 이번에는 training dataset의 어떤 실제 distribution, \(p_{train}(s_t)\)에서 sampling될 수 있는 어떠한 state들에 대해서 계산을 해보는 겁니다. “최대 얼만큼 못할 수 있는지?”
이번에는 좀 더 현실적인 가정이기 때문에 해당 state에서 정답이 아닌 action을 할 expected value가 \(\epsilon\)보다 작다고 가정합시다.
\[\mathbb{E}_{p_{trarin}(s)} [ \pi_{\theta} (a \neq \pi^{\ast}(s) \vert s) ] \leq \epsilon\]당연하겠지만 아무리 학습을 잘해도 BC는 \(p_{train}(s) \neq p_{\theta}(s)\)일 겁니다. 그렇다면 timestep t 시점까지 trajectory가 진행됐을 때 \((s_t)\)의 distribution은 앞서 계산했던것과 비슷하게 실수를 하나도 저지르지 않았을 경우와 실수를 저질렀을 경우의 확률 분포의 합이 되겠습니다. (당연히 \(p_{mistake}\)는 어떻게 생겼는지도 모릅니다)
\[p_{\theta}(s_t ) = \color{red}{ (1-\epsilon)^t } p_{train}(s_t) + ( 1 - \color{red}{ (1-\epsilon)^t } ) p_{mistake}(s_t)\]여기서 \(\epsilon\)이 매우작다면 첫 번째 term이 dominant해지겠군요. 이제 \(p_{train}\)와 \(p_{\theta}\)을 서로 연관지으려고 합니다. 지금부터 쓸 것은 Total Variation Divergence (TVD)라는 것인데, 가능한 모든 state에 대해서 두 확률 분포의 차이값을 더한 것으로 KL Divergence처럼 두 확률 분포의 차이를 measure하는 수학적 tool이라고 보시면 됩니다.
그런데 지금은 한 state, \(s_t\)에 대해서만 이를 measure해보려고 합니다. State, \(s_t\)에 대한 \(p_{\theta}(s_t)\)와 \(p_{train}(s_t)\)값의 차이를 계산해서 절대값을 씌우면 되는데, 우리가 앞서 구한 수식에서 양변에 \(p_{train}(s_t)\)를 빼면 이를 쉽게 구할 수 있습니다.
\[\vert p_{\theta}(s_t ) - p_{train}(s_t) \vert = ( 1 - (1-\epsilon)^t ) \vert p_{mistake}(s_t) - p_{train}(s_t) \vert\]아직까지는 수수께끼 같은 (cryptic) equation 이지만 적어도 이 값이 최대 어떤값이 되겠다 정도는 구할 수 있습니다. 이를 위해 먼저 TDV (혹은 \(D_{TV}\))에 대해 알아야 하는데, 이는 다음의 수식을 따릅니다.
\[\begin{aligned} & D_{TV} = \frac{1}{2} \sum_i \vert p_i - q_i \vert \\ & cf) D_{KL} = \sum_i p_i (\log p_i - \log q_i) \\ \end{aligned}\]모든 확률 변수는 0~1사이의 값을 갖기 때문에 total variation divergence는 최대 2라는 값이 될 수 있는데, 이는 t시점에 존재하는 agent가 존재할 수 있는 모든 \(s_t\)중 \(p_{mistake}(s_{t,1})\)값만 1일이고 나머지는 0이고, \(p_{train}(s_t)\)의 경우는 \(p_{train} (s_{t,2})\)만 1이고 나머지는 0이거나 하면 극단적으로 확률의 값 차이가 2가 되기 때문에 그렇습니다. (지금 수식 상으로는 \(1/2 \vert p_i - q_i \vert\)가 아니라 \(p_i - q_i\)라 2인듯 합니다.)
그러므로 특정 state에 대해 이 divergence는 worst case일 때의 divergence값인 \(2(1-(1-\epsilon)^t)\)보다 항상 작다는 것을 알 수 있습니다.
\[\begin{aligned} & \vert p_{\theta}(s_t ) - p_{train}(s_t) \vert = ( 1 - (1-\epsilon)^t ) \vert p_{mistake}(s_t) - p_{train}(s_t) \vert \\ & \quad \leq \color{red}{2} ( 1 - (1-\epsilon)^t ) \\ \end{aligned}\]
Slide. 37.
여기에 어떤 항등식 (useful identity)을 이용하려고 합니다. 0~1사이의 값 \(\epsilon\)에 대해서 아래가 성립합니다.
\[(1-\epsilon)^t \geq 1 - \epsilon t \text{ for } \epsilon \in [0,1]\]이를 적용하면 다시한 번 \(s_t\)에서의 divergence 값은 다음과 같게 됩니다.
\[\begin{aligned} & \vert p_{\theta}(s_t ) - p_{train}(s_t) \vert = ( 1 - (1-\epsilon)^t ) \vert p_{mistake}(s_t) - p_{train}(s_t) \vert \\ & \quad \leq 2 ( 1 - (1-\epsilon)^t ) \\ & 2 \epsilon t \\ \end{aligned}\]이러면 좀 더 bound가 느슨해지지지만 (loser) 더 생각하기 쉬워지기 때문에 일단 이렇게 합니다. 이제 다음의 cost를 계산해 봅시다. 특정 state에서의 cost에 대한 기대값을 모든 timestep에 대해서 계산해 더하는 겁니다.
\[\sum_{t} \mathbb{E}_{p_{\theta}(s_t)} [c_t] = \sum_t \sum_{s_t} p_{\theta}(s_t) c_t(s_t)\]이 기대값은 다음과 같이 표현될 수 있는데
\[\begin{aligned} & \sum_{t} \mathbb{E}_{p_{\theta}(s_t)} [c_t] = \sum_t \sum_{s_t} p_{\theta}(s_t) c_t(s_t) \\ & \quad \leq \sum_t \sum_{s_t} \color{red}{p_{train}(s_t)} c_t (s_t) + \vert \color{blue}{ p_{\theta} (s_t) } - \color{red}{p_{train}(s_t)} \vert c_{max} \\ \end{aligned}\]이는 \(A = A + (B-B)\)이라는 항등식을 이용하고 절대값을 씌워 얻은 부등식 입니다. 여기서 \(c_{max}\)는 각 state에서 발생할 수 있는 cost의 최대 값입니다. 우리가 원하는 것은 특정 state에 대한 bound 값이 아니라 모든 timestep에서의 state에 대한 bound값이므로 \(\sum_t\)을 취했으며, 특정 state에서 cost의 최대값은 언제나 1이기 때문에 위의 부등식은 결국 \(\sum_t \epsilon + 2 \epsilon t\)로 bound 됩니다.
\[\begin{aligned} & \sum_{t} \mathbb{E}_{p_{\theta}(s_t)} [c_t] = \sum_t \sum_{s_t} p_{\theta}(s_t) c_t(s_t) \\ & \quad \leq \sum_t \sum_{s_t} p_{train}(s_t) c_t (s_t) + \vert p_{\theta} (s_t) - p_{train}(s_t) \vert c_{max} \\ & \quad \leq \sum_t \epsilon + 2 \epsilon t \leq \epsilon T + 2 \epsilon T^2 \\ \end{aligned}\]Bound되는 값은 linear term 하나 quadratic term 하나이므로 최종적으로 order는 \(\color{red}{O(\epsilon T^2)}\)가 됩니다. 앞서 외줄타기 예제로 구했던 값과 같은것이죠.
Why is This Rather Pessimistic
그런데 또 현실이 그렇게 냉혹하지는 않습니다. 외줄타기의 경우 한번만 실수를 해도 unrecoverable situation에 놓이게 되지만 자율주행 같은 real world problem에서는 실수를 해도 recover를 할 수 있기 때문입니다. 하지만 문제는 BC가 그 방법을 자연스럽게 배우지는 못한다는 겁니다.
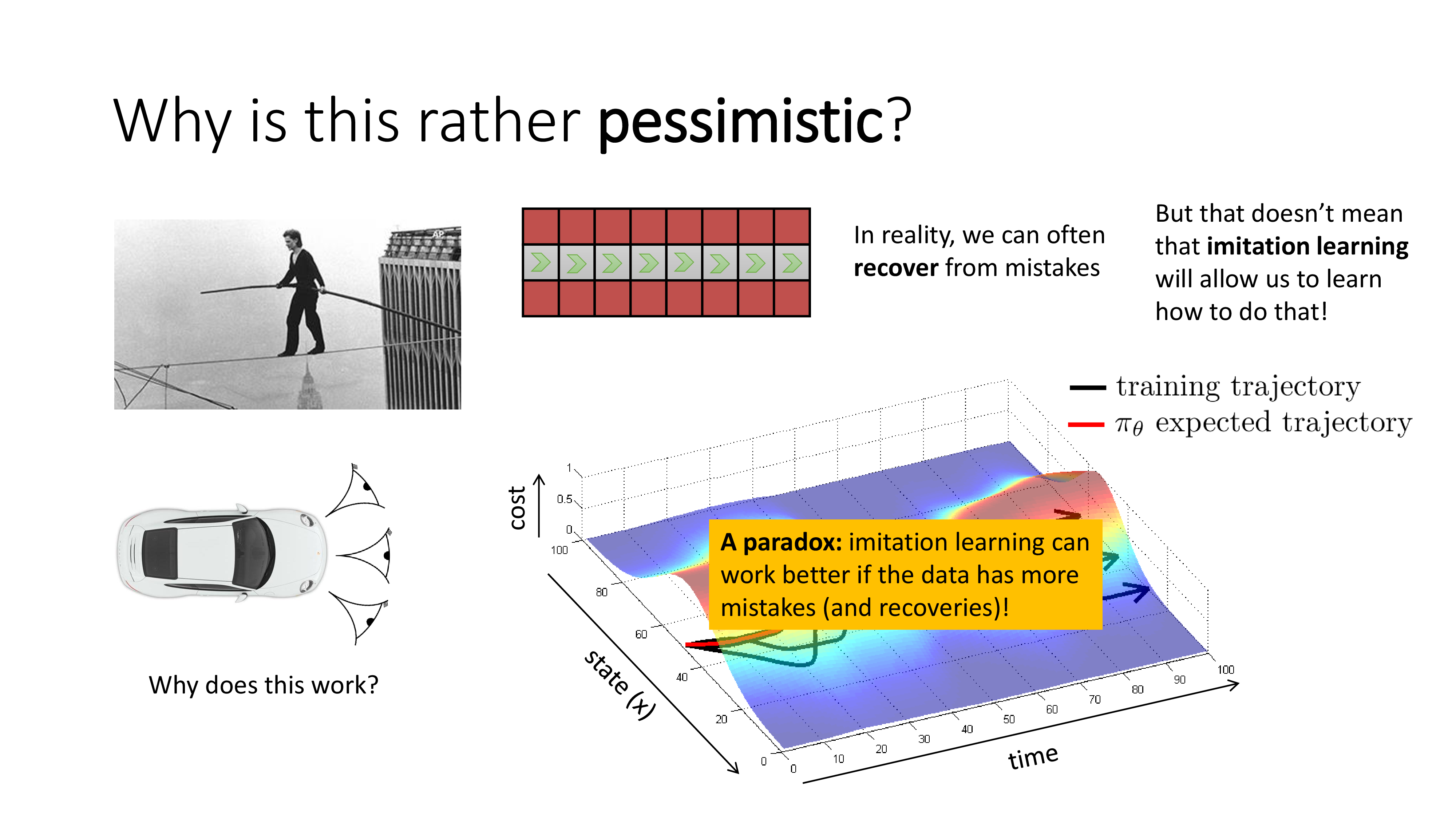
앞서 cam을 여러개 다는것도 recover하는 방법을 배우는 것과 다름없다고 하며, training trajectory를 조금 수정해서 일부러 실수를 만든 뒤 이 실수를 수정하는 방법을 (feedback to correct) policy가 배우게 하는 approach도 있다고 합니다. BC가 잘 working 하도록 하는 과정에서 수 많은 analysis와 trick들이 있었음을 알 수 있습니다.
Addressing the problem in practice
이제 왜 naive BC가 잘 안되는지 알았으니 BC가 잘 되게 하기 위한 method들에 어떤 것들이 있는지 알아봅시다.
1. Be smart about how we collect our data
먼저 첫 번째 방법은 아까 말씀드린 것 처럼 data collection과정에 일부러 틀린 action을 하고 이를 바로잡는 action을 넣는겁니다. 이러면 성능이 떨어질 것 같지만 더 많은 state를 cover하게 돼서 agent가 처음보는 state를 마주하게될 확률이 많이 줄어듭니다. 그리고 어차피 해당 state에서 최적의 수 (optimal action)의 확률이 가장 높다는 것은 변하지 않을거라고 하니 그렇게 걱정할 필요가 없다고 합니다.
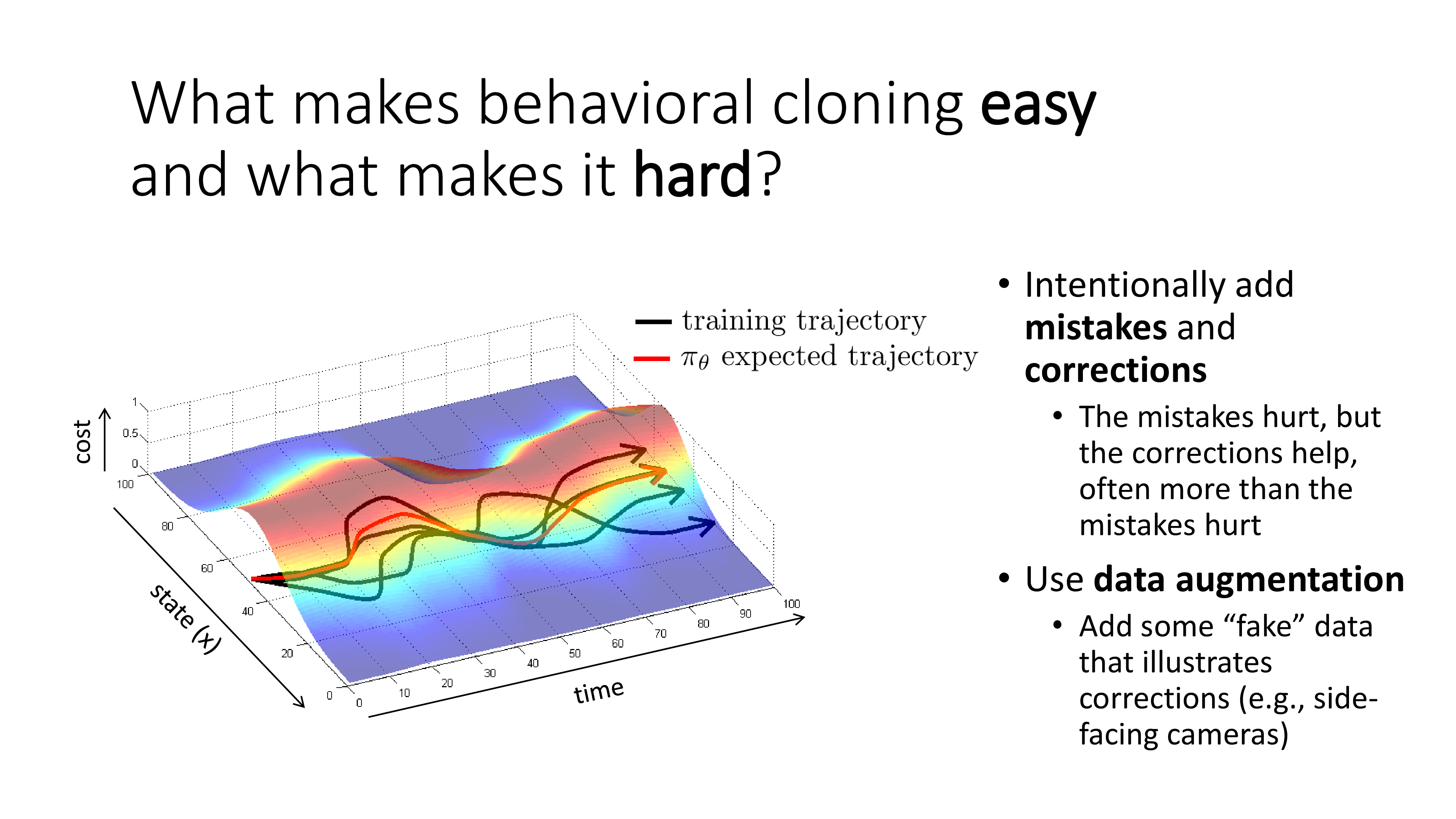
혹은 거듭 말씀드린 것 처럼 side-cam을 달아서 같이 학습하는 것인데 이를 data augmentation이라고 표현하네요. 이어서 Sergey가 몇 가지 case study를 하는데요, 드론에 cam을 여러개 달아 BC를 하는것으로 숲속에서 자율주행하는 드론을 보여줍니다. 매 state마다 할 수 있는 action은 (left, front, right)이며 후진은 없기 때문에 3차원 catgorical distribution이 target distribution입니다.
사람이 머리에 cam이 달린 밴드를 달고 data collection을 했으며 cam중에 오른쪽 cam은 항상 왼쪽으로 가는 게 정답이겠죠? 이런식으로 data를 많이 collection했다고 합니다. (사람이 data collection을 해도 drone을 학습할 수 있다니 좀 재밌는 것 같습니다.)
(몇 가지 case study를 더 알려주는데 이는 생략하겠습니다)
2. Use very powerful models that make very few mistakes
그 다음은 매우 강력 model을 쓰는겁니다. 논지는 앞서 BC의 upper bound cost가 \(\epsilon T^2\)였고 이 \(\epsilon\)은 human expert가 알려준 정답 action 외의 action을 할 확률이었는데, model이 너무 강력해서 이를 잘 학습한다면 cost가 클 여지도 없다는 겁니다. 이 얘기는 model을 overfitting 시켜서 training sample에 있는 state에 대해서 \(\epsilon\)을 최소화 하자는 얘기는 아닙니다.
Sergey는 왜 human expert data를 학습하는게 어려운지? 에 대해서 두 가지를 꼽습니다.
- Non-markovian behavior
- human expert는 내가 여태 주행해왔던 길 까지 고려해서 다음 action을 하지 현재 state만 보고 action을 결정하는 것이 아닌데 우리는 markov property를 적용한 문제만 풀고 있다는 소리
- Multimodal behavior
- 보통 model을 학습할 때는 정해진 state에서 정답 action 하나의 확률만 1에 가깝게 만드는데, 즉 이는 언제나 1가지만 정답이라고 치는 것인데 실제로는 그렇지 않을 수 있음.
Non-Markovian behavior
1번에 대해서 먼저 생각해봅시다. 우리가 실제로 modeling 해야 할 것은 \(\pi_{\theta} (a_t \vert o_t)\)가 아니라 \(\pi_{\theta} (a_t \vert o_1, \cdots, o_t)\)인 겁니다 (여러 observation이 현재 action에 영향을 주니, 즉 독립이 아니므로 markovian이 아닌겁니다).
어떻게하면 과거 history까지 다 보면서 decision making을 할 수 있을까요? 이미 DL에 익숙하신 분들이라면 solution은 너무나 자명할 겁니다. 바로 Recurrent Neural Networks (RNNs)나 Transformer 같은 sequence model을 쓰는겁니다.
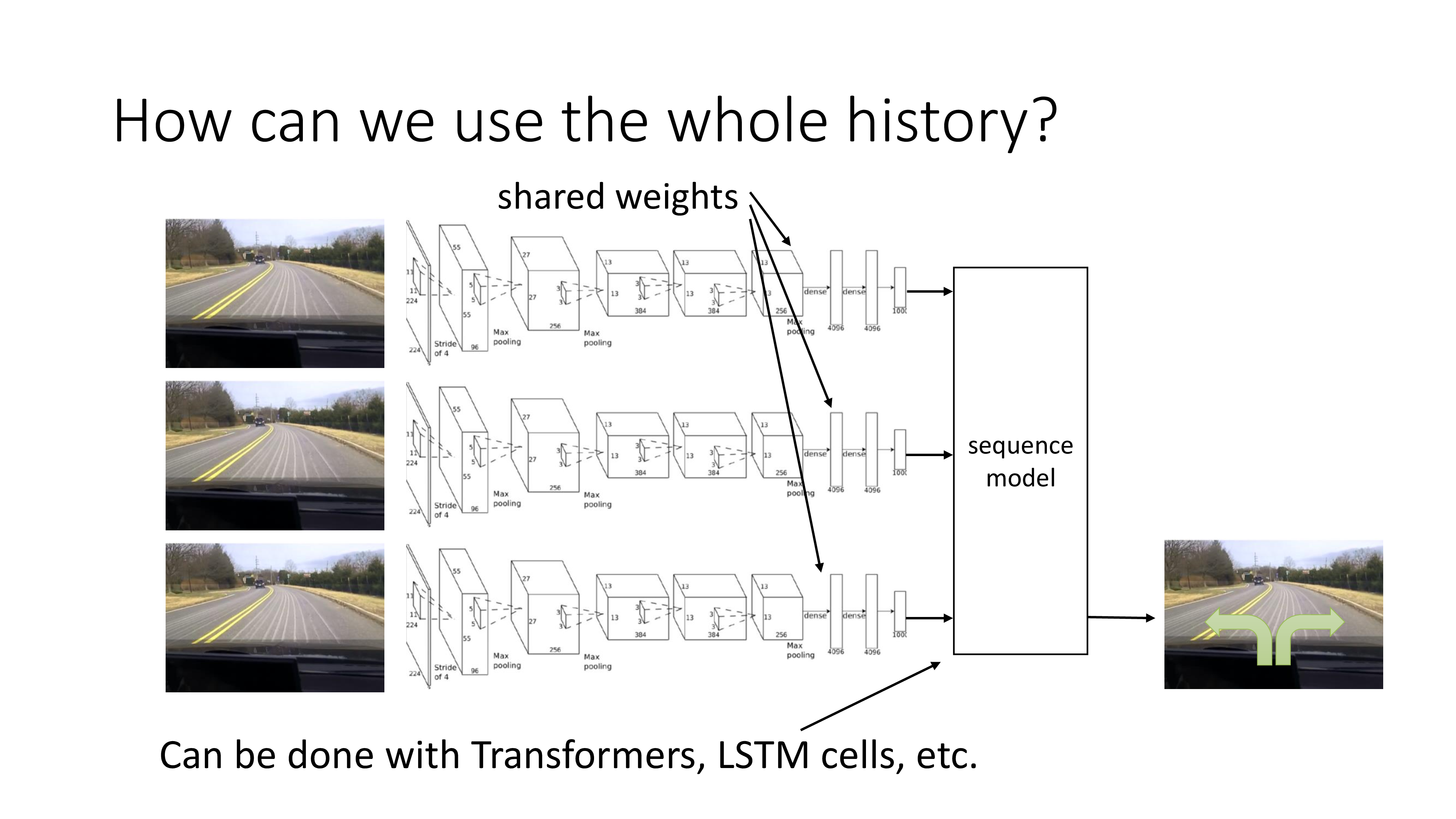
(자율 주행을 하는 상황에서는 주행 image가 들어오므로 fron-end에 Convolutional Neural Networks (CNNs) 같은거도 좀 넣어주고요) 하지만 이런방식이 잘 작동하는 것은 아닐 수 있다고 하는데 그 이유는 너무나 관련성이 큰 frame들이 연속적으로 들어오기 때문입니다. 아래의 예시를 한 번 보도록 하겠습니다.
마찬가지로 자율주행을 하는 상황에서 agent의 camera가 전면 유리 안쪽에 위치해 있어 dashboard, handle, 그리고 창 밖의 상황을 전부 관측 (observe)할 수 있는 상황이라고 칩시다. 그리고 brake를 밟으면 dashboard에 어떤 불이 들어오는 상황입니다. 만약 주행중인 차량에 사람이 뛰어든다면 agent는 사람을 인지하여 brake를 누를 것이고 불빛이 들어올겁니다. 하지만 연속적인 image frame을 받아 decision을 하는 경우 agent입장에서 현재 observation은 앞에 사람은 있는데 또 brake는 밟혀있기 때문에 어떤 action을 해야 하는지 햇갈리 겁니다. 이런 경우 model은 잘못된 인과 관계 를 학습하게 될 수도 있습니다. 이를 Causal Confusion 이라고 하는데, Observation에 너무 많은 정보가 포함되어있어 agent를 혼동시키므로 차라리 없는게 낫다 라는 것이며 꼭 history가 포함된다고 해서 이것이 발생하는건 아닙니다. Causal confusion은 Sergey가 참여한 논문인데 논문에는 history를 같이 보는 것이 causal confusion에 좋은지? 나쁜지? 아니면 바로 뒤에 배울 DAgger가 casual confusion에 좋은지 나쁜지?를 다루니 관심이 더 있으신 분들은 이를 참고하시면 좋을 것 같습니다.
Multimodal behavior
이번에는 real-world의 action은 정답이 1개가 아니고 선택지가 많다는 것입니다. 자율 주행을 하는 expert가 아래와 같이 나무를 만났다고 칩시다.
Additive Fig.
당연하게도 expert는 나무를 피할 것이지만 여기서 정답은 하나가 아닙니다. 왼쪽으로 가도 되고 오른쪽으로 가도 되죠. 그런데 어떤 expert data는 왼쪽으로 가고 어떤 expert data는 오른쪽으로 갈겁니다. 같은 state에 대해서 말이죠. 즉 매우 유사한 state에 대해서 완전히 다른 action을 label로 주게 되는 것인데, 이것이 discrete action space인 상황에서는 문제가 안됩니다.
Additive Fig.
왜냐하면 discrete action space의 경우 한쪽으로 확률이 쏠리지 않겠지만 그래도 가운데로 직진 (front)한다는 확률이 커지진 않거든요. 나무를 마주치면 Argmax sampling해서 왼쪽이든 오른쪽이든 가면 그만입니다. 하지만 continuous action space에서는 그렇지 않습니다. 만약 드론이 (left, front, right) 세 가지 중 하나를 고르는게 아니라, 왼쪽으로 handle을 몇도 이런식으로 학습을 한다고 하면 같은 state에서의 서로 다른 두 action은 결국 가운데로 직진 (front) 한다는 이상한 distribution을 줄 겁니다.
Additive Fig.
이 문제는 어느쪽으로 handle을 기울일 것인지를 봉우리가 하나인 단봉 가우시안 분포 (unimode normal distribution)을 사용했기 때문에 생기는 것으로, 봉우리가 여러개인 분포, 즉 multimodal normal distribution을 사용하면 해결할 수 있습니다. 혹은 high dimensional action space 를 discretization 함으로써 해결할 수 있다고 합니다.
Slide. 21.
그럼 어떻게 해야 multimodal 을 갖는 복잡한 distribution을 modeling할 수 있을까요? 사실 이를 제대로 cover하기에는 이것이 Imitation Learning의 main problem도 아니라 현재 lecture의 coverage를 넘어 서기 때문에 따로 찾아보시면 될 것 같은데, 대표적으로 아래의 세 가지가 있습니다.
Mixture of Gaussian (MoG)이란 gaussian 분포 여러개를 weighted sum 한 것으로 Expectation Maximization (EM) algorithm으로 학습하는 것이고 latent variable model은 변분법 (variational method)을 사용해서 복잡한 distribution을 학습하는 것이며 diffusion model은 latent variable model을 확장한 것이라고 할 수 있습니다.
(diffusion까지 언급하는건 진짜 뇌절인거 같으나 Sergey가 diffusion으로 planning하는 paper를 썼기 때문에 넣은 것 같습니다.)
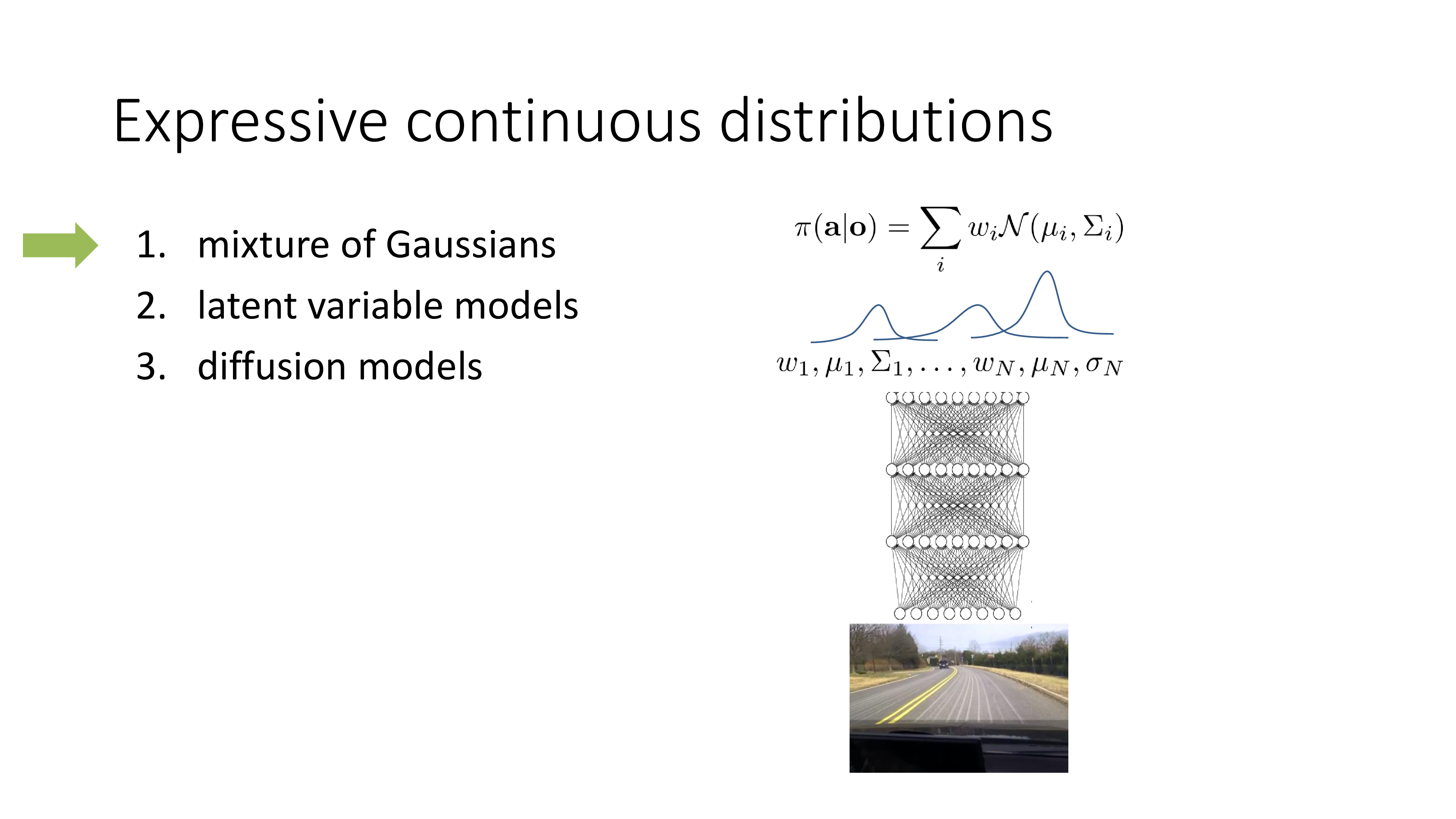
MoG는 매우 간단합니다. 여러 개의 mean, variance와 각 gaussian distribution을 weighted sum할 때 쓰는 weight을 trainable parmeter로 두고\((w_1, \mu_1, \sigma_1, \cdots, w_{N}, \mu_{N}, \sigma_{N})\), objective function을 최적화 하면 됩니다.
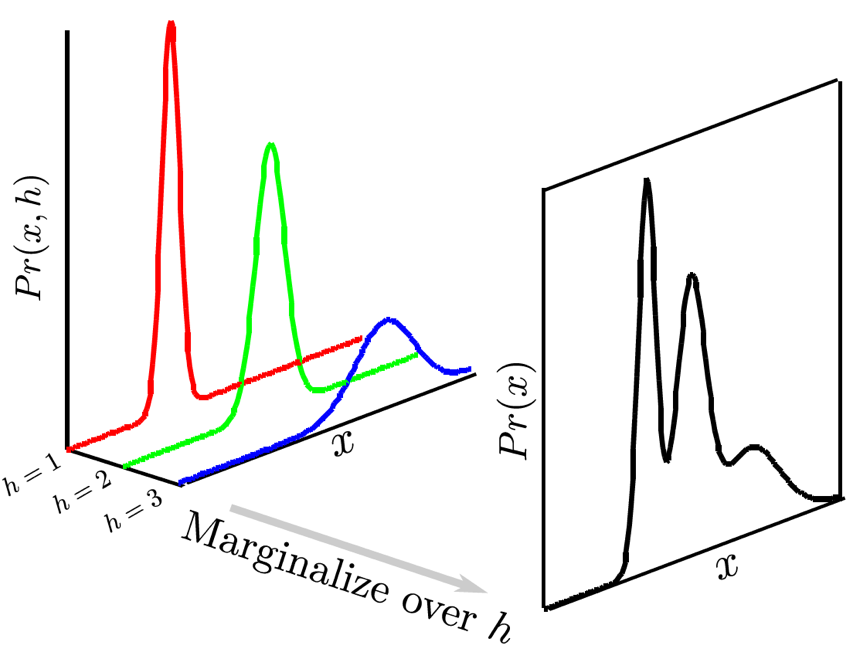Fig. MoG (GMM)은 여러개의 unimode normal distribution을 weighted sum 한 것이고 각 distribution의 mean값과 weight값을 예측하는 것이 핵심이다
가장 간단하지만 단점이 있다면 몇개의 distribution을 쓸 것인지? 같은걸 정해야 하며 이는 task가 어려워질 수록 1000개의 mode가 필요할 수도 있어 문제가 있습니다. latent variable model은 이런 문제를 해결한 것입니다.
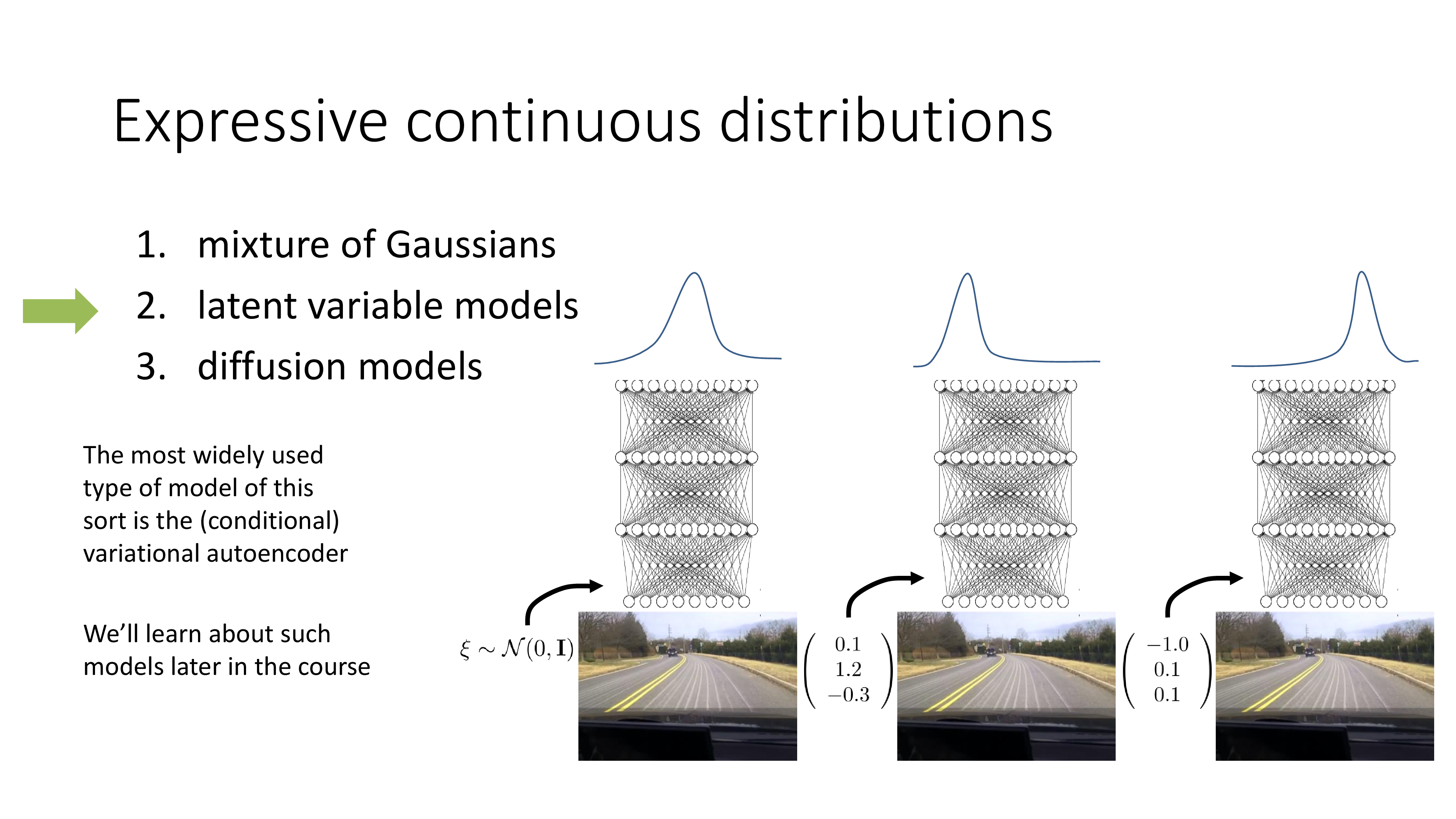
(점점 상황이 복잡해지는데, generative model을 처음 접하시는 분들은 느낌만 보시면 됩니다)
Latent variable model은 NN output이 여전히 봉우리가 하나인 unimode gaussian distribution입니다.
하지만 NN이 input으로 받는 것은 camera image뿐만 아니라 어떤 random seed (vector)도 있습니다.
이 random seed가 달라질 때마다 다른 mode를 갖는 distribution을 NN은 출력합니다.
Latent variable model은 직관적으로는 MoG와 비슷하다고 생각할 수 있습니다.
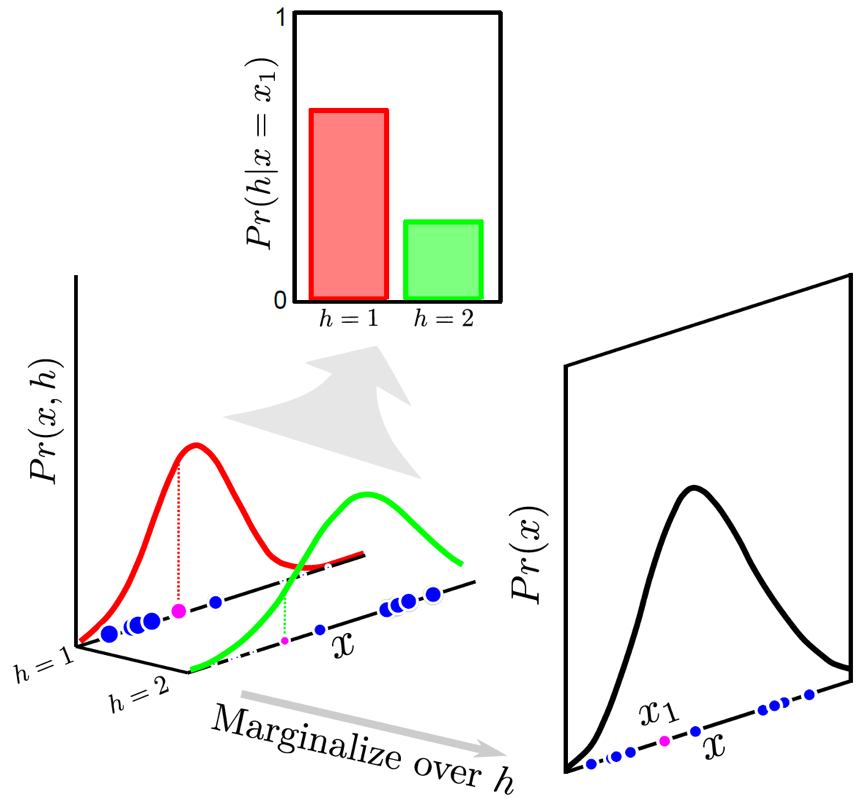
위의 figure를 보시면 h가 의미하는것이 random seed이며 random seed의 분포가 discrete한 걸 볼 수 있습니다. (물론 contiunous해도 됩니다)
MoG처럼 여러개의 unimode gaussian distribution을 합칠것은 맞는데, 어떤 image input이 들어왔을때 그 image input이 어떤 random seed에 할당될지? 그 random seed에 대한 distribution이 학습을 통해 modeling되고 (지금은 discrete), 더 높은확률의 random seed가 뽑혔으면 그 random seed가 가리키는 unimode distribution으로 가는 것이죠. Intuition은 학습 때 같은 training sample image에 대해서도 어떤 sample은 left로 어떤 sample은 right으로 가는데, 이를 서로 다른 random seed에 mapping시켜줘서 어떤 sample은 left mode를 갖고 또 다른 sample은 right mode를 갖을 수 있게 하는겁니다. 즉 같은 image가 들어오더라도 seed vector가 어떠냐에 따라서 어떤 mode를 선택할지가 달라진다는 것이므로 같은 state에서 서로 다른 label을 정답으로 치는 일이 없어지고, 실제 주행을 하는 test time에는 seed vector를 random하게 하나뽑으면 그것이 왼쪽으로 가라고 알려주게 될 거라는 겁니다. 우리는 완벽하게 expert가 하는 trajectory를 따라하는게 목표가 아니라 나무가 앞에 있을때 그걸 우회하기만 하면 되니까 왼쪽 오른쪽 중 어떤 방향에 해당하는 seed가 뽑혀도 전혀 상관하지 않습니다.
하지만 이것을 학습하는것이 쉽지는 않습니다. 아무 input frame과 상관없는 random seed를 같이 넣어 unimode distribution을 출력하라고 학습하면 NN은 이를 무시할 수도 있기 때문에 학습이 어렵습니다. 이를 해결하는 technique들이 있지만 이는 lecture 18쯤에 더 자세히 다룰 것이니 신경쓰지 않아도 됩니다.
이하는 diffusion model에 대한 slide인데 대부분 생략하려고 합니다. 왜냐하면 diffusion model은 latent variable model의 한 종류로 latent variable model의 application으로 유명한 Variational Auto Encoder (VAE)을 여러 번 반복하는 확장판이라고 할 수 있는데, 이를 제대로 설명하는 것은 논지를 한참 벗어나기 때문입니다 (개인적으로 생각할 때).
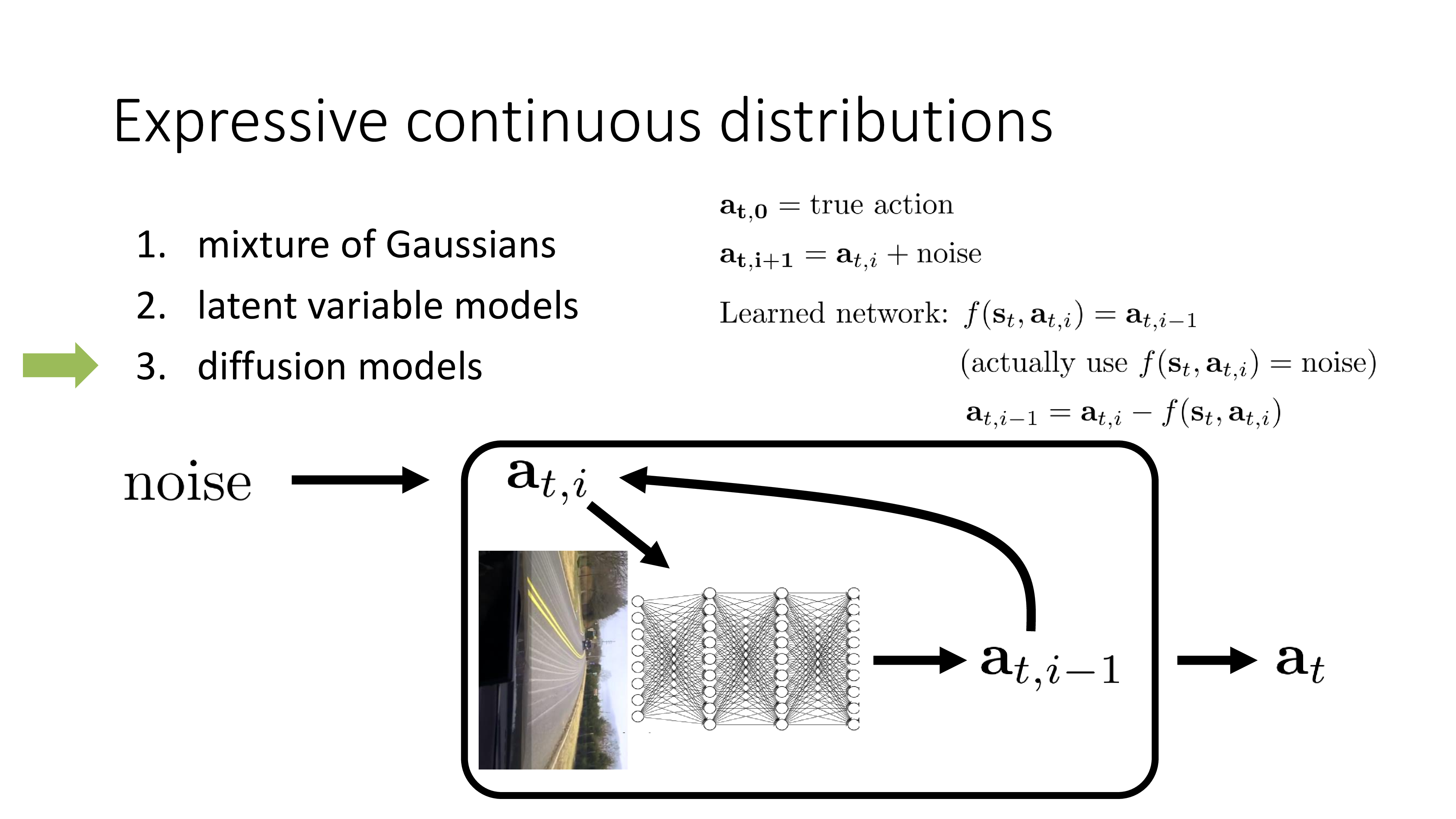
더 관심이 있으신 분들은 Sergey가 쓴 Planning with Diffusion for Flexible Behavior Synthesis를 보시길 추천드리며, 결론은 diffusi on based model 또한 latent variable model의 한 종류이기 때문에 매우 복잡한 multimodal distribution을 modeling할 수 있으며 아까의 나무에 부딪히는 문제를 해결할 수 있다는 겁니다. (diffusion model은 VAE를 여러 번 해야 하기 때문에 inference 비용이 매우 비쌉니다.)
(Sergey가 Diffusion으로 robotics 문제를 푸는 demo를 보여주는데 이건 좀 신기해서 첨부합니다)
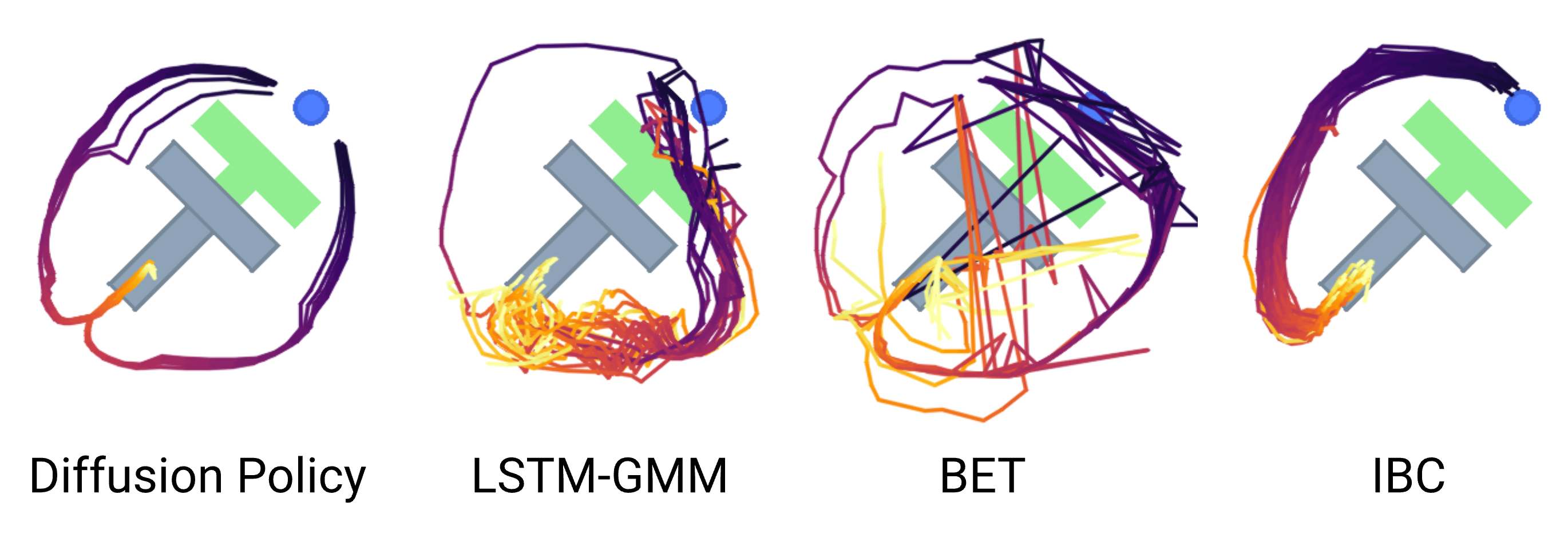
Fig. 시간이 좀 오래 걸리지만 서서히 random noise로부터 denoising과정을 거쳐 action sequence를 만들어낸다. 이를 planning이라고 한다. BC의 범주를 벗어나지만 복잡한 distribution modeling을 할 수 있다는 걸 이해하면 될 것 같다. Source from here
그 다음은 Autoregressive Discretization입니다.
(처음 들어보는 용어라서 googling을 해보니 Sergey가 만든 term인 것 같습니다. Reddit)
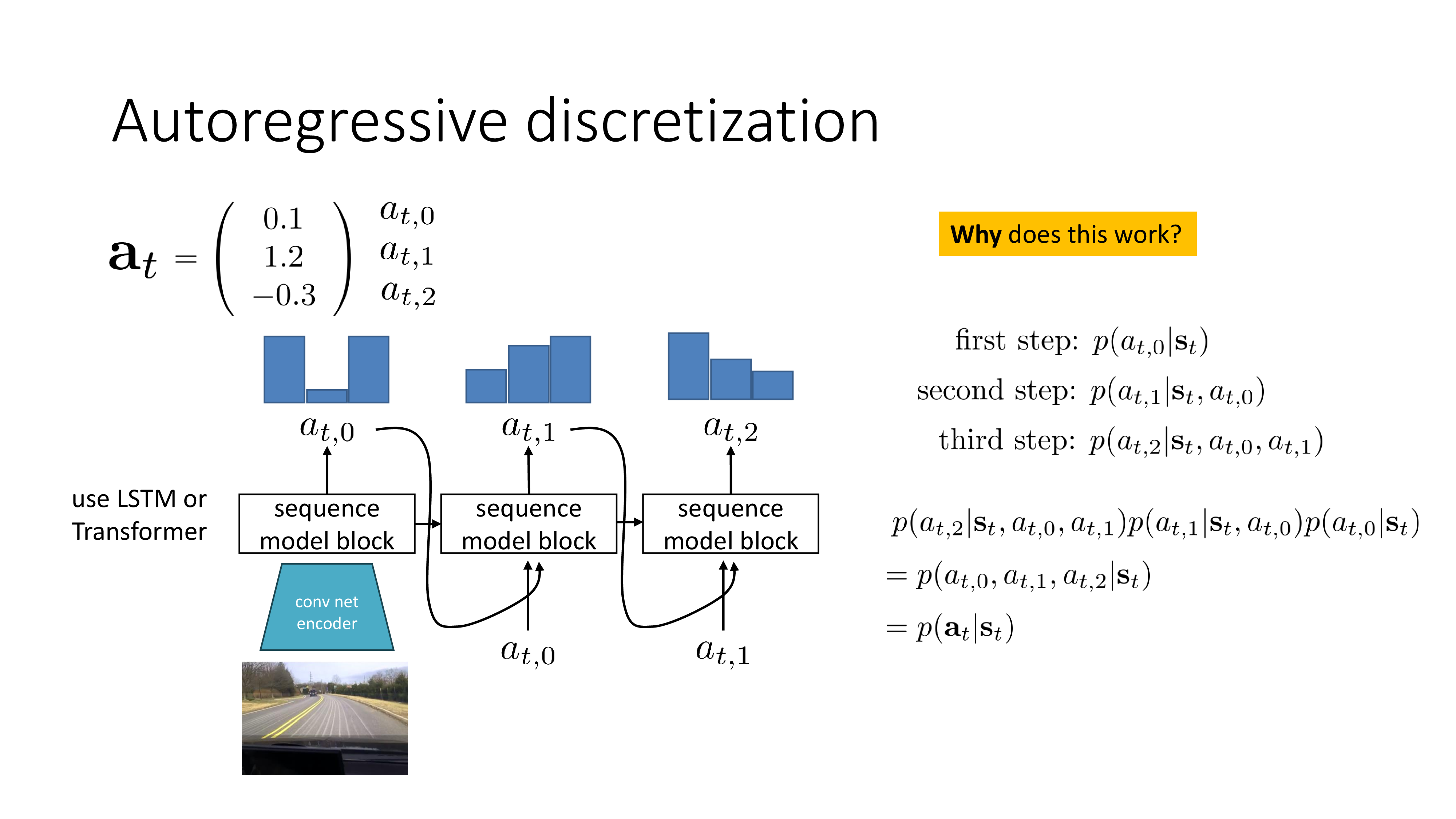
양자화 (Discretization) 자체는 간단한 개념입니다. 앞서 나무를 피하는 예제를 생각해보면 1차원 action space를 3차원으로 쪼갠 것이나 다름 없습니다. Discrete action space를 쓴다는 개념 자체가 이미 양자화의 예제였던 것이죠. Discrete action space를 쓰면 나무에 부딪힐 문제가 없었죠? 그런데 문제는 1차원 이상의 continuous action space를 쪼개는 것이 어렵다는 겁니다.
High dim에서 discretization을 하려면 어떤 trick이 필요한데, 바로 언어 모델 (languge modeling)처럼 modeling을 하는 겁니다. 우리가 어떤 “hello, how are you?” 라는 4~5개 단어로 이루어진 sentence를 modeling할 때 우리는 sentence를 한번에 modeling하지 않고 (\(p(x_1,x_2,x_3,x_4,x_5)\)), 이를 chain rule을 사용해 쪼개서 modeling 합니다.
\[\begin{aligned} & p(x_1,x_2,x_3,x_4,x_5) = p(x_1) \\ & \quad \cdot p(x_2 \vert x_1) \\ & \quad \cdot p(x_3 \vert x_2, x_1) \\ & \quad \cdot p(x_4 \vert x_3, x_2, x_1) \\ & \quad \cdot p(x_5 \vert x_4, x_3, x_2, x_1) \\ \end{aligned}\]이처럼 복잡한 distribution의 차원을 쪼개서 간단한 discrete distribution 여러개로 두고 학습한 뒤에, chain rule에 의해 각 차원의 distribution들을 곱하면 복잡한 원래의 joint distribution이 recover되는겁니다. (이것 또한 inference 시 주어진 state에 대한 action distribution을 얻기 위해서는 예제에서는 최소 3step inference를 해서 곱해야 하므로 computational cost가 많이 듭니다.)
한 편, Autoregressive discretization는 이렇게도 생각할 수 있습니다. Action차원이 (brake를 밟는 정도, accel을 밟는 정도, handle을 꺾는 정도) 이렇게 3차원인 겁니다. 이 3가지의 차원을 각각 양자화 하기 위해서 각 차원을 autoregressive하게 나눈 것인데, autoregressive sequence modeling의 관점에서 보면 brake를 밟는 정도를 먼저 정하고, 그 다음 accel의 압력을 정하고, 마지막으로 handle을 꺾는 정도를 정한다는 것이죠. 이렇게 해석할 수도 있습니다.
이어서 Sergey가 본인이 참여한 paper들 몇 개 광고하고 subsection이 마무리되는데, paper demo들은 생략하도록 하겠습니다
3. Use multi-task learning
이번 subsection에서 언급하는 내용도 사실 diffusion 만큼이나 어려운 내용입니다. BC는 사실 lecture 15~16 쯤에서 배울 Offline RL이나 Goal Conditioned RL등과 비견됩니다. 이 셋의 공통점은 human expert data같은걸 쓴다는 것인데, naive BC는 그냥 SL을 하는 것이고 뒤의 두 개는 RL을 한다는 차이점이 있습니다. BC는 일반적으로 expert의 성능을 뛰어넘을 수 없는 반면 나머지 두개는 그렇지 않다고 알려져 있습니다.
Sergey는 지금 Goal Conditioned Behavior Cloning (GCBC)를 얘기하려고 하는겁니다.
본인도 얘기하길 “처음에는 내가 말하는게 굉장히 역설적일 수 있지만 곧 이해될거다” 라는 식으로 얘기합니다 (…).
그러므로 깊게 이해가 안되더라도 이번에는 느낌만 가져가면 될 것 같습니다.
이번에는 multi-task learning으로 BC의 단점을 보완한다고 되어있는데 title부터가 와닿지 않을 수 있지만 한 번 얘기해보도록 하겠습니다. 현재 BC setting은 다음과 같습니다. Human expert가 여러 주행을 해서 trajectory들을 모아주면 그걸 바탕으로 학습하는건데, 이 때 목적지는 \(p_1\) 하나였습니다.
하지만 만약 expert data가 없다면 어떻게 될까요? expert수준은 아니지만 대충 주행을 해서 demo data를 모으긴 모았는데 각 trajectory들의 목적지 (goal)들이 제각각인 경우를 생각해봅시다. 이런 경우에도 학습을 할 수 있는데, 바로 model에 goal을 같이 condition으로 주는겁니다.
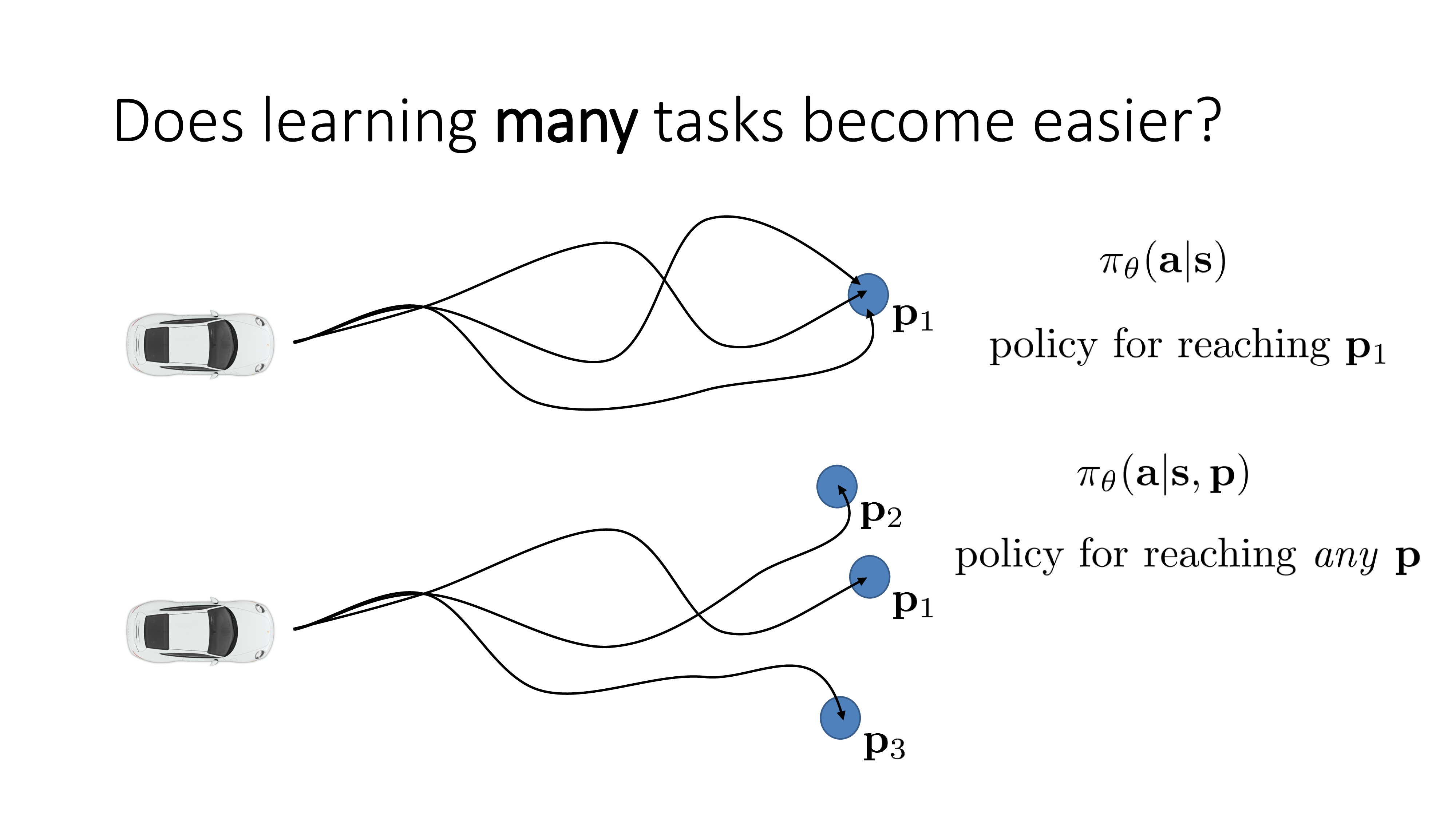
Goal이 어떤것이냐에 따라서 다른 task를 푸는 것이 되기 때문에 multi-task learning이라고 이름 지은 것 같고, 간단히 말해서 sergey는 이런식으로 data를 수집할 경우 unseed state를 더 많이 줄일 수 있고 (더 많은 state를 cover), 그러므로 distribution shift가 일어났을 때 recover를 할 수 있기 때문에 성능이 좋아진다고 합니다 (?).
그리고 몇 가지 case study를 보여주는데, 첫 번째는 robot arm을 가지고 서랍을 닫고 물건을 집고… 등등의 행위를 하는겁니다.
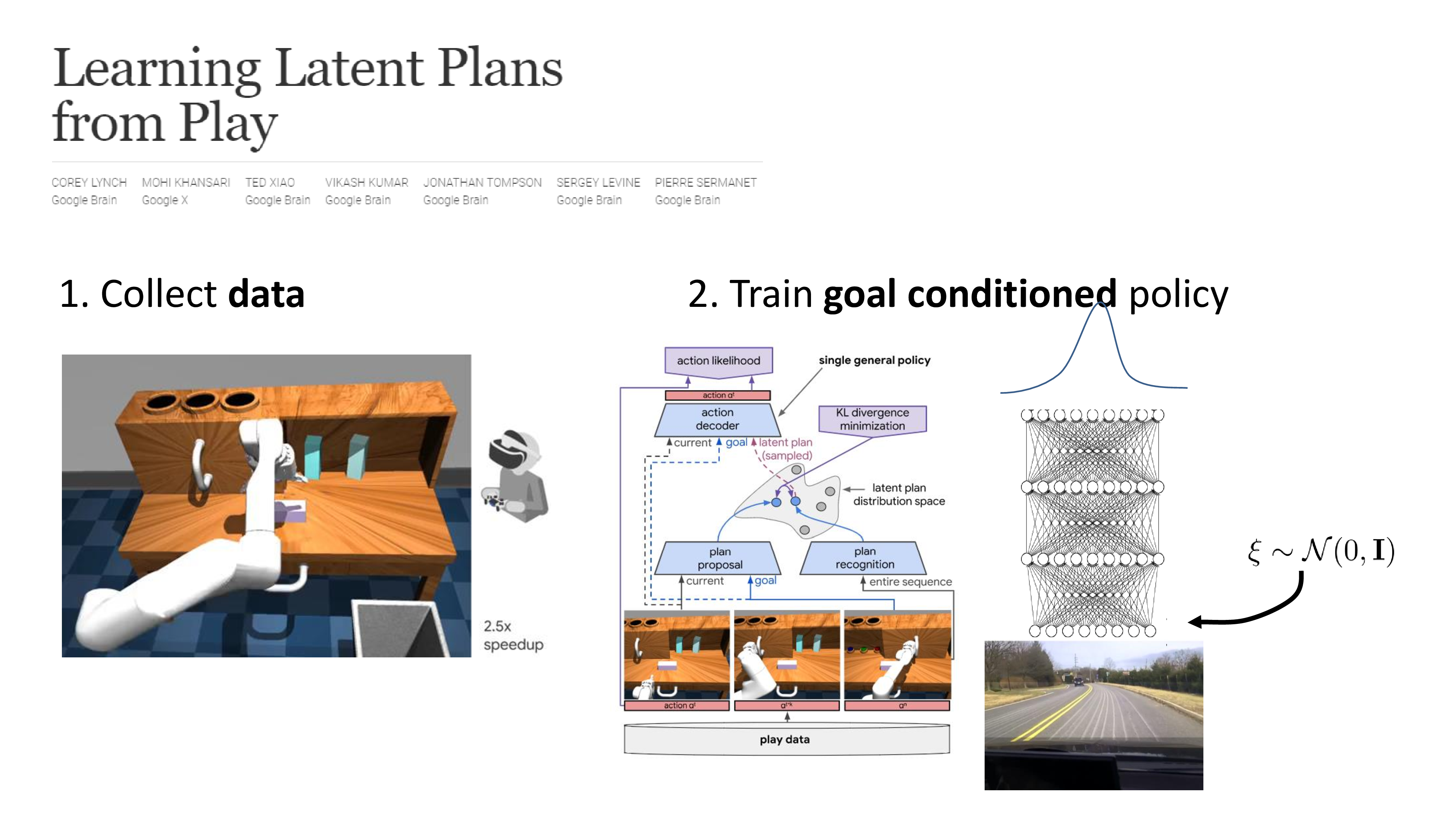
앞서 설명드린 latent variable model을 사용해서 modeling한 것 같은데, 핵심은 그것이 아니라 random하게 혹은 expert가 조종을 해서 robot arm을 무작정 움직인 뒤에 조작이 다 끝났으면 마지막 scene을 정답지로 해서 학습할 때 맨 처음에 그 frame을 같이 condition주면 그 demo를 따라하는 겁니다. 여기서 서랍을 연다던가 물건을 집는다던가 하는 것이 각각 goal이며 task인 것이기 때문에 이번 subsection에 multi-task learning이라는 이름이 붙은 것 같습니다.
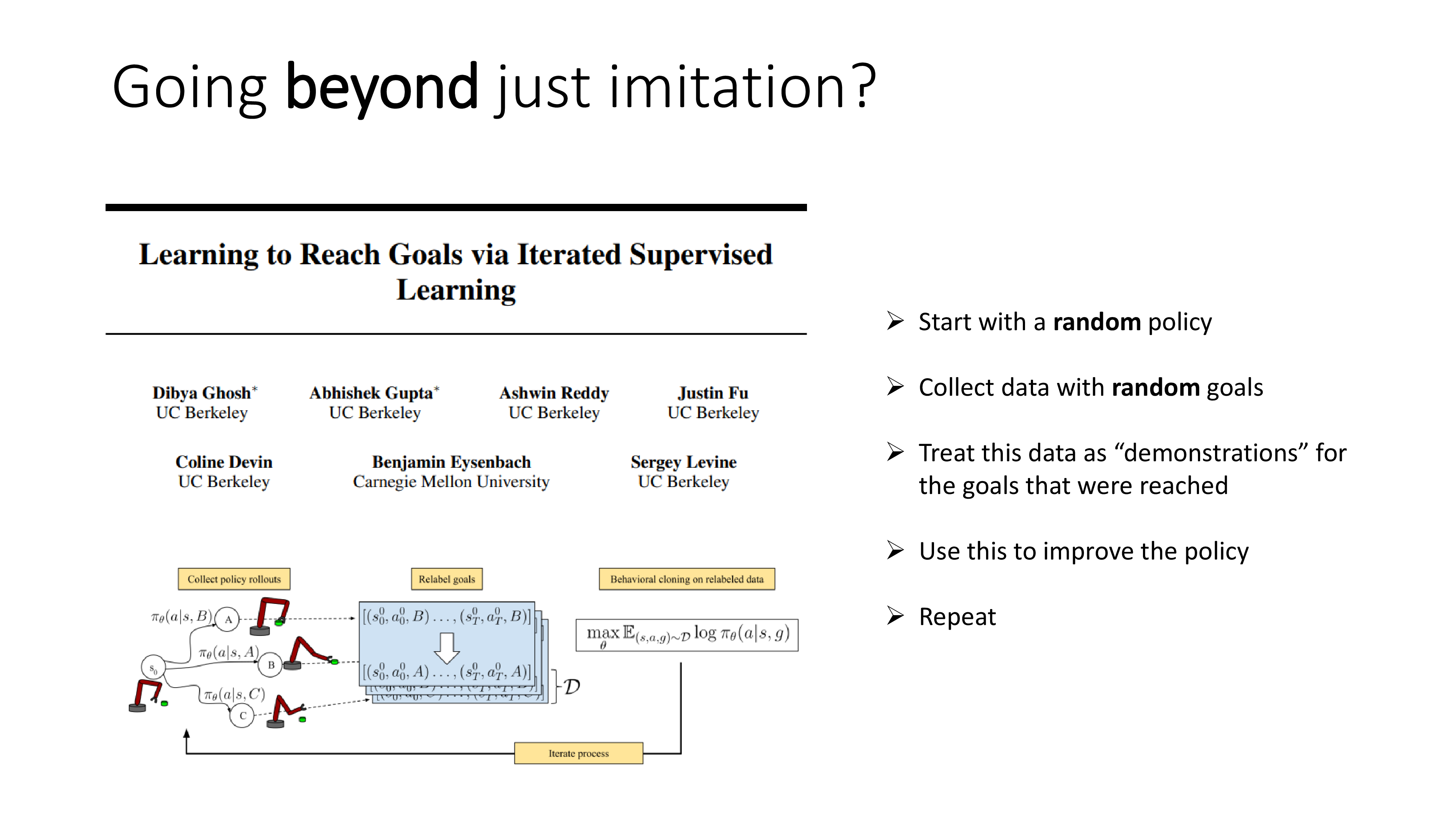
그 다음 예시에서는 robot arm을 움직이는 task로 random policy를 이용해 처음에는 마구잡이로 demo를 만든 뒤에 그 goal을 condition으로 GCBC를 하게 했더니 policy가 점점 좋아지고, 좋아진 policy로 demo를 또 만들고…를 반복했더니 “이 일 (goal) 을 해줘”라고 하면 실제로 그 일을 수행하는 agent를 만들 수 있었다고 합니다.
(왜 GCBC가 성능이 좋아지는건지 직관적으로 이해가 잘 안가서 나중에 revisit 하겠습니다.)
4. DAgger
DAgger (Dataset Aggregation)는 말 그대로 Data를 추가하는 겁니다. 여태까지 우리는 어떻게하면 \(p_{\theta}\)를 \(p_{data}\)에 조금이라도 더 비슷하게 만들까 노력했습니다. 이번에는 역으로 \(p_{\pi_{\theta}}(o_t)\) 에서 뽑아 보자는 idea로 \(p_{\theta}\)를 실제로 사용해서 data를 만들고 그 data를 human expert가 직접 고쳐서 원래 dataset에 합치는 (aggregate) 겁니다.
매우 간단하면서 실제로도 잘 된다고 하는데 사실 DAgger는 별로 좋은 algorithm이 아니라고 합니다.
그 이유는 중간에 사람이 개입해서 다시 label을 해 줘야 하는, 이른 바 human in the loop alogirhtm이기 때문이죠.
What's the problem of Imitation Learning ? (A preview of what comes next)
Imitation Learning, 그 중에서도 BC는 안좋습니다. Distributional shift가 일어나기 쉽고 expert data를 모으기도 어려우며 잘 working 하게 하려면 resource가 많이들기 때문이죠.
그 밖에도 사람은 부모나 선생을 모방하는 것 외에도 자연스럽게 경험 (experience)를 통해서 학습을 하는데, 왜 machine은 그렇게 할수 없는가? 같은 본질적인 질문이 BC보다 더 좋은, 그리고 무한히 자기 발전 (self-improvement) 하여 human expert를 뛰어넘는 algorithm에 대한 갈증을 불러일으키는데, 이것이 이후 20개에 달하는 lecture를 통해 배우게 될 Reinforcement Learning (RL)입니다.
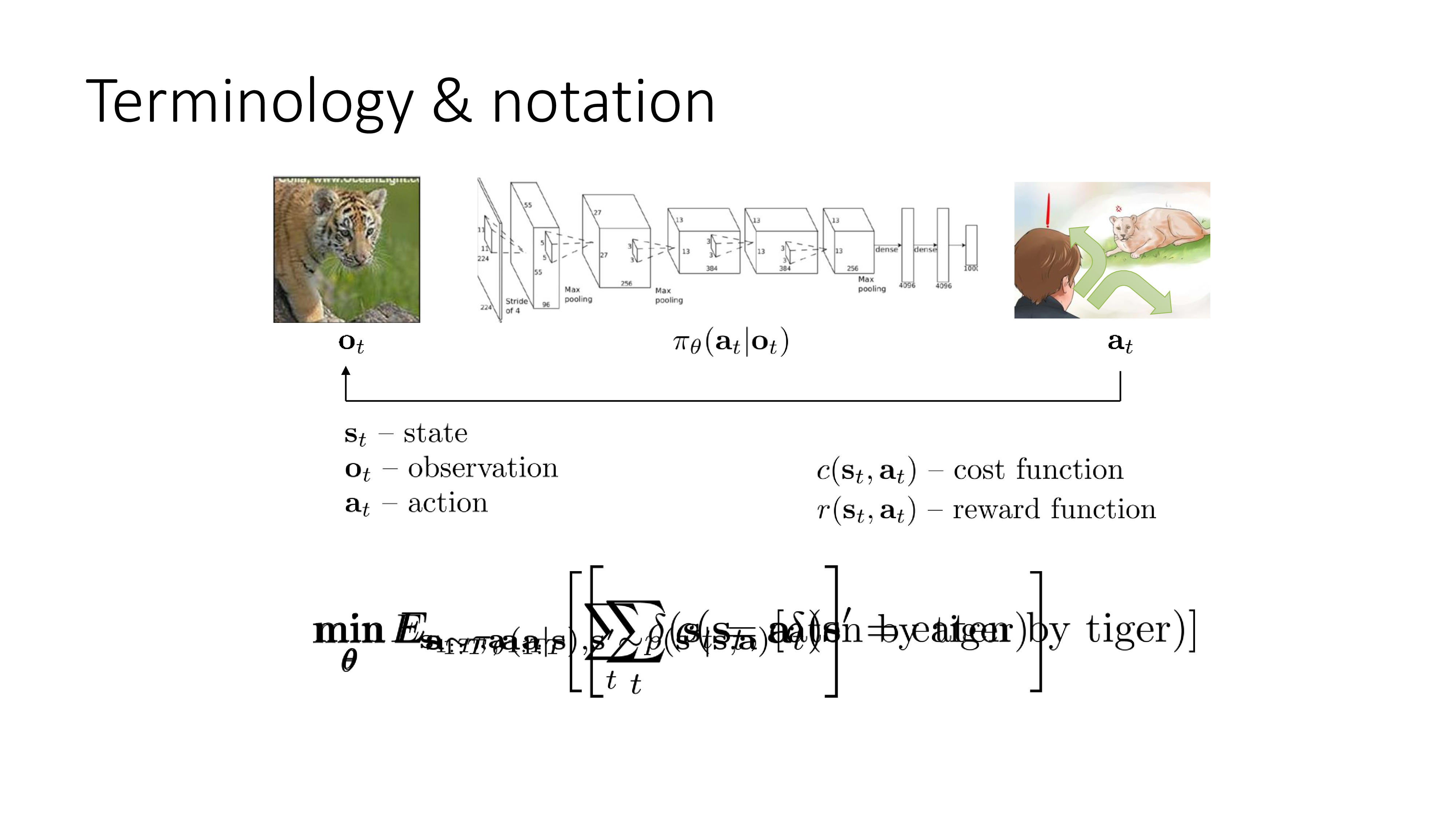
다시 위에서 다뤘던 호랑이에 쫓기는 상황을 생각해볼까요? 우리가 observation을 action으로 mapping하는 model 가진 상황에서 과연 어떤식으로 mapping하는게 좋고 나쁜지에 대해서 정한 적은 없습니다. 그저 SL처럼 주어진 정답이 있고 maximum likelihood estimation을 했을 뿐이죠.
그런데 실제로 우리가 원하는 것은 likelihood를 최대화 하는 것이 아닐겁니다. 단지 호랑이한테 먹히지 않고 살아남는 것이 목적이겠죠. 이는 수학적으로 아래의 식으로 나타낼 수 있습니다.
\[\min_{\theta} \mathbb{E}_{a \sim \pi_{\theta}(a \vert s), s' \sim p(s' \vert s,a)} [ \delta (s'= \text{eaten by tiger})]\]호랑이한테 먹히는 경우에 대한 기대 값 (Expectation)을 최소화 하는게 바로 진정한 목적 (objective)이 될 수 있는거죠. (여기서 delta function, \(\delta\)을 사용했기 때문에 먹힐 경우만 1이고 나머진 전부 0입니다.)
수식은 “현재 state에서 어떤 action을 취했을 때, 내가 잡아먹힐까?”를 의미합니다. 수식에 expectation이 있는데 expectation의 정의는 모든 outcome들에 대해서 다 확률을 곱해서 더하는 것으로
\[\mathbb{X} = \sum_{i=1}^k x_i p_i = x_1 p_1 + x_2 p_2 + \cdots + x_k p_k\]현재 내가 할 어떤 action이 초래하게될 다음 state, \(s'\)가 호랑이 뱃속이 아니면 되기 때문에 그렇게 만들 action이 안좋다고 판단해서 확률을 0에 가깝게 낮춰버리면 됩니다.
조금 더 일반화하면 \(\delta\) 함수를 다른 다양한 손실 함수 (Cost Function)로 나타낼 수 있습니다.
혹은 이를 보상 함수 (Reward Function)라고 부르기도 하기 때문에 보상 함수로 대체하고 보상은 높을수록 좋은 것이기 때문에 min term을 max로 교체하면 다음을 얻을 수 있습니다.
이것이 RL의 Objective Function입니다.
여기서 중요한 점은 \((s_{1:T}, a_{1:T})\)가 고정되어있는 data가 아니라 현재 policy를 따라서 만들어진 trajectory라는 겁니다.
policy가 발전할 때마다 새로운 policy로부터 data가 만들어집니다.
이러면 어떤 장점이 있는가?
앞서 BC가 \(p_{data}\)로만 학습하고 평가할 때는 \(p_{\pi}\)하에서 action을 해 나가니 문제가 됐었죠. DAgger같은 방법이 \(p_{\pi}\)에서 뽑은 observation (혹은 state)를 가지고 학습함으로써 training과 test의 distributional shift를 완화한 것인데, 매 번 최신의 policy를 가지고 만든 data로 학습을 하니 이 문제도 사라지는 겁니다.
다음 chapter부터는 본격적으로 maximum likelihood estimation이 아니라 RL이 무엇인지에 대해 본격적으로 얘기해 보도록 하겠습니다.