(CS285) Lecture 7 - Value Function Methods

이 글은 UC Berkeley 의 교수, Sergey Levine 의 심층 강화 학습 (Deep Reinforcement Learning) 강의인 CS285를 듣고 작성한 글 입니다.

Lecture 7의 강의 영상과 자료는 아래에서 확인하실 수 있습니다.

• Fall 2020 ver.
  • Lecture Video Link (Youtube)
  • Lecture Slide Link

Additional) Sergey의 강의도 좋지만 좀 더 Pieter Abbeel의 Foundations of Deep RL Series가 조금 더 이해하기 쉬운 것 같으니 아래의 video들도 참고하시면 좋을 것 같습니다.

• Foundations of Deep RL Series
  • L1 MDPs, Exact Solution Methods, Max-ent RL
  • L2 Deep Q-Learning

< 목차 >

• Introduction and Motivation
• Recap
• Can we omit policy gradient entirely?
  • Policy Iteration
  • Value Iteration
• Examples of DP-based Methods
  • Value Iteration Example - Grid World
  • Q-Iteration
  • Policy Iteration Example - 4x4 Grid World
  • Effect of Discount and Noise
  • Andrej Karapthy's Demo for DP method
• Fitted Value Iteration & Q-Iteration
  • Model-Free Value-based Methods: Q-Iteration
• From Q-Iteration to Q-Learning
  • Q-Iteration and Off-Policy Algorithm
  • Design of Q-Network
  • Online Q-iteration: Q-Learning
  • Exploration in Q-Learning
  • Temporal Difference (TD) Learning: Q-Learning vs SARSA
• Value Functions in Theory (About Convergence Guarantees)
  • Theory in Tabular Value-based Algorithm
  • Theory in Non-Tabular Value-based Algorithm
• Reference

이번 chapter에서 다룰 내용은 Value Function based Method입니다.

Slide. 1.

Lecture 9과 그 이후에 Policy-based Method를 몇번 더 다룰 것 같으나, chapter 7,8에서는 Value-based를 집중적으로 배울겁니다. Value-based method의 기본 concept을 이해하기 위해 Value Iteration 부터 알아보고, 더 나아가서는 (Deep) Q-Learning (DQN)에 대해서 배우는 것이 목표입니다. 앞서 2, 4장에서도 말씀드렸지만 value-based 방법론들의 Goal도 언제나 좋은 policy를 학습하는 겁니다. 다만 value-based의 경우 policy를 implicit 하게배웁니다. 즉 policy를 의미하는 Neural Network (NN)이라는 것이 없습니다.

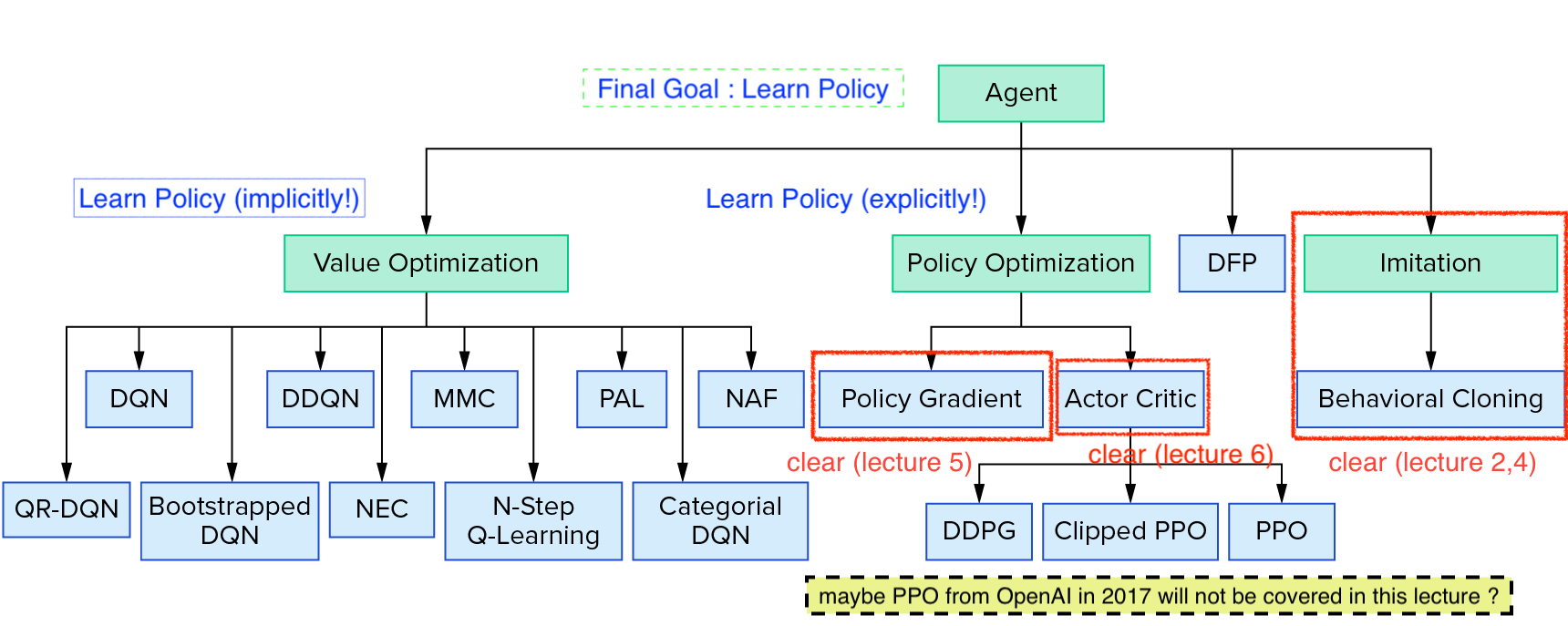Source From Reinforcement Learning Coach from Intel Lab

Introduction and Motivation

본격적으로 Policy Iteration과 Value Iteration 등에 대해서 본격적으로 알아보기 전에 알아둬야 할 것이 있습니다. 이 두 방법론은 테이블 형식으로나 표현이 가능한 state나 (state, action) tuple에 대한 가치 (Value) 를 Dynamic Programming (DP)을 이용해 정확하게 구해내는 과정을 반복함으로써 최적의 policy를 결국 찾아내는 오래된 RL 방법론입니다.

RL이긴 한데요, 그러니까 iteration을 통해 개선을 하는것은 맞는데, 이 방법론들은 학습을 할 parameter가 없습니다. 그럼에도 불구하고 “왜 이 오래된 알고리즘들을 알아야하는가?”에 대해서는 이렇게 DP를 통해서 솔루션을 구하는 아이디어가 현대의 강화학습에 지대한 영향을 끼쳤기 때문이라고 합니다. (이는 Pieter Abbeel의 Foundation of Deep RL 강의에도 언급이 됩니다.)

이번 chapter에서는 앞으로 RL을 이해하기 위한 insight를 얻는 목적으로 보시면 좋을 것 같습니다.

Recap

먼저 지난 강의에서 다뤘던 내용을 복습하면서 강의를 시작합니다.

Slide. 2.

지난 강의까지 정책 경사 (Policy Gradient; PG)기반의 algorithm들을 주로 알아봤습니다. Policy를 나타내는 Actor뿐 아니라, variance를 줄이기 위해 Critic도 도입해서 Actor-Critic까지 알아봤죠. 그리고 언제나 PG algorithm들의 목표는 아래의 3가지 main problem을 해결하는 것이었습니다.

• PG의 3가지 Main Problem
  • High Variance 하다.
  • 최적화 시 Step Size, \(\alpha\) 를 고르기 어렵다.
  • Sample Inefficiency 하다.

Graident estimator가 unbias하면 더 좋았죠.

Can we omit policy gradient entirely?

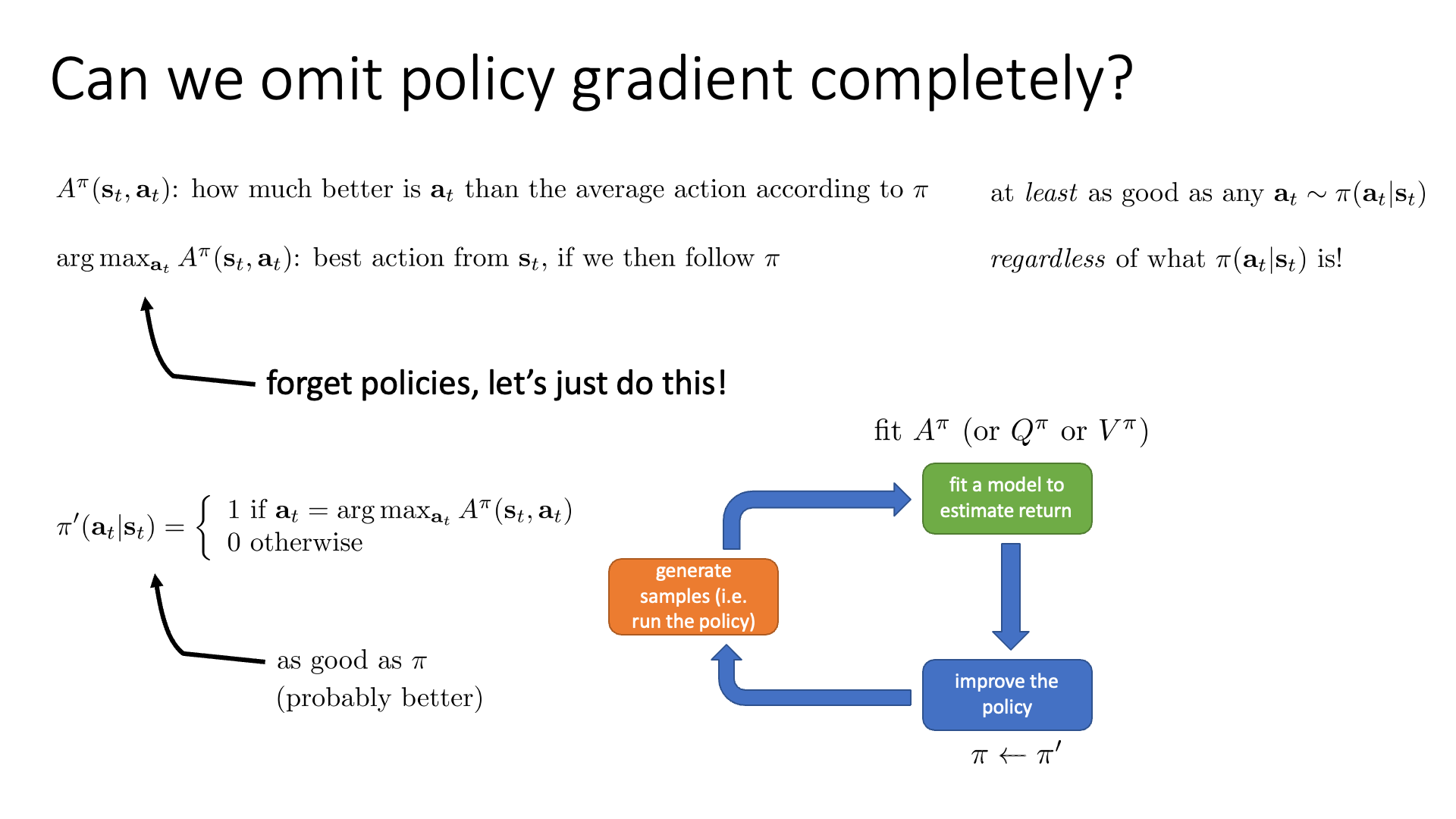
7장의 주제인 Value Function based Method은 “Value Function을 잘 학습시켜서 이를 통해 어떻게 행동할지?를 결정할 순 없을까?” 라는 idea에서 출발합니다.

이게 가능한 이유가 뭘까요?

우리가 어떤 state에 놓여져 있을때 좋은 action이라는 것은 policy를 실제로 PG로 학습시켰을 경우 action에 대한 확률 분포가 나오므로 가장 확률이 높은 action을 고르는 것이었습니다. 그런데 만약 우리가 모든 state마다 “이 state가 얼마나 좋은지?”를 의미하는 value를 부여할 수 있다고 칩시다. 그러면 어떤 state, \(s_{t}\) 에서 좋은 action이라는 것은 내가 할수 있는 action들을 실행함으로써 그 다음 state, \(s_{t+1}\)로 갔을 때 그 state의 value가 가장 높은 action을 말합니다.

그러니까 매 순간 다 해보고 value가 높은 것들을 찾아가면 그것이 곧 optimal policy 이기 때문에 명시적인 (explicit) policy는 더이상 필요가 없다는 것이죠.

Slide. 3.

앞서 많이 다뤘던 Advantage Function, \(A\)는 “현재 상태에서 \(a_t\) 라는 행동을 하는게 다른 옵션들을 골랐을때의 평균보다 얼마나 좋은가?”를 의미 했습니다.

만약 \(A^{\pi}\)의 가장 높은 값 (argmax)을 나타내는 행동을 하나 뽑으면 \(\pi\) 정책을 계속 따른다는 가정하에 \(s_t\)상황에서 최선의 선택이 될겁니다. (모든 가능한 행동을 고려해서 평균적인 가치를 계산한 것 보다 지금 행동이 얼마나 좋은지를 나타내는 \(A\) 중에서도 최대값을 return할 행동을 골랐으니까요)

하지만 policy가 명시적 (explicit)으로가 아니라 암시적 (implicit)으로 존재할 경우에도, 우리는 policy를 계속해서 업데이트 해 나가야 합니다.

아니, policy가 명시적으로 존재하지 않는다면서 무슨말일까요? 거듭 이야기하지만 따로 network가 있는건 아닌게 맞습니다. 그런데 우리는 어떤 state에서 어떤 action을 할지를 표현하는 policy를 다음과 같이 정의할 수는 있습니다.

현재 policy를 따랐을 때 Advantage가 가장 큰 값만 확률이 1인 policy이므로 다른 action을 할 확률이 없는 deterministic한 policy이죠. 다르게말하면 greedy policy입니다. (맨 처음에는 policy가 모든 action에 대해 균일한 분포를 가지는 random 분포를 갖습니다)

즉 앞서 말한 policy를 개선해 나간다는 말의 의미는 다음의 절차를 의미합니다.

• 1.현재 greedy policy를 사용해서 모든 state에 대해서 먼저 value 값을 구한다.
• 2.각 state의 value값을 기반으로 advantage값을 계산한다.
• 3.각 state에서 advantage가 가장 높은 action의 확률을 1로 만든다 (개선, update)

이를 반복하면 됩니다.

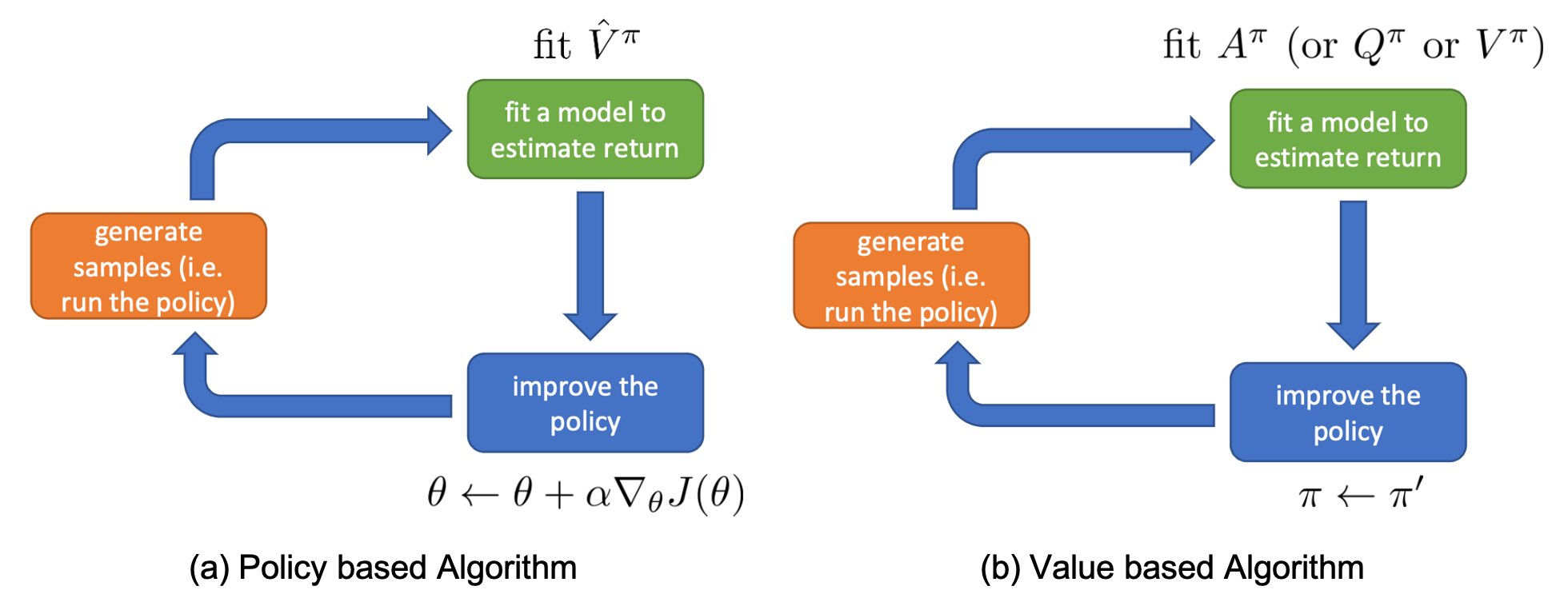Fig. Blue Box가 다른것을 알 수 있다. 정책 경사 알고리즘과 다르게 가치 기반 알고리즘은 더이상 Blue Box에서 정책을 학습하지 않는다.

Policy Iteration

이런 방식을 Policy Evaluation (Advantage 계산) 과 Update가 반복되기 때문에 Policy Iteration이란 이름으로 부릅니다.

Slide. 4.

다시 policy iteration을 정리해봅시다.

• 1.현재 policy하의 Advantage Function 값을 계산 (Policy Evaluation) 한다.
• 2.policy을 업데이트한다. (Advantage 제일 높은 action에 확률 1 할당)
• 3.더이상 policy가 변하지 않을 때 까지, 즉 수렴할 때 까지 1,2를 반복.

그런데 여기서 1번은 어떻게 계산해야 할까요? 어떻게 매 상태마다의 행동이 야기하는 Advantage 값, \(A^{\pi}\)를 평가해야 하는걸까요?

다시, Q,V,A는 아래와 같습니다.

• V Function

• Q Function

• A Function

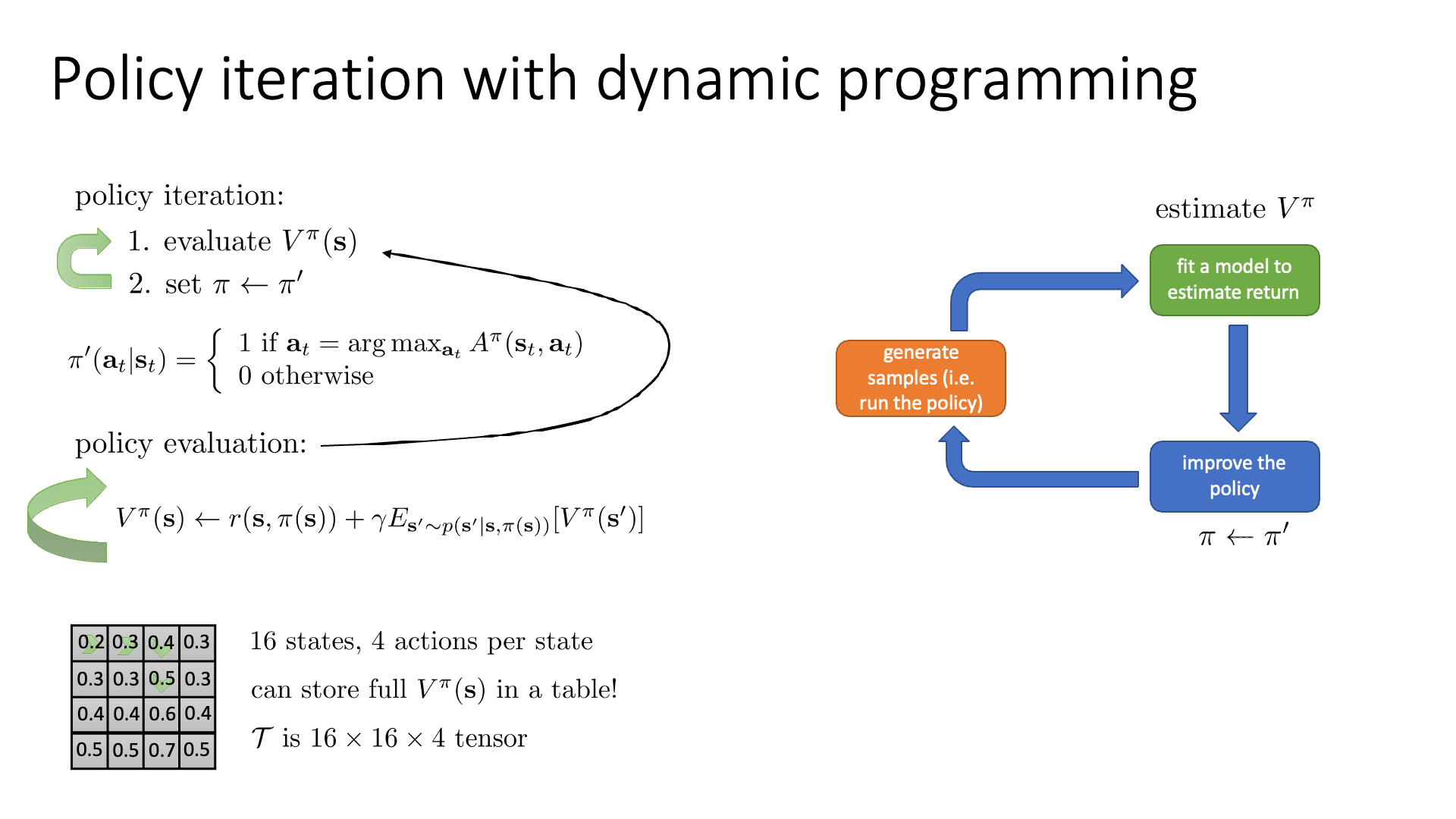
Advantage, \(A\)는 결국 \(V\)만으로 표현이 되기 때문에 \(V\)를 계산해야 하는데, \(V^{\pi}(s)\)를 구하기 위해서는 동적 프로그래밍 (Dynamic Programming, DP)를 사용해야 합니다.

Slide. 5.

여기서 DP로 문제를 푼 다는 것은 하나의 큰 문제를 여러 개의 작은 문제 (sub-problem)로 쪼개서 푸는 것을 말합니다. 즉 하나의 값을 구하기 위해서 그 앞의 값, 앞의 값…을 알아야 하는거죠. DP는 완벽하게 환경을 알 경우 (Transition Matrix 등) optimal solution을 계산할 수 있게 해준다고 합니다.

Sergey가 얘기하는 것 처럼 미로를 탈출하는 example을 생각해 봅시다. 매우 작은 이산적인 (Very Small Discrete) state, action으로 정의된 MDP일 경우 입니다.

• State Space : \(s\) - 미로 16칸
• Action Space : \(a\) - 상,하,좌,우
• State Transition Probability : \(p(s' \vert s,a)\)

여기서 Transition Matrix는 \(16 \times 16 \times 4\)으로 3차원 Tensor가 됩니다. 또한 매 상태마다 가치가 매겨질테니 \(V^{\pi}(s)\)는 16개가 됩니다. 이런 setting에서는 action space 와 state space 모두 몇 안되기에 표 형태 (tabular form, table form)로 value 값을 다 표현할 수 있고 매 state마다 가치를 직접적으로 부여할 수 있다고 합니다.

한 번 계신을 해보죠. (lecture 6에서도 봤던) Value Function에 대한 Bootstrapped update는 다음과 같이 쓸 수 있습니다.

여기서, policy \(\pi\)는 어떤 것이었죠? 맨 처음에는 random policy 였을겁니다 (상,하,좌,우 모두 0.25), 그런데 1 iteration만 지나도 계산한 Advantage 를 가지고 argmax를 취해 가장 A가 큰 action만 확률이 1.0이고 나머지는 0.0인 one-hot policy입니다.

즉 모든 가능한 액션을 다 해본다는 기대값은 아래와 같이 정리가 되는겁니다.

더이상 policy가 좌로 갈확률 0.21, 우로 갈 확률 0.37 ... 처럼 확률적 (stochastic)으로 주어지지 않고 원핫 형태, \([1,0,0,0]\) 처럼 주어져 어떤 상태에서 취할 행동은 정해져 (deterministic)있기 때문입니다.

Slide. 6.

이제 모든 state별로 value를 부여했습니다. 우리가 policy를 업그레이드 하기 위해서는 A를 구해야 하므로 아래의 값을 또 다 계산하고 그 state에서 가능한 action중 가장 A가 큰 action의 확률값만 1로 만듭니다.

이는 직관적으로 아래와같이 모든 tile에 value를 부여하고 인접한 tile간의 value값들을 비교함으로써 더 나은 state로 가는 action만 확률을 1로 부여한다는 걸 의미합니다.

Fig. 녹색 화살표가 의미하듯 각 state에서 최적의 action은 가능한 action중 그 다음 state의 value가 가장 높은 action 뿐이다.

Value Iteration

Policy Iteration이 explicit한 정책 없이 잘 작동하는 것 처럼 보이지만 사실 이는 몇가지 문제점을 안고 있습니다. 강화학습 분야의 세계적인 석학 Richard S. Sutton 의 책이자 강화학습 입문서로 유명한 Reinforcement Learning: An Introduction.를 보면 이에 대한 내용이 나와있습니다.

One drawback to policy iteration is that each of its iterations involves policy evaluation, 
which may itself be a protracted iterative computation requiring multiple sweeps through the state set. 

If policy evaluation is done iteratively, then convergence exactly to v_{\pi} occurs only in the limit. 
Must we wait for exact convergence, or can we stop short of that? 

The example in Figure 4.1 certainly suggests that it may be possible to truncate policy evaluation. 
In that example, policy evaluation iterations beyond the first three have no effect 
on the corresponding greedy policy.

요약하자면 Policy Iteration이 정책 평가를 하는데 시간이 너무 오래걸리며 (A를 계산하는 데), 이를 계속 반복적으로 수행해서 최적의 정책으로 수렴하는 데 너무 많은 시간이 걸린다는 겁니다.

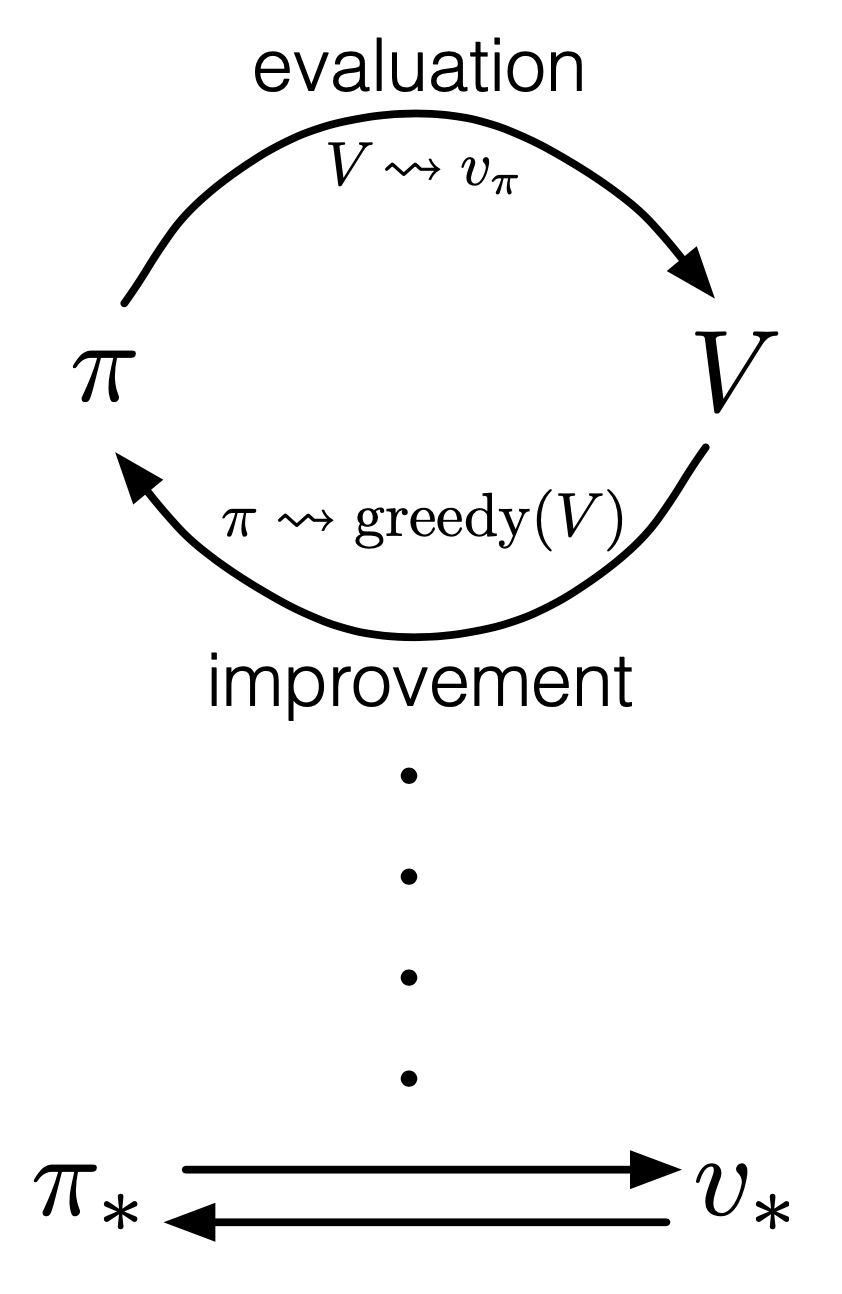Fig. 반복적으로 evaluation, update를 해야하는 Policy Evaluation

그래서 Policy Iteration의 두 가지 스텝을 합쳐서 보다 단순하게 만든 algorithm이 있는데 바로 가치 반복 (Value Iteration)입니다.

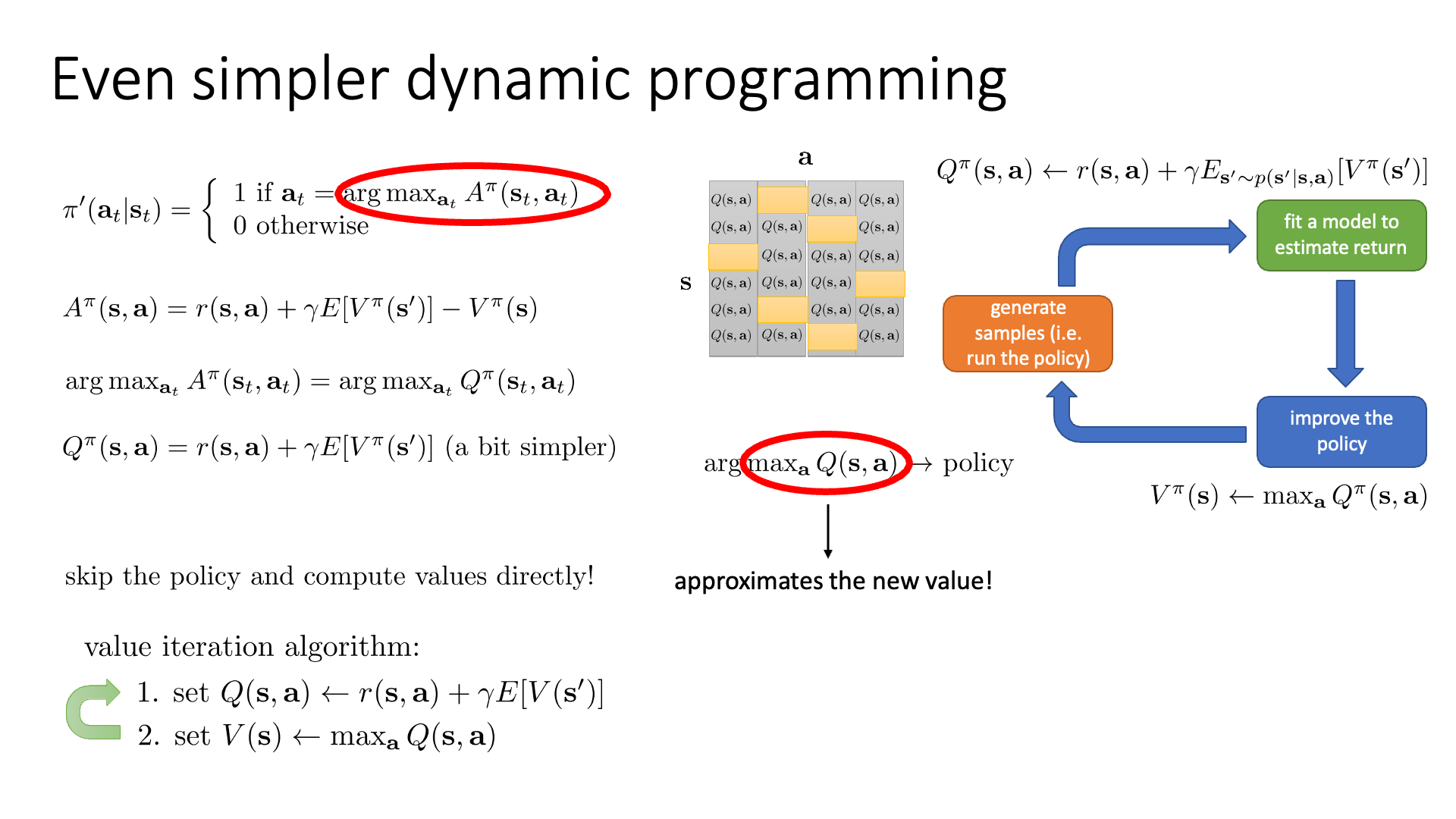Slide. 7.

우리가 policy를 update한다는 것은 A값을 다 구하고 argmax를 구하는 것인데,

사실 여기서 argmax 할 때 action에 dependent하지 않은 현재 state의 value는 영향을 주지 않습니다. 그 다음 state의 value에 현재 state의 value를 모두 공통적으로 빼는것은 있으나 마나 하니까요.

다시 말해서 \(V^{\pi}(s)\)를 빼고 \(Q\)값만으로 판단해도 된다는 말입니다.

Value Iteration은 아래의 Policy Iteration procedure에서

• Policy Iteration
  • 1.state별로 현재 policy를 따라 V를 다 계산
  • 2.V값들로 A=Q-V 계산
  • 3.policy update

1번을 한 뒤에 2번의 A계산을 조금 더 간단하게 \(Q=r+V\)를 계산하는 것으로 (모든 \(s,a\)에 대해서) 대체하고, 마지막 policy를 update하는 부분도 각 state의 value를 \(V(s)=\max_a Q(s,a)\)로 update하는것으로 바꾸면 됩니다.

• Value Iteration
  • 1.모든 \(s,a\) 조합에 대해서 \(Q(s,a)\)를 계산한다.
  • 2.각 \(s\)에서 가능한 \(a\) 중 \(Q(s,a)\) 값이 가장 큰 (max) 값으로 \(V(s)\)를 update한다.

A를 Q로 대체한건 알겠는데 왜 \(V(s)\)를 \(\max_a Q\)로 대체해도 되는걸까요?

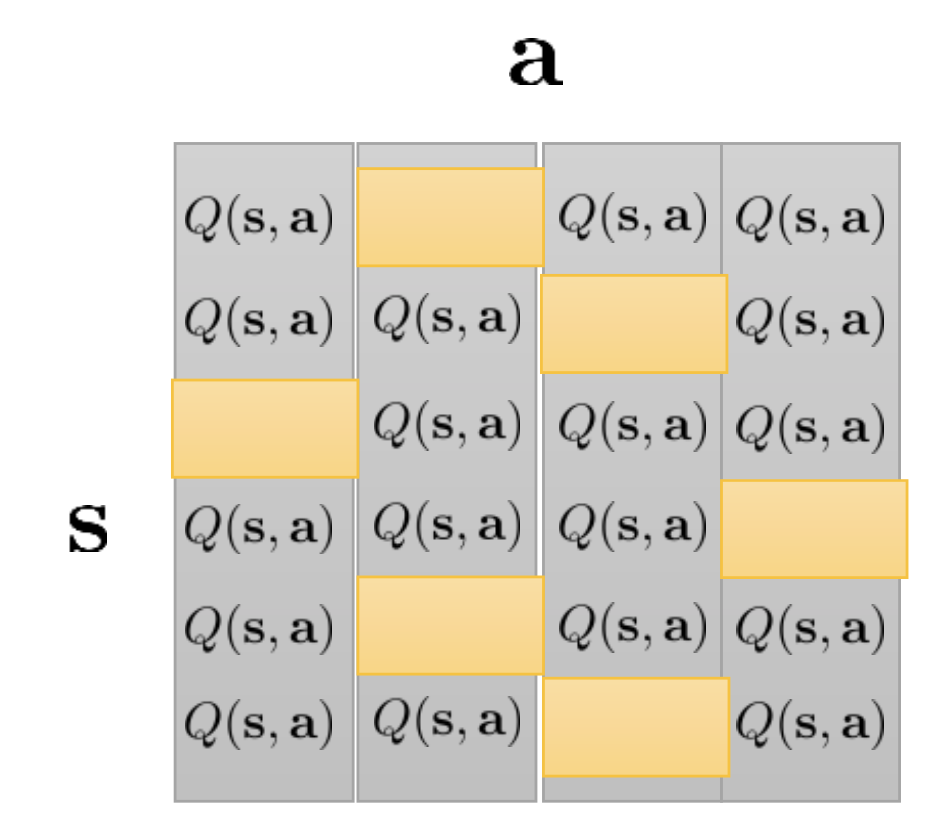Fig. (s,a)를 다 구해야 함. 예를 들어 state수가 16개인 미로이며, 행동이 ‘up,down,left,right’ 4개면, 4x16 = 64

그 이유는 Policy Iteration의 policy update하는 부분이 해당 \(s\)에서 가능한 \(a\)중에서 \(A(s,a)\)값이 가장 큰 action의 혹률만 1로 만드는 것이기 때문입니다. 마찬가지로 원래 value 값은 \(V(s) \leftarrow \mathbb{E}_{a \in \text{<action space>}} [Q(s,a)]\) 인데 policy evaluation의 철학에 따라 가장 좋은 action 하나만 확률이 1이므로 이 기대값은 \(\max_a Q\)가 됩니다.

Fig. Policy Iteration VS Value Iteration. Value Iteration은 policy update과정이 없다.

모든 (s,a) 조합에 대한 value를 알면, 즉 \(Q^{\pi} (s_t,a_t)\)만 계산하면 나중에 inference할 때는 그 state에서 고를 수 있는 action 중 가장 Q값이 큰 action을 고르면 그것이 policy인 것이 되는겁니다.

정리해 보겠습니다. Policy Iteration을 하면 optimal policy를 직접 계산해서 구할 수 있기 때문에 어떤 explicit parameteric policy가 필요가 없습니다. 여기에 Value Iteration으로 가면서 추가로 policy update를 하는 과정까지 빼버렸습니다. 그냥 이제는 V하나만 가지고 지지고 복는거죠. (왜냐하면 Q도 결국 Q=r+V 이므로)

Sergey는 여기서 프로세스가 한단계 더 간단해 질 수 있다고 합니다. 그 이유는 Value Iteration의 step 2를 step 1에 넣을 수 있기 때문인데, Step 1에 Value Function이 들어가는 요소는 \(V^{\pi}(s')\)뿐이고 이를 \(\max_{a} Q^{\pi}(s,a)\)로 대체하면 algorithm을 한 줄로 정리할 수 있게 됩니다. 이것이 바로 Q-Iteration, 더 나아가서 Q-Learning로 발전하게 되며 여기에 Deep Learning 을 결합한 Deep Q-Learning (DQN)이 바로 Deep RL분야의 value-based method 중 가장 핵심적이고 중추적인 algorithm입니다. (곧 나옴)

Policy Iteration과 Value Iteration 둘을 Sergey가 만든 Anatomy로 비교하면 아래와 같습니다.

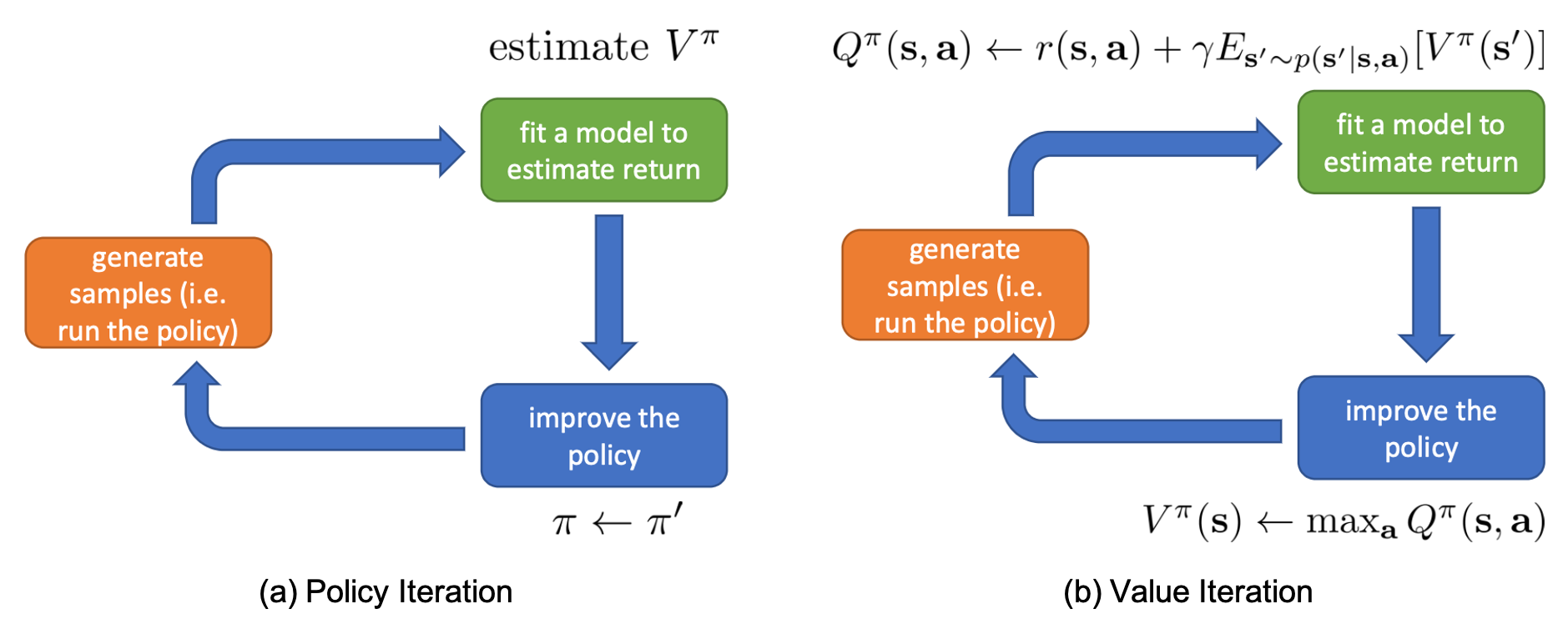Fig. Policy Iteration VS Value Iteration with Deep RL Anatomy

다시 한 번 강조하자면 지금의 상황은 모든 state에 대해 value를 DP를 통해 계산할 수 있기에 가능한 것이며, 이는 당연하게도 real-world에서는 먹히지 않습니다. 실제 보스턴 boston dynamics의 로봇 개인 spot이 움직이기 위해서 이동가능한 모든 state의 value를 다 계산한다는 건 말이 안되잖아요? 이번 chapter의 후반부에 나올 DQN은 이런 문제를 해소했고 엄청난 당시 불가능 할 것이라 여겨지던 video game을 play하는 agent를 학습하는 데 성공해 machine learning 계의 하나의 커다란 이정표가 되었습니다.

Fig. DQN은 Deep Learning, Deep RL 분야에 크게 한 획을 그었다. Source from Pieter’s Lecture

Examples of DP-based Methods

그런데 DP니 뭐니 하면서 수식만 가지고 얘기하면 확실하게 와닿지 않을 것 같아서 (사실 제가 안 와닿습니다), 자료를 조금 더 준비 해 봤습니다.

Value Iteration Example - Grid World

Value Iteration의 example은 Pieter Abbeel의 Foundations of Deep RL Series를 보도록 하겠습니다.

문제 상황은 robot이 함정(-1)로 빠지지 않고 도착 지점(+1)으로 가는 겁니다.

Fig.

Value Iteration에 대한 수식을 이미 정의했지만 더 직관적으로 이해하기 위해 다음과 같이 새롭게 Optimal Value Function을 정의하도록 합시다. 이는 state s에서 시작했을 때 최적의 action을 했을 때 (optimal policy 를 따라 action했을 때) 얻을 수 있는 (discount된) return의 기대값을 의미합니다.

Fig.

Optimal Value Function과 Value Function은 어떤 policy를 따르냐가 다르지만 Value Iteration의 concept을 이해하는데는 어떤 Function을 쓰던 상관이 없는 것으로 보입니다.

Fig. V vs Q. V vs Optimal V .Source from link

우선 action을 하면 무조건 성공한다고 생각하고 (성공 확률= 1.0), discount factor= 1 인 경우에 대해서 생각해봅시다.

Fig.

그럴 경우 다양한 state에서 시작했을 때의 optimal value 값을 구해봅시다.

Fig.

• (4,3)에서 시작: 1. 그자체로 goal에 도착한 셈이기 때문에 움직일 필요가 없음.
• (3,3)에서 시작: 1. right으로 1번 가야하는데 1회 action (t = t+1)에 대해 discount가 되지 않기때매 여전히 value는 1임.
• (4,2)에서 시작: -1. -1에 빠지면 빠져나올 수 없는데 -1에서 시작했으니 여전히 -1임.

나머지 어느 state에서 시작해도 optimal 하게 최단경로로 움직여도 가치는 모두 1입니다.

이번에는 discount factor, \(\gamma=0.9\)인 경우에 대햇 생각해 봅시다.

Fig.

처음부터 계산해 봅시다.

Fig.

• (4,3)에서 시작: 1. 그자체로 goal에 도착한 셈이기 때문에 움직일 필요가 없음.
• (3,3)에서 시작: 0.9. right으로 1번 가야하는데, discount factor가 적용됨
• (2,3)에서 시작: up -> right 2번 가야하므로, 2번 discount됨
• (1,1)에서 시작: up -> up -> right -> right -> right, 5번

이제 discount factor가 적용됨으로써 각 state별로 optimal value 값이 다양해지기 시작했습니다.

이제 여기에 추가로 어떤 action을 할 때 성공 확률이 0.8 로 줄어든 경우입니다.

Fig.

다시 여러 state의 경우에 대해 optimal value를 계산해보겠습니다.

Fig.

먼저 (4,3)에서 출발할 때는 똑같습니다. 그 다음 (3,3)에서 시작할 때는

Fig.

optimal action이 right으로 가는 것 이지만, success rate이 0.8로 줄어들었습니다. 그러므로 다음 state, (4,3)의 value에 success rate, discount factor를 곱한 값을 계산해줍니다. 그런데 여기에 0.2확률이 추가로있죠. 0.1은 down으로 갈 확률, 0.1은 up으로 갈 확률이라고 칩시다.

Fig.

Down으로 가면 (3,2)로 가게되니까 다시 (3,3), (4,3)으로 가야됩니다. Up으로 가면 벽에부딪히기 때문에 여전히 (3,3)이므로 (4,3)으로 한번 더 가야합니다.

Fig.

여기서 수식이 이전과 다른 형태임을 알 수 있습니다. V(3,3)를 구하려면 이제 V(3,3)가 필요하게 된거죠.

이 수식을 일반화 해보면 우리가 앞서 배운 Value Iteration이 됩니다.

Fig.

사실 여태까지 언급하지 않았으나 위에서 value 값을 계산하는데 쓰인 수식은 Bellman Equation이라고 부릅니다. 즉 Value Iteration은 Bellman Equation을 iterative하게 풀게 됨으로써 Optimal Value Function을 찾는 것이라고 할 수 있습니다.

강의 내내 똑같은 수식을 다루긴 했는데 왜인지 Sergey는 이것이 Bellman Equation이라고 언급조차 하지 않습니다. 이는 RL에서 매우 중요한 개념이며, 다른 서적들에서는 맨 처음에 다루고 넘어갈 정도인데 Sergey는 일부러 언급을 하지 않은건지? 아니면 다 안다고 생각하고 그런건지 모르겠습니다. 게다가 이 강의는 value-based를 먼저 설명하는 다른 책들과 달리 policy-based부터 설명 한다는 차이도 있습니다.

아무튼 이 value update에 쓰이는 수식은 Bellman Optimality Equation이라고 하며 (왜냐면 optimal function을 썼기 때문?), 아래의 for loop algorithm은 Value Update 혹은 Bellman update/back-up이라고 합니다.

Fig.

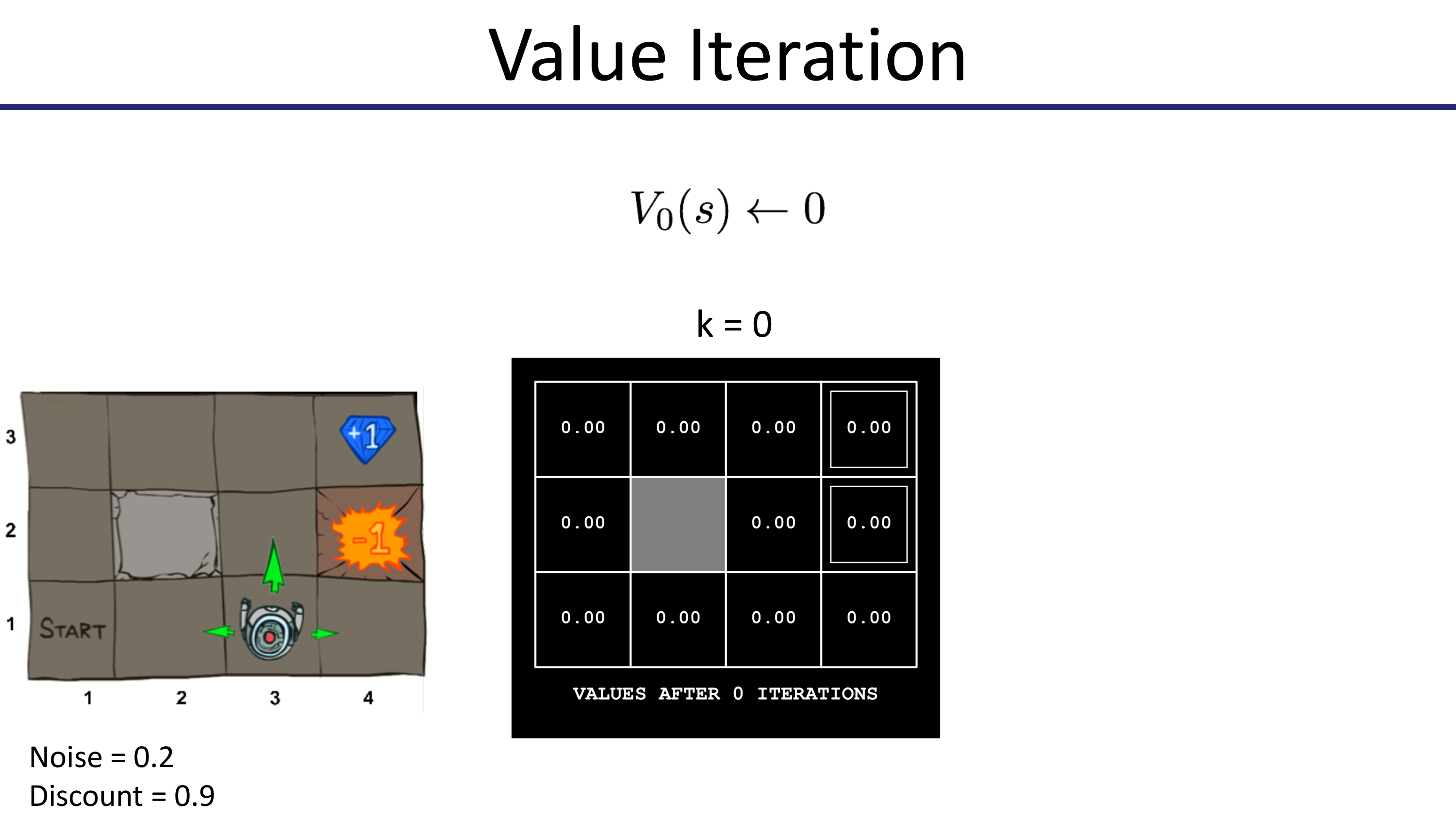
이제 Value Iteration을 통해 어떻게 state별 value update가 되는지 봅시다. 맨 처음엔 모든 state의 value가 0으로 초기화 됩니다.

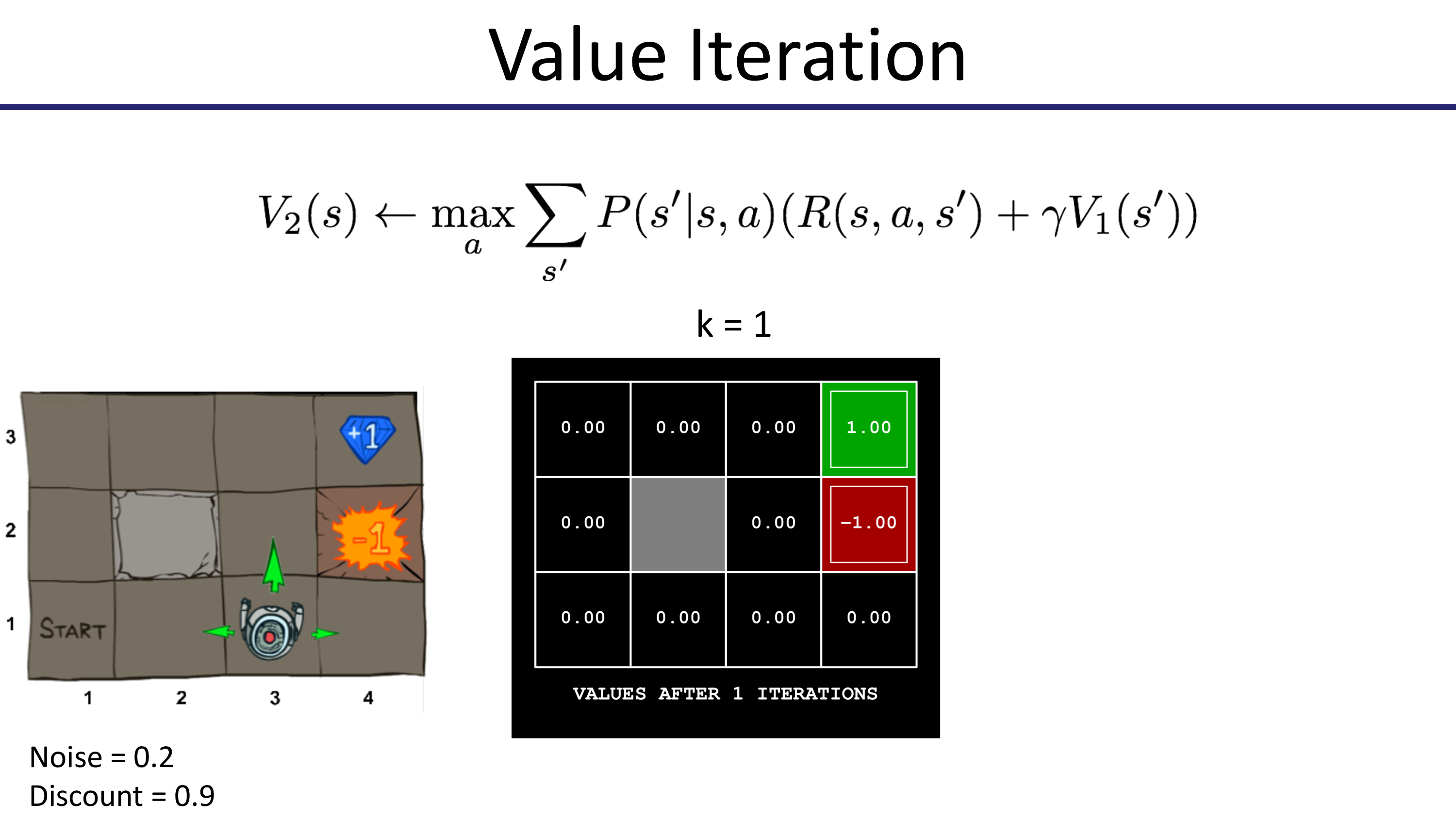
이제 더이상 값이 변하지 않습니다. 100 step 더 해봐야 바뀌지 않습니다. 수렴을 한 것이죠.

이제 현재 state에서 갈 수 있는 다음 state들 중 가장 value가 높은 곳으로 가면 그것이 최적의 action인 것이 됩니다.

Q-Iteration

한 편, CS285에 나오는 Value Iteration은 \(Q\)값을 구하고 \(\max_a Q\)로 \(V\)를 update하는 형태로 실제로는 Q-Value Iteration 이라고 하는게 맞는 것 같습니다.

Fig. Pieter Abbeel Lecture에서는 Optimal Q를 사용해서 표현함. Max Operator로 Value function을 update하는 것이 Value를 계산하는 수식에 포함된 형태임.

앞서 우리가 얘기했던 것 처럼, 모든 \(s,a\)에 대해서 Q값을 계산해야 하고 이를 계속 update함으로써 optimal policy를 찾습니다.

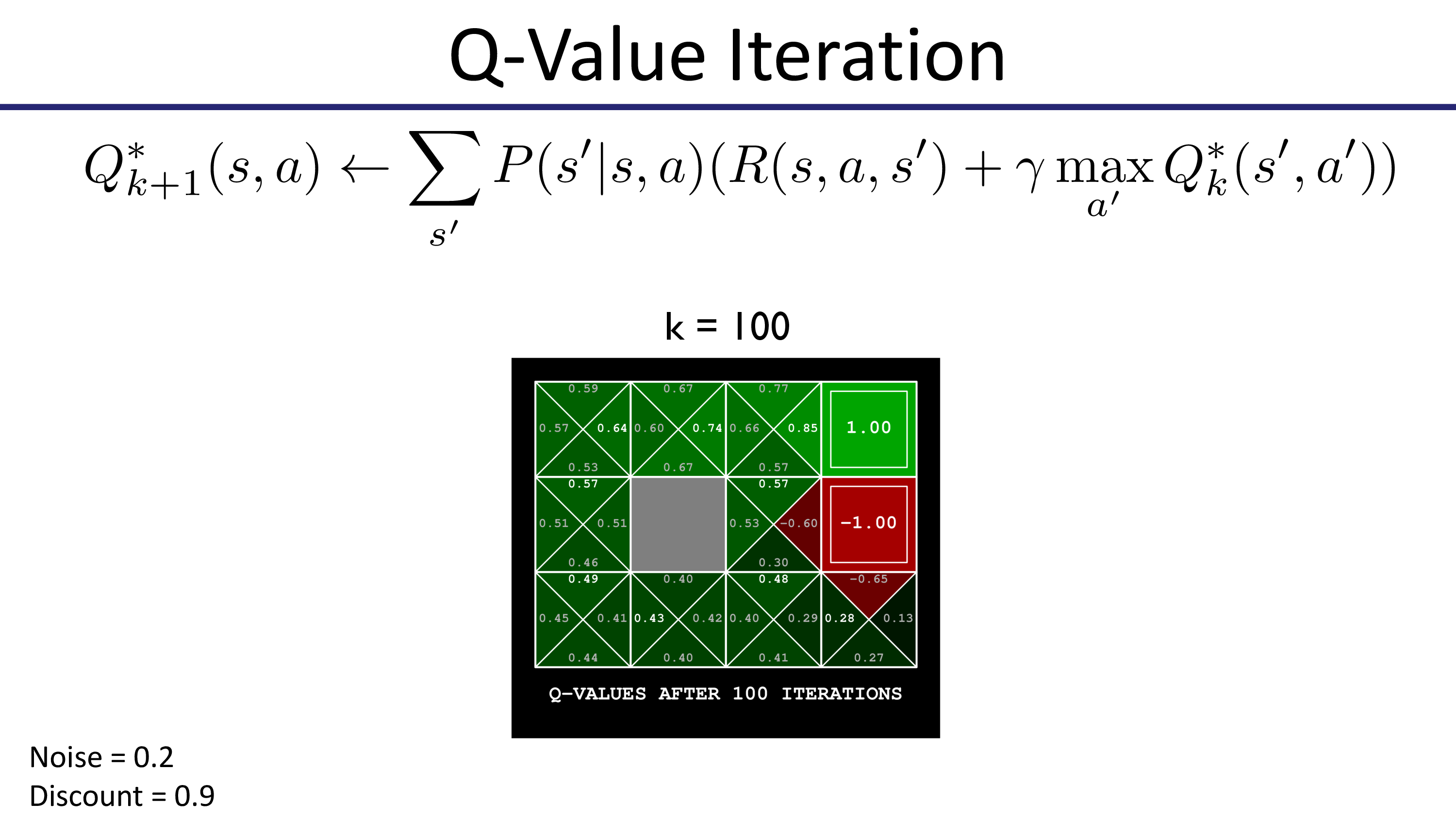Fig.

Policy Iteration Example - 4x4 Grid World

Policy Iteration의 예제로는 Richard S. Sutton 의 책이자 강화학습 입문서로 유명한 Reinforcement Learning: An Introduction.를 보도록 하겠습니다.

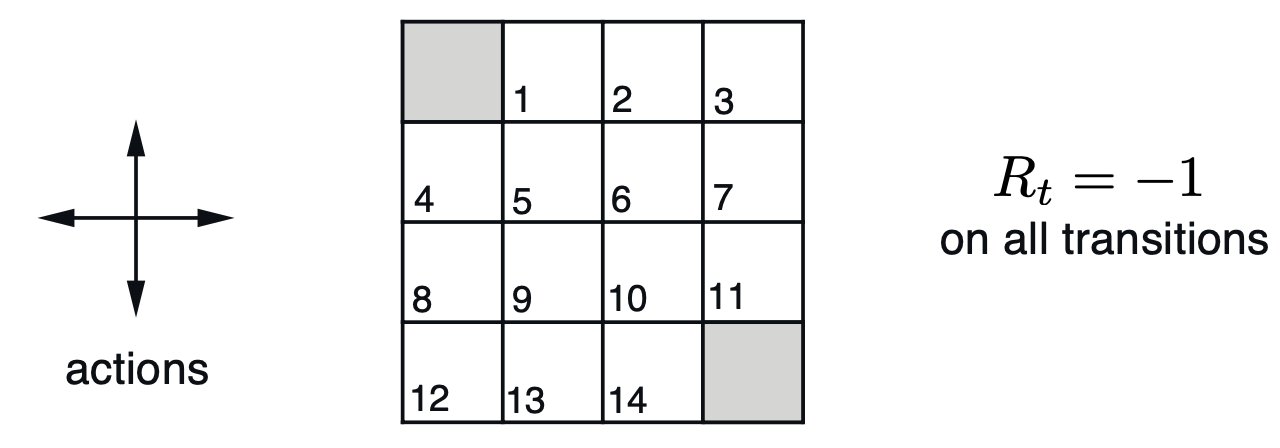Fig. 4x4 Grid World에서 음영 부분으로만 가면 되고, 매번 이동할 때 마다 -1점씩 점수를 까먹으므로 최단경로로 가는게 제일 좋은 정책일 것이다.

Policy Iteration을 통해서 k번째 스텝의 \(V^k\)와 이를 argmax한 \(\pi\)를 보면 아래와 같습니다.

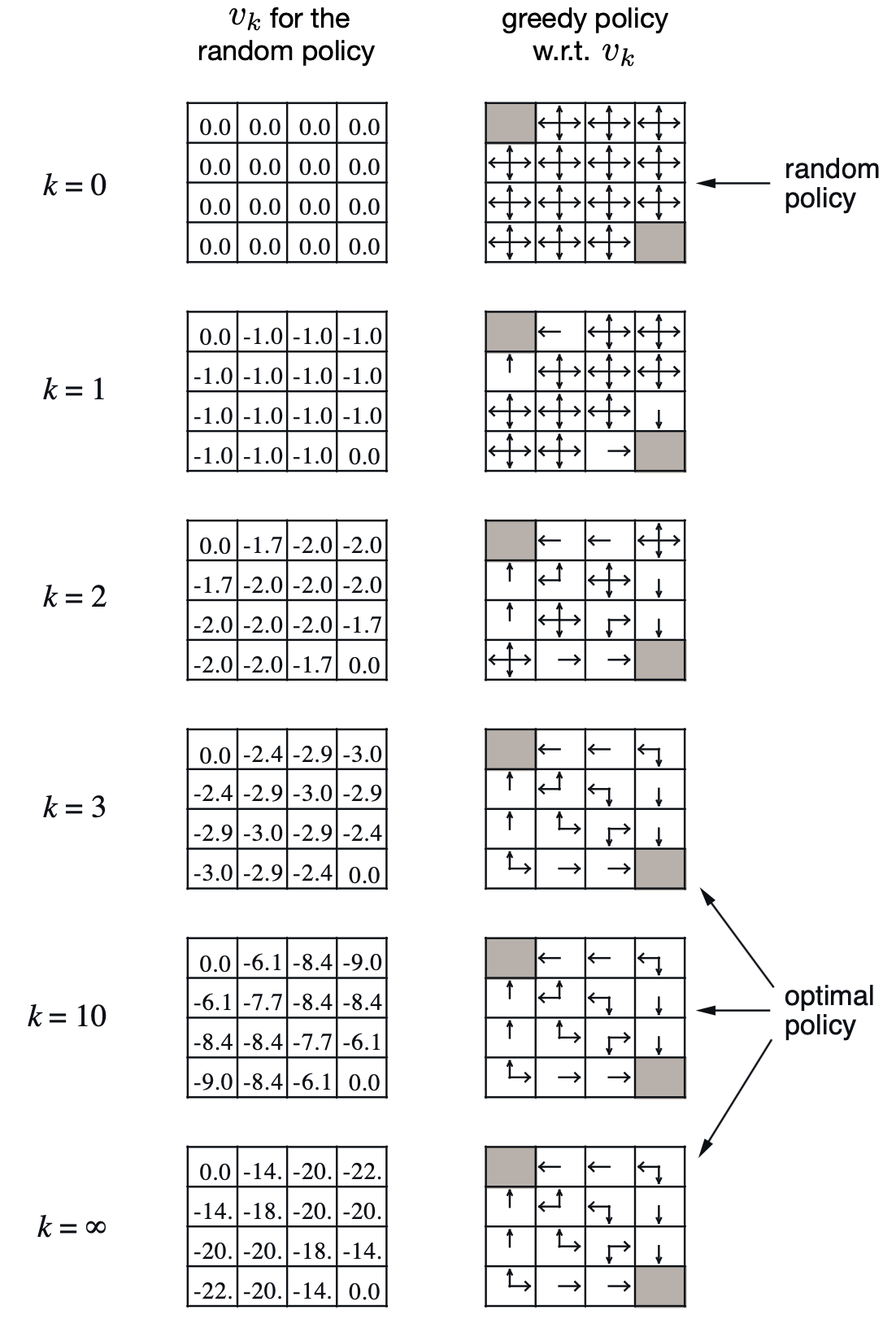Fig. 반복하다보면 결국 어떤 상태에서 어떤 행동을 해야 하는지에 대한 deterministic optimal policy를 얻게 된다.

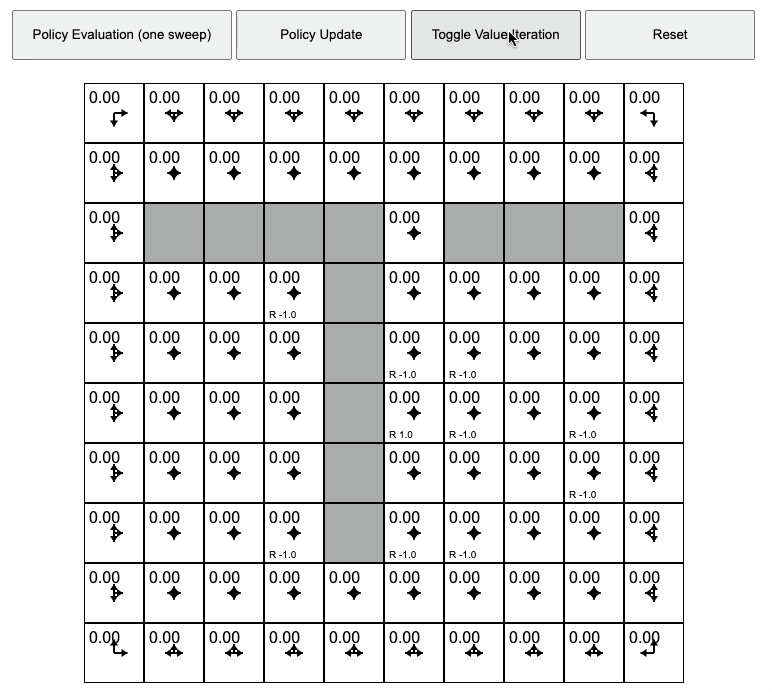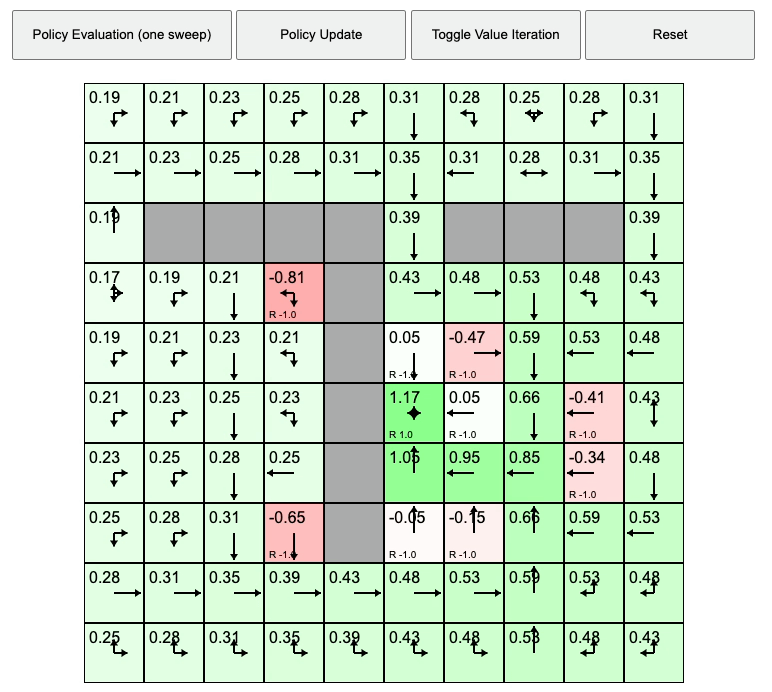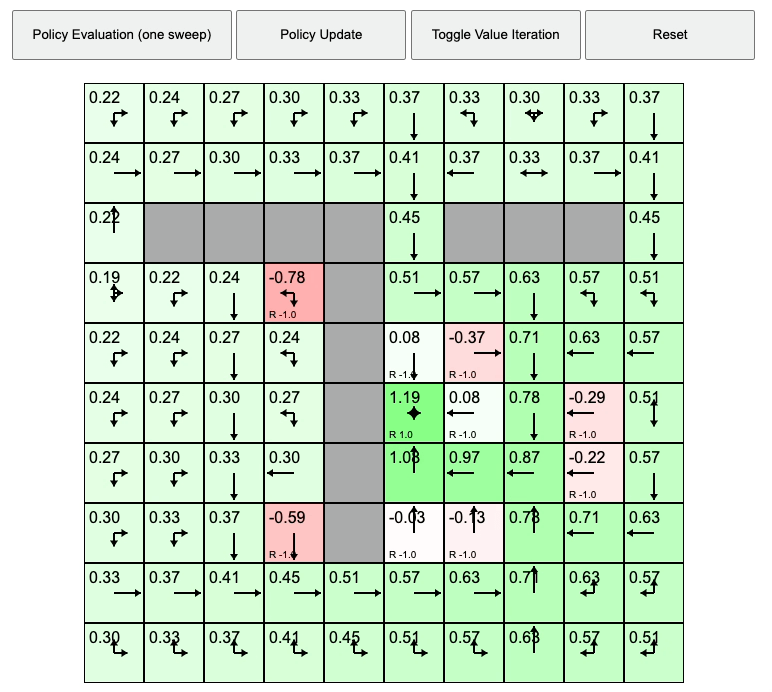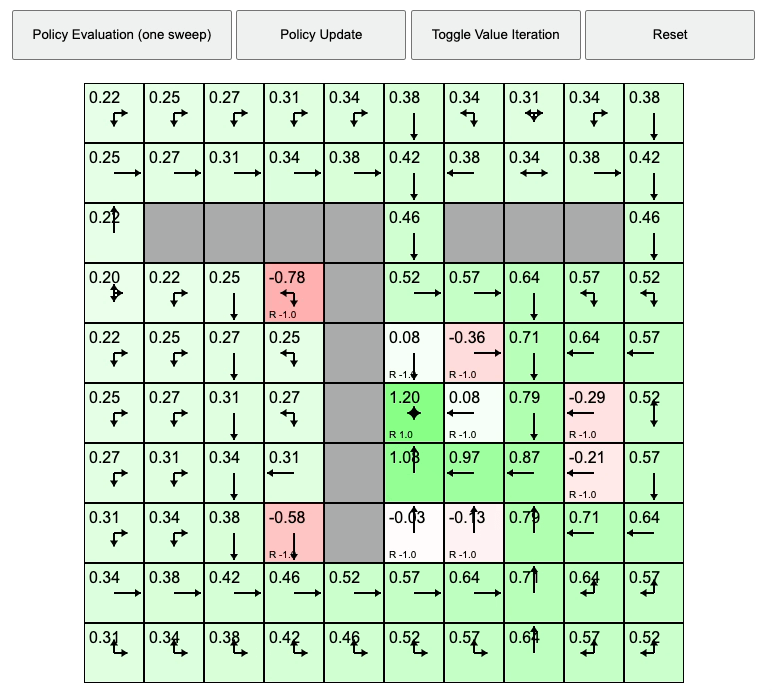
한번 Policy Iteration을 직접 수행해 봅시다. 맨 처음 policy는 random 입니다. ‘상,하,좌,우’로 움직일 확률이 모두 0.25나 되는 것이죠.

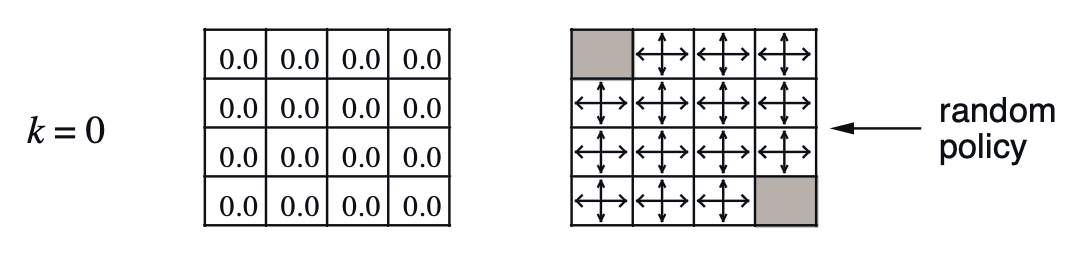Fig. Intial Policy and Values

이를 통해서 6번 tile의 value 값을 계산 해 봅시다.

6번 tile에서 할 수 있는 action은 up, down, left, right 4개이며 각각의 확률은 0.25입니다. 그리고 어떤 state에서 action을 했을 때 transition 확률은 일단 1.0 이며 discount factor, \(\gamma\) 또한 1이라고 생각해 보겠습니다 (noise 없음). up을 했을 때의 경우를 생각해 보겠습니다. 당연히 3번 tile은 goal이 아니므로 받는 reward는 -1 이며 (한번 움직일 때마다 -1), \(V(3)\) 또한 0입니다. 즉 상하좌우 어디로 가든 -1밖에 못받으므로

이처럼 모든 state에 대해서 value 값을 계산하면 아래와 같이 첫 번째 random policy로 인한 각 state들의 value를 얻을 수 있습니다.

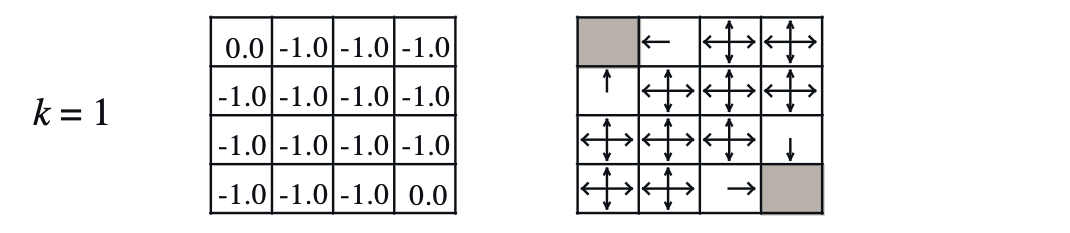Fig. Policy and Values for step 1

오른쪽에 보면 policy가 value에 따라서 update된 것이 보입니다. 어떻게 policy가 update 되었는지는 앞서 설명드린 것 처럼 각 state와 그 때 선택 가능한 action들에 대한 A 값들을 따라서 계산해서 가장 큰 A값을 가지는 action에 대해 확률을 1로 주면 됩니다. (만약 최대값이 여러개면 확률이 분산됨)

이제 \(\pi_1\)과 \(V_{1}^{\pi}\)를 가지고 한번 더 V를 구하고 update하는 과정을 가져봅시다. 또 6번 tile입니다.

6번 tile은 또 값이 작아진 걸 알 수 있습니다. 이번에는 2번 tile에 대해서 계산해 보겠습니다.

또 policy를 update 해야겠죠?

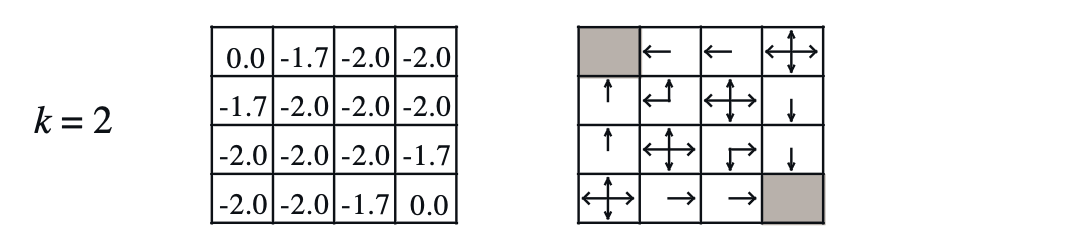Fig. Policy and Values for step 2

이를 무수히 많이 반복한다고 하면 아래와 같이 각 타일의 value값들과 policy가 update 될 겁니다. 그리고 언젠가는 수렴해서 더 이상 변하지 않겠죠. 이제 우리는 각 state별로 어떻게 action해야 하는지 (policy)에 대해서 알게된 겁니다.

Fig. 반복적으로 evaluation, update를 해야하는 Policy Evaluation

Fig. 결국 수렴하는 Policy Iteration. 수렴성에 대한 얘기는 후술할 것.

Effect of Discount and Noise

추가적으로 Discount factor와 Noise가 policy에 어떤 영향을 미치는지 알아보도록 하겠습니다. 아래와 같은 example을 생각해 보도록 하겠습니다.

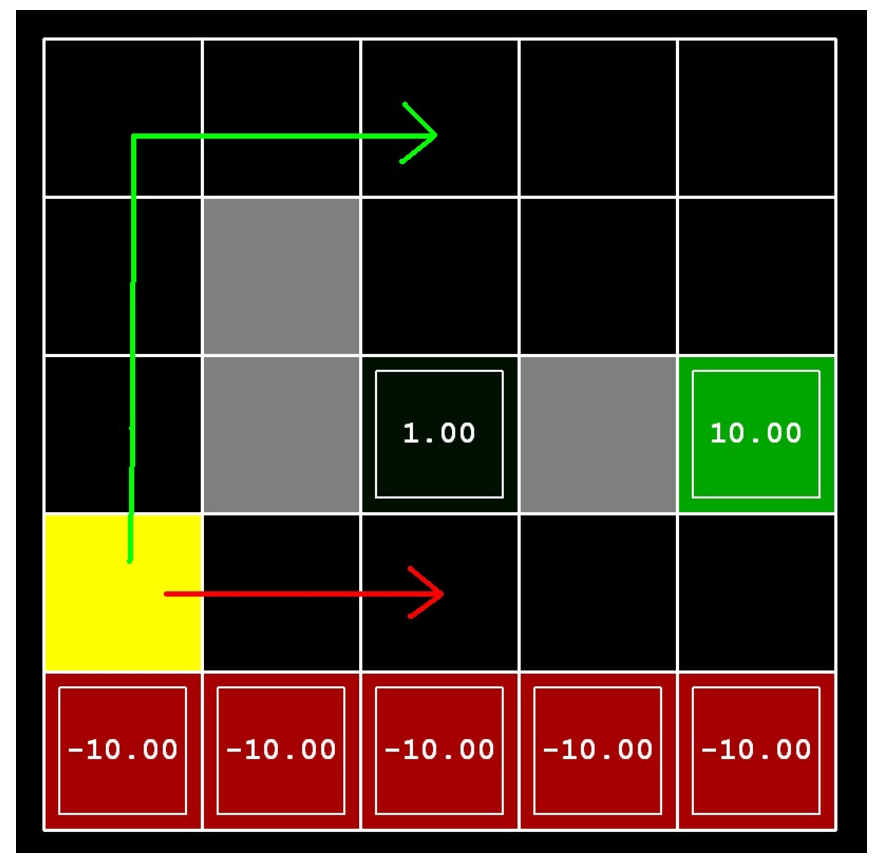
두 가지 탈출 루트가 있는데 가까운 루트 (close exit)는 +1점을 return, 먼 루트 (distant exit)는 +10점을 return합니다. Agent가 어떤 경로로 전진해서 어느 goal로 가는지는 discount factor \(\gamma\)와 noise 확률에 따라 달라진다고 하는데요, \(\gamma\)가 1에 가까울수록, action이 실패할 확률이 있을 수록 어떤 루트가 optimal이 되는지 생각해 봅시다.

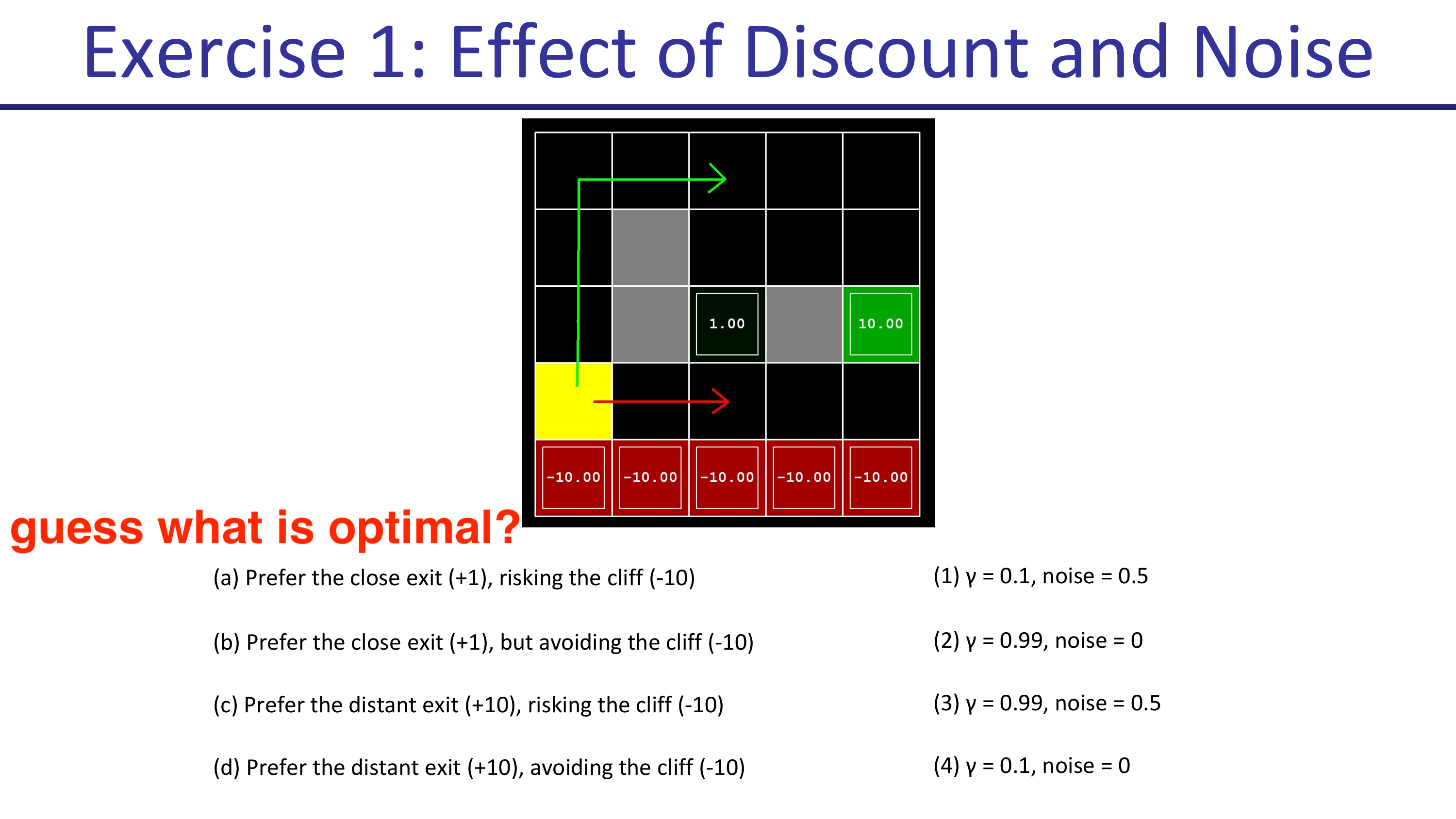
먼저 (a)의 경우입니다. 가까우면서도 벼랑 끝 위험을 무릎쓰는 (risking cliff) 루트를 선호하는 것은 \(\gamma=0.1, \text{noise}=0\)일 때 입니다. 직관적으로 생각했을 때 action을 실패할 확률이 없기 때문에 (좌, 우로 갑자기 튼다던가?), 절벽으로 떨어질 가능성이 없으므로 절벽을 끼면서 갈 수 있는것이며 먼 미래의 reward보다는 가까운 미래의 reward를 더 선호하기 때문에 가까운 경로로 가게 되는 것입니다.

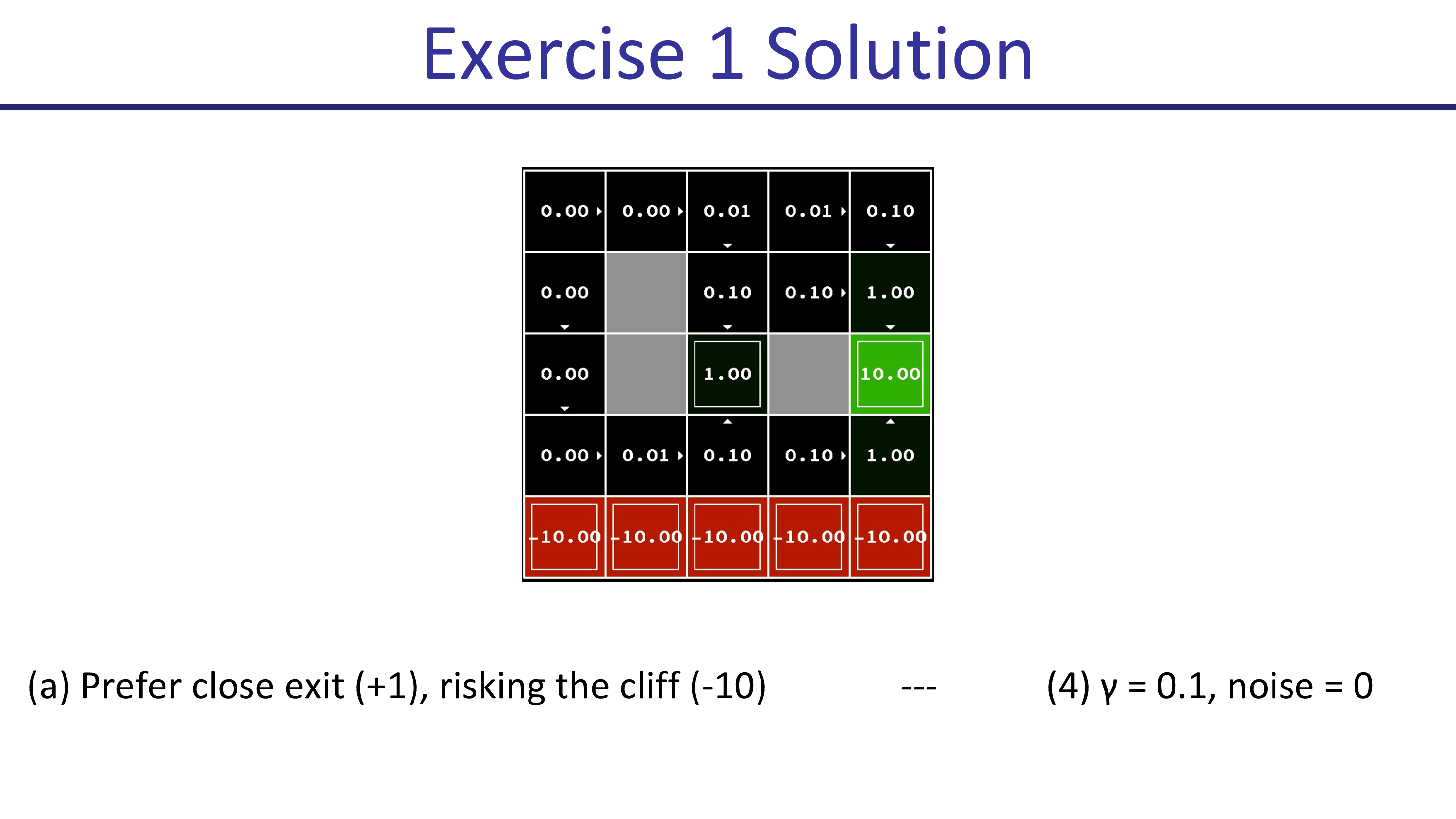
그 다음은 \(\gamma=0.1,\text{noise}=0.5\)인 경우입니다. 이제는 절벽 쪽의 state들의 action들이 모두 위를 향하는 것을 볼 수 있습니다. 실패할 위험이 생겼기 때문에 바로 회피를 해버리는 것이죠. 그러므로 절벽을 우회해서 가까운 경로로 가게 됩니다. (마찬가지로 미래 reward가 너무 discount되어 +10으로 가지 못함)

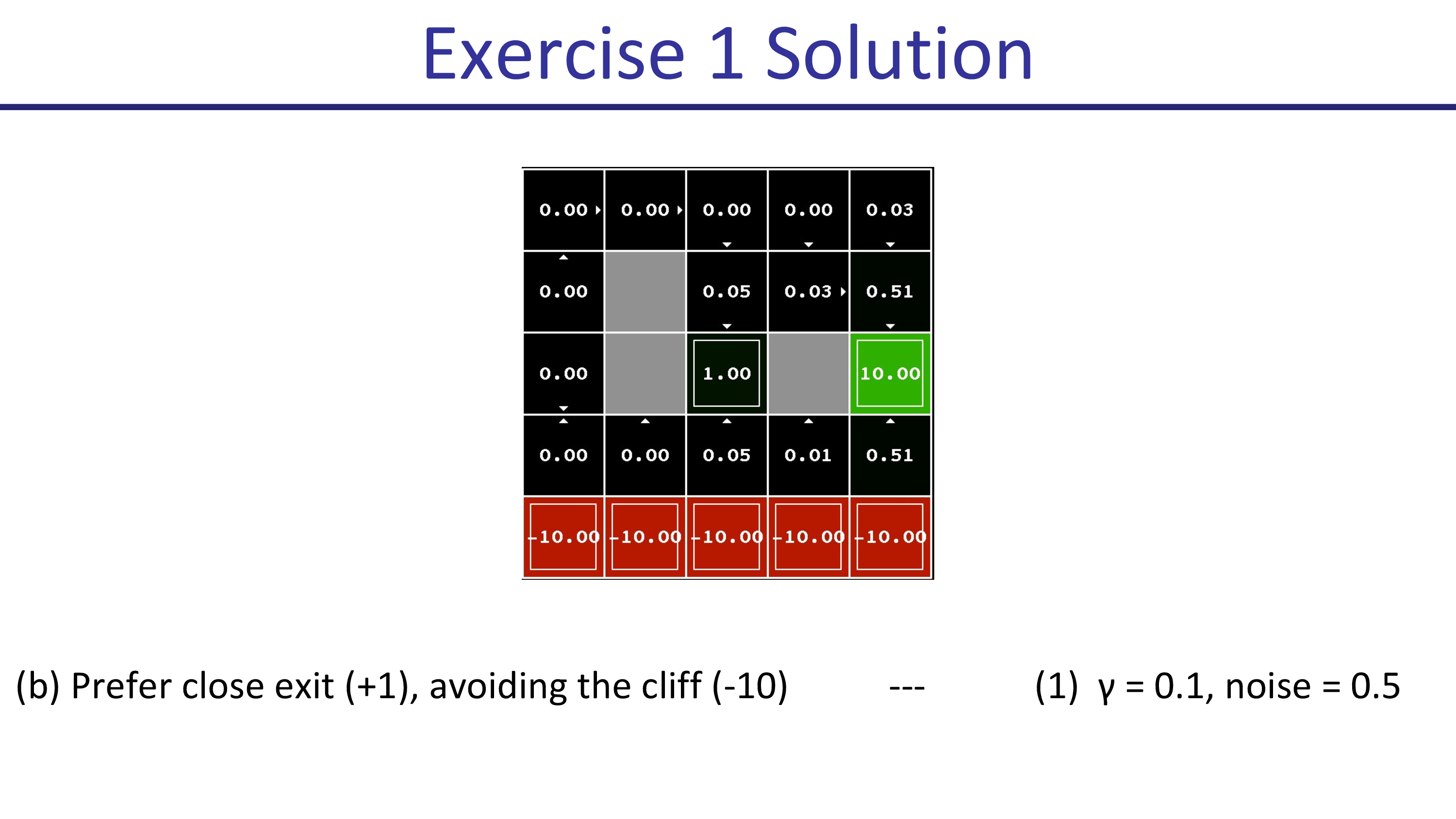
discount factor가 0.99일 때는 아래와 같습니다. 마찬가지로 noise 확률에 따라서 절벽을 우회하느냐 마느냐가 정해지죠.

Andrej Karapthy's Demo for DP method

Policy Iteration Animation. Source from REINFORCEjs

Value Iteration Animation. Source from REINFORCEjs

(이하 Andrej’s comment on DP methods)

실제로 강화 학습 문제를 해결하기 위해 DP를 사용하는 사람들을 자주 볼 수 없을겁니다. 이에는 여러 가지 이유가 있지만, 가장 큰 두 가지 이유는 다음과 같습니다.

• continuous action space와 continuous state space로 확장하는 방법이 명확하지 않다.
• 이러한 업데이트를 계산하려면 environment model (dynamics)인 \(P_{ss'}^a\)에 access할 수 있어야 하는데, 이는 실제로는 거의 사용할 수 없습니다. 우리가 기대할 수 있는 최선의 경우는 Agent가 environment와 상호 작용을하면서 experience를 수집함으로써 이 분포로부터 sample을 얻는 것입니다. 이를 통해 expectation을 sampling으로 대략 평가할 수 있습니다.

그러나 장점도 있긴 합니다.

• 모든 것이 수학적으로 정확하며, 표현 가능하고 분석 가능하다.
• 문제가 상대적으로 작다면 (몇 천 개의 상태와 수십/백 개의 행동까지), DP 방법이 가장 안정적이고, 가장 안전하며, 가장 단순한 수렴 보장이 따르기 때문에 당신에게 최적의 해결책일 수 있다.

Fitted Value Iteration & Q-Iteration

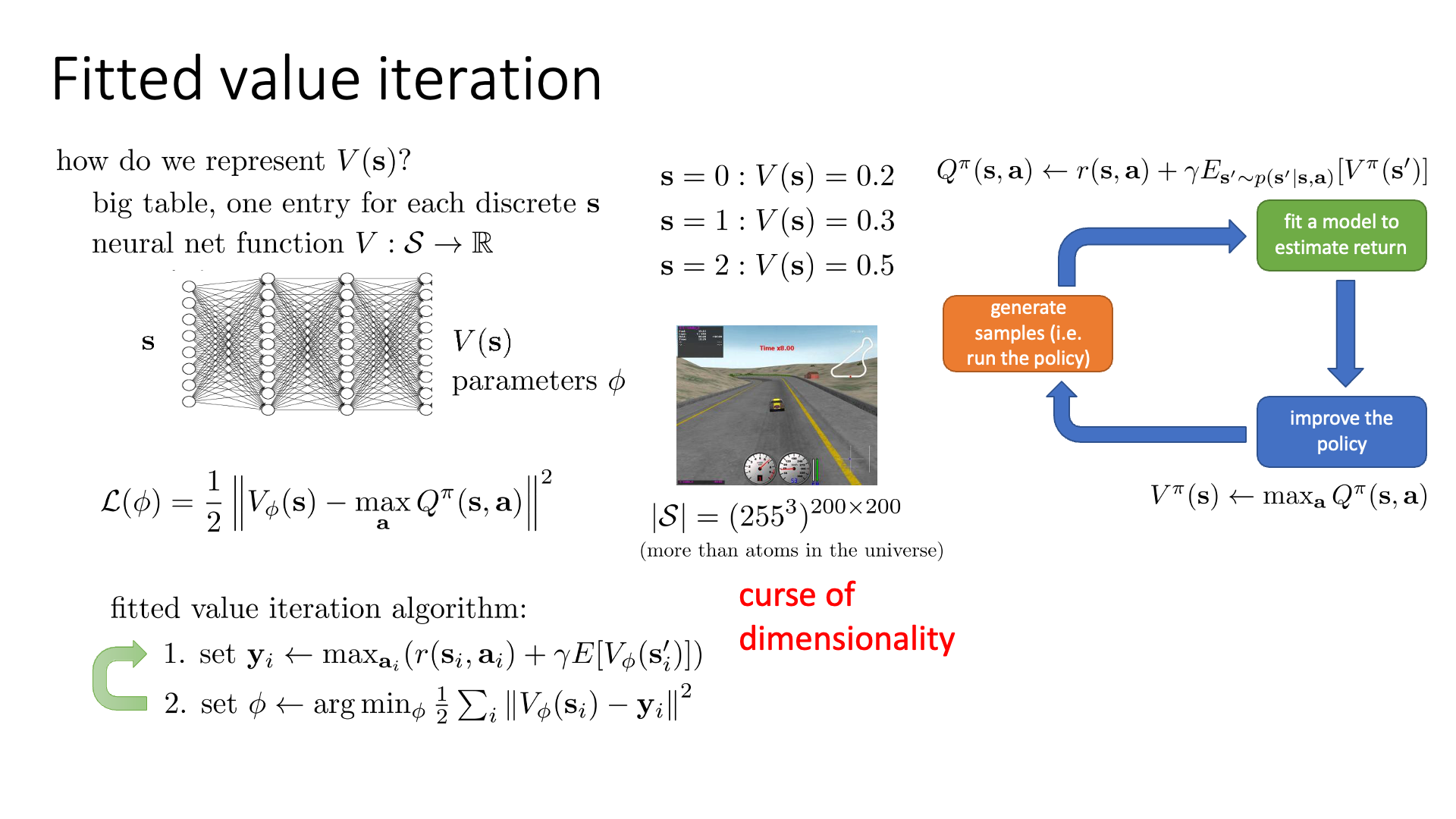
다시 돌아와서, 지금까지 우리는 매우 작은 state-action space 를 갖는 MDP 문제에 대해 어떻게 tabular 형식으로 표현이 가능한 Value Function을 계산하는지?에 대해서 알아봤습니다. 하지만 당연히 real-world problem은 table 형식으로 표현할 수 없으므로 모든 value 값을 다 구해서 optimal solution을 완벽하게 찾아내는 것이 불가능 하다고 합니다.

어떤 racing video game을 한다고 생각해보면 표현 가능한 총 state수가 우주에 존재하는 원자의 수 보다 많은 문제를 풀어야 하는데,
심지어 action space까지 continuous하다면 그 수는 더 커지게 됩니다.

Fig. Tabular 폼으로 나타낼 수 없는 경우. video game에서 agent가 주행을 하면서 변환되는 장면 (frame)들은 결국 pixel의 RGB값이 변하는 것이므로, game에서 마주칠 수 있는 모든 state의 수는 RGB color로 표현한다고 칠 때 frame 비율이 200x200이면 255^3x200x200 이 된다.

Fig. Tabular 폼으로 나타낼 경우 (Value Iteration으로 해결 가능)

이렇게 말도안되는 차원에 대해서 계산을 해야 하는 것을 차원의 저주 (Curse of Dimensionality)라고 합니다. ML에서 쓰이는 것과 거의 맥락이 같은데 RL에서는 이를 특히 Tabular RL을 할 경우 state가 굉장히 높은 차원을 가지고 있어 entry 숫자가 그 차원의 지수승 (exponential) 이 된다는 것을 의미한다고 합니다.

Slide. 9.

우리는 모든 \(s,a\) 에 대해 value를 계산할 수 없고, 어떤 mapping function이 필요합니다. 비슷한 state에 대해서 비슷한 value를 return해 줄 generalization 능력 까지 있으면 좋죠. 바로 Neural Network (NN)입니다.

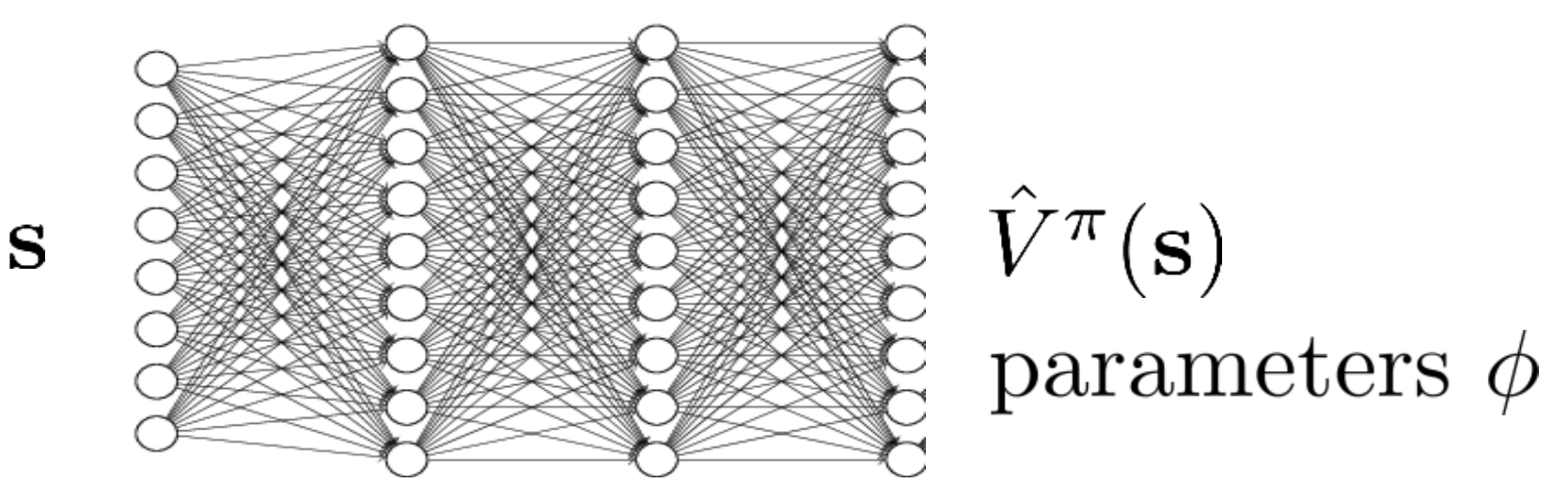Fig. Neural Netowrk as a Function Approximator

이 NN을 학습하려면 당연히 Target Value가 필요하죠? 우리가 Value Iteration을 사용했을 때를 생각 해 봅시다. 우리가 \(V(s)\)를 update할 때 쓴 값은 \(\max_a Q^{\pi} (s,a)\) 였습니다. 그러므로 이 때의 Target Value는 \(Q\)가 될겁니다.

이런 방식을 lecture에서는 Fitted Value Iteration이라고 합니다. (아직까지는 Value Iteration의 틀안에 있는것임)

Fig. Value Iteration VS Fitted Value Iteration

Actor-Critic에서 봤듯 여기서 눈치챌 수 있는 것이 있는데, 바로 NN의 output을 사용해서 계산한 값을 또 target으로 쓴다는 겁니다. 즉 bootstrapped target을 쓰는 것이죠. Fitted Value iteration의 학습 과정을 요약하자면 다음과 같습니다.

• 1.모든 state에 대해서 계산할 순 없으니 sample state에 대해서 가능한 action들에 대해서 \(Q\)값을 계산함 (action space가 discrete 하고 별로 크지 않음을 가정)
• 2.계산한 \(Q\)값 중 가장 큰 값을 target으로 삼고 regression 으로 NN을 update함.

하지만 여기에는 크나큰 문제가 있습니다. 바로 1 step 을 계산하기 위해서는 어떤 \(s\)에서 \(a\)를 했을 때 어떤 \(s'\)으로 움직이는지에 대한 Transition Dynamics, \(p(s' \vert s,a)\)를 알아야만 한다는 겁니다. Value Iteration에서는 이것이 가능했습니다. Karpathy가 말하듯 이것은 model (dynamics)을 안다는 가정이 깔려있기 때문이죠.

과연 어떻게 Transition Dynamics를 모르면서도 Value Iteration 학습을 할 수 있을까요?

Model-Free Value-based Methods: Q-Iteration

우리가 real-world problem에 Value Iteration을 사용하는 데 있어 현재까지 직면한 문제는 3가지 입니다.

• 1.Value를 부여해야 하는 state가 너무 많다.
• 2.Transition dynamics를 모른다.
• 3.같은 state로 돌아가서 action을 여러번 해 볼 수 없다. (V를 계산하려면 필수)

1번은 NN을 도입함으로써 해결했지만 NN의 target을 만들려고 할 때 2, 3번이 문제가 됩니다.

이는 Actor-Critic 때와 비슷하다고 볼 수 있는데, 위의 수식에서 2, 3번은 각각 아래의 point가 문제입니다.

• 기대값을 계산해야 하는데 이를 위해서는 다음 state로의 선택지에 대해 알아야 하며 그 state들이 될 확률이 몇인지 각각 알아야 하며
• 가능한 action들에 대해서 다 해보고 max를 하려면 현재 state에서 가능한 action들을 여러 번 수행해야 하므로 현재 state로 여러 번 되감기를 해서 outcome을 계산해야 한다.

특히 2번에 대해서, 우리가 target, \(y_i\)로 삼기위해서는 현재 state, s 에서 가능한 action, a 에 대해서 그 action을 했을 때의 quantity를 측정해야 함으로 같은 state로 여러번 simulator를 reset하던지 해야하는데, 그게 허용되지 않는 (대부분의) simulator의 경우 \(Q(s,a)\)를 다 구해보고 이 값이 가장 큰 action의 Q값을 target으로 하기가 어려운 겁니다.

그리고 1번에 대해서는 말씀드린 것 처럼 dynamics를 몰라서 정확히 \(Q(s,a)\)를 계산할 수 없다는 것인데, 그러므로 우리는 NN이 표현하고자 하는 값을 수정해야 할 필요가 있습니다.

Slide. 10.

이를 해결하기 위해서 다시 Policy Iteration으로 돌아가 생각을 해 보도록 하겠습니다. Policy Iteration은 위 slide의 좌측하단을 보면 V(s) 계산, policy update를 반복하는 것이었습니다. (원래 V계산하고 A계산한다음에 policy update 했는데, 앞서 말씀드린 것 처럼 A를 max하는 것은 곧 Q를 max하는 것이라고 앞서 얘기했으므로, 아예 Q로 simplification 한 것 같기도 하고… Value iteration과 좀 짬뽕이 되어있는 것 같습니다)

여기서 1번 policy evaluation (V 계산) 하는 과정은 모든 state에 대해서 \(V\)를 recursive하게 계산해야 합니다.

Sergey는 우리가 1번의 \(V\) function recurrence를 하는 과정을 \(Q\) function recurrence를 수행하는 것으로 대체해보자고 합니다. 말이 안될것은 없는것이 \(Q=r+V\) 같은 꼴이기에 NN을 학습하기 위해 V를 구하고, Q를 계산하는 것이나 Q를 계산하는걸 바로 수행하는 것은 결국 같다고 할 수 있습니다.

V나 Q를 계산하는 과정인 Policy Evaluation을 바꾸는것이 어떤 의미가 있는데? 라고 하실 수 있겠지만, 앞서 lecture 6에서 Online Actor-Critic에 대해서 잘 이해했다면 이 둘은 비슷한 맥락임을 느끼실 수 있습니다.

간단히 말하자면 \(V(s)=\mathbb{E}[Q(s,a)]\)는 그 state에서 가능한 모든 action을 했을때 각 \(Q(s,a)\)값의 weighted sum을 한 것이죠, 그러므로 그 state에서 여러번 action을 해서 값을 평균내고 그 과정에서 transition dynamics가 필요했던 것입니다.

반면에 \(Q(s,a)\)는 그 state에서 그 action을 했을 때의 값입니다. 이는 그 state에서 action을 해보고 또 다른 action에 대해 값을 계산하기 위해서 다시 simulator를 reset시킬 필요가 없으며, 우리가 \(V\)와 다르게 \(Q\)는 \((s,a)\)에 대한 함수로 그 state에서 action을 했을때의 값을 추정하기만 하면 되므로, 여러번 계산을 위해 \(a\)를 바꿔가며 계산하고 평균 내는 행위를 하지 않아도 됩니다 (다시 current state, \(s\)로 돌아갈 필요 없음).

(Sergey가 여러 과정을 생략한 것 같아서 좀 헷갈리실 수 있는데, Q와 V사이의 관계와 bellman equation을 잘 생각해보시면 설득이 되실 것 같습니다.)

다시 정리해봅시다.

Fig. From Policy Iteration to Fitted Value Iteartion

우리는 Policy Iteration을 간단히 해서 Value Iteration으로 바꿨다가, 너무 state가 많아서 state마다의 value를 출력해주는 NN을 학습하는 Fitted Value Iteration까지 왔습니다. 여기서 1번에 대해 어떤 state에 대해서 모든 action에 대해 \(\color{blue}{Q(s,a)}\)값을 계산하고 그 중 max가 되는 값으로 \(V_{\color{red}{\phi}}(s)\)를 fitting하려 했으나 장벽에 가로막혔기 때문에, \(Q_{\color{red}{\phi}}(s,a)\)를 각 \(\color{blue}{Q(s,a)}\)로 fitting 하기로 했습니다.

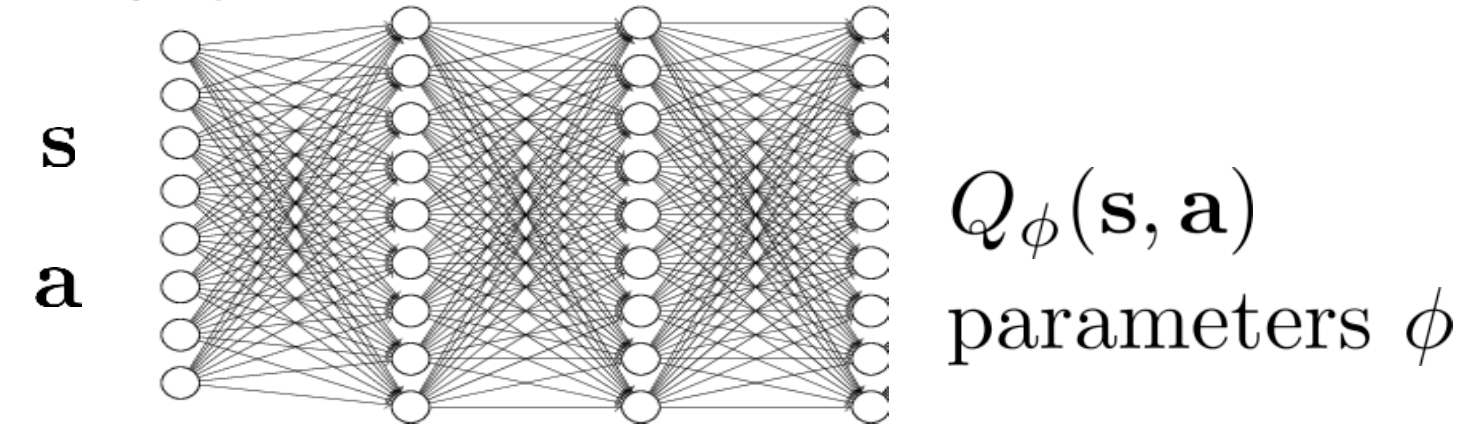Fig. Neural Network for Fitted Q Iteration

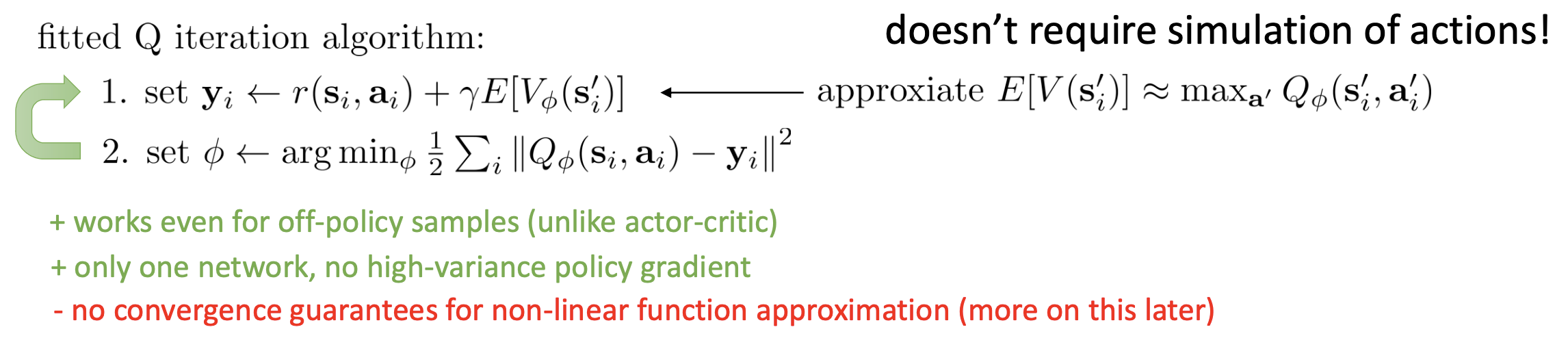Fig. Fitted Q Iteration

변경된 algorithm인 fitted q iteration을 보시면 (바로 위 slide) 1번 수식에 \(\max_{a_i}\)가 빠졌으며, network가 더이상 \(V\)에 대한 network가 아니라 \(Q(s,a)\)에 대한 network임을 알 수 있습니다. 그리고 NN의 target을 계산하는 부분에 원래라면 \(Q=r+\mathbb{E}[V]\) 형태이므로 transition dynamics 분포에 대한 기대값이 필요하지만, 이를 한 step 실제로 가 보는 것으로 대체해 줍니다 (dynamics 모르면 기대값을 계산할 수 없다는 부붑은 어쩔 수 없는 듯).

Fitted Q Iteration은 몇 가지 중요한 특성이 있는데,

• 현재 policy가 아닌 다른 behavior policy가 있어서 그 policy가 뽑은 transition sample들에 대해서도 (s,a,s’) 잘 학습이 됨 (off-policy)
• 수렴성이 보장되지 않음

곧 이 두가지에 대해서 말씀드리도록 하겠습니다.

이렇게 해서 Full fitted Q iteration 알고리즘을 정의했는데, 이 alogirhtm이 학습되는 과정은 다음과 같습니다.

Slide. 12.

가장 최근의 (현재) policy를 따라서 (다시 강조하지만 이는 다른 policy를 써도 됩니다 : off-policy) 데이터를 뽑고, Q 네트워크를 학습하는 과정을 k번 반복하고, 다시 정책을 업데이트하고 이를 바탕으로 샘플링을 하고, … 를 반복하는 겁니다. 여기서 새로운 transition data를 매 번 뽑기보다는 주어진 data로 Q network를 K 번 fitting 하는 과정이 필요하다고 합니다. (바로바로 sample 추가하면 잘 안됨)

Slide. 13. Review는 생략

From Q-Iteration to Q-Learning

Q-Iteration and Off-Policy Algorithm

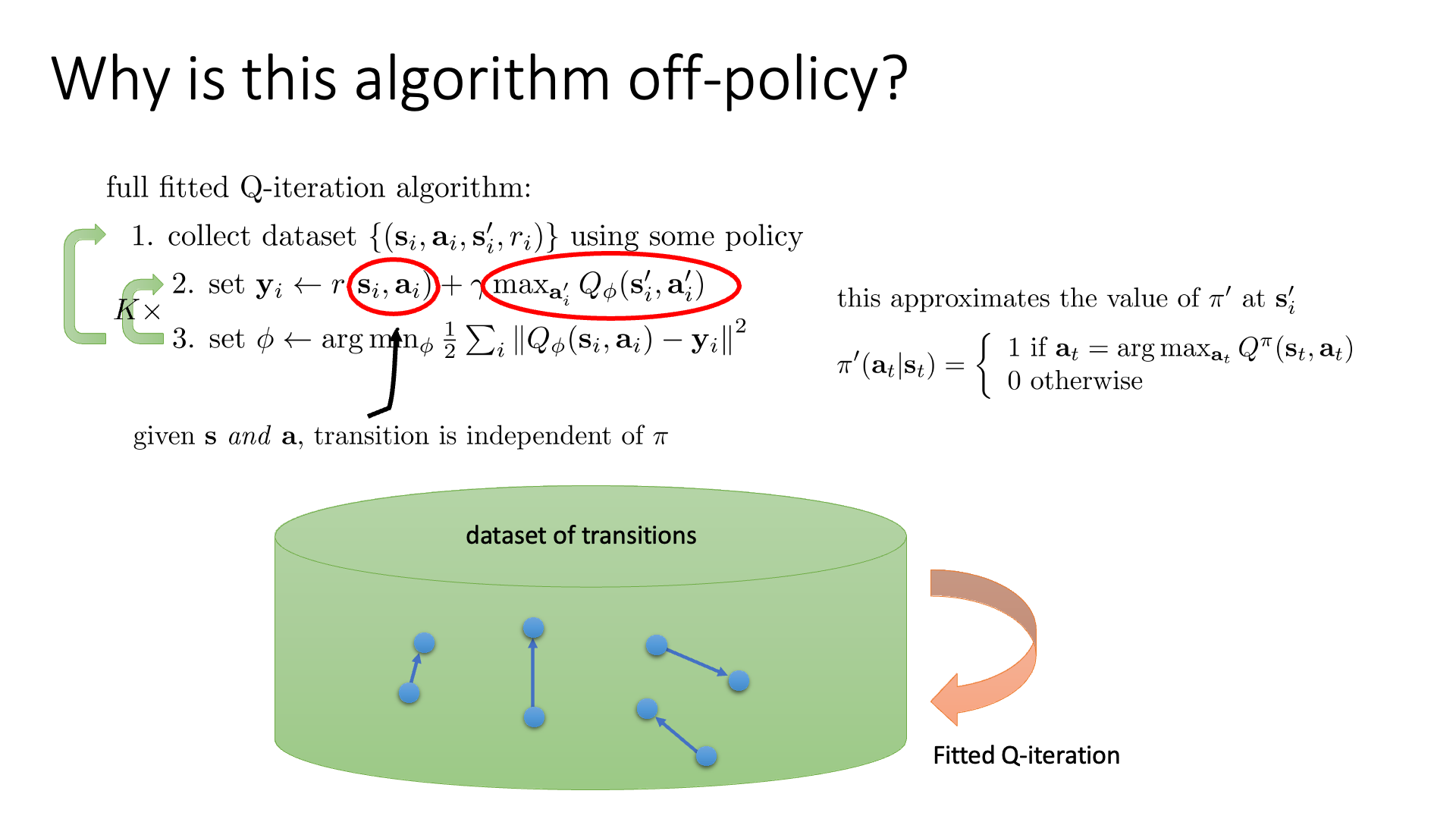
바로 직전에 Q-Iteration의 Off-Policy 특성에 대해 잠깐 언급했습니다. 원래같으면 Actor Critic에서도 그렇고 바로 직전 update step의 policy를 활용해서 sample을 해야 했는데 (지금의 value-based의 경우엔 명시적인 policy가 없긴 하나 각 state에서 가능한 action들 중 Q값이 가장 큰 action이 확률이 1인 것이 policy임), off-policy는 아예 쌩뚱맞은 policy에서 뽑은 sample을 학습에 써도 됐습니다.

그러므로 off-policy는 재활용을 하기 때문에 on-policy에 비해서 sampling이 덜 필요하므로 학습과정이 더 efficient 해질 수 있습니다. (하지만 sample efficiency하다고는 장담할 수 없을 것 같습니다. 왜냐하면 sample efficiency는 good policy를 만들기 위해서 얼마나 많은 sample이 필요한가?를 의미하는 것이지 environment와 interaction해서 sampling을 하는 행위를 덜 한다는걸 의미하지는 것은 아니기 때문입니다.)

Slide. 15.

Q-Iteration에서 이게 되는 이유는 실제로 policy가 사용되는 부분은 수식에서 \(\max_{a_{i'}} Q_{\phi} (s'_i,a'_i)\) 밖에 없기 때문입니다.

우선 어떤 sampling된 transition data는 \((s,a,s')\)가 있어서 이는 replay buffer에 들어가 변하지 않습니다. 그런데 Q Network의 target을 구하기 위해서는 \(s'\)에서 \(a'\)이라는 한 수를 둬 봐야 하는데, 이 값은 policy가 update 됨에 따라서 변할 것이며, 그 때 그 때 Q network에 가능한 action들에 대해서 \((s',a')\)들을 network에 넣어 계산하고 그 중 큰 값을 고르면 됩니다. 그러니까 우리가 replay buffer에서 sampling할 \((s,a,s')\)가 어떤 behavior policy, \(\color{blue}{\pi_{b}}\)에서 뽑혔고 현재 optimization step의 policy는 \(\color{red}{\pi_{k}}\)라고 하면 어떤 behavior policy에서 뽑힌 transition sample이든 \(\pi_{k}\)학습에 쓸 수가 있는 것입니다. (곧 자세히 설명 드리겠습니다.)

Slide. 16. Tabular form을 벗어나면 Fitted Q-Iteration은 regression 의 error값이 0으로 되기 힘든데, 즉 이는 optimal policy로 갈 수 없다는 내용.

Design of Q-Network

추가로 Q-Network의 디자인에 대해서는 아래 왼쪽과 같이 \((s,a)\) 를 input으로 하는 design을 할 수도 있고 아니면 오른쪽과 같이 \(s\)를 받아 \(a\)의 갯수만큼 value를 return해 줄 수도 있습니다. 어차피 푸는 objective는 같은데, 우리가 \((s,a,s',r)\)이 주어졌을 때 \(s'\)에서의 action \(a'\)중 Q가 가장 큰 값을 골라야 하기 때문에 실제 inference를 해봐야 하고, 그 과정에서는 아래 오른쪽 처럼 design하는 것이 좋을 것 같기도 합니다.

Fig. Source from Bowen Xu’s slide

Online Q-iteration: Q-Learning

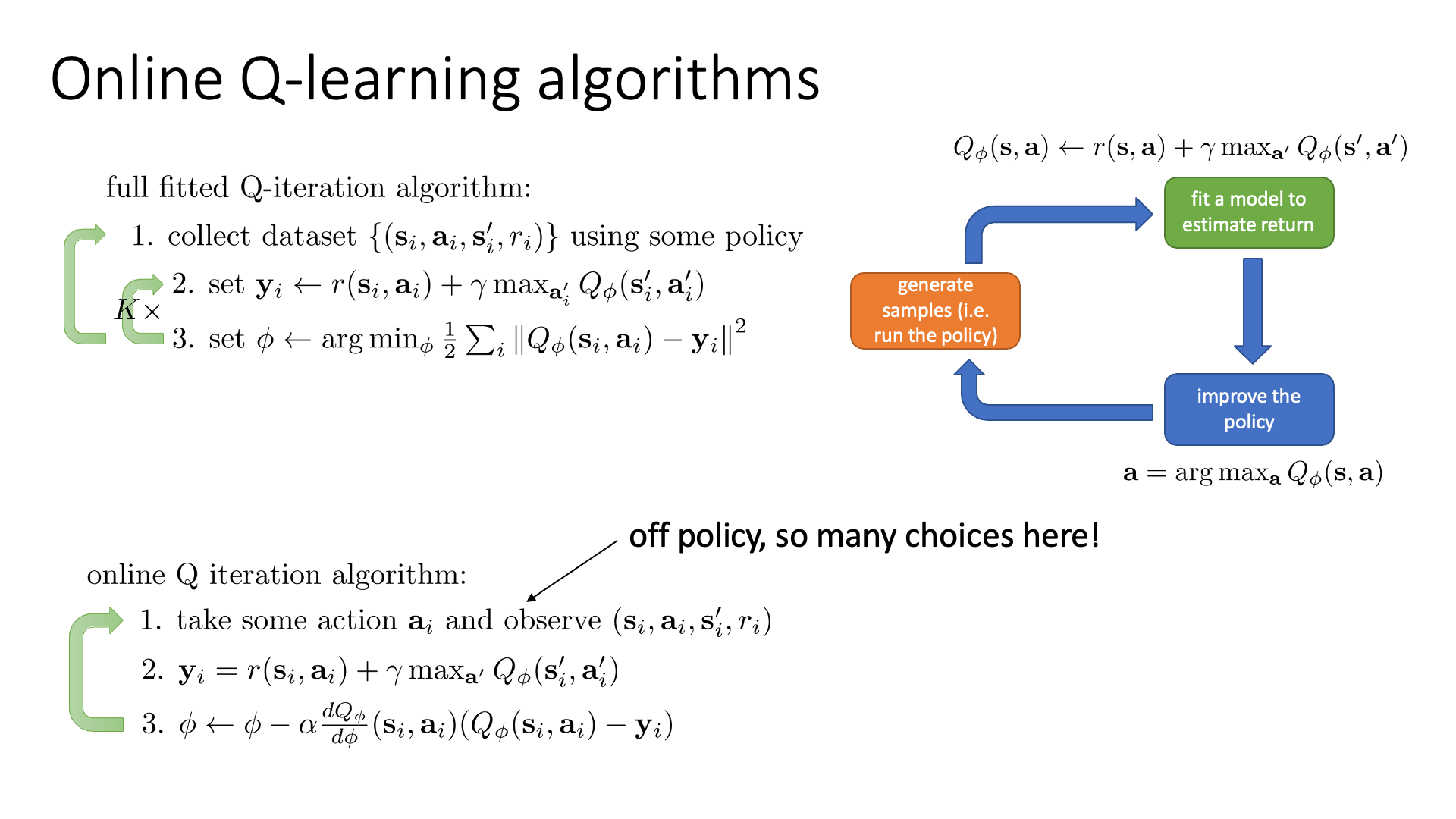
Actor-Critic에서와 마찬가지로 모종의 이유로 (episode가 안끝난다던가 했죠) 1 step씩 계속 update를 한다고 칩시다. 이를 당연히 Online Fitted Q-Iteration라고 합니다. 그리고 이를 (다음장에서 배울) Q-Learning의 classic version으로 1989년에 Watkins라는 연구자가 제안한 Watkins Q-Learning 이라고 한다고 합니다.

Slide. 17.

Online Q-Learning은 1 step transition에 대해서만 바로 update를 하고… 이 과정을 반복하는데, 이 또한 off-policy manner로 할 수 있다고 합니다.

Exploration in Q-Learning

Slide. 18.

우리가 NN을 학습하는데 사용해온 것은 greedy policy (one-hot으로 표현됨) 이었습니다. 하지만 학습을 하는 동안 greedy policy를 쓰는 것은 좋지 않은 idea가 될 수 있다고 합니다. 그 이유는 Iteration의 초반에 행동이 좋지 않았다면 (대개 random policy이므로 안좋을 것) 이 굴레를 빠져나오기 어렵기 때문입니다. 그러니까 “내가 지금 가지고 있는 정책이 뱉는 행동이 최선이 아니며 더 좋은 수가 있지 않을가?”라는 것을 염두에 두고 새로운 수를 탐색 (Exploration) 하거나 아니면 그 수를 그대로 쓰거나 착취? (Exploitation) 하는 두 가지를 조화롭게 사용할 필요가 있습니다.

강화학습을 관통하는 주요 Keyword들은 다음과 같은 것들이 있는데,

• Policy-based vs Value-based
• Model-based vs Model-Free
• On-Policy vs Off-Policy
• Online Learning vs Offline Learning
• Expolration vs Exploitation

이 중에서도 “Expolration vs Exploitation”을 얼만큼의 비중으로 할것이냐 또한 굉장히 중요하다고 할 수 있습니다. 이렇게 매 순간 랜덤성 (randomness)을 조금씩 섞어주는 것이 RL을 굉장히 강력한 policy로 도달할 수 있게 해줍니다.

Greedy Policy를 개선한 방법이 몇 가지 아래에 수식으로 나타나 있는데,

그 중 Epsilon Greedy Algorithm라는 것을 먼저 보겠습니다. 원래는 100 percent의 확률로 Q가 가장 큰 action을 고르는 행위만 했으나 이제는 다른 행동을 샘플할 확률이 \(\epsilon\)정도는 되는겁니다 (물론 매우 작은 숫자). 학습을 하는 동안에는 \(\epsilon\)에 다양한 변화를 주는데, 그 이유는 학습 초기에는 정책이 별로 좋지 못할 가능성이 큰데 반해 policy가 잘 학습되면 너무 자주 Exploration을 할 필요가 없기 때문이죠. 처음에는 Exploitation 비율을 크게 주다 점점 줄여주는 겁니다.

두 번째는 Q-Value에 Exponential을 취하는 Boltzmann Exploration 기법이라고 하는데, ML에서 많이 쓰이는 방법으로, Softmax 를 구할 때 처럼 exponential을 취해 값을 양수로 유지하면서 random성을 부여하는 겁니다. 이는 당연히 optimal action이 아닌 action들은 0에 가까운 값이 할당되므로 매우 적은 확률로 sampling이 되는 상황일테지만, 언제나 argmax를 하는 상황은 이제 아니기 때문에 마찬가지로 탐색의 여지가 남게 됩니다.

Epsilon Greedy가 많이 쓰이긴 하지만 Boltzmann Exploration도 좋은게, 예를 들어 어떤 정책이 어떤 상태에서의 행동들에 대한 확률을 리턴할 때 첫 번째 best action이 Q값이 \(31\)이고 두 번째 action의 Q 값이 \(30\)일 경우 Epsilon Greedy의 경우 Q=31인 action을 뽑을 확률이 1에 가깝고 그와 비슷한 Q=30인 action은 0에 가까운 데 반해, Bolzmann은 이 둘이 비슷한 확률을 할당하게 됩니다.

Exploration & Exploitation 은 RL의 핵심 요소이기 때문에, 강의를 꽤 진행하고 나서 다시 한 번 다룬다고 합니다. (lecture 13 & 14 참고)

Slide. 19. 리뷰는 넘어가도록 하겠습니다.

Temporal Difference (TD) Learning: Q-Learning vs SARSA

새삼스럽지만 강의 중간에 갑자기 여기서 Sergey가 시간차 (Temporal Difference; TD)라는 용어를 씁니다. 그런데 이는 새로운 것이 아니라 우리가 여태까지 배운 것으로 \(r(s,a) + \gamma \max_{a'} Q_{\phi}(s',a')\) 같은 걸 의미합니다. 앞서 Bootstrapped Actor-Critic에서도 비슷한 방식이었고 Q-Iteration또한 이렇게 해왔는데, 현재 상태의 가치 \(V(s_t)\)를 그 다음 스텝의 가치 \(V(s_{t+1})\)를 사용해서 업데이트 하는, \(t\)와 \(t+1\)의 시간차이를 이용해 미래의 가치를 앞으로 가져와 학습하는 것을 시간차 학습을 바로 Temporal Difference (TD) Learning이라고 합니다.

Sergey나 Pieter Abbeel처럼 RL의 대가인 David Silver의 slide를 보면 Monte Calro (MC)나 Temporal Difference (TD), 그리고 Dynamic Programming (DP)이 어떤 값을 현재 state의 value로 땡겨오는지에 대한 figure가 있습니다. (딱봐도 할수있다면 DP를 해야할것 같고, MC는 너무 naive해보입니다)

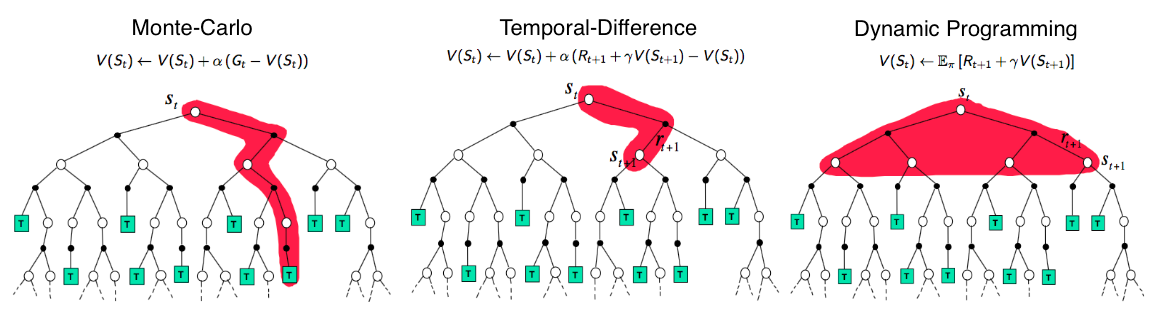Fig. Image From David Silver

본 lecture에서는 제대로 언급하거나 다루지 않지만, value-based method 중 Q Function을 사용한 TD Learning은 사실 두 가지 형태로 쓸 수 있는데 이는 다음과 같습니다.

• On-Policy TD Control : SARSA

• Off-Policy TD Control : Q-Learning

여기서 On-policy TD algorithm을 특별히 SARSA라고 부르는데, 그 이유는 \(s_t,a_t,r_t,s_{t+1},a_{t+1}\) 을 사용하기 때문입니다. 그리고 Off-policy TD algorithm은 방금까지 살펴 본 (Watkins의)Q-Learning이라고 부르며 이 둘의 단 하나의 차이는 max operator의 유무입니다.

하지만 이 max operator가 있음으로써 이 두 algorithm은 극명한 차이가 발생하게 되는데, 이 것 때문에 하나는 on-policy이며 다른 하나는 off-policy가 됩니다. 그리고 SARSA는 더 안전하고 정책에 일관성을 유지하지만, 수렴 속도가 느리고 데이터 효율성이 낮은 반면에, Q-Learning은 빠른 수렴과 최적성을 제공하지만, 과대 추정과 위험한 행동을 취할 수 있는 차이가 발생합니다.

왜 그럴까요?

먼저 왜 SARSA는 on-policy이고 Q-Learning은 off-policy인가?에 대해서 얘기해봅시다.

Fig. SARSA. SARSA는 S,A,R,S’,A’을 사용해서 update한다.

Fig. SARSA. Q-Learning은 S,A,R,S’을 사용해서 update한다. 즉 A’은 나중에 채워넣으면 된다.

아래와 같은 \(4x4\) grid world에서 목표지점 (하트 모양)에 도달하는 것이 goal 이라고 생각해 봅시다. 그리고 한번 이동할때마다 reward=0 이며, 번개 모양 함정에 빠지면 -100점이 됩니다. 현재 policy 를 가지고 \((4,2)\)에서 위로가는 action을 했다고 칩시다. 그러면 환경은 즉각적으로 reward를 줄것이고 (0점), 그 다음 state, \(s'\)은 매우 높은확률로 \((3,2)\)가 된다고 칩시다. 여기서 다음 state가 \((3,2)\)가 될 확률이 완전 1은 아니고 거의 1이며 transition dyanmics는 모른다고 칩시다. (높은 확률로 그 곳에 도달할겁니다.)

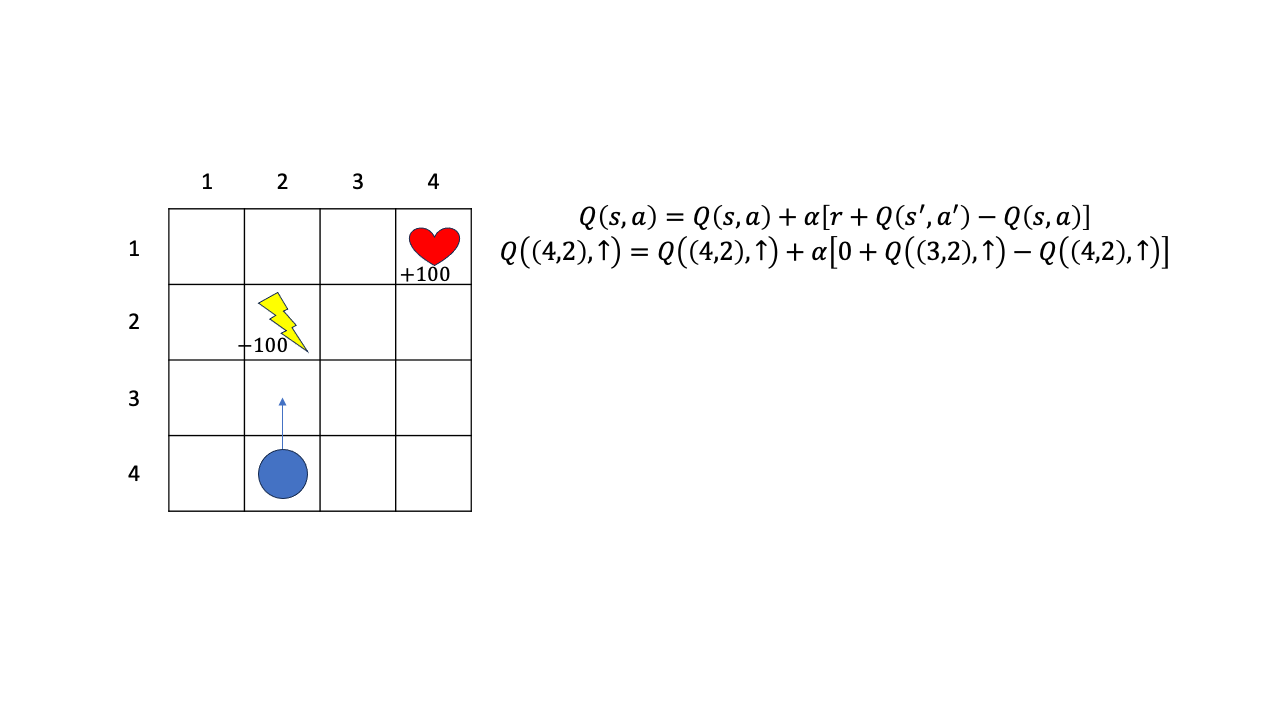Fig.

그리고 \((3,2)\)에서 할만한 action이 current policy가 초기단계에 가까워서 위로 가는 action에 높은 Q를 할당했다고 칩시다.

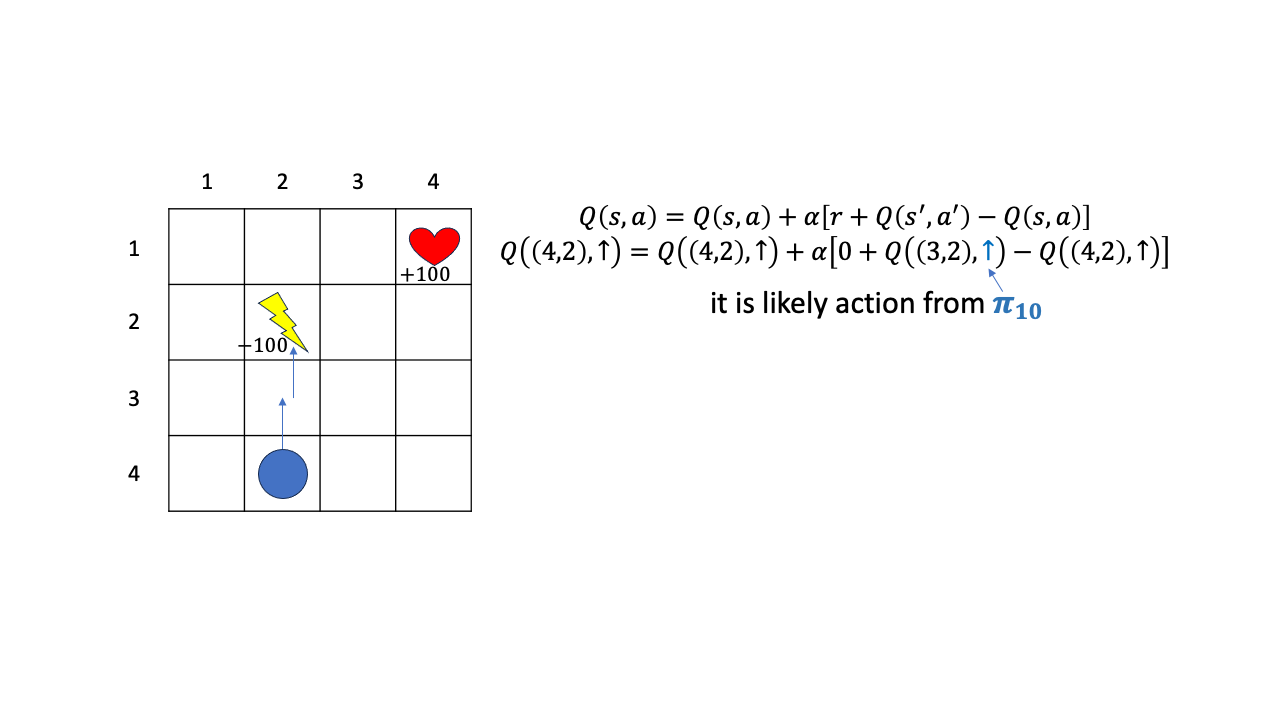Fig.

그러면 이 policy, \(\pi_{10}\)으로 뽑은 transition을 나중에도 학습에 쓸 수 있을까요?? 일단 어떤 buffer에 caching해 둔다고 칩시다.

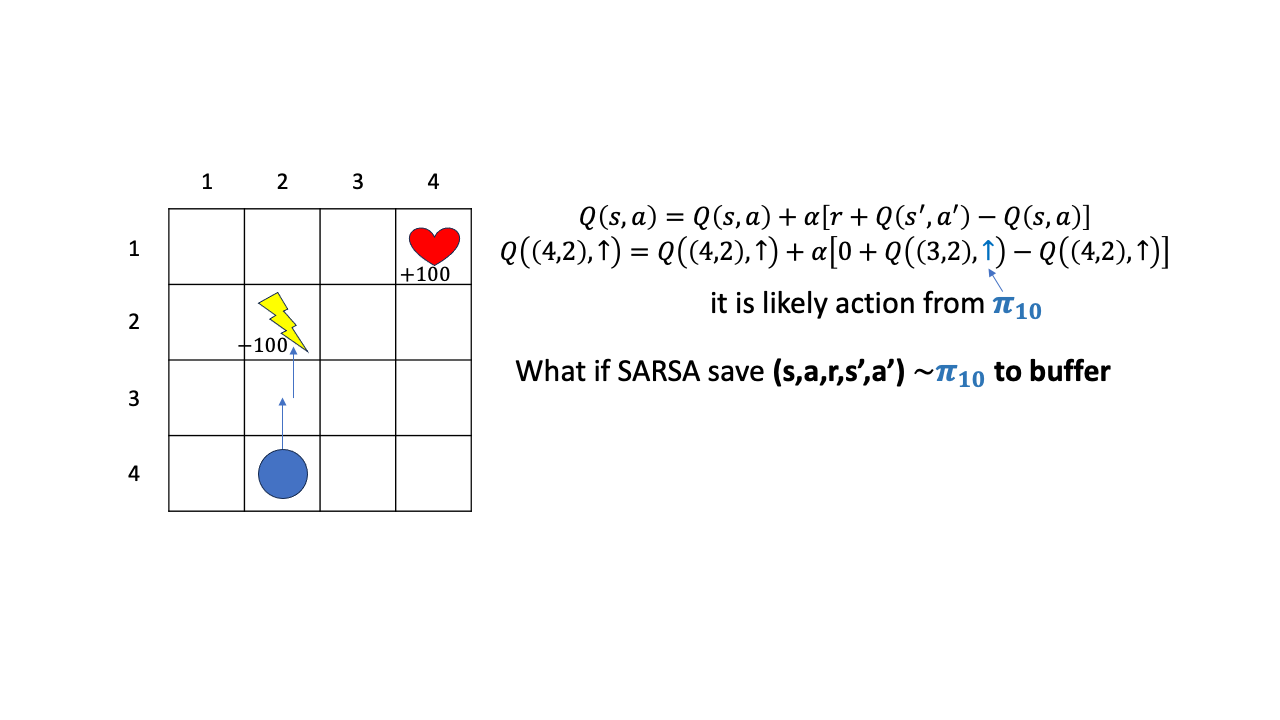Fig.

그리고 이 transition \((s,a,r,s',a')\)을 policy가 꽤 update된 시점인 \(\pi_{100}\)에 학습용으로 쓴다고 칩시다.

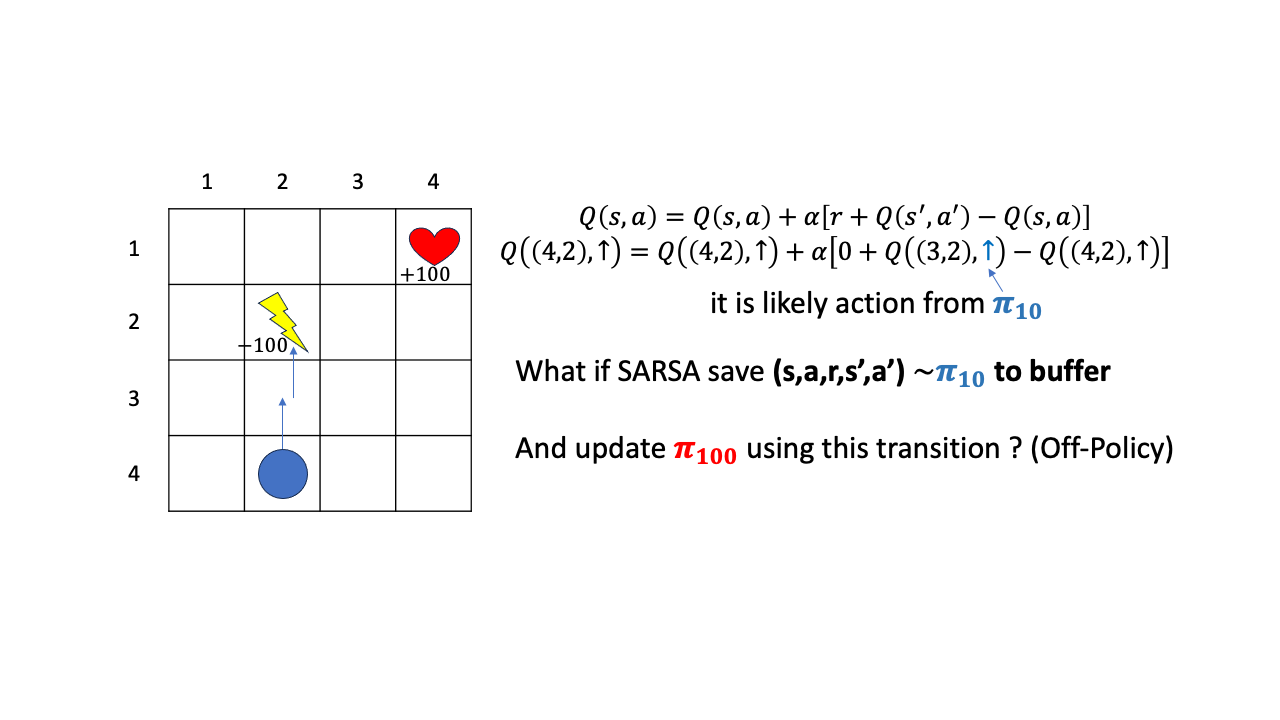Fig.

그러면 sampling을 수행한 behavior policy와 update 하려는 policy가 다르므로 off-policy인 상황이겠죠? 이러면 학습이 될까요?

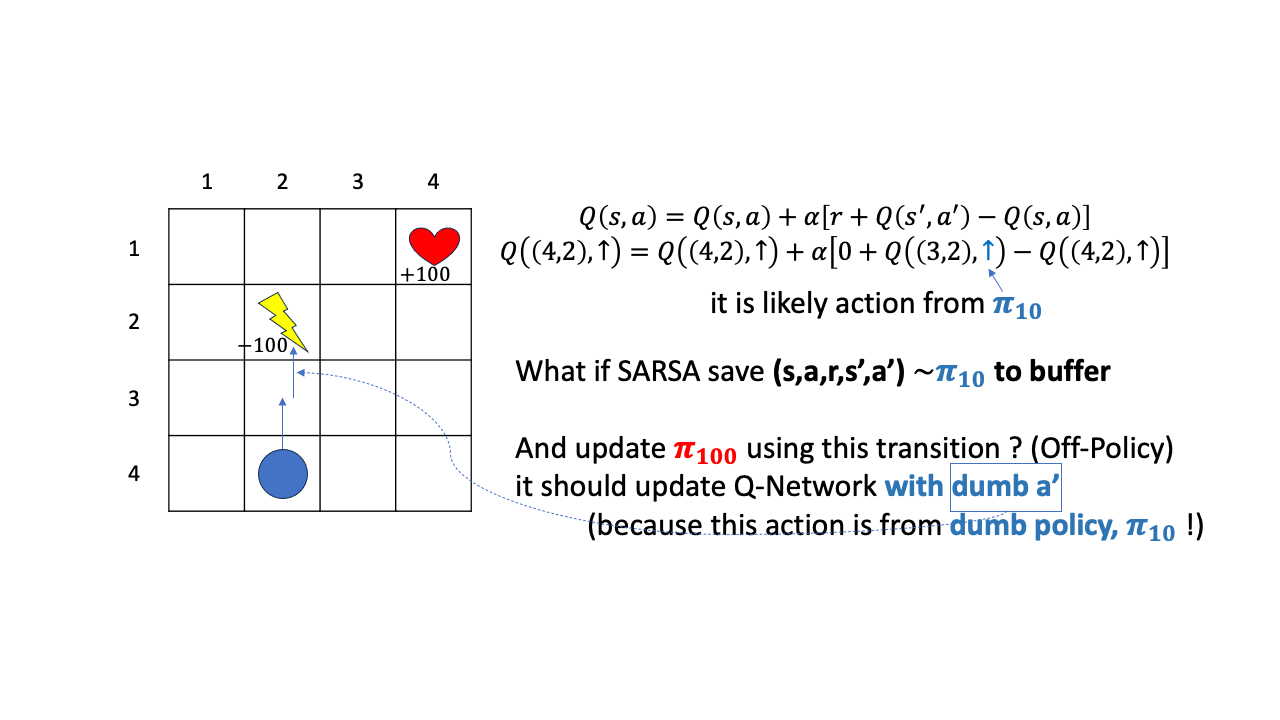Fig.

안타깝지만 학습이 잘 안될겁니다. 왜냐하면 \((3,2)\)에서 위로 간다는 판단은 \(\pi_{10}\)이 내릴만한 판단이지 여러번 Q값이 update된 \(\pi_{100}\)이 할만한 행동이 아니기 때문입니다. 처음에 했던 실수를 계속 가지고 갈수는 없는 노릇이죠. 계속 위로가서 -100점을 받아 그 값을 \(Q(4,2)\)에 propagate 시키는건 이상하겠죠?

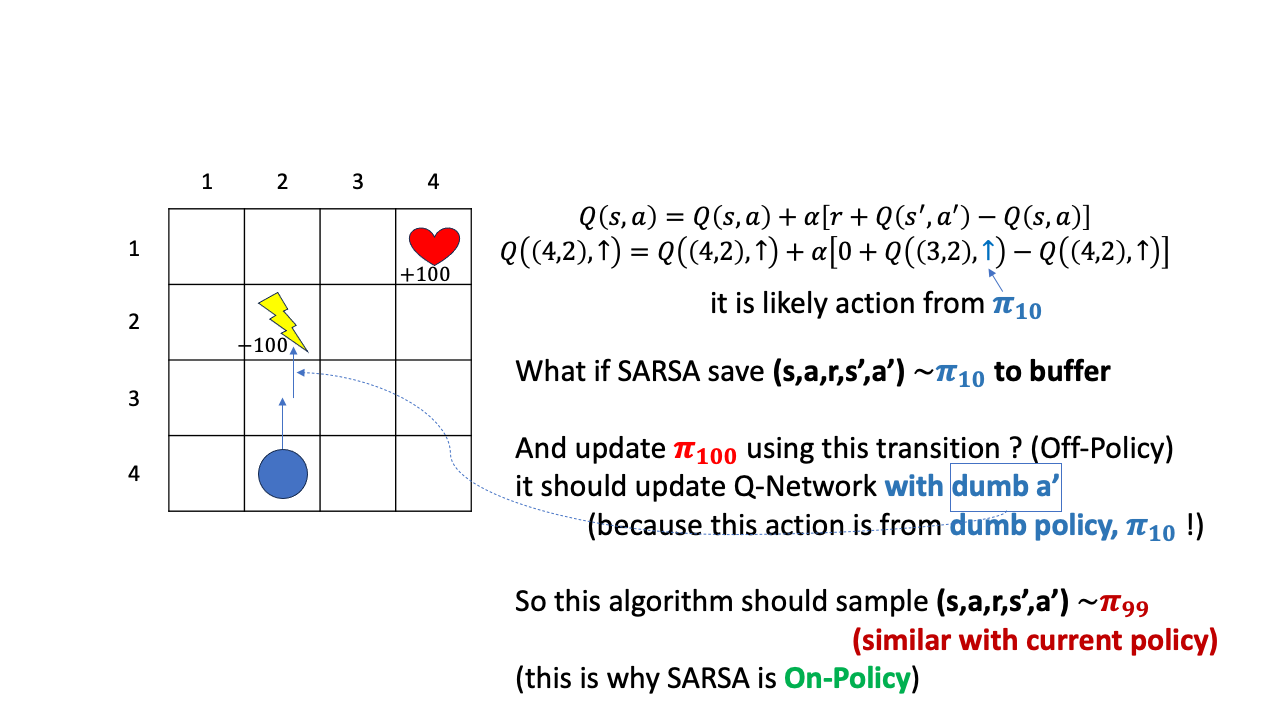Fig.

그래서 이 경우에는 \(\pi_{100}\)를 update하기 위해 바로 직전 \(\pi_{99}\)이 sample한 transition을 써야 하는겁니다. 이를 우리는 On-policy라고 부르며 이게 SARSA입니다.

그러면 Q-Learning은 어떨까요?

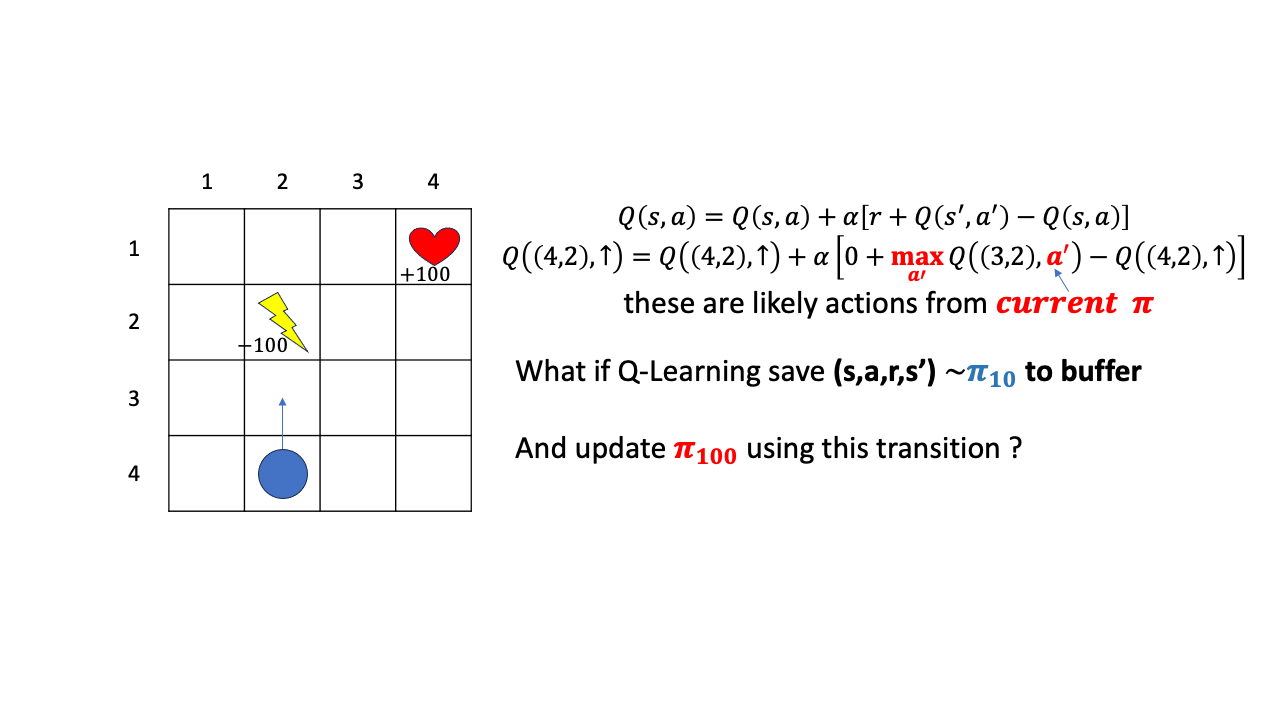Fig.

Q-Learning는 \(s'\)에서의 action으로 current step의 Q-Network가 판단하는 Q값중 max인 것을 고릅니다. 그리고 Q-Learning이 만약 어떤 buffer에 이 transition을 저장한다면 \((s,a,r,s')\)까지만 저장을 하게 됩니다. 여기서 point는 \(a'\)은 저장하지 않고 policy가 update되면 그 update된 policy의 Q값을 따라 \(a'\)을 정한다는 겁니다.

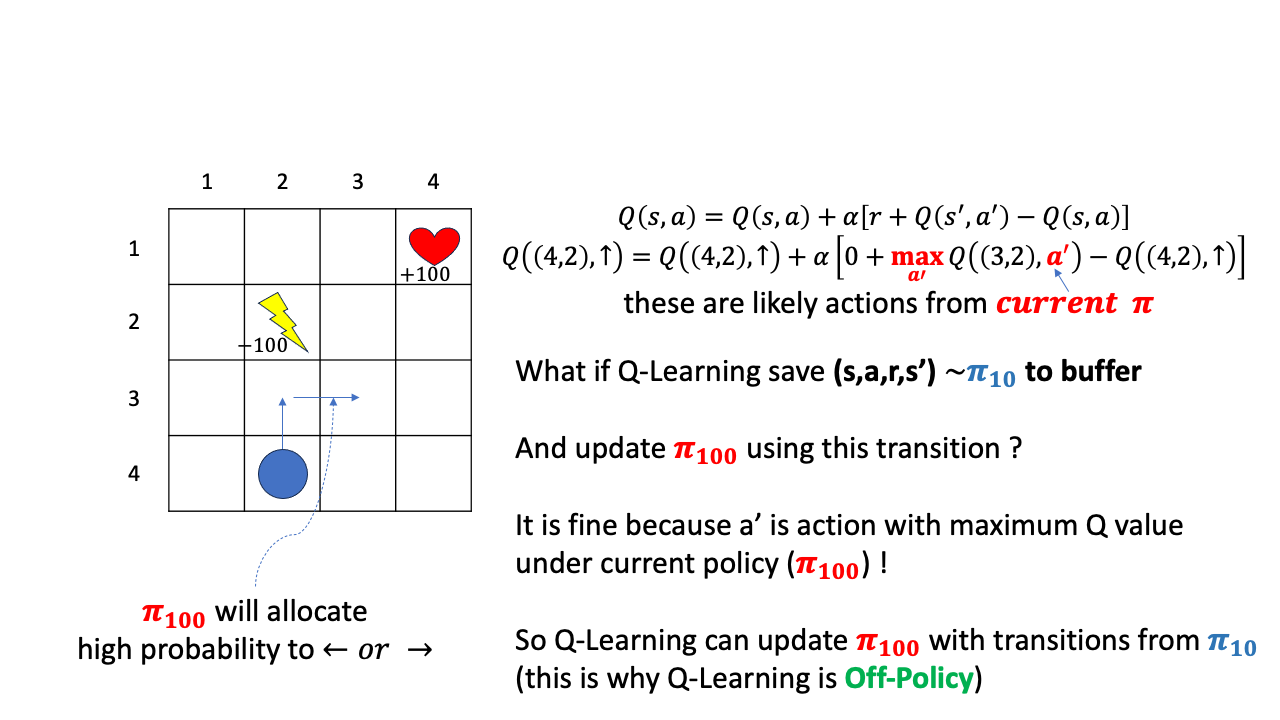Fig.

즉 \(\pi_{10}\)으로 \((s,a,r,s')\)을 뽑아두고 \(\pi_{100}\)을 update할 때 이 transition을 사용하는것도 가능한 이유는, 어차피 \(Q(4,2)\)에서 위로가는 행위에 대한 평가가 current policy 하의 \(Q(s',a')\)이 가장 큰 값을 사용해서 이뤄지기 때문입니다. 이제 더이상 \((3,2)\)에서 위로가지 않고 (왜냐하면 \((2,2)\)의 value 값이 매우 작을 것이기 때문에) 좌 우로 가는 action의 값이 더 클 것이고, 그 때의 Q값을 propagate하게 될 겁니다.

즉 Q-Learning은 \(\pi_{10}\)을 \(\pi_{100}\)이나 \(\pi_{200}\)에 쓸 수 있는 Off-policy algorithm인 것입니다.

두 번째로, 왜 SARSA와 Q-Learning은 서로 배우는 policy의 양상이 다른가?에 대해서 얘기해 보겠습니다. 이번에는 굉장히 잘 알려진 Sutton 책의 예제로 설명드려보겠습니다. 어떤 Agent가 마찬가지로 grid world 에서 cliff (낭떠러지)를 피해 goal에 무사히 도착하는 방법을 배운다고 칩시다. 이 때 두 algorithm이 배우는 최적 경로는 달라지는데, SARSA는 멀리 에둘러 가는 (roundabout) policy를 배우게 되고, Q-Learning은 상남자처럼 절벽을끼고 직진하게 됩니다.

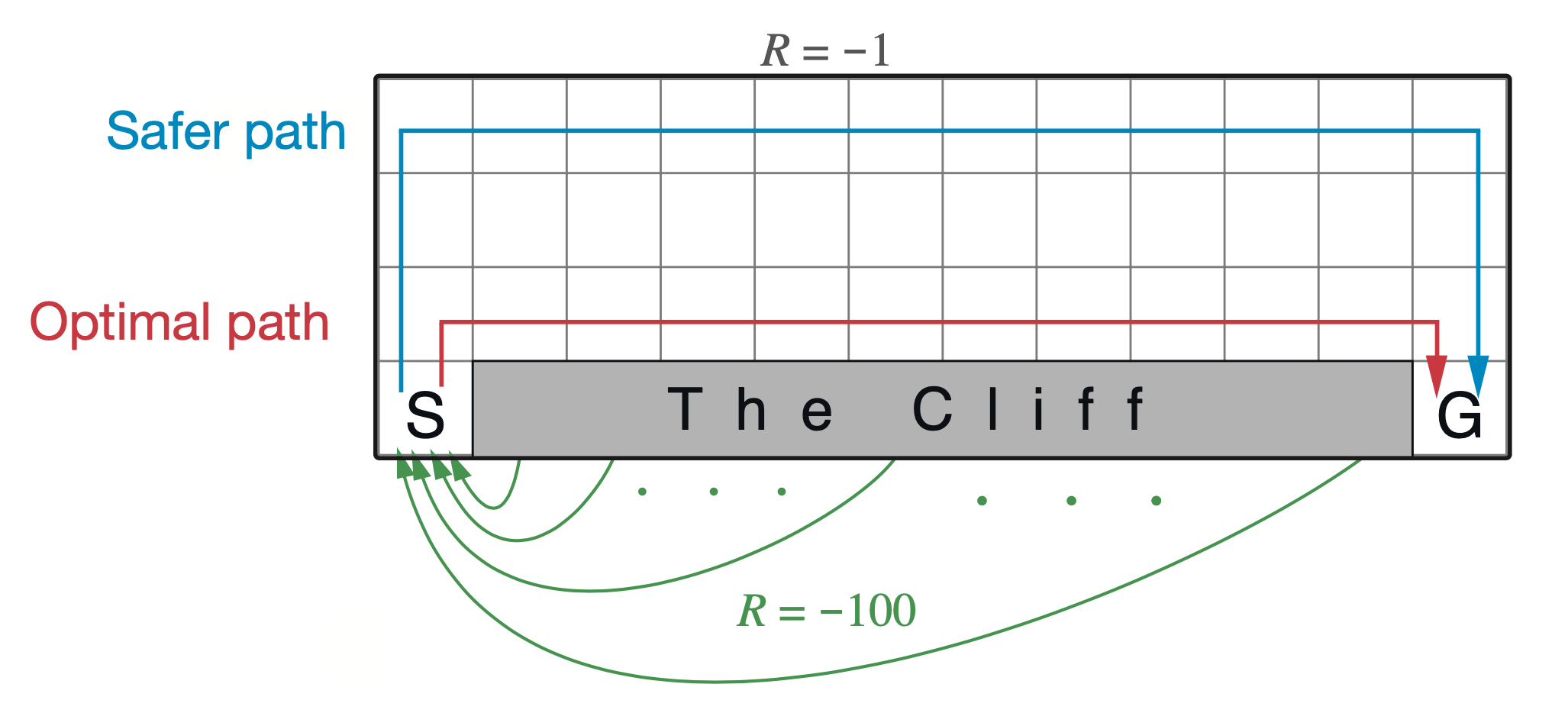Fig.

(Watkins의) Q-Learning의 경우 언제나 그 state에서 optimal action에 대한 값을 계속 update에 사용합니다. 예를 들어 cliff바로 근처 지점, \(s_t\)에서 또 cliff를 따라가는 행동 \(a_t\)을 해서 또 cliff 옆, \(s_{t+1}\)에 위치할 경우에 경우에 대해서, 떨어지면 -100점임에도 불구하고 그 떨어지는 경우의 수를 전혀 고려하지 않고 어차피 여기서 optimal action은 떨어지는게 아니라 왼쪽으로 가는거야 라는 생각으로 update를 합니다. 반면 SARSA는 아 떨어질 수도 있겠는걸? 이라는 생각을 하게 됩니다. SARSA는 update에 사용하는 값이 \(\max_{a_i} Q(s_{t+1},a_{t+1})\)가 아니라 현재 policy를 따라 실제 action을 해 보고 \(a_{t+1}\), 그 값을 쓰기 때문에 실제로 action을 해 보니 -100을 받을 수 도 있기 때문입니다.

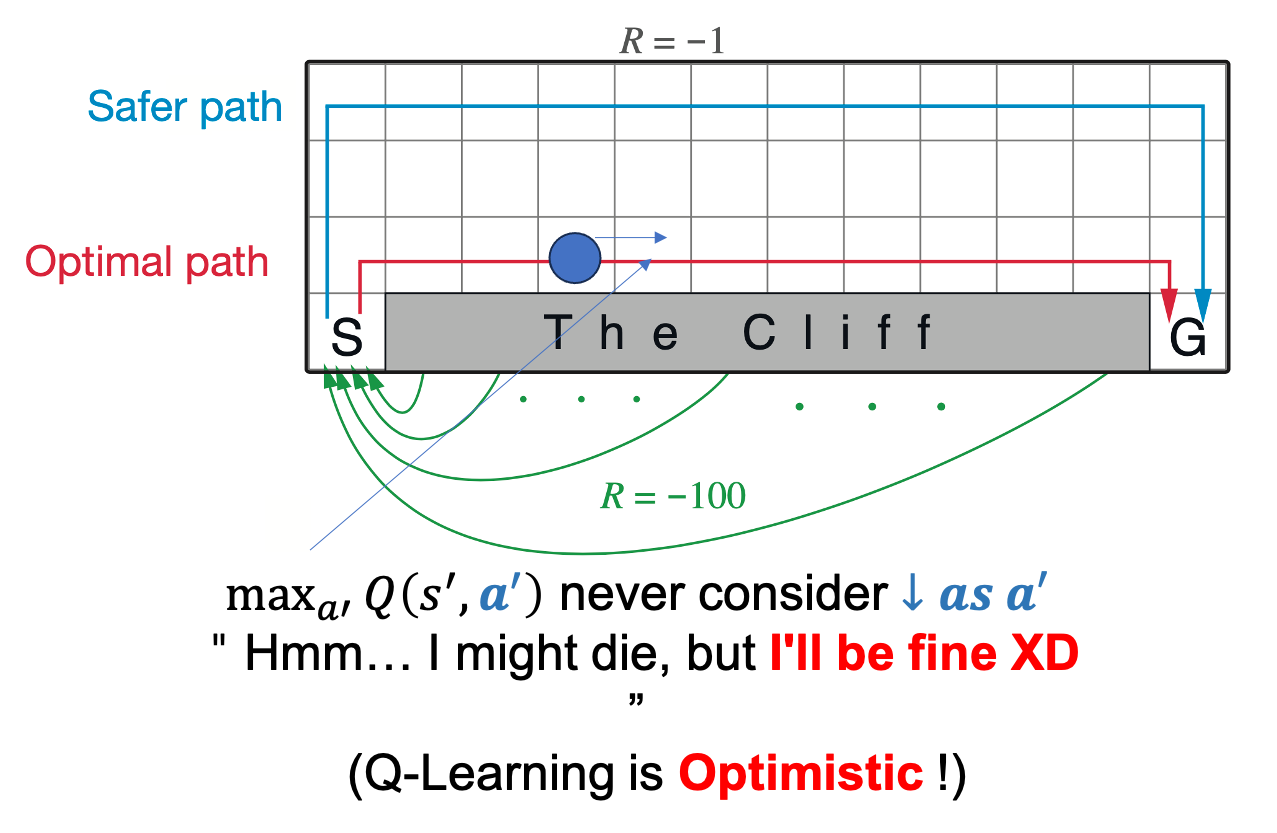
그래서 Q-Learning을 보통 낙천적인 (Optimistic) algorithm이라고도 합니다. 이는 더 나아가서 action을 너무 좋게 (과하게) 평가한다고 해서 Overestimatation 한다고도 하는데 lecture 8에서 왜 이것이 문제이며 어떻게 해결해야 되는지 언급합니다.

아래는 episode별 평균 reward의 합이 SARSA가 Q-Learning 보다 더 큰것을 알 수 있습니다.

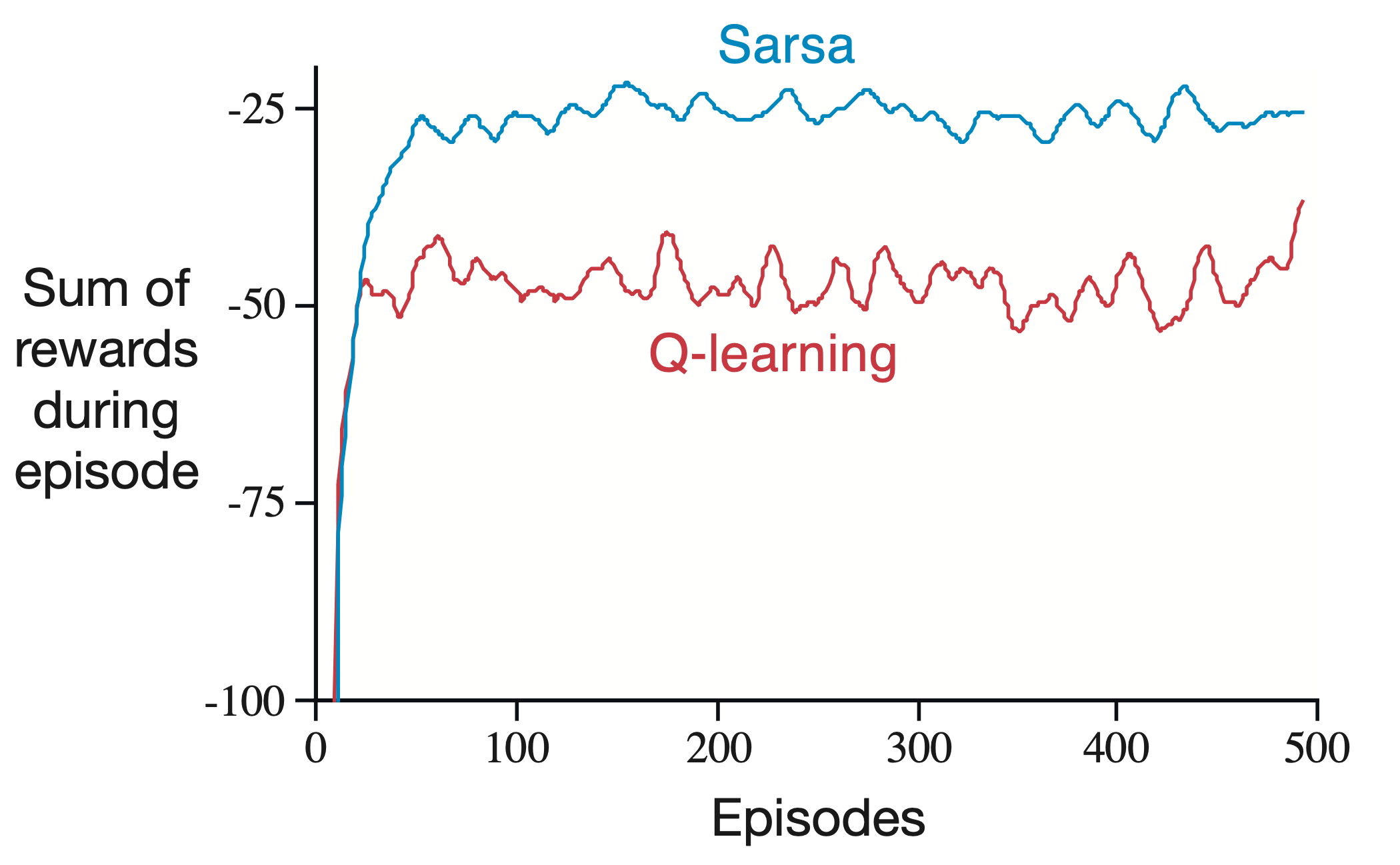Fig.

당연히 그러면 어떤 algorithm이 좋은가?가 궁금하실 수 있을 것 같습니다. 이는 당연히 모든 algorithm들이 그렇듯 각자 장단점이 있어 판단하기 어렵습니다.

• SARSA (On-Policy Learning)
  • Pros
    • 정책 일관성 (Consistent with Policy): SARSA는 학습 중 사용되는 정책과 평가에 사용되는 정책이 일치합니다. 즉, 학습하는 동안 탐험적인 행동을 하면 평가도 이러한 탐험적인 행동을 기반으로 이루어집니다.
    • 안전성 (Safety): 불확실한 환경에서 SARSA는 보다 안전한 행동 경향을 보입니다. 예를 들어, 위험을 피하는 경로를 학습할 수 있습니다.
    • 행동의 순차성 (Sequential Dependency): 이 알고리즘은 행동의 순차적 연관성을 고려합니다. 즉, 현재 행동이 다음 상태에 영향을 미친다는 점을 반영합니다.
  • Cons
    • 속도 문제 (Slower Convergence): 학습 과정이 탐험적인 행동에 의존하기 때문에, 최적 정책으로 수렴하는 데 더 많은 시간이 걸릴 수 있습니다.
    • 데이터 효율성 (Data Efficiency): 최적의 해를 찾기 위해 더 많은 데이터가 필요할 수 있습니다.
• Q-Learning (Off-Policy Learning)
  • Pros
    • 빠른 수렴 (Faster Convergence): 최적 정책을 학습하기 위해 탐욕적인 방식을 사용합니다. 이는 일반적으로 더 빠른 수렴으로 이어집니다.
    • 최적성 (Optimality): Q-Learning은 최적의 Q-값을 찾는 것을 목표로 하며, 이론적으로 최적 정책으로 수렴합니다.
    • 유연성 (Flexibility): 학습 과정에서 다른 정책을 사용할 수 있어, 학습 데이터가 다른 정책으로부터 얻어진 경우에도 사용할 수 있습니다.
  • Cons
    • 과대 추정 (Overestimation): Q-Learning은 때때로 Q값을 과대 추정할 수 있습니다. 즉, 실제보다 높은 가치를 부여하는 경향이 있어, 최적이 아닌 행동을 선택할 수 있습니다.
    • 정책 불일치 (Policy Inconsistency): 학습하는 동안의 정책과 평가하는 정책이 다를 수 있습니다. 이는 학습된 정책이 실제 사용 환경과 다르게 동작할 가능성을 의미합니다.
    • 위험한 행동 (Riskier Behavior): 최적화된 경로를 찾기 위해 위험한 행동을 선택할 수 있습니다, 특히 환경이 위험을 포함하는 경우에 그렇습니다.

(출처는 RL Book from Richard Sutton 과 GPT-4)

둘다 epsilon greedy를 잘 설정해주면 수렴한다고 내가 풀어야하는 문제를 MDP로 정의할 수 있고, value-based로 풀만한 상황이라고 하면 둘 다 해볼 수 있을 것 같습니다. 하지만 real-world에서는 현재 SARSA는 거의 쓰이지 않는 것 같고, Deepmind의 Atari를 푼 agent도 Deep Q Network (DQN)이며 그 후에도 Double Deep Q Network (DDQN) 등 계속 Q-Learning이 쓰이고 있으므로 Q-Learning을 쓰는것이 가장 처음 시도해 볼 만한 방법인 것 같습니다.

Value Functions in Theory (About Convergence Guarantees)

이제 lecture 7의 마지막 section 입니다. 이 section에서는 value-based method의 수렴성에 대해서 알아봅니다. (Q) Value iteration 과 Q-Learning 같은 algorithm이 수렴을한다는 것은 여러번 반복하다보면 결국 policy가 점진적으로 개선돼서 (improved) optimal policy로 수렴 하는가?를 의미합니다.

먼저 Q Iteration에 대해서 그것을 증명하고 Fitted Q-Learning의 경우에도 그러한가를 알아보는데요, 둘의 차이는 NN을 사용해서 Q Function을 근사하는가? 였죠. 그런데 NN은 non-lineary function이 포함되어 있기 때문에 optimal policy로 수렴하지 않을 수도 있습니다. 그렇기때문에 보통 Deep Learning에서도 NN을 학습하려면 iterative optimization을 하게 되고, 경우에 따라서 globa loptimum이 아니라 local optimum 에서 학습이 끝나는 경우가 있습니다. 그럼에도 불구하고 (Deep) Q-Learning은 실전에서 쓸만하다이라는 것이 결론이긴합니다.

사실 이 subsection은 RL을 처음 접하는 입장에서는 그리 중요하지 않을 수 있습니다. 수많은 석학들이 각 paper에서 이를 증명해왔고 2022년 현재에는 가장 stable 하고 정책 개선이 일어날법한 한 algorithm을 쓸 것이기 때문에 그렇죠. 그런데 언제가 문제에 내가 design한 문제에 Q-Learning이 안먹힌다거나? 하는 문제에 부딪히면 이 부분도 한번 되돌아 봐야 할겁니다. 그렇기 때문에 아직 여기까지 알 필요가 없다고 생각하시는 분들은 과감하게 넘어가셨다가 나중에 다시 돌아오셔도 좋을 것 같습니다.

Theory in Tabular Value-based Algorithm

Tabular Value Iteration은 아래의 2 step을 반복하면서 policy를 점점 optimal policy에 가깝게 개선시키는 방식이었습니다.

• set \(Q(s,a) \leftarrow r(s,a) + \gamma \mathbb{E} [V(s')]\)
• set \(V(s) \leftarrow \max_a Q(s,a)\)

Slide. 21.

우리가 궁금한 것은, “이게 수렴하는가? 수렴하면 어디로 수렴하는가?” 입니다. 이를 분석하기 위해 lecture 어떤 operator 하나를 정의하는데, 이 operator를 사용할 경우 다음이 성립하며,

이 때 operator를 바로 Bellman Operator, B 라고 합니다. 각 term들이 의미하는 바는 slide 21을 참고해 주시면 되고, 여기서 \(\max_a\)는 요소마다 적용되기 때문에 모든 state마다 max를 취하게 됩니다. 이를 Bellman Backup이라고 하는데요, 이는 원래의 Value Iteration 을 그냥 \(B\)를 가지고 표현한 것으로,

Value Iteration 는 \(BV\)를 반복적으로 수행하는 것과 같습니다.

여기서 Optimal Policy를 나타내는 어떤 \(V^{\ast}\)는 \(B\)의 fixed point가 된다는 겁니다.

이제 우리가 보여야할 것은 “\(V^{\ast}\)가 항상 존재하며 해는 유일한가? 그리고 \(V^{\ast}\)가 optimal polciy에 대응하는가?” 인데, 이는 항상 옳다고 하며 남은 한가지 질문은 “BV를 반복적으로 수행 하면 그 지점으로 가는가?” 라고 합니다.

Slide. 22.

여기서 B가 수축 (contraction) 하다는 것을 통해서 \(V^{\ast}\)에 도달할 수 있음을 보일 수 있는데, contraction 이라는 것은 다음과 같다고 합니다.

의미 그대로 어떤 operation (최적화 step)을 한번 거치면 내가 원하는 방향으로 지렁이처럼 조금이라도 꿈틀 (수축) 거리면서 갈 수 있는가? 라고 보면 될 것 같은데, 정의에 의하면 contraction이란 “우리가 만약 어떤 두 가지 vector \(V,\bar{V}\)를 가지고 있을 때 \(B\)를 두 벡터에 적용하는 것이 두 벡터가 (infinity norm 크기에 대해) 적어도 \(\gamma\) 만큼 가까워지는 결과를 가져온다”를 의미한다고 합니다.

(여기서 infinity norm을 사용했다는 것과 우변에 \(\lambda\)가 곱해져 있다는 것에 주의하라고 하네요)

Bellman Operator를 적용하는 것이 그런 결과를 가져오는가?, 즉 B가 “contraction” 한가? 에 대한 증명이 그렇게 어렵지는 않으나 본 강의에서 다루지는 않는다고 합니다. 우리가 알고싶은 내용은 optimal policy를 나타내는 point, \(V^{\ast}\)로 적어도 조금씩 움직이는가? 일텐데, 이는 Value Iteration (NN을 안 씀) 에 대해서 성립한다고 합니다.

Theory in Non-Tabular Value-based Algorithm

“Non-Tabular form의 경우에도 이것이 성립할까?”

• Value Iteration (Tabular)

1. set \(Q(s,a) \leftarrow r(s,a) + \gamma \mathbb{E} [V(s')]\)
2. set \(V(s) \leftarrow \max_a Q(s,a)\)

• Fitted Value Iteration (Non-Tabular)

1. set \(y_i \leftarrow \max_{a_i} ( r(s_i,a_i) + \gamma \mathbb{E} [ V_{\phi}(s'_i) ] )\)
2. set \(\phi \leftarrow \arg \min_{\phi} \frac{1}{2} \sum_i \parallel V_{\phi}(s_i) - y_i \parallel\)

Slide. 23.

Fitted Value Iteration은 어떤 target값으로 Q Network를 regress하는 step이 있습니다. step 1은 Value Iteration에서와 같이 Bellman Backup으로 표현할 수 있는데, step 2는 Neural Network를 학습하는 것 인데 이는 Q Function을 표현할 수 있는 parameter set 중 (continuous space에서 정의되므로 사실상 무한대에 가까움) optimal point를 찾는다는 것이 됩니다.

• Fitted Value Iteration (Non-Tabular)

1. set \(y_i \leftarrow \max_{a_i} ( r(s_i,a_i) + \gamma \mathbb{E} [ V_{\phi}(s'_i) ] )\)
2. set \(\phi \leftarrow \arg \min_{\phi} \frac{1}{2} \sum_i \parallel V_{\phi}(s_i) - y_i \parallel\)

이 parameter set (hypothesis set)을 \(\Omega\)라고 하면 Regression Error를 최소화 하는 파라메터를 찾는 것은 아래와 같이 나타낼 수 있다고 합니다.

여기서 Target Value는 step 1 이므로 당연히 BV로 표현할 수 있겠죠.

즉, Fitted Value Iteration은 매 optimization step마다 새로운 Value Function \(\color{red}{V'}\)를 set \(\Omega\) 안에서 Squared Error \(\sum \parallel V'(s) - (BV)(s) \parallel^2\)이 가장 작은 parameter를 찾는 것이라고 할 수 있겠습니다. 여기서 BV는 이전 Value Function을 의미합니다.

즉 우리가 이런 Supervsied Learning을 하는것은 old V가 있고, 가능한 뉴럴 네트워크로 표현되는 set을 직선으로 나타낼 때 (\(\Omega\)는 직선의 모든 점들이 되는데, 그렇다고 이게 모든 가능한 Value Function을 나타내지는 않는다고 합니다.)

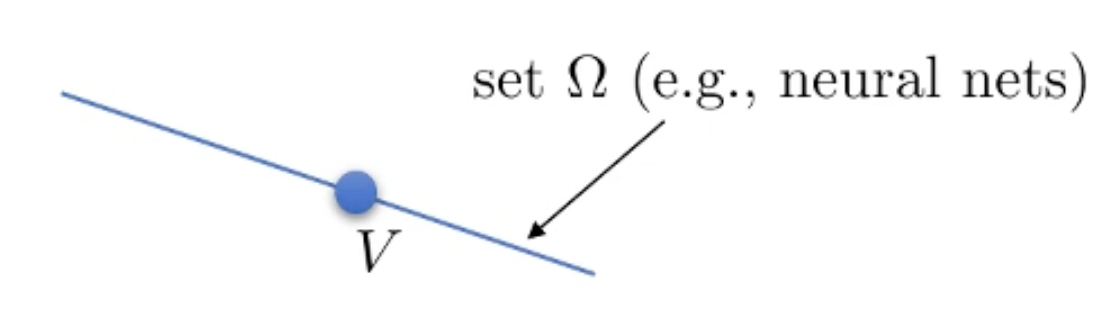Fig.

우리가 여기서 BV를 하면 이 직선을 벗어나게 되고 (더이상 \(\Omega\)에 있지 않습니다.)

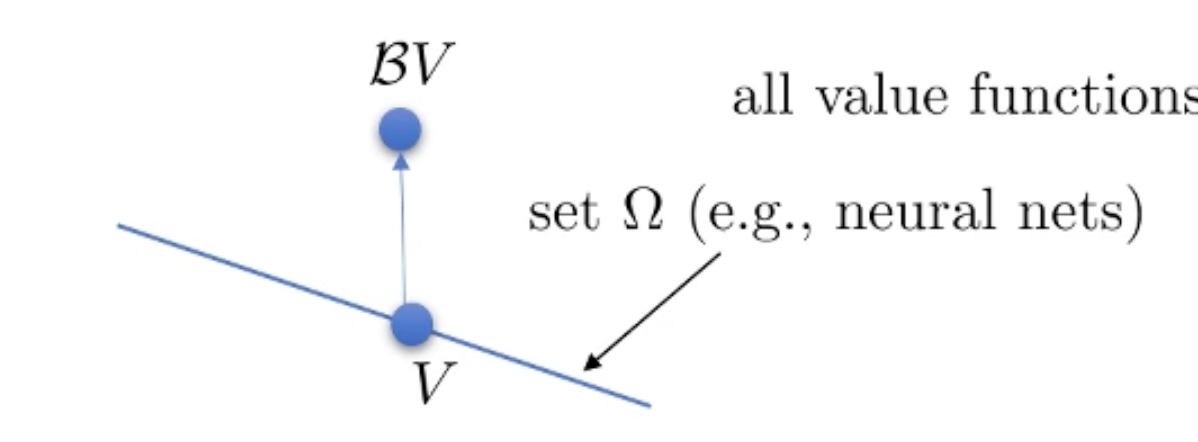Fig.

우리가 step 2의 Supervised Learning을 하면 다시 \(\Omega\) 내에 있는 어떠한 점으로 projection을 하는게 되는겁니다.

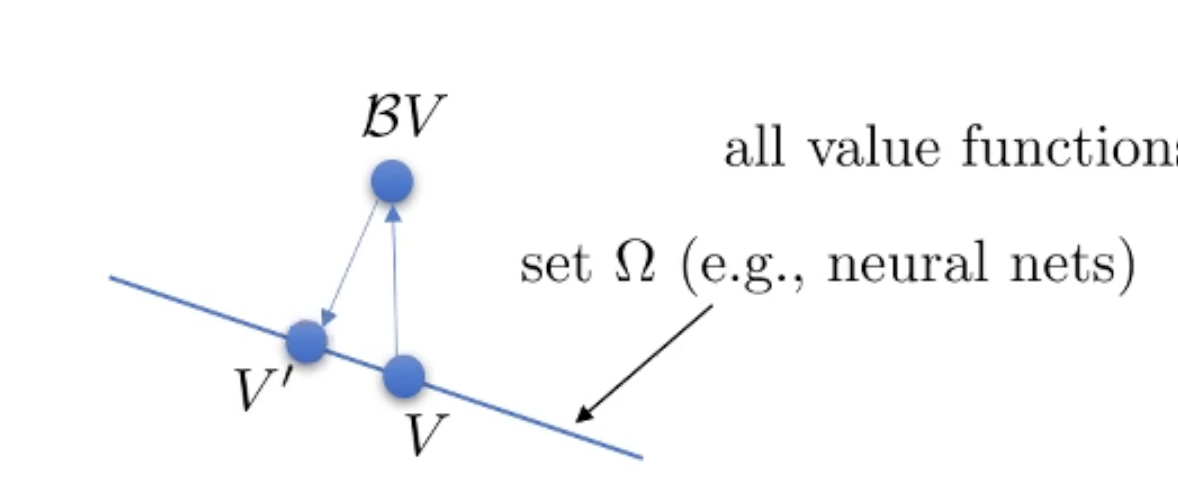Fig.

이를 반복하는게 일반적인 딥러닝에서의 최적화 인데요, 이를 종합해서 다시 Fitted Value Iteration을 나타내면 아래와 같습니다.

• Value Iteration (Tabular)

1. set \(Q(s,a) \leftarrow r(s,a) + \gamma \mathbb{E} [V(s')]\)
2. set \(V(s) \leftarrow \max_a Q(s,a)\)

• Fitted Value Iteration (Non-Tabular)

1. set \(y_i \leftarrow \max_{a_i} ( r(s_i,a_i) + \gamma \mathbb{E} [ V_{\phi}(s'_i) ] )\)
2. set \(\phi \leftarrow \arg \min_{\phi} \frac{1}{2} \sum_i \parallel V_{\phi}(s_i) - y_i \parallel\)

정리된 수식을 보면 Fitted Value Itearion에는 새로운 Operator \(\color{red}{\Pi}\)가 추가된 것을 볼 수 있습니다. 이는 Projection Operator로 l2 norm 에 대해서 \(\Omega\)라는 곳으로 어떤 벡터를 사영시키는 operator입니다. \(\Pi V\)는 \(\Omega\) 내에서 step 2의 Objective 의 argmin이 됩니다.

여기서 \(\Pi\) 또한 contraction이라고 하는데요, 왜냐하면 어떤 벡터를 l2 norm 하에서 사영시키면 그 점들은 가까워 질 수 밖에 없기 때문이라고 합니다.

Slide. 24.

다시 정리하자면

• \(B\) 는 \(\infty\)-norm 에 대해서 contraction 임 (“max” norm).
  • \[\parallel B V - B \bar{V} \parallel_{\infty} \leq \gamma \parallel V- \bar{V} \parallel_{\infty}\]
• \(\Pi\) 는 \(l_2\)-norm에 대해서 contraction 임 (Euclidean distance).
  • \[\parallel \Pi V - \Pi \bar{V} \parallel^{2} \leq \parallel V- \bar{V} \parallel^{2}\]

이 된다고 합니다.

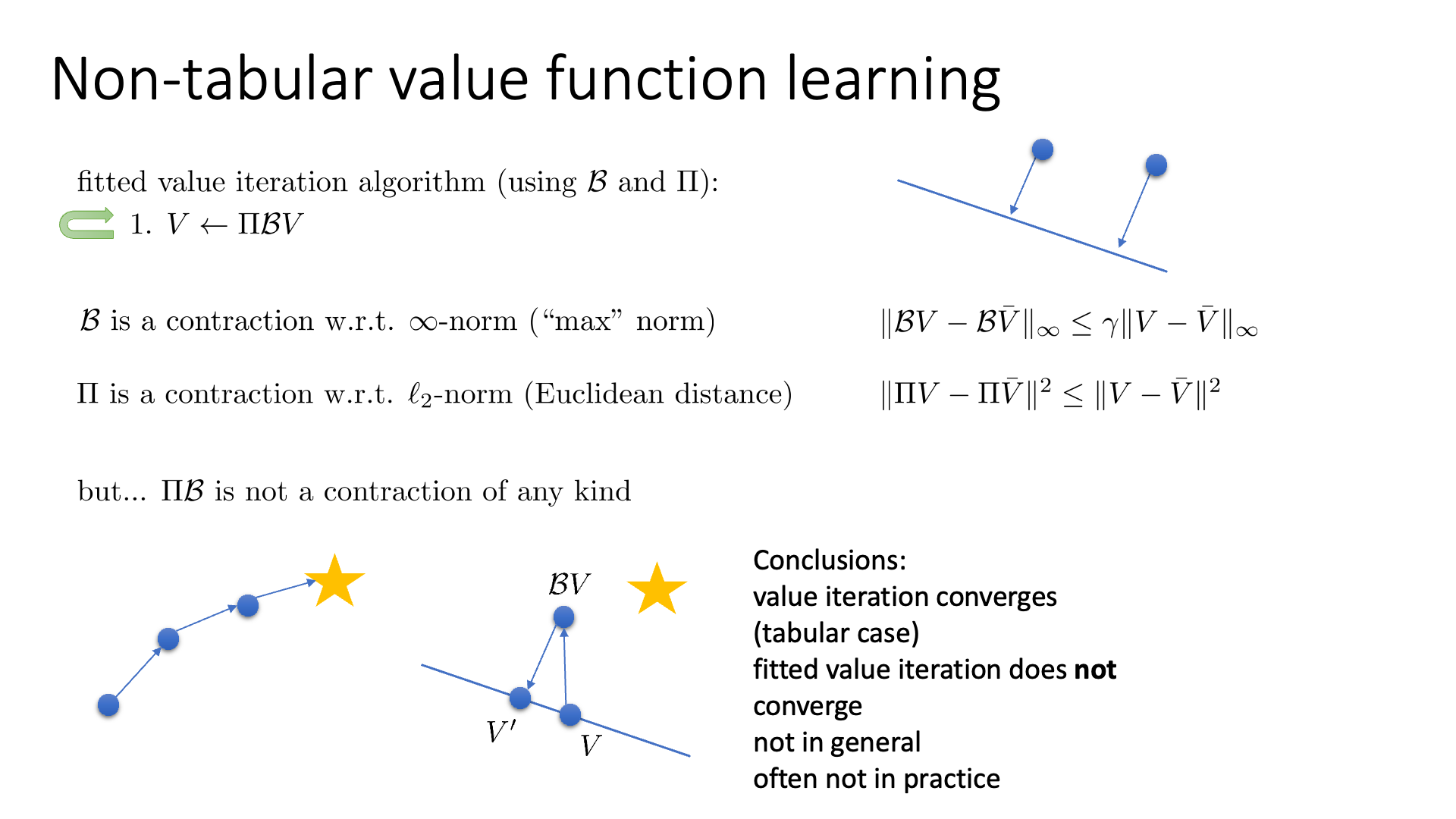
하지만 여기서 문제가 생기는데, Fitted Value Iteration의 수식은 아래와 같은데,

여기서 \(\color{red}{\Pi B}\)는 contraction이 아니라는 데 있다고 합니다. 이게 둘 다 contraction인 연산이기에 둘 다 contract 되어야 하는것이 아닌지? 라고 생각할 수 있으나, 이 두가지가 다른 norm에 대해서 contraction이라서 \(\Pi B\)는 contraction이 아니게 된다고 합니다. 즉 Fitted Value Iteration 은 수렴 (convergence)가 보장되어 있지 않다는 겁니다.

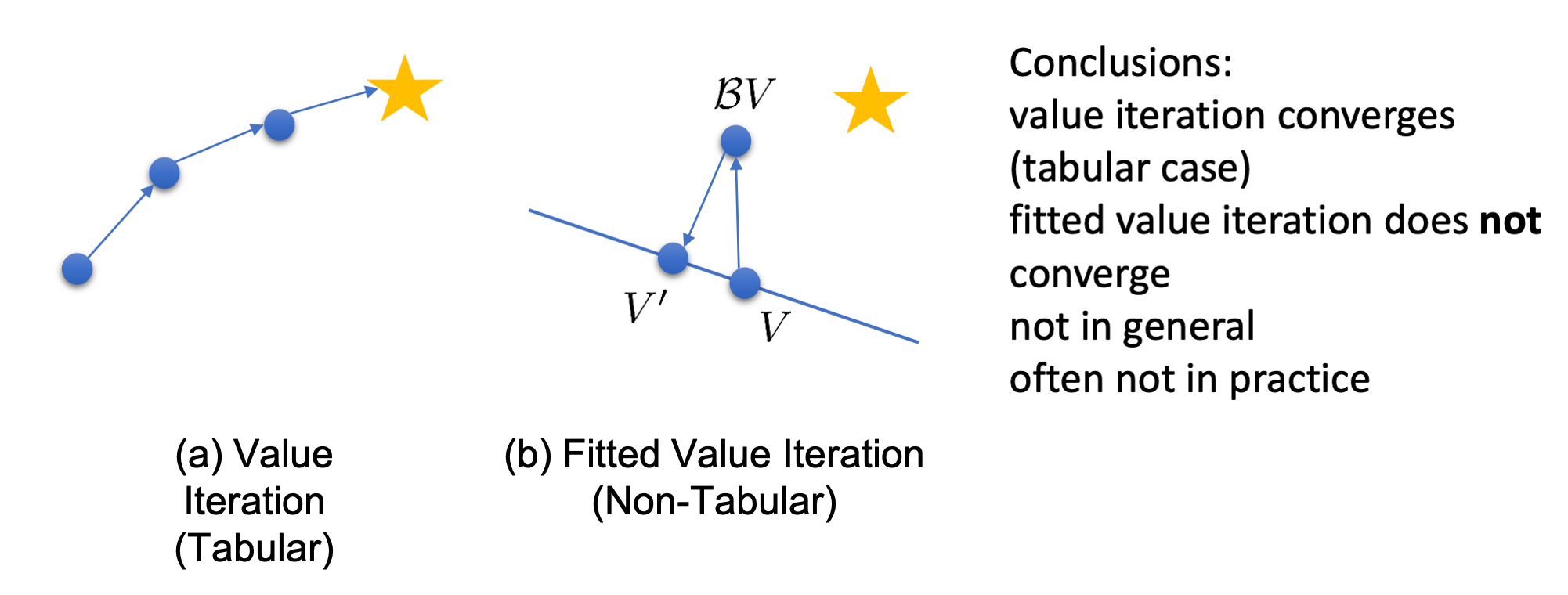Fig.

위의 그림을 보시면 Fitted Value Iteration 에서 \(V\) 를 \(BV\)로 이동시키고, 다시 이를 사영시켜 \(V'\)을 얻었음에도 불구하고 \(V'\)는 \(V^{\ast}\)로부터 오히려 멀어지는 것을 볼 수 있습니다.

이는 Fitted Q-Iteration 에서도 마찬가지가 된다고 합니다.

Slide. 25.

마찬가지로 \(B, \Pi\)는 각각 \(\infty\)-norm과 \(l_2\)-norm 에 대해서 contraction 이지만 둘 다 적용할 경우는 아니라고 합니다.

그런데 Contraction이고 뭐고 잘 모르겠고… Q-Learning은 단순히 gradient descent를 하는 ML의 regression 을 하는 task인데, 왜 이게 안되는거지? 라는 생각이 드실 것 같습니다. Sergey는 이 부분에 대해서 Q-Learning 은 사실 잘 정의된 Objectvie에 대해 gradient descent를 하는건 아니다 라고 얘기합니다.

Slide. 26.

모양새가 regression 하는 것 처럼 생겼는데 대체 왜 그러는 걸까요? 그 이유는 Q-Learning의 target은 Q-Network의 출력값에 의존하기 때문 입니다. 그리고 이 Q-Network는 계속 학습이되면서 다른 값을 바꿀 것이기 때문이죠. 즉, 같은 \((s,a,r,s')\)에 대해서 target값이 training time이 경과될수록 계속 변하는 겁니다.

일반적인 deep learning 의 supervised learning의 경우 training dataset이 fix되어 있고 (더 추가되지 않고), 그리고 model의 모양새 (parameter)가 정해져있습니다. 그러니까 우리는 어떤 parameter set에서 어떤 data sample들이 들어오면 어떤 loss를 반환한다는 것이 처음에 정해지는 것입니다. 즉 loss surface가 최초에 정해지고 그것이 너무나 고차원이어서 어떻게 생겼는지는 모르겠으나, input date에 대해서 loss를 구하고, 그 point에서 가장 가파른 기울기를 계산 해 한 step 전진 하는 것이 (steepest) gradient descent인데, 매번 값이 달라지고 loss surface가 달라지므로 gradient descent라 하기 어려운 것입니다.

그러니까 우리가 어떤 optimal value function을 의미하는 parameter set을 향한 아름다운 objective surface가 존재하고, 이에 대해서 정확하게 gradient를 계산한 것이 아니기 때문에 Q-Learning을 통해 매 순간 전진하는 한 step 한 step 이 optimal point로 우리를 데려가는 것이 보장되지 않는 것이죠.

Sergey는 Q-Learning algorithm을 좀 수정함으로써 이를 gradient descent로 바꿀 수 있다고 하는데요, target에 gradient가 흐르게 algorithm을 수정하면 된다고 합니다 (이렇게 하면 왜 gradient descent 가 된다는건지 잘은 모르겠습니다 관련 논문을 찾아보시길 바랍니다…). key idea는 target에도 Q-Network가 사용되고 있으니 여기에도 gradient를 흐르게 하는것인데, arg max operation은 미분이 불가능하기 때문에 Residual Algorithm 이라는 것을 사용해야 한다고 합니다. 하지만 이는 poor numerical property를 가지기 때문에 실제로는 잘 안된다고 하며, Q-Learning이 실제로는 더 잘 작동한다고 합니다.

사실 우리가 Lecture 6 에서 다뤘던 Actor-Critic도 사실은 같은 이유로 수렴이 보장되지 않는다고 합니다.

Slide. 27.

Slide. 28. Review는 생략

Reference

• Lectures
  • CS 285 at UC Berkeley : Deep Reinforcement Learning
  • Foundations of Deep RL Series
    • L1 MDPs, Exact Solution Methods, Max-ent RL
    • L2 Deep Q-Learning
  • CS224R
    • Q-Learning
• Blogs
  • Nuts & Bolts of Reinforcement Learning: Model Based Planning using Dynamic Programming
  • Deep Learning in a Nutshell: Reinforcement Learning By Tim Dettmers
  • A (Long) Peek into Reinforcement Learning
  • On-Policy VS Off-Policy in Reinforcement Learning from Lei Mao