Rescent Advances in Deep Generative Model (3/4) Generative Modeling by Estimating Gradients of the Data Distribution (Score-Based Model)
10 Aug 2022< 목차 >
- Motivation (Explicit, Implicit Generative Models vs Score-based Generative Models)
- The Score Function, Score-based Models, and Score Matching
- Score-based Generative Modeling
- References
앞선 2개의 post 로 기본적인 Diffusion-based Generative Model 이 어떻게 작동하는지에 대해 이해할 수 있었습니다.
이번에는 Score Function 이라는 개념에 대해서 알아보고 어떻게 Score Function 을 통해 Data Distribution 을 학습하는 생성 모델, Score-based Model을 만들 수 있으며, 이 알고리즘의 diffusion model 과의 관계는 어떻게 되는가? 에 대해 알아보도록 하겠습니다.
본 post 는 Generative Modeling by Estimating Gradients of the Data Distribution 논문과 해당 논문의 저자 Yang Song 의 Blog Post 와 Seminar Video를 기반으로 해서 작성 했습니다.
Motivation (Explicit, Implicit Generative Models vs Score-based Generative Models)
생성 모델 (Generative Model) 이란 현재 가지고 있는 Training Dataset 이 Sampling 된 알수 없는 분포 (Unknown Distribution) 이 있다고 가정하고 그걸 찾는 것이 목적입니다.
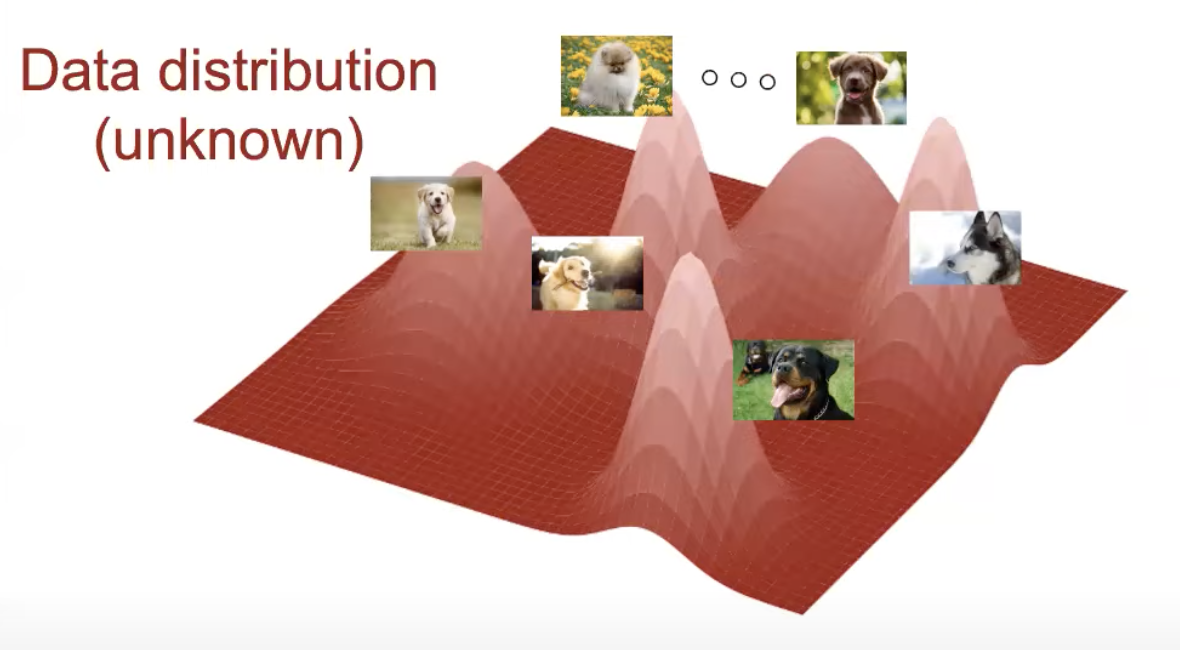 Fig. Nerual Network 가 찾아낸 Data Distribtution 로부터 확률이 높은 (봉우리가 큰; Likely) 부분을 샘플링하면 새로운 데이터를 얻을 수 있다.
Fig. Nerual Network 가 찾아낸 Data Distribtution 로부터 확률이 높은 (봉우리가 큰; Likely) 부분을 샘플링하면 새로운 데이터를 얻을 수 있다.
본 Post 의 주제인 Score-based Method 도 이런 분포를 찾는다는 목적 자체는 같습니다.
하지만 기존의 Variational AutoEncoders (VAEs) 나 Generative Adverserial Networks (GANs) 등과는 차이점이 있습니다.
- Explicit Models (likelihood-based models) : EBMs, VAEs, Autoregressive Models, Normalizing Flows
- Implicit Models : GANs
- Score-based Models :
We don't know yet
Explicit Model은 VAE 처럼 우리가 실제로 알 수 없는 Data Distribution 이 가우시안 일것이다 라고 하는 등 분포를 명시적으로 세팅 (가정) 하고 그 분포의 파라메터를 학습하로 찾아내는 방법이고, Implicit Model 은 이런걸 정의해주지 않지만 모델이 알아서 배우는 것으로 GANs 같은 방식이 대표적이며 이는 Sampling 기반의 방법이라고 부르기도 합니다.
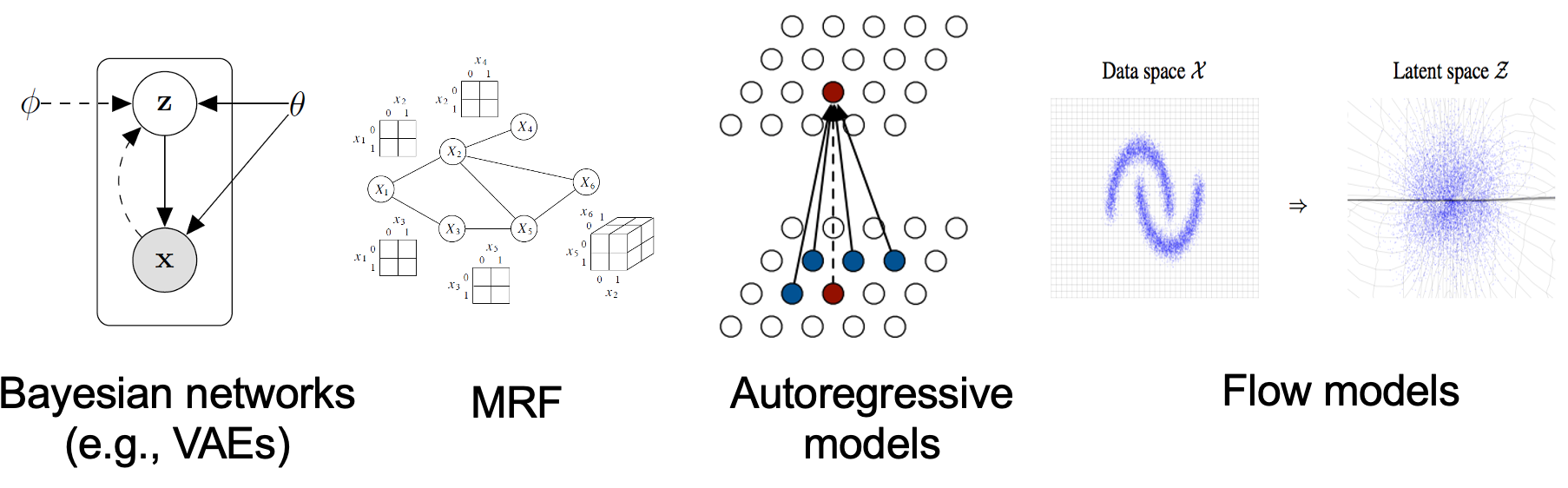 Fig. EBMs, VAEs, AR Models 등 + Diffusion Models (사진에는 없음) 은 전부 Explicit 생성 모델이다.
Fig. EBMs, VAEs, AR Models 등 + Diffusion Models (사진에는 없음) 은 전부 Explicit 생성 모델이다.
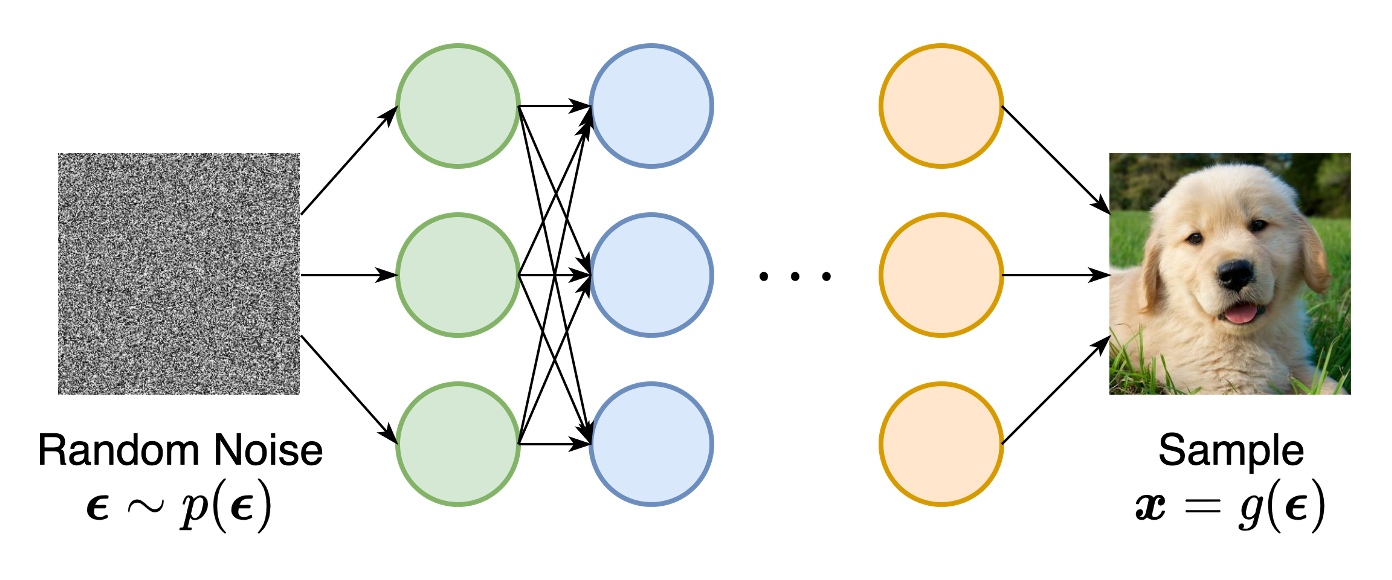 Fig. GAN 은 샘플링 기반의 Implicit 생성 모델이다.
Fig. GAN 은 샘플링 기반의 Implicit 생성 모델이다.
어떤 방식으로든 학습을 통해 Data 의 실제 Disribution 을 잘 근사해내면
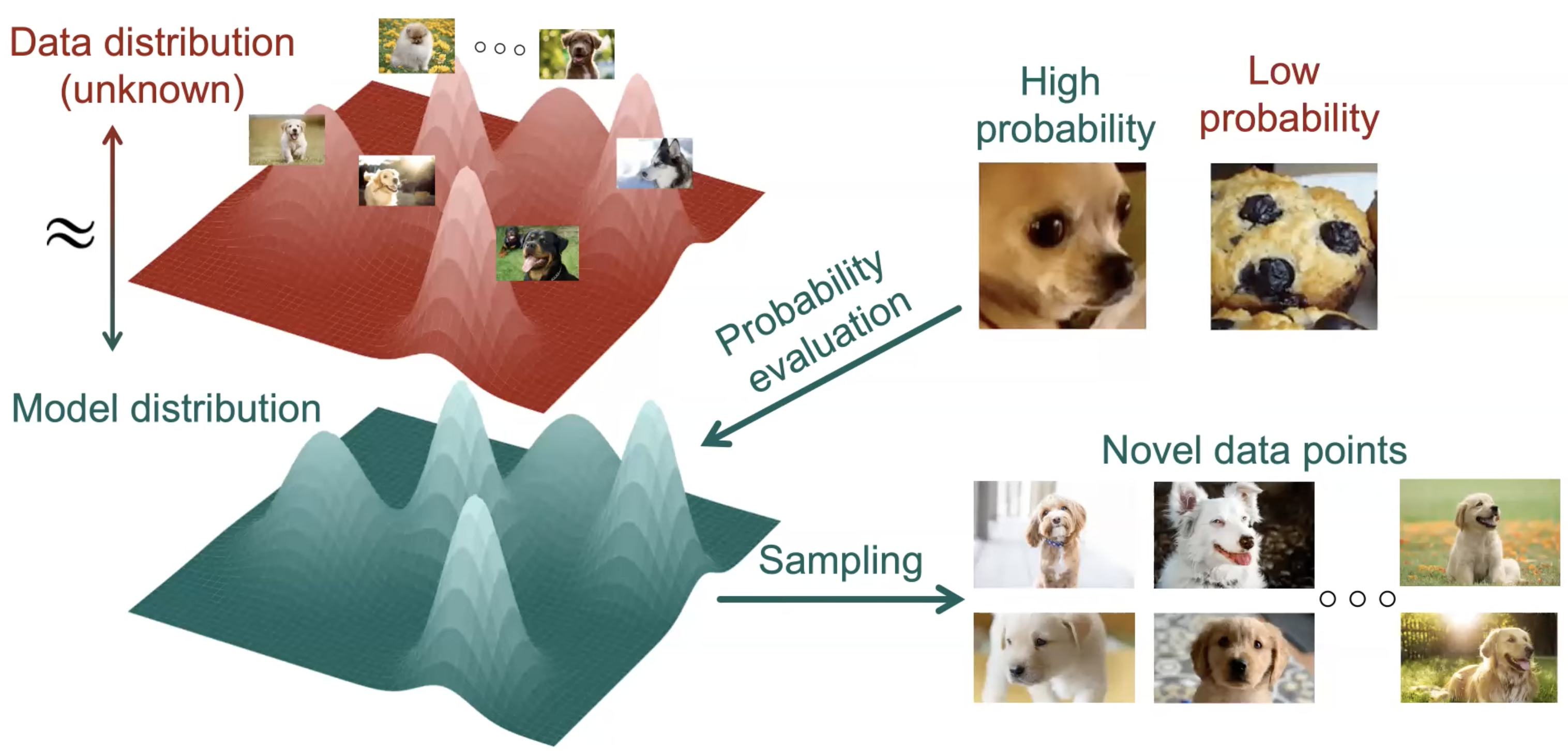
이로부터 새로운 이미지를 생성할 수 있습니다. 하지만 이런 방식으로 학습하는데는 몇가지 문제점이 존재합니다.
Challenge of Training Generative Models
Generative Model 을 학습한다는 것은 원래의 Data Distribution 을 찾는 것이라고 했는데요, 과연 어떻게 이 복잡한 분포를 알지도 못하는데 근사할 수 있을까요?

가장 단순한 방법으로 우리는 이 Target Data Distribution 이 봉우리 (Mode) 가 한개인 Gaussian Distribution 이라고 생각하고 문제를 풀 수 있겠습니다.
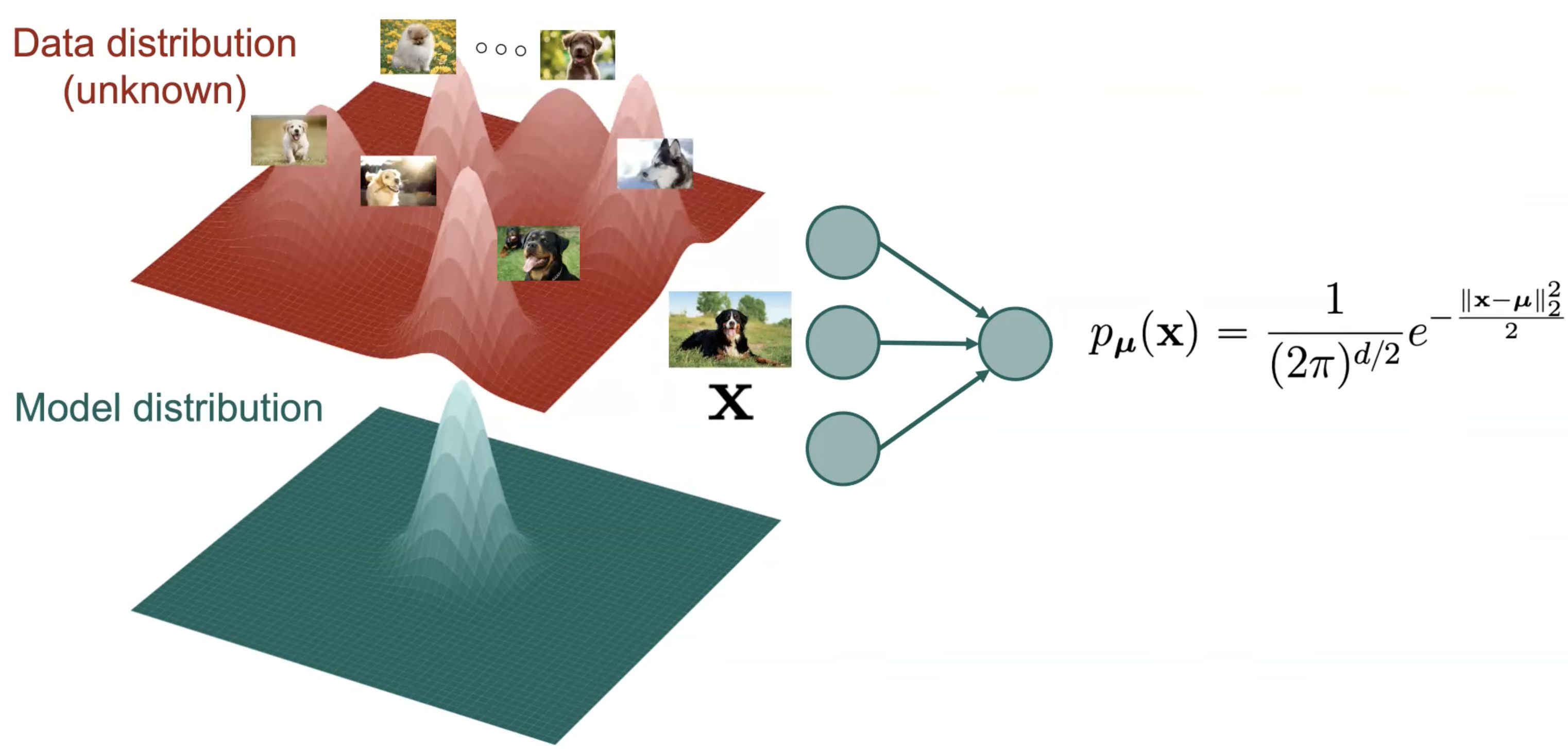
이는 계산이 쉽다는 장점과 2개의 Layer 를 갖는 Neural Network 만으로도 모델링 할 수 있다는 장점이 있지만 지나치게 단순하다는 단점이 있습니다.
그래서 우리는 층이 더 깊은 Deep Neural Network 로 Deep Generative Model을 모델링 하게 되는데요,
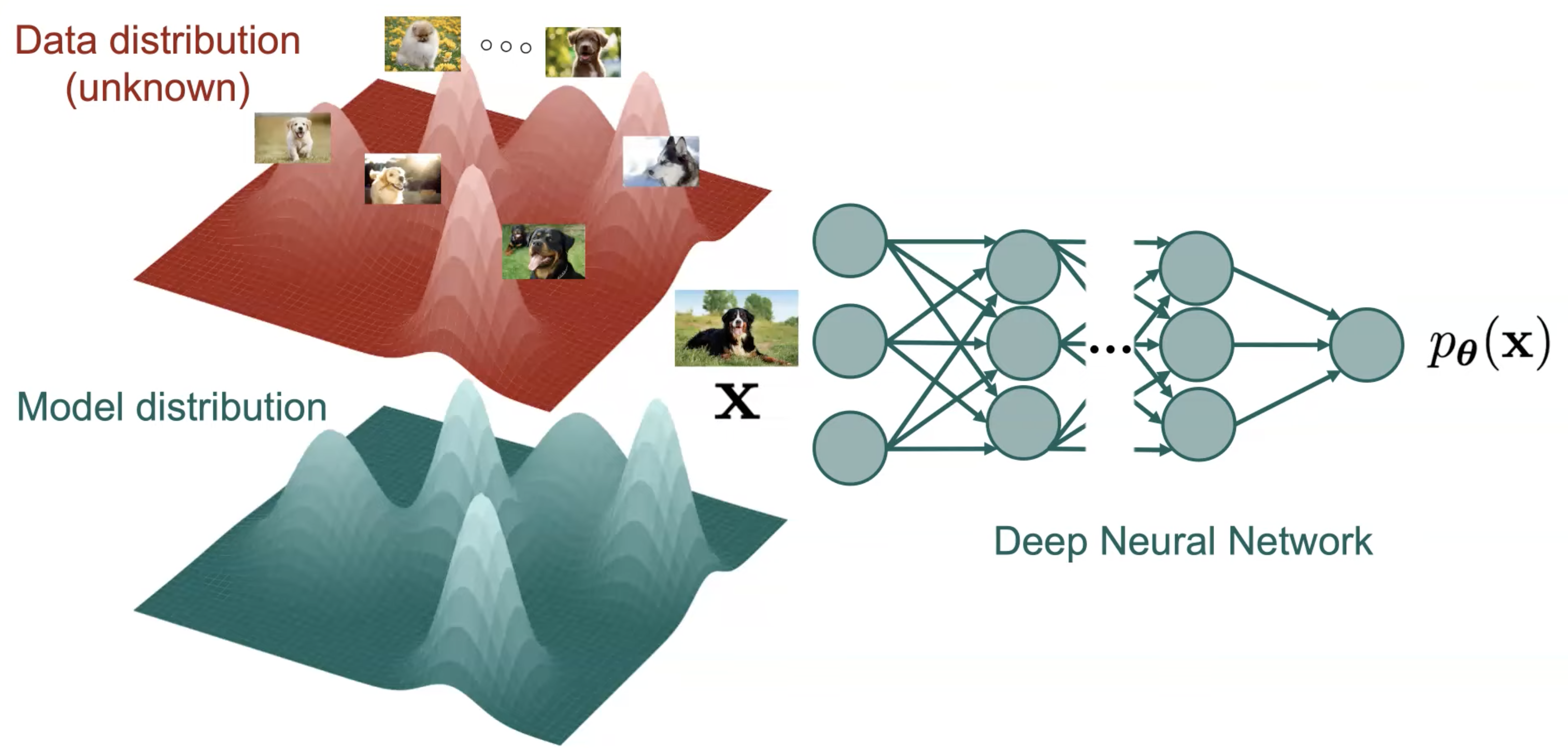 Fig. 아마 정확히는 Latent Variable Model 을 가정하고 문제를 풀어야 위 처럼 될 것 같습니다.
Fig. 아마 정확히는 Latent Variable Model 을 가정하고 문제를 풀어야 위 처럼 될 것 같습니다.
여기서 입력 이미지 (Input Image) 를 받아 Target Data Distribution 을 표현하는 파라메터 (가우시안일 때는 mean) 를 계산해야 하는데 Deep Neural Network 는 단층의 고전 머신 러닝 모델이 아니라 여러 층으로 이루어져 있으며 Non Linear Activation Function 을 수없이 통과하기 때문에 출력 Vector 에는 양수가 아닌 값들이 존재할 수 있고
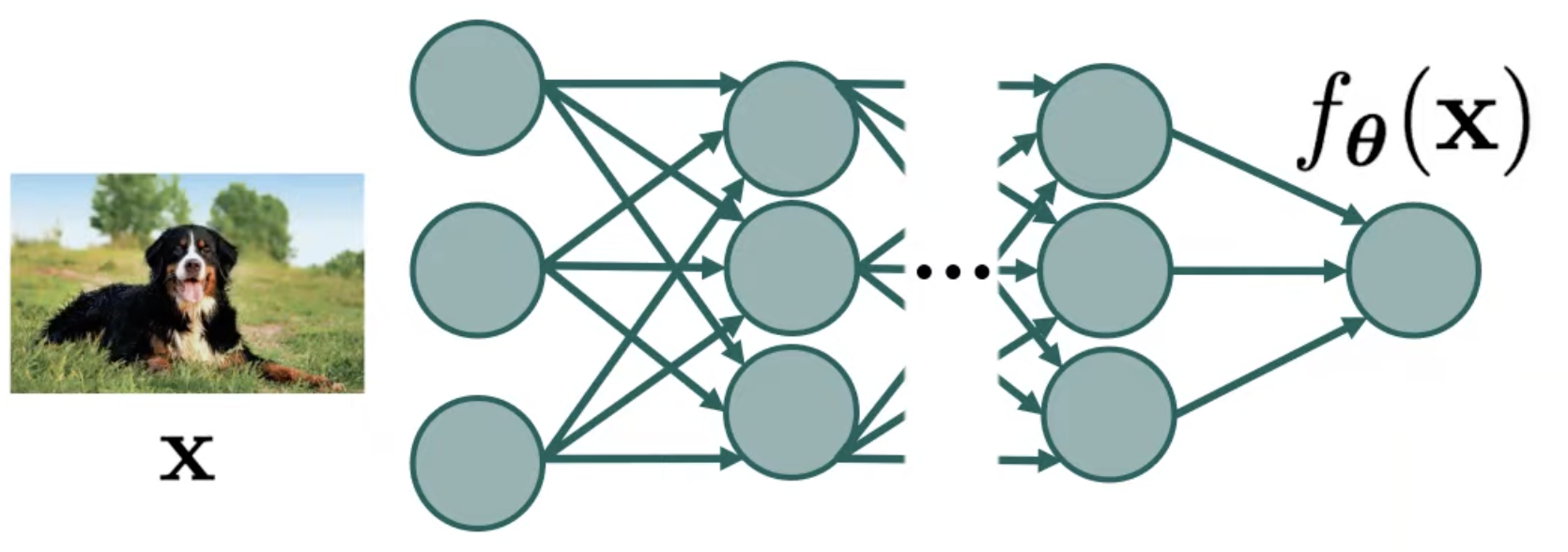
따라서 \(f_{\theta}\) 를 확률 분포로 나타내기 위해서는 출력 값에 exponential 을 취해 출력 값들을 모두 양수 값들로 바꾸고
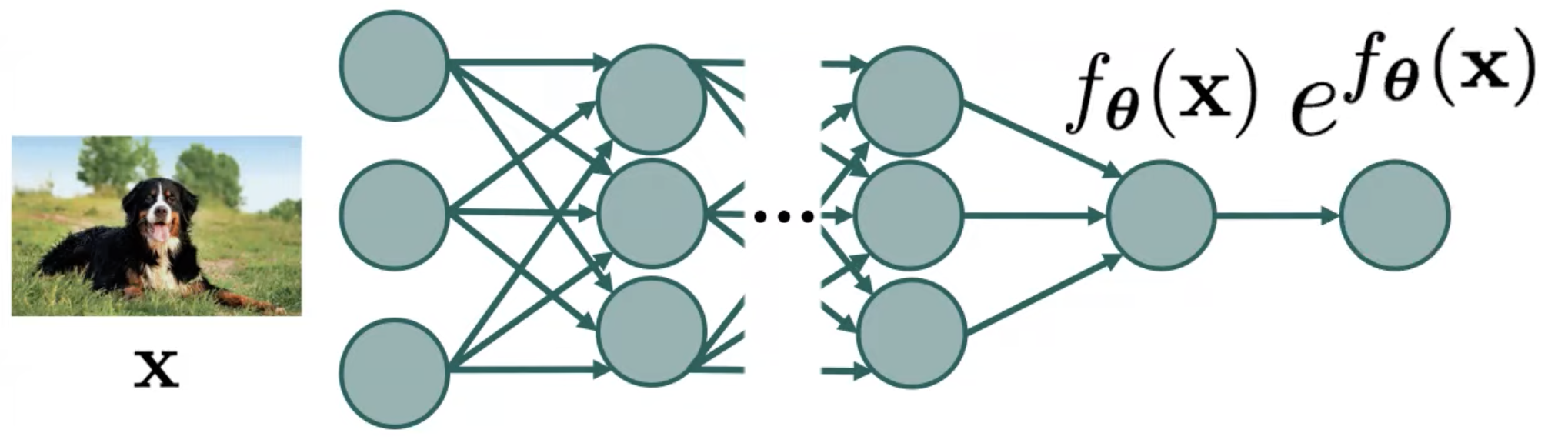
여기에 어떤 값 \(Z_{\theta}\) 를 나눠주어야 합니다.
이제 이를 최적화 하면 모델이 학습되는 것이겠죠?
하지만 여기서 이 \(Z_{\theta}\) term 이 문제가 되는데요, 이를 바로 Normalizing Constant 라고 부릅니다.
(Normalizing Constant 로 나눠줘야 최종 출력을 합이 1인 확률 분포로 나타낼 수 있으니)

이 값은 가능한 모든 네트워크 출력값을 모든 x 에 대해 적분한 것과 같습니다.
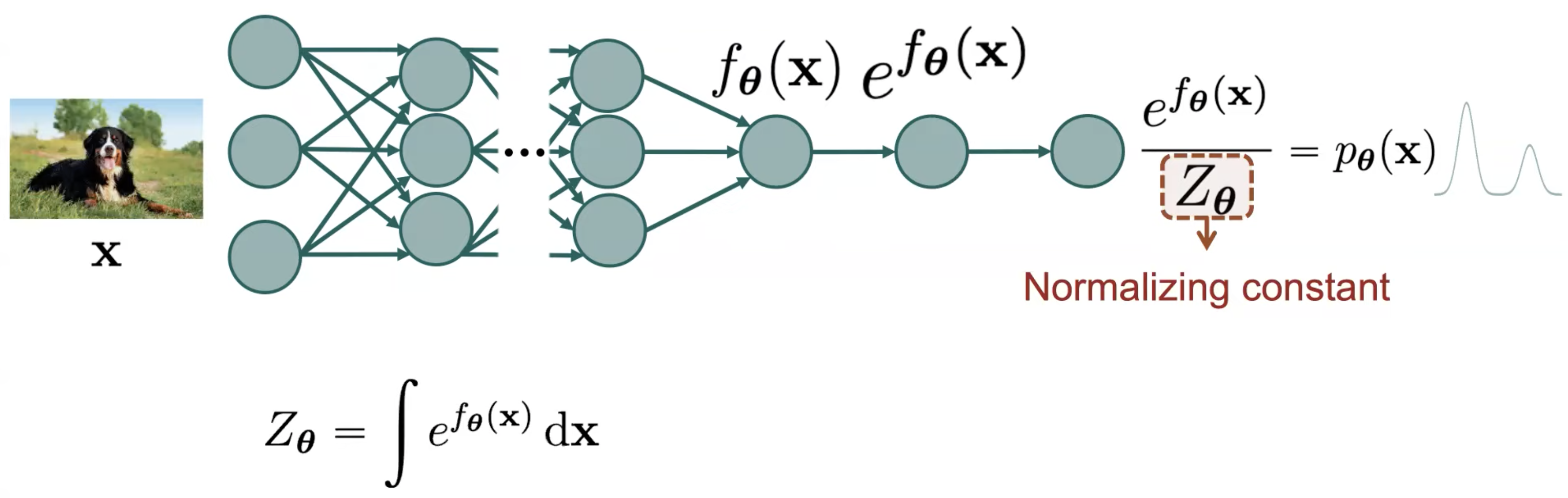
우리가 근사하려고 명시적으로 정해준 분포 \(f_{\theta}\) 가 Gaussian Distribution 이라면 이 term 은 아래처럼 간단하게 정의될 수 있다고 하는데요,
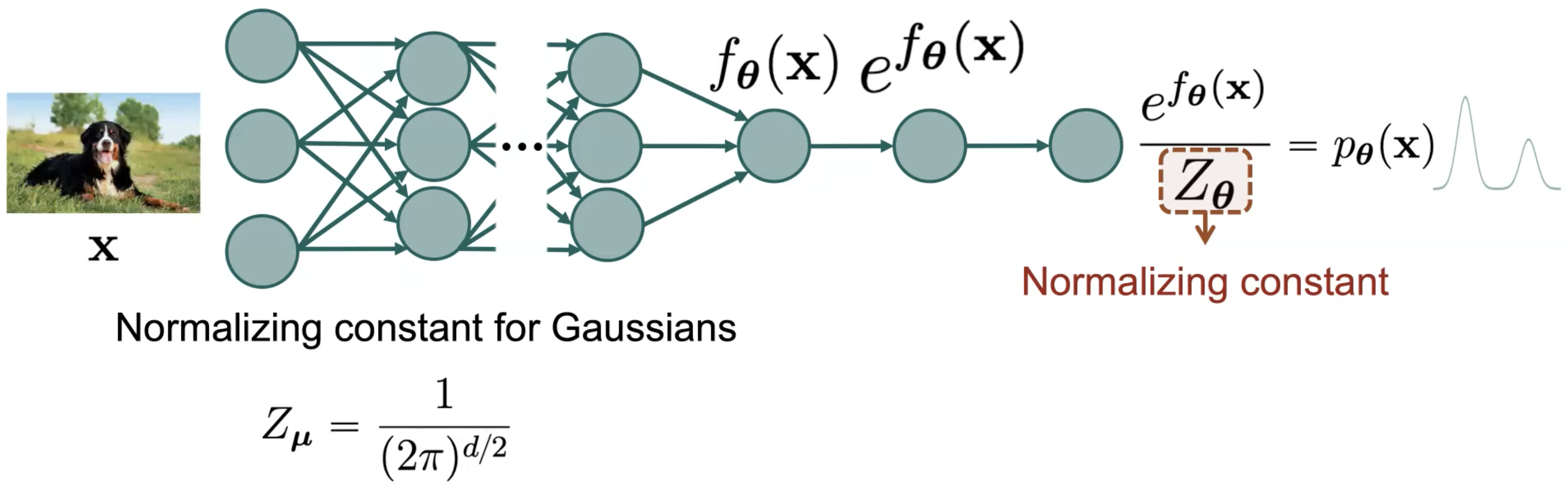
이런 경우를 풀기 쉬운 (tractable) 한 경우라고 얘기합니다.
하지만 Deep Neural Network 를 쓰는 대부분의 경우에 이 값을 계산하는 것 자체가 거의 불가능한, 즉 intractable 하게 되는데요,
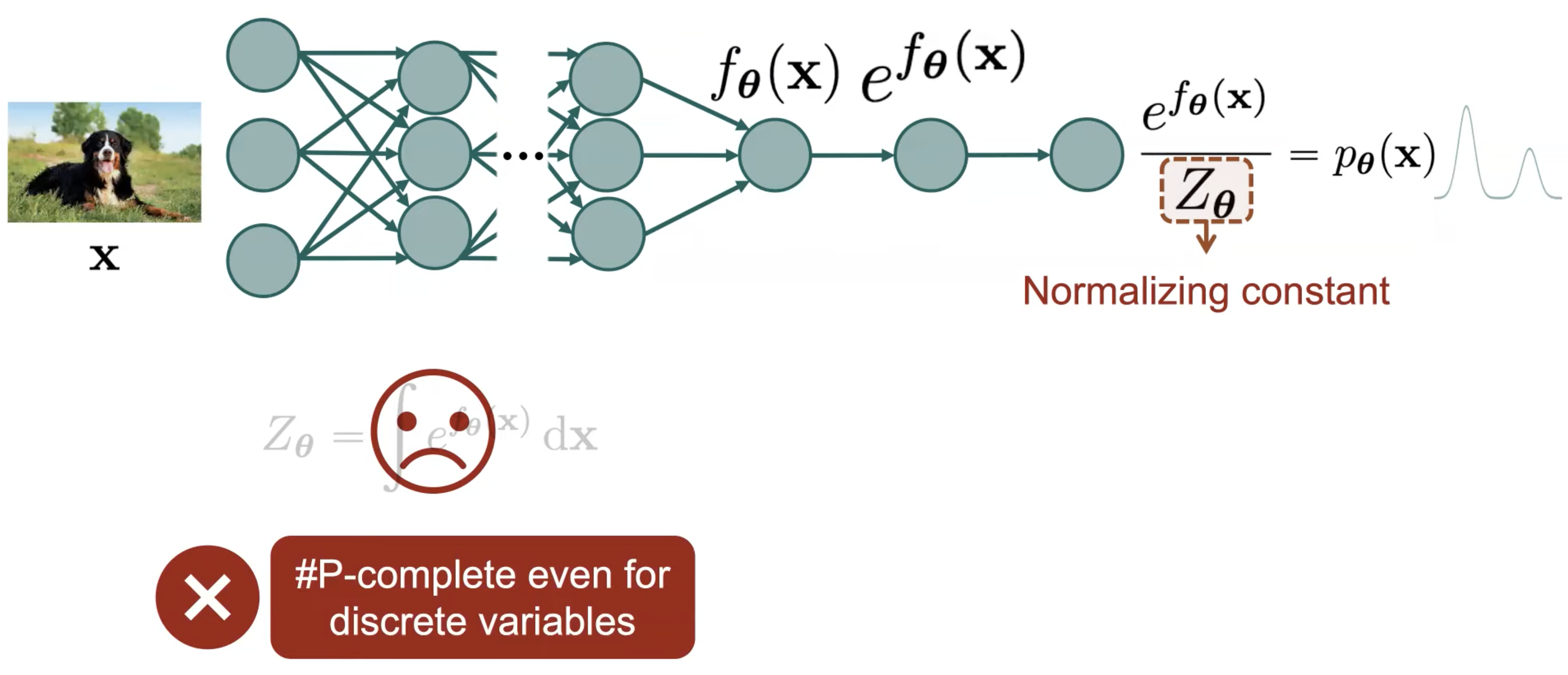
대부분의 VAEs 를 비롯한 현대의 Deep Generative Models 는 이 문제를 해결하기 위한 방법론들 이었던 겁니다.
- VAEs 등의 Latent Variable Models
- asd
- Transformer Decoder 스타일의 Autoregressive Models
- asd
- GANs
- 아예 샘플링을 통해 데이터의 분포를 Implicit 하게 학습하는 것으로, Normalizing Constant 문제점을 우회 (bypass) 해버림.
하지만 이런 방법들은 Normalizing Constant 를 계산하지 않기 위해서 Variational Inference 를 쓴다던가, 아예 GAN 같은 독자노선을 타는 등의 방법을 취하며 각각 한계점을 지니고 있다고 저자는 이야기 합니다.
 Fig. Deep Generative Models 의 한계점
Fig. Deep Generative Models 의 한계점
Score-based Generative Model 는 GAN 이 그랬던 것 처럼 아예 Normalizing Constant 를 계산하지 않고 우회해버리는 방법을 택하는데요, 데이터의 분포를 배운다는 목표는 같습니다만 Score Function 이란걸 따로 정의하게 됩니다.
The Score Function, Score-based Models, and Score Matching
Score Function
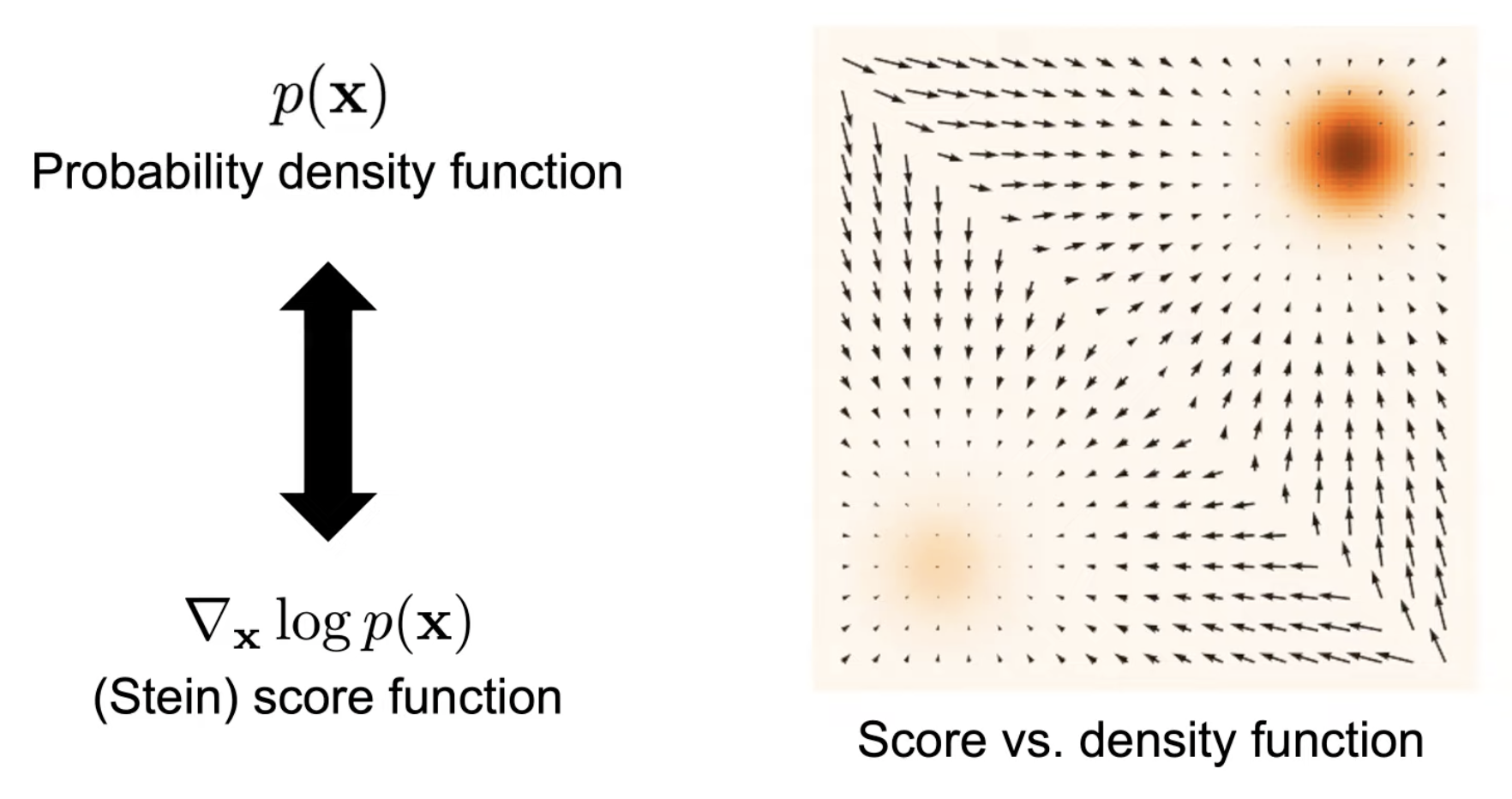
Score Function 이 뭘까요? 예를 들어 어떤 데이터의 분포 \(p(x)\) 가 2개의 이변량 가우시안 분포 (Bivariate Gaussian Distribution) 을 합친 Mixture of Gaussian (MoG) 라고 해보겠습니다. Score Function 은 단지 \(p(x)\) 를 모델의 파라메터 \(\theta\) 가 아니라 데이터 x 에 대해서 미분한 걸 말합니다.
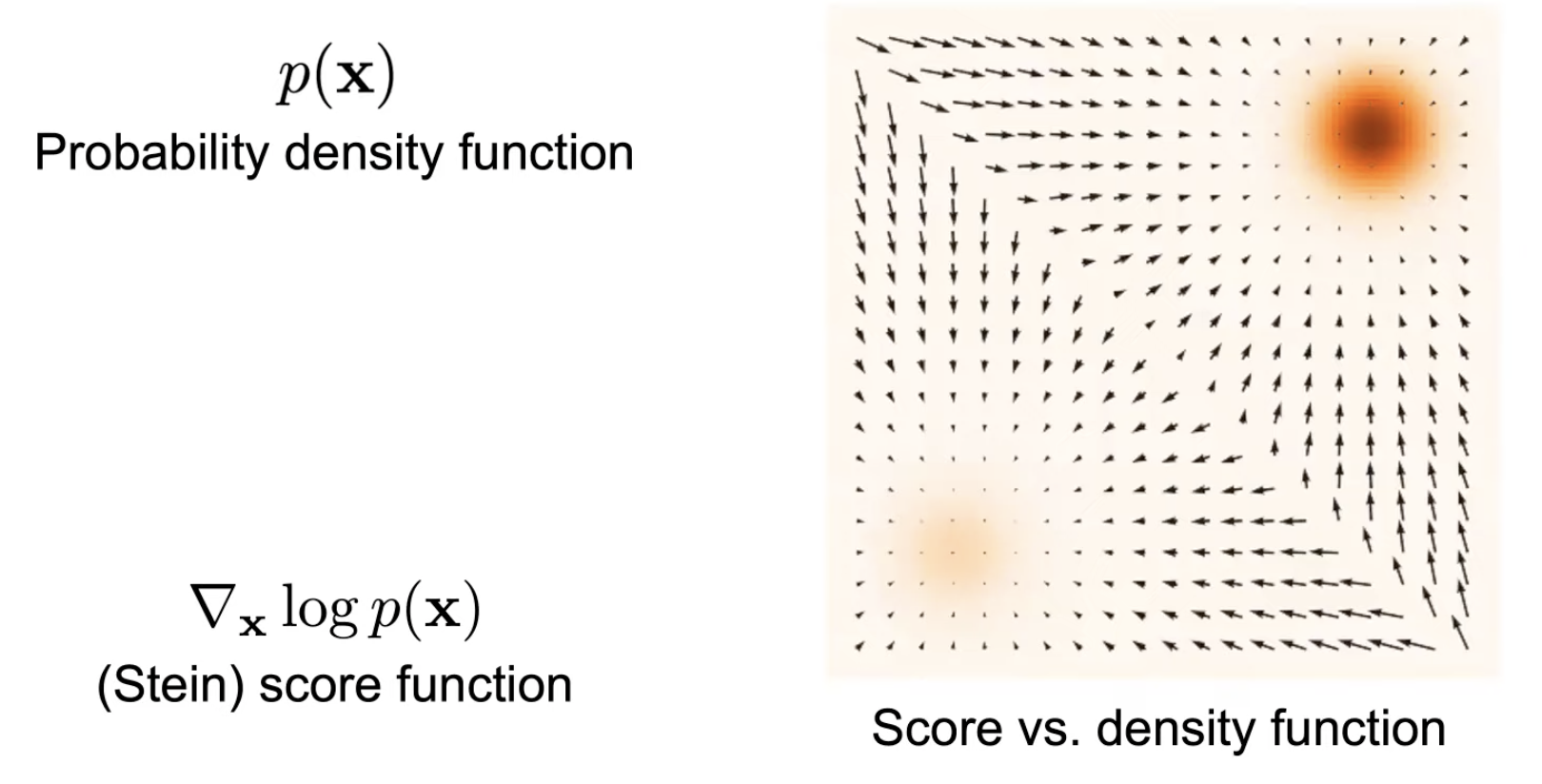
위의 Figure 는 2차원 MoG 에 대해서 실제로 Score Function 을 계산해서 시각화 한 것인데요, 사진에서는 더 어두울수록 밀도 (density) 가 높은것이고 화살표의 방향과 크기가 \(p(x)\) 곡면의 기울기의 방향과 크기를 나타낸다고 합니다.
이렇게 Density Function \(p(x)\) 가 주어지면 미부늘 취함으로써 Score Function 을 구할 수 있고 반대로 Score Function 을 적분하면 \(p(x)\) 를 구할 수 있습니다.
왜 Score-based Model 이 GAN 같은 Normalizing Constant 를 계산하는 것을 우회한게 되는걸까요? 그 이유는 아까 말씀드린 것 처럼 원래 확률 분포를 만들기 위해 Network Output 을 적분하는 intractable 한 연산을 하는것을
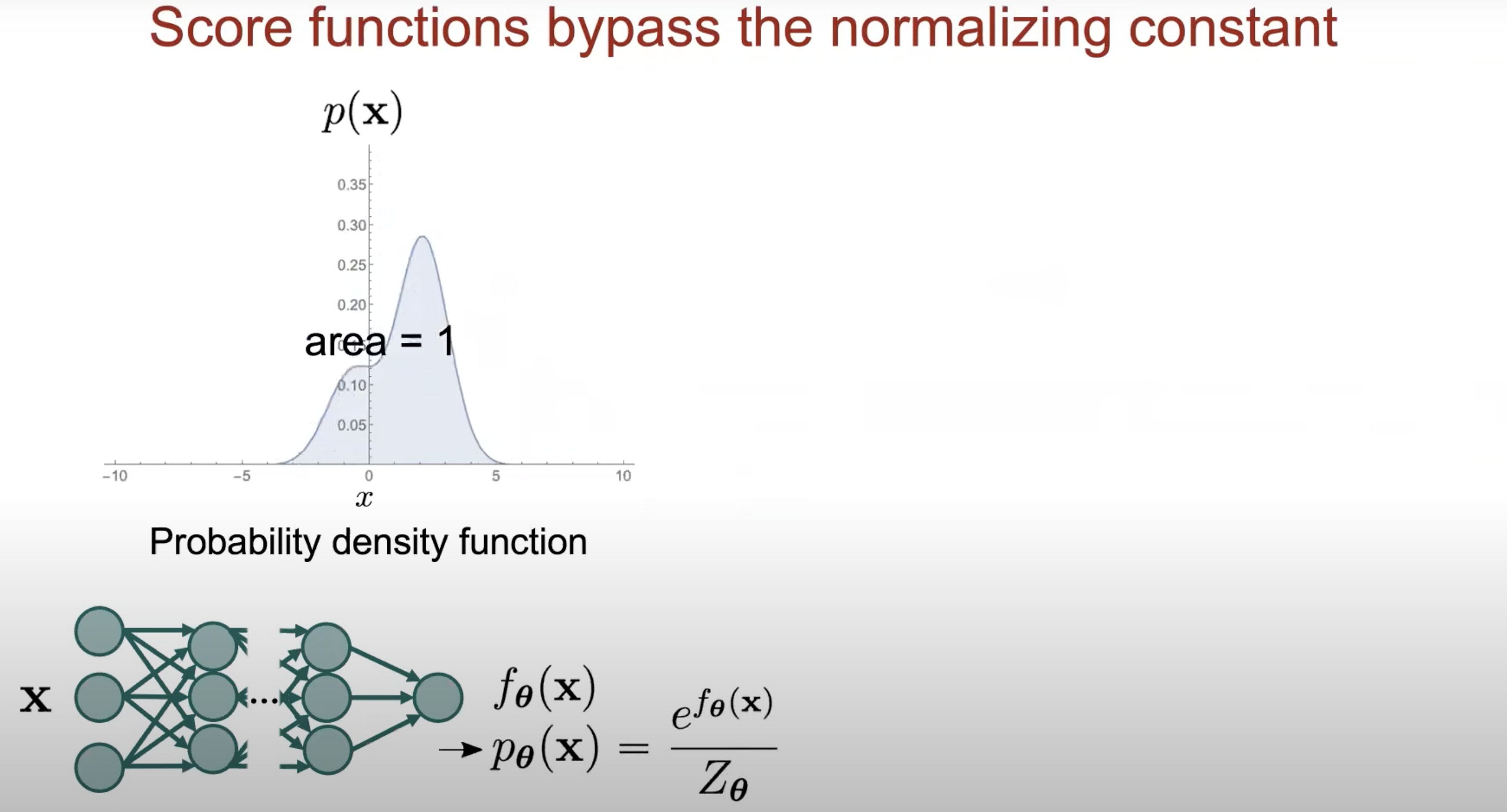
Score Function 의 정의에 따라 \(x\) 에 대해 미분하면 \(Z_{\theta}\) term 자체를 무시해버려도 되기 때문입니다.
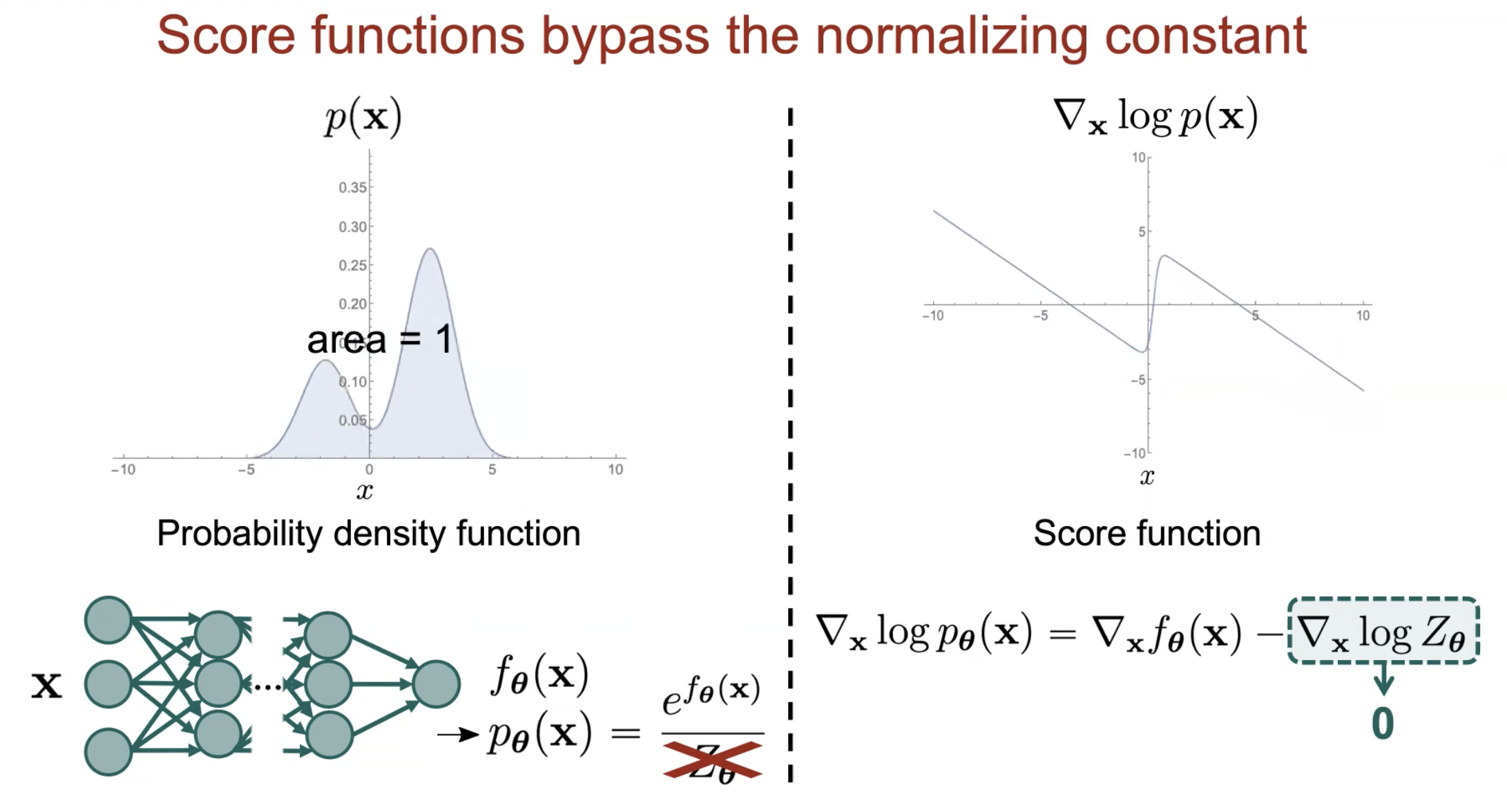
데이터의 확률 밀도 분포 와 이를 x 에 대해 미분한 것은 1차원 데이터에 대해 생각해볼 때 아래와 같습니다.
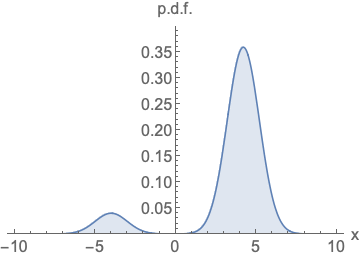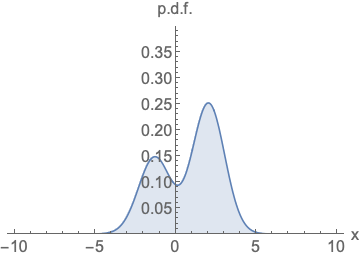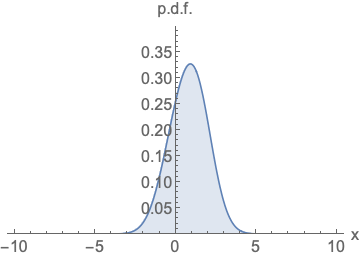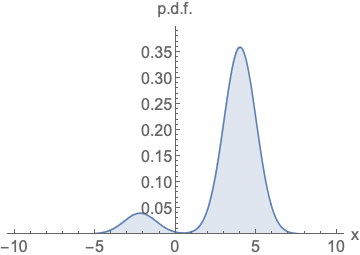 Fig. Parameterizing probability density functions. No matter how you change the model family and parameters, it has to be normalized (area under the curve must integrate to one).
Fig. Parameterizing probability density functions. No matter how you change the model family and parameters, it has to be normalized (area under the curve must integrate to one).
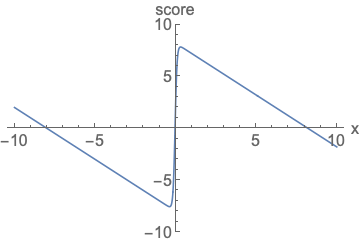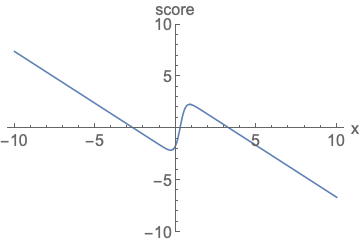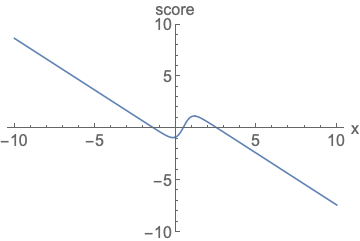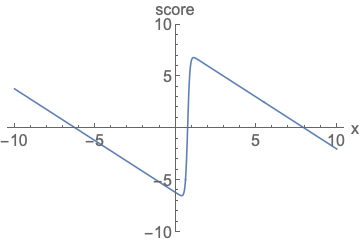 Fig. Parameterizing score functions. No need to worry about normalization.
Fig. Parameterizing score functions. No need to worry about normalization.
여기서 주의할 점은 당연히 실제로는 \(p_{data}(x)\) 는 어떻게 생겼는지 알 수 없고 우리가 가지고 있는 것은 이 분포로부터 뽑힌 샘플들, \(\{ x_i \in \mathbb{R}^D \}^{N}_{i=1}\)밖에 없으며, 우리가 하고싶은 것은 \(\theta\) 로 표현되는 Neural Network \(s_{\theta} : \mathbb{R}^D \rightarrow \mathbb{R}^D\) 가 이를 근사하는 것이 된다는 겁니다.
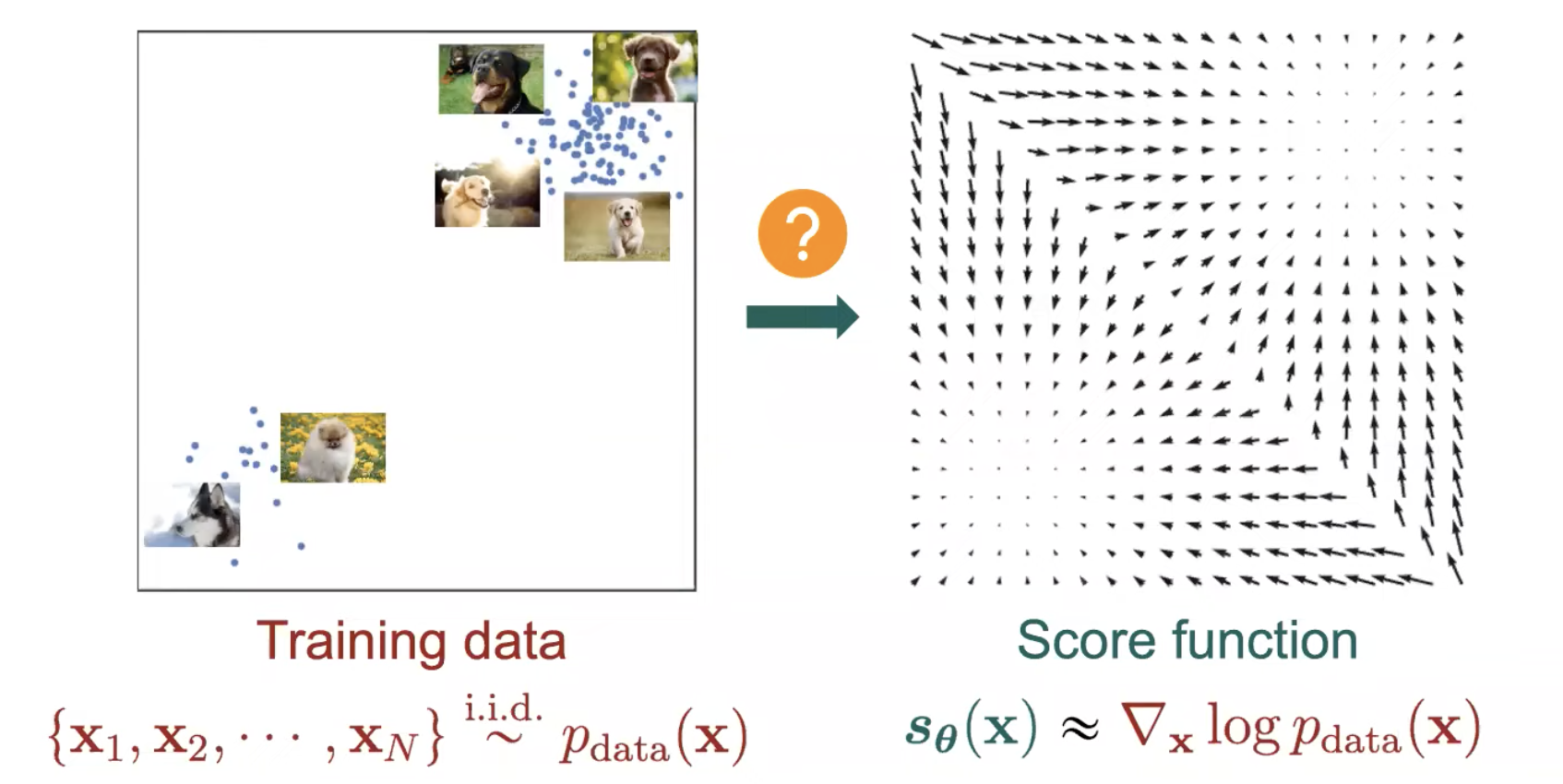 Fig. \(s_{\theta}\) 를 적분하면 p_{\theta}(x) 가 됨.
Fig. \(s_{\theta}\) 를 적분하면 p_{\theta}(x) 가 됨.
이 때 필요한 두가지 ingredient 들이 있는데요, 바로
- Score Matching
- Langevin Dynamics
입니다.
이제 이것들에 대해 알아볼 것인데요, 그 전에 Score-based 가 다른 기법들에 비해 어떤 장점이 있는지 조금 더 생각해 봅시다.
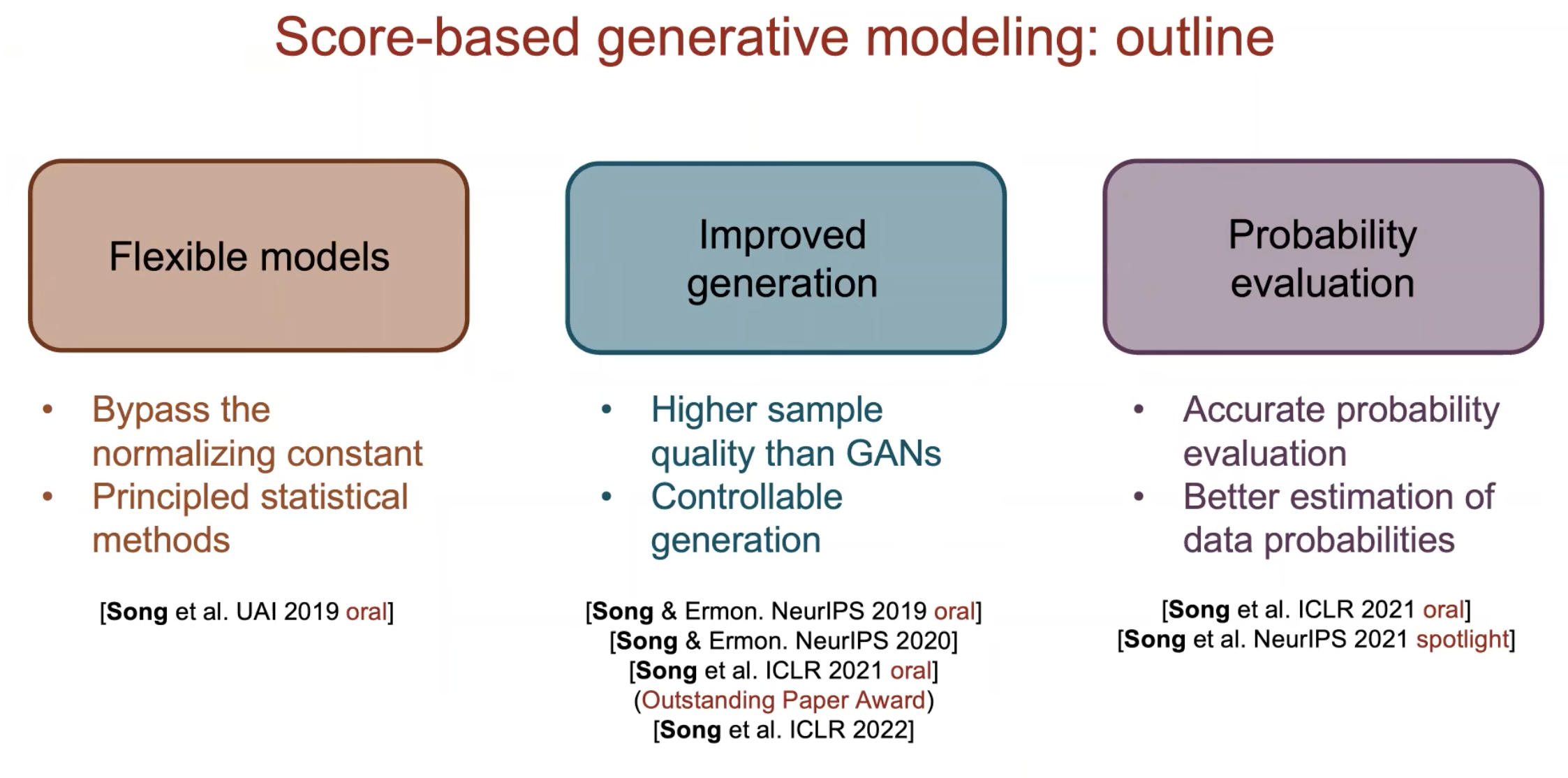 Fig.
Fig.
From Fisher Divergence to Score Matching
우리는 앞서 Score Function 이라는 것을 정의했는데요, 우리가 할 일은 데이터의 실제 분포와 이 vector field 를 매칭시키도록 네트워크의 파라메터를 조정하는 것이 되겠습니다.

어떻게 하면 될까요? 가장 간단하게 생각할 수 있는 방식은 데이터의 실제 분포를 우리가 가지고 있는 학습 데이터 \(x_1, x_2, \cdots, x_N\) 에 대해서 각각 미분을 해서 vector 들을 구하고

이를 모델이 각 지점에서 예측한 vector 와 거리를 계산하는 것을

 Fig. Animation of Fisher Divergence
Fig. Animation of Fisher Divergence
전체 샘플에 대해 하고 이를 평균을 내서 이를 줄이는 방식으로 학습을 하면 되겠습니다.
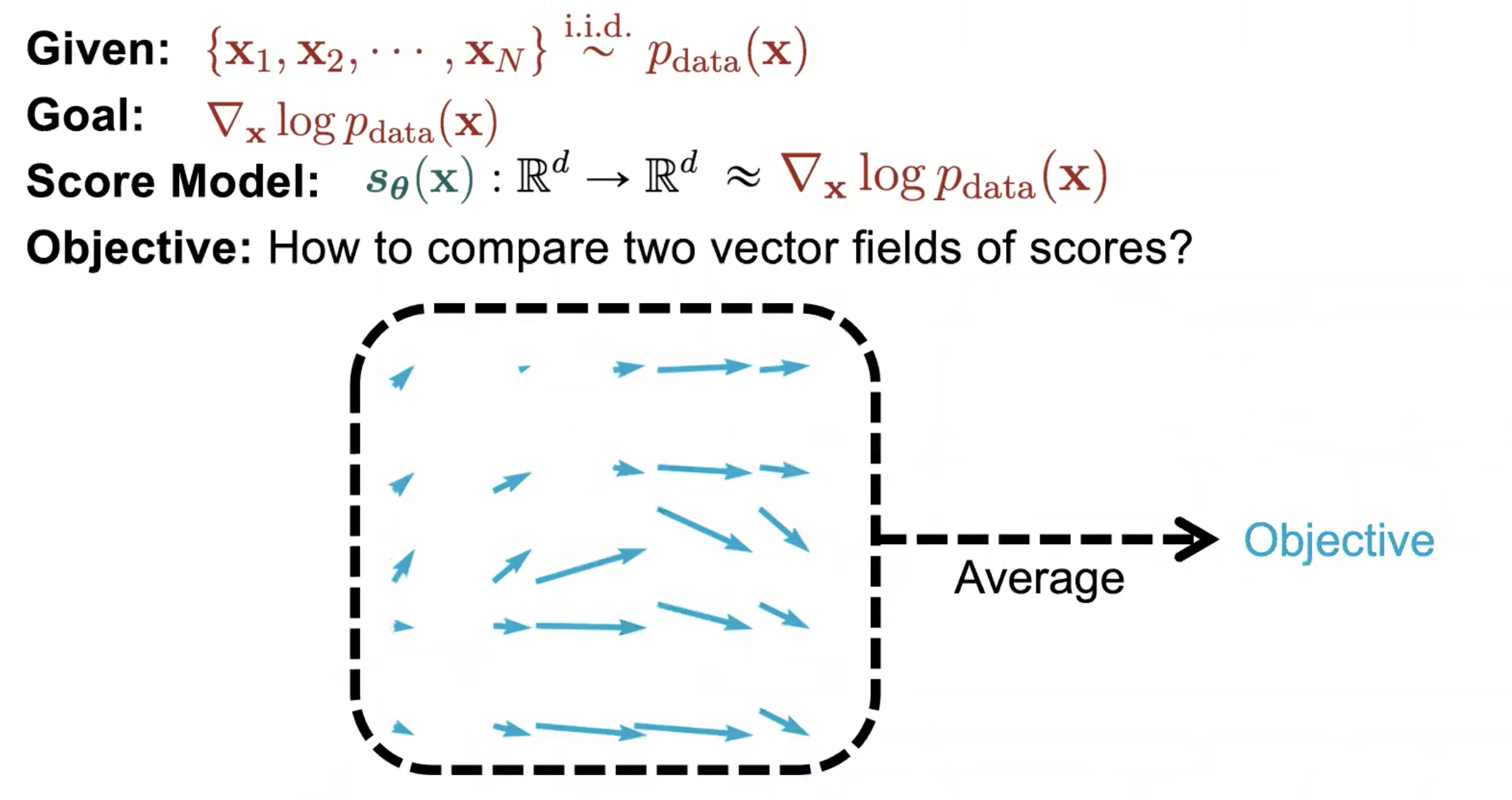
이 때 우리는 거리가 재고 싶으니 아래의 수식을 쓰면 되는데요,
\[\frac{1}{2} \mathbb{E}_{p_{data}} [ \parallel \nabla_x \log p_{data}(x) - s_{\theta}(x) \parallel^2_2 ]\]이렇게 실제 거리를 재는 것을 Fisher Divergence 라고 합니다.
하지면 이 방식에는 큰 문제점이 있으니 바로 실제 데이터 분포를 우리가 당연히 알 리가 없다는 겁니다.

그래서 논문의 저자들은 이를 해결하기 위해 2005년에 이미 알려진 방법인 Score Matching 이라는 방법을 이용해서 실제 vector 들 간의 거리를 재는것과 같은 효과를 내는 것을 사용하기로 하는데요,
여기서 우리가 거의 모든 머신러닝/딥러닝에서 하는 것 처럼 당연히 모든 데이터에 대해서 거리를 잴 수 없고 우리가 가지고 있는 데이터는 유한 (finite) 하기 때문에 기대값 \(\mathbb{E}\)을 \(\sum\) 으로 바꾸면

아래와 같은 수식을 얻을 수 있습니다.
\[\approx \sum_{i=1}^N [ tr( \nabla_x s_{\theta}(x_i) ) + \frac{1}{2} \parallel s_{\theta}(x_i)\parallel^2_2 ]\]하지만 아직 끝난 것이 아닌데요, 수식을 보시면 Loss 를 계산하기 위해서는 Score Function 의 1차 미분 (Jacobian) 행렬을 구한 뒤에 이것의 Trace 를 구해야 합니다. 기본 몇 천만 (xx M) 에서 억 (xxx M) 단위를 넘어가는 요즘 딥러닝 모델에 대한 Jacobian 을 구하고 역전파 (Back Propagation) 까지 계산한다고 생각하면 이는 모델 학습에 있어 굉장한 Bottleneck 이 될겁니다.

즉 모델의 크기를 키우기가 힘든, Scalable 하지 않은거죠.
그래서 논문의 저자들은 아주 기발한 (Novel) 방법을 제안하는데요, 바로 차원의 수를 확 줄여서 일 부분에 대해서만 연산을 수행하자는 겁니다. 즉 Projection 시켜서 계산 하자는 것이었죠.
 Fig. Animation of Fisher Divergence
Fig. Animation of Fisher Divergence
asd
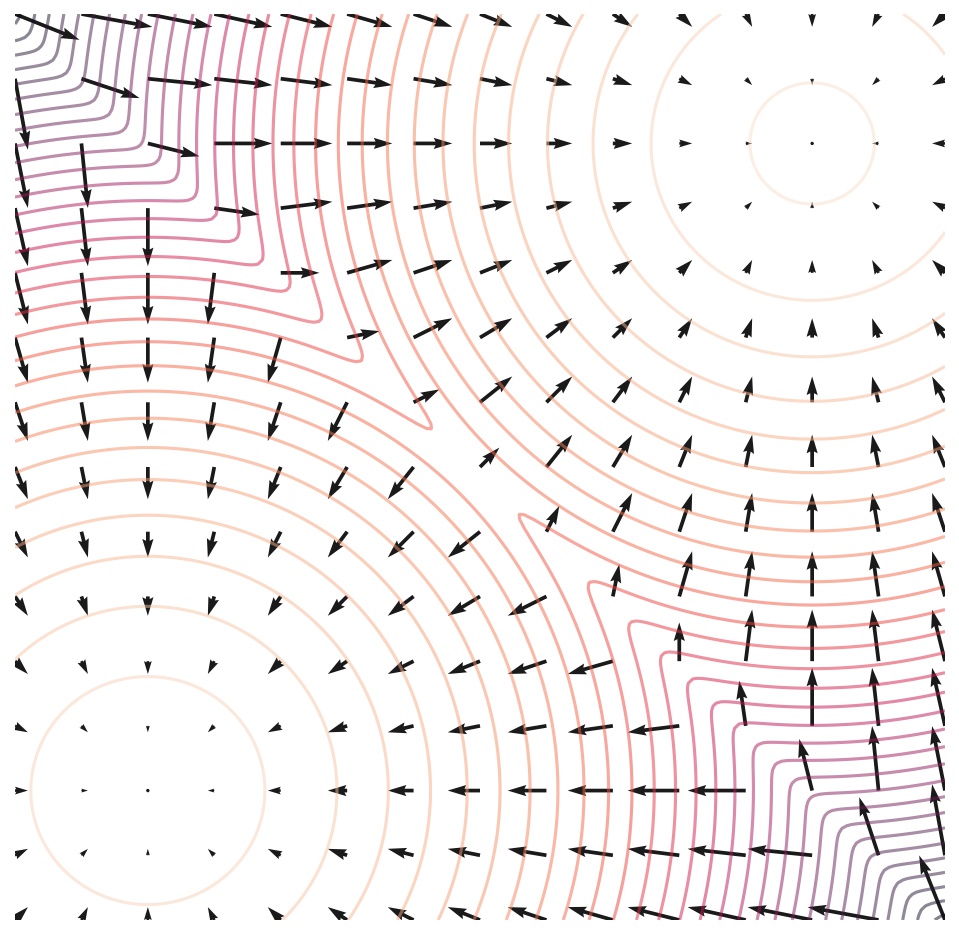 Fig. 2개의 2D-Gaussian Distribution 을 섞은 (Mixture) 간단한 분포에 대한 Score Function (the Vector Field) 와 Density Function (Contours)
Fig. 2개의 2D-Gaussian Distribution 을 섞은 (Mixture) 간단한 분포에 대한 Score Function (the Vector Field) 와 Density Function (Contours)
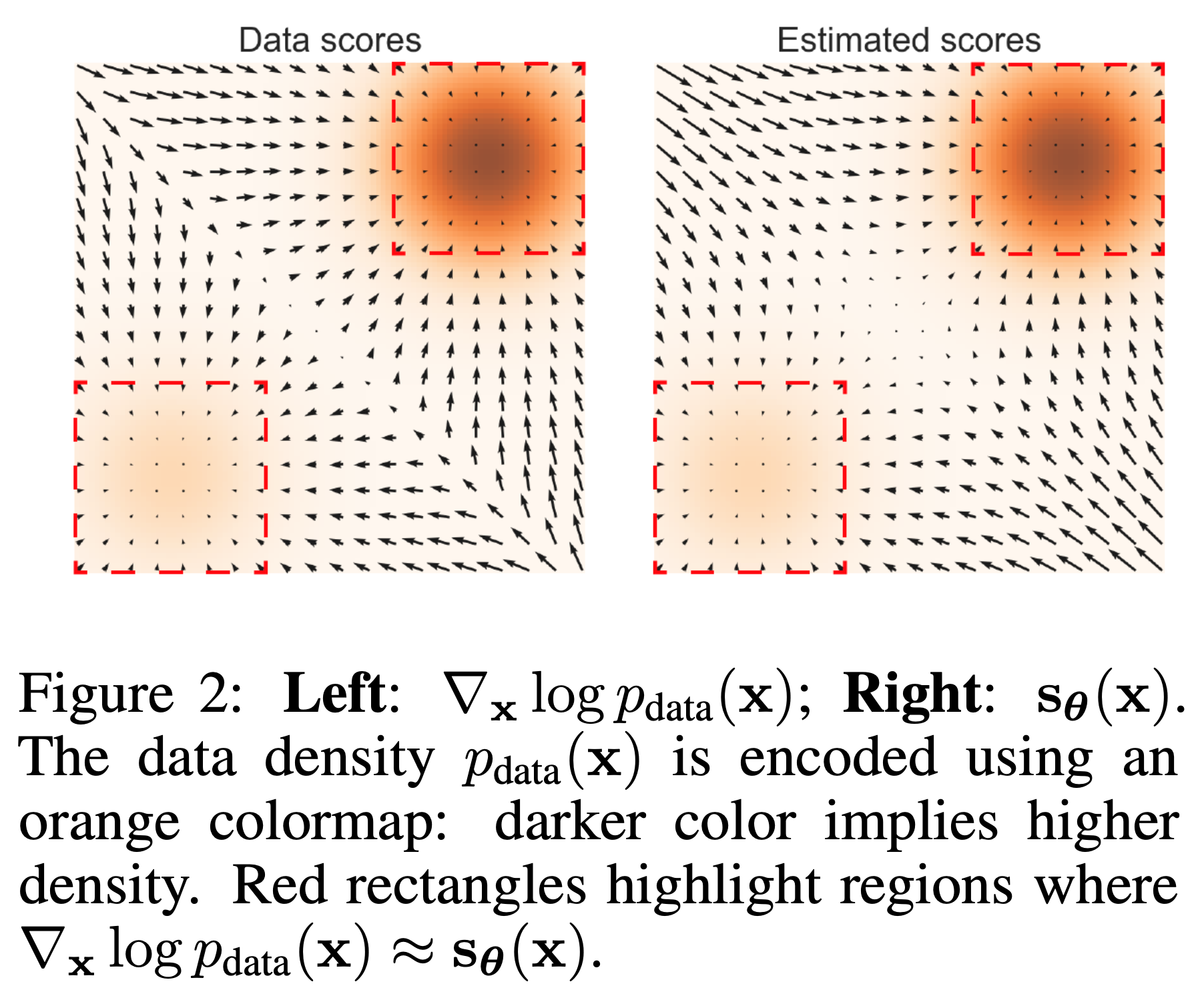 Fig.
Fig.
Sampling (Generation) From Score Function (Langevin dynamics)
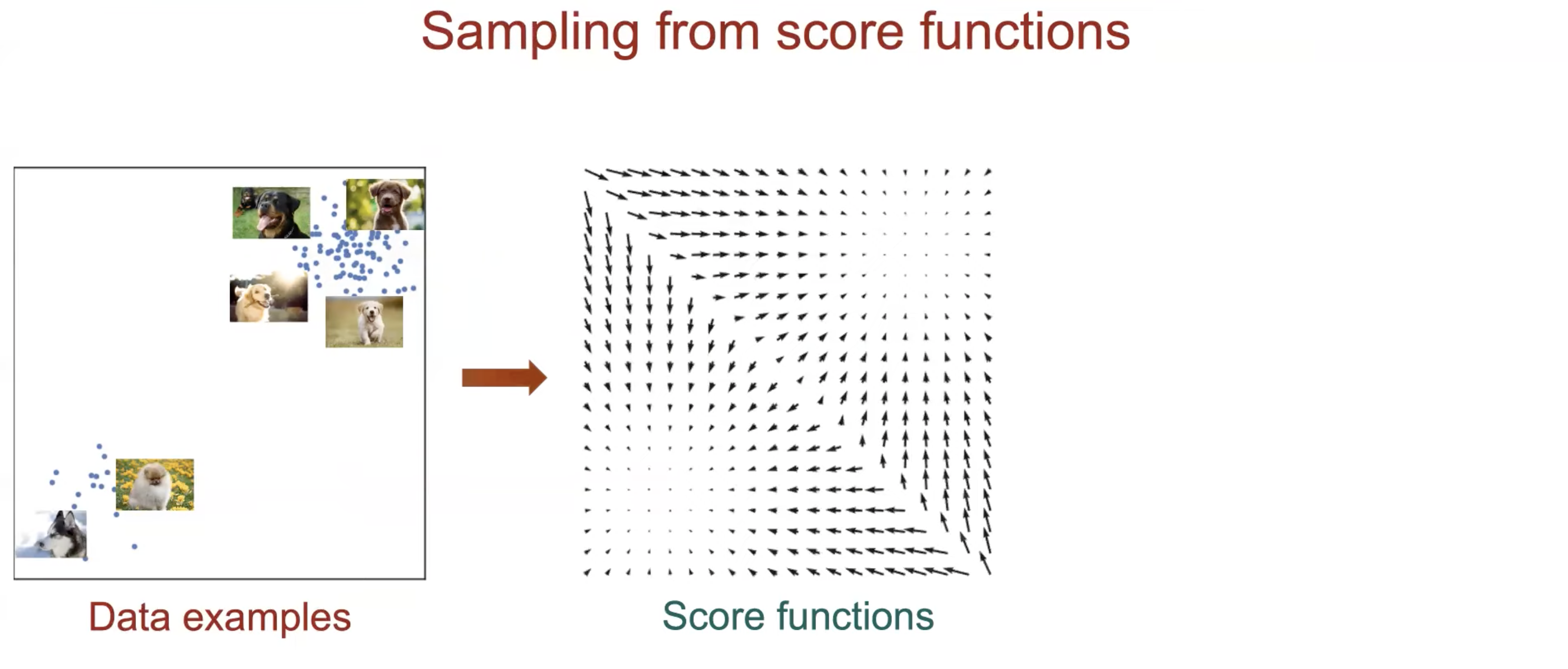 Fig.
Fig.
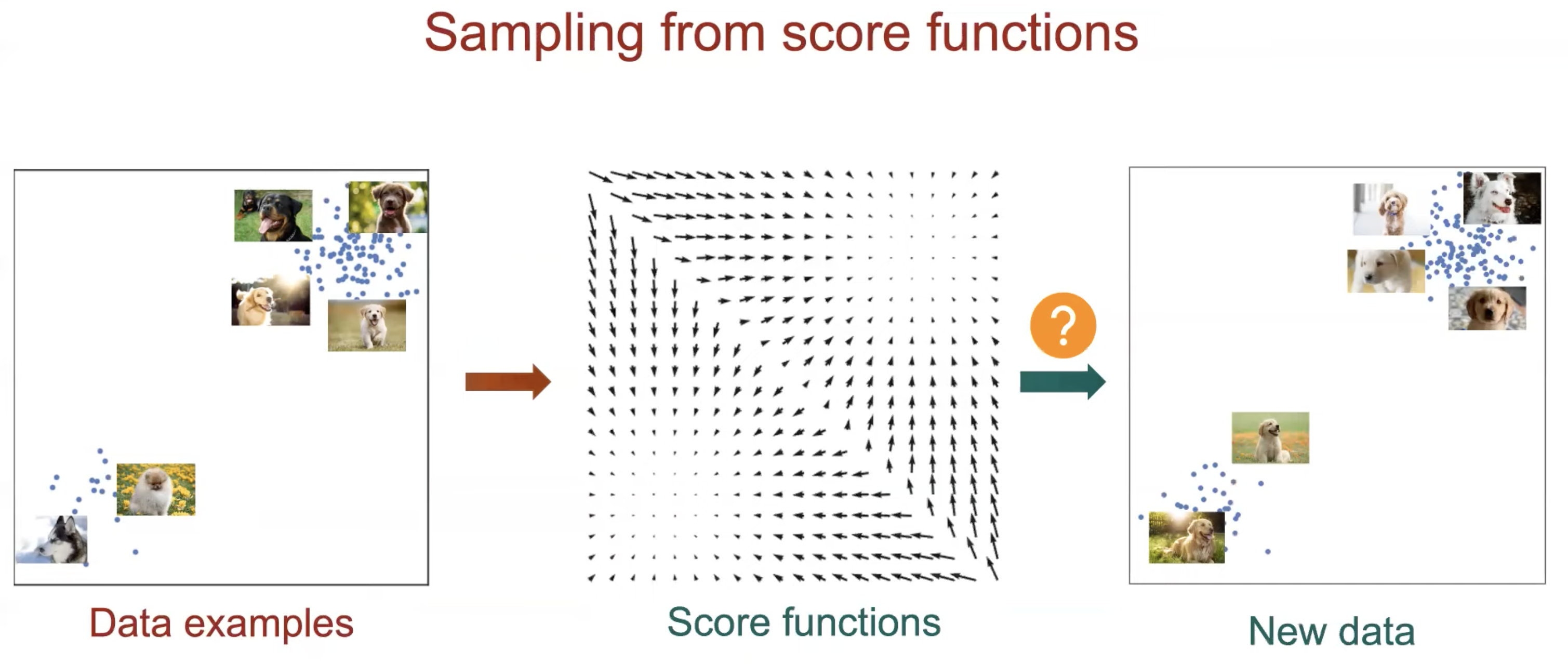 Fig.
Fig.
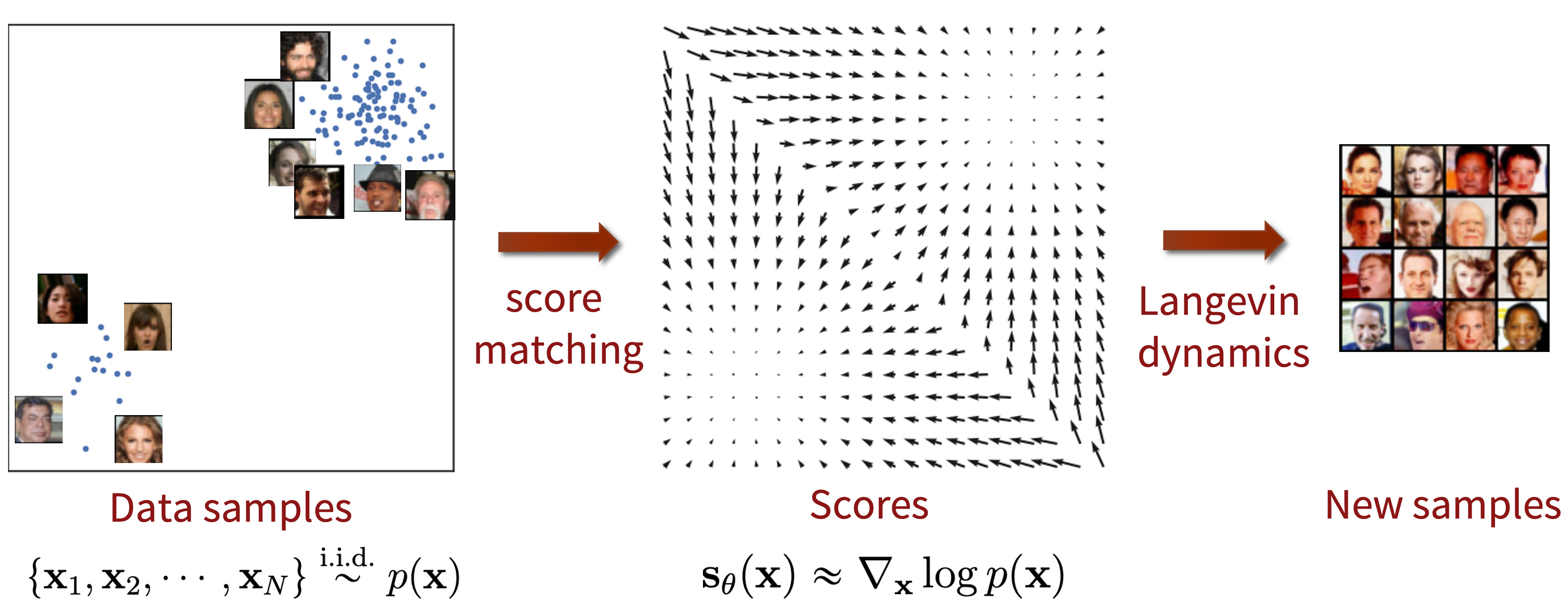 Fig. Score-based generative modeling with score matching + Langevin dynamics.
Fig. Score-based generative modeling with score matching + Langevin dynamics.
 Fig. Using Langevin dynamics to sample from a mixture of two Gaussians.
Fig. Using Langevin dynamics to sample from a mixture of two Gaussians.
Score-based Generative Modeling
Naive Score-based Generative Modeling and its Pitfalls
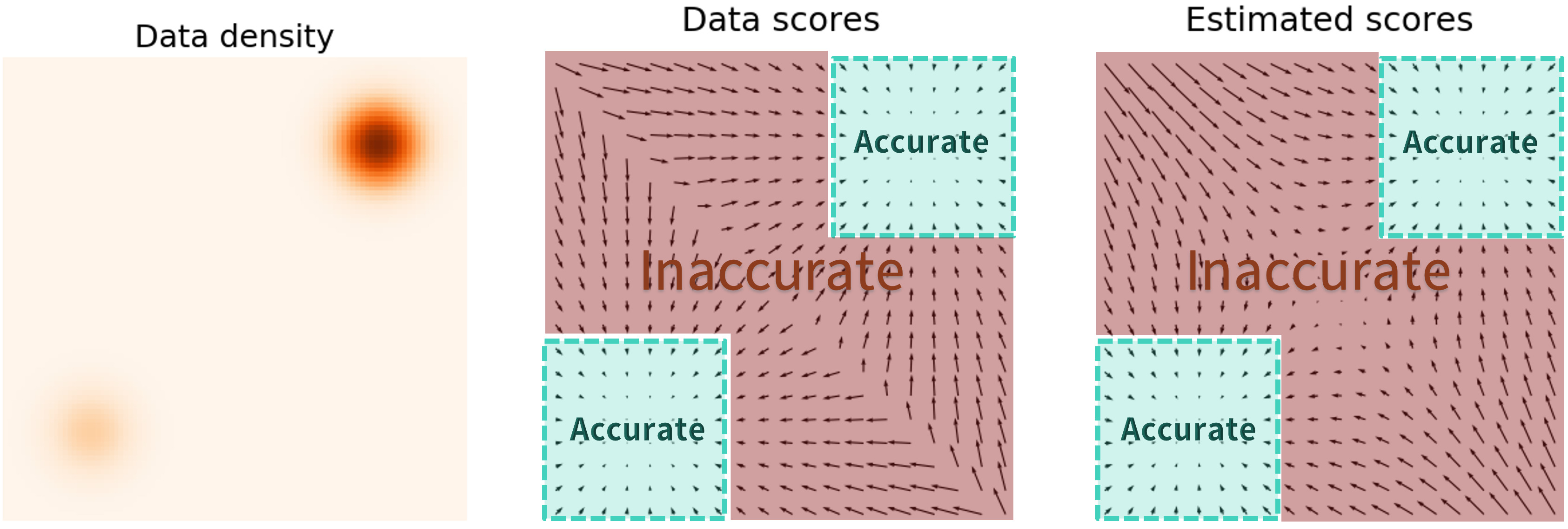 Fig.
Fig.
Score-based Generative Modeling with Multiple Noise Perturbations
 Fig.
Fig.
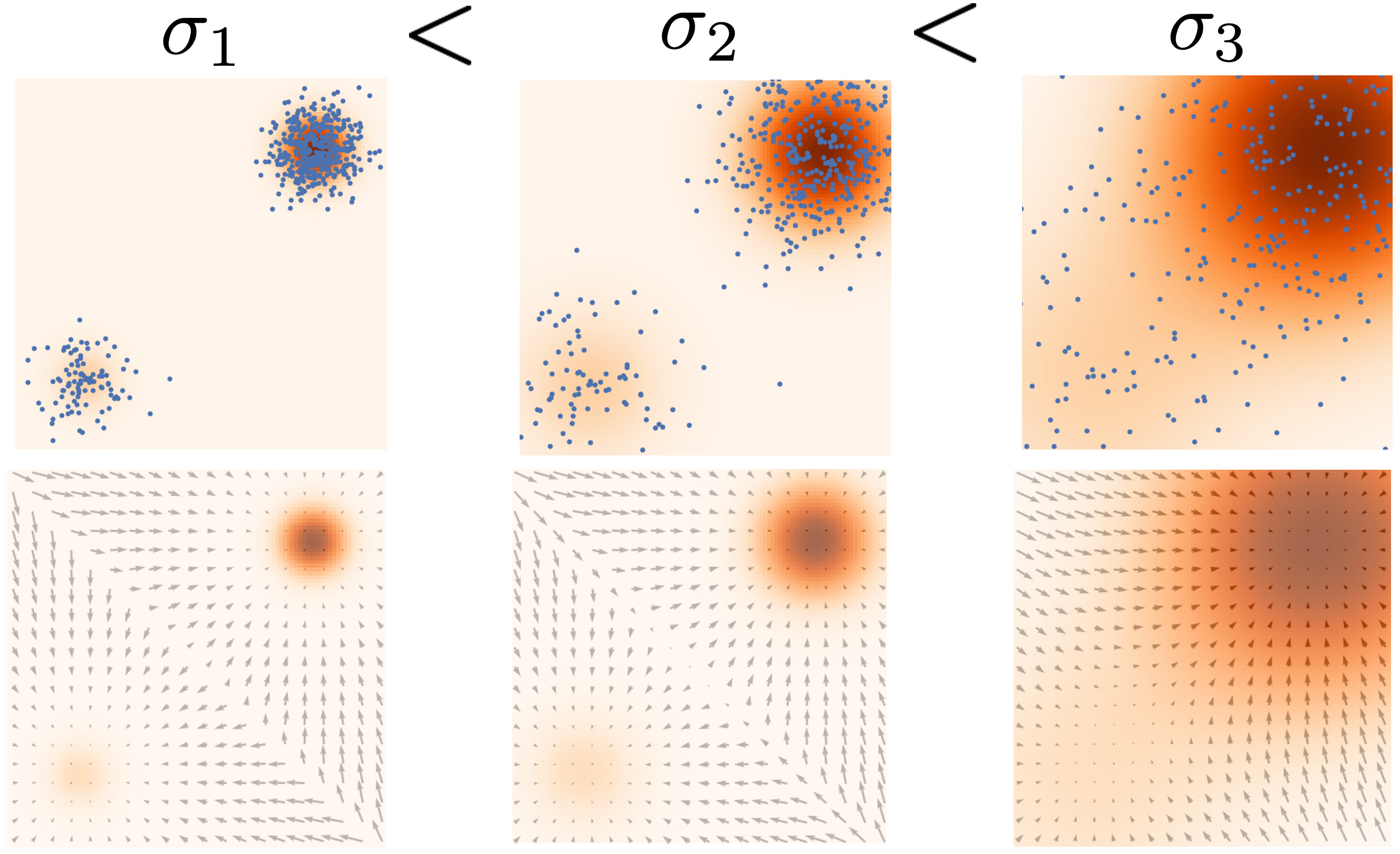 Fig.
Fig.
 Fig.
Fig.
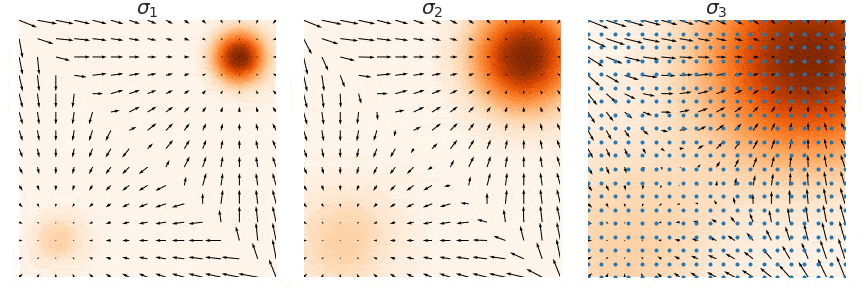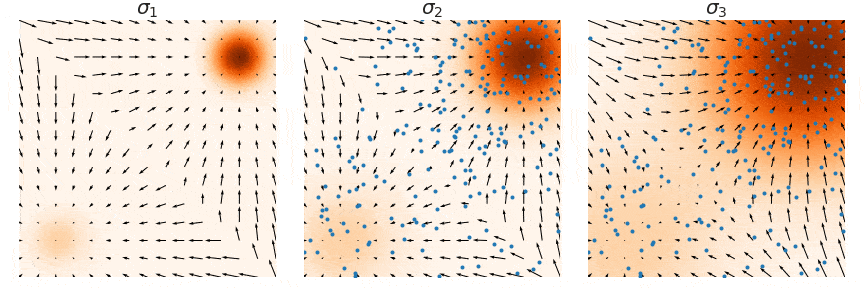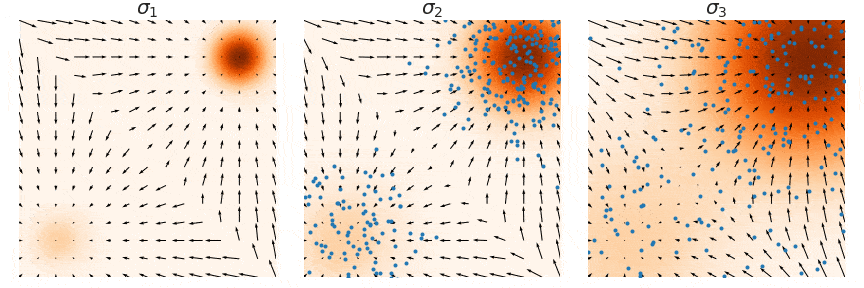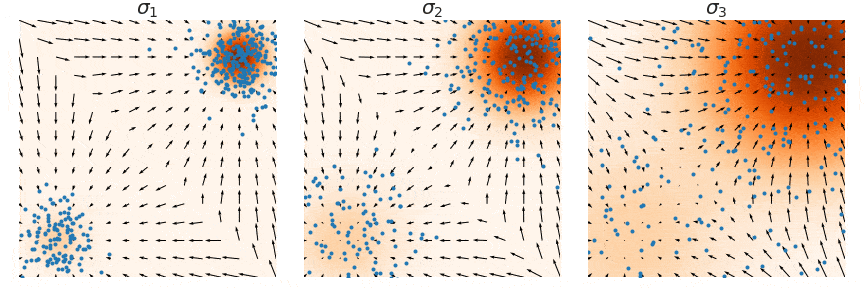 Fig.
Fig.
 Fig.
Fig.
 Fig.
Fig.
References
- Papers
- 2019 NIPS, Generative Modeling by Estimating Gradients of the Data Distribution
- 2020 NIPS, Improved Techniques for Training Score-Based Generative Models
- 2021 ICLR, Score-Based Generative Modeling through Stochastic Differential Equations
- 2021 NIPS, Maximum Likelihood Training of Score-Based Diffusion Models
- Blogs
- Videos
- Learning to Generate Data by Estimating Gradients of the Data Distribution (Yang Song, Stanford)
- Diffusion and Score-Based Generative Models
- Generative Modeling by Estimating Gradients of the Data Distribution - Stefano Ermon
- PR-385: Generative Modeling by Estimating Gradients of the Data Distribution from Jaejun Yoo
- PR-400: Score-based Generative Modeling Through Stochastic Differential Equations from Jaejun Yoo
- Others