L1 & L2 Regularization
03 Nov 2023< 목차 >
L1, L2 Regularization
Machine Learning (ML), Deep Learning (DL) model을 practical하게 학습하려면 과적합 (over-fitting)을 방지하는 technique들이 필요합니다.
보통 정규화 (Regularization) method들 이라고 부르는데, 이 중 L1, L2 Regularization이라는 것들이 있습니다.
이는 우리가 최적화 하려는 objective가 다음과 같을 때
추가적인 term이 다음과 같이 붙는 형태입니다.
\[L(\theta) = \frac{1}{2} \sum_{n=1}^N ( y_n - \theta^T x_n )^2 + \color{red}{ \frac{\lambda}{2} \sum_{j=1}^M \vert \theta_j \vert^q }\]Geometric Interpretation
L1, L2 Regularization은 기하학적으로 설명하는 자료들이 많은데 bishop의 PRML을 보면 아래와 같은 Figure가 있습니다.
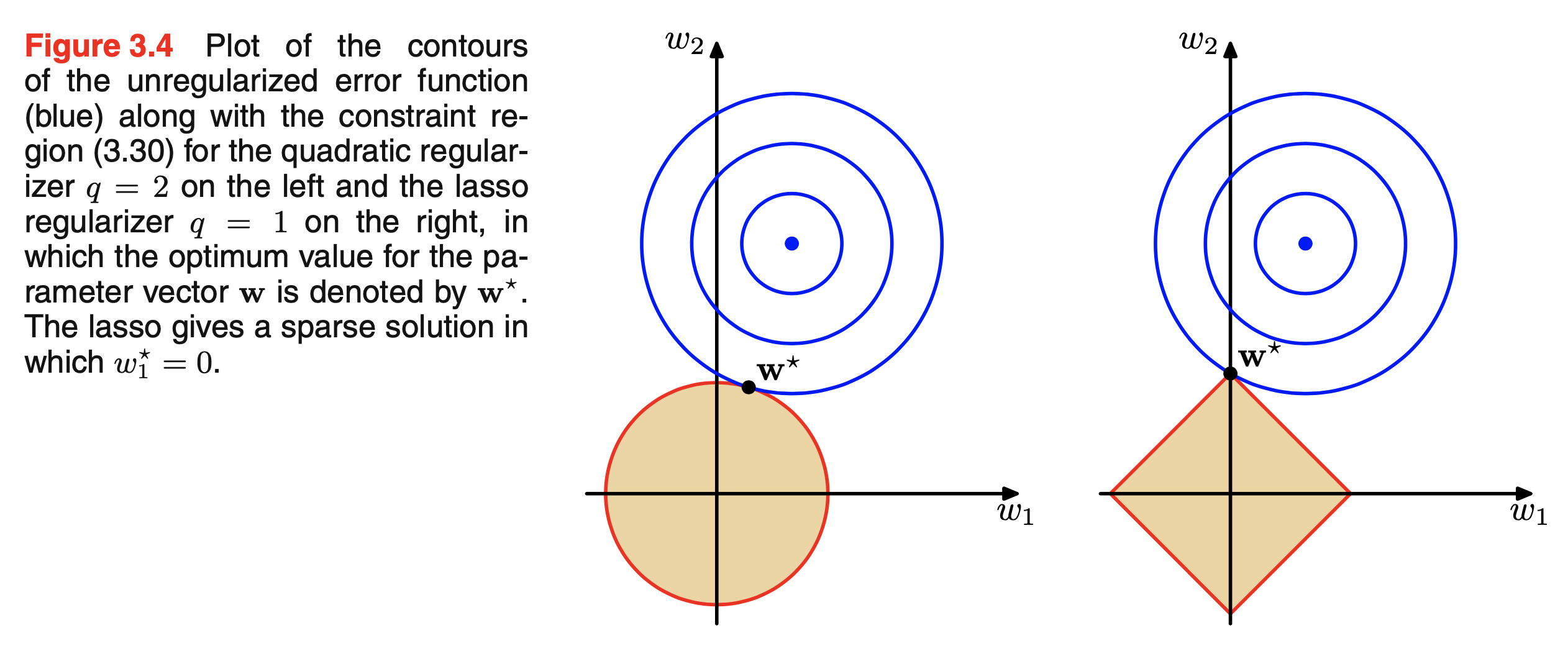 Fig.
Fig.
이는 model parameter가 2차원일 때 파란색의 objective surface안에서 최적화가 되면서 동시에 노란색 regularization surface에서도 동시에 최적화 되어야 한다는 의미를 갖고있으며, \(\lambda\)가 충분히 크면 parameter들 중 어떤 값들은 0이 되는 sparse solution을 얻을 수도 있습니다.
L1 (오른쪽)의 경우를 보면 두가지를 만족하는 solution은 보통 어떤 parameter는 0이 되는 형태라는 걸 볼 수 있습니다.
이는 data를 따르면서 최적화를 하면서도 weight value를 0으로 decay 시키기에 weight decay라고도 합니다.
q에 따라 다양한 형태의 regularization을 줄 수 있습니다.
\[L(\theta) = \frac{1}{2} \sum_{n=1}^N ( y_n - \theta^T x_n )^2 + \color{red}{ \frac{1}{2} \sum_{j=1}^M \vert \theta_j \vert^q }\]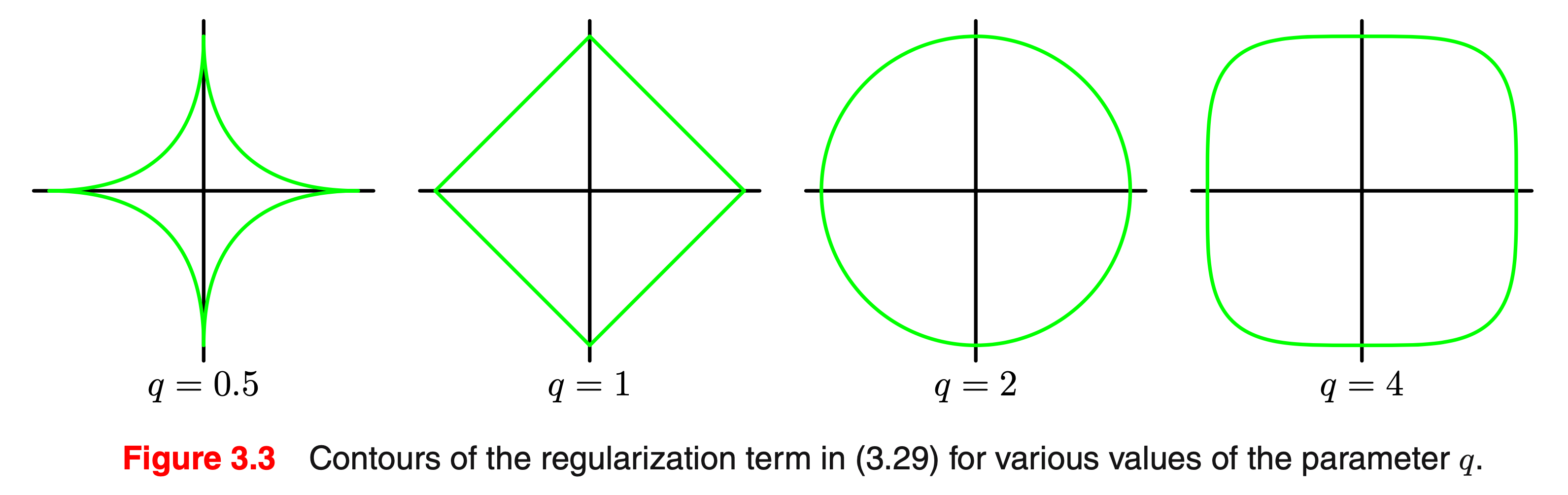 Fig.
Fig.
Bayesian Interpretation
그런데 우리가 앞서 얘기한 objective인 Mean Squared Error (MSE)는 target likelihood distribution 이 gaussian distribution인 경우에 대해 log likelihood로 수식을 전개한 형태입니다. 이를 maximize 하는 것이 결국 학습을 하는 것이었죠. likelihood를 써 봅시다. variance 가 1이라고 생각하면 아래와 같습니다.
\[p(y_n \vert x_n, \theta) = N(\theta^T x_n, \beta^{-1}I)\]그런데 여기에 parameter에 대한 prior 분포를 주면 어떻게 될까요?
- likelihood : \(p(x\mid\theta)\)
- posterior \(\propto\) likelihood \(\times\) prior : \(p(\theta \mid x) \propto p(x \mid \theta)p(\theta)\)
likelihood, prior 그리고 posterior는 위의 관계가 성립함이 기억나실겁니다. 만약 prior를 zero-mean 가우시안 분포로 적당히 정해보면 어떨까요?
\[p(\theta \vert \alpha) = N (\theta \vert 0, \alpha^{-1} I)\]그러면 posterior는 다음과 같습니다.
\[p(y_n \vert x_n, \theta) \cdot p(\theta \vert \alpha) = N(\theta^T x_n, \beta^{-1}I) \cdot N (\theta \vert 0, \alpha^{-1} I)\]이제 이를 전개해 봅시다.
\[\begin{aligned} & p(y_n \vert x_n, \theta) \cdot p(\theta \vert \alpha) = \frac{1}{ \beta^{-1} \sqrt{2\pi}} \exp [ -\frac{1}{2} (\frac{y_n - \theta^T x_n}{\beta^{-1/2}})^2 ] \cdot \frac{1}{ \alpha^{-1} \sqrt{2\pi}} \exp [ -\frac{1}{2} (\frac{\theta - 0}{\alpha^{-1/2}})^2 ] \\ & = \frac{\beta \alpha}{2\pi} \exp \{ -\frac{1}{2} [ \beta \cdot (y_n - \theta^T x_n)^2 + \alpha \cdot \theta^T \theta] \} \\ \end{aligned}\]여기에 -log를 씌우면
\[- \log [ p(y_n \vert x_n, \theta) \cdot p(\theta \vert \alpha) ] = \frac{\beta}{2} (y_n - \theta^T x_n)^2 + \frac{\alpha}{2} \theta^T \theta + const.\]가 됩니다.
이 수식은 앞서 L2 regularization과 정확히 동일한 수식입니다. regularization의 정도를 의미하는 \(\lambda = \frac{\alpha}{\beta}\)로 만약 likelihood의 variance가 1로 고정이라면 regularization의 정도는 \(\alpha\)가 커질수록, 즉 prior가 좁아질수록 더 세게 작용한다고 볼 수 있습니다.
이는 직관적으로도 prior가 weight은 0에 많이 분포할 것이다를 나타내고 얼마나 그 prior에 강한 확신이 있는지?를 variance로 control 하는 것이기 때문에 완전히 부합한다고 볼 수 있습니다.
L1의 경우는 model weight 에 대한 prior가 gaussian 이 아닌 Laplace Distribution 이라면 동일하게 유도할 수 있는데,
laplace가 gaussian 보다 0에 확률이 더 확률이 크게 할당되기 때문에 0인 weight이 더 많아서 L2보다 sparse한 solution을 갖게 된다는 해석을 할 수도 있습니다.
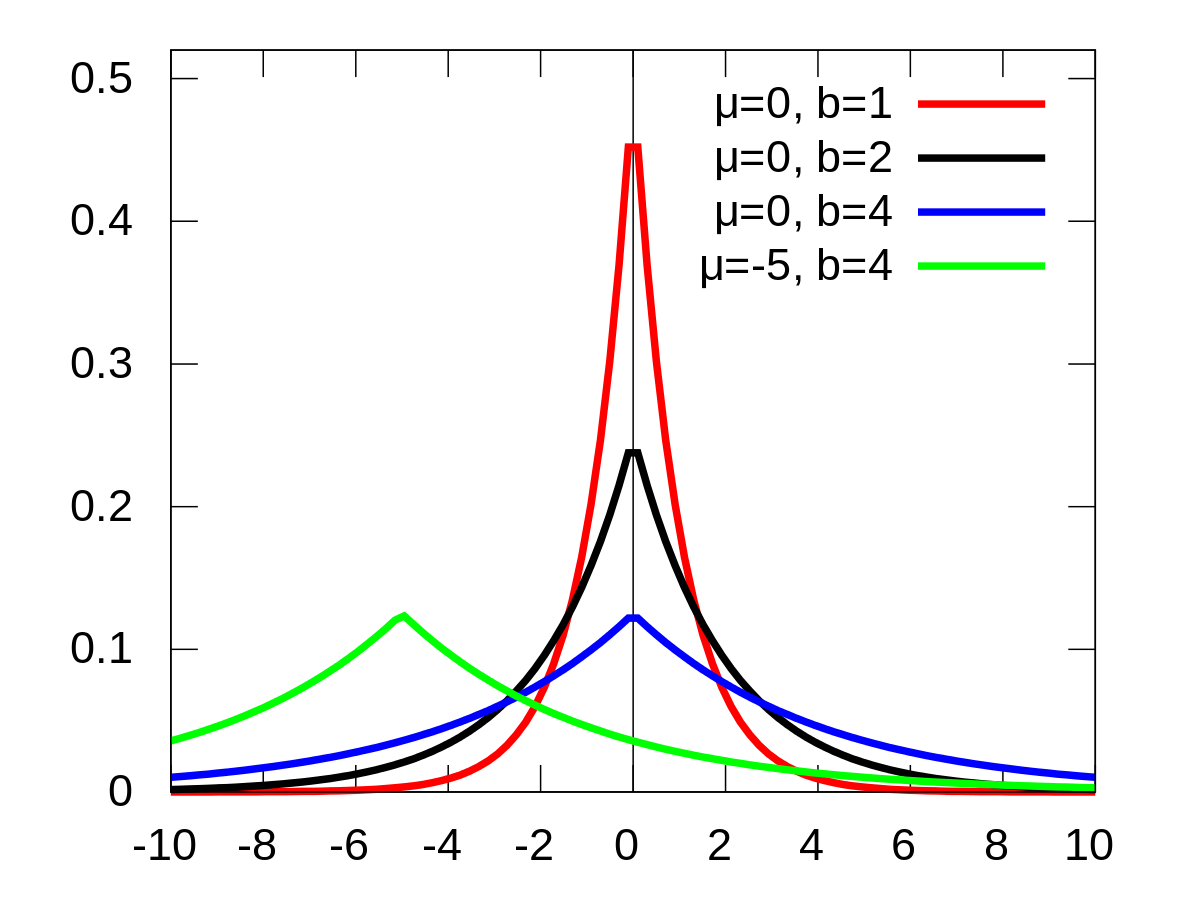 Fig. Laplace Distribution
Fig. Laplace Distribution
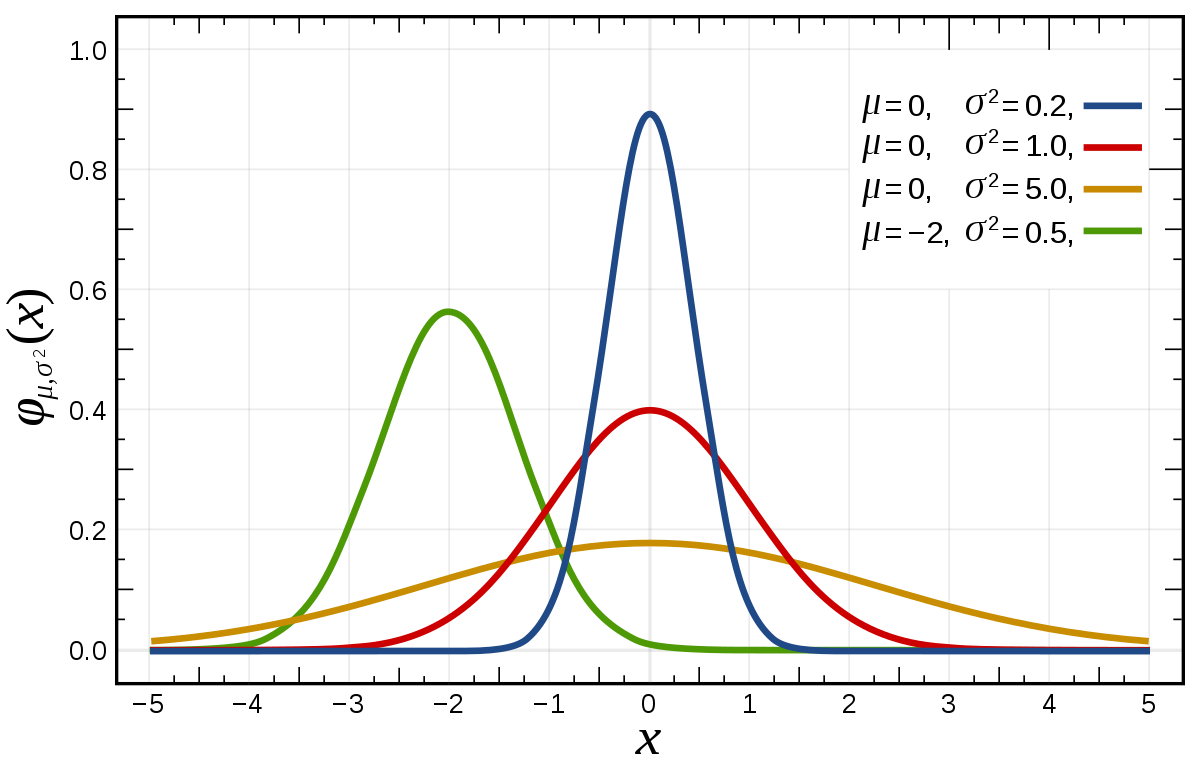 Fig. Gaussian Distribution
Fig. Gaussian Distribution
Loss Surface
Regularization term을 추가하는 것은 loss surface 관점에서 해석을 할 수도 있습니다. 예를 들어 Ridge를 적용하면 아래처럼 loss surface가 stable해질 수 있는데 앞서 우리가 얘기한 것과 다른 맥락인 것은 아닙니다.
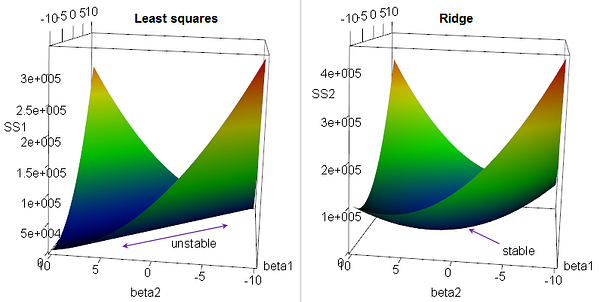 Fig. Source from here
Fig. Source from here