(WIP) Iterative Optimization Algorithms for ML

< 목차 >

• How to Find The Optimal Parameter of ML Model
• Basic Algorithms
  • Steepest Gradient Descent (1st Order Method)
    • Convexity
    • Downsides of 1st Order Method
    • Additioanl) Skip Connection makes Surface Smooth
  • Newton’s Method (Newton-Raphson; 2nd Order Method)
• Momentum
  • Nesterov Accelerated Gradient (NAG)
  • What if We Pass Minima because of Momentum ?
  • Additioanl) Why Mometum rly Works?
• Gradient Scale
  • Root Mean Squared Propagation (RMSProp)
  • Adaptive Subgradient Methods (AdaGrad)
• Intuitive Animations of Various Algorithms
• ADAptive estimates of lower-order Moments (Adam)
• Stochastic Optimization
  • Stochatic Gradient Descent (SGD)
  • Hyperparameter Tuning for SGD
• Important Intuition for Gradient Based Method
• Addtional Things (for Modern DL)
  • Memory Consumption of Adam
  • LR vs Batch Size
  • Sometimes SGD would be better
  • AdamW
• More Intuition from DeepMind x UCL Lecture
  • Revisit Steepest Gradient Descent
  • Convergence Theory
  • Revisit Momentum Methods
  • Revisit 2nd Order Methods
  • Revisit Stochastic Methods
• References

Core resources that i refered to are

• (CS 182) Lecture 4: Optimization
• (DeepMind x UCL Deep Learning Lectures) Lecture 5: Optimization for Machine Learning
• (Stanford CS231n) Lecture 7: Training Neural Networks II

이번 post는 고전 Machine Learning (ML)이라기에는 Deep Learning (DL)내용이 많지만, ML에도 다 적용되는 얘기이기 때문에 category는 ML로 정했다. Post를 시작하기에 앞서 최적화 이론 (Optimization Theory) 분야는 그 자체로 어떤 박사과정의 평생 연구주제가 될 정도로 굉장히 거대한 분야이다. 그 중에서도 이 post는 ML과 관련된 optimization만 알아보는 것이고, 그마저도 너무 algorithm이 다양하기 때문에 핵심이 되는 개념들만 정리 했다. 최대한 친절하지만 중요한 내용을 모두 포함하려고 노력했음에도 불구하고 부족한 점이 있을 수 있음을 미리 알린다 (본인은 optimization 전공이 아니니).

How to Find The Optimal Parameter of ML Model

일반적으로 Machine Learning (ML) algorithm을 활용해 문제를 풀려면 원하는 task의 objective function을 정의하고, 이에 맞는 Neural Network (NN)를 design 한 뒤에 objective를 가장 잘 만족하는 (negative log likelihood같은 cost function이면 minimize) parameter (weight)를 찾게 된다. 보통 NN을 사용하면 미분을 해서 극소, 극대 값을 찾는 방식으로 한번에 solution을 구할 수 없기 때문에 (no closed form), 최적화 (Optimization)를 통해 parameter tuning을 해야 한다.

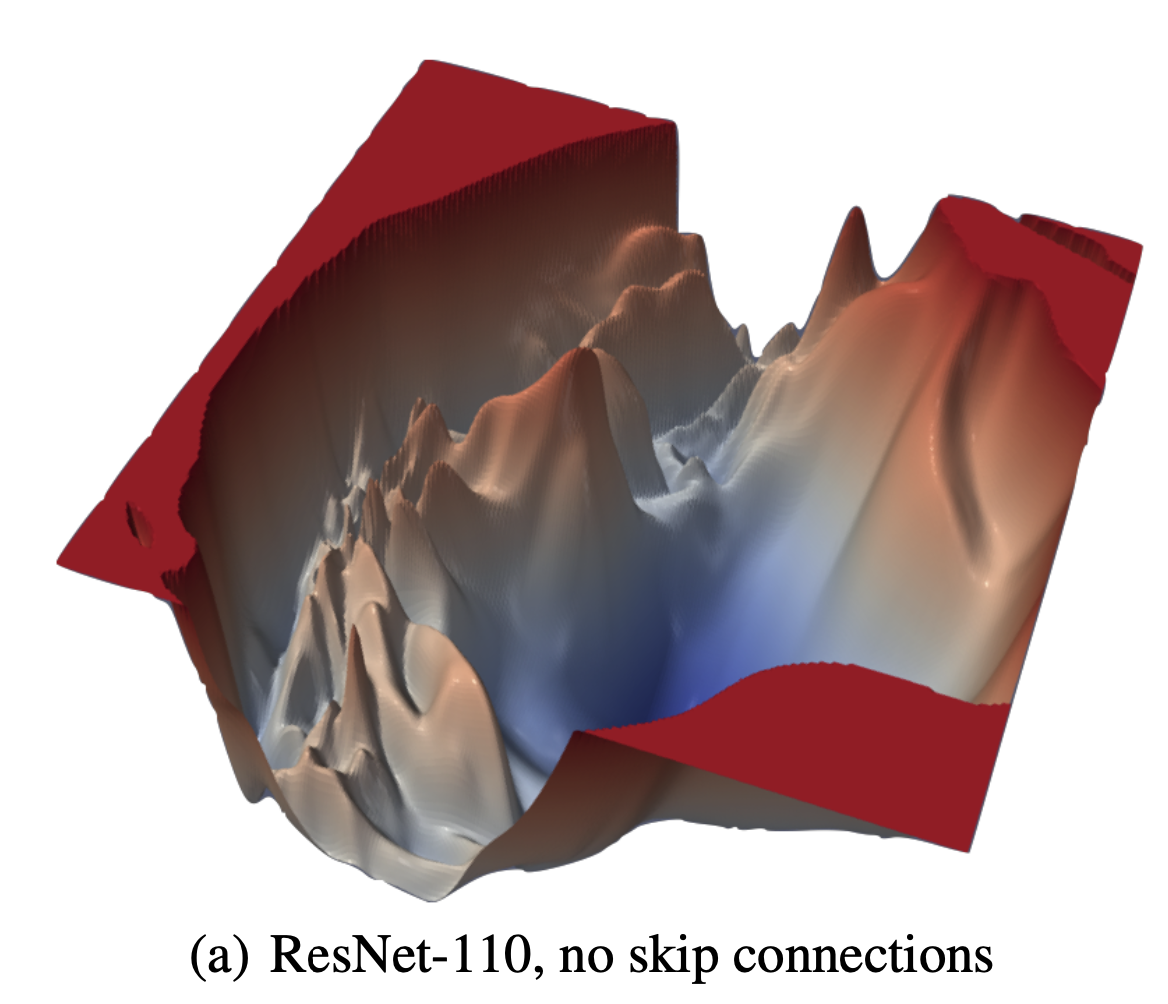Fig. Residual Connection 이 없는 ResNet 의 Loss Surface. Source From Visualizing the Loss Landscape of Neural Nets

일단 model의 복잡도 (차원), objective function, 그리고 dataset이 정해지면 전체 dataset에 대해서 Loss Surface가 정해진다. 그리고 주어진 objective (Loss) surface에서 iterative하게 direction (어디로 갈지?)와 step size (그 방향으로 얼만큼 갈지?)를 iterative하게 계산해서 optimal solution으로 다가간다. 이는 NN의 복잡도와 비 선형성 (non-linearity) 때문에 loss surface는 non-convex하며 optimal solution으로 간다는 것이 보장되지는 않고, 무수히 많은 local minima들이 존재한다고 알려져 있다. 그럼에도 불구하고, optimization을 동반한 Deep Learning (DL) 방법론들은 좋은 성능을 보이는데, 왜 non-convex함에도 불구하고 DL이 잘될까? 심지어 generalization까지 (test accuracy마저 좋음) 꽤 잘된다는 부분에 대한 답변은 또 하나의 거대한 research domain이다.

본 post에서는 왜 DL이 good solution을 찾을 수 있는가? 까지는 가지 않겠지만, iterative optimization algorithm들에는 어떤 것들이 있는지 이들의 발전사와 장단점에 대해서 알아보려 한다.

Basic Algorithms

Steepest Gradient Descent (1st Order Method)

가장 간단한 approach에 대해서 알아보자. 어떤 model이 \(\theta\)로 parameterize 되었을 때 우리가 원하는 바는 모든 data sample들에 대해서 likelihood를 maximize하는 것, 혹은 negative log likleihood를 minimize하는 것이고 이는 다음과 같이 수식으로 나타낼 수 있다.

이를 보통 loss or cost function, \(L(\theta)\) 이라고 표현한다.

단순하게 model parameter, \(\theta\) 가 2차원이라고 생각해보자. 그럼 두 parameter, \(\theta_1, \theta_2\)에 대한 loss 값을 그릴 수 있기 때문에 총 3차원으로 loss surface를 나타낼 수 있다.

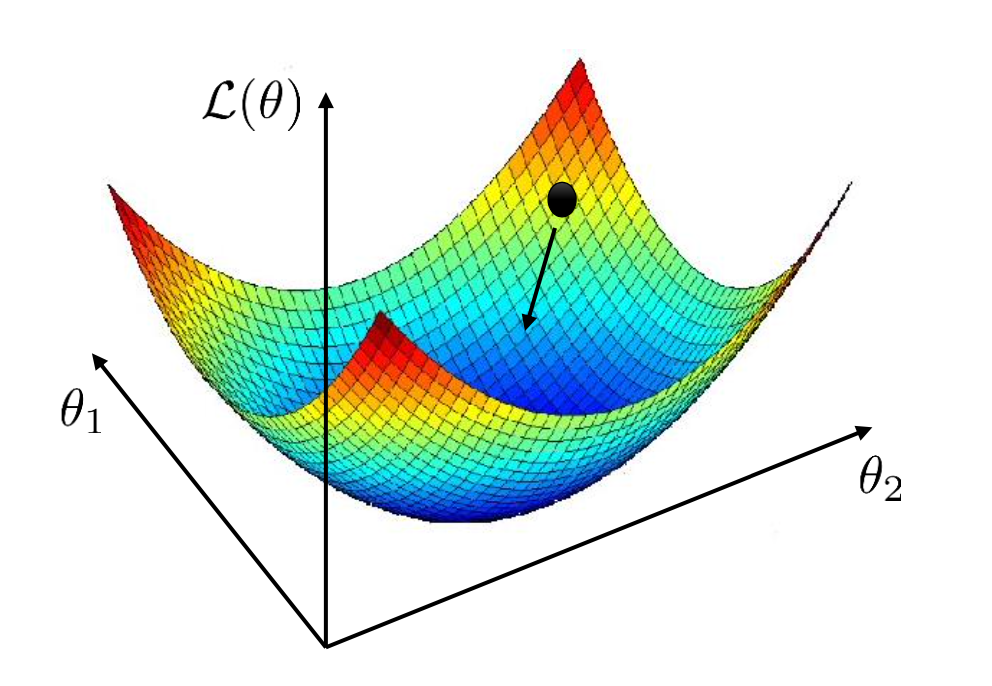
일단 우리는 loss function의 parameter에 대한 closed form solution을 찾을 수 없는 상태라고 가정하겠다. 그렇다면 어떻게 해야 model의 initial parameter가 검은 점이라고 할 때 loss가 가장 optimal solution에 도달할 수 있을까? 방법은 간단하다.

• Current parameter point에서 움직일 방향 (direction), \(v\)을 계산한다.
• 해당 direction으로 parameter를 얼만큼 움직일지 (step size or learning rate) 정하고 그 만큼 움직인다.
  • 이를 update 한다고 표현한다. (\(\theta \leftarrow \theta + \alpha v\))
  • 적절한 step size를 찾기 위해서 line search라는 걸 할 수 있지만 fixed value를 쓸 수도 있다.
  • 너무 크거나 작으면 optimal로 가지 못할 수 있다.

여기서 step size는 고정하여 쓴다고 가정해도 되는데, 어떻게 direction을 정할지가 관건이다. 잘 알려진 방식은 바로 해당 지점에서 1차 미분항 (1st order derivative)을 계산하는 것이다.

우리는 current parameter point에서 1차 미분을 하면 그 point에서의 기울기 (Gradient)를 얻을 수 잇는데, 단순하게 gradient가 양수이면 아래의 그림에서 곡선의 오른편에 있다는 뜻이므로 왼쪽으로 가면 되고, gradient가 음수이면 왼쪽에 있다는 신호이므로 또 반대로 (오른쪽) 가면 된다. 즉 언제나 gradient의 반대방향으로 가기만 하면 된다.

만약 gradient가 +2 였다고 하면 위의 그림처럼 gradient에 -를 붙혀 원래 지점 (x1) 에 step_size X gradient의 음수 를 곱한 만큼 이동하면 된고, 이로써 parameter를 1 step update한 것이 된다.
Model parameter가 1차원이라면 \(\theta_1\)에 대해서만 미분을 하면 되는데,

만약 2차원이라면 각 parameter에 대해서 모두 gradient 구해야 한다.

2변수를 넘어 수백만 차원 이상의 다변수 (multivariate)인 경우로 확대해도 각 parameter에 대해서 편 미분 (partial derevitave)를 계산하여 각각의 gradient를 구하면 된다.

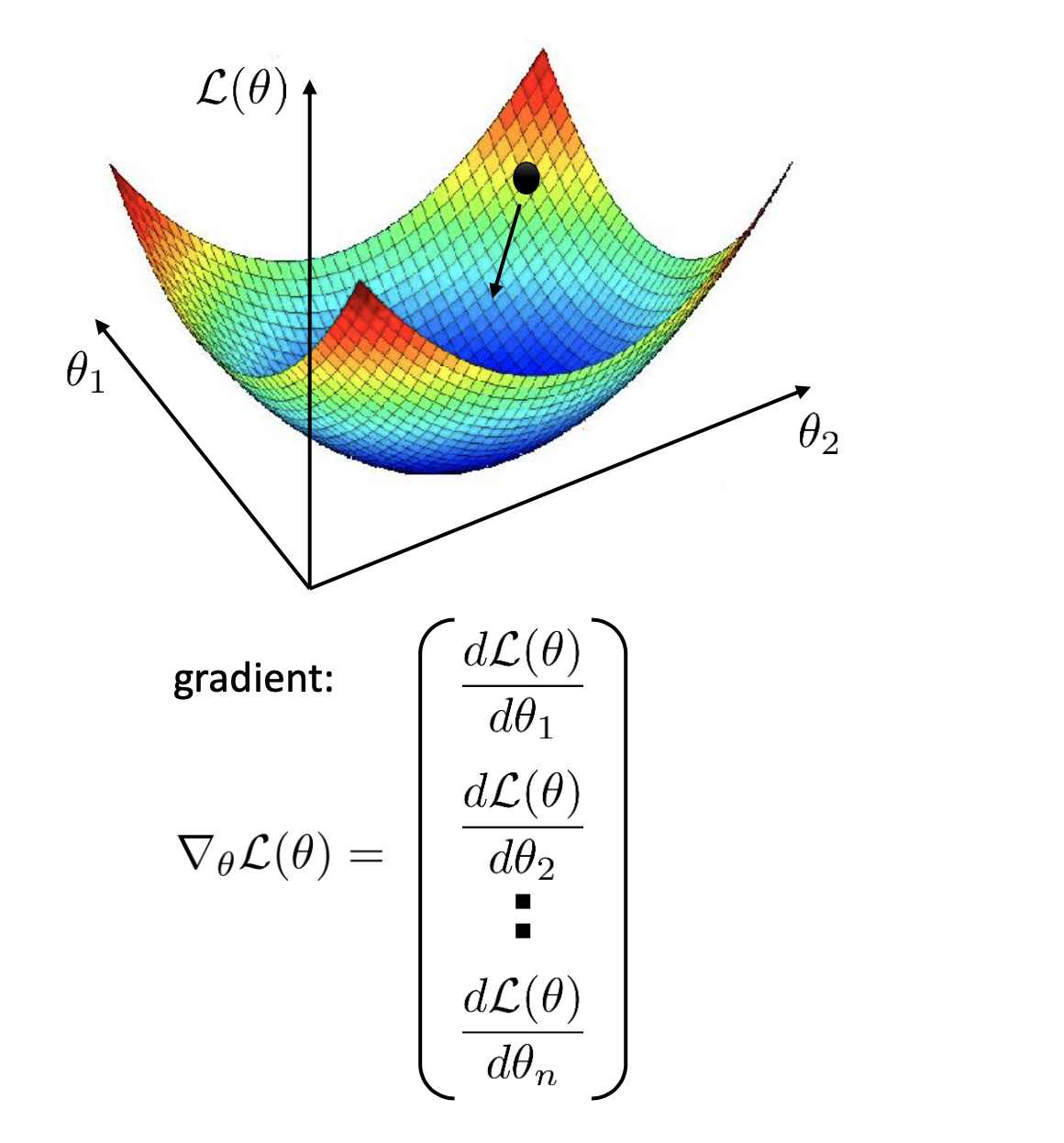
이를 gradient의 반대방향으로 loss 를 minimize하는 방향으로 내려온다고 해서 (descent), 경사 하강법 (Gradient Descent)이라고 한다. 이는 언제나 가장 가파른 (Steepest) 방향을 찾아 움직이기 때문에 Steepest Gradient Descent 라고도 한다.

Convexity

그런데 가장 가파른 방향으로 descent를 하다보면 optimal solution을 얻을 수 있을까? 만약 loss surface가 convex하다면 그러할 것이다. Convex optimization 은 하나의 큰 분야이지만 단순하게 이해해보자. 아래 그림의 1번 처럼 두 점을 찍어 이었을 때 그 line 이 언제나 정의된 함수 위에 존재하면 보통 convex 하다고 한다. 이 경우 optimal solution으로 수렴하는 것이 매우 강하게 보장되어 있음 (strong guarantee)이 알려져있다고 한다.

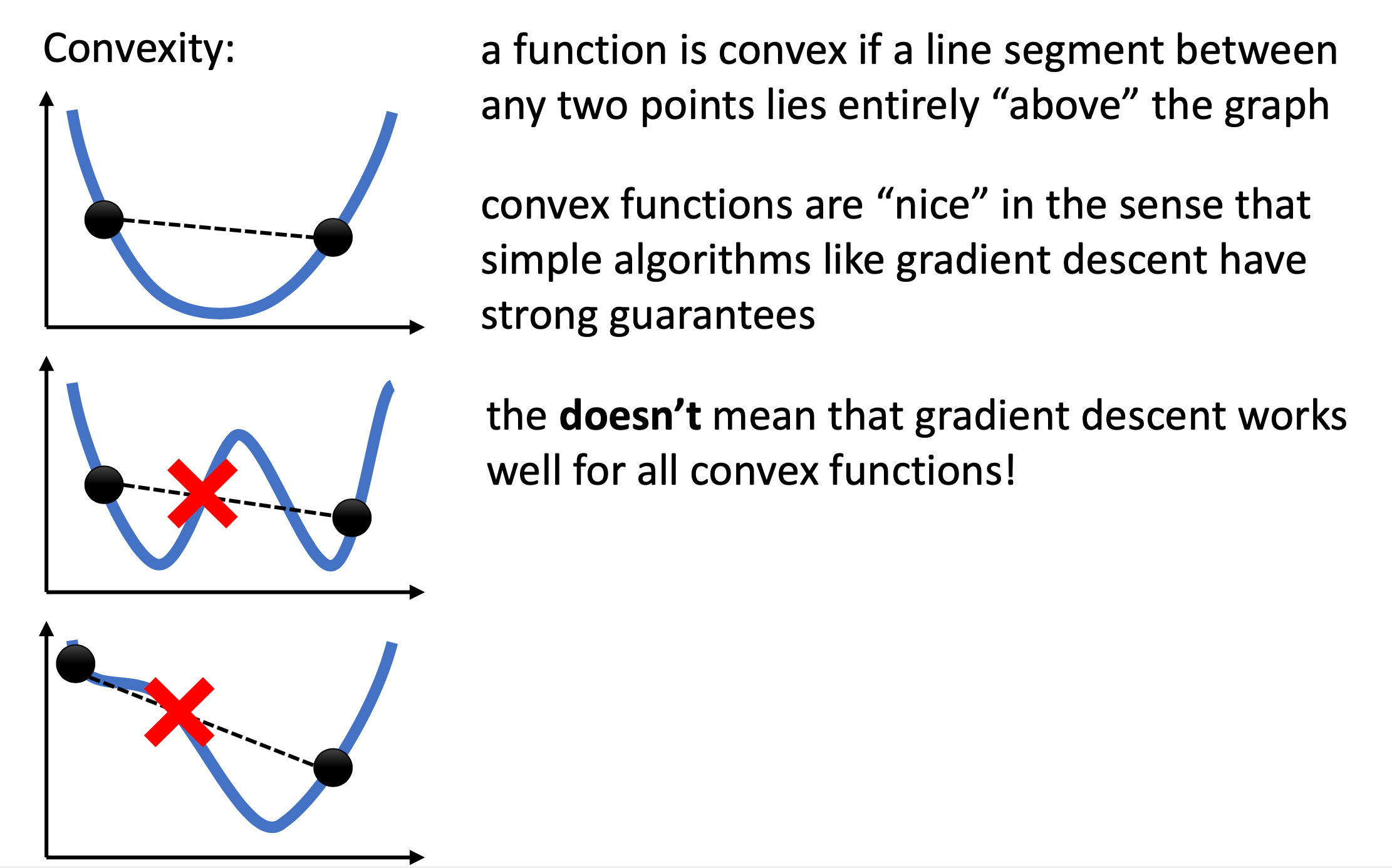
하지만 위 figure의 아래 두 예시는 각각 두 점을 이었을 때 함수의 곡선을 관통하기 때문에 non-convex 하다고 한다. 이 중 2번 예시는 surface의 극소값이 한개가 아니고 두개로 optimal minimum가 두 개 처럼 보이는데, 실제로는 optimum은 하나이며 나머지는 그 지역부근에서 최소점이라고 해서 지역 최소해 (local optimum)이라고 한다. 마지막 3번 예시는 gradient가 0이 되는 부근 (평탄한 부근; plateau) 를 가지고 있기 때문에 두 점을 이었을 때 마찬가지로 함수의 곡선과 교차하는 부분이 살짝 생긴다. 이런 경우에도 non-convex 하다고 얘기하며, 이는 gradient based optimization을 하는 데 있어 큰 문제를 일으키는데 곧 살펴보도록 하겠다.

고전 ML algorithm의 경우 linear regression이나 logistic regression은 convexity가 증명되어 있다고 한다. 이런 경우 closed form solution이 존재할 수도 있지만 (logistic regression도 마찬가지) iterative optimization을 하는 것이 성능이 더 좋다고 하기도 한다.

Fig. Source From here

Downsides of 1st Order Method

하지만 언제나 가장 가파른 방향으로 한 step가는 gradient descent는 그리 좋지 않다는 것이 알려져 있다. 이는 곡면이 convex하다고 해도 예외는 아니다. 아래의 예시를 보자.

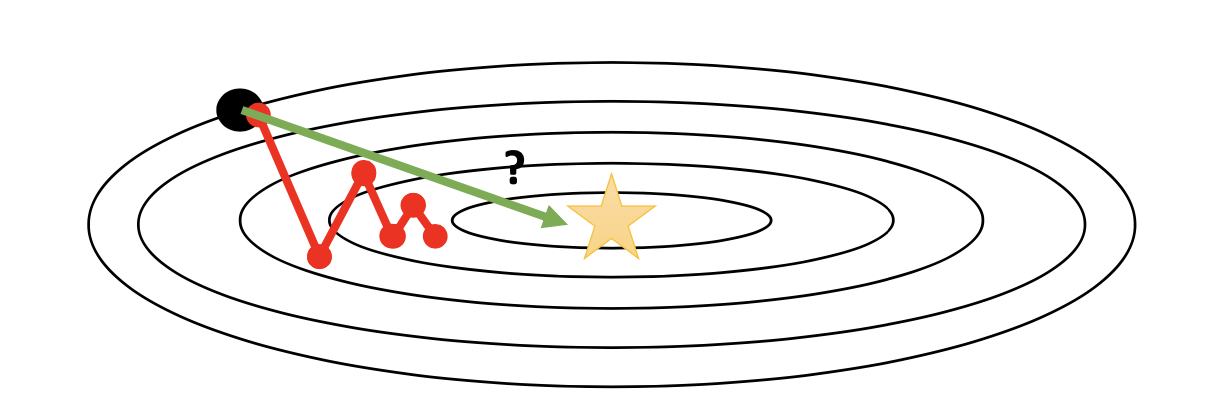
단순히 model parameter가 2차원에 불과한 예제임에도 불구하고 black point에서 gradient descent를 시작해서 update를 할 때마다 방향이 zigzag로 바뀌는 걸 볼 수 있다. 물론 언젠가는 optimal point에 도달할 수는 있겠으나 이런식으로는 매우 오랜 시간이 걸릴 것이다. 이는 어떤 parameter의 gradient는 매우 가파른데 반해 다른 parameter는 그렇지 않기 때문에 발생하는 문제이다.

그러면 step size를 잘 조절해 주면 되지 않을까? 싶겠지만 모든 parameter에 대해서 잘 먹히는 (공통으로 적용되는) learning rate를 찾기란 쉽지않다. 너무 크면 발산 (diverge, overshoot) 해버리고, 너무 작으면 정해진 시간 내에 optimal에 도달할 수 없다. (아래 animation의 momentum 이라는 것은 gradient based optimization을 개선하면서 등장하는 개념인데 곧 다룰 예정임)

fig. Visualization of Gradient Descent according to Learning Rate. Source from here

Gradient based optimization의 몇 가지 문제점은 아래와 같이 요약할 수 있겠다.

• parameter별로 gradient scale이 달라 learning rate를 정하기 어려움
• local optimum이 많이 존재해 local optimum으로 빠진 뒤 빠져나올 수 없음 (수렴해버림)
• plateau가 존재함
• saddle point가 존재함

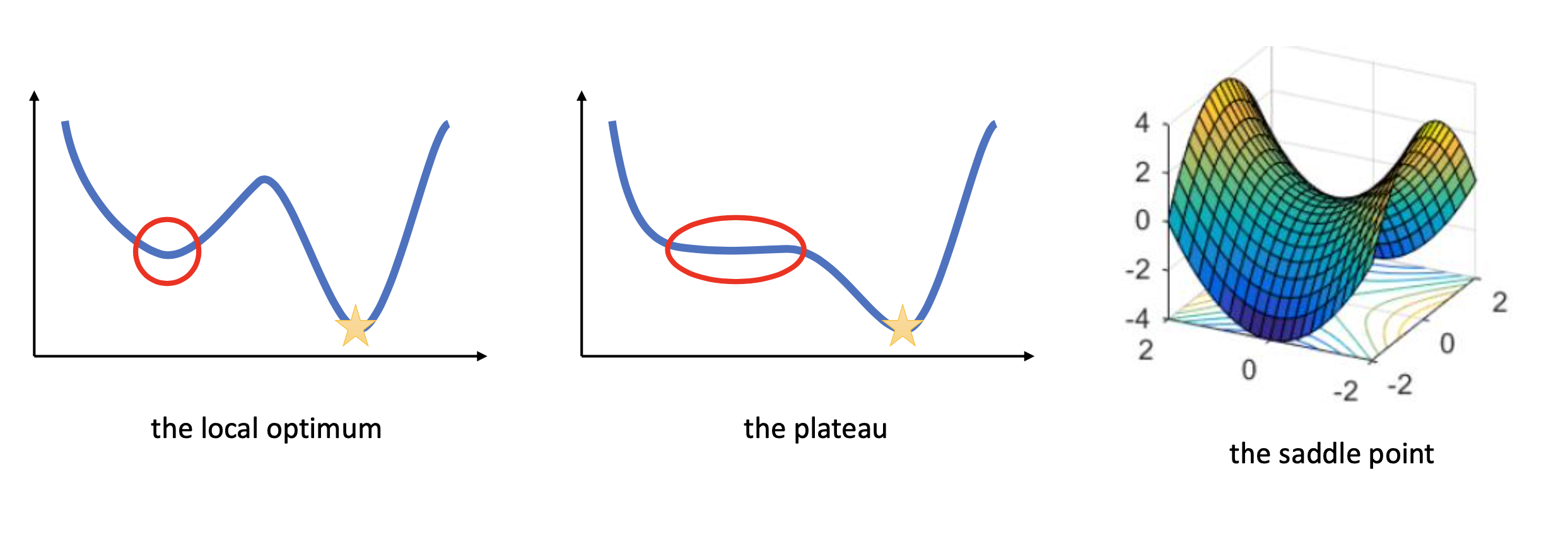Fig.

이 중에서 먼저 parameter별로 scale이 달라 zigzag 하는 경향을 보이는 것은 후에 다루도록 하고, 먼저 local mimimum에 대해서 생각해보자.

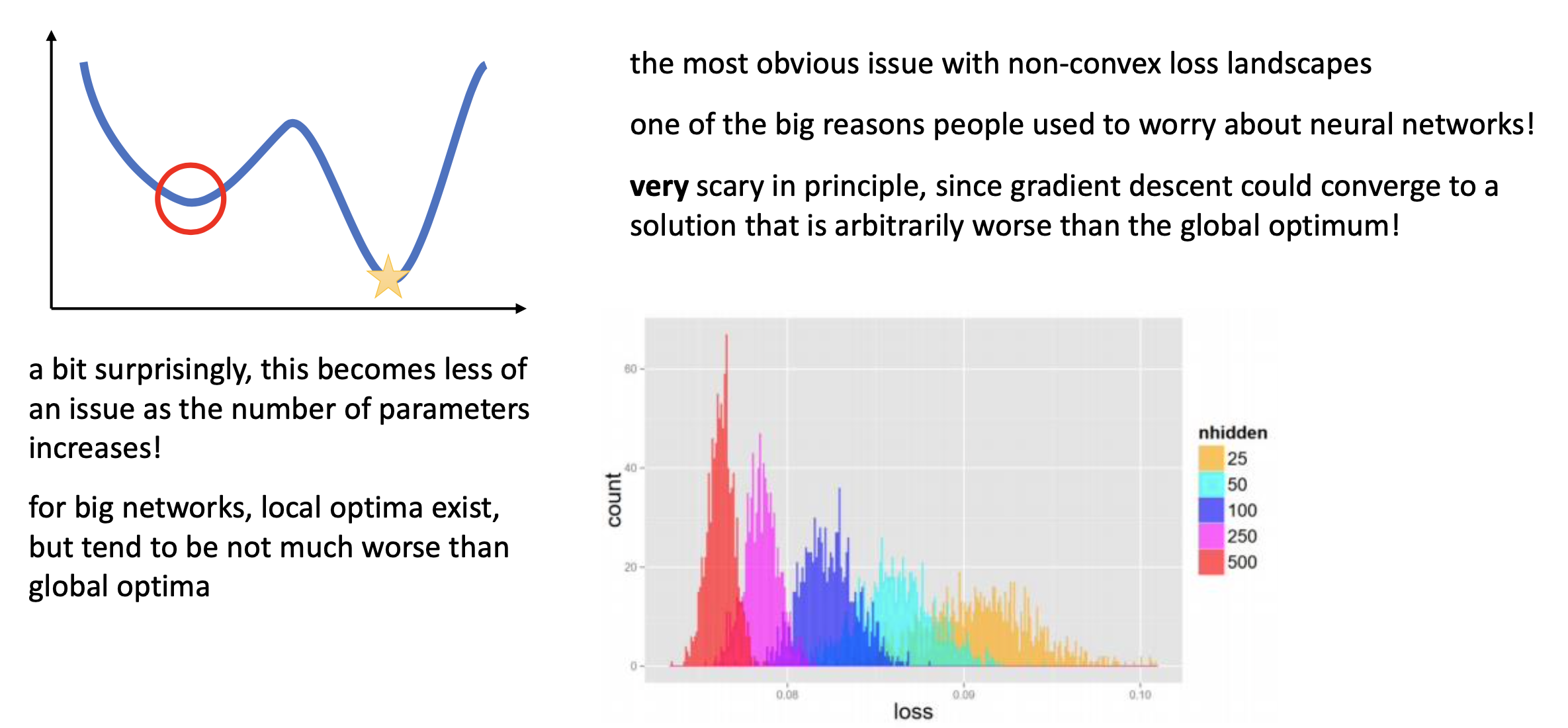Fig.

Objective surface가 non-convex하기 때문에 곳곳에 local minimum이 존재하게 된다. Optimization이 진행되면서 이런 minimum에 빠졌다가 탈출하지 못한 채 학습이 끝날 수 있는데, 사실 이는 model size가 커지면서 놀랍게도 크게 문제는 아니게 되었다고 한다. (아마 Measuring the Intrinsic Dimension of Objective Landscapes의 내용과도 관련이 있을 것 같은데, model size가 커지다보면 optimal solution과 유사한 parameter set이 훨씬 늘어나게 되면서 모로가도 서울이라고 비슷한 성능의 minimum 중 어디로든 가게 돼서 그런 것 같다)

그 다음은 plateau인데, 이 부근에서는 saddle point와 비슷하게 gradinet가 0에 가까워지면서 벗어나기 힘들어진다.

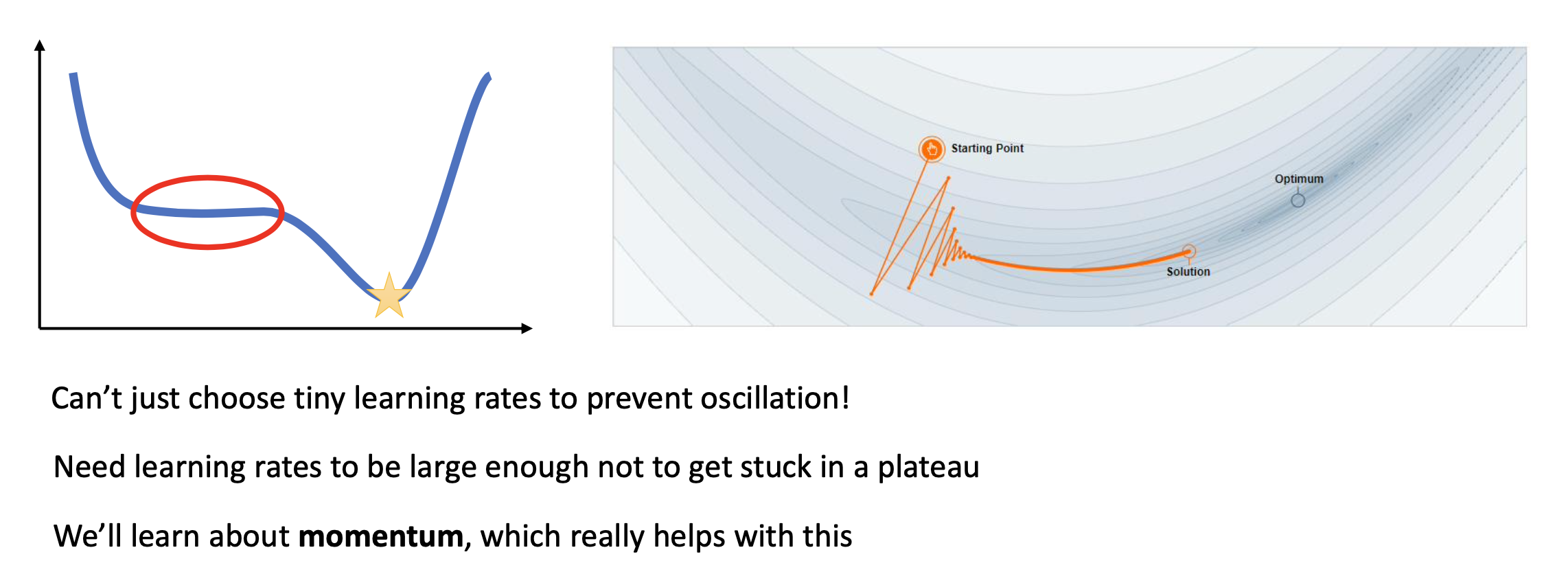Fig.

이런 경우 learning rate를 키워야 하는데, 어떻게 현재 optimization step이 plateau에 빠졌는지 알고 이를 올리겠는가? 다양한 방법이 있을 수 있지만 이를 해결하는 대표적인 방법은 후에 소개할 momentum이라는 개념이다. TL;DR하자면 기존 optimization step들의 history를 참고해 이전까지 이 direction으로 가파르게 내려오고 있었으면, 계속해서 가속을 받아 이 direction을 유지하게 하는 것이다.

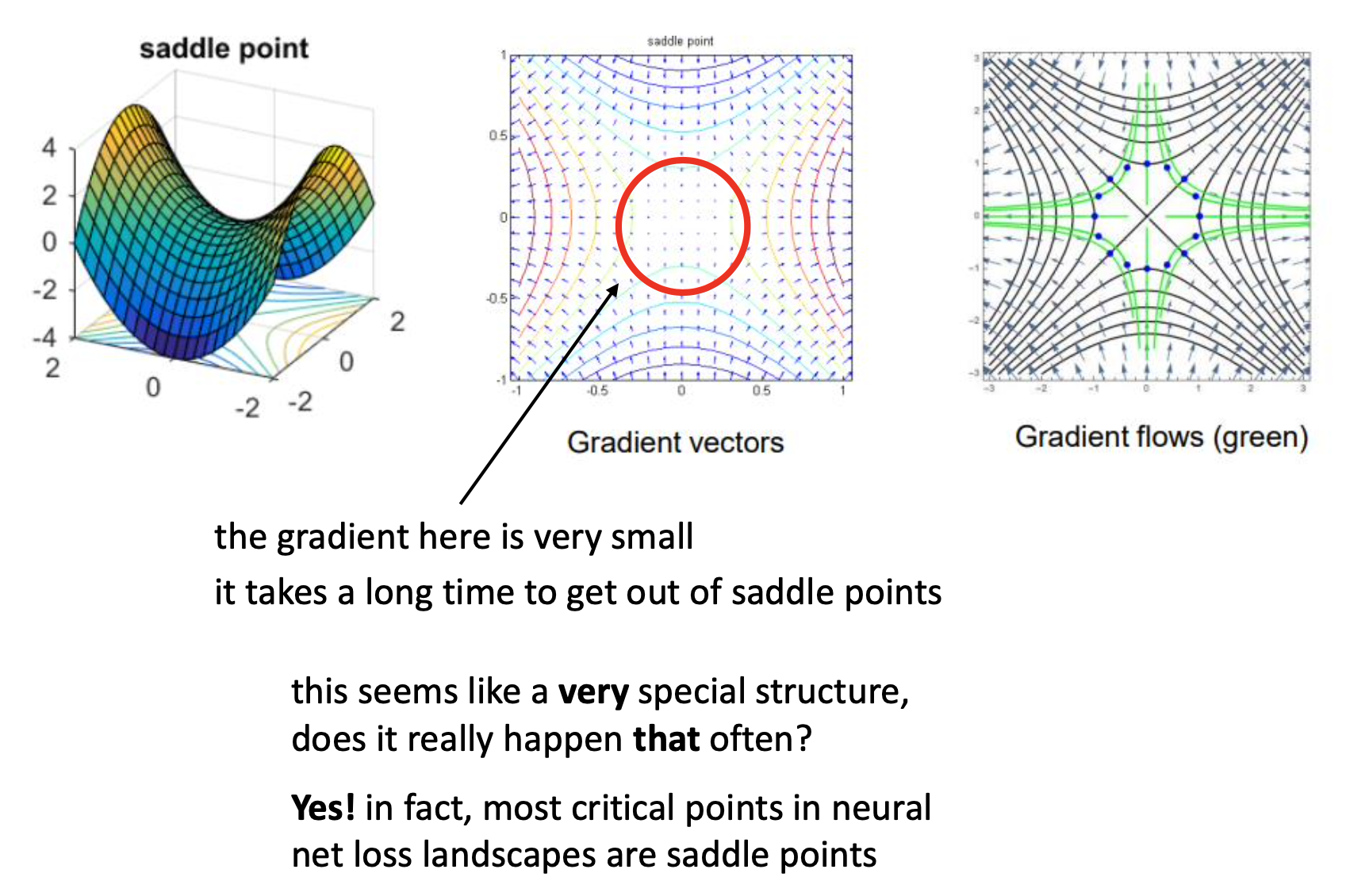Fig.

마지막은 saddle point인데 여기서는 모든 parameter에 대해서 gradient가 거의 0에 수렴한다. plateau 보다 더 한 것이다. 그리고 이것이 NN을 학습하는 데 있어 가장 critical한 point가 된다고 한다. 물론 gradient가 0이라는 signal은 minimum을 의미할 수도 있지만 이것이 saddle point인지 누가알겠는가?

이건 어떻게 해결해야할까?

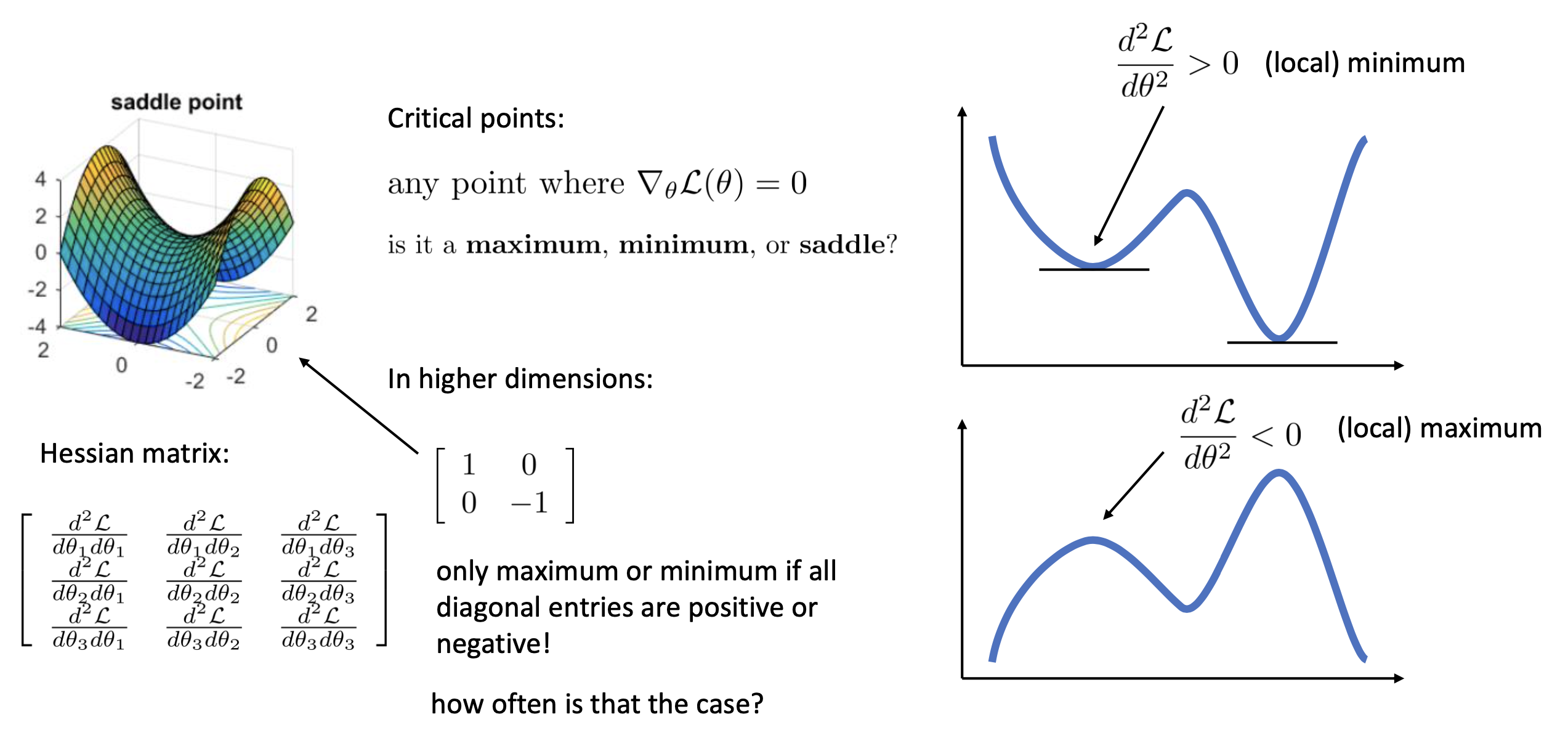Fig.

마찬가지로 여러 방법이 있을 수 있지만, loss의 parameter에 대한 2차 미분항인 hessian matrix를 계산하는 것이 이를 진단하기 좋다는 것이 알려져 있다. 2차 미분을 해서 대각 성분 (diagonal entries)를 보면 이것이 양수이거나 음수일 때만 maximum, minimum이 되기 때문이다. (saddle point는 그렇지 않을테니)

그럼 앞으로 어떻게 이런 문제점들을 벗어날 수 있는 trick들을 활용해 좋은 optimizer를 design할 수 있는지 알아보자.

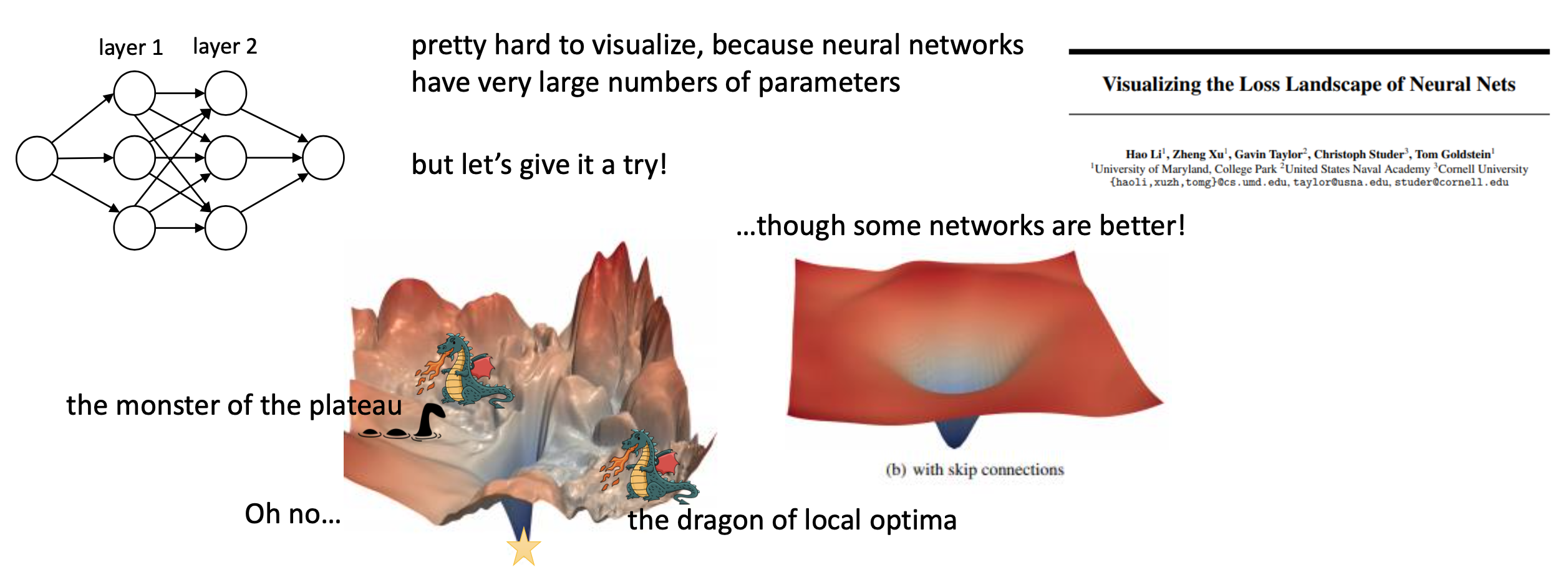
Additioanl) Skip Connection makes Surface Smooth

한 편, model parameter가 수십억개 (billion order)에 달하는 요즘의 DL model들은 층이 깊어지면서 또다른 문제가 발생한다. 바로 backprop과정에서 gradient가 소실되는 gradient vanishing문제 같은 것이다. 이를 해결하기 위해 skip connection (residual connection)이라는 것이 제안되었는데, 이는 Visualizing the Loss Landscape of Neural Nets라는 paper에 의해서 loss surface를 부드럽게 만든다는 것으로 해석할 여지가 있다는 것이 알려졌다. 즉 local minima, plateau, saddle point가 덜해질 수 있는 것이다. (이는 나중에 따로 다루도록 하겠으나 언급만 하고 넘어간다)

Newton’s Method (Newton-Raphson; 2nd Order Method)

다시 본론으로 돌아와 생각해보자. 어떻게 해야 더 좋은 optimizer를 얻을 수 있을까? 좋은 optimizer란 다음과 같을 것이다.

• zigzag 하지 말아야 (덜 해야) 할 것
• local optimum에서 잘 빠져나와야 할 것
• saddle point, plateau를 잘 탈출할 것

1번의 경우에 대해 먼저 생각해보자. Zigzag는 사실 gradient scale이 각 parameter별로 달라서 일어나는 문제이다. 그런데 zigzag 하는 경향을 보이는 경우, 더 나쁜것은 optimization하는 trend를 봤을때 심지어 optimal point를 향하지도 않는다.

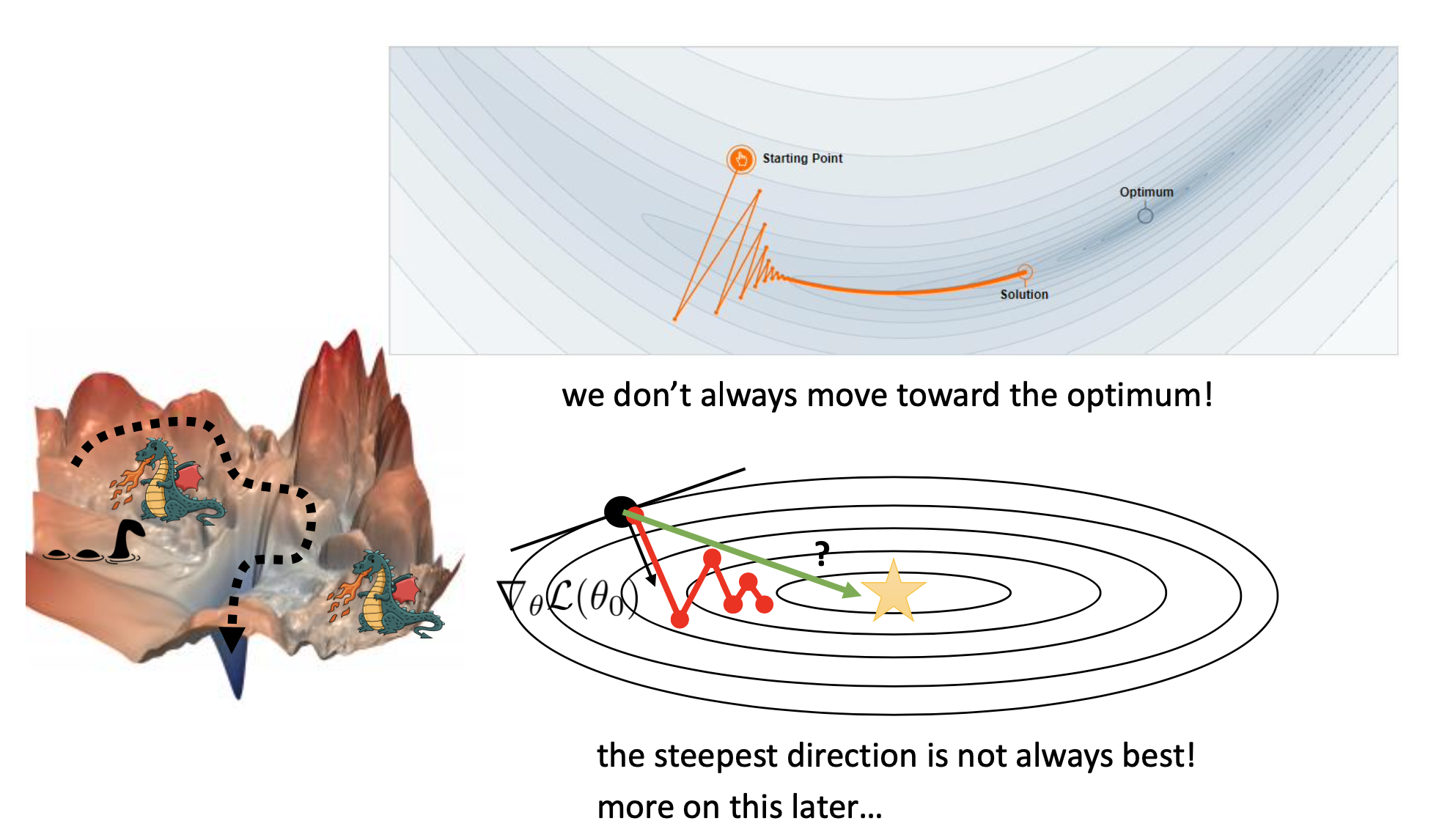Fig.

이를 해결하는 방법 중 이번에 소개할 내용의 key idea는 바로 2차 테일러 근사 (2nd order taylor approximation)를 쓰자는 것이다. 왜 갑자기 taylor approximation인가?

사실 1차 미분항 (gradient)을 구하는 것 자체가 어떤 parameter point에 대해 loss surface를 지역적으로 (locally) 1st order taylor approximation한 것이다. 이번에는 2nd order approximation을 시도해 보자. 어떤 미지의 함수 \(f(x)\)를 p 점에 대해 taylor expnasion을 할 경우 다음과 같이 표현할 수 있는데,

objective function을 현재 parameter point에 대해 2nd order approximaion 까지만 남기면 다음을 얻을 수 있다.

그리고 이를 시각화 하면 아래 figure에서 처럼 pink curve가 원함수 일 때 blue curve를 얻을 수 있다.

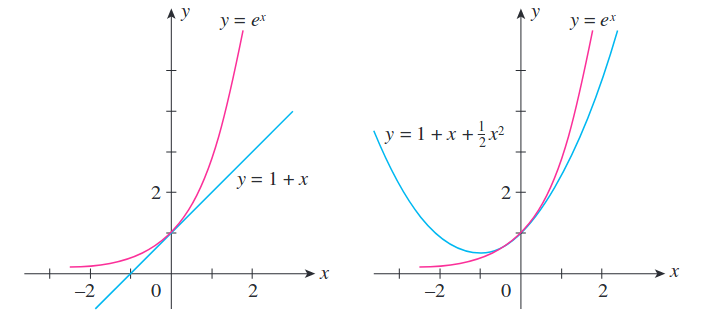Fig.

2nd order approximation을 할 경우 근사된 function은 볼록하기 때문에 (convex), 미분해서 0인 지점 (극솟값; local minimum)을 구해보자.

그러면 우리는 놀랍게도 어떤 direction으로 얼만큼의 step size로 가야하는지를 정할 수 있게 되는데, 이런 2nd order method를 Newton’s method (or Newton Raphson Method)라고 한다.

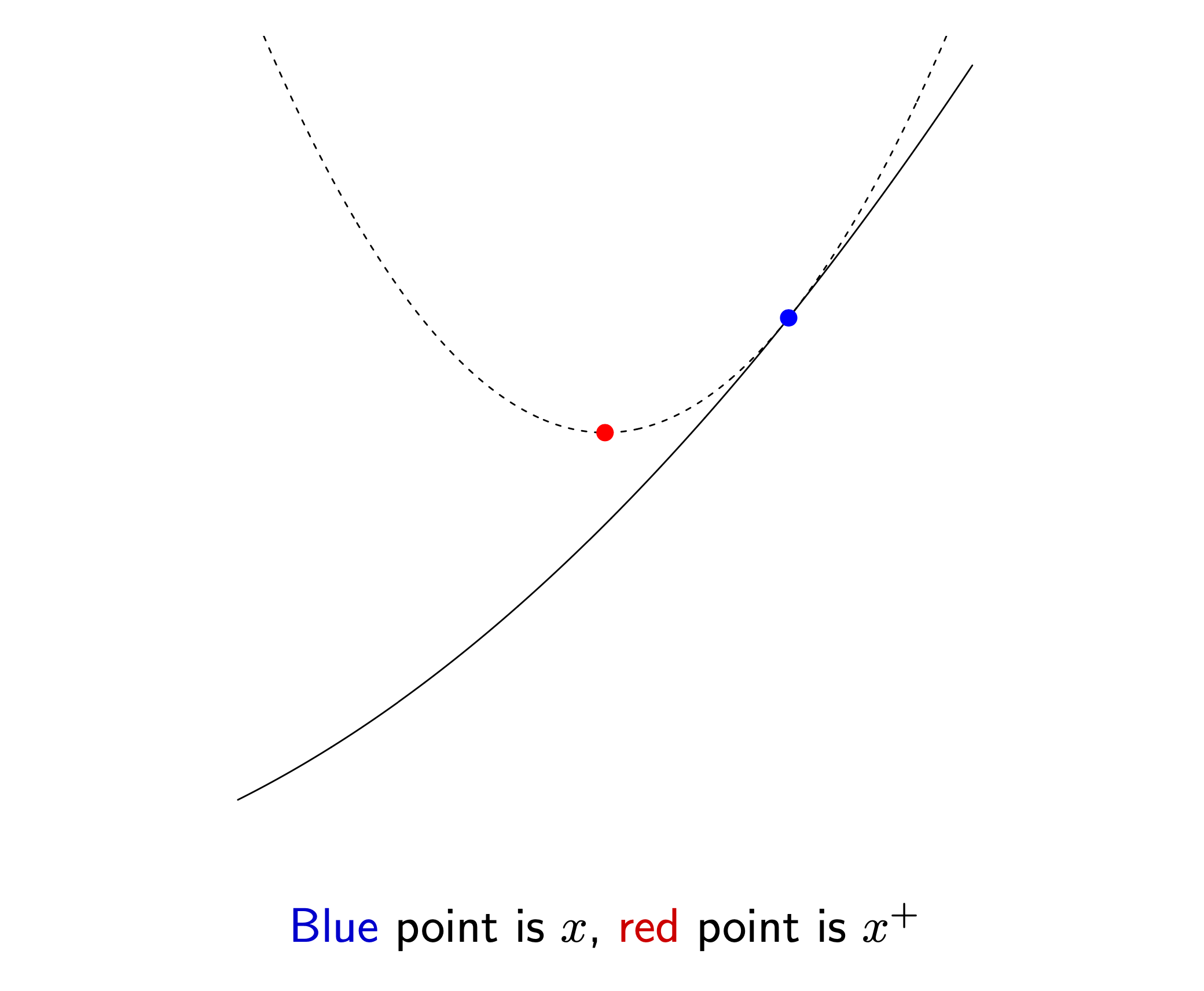Fig. blue point에서 2차 taylor 근사를 한 뒤에 극소값을 찾아서 그곳으로 옮기면 된다.

앞선 gradient descnet와 비교해서 2차 미분항의 역수가 step size로 추가된 것이나 다름 없는데, 2차 미분항이 크면 조금 가고, 작으면 많이 간다는 것을 알 수 있다.

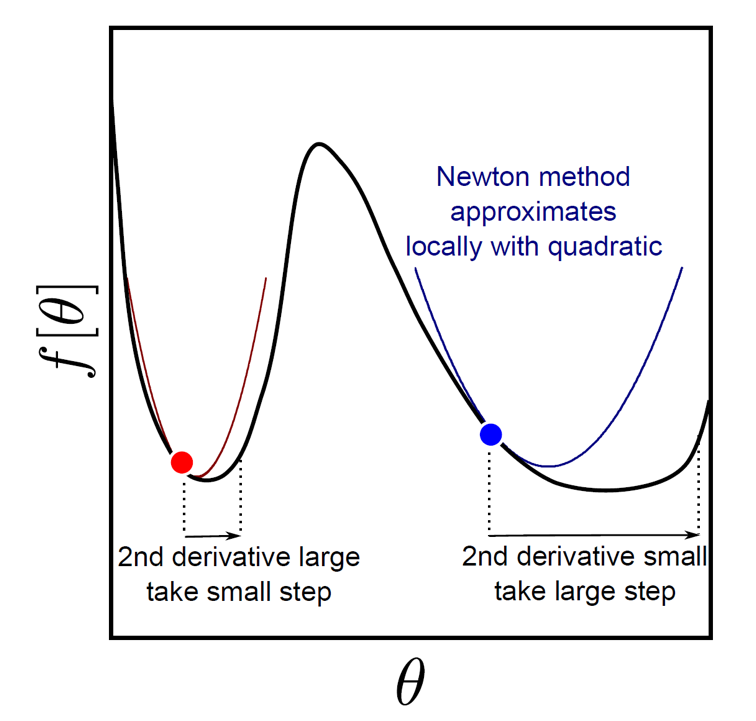Fig.

Newton’s method는 좋은 algorithm이긴 하다. 왜냐하면 optimal point로 향하는 direction을 거의 찾을 수 있기 때문이다. 하지만 그 이면에는 매우 큰 단점이 존재한다.

Fig.

바로 2nd derivative term을 구하기 위해서 엄청난 computational cost를 요구된다는 것이다.

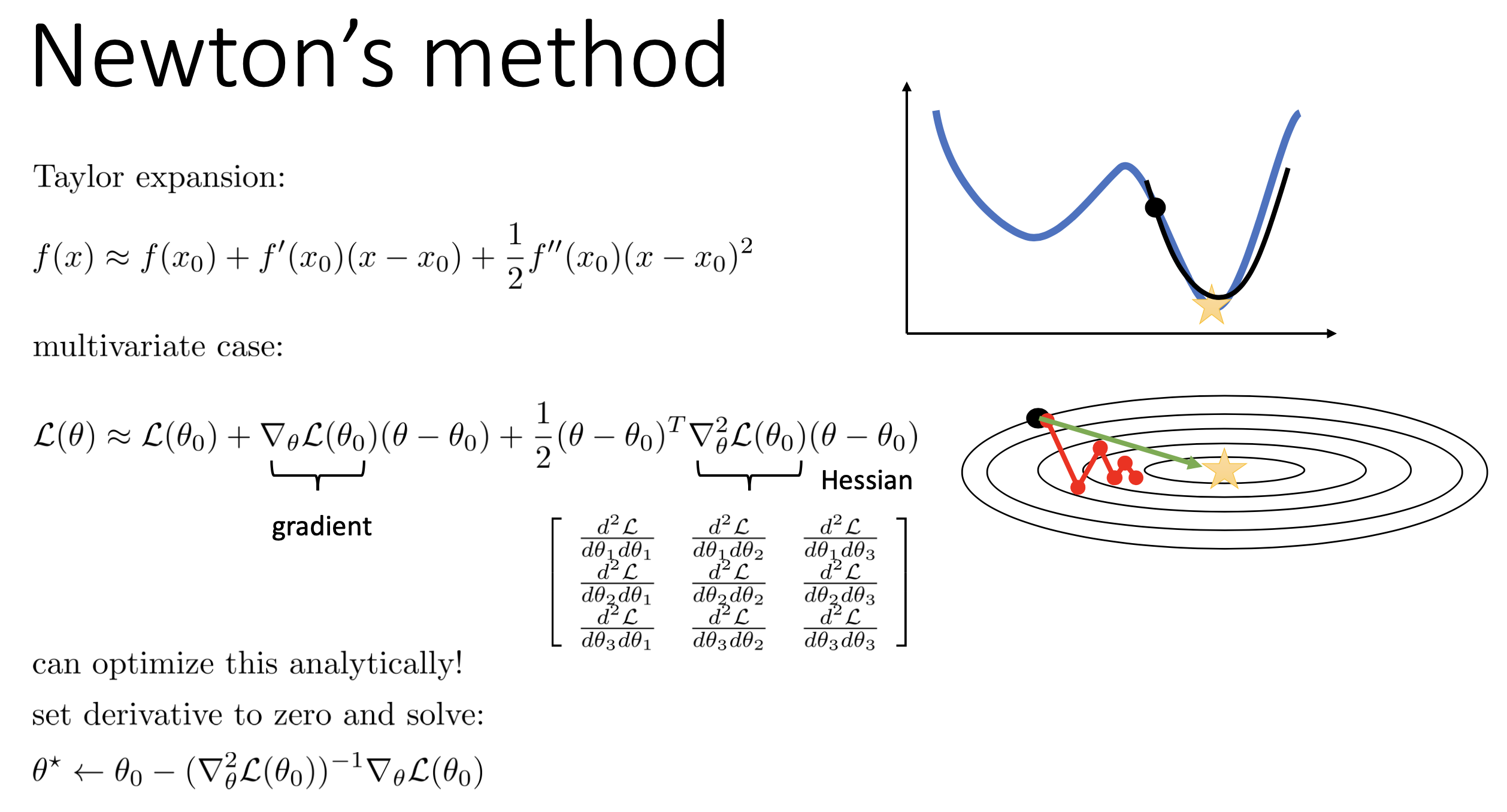Fig.

이는 parameter size가 \(n\)일 때 \(O(n^3)\)의 computational cost를 필요로 한다.

Fig.

최근 DL model들은 날이갈수록 size가 커지고 있기 때문에 Newton’s method를 바로 쓰기에는 더더욱 나쁜 상황이 되었다. 여기에 2nd order method가 무조건 좋은것만은 아닌 것이 step size는 꽤 잘 정해줄 수 있지만 \(f''=0\)인 변곡점 근처에서는 방향을 잘 못찾기도 한다는 단점도 있다고 한다. 그럼에도 이와 유사한 idea자체는 쓰고 싶지 않은가? 그래서 제안된 것이 바로 Momentum이다.

Momentum

우리가 지금부터 알아볼 것은 accelerated gradient descent이다. 그 중 우리가 알아볼 첫 번째 acceleration technique 이 momentum이다. (앞서 newton method의 특징을 가져오고 싶다고 했지만, 이것이 정확히 newton method와 일치한다는 근거는 찾지 못해다.)

이름에서도 알 수 있듯 idea는 간단한데, 몇 번의 누적된 gradient 들을 보고 “음 zigzag로 oscillate하긴 하지만 평균적으로는 이 방향으로 가려고하네?”를 추정하는 것이다. 즉 gradient history를 보고 이들을 averaging하는 특수한 term을 두는 것인데 이것이 momentum이다. 물리학을 공부할 때 어떤 물체가 원래의 운동 상태를 유지하려는 경향을 관성이라고 해석할 수 있겠다.

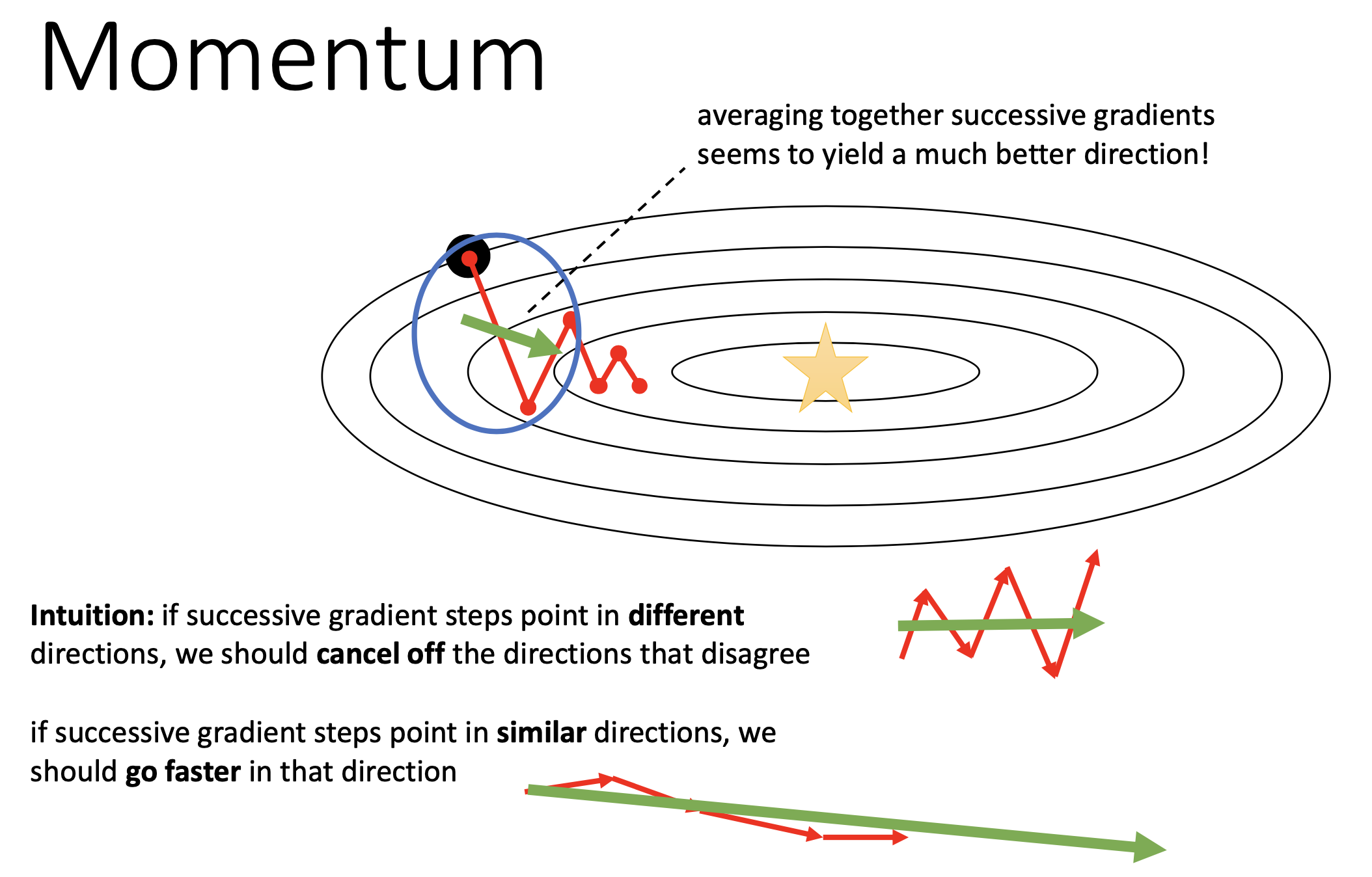Fig.

만약 매 optimization step마다 서로 다른 direction의 gradient가 나온다면 averaging함으로써 disagree하는 direction을 cancel할 수 있고, 매 step마다 similar direction의 gradient를 얻는다면 averaging해봐야 같은 direction이 나오므로 더 탄력을 받아 이동하는 것이다. (후자의 경우 saddle point의 돌파구를 찾는데 도움이 될 것이다.)

이것이 가능한 이유는 momentum을 사용할 경우 momentum은 여태 gradient를 averaging한 vector이고, 현재 step의 gradient vector와 더해져서 최종적인 grdaient를 얻기 때문이다.

Fig.

바뀐 update rule을 써보면 다음과 같다.

여기서 averaging을 하는 coefficient인 \(\mu\)는 \(0.9, 0.99\)정도로 설정하는 것이 일반적이다. Lecturer Sergey는 이런 accelerated gradient descent 가 Newton method의 어떤 benefit을 많은 cost없이 얻을 수 있다 라고 한다.

우리가 추가적으로 필요한 memory, computation cost는 gradient와 동일한 크기의 (parameter size와 같음) momentum을 training 내내 가지고 있어야 한다는 것과 두 gradient를 더하는 연산을 추가로 한다는 것 뿐이다. (이것이 나중에 large scale model을 다룰 대는 매우매우 큰 문제가 될 수 있는데, 나중에 따로 다루도록 하겠다)

Nesterov Accelerated Gradient (NAG)

추가로 momentum을 더하는 방식에는 Nesterov 가 제안한 더 나은 방식이 있다고 한다. 이것은 convex problem 일 때 수렴성을 보장하기 때문에 optimization theory에 더 관심이 있는 사람이라면 찾아보면 좋겠으나, 좀 더 복잡하기 때문에 modern DL algorithm들은 이를 쓰지 않는다고 한다.

Fig.

그래도 간단하게 말하자면 Nesterov 가 제안한 momentum 계산 방식을 접목시킨 Nesterov Accelerated Gradient (NAG)은 2012년 Ilya Sutskever에 제안되었다. TL;DR 하자면 current point에서 gradient를 계산해서 momentum과 더해서 한 step가지 말고, momentum방향으로 한 step 간 뒤에 gradient를 계산해서 한 step 더 가겠다는 것이다. 일단 가보고 실수를 보정하는게 더 낫다는 intuition이라고 한다.

Fig.

아래의 figure를 보면 실제로 서로 다른 optimization이 진행되면서 어떤 차이가 생기는 지 알 수 있다.

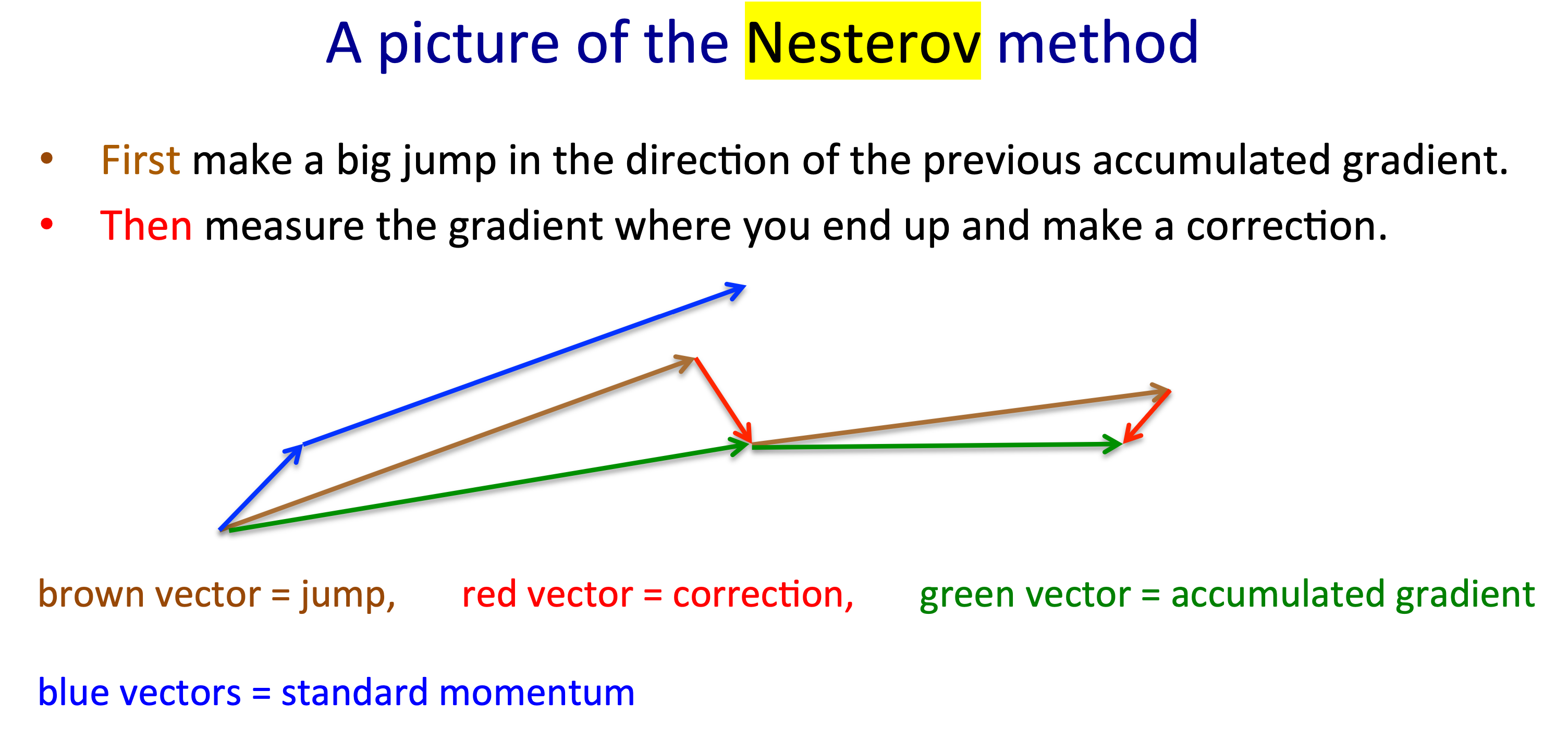Fig.

What if We Pass Minima because of Momentum ?

cs231n의 lecturer Justin가 momentum 얘기를 하면서 재밌는 질문을 받는다. 어떤 학생이 ‘SGD + momentum을 하면 어떤 narrow한 optimal point가 존재하는 valley를 지나칠 수도 있나요?’라는 질문을 하는데, lecturer는 그렇다고 하는데 오히려 그게 좋다고 한다. 왜냐하면 그런 좁은 (혹은 sharp) minima는 일반적으로 loss값은 낮긴 한데 training dataset에만 overfitting하는 지점일 수 있고, 실제로 우리가 찾는 것은 flat minmima이기 때문에 지나치는 것이 오히려 좋다는 것이다. (관련 paper들이 있는데 넘어가도록 하겠다)

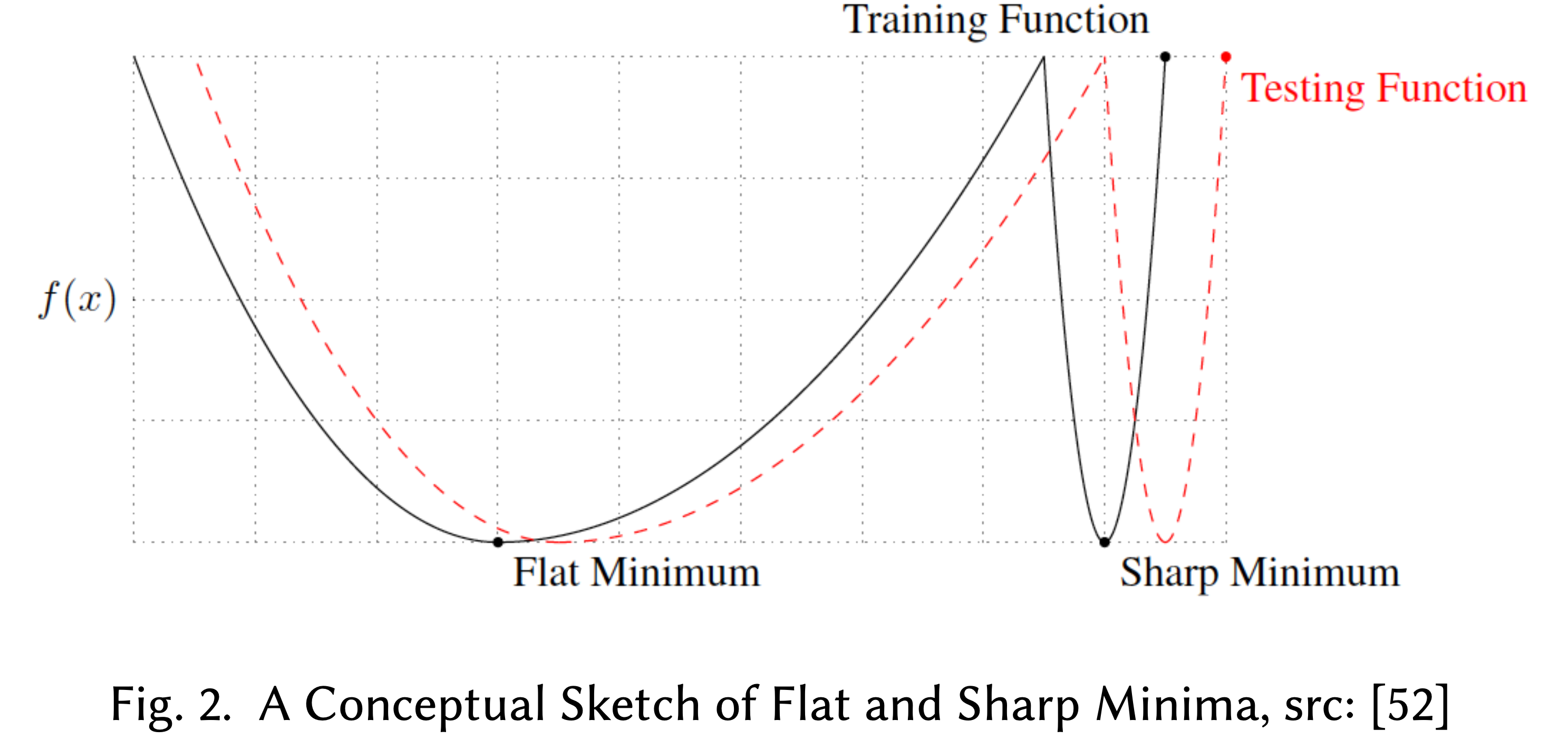Fig. sharp minima에 빠지면 landscape이 조금만 바뀌어도 loss가 확 증가한다 (eval set이 들어온다거나 하면 surface가 바뀜)

Additioanl) Why Mometum rly Works?

왜 momentum같은 가속화 기법이 실제로 잘 되는걸까? 수많은 ML blog post로 유명한 distill의 ‘Why Momentum Really Works’라는 post가 있다. 내용이 많고 어려워서 지금 다루진 않겠지만 관심이 있는 사람이 있다면 읽어보는 것도 좋을 것 같아 언급만 한다.

Gradient Scale

아무튼 monemtum은 gradient가 oscillate하면서 더 늦게 수렴하는걸 막아주는데, 여전히 문제가 있는 것이 gradient의 scale이 parameter별로 달라서 step size를 고르기 어렵다는 것이다. 혹은 optimization이 진행되면서 gradient의 scale이 갑자기 바뀌는 곤혹스러운 경우도 생긴다고 한다. 이런 경우 어떻게 해야할까?

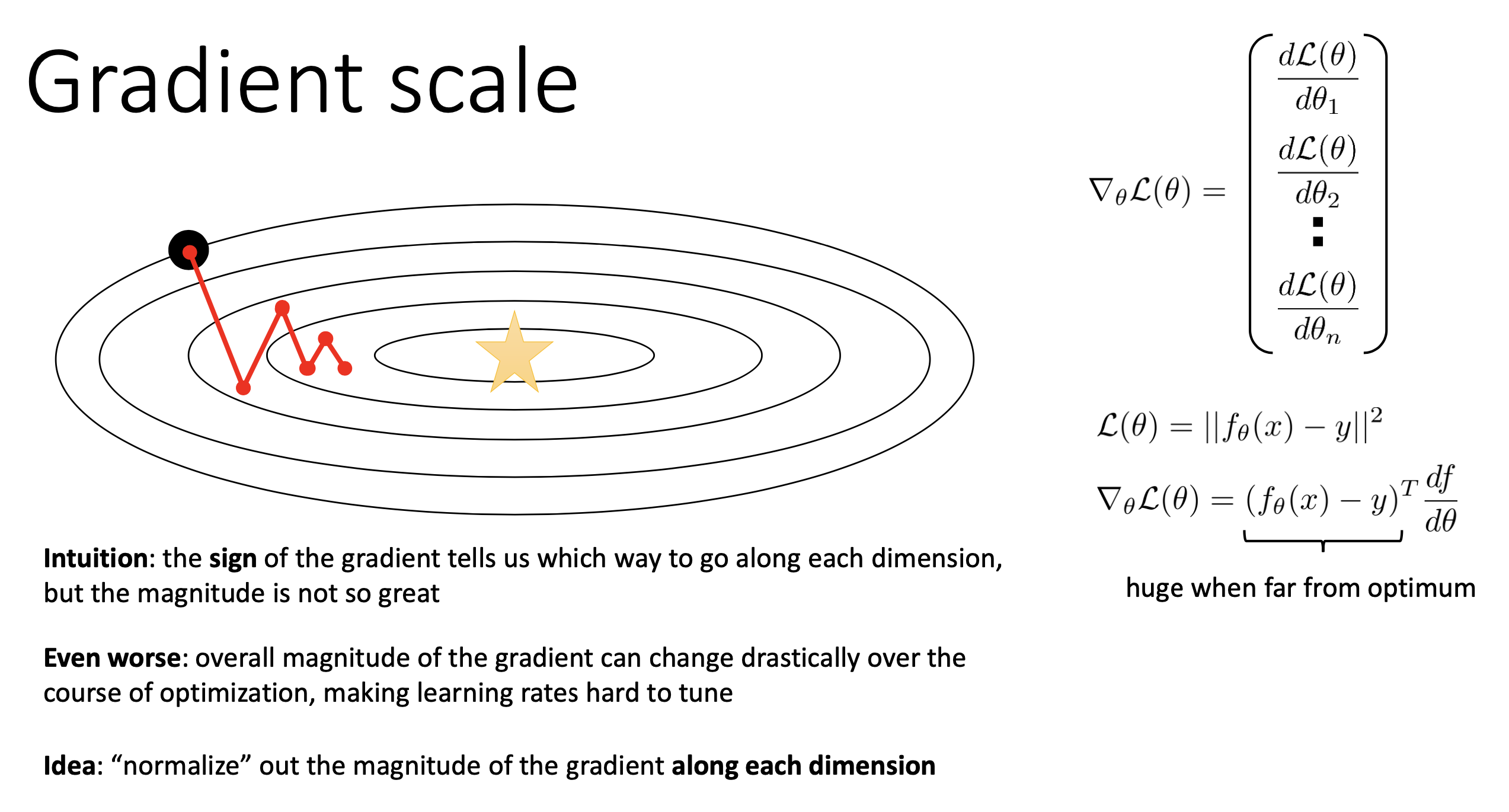Fig.

예를 들어 우리가 Mean Squared Error (MSE) Loss를 최적화 한다고 치자.

이것의 gradient는 다음과 같은데,

gradient는 predicted value와 gold label간의 차이인 loss에 비례함을 알 수 있다. 만약 error가 너무 크다면 어떻게 될까? 각 parameter별로 gradient vector의 direction은 고사하고 일단 크기가 너무 크기때문에 발산 (overshoot)할 가능성이 있다. 그런데 이를 고려해서 step size를 작게 할당하자니 loss가 점점 줄어들면서 gradient scale이 줄어들면 이때는 어떻게 할 것인가? 또한 loss를 계산할 때 위 figure의 예시를 볼 때 \(\theta = [\theta_1 \theta_2]\) 2차원으로 이루어져 있는데, \(\theta_1\) 기준 (대충 y축이라고 치자)으로는 loss값이 작은데, \(\theta_2\)기준으로는 매우 큰 경우 두 parameter별로의 gradient scale도 다른 문제가 생길 것이다.

어떻게 해결할까? 잘 알려져있는 solution은 (각 parameter dimension 별로의) gradient vector를 각각 상황에 맞게 normalization을 하는 것이다.

Root Mean Squared Propagation (RMSProp)

Gradient를 normalize하는 가장 간단한 방법 중 하나는 Root Mean Squared Propagation (RMSProp)이다. Hinton의 lecture slide를 제외하고 reference를 못 찾겠어서 아마 Hinton이 개발한 것으로 보이는데, RMSProp은 heuristic하게 normalizing 하는 것이기 때문에 별로 좋은 gaurantee는 없다고 한다.

Fig.

RMSProp은 momentum처럼 여태까지의 gradient vector들의 크기를 누적해서 평균을 취하는 것이다. 즉 moving average를 계산하는 것인데, Root Mean Square (RMS)를 사용해서 계산하기 때문에 method이름이 RMSProp이 되는 것이다.

직관적으로 위의 \(s_k\)를 update하는 rule의 gradient의 제곱항을 아래 weight update항의 제곱근에 넣으면 여태까지 누적된 gradient vector 각 parameter 차원별로의 length를 expoential weighted sum해서 나눠주는 것이라고 생각할 수 있다.

Adaptive Subgradient Methods (AdaGrad)

그 다음은 Adaptive Subgradient Methods for Online Learning and Stochastic Optimization (AdaGrad)이다. 이름에서 알 수 있듯 이것도 상황에 맞게 (adaptive 하게) step size를 각 parameter별로 정해주는 method이다. RMSprop과 유사하게 생겼지만 AdaGrad는 convex optimization을 할 때 수렴이 보장된다는 점에서 장점이 있지만, 현대 DL에서는 RMSProp이 더 무난하게 쓰인다는 것 같다. (마치 NAG보단 naive momentum이 더 쓰이는 것 처럼)

Fig.

AdaGrad의 update rule은 RMSProp 보다 더 간단하다.

(수렴성이 궁금한 사람은 paper를 읽어보도록 하자)

Intuitive Animations of Various Algorithms

앞서 momentum과 gradient scale을 이용한 optimizer들을 살펴봤다. 이 둘을 결합한 advanced optimizer를 알아보기 전에 Alec Randford가 예전에 reddit에 공유했던 optimizer들의 behavior를 잘 설명하는 animation을 보자. (Alec은 OpenAI의 research scientist로 GPT-3와 whisper를 포함한 OpenAI model들의 core contributer이다. 그런 그가 커리어 초기에 optimizer에 대해서 이런 자료를 만든 것을 보면 optimizer나 backprop을 제대로 이해하는 것이 얼마나 중요한지 유추할 수 있따. 아님말고;)

첫 번째 예시를 보자.

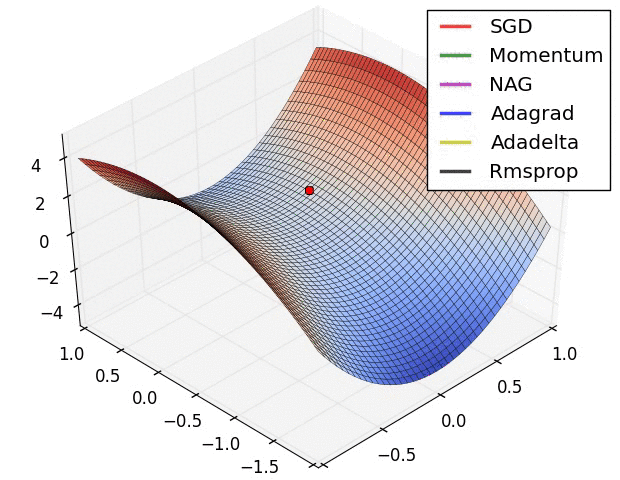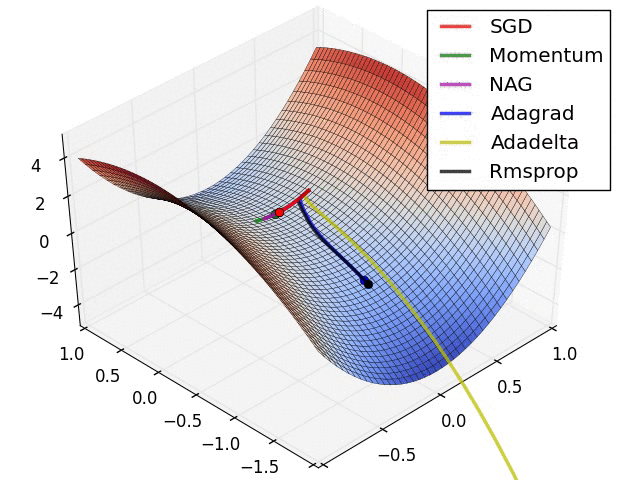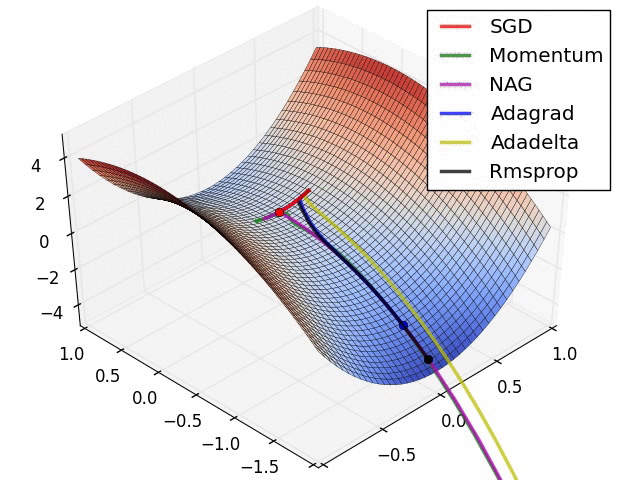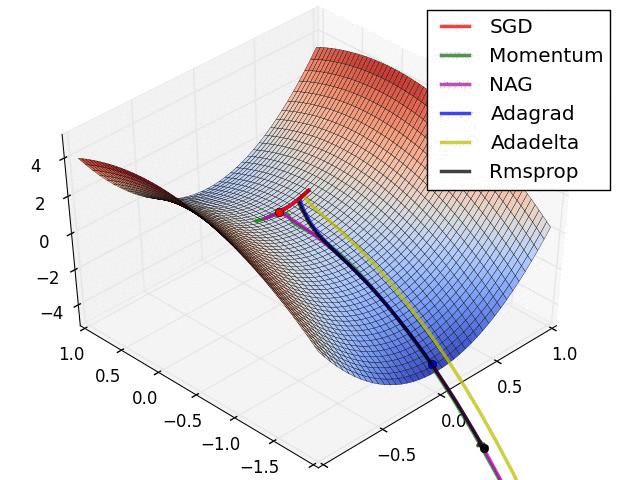Fig. Algos without scaling based on gradient information really struggle to break symmetry here - SGD gets no where and Nesterov Accelerated Gradient / Momentum exhibits oscillations until they build up velocity in the optimization direction. Algos that scale step size based on the gradient quickly break symmetry and begin descent. Source from Alec Randford

(Stochastic Gradient Descent (SGD)는 곧 다룰 건데 우선은 vanilla gradient descent라고 생각하면 된다.)

주석에 써있지만 SGD는 거의 saddle point를 탈출하지 못하는데, 그 이유는 gradient가 0이 되기 때문이다. 그리고 momentum만 적용된 SGD + momenttum은 빠르게 saddle point를 탈출하지는 못하는데, 왜냐하면 맨 처음에는 velocity가 0이고 이를 점차 update하기 때문이다. 따라서 warming up하는 시간이 필요하지만 결국 탈출하게 된다. 그 다음 Adagrad나 RMSProp같은 경우에는 곧장 탈출하는 걸 볼 수 있다.

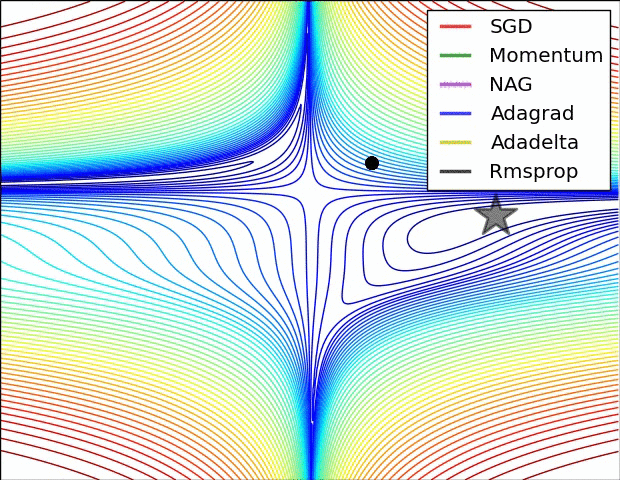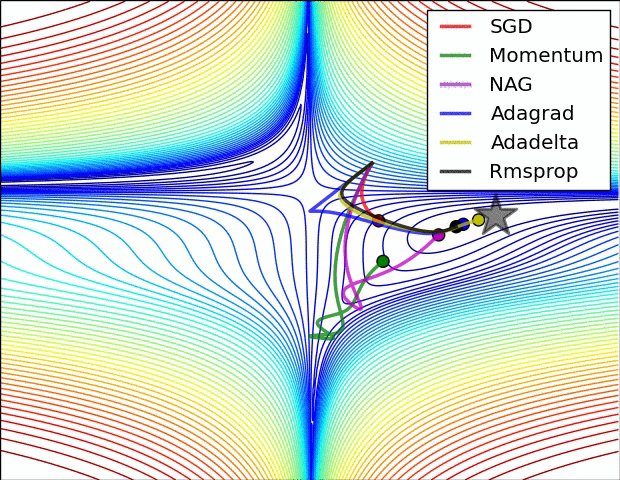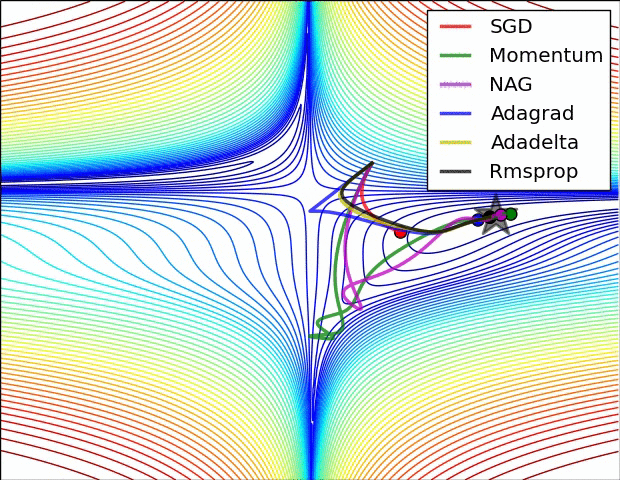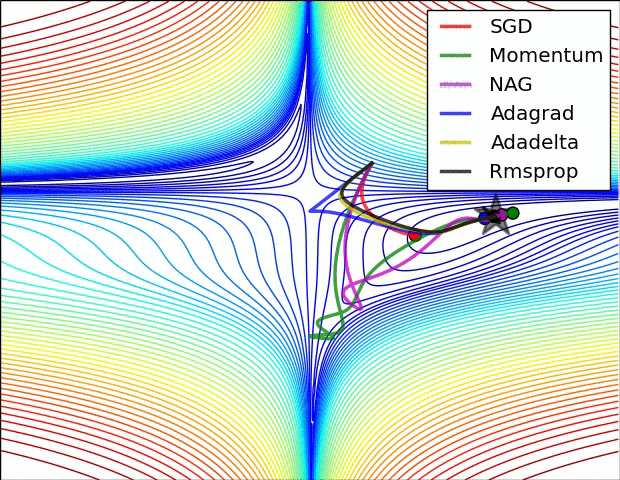Fig. Due to the large initial gradient, velocity based techniques shoot off and bounce around - adagrad almost goes unstable for the same reason. Algos that scale gradients/step sizes like adadelta and RMSProp proceed more like accelerated SGD and handle large gradients with more stability. Source from Alec Randford

다음 예시에서는 (위) initial point에서 gradient가 매우 컸기 때문에 momentum만 적용된 algorithm들은 초반에 팍 튀는 경향이 있고 Adagrad도 그러하다고 한다. 반면 RMSProp이나 AdaDelta등은 안정적으로 optimal point로 향하는 것을 볼 수 있다.

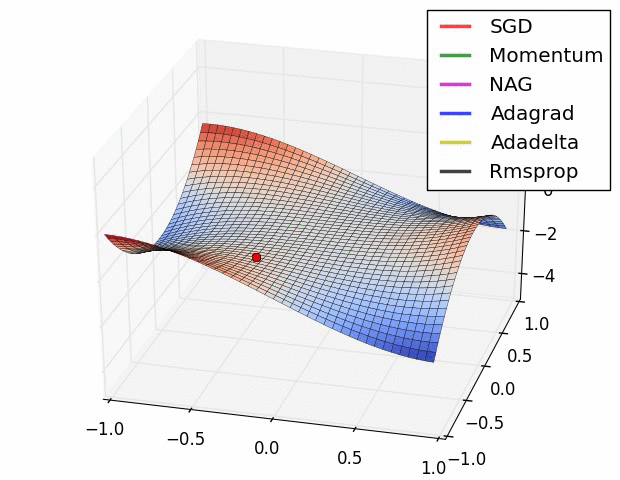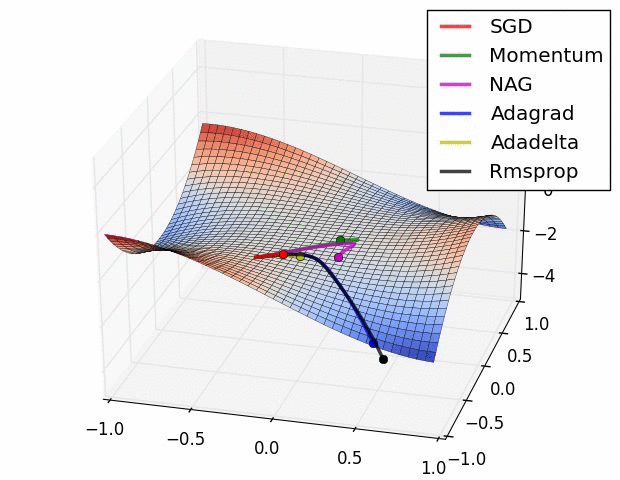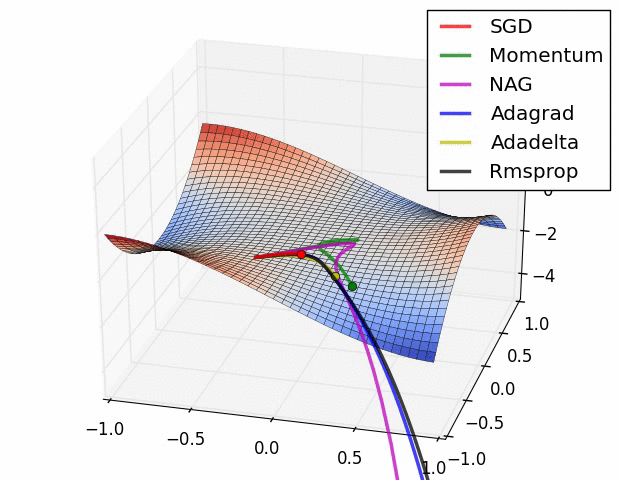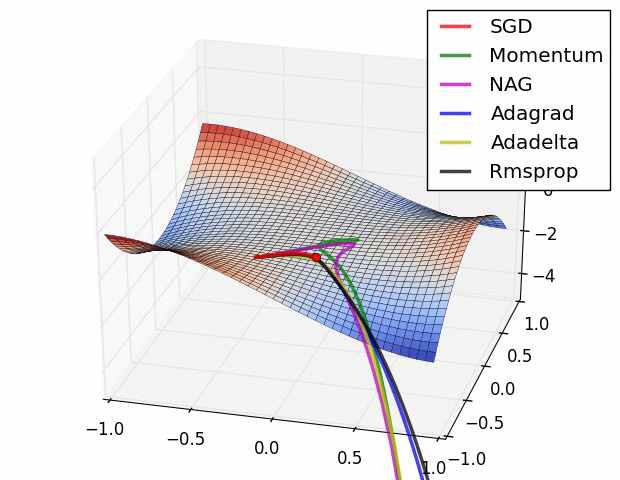Fig. Behavior around a saddle point. NAG/Momentum again like to explore around, almost taking a different path. Adadelta/Adagrad/RMSProp proceed like accelerated SGD. Source from Alec Randford

마지막 예시에서도 마찬가지로 momentum 만 적용된 algorithm들은 탐색하기를 좋아하는 것 처럼 보이는데, 아예 초기에는 다른 방향으로 갔다가 결국에는 saddle point를 빠져나오게 되며 plain SGD는 가망이 없어보인다.

ADAptive estimates of lower-order Moments (Adam)

마지막으로 알아볼 algorithm은 Adam이다. (Variational AutoEncoder (VAE)가 처음 제안된 Auto-Encoding Variational Bayes (AEVB)를 비롯해 다수의 impact를 남긴 DP Kingma의 작품이다)

Adam은 momentum과 gradient scale을 합친 algorithm으로, 왠만한 DL algorithm들은 대부분 이것으로 학습되었다고 할 정도로 DL optimizer계의 standard라고 해도 과언이 아니다. (2010년대 후반부터는 AdamW에 밀렸지만)

We propose Adam, a method for efficient stochastic optimization 
that only requires first-order gradients with little memory requirement. 

The method computes individual adaptive learning rates for different parameters 
from estimates of first and second moments of the gradients; 
the name Adam is derived from adaptive moment estimation. 

Our method is designed to combine the advantages of two recently popular methods: 
AdaGrad (Duchi et al., 2011), which works well with sparse gra- dients, 
and RMSProp (Tieleman & Hinton, 2012), which works well in on-line and non-stationary settings;

An important property of Adam's update rule is its careful choice of stepsizes

Fig.

Adam은 위 slide에 나와있는 것처럼 아래의 과정을 거치는데, momentum을 통해 gradient acceleration을 하고 이를 squared length의 running average로 나눠서 normalize한다.

• gradient, \(\nabla_{\theta} L(\theta_k)\)를 계산
• mean, variance \(m_k, v_k\)를 먼저 추정 (estimate)
• mean, variance를 \(\hat{m_k}, \hat{v_k}\)로 보정 (correct)
• parameter update

Algorithm은 매우 간단하다. momentum같아보이는 \(m_k\)와 gradient의 squared legnth를 의미하는 \(v_k\)를 과거의 값들과 interpolation해서 계속 추적하는 것이다. 몇 가지 차이점은 이전의 momentum based method, RMSprop과 다르게 \(m_k\)라는 term이 momentum 같아 보여도 수식적으로 살짝 다르다는 점 (Exponential Moving Average (EMA)를 사용함), (momentum은 \(1-\beta\)를 current gradient에 곱해주지 않음)

moment를 두 번 계산하는데 (first, second moment) 이 둘은 mean, variance라고 부르는 점, 그리고 마지막으로 correction 과정을 거친다는 것이다. Correction을 하는 것은 paper에는 초기화 편향 보정 (initialization bias correction)이라고 되어있는데, 이 과정을 거치는 이유는 우리가 training을 시작할 때 문제가 있기 때문이다. 보통 Adam을 쓰면 \(\color{red}{m_0=0,v_0=0}\)으로 초기화하고, hparam은 \(\color{blue}{\beta_1 = 0.9, \beta_2=0.999}\)로 setting한다. 그렇다면 맨 처음 gradient는 아래와 같이 계산될 것이다.

이러면 당연히 early training step에서는 gradient가 매우 작게 되고, 시간이 경과할수록 이 값은 점점 커질 것이다. 그래서 아래와 같이 correction을 해 주는 것인데,

이러면 \(k\)가 작은 early step에서는 \(m_k, v_k\)를 current gradient와 거의 동일하게 만들어주고 (어차피 더할게 없으니 현재에 의존함), timestep, \(k\)가 커지면 correction하는 분모의 \(1-\beta_1^k\)가 1에 가까워지므로 \(\hat{m_k} \approx m_k\)가 되니 문제가 없어진다. 실제 Adam paper의 algorithm은 아래와 같은데, paper에는 수렴성 증명 (convergence analysis)와 더불어 더 자세한 내용이 있으니 관심있는 사람들은 paper를 직접 읽어보길 바란다.

Fig.

(paper에는 Adam의 variant인 AdaMax와 이에대한 discussion도 있으니 깊이를 더하고싶다면 꼭 paper를 읽어보도록 하자)

Fig.

Stochastic Optimization

Stochatic Gradient Descent (SGD)

한 편, DL model들을 학습할 때 Stochatic Gradient Descent (SGD)이라는 term이 많이 등장한다. 우리가 real world 에서 작동하는 DL 기반 application 을 만들고 싶다고 치자. 그러면 엄청나게 많은 dataset (large scale dataset)을 구축하고 objective를 정의해 optimization을 해야할 것이다. 하지만 우리가 앞서 알아봤던 optimization algorithm들은 모두 Full Batch GD인데, 이를 사용하는건 바보같은 짓이다.Training dataset sample이 100만개라고 쳐보자. 100만개에 대해서 다 gradient를 계산해서 sum한 값으로 한 번 update를 하는 것과, 128개 정도에 대해서 gradient를 계산하고 update한 다음, update된 parameter로 또 128개에 대해 gradient를 재고… 이렇게 하는 것 중에서 어떤 것이 더 좋을까?

사실 full batch를 본 것과 128개를 본 것의 gradient는 크게 다르지 않을 수 있다. 만약 이게 사실이라면 data sample을 128개만 보고 parameter update를 하고, 개선된 parameter로 gradient를 재고 또 update를 하고… 하면 훨씬 더 좋은 model을 얻는 장점까지 있을 것이다. 그러니까 우리는 full batch gradient를 계산할 필요가 없고 128개 정도의 mini batch에 대해 계산하는 것이 훨씬 경제적이며 좋은데, 이를 Mini Batch GD라고 한다.

Fig.

그래서 기본적으로 deep learning에서는 full batch를 여러개로 나눠 mini batch training을 하는데, 매 epoch마다 training data sample의 순서를 random하게 바꿔가면서 random access하는 효과를 내기 때문에 Stochastic GD (SGD)라고 하기도 한다. 물론 momentum이나 gradient scale같은 trick은 당연히 사용할 수 있다.

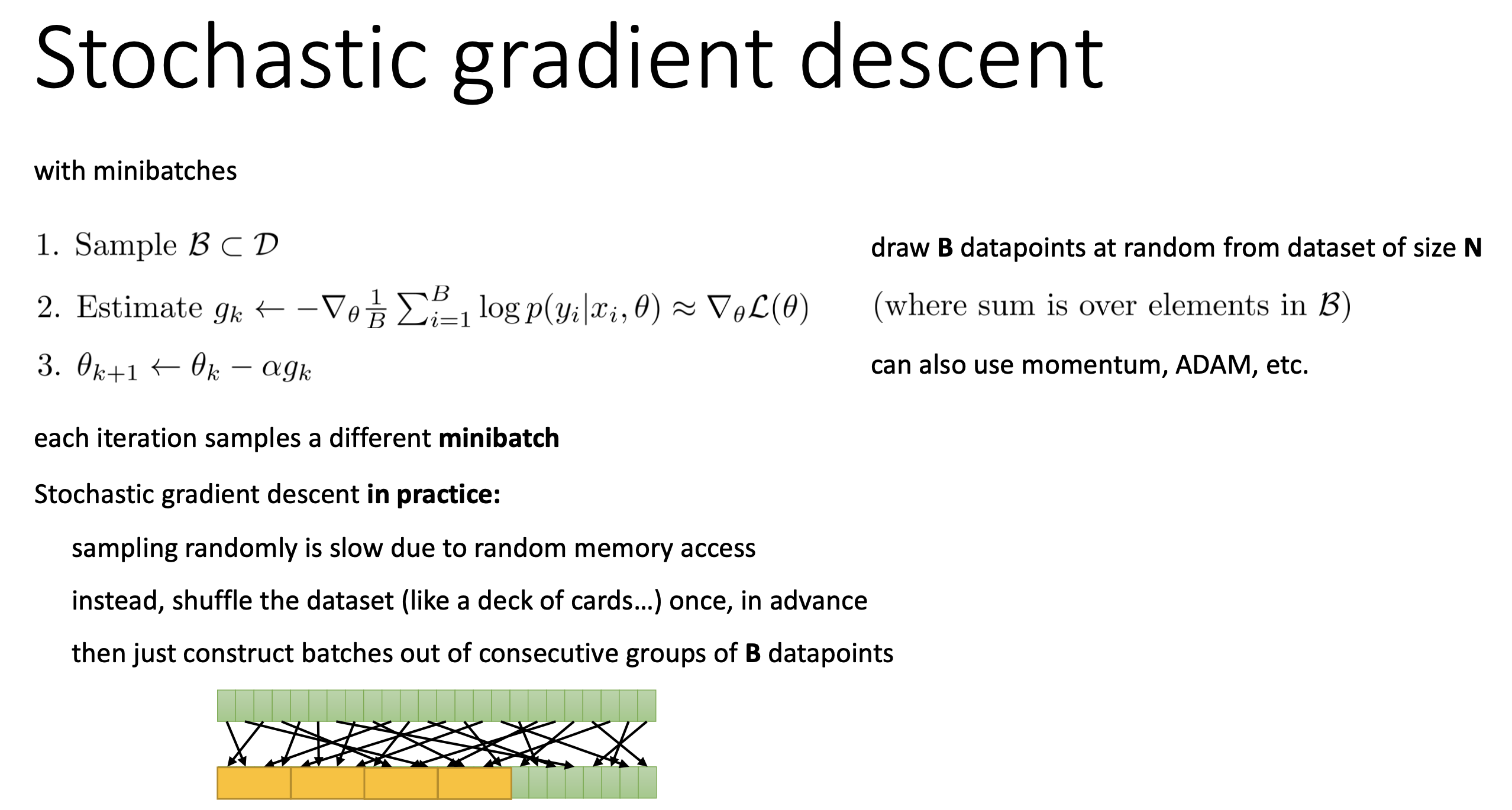Fig.

추가적으로 PRML에 따르면 SGD를 Online Gradient Descent라고 부르기도 하는데, 이는 sample 1개만 사용해서 update하는 것을 의미한다 (즉 mini batch size = 1).

On-line gradient descent, also known as sequential gradient descent 
or stochastic gradient descent, 
makes an update to the weight vector based on one data point at a time.

(from PRML)

그런데 DL에서 SGD는 일반적으로 mini batch GD를 말하는 것이니 헷갈리지 않도록 주의해야 한다.

Hyperparameter Tuning for SGD

Optimization을 할 때 중요하게 생각해야 하는 것이 또 하나 있는데, 바로 learning rate (lr) 를 controll 하는 것이다. “?? 앞에서 Adaptive optimizer들이 알아서 lr 고르는 거 아니었나요?” 라고 할 수 있는데, 그럼에도 불구하고 이것을 사용하는게 성능이 더 좋다고 알려져 있다.

물론 plain SGD를 쓸 경우 당연하게도 step size를 adaptive하게 정해주지 않으니 이것은 선택이 아닌 필수다.

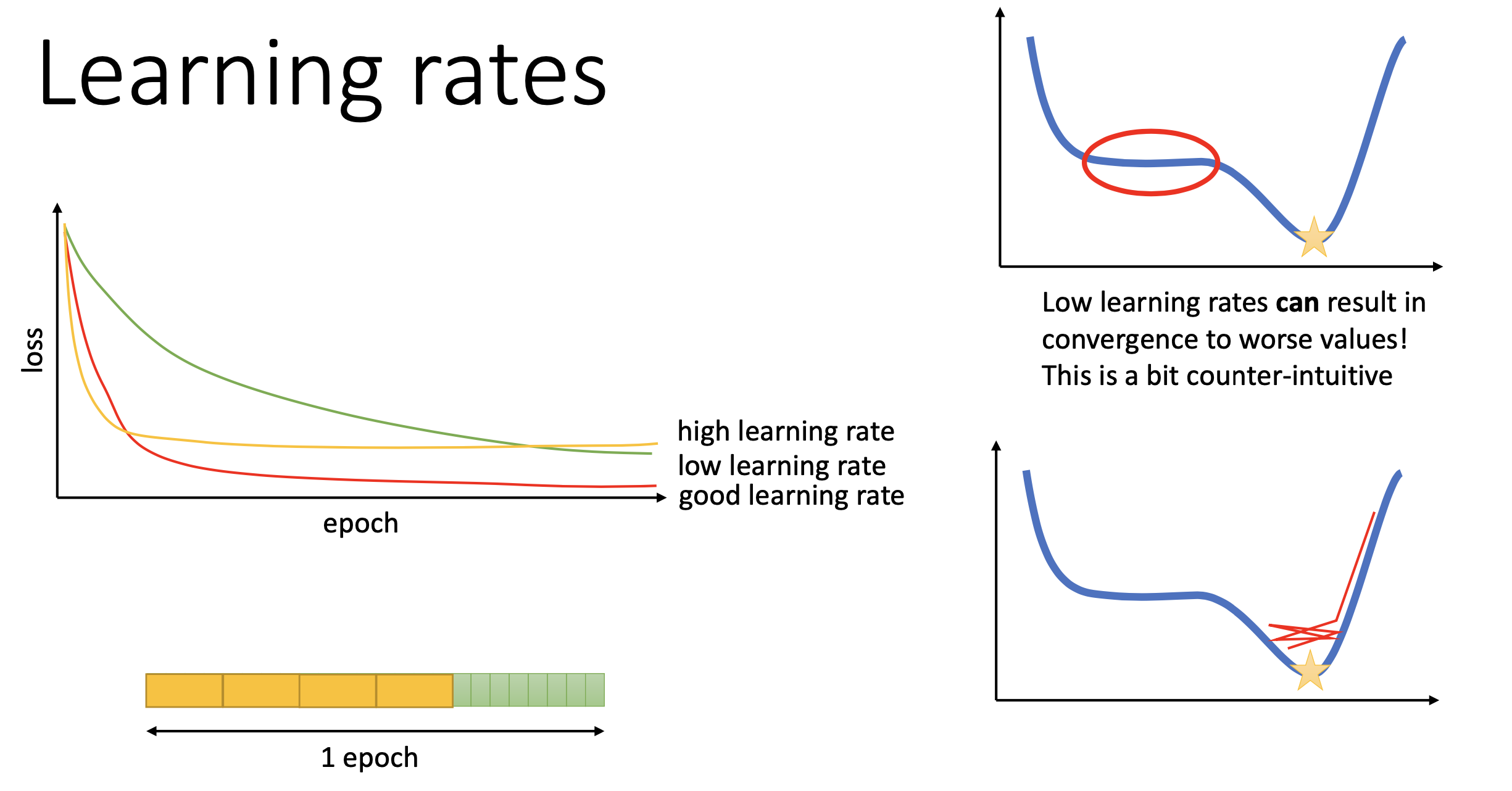Fig.

Lr을 감쇠시키는 (decay) 방법에는 여러가지가 있는데, 주기함수를 쓴다거나 optimization timestep에 대해 linear하게 감쇠시킨다거나, sqrt하게 감쇠시킨다거나… 등등이 있다. 아래 slide 에도 쓰여있지만 Adam같은 optimizer는 알아서 lr을 조절해주기 때문에 필요없다고 하나, 현실은 그렇지 않다. (경우에 따라 다르기 때문에 Adam이어도 constant lr을 안 쓸수도 있고 constant lr을 쓰는게 더 좋을 수도 있다.)

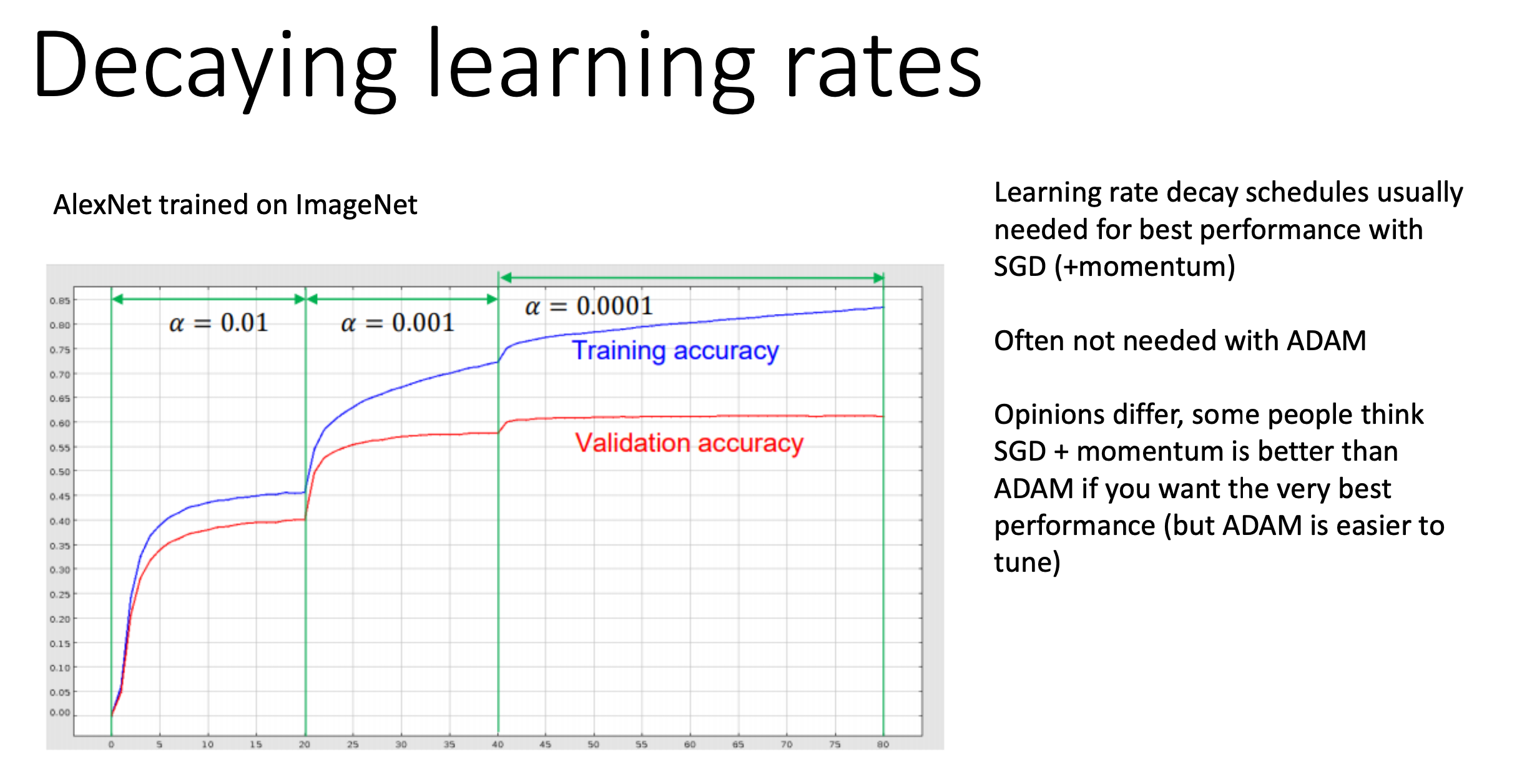Fig.

마지막으로 hyperparameter tuning에 대한 얘기인데, 마지막에 '어떤이들은 L2 등의 regularization과 GD는 서로 충돌할 수도 있다'라는 문구가 있는데, 곧 이에 대해서 알아볼 것이다.

Fig.

Important Intuition for Gradient Based Method

그런데 왜 loss function을 \(\theta\) point에 대해서 미분을 해야 하는걸까? 엄밀히 말하면 1차 미분은 1차 테일러 근사 (1st order taylor expansion, taylor approximation)를 하는 것이다. 이것이 갖는 의미가 뭘까?

우리가 전체 data point와 model parameter에 대해서 loss surface가 어떻게 생겼는지 알 길은 없겠지만, 만약 이를 알 수 있다면 현재 parameter point의 부근에서 어느 방향으로 얼만큼 가는것이 cost를 가장 많이 낮추는 것인지 알 수 있을것이다. 하지만 아무리 전체 surface가 어떻게 생겼는지 모른다고 하더라도 우리는 direction을 정할 수 있었다. 이게 가능한 이유는 사실 현재 parameter point 근처에서 loss function이 어떻게 생겼는가?를 taylor approximation으로 알 수 있기 때문이다. 즉 현재 parameter 부근에서만 어떻게 생겼는지 알면 되는데, 이 때 쓰는 것이 taylor expansion이다. Taylor expansion은 다항식이 아닌 미지의 함수를 다항식으로 표현하는 방법으로, 어떤 함수가 너무 어려워 그대로 사용하기 힘들 때 그 함수를 근사해서 연산에 사용하기 위해서 ML이나 여러 분야에서 많이 쓰이는 수학적 Tool 중 하나이다. 아래와 같이 cyan색 curve에 대해서 1차 근사 (first order approximation)를 하면 우리는 pink색 근사된 curve를 얻을 수 있다.
이것을 우리는 gradient를 구한다라고 얘기하고 SGD, Adam 모두가 이런 방식으로 작동하는 것은 앞서 배웠기 때문에 납득이 갈 것이다.

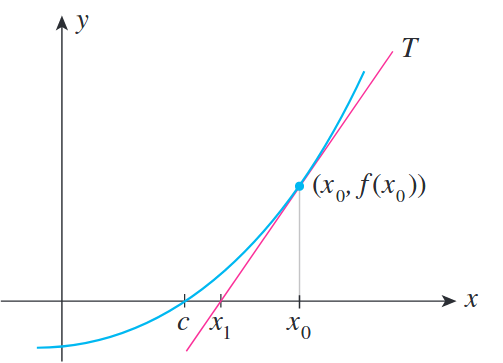Fig.

중요한 점은 current point에서 많이 벗어나게 되면 더이상 이 pink와 cyan curve는 유사하지 않다는 것이다. 즉 오차가 커지는 것이다. 하지만 그럼에도 안정적인 optimization을 할 수 있는데, 그 이유는 정해진 반경 (radius), \(\epsilon\) 내에서만 그 다음 parameter를 고르는 전략을 쓰면 되기 때문이다. 그러면 더이상 우리는 정해진 범위 밖이 어떻게 생겼는지 알바가 아니다. 이렇게 parameter space에서 euclidean distance가 \(\epsilon\)인 원 모양의 region을 신뢰할 만한 구간 (trust region)이라고 한다.

Fig. Source from DeepMind X UCL Lecture

그래서 gradient descent랑 이것이 무슨 상관이냐? 사실 current parameter point에서 radius가 \(\alpha \parallel \nabla_{\theta} L(\theta) \parallel\)인 제한 조건 (constraint)를 걸어서 constraint optimization problem의 해를 구하는 것은 정확히 gradient descent와 같다.

이러한 제한 조건이 걸린 최적화 (constraint)를 푸는 방법은 먼저 Lagrangian Multiplier를 이용해 constraint를 objective term과 결합시키고, objective는 1차 근사를 하고 constraint 에 대해서는 2차 근사한 뒤, 근사된 수식을 미분해서 0으로 두고 문제를 풀면 된다. 왜냐하면 우리가 원하는 것이 trust region에 놓여진 parameter 후보군 중 cost가 가장 낮은 parameter이기 때문이다. 이를 풀면 놀랍게도 우리가 앞서 봤던 gradient descent 수식이 나온다.

우리가 full batch gradient가 아닌 SGD를 쓰기 때문에 원래 objective function이 아니라 이를 근사한 대리 손실 함수 (Surrogate Loss Function)라는 걸 쓰는 격이 된다. 여기서 주의할 점은 1st order, 2nd order모두 optimal point로 향하지 않는다는 것이다. 특히 2nd order method의 경우 surrogate loss function이 많이 다른 경우에 surrogate surface의 optimal point를 향하게 되는데, 이것이 오히려 치명적일 수 있다.

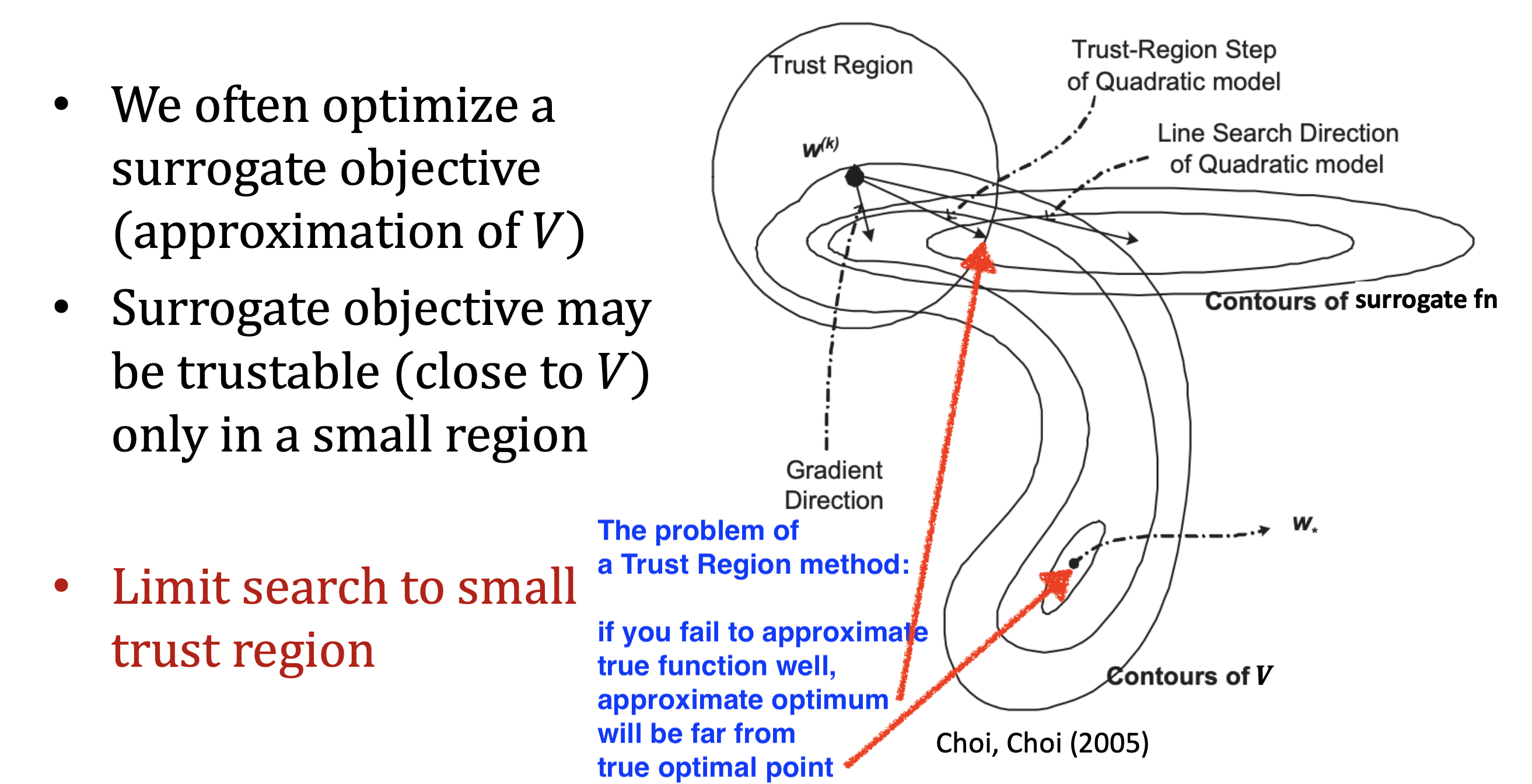Fig. Source from CS885 by Pascal Poupart

위 figure에서 trust region method와 gradient descent의 direction이 다른 것은 constraint이 달라서 그런거라고 생각하면 될 것 같다.

Addtional Things (for Modern DL)

Memory Consumption of Adam

완벽할 것 같은 Adam에도 몇 가지 단점이 있는데, 그 중 하나를 한 가지 언급하고 넘어가려고 한다. 그것은 바로 GPU memory를 너무 많이 먹는다는 것이다. 왜냐하면 model parapeter와 동일한 크기의 momentum, variance를 따로 caching하고 있어야 하기 때문이다. Parameter 1개당 floating point 32 (fp32)면 4bytes, floating point 16 (fp16)이면 2bytes 이기 때문에 만약 parameter 개수가 10억 개 (1 Billion, 1B)라면 fp16일 때 model parameter만 2GB의 GPU memory를 필요로 한다. 그런데 model parameter 2GB있고, forward activation을 또 2GB 저장해야 하고 (parameter마다 output들), backward로 gradient를 계산하면서 2GB 를 또 저장하고 마지막에 parameter를 update하기 위해서 momentum 2GB, variance 2GB를 사용한다. 그러니까 실제로는 10GB정도가 필요한 것이다.

이는 엄청나게 큰 model들을 분산 학습하기 위한 Zero Redundancy Optimizer (ZeRO)라는 algorithm의 paper에 언급이 되어있는데, model의 크기가 커질수록 엄청난 redundancy가 발생한다. 왜냐하면 gpu device별로 model크기의 12배에 달하는 optimizer state를 모두 들고 있어야 하기 때문이다. 즉 Adam은 space complexity 관점에서 결코 좋은 algorithm은 아니라는 것이다.

LR vs Batch Size

일반적으로 batch size가 2배 커지면 learning rate은 linear하게, 혹은 sqrt만큼 배수를 취해준다. 왜냐하면 mini-batch training을 할 때 그만큼 gradient estimator의 noise가 감소하고, optimization step수도 같은 epoch을 기준으로 2배 감소했기 때문에, 그 scale을 맞추기 위해서 그런 것이다. 이에 대해 더 살펴보고 싶다면 blog 내 large batch training에 관한 post를 보는 것을 추천한다.

(조금 오래되긴 했으나 lr과 batch size에 관해서 Don’t Decay the Learning Rate, Increase the Batch Size라는 paper도 있으니 참고하면 좋을 것 같다)

Sometimes SGD would be better

이쯤에서 ‘아니 그냥 Adam 쓰면 되는 거 아니야? 왜 복잡하게 모든 mechanism을 알아야 하지? 알아서 해주는데?’ 라는 생각이 들 수 있다. 하지만 optimizer를 잘 이해하지못하면 NN을 학습하면서도 ‘왜 내 model은 제대로 학습되지않을까?’같은 생각이 들 수 있다.

조금 어려운 내용이지만 motivation을 위해 강화 학습 (Reinforcement Learning)의 algorithm을 예시로 들겠다. Proximal Policy Optimization (PPO)이라는 algorithm은 model (actor라고 하긴하는데)의 parameter를 최대한 보수적으로 update하는 rule을 사용한다. Gradient를 계산한 뒤에 신뢰 구간 (trust region) 내에서 가장 크게 한 step 가는 것이다. 그런데 실제로는 PPO가 clip 이라고 하는 trick을 사용해서 trust region내에서 param update가 행해지는지를 판단해서, clip range를 넘어가면 gradient를 0으로 만들어버린다. 이를 계산할 때는 model의 log probability 를 이전 step의 parameter를 썼을때의 model의 log prob과 비교하는데, 만약 log prob의 비율 (ratio)를 기준으로는 clip range를 넘어가지 않아 gradient가 0이되지 않았는데 (이정도면 보수적이라고 한 것), 여기에 update를 할 때는 momentum이 더해지게 된다. 그러면 실제로는 clip range를 벗어나는 behavior였음에도 불구하고 이를 분간하지 못하게 될 수 있는것이다.

이럴 때는 SGD를 써야 하지 않을까? 하지만 paper를 확인해본 결과 PPO를 Adam과 쓰는 경우도 종종 있다고 한다. 물론 실험적으로 Adam이 더 좋으면 쓰는게 맞지만, 향후 내 model의 training dynamics가 어떻게 될지는 알 수 없는 노릇이다. 그러므로 optimizer들에 대해서 제대로 이해해야만 왜 내 model이 학습이 되지 않는지 알 수 있을 것이고, 다른 optimizer나 regularization을 쓴다던가 하는 option을 생각해 볼 수 있을 것이다.

이런 의미에서 optimizer를 공부하는건 매우 중요하며 Adam이 항상 정답이 아닐 수도 있음을 명시하고 항상 모든걸 의심해야 할 것이다.

AdamW

그 다음은 AdamW에 대해서 잠깐 알아보자. 2010년대 중 후반까지만 해도 어떤 model을 학습하던 adam optimizer를 사용했다. 하지만 10년대 후반부터 20년대에는 AdamW를 쓰는 것이 거의 사실상의 baseline (de facto)이 되었다. AdamW paper의 원 제목은 Decoupled Weight Decay Regularization으로 ICLR 2019 (preprint는 2017)에 발표되었는데, 이름에서도 알 수 있듯 weight decay regularization과 adam을 분리하자는 게 point이다. Paper에서는 pytorch등의 ML framework에서 adam과 regularization이 같이 구현되어 있는데 이것이 문제를 일으킨다는 것이다. 결과적으로 regularization 효과가 떨어져 generalization이 잘 안되다는 것이다.

Fig.

Fig.

More Intuition from DeepMind x UCL Lecture

앞서 cs182와 cs231n를 기반으로 optimization algorithm들에 대해 주욱 살펴봤다. 여기에 조금 수학적이지만 훌륭한 또 하나의 lecture (from DeepMind x UCL)를 통해 추가 insight를 얻어 보도록 하자. (여기서부터는 관심 없는 분들은 page를 닫아도 됨)

Revisit Steepest Gradient Descent

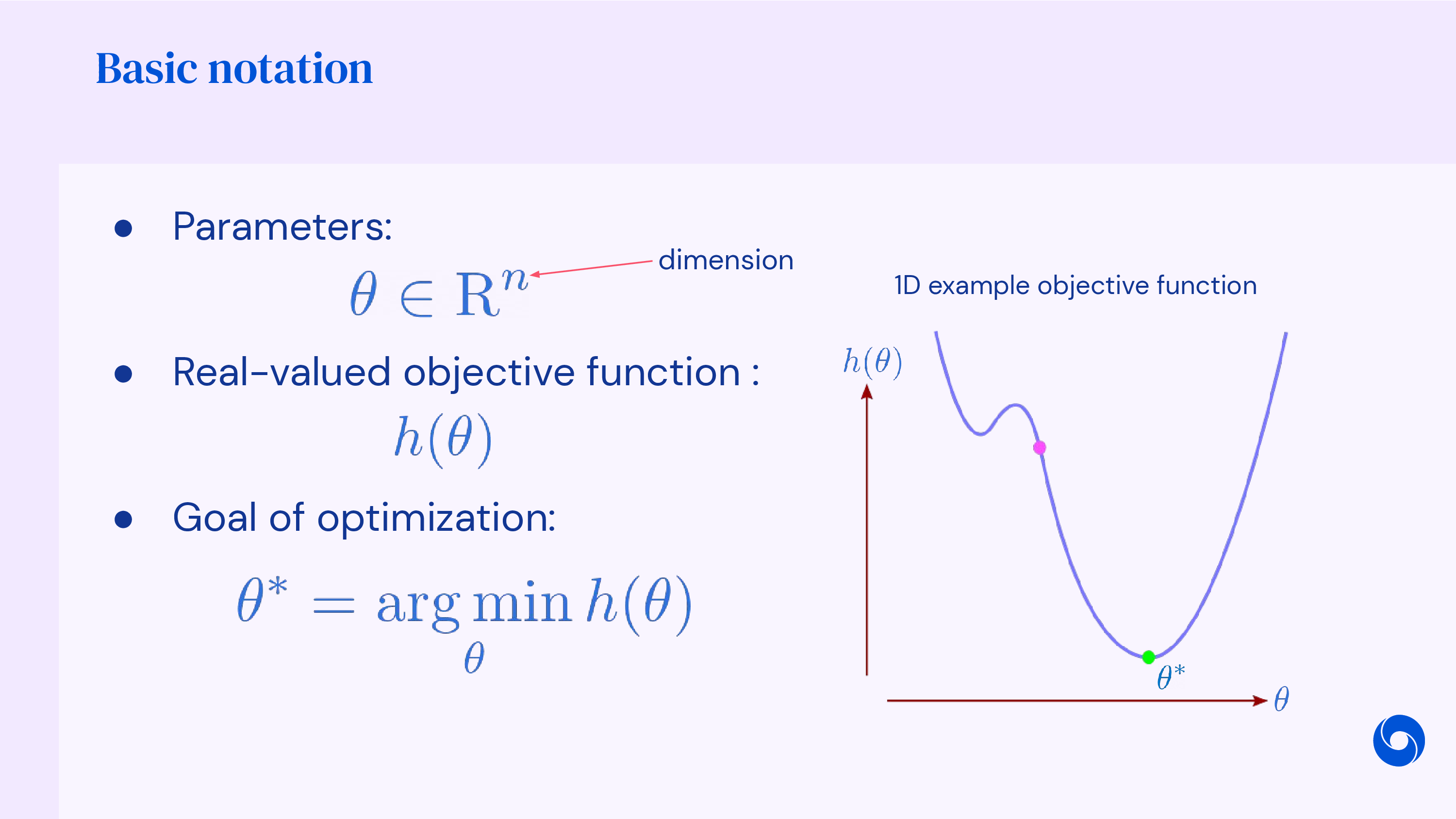Fig.

Fig.

Fig.

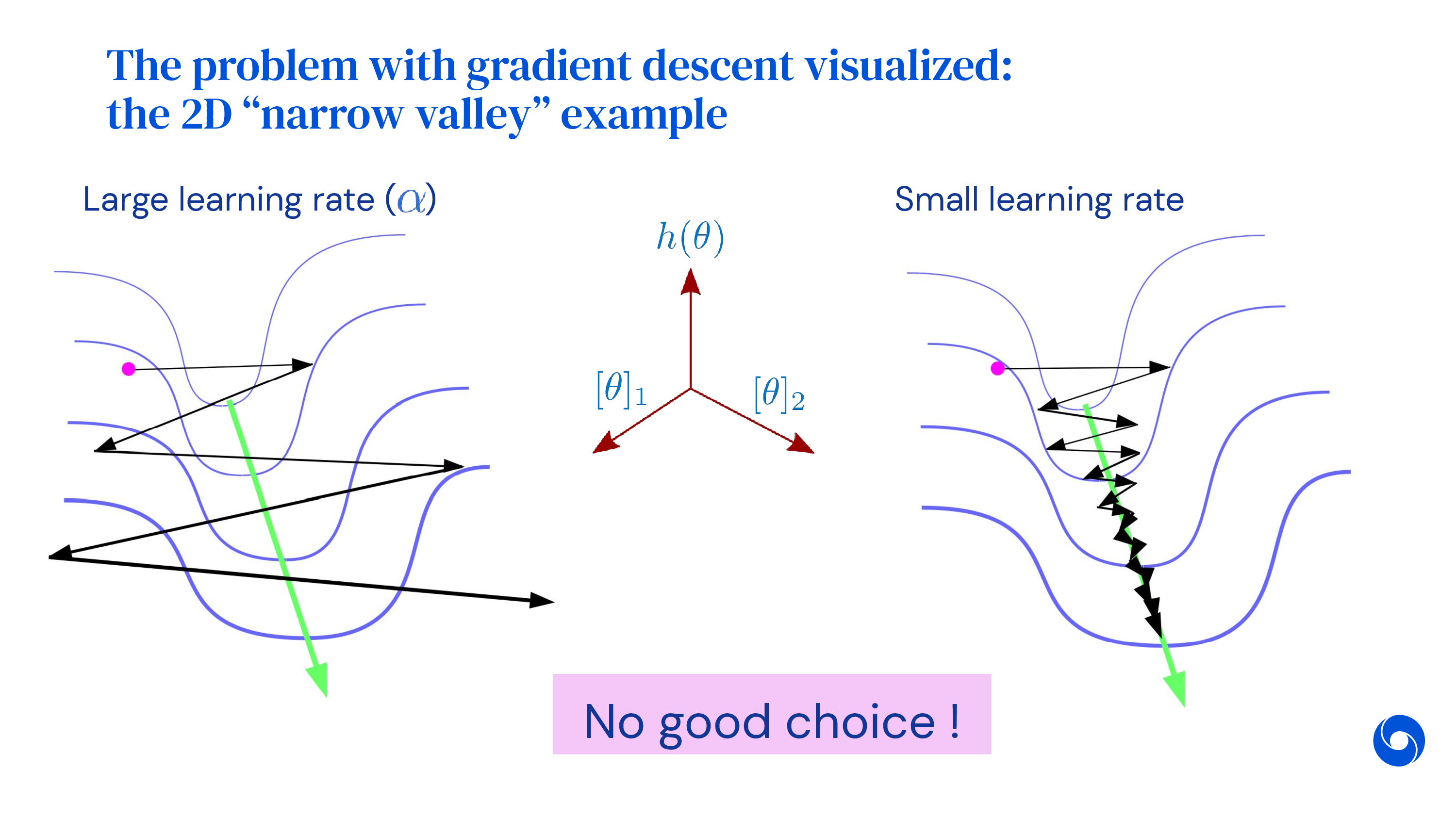Fig.

Fig.

Convergence Theory

Fig.

Fig.

Fig.

Revisit Momentum Methods

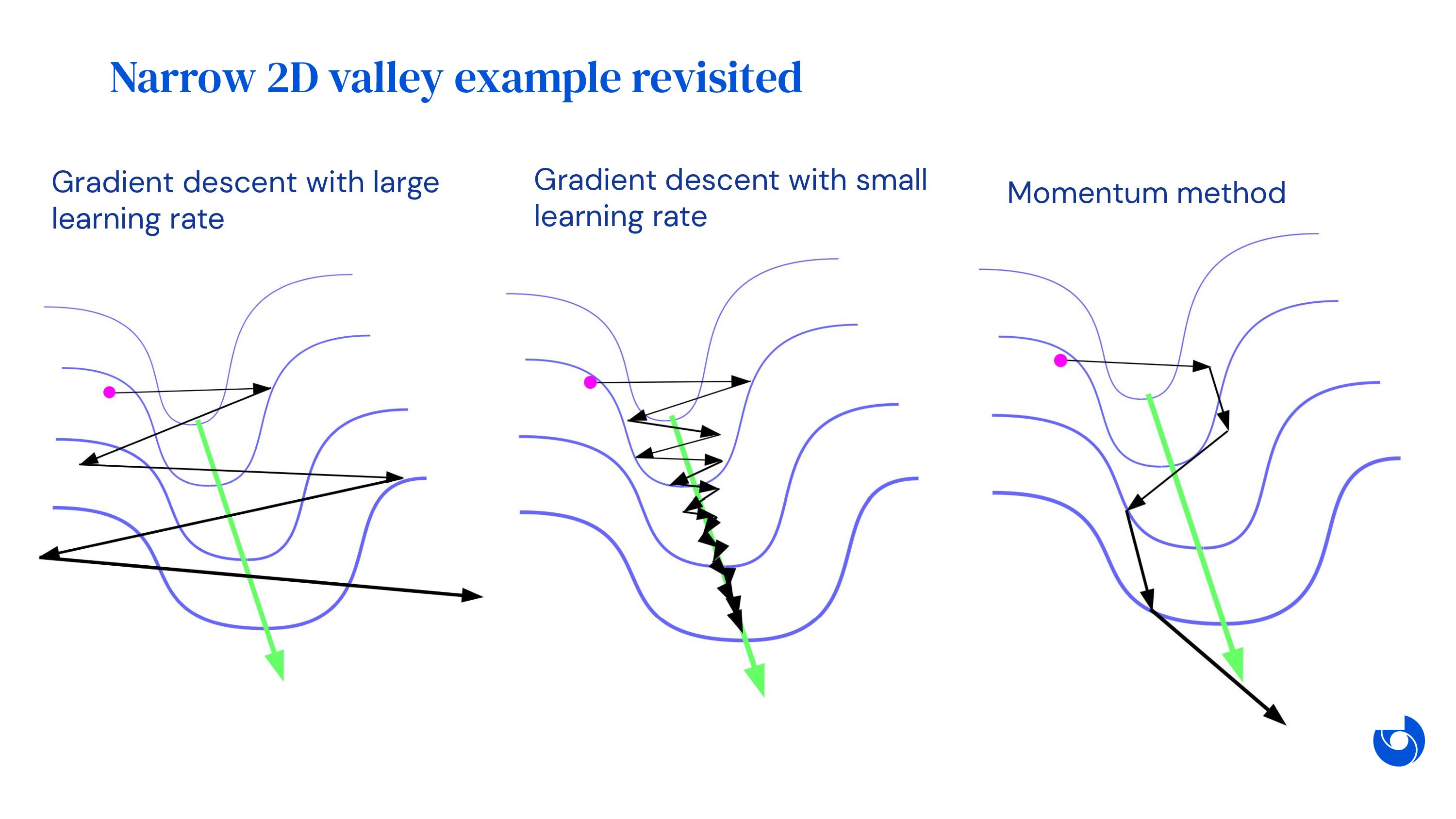Fig.

Fig.

Fig.

Fig.

Fig.

Fig.

Fig.

Revisit 2nd Order Methods

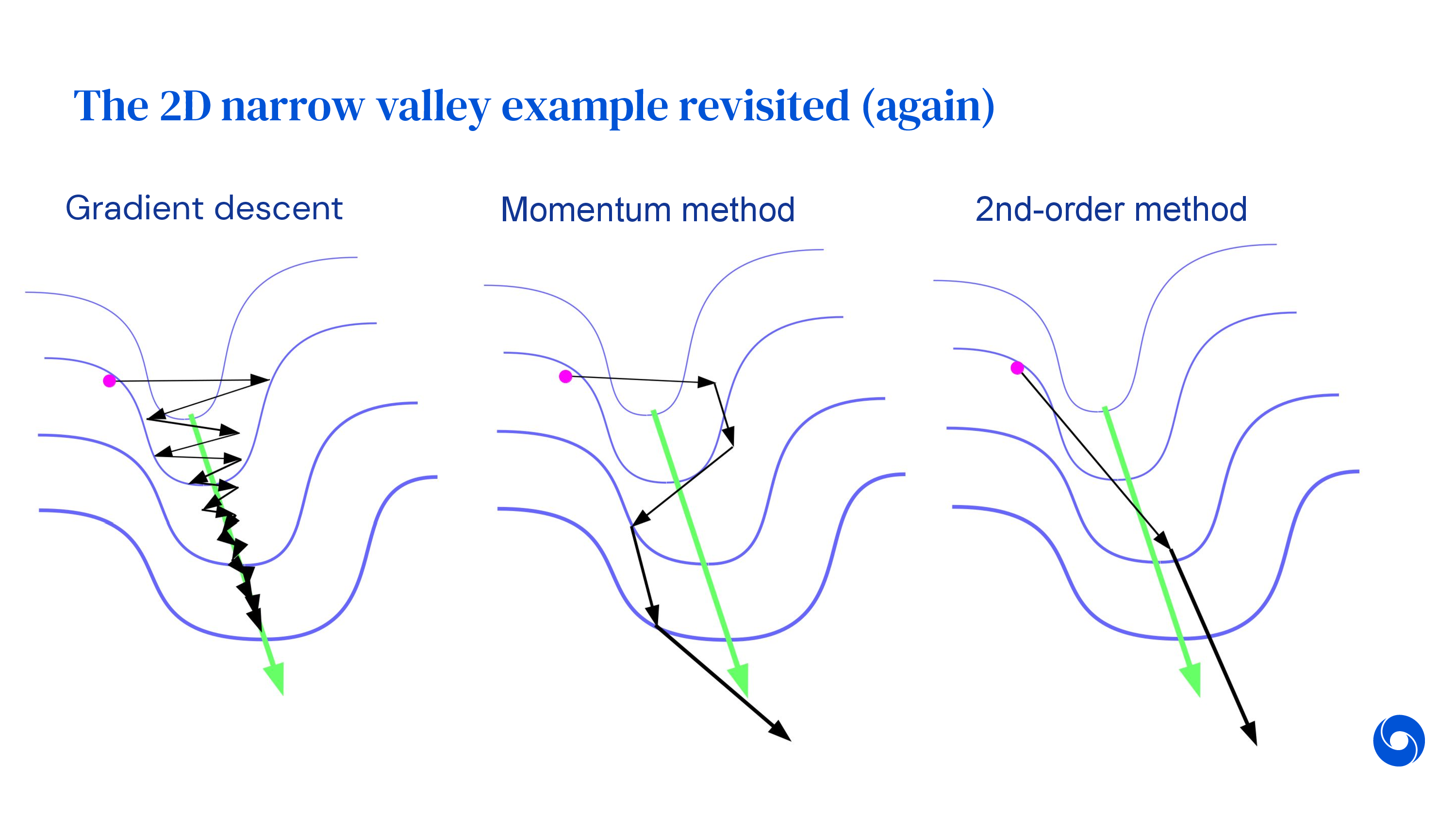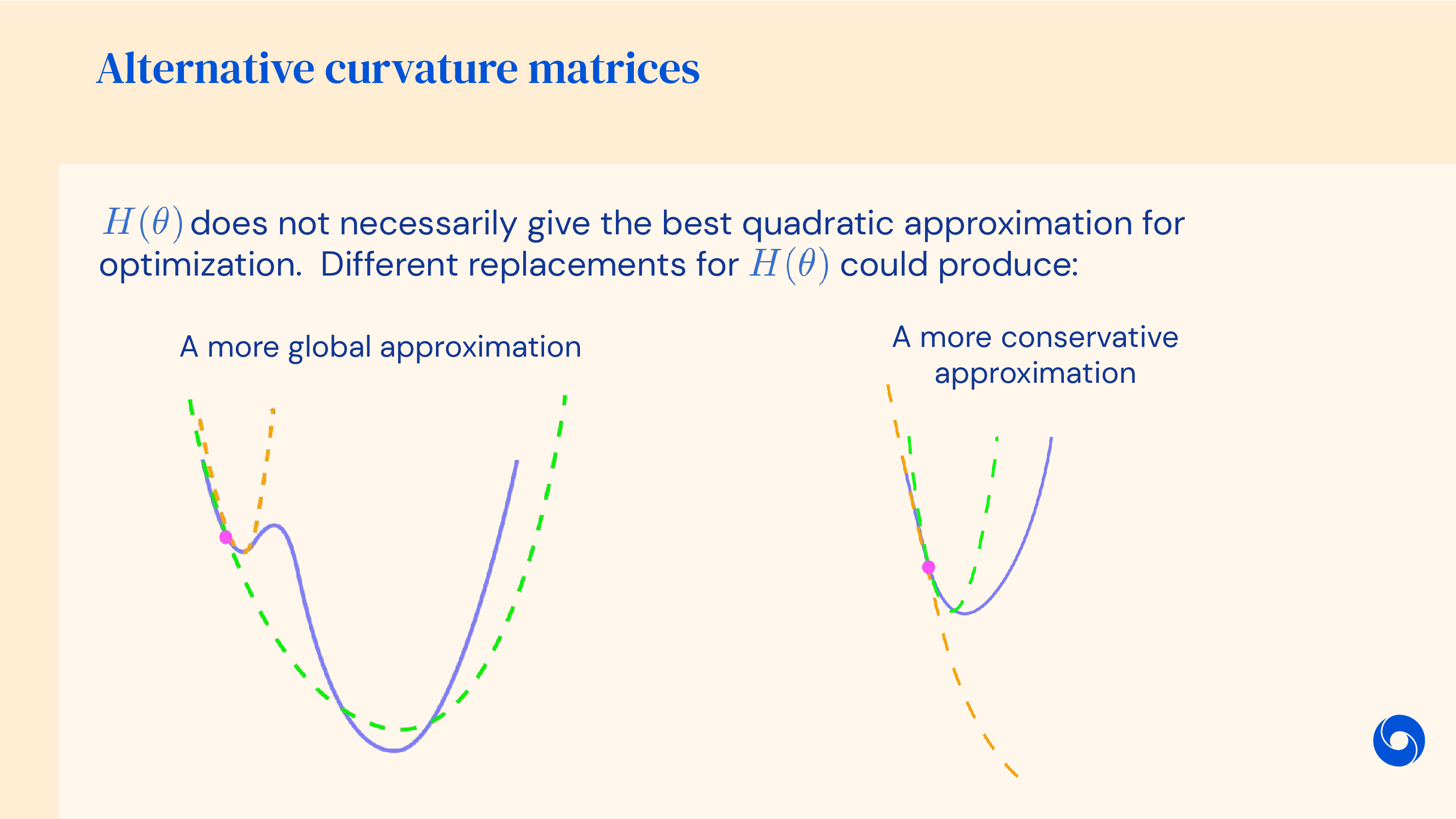Fig.

Fig.

Fig.

Fig.

Fig.

Fig.

Fig.

Fig.

Fig.

Fig.

Fig.

Fig.

Revisit Stochastic Methods

Fig.

Fig.

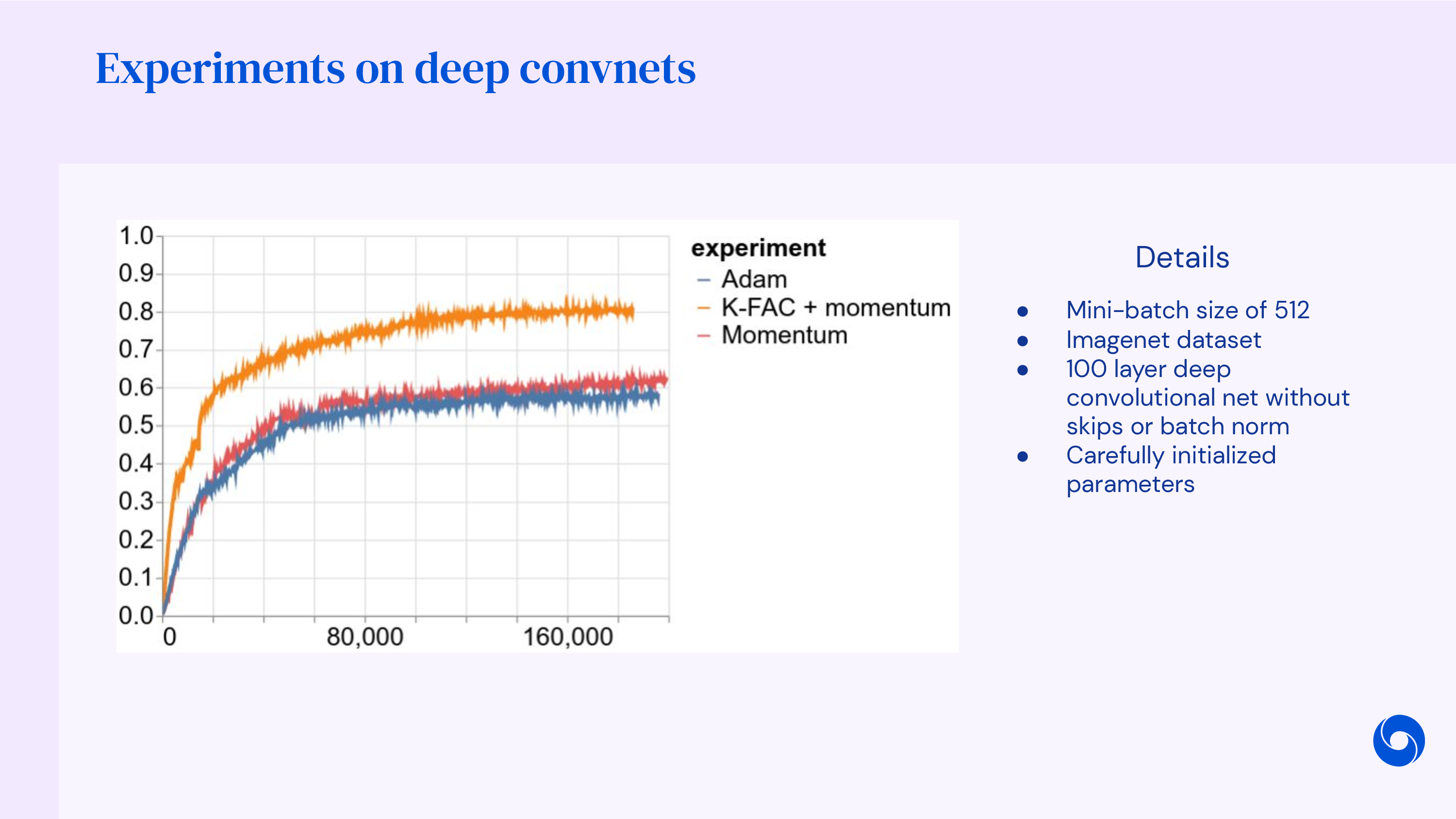Fig.

Fig.

Fig.

Fig.

Fig.

Fig.

References

• Lecture Videos
  • CS 182: Lecture 4, Optimization
    • Lecture Slide
  • DeepMind x UCL, Deep Learning Lectures, 5/12, Optimization for Machine Learning
    • Lecture Slide
  • Stanford CS231n, Lecture 7, Training Neural Networks II
    • Lecture Slide
  • CMU Convex Optimization, Fall 2019
    • Gradient descent
    • Newton’s method
  • Week 5 – Lecture: Optimisation

  • General Sequence Learning using Recurrent Neural Networks

  • CSC 2541: Neural Net Training Dynamics - Lecture 7
  • Stochastic Gradient Descent from KAIST EE807: Recent Advances in Deep Learning Lecture 2
• Blog Posts
  • An overview of gradient descent optimization algorithms
  • Why Momentum Really Works (distill)
  • A journey into Optimization algorithms for Deep Neural Networks
  • 최적화 기법의 직관적 이해 from 다크 프로그래머
  • [딥러닝] 딥러닝 최적화 알고리즘 알고 쓰자. 딥러닝 옵티마이저(optimizer) 총정리
  • AdamW에 대해 알아보자! Decoupled weight decay regularization 논문 리뷰(1) form HiddenBeginner (이동진)
  • The N Implementation Details of RLHF with PPO
• Papers
  • Don’t decay the learning rate, increase the batch size