Error BackPropagation
04 May 2022< 목차 >
- What is Deep Learning? and How to train Neural Network?
- Why Error Backpropagation?
- Error Backpropagation
- "Yes you should understand backprop" from Andrej Karpathy
- Jacobian and Hessian
- References
What is Deep Learning? and How to train Neural Network?
Machine Learning (ML), Deep Learning (DL) algorithm으로 문제를 푼다는 것은 input, output data가 충분히 존재할 때 input, output 사이의 mapping function, \(f\)을 최대한 잘 approximate하는 \(f'\)을 찾는 것이라고 할 수 있다. 이 function을 얻기 위해서는 target data의 distribution이 어떤 shape인지를 정해고, 그에 따라 objective function을 정하고 objective의 값 (보통 likelihood)가 최대가 되는 parameter를 찾으면 된다.
고전적인 ML algorithm들은 이 objective를 미분함으로써 극값을 구해 한번에 닫힌 해 (closed-form solution)를 찾을 수 있다. 하지만 model이 복잡하고 비선형성 (non-linearity)이 추가된 DL algorithm들은 그렇지 않다. 그렇기 때문에 어떤 initial parameter부터 시작해 매 순간 그 시점에서 objective를 최대화 하는 방향으로 parameter를 점진적으로 update 하는, 이른 바 반복적 최적화 (iterative optimization) method를 사용해야 한다.
 Fig. Traditional Gradient based Optimization for Deep Learning.
Fig. Traditional Gradient based Optimization for Deep Learning.
Why Error Backpropagation?
그렇다면 어떻게 iterative optimization으로 network parameter를 update해야할까?
우리가 설정한 objective function에 대해 gradient descent 같은 algorithm을 쓰기 위해서는 현재 parameter와 data point들을 가지고 objective (혹은 loss) function 값을 먼저 계산해 본 뒤,
그 값을 parameter에 대해서 1차 미분값 (1st order taylor approximation)을 구해야 한다.
미분 (differentiation)이라는 것은 어떤 변수가 조금 변했을 때 그 function이 얼마나 변하는지를 보는 것으로,
즉 function의 그 변수에 대한 민감도를 측정하는 것정도로 해석할 수 있다.
우리는 지금 loss function을 각 prameter에 대해 미분을 하는 것이므로 각 parameter들이 이 loss값을 내는데 얼마나 기여했는지를 측정하게 되는 것인데, 이 값이 크면 parameter에 penalty를 많이 부여해 값을 크게 변화시키는 식으로 update를 해 나가는 것이 바로 gradient based optimization method이다. 그리고 이를 효율적으로 계산하는 alogirhtm이 바로 오차 역전파 (Error Back Propagation) algorithm 이다.
 Fig. Animation of Backpropagation
Fig. Animation of Backpropagation
오차 역전파에 대해서 알아보기 전에 먼저 미분을 하는 다른 방법에는 뭐가 있고 왜 이것이 비 효율적인지에 대해 알아보기 위해서는 앞서 설명한 미분을 계산하는 전체 flow를 2가지로 구분지어 생각하는 것이 중요하다.
- 1.Loss Function를 통해서 정답과 추정치의 차이 값을 계산한다.
- 2.
Loss를 parameter에 대해서 미분해서 각 parameter 별 미분 값 (derivative)를 모두 구한다. - 3.
Gradient를 사용해서 parameter를 업데이트한다.
여기서 3번은 2번에서 구한 loss의 각 parameter에 대한 derivative를 모두 구하고, parameter값과 derivative를 weighted sum 해서 update하는 gradient descent를 사용하는 것이 가장 일반적이다.
\[\theta_{t+1} = \theta_{t} + \alpha \nabla_{\theta} L(\theta)\]여기서 2번 step이 많은 computational cost를 요구하는데, backpropagation은 이를 tackle하는 것이다. 왜 2번이 cost가 많이들까? 이에 대해 생각해보자.
Symbolic and Numerical Approaches
Loss에 대한 어떤 parameter의 derivative를 구하는 방법은 크게 두 가지로 나뉠 수 있다. 먼저 우리가 정의한 NN이 input과 output loss간의 function을 의미하므로 이 function의 derivative를 직접 유도하는 것이다.
 Fig. Source from here
Fig. Source from here
당연히 이는 NN의 layer수가 많아지면 난이도가 기하급수적으로 올라갈 것이므로 쓸 수 없는 방법이다.
이를 Symbolic Approach라고 부른다.
다른 방법으로는 유한 차분법 (Finite Difference Method)을 쓰는 방법이 있다.
우리가 가진 어떤 network의 parameter가 \(W\)개 라고 가정해 보자.
우선 현재 parameter를 평가하기 위해서 순전파 (Forward Propagation)를 하면 W가 충분히 큰 경우에 대해서,
loss을 계산하는 데 \(O(W)\) 만큼의 연산이 필요하다고 한다.
왜냐하면 굉장히 희박한 (sparse) 연결을 가진 network를 제외하면 weight의 수가 보통 unit들의 숫자보다 훨씬 크며,
따라서 forward propagation 시에 필요한 대부분의 계산은 이전 단계의 output (현재 단계의 input)과 weight간 matrix multiplication 연산이 되기 때문이라고 한다.
여기에 활성 함수 (activation function)를 통과시키는 비용이 약간 추가될 수 있겠으나,
어쨌든 계산 비용은 대충 \(O(W)\) 라고 할 수 있다.
이제 optimization을 하기 위해서 \(W\)개 parameter 각각이 현재 loss를 내는데 어떤 영향을 미쳤는지를 알아야 한다. 여기에 finite difference method를 쓴다고 생각해보자.
\[\frac{\partial E_n}{\partial w_{ji}} = \frac{E_n (w_{ji}+\epsilon) - E_n(w_{ji})}{ \epsilon} + O({\epsilon})\]여기서 \(E_n\)은 loss function 이고 \(\epsilon \ll 1\)인 매우작은 숫자이며, \(w_{ji}\)는 전체 가중치 중 element 하나이며 \(\epsilon\)값이 작아질수록 더 정확한 미분 결과를 얻을 수 있다. (모든 notation은 Bishop의 PRML을 따른다)
finite difference method은 수식에서도 알 수 있듯 큰 문제가 있다.
전체 parameter 중의 딱 한개인 \(w_{ji}\)의 미분 값을 구하기 위해서는 parameter를 \(\epsilon\)만큼 수정한 뒤 (실제로 가본 뒤) forward propagation을 해본 결과가 필요하기 때문에 forward propagation을 두 번이나 해야 한다 (\(E_n (w_{ji}+\epsilon)\) 와 \(E_n(w_{ji})\)).
그래야 특정 weight이 얼만큼 변한게 loss를 변화시키는 걸 관찰하고 이를 통해 미분 값을 구할 수 있기 때문이다.
그런데 forward propagation은 1회마다 O(W) 만큼의 연산이 들어간다.
이를 모든 weight parameter 마다 한 번씩 해야 하니 \(O(W^2)\) 만큼의 계산 복잡도를 요구하는 것이다.
이런 접근 방식을 Numerical Approach라고 부른다.
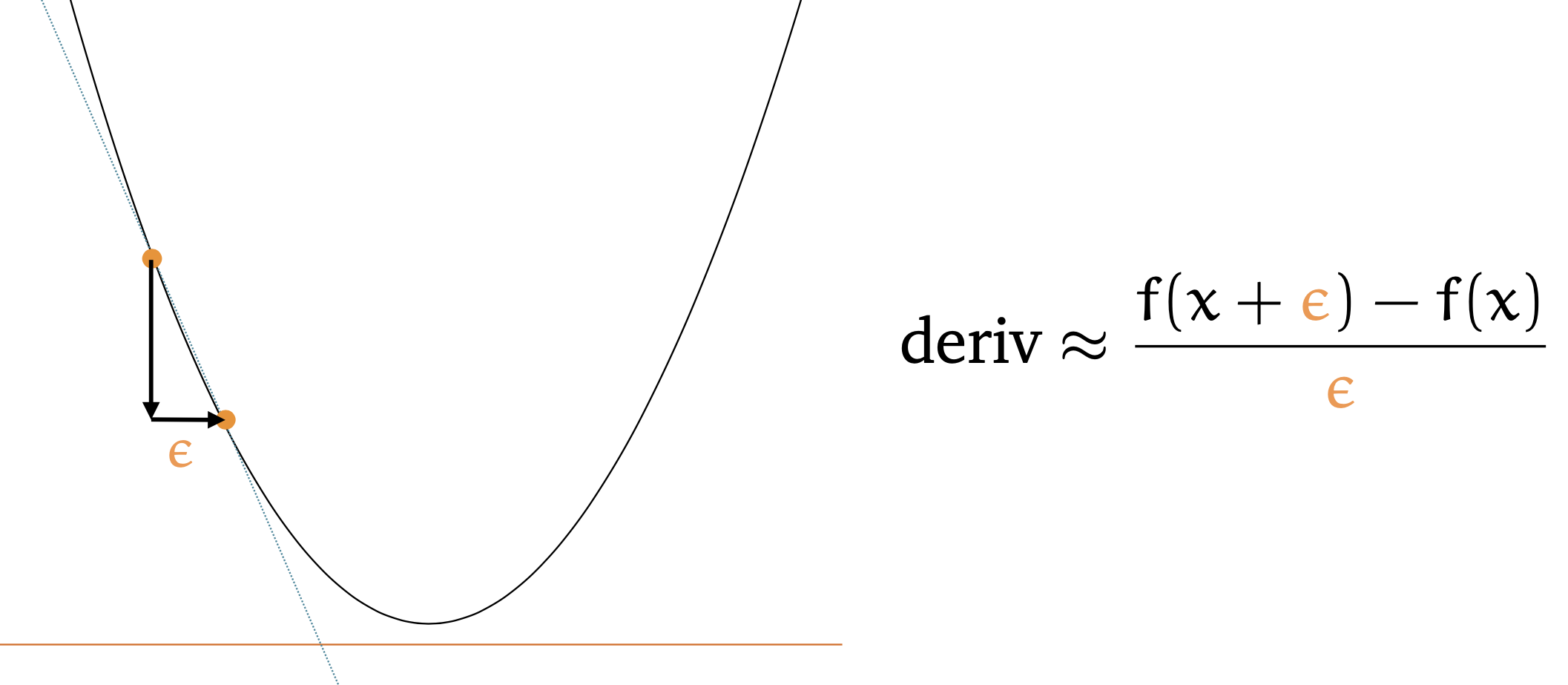 Fig. Source from here
Fig. Source from here
이 방법은 symbolic method보다는 간단해 보이지만 computational cost가 많이 들 것으로 보인다. 어떻게 해야 효율적으로 loss의 parameter에 대한 derivative를 구할 수 있을까?
Error Backpropagation
Efficent Way to Compute Partial Differentiation using Chain Rule
결론부터 말하자면 error backpropagation은 아래와 같은 절차를 따른다.
Error Backpropagation- 1.Forward propagation을 현재 weight으로 1회 시행
- 2.Loss를 계산했으면 끝에서 부터 시작 지점까지 (input 까지) 연쇄 법칙 (chain rule)을 통해 parameter에 대한 미분 값을 점진적으로 계산하여 뒤로 전파 (역 전파; back propagation) 한다.
- 이 때 parameter 각각에 대해서 수치 미분을 일일히 하는 것이 아니므로 forward propagation을 다시 시행할 필요가 없음
- 3.얻은 미분값으로 parameter 갱신 (update)
Finite Difference Method- 1.모든 W개의 parameter, \(\theta\) (weight, bias)에 대해서 미분 시행
- 이 때 미분값을 계산하기 위해서 parameter 한 개당 forward propagation을 두 번씩 시행하게 된다.
- 그 이유는 \(E_n (w_{ji}+\epsilon)\) 와 \(E_n(w_{ji})\) 를 둘 다 알아야 빼서 parameter 한개의 loss에 대한 미분 값을 구할 수 있기 때문이다.
- 이 과정이 굉장히 비효율적이라고 할 수 있는데, 즉 순전파 당 \(O(W)\) 만큼의 계산 복잡도가 필요하기 때문에 전체 계산 복잡도는 \(O(W^2)\)가 된다.
- 2.얻은 미분값으로 parameter 갱신 (update)
- 1.모든 W개의 parameter, \(\theta\) (weight, bias)에 대해서 미분 시행
Chain rule을 써서 뒤로 전파한다는게 무슨 말일까? 왜 이게 효율적일까? 이에 대해서 알아보도록 하자.
먼저 간단한 ML architecture를 표현해보자. 보통 NN의 computational graph는 아래처럼 한 방향으로만 향하는 Directed Acyclic Graph (DAG)로 표현하곤 하는데, 아래는 어떤 2차원 vector input \(x\) 에 대해서 parameter, \(\theta\)를 곱하고 regression loss를 계산하는 것 까지 표현한 것이다.
\[|| (x_1 \theta_1 + x_2 \theta_2) - y ||^2\]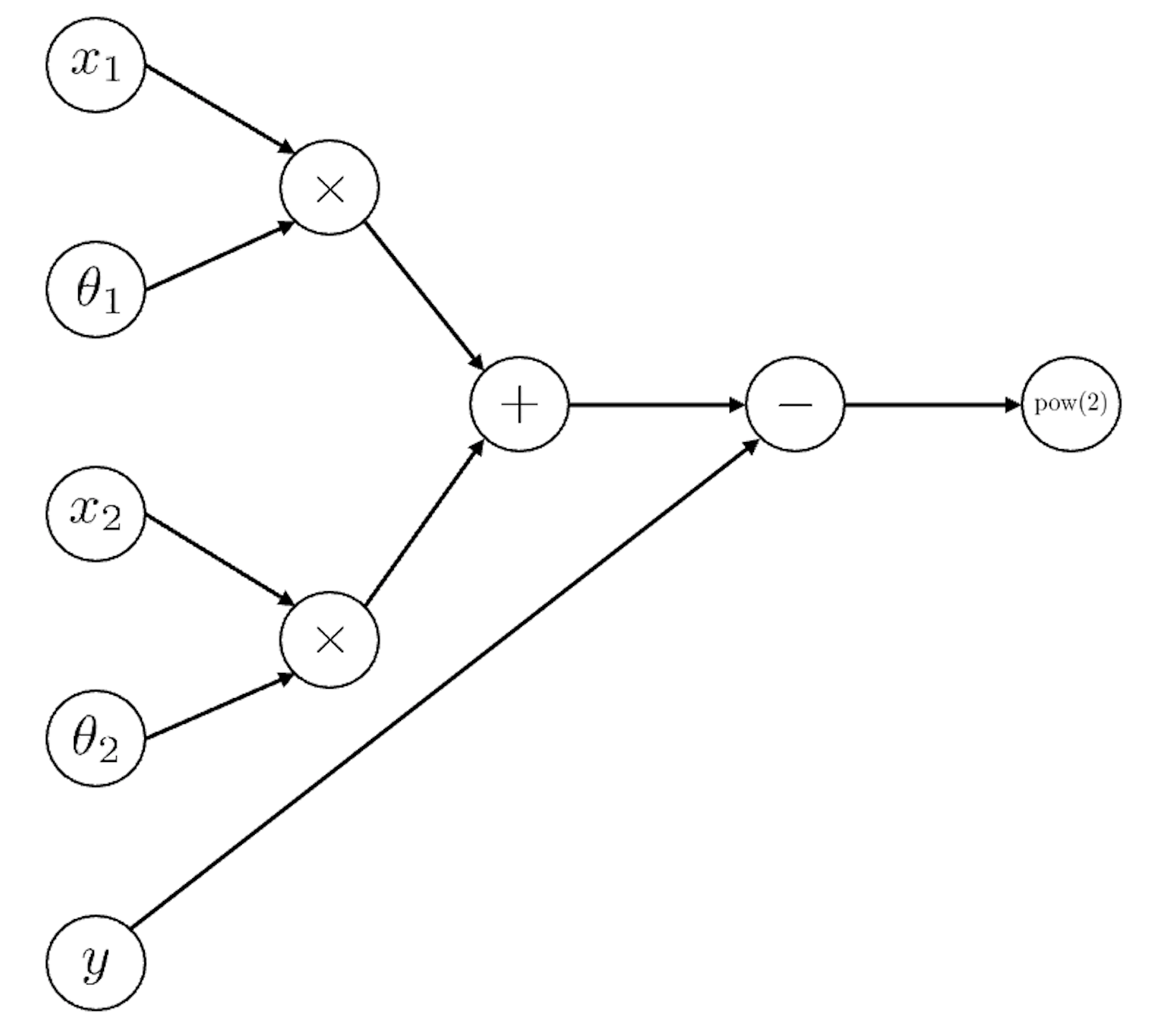
Hidden layer가 없기 때문에 linear regression을 한다고 할 수 있는데, 이를 vector 형태로 표현하면 아래처럼 그릴 수 있다.
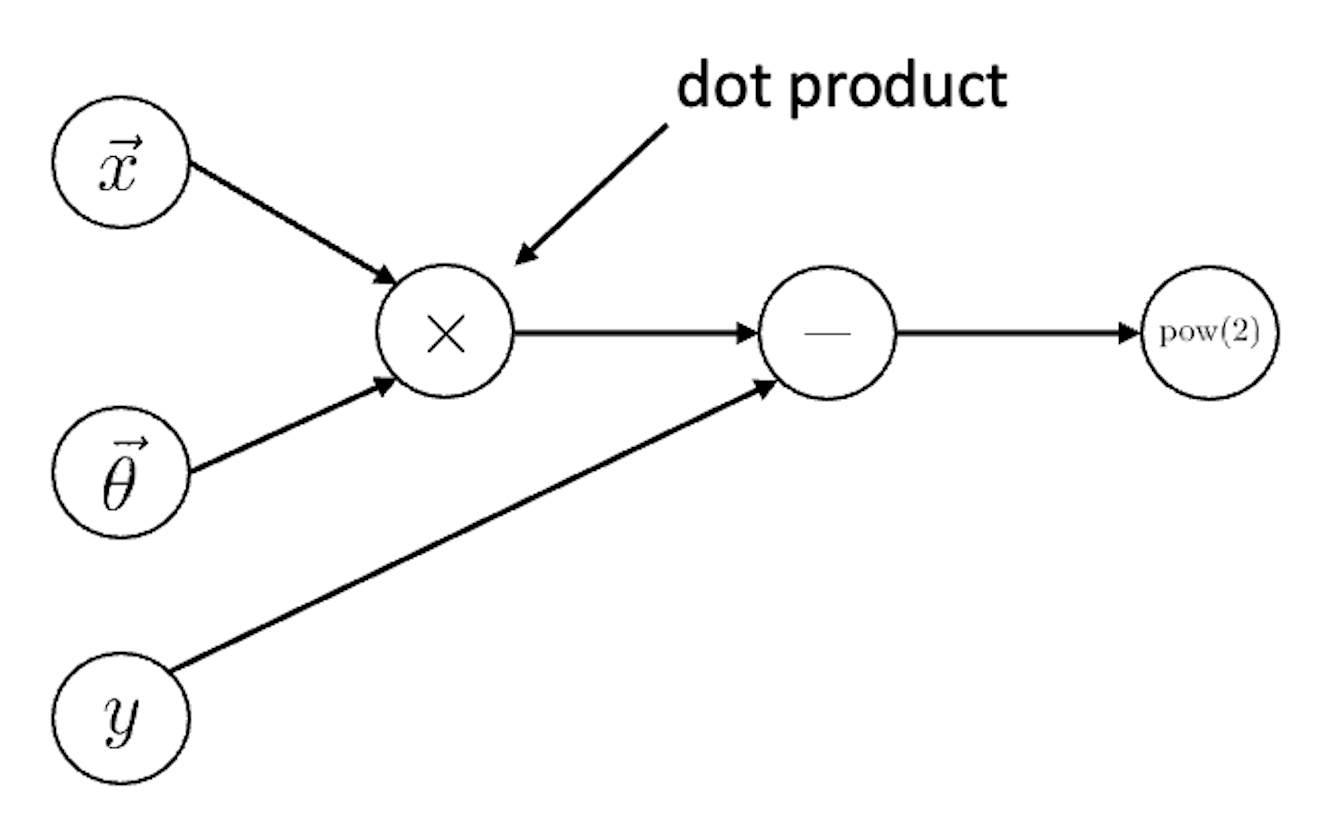
만약 classification task를 푼다면 아래와 같은 graph가 필요하다.
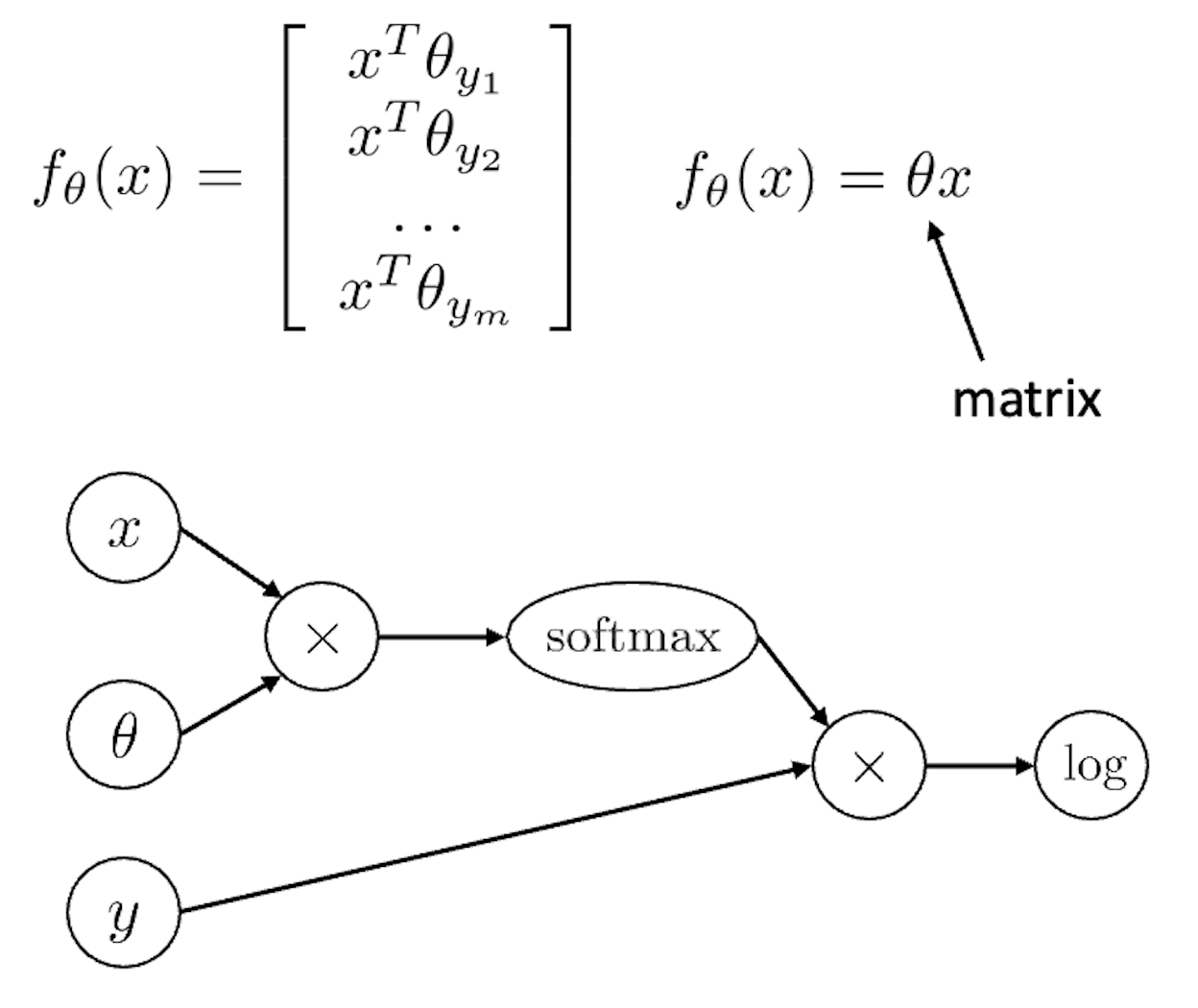
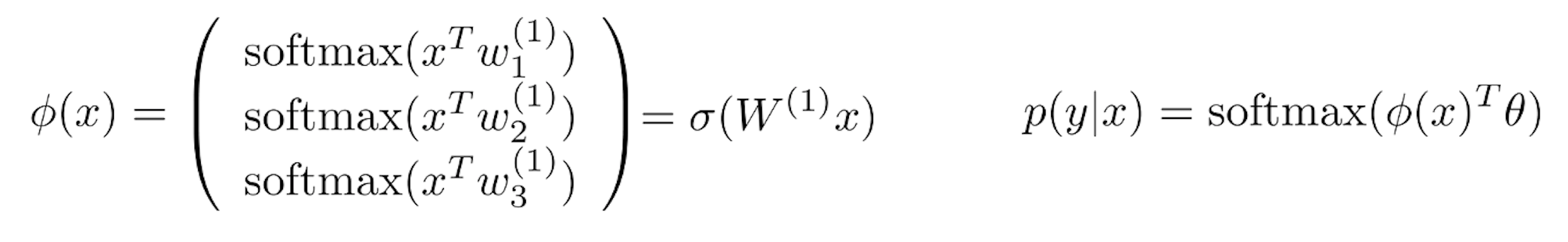
Sofmtax로 normalize하고 one hot vector인 y를 곱해 정답에 해당하는 부분만 pick한 뒤 log를 씌우는 것이다. 이를 좀 더 간소화 해서 아래와 같이 나타낼 수 있다.
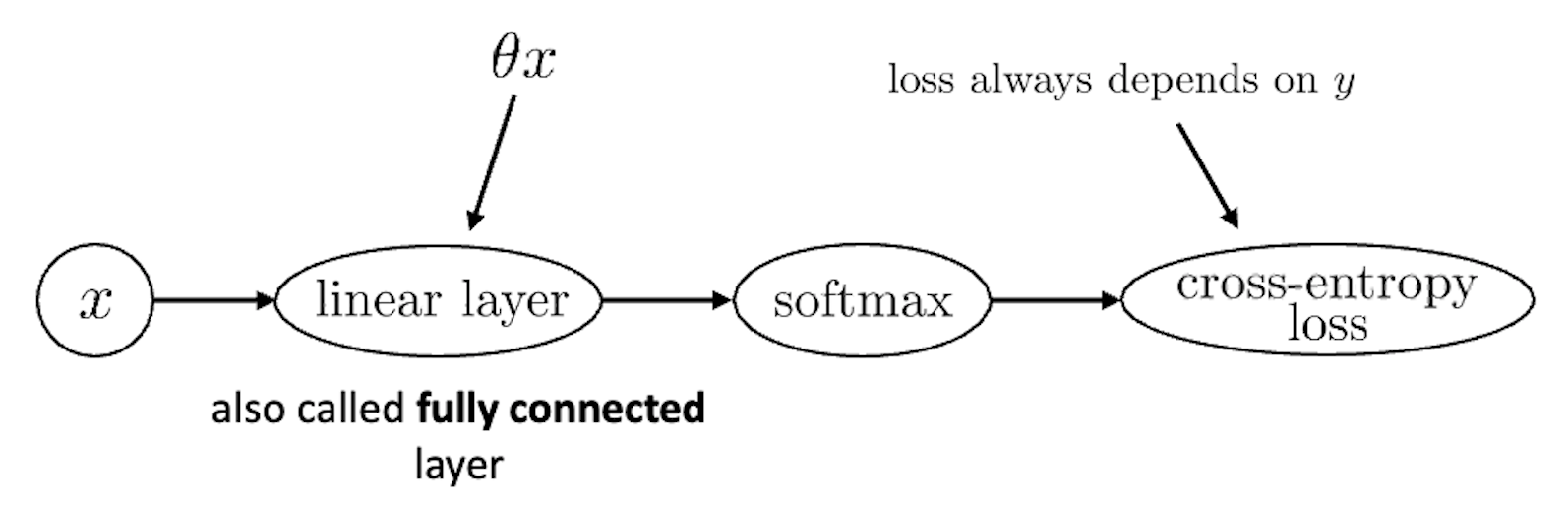
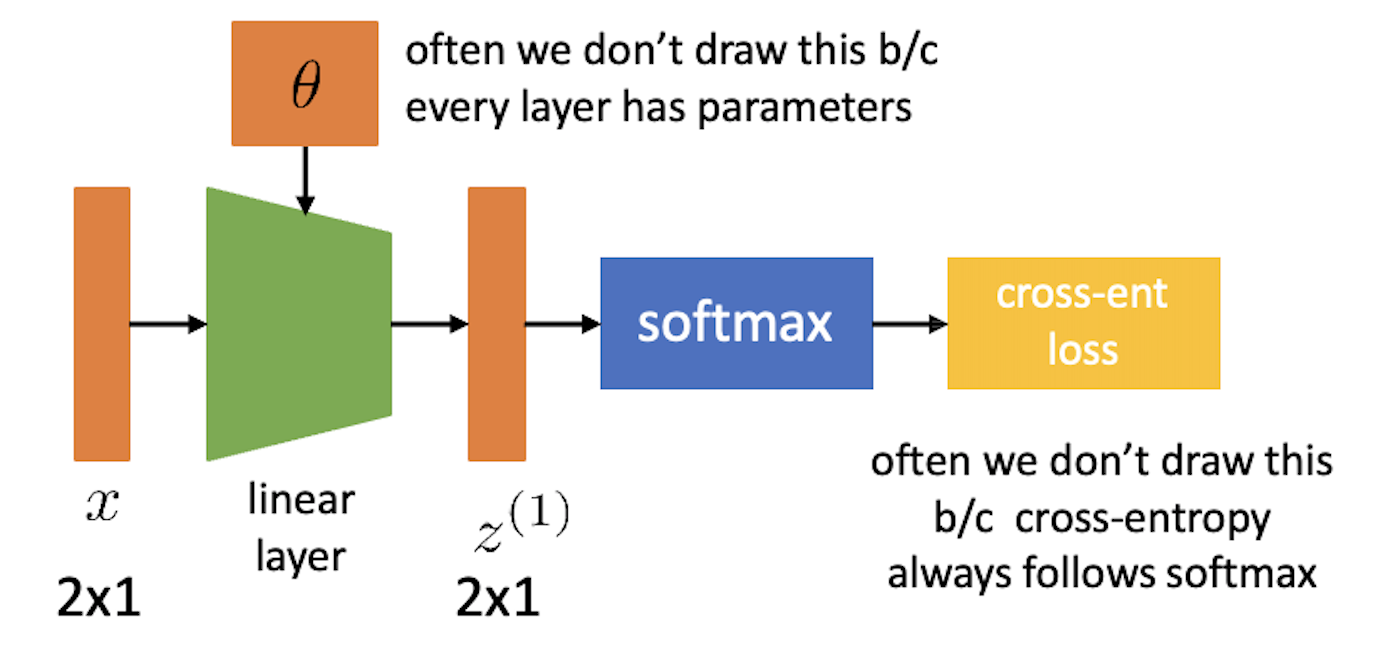
이제 이를 Nerual Network (NN)으로 확장시켜보자. Non-linear activation 을 통과하는 2 layer이상의 architecture가 NN이기 때문에 2 layer인 경우를 그려보자.

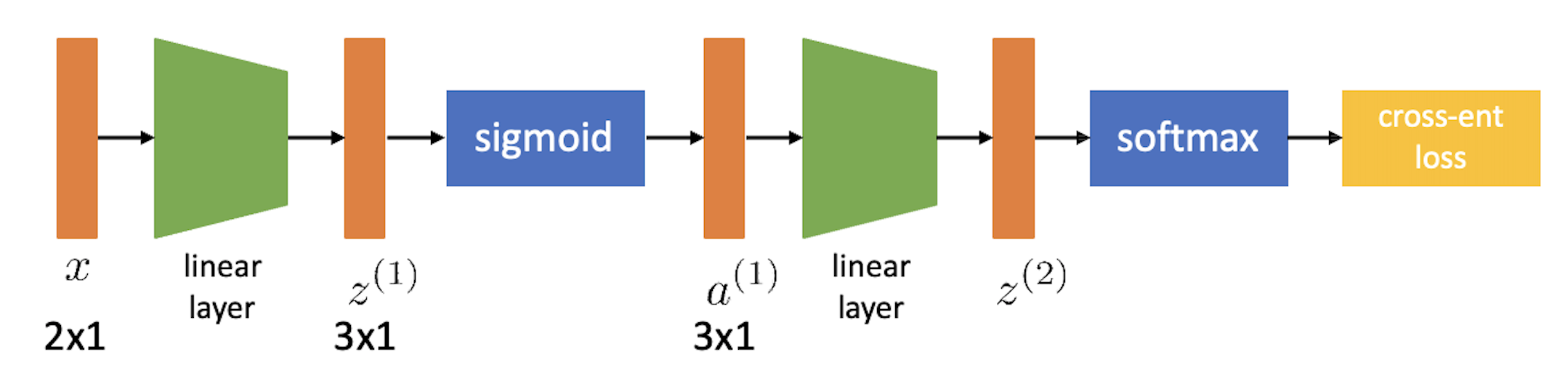
여기서 activation function (sigmoid 등) 같은 부분은 각 layer별 input과 parameter를 곱하는 block diagram 으로 편입시키면 아래와 같이 최종적으로 표현할 수 있다.
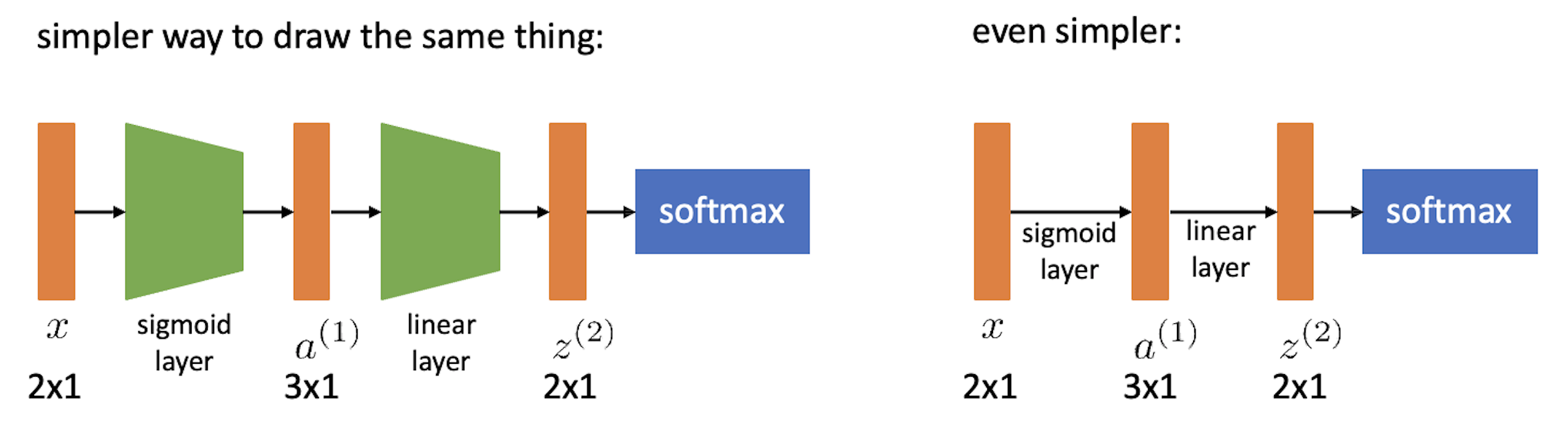
이런식으로 모든 ML architecture는 DAG로 나타낼 수 있고, 이로써 어떻게 backpropagation이 수행되는지를 직관적으로 이해할 기본 setting이 된 것이라고 할 수 있다.
우리는 지금 finite difference method처럼 각 parameter가 loss 에 얼마나 기여했는지를 알고싶다. 즉 아래 objective function에 대해서 \(\frac{dL}{dW^{(2)}}, \frac{dL}{dW^{(1)}}\)을 구해야 하는 것인데, 여기서 weight들은 \(W^{(1)} \in \mathbb{R}^{3 \times 2}\)같은 matrix이므로 모든 weight의 element마다 미분값을 다 구해야 한다.
\[\begin{aligned} & \hat{y} = softmax (\sigma ( W^{(2)} (\sigma (W^{(1)} x)))) & \\ & \mathcal{L} = CE(y,\hat{y}) & \\ \end{aligned}\]
먼저 \(\frac{dL}{dW^{(1)}}\)에 대해서 생각해보자. 사실 이는 finite difference method처럼 parameter를 조금 수정하고 forward propagation을 해서 두 값의 차이를 구하는 식으로 계산할 필요가 없이 chain rule을 사용해서 아래와 같이 분해 (factorization)해서 표현할 할 수 있다.
\[\frac{d \mathcal{L}}{d W^{(1)}}=\frac{d z^{(1)}}{d W^{(1)}} \frac{d a^{(1)}}{d z^{(1)}} \frac{d z^{(2)}}{d a^{(1)}} \frac{d \mathcal{L}}{d z^{(2)}}\]그리고 \(\frac{dL}{dW^{(2)}}\)도 마찬가지로 아래처럼 쓸 수 있다.
\[\frac{d \mathcal{L}}{d W^{(2)}}=\frac{d z^{(2)}}{d W^{(2)}} \frac{d \mathcal{L}}{d z^{(2)}}\]여기서 두 가지 정도 finite difference method와의 차이를 발견할 수 있는데, 먼저 \(W^{(1)}\) weight의 미분 값을 구하기 위해서 loss를 맨 마지막 2nd layer의 output \(z\)에 대해 미분한 값을 구하고, 그 다음 \(z\)를 2nd layer의 input \(a\)로 미분한 값을 구하고… 같은 방법으로 끝에서부터 순차적으로 구한 미분 값을 곱한다는 점과 이런식으로 계산을 하기 때문에 \(W^{(2)}\)의 미분 값을 구하는데 쓰인 \(\frac{d \mathcal{L}}{d z^{(2)}}\)가 \(\frac{dL}{dW^{(1)}}\)을 구하는데도 중복해서 쓸 수 있다는 것이다.
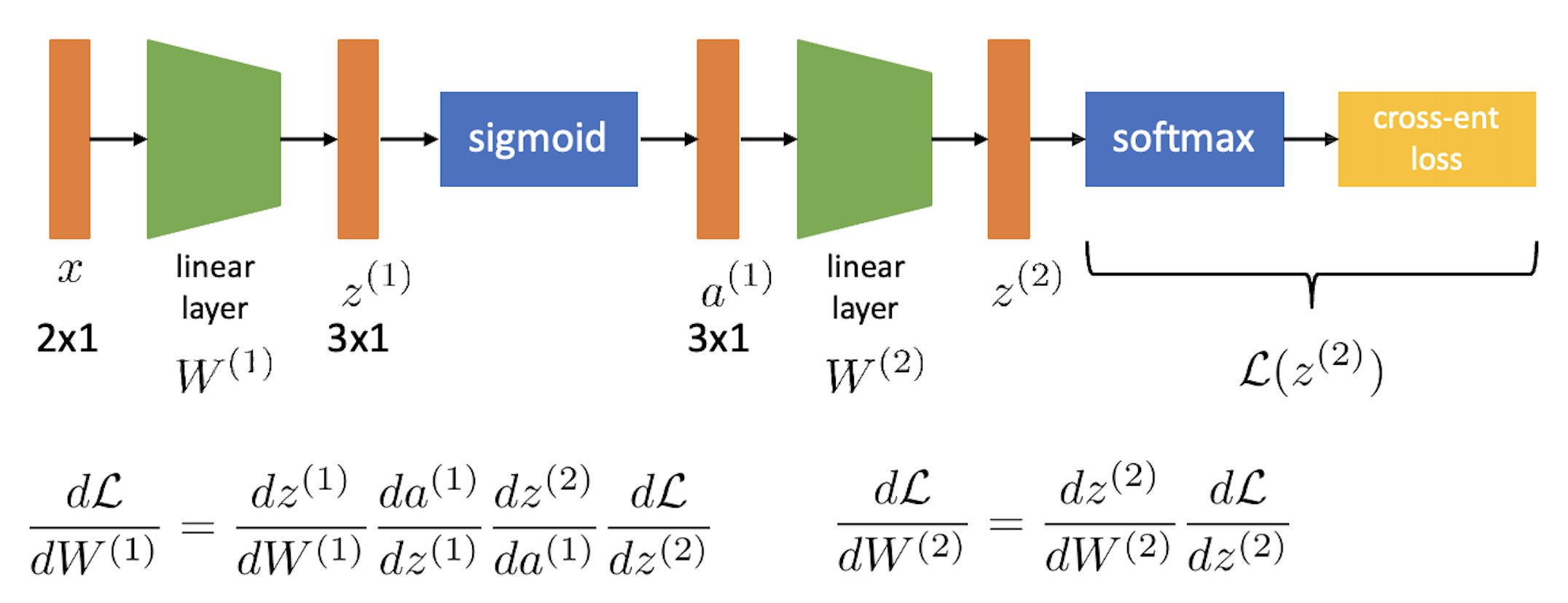
Doing it More Efficiently
그런데 실제로 data input 쪽의 (가장 아래 부분 layer) weight의 미분 값을 구할 때 연산을 아무렇게나 하면 안된다.
\[\frac{d \mathcal{L}}{d W^{(1)}}=\frac{d z^{(1)}}{d W^{(1)}} \frac{d a^{(1)}}{d z^{(1)}} \frac{d z^{(2)}}{d a^{(1)}} \frac{d \mathcal{L}}{d z^{(2)}}\]먼저 chain rule에 대해 다시 생각해보자. 예를 들어 \(x \rightarrow y \rightarrow z\)로 이루어진 간단한 module에 대해서 이를 미분할 경우 아래와 같이 편 미분 (Partial Derivative)의 곱으로 나눌 수 있다.
\[\frac{d}{d x} f(g(x)) =\frac{d z}{d x} =\frac{d y}{d x} \frac{d z}{d y}\]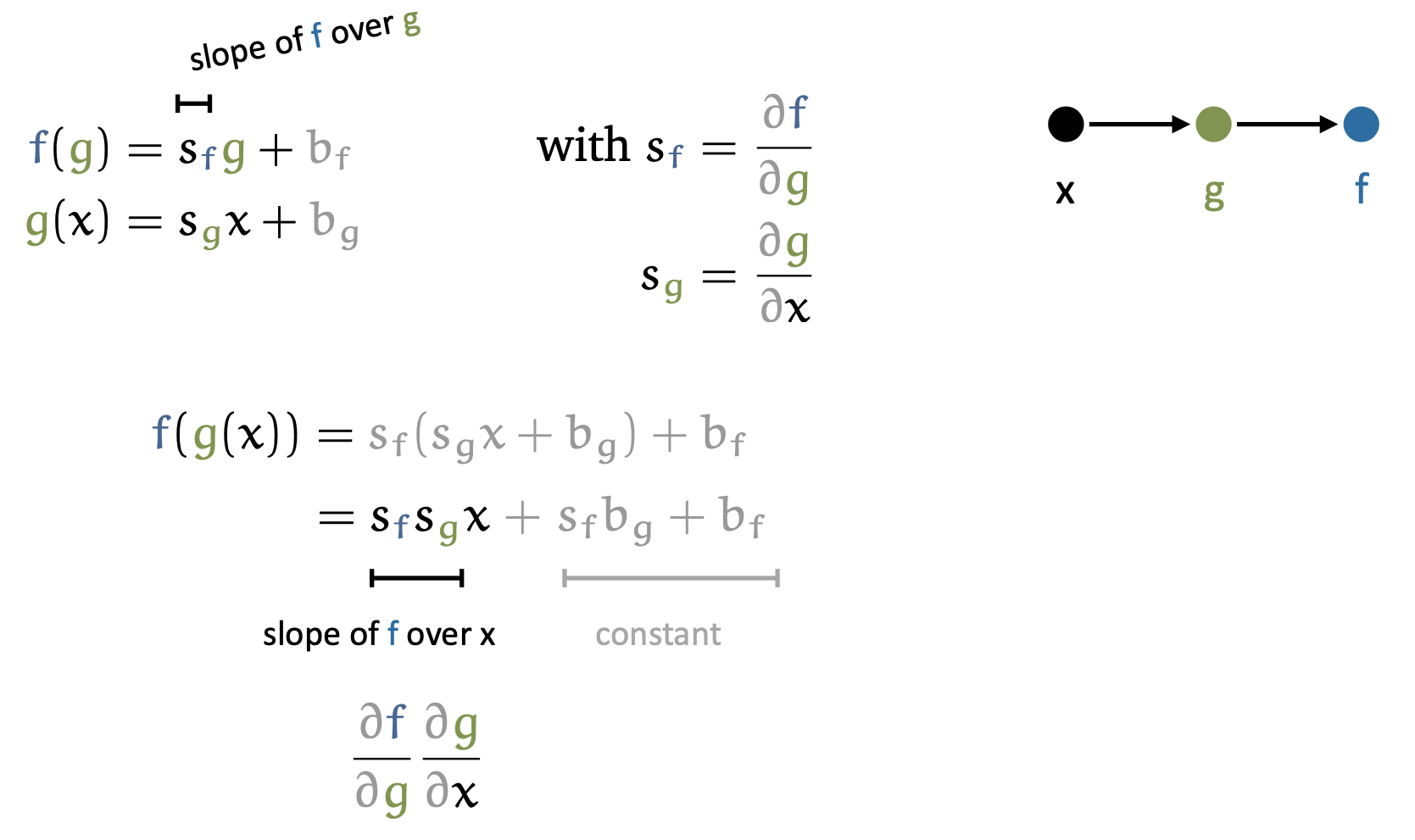 Fig.
Fig.
위 예시는 scalar 값에 대한 편 미분 얘기이기 때문에, 이를 multivariate case인 어떤 2 layer NN에 대해 확장해야한다. NN은 어떤 input element가 다음 layer의 수 많은 neuron과 fully connected인 경우가 대부분인다. 만약 neuron이 2개라고 치면 다음처럼 계산해야 할 것이다.
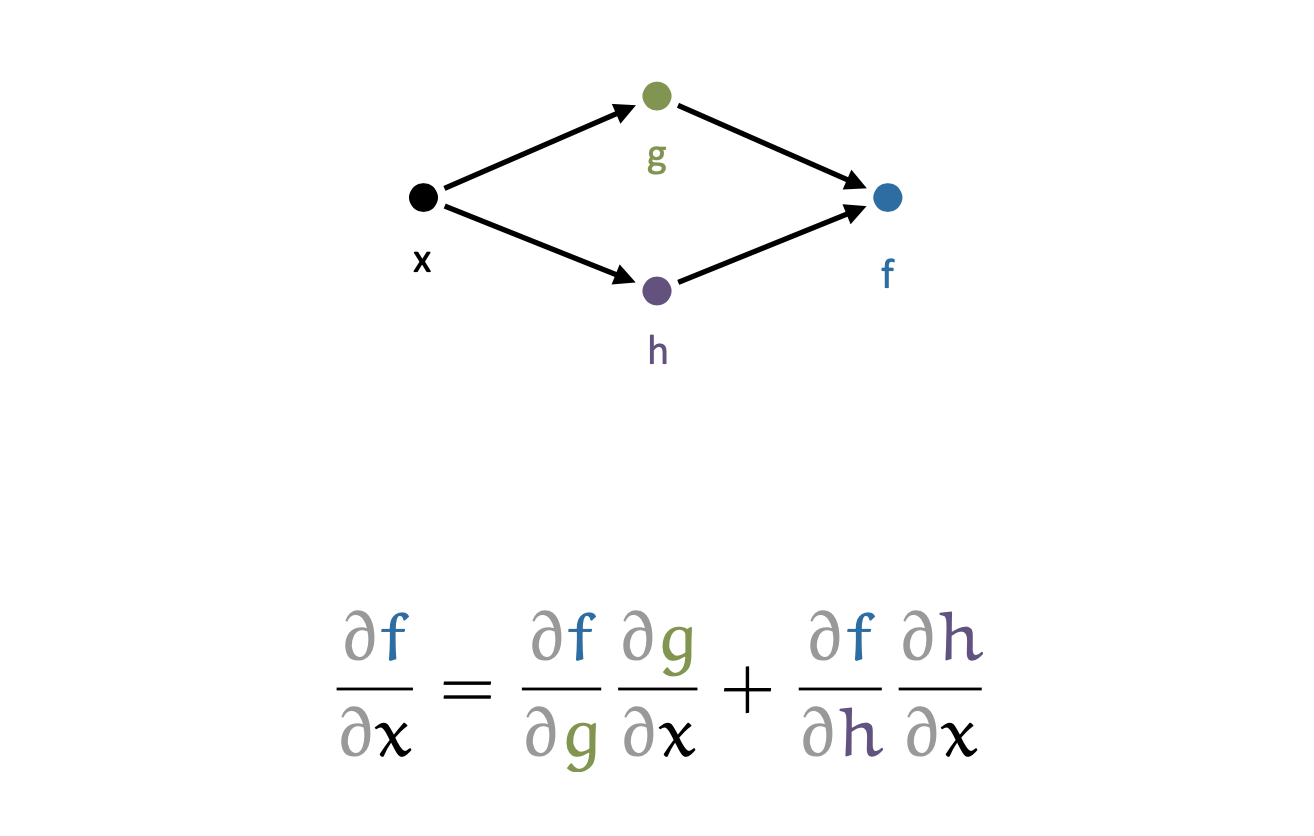 Fig.
Fig.
이것을 n개로 확장하면 input x 하나에 대해서 아래처럼 summation으로 간단히 표현할 수 있을 것이다.
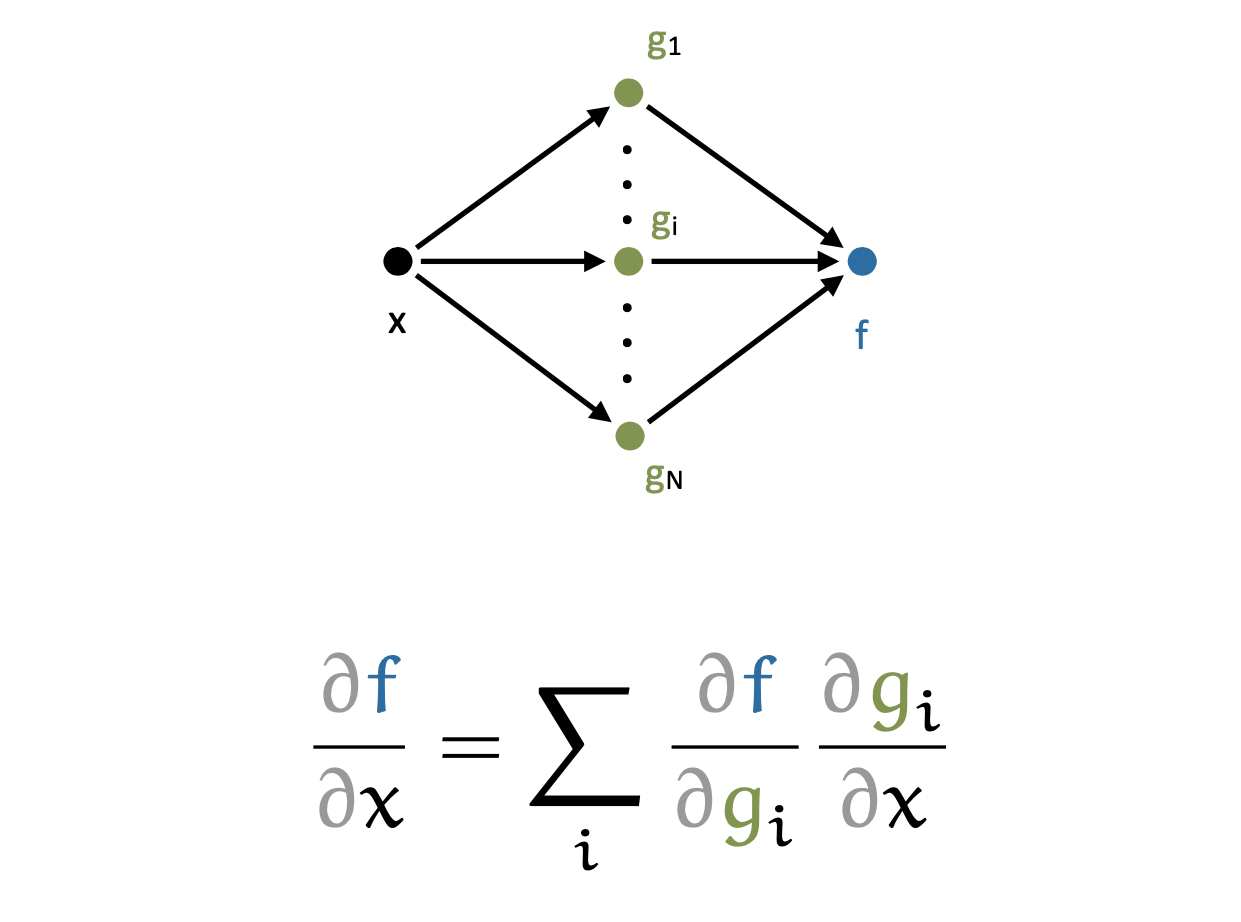 Fig.
Fig.
그런데 실제로는 function, \(g\)가 n차원 vector를 m차원 vector로 mapping해줄 수도 있다.
여전히 function, \(f\)는 m차원 vector를 scalar로 mapping 한다고 치자.
그러면 \(\frac{dz}{dy}\)는 y와 크기가 같은 vector이고 \(\frac{dy}{dx}\)는 \(n \times m\)차원의 matrix가 된다.
이 때 각 partial derivative 값을 g와 y의 Jacobian이라고 한다고 한다.
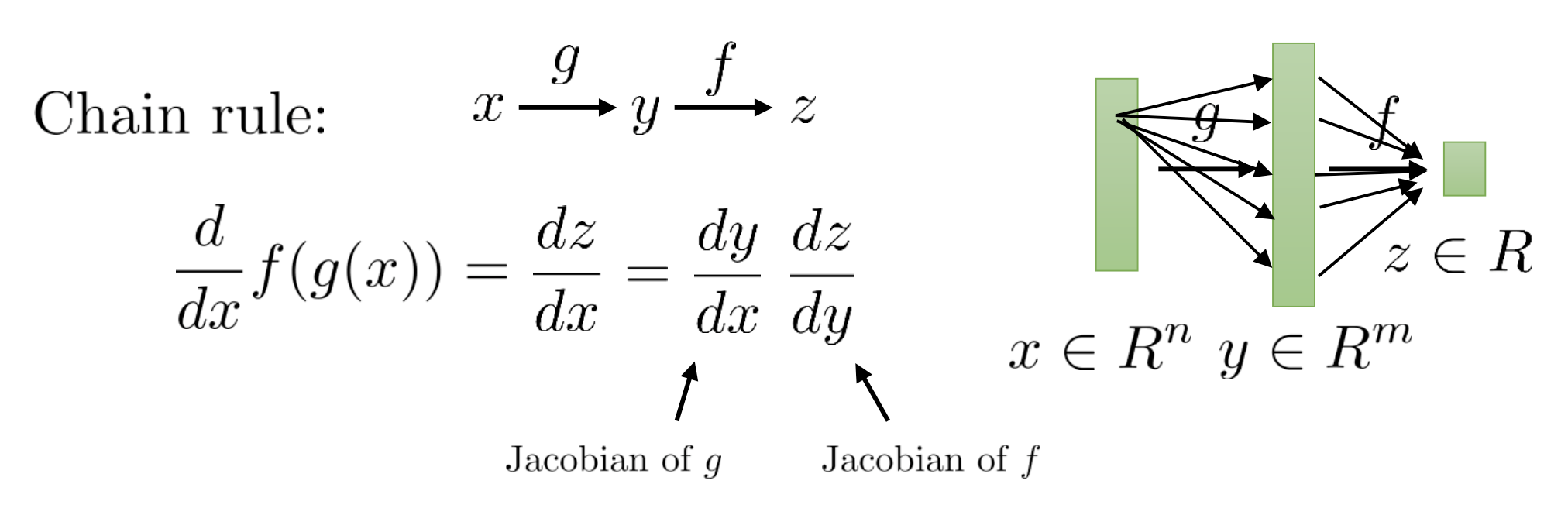 Fig.
Fig.
이것이 matrix, vector 형태인 이유는 뭘까?
당연하게도 \(\frac{dz}{dy}\)는 vector \(y\)의 각 element들이 scalar z에 대한 영향을 끼치는 정도가 다 다를 것이기 때문에 function, \(f\)의 input인 \(y\)와 같은 크기인 \(m \times 1\)를 갖게 되며, \(\frac{dy}{dx}\)는 n차원 vector \(x\)의 모든 element가 m차원 vector를 만드는 데 끼치는 영향을 일일히 다 알아야 하므로 \(n \times m\)크기인 것이다. 최종적으로 우리가 구하고 싶은 \(\frac{dz}{dx}\)는 따라서 이 둘을 곱한 \(n \times 1\)로 input, \(x\)와 같은 크기이다.
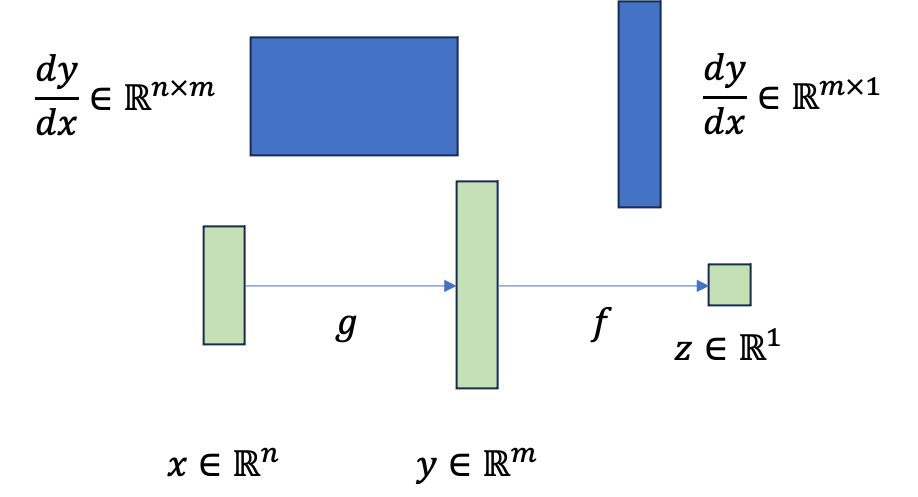 Fig.
Fig.
보통 scalar to scalar 연산에 대한 derivative는 미분체 또한 scalar이며 regular derivative라고 하며,
vector to scalr 에 대한 derivative는 operator (function)의 input과 같은 차원이 되며 gradient 라고 부르며,
마지막으로 vector to vector 연산의 미분체는 jacobian이라고 부른다고 한다.
(그런데 왜 cs182 lecture slide에는 vector to scalar의 미분 체를 jacobian이라고 부르는 지 모르겠으나 우선은 넘어가도록 하자)
 Fig.
Fig.
Sergey는 여기서 multivariate에 대한 직관이 오지 않으면 우선 n차원 입력 \(x\)의 element 하나인 scalar, \(x_i\)에 대한 derivative만 생각해 보자고 한다. 이제 \(\frac{dy}{dx_i}\)는 더이상 2차원 matrix가 아니라 \(1 \times m\) vector이지만 \(\frac{dz}{dy}\)는 여전히 \(m \times 1\)의 vector이고, 이 둘을 곱한 \(\frac{dz}{dx_i}\)는 1차원 scalar이다.
\[\frac{d}{d x_{i}} f(g(x)) =\sum_{j=1}^{m} \frac{d y_{j}}{d x_{i}} \frac{d z}{d y_{j}} =\frac{d y}{d x_{i}} \frac{d z}{d y}\]이를 모든 element로 확장하면 vector to scalar derivative를 구할 수 있는데, 여기서 중요한 점은 \(\frac{dz}{dx}\)가 결국은 matrix와 vector의 연산이라는 것이다. 다시 아까로 돌아가서 classification task를 풀기 위한 2 layer NN을 생각해보자.

여기서 loss의 \(W^{(1)}\)에 대한 derivative, \(\frac{dL}{dW^{(1)}}\)는 computational cost가 얼마나 될까?
\[\frac{d \mathcal{L}}{d W^{(1)}} =\frac{d z^{(1)}}{d W^{(1)}} \frac{d a^{(1)}}{d z^{(1)}} \frac{d z^{(2)}}{d a^{(1)}} \frac{d \mathcal{L}}{d z^{(2)}}\]편의를 위해 \(z^{(i)}\) 와 \(a^{(i)}\) 가 각각 n 차원이라고 생각해 보자. 마지막 loss는 언제나 scalar 값이다. 그러므로 \(\frac{d\mathcal{L}}{dz}\) 부분은 \(n \times 1\)임이 자명하다. 하지만 나머지 vector to vector derivative인 jacobian들은 모두 \(n \times n\)차원을 갖는다. 그래서 실제로 \(\frac{d \mathcal{L}}{d W^{(1)}}\)의 computational cost는 \(O(n^3)\)가 된다고 한다.
그런데 대체 뭐가 그리 비싼 연산인걸까? 사실 \(O(n^3)\)는 jacobian 2개를 곱하는 경우에 발생한다. 그런데 우리는 layer의 최종 output 쪽, 즉 loss를 계산한 부근에서의 derivative는 \(n \times 1\)의 gradient임을 안다 (vector 형태). 그리고 vector와 matrix의 곱은 \(O(n^2)\)밖에 되질 않는다 (당연하게도 \(n \times n\)의 vector dot product를 n번 하는 것이기 때문에).
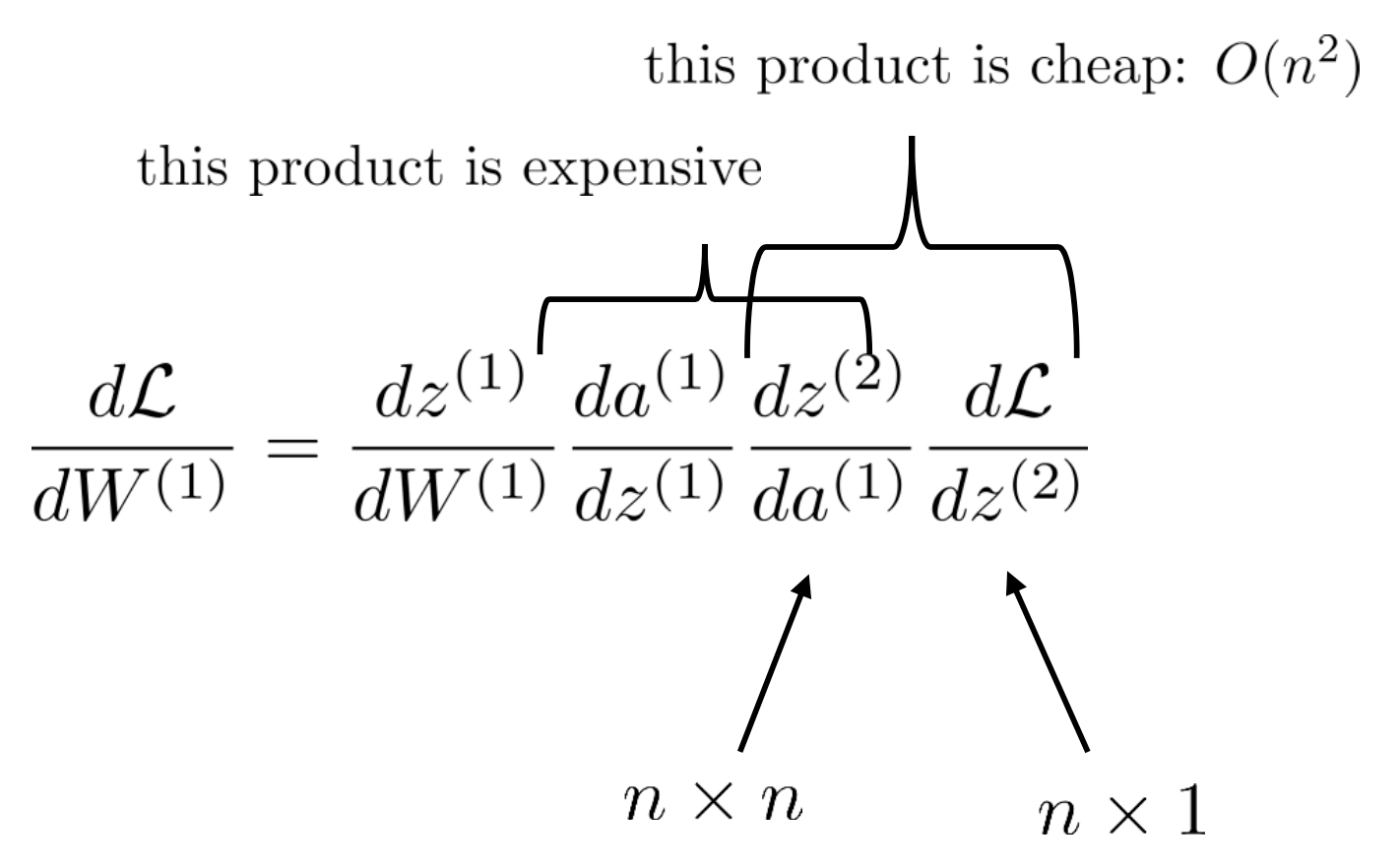
그런데 당연하게도 \(n \times n\) jacobian과 \(n \times 1\)의 vector를 곱하면 또 \(n times 1\)의 vector가 된다. 즉 우리는 같은 derivative, \(\frac{d \mathcal{L}}{d W^{(1)}}\) 를 구하더라도 맨 끝단 (end)에서부터 역 방향으로 (backward) gradient와 jacobian을 곱해나가면 \(O(n^2)\)의 복잡도 밖에 안 필요하다는 것이 된다. 즉 AlexNet같이 \(n=4096\)인 경우를 예로 들면 4096배의 시간을 아낄 수 있다는 말이 될 수도 있다는 것이다.
즉 아래의 수식을 오른쪽에서 부터 계산하면 되는데,
이 모양새가 마치 forward를 끝내서 얻은 loss 값 부터 다시 input쪽으로 역으로 전파한다고 하여 오차 역전파 (Error Backpropagation)라고 하는 것이다.
Backpropagation을 수행할 때 전체 derivative를 global derivative, 중간에 activation에 대한 gradient를 local derivative 라고 부르는데,
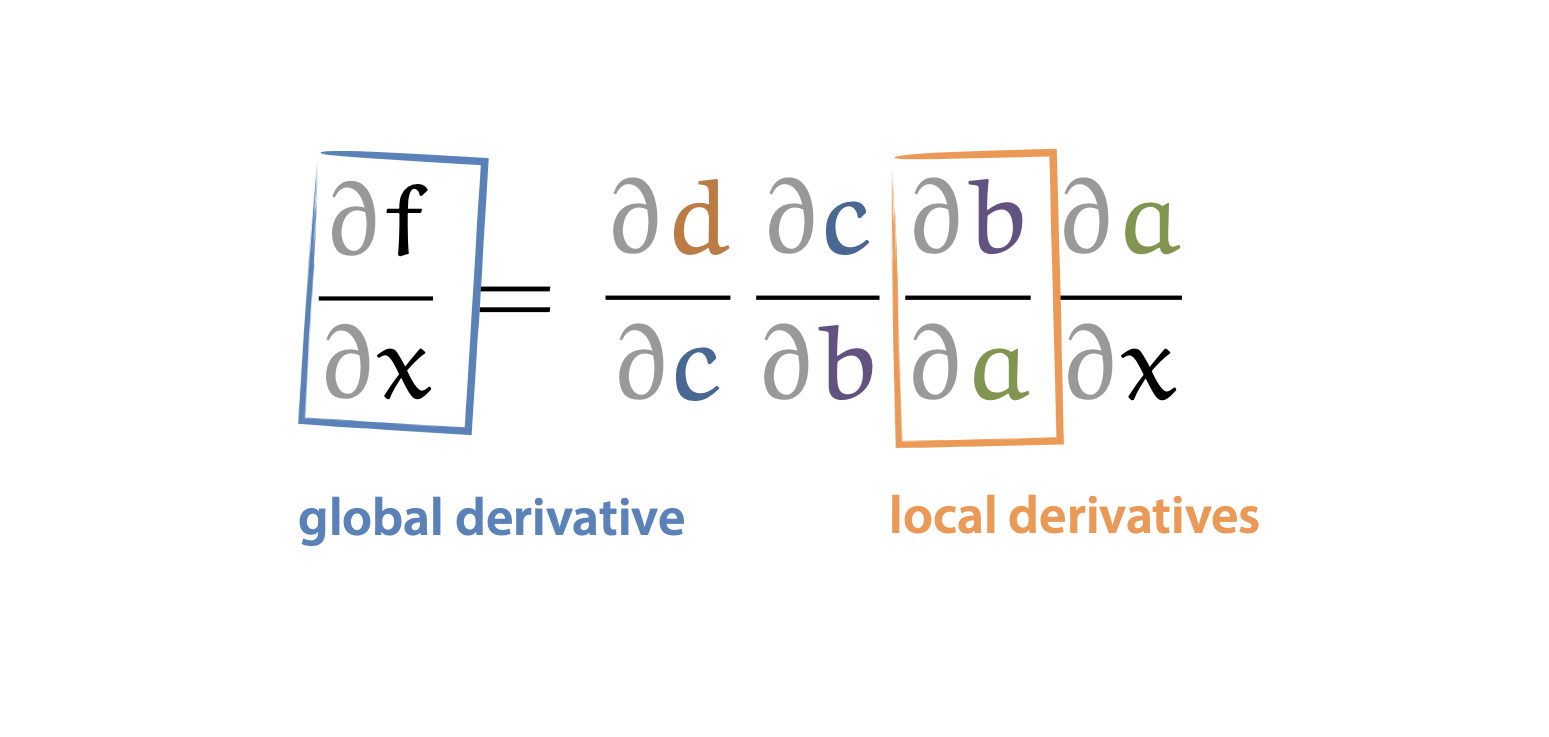 Fig.
Fig.
backpropagation은 local derivative를 symbolic하게 계산하고 global derivative는 numerical하게 계산한다고 하기도 하는 것 같다.
 Fig.
Fig.
우리는 local derivative에 대해서만 미분체가 어떻게 계산되는지 알면 되기 때문에, 아래보다 훨씬 복잡한 function에 대해서도 쉽게 미분을 구할 수 있다.
 Fig. An example of how to compute global derivative (1/5)
Fig. An example of how to compute global derivative (1/5)
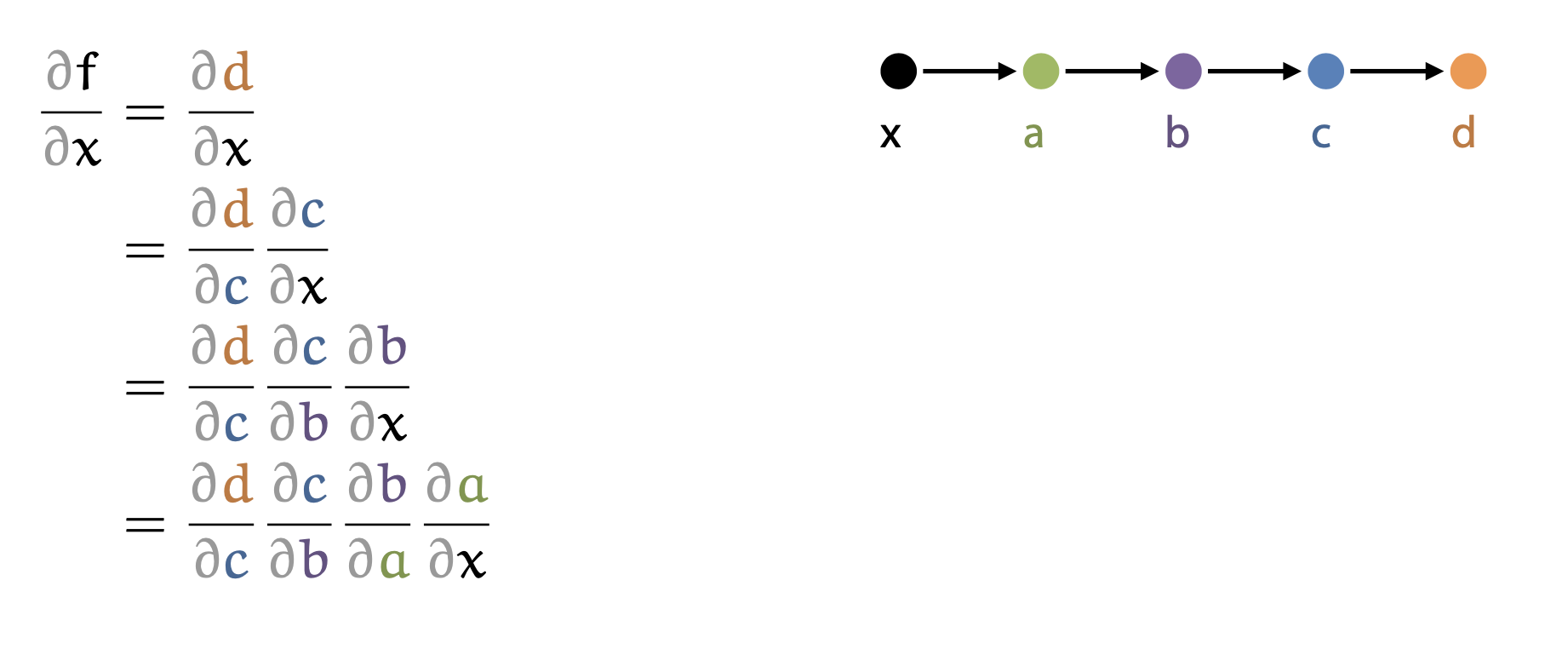 Fig. An example of how to compute global derivative (2/5)
Fig. An example of how to compute global derivative (2/5)
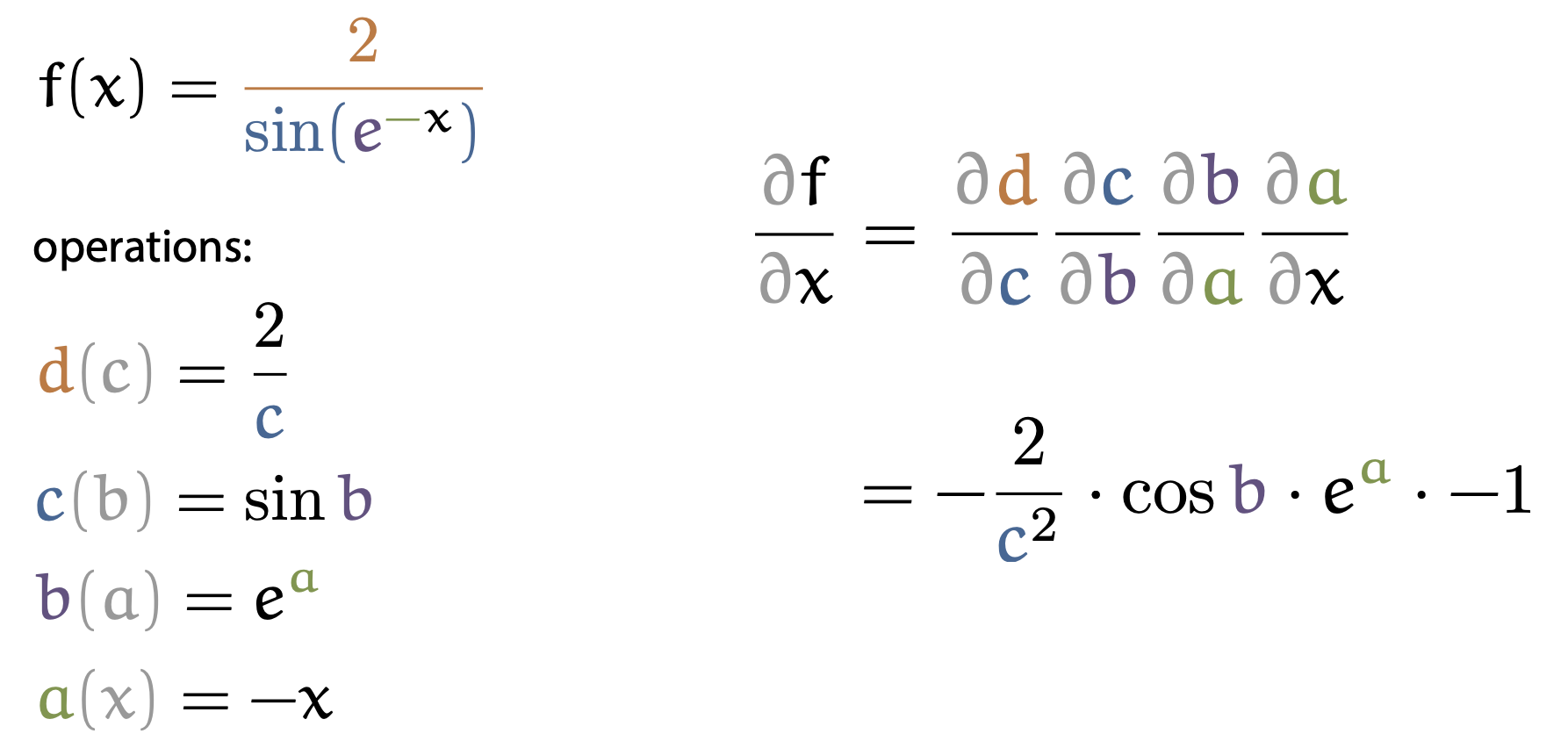 Fig. An example of how to compute global derivative (3/5)
Fig. An example of how to compute global derivative (3/5)
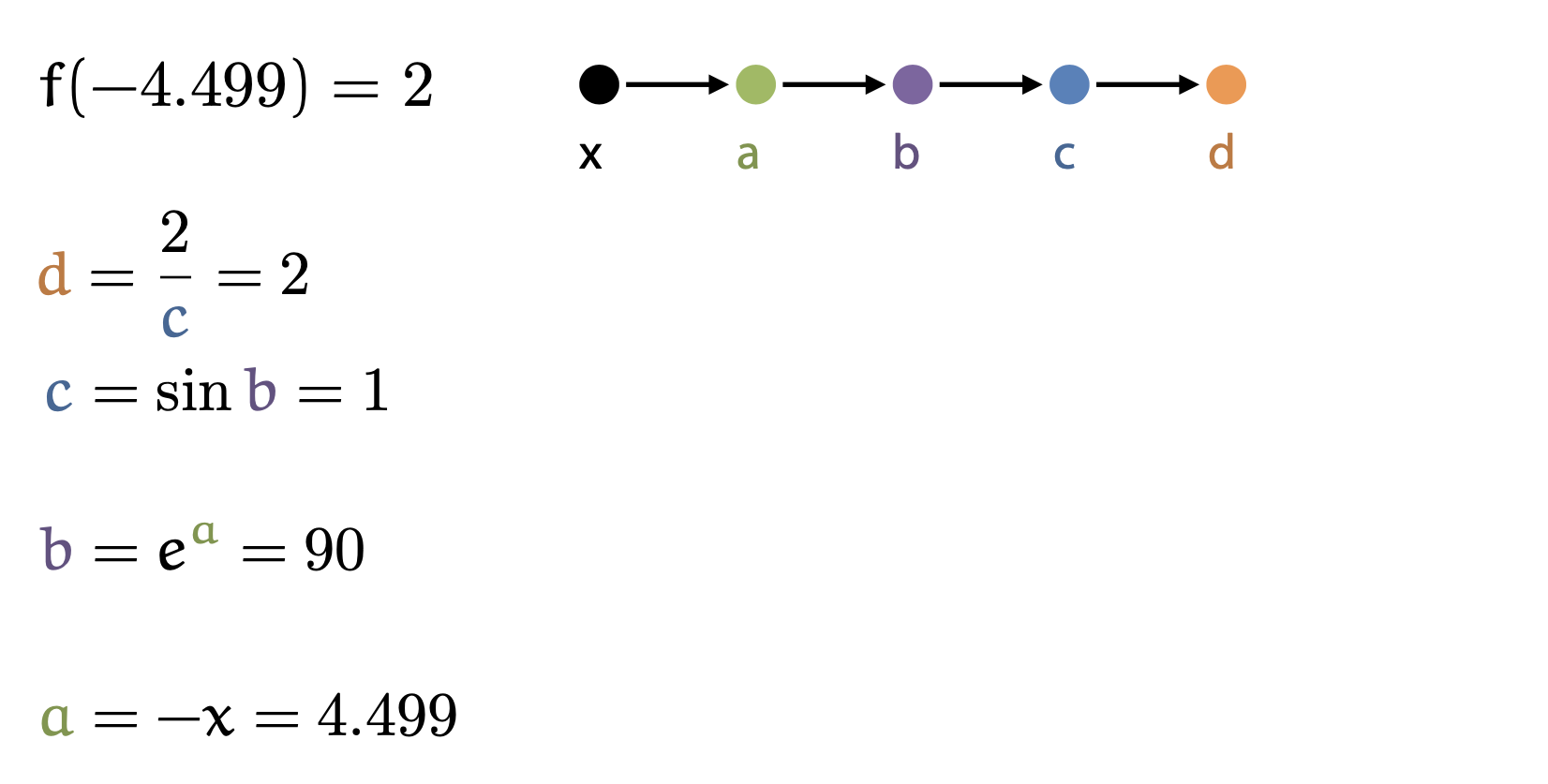 Fig. An example of how to compute global derivative (4/5)
Fig. An example of how to compute global derivative (4/5)
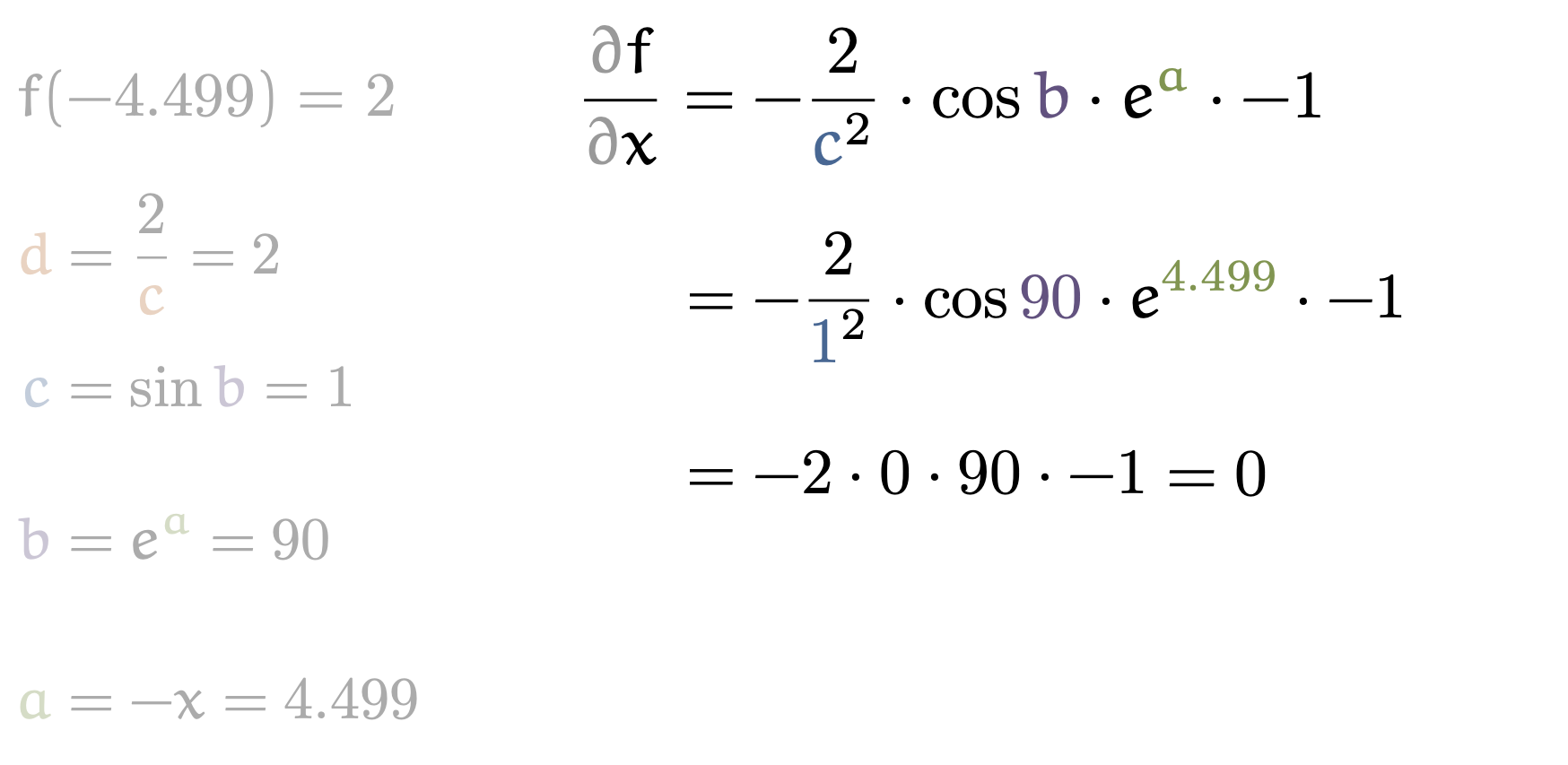 Fig. An example of how to compute global derivative (5/5)
Fig. An example of how to compute global derivative (5/5)
Practical Implementation of Backprop
Vector Derivatives
이번에는 실제로 어떻게 backprop 연산이 수행해야 하는지 알아보자. (이하 내용은 cs231n을 참고했는데 관심이 있는 사람들은 Justin Johnson과 Yann Lecun의 material을 참고하면 좋을 것 같다: Linear backprop example, Derivatives notes, Efficient backprop)
앞서 derivative를 계산하는 데에는 여러 형태가 있다고 잠시 언급했었다.
- Scalar to Scalar : Regular Derivative
Vectorto Scalar : GradientVectortoVector: Jacobian
 Fig.
Fig.
사실 scalar to scalar와 다르게 vector to scalar나 vector to vector derivative는 실제 backprop을 수행할 때 최적화할 여지가 있다. 반대로 말하면 무식하게 계산했다가는 GPU memory가 부족해서 학습을 할 수가 없다. 대부분의 경우 loss 값은 scalar이고 backprop은 loss쪽부터 미분을 구해 전파하기 때문에 vector to scalar derivative인 gradient를 계산하게 된다.
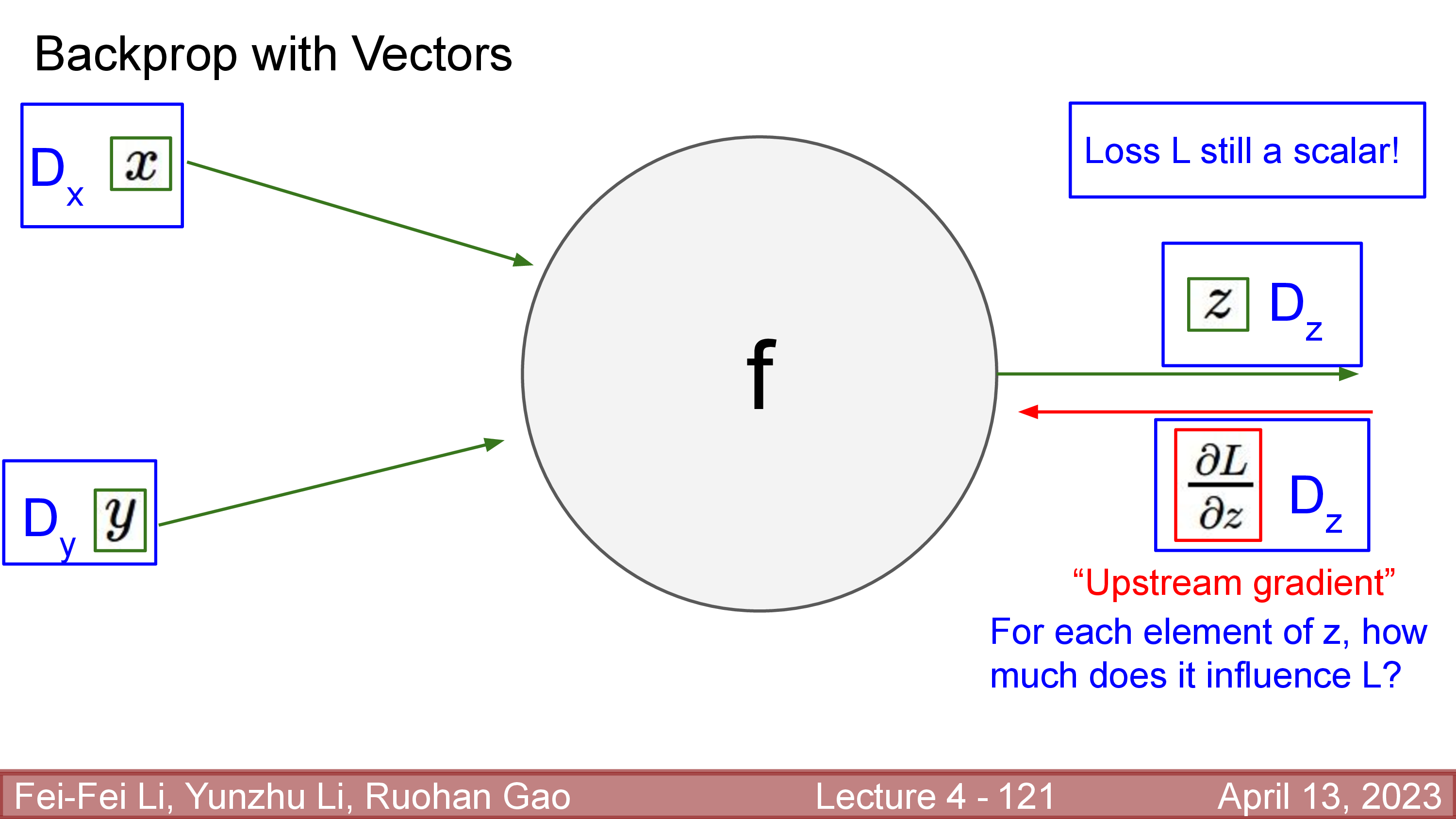 Fig.
Fig.
여기서 몇 가지 term들이 추가되는데,
어떤 한 layer가 (function이) \(z = f(x,y)\)와 같은 연산을 한다면 loss를 output, \(z\)에 대해 미분한 \(\frac{dL}{dz}\)를 \(f\)기준으로 위에서 오기 때문에 upstream gradient라고 부르며, \(\frac{dz}{dx}, \frac{dz}{dy}\)는 local gradient, 그리고 \(\frac{dL}{dx}, \frac{dL}{dy}\)를 downstream gradient라고 한다.
(local, downstream gradient는 앞서 살짝 언급했다)
- Operation : \(z = f(x,y)\)
- Upstream gradient : \(\frac{dL}{dz}\)
- Local gradient : \(\frac{dz}{dx}, \frac{dz}{dy}\)
- Downstream gradient (or Global gradient): \(\frac{dL}{dx}, \frac{dL}{dy}\)
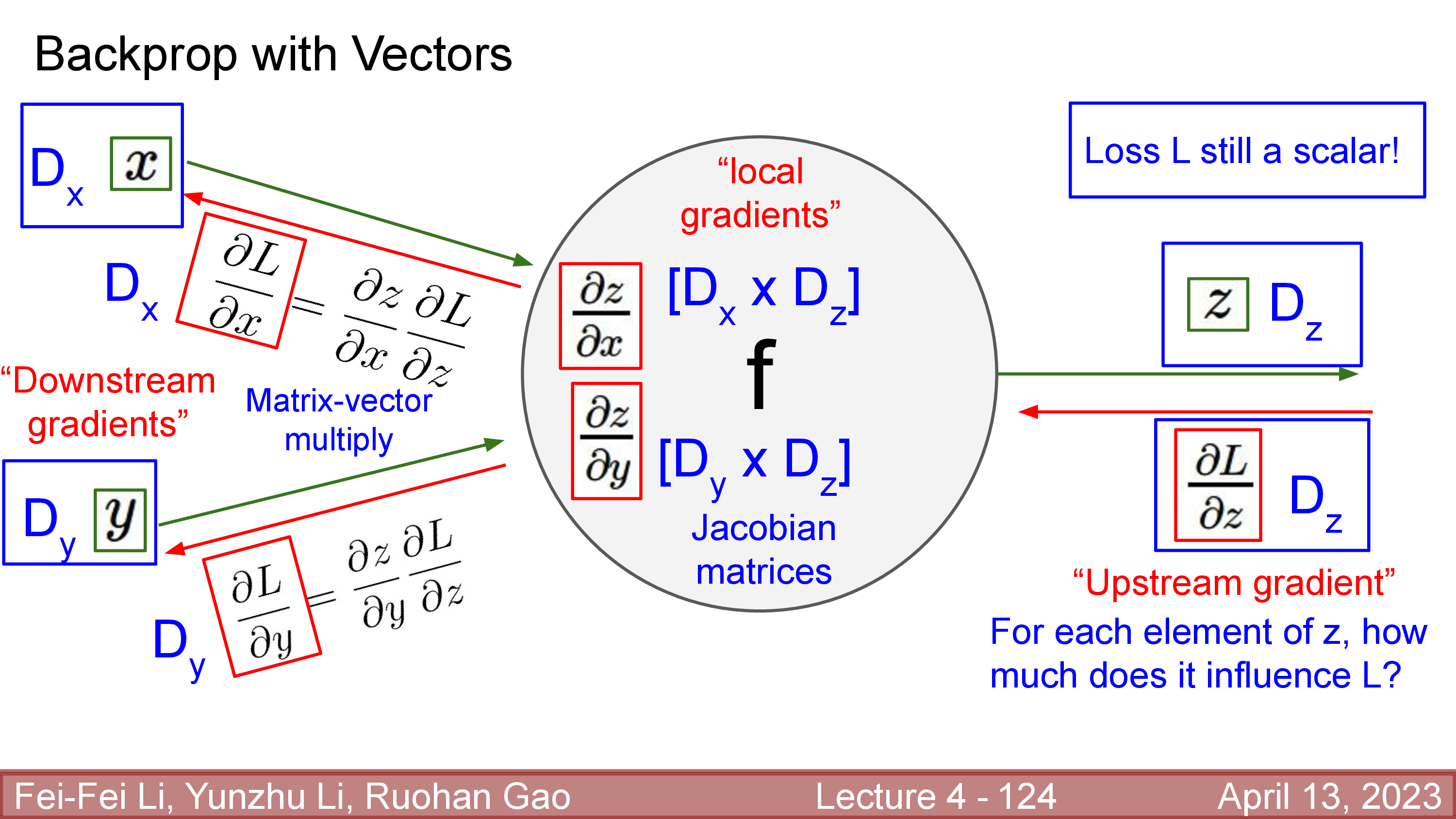 Fig.
Fig.
여기서 문제는 upstream gradient와 곱할 local gradient를 계산하는 것인데, 예를 들어 \(x, z \in \mathbb{R}^{4 \times 1}\)라고 하자. 즉 어떤 function은 input, output 차원이 같은 activate function 같은 것인데 예를 들어 이것이 ReLU function라고 생각해보자.
 Fig.
Fig.
Upstream gradient가 어떻게 계산됐는지는 대충 loss값이 scalar이고 output, \(z\)가 4차원이므로 gradient도 4차원이다. Gradient, \(\frac{dL}{dz}\) loss를 계산할 때 z의 element가 각각 어떤 영향을 미쳤는가?를 의미한다.
 Fig.
Fig.
Local gradient, \(\frac{dz}{dx}\)는 그렇다면 \(4 \times 4\)차원이 되는데, 이는 자명하게도 input vector, \(x\)의 각 element가 output \(z\)의 각 element에 어떤 영향을 끼쳤는지를 의미한다.
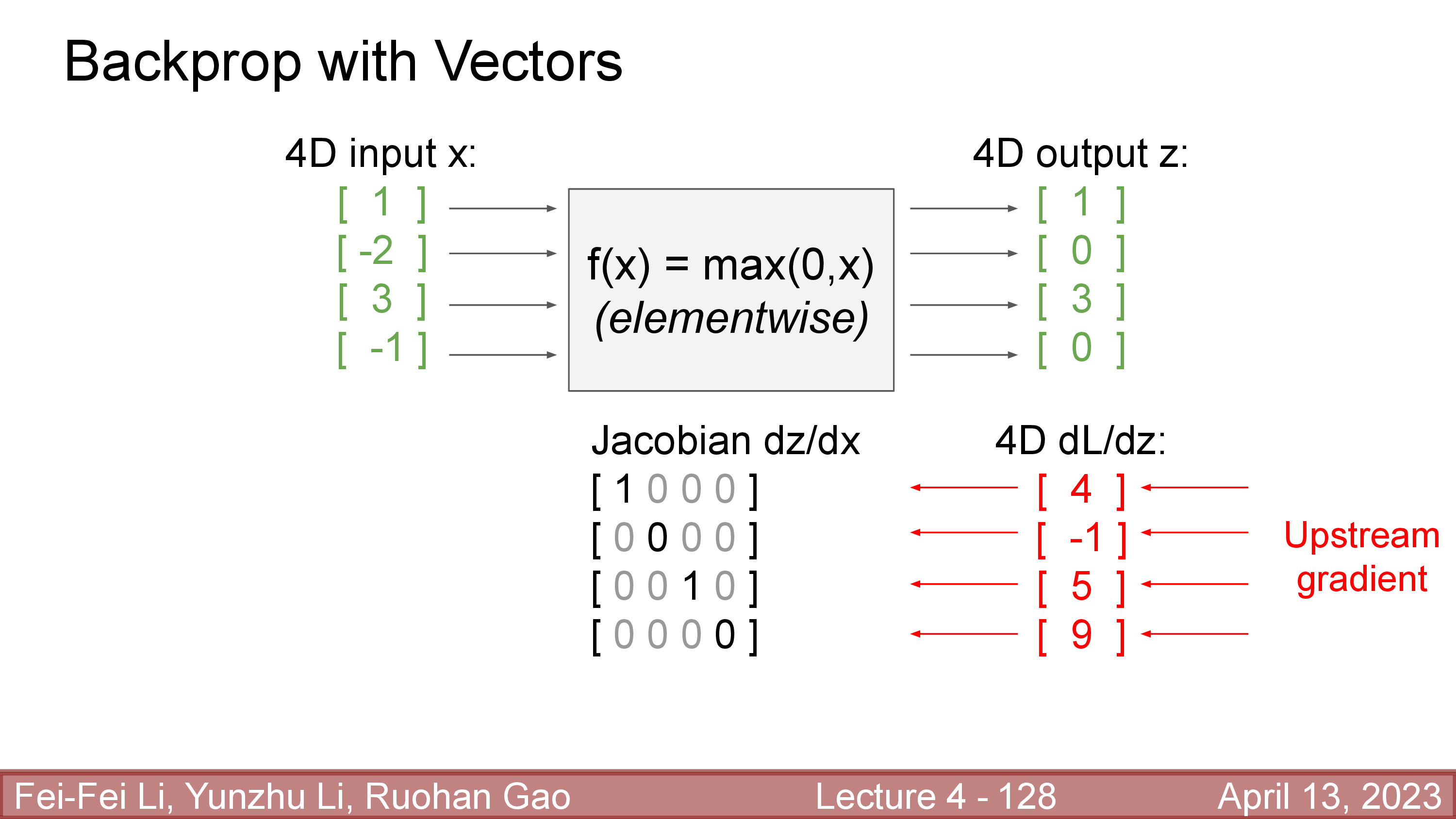 Fig.
Fig.
이제 upstream gradient와 local gradient를 곱하면 input vector와 동일한 size를 갖는 global gradient (downstream gradient)를 얻을 수 있다.
 Fig.
Fig.
여기서 local gradient가 input, output이 \(n\)차원일 경우 \(n \times n\)을 갖기 때문에 GPU memory관점에서 매우 비싸다는 걸 알 수 있는데, figure에 나타나 있는 것 처럼 ReLU function에 대한 local gradient 매우 sparse 한 것을 넘어서서 off-diagonal 성분이 항상 0이기 때문에 full matrix를 구할 필요가 없다. (ReLU는 각 element별로 양수이면 input자신을 return하고 음수이면 0을 return한다)
 Fig.
Fig.
Local gradient는 다른 layer에서는 쓰이지 않기 때문에 결국 downstream gradient를 계산하기 위해서는 explicit multiplication을 할 필요가 없고,
위 figure에 나와있는 것 처럼 input이 양수면 upstream을 그대로 전파하고 음수이면 0을 전파하는 implicit multiplication을 수행하면 된다.
Matrix (Tensor) Derivatives
그러면 2차원 matrix, 더 나아가서 3차원, 4차원 tensor에 대한 derivative는 어떻게 계산해야 할까? 이는 앞서 jacobian을 efficient하게 계산했던 것을 generlize하면 된다.
- Scalar to Scalar : Regular Derivative
Vectorto Scalar : GradientVectortoVector: Jacobian- Tensor to Tensor : Generalized Jacobian
이번에도 마찬가지로 loss를 input, \(x\)에 대해 미분한 값인 \(\frac{dL}{dx}\)는 \(x\)와 같은 size의 matrix여야 한다.
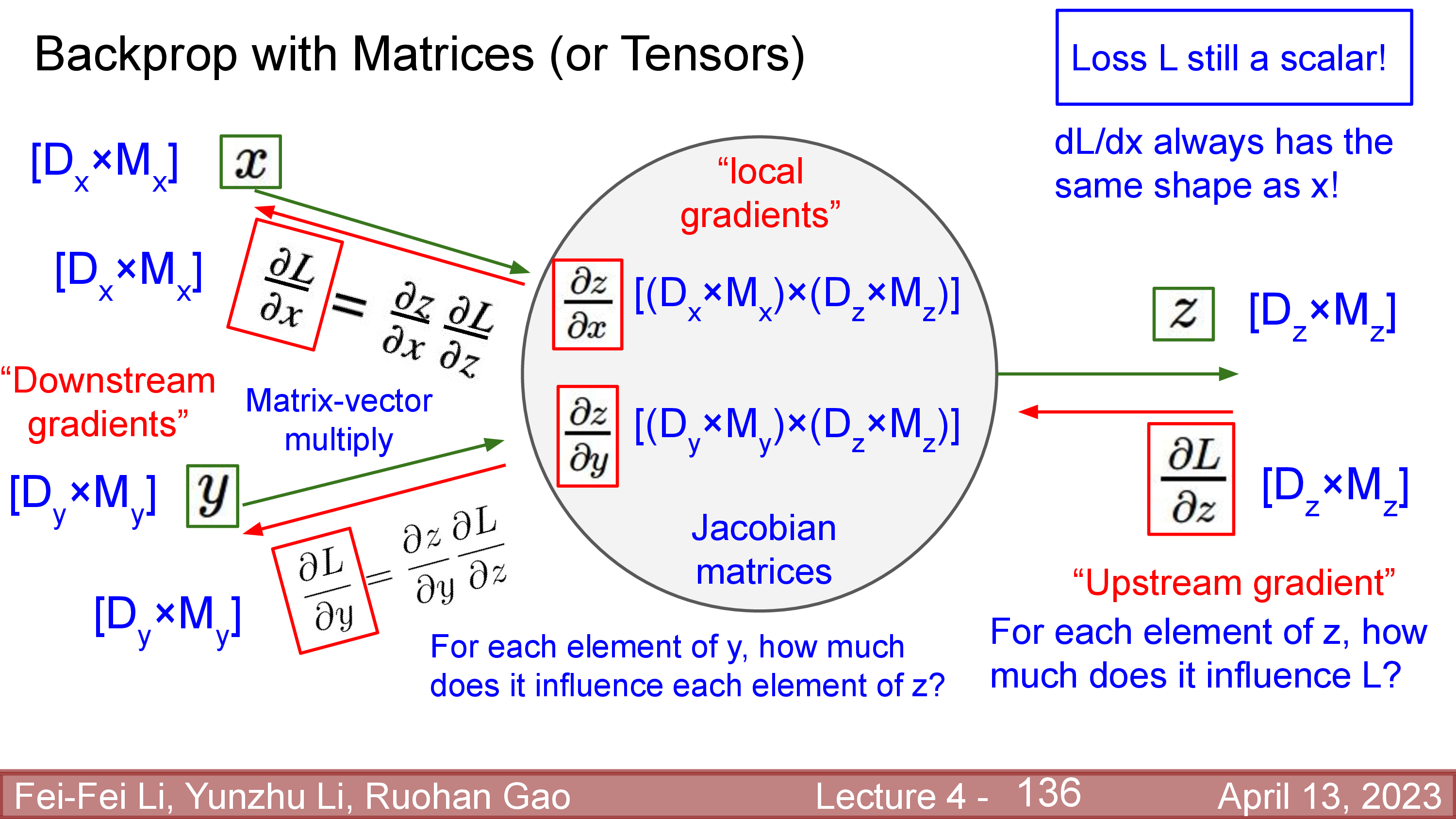 Fig.
Fig.
이제 ML스럽게 function을 바꿔보자. 어떤 function이 아래의 matrix multiplication 연산을 한다.
\[y = Wx\]Vector to scalar와 마찬자기로 matrix to scalar jacobian도 derivative가 input과 같은 차원을 갖게 되는데, input, weight matrix, output이 아래와 같은 size 일 때 derivative는 다음과 같다.
\[\begin{aligned} & \text{let } x \in \color{red}{ \mathbb{R}^{N \times D} }, W \in \color{blue}{ \mathbb{R}^{D \times M} } & \\ & \text{then } y \in \mathbb{R}^{N \times M} & \\ & \frac{dL}{dx} = \frac{dL}{dy} \frac{dy}{dx}\in \color{red}{ \mathbb{R}^{N \times D} } & \\ & \frac{dL}{dW} = \frac{dL}{dy} \frac{dy}{dW}\in \color{blue}{ \mathbb{R}^{N \times M} } & \\ \end{aligned}\]Explicit multiplication을 하기 위해서는 \(N=64, D,M = 4096\)일 경우 local gradient는 \([(N \times D) \times (N \times M)]\), \([(D \times M) \times (N \times M)]\)의 matrix를 형성해야 하는데, 이는 각각 256GB 정도의 memory를 필요로 한다고 한다. (각 matrix별로 single precision (32-bit floating point)일 경우 4 bytes 이기 때문)
>>> 4*((64*4096)*(64*4096))/pow(1024,3)
256.0
그리고 이러한 \(N,D,M\) setting은 modern DL era에서는 흔한 setting이며 이것보다 더 거대한 NN layer도 많다.
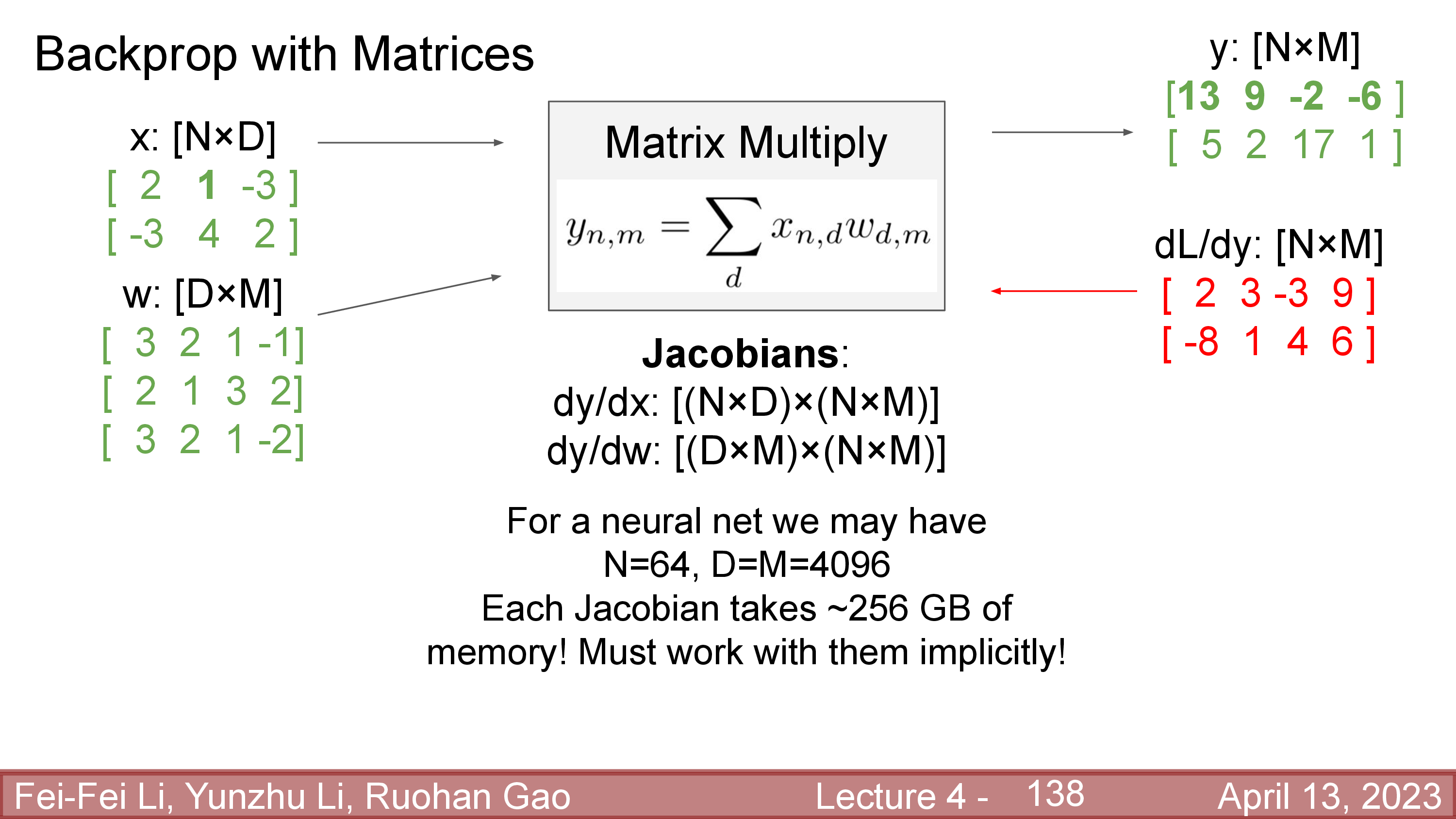 Fig.
Fig.
그런데 당연하게도 tesnro backprop도 full matrix를 형성할 필요는 없다. 아래 예시처럼 input matrix, \(x\)의 한 element, \(x_{n,d} = x_{1,2}\)가 layer output, \(y\)에 영향을 끼치는 것은 사실 일부분밖에 안된다.
 Fig.
Fig.
정확히는 output matrix의 첫 번째 row인데, 이 row의 각 element중 \(y_{n,m} = y_{1,3}\)은 정확히 \(x_{n,d}\)의 얼만큼의 영향을 받았을까?를 결정하는 요인은 \(w_{d,m} = w_{2,3}\)이 된다.
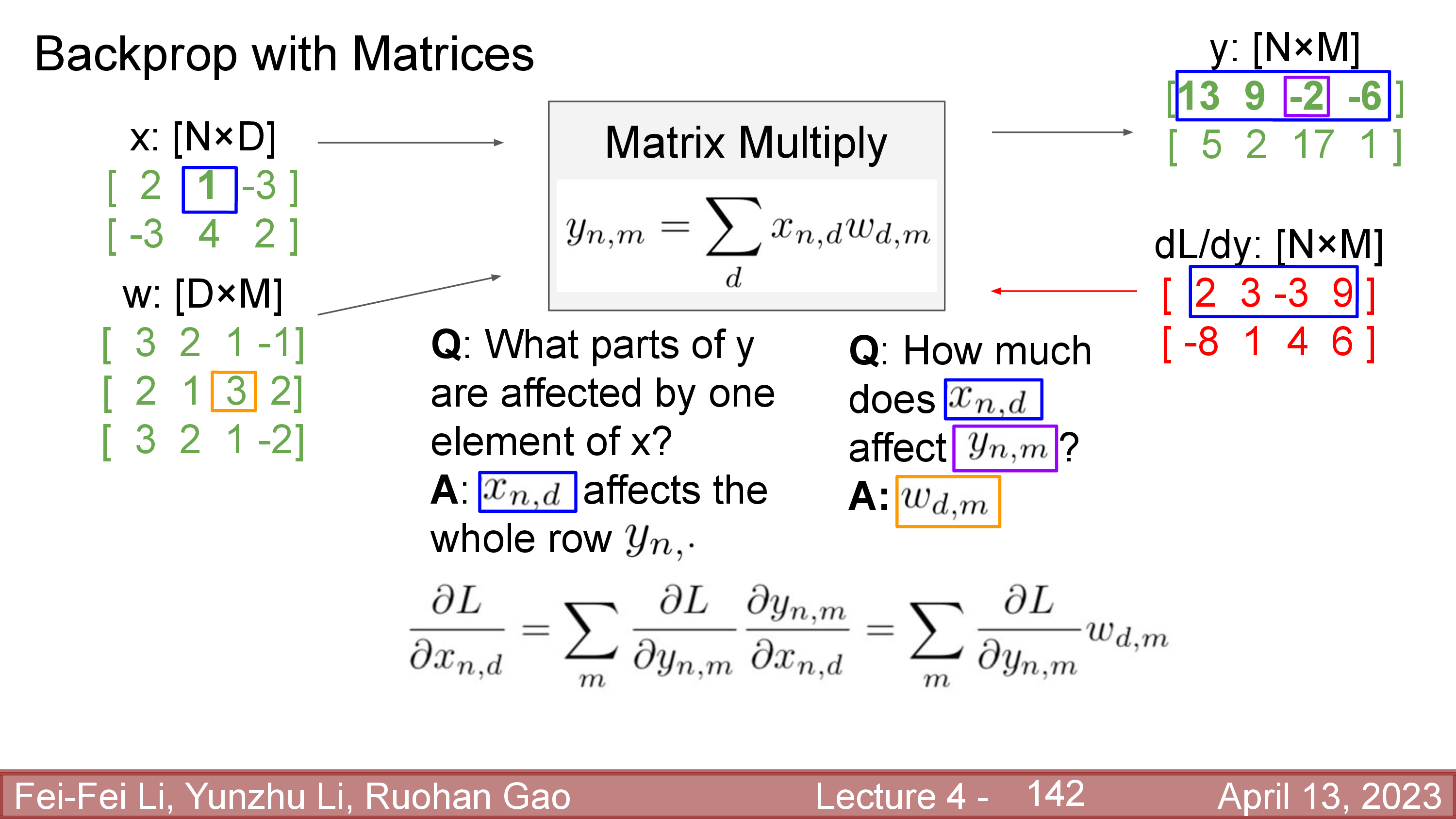 Fig.
Fig.
즉 matrix (나아가서는 tensor) backprop의 경우에도 downstream을 계산하는 것은 upstream gradient와 weight matrix를 적당히 연산해주는 것으로 대체가 가능하다는 것이다. 결과적으로 downstream gradient는 결과적으로 아래와 같이 간단한 연산으로 구할 수 있다.
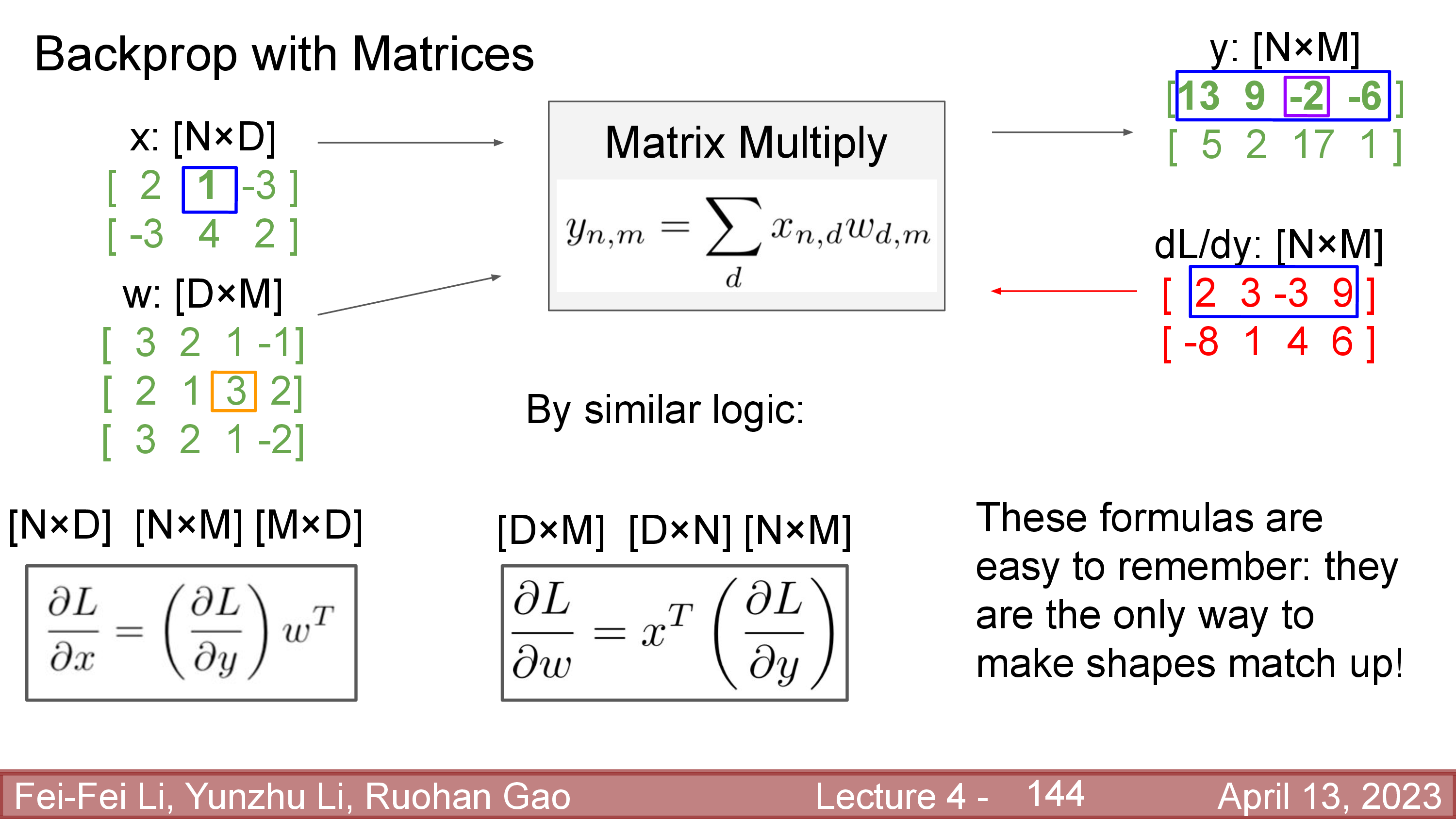 Fig.
Fig.
어떻게 유도가 된 것인지는 서두에 언급했던 notes를 확인하면 되는데, 요약하자면 아래와 같다.
 Fig. Credit is for Justin Johnson.
Fig. Credit is for Justin Johnson.
이렇게 gradient를 구하는 방식은 외적 (outer product)을 쓴다고 얘기할 수도 있다. (몇몇 문헌에서 언급됨)
\[\displaystyle \mathbf {u} \otimes \mathbf {v} =\mathbf {u} \mathbf {v} ^{\textsf {T}} ={ \begin{bmatrix}u_{1}\\u_{2}\\u_{3}\\u_{4}\end{bmatrix} }{ \begin{bmatrix}v_{1}&v_{2}&v_{3}\end{bmatrix} } ={ \begin{bmatrix}u_{1}v_{1}&u_{1}v_{2}&u_{1}v_{3}\\u_{2}v_{1}&u_{2}v_{2}&u_{2}v_{3}\\u_{3}v_{1}&u_{3}v_{2}&u_{3}v_{3}\\u_{4}v_{1}&u_{4}v_{2}&u_{4}v_{3}\end{bmatrix} }\]Activation Functions and Bias Term
이번에는 실제 backprop을 할 때 주의해야 할 점 몇가지에 대해 알아볼 것인데, key topic은 다음과 같다.
- 어떤 activation function을 쓸 것인가?
- Bias가 들어간 Linear Layer를 고려해볼 것
- 미분 가능한 연산들로 NN을 구성할 것
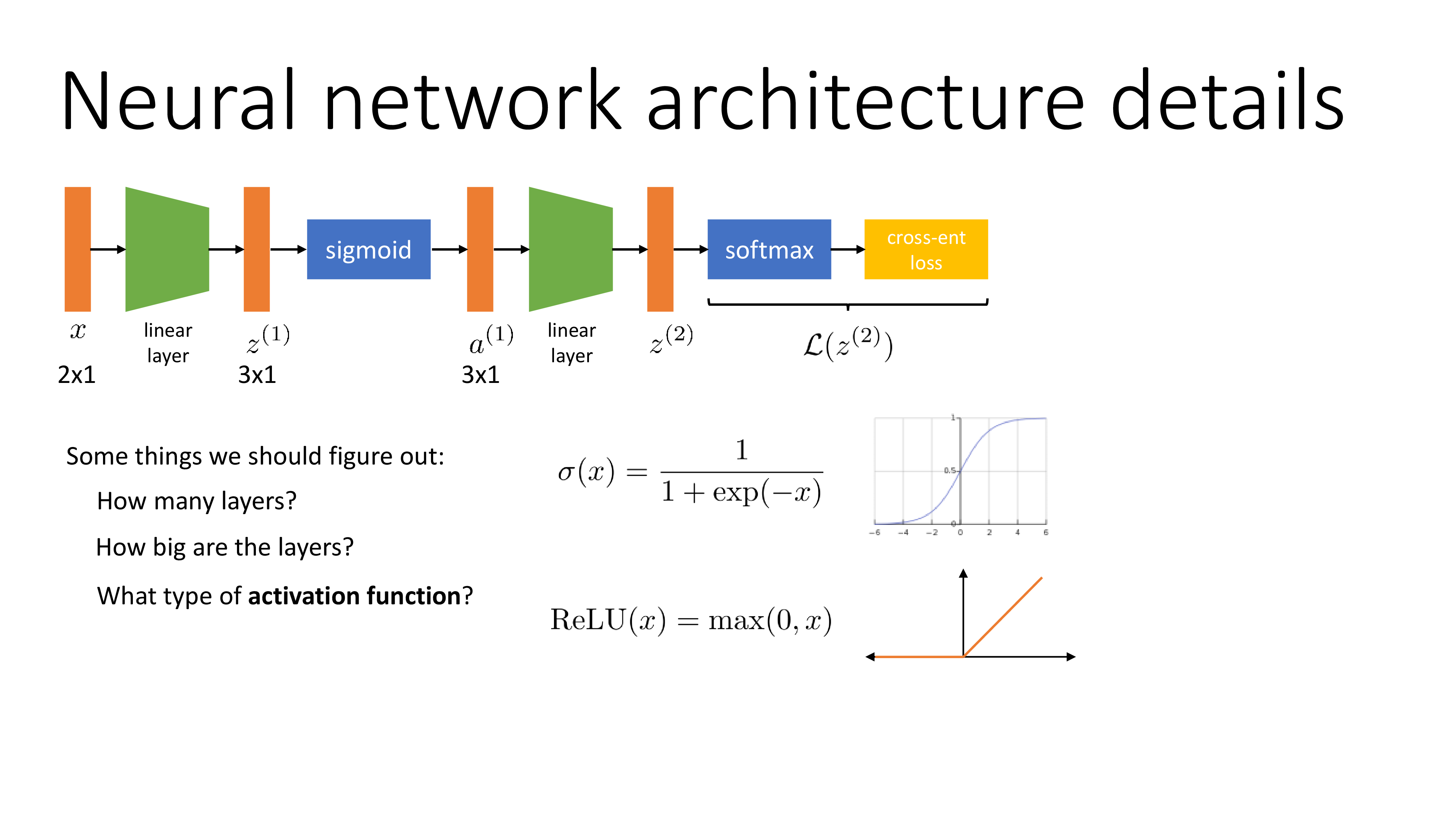 Fig.
Fig.
먼저 activation function에 대한 얘기를 해보자. Logistic regression 같은 경우 sigmoid function을 사용해 probability distribution을 추정한다. 이에 따라 NN을 쓸 때도 hidden layer의 activation function을 sigmoid로 쓰는 경우가 있는데, 이는 gradient가 0이 되는 지점이 있기 때문에 학습이 경과되면서 점점 parameter update가 안될 수도 있다. Sergey는 그러므로 Rectifier Linear Unit (ReLU)를 쓰는게 좋다고 하는데 (요즘 DL에서는 gelu, silu 이런걸 쓴다) 또 다른 ReLU의 장점은 바로 미분 계산 자체가 cheap하다는 것이다. 왜냐면 양수값에 대해서 기울기가 1이라 다른 연산이 필요하지 않기 때문이다.
\[f'(x) = \begin{cases} 1 & \text{ if } x>0 \\ 0 \text{ or } 1 & \text{ otherwise } \end{cases}\]그 다음은 bias가 들어간 linear layer를 고려해보는 것인데,
multi layer NN 을 학습할 때, 중간에 어떤 layer의 입력이 전부 0이 되어버린다면 그 뒤로도 모두 0이 되기 때문에 정상적인 학습이 불가능해진다. 이 때 bias를 더하는 것이 해결책이 될 수 있다고 한다.
Bias에 대한 derivation은 bias가 vector이기 때문에 vector to scalar derivation을 구하는 것이 될 것인데, 이는 어떠한 operation도 아니고 사실 덧셈을 하는 것이기 때문에 사실 upstream gradient와 동일하다.
\[\frac{dL}{db} = \frac{dL}{dz} \frac{dz}{db} = \frac{dL}{dz}\]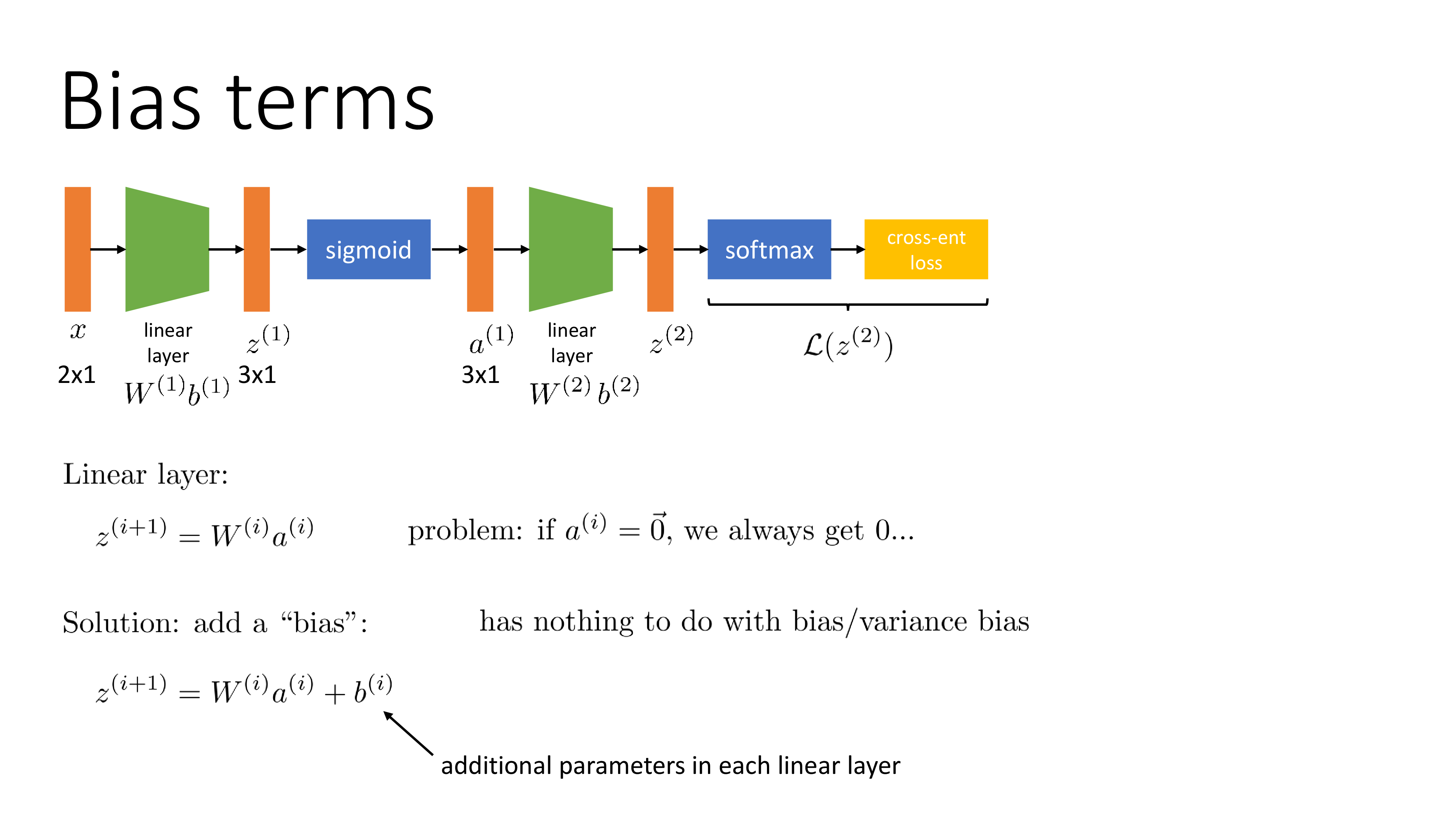 Fig. 여기서 bias는 bias/variance decomposition과는 관련이 없다. 1차원 linear regression을 할 때 y절편을 학습한다는 것이라고 이해하면 된다.
Fig. 여기서 bias는 bias/variance decomposition과는 관련이 없다. 1차원 linear regression을 할 때 y절편을 학습한다는 것이라고 이해하면 된다.
마지막으로 미분 가능한 (differntiable) 연산들로 NN을 구성하는 것인데, 당연하게도 backprop는 jacobian들을 수없이 곱하는 것이지만 어떤 advanced DL algorithm 들은 이를 불가능하게 하는 연산을 포함하고 있다. 지금 다루진 않겠으나 이런 (argmax) sampling operator 같은걸 사용하는 경우가 대표적인데, 이런 경우 REINFORCE algorithm, Gumbel Softmax 혹은 Reparametrization Trick 등을 사용해 해결할 수 있다.
Placeholder for CS182 slides
같은 내용이지만 누군가는 Sergey style을 선호할 수도 있으므로 이 subsection을 추가한다. 전반적으로 내용이 같지만 weight matrix에 대한 미분을 tensor로 설명한다던가 하는 부분이 더 직관적일 수 있다.
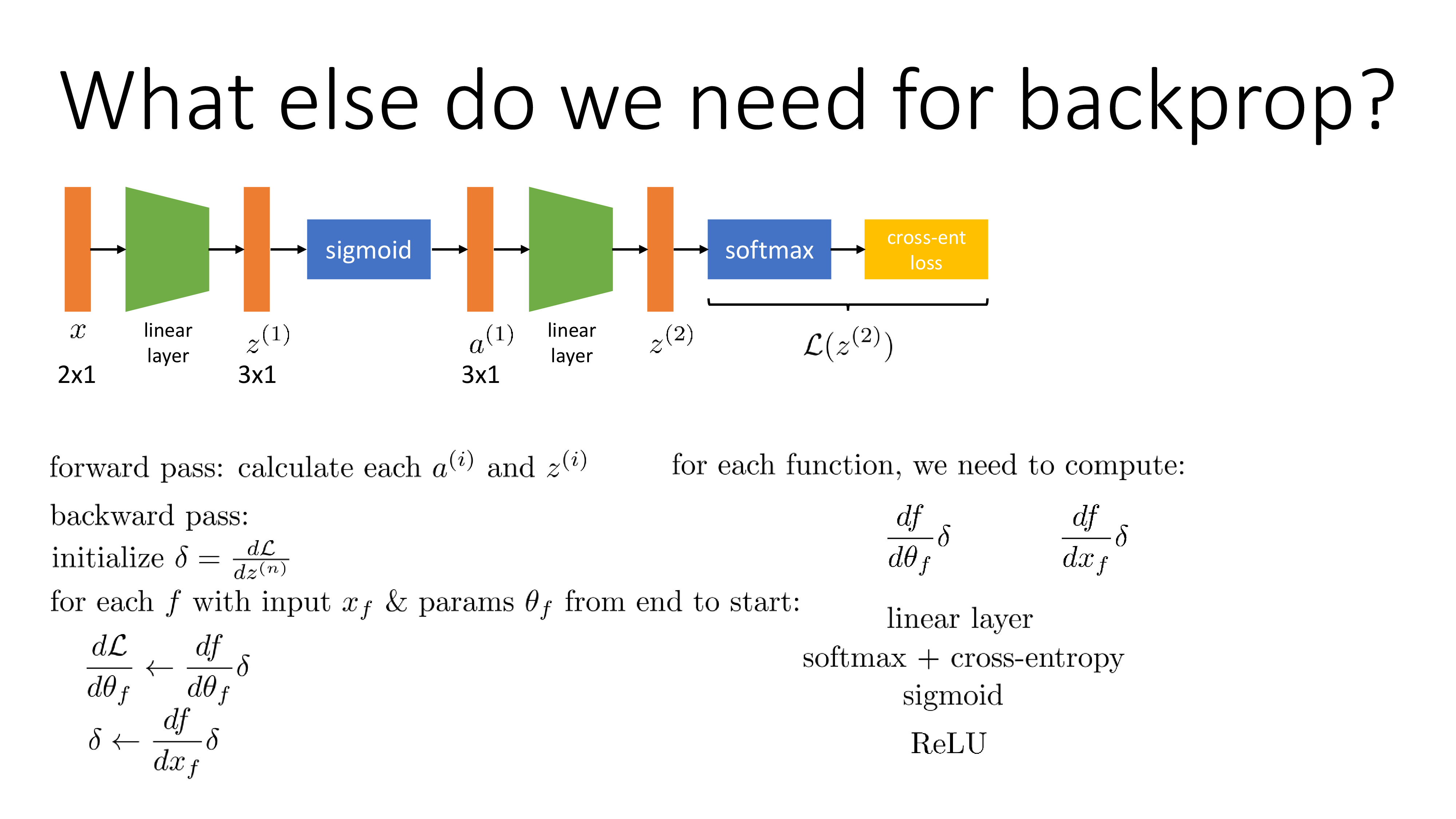 Fig. efficient backprop from cs182 (1/8)
Fig. efficient backprop from cs182 (1/8)
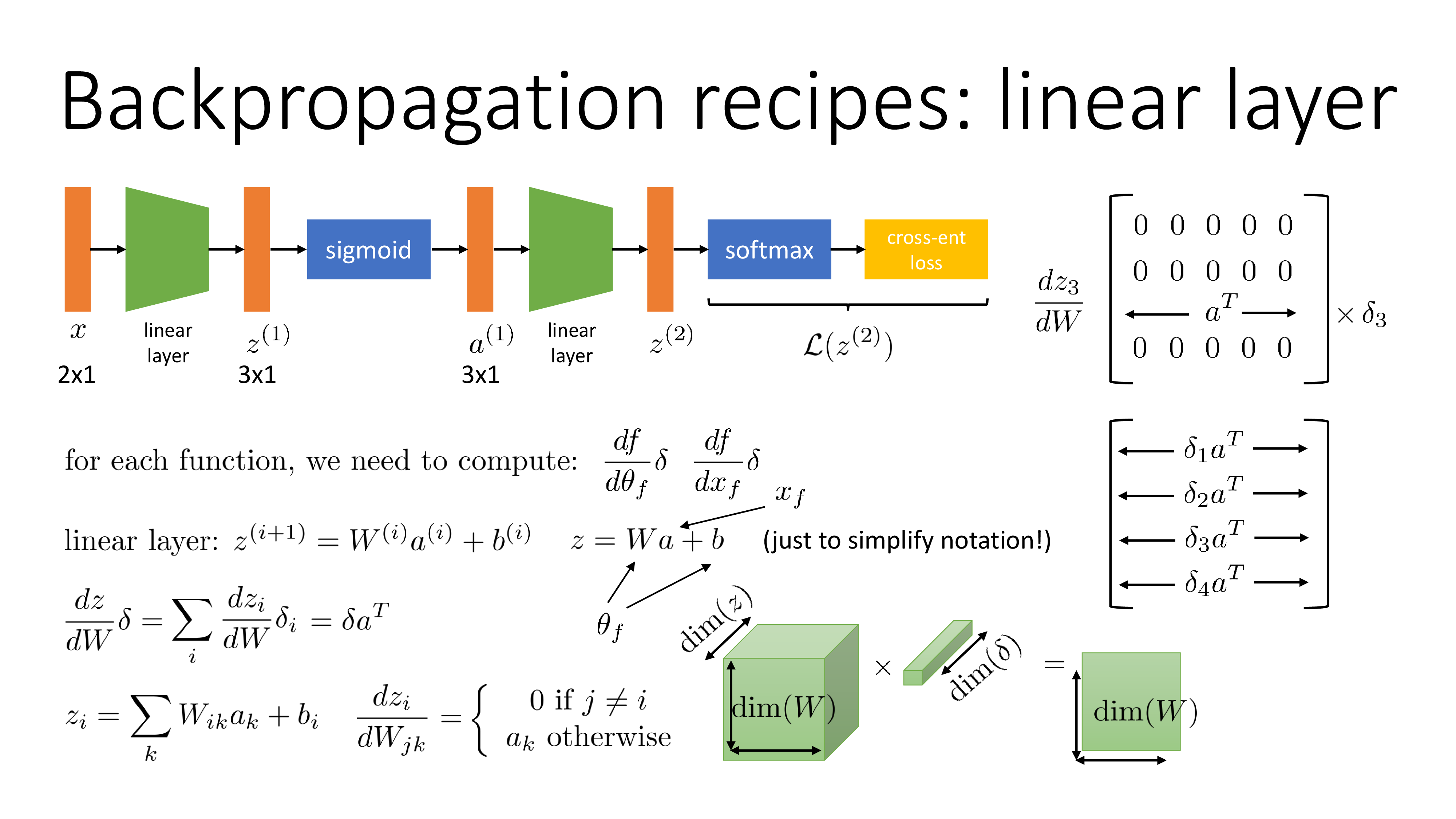 Fig. efficient backprop from cs182 (2/8)
Fig. efficient backprop from cs182 (2/8)
 Fig. efficient backprop from cs182 (3/8)
Fig. efficient backprop from cs182 (3/8)
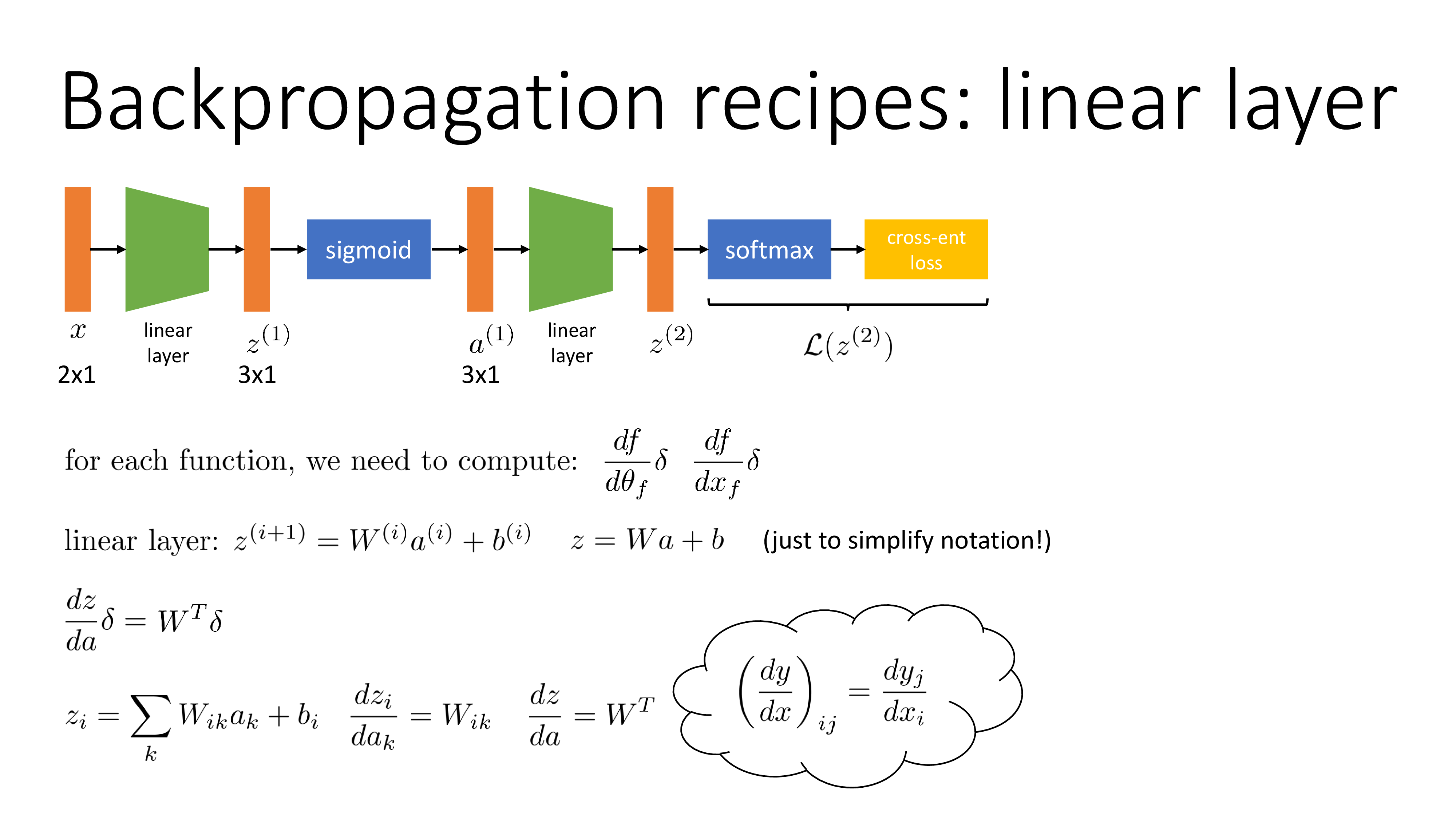 Fig. efficient backprop from cs182 (4/8)
Fig. efficient backprop from cs182 (4/8)
 Fig. efficient backprop from cs182 (5/8)
Fig. efficient backprop from cs182 (5/8)
 Fig. efficient backprop from cs182 (6/8)
Fig. efficient backprop from cs182 (6/8)
 Fig. efficient backprop from cs182 (7/8)
Fig. efficient backprop from cs182 (7/8)
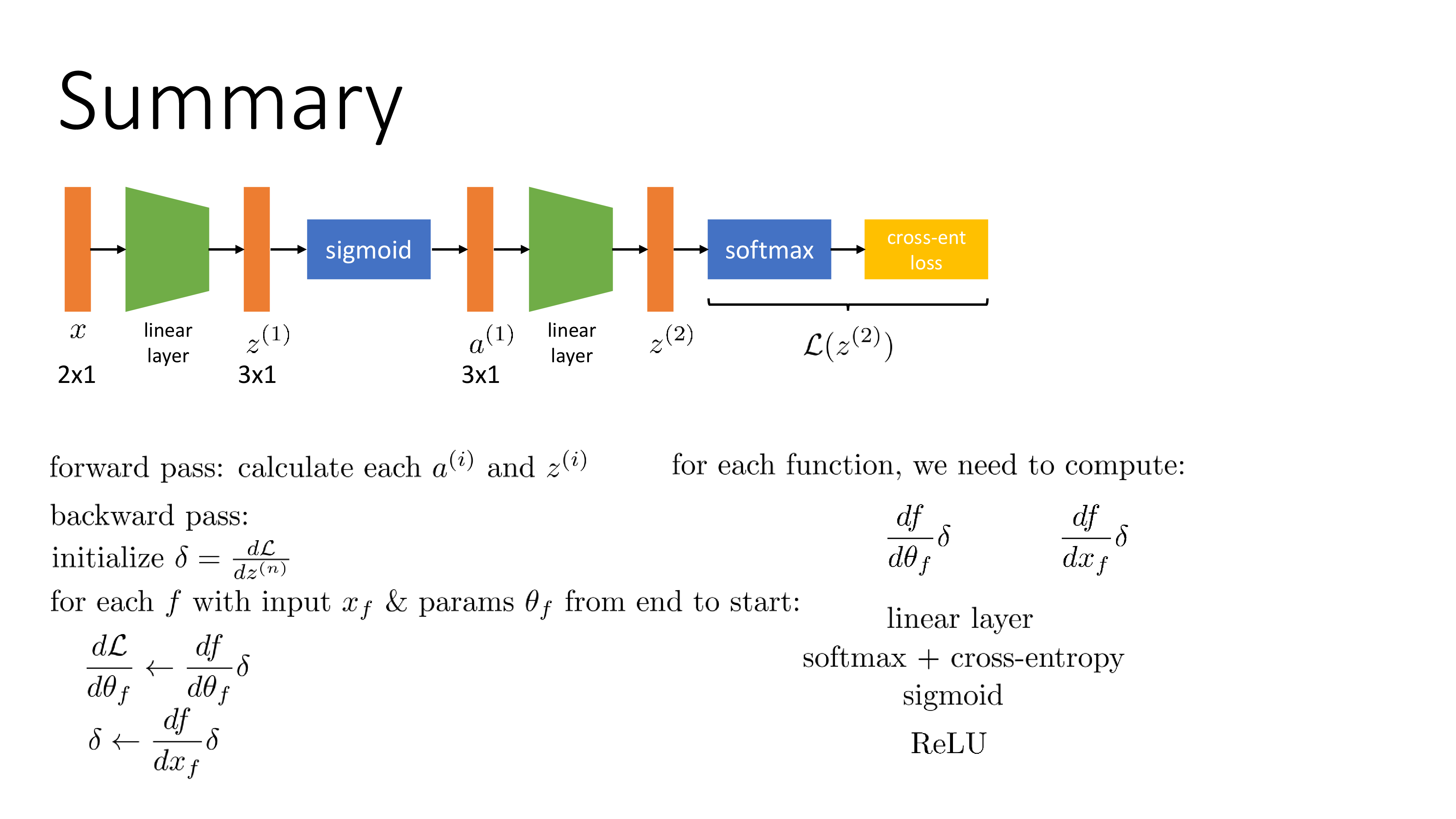 Fig. efficient backprop from cs182 (8/8)
Fig. efficient backprop from cs182 (8/8)
Example Implementation with Pure Numpy
Logistic Regression (1 Layer)
이제 간단한 NN의 backpropagation을 직접 수행해보자. 예를 들어보자면 bernoulli distribution을 target distribution으로 해서 학습하는 logistic regression은 단 두 줄로 쉽게 gradient를 구할 수 있다. (물론 logistic regression은 NN이 아니지만 굳이 따지자면 1 layer NN정도로 생각할 수 있겠다)
우리가 구성하는 network들은 아무리 복잡해도 간단한 layer 몇 개의 연속이다.
- Lienar layer (matrix multiplication 연산이 전부임)
- Sigmoid, softmax 등 activation function (gradient 형태가 굉장히 단순함)
즉 backpropagation을 실제로 구현하기 위해서 몇 가지 operation의 local gradient를 구하는 pattern만 기억하고 있으면 된다.
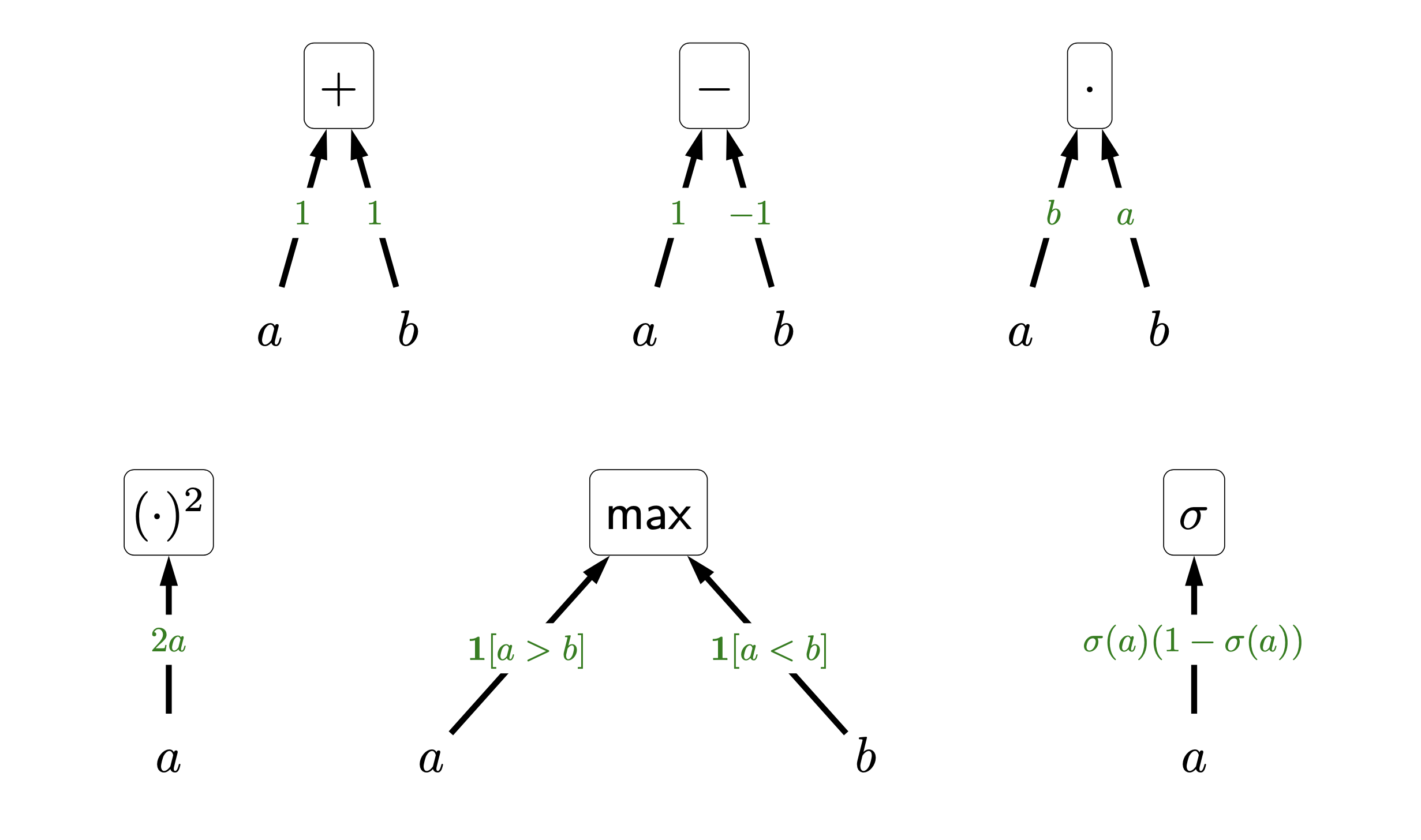 Fig. 몇가지 derivative의 pattern
Fig. 몇가지 derivative의 pattern
먼저 logistic regression은 \(x\)와 \(W\)를 matrix multiplication 하고 activation을 통과시켜 lgoit, \(z\)를 계산해야 한다.
\[\begin{aligned} & y=Wx & \\ & z = \sigma(y) = \frac{1}{1+\exp^{-(Wx)}} & \\ \end{aligned}\]Sigmoid function의 gradient는 먼저 아래와 같이 간단한 pattern을 가지고 있다.
\[\frac{dz}{dy} =z(1-z)\]여기서 \(y = Wx\)의 미분형태는 아래와 같기 때문에
\[\frac{dy}{dx} = W^T\]activation, \(z\)의 \(x\) 대한 gradient는 다음과 같이 계산할 수 있다.
\[\frac{dz}{dx} = \frac{dy}{dx} \cdot \frac{dz}{dy} = W^T z(1-z)\]마지막으로 우리가 최종적으로 원하는 것은 activation output을 \(W\)에 대해 미분한 것인데,
\[\frac{dz}{dW} = \frac{dx}{dW} \cdot \frac{dz}{dx} = z(1-z) x^T\]Logistic regression의 weight matrix \(W\)의 gradient는 아래처럼 간단히 두 줄로 구현할 수 있다. (지금은 loss를 따로 명시하지 않았음)
x = np.random.rand(10)
W = np.random.rand(1,10)
z = 1/(1 + np.exp(-np.dot(W, x))) # forward pass
dx = np.dot(W.T, z*(1-z)) # backward pass: local gradient for x
dW = np.outer(z*(1-z), x) # backward pass: local gradient for W
NN for Binary Classification (more than 2 layers)
이번에는 2 layer 이상 NN의 backprop을 구현해보자. 먼저 activation function의 forward backward 를 아래처럼 정의해 준다.
def sigmoid(Z):
return 1/(1+np.exp(-Z))
def relu(Z):
return np.maximum(0,Z)
def sigmoid_backward(dA, Z):
sig = sigmoid(Z)
return dA * sig * (1 - sig)
def relu_backward(dA, Z):
dZ = np.array(dA, copy = True)
dZ[Z <= 0] = 0;
return dZ
여기서 ReLU activation같은 경우 0인 지점에서 derivative가 0이라는 점에 주읳자. 그리고 linear layer 하나의 forward는 먼저 다음과 같이 구현되어 있는데, 경우에 따라서 2~5 layer 정도를 쌓으면 된다.
def single_layer_forward_propagation(A_prev, W_curr, b_curr, activation="relu"):
# calculation of the input value for the activation function
Z_curr = np.dot(W_curr, A_prev) + b_curr
# selection of activation function
if activation is "relu":
activation_func = relu
elif activation is "sigmoid":
activation_func = sigmoid
else:
raise Exception('Non-supported activation function')
# return of calculated activation A and the intermediate Z matrix
return activation_func(Z_curr), Z_curr
한 layer 에서 수행되는 operation은 이전 layer의 activation output, \(\boldsymbol{A}^{[l-1]}\)와 현재 layer의 weight matrix, \(\boldsymbol{W}^{[l]}\)를 곱하고, biase term, \(\boldsymbol{b}^{[l]}\)를 더해 \(\boldsymbol{Z}^{[l]}\)f를 얻고, 최종적으로 activation 을 통과시켜 \(\boldsymbol{A}^{[l]}\)를 얻는 것이다. 이에 따른 각 gradient, jacobian는 아래와 같을 것이다.
\[\begin{aligned} & \boldsymbol{d} \boldsymbol{W}^{[l]} =\frac{\partial L}{\partial \boldsymbol{W}^{[l]}}=\frac{1}{m} \boldsymbol{dZ}^{[l]} \boldsymbol{A}^{[l-1] T} & \\ & \boldsymbol{d} \boldsymbol{b}^{[l]} =\frac{\partial L}{\partial \boldsymbol{b}^{[l]}}=\frac{1}{m} \sum_{i=1}^{m} \boldsymbol{dZ}^{[l](i)} & \\ & \boldsymbol{d} \boldsymbol{A}^{[l-1]} =\frac{\partial L}{\partial \boldsymbol{A}^{[l-1]}}=\boldsymbol{W}^{[l] T} \boldsymbol{d} \boldsymbol{Z}^{[l]} & \\ & \boldsymbol{d} \boldsymbol{Z}^{[l]} =\boldsymbol{d} \boldsymbol{A}^{[l]} * g^{\prime}\left(\boldsymbol{Z}^{[l]}\right) & \\ \end{aligned}\]def single_layer_backward_propagation(dA_curr, W_curr, b_curr, Z_curr, A_prev, activation="relu"):
# number of examples
m = A_prev.shape[1]
# selection of activation function
if activation is "relu":
backward_activation_func = relu_backward
elif activation is "sigmoid":
backward_activation_func = sigmoid_backward
else:
raise Exception('Non-supported activation function')
# calculation of the activation function derivative
dZ_curr = backward_activation_func(dA_curr, Z_curr)
# derivative of the matrix W
dW_curr = np.dot(dZ_curr, A_prev.T) / m
# derivative of the vector b
db_curr = np.sum(dZ_curr, axis=1, keepdims=True) / m
# derivative of the matrix A_prev
dA_prev = np.dot(W_curr.T, dZ_curr)
return dA_prev, dW_curr, db_curr
위 numpy 구현체는 SkalskiP의 notebook을 가져온 것인데, loss를 계산하는 부분과 weight update를 하는 부분까지 구현해 실제로 backprop, gradient descent를 통해 pure numpy로 구성된 NN을 학습하면 decision boundary가 아래처럼 잘 학습되는 것을 확인할 수 있다.
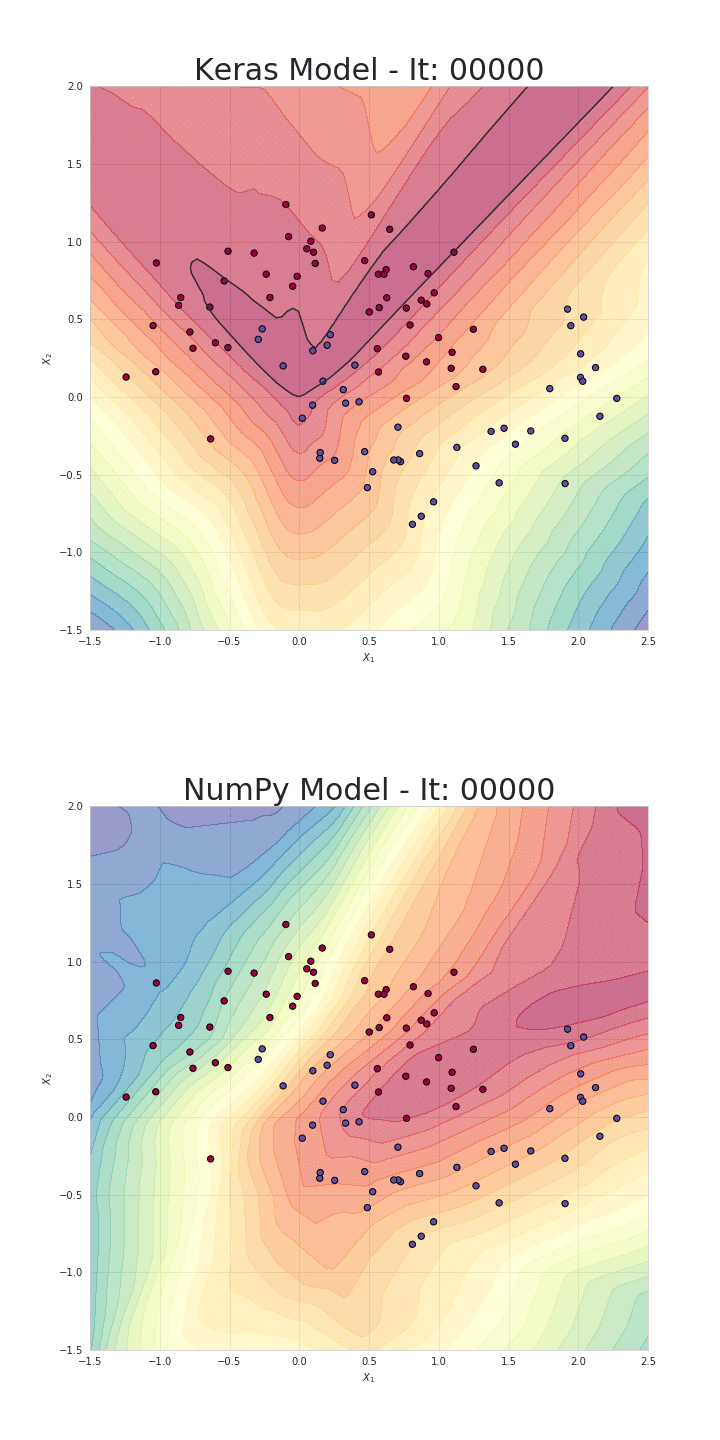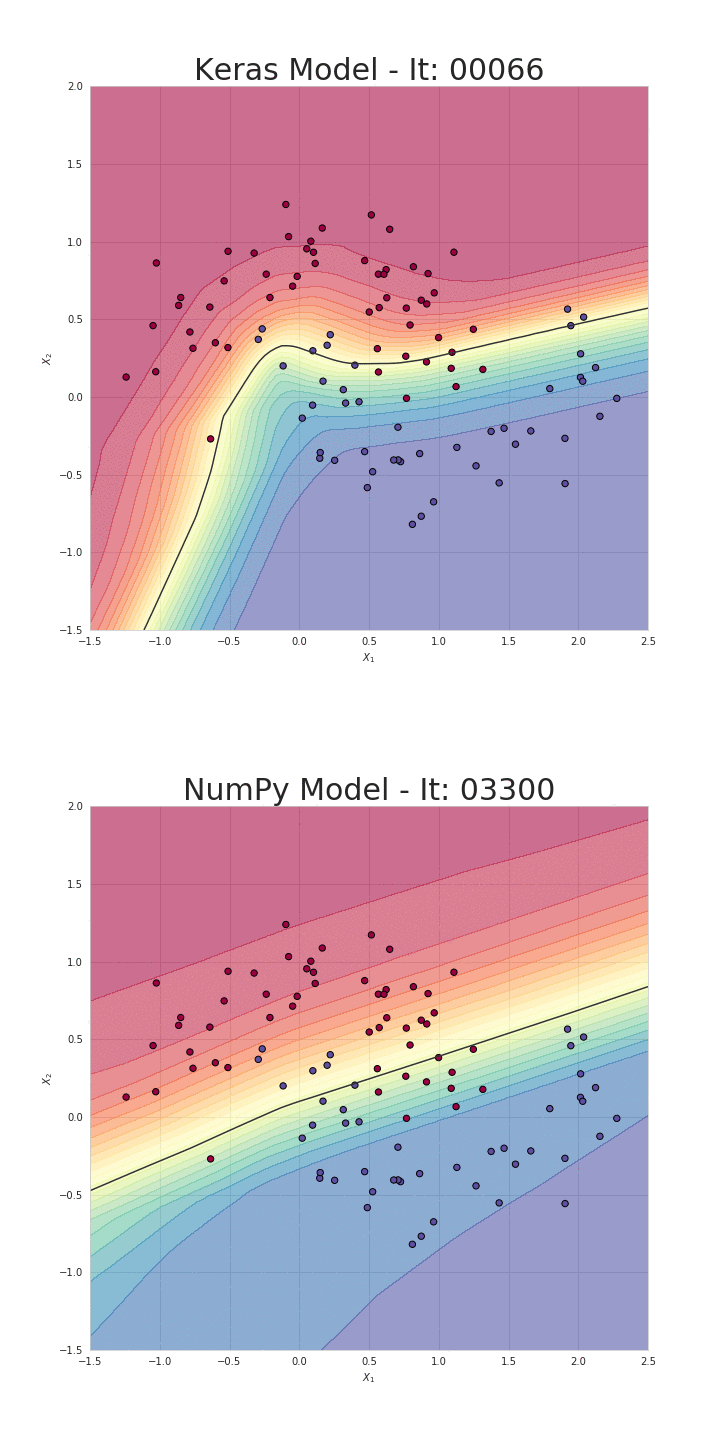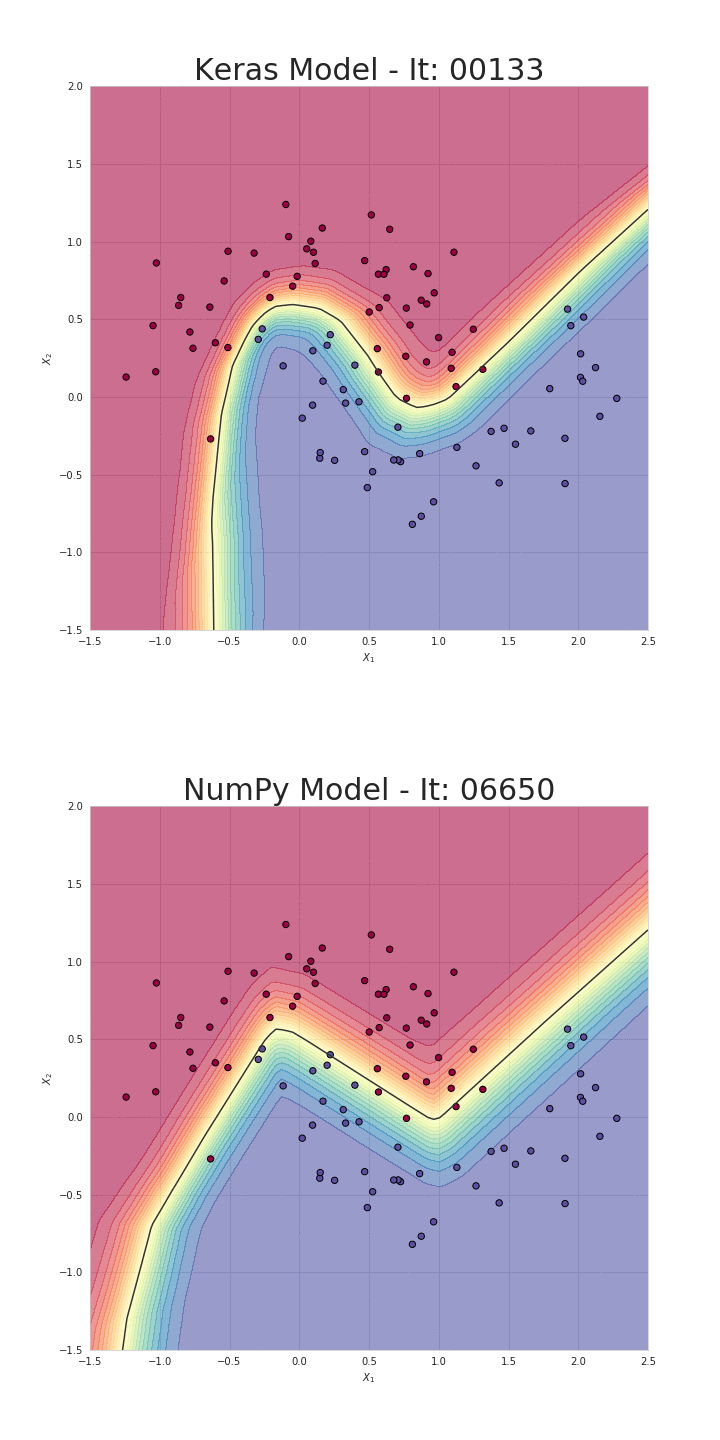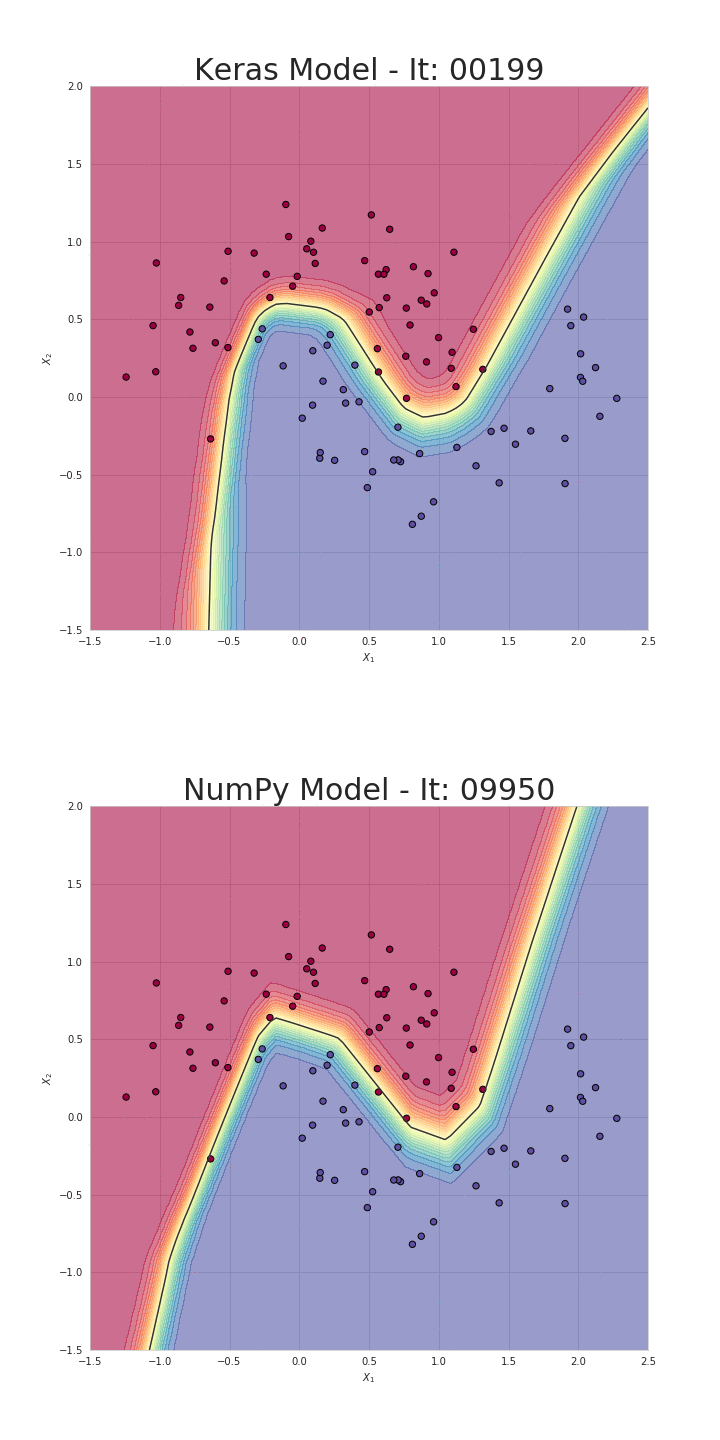 Fig.
Fig.
Pytorch Autograd (vs Manual Backprop)
그런데 실제로는 우리가 직접 backward pass의 연산을 다 구현할 필요는 없다. Tensorflow나 Pytorch같은 open source framework에 이 모든것들이 구현되어 있기 때문이다. 실제로 거의 모든 pattern에 대한 backward pass가 구현이 되어있는 것으로 알고 있는데,
 Fig.
Fig.
예를 들어 sigmoid function에 대해서 forward, backward가 아래처럼 c++로 구현되 있는 걸 확인할 수 있다.
 Fig.
Fig.
 Fig.
Fig.
물론 왠만한 ML researcher들은 이를 까볼 일은 거의 없다. 그렇다면 Pytorch의 Automatic differentiation package는 얼마나 정확할까. 아래의 example module을 만들어 직접 확인해 볼 수 있다.
import torch
import torch.nn as nn
import torch.nn.functional as F
def compare_outputs(out1, out2):
print(f'''
=========================
autograd : {out1}
manual grad : {out1}
all close : {torch.allclose(out1, out2, atol=1e-2, rtol=0)}
diff max : {(out1-out2).abs().max()}
diff mean : {(out1-out2).abs().mean()}
=========================
''')
class Model(nn.Module):
def __init__(self, input_dim, output_dim):
super().__init__()
self.layer = nn.Linear(input_dim, output_dim, bias=False)
def forward(self, x):
return torch.sigmoid(self.layer(x))
model = Model(10,1)
input = torch.rand(1,10)
# Manual Backprop from Andrej Karpathy
import numpy as np
x = input[0].detach().numpy()
W = model.layer.weight.detach().numpy()
z = 1/(1 + np.exp(-np.dot(W, x)))
dx = np.dot(W.T, z*(1-z))
dW = np.outer(z*(1-z), x)
# impl autograd
model(input).backward()
# comparison
compare_outputs(model.layer.weight.grad, torch.tensor(dW))
수행결과 아예 exact same임을 확인할 수 있지만 GPU로 계산을 한다던가, floating point precision을 바꾼다던가 하면 실제로는 아예 값이 같지는 않을 수 있을 것이다.
=========================
autograd : tensor([[1.8779e-01, 1.2162e-01, 1.8585e-04, 1.9439e-01, 5.5930e-02, 1.8423e-01,
1.1678e-01, 2.2812e-01, 1.8726e-01, 7.0697e-02]])
manual grad : tensor([[1.8779e-01, 1.2162e-01, 1.8585e-04, 1.9439e-01, 5.5930e-02, 1.8423e-01,
1.1678e-01, 2.2812e-01, 1.8726e-01, 7.0697e-02]])
all close : True
diff max : 0.0
diff mean : 0.0
=========================
When to use Numerical Approach?
추가로 DL을 할 때는 그럼 finite difference method은 쓸 일이 아예 없을까?에 대해 생각하는 사람이 있을 수 있다. Bishop의 PRML에는 검증하는 데 쓰인다고 하니 참고차 알아두기만 하면 좋을 것 같다.
 Fig. PRML p.246
Fig. PRML p.246
"Yes you should understand backprop" from Andrej Karpathy
'왜 Error Backpropagation을 잘 이해해야할까?'
사실 여기까지 post를 읽는 사람 중에 error backprop을 처음 본 사람은 거의 없을 것이다. 대다수의 독자들은 ‘음, 그래 나도 체인룰로 편미분을 계산하는 건 알고 있었어, 그래서 뭐?’ 라고 할 것이다. 사실 나도 그렇다. ‘나는 빨리 model을 학습하고 싶지 이런 detail까지 알고싶은건 아니야, 어차피 pytorch가 다 해주잖아?’라고 생각하기도 했다.
하지만 2022년 현재 미친 주가를 달리고 있는 Tesla 의 Computer Vision Team Leader 이자 박사과정 때도 스탠포드의 cs231n 강의의 조교로 유명했던 Andrej Karpathy는 본인이 작성한 blog post에서 backprop을 심도 깊게 이해하고,
또 직접 코드로 짜볼 필요성에 대해 역설했다.
요약하자면 open source framework가 자동 미분 (Autograd)을 다 해주는 시대에 단순히 지적 호기심 때문만이 아니라 backprop을 제대로 이해해야 NN을 만들 때 더 효율적이게 만들 수 있으며 debugging도 효율적으로 할 수 있기 때문이라는 것이다.
If you try to ignore how it works under the hood
because “TensorFlow automagically makes my networks learn”,
you will not be ready to wrestle with the dangers it presents,
and you will be much less effective at building and debugging neural networks.
- Andrej Karpathy
사실 Karpathy가 이 글을 투고한 이유는 어떤 한 구현체때문이라고 한다. 2014 DeepMind가 사람 수준의 video game 을 play하는 agent를 학습한 데 쓰인 Deep Q Learning (DQN)을 세상에 발표했다. Karpathy는 carpedm20 으로 유명한 김태훈님의 DQN 구현체의 특정 부분에 문제점을 지적했었다. 아래의 code가 그것인데 무엇이 문제인지 알겠는가?
self.delta = self.target_q_t - q_acted
self.clipped_delta = tf.clip_by_value(self.delta, self.min_delta, self.max_delta, name='clipped_delta')
self.global_step = tf.Variable(0, trainable=False)
self.loss = tf.reduce_mean(tf.square(self.clipped_delta), name='loss')
DQN algorithm을 지금 설명하는 것은 적절치 않으니 넘어가고, 요지는 DQN이 Q값을 계산하고 이를 target Q라는 값과 계산해서 differnce를 계산한 뒤 clipping을 하고 있다는 것이다. Q값은 NN이 출력한 scalar값이고 target과의 차이에 4번째 줄의 제곱을 계산하면 이는 regression을 한다는 것으로 충분히 설명을 할 수 있을 것이다.
\[\parallel Q - Q_{\text{targ}}\parallel^2\]Karpathy는 여기서 min, max 범위를 지나가면 값이 0이 되어 gradient 계산이 안될거라고 지적했다. 그래서 저자가 의도했을지도 모르지만 이 방법은 일반적인 것은 아니기 때문에 아래처럼 고치면 어떻겠냐는게 것이 그의 주장이었다. (Huber Loss 참고)
def clipped_error(x):
return tf.select(tf.abs(x) < 1.0, 0.5 * tf.square(x), tf.abs(x) - 0.5) # condition, true, false
즉 gradient가 흐르는 operation이냐 아니냐? 혹은 쉽게 gradient가 0이 되도록 code를 작성했는가? 등 backprop을 자세히 모르면 어디가 잘못돼서 내 model이 잘 학습이 안되는지 단서를 찾을 수가 없는 것이다. 이러면 debugging에만 한 세월 걸리거나 최악의 경우 project 자체를 포기해버릴 수도 있다.
Karpathy가 지적한 내용은 몇 가지가 더 있는데, 예를 들어 아래와 같은 1층짜리 NN layer를 만들었다고 쳐보자. (앞서 계속 내가 썼던 example이 사실은 karpathy 꺼였다.)
z = 1/(1 + np.exp(-np.dot(W, x))) # forward pass
dx = np.dot(W.T, z*(1-z)) # backward pass: local gradient for x
dW = np.outer(z*(1-z), x) # backward pass: local gradient for W
만약 weight matrix, \(W\)를 random initialization 했는데 너무 큰 값이 할당돼서 weight matrix와 input을 곱한 값이 \(-400 \sim 400\)사이로 떨어졌다고 치자. 그러면 \(z\)값은 대부분 \(0\) or \(1\)이 나올 것이고. 이런 경우 sigmoid output의 local gradient 인 \(z(1-z)\)는 0이나 다름 없는 값이 나온다. 이럴 경우 NN은 아예 학습이 안된다.
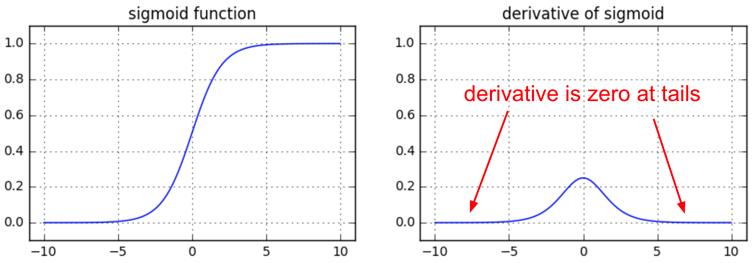 Fig. sigmoid의 미분체는 무조건 0보다 작고 0인 부분이 많다.
Fig. sigmoid의 미분체는 무조건 0보다 작고 0인 부분이 많다.
앞서 ReLU같은걸 쓰면 해결이 될 수 있다고 했으나 ReLU도 완벽한 해결책은 아닐 수 있다. 왜냐하면 아래 figure처럼 ReLU가 0보다 큰 activation 값에 대해서는 미분값이 1로 gradient를 정상적으로 흘려주지만 0 이하인 경우는 gradient가 0이되어 해당 neuron이 영원히 update되지 않는 dead ReLU 문제를 가지고 있기 때문이다. 이는 NN을 학습하다보면 흔히 발생하는 문제 중 하나라고 한다.
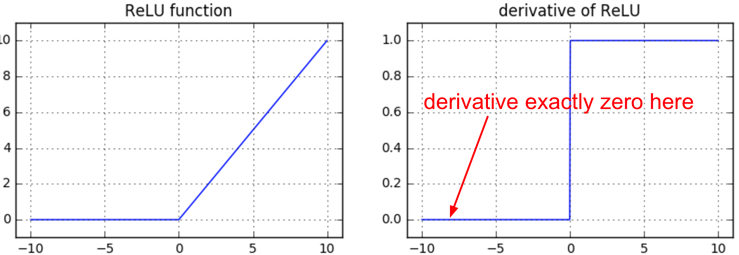 Fig. Gradient Vanishing, Exploding 문제를 해결하기 위해 sigmoid 대신 ReLU를 쓰는 방법도 있지만, 이는 근본적인 해결책은 아니다.
Fig. Gradient Vanishing, Exploding 문제를 해결하기 위해 sigmoid 대신 ReLU를 쓰는 방법도 있지만, 이는 근본적인 해결책은 아니다.
또한 init을 문제없이 해줘도 여러 문제가 생길 수 있는것이, NN의 layer가 많아질수록 chain rule로 곱해지는 횟수가 증가하는데 1보다 작은 gradient들이 누적되면 결국 layer의 앞부분은 gradient가 0이 되면서 학습이 안되게 된다. 혹은 1보다 큰 수가 계속 곱해져도 문제인데, 바로 이런 문제들이 DL을 하면 누구나 들어봤을 법한 grdaident exploding, vanishing이다.
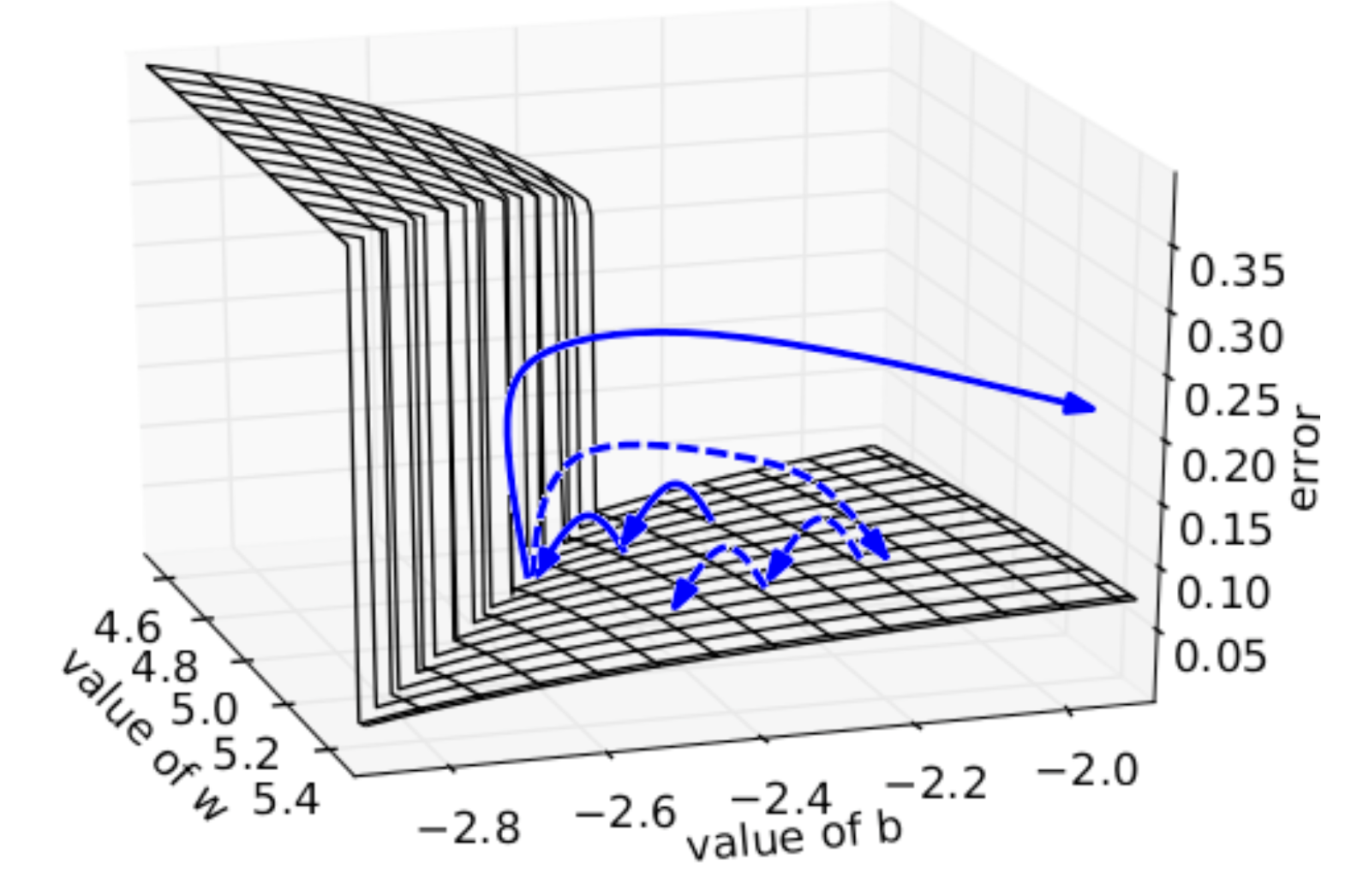 Fig. Gradient Exploding. 일정 theshold를 넘어서는 gradient는 rescaling 해준 결과 (dotted line) 발산하지 않는다.
Fig. Gradient Exploding. 일정 theshold를 넘어서는 gradient는 rescaling 해준 결과 (dotted line) 발산하지 않는다.
이런 상황에서 researcher들이 backprop을 제대로 이해하지 못했다면 He init, Gradient Clipping, ReLU 같은 solution들은 아마 나오지 않았을 것이고 DL의 발전속도는 줄어들었을 것이다.
사실 내가 이 post를 다시 작성하게 된 이유도 debugging 때문이었다.
나는 mixed precision으로 transformer를 학습하던 중 NaN (Not a Number)이나 -inf같은 model이 표현할 수 있는 값을 넘어서기 때문에 발생하는 문제에 직면했었다 (당연히 학습이 안된다).
물론 이는 흔한 일이긴하다.
단순히 random seed를 바꿔 돌리는 soltuion을 쓰는 사람들도 있지만 이는 물 떠놓고 기도하는 것이나 다름이 없다.
문제를 해결하기 위해서는 내 model이 어떤 연산들로 이루어져있고? (self-attention 등) 어떤 weight distribution이나 activation distribution을 갖고있고 학습이 진행되면서 이들이 어떻게 변하는지 등 chain rule로 gradient를 계산하는 backprop을 중심으로 여러가지를 확인해 봐야 근본적인 solution을 제시할 수 있다.
- 0으로 tensor값들을 나눈다거나 (
nan) - 너무 크거나 작은 값을 torch.exp, torch.log 등의 연산을 취해준다던가 (
-inf) - fp16으로 학습하는데 \(\frac{(q^T \cdot k)}{\sqrt{d_{model}}}\)인 self-attention 연산이 fp16 범위를 넘어가 버린다던가
- (이럴 경우 \(\frac{(q^T)}{\sqrt{d_{model}}}\) 을 먼저 계산한 뒤에 \(k\) 를 곱하는 식으로 해결 가능)
- self-attention 의 padding mask 가
-inf인데 fp16을 쓰는 경우 attention score와 더해져nan을 리턴한다던가 - forward 과정에선 멀쩡했지만 backward 과정에서
nan이 발생한다던가.( torch.norm, torch.sqrt 연산을 쓸 때 연산자 안의 값이 0 이되면 빈번하게 발생한다는 것 같다.)
추가적으로 이런 backpropagation을 유도해보는 것이 algorithm을 더 효율적으로 design할 수 있게 해주는데, 일례로 DL을 하는 사람이라면 지금은 꽤 주목을 받아 모르는 사람이 없을 Low Rank Adaptation (LoRA)라는 method가 있다. LoRA는 대표적인 Parameter Efficient Fine-Tuning (PEFT) method인데 paper에 직접적으로 언급이 되지 않아 모르는 사람이 많지만 memory efficient backpropgation을 하기 위해 구현에 신경을 쓴 부분이 있다. (이는 나중에 다른 post에서 자세히 다루도록 하겠다)
Jacobian and Hessian
마지막으로 Hessian Matrix에 대한 이야기다. 여태까지 우리는 gradient, jacobian에 대해 다뤘다. Jacobian은 vector나 tensor간의 입출력 관계를 나타내는 함수를 1번 미분한 것이었다. 그런데 경우에 따라 2번 미분한 matrix를 필요로 하기도 하는데, 이를 Hessian Matrix이라고 부른다. PRML에 따르면 몇 가지 이유에서 Hessian을 쓸 수 있다고 한다.
- 1.일부 optimization algorithm 들에서는 Hessian 쓴다.
- e.g. Newton’s Method
- 2.Network의 weight들 중 결과에 별로 중요한 영향을 끼치지 않는 값들은 쳐내는 pruning이라는 작업에 사용된다.
- 정확히는 Hessian의 역행렬을 쓴다고 한다.
- 3.Training data에 적은 변화가 생겼을 경우에 빠르게 network를 재훈련 하는 과정에 사용된다.
- 4.Bayesian NN에서 사용되는 Laplace Approximation을 할 때 쓰인다.
- 추가) 5.Objective function의 곡률을 측정하기 위해 Hessian이 사용된다.
- Hessian의 expectation을 Fisher Information Matrix라고 하는데 TRPO같은 advanced Reinforcement Learning (RL) algorithm의 핵심으로 사용된다.
사실 Hessian을 구하는 것 자체가 computational cost가 너무 크기 때문에 modern DL era는 거의 쓰이지 않는다. 1번의 Newton’s method는 실제로 쓰는 사람을 필자는 본 적이 없을 정도이다. 다만 5번의 경우 modern Reinforcement Learning (RL) algorithm인 TRPO같은 데서도 쓰는데, 이는 나중에 기회가 되면 따로 다뤄보도록 하겠다.
References
- Lectures
- cs231n Winter 2016, Lecture 4, Backpropagation, Neural Networks
- cs182 Lecture 5, Part 2, Backpropagation
- cs231n Lecture 4: Neural Networks and Backpropagation
- Backpropagation from Justin Johnson
- Lecture 2: Backpropagation - Peter Bloem
- Machine Learning 9 - Backpropagation from Stanford CS221: AI (Autumn 2021)
- Book and Papers
- Others (Blogs)
- Yes you should understand backprop (Medium)
- Hacker’s guide to Neural Networks
- Backpropagation through a fully-connected layer from Eli Bendersky
- Understanding the backward pass through Batch Normalization Layer
- Recurrent Neural Networks Tutorial, Part 3 – Backpropagation Through Time and Vanishing Gradients from Denny
- Learning with Backpropagation from Yani Ioannou
- Fisher Information from Hohyun Kim