(WIP) Regression (4/7) - Kernelization and Gaussian processes
11 Mar 2021< 목차 >
- Recap
- Bayesian Non-Linear Regression
- Two Different Ways to Explain Gaussian Process (GP)
- GP Explanation (1)
- Bayesian Linear Regression (BLR) vs GP
- GP Regression as Bayesian Inference
- GP Prior
- Gaussian Mean Function
- (Gaussian) Covariance Funtion
- Amplitude Parameter & Length-Scale Parameter
- (Gaussian) Likelihood
- Marginal Likelihood
- GP Posterior
- Sampling from the GP Prior
- GP Prediction (Posterior)
- Sanity Check
- Illustration: Inference with Gaussian Processes
- GP Explanation (2)
- 2D Gaussian Example
- 2D Gaussian Example : Conditional Probability
- 2D Gaussian Example : New Representation
- Higher Dimension : 5D Gaussian
- Higher Dimension : 20D Gaussian
- GP is Non-Parametric Model (vs Parametric Model)
- Mathematical Foundations, Definition
- GP for Regression
- Marginalisation
- GP's Prediction (vs Parametric Model's Prediction)
- GP's Limitation
- References
이번 글에서 다루고 싶은 내용은 아래의 그림에서 가우시안 과정 (Gaussian Process; GP) Regression 으로,
회귀 곡선을 예측할 때 비 선형성 (non-linearity)를 추가하고 여기에 베이지안 추론 (bayesian inference)을 합치는 것이다.
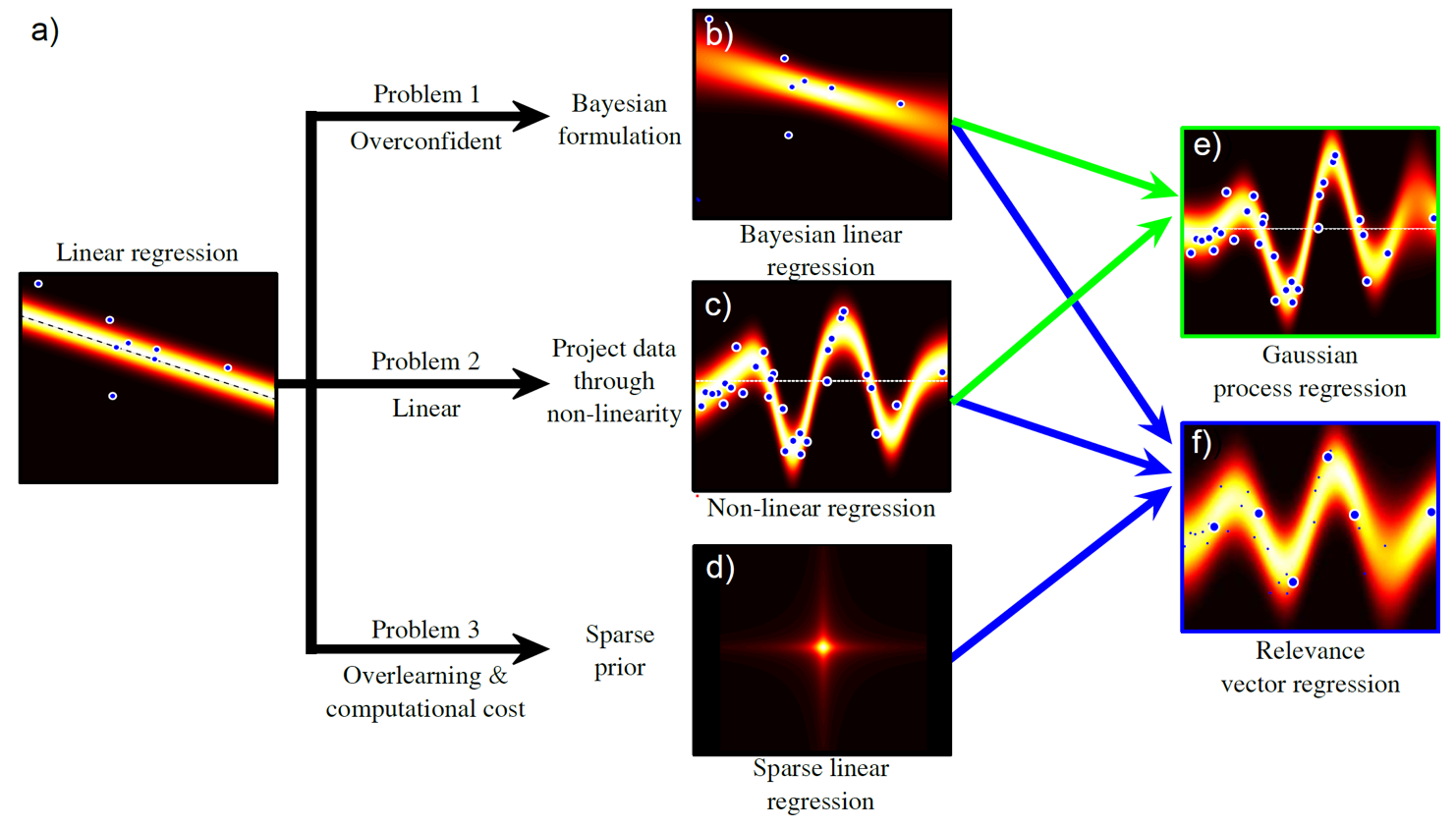 Fig.
Fig.
Recap
Bayeisan Linear Regression
이전의 linear regression에 대해서 recap 해보자. 다음과 같이 Likelihood 와 Prior 를 둘 다 gaussian으로 정의했다고 치자.
- Likelihood : \(Pr (w \vert X, \phi) = Norm_w [X^T \phi \sigma^2 I]\)
- Prior : \(Pr(\phi) = Norm_w[0, \alpha_p^2 I]\)
- Posterior (using Bayes’ Rule) : \(Pr(\phi \vert X,w) = \frac{ Pr(w \vert X,\phi) Pr(\phi) }{ Pr(w \vert X) }\)
Posterior 는 gaussian distribution 두개의 곱으로 표현된 것이나 다름 없으니, 아래 처럼 나타낼 수 있다.
\[\begin{aligned} & \text{Posterior} \sim \text{Likelihood} \times \text{Prior} \\ & Pr(\phi \vert X,w) = Norm_{\phi} [ \frac{1}{\sigma^2} A^{-1} X w, A^{-1} ] \\ & \text{where } A = \frac{1}{\sigma^2} XX^T + \frac{1}{\sigma^2_p} I \\ \end{aligned}\]즉 우리는 Maximum Likelihood Estimation (MLE)에 추가적으로 \(\phi\) 라는 parameter, ‘gaussian distribution의 mean을 나타내는 \(\mu\) 값이 어떤 값일 확률이 몇이다’ 라는 parameter space 상의 사전 정보를 probabilistic distribution을 같이 modeling 한 것이다.
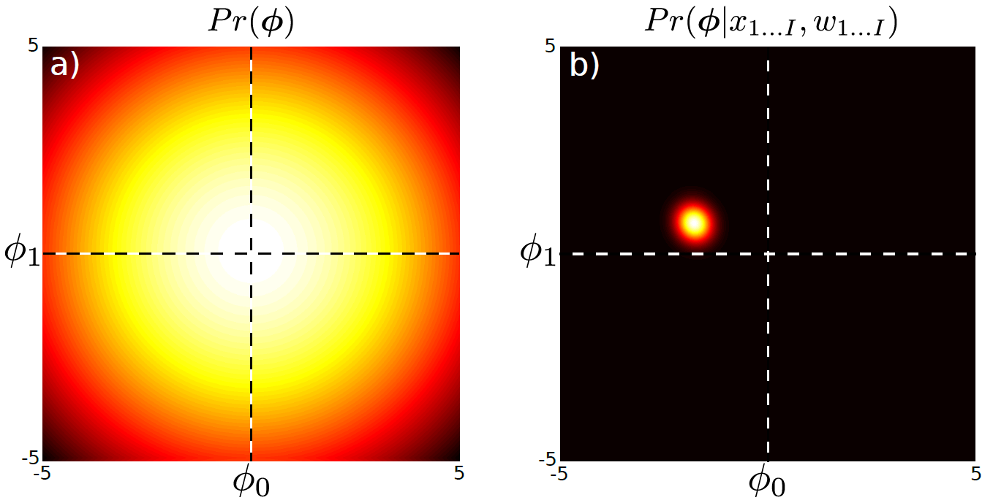 Fig. Prior는 Parameter 를 distribution으로 나타낸 것 (왼쪽) 이고 여기에 data 의 likelihood을 추가한 posterior는 오른쪽과 같이 생겼다.
Fig. Prior는 Parameter 를 distribution으로 나타낸 것 (왼쪽) 이고 여기에 data 의 likelihood을 추가한 posterior는 오른쪽과 같이 생겼다.
Bayesian Approach 가 이처럼 posterior를 modeling하지만,
Maximum A Posteriori (MAP)는 MLE처럼 여전히 posterior를 maximize하는 parameter 하나만을 찾는데 (즉 point estimation 함)
Bayesian Inference는 test sample, \(x\) 가 들어왔을 때 Posterior 를 fitting한 뒤에 Max 가 되는 값 하나만으로 추론결과를 내는 것이 아니라 parameter space 상의 가능한 모든 parameter를 사용해 target distribution을 그리고, 이를 weighted sum 한다.
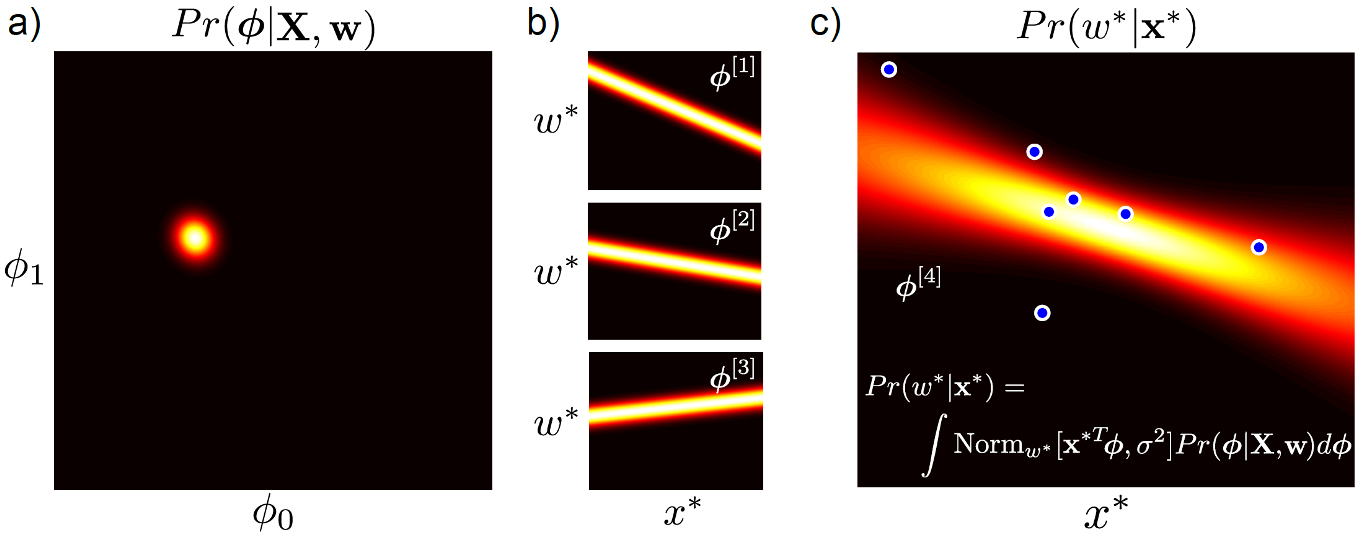 Fig.
Fig.
즉 실체 inference result인 bayesian regession curve를 얻기 위해서는 모든 parameter를 고려해야 하므로 적분을 해야한다.
\[\begin{aligned} & Pr(w^{\ast}|x^{\ast},X,w) = \int Pr(w^{\ast} \vert x^{\ast}, \phi) Pr(\phi \vert X, w) d\phi \\ & = \int Norm_{w^{\ast}}[\phi^T x^{\ast},\sigma^2] Norm_{\phi}[\frac{1}{\sigma^2} A^{-1}Xw, A^{-1}] d\phi \\ & = Norm_{w^{\ast}}[\frac{1}{\sigma^2}x^{\ast T}A^{-1}Xw,x^{\ast T}A^{-1}x^{\ast} + \sigma^2] \\ & \text{where } \space A = \frac{1}{\sigma^2} XX^T + \frac{1}{\sigma_p^2}I \\ \end{aligned}\]위의 수식을 정리하면 아래와 같은데 (이전 post 참고),
\[Pr(w^{\ast} \vert x^{\ast}, X, W) = Norm_w[ \frac{\sigma_p^2}{\sigma^2} x^{\ast T} X w - \frac{\sigma_p^2}{\sigma^2} x^{\ast T} X (X^TX + \frac{\sigma^2}{\sigma_p^2} I)^{-1} X^TXw, \\ \space \sigma_p^2 x^{\ast T} x^{\ast} - \sigma_p^2 x^{\ast T} X (X^TX + \frac{\sigma^2}{\sigma_p^2} I)^{-1} X^T x^{\ast} + \sigma^2 ]\]자세히 보면 수식에 모델 파라메터 \(phi\) 는 아예 없어진 걸 볼 수 있고, variance term인 \(\sigma, \sigma_p\) 만 존재한다. 여기서 \(\sigma_p\) 는 상수이니까 \(\sigma\) 만 찾아내면 되는데, 이를 위해 optimization 해야 할 수식은 아래와 같다.
\[\begin{aligned} & Pr(w \vert X, \sigma^2) = \int Pr(w \vert X, \phi, \sigma^2) Pr(\phi) d \phi & \\ & = \int Norm_w [X^T \phi, \sigma^2 I] Norm_{\phi}[0,\sigma^2_p I] d\phi & \\ & = Norm_w [0, \sigma^2_p X^T X + \sigma^2 I] & \\ \end{aligned}\]즉 MAP를 통해 posterior를 가장 크게 해주는 variance까지 찾았으면, 매 test input이 들어올 때 마다 적분을 해주면 된다.
Non-Linear Regression
Non-Linear Regression 을 하기 위해서는 아래의 그림처럼 먼저 Non-Linear Function을 사용해 x 를 다른 high dim space로 mapping 해야 한다.
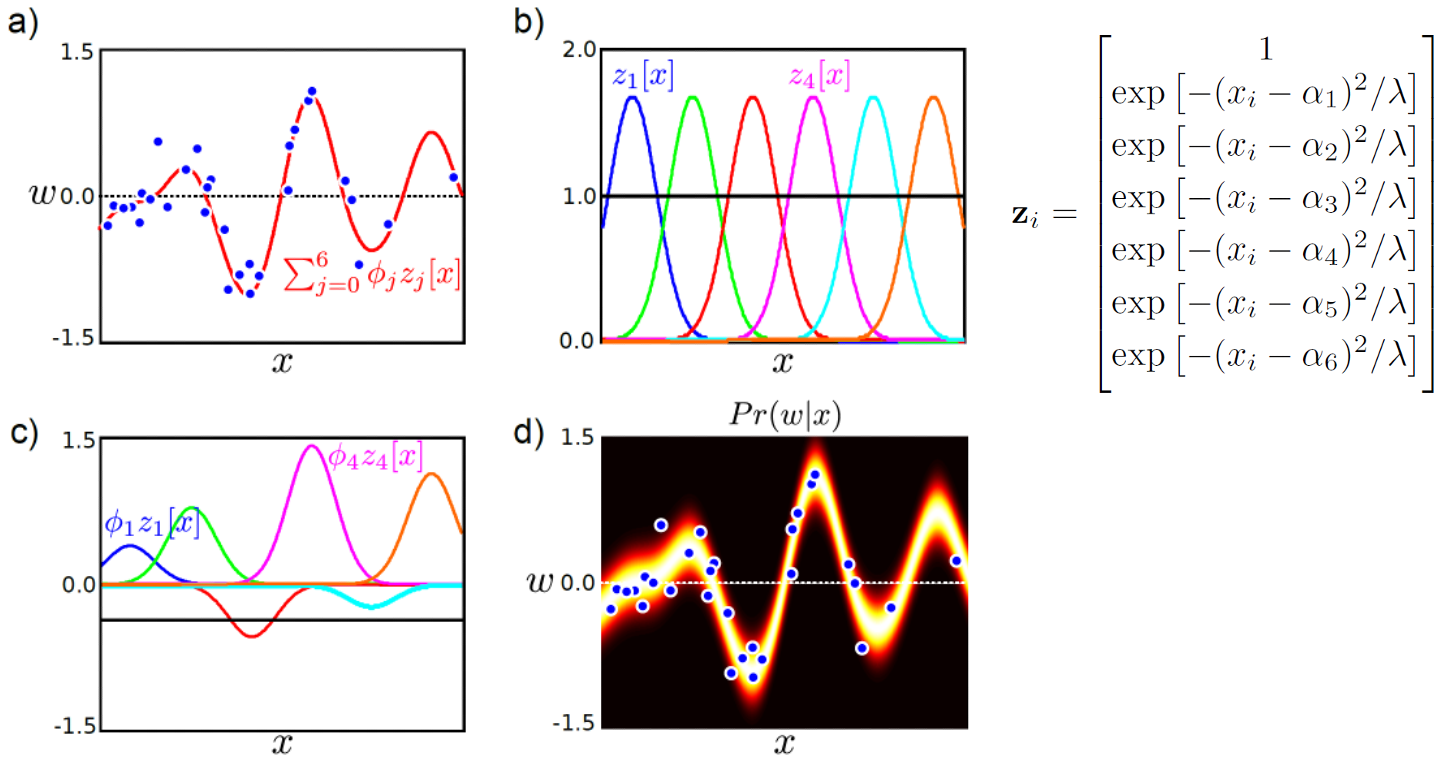 Fig.
Fig.
문제가 복잡해질 것 같지만 원래의 likelihood를,
\[Pr(w_i \vert x_i, \theta) = Norm_{w_i}[\theta^T x_i, \sigma^2]\]아래처럼 변형시키고 문제를 풀면 된다 (이전 post 참조).
\[\begin{aligned} & Pr(w_i \vert \color{red}{z_i}, \theta) = Norm_{w_i}[\theta^T \color{red}{z_i}, \sigma^2] \\ & \text{where } \space \color{red}{z_i} = f[x_i] \\ \end{aligned}\]Bayesian Non-Linear Regression
이제 위의 두 가지, non-linearity 와 bayesian approach를 합쳐보자. 새로운 data point 인 \(z^{\ast}\)가 test-time 에 들어왔을 때 label w 의 distribution는 어떻게 될까.
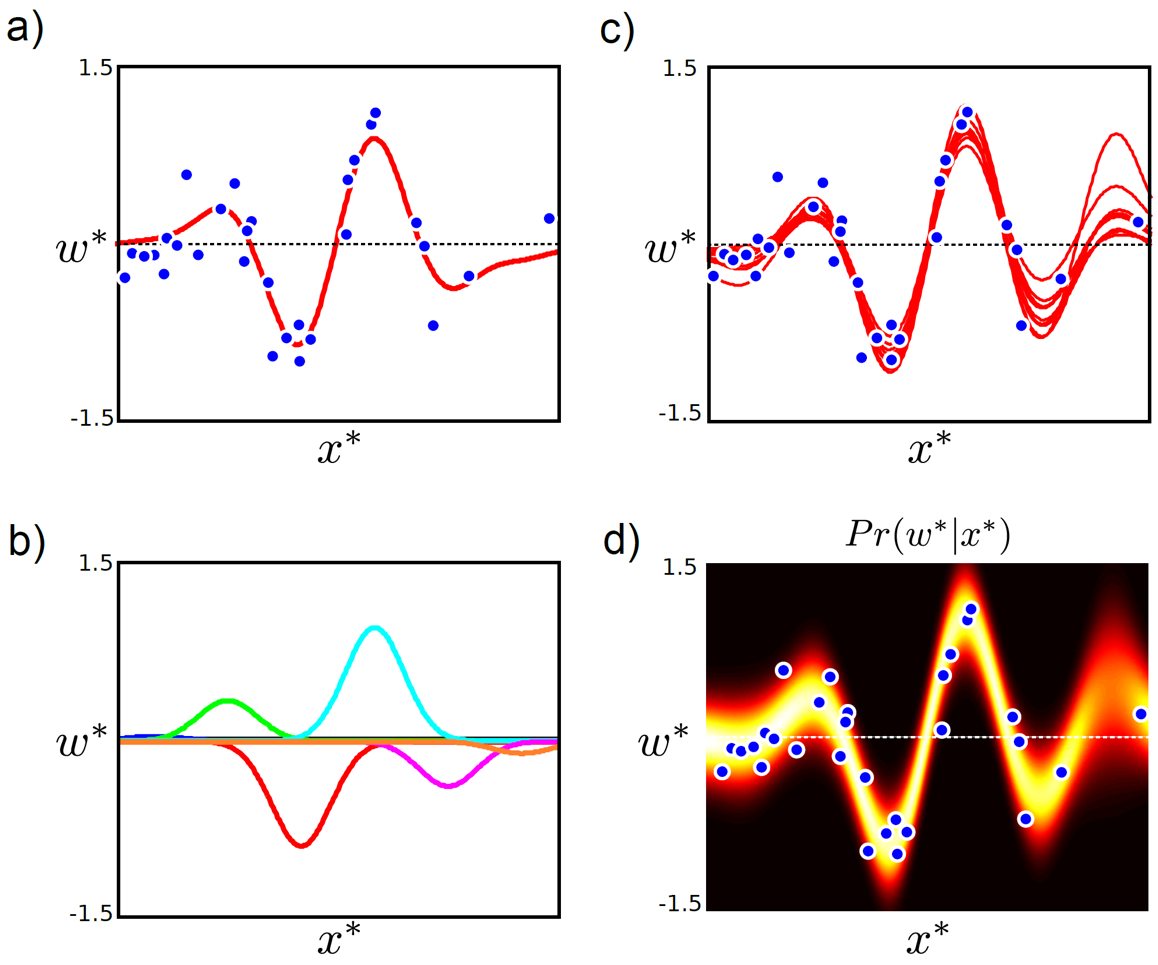 Fig.
Fig.
이 두 가지를 합치면 inference시 test data의 output label에 대한 distribution을 아래의 수식처럼 얻을 수 있다.
\[Pr(w^{\ast} \vert z^{\ast}, X, W) = Norm_w[ \frac{\sigma_p^2}{\sigma^2} z^{\ast T} Z w - \frac{\sigma_p^2}{\sigma^2} z^{\ast T} Z (Z^TZ + \frac{\sigma^2}{\sigma_p^2} I)^{-1} Z^TZw, \\ \sigma_p^2 z^{\ast T} z^{\ast} - \sigma_p^2 z^{\ast T} Z (Z^TZ + \frac{\sigma^2}{\sigma_p^2} I)^{-1} Z^T z^{\ast} + \sigma^2 ]\]근데 여기서 불편한 게 있다. 왜냐하면 원래도 \(X\)라는 input data matrix와 이것을 Transpose 한 \(X^T\) 를 연산하는게 여간 쉬운일이 아니었는데, 여기에 \(z = f(x)\)라는 non linear function까지 적용하려니 상당히 부담스럽기 때문이다. 어떻게 해결할 수 있을까?
이것이 지금부터 알아보게 될 가우시안 과정 (Gaussian Process; GP)의 핵심인 커널화 (Kernelization)라는 개념이다.
Kernelization
지금 중요한 점은 아래의 수식에서 data 그 자체는 필요하지 않고 data sample들 간의 관계를 의미하는 term인 \(z_iT^ z_j\) 라는 것이다.
즉 dot product (inner product)을 하므로 data간의 유사도 (similarity)를 측정한다는 것이다.
만약 data point가 100개면 100개끼리 dot product를 한 결과를 얻으면 된다. 그런데 우리는 \(x\)가 아니라,
\[X X^T = \begin{pmatrix} x_1 \cdot x_1 && x_1 \cdot x_2 && x_1 \cdot x_3 && \cdots && x_1 \cdot x_N \\ x_2 \cdot x_1 && x_2 \cdot x_2 && x_1 \cdot x_3 && \cdots && x_2 \cdot x_N \\ \vdots && \vdots && \ddots && \vdots \\ x_{N-1} \cdot x_1 && x_{N-1} \cdot x_2 && x_{N-1} \cdot x_3 && \cdots && x_{N-1} \cdot x_N \\ x_N \cdot x_1 && x_N \cdot x_2 && x_N \cdot x_3 && \cdots && x_N \cdot x_N \\ \end{pmatrix}\]이를 변형한 \(z\)간의 dot product를 쓰고 있다.
\[Z Z^T = \begin{pmatrix} z_1 \cdot z_1 && z_1 \cdot z_2 && z_1 \cdot z_3 && \cdots && z_1 \cdot z_N \\ z_2 \cdot z_1 && z_2 \cdot z_2 && z_1 \cdot z_3 && \cdots && z_2 \cdot z_N \\ \vdots && \vdots && \ddots && \vdots \\ z_{N-1} \cdot z_1 && z_{N-1} \cdot z_2 && z_{N-1} \cdot z_3 && \cdots && z_{N-1} \cdot z_N \\ z_N \cdot z_1 && z_N \cdot z_2 && z_N \cdot z_3 && \cdots && z_N \cdot z_N \\ \end{pmatrix}\]만약 아래와 같은 function을 썼다면,

우리는 input data를 아래 처럼 변형해야 하는데, 이는 많은 연산 비용을 요구할 것이다.
\[z_i = \left[ \begin{matrix} 1 \\ z_1[x_i] \\ z_2[x_i] \\ z_3[x_i] \\ z_4[x_i] \\ z_5[x_i] \\ z_6[x_i] \\ \end{matrix} \right] = \left[ \begin{matrix} 1 \\ \exp[-(x_i - \alpha_1)^2 / \lambda] \\ \exp[-(x_i - \alpha_2)^2 / \lambda] \\ \exp[-(x_i - \alpha_3)^2 / \lambda] \\ \exp[-(x_i - \alpha_4)^2 / \lambda] \\ \exp[-(x_i - \alpha_5)^2 / \lambda] \\ \exp[-(x_i - \alpha_6)^2 / \lambda] \\ \end{matrix} \right]\]근데 이 과정을 생략하면 안되는 걸까 하는 생각이 들 수 있다. 혹시 \(x\)끼리 비교하면 안될까?
어쩌면 data간의 관계를 잘 정의하기만 하면 우리가 어떤 함수를 통해 x 를 z 로 변환시켰는지 명시적으로 알 필요는 없지 않을까?
즉 어떤 function, \(z=f[x]\)에 대해서는 similarity를 재기 위해 \(z\)까지 갈 필요가 없다는 건데, 어떤 function이 이를 만족할까?
이 idea가 바로 커널화 (Kernelization)이다.
Kernelization의 장점은 어떤 \(x\)가 어떠한 기저 함수 (basis function)를 타고 \(z\) 로 mapping이 되는지 명시적으로 (\explicit) 하게 정하지 않아도 되고,
심지어 low dimensional의 data (원래 2차원 이라고 생각) \(x\)가 우리가 정의한 커널 함수를 통해 암시적 (implicit) 으로 알게된 어떠한 기저 함수 (basis function)를 통해 매우 높거나 (10차원) 혹은 심지어 무한 차원 (infinite dimension)의 \(z\)로 mapping이 될 수도 있다는 것이다.
원 data를 무한 차원으로 mappin하여 dot product을 취한 값을 알 수 있는 것이다.
이럴 경우 우리는 원래의 수식을 아래와 같이 바꿀 수 있다.
- Before
- After
여기서 \(\color{red}{K}[X,X]\)는 dot product한 data들의 값을 나타내는 matrix이며 \((i,j)\) 번째 element는 \(k[x_i,x_j]\)에 대한 것이다.
\[k[X,X] = \begin{pmatrix} k[x_1,x_1] & \cdots & k[x_1,x_n] \\ \vdots & \ddots & \vdots \\ k[x_n,x_1] & \cdots & k[x_n,x_n] \end{pmatrix}\]만약에 우리가 학습 data를 100개 가지고 있으면 \(K[X,X]\) 는 100x100 차원을 갖게 된다.
What is Kernel and Why it works?
왜 이게 되는걸까? 우리가 2차원 input data \(x \in \mathbb{R}^2\) 를 가지고 있다고 생각해 보자. 이제 이 data를 3차원으로 mapping 시켜주는 어떤 function이 존재한다고 하자.
\[\begin{aligned} & z = f (x) \\ & \begin{pmatrix} x_1^2 \\ \sqrt{2} x_1x_2 \\ x_2^2 \end{pmatrix} = f ( \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} ) \\ \end{aligned}\]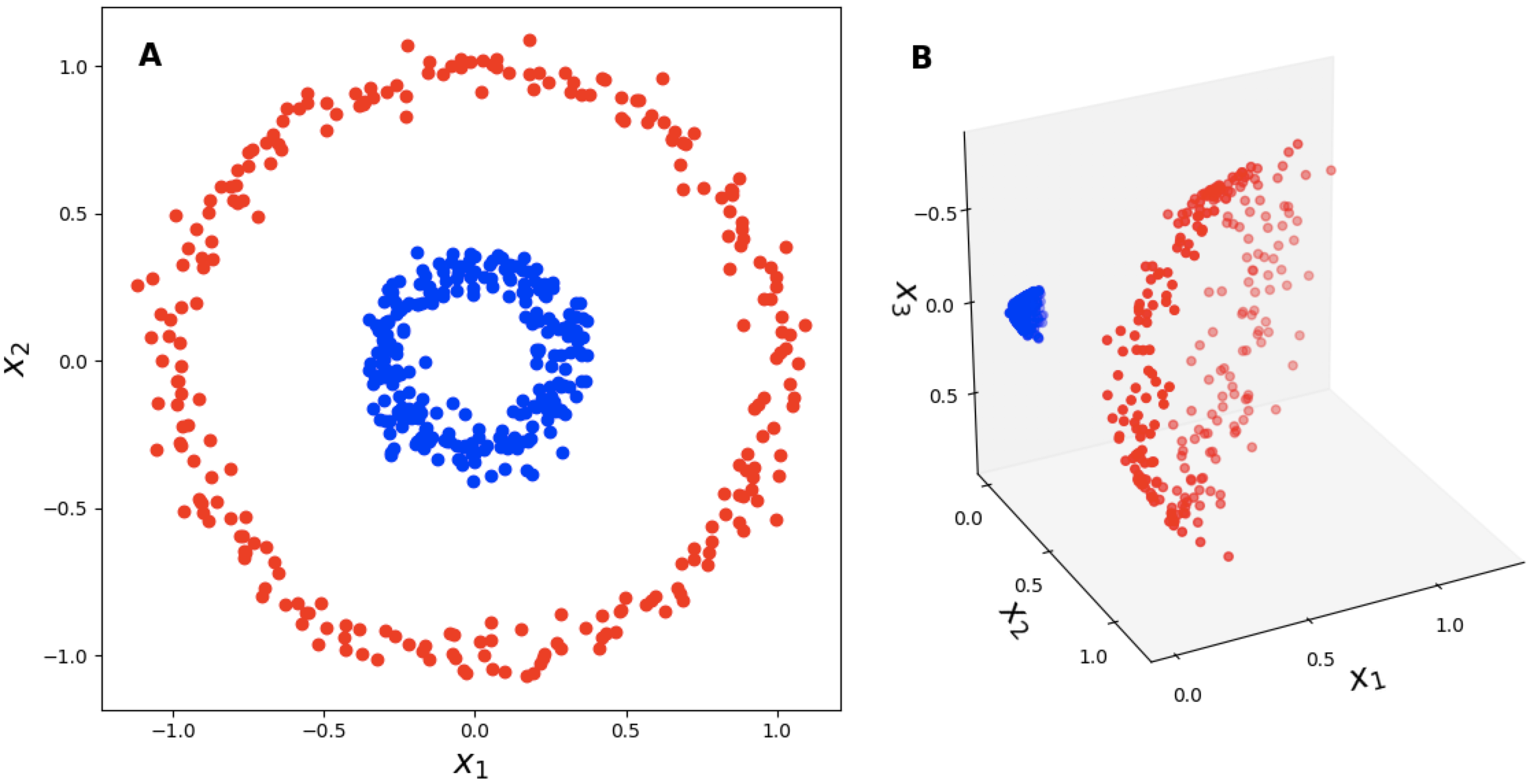 Fig. 2d to 3d. Source from link
Fig. 2d to 3d. Source from link
이제 차원이 추가된 어떤 두 개 data point 간 dot product을 구해보자.
\[\begin{aligned} & f(x_1) \cdot f(x_2) = \begin{pmatrix} x_{11}^2 \\ \sqrt{2} x_{11}x_{12} \\ x_{12}^2 \end{pmatrix} \cdot \begin{pmatrix} x_{21}^2 \\ \sqrt{2} x_{21}x_{22} \\ x_{22}^2 \end{pmatrix} = x_{11}^2x_{21}^2 + 2 x_{11} x_{21} x_{12} x_{22} + x_{12}^2 x_{22}^2 \\ & = (x_{11} x_{21} + x_{12} x_{22})^2 = (x_1^T \cdot x_2)^2 \\ \end{aligned}\]우리는 수식에서 2차원을 3차원으로 mapping해서 dot product해도 그냥 원래 2차원 data를 dot product해서 제곱을 하는것에 지나지 않으니, 굳이 우리가 \(f\)로 갔다가 dot product을 할 필요가 없다는 사실을 알게 된다.
\[k[x_i,x_j] = x_i^T x_j\]이 커널을 Polynomial Kernel, \(k_{poly}[x_i,x_j]\) 이라고 부른다.
이제 또 다른 커널을 보자. 어떤 커널은 아래와 같이 생겼는데,
\[k[x_i,x_j] = \exp [ - 0.5 ( \frac{ ( x_i - x_j)^T (x_i - x_j) }{ \lambda^2 } ) ]\]굉장히 gaussian distribution 같이 생겼음을 느낄 수 있다. Mean 이 \(x_i\) 고 퍼진 정도를 나타내는 variance가 \(\lambda^2\) 인 gaussian 이다. 이번에는 역으로 이 커널이 어떤 mapping function f 를 사용한 것인지 알아보자.
\[\begin{aligned} & k[x, x'] = \exp ( - \frac{1}{2} \parallel ( x - x') \parallel^2 ) \\ & = \exp ( \frac{2}{2} x^T x' - \frac{1}{2} \parallel x \parallel^2 - \frac{1}{2} \parallel x' \parallel^2 ) \\ & = \exp (x^T x') \exp(-\frac{1}{2} \parallel x \parallel^2) \exp(-\frac{1}{2} \parallel x' \parallel^2 ) \\ \end{aligned}\]위의 수식에서 Taley Expansion 의 를 사용해 보자.
\[e^{f(x)} = \sum_{r=0}^{\infty} \frac{[f(x)]^r}{r!}\]그 결과 우리는 위의 kernel을 아래처럼 다시 쓸 수 있다.
\[k[x, x'] = \exp(-\frac{1}{2} \parallel x \parallel^2) \exp(-\frac{1}{2} \parallel x' \parallel^2 ) \sum_{r=0}^{\infty} \frac{(x^Tx')^r}{r!}\]여기서 익숙한 커널이 하나 보이는데, 바로 polynomial kernel 이다.
\[k[x, x'] = \exp(-\frac{1}{2} \parallel x \parallel^2) \exp(-\frac{1}{2} \parallel x' \parallel^2 ) \sum_{r=0}^{\infty} \frac{k_{poly(r)}[x,x']}{r!}\]여기서 \(r\) 이 증가할수록 polynomial kernel 은 data를 더욱 high dimension 변환한ㄷ. 즉 위의 kernel은 polynomial kernel 을 무한번 연산한 것과 같이 되며, 사실상 infinite dimension의 data로 mapping한 뒤 data간의 similarity를 계산하는 것이 된다.
근데 우리가 이 infinite dimension으로 변환할 function을 명시적 (\explicit)으로 알 필요는 전혀 없는 것이다.
이를 Radial Basis Function (RBF) Kernel 이라고 한다.
이런식으로 우리가 굳이 원래 차원의 data를 high dimension으로 변환 한 뒤 dot product을 쉽게 (cheap) 구하는 것을 Kernel Trick 이라고 하며,
이는 수학적으로 James Mercer 라는 수학자에 의해 증명되었다고 한다.
다만 아무거나 다 커널이 되는건 아니고 몇가지 조건이 충족 돼야 한다.
Some kinds of Kernels
대표적인 Kernel로는 아래와 같은 것들이 있다.
- Linear Kernel : \(k[x_i,x_j] = x_i^T x_j\)
- Degree p Polynomial Kernel : \(k[x_i,x_j] = ( x_i^T x_j + 1)^p\)
- Radial Basis Function (RBF) or Gaussian Kernel : \(k[x_i,x_j] = \exp [ - 0.5 ( \frac{ ( x_i - x_j)^T (x_i - x_j) }{ \lambda^2 } ) ]\)
만약 여기서 RBF Kernel 을 쓴다면 아래와 같은 결과를 얻을 수 있는데,
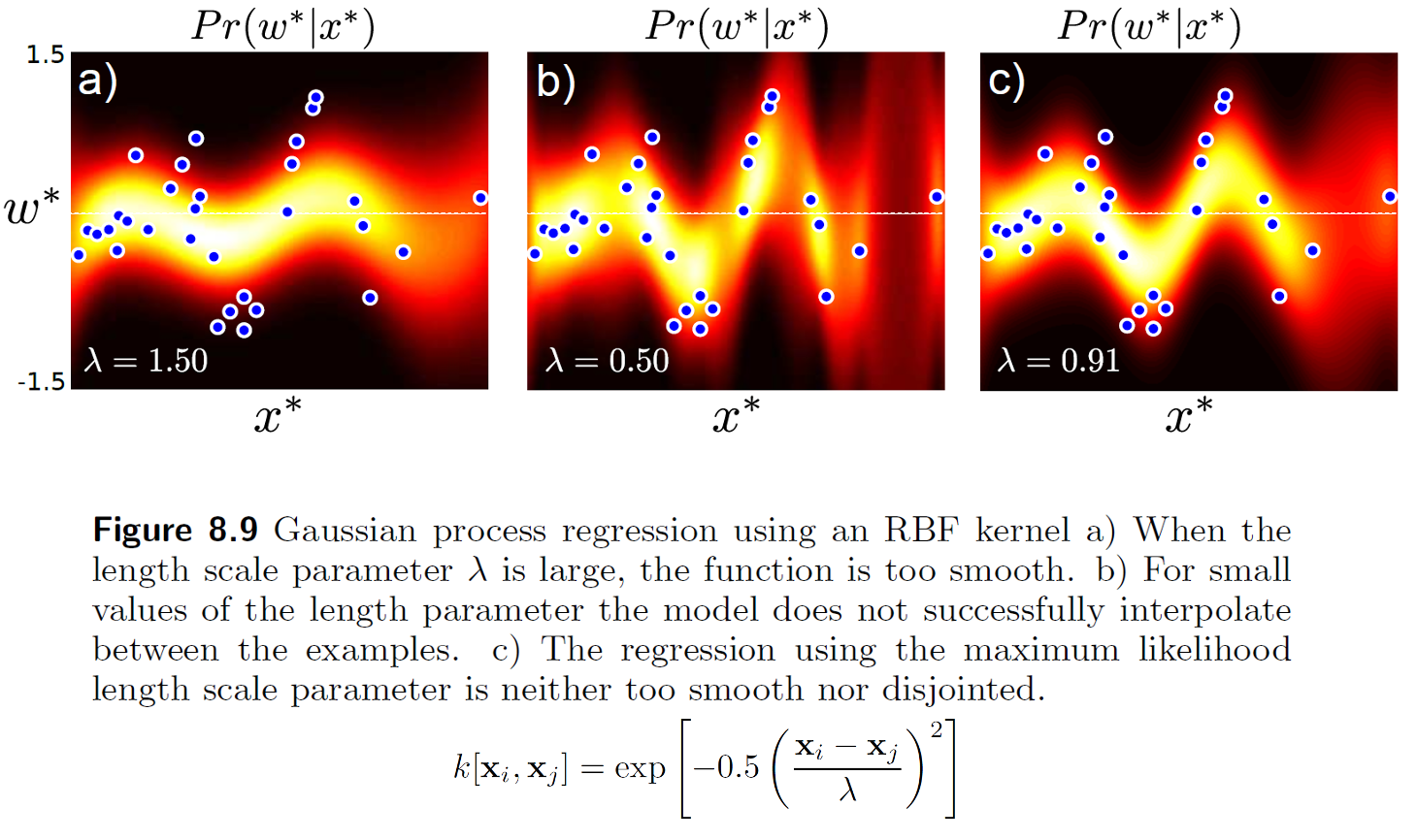 Fig.
Fig.
여기서 Kernel 의 파라메터 \(\lambda\) 는 함수의 smoothness 를 결정하며 (variance에 해당함), marginal likelihood (evidence) 를 최대화 하는 방향으로 파라메터를 학습할 수 있다.
\[\begin{aligned} & \hat{\lambda} = arg max_{\lambda} [ Pr(w \vert X, \sigma^2)] \\ & = arg max_{\lambda} [ \int Pr( w \vert X, \phi, \sigma^2) Pr(\phi) d \phi ] \\ & = arg max_{\lambda} [ Norm_w [0, \sigma_p^2 K[X,X] + \sigma^2 I] ] \\ \end{aligned}\]그리고 이는 gradient descent 등의 iterative optimization method로 학습할 수 있다.
이렇게 kernel trick 과 bayesian inference 를 결합해서 곡선을 그리는 model을 Gaussian Process Regression (GPR)이라고 부른다.
Two Different Ways to Explain Gaussian Process (GP)
이제 본격적으로 Gaussian Process (GP)에 대해서 알아보도록 하자. 이는 꽤 어려운 개념으로, 고전 ML의 거의 끝판왕이라고 할 수 있을 정도이다. 그래서 GP만 다루는 248 페이지 분량의 책이 따로 있을 정도이다.
 Fig. Gaussian Processes for Machine Learning
Fig. Gaussian Processes for Machine Learning
문헌 조사를 하다보면 결과 GP 를 설명하는 방법이 두 가지 정도 있음을 알 수 있다.
- Regression curve의 distribution 자체를 예측하는 것으로 설명하는 가장 기본적인 해석 방법
- 다변수 (multivariate) gaussian distribution를 새롭게 해석하는 방법으로 좀 더 직관적인 해석 방법
이 두 가지를 활용한 앞으로의 GP에 대한 내용은 DeepMind의 Chair 인 Marc Deisenroth가 UCL 에서 강의한 lecture 1과
 Fig. Lecture from Marc Deisenroth
Fig. Lecture from Marc Deisenroth
Richard Turner가 Imperial College 에서 강의한 lecture 2와 이를 옮겨 적은 Yuge Shi라는 phd student의 post를 참고해서 작성하였음을 알린다.
 Fig. Lecture from Richard Turner
Fig. Lecture from Richard Turner
GP Explanation (1)
먼저 첫 번째 관점으로 GP에 대해 생각해보자. (근데 GP로 Regression Classification 둘 다 할 수 있음에 주의하자)
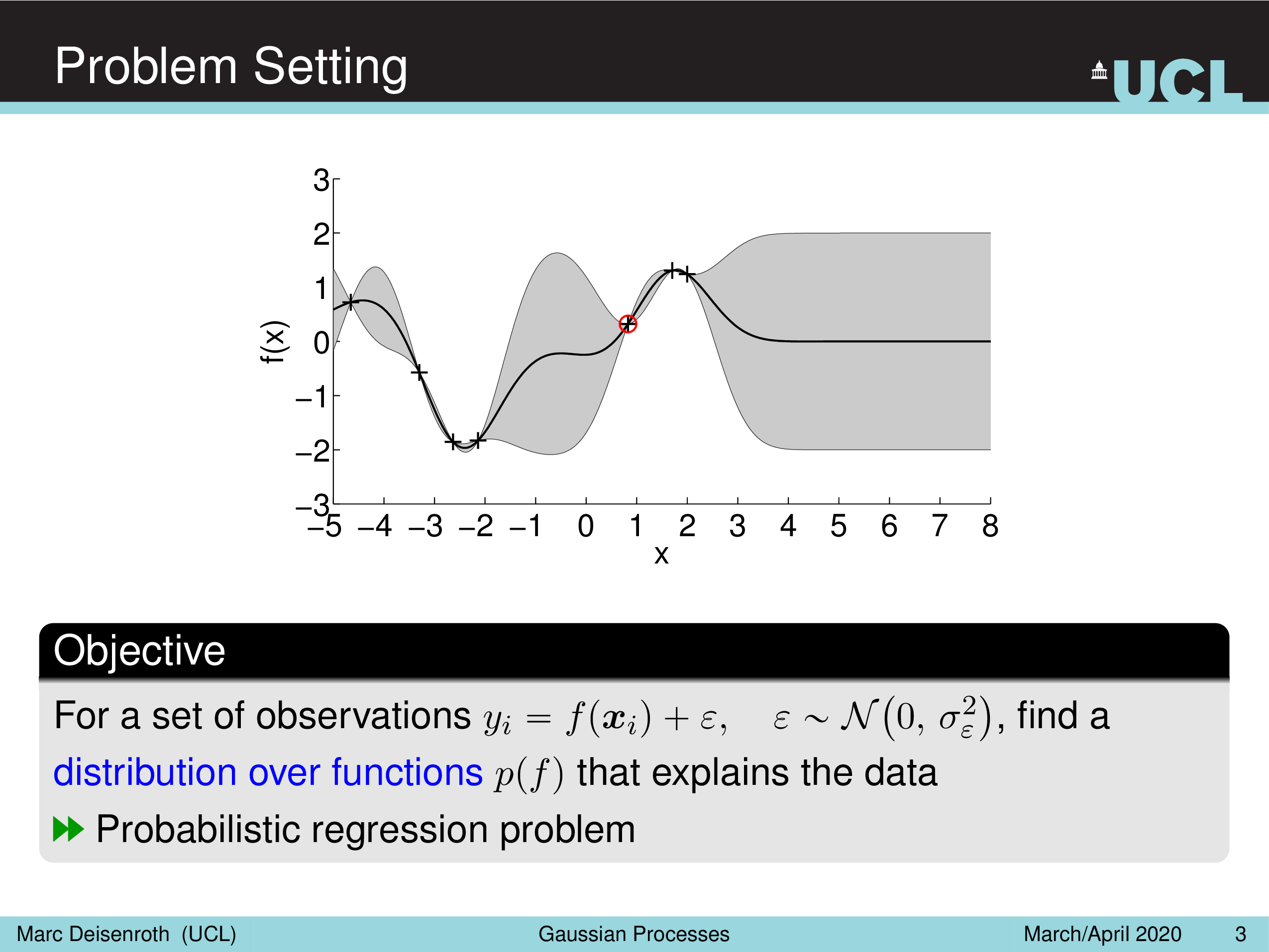 Fig.
Fig.
우리가 아는 linear regression은 target distribution 을 gaussian distribution으로 modeling 하는데, 이는 다음과 같은 term 으로 표현이 가능하다.
\[y_i = f(x_i) + \epsilon, \text{where } \epsilon \sim N(0,\sigma_{\epsilon}^2)\]어떤 sample, \(x_i^{\ast}\) 들어왔을때 \(y_i^{\ast}\) 의 mean 값을 예측하고, variance, \(\sigma\)는 보통 고정으로 가지고 있다 (학습해도 됨). 위의 수식이 나타내는 바가 같은 의미를 내포하고 있다.
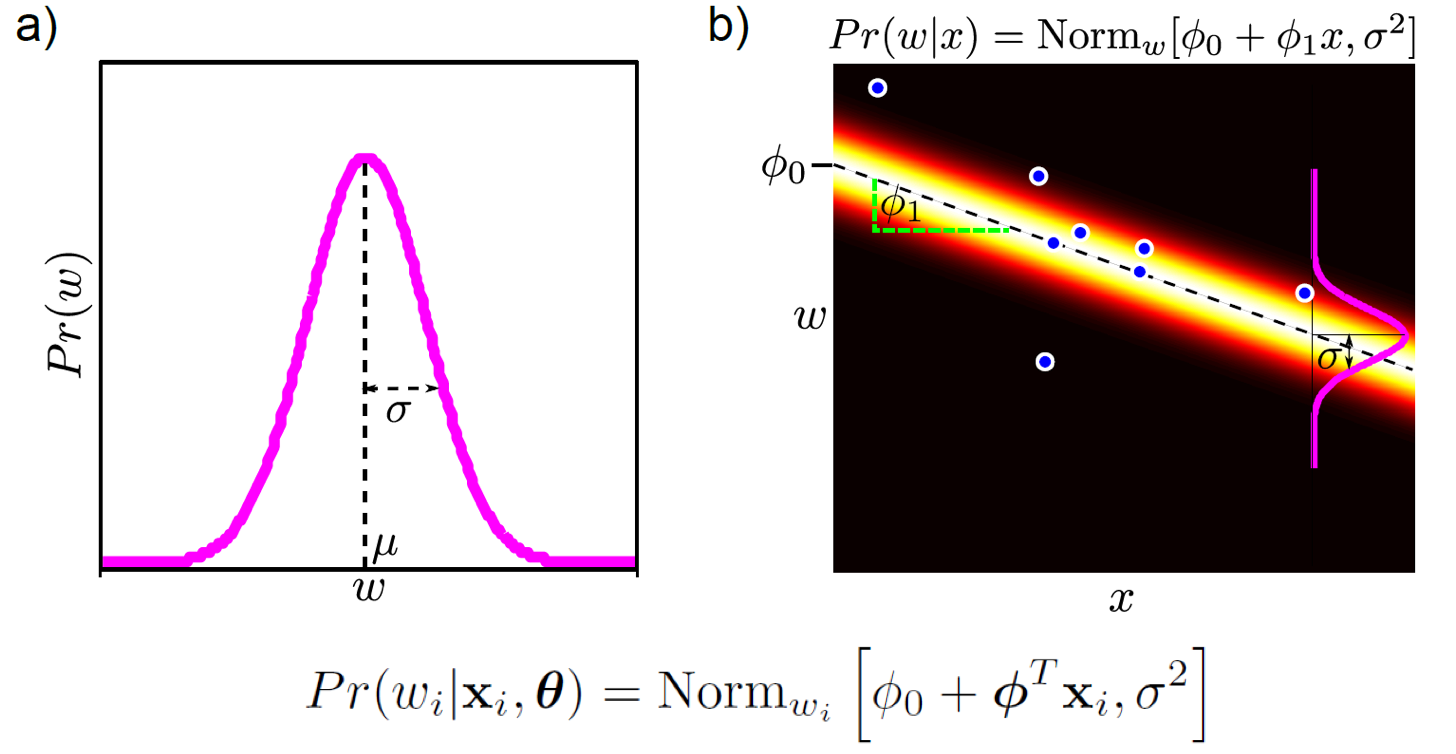
GP의 motivation 은 bayesian approach에서 출발하는데,
bayesian approach가 어차피 parameter의 distribution을 모델링 한 뒤 거기서부터 sampling가능한 모든 parameter로 inference해서 weighted sum 하는것인데,
이럴거면 차라리 아예 함수 f 의 distribution를 modeling 하는건 어떨까?라는 생각을 하게 된다.
 Fig.
Fig.
어떤 function 이라는 것은 \(x\) 가 들어가면 output, \(y\) 를 뱉어주는 것인데
\[y_i = f(x_i)\]만약 \(i\)$가 무수히 많이 있으면 function \(f\) 를 정의할 수 있을 것이다. 즉 어떤 function는 무수히 많은 (무한개의) function value 정의할 수 있다는 것이다.
 Fig.
Fig.
GP 를 관통하는 키워드 중 하나는 non-parametric이다.
보통 parameteric method라는 것은 우리가 가진 data point가 100개인데 어떤 정해진 10개 혹은 1000개의 parameter으로 input output간의 관계를 modeling하는 것이다.
Neural Network (NN)나 linear regression 모두 이런 방식이고,
만약 data point보다 model parameter가 더 많으면 overparameterized 라고 얘기한다.
그런데 non-parameteric은 이런게 아니다.
GP같은 경우 data point가 100개면 100개의 관계식? 같은게 정의된다.
10000개면 10000개 element간의 관계를 나타내는 \(10000^2\)의 어떤 matrix가 있는 것이고,
이걸 통해 10001번째 sample이 들어오면 그것을 예측하는 것이 non-parameteric이다.
이는 다른 말로 \(\infty\)-parameter 라고도 한다.
Non-parameteric method는 data가 복잡해 질 수록 더 많은 parameter 가 필요하다는 기존의 parametric method에 비해 장점이 있지만, data의 크기에 따라 parameter의 수가 늘어나는 단점이 있어 일반적으로 large scale dataset 에 적용하기 어려운 것으로 알려져 있다. (후에 다시 다루도록 할 것)
Bayesian Linear Regression (BLR) vs GP
다시, Bayesian Linear Regression (BLR) 이 수식적으로 어떻게 표현됐는지 생각해보자. 이는 parameter 값이 정해지면 (fixed) 함수 \(f\) 가 정해지는 것이라고 할 수 있다.
\[p(y^{\ast} \vert x^{\ast}) = \underbrace{\int p(y^{\ast} \vert x^{\ast}, \color{red}{\theta}) p(\color{red}{\theta}) d \color{red}{\theta}}_{\text{consider all plausable } (\infty) \text{ values/settings of } \color{red}{\theta}}\]그런데 앞서 말한 것 처럼 우리가 원하는것은 이제 \(\theta\) 에 대한 distribution가 아니라 \(f\)자체의 distribution이다.
\[p(y^{\ast} \vert x^{\ast}) = \underbrace{\int p(y^{\ast} \vert x^{\ast}, \color{blue}{f}) p(\color{blue}{f}) d \color{blue}{f}}_{\text{consider all plausable } (\infty) \text{ values/settings of } \color{blue}{f}}\]두 likelihood와 prior를 곱한 posterior는 이제 \(p(\theta \vert x, y)\)가 아닌 \(p(f \vert x, y)\)가 되겠다.
그리고 어떤 function \(f\) 는 function value들로 이뤄진 긴 vector \([f_1, f_2, f_3, \cdots,]\)로 표현이 가능한데,
GP 는 이 무수히 많은 variable 에 대한 Multivariate Gaussian Distribution으로 표현이 되고 (무수히 많으면 좋겠지만 가지고 있는 data point 한정되어 있으니 data point 개수 만큼의 크기를 갖음),
이 때 바로 Kernel Trick이 사용 된다.
 Fig.
Fig.
GP Regression as Bayesian Inference
GP 의 목표는 학습 data data point (observation) 이 있을 때 함수에 대한 prior \(p(f(\cdot))\) 와 학습 data를 이용해 함수에 대한 Posterior \(p(f(\cdot) \vert X,y)\) 를 구하는 것이다.
 Fig.
Fig.
언제나처럼 Bayes' Rule 을 사용해 Posterior 를 Likelihood, Prior 그리고 Marginal Likelihood (Evidence) 이 세 가지로 표현할 수 있다.
 Fig.
Fig.
각각의 term 들은 아래처럼 표현이 된다.
 Fig.
Fig.
보시면 Prior 에도 GP 라고 되어있고 Posterior 도 GP 라고 되어있는것을 볼 수 있는데, 함수 f 에 대한 Gaussian Distribution 을 GP 라고 하니 둘 다 GP 라고 부를 수 있는 것이다.
GP Prior
Prior 에 대해 먼저 생각 해 보자.
 Fig.
Fig.
GP 는 이 함수의 distribution가 대충 이럴 것이다 라는 걸 정의한 prior 를 GP Prior라고 한다.
그리고 Likelihood 를 Prior 결합해 최종적으로 \(\mu_{post}, k_{post}\) 로 표현되는 GP Posterior를 얻는다.
둘 다 gaussian 형태로 정의 된다. 여기서 prior 는 좀 더 detail하게 쓰면 현재 dataset \(X\) \(N\)개를 가지고 kernel 을 계산해서 \(N \times N\) 차원의 Covariance 와 \(N\)차원의 mean vector 를 가지는 \(p(f \vert X)\) 로 쓸 수 있다.
\[\begin{aligned} & GP_{prior} = p(f \vert X) \\ & = N(f \vert \mu, K) \\ & \text{where } \color{red}{f} = (f(x_1), \cdots, f(x_N)), \color{red}{\mu} = (m(x_1), \cdots, m(x_N)), \color{red}{K_{ij}} = k(x_i,x_j) \\ \end{aligned}\]하지만 Prior 라고 하는 것은 일반적으로 실제 우리가 가지고 있는 real world 의 noisy data point 들을 반영한 것이 아니다.
이는 얘기했던 것 처럼 기존의 Linear Regression (parametric setting) 에서는 아 parameter 2개가 0일 확률이 높지만 variance 가 좀 있겠구나 라는 사전 정보를 모델에 전달할 뿐 data가 반영되기 전 단계를 바로 prior 라고 했다.
이 세팅에서는 prior를 parameter, \(\theta\) 가 2개 이런식으로 정해져있고 이 2개에 대해 gaussian distribution 을 정의했다면 prior 는 \(N(\theta \vert 0, I)\) 처럼 정의됐다.
근데 GP Prior 를 보면 X 를 통해서 이 data point 들간의 연산을 통해 (Kernel) Covariance Matrix 구하는데요 이 때 사용된 X는 대체 무엇일까? training data 일까?
아니다.
이 X는 정해진 범위 내에 일정한 간격으로 data point 들을 쭉 뽑은 것이다.
즉 [-5, 5] 범위 내에 0.2의 간격으로 data를 뽑으면 50개 정도의 data point 를 얻을 수 있다.
이제 이들 간의 관계를 kernel 연산을 해서 covaraince 를 구하고 mean vector 는 정보가 없으니 0 으로 두면 우리는 50차원의 Multivariate Gaussian Distribution 인 Prior 를 얻을 수 있는 것이다.
아래는 구현 예시인데,
# Finite number of points
X = np.arange(-5, 5, 0.2).reshape(-1, 1)
# Mean and covariance of the prior
mu = np.zeros(X.shape)
cov = kernel(X, X)
# Draw three samples from the prior
samples = np.random.multivariate_normal(mu.ravel(), cov, 3)
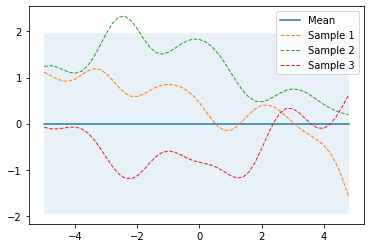 Fig. Source From here
Fig. Source From here
실제로 함수를 정의하려면 모든 실수구간 x 에서 그에 대응하는 함수 값 y, f(x) 를 알아야 하는데 이는 불가능 하기 떄문에
유한한 개수 (finite number) 의 아무 sample을 가지고 Prior 를 만들어서 함수를 구성하고 이 함수가 어디서 뽑혔을까를 kernel trick 으로 만든다는 것이다.
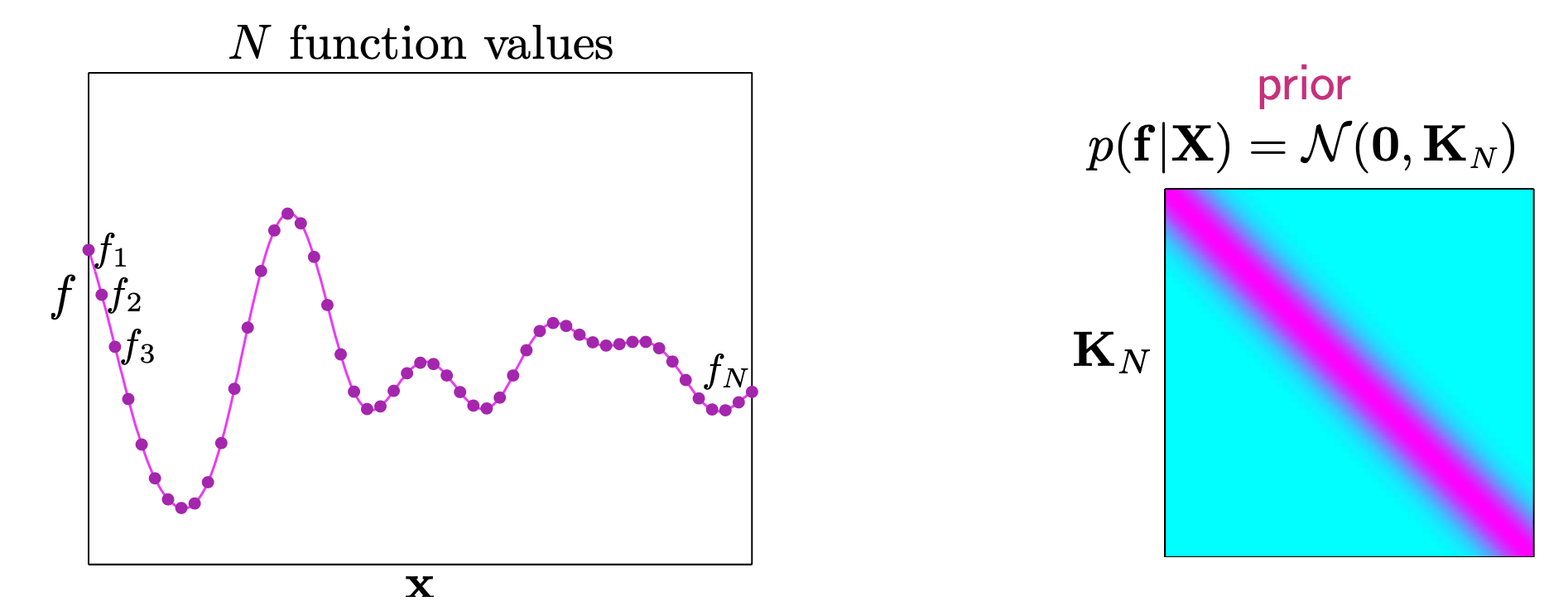 Fig. RBF 커널을 썼을 시 Covariance 의 대각 성분 값이 크게 나타난다.
Fig. RBF 커널을 썼을 시 Covariance 의 대각 성분 값이 크게 나타난다.
20개를 가지고 만들면 20 차원의 Multivariate Gaussian Distribution 이 만들어지고 그로부터 몇개를 sample링 해보면 아래와 같은 함수 개형을,
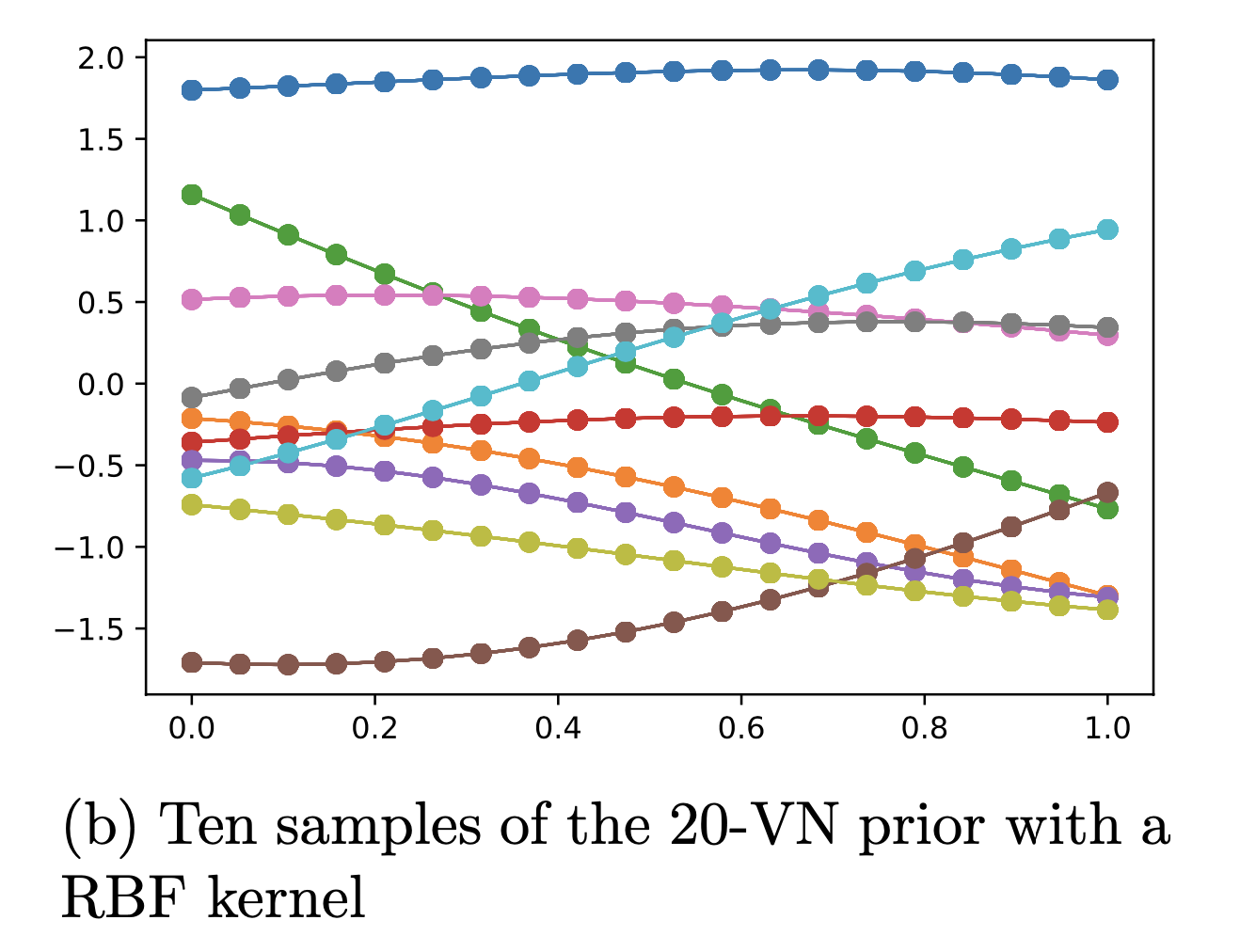 Fig.
Fig.
200개를 가지고 만들면 아래와 같은 sample 을 얻을 수 있다.
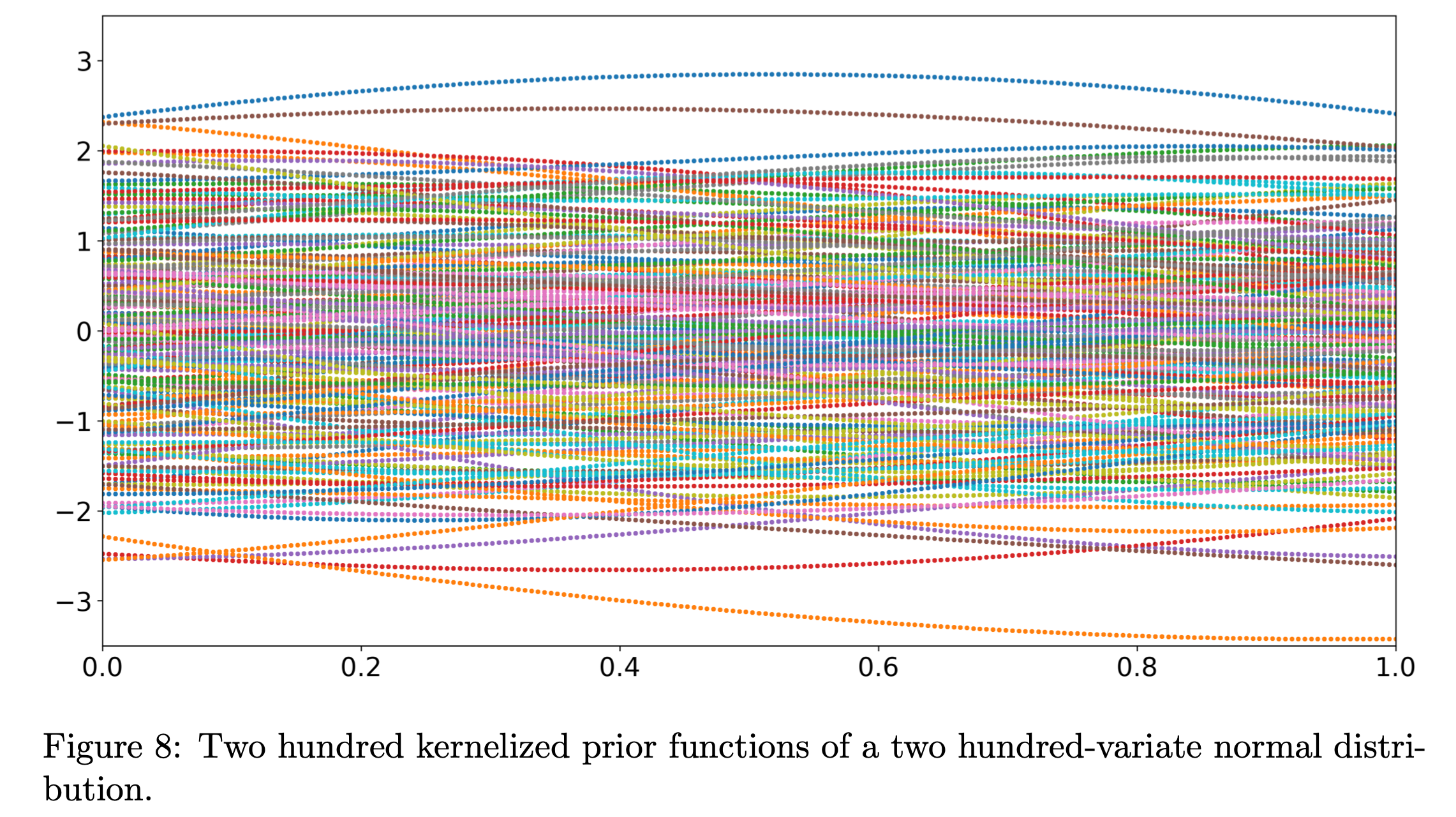 Fig.
Fig.
Gaussian Mean Function
GP Prior 는 의 mean vector는 모든 값을 0 으로 (mean vector 자체가 0 벡터가 되어버림) 설정하는 것이 일반적이라고 하는데,
\[\mu = (m(x_1), \cdots, m(x_N)) = (0, \cdots, 0)\]우리가 앞서 배운 linear regression 을 통해서 하나의 함수를 점 추정해서 이 함수를 \(m(\cdot)\) 쓸 수도 있다고 한다. robotics 같은 분야에서는 잘 알려진 함수?로 설정하는 등 domain knowledge 가 들어갈 수도 있다고 하는 것 같다.
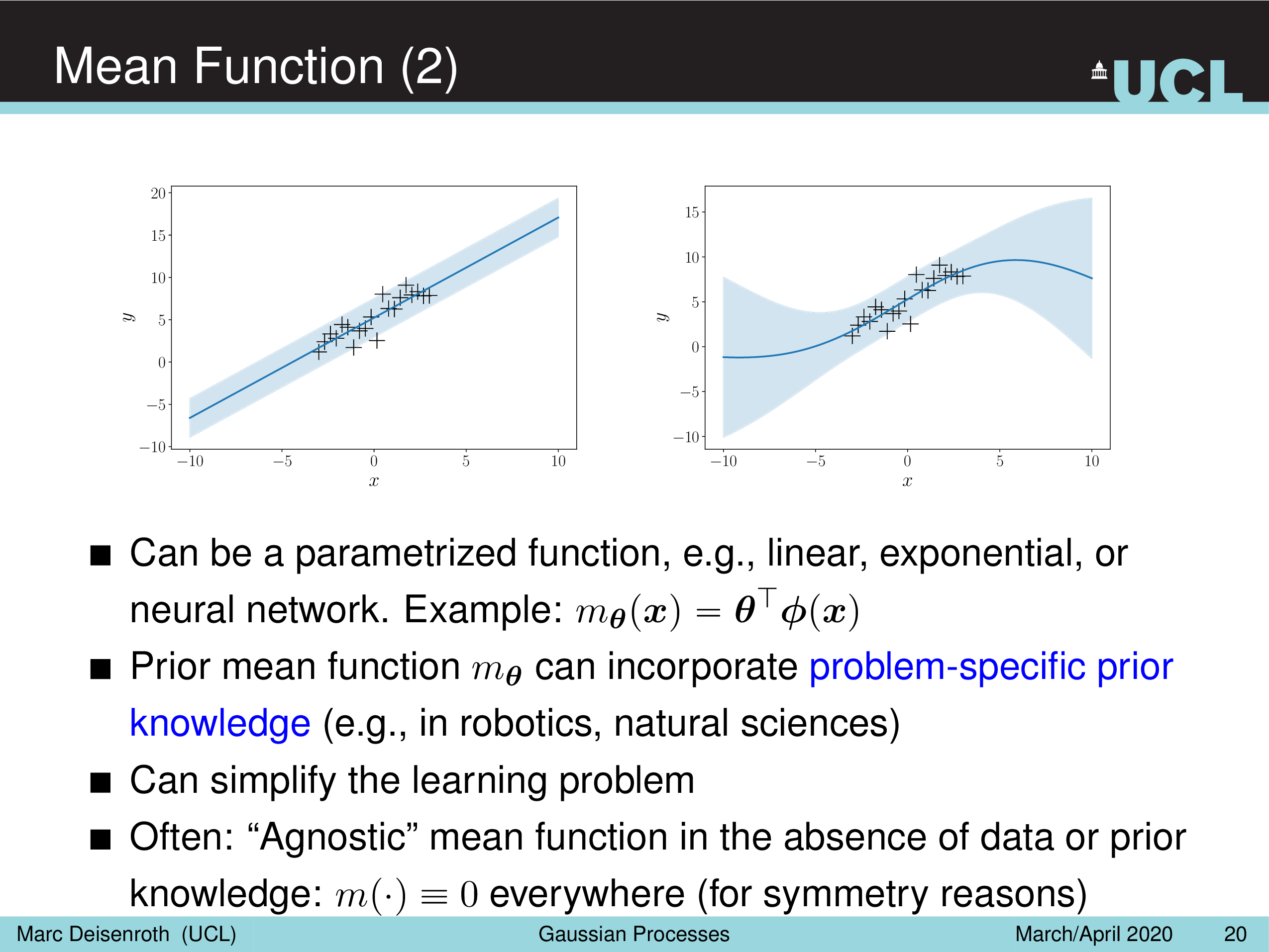 Fig.
Fig.
(Gaussian) Covariance Funtion
Covariance Matrix 는 먼저 말씀드린 것 처럼 data들 간의 상관 관계 (correlation)를 나타 내는데, 일반적으로 data point 가 유사하면 (유사한 벡터면) 그 값이 높은 값을 갖게 되며 이는 Kernel 을 사용해서 계산한다.
 Fig.
Fig.
커널 종류는 특정 조건을 만족하는 어떤 함수라도 쓸 수 있다고 얘기 했었다.
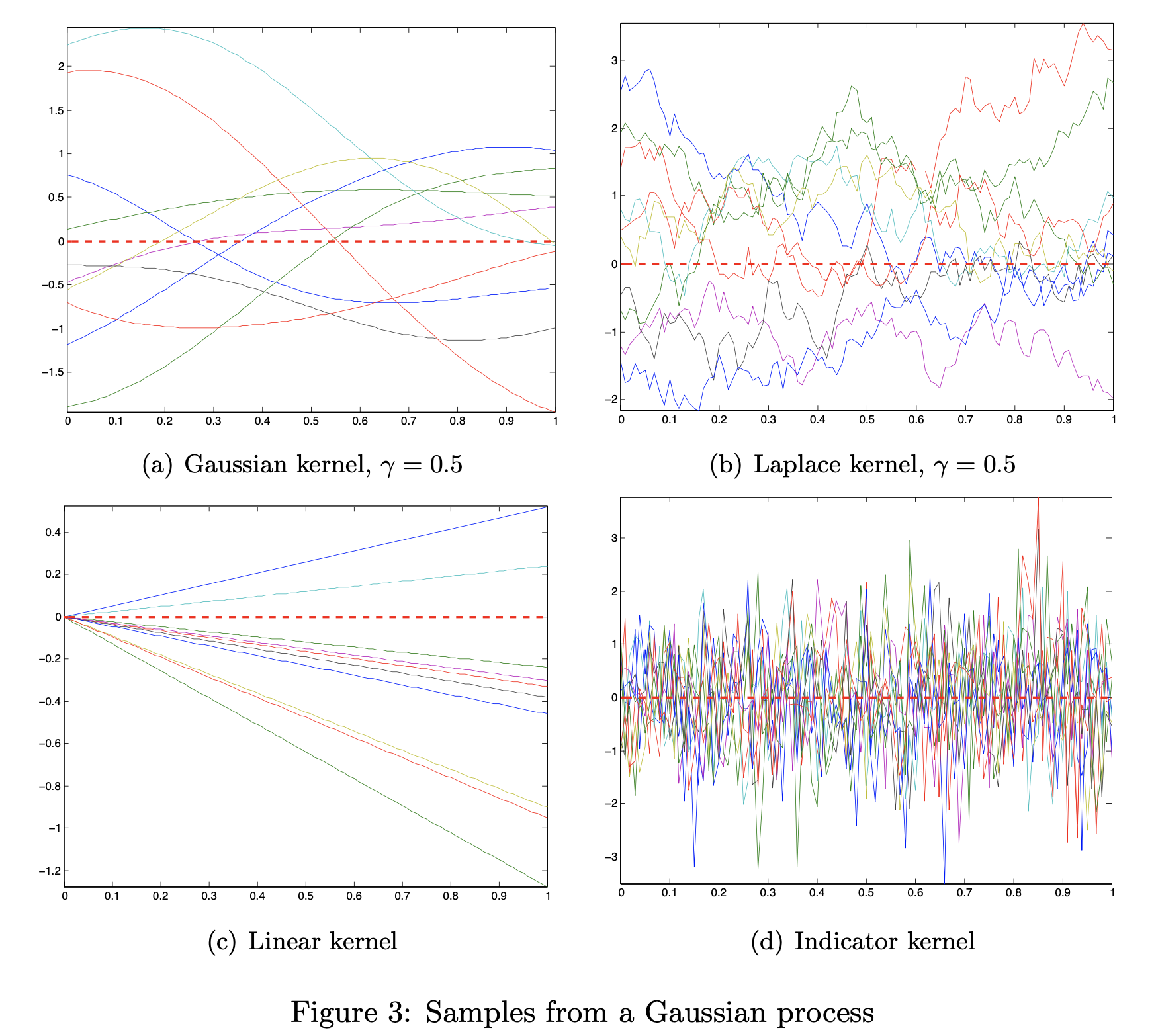 Fig. Gaussian Kernel 이 RBF Kernel
Fig. Gaussian Kernel 이 RBF Kernel
그 중 무한차원으로 implicit 하게 lifting 할 수 있는 RBF 커널은
 Fig.
Fig.
다음 두 개의 하이퍼 파라메터를 가지고 있다.
- Amplitude Parameter, \(\sigma_f^2\)
- Length-Scale Parameter, \(l^2\)
Amplitude Parameter & Length-Scale Parameter
말 그대로 Amplitude Parameter, \(\sigma_f^2\) 는 GP prior function 들의 진폭을 나타내는데, 즉 이 값이 작을수록 variation 이 줄어들게 되고
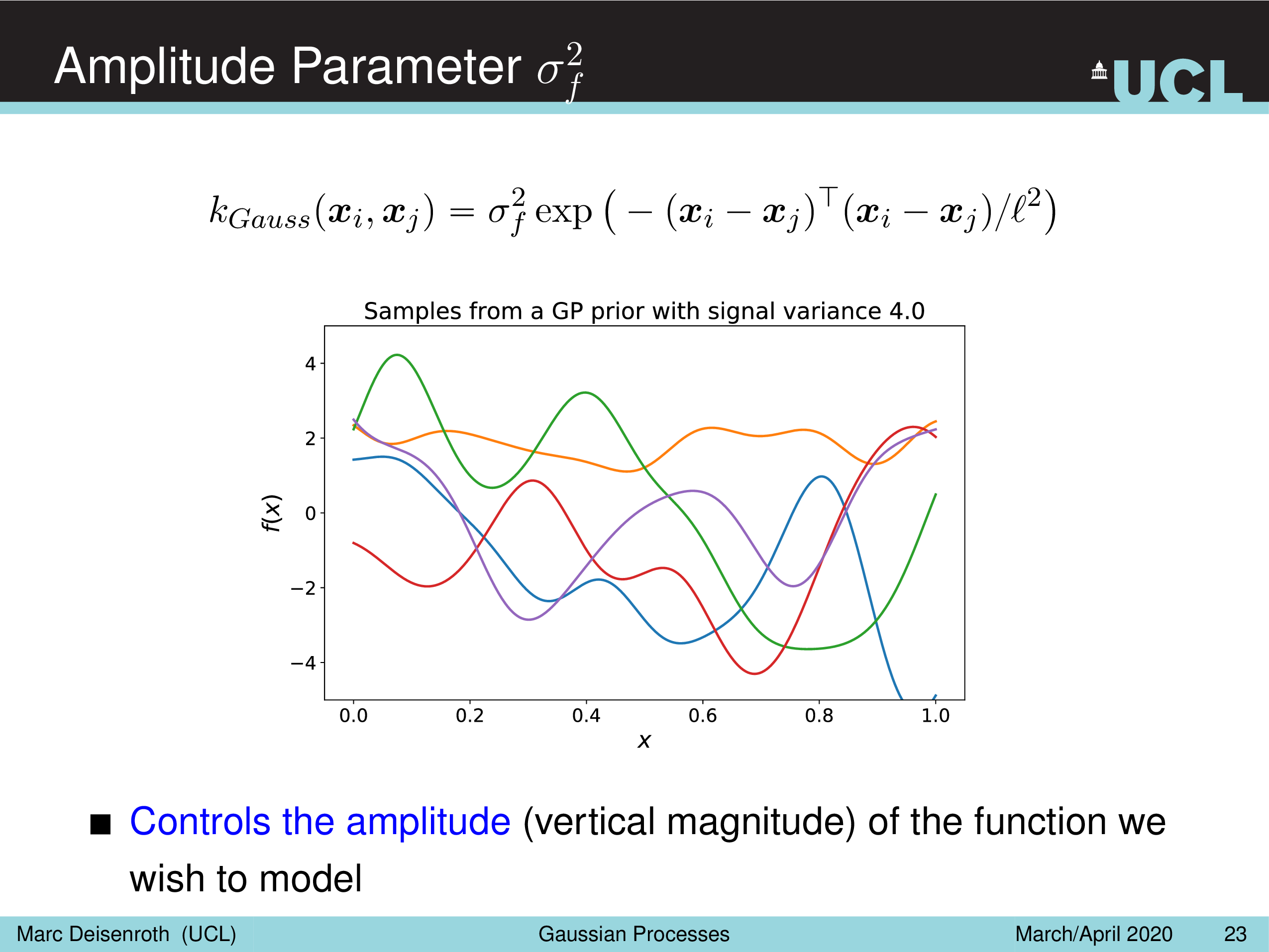
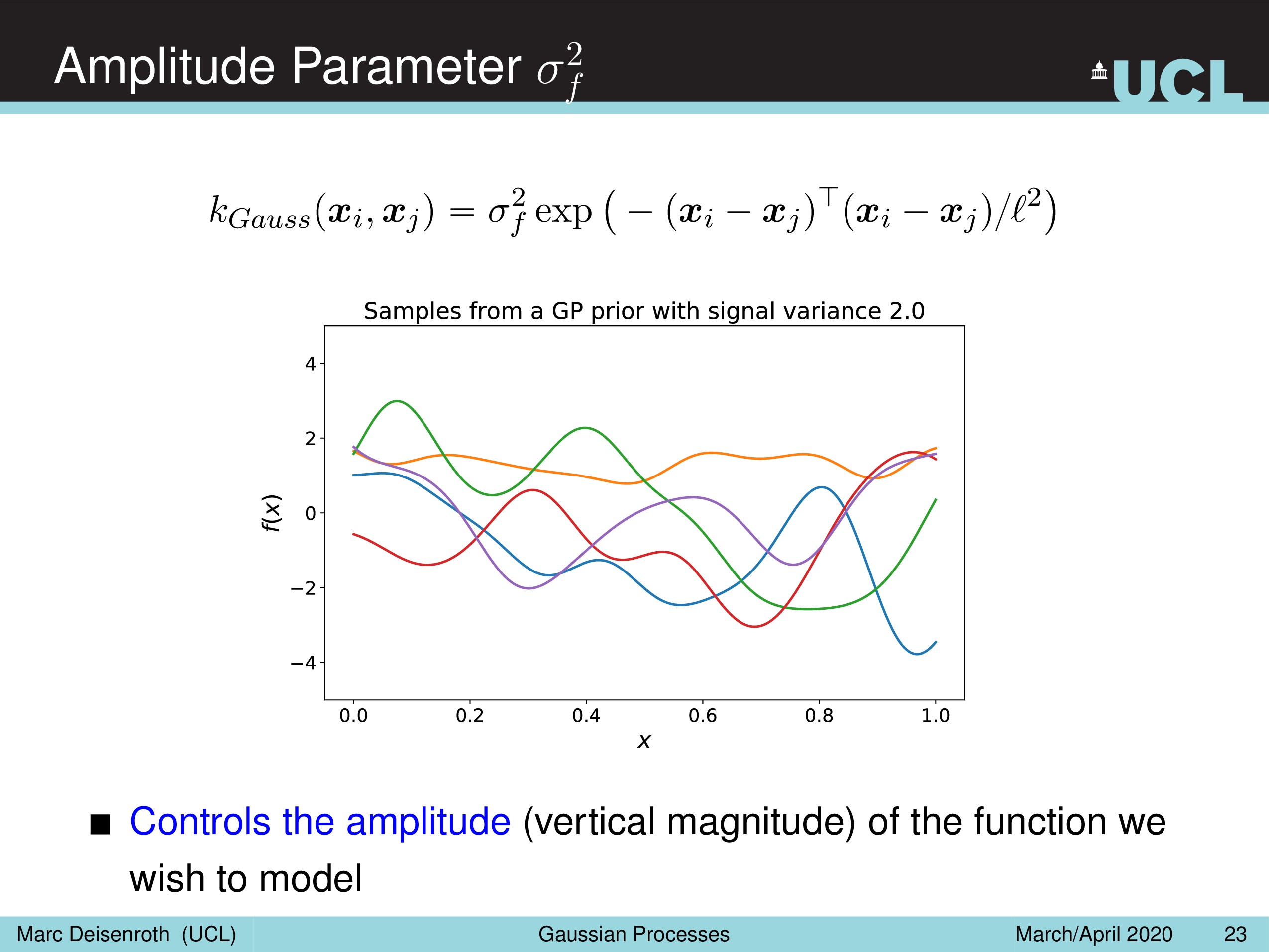
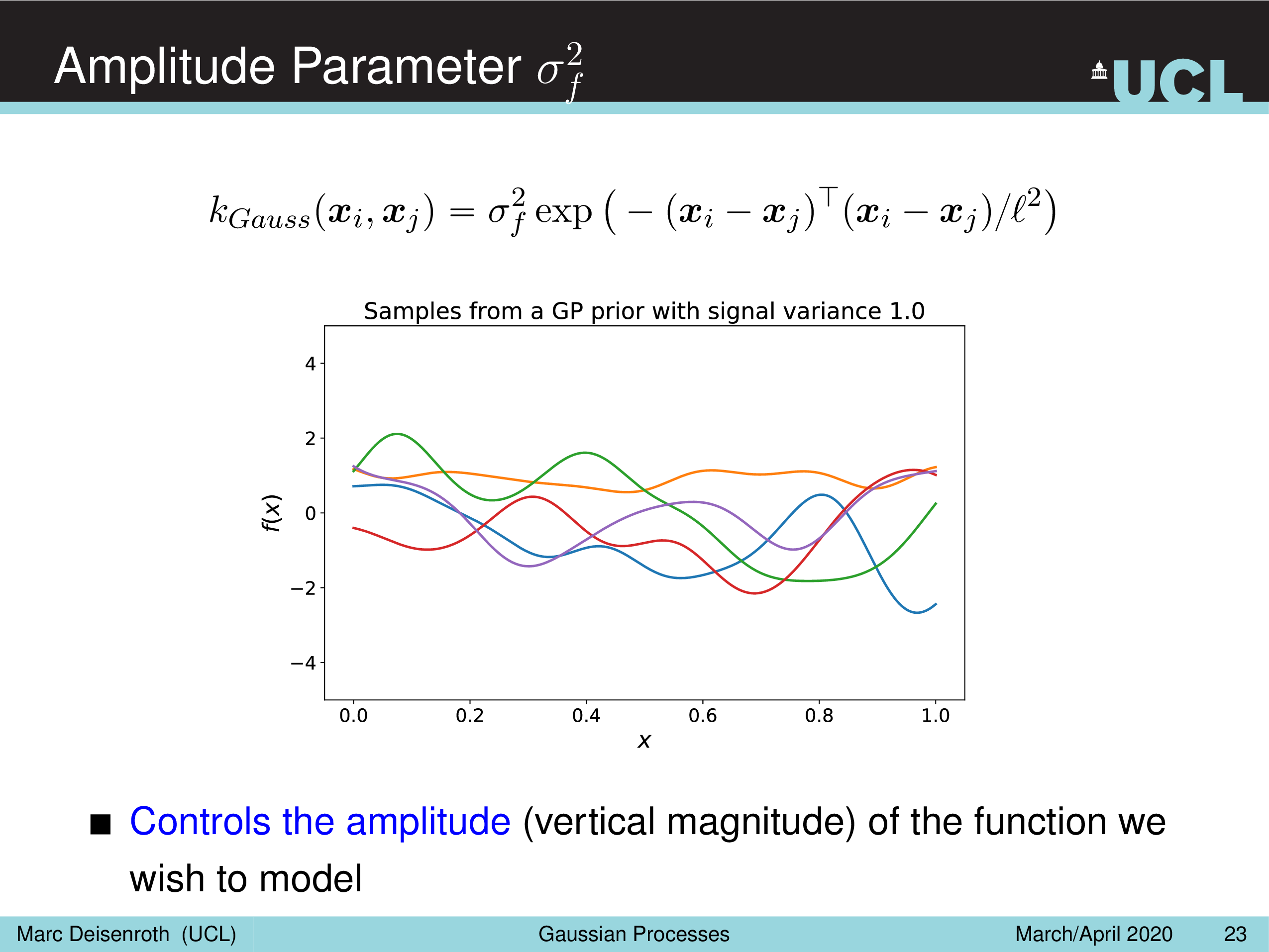
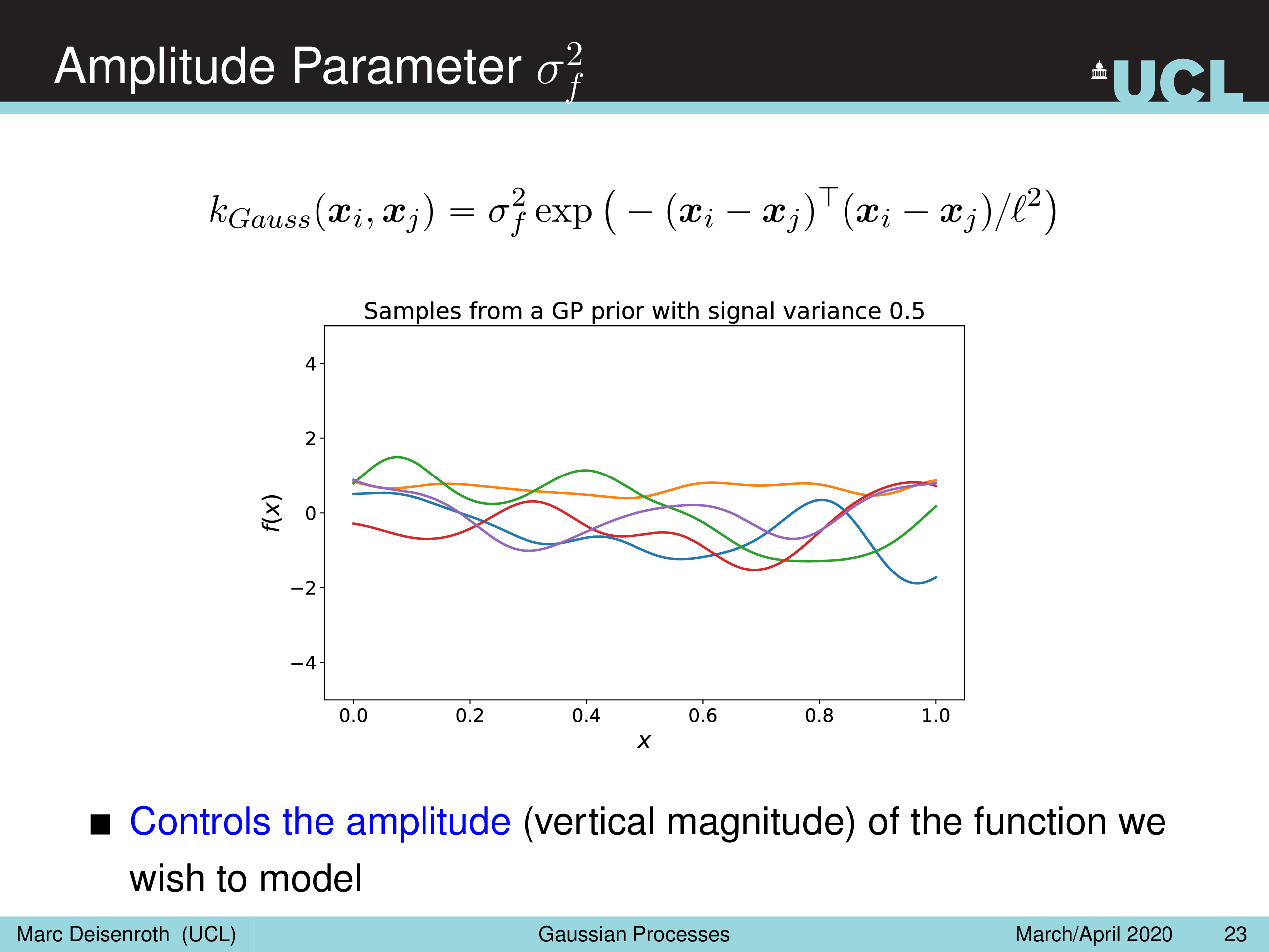
Length-Scale Parameter, \(l^2\) 을 따라서 함수가 좌우로 늘어나면서 얼마나 GP prior function 가 꾸불거리느냐 (wiggly), 즉 부드러워지냐를 결정할 수 있게 된다.

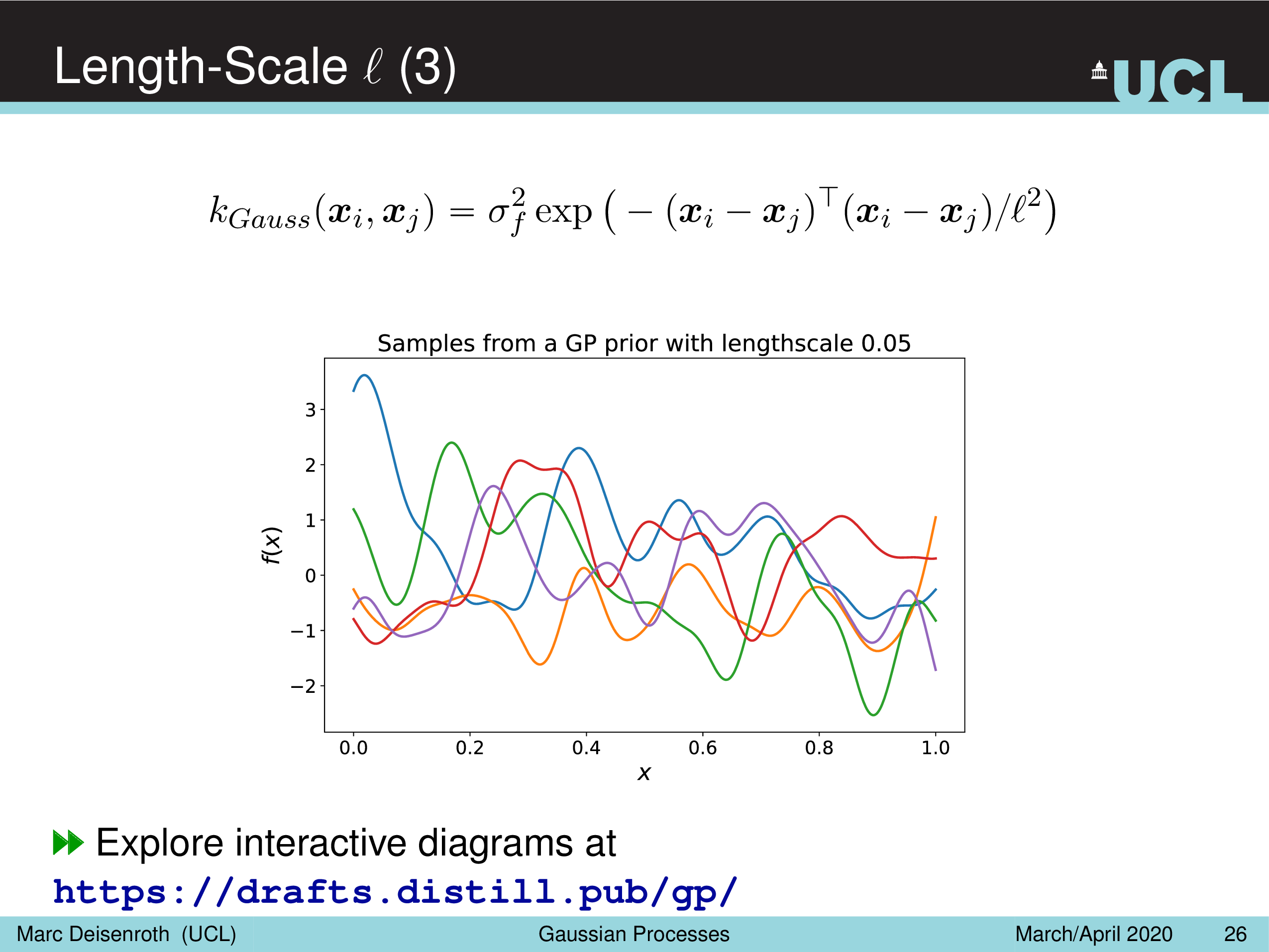
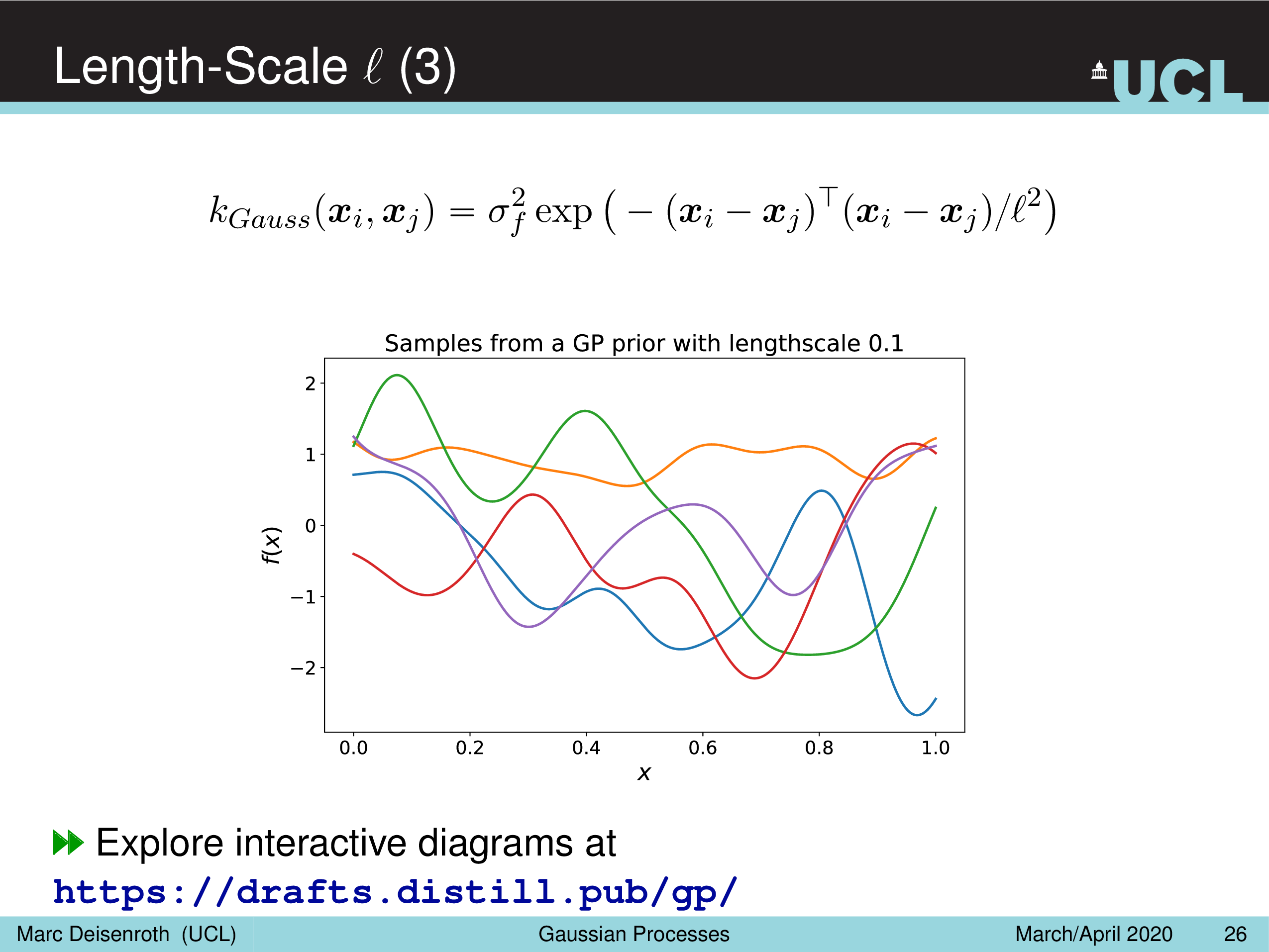
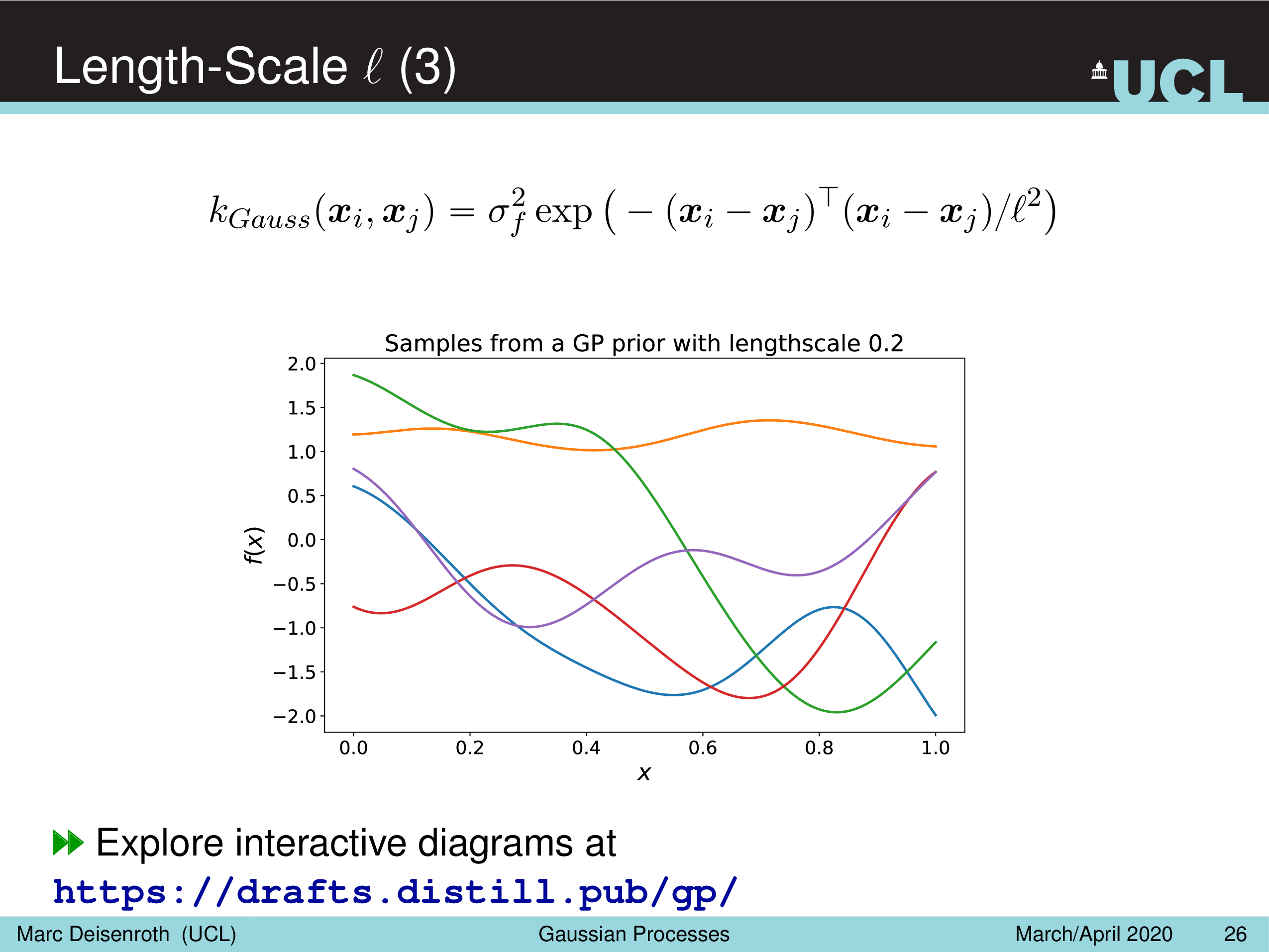
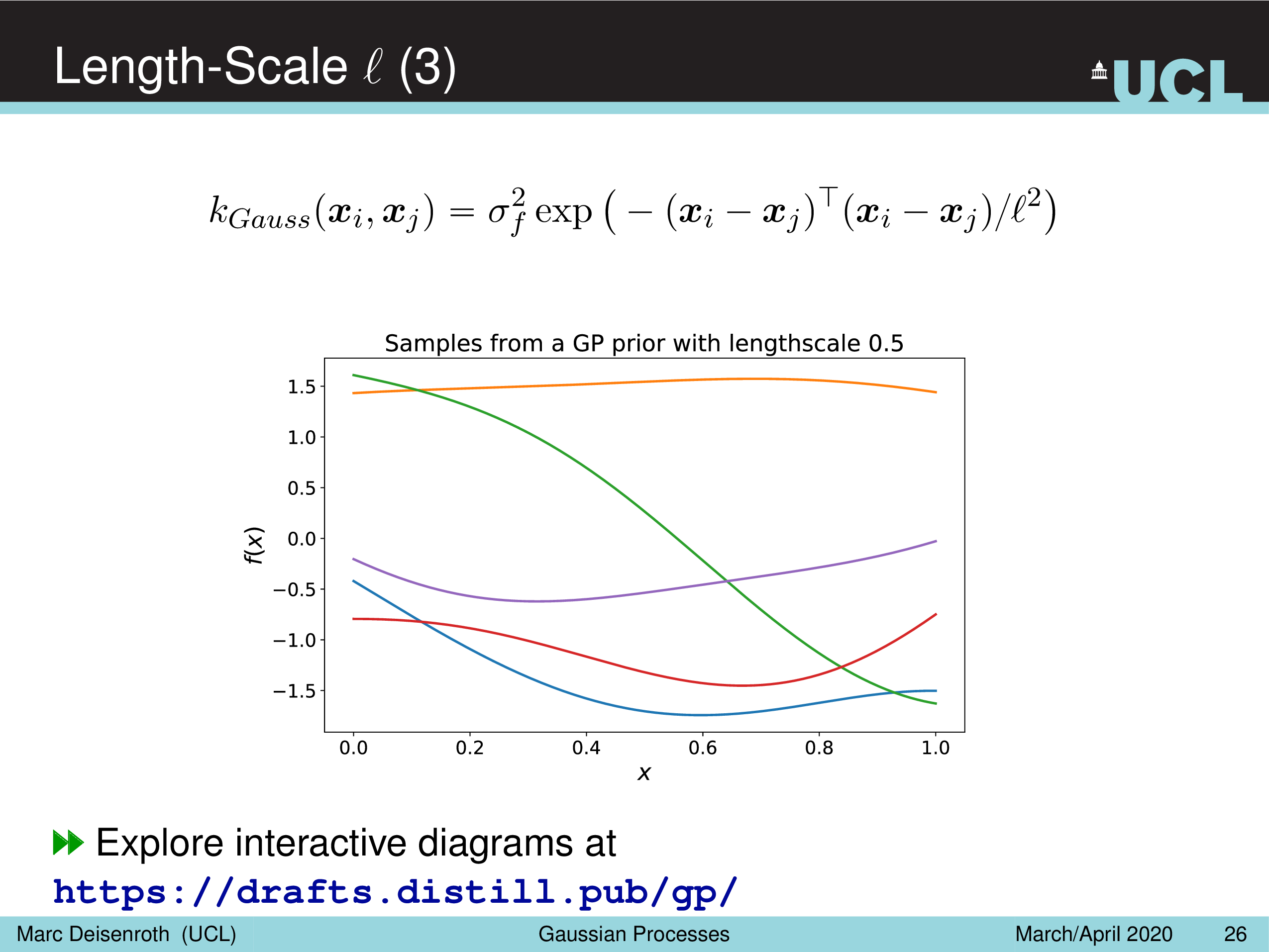
(Gaussian) Likelihood
이제 likleihood에 대해 알아보자. 이제 우리가 가지고 있는 training dataset을 반영하는 것이다.
 Fig.
Fig.
 Fig.
Fig.
Marginal Likelihood
 Fig.
Fig.
 Fig.
Fig.
 Fig.
Fig.
 Fig.
Fig.
 Fig.
Fig.
 Fig.
Fig.
 Fig.
Fig.
GP Posterior
이제 마지막으로 Posterior를 계산할 차례이다. Posterior는 prior 와 likelihood 의 곱한 것을 marginal likelihood 로 normalize 해주는 것이다.
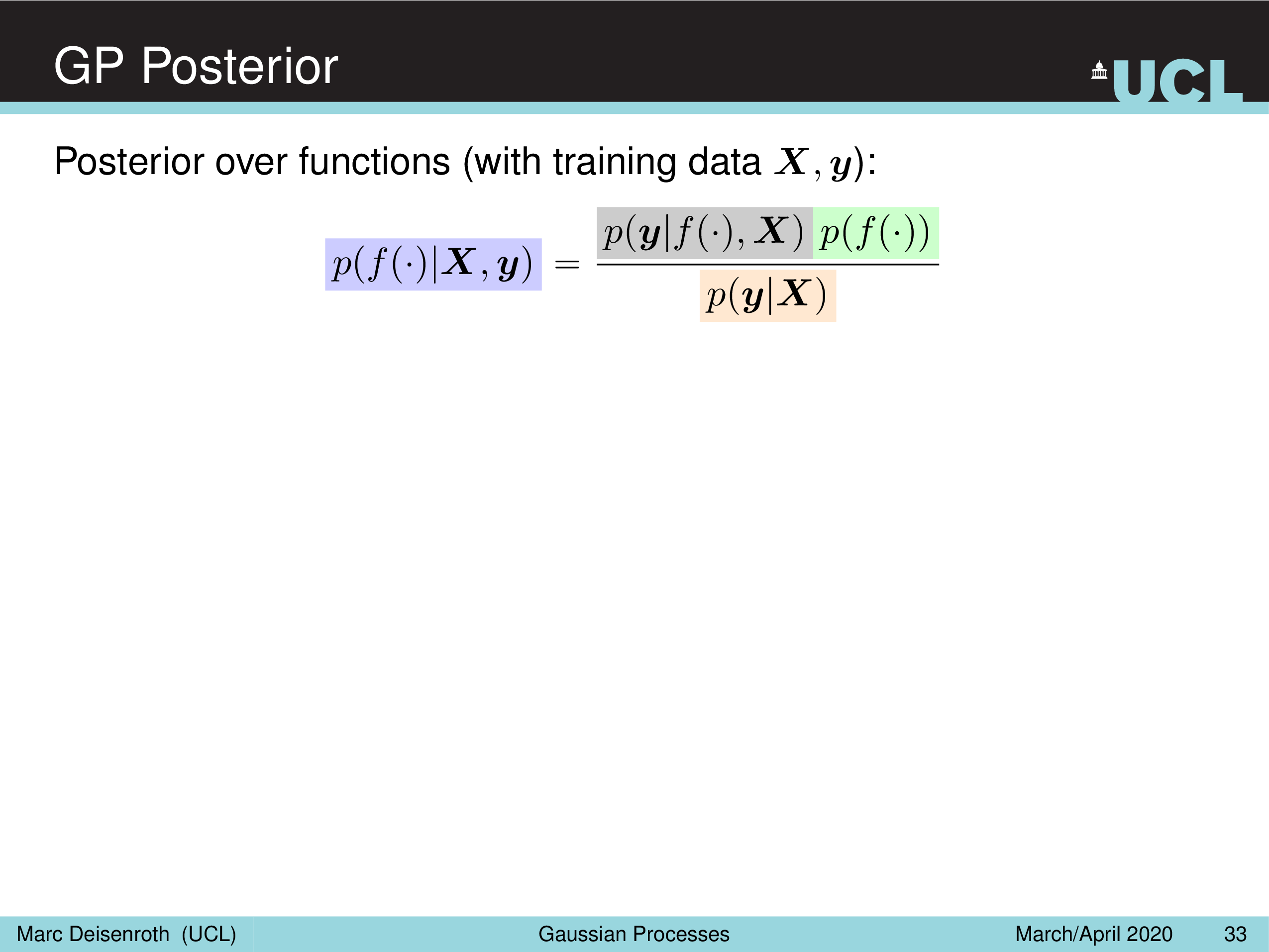 Fig.
Fig.
 Fig.
Fig.
 Fig.
Fig.
 Fig.
Fig.
Sampling from the GP Prior
 Fig.
Fig.
 Fig.
Fig.
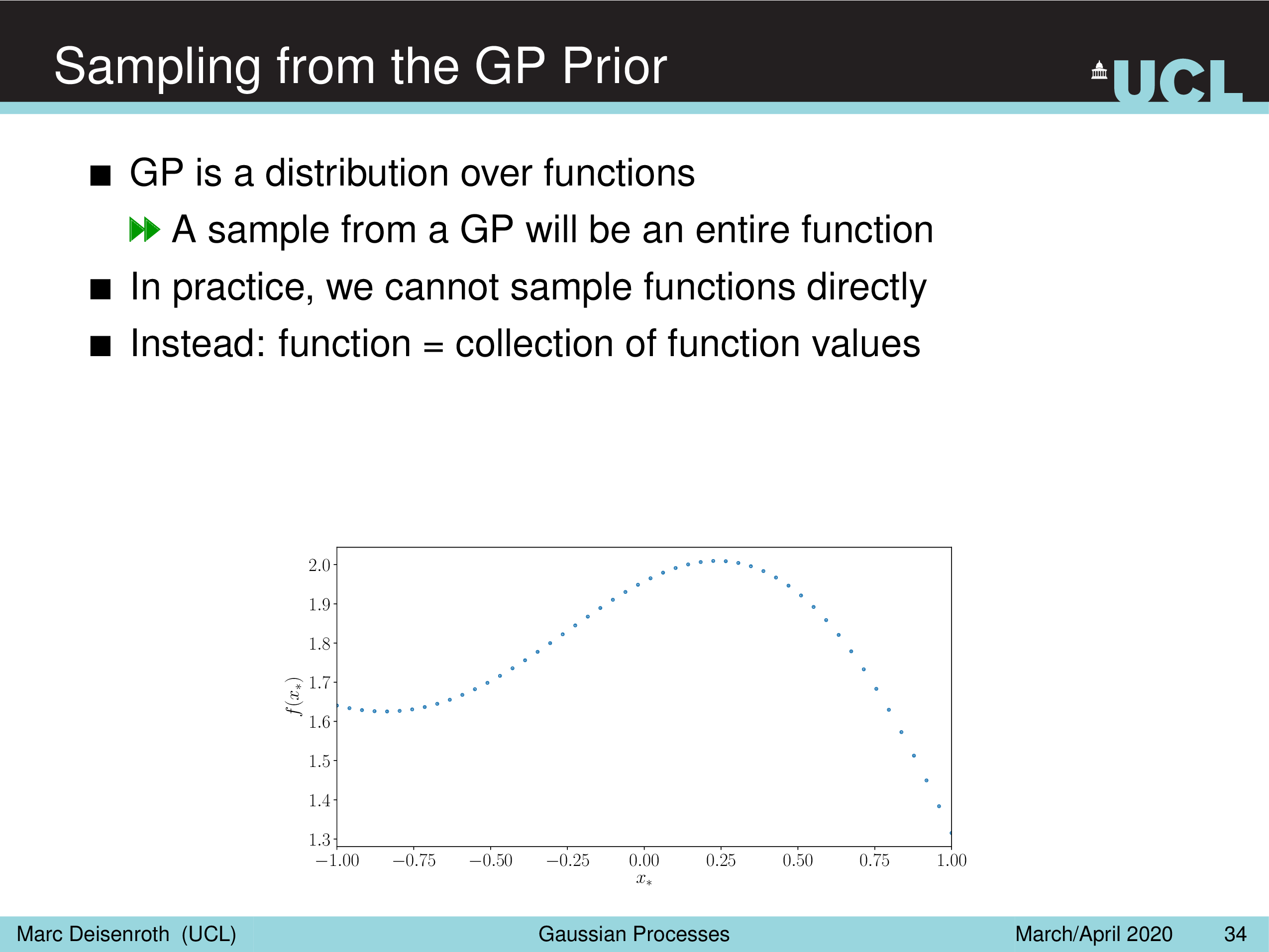 Fig.
Fig.
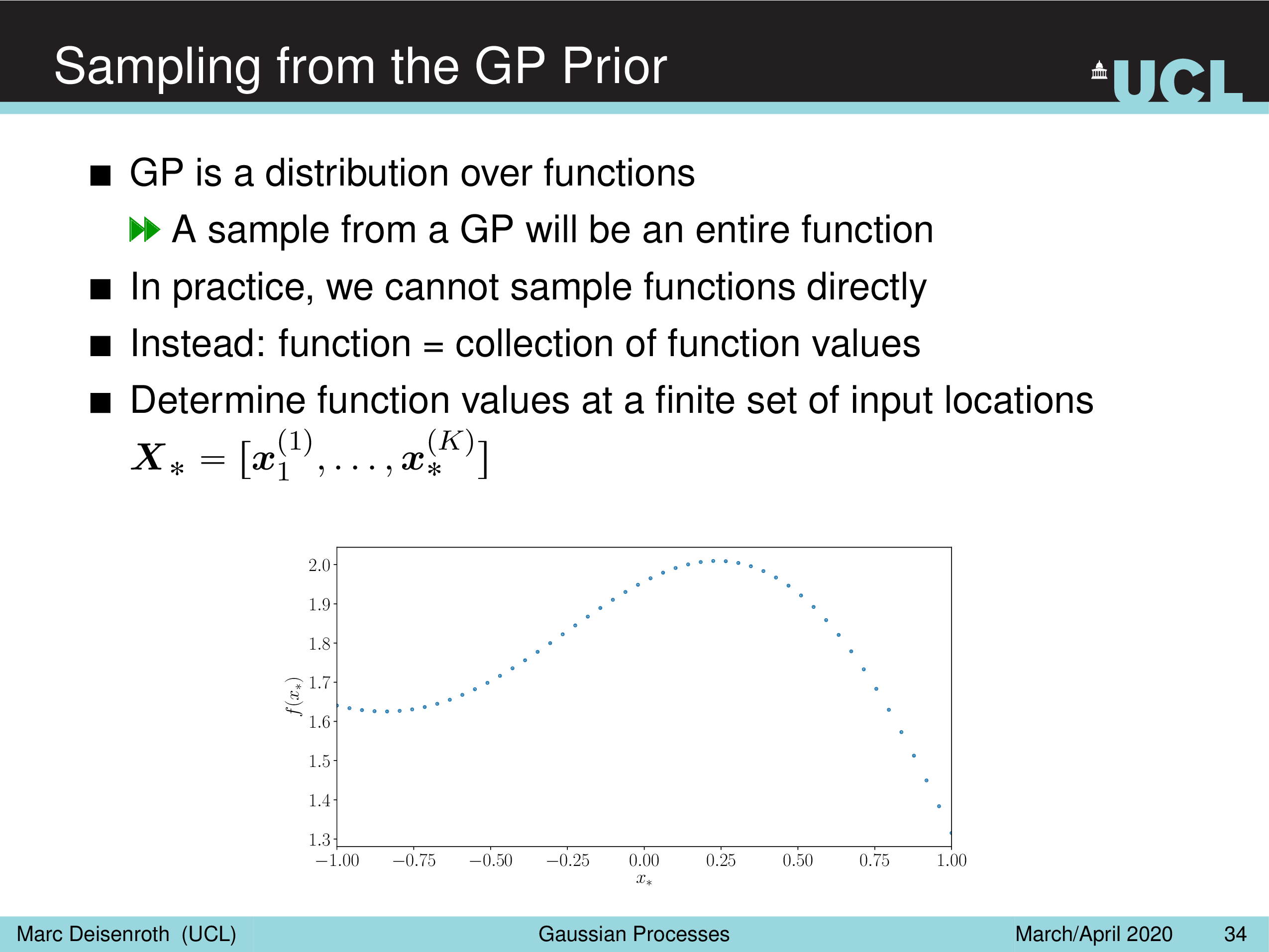 Fig.
Fig.
 Fig.
Fig.
 Fig.
Fig.
 Fig.
Fig.
 Fig.
Fig.
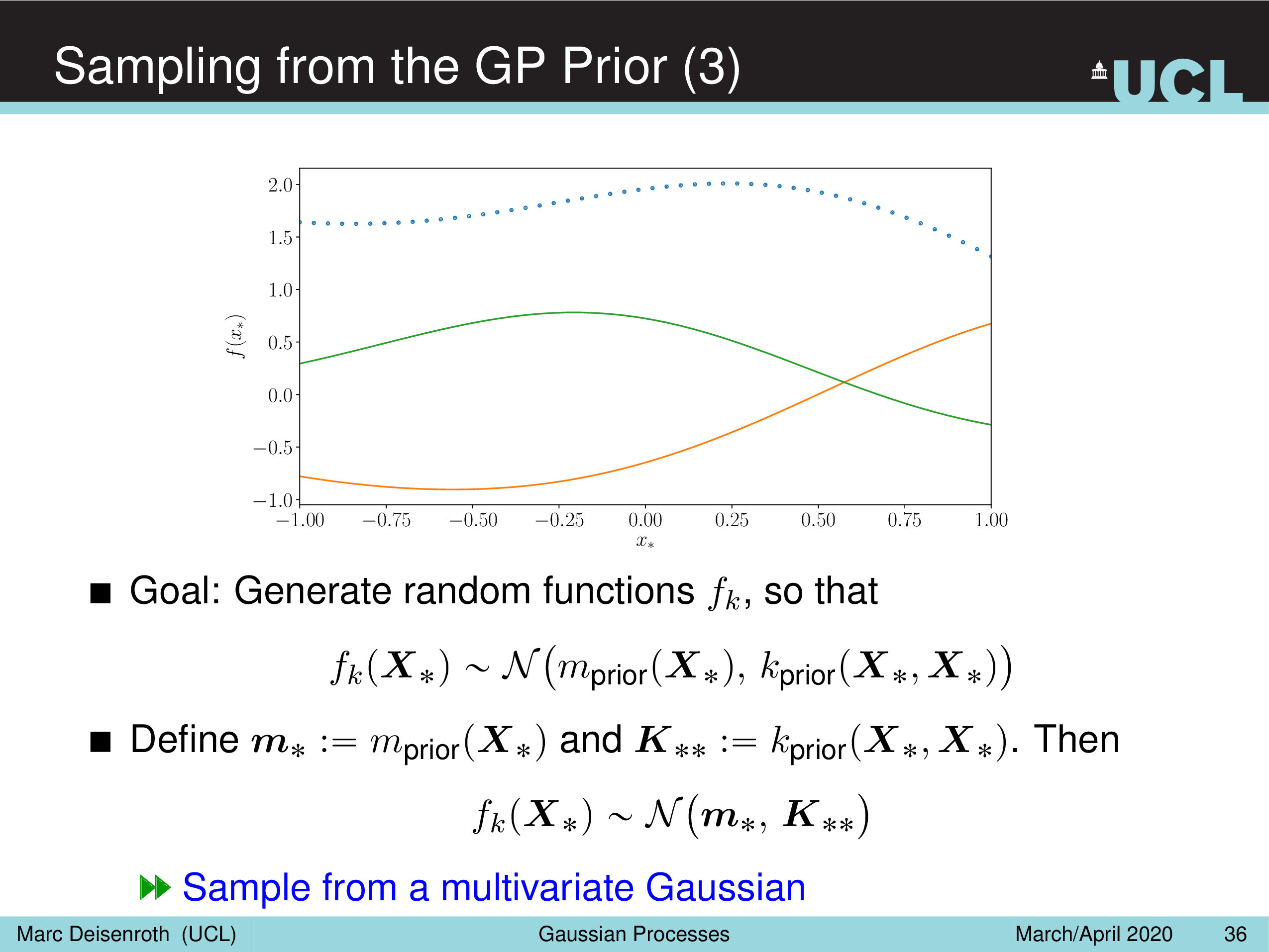 Fig.
Fig.
GP Prediction (Posterior)
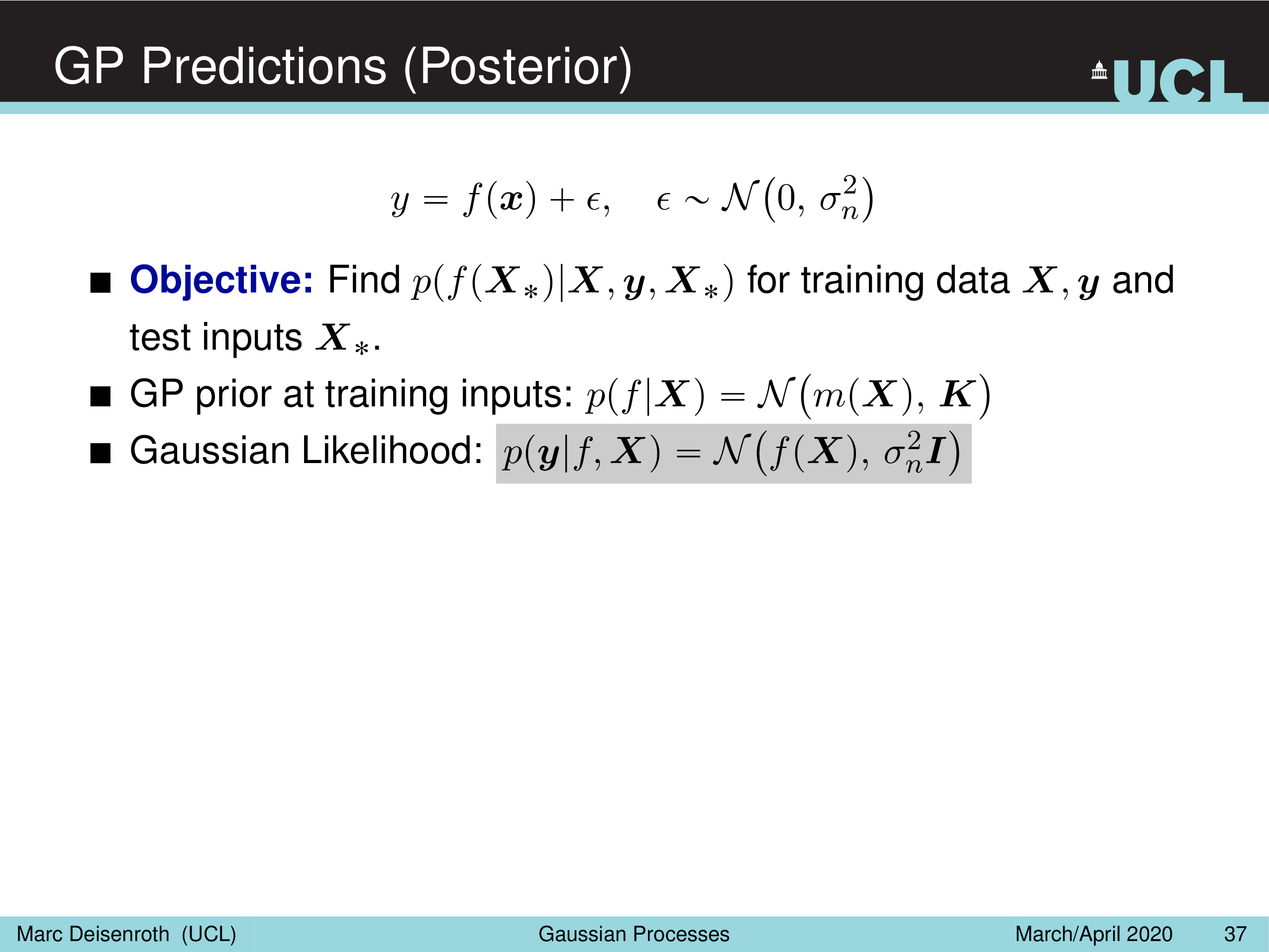 Fig.
Fig.
 Fig.
Fig.
 Fig.
Fig.
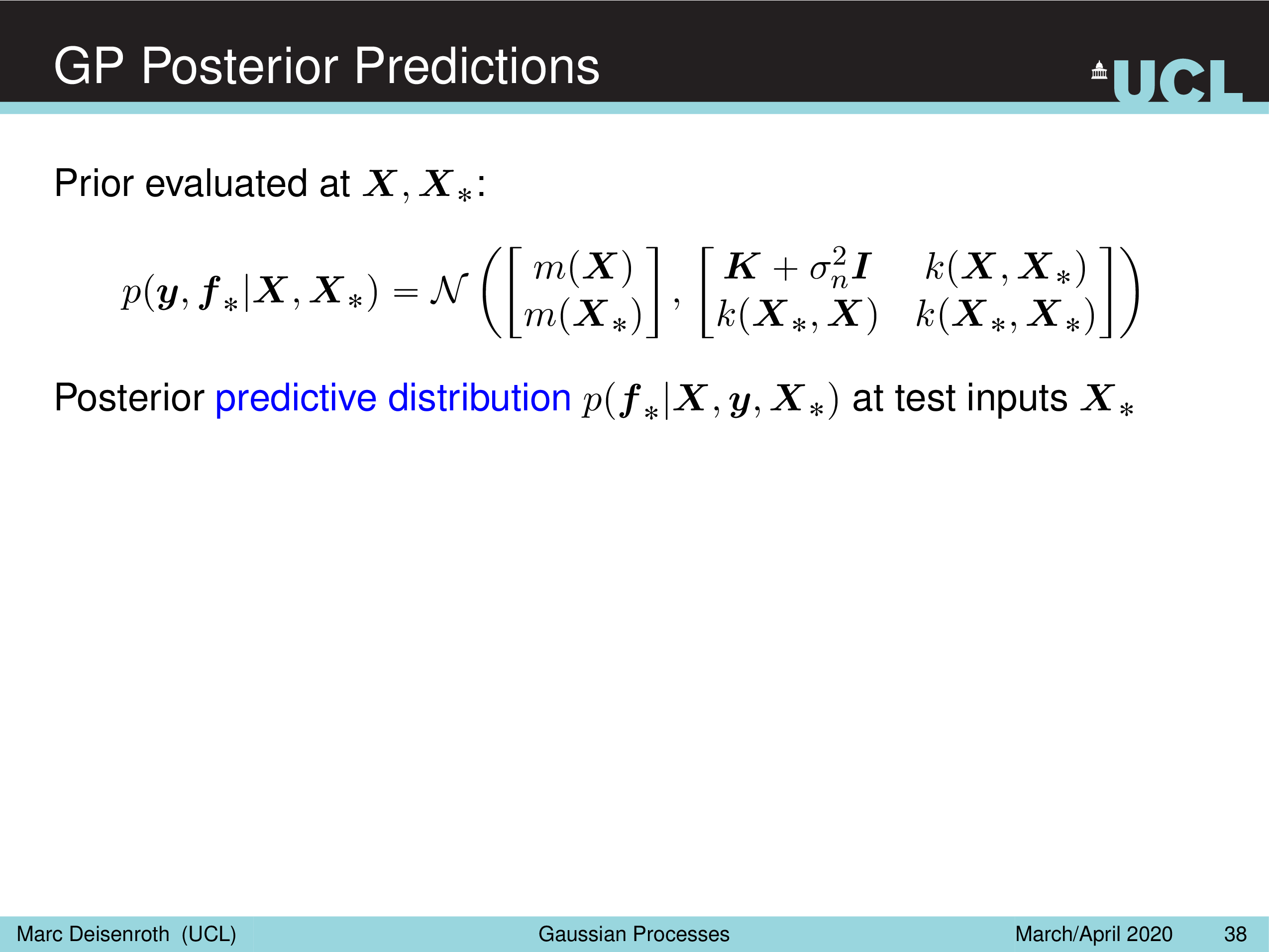 Fig.
Fig.
 Fig.
Fig.
 Fig.
Fig.
Sanity Check
 Fig.
Fig.
 Fig.
Fig.
 Fig.
Fig.
Illustration: Inference with Gaussian Processes
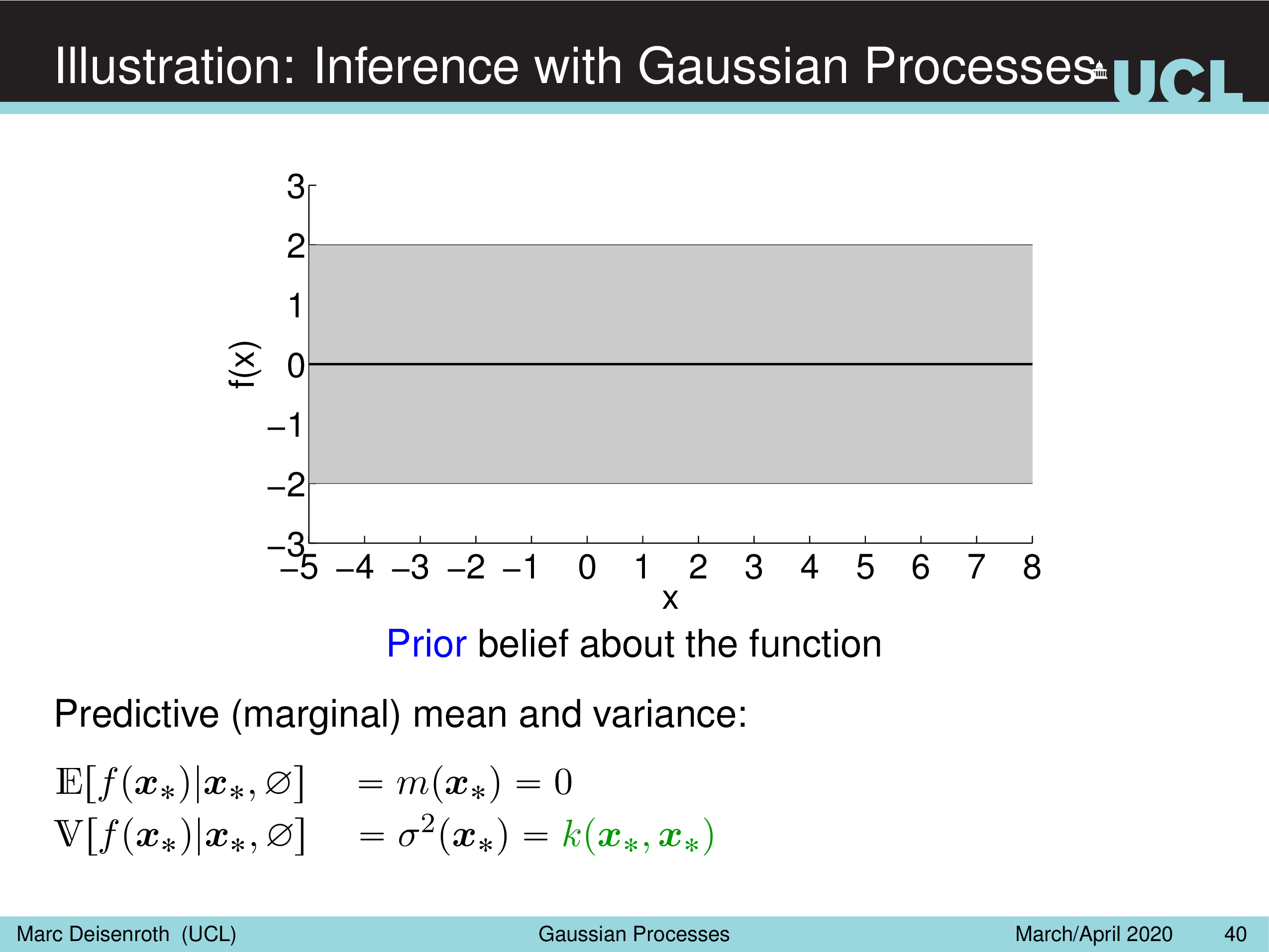 Fig.
Fig.
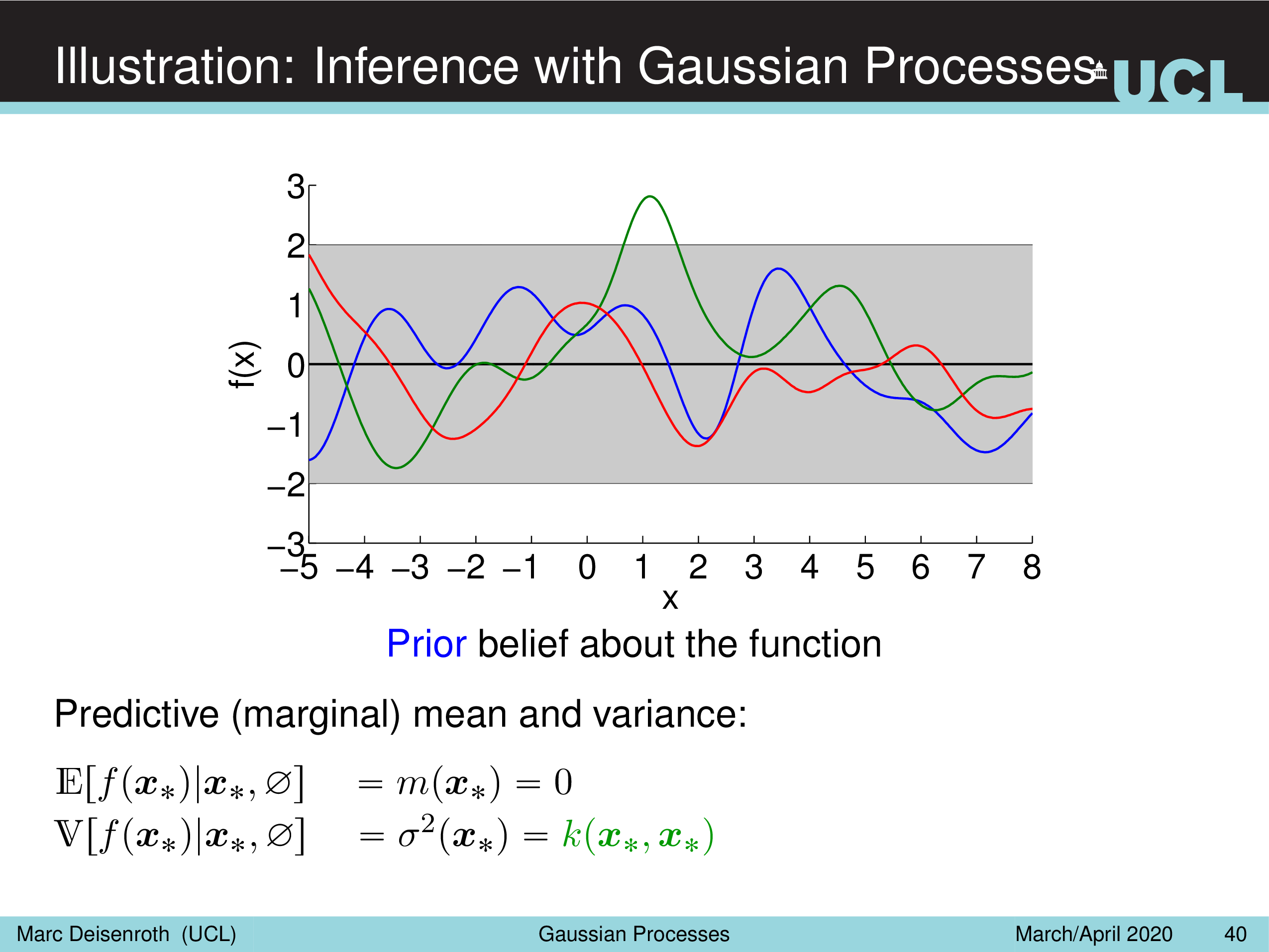 Fig.
Fig.
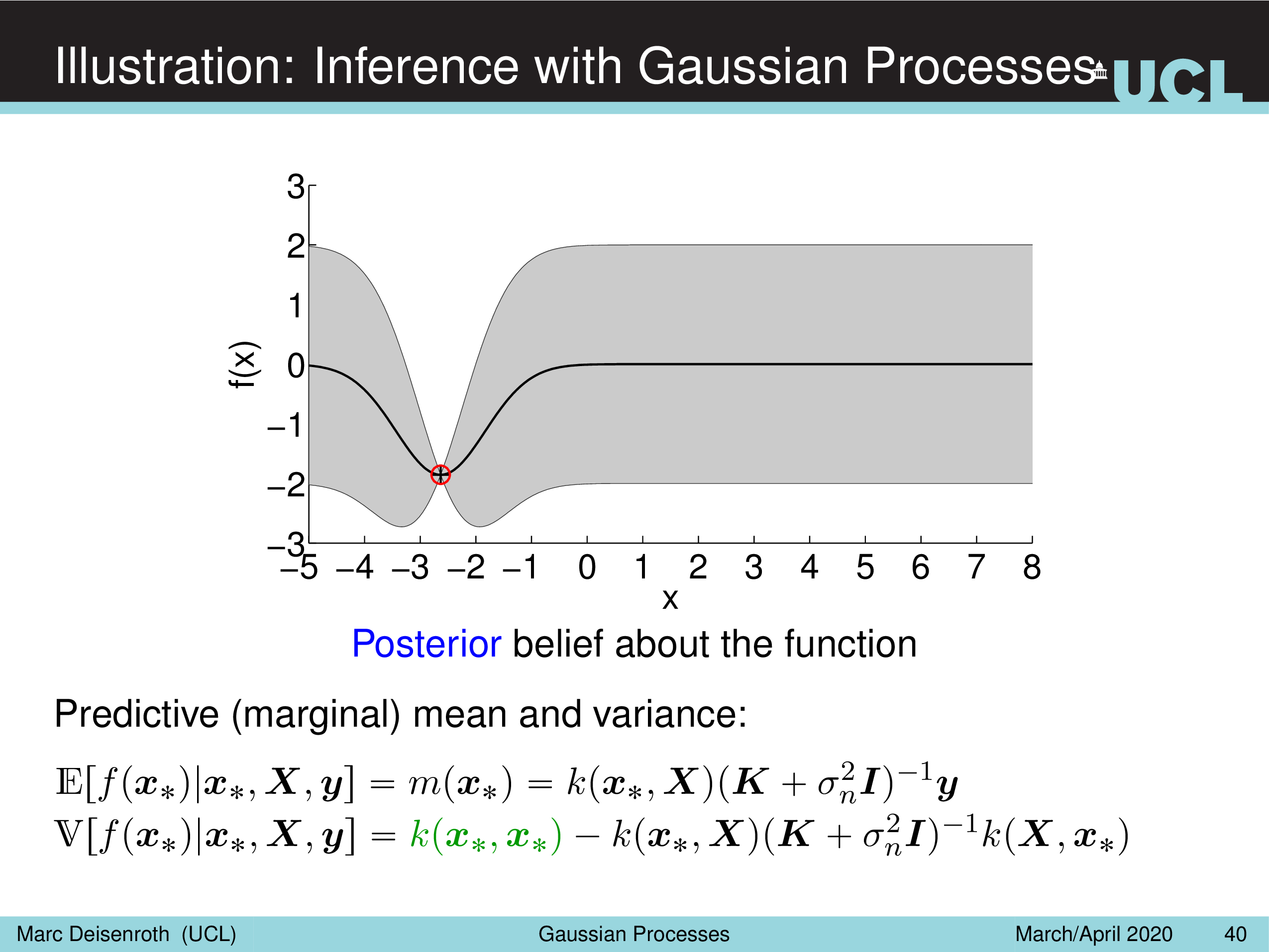 Fig.
Fig.
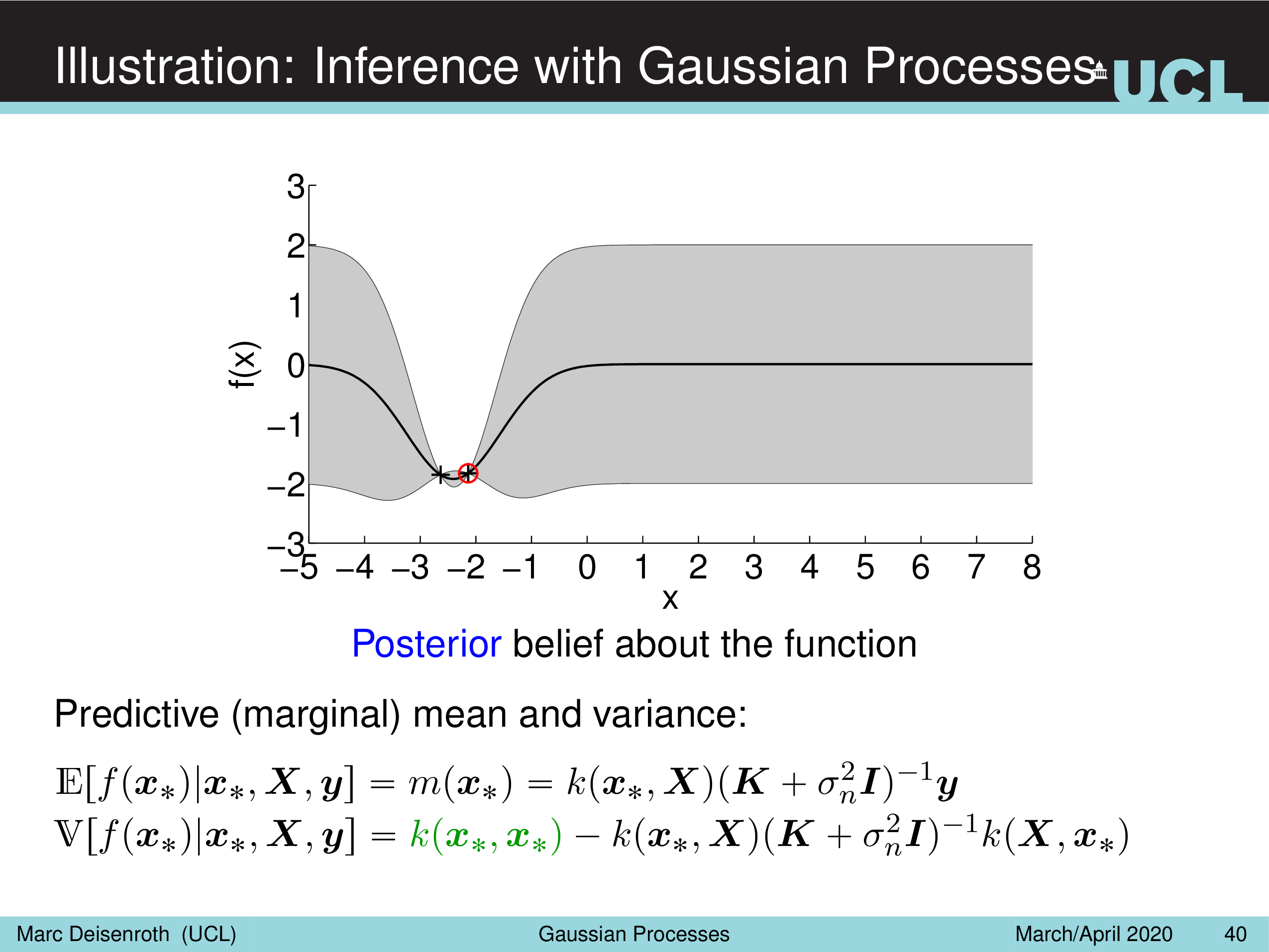 Fig.
Fig.
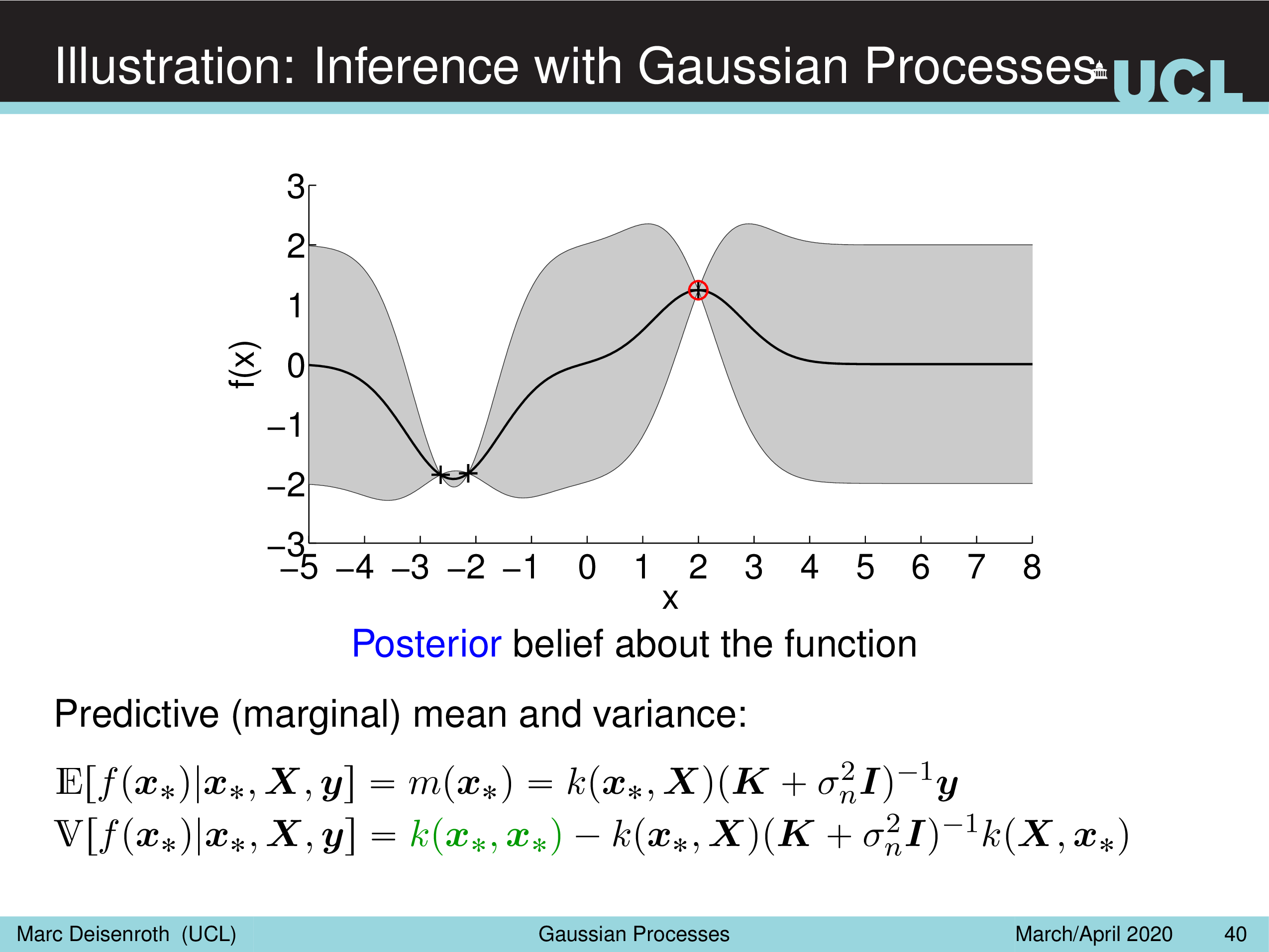 Fig.
Fig.
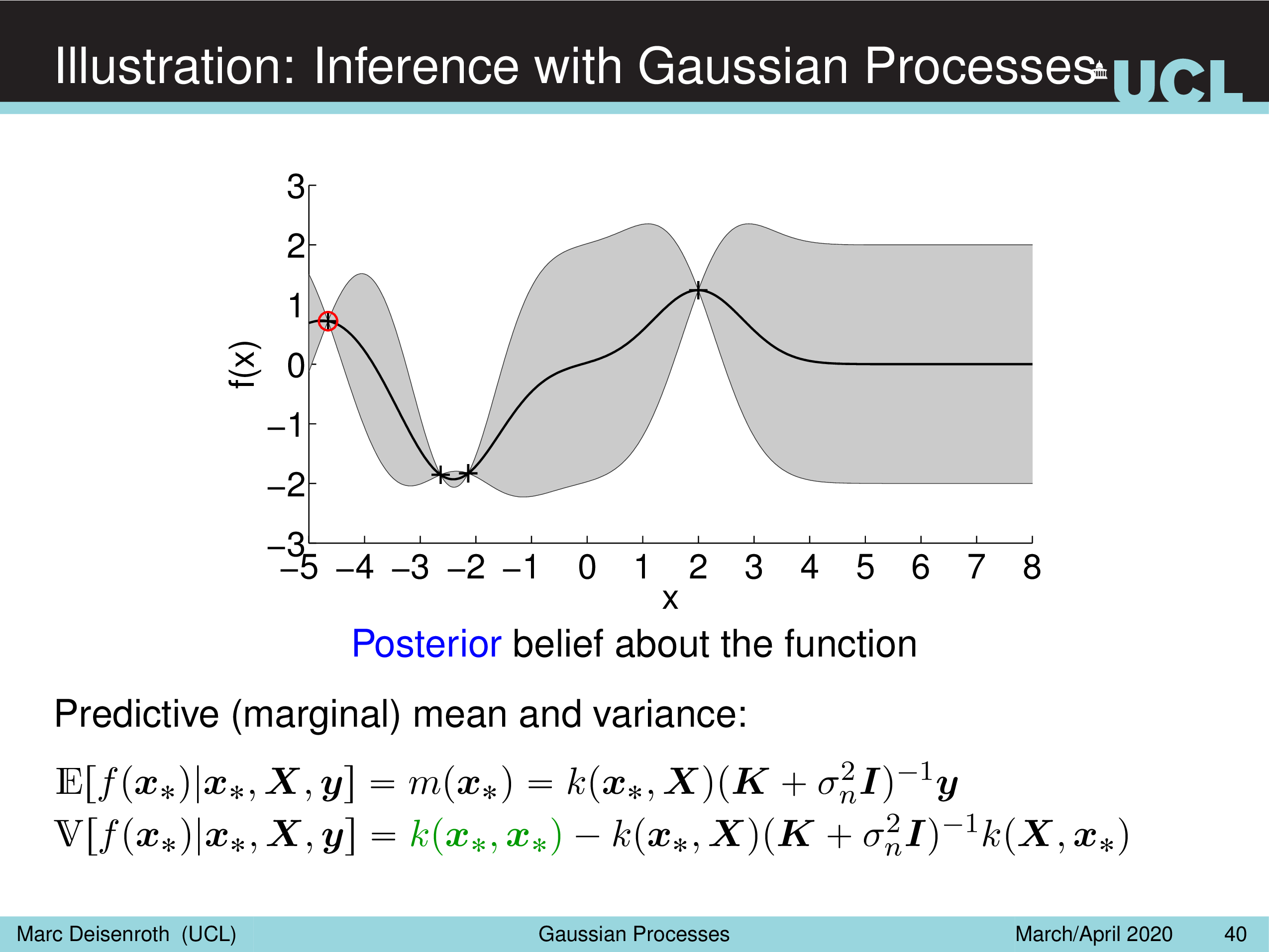 Fig.
Fig.
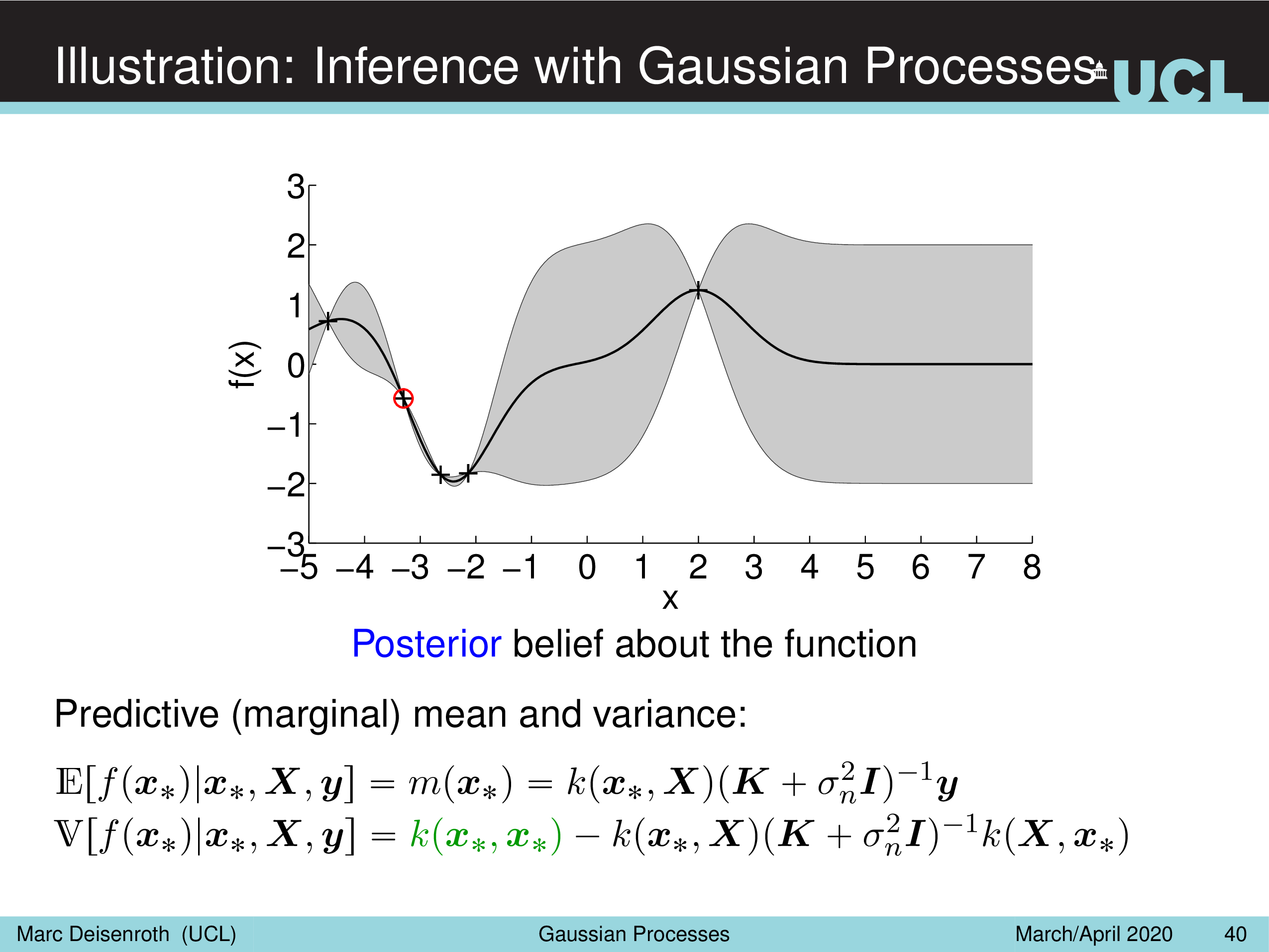 Fig.
Fig.
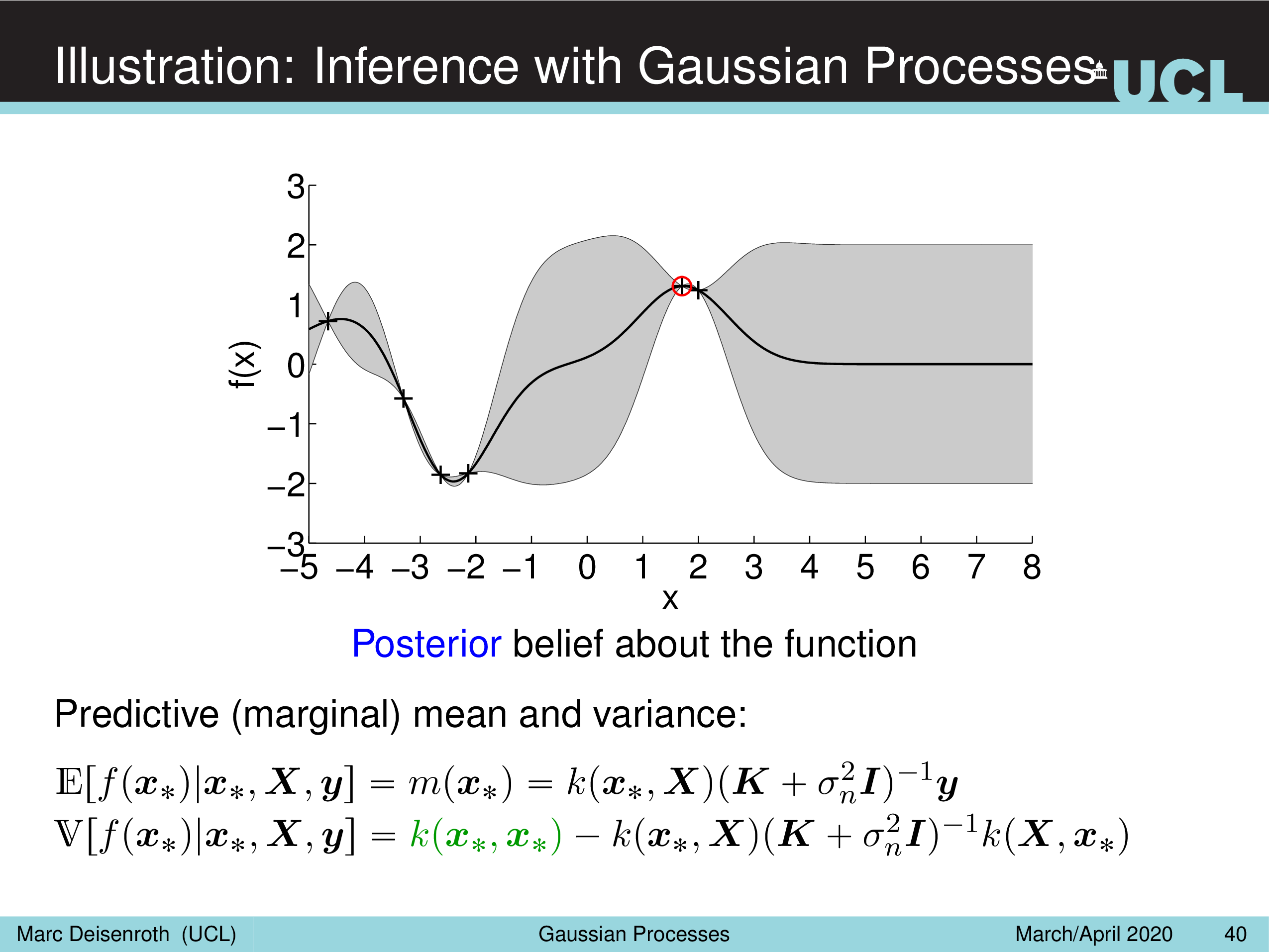 Fig.
Fig.
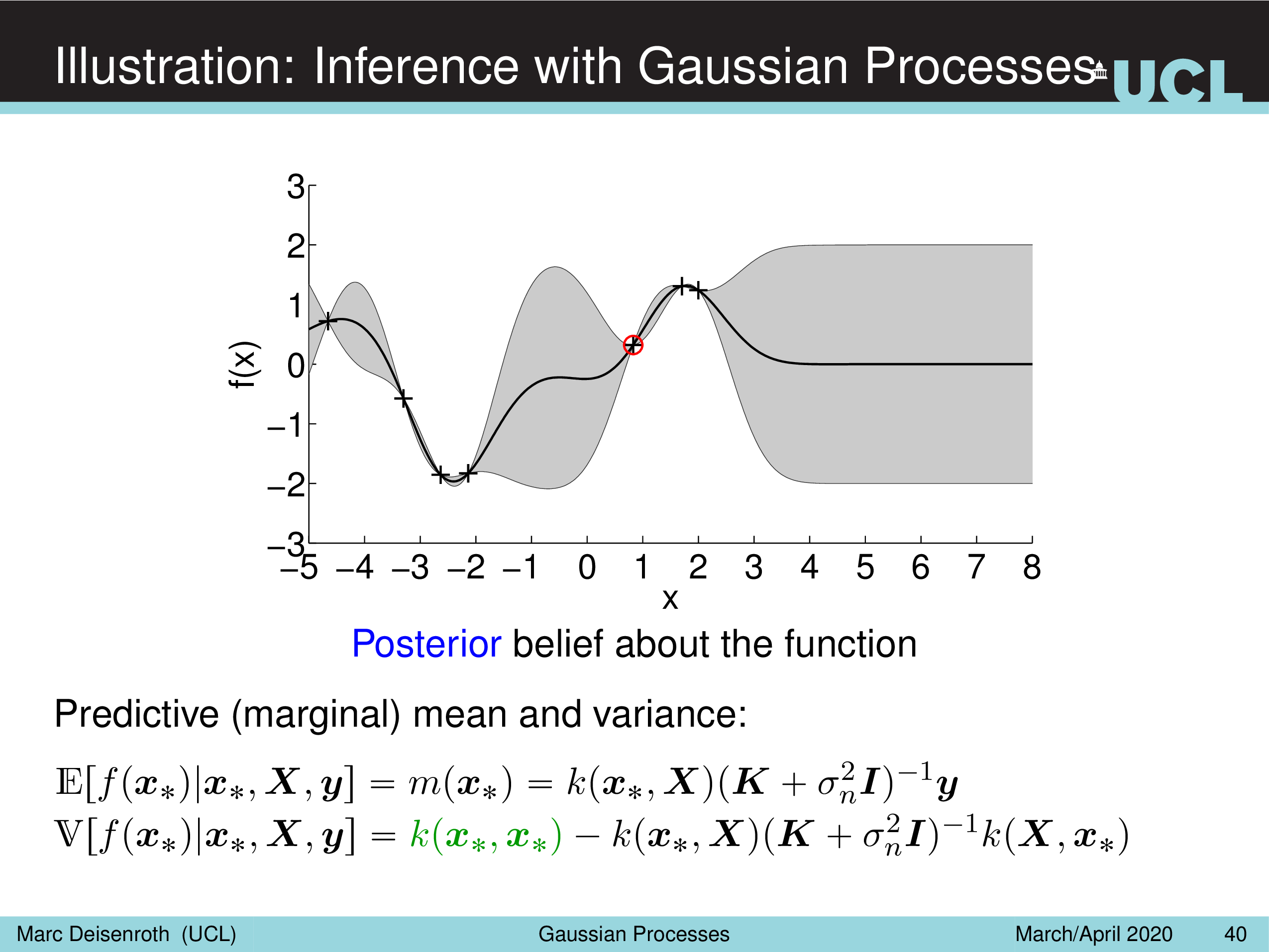 Fig.
Fig.
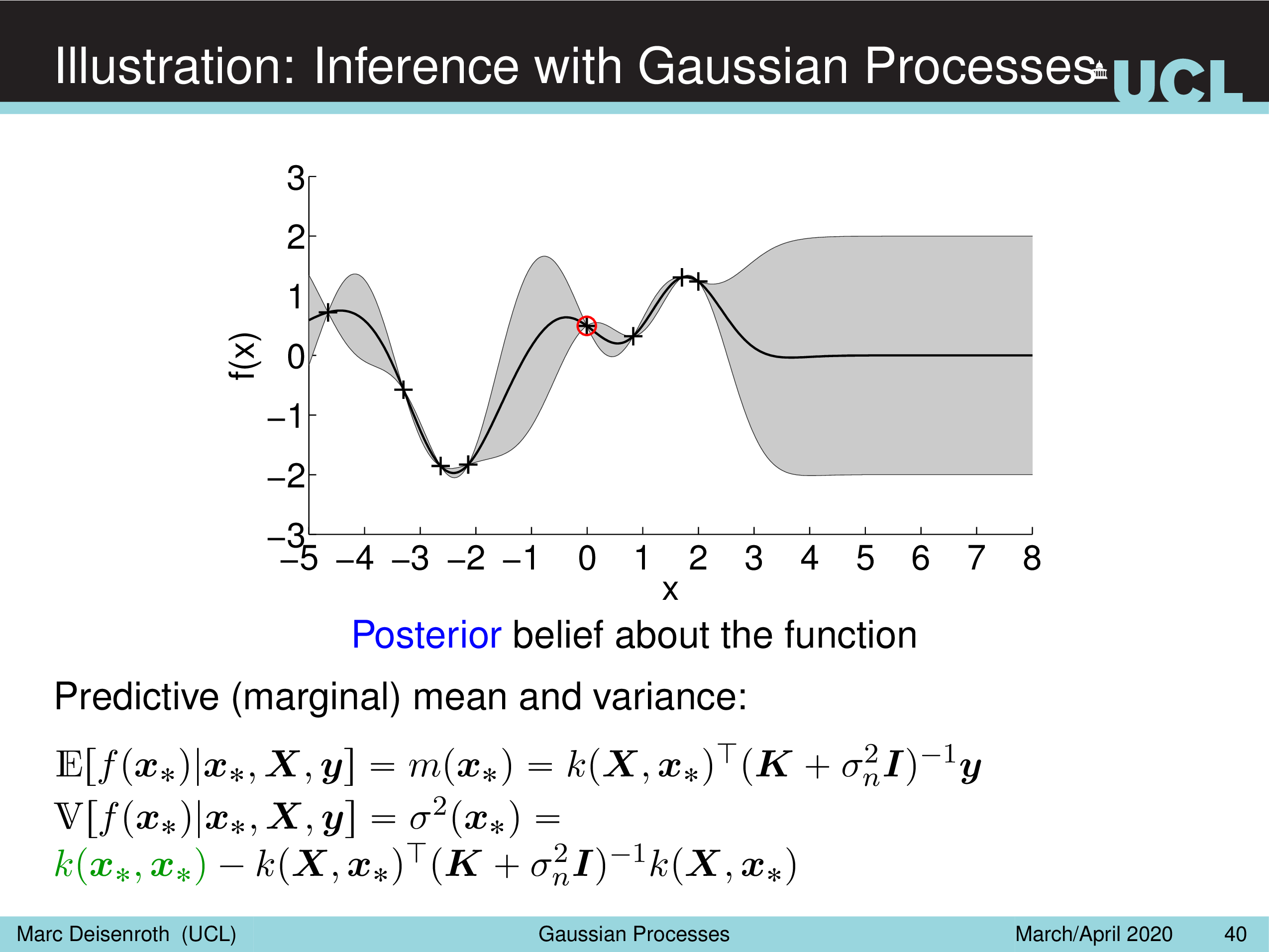 Fig.
Fig.
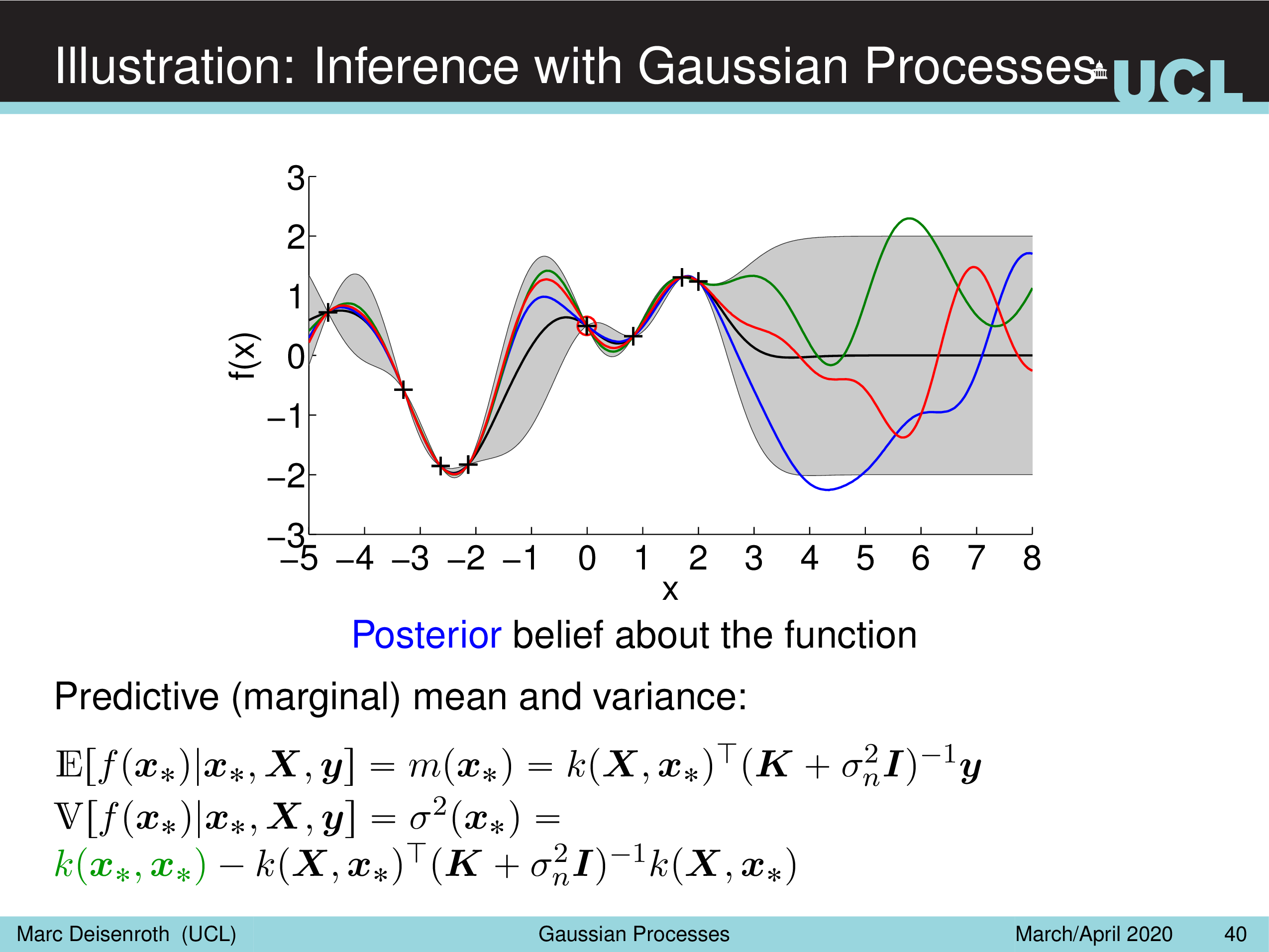 Fig.
Fig.
GP Explanation (2)
두 번째 방법은 다 변수 (multivariate) gaussian distribution를 새롭게 해석해서 GP 를 이해하는 방법이다.
2D Gaussian Example
ML에서는 low dimension에서 개념을 이해하고 이를 high dimension으로 확장시키는게 중요하다.
먼저 변수가 \(y_1, y_2\) 두 개 일 때 2차원 gaussian distribution에 대해 생각해 보자.
2차원 이상의 gaussian distribution는 공분산 행렬 (Covariance Matrix) 에 따라서 distribution의 생김새가 다른데,
covariance Matrix 는 변수들 간의 상관 관계 (correlation) 을 나타낸 것 이다.
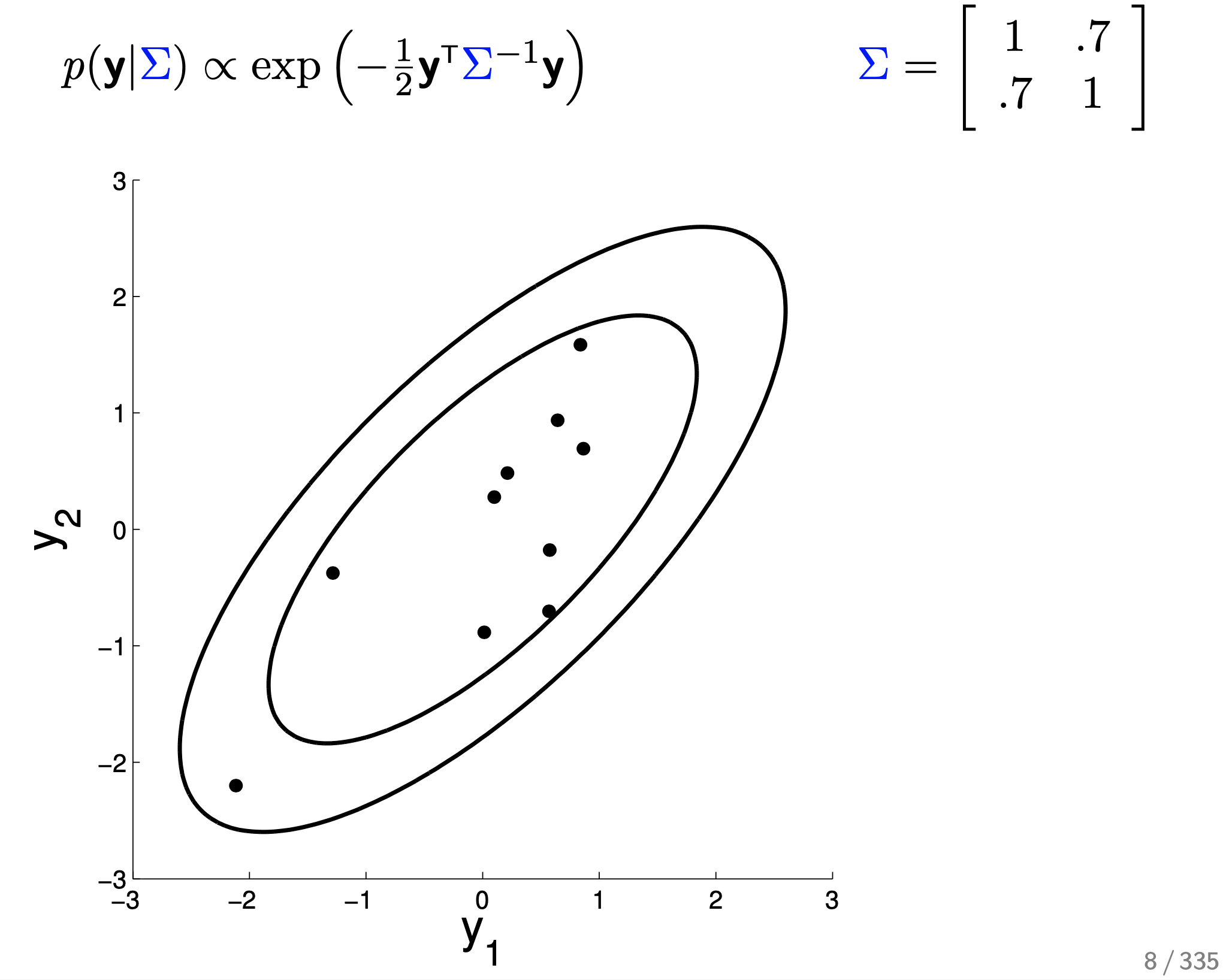 Fig.
Fig.
위의 예시를 보자.
타원형으로 조금 퍼져있는데,
수식이 나타내는 바는 Mean Vector 가 \(\begin{bmatrix} 0 \\ 0 \end{bmatrix}\) 이고 Covariance Matrix 가 \(\begin{bmatrix} 1 & 0.7 \\ 0.7 & 1 \end{bmatrix}\) 라는 의미로, 지금의 경우에는 mean이 0이기 때문에 covariance 행렬이 확률 distribution에 대한 정보를 모두 담고 있다.
지금은 각 변수 \(y_1, y_2\) 방향으로 얼마나 퍼져있는지에 대한 정도 (분산)는 1 로 같은 상태고 두 변수가 얼마나 관련이 있는 변수냐에 대한 정도 (covariance)는 0.7 인 상태로 y1 이 mean보다 큰 값을 가지는, 증가하는 경향을 보일 때 y2 도 0.7 만큼 비슷하게 증가하는 경향을 보인다 는 의미를 공분상 행렬이 가지고 있다.
나머지는 다 같다고 치고 (각각의 분산은 1, mean은 0) correlation에 대해서만 좀 더 살펴보자. 만약 0.6이라면 distribution는 어떻게 변할까?
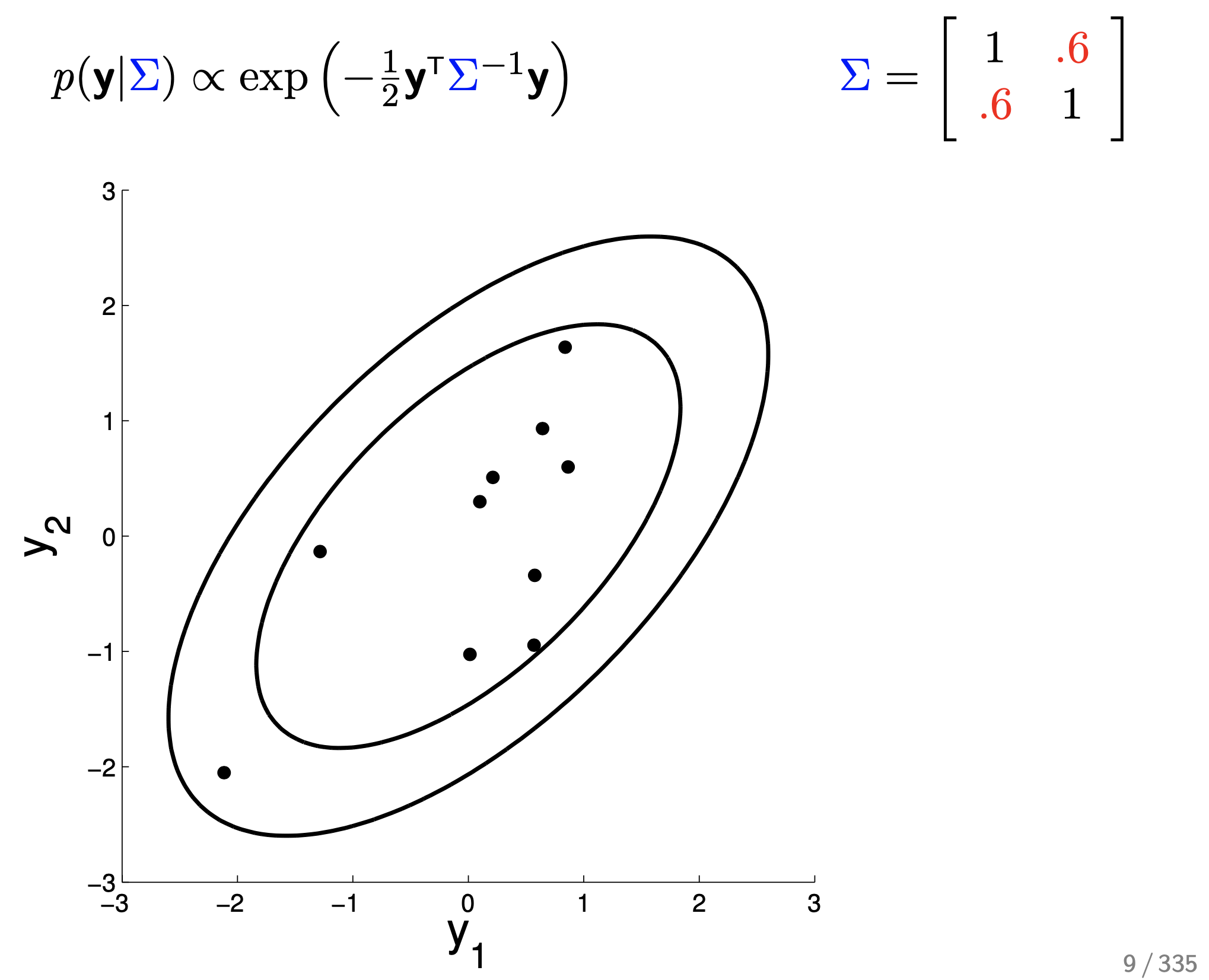 Fig.
Fig.
0.1인 경우에는 거의 두 변수가 correlation가 없어졌다가,
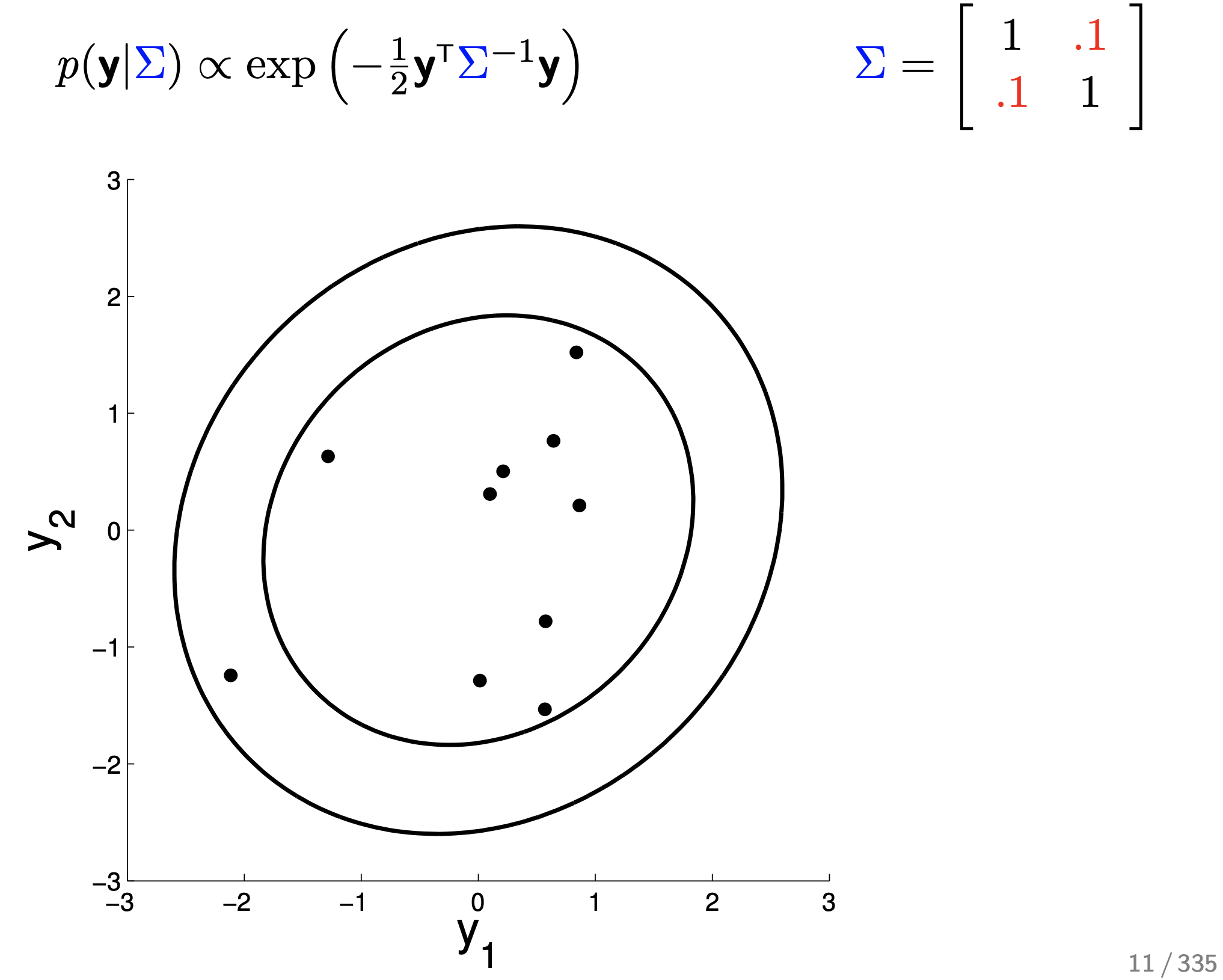 Fig.
Fig.
두 변수가 서로 변하든 말든 서로 correlation가 없으면 값은 0이 되어 아래와 같은 모양이 된다.
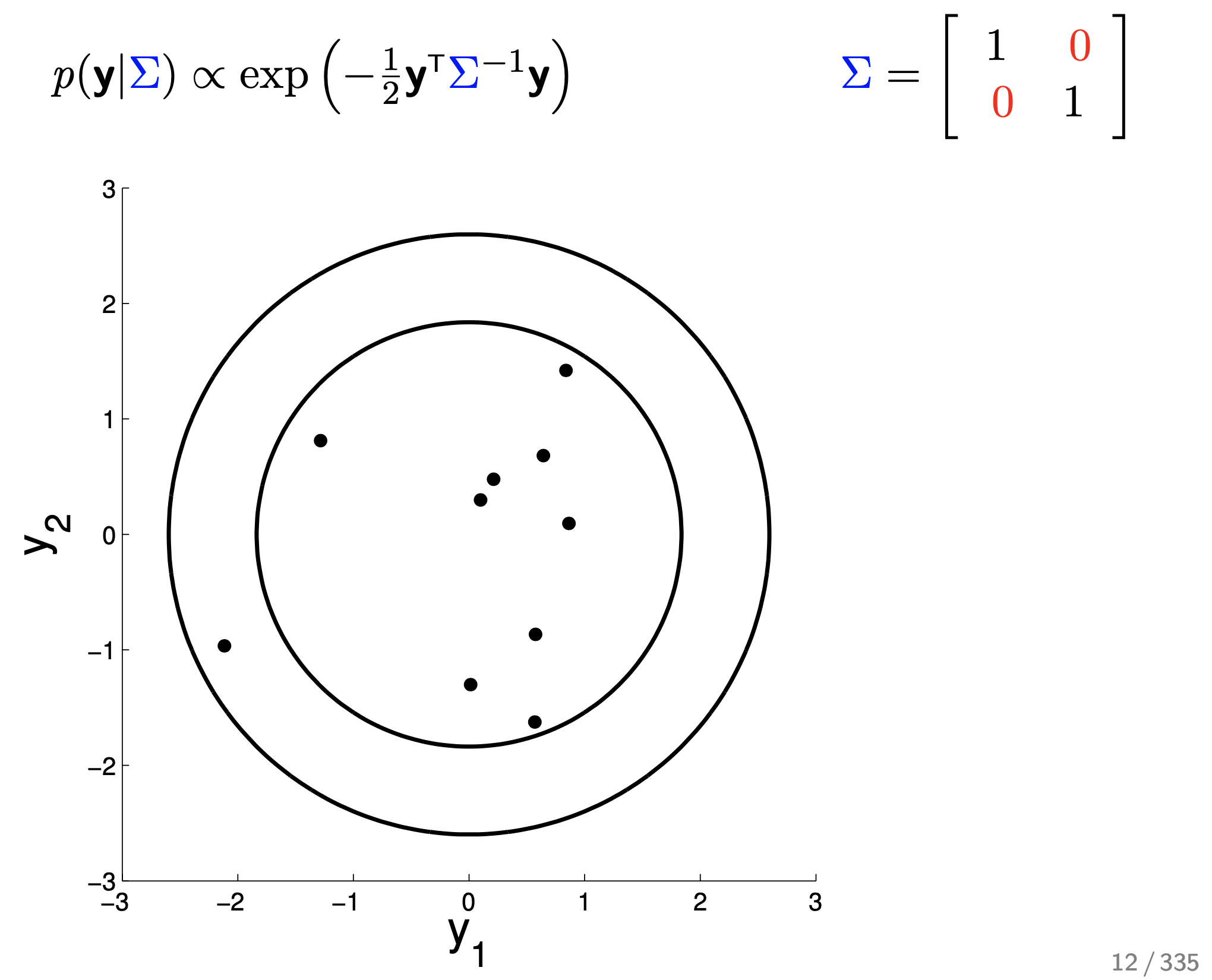 Fig.
Fig.
이런 경우 그냥 \(y_1\) 이 mean보다 큰 쪽에 있을 때 \(y_2\) 도 mean보다 큰쪽에 있을 확률 (correlation)은 아예 없는 것이 된다.
covariance 값은 양수, 0 일수도 있고 음수 일수도 있다.
이를 각 변수의 분산으로 normalize 한 상관 계수 (Correlation Coefficient), \(\rho\) 를 기준으로
아래처럼 다양한 type의 distribution를 표현할 수 있다.
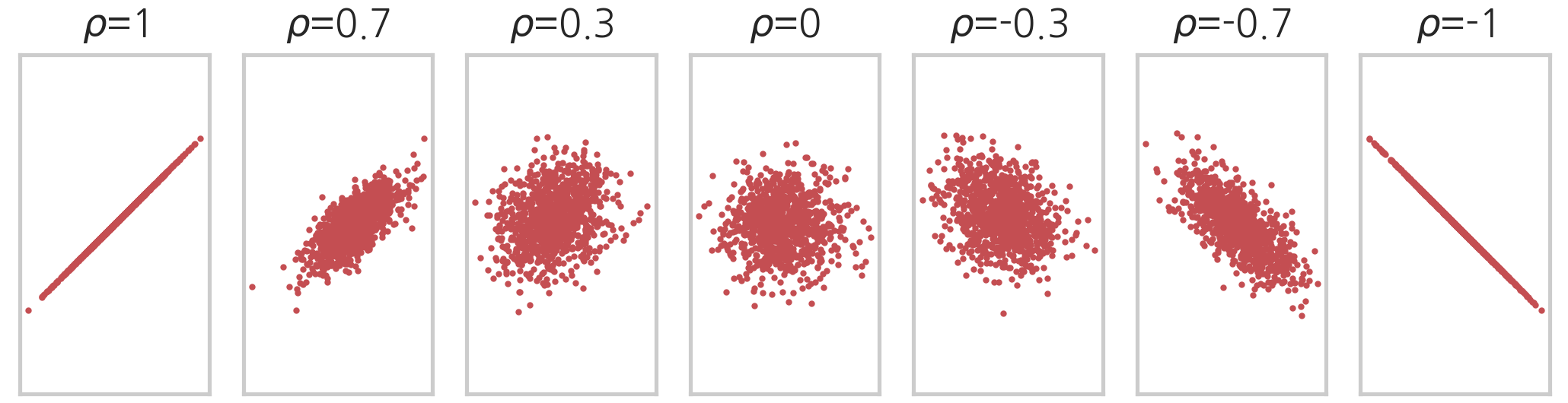 Fig. Source From link
Fig. Source From link
2D Gaussian Example : Conditional Probability
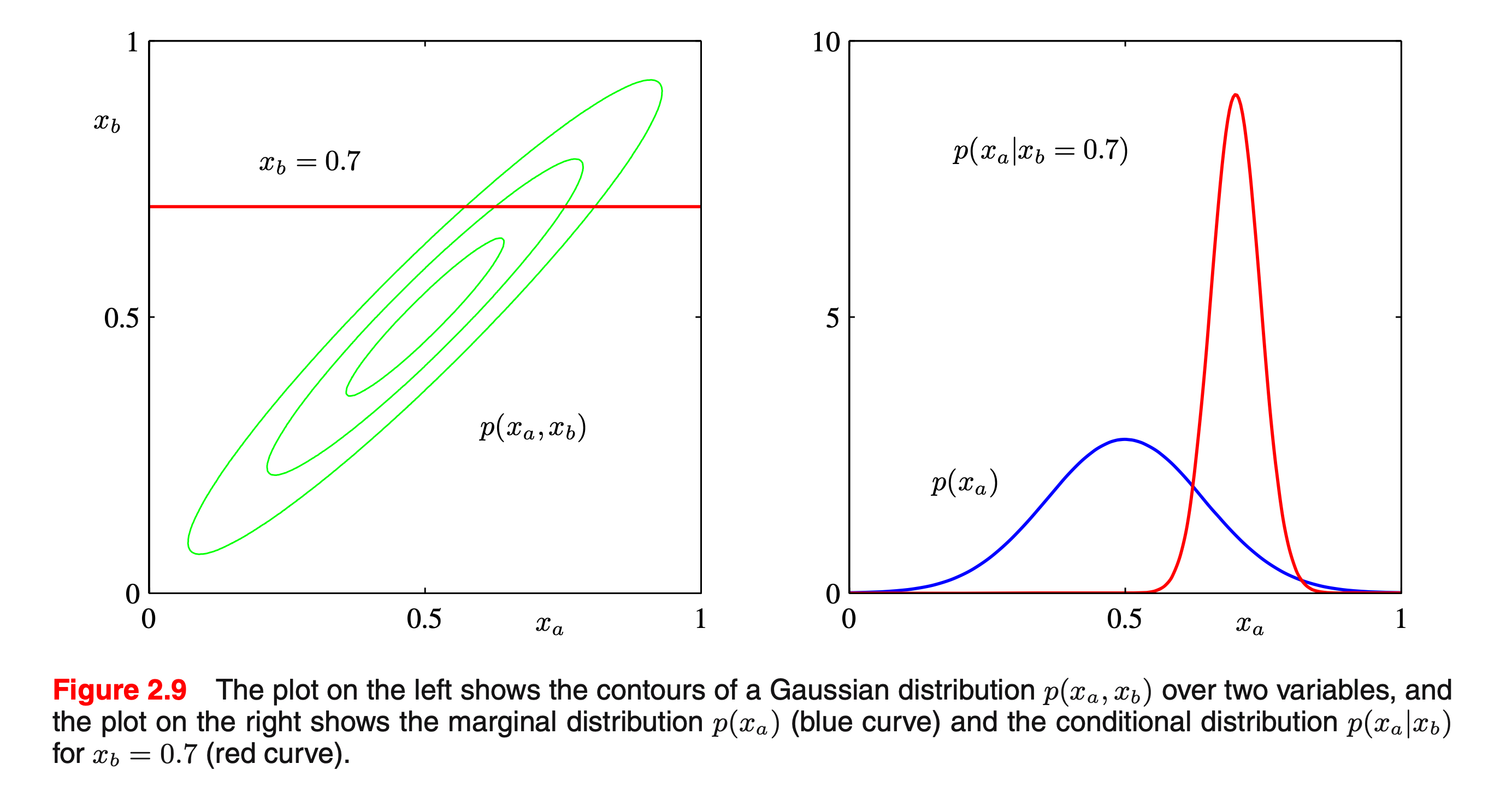 Fig.
Fig.
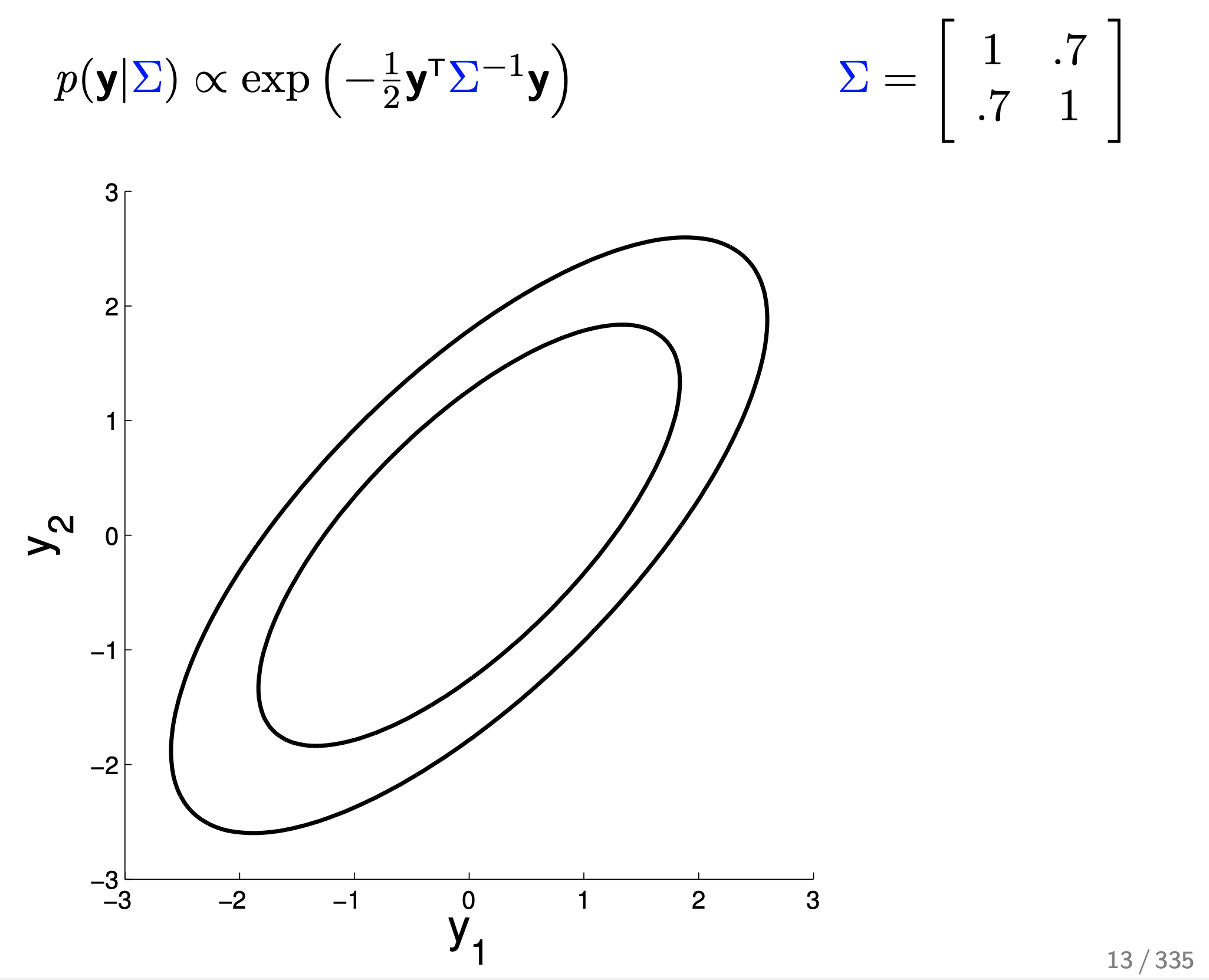 Fig.
Fig.
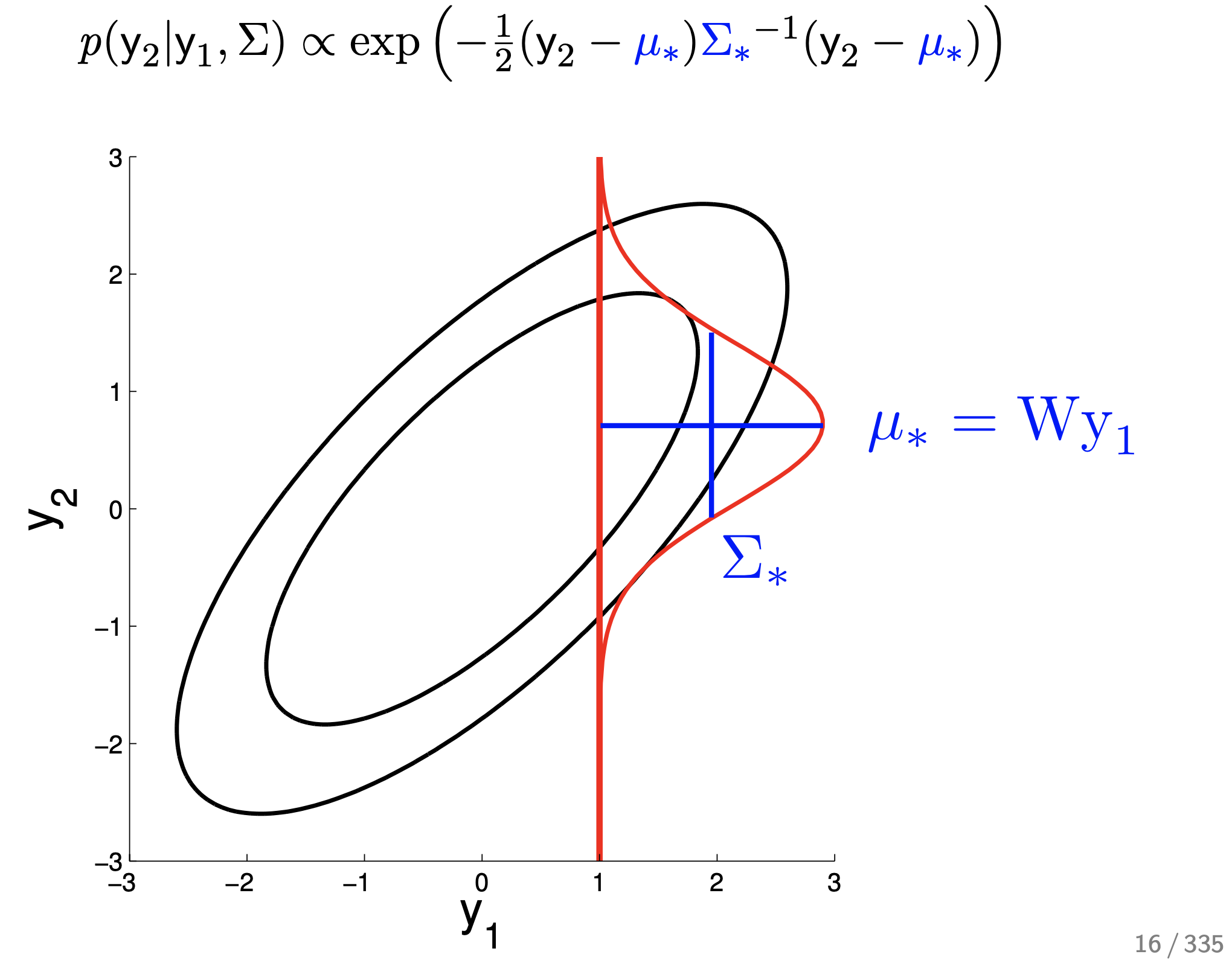 Fig.
Fig.
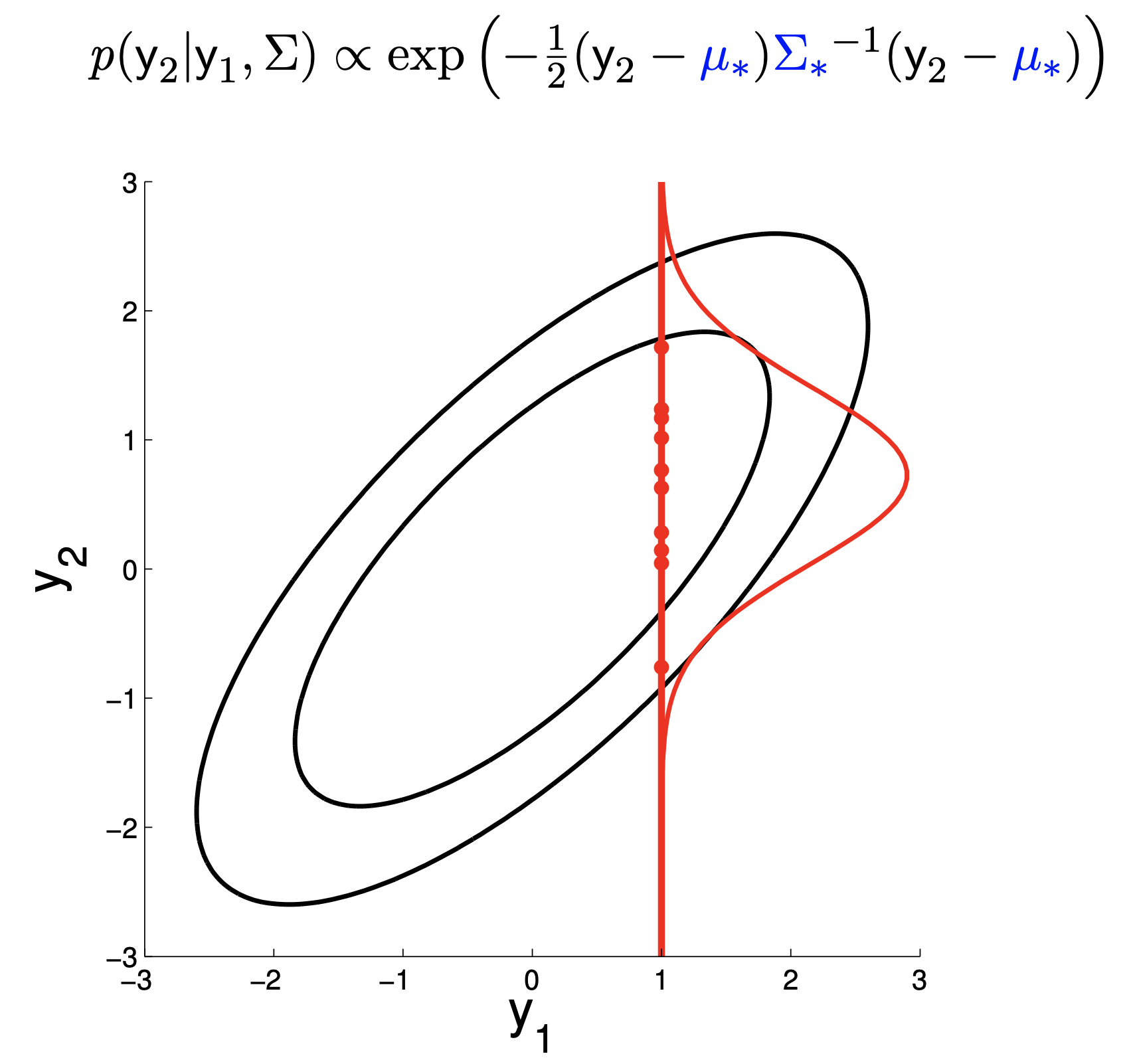 Fig.
Fig.
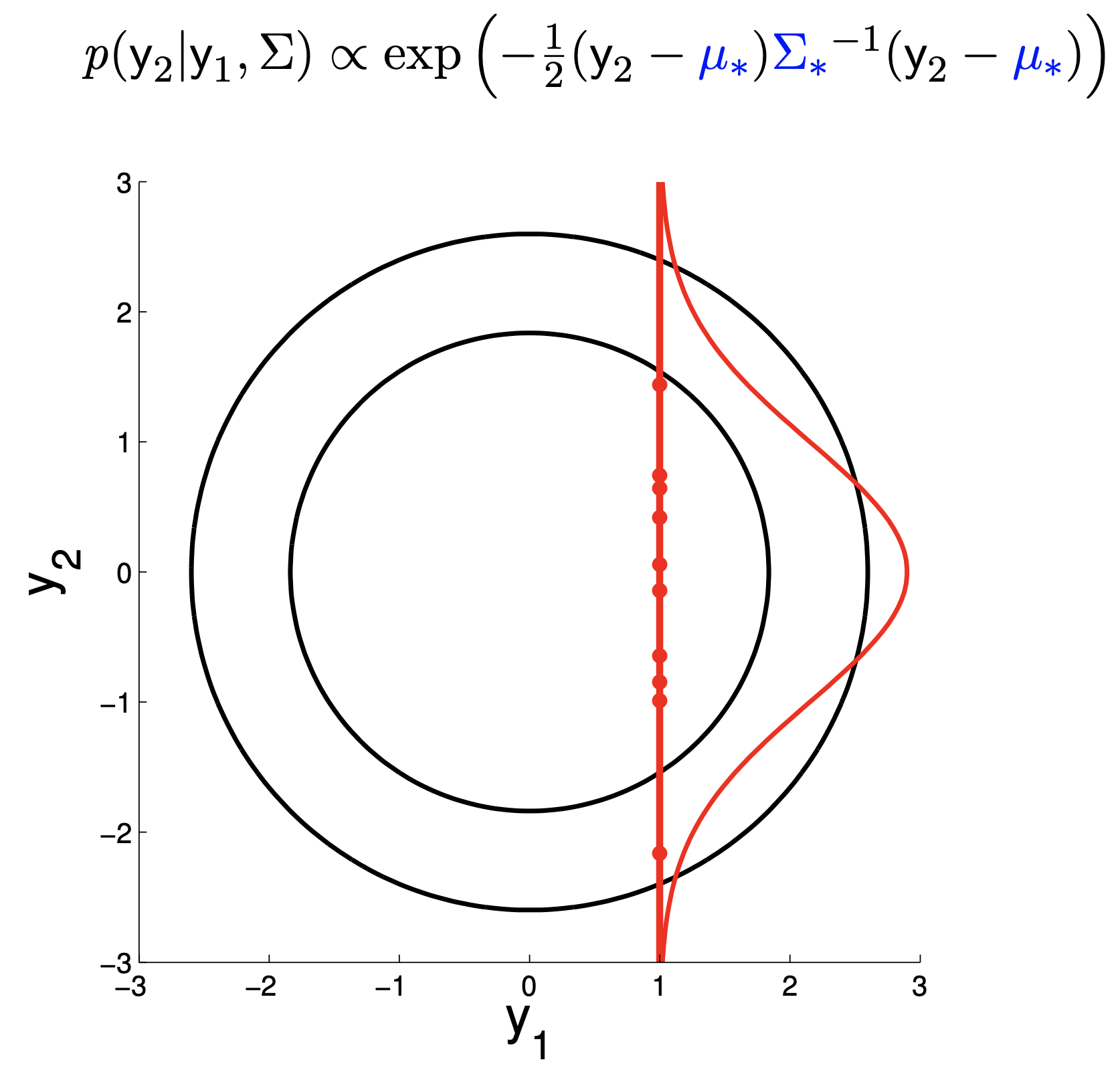 Fig.
Fig.
2D Gaussian Example : New Representation
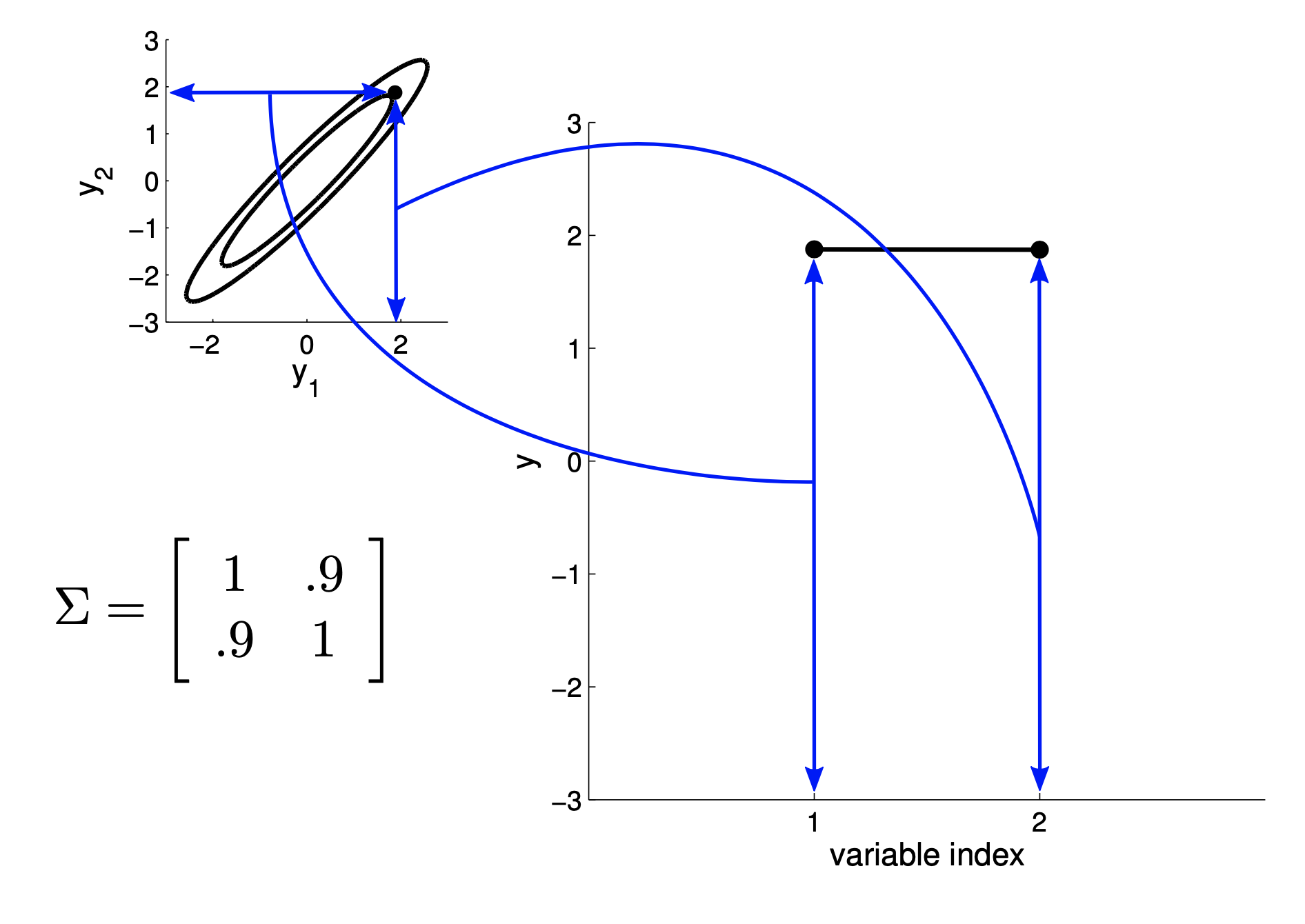 Fig.
Fig.
Higher Dimension : 5D Gaussian
Higher Dimension : 20D Gaussian
GP is Non-Parametric Model (vs Parametric Model)
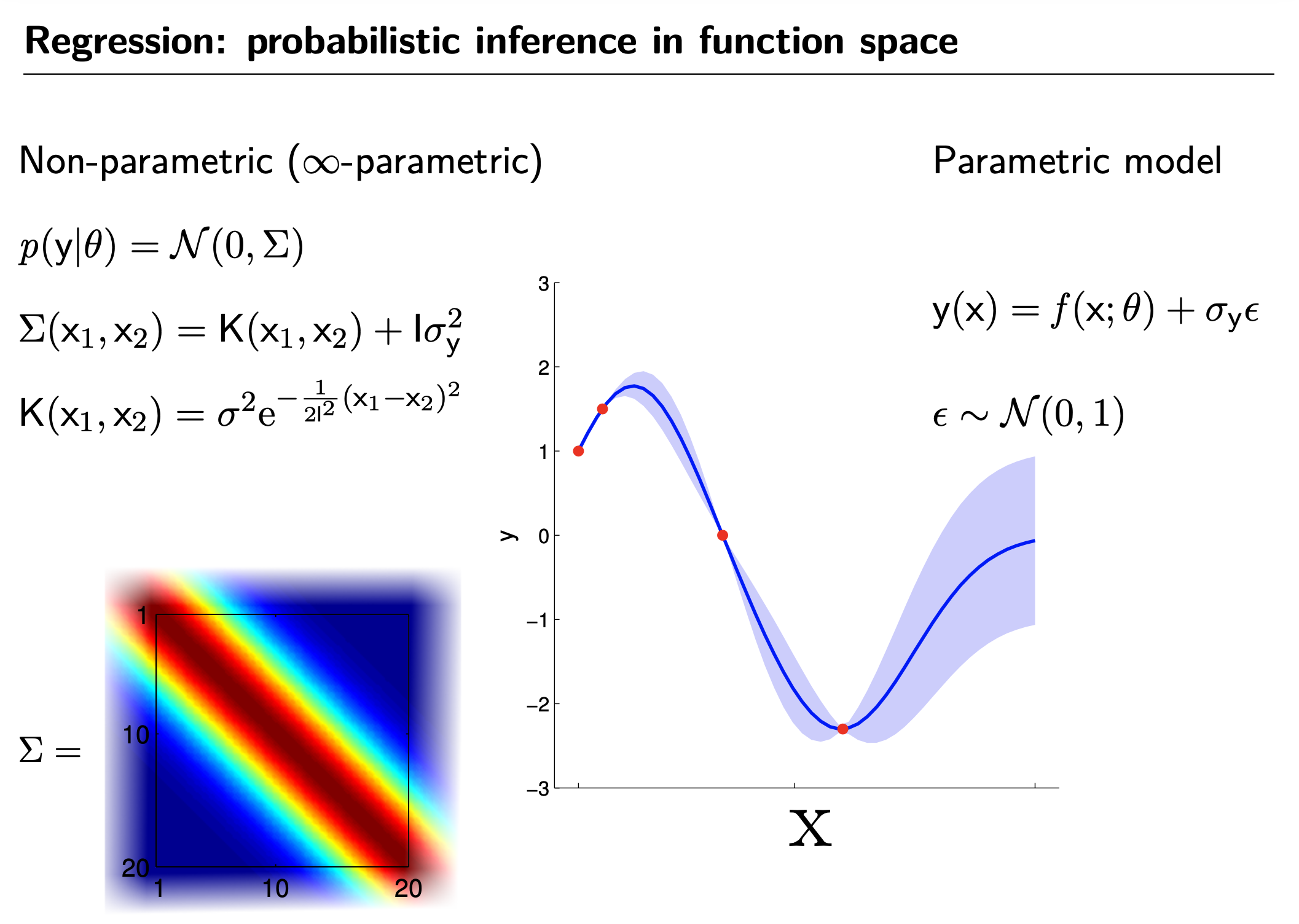 Fig.
Fig.
Mathematical Foundations, Definition
 Fig.
Fig.
GP for Regression
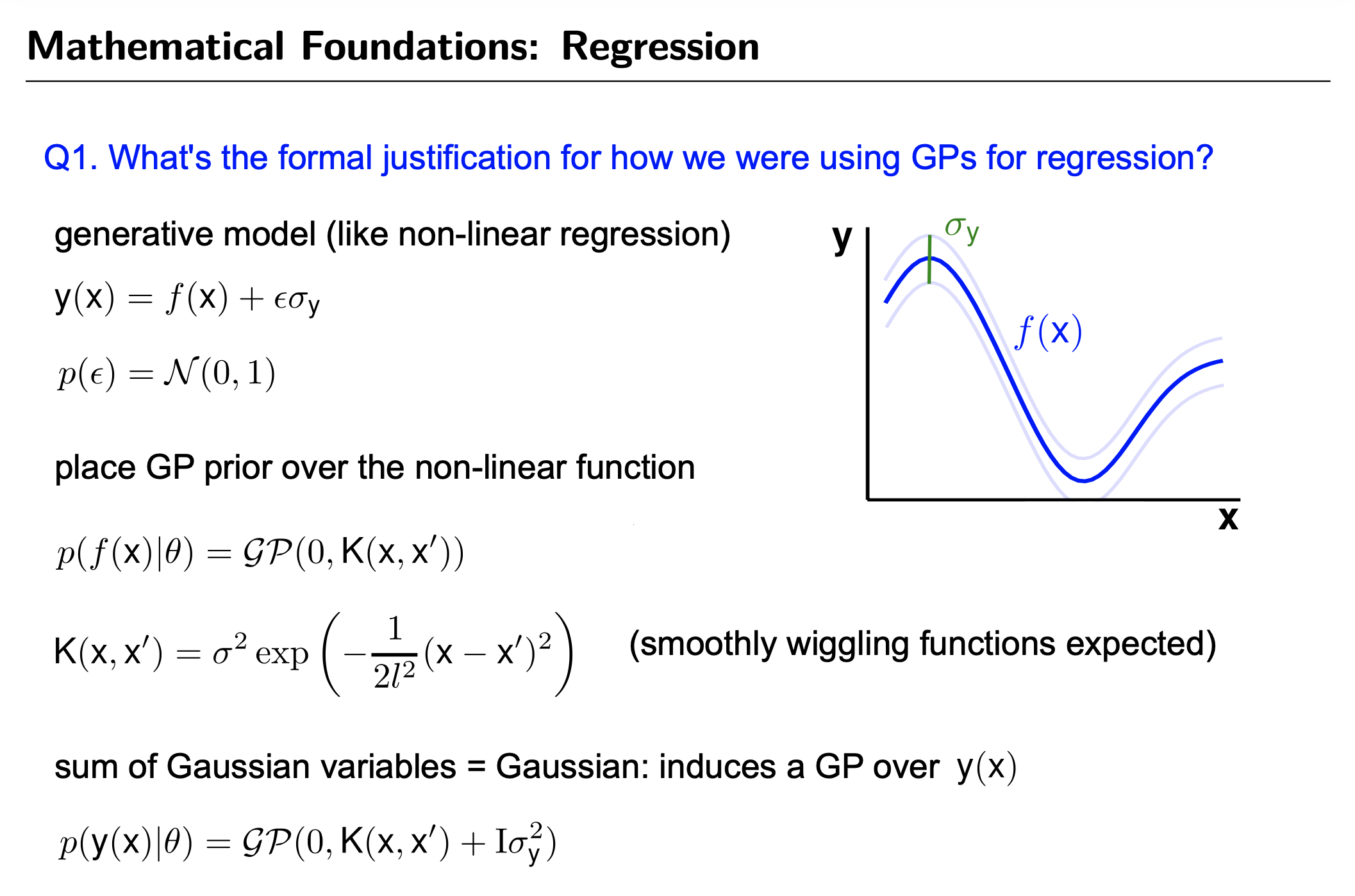 Fig.
Fig.
Marginalisation
 Fig.
Fig.
GP's Prediction (vs Parametric Model's Prediction)
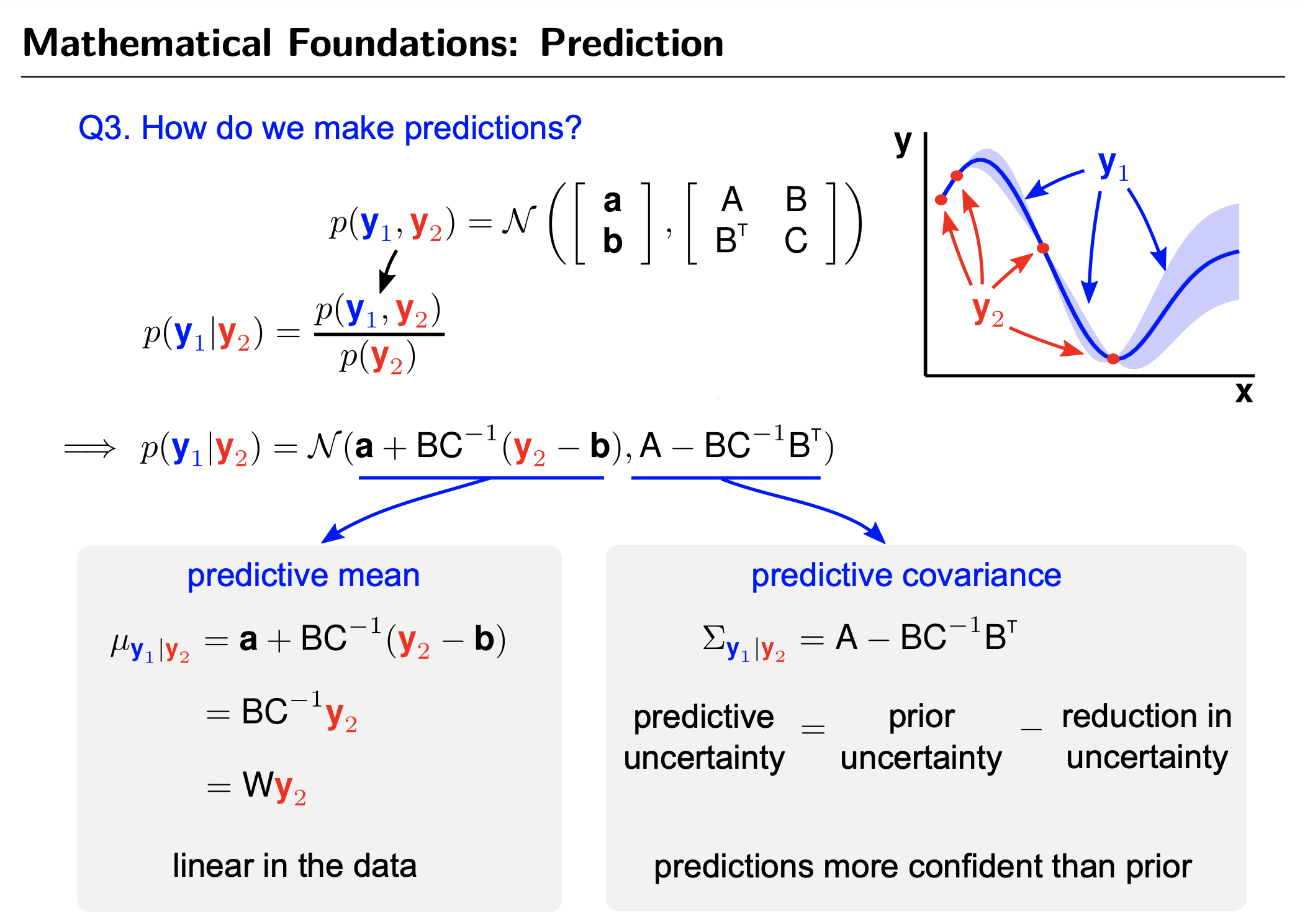 Fig.
Fig.
GP's Limitation
Pros and Cons
 Fig.
Fig.
Applications
 Fig.
Fig.
GP in Modern Deep Learning Era
tmp
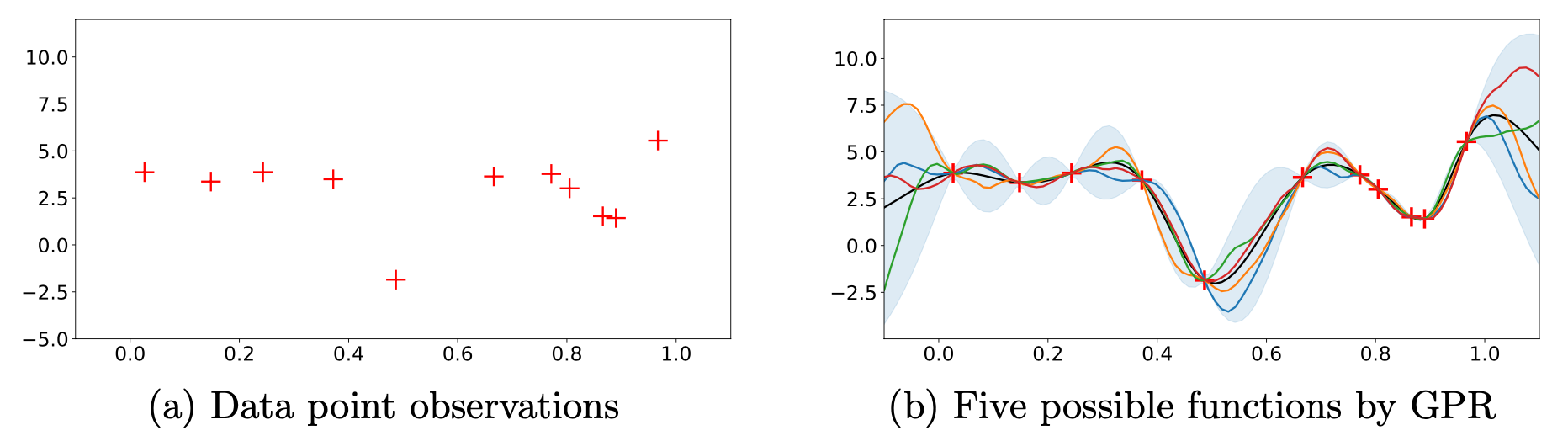 Fig.
Fig.
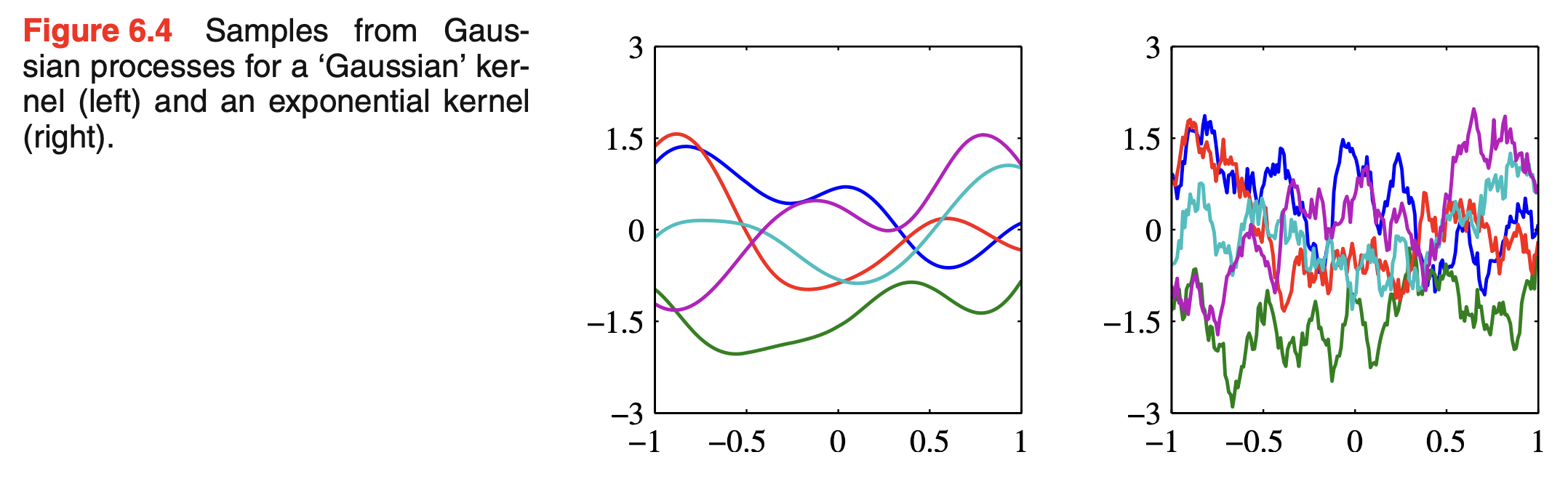 Fig. 6.4.
Fig. 6.4.
References
- Books
- Papers
- Blog and Others
- What My Deep Model Doesn’t Know… (Yarin Gal)
- A Visual Exploration of Gaussian Processes (Distill)
- Lecture 15: Gaussian Processes from Cornell University
- Gaussian processes (1/3) - From scratch
- Gaussian Process, not quite for dummies
- Gaussian Process 설명
- https://sonsnotation.blogspot.com/2020/11/11-2-gaussian-progress-regression.html
- [머신러닝/딥러닝] 11-1. Kernel의 이해와 종류
- What is the essential difference between a neural network and nonlinear regression?
- tmp
- Implicit Lifting and the Kernel Trick from Gregory Gundersen
- Gaussian processes from Martin Krasser
- Videos