MLE & Bayesian Series (3/3) - Bayesian Approach
11 Mar 2021- MLE & Bayesian Series (1/3) - Maximum Likelihood Estimation (MLE)
- MLE & Bayesian Series (2/3) - Maximum A Posteriori (MAP)
- MLE & Bayesian Series (3/3) - Bayesian Approach
< 목차 >
Bayesian Approach
- likelihood : \(p(x\mid\theta)\)
- posterior : \(\text{posterior} \propto \text{likelihood} \times \text{prior} = p(\theta \mid x) \propto p(x \mid \theta)p(\theta)\)
Posterior distribution 이란 likelihood에 parameter에 대한 사전 정보, prior distribution을 추가한 것이었다.
그리고 posterior distribution에서 최대값을 갖는 parameter 하나만을 취하는 것 (point estimation)이 바로 Maximum A Posterior (MAP)라는 method였다.
반면에 가능한 모든 parameter를 고려해서 output distribution을 뽑는것이 베이지안 방법론 (Bayesian Approach)라고 앞서 짧게 언급했었다.
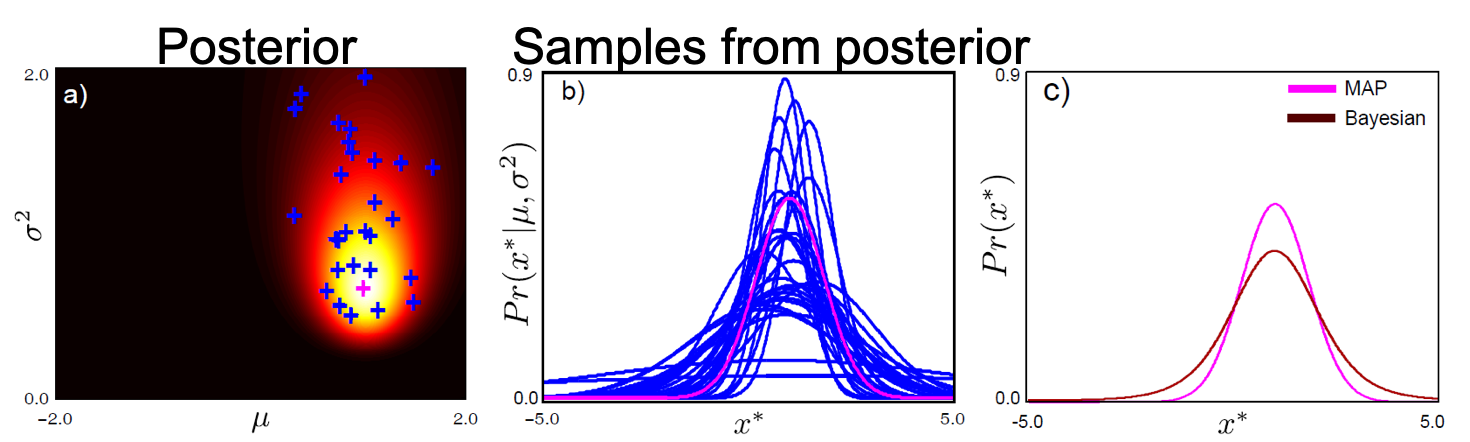 Fig. MAP vs Bayesian
Fig. MAP vs Bayesian
앞서 poseterior distribution은 제가 알기 쉽게 likelihood와 prior의 곱으로 쉽게 표현할 수 있다고 얘기했지만, 이를 제대로 계산하려면 사실 베이즈 룰 (Bayes’ Rule)에 의거해 정확하게 계산해야 한다.
\[\begin{aligned} & \text{posterior} \propto \text{likelihood} \times \text{prior} : p(\theta \vert x) \propto p(x \vert \theta)p(\theta) & \\ & p(\theta \vert x) = \frac{p(x \vert \theta)p(\theta)}{p(x)} & \\ \end{aligned}\]이번에도 likelihood는 Gaussian distribution (Normal distribution)으로 정하고 prior는 계산을 용이하게 하기 위해 Normal Inverse Gamma distribution 으로 정할 것이다. 그러면 posterior distribution의 full derivation은 다음과 같다.
\[\begin{aligned} & p(\theta \vert x) = \frac{p(x \vert \theta)p(\theta)}{p(x)} & \\ & p(\mu,\sigma^2 \vert x_{1,\cdots, I}) = \frac{ \prod_{i=1}^I p(x_i \vert \mu, \sigma^2) p(\mu,\sigma^2) }{ p(x_{1,\cdots,I}) } & \\ & = \frac{ Norm_{x_i} [\mu,\sigma^2] NormInvGam_{\mu,\sigma^2}[\alpha,\beta,\gamma,\delta] }{ p(x_{1,\cdots,I}) } & \\ & = \frac{ \kappa(\alpha,\beta,\gamma,\delta,x_{1,cdots,I}) NormInvGam_{\mu,\sigma^2}[\tilde{\alpha},\tilde{\beta},\tilde{\gamma},\tilde{\delta}] }{ p(x_{1,\cdots,I}) } & \\ & = NormInvGam_{\mu,\sigma^2} [\tilde{\alpha},\tilde{\beta},\tilde{\gamma},\tilde{\delta}] & \\ \end{aligned}\]여기서 \(\tilde{\alpha}, \tilde{\beta}, \tilde{\gamma}, \tilde{\delta}\)는 각각 다음과 같다.
\[\begin{aligned} & \tilde{\alpha} = \alpha + \frac{I}{2} & \\ & \tilde{\gamma} = \gamma + I & \\ & \tilde{\delta} = \frac{ \gamma \delta + \sum_i x_i }{ \gamma +I } & \\ & \tilde{\beta} = \frac{\sum_i x_i^2}{2} + \beta + \frac{\gamma \delta^2}{2} - \frac{ (\gamma \delta + \sum_i x_i )^2}{ 2(\gamma +I) } & \\ \end{aligned}\]복잡해 보여도 prior를 likelihood의 conjugage인 것으로 선정했기 때문에 그나마 간단한 distribution가 도출된 것이다. 이제 우리는 모든 parameter \(\theta=\mu,\sigma^2\)에 대해 고려해서 output distribution을 구하면 되는데, 모두 고려한다는 의미는 적분을 한다는 것이기 때문에 완전한 posterior수식을 계산한 것이다.
\[\begin{aligned} & p(x^{\ast} \vert x_{1,\cdots,I}) = \int p(x^{\ast} \vert \theta) p(\theta \vert x_{1,\cdots,I}) d \theta & \\ & p(x^{\ast} \vert x_{1,\cdots,I}) = \int \int p(x^{\ast} \vert \mu,\sigma^2) p(\mu,\sigma^2 \vert x_{1,\cdots,I}) d \mu d \sigma & \\ \end{aligned}\]위의 수식의 좌변이 의미하는 바는 모든 data point \(x_{1, \cdots, I}\)개로부터 posterior distribution을 구하고,
training data가 아니라 새로운 test data가 들어왔을 때 posterior distribution 하의 모든 parameter 를 사용해서 그 data가 어떤 값이 확률이 몇이나 된다?를 계산하겠다 라는 것이다.
그래서 Bayesian Approach는 Bayesian Inference라고도 불린다.
왜냐하면 posterior distribution을 구하는 것은 맞지만 test data가 들어왔을 때 비로소 적분을 해서 output을 만들어 내기 때문이다.
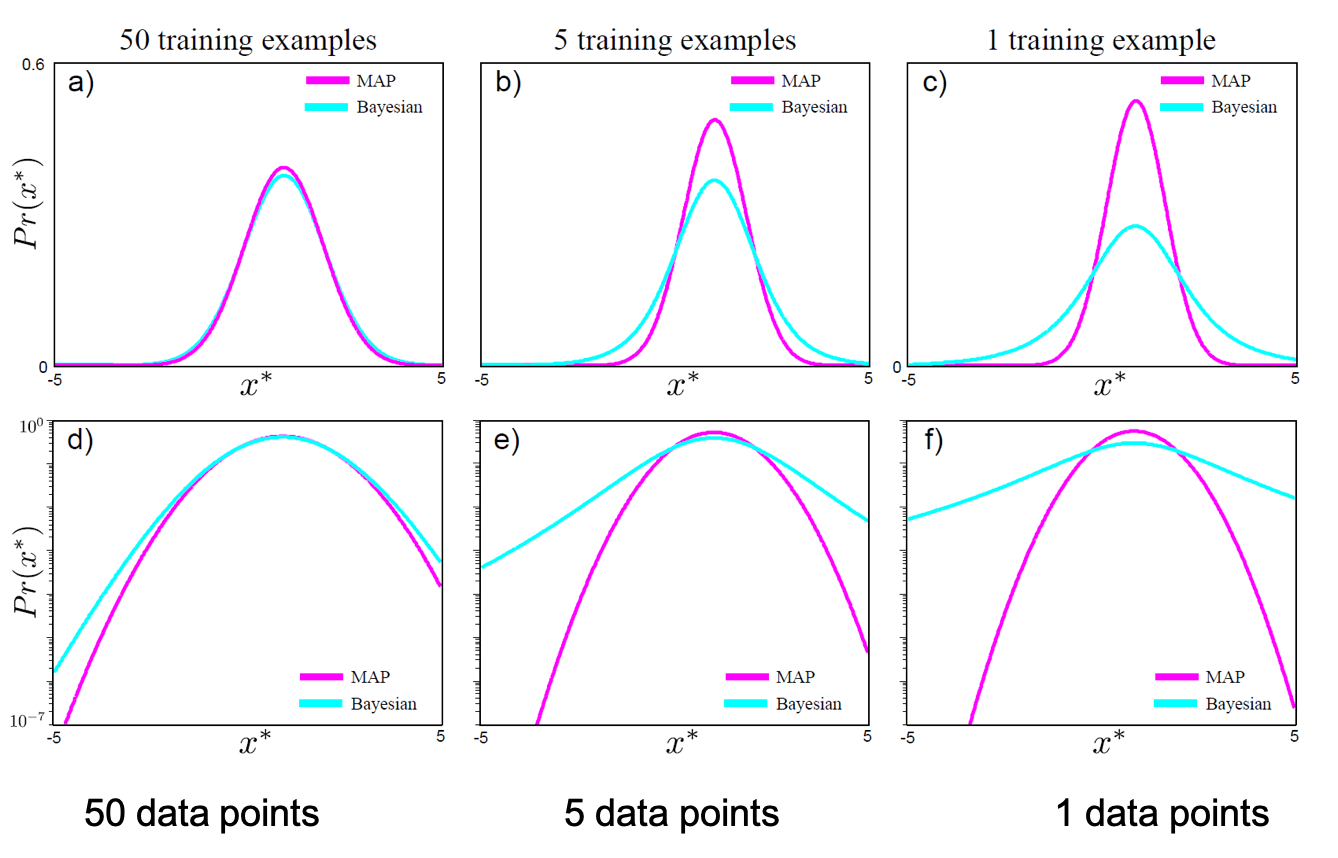 Fig.
Fig.
이러한 Bayesian Approach는 ML/DL의 다양한 회귀 (Regression), 분류 (Classificaion) 문제를 풀 때 적용될 수 있는데, 이 때 발생하는 적분을 계산하는 문제를 완화하기 위해서 다양한 algorithm들이 제안되어 왔다.
다음 post들에서는 본격적으로 regression, classification 등의 task를 푸는 방법과 DL의 핵심인 Neural Network (NN) 등에 대해서 알아보도록 하겠다.