Regression (3/7) - Non-linear regression
15 Feb 2021< 목차 >
- Non-Linear Regression
- Basis Functions
- MLE Solution for Non-Linear Regression
- Bayesian Approach
- References
Non-Linear Regression
이번 post의 주제인 비선형 회귀 (Non-linear Regression)의 motivation는 ‘만약 우리가 가진 data를 도저히 직선 (linear regression의 결과) 으로 표현하기 힘들다면 어떡하지?’ 이다.
그러면 우리 model이 만들어낼 curve가 직선이 아니라 구불거리는, 즉 non-linear 해야하지 않을까??
(여기서 중요한 점은 non linear regression의 ‘비선형 (non linearity)’라는 용어는 독립 변수와 종속 변수 간의 관계가 non linear하다는 것을 의미한다는 것이다. 매개변수 간에는 선형성이 성립할 수 있지만 중요한 것은 그게 아니다.)
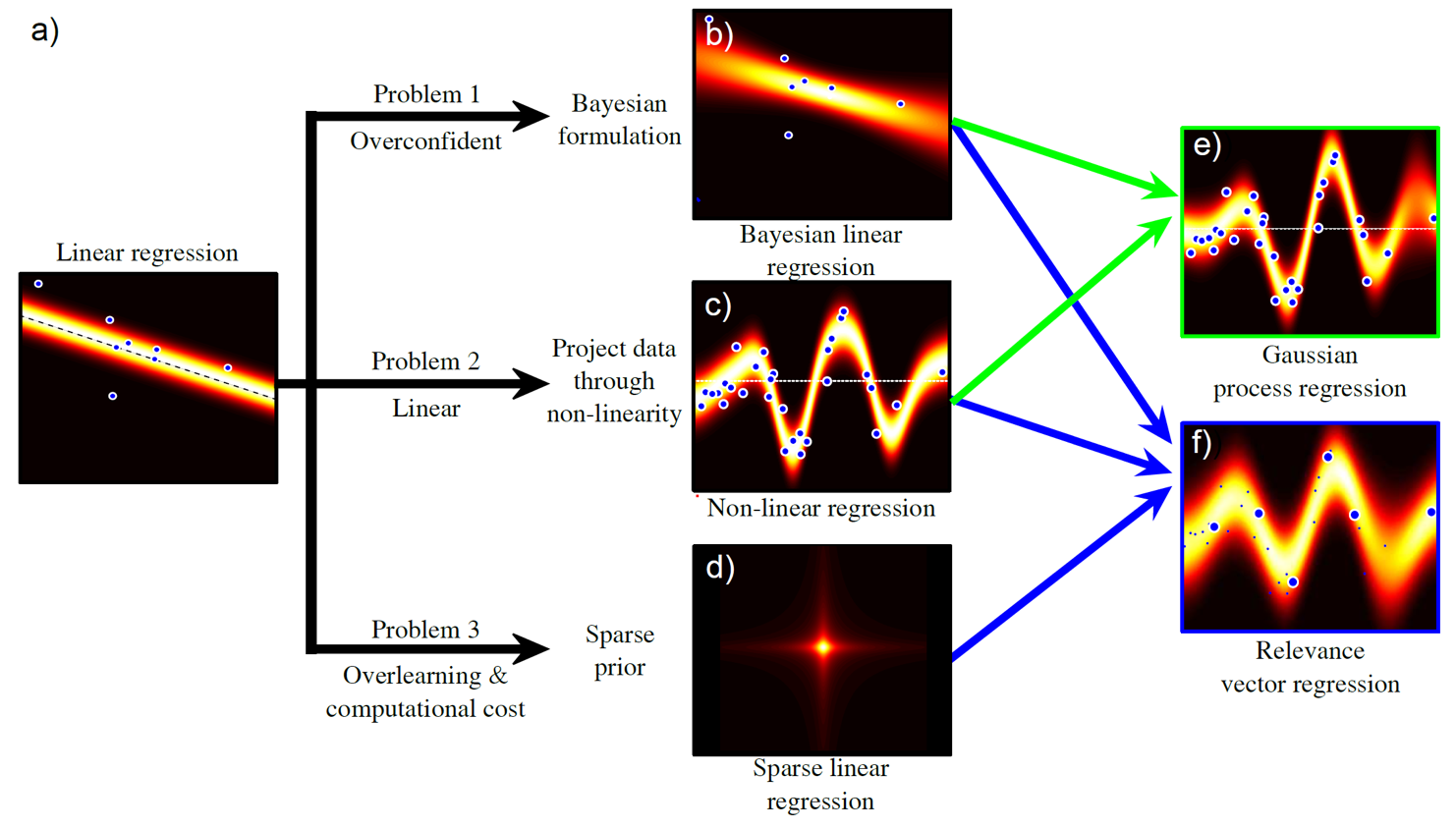 Fig. Regression problem의 variations
Fig. Regression problem의 variations
우리가 지금까지 다룬 linear regression의 경우, target, \(w\)에 대한 distribution을 gaussian distribution으로 설정했고, 이 때의 likelihood는 다음과 같이 쓸 수 있었다.
\[Pr(w_i \vert x_i, \theta) = Norm_{w_i}[\theta^T x_i, \sigma^2]\]여기서 비선형성 (non-linearlity)를 주기위해서는 input data를 어떠한 nonlinear function에 통과시켜야 한다.
\[\begin{aligned} & Pr(w_i \vert \color{red}{z_i}, \theta) = Norm_{w_i}[\theta^T \color{red}{z_i}, \sigma^2] \\ & \text{where } \color{red}{z_i} = f[x_i] \\ \end{aligned}\]여기서 \(x\)를 \(z\)로 mapping해주는 function을 기저 함수 (Basis Function)라고 한다.
Basis Functions
Basis function에는 다양한 종류가 있는데, 이번 post에서는 두 가지 정도만 알아볼 것이다.
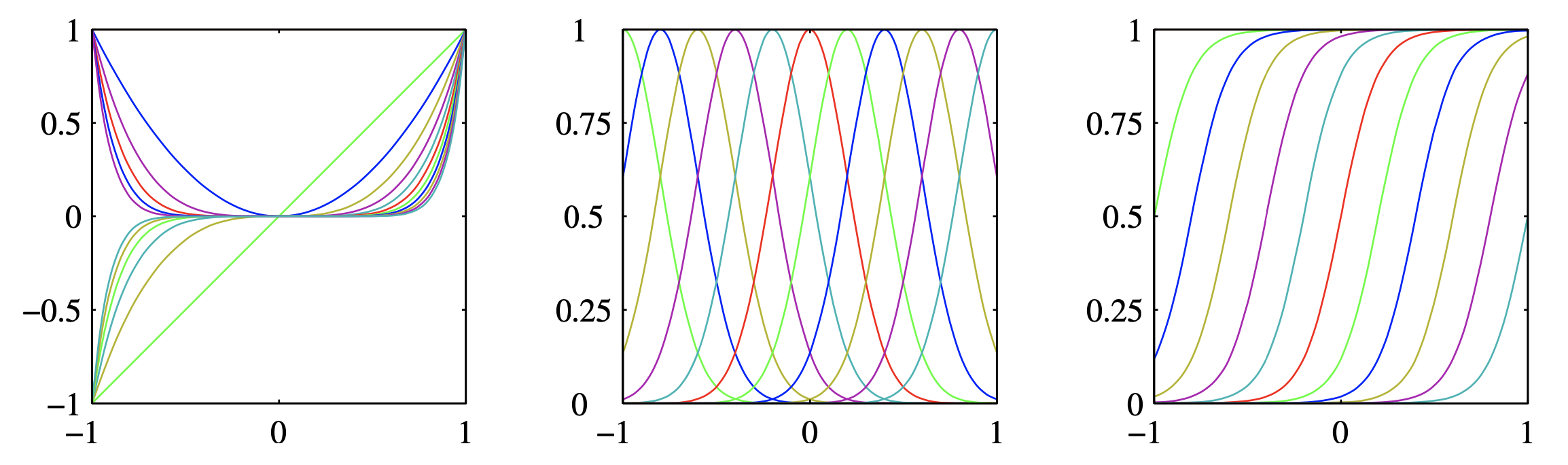 Fig. basis function의 예시들. 왼쪽부터 다항 기저 함수 (polynomial basis function), gaussian, sigmoid.
Fig. basis function의 예시들. 왼쪽부터 다항 기저 함수 (polynomial basis function), gaussian, sigmoid.
Polynomial Regression
우선 polynomial basis function을 쓰는 경우에 대해서 알아보자. 이를 사용해 curve fitting한 것을 polynomial regression라고 하는데, 이는 input, \(x_i\)에 대해서 이것의 대한 제곱항, 세제곱항에 해당하는 curve를 weighted sum 하는걸 말한다.
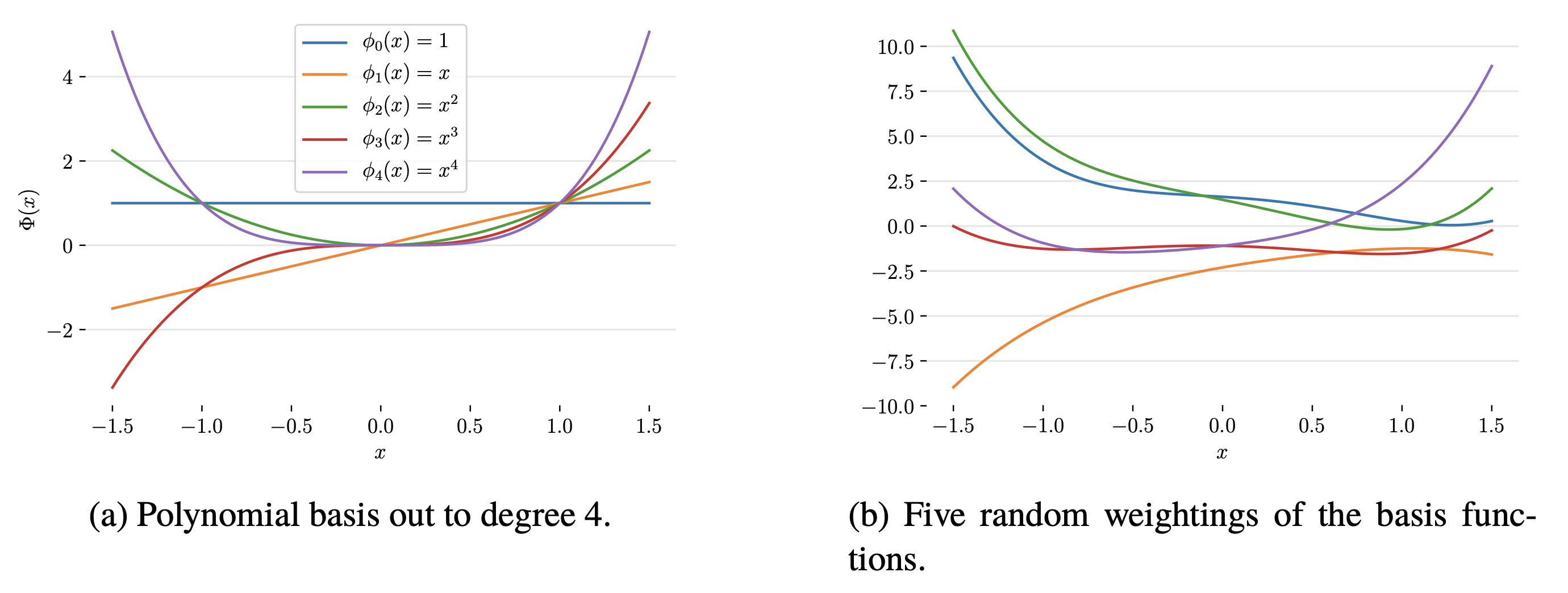 Fig. polynomial basis function의 몇가지 예시(좌)와 이에 random하게 weight을 곱한 결과(우)
Fig. polynomial basis function의 몇가지 예시(좌)와 이에 random하게 weight을 곱한 결과(우)
이를 수식으로 나타내면 아래와 같다.
\[Pr(w_i \vert x_i, \theta) = Norm_{w_i}[\theta_0 + \theta_1 x_i + \theta_2 x_i^2 + \theta_3 x_i^3, \sigma^2 ]\]Radial Basis Functions
너무 중요한 basis function에 대해서 하나만 더 알아보도록 하자.
바로 방사 basis function (Radial Basis Function; RBF)이다.
이는 gaussian basis function 이라고 불리기도 한다.
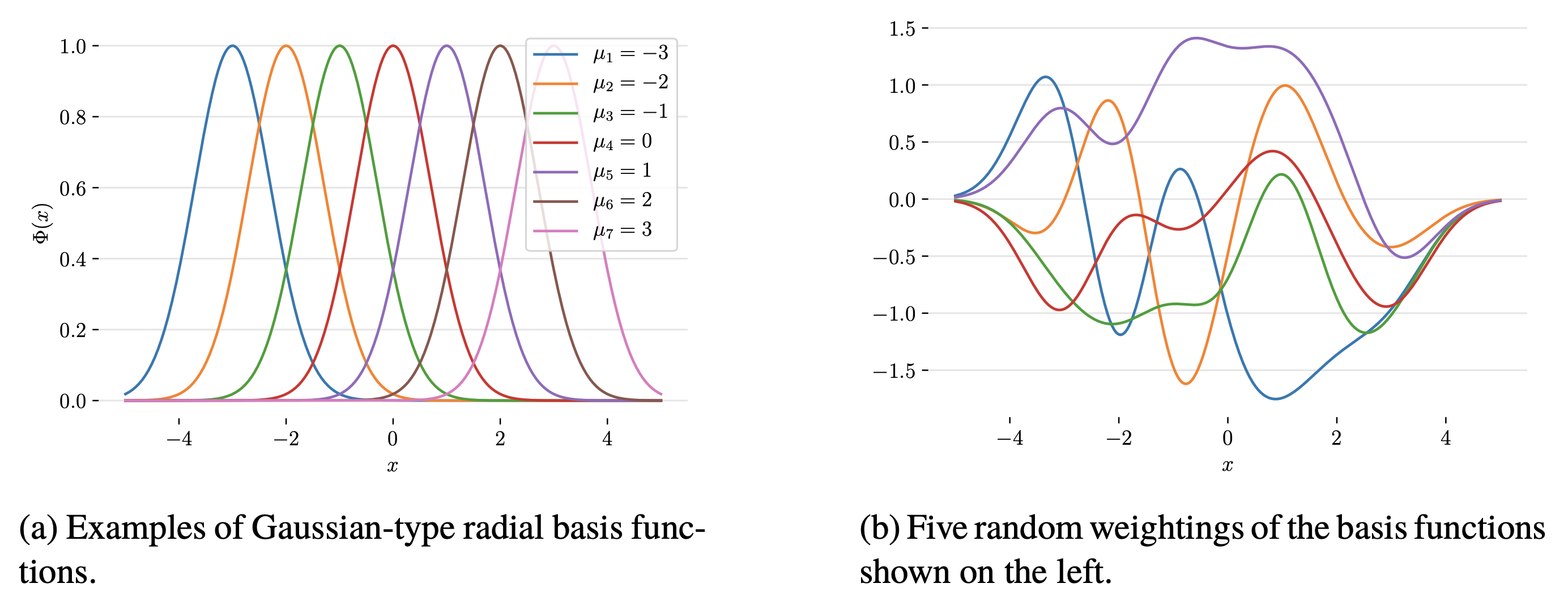 Fig. 방사 (gaussian) basis function의 몇가지 예시(좌)와 이에 random하게 weight을 곱한 결과(우)
Fig. 방사 (gaussian) basis function의 몇가지 예시(좌)와 이에 random하게 weight을 곱한 결과(우)
그런데 이 basis function을 어떻게 해야 data에 fitting하는 curve를 얻을 수 있을까? 직관적으로 bayesian inference를 하는 것이 여러 linear curve를 합치는 것 처럼, 각 basis를 잘 합쳐주기만 하면 우리는 굉장히 복잡한 data distribution에도 fit하는 curve를 만들어 낼 수 있을 것 같다. 문제는 각 basis별로 어떤 weight을 곱해줄것인가? 인데, 당연히 Maximum Likelihood Estimation (MLE)로 학습하면 되겠다.
이하는 각 basis에 어떤 weight을 줄 것인지 학습한 뒤 각 curve를 weighted sum한 결과다.
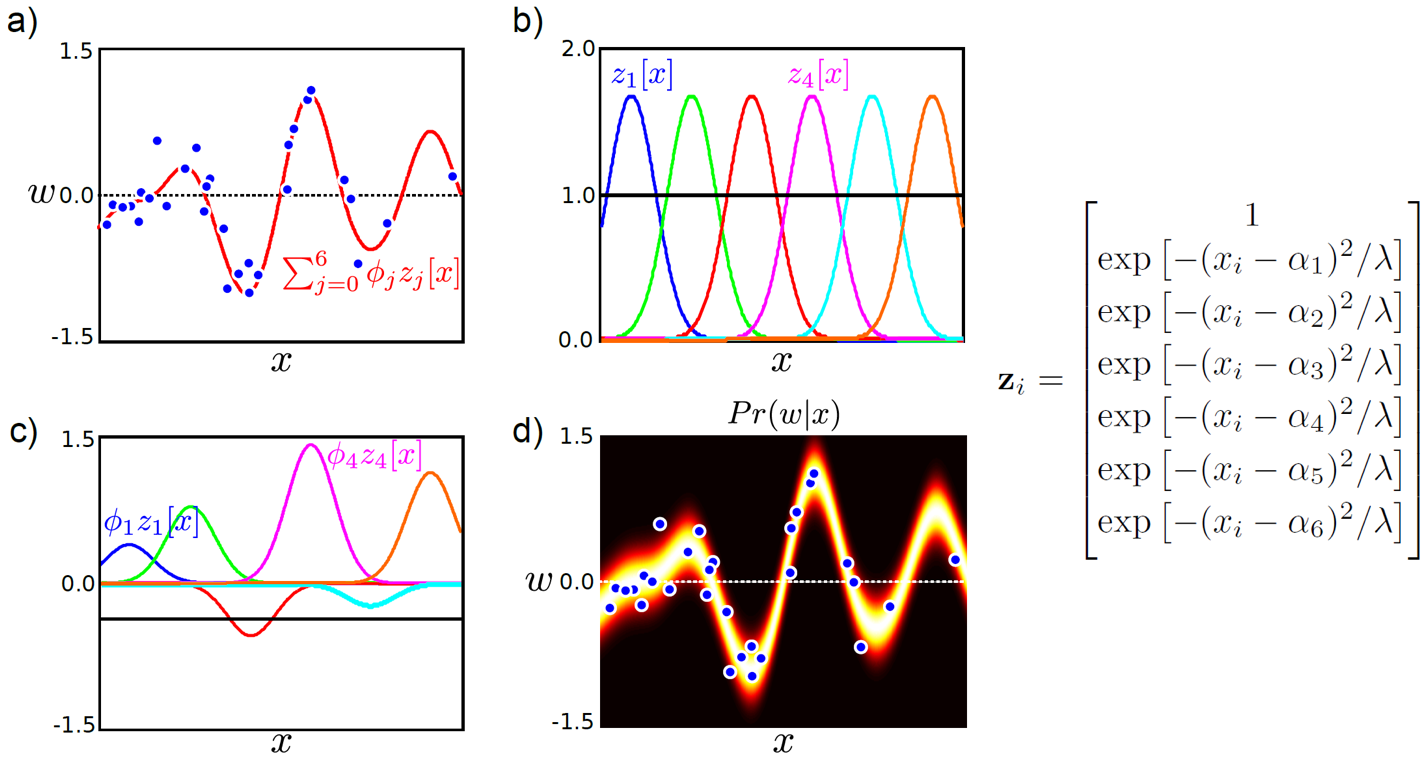 Fig. 각 basis function과 그에 해당하는 학습된 weight을 곱해 만들어 낸 curve 모양은 (d)와 같다.
Fig. 각 basis function과 그에 해당하는 학습된 weight을 곱해 만들어 낸 curve 모양은 (d)와 같다.
Other basis functions
이하는 다른 basis function들의 예시인데, 본 post에서는 다루지 않는다.
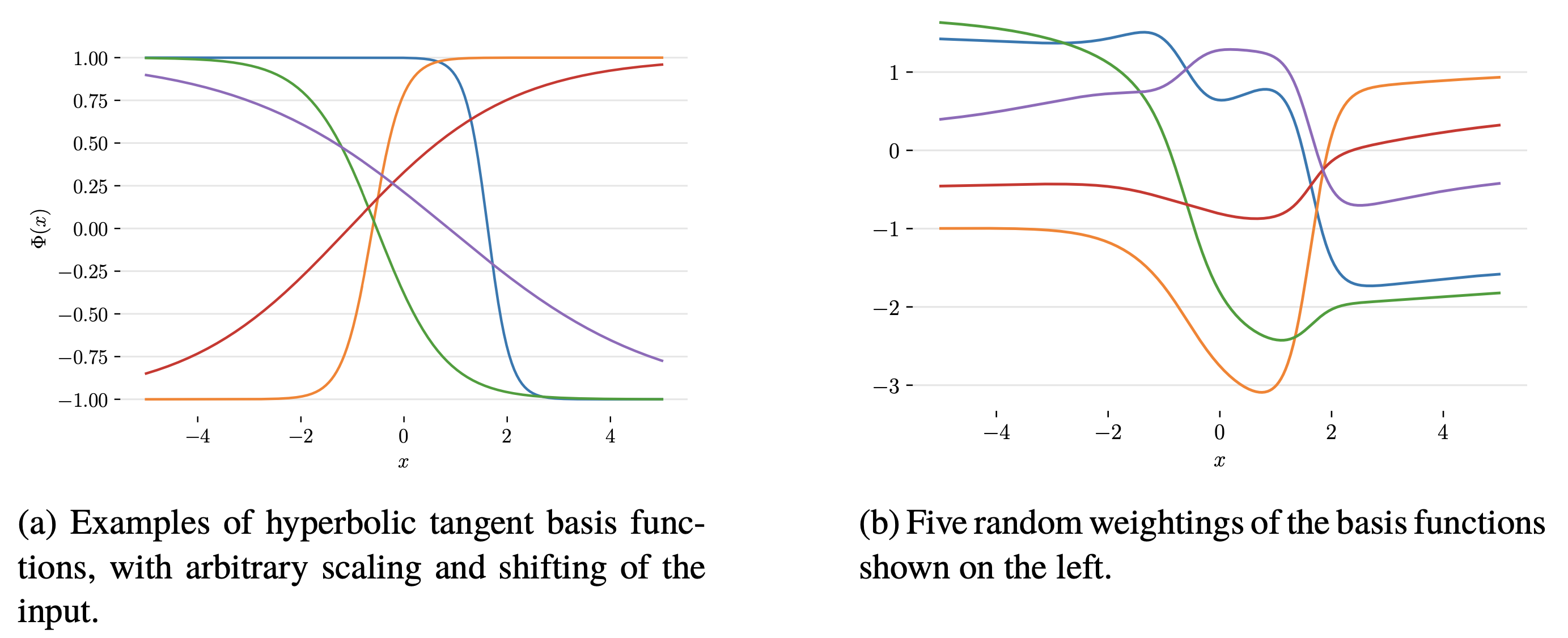 Fig. tanh basis function의 몇가지 예시(좌)와 이에 random하게 weight을 곱한 결과(우)
Fig. tanh basis function의 몇가지 예시(좌)와 이에 random하게 weight을 곱한 결과(우)
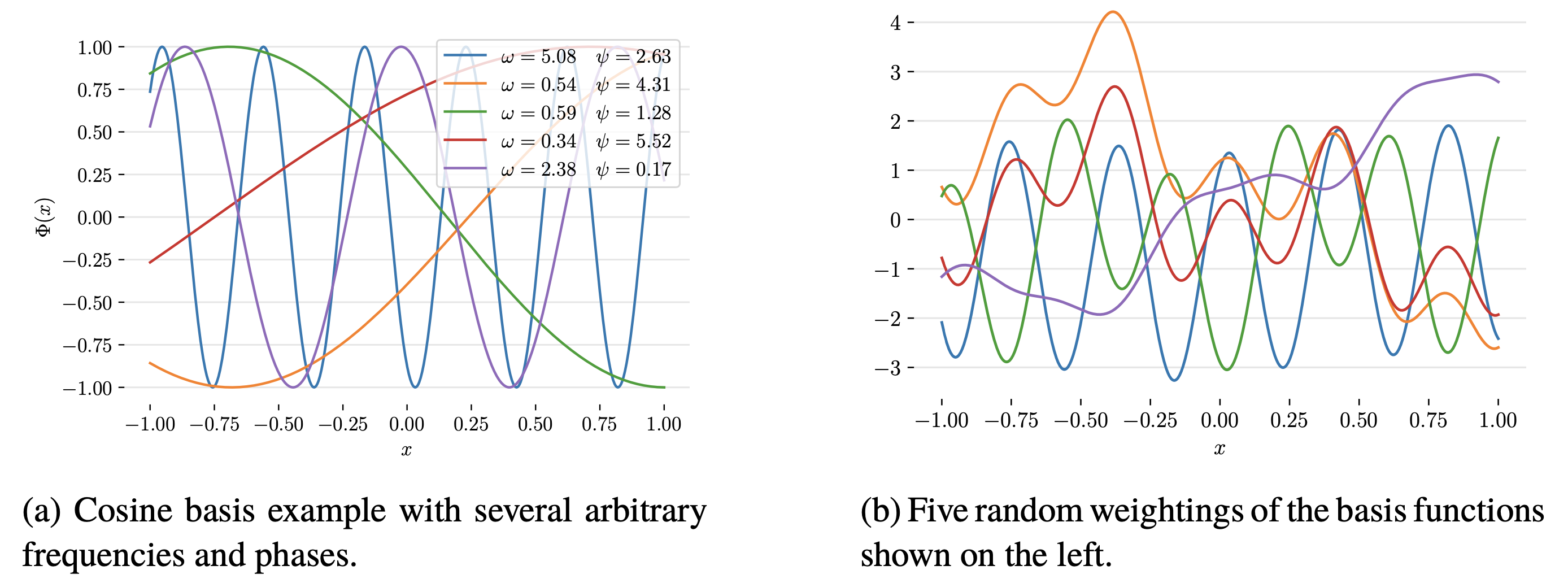 Fig. cosine basis function의 몇가지 예시(좌)와 이에 random하게 weight을 곱한 결과(우)
Fig. cosine basis function의 몇가지 예시(좌)와 이에 random하게 weight을 곱한 결과(우)
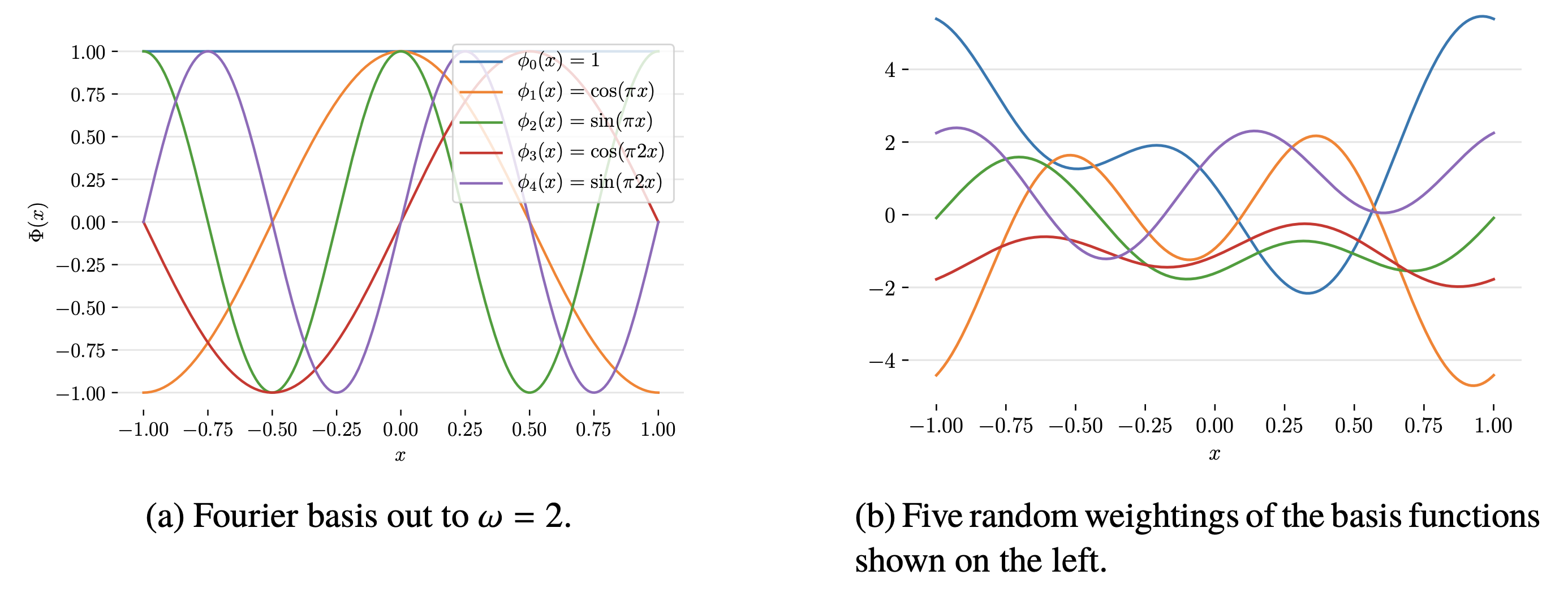 Fig. fourier basis function의 몇가지 예시(좌)와 이에 random하게 weight을 곱한 결과(우)
Fig. fourier basis function의 몇가지 예시(좌)와 이에 random하게 weight을 곱한 결과(우)
MLE Solution for Non-Linear Regression
이제 아래와 같은 polynomial regression의 solution을 구해보자.
\[\begin{aligned} & Pr(w_i \vert x_i,\theta) = Norm_{w_i}[\theta^T z_i, \sigma^2] \\ & \text{where } z_i = \left[ \begin{matrix} 1 \\ x_i \\ x_i^2 \\ x_i^3 \end{matrix} \right] \\ \end{aligned}\]앞서 gaussian distribution을 target distribution으로 가정한 경우, log를 취한 log-likelihood의 미분체를 구해 0이 되는 solution을 구했다. 즉 닫힌 해(closed-form solution)를 구할 수 있었다. 마찬가지로 해보자.
\[\begin{aligned} & \hat{\phi} = (ZZ^T)^{-1}Zw \\ & \hat{\sigma^2} = \frac{(w-Z^T\phi)^T(w-Z^T \phi)}{I} \\ \end{aligned}\]여기서 \(Z\) matrix는 training data sample수가 \(N\)개, input dimension이 \(M\)일 경우 \(N \times M\) 차원을 갖는다.
\[Z = \left[ \begin{matrix} f_0[x_1] && f_1[x_1] && \cdots && f_{M-1}[x_1] \\ f_0[x_2] && f_1[x_2] && \cdots && f_{M-1}[x_2] \\ \vdots && \vdots && \ddots && \vdots \\ f_0[x_N] && f_1[x_N] && \cdots && f_{M-1}[x_N] \end{matrix} \right]\]위의 matrix를 설계 행렬 (design matrix) 라고 부르며, 우리가 구한 식의 \((ZZ^T)^{-1}Z\)를 무어-펜로즈 수도 인버스 (Moor-Penrose Pseudo Inverse)라고 하여 \(Z^{-1}=(ZZ^T)^{-1}Z\) 가 성립한다고 한다.
\[\begin{aligned} & \hat{\phi} = (ZZ^T)^{-1}Zw \\ & Z^{-1}=(ZZ^T)^{-1}Z \\ \end{aligned}\]그러므로 우리는 optimal solution을 아래와 같이 간단하게 얻을 수 있다.
\[\hat{\phi} = (Z)^{-1}w\]Bayesian Approach
여기서 끝이 아니다. 앞서 MLE를 MAP, bayesian inference로 확장했던 것이 기억날 것이다.
\[Pr(w^{\ast} \vert z^{\ast}, X, W) = \int Pr(w^{\ast} \vert z^{\ast}, \theta) Pr(\theta \vert X,W) d \theta\]당연히 이번에도 확장할 수 있지 않을까?
이것이 다음 post에서 알아보게 될 Gaussian Process Regression이다.
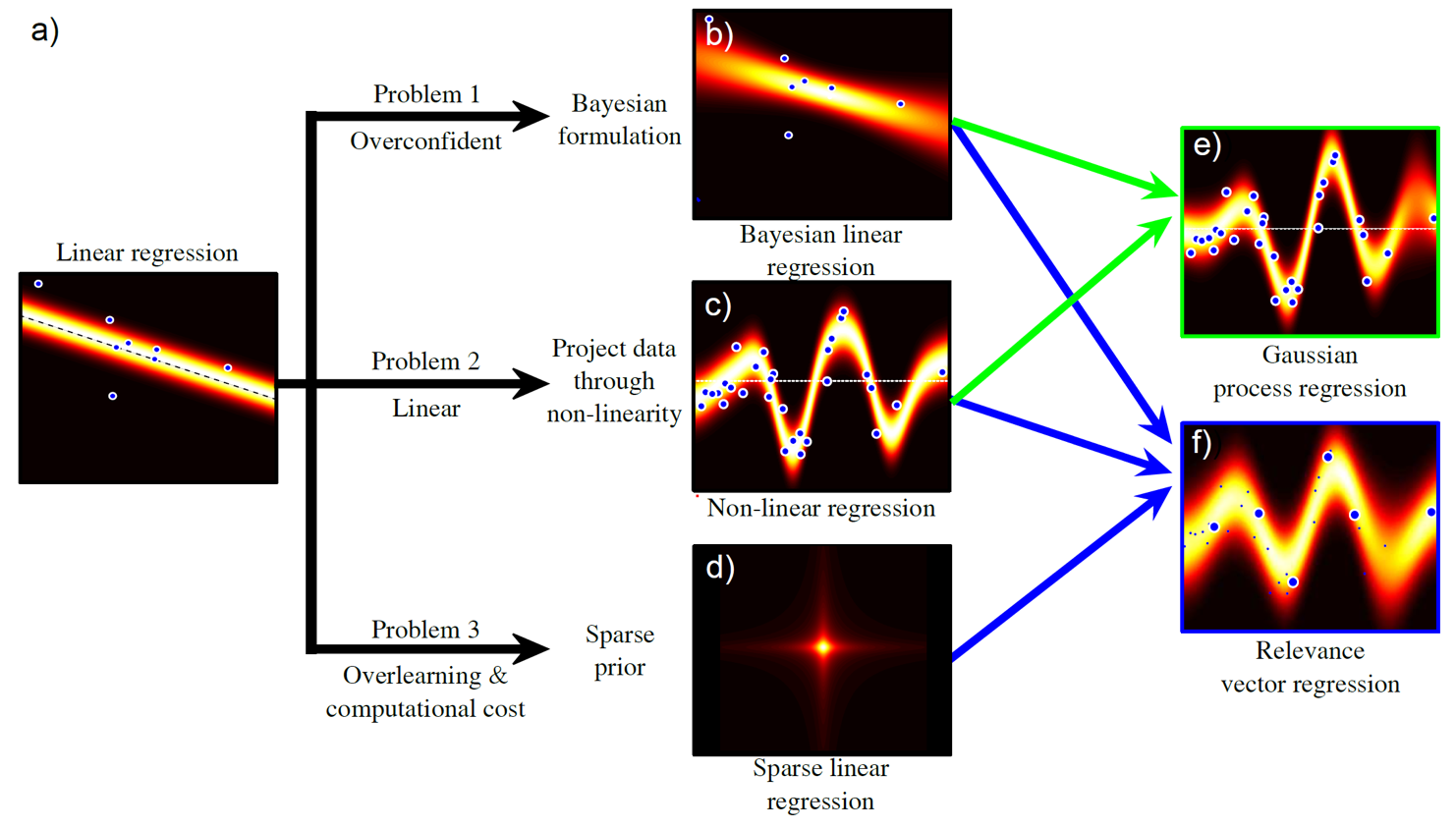 Fig. Bayesian Approach for Regression using RBF
Fig. Bayesian Approach for Regression using RBF