Regression (2/7) - Bayesian Linear Regression
26 Jan 2021< 목차 >
- ML solution for Modeling Gaussian Dist over Output, W
- Bayesian Linear Regression (BLR)
- MLE, MAP and Bayesian Inference according to the number of data points
- Limitation
- References
ML solution for Modeling Gaussian Dist over Output, W
이전 post에서 우리는 회귀 (Regression) 문제를 어떻게 푸는지에 대해 알아봤다. 그 중에서도 parameter들에 대한 선형 결합 (linear combination)으로 회귀 곡선 (regression curve)를 표현하는 선형 회귀 (Linear Regression)에 대해 알아봤다. Curve를 fitting하기 위해서는 (data를 가장 잘 설명하는 curve를 찾기 위해서는) 가장 먼저 output, \(w\)에 대한 distribution을 gaussian distribution 으로 정의해야 했다. 그리고 likelihood, \(Pr(y \mid x,\theta)\)를 maximize하는 Maximum likelihood Estimation (MLE)를 통해 curve를 나타내는 parameter를 추정해서 찾아냈다.
더 나아가 \(\theta\)에 대한 prior distribution을 정의해서 likelihood와의 곱을 통해 posterior, \(Pr(\theta \mid x,y)\)를 정의할 수 있었고, 이를 maximize하는 Maximum A Posterior (MAP)를 통해 posterior space에서도 parameter를 찾을 수 있음에 동의했다. 아래는 MAP로 posterior가 자장 큰 값을 가질 때의 parameter를 구했을 때 curve를 나타낸 것이다.
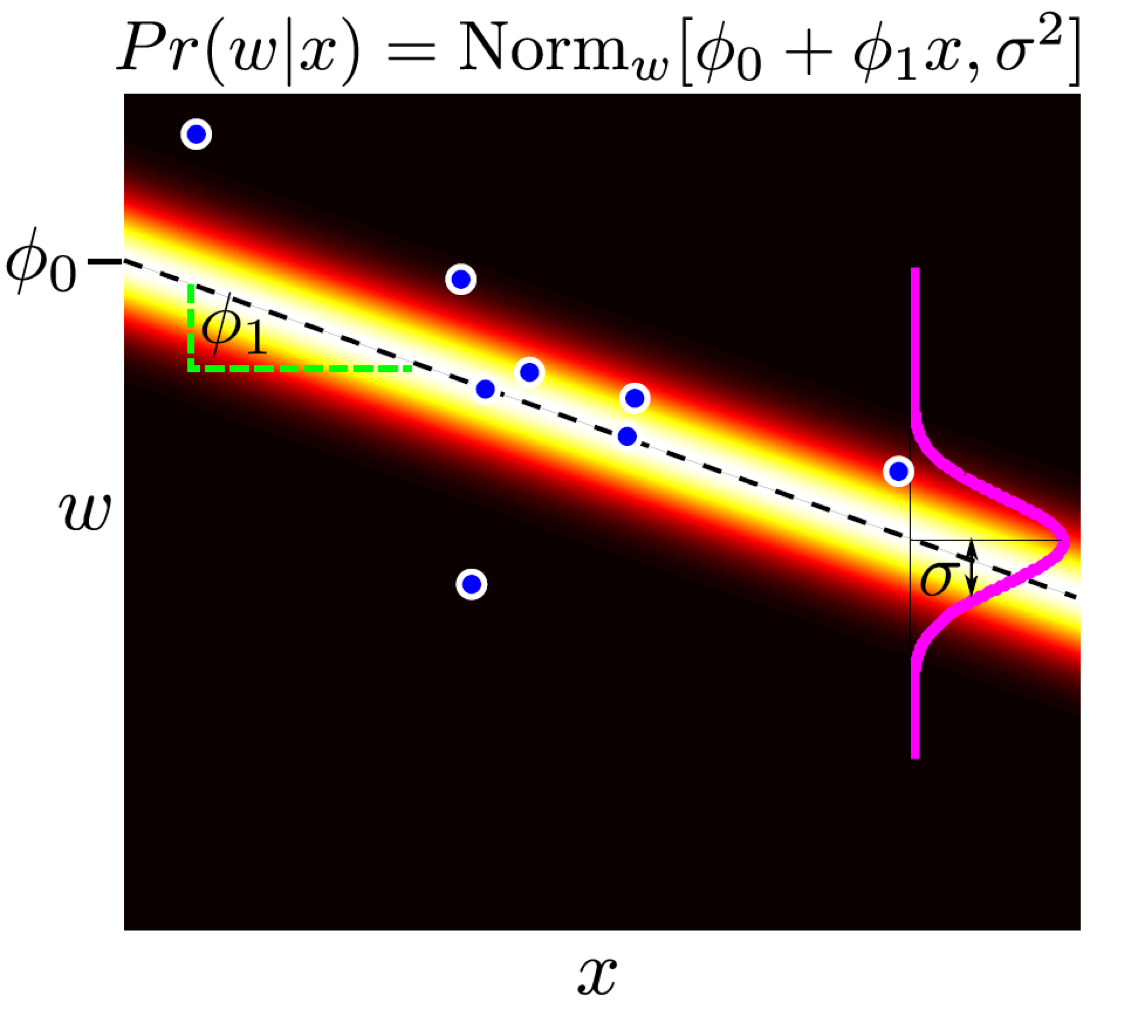 Fig. 일반적인 점 추정 방식의 회귀 곡선
Fig. 일반적인 점 추정 방식의 회귀 곡선
그런데 위의 curve는 뭔가 불편한 구석이 있다.
Curve의 밝은 부분은 어떤 input \(x_i\)를 paramter와 연산했을 때 \(y_i\)의 distribution을 나타낸 것으로,
variance를 의미한다.
그런데 어떻게 모든 구간에서 variance가 같은걸까?
직관적으로 위의 figure에서 data가 많이 존재하는 중간 부분 (밀도가 큼)은 data로 부터 얻은 정보가 많으니 다른 구간보다 variance가 작고,
어떤 부분은 data point가 하나도 없으니 variance가 크게 나와야 하는게 아닐까?
즉 전 구간에 있어 동일한 자신감 (confidence)을 가지고 distribution을 알려주는 model 자체가 불만인 것이다.
어떻게 해결해야할까?
우리는 model이 tarining data point가 없는 부분에 대해서는 적어도 ‘저는 이부분은 data를 본적이 별로 없어서 모르겠는데요?’라고 했으면 한다.
즉 불확실성 (uncertainty)을 나타냈으면 좋겠는데,
이는 구간별로 variance를 다르게 하는것으로 충분할 수 있다.
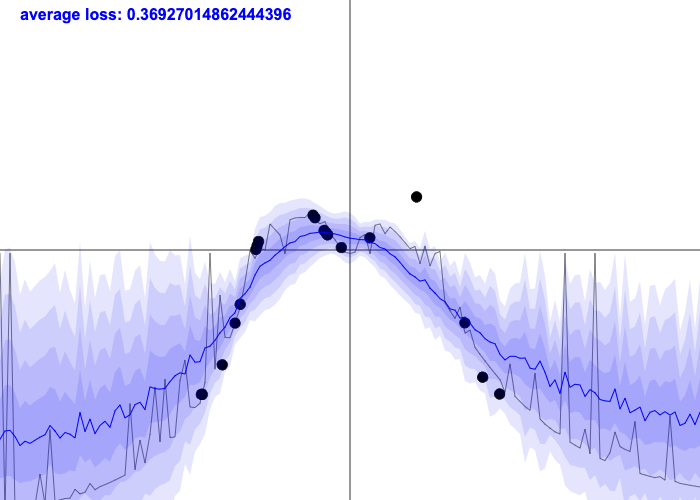 Fig. 밀도 (density)에 따라서 confident가 달라지는 경우.
Fig. 밀도 (density)에 따라서 confident가 달라지는 경우.
해결책은 Bayesian Approach를 적용하는 것이다.
앞서 MLE, MAP post에서도 말했지만 MAP도 posterior를 modeling하는 bayesian approach라고 할 수 있는데,
지금 말하는 것은 bayesian inference를 하자는 것이다.
MLE와 MAP는 각각 likelihood와 posterior space에서 그 값을 maximize하는 parameter 딱 하나만을 찾아내는 이른 바 점 추정 (point estimation)을 하는 것이라고 했는데,
bayesian approach는 어떤 test sample data가 들어왔을 때,
training data로부터 얻어낸 posterior distribution의 모든 parameter가 나타내는 각 curve를 weighted sum (parameter 개수가 무한에 가깝기 때문에 integral)을 해서 표현한다.
\[y^{\ast} = p(y^{\ast} \vert x^{\ast}, X,Y) = \int p(y^{\ast} \vert x^{\ast}, \theta ) p(\theta \vert X,Y)\]그 결과 data point의 수나 밀도에 따라 아래와 같은 curve를 얻을 수 있다.
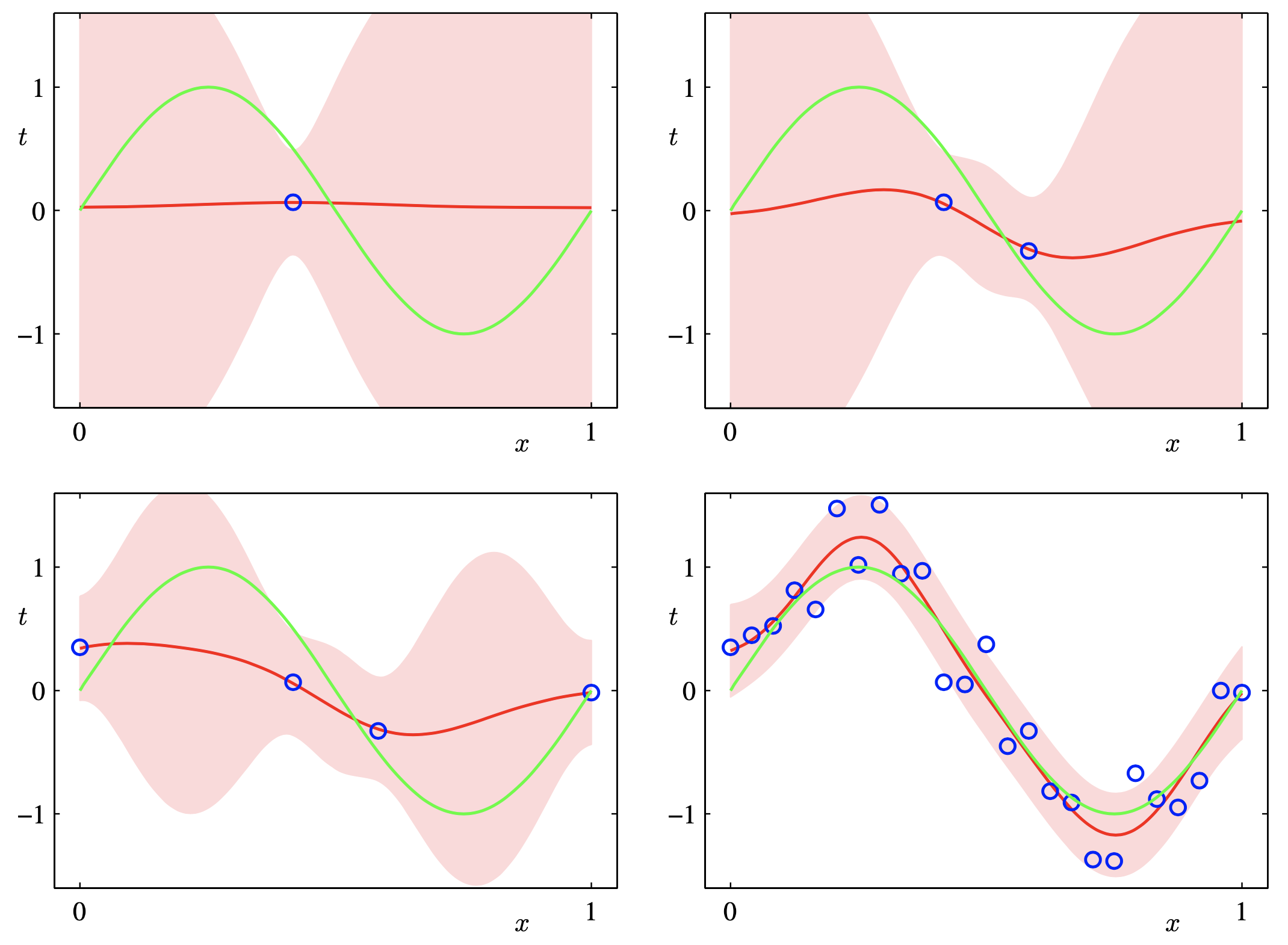 Fig. uncertainty는 data 수에 dependent함. (분홍색 음영이 큰 것은 그 data point, x에서 uncertainty가 크다는 것을 의미함)
Fig. uncertainty는 data 수에 dependent함. (분홍색 음영이 큰 것은 그 data point, x에서 uncertainty가 크다는 것을 의미함)
Bayesian Linear Regression (BLR)
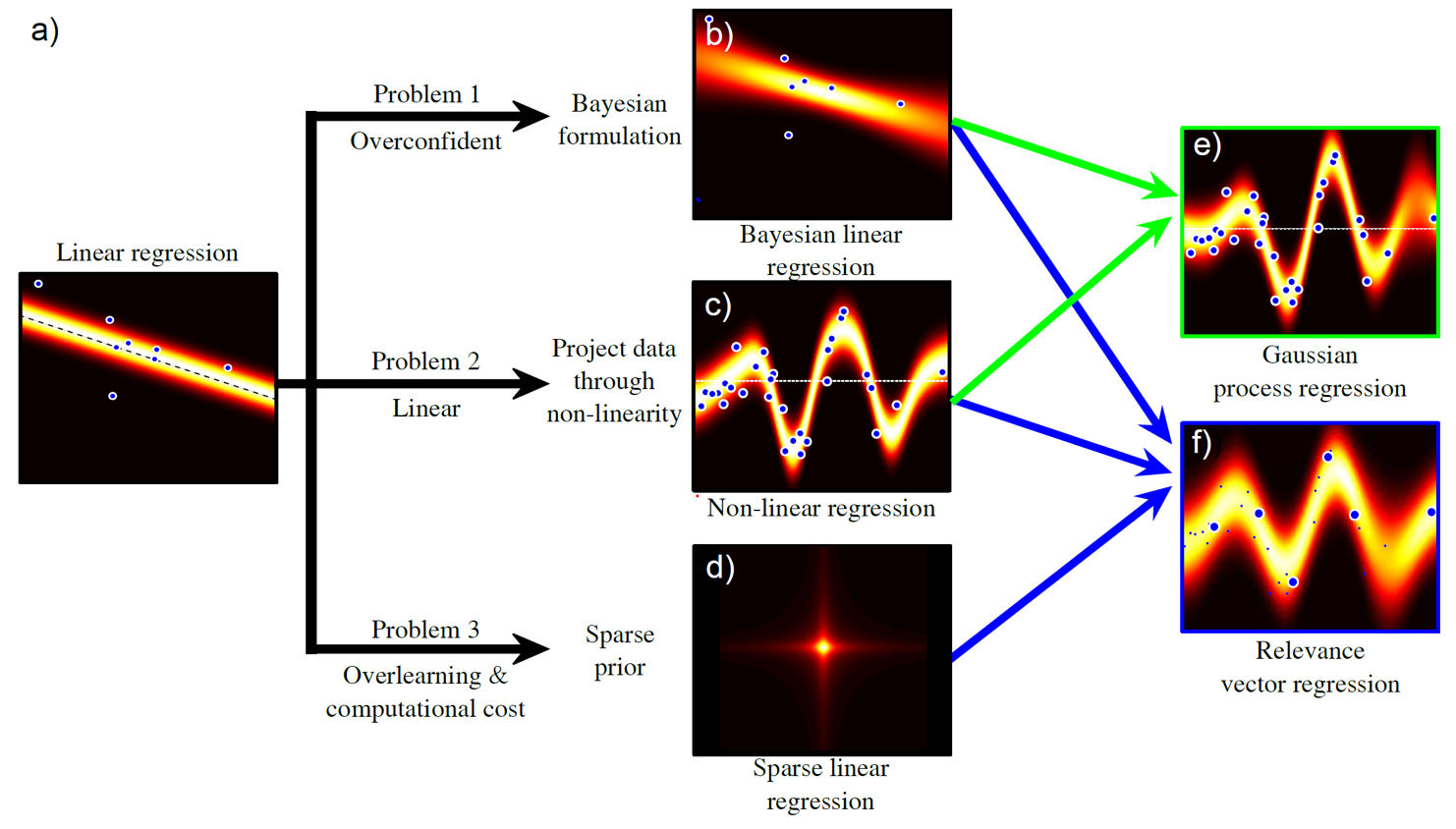 Fig. 다양한 regression algorithm. 이번 post에서는 Bayesian Linear Regression만 다룬다.
Fig. 다양한 regression algorithm. 이번 post에서는 Bayesian Linear Regression만 다룬다.
Posterior는 엄밀히 bayes rule에 의해 계산되어야 하지만 likelihood와 prior의 곱에 비례하기 때문에 둘의 곱으로 표현한다 (원래 normalized term으로 나눠줘야함). 편의를 위해 likelihood와 prior를 모두 gaussian distribution로 정의하자. (왜냐하면 gaussian 두개의 곱은 gaussian이라 다루기 쉽기 때문)
\[\begin{aligned} & \text{likelihood} : Pr(w|X) = Norm_w[X^T\phi,\sigma^2I] & \\ & \text{prior} : Pr(\phi) = Norm_\phi[0,\sigma_p^2I] & \\ \end{aligned}\]여기서 헷갈리지 말아야 할 점은 prior에 존재하는 variance은 \(\sigma_p^2\)라는 것이다. 위의 posterior를 구하기 위해 두 gaussian을 곱하면 다음을 얻는다.
\[\begin{aligned} & \text{posterior} : Pr(\phi|X,w) = Norm_\phi[\frac{1}{\sigma^2} A^{-1}Xw, A^{-1}] & \\ & \text{where } A = \frac{1}{\sigma^2} XX^T + \frac{1}{\sigma_p^2}I & \\ \end{aligned}\]아래 그림의 (a)는 원래 추정하고자 했던 \(\phi\)의 prior를 나타내고, (b)는 \(\phi\)의 distribution, 즉 posterior distribution을 나타낸다. (variance는 나중에 다룰 예정)
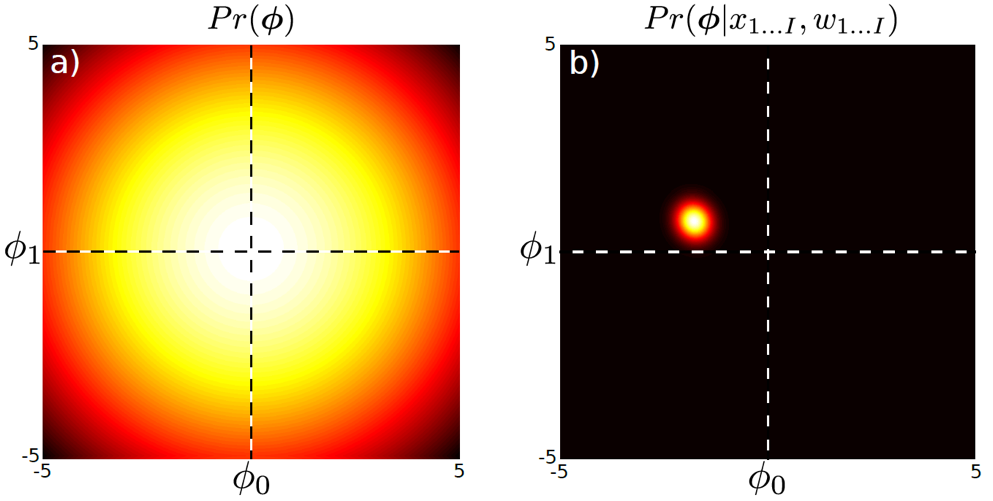 Fig.
Fig.
Inference
한편 bayesian infernce는 정확히 무슨 의미를 가지고 있을까? Bayesian Deep Learning으로 유명한 Yarin Gal의 학위 논문 (thesis)를 보면 bayesian modeling에서의 inference를 아래와 같이 정의한다.
Note that “inference” in Bayesian modelling has a different meaning to that in deep learning.
In Bayesian modelling “inference” is the process of integration over model parameters.
This means that “approximate inference” can involve optimisation at training time (approximating this integral).
This is in contrast to deep learning literature where “inference” often means model evaluation at test time alone.
즉 bayesian approach 에서의 inference 는 posterior distribution을 유저가 구했으면 이를 intergral 하는 것을 의미하고, 경우에 따라서 이 posterior distribution을 정확하게 계산할 수 없다면 이를 approximate한 distribution를 학습할 수 있다. 이는 일반 Deep Learning (DL)의 inference가 model parameter와 test input data를 matrix multiplication 하는 것에 불과한 것과는 대조적이라는 겁니다.
이제 어떻게 bayesian inference를 하는지 알아보자. 먼저 training dataset은 input과 output pair가 각각 \(X,W\)로 정의된다. 그리고 우리는 training data에 존재하지 않는 어떤 test data, \(x^{\ast}\)를 넣었을 때 그 output의 distribution, \(w^{\ast}\)를 얻고 싶다고 하자.
\[Pr(w^{\ast}|x^{\ast},X,W)\]이는 주변화 (marginalization) technique을 통해 아래와 같이 나눌 수 있는데,
\[Pr(w^{\ast}|x^{\ast},X,W) = \int Pr(w^{\ast}|x^{\ast},\phi) Pr(\phi|X,W) d\phi\]우리는 이미 likelihood, \(Pr(w \mid x,\phi)\)와 posterior, \(Pr(\phi \mid X,W)\)가 모두 gausisan distribution인 경우에 대해 정의한 바 있다. 이를 사용해서 전개하면 우리는 아래와 같은 수식을 얻을 수 있다.
\[\begin{aligned} & Pr(w^{\ast}|x^{\ast},X,W) = \int Norm_{w^{\ast}}[\phi^T x^{\ast},\sigma^2] Norm_{\phi}[\frac{1}{\sigma^2} A^{-1}Xw, A^{-1}] d\phi \\ & = Norm_{w^{\ast}}[\frac{1}{\sigma^2}x^{\ast T}A^{-1}Xw,x^{\ast T}A^{-1}x^{\ast} + \sigma^2] \\ & \text{where } A = \frac{1}{\sigma^2} XX^T + \frac{1}{\sigma_p^2}I \\ \end{aligned}\]이 수식에는 놀라운 부분이 있는데, 잘 보면 model parameter, \(\phi\)가 없다. 이는 우리가 dataset \((X,W)\)와 정의한 likelihood, prior distribution만 있다면 어떤 test data, \(x^{\ast}\)의 output distribution은 주어진 dataset과 \(\sigma\)에만 depedent하다는 걸 의미한다. 일반적으로 이 값은 `정해져있거나 (fixed variance), 계산 (혹은 최적화)’으로 구할 수 있는 값이다.
이제 최종적으로 test data가 들어오면 이 posterior distribution을 이용해 적분을 하면 된다.
\[Pr(w^{\ast}|x^{\ast},X,W) = \int Pr(w^{\ast}|x^{\ast},\phi) Pr(\phi|X,W) d\phi\]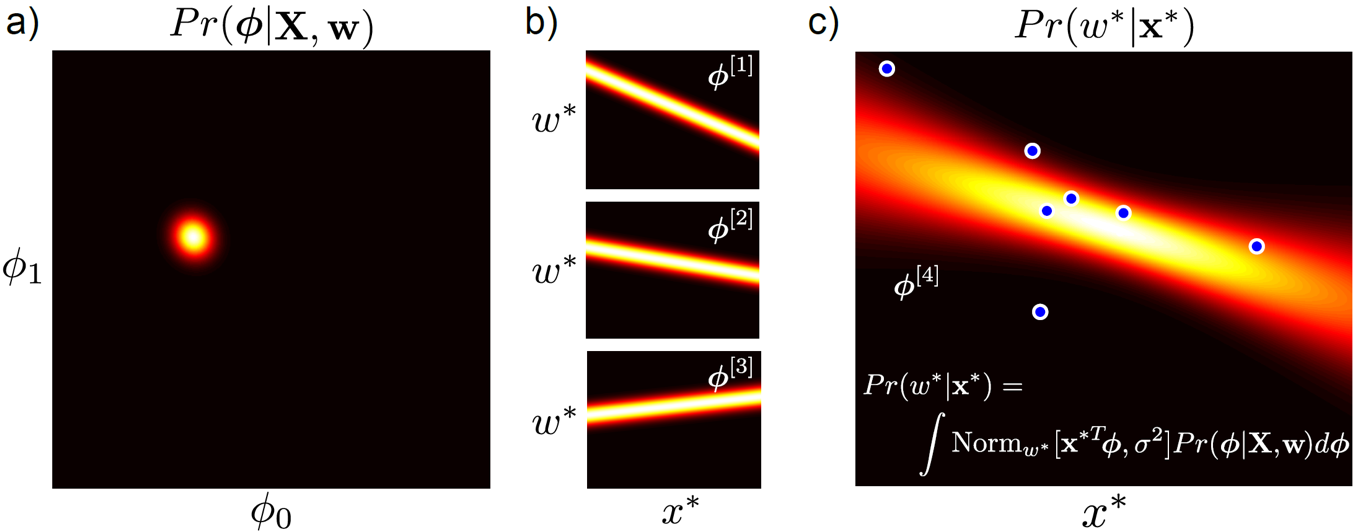 Fig. (a)는 추정하고자 하는 parameter set, \(\phi_0,\phi_1\)의 distribution를 나타내는 것이다. (b) 모든 parameter, \(\phi_{1}\), \(\phi_{2}\), \(\phi_{3}\) … 가 각자 만들어내는 curve를 합치면 (c)가 된다. MAP는 이 중 하나의 curve만 고르는 method
Fig. (a)는 추정하고자 하는 parameter set, \(\phi_0,\phi_1\)의 distribution를 나타내는 것이다. (b) 모든 parameter, \(\phi_{1}\), \(\phi_{2}\), \(\phi_{3}\) … 가 각자 만들어내는 curve를 합치면 (c)가 된다. MAP는 이 중 하나의 curve만 고르는 method
마지막으로 우리가 구한 수식을 전부 풀어쓰면 아래와 같아진다.
\[Pr(w^{\ast} \vert x^{\ast}, X, W) = Norm_w[ \frac{\sigma_p^2}{\sigma^2} x^{\ast T} X w - \frac{\sigma_p^2}{\sigma^2} x^{\ast T} X (X^TX + \frac{\sigma^2}{\sigma_p^2} I)^{-1} X^TXw, \\ \space \sigma_p^2 x^{\ast T} x^{\ast} - \sigma_p^2 x^{\ast T} X (X^TX + \frac{\sigma^2}{\sigma_p^2} I)^{-1} X^T x^{\ast} + \sigma^2 ]\]Fitting Variance
그런데 만약 variance를 구할거면 어떻게 해야할까? 아래의 최종 수식을 보자.
\[Pr(w^{\ast} \vert x^{\ast}, X, W) = Norm_w[ \frac{\sigma_p^2}{\sigma^2} x^{\ast T} X w - \frac{\sigma_p^2}{\sigma^2} x^{\ast T} X (X^TX + \frac{\sigma^2}{\sigma_p^2} I)^{-1} X^TXw, \\ \space \sigma_p^2 x^{\ast T} x^{\ast} - \sigma_p^2 x^{\ast T} X (X^TX + \frac{\sigma^2}{\sigma_p^2} I)^{-1} X^T x^{\ast} + \sigma^2 ]\]여기에 parameter는 \(\sigma, \sigma_p\) 두 개가 존재하는데,
이 중에서 prior의 variance, \(\sigma_p\)는 보통 1로 고정되어 있다 (prior느 보통 zero mean unit variance).
우리는 \(\sigma\)를 구해야 하므로 아래의 수식을 maximize하는 \(\sigma\)를 단순히 구하면 되겠다.
이는 MLE를 하는것으로 구할 수 있는데, 이 \(\sigma\)를 구하기 위한 term을 marginal likelihood라고 한다.
(왜냐면 mean을 나타내는 parameter가 사라졌기 때문인데 이를 통계쪽에서 marginalization 이라고 한다)
이 수식은 단순히 gaussian distribution이기 때문에, 앞서 했던 것 처럼 log를 씌우고 미분을 하는 식으로 계산할 수 있을 것이다 (계산 생략).
MLE, MAP and Bayesian Inference according to the number of data points
이번에는 data point 개수에 따른 각 method들의 차이에 대해 알아보자. 먼저 training dataset의 규모가 작은 경우다. 아래는 MLE solution을 나타낸다.
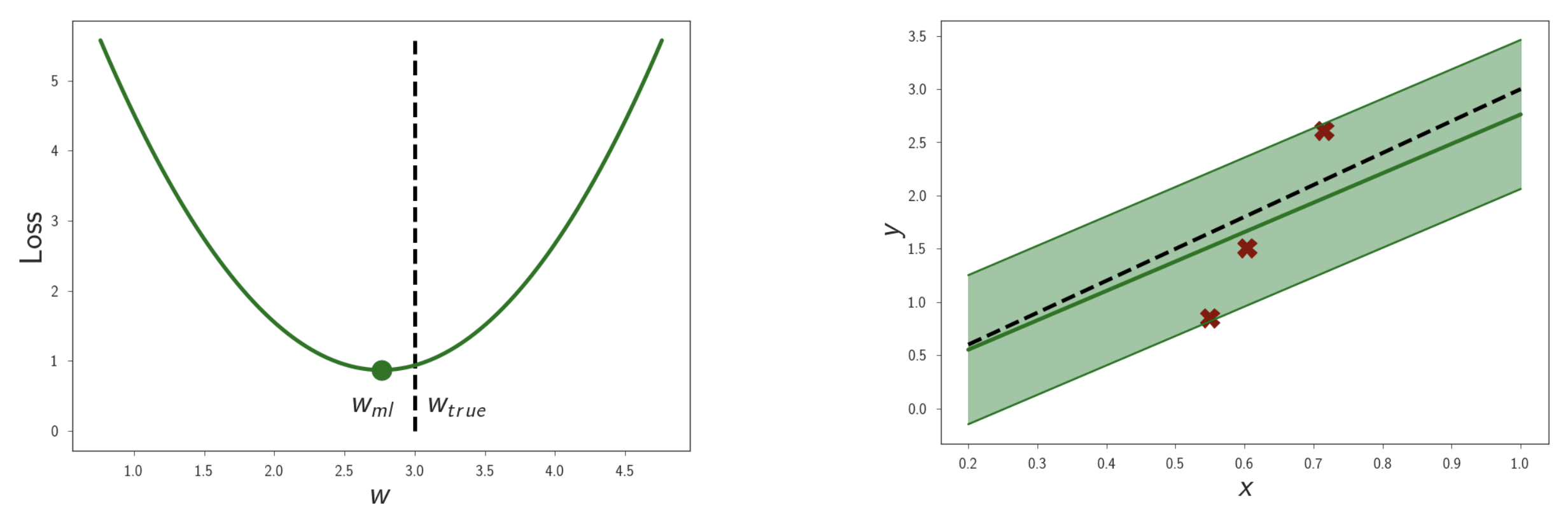 Fig. MLE solution이 나타내는 curve. (Loss를 최소화 == Likleihood를 최대화)
Fig. MLE solution이 나타내는 curve. (Loss를 최소화 == Likleihood를 최대화)
그리고 아래는 bayesian inference를 위해 계산한 posterior distribution를 나타낸다. Distribution에서 확률이 높은 parameter (yellow, purple)와 아닌 것들 (blue, green 등)의 curve의 생김새 차이를 있음을 알 수 있다. 실제로는 모든 curve를 다 합쳐야 bayesian inference가 될 것이다.
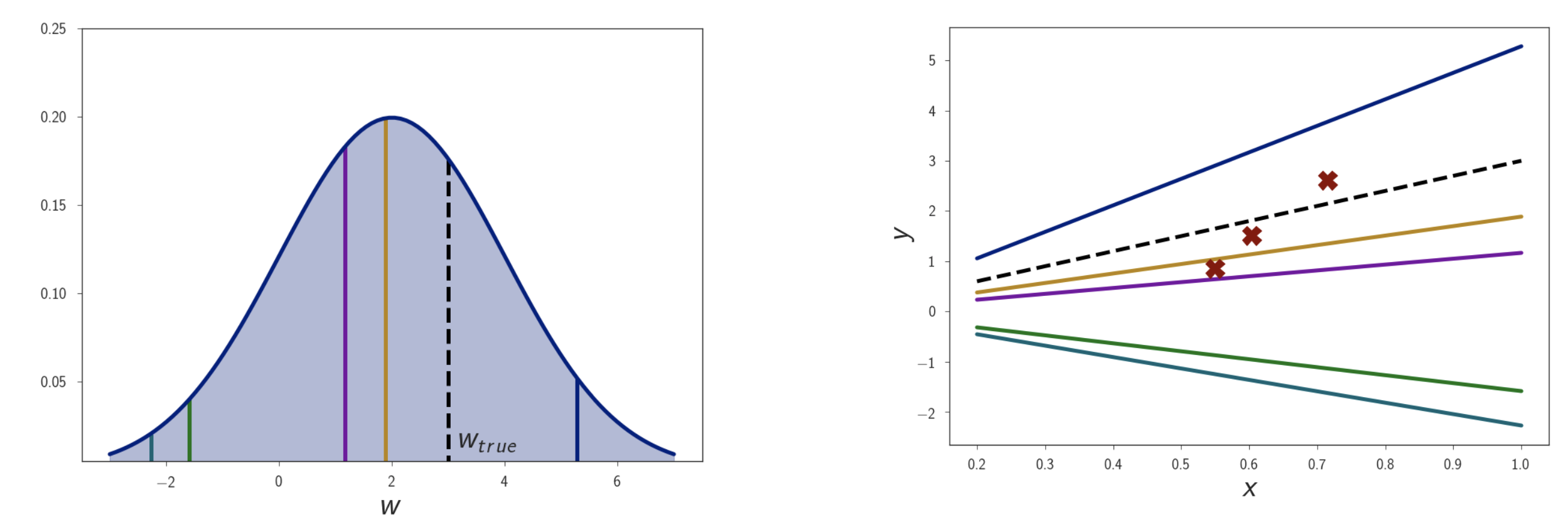 Fig.
Fig.
여기에 점점 data point 수를 늘려보자. 그러면 점점 posterior distribution이 굉장히 좁아지는 걸 볼 수 있는데, 이는 굉장히 작은 범위의 parameter에 모든 확률을 몰빵하는 거라고 볼 수 있다. Prior는 가만히 있겠지만 datapoint가 많아지면서 likelihood가 정교해지고 결국 posterior도 likelihood에 dominant해진 것이다.
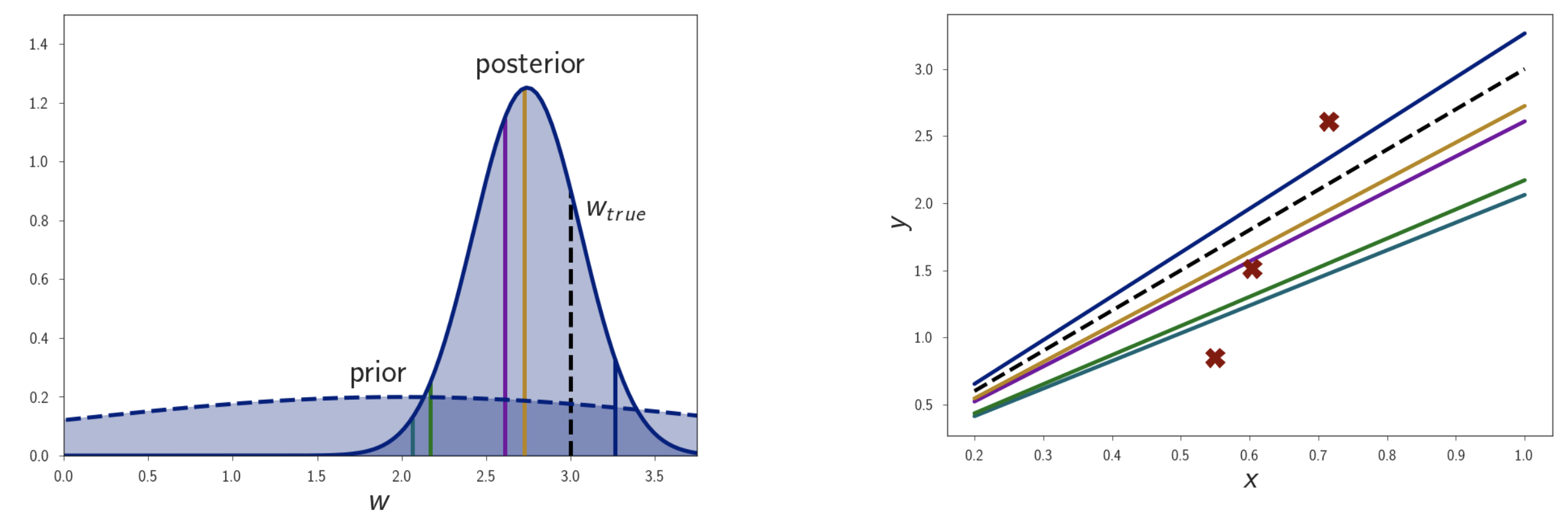
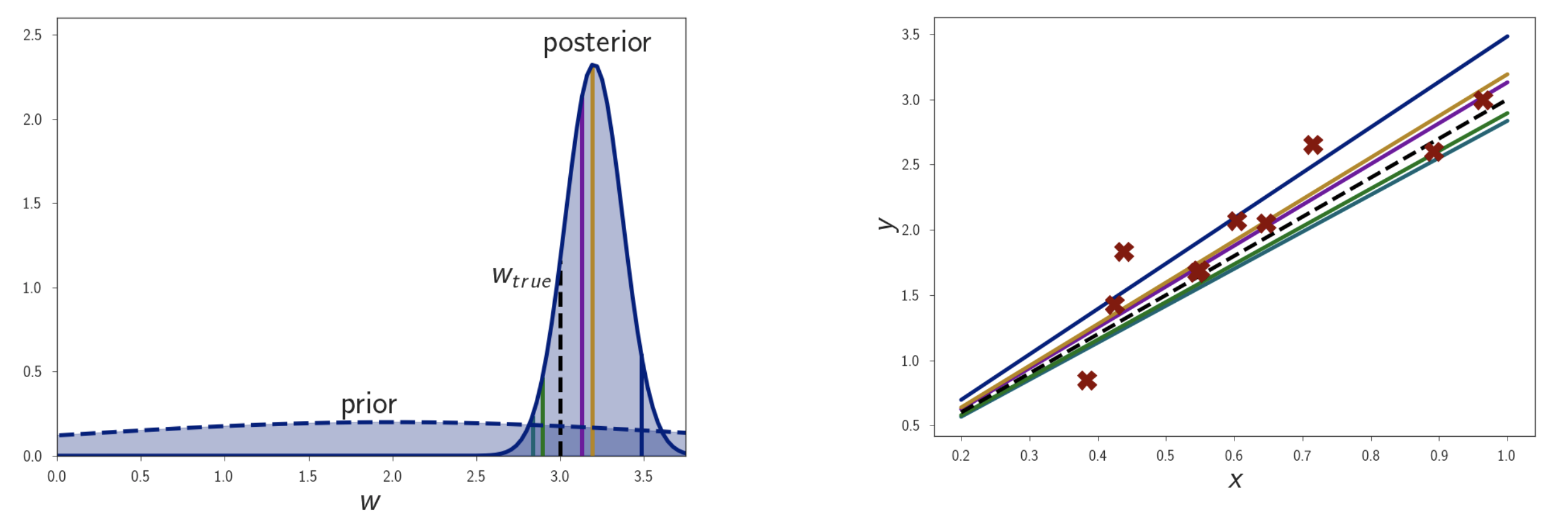
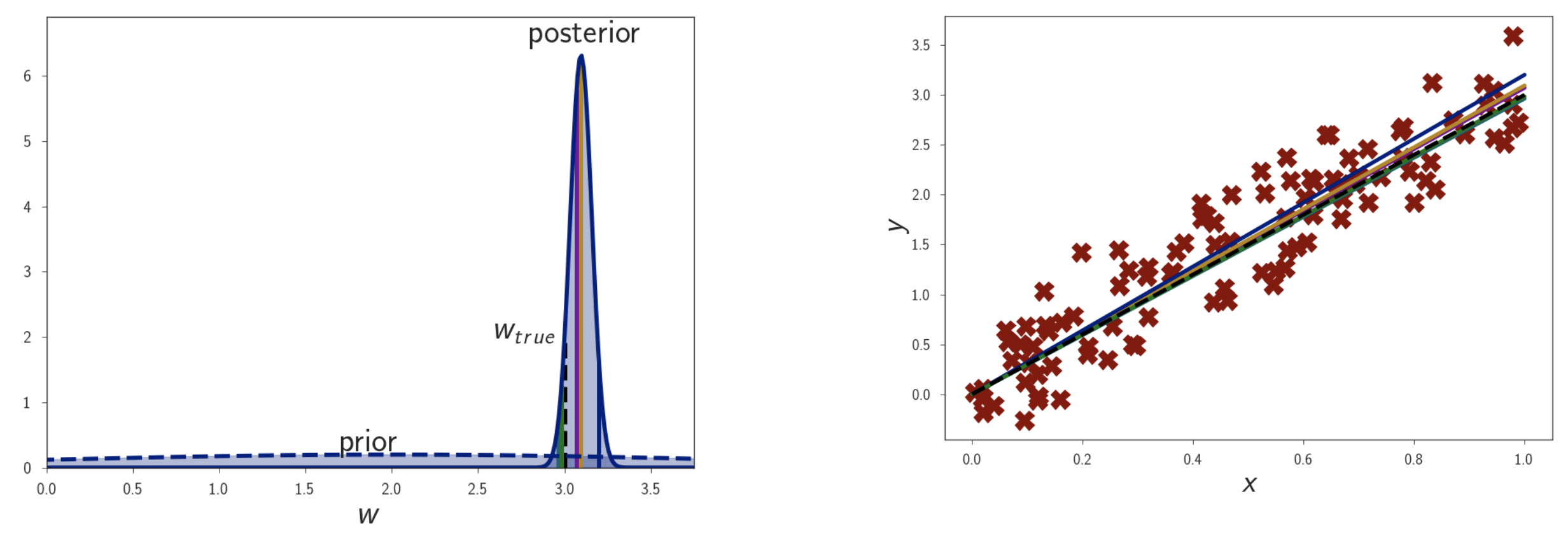 Fig. dataset 규모가 커질수록 posterior가 delta function 가까워진다.
Fig. dataset 규모가 커질수록 posterior가 delta function 가까워진다.
이럴 경우 bayesian inference를 한 것이나 MLE, MAP한 것이나 모두 같은 결과를 내게 된다. 즉 data가 많은 경우에는 굳이 MLE만으로도 충분할 수 있다는 생각을 해볼 수 있는 것이다.
Limitation
이번에는 bayesian approach의 단점에 대해 알아보자.
Bayesian inferene는 꽤 괜찮은 idea로 보인다. Model이 모르면 모른다 하는 것이 얼마나 편리할까? 하지만 실제로는 posterior distribution을 제대로 구하기 힘들다. 앞서 우리는 posterior를 likelihood와 prior의 곱으로 표현했지만 실제로는 bayes’ rule에 의해서 이를 제대로 구해야 하는데 model이 복잡해질수록 이를 계산하는 것은 불가능에 가까워 진다.
Bayes' Rule
왜 계산이 어려워질까?
\[\begin{aligned} & \text{posterior} : p(\theta \mid X,W) = \frac{p(W \mid X, \theta)p(\theta)}{\color{red}{p(W \mid X)}} \\ & \color{red}{p(W \mid X)} = \int p(W|X,\theta)p(\theta)d\theta \\ \end{aligned}\]위의 수식에서 보는 바와 같이 실제 posterior를 구하기 위해서는 분모의 normalizer term (model evidence)를 제대로 계산해야 한다. 이를 구하는 것을 ‘marginalising the likelihood over \(\theta\)’ 혹은 ‘marginal likelihood’라고 얘기한다.
우리가 지금까지 해결한 것은 고작 linear regression 문제였고, 여기서 likelihood와 prior를 둘 다 gaussian distribution로 적당히 가정했기 때문에 (둘은 conjugate 관계임) 이 적분을 계산하는게 상대적으로 쉬웠다. 하지만 model이 조금만 복잡해져도 (e.g. basis function이 고정되어 있지 않은 basis function regression이라던가, Neural Network (NN) 라던가) 위의 적분을 계산하는 난이도는 확 올라가게 된다.
이런 경우를 보통 ML에서는 아래처럼 표현한다.
- The
true posteriorcannot usually be evaluated analytically. - The
true posteriorisintractable.
이를 해결하기 위해서는 true posterior를 구할 수 없기 때문에, 이를 쉬운 distribution로 근사 (approximate)해서 문제를 풀게 된다. 이런 approximation에는 Laplace Approximation이나 Variational Inference (VI)같은 방법들이 있는데, VI가 그 유명한 Deep Learning (DL)의 generative model application인 Variational Auto Encoder (VAE)의 key idea이다.
그런데 이렇게 true posterior와 비슷한 approximation을 얻더라도 우리가 최종적으로 아래의 integral을 계산해야 하는데 사실 이것 또한 계산이 어렵다는 문제가 있다.
\[Pr(w^{\ast}|x^{\ast},X,W) = \int Pr(w^{\ast}|x^{\ast},\phi) Pr(\phi|X,W) d\phi\]어떻게 이를 해결해야 DL model들에 대해서도 bayesian inference를 할 수 있을까? bayesian inference를 하는 것이 요즘같은 시대에도 효과가 있을까? 이는 다른 post에서 다뤄보도록 하겠다.
References
- Books
- Others