Classification (1/4) - Logistic Regression and Optimization

< 목차 >

• Regression VS Classification
• Target Distributions for Classification
  • Bernoulli Distribution
  • Categorical Distribution (for Multi-Class Classification)
• Logistic Regression
  • Decision Boundary
  • Maximum Likelihood
• Optimization
  • Gradient Based Optimization
    • Why does it work? (gradient descent is minimizing a local approximation)
  • Problem of (Steepest) Gradient Descent
  • Newton’s Method (Newton-Raphson)
  • Line Search
  • Optimization Result
• Intuitive Things
  • Multi Class Classification
  • Modeling Categorical Distribution over Model Output VS Cross Entropy Loss
  • Another Perspective of Classification
• References

Regression VS Classification

일반적으로 회귀 (regression)과 분류 (classification) 문제를 구분하려면 아래의 두 가지를 기억하시면 됩니다.

1.입력값이 continuous 한데 결과값이 continuous하면 regression 문제
2.입력값이 continuous 한데 결과값이 discrete하면 classification 문제

물론 Input data가 discrete 할 수도 있겠으나 일반적으로 image input 등 대부분의 input들은 continuous 합니다. 개, 고양이, 비행기 같은 image들을 class가 3개로 나눈다면 개=1 ([1 0 0]), 고양이=2 ([0 1 0]), 비행기=3 ([0 0 1]) 일 확률이 각각 몇인지? 에 대한 이산적인 분포 (discrete distribution)로 modeling 하는 것을 바로 분류 (classification) 문제라고 합니다.

Fig. Regression vs Classification Table

Target Distributions for Classification

앞서 Regression 문제에서와 마찬가지로 우리는 연속적인 입력 변수에 대해서 대상 y (or world state w라고 정의하는 책도 있음)의 분포를 modeling 할 수 있습니다. 선형 회귀에서는 y를 가우시안 분포로 정의하여 문제를 풀었습니다. 이번에는 y의 분포를 discrete distribution 중 하나인 베르누이 분포 (Bernoulli Distribution)로 modeling 해보도록 하겠습니다.

왜 discrete distribution가 분류 문제를 위한 distribution가일까요? 그 이유는 model이 x 라는 image를 입력으로 받았을 경우 개일 확률 \(p(dog \vert x) = 0.4\), 고양이일 확률 \(p(cat \vert x) = 1 - p(dog \vert x) = 0.6\) 같이 어떤 class에 대한 확률값을 이산적으로 뱉길 원하기 때문입니다.

Bernoulli Distribution

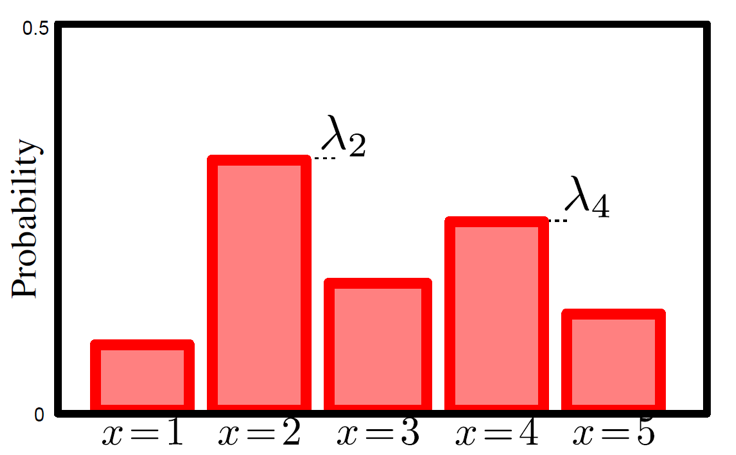
Bernoulli distribution에 대해 쉽게 설명하기 위해 그림을 먼저 보도록 하겠습니다.

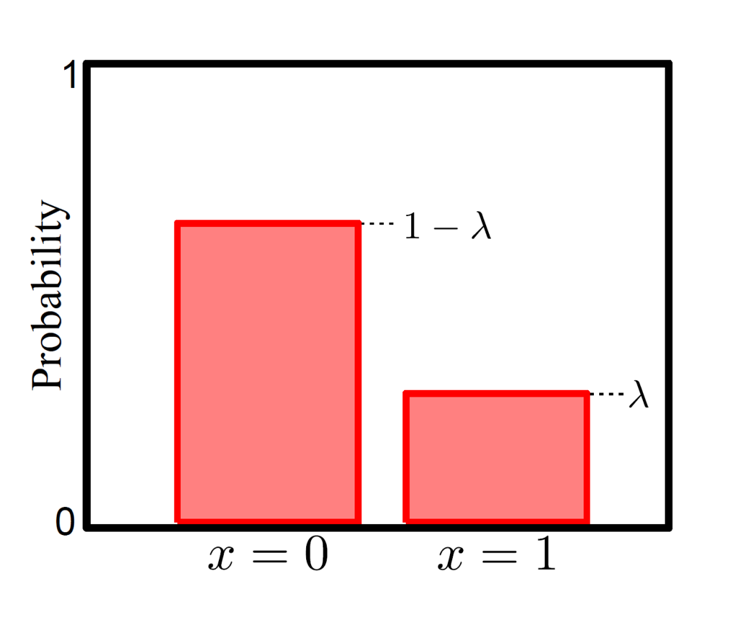
Bernoulli distribution는 ‘\(x=0/x=1\)’ 이나 ‘성공/실패’ 등 두 가지 가능한 경우에 대한 상황을 나타냅니다. 수식으로 나타내면 \(x=1\)일 확률이 \(\lambda\) 이고, Bernoulli distribution는 두 가지 경우에 대해서만 생각하기 때문에 반대로 \(x=0\) 이 될 확률은 \(1-\lambda\)로 아래와 같이 쓸 수 있습니다. (예를 들어 어떤 x(이미지 픽셀값)가 \(x=0\)(강아지)일 확률이 \(\lambda\)(0.64)면 \(x=1\)(고양이)일 확률은 \(1-\lambda\)(1-0.64=0.34)가 됩니다.)

위의 수식을 보면 Bernoulli distribution를 한번에 \(\lambda^{x}(1-\lambda)^{1-x}\)로 표현하는 걸 알 수 있습니다. 이는 x가 1이면 \(\lambda\)가 되고 x가 0이면 \((1-\lambda)\)가 되는 수식입니다.

이 때 추정하고자 하는 parameter는 가우시안 분포에서 평균,\(\mu\)와 분산,\(\sigma^2\) 인 것처럼 Bernoulli distribution에서는 성공 확률 \(\lambda\)가 됩니다. parameter가 2개에서 1개로 줄었습니다. (사실 gaussian 을 추정하는 regression 도 보통 variance, \(\sigma\)는 1로 고정해두고 mean, \(\mu\)만 학습하면 둘다 1개인건 마찬가지)

Categorical Distribution (for Multi-Class Classification)

Bernoulli distribution와 유사한 분포로 범주형 (Categorical) 분포가 있습니다.

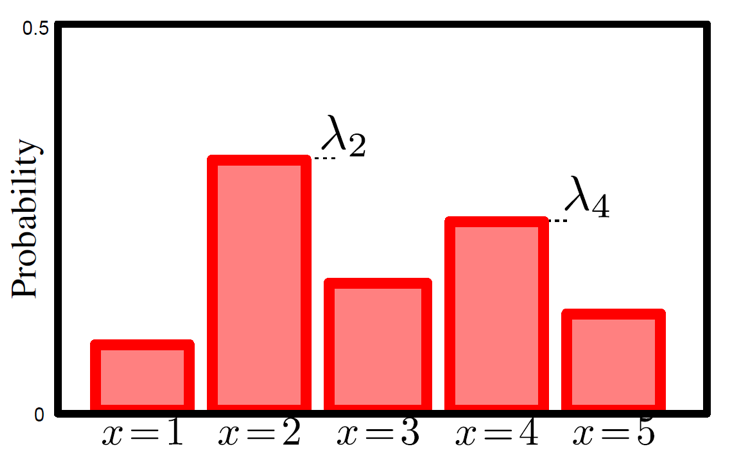
Categorical distribution는 Bernoulli distribution와 크게 다르지 않지만, 발생 가능한 case가 두 가지 이상이 된 경우에 대한 이야기를 합니다. 아래의 수식은 Categorical distribution에 대한 수식을 나타냅니다.

Bernoulli distribution에서는 두 가지 case중 한 가지 case로 분류될 확률 \(\lambda\)만 찾아내면 확률 분포의 합이 1이 되는것을 이용하여 자동으로 나머지 case로 분류될 확률이 정해졌습니다. 하지만 Categorical distribution는 예를들어 x=0~x=4 (5가지 가능한 경우)에 대한 확률을 전부 다 찾아내야 함으로 전체 경우에 대한 가능한 확률 값을 추정해야 합니다. (근데 이제 확룰의 합은 1이어야 하므로 \(\sum{\lambda_{0...I}} = 1\) 이 되는거죠)

Logistic Regression

Bernoulli distribution의 parameter 를 학습 (추정) 하는 것에 대해 살펴봅시다. Bernoulli distribution은 2개 class에 대한 예측을 하므로 이진 분류 (binary classification) 한다고 합니다. Deep Learning (DL)의 Neural Network (NN)도 이진 분류를 할 수 있지만 만약 NN이 없이 1 layer로 분류기를 만든다고 하면 Logistic Regression 이라고 합니다. Logistic Regression은 설명한 대로 Bernoulli distribution으로 world state, \(w\)를 modeling 하는데, 이때 likelihood 를 최대화 하는 \(\lambda\) 를 찾으면 주어진 data sample들을 잘 분류하는 것이 됩니다.

Regression 에서 결국 input data \(x_1, \cdots, x_N\) 들과 \(\theta\) 를 dot product 해서 \(\mu\) 를 표현하기로 하고, likelihood 가 높아지는 \(\mu\) 를 찾았습니다. 즉 \(\theta\) 를 바꾸다보면 \(\mu\) 가 변하는거죠. 마찬가지로 여기서 \(\lambda\) 를 입력 데이터 x와 어떤 learnable parrameter 의 연산 (함수)로 표현을 해봅시다.

여기서 input data는 \(x\), 정답 label은 world state라고도 하는데 (제가 reference로 삼은 JD책에서 그렇습니다) 이를 \(w\)라고 표시합니다. 그리고 우리가 추정하려는 값은 \(\lambda\)이긴 한데 \(\phi\)로 parameterized 되어 있기 때문에 \(\phi\)를 추정하면 됩니다. 위의 수식에서 \(a\)는 \(x\)에 \(\phi\)를 선형 결합한 것이고, \(\sigma[a]\)는 a를 sigmoid 라는 함수에 넣은 결과값입니다. 여기서 이 함수는 활성 함수 (activation function)라고 불립니다. Sigmoid 함수는 아래의 그림처럼 \([-\infty,\infty]\) 사이의 입력값을 \([0,1]\) 사이의 값으로 mapping해줍니다.

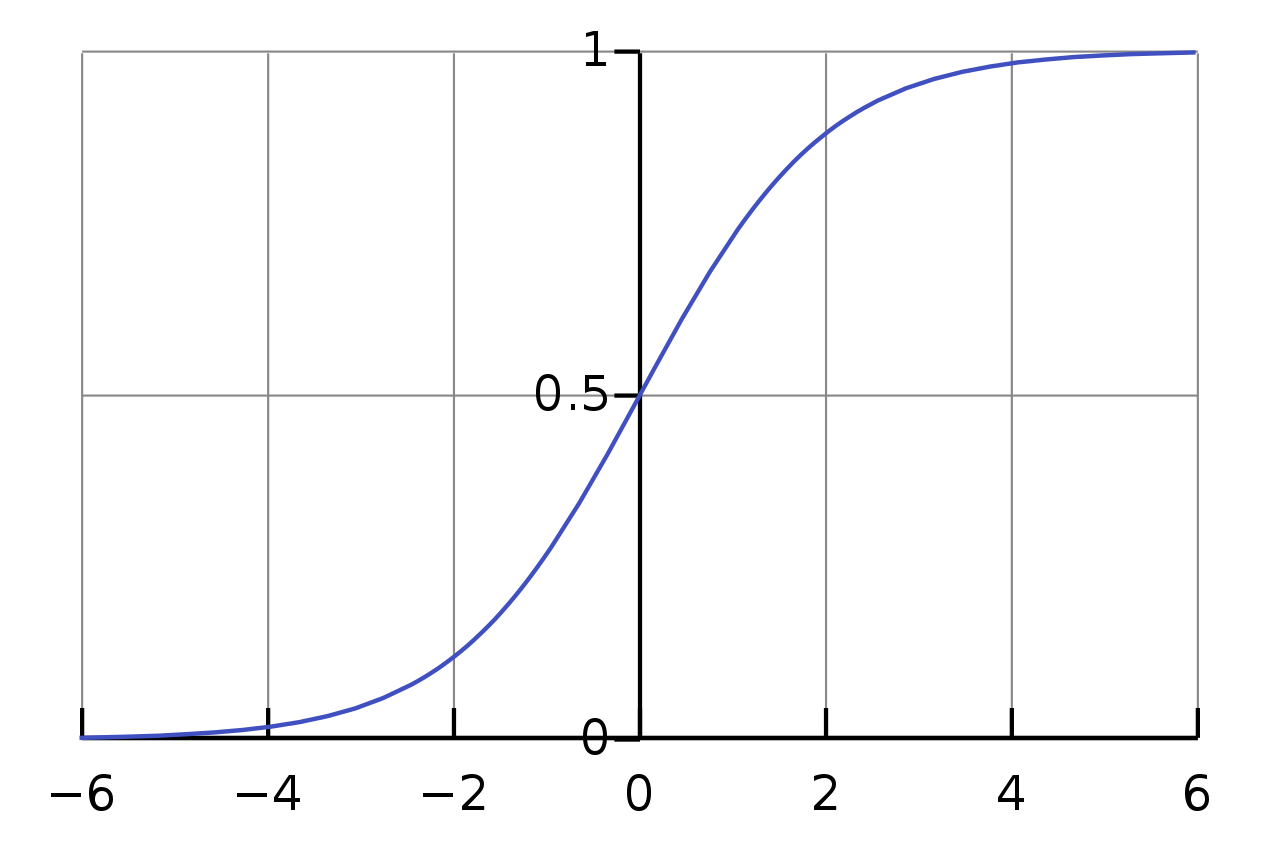Fig. Source From link

이렇게 하는 이유는 우리가 출력 분포를 bernoulli 분포로 가정했으며, 이때 bernoulli 분포의 매개변수인 \(\color{red}{\lambda}\) 는 \(0~1\) 사이의 값이여야하기 때문입니다. Gaussian 분포를 Target 분포로 가정하고 그 때의 Mean 값이 어떤 값이어도 되는 Regression과는 조금 다른 상황이죠.

입력값을 Model weight 와 연산한 뒤에 sigmoid 함수에 넣어 최종 출력값으로 나타내는 것은 여러가지 의미가 있습니다. 나중에 다루겠으나 Neural Network가 인간의 신경망을 motive로 만들었다는 것 같이, sigmoid가 neural firining을 나타내는 것이라고 해석하는 사람도 있고, 확률로 modeling 하기 위해서 출력값을 확률처럼 나타내기 위해서 라는 해석도 있습니다. (지금은 이부분에 초점)

이 과정을 그림으로 나타내면 다음과 같습니다.

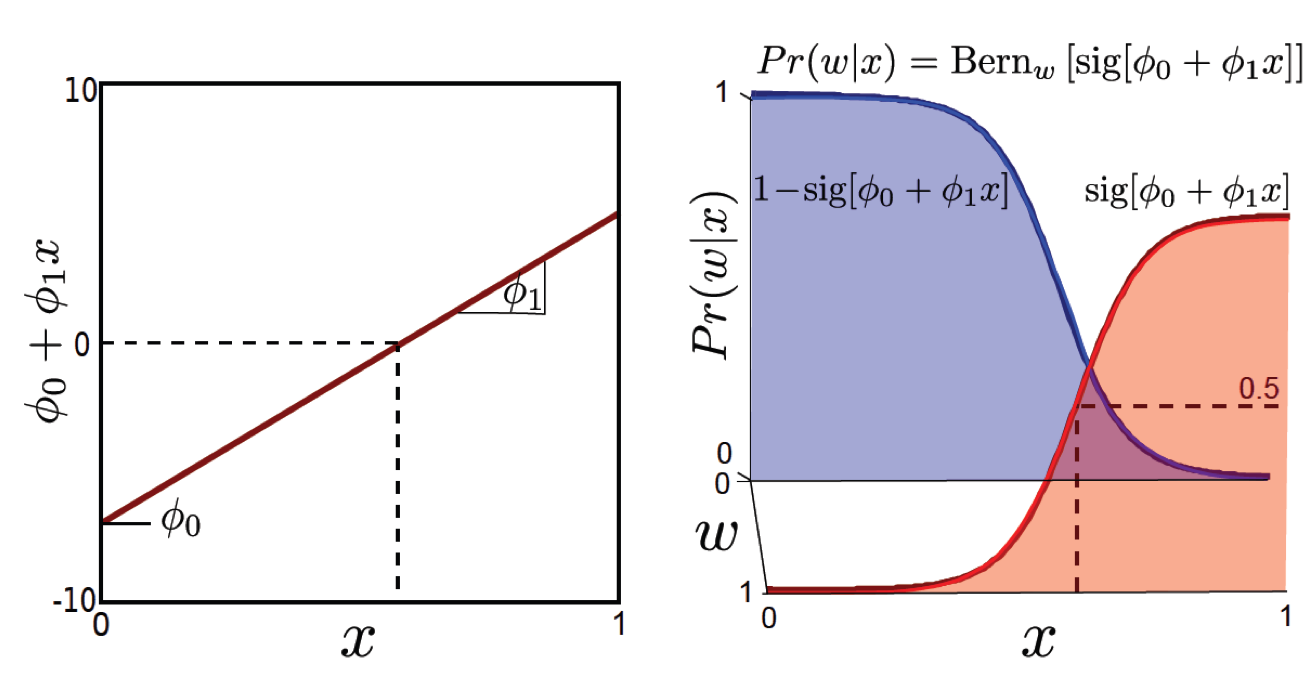
조금 더 notation을 깔끔하게 써보겠습니다.

를 더 쉽게 쓰기 위해서 입력 데이터 \(x\) vector 에 scalar 1을 붙혀봅시다. 원래 \(x\)가 2차원이라면 3차원이 되는것이죠. 그러면 전체 dataset 중 하나의 sample 을 다음과 같이 표현할 수 있습니다.

추정하고자 하는 parameter도 간단하게 쓰기위해서 \(\phi_0\) 과 \(\phi\)를 붙혀봅니다.

이렇게하면 notation을 깔끔하게 다시 쓸 수 있습니다.

Decision Boundary

이제 Regression 에서와 마찬가지로 Likelihood 를 가장 크게 만들기 위해 parameter 를 잘 바꿨다고 생각해 보겠습니다. 그렇다면 우리는 아래와 같은 결과를 얻을 수 있는데, 왼쪽은 input data \(x\)가 1차원, 오른쪽은 2차원인 경우입니다.

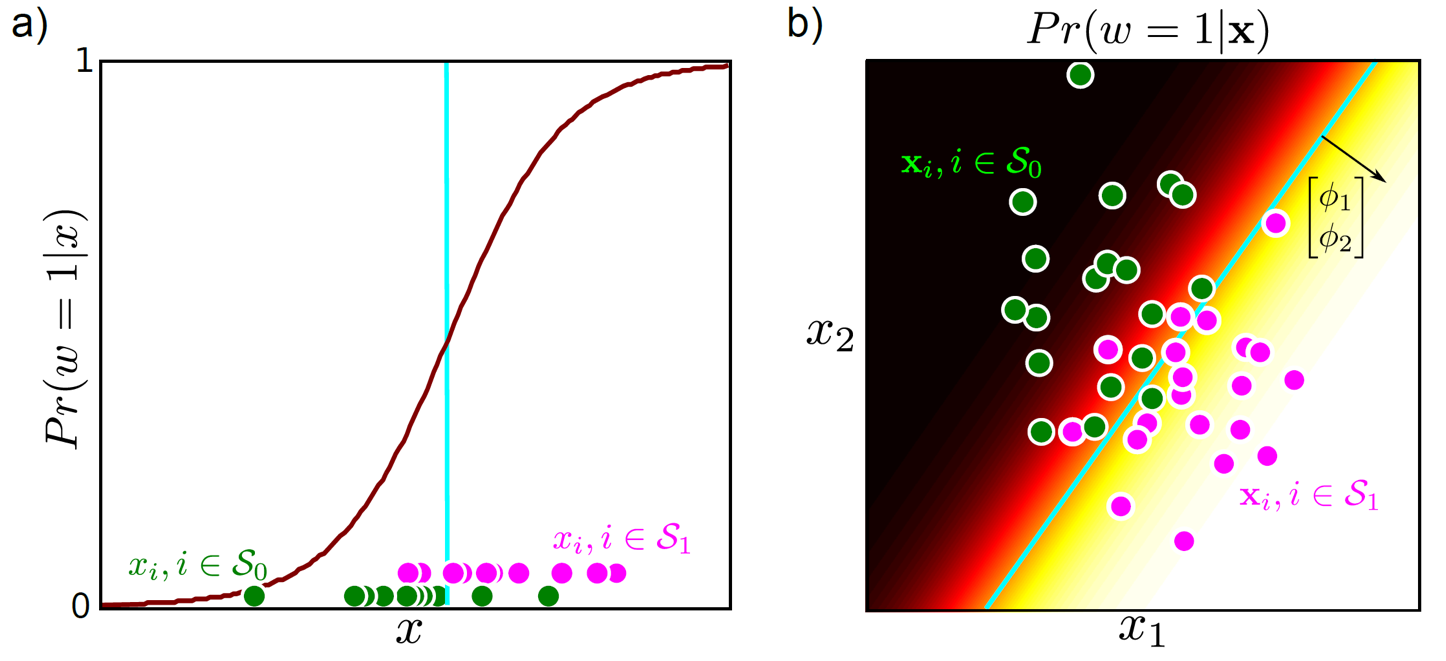
분류 문제를 푼다고 생각할 때, 베르누이 확률 분포가 0.5가 되는 지점을 두 class가 어떤 것인지 결정하는 Decision Boundary라고 정하게 됩니다. 그림에서는 파란(cyan)색이 decision boundary입니다. 여기에 우리가 학습때 보지 못했던 test data 가 들어오게 되면 input data 의 space 에서 Decision Boundary 를 기준으로 어디에 놓여지느냐? 에 따라서 class가 자연스럽게 분류 (classification) 됩니다. 그래서 Bernoulli 분포를 가정하고 문제를 푼다는 것이 분류를 하는 것이 되는겁니다.

사실 2차원 데이터도 아래의 그림처럼 생각하는게 더 직관적입니다. z축이 class를 나누는 Bernoulli distribution의 확률 분포가 될 겁니다.

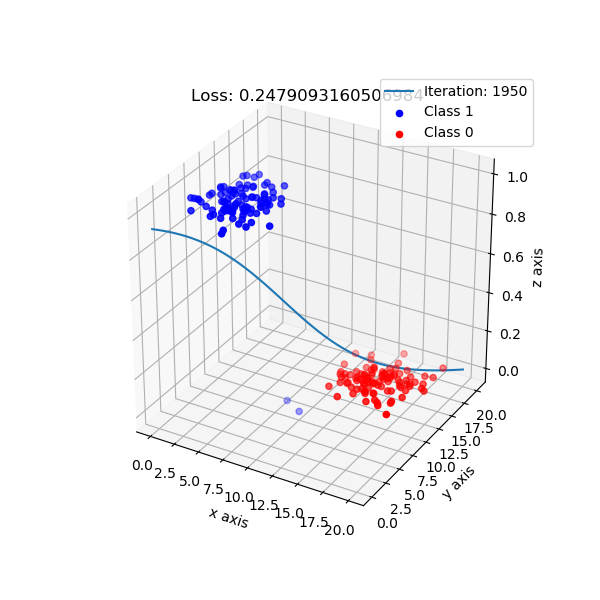Fig. Source From link

Logistic Regression은 사실 간단히 말해서 한마디로 정리할 수 있습니다. 바로 데이터로부터 학습을 최적의 Decistion Boundary를 정하는 것 입니다. 이 때 경계선은 확률 분포가 0.5인 지점을 고르는 것이 일반적이지만 경우에 따라 0.3, 0.7 을 기준으로 할 수 도 있습니다. 예를 들어 사람이 암에 걸렸느냐 아니냐 등을 판단할 때 암에 안걸렸어도 걸렸다고 하는것이, 걸렸는데 안걸렸다고 하는거보다 낫기 때문에 암이 걸렸다는 결과를 낼 좀 더 관대하게 내도록 할 수도 있는거죠.

Maximum Likelihood

이제 어떻게 하면 위의 그림처럼 데이터로부터 최적의 Decision Boundary를 찾아낼 수 있는지, 그러니까 최적의 parameter \(\phi\) (1차원이면 \(\phi_0, \phi_1\)) 를 찾아낼 수 있을지를 알아봅시다. 이전에 Regression 에서 본 것 처럼 MLE, MAP 들 중 하나를 쓰면 되는데, 먼저 간단하게 Maximum Likelihood Estimation (MLE) 방법을 쓸 경우를 생각해 봅시다. MLE는 Likelihood가 가장 커지는 (maximum likeliihod) 어떤 parameter를 (point) 찾아내면 (estimation) 되는거죠. Regression 때와 마찬가지로 아래의 절차를 따르면 됩니다.

1.likelihood를 정의한다.
2.전체 식에 log를 취한다.
3.미분을 취해 0인 지점을 찾는다.

Likelihood 수식은 이미 우리가 bernoulli 분포를 가정했으므로 이미 알고있는 겁니다.

여기에 Log를 취하고 -를 붙히면 최종적으로 Negative Log Likelihood (NLL)을 얻게 됩니다.

이제 negative likelihood이니 미분을해서 0인 지점을 찾으면 우리는 주어진 dataset에 대한 optimal solution을 얻을 수 있습니다..

여기서 미분을 할 때 chain rule 에 의해 \(\sigma [\phi^T x] = \frac{1}{1 + \\exp[- \phi^T x]}\) 를 미분한 \(\sigma' [\phi^T x]\) 를 계산해야 하는데 이 값은 아래와 같이 계산이 되었습니다.

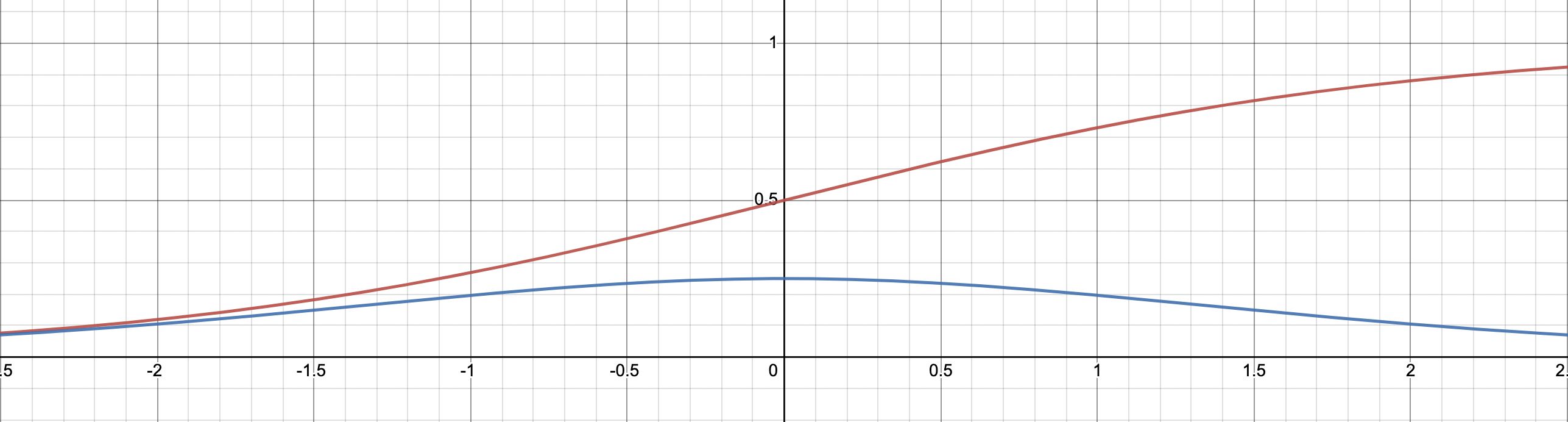Fig. sigmoid (red line) vs derivative of sigmoid (blue line). sigmoid 를 미분한 수식은 아래와 같이 종을 뒤집은 bell shape 인데, 이것은 나중에 Deep Learning에서 굉장히 중요한 정보를 제공합니다

하지만 안타깝게도 NLL Loss인 \(L(\phi)\) 의 미분값 \(\frac{\partial L(\phi)}{\partial \phi}\) 가 0이되는 지점을 통해 최적 해 (optimal solution)을 구할 수는 없습니다. 왜냐하면 Logistic Regression에 non-linearity가 포함되어 있기 때문입니다. Logistic Regression은 \(\phi\)를 x와 w에 대해 한방에 정리해 그 식을 최소화 하는 해를 구할 수 없다고 하는데, 다른 말로는 닫힌 형태의 해(Closed-form Solution)를 구할 수 없다, Analytic Solution이 존재하지 않는다고도 합니다. (Analytic Solution의 반대는 Numerical Solution)

Optimization

그러면 어떤 방법을 사용해야 나하의 parameter 셋을 찾는 Logistic Regression의 likelihood가 가장 커지는 point, optimal solution를 구할 수 있을까요? 이런 경우에는 최적화 (Opitmization)를 통해 문제를 푸는 것이 일반적입니다. ML뿐만 아니라 다양한 분야에서 쓰이는 하나의 거대한 분야이며 (최적화만으로 학위를 하는 분들이 있을 정도로), 앞으로 우리가 Logistic Regression을 넘어 더 거대한 NN architecture로 더 복잡한 문제를 풀 때도 항상 사용하게될 방법론입니다. 우리가 이번에 알아볼 optimization은 시작 점 (initial point)에서 출발해 data들로부터 얻은 loss (NLL) 정보를 바탕으로, loss를 최소화 할 수 있는 방향 (direction)이 어딘지 계산하고 그 direction으로 적당히 한 step가는것을 무한히 반복해서 최종적으로 가장 loss가 낮은 지점으로 가는 이른 바 반복적인 비선형 최적화 (Iterative Non-linear Opitmization) 입니다.

예시를 가지고 iterative optimization에 대해 이해해봅시다. 우리가 어떤 미지의 함수 \(f[\theta]\) 를 가지고 있다고 칩시다. 우리의 목적 (objective) 은 다음과 같습니다.

말로 다시 풀어쓰면 ‘\(f[\theta]\) 라는 함수값을 가장 작게 만드는 \(\theta\) 를 찾고싶다.’ 입니다. 이 \(f\)함수를 우리가 목표로 하는 함수라고 해서 목적 함수 (objective function) 혹은 손실 함수 (cost function) 이라고도 하는데, 앞서 말씀드린 negative log likelihood가 목적 함수로 쓰면 우리는 MLE를 하는것이 됩니다.

Iterative optimization의 idea를 4가지 step으로 반복하면 다음과 같은데,

1. 어떤 랜덤한 값 \(\theta^{[0]}\) 에서 시작한다.
   
2. 그 다음 \(\theta^{[1]}\), 그 다음 \(\theta^{[2]}\), \(\theta^{[3]}\) … 으로 조금씩 이동한다.
   
3. 조금씩 이동하는 것이 cost를 감소시킨다는걸 보장한다.
   
4. 더이상 나아질 수 없을 때, 그 지점이 바로 최소값이어야 한다.
   

이 idea를 그림으로 나타내면 다음과 같습니다.

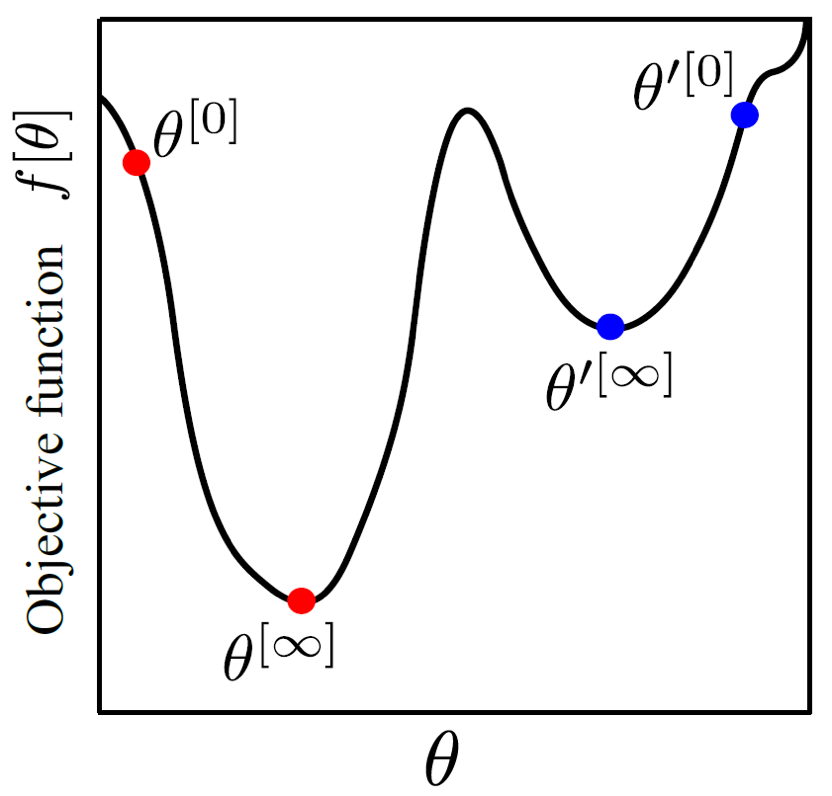
하지만 위의 figure에서도 알 수 있듯 이런 방식에는 문제점이 있는데, 바로 시작 지점이 red point냐 blue point냐에 따라서 도달하는 지점이 다를 수 있다는 것입니다. 이런 경우 최적화 하고자 하는 function이 Non Convex 하다고 하는데, 바로 아래 figure의 2, 3번째 같이 두 점을 이었을 때 걸리적 거리는게 있는 경우를 Convex 하지 않다고 얘기합니다.

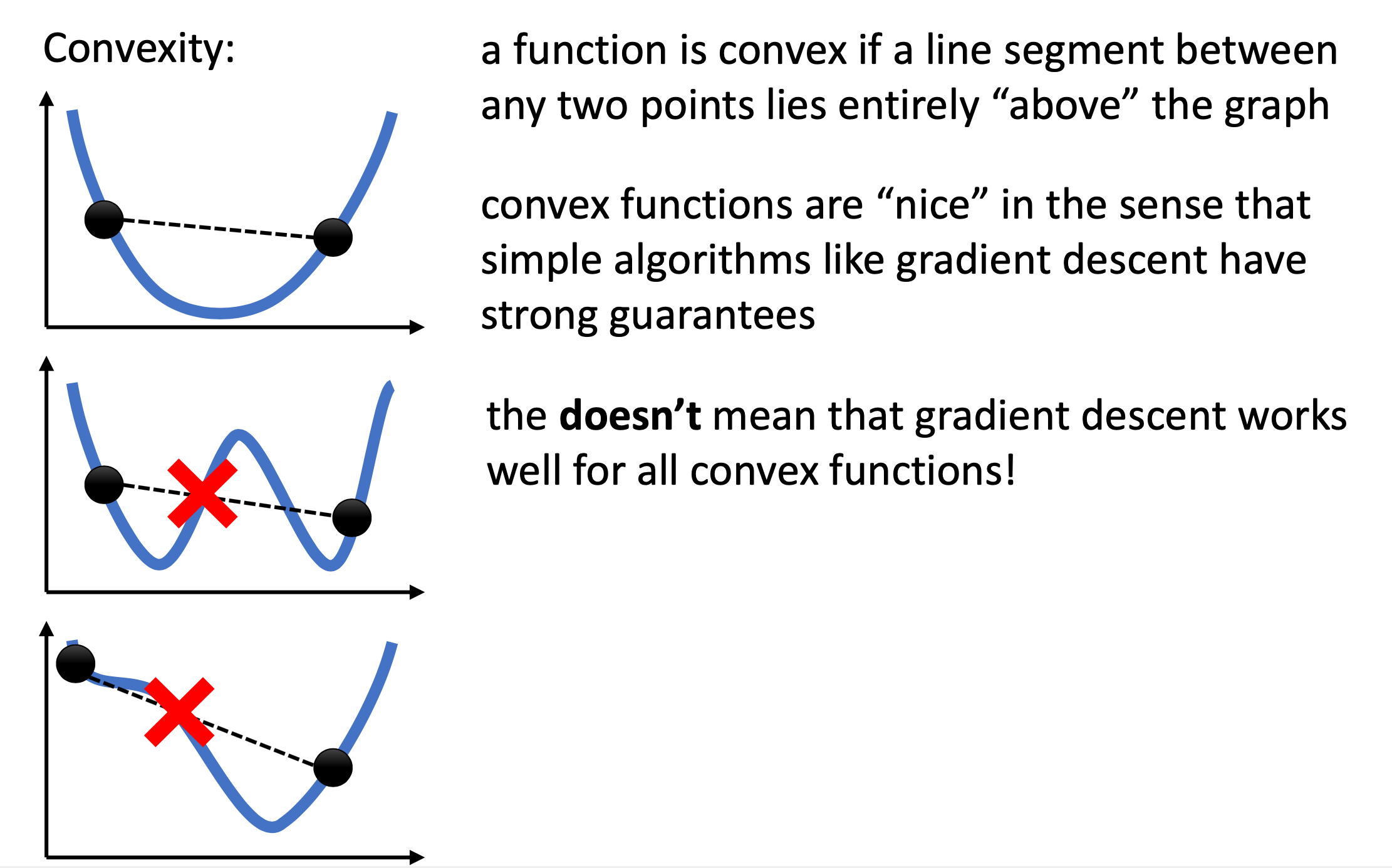
이럴 경우 운이 나쁘면 시작하는 지점과 최적화 parameter의 값에 따라 최적해 (Global Minimum, Optimal Solution) 근처에 가지 못할 수가 있습니다. 다만 최적이 아니어도 적당히 괜찮은 지역해 (Local Minimum, Sub-optimal Solution)정도에 도달 할 수는 있죠. 반면 맨 1번째 sub figure는 소위 밥 공기 뒤짚은 듯한 (bowl-shaped) 모양으로 Convex 하다고 얘기하는데, 이 경우에는 Local Minimum 이 존재하지 않고 최적해에 도달하는 것이 보장됩니다.

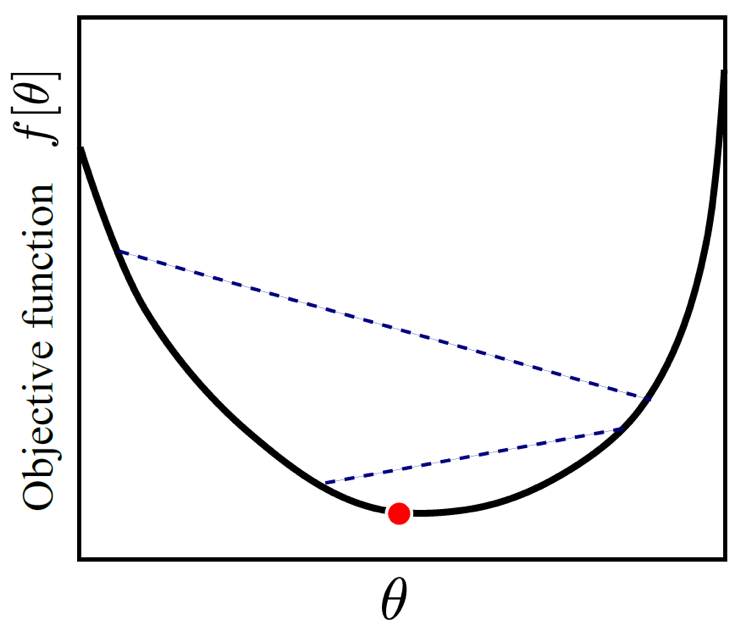
다행히 현재 우리가 다루는 문제인 Logistic Regression 은 Likelihood 를 Bernoulli distribution로 설정하고 그것에 Log 를 씌움으로써 Convexity가 보장된다고 합니다.

Fig. Source From UCB CS194 Lecture 6, Logistic Regression - CS 194-10, Fall 2011

하지만 우리가 2022년 현재 대다수의 분야에 사용하고 있는 수십층으로 이루어진 Nerual Network (NN) 기반의 algorithm들은 대부분이 Non-Convex Surface 를 가지게 됩니다.

다시 Logistic Regression으로 돌아와서, likelihood와 log likelihood를 각각 아래 (a, b)처럼 시각화 했을 때, b) 1번 점에서 출발해 cost를 줄이는 방향으로 2번, 3번으로 parameter가 update 되는 최적화 과정에 따라서 c) Decision Boundary 가 어떻게 움직이는가를 볼 수 있습니다.

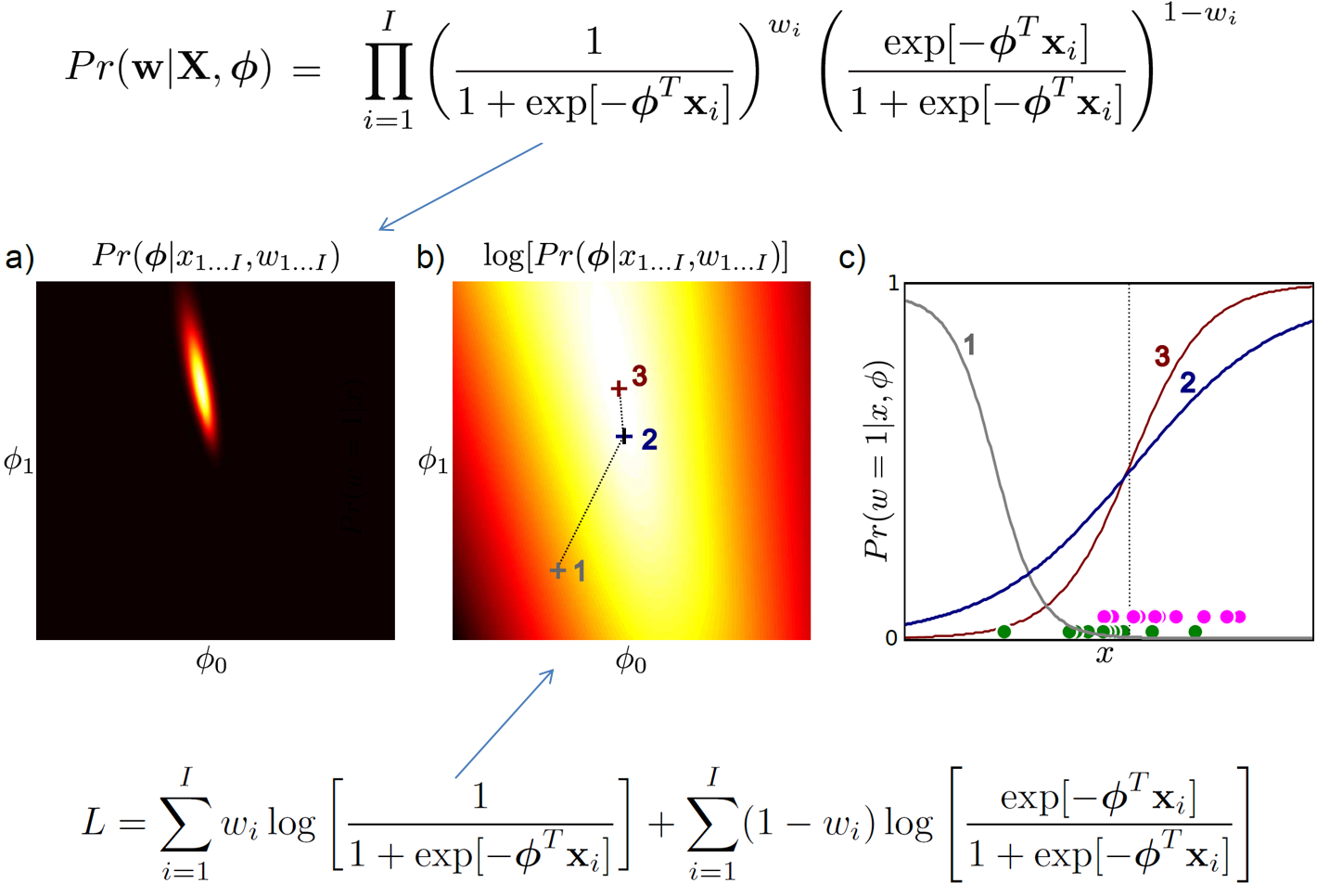
그런데 어떻게, 어느 시점 t의 \(\theta^{[t]}\)에 대해서 그 때 마다 어떤 direction으로 가야 cost가 조금씩이라도 감소하는걸 보장하는 방향으로 가게될까요? 이에 대해 알아봅시다.

Gradient Based Optimization

우리가 지금 알아야 할 것은 아래의 두 가지 입니다.

1.Search direction s를 함수 f의 특성에 따라 정합니다. (어느 방향으로 이동할것인가?) 2.여러 \(\lambda\) 중 다음의 식을 만족하는 최적의 \(\lambda\)를 찾아냅니다. 이를 line search라고 합니다. (얼만큼 이동할 것인가?)

즉 어느방향으로?, 얼만큼 갈지? 를 정하고 나면 이 정보를 바탕으로 아래의 수식을 사용해 parameter를 update하면 됩니다.

일단 \(\lambda\) 에 대해서는 생각하지 말고 (적당한 상수값으로 고정시키고) direction만 생각해 봅시다.

Solution부터 말씀드리면 loss function, \(L(\theta)\)을 현재 parameter에 대해서 미분을 해 기울기를 계산하는 겁니다. 예를 들어 아래와 같이 parameter space 가 1차원일 경우 loss값을 1차원 더해 총 2차원으로 생각해 봅시다. 이 setting에서 기울기가 음수라면 현재 parameter 가 있는 지점에서 오른쪽으로 가면되고 기울기가 양수일 때는 그 반대 방향인 왼쪽으로 가면 됩니다.

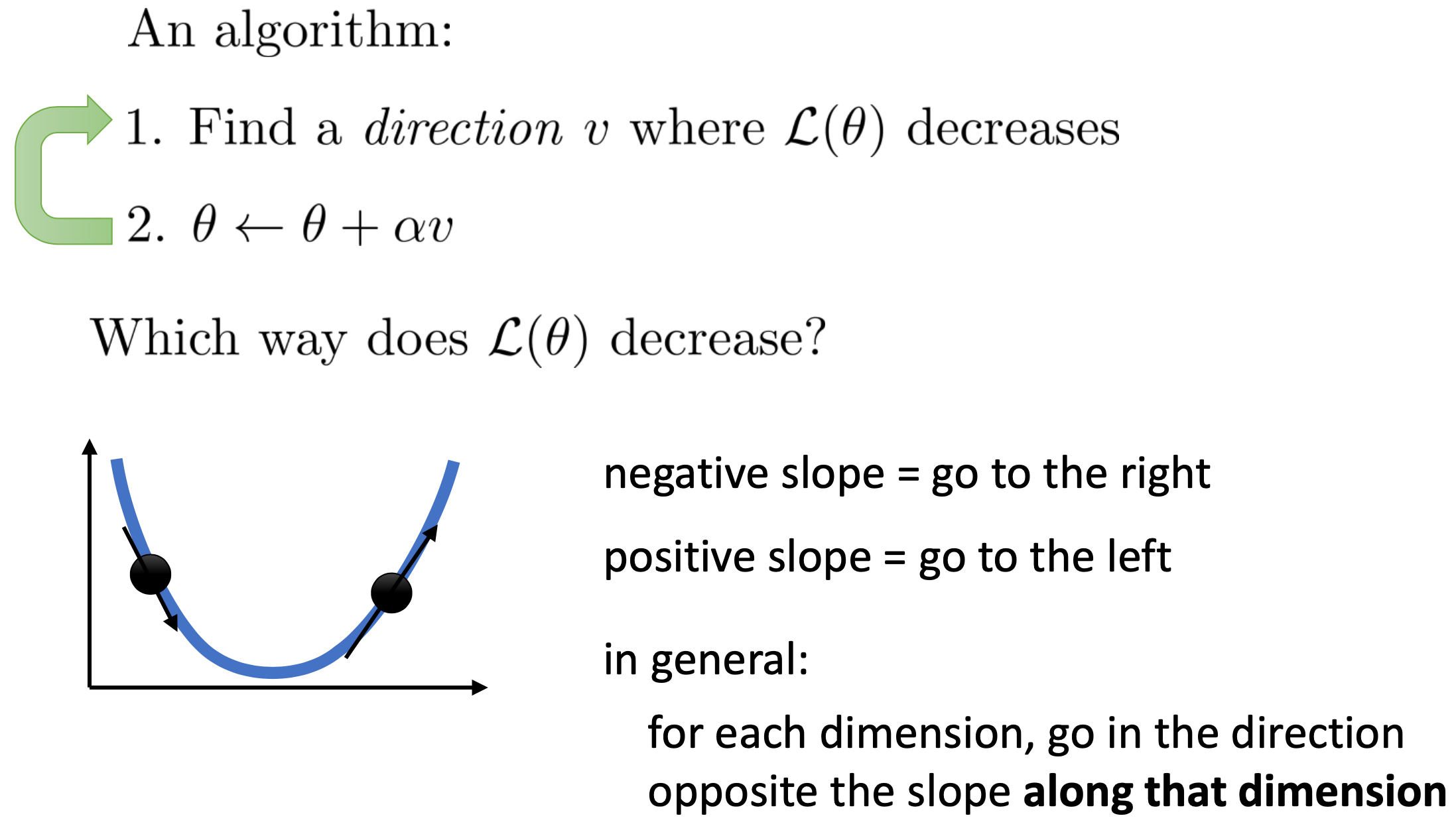Fig. Source From cs182

즉 언제 어디서나 기울기 (Graident)를 구하고 그 반대 방향으로 가면 되는겁니다.

• parameter space 1차원 (\(\theta\) 의 이동 방향은 양수, 음수 방향 밖에 없음)
  • 기울기가 양수면 음의 방향으로 이동
  • 기울기가 음수면 양의 방향으로 이동

이것을 차원을 2차원, 3차원 ... N차원 으로 늘려도 동일한데, parameter space 가 N차원이면 N개의 parameter 에 대해 모두 편 미분 (Partial Derivative)을 해서 각 차원별로 전진을 하면 됩니다.

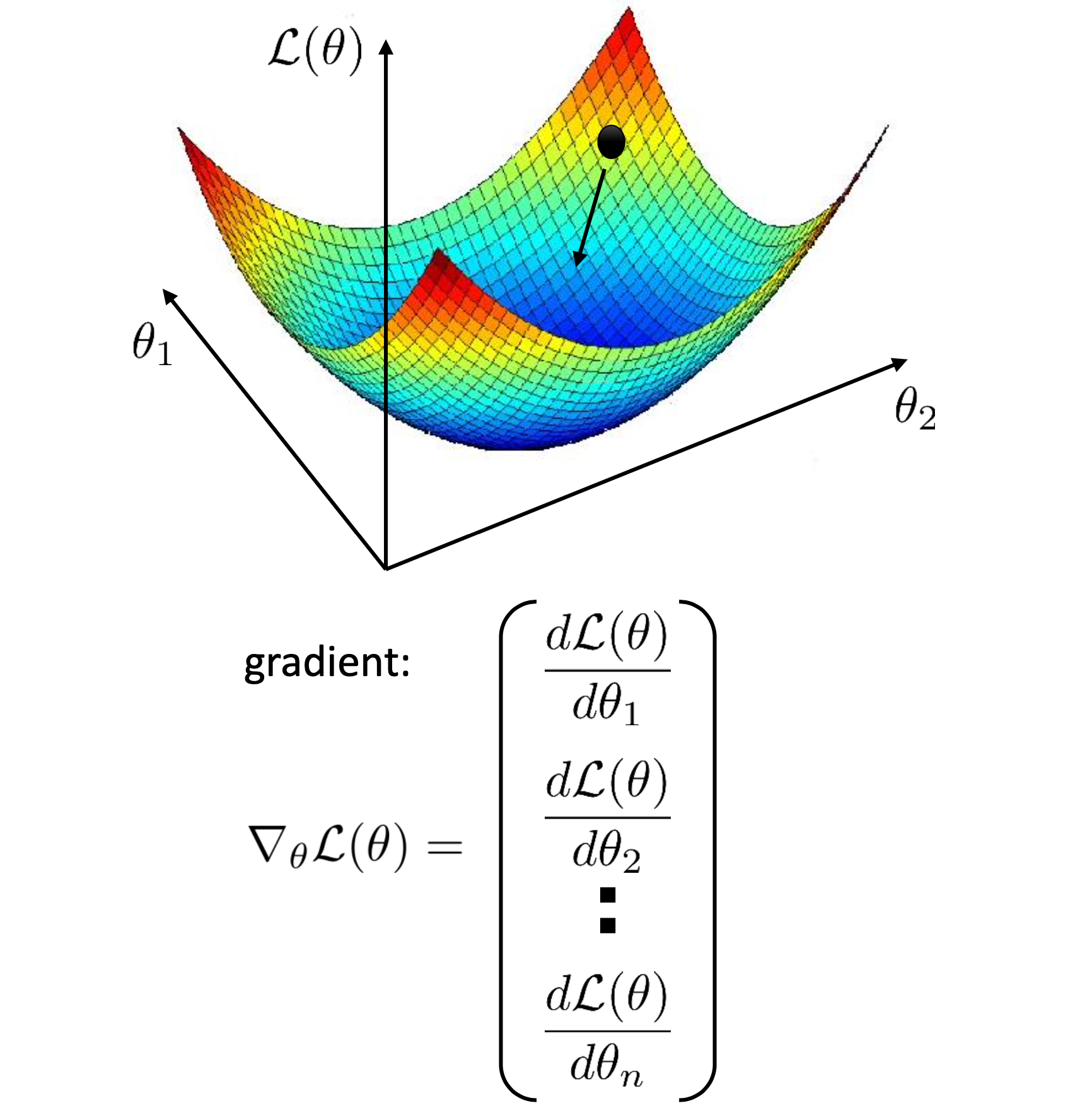Fig. Logistic Regression 의 Convex Loss Surface

이를 기울기 (gradient)를 따라서 loss surface를 내려간다 (하강한다)고 해서 경사 하강법 (Gradient Descent)이라고 부릅니다.

Why does it work? (gradient descent is minimizing a local approximation)

그런데 왜 미분을 해야하는걸까요? 이것이 갖는 의미가 뭘까요?

사실 loss function의 현재 parameter 에 대해서 gradient를 구하는 것은 loss function을 테일러 전개 (taylor expansion, taylor approximation) 하는 의미를 가지고 있습니다.

그럴 일은 없겠지만 Loss function이 어떤 모양인지 만약 우리가 알고있다면 현재 parameter point의 부근에서 어느 방향으로 얼만큼 가는것이 cost를 가장 많이 낮추는 것인지 알겁니다 (반경 \(\epsilon\)내에서 고른다고 칩시다). 그런데 loss function이 어떻게 생겼는지 모르고 실제로는 매우 복잡하게 생겼을 것이므로 우리는 이를 알지 못합니다. 하지만 우리가 원하는 것은 전체 function이 어떻게 생겼는지가 아니라 현재 parameter point 근처에서 loss function이 어떻게 생겼는가?입니다. 다 알필요가 없는거죠. 정해진 반경 \(\epsilon\) 내에서만 그 다음 parameter를 고를 것이기 때문에 정해진 범위 밖은 어떻게 생겼는지 알바가 아니거든요. 그러므로 우리는 현재 parameter 부근에서만 어떻게 생겼는지 알면 되는데, 이 때 쓰는 것이 taylor expansion 입니다. Taylor expansion은 다항식이 아닌 미지의 함수를 다항식으로 표현하는 방법으로, 어떤 함수가 너무 어려워 그대로 사용하기 힘들 때 그 함수를 근사해서 연산에 사용하기 위해서 ML이나 여러 분야에서 많이 쓰이는 수학적 Tool 중 하나 입니다. 아래와 같이 cyan색 curve에 대해서 1차 근사 (first order approximation)를 하면 우리는 pink색 근사된 curve를 얻을 수 있습니다.

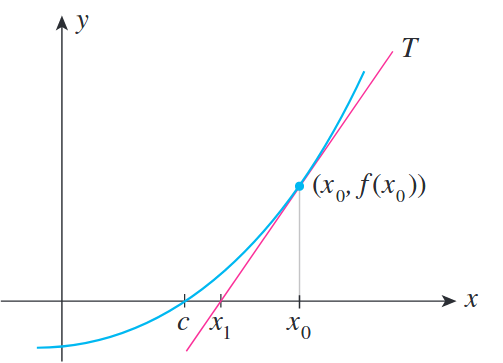Fig.

Order수를 늘리수록 해당 point에서 더 원래의 함수와 비슷한 형태를 갖추게 됩니다.

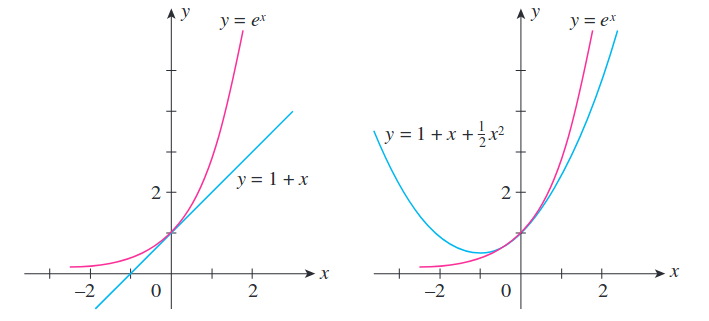Fig.

Taylor approximation은 보시는 바와 같이 근사를 한 point에서 멀어지게 되면 원래 function과의 오차가 증가하게 됩니다. 하지만 말씀드린 것 처럼 우리는 어떤 정해진 지점에서만 다음 parameter를 고를 것이므로 이는 완벽하진 않아도 꽤 괜찮은 approxmiation이 됩니다. 우리가 정의한 objective function에 대해서 first order taylor approximation을 하는것은 gradient를 계산하는 것과 같습니다. 그런데 small region을 정해줘야 비로소 괜찮은 optimization이 될거라고 했습니다.

Fig. Source from DeepMind X UCL Lecture

Gradient descent는 그래서 내가 현재 parameter point에서 radius가 \(\alpha \parallel \nabla_{\theta} L(\theta) \parallel\)인 제한 조건 (constraint)를 걸어주는 것과 다름 없습니다. 이러한 제한 조건이 걸린 최적화 (constraint)를 푸는 방법은 먼저 Lagrangian Multiplier를 이용해 constraint를 objective term과 결합시키고, objective는 1차 근사를 하고 constraint 에 대해서는 2차 근사해줍니다. 그리고 우리가 원하는 것은 cost가 가장 낮은 parameter로 update를 하는 것이므로 근사된 수식을 미분해서 0으로 두고 문제를 풀면 됩니다. 그러면 우리가 앞서 봤던 gradient descent 수식이 나옵니다.

(수식으로 길게 풀어쓰기에는 post의 주제가 classification이기 때문에 범위를 벗어나는 것 같아 구두로만 설명했습니다. 더 관심이 있으신 분들은 DeepMind X UCL Lecture를 보시면 좋을 것 같습니다.)

Problem of (Steepest) Gradient Descent

앞서 설명 드린 방법이 바로 가장 가파른 (Steepest) direction을 찾아 내려간다고 해서 Steepest Gradient Descent 라고도 합니다.

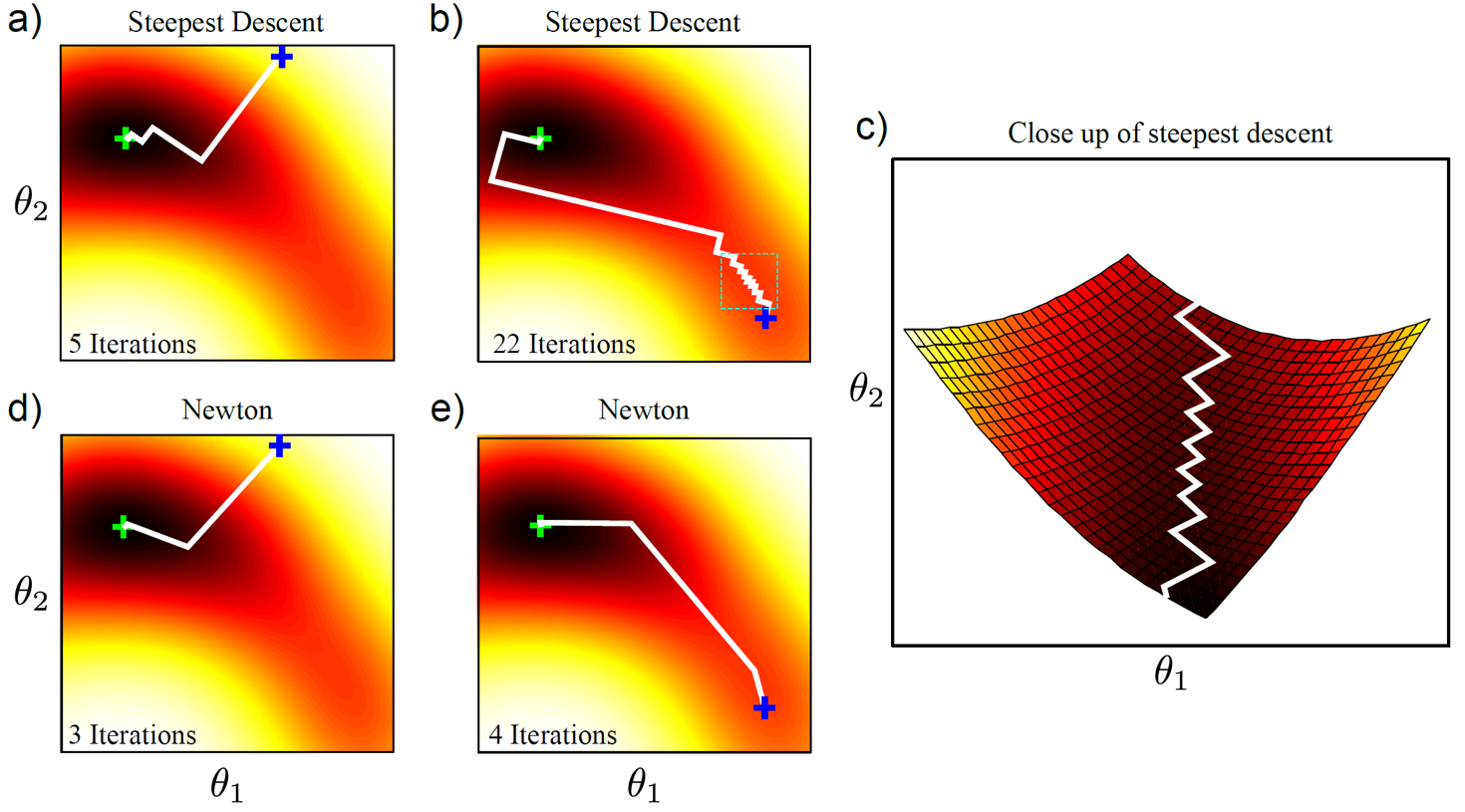
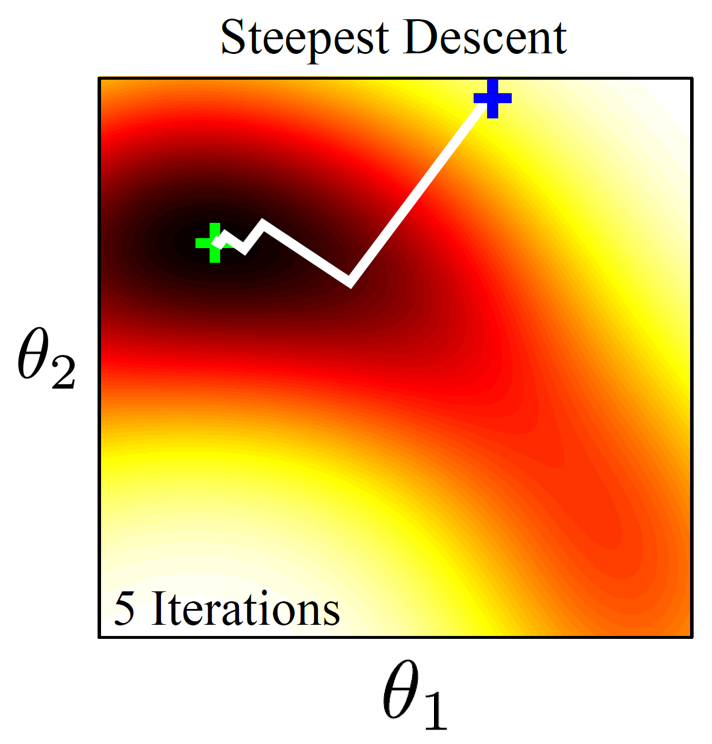Fig. 2 dimensional Gradient Descent

그런데 Steepest Descent 는 몇 가지 잘 알려진 문제점들이 있습니다. 첫 번째는 non-convex인 loss function를 optimize하는데 어려움이 있을 수 있다는 겁니다.

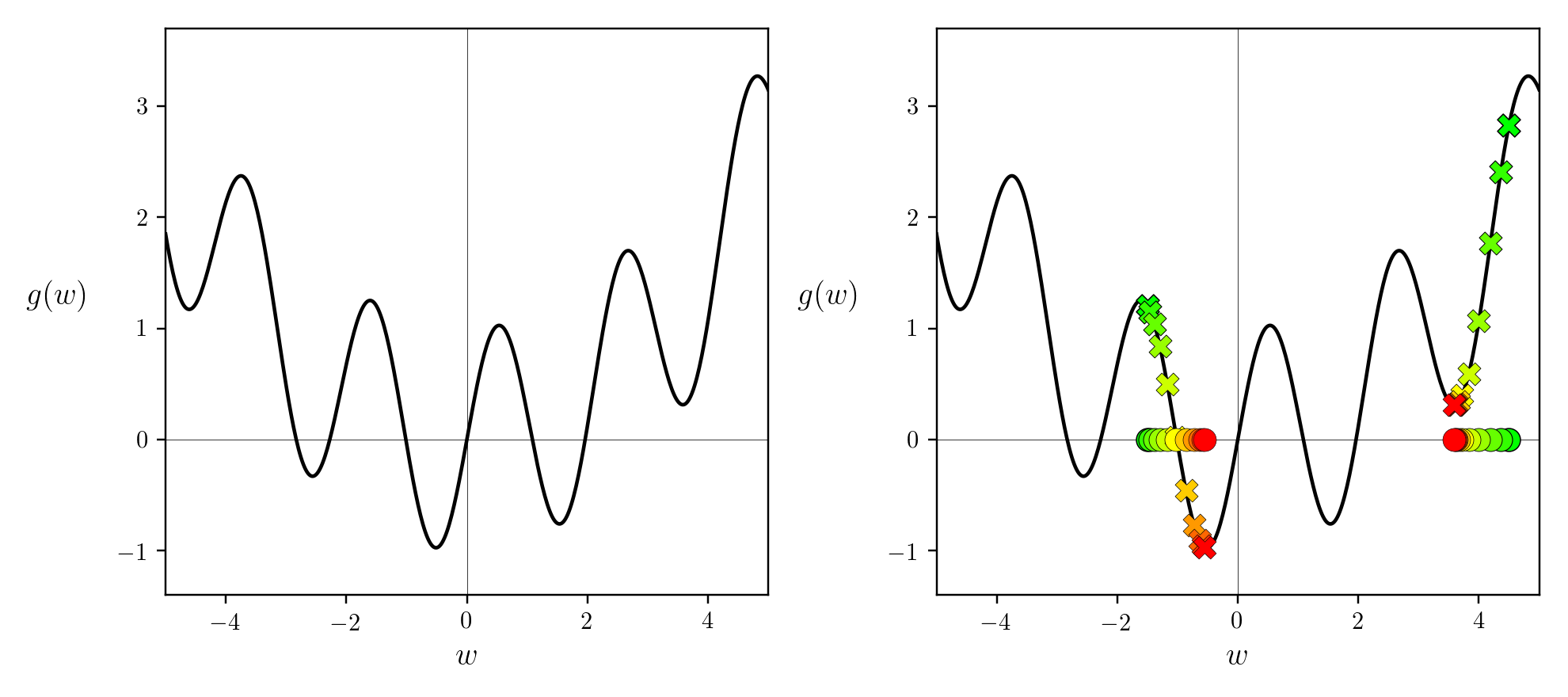Fig. Source from here

Non-convex하기 때문에 naive gradient descent를 하면 optimal minima가 아니라 local minima로 가는 경향이 있지만 그래도 cost는 감소하는 방향으로 optimize되었기 때문에 이는 별 문제가 안될 수 있습니다. 진짜 문제는 바로 아래처럼 초반에 비해서 optimal value 근처에서 너무 오래 머물러 있는다는 겁니다. 다시 말해서 너무 많은 반복 횟수 (iteration)가 필요한 거죠.

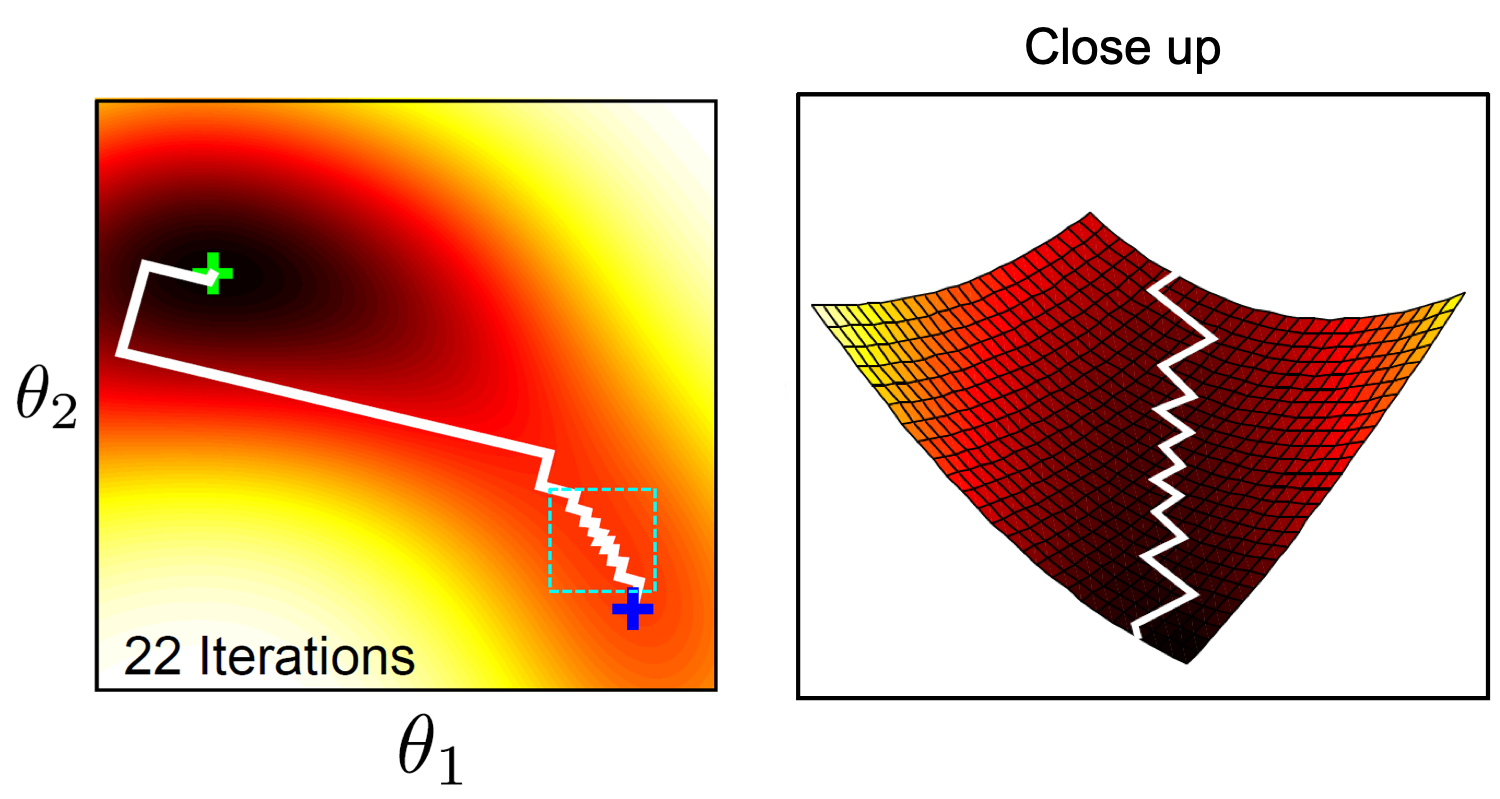
이는 특히 Saddle Point에서 벗어나지 못하는 치명적인 문제를 야기할 수 있습니다.

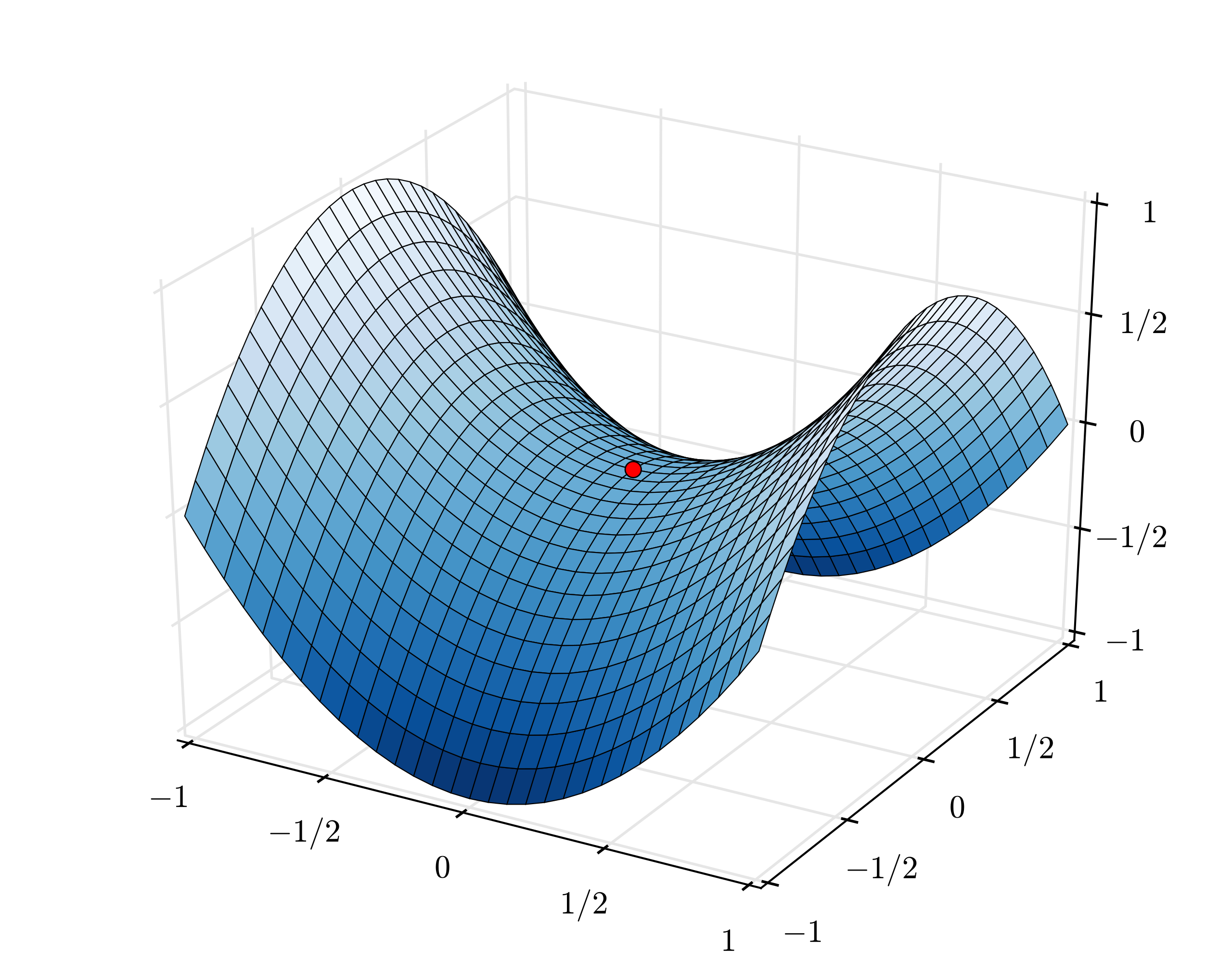Fig. 안장점 (Saddle Point)는 실제로 말의 안장같이 생겨서 붙은 이름이다. Source from wiki

실제로 아래 gradient descent를 통한 optimization과정을 보면 결국 saddle point에서 벗어나지 못하고 training이 끝나는 것을 볼 수 있는데, 이는 saddle point지점에서 1차 미분값이 거의 0이기 때문에 발생하는 문제입니다.

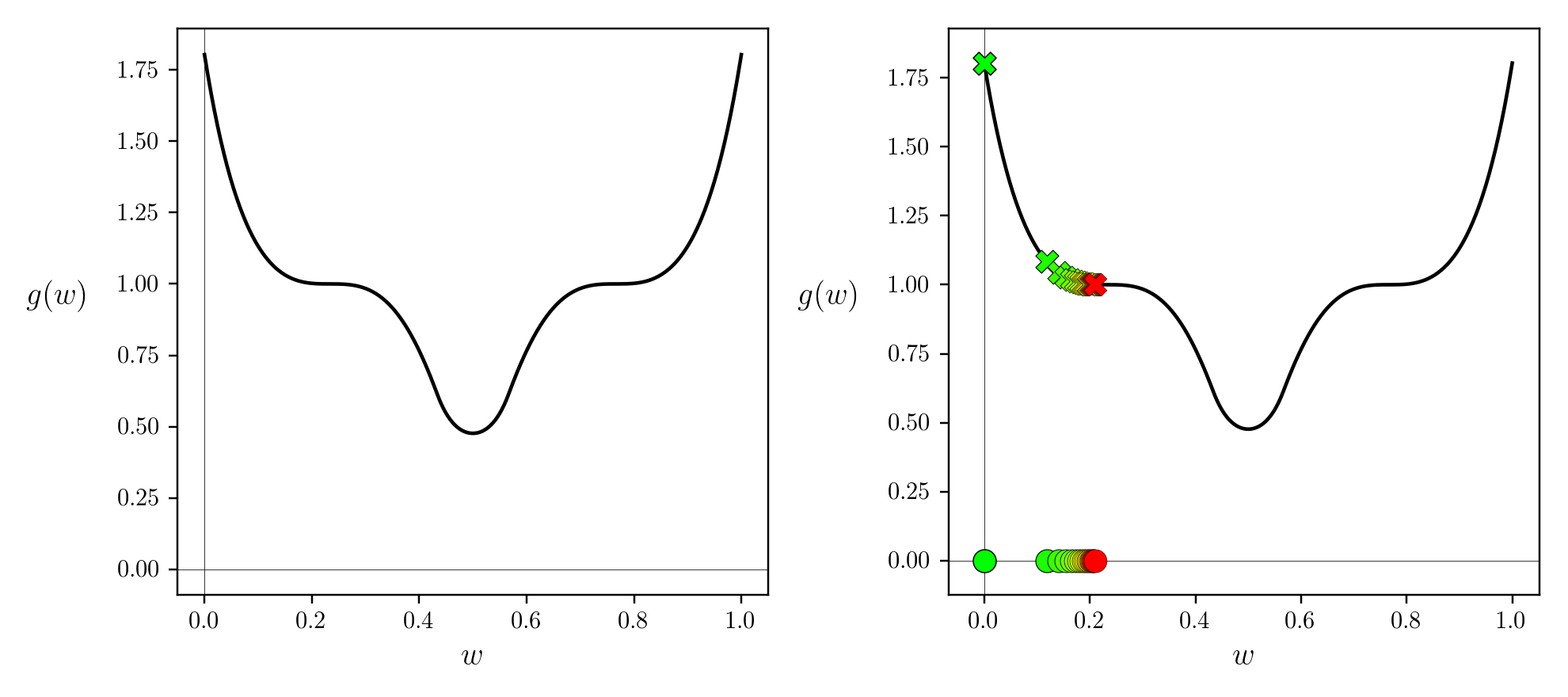Fig. Source from here

이를 해결할 수 있는 방법이 몇 가지 있겠지만 가장 단순한 방법 중 하나는 해당 방향으로 얼마나 이동할 것인가? 를 결정하는 step size (or learning rate)를 잘 정하는 겁니다.
Naive gradient descent는 이 step size, \(\lambda\) 를 고정해서 쓰니 더욱 문제가 되는겁니다. 하지만 step size를 너무 작거나 큰 값으로 설정해주는게 능사는 아닙니다. 크면 saddle point를 탈출할 수는 있겠으나 너무 크게 설정하면 아예 발산해서 optimal solution에 다가가기는 커녕 멀어져 버리는 수가 있습니다.

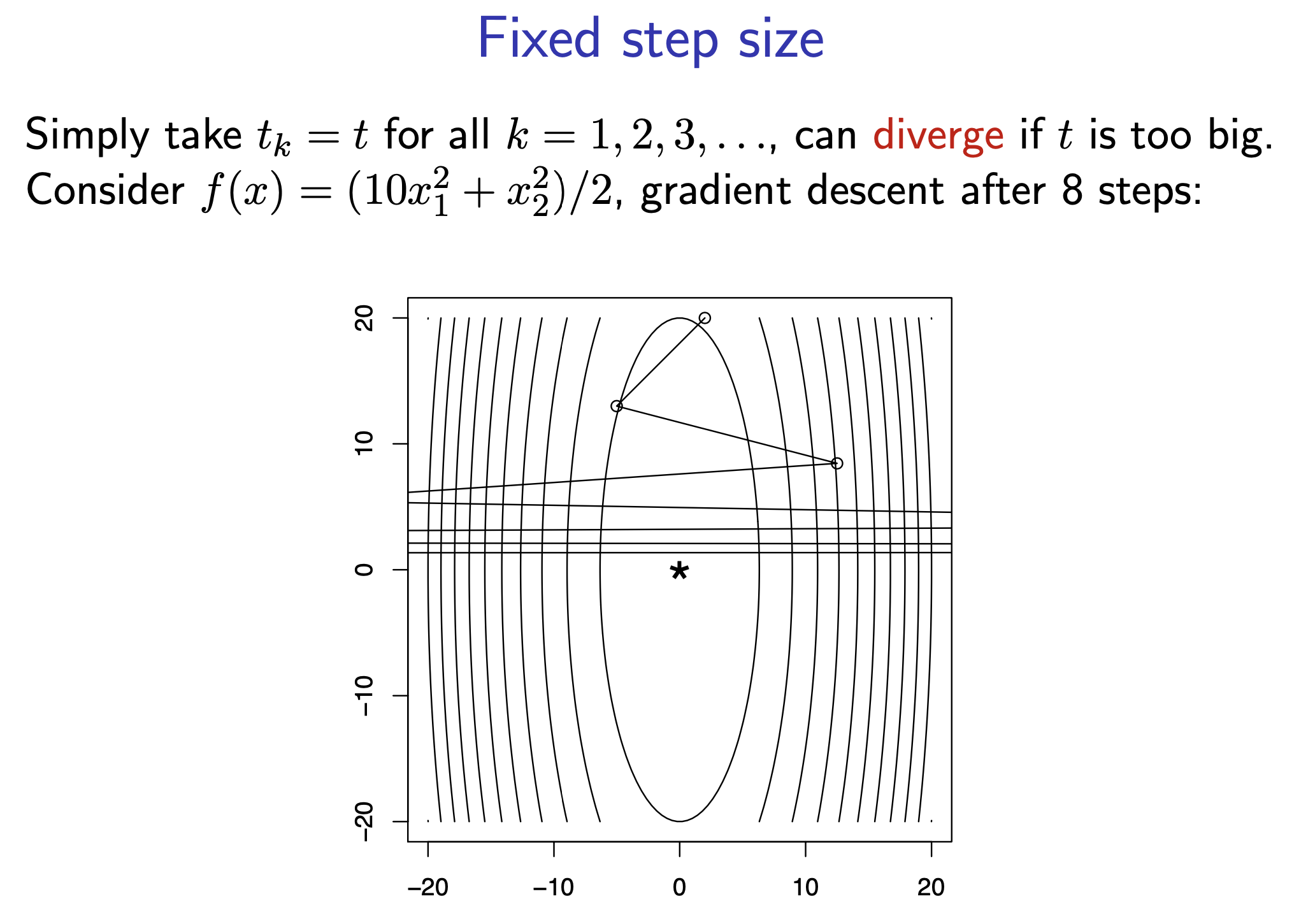Fig. step size가 너무 큰 경우

반면에 이 값을 너무 작게 설정하면 수렴속도가 너무 느려지게 됩니다.

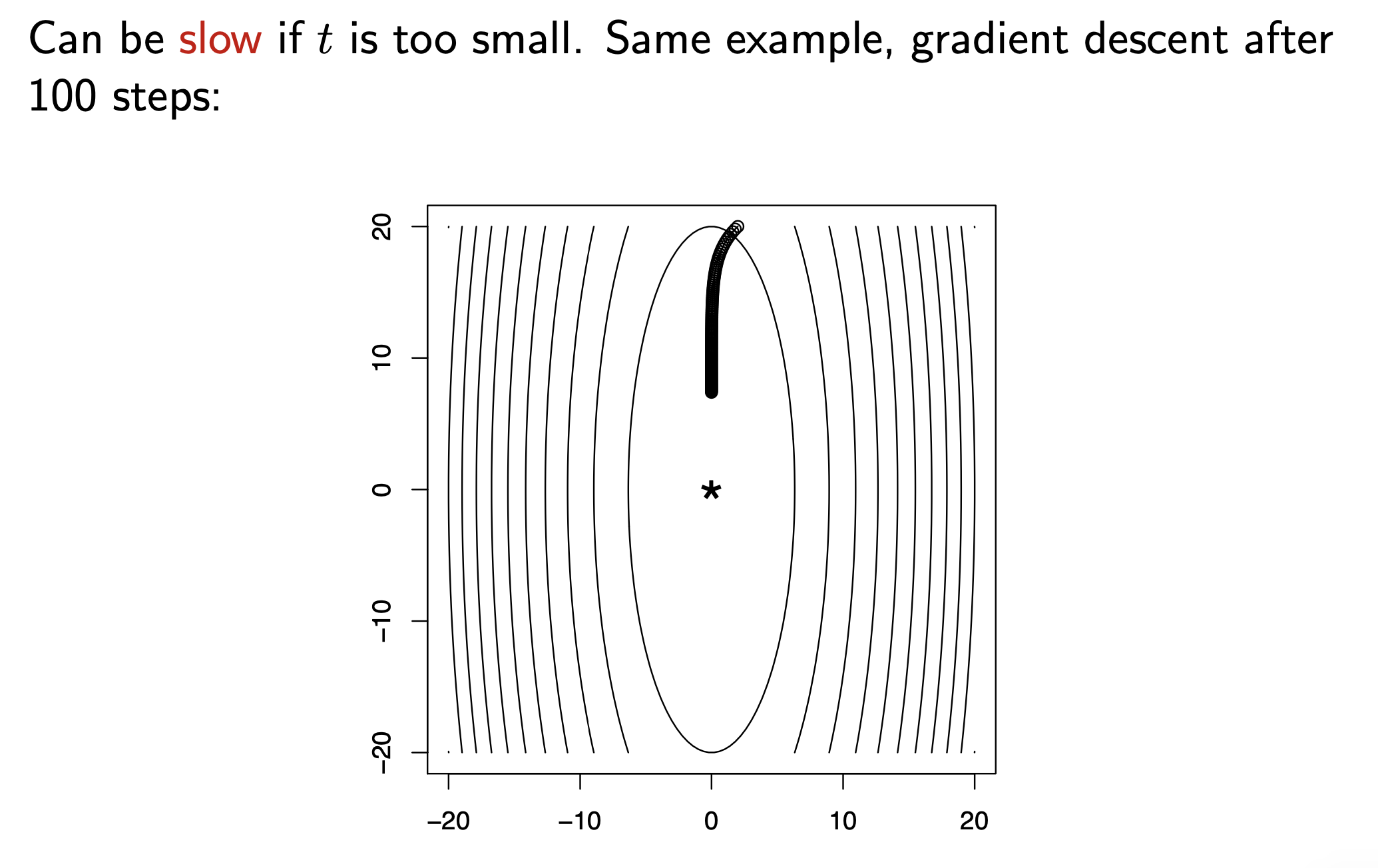Fig. step size가 너무 작은 경우

따라서 적절한 step size를 상황에 맞게 (adaptive) 정해줘야 하는데 어떤 기준으로 이를 정해야 할까요?

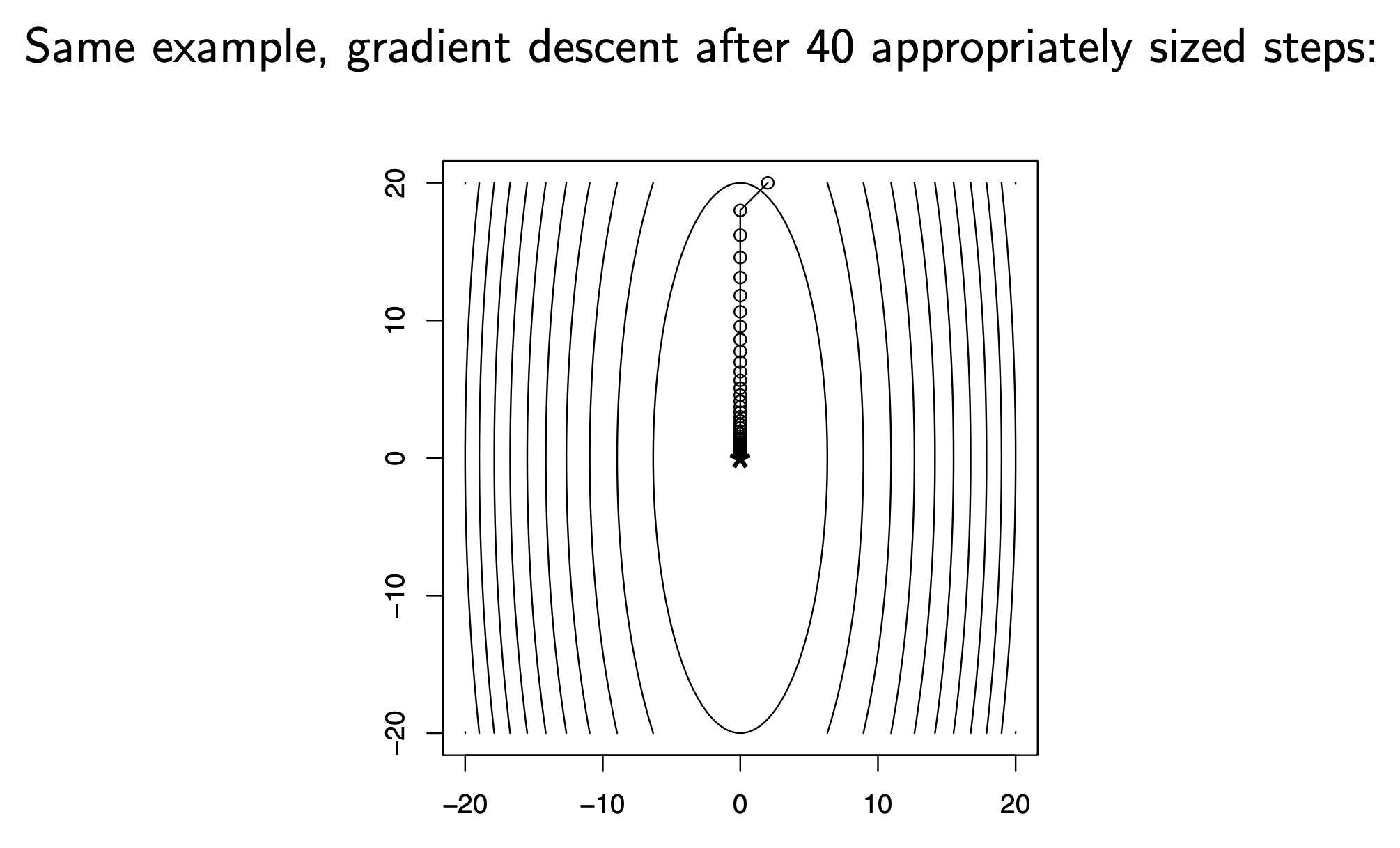Fig. 매 순간 적당한 step size를 고를 경우

Newton’s Method (Newton-Raphson)

앞서 현재 parameter 에서 어떤 direction으로 optimization step을 수행해야 하는지를 알려면 objective function을 근사해야 한다고 했습니다. 그런데 꼭 first order approximation를 할 필요는 없습니다. 2nd order approximaion을 사용해도 되죠.

Fig.

한 번, 2nd order approximaion을 해봅시다. 어떤 미지의 함수 \(f(x)\)를 p 점에 대해 taylor expnasion을 할 경우 다음과 같이 표현할 수 있는데,

objective function을 현재 parameter point에 대해 2nd order approximaion 까지만 하면 2차항 까지만 남습니다.

2nd order approximation을 할 경우 근사된 function이 볼록하기 때문에 이번에는 small region이라는 constraint를 주지 않고, 미분해서 0인 지점 (극솟값; local minimum)을 구해보겠습니다.

그러면 우리는 아래와 같이 blue point에서 어느 방향으로 얼만큼 가야하는지를 동시에 알 수 있게 됩니다. 즉 골칫거리였던 step size문제가 해결이 된 것이죠. 이를 Newton’s method (or Newton Raphson Method)라고 합니다.

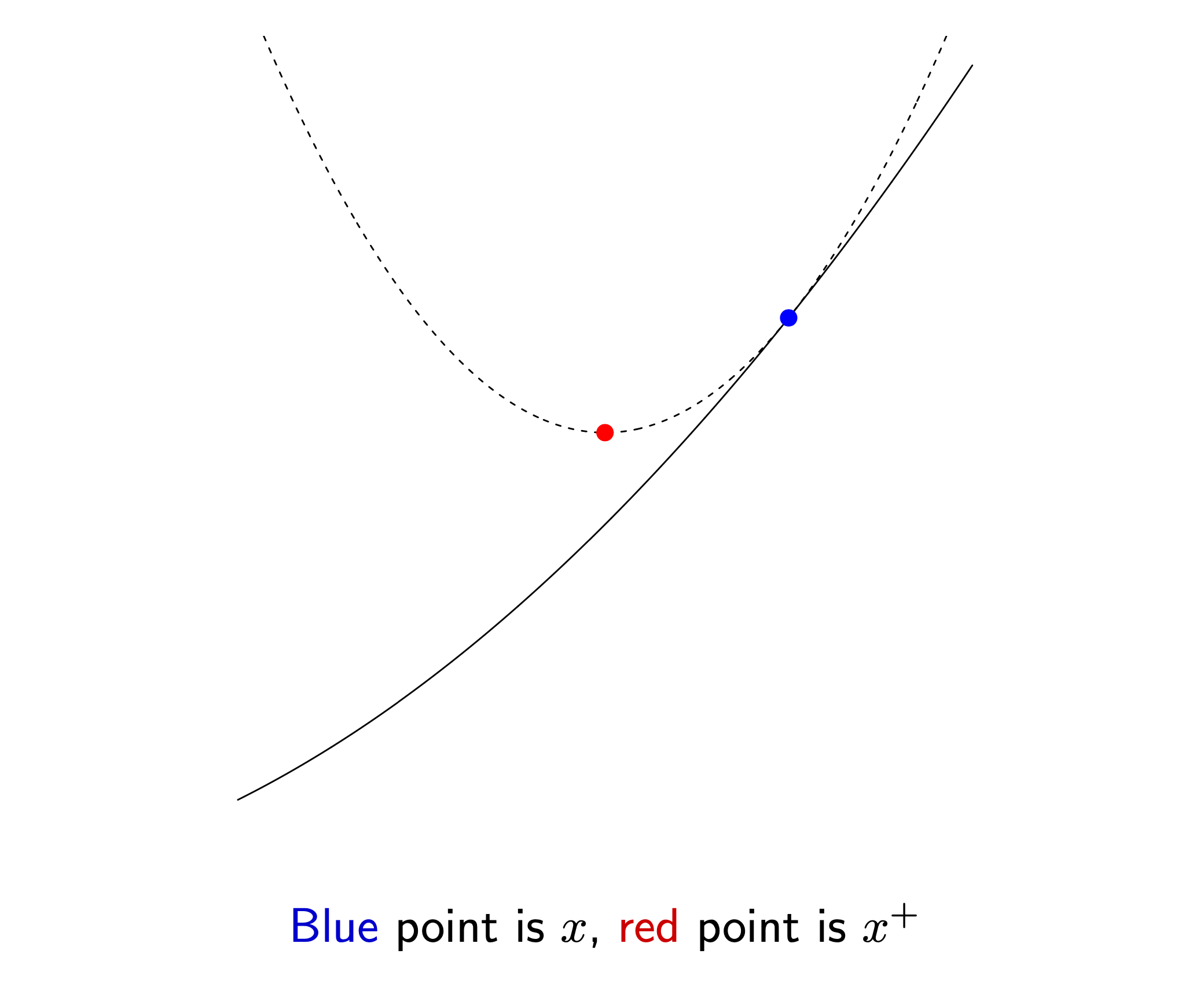
앞선 Gradient Descent와 비교해서 2차 미분항의 역수가 step size로 추가된 것이나 다름 없는데, 2차 미분항이 크면 조금 가고, 작으면 많이 간다는 것을 알 수 있습니다.

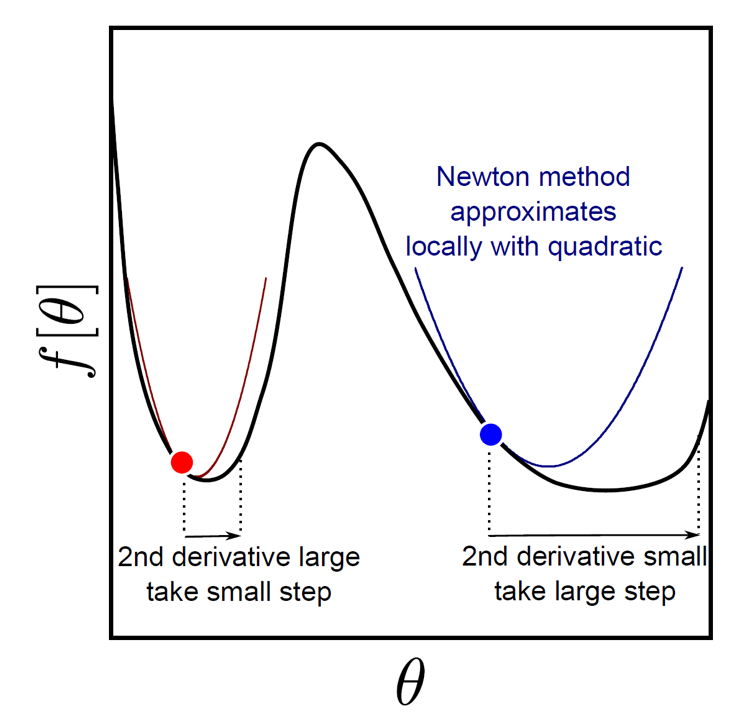
Step size를 알긴 했지만 여기에 추가로 \(\lambda\)를 결합할 수도 있습니다. (또 어떤 step size를 곱해준 다는 것인데 이는 바로 아래 Line search와 연결됨)

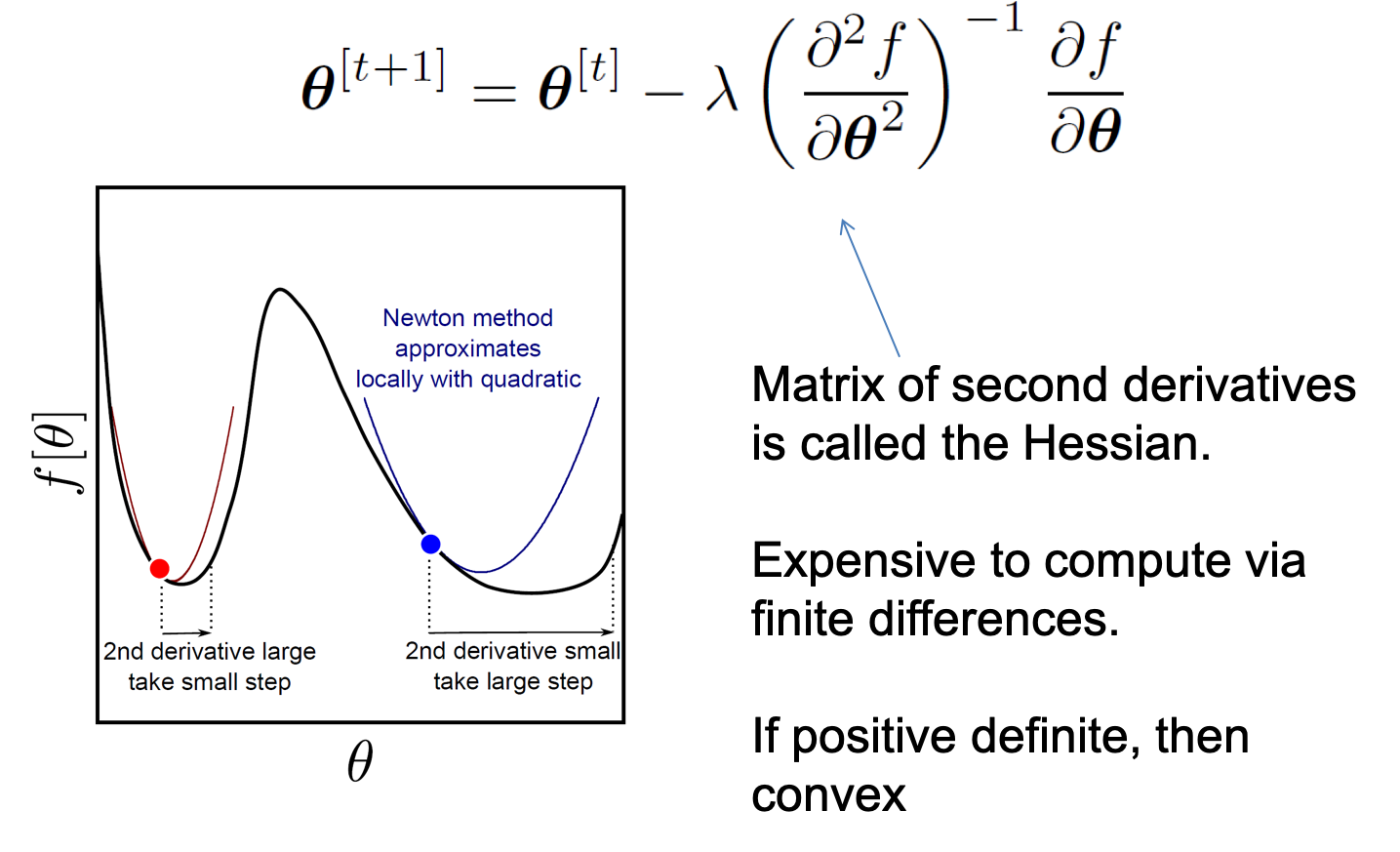
Newton’s method는 2차 미분 항인 Hessian을 계산해야 하므로 computational cost가 많이 들지만 어느 지점에서 시작하더라도 optimal point를 꽤 잘 찾아가는 좋은 algorithm 입니다.

Line Search

말씀드린 것 처럼 Newton Method 도 완벽하지만은 않습니다.

• 1차 미분 활용 (Steepest)
  • 방향은 잘 찾지만 adaptive step size 를 갖기 힘듬
• 2차 미분 활용 (Newton)
  • Hessian 을 구해줘야 하는데 이 연산 자체가 비쌈
  • step size는 꽤 잘 정하지만 \(f''=0\) 인 변곡점 근처에서 방향을 잘 못 찾음.

Pure Newton’s method는 아래의 수식에서 \(\lambda=1\)인 경우인데, 이러면 잘 수렴하지 않는다고 합니다.

그래서 \(\lambda\)를 search하는 과정을 가져야 하는데, 이를 Line Search라고 합니다. 이는 Newton’s Method나 Gradient Descent에 모두 사용할 수 있습니다.

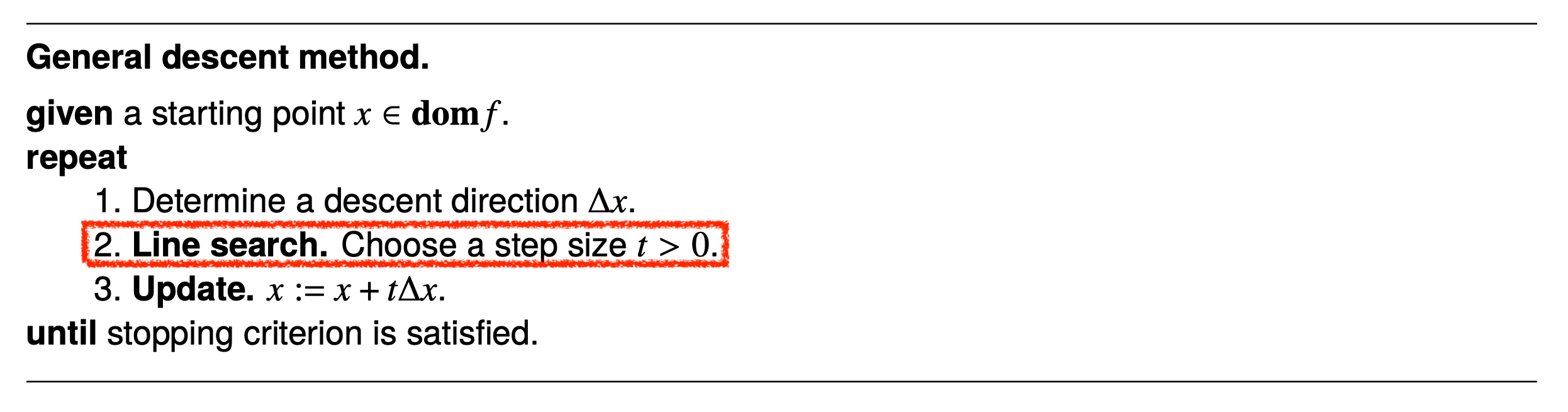Fig. Vanilla Gradient Descent는 step size가 고정이다.

Fig. Gradient Descent에 Line Search를 결합하면 매 순간 step size를 계산해야 한다.

Line search 의 종류중에는 Exact Line Search와 Backtracking Line Search가 유명한데, line Search까지 cover하기에는 classification이라는 주제를 너무 벗어나는 것 같아 개념만 소개해드리는 선에서 끝내려고 합니다. Line search는 간단하게 말하면 step size \(\lambda\)를 \(\lambda, \frac{\lambda}{2}, \frac{\lambda}{4}, \cdots\) 처럼 여러 개를 해보고 이 중에서 가장 cost가 많이 줄어드는 쪽으로 한 step가보는 식으로 단순하게 step size를 정하는 방법이라고 생각하시면 됩니다. Newton’s method가 이미 2차 미분항으로 step size를 구했지만 더 optimal한 step size를 구하기 위한 절차라고 생각하시면 될 것 같습니다. 더 내용이 궁금하신 분들은 Reference를 참고해주시길 바랍니다.

Fig. Various Types of Line Search

Optimization Result

마지막으로 optimization step을 거치면서 어떻게 Logistic Regression의 decision boundary가 변하는지 보도록 합시다. Logistic Regression의 likelihood surface와 log likelihood의 surface가 (a)와 (b)에 나타나 있습니다. optimization step을 1->2->3 거칠수록 (c)의 decision boundary도 점점 좋아지는 걸 볼 수 있습니다.

Loss function에 대한 1, 2차 미분항은 다음과 같으니 참고하시길 바랍니다.

Intuitive Things

Logistic Regression의 solution을 구했다고 생각해봅시다. 이 solution은 decision boundary를 나타낸다고 말씀드렸는데 \(\phi\) 아래와 같이 cyan색의 직선으로 표현되는걸 알 수 있습니다. 이 직선의 출처는 Logistic Regression의 결과물의 확률이 0.5인 지점을 의미합니다. 왜냐하면 class 1에 대한 확률이 0.5를 넘어가면 class 1, 못넘어가면 class 2로 분류하는 것이 일반적이기 때문이죠.

Decision boundary는 사실 3D로 보면 더 직관적으로 이해하기 쉽습니다. Logistic Regression이 학습되는 과정을 animation으로 재생하면 아래와 같은데, input data 2차원에 class 1로 분류될 확률을 1차원 추가 표현을 한 것입니다. 우리가 modeling 하는 것은 sigmoid로 표현되는 한 class의 확률이기 때문에 실제로는 이런 식으로 decision boundary가 학습되는 것이죠. 어디서 직선이 갑자기 튀어나온것이 아닙니다.

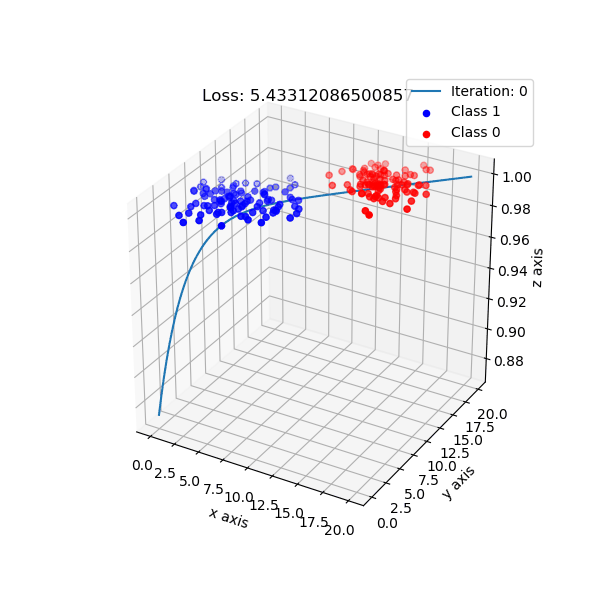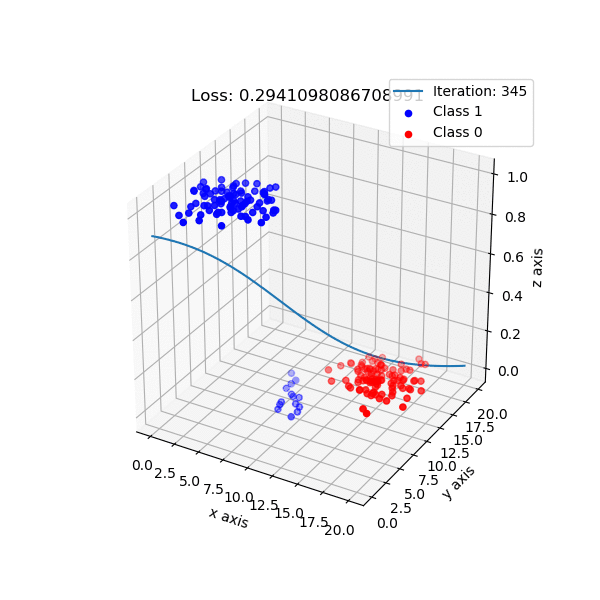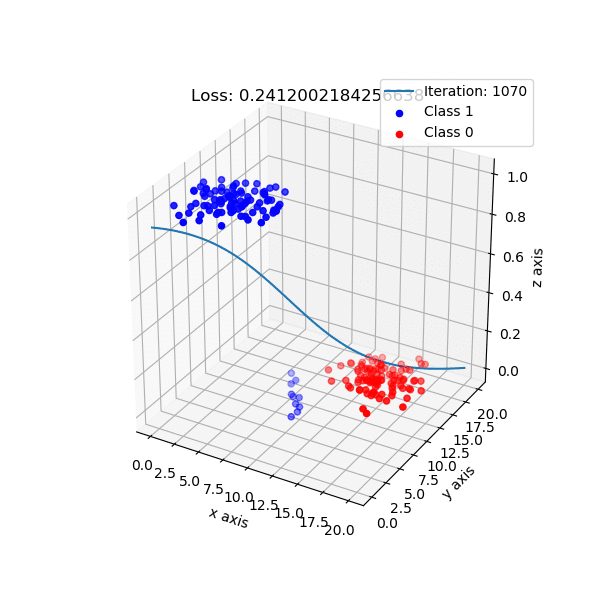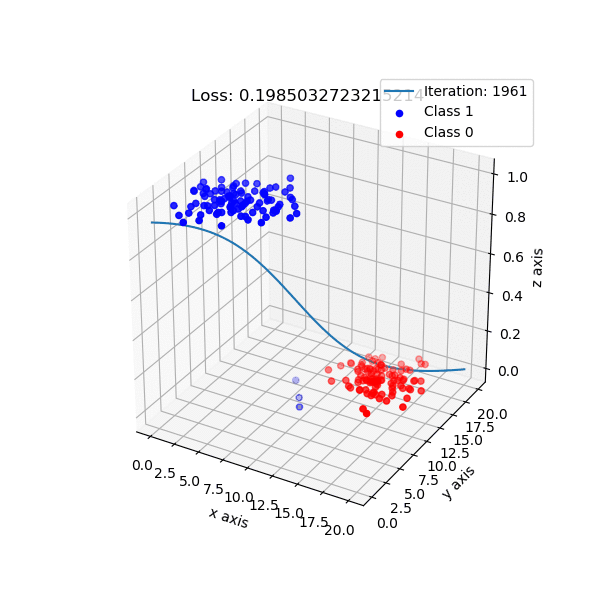Fig. Source From link

Multi Class Classification

한편 우리가 실제 real-world 에서 많이 사용한는 것은 어떤 image가 사람의 얼굴인지? 아닌지? 하는 Binary Classification 같은 것 보다는 사람인지? 사람이면 어떤 사람인지? 아니면 다른 물체인지? 등 2개 이상의 class를 구분하는 다중 분류 (Multi Class Classification)일겁니다. 여러개의 class를 분류하는 문제의 경우 이진 class를 분류하는 경우와 거의 같지만 출력값을 Bernoulli 분포가 아닌 Categorical distribution로 modeling 하는 부분만 다릅니다.

Categorical distribution의 Likelihood 는 다음과 같이 쓸 수 있는데

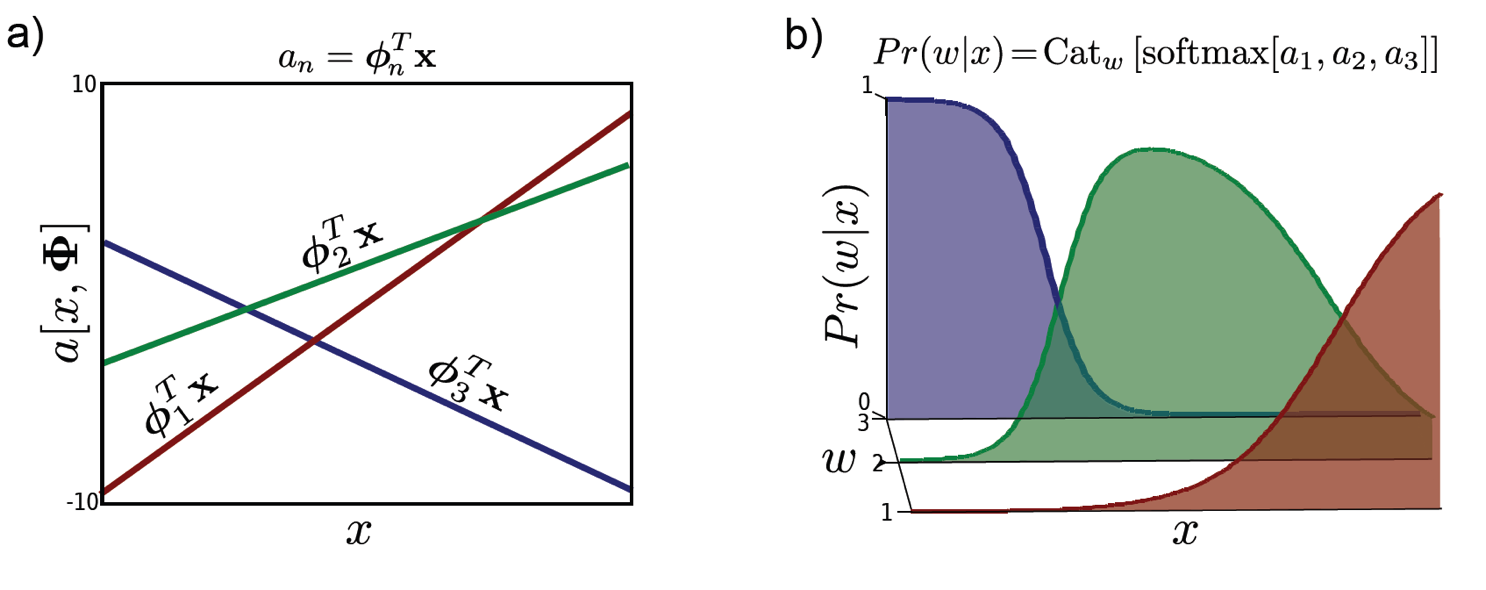
여기서 \(\lambda\)는 전체 합이 합이 1이 되는 각 class들에 대한 확률 값을 나타내는 vector이고 이를 수식으로 나타내면 다음과 같습니다.

확률 분포의 합은 언제나 1이기 때문에 앞선 Bernoulli distribution으로 modeling할 때 sigmoid 함수가 하나의 입력값을 0~1 사이의 값으로 mapping 해주어 두 class로 분류될 확률의 합이 1이 되게 한 것처럼 장치를 해 준 겁니다. 3개 class가 있는 경우를 예로 들면 아래와 같이 수식을 적을 수 있겠습니다.

우리가 추정하고자 하는 parameter는 n개의 vector들 \(\theta_n\) 입니다.

마찬가지로 이제 negative log likelihood를 구한 뒤에 optimization step을 여러 번 거치면 각각의 class에 대한 개별적인 decision boundary를 구할 수 있게 됩니다.

Modeling Categorical Distribution over Model Output VS Cross Entropy Loss

아마 DL로 ML에 입문하신 분들은 classification 문제를 풀기 위해서는 Cross Entropy (CE) Loss 가 사용된다는것에 익숙하실 겁니다. 그런데 사실 CE Loss는 이번 post에서 설명한 Bernoulli distribution 혹은 Categorical distribution을 target distribution이라고 정의하고 NLL을 취한 것과 정확하게 동치입니다.

그러니까 우리가 실제로 하고 있었던 것은 probabilistic modeling 이었던 겁니다.

Another Perspective of Classification

Classification 문제를 풀면 우리는 decision boundary를 얻을 수 있다고 했습니다. 이는 또다른 방식으로도 해석할 수 있는데, 우리가 얻는 것은 각 class를 대표하는 class vector라는 겁니다. 그니까 우리는 학습의 결과물로 class vector가 나오고 input data를 이 class vector와 내적해서 vector간 similarity가 가장 높은 것으로 input이미지를 분류한다고 생각할 수 있는겁니다.

아래의 예시에서 우리는 개, 고양이, 배 … 등 다양한 class의 이미지가 포함된 데이터셋을 분류하는 task인 다중 분류 문제를 풀고 싶습니다. Model은 이미지 분류에서 유명한 DL model인 ResNet과 classifier를 결합해만든 image classifer입니다.

• Input image 수 : \(B\)
  
• Width of input image : \(W\)
  
• Height of input image : \(H\)
  
• ResNet이라는 feature extractor를 통과한 encoding vector의 차원 : \(Z\)
  
• Class 갯수: \(C\)

Input이 \(\mathbb{R}^{B \times W \times H \times 1}\)의 4차원 Tensor라고 칩시다.

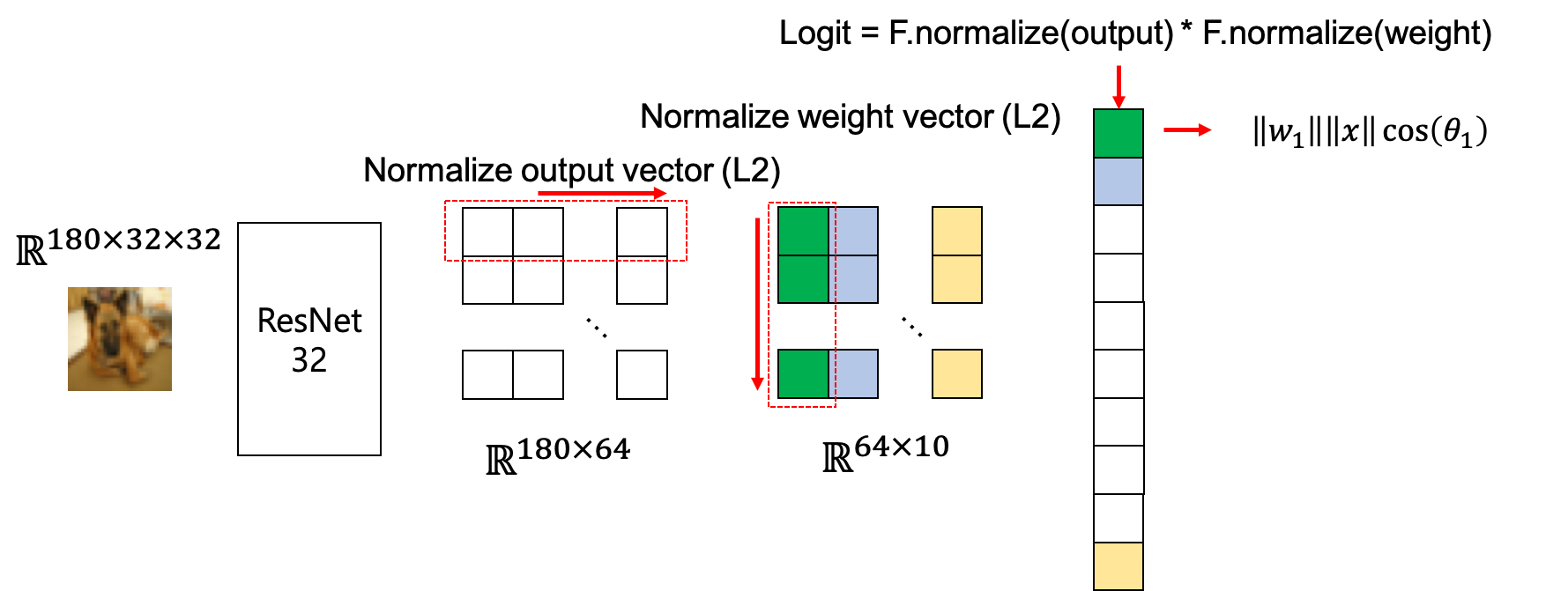
Image가 model에 들어가 feature extraction 단계를 거치면 마지막에 \(\mathbb{R}^{B \times Z}\) 형태가 되고, 최종적으로 feature를 classifier에 넣는데, classifier는 \(\mathbb{R}^{Z \times C}\)라는 weight matrix를 가지고 있고 이를 feature와 행렬 곱 (matrix multiplication)을 해줍니다. 이 classifier의 weight matrix는 다시 생각해보면 \(\mathbb{R}^Z\)차원의 class vector가 \(C\)개 있는 것과 다름 없습니다. 그러니까 실제로 classifer가 하는 일은 주어진 feature를 각 class를 대표하는 vector들과 일일이 대조해보고 어떤 class에 가까운지 대보는 것과 다름이 없습니다.

수식으로 생각해봅시다. Image data 1개에 대해서 CE Loss는 아래와 같았습니다.

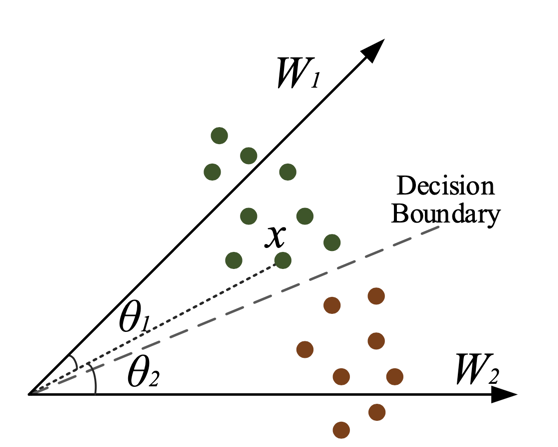
여기서 \(t_i\)는 input image에 대한 정답 (true) label 입니다. CE Loss를 class vector들과의 유사도 계산, 즉 내적 (inner product)이라고 말씀드렸는데, 실제로 CE Loss를 아래처럼 내적으로 표현해도 아무런 차이가 없습니다.

이렇게 classification을 class vector들과의 내적으로 생각하게 되면 \(\cos{\theta}\)에 변형을 주어 class를 구분짓는 decision boundary를 조정할 수 있다는 걸 알게되고, 이를 loss에 반영하여 학습을 하여 data imbalance상황을 타개한다거나 할 수도 있습니다.

• Large Margine Loss
• Additive Margin Softmax for Face Verification
• Label-Distribution-Aware Margin Loss

Large Margine Loss에서는 원래의 CE Loss수식을

아래처럼 변형해서 학습하게 됩니다.

그 결과 decisoun boundary가 변하게 되는데, 이는 dataset 규모가 작고 불균형 (imbalance) 해서 (특히 어느 class가 특히 적음) decisoun boudary를 그릴 때 "아 이 class는 데이터가 적으니까 좀 더 있다는 가정하에 margin을 좀 남겨두자"라는 의도를 반영해서 학습이 된 결과입니다.

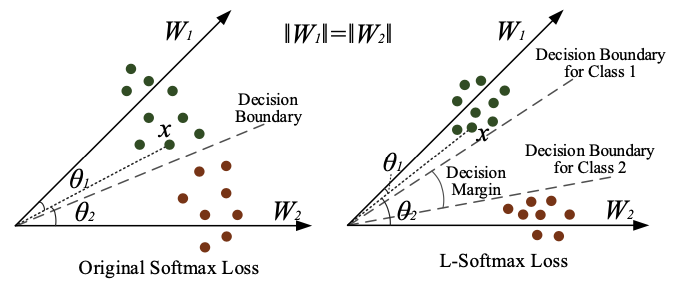Fig. Source From Large Margine Loss

그 다음 예시는 Label-Distribution-Aware Margin (LDAM) Loss 인데, 이것도 마찬가지로 CE Loss에 class 개수 \(n_j\)의 역수를 인자로 추가해 (즉 개수가 적을수록 margin을 더 갖게 됨), class가 적은 쪽에는 decision boundary를 널널하게 형성되게 하는겁니다. 왜냐하면 class가 적기 때문에 "아 별로 없는 이 data근처에 비슷한 data들이 더 많이 포진해 있겠지? 고려해서 boundary를 치자"라는 의도를 model이 주입받게 되기 때문입니다.

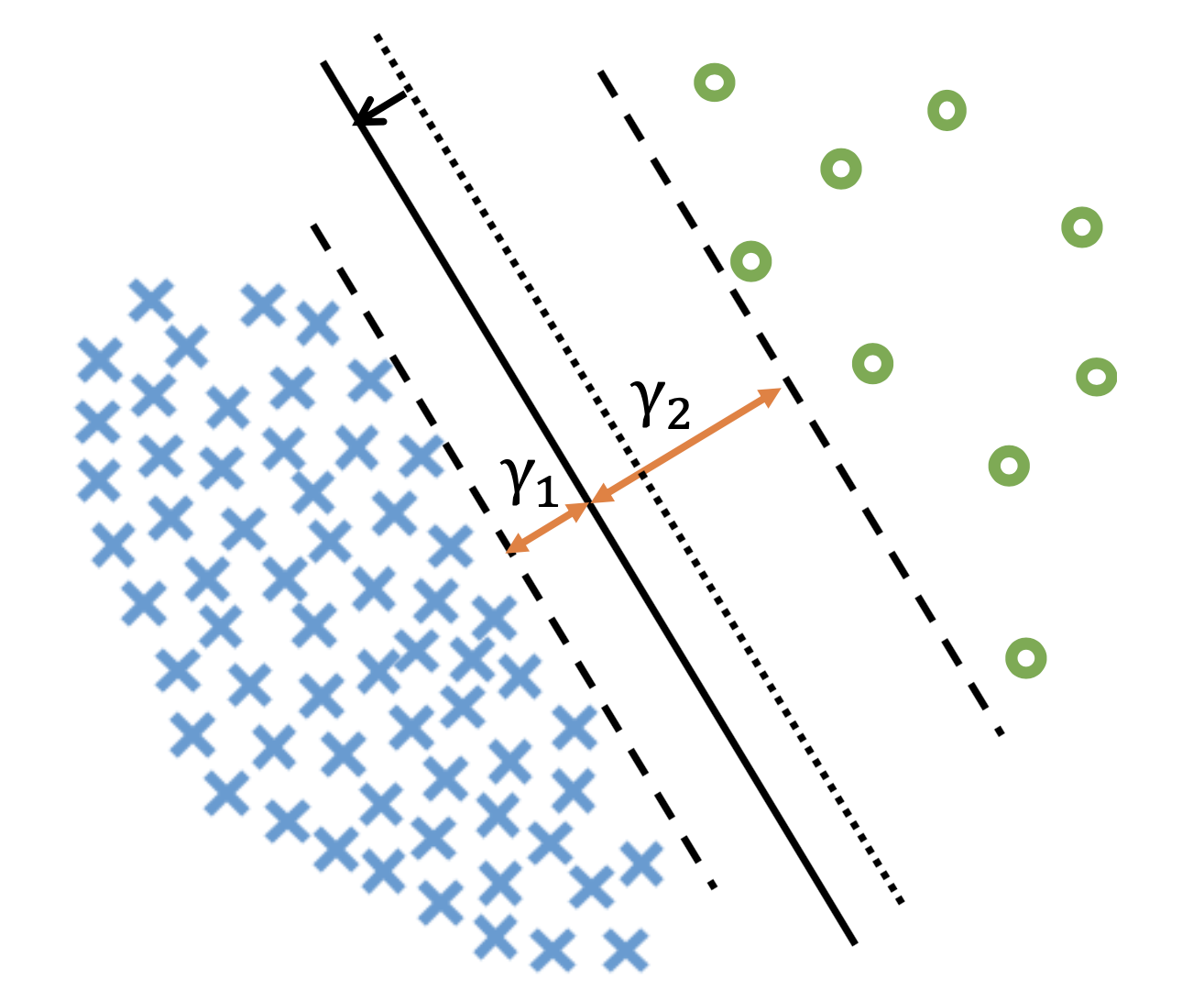Fig. Source From LDAM Loss

이런 식으로 classifier 를 해석하는 것도 algorithm을 연구하는데 도움이 될 수 있습니다.

References

• Books
  • Prince, Simon JD. Computer vision: models, learning, and inference. Cambridge University Press, 2012.
    • Lecture_Slide_09_Classification
  • Bishop, Christopher M. Pattern recognition and machine learning. springer, 2006.
• Blog Posts and Others
  • Logistic Regression
    • Solving Logistic Regression with Newton’s Method
    • Lecture 3: Logistic Regression (Draft: version 0.8.7) from Hyeong In Choi
  • Optimization
    • Taylor Series approximation, newton’s method and optimization
    • Are line search methods used in deep learning? Why not?
    • 최적화 기법의 직관적 이해
    • When is logistic regression solved in closed form?
    • The Gradient: A Visual Descent
    • 6.4 Gradient descent
    • 4.3 Newton’s Method
    • jermwatt/machine_learning_refined/notes/4_Second_order_methods
• Lecture Slides and Videos
  • Optimization
    • CS 182: Lecture 4, Optimization
      • Lecture Slide
    • CMU Convex Optimization, Fall 2019 from Geoff Gordon and Ryan Tibshirani
      • Gradient descent
      • Newton’s method
      • Gradient descent revisited
    • Convex Optimization from Stephen Boyd and Lieven Vandenberghe