MLE & Bayesian Series (1/3) - Maximum Likelihood Estimation (MLE)
19 Jan 2021- MLE & Bayesian Series (1/3) - Maximum Likelihood Estimation (MLE)
- MLE & Bayesian Series (2/3) - Maximum A Posteriori (MAP)
- MLE & Bayesian Series (3/3) - Bayesian Approach
Machine Learning (ML), Deep Learning (DL) 을 제대로 공부하게 되면 Maximum Likelihood Estimation (MLE), Maximum A Posterior (MAP), Bayesian Approach 에 대해 들어보게 될 것이다.
특히 대부분의 DL algorithm들은 이 MLE 문제를 푸는 것이기 때문에 Likelihood가 무엇인지 이해하는 것이 매우 중요하다.
< 목차 >
What is Maximum Likelihood Estimation (MLE) ?
In statistics, the likelihood function (often simply called the likelihood)
measures the goodness of fit of a statistical model to a sample of data
for given values of the unknown parameters.
(Source from link)
통계학적으로 likelihood란 어떠한 통계적 모형(분포)가 주어진 샘플 data에 대해 얼마나 잘 맞는가? 를 나타내는 것을 의미한다. Maximum Likelihood Estimation(MLE)란 말 그대로 어떤 parameter가 likelihood를 최대화 하는지 찾아내는 (추정하는) 걸 말한다. 즉 주어진 data sample들을 가장 잘 설명하는 통계적 모형의 parameter를 찾는 것이다.
Maximum Likelihood Estimation (MLE)
ML을 처음접하시거나 ML을 접했더라도 확률적 관점 (probabilistic perspective)에서 생각해보지 않은 분들은 likelihood가 무엇인지 감이 오지 않을 수 있다. 그래서 먼저 아래 figure를 통해 likelihood에 대해서 알아보자.
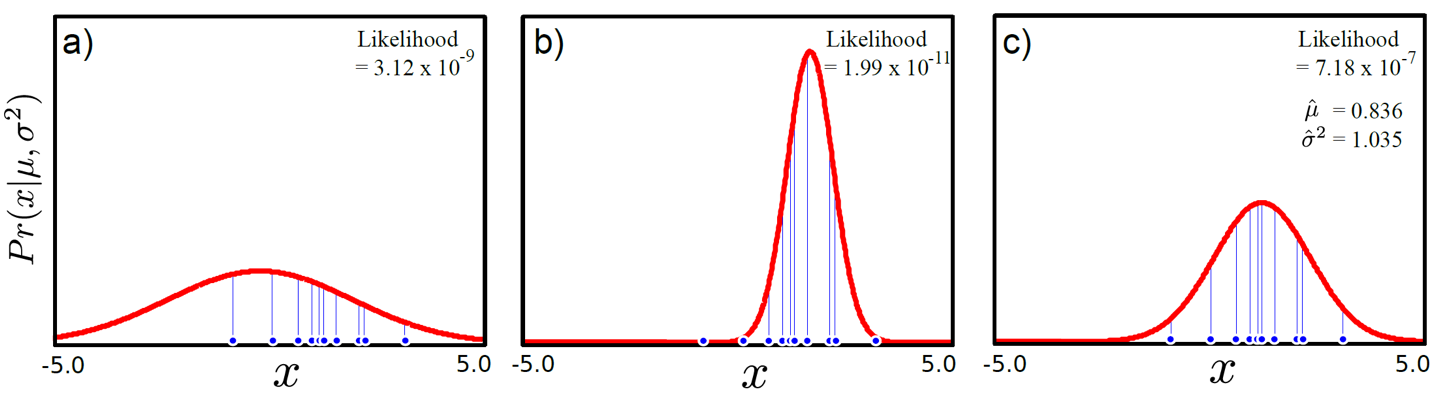 Fig. 위의 그림들 (분포들) 중 data를 가장 잘 설명하는 분포는 과연 뭘까?
Fig. 위의 그림들 (분포들) 중 data를 가장 잘 설명하는 분포는 과연 뭘까?
위의 그림에 나와있는 likelihood 값은 어떤 data가 존재할 때 (지금은 1차원 data가 x축 상에 뿌려졌 있음), 이에 대응하는 확률 분포(지금은 Gaussian distribution)의 확률 y값을 전부 곱한 값을 나타낸다. 각 a,b,c 그림은 Gaussian distribution의 평균,분산 값이 어떠냐에 따라서 확률분포가 달라진다는 걸 보여주며 그때 마다의 likelihood 값을 의미한다.
최대 가능도 측정 (Maximim likelihood estimation, MLE)는 바로 data에 대응하는 확률 값들을 가장 높게 만들어주는,
즉 data x의 분포를 가장 잘 표현하는, 그러니까 가장 그럴듯한(likely) 확률 분포 (probability distribution)의 parameter(여기서는 평균,분산)를 학습 (training)을 통해 찾아내는 것이라고 할 수 있다.
여기서는 가장 likelihood가 높은 것이 c가 될 것인데 이 때의 Gaussian distribution parameter는 mean=0.836, variance=1.035가 된다.
우리가 추정하고자 하는 parameter가 Gaussian distribution mean, variance이기 두 개이기 때문에 이 값이 만들어내는 likelihood값을 2차원 평면에 다음과 같이 나타낼 수 있다.
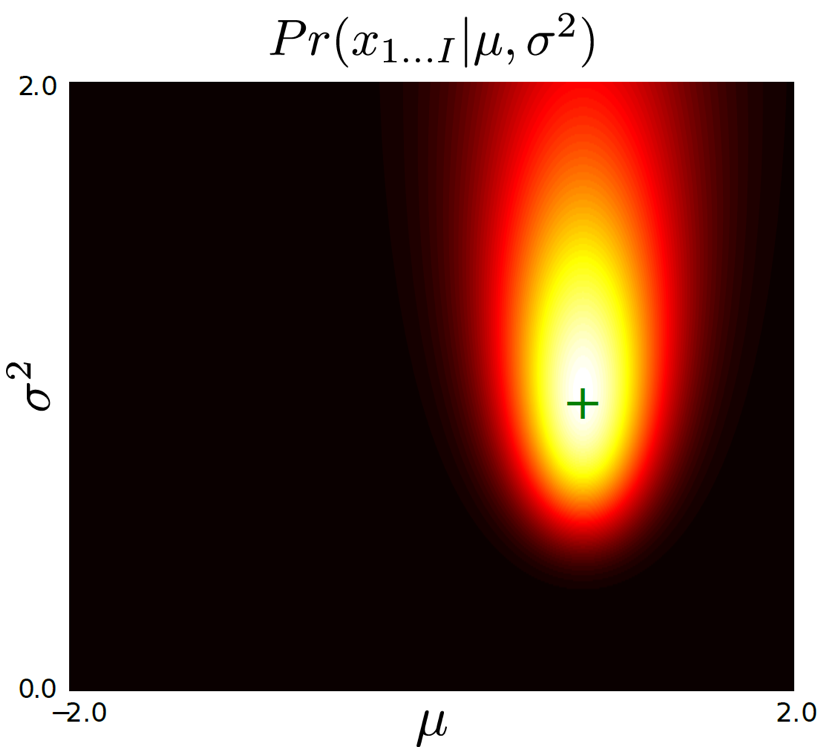 Fig. data를 표현하는 분포는 Gaussian distribution거라고 가정했으므로, likelihood는 \(\sigma\),\(\mu\)로 이루어진 2차원이다.
Fig. data를 표현하는 분포는 Gaussian distribution거라고 가정했으므로, likelihood는 \(\sigma\),\(\mu\)로 이루어진 2차원이다.
위의 그림에서 peak 값을 나타내는 parameter를 찾으면 그게 바로 data를 가장 잘 설명하는 지점이 될것이다.
그리고 이 지점이 바로 likelihood가 가장 높은 지점이 된다.
이를 찾는 과정이 바로 최대 우도 측정 (Maximum Likelihood Estimation, MLE)이라고 한다.
어떻게 그 parameter 한 점을 찾느냐 (point estimation)? 크게 두 가지 방법이 있을 수 있는데, 하나는 likelihood를 나타내는 목적 식 (objective function)을 정의하고 이를 미분해서 0인 지점을 찾아 극소값 (local minimum)을 찾는 것이다. 이를 closed-form solution 혹은 analytic solution을 찾는다고 한다. 하지만 DL을 하면 이 likelihood와 input data간의 mapping function이 매우 복잡한 Neural Network (NN)으로 구성 될 수도 있는데, 이런 경우 미분을 해서 한번에 solution을 찾을 수는 없다. 이럴 때는 Gradient descent 등의 반복적 비선형 최적화 (Iterative Non-Linear Optimization)을 통해 likelihood가 max가 되는 지점을 찾아야 하는데, 이를 Numerical Solution이라고 한다.
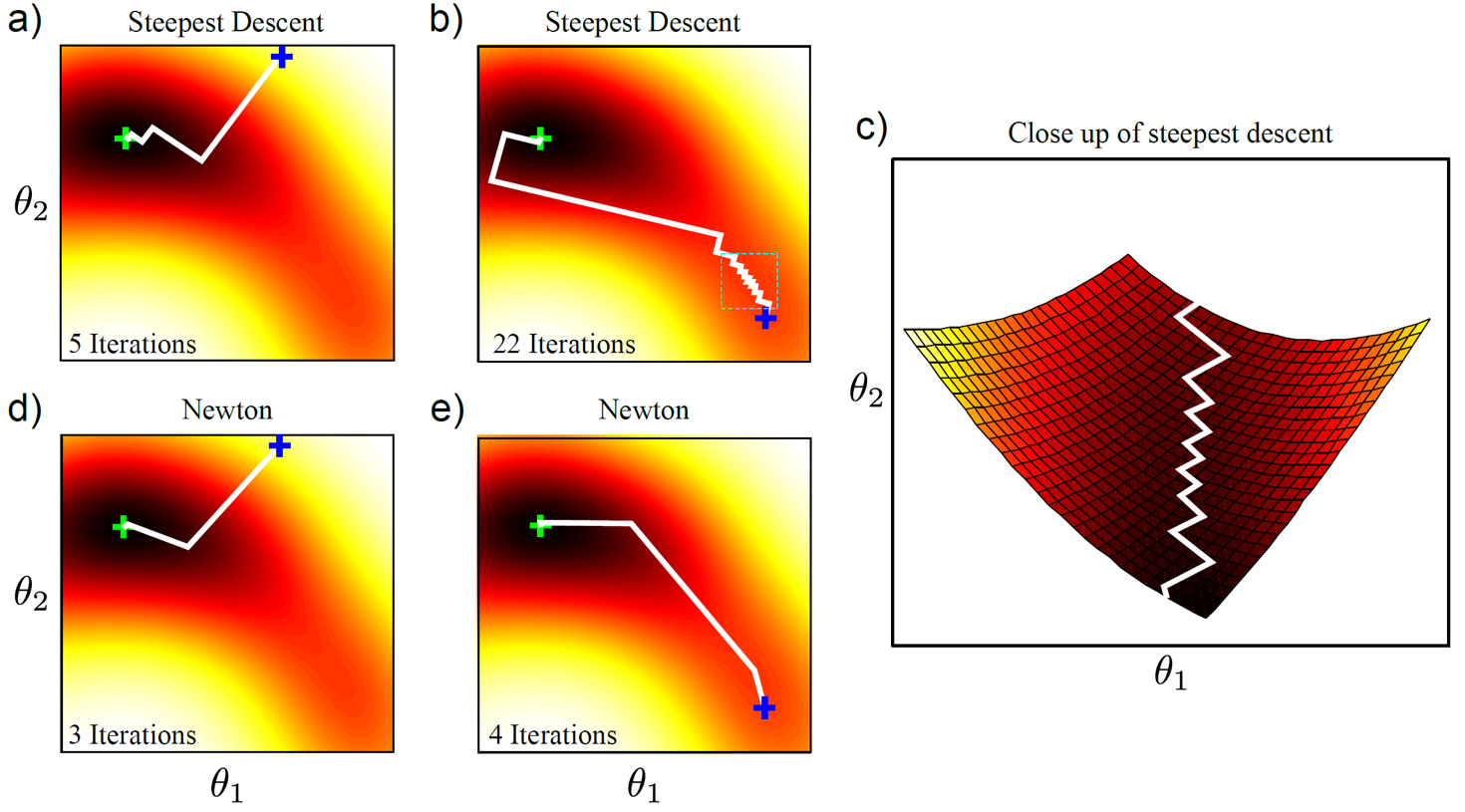 Fig. 최적화를 통해 점진적으로 최적의 parameter를 찾아낼 수도 있다.
Fig. 최적화를 통해 점진적으로 최적의 parameter를 찾아낼 수도 있다.
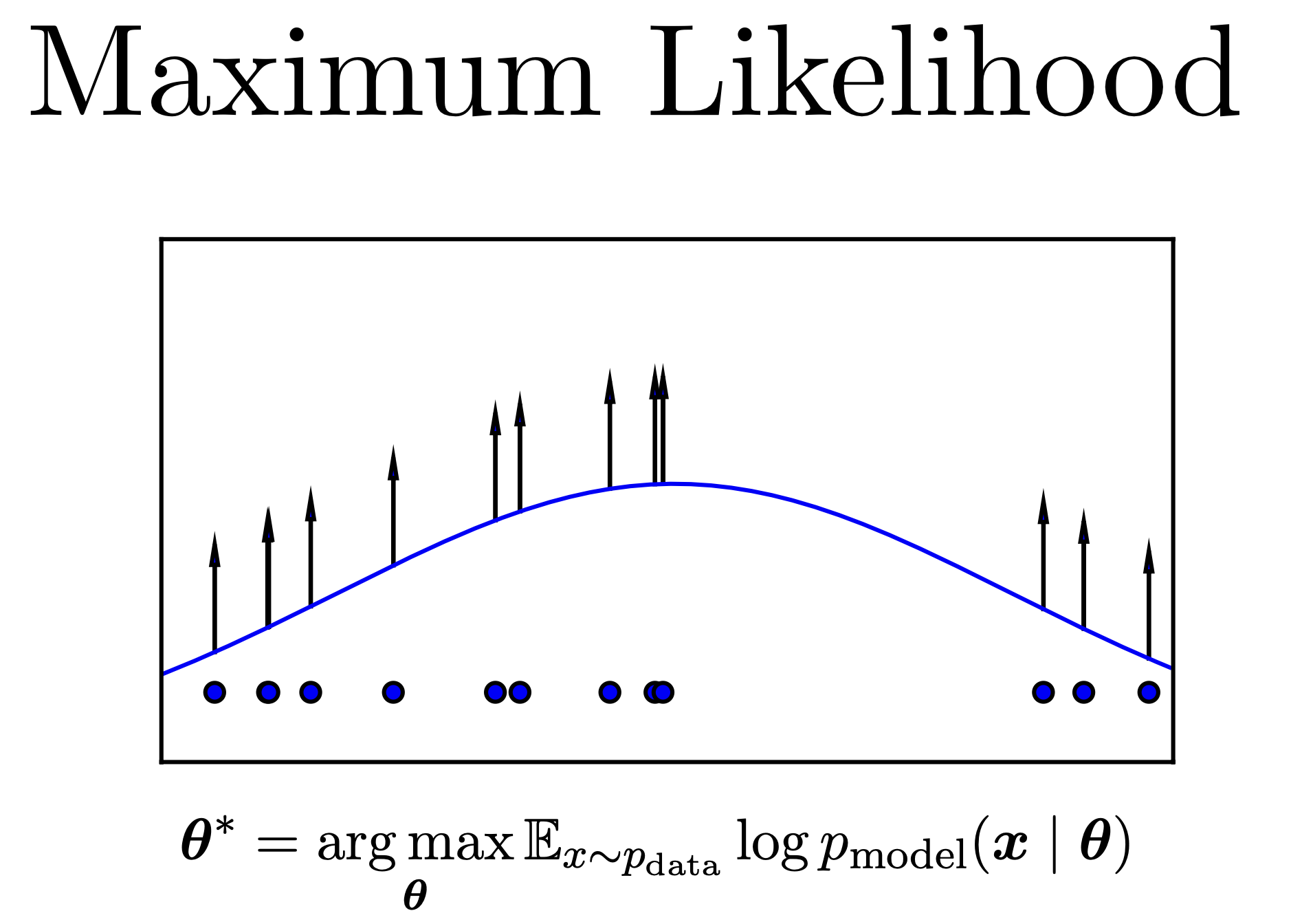 Fig. 점점 초기의 분포는 Likelihood가 최대가 되는 분포로 변하게 된다.
Fig. 점점 초기의 분포는 Likelihood가 최대가 되는 분포로 변하게 된다.
MLE in formula
이번에는 MLE를 수식으로 표현해 보자.
먼저 MLE를 하려면 우리가 traget 하는 data distribution이 어떤 모양인지를 정한다.
앞선 예제들 처럼 Gaussian distribution이라고 해보자.
이제 input data와 우리가 추정하고자 하는 target distribution과의 목적 함수 (Objective Function)라는 걸 정의해야 한다.
우리가 추정하고자 하는 것은 전체 data sample에 대해서 가장 잘 맞는 distribution 이므로 모든 data를 고려해야 하고, 이는 결합 분포 (joint distribution)으로 나타난다.
그런데 각각의 data point (sample)들이 독립이라고 가정하면 (i.i.d) 위의 수식은 아래처럼 모든 data point들의 확률의 곱으로 다시 쓸 수 있다.
\[\hat{\Theta}=\arg \max_\theta[\prod_{i=1}^{I}Pr(x_{i}\mid\theta)]\]우리는 Gaussian distribution 을 찾고 싶은 것이므로, 찾아아할 parameter, \(\Theta\)는 mean, variance가 된다.
\[Pr(x_{1...I}\mid\theta) = Pr(x_{1...I}\mid\mu,\sigma^2)\] \[\hat{\mu},\hat{\sigma^2}=\arg \max_{\mu, \sigma^2}[\prod_{i=1}^{I}Pr(x_{i}\mid\mu,\sigma^2)]\]위의 수식에서 \(\arg \max\)란 가능한 모든 parameter에서 주어진 function을 최대화 하는 parameter를 찾는다는 의미이다. 다시 Gaussian distribution을 풀어서 전개하면 다음과 같고
\[Pr(x\mid\mu,\sigma^2)=Norm_x[\mu,\sigma^2]=\frac{1}{\sqrt{2\pi\sigma^2}}exp[-0.5\frac{(x-\mu)^2}{\sigma^2}]\]이를 모든 data로 확장하면 다음과 같은 수식을 얻을 수 있다.
\[Pr(x_{1...I}\mid\theta) = \frac{1}{(2\pi\sigma^2)^{I/2}}exp[-0.5\sum_{i=1}^{I}\frac{(x_i-\mu)^2}{\sigma^2}]\]마지막으로 깔끔하게 정리하면 아래의 식을 얻을 수 있다.
\[\hat{\mu},\hat{\sigma^2}=\arg \max_{\mu,\sigma^2}[\prod_{i=1}^{I}Pr(x_{i}\mid\mu,\sigma^2)]\] \[\hat{\mu},\hat{\sigma^2}=\arg \max_{\mu,\sigma^2}[\prod_{i=1}^{I}\frac{1}{(2\pi\sigma^2)^{I/2}}exp[-0.5\sum_{i=1}^{I}\frac{(x_i-\mu)^2}{\sigma^2}]]\]How Can We Estimate Optimal Parameter Maximizing Likelihood?
우리는 위의 objective function을 최대화 하는 Gaussian distribution의 parameter인 mean, variance를 찾으면 된다. 어떻게 찾아야 하띾?
우선 계산을 쉽게 하기 위해서 log를 취한다. 왜냐하면 log가 단조 증가 함수이기 때문에 log를 취한 식을 maximize하는것이 원래의 수식을 maximize 하는 것과 같고, log를 취하는 것이 계산상 편의성이 높기 때문이다.
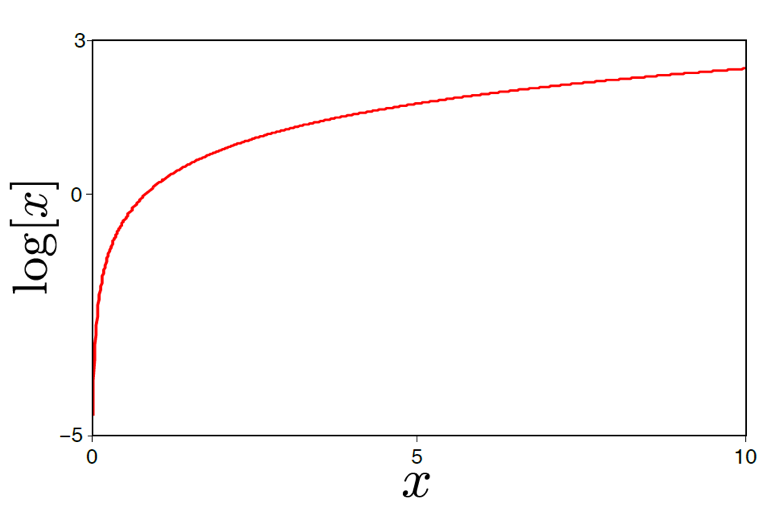 Fig. Logarithm을 취해도 문제를 푸는데 문제가 없다.
Fig. Logarithm을 취해도 문제를 푸는데 문제가 없다.
log를 씌우면 저희가 최대화 하고자 하는 수식은 다음과 같이 전개된다.
\[\hat{\mu},\hat{\sigma^2}=\arg \max_{\mu,\sigma^2}[\sum_{i=1}^{I} \log [Norm_{x_i}[\mu,\sigma^2]]]\] \[\hat{\mu},\hat{\sigma^2}=\arg \max_{\mu,\sigma^2}[ -0.5I \log [2\pi] - 0.5I \log \sigma^2 - 0.5 \sum_{i=1}^{I}\frac{(x_i-\mu)^2}{\sigma^2} ]\]위의 식에서 우리가 구하고자 하는 parameter와 관련 없는 term을 제외하고 나머지를 미분해서 0인 지점을 찾는다.
그러면 우리는 likelihood를 maximize하는 parameter를 구할 수 있게 된다.
우리는 현재 두 가지의 parameter를 가지고 있으므로 둘 다 계산해야 하기 때문에 한번은 mean에 대해 미분하고 한번은 variance에 대해 미분을 해서 둘 다 구하면 된다. 이를 수식으로 나타내면 아래처럼 나타낼 수 있게 된다.
\[\frac{\partial L}{\partial \mu} = \sum_{i=1}^{I}\frac{x_i-\mu}{\sigma^2}\] \[\frac{\sum_{i=1}^{I}x_i}{\sigma^2}-\frac{I\mu}{\sigma^2}=0\] \[\hat{\mu}=\frac{\sum_{i=1}^{I}x_i}{I}\]variance에 대해서 유사하게 구하면 다음과 같다.
\[\hat{\sigma^2}=\frac{\sum_{i=1}^{I}(x_i-\hat{\mu})^2}{I}\]하지만 이것은 앞으로 우리가 배울 선형 회귀 (Linear regression)까지만 적용되는 방법이다. 말씀드린 것처럼 대부분의 DL algorithm들은 이런식으로 해를 구할 수 없고, optimization 기법을 사용해야 합니다만 이는 현재 post의 coverage를 넘어가도록 하자.
Solution for the Normal Distribution
사실 위에서 유도한 식을 잘 정리하면 이것이 ML, DL을 이미 접한 사람들에게는 이미 익숙할 Least Squares Solution (혹은 mean square error, MSE)과 유사하다는 걸 알 수 있다.
즉 data를 설명하는 distribution이 Gaussian distribution이라고 정의를 하고 MLE로 parameter를 찾는 과정은 MSE loss를 objective function으로 쓰는 것과 같다는 것이다. 이는 나중에 linear regression을 다룰 때 다시 알아보도록 하자.
Problems of MLE
MLE 방법은 문제없는 algorithm처럼 보이지만 몇 가지 단점이 존재한다. 아래의 figure을 예시로 들어 설명해 보도록 하자.
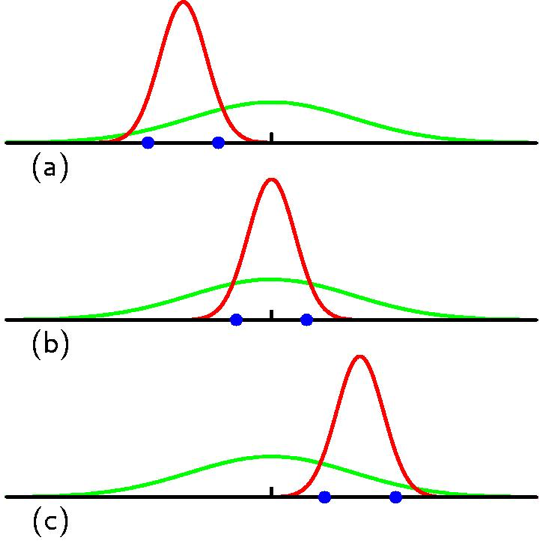 Fig. 실제 분포인 녹색 분포에서 샘플링 된 2개의 data 포인트를 기준으로 MLE를 할 경우, 머신러닝의 궁극적인 목적인 실제 분포를 찾는 것과는 다른 솔루션을 얻을 수 밖에 없다. (data가 좋지않으면, 적으면)
Fig. 실제 분포인 녹색 분포에서 샘플링 된 2개의 data 포인트를 기준으로 MLE를 할 경우, 머신러닝의 궁극적인 목적인 실제 분포를 찾는 것과는 다른 솔루션을 얻을 수 밖에 없다. (data가 좋지않으면, 적으면)
녹색의 distribution에서 data를 무작위로 두 개 sampling했다고 생각해 보자.
data는 (a)(b)(c) 처럼 수평선 위에 뿌려질 수 있다 (1차원 data).
우리가 추정하고자 하는 분포가 Gaussian distribution고 생각해보자.
MLE로 가장 likelihood 값이 높은 경우의 parameter를 구하고 그 확률분포를 그린게 빨간색 선으로 표현된 분포가 된다.
그런데 figure에서 알 수 있듯이 MLE는 data가 어떻게 sampling되느냐에 따라서 매우 다른 결과가 나타나는걸 나올 수 있다는 문제가 존재한다. 실제로 (b)를 제외하고는 녹색 선의 진짜 분포와는 굉장히 다르게 생겼다는 걸 알 수 있다. 즉 우리는 주어진 data들로 녹색 선과 유사한 분포를 얻고싶은건데 data가 희소하거나 질이 나쁘다면 그게 안된다는 것이다.
이런 MLE의 단점을 보완하기 위해서 내가 구하고자하는 확률 분포의 parameter들에 대한 사전 분포 (prior distribution)를 정하고 이를 likelihood와 곱한 사후 분포 (posterior)를 추정하는 방법이 있다.
prior란 학습이 실제로 되는 parameter에 대한 사전 지식으로,
“음 mean,variance가 어떤 값을 가질지는 모르겠지만 대충 0~0.5 사이 값이던데?”
라는 선입견 (prior) 정보를 모델에게 주는 것이다.
이럴 경우 data가 적을 때는 prior의 영향력이 커서 추정 값이 너무 편향되지 않게 잡아주고,
data가 많을 경우 likelihood의 영향력이 커지게 되는 효과가 있다.
Posterior distribution 중에서 가장 posterior 값이 큰 parameter 하나만을 선택하는 것이 Maximum A Posteriori (MAP)이고,
모든 parameter들을 고려해서 weighted sum한 결과를 최종 결과로 취하는 것이 Bayesian Approach라고 한다.
Data point 수에 따라 MLE, MAP solution이 어떻게 다른지는 다음과 같다.
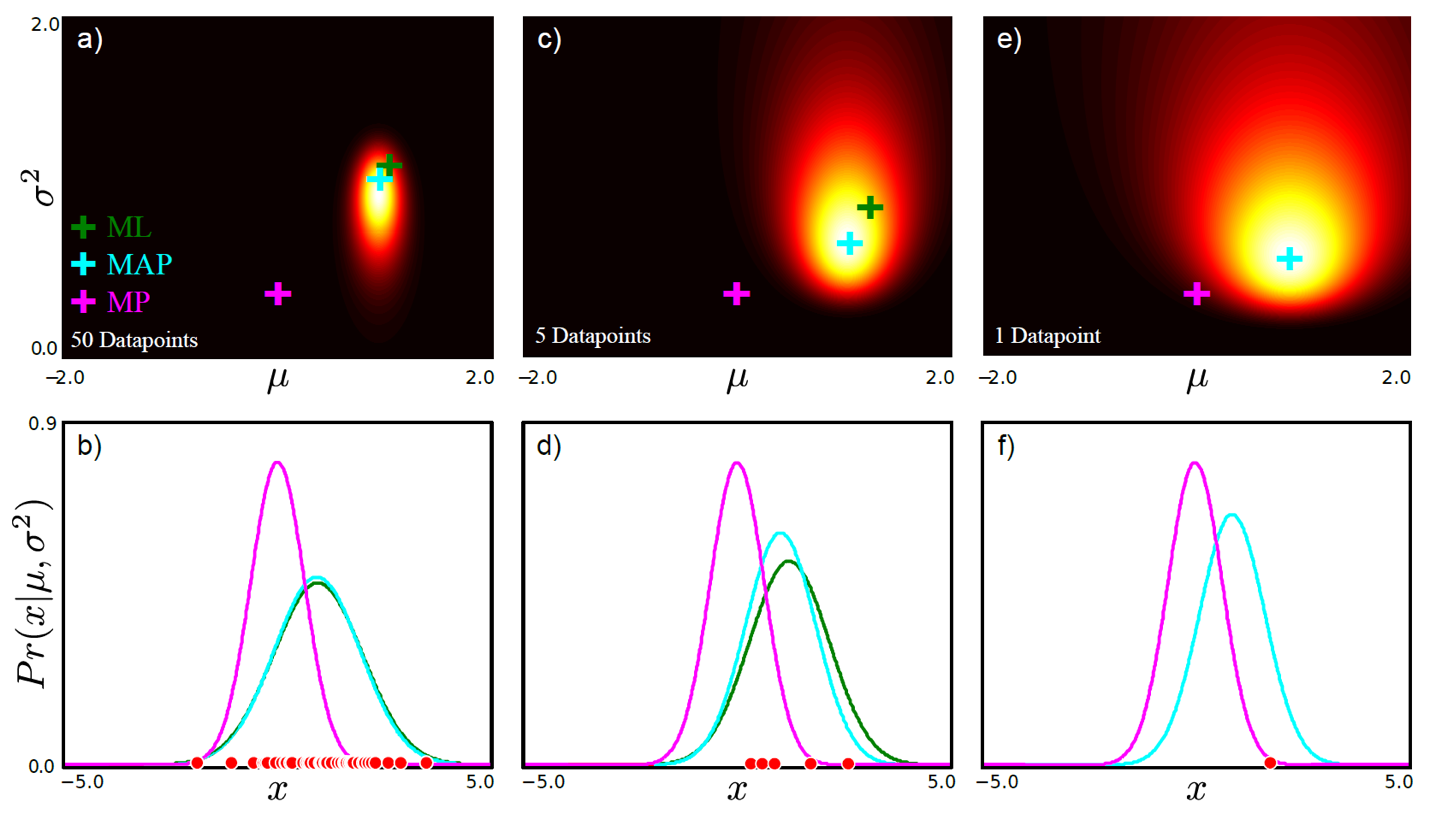 Fig. data 갯수에 따른 MLE와 MAP 방법론의 결과 차이. 그림에서 분홍색 cross가 나타내는 것은 사전 분포로, “mean=0, variance=0 일 확률이 높더라” 라는 정보를 주고 있으며, 이에 영향받은 MAP와 영향을 받지 않는 MLE는 data가 적을때는 값이 차이가 많이 나지만 data가 많을 때는 차이가 별로 없어진다.
Fig. data 갯수에 따른 MLE와 MAP 방법론의 결과 차이. 그림에서 분홍색 cross가 나타내는 것은 사전 분포로, “mean=0, variance=0 일 확률이 높더라” 라는 정보를 주고 있으며, 이에 영향받은 MAP와 영향을 받지 않는 MLE는 data가 적을때는 값이 차이가 많이 나지만 data가 많을 때는 차이가 별로 없어진다.
MAP, Bayesian 각각은 다른 post에서 다루도록 하겠다.