(almost) The Comparison of Positional Embedding Methods

< 목차 >

• Why Another Positional Encoder is needed ?
  • Positional Encoding vs Positional Embedding
  • Sinusoidal Position Encodings is Enough?
    • Relationship between Sinusoidal Embedding Vectors
    • Decomposition of Adding Position Vectors in Self-Attention
    • Similarity between Sinusoidal Embedding Vectors
• Additive Relative Positional Embedding (RPE)
  • Shaw RPE
  • Music-Transformer RPE
  • Transformer-XL RPE
  • RPE in T5
  • Convolutional Positional Embeddings
• Multiplicative RPE
  • PE in Complex Space
  • Rotary Positional Embedding (RoPE)
    • Position Encoded Q, K is just Rotated Q, K
    • Linearized Attention with RoPE
    • Long-term decay of RoPE
• Attention with Linear Biases (ALiBi)
  • Why does it works well?
• Additional
  • Do Transformer Really Need RPE ?
• References

이번 post 에서는 Transformer 의 핵심 module들 중에서 Positional Encoding (PE) metdhos에 대해서 조금 더 자세히 알아보자.

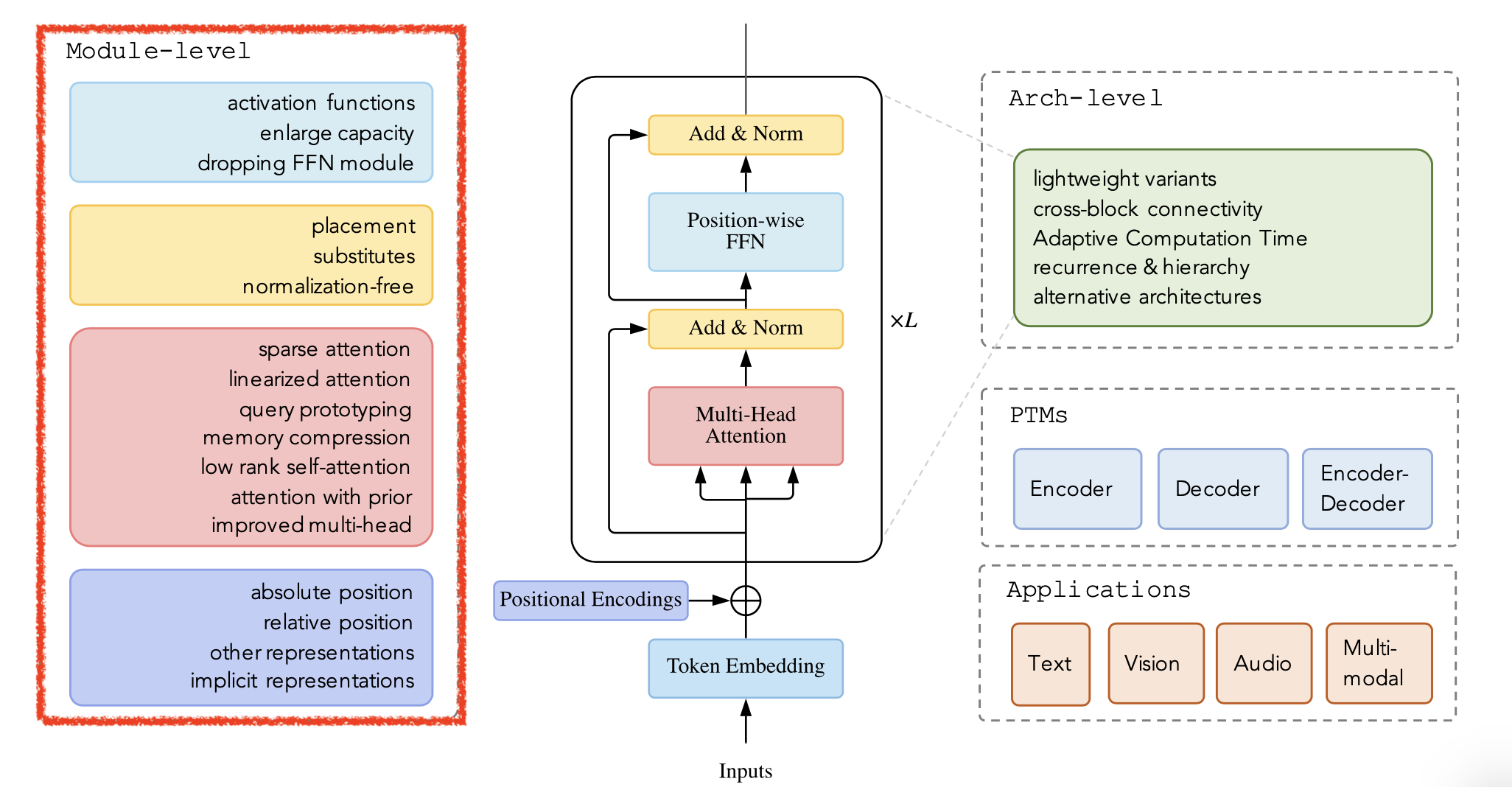Fig. Various Transformer. Module-Level. Source From 2021, A Survey of Transformers

Why Another Positional Encoder is needed ?

Sequence Modeling을 할 때 맥락 (Context) 정보를 잘 녹인 embedding 을 만들기 위해서 한 방향으로 정보를 encoding 하는 Recurrent Neural Network (RNN)이나 Convolutional Neural Network (CNN) 기반의 method들과는 다르게, Transformer based model들은 병렬적으로 모든 token embedding을 한 번에 만들게 된다. Transformer based model들은 이런 특성 때문에 예를 들어 token이 10개가 있으면 순차적으로 hidden state을 propagate하거나 convolving (sliding)하면서 encoding을 만드는 것이 아니기 때문에, 다시 말하면 정해진 방향이 없기 때문에 Positional Information을 주입해주지 않으면 동일한 Token이 어느 위치에 있는지 전혀 구분할 수가 없다고 (Permutation-Invariant) 알려져 있다. 그래서 Token 들에 상대적인 위치 (Relative Position) 정보를 주입하기 위해 Positional Encoding (or Embedding)이 기본적으로 모델에 주입되는데, 기본적으로 Vanilla Transformer 에는 Sin, Cos 함수를 이용한 Trigonometric (Sinusoidal) Positional Encoding 이 사용된다.

하지만 2017년 Transformer가 제안되면서 같이 제안된 Sinusoidal Positional Encoding (PE)는 대부분의 Sequence Modeling Task에서 문제가 있음이 드러났는데, 바로 학습시 본 Sequnece data 의 길이보다 긴 Sequence 를 추론시에 마주치는 경우 성능이 좋지 못하다는 것이다. 이를 해결하기 위해 2022년 지금까지 지속적으로 더 긴 문장에 잘 대응하는 Method 들이 제안되어 왔는데, 그 중 핵심적인 몇가지를 이번 post 에서 알아보도록 하자.

Positional Encoding vs Positional Embedding

본격적으로 알고리즘들을 살펴 보기 전에 얘기 하고 싶은 것이 있다. 나는 PE 관련 paper들을 읽으면서 Positional Encoding 혹은 Embedding 이 혼용되어 좀 헷갈렸는데, Positional Embedding 이란 Discrete Space 에 있는 One-hot Token 을 Continuous Space 로 mapping 시켜주는 Word Embedding 처럼 어떤 mapping function 을 학습하는 layer를 말한다. 하지만 Positional Encoding 는 학습이 되는 Layer가 아니라 사용자가 정의한 함수 (Chosen mathmetical function) 를 의미한다. 둘의 역할은 같지만 Learnable 한가? 의 차이가 있는 것이다. Transformer 의 원 논문인 Attention Is All You Need 에 사용되는 것은 \(sin(\cdot)\), \(cos(\cdot)\) 함수로 이루어진 것으로 학습이 되는것이 아니기 때문에 Positional Encoding 이라고 표기하는 것 같다.

(In Paper)

...
To this end, we add "positional encodings" to the input embeddings
...
positional embedding instead of sinusoids
...

하지만 본 post에서는 Positional Encoding 이나 Embedding 모두 PE로 통일해서 부르도록 하겠다. (틀릴 수도 있으니 정확한 정보가 있다면 알려주면 감사드리겠습니다.)

Sinusoidal Position Encodings is Enough?

기존의 Sinusoidal PE 은 우리가 원하는 Position Embedding Vector 가 예를 들어 768 차원일 때, 768개의 element 를 아래 처럼 다양한 주기의 Sin, Cos 함수로부터 t 번째 시점의 값을 sample 해서 사용했다.

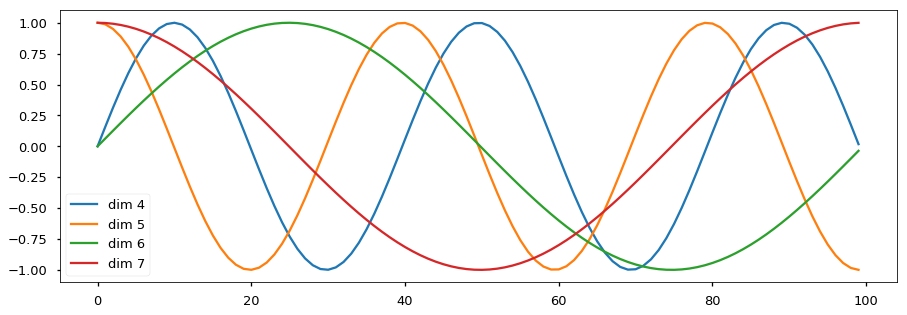
실제 만들어지는 벡터는 수식으로 쓰면 아래와 같다.

예를 들어 Token 개수가 10개일 때 각 row 별로 PE vector 는 아래와 같은 pattern을 나타내게 된다.

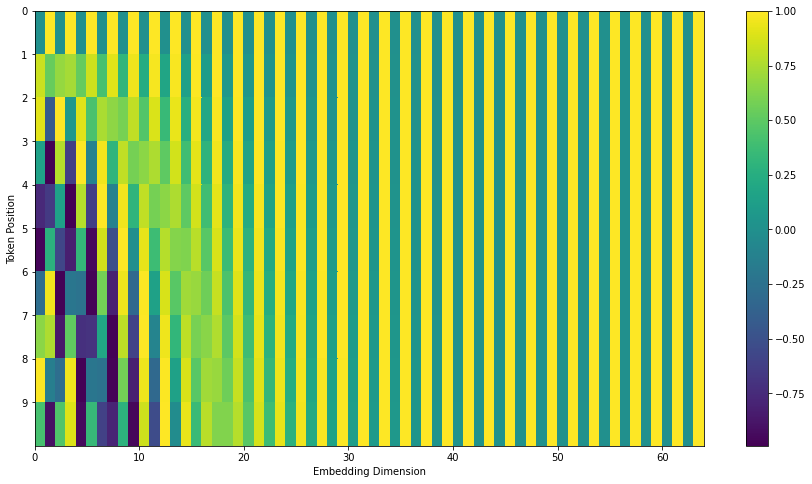Fig. token 10 개의 Position Vector 들 (row) 이 전부 다른걸 알 수 있다. Source From The Illustrated Transformer

이를 엄청나게 확대해서 만약에 우리가 처리하고 싶은 문장 길이가 500개 이고 Embedding Dimension 도 꽤 늘려준다면 (768) 아래와 같은 결과를 얻을 수 있다.

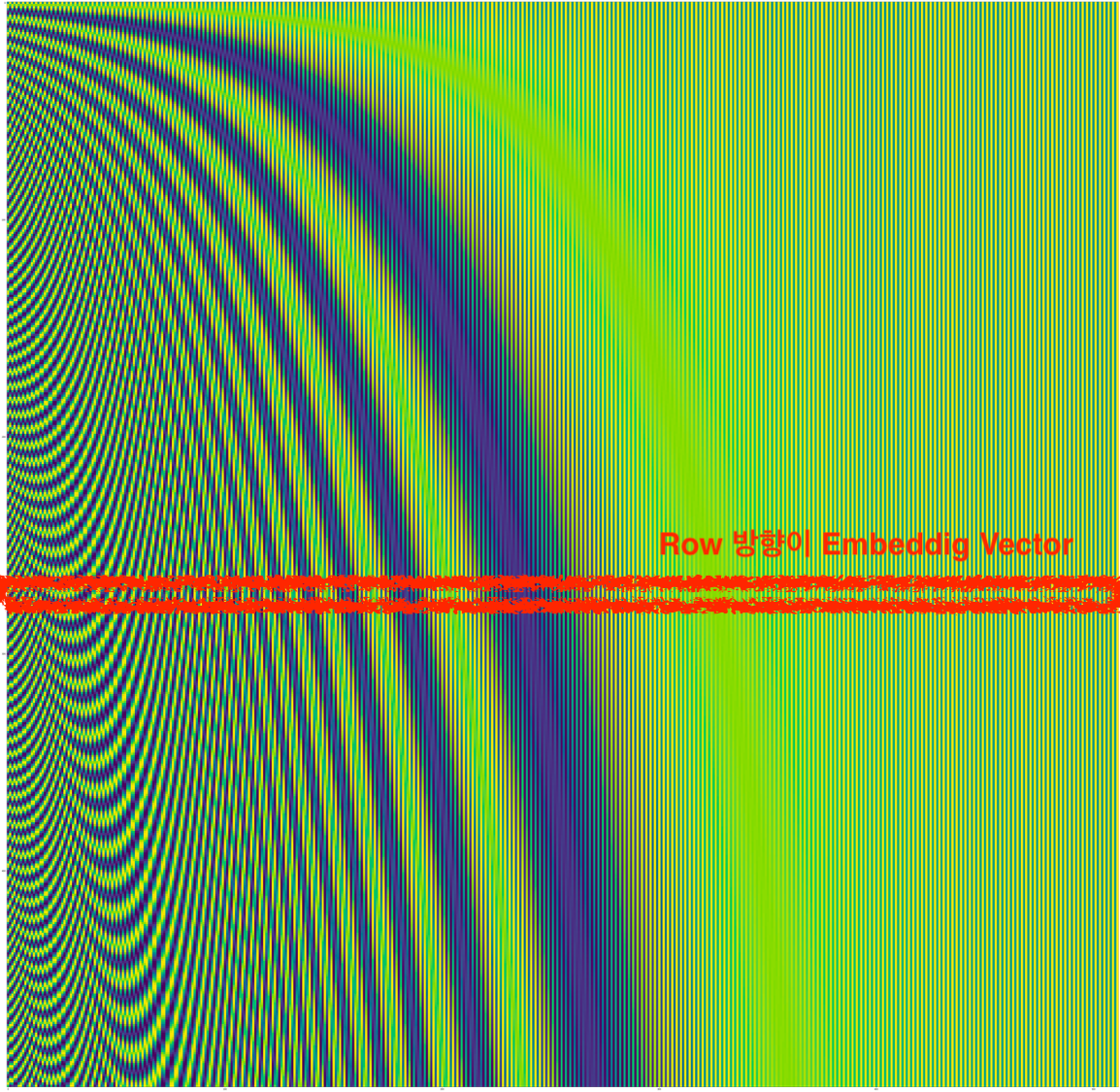Fig. 문장 길이가 500인 경우

문장 길이가 길어져도 각 timestep 별로의 Token 에 다른 Vector 가 더해지기 때문에 일단 큰 문제는 없어보인다. 그런데 Sin, Cos 함수는 일정한 pattern이 반복되는 주기함수이기 때문에 만약 사전에 정의한 이 function의 maximum length를 넘어가면 (위의 경우 10000 개) 문제가 생길 것이다 (예를 들어 1번째와 10001를 구분할 수 없다). 하지만 보통 임계치를 정해두고 그 이상은 system이 받아들이지 못하도록 구현하기 때문에 문제가 되지는 않는다. 이제 조금 더 Sinusoidal PE 을 조금 분석해 보자.

Relationship between Sinusoidal Embedding Vectors

Sinusoidal PE는 그렇다면 얼마나 좋을까?

Transformer의 paper에는 sin, cos을 사용한 vanilla PE가 token 들 간의 상대적인 Position 에 집중하는 방법을 모델이 잘 배울 수 있도록 해주며, 학습 때 보지 못한 길이의 (보통 더 긴) 문장이 들어와도 문제없이 위치를 추론할 수 있게 해준다고 한다.
이는 서로 다른 위치의 Token 들의 PE Vector 들의 인자들이 서로 어떤 선형 관계에 놓여져 있기 때문이라고 paper에 쓰여있다.

we must inject some information about the relative 
or absolute position of the tokens in the sequence.
...
We chose this function because we hypothesized 
it would allow the model to easily learn to attend by relative positions, 
since for any fixed offset k, PEpos+k can be represented as a linear function of PEpos.
...
We chose the sinusoidal version because it may allow the model to extrapolate to sequence lengths 
longer than the ones encountered during training.

이것이 사실인지 알아보기 위해 PE Vector 을 \(\vec{p}\) 이라고 하고 t 번째 token 에 대한 PE 를 \(\vec{p}(t)\) 라고 하고 전개를 해보자. PE 의 중요한 특성중 하나는 Sin Cosine 으로 이루어진 PE Vector 들에 대해서, 예를 들어 어떤 \(t,k\) 에 대해 \(\vec{p}(t+k)\) 와 \(\vec{p}(t)\) 사이에는 Rotation 관계가 있다는 것이다. (Reference 참고)

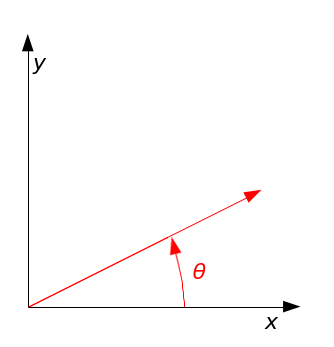Fig. Counter Clock Wise Rotation in 2-dim Space

어떤 vector를 회전시켜주는 rotation matrix는 아래와 같은 form 으로 정의된다.

이 두 번째 특성이 바로 Model 이 상대적인 position의 token 정보를 배울 수 있게 해준다고 하는데, 두 k만큼의 거리가 있는 token 들의 PE 인 \(\vec{p}(t)\), \(\vec{p}(t+k)\)에 대해서 생각해 보자. PE 의 \(m\) 번째 element 들이 sin, cos 값들에 대해서

아래의 관계가 성립하는

어떤 linear transformation이 있다고 생각해 보자. 이 matrix, \(M\) 가 \(\begin{bmatrix} u_1 & v_1 \\ u_2 & v_2 \end{bmatrix}\) 일 때, 수식은 우변에 결합 법칙을 사용할 경우 다음과 같이 정리된다.

수식을 다시 쓰면 아래가 성립한다는 걸 알 수 있는데,

위의 방정식을 풀면 matrix, \(M\)은 아래 처럼 어떤 offset 을 기준으로 \(k\) 만큼 떨어진 PE vector 는 서로를 회전한 것에 지나지 않는다는 것을 알 수 있다.

이를 확장하면

를 만족하는 \(T_k\)라는 것이 있다는걸 알 수 있다. 즉 sin, cos 으로 이루어진 PE vector들 끼리는 서로 rotation 관계에 놓여져 있는 것이다. 만약 model이 잘 학습되었다면 training data 내에서 서로 다른 position에 있는 token들을 통해 rotated PE vector들을 이해하는 능력이 생기므로 (?), 학습때 본 것 보다 더 긴 sequence의 token들이 들어와도 추론을 할 수 있을 것이다. 하지만 후속 논문들에서 성능상으로는 Sinusoidal PE 가 학습때보다 긴 문장에 대해서는 성능이 급격하게 감소하는 경우가 많다고 했다.

Decomposition of Adding Position Vectors in Self-Attention

이번에는 Vanilla Transformer 의 Scaled Dot Product Attention (SDPA)와 같이 PE를 생각해 보자. SDPA의 수식은 아래와 같다.

여기서 attention score, \(A\)는 \(QK^T\) 연산으로 구할 수 있고, 이 Query (Q), Key (K)를 만들기 전에 position information이 input token vector에 흘러들어가게 된다. 만약 우리가 \(L\) 개의 token을 갖는 sequence를 갖고 있다고 치면 \(L \times L\) 크기의 Matrix 는 다음과 같이 정의 된다.

위의 수식에서 \(e_i\) 는 \(i\) 번째 continuous word embedding vector 고 \(p_i\) 는 그에 대응하는 Position 정보다. 이를 간단하게 전개하면 아래와 같은 수식을 얻을 수 있는데,

이는 word embedding 간의 관계 혹은 position embedding vector 간의관계 혹은 그 둘의 정보가 섞인 term 등 총 4가지 term 으로 구성되어 있다.

• a : i 번째 단어가 j 번째 단어에 얼마나 Attend 해야 하는가
• b : i 번쨰 단어가 j 번째 단어의 위치에 얼마나 Attend 해야 하는가
• c : i 번째 단어의 위치가 j 번째 단어에 Attend 해야 하는가
• d : i 번쨰 단어의 위치가가 j 번째 단어의 위치에 얼마나 Attend 해야 하는가

즉 모델은 word embedding 정보가 q,k 로 mapping되고, 그들간의 similarity만 측정하는 것이 아니라, position information과의 similarity도 측정하는 것이 된다. 이는 앞으로 전개될 Relative Positional Embeddings (RPE)는 대부분이 위의 수식의 특정 term 들을 다른 것들로 근사, 대체하는 것들이므로 이 form 을 잘 기억해야 한다.

Similarity between Sinusoidal Embedding Vectors

Sinusoidal PE의 특성을 하나 더 알아볼 것인데, 이는 인접한 PE vector들 끼리 굉장히 similarity 가 높다는 건이다. 즉 \(\vec{p}(t)\) 와 \(\vec{p}(t-1), \vec{p}(t+1)\)같은 것들이 굉장히 유사하다는 것이다.

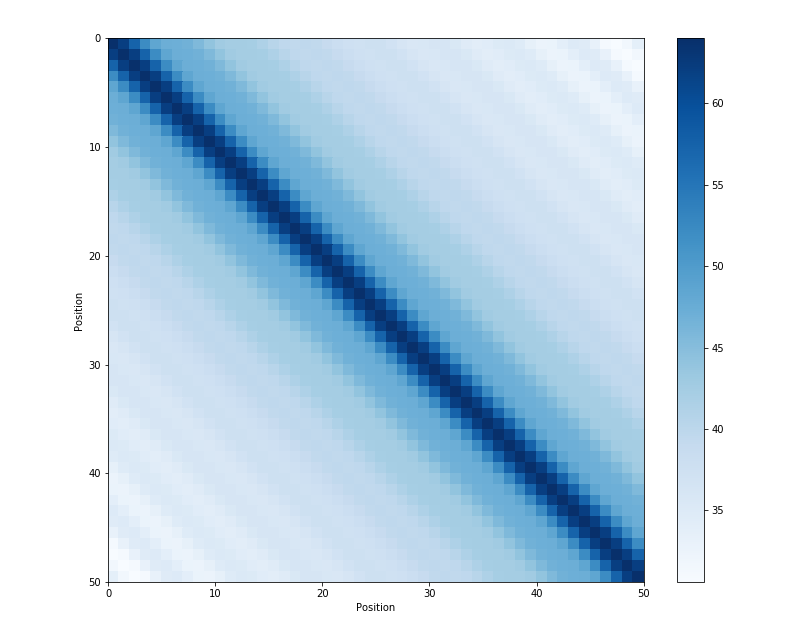Fig. Dot product of position embeddings for all time-steps. Source from here

사실 위의 subsubsection의 수식에서 \(p_i \cdot p_j\)가 direct로 쓰이지는 않고 \({p_i}^T W_q^T W_k p_j\) 처럼 Q, K vector들로 linear transform된 결과가 내적된 결과인 \(QK^T\)에 더해지는 형태로 쓰이는 것을 볼 수 있다. 비록 linear transform된 결과들끼리의 similarity score가 쓰이지만 원래 \(\vec{p}\)들끼리의 dot product 결과물이, 실제로는 인접한 vector들 간 similarity가 매우 높고 symmetric 하다는 property 가 나중에 PE를 design하는 데 좋은 힌트가 될 수 있기 때문에 미리 언급을 하고 싶었다.

Additive Relative Positional Embedding (RPE)

Shaw RPE

그래서 어떻게 PE가 발전하게 되었을까? 가장 먼저 Shaw et al.는 트랜스포머에서 가장 먼저 상대적인 위치를 고려한 PE 를 제시했다고 알려져 있다. (이 논문의 저자들은 Transformer 를 제안한 Google Brain 저자진과 거의 동일하다. 본인들도 논문을 내놓고 실제로 학습때보다 긴 문장에 대해 추론할 때 대해 성능이 안좋으니 보완한 것 같다)

Shaw et al.의 Relation-aware Self-Attention (RPE) algorithm은 간단하다. 먼저 Q, K를 구하고 이를 통해 얻은 \(\mathbb{R}^{n \times n}\)차원의 score matrix (문장길이 n 일 때)를 구한다. 여기에 Value, V를 연산해줄 때 token간의 상관 관계 정보를 넣어주는 것이다. 즉 vanilla transformer 의 SDPA을 통해서 context vector, \(z\) 를 만드는 과정은 아래와 같은데,

여기에 relative position 정보를 K쪽에 먼저 넣어준다.

그리고 V쪽에도 비슷하게 정보를 넣어준다.

위의 수식에서 \(a_{i j}^{K}, a_{i j}^{V}\)가 단어간의 상대 위치 정보를 반영해주게 된다. 주의 해야 할 점은 원래 sinusoidal PE의 경우 token embedding, \(x\) 에 이미 PE 를 더해주고 Q, K, V projection 을 했고 각 PE vector들은 learnable하지 않았으나

지금의 경우에는 K, V에만 learnable position information이 들어간다는 것이다. 직관적으로 \(a_{i j}^{K}, a_{i j}^{V}\)는 아래 figure처럼 token간 정보를 상대적으로 (자기 자신 기준으로 양옆으로 갈수록 1, 2, … 처럼) modeling 하게 된다.

Fig. Vanilla PE vs RPE

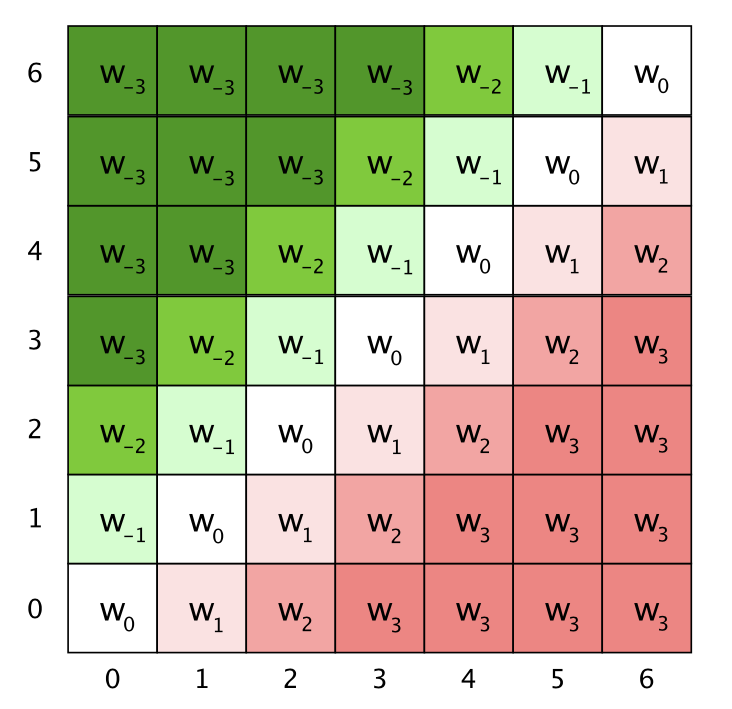
위 figure는 이해를 돕기위한 것이지 실제로 -3, -2 이렇게 단순하게 scalar 값으로 되어있지는 않고, 각 \(a_{i j}^{K}, a_{i j}^{V}\)는 \(\mathbb{R}^{d_a}\)차원의 vector 형태이다. 다시 말해 이 방법을 쓰는 목적 자체가 서로 상대적인 position 정보를 모델에 주고싶은 것이기 때문에, 예를 들어 어떤 token 이 3번째 있다면 attention 할 때 자기 자신을 Q,K 로 변환한 vector들끼리 내적할 때는 가장 가깝다는 정보를 (0), 양옆은 그 다음으로 가깝다는 정보를 (+-1) … vector 간 내적의 정보로 주게 되는데 그것이 현재 query 의 위치와 position vector 들끼리의 내적으로 주어지는 것이 된다.

그런데 저자들은 여기에 추가로 attention 하려는 token 기준 양옆 +-k 이후로는 별로 안중요할거같은데?라는 생각을 했다. 그래서 embedding 하려는 Q token 기준으로 +-k, 예를 들어 +-3 이후의 K들에 대해서는 똑같이 +-3 에 해당하는 vector 들을 할당하게 된다. 그러니까 우리는 \(a_{ij}^K, a_{ij}^V\) vector 들은 그러면 양쪽으로 +-k 만큼이니까 \(2k+1\) 개 만큼만 있으면 \(QK^T\)에 더해줄 position tensor 를 만들 수 있으므로 (Q가 바뀔때마다 재탕할 수 있음), vanilla transformer 모델 만큼의 parameter 외에 우리가 추가로 갖고있어야할 learable parameter는 \(\mathbb{R}^{(2k+1) \times d_a}\) 가 \(a^K, a^V\) 에 대해 한쌍씩 있는 것이 된다. 다시 말해, \(QK^T \in \mathbb{R}^{n \times n \times d_a}\)만큼 전부 다 필요한건 아닌 것이다.

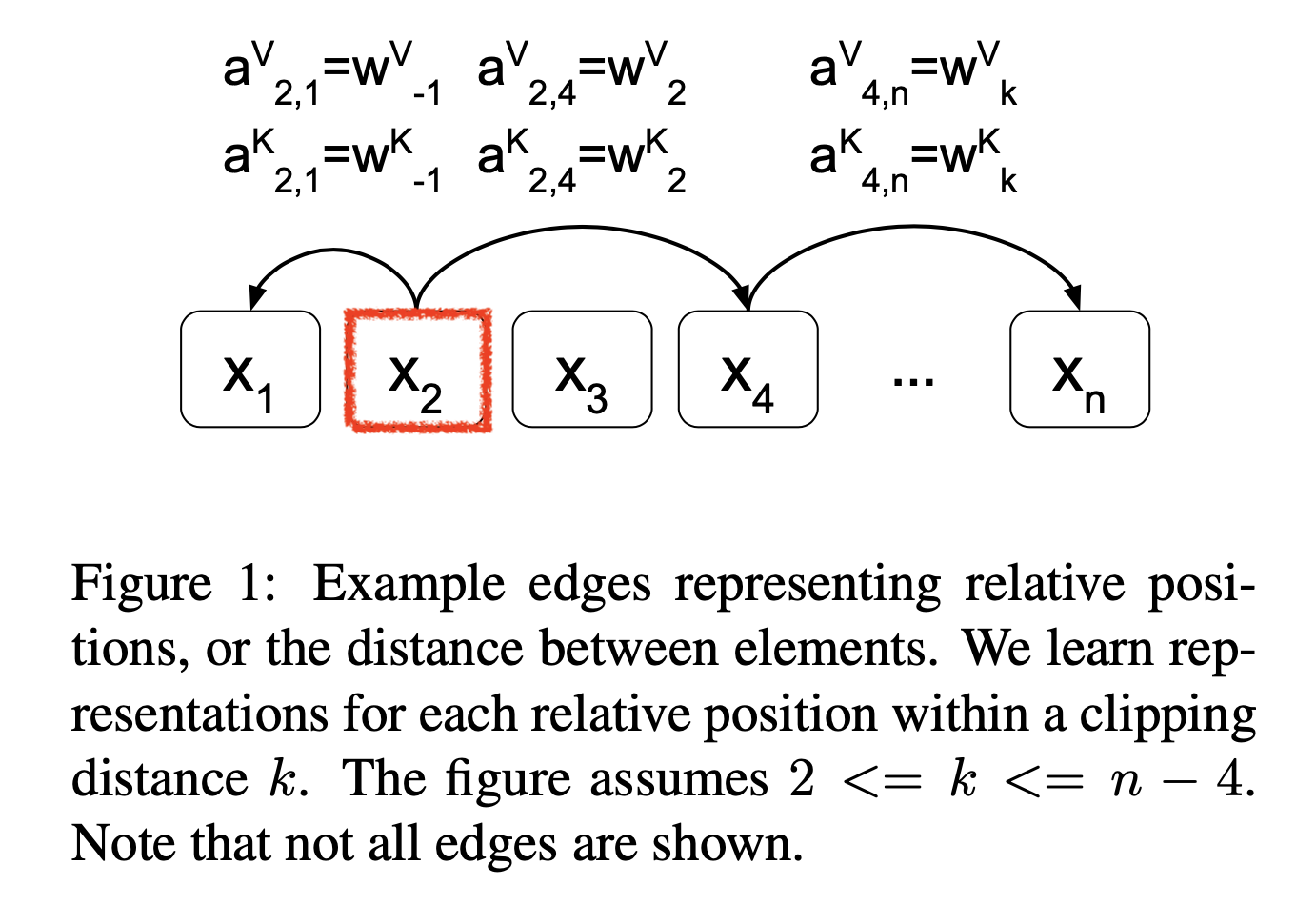Fig. 실제 Shaw 의 논문에서의 Figure

Vanilla transformer 와 또 다른 점은 sinusoidal PE는 model의 가장 앞쪽인 (front-end) input 부근에서 최초로 한 번 token embedding과 더해지는 것 이었으나 지금의 경우에는 매 block마다, 즉 self attention을 할 때마다 PE Matrix를 계산해 더해줘야 하므로 연산량이 늘어나고 (Time Complexity 증가), 추가로 learnable vector 들을 가지고 있어야 하므로 Space Complexity 도 늘어난다는 것이다. Pseudo Code로 써보자면 아래와 같습니다.

x = embedding(input_tokens)
pos = relative_positional_embedding(x)

for layer in range(transformer_encoder_layers)
    x = layer(
        layer_input = x,
        positional = pos
    )

최초에 계산한 상대적인 Positional Encoding Matrix 를 계속 재사용해서 더해준다. 저자들은 모든 Multi Head Attention (MHA)의 head마다 RPE에 대한 파라메터를 공유하는 것으로 space complexity를 줄이고, \(QK^T\)연산을 decomposition하여 time complexity를 줄였다. 이렇게 하면 \(QK^T\)는 원래대로 계산하고 position 정보는 \(Q\)와 \(a^K\)는 한번만 곱한걸 더해주기만 하면 된다.

그런데 이렇게 decomposition 하는 것을 아마 앞에서 본적이 있을 것이다. 바로 sinusoidal PE를 쓸 때 attention score Matrix 를 4개 term 으로 decomposition 했던 것과 크게 다르지 않은 형태가 된 것이다.

이를 비교해보면 Shaw et al의 방법론은 위의 b,c,d term 을 query \(q_i \in \mathbb{R}^{d}\) 와 \(a_{ij}^k \in \mathbb{R}^d\) 의 연산으로 근사한 방법이라는 것이 된다. Sequence modeling 시, 양쪽 Q,K token에 정보를 주입할게 아니라 둘 간의 상대적인 차이만 고려하면 되는데, 이 정보를 \(a^k\) 에 담아서 학습하게 하고, 추론시에는 Q와 내적 시켜 아 이 Q와 K는 현재 이만큼 떨어져있구나?를 모델이 추론하게 되는것이다. Vanilla transformer와 RPE를 쓰는 transformer를 diagram으로 나타내면 아래와 같을 것이다.

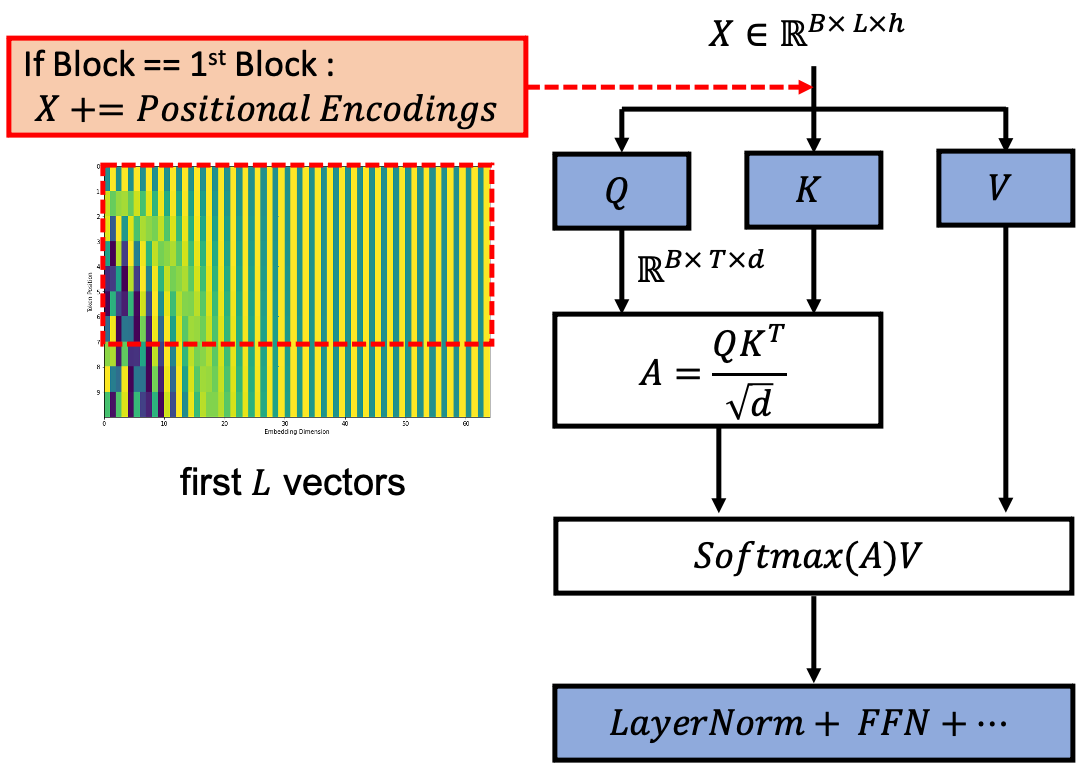Fig. Absoulite Positional Encoding 을 쓰는 Vanilla Transformer. 첫 번째 Layer 에만 Position Information 이 들어간다.

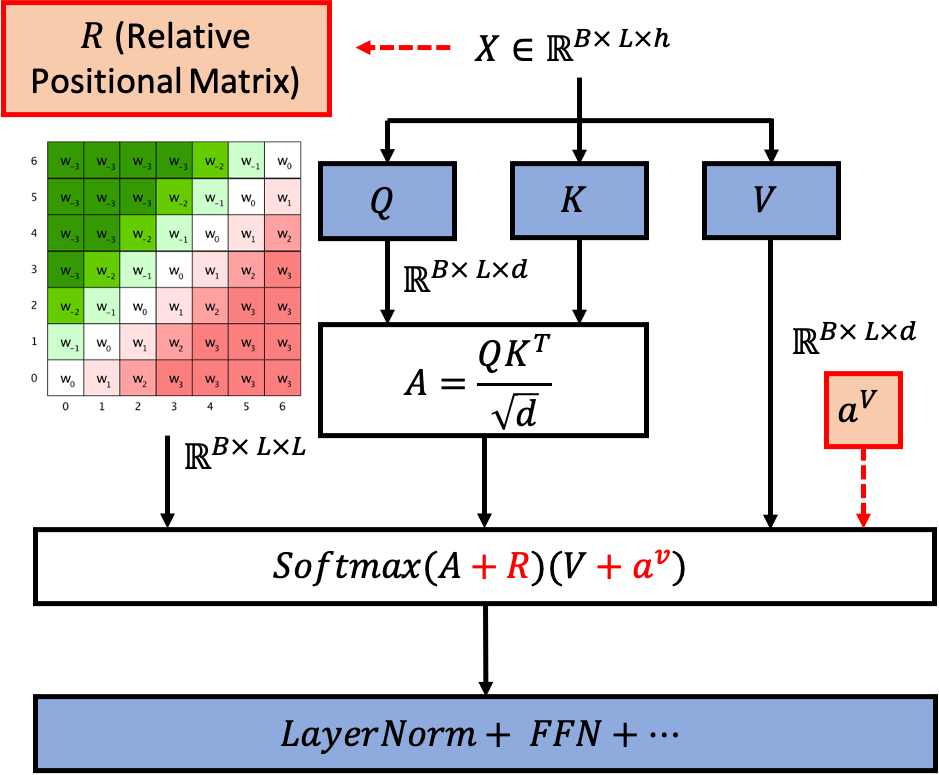Fig. Shaw et al. 이 제안한 RPE 방식, 사실상 bias 를 Attention Score 에 더해주는 것과 같다.

저자들이 제안한 clipping 된 형태의 position bias가 \(QK^T\)에 더해지는 형태를 최대한 표현하려고 했다.

Fig.

그런데 이는 앞서 살펴본 sinusoidal PE가 서로 거리가 비슷할 경우 correlation이 굉장히 높고 symmetric했던 것과 연관지어 생각할 수 있을 것이다. 즉 애초에 sinusoidal PE 가 거리가 먼 Q, K 끼리는 정보가 없는셈이나 다름 없기 때문에 이런것이 반영된게 아닌가 생각해볼 수 있는것이다. (정확히 대응되는지는 모르겠다. 확실한건 vanilla transformer 논문에만 PE를 포함한 엄청나게 많은 insight가 존재한다는 것이다.)

Fig. Dot product of position embeddings for all time-steps. Source from here

이런식으로 \(QK^T\)에 뭔가를 더하는 형태를 attention bias를 더하는 형태라고 해서 additive PE라고 하며, 이런 종류의 RPE는 후술할 Rotarty Positional Embedding (RoPE)와 결정적인 차이를 보이기도 한다. 어쨌든 Shaw et al.의 method는 token간의 절대적인 (absolute) 위치보다 상대적인 (relative) 위치를 고려한 것이고, 그 결과 기계번역 (Neural Machine Translation; NMT) task 에서 성능 향상이 있었으나,

Fig.

window size 가 \(k\) 일 때 \((2k-1) \times d\) 짜리 matrix 학습하고 추론시에도 이만큼을 더해줘야 하기 때문에 초당 step 수 가 7% 감소하게 됐으며 (매 층마다 더해줘야 하기 때문), model parameter가 커진건 어쩔 수 없었으며, 실험 결과가 딱히 학습때보다 더 긴 sequence 들에 대해서만 평가한 결과는 없기 때문에 이게 길이에 대해서 generatlization 이 더 잘되나?에 대한 의문을 남기게 된다.

Music-Transformer RPE

다음은 Shaw et al.의 RPE를 개선한 논문들 중 음악 midi generation (music generation)을 위한 것으로, Music Transformer이다. 뜬금없이 무슨 music transformer냐 할 수 있지만 한 번 생각해보자. 원래의 SDPA이 아래와 같았고,

Shaw et al.이 제안한 RPE 는 아래처럼 query 와의 interaction 을 통해 생성된 relative position information을 담고 있는 matrix가 추가된 격이었다. (여러 논문에서 수식을 가져오다보니 Notation 이 살짝 달라진 점 주의)

하지만 이 방법에는 space compleixty 에 대한 문제가 있었다. 앞서 얘기한 것 처럼 아래의 \(L \times L\) 크기로 보이는 \(S^{rel}\)은 사실 2차원 Matrix 가 아닌 3차원 Tensor, \(L \times L \times d\)이다. (물론 learnable parameter 는 \((2k+1) \times d\) 밖에 안되지만, 실제 \(QK^T\)에 더해지고 backprop이 되는 tensor의 크기는 \(L \times L \times d\)인 것이 문제인 것이다.)

그런데 music generation을 위해서는 수십초에서 2~3분에 해당하는 음악 sequence를 transformer input으로 써야한다. 이 경우 token 으로 따지면 L 이 엄청 큰 것으로, GPU memory가 당연히 부족할 것이다.

여기에 기본적으로 transformer의 self attention의 memory requirement는 sequence length에 quadratic하므로 GPU memory를 \(O(\color{red}{L^2d} + L^2)\)만큼 먹게되는데 (\(QK^T\) 부분만), music transformer 에서는 이를 개선해서 \(O(\color{red}{Ld} + L^2)\) 로 만들기위한 method 를 제안한다.

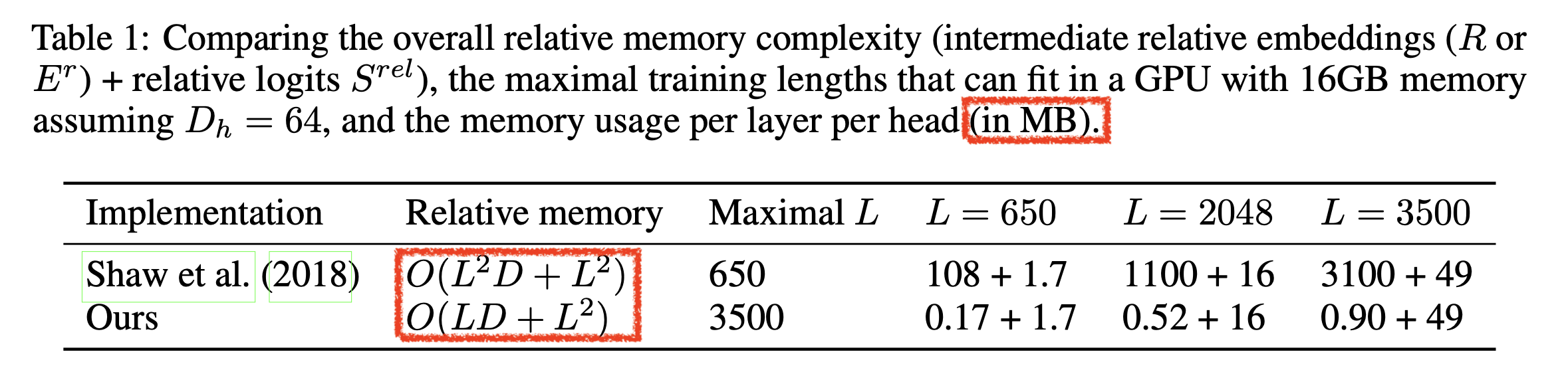Fig.

방법은 간단하다. 우리가 필요한건 Q, \(Q' \in \mathbb{R}^{L \times 1 \times d}\) (\((L,d)\) 를 torch.unsqueeze 해서 Reshape한거임)와 연산을 할 \(\color{red}{ R } \in \mathbb{R}^{L \times L \times d}\) tensor이다. 이 tensor를 만들기 위해서는 상대 정보를 표현할 \(d\) 차원의 learnable vector들인 \(E^r\)를 \(L \times L\)로 늘어놓아야 하고, 최종적으로 Q와 곱해서 \(L \times L\)의 \(S^{rel}\)을 만들어야 한다.

여기서 우리가 원하는 task는 음악을 autoregressive 하게 생성하는 것이기 때문에 transformer decoder를 모델로 사용할 것이고, decoder를 학습하기 위해서는 이전 token 들에만 attention이 걸리는 unidirectional 상황이라는 가정을 추가한다. 이를 위해서는 future token을 마스킹 하는 upper triangle mask를 만들어 attention score matrix에 더해야 한다. 바로 이 특성 때문에 아래와 같은 \(S^{rel}\)을 고안해 낼 수 있었던 것이다.

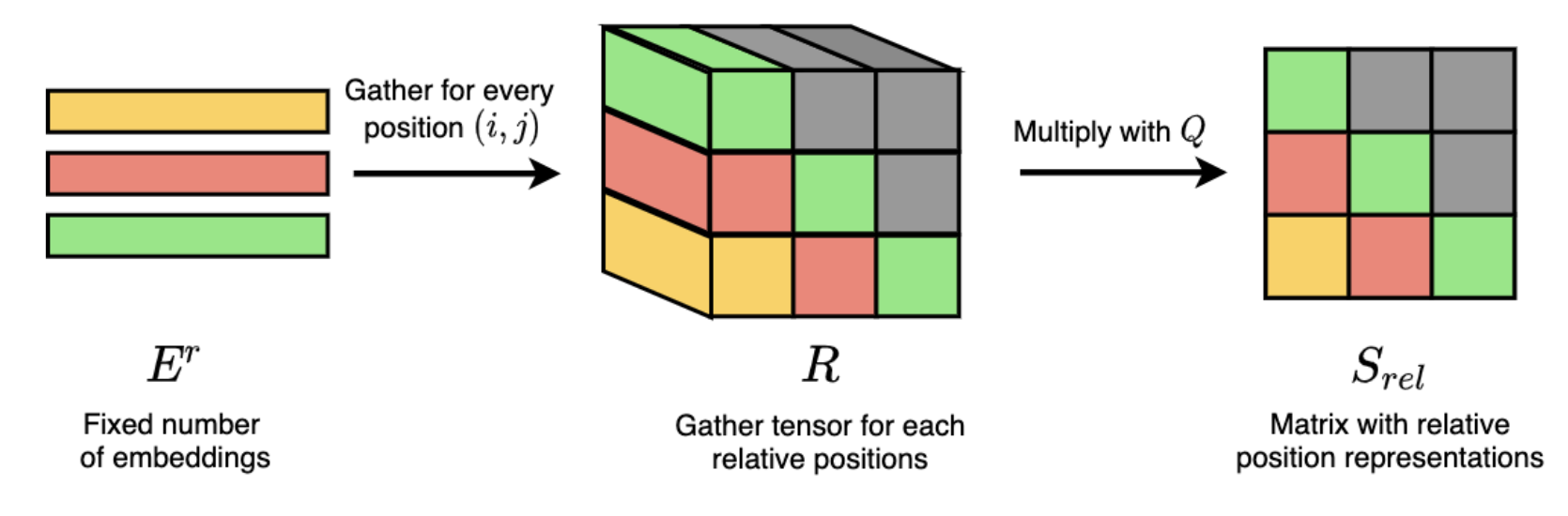Fig.

이를 계산하기 위해 굳이 \(\color{red}{ R } \in \mathbb{R}^{L \times L \times d}\)이라는 3차원 tensor가 필요할까? 그렇지 않다.

어떤 L개 vector들 \(E_r \in \mathbb{R}^{(L, d)}\)와 마찬가지의 reshape하기 전의 L개 vector들, \(Q \in \mathbb{R}^{(L,d)}\) 를 \(E^r Q^T\) 로 곱합니다. 그리고 이를 아래 네 가지 과정을 거친다.

• left padding
• flatten
• reshape
• trim

그러면 우리는 원래의 \(S^{rel}\)와 같은 결과를 얻게 되므로 \(R\) 이라는 거대한 memory를 저장할 필요 자체가 없어진다. 생각해보면 3차원 tensor, \(R\)은 query가 바뀔때마다 vector들을 한칸씩 shift 해서 재탕하기때문에 이런 접근이 가능한 것이다.

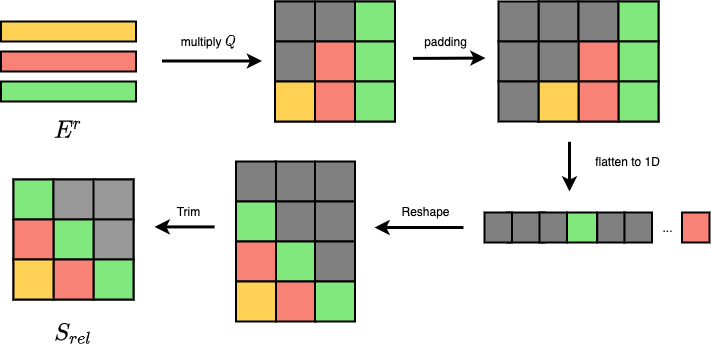Fig.

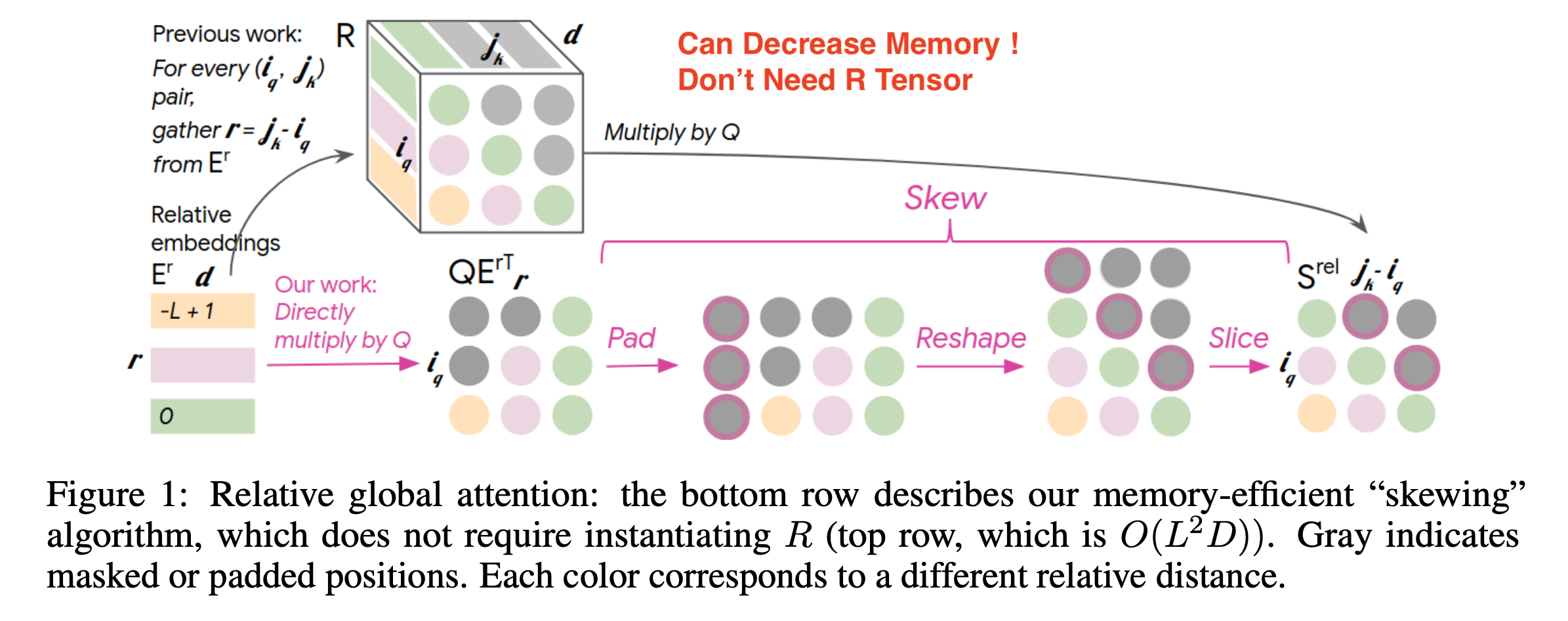Fig. 실제 paper의 Figure

저자들은 추가적으로 global context가 아닌 local에만 attention 하는 local attention에 대해서도 효과적인 방법을 제안하는데, 관심이 더 있으신 분들은 따로 paper를 읽어보길 바란다.

Fig. Optimized Relative Local Attention from Music Transformer

Transformer-XL RPE

Music transformer의 다음으로 제안된 Additive RPE는 Transformer-XL, Attentive Language Models Beyond a Fixed-Length Context라는 paper에서 제안되었고 이것이 당대에 나온 RPE들 중에서는 사실상 가장 유명했다. 앞선 method들을 잘 따라오셨다면 크게 다른 점이 없다. 다만 여기서는 RPE 가 학습때보다 더 긴 문장을 잘 추론하기 위해서도 있지만, transformer 구조에 엄청나게 긴 (extra long) Context 를 보는 학습, 추론이 가능하게 하기 위해서 Memory Caching 방식을 제안했는데, 이를 위해서 RPE가 필수이다. 논문의 요지는 다음과 같다.

우선 transformer model로 Langugae Modeling (LM) task를 푸는 상황이다. 어떤 문장이 10000개 token을 가지고 있다고 생각해 봅시다. 그런데 model이 GPU memory의 한계로 한 번에 최대로 볼 수 있는 token들은 기껐해야 512개 정도 밖에 안될 것이다. 그러므로 우리는 엄청 긴 sequence를 학습하기 위해서 문장을 512개 Token씩 모아서 분리 (segment) 해야 할 것이다. 그리고 dataloader를 구성할 때 이 segment들을 sequential하게 구성해서 hidden 정보를 concat해주는 식으로 학습하는 전략을 쓸 수 있을 것이다.

그러면 첫 번째 segment에 대해서 먼저 model forward를 한다. 그러면 1층부터 예를 들어 12층까지 layer별로 \(K,V\)같은 것들이 512개씩 있을 것이다. 그리고 그 다음 2번째 segment 에 대해서 계산할때는 우리가 long sequence modeling을 하기로 했으니 이전 segment의 vector들을 caching해서 가지고있다가 다음 token들을 연산할 때 concat해서 연산해볼 수 있을 것이다. 즉 다음 512개 token 들에 대해서 attention 을 할 때는 앞서 caching 한 \(K_512, V_512\)에 추가로 attention이 걸리므로 이전 segment의 context 정보가 흘러들어오는 것을 model이 이해할 수도 있을 것이다. 이 때 이전 시점의 Token 들은 500개 1000개 … 등 정하기 나름인데요, caching된 tensor를 불러와서 쓸 때 해당 tensor는 gradient가 흐르지 않게 되어 있다 (GPU memory 때문인듯).

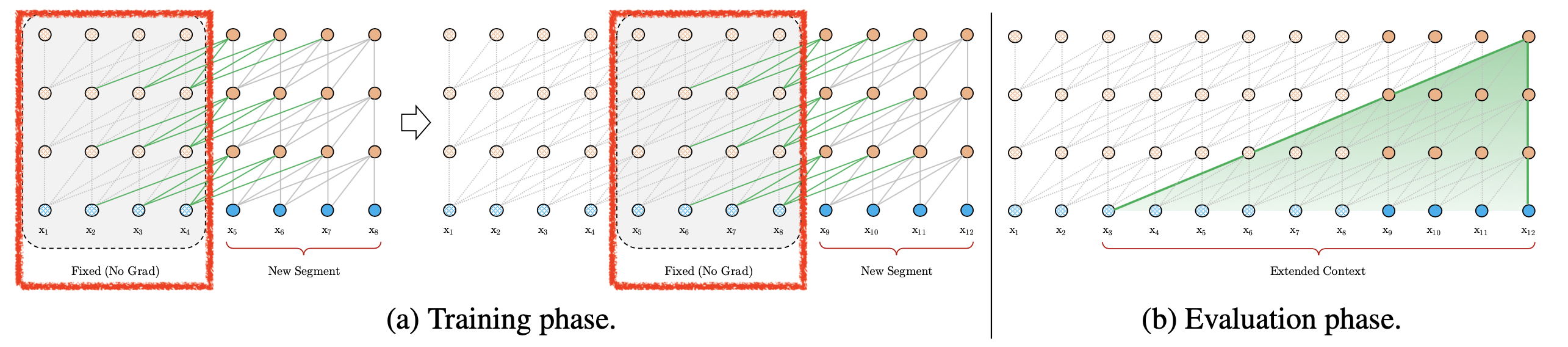Fig. Training and Evaluation Phase of Transformer-XL

여기서 왜 RPE를 쓰는 이유는 명호가한데, 바로 caching된 K,V 는 이미 PE가 이미 적용되어있는 상태이며 이 때, absolute PE 정보를 넣어주게 되면 이전 segment와 현재 segment의 position information이 무의미해지기 때문이다.

그래서 어떻게 RPE 를 개선해서 적용했느냐? 이를 위해 먼저 다음을 정의한다.

두 개의 연속적인 (consecutive) segment block을 \(s_{\tau}, s_{\tau+1}\)로 표현했는데, 여기서 \(\tau\)번째 segment의 n 번째 layer의 hidden state sequence (n+1 번째 Layer 의 input 이 되겠네요)를 \(h_{\tau}^{n} \in \mathbb{R}^{L \times d}\)라고 정의할 수 있겠다. 그러면 앞서 Transformer-XL (TFXL) 의 model Foward는 다음과 같이 정의할 수 있다.

SG는 Stop Gradient의 약자로 앞서 말한 것 처럼 이 부분에는 back propagation을 하지 않겠다는 것을 의미하며, 여기서 \(\circ\)는 두 tensor 를 붙힌다는 concat operation을 표현한 것이다. 수식을 보면 Q를 만들때는 현재 segment의 정보만 사용하고, K, V 를 만들 때는 이전 segment (\(s_{\tau}, s_{\tau-1}, \cdots\))들의 정보를 끌어다 쓴다고 볼 수 있다. (한개만 쓰면 \(s_{\tau}\) 만, 근데 어차피 \(s_{\tau}\) 가 \(s_{\tau-1}\) 정보를 가지고 있기 때문에 RNN이 하는 것 처럼 context 정보는 segment가 새로 붙을 수록 사실상 무한대로 전파된다고 볼 수 있다)

이제 각 Token들에 주입해줄 어떤 PE를 다음과 같이 정의하겠다.

그리고 \(\tau\) 번째 segment 의 input word embedding sequence를 아래처럼 정의하겠다.

그러면 다시 아까의 각 segment 별 hidden state sequence는 다음과 같이 쓸 수 있을 것이다.

여기서도 Shaw et al.등과 마찬가지로 input token들에 \(U\)를 더하는, addtive 방식을 차용한 것을 알 수 있다. 여기서 만약 \(U\)가 vanilla transformer 의 sinusoidal PE라고 생각하고 SPDA를 첫 번째 layer에 대해서 수행해보자.

이제 우리가 앞서 몇번 경험했던 것 처럼 decompoisition 해보도록 하자.

현재 Segment 에 대해서 \(i,j\) 번째 Token 들, \(x_i\) 와 \(x_j\)간의 attention map 값은 위 처럼 계산할 수 있게 되는 것이고, 각 term은 token-token 간의 정보, token-position, position-position의 정보를 나타낸다. TFXL RPE는 이를 다음과 같이 바꾸는데, position을 나타내는 vector들인 \(u\)를 learnable 한 \(u,v\)와 어떤 \(R\) 이라는 것으로 대체하게 된다.

또 바뀐 점은 \(W_k\)라는 input token을 key space로 projection 해주는 layer가 \(W_{k,R}, W_{k,E}\), 2개로 분리됐다는 것이다. 여기서 \(u,v\)는 각각 원래 \(U\)를 \(W_q\)와 연산하는 등의 행위를 그냥 vector 하나로 대체한 것이다. 이는 사실 sin, cos 함수에서 뽑은 vector를 \(W_q\)로 선형 변환을 해주나, 애초부터 parameter 로 두고 학습을 하나 비슷비슷 하기 때문인 것 같다.

그럼 여기서 \(R_{i-j}\) 은 뭘까? 이는 vanilla transformer 의 sinusoidal encoding을 각 Q,K의 현재 position \(i,j\)에 대해서 구하고, 그 둘의 차이를 나타내는 vector를 의미한다. Shaw et al.의 방식처럼 \(w_{-k}, \cdots, w_{0}, \cdots w_{+k}\)으로 표현 할 수도 있겠으나, sinusoidal encoding 이라는 이미 잘 design 되었으므로 vanilla transformer의 inductive bias를 재사용해보자 라는 취지에서 추가된 term으로 생각할 수 있겠다. 이렇게 새롭게 parameterization 을 함으로써 저자들은 각각의 term 을 수식에 적어둔 것 처럼 직관적으로 해석할 수 있다고 주장했다. (사실 그냥 썰 푼것 같다는 생각이 든다)

최종적으로 TFXL는 아래 수식처럼 이전 segment 하면서 얻은 층별 hidden vector들을 (예를 들어 512개 token 을 transformer 에 forwarding 하면서 얻은 것), memory, \(m_{\tau}\) 라고 하며, 학습시에 이 memory까지 attention 을 걸어서 정보를 끌어다 쓰지만 과거 segment 에 대해서는 학습을 하지 않기위해 Stop Gradient (SG)를 해줍니다.

그리고 attention은 relative position이 가미된 MHA이기 때문에 아래와 같은 수식을 따르며,

나머지는 LM task라면 future context를 보지 않아야 하기 때문에 upper triangle mask 를 씌워주고 최종적으로 layernorm, FFN operation을 해주는 것을 표현한 수식이다.

마찬가지로 TFXL도 diagram으로 아래처럼 표현할 수 있겟다.

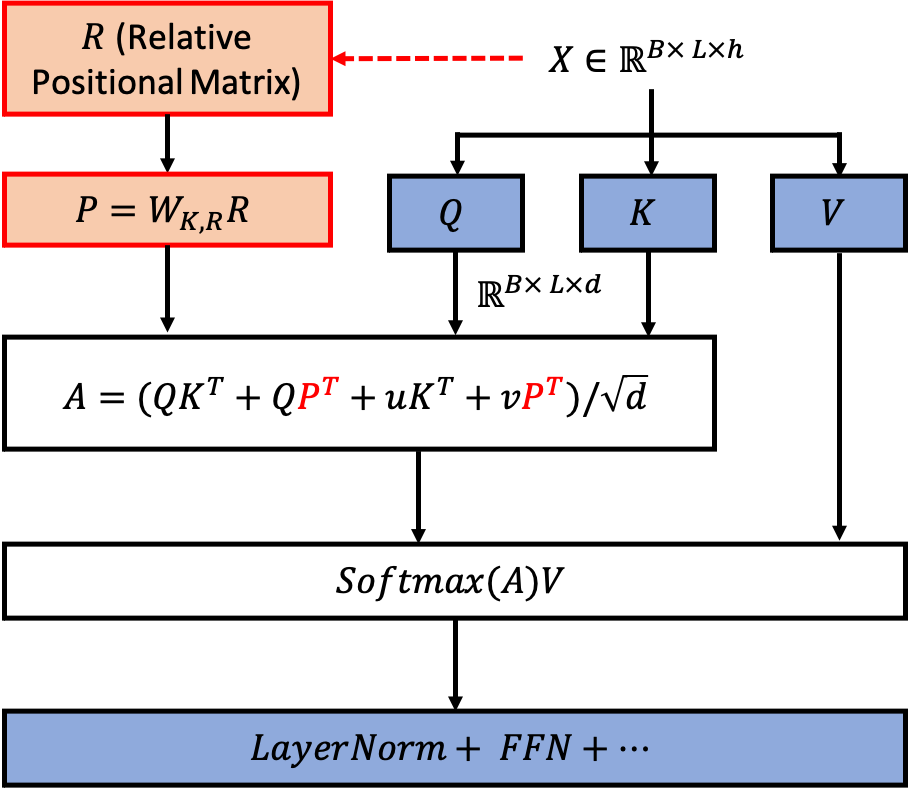Fig.

그런데 수식을 잘 보시면 attention score 를 계산할 때 Shaw et al.처럼 효율적으로 묶어서 계산할 수 있는 여지가 있기 때문에, 실제 구현은 아래와 같다.

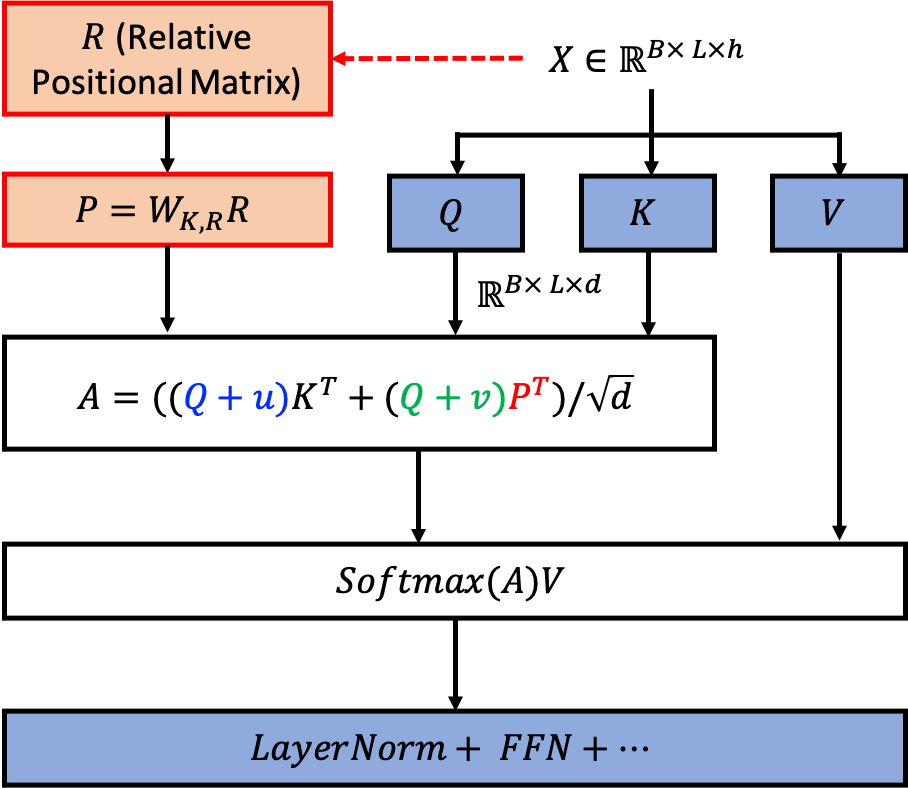Fig.

즉 원래의 \(q,k\)에 \(u, v\) 만큼이 더해진 Biased Query, Value를 K와 한번, positon information, P 와 한 번 계산해서 서로 더한 것이다. 마지막으로 저자들은 \(W_{k,R} R_{i-j}\) 를 모든 \(i,j\) 에 대해 계산해야하는 점이 Sequence Length 에 제곱에 달하는 연산, 즉 Quadratic Cost 를 갖는 다는 점을 문제 삼는다. 왜냐하면 실제로 연산을 수행하려면 \(L\)길이의 Seuqnece 가 들어오면 (cache memory 없다고 가정) 먼저 sinusoidal vector 들을 가지고 덧셈, 뺄셈을 하면서 \(R \in \mathbb{R}^{L \times L \times d}\) 차원의 Tensor 를 만들고, \(W_{K,R} \in \mathbb{R}^{d \times d}\)를 곱해서 \(P \in \mathbb{R}^{L \times L \times d}\)를 만들어 \(P_{i, j } \in \mathbb{R}^{d}\)차원의 vector 를 \(i\) 번째 query 와 \(j\) 번째 key 간의 상관관계를 구할 때 써야하기 때문이다. 저자들은 이 quadratic 연산을 linear로 바꾸는 trick 을 제안합니다.

Query matrix, \(Q\) 는 \(L \times d\) 크기였다. 첫 번째 query vector \(q_1 \in \mathbb{R}^{1 \times d}\) 에 Relative Infromation 을 주입하려면 필요한 정보는 아래와 같다.

그런데 2번째 query vector에 대해서는 위의 Q를 한번씩 shift 하면 된다.

이를 반복하면서 query vector \(q_1 \sim q_L\) 에 대해 모든 \(Q\) 를 구하면 우리가 원하는 (b) term 을 계산하는 것이 된다.

그리고 b term은 최종적으로 아래처럼 나타낼 수 있다.

이는 생각해보면 단순히 \(q \in \mathbb{R}^{L \times d}\) 와 \(Q \in \mathbb{R}^{L \times d}\)를 단순히 matrix multiplication을 한번만 한 뒤,

계산된 \(L \times L\) 차원의 matrix의 row를 왼쪽으로 shift하는 것이나 마찬가지라고 할 수 있다.

그러니까 우리는 꽤 간단하게 전체 \(B\) 를 구할 수 있게 된 것이다.

이게 왜 Linear 일까? 써야함. 
(TBC)

RPE in T5

T5 RPE 는 Google 의 T5라는 여러개의 NLP Task들을 수행하기 위한 Transformer에서 제안되어 보통 T5 Bias 라고 부릅니다.

Shaw et al. 의 RPE 를 더욱 간단하게 만들어 상대적인 postition 를 vector 를 두는 것도 아니고 scalar 를 두는 것으로 간단히 해결했습니다.

Fig. Phrase in T5 paper

이 Matrix는 학습이 되는 Learable Paramter 입니다.

이렇게 단순하게 attention bias 를 넣어줘도 잘된다는걸 보면 사실 decomposition 하고 이런것들은
논문을 풀기위한 썰일 수도 있으니 너무 맹신하지는 말아야 한다는 생각이 들기도 합니다.

Convolutional Positional Embeddings

마지막으로 알아볼 것은 Convolutional PE 입니다. 이는 상대적인 Position 정보를 Neural Network인 Convolution Neural Network (CNN)으로부터 얻겠다는 것인데, Shaw et al. 의 논문에서도 이를 언급한 부분이 있습니다.

Fig. Phrase in Shwa et al. paper

왜냐하면 1D CNN 의 경우 Kernel Size 안의 Token 들만 보고 output을 내게 되는데, 이것이 정해진 window 내에 강한 bias를 주는 것 (사실상 window밖은 무시될 수도 있는)의 극단적인 (?) case라고 생각할 수도 있기 때문입니다.

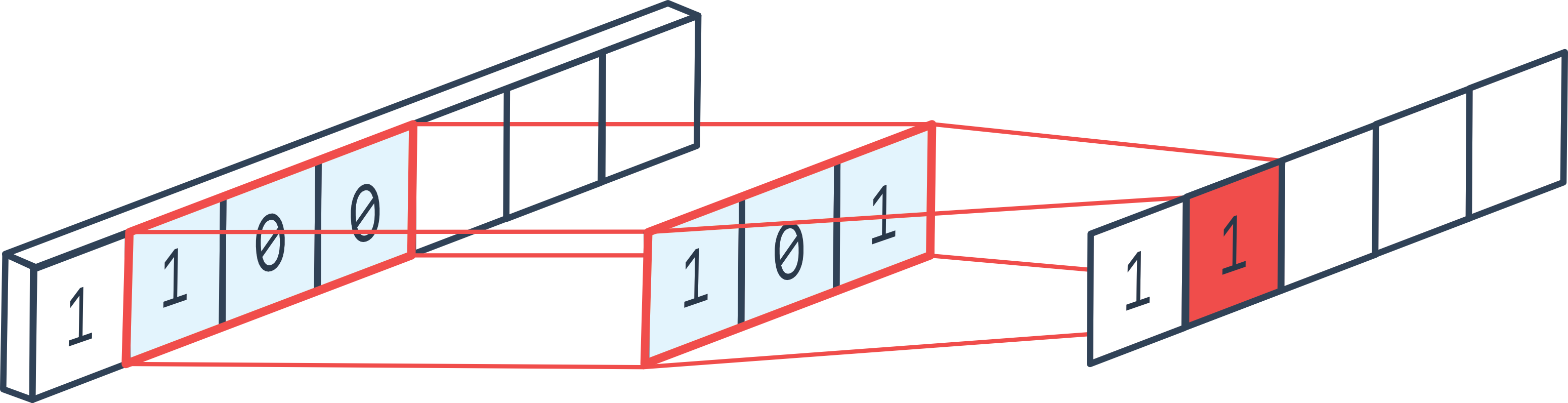Fig. 1d CNN Example. Source from here

이에 영감을 받아 Speech 분야의 BERT 라고 할 수 있는 Wav2Vec 2.0에서는 Convolutional Positional Embedding 을 사용하는데,

Group Convolution 을 사용해서 만든 값을 Transformer 의 가장 처 부분에 Input sequence 와 더해주는 것으로 position 정보를 주게 됩니다.

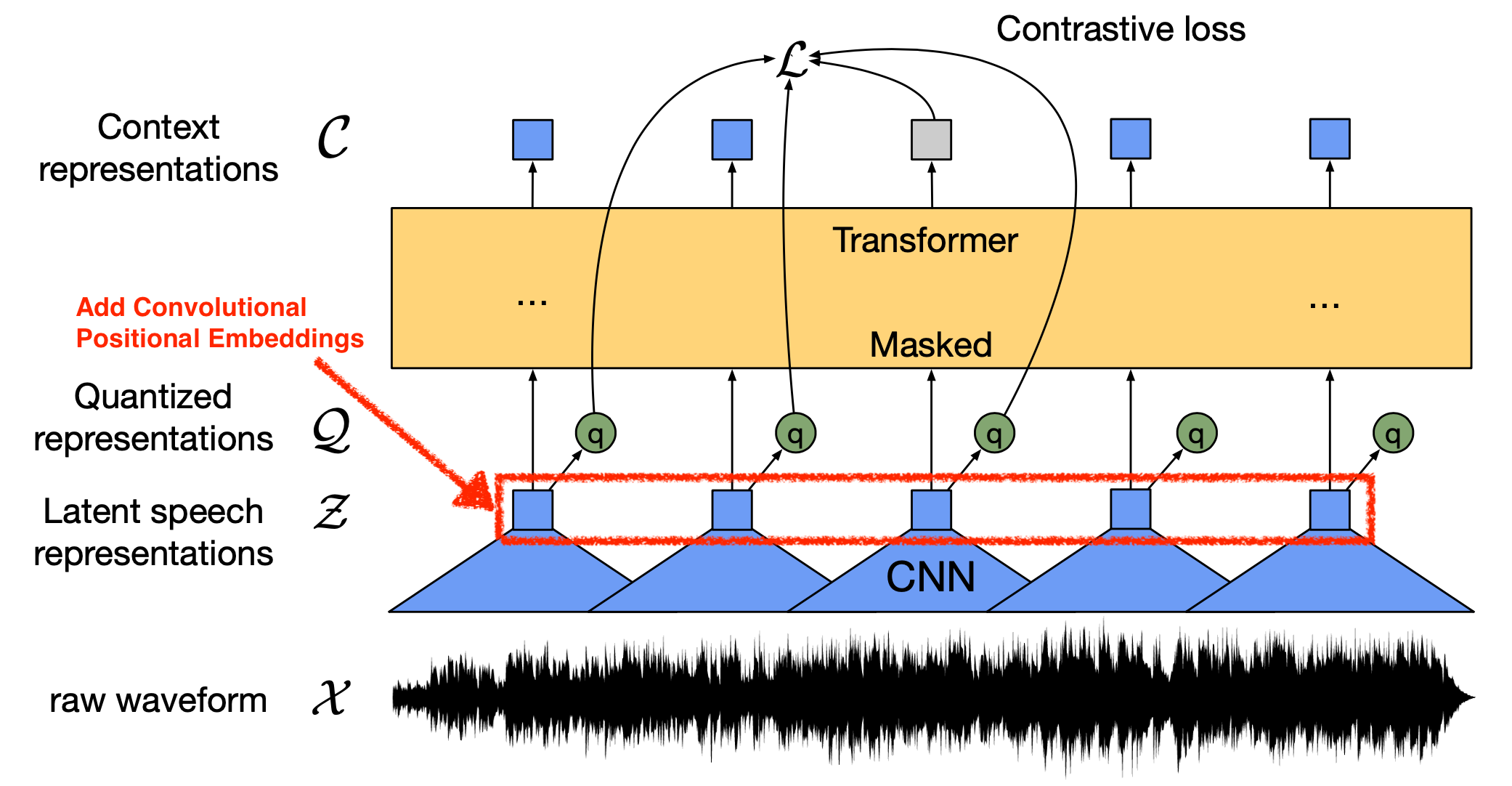Fig. Wav2Vec 2.0 Model Architecture

Sinusoidal PE 처럼 그냥 더하는거죠.

## Pseudo Code
def forward(x):
    pos_conv =  nn.Sequential( # group conv
        nn.Conv1d(
            embedding_dim,
            embedding_dim,
            kernel_size=kernel_size,
            padding=padding // 2,
            groups=groups,
        ),
        SamePad(kernel_size), # for padding
        nn.GELU() # activation
    )
    x_conv = pos_conv(x)
    x = x + x_conv # addition like sinusoidal embedding 

Multiplicative RPE

앞선 RPE method 들은 요약하자면 \(QK^T\)에 Position 정보 (attention bias) 를 더해주는 Additive RPE 형태들 이었습니다. 각 논문들에서 성능 개선이 있었다고 하니 Sequence Modeling 을 하는사람들은 앞선 방법들중에서 PE를 골라 쓰곤 했습니다. 하지만 이들에게 문제점이 있었으니, 바로

• 여전히 학습때보다 더 긴 Sequence 에서 잘 안된다 (영원히 거론될듯…)
• Flash Attention 이나 Linearized Transformer 랑 결합이 잘 안된다.

같은 것들 이었습니다.

Flash Attention은 무엇이냐? 바로 Vanilla SDPA의 경우 \(QK^T\) 를 계산하고 이를 Softmax, Scaling 해주고, 마지막으로 V와 계산을 해줘야 하는데 이 연산 속도를 가속화한 Cuda Kernel을 만든 것이라고 생각하시면 됩니다. 즉 한번에 연산을 수행하는 Kernel Fusion을 한 것인데, Additive RPE 들의 치명적인 단점이 바로 \(QK^T\) 에 뭔가를 더해주는 번거로움이 추가된다는 겁니다. RPE 중에는 이런 덧셈 형태가 아닌데다가 학습시 수렴까지 더 빨리하는 RPE가 존재하는데, 바로 곱셈 형태 (Multiplicative)로 상대 정보를 주입하겠다는 Rotary Positional Embedding (RoPE)입니다.

PE in Complex Space

RoPE를 이해하기 위해서는 PE Vector 를 Complex Vector Space에서 한 번 볼 필요가 있습니다. 이렇게 하면 더 풍부한 정보 (richer information) 을 가지고 q, k, v 를 분석할 수 있다고 합니다. (대부분의 좀 복잡하다싶은 PE 들은 다 이런식으로 논문을 전개를 하더군요)

이 방법의 핵심은 원래 \(d\)차원의 실 벡터 공간 (Real Vector Space) 에 정의되어 있던 Vector, 즉 \(\vec{q} \in \mathbb{R}^d\) 를

복소 벡터 공간 (Complex Vector Space), \(\mathbb{C}^{d/2}\) 에 정의되는 벡터

같이 보겠다는 겁니다. 왜 이것이 가능할까요? 이를 위해서는 먼저 2-dim Vector 를 복소수 (Complex Numbers) 로 생각하는 것이 중요합니다. 우리가 알고 있는 2차원 직각 좌표계의 어떤 2차원 Vector \(\vec{v}\)는 만약 이 평면이 허수부 (Imaginary ; im) 와 실수부 (Real; Re) 로 표현되는 복소 평면 (Complex plane) 이었다면 다음과 같이 표현할 수 있습니다.

이렇게 2차원 좌표값을 복소수로 생각하는 것은 수, 함수의 회전 특성 같은걸 분석하기 유리해지기 때문에 전자공학의 신호처리 같은데서 많이 쓰이는데요, 이는 또한 아래의 수식으로도 나타낼 수 있습니다.

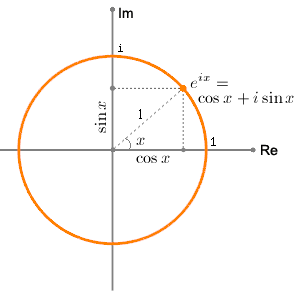Fig. Source From here

만약의 길이 \(r\)이 1일 때 이를 각도 \(x\) 에 따른 변화를 보기 위해 3차원 (x - Real - Imaginary) 으로 확장 시켜서 생각해보면 아래와 같게 됩니다.

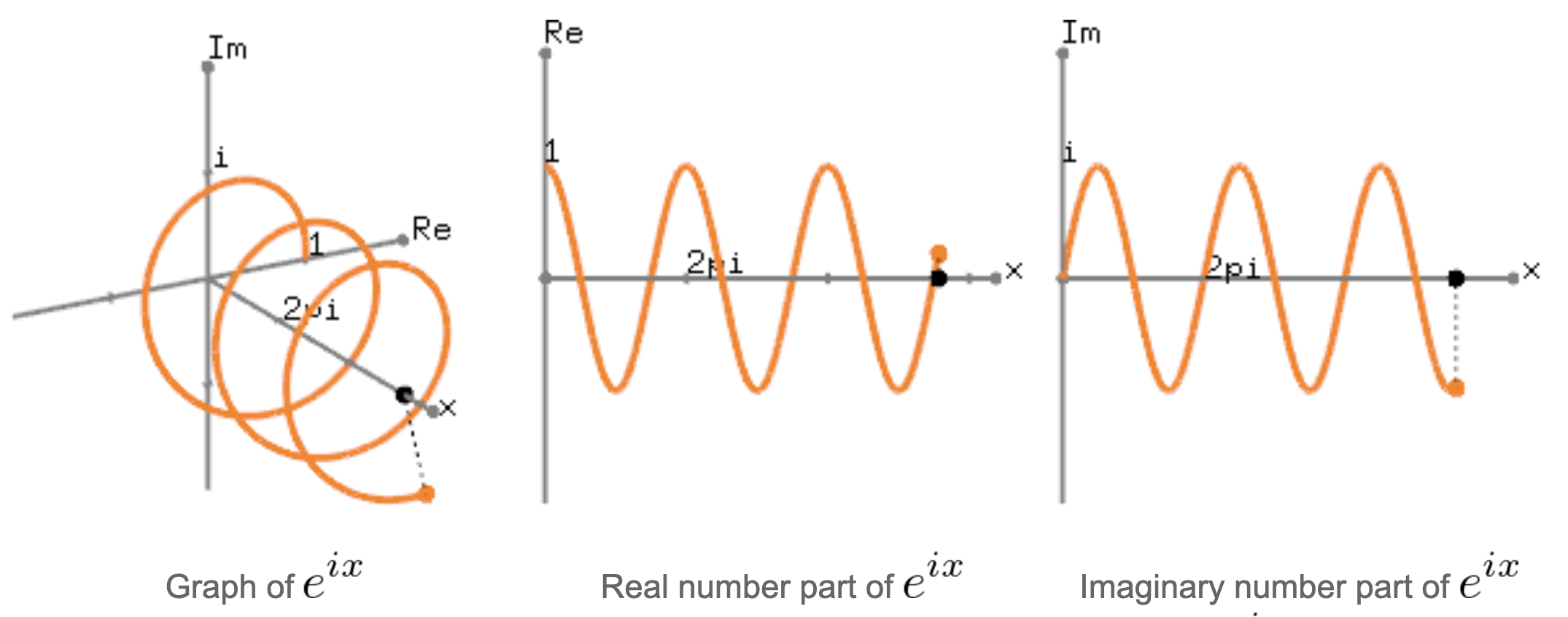Fig. Source From here

위의 그림에서 (중간)에 해당하는것은 각도에따른 Real Value 의 변화로 이 벡터의 실수부만 취하면 sin 파가 된다는 것을 의미하고, (우)에 해당하는 것은 허수부 \(i\) 만을 취하면 cos 파가 된다는 것을 의미합니다.

여기서 벡터의 길이 \(r\) 을 magnitude, 각도 \(x\) (혹은 \(\theta\) 로 많이 씀) 을 phase 라고 표현합니다.

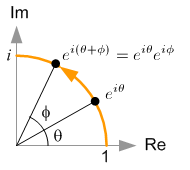Fig. Source From here

말씀드린 것 처럼 수 체계에서 허수를 도입하는 이유는 수의 회전을 표현하기 위해서 였다고 하는데요, \(\vert z \vert e^{i \theta}\) 가 길이 \(\vert z \vert\) 를 갖는 벡터가 기준점부터 \(\theta\) 만큼 회전한 것을 나타내기 때문에, 여기에 추가적으로 \(e^{i\phi}\) 만큼을 곱하는 것은 \((\theta + \phi)\) 만큼 회전하는, 즉 \(\phi\) 만큼 더 이동하는 것이 됩니다.

이를 행렬로 표현하면 아래와 같은데요,

바로 우리가 잘 아는 Rotation Matrix 를 통해 Original Vector 를 선형 변환하는 것이 바로 2차원 Vector 를 복소수로 해석함으로써 얻을 수 있는 특성 이었던 것이죠.

여기서 주의할 점은 우리가 Complex Space 에서 Vector를 본다고 해서 768차원짜리 Vector가 그의 절반인 368 차원이 된다는 것은 아닙니다. 그냥 2차원 Vector \((x,y)\) 를 \((x, iy)\)로 놓고 복소수 특성을 사용하겠다는 것만 기억하시면 됩니다.

Rotary Positional Embedding (RoPE)

RoPE 의 핵심 아이디어는 다음과 같습니다.

• 먼저 Word Embedding 을 Complex Numbers 로 생각해봤더니 여기에 Position 정보를 주입하는것은 position 이 0일 때의 원본 Vector 를 사실상 Rotation 과 다름이 없더라. (논문에서 수학적으로 꽤 엄밀하게 보임.)
• 그래서 만약 어떤 Word Embedding 이 똑같은 position 을 갖고있다면 이 둘의 차이는 position 이 0인 지점에서 dot product 를 하는 것과 다름 없고, 즉 둘 다 Absolute Position 은 변화했겠지만 Relative Position 의 차이는 0일때와 다름 없다.
• 그러므로 이 둘의 position 차이가 \((m-n)\) 만큼 났다면 \(q,k\) 의 길이의 곱에 원래 둘의 차이 \(\theta_{qk}\) 보다 \(\theta_{(m-n)}\) 만큼이 더 차이나는 \(\theta_{qk + (m-n)}\) 이 돼서 멀어질수록 원래의 dot product 값이 컸어도 그만큼 discount 된다.

Position Encoded Q, K is just Rotated Q, K

다시 SDPA를 봅시다. 어떤 word embedding vector, \(x\) 가 있습니다. 우리가 원하는 것은 이 \(x\)가 어떤 특정 position, \(t\)에 있을때 입니다. 즉 원래 vector \(x\)에 포지션을 주입해주는 어떠한 Positional Embedding Function이 있다고 칩시다. 그걸 \(f(x,t)\) 라고 부르겠습니다. 그런데 실제 SDPA 에서 사용하는것은 vector \(x\)에 position 정보를 주입하면서 Q,K,V Projection 까지 해주는 경우이므로 마지막으로 \(f_{q,k,v}\)를 정의하도록 하겠습니다. 우리의 목적은 이 \(f\)를 찾는것인데, 만약 우리가 Sinusoidal PE 를 쓴다고 생각하면 이 \(f_{q}\) 함수는 예를들어 아래처럼 표현할 수 있을겁니다.

그런데 우리가 하고 싶은것은 당연히 Sinusoidal PE를 쓰는것이 아니고 어떤 nice한 \(f\)를 새롭게 discovery 하는 겁니다. 이제 어떤 Token \(x\)가 \(m\)번째 위치에 있는데 Q 로 mapping 된 vector, \(f_q (x_m, m)\)가 하나 있고, \(n\)번째 위치에 있을 때 K로 mapping 된 또다른 vector,\(f_k (x_n, n)\)가 있습니다. 이제 이 둘의 내적을 통해서 새로운 \(f\)를 도출하려고 합니다.

먼저 Q,K vector를 생각하기 쉽게 2차원이라고 가정하고 complex space 에서 이 2차원 vector를 생각해보도록 하겠습니다.

어떤 2차원 Vector 는 그 Vector 의 크기 (Norm)를 나타내는 Radial Component와 원점으로부터의 각도를 나타내는 Angular Component의 곱으로 나타낼 수 있었죠.

여기서 \(R\)이 Radial을 나타내는 함수, \(\Theta\)가 Angle을 나타내는 함수입니다. 그런데 우리가 궁극적으로 원하는 것은 Q,K의 내적이죠? 이 두 Q, K 의 내적의 결과를 나타내는 어떤 함수 \(g\) 가 또 존재한다고 생각해 봅시다. 이 떄 두 Word Token 들 간의 거리는 \(m-n\) 입니다.

그럼 이 \(g\) function 또한 Radial, Angular Component 의 곱으로 나타낼 수 있다고 합니다.

여기서 두 vector 간의 내적 결과는 scalar 값인데 어떻게 각도가 있지? 라는 생각이 드실 거 같습니다. (저도 그랬습니다) 제 생각에는 두 vector의 내적과 동일한 vector 결과물을 나타낼 수는 있습니다.

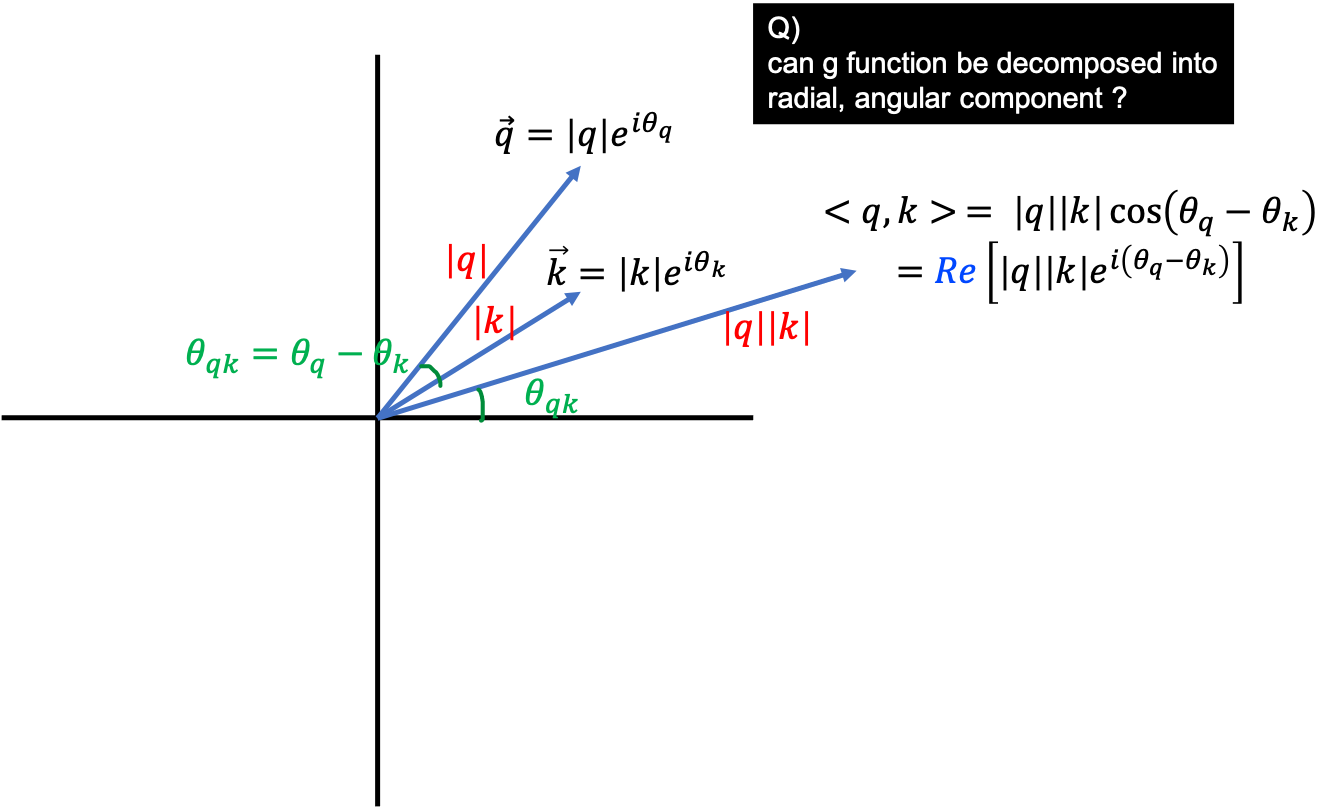
왜냐면 두 vector간 내적의 결과물은 결국 두 vector의 크기와 둘의 끼인각에 대한 cos 함수값이 되기 때문이죠. 그런데 내적을 표현하려면 이 vector의 projection된 값, 즉 Real Value 만 나타내야 하는데 이를 빼먹은 것 같습니다. 논문에 typo도 꽤 있는 편이라 일단 넘어가도록 하겠습니다.

이제 \(f_q(x_q,m), f_k(x_k,n)\)둘을 내적하면 \(g\)가 된다는 점에서 아래와 같은 관계식을 얻을 수 있습니다.

그리고 RoPE 를 도출하기위한 마지막 준비로 어떤 Token x가 position 정보 없이 embedding될 경우인 initial condition 을 다음과 같이 정의하도록 하겠습니다.

(지금 정의한 position 정보가 없을때의 query vector의 각도와 크기는 나중에 사용됩니다.)

이제 어떤 Q,K 로 mapping 될 \(x_q,x_k\) token 들이 서로 같은 위치 \(m=n\) 에 있는 경우를 생각해 봅시다. 그러면 우리는 먼저 Radial Component에 대해서 아래가 성립하는것을 알 수 있습니다.

이는 \(m=n\)이 무엇이든 성립하는 것이기 때문에

라는 결론을 얻을 수 있다고 합니다. 여기서 얻을 수 있는 중요한 property 하나는 바로 x_q 가 q 가 될때 어느 position에 놓여있던 그 vector의 길이는 변하지 않는다 라는 겁니다. 즉 길이는 position invarient 하다고 할 수 있습니다.

그 다음 Angular Component 를 보도록 하겠습니다. 마찬가지로 \(m=n\)일 경우 아래가 성립합니다.

여기서 우리는 아래의 수식을 얻을 수 있는데,

이 수식이 의미하는 바는 \(x_q\)가 0 position (initial condition)과 m position에 있을때의 각도차이가 \(x_k\)가 0 position과 m position 에 있을때의 각도차가 서로 같다는 의미이므로 Angular Component 는 embedding 될 token vector가 무엇이든 상관없이 오직 position에 의해서만 결정된다 라는 겁니다.

좀 더 전개해보자면 \(\Theta_f(x_{\{q,k\}}, m) - \theta_{\{q,k\}}\) 를 어떤 position m에 대한 함수 \(\color{red}{\phi(m)}\) 이라고 두면 우리는 \(\Theta_f(x_{\{q,k\}},m)\) 를

로 나타낼 수 있습니다. 만약 \(n=m\)이 아니라 \(n=m+1\)인 상황을 생각해보면 우리는 다음의 수식을 얻을 수 있습니다.

이를 등차수열처럼 나타내면

가 되기 때문에 이로부터 다음과 같이 position이 2만큼 차이나면 \(\color{red}{\phi(m)} = \Theta_f(x_{\{q,k\}}, m) - \theta_{\{q,k\}}\) 끼리는 어떤 각도 \(\theta\)의 2배 만큼이 차이가 남을 알 수 있습니다.

이를 일반화하면 position 정보를 안넣어준 initial \(q\) 와 position 정보 m이 들어간 q는 \(\phi(m) = m \theta + \gamma\) 만큼의 각도 차이가 나는것이고 이는 input token이 어떤 것이든 상관없이 동일하게 적용되는 겁니다. 편하게 생각하기 위해서 \(\gamma=0\)으로 두고 앞서 우리가 새롭게 발견한 특성들을 종합하면 우리는 최종적으로 어떤 position 정보를 주입하면서 projection해주는 함수, \(f\)를 얻은 것이나 다름없습니다. 즉 어떤 token 에 position을 주입해서 q나 k로 projection하는 경우, vector의 길이는 position이 없을때와 동일하게 변하지않고 만약 position이 m이라면 vector가 initial point 에서부터 theta의 m배 만큼 회전된 것인 셈인겁니다.

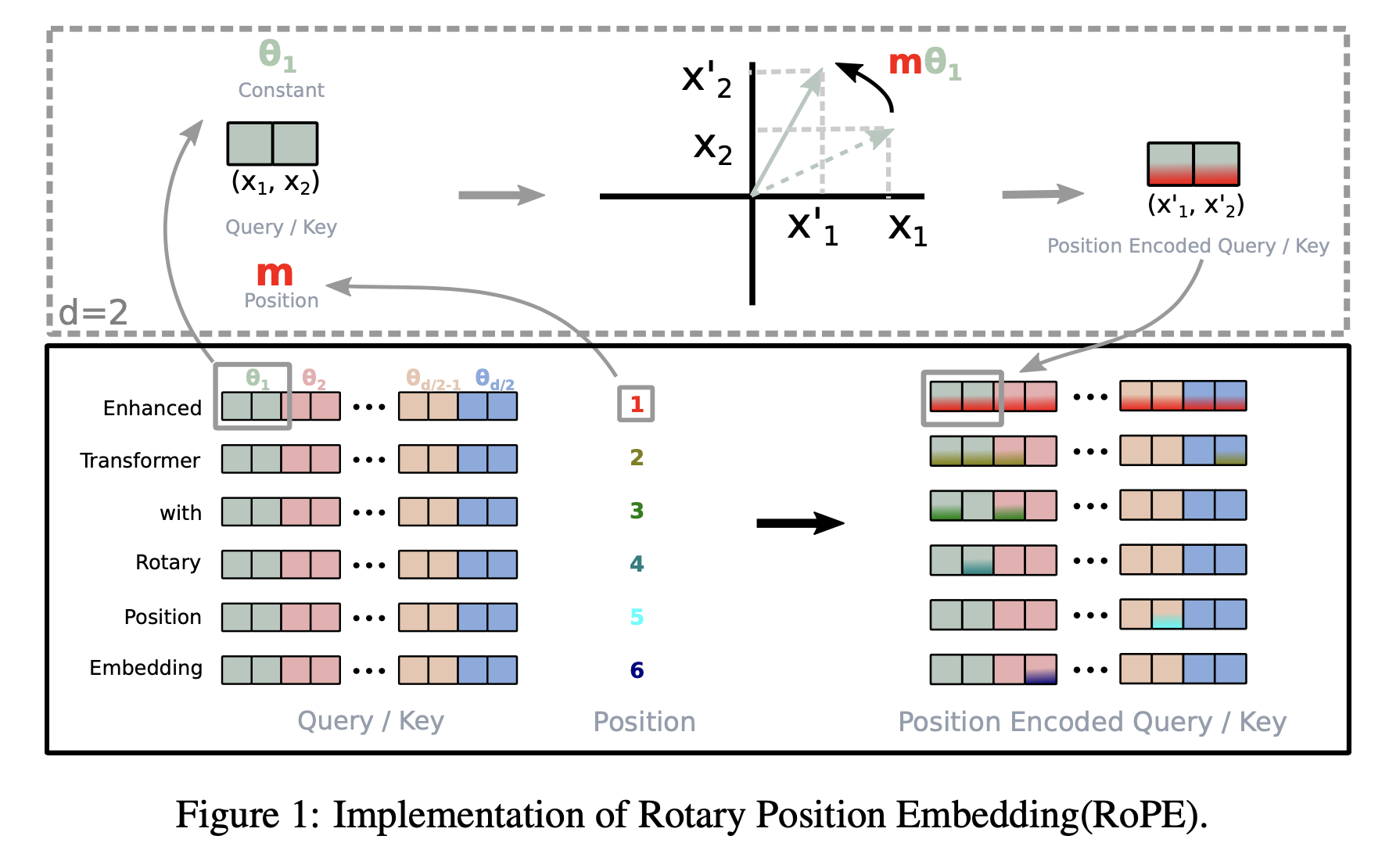Fig. Position Encoded Q is just Rotated Q

이 Euler Form 은 matrix form으로 나타내면 Q, K vector에 Rotation Matrix 를 행렬 곱 해주는 것이 됩니다.

우리가 직관적으로 이해하기 위해서 2차원에서 생각했지만 이를 \(\mathbb{R}^d\) 차원으로 확장하면 우리는 d차원을 d/2 의 sub-space 들로 나누고 이들을 합치면 되는데, 이것이 가능한 이유는 내적의 선형성 때문이라고 합니다.

In order to generalize our results in 2D to any xi ∈ Rd where d is even, 
we divide the d-dimension space into d/2 sub-spaces and combine them 
in the merit of the linearity of the inner product

즉 d차원으로 일반화했을 경우 아래와 같이 되는데,

여기서 \(\color{red}{R_{\Theta,m}^d}\)는 \(\Theta = \{ \theta_i = 10000^{-2(i-1)/d}, i \in [1,2,\cdots,d/2]\}\) 가 이미 정의된 parameter 일 때 (sinusoidal를 생각하시면 됩니다), 다음과 같이 정의됩니다.

그런데 딱 보기에도 \(R\) Tensor 는 0이 굉장히 많은 Sparse Matrix라는 걸 알 수 있습니다. 왜냐하면 이것들은 2차원씩 구성된 subspace를 combine 한 것이라서 그렇죠. 그래서 이것을 좀 더 efficient 하게 처리할 수 있는데, 바로 elemenet-wise product를 하는 겁니다. 어떤 \(q\)에 대해서 \(R_{\Theta,m}^d\) 를 곱해주는 경우에 대해서 다음과 같이 처리하는거죠.

그러니까 적당히 reorder (torch.view) 해주고 element-wise 곱 해주고, QK 곱을 해주면 끝인 겁니다. 이를 간단하게 코드로 작성하면 다음과 같습니다.

# reference : meta's llama coda-base (https://github.com/facebookresearch/llama/blob/main/llama/model.py)
import torch
import torch.nn.functional as F

def precompute_freqs_cis(
    dim: int, 
    end: int, 
    theta: float = 10000.0
):
    freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim))
    t = torch.arange(end, device=freqs.device)  # type: ignore
    freqs = torch.outer(t, freqs).float()  # type: ignore
    freqs_cis = torch.polar(torch.ones_like(freqs), freqs)  # complex64
    return freqs_cis


def reshape_for_broadcast(
    freqs_cis: torch.Tensor, 
    x: torch.Tensor
):
    ndim = x.ndim
    assert 0 <= 1 < ndim
    assert freqs_cis.shape == (x.shape[1], x.shape[-1])
    shape = [d if i == 1 or i == ndim - 1 else 1 for i, d in enumerate(x.shape)]
    return freqs_cis.view(*shape)


def apply_rotary_emb(
    xq: torch.Tensor,
    xk: torch.Tensor,
    freqs_cis: torch.Tensor,
):
    xq_ = torch.view_as_complex(xq.float().reshape(*xq.shape[:-1], -1, 2))
    xk_ = torch.view_as_complex(xk.float().reshape(*xk.shape[:-1], -1, 2))
    freqs_cis = reshape_for_broadcast(freqs_cis, xq_)
    xq_out = torch.view_as_real(xq_ * freqs_cis).flatten(3)
    xk_out = torch.view_as_real(xk_ * freqs_cis).flatten(3)
    return xq_out.type_as(xq), xk_out.type_as(xk)

bsz = 4
n_heads = 16
dim = 1024
max_seq_len = 2048

seq_len = 256
q = torch.FloatTensor([bsz, seq_len, n_heads, dim/n_heads])
k = torch.FloatTensor([bsz, seq_len, n_heads, dim/n_heads])
v = torch.FloatTensor([bsz, seq_len, n_heads, dim/n_heads])

freqs_cis = precompute_freqs_cis(
    dim // n_heads, 
    max_seq_len * 2
)

q,k = apply_rotary_emb(q, k, freqs_cis)
attn_weight = torch.softmax(q @ k.transpose(-2, -1) / math.sqrt(q.size(-1)), dim=-1)
out = (attn_weight @ v)

이렇게 position applied \(Q,K\) 를 각각 만드는 형태는 또 Flash Attention 같은 Efficient SPDA Kernel을 사용하거나 Time Compleixty 가 Sequence Length L 의 \(O(Lrd)\) 혹은 \(O(L^d)\)로 L에 대해 선형인 Linearized Attention에 결합될 수 있어서 추가로 건드릴 게 없지만, 만약 그냥 단순히 \(Softmax(QK^T/ \sqrt{d_k}) V\) 를 할 거라면 \(QK^T\)만 구하는 것 자체는

의 형태로 나타낼 수 있습니다.

Linearized Attention with RoPE

마지막으로 RoPE이 왜 additive bias 들과 다르게 Linearized Attention에 결합될 수 있는지 알아봅시다. 설명드린 것 처럼 Linearized Attention 은 Time Compleixty 가 Sequence Length L 의 \(O(Lrd)\) 혹은 \(O(L^d)\)로 L에 대해 선형인 것을 말합니다.

Linearized Attention 을 이해하기 위해서 다시 SDPA 수식을 봅시다.

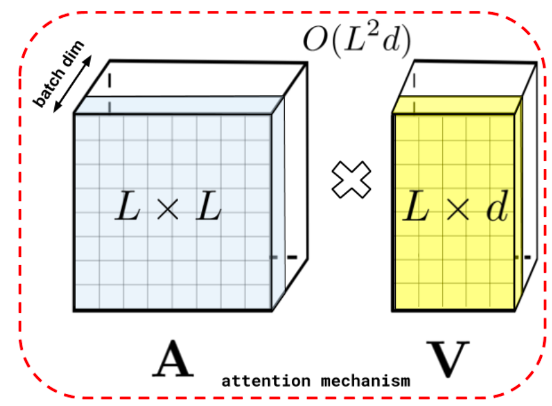Fig.

여기서 attention 이 된 context matrix \(V' \in \mathbb{R}^{L \times d}\) 의 i번째 vector 하나만 봅시다. 그러면 Softmax operator를 풀어쓰면 아래와 같이 나타낼 수 있습니다.

이 때 \(\color{red}{sim(q_i,k_j)} = \exp( \frac{q_i^T k_j}{\sqrt{D}} )\)로 볼 수 있는데, 이 때 고전 ML의 Kernel Trick 을 연관지을 수 있습니다. Kernel Trick이라는 것은 아주 단순하게 말해서 어떤 원래 차원의 feature를 다른 차원으로 (보통 고차원으로) lift up시킨뒤에 그 고차원 공간에서 similarity 를 재는 것이, 사실상 원래 차원에서의 feature끼리 similarity 를 재는것과 비슷하게 해주는 어떤 Kernel이 존재한다는 내용입니다.

예를 들어 원래 2차원이 feature가 있었는데 이를 다음의 function을 통해서 3차원으로 lift up 시켜봅시다.

Fig.

그러면 이 3차원 공간의 z끼리 dot product를 통해 similarity 를 재봅시다.

그런데 우리는 SDPA를 할 때 이미 expoenetial operator를 사용하는 특정 Kernel을 쓰고있었다고 볼 수 있습니다. 그러면 반대의 경우도 가능하겠죠? 즉 원래 d 차원의 q,k 를 다른 차원으로 보내서 dot product를 하는 것 말이죠. 만약 그 함수가 \(\phi\) 라고 생각해보면 우리는 SDPA를 다음처럼 나타낼 수 있습니다.

이렇게 kernel을 분해하면 어떤 장점이 생기느냐? QK 를 먼저 계산하는것이 아니라 KV 를 먼저 계산할 수 있는 장점이 생기는데, 만약 이 함수가 원래 차원으로 mapping 해주는 함수, \(\phi : \mathbb{R}^d -> \mathbb{R}^d\)라면 시간복잡도는 \(O(L^d)\)가 되고 d보다 낮은 r차원으로 mapping 해주는 함수, \(\phi : \mathbb{R}^d -> \mathbb{R}^r \text{, where} \quad r << d\)라면 \(O(Lrd)\) 가 되어 L에 선형인 연산이 됩니다.

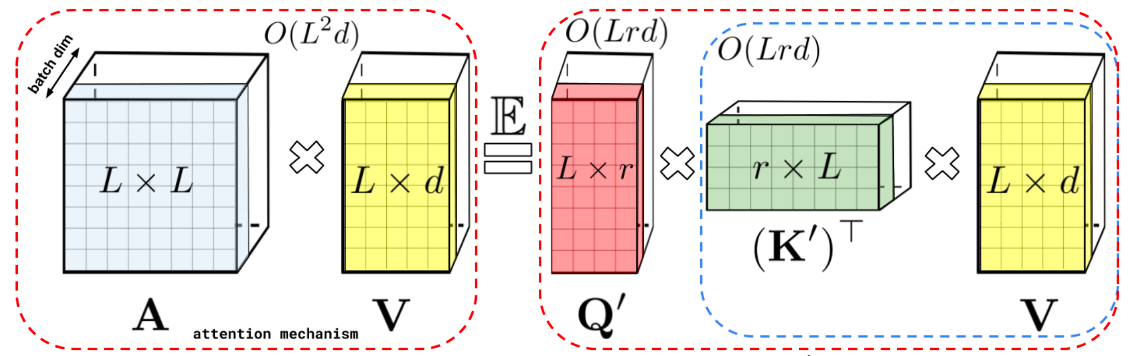Fig.

(사실 좀 더 복잡한 개념이기 때문에 자세한 내용은 Roformer 본문이나 Performer논문을 찾아보시길 바랍니다)

바로 이렇게 Kernel 을 분해하려고 할 때 additive bias 들은

와 같은 형태를 하고 있어서 분해하기가 어렵지만 (되는지도 모르겠음), RoPE의 경우

만 해주면 되기 때문에

Long-term decay of RoPE

tbc

Attention with Linear Biases (ALiBi)

RoPE 도 Meta의 LLAMA 에 사용 되는 등 많이 채택되는 것이지만, ICLR 2022 에 발표돼 각광받는 method가 있으니 바로 Attention with Linear Biases (ALiBi) 입니다. 이는 Train Short, Test Long: Attention with Linear Biases Enables Input Length Extrapolation 라는 논문에서는 제안되었습니다.

tbc

Why does it works well?

• 어쩌면 TF-XL RPE의 경우 PE vector 를 가지고 선형변환을 하는 term이 3개고 이 3개를 QK^T 에 더하는데 너무 뻘짓인게 아닐까?
• MHA 가 Global, Local Context 를 모두 볼 수 있는 potential이 있지만 실제로는 local을 보게끔 명시적으로 해준것이 전부가 아닐까?

Additional

Do Transformer Really Need RPE ?

그런데 RPE 가 논문들에서 주장하는 대로 진짜 필요한걸까요? Meta의 CAPE: Encoding Relative Positions with Continuous Augmented Positional Embeddings 라는 논문이 있습니다. 논문에서는 Absoulte Postional Encoding 은 길이에 대한 Generalization 이 안좋아 RPE 를 쓰는게 좋긴 하나, 너무 복잡하고 연산량이 많이 들어 Continuous Augmented Positional Embeddings (CAPE) 라는 새로운 기법을 제안합니다. 하지만 여기서 제가 하고싶은 얘기는 사실 CAPE 가 아니라 Positional Encoding 이 없는 경우의 성능 분석 입니다.

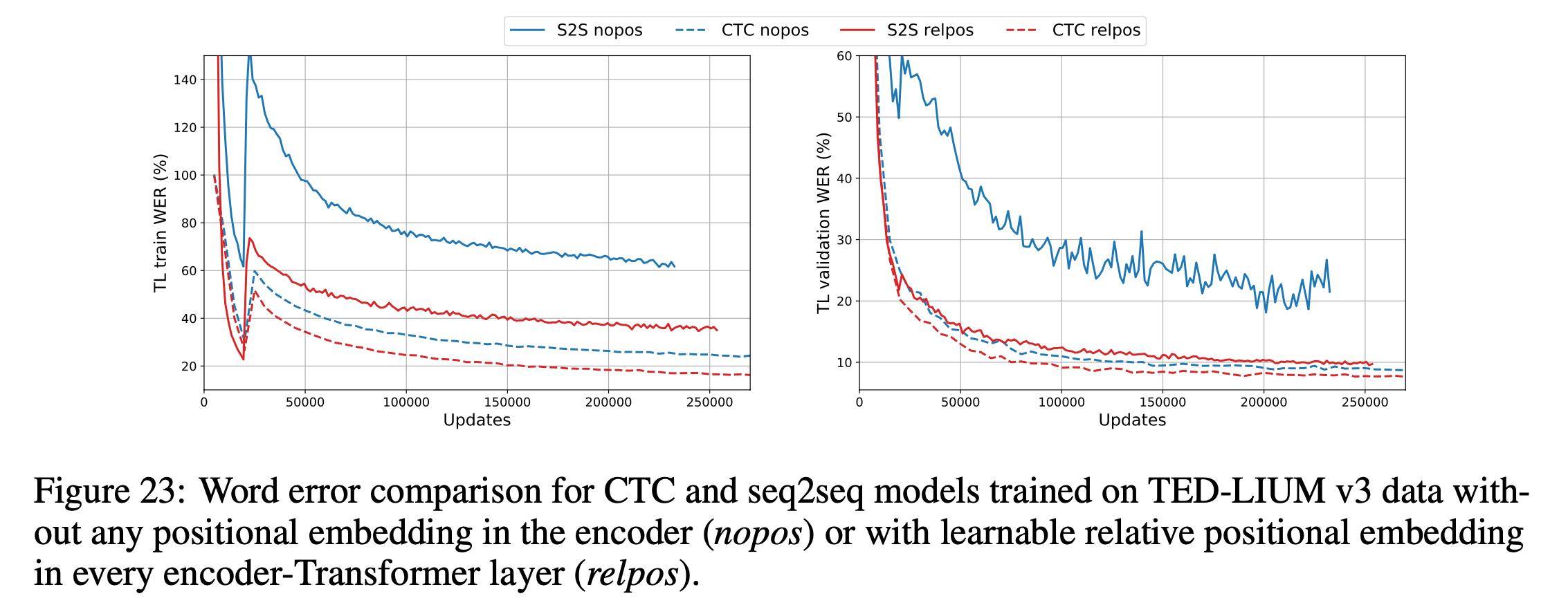
논문에서는 아래와 같이 음성 인식 (Automatic Speech Recogniton; ASR) 에서 Positional Embedding 을 아예 삭제하는 것이 (입력단에서도 넣어주지 않음) 오히려 Sinusoidal Positional Embeddings 을 넣어준 것 보다 긴 음성에 대해서 더 좋은 성능 (더 낮은 Word Error Rate (WER) 을 보임) 을 보이는 걸 보여줍니다.

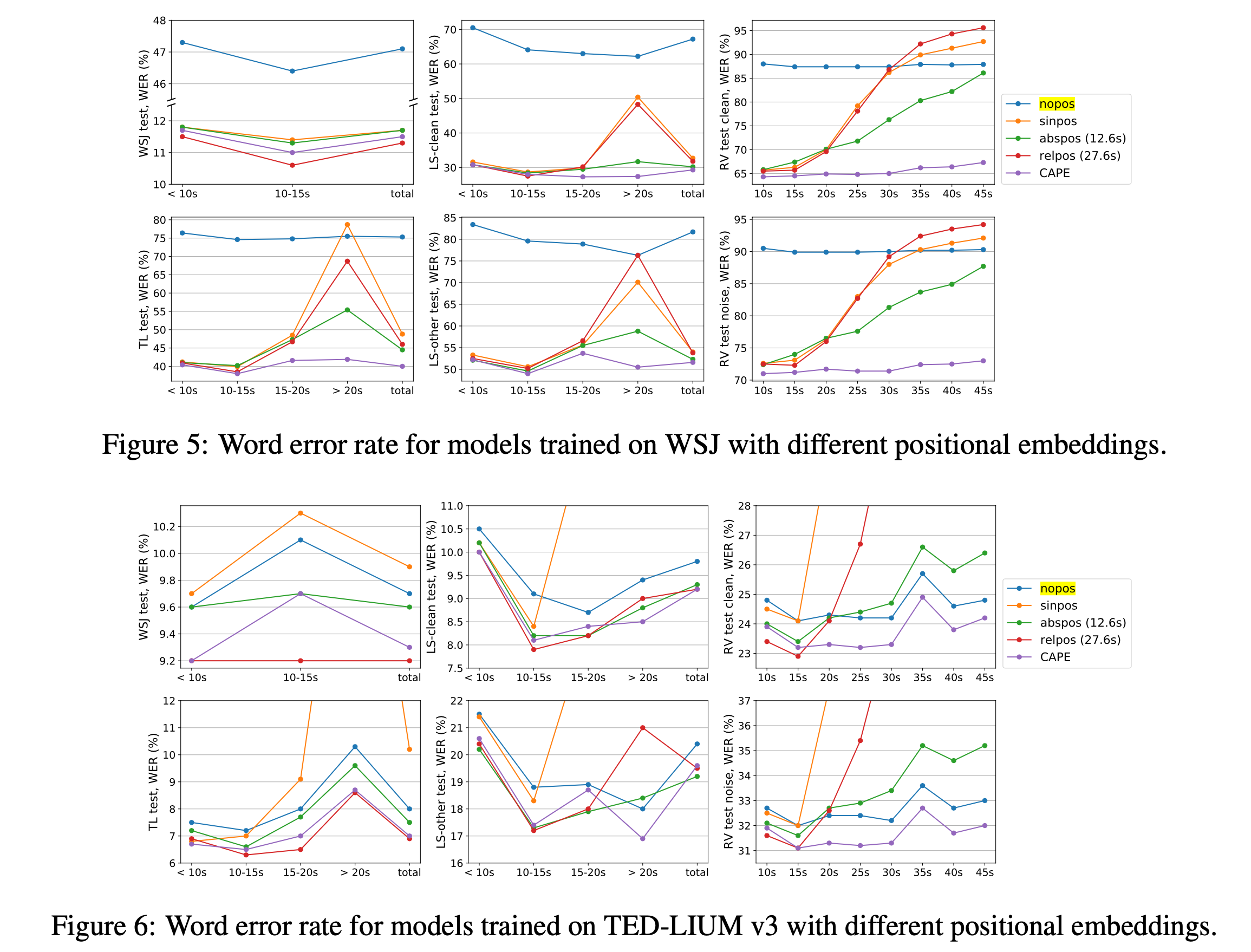Fig. WER이 낮을수록 좋음. y 축 WER, x 축 입력 길이

어떻게 이럴 수 있는 걸까요?? 저자들은 이에 대해 분석한 것을 Appendix 에 실었는데요, 핵심은 바로 ASR 분야의 저명한 Objective Function 인 Connectionist Temporal Classification (CTC) Loss 때문이었습니다.

또 다른 이유로는 충분한 데이터가 있었기 때문이라고 하는데요, CTC 라는 것이 원래 입력 sequence 와 정답 sequence 의 길이가 서로 다를 때 이들의 alignemnt 정보를 스스로 학습하는 Loss 이기 때문에

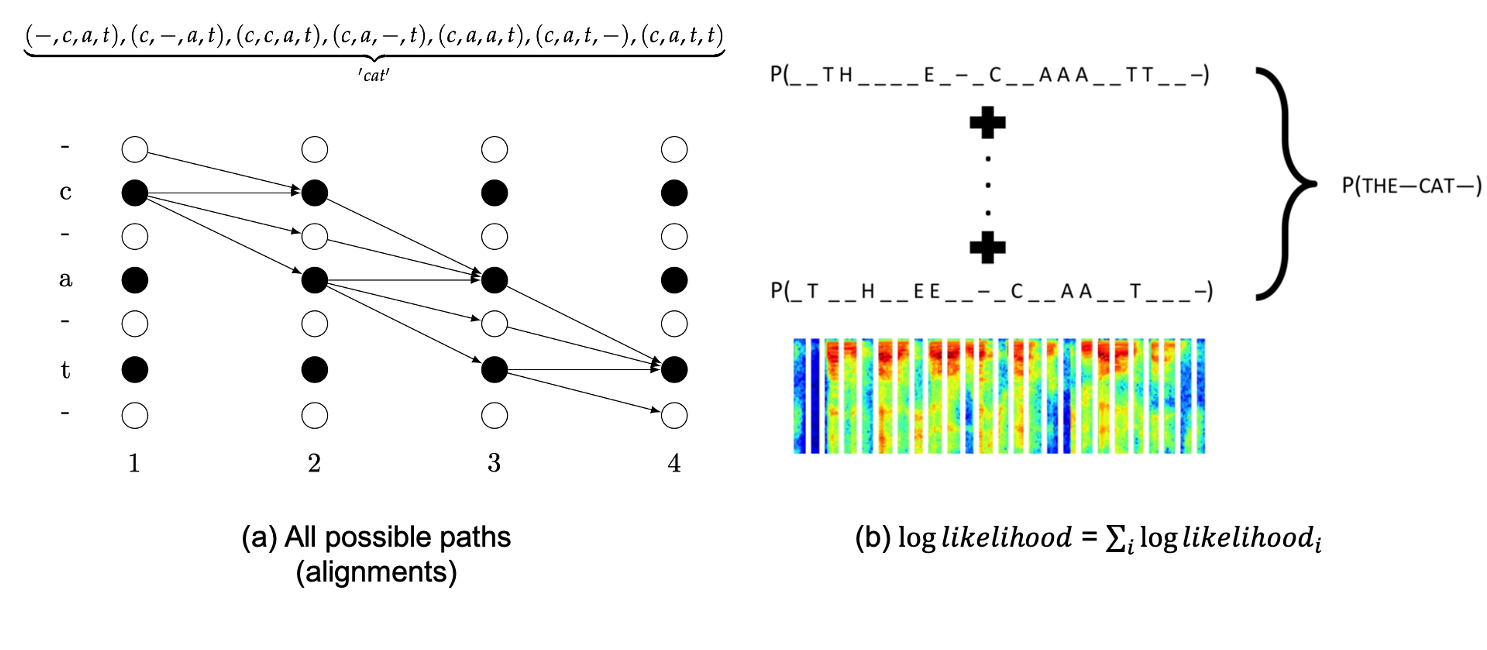Fig. CTC는 frame 별 정답은 없고 전체 정답만 있을 때, 그리고 alignment가 monotonic할 때 Classification 에 쓸 수 있는 Objective 이다.

그 과정에서 Position 정보를 학습한 게 아닌가 싶다는 내용입니다.

저자들은 가설이 맞는지 확인하기 위해 Encoder + CTC Loss 구조를 Encoder + Decoder + CE Loss, 즉 Seq2Seq 구조로 바꿔 실험해봤다고 하는데요,

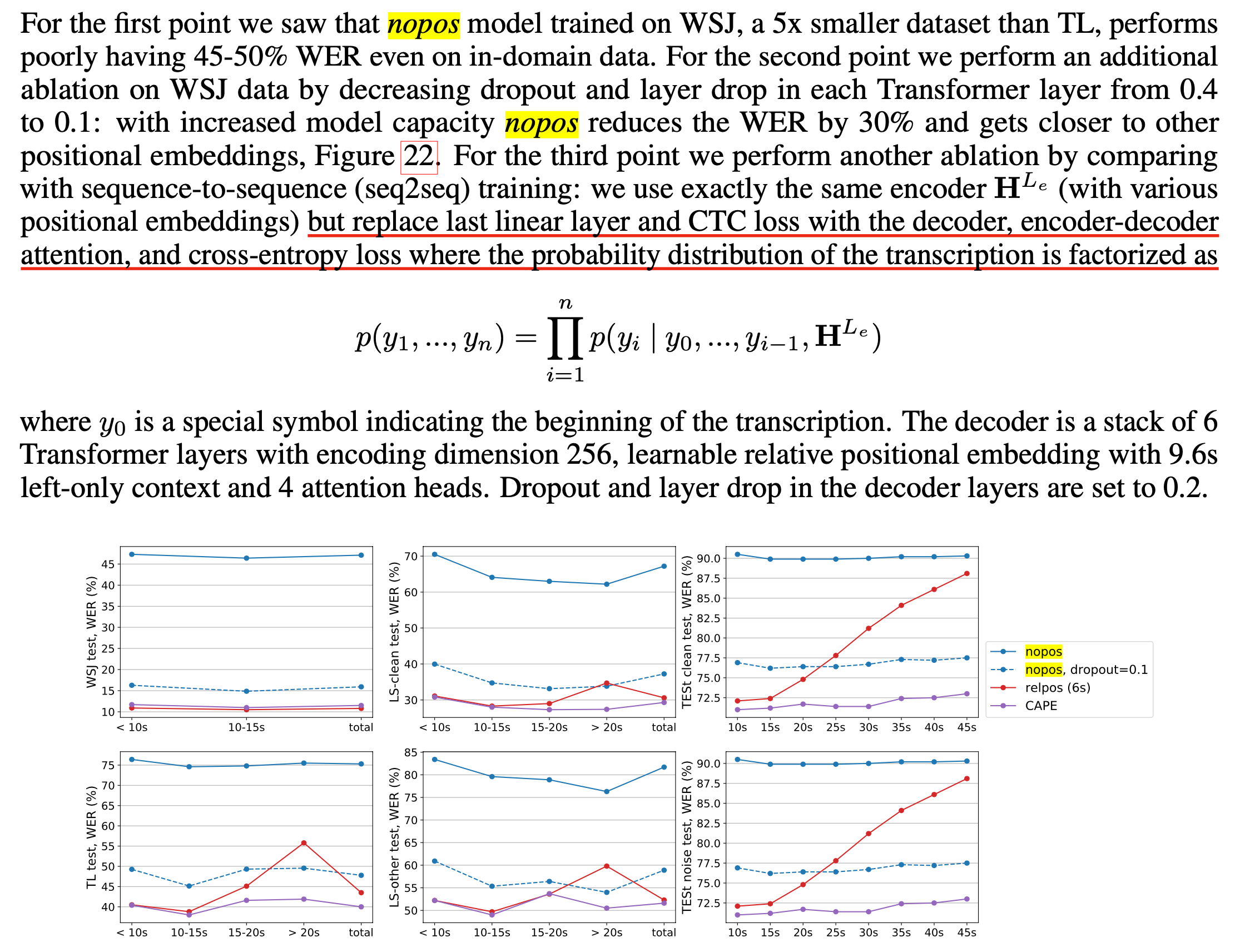
Seq2Seq 의 경우 PE가 없으면 성능이 확 나빠지는데 반해서

CTC는 성능 drop이 거의 없음을 볼 수 있었습니다. 제가 첨부한 Figure 에는 Convlution 자체가 RPE 역할을 한다는 것이 또 언급이 되는데, 보통 음성의 경우 Sequence 가 길어 1D Conv 를 쌓아 길이를 줄이는데 (Reducing Temporal Resolution), 왜 이 실험에서는 그런게 없냐? 있는데도 Seq2Seq는 망한것인가? 라고 생각하실 수 있겠으나 본 실험에서는 1D CNN 1층 + 다층의 Transformer 만 사용했다고 합니다.

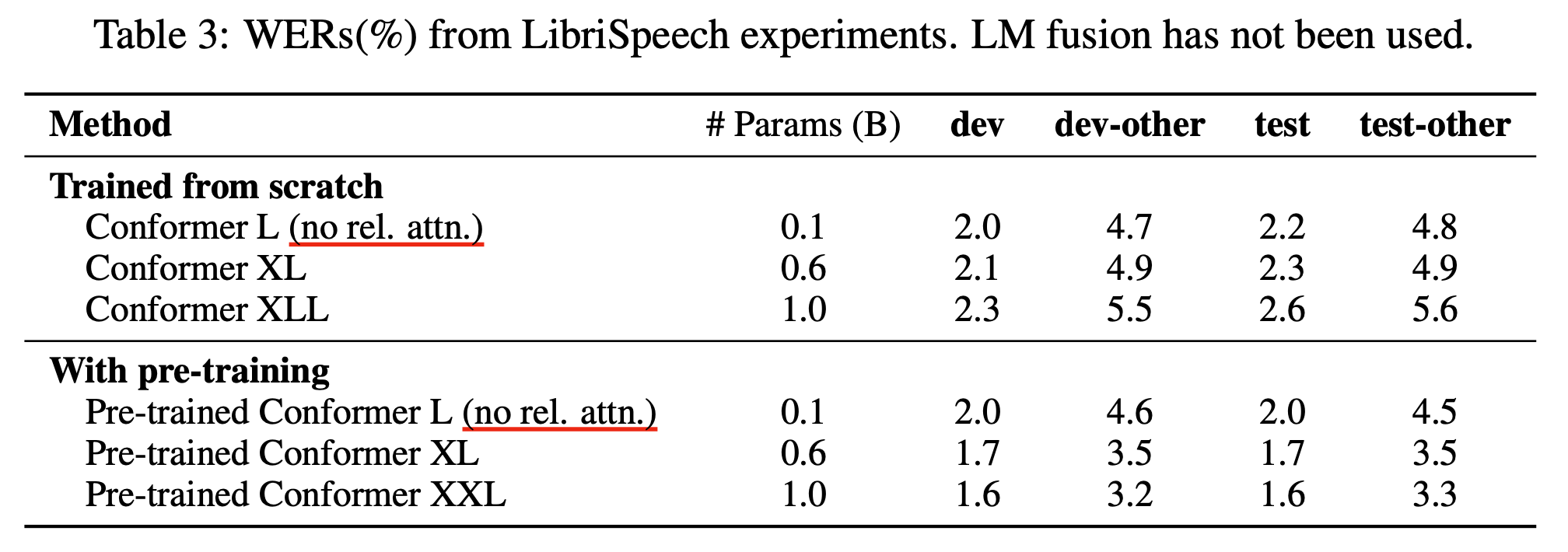
이 밖에 Google 이 발표한 Pushing the Limits of Semi-Supervised Learning for Automatic Speech Recognition 라는 논문에서도 데이터와 모델 크기가 충분할 경우 RPE 를 빼도 Performance 손해를 보지 않는다고 report 하는데, 이 또한 CTC와 비슷한 Transducer Objective 를 사용해서 그렇습니다.

여기서 우리가 얻어갈 수 있는 점은, Task에 따라서 Space, Time Complexity 가 추가로 드는 RPE 는 없어도 된다는 겁니다. 역시 Model을 디자인할 때는 Domain, Task 등 여러가지를 고려해야 한다는 생각이 들었습니다.

References

• Fundamentals
  • Let’s use sinusoidal functions to inject the order of words in our model from Amirhossein Kazemnejad’s Blog
  • Linear Relationships in the Transformer’s Positional Encoding from Timo Denk’s Blog
  • Master Positional Encoding: Part I
• Additive RPE
  • Papers
    • Self-Attention with Relative Position Representations
    • Music Transformer
    • Transformer-XL, Attentive Language Models Beyond a Fixed-Length Context
    • Exploring the Limits of Transfer Learning with a Unified Text-to-Text Transformer
    • (Alibi) Train Short, Test Long: Attention with Linear Biases Enables Input Length Extrapolation
  • Blogs
    • Generating Piano Music with Music Transformer (wandb)
    • The Transformer Family Version 2.0 from Lilian Weng
• Multiplicative RPE (Rotary Positonal Embedding; RoPE)
  • Papers
    • RoFormer, Enhanced Transformer with Rotary Position Embedding
  • Blogs
    • A gentle introduction to Rotary Position Embedding Intuition and implementation from Martin Krasser
    • Rotary Embeddings, A Relative Revolution (eleuther.ai)
• Others
  • Papers
    • What Do Position Embeddings Learn? An Empirical Study of Pre-Trained Language Model Positional Encoding
    • Big Bird, Transformers for Longer Sequences
    • CAPE: Encoding Relative Positions with Continuous Augmented Positional Embeddings
    • Position Information in Transformers: An Overview
  • Blogs
    • How Positional Embeddings work in Self-Attention (code in Pytorch), AI Summer School
  • Lecture Notes
    • cs182/sp23/assets/section/dis10/sol10.pdf
• Code Implementations
  • kimiyoung/transformer-xl/pytorch/mem_transformer.py
  • espnet/espnet/espnet/nets/pytorch_backend/transformer/attention.py
  • fairseq/fairseq/modules/positional_embedding.py
  • fairseq/fairseq/models/wav2vec/wav2vec2.py
  • fairseq/fairseq/modules/espnet_multihead_attention.py
  • Transformer Encoder and Decoder Models from labml.ai
  • Multi-Headed Attention (MHA) from labml.ai
  • Transformer XL from labml.ai
  • Relative Multi-Headed Attention from labml.ai
  • Rotary Positional Embeddings (RoPE) from labml.ai
  • T5 Bias Implementation